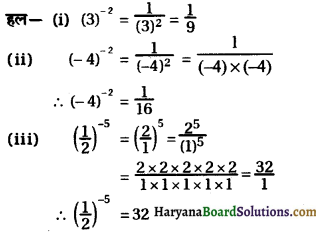Author name: Bhagya

Haryana State Board HBSE 10th Class Maths Solutions Chapter 4 Quadratic Equations Ex 4.3 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 4 Quadratic Equations Ex 4.3

Question 1.
Find the roots of the following quadratic equations, if they exist, by the method of completing the squsire :
(i) 2x² – 7x + 3 = 0
(ii) 2x² + x – 4 = 0
(iii) 4x² + 4√3x + 3 = 0
(iv) 2x² + x + 4 = 0
Solution :
(i) The given equation is :
2x² – 7x + 3 = 0
⇒ x² – \(\frac{7}{2}\)x + \(\frac{3}{2}\) = 0
[Dividing throughout by 2]
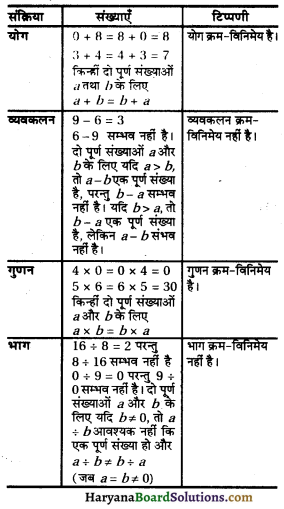
⇒ x² – \(\frac{7}{2}\)x = – \(\frac{3}{2}\)
⇒ x² \(\frac{7}{2}\)x + (\(\frac{7}{4}\))² = – \(\frac{3}{2}\) + (\(\frac{7}{4}\))²
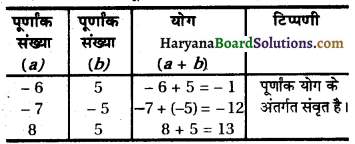
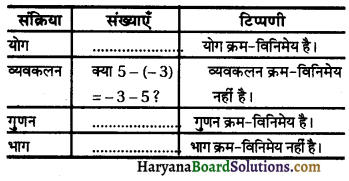
[Adding (\(\frac{1}{2}\) coeff. of x)² of both sides]

(ii) The given equation is:
2x² + x – 4 = 0
x² + \(\frac{x}{2}\) – 2 = 0
[Dividing throughout by 2]
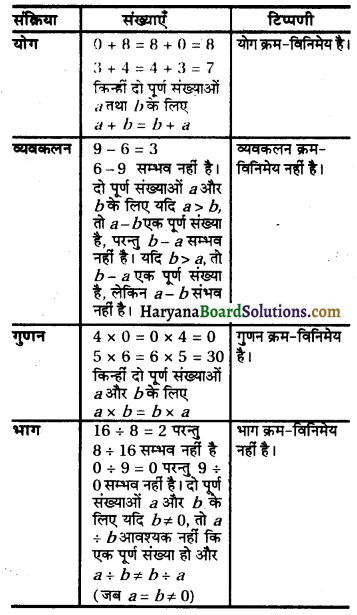
x² + \(\frac{x}{2}\) = 2

Hence, the roots of the equation are \(\frac{-1+\sqrt{33}}{4}\) and \(\frac{-1-\sqrt{33}}{4}\).

(iii) The given equation is :
4x² + 4√3x + 3 = 0
⇒ x² + √3x + \(\frac{3}{4}\) = 0
[Dividing throughout by 4]
x² + √3x = – \(\frac{3}{4}\)
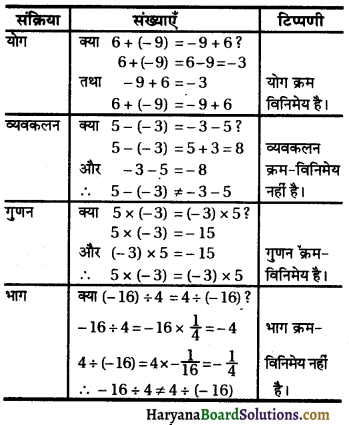
[Adding (\(\frac{1}{2}\) coeff. of x)² of both side]
(x + \(\frac{\sqrt{3}}{2}\))² = \(-\frac{3}{4}+\frac{3}{4}\)
(x + \(\frac{\sqrt{3}}{2}\))² = 0
∴ The roots of the equation exist.
∴ (x + \(\frac{\sqrt{3}}{2}\))² = 0
x = – \(\frac{\sqrt{3}}{2}\), – \(\frac{\sqrt{3}}{2}\)
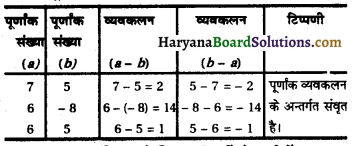
Hence, the roots of the equation are – \(\frac{\sqrt{3}}{2}\) and – \(\frac{\sqrt{3}}{2}\).

(iv) The given equation is :
2x² + x + 4 = 0
⇒ x² + \(\frac{x}{2}\) + 2 = 0
[Dividing throughout by 2]
x² + \(\frac{x}{2}\) = – 2
\(x^2+\frac{x}{2}+\left(\frac{1}{4}\right)^2=-2+\left(\frac{1}{4}\right)^2\)
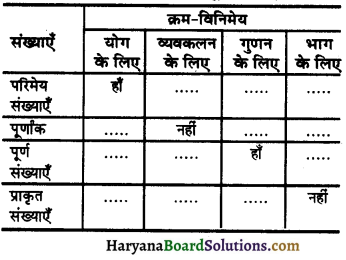
[Adding (\(\frac{1}{2}\) coeff. of x)² of both sides]
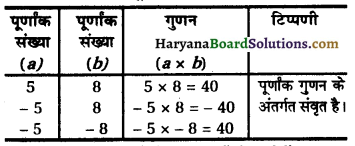
\(\left(x+\frac{1}{4}\right)^2=-2+\frac{1}{16}\)
\(\left(x+\frac{1}{4}\right)^2=\frac{-32+1}{16}\)
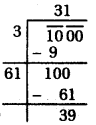
\(\left(x+\frac{1}{4}\right)^2=\frac{-31}{16}\) < 0
∴ The roots of the equation do not exist.

Question 2.
Find the roots of the quadratic equations given in question 1 above by applying the quadratic formula.
Solution :
(i) The given equation is :
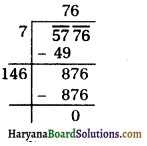
2x² – 7x + 3 = 0
Here, a = 2, b = – 7, c = 3
∴ D = b² – 4ac
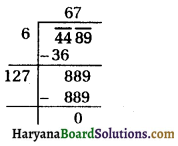
⇒ D = (- 7)² – 4 × 2 × 3
⇒ D = 49 – 24
⇒ D= 25
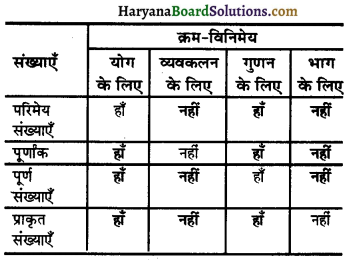
D > 0
∴ The equation has real roots.

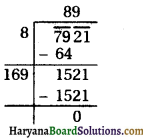
(ii) The given equation is 2x² + x – 4 = 0
Here, a = 2, b = 1, c = – 4
∴ D = b² – 4ac
⇒ D = (1)² – 4 × 2 × (- 4)
⇒ D = 1 + 32
⇒ D = 33
∵ D > 0
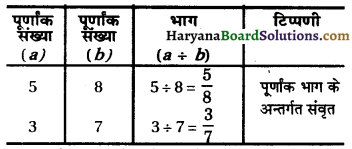
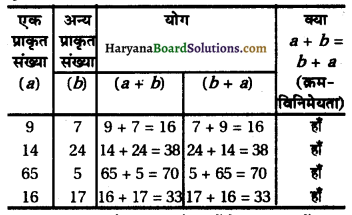
∴ The equation has real roots.

Hence, the roots of the equation are \(\frac{-1+\sqrt{33}}{4}\) and \(\frac{-1-\sqrt{33}}{4}\).

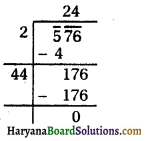
(iii) The given equation is :
4x² + 4√3 + 3 = 0
Here, a = 4, b = 4√3 , c = 3
∴ D = b² – 4ac
⇒ D = (4√3)² – 4 × 4 × 3
⇒ D = 48 – 48
∵ D = 0
∴ The equation has real roots.
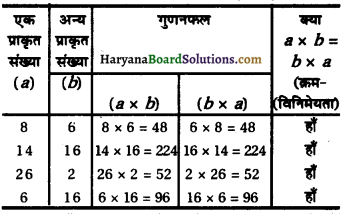
∴ x = \(\frac{-b \pm \sqrt{\mathrm{D}}}{2 a}\)
x = \(\frac{-4 \sqrt{3} \pm 0}{2 \times 4}\)
x = \(-\frac{\sqrt{3}}{2}\)
Hence, the roots of the equation are \(-\frac{\sqrt{3}}{2}\) and \(-\frac{\sqrt{3}}{2}\).

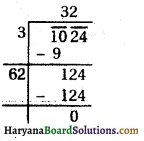
(iv) The given equation is :
2x² + x + 4 = 0
Here, a = 2, b = 1, c = 4
D = b² – 4ac
⇒ D= (1)² – 4 × 2 × 4
⇒ D = 1 – 32
⇒ D = – 31
∵ D < 0
∴ Roots of the equation do not exist.
Hence, the equation has no real roots.

Question 3.
Find the roots of the following equations:
(i) x – \(\frac{1}{x}\) = 3, x ≠ 0
(ii) \(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\), x ≠ – 4, 7
Solution:
(i) The given equation is
x – \(\frac{1}{x}\) = 3
Multiplying both sides by x, we get
⇒ x² – 1 = 3x
⇒ x² – 3x – 1 = 0
Here, a = 1, b = – 3, c = – 1
∴ D = b² – 4ac
D = (- 3)² – 4 × 1 × (- 1)
D = 9 + 4
D = 13
∵ D > 0
∴ The equation has real roots.
x = \(\frac{-b \pm \sqrt{D}}{2 a}\)
x = \(\frac{3 \pm \sqrt{13}}{2 \times 1}\)
x = \(\frac{3+\sqrt{13}}{2}\) or x = \(\frac{3-\sqrt{13}}{2}\)
Hence, the roots of the equation are \(\frac{3+\sqrt{13}}{2}\) and \(\frac{3-\sqrt{13}}{2}\).

(ii) The given equation is:
\(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\)
\(\frac{x-7-x-4}{(x+4)(x-7)}=\frac{11}{30}\)
\(\frac{-11}{x^2-3 x-28}=\frac{11}{30}\)
11x² – 33x – 308 = – 330
11x² – 33x – 308 + 330 = 0
11x² – 33x + 220 = 0
x² – 3x + 2 = 0
Here, a = 1, b = – 3, c = 2
∴ D = b² – 4ac
D = (- 3)² – 4 × 1 × 2
D = 9 – 8
D = 1
∵ D > 0
∴ The equation has real roots.

x = 2 or x = 1
Hence, the roots of the equation are 2 and 1.

Question 4.
The sum of the reciprocals of Rehman’s ages (in years) 3 years ago and 5 years from now is Find his present age.
Solution :
Let the present age of Rehman be x years
3 years ago Rehmans age = (x – 3) years
After 5 years Rehxnan’s age = (x + 5) years
According to question,
\(\frac{1}{x-3}+\frac{1}{x+5}=\frac{1}{3}\)
\(\frac{x+5+x-3}{(x-3)(x+5)}=\frac{1}{3}\)
\(\frac{2 x+2}{x^2+2 x-15}=\frac{1}{3}\)
= x² + 2x – 15 = 6x + 6
x² + 2x – 15 – 6x – 6 = 0
x² – 4x – 21 = 0
Here, a = 1, b = – 4, c = – 21.
∴ D = b² – 4ac
D = (- 4)² – 4 × 1 × (- 21)
D = 16 + 84
D = 100
∵ D > 0
Then, roots of the equation are given by
∴ x = \(\frac{-b \pm \sqrt{D}}{2 a}\)
x = \(\frac{4 \pm \sqrt{100}}{2 \times 1}\)
x = \(\frac{4 \pm \{10}}{2 }\)
⇒ x = 2 ± 5
⇒ x = 2 + 5 or x = 2 – 5
⇒ x = 7 or x = – 3.
Since, x is the present age ofRehman. It cannot be negative.
Therefore, x = 7.
Hence, the present age of Rehman = 7 years.

Question 5.
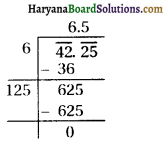
In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subject?.
Solution:
Let the marks obtained by Shefali in Mathematics be x
Then, marks obtained by Shefali in English = 30 – x .
According to question,
(x + 2)(30 – x – 3) = 210
⇒ (x + 2) (27 – x)= 210
⇒ 27x – x² + 54x – 2x = 210
⇒ – x² + 25x + 54 – 210 = 0
⇒ – x² + 25x – 156 = 0
⇒ x² – 25x + 156 = 0
Here, a = 1, 6 = – 25, c = 156
∴ D =b² – 4ac
⇒ D = (- 25)² – 4 x 1 x 156
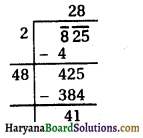
⇒ D= 625 – 624
⇒ D = 1
∵ D > 0
Then roots of the equation are given by

Hence, Marks in Mathematics = 12, Marks in English = 30 – 12 = 18.
Or Marks in Mathematics = 13,
Marks in English 30 – 13 = 17.

Question 6.
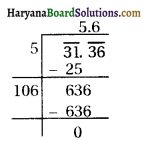
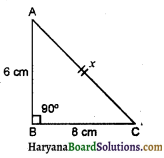
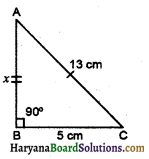
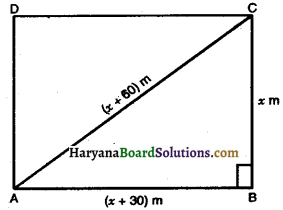
The diagonal of a rectangular field is 60 m more than the shorter side. If the longer side is 30 m more than the shorter side. Find the sides of the field.
Solution :
Let the shorter side of the rectangular field be x m.
Then diagonal = (x + 60) m
and longer side = (x + 30) m
In a right triangle ABC.
By Pythagoras theorem, we get
(x + 60)² = (x + 30)² + x²
x² + 120x + 3600 = x² + 60x + 900 + x²
x² + 120x + 3600 – 2x² – 60x – 900 = 0
– x² + 60x+ 2700 = 0
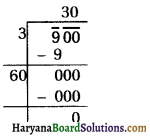
x² – 60x – 2700 = 0

Here, a = 1, b = – 60, c = – 2700
⇒ D = b² – 4oc
⇒ D = (- 60)² – 4 × 1 × (- 2700)
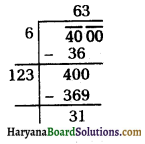
⇒ D = 3600 + 10800
⇒ D = 14400
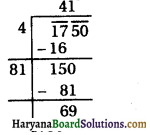
Then, the roots of the equation are given by

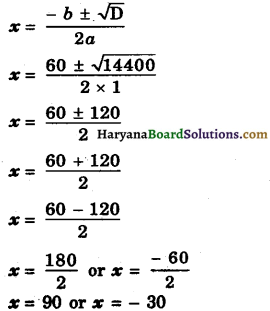
Since, x is the shorter side of a rectangular field. It cannot be negative.
Therefore, x = 90
Hence, the sides of the rectangular field are 90 m and (90 + 30)m = 120 m.

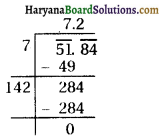
Question 7.
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Solution :
Let the larger number be x and smaller number be y.
Then, according to question,
x² – y² = 180 ……………….(1)
and y² = 8x …………………(2)
Substituting the value of y² in equation (1), we get
x² – 8x = 180
⇒ x² – 8x – 180 = 0
Here, a = 1, b = – 8, c = – 180
D = b² – 4ac
⇒ D = (- 8)² – 4 × 1 × (- 180)
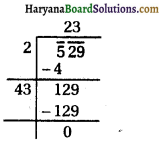
⇒ D = 64 + 720
⇒ D = 784
∵ D > 0
Then, the roots of the equation are given by
x = \(\frac{-b \pm \sqrt{D}}{2 a}\)
x = \(\frac{8 \pm \sqrt{784}}{2 \times 1}\)
x = \(\frac{8 \pm 28}{2}\)
⇒ x = – 4 ± 14
⇒ x = 4 + 14 or x = 4 – 14
⇒ x = 18 or x = – 10
Substituting the values of x in equation (2), we get
If x = 18,
y² = 8 x 18
⇒ y² = 144
⇒ y = ± 12
If x = – 10,
y² = 8 x -10
⇒ y² = – 80
⇒ y = √-80
We cannot find the value of √-80 .
Hence, the two numbers are 18, 12 or 18, – 12.

Question 8.
A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for same journey. Find the speed of the train.
Solution :
Let the speed of train be x km/h.
Time taken by the train = \(\frac{360}{x}\) hours
[Time = \(\frac{\text { Distance }}{\text { Speed }}\)]
If the speed of the train is 5 km/h more
Then new speed of the train = (x + 5) km/h
and time taken by the train = \(\frac{360}{x+5}\) hours
According to question,
\(\frac{360}{x}-\frac{360}{x+5}\) = 1
⇒ \(\frac{360(x+5)-360 x}{x(x+5)}\) = 1
⇒ \(\frac{360 x+1800-360 x}{x^2+5 x}\) = 1
⇒ \(\frac{1800}{x^2+5 x}\) = 1
⇒ x² + 5x = 1800
⇒ x² + 5x – 1800 = 0
Here, a = 1, b = 5, c = – 1800
∴ D = b² – 4ac
⇒ D = (5)² – 4 × 1 × (- 1800)
⇒ D = 25 + 7200
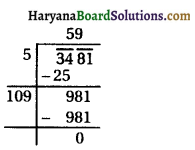
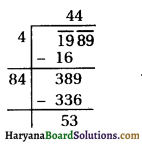
⇒ D = 7225
∵ D > 0
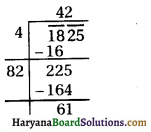
Then, the roots of the equation are given by

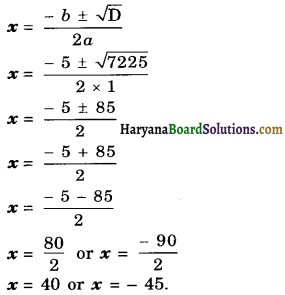
Since x is the speed of a train. It cannot be negative.
Therefore, x = 40.
Hence, the speed of train = 40 km/h.

Question 9.
Two water taps together can fill a tank in 9\(\frac{3}{8}\) hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution :
Let time taken by smaller tap be x hours
and time taken by larger tap be (x -10) hours.
Time taken by both taps together be 9\(\frac{3}{8}\) hours
The portion of tank filled by smaller tap in 1 hour = \(\frac{1}{x}\)
The portion of tank filled by larger tap in 1 hour = \(\frac{1}{x-10}\)
The portion of tank filled by both taps together in 1 hour = \(\frac{1}{9 \frac{3}{8}}\)
According to question,
\(\frac{1}{x}+\frac{1}{x-10}=\frac{1}{9 \frac{3}{8}}\)
\(\frac{x-10+x}{x(x-10)}=\frac{1}{\frac{75}{8}}\)
\(\frac{2 x-10}{x^2-10 x}=\frac{8}{75}\)
⇒ 8x² – 80x = 150x – 750
⇒ 8x² – 80x – 150x + 750 = 0
⇒ 8x² – 230x + 750 = 0
Here, a = 8, b = – 230, c = 750
∴ D = b² – 4ac
⇒ D = (- 230)² – 4 × 8 × 750
⇒ D = 52900 – 24000
D = 28900
D > 0
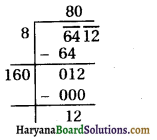
Then, the roots of the equation are given by

We reject x = \(\frac{15}{4}\)
Therefore, x = 25
Hence, the smaller tap takes time = 25 hours
And the larger tap takes time = 25 – 10 = 15 hours.

Question 10.
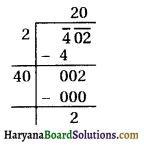
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (Without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km)h more than that of the passenger train. Find the average speed of the two trains.
Solution:
Let the average speed of passenger train be x km/h.
Then the average speed of express train = (x + 11) km/h
Time taken by passenger train to cover 132 = 132 hours
[∵ Time = Distance/ Speed]
Time taken by express train to cover 132 km = \(\frac{132}{x+11}\) hours
According to question,
\(\frac{132}{x}-\frac{132}{x+11}\) = 1
\(\frac{132(x+11)-132 x}{x(x+11)}\) = 1
\(\frac{132 x+1452-132 x}{x^2+11 x}\) = 1
\(\frac{1452}{x^2+11 x}\) = 1
x² + 11x = 1452
x²+ 11x – 1452 = 0
Here, a = 1, b = 11, c = – 1452
∴ D = b² – 4ac
D = (11)² – 4 × 1 × (- 1452)
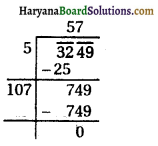
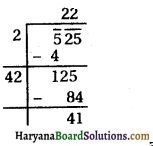
D = 121 + 5808
D = 5929
D > 0
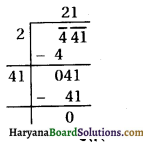
Then, the roots of the equation are given by

Since, x is the average speed of the passenger train. It cannot be negative.
Therefore, x = 33
Hence, the average speed of passenger train = 33 km/h
and average speed of express train = 33 + 11 = 44km/h.

Question 11.
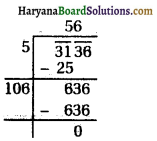
The sum of the areas of two squares is 468 m². If the difference of their perimeters is 24 m. Find the sides of the two squares.
Solution :
Let the side of larger square be x m and side of smaller square be y m.
According to question,
x² + y² = 468 ……………..(1)
and 4x – 4y = 24
x – y = 6
⇒ x = 6 + y ………………..(2)
Substituting the value of x in equation (1), we get
(6 + y)² + y² = 468
⇒ 36 + 12y + y² + y² = 468
⇒ 2y² + 12y + 36 – 468 = 0
⇒ 2y² + 12y – 432 = 0
⇒ y² + 6y – 216 = 0
Here, a = 1, b = 6, c = – 216
D = b² – 4ac
D = (6)² – 4 × 1 × (- 216)
D = 36 + 864
D = 900
D > 0
Then, the roots of the equation are given by

Since, y is the side of smaller square. It cannot be negative.
Therefore, y = 12
Substituting the value of y in equation (2), we get
x = 6 + 12
⇒ x = 18
Hence, the sides of the two squares are 18 m and 12 m.

Haryana State Board HBSE 8th Class Maths Solutions Chapter 14 गुणनखंडन Ex 14.4 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 14 गुणनखंडन Ex 14.4

निम्नलिखित गणितीय कथनों में त्रुटि ज्ञात करके उसे सही कीजिए

प्रश्न 1.
4(x – 5) = 4x – 5
हल:
4(x – 5) = 4x – 5
4(x – 5) = 4x – 20
∵ कोष्ठक खोलते समय किसी संख्या को गुणा करने पर कोष्ठक की दोरों संख्याओं में गुणा किया जाता है ।

प्रश्न 2.
x(3x + 2) = 3x² + 2
हल:
x(3x + 2) = 3x² + 2x

प्रश्न 3.
2x + 3y = 5xy
हल:
2x + 3y = 2x + 3y

प्रश्न 4.
x + 2x + 3x = 5x
हल:
x + 2x + 3x = 6x

प्रश्न 5.
5y + 2y + y – 7y = 0
हल:
5y + 2y + y – 7y = y

प्रश्न 6.
3x + 2x = 5x²
हल:
3x + 2x = 5x

प्रश्न 7.
(2x)² + 4(2x) + 7 = 2x² + 8x + 7
हल:
(2x)² + 4(2x) + 7 = 4x² + 8x + 7

प्रश्न 8.
(2x)² + 5x = 4x + 5x = 9x
हल:
(2x)² + 5x = 4x² + 5x

प्रश्न 9.
(3x + 2)² = 3x² + 6x + 4
हल:
(3x + 2)² = (3x)² + 2 × 3x × 2 + 2²
= 9x² + 12x + 4

प्रश्न 10.
x = -3 प्रतिस्थापित करने पर प्राप्त होता है।
(a) x² + 5x + 4 से (- 3)² + 5(- 3) + 4 = 9 + 2 + 4 = 15 प्राप्त होता है।
(b) x² – 5x + 4 से (- 3)² – 5(- 3) + 4 = 9 – 15 + 4 = -2 प्राप्त होता है।
(c) x² + 5x से (-3)² + 5(- 3) = – 9 – 15 = – 24 प्राप्त होता है।
हल:
(a) x² + 5x + 4 ………….(i)
x = – 3 समी. (i) में रखने पर,
= (- 3)² + 5(-3) + 4
= 9 – 15 + 4
= 13 – 15 = – 2.
∴ x² + 5x + 4 = -2

(b) x² – 5x + 4 …………..(ii)
x² – 5x + 4
x = – 3 समी. (ii) में रखने पर,
= (-3)² – 5(-3) + 4
= 9 + 15 + 4 = 28
x² – 5x + 4 = 28

(c) x² + 5x
समी (iii) में x = -3 रखने पर,
= (-3)² + 5(- 3)
= 9 – 15
= – 6
∴ x² + 5x = -6

प्रश्न 11.
(y – 3)² = y² – 9
हल:
(y – 3)² = y² – 2 × y × 3 + (-3)²
= y² – 6y + 9
अतः (y – 3)² = y² – 6y + 9
अर्थत (y – 3)² ≠ y² – 9

प्रश्न 12.
(z + 5)² = z² + 25
हल:
(z + 5)² = z² + 2 × z × 5 + 5²
= z² + 10z + 25
∴ (z + 5)² = z² + 10z + 25 ≠ z² + 25

प्रश्न 13.
(2a + 3b)(a – b) = 2a² – 3b²
हल:
L.H.S. = (2a + 3b)(a – b)
= 2a(a – b) + 3b(a – b)
= 2a² – 2ab+ 3ab – 3b²
= 2a² + ab – 3b²
(2a + 3b)(a – b) = 2a² + ab – 3b² ≠ 2a² – 3b²

प्रश्न 14.
(a + 4)(a + 2) = a² + 8
हल:
L.H.S. = (a + 4)(a + 2)
= a² + (4 + 2) a + 4 × 2
= a² + 6a + 8
(a + 4)(a + 2) = = a² + 6a + 8

प्रश्न 15.
(a – 4)(a – 2) = a² – 8
हल:
L.H.S. = (a – 4) (a – 2)
= a² – (4 + 2)a + (-4 × – 2)
= a² – 6a + 8
(a – 4) (a – 2) = a² – 6a + 8

प्रश्न 16.
\(\frac{3 x^{2}}{3 x^{2}}\) = 0
हल:
L.H.S. = \(\frac{3 x^{2}}{3 x^{2}}\) = 1 ≠ 0
∴ \(\frac{3 x^{2}}{3 x^{2}}\) = 1

प्रश्न 17.
\(\frac{3 x^{2}+1}{3 x^{2}}\) = 1 + 1 = 2
हल:
L.H.S. = \(\frac{3 x^{2}+1}{3 x^{2}}\) = \(\frac{3 x^{2}}{3 x^{2}}\) + \(\frac{1}{3 x^{2}}\)
⇒ (1 + \(\frac{1}{3 x^{2}}\)) ≠ 1 + 1 = 2
∴ \(\frac{3 x^{2}+1}{3 x^{2}}\) = (1 + \(\frac{1}{3 x^{2}}\))

प्रश्न 18.
\(\frac{3x}{3x+2}\) = \(\frac{1}{2}\)
हल:
\(\frac{3x}{3x+2}\) = \(\frac{3x}{3x+2}\) ≠ \(\frac{1}{2}\)
∴ \(\frac{3x}{3x+2}\) = \(\frac{3x}{3x+2}\)

प्रश्न 19.
\(\frac{3x}{4x+3}\) = \(\frac{1}{4x}\)
हल:
L.H.S. \(\frac{3x}{4x+3}\) = \(\frac{3x}{4x+3}\) ≠ \(\frac{1}{4x}\)
∴ \(\frac{3x}{4x+3}\) = \(\frac{3x}{4x+3}\)

प्रश्न 20.
\(\frac{4x+5}{4x}\) = 5
हल:
L.H.S. \(\frac{4x+5}{4x}\) = \(\frac{4x}{4x}\) + \(\frac{5}{4x}\)
= (1 + \(\frac{5}{4x}\)) ≠ 5
∴ \(\frac{4x+5}{4x}\) = (1 + \(\frac{5}{4x}\))

प्रश्न 21.
\(\frac{7x+5}{5}\) = 7x
हल:
\(\frac{7x+5}{5}\) = \(\frac{7x}{5}\) + \(\frac{5}{5}\)
⇒ \(\frac{7x}{5}\) + 1 ≠ 7x
∴ \(\frac{7x+5}{5}\) = \(\frac{7x}{5}\) + 1

Haryana State Board HBSE 8th Class Maths Solutions Chapter 14 गुणनखंडन Ex 14.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 14 गुणनखंडन Ex 14.1

प्रश्न 1.
दिये गये पदों में सार्व गुणनखण्ड ज्ञात कीजिए-
(i) 12x, 36
(ii) 2y, 22xy
(iii) 14pq, 28 p²q²
(iv) 2x, 3x², 4
(v) 6abc, 24 ab², 12a²b
(vi) 16x³, -4x², 32x
(vii) 10pq, 20qr, 30rp
(viii) 3x²y³, 10x³y², 6x²y²z
हल:
(i) 12x = 2 × 2 × 3 × x
36 = 2 × 2 × 3 × 3
सार्व गुणनखण्ड = 2 × 2 × 3 = 12
∴ सार्व गुणनखण्ड = 12

(ii) 2y, 22xy
2y = 2 × y
22xy = 2 × 11 × x × y
सार्व गुणनखण्ड 2 व y है। तो
सार्व गुणनखण्ड = 2 × y = 2y

(iii) 14pq, 28 p²q²
14pq = 2 × 7 × p × q
28 p²q² = 2 × 2 × 7 × p × p × q × q
∴ सार्व गुणनखण्ड = 2 × 7 × p × q
= 14 pq
∴ सार्व गुणनखण्ड = 14 pq

(iv) 2x, 3x², 4
2x, 3x², 4
2x = 2 × x
3x² = 3 × x × x
4 = 2 × 2 × 1
∴ सार्व गुणनखण्ड = 1

(v) 6abc, 24 ab², 12a²b
6abc = 2 × 3 × a × b × c
24 ab² = 2 × 2 × 2 × 3 × a × b × b
12a²b = 2 × 2 × 3 × a × a × b
सार्व गुणनखण्ड 2, 3, a और b हैं।
∴ सार्व गुणनखण्ड = 2 × 3 × a × b
= 6ab

(vi) 16x³, -4x², 32x
16x³ = 2 × 2 × 2 × 2 × x × x × x
-4x² = -1 × 2 × 2 × x × x
32x = 2 × 2 × 2 × 2 × 2 × x
सार्व गुणनखण्ड 2, 2, और x हैं।
∴ सार्व गुणनखण्ड = 2 × 2 × x = 4x

(vii) 10pq, 20qr, 30rp
10pq = 2 × 5 × p × q
20qr = 2 × 2 × 5 × q × r
30rp = 2 × 3 × 5 × r × p
सार्व गुणनखण्ड 2 और 5 हैं।
∴ सार्व गुणनखण्ड = 2 × 5 = 10

(viii) 3x²y³, 10x³y², 6x²y²z
3x²y³ = 3 × x × x × y × y × y
10 x³ y² = 2 × 5 × x × x × x y × y
6x²y²z = 2 × 3 × x × x × y × y × z
सार्व गुणनखण्ड x, x, y और y हैं।
= x × x × y × y
सार्व गुणनखण्ड = x²y²

प्रश्न 2.
निम्नलिखित व्यंजकों के गुणनखंड कीजिए
(i) 7x – 42
(ii) 6p – 12q
(iii) 7a² + 14a
(iv) -16z + 20z³
(v) 20l²m + 30alm
(vi) 5x²y – 15xy²
(vii) 10a² – 15b² + 20c²
(viii) -4a² + 4ab – 4ca
(ix) x²yz + xy²z + xyz²
(x) ax²y + bxy² + cxyz
Solution:
(i) 7x – 42
= 7x – 7 × 6
= 7(x – 6)
∴ 7x – 42 = 7(x – 6)

(ii) 6p – 12q
= 6p – 6 × 2q
= 6 (p – 2q)
∴ 6p – 12q = 6 (p – 2q)

(iii) 7a² + 14a
= 7a² + 7 × 2a
= 7a (a + 2)
∴ 7a² + 14a = 7a (a + 2)

(iv) -16z + 20z³
= 42 (-4z + 5z²)
= 4z (5z² – 4z)
∴ -16z + 20z³ = 4z (5z² – 4z)

(v) 20l²m + 30alm
= (2 × 2 × 5 × l × l × m) + (3 × 2 × 5 × a × l × m)
= 2 × 5 lm (2 × l + 3 × a)
= 10lm (2l + 3a)
∴ 20l²m + 30alm = 10lm (2l + 3a)

(vi) 5x²y – 15xy²
= (5 × x × x × y) – (3 × 5 × x × y)
= 5 xy (x – 3y)
∴ 5x²y – 15xy² = 5xy (x – 3y)

(vii) 10a² – 15b² + 20c²
= (2 × 5 × a × a) – (3 × 5 × b × b × b) + (2 × 2 × 5 × c × c)
= 5 × (2 × a × a – 3 × b × b + 4 × c × c)
= 5 (2a² – 3b² + 4c²)
∴ 10a² – 15b² + 20c² = 5 (2a² – 3b² + 4c²)

(viii) -4a² + 4ab – 4ca
= – (4 × a × a) + (4 × a × b) – (4 × c × a)
= 4a(-a + b – c)
∴ -4a² + 4ab – 4ca = 4a(-a + b – c)

(ix) x²yz + xy²z + xyz²
= (x × x × y × z) + (x × y × y × z) + (x × y × z × z)
= xyz (x + y + z)
∴ x²yz + xy²z + xyz² = xyz (x + y + z)

(x) ax²y + bxy² + cxyz
= (a × x × x × y) + (b × x × y × y) + (c × x × y × z)
= xy (ax + by + cz)
∴ ax²y + bxy² + cxyz = xy (ax + by + cz)

प्रश्न 3.
गुणनखंड कीजिए
(i) x² + xy + 8x + 8y
(ii) 15xy – 6x + 5y – 2
(iii) ax + bx – ay – by
(iv) 15pq + 15 + 9q + 25p
(v) z – 7 + 7xy – xyz
हल:
(i) x² + xy + 8x + 8y
= (x² + xy) + (8x + 8y)
= x (x + y) + 8 (x + y)
= (x + y)(x + 8)

(ii) 15xy – 6x + 5y – 2
= (15xy – 6x) + (5y – 2)
= 3x (5y – 2) + 1 (5y – 2)
= (5y – 2) (3x + 1)

(iii) ax + bx – ay – by
= (ax + bx) – (ay – by)
= x(a + b) – y (a + b)
= (a + b) (x – y)

(iv) 15pq + 15 + 9q + 25p
= (15pq + 15) + (9q + 25p)
= 15pq + 9q + 25p + 15
= 3q + (5p + 3) + 5 (5p + 3)
= (5p + 3) (3q + 5)

(v) z – 7 + 7xy – xyz
= (z – 7) + (7xy – xyz)
= 1 (z – 7) – xy (z – 7)
= (z – 7)(1 – xy)

Haryana State Board HBSE 8th Class Maths Solutions Chapter 15 आलेखों से परिचय Ex 15.3 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 15 आलेखों से परिचय Ex 15.3

प्रश्न 1.
उपयुक्त पैमाने प्रयोग करते हए, निम्न तालिकाओं में दी गई राशियों के लिए आलेख बनाइए
(a) सेबों का मूल्य

(b) कार द्वारा तय की गई दूरी

(i) 7.30 बजे प्रातः व 8 बजे प्रातः के अंतराल में कार द्वारा कितनी दूरी तय की गई?
(ii) कार के 100 km दूरी तय कर लेने पर समय क्या था?
(c) जमा धन पर वार्षिक ब्याज

(i) क्या आलेख मूल बिन्दु से गुजरता है?
(ii) आलेख से 2500 रुपए का वार्षिक ब्याज ज्ञात कीजिए।
(iii) 280 रुपए ब्याज प्राप्त करने के लिए कितना धन जमा करना होगा?
हल :
(a) सेबों का मूल्य X-अक्ष पर सेबों की संख्या दर्शाई गई है तथा Y-अक्ष पर उनका मूल्य दर्शाया गया है।

(b) कार द्वारा तय की गई दूरी-आलेख में x-अक्ष पर समय तथा Y-अक्ष पर दूरी को दर्शाया गया है।

(i) आलेख से स्पष्ट है कि, प्रात: 7:30 बजे व 8 बजे के अन्तराल में कार द्वारा (120 – 100) km = 20 km की दूरी तय की गई।
(ii) कार के 100 km दूरी तय करने के लिए समय प्रात: 7:30 बजे का था।

(c) जमा धन पर वार्षिक ब्याज-

(i) हाँ, आलेख मूल बिन्दु से गुजरता है।
(ii) आलेख से स्पष्ट है कि, ₹ 2500 का वार्षिक ब्याज ₹200 होगा।
(iii) आलेख से स्पष्ट है कि, 280 रु. व्याज प्राप्त करने के लिए उसे ₹3500 का धन जमा करना होगा।

प्रश्न 2.
निम्न तालिकाओं के लिए आलेख खीचिये।
(i)

क्या यह रैखिक आलेख है ?
हल :

(ii)

नहीं, यह एक रैखिक आलेख नहीं है-

Haryana State Board HBSE 8th Class Maths Solutions Chapter 12 घातांक और घात Ex 12.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 12 घातांक और घात Ex 12.2

प्रश्न 1.
निम्न संख्याओं को मानक रूप में व्यक्त कीजिए
(i) 0.0000000000085.
(ii) 0.00000000000942
(iii) 6020000000000000
(iv) 0.000000008
(v) 31860000000
हल:
(i) 0.0000000000085 = \(\frac{85}{10^{13}}\)
= \(\frac{85 \times 10}{10^{13}}\)
= 8.5 × 10¹ × 10^-13
= 8.5 × 10^-12

(ii) 0.00000000000942 = \(\frac{942}{10^{14}}\)
= \(\frac{9.42 \times 100}{10^{14}}\)
= 9.42 × 10² × 10^-14
= 9.42 × 10^-12

(iii) 6020000000000000 = 602 × 1013
= 6.02 × 100 × 10¹³
= 6.02 × 10² × 10¹³
= 6.02 × 10¹⁵

(iv) 0.000000008 =\(\frac{837}{10^{11}}\)
= \(\frac{8.37 \times 100}{10^{11}}\)
= 8.37 × 10² × 10
= 8.37 × 10^-9

(v) 31860000000 = 3186 × 1013
= 3.186 × 10⁷
= 3.186 × 1000 × 10⁷
= 3.186 × 10¹⁰

प्रश्न 2.
निम्न संख्याओं को सामान्य रूप में व्यक्त कीजिए
(i) 3.02 × 10^-6
(ii) 4.5 × 10⁴
(iii) 3 × 10^-8
(iv) 1.0001 × 10⁹
(v) 5.8 × 10¹²
(vi) 3.61492 × 10⁶.
हल:
(i) 3.02 × 10^-6
= \(\frac{3.02}{10^{6}}\)
= \(\frac{302 \times 100}{10^{6}}\)
= 302 × 10^-2 × 10^-6
= 302 × 10^-8
= 0.00000302

(ii) 4.5 × 10⁴ = \(\frac{45}{10}\) × 10⁴
= 45 × 10⁴ × 10^-1
= 45 × 10³
= 45000

(iii) 3 × 10^-8
= \(\frac{3}{10^{8}}\)
= \(\frac{3}{100000000}\)
= 0.00000003

(iv) 1.0001 × 10⁹
= \(\frac{10001}{10000}\) × 10⁹
= 10001 × 10⁹ × 10^-4
= 10001 × 10⁵
= 1000100000

(v) 5.8 × 10¹² = \(\frac{58}{10}\) × 10¹²
= 58 × 10¹² × 10^-1
= 58 × 10¹²
= 5800000000000

(vi) 3.61492 × 10⁶ = \(\frac{361492}{100000}\) × 10⁶
= \(\frac{361492}{10^{5}}\) × 10⁶
= 361492 × 10⁶ × 10^-5
= 361492 × 10¹
= 3614920

प्रश्न 3.
निम्नलिखित कथनों में जो संख्या प्रकट हो रही है उन्हें मानक रूप में व्यक्त कीजिए-
(i) 1 माईक्रॉन \(\frac{1}{1000000}\) m के बराबर होता है।
(ii) एक इलेक्ट्रॉन का आवेश 0.000,000,000,000,000,000,16 कुलंब होता है।
(iii) जीवाणु की माप 0.0000005 m है।
(iv) पौधों की कोशिकाओं की माप 0.00001275 m है।
(v) मोटे कागज की मोटाई 0.07 mm है।
हल:
(i) 1 माइक्रॉन =\(\frac{1}{1000000}\) m = \(\frac{1}{10^{6}}\)
= 1 × 10^-6 m

(ii) एक इलेक्ट्रॉन का आवेश = 0.000,000,000,000,000,000,16
= \(\frac{16}{10^{20}}\) = 16 × 10^-20
= 1.6 × 10 × 10^-20
= 1.6 × 10^-19
अतः एक इलैक्ट्रोन का आवेश = 1.6 10^-19 कूलम्ब होता है ।

(iii) जीवाणु की माप = 0.0000005 m
= \(\frac{5}{10^{7}}\)
= 5 × 10^-7
अतः जीवाणु की माप 5 × 10^-7 m है।

(iv) कोशिकाओं की माप = 0.00001275 m
= \(\frac{1275}{10^{7}}\)
= \(\frac{1.275 \times 10^{7}}{10^{8}}\)
= 1.275 × 10³ × 10^-8
= 1.275 × 10^-5 m है।

(v) मोटे कागज की मोटाई = 0.07 mm.
= \(\frac{7}{100}\)
= 7 × 10^-2
अतः मोटे = 7 × 10^-2 mm

प्रश्न 4.
एक ढेर में पाँच किताबें हैं जिनमें प्रत्येक की मोटाई 20 mm तथा पाँच कागज की शीटें हैं जिनमें प्रत्येक की मोटाई 0.016 mm है। इस ढेर की कुल मोटाई ज्ञात कीजिए।
हल:
एक किताब की मोटाई = 20 mm
5 किताबों की मोटाई = 5 × 20 = 100 mm
इस प्रकार,
एक शीट की मोटाई = 0.016 mm
∴ 5 शीटों की मोटाई = 5 × 0.016 mm = 0.08 mm
कुल मोटाई = 100 mm + 0.08 mm
= 100.080 mm
= \(\frac{100080}{10^{3}}\)
= \(\frac{1.00080 \times 10^{5}}{10^{3}}\)
= 1.00080 × 10⁵ × 10^-3
= 1.0008 × 10²
अतः ढेर की मोटाई = 1.0008 × 10² mm

Haryana State Board HBSE 8th Class Maths Solutions Chapter 13 सीधा और प्रतिलोम समानुपात Ex 13.1 Text Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 13 सीधा और प्रतिलोम समानुपात Ex 13.1

प्रश्न 1.
एक रेलवे स्टेशन के निकट कार पार्किंग शुल्क इस प्रकार है.
4 घंटों तक – 60 रुपए
8 घंटों तक – 100 रुपए
12 घंटों तक – 140 रुपए
24 घंटों तक – 180 रुपए
जाँच कीजिए कि क्या कार पार्किंग शुल्क पार्किंग समय के प्रत्यक्ष अनुपात में है?
हल :
हम देखते हैं कि जैसे-जैसे समय में वृद्धि हो रही है, उसी प्रकार पार्किग शुल्क में भी वृद्धि हो रही है, लेकिन इनका अनुपात का मान समान नहीं है। इसलिए, पाकिग शुल्क पारिंग समय के प्रत्यक्ष अनुपात में नहीं है।

प्रश्न 2.
एक पैंट के मूल मिभण के 8 भागों में जाल रंग के पदार्थ का 1 भाग मिताकर मिश्न सैयार किया आता है, निम्नलिखित सारणी में, मूल मिश्रण के वे मान ज्ञात कीजिए, जिनें मिलाये जाने की आवश्यका है-

हुल :
मान लीजिए कि, लाल रंग के पदार्थ का भाग x है, तथा मूल मिश्रण के भाग y है।

जैसे-जैसे लाल रंग के पदार्थ के भागों में वृद्धि होती है। अत: यह एक प्रत्यक्ष अनुपात की स्थिति है। अतः

(i) यहाँ x₁ = 1
x₂ = 4
y₁ = 8
y₂ = ?

∴ \(\frac{x_{1}}{x_{2}}=\frac{y}{y_{2}}\)
\(\frac{1}{4}=\frac{8}{y_{2}}\) अर्थात, y₂ = 32 ………(i)

(ii) यहाँ x₂ = 4
x₃ = 7
y₂ = 32
y₃ = ?

∴ \(\frac{x_{2}}{x_{3}}=\frac{y_{2}}{y_{3}}\)
= \(\frac{4}{7}=\frac{32}{y_{3}}\)
4y₃ = 32 × 7
y₃ = \(\frac{32 \times 7}{4}\)
y₃ = 56 …………..(ii)

(iii) यहाँ x₃ = 7
x₄ = 12
y₃ = 56
y₄ = ?

∴ \(\frac{x_{3}}{x_{4}}=\frac{y_{3}}{y_{4}}\)
= \(\frac{7}{12}=\frac{56}{y_{4}}\)
7y₄ = 56 × 121
y₄ = \(\frac{56 \times 12}{7}\) = 8 × 12
y₄ = 96 ……………(iii)

(iv) यहाँ x₄ = 12
x₅ = 20
y₄ = 96
y₅ = ?

∴ \(\frac{x_{4}}{x_{5}}=\frac{y_{4}}{y_{5}}\)
= \(\frac{12}{20}=\frac{96}{y_{5}}\)
12y₅ = 96 × 20
y₅ = \(\frac{96 \times 20}{12}\)
y₅ = 160 ……………(iv)
अतः

प्रश्न 3.
प्रश्न 2 में यदि लाल रंग के पदार्थ के 1 भाग के लिए 75 ml मूल मिश्रण की आवश्यकता है, तो मूल मिश्रण के 1800 ml में हमें कितना लाल रंग का मिश्रण मिलाना चाहिए?
हल :
माना 1800ml में लाल रंग के पदार्थ में भाग की आवश्यकता होगी । तब,

लाल रंग के पदार्थ के मान में जितनी वृद्धि होगी, उसके मूल मिश्रण में भी उतनी ही वृद्धि होगी । अर्थात्
∴ \(\frac{x_{1}}{x_{2}}=\frac{y_{1}}{y_{2}}\)
\(\frac{1}{x}=\frac{75}{1800}\)
x = \(\frac{1800}{75}\)
∴ x = 24
अत: मूल मिश्रण के 1800 ml में हमें 24 भाग लाल रंग के पदार्थ की आवश्यकता होगी।

प्रश्न 4.
किसी सॉफ्ट ड्रिंक फैक्ट्री में एक मशीन 840 बोतलें 6 घंटे में भरती हैं। वह मशीन 5 घंटे में कितनी बोतलें भरेगी।
हल :
माना, वह मशीन 5 घंटे में x बोतलें भरेगी।

हम देखते हैं कि जैसे बोतलों की संख्या घटेगी, उसी प्रकार समय भी घटेगा।
अर्थात्,
∴ \(\frac{x_{1}}{x_{2}}=\frac{y_{1}}{y_{2}}\)
\(\frac{840}{x}=\frac{6}{5}\)
6x = 840 × 5
∴ x = \(\frac{840 \times 5}{6}\) = 140 × 5
∴ x = 700

अत: 5 घंटे में 700 बोतलें भरी जायेंगी ।

प्रश्न 5.
एक बैक्टीरिया या जीवाणु के फोटोग्राफ को 50,000 गुना आवर्धित करने पर उसकी लम्बाई 5 cm हो जाती है । इस बैक्टीरिया की लम्बाई क्या है ? यदि फोटोग्राफ को केवल 20,000 गुना आवर्षित किया जाये, तो उसकी आवर्धित लम्बाई क्या होगी?
हल :

(i) जैसे-जैसे जीवाणु के फोटोग्राफ को आवर्धित करना पड़ेगा, उसी प्रकार उसकी लम्बाई में भी वृद्धि होगी।
अर्थात,
∴ \(\frac{x_{1}}{x_{2}}=\frac{y_{1}}{y_{2}}\)
\(\frac{20000}{50000}=\frac{x}{5}\)
50000x = 20000 × 5
∴ x = \(\frac{20000 \times 5}{50000}\)
∴ x = 2 cm.

(ii) बैक्टीरिया की वास्तविक लम्बाई = \(\frac{x}{50000}\)
= \(\frac{1}{10000}\) = 10^-4 cm.

प्रश्न 6.
एक जहाज के मॉडल में, उसका मस्तूल 9 cm ऊँचा है, जबकि वास्तविक जहाज का मस्तूल 12 m ऊंचा है। यदि जहाज की लम्बाई 28 m है तो उसके मॉडल की लम्बाई कितनी है ?
हल :
माना जहाज के मॉडल की लम्बाई y cm है।

∴ \(\frac{x_{1}}{x_{2}}=\frac{y_{1}}{y_{2}}\)
\(\frac{9}{y}=\frac{12}{28}\)
28 × 9 = 12y
∴ y = \(\frac{28 \times 9}{12}\)
∴ y = 12 cm.
अत: मॉडल की लम्बाई 21 cm होगी।

प्रश्न 7.
मान लीजिए 2 kg. चीनी में 9 × 10⁶ क्रिस्टल हैं। निम्नलिखित kg. चीनी में कितने क्रिस्टल होंगे?
(i) 5 kg
(ii) 1.2 kg
हल :
(i) माना, 5kg चीनी में y क्रिस्टल हैं।

∴ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
\(\frac{2}{9 × {10^{6}}=\frac{5}{y}\)
\(\frac{9}{y}=\frac{12}{28}\)
2y = 5 × 9 × 10⁶
y = \(\frac{5 \times 9 \times 10^{6}}{2}\)
∴ y = \(\frac{45}{2}\) × 10⁶
⇒ 22.5 × 10⁶
⇒ 2.25 x 10⁷
अत: 5 kg. चीनी में 2.25 ×10⁶ क्रिस्टल है।

(ii) माना, 1.2 kg. में x क्रिस्टल हैं।

∴ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
\(\frac{2}{9 × {10^{6}}=\frac{1.2}{x}\)
2x = 1.2 × 9 × 10⁶
x = \(\frac{1.2 \times 9 \times 10^{6}}{2}\)
∴ x = 5.4 × 1010⁶
अतः 1.2 kg चीनी में 5.4 x 10 क्रिस्टल है।

प्रश्न 8.
रश्मि के पास एक सड़क का मानचित्र है, जिसके पैमाना 1 cm की दूरी 18 km. निरूपित करती है । वह सड़क पर अपनी गाड़ी से 72 km की दूरी तय करती है। उसके द्वारा तय की गई दूरी मानचित्र में क्या होगी?
हल :
माना गाड़ी द्वारा तय की गई दूरी मानचित्र में x cm है।

अर्थात् हम
∴ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
\(\frac{18}{1}=\frac{72}{x}\)
18x = 72 × 1
x = \(\frac{72}{18}\) = 4
अत: मानचित्र में यह दूरी 4 cm होगी।

प्रश्न 9.
एक 5 m 60 cm ऊंचे ऊर्ध्वाधर खम्भे की छाया की लम्बाई 3 m 20 cm है। उसी समय पर ज्ञात कीजिए
(i) 10 m 50 cm ऊँचे एक अन्य खम्भे की अया की लम्बाई,
(ii) उस खम्भे की ऊंचाई, जिसकी अया की लम्बाई 5 m है।
हल :
(i) माना कि 10 m 50 cm ऊँचे खम्भे की छाया की लम्बाई x m है।

अर्थात, हम \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\) का उपयोग करेंगे।
\(\frac{5.60}{3.20}\) = \(\frac{10.50}{x}\)
कैंची गुणा करने पर-
5.60x = 10.50 × 3.20
x = \(\frac{10.52 \times 3.20}{5.60}\) = \(\frac{10.50 \times 3.20}{5.60 \times 100}\)
x = 6 m
अत: 10 m 50 cm ऊंचे एक खम्भे की छाया की लम्बाई 6 m होगी।

(ii) माना खम्भे की ऊँचाई x मीटर है-

अत: जैसे-जैसे छाया की लम्बाई में वृद्धि होती है, वैसे-वैसे खम्भे की ऊँचाई में भी वृद्धि होगी।
अतः \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
\(\frac{5.60}{3.20}\) = \(\frac{x}{5}\)
⇒ 5.60 × 5 = 3.20x
⇒ x = \(\frac{5.60 \times 5}{3.20}\) ⇒ \(\frac{560 \times 5}{320}\) = 8.75
अत: खम्भे की ऊँचाई 8 m 75 cm, होगी ।

प्रश्न 10.
माल से लदा हुआ एक टुक 25 मिनट में 14 km चलता है । यदि चाल वही रहे, तो वह 5 घंटे में कितनी दूरी तय कर पायेगा?
हल :
माना ट्रक 5 घंटे में दूरी तय करेगा ।
1 घंटा = 60 मिनट
5 घंटे = 300 मिनट

अत: जैसे-जैसे समय में वृद्धि हो रही है, वैसे-वैसे दूरी में भी वृद्धि होगी।
अर्थात् –
\(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
\(\frac{14}{x}\) = \(\frac{25}{300}\)
कैंची गुणा करने पर-
25x= 300 × 14
∴ x = \(\frac{300 \times 14}{25}\)
x = 168 km
अतः वह ट्रक 5 घंटे में 168 km दूरी तय करेगा ।

Haryana State Board HBSE 8th Class Maths Solutions Chapter 12 घातांक और घात Ex 12.1 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 12 घातांक और घात Ex 12.1

प्रश्न 1.
मान ज्ञात कीजिए-
(i) 3^-2
(ii) (-4)^-2
(iii) (\(\frac{1}{2}\))^-5

प्रश्न 2.
सरल कीजिए और उत्तर को धनात्मक घातांक के रूप में व्यक्त कीजिए।
(i) (- 4)⁵ ÷ (- 4)⁸
(ii) \(\left(\frac{1}{2^{3}}\right)^{2}\)
(iii) (-3)⁴ × \(\left(\frac{5}{3}\right)^{4}\)
(iv) (3^-7 ÷ 3^-10) × 3^-5
(v) 2^-5 × (-7)^-3.
हल:

प्रश्न 3.
मान ज्ञात कीजिए-
(i) (3⁰ + 4^-1) × 2²
(ii) (2^-1 × 4^-1), 2^-2
(iii) \(\left(\frac{1}{2}\right)^{-2}\) + \(\left(\frac{1}{3}\right)^{-2}\) + \(\left(\frac{1}{4}\right)^{-2}\)
(iv) (3^-1 + 4^-1 + 5^-1)⁰
(v) \(\left\{\left(\frac{-2}{3}\right)^{-2}\right\}^{2}\)
हल:

प्रश्न 4.
मान ज्ञात कीजिए
(i) \(\frac{8^{-1} \times 5^{3}}{2^{-4}}\)
(ii) (5^-1 × 2^-1) × 6^-1
हल:
(i) \(\frac{8^{-1} \times 5^{3}}{2^{-4}}\)
= \(\frac{5^{3} \times 2^{4}}{8^{1}}\)
= \(\frac{5^{3} \times 16}{8}\)
= 5 × 5 × 5 ×2
= 125 × 2
= 250

(ii) (5^-1 × 2^-1) × 6^-1
= \(\frac{1}{5}\) × \(\frac{1}{2}\) × \(\frac{1}{6}\)
= \(\frac{1}{60}\)

प्रश्न 5.
m का मान ज्ञात कीजिए जिसके लिए 5^m ÷ 5^-3 = 5⁵
हल:
∴ 5^m ÷ 5^-3 = 5⁵
\(\frac{5^{m}}{5^{-3}}\) = 5⁵
5^m = 5⁵ × 5^-3
5^m = 5²
∵ दोनों ओर के घातों के आधार समान हैं। तुलना करने पर,
∴ m = 2

प्रश्न 6.
मान ज्ञात कीजिए
(i) \(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)
(ii) \(\left(\frac{5}{8}\right)^{-7} \times\left(\frac{8}{5}\right)^{-4}\)
हल:
(i) \(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)
= (3 – 4)^-1 = (-1)^-1
= \(\frac{1}{-1^{1}}\)
= \(\frac{1}{-1}\)
= -1

(ii) \(\left(\frac{5}{8}\right)^{-7} \times\left(\frac{8}{5}\right)^{-4}\)
= \(\left(\frac{5}{8}\right)^{-7} \times\left(\frac{5}{8}\right)^{4}\)
= \(\left(\frac{5}{8}\right)^{-3}\)
= latex]\left(\frac{8}{5}\right)^{3}[/latex]
= \(\frac{8 \times 8 \times 8}{5 \times 5 \times 5}\)
= \(\frac{512}{125}\)

प्रश्न 7.
सरल कीजिए-
(i) \(\frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}}\) (t ≠ 0)
(ii) \(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\)
हल:

Haryana State Board HBSE 10th Class Maths Solutions Chapter 2 Polynomials Ex 2.4 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 2 Polynomials Exercise 2.4

Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and coefficients in each case :
(i) 2x³ + x² – 5x + 2; \(\frac{1}{2}\), 1, – 2,
(ii) x³ – 4x² + 5x – 2; 2, 1, 1.
Solution :
(i) We have,
f(x) = 2x³ + x² – 5x + 2
On comparing f(x) with standard form of cubic polynomial ax³ + bx² + cx + d,
We get a = 2, b = 1, c = – 5, d = 2 and the
given zeroes are \(\frac{1}{2}\), 1, – 2.
∴ f(\(\frac{1}{2}\)) = 2 × (\(\frac{1}{2}\))³ + (\(\frac{1}{2}\))² – 5 × \(\frac{1}{2}\) + 2

= 2 × \(\frac{1}{8}+\frac{1}{4}-\frac{5}{2}\) + 2

= \(\frac{1}{4}+\frac{1}{4}-\frac{5}{2}\) + 2

= \(\frac{2}{4}-\frac{5}{2}\) + 2

= \(\frac{1}{2}-\frac{5}{2}\) + 2

= = \(\frac{1-5+4}{2}=\frac{5-5}{2}\) = 0
f(1) = 2 × (1)³ + (1)² – 5 × 1 + 2
= 2 + 1 – 5 + 2
= 5 – 5 = 0
f(- 2) = 2 × (- 2)³ + (- 2)² – 5 × (- 2) + 2
= 2 × (- 8) + 4 + 10 + 2
= – 16 + 16 = 0.
Therefore, \(\frac{1}{2}\), 1 and – 2 are the zeroes of given polynomial.
∴ α = \(\frac{1}{2}\), β = 1 and γ = – 2
Now,
α + β + γ = \(\frac{1}{2}\) + 1 – 2
= \(\frac{1+2-4}{2}\)
= \(-\frac{1}{2}=-\frac{b}{a}\)
= \(-\frac{\text { Coefficient of } x^2}{\text { Coefficient of } x^3}\)

αβ + βγ + αγ = \(\frac{1}{2}\) × 1 + 1 × (- 2) + (- 2) × \(\frac{1}{2}\)
= \(\frac{1}{2}\) – 2 – 1
= \(\frac{1}{2}\) – 3
= \(\frac{c}{a}=\frac{\text { Coefficient of } x}{\text { Coefficient of } x^3}\)

αβγ = \(\frac{1}{2}\) × 1 × (- 2) = – \(\frac{2}{2}\)
= \(-\frac{d}{a}=-\frac{\text { Constant term }}{\text { Coefficient of } x^3}\).

(ii) We have,
f(x) = x³ – 4x² + 5x – 2
On comparing f(x) with standard form of cubic polynomial ax³ + bx² + cx + d,
We get, a = 1, b = – 4, c = 5 and d = – 2
The given zeroes are 2, 1, 1.
f(x) = (2)³ – 4 × (2)² + 5 × 2 – 2
= 8 – 16 + 10 – 2
= 18 – 18 = 0

f(x) = (1)³ – 4 × (1)² + 5 × 1 – 2
= 1 – 4 + 5 – 2
= 6 – 6 = 0
Again f(1) = 0 (solved above).
Therefore, 2, 1 and 1 are zeroes of the given polynomial.
∴ α = 2, β = 1 and γ = 1.
Now, α + β + γ = 2 + 1 + 1 = 4 = \(\frac{-(-4)}{1}\)
= \(-\frac{b}{a}=-\frac{\text { Coefficient of } x^2}{\text { Coefficient of } x^3}\)

αβ + βγ + γα = 2 × 1 + 1 × 1 + 1 × 2
= 2 + 1 + 2
= \(\frac{5}{1}=\frac{c}{a}=\frac{\text { Coefficient of } x}{\text { Coefficient of } x^3}\)

Question 2.
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, – 7, – 14 respectively.
Solution:
Let α, β and γ are the zeroes of cubic polynomial f(x).
According to question,
α + β + γ = 2
αβ + βγ + γα = – 7
αβγ = – 14
Then cubic polynomial is
f(x) = x³ – (α + β + γ) x² + (αβ + βγ + γα)x – αβγ
= x³ – 2x² – 7x – (- 14)
= x³ – 2x² – 7x + 14

Question 3.
If file zeroes of the polynomial x³ – 3x² + x + 1 are a – b, a, a + b, find a and b.
Solution :
We have,
f(x) = x³ – 3x² + x + 1 and zeroes of the, polynomial are a – b, a, a + b , ’
Sum of zeroes = – \(\frac{b}{a}\)
⇒ a – b + a + a + b = – \(\frac{b}{a}\)
⇒ 3a = 3
⇒ a = 1.
and, Product of zeroes = – \(\frac{d}{a}\)
⇒ (a – b) a (a + b) = – \(\frac{1}{1}\)
⇒ (1 – b) × 1 (1 + b) = – 1
⇒ – b² = – 1.
⇒ b² = 1 + 1 = 2
⇒ b = ± √2
Hence, a = 1, b = ± √2.

Question 4.
If two zeroes of the polynomial x⁴ – 6x³ – 26x² + 138x – 35 are 2 ± √3 , find other zeroes.
Solution :
We have,
f(x) = x⁴ – 6x³ – 26x² + 138x – 35
∴ 2 ± √3 are the zeroes of given polynomial.
∴ (x – 2 – √3) (x – 2 + √3) = (x – 2)²
– (√3)² = x² – 4x + 1 is a factor of f(x).
Now, we divide given polynomial f(x) by x² – 4x + 1 to obtain the other zeroes as follows :

According to division algorithm of polynomials,
x⁴ – 6x³ – 26x² + 138x + 10 = (x² – 4x + 1) (x² – 2x – 35) + 0
= (x² – 4x + 1) [x² – (7 – 5)x – 35]
= (x² – 4x + 1) [x² – 7x + 5x – 35]
= (x² – 4x + 1) [x (x – 7) + 5(x – 7)]
= (x – 2 – √3)(x – 2 + √3) (x – 7)(x + 5)
For the zeroes of polynomial f(x) = 0.
⇒ (x – 2 – √3)(x – 2 + √3) (x – 7)(x + 5) = 0
⇒ x = 2 + √3, 2 – √3, 7, – 5.
Hence, other zeroes of polynomial are 7, – 5.

Question 5.
If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a, find k and a.
Solution :
We have,
f(x) = x⁴ – 6x³ + 16x² – 25x + 10
g(x) = x² – 2x + k
r(x) = x + a
According to division algorithm of polynomials f(x) = g(x) x q(x) + r(x)
⇒ f(x) – r(x) = g(x) × q(x)
⇒ x⁴ – 6x³ + 16x² – 25x + 10 – x – a = g(x) × q(x)
⇒ x⁴ – 6x³ + 16x² – 25x + 10 – a = g(x) × q(x)
Now, f(x) – r(x) is divisible by g(x).
Now, we divide x⁴ – 6x³ + 16x² – 26x + 10 – a by x² – 2x + k as follows.

But f(x) – r(x) is exactly divisible by g(x), therefore, remainder will be zero.
∴ (- 10 + 2k) x + (10 – a – 8k + k²) = 0 × x + 0.
On equating the coefficient of x and constant term
⇒ – 10 + 2k = 0
⇒ k = \(\frac{10}{2}\) = 5
and 10 – a – 8k + k² = 0
⇒ 10 – a – 8 × 5 + (5)² = 0 [∵ k = 5]
⇒ 10 – a – 40 + 25 = 0
⇒ – a – 5 = 0
⇒ a = – 5
Hence, k = 5 and a = – 5

Haryana State Board HBSE 8th Class Maths Solutions Chapter 6 वर्ग और वर्गमूल Ex 6.4 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 6 वर्ग और वर्गमूल Ex 6.4

प्रश्न 1.
निम्नलिखित संख्याओं का वर्गमूल, भाग विधि से ज्ञात कीजिए
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900
हल:
भाग विधि द्वारा संख्याओं का वर्गमूल ज्ञात करना|

(i) 2304 ⇒

∴ √2304 = 48

(ii) 4489

∴ √4489 = 67

(iii) 3481

∴ √3481 = 59

(iv) 529

∴ √529 = 23

(v) 3249

∴ √3249 = 57

(vi) 1369

∴ √1369 = 37

(vii) 5776

∴ √5776 = 76

(viii) 7921

∴ √7921 = 89

(ix) 576

∴ √576 = 24

(x) 1024

∴ √1024 = 32

(xi) 3136

∴ √3136 = 56

(xii) 900

∴ √900 = 30

प्रश्न 2.
निम्नलिखित संख्याओं में से प्रत्येक के वर्गमूल के अंक ज्ञात कीजिए । (बिना गणना के)।
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625
हल:
(i) 64 – संख्या में बार लगाने पर \(\overline{64}\) – (1 बार)
इस संख्या में 1 बार है, अत: वर्गमूल 1 अक का होगा ।

(ii) 144 – संख्या में बार लगाने पर \(\overline{1}\) \( \overline{44}\) – (2 बार)
इस संख्या में 2 बार हैं, अतः वर्गमूल 2 अंक का होगा ।

(iii)4489 – संख्या में बार लगाने पर \(\overline{44}\) \(\overline{89}\) – (2 बार)
अत: वर्गमूल 2 अंक का होगा ।

(iv) 27225 – संख्या में बार लगाने पर \(\overline{2}\) \(\overline{72} \) \(\overline{25}\) – (3 बार)
अत: वर्गमूल 3 अंक का होगा ।

(v) 390625-संख्या में बार लगाने पर \(\overline{39}\) \( \overline{06}\) \(\overline{25}\) – (3 बार)
अत: वर्गमूल 3 अंक का होगा ।

प्रश्न 3.
निम्नलिखित देशमलव संख्याओं के वर्गमूल ज्ञात कीजिए
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
हल:
(i) 2.56

∴ √2.56 = 1.6

(ii) 7.29

∴ √7.29 = 2.7

(iii) 51.84

∴ √51.84 = 7.2

(iv) 42.25

∴ √42.25 = 6.5

(v) 31.36

∴ √31.36 = 5.6

प्रश्न 4.
निम्नलिखित संख्याओं में से प्रत्येक में न्यूनतम संख्या क्या घटाई जाये कि एक पूर्ण वर्ग संख्या प्राप्त हो जाये । इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का वर्गमूल भी ज्ञात कीजिए।
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
हल :
(i) 402 का वर्गमूल ज्ञात करने पर हमें 2 शेषफल प्राप्त होता है।

इसलिए (20)², 402 से 2 कम है।
यदि, संख्या से शेषफल (2) घटा की देते हैं, तो हमें पूर्ण वर्ग संख्या प्राप्त होती है।
∴ 402 – 2 = 400
∴ √400 = 20

(ii) 1989

वर्गमूल ज्ञात करने पर-
53 शेषफल प्राप्त होता है।
अत: संख्या में से 53 घटायें,
तो एक पूर्ण वर्ग संख्या प्राप्त होगी ।
अत: 1989 – 53 = 1936
∴ √1936 = 44

(iii) 3250

वर्गमूल ज्ञात करने पर 1 शेषफल प्राप्त होता है।
अत: संख्या में से 1 घटायें,
तो एक पूर्ण वर्ग संख्या प्राप्त होगी ।
अत: 3250 – 1 = 3249
∴ √3249 = 55

(iv) 825

वर्गमूल ज्ञात करने पर 41 शेषफल प्राप्त होता है।
अत: संख्या में से 41 घटायें,
तो एक पूर्ण वर्ग संख्या प्राप्त होगी ।
अत: 825 – 41 = 784
∴ √784 = 28

(v) 4000

वर्गमूल ज्ञात करने पर 31 शेषफल प्राप्त होता है।
अत: संख्या में से 31 घटायें,
तो एक पूर्ण वर्ग संख्या प्राप्त होगी ।
अत: 4000 – 31 = 3969
∴ √3969 = 63

प्रश्न 5.
निम्नलिखित संख्याओं में से प्रत्येक में कम से कम कितना जोड़ा जाये कि एक पूर्ण वर्ग संख्या प्राप्त हो जाये । इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का वर्गमूल भी ज्ञात कीजिए।
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
हल :
(i) 525
525 का वर्गमूल ज्ञात करने पर शेषफल पर हम देखते हैं कि
(22)² < 525 < (23)².

अतः, पूर्ण वर्ग बनाने के लिये कम से कम जोड़ी जाने वाली संख्या = (23)² -525
अत: अभीष्ट संख्या = 529 – 525 = 4
अतः प्राप्त पूर्ण वर्ग संख्या = 525 + 4 = 529
तथा, √1529 = 23

(ii) 1750
1750 का वर्गमूल ज्ञात करने पर यहाँ हम देखते हैं कि
(41)² < 1750 < (42)²

अतः पूर्ण वर्ग बनाने के लिए कम से कम जोड़ी जाने वाली संख्या = (42)²
= 1764 – 1750
= 14
अतः प्राप्त पूर्ण वर्ग संख्या = 1750 + 14 = 1764
तथा, √1764 = 42

(iii) 252
252 का वर्गमूल ज्ञात करने पर यहाँ पर हम देखते हैं कि
(15)² < 252 < (16)²

अतः पूर्ण वर्ग बनाने के लिए कम से कम जोड़ी जाने वाली संख्या = (16)² – 252
अत: अभीष्ट संख्या = (16)² – 252
= 256 – 252
= 4

अतः प्राप्त पूर्ण वर्ग संख्या = 252 +4
= 256
तथा, √256 = 16

(iv) 1825
1825 का वर्गमूल ज्ञात करने पर यहाँ पर हम देखते हैं कि
(42)² < 1825 < (43)²

अतः पूर्ण वर्ग बनाने के लिए कम से कम जोड़ी जाने वाली संख्या = (43)² – 1825
अतः अभीष्ट संख्या = (43)² – 1825
= 1849 -1825 = 24
अतः प्राप्त पूर्ण वर्ग संख्या = 1825 + 24
= 1849
तथा, √1849 = 43

(v) 6412
80 यहाँ पर हम देखते हैं कि (80)² < 6412 < (81)²

अत: पूर्ण वर्ग बनाने के लिए कम से कम जोड़ी जाने वाली संख्या = (81)² – 6412
= 6561 – 6412
= 149
अतः प्राप्त पूर्ण वर्ग संख्या = 6412 + 149
= 6561
तथा, √16561 = 81

प्रश्न 6.
किसी वर्ग की भुजा की लम्बाई ज्ञात करो जिसका क्षेत्रफल 441 m² है।।
हल:

वर्ग का क्षेत्रफल = 441 m²
वर्ग की भुजा = √वर्ग का क्षेत्रफल
∴ भुजा = √441 – 21
∴ भुजा = 21 m

प्रश्न 7.
किसी समकोण त्रिभुज ABC में, ∠B = 90°.
(a) यदि AB = 6cm, BC = 8cm है, तो AC ज्ञात कीजिए।
(b) यदि, AC= 13 cm, BC = 5 cm है, तो AB ज्ञात कीजिए।
हल :

(a) AB = 6cm
BC = 8cm
AC = ? (x) माना
पाइथागोरस प्रमय स-
∴ AC² = AB² + BC²
x² = 6² + 8²
x² = 36 + 64
x² = 100
x = \(\sqrt {100}\) = 10 cm
∴ AC = 10 cm

(b) AC = 13 cm
BC = 5 cm
AB = ? (x) माना ।

पाइथागोरस प्रमेय से
∴ AB² = AC² – BC²
x² = (13)² – (5)²
x² 169 – 25
x² 169 – 25
x² = 144
∴ x = \(\sqrt {144}\) = 12 cm
अत: AB = 12 cm

प्रश्न 8.
एक माली के पास 1000 पौधे हैं। इन पौधों को वह इस प्रकार लगाना चाहता है कि पंक्तियों की संख्या और कॉलम की संख्या समान रहे । इसके लिए कम से कम पौधों की संख्या ज्ञात कीजिए, जिसकी उसे आवश्यकता हो ।
हलः
माना, पंक्तियों की संख्या = x
कॉलम की संख्या = x

तब, कुल पौधों की संख्या = x × x
अब, x × x = 1000
x² = 1000
x = \(\sqrt {1000}\)
वर्गमूल करने पर 39 शेष आता है । अत: संख्या 1000 पूर्ण वर्ग नहीं है।
अतः (31)² < 1000 < (32)²
अतः कम से कम और पौधे चाहिए
= (32)² – 1000
= 1024 – 1000
= 24
अतः कम से कम 24 और पौधों की आवश्यकता होगी।

प्रश्न 9.
एक विद्यालय में 500 विद्यार्थी हैं, पी.टी. के अभ्यास के लिए इन्हें इस तरह से खड़ा किया गया कि पंक्तियों की संख्या कॉलम की संख्या के समान रहे। . इस व्यवस्था को बनाने में कितने विद्यार्थियों को बाहर जाना होगा?
हल:
माना पंक्तियों की संख्या = x
तथा कॉलम की संख्या = x

तब कुल विद्यार्थियों की संख्या = x × x
अतः x × x = 500
x² = 500
x = \(\sqrt {500 }\)
अत: वर्गमूल करने पर शेषफल 16 प्राप्त होता है ।
अत: इस व्यवस्था को बनाने के लिए 16 विद्यार्थी अतिरिक्त हैं।
अत: 16 विद्यार्थियों को बाहर जाना होगा।

Haryana State Board HBSE 8th Class Maths Solutions Chapter 2 एक चर वाले रैखिक समीकरण Ex 2.2 Textbook Exercise Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 2 एक चर वाले रैखिक समीकरण Exercise 2.2

प्रश्न 1.
अगर आपको किसी संख्या से 7 घटाने और परिणाम को 7 से गुणा करने पर प्राप्त होता है, तो वह संख्या क्या है?
हल :
माना कि वह संख्या x है।
x से \(\frac {1}{2}\) घटाने पर x – \(\frac {1}{2}\) प्राप्त होता है = (x –\(\frac {1}{2}\))
अब प्रश्नानुसार \(\frac {1}{2}\) से गुणा करने पर,
\(\frac {1}{2}\) (x – \(\frac {1}{2}\)) = \(\frac {1}{8}\)
⇒ \(\frac {1}{2}\)(\(\frac {2x – 1}{2}\)) = \(\frac {1}{8}\)
⇒ \(\frac {2x – 1}{2}\) = \(\frac {1}{8}\) कैंची गुणा करने पर,
8(2x – 1) = 4
⇒ 16x – 8 = 4
-8 का दायें पक्ष में स्थानांतरण करने पर
⇒ 16x= 4+ 8 = 12
x = \(\frac {12}{16}\)) = \(\frac {3}{4}\)
∴ x = \(\frac {3}{4}\)
अत: वह संख्या = \(\frac {3}{4}\)

प्रश्न 2.
एक आयताकार तरण-ताल की लम्बाई उसकी चौड़ाई के दुगुने से 2 मीटर अधिक है। यदि इसका परिमाप 154 मीटर है, तो इसकी लम्बाई व चौड़ाई ज्ञात कीजिए।
हल:
माना कि आयताकार तरण-ताल की चौड़ाई =x मी० है।
तब उसकी लम्बाई 2x + 2 मी०
आयताकार तरण-ताल का परिमाप = 2 (लम्बाई + चौड़ाई)
∴ 154 = 2(2x + 2 + 3)
= 2 (3x + 2)
⇒ 154 = 6x + 4
⇒ 154 – 4 = 6x
⇒ 150 = 6x
⇒ x = \(\frac {150}{6}\) = 25
∴ x = 25
अत: तरण-वाल की लम्बाई = 2x + 2 = 2 × 25 + 2
= 50 + 2 = 52 मीटर
तथा चौड़ाई x = 25 मीटर

प्रश्न 3.
एक समद्विबाहु त्रिभुज का आधार \(\frac {4}{3}\) सेमी. तथा उसका परिमाप 4\(\frac {2}{15}\) सेमी. है । उसकी दो बराबर भुजाओं की माप ज्ञात कीजिए।
हल :
माना कि समद्विबाहु त्रिभुज की बराबर भुजाओं की माप = सेमी.।
त्रिभुज का आधार = \(\frac {4}{3}\) सेमी.
परिमाप = 4\(\frac {2}{15}\) ⇒ \(\frac {62}{15}\) सेमी.
अतः समद्विबाहु त्रिभुज का परिमाप = आधार + भुजा + भुजा
⇒ \(\frac {62}{15}\) = \(\frac {4}{3}\) + x + x
⇒ \(\frac {4 + 3x + 3x}{3}\) = \(\frac {62}{15}\)
⇒ \(\frac {6x + 4}{3}\) = \(\frac {62}{15}\)
कैंची गुण करने पर,
15(6x + 4) = 62 × 3
90x + 60 = 186 (+ 60 को पक्षोतरित करने पर)
​⇒ 90x = 186 – 60 = 126
⇒ x = \(\frac {126}{90}\) = \(\frac {7}{5}\)
∴ x = \(\frac {7}{5}\) ⇒ \(1 \frac {2}{5}\)
​​अत: समद्विबाहु त्रिभुज की बराबर भुजाएँ = \(1 \frac{2}{5}\) सेमी

​प्रश्न 4.
दो संख्याओं का योग 95 है । यदि एक संख्या दूसरी से 15 अधिक है, तो दोनों संख्याएँ ज्ञात कीजिए।
हल :
माना कि पहली संख्या = x
तो दूसरी संख्या = (x + 15)
दोनों संख्याओं का योग = (x + 15) + x=95
प्रश्नानुसार, 2x + 15 = 95
⇒ 2x = 95 – 15 = 80 (15 को दायें पक्ष में पक्षांतरण करने पर)
⇒ 2x = 80
∴ x = \(\frac {80}{2}\) = 40
अत: पहली संख्या =40
तथा दूसरी संख्या = 40+ 15 = 55

प्रश्न 5.
दो संख्याओं में 5:3 का अनुपात है । यदि उनमें अन्तर 18 है, तो संख्याएँ ज्ञात कीजिए।
हल :
दो संख्याएँ 5:3 के अनुपात में हैं।
माना कि एक संख्या 5 तथा दूसरी संख्या 3x है।
अतः प्रश्नानुसार, 5x – 3x = 18
या 2x = 18
या x = \(\frac {18}{2}\) = 9
∴ x = 9

अत: पहली संख्या = 5x = 5 × 9 = 45
तथा दुसरी संख्या = 3x = 3 × 9 = 27

प्रश्न 6.
तीन लगातार पूर्णाकों का योग 51 है। पूर्णाक ज्ञात कीजिए।
हल:
माना कि पहली पूर्णांक संख्या = x .
दूसरी पूर्णांक संख्या = x + 1
तीसरी पूर्णांक संख्या = x + 2
तीनों पूर्णांक संख्याओं का योग = 51

अत: x + x + 1 + x + 2 = 51
या, 3x + 3 = 51
या, 3x = 51 – 3 = 48
x = \(\frac {48}{3}\) = 16

अत: पहली पूर्णांक संख्या = 16
दूसरी पूर्णांक संख्या = x + 1 = 16 + 1 = 17
तीसरी पूर्णांक संख्या = x+ 2 = 16 +2 = 18.

प्रश्न 7.
8 के तीन लगातार गुणजों का योग 888 है। गुणजों को ज्ञात कीजिए।
हल :
माना कि 8 के तीन लगातार गुणज = x, (x+8), (x+ 16)
उनका योग = 888
अतः x + (x + 8) + (x + 16) = 888
या, 3x + 24 = 888
या, 3x = 888 – 24 = 864
∴ x = \(\frac {864}{3}\) = 288
अतः पहला गुणज (x) = 288
दूसरा गुणज (x + 8) = 288 +8 = 296
तीसरा गुणज (x + 16) = 288 + 16 = 304

प्रश्न 8.
तीन लगातार पूणांक बढ़ते क्रम में लेकर में क्रमश: 2,3 और 4 से गुणा कर योग करने पर योगफल 74 प्राप्त होता है। तीनों पूर्णाक ज्ञात कीजिए।
हल :
माना कि पहला पूर्णांक =x.
दूसरा पूर्णांक = x + 1
तीसरा पूर्णाक = x + 2
अब प्रश्नानुसार, 2x + 3(x + 1) + 4(x + 2) = 74
या 2x + 3x + 3 + 4x + 8 = 74
या, 9x + 11 = 74
or, 9x = 74 – 11 = 63
∴ x = \(\frac {63}{9}\) = 7

अत: पहली पूर्णाक संख्या x = 7
दूसरी पूर्णांक संख्या = x + 1 = 7 + 1 = 8
तीसरी पूर्णांक संख्या = x + 2 = 7 + 2 = 9

प्रश्न 9.
राहुल और हारून की वर्तमान आयु में अनुपात 5:7814 वर्ष बाद उनकी आयु का योग 56 वर्ष हो जायेगा। उनकी वर्तमान आयु क्या है?
हल :
माना कि राहुल की वर्तमान आयु = 5x
तथा हारून की वर्तमान आयु = 7x
4 वर्ष बाद दोनों की आयु क्रमशः (5x + 4) तथा (7x + 4) वर्ष होगी।
प्रश्नानुसार, दोनों की आयु का योग,
(5x + 4) + (7x + 4) = 56
या 12x + 8 = 56
या 12x = 56 – 8
∴ 12x = 48
या x = \(\frac {48}{12}\) = 4

अत: x = 4
अत: राहुल की वर्तमान आयु = 5x = 5 × 4 = 20 वर्ष
तथा हारून की वर्तमान आयु = 7x = 7 × 4 = 28 वर्ष

प्रश्न 10.
किसी कक्षा में बालक और बालिकाओं की संख्याओं में अनुपात 7:5है। यदि बालकों की संख्या बालिकाओं की संख्या से 8 अधिक है, तो कक्षा में कुल कितने विद्यार्थी ?
हल :
माना, कक्षा में बालकों की संख्या = 7x
तथा बालिकाओं की संख्या = 5x
बालकों की संख्या बालिकाओं की संख्या से 8 अधिक है।
अत: 7x = 5x + 8
या 7x – 5x = 8 .
या 2x = 8
या x = \(\frac {8}{2}\) = 4
∴ x = 4

अतः बालकों की संख्या,7x = 7 × 4 = 28
तथा, बालिकाओं की संख्या, 5x = 5 × 4 = 20
अत: कुल विद्यार्थियों की संख्या = 28 + 20 = 48

प्रश्न 11.
बाइचुंग के पिताजी उसके दादाजी से 26 वर्ष छोटे हैं और उससे 29 वर्ष बड़े हैं । यदि उन तीनों की आयु का योग 135 वर्ष है, तो उनकी आयु अलग-अलग ज्ञात कीजिए।
हल :
माना कि बाइचुंग की आयु =x वर्ष
तो उसके पिताजी की आयु = (x + 29) वर्ष होगी
दादाजी की आयु, उसके पिता की आयु से 26 वर्ष अधिक

अत: उसके दादाजी की आयु = (x + 29) + 26 = (x + 55) वर्ष
​तीनों की आयु का योग = 135 वर्ष
अत: x + (x + 29) + (x + 55) = 135
या 3x + 84 = 51
या 3x = 135 – 84 = 51
∴ x = \(\frac {51}{3}\) = 17

अत: बाइचुंग की आयु (x) = 17 वर्ष
पिताजी की आयु (x + 29) = 17 + 29 = 46 वर्ष
दादाजी की आयु (x + 55) = 17 + 55 = 72 वर्ष

प्रश्न 12.
15 वर्ष वाद रवि की आयु, उसकी वर्तमान आयु से चार गुनी हो जायेगी । रवि की वर्तमान आयु क्या है ?
हल :
माना कि रवि की वर्तमान आयु = x वर्ष
15 वर्ष बाद उसकी आयु = (x+ 15) वर्ष
अब प्रश्नानुसार, x + 15= 4x
या 15 = 4x – x
या 15 = 3x
अत: 3x = 15
∴ x = \(\frac {15}{3}\) = 5

अतः रवि की वर्तमान आयु = 5 वर्ष

प्रश्न 13.
एक परिमेय संख्या को \(\frac{5}{2}\) से गुणा कर जोड़ने पर \(\frac{2}{3}\) प्राप्त होता है \(\frac{-7}{12}\) वह संख्या क्या है ?
हल :
माना कि संख्या = x
प्रश्नानुसार, \(\frac{5}{2}\) x + \(\frac{2}{3}\) = \(\frac{-7}{12}\)
\(\frac{5x}{2}\) = \(\frac{-7}{12}\) – \(\frac{2}{3}\) = \(\frac{-7-8}{12}\)
या \(\frac{5x}{2}\) = \(\frac{-15}{12}\)
या 12 × 5x = -15 × 2 (कैंची गुणा करने पर)
x = \(\frac{-15 \times 2}{12 \times 5}=-\frac{1}{2}\)
∴ x = \(\frac{-1}{12}\)
अत: परिमेय संख्या = \(\frac{-1}{12}\)

प्रश्न 14.
लक्ष्मी एक बैंक में खजांची है । उसके पास नकदी के रूप में 100 रुपये, 50 रुपये व 10 रुपये वाले नोट हैं । उनकी संख्याओं में क्रमश: 2 : 3 : 5 का अनुपात और उनका कुल मूल्य 4,00,000 रुपये है । उसके पास प्रत्येक प्रकार के कितने-कितने नोट हैं ?
हल :
माना कि 100 रुपये, 50 रुपये व 10 रुपये के नोटों की संख्या क्रमश: 2x, 3x व 5x हैं।
100 रु. वाले नोटों का मूल्य =2x × 100 = 200 रुपये
50 रु. वाले नोटों का मुल्य =3x × 50 = 150x
रुपये 10रु.वाले नोटों का मूल्य = 5x × 10=50x
रुपये नोटों का कुल मूल्य = 4,00,000
अतः 200x + 150x + 50x = 400000
या 400x = 400000
या x = \(\frac{400000}{400}\)
∴ x = 1000
अत: 100 रुपये वाले नोटों की संख्या =2 × 1000=2000
50 रुपये वाले नोटों की संख्या =3 × 1000 = 3000
10 रुपये वाले नोटों की संख्या = 5 × 1000 = 5000

प्रश्न 15.
मेरे पास 300 रुपये मूल्य के 1 रुपये, 2 रुपये और 5 रुपये वाले सिक्के हैं । 2 रुपये वाले सिक्कों की संख्या 5 रुपये वाले सिक्कों की संख्या की तिगुनी है और सिक्कों की कुल संख्या 160 है। मेरे पास प्रत्येक प्रकार के कितने-कितने सिक्के हैं ?
हल :
माना कि 5 रुपये वाले सिक्कों की संख्या = x
2 रुपये वाले सिक्कों की संख्या = 3x
दिया है कुल सिक्कों की संख्या = 160
1 रुपये वाले सिक्कों की संख्या = 160 – (2 रुपये के सिक्कों की संख्या + 5 रुपये के सिक्कों की संख्या)
= 160 – (3x + x) = (160 – 4x)
अत: 1 रुपये वाले सिक्कों की संख्या = 160 – 4x
अब 1 रुपये वाले सिक्कों का कुल मूल्य = (160-4x) × 13 (160 – 4x)
रुपये 2 रुपये वाले सिक्कों का कुल मुल्य =3x × 2=6x
रुपये 5 रुपये वाले सिक्कों का कुल मूल्य = x × 5= 5x
रुपये अतः कुल रुपये = (160 – 4x) + 6x + 5x = 160 + 7x
रुपये परन्तु सभी सिक्कों का कुल मूल्य = 300 रुपये अतः प्रश्नानुसार, 160 + 7x = 300
7x = 300 – 160 = 140
∴ x = \(\frac{140}{7}\) = 20

अत:5 रुपये वाले सिक्कों की संख्या (x) = 20
2 रुपये वाले सिक्कों की संख्या (3x) = 60
1 रुपये वाले सिक्कों की संख्या (160 – 4x) = = 160 – 4 × 20 = 160 – 80
= 80

प्रश्न 16.
एक निबन्ध प्रतियोगिता में आयोजकों ने तय किया कि प्रत्येक विजेता को 100 रुपये और विजेता को छोड़कर प्रत्येक प्रतिभागी को 25 रुपये पुरस्कार के रूप में दिये जायेंगे । यदि पुरस्कारों में बाँटी गयी राशि 3000 रुपये थी, तो कुल 63 प्रतिभागियों में विजेताओं की संख्या ज्ञात कीजिए।
हल :
माना कि विजेताओं की संख्या = x
कुल प्रतिभागियों की संख्या = 63
∴ शेष प्रतिभागियों की संख्या (63 – x)
प्रत्येक विजेता को दी गई राशि = 100 रुपये
∴ x विजेताओं को दी गई राशि = 100x रुपये
चूँकि विजेताओं को छोड़कर प्रत्येक प्रतिभागी को दी गई राशि = 25 रुपये
अत: विजेता को छोड़कर सभी प्रतिभागीर्यों को दी गई कुल राशि =(63 – x) × 25
= (1575 – 250x)
अतः कुल दी गई राशि = 100x + (1575 – 25.x) = (1575 + 75x)
अब, प्रश्नानुसार, कुल दी गई राशि = 3000
1575 + 75x = 3000
या 75x = 3000 – 1575 ⇒ 1425
x = \(\frac{1425}{75}\) = 19
विजेताओं की संख्या (x) = 19

Haryana State Board HBSE 8th Class Maths Solutions Chapter 1 परिमेय संख्याएँ InText Questions and Answers.

Haryana Board 8th Class Maths Solutions Chapter 1 परिमेय संख्याएँ InText Questions

संवृत (पृष्ठ 2)

प्रश्न 1.
पूर्ण संख्याओं के लिए सभी संक्रियाओं पर संवृत्त गुणधर्म की जाँच-
हल:

प्रश्न 2.
पूर्णाक संख्याओं के लिए सभी संक्रियाओं के लिए संघृत गुणधर्म की जाँच-
हल :
(i) योग संक्रिया के लिए-
किन्हीं दो पूर्णाकों तथा bके लिए a + b एक पूर्णांक संख्या होगी।

(ii) व्यवकलन संक्रिया के लिए-
किन्हीं दो पूर्णाक a तथा b के लिए a-bभी एक पूर्णांक संख्या होगी। तथा b – a भी एक पूर्णाक संख्या होगी।

(iii) गुणन संक्रिया के लिए-किन्हीं दो पूर्णाकों तथा । के लिए a × b भी एक पूर्णांक संख्या होगी।

(iv) भाग संक्रिया के लिए-किन्हीं दो पूर्णाकों तथा b के लिए पूर्णांक संख्या नहीं होगी।

स्पष्ट है कि पूर्ण संख्याएँ योग और गुणन के अंतर्गत संवृतु है परन्तु भाग और व्यवकलन के अंतर्गत नहीं है। तथापि पूर्णाक योग, व्यवकलन एवं गुणन के अंतर्गत संवृत है लेकिन भाग के अंतर्गत संवृत नहीं हैं।

पृष्ठ 2

प्रश्न 3.
प्राकृत संख्याओं के लिए सभी चार संक्रियाओं के अन्तर्गत संवृत गुण की जाँच कीजिए।
हल :
(1) योग संक्रिया:
प्राकृत संख्याएँ योग संक्रिया के अन्तर्गत संवृत है अर्थात् और b दो प्राकृत संख्याएँ हैं, तो a + b भी प्राकृत संख्या होगी।

(2) व्यवकलन संक्रिया:
प्राकृत संख्याएँ व्यवकलन संक्रिया के अन्तर्गत संवत नहीं हैं। यदि aऔर दो प्राकृत संख्याएँ हैं,तो a > b होने पर a – b एक प्राकृत संख्या होगी, किन्तु a < b अथवा ab होने पर प्राप्त संख्या प्राकृत संख्या नहीं होगी।

(3) गुणन संक्रिया:
प्राकृत संख्याएँ गुणन संक्रिया के अन्तर्गत संवृत हैं अर्थात् ३और bदो प्राकृत संख्याएँ हैं, तो उनका गुणनफल भी प्राकृत संख्या होगी।
उदाहरण द्वारा जांच-

(4) भाग संक्रिया:
प्राकृत संख्याएँ भाग संक्रिया के अन्तर्गत संवृत नहीं है।
उदाहरण द्वारा जाँच-

प्रयास कीजिए (पृष्ठ 5)

निम्नलिखित सारणी में रिक्त स्थानों की पूर्ति कीजिए-

उत्तर:

क्रमविनिमेयता

प्रश्न 1.
निम्नलिखित सारणी के रिक्त स्थानों को भरते हुए विभिन्न संक्रियाओं के अन्तर्गत पूर्ण संख्याओं की क्रम विनिमेयता का स्मरण कीजिए-

हल :

जाच कीजिए कि क्या प्राङृत संख्याओं के लिए भी ये संक्रियाएँ क्रम-विनिमेय हैं-

जांच कीजिए कि क्या प्राकृत संख्याओं के लिए भी ये संक्रियाएँ कम-विनिमेय हैं-

प्राकृत संख्याओं के लिए क्रम-विनिमेयता की जांच

(1) योग में- यदि और b कोई दो प्राकृत संख्याएँ है, तो (a + b) = (b + a) (योग में क्रम-विनिमेयता है।)
जाँच- इस गुण की जाँच के लिए कुछ प्राकृत संख्याओं के युग्म लेकर उन्हें भिन्न-भिन्न क्रम में जोड़ेंगे-

(2) व्यवकलन में- प्राकृत संख्याओं के व्यवकलन में क्रमविनिमेयता नहीं होती है अर्थात् यदि और b दो प्राकृत संख्याएँ है,तो सामान्यतः (a – b) ≠ (b – a)
हम जानते है कि 9 – 4 = 5, लेकिन 4 – 9 सम्भव नहीं है। इसी प्रकार 110 – 35 = 75, लेकिन 35 – 110 सम्भव नहीं है।

(3) गुणन में- यदि और कोई दो प्राकृत संख्याएँ है, तो (a × b) = (b × a) (गुणन में क्रम-विनिमेयता है।)
जाँच- इस गुणन की जाँच के लिए प्राकृत संख्याओं के कुछ युग्म लेकर उन्हें भिन्न-भिन्न क्रम में नियमानुसार गुणन करेंगे-

हम पाते हैं कि दो प्राकृत संख्याओं को किसी भी क्रम में गुणा करने पर गुणनफल सदैव समान ही आता है।

(4) भाग में- यदि a और b दो प्राकृत संख्याएँ है, तो a+b ÷ b+a (भाग में क्रम-विनिमेयता नहीं है।)
जाँच- इस गुण की जाँच हम कुछ युग्म लेकर निम्नानुसार करेंगे-

प्रश्न 2.
निम्नलिखित सारणी के रिक्त स्थानों को भरिए और पूर्णाकों के लिए विभिन्न संक्रियाओं की क्रमविनिमेयता जाँचिए-

हल:

प्रयास कीजिए (पृष्ठ 7)

प्रश्न 1.
निम्नलिखित सारणी को पूरा कीजिए-

हल:

साहचर्यता (सहचारिता)

प्रश्न 1.
निम्नलिखित सारगी के माध्यम से पूर्ण संख्याओं के लिए चार संक्रियाओं की साहचर्यता को स्मरण कीजिए-

इस सारणी को भरिए और अन्तिम स्तम्भ में दी गई टिप्पणियों को सत्यापित कीजिए। प्राकृत संख्याओं के लिए विभिन्न संक्रियाओं की साहचर्यता की स्वयं जाँच कीजिए।
हल:

प्राकत माताओं ने लिए विभिन्न संक्रियाओं की साहचर्य।

(1) योग-किन्हीं तीन प्राकृत संख्याओं abऔर C के लिए
(a + b) + c = a + (b + c)
जाँच-

अत: प्राकृत संख्याओं का योग साहचर्य है।

(2) व्यवकलन- किन्हीं तीन प्राकृत संख्याओं a, bऔर c के लिए सामान्यतः
a – (b – c) = (a – b) – c
जाँच-

अतः प्राकृत संख्याओं का व्यवकलन साहचर्य नहीं है।

(3) गुणन- किन्हीं तीन प्राकृत संख्याओं a bऔर C के लिए सामान्यतः
a × (b × a) = (a × b) × c
जाँच-

अत: प्राकृत संख्याओं का गुणन साहचर्य है।

(4) भाग- किन्हीं तीन प्राकृत संख्याओं a, b और c के लिए सामान्यतः
a ÷ (b ÷ a) = (a ÷ b) ÷ c
जाँच-

अत: प्राकृत संख्याओं का भाग साहचर्य है।

प्रश्न 2.
पूर्णाकों के लिए चार संक्रियाओं की साहचर्यता निम्नलिखित सारणी से जाँचिए

हल:

प्रयास कीजिए (पृष्ठ 10)

निम्नलिखित सारणी को पूरा कीजिए-

हल:

सोचिए, चर्चा कीजिए और लिखिए (पृष्ठ 12)

प्रश्न 1.
यदि कोई गुणधर्म परिमेय संख्याओं के लिए सत्य है, तो क्या वह गुणधर्म पूर्णांकों, पूर्ण संख्याओं के लिए भी सत्य होगा? कौन-से गुणधर्म इनके लिए सत्य होंगे और कौन-से सत्य नहीं होंगे?
हल:
(1) निम्नांकित गुण को छोड़कर परिमेय संख्याओं की क्रियाओं के गुण पूर्णाकों में भी होंगे-
a ÷ b एक परिमेय संख्या है यदि b ≠ 0, लेकिन a ÷ b जरूरी नहीं है कि एक पूर्णांक हो यदि a, b ∈ I

(2) निम्नांकित गुणों को छोड़कर परिमेय संख्याओं के सभी गुण पूर्ण संख्याओं में भी होंगे-
(i) यदि a और b परिमेय संख्याएँ हैं, तो a – b भी परिमेय संख्या होगी। लेकिन यदि और b पूर्ण संख्याएँ हैं, तो (a – b) पूर्ण संख्या हो भी सकती है और नहीं भी।
(ii) यदि और b परिमेय संख्याएँ हैं, तो a ÷ b(b ≠ 0) एक परिमेय संख्या होगी। लेकिन और संपूर्ण संख्याएँ हों, तो a ÷ b(b = 0) जरूरी नहीं कि एक पूर्ण संख्या हो।
निम्नलिखित तालिका दर्शाती है कि परिमेय संख्याओं, पूर्णाकों तथा पूर्ण संख्याओं में कौन-सा गुण उभयनिष्ठ है/नहीं है-

प्रयास कीजिए (पृष्ठ 14)

प्रश्न 1.
वितरकता के उपयोग से निम्नलिखित का मान ज्ञात कीजिए
(i) \(\left\{\frac{7}{5} \times\left(\frac{-3}{12}\right)\right\}\) + \(\left\{\frac{7}{5} \times \frac{5}{12}\right\}\)
(ii) \(\left\{\frac{9}{16} \times \frac{4}{12}\right\}\) + \(\left\{\frac{9}{16} \times \frac{-3}{9}\right\}\)
हल:

प्रयास कीजिए (पृष्ठ 18)

प्रश्न 1.
अक्षर द्वारा अंकित प्रत्येक बिन्दु के लिए परिमेय संख्या लिखिए-

हल:
(i) अक्षर द्वारा अंकित बिन्दुओं के सम्मुख परिमेय संख्याएँ निम्नलिखित हैं-
A : \(\frac{1}{5}\)
B : \(\frac{4}{5}\)
C : \(\frac{5}{5}\)
D : \(\frac{8}{5}\)
E : \(\frac{9}{5}\)

(ii) अक्षर द्वारा अंकित बिन्दुओं के सम्मुख परिमेय संख्याएँ निम्नलिखित हैं-
J : \(\frac{-11}{6}\)
I : \(\frac{-8}{6}\)
H : \(\frac{-7}{6}\)
G : \(\frac{-5}{6}\)
F : \(\frac{-2}{6}\)