HBSE 10th Class Maths Solutions Chapter 2 Polynomials Ex 2.4

Haryana State Board HBSE 10th Class Maths Solutions Chapter 2 Polynomials Ex 2.4 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 2 Polynomials Exercise 2.4

Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and coefficients in each case :
(i) 2x³ + x² – 5x + 2; \(\frac{1}{2}\), 1, – 2,
(ii) x³ – 4x² + 5x – 2; 2, 1, 1.
Solution :
(i) We have,
f(x) = 2x³ + x² – 5x + 2
On comparing f(x) with standard form of cubic polynomial ax³ + bx² + cx + d,
We get a = 2, b = 1, c = – 5, d = 2 and the
given zeroes are \(\frac{1}{2}\), 1, – 2.
∴ f(\(\frac{1}{2}\)) = 2 × (\(\frac{1}{2}\))³ + (\(\frac{1}{2}\))² – 5 × \(\frac{1}{2}\) + 2

= 2 × \(\frac{1}{8}+\frac{1}{4}-\frac{5}{2}\) + 2

= \(\frac{1}{4}+\frac{1}{4}-\frac{5}{2}\) + 2

= \(\frac{2}{4}-\frac{5}{2}\) + 2

= \(\frac{1}{2}-\frac{5}{2}\) + 2

= = \(\frac{1-5+4}{2}=\frac{5-5}{2}\) = 0
f(1) = 2 × (1)³ + (1)² – 5 × 1 + 2
= 2 + 1 – 5 + 2
= 5 – 5 = 0
f(- 2) = 2 × (- 2)³ + (- 2)² – 5 × (- 2) + 2
= 2 × (- 8) + 4 + 10 + 2
= – 16 + 16 = 0.
Therefore, \(\frac{1}{2}\), 1 and – 2 are the zeroes of given polynomial.
∴ α = \(\frac{1}{2}\), β = 1 and γ = – 2
Now,
α + β + γ = \(\frac{1}{2}\) + 1 – 2
= \(\frac{1+2-4}{2}\)
= \(-\frac{1}{2}=-\frac{b}{a}\)
= \(-\frac{\text { Coefficient of } x^2}{\text { Coefficient of } x^3}\)

αβ + βγ + αγ = \(\frac{1}{2}\) × 1 + 1 × (- 2) + (- 2) × \(\frac{1}{2}\)
= \(\frac{1}{2}\) – 2 – 1
= \(\frac{1}{2}\) – 3
= \(\frac{c}{a}=\frac{\text { Coefficient of } x}{\text { Coefficient of } x^3}\)

αβγ = \(\frac{1}{2}\) × 1 × (- 2) = – \(\frac{2}{2}\)
= \(-\frac{d}{a}=-\frac{\text { Constant term }}{\text { Coefficient of } x^3}\).

(ii) We have,
f(x) = x³ – 4x² + 5x – 2
On comparing f(x) with standard form of cubic polynomial ax³ + bx² + cx + d,
We get, a = 1, b = – 4, c = 5 and d = – 2
The given zeroes are 2, 1, 1.
f(x) = (2)³ – 4 × (2)² + 5 × 2 – 2
= 8 – 16 + 10 – 2
= 18 – 18 = 0

f(x) = (1)³ – 4 × (1)² + 5 × 1 – 2
= 1 – 4 + 5 – 2
= 6 – 6 = 0
Again f(1) = 0 (solved above).
Therefore, 2, 1 and 1 are zeroes of the given polynomial.
∴ α = 2, β = 1 and γ = 1.
Now, α + β + γ = 2 + 1 + 1 = 4 = \(\frac{-(-4)}{1}\)
= \(-\frac{b}{a}=-\frac{\text { Coefficient of } x^2}{\text { Coefficient of } x^3}\)

αβ + βγ + γα = 2 × 1 + 1 × 1 + 1 × 2
= 2 + 1 + 2
= \(\frac{5}{1}=\frac{c}{a}=\frac{\text { Coefficient of } x}{\text { Coefficient of } x^3}\)

Question 2.
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, – 7, – 14 respectively.
Solution:
Let α, β and γ are the zeroes of cubic polynomial f(x).
According to question,
α + β + γ = 2
αβ + βγ + γα = – 7
αβγ = – 14
Then cubic polynomial is
f(x) = x³ – (α + β + γ) x² + (αβ + βγ + γα)x – αβγ
= x³ – 2x² – 7x – (- 14)
= x³ – 2x² – 7x + 14

Question 3.
If file zeroes of the polynomial x³ – 3x² + x + 1 are a – b, a, a + b, find a and b.
Solution :
We have,
f(x) = x³ – 3x² + x + 1 and zeroes of the, polynomial are a – b, a, a + b , ’
Sum of zeroes = – \(\frac{b}{a}\)
⇒ a – b + a + a + b = – \(\frac{b}{a}\)
⇒ 3a = 3
⇒ a = 1.
and, Product of zeroes = – \(\frac{d}{a}\)
⇒ (a – b) a (a + b) = – \(\frac{1}{1}\)
⇒ (1 – b) × 1 (1 + b) = – 1
⇒ – b² = – 1.
⇒ b² = 1 + 1 = 2
⇒ b = ± √2
Hence, a = 1, b = ± √2.

Question 4.
If two zeroes of the polynomial x⁴ – 6x³ – 26x² + 138x – 35 are 2 ± √3 , find other zeroes.
Solution :
We have,
f(x) = x⁴ – 6x³ – 26x² + 138x – 35
∴ 2 ± √3 are the zeroes of given polynomial.
∴ (x – 2 – √3) (x – 2 + √3) = (x – 2)²
– (√3)² = x² – 4x + 1 is a factor of f(x).
Now, we divide given polynomial f(x) by x² – 4x + 1 to obtain the other zeroes as follows :

According to division algorithm of polynomials,
x⁴ – 6x³ – 26x² + 138x + 10 = (x² – 4x + 1) (x² – 2x – 35) + 0
= (x² – 4x + 1) [x² – (7 – 5)x – 35]
= (x² – 4x + 1) [x² – 7x + 5x – 35]
= (x² – 4x + 1) [x (x – 7) + 5(x – 7)]
= (x – 2 – √3)(x – 2 + √3) (x – 7)(x + 5)
For the zeroes of polynomial f(x) = 0.
⇒ (x – 2 – √3)(x – 2 + √3) (x – 7)(x + 5) = 0
⇒ x = 2 + √3, 2 – √3, 7, – 5.
Hence, other zeroes of polynomial are 7, – 5.

Question 5.
If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a, find k and a.
Solution :
We have,
f(x) = x⁴ – 6x³ + 16x² – 25x + 10
g(x) = x² – 2x + k
r(x) = x + a
According to division algorithm of polynomials f(x) = g(x) x q(x) + r(x)
⇒ f(x) – r(x) = g(x) × q(x)
⇒ x⁴ – 6x³ + 16x² – 25x + 10 – x – a = g(x) × q(x)
⇒ x⁴ – 6x³ + 16x² – 25x + 10 – a = g(x) × q(x)
Now, f(x) – r(x) is divisible by g(x).
Now, we divide x⁴ – 6x³ + 16x² – 26x + 10 – a by x² – 2x + k as follows.

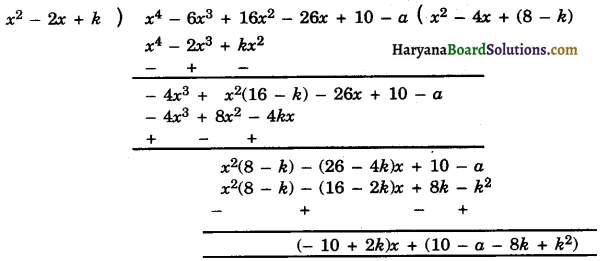
But f(x) – r(x) is exactly divisible by g(x), therefore, remainder will be zero.
∴ (- 10 + 2k) x + (10 – a – 8k + k²) = 0 × x + 0.
On equating the coefficient of x and constant term
⇒ – 10 + 2k = 0
⇒ k = \(\frac{10}{2}\) = 5
and 10 – a – 8k + k² = 0
⇒ 10 – a – 8 × 5 + (5)² = 0 [∵ k = 5]
⇒ 10 – a – 40 + 25 = 0
⇒ – a – 5 = 0
⇒ a = – 5
Hence, k = 5 and a = – 5