Haryana State Board HBSE 9th Class Maths Solutions Chapter 8 Quadrilaterals Ex 8.2 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 8 Quadrilaterals Exercise 8.2
Question 1.
ABCD is a quadrilateral in which P, Q, R and S are mid points of the sides AB, BC, CD and DA (see figure 8.29). AC is a diagonal. Show that:
(i) SR || AC and SR = \(\frac{1}{2}\)AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.

Solution:
Given : ABCD is a quadrilateral in which P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively. AC is a diagonal.
To prove : (i) SR || AC and SR = \(\frac{1}{2}\)AC,
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Proof : (i) In ΔACD, we have
∴ S and R are the mid points of AD and CD respectively.
∴ SR || AC and SR = \(\frac{1}{2}\)AC
(ii) In ΔABC, we have
∴ P and Q are the mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac{1}{2}\)AC,
[By theorem 8.9] …(ii)
From (i) and (i), we get
PQ || SR and PQ = SR.
(iii) ∵ PQ || SR and PQ = SR,
(As proved above)
∴ PQRS is a parallelogram.
Hence proved
![]()
Question 2.
ABCD is a rhombus and P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
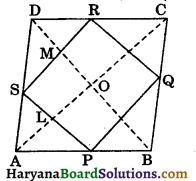
Given: A rhombus ABCD in which P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively.
To prove: Quadrilateral PQRS is a rectangle.
Construction: Join AC and BD.
Proof: In ΔADC, we have S and R are the mid points of AD and CD respectively.
∴ SR || AC and SR = \(\frac{1}{2}\)AC ……(1)
and in ΔABC, we have
P and Q are the mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac{1}{2}\)AC,
[By theorem 8.9] …….. (ii)
From (i) and (ii), we get
PQ || SR and PQ = SR
∴ PQRS is a parallelogram.
[By theorem 8.8]
Again in ΔDAB, we have
S and P are the mid points of AD and AB respectively.
SP || BD
⇒ SL || MO
and SR || AC [From (i)]
⇒ SM || LO
∴ SLOM is a parallelogram.
Since, diagonals of a rhombus bisect each other at 90°.
∴ ∠AOD = 90°
∠MOL = 90°
But, ∠LSM = ∠MOL,
(Opposite angles of a parallelogram)
⇒ ∠LSM = 90°
⇒ ∠PSR = 90°
Since, one angle of a parallelogram PQRS is 90°.
Therefore, quadrilateral PQRS is a rectangle.
Hence proved
Question 3.
ABCD is a rectangle and P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
Given: A rectangle ABCD in which P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively.
To prove : Quadrilateral PQRS is a rhombus.
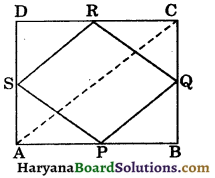
Construction: Join AC.
Proof: In ΔADC, S and R are the mid points of AD and CD respectively.
∴ SR || AC and SR = \(\frac{1}{2}\)AC …(i)
[By thoerem 8.9]
In ΔABC, P and Q are the mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac{1}{2}\)AC …..(ii)
From (i) and (ii), we get
PQ || SR and PQ = SR
∴ PQRS is a parallelogram.
[By theorem 8.8]
∵ ABCD is a rectangle.
∠A = ∠B = 90° …(ii)
and AD = BC, (Opposite sides of a rectangle)
⇒ \(\frac{1}{2}\)AD = \(\frac{1}{2}\)BC
⇒ AS = BQ,
[∵ S is the mid point of AD and Q is the mid point of BC]
∴ AS = \(\frac{1}{2}\)AD and BQ = \(\frac{1}{2}\)BC]
Now in ΔSAP and ΔQBP, we have
AS = BQ, [As proved above]
∠SAP = ∠QBP,
[From (iii), Each = 90°]
and AP = BP,
[∵ P is the mid point of AB]
∴ ΔSAP ≅ ΔQBP,
(By SAS congruence rule)
⇒ SP = PQ, (CPCT)
Thus, adjacent sides of a parallelogram PQRS are equal.
Therefore, PQRS is a rhombus.
Hence proved
![]()
Question 4.
ABCD is a trapezium in which AB || CD, BD is a diagonal and E is the mid point of AD. A line is drawn through E parallel to AB intersecting BC at F(see figure 8.30). Show that F is the mid point of BC.
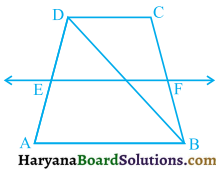
Solution:
Given: ABCD is a trapezium in which AB || CD, EF || AB and E is the mid point of AD.
To prove: F is the mid point of BC.
Proof: Let line EF intersecting BD at G.
In ΔDAB, we have
EG || AB (∵ EF || AB)
and E is the mid point of AD.
∴ G is the mid point of BD.
Now, AB || CD and AB || EF, (Given)
⇒ EF || CD
⇒ GF || CD
and G is the mid point of BD. (As proved above)
∴ F is the mid point of BC.
Hence proved
Question 5.
In a parallelogram ABCD, E and Fare the mid points of sides AB and CD respectively (see figure 8.31). Show that the line segments AF and EC trisect the diagonal BD.
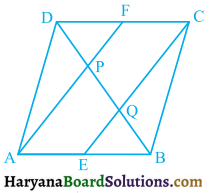
Solution:
Since, ABCD is a parallelogram.
∴ AB = CD,
(Opposite sides of parallelogram)
\(\frac{1}{2}\)AB = \(\frac{1}{2}\)CD
AE = FC,
[∵ E and F are mid points of AB and CD respectively
∴ AE = \(\frac{1}{2}\)AB and FC = \(\frac{1}{2}\)CD]
and AB || CD
⇒ AE || FC
∴ AECF is a parallelogram.
⇒ AF || EC …..(i)
In ΔABP, we have
E is the mid point of AB.
and EQ || AP [∵ AF || EC]
∴ Q is the mid point of BP
⇒ BQ = PQ …….(ii)
In ΔCQD, we have
F is the mid point of CD.
and PF || CQ [∵ AF || EC]
∴ P is the mid point of DQ.
⇒ DP = PQ ……..(iii)
From (ii) and (iii), we get
DP = PQ = BQ
Hence, line segments AF and EC trisect the diagonal BD.
Hence proved
![]()
Question 6.
Show that the line segments joining the mid points of the opposite sides of a quadrilateral bisect each other.
Solution:
Given: ABCD is a quadrilateral in which EG and FH are the line segments joining the mid points of opposite sides of a quadrilateral.
To prove: EG and FH bisect each other.
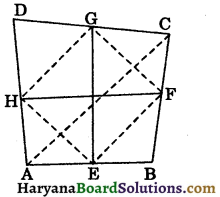
Construction: Join EF, FG, GH, HE and AC.
Proof: In ΔABC, E and F are mid points of AB and BC.
∴ EF || AC and EF = \(\frac{1}{2}\)AC
[By mid point theorem]
In ΔADC, H and G are mid points of AD and CD.
∴ HG || AC and HG = \(\frac{1}{2}\)AC ……(ii)
From (i), (ii), we get
EF || HG and EF = HG
∴ EFGH is a parallelogram. [By theorem 8.8]
We know that diagonals of a parallelogram bisect each other.
Therefore EG and FH bisect each other.
Hence proved
Question 7.
ABC is a triangle right angled at C. A line through the mid point M of hypotenuse AB and parallel to BC intersects AC at D. Show that:
(i) D is the mid point of AC,
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac{1}{2}\)AB.
Solution:
Given: A ΔABC in which ∠C = 90°,
M is the mid point of AB and MD || BC.
To prove : (i) D is the mid point of AC.
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac{1}{2}\)AB.
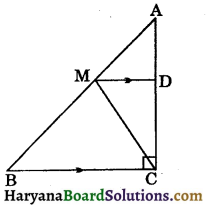
Proof: (i) In ΔABC, M is the mid point of AB.
and MD || BC, (Given)
∴ D is the mid point of AC.
(By theorem 8.10)
(ii) Since, MD || BC and ∠ACB = 90°
∴ ∠ADM = 90°
(Corresponding angles) …(i)
(iii) But, ∠DM + ∠CDM = 180°, (Linear pair)
⇒ 90° + ∠CDM = 180°, [Using (i)]
⇒ ∠CDM = 180° – 90° = 90° … (ii)
Now, ΔADM and ΔCDM, we have
AD = CD,
(As proved above, D is the mid point of AC)
∠ADM = ∠CDM, [From (i) and (ii), Each = 90°]
and MD = MD, (Common)
∴ ΔADM ≅ ΔCDM,
(By SAS congruence rule)
⇒ AM = CM, (CPCT)
But, AM = BM, (∵ M is the mid point of AB)
∴ AM = CM = \(\frac{1}{2}\)AB.
Hence proved