Haryana State Board HBSE 9th Class Maths Solutions Chapter 7 Triangles Ex 7.3 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 7 Triangles Exercise 7.3
Question 1.
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure 7.56). If AD is extended to intersect BC at P, show that:
(i) ΔABD ≅ ΔACD,
(ii) ΔABP ≅ ΔACP,
(iii) AP bisects ∠A as well as ∠D,
(iv) AP is the perpendicular bisector of BC.

Solution:
(i) In ΔABD and ΔACD, we have
AB = AC, (∵ ΔABC is an isosceles triangle)
DB = DC, (∵ ΔDBC is an isosceles triangle)
and AD = AD, (Common)
∴ ΔABD ≅ ΔACD,
(By SSS congruence rule)
⇒ ∠BAD = ∠CAD, (CPCT) …(i)
Hence proved
(ii) In ΔABP and ΔACP, we have
AB = AC, (Given)
∠BAP = ∠CAP,
[from (i), ∠BAD = ∠CAD]
and AP = AP, (Common)
∴ ΔABP ≅ ΔACP, …(ii)
(by SAS congruence rule)
⇒ BP = CP (CPCT) …(iii)
Hence proved
(iii) From (i), we have
∠BAD = ∠CAD
⇒ ∠BAP = ∠CAP
⇒ AP is the bisector of ∠A.
In ΔBPD and ΔCPD, we have
BD = CD, (Given)
BP = CP, [from (iii)]
and PD = PD, (Common)
∴ ΔBPD ≅ ΔCPD,
(by SSS congruence rule)
⇒ ∠BDP = ∠CDP, (CPCT)
⇒ DP is the bisector of ∠D.
Hence, AP is the bisector of ∠A as well as ∠D
Hence proved
(iv) From (ii), we have
ΔABP ≅ ΔACP (from (iii)]
⇒ BP = CP, [From (iii)]
and ∠APB = ∠APC, (CPCT) …(iv)
∠APB + ∠APC = 180°, (linear pair)
⇒ ∠APB + ∠APB = 180, [(Using (iv)]
⇒ 2∠APB = 180°
⇒ ∠APB = \(\frac {180°}{2}\) = 90°
Hence, AP is the perpendicular bisector of BC.
Hence proved
![]()
Question 2.
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that:
(i) AD bisects BC,
(ii) AD bisects ∠A.
Solution:
In ΔADB and ΔADC, we have
∠ADB = ∠ADC, (Each = 90°)
Hyp. AB = Hyp. AC, (Given)
and AD = AD, (Common)
∴ ΔADB ≅ ΔADC,
(by RHS congruence rule)
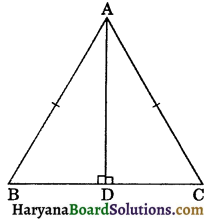
(i) ⇒ DB = DC, (CPCT)
OR AD bisects BC.
Hence proved
(ii) ∠BAD = ∠CAD, (CPCT)
Or AD bisects ∠A.
Hence proved
Question 3.
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see figure 7.58). Show that:
(i) ΔABM ≅ ΔPQN,
(ii) ΔABC ≅ ΔPQR.

Solution:
We have, AM is the median of ΔABC.
⇒ BM = CM ……(i)
PN is the median of ΔPQR.
∵ QN = RN ……(ii)
BC = QR (Given)
⇒ \(\frac {1}{2}\) BC = \(\frac {1}{2}\) QR
(Multiplying by 1/2 on both sides)
⇒ BM = QN …….(iii)
(i) In ΔABM and ΔPQN, we have
AB = PQ, (Given)
BM = QN, [from (iii)]
and AM = PN, (Given)
∴ ΔABM ≅ ΔPQN, (by SSS congruence rule)
Hence proved
⇒ ∠B = ∠Q. (CPCT) …(iv)
(ii) In ΔABC and ΔPQR, we have
AB = PQ, (Given)
∠B = ∠Q, [from (iv)]
and BC = QR (Given)
∴ ΔABC ≅ ΔPQR, (by SAS congruence rule)
Hence proved
![]()
Question 4.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Solution:
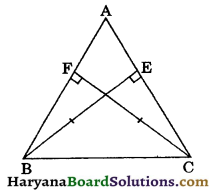
We have,
BE ⊥ AC and CF ⊥ AB
i.e., ∠CFB= 90° and ∠BEC = 90° ………(i)
In ΔBFC and ΔCEB, we have
∠CFB = ∠BEC,
[from (i), Each = 90°]
Hyp. BC = Hyp. BC, (Common)
and CF = BE (Given)
∴ ΔBFC ≅ ΔCEB,
(by RHS congruecne rule)
⇒ ∠FBC = ∠ECB, (CPCT)
⇒ ∠B = ∠C
Now in ΔABC, we have
∠B = ∠C, (As proved above)
⇒ AB = AC, (∵ Sides opposite to equal angles are equal)
Or ΔABC is an isosceles triangle.
Hence proved
Question 5.
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Solution :
In ΔAPB and ΔAPC, we have
∠APB = ∠APC,
(∵ AP ⊥ BC, ∴ Each = 90°)
Hyp. AB = Hyp. AC, (Given)
and AP = AP (common)
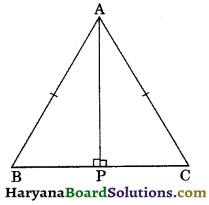
∴ ΔAPB ≅ ΔAPC,
(by RHS congruence rule)
⇒ ∠B = ∠C, (CPCT)
Hence proved