Haryana State Board HBSE 9th Class Maths Solutions Chapter 14 Statistics Ex 14.2 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 14 Statistics Exercise 14.2
Question 1.
The blood groups of 30 students of Class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
Represent this data in the form of a frequency distribution table. Which is the most common, and which is the rarest, blood group among these students?
Solution:
The frequency distribution table is given below :
Frequency distribution of blood groups
| Blood Groups | Numbers of students |
| A | 9 |
| B | 6 |
| O | 12 |
| AB | 3 |
| Total | 30 |
Most common blood group is O and rarest blood group is AB.
Question 2.
The distance (in km) of 40 engineers from their residence to their place of work were found as follows:

Construct a grouped frequency distribution table with class size 5 for the data given above taking the first interval as 0 – 5 (5 is not included). What main features do you observe from this tabular representation?
Solution :
Minimum and maximum observations are 2 and 32. And class size is 5, first class interval is 0 – 5.
So, class intervals of same size are 0 – 5, 5 – 10, 10 – 15, 15 – 20, 20 – 25, 25 – 30 and 30 – 35. The frequency distribution table is given below
Frequency distribution of distance
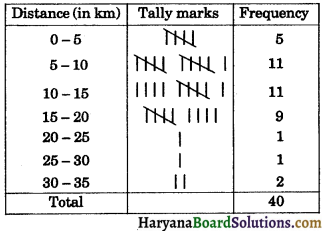
We observe that:
(i) The residence of 36 engineers are within 5 km to 20 km.
(ii) The residence of 4 engineers are within 20 km to 35 km.
![]()
Question 3.
The relative humidity (in %) of a certain city for a month of 30 days was as follows:

(i) Construct a grouped frequency distribution table with classes 84 – 86, 86 – 88, etc.
(ii) Which month or season do you think this data is about?
(iii) What is the range of this data?
Solution :
Minimum and maixmum observations are 84.9 and 99.2 respectively.
∴ Class intervals of same size are 84 – 86, 86 – 88, 88 – 90, 90 – 92, 92 – 94, 96 – 98 and 98 – 100.
Frequency distribution table of relative humidity is given below :
(i) Frequency distribution of relative humidity :
| Relative humidity (in %) | Frequency |
| 84 – 86 | 1 |
| 86 – 88 | 1 |
| 88 – 90 | 2 |
| 90 – 92 | 2 |
| 92 – 94 | 7 |
| 94 – 96 | 6 |
| 96 – 98 | 7 |
| 98 – 100 | 4 |
| Total | 30 |
(ii) The data appears to be taken in the rainy season as the relative humidity is high.
(iii) Range = 99.2 – 84.9 = 14.3.
Question 4.
The heights of 50 students, measured to the nearest centimeters, have been found to be as follows:

(i) Represent the data given above by a grouped frequency distribution table, taking the class intervals as 160 – 165, 165 – 170 etc.
(ii) What can you conclude about their heights from the table?
Solution :
Minimum and maximum observations are 150 and 173 respectively. So, class intervals of same size are
150 – 155, 155 – 160, 160 – 165, 165 – 170 and 170 – 175
The frequency distribution table of heights of 50 students is given below.
(i) Frequency distribution of heights.
| Heights (in cm) | Frequency |
| 150 – 155 | 12 |
| 155 – 160 | 9 |
| 160 – 165 | 14 |
| 165 – 170 | 10 |
| 170 – 175 | 5 |
| Total | 50 |
(ii) One conclusion that we can draw from the above table is that more than 50% of students are shorter than 165 cm. Ans.
![]()
Question 5.
A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows:
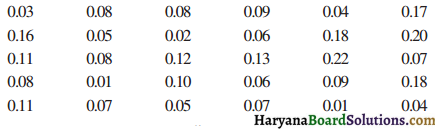
(i) Make a ground frequency distribution table for this data with class intervals as 0.00 – 0.04, 0.04 – 0.08 and so on.
(ii) For how many days, was the concentration of sulphur dioxide more than 0.11 parts per million?
Solution :
Minimum and maximum observations are 0.01 and 0.22.
Class intervals of same size are 0.00 – 0.04, 0.04 – 0.08, 0.08 – 0.12, 0.12 – 0.16, 0.16 – 0.20 and 0.20 – 0.24.
Frequency distribution table of concentration of sulphur dioxide in the air is given below :
(i) FREQUENCY DISTRIBUTION OF CONCENTRATION OF SULPHUR DIOXIDE
| Concentration of sulphur dioxide (in ppm) | Frequency |
| 0.00 – 0.04 | 4 |
| 0.04 – 0.08 | 9 |
| 0.08 – 0.12 | 9 |
| 0.12 – 0.16 | 2 |
| 0.16 – 0.20 | 4 |
| 0.20 – 0.24 | 2 |
| Total | 30 |
(ii) The concentration of sulphur dioxide was more than 0.11 ppm for 8 days.
Question 6.
Three coins were tossed 30 times simultaneously. Each time the number of heads occurring was noted down as follows :

Prepare a frequency distribution table for the data given above.
Solution :
Frequency distribution table for the given data is given below :
Frequency distribution table of coins
| Number of heads | Frequency |
| 0 | 6 |
| 1 | 10 |
| 2 | 9 |
| 3 | 5 |
| Total | 30 |
![]()
Question 7.
The value of π up to 50 decimal places is given below :
3.14159265358979323846264338327950288419716939937510
(i) Make a frequency distribution of the digits from 0 to 9 after the decimal point.
(ii) What are the most and the least frequently occurring digits?
Solution:
(i) Frequency distribution table of digits from 0 to 9 after the decimal point is given below:
Frequency distribution of digit from 0 to 9
| Digits | Frequency | Digits | Frequency |
| 0 | 2 | 5 | 5 |
| 1 | 5 | 6 | 4 |
| 2 | 5 | 7 | 4 |
| 3 | 8 | 8 | 5 |
| 4 | 4 | 9 | 8 |
| Total | 50 |
(ii) The most frequently occurring digits are 3 and 9. The least occurring is 0.
Question 8.
Thirty children were asked about the number of hours they watched TV programmes in the previous week. The results were found as follows:

(i) Make a grouped frequency distribution table for this data, using class width 5 and one of the class intervals as 5 – 10.
(ii) How many children watched television for 15 or more hours a week?
Solution :
Minimum and maximum observations are 1 and 17 respectively.
Class width = 5 and one of the class interval is 5 – 10.
So, class intervals of the following data are 0 – 5, 5 – 10, 10 – 15 and 15 – 20.
(i) Frequency distribution table of hours of T.V. programme is given below :
Frequency distribution of hours of T.V. programme
| Number of hours | Frequency |
| 0 – 5 | 10 |
| 5 – 10 | 13 |
| 10 – 15 | 5 |
| 15 – 20 | 2 |
| Total | 30 |
(ii) Number of children watched television for 15 or more hours a week = 2.
![]()
Question 9.
A company manufactures car batteries of a particular type. The lives (in years) of 40 such batteries were recorded as follows:

Construct a grouped frequency distribution table for this data, using class intervals of size 0.5 starting from the interval 2 – 2.5.
Solution :
The minimum and maximum observations of the data are 2.2 and 4.6 respectively.
Class size = 0.5 and one of the class interval is 2 – 2.5.
So, class intervals of the following data are :
2 – 2.5, 2.5 – 3.0, 3.0 – 3.5, 3.5 – 4.0, 4.0 – 45 and 4.5 – 5.0.
The frequency distribution table of car batteries is given below :
Frequency distribution of car batteries
| Life of batteries (in years) | Frequency |
| 2.0 – 2.5 | 2 |
| 2.5 – 3.0 | 6 |
| 3.0 – 3.5 | 14 |
| 3.5 – 4.0 | 11 |
| 4.0 – 4.5 | 4 |
| 4.5 – 5.0 | 3 |
| Total | 40 |