Haryana State Board HBSE 9th Class Maths Solutions Chapter 11 रचनाएँ Ex 11.1 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 11 रचनाएँ Exercise 11.1
प्रश्न 1.
एक दी हुई किरण के प्रारंभिक बिंदु पर 90° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
हल :
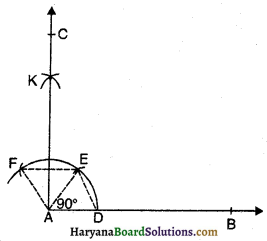
रचना के चरण-
- एक किरण AB खींचिए।
- A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
- परकार को इतना ही खुला रखकर D से चाप DE लगाओ। इसी प्रकार E से चाप EF लगाओ।
- अब परकार कुछ अधिक खोलकर E तथा F से चापें लगाओ जो परस्पर K पर काटें।
- अब K से गुजरती हुई एक किरण AC खींचिए।
- ∠CAB, अभीष्ट कोण है जो 90° का है।
सत्यापन- रचना से EA = AD = ED
∴ AED एक समबाहु त्रिभुज है।
अतः ∠EAD = 60° …….(i)
इसी प्रकार, AE = EF = FA
⇒ AEF एक समबाहु त्रिभुज है।
∠EAF = 60°
क्योंकि AC, ∠EAF का समद्विभाजक है।
∴ ∠EAC = \(\frac{1}{2}\) × 60° = 30° …….(ii)
समीकरण (i) व (ii) से,
∠CAB = ∠EAC + ∠EAD
= 30° + 60° = 90°
![]()
प्रश्न 2.
एक दी हुई किरण के प्रारंभिक बिंदु पर 45° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
हल :
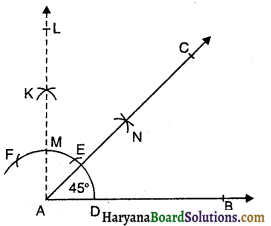
रचना के चरण-
- एक किरण AB खींचिए।
- A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
- परकार को इतना ही खुला रखकर D से चाप DE लगाओ। इसी प्रकार E से चाप EF लगाओ। अब परकार कुछ अधिक खोलकर E तथा F से चापें लगाओ जो परस्पर K पर काटें।
- अब K से गुजरती हुई एक किरण AL खींचो। ∠LAB का माप 90° होगा।
- अब M तथा D से चापें लगाओ जो परस्पर N पर काटें।
- अब N से गुजरती हुई एक किरण AC खींचिए।
- ∠CAB, अभीष्ट कोण है जो 45° का है।
सत्यापन- रचना में ∠LAB = 90° है और AC, ∠LAB का समद्विभाजक है।
∠CAB = \(\frac{1}{2}\)∠LAB = \(\frac{1}{2}\) × 90° = 45°
प्रश्न 3.
निम्न मापों के कोणों की रचना कीजिए- [B.S:E.H. March, 2018]
(i) 30°
(ii) \(22 \frac{1^{\circ}}{2}\)
(iii) 15°
हल :
(i) रचना के चरण-
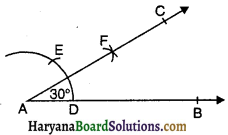
- एक किरण AB खींचिए।
- A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
- परकार को इतना ही खुला रखकर D से DE चाप लगाओ।
- अब परकार कुछ अधिक खोलकर D व E से चापें लगाओ जो परस्पर F पर काटें।
- F में से गुजरती हुई एक किरण AC खींचिए।
- ∠CAB, अभीष्ट कोण है जो 30° का है।
(ii) रचना के चरण- [B.S.E.H. March, 2019]
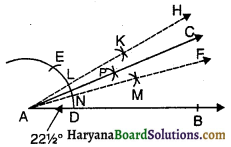
- एक किरण AB खींचिए।
- A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
- परकार को इतना ही खुला रखकर D से DE चाप लगाओ।
- अब परकार कुछ अधिक खोलकर D व E से चापें लगाओ जो परस्पर K पर काटें।
- K से गुजरती हुई एक किरण AH खींचिए। इस प्रकार ∠HAB = 30° का होगा।
- अब D व L से चापें लगाओ जो परस्पर M पर काटें।
- M से गुजरती हुई किरण AF खींचिए। इस प्रकार ∠FAB = 15° का होगा।
- अब N तथा L से चापें लगाओ जो परस्पर P पर काटें।
- P में से गुजरती हुई किरण AC खींचिए।
- ∠CAB, अभीष्ट कोण है जो \(22 \frac{1^{\circ}}{2}\) का है।
(iii) रचना के चरण-
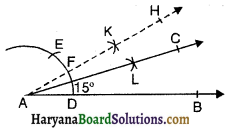
- एक किरण AB खींचिए।
- A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
- परकार को इतना ही खुला रखकर D से DE चाप लगाओ।
- अब परकार कुछ अधिक खोलकर D व E से चापें लगाओ जो परस्पर K पर काटें।
- K से गुजरती हुई एक किरण AH खींचिए। इस प्रकार ∠HAB = 30° का होगा।
- अब F व D से चापें लगाओ जो परस्पर L पर काटें।
- L में से गुजरती हुई एक किरण AC खींचिए।
- ∠CAB, अभीष्ट कोण है जो 15° का है।
![]()
प्रश्न 4.
निम्न कोणों की रचना कीजिए और चाँदे द्वारा मापकर पुष्टि कीजिए-
(i) 750
(ii) 105° [March, 2020]
(iii) 135°
हल :
(i) रचना के चरण-
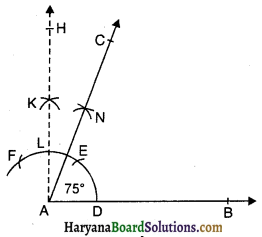
- एक किरण AB खींचिए।
- A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
- परकार को इतना ही खुला रखकर D से DE चाप लगाओ। इसी प्रकार E से चाप EF लगाओ।
- अब परकार कुछ अधिक खोलकर E व F से चापें लगाओ जो परस्पर K पर काटें।
- K से गुजरती हुई एक किरण AH खींचिए।
- बिंदु L व E से चापें लगाओ जो परस्पर N पर प्रतिच्छेद करें।
- N से गुजरती हुई एक किरण AC खींचिए।
- ∠CAB, अभीष्ट कोण है जो 75° का है।
- ∠CAB को चाँदे से नापने पर पता चलता है कि यह 75° का है।
(ii) रचना के चरण-
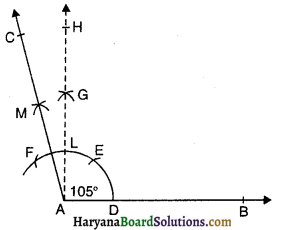
- एक किरण AB खींचिए।
- A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
- परकार को इतना ही खुला रखकर D से DE चाप लगाओ। इसी प्रकार E से चाप EF लगाओ।
- अब परकार कुछ अधिक खोलकर E व F से चापें लगाओ जो परस्पर G पर काटें।
- G से गुजरती हुई एक किरण AH खींचिए।
- बिंदु F तथा L से चापें लगाओ जो परस्पर M पर काटें।
- M से गुजरती हुई किरण AC खींचिए।
- ∠CAB, अभीष्ट कोण है जो 105° का है।
- इस कोण को चाँदे से नापने पर पता चलता है कि यह 105° का है।
(iii) रचना के चरण-
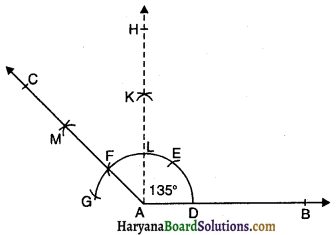
- एक किरण AB खींचिए।
- A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
- परकार को इतना ही खुला रखकर D से DE चाप लगाओ। इसी प्रकार E से EF तथा F से FG चाप लगाओ।
- अब परकार को पहले से अधिक खोलकर E व F से चापें लगाओ जो परस्पर K पर काटें।
- K में से गुजरती हुई एक किरण AH खींचिए।
- बिंदु L तथा G से चापें लगाओ जो परस्पर M पर काटें।
- अब M से गुजरती हुई एक किरण AC खींचिए।
- ∠CAB, अभीष्ट कोण है जो 135° का है।
- ∠CAB को चाँदे से नापने पर पता चलता है कि यह 135° का है।
![]()
प्रश्न 5.
एक समबाहु त्रिभुज की रचना कीजिए, जब इसकी भुजा दी हो तथा कारण सहित रचना कीजिए।
हल :
रचना के चरण-
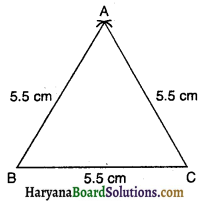
- एक रेखाखंड BC = 5.5 cm खींचिए।
- B और C को केंद्र मानकर BC = 5.5 cm त्रिज्या की परकार खोलकर दो चापें लगाएँ जो परस्पर A पर प्रतिच्छेद करें।
- A को B व C से मिलाओ।
- इस प्रकार ABC अभीष्ट समबाहु त्रिभुज है।
सत्यापन-क्योंकि रचना द्वारा AB = BC = CA = 5.5 cm
⇒ ∠C = ∠B = ∠A = 60°
∴ ΔABC समबाहु त्रिभुज है।