Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 Circles Ex 10.5 Textbook Exercise Questions and Answers.
Haryana Board 9th Class Maths Solutions Chapter 10 Circles Exercise 10.5
Question 1.
In Fig. 10.36, A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC. find ∠ADC.
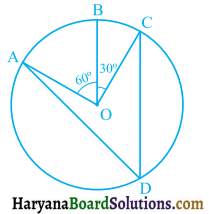
Solution:
∠AOC = ∠AOB + ∠BOC
∠AOC = 60° + 30°
∠AOC = 90°
∠AOC is an angle subtended by an arc AC on centre and ∠ADC on the remaining part of the circle.
∴ ∠AOC = 2 × ∠ADC [By theorem 10.8]
⇒ 90° = 2 × ∠ADC
⇒ ∠ADC = \(\frac{90^{\circ}}{2}\) = 45°3
Hence, ∠ADC = 45°.
Question 2.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
Let AB be a chord which is equal to radius. Join OA and OB, where O is the centre of the circle.
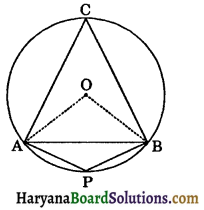
∵ AO = OB = AB (given)
∴ AOB is an equilateral triangle.
⇒ ∠AOB = 60°
Reflex ∠AOB = 360° – 60° = 300°
∠AOB = 2 × ∠ACB [By theorem 10.8]
⇒ 60° = 2 × ∠ACB
⇒ ∠ACB = \(\frac{60^{\circ}}{2}\) = 30°
and Reflex (∠AOB) = 2 × ∠APB [By theorem 10.8]
⇒ 300° = 2 × ∠APB
⇒ ∠APB = \(\frac{300^{\circ}}{2}\) = 150°
Hence, angle subtended by the chord at a point on the minor arc is 150° and major arc is 30°.
![]()
Question 3.
In Fig. 10.37, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.

Solution:
Since, reflex ∠POR is an angle subtended by an arc PR at the centre and ∠PQR at the remaining part of the circle.
∴ Reflex ∠POR = 2 × ∠PQR
⇒ Reflex ∠POR = 2 × 100° = 200°
∠POR = 360° – Reflex ∠POR
⇒ ∠POR = 360° – 200° = 160°
In ΔPOR, OP = OR [Radii of the same circle]
⇒ ∠OPR = ∠ORP [Angles opposite to equal sides are equal]
Let ∠OPR = ∠ORP = x°
In ΔPOR, we have
∠OPR + ∠ORP + ∠POR = 180° [∵ Sum of angles of a triangle is 180°]
⇒ x° + x° + 160° = 180°
⇒ 2x° = 180° – 160° = 20°
⇒ x° = \(\frac{20^{\circ}}{2}\) = 10°
Hence, ∠OPR = 10°.
Question 4.
In Fig. 10.38, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
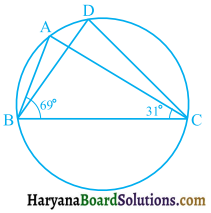
Solution:
In ΔBAC, we have
∠ABC + ∠BCA + ∠BAC = 180° [∵ Sum of angles of a triangle = 180°]
⇒ 69° + 31° + ∠BAC = 180°
⇒ 100° + ∠BAC = 180°
⇒ ∠BAC = 180° – 100°
⇒ ∠BAC = 80°
∠BDC = ∠BAC
[∵ Angles in the same segment are equal]
Hence ∠BDC = 80°.
Question 5.
In Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.

Solution:
In ΔECD, we have
∠BEC = ∠EDC + ∠ECD [∵ Exterior angle is equal to sum of its opposite two interior angles]
⇒ 130° = ∠EDC + 20°
⇒ ∠EDC = 130° – 20°
⇒ ∠EDC = 110°
⇒ ∠BDC = 110°
∠BAC = ∠BDC [∵ Angles in the same segment are equal]
Hence, ∠BAC = 110°.
![]()
Question 6.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Solution:
In ΔABC,
AB = BC (given)
⇒ ∠BAC = ∠BCA [∵ Angles opp. to equal sides are equal]
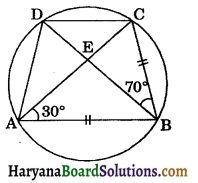
30° = ∠BCA
⇒ ∠BCA = 30°
In ΔABC, we have
∠BAC + ∠BCA + ∠ABC = 180°
⇒ 30° +30° +70° + ∠ABE = 180°
⇒ 130° + ∠ABE = 180°
⇒ ∠ABE = 180° – 130° = 50°
⇒ ∠ABD = 50°
∠ACD = ∠ABD [∵ Angles in the same segment of a circle are equal]
⇒ ∠ACD = 50°
⇒ ∠ECD = 50°
⇒ ∠BCD = ∠BCA + ∠ACD
⇒ ∠BCD = 30° +50°
⇒ ∠BCD = 80°
Hence, ∠BCD = 80° and ∠ECD = 50°.
Question 7.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Solution:
Given: Diagonals AC and BD of cyclic quadrilateral are thediameters of the circle through the vertices of the quadrilateral ABCD.
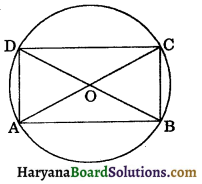
To prove: Quadrilateral ABCD is a rectangle.
Proof: Since BD is a diameter.
∠C = ∠A = 90°
[Angle in a semicircle is 90°]
Similarly, AC is a diameter.
∠B = ∠D = 90°
[Angle in a semicircle is 90°]
Thus, in a quadrilateral ABCD
∠A = ∠B = ∠C = ∠D = 90°
Hence, quadrilateral ABCD is a rectangle
Proved.
![]()
Question 8.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Solution:
A trapezium ABCD in which AB || CD and AD = BC.
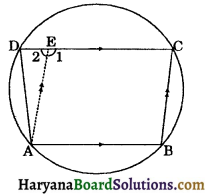
To prove: Trapezium ABCD is cyclic.
Construction: Draw AE || BC.
Proof: Since, AB || CD (given)
and AE || BC (By construction)
∴ AE = BC …..(i) (Opposite sides of a parallelogram)
AD = BC (given) … (ii)
From (i) and (ii), we get
AE = AD
⇒ ∠2 = ∠D …..(iii)
[Angles opposite to equal sides are equal]
∠B = ∠1 …..(iv)
[Opposite angles of a parallelogram]
But, ∠1 + ∠2 = 180°
[By linear pair axiom]
∠B + ∠D = 180° [Using (iii) and (iv)]
⇒ ABCD is a cyclic.
Hence, trapezium ABCD is cyclic.
Proved
Question 9.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP = ∠QCD.

Solution:
∠ABP = ∠ACP ……(i)
[Angles in a same segment are equal]
∠QBD = ∠QCD …..(ii)
[Angles in a same segment are equal]
∠ABP = ∠QBD …..(iii)
(Vertically opposite angles)
From (i), (ii) and (iii), we get
∠ACP = ∠QCD. Hence proved
Question 10.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Solution:
Given: Two circles are drawn with sides AB and AC of ΔABC as diameters. The circles intersect each other at D.
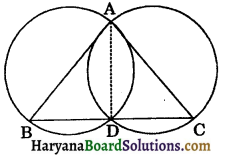
To prove: Point D lies on BC i.e., BDC is a straight line.
Construction: Join AD.
Proof: Since AB and AC are diameters of two circles.
∴ ∠ADB = 90° …..(i)
[Angle in semicircle is 90°]
and ∠ADC = 90° …..(ii)
[Angle in a semicircle is 90°]
Adding (i) and (ii), we get
∠ADB + ∠ADC = 90° + 90°
⇒ ∠ADB + ∠ADC = 180°
⇒ BDC is a straight line.
Hence, D lies on BC. Proved.
![]()
Question 11.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Solution:
∠ABC = ∠ADC = 90° (given)
In a quadrilateral ABCD,
∠ABC + ∠ADC = 90° + 90°
= 180°
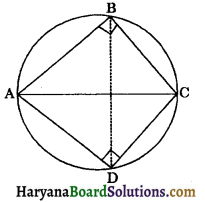
Therefore, ABCD is a cyclic quadrilateral.
∠CAD = ∠CBD [Angles in a same segment are equal]
Hence proved
Question 12.
Prove that a cyclic parallelogram is a rectangle.
Solution:
Given: A cyclic parallelogram ABCD.
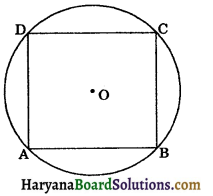
To prove: ABCD is a rectangle.
Proof : Since ABCD is a parallelogram. (given)
∴ ∠A = ∠C
(Opposite angles of a || gm) …(i)
But, ∠A + ∠C = 180° [By theorem]
⇒ ∠A + ∠A = 180° [Using (i)]
⇒ 2∠A = 180°
⇒ ∠A = \(\frac{180^{\circ}}{2}\)
So, ∠A = ∠C = 90°
Thus, ABCD is a parallelogram in which
∠A = ∠C = 90°.
Hence, ABCD is a rectangle. Proved