HBSE 9th Class Maths Solutions Chapter 10 वृत्त Ex 10.4

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 वृत्त Ex 10.4 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 वृत्त Exercise 10.4

प्रश्न 1.
5 सें०मी० तथा 3 सें०मी० त्रिज्या वाले दो वृत्त दो बिंदुओं पर प्रतिच्छेद करते हैं तथा उनके केंद्रों के बीच की दूरी 4 सें०मी० है। उभयनिष्ठ जीवा की लंबाई ज्ञात कीजिए।
हल :

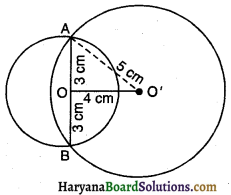
माना O व O’ केंद्र वाले दो वृत्त हैं जिनकी त्रिज्याएं क्रमशः 3 सें०मी० व 5 सें०मी० हैं।
∴ O’A = 5 सें०मी, OO’ = 4 सें०मी
समकोण त्रिभुज AOO’ में,
AO’² = AO² + OO’²
⇒ (5)² = AO² + (4)²
⇒ AO² = 25 – 16
⇒ AO² = 9
⇒ AO = 3
अतः उभयनिष्ठ जीवा AB है अर्थात 2AO या 2 × 3 = 6 सें०मी० उत्तर

प्रश्न 2.
यदि एक वृत्त की दो समान जीवाएं वृत्त के अंदर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खंड दूसरी जीवा के संगत खंडों के बराबर हैं।
हल :

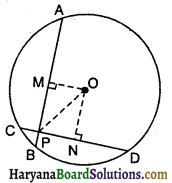
दिया है : AB तथा CD वृत्त की दो समान जीवाएं हैं, O वृत्त का केंद्र है। AB तथा CD, P पर प्रतिच्छेद करती हैं।
सिद्ध करना है:
(i) AP = PD
(ii) PB = CP
रचना : OM ⊥ AB, ON ⊥ CD खींचिए। OP को मिलाओ।
प्रमाण: AM = MB = \(\frac{1}{2}\) AB [∵ वृत्त के केंद्र से जीवा पर खींचा गया लंब जीवा को समद्विभाजित करता है]
इसी प्रकार CN = ND = \(\frac{1}{2}\)CD [वृत्त के केंद्र से जीवा पर खींचा गया लंब जीवा को समद्विभाजित करता है]
⇒ AM = ND तथा MB = CN …..(i) [∵ AB = CD दिया है]
अब ΔOMP तथा ΔONP में,
OM = ON [एक वृत्त की समान जीवाएं केंद्र से समान दूरी पर होती हैं।
∠OMP = ∠ONP [∵ प्रत्येक 90°]
OP = OP [उभयनिष्ठ]
∴ ΔΟΜΡ ≅ ΔΟΝΡ [समकोण-कर्ण-भुजा सर्वांगसमता]
⇒ MP = PN ….. (ii) [सर्वांगसम त्रिभुजों के संगत भाग]
समीकरण (i) तथा (ii) को जोड़ने पर,
AM + MP = ND + PN
⇒ AP = PD [इति सिद्धम]
समीकरण (i) में से समीकरण (ii) घटाने पर,
MB – MP = CN – PN
⇒ PB = CP [इति सिद्धम]

प्रश्न 3.
यदि एक वृत्त की दो समान जीवाएं वृत्त के अंदर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिंदु को केंद्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
हल :

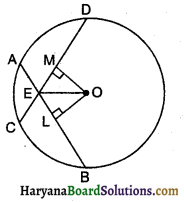
दिया है : केंद्र O वाले वृत्त की दो समान जीवाएं AB तथा CD वृत्त के अंदर परस्पर बिंदु E पर प्रतिच्छेदित होती हैं।
सिद्ध करना है : ∠OEB = ∠OED
रचना : O से OL ⊥ AB तथा OM ⊥ CD खींचिए।
प्रमाण : ∵ AB = CD [दिया है]
⇒ OL = OM [समान जीवाएं केंद्र से समान दूरी पर होती हैं]
ΔOEL तथा ΔOEM में,
OL = OM [प्रमाणित]
OE = OE [उभयनिष्ठ]
∠OLE = ∠OME [प्रत्येक = 90°]
∴ ΔOEL ≅ ΔOEM [समकोण-कर्ण-भुजा सर्वांगसमता]
∴ ∠OEL = ∠OEM [सर्वांगसम त्रिभुजों के संगत भाग]
या ∠OEB = ∠OED [इति सिद्धम]

प्रश्न 4.
यदि एक रेखा दो संकेंद्री वृत्तों (एक ही केंद्र वाले वृत्त) को, जिनका केंद्र O है, A,B,C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB =CD है (आकृति अनुसार)।

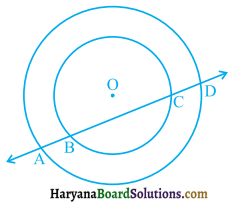
हल :

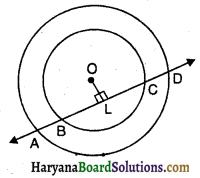
दिया है : दो संकेंद्री वृत्त जिनका केंद्र O है। एक रेखा इन्हें A, B, C तथा D बिंदुओं पर प्रतिच्छेद करती है।
सिद्ध करना है : AB = CD
रचना : O से OL ⊥ AD खींचिए।
प्रमाण : बड़े वृत्त में,
OL ⊥ AD
∴ AL = LD …(i) [∵ केंद्र से जीवा पर खींचा गया लंब उसे समद्विभाजित करता है]
इसी प्रकार छोटे वृत्त में,
OL ⊥ BC
∴ BL = LC …(ii) [∵ केंद्र से जीवा पर खींचा गया लंब उसे समद्विभाजित करता है]
समीकरण (ii) को (i) में से घटाने पर,
AL – BL = LD – LC
⇒ AB = CD [इति सिद्धम]

प्रश्न 5.
एक पार्क में बने 5 मी० त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियां रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 मी० हो, तो रेशमा और मनदीप के बीच की दूरी क्या है ?
हल :
माना तीन लड़कियां रेशमा, सलमा तथा मनदीप एक वृत्त की परिधि पर क्रमशः बिंदु A, B तथा C पर खड़ी हैं। वृत्त की त्रिज्या 5 मी० है।
प्रश्नानुसार AB = BC = 6 मी०
AC = ? OA, OB तथा OC को मिलाओ।
AB = BC [दिया है]
∴ बिंदु B, AC के लंबार्धक पर स्थित है।
OA = OC [एक ही वृत्त की त्रिज्याएं]
∴ बिंदु O, AC के लंबार्धक पर स्थित है।
∴ OB, AC का लंबार्धक है जो AC को D बिंदु पर प्रतिच्छेदित करती है।
∴ AD = DC
∴ AC = 2 AD
माना OD = x मी०

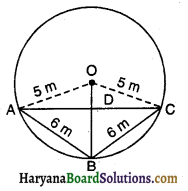
तो DB = (5 – x) मी०
समकोण ΔOAD में,
AD² = OA² – OD²
= (5)² – (x)² …….(i)
समकोण ΔABD में,
AD² = AB² – DB²
= (6) – (5 – x)²
समीकरण (i) तथा (ii) की तुलना से,
(5)² – (x)² = (6)² – (5 – x)²
या 25 – x² = 36 – (25 + x² – 10x)
या 25 – x² = 36 – 25 – x² + 10x
या -10 x = 36 – 25 – 25
या -10x = -14
या x = \(\frac{14}{10}\) = 1.4 मी०
अतः OD = 1.4 मी०
अब AD² = (5)² – (x)²
= 25 – (1.4)²
= 25 – 1.96 = 23.04
AD = \(\sqrt{23.04}\) = 4.8 मी०
⇒ AC = 2AD = 2 × 4.8 = 9.6 मी०
अतः रेशमा व मनदीप के मध्य की दूरी = 9.6 मी० उत्तर

प्रश्न 6.
20 मी० त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लंबाई ज्ञात कीजिए।
हल :
माना तीन लड़के अंकुर, सैय्यद तथा डेविड वृत्त की परिधि पर एक-दूसरे से बराबर दूरी पर बिंदु A, B व C पर बैठे हैं। इसलिए ABC समबाहु त्रिभुज है। वृत्त की त्रिज्या 20 मी० है। A से AL ⊥ BCखींचिए। क्योंकि त्रिभुज समबाहु है इसलिए यह लंब केंद्र O में से भी गुजरता है।
माना समबाहु त्रिभुज की प्रत्येक भुजा = 2x मी० है
तो BL = \(\frac{\mathrm{BC}}{2}=\frac{2 x}{2}\) = x मी० [∵ OL ⊥ BC है]
समकोण ΔABL में

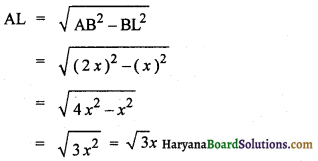
OL = AL – AO = (\(\sqrt{3}\)x – 20) मी०
समकोण ΔOBL में

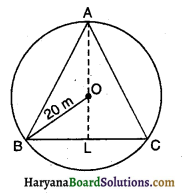
OB² = OL² + BL²
(20)² = (\(\sqrt{3}\)x – 20) + (x)²
400 = 3x² + 400 – 40\(\sqrt{3}\)x + x²
4x² – 40\(\sqrt{3}\)x = 0
4x (x – 10\(\sqrt{3}\)) = 0
⇒ 4x = 0
⇒ x = \(\frac{0}{4}\) = 0 जो कि संभव नहीं है।
या x – 10\(\sqrt{3}\) = 0
x = 10\(\sqrt{3}\)
∴ BC = 2 BL = 2 × 10\(\sqrt{3}\) = 20\(\sqrt{3}\) मी०
अतः प्रत्येक फोन की डोरी की लंबाई = 20\(\sqrt{3}\) मी० उत्तर