Haryana State Board HBSE 9th Class Maths Notes Chapter 11 Constructions Notes.
Haryana Board 9th Class Maths Notes Chapter 11 Constructions
Introduction
In previous chapters, we have drawn rough diagrams to prove theorems or solving exercise. But sometimes we need to construct accurate figures. For example, to draw a map of building to be constructed, to design the parts of machine and tools etc. To draw such figures the following geometrical instruments are needed:
(i) A graduated scale, (ii) a pair of set squares, (iii) a pair of dividers, (iv) a pair of compasses, (v) a protractor (see in the figure below).
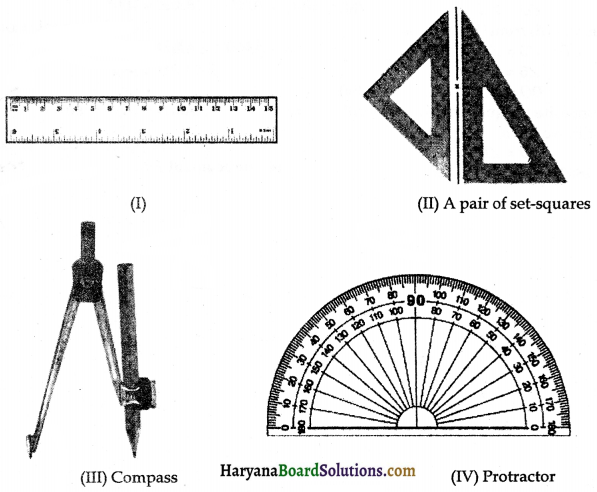
These instruments are used in drawing a geometrical figure, such as a triangle, quadrilateral, trapezium, circle etc. In this chapter we will learn about some simple and basic constructions such as bisector of a line segment, bisector of a given angle, constructions of some standard angle and some constructions of triangles with the help of graduated scale, compass and protractor.
![]()
Key Words
→ Geometrical Construction: A geometrical construction is the process of drawing a geometrical figure using only two instruments-an ungraduated ruler and compass.
→ Perpendicular bisector: A line which divides the given line in two equal parts and is perpendicular to the line segment is called the perpendicular bisector.
→ Corresponding: Angles, lines and points in one figure which bear a similar relationship, each to each, to angles, lines and points in another figure.
→ Triangle: A closed figure which bounded by three line segments is called a triangle.
→ Isosceles triangle: If at two sides of a triangle are equal, it is called an isosceles triangle.
→ Equilateral triangle: If all three sides of a triangle are equal, it is called an equilateral triangle.
→ Perimeter of a triangle: Sum of the all sides of a triangle is called the perimeter of a triangle.
→ Median: The median of a triangle, corresponding to any side, is the line joining the midpoint of that side with the opposite vertex.
→ Altitude: An altitude of a triangle, corresponding to any side, is the length of perpendicular drawn from the opposite vertex to that side.
Basic Concepts
Basic Constructions
(a) Construction 11.1: To construct the bisector of a given angle.
We have an ∠ABC, we need to construct its bisector.
Steps of construction:
Step – I: Taking B as centre and any suitable radius draw an arc cutting AB and BC at P and Q respectively.
Step – II: Taking P and Q as centres and radius more than \(\frac{1}{2}\)PQ, draw two arcs intersecting each other at R.
Step-III: Draw the ray BR. The ray BR is the required bisector of the angle ABC.
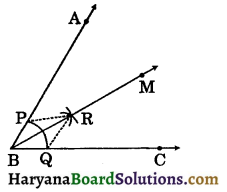
Justification: Join PR and QR.
In ΔBPR and ΔBQR, we have
PB = QB [Radii of the same arc]
PR = QR [Arcs of equal radii]
BR = BR [Common]
ΔBPR ≅ ΔBQR [By SSS congruence rule]
⇒ ∠PBR = ∠QBR [CPCT]
Hence, BR is the bisector of ∠ABC.
![]()
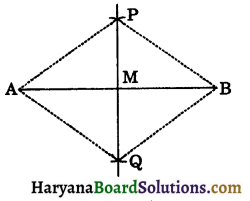
Construction 11.2:
To construct the perpendicular bisector of a given line segment.
We have a line segment AB, we need to construct its perpendicular bisector.
Steps of construction:
Step-I: Draw a line segment AB of given length.
Step-II: Taking A as centre and radius more than \(\frac{1}{2}\)AB, draw arcs one on each side of AB.
Step-III: Taking B as centre and the same radius as in Step (II), draw arcs intersecting previous arcs at P and Q.
Step-IV: Join PQ intersecting AB at M. Then line PQ is the perpendicular bisector of AB.
Justification: Join AP, BP, AQ and BQ.
In ΔPAQ and ΔPBQ, we have
AP = BP Arcs of equal radii]
AQ = BQ [Arcs of equal radii]
PQ = PQ [Common]
∴ ΔPAQ ≅ ΔPBQ [By SSS congruence rule]
⇒ ∠APQ ≅ ∠BPQ [CPCT]
⇒ ∠APM = ∠BPM ……(i)
In ΔPMA and ΔPMB, we have
PA = PB [Arcs of equal radii]
∠APM = ∠BPM [As proved in (i)]
PM = PM [Common]
ΔPMA ≅ ΔPMB (By SAS congruence rule)
⇒ AM = BM
and ∠PMA = ∠PMB (CPCT)
But, ∠PMA + ∠PMB = 180° [By linear pair axiom]
∠PMA + ∠PMA = 180°
2∠PMA = 180°
∠PMA = \(\frac{180^{\circ}}{2}\) = 90°
∠PMA = ∠PMB = 90°.
Hence, PM is the perpendicular bisector of AB.
Construction 11.3:
To construct an angle of 60° at the initial point of a given ray.
Let us take a ray AB with initial point A.
We need to construct a ray AC such that
∠CAB = 60°.
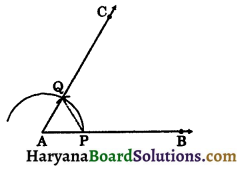
Steps of construction:
Step-I: Draw a ray AB with initial point A.
Step-II: Taking A as centre and suitable radius, draw an arc which intersects AB at P.
Step-III: Taking P as centre and same radius as before, draw an arc intersecting the previous are at point Q.
Step-IV: Draw a ray AC passing through Q. Then ∠CAB is the required angle of 60°.
Justification: Join PQ.
AP = PQ = AQ [By construction]
⇒ ΔPAQ is an equilateral triangle.
∴ ∠QAP = 60°
⇒ ∠CAB = 60°.
![]()
Some Constructions of Triangles:
Construction 11.4 To construct a triangle, given its base, a base angle and sum of other two sides.
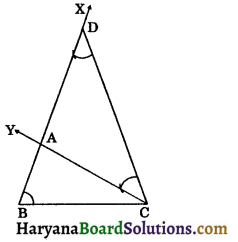
Given: The base BC, a base angle, say ∠B and the sum AB + AC of the other two sides of a triangle ABC, we need to construct ΔABC.
Steps of construction:
Step-I: Draw the given base BC and the point B construct an angle ∠CBX equal to the given angle with BC.
Step-II: From the ray BX,
cut BD = AB + AC.
Step-III: Join DC and construct
∠DCY = ∠BDC.
Step-IV: Let CY intersects BX at A.
Then, ABC is the required triangle.
Justification: Since,
∠BDC = ∠DCY (By construction)
⇒ ∠ADC = ∠ACD
⇒ AD = AC
[Sides opp. to equal angles are equal]
Now, AB = BD – AD
⇒ AB = BD – AC [∵AD = AC]
⇒ AB + AC = BD
⇒ BD = AB + AC.
Alternative method
Steps of construction:
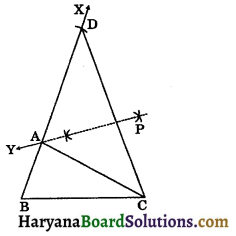
Step-I: Draw the given base BC and at the point B construct ∠CBX equal to the given angle with BC.
Step-II: From the ray BX, cut BD = AB + AC.
Step-III: Join DC and draw perpendicular bisector PY of CD intersecting BD at point A. Join AC.
Remarks: The construction of the trinagle is not possible if the sum AB + AC ≤ BC.
![]()
Construction 11.5: To construct a triangle given its base, a base angle and the difference of the other two sides.
Given: Base BC and a base angle, say ∠B and the difference of other two sides AB – AC or AC – AB. We need to construct AABC. There are following two cases arise:
Case I: If AB > AC that is AB – AC is given.
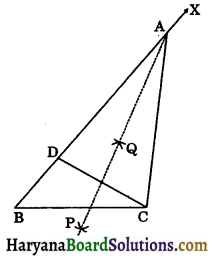
Steps of construction:
Step-I: Draw the given base BC. At the point B, construct ∠CBX equal to the given angle with BC.
Step-II: From ray BX, cut the line segment BD is equal to AB – AC.
Step-III Join DC and draw perpendicular bisector of CD intersecting BX at A.
Step-IV: Join AC. Then ABC is required triangle.
Justification: Since AP is the perpendicular to CD.
∴ AD = AC
So, BD = AB – AD
⇒ BD = AB – AC.
Case II: If AB < AC that is AC – AB is given.
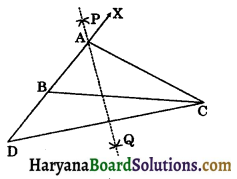
Steps of construction:
Step-I: Draw the given base BC. At the point B, construct ∠CBX equal to the given angle with BC.
Step-II: Extend XB to D to the opposite side of BC such that
BD = AC – AB.
Step-III: Join CD and draw perpendicular bisector PQ of CD intersecting BX at A.
Step-IV: Join AC, then ABC is required triangle.
Justification: Since PQ is the perpendicular bisector of CD.
∴ AD = AC
Now, BD = AD – AB
⇒ BD = AC – AB.
![]()
Construction 11.6:
To construct a triangle, given its perimeter and its two base angles.
Given: Base angles ∠B and ∠C and perimeter of a triangle ABC (ie., BC + CA + AB) are given. We need to construct the triangle ABC.
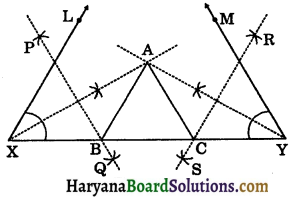
Steps of construction:
Step – I: Draw a line segment XY equal to BC + CA + AB.
Step – II: Construct ∠LXY equal to ∠B and ∠MYX equal to ∠C with XY.
Step – III: Draw the bisectors of ∠LXY and ∠MYX intersecting at A.
Step – IV: Draw perpendicular bisectors PQ of AX and RS of AY.
Step – V: Let perpendicular bisectors PQ and RS intersect XY at B and C respectively.
Step – VI: Join AB and AC, then ABC is the required triangle.
Justification: Since PQ is the perpendicular bisector of AX.
∴ XB = AB …..(i)
Similarly, RS is the perpendicular bisector of AY.
∴ CY = AC ……(ii)
Now, XY = XB + BC + CY
XY = AB + BC + AC [Using (i) & (ii)]
Since, XB = AB
⇒ ∠AXB = ∠XAB ……(iii)
and CY = AC
⇒ ∠CAY = ∠CYA …..(iv)
∠ABC = ∠AXB + ∠XAB
[∵ Exterior angle is equal to its opp. two interior angles]
⇒ ∠ABC = ∠AXB + ∠AXB [Using (iii)]
⇒ ∠ABC = 2∠AXB
⇒ ∠ABC = ∠LXY
Similarly, ∠ACB = ∠MYX.