HBSE 9th Class Maths Important Questions Chapter 5 Introduction to Euclid’s Geometry

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 5 Introduction to Euclid’s Geometry Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 5 Introduction to Euclid’s Geometry

Very Short Answer Type Questions

Question 1.
From the adjoining figure, name the following:

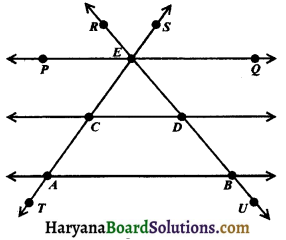
(i) Four lins segments.
(ii) Three parallel lines.
(iii) Three pairs of collinear points.
(iv) Two pairs of intersecting lines.
(v) Four rays.
Solution :
(i) \(\overline{E C}, \overline{A C}, \overline{E D}\) and \(\overline{D B}\).
(ii) Three parallel lines are \(\stackrel{\leftrightarrow}{A B}\), \(\stackrel{\leftrightarrow}{C D}\) and
(iii) Three pairs of collinear points are (A, C, E), (B, D, E) and (P, E, Q).
(iv) Two pair of intersecting lines are (\(\overleftrightarrow{A E}\), \(\overleftrightarrow{B E}\)) and (\(\overleftrightarrow{C D}\), \(\overleftrightarrow{E B}\)).
(v) Four rays are \(\overrightarrow{E R}\), \(\overrightarrow{E S}\), \(\overrightarrow{A T}\) and \(\overrightarrow{B U}\)

Question 2.
From the adjoining figure, name the following:

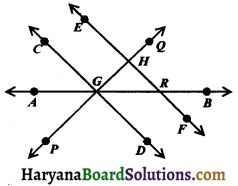
(i) Four lines.
(ii) Three concurrent lines and their point of intersection.
(iii) Three pairs of intersecting lines and their corresponding points of intersection.
(iv) Six points.
Solution :
(i) Four lines are \(\stackrel{\leftrightarrow}{P Q}, \stackrel{\leftrightarrow}{C D}, \stackrel{\leftrightarrow}{E F}\) and \(\overleftrightarrow{A B}\).
(ii) Three concurrent lines and their point of intersection are \(\stackrel{\leftrightarrow}{A B}, \stackrel{\leftrightarrow}{P Q}, \stackrel{\leftrightarrow}{C D}\), G.
(iii) Three pairs of intersecting lines and their corresponding points of intersection are (\(\stackrel{\leftrightarrow}{P Q}, \stackrel{\leftrightarrow}{E F}\), H), (\(\stackrel{\leftrightarrow}{A B}, \stackrel{\leftrightarrow}{E F}\), R) and (\(\stackrel{\leftrightarrow}{C D}, \stackrel{\leftrightarrow}{A B}\), G).
(iv) Six points are A, B, C, D, E, F.

Question 3.
In the given figure, if C is the midpoint of AB and PC = CQ, then prove that AQ = BP.

Solution :
We have C is the mid point of
⇒ AC = BC
⇒ AC + CQ = BC + CQ,
[Adding CQ on both sides]
⇒ AC + CQ = BC + PC,
[It is given PC = CQ]
According to Axiom 2, if equals are added to equals, then whole are equal.
⇒ AQ = BP
Hence, AQ = BP. Hence proved.

Question 4.
In the figure, we have x and y are the midpoints of AC and BC and Ax = Cy. Show that AC = BC.
[NCERT Exemplar Problems]

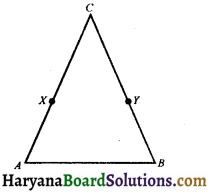
Solution :
Since x is the mid point of AC
∴ AC = 2Ax
Again y is the mid point of BC
∴ BC = 2Cy
Also, Ax = Cy (given)
Therefore, AC = BC, because by axiom 6, things which are double of the same things are equal to one another.

Short Answer Type Questions

Question 1.
In the fig, we have ∠ABC = ∠ACB, ∠3 = ∠4. Show that ∠1 = ∠2. [NCERT Exemplar Problems]

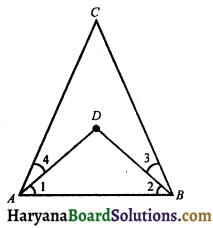
Solution :
We have
∠ABC = ∠ACB ……….(i)
and ∠3 = ∠4 ……….(ii)
Substracted (ii) from (i), we get
∠ABC – ∠3 = ∠ACB – ∠4
⇒ ∠1 = ∠2
[∵ By axiom 3, if equals are subtracted from equals remainders are equal]
Hence ∠1 = ∠2. Proved

Question 2.
Two lines which are both parallel to the same line, are parallel to each other.
Solution :
Given: Three lines l, m, n in a plane such that l || m and n || m.

To prove : l || n.
Proof : If possible, let line l is not parallel to linen, then lines l and n intersect in a unique point, say P. Now P is not on m. Since P is on l and l || m.
∴ Through a point P out side m, there are two lines l, n both parallel to m. This is not possible (parallel axiom).
∴ Our suposition is wrong.
Hence, l || n. Hence proved

Question 3.
(a) If C lies between A and B and AB = 9 cm and BC = 4 cm, what is AC and AC²?
(b) If C lies between A and B and AB = 8 cm and BC = 4 cm, what is AC³?
Solution :
∵ C lies between A and B.
∴ AC + BC = AB

(a) AB = 9 cm and BC = 4 cm
∴ AC + 4 = 9 ⇒ AC = 9 – 4 = 5cm
AC² = 5² = 25 cm².

(b) AB = 8 cm and BC = 4 cm
AC + 4 = 8 ⇒ AC = 8 – 4 = 4 cm
AC³ = 4³ = 64 cm³.

Multiple Choice Questions

Choose the correct option in each of the following :

Question 1.
If equals be added to equals, then whole are :
(a) unequal
(b) twice of each other
(c) half of the other
(d) equal
Solution :
(d) equal

Question 2.
If equals be subtracted from equals, then remainders are equal, is stated in the form of :
(a) an axiom
(b) a definition
(c) a postulate
(d) a proof
Solution :
(a) an axiom

Question 3.
A circle can be drawn with any centre and any radius, is stated in the form of :
(a) an axiom
(b) a postulate
(c) a definition
(d) a theorem
Solution :
(b) a postulate

Question 4.
Things which coincide with another are equal to one another, is stated in the form of:
(a) a postulate
(b) an axiom
(c) a definition
(d) a theorem
Solution :
(b) an axiom

Question 5.
Lines are parallel, if they do not intersect is stated in the form of:
(NCERT Exemplar Problems)
(a) a postulate
(b) an axiom
(c) a definition
(d) a proof
Solution :
(c) a definition

Question 6.
Euclid first axiom is :
(a) If equals are added to equals, the wholes are equal
(b) The whole is greater than part
(c) Things which are equal to the same things are equal to one another
(d) Things which coincide with another are equal to one another
Solution :
(c) Things which are equal to the same things are equal to one another

Question 7.
Euclid’s third postulate is :
(a) A circle can be drawn with any centre and any radius
(b) A straight line may be drawn from any one point to any other point
(c) All right angles are equal to one another
(d) A terminated line can be produced infinitely
Solution :
(a) A circle can be drawn with any centre and any radius

Question 8.
Euclid divided his famous book, ‘Elements’ into: [NCERT Exemplar Problems]
(a) 10 chapters
(b) 13 chapters
(c) 11 chapters
(d) 12 chapters
Solution :
(b) 13 chapters

Question 9.
Euclid belongs to the country:
[NCERT Exemplar Problems]
(a) Egypt
(b) Babylonia
(c) India
(d) Greece
Solution :
(d) Greece

Question 10.
Thales belongs to the country:
[NCERT Exemplar Problems]
(a) Egypt
(b) China
(c) Greece
(d) Babylonia
Solution :
(c) Greece

Question 11.
Bhrahmgupta discovered the formula for finding the area of :
(a) Isosceles triangle
(b) Square
(c) Equilateral triangle
(d) Cyclic quadrilateral
Solution :
(d) Cyclic quadrilateral

Question 12.
The Indian Mathematician Bhaskara II born in :
(a) 598 AD
(b) 1114 AD
(c) 476 AD
(d) 1185 AD
Solution :
(b) 1114 AD

Question 13.
Pythagoras was a famous pupil of:
[NCERT Exemplar Problems]
(a) Euclid
(b) Aryabhatt
(c) Thales
(d) Newton
Solution :
(c) Thales

Question 14.
The total number of propositions in the elements are: [NCERT Exemplar Problems]
(a) 465
(b) 450
(c) 13
(d) 55
Solution :
(a) 465