HBSE 9th Class Maths Important Questions Chapter 11 Constructions

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 11 Constructions Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 11 Constructions

Very Short Answer Type Questions

Question 1.
With the help of protractor, draw an angle of 110°. Bisect it to get an angle of measure 55°. [NCERT Exemplar Problems]
Solution:
Steps of construction:
Step – I: Draw a ray BC.
Step – II: Construct ∠ABC = 110°, with the help of protractor.

Step – III: Taking B as centre and a suitable radius, draw an arc intersecting ray AB and BC at Q and P respectively.
Step – IV: Taking P and Q as the centres and radius more than \(\frac{1}{2}\)PQ, draw two arcs intersecting each other at D.
Step – V: Draw ray BD. Ray BD is required bisector of ∠ABC. On measuring with the help of the protractor, we get ∠CBD = ∠ABD = 55°.

Question 2.
Draw adjacent supplementary angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Solution:
Steps of construction :
Step – I: Draw ∠AOB = 180°.

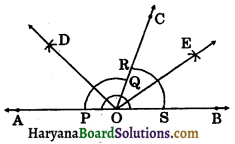
Step – II: Draw ray OC such that it divides ∠AOB into two adjacent supplementary angles.
i.e., ∠AOC + ∠BOC = 180°.
Step – III: Draw the bisector OD of ∠AOC as followed by the steps in 1.
Step – IV: Draw the bisector OE of ∠BOC as followed by the steps in 1.
Verification: Since ray OD is the bisector of ∠AOC.
∴ ∠AOD = ∠COD = \(\frac{1}{2}\)∠AOC…(i)
Similarly, QE is the bisector of ∠BOC.
∴ ∠BOE = ∠COE = \(\frac{1}{2}\)∠BOC …..(ii)
Adding (i) and (ii), we get
∠COD + ∠COE = \(\frac{1}{2}\)∠AOC + \(\frac{1}{2}\)∠BOC
⇒ ∠COD + ∠COE = \(\frac{1}{2}\)(∠AOC + ∠BOC)
⇒ ∠DOE = \(\frac{1}{2}\) × 180°
[∵ ∠AOC and ∠BOC are supplementary angles]
⇒ ∠DOE = 90°
DO ⊥ OE
Yes, bisecting rays are perpendicular to each other.

Question 3.
Draw a circle whose centre is O. Draw its chord AB, draw the perpendicular bisector of line segment AB. Does it pass through the centre of the circle.
Solution:
Steps of construction:
Step – I: With the help of compass and scale draw a circle of radius 4.5 cm (say) whose centre is O.
Step – II: Draw chord AB of suitable length.
Step – III: Taking A as the centre and radius more than \(\frac{1}{2}\)AB draw two arcs one on each side of AB.

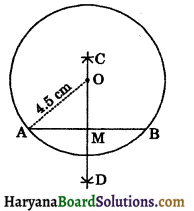
Step – IV: Taking B as the centre and same radius as before, draw two arcs intersecting previous arc at C and D respectively.
Step – V: Join CD, intersecting AB at M. So, CD is the perpendicular bisector of AB. Yes, perpendicular bisector CD passes through the centre of the circle.

Question 4.
Draw a circle whose centre is O. Draw its two chords PQ and QR such that PQ ≠ RS. Do they intersect at point O?
Solution:
Steps of construction:
Step – I: Draw a circle of suitable radius whose centre is O.
Step – II: Draw two chords PQ and QR of suitable lengths.

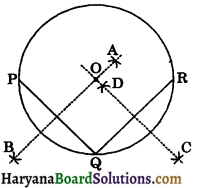
Step – III: Draw the perpendicular bisector AB of chord PQ as followed by the steps in 3.
Step – IV: Similarly draw the perpendicular bisector CD of chord QR.
Step – V: AB and CD intersect each other at point O.
Yes, perpendicular bisectors of chord PQ and chord QR intersect each other at point O.

Question 5.
Draw a line segment of length 10 cm with the help of ruler and compass to obtain a length of 7.5 cm.
Solution:
Steps of construction :
Step – I: Draw a line segment of length 10 cm.
Step – II: Draw the perpendicular bisector PQ of line AB as followed by the steps in 3 intersecting AB at M.
∴ AM = MB = \(\frac{10}{2}\) = 5 cm.

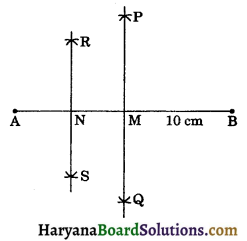
Step – III: Similarly, draw the perpendicular bisector of AM intersecting AM at N.
∴ AN = NM = \(\frac{5}{2}\) = 2.5 cm
Now, BN = BM + NM
⇒ BN = 5 cm + 2.5 cm
⇒ BN = 7.5 cm
Hence, we obtain BN of length 7.5 cm.

Question 6.
Using ruler and compass only, construct the following angles :
(a) 120° (b) 150° (c) 37\(\frac{1^{\circ}}{2}\)
Solution:
(a) Steps of construction:
Step – I: Draw a ray AB with initial point A.
Step – II: Taking A as centre and a suitable radius, draw an arc intersecting AB at P.
Step – III: Taking P as centre and same radius as before, draw an arc intersecting the previous arc at Q.

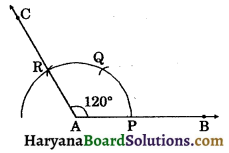
Step – IV: Taking Q as centre and same radius as before, draw an arc intersecting the previous arc at R.
Step – V: Join AR and produced it to C. Then ∠CAB = 120° is required angle.

(b) Steps of construction:
Step – I: Draw a ray AB with initial point A.
Step – II: Taking A as centre and a suitable radius, draw an arc intersecting AB at P.
Step – III: Taking P as centre and same radius as before, draw an arc intersecting previous arc at Q.

Step – IV: Taking Q as centre and same radius as before, draw an arc intersecting previous arc at R. Join AR and produced it to C. Then ZCAB = 120°.
Step – V: Taking R as centre and same radius as before, draw an arc intersecting previous arc at S. Join AS. Then ∠CAS = 180° – 120° = 60°.
Step – VI: Draw bisector AD of ∠CAS.
∴ ∠CAD = \(\frac{1}{2}\) × ∠CAS
⇒ ∠CAD = \(\frac{1}{2}\) × 60° = 30°
∠DAB = 120° + 30° = 150°.
Hence, ∠DAB = 150° is the required angle.

(c) Steps of construction:
Step – I: Draw a ray AB with initial point A.
Step – II: Draw ∠CAB = 60° as followed by the steps in Construction 11.3.
Step – III: Draw ∠DAB = 90° as followed by the steps in 1. of Ex. 11:1. Then
∠DAC = 90° – 60° = 30°.

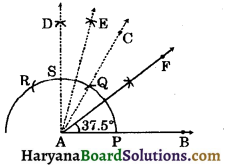
Step – IV: Draw bisector AE of ∠DAC.
∴ ∠DAE = ∠CAE = \(\frac{30^{\circ}}{2}\) = 15°
∠EAB = 90° – ∠DAE
⇒ ∠EAB = 90° – 15° = 75°.
Step – V: Draw the bisector AF of ∠EAB.
∴ ∠FAB = \(\frac{1}{2}\)∠EAB
⇒ ∠FAB = \(\frac{75^{\circ}}{2}\) = 37\(\frac{1^{\circ}}{2}\)
Hence, ∠FAB = 37\(\frac{1^{\circ}}{2}\) is the required angle.

Question 7.
Construct an equilateral triangle, if one of its altitude is 3.2 cm. [NCERT Exemplar Problems]

Solution:
Steps of construction:
Step – I: Draw a line l.
Step – II: Mark any point D on the line l.
Step – III: At point D, draw DX ⊥ l and cut off AD = 3.2 cm.
Step – IV: Construct ∠DAB = 30° and ∠DAC = 30° intersecting l at B and C respectively.
Then ABC is the required triangle.

Question 8.
Construct a triangle ABC such that AB = 6 cm, BC = 6 cm and median CM = 4.3 cm.
Solution:
Steps of construction:
Step – I: Draw a line segment AB = 6 cm.
Step – II: Draw the bisector of AB intersecting AB at M.

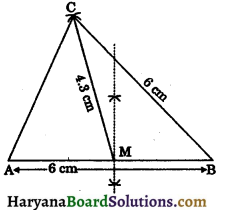
Step – III: Taking M as the centre and radius 4.3 cm draw an arc.
Step – IV: Taking B as the centre and radius 6 cm, draw another arc which intersects the previous arc at point C.
Step – V: Join AC and BC, then ABC is the required triangle.

Question 9.
Construct an isosceles triangle whose base 6 cm and vertical angle is 60°.
Solution:
Steps of construction:
Step – I: Draw a line segment BC = 6 cm.

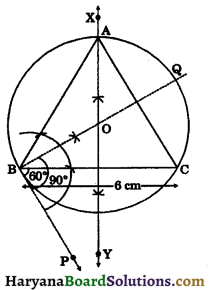
Step – II: Construct ∠CBP = 60°, below the line segment BC.
Step – III: Construct ∠PBQ = 90°.
Step – IV: Draw the perpendicular bisector XY of BC, intersecting BQ at O.
Step – V: Taking O as the centre and radius OB, draw a circle intersecting XY at A.
Step – VI: Join AB and AC, then ABC is the required triangle.

Question 10.
Construct right angled triangle whose hypotenuse measures 7 cm and the length of one of whose sides containing the right angle is 5 m.
Solution:
Steps of construction:
Step – I: Draw a line segment BC = 7 cm.
Step – II: Draw the perpendicular bisector of BC intersecting BC at O.

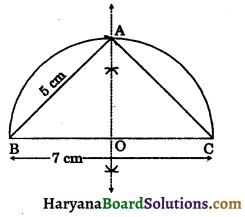
Step – III: Taking O as centre and radius OB, draw a semi-circle on BC.
Step – IV: Taking B as the centre and radius equal to 5 cm, draw an arc, interscting the semicircle at A.
Step – V: Join AB and AC. Then ABC is the required triangle.

Question 11.
Construct a right angled triangle in which ∠B = 90°, hypotenuse AC = 13 cm and the sum of the remaining sides AB and BC is 17 cm.
Solution:
Sum of the remaining two sides = 17 cm (given)
Let one of its side be x, then other its side is (17 – x) cm
hypotenuse = 13 cm
In right triangle, we have
(hypotenuse)² = (one side)² + (other side)²
⇒ 132 = x² + (17 – x)²
⇒ 169 = x² + 289 + 32 – 34x
⇒ 0 = 2x² – 34x + 289 – 169
⇒ 2x² – 34x + 120 = 0
⇒ x² – 17x + 60 = 0
⇒ x² – 12x – 5x + 60 = 0
⇒ x(x – 12) -5 (x – 12) = 0
⇒ (x – 12) (x – 5) = 0
⇒ x – 12 = 0 or x – 5 = 0
x = 12 or x = 5
So, sides are 12 cm and 17 – 12 = 5 cm.
So, we construct a right triangle in which ∠B = 90°, hypotenuse (AC) = 13 cm and other sides AB = 12 cm and BC = 5 cm.

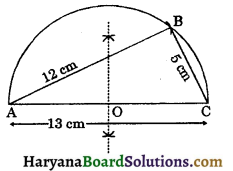
Steps of construction:
Step – I: Draw a line segment AC = 13 cm.
Step – II: Draw the perpendicular bisector of AC intersecting AC at O.
Step – III: Taking O as the centre and radius AO, draw a semicircle on AC.
Step – IV: Taking A as the centre and radius equal to 12 cm, draw an arc interscting the semicircle at B.
Step – V: Join AB and BC. The ABC is the required triangle.

Question 12.
Construct a triangle ABC whose perimeter is 12 cm and sides are in the ratio 3 : 4 : 5.
Solution:
Steps of construction:
Step – I: Draw a line segment PQ = 12 cm (= perimeter).
Step – II : At the point Q, draw an acute ∠PQX with PQ.
Step – III: Divide QX into 3 + 4 + 5 = 12 equal parts.

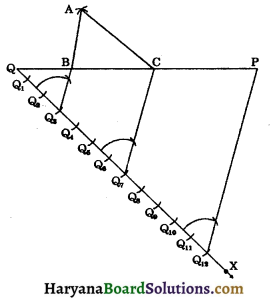
Step – IV: Join Q₁₂ to P.
Step – V: From Q₃, draw BQ₃ || PQ₁₂ intersecting PQ at B.
Step – VI: From Q₇, draw CQ₇ || PQ₁₂ intersecting PQ at C.
Step – VII: Taking B as centre and radius as QB, draw an arc.
Step – VIII: Taking C as the centre and radius as CP, draw another arc, which intersects the previous arc at A.
Step – IX: Join AB and AC, then ABC is the required triangle.

Question 13.
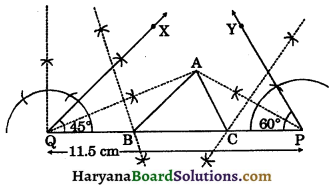
Construct a triangle having its perimeter 11.5 cm and ratio of the angles as 3 : 4 : 5.
Solution:
Ratio of angles = 3 : 4 : 5
Sum of ratios = 3 + 4 + 5 = 12

Ist angle = \(\frac{13}{2}\) × 180°
[∵ Sum of angles of a triangle is 180°]
⇒ I^st angle = 45°
⇒ II^nd angle = \(\frac{4}{12}\) × 180°
⇒ II^nd angle = 60°
III^rd angle = \(\frac{5}{12}\) × 180°
⇒ III^rd angle = 75°.
Let base angles be 45° and 60° and perimeter of triangle is 11.5 cm (given).
Now we construct a ΔABC as follows:
Steps of construction:
Step – I: Draw a line segment PQ = 11.5 cm.
Step – II: At the point Q construct ∠PQX = 45° and at the point P construct ∠QPY = 60°.
Step – III: Draw the bisectors of ∠PQX and ∠QPY intersecting at A.
Stop – IV: Draw the perpendicular bisectors of AQ and AP intersecting PQ at B and C respectively.
Step – V: Join AB and AC, then ABC is the required triangle.

Question 14.
Construct a triangle ABC, the lengths of whose medians are 5 cm, 5 cm and 6 cm. Measure the length of sides of ΔABC.
Solution:
In a ΔABC, let medians AD = 5 cm, BE = 6 cm and CF = 5 cm. We need to construct a ΔABC.
Steps of construction:
Step – I: Construct a triangle AXD with sides AX = 5 cm, AD = 5 cm and XD = 6 cm.

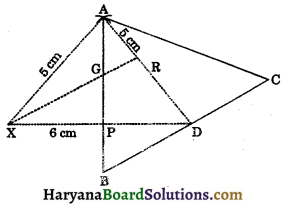
Step – II: Draw the medians AP and XR intersecting each other at point G.
Step – III: Extend GP to B such that GP = PB.
Step – IV: Join BD and produced to it C such that BD = CD.
Step – V: Join A to C, then ABC is the required triangle and AD its median.
On measuring the sides of ΔABC, we get AB = 5.95 cm, AC = 6.5 cm, BC = 6.5 cm.

Question 15.
Construct a rhombus whose diagonals are 4 cm and 6 cm in lengths. [NCERT Exemplar Problems]
Solution:
We know that, diagonals of a rhombusbisect each other at right angles.
Let AC and BD are diagonals of a rhombus and bisect each other at O.
Steps of construction:
Step – I: Draw diagonal AC of length 6 cm.
Step – II: Draw perpendicular bisector XY of AC intersecting AC at O.

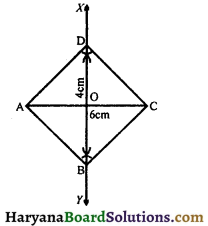
Step – III: From O, cuts OB = OD = 2 cm.
Step – IV: Join AB, BC, CD and DA. Then ABCD is the required rhombus.

Multiple Choice Questions

Choose the correct option in each of the following:

Question 1.
Which of the following angle cannot be constructed using ruler and compass only: [NCERT Exemplar Problems]
(a) 22°\(\frac{1^{\circ}}{2}\)
(b) 67\(\frac{1^{\circ}}{2}\)
(c) 40°
(d) 37\(\frac{1^{\circ}}{2}\)
Answer:
(c) 40°

Question 2.
Which of the following angle cannot be constructed using ruler and compass only:
(a) 60°
(b) 150°
(c) 65°
(d) 22\(\frac{1^{\circ}}{2}\)
Answer:
(c) 65°

Question 3.
Which of the following angle can be constructed using ruler and compass only:
(a) 85°
(b) 115°
(c) 47\(\frac{1^{\circ}}{2}\)
(d) 75°
Answer:
(d) 75°

Question 4.
Which of the following angle can be constructed using ruler and compass only:
(a) 82\(\frac{1^{\circ}}{2}\)
(b) 92°
(c) 100°
(d) 122\(\frac{1^{\circ}}{2}\)
Answer:
(a) 82\(\frac{1^{\circ}}{2}\)

Question 5.
It is not possible to construct a triangle when its sides are :
(a) 4 cm, 2 cm and 6 cm
(b) 7 cm, 4 cm and 5 cm
(c) 4 cm, 5 cm and 8 cm
(d) 5 cm, 12 cm and 13 cm
Answer:
(a) 4 cm, 2 cm and 6 cm

Question 6.
It is possible to construct a triangle when its sides are :
(a) 5 cm, 6 cm and 13 cm
(b) 5 cm, 7 cm and 12 cm
(c) 6 cm, 4 cm and 9 cm
(d) 3 cm, 5 cm and 10 cm
Answer:
(c) 6 cm, 4 cm and 9 cm

Question 7.
It is possible to construct a triangle when its angles are :
(a) 40°, 55°, 60°
(b) 55°, 60°, 65°
(c) 50°, 70°, 80°
(d) 67°, 63°, 51°
Answer:
(b) 55°, 60°, 65°

Question 8.
The construction of ΔABC in which BC = 8 cm, ∠C = 50° is possible when (AC + BC) is :
(a) 10 cm
(b) 8 cm
(c) 7 cm
(d) 6 cm
Answer:
(a) 10 cm

Question 9.
The construction of ΔABC in which AB = 5 cm, ∠B = 70° is not possible when (BC + AC) is :
(a) 7 cm
(b) 8.5 cm
(c) 4.5 cm
(d) 9 cm
Answer:
(c) 4.5 cm

Question 10.
The construction of a triangle ABC in which AB = 4 cm, ∠A = 60° is not possible when difference of BC and AC is equal to: [NCERT Exemplar Problems]
(a) 3.5 cm
(b) 4.5 cm
(c) 3 cm
(d) 2.5 cm
Answer:
(b) 4.5 cm

Question 11.
The construction of a triangle ABC, given that BC = 6 cm, ∠B = 45° is not possible when difference of AB and AC is equal to : [NCERT Exemplar Problems]
(a) 6.9 cm
(b) 5.2 cm
(c) 5.0 cm
(d) 4.0 cm
Answer:
(a) 6.9 cm

Question 12.
The construction of triangle ABC, given that BC = 3 cm, ∠C = 60° is possible when difference of AB and AC is equal to : [NCERT Exemplar Problems]
(a) 3.2 cm
(b) 31 cm
(c) 3 cm
(d) 2.8 cm
Answer:
(b) 31 cm