Haryana State Board HBSE 8th Class Maths Solutions Chapter 10 ठोस आकारों का चित्रण Intext Questions and Answers.
Haryana Board 8th Class Maths Solutions Chapter 10 ठोस आकारों का चित्रण Intext Questions
(इन्हें कीजिए – पृष्ठ 163-164)
प्रश्न 1.
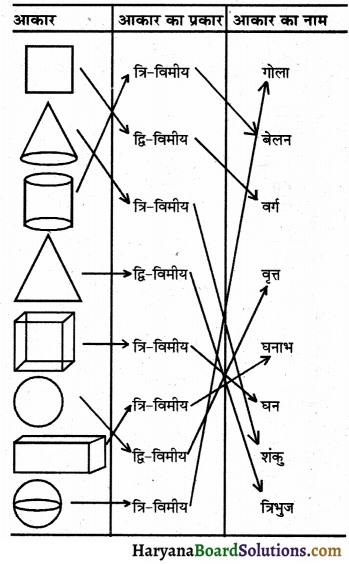
निम्नलिखित का मिलान कीजिए (आपके लिए, पहला मिलान किया हुआ है)-
हल:
मिलान निम्न प्रकार है-
![]()
(पृष्ठ 164-165)
प्रश्न 1.
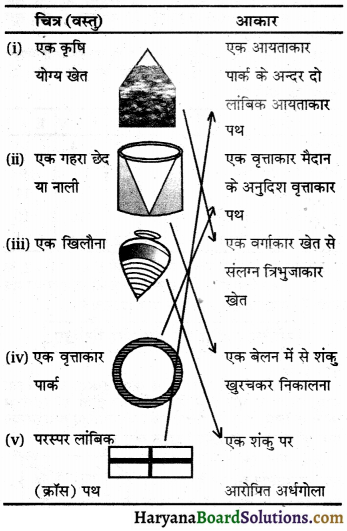
निम्नलिखित चित्रों (वस्तुओं) का उनके आकारों से मिलान कीजिए-
हल :
मिलान निम्न प्रकार है-
(पृष्ठ 166)
प्रश्न 1.
अपने आस-पास की विभिन्न वस्तुओं को विभिन्न स्थितियों से देखिए। अपने मित्रों के साथ उनके विभिन्न दूश्यों की चर्चा कीजिए।
संकेत- कुछ चात्र ग्रुप बनाकर स्वयं अवलोकन करें।
![]()
(पृष्ठ 175)
प्रश्न 1.
निम्नलिखित बहुफलकों के लिए फलकों (faces), किनारों (edges) और शीर्षों (vertices) की संख्याओं को सारणीबद्ध कीजिए-(यहाँ V शीर्षों की संख्या, F फलकों की संख्या तथा E किनारों की संख्या प्रदर्शित करता है।)
| ठोस | F | V | E | F + v | E + 2 |
| घनाभ | |||||
| त्रिभुजाकार पिरामिड | |||||
| त्रिभुजाकार प्रिज्म | |||||
| वर्ग आधार वाला पिरामिड | |||||
| वर्ग आधार वाला प्रिज्म |
आप अन्तिम दो स्तम्भों से क्या निष्कर्ष निकालते हैं? क्या प्रत्येक स्थिति में आप F + V = E + 2, अर्थात् F + V – E = 2 प्राप्त करते हैं? यह सम्बन्ध ऑयलर सूत्र (Euler’s Formula) कहलाता है। वास्तव में यह सूत्र प्रत्येक बहुफलक के लिए सत्य है।
हल:
निम्नलिखित बहुफलकों के लिए फलकों की संख्या (F), किनारों की संख्या (E) तथा शीर्षों की संख्या (V) को सारणीबद्ध करने पर,
| ठोस | F | V | E | F + v | E + 2 |
| घनाभ | 6 | 8 | 12 | 14 | 14 |
| त्रिभुजाकार पिरामिड | 4 | 4 | 6 | 8 | 8 |
| त्रिभुजाकार प्रिज्म | 5 | 6 | 9 | 11 | 11 |
| वर्ग आधार वाला पिरामिड | 5 | 5 | 8 | 10 | 10 |
| वर्ग आधार वाला प्रिज्म | 6 | 8 | 12 | 14 | 14 |
अन्तिम दो स्तम्भों से प्रत्येक स्थिति में हमें F + V= E + 2, या F + V – E = 2 प्राप्त होता है। इस समीकरण को ऑयलर का सूत्र कहते हैं। तथा यह सूत्र बहुफलक के लिए सत्य है।
![]()
(सोचिए, चर्चा कीजिए और लिखिए – पृष्ठ 175)
प्रश्न 1.
यदि किसी ठोस में से कोई टुकड़ा काट दिया जाए, तो F, V और E में क्या परिवर्तन होता है? (प्रारम्भ करने के लिए, एक प्लास्टिसीन का घन लीजिए तथा उसका एक कोना काटकर इसकी खोज कीजिए।)
हल:
माना कि ABCDHEFG एक प्लास्टिसीन का घन है। इसमें से एक टुकड़ा PQR काट लिया जाता है। यहाँ PQR क्रमशः किनारा FG, FE तथा FB पर हैं। दी गई आकृति से,
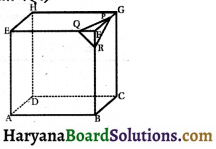
स्थिति I :
घन ABCDHEFG में,
फलकों की संख्या (F) = 6
शीर्षों की संख्या (V) = 8
किनारों की संख्या (E) = 12
स्पष्टतः F + V = E + 2 = 6 + 8 – 12
= 2
इस प्रकार ऑयलर सूत्र सत्यापित होता है।
स्थिति II :
जब तल PQR घन में से काटकर निकाल दिया ता है, तब
फलकों की संख्या F = 7
शीर्षों की संख्या V = 10
किनारों की संख्या E = 15
स्पष्टतः F + V = E + 2 = 7 + 10 = 15
इस प्रकार, इस स्थिति में भी ऑयलर का सूत्र सत्यापित होता है।