Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 प्रायोगिक ज्यामिती InText Questions and Answers.
Haryana Board 7th Class Maths Solutions Chapter 10 प्रायोगिक ज्यामिती InText Questions
इन्हें कीजिए (पृष्ठ सं. 214)
प्रश्न 1.
अब एक अन्य त्रिभुज DEF की रचना करें, जिसमें DE = 5 सेमी, EF = 6 सेमी और DF = 7 सेमी है। ΔDEF को काट कर उसे ΔABC पर रखिए।
हल :
पहले दी गई मापों के अनुसार त्रिभुज DEF की रफ आकृति बनाते हैं।
रचना के पद :
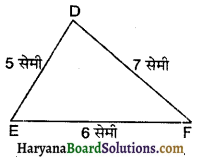
1. EF रेखाखण्ड 6 सेमी खींचा।
2. बिन्दु E को केन्द्र मानकर 5 सेमी त्रिज्या का चाप EF के ऊपर की ओर लगाया।
3. अब बिन्दु F को केन्द्र मानकर 7 सेमी त्रिज्या का चाप लेकर खींचा जो चरण 2 वाले चाप को D बिन्दु पर काटता है।
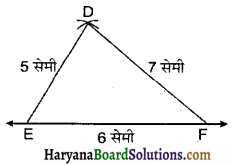
4. DE और DF को मिलाया।
5. इस प्रकार अभीष्ट ΔDEF प्राप्त हुआ।
यदि ΔDEF को काटकर उसे ΔABC के ऊपर [पुस्तक में आकृति 10.3] रखें तो ΔDEF की भुजाएँ, ΔABC की भुजाओं के बराबर हैं। इसलिए दोनों त्रिभुज सर्वांगसम होंगे। यह S.S.S. सर्वांगसमत नियम है।
![]()
पृष्ठ सं. 216
प्रश्न 1.
अब एक अन्य त्रिभुज ABC की रचना करें ताकि AB = 3 सेमी, BC = 5.5 सेमी और ∠ABC = 60° हो। इस ΔABC को काटकर ΔPQR पर रखिए। हम क्या देखते हैं ?
हल :
रचना के पद :
पद 1 : BC = 5.5 सेमी की एक रेखा खींचते हैं।
![]()
पद 2 : B पर BC के साथ 60° का कोण बनाते हुए BX किरण खींची।
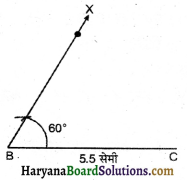
पद 3 : B को केन्द्र मानकर 3 सेमी की त्रिज्या का चाप खींचा जो BX को A पर काटता है।
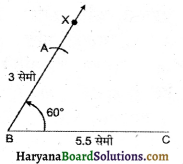
पद 4 : AC को मिलाया।
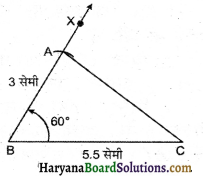
इस प्रकार अभीष्ट ΔABC प्राप्त होगा।
हम देखते हैं कि ΔABC व ΔPQR (पुस्तक आकृति 10.5) समान हैं। यदि एक त्रिभुज की दो भुजाएँ और एक कोण, दूसरे त्रिभुज की दो भुजाएँ और एक कोण के बराबर हैं तो त्रिभुज सर्वांगसम होंगे। यह S.A.S. सर्वांगसमता का नियम है।
![]()
पृष्ठ सं. 218
प्रश्न 1.
अब एक अन्य त्रिभुज LMN खींचिए, जिसमें m∠NLM = 30°, LM = 6 सेमी और m∠NML = 100° हो। इस त्रिभुज LMN को काटकर त्रिभुज XYZ पर रखिए।
हल :
रचना के पद :
पद 1 : एक रेखाखण्ड LM = 6 सेमी खींचा।
![]()
पद 2 : बिन्दु L पर ∠XLM = 30° का कोण बनाया तथा M पर ∠YML = 100° का कोण बनाया।

पद 3 : LX और MY आगे बढ़ाने पर आपस में N पर काटते है।
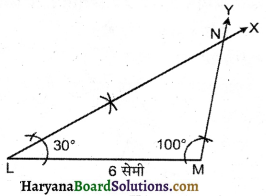
इस प्रकार अभीष्ट ΔLMN प्राप्त होगा।
इस प्रकार हम देखते हैं कि ΔLMN व ΔXYZ (पुस्तक में आकृति 10.6) सम्पाती हैं। यदि एक त्रिभुज के दो कोण और एक भुजा दुसरे त्रिभुज के दो कोण और एक भुजा के बराबर हैं तो दोनों त्रिभुज सर्वांगसम होंगे। यह A.S.A. का नियम है।