HBSE 12th Class Physics Important Questions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्र

Haryana State Board HBSE 12th Class Physics Important Questions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्र Important Questions and Answers.

Haryana Board 12th Class Physics Important Questions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्र

वस्तुनिष्ठ प्रश्न:

प्रश्न 1.
वस्तु का आभासी तथा बड़ा प्रतिबिम्ब बनाता है:
(अ) उत्तल दर्पण में
(ब) अवतल दर्पण में
(स) समतल दर्पण में
(द) इनमें से किसी में नहीं
उत्तर:
(ब) अवतल दर्पण में

प्रश्न 2.
प्रायः मोटर ड्राइवर की सीट के आगे लगा दर्पण होता है-
(अ) समतल
(ब) उत्तल
(स) अवतल
(द) इनमें से कोई नहीं
उत्तर:
(ब) उत्तल

प्रश्न 3.
जब प्रकाश हवा से काँच में प्रवेश करता है तो किस रंग के लिए विचलन कोण अधिकतम है?
(अ) लाल
(ब) पीला
(स) नीला
(द) बैंगनी
उत्तर:
(द) बैंगनी

प्रश्न 4.
प्रकाश का अपवर्तन होता है:
(अ) प्रकाश की चाल में परिवर्तन के कारण
(ब) प्रकाश की चाल में परिवर्तन न होने के कारण
(स) प्रकाश के रंग में परिवर्तन के कारण
(द) इनमें से किसी के भी कारण नहीं
उत्तर:
(अ) प्रकाश की चाल में परिवर्तन के कारण

प्रश्न 5.
एक अवतल दर्पण की वक्रता त्रिज्या 80 सेमी है, इसकी फोकस दूरी मीटर में होगी:
(अ) 0.40 मीटर
(ब) 0.20 मीटर
(स) 0.80 मीटर
(द) 0.10 मीटर
उत्तर:
(अ) 0.40 मीटर

प्रश्न 6.
सर्चलाइट में निम्न में से कौनसा दर्पण प्रयुक्त करते हैं:
(अ) अवतल
(ब) समतल
(स) उत्तल
(द) बेलनाकार
उत्तर:
(अ) अवतल

प्रश्न 7.
निम्न में से कौनसा दर्पण सदैव आभासी तथा छोटा प्रतिबिम्ब बनाता है:
(अ) समतल दर्पण
(ब) अवतल दर्पण
(स) समतल व अवतल दर्पण
(द) उत्तल दर्पण
उत्तर:
(द) उत्तल दर्पण

प्रश्न 8.
एक अवतल दर्पण की फोकस दूरी 10 सेमी. है। दर्पण के सामने 10 सेमी. पर एक वस्तु रखने पर उसका प्रतिबिम्ब बनेगा:
(अ) अनन्त पर
(स) फोकस पर
(ब) वक्रता त्रिज्या पर
(द) ध्रुव पर
उत्तर:
(अ) अनन्त पर

प्रश्न 9.
गोलीय दर्पण द्वारा प्रतिबिम्ब निर्माण में केवल अक्ष समानान्तर किरणें ही प्रयुक्त की जाती हैं; क्योंकि ये
(अ) ज्यामिति को आसान बना देती हैं।
(ब) न्यूनतम विक्षेपण दर्शाती हैं।
(स) अधिकतम तीव्रता दर्शाती हैं।
(द) एक बिन्दु बिम्ब का बिन्दु प्रतिबिम्ब निर्मित करती हैं।
उत्तर:
(द) एक बिन्दु बिम्ब का बिन्दु प्रतिबिम्ब निर्मित करती हैं।

प्रश्न 10.
किसी समतल दर्पण पर प्रकाश की किरण अभिलम्बवत् आपतित होती है तो परावर्तन कोण का मान होता है-
(अ) 90°
(ब) 180°
(स) 0°
(द) 45°
उत्तर:
(स) 0°

प्रश्न 11.
f फोकस दूरी वाला एक अवतल दर्पण यदि किसी वस्तु का m आवर्धन का प्रतिबिम्ब बनाता है तो वस्तु की दर्पण से दूरी है:
(अ) \(\frac{(m-1) f}{m}\)
(ब) \(\frac{(m+1) f}{m}\)
(स) (m – 1)f
(द) (m + 1)f
उत्तर:
(अ) \(\frac{(m-1) f}{m}\)

प्रश्न 12.
किसी माध्यम से निर्वात में पूर्ण आन्तरिक परावर्तन के लिए क्रान्तिक कोण 30° है। माध्यम में प्रकाश की चाल होगी:
(अ) 3 x 10⁸ m/s
(ब) 1.5 x 10⁸ m/s
(स) 6 × 10⁸ m/s
(द) √3 x 10⁸ m/s
उत्तर:
(ब) 1.5 x 10⁸ m/s

प्रश्न 13.
एक 1 अपवर्तनांक के पारदर्शी माध्यम में चलती हुई प्रकाश किरण एक पृष्ठ पर आपतित होती है, जो इस माध्यम को वायु से पृथक कर रही है। आपतन कोण 45° है। n के किस मान आन्तरिक परावर्तन हो सकता है ?
के लिए इस किरण का पूर्ण
(अ) n = 1.33
(ब) n = 1.40
(स) n = 1.50
(द) n = 1.25
उत्तर:
(स) n = 1.50

प्रश्न 14.
हीरे के चमकने का प्रमुख कारण है:
(अ) परावर्तन
(ब) विवर्तन
(स) पूर्ण आंतरिक परावर्तन
(द) विसरण
उत्तर:
(स) पूर्ण आंतरिक परावर्तन

प्रश्न 15.
यदि ∠i = 60° तथा ∠r = 90° हो तो अपवर्तनांक n2 होगा:
(अ) \(\frac{\sqrt{3}}{2}\)
(ब) \(\frac{2}{\sqrt{3}}\)
(स) \(\sqrt{3}\)
(द) \(\frac{1}{\sqrt{3}}\)
उत्तर:
(अ) \(\frac{\sqrt{3}}{2}\)

प्रश्न 16.
धुएँ के आर-पार किसी दूर स्थित प्रकाश स्रोत को देखने पर उसके झिलमिल करते हुए दिखाई देने का कारण है:
(अ) परावर्तन
(ब) अपवर्तन
(स) विवर्तन
(द) वर्ण विक्षेपण
उत्तर:
(ब) अपवर्तन

प्रश्न 17.
किसी गोलीय लेन्स के लिए निम्न में से कौनसा सूत्र सही है:
(अ) \(\frac{1}{f}\) = \(\frac{1}{u}\) + \(\frac{1}{v}\)
(ब) \(\frac{1}{f}\) = \(\frac{1}{v}\) – \(\frac{1}{u}\)
(स) \(\frac{1}{u}\) = \(\frac{1}{v}\) + \(\frac{1}{f}\)
(द) f = \(\frac{u v}{u+v}\)
उत्तर:
(ब) \(\frac{1}{f}\) = \(\frac{1}{v}\) – \(\frac{1}{u}\)

प्रश्न 18.
+ 2.50 D और – 3.75 D क्षमता वाले लेन्सों को मिलाकर एक संयुक्त लेन्स निर्मित किया गया है। इसकी फोकस दूरी का मान सेमी. में होगा:
(अ) 40
(ब) 40
(स) 80
(द) 160
उत्तर:
(स) 80

प्रश्न 19.
उत्तल लेन्स की शक्ति होती है:
(अ) ऋणात्मक
(ब) धनात्मक
(स) शून्य
(द) काल्पनिक
उत्तर:
(ब) धनात्मक

प्रश्न 20.
किसी लेन्स का आधा भाग काले कपड़े में लपटने पर लेन्स द्वारा निर्मित प्रतिबिम्ब पर क्या प्रभाव पड़ेगा?
(अ) प्रतिबिम्ब लुप्त हो जाएगा
(ब) कोई प्रभाव नहीं पड़ेगा
(स) प्रतिबिम्ब पहले से नाप में आधा हो जाएगा
(द) प्रतिबिम्ब की चमक कम हो जाएगी
उत्तर:
(द) प्रतिबिम्ब की चमक कम हो जाएगी

प्रश्न 21.
प्रकाश की एक किरण √2 अपवर्तनांक वाले प्रिज्म से इस प्रकार गुजरती है कि उसका आपतन कोण, अपवर्तन कोण का दो गुना है तथा किरण में न्यूनतम विचलन होता है। प्रिज्म का कोण होगा:
(अ) 45°
(ब) 90°
(स) 0°
(द) इनमें से कोई नहीं
उत्तर:
(ब) 90°

प्रश्न 22.
एक उत्तल लेन्स की वक्रता त्रिज्यायें क्रमशः 15 सेमी तथा 30 सेमी हैं। इसका अपवर्तनांक 1.5 है लेन्स की फोकस दूरी होगी:
(अ) 20 सेमी.
(ब) -20 सेमी.
(स) 60 सेमी.
(द) – 60 सेमी.
उत्तर:
(अ) 20 सेमी.

प्रश्न 23.
किसी उत्तल लेन्स की फोकस दूरी 2.5 सेमी है इसकी अधिकतम आवर्धन क्षमता का मान होगा:
(अ) 25
(ब) 52
(स) 11
(द) 1.1
उत्तर:
(स) 11

प्रश्न 24.
एक प्रिज्म का अपवर्तनांक √2 तथा अपवर्तन कोण 60° है तो इसका न्यूनतम विचलन कोण होगा:
(अ) 15°
(ब) 30°
(स) 450
(द) 60°
उत्तर:
(ब) 30°

प्रश्न 25.
जब 1.47 अपवर्तनांक वाले काँच के उभयोत्तल लेन्स को किसी द्रव में डुबाया जाता है, तब यह एक काँच की समतल शीट की भाँति व्यवहार करता है, इसका तात्पर्य है कि द्रव का अपवर्तनांक है:
(अ) काँच के अपवर्तनांक के बराबर
(ब) एक से कम
(स) काँच के अपवर्तनांक से अधिक
(द) काँच के अपवर्तनांक से कम
उत्तर:
(अ) काँच के अपवर्तनांक के बराबर

प्रश्न 26.
एक दूरदर्शी की आवर्धन क्षमता M है। यदि अभिनेत्र लेन्स की फोकस दूरी दो गुनी कर दी जाये तब आवर्धन क्षमता होगी:
(अ) 2M
(ब) 1/2M
(स) √2M
(द) 3M
उत्तर:
(ब) 1/2M

प्रश्न 27.
एक सूक्ष्मदर्शी के अभिदृश्यक और नेत्र लेन्स की फोकस दूरियाँ क्रमशः 4 सेमी और 8 सेमी हैं तथा वस्तु की अभिदृश्यक से दूरी 4.5 सेमी है, तो आवर्धन क्षमता होगी:
(अ) 18
(ब) 32
(स) 64
(द) 20
उत्तर:
(ब) 32

प्रश्न 28.
एक व्यक्ति के चश्मे के लेन्स की क्षमता 2D है। वह निम्न में से किस दोष से पीड़ित है:
(अ) दूर दृष्टिदोष से
(ब) निकट दृष्टिदोष से
(स) वर्णान्धता से
(द) जरा दूर दृष्टिदोष से
उत्तर:
(अ) दूर दृष्टिदोष से

प्रश्न 29.
एक निकट दृष्टिदोष से पीड़ित व्यक्ति स्पष्ट नहीं देख सकता:
(अ) निकट की वस्तुओं को
(ब) दूर की वस्तुओं को
(स) न निकट तथा न ही दूर की वस्तुओं को
(द) क्षैतिज तथा ऊर्ध्वाधर रेखाओं को
उत्तर:
(ब) दूर की वस्तुओं को

प्रश्न 30.
एक सूक्ष्मदर्शी के अभिदृश्यक और नेत्र लेन्स की फोकस दूरियाँ क्रमशः 4 सेमी और 8 सेमी हैं तथा वस्तु की अभिदृश्यक से दूरी 4.5 सेमी है, तो आवर्धन क्षमता होगी:
(अ) 18
(ब) 32
(स) 64
(द) 20
उत्तर:
(ब) 32

प्रश्न 31.
जब किसी सूक्ष्मदर्शी के नलिका की लम्बाई बढ़ाई जाती है तो आवर्धन क्षमता:
(अ) घटती है
(ब) बढ़ती है
(स) अपरिवर्तित रहती है।
(द) कम व अधिक हो सकती है
उत्तर:
(अ) घटती है

प्रश्न 32.
प्रकाश की एक किरण काँच (अपवर्तनांक = 3/2) से पानी (अपवर्तनांक = 4/3) में संचरण करती है। क्रान्तिक कोण का मान होगा:
(अ) sin^-1(1/2)
(ब) sin^-1\(\left(\sqrt{\frac{8}{9}}\right)\)
(स) sin^-1(8/9)
(द) sin^-1(5/7)
उत्तर:
(स) sin^-1(8/9)

प्रश्न 33.
एक दूरदर्शक के अभिदृश्यक लेन्स तथा अभिनेत्र लेन्स की फोकस दूरियाँ क्रमश: f तथा हैं। इसकी आवर्धन क्षमता लगभग है:
(अ) f0/fc
(ब) fo – fe
(स) fofe
(द) fc + fc/2
उत्तर:
(अ) f0/fc

प्रश्न 34.
एक सूक्ष्मदर्शी में अभिदृश्यक लेन्स की फोकस दूरी, अभिनेत्रक लेन्स की फोकस दूरी से होती है:
(अ) कम
(ब) अधिक
(स) बराबर
(द) कुछ कहा नहीं जा सकता
उत्तर:
(अ) कम

प्रश्न 35.
परावर्तक दूरदर्शी में अभिदृश्यक के रूप में प्रयोग किया जाता है:
(अ) समतल दर्पण
(ब) अवतल दर्पण
(स) उत्तल लेन्स
(द) प्रिज्म
उत्तर:
(ब) अवतल दर्पण

प्रश्न 36.
दूरस्थ वस्तु को खगोलीय दूरदर्शी द्वारा देखने पर इसका प्रतिबिम्ब होता है:
(अ) सीधा
(ब) उल्टा
(स) विकृत
(द) उपर्युक्त में से कोई नहीं
उत्तर:
(ब) उल्टा

प्रश्न 37.
संयुक्त सूक्ष्मदर्शी में अन्तिम प्रतिबिम्ब बनता है:
(अ) वास्तविक एवं सीधा
(ब) आभासी एवं उल्टा
(स) आभासी एवं सीधा
(द) वास्तविक एवं उल्टा
उत्तर:
(ब) आभासी एवं उल्टा

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1.
एक प्रकाश किरण समतल दर्पण पर लम्बवत् आपतित होती है। आपतन कोण तथा परावर्तन कोण के मान क्या होंगे?
उत्तर:
आपतन कोण = 90° तथा परावर्तन कोण r = 0°

प्रश्न 2.
समतल दर्पण की फोकस दूरी कितनी होती है?
उत्तर:
शून्य।

प्रश्न 3.
उत्तल दर्पण का प्रयोग कारों में पीछे की साइड देखने के दर्पण बनाने में क्यों किया जाता है?
उत्तर:
इसका दृष्टि क्षेत्र विस्तृत होने तथा इसके द्वारा सीधा प्रतिबिम्ब बनने के कारण।

प्रश्न 4.
प्रकाश का परावर्तन से क्या तात्पर्य है?
उत्तर:
जब कोई किरण किसी सतह पर आपतित होकर उसी माध्यम में पुनः वापस लौटती है, तो इस परिघटना को परावर्तन कहते हैं। सघनता से पॉलिश किया हुआ सतह या दर्पण प्रकाश का परावर्तन करता है।

प्रश्न 5
परावर्तन के नियम को लिखिए।
उत्तर:
(i) आपतित किरण परावर्तित किरण तथा अभिलम्ब तीनों एक ही समतल में होते हैं।
(ii) नियमित परावर्तन में आपतन कोण Zi सदैव परावर्तन कोण Zr के बराबर होता है।

प्रश्न 6.
दर्पण तथा उसके प्रकार लिखिए।
उत्तर:
दर्पण – उच्च पॉलिश की हुई परावर्तक सतह को दर्पण कहते हैं। दर्पण तीन प्रकार के होते हैं:
(i) समतल दर्पण
(ii) अवतल दर्पण
(iii) उत्तल दर्पण|

प्रश्न 7.
अवतल दर्पण तथा उत्तल दर्पण की परिभाषा लिखिए।
उत्तर:
अवतल दर्पण-यदि बाहरी भाग को कलई किया जाये और भीतरी भाग से प्रकाश का परावर्तन हो तो उसे अवतल दर्पण कहते हैं।
उत्तल दर्पण – यदि किसी गोलीय दर्पण का आन्तरिक भाग कलई कर दिया जाये और बाहरी भाग से प्रकाश का परावर्तन हो तो उसे उत्तल दर्पण कहते हैं।

प्रश्न 8.
गोलीय दर्पण का सूत्र लिखिए और उसे समझाइए।
उत्तर:
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{u}}\) + \(\frac{1}{\mathrm{v}}\) जहाँ f, v तथा u क्रमशः फोकस दूरी, प्रतिबिम् की दूरी और वस्तु की दूरी है f, वक्रता त्रिज्या R की आधी होती है। अवतल दर्पण के लिए ऋणात्मक तथा उत्तल दर्पण के लिए f धनात्मक होता है।

प्रश्न 9.
किसी गोलीय दर्पण की आवर्धन को परिभाषित कीजिए।
उत्तर:
आवर्धन (m) – प्रतिबिम्ब का आकार (h) और बिम्ब के आकार (h) के अनुपात को गोलीय दर्पण का आवर्धन कहते हैं अर्थात्

प्रश्न 10.
न्यूनतम विचलन की अवस्था में प्रिज्म के पदार्थ के अपवर्तनांक ज्ञात करने का सूत्र लिखो।
उत्तर:
n2 = \(\frac{\sin \left(\frac{A+D_m}{2}\right)}{\sin \frac{A}{2}}\)
जहाँ n2 = हवा के सापेक्ष प्रिज्म के पदार्थ का अपवर्तनांक
A = प्रिज्म कोण
Dm = न्यूनतम विचलन कोण

प्रश्न 11.
अपवर्तन का मूल कारण क्या है?
उत्तर:
भिन्न-भिन्न माध्यमों में प्रकाश के वेग का भिन्न-भिन्न होना अपवर्तन का मूल कारण है।

प्रश्न 12.
उत्तल दर्पण में आवर्धन (m) का मान वास्तविक प्रतिबिम्ब और आभासी प्रतिबिम्ब के लिए कैसा होता है?
उत्तर:
वास्तविक प्रतिबिम्ब के लिए ऋणात्मक और आभासी प्रतिबिम्ब के लिए धनात्मक होता है।

प्रश्न 13.
अवतल दर्पण में आवर्धन (m) का मान किस पर निर्भर करता है और उत्तल दर्पण में (m) का मान सदैव किस तरह का होता है?
उत्तर:
प्रतिबिम्ब की स्थिति पर निर्भर करता है और आवर्धन (m) उत्तल दर्पण के लिए हमेशा +ve होता है।

प्रश्न 14.
एक समतल दर्पण पर प्रकाश की किरण 45° कोण पर आपतित होती है तो परावर्तित एवं आपतित किरण के मध्य कोण कितना होगा?
उत्तर:
90°।

प्रश्न 15.
प्रकाश का अपवर्तन परिभाषित कीजिए।
उत्तर:
जब कोई प्रकाश की किरण एक माध्यम से दूसरे माध्यम में प्रवेश करती है तो उसका पथ विचलित हो जाता है। इस परिघटना को अपवर्तन कहते हैं।

प्रश्न 16.
अपवर्तन के नियम लिखिए।
उत्तर:
(i) आपतित किरण, अपवर्तित किरण तथा दोनों माध्यमों को अलग करने वाले पृष्ठ पर अभिलम्ब एक ही तल में होते हैं।
(ii) किन्हीं दो माध्यमों के लिए तथा एक निश्चित रंग (तरंगदैर्ध्य ) के प्रकाश के लिए आपतन कोण की ज्या तथा अपवर्तन कोण की ज्या की निष्पत्ति एक नियतांक होती है।
यदि आपतन कोण व अपवर्तन कोण है, तो sini/sin r = नियतांक

प्रश्न 17.
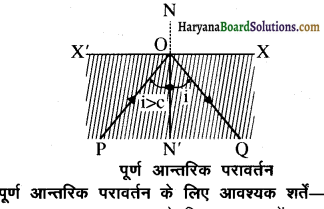
पूर्ण आन्तरिक परावर्तन की घटना को परिभाषित कीजिए।
उत्तर:
र-पूर्ण आन्तरिक परावर्तन (Total Internal Reflection ): जब सघन माध्यम में आपतन कोण का मान क्रान्तिक कोण से आगे थोड़ा-सा ही बढ़ाया जाता है, तो सम्पूर्ण आपतित प्रकाश, परावर्तन के नियमों के अनुसार परावर्तित होकर सघन माध्यम में ही वापस लौट आता है। इस घटना को प्रकाश का पूर्ण आन्तरिक परावर्तन कहते हैं।

प्रश्न 18.
क्रान्तिक कोण किसे कहते हैं?
उत्तर:
सघन माध्यम में बना वह आपतन कोण जिसके लिए विरल माध्यम में बना अपवर्तन कोण समकोण अर्थात 90° होता है, दोनों माध्यमों के अन्तरापृष्ठ के लिए क्रान्तिक कोण कहलाता है।

प्रश्न 19.
पूर्ण आन्तरिक परावर्तन के लिए कोई दो शर्तें लिखिए।
उत्तर:
(i) प्रकाश सघन माध्यम से विरल माध्यम की ओर गतिमान होना चाहिए।
(ii) आपतन कोण का मान दिए गए माध्यम में क्रान्तिक कोण से अधिक होना चाहिए।

प्रश्न 20.
किसी गोलीय पृष्ठ पर अपवर्तन के लिए सूत्र लिखिए।
उत्तर:
n2/v – n1/v = n2 – n1/R

प्रश्न 21.
किसी लेन्स द्वारा अपवर्तन के लिए सूत्र को लिखिए।
उत्तर:
\(\frac{1}{\mathrm{f}}\) = n21 – 1 (\(\frac{1}{\mathrm{R1}}\) – \(\frac{1}{\mathrm{R2}}\))

प्रश्न 22.
लेन्स को परिभाषित करते हुए इसके लिए सूत्र
उत्तर:
दो पृष्ठ से घिरा हुआ कोई पारदर्शी माध्यम, जिसका एक या दोनों पृष्ठ गोलीय हैं, लेन्स कहलाता है लेन्स दो प्रकार के होते हैं:
(1) उत्तल लेन्स
(2) अवतल लेन्स
वस्तु की दूरी, प्रतिबिम्ब की दूरी और लेन्स की फोकस दूरी के मध्य सम्बन्ध लेन्स सूत्र कहलाता है।
अर्थात् –\(\frac{1}{\mathrm{u}}\) + \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\)

प्रश्न 23.
उत्तल अथवा अवतल लेन्स द्वारा बने सीधे (तथा आभासी) प्रतिबिम्ब के लिए m का मान कैसा होता है?
उत्तर:
धनात्मक

प्रश्न 24.
उत्तल अथवा अवतल लेन्स द्वारा बने किसी उलटे (तथा वास्तविक) प्रतिबिम्ब के लिए m का मान किस तरह का होता है?
उत्तर:
m का मान ऋणात्मक होता है।

प्रश्न 25.
एक 1.45 अपवर्तनांक वाला काँच का लेन्स जब किसी द्रव में डुबोया जाता है, तो वह दिखाई नहीं देता है। द्रव का अपवर्तनांक क्या होगा?
उत्तर:
लेन्स के पदार्थ (काँच) के अपवर्तनांक के बराबर अर्थात्

प्रश्न 26.
एक अपवर्तनांक वाला एक उत्तल लेन्स एक ऐसे माध्यम में रखा जाता है, जिसका अपवर्तनांक लेन्स के अपवर्तनांक के बराबर है। इस माध्यम में लेन्स की फोकस दूरी क्या होगी?
उत्तर:
इस दशा में लेन्स काँच की समतल प्लेट की भाँति व्यवहार करेगा अतः इसकी फोकस दूरी अनन्त होगी।

प्रश्न 27.
अभिसारी लेन्सों की क्षमता लेन्स की क्षमता होती “होती है और अपसारी है।
उत्तर:
धनात्मक, ऋणात्मक।

प्रश्न 28.
लेन्स की क्षमता को परिभाषित कीजिए।
उत्तर:
किसी लेन्स की क्षमता को लेन्स की फोकस दूरी के व्युत्क्रम के रूप में परिभाषित किया जाता है।
अर्थात् P = \(\frac{1}{\mathrm{f}}\) (m)

प्रश्न 29.
यदि f1. f2 f3 …… फोकस दूरियों के बहुत से लेन्स एक-दूसरे के सम्पर्क में रखे हैं, तो इस संयोजन की प्रभावी फोकस दूरी क्या होगी?
उत्तर:
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{f1}}\) + \(\frac{1}{\mathrm{f2}}\) + \(\frac{1}{\mathrm{f3}}\) + …………..
क्षमता के पदों में P = P1 + P2 + P3 + …………

प्रश्न 30.
किसी दिए हुए प्रिज्म के लिए विचलन कोण का मान किस पर निर्भर करता है?
उत्तर:
किसी दिए हुए प्रिज्म के लिए विचलन कोण का मान प्रिज्म पर आपतित प्रकाश किरण के आपतन कोण पर निर्भर करता है।

प्रश्न 31.
किस रंग के लिए विचलन कोण का मान अधिकतम और न्यूनतम होता है?
उत्तर:
बैंगनी रंग के लिए अधिकतम और लाल रंग के लिए न्यूनतम होता है

प्रश्न 32.
न्यूनतम विचलन कोण को परिभाषित कीजिए।
उत्तर:
एक विशेष आपतन कोण पर विचलन कोण का मान न्यूनतम होता है। उसे न्यूनतम विचलन कोण कहते हैं।

प्रश्न 33.
वर्ण विक्षेपण (Dispersion) को परिभाषित कीजिए।
उत्तर:
प्रिज्म के द्वारा श्वेत प्रकाश की किरण का सात रंगों में विभाजित होना वर्ण विक्षेपण कहलाता है

प्रश्न 34.
वर्ण विक्षेपण का क्या कारण है?
उत्तर:
वर्ण विक्षेपण का कारण पारदर्शी माध्यम में भिन्न-भिन्न रंगों के लिए प्रकाश की चाल भिन्न-भिन्न होना है।

प्रश्न 35.
वर्णक्रम या स्पेक्ट्रम किसे कहते हैं?
उत्तर:
प्रिज्म से श्वेत प्रकाश के विक्षेपण के कारण प्राप्त रंगों की पट्टिकाओं (Bands) को वर्णक्रम या स्पेक्ट्रम कहते हैं। इस स्पेक्ट्रम में रंगों का क्रम VIBGYOR या बैंनी आहपीनाला होता है।

प्रश्न 36.
प्रिज्म की विक्षेपण क्षमता को लिखिए।
उत्तर:
किसी प्रिज्म की वर्ण विक्षेपण क्षमता जितनी अधिक होगी, उस पदार्थ से निर्मित प्रिज्म से प्राप्त स्पेक्ट्रम उतना ही विस्तृत होगा।

प्रश्न 37.
किसी प्रिज्म की वर्ण विक्षेपण क्षमता किस पर निर्भर करती है?
उत्तर:
प्रिज्म की वर्ण विक्षेपण क्षमता उसके पदार्थ पर निर्भर करती है अपवर्तन कोण पर नहीं।

प्रश्न 38.
किसी त्रिभुजाकार प्रिज्म के लिए आपतन कोण (i) तथा विचलन कोण (8) के बीच ग्राफ को खींचिए।
उत्तर:

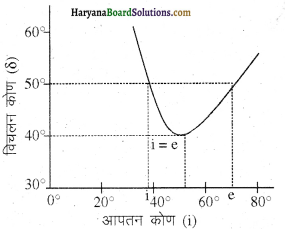
(i) तथा विचलण कोण (8) के बीच एक ग्राफ।

प्रश्न 39.
एक उत्तल लेन्स जिसका अपवर्तनांक n2. है. को एक तरल जिसका अपवर्तनांक 11 है, में डुबोया जाता है (n2 > n1 )। लेन्स की कार्य- शैली में क्या अन्तर आयेगा ?
उत्तर;
यह लेन्स अवतल लेन्स की भाँति कार्य करेगा।

प्रश्न 40.
एक उत्तल लेन्स (n = 1.5) की फोकस दूरी पर क्या प्रभाव पड़ेगा जब इसको जल में डुबोया जाता है?
उत्तर:
∴ Whg < ang, अतः जल में लेन्स की फोकस दूरी बढ़ जायेगी परन्तु प्रकृति नहीं बदलेगी।

प्रश्न 41.
क्राउन काँच की विक्षेपण क्षमता फ्लिन्ट काँच से कम होती है या अधिक? लिखिए।
उत्तर:
कम होती है।

प्रश्न 42
प्रकाशीय उपकरण किसे कहते हैं?
उत्तर:
वे उपकरण जो मानव को समीप तथा दूर की वस्तुओं को देखने में सहायता करते हैं, प्रकाशीय उपकरण या यंत्र कहलाते हैं।

प्रश्न 43.
अभिदृश्यक लेन्स की आवर्धन क्षमता को लिखिए।
उत्तर:
अभिदृश्य लेन्स की आवर्धन क्षमता का मान mo =v/u से ज्ञात करते हैं।

प्रश्न 44.
अभिकेन्द्र लेन्स की आवर्धन क्षमता का सूत्र लिखिए।
उत्तर:
me = D/VC[1 + Ve/fe]

प्रश्न 45.
एक संयुक्त सूक्ष्मदर्शी तथा एक दूरदर्शी की रचना को देखकर आप कैसे भेद करेंगे कि कौन किस प्रकार का प्रकाशिक यन्त्र है?
उत्तर:
संयुक्त सूक्ष्मदर्शी के अभिदृश्यक का द्वारक बहुत छोटा तथा दूरदर्शी लेन्स का द्वारक बहुत बड़ा होता है। अतः अभिदृश्यक के द्वारकों को देखकर दोनों प्रकार के प्रकाशिक यन्त्रों में भेद किया जा सकता है।

प्रश्न 46.
सामान्य समायोजन में दूरदर्शी की लम्बाई कितनी होती है?
उत्तर:
(fo + fe)

प्रश्न 47.
मोटर वाहनों में पीछे के ट्रैफिक को देखने हेतु चालक किस दर्पण को उपयोग में लेता है और क्यों ?
उत्तर:
चालक उत्तल दर्पण का उपयोग लेता है। चूँकि इससे बनने वाला प्रतिबिम्ब सीधा, आभासी एवं छोटा होता है, जिसके फलस्वरूप पश्च दृश्य क्षेत्र बड़ा हो जाता है।

प्रश्न 48.
दो पतले लेंस, जिनकी क्षमता + 5D एवं 3D है, परस्पर सम्पर्क में रखे हैं। संयोजन की फोकस दूरी ज्ञात कीजिए।
उत्तर:
प्रश्नानुसार
P1 = + 5D
P2= – 3D
∴ P = P1 + P2
= + 5D – 3D = + 2D
फोकस दूरी
f = \(\frac{1}{\mathrm{p}}\) (मीटर में)
= \(\frac{1}{\mathrm{2}}\) मीटर = \(\frac{1}{\mathrm{2}}\) x 100 = 50 सेमी.

प्रश्न 49.
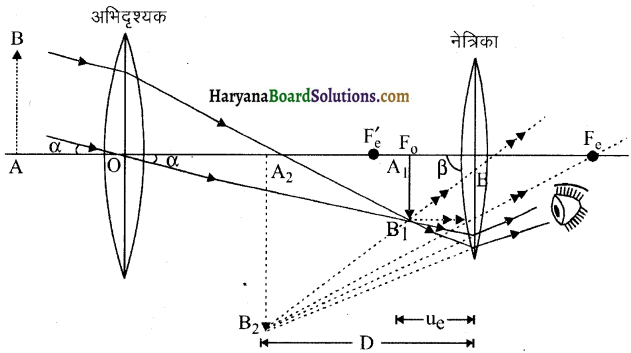
खगोलीय दूरदर्शी का नामांकित चित्र बनाइए।
उत्तर:

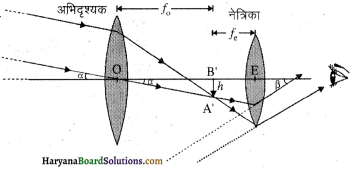
प्रश्न 50.
प्राथमिक इन्द्रधनुष तथा द्वितीयक इन्द्रधनुष में बूँद के अन्दर कितनी बार पूर्ण आन्तरिक परावर्तन होता है?
उत्तर:
प्राथमिक इन्द्रधनुष का निर्माण पानी की बूँदों पर सूर्य की किरणों के दो अपवर्तन तथा एक पूर्ण आन्तरिक परावर्तन से होता है, जबकि द्वितीयक इन्द्रधनुष का निर्माण पानी की बूँदों पर प्रकाश के दो अपवर्तन तथा दो पूर्ण आन्तरिक परावर्तन से होता है।

प्रश्न 51.
अवतल दर्पण के लिए बिंब दूरी u, प्रतिबिंब दूरी (v) एवं फोकस दूरी (f) में संबंध लिखिए।
उत्तर:
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{u}}\) + \(\frac{1}{\mathrm{v}}\)

प्रश्न 52.
जब प्रकाश किसी प्रकाशतः सघन माध्यम से विरल माध्यम में गमन करता है, तब आपतन का क्रांतिक कोण प्रकाश के वर्ण (रंग) पर निर्भर क्यों करता है?
उत्तर:
भिन्न-भिन्न रंग की तरंगदैर्ध्य के लिये अपवर्तनांक भिन्न-भिन्न होते हैं। u = a + b/λ² होता है, इसलिये क्रान्तिक कोण sin ic = 1/μ का मान भी भिन्न-भिन्न रंग के लिये भिन्न-भिन्न होता है।

लघुत्तरात्मक प्रश्न:

प्रश्न 1.
सिद्ध कीजिए n12 = 1/n21
उत्तर:
सामने के चित्र में यदि n21 माध्यम 2 का माध्यम 1 के सापेक्ष अपवर्तनांक है तब स्नेल नियम से
n21 = sini/sin r1 …..(i)

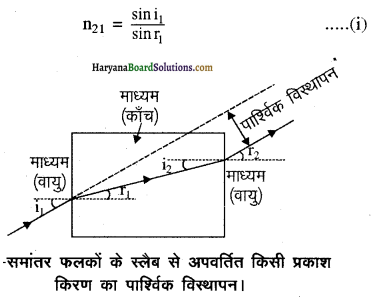
इसी तरह से यदि n12 माध्यम 1 का माध्यम 2 के सापेक्ष अपवर्तनांक है तब स्नेल नियम से
n12 = sini2/sin r2 ……….. (ii)
समीकरण (i) तथा (ii) का गुणा करने पर
n21 × n12 = \(\frac{\sin i_1}{\sin r_1}\) × \(\frac{\sin i_2}{\sin r_2}\)
चित्र से ∠r1 = ∠i2
और ∠i1 = ∠r2
∴ n1 x n12 = sini/sin r1 x sini2/sin r2
या
n21 x n12 = 1
या
n12 = 1/n21 इतिसिद्धम्

प्रश्न 2.
जब कोई प्रकाश किरण वायुमण्डल (a) से दो माध्यमों जल (b) तथा काँच (c) के संयोजन से होकर जाती है, तो तीन माध्यमों के अपवर्तनांकों में सम्बन्ध ज्ञात कीजिए।
उत्तर:
बिन्दुओं A, B तथा C पर स्नेल का नियम को लगाने पर:

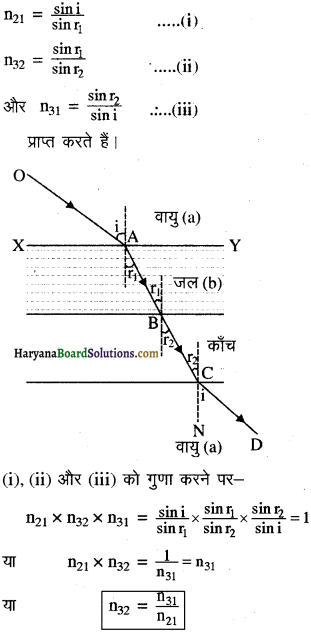
प्रश्न 3.
एक प्रकाश किरण माध्यम (1) से माध्यम (2) में अपवर्तित होती है। इनके अपवर्तनांक क्रमश: n1 तथा n2 हैं तथा n2 < n1 क्रान्तिक आपतन कोण के लिए व्यंजक लिखिए।
उत्तर:
जब आपतन कोण = क्रान्तिक कोण c तो इसके लिए
अपवर्तन कोण r = 90°
परन्तु स्नेल के नियम से n sini = n2 sin r
∴ n1 sin c = n2. sin 90° = n2 x 1 = n2
या sin c = (n2/n1) c = sin^-1(n2/n1)

प्रश्न 4.
क्या किसी माध्यम का दूसरे माध्यम के सापेक्ष अपवर्तनांक 1 से कम हो सकता है?
उत्तर:
हाँ।
उदाहरणार्थ-काँच के सापेक्ष जल का अपवर्तनांक
gn_w = n_w/n_g = 4/3/3/2 = 8/9
जो कि एक से कम है।

प्रश्न 5.
सिद्ध कीजिए कि n12 = 1/sin ic जहाँ पर Ic क्रान्तिक कोण है।
उत्तर:
वह आपतन कोण जिसका तदनुरूपी अपवर्तन कोण 90° होता है, वह दिए हुए माध्यमों के युगल के लिए क्रान्तिक कोण ic कहलाता है। स्नेल के नियम n21 = sini/sinr से हम देखते हैं कि यदि आपेक्षिक अपवर्तनांक एक से कम है, तो क्योंकि sinr का अधिकतम मान एक होता है अतः sini के मान की कोई ऊपरी सीमा है जिस तक यह नियम लागू किया जा सकता है। यह है i = ic इस प्रकार
sinic = n21
i के ic से अधिक मानों के स्नेल के अपवर्तन के नियम को लागू नहीं किया जा सकता है अतः कोई अपवर्तन संभव नहीं होता। सघन माध्यम 2 का विरल माध्यम 1 के सापेक्ष अपवर्तनांक होगा।
n12 = 1/sinic

प्रश्न 6.
क्या कारण है कि सूर्य वास्तविक सूर्योदय से कुछ पहले दृष्टिगोचर होने लगता है तथा वास्तविक सूर्यास्त के कुछ समय पश्चात् तक दृष्टिगोचर होता है? समझाइए।
उत्तर:
इसका मुख्य कारण प्रकाश का अपवर्तन है। वास्तविक सूर्योदय से हमारा तात्पर्य है क्षितिज से सूर्य का ऊपर उठना चित्र में क्षितिज के सापेक्ष सूर्य की वास्तविक एवं आभासी स्थितियाँ दर्शायी गई हैं। चित्र में इस प्रभाव को समझने की दृष्टि से आवर्धित करके दर्शाया गया है। निर्वात के सापेक्ष वायु का अपवर्तनांक 1.00029 है। इसके कारण सूर्य की दिशा में लगभग आधे डिग्री ( 1/2°) का आभासी विस्थापन होता है जिसका वास्तविक सूर्यास्त तथा आभासी सूर्यास्त में तदनुरूपी अंतर लगभग 2 मिनट है। सूर्यास्त तथा सूर्योदय के समय सूर्य का आभासी चपटापन (अंडाकार आकृति) भी इसी परिघटना के कारण ही है।

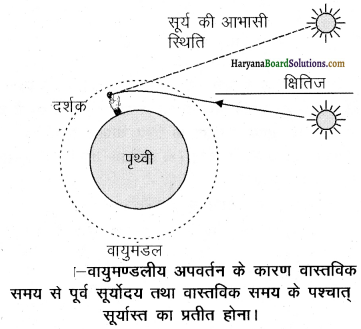
प्रश्न 7.
किसी उत्तल लेन्स के पदार्थ का अपवर्तनांक 1.5 है तथा इसकी दोनों सतहों की वक्रता त्रिज्यायें बराबर हैं सिद्ध कीजिए कि उसकी फोकस दूरी वक्रता त्रिज्या के बराबर है।
उत्तर:
\(\frac{1}{\mathrm{f}}\) = (n – 1)(\(\frac{1}{\mathrm{R1}}\) – \(\frac{1}{\mathrm{R2}}\))
\(\frac{1}{\mathrm{f}}\) = (1.5 – 1)(\(\frac{1}{\mathrm{R}}\) – \(\frac{1}{\mathrm{R}}\))
⇒ \(\frac{1}{\mathrm{f}}\) = 0.5 × (\(\frac{2}{\mathrm{R}}\)) = \(\frac{1}{\mathrm{R}}\)
अथवा f = R

प्रश्न 8.
वायु का बुलबुला जल में किस प्रकार के लेन्स की भाँति व्यवहार करेगा?
उत्तर:
वायु के बुलबुले के दोनों पृष्ठ उत्तल होते हैं। अतः यह एक उत्तल लेन्स की भाँति व्यवहार करता है लेकिन जल का अपवर्तनांक वायु के अपवर्तनांक से अधिक होता है। अतः जल की टंकी में स्थित वायु के बुलबुले की प्रकृति बदल जाने के कारण यह अवतल लेन्स की भाँति कार्य करेगा।

प्रश्न 9.
एक उत्तल लेन्स की फोकस दूरी किस प्रकार परिवर्तित होगी यदि बैंगनी प्रकाश के स्थान पर लाल प्रकाश प्रयुक्त किया जाये?
उत्तर:
∵ f α \(\frac{1}{(n-1)}\)
तथा nv > nR, अतः बैंगनी प्रकाश के स्थान पर लाल प्रकाश प्रयुक्त करने से लेन्स की फोकस दूरी बढ़ जायेगी।

प्रश्न 10.
प्रकाशिक तंतुओं के बंडल का उपयोग किस प्रकार से किया जा सकता है? समझाइए
उत्तर:
प्रकाशिक तंतुओं के बंडल (गुच्छ) का कई प्रकार से उपयोग किया जा सकता है। प्रकाशिक तंतुओं का बड़े पैमाने पर वैद्युत संकेतों, जिन्हें उचित ट्रांसड्यूसरों द्वारा प्रकाश में परिवर्तित कर लेते हैं, के प्रेषण तथा अभिग्रहण में उपयोग किया जाता है। स्पष्ट है कि प्रकाशिक तंतुओं का उपयोग प्रकाशिक संकेत प्रेषण के लिए भी किया जा सकता है। उदाहरण के लिए, इन्हें आंतरिक अंगों जैसे ग्रसिका आमाशय तथा आंत्रों के दृश्य अवलोकन के लिए ‘लाइट पाइप’ के रूप में प्रयोग किया जाता है।

प्रश्न 11.
यदि हम किसी अवतल दर्पण के परावर्तक पृष्ठ के नीचे का आधा भाग किसी अपारदर्शी (अपरावर्ती) पदार्थ से ढक देते हैं तब दर्पण के सामने स्थित किसी बिंब के दर्पण द्वारा बने प्रतिबिंब पर इसका क्या प्रभाव पड़ेगा?
उत्तर:
आप सोच सकते हैं कि प्रतिबिंब में बिंब का आधा भाग दिखाई देगा। परंतु यह मानते हुए कि परावर्तन के नियम दर्पण के शेष भाग पर भी लागू होते हैं, अतः दर्पण द्वारा बिंब का पूर्ण प्रतिबिंब बनेगा। तथापि, क्योंकि परावर्ती पृष्ठ का क्षेत्रफल कम हो गया है इसलिए प्रतिबिंब की तीव्रता कम हो जाएगी अर्थात् आधी हो जाएगी।

प्रश्न 12.
किसी अवतल दर्पण के मुख्य अक्ष पर एक मोबाइल फोन रखा है। उचित किरण आरेख द्वारा प्रतिबिंब की रचना दर्शाइए। व्याख्या कीजिए कि आवर्धन एकसमान क्यों नहीं है क्या प्रतिबिंब की विकृति दर्पण के सापेक्ष फोन की स्थिति पर निर्भर करती है?
उत्तर:

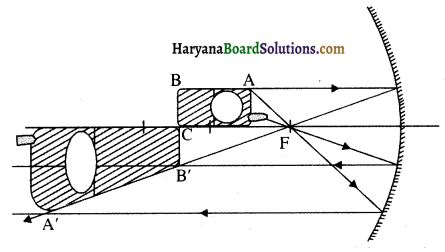
चित्र में फोन के प्रतिबिंब की रचना का प्रकाश-किरण आरेख दर्शाया गया है। मुख्य अक्ष के लंबवत् समतल में स्थित भाग का प्रतिबिंब उसी समतल में होगा। यह उसी साइज का होगा, अर्थात् BC = BC।

प्रश्न 13.
उत्तल लेन्स तथा अवतल लेन्स से गुजरने वाली प्रकाश किरणों का अनुरेखन कीजिए।
उत्तर:

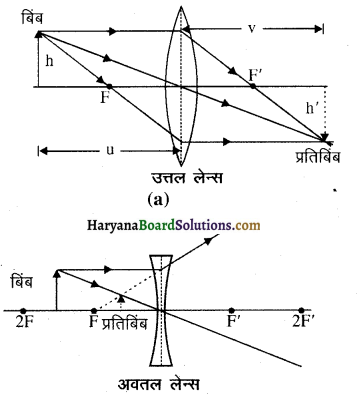
प्रश्न 14.
लेन्स की क्षमता से क्या तात्पर्य है? इसे समझाइए।
उत्तर:
लेन्स की क्षमता किसी लेन्स की क्षमता P को उस कोण की स्पर्शज्या से परिभाषित करते हैं, जिससे यह किसी प्रकाश पुंज को जो प्रकाशिक केंद्र से एकांक दूरी पर आकर गिरता है, अभिसरित या अपसरित करता है। जैसा कि चित्र में दिखाया गया है।
tanδ = h/f; यदि h = 1 tanδ = 1/f
δ = 1⁄2 (δ के लघु मान के लिए)।
अथवा
अतः
p = \(\frac{1}{\mathrm{f}}\) यहाँ पर f को मीटर में लिया गया है।

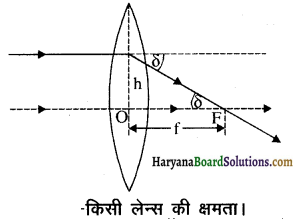
लेन्स की क्षमता का SI मात्रक डाइऑप्टर (D) = 1D=1m^-1 है।
अतः 1m फोकस दूरी के लेन्स की क्षमता एक डाइऑप्टर है। अभिसारी लेसों की क्षमता धनात्मक तथा अपसारी लेंस की क्षमता ऋणात्मक होती है। इस प्रकार जब कोई नेत्र चिकित्सक + 2.5 D क्षमता का संशोधक लेन्स निर्धारित करता है, तब + 40 cm फोकस दूरी के उत्तल लेन्स की आवश्यकता होती है। 4.0 D क्षमता के लेन्स से तात्पर्य – 25 cm फोकस दूरी का अवतल लेन्स होता है।

प्रश्न 15.
शुद्ध एवं अशुद्ध स्पैक्ट्रम से क्या अभिप्राय है?
उत्तर:
शुद्ध स्पैक्ट्रम – जब श्वेत प्रकाश की किरणें किसी प्रिज्म में से गुजरती हैं तो प्रत्येक किरण पर्दे पर स्पैक्ट्रम बनाती है। यदि स्पैक्ट्रम में प्रत्येक रंग अलग-अलग रूप से दिखाई दे तो इस प्रकार के स्पैक्ट्रम को ‘शुद्ध स्पैक्ट्रम’ कहते हैं शुद्ध स्पैक्ट्रम प्राप्त करने की निम्न शर्तें होती हैं:
(i) रेखा छिद्र संकरा तथा अभिसारी लेन्स के फोकस पर स्थित होना चाहिये।
(ii) प्रिज्म न्यूनतम विचलन की स्थिति में होना चाहिए।
(iii) प्रिज्म से निर्गत एक ही रंग की किरणें अभिसारी लेन्स द्वारा एक ही स्थान पर फोकसित होनी चाहिये।
(iv) आपतित किरणें समान्तर होनी चाहिये।
अशुद्ध स्पैक्ट्रम जब श्वेत प्रकाश की किरणें किसी प्रिज्म में से गुजरती हैं तो प्रत्येक किरण पर्दे पर स्पैक्ट्रम बनाती है। भिन्न-भिन्न रंगों के अतिव्यापन के कारण पर्दे पर ये रंग पृथक् पृथक् दिखाई नहीं देते हैं, इस प्रकार के स्पैक्ट्रम को ‘अशुद्ध स्पैक्ट्रम’ कहते हैं।

प्रश्न 16.
प्रकाश के प्रकीर्णन से क्या अभिप्राय है? इसका दैनिक जीवन में उपयोग बताइये।
उत्तर:
प्रकाश का प्रकीर्णन जब प्रकाश किसी माध्यम में से संचरित होता है तो वह उस माध्यम के कणों के साथ अन्योन्य क्रिया करता है। ये कण आपतित प्रकाश से कुछ ऊर्जा ले लेते हैं तथा उसे पुनः उत्सर्जित कर देते हैं। इस प्रक्रिया को प्रकीर्णन कहते हैं। प्रकाश के प्रकीर्णन का उपयोग प्रकाश के प्रकीर्णन से हमें वस्तुएँ दिखाई देती हैं। जब प्रकाश की किरणें किसी खुरदरे पृष्ठ पर गिरती हैं तो परावर्तित किरणें विभिन्न दिशाओं में बिखर जाती हैं। इस बिखरे प्रकाश या प्रकीर्णन प्रकाश के कारण ही हमें अपने कमरे में जबकि सूर्य की किरणें प्रत्यक्ष नहीं आती हैं फिर भी सभी वस्तुयें दिखाई देती हैं। आकाश का रंग नीला दिखाई देना, सूर्योदय एवं सूर्यास्त पर सूर्य का लाल दिखाई देना भी प्रकाश प्रकीर्णन की घटना के कारण हैं।

प्रश्न 17.
समान फोकस दूरी का एक अभिसारी लेन्स तथा एक अपसारी लेन्स समाक्षीय रूप से परस्पर सम्पर्क में रखे गये हैं। संयोजन की फोकस दूरी तथा क्षमता ज्ञात कीजिए।
उत्तर:
र-संयोजन की फोकस दूरी F हो, तो
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{f1}}\) + \(\frac{1}{\mathrm{f2}}\) = \(\frac{1}{\mathrm{f}}\) + \(\frac{1}{\mathrm{f}}\)
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{f}}\) – \(\frac{1}{\mathrm{f}}\) = 0
अतः
F = \(\frac{1}{\mathrm{0}}\) = ∞ अर्थात्
F= अनन्त अतः क्षमता P = \(\frac{1}{\mathrm{f}}\)
P = 1/∞ = 0
अतः संयोजन लेन्स की फोकस दूरी अनन्त होगी और संयोजन लेन्स की क्षमता P = शून्य होगी।

प्रश्न 18.
सरल सूक्ष्मदर्शी की आवर्धन क्षमता किस रंग के प्रकाश के लिए अधिकतम तथा किस रंग के प्रकाश के लिए न्यूनतम होगी?
उत्तर:
fv < fgRअतः सूत्र m = (1 + D/f) स्पष्ट है कि बैंगनी रंग के लिए आवर्धन क्षमता अधिकतम तथा लाल रंग के लिए न्यूनतम होगी।

प्रश्न 19.
दूरदर्शी द्वारा अन्तिम प्रतिबिम्ब जब अनन्त पर बन रहा हो तब उसकी नली की लम्बाई कितनी होती है? यदि प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने तब लम्बाई पहले से कम होगी अथवा अधिक?
उत्तर:
जब प्रतिबिम्ब अनन्तता पर बनेगा तो नली की लम्बाई (fo + fe) होगी। यहाँ fo अभिदृश्यक लेन्स की फोकस दूरी है तथा fe नेत्रिका की फोकस दूरी है परन्तु यदि अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है तब नली की लम्बाई (fo + ue) होगी, जहाँ u अभिदृश्यक लेन्स से बने प्रतिबिम्ब की नेत्रिका से दूरी है। यह लम्बाई (fo + fe) से कम होगी।

प्रश्न 20.
दूरदर्शी का अभिदृश्यक बड़ा और नेत्रिका छोटा है, जबकि सूक्ष्मदर्शी का अभिदृश्यक छोटा तथा नेत्रिका बड़ा होता है। यदि किसी दूरदर्शी को उलट दें, तो क्या वह सूक्ष्मदर्शी की भाँति प्रयुक्त की जा सकती है? क्या इसी प्रकार सूक्ष्मदर्शी को दूरदर्शी की तरह प्रयुक्त कर सकते हैं?
उत्तर:
नहीं। क्योंकि दूरदर्शी के लेन्सों की फोकस – दूरियों में अन्तर सूक्ष्मदर्शी के लेन्सों की फोकस दूरियों में अन्तर की अपेक्षा बहुत अधिक होता है। इस प्रकार दूरदर्शी को उलटकर सूक्ष्मदर्शी की भाँति प्रयुक्त करने पर उसकी आवर्धन क्षमता बहुत कम होगी। इसी तरह सूक्ष्मदर्शी को उलटकर दूरदर्शी की भाँति प्रयुक्त करने पर उसकी आवर्धन क्षमता कम हो जायेगी।

प्रश्न 21.
(a) बहुत दूर स्थित तारे जिन्हें नेत्र द्वारा नहीं देखा जा सकता, वे दूरदर्शी द्वारा देखे जा सकते हैं। क्यों?
(b) दो दूरदर्शियों की आवर्धन क्षमता समान है लेकिन इनके अभिदृश्यक लेन्सों के द्वारक अलग-अलग हैं। इनके द्वारा बनने वाले अंतिम प्रतिबिम्बों में क्या परिवर्तन होगा?
उत्तर:
(a) नेत्र के लेन्स का द्वारक बहुत छोटा होता है तथा बहुत अधिक दूर स्थित तारे से आने वाला प्रकाश बहुत कम होता है तथा हमारे नेत्र के रेटिना को उत्तेजित करने में असमर्थ होता है परन्तु दूरदर्शी का द्वारक, नेत्र की तुलना में बहुत बड़ा होता है। इस कारण यह दूरस्थ तारे से उचित प्रकाश प्राप्त कर सकता है तथा तारे का चमकीला प्रतिबिम्ब बनाता है, जिसे देखा जा सकता है।
(b) प्रतिबिम्बों की चमक अलग-अलग होगी; क्योंकि यह द्वारक के व्यास पर निर्भर करती है। बड़े द्वारक के अभिदृश्यक लेन्स युक्त दूरदर्शी द्वारा बना प्रतिबिम्ब अधिक चमकीला होगा। साथ ही इस दूरदर्शी की विभेदन क्षमता (1.222) भी छोटे द्वारक के अभिदृश्यक लेन्स युक्त दूरदर्शी की तुलना में अधिक होगी।

प्रश्न 22.
(a) किसी दूरदर्शी को उलटकर अभिदृश्यक की ओर देखने पर बहुत छोटी प्रतीत होती है, क्यों?
(b) सूक्ष्मदर्शी में ऐसा क्यों नहीं होता है?
उत्तर:
(a) दूरदर्शी में अभिदृश्यक लेन्स की फोकस दूरी (f0) नेत्रिका की फोकस दूरी (fc) से कहीं अधिक होती है तथा इसकी आवर्धन क्षमता f0/fc होती है। पलटकर देखने पर आवर्धन क्षमता fc/f0 हो जाएगी क्योंकि fo << fc अतः अब वस्तु बहुत ही छोटी दिखाई देगी।
क्योंकि
(b) संयुक्त सूक्ष्मदर्शी की आर्धन क्षमता का सूत्र v0/u0 × D/fe है; क्योंकि v0 का मान सूक्ष्मदर्शी के अभिदृश्यक की फोकस दूरी f0 से थोड़ा सा ही अधिक होता है, अतः आवर्धन v0/f0 × D/fe माना जा सकता है; fo तथा दोनों के ही मान कम होते हैं। अतः सूक्ष्मदर्शी को उलटने पर भी vo के मान में कोई विशेष अन्तर न होने से आवर्धन क्षमता लगभग अपरिवर्तित रहती है।

प्रश्न 23.
“सूक्ष्मदर्शी एवं दूरदर्शी में उच्च आवर्धन क्षमता के साथ-साथ पर्याप्त विभेदन क्षमता भी होनी चाहिए।” उपर्युक्त कथन का आशय स्पष्ट कीजिए।
उत्तर:
आवर्धन क्षमता अधिक होने से वस्तु बड़ी एवं स्पष्ट दिखाई देती है, किन्तु यदि विभेदन क्षमता कम है तो उसकी संरचना को स्पष्ट नहीं देखा जा सकता है।

प्रश्न 24.
सुमेलित कीजिए:

कॉलम I	कॉलम II
A μ  = tanip	P स्नैल का नियम
B μ = 1/sinic	Q ब्रुस्टर का नियम प्रिज्म
C μ = sini/sinr	R पूर्ण
D μ =  \(\frac{\sin \left(\frac{A+D_m}{2}\right)}{\sin \frac{A}{2}}\)	S आन्तरिक परावर्तन

उत्तर:

A	Q
B	S
C	P
D	R

प्रश्न 25.
निम्न को परिभाषित कीजिए:
(a) पूर्ण आन्तरिक परावर्तन
(b) प्रकाश का विवर्तन
(c) प्रकाश का अपवर्तन।
उत्तर:
(a) पूर्ण आन्तरिक परावर्तन (Total Internal Reflection): जब सघन माध्यम में आपतन कोण का मान क्रान्तिक कोण से आगे थोड़ा-सा ही बढ़ाया जाता है, तो सम्पूर्ण आपतित प्रकाश, परावर्तन नियमों के अनुसार परावर्तित होकर सघन माध्यम में ही वापस लौट आता है जैसा कि नीचे चित्र में दिखाया गया प्रकाश का पूर्ण आन्तरिक परावर्तन कहते हैं।

पूर्ण आन्तरिक परावर्तन के लिए आवश्यक शर्तें:
(1) प्रकाश सघन माध्यम से विरल माध्यम में जाना चाहिए।
(2) सघन माध्यम में आपतन कोण का मान क्रान्तिक कोण से बड़ा होना चाहिए।

(b) प्रकाश का विवर्तन (Diffraction of light): विवर्तन तरंगों का एक अभिलाक्षणिक गुण है। जब तरंगों के मार्ग में कोई अवरोध आता है अथवा तरंगें किसी सूक्ष्म छिद्र से गुजरती हैं तो वे अवरोध या छिद्र के किनारे पर ‘आंशिक रूप से मुड़ जाती हैं। इस घटना को विवर्तन कहते हैं। विवर्तन की घटना सभी प्रकार की तरंगों, जैसे प्रकाश तरंगें, ध्वनि तरंगें इत्यादि में देखने को मिलती है। तरंगों का विवर्तन होने के लिये अवरोध का आकार तरंगों की तरंगदैर्घ्य की कोटि का होना चाहिये।

(c) प्रकाश का अपवर्तन (Refraction of light): प्रकाश की किरणें किसी समांगी (homogeneous ) एवं पारदर्शी माध्यम में सीधी रेखाओं में चलती हैं, परन्तु जब प्रकाश की कोई किरण इस प्रकार के एक पारदर्शी माध्यम से दूसरे पारदर्शी माध्यम में जाती है तो किरण का कुछ भाग माध्यमों के सीमा पृष्ठ (boundary surface) पर परावर्तित होकर पहले माध्यम में ही लौट आता है और शेष भाग दूसरे माध्यम में चला जाता है। दूसरे माध्यम में जाने पर प्रायः किरण की दिशा बदल जाती है अर्थात् प्रकाश की किरण अपने प्रारम्भिक मार्ग से विचलित (deviate) हो जाती है। “प्रकाश किरण का एक पारदर्शी माध्यम से दूसरे पारदर्शी माध्यम में जाने पर अपने पथ से विचलित हो जाना प्रकाश का अपवर्तन (Refraction) कहलाता है।”

प्रश्न 26.
तरंगाय की परिभाषा लिखिए। हाइगेन्स के सिद्धान्त का उपयोग करके किसी उत्तल लेंस पर आपतित समतल तरंग के अपवर्तित तरंगाय की आकृति खींचिए।
अथवा
(a) जब कोई तरंग किसी विरल माध्यम से किसी सघन माध्यम संचरण करती है, तब उस तरंग का कौन-सा अभिलक्षण परिवर्तित नहीं होता और क्यों?
(b) दो माध्यमों के अपवर्तनांक μ1 और μ2 हैं, उनमें तरंग के वेगों का अनुपात क्या होगा?
उत्तर:
जब किसी माध्यम में स्थित तरंग स्रोत से तरंगें निकलती हैं तो इसके चारों ओर स्थित माध्यम के कण कम्पन करने लगते हैं। माध्यम में वह पृष्ठ जिसमें स्थित सभी कण कम्पन की समान कला में हों, तरंगाग्र कहलाता है।

(a) आवृत्ति स्थिर रहती है क्योंकि दो माध्यमों में प्रति सेकण्ड प्रवेश करते समय तरंगों की संख्या समान होती है।
(b) भिन्न-भिन्न माध्यमों में वेग का मान इस प्रकार दिया जा सकता है और इस प्रकार से प्रकाश की चाल अपवर्तनांक के माध्यम के व्युत्क्रमानुपाती होती है।

प्रश्न 27.
(a) प्रकाश की एक किरण अपवर्तनांक aμg = 1.5 के काँच के समकोणिक प्रिज्म के फलक AB पर अभिलम्बवत आपतित है। यह प्रिज्म किसी अज्ञात अपवर्तनांक के द्रव में आंशिक डूबा है। द्रव के अपवर्तनांक का मान ज्ञात कीजिए ताकि प्रिज्म से अपवर्तन के पश्चात् प्रकाश की किरण फलक BC के अनुदिश पृष्ठसर्पी हो।

(b) उस प्रकरण में किरण का पथ खींचिये जब यह किरण फलक AC पर अभिलम्बवत आपतन करती है।
उत्तर:
(a) स्नेल के नियम से
aμg sinic = aμ1 sin90°
1.5 × 60° =aμ1
aμ1 = 1.5 × 3/2
= 1.3

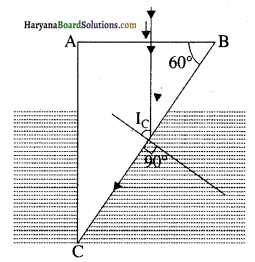
(b) आपतित किरण 30° के कोण पर टकराती है जो कि ic से कम है। इस कारण से प्रकाश किरण अभिलम्ब से दूर हट जाती है।

आंकिक प्रश्न:

प्रश्न 1.
एक अवतल दर्पण की फोकस दूरी 36 सेमी. हो तो इसकी वक्रता त्रिज्या ज्ञात कीजिए।
उत्तर:
प्रश्नानुसार
f = 36 सेमी.
हम जानते हैं-फोकस दूरी और वक्रता त्रिज्या में सम्बन्ध
f = 1⁄2R
∴ R = 2f
या
R = 2 × 36 = 72 सेमी.

प्रश्न 2.
3 सेमी. ऊँची एक वस्तु 30 सेमी. फोकस दूरी के उत्तल दर्पण के सम्मुख इससे 60 सेमी. की दूरी पर रखी है। प्रतिबिम्ब की प्रकृति, स्थिति तथा आकार ज्ञात कीजिए।
उत्तर:
दिया गया है:
वस्तु की ऊँचाई h = 3 सेमी.
उत्तल दर्पण की फोकस दूरी f = 30 सेमी.
दर्पण से वस्तु की दूरी u = – 60 सेमी.
दर्पण के सूत्र से
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{U}}\) + \(\frac{1}{\mathrm{V}}\)
या
\(\frac{1}{\mathrm{V}}\) = \(\frac{1}{\mathrm{f}}\) – \(\frac{1}{\mathrm{U}}\)
= \(\frac{1}{\mathrm{30}}\) – \(\frac{1}{\mathrm{-60}}\)
= \(\frac{1}{\mathrm{30}}\) + \(\frac{1}{\mathrm{60}}\)
⇒ v = 20 सेमी. 20
अतः प्रतिबिम्ब आभासी व सीधा बनेगा अतः दर्पण के पीछे अर्थात्
वस्तु की विपरीत दिशा में दर्पण से 20 सेमी. दूरी पर बनेगा
आवर्धन m = h/n = v/u
h/3 = – (20 सेमी/−60 सेमी) = 1/3
h’ = 1 सेमी.
अतः प्रतिबिम्ब की ऊँचाई 1 सेमी. होगी।

प्रश्न 3.
एक उत्तल लेन्स द्वारा एक वस्तु का सीधा प्रतिबिम्ब बनता है तथा इसकी लम्बाई वस्तु की लम्बाई की चार गुनी है। यदि लेन्स की फोकस दूरी 20 सेमी. है तो वस्तु के प्रतिबिम्ब की दूरियाँ ज्ञात कीजिए।
उत्तर:
दिया है:
f = 20 सेमी. तथा m = 4
∵h’ = 4h दिया
u तथा f के पदों में m का सूत्र
m = f/u+f
⇒ 4 = 20 सेमी/u + 20 सेमी.
4u + 80 = 20
4u = (20 – 80) सेमी.
4u = – 60 सेमी.
लेन्स से वस्तु की दूरी = -15 सेमी.
v तथा f के पदों में m का सूत्र
m = f – v/f
⇒ 4 = 20 सेमी – v/20 सेमी.
80 = 20 – v
v = ( 20 – 80 ) सेमी.
= 60 सेमी.
∴ लेन्स से प्रतिबिम्ब की दूरी v = – 60 सेमी.

प्रश्न 4.
10 सेमी. फोकस दूरी वाला एक उत्तल लेन्स समाक्षीय रूप से एक 10 सेमी. फोकस दूरी वाले अवतल लेन्स से 5 सेमी. दूरी पर रखा है। यदि एक वस्तु उत्तल लेन्स के सम्मुख 30 सेमी. दूरी पर रखी है तो संयुक्त निकाय द्वारा बने अन्तिम प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
उत्तर:
यहाँ पर उत्तल लेन्स के लिए
f= + 10 सेमी. तथा u = – 30 सेमी.
\(\frac{1}{\mathrm{V}}\) – \(\frac{1}{\mathrm{U}}\) = \(\frac{1}{\mathrm{f}}\) से,
\(\frac{1}{\mathrm{V}}\) = \(\frac{1}{\mathrm{f}}\) + \(\frac{1}{\mathrm{U}}\)
= \(\frac{1}{\mathrm{10}}\) + \(\frac{1}{\mathrm{-30}}\)
= \(\frac{1}{\mathrm{10}}\) – \(\frac{1}{\mathrm{-30}}\)
= 3-\(\frac{1}{\mathrm{30}}\)
= \(\frac{2}{\mathrm{30}}\)
= \(\frac{1}{\mathrm{15}}\)
v = 15 सेमी.
नीचे चित्र में उत्तल लेन्स द्वारा वस्तु O का बना प्रतिबिम्ब I’ अवतल लेन्स के लिए आभासी वस्तु का कार्य करेगा जिसकी अवतल लेन्स से दूरी u = (15 – 5) सेमी = 10 सेमी.

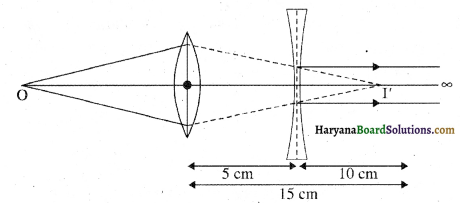
इसकी फोकस दूरी f = -10 सेमी.
\(\frac{1}{\mathrm{V}}\) – \(\frac{1}{\mathrm{U}}\) = \(\frac{1}{\mathrm{f}}\) से
\(\frac{1}{\mathrm{V}}\) = \(\frac{1}{\mathrm{f}}\) + \(\frac{1}{\mathrm{U}}\) = \(\frac{1}{\mathrm{-10}}\) + \(\frac{1}{\mathrm{10}}\) = 0
अतः संयुक्त निकाय द्वारा बना अन्तिम प्रतिबिम्ब अनन्त पर होगा।

प्रश्न 5.
खगोलीय दूरदर्शक के अभिदृश्यक तथा नेत्रिका लेन्सों की फोकस दूरियाँ क्रमशः 2 मीटर तथा 0.05 मीटर हैं। अन्तिम प्रतिबिम्ब यदि (i) स्पष्ट दृष्टि की न्यूनतम दूरी पर (ii) अनन्तता पर बने तो प्रत्येक दशा में दूरदर्शी की आवर्धन क्षमता तथा लम्बाई ज्ञात कीजिए।
उत्तर:
(i) जब अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है, तो
आवर्धन क्षमता m = – \(\left[\frac{\mathrm{f}_{\mathrm{o}}}{\mathrm{f}_{\mathrm{e}}}\left(1+\frac{\mathrm{f}_{\mathrm{e}}}{\mathrm{D}}\right)\right]\)
यहाँ अभिदृश्यक की फोकस दूरी f = 2 मीटर = 200 सेमी. तथा नेत्रिका की फोकस दूरी = 0.05 मीटर = 5 सेमी एवं स्पष्ट दृष्टि की न्यूनतम दूरी D = 25 सेमी.
m = – 200/5(1 + 5/25) = -48
नेत्रिका के लिए fe = 5 सेमी. तथा Ve = 25 सेमी.
∴ \(\frac{1}{\mathrm{fe}}\) = \(\frac{1}{\mathrm{ve}}\) – \(\frac{1}{\mathrm{ue}}\)
\(\frac{1}{\mathrm{ue}}\) = \(\frac{1}{\mathrm{v}}\) – \(\frac{1}{\mathrm{fe}}\) = \(\frac{1}{\mathrm{-2.5}}\) – \(\frac{1}{\mathrm{5}}\)
= \(\frac{-1}{\mathrm{25}}\) + \(\frac{1}{\mathrm{5}}\) = -(\(\frac{6}{\mathrm{-25}}\))
∴ u = (25/6) सेमी. 4.167 सेमी.
दूरदर्शी की लम्बाई L = fo + ue
= (200 सेमी. + 4.167 सेमी.) = 204.167 सेमी.
(यहाँ ue का मान चिन्ह छोड़कर रखना होता है)

(ii) जब अन्तिम प्रतिबिम्ब अनन्तता पर बनता है, तो
आवर्धन क्षमता m = -(f0/fe) = -(\(\frac{200}{\mathrm{5}}\))
= -40
इस दशा में
दूरदर्शी की लम्बाई L = f0 + fe = (200 + 5) सेमी.
= 205 सेमी.

प्रश्न 6.
एक सरल सूक्ष्मदर्शी में प्रयुक्त लेन्स की फोकस दूरी 5 सेमी है। स्पष्ट दृष्टि की न्यूनतम दूरी 25 सेमी. है। इसकी आवर्धन क्षमता ज्ञात कीजिए:
(i) जबकि अन्तिम प्रतिबिम्ब अनन्त पर बने,
(ii) स्पष्ट दृष्टि की न्यूनतम दूरी पर बने।
उत्तर:
यहाँ f = 5 सेमी. D = 25 सेमी.
(i) आवर्धन क्षमता m = D/f = 25 सेमी/5 सेमी. = 5

(ii) आवर्धन क्षमता m = 1+ D/f 1 + 25 सेमी/5 सेमी. = 6

प्रश्न 7.
एक यौगिक सूक्ष्मदर्शी के अभिदृश्यक तथा नेत्रिका की फोकस दूरियाँ क्रमशः 1.0 सेमी. तथा 5.0 सेमी हैं। एक वस्तु अभिदृश्यक से 1.1 सेमी. की दूरी पर रखी जाती है। सूक्ष्मदर्शी की आवर्धन क्षमता तथा लम्बाई ज्ञात कीजिए, जबकि अन्तिम प्रतिबिम्ब (i) अनन्त पर बन रहा हो, (ii) स्पष्ट दृष्टि की न्यूनतम दूरी पर बन रहा हो।
उत्तर:
(i) यहाँ fo = 1.0 सेमी. fe = 5.0 सेमी. तथा g = -1.1 सेमी. D = 25 सेमी.
सूत्र \(\frac{1}{\mathrm{v0}}\) – \(\frac{1}{\mathrm{u0}}\) = \(\frac{1}{\mathrm{f0}}\) से,
\(\frac{1}{\mathrm{v0}}\) = \(\frac{1}{\mathrm{f0}}\) + \(\frac{1}{\mathrm{u0}}\) = \(\frac{1}{\mathrm{1.0}}\) + \(\frac{1}{\mathrm{-1.1}}\) = 1 – \(\frac{10}{\mathrm{11}}\) = \(\frac{1}{\mathrm{11}}\)
Vo = 11 सेमी.
अतः आवर्धन क्षमता m
= –\(\left[\frac{v_o}{u_o}\left(1+\frac{D}{f_e}\right)\right]\) = –\(\left[\frac{11}{1.1}\left(1+\frac{25}{5}\right)\right]\) = -60
सूक्ष्मदर्शी की लम्बाई L = Vo + f = (11 + 5) सेमी.
= 16 सेमी

(ii) नेत्रिका के लिए f = 5 सेमी. तथा Ve = -25सेमी.
∴ \(\frac{1}{\mathrm{fe}}\) = \(\frac{1}{\mathrm{ve}}\) – \(\frac{1}{\mathrm{ue}}\) से,
\(\frac{1}{\mathrm{ue}}\) = \(\frac{1}{\mathrm{ve}}\) – \(\frac{1}{\mathrm{fe}}\) = \(\frac{1}{\mathrm{-25}}\) – \(\frac{1}{\mathrm{5}}\) = \(\frac{-6}{\mathrm{5}}\)
अतः आवर्धन क्षमता m =
= \(-\left[\frac{v_0}{u_o}\left(\frac{D}{f_e}\right)\right]\) = \(\left[\frac{11}{1.1}\left(\frac{25}{5}\right)\right]\) = -50
सूक्ष्मदर्शी की लम्बाई L = Vo + ue
= (11 + 4.167) सेमी.
= 15.167 सेमी.

प्रश्न 8.
एक उत्तल लैंस जिसकी वक्रता त्रिज्या R1 = R2 = 24 cm है एवं जिसके पदार्थ का अपवर्तनांक 1.6 है।
(a) वायु में इस लेंस की फोकस दूरी की गणना करो।
(b) यदि इस लैंस को दो समान ऊर्ध्वाधर भागों में बाँट लिया जाये तो प्रत्येक भाग की फोकस दूरी की गणना करिये।
उत्तर:
दिया गया है:
R1 = 24 cm
R2 = – 24 cm
n2 = 1.6, n1 = 1.0
(a) वायु में इस लैंस की फोकस दूरी f का मान निम्न सूत्र से ज्ञात करते हैं
\(\frac{1}{\mathrm{f}}\) = (n2 – n1/n1)[\(\frac{1}{\mathrm{R1}}\) – \(\frac{1}{\mathrm{R2}}\)]
मान रखने पर-
\(\frac{1}{\mathrm{f}}\) = (1.6 – 1)/1 [\(\frac{1}{\mathrm{24}}\) + \(\frac{1}{\mathrm{24}}\)]
= 0.6 × 2/24 = 24 = 240
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{20}}\)
∴ f = 20 cm
(b) n2 = 1.6, n1 = 1.0
मान रखने पर
R1 = 24 cm, R2 = ∞
\(\frac{1}{\mathrm{f1}}\) = (n2 – \(\frac{n1}{\mathrm{n2}}\))[\(\frac{1}{\mathrm{R1}}\) – \(\frac{1}{\mathrm{R2}}\)]
मान रखने पर
\(\frac{1}{\mathrm{f}}\) = (1.6 – 1)/1 [\(\frac{1}{\mathrm{24}}\) + \(\frac{1}{\mathrm{∞}}\)]
= 0.6 × \(\frac{1}{\mathrm{24}}\) = \(\frac{6}{\mathrm{240}}\) = \(\frac{1}{\mathrm{40}}\)
f1 = 40cm

प्रश्न 9.
निम्न चित्र में दर्शाये लैंस के लिए

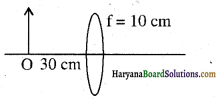
(i) प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
(ii) प्रतिबिम्ब की स्थिति को लेंस से और दूर करने हेतु एक अन्य लैंस उपर्युक्त लैंस के सम्पर्क में रखा जाता है। इस द्वितीय लैंस की प्रकृति क्या होगी?
उत्तर:
(i) दिया गया है:
f = 10 cm, U = 30 cm, v = ?
सूत्र \(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{V}}\) – \(\frac{1}{\mathrm{u}}\) से
मान रखने पर
\(\frac{1}{\mathrm{10}}\) = \(\frac{1}{\mathrm{V}}\) – (\(\frac{-1}{\mathrm{30}}\))
⇒ \(\frac{1}{\mathrm{10}}\) = \(\frac{1}{\mathrm{V}}\) + \(\frac{1}{\mathrm{30}}\)
⇒ \(\frac{1}{\mathrm{V}}\) = \(\frac{1}{\mathrm{10}}\)– \(\frac{1}{\mathrm{30}}\) = \(\frac{2}{\mathrm{30}}\)
या \(\frac{1}{\mathrm{V}}\) = \(\frac{1}{\mathrm{15}}\)
∴ v = 15 cm
अतः प्रतिबिम्ब की स्थिति 15 cm की दूरी पर है।
(ii) प्रतिबिम्ब की स्थिति को लेंस से दूर करने हेतु अवतल

प्रश्न 10.
कोई वस्तु 15 सेमी. वक्रता त्रिज्या के अवतल दर्पण से (i) 10 cm तथा (ii) 5 cm दूरी पर रखी है। प्रत्येक स्थिति में प्रतिबिम्ब की स्थिति, प्रकृति तथा आवर्धन परिकलित कीजिए।
उत्तर:
दिया गया है:
वक्रता त्रिज्या = 15 cm.
फोकस दूरी f = 15/2 = -7.5 cm.
(i) बिम्ब की दूरी दर्पण के सूत्र
u = – 10 cm.
\(\frac{1}{\mathrm{V}}\) + \(\frac{1}{\mathrm{u}}\) = \(\frac{1}{\mathrm{f}}\)
मान रखने पर
∴ \(\frac{1}{\mathrm{V}}\) + \(\frac{1}{\mathrm{-10}}\) = \(\frac{1}{\mathrm{-5}}\)
या \(\frac{1}{\mathrm{V}}\) – \(\frac{1}{\mathrm{10}}\) = \(\frac{-10}{\mathrm{75}}\) = \(\frac{-2}{\mathrm{15}}\)
या \(\frac{1}{\mathrm{V}}\) = \(\frac{-2}{\mathrm{15}}\) + \(\frac{1}{\mathrm{10}}\) = \(\frac{-4+3}{30}\) = \(\frac{-1}{\mathrm{30}}\)
या v = – 30cm.
प्रतिबिम्ब बिम्ब की दिशा में दर्पण से 30 cm. दूरी पर बनेगा।
आवर्धन m = v/u = \(\frac{-30}{\mathrm{10}}\)
m =-3
प्रतिबिम्ब आवर्धित वास्तविक तथा उल्टा है।
(ii) बिम्ब दूरी u = -5cm. तब दर्पण सूत्र से
\(\frac{1}{\mathrm{V}}\) + \(\frac{1}{\mathrm{-5}}\) = \(\frac{1}{\mathrm{-7.5}}\)
या
\(\frac{1}{\mathrm{V}}\) – \(\frac{1}{\mathrm{5}}\) = \(\frac{-1}{\mathrm{10}}\) = \(\frac{-2}{\mathrm{15}}\)
या
\(\frac{1}{\mathrm{V}}\) = \(\frac{-2}{\mathrm{15}}\) + \(\frac{1}{\mathrm{5}}\)
या
\(\frac{1}{\mathrm{V}}\) = \(\frac{-2+3}{15}\) = \(\frac{1}{\mathrm{15}}\)
v = 15 cm.
प्रतिबिम्ब दर्पण के पीछे 15 cm दूरी पर बनता है। यह प्रतिबिम्ब आभासी है।
आवर्धन m = \(\frac{-v}{\mathrm{u}}\) = \(\frac{-15}{\mathrm{5}}\) = 3
यह प्रतिबिम्ब आवर्धित, आभासी तथा सीधा है

प्रश्न 11.
3 सेमी आकार की कोई वस्तु 40 सेमी वक्रता त्रिज्या के किसी अवतल दर्पण से 30 सेमी दूरी पर स्थित है। दर्पण से प्रतिबिम्ब की दूरी व आकार ज्ञात करें एवं प्रतिबिम्ब की प्रकृति बताइए।
उत्तर:
यहाँ पर वस्तु का आकार h = 3 सेमी
अवतल दर्पण की वक्रता त्रिज्या R = 40 सेमी
अतः दर्पण की फोकस दूरी f = 1\(\frac{1}{\mathrm{2r}}\)
R = \(\frac{-40}{\mathrm{20}}\)
= – 20 सेमी
दर्पण से वस्तु की दूरी u = – 30 सेमी
अतः दर्पण के सूत्र
\(\frac{1}{\mathrm{V}}\) + \(\frac{1}{\mathrm{U}}\) = \(\frac{1}{\mathrm{F}}\) में ज्ञात मान रखने पर
\(\frac{1}{\mathrm{V}}\) + \(\frac{1}{\mathrm{-30}}\) = \(\frac{1}{\mathrm{-20}}\)
\(\frac{1}{\mathrm{V}}\) = \(\frac{-1}{\mathrm{20}}\) + \(\frac{1}{\mathrm{30}}\) = \(\frac{-3+2}{60}\) = \(\frac{-1}{\mathrm{60}}\)
v = 60 सेमी
इसलिये दर्पण से वस्तु के प्रतिबिम्ब की दूरी v = – 60 सेमी अतः प्रतिबिम्ब दर्पण से 60 सेमी वस्तु की ओर (अर्थात् दर्पण के सामने) बनेगा।
प्रतिबिम्ब के आवर्धन के लिये m = h/h = -(\(\frac{V}{\mathrm{U}}\))
इसलिये प्रतिबिम्ब का आकार h’ = – (\(\frac{V}{\mathrm{U}}\)) h
= \(-\left[\frac{-60}{-30}\right]\) × 3
h’ = – 6 सेमी
अर्थात् प्रतिबिम्ब उल्टा ( वास्तविक ) तथा 6 सेमी ऊँचा बनेगा, जो कि वस्तु से बड़ा होगा।