HBSE 11th Class Physics Important Questions Chapter 3 सरल रेखा में गति

Haryana State Board HBSE 11th Class Physics Important Questions Chapter 3 सरल रेखा में गति Important Questions and Answers.

Haryana Board 11th Class Physics Important Questions Chapter 3 सरल रेखा में गति

बहुविकल्पीय प्रश्न:

प्रश्न 1.
एक गेंद को ऊर्ध्वाधर ऊपर की ओर 19.6 मी/सेकण्ड के वेग से फेंका जाता है। गेंद अधिकतम ऊँचाई तक कितने सेकण्ड में पहुँचेगी?
(a) 1
(b) 2
(c) 3
(d) 4
उत्तर:
(b) 2

प्रश्न 2.
एक कण का वेग \(\vec{v}=k(y \hat{i}+x \hat{j})\) से गतिशील है, जहाँ k एक स्थिरांक है। इसके पथ का व्यापक समीकरण है:
(a) y = x² + स्थिरांक
(b) y² = x + स्थिरांक
(c) xy = स्थिरांक
(d) y² = x²+ स्थिरांक
उत्तर:
(d) y² = x²+ स्थिरांक

प्रश्न 3.
मन्दित गति के लिए वेग समय ग्राफ का ढाल है:
(a) धनात्मक
(b) ऋणात्मक
(c) शून्य
(d) धनात्मक, ऋणात्मक, शून्य या कुछ भी।
उत्तर:
(b) ऋणात्मक

प्रश्न 4.
एक ट्रक एवं एक कार दोनों समान वेग से चल रहे हैं। ब्रेक लगाने के बाद।
(a) ट्रक कम दूरी तय करेगा
(b) कार कम दूरी तय करेगी
(c) दोनों समान दूरी तय करेंगे
(d) उपर्युक्त में से कोई नहीं
उत्तर:
(b) कार कम दूरी तय करेगी

प्रश्न 5.
किसी वस्तु का विस्थापन समय के वर्ग के अनुक्रमानुपाती होता है तो वस्तु की गति होती है।
(a) एकसमान त्वरण से
(b) असमान त्वरण से
(c) एकसमान वेग से
(d) असमान त्वरण परन्तु एकसमान चाल से।
उत्तर:
(a) एकसमान त्वरण से

प्रश्न 6.
स्वतन्त्रतापूर्वक गिर रही एक वस्तु द्वारा अपने प्रथम तथा द्वितीय सेकण्ड में पार की गयी दूरियों में अनुपात है।
(a) 1 : 2
(b) 1 : 3
(c) 3 : 2
(d) 1 : √3
उत्तर:
(b) 1 : 3

प्रश्न 7.
यदि दो राशियों के परस्पर ग्राफ सरल रेखा में हों, तो दोनों राशियाँ।
(a) अचर होती हैं
(b) बराबर होती हैं।
(c) अनुक्रमानुपाती होती हैं।
(d) व्युत्क्रमानुपाती होती हैं।
उत्तर:
(c) अनुक्रमानुपाती होती हैं।

प्रश्न 8.
1.0m त्रिज्या के अर्द्धवृत्त में गतिमान एक कण 1 सेकण्ड में बिन्दु A से बिन्दु B तक जाता है, औसत वेग का परिमाण है:

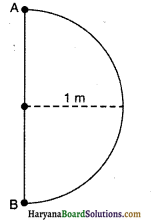
(a) 3.14m/s
(b) 2.0m/s
(c) 1.0m/s
(d) शून्य
उत्तर:
(b) 2.0m/s

प्रश्न 9.
x अक्ष के अनुदिश एक कण की स्थिति x समय t के पदों में दी जाती है, x = at² – t³ जिसमें ‘x’ में तथा सेकण्ड में है। जब कण की चाल अधिकतम है तो कण की स्थिति (x) होगी:
(a) \(\frac{2 a^3}{27}\)मी
(b) \(\frac{4 a^3}{27}\)मी
(c) \(\frac{2 a}{27}\)मी
(d) \(\frac{4 a}{27}\)मी
उत्तर:
(c) \(\frac{2 a}{27}\)मी

प्रश्न 10.
एक पिण्ड विरामावस्था से चलना प्रारम्भ करके ऋजुरेखीय पथ पर अचर त्वरण से गति करता है। वेग का विस्थापन के साथ परिवर्तन होगा:

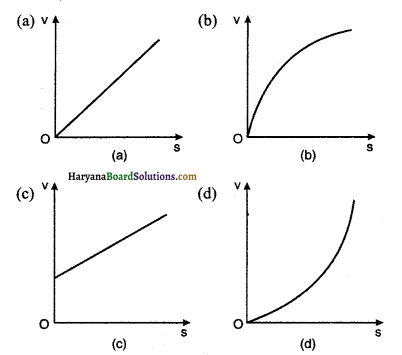
उत्तर:

प्रश्न 11.
दो पिण्ड जिनके द्रव्यमान तथा m₁ m₂ हैं, क्रमश: h₁ तथा h₂ ऊँचाई से गिरते हैं। पिण्डों द्वारा धरातल से टकराने में लगे समय का अनुपात है:
(a) h₁ : h₂
(b) \(\sqrt{h_1}: \sqrt{h_2}\)
(c) m₂ h₁ : m₂h₂
(d) \(\sqrt{m_1 h_1}: \sqrt{m_2 h_2}\)
उत्तर:
(b) \(\sqrt{h_1}: \sqrt{h_2}\)

प्रश्न 12.
एक पिण्ड का विस्थापन समय के अनुक्रमानुपाती है। पिण्ड के त्वरण का परिमाण:
(a) समय के साथ बढ़ रहा है
(b) समय के साथ घट रहा है
(c) शून्य
(d) अचर है, लेकिन शून्य नहीं है
उत्तर:
(a) समय के साथ बढ़ रहा है

अति लघु उत्तरीय प्रश्न:

प्रश्न 1.
बिन्दु वस्तु क्या हैं?
उत्तर:
यदि गतिशील वस्तु द्वारा तय की गयी दूरी वस्तु के आकार की तुलना में बहुत अधिक हो तो उसे बिन्दु वस्तु कहते हैं।

प्रश्न 2.
कणों के गतिकीय व्यवहार से सम्बन्धित अध्ययन की भौतिकी की शाखा क्या कहलाती है?
उत्तर:
गतिकी।

प्रश्न 3.
एक विमीय, द्विविमीय एवं त्रिविमीय गति में कितने-कितने निर्देशांक होते हैं?
उत्तर:
एक विमीय गति में 1 निर्देशांक द्विविमीय गति में 2 निर्देशांक तथा त्रिविमीय गति में 3 निर्देशांक होते हैं।

प्रश्न 4.
जब कोई कण या कणों का निकाय किसी निश्चित अक्ष के परितः घूर्णन करे तो वह कौन सी गति कहलाती है?
उत्तर:
घूर्णन गति।

प्रश्न 5.
वृत्ताकार गति में एक चक्र में विस्थापन कितना होता है?
उत्तर:
वृत्तीय गति में एक चक्र पूरा करने पर प्रारम्भिक एवं अंतिम स्थितियाँ समान हो जाती है, अतः विस्थापन शून्य हो जाता है।

प्रश्न 6.
चाल का सूत्र लिखिए।
उत्तर:
चाल =

प्रश्न 7.
वाहनों का स्पीडोमीटर क्या नापता है?
उत्तर:
तात्क्षणिक चाल।

प्रश्न 8.
चाल कैसी राशि है? S.I. प्रणाली में चाल का मात्रक क्या है?
उत्तर:
चाल अदिश राशि है एवं इसका S. I. प्रणाली में मात्रक मीटर / सेकण्ड (ms^-1) है।

प्रश्न 9.
वर्षा की बूँदें एक समान वेग से गिरती है या समान त्वरण से?
उत्तर:
वर्षा की बूँदें एकसमान वेग से गिरती हैं।

प्रश्न 10.
मन्दन किसे कहते हैं?
उत्तर:
समय के साथ वेग घटने की दर को मन्दन कहते हैं अर्थात् ऋणात्मक त्वरण ही मन्दन होता है।

प्रश्न 11.
क्या गतिशील वस्तु की दूरी व विस्थापन शून्य हो सकता है?
उत्तर:
गतिशील वस्तु का विस्थापन शून्य हो सकता है दूरी नहीं।

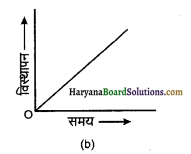
प्रश्न 12.
संलग्न चित्र (a) व (b) में प्रदर्शित वक्रों द्वारा वस्तु के वेग व त्वरण के बारे में क्या निष्कर्ष निकलता है?

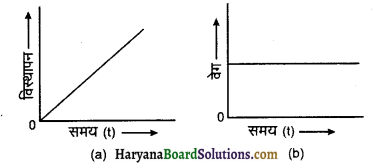
उत्तर:
दोनों वक्रों द्वारा एकसमान वेग की गति प्रदर्शित है अत: त्वरण शून्य होगा।

प्रश्न 13.
यदि एक व्यक्ति 4 मीटर पूर्व फिर 3 मीटर दक्षिण तथा पुनः वहाँ से 4 मीटर पश्चिम चले तो उसका विस्थापन कितना होता?
उत्तर:
व्यक्ति का विस्थापन s = 33m दक्षिण में।

प्रश्न 14.
ऋणात्मक त्वरण को क्या कहते हैं?
उत्तर:
मन्दन।

प्रश्न 15.
एकांक समय में तय विस्थापन को क्या कहते हैं?
उत्तर:
वेग

प्रश्न 16.
विस्थापन समय वक्र का ढाल क्या बताता है?
उत्तर:
वेग

प्रश्न 17.
वेग समय वक्र का ढाल क्या बताता है?
उत्तर:
त्वरण।

प्रश्न 18.
वेग समय वक्र का क्षेत्रफल क्या दर्शाता है?
उत्तर:
दूरी।

प्रश्न 19.
यदि कोई कण एक नियत वेग से गतिशील है तो उसका त्वरण कितना होगा?
उत्तर:
∵ त्वरण a = \(\frac{\Delta v}{\Delta t}\)
∴ वेग नियत होने पर ∆v = 0
अतः त्वरण a = 0 (शून्य)

प्रश्न 20.
स्वतन्त्रता पूर्वक गिर रही वस्तु द्वारा प्रथम व द्वितीय सेकण्ड में पार की गई दूरियों का अनुपात क्या है?
उत्तर:
n वें सेकण्ड में चली गई दूरी,
X_n^th = u + a (2n – 1)
∴ x₁ = 0 + \(\frac{1}{2}\)g(2 × 1 – 1) = \(\frac{1}{2}\)g
x₂ = 0 + \(\frac{3}{2}\)g(2 × 1 – 1) = \(\frac{3}{2}\)g
∴ x₁ : x₂ = 1 : 3

प्रश्न 21.
धनात्मक दिशा में गतिशील मंदित कण के लिए विस्थापन समय ग्राफ बनाइये।
उत्तर:
अभीष्ट ग्राफ संलग्न चित्र में प्रदर्शित है।

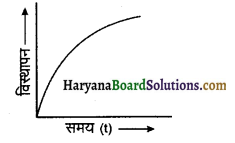
प्रश्न 22.
क्या किसी वस्तु की चाल ऋणात्मक हो सकती है?
उत्तर:
नहीं; क्योंकि दूरी कभी भी ऋणात्मक नहीं हो सकती।

प्रश्न 23.
दो गतिमान वस्तुओं का आपेक्षिक वेग कब शून्य हो सकता है?
उत्तर:
जब दोनों वस्तुएँ समान चाल से एक ही दिशा में गतिशील हों।

प्रश्न 24.
संलग्न चित्र में प्रदर्शित विस्थापन समय ग्राफ पर टिप्पणी कीजिए।

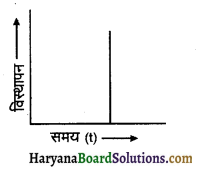
उत्तर:
दिया गया ग्राफ सम्भव नहीं है क्योंकि ग्राफ के अनुसार समय परिवर्तन के बिना विस्थापन परिवर्तित होता है।

प्रश्न 25.
क्या किसी वस्तु की चाल स्थिर व वेग परिवर्ती हो सकती है?
उत्तर:
हाँ; एक समान वृत्तीय गति यह सम्भव है।

प्रश्न 26.
क्या किसी वस्तु की औसत चाल शून्य हो सकती है? क्या औसत वेग शून्य हो सकता है?
उत्तर:
नहीं; गतिशील वस्तु की औसत चाल शून्य नहीं हो सकती है लेकिन औसत वेग शून्य हो सकता है।

प्रश्न 27.
किस परिस्थिति में औसत वेग तात्कालिक वेग के तुल्य होता है?
उत्तर:
जब वस्तु एकसमान वेग से गति करती है।

प्रश्न 28.
क्या किसी समय पिण्ड स्थिर एवं गतिशील दोनों स्थितियों में हो सकता है?
उत्तर:
हाँ, क्योंकि गति आपेक्षिक है।

प्रश्न 29.
किसी पिण्ड का वेग नियत होने पर क्या उसकी चाल परिवर्ती हो सकती है?
उत्तर:
नहीं, वेग नियत होने पर उसका परिमाण एवं दिशा दोनों अपरिवर्तित रहते हैं; अतः चाल परिवर्ती नहीं हो सकती।

प्रश्न 30.
एक कण का समय विस्थापन ग्राफ संलग्न चित्र में प्रदर्शित है। कण का तात्कालिक वेग किस बिन्दु पर ऋणात्मक होगा?

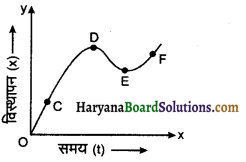
उत्तर:
बिन्दु E पर क्योंकि इस बिन्दु पर वक्र की प्रवणता ऋणात्मक है।

प्रश्न 31.
गति के समीकरणों को किस वैज्ञानिक ने ज्ञात किया था?
उत्तर:
गैलीलियो ने।

प्रश्न 32.
एक पिण्ड नियत वेग से गतिमान है, इसके लिए विस्थापन और समय में सम्बन्ध बताइये।
उत्तर:
विस्थापन ∝ समय।

लघु उत्तरीय प्रश्न:

प्रश्न 1.
दूरी तथा विस्थापन में क्या अन्तर हैं? लिखिए।
उत्तर:

1. दूरी अदिश राशि है जबकि विस्थापन सदिश राशि है।
2. दो बिन्दुओं के मध्य वस्तु द्वारा अपनाए गये पथ की वास्तविक लम्बाई दूरी होती है, जबकि उन बिन्दुओं के मध्य न्यूनतम दूरी विस्थापन कहलाती है।

प्रश्न 2.
स्थानान्तरीय गति का विवरण देते हुए इसे उदाहरण सहित समझाइये।
उत्तर:
स्थानान्तरीय गति- जब कोई कण किसी निर्देश तन्त्र के सापेक्ष एक स्थान से दूसरे स्थान पर स्थानान्तरित होता है तो इस प्रकार की गति को स्थानान्तरीय गति कहते हैं।
उदाहरण: सीधी सड़क पर चलने वाली गाड़ी की गति।

प्रश्न 3.
एक व्यक्ति 4 मीटर पूर्व में चलकर 5 मीटर उत्तर की ओर जाता है तथा वहाँ से चलकर पुनः दायीं ओर मुड़कर 8 मीटर सीधा जाता है। व्यक्ति द्वारा चली गई दूरी तथा उसका विस्थापन ज्ञात कीजिए।

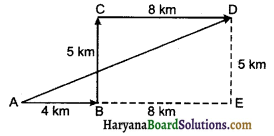
उत्तर:
व्यक्ति द्वारा चली गई दूरी = 4 + 5 + 8 = 17km
तथा विस्थापन

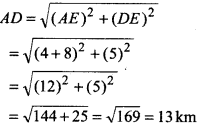
या
AD = 13 km

प्रश्न 4.
किसी पिण्ड द्वारा तय की गई दूरी समय वर्ग के अनुक्रमानुपाती होती है। इस पिण्ड में किस प्रकार की गति होती है?
उत्तर:
दिया है:
x ∝ t²
या
x = kt²
∴ पिण्ड का वेग
जहाँ k एक नियतांक है।
v = \(\frac{d x}{d t}\) = \(\frac{d}{d t}\) = (kt²) = 2kt
और त्वरण a = \(\frac{d x}{d t}\) = \(\frac{d}{d t}\) = (2kt) = 2k
या a = 2k = नियतांक
अतः पिण्ड गति एकसमान त्वरित गति है।

प्रश्न 5.
एक गेंद को ऊर्ध्वाधर ऊपर की ओर फेंका जाता है। कुछ समय पश्चात् यह धरती पर लौट आती है। गेंद के लिए चाल – समय ग्राफ खींचिए। (वायु का प्रतिरोध नगण्य मानिए।)
उत्तर:
जब कुछ प्रारम्भिक वेग देकर किसी गेंद को ऊर्ध्वाधर ऊपर की ओर फेंका जाता है उसका वेग नियत दर से कम होता रहता है और एक स्थिति में शून्य हो जाता है। यहीं से वस्तु नीचे गिरना प्रारम्भ करती है और उसका वेग उसी दर से बढ़ता है जिस दर से ऊपर जाने पर घटा था। अतः भूमि पर पहुँचते समय उसका वेग प्रारम्भिक वेग के तुल्य जायेगा। अतः वेग- समय ग्राफ चित्र की भांति होगा।

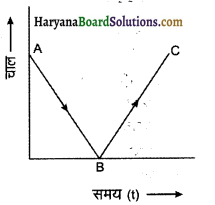
प्रश्न 6.
यदि किसी कण का तात्क्षणिक वेग शून्य हो तो क्या इसका तात्क्षणिक त्वरण भी शून्य होना चाहिए?
उत्तर:
नहीं; जब कोई कण ऊपर की ओर फेंका जाता है तो उच्चतम बिन्दु पर कण का तात्क्षणिक वेग तो शून्य हो जाता है लेकिन गुरुत्वीय त्वरण (g) तब भी प्रभावी रहेगा।

प्रश्न 7.
यदि किसी गतिमान वस्तु द्वारा चली गई दूरी समय के अनुक्रमानुपाती हो तो वस्तु की गति किस प्रकार की होती है?
उत्तर:
दिया है: x ∝ t
∴ x = kt
जहाँ k एक नियतांक है।
∴ वस्तु का वेग
v = \(\frac{d x}{d t}\) = \(\frac{d}{d t}(k t)\)
या
v = k = नियतांक
जहाँ k एक नियतांक है।
अतः वस्तु की गति एकसमान वेग की गति होगी।

प्रश्न 8.
एक रेलगाड़ी के इंजन तथा आखिरी डिब्बे के एक खम्भे से गुजरते हुए वेग क्रमशः तथा हैं। रेलगाड़ी के मध्य में स्थित डिब्बे का वेग क्या होगा?
उत्तर:
इंजन तथा मध्य डिब्बे के लिए गति का समीकरण
v² – u² = 2ax …(1)
आखिरी डिब्बे एवं मध्य डिब्बे के लिए गति का समीकरण
v² – u² = 2ax …(2)

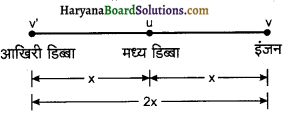
समीकरण (1) से (2) को घटाने पर
v² – u² – u² + v² = 0
v² – 2u² + v² = 0
2u² = v² + v²
या
u = \(\sqrt{\frac{v^2+v^{\prime 2}}{2}}\)

प्रश्न 9.
किसी गतिमान वस्तु का वेग-समय ग्राफ चित्र (a) में प्रदर्शित है। वस्तु का त्वरण क्या है? वस्तु की गति के लिए विस्थापन समय ग्राफ भी बनाइये।

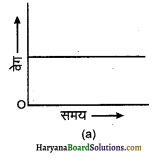
उत्तर:
वेग समय ग्राफ में समय के साथ वेग नियत है अतः
त्वरण = \(\frac{\Delta v}{\Delta t}\) = 0 (शून्य)
वस्तु की गति के लिए विस्थापन समय ग्राफ चित्र (b) में प्रदर्शित है।

प्रश्न 10.
संलग्न चित्र ग्राफ एक कण का वेग समय ग्राफ दर्शाता है तो ग्राफ के छायांकित भाग का क्षेत्रफल क्या प्रदर्शित करेगा?

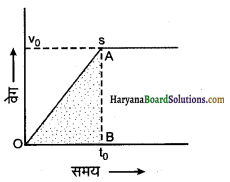
उत्तर:
छायांकित भाग का क्षेत्रफल = ∆OAB का क्षेत्रफल
= \(\frac{1}{2}\) × OB × AB
= \(\frac{1}{2}\) × t₀ × v₀
= \(\frac{1}{2}\) V₀ – f₀
= कण द्वारा चली गई दूरी
अतः छायांकित भाग का क्षेत्रफल कण द्वारा चली दूरी प्रदर्शित

प्रश्न 11.
क्या संलग्न ग्राफ किसी कार के एक स्थान से दूसरे स्थान तक जाने तथा वापस आने का विस्थापन समय ग्राफ हो सकता है?

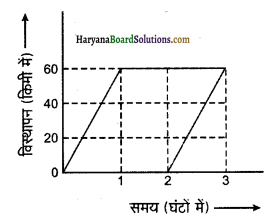
उत्तर:
नहीं; क्योंकि ग्राफ के अनुसार 2 व 3 घंटे के बीच कार एक ही समय पर दो स्थानों पर है जोकि सम्भव नहीं है।

प्रश्न 12.
एक कण का त्वरण समय के साथ समीकरण a = bt के अनुसार बढ़ता है। यदि कण का प्रारम्भिक वेग v0 हो तो t समय में कण का विस्थापन ज्ञात कीजिए।
उत्तर:
त्वरण a = bt
∴ \(\frac{d v}{d t}\) = bt => dv = bt.dt
=> \(\int d v= \int b t \cdot d t\)
समाकलन करने पर
v = \(\frac{1}{2}\)bt² + c
जहाँ c = समाकलन नियतांक
दिया है जब t = 0 तो v = v0
∴ vo = 0 + c अर्थात् c = Vo
∴ v = \(\frac{1}{2}\)bt² + vo
या
\(\frac{d x}{d t}\) = \(\frac{1}{2}\)bt² + vo
या
dx = \(\frac{1}{2}\)bt² .dt + vodt
पुनः समाकलन करने
\(\int d x=\int \frac{1}{2} b t^2 \cdot d t+\int v_0 d t\)
या
x = \(\frac{1}{2}\)b × \(\frac{t^3}{3}\) + vot
या
x = \(\frac{1}{6}\)bt³ + vot
या
x = vot + \(\frac{1}{6}\)bt³

प्रश्न 13.
त्वरण के प्रदर्शन में समय को दो बार क्यों कहा जाता है?
उत्तर:
क्योंकि त्वरण विस्थापन का द्वितीय अवकलन है।
a = \(\frac{d^2 x}{d t^2}\)
अतः त्वरण के प्रदर्शन में समय को दो बार पुकारा जाता है।

प्रश्न 14.
जब दो ट्रेनें समान वेग से एक-दूसरे के समान्तर गतिशील होती हैं तो एक ट्रेन में बैठे व्यक्ति को दूसरी ट्रेन स्थिर क्यों प्रतीत होती है?
उत्तर:
यह अनुभव सापेक्ष वेग के कारण होता है, क्योंकि दोनों ट्रेनों का वेग बराबर है, अतः उनका एक-दूसरे के सापेक्ष वेग शून्य होगा। उदाहरणार्थ: यदि दो ट्रेनों के वेग 50 km.hr^-1 है अर्थात्
V_A = V_B = 50km.hr^-1
∴ A के सापेक्ष B का आपेक्षिक वेग
V_BA = V_B – V_A = 50 – 50 = 0 (शून्य)

प्रश्न 15.
किसी कण की चाल नियत रहने पर क्या उसमें त्वरण हो सकता है?
उत्तर:
हाँ, यह एक समान वृत्तीय गति में सम्भव है, क्योंकि इस गति में कण की चाल तो नियत रहती है पर प्रति क्षण उसकी दिशा बदलने से उसका वेग बदलता रहता है, अतः उस पर अभिकेन्द्रीय त्वरण कार्य करता है।

प्रश्न 16.
क्या यह सम्भव है कि किसी वस्तु का औसत वेग शून्य हो परन्तु औसत चाल शून्य न हो? क्या इसका विपरीत भी सम्भव है?
उत्तर:
हाँ, यदि एक पिण्ड को ऊर्ध्वाधर ऊपर की ओर फेंका जाये तथा वह अपने प्रारम्भिक बिन्दु पर लौट आये तो उसका औसत वेग शून्य होगा लेकिन औसत चाल शून्य नहीं होगी। माना कोई गेंद पृथ्वी तल से ऊर्ध्वाधरत: ऊपर की ओर फेंकी गयी है और वह कुछ ऊँचाई (माना मीटर) तक ऊपर जाकर कुछ समय पश्चात् पृथ्वी पर वापस लौट आती है। उसके द्वारा चली गई दूरी 2h तथा उसका विस्थापन 01 चूँकि औसत चाल दूरी / समय तथा औसत वेग विस्थापन / समय, अतः गेंद में औसत चाल होगी, जबकि इसका औसत वेग शून्य होगा। इसका विपरीत सम्भव नहीं है।

प्रश्न 17.
यदि एक कण की गति को x = ut + \(\frac{1}{2}\) a₁ t² में बनाया गया है, जहाँ x स्थिति है, t समय है और u व a₁ दर्शाइये कि कण का त्वरण नियत है।
उत्तर:
दिया है:
x = ut + \(\frac{1}{2}\) a₁ t²
अतः वेग v = \(\frac{d x}{d t}\) =\(\frac{d}{d t}\)[ut + \(\frac{1}{2}\) a₁ t²]
= u +\(\frac{1}{2}\) a₁.2t
या v = u + at
त्वरण a = \(\frac{d x}{d t}\) =\(\frac{d}{d t}\)[u + a₁t]
= 0 + a₁
या
a = a₁ = नियतांक
अतः कण का त्वरण नियत है।

दीर्घ उत्तरीय प्रश्न:

प्रश्न 1.
एक समान त्वरित गति हेतु गणितीय विधि से गति के तीनों समीकरण व्युत्पन्न कीजिए।
उत्तर:
(ii) कलन विधि (Calculus Method):
(a) प्रथम समीकरण: त्वरण की परिभाषा से
a = \(\frac{d v}{d t}\)
या
dv = adt
इस समीकरण के दोनों पक्षों का t = 0 पर वेग = u एवं समय पर वेग = v की सीमा में समाकलन करने पर
\(\int_u^v d v=\int_0^t a d t\)
या
[v]^v_u = a[t]^t₀
या
v – u = a [ t – 0] = at
∴ v = u + at

(b) द्वितीय समीकरण: वेग की परिभाषा से
v = \(\frac{d s}{d t}\)
या
ds = V. dt (u + at )dt
उक्त समीकरण का समाकलन t = 0 पर s = 0 एवं t = t पर s = s
सीमा के अन्तर्गत करने पर
\(\int_0^s d s=\int_0^t(u+a t) d t=\int_0^t u d t+\int_0^t a t d t\)
या
[s]^s₀ = u[t]^t₀ + a\(\left[\frac{t^2}{2}\right]_0^t\)
या
s – 0 = u(t – 0) + \(\frac{a}{2}\)[t² – 0]
या
S = ut + \(\frac{a}{2}\)at²

(c) तृतीय समीकरण: त्वरण की परिभाषा से
a = \(\frac{d v}{d t}\) = \(\frac{d v}{d s} \cdot \frac{d s}{d t}\)
या
a = v\(\frac{d v}{d t}\)
या
a.ds = vdv
इस समीकरण का भी पूर्व में दी गई सीमाओं के अन्तर्गत समाकलन करने पर
\(\int_0^s a d s=\int_u^v v \cdot d v\)
या
\(a[s]_0^s=\left[\frac{v^2}{2}\right]_u^v\)
या
a[s – 0] = \(\left[\frac{v^2}{2}-\frac{u^2}{2}\right]\)
या
as = \(\frac{1}{2}\) [v² – u²]
या
2as = v² – u²
या
v² = u² + 2as

प्रश्न 2.
निम्न की परिभाषा दीजिए
(i) विस्थापन
(ii) वेग
(iii) त्वरण
(iv) चाल
(v) औसत वेग
(vi) तात्क्षणिक वेग
(vii) औसत त्वरण
(viii) तात्क्षणिक त्वरण
उत्तर:
(i) विस्थापन(displacement):
दूरी तथा विस्थापन में अन्तर समझने के लिए एक सामान्य उदाहरण पर विचार करते हैं। माना कोई वस्तु A बिन्दु से पहले पूर्व दिशा में 4m चलकर B बिन्दु पर पहुँचती है और फिर वहाँ से 3m उत्तर की ओर चलकर C बिन्दु पर पहुँचती है। इस यात्रा में वस्तु के द्वारा तय किये गये पथ की वास्तविक लम्बाई 4 + 3 = 7m है जिसे ‘दूरी’ कहते हैं। प्रारम्भिक बिन्दु A से अंतिम बिन्दु C के मध्य सीधी लम्बाई AC(5m) है जिसे ‘विस्थापन’ कहते हैं। AC की लम्बाई निम्न प्रकार प्राप्त है

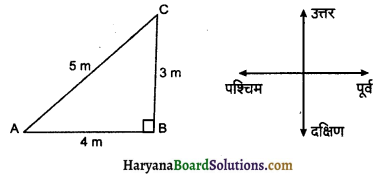
समकोण ∆A B C में, पाइथागोरस प्रमेय से,
AC² = AB² + BC²
AC = \(\sqrt{(4)^2+(3)^2}\) = \(\sqrt{16+9}\) = \(\sqrt{25}\)
∴ AC = 5m

(ii) वेग(velocity): “निश्चित दिशा में एकांक समय में तय की गई दूरी को वेग कहते हैं।” दिशा सहित दूरी को विस्थापन कहते हैं, अत: वेग की परिभाषा इस प्रकार भी की जा सकती है, “समय के साथ विस्थापन परिवर्तन की दर को वेग कहते हैं।” यह सदिश राशि है।
∴ वेग = चाल + दिशा
और
या \(\vec{v}\) = \(\frac{\vec{s}}{t}\) = \(\frac{\Delta \vec{s}}{\Delta t}\)
∴ वेग का M.K.S. पद्धति में मात्रक ms^-1 एवं C.G.S. प्रद्धति में cms^-1 होता है तथा विमीय सूत्र [M⁰L¹T^-1] है।

(iii) त्वरण (Acceleration): यदि किसी वस्तु का वेग विभिन्न समयों पर भिन्न-भिन्न होता है तो वस्तु की गति को असमान गति कहते हैं। यदि समय बढ़ने के साथ-साथ वेग बढ़ता है तो गति त्वरित कहलाती है। इसके विपरीत यदि समय बढ़ने के साथ वस्तु का वेग घटता है तो वस्तु की गति अवमंदित गति कहलाती है। अर्थात्
“समय के साथ वेग परिवर्तन की दर को त्वरण कहते हैं।”
इसे ‘a’ से प्रदर्शित करते हैं।
∴ त्वरण =
या \(\vec{a}=\frac{\Delta \vec{v}}{\Delta t}\)
त्वरण का M.K.S पद्धति में मात्रक मीटर/सेकण्ड² ms^-1 होता है। त्वरण एक सदिश राशि है। जिसकी दिशा वेग परिवर्तन की दिशा होती है।
माना कोई वस्तु प्रारम्भिक वेग u से चलना प्रारम्भ करती है और t समय के बाद उसका वेग v हो जाता है तो

(iv) चाल (speed): किसी वस्तु की चाल वह भौतिक राशि है, जो वह अनुभव कराती है कि वस्तु कितनी तेजी से गति कर रही है। ” किसी गतिमान वस्तु द्वारा एकांक समय में तय की गई दूरी को चाल कहते हैं।” अथवा ” समय के साथ दूरी परिवर्तन की दर को चाल कहते हैं।'” यदि किसी गतिमान वस्तु द्वारा। समय में s दूरी तय की जाती है तो उसकी,
चाल =
या
\(v=\frac{s}{t}\)
चाल का M.K.S. पद्धति में मात्रक ms^-1 एवं C.G.S. पद्धति में cms^-1 है।

= [M⁰L¹T^-1]

(v) औसत वेग (Average Velocity): किसी गतिमान वस्तु का औसत वेग कुल विस्थापन परिवर्तन तथा कुल समयान्तराल का अनुपात होता है।

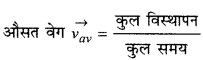
(vi) तात्क्षणिक वेग (Instantaneous Velocity): यदि गतिमान वस्तु का वेग परिवर्ती वेग है तो, “किसी क्षण विशेष पर उसका वेग तात्कालिक वेग कहलाता है।’ इसकी गणना के लिए समयान्तराल को अत्यन्त छोटा ∆t → 0 माना जाता है।
∴ तात्कालिक वेग \((\vec{v})=\lim _{\Delta t \rightarrow 0} \frac{\overrightarrow{\Delta s}}{\Delta t}=\frac{d \vec{s}}{d t}\)
यहाँ \(\frac{d \vec{s}}{d t}\), \(\vec{s}\) का t के सापेक्ष अवकलन है जिसे अवकलन गणित की सहायता से ज्ञात कर सकते हैं। एक समान वेग से गति की स्थिति में औसत वेग व तात्कालिक वेग का मान एवं औसत वेग का मान समान होता है। वेग का मान धनात्मक, शून्य या ऋणात्मक हो सकता है।

(vii) औसत त्वरण (Average Acceleration):यदि गतिमान वस्तु परिवर्ती त्वरण से गति करती है तो वस्तु के वेग में कुल परिवर्तन ∆v एवं समयान्तराल ∆t के अनुपात को औसत त्वरण कहते हैं अर्थात्

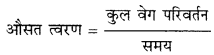
या
\(\overrightarrow{a_{a v}}=\frac{\Delta \vec{v}}{\Delta t}\)
यदि समय t1 पर वेग \(\overrightarrow{v_1}\) एवं t2 पर वेग \(\overrightarrow{v_2}\) हो तो
\(\overrightarrow{a_{a v}}=\frac{\overrightarrow{v_2}-\overrightarrow{v_1}}{t_2-t_1}\)
\(\frac{\Delta \vec{v}}{\Delta t}\)

(viii) तात्क्षणिक या तात्कालिक त्वरण (Instantaneous Acceleration): “किसी निश्चित समय या क्षण पर वस्तु के त्वरण को तात्कालिक त्वरण कहते हैं।” इसके लिए समयान्तराल अत्यन्त छोटा लेते हैं अर्थात् ∆t = 0
तात्क्षणिक त्वरण
\(\vec{a}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \vec{v}}{\Delta t}=\frac{d \vec{v}}{d t}\)
या
\(\vec{a}=\frac{d \vec{v}}{d t}\)
परन्तु
\(\vec{v}=\frac{d \vec{s}}{d t}\)

प्रश्न 3.
आलेखीय विधि द्वारा गति के समीकरणों की व्युत्पत्ति कीजिए।
उत्तर:
(i) आलेखीय विधि (Graphical Method): माना किसी गतिशील वस्तु का प्रारम्भिक वेग 14 है और त्वरण a है। इसका वेग समय ग्राफ AB संलग्न चित्र 3.13 में प्रदर्शित है। बिन्दु B के संगत समय एवं वेग v है।
(a) प्रथम समीकरण: गति का प्रथम समीकरण
v = u + at
उपपत्ति: ∵ त्वरण वेग-समय ग्राफ की प्रवणता

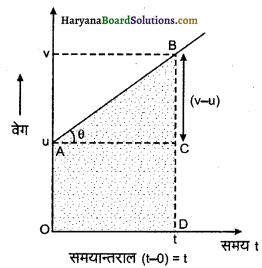
समयान्तराल (t – 0) = t
∴ a = tan θ = \(\frac{B C}{A C}\)
या
a = \(\frac{v-u}{t-0}=\frac{v-u}{t}\)
या at = v – u
∴ v = u + at …………(1)

(b) द्वितीय समीकरण – गति का द्वितीय समीकरण
s = ut + \(\frac{1}{2}\) at²
जहाँ s = t समय में वस्तु द्वारा तय की गई दूरी
उपपत्ति: वेग समय ग्राफ में ग्राफीय रेखा एवं समय-अक्ष के मध्य घिरा क्षेत्रफल विस्थापन अर्थात् तय की गई दूरी प्रदान करता है। अत:
s = समलम्ब चतुर्भुज OABD का क्षेत्रफल

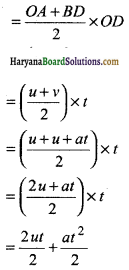
[समी० (1) से]
या
s = ut + \(\frac{1}{2}\) at² …….(2)

(c) तृतीय समीकरण: गति का तृतीय समीकरण
v² = u² + 2as (v – u)
उपपत्ति – समी० (1) से, \(t=\frac{(v-u)}{a}\)
समी० (2) में का यह मान रखने पर
s = \(u \frac{(v-u)}{a}+\frac{1}{2} a \frac{(v-u)^2}{a^2}\)
या
= \(\frac{\left(u v-u^2\right)}{a}+\frac{1}{2 a}\) [v² + u² – 2uv]
या
s = [2uv – 2u² + v² + u² – 2uv]
या
2as = v² – u²
या
v²= u² + 2as

प्रश्न 4.
नियत त्वरण से गतिमान पिण्ड के लिए वेग-समय ग्राफ खींचिए एवं इस ग्राफ की सहायता से गति के समीकरणों की स्थापना कीजिए।
उत्तर:
(i) आलेखीय विधि (Graphical Method): माना किसी गतिशील वस्तु का प्रारम्भिक वेग 14 है और त्वरण a है। इसका वेग समय ग्राफ AB संलग्न चित्र 3.13 में प्रदर्शित है। बिन्दु B के संगत समय एवं वेग v है।
(a) प्रथम समीकरण: गति का प्रथम समीकरण
v = u + at
उपपत्ति: ∵ त्वरण वेग-समय ग्राफ की प्रवणता

समयान्तराल (t – 0) = t
∴ a = tan θ = \(\frac{B C}{A C}\)
या
a = \(\frac{v-u}{t-0}=\frac{v-u}{t}\)
या at = v – u
∴ v = u + at …………(1)

(b) द्वितीय समीकरण – गति का द्वितीय समीकरण
s = ut + \(\frac{1}{2}\) at²
जहाँ s = t समय में वस्तु द्वारा तय की गई दूरी
उपपत्ति: वेग समय ग्राफ में ग्राफीय रेखा एवं समय-अक्ष के मध्य घिरा क्षेत्रफल विस्थापन अर्थात् तय की गई दूरी प्रदान करता है। अत:
s = समलम्ब चतुर्भुज OABD का क्षेत्रफल

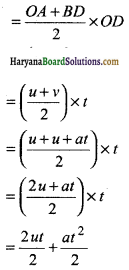
[समी० (1) से]
या
s = ut + \(\frac{1}{2}\) at² …….(2)

(c) तृतीय समीकरण: गति का तृतीय समीकरण
v² = u² + 2as (v – u)
उपपत्ति – समी० (1) से, \(t=\frac{(v-u)}{a}\)
समी० (2) में का यह मान रखने पर
s = \(u \frac{(v-u)}{a}+\frac{1}{2} a \frac{(v-u)^2}{a^2}\)
या
= \(\frac{\left(u v-u^2\right)}{a}+\frac{1}{2 a}\) [v² + u² – 2uv]
या
s = [2uv – 2u² + v² + u² – 2uv]
या
2as = v² – u²
या
v²= u² + 2as

प्रश्न 5.
आपेक्षिक गति की विवेचना करते हुए आपेक्षिक वेग के सूत्र प्राप्त कीजिए।
उत्तर:
आपेक्षिक गति (Relative Motion): “किसी कण की गति की अवस्था का अनुमान सदैव किसी अन्य निर्देश वस्तु या तन्त्र के सापेक्ष ही कर सकते हैं; निरपेक्ष रूप से गति की अवस्था को प्रेक्षित नहीं किया जा सकता है। यही आपेक्षिक गति कहलाती है।’ गति से तात्पर्य सदैव आपेक्षिक गति से ही होता है तथा निर्देश तन्त्र की स्थितियों के कारण किसी वस्तु की गति भिन्न-भिन्न निर्देश तन्त्रों के सापेक्ष परिस्थिति के अनुसार समान या भिन्न-भिन्न प्रतीत हो सकती हैं।

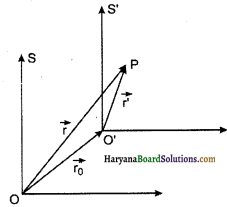
संलग्न चित्र 3.14 के अनुसार दो निर्देश तन्त्रों S व \(S^{\prime}\) पर विचार करते हैं, जिनके मूल बिन्दु प्रेक्षकों O व \(O^{\prime}\) के सम्पाती हैं। प्रेक्षक O के निर्देश तन्त्र में बिन्दु P का स्थिति सदिश है एवं प्रेक्षक \(\vec{r}\) के निर्देश तन्त्र में उसी बिन्दु का स्थिति सदिश \(\vec{r}\) है। \(O^{\prime}\) का O के सापेक्ष स्थिति सदिश
\(\vec{r}_0\) है, तो
\(\overrightarrow{r_0}+\overrightarrow{r^{\prime}}=\vec{r}\)
∴ \(\overrightarrow{r^{\prime}}=\vec{r}-\overrightarrow{r_0}\) ……….(1)
इस समी० (1) का समय के सापेक्ष अवकलन करने पर
\(\frac{d}{d t} \overrightarrow{r^{\prime}}=\frac{d \vec{r}}{d t}-\frac{d \overrightarrow{r_0}}{d t}\)
या
\(\overrightarrow{v^{\prime}}=\vec{v}-\overrightarrow{v_0}\) ………….(2)
यहाँ निर्देश तन्त्र S’ का S के सापेक्ष वेग है।
समी० (2) S व S’ में वेग सदिशों का सम्बन्ध प्रदर्शित करता है।
समीकरण (2) का t के सापेक्ष अवकलन करने पर,
\(\frac{d \overrightarrow{v^{\prime}}}{d t}=\frac{d \vec{v}}{d t}-\frac{d \overrightarrow{v_0}}{d t}\)
या
\(\overrightarrow{a^{\prime}}=\vec{a}-\overrightarrow{a_0}\) …………(3)
यहाँ निर्देश तन्त्र S’ का s के सापेक्ष त्वरण है। यदि a0 = 0 अर्थात् यदि फ्रेम s एवं S’ एक-दूसरे के सापेक्ष नियत वेग से गति कर रहे हों, तो
\(\overrightarrow{a^{\prime}}=\vec{a}\)
अतः इस अवस्था में किसी कण का दोनों निर्देश तन्त्रों में नापा गया त्वरण समान प्राप्त होता है।
यदि एक विमीय गति पर विचार करें तो माना दो वस्तुएँ A व B -अक्ष की दिशा में नियत वेग V_A व V_B से गतिमान हैं। यदि किसी क्षण वस्तुओं की स्थितियाँ क्रमशः X_A व X_B; हैं तो वस्तु A के सापेक्ष B की स्थिति
X_BA = X_B – X_A ……(4)

प्रश्न 6.
औसत चाल से क्या समझते हो? विभिन्न परिस्थितियों में इसकी विवेचना कीजिए।
उत्तर:
चाल (speed): किसी वस्तु की चाल वह भौतिक राशि है, जो वह अनुभव कराती है कि वस्तु कितनी तेजी से गति कर रही है। ” किसी गतिमान वस्तु द्वारा एकांक समय में तय की गई दूरी को चाल कहते हैं।” अथवा ” समय के साथ दूरी परिवर्तन की दर को चाल कहते हैं।'” यदि किसी गतिमान वस्तु द्वारा। समय में s दूरी तय की जाती है तो उसकी,
चाल =
या
\(v=\frac{s}{t}\)
चाल का M.K.S. पद्धति में मात्रक ms-1 एवं C.G.S. पद्धति में cms-1 है।

= [M⁰L¹T^-1]

चाल के प्रकार (Types of Speed):
(a) एक समान चाल (Uniform Speed)-यदि कोई गतिमान वस्तु समान समयान्तरालों में समान दूरी तय करती है तो उसकी चाल को एक समान चाल कहते हैं। उदाहरणार्थ-घड़ी की सुइयों की चाल।
(b) परिवर्ती चाल (Variable Speed)-यदि कोई गतिमान वस्तु समान समयान्तरालों में भिन्न-भिन्न दूरी तय करती है तो उसकी चाल परिवर्ती चाल कहलाती है। उदाहरण के लिए-भीड़ भाड़ वाले स्थानों पर वाहनों की चाल।
(c) औसत चाल (Average Speed)-गतिमान वस्तु द्वारा तय की गई कुल दूरी एवं कुल समय के अनुपात को औसत चाल कहते हैं।

∴ औसत चाल =
या \(\vec{v}=\frac{\Delta s}{\Delta t}\)
औसत चाल को समझने के लिए एक उदाहरण पर विचार करते हैं। माना किन्हीं दो स्थानों के मध्य दूरी 300km है तथा इसे तय करने में किसी कार को 5 घंटे का समय लगता है, तो कार की, औसत चाल
\(\vec{v}=\frac{300}{5}\) = 60Kmhr^-1

पूरी यात्रा के दौरान कार की चाल 60Kmhr^-1 रहना आवश्यक नहीं है और न ही यह आवश्यक है कि कार लगातार चलती रही हो। उपलब्ध मार्ग के अनुसार कार की चाल घट/बढ़ सकती है और कुछ समय के लिए कार विश्राम की स्थिति में रह सकती है।

प्रश्न 7.
निर्देश तन्त्र से क्या अभिप्राय है? वामावर्त एवं दक्षिणावर्त निर्देशांक निकाय की व्याख्या कीजिए।
उत्तर:
संसार में कोई वस्तु निरपेक्ष रूप से स्थिर नहीं है, सभी वस्तुएँ सापेक्षिक रूप से स्थिर व गतिशील होती हैं। एक वस्तु किसी निकाय के सापेक्ष स्थिर तो किसी अन्य निकाय के सापेक्ष गतिशील हो सकती है। उदाहरणार्थ-गतिशील बस में बैठा यात्री अपने पड़ोसी यात्रियों के सापेक्ष तो स्थिर होता है लेकिन सड़क के किनारे खड़े किसी दर्शक के सापेक्ष गतिशील होता है। इसी प्रकार चलती बस का रेलगाड़ी में बैठा यात्री जब खुद को स्थिर मानता है तो मार्ग के किनारे खड़े पेड़ उसे पीछे भागते दिखायी देते हैं और जब पेड़ों को स्थिर मानता है तो स्वयं को गतिशील अनुभव करता है। इसी प्रकार एक ही दिशा में दो कारें A व B क्रमश: 50 km hr^-1 एवं 40km hr^-1 की चालों से गतिशील हैं तो कार B में बैठे यात्री को कार 4 की चाल 10km hr^-1 प्रतीत होती है, जबकि सड़क पर खड़े व्यक्ति को कार 4 की चाल 50 km hr प्रतीत होती है। उक्त उदाहरणों से स्पष्ट है कि गति सापेक्ष होती है और वस्तु की गति का अध्ययन करने के लिए किसी न किसी सन्दर्भ वस्तु निकाय की आवश्यकता होती है, जिसके सापेक्ष हम वस्तु की स्थिति का अध्ययन कर सकें। अतः, “वह निकाय जिसके सापेक्ष कण की स्थिति का अध्ययन किया जाता है, निर्देश तन्त्र कहलाता है।”

निकायों का प्रयोग किया जाता है:

1.  वामावर्ती निर्देशांक पद्धति
2. दक्षिणावर्ती निर्देशांक पद्धति
   
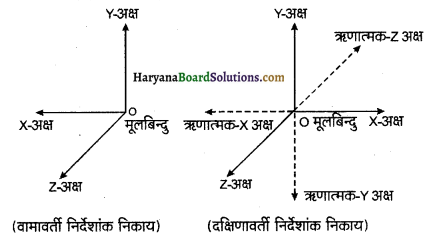
   सामान्यतः हम दक्षिणावर्ती कार्तीय निर्देश तन्त्र का प्रयोग करते हैं। जिसके अनुसार दाहिने हाथ की अंगुलियों को यदि OX अक्ष के समान्तर करके OY की ओर घुमाएं तो अंगुलियों के लम्बवत् रखने पर अंगूठा OZ की दिशा बताता है। इसके अनुसार किसी कण की गति का अध्ययन x, y, 2 निर्देशांकों के आधार पर किया जाता है।

आंकिक प्रश्न:

प्रश्न 1.
एक धावक 50 m त्रिज्या के वृत्ताकार पथ पर दौड़ता है। धावक द्वारा तीन चौथाई पथ तय करने में विस्थापन एवं दूरी की गणना कीजिए।
उत्तर:
70.7m 235.7m

प्रश्न 2.
एक कण को 20 ms^-1 की प्रारम्भिक चाल से ऊपर की ओर फेंका जाता है। 3.0 बाद कण द्वारा तय की गई दूरी तथा विस्थापन की गणना कीजिए। (g = 10ms^-2)
उत्तर:
दूरी = 25m; विस्थापन = 15m]

प्रश्न 3.
पद्मा अपने घर से स्कूल 50 km की दूरी एक समान चाल से 50km. hr^-1 की चाल से जाती है। छुट्टी होने पर वह भीड़ भाड़ होने के कारण 30km.hr^-1 की औसत चाल से घर पहुँचती है। यात्रा के दौरान कुल औसत चाल की गणना कीजिए।
उत्तर:
37.5 km.hr^-1

प्रश्न 4.
एक वस्तु X- अक्ष की दिशा में गति कर रही है जिसका विस्थापन निम्न प्रकार प्रदर्शित होता है x = 30 + 20t², जहाँ x, m एवं t,s में है।
1. वस्तु का वेग तथा त्वरण ज्ञात कीजिए।
2. वस्तु का प्रारम्भिक वेग तथा स्थिति ज्ञात कीजिए।
उत्तर:

1. 40rms^-1; 40ms^-2
2. 0ms^-1; 30m

प्रश्न 5.
एक कण विरामावस्था से चलना आरम्भ करके t समय में स्थिर त्वरण से s₁ दूरी तय करता है। यदि कण अगले ‘t समय में s₂ दूरी तय कर ले तो दर्शाइये कि
उत्तर:
s₂ = 3s₁

प्रश्न 6.
एक गतिमान वस्तु प्रथम 25 में 200m दूरी तय करती अगले 4 में वह 220m की दूरी तय करती है। गतिमान वस्तु का वेग सातवें सेकण्ड के अन्त में ज्ञात कीजिए।
उत्तर:
10ms^-1

प्रश्न 7.
एक कार 15 ms^-1 के वेग से सड़क पर चल रही है। ब्रेक लगाने पर इसकी अवरोधन दूरी 18m है। यदि इसी कार का वेग 25ms^-1 हो तथा ब्रेक लगाने पर वही मन्दन उत्पन्न किया जाये तो
कार की नयी अवरोधन दूरी ज्ञात कीजिए।
उत्तर:
50m

प्रश्न 8.
एक कण 5वें सेकण्ड में 25 m तथा 7वें सेकण्ड में 33 mm की दूरी तय करता है। यदि गति समान रूप से त्वरित हो तो यह अगले 35 में कितनी दूर चलेगा।
उत्तर:
123m

प्रश्न 9.
किसी क्षण पर एक कण का विस्थापन निम्नलिखित सूत्र द्वारा दिया जाता है:
x = – 15t² + 20t + 30
जहाँ x मीटर में तथा सेकण्ड में है। t = 0 पर कण की स्थिति, वेग तथा त्वरण ज्ञात कीजिए।
उत्तर:
Xo = 30m; v0 = 20 ms^-1; a0 = 30ms^-2

प्रश्न 10.
किसी पिण्ड का त्वरण समय का फलन है, चित्र के अनुसार यदि t = 0 पर पिण्ड का वेग u = 0 हो:
(a) बाद वाले समय पर पिण्ड का वेग क्या है?
(b) t समय में पिण्ड कितनी दूरी तय करेगा?

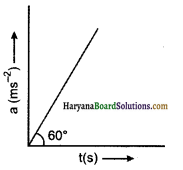
उत्तर:
\(\frac{\sqrt{3}}{2}\)t² ms^-1 \(\sqrt{3} \frac{t^3}{6}\)m

प्रश्न 11.
एक 80 m लम्बी ट्रेन 60ms^-1 के वेग से एक अन्य 100 m लम्बी ट्रेन से आगे निकलती है। दूसरी ट्रेन की चाल 40 ms^-1 है। पहली ट्रेन द्वारा दूसरी ट्रेन से आगे निकलने में कितना समय लगेगा?
उत्तर:
9s

प्रश्न 12.
दो समान्तर सीधी रेल की पटरियों में एक पर एक मालगाड़ी 72 km. hr^-1 की चाल से और दूसरी पर एक सवारी गाड़ी 108 km.hr^-1 की चाल से चल रही है। मालगाड़ी की लम्बाई 150m और सवारी गाड़ी की लम्बाई 90m है। यदि:
1. दोनों गाड़ियाँ एक ही दिशा में हैं;
2. दोनों विपरीत दिशा में हैं तब एक-दूसरे को पार करने में कितना समय लगेगा?
उत्तर:

1. 24s
2.  4.8s

प्रश्न 13.
एक कण की स्थिति \(\vec{r}=\left(3 t \hat{i}+4 t^3 \hat{j}+5 \hat{k}\right)\) द्वारा दी जाती है। ज्ञात कीजिए।
1. कण का वेग तथा त्वरण
2. t = 5s पर कण के वेग और त्वरण का परिमाण बताओ।
उत्तर:

1. \(\left(3 \hat{i}+12 t^2 \hat{j}\right)\) ms^-1; \((24 t \hat{j})\) ms^-2
2. 300 ms^-1; 120 ms^-2

प्रश्न 14.
एक कण के निर्देशांक x = (4t – 1) m तथा y = 8t² m है। निम्न की गणना कीजिए।
1. कण का t = 1s से t = 2s समयान्तराल में औसत वेग तथा
2. t = 2s पर कण का तात्क्षणिक वेग
उत्तर:

1.  \(\overrightarrow{v_{a v}}=(4 \hat{i}+24 \hat{j})\) ms^-1
2. 32.25ms^-1

Must Read:

LTTS Pivot Point Calculator