Haryana State Board HBSE 10th Class Maths Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Ex 9.1 Textbook Exercise Questions and Answers.
Haryana Board 10th Class Maths Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Exercise 9.1
प्रश्न 1.
सर्कस का एक कलाकार एक 20m लंबी डोर पर चढ़ रहा है जो अच्छी तरह A से तनी हुई है और भूमि पर सीधे लगे खंभे के शिखर से बंधा हुआ है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो तो खंभे की ऊँचाई ज्ञात कीजिए (देखिए संलग्न आकृति)।
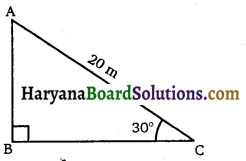
हल :
प्रश्नानुसार,
AB उर्ध्वाधर खंभा है तथा CA एक 20m लंबी डोर है जिसका एक छोर खंभे AB के 7 शिखर से तथा दूसरा छोर भूमि पर स्थित एक बिंदु C से बंधा है।
ΔABC में,
sin 30° = \(\frac{A B}{A C}\)
\(\frac{1}{2}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
\(\frac{1}{2}=\frac{\mathrm{AB}}{20}\)
AB = \(\frac{20}{2}\) = 10m
अतः खंभे की ऊँचाई 10m
![]()
प्रश्न 2.
आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिंदु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8m है। पेड़ की ऊँचाई ज्ञात कीजिए।
हल :
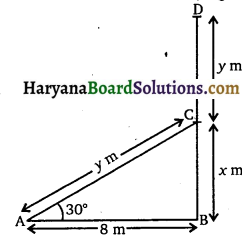
माना BD एक पेड़ है जो बिंदु C से टूटने के बाद CD के स्थान पर CA की स्थिति में आ जाता है अर्थात् बिंदु A पर पेड़ का शिखर D जमीन को छूता है।
प्रश्नानुसार, ∠BAC = 30°
माना BC = x m
CD = CA = y m
अब समकोण ΔABC में,


प्रश्न 3.
एक ठेकेदार बच्चों के खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है. 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर 1.5 m की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3 m की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लंबाई क्या होनी चाहिए?
हल :
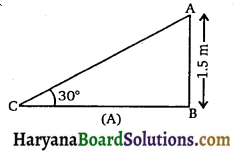
स्थिति (A) 5 वर्ष से कम उम्र के बच्चों के लिए फिसलनपट्टी की लंबाई ज्ञात करना।
माना AC फिसलनपट्टी की लंबाई 1 m तथा ऊँचाई AB = 1.5 m तथा ∠ACB = 30°
समकोण ΔABC में,
\(\frac{\mathrm{AB}}{\mathrm{AC}}\) = sin 30°
\(\frac{1.5}{l}=\frac{1}{2}\)
या l = 1.5 x 2 = 3.0 m या 3 m
अतः 5 वर्ष से कम उम्र के बच्चों के लिए फिसलनपट्टी की लंबाई = 3 m
स्थिति (B) 5 वर्ष से अधिक उम्र के बच्चों के लिए फिसलनपट्टी की लंबाई ज्ञात करना।
माना DF फिसलनपट्टी की लंबाई x m तथा ऊँचाई DE = 3 m तथा ∠DFE = 60°
समकोण ΔDEF में,
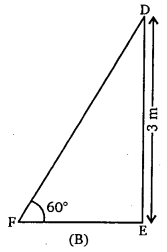
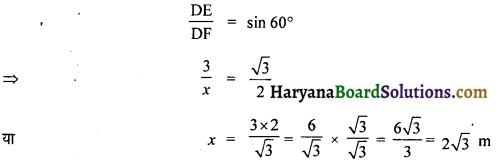
अतः 5 वर्ष से अधिक उम्र के बच्चों के लिए फिसलनपट्टी की लंबाई = 2√3 m
प्रश्न 4.
भूमि के एक बिंदु से, जो मीनार के पाद-बिंदु से 30 m की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
हल :
माना मीनार AB का शिखर A तथा पाद-बिंदु B है जिसकी ऊँचाई hm है। बिंदु C मीनार के पाद-बिंदु B से 30 m की दूरी पर है।
प्रश्नानुसार,
AB = h m
BC = 30 m
∠ACB = 30°
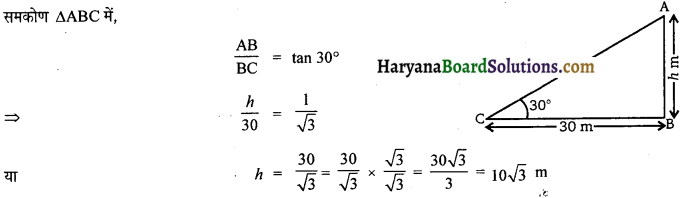
अतः मीनार की ऊँचाई (AB) = 10√3 m
प्रश्न 5.
भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिंदु से बांध दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर कि डोरी में कोई ढील नहीं है, डोरी की लंबाई ज्ञात कीजिए।
हल :
माना A पतंग की स्थिति जिसकी डोरी का दूसरा सिरा बिंदु C पर बंधा है। पतंग की ऊँचाई (AB) = 60 m तथा ∠ACB = 60°
अब समकोण ΔABC में,
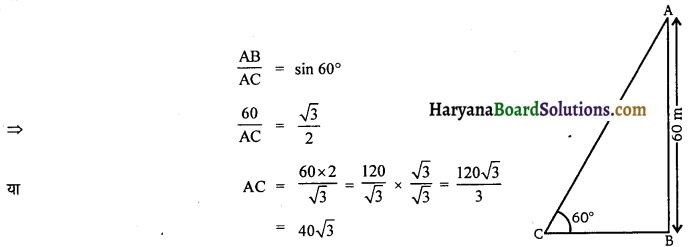
अतः डोरी की लंबाई (AC) = 40√5 m
![]()
प्रश्न 6.
1.5 m लंबा एक लड़का 30m ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है तब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है।
हल :
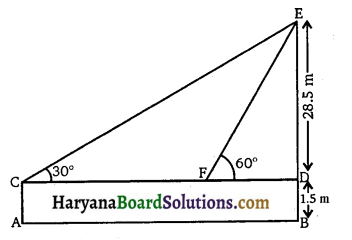
माना AC एक लड़का है जिसकी ऊँचाई 1.5 m है जो 30 m ऊँचे भवन BE से कुछ दूरी पर खड़ा है। जहाँ से शिखर का उन्नयन कोण 30° भवन की ओर F तक चलने के बाद उन्नयन कोण 60° हो जाता है।
प्रश्नानुसार,
∠ECD = 30°
∠EED = 60°
माना CF = x m तथा FD = y m
अब समकोण ΔEDF में,
\(\frac{\mathrm{DE}}{\mathrm{DF}}\) = tan 60°
\(\frac{28.5}{y}=\frac{\sqrt{3}}{1}\)

अतः भवन की ओर चली गई वांछित दूरी = 19√3 m
प्रश्न 7.
भूमि के एक बिंदु से एक 20 m ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः 45° और 60° है। संचार मीनार की ऊँचाई ज्ञात कीजिए।
हल :
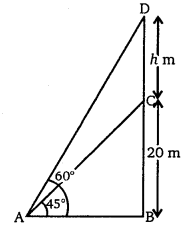
माना CD एक संचार मीनार है जिसकी ऊँचाई hm है जोकि 20 m ऊँचे भवन BC पर लगी है।
अर्थात्
CD = h m
BC = 20 m
प्रश्नानुसार,
∠BAC = 45°
∠BAD = 60°
अब समकोण ΔABC में,
\(\frac{\mathrm{BC}}{\mathrm{AB}}\) = tan 45°
\(\frac{20}{\mathrm{AB}}\) = 1
AB = 20 m ………..(i)
इसी प्रकार, समकोण ΔABD में,
\(\frac{\mathrm{BD}}{\mathrm{AB}}\) = tan 60°
\(\frac{20+h}{20}\) = √3 [समीकरण (i) से AB = 20 लेने पर]
20 + h = 20√3
h = 20√3 – 20
= 20 (√3 – 1)
अतः संचार मीनार की ऊँचाई = 20 (√3 – 1) m
प्रश्न 8.
एक पेडस्टल के शिखर पर एक 1.6 m ऊँची मूर्ति लगी है। भूमि के एक बिंदु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिंदु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
हल :
माना पेडस्टल BD की ऊँचाई h m है जिसके ऊपर मूर्ति CD = 1.6 m लगी है। भूमि पर स्थित बिंदु A से C का उन्नयन कोण 60° तथा D का उन्नयन 45° है।
प्रश्नानुसार,
∠CAB = 60°
∠DAB = 45°
CD = 1.6 m
BD = h m
अब समकोण ΔABD में,
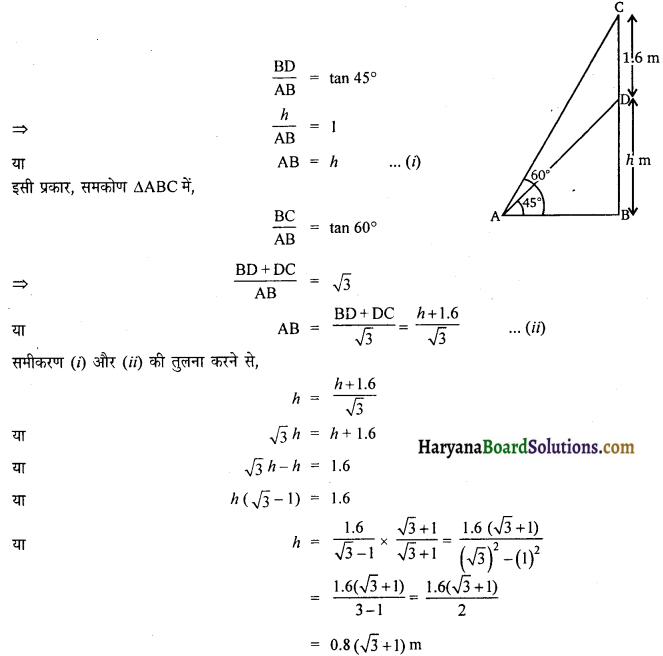
अतः पेडस्टल BD की ऊँचाई = 0.8 (√3 +1) m
![]()
प्रश्न 9.
एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद-बिंद्र से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन की ऊँचाई ज्ञात कीजिए।
हल :
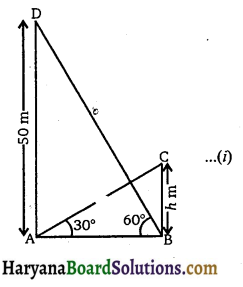
माना BC = h m ऊँचाई का एक भवन है तथा AD = 50 m ऊँची एक मीनार है।
प्रश्नानुसार,
∠ABD = 60°
तथा ∠BAC = 30°
अब समकोण ΔABD में,

अतः भवन की ऊँचाई = 16\(\frac{2}{3}\) m
प्रश्न 10.
एक 80 m चौड़ी सड़क के दोनों ओर आमने-सामने समान लंबाई वाले दो खंभे लगे हुए हैं। इन दोनों खंभों के बीच सड़क के एक बिंदु से खंभों के शिखर के उन्नयन कोण क्रमशः 60° और 30° हैं। खंभों की ऊँचाई और खंभों से बिंदु की दूरी ज्ञात कीजिए।
हल :
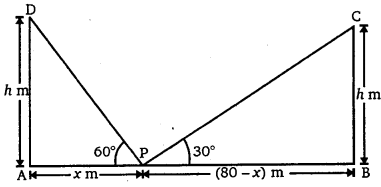
माना AD और BC समान ऊँचाई hm के दो खंभे हैं तथा AB = 80 m चौड़ी एक सड़क है जिसके बीच बिंदु P है।
माना AP = x m तो
BP = (80-x) m
प्रश्नानुसार, ∠APD = 60° तथा
∠BPC = 30°
अब समकोण ΔAPD में,
\(\frac{\mathrm{AD}}{\mathrm{AP}}\) = tan 60°
\(\frac{h}{x}=\sqrt{3}\)
x = \(\frac{h}{\sqrt{3}}\) ………..(i)
x = इसी प्रकार, समकोण ΔBPC में,
\(\frac{\mathrm{BC}}{\mathrm{BP}}\) = tan 30°
\(\frac{h}{80-x}=\frac{1}{\sqrt{3}}\)
80 – x = √3h
x = 80 – √3h ……….(ii)
समीकरण (i) और (ii) की तुलना करने से,
\(\frac{h}{\sqrt{3}}\) = 80 – √3h
h = 80√3 – 3 h
h + 3h = 80√3
4 h = 80√3
h = \(\frac{80 \sqrt{3}}{4}\) = 20√3
h का मान समीकरण (i) में रखने पर,
x = \(\frac{20 \sqrt{3}}{\sqrt{3}}\) = 20
AP = 20m और BP = 80 – 20 = 60m
अतः खंभों की ऊँचाई = 20√3 m.
खंभों से बिंदु की दूरी = 20 m और 60 m
प्रश्न 11.
एक नहर के एक तट पर एक टी०वी० टॉवर ऊर्ध्वाधरतः खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिंदु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिंद्र से टॉवर के शिखर का उन्नयन कोण 30° है। (देखिए संलग्न आकृति)। टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।
हल :
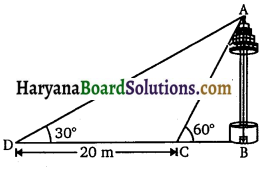
माना टी०वी० टॉवर AB की ऊँचाई hm है जोकि नहर के एक तट D -20m पर खड़ा है। दूसरे तट पर बिंदु C की टॉवर के पाद-बिंदु B से दूरी BC=xm है। बिंदु C से 20 m की दूरी चलने पर माना बिंदु D आता है।
प्रश्नानुसार, ∠ACB = 60°, ∠ADB = 30°, CD = 20 m
BC = xm, BD = (20 + x) m
अब समकोण ΔABC में,

इसी प्रकार, समकोण ΔABD में,
\(\frac{\mathrm{AB}}{\mathrm{BD}}\) = tan 30°
\(\frac{h}{20+x}=\frac{1}{\sqrt{3}}\)
20 + x = √3h
x = √3h – 20 ……………(ii)
समीकरण (i) और (ii) की तुलना करने से,
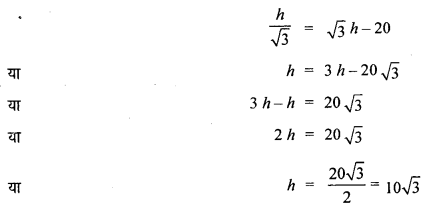
h का मान समीकरण (i) में रखने पर,
x = \(\frac{h}{\sqrt{3}}=\frac{10 \sqrt{3}}{\sqrt{3}}\) = 10
अतः टी०वी० की ऊँचाई = 10√3 m तथा नहर की चौड़ाई = 10 m
![]()
प्रश्न 12.
7 m ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
हल :
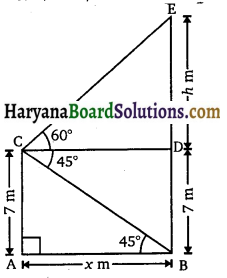
माना AC = 7 m ऊँचा एक भवन है तथा BE एक केबल टॉवर है। प्रश्नानुसार,
∠DCE = 60° और
∠BCD = ∠ABC = 45°
AC = BD = 7 m
माना DE = h m
अब समकोण ΔABC में,
\(\frac{\mathrm{AC}}{\mathrm{AB}}\) = tan 45°
\(\frac{7}{\mathrm{AB}}\) = 1
AB = 7
AB = CD = 7 … (i)
इसी प्रकार, समकोण ΔDCE में,
\(\frac{\mathrm{DE}}{\mathrm{CD}}\) = tan 60°
\(\frac{h}{7}\) = 75
अतः केबल टॉवर की ऊँचाई (BE) = BD + DE
= (7 + 7√3) m
= 7 (1 + √3) m
प्रश्न 13.
समुद्र-तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बीच की दूरी ज्ञात कीजिए।
हल :
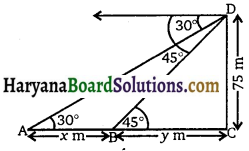
माना D एक लाइट हाऊस जो समुद्र के तल C से 75 m ऊँचा है। समुद्र तल पर दो जहाज A और B के अवनमन कोण क्रमशः 30° और 45° हैं।
माना AB = x m तथा BC = y m
प्रश्नानुसार, ∠DAC = 30° और ∠DBC = 45°
अब समकोण ΔBCD में,

x + y = 75√3
x + 75 = 75√3 [समीकरण (i) से]
x = 75√3 – 75
= 75 (√3 – 1)
अतः दोनों जहाजों के बीच की दूरी = 75 (√3 – 1)
![]()
प्रश्न 14.
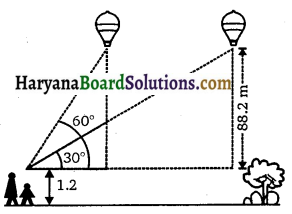
1.2 m लंबी एक लड़की भूमि से 88.2 m की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण 60° है। कुछ समय बाद उन्नयन कोण घटकर 30° हो जाता है (देखिए संलग्न आकृति)। इस अंतराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।
हल :
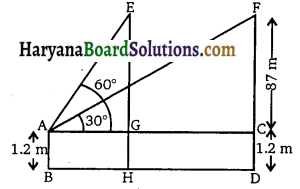
माना AB = 1.2 m लंबी एक लड़की है। E तथा F गुब्बारे की दो विभिन्न स्थितियाँ हैं जिनके लड़की की आँख से उन्नयन कोण क्रमशः । 60° और 30° हैं।
प्रश्नानुसार,
EH = FD = 88.2 m
EG = FC = (88.2 – 1.2) m
= 87 m
अब समकोण ΔEAG में,

प्रश्न 15.
एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जोकि मीनार के पाद की ओर एक समान चाल से जाता है। छः सेकेंड बाद कार का अवनमन कोण 60° हो गया। इस बिंदु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
हल :
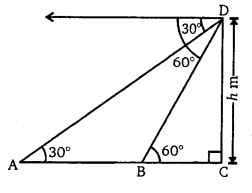
माना CD एक मीनार है जिसकी ऊँचाई h m है। इसके शिखर D से कार की स्थिति A और B के क्रमशः अवनमन कोण 30° और 60° है अर्थात् ∠DAC = 30° और ∠DBC = 60°
माना कार की चाल = x m/s
तो 6 सेकेंड में कार द्वारा चली गई दूरी AB = 6x m
माना B से C तक पहुँचने में लिया गया समय = n सेकेंड
तो दूरी BC = nx m
अब समकोण ΔACD में,

\(\frac{h}{n x}\)= √3
या h = nx√3 …..(ii)
समीकरण (i) और (ii) की तुलना करने से,
\(\frac{6 x+n x}{\sqrt{3}}=n x \sqrt{3}\)
6x + nx = 3nx
6x = 3nx – nx
6x = 2nx
अतः कार द्वारा B से C तक पहुँचने में लगा समय = 3 सेकेंड
![]()
प्रश्न 16.
मीनार के आधार से और एक सरल रेखा में 4m और 9 m की दूरी पर स्थित दो बिंदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए कि मीनार की ऊँचाई 6 m है।
हल :
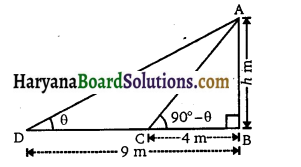
माना AB = hm ऊँचाई की मीनार है जिसके आधार B से बिंदु C और D की क्रमशः दूरी 4 m और 9 m है।
माना, ∠ADB = θ
तो ∠ACB = 90° – θ
अब समकोण ΔABC में,
\(\frac{\mathrm{AB}}{\mathrm{BC}}\) = tan (90° – θ)
\(\frac{h}{4}\) = cot θ
इसी प्रकार, समकोण ΔABD में,

h2 = 36
h = ±6
परंतु h = – 6 असंभव है।
∴ मीनार की ऊँचाई = 6 m