HBSE 10th Class Maths Solutions Chapter 14 सांख्यिकी Ex 14.2

Haryana State Board HBSE 10th Class Maths Solutions Chapter 14 सांख्यिकी Ex 14.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 14 सांख्यिकी Exercise 14.2

प्रश्न 1.
निम्नलिखित सारणी किसी अस्पताल में एक विशेष वर्ष में भर्ती हुए रोगियों की आयु को दर्शाती है :

उपरोक्त आँकड़ों के बहुलक और माध्य ज्ञात कीजिए। दोनों केंद्रीय प्रवृत्ति की मापों की तुलना कीजिए और उनकी व्याख्या कीजिए।
हल :
यहाँ पर अधिकतम वर्ग बारंबारता 23 है तथा इसका बारंबारता संगत वर्ग 35-45 है।
बहुलक वर्ग = 35 – 45
बहुलक वर्ग की निम्न सीमा (l) = 35
वर्ग-माप (h) = 10
बहुलक वर्ग की बारंबारता (f₁) = 23
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f₀) = 21
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f₂) = 14
अब बहुलक = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) x h
= 35 + \(\left(\frac{23-21}{2 \times 23-21-14}\right)\) x 10
= 35 + \(\frac{2}{11}\) x 10
= 35 + 1.8 = 36.8 (लगभग) वर्ष
माध्य ज्ञात करने के लिए-
माना कल्पित माध्य (a) = 30
वर्ग-माप (h) = 10
u_i = \(\frac{x_{i}-a}{h}=\frac{x_{i}-30}{10}\)

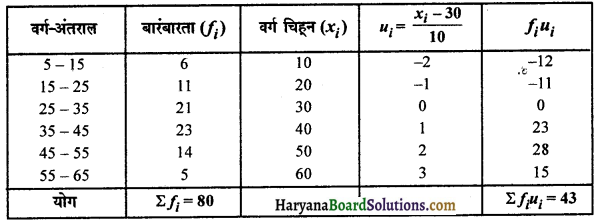
अब माध्य \((\bar{x})=a+\left(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\right) \times h\)
= 30 + \(\frac{43}{80}\) x 10
= 30 + 5.37 = 35.37 वर्ष
अतः अस्पताल में भर्ती अधिकतम रोगी 36.8 वर्ष आयु (लगभग) के हैं जबकि औसतन अस्पताल में भर्ती किए गए रोगियों की आयु 35.37 वर्ष है।

प्रश्न 2.
निम्नलिखित आँकड़े, 225 बिजली उपकरणों के प्रेक्षित जीवनकाल (घंटों में) की सूचना देते हैं-

उपकरणों का बहुलक जीवनकाल ज्ञात कीजिए।
हल :
यहाँ पर अधिकतम वर्ग बारंबारता 61 है तथा इस बारंबारता का संगत वर्ग 60-80 है।
बहुलक वर्ग = 60-80
बहुलक वर्ग की निम्न सीमा (1) = 60
वर्ग-माप (h) = 20
बहुलक वर्ग की बारंबारता (f₁) = 61
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f₀) = 52
बहलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f₂) = 38
अब बहुलक = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) x h
= 60 + \(\left(\frac{61-52}{2 \times 61-52-38}\right)\) x 20 = 60 + \(\frac{9}{32}\) x 20
= 60 + 5.625 = 65.625
अतः दिए आँकड़ों के उपकरणों का बहुलक जीवनकाल 65.625 घण्टे है।

प्रश्न 3.
निम्नलिखित आँकड़े किसी गाँव के 200 परिवारों के कल मासिक घरेल व्यय के बंटन को दर्शाते हैं। इन परिवारों का बहुलक मासिक व्यय ज्ञात कीजिए। साथ ही, माध्य मासिक व्यय भी ज्ञात कीजिए।

व्यय (रुपयों में)	परिवारों की संख्या
1000-1500	25
1500-2000	40
2000-2500	33
2500-3000	28
3000-3500	30
3500-4000	22
4000-4500	16
4500-5000	7

हल :
यहाँ पर अधिकतम वर्ग बारंबारता 40 है तथा इस बारंबारता का संगत वर्ग 1500 -2000 है।
बहुलक वर्ग = 1500-2000
बहुलक वर्ग की निम्न सीमा (l) = 1500
वर्ग-माप (h) = 500
बहुलक वर्ग की बारंबारता (f₁) = 40
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f₀) = 24
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f₂) = 33
अब बहुलक = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) x h
= 1500 + \(\left(\frac{40-24}{2 \times 40-24-33}\right)\) x 500
= 1500 + \(\frac{16}{23}\) x 500
= 1500 + 347.83
= 1847.83
अतः परिवारों का बहुलक मासिक व्यय = 1847.83 रु०
माध्य मासिक व्यय के लिए-
माना कल्पित माध्य (a) = 2750
वर्ग-माप (h) = 500
u_i = \(\frac{x_{i}-a}{h}\)
= \(\frac{x_{i}-2750}{500}\)

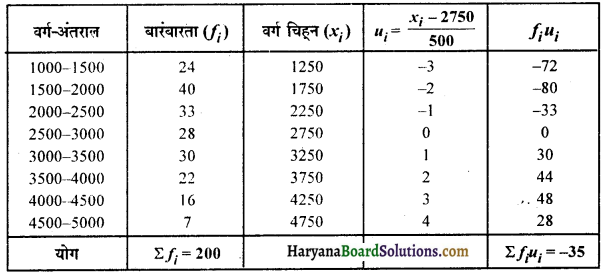
अब माध्य \(a+\left(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\right) \times h\)
= 2750 + \(\left(\frac{-35}{200}\right)\) x 500
= 2750 – 87.5 = 2662.5
अतः परिवार का माध्य मासिक व्यय = 2662.50 रु०

प्रश्न 4.
निम्नलिखित बंटन भारत के उच्चतर माध्यमिक स्कूलों में, राज्यों के अनुसार, शिक्षक-विद्यार्थी अनुपात को दर्शाता है। इन आँकड़ों के बहुलक और माध्य ज्ञात कीजिए। दोनों मापकों की व्याख्या कीजिए।

प्रति शिक्षक विद्यार्थियों की संख्या	राज्य/संघीय क्षेत्रों की संख्या
15-20	3
20-25	8
25-30	9
30-35	10
35-40	3
40-45	0
45-50	0
50-55	2

हल :
यहाँ पर अधिकतम वर्ग वारंवारता 10 है तथा इस वारंबारता का संगत वर्ग 30-35 है।
बहुलक वर्ग = 30-35
बहुलक वर्ग की निम्न सीमा (l) = 30
वर्ग-माप (h) = 5
बहुलक वर्ग की बारंबारता (f₁) = 10
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f₀) = 9
बहलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f₂) = 3
अब बहुलक = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) x h
= 30 + \(\left(\frac{10-9}{2 \times 10-9-3}\right)\) x 5 = 30 + \(\frac{1}{8}\) x 5
= 30 + 0.625 = 30.625 = 30.6 (लगभग)

माध्य के लिए-
माना कल्पित माध्य (a) = 32.5
वर्ग-माप (h) = 5
u_i = \(\frac{x_{i}-a}{h}=\frac{x_{i}-32.5}{5}\)

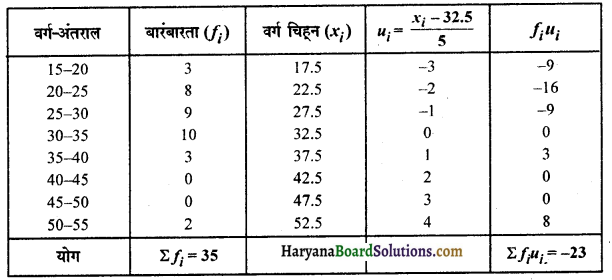
माध्य \((\bar{x})\) = a + \(\left(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\right)\) x h
= 32.5 + \(\left(\frac{-23}{35}\right)\) x 5
= 32.5 – 3.3 = 29.2
अतः अधिकांश राज्यों/U.T. में छात्र और अध्यापक का अनुपात 30.6 है तथा औसतन छात्र व अध्यापक अनुपात. 29.2 है।

प्रश्न 5.
दिया हुआ बंटन विश्व के कुछ श्रेष्ठतम बल्लेबाज़ों द्वारा एकदिवसीय अंतर्राष्ट्रीय क्रिकेट मैचों में बनाए गए रनों को दर्शाता है-

बनाए गए रन	बल्लेबाज़ों की संख्या
3000-4000	4
4000-5000	18
5000-6000	9
6000-7000	7
7000-8000	6
8000-9000	3
9000 – 10,000	1
10,000 – 11,000	1

इन आँकड़ों का बहुलक ज्ञात कीजिए।
हल :
यहाँ पर अधिकतम वर्ग बारंबारता 18 है तथा इस बारंबारता का संगत वर्ग 4000 -5000 है।
बहुलक वर्ग = 4000 – 5000
बहुलक वर्ग की निम्न सीमा (l) = 4000
वर्ग-माप (h) = 1000
बहुलक वर्ग की बारंबारता (f₁) = 18
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f₀) = 4
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f₂) = 9
अब बहुलक = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) x h
= 4000 + \(\frac{14}{23}\) x 1000
= 4000 + 52 x 1000
= 4000 + 608.695
= 4608.695 ≅ 4608.7 (लगभग)
अतः दिए गए आँकड़ों का बहुलक = 4608.7 रन (लगभग)

प्रश्न 6.
एक विद्यार्थी ने एक सड़क के किसी स्थान से होकर जाती हुई कारों की संख्याएँ नोट की और उन्हें नीचे दी हुई सारणी के रूप में व्यक्त किया। सारणी में दिया प्रत्येक प्रेक्षण 3 मिनट के अंतराल में उस स्थान से होकर जाने वाली कारों की संख्याओं से संबंधित है। ऐसे 100 अंतरालों पर प्रेक्षण लिए गए। इन आँकड़ों का बहुलक ज्ञात कीजिए।

हल :
यहाँ पर अधिकतम वर्ग बारंबारता 20 है तथा इस बारंबारता का संगत वर्ग 40-50 है।
बहुलक वर्ग = 40-50
बहुलक वर्ग की निम्न सीमा (l) = 40
वर्ग-माप (h) = 10
बहुलक वर्ग की बारंबारता (f₁) = 20
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f₀) = 12
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f₂) = 11
अब बहुलक = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) x h
= 40 + \(\left(\frac{20-12}{2 \times 20-12-11}\right)\) x 10
= 40 + \(\frac{8}{17}\) x 10
= 40+ 4.7 = 44.7
अतः दिए गए आँकड़ों का बहुलक = 44.7 कारें