HBSE 7th Class Science Solutions Chapter 18 अपशिष्ट जल की कहानी
Haryana State Board HBSE 7th Class Science Solutions Chapter 18 अपशिष्ट जल की कहानी Textbook Exercise Questions and Answers.
Haryana Board 7th Class Science Solutions Chapter 18 अपशिष्ट जल की कहानी
HBSE 7th Class Science अपशिष्ट जल की कहानी InText Questions and Answers
बूझो/पहेली
प्रश्न 1.
अपशिष्ट जल उपचार संयंत्र का बोझ मत बढ़ाइए। पहेली जानना चाहती है कि यह कैसे सम्भव होगा?
उत्तर:
(i) नालियों में चिकनाई न बहाकर ।
(ii) रासायनिक पदार्थ तथा औषधियाँ न बहाकर इनसे शुद्धिकरण में सहायक सूक्ष्म जीव मर सकते हैं।
(iii) कोई भी ठोस पदार्थ नाली में न बहाकर।
प्रश्न 2.
बूझो जानना चाहता है कि हवाई जहाज में वाहित मल का निबटान कैसे होता है ?
उत्तर:
इसे एक टैंक में एकत्रित करके हवाई अड्डे पर लाकर संयंत्र में डाला जाता है जहाँ इसका निबटान किया जाता है।
![]()
HBSE 7th Class Science अपशिष्ट जल की कहानी Textbook Questions and Answers
प्रश्न 1.
रिक्त स्थानों की पूर्ति कीजिए
(क) जल को स्वच्छ करना ……………………. को दूर करने का प्रक्रम है।
(ख) घरों द्वारा निर्मुक्त किये जाने वाला अपशिष्ट जल ……………………. कहलाता है।
……………………. का उपयोग खाद के रूप में किया जाता है।
(घ) नालियाँ ……………………. और ……………………. के द्वारा अवरुद्ध हो जाती हैं।
उत्तर:
(क) संदूषकों
(ख) वाहित मल
(ग) गोबर
(घ) पॉलीथीन, आपंक।
प्रश्न 2.
वाहित मल क्या है ? अनुपचारित वाहित मल को नदियों अथवा समुद्र में विसर्जित करना हानिकारक क्यों है, समझाइए।
उत्तर:
वाहित मल अपशिष्ट जल होता है जो कि घरों, उद्योगों, अस्पतालों आदि द्वारा उपयोग के बाद प्रवाहित होता है। तेज वर्षा के समय गलियों, सड़कों तथा छतों से बहकर आने वाला वर्षा जल भी इसमें शामिल है जो अपने साथ हानिकारक पदार्थों को भी बहा ले जाता है। वाहित मल में धुले हुए तथा निलम्बित अपद्रव्य युक्त जल होता है। ये अपद्रव्य संदूषक कहलाते हैं।
प्रश्न 3.
तेल और वसाओं को नाली में क्यों नहीं बहाना चाहिए ? समझाइए।
उत्तर:
तेल या वसा हल्का होने के कारण जल की सतह पर तैरता रहता है। इसके कारण वायु जल के अन्दर प्रवेश नहीं कर पाती है। फलस्वरूप ऐसे जल में रहने वाले जीवों को ऑक्सीजन की आपूर्ति नहीं हो पाती और श्वसन के अभाव में उनकी मृत्यु हो जाती है।
प्रश्न 4.
अपशिष्ट जल से स्वच्छ जल प्राप्त करने के प्रक्रम में सम्मिलित चरणों का वर्णन कीजिए।
उत्तर:
स्वच्छ जल प्राप्त करने के प्रक्रम में सर्वप्रथम जल को बार-बार शलाका छन्नों (बार स्क्रीन) से गुजारा जाता है जिससे कि बड़े आकार के सन्दूषक पृथक हो जाते हैं। अब वाहित अपशिष्ट जल को इस टंकी के अपशिष्ट जल से कम प्रवाह से छोड़ा जाता है, जिससे उसमें उपस्थित बालू, ग्रिट, कंकड़, पत्थर उसकी पेंदी में बैठ जाते हैं। फिर आपंक को अलग किया जाता है। उपचारित जल में अल्प मात्रा में कार्बनिक पदार्थ और निलम्बित अशुद्धियाँ होती हैं। इसे समुद्र, नदी अथवा भूमि में विसर्जित कर दिया जाता है।
![]()
प्रश्न 5.
आपंक क्या है ? समझाइए कि इसे कैसे उपचारित किया जाता है ?
उत्तर:
जल शोधन के समय टंकी की तली में बैठ जाने वाली अशुद्धियों (मल आदि) खुरचकर बाहर निकाली जाती हैं जिन्हें आपंक कहते हैं। आपंक को पृथक् टंकी में स्थानान्तरित करके जीवाणुओं द्वारा अपघटित कराया जा सकता है। जल को बालू बिछाकर बनाये शुष्कन तलों अथवा मशीनों द्वारा हटा दिया जाता है। शुष्क अपंक का प्रयोग खाद के रूप में कृषि में किया जाता है।
प्रश्न 6.
अनुपचारित मानव मल एक स्वास्थ्य संकट है। समझाइए।
उत्तर:
अनुपचारित मानव मल, जल तथा मृदा प्रदूषण का कारण बन सकता है। इससे भौमजल तथा सतही जल दोनों ही प्रदूषित हो सकते हैं। अनुपचारित मानव मल से भयंकर बीमारियों के फैलने की अत्यधिक संभावनाएँ होती हैं। इसीलिये यह एक स्वास्थ्य संकट है।
प्रश्न 7.
जल को रोगाणुनाशित (रोगाणुमुक्त) करने के लिये उपयोग किये जाने वाले दो रसायनों के नाम बताइए।
उत्तर:
(i) क्लोरीन
(ii) ओजोन।
प्रश्न 8.
अपशिष्ट जल उपचार संयन्त्र में शलाका छन्नों के कार्यों को समझाइए।
उत्तर:
अपशिष्ट जल को शलाका छन्नों से गुजारे जाने पर बड़े आकार के सभी सन्दूषक अलग हो जाते हैं।
प्रश्न 9.
स्वच्छता और रोग के बीच सम्बन्ध को समझाइए।
उत्तर:
स्वच्छता और रोग के बीच निम्न सम्बन्ध हैं
- गन्दगी के कारण रोगाणु तथा रोग फैलते हैं।
- साफ तथा स्वच्छ शरीर से रोगाणु दूर रहते हैं।
- जहाँ स्वच्छता होती है वहाँ रोग नहीं होते।
![]()
प्रश्न 10.
स्वच्छता के सन्दर्भ में एक सक्रिय नागरिक के रूप में अपनी भूमिका को समझाइए।
उत्तर:
स्वच्छता के सन्दर्भ में एक सक्रिय नागरिक के रूप में हम निम्न कार्य कर सकते हैं
(i) हम सबसे पहले अपने शरीर को साफ एवं स्वच्छ रखेंगे।
(ii) हम अपने घर तथा इसके आस-पास के वातावरण को स्वच्छ रखेंगे।
(iii) हम अपने पड़ोसियों के साथ मिलकर जल निकास की उचित व्यवस्था करेंगे।
(iv) मल-मूत्र को खले में नहीं छोड़ेंगे।
(v) हम सम्बन्धित नगरपालिका को साफ-सफाई के सम्बन्ध में सहयोग करेंगे।
प्रश्न 11.
प्रस्तुत वर्ग पहेली को दिये गये संकेतों की सहायता से हल कीजिए।
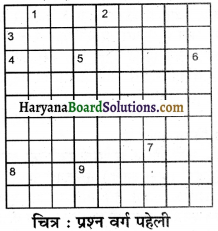
बाएँ से दाएँ-
2. वाहित मल उपचार संयन्त्र से प्राप्त गैसीय उत्पाद.
4. इस प्रक्रम में प्रदूषित जल से वायु को गुजारा जाता है।
7. वाहित मल ले जाने वाले पाइपों की व्यवस्था
8. उपयोग के बाद नालियों में बहता जल।
ऊपर से नीचे
1. जल उपचार में रोगाणुनाशन के लिए प्रयुक्त एक रसायन
3. वह सूक्ष्मजीव, जो ऑक्सीजन की अनुपस्थिति में जैव पदार्थों का विघटन करते हैं।
5. सन्दूषित जल
6. यह स्थान, जहाँ वाहित मल से प्रदूषक पृथक किये जाते हैं।
19. अनेक व्यक्ति इसका विसर्जन खुले स्थानों में करते हैं।
उत्तर:

प्रश्न 12.
ओजोन के बारे में निम्नलिखित वक्तव्यों को ध्यानपूर्वक पढ़िए-
(क) यह सजीव जीवों के श्वसन के लिये अनिवार्य
(ख) इसका उपयोग जल को रोगाणु रहित करने के लिये किया जाता है।
(ग) यह पराबैंगनी किरणों को अवशोषित कर लेती
(घ) वायु में इसका अनुपात लगभग 3% है। इनमें से कौन से वक्तव्य सही हैं।
(i) (क), (ख) और (ग)
(ii) (ख) और (ग)
(iii) (क) और (ग)
(iv) सभी चार
उत्तर:
(i) (ख) और (ग)।
![]()
HBSE 7th Class Science अपशिष्ट जल की कहानी Important Questions and Answers
वस्तुनिष्ठ प्रश्न
I. बहुविकल्पीय प्रश्न
निम्नलिखित प्रश्नों में से सही विकल्प का चयन कीजिए
1. ‘जीवन के लिए जल’ पर कार्य के लिए अन्तर्राष्ट्रीय दशक के रूप में घोषित किया गया
(क) वर्ष 1990 से 2000
(ख) वर्ष 1995 से 2005
(ग) वर्ष 2005 से 2015
(घ) वर्ष 2010 से 2020
उत्तर:
(ग) वर्ष 2005 से 2015
2. जल में कार्बनिक अशुद्धियाँ हो सकती हैं
(क) मानव मल
(ख) पीड़कनाशी
(ग) तेल
(घ) ये सभी
उत्तर:
(घ) ये सभी
3. प्रदूषित जल में हानिकारक जीव हो सकते हैं
(क) जीवाणु
(ख) प्रोटोजोआ
(ग) बीजाणु
(घ) ये सभी
उत्तर:
(घ) ये सभी
4. जल शोधक पदार्थ है
(क) मेथेन
(ख) क्लोरीन
(ग) सैकरीन
(घ) फीनॉल
उत्तर:
(ख) क्लोरीन
5. जैव निम्नीकरणीय जल प्रदूषक है
(क) प्लास्टिक की थैली
(ख) शाकनाशी
(ग) पीड़कनाशी
(घ) मानव मल
उत्तर:
(घ) मानव मल
![]()
II. रिक्त स्थान
निम्नलिखित वाक्यों में रिक्त स्थान भरिए
1. अपशिष्ट जल के उपचार का प्रक्रम सामान्य रूप से ……………….. कहलाता है।
2. सीवर मिलकर ………… की व्यवस्था करता है।
3. निर्मलीकृत जल में पंप द्वारा वायु को गुजारा जाता है जिससे उसमें ………… की वृद्धि होती है।
4. ………… उन स्थानों के लिए उपयुक्त हैं जहाँ मल वहन की व्यवस्था नहीं है।
उत्तर;
1. वाहित मल उपचार
2. मल विसर्जन
3. वायवीय जीवाणु
4. सैप्टिक टैंक।
III. सुमेलन
कॉलम A तथा कॉलम B के शब्दों का मिलान कीजिए
| कॉलम A | कॉलम B |
| 1. टाइफाइड | (a) वायुवीय जीवाणु |
| 2. जल निर्मलीकरण | (b) प्रदूषित जल का उपयोग |
| 3. कीटनाशक | (c) वाहित मल उपचार संयंत्र |
| 4. वातित्र | (d) जल प्रदूषक |
उत्तर:
| कॉलम A | कॉलम B |
| 1. टाइफाइड | (b) प्रदूषित जल का उपयोग |
| 2. जल निर्मलीकरण | (a) वायुवीय जीवाणु |
| 3. कीटनाशक | (d) जल प्रदूषक |
| 4. वातित्र | (c) वाहित मल उपचार संयंत्र |
IV. सत्य/असत्य
निम्नलिखित वाक्यों में से सत्य एवं असत्य कथन छाँटिए
1. वह जल जो शौचालयों, लान्ड्री, सिंक, कारखानों आदि से निकलता है, अपशिष्ट जल कहलाता है।
2. हैजा और टाइफाइड रोग के रोग कारक क्रमशः विनियो कोलेरा एवं साल्मानेला पैराटाइफी जीवाणु हैं।
3. अपशिष्ट जल में तैरने वाले तेल और ग्रीज को हटाने के लिए अपमथित्र (स्किमर) का उपयोग किया जाता है।
4. बायोगैस का उपयोग ऊर्जा के स्रोत के रूप में नहीं किया जा सकता है।
उत्तर:
1, सत्य
2. सत्य
3. सत्य
4. असत्य।
![]()
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
जल के शुद्धिकरण से आप क्या समझते हैं ?
उत्तर:
शुद्धिकरण की प्रक्रिया जिसमें जल से पानी व सन्दूषित पदार्थों को पृथक् कर दिया जाता है।
प्रश्न 2.
वाहित मल क्या होता है ?
उत्तर:
वाहित मल घरों, उद्योगों, अस्पतालों, कार्यालयों और अन्य उपयोगों के बाद प्रवाहित किया जाने वाला जल होता है।
प्रश्न 3.
सन्दूषक किसे कहते हैं ?
उत्तर;
जल में घुले हुए तथा निलम्बित अपद्रव्य होते हैं जिन्हें सन्दूषक कहते हैं।
प्रश्न 4.
वाहित मल जल में कौन-कौन से पदार्थ हो सकते हैं? (क्रियाकलाप)
उत्तर:
- सूक्ष्म जीव
- रासायनिक अपशिष्ट
- धातुओं के कण
- सीसा के कण।
प्रश्न 5.
सन्दूषित जल के प्रयोग से किन रोगों के होने की सम्भावना होती है ?
उत्तर:
हैजा, टाइफाइड, पोलियो, मेनिन्जाइटिस, हेपैटाइटिस और पेचिश।
प्रश्न 6.
उस जीव का नाम लिखिये जिसका प्रयोग जल के शुद्धिकरण में किया जाता है ?
उत्तर:
जीवाणु (बैक्टीरिया)।
प्रश्न 7.
दो ऐसे पदार्थों के नाम लिखिए जिनसे जल को कीटाणु मुक्त किया जा सकता है? (क्रियाकलाप)
उत्तर:
(i) फिटकरी
(ii) क्लोरीन।
![]()
प्रश्न 8.
नदियों में जल प्रदूषण के दो कारक लिखिए।
उत्तर:
(i) घरेलू बाहित मल
(ii) उद्योगों का कचरा।
प्रश्न 9.
अपशिष्ट जल को कहाँ उपचारित किया जाता है ?
उत्तर:
अपशिष्ट जल को वाहित मल उपचार संयन्त्र में उपचारित किया जाता है।
प्रश्न 10.
हमारे लिये जल के स्रोत क्या हैं ?
उत्तर:
नदियाँ, कुएँ, ट्यूबवैल, झरने आदि।
लघु उत्तरीय प्रश्न
प्रश्न 1.
निम्नलिखित आरेख में खाली स्थानों में उपयुक्त शब्द भरिए। (क्रियाकलाप)
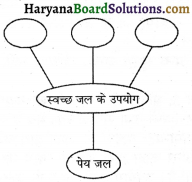
उत्तर:
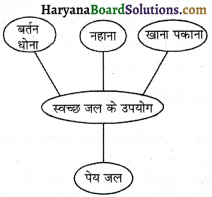
प्रश्न 2.
ऐसे चार क्रियाकलापों की सूची बनाइए जिसे न करने पर आप जल को सन्दूषणरहित बनाने में योगदान कर सकते हैं?
उत्तर:
- हमें खुले स्थानों पर मल विसर्जन नहीं करना चाहिए।
- रसोईघर के अपशिष्ट पदार्थ, जैसे सब्जियों के छिलके आदि को नालियों में नहीं डालना चाहिए।
- खाना पकाने के तेल एवं बर्तन साफ करने से निकले मैले को जल में नहीं डालना चाहिए।
- कीटनाशकों, औषधियों, पेंट, विलायक आदि को जल में नहीं फेंकना चाहिए।
प्रश्न 3.
कृमि प्रसंस्करण शौचालय का क्या महत्व
उत्तर:
भारत में ऐसे शौचालयों की रूपरेखा का परीक्षण किया गया है, जिसमें मानव मल को केंचुओं द्वारा उपचारित किया जाता है। यह तकनीक मानव मल के सुरक्षित प्रसंस्करण के लिये आदर्श सिद्ध हो सकती है, क्योंकि इसके उपयोग में जल की बहुत कम मात्रा की आवश्यकता होती है। शौचालय का संचालन बहुत सरल और स्वच्छ है। मानव मल पूर्णत: कृमि केकों में परिवर्तित हो जाता है जो मृदा के लिये अति समृद्ध पोषक है।
प्रश्न 4.
वाहित जल में पाई जाने वाली विभिन्न अशुद्धियों का विवरण दीजिए।
उत्तर:
वाहित जल में पाई जाने वाली अशुद्धियाँ निम्न प्रकार हैं
(1) कार्बनिक अशुद्धियाँ-मानव मल, जैविक अपशिष्ट पदार्थ, तेल, यूरिया (मूत्र), पीड़कनाशी, शाकनाशी, फल एवं सब्जी का कचरा आदि।
(2) अकार्बनिक अशुद्धियाँ-नाइट्रेट, फॉस्फेट, धातुएँ।
(3) पोषक तत्व-फॉस्फोरस और नाइट्रोजनयुक्त पदार्थ।
(4) जीवाणु-हैजा और टाइफाइड आदि रोग उत्पन्न करने वाले।
(5) अन्य सूक्ष्म जीव पेचिश आदि रोग उत्पन्न करने वाले।
प्रश्न 5.
मल विसर्जन व्यवस्था क्या होती है ?
उत्तर:
घरों तथा सार्वजनिक भवनों को स्वच्छ जल की आपूर्ति सामान्यत: पाइपों के जाल द्वारा की जाती है। पाइपों के एक अन्य जाल द्वारा उपयोग किये जा चुके जल को ले जाया जाता है। उपयोग किये जा चुके जल को ले जाने वाली पाइप लाइनों को सीवर कहते हैं जो मल विसर्जन की व्यवस्था करता है। यह एक परिवहन तन्त्र की तरह है जो वाहित मल को उसके उद्गम स्थल से उसके निबटान के स्थान अर्थात् उपचार संयन्त्र तक ले जाता है।
![]()
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
अपशिष्ट जल उपचार संयन्त्र का वर्णन कीजिए।
उत्तर:
अपशिष्ट जल के उपचार में भौतिक, रासायनिक और जैविक प्रक्रम सम्मिलित होते हैं। यह प्रक्रम जल को सन्दूषित करने वाले भौतिक, रासायनिक और जैविक द्रव्यों को पृथक् करने में सहायता करते हैं।
(1) सबसे पहले अपशिष्ट जल को ऊर्ध्वाधर लगी छड़ों से बने शलाका छन्ने (बार स्क्रीन) से गुजारा जाता है। इससे अपशिष्ट जल में उपस्थित कपड़ों के टुकड़े, डण्डियाँ, डिब्बे, प्लास्टिक के पैकेट, नैपकिन आदि जैसे बड़े साइज के सन्दूषक अलग हो जाते हैं।
(2) अब वाहित अपशिष्ट जल को ग्रिट और बालू अलग करने की टंकी में ले जाया जाता है। इस टंकी में अपशिष्ट जल को कम प्रवाह से छोड़ा जाता है, जिससे उसमें उपस्थित बालू, ग्रिट और कंकड़-पत्थर उसकी पेंदी में बैठ जाते हैं।
(3) फिर जल को एक ऐसी बड़ी टंकी में ले जाया जाता है जिसका पेंदा मध्य भाग की ओर ढलान वाला होता है। जल को इस टंकी में कई घण्टों तक रखा जाता है, जिसमें मल जैसे ठोस उसकी तली के मध्य भाग में बैठ जाते हैं। इन अशुद्धियों को खुरचकर बाहर निकाल दिया जाता है। यह आपंक (स्लज) होता है। अपशिष्ट जल में तैरने वाले तेल और ग्रीस जैसी अशुद्धियों को हटाने के लिये अपमथित्र (स्किमर) का उपयोग किया जाता है। इस प्रकार साफ किया गया जल निर्मलीकृत होता है।
(4) निर्मलीकृत जल में पम्प द्वारा वायु को गुजारा जाता है जिससे जीवाणुओं की वृद्धि होती है। ये अनेक अपशिष्ट पदार्थों का विघटन कर देते हैं।
कई घण्टों के पश्चात् जल में निलम्बित सूक्ष्म जीव टंकी की पेंदी में सक्रिय आपंक के रूप में बैठ जाते हैं। अब शीर्ष भाग से जल को निकाल दिया जाता है। सक्रिय आपंक लगभग 97% जल है। जल को बालू बिछाकर बनाये शुष्कन तो अथवा मशीनों द्वारा हटा दिया जाता है। शुष्क आपंक का उपयोग खाद के रूप में किया जाता है जिससे कार्बनिक पदार्थ और पोषक तत्व पुनः मृदा में वापस चले जाते हैं।
उपचारित जल में अल्प मात्रा में कार्बनिक पदार्थ और निलम्बित तत्व होते हैं। इसे समुद्र, नदी अथवा भूमि में विसर्जित कर दिया जाता है। कभी-कभी जल को वितरण तन्त्र में निर्मुक्त करने से पहले उसमें क्लोरीन अथवा ओजोन मिलाकर रोगाणुमुक्त किया जाता है।
प्रश्न 2.
अपने संदूषक सर्वेक्षण के आधार पर वाहित मल के प्रकार, उत्पत्ति स्थल, उपस्थित संदूषक पदार्थों की तालिका बनाइए। (क्रियाकलाप)
उत्तर:
सारणी सन्दूषक सर्वेक्षण
| वाहित मल का प्रकार | उत्पत्ति स्थल | संदूषक पदार्थ | कोई अन्य टिप्पणी |
| कूड़ा-करकट/मलिन जल | रसोई | शाकनाशी | ज्यादा प्रदूषित नहीं |
| दुर्गन्ध युक्त अपशिष्ट | शौचालय | मल | बहुत प्रदूषित |
| व्यावसायिक अपशिष्ट | औद्योगिक और व्यावसायिक संस्थान | रसायन | अत्यधिक प्रदूषित |
![]()
वन: हमारी जीवन रेखा Class 7 HBSE Notes in Hindi
→ झाग से भरपूर, तेल मिश्रित, काले, भूरे रंग का जल जो सिंक, शौचालय, लॉन्ड्री आदि से नालियों में जाता है, वह अपशिष्ट जल कहलाता है।
→ जल समस्या की गंभीरता को समझते हुए विश्व जल दिवस 22 मार्च 2005 को संयुक्त राष्ट्र की जनरल एसेम्बली ने 2005-2015 को जीवन के लिए जल पर कार्य के लिए अन्तर्राष्ट्रीय दशक के रूप में घोषित किया है।
→ वाहित मल घरों, उद्योगों, अस्पतालों, कार्यालयों और अन्य उपयोगों के बाद प्रवाहित किए जाने वाला जल अपशिष्ट जल होता है।
प्रयुक्त जल अपशिष्ट जल कहलाता है, जिसका पुन: उपयोग किया जा सकता है।
→ वाहित मल द्रवरूपी अपशिष्ट पदार्थ होता है जो जल और मृदा का प्रदूषण उत्पन्न करता है।
→ छोटे एवं बड़े पाइपों की भूमि के अन्दर बनायी गयी व्यवस्था जो मिलकर मल विसर्जन की व्यवस्था करती है, सीवर कहलाती है।
अपशिष्ट जल उपचार के सह-उत्पाद, आपंक और बायो गैस हैं।
→ खुली (मुक्त) नाली व्यवस्था, मक्खी, मच्छर और अन्य ऐसे जीवों के लिए प्रजनन स्थल प्रदान करती है, जो रोग उत्पन्न करते हैं।
→ हमें खुले में मलत्याग नहीं करना चाहिये। कम लागत विधियों को अपनाकर मल का सुरक्षित निबटान सम्भव है।
→ अपशिष्ट जल – उपयोग के बाद बचा प्रदूषित जल अपशिष्ट जल कहलाता है।
→ वाहित मल – नालियों से बहता हुआ जल जिसमें घरेल, औद्योगिक अपशिष्ट पदार्थ होते हैं।
→ सीवर – वह व्यवस्था जो नालियाँ एवं पाइपों को जोड़कर मल विसर्जन के लिए बनायी जाती है।
→ वातन – वाहित मल में वायु का संचरण करना।
→ अपशिष्ट पदार्थ – ऐसे पदार्थ जो प्रयोग करने के बाद व्यर्थ बच जाते हैं।
→ आपंक – जब अपशिष्ट जल को साफ करने के लिये टंकी में ले जाया जाता है तो अपशिष्ट ठोस उसकी तली में बैठ जाते हैं, यह आपंक कहलाता है।
→ अवायवीय जीवाणु – जीवाणु जिन्हें ऑक्सीजन की आवश्यकता नहीं होती है।
→ वायवीय जीवाणु – जीवाणु जिन्हें जीवित रहने के लिये ऑक्सीजन की आवश्यकता होती है।
→ जैवनिम्नीकरण – ऐसे अपशिष्ट पदार्थ जिन्हें सूक्ष्म जीवों द्वारा अपघटित (निम्नीकृत) किया जा सकता है।
→ बायो गैस – अवायवीय जीवाणुओं द्वारा आपंक को अपघटित करने पर एक ज्वलनशील गैस उत्पन्न होती है जो बायो गैस कहलाती है।
→ जल शोधन – अपशिष्ट जल का शुद्धीकरण।
HBSE 7th Class Science Solutions Chapter 18 अपशिष्ट जल की कहानी Read More »