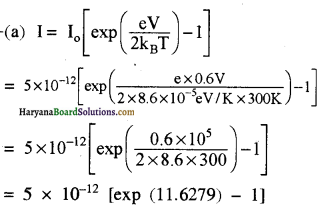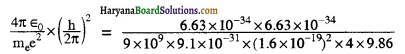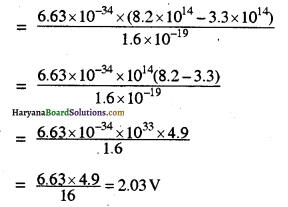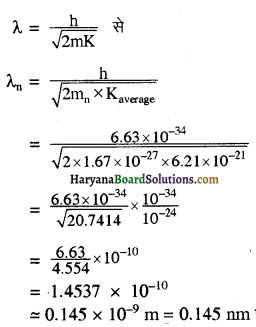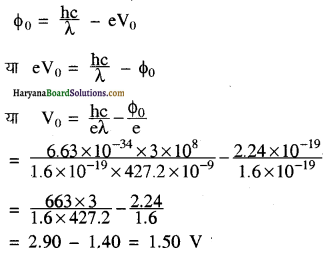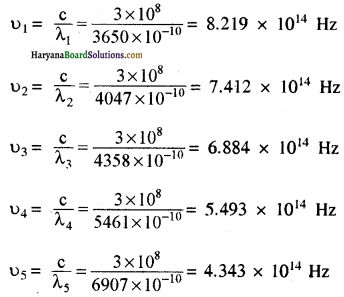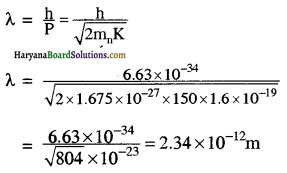Haryana State Board HBSE 12th Class Physics Solutions Chapter 11 विकिरण तथा द्रव्य की द्वैत प्रकृति Textbook Exercise Questions and Answers.
Haryana Board 12th Class Physics Solutions Chapter 11 विकिरण तथा द्रव्य की द्वैत प्रकृति
प्रश्न 11.1.
30 kV इलेक्ट्रॉनों के द्वारा उत्पन्न X – किरणों की (a) उच्चतम आवृत्ति तथा (b) निम्नतम तरंगदैर्ध्य प्राप्त कीजिए।
उत्तर:
(a) दिया गया है:
V = 30 KV = 30 × 1000 = 30,000 v
= 3 × 104
हम जानते हैं- E = hv = eV
∴ Vmax = ev/h
जहाँ पर
h = 6.63 × 10-34 Js
e = 1.6 x 10-19 C
Umax = \(\frac{1.6 \times 10^{-19} \times 3 \times 10^4}{6.63 \times 10^{-34}}\)
= 7.24 × 1018 Hz
(b) माना उत्पन्न न्यूनतम X – किरण तरंगदैर्घ्य = λmin = ?
∴ λmin = c/vmax
मान रखने पर λmin = \(\frac{3 \times 10^8}{7.24 \times 10^{18}}\)
= 4.14 × 1011 m
= 4.14 × 10-11 x 1010A
= 4.14 × 10-1 A
= 0.414 A = 0.0414 nm

प्रश्न 11.2.
सीजियम धातु का कार्य फलन 2.14ev है। जब 6 × 1014 Hz आवृत्ति का प्रकाश धातु-पृष्ठ पर आपतित होता है, इलेक्ट्रॉनों का प्रकाशिक उत्सर्जन होता है।
(a) उत्सर्जित इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा,
(b) निरोधी विभव, और
(c) उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम चाल कितनी
उत्तर:
दिया गया है:
सीजियम धातु का कार्य फलन Φ = 2.14 ev
तथा
= 2.14 × 1.6 x 10-19 J
आवृत्त = 0 = 6 × 1014 Hz
h = 6.63 Js
(a) उत्सर्जित इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा = Kmax = ?
आइन्सटीन के प्रकाश विद्युत समीकरण से
hv = Kmax + Φ0
∴ kmax = hv – Φ0
मान रखने पर
Kmax = 6.63 × 1034 x 6 x 104 – 2.14
× 1.6 × 10-19
= 6.63 × 6 × 10-20 – 2.14 x 1.6 x 10-19
= 39.78 × 10-20 – 3.424 x 10-19
= 3.978 x 10-19 – 3.424 x 10-19
= 0.554 × 10-19 J
∴ Kmax = \(\frac{0.554 \times 10^{-19}}{1.6 \times 10^{-19}}ev\)
= 0.34 ev/e
(b) निरोधी विभव Vo = 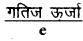
= 0.34 eV
= 0.34V
(c) उत्सर्जित प्रकाशिक इलेक्ट्रॉन की अधिकतम चाल = V
इलेक्ट्रॉन का द्रव्यमान = m = 9.1 x 10-31 kg

= 3.44 x 105 m/s
= \(\frac{3.44 \times 10^5}{10^3}km/s\)
= 344 km/s
प्रश्न 11.3.
एक विशिष्ट प्रयोग में प्रकाश-विद्युत प्रभाव की अंतक वोल्टता 1.5 V है। उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा कितनी है?
उत्तर:
अंतक वोल्टता या निरोधी विभव
Vo= 1.5 V
एक इलेक्ट्रॉन पर आवेश = Kmax = ?
उत्सर्जित अधिकतम गतिज ऊर्जा = e= 1.6 x 10-19 C
सम्बन्ध
K.E = Kmax = eVo से
Kmax = 1.6 x 10-19 x 1.5 V J
= 2.40 × 10-19 J
= \(\frac{2.40 \times 10^{-19}}{1.6 \times 10^{-19}}ev\)
= 1.5 इलेक्ट्रॉन-वोल्ट
प्रश्न 11.4.
632.8 nm तरंगदैर्घ्य का एकवर्णी प्रकाश एक हीलियम-नियॉन लेसर के द्वारा उत्पन्न किया जाता है। उत्सर्जित शक्ति 9.42mW है।
(a) प्रकाश के किरण-पुंज में प्रत्येक फोटॉन की ऊर्जा तथा संवेग प्राप्त कीजिए,
(b) इस किरण-पुंज के द्वारा विकिरित किसी लक्ष्य पर औसतन कितने फोटॉन प्रति सेकंड पहुँचेंगे? (यह मान लीजिए कि किरण-पुंज की अनुप्रस्थ काट एकसमान है जो लक्ष्य के क्षेत्रफल से कम है), तथा
(c) एक हाइड्रोजन परमाणु को फोटॉन के बराबर संवेग प्राप्त करने के लिए कितनी तेज चाल से
उत्तर:
दिया गया है:
चलना होगा ?
λ = 632.8 nm
= 632.8 x 10-9 m
शक्ति P = 9.42 mW
= 9.42 × 10-3 W
(a) प्रत्येक फोटॉन की ऊर्जा
= K= ?
प्रत्येक फोटॉन का संवेग = p= ?
h = 6.63 × 10-34 J
c= 3 x 10-8 m/s
सम्बन्ध E = hv = hc/λ का उपयोग करने पर
मान रखने पर
= \(\frac{2.40 \times 10^{-19}}{1.6 \times 10^{-19}}ev\)
= 3.14 × 10-19 J
= \(\frac{3.14 \times 10^{-19}}{1.6 \times 10^{-19}}\)
= 1.96eV
तथा संवेग (p) = h/λ से
= \(\frac{6.63 \times 10^{-34}}{632.8 \times 10^{-9}}\)
= 1.05 x 10-27 kg m/s
(b) फोटॉन प्रति सेकण्ड उत्सर्जित की दर

= 3 x 1016 फोटॉन/s
(c) माना हाइड्रोजन परमाणु की चाल = VH = ?
हाइड्रोजन परमाणु का द्रव्यमान = my = 1.67 x 10-27 kg
माना हाइड्रोजन परमाणु का संवेग p’ = MHVн
प्रश्नानुसार p = p = फोटॉन का संवेग
या mHVH = 1.05 x 10-27
∴ VH = \(\frac{1.05 \times 10^{-27}}{\mathrm{~m}_{\mathrm{H}}}\)
= \(\frac{1.05 \times 10^{-27}}{1.67 \times 10^{-27}}\)
= 0.628m/s
= 0.63 m/s
प्रश्न 11.5.
पृथ्वी के पृष्ठ पर पहुँचने वाला सूर्य प्रकाश का ऊर्जा – अभिवाह (फ्लक्स) 1.388 x 10 W/m2 है। लगभग कितने फोटॉन प्रति वर्ग मीटर प्रति सेकंड पृथ्वी पर आपतित होते हैं? यह मान लें कि सूर्यप्रकाश में फोटॉन का औसत तरंगदैर्घ्य 550 nm है।
उत्तर:
दिया गया है:
ऊर्जा फ्लक्स Φ = = 1.388 x 103 W/m2
फोटॉन का औसत तरंगदैर्घ्य
λ = 550nm
A = 550 x 10-9 m
h = 6.23 x 10-34 Js
c = 3 x 108 m/s2
∴ प्रत्येक फोटॉन की ऊर्जा E = hc/λ से
= \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{550 \times 10^{-9}}\)
= 3.62 × 10-19 J
∴ प्रोटॉन प्रति वर्ग मीटर प्रति सेकण्ड पृथ्वी पर
n = Φ/E
= \(\frac{1.388 \times 10^3}{3.62 \times 10^{-19}}\)
= 3.8 × 1021
= 4 x 1021

प्रश्न 11.6.
प्रकाश – विद्युत प्रभाव के एक प्रयोग में, प्रकाश आवृत्ति के विरुद्ध अंतक वोल्टता की ढलान 4.12 x 10-15 V s प्राप्त होती है। प्लांक स्थिरांक का मान परिकलित कीजिए।
उत्तर:
VS = V की प्रवणता
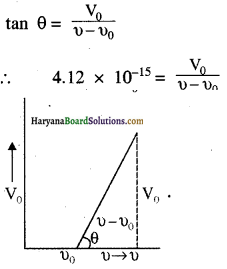
हम जानते हैं:
eV0 = h (v – v0)
=> h = \(\frac{\mathrm{eV}_0}{v-v_0}\) = \(\left(\frac{V_0}{v-v_0}\right)\)
h = 1.6 × 10-19 x 4.12 x 10-15
= 6.592 × 1034 Js
प्रश्न 11.7.
एक 100 W सोडियम बल्ब (लैंप) सभी दिशाओं में एकसमान ऊर्जा विकिरित करता है। लैंप को एक ऐसे बड़े गोले के केंद्र पर रखा गया है जो इस पर आपतित सोडियम के संपूर्ण प्रकाश को अवशोषित करता है। सोडियम प्रकाश का तरंगदैर्ध्य 589 nm है। (a) सोडियम प्रकाश से जुड़े प्रति फोटॉन की ऊर्जा कितनी है ? (b) गोले को किस दर से फोटॉन प्रदान किए जा रहे हैं?
उत्तर:
दिया गया है:
सोडियम लैम्प की शक्ति P = 100 W
सोडियम प्रकाश का तरंगदैर्घ्य
λ = 589nm
A = 589 x 10-9 m
(a) फोटॉन की ऊर्जा
E = hc/λ
मान रखने पर
E = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{589 \times 10^{-9}}\)
= 3.38 × 10-19 J
= 2.11 eV
(b) गोले को किस दर से फोटॉन प्रदान किये जा रहे हैं ?
n = p/E
= \(\frac{100}{3.38 \times 10^{-19}}\)
= 2.96 × 1020
= 3.0 x 1020 फोटॉन/s
प्रश्न 11.8.
किसी धातु की देहली आवृत्ति 3.3 x 1014 Hz है। यदि 8.2 x 1014 Hz आवृत्ति का प्रकाश धातु पर आपतित हो, तो प्रकाश-विद्युत उत्सर्जन के लिए अंतक वोल्टता ज्ञात कीजिए।
उत्तर:
दिया गया है:
आवृत्ति v = 8.2 x 1014 Hz
देहली आवृत्ति vo = 3.3 x 1014 Hz
h = 6.63 × 10-34 Js
इलेक्ट्रॉन पर आवेश
e = 1.6 x 10-19 C
आइन्सटीन के प्रकाश विद्युत प्रभाव के समीकरण से
hv – hv0 = eVo
∴ h(v – v0) = ev0
v0 = h(v – v0)/e
मान रखने पर
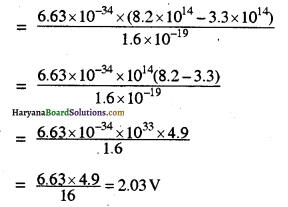
प्रश्न 11.9.
किसी धातु के लिए कार्य फलन 4.2 ev है। क्या यह धातु 330nm तरंगदैर्घ्य के आपतित विकिरण के लिए प्रकाश-विद्युत उत्सर्जन देगा?
उत्तर:
दिया गया है:
कार्यफलन 40 = 4.2 ev
= 4.2 x 1.6 × 10-19 J
= 6.72 x 10-19 J
तरंगदैर्घ्य A = 330 nm = 330 x 10-9 nm
कार्यफलन Φo = hov0 का उपयोग करने पर
∴ देहली आवृत्ति v0 = Φo/h
मान रखने पर
vo = \(\frac{6.72 \times 10^{-19}}{6.63 \times 10^{-34}}\)
Vo = 1 x 1015 Hz
c = vλ का भी उपयोग करने पर
आपतित विकिरण की आवृत्ति
v = c/λ
मान रखने पर
v = \(\frac{3 \times 10^8}{330 \times 10^{-9}}\)
= 9 × 1014 Hz …………. (ii)
अब समीकरण (i) व (ii) से यह स्पष्ट है कि आपतित विकिरण की आवृत्ति 1 देहली आवृत्ति 00 से कम है अतः इस विकिरण के लिए प्रकाश वैद्युत उत्सर्जन नहीं हो सकता।
प्रश्न 11.10.
7.21 × 1014 Hz आवृत्ति का प्रकाश एक धातु-पृष्ठ पर आपतित है इस पृष्ठ से 6.0 x 105 m/s की उच्चतम गति से इलेक्ट्रॉन उत्सर्जित हो रहे हैं। इलेक्ट्रॉनों के प्रकाश उत्सर्जन के लिए देहली आवृत्ति क्या है?
उत्तर:
दिया गया है:
प्रकाश की आवृत्ति
= 7.21 × 1014 Hz
पृष्ठ से निकले इलेक्ट्रॉन की अधिकतम चाल
Vmax = 6.0 x 10 m/s
इलेक्ट्रॉन का द्रव्यमान = m = 9.1 x 10-31 kg
देहली आवृत्ति = Up = ?
प्लांक का नियतांक = h = 6.63 × 10-34 Js
आइन्सटीन के प्रकाश-वैद्युत समीकरण का उपयोग करने पर

प्रश्न 11.11.
488 nm तरंगदैर्ध्य का प्रकाश एक ऑर्गन लेसर से उत्पन्न किया जाता है, जिसे प्रकाश-विद्युत प्रभाव के उपयोग में लाया जाता है जब इस स्पेक्ट्रमी रेखा के प्रकाश को उत्सर्जक पर आपतित किया जाता है तब प्रकाशिक इलेक्ट्रॉनों का निरोधी (अंतक) विभव 0.38 V है। उत्सर्जक के पदार्थ का कार्य-फलन ज्ञात करें।
उत्तर:
तरंगदैर्ध्य λ = 488 nm
= 488 × 109 m
निरोधी विभव Vo = 0.38 V
उत्सर्जक के पदार्थ का कार्यफलन Φ0 = ?
प्रकाश-विद्युत समीकरण को इस प्रकार से उपयोग करने पर
eV0 = ho – po
∴ Φo = ho – eVo
= hc/λ – evo
मान रखने पर
Φo = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{488 \times 10^{-9}}\) – 1.6×10-19 × 0.38
= 4.08 × 10-19 – 0.608 × 10-19
= 3.472 × 10-19 J
= \(\frac{3.472 \times 10^{-19}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 2.17 eV
प्रश्न 11.12.
56 V विभवांतर के द्वारा त्वरित इलेक्ट्रॉनों का
(a) संवेग, और
(b) दे- बॉली तरंगदैर्घ्य परिकलित कीजिए।
उत्तर:
(a) दिया गया है:
लगाया गया विभवांतर = V = 56 V
इलेक्ट्रॉन का संवेग = p = ?
दे-ब्रॉग्ली तरंगदैर्घ्य = λ = ?
इलेक्ट्रॉन का द्रव्यमान m = 9.1 x 10-31 kg
हम जानते हैं:
संवेग p = √2meV
मान रखने पर
\(\sqrt{2 \times 9.1 \times 10^{-31} \times 1.6 \times 10^{-19} \times 56}\)
या p= 4.04 x 10-24 kg m/s
(b) दे-ब्रॉग्ली तरंगदैर्ध्य
λ = h/p = \(\frac{6.63 \times 10^{-34}}{4.04 \times 10^{-24}}\)
= 1.64 x 10-10 mn
= 0.164 nm
= 1.64 Å

प्रश्न 11.13.
एक इलेक्ट्रॉन जिसकी गतिज ऊर्जा 120 ev है, उसका
(a) संवेग, (b) चाल और (c) दे-ब्रॉग्ली तरंगदैर्ध्य क्या है?
उत्तर:
दिया गया है:
K = 120 ev
(a) अतः संवेग
P = √2mK
= \(\sqrt{2 \times 9.1 \times 10^{-31} \times 120 \mathrm{eV}}\)
= \(\sqrt{2 \times 9.1 \times 10^{-31} \times 120 \times 1.6 \times 10^{-19}}\)
= \(\sqrt{2 \times 9.1 \times 120 \times 1.6 \times 10^{-50}}\)
= 5.91 × 10-24 kg m/s
(b) चाल v = imm
v = \(\frac{5.91 \times 10^{-24}}{9.1 \times 10^{-31}}\)
= 6.5 × 106 m/s
(c) डी-ब्रॉग्ली तरंगदैर्घ्य λ = h/p
= 1.12 × 10-10m
= 1.12Å
= 0.112 nm
प्रश्न 11.14.
सोडियम के स्पेक्ट्रमी उत्सर्जन रेखा के प्रकाश का तरंगदैर्ध्य 589 nm है। वह गतिज ऊर्जा ज्ञात कीजिए जिस पर
(a) एक इलेक्ट्रॉन, और (b) एक न्यूट्रॉन का दे-बॉली तरंगदैर्घ्य समान होगा।
उत्तर:
दिया गया है:
प्रकाश का तरंगदैर्घ्य = λ = 589nm
λ = 589 x 10-9 m
हम जानते हैं:
इलेक्ट्रॉन का द्रव्यमान = mc = 9.1 x 10-31 kg
न्यूट्रॉन का द्रव्यमान = mg = 1.67 x 10-27 kg
प्लांक का नियतांक = h = 6.63 x 10-34 Js
(a) माना इलेक्ट्रॉन की गतिज ऊर्जा (K.E) = K1 = ?
सम्बन्ध λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{~m}_{\mathrm{c}} \mathrm{K}_1}}\) का उपयोग करके
हम
λ2 = \(\frac{\mathbf{h}^2}{2 \mathrm{~m}_{\mathrm{e}} \mathbf{K}_1}\) प्राप्त करते हैं।
∴ K1 = \(\frac{h^2}{2 m_e \lambda^2}\)
मान रखने पर
K1 = \(\frac{\left(6.63 \times 10^{-34}\right)^2}{2 \times 9.1 \times 10^{-31} \times\left(589 \times 10^{-9}\right)^2}\)
= 6.94 × 10-25 J
= \(\frac{6.94 \times 10^{-25}}{16 \times 10^{-19}} \mathrm{eV}\)
K1 = 4.34 × 10-6 eV
= 4.34 HeV
(b) न्यूट्रॉन की गतिज ऊर्जा (KE) = K2 = ?
K2 = \(\frac{h^2}{2 m_n \lambda^2}\)
मान रखने पर
= \(\frac{\left(6.63 \times 10^{-34}\right)^2}{2 \times 1.67 \times 10^{-27} \times\left(589 \times 10^{-9}\right)^2}\)
= 3.79 × 10-28 J
= \(\frac{3.79 \times 10^{-28}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 2.36 × 10-9 eV
= 2.36 neV
प्रश्न 11.15.
(a) एक 0.040 kg द्रव्यमान का बुलेट जो 1.0km/s की चाल से चल रहा है, (b) एक 0.060 kg द्रव्यमान की गेंद जो 1.0 km/s की चाल से धूल-कण जिसका द्रव्यमान 1.0 x 10-9 kg चल रही है, और (c) एक kg और जो 2.2 m/s की चाल से अनुगमित हो रहा है, का दे-बॉग्ली तरंगदैर्ध्य कितना होगा?
उत्तर:
दिया गया है:
(a) बुलेट का द्रव्यमान = mg = 0.040 kg
बुलेट का वेग = Vo = 1.0 km/s = 1000 m/s
माना बुलेट का दे-ब्रॉग्ली तरंगदैर्ध्य = λb = ?
हम जानते हैं।
λ = h/p = h/mv का उपयोग करने पर
∴ λb = h/mbvb
समीकरण के मान रखने पर λb = \(\frac{6.63 \times 10^{-34}}{0.040 \times 1000}\)
= 1.655 x 10-35
= 1.7 x 10-35 m
(b) यहाँ पर दिया गया है ( गेंद के लिए)
m = 0.060 kg = 60 x 10-13 kg
v = 1.00 m/s
λ = ?
∴ λ = h/mv = \(\frac{6.63 \times 10^{-34}}{60 \times 10^{-3} \times 1.0}\)
= 1.1 x 10-2m
(c) दिया गया है: ( धूल कण के लिए)
m = 1.0 × 10-9 kg
v = 2.2m/s
दे-ब्रॉग्ली तरंगदैर्घ्य λ = ?
λ = \(\frac{6.63 \times 10^{-34}}{1.0 \times 10^{-9} \times 2.2}\)
= 3.01 × 10-25m
प्रश्न 11.16.
एक इलेक्ट्रॉन और एक फोटॉन प्रत्येक का तरंगदैर्घ्य 1.00nm है।
(a) इनका संवेग,
(b) फोटॉन की ऊर्जा, और
(e) इलेक्ट्रॉन की गतिज ऊर्जा ज्ञात कीजिए।
उत्तर:
दिया गया है:
= λc = 1.0nm
∴ λc = 1 × 10-9 m
फोटॉन का तरंगदैर्घ्य = λp = 10-9 m
हम जानते हैं:
प्लांक नियतांक h = 6.63 x 10-34 Js
c = 3 x 108 m/s
(a) माना इलेक्ट्रॉन का संवेग = Pe = ?
हम जानते हैं
λ = h/p = सूत्र से
∴ Pc = h/λe
मान रखने पर
Pe = \(\frac{6.63 \times 10^{-34}}{10^{-9}}\)
= 6.63 × 10-25 kg m/s
इलेक्ट्रॉन और फोटॉन के लिए समान है।
(b) फोटॉन की ऊर्जा
Ep = \(\frac{\mathrm{hc}}{\lambda_P}\)
या
Ep = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{10^{-9}}\)
= 1.99 × 10-16 J
= \(\frac{1.99 \times 10^{-16}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 1.24 × 103 ev
= 1.24 Kev
1KeV = 10 eV
(c) इलेक्ट्रॉन की गतिज ऊर्जा = Kc = ?
सूत्र λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{mK}}}\)q से
या λ2 = \(\frac{h^2}{2 \mathrm{mK}}\)
∴ K = \(\frac{h^2}{2 m \lambda^2}\)
चूँकि इलेक्ट्रॉन की गतिज ऊर्जा के लिए है।
∴ Ke = \(\frac{\mathrm{h}^2}{2 m_e \lambda_e^2}\)
मान रखने पर
Ke = \(\frac{\left(6.63 \times 10^{-34}\right)^2}{2 \times 9.1 \times 10^{-31} \times\left(10^{-9}\right)^2}\)
= \(\frac{43.9569 \times 10^{-68}}{18.2 \times 10^{-49}}\)
= 2.415 x 10-19 ev
= \(\frac{2.415 \times 10^{-19}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 1.51 ev
प्रश्न 11.17.
(a) न्यूट्रॉन की किस गतिज ऊर्जा के लिए दे- बॉली तरंगदैर्घ्य 1.40 x 10-10 m होगा?
(b) एक न्यूट्रॉन, जो पदार्थ के साथ तापीय साम्य में है और जिसकी 300 K पर औसत गतिज ऊर्जा 3/2KT है, का भी दे ब्रॉग्ली तरंगदैर्ध्य ज्ञात कीजिए।
उत्तर:
(a) दिया गया है:
दे-ब्रॉग्ली तरंगदैर्घ्य = λ = 1.40 x 10-10 m
न्यूट्रॉन की गतिज ऊर्जा = K = ?
हम जानते हैं
न्यूट्रॉन का द्रव्यमान = mg = 1.67 x 10-27 kg
h = 6.63 x 1034 Js
सूत्र: λ = \(\frac{h}{\sqrt{2 \mathrm{mK}}}\) का उपयोग करने पर
हम K = \(\frac{h^2}{2 \mathrm{~m} \lambda^2}\) प्राप्त करते हैं।
न्यूट्रॉन के लिए K = \(\frac{h^2}{2 m_n \lambda_n^2}\)
मान रखने पर

(b) यहाँ पर परम ताप = T = 300K.
वोल्ट्जमान नियतांक = k = 1.38 x 10-23 JK-1
दिया गया है औसत गतिज ऊर्जा
Kaverage = 3/2KT
= 1.5 × 1.38 × 10-23 x 300
Kaverage = 6.21 × 10-21 J.
न्यूट्रॉन का द्रव्यमान = m = 1.67 x 10-27 kg
माना न्यूट्रॉन का तरंगदैर्घ्य = λn = ?
सम्बन्ध सूत्र:
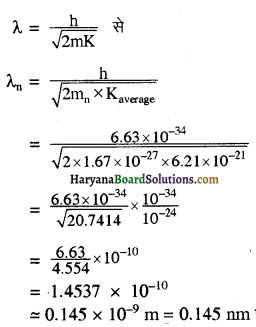
प्रश्न 11. 18.
यह दर्शाइए कि वैद्युतचुंबकीय विकिरण का तरंगदैर्ध्य इसके क्वांटम ( फोटॉन) के तरंगदैर्घ्य के बराबर है।
उत्तर:
वैद्युत चुम्बकीय विकिरण के लिए
c = Uλ
या
λ = c/v …..(i)
तथा फोटॉन के लिए
λ = h/p
लेकिन
E = pc होता है
p = E/c से λ का
λ = h/Ec = hc/E
λ = hc/hv
E = hv
λ = c/v ………(ii)
इस प्रकार डी ब्रोग्ली सम्बन्ध से तथा वैद्युत चुम्बकीय विकिरण के लिए A का मान समान है।

प्रश्न 11.19.
वायु में 300 K ताप पर एक नाइट्रोजन अणु का दे-ब्रॉग्ली तरंगदैर्ध्य कितना होगा? यह मानें कि अणु इस ताप पर अणुओं के चाल वर्ग माध्य से गतिमान है (नाइट्रोजन का परमाणु द्रव्यमान = 14.0076 u )
उत्तर:
दिया गया है:
तापमान T = 300 K
नाइट्रोजन के अणु का द्रव्यमान = m = 2 x 14.0076 u
= 2 × 14.0076 × 1.6606 x 10-27 kg
= 46.52 × 10-27 kg
डी- ब्रोग्ली तरंगदैर्घ्य =

अतिरिक्त अभ्यास प्रश्न (NCERT):
प्रश्न 11.20.
(a) एक निर्वात नली के तापित कैथोड से उत्सर्जित इलेक्ट्रॉनों की उस चाल का आकलन कीजिए जिससे वे उत्सर्जक की तुलना में 500V के विभवांतर पर रखे गए एनोड से टकराते हैं इलेक्ट्रॉनों के लघु प्रारंभिक चालों की उपेक्षा कर दें। इलेक्ट्रॉन का आपेक्षिक आवेश अर्थात् e/m = 1.76 x 1011 Ckg-1 है।
(b) संग्राहक विभव 10MV के लिए इलेक्ट्रॉन की चाल ज्ञात करने के लिए उसी सूत्र का प्रयोग करें, जो (a) में काम में लाया गया है। क्या आप इस सूत्र को गलत पाते हैं? इस सूत्र को किस प्रकार सुधारा जा सकता है?
उत्तर:
(a) दिया गया है:
विभवान्तर V = 500 Volt
e/m = 1.76 x 1011 C kg-1
हम जानते हैं
वेग \(\sqrt{\frac{2 \mathrm{eV}}{\mathrm{m}}}\)
∵ 1/2 mv2 = eV
मान रखने पर
वेग v = \(\sqrt{2 \times 1.76 \times 10^{11} \times 500}\)
= 1.33 × 107 m/s
V = 10 MV = 10 x 106 v
= 107 V
(b) दिया गया है:
वेग v = \(\sqrt{2 \times\left(\frac{\mathrm{e}}{\mathrm{m}}\right) \mathrm{V}}\)
= \(\sqrt{2 \times 1.76 \times 10^{11} \times 10^7}\)
= \(\sqrt{3.52 \times 10^{18}}\)
= 1.88 x 109 m/s
यदि हम V = 107 V के लिए उसी सूत्र का प्रयोग करें, तो “v = 1.88 × 109 ms-1 आता है। यह स्पष्ट रूप से गलत है, क्योंकि कोई भी द्रव्य कण प्रकाश के वेग ( c = 3 x 108 ms-1) से अधिक वेग से नहीं चल सकता। वस्तुतः गतिज ऊर्जा के लिए उपर्युक्त सूत्र (mv2/ 2 ) केवल (v/c) << 1 के लिए वैध है। बहुत अधिक चाल पर, जब (v/c) के लगभग तुल्य (यद्यपि हमेशा 1 से कम ) होता है, तो आपेक्षिकीय प्रभाव क्षेत्र के कारण निम्नलिखित सूत्र वैध होते हैं
आपेक्षिकीय संवेग p = mv
कुल ऊर्जा E = mc2
गतिज ऊर्जा K = mc72 – moc2
जहाँ आपेक्षिकीय द्रव्यमान ॥ निम्नानुसार दिया जाता है:
m = m0\(m_0\left(1-\frac{v^2}{c^2}\right)^{-1 / 2}\)
m0 कण का विराम द्रव्यमान कहलाता है। इन संबंधों से प्राप्त होता है:
E = \(\left(p^2 c^2+m_0^2 c^4\right)^{1 / 2}\)
ध्यान दीजिए कि आपेक्षिकीय प्रभाव क्षेत्र में, जब V/c लगभग 1 के बराबर होता है, तो कुल ऊर्जा E > m0c2 (विराम द्रव्यमान ऊर्जा)। इलेक्ट्रॉन की विराम द्रव्यमान ऊर्जा लगभग 0.51 Mev होती है। इसलिए 10 MeV की गतिज ऊर्जा, जो इलेक्ट्रॉन की विराम द्रव्यमान ऊर्जा से बहुत अधिक है, आपेक्षिकीय प्रभाव क्षेत्र को व्यक्त करती है। आपेक्षिकीय सूत्रों के प्रयोग से (10 Mev गतिज ऊर्जा के लिए) = 0.999 c
प्रश्न 11.21.
(a) एक समोर्जी इलेक्ट्रॉन किरण-पुंज जिसमें इलेक्ट्रॉन की चाल 5.20 x 106 ms-1 है, पर एक चुंबकीय क्षेत्र 1.30 x 10-4 T किरण-पुंज की चाल के लंबवत् लगाया जाता है। किरण-पुंज द्वारा आरेखित वृत्त की त्रिज्या कितनी होगी, यदि इलेक्ट्रॉन के e/m का मान 1.76 x 1011 Ckg है?
(b) क्या जिस सूत्र को (a) में उपयोग में लाया गया है। वह यहाँ भी एक 20 Mev इलेक्ट्रॉन किरण-पुंज की त्रिज्या परिकलित करने के लिए युक्तिपरक है? यदि नहीं तो किस प्रकार इसमें संशोधन किया जा सकता है?
उत्तर:
(a) दिया गया है:
इलेक्ट्रॉन की चाल = v = 5.20 x 106 m/s
चुम्बकीय क्षेत्र = B = 1.30 × 10-4 T
तथा
m = 1.76 x 1011 C kg-1
θ = 90°
इलेक्ट्रॉन पर चुम्बकीय क्षेत्र B द्वारा आरोपित बल
या
= qvB sin θ
= qvB × 1
∵ θ = 90°
F= qvB
यह बल वृत्त खींचने के लिए आवश्यक अभिकेन्द्रीय बल प्रदान करता है।
∴ qvB = mv2/r
या
r = mv2/qvB
या
r = mv/qB
या
r = mv/eB
∵ q = e
या
r = \(\frac{v}{\left(\frac{e}{m}\right) \times B}\)
मान रखने पर
r = \(\frac{5.20 \times 10^6}{1.76 \times 10^{11} \times 1.30 \times 10^{-4}}\)
= 0.227 m = 22.7 cm
(b) यहाँ पर दिया गया है
K = ऊर्जा = 20 Mev
K = 20 × 1.6 × 10-19 J
सम्बन्ध K = 1/2mv2 का उपयोग करने पर
या v = \(\) = \(\)
= 2.65 x 109 m/s
जो कि प्रकाश के वेग से अधिक है।
इसलिए 20 Mev इलेक्ट्रॉन किरण पुंज के r का आकलन करने के लिए स्थिति (a) में प्रयुक्त सूत्र अर्थात् r = mv/eB मान्य नहीं है या प्रामाणिक नहीं है; क्योंकि इतनी अधिक ऊर्जा के इलेक्ट्रॉन का वेग आपेक्षिकता क्षेत्र में है अर्थात् प्रकाश वेग के तुलनीय है तथा द्रव्यमान वेग बढ़ने के साथ परिवर्तित होता है; परन्तु हमने इसे स्थिर लिया है।
∴ m = \(\frac{\mathrm{m}_0}{\sqrt{1-\frac{\mathrm{v}^2}{\mathrm{c}^2}}}\) पर विचार किया जाना है।
अतएव रूपान्तरित किया हुआ समीकरण
r = \(\left(\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\right) \frac{v}{e B}\) हो जाता है।
प्रश्न 11.22.
एक इलेक्ट्रॉन गन जिसका संग्राहक 100 v विभव पर है, एक कम दाब (~10-2mm Hg) पर हाइड्रोजन से भरे गोलाकार बल्ब में इलेक्ट्रॉन छोड़ती है। एक चुंबकीय क्षेत्र जिसका मान 2.83 x 10-4 T है, इलेक्ट्रॉन के मार्ग को 12.0 cm त्रिज्या के वृत्तीय कक्षा में वक्रित कर देता है (इस मार्ग को देखा जा सकता है क्योंकि मार्ग में गैस आयन किरण-पुंज को इलेक्ट्रॉनों को आकर्षित करके और इलेक्ट्रॉन प्रग्रहण के द्वारा प्रकाश उत्सर्जन करके फोकस करते हैं: इस विधि को ‘परिष्कृत किरण-पुंज नली’ विधि कहते हैं।) आँकड़ों से e/m का मान निर्धारित कीजिए।
उत्तर:
दिया गया है:
V = 100 Volt
B = 2.83 × 10-4 T
r = 12.0 cm = 12 x 10-2 m
अब
K = 1⁄2mv-2 = eV
∴ mv-2 = 2eV
v 2 = 2ev/m ………… (i)
तथा वृत्ताकार पथ के लिए आवश्यक अभिकेन्द्रीय बल
mv2/r = evB
या
V = eBr/m
v2 = e2b2r2/m2 ………….. (ii)
समीकरण (i) व (ii) से
e2b2r2/m2 = 2ev/m
= e/m = 2v/b2r2 = \(\frac{2 \times 100}{\left(2.83 \times 10^{-4}\right) \times\left(12 \times 10^{-2}\right)^2}\)
= 1.734 × 1011 कूलॉम / किग्रा.

प्रश्न 11.23.
(a) एक X-किरण नली विकिरण का एक संतत स्पेक्ट्रम जिसका लघु तरंगदैर्घ्य सिरा 0.45 पर है, उत्पन्न करता है। विकिरण में किसी फोटॉन की उच्चतम ऊर्जा कितनी है? (b) अपने (a) के उत्तर से अनुमान लगाइए कि किस कोटि की त्वरक वोल्टता (इलेक्ट्रॉन के लिए) की इस नली में आवश्यकता है?
उत्तर:
(a) दिया गया है:
λmin = 0.45 A
= 0.45 x 10-10 m
∴ Emax = hc/λmin
लेकिन हम जानते हैं:
h= 6.63 × 10-4 Js.
c = 3 x 108 m/s
मान रखने पर
Emax = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{0.45 \times 10^{-10}}\)
= \(\frac{6.63 \times 3 \times 10^{-16}}{0.45}\)
= \(\frac{19.89 \times 10^{-15}}{4.5}\)
= 4.42 × 10-15 J
= \(\frac{4.42 \times 10^{-15}}{1.6 \times 10^{-16}} \mathrm{KeV}\)
= 27.6 KeV
(b) Kmax = eV
∴ V = kmax/e
= \(\frac{4.42 \times 10^{-15}}{1.6 \times 10^{-19}} \mathrm{~V}\)
= 27.61 × 103‘ v
= 27.61 KV
∴ त्वरण विभव की कोटि = 30 KV है।
प्रश्न 11.24.
एक त्वरित्र (accelerator) प्रयोग में पाजिट्रॉनों (e) के साथ इलेक्ट्रॉनों के उच्च ऊर्जा संघट्टन पर, एक विशिष्ट घटना की व्याख्या कुल ऊर्जा 10.2 Bev के इलेक्ट्रॉन- पाजिट्रॉन युग्म के बराबर ऊर्जा की दो -किरणों में विलोपन के रूप में की जाती है। प्रत्येक y-किरण से संबंधित तरंगदैघ्यों के मान क्या होंगे? (1 BeV = 109 ev)
उत्तर:
y – किरणों के युग्म द्वारा ले जाने वाली ऊर्जा की मात्रा
= 10.2 BeV
∴ प्रत्येक किरण की ऊर्जा है।
E = 102/2 = 5.1 BeV
= 5.1 × 109 ev
= 5.1 x 109 x 1.6 x 10-19 J = 8.16 × 10-10 J
हम जानते हैं:
E = hc/λ का उपयोग करने पर
λ = hc/E
मान रखने पर
λ = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{8.16 \times 10^{-10}}\)
= \(\frac{19.89 \times 10^{-16}}{8.16}\)
= 2.44 x 10-16m
प्रश्न 11.25
आगे आने वाली दो संख्याओं का आकलन रोचक हो सकता है। पहली संख्या यह बताएगी कि रेडियो अभियांत्रिक फोटॉन की अधिक चिंता क्यों नहीं करते। दूसरी संख्या आपको यह बताएगी कि हमारे नेत्र ‘फोटॉनों की गिनती क्यों नहीं कर सकते, भले ही प्रकाश साफ-साफ संसूचन योग्य हो।
(a) एक मध्य तरंग (medium wave) 10 kW सामर्थ्य के प्रेषी, जो 500m तरंगदैर्ध्य की रेडियो तरंग उत्सर्जित करता है, के द्वारा प्रति सेकंड उत्सर्जित फोटॉनों की संख्या।
(b) निम्नतम तीव्रता का श्वेत प्रकाश जिसे हम देख सकते हैं (~10-10 Wm2) के संगत फोटॉनों की संख्या जो प्रति सेकंड हमारे नेत्रों की पुतली में प्रवेश करती है। पुतली का क्षेत्रफल लगभग 0.4 cm2 और श्वेत प्रकाश की औसत आवृत्ति को लगभग 6 x 1014 Hz मानिए।
उत्तर:
दिया गया है;
P = 10 kW = 10 x 1000 W
= 104 W
λ = 500m
(a) प्रति सेकण्ड उत्सर्जित फोटॉन की संख्या

∴ n = p/E
हम जानते हैं:
E = hc/λ
= \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{500}\)
= 3.98 × 10-28 J
∴ n = p/E = \(\frac{10^4}{3.98 \times 10^{-28}}\)
= 10/3.98 × 1031
= 2.52 × 1031 = 3 x 1031 S-1
हम देखते हैं कि रेडियोफोटॉन की ऊर्जा बहुत कम है और रेडियो पुंज में प्रति सेकंड उत्सर्जित फोटॉनों की संख्या बहुत अधिक है। इसलिए यहाँ ऊर्जा के न्यूनतम क्वांटम ( फोटॉन) के अस्तित्व को उपेक्षित करने और रेडियो तरंग की कुल ऊर्जा को सतत मानने में नगण्य त्रुटि आती है।
(b) न्यूनतम तीव्रता का मान 1= 10-10 Wm-2
आँख की पुतली का क्षेत्रफल = A = 0.4 cm2
∴ A = 0.4 x 10-4 m-2
माध्य आवृत्ति V = 6 × 1014 Hz
∴ प्रत्येक फोटॉन की ऊर्जा का मान = E = hv
E = 6.63 × 1034 x 6 × 1014
= 39.78 x 10-20
= 3.98 × 10-19 J = 4 x 10-19 J
आवृत्ति v = 6 × 1014 Hz के लिए E = 4 x 10-19 J
न्यूनतम तीव्रता के संगत फोटॉनों का अभिवाह (फ्लक्स)
Φ = T/E = \(\frac{10^{-10}}{4 \times 10^{-19}}\) = 25 x 108
4 = 2.5 x 108 m-2 S-1
आँख की पुतली में प्रवेश करने वाले फोटॉनों की संख्या प्रति सेकंड sal 10ts- यद्यपि यह फोटॉनों = 2.5 × 108 x 0.4 x 10-4 S-1 की संख्या (a) की तरह अत्यधिक नहीं है, फिर भी हमारे लिए यह काफी अधिक है, क्योंकि हम कभी भी अपनी आँखों से फोटॉनों को न तो अलग-अलग देख सकते हैं, न ही गिन सकते हैं।

प्रश्न 11.26.
एक 100 W पारद (Mercury) स्रोत से उत्पन्न 2271 Å तरंगदैर्घ्य का पराबैंगनी प्रकाश एक मालिब्डेनम धातु से निर्मित प्रकाश सेल को विकिरित करता है। यदि निरोधी विभव 1.3 V हो, तो धातु के कार्य फलन का आकलन कीजिए। एक He Ne लेसर द्वारा उत्पन्न 6328 A के उच्च तीव्रता (10<sup5 w m2 ) के लाल प्रकाश के साथ प्रकाश सेल किस प्रकार अनुक्रिया करेगा?
उत्तर:
दिया गया है:
शक्ति P = 100 W
निरोधी विभव Vo = 1.3 V (परिमाण)
अवरक्त प्रकाश का तरंगदैर्घ्य = 6328 x 10-10 m
प्लांक नियतांक = h = 6.63 × 10-4 JS
c = 3 × 108m/s
UV प्रकाश का तरंगदैर्घ्य = u = 2271 Å
= 2271 × 10-10 m
धातु का कार्यफलन = Φo = ?
आइन्सटीन का प्रकाश विद्युत समीकरण का उपयोग करने पर
hv = Φ0 + ev0
∴ Φ0 = hv – ev0
या
Φ0 = hc/λ – eV0
= \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{2271 \times 10^{-10}}\) – 1.6 × 10-19 × 1.3
= 8.76 x 10-19 – 2.08 x 10-19
= 6.68 × 10-19 J
= \(\frac{6.68 \times 10^{-19}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 4.175 eV = 4.2 ev
पुनः तरंगदैर्घ्य λ1 = 6328 A = 6328 x 10-10 मी. के संगत
फोटॉन ऊर्जा
E1 = hc/λ1 = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{6328 \times 10^{-10}}\)
= 3.14 × 10-19 J
= \(\frac{3.14 \times 10^{-19}}{1.6 \times 10^{-19}}\)
= 1.97 ev
स्पष्टतः E1 < Φ0 अतः इस लाल प्रकाश के लिए प्रकाश सेल, फोटो इलेक्ट्रॉन उत्सर्जित नहीं करेगा चाहे इसकी तीव्रता कितनी ही क्यों न हो।
प्रश्न 11.27.
एक नियॉन लैंप से उत्पन्न 640.2nm (1nm = 10-9 m ) तरंगदैर्घ्य का एकवर्णी विकिरण टंग्स्टन पर सीजियम से निर्मित प्रकाशसंवेदी पदार्थ को विकिरित करता है। निरोधी वोल्टता 0.54 मापी जाती है। स्रोत को एक लौह-स्रोत से बदल दिया जाता है। इसकी 427.2nm वर्ण-रेखा उसी प्रकाश सेल को विकिरित करती है। नयी निरोधी बोल्टता ज्ञात कीजिए ।
उत्तर:
दिया गया है:
A = 640.2 nm
= 640.2 × 10-9m
निरोधी वोल्टता = Vo = 0.54 V
आइन्सटीन का विद्युत प्रभाव समीकरण से
पहले स्रोत के लिए eV0 = ho – Φ0 का उपयोग करने पर
या
Φ0 = hv – eVo
= hc/λ – eVo
मान रखने पर =
= \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{640.2 \times 10^{-9}}\) – 1.6 x 10-19 × 0.54
= 3.10 x 10-19 – 8.64 × 10-20
= 3.10 × 10-19 – 0.864 x 10-19
= 2.236 × 10-19 = 2.24 × 10-19 J
∴ Φo = \(\frac{2.24 \times 10^{-19}}{1.6 \times 10^{-19}} \mathrm{eV}\)eV = 1.40 V
दूसरे स्रोत के लिए
λ = 427.2nm
= 427.2 × 10-9 m
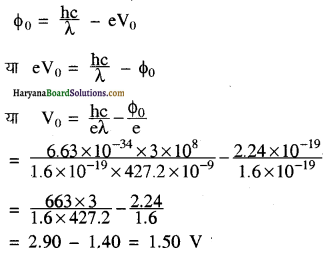
प्रश्न 11. 28.
एक पारद लैंप, प्रकाश-विद्युत उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्रोत है, क्योंकि यह दृश्य – स्पेक्ट्रम के पराबैंगनी (UV) से लाल छोर तक कई वर्ण-रेखाएँ उत्सर्जित करता है। रूबीडियम प्रकाश सेल के हमारे प्रयोग में, पारद (Mercury) स्रोत की निम्न वर्ण-रेखाओं का प्रयोग किया गया:
λ1 = 3650Å, λ2 = 4047 Å, λ3 = 4358 Å. λ4 = 5461 Å, λ5 = 6907 Å,
निरोधी वोल्टताएँ, क्रमशः निम्न मापी गई:
V01 = 1.28 V, Vo2 = 0.95 V, Vo3 = 0.74 V, V04 = 0.16 V, Vo5 = 0V
(a) प्लॅक स्थिरांक h का मान ज्ञात कीजिए।
(b) धातु के लिए देहली आवृत्ति तथा कार्य-फलन का आकलन कीजिए।
[नोट-उपर्युक्त आँकड़ों से h का मान ज्ञात करने के लिए आपको e = 1.6 x 10-19 C की आवश्यकता होगी। इस प्रकार के प्रयोग Na, Li, K आदि के लिए मिलिकन ने किए थे। मिलिकन ने अपने तेल बूँद प्रयोग से प्राप्त के मान का उपयोग कर आइंस्टाइन के प्रकाश-विद्युत समीकरण को सत्यापित किया तथा इन्हीं प्रेक्षणों से h के मान के लिए पृथक् अनुमान लगाया।]
उत्तर:
(a) दिये गये तरंगदैर्घ्य के मान से विकिरण आवृत्ति ज्ञात करने पर
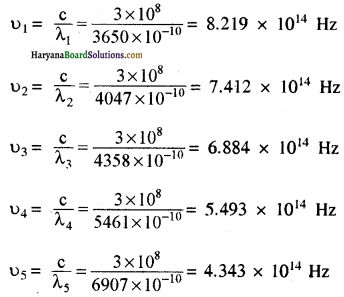
प्रकाश विद्युत समीकरण से
eV0 = ho – ¢o ………… (1)
∴ Vo = hv/e – ¢o/e
यह एक सरल रेखा का समीकरण है अतः v तथा Vo बीच ग्राफ सरल रेखा प्राप्त होगी, जिसका ढाल होगा
h/e = ∆v0/∆v = \(\frac{V_{01}-V_{04}}{v_1-v_4}\)
= \(\frac{1.28-0.16}{(8.219-5.493) \times 10^{14}}\)
= 4.15 × 10-15 Vs
h = 4.15 × 10-15 x e
= 4.15 × 10-15 x 1.6 x 10-19
= 6.64 × 10-34 Js
(b) समीकरण (1) का उपयोग करने पर कार्यफलन
¢o = hv – eVo
= hc/λ – eVo
या
¢o = hc/λ2 – ev02
= \(\frac{6.64 \times 10^{-34} \times 3 \times 10^8}{4047 \times 10^{-10}}\) – 1.6 x 10-19 × 0.95
= 4.89 × 10-19 – 1.52 x 10-19
= 3.37 × 10-19J = \(\frac{3.37 \times 10^{-19}}{1.6 \times 10^{-19}}\) = 2.11ev
देहली आवृत्ति vo = ¢o/h = \(\frac{3.37 \times 10^{-19}}{6.64 \times 10^{-34}}\)
= 5.11 × 1014 Hz

प्रश्न 11.29.
निम्न धातुओं के कार्य-फलन निम्न प्रकार दिए गए हैं:
Na: 2.75 eV; K: 2.30 eV; Mo: 4.17 eV; Ni: 5.15 EV इनमें धातुओं में से कौन प्रकाश सेल से 1m दूर रखे गए He Cd लेसर से उत्पन्न 3300 À तरंगदैर्ध्य के विकिरण के लिए प्रकाश-विद्युत उत्सर्जन नहीं देगा? लेसर को सेल के निकट 50 cm दूरी पर रखने पर क्या होगा?
उत्तर:
दिया गया है:
λ = 3300 A = 3300 x 10-10 m
= 33 × 10-8 m
दूरी r = 1m
तथा r’ = 50 cm = 1/2
E = hv = उपयोग करने पर
E = hc/λ
मान रखने पर
E = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{33 \times 10^{-8}}\)
= 663/11 × 10-18
= 6.02 × 10-19 J
= \(\frac{6.02 \times 10^{-19}}{1.6 \times 10^{-19}} \mathrm{eV}\)
E = 3.76 eV
जो Na और K के से छोटा इसलिए Na और r’ = 50 cm = 0.50m लिए 40 से बड़ा है और Mo और Ni K में उत्सर्जन होगा। अब r = 1m, यदि लेसर को निकट लाया जाये, आपतित विकिरण की तीव्रता बढ़ जाती है। यह Mo और Ni धातुओं के परिणामों को प्रभावित नहीं करता, जबकि Na और K से उत्सर्जित प्रकाश वैद्युत बढ़ जायेगा जो तीव्रता के अनुपाती है।
∵ I α 1/R2 होता है।
और 4 गुना हो जाता है जबकि r1 = 1⁄2r
प्रश्न 11.30
10-5 Wm-2 तीव्रता का प्रकाश एक सोडियम प्रकाश सेल के 2 cm2 क्षेत्रफल के पृष्ठ पर पड़ता है। यह मान लें कि ऊपर की सोडियम की पाँच परतें आपतित ऊर्जा को अवशोषित करती हैं, तो विकिरण के तरंग चित्रण में प्रकाश-विद्युत उत्सर्जन के लिए आवश्यक समय का आकलन कीजिए धातु के लिए कार्य फलन लगभग 2 ev दिया गया है। आपके उत्तर का क्या निहितार्थ है?
उत्तर:
दिया गया है:
I = 10-3 Wm-2
A = 2 cm2 = 2 x 10-4m2
Φ0 = 2ev
= 2 × 1.6 × 10-19 J
= 3.2 × 10-19 J
परमाणु की लगभग त्रिज्या 10-10 m लेने पर सोडियम परमाणु
का प्रभावी क्षेत्रफल r2 = 10-20 m
∴ Na की 5 परतों में परमाणुओं की संख्या

= \(\frac{5 \times 2 \times 10^{-4}}{10^{-20}}\)
आपतित शक्ति P = IA
P = 105 × 2 × 104
= 2 × 10-9 w
तरंग चित्रण (प्रकृति) में आपतित शक्ति सभी इलेक्ट्रॉनों द्वारा सतत रूप से एकसमान अवशोषित होती है। परिणामस्वरूप प्रति इलेक्ट्रॉन प्रति सेकण्ड अवशोषित ऊर्जा
= \(\frac{2 \times 10^{-9}}{10^{17}}\) = 2 ×10-26 W
प्रकाश विद्युत उत्सर्जन के लिए आवश्यक समय
= \(\frac{3.2 \times 10^{-19}}{2 \times 10^{-26}}\)
= 1.6 x 107 S
जो कि लगभग आधा (0.5) वर्ष है।
महत्त्व – प्रायोगिक रूप से, प्रकाश-विद्युत उत्सर्जन लगभग तात्क्षणिक (-109 S) प्रेक्षित होता है। इसलिए तरंग प्रकृति प्रयोग से पूर्ण असहमति में है। फोटॉन-चित्रण में, ऊपरी सतह में विकिरण की ऊर्जा सभी इलेक्ट्रॉनों द्वारा समान रूप से साझित नहीं होती है बल्कि ऊर्जा असतत ‘क्वांटा’ के रूप में आती है और ऊर्जा का अवशोषण धीरे- धीरे नहीं होता। फोटॉन या तो अवशोषित नहीं होता है, या लगभग तात्क्षणिक रूप से इलेक्ट्रॉन द्वारा अवशोषित होता है।
प्रश्न 11.31.
X – किरणों के प्रयोग अथवा उपयुक्त वोल्टता से त्वरित इलेक्ट्रानों से क्रिस्टल- विवर्तन प्रयोग किए जा सकते हैं। कौन-सी जाँच अधिक ऊर्जा संबद्ध है? [परिमाणिक तुलना के लिए, जाँच के लिए तरंगदैर्घ्य को 1 Å लीजिए, जो कि जालक (लेटिस) में अंतर- परमाणु अंतरण की कोटि का है ] (me = 9.11 x 10-31 kg )।
उत्तर:
दिया गया है:
तरंगदैर्घ्य = λ = 1 Å = 10-10 m
mc = 9.11 x 10-31 kg
फोटॉन की ऊर्जा
= E = hv = hc/λ
E = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{10^{-10}}\)
= 19.89 × 10-16 J
= \(\frac{19.89 \times 10^{-16}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 12.43 Kev
इलेक्ट्रॉन की स्थिति में

λ = 1 Å के लिए, इलेक्ट्रॉन की ऊर्जा = 150 ev समान तरंगदैर्ध्य के लिए फोटॉन की ऊर्जा, इलेक्ट्रॉन की ऊर्जा से काफी अधिक होती है।
प्रश्न 11.32.
(a) एक न्यूट्रॉन, जिसकी गतिज ऊर्जा 150 ev है, का दे-ब्रॉग्ली तरंगदैर्घ्य प्राप्त कीजिए। जैसा कि आपने अभ्यास 11.31 में देखा है, इतनी ऊर्जा का इलेक्ट्रॉन किरण-पुंज क्रिस्टल विवर्तन प्रयोग के लिए उपयुक्त है क्या समान ऊर्जा का समान रूप में उपयुक्त एक न्यूट्रॉन किरण-पुंज इस प्रयोग के लिए होगा? स्पष्ट कीजिए। (ma = 1.675 × 10-27kg )
(b) कमरे के सामान्य ताप (27 °C) पर ऊष्मीय न्यूट्रॉन से जुड़े दे-ब्रॉग्ली तरंगदैर्ध्य ज्ञात कीजिए। इस प्रकार स्पष्ट कीजिए कि
क्यों एक तीव्रगामी न्यूट्रॉन को न्यूट्रॉन-विवर्तन प्रयोग में उपयोग में लाने से पहले वातावरण के साथ तापीकृत किया जाता है।
हल
दिया गया है:
न्यूट्रॉन की गतिज ऊर्जा =
K = 150eV = 150 x 1.6 x 109 J
λ = ?
m, = 1.675 x 10-27 kg
T = (27 + 273 ) K = 300K
(a) हम जानते हैं
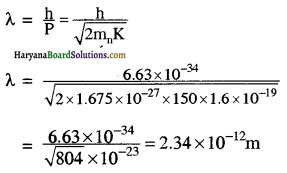
= 2.34 x 10-12 m
अंतरापरमाण्विक (Interatomic) दूरियाँ इससे लगभग सौ गुना बड़ी हैं। इसलिए 150eV ऊर्जा का न्यूट्रॉन-पुंज विवर्तन प्रयोगों के लिए उपयुक्त नहीं है।
(b) T = (27 + 273) K = 300K
न्यूट्रॉन की ऊर्जा (कक्ष ताप पर )
गतिज ऊर्जा (K) = E = 3/2KT
E = 3/2KT
λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{mK}}}\)
λ = \(\frac{\mathrm{h}}{\sqrt{3 \mathrm{mkT}}}\)
= \(\frac{6.63 \times 10^{-34}}{\sqrt{3 \times 1.675 \times 10^{-27} \times 1.38 \times 10^{-23} \times 300}}\)
λ = \(\frac{6.63 \times 10^{-34} \times 10^{24}}{\sqrt{9 \times 1.675 \times 1.38}}\)
= 1.45 × 10-10 m = 1.45 A
यह तरंगदैर्घ्य, परमाण्वीय दूरी 1 (10-10 मी.) की कोटि की है। अतः विवर्तन प्रयोग में ये तापीय ऊर्जा के न्यूट्रॉन उपयुक्त हैं यही कारण है कि उच्च ऊर्जा के न्यूट्रॉन पुंज से विवर्तन प्रयोग के लिए पहले उन्हें वातावरण के साथ तापीकृत किया जाता है।

प्रश्न 11.33.
एक इलेक्ट्रॉन सूक्ष्मदर्शी में 50kV वोल्टता के द्वारा त्वरित इलेक्ट्रॉनों का उपयोग किया जाता है। इन इलेक्ट्रॉनों से जुड़े दे-ब्रॉग्ली तरंगदैर्ध्य ज्ञात कीजिए। यदि अन्य बातों (जैसे कि संख्यात्मक द्वारक, आदि) को लगभग समान लिया जाए, इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन क्षमता की तुलना पीले प्रकाश का प्रयोग करने वाले प्रकाश सूक्ष्मदर्शी से किस प्रकार होती है?
उत्तर:
दिया गया है:
त्वरण विभव = V = 50 kV
= 50 x 103 V = 5 x 104 v
mg = 9.1 × 10-31 kg
e = 1.6 x 10-19 C
h = 6.63 × 10-34 J
इलेक्ट्रॉन का तरंगदैर्घ्य = λ = ?
इलेक्ट्रॉन की ऊर्जा = K = ?
K = 1⁄2mv2 = eV
द्वारा इलेक्ट्रॉन की ऊर्जा दी जाती है।
K = 1.6 x 10-19 x 5 x 104
= 8 × 10-15 J
सूत्र λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{mK}}}\) का उपयोग करने पर
λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{~m}_{\mathrm{e}} \mathrm{K}}}\) प्राप्त करते हैं।
या
λ = \(\frac{6.63 \times 10^{-34}}{\sqrt{2 \times 9.1 \times 10^{-31} \times 8 \times 10^{-15}}}\)
λ = \(\frac{6.63 \times 10^{-34}}{12.07 \times 10^{-23}}\)
= 5.5 x 10-12 m
पीले प्रकाश के लिए भी λy = 5990A
= 5990 x 10-10 m
हम जानते हैं कि सूक्ष्मदर्शी की विभेदन क्षमता उपयुक्त प्रकाश विकिरण के तरंगदैर्घ्य के व्युत्क्रमानुपाती होती है।
अर्थात् R.P. (Resolving Power) α 1/λ
इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन क्षमता प्रकाशिक सूक्ष्मदर्शी की विभेदन क्षमता

= 1.1 × 105
अर्थात् इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन क्षमता (Resolving Power) प्रकाशिक सूक्ष्मदर्शी की विभेदन क्षमता से 105 गुणा अधिक होती है।
प्रश्न 11.34.
किसी जाँच की तरंगदैर्घ्य उसके द्वारा कुछ विस्तार में जाँच की जा सकने वाली संरचना के आकार की लगभग आमाप है। प्रोटॉनों तथा न्यूट्रॉनों की क्वार्क (quark) संरचना 10-15m या इससे भी कम लंबाई के लघु पैमाने की है। इस संरचना को सर्वप्रथम 1970 के दशक के प्रारंभ में, एक रेखीय त्वरित्र (Linear accelerator) से उत्पन्न उच्च ऊर्जा इलेक्ट्रॉनों के किरण-पुंजों के उपयोग द्वारा, स्टैनफोर्ड, संयुक्त राज्य अमेरिका में जाँचा गया था। इन इलेक्ट्रॉन किरण-पुंजों की ऊर्जा की कोटि का अनुमान लगाइए (इलेक्ट्रॉन की विराम द्रव्यमान ऊर्जा 0.511 Mev है।)
उत्तर:
दिया गया है:
A = 10-15 m
इलेक्ट्रॉन की विराम द्रव्यमान ऊर्जा = mc2 = 0.511
M0C2 = 0.511 × 100 × 1.6 x 10-19 J
= 8.18 x 10-14J
सूत्र λ = h/p का उपयोग करने पर
या
p = h/λ
= 6.63 x 10-19 kgms-1
कण के लिए ऊर्जा का आपेक्षिक सूत्र का उपयोग करने पर
E2 = m02c4 + p2c2
E2 = (m0c2 )2 + p2c2
= (8.18 x 10-14) 2 + ( 6.63 x 10-19)2 x (3 × 108)2
= 66.91 × 10-28 + 43.96 x 10-38 x 9 x 1016
= 0.6691. x 10-26 + 3.96 x 10-20
प्रथम पद, द्वितीय पंद की तुलना में नगण्य है अतः
E2= 3.96 × 10-20
E = \(\sqrt{3.96 \times 10^{-20}}\)
= 1.99 × 10-10 J
= \(\frac{1.99 \times 10^{-10}}{1.6 \times 10^{-19}} \mathrm{eV}\)
= 1.24 × 109 ev
∴ E = 1.24 BeV
( ∵ 1 BeV = 109 eV)
अतः त्वरक (Accelerator) से निकले इलेक्ट्रॉन की ऊर्जा कुछ BeV की कोटि की अवश्य होनी चाहिए।
प्रश्न 11.35.
कमरे के ताप (27 °C) और 1 atm दाब पर He परमाणु से जुड़े प्रारूपी दे ब्रॉग्ली तरंगदैर्ध्य ज्ञात कीजिए और इन परिस्थितियों में इसकी दूरी से कीजिए।
उत्तर:
दिया गया है:
T = (27 + 273) K = 300K
तुलना दो परमाणुओं के बीच औसत
He परमाणु के लिए
m = 4mg
जहाँ mn एक न्यूक्लिऑन का द्रव्यमान है।
mg = 1.675 x 10-27 kg
∴ m = 4 × 1.675 × 10-27 kg
= 6.67 x 10-27 kg
गतिज ऊर्जा
K = 3/2kT
= 3/2 x 1.38 × 1023 x 300 J
हम जानते हैं:
λ = \(\frac{h}{\sqrt{2 \mathrm{mK}}}\) = \(\frac{h}{\sqrt{2 m \times \frac{3}{2} k T}}\)
मान रखने पर
λ = \(\frac{6.63 \times 10^{-34}}{\sqrt{2 \times 6.67 \times 10^{-27} \times \frac{3}{2} \times 1.38 \times 10^{-23} \times 300}}\)
= \(\frac{6.63 \times 10^{-34} \times 10^{24}}{\sqrt{6.67 \times 9 \times 1.38}}\)
= \(\frac{6.63 \times 10^{-10}}{\sqrt{82.84}}\)
= 0.73 Å
अब PV = RT = kNT
या V/N = KT/P
परमाणुओं के बीच माध्य पृथक्करण
r0 = (V/N)1/3 = (kT/P)1/3
यहाँ पर P = 1.01 x 105 Nm2 (परमाणुक दाब है)
ro = 3.4 x 109 m
ro = 34 A
समीकरण (i) तथा (ii) से
ro/λ = 34/0.73 = 3400/73 46.58
= 46.58
स्पष्टतः हीलियम परमाणुओं के बीच की दूरी, डी-ब्रॉग्ली तरंगदैर्घ्य की तुलना में बहुत अधिक होती है।

प्रश्न 11.36.
किसी धातु में (27 °C) पर एक इलेक्ट्रॉन का प्रारूपी दे-ब्रॉग्ली तरंगदैर्घ्य परिकलित कीजिए और इसकी तुलना धातु में दो इलेक्ट्रॉनों के बीच औसत पृथक्य से कीजिए जो लगभग 2 x 10-10 m दिया गया है।
[नोट- अभ्यास 11.35 और 11.36 प्रदर्शित करते हैं कि जहाँ सामान्य परिस्थितियों में गैसीय अणुओं से जुड़े तरंग पैकेट अ- अतिव्यापी हैं किसी धातु में इलेक्ट्रॉन तरंग पैकेट प्रबल रूप से एक-दूसरे से अतिव्यापी हैं। यह सुझाता है कि जहाँ किसी सामान्य गैस में अणुओं की अलग पहचान हो सकती है, किसी धातु में इलेक्ट्रॉन की एक-दूसरे से अलग पहचान नहीं हो सकती। इस अप्रभेद्यता की कई मूल निहितार्थताएँ हैं जिन्हें आप भौतिकी के अधिक उच्च पाठ्यक्रमों में जानेंगे ।]
उत्तर:
दिया गया है:
t = 27 °C
T = 27 + 273 = 300 K
धातु में दो इलेक्ट्रॉनों के बीच औसत पृथक्कीकरण
r0 = 2 × 10-10 m
= 2 A
दे- ब्रॉग्ली तरंगदैर्घ्य = λ = ?
हम जानते हैं
इलेक्ट्रॉन का द्रव्यमान = mc = 9.1 x 10-31 kg
h = 6.63 × 10-34 JS
वोल्ट्जमान नियतांक k = 1.38 x 10-23 JK-1 mol-1
T पर इलेक्ट्रॉन की गतिज ऊर्जा = K = 3/2T
∴ इलेक्ट्रॉन का दे ब्रॉग्ली तरंगदैर्ध्य
λ = \(\frac{h}{\sqrt{2 m K}}\) के उपयोग से
λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{~m}_{\mathrm{c}} \times \frac{3}{2} \mathrm{kT}}}\) = \(\frac{\mathrm{h}}{\sqrt{3 m_{\mathrm{e}} \mathrm{kT}}}\)
मान रखने पर λ = \(\frac{6.63 \times 10^{-34}}{\sqrt{3 \times 9.1 \times 10^{-31} \times 1.38 \times 10^{-23} \times 300}}\)
= 6.2 × 10-9 m
= 62 × 10-10 m
∴ λ/r0 = \(\frac{62 \times 10^{-10}}{2 \times 10^{-10}}\)
अतः λ >> ro
अर्थात् धातुओं में तरंग पैकेट एक-दूसरे को अतिव्यापित करते हैं। गैसीय परमाणुओं में यह नहीं होता है।
प्रश्न 11.37.
निम्न प्रश्नों के उत्तर दीजिए:
(a) ऐसा विचार किया गया है कि प्रोटॉन और न्यूट्रॉन भीतर क्वार्क पर आंशिक आवेश होते हैं [ ( +2/3)e; (-1/3)e ]। यह मिलिकन तेल-बूँद प्रयोग में क्यों नहीं प्रकट होते?
(b) e / m संयोग की क्या विशिष्टता है? हम e तथा m के विषय में अलग-अलग विचार क्यों नहीं करते?
(c) गैसें सामान्य दाब पर कुचालक होती हैं परंतु बहुत कम दाब पर चालन प्रारंभ कर देती हैं। क्यों?
(d) प्रत्येक धातु का एक निश्चित कार्य फलन होता है। यदि आपतित विकिरण एकवर्णी हो तो सभी प्रकाशिक इलेक्ट्रॉन समान ऊर्जा के साथ बाहर क्यों नहीं आते हैं? प्रकाशिक इलेक्ट्रॉनों का एक ऊर्जा वितरण क्यों होता है?
(e) एक इलेक्ट्रॉन की ऊर्जा तथा इसका संवेग इससे जुड़े पदार्थ तरंग की आवृत्ति तथा इसके संबंधित होते हैं
तरंगदैर्घ्य के साथ निम्न प्रकार
E = ho, p = h/v
परंतु 2 का मान जहाँ भौतिक महत्त्व का है, 0 के मान (और इसलिए कला चाल 02 का मान ) का कोई भौतिक महत्त्व नहीं है। क्यों?
उत्तर:
(a) क्वार्क, न्यूट्रॉन या प्रोटॉन में ऐसे बलों से बँधे माने जाते हैं, जो उनको दूर खींचने पर प्रबल होते हैं। इसलिए ऐसा प्रतीत होता है कि यद्यपि प्रकृति में भिन्नात्मक आवेश हो सकते हैं, तथापि प्रेक्षणीय आवेश के पूर्ण गुणज होते हैं।
(b) विद्युत तथा चुम्बकीय क्षेत्रों के लिए क्रमशः दोनों मूल सम्बन्ध eV = (1/2) mv2 या eE = ma तथा eBv=mv2 / r, प्रदर्शित करते हैं कि इलेक्ट्रॉन की गतिकी एवं m दोनों द्वारा अलग-अलग निर्धारित नहीं होती, बल्कि e/m द्वारा निर्धारित होती है।
(c) निम्न दाबों पर आयनों की उनके संगत इलेक्ट्रोडों पर पहुँचने और धारा की रचना करने की सम्भावना होती है। सामान्य दाबों पर, गैस अणुओं से टक्कर और पुनर्संयोजन के कारण आयनों की ऐसी कोई सम्भावना नहीं होती।
(d) कार्य फलन, इलेक्ट्रॉन को चालन बैंड के ऊपरी स्तर से धातु से बाहर निकालने के लिए आवश्यक न्यूनतम ऊर्जा मात्र है। धातु के सभी इलेक्ट्रॉन इस स्तर (ऊर्जा अवस्था) में नहीं होते। वे स्तरों की संतत बैंड में रहते हैं। परिणामस्वरूप एक ही आपतित विकिरण के लिए विभिन्न स्तरों से निकले इलेक्ट्रॉन, विभिन्न ऊर्जाओं के साथ निर्गत होते हैं।
(e) किसी कण की ऊर्जा E (न कि संवेग p) का परम मान एक योगात्मक स्थिरांक के अधीन स्वतंत्र है इसलिए जहाँ भौतिक रूप से महत्वपूर्ण है, वहीं एक इलेक्ट्रॉन की द्रव्य तरंग के लिए के परम मान का कोई सीधा भौतिक महत्व नहीं होता है। इसी तरह कला चाल vi भी भौतिक कण से महत्वपूर्ण नहीं है समूह चाल भौतिक रूप से अर्थपूर्ण है।
![]()
![]()
![]()
![]()

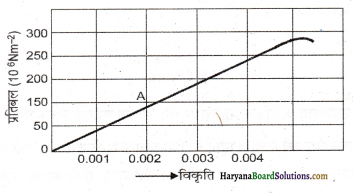
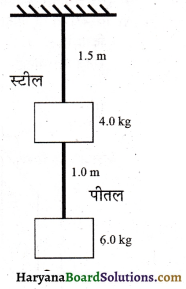
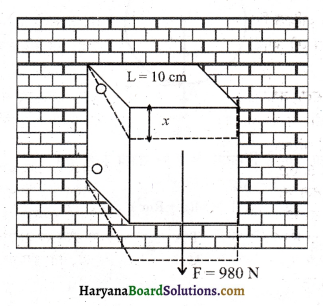


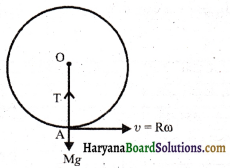
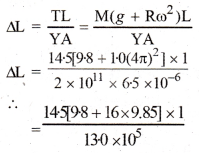
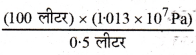

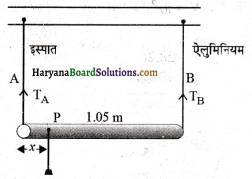
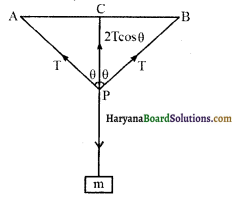

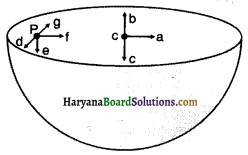
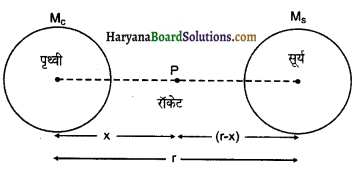



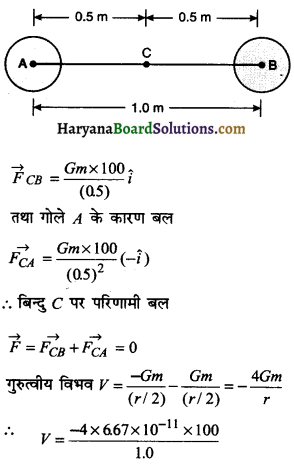

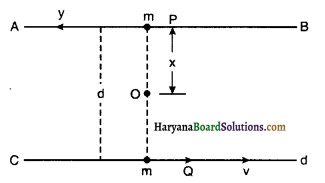
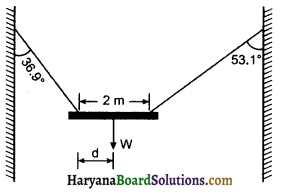
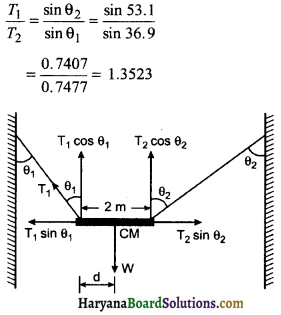
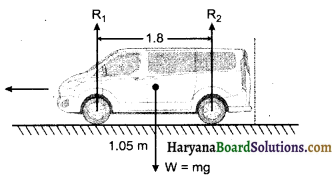
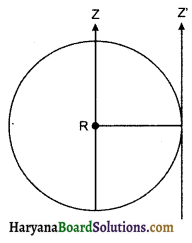
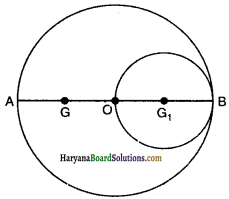
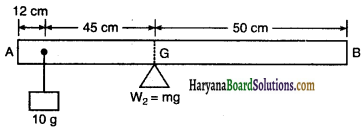
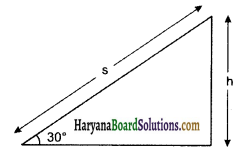

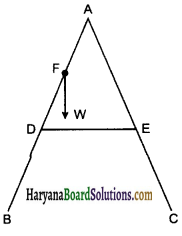
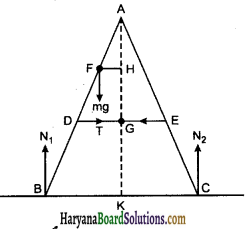
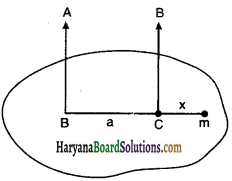
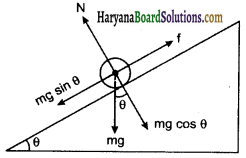
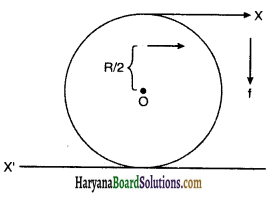
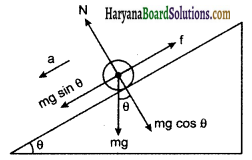
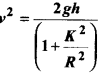 को गतिकीय दृष्टि (अर्थात् बलों तथा बल आघूर्णो के विचार) से व्युत्पन्न कीजिए। जहाँ लोटनिक गति करते पिण्ड (वलय, डिस्क, बेलन या गोला) का आनत तल की तली में वेग है। आनत तल पर वह ऊँचाई है जहाँ से पिण्ड गति प्रारम्भ करता है। K सममित अक्ष के परितः पिण्ड की घूर्णन त्रिज्या है और R पिण्ड की त्रिज्या है।
को गतिकीय दृष्टि (अर्थात् बलों तथा बल आघूर्णो के विचार) से व्युत्पन्न कीजिए। जहाँ लोटनिक गति करते पिण्ड (वलय, डिस्क, बेलन या गोला) का आनत तल की तली में वेग है। आनत तल पर वह ऊँचाई है जहाँ से पिण्ड गति प्रारम्भ करता है। K सममित अक्ष के परितः पिण्ड की घूर्णन त्रिज्या है और R पिण्ड की त्रिज्या है।