HBSE 11th Class Physics Solutions Chapter 6 कार्य, ऊर्जा और शक्ति

Haryana State Board HBSE 11th Class Physics Solutions Chapter 6 कार्य, ऊर्जा और शक्ति Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 6 कार्य, ऊर्जा और शक्ति

प्रश्न 6.1.
किसी वस्तु पर किसी बल द्वारा किये गये कार्य का चिह्न समझना महत्त्वपूर्ण है। सावधानीपूर्वक बताइए कि निम्नलिखित राशियाँ धनात्मक हैं या ऋणात्मक:
(a) किसी व्यक्ति द्वारा किसी कुएँ में से रस्सी से बँधी बाल्टी को रस्सी द्वारा बाहर निकालने में किया गया कार्य।
(b) उपर्युक्त स्थिति में गुरुत्वीय बल द्वारा किया गया कार्य।
(c) किसी आनत तल पर फिसलती हुई किसी वस्तु पर घर्षण द्वारा किया गया कार्य।
(d) किसी खुरदरे क्षैतिज तल पर एक समान वेग से गतिमान किसी वस्तु पर लगाये गये बल द्वारा किया गया कार्य।
(e) किसी दोलायमान लोलक को विरामावस्था में लाने के लिए वायु के प्रतिरोधी बल द्वारा किया गया कार्य।
उत्तर:
(a) धनात्मक, क्योंकि व्यक्ति द्वारा बाल्टी पर लगाया गया बल व विस्थापन दोनों ऊपर की ओर समान दिशा में अर्थात् θ = 0
(b) ऋणात्मक, इस स्थिति में गुरुत्वीय बल नीचे की ओर कार्य करता है, अत: θ = 180°.
(c) ऋणात्मक वस्तु नीचे की ओर विस्थापित होगी, जबकि घर्षण विपरीत दिशा में कार्य करेगा, अतः θ = 180°.
(d) धनात्मक, वस्तु पर लगाया गया बल व विस्थापन एक ही दिशा में हैं, θ = 80.
(e) ऋणात्मक, वस्तु का प्रतिरोध बल गति को रोकने को प्रयास करता है, अत: θ = 180°

प्रश्न 6.2.
2 kg द्रव्यमान की कोई वस्तु जो आरम्भ में विरामावस्था में है, 7N के किसी क्षैतिज बल के प्रभाव से एक मेज पर गति करती है। मेज का गतिज घर्षण गुणांक 0.1 है। निम्नलिखित का परिकलन कीजिए और अपने परिणामों की व्याख्या कीजिए:
(a) लगाए गये बल द्वारा 10s में किया गया कार्य।
(b) घर्षण द्वारा 10s में किया गया कार्य।
(c) वस्तु पर कुल बल द्वारा 10s में किया गया कार्य।
(d) वस्तु की गतिज ऊर्जा में 10s में परिवर्तन।
उत्तर:
m = 2kg; u = 0; F = 7N; μ = 0.1; t = 10s
बल द्वारा उत्पन्न त्वरण
a₁ = F /m = 7 /2 = 3.5ms^-2
घर्षण बल
f_f= μR = μmg = 0.1 x 2 x 9.8 = 1.96 N
घर्षण बल द्वारा उत्पन्न त्वरण
a₂ = -f_f/m = – \(\frac{1.96}{2}\)
∴ वस्तु पर परिणामी त्वरण
a = a₁ + a₂ = 3.5 – 0.98 = 2.52 ms^-2
∴ वस्तु द्वारा 10s में तय की गयी दूरी
s = ut + \(\frac{1}{2}\)at²
= 0 +\(\frac{1}{2}\) × 2.52 × (10)²
= 126m
(a) 10s में बल द्वारा किया गया कार्य W1 = Fscosθ
= 7 x 126 = +882J
(b) घर्षण द्वारा 10s में किया गया कार्य W2 = f1scos180°
= 1.96 × 126 × (- 1) = – 247J
(c) कुल बल द्वारा किया गया कार्य
W = W₁ + W₂
= 882 – 247 = 635 J
(d) कार्य ऊर्जा प्रमेय से,
गतिज ऊर्जा में परिवर्तन ∆K = किया गया कुल कार्य
= 635 J

प्रश्न 6.3.
चित्र में कुछ एकविमीय स्थितिज ऊर्जा फलनों के उदाहरण दिये गये हैं। कण की कुल ऊर्जा कोटि-कक्ष पर क्रॉस द्वारा निर्देशित की गई है। प्रत्येक स्थिति में, कोई ऐसे क्षेत्र बताइए, यदि कोई हैं तो, जिनमें दी गई ऊर्जा के लिए, कण को नहीं पाया जा सकता है। इसके अतिरिक्त, कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिए। कुछ ऐसे भौतिक सन्दर्भों के विषय में सोचिए जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हों।

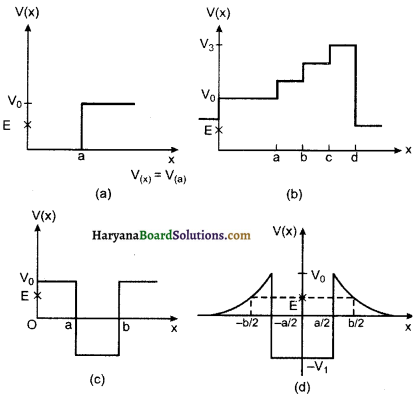
उत्तर:
कण की गतिज ऊर्जा ऋणात्मक नहीं हो सकत है अतः जिस स्थिति में कण की गतिज ऊर्जा ऋणात्मक होगी, कण नहीं पाया जा सकता है।
(a) x > a में Vo > E
∵ K = E – V
अतः गतिज ऊर्जा ऋणात्मक होगी।
अतः
कण > a में नहीं पाया जा सकता।
कण की कुल न्यूनतम ऊर्जा E = 0
(b) सम्पूर्ण मान में > E, अतः कहीं नहीं जायेगा। की कुल न्यूनतम
ऊर्जा E = V₁
(c) x < a तथा x > b के मध्य Vo < E
अतः कण इस क्षेत्र में रहेगा। कण की कुल न्यूनतम ऊर्जा
E = -V₁
(d) \(-\frac{d}{2}\) < x < \(-\frac{a}{2}\) तथा \(\frac{a}{2}\) < x < \(\frac{b}{2}\) में कण नहीं रहेगा, कण की
कुल न्यूनतम ऊर्जा E = -V₁

प्रश्न 6.4.
रेखीय सरल आवर्त गति कर रहे किसी कण का स्थितिज ऊर्जा फलन v(x) = \(\frac{k x^2}{2}\) है, जहाँ दोलक का बल नियतांक है। k = 0.5 Nm^-1 के लिए V(x) व x के मध्य ग्राफ चित्र में दिखाया गया है। यह दिखाइए कि इस विभव के अन्तर्गत गतिमान कुल 1J ऊर्जा वाले कण को अवश्य ही ‘वापस आना चाहिए जब यह x = +2m पर पहुँचता है।

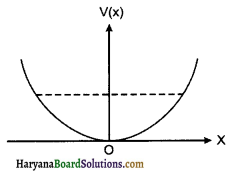
उत्तर:
स्थितिज ऊर्जा फलन V(x) = \(\frac{k x^2}{2}\)
सरल आवर्त गति में कुल ऊर्जा E = \(\frac{1}{2}\)mv² + \(\frac{1}{2}\)kx²
परन्तु कण उस स्थिति से वापस लौटेगा जब उसकी गतिज ऊर्जा शून्य हो जायेगी।
अत:
E = \(\frac{1}{2 k x^2}\)
या
1 = \(\frac{1}{2}\) x 0.5 x x²_m
या
x²_m = \(\frac{2}{0.5}\) = 4
x_m = ±2m
अतः कण 2m से वापस आयेगा।
∵ E = 1J, 1 = 0.5 Nm²

प्रश्न 6.5.
निम्नलिखित का उत्तर दीजिए:
(a) किसी रॉकेट का बाह्य आवरण उड़ान के दौरान घर्षण के कारण जल जाता है। जलने के लिए आवश्यक ऊष्मीय ऊर्जा किसके व्यय पर प्राप्त की गई रॉकेट या वातावरण?
(b) धूमकेतु सूर्य के चारों ओर बहुत ही दीर्घवृत्तीय कक्षाओं में घूमते हैं। साधारणतः धूमकेतु पर सूर्य का गुरुत्वीय बल धूमकेतु के लम्बवत् नहीं होता। फिर भी धूमकेतु की सम्पूर्ण कक्षा में गुरुत्वीय बल द्वारा किया गया कार्य शून्य होता है। क्यों?
(c) पृथ्वी के चारों ओर बहुत ही क्षीण वायुमण्डल में घूमते हुए किसी कृत्रिम उपग्रह की ऊर्जा धीरे-धीरे वायुमण्डलीय प्रतिरोध (चाहे यह कितना ही कम क्यों न हो) के विरुद्ध क्षय के कारण कम होती जाती है फिर भी जैसे-जैसे कृत्रिम उपग्रह पृथ्वी के समीप आता है तो उसकी चाल में लगातार वृद्धि क्यों होती है?
(d) चित्र (i) में एक व्यक्ति अपने हाथों में 15 kg का कोई द्रव्यमान लेकर 2m चलता है। चित्र (ii) में वह उतनी ही दूरी अपने पीछे रस्सी को खींचते हुए चलता है। रस्सी घिरनी पर चढ़ी हुई है और उसके दूसरे सिरे पर 15 kg का द्रव्यमान लटका हुआ है। परिकलन कीजिए कि किस स्थिति में किया गया कार्य अधिक है?

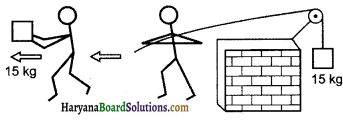
उत्तर:
(a) रॉकेट की कुल ऊर्जा = mgh + \(\frac{1}{2}\) mv² जलने पर द्रव्यमान घटने से कुल ऊर्जा भी घटेगी अतः जलने के लिए आवश्यक ऊष्मीय ऊर्जा रॉकेट की ऊर्जा से ही प्राप्त होगी।
(b) धूमकेतु द्वारा सूर्य पर आरोपित गुरुत्वाकर्षण बल संरक्षी बल है। तथा संरक्षी बल द्वारा बन्द पथ में किया गया परिणामी कार्य शून्य होता है। अतः धूमकेतु की सम्पूर्ण कक्षा में गुरुत्वीय बल द्वारा किया गया कार्य शून्य होता है।
(c) जब उपग्रह पृथ्वी के समीप आता है तो उसकी स्थितिज ऊर्जा घटती है जबकि गतिज ऊर्जा बढ़ती है, अतः उसकी चाल में वृद्धि होगी।
(d) प्रथम स्थिति (i) में द्रव्यमान को उठाये रखने के लिए भार के विरुद्ध ऊपर की ओर बल लगता है जबकि विस्थापन क्षैतिज दिशा में है।
∴ θ = 90°
किया गया कार्य W = Fdcos 90°
= 0
∴ द्वितीय स्थिति (ii) में व्यक्ति द्वारा लगाया गया बल क्षैतिज दिशा में है व विस्थापन भी क्षैतिज दिशा में है।
θ = 0°
W = Fdcos 0° = mgdcos 0°
= 15 × 98 x 2 x 1
= 294 J
अतः दूसरी स्थिति में कार्य अधिक है।

प्रश्न 6.6.
सही विकल्प को रेखांकित कीजिए:
(a) जब कोई संरक्षी बल किसी वस्तु पर धनात्मक कार्य करता है तो वस्तु की स्थितिज ऊर्जा बढ़ती है/ घटती है/ अपरिवर्ती रहती है।
(b) किसी वस्तु द्वारा घर्षण के विरुद्ध किये गये कार्य का परिणाम हमेशा इसकी गतिज स्थिति ऊर्जा में क्षय होता है।
(c) किसी बहुकण निकाय के कुल संवेग परिवर्तन की दर निकाय के बाह्य बल / आन्तरिक बलों के जोड़ के अनुक्रमानुपाती होती है।
(d) किन्हीं दो पिण्डों के अप्रत्यास्थ संघट्ट में वे राशियाँ, जो संघट्ट के बाद नहीं बदलती हैं, निकाय की कुल गतिज ऊर्जा / कुल रेखीय संवेग / कुल ऊर्जा हैं।
उत्तर:
(a) घटती है, क्योंकि धनात्मक कार्य के कारण वस्तु, बल की दिशा में विस्थापित होकर बल केन्द्र की ओर विस्थापित होती है। अतः इस स्थिति में x कम होगा तथा स्थितिज ऊर्जा kr² घटेगी।
(b) गतिज घर्षण, वस्तु की गति में ही कार्य करता है, अतः इसकी गतिज ऊर्जा में क्षय होता है।
(c) बाह्य बल, क्योंकि आन्तरिक बल संवेग में परिवर्तन नहीं करते हैं।
(d) कुल रेखीय संवेग, प्रत्येक संघट्ट में कुल रेखीय संवेग सदैव संरक्षित रहता है। प्रत्यास्थ संघट्ट में गतिज ऊर्जा भी संरक्षित रहती है।

प्रश्न 6.7.
बतलाइए कि निम्नलिखित कथन सत्य हैं या असत्य। अपने उत्तर के लिए कारण भी दीजिए:
(a) किन्हीं दो पिण्डों के प्रत्यास्थ संघट्ट में, प्रत्येक पिण्ड का संवेग व ऊर्जा संरक्षित रहती है।
(b) किसी पिण्ड पर चाहे कोई भी आन्तरिक व बाह्य बल क्यों न लग रहा हो, निकाय की कुल ऊर्जा सर्वदा संरक्षित रहती है।
(c) प्रकृति में प्रत्येक बल के लिए किसी बन्द लूप में, किसी पिण्ड की गति में किया गया कार्य शून्य होता है।
(d) किसी अप्रत्यास्थ संघट्ट में, किसी निकाय की अन्तिम गतिज ऊर्जा, आरम्भिक गतिज ऊर्जा से हमेशा कम होती है।
उत्तर:
(a) असत्य, टक्कर से पूर्व व टक्कर के पश्चात् निकाय का संवेग व गतिज ऊर्जा संरक्षित रहती है न कि प्रत्येक पिण्ड की।
(b) असत्य, कुल ऊर्जा सदैव संरक्षित है परन्तु बाह्य बल वस्तु की ऊर्जा परिवर्तित कर सकते हैं।
(c) असत्य, केवल संरक्षी बलों में बन्द लूप में किया गया कार्य शून्य होता है।
(d) असत्य, प्रत्यास्थ टक्कर में सामान्यतः ऊर्जा की हानि होती है परन्तु विशेष परिस्थिति में ऊर्जा बढ़ भी सकती है।

प्रश्न 6.8.
निम्नलिखित का उत्तर ध्यानपूर्वक, कारण सहित दीजिए:
(a) किन्हीं दो बिलियर्ड गेंदों के प्रत्यास्थ संघट्ट में, क्या गेंदों के संघट्टकी अल्पावधि में (जब वे सम्पर्क में होती हैं) कुल गतिज ऊर्जा संरक्षित रहती है?
(b) दो गेंदों के किसी प्रत्यास्थ संघट्ट की लघु अवधि में क्या कुल रेखीय संवेग संरक्षित रहता है?
(c) किसी अप्रत्यास्थ संघट्ट के लिए प्रश्न (a) व (b) के लिए आपके उत्तर क्या हैं?
(d) यदि दो बिलियर्ड गेंदों की स्थितिज ऊर्जा केवल उनके केन्द्रों के मध्य, पृथक्करण दूरी पर निर्भर करती है तो संघट्ट प्रत्यास्थ होगा या अप्रत्यास्थ? ( ध्यान दीजिए कि यहाँ हम संघट्ट के दौरान बल के संगत स्थितिज ऊर्जा की बात कर रहे हैं, न कि गुरुत्वीय स्थितिज ऊर्जा की )।
उत्तर:
(a) नहीं, संघट्ट के समय गतिज ऊर्जा, स्थितिज ऊर्जा में परिवर्तित हो जाती है।
(b) हाँ, रेखीय संवेग संरक्षित रहता है।
(c) अप्रत्यास्थ टक्कर होने पर भी समान उत्तर होंगे।
(d) प्रत्यास्थ, चूँकि स्थितिज ऊर्जा दूरी पर निर्भर करती है, अतः पिण्डों के बीच लगने वाला बल संरक्षी बल है।

प्रश्न 6.9.
कोई पिण्ड जो विरामावस्था में है, अचर त्वरण से एकविमीय गति करता है। इसको किसी समय पर दी गई शक्ति अनुक्रमानुपाती है।
(i) t^1/2
(ii) t
(iii) t^3/2
(iv) t²
उत्तर:
त्वरण अचर है, u = 0,
v = at से,
बल F = ma (अचर)
शक्ति P = F.v = ma.at = ma²t
P ∝t

प्रश्न 6.10.
एक पिण्ड अचर शक्ति के स्रोत के प्रभाव में एक ही दिशा में गतिमान है। इसका समय में विस्थापन, अनुक्रमानुपाती है।
(i) t^1/2
(ii) t
(iii) t^3/2
(iv) t²
उत्तर:
P = F.v
शक्ति की विमा, [ML²T^-3 ] नियत
∴ L²T^-3 = नियत
या L² ∝ T³
या L ∝ T^3/2
उत्तर: (iii)
∴ विस्थापन x ∝ t^3/2

प्रश्न 6.11.
किसी पिण्ड पर नियत बल लगाकर उसे किसी निर्देशांक प्रणाली के अनुसार Z-अक्ष के अनुदिश गति करने के लिए बाध्य किया गया है, जो इस प्रकार है।
\(\vec{F}=(-\hat{i}+2 \hat{j}+3 \hat{k}) \mathrm{N}\)
जहाँ, \(\hat{i}\) तथा \(\hat{j}\) क्रमश: X, Y एवं Z – अक्षों के अनुदिश एकांक सदिश हैं। इस वस्तु को Z-अक्ष के अनुदिश 4m की दूरी तक गति कराने के लिए आरोपित बल द्वारा किया गया कार्य कितना होगा?
उत्तर:
\(\vec{F}=(-\hat{i}+2 \hat{j}+3 \hat{k}) \mathrm{N}\)
\(\vec{d}=4 \hat{k}\)
(वस्तु Z – अक्ष के अनुदिश गति करती है।)
W = \(\vec{F} \cdot \vec{d}\) = \((-\hat{i}+2 \hat{j}+3 \hat{k}) \cdot(4 \hat{k})\)
= 12 J

प्रश्न 6.12.
किसी अन्तरिक्ष किरण प्रयोग में एक इलेक्ट्रॉन और एक प्रोटॉन का संसूचन होता है जिसमें पहले कण की गतिज ऊर्जा 10 keV है और दूसरे कण की गतिज ऊर्जा 100 keV है। इनमें कौन-सा तीव्रगामी है – इलेक्ट्रॉन या प्रोटॉन? इनकी चालों का अनुपात ज्ञात कीजिए (इलेक्ट्रॉन का द्रव्यमान = 9.11 x 10^-31 kg. प्रोटॉन का द्रव्यमान = 1.67 x 10^-27 kg, 1eV = 1.60 x 10^-19 J
उत्तर:
इलेक्ट्रॉन की गतिज ऊर्जा
E₁ = \(\frac{1}{2}\)m_ev_e²
= 10 kev
= 10 x 16 × 10^-16 J
प्रोटॉन की गतिज ऊर्जा
E₂ = \(\frac{1}{2}\)m_pv²_p
= 100 kev
= 100× 1.6 × 10^-16 J

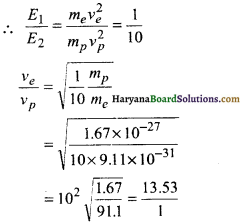
V_e = 13.5vp
अर्थात् इलेक्ट्रॉन तीव्रगामी है

प्रश्न 6.13.
2mm त्रिज्या की वर्षा की कोई बूँद 500m की ऊँचाई से पृथ्वी पर गिरती है। यह अपनी आरम्भिक ऊँचाई के आधे हिस्से तक (वायु के श्यान प्रतिरोध के कारण) घटते त्वरण के साथ गिरती है और अपनी अधिकतम (सीमान्त) चाल प्राप्त कर लेती है और उसके बाद एकसमान चाल से गति करती है। वर्षा की बूँद पर उसकी यात्रा के पहले व दूसरे अर्ध भागों में गुरुत्वीय बल द्वारा किया गया कार्य कितना होगा? यदि बूँद की चाल पृथ्वी तक पहुँचने पर 10ms^-1 हो तो सम्पूर्ण यात्रा में प्रतिरोधी बल द्वारा किया गया कार्य कितना होगा?
उत्तर:
r = 2 mm = 2 x 10^-3
g = 9.8ms^-2
h = 500mm
∴ अर्ध भाग की लम्बाई h₁ = h₂ = 250m
पानी का घनत्व p= 10³ kg m^-3
बूँद का द्रव्यमान m = \(\frac{4}{3}\)πr³ × p
= \(\frac{4}{3}\) × 3.14 × (2 × 10^-3)³ x 10³
= 3.35 × 10^-5 kg
बूँद पर भार (गुरुत्वीय बल)
F₁ = mg
= 3,35 × 10^-5 × 9.8
= 3,35 × 10^-4 N
कार्य: W = mg x h₁ = 3.35 × 10^-4 x 250 = 0.082J
गुरुत्वीय बल द्वारा दोनों स्थितियों में किया गया कार्य समान ही होगा।
कुल कार्य W = 2 x W₁ = 2 × 0.082 = 0.164J
गतिज ऊर्जा E = mv²
बूँद की चाल = 10ms^-1
= \(\frac{1}{2}\) × 3.35 × 10^-1 x (10)²
= 1.675 × 10^-3 J = 0.001675
∴ सम्पूर्ण भाग में प्रतिरोध बल द्वारा किया गया कार्य
= E – W
= 0.001675 – 0.164
= – 1.63 J

प्रश्न 6.14.
किसी गैस पात्र में कोई अणु 200ms^-1 की चाल से अभिलम्ब के साथ 30° का कोण बनाता हुआ क्षैतिज दीवार से टकराकर पुन: उसी चाल से वापस लौट जाता है। क्या इस संघट्ट में संवेग संरक्षित है? यह संघट्ट प्रत्यास्थ है या अप्रत्यास्थ?
उत्तर:
v = 200 ms^-1
u = 200ms^-1: θ = 30°
प्रत्येक टक्कर में संवेग सदैव संरक्षित रहता है।
टक्कर से पूर्व गतिज ऊर्जा E₁ = \(\frac{1}{2}\)mu²
= \(\frac{1}{2}\)m × (200)²
टक्कर के पश्चात् गतिज ऊर्जा Ex = \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\)m(200)²
स्पष्ट है कि गतिज ऊर्जा संरक्षित रहती है। अतः टक्कर प्रत्यास्थ है।

प्रश्न 6.15.
किसी भवन के भूतल पर लगा कोई पम्प 30m³ आयतन की पानी की टंकी को 15 मिनट में भर देता है। यदि टंकी पृथ्वी तल से 40m ऊपर हो और पम्प की दक्षता 30% हो तो पम्प द्वारा कितनी विद्युत् शक्ति का उपयोग किया गया?
उत्तर:

पानी का द्रव्यमान = आयतन x घनत्व
= 30 x 10³ kg
समय t = 15 मिनट 15 x 60 सेकण्ड = 900s;
निर्गत शक्ति

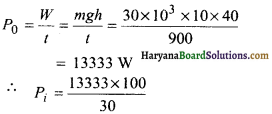
= 44443W
= 44.443 kW
= 44.4kW

प्रश्न 6.16.
दो समरूपी बॉल-बियरिंग एक-दूसरे के सम्पर्क में हैं और किसी घर्षणरहित मेज पर विरामावस्था में हैं। इनके साथ समान द्रव्यमान का कोई दूसरा बॉल-बियरिंग, जो आरम्भ में v चाल से गतिमान है, सम्मुख संघट्ट करता है। यदि संघट्ट प्रत्यास्थ है तो संघट्ट के पश्चात् निम्नलिखित चित्र में से कौन-सा परिणाम सम्भव है?

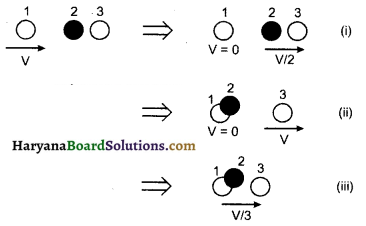
उत्तर:
(i) माना प्रत्येक बॉल-बियरिंग का द्रव्यमान m है। संघट्ट से पूर्व निकाय की गतिज ऊर्जा
= \(\frac{1}{2}\)mV² + 0 + 0
(ii) स्थिति में गतिज ऊर्जा
= 0 + 0 + \(\frac{1}{2}\)mV² = 2mv²
अर्थात् गतिज ऊर्जा समान प्राप्त होती है।
अन्य सभी स्थितियों में गतिज ऊर्जा कम हो रही है।

प्रश्न 6.17.
किसी लोलक के गोलक 1 को, जो ऊर्ध्वाधर से 30° का कोण बनाता है, छोड़े जाने पर मेज पर, विरामावस्था में रखे दूसरे गोलक 8 से टकराता है जैसा कि चित्र में प्रदर्शित है। ज्ञात कीजिए कि संघट्ट के पश्चात् गोलक 4 कितना ऊँचा उठता है? गोलकों के आकारों की उपेक्षा कीजिए और मान लीजिए कि संघट्ट प्रत्यास्थ है।

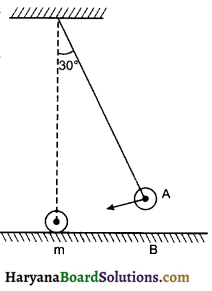
उत्तर:
समान द्रव्यमान के पिण्डों की प्रत्यास्थ टक्कर में टक्कर के पश्चात् पिण्डों के वेग परिवर्तित हो जाते हैं अतः टक्कर के पश्चात् 4 पिण्ड स्थिर हो जायेगा व B पिण्ड, A के वेग से ऊपर उठेगा।

प्रश्न 6.18.
किसी लोलक के गोलक को क्षैतिज अवस्था में छोड़ा गया है। यदि लोलक की लम्बाई 1.5 m है तो निम्नतम बिन्दु पर आने पर गोलक की चाल क्या होगी? यह दिया गया, कि इसकी आरम्भिक ऊर्जा का 5% अंश वायु प्रतिरोध के विरुद्ध क्षय हो जाता है।
उत्तर:
h = 1.5m u = 0
बिन्दु A पर गोलक की कुल ऊर्जा = mgh
= m x 9.8 × 1.5
= 14.7 mJ
∵ 5% ऊर्जा क्षय हो जाती है
∴ शेष ऊर्जा = 95%
= \(\frac{95}{100}\) x 14.7m

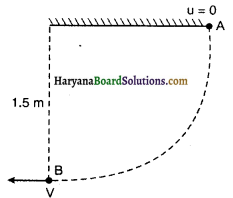
माना बिन्दु B पर वेग हो तो ऊर्जा संरक्षण से,
\(\frac{1}{2}\)mV² = \(\frac{95}{100}\) × 14.7cm
v = \(\\sqrt{\frac{95}{100} \times 14.7 \times 2}\) = \(\\sqrt{27.93}\)
v = 5.285ms^-1

प्रश्न 6.19.
300 kg द्रव्यमान की कोई ट्रॉली, 25 kg रेत का बोरा लिये हुए किसी घर्षणरहित पथ पर 27 kmh की एकसमान चाल से गतिमान है। कुछ समय पश्चात् बोरे में किसी छिद्र से रेत 0.05 kgs^-1 की दर से निकलकर ट्रॉली के फर्श पर रिसने लगती है। रेत का बोरा खाली होने के पश्चात् ट्रॉली की चाल क्या होगी?
उत्तर:
ट्रॉली एकसमान चाल से चल रही है। अतः बाह्य बल F = 0 अतः निकास का रेखीय संवेग नियत रहेगा। अतः ट्रॉली की चाल 27 kmh^-1 ही रहेगी।

प्रश्न 6.20
0.5 kg द्रव्यमान का एक कण v = ax^3/2 सरल रेखीय गति करता है। जहाँ a = 5m^1/2g^-1 है। x = 0 से x = 2m तक इसके विस्थापन में कुल बल द्वारा किया गया कार्य कितना होगा?
उत्तर:
x = 0 पर, V₁ = 0
x = 2 पर, V₂ = 5 x (2)^3/2
कार्य = गतिज ऊर्जा में वृद्धि = \(\frac{1}{2}\)mv₂² – \(\frac{1}{2}\)m₁²
= 2m2v7
= \(\frac{1}{2}\)m₂² [∵ V₁ = 0]
= 2 × 0.5 × 25 × (2)³
= 50J

प्रश्न 6.21.
किसी पवनचक्की के ब्लेड, क्षेत्रफल 4 के वृत्त जितना क्षेत्रफल प्रसर्प करते हैं:
(a) यदि हवा, वेग से वृत्त के लम्बवत् दिशा में बहती है तो समय में इससे गुजरने वाली वायु का द्रव्यमान क्या होगा? (b) वायु की गतिज ऊर्जा क्या होगी? (c) मान लीजिए कि पवनचक्की हवा की 25% ऊर्जा को विद्युत् ऊर्जा में रूपान्तरित कर देती है। यदि A = 30m², और V = 36kmh^-1 और वायु का घनत्व 1.2kgm^-3 ‘है तो उत्पन्न विद्युत् शक्ति का परिकलन कीजिए।
उत्तर:
A = 30m²;
v = 36kmh^-1
= 10ms^-1
वायु का घनत्व p = 1.2kgm^-3
(a) t समय में वृत्त से गुजरी वायु का आयतन = Avt
(आयतन = क्षेत्रफल x दूरी)
∴ वायु का द्रव्यमान ( t समय में) = Avtp
(b) वायु की गतिज ऊर्जा
K = 2m² = 2 Avtpv² = Aptv²
(c) t समय में उत्पन्न विद्युत ऊर्जा
E = \(\frac{25}{100}\) × \(\frac{1}{8}\) Apv³t
विद्युत शक्ति P = \(\frac{E}{t}\) = \(\frac{1}{8}\)Aptv³
P = \(\frac{1}{8}\) × 30 × 1.2 × (10)³
= 4500W
= 4.5 kW

प्रश्न 6.22.
कोई व्यक्ति वजन कम करने के लिए 10 kg द्रव्यमान को 0.5m की ऊँचाई तक 1000 बार उठाता है। मान लीजिए कि प्रत्येक बार द्रव्यमान को नीचे लाने में खोई हुई ऊर्जा क्षयित हो जाती है। (a) वह गुरुत्वाकर्षण के विरुद्ध कितना कार्य करता है? (b) यदि वसा 3.8 x 10⁷ J ऊर्जा प्रति किलोग्राम आपूर्ति करती हो जो कि 20% दक्षता की दर से यान्त्रिक ऊर्जा में परिवर्तित हो जाती है तो वह कितनी वसा खर्च कर डालेगा?
उत्तर:
m = 10kg; h = 0.5m n = 1000
(a) मनुष्य द्वारा 1000 बार ऊपर उठाने में किया गया कार्य
W = n (mgh)
= 1000 x 10 x 9.8 x 0.5 = 49000 J
(b) 1 kg वसा द्वारा प्रदान की गई यान्त्रिक ऊर्जा
= 3.8 x 10⁷J का 20%
= 3.8 × 10⁷ x \(\frac{20}{100}\)
= 3.8 × 10⁷ (J)
= \(\frac{3.8 \times 10^7}{5}\) (J)
= \(\frac{3.8 \times 10^7}{5}\) J ऊर्जा प्राप्त होगी = 1 kg वसा से
∴ 49000J ऊर्जा प्राप्त होगी
= \(\frac{5}{3.8 \times 10^7}\) x 49000kg वसा से
= 6.45 × 10^-3 kg वसा से
अतः व्यक्ति 6.45 x 10^-3 kg वसा खर्च कर देगा।

प्रश्न 6.23.
कोई परिवार 8 kW विद्युत शक्ति का उपभोग करता है। (a) किसी क्षैतिज सतह पर सीधे आपतित होने वाले सौर ऊर्जा की औसत दर 200 Wm^-2 है। यदि इस ऊर्जा का 20% भाग लाभदायक विद्युत् ऊर्जा में रूपान्तरित किया जा सकता है तो 8KW की विद्युत् आपूर्ति के लिए कितने क्षेत्रफल की आवश्यकता होगी? (b) इस क्षेत्रफल की तुलना किसी विशिष्ट भवन की छत के क्षेत्रफल से कीजिए।
उत्तर:
(a) शक्ति P = 8kW = 8000W,
सौर ऊर्जा की औसत दर = 200Wm^-2
इसका 20% भाग विद्युत् ऊर्जा में रूपान्तरित होता है।
= 200 x \(\frac{20}{100}\) = 40W
∴ 40W उपयोगी शक्ति प्राप्त होगी
= 1m2 क्षेत्रफल से
IW शक्ति प्राप्त होगी = \(\frac{1}{40}\) m² क्षेत्रफल से
8000 W शक्ति प्राप्त होगी
= \(\frac{1}{40}\) x 8000m² क्षेत्रफल से
= 200m² क्षेत्रफल
अतः 8kW शक्ति प्राप्त करने के लिए 200m² क्षेत्रफल की आवश्यकता होगी।
(b) इसके लिए लगभग 15m x 14m आकार का भवन उपयुक्त होगी।

अतिरिक्त अभ्यास (Additional Exercise):

प्रश्न 6.24
0.012 kg द्रव्यमान की कोई गोली 70ms^-1 की क्षैतिज चाल से चलते हुए 0.4 kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरन्त ही विरामावस्था में आ जाती है। गुटके को छत से पतली तारों द्वारा लटकाया गया है। परिकलन कीजिए कि गुटका किस ऊँचाई तक ऊपर उठता है? गुटके में पैदा ऊष्मा की मात्रा का भी अनुमान लगाइए।
उत्तर:
m₁ = 0.012kg m₂ = 0.4kg v = ?
u₁ = 70ms^-1; u₂ = 0
या
v= \(\frac{m_1 u_1+m_2 u_2}{\left(m_1+m_2\right)}=\frac{0.012 \times 70+0}{(0.012+0.4)}\)
= \(\frac{0.012 \times 70}{0.412}\)
= 2.04ms-1
माना गुटका ऊँचाई तक ऊपर जाता है।
∴ v² = 2gh
या
h = \(\frac{v^2}{2 g}\)
= \(\frac{2.04 \times 2.04}{2 \times 9.8}\)
= 0.212m = 21.2cm
इस क्रिया में ऊर्जा हानि ऊष्मा में परिवर्तित होगी।
अतः
W = \(\frac{1}{2}\) m₁u₁² – \(\frac{1}{2}\)(m₁ + m₂)v²
= \(\frac{1}{2}\) × 0.012 × (70)² – \(\frac{1}{2}\) × (0.412) × (2.04)²
= 29.4 – 0.86
= 28.52 जूल

प्रश्न 6.25.
दो घर्षण रहित आनत पथ, जिनमें से एक की ढाल अधिक है और दूसरे की ढाल कम है, बिन्दु पर मिलते हैं। बिन्दु से प्रत्येक पथ पर एक-एक पत्थर को विरामावस्था से नीचे सरकाया जाता है। चित्रानुसार क्या ये पत्थर एक ही समय पर नीचे पहुँचेंगे? क्या वे वहाँ एक ही चाल से पहुँचेंगे? व्याख्या कीजिए। यदि θ₁ = 30°, θ₂ = 60° और h = 10m दिया है तो दोनों पत्थरों की चाल एवं उनके द्वारा नीचे पहुँचने में लिए गये समय क्या हैं?

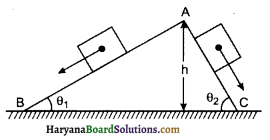
उत्तर:
चूँकि दोनों आनत पथ की ऊँचाई समान है। अतः दोनों वस्तुएँ एक ही चाल से नीचे पहुंचेंगी।
त्वरण a₁ = g sinθ₁ तथा a₂ = gsinθ₂
∵ θ₁ < θ₂
∴ a₁ < a₂
∴ v = u + at से u = 0 हो तो t =
t₁ < t₂ या t₂ < t₁
अतः दूसरा पत्थर पहले की तुलना में पहले नीचे आयेगा।
h = 10m हो, तो वेग v = √2gh
= \(\sqrt{2 \times 9.8 \times 10}\) = 14 ms¹
θ₁ = 30° के लिए समय
v = u + at, v = gsinθ₁t₁

प्रश्न 6.26.
किसी रूक्ष आनत तल पर रखा हुआ 1kg द्रव्यमान का गुटका किसी 100Nm स्प्रिंग नियतांक वाले स्प्रिंग से दिये गये चित्र के अनुसार जुड़ा है। गुटके को स्प्रिंग की बिना खिंची स्थिति में, विरामावस्था से छोड़ा जाता है। गुटका विरामावस्था में आने से पहले आनत तल पर 10 cm नीचे खिसक जाता है। गुटके और आनत तल के म घर्षण गुणांक ज्ञात कीजिए। मान लीजिए कि स्प्रिंग का द्रव्यमान उपेक्षणीय है और घिरनी घर्षणरहित है।

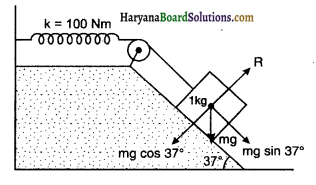
उत्तर:
चित्र में गुटके पर लगने वाले बल प्रदर्शित हैं।
प्रतिक्रिया R = mg cos 37
∴ घर्षण f = μR = μmg cos 37° गुटके पर नीचे की ओर परिणामी बल
= mg sin 37° – μmg cos 37°
= mg [sin 37°- μcos 37°]
x विस्थापन में किया गया कार्य
W = mg (sin 37° – μcos 37° ) x x ……..(1)
इस स्थिति में स्प्रिंग 10cm विस्थापित होती है। अतः स्प्रिंग द्वारा किया गया कार्य
∵ x = 10cm = 0.1m; ∴ k = 10Nm^-1
समी० (1) व (2) से,
\(\frac{1}{2}\)kx² = mg [sin 37° – μcoscos 37°) x x
या \(\frac{1}{2}\) x 100 x (0.1) = 1 x 10 x [0.601 – μ0.798]
[∵ sin 37° = 0.6017 cos 37° = 0.798]
या
\(\frac{1}{2}\) = [0.601 – μ × 0.798]
या μ × 0.798 = [ 0.601 – 0.5]
∴ μ = \(\frac{0.101}{0.798}\)
= 0.126

प्रश्न 6.27
0.3 kg द्रव्यमान का कोई बोल्ट 7ms^-1 की एकसमान चाल से नीचे आ रही किसी लिफ्ट की छत से गिरता है। यह लिफ्ट के फर्श से टकराता है (लिफ्ट की लम्बाई 3m) और वापस नहीं लौटता है। टक्कर द्वारा कितनी ऊष्मा उत्पन्न हुई? यदि लिफ्ट स्थिर होती तो क्या आपका उत्तर इससे भिन्न होता?
उत्तर:
m = 0.4 kg; μ = 7ms^-1; h = 3m
लिफ्ट की छतपर बोल्ट की स्थितिज ऊर्जा
= mgh
= 0.3 × 9.8 × 3
= 8.82 J
टक्कर के पश्चात् वोल्ट वापस नहीं लौटता है, अतः सम्पूर्ण स्थितिज ऊर्जा, ऊष्मा में परिवर्तित हो जाती है = 8.82J
लिफ्ट एकसमान चाल से गति कर रही है। अतः त्वरण a = 0, अतः लिफ्ट स्थिर होने पर भली उत्तर अपरिवर्तित रहेगा। लिफ्ट जड़त्वीय निर्देश तन्त्र की भाँति व्यवहार करेगा।

प्रश्न 6.28.
200 kg द्रव्यमान की कोई ट्रॉली किसी घर्षणरहित पर 36 kmh की एकसमान चाल से गतिमान है। 20 kg द्रव्यमान का कोई बच्चा ट्रॉली के एक सिरे से दूसरे सिरे तक (10m दूर) ट्रॉली के सापेक्ष 4ms^-1 चाल से ट्रॉली की गति की विपरीत दिशा में दौड़ता है और ट्रॉली से बाहर कूद जाता है। ट्रॉली की अन्तिम चाल क्या है? बच्चे के दौड़ना आरम्भ करने के समय से ट्रॉली ने कितनी दूरी तय की?
उत्तर:
ट्रॉली का द्रव्यमान
m₁ = 200kg
चाल u₁ = 36km h
= 36 x \(\frac{5}{18}\)
= 10ms^-1
बच्चे का द्रव्यमान
m₂ = 20kg
माना बच्चे की चाल = x
ट्रॉली के सापेक्ष बच्चे की चाल
V₂ = 4ms^-1
V₂ = V₁ – x
माना ट्रॉली की अन्तिम चाल
∴ बच्चे की वास्तविक चाल x = V₁ – V₂
संवेग संरक्षण से,
बच्चे के दौड़ना प्रारम्भ करने से पूर्व निकाय का संवेग = ट्रॉली से कूदते समय निकाय का संवेग
(m₁ + m₂) u₁ = m₁v₁ + m₂(V₁ – V₂ )
या (200 + 20) x 10 = 200 v₁ + 20(v₁ – 4)
या 220v₁ – 80 = 2200
∴ v₁ = \(\frac{2280}{220}\)
= 10.36ms^-1

प्रश्न 6.29.
चित्र में दिये गये स्थितिज ऊर्जा वक्रों में से कौन-सा वक्र सम्भवतः दो बिलियर्ड गेंदों के प्रत्यास्थ संघट्ट का वर्णन नहीं करेगा? यहाँ गेंदों के केन्द्रों के मध्य की दूरी है और प्रत्येक गेंद का अर्द्धव्यास R है।

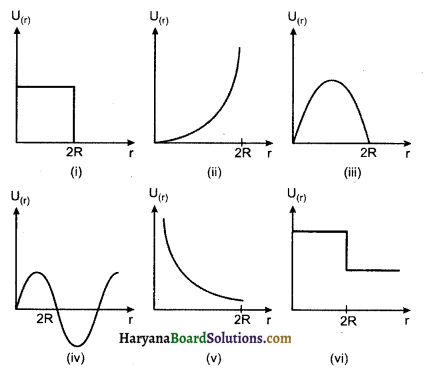
उत्तर:
(i), (ii), (iii), (iv), (vi) ये संघट्ट का वर्णन नहीं करेंगे।
व्याख्या: जब दो गेंद संघट्ट करेंगी तो एक-दूसरे को संपीडित करेंगी जिससे दूरी घटेगी तथा स्थितिज ऊर्जा बढ़ेगी। परन्तु टक्कर के पश्चात् गेंदें दूर हटेंगी तो उनकी स्थितिज ऊर्जा घटेगी। पुन: प्रारम्भिक आकार प्राप्त करने पर स्थितिज ऊर्जा शून्य हो जायेगी। अतः (v) स्थिति इसकी सही व्याख्या करता है (टक्कर के पश्चात्)। अन्य वक्र संघट्ट का वर्णन नहीं करेंगे।

प्रश्न 6.30.
विरामावस्था में किसी मुक्त न्यूट्रॉन के क्षय पर विचार कीजिए n → p + e प्रदर्शित कीजिए कि इस प्रकार के द्विपिण्ड क्षय से नियत ऊर्जा का कोई इलेक्ट्रॉन अवश्य उत्सर्जित होना चाहिए, और इसलिए यह किसी न्यूट्रॉन या किसी नाभिक के 3-क्षय में प्रेक्षित सतत ऊर्जा वितरण का स्पष्टीकरण नहीं दे सकता।

उत्तर:
इस अभिक्रिया में वैज्ञानिक पॉली ने सुझाव दिया कि इसमें एक अन्य कण जिसे न्यूट्रिनों (v) कहा जाता है उत्सर्जित होता है। यह उदासीन व द्रव्यमान रहित कण है। इसका चक्रण \(\frac{1}{2}\) है।
अतः सही अभिक्रिया निम्न है n → p + e + v