HBSE 12th Class Physics Solutions Chapter 14 अर्द्धचालक इलेक्ट्रॉनिकी-पदार्थ, युक्तियाँ तथा सरल परिपथ

Haryana State Board HBSE 12th Class Physics Solutions Chapter 14 अर्द्धचालक इलेक्ट्रॉनिकी-पदार्थ, युक्तियाँ तथा सरल परिपथ Textbook Exercise Questions and Answers.

Haryana Board 12th Class Physics Solutions Chapter 14 अर्द्धचालक इलेक्ट्रॉनिकी-पदार्थ, युक्तियाँ तथा सरल परिपथ

प्रश्न 14.1.
किसी n प्रकार के सिलिकॉन में निम्नलिखित में से कौन-सा प्रकथन सत्य है?
(a) इलेक्ट्रॉन बहुसंख्यक वाहक हैं और त्रिसंयोजी परमाणु अपमिश्रक हैं।
(b) इलेक्ट्रॉन अल्पसंख्यक वाहक हैं और पंचसंयोजी परमाणु अपमिश्रक हैं।
(c) होल (विवर) अल्पसंख्यक वाहक हैं और पंचसंयोजी परमाणु अपमिश्रक हैं।
(d) होल (विवर) बहुसंख्यक वाहक हैं और त्रिसंयोजी परमाणु अपमिश्रक हैं।
उत्तर:
(c) होल (विवर) अल्पसंख्यक वाहक हैं और पंचसंयोजी परमाणु अपमिश्रक हैं।

प्रश्न 14.2.
अभ्यास 14.1 में दिए गए कथनों में से कौन-सा p- प्रकार के अर्धचालकों के लिए सत्य है?
उत्तर:
(d) होल (विवर) बहुसंख्यक वाहक हैं और त्रिसंयोजी परमाणु अपमिश्रक हैं।

प्रश्न 14.3.
कार्बन, सिलिकॉन और जर्मेनियम, प्रत्येक में चार संयोजक इलेक्ट्रॉन हैं। इनकी विशेषता ऊर्जा बैंड अंतराल द्वारा पृथक्कृत संयोजकता और चालन बैंड द्वारा दी गई हैं, जो क्रमशः (E^g)C (E^g) si तथा (E^g)Ge के बराबर हैं। निम्नलिखित में से कौन-सा प्रकथन सत्य है?
(a) (E^g)si < (E^g)Ge < (E^g)C
(b) (E^g)C < (E^g)Ge > (E^g)si
(c) (E^g)C > (E^g)si > (E^g)Ge
(d) (E^g)C = (E^g)si = (E^g) Ge
उत्तर:
(c) (E^g)C > (E^g)si > (E^g)Ge

प्रश्न 14.4.
बिना बायस p-n संधि से होल p- क्षेत्र में n क्षेत्र की ओर विसरित होते हैं, क्योंकि
(a) n क्षेत्र में मुक्त इलेक्ट्रॉन उन्हें आकर्षित करते हैं।
(b) ये विभवांतर के कारण संधि के पार गति करते हैं।
(c) p- क्षेत्र में होल-सांद्रता 1- क्षेत्र में इनकी सांद्रता से अधिक है।
(d) उपर्युक्त सभी।
उत्तर:
(c) p- क्षेत्र में होल सांद्रता n क्षेत्र में इनकी सांद्रता से अधिक है।

प्रश्न 14.5.
जब p-n संधि पर अग्रदिशिक बायस अनुप्रयुक्त किया जाता है, तब यह
(a) विभव रोधक बढ़ाता है।
(b) बहुसंख्यक वाहक धारा को शून्य कर देता है।
(c) विभव रोधक को कम कर देता है।
(d) उपरोक्त में से कोई नहीं।
उत्तर:
(c) विभव रोधक को कम कर देता है।

प्रश्न 14.6.
अर्ध-तरंगी दिष्टकरण में, यदि निवेश आवृत्ति 50 Hz है तो निर्गम आवृत्ति क्या है? समान निवेश आवृत्ति हेतु पूर्ण तरंग दिष्टकारी की निर्गम आवृत्ति क्या है?
उत्तर:
अर्ध-तरंगी दिष्टकरण केवल आधा निवेशी A. C. को दिष्ट में करती है।
∴ निर्गत A. C. की आवृत्ति = निवेशी AC की आवृत्ति = 50 Hz
पूर्ण तरंगी दिष्टकरण, AC निवेशी के दोनों अद्धों को दिष्ट करता है।
∴ निर्गत AC की आवृत्ति = 2 x निवेशी AC की आवृत्ति
= 2 × 50 = 100 Hz

प्रश्न 14.7.
कोई p-n फोटोडायोड 2.8eV बैंड अंतराल वाले अर्धचालक से संविरचित है। क्या यह 6000 nm की तरंगदैर्ध्य का संसूचन कर सकता है?
उत्तर:
बैण्ड अंतराल Eg = 2.8 ev
6000 nm की तरंगदैर्ध्य संगत ऊर्जा बैण्ड अन्तराल माना E
∴ हम जानते हैं:

बैण्ड अन्तराल Eg का मान E से अधिक ही है। अतः यह 6000 nm की तरंगदैर्घ्य का संसूचन नहीं कर सकता है।

अतिरिक्त अभ्यास प्रश्न (NCERT):

प्रश्न 14.8.
सिलिकॉन परमाणुओं की संख्या 5 x 10²⁸ प्रति m” है। यह साथ ही साथ आर्सेनिक के 5 x 10²² परमाणु प्रति ms और इंडियम के 5 x 10²⁰ परमाणु प्रतिm से अपमिश्रित किया गया है। इलेक्ट्रॉन और होल की संख्या का परिकलन कीजिए दिया है कि n = 1.5 x 10¹⁶ m ” दिया गया पदार्थ n प्रकार का या p प्रकार का?
उत्तर:
दिया गया है:
N_D = 5 x 10²² परमाणु / मीटर³
N_a = 5 × 10²⁰ परमाणु / मीटर³
ni = 1.5 x 10¹⁶ प्रति / मीटर³
यहाँ पर स्पष्ट है कि ni << ND और भी << NA
ND – NA = ne – nh और nenh = ni²
या
nh = ni²/ne
या
ND – NA = ne – ni²/ne
(ND – NA) x ne = ne² – ni²
या ne² – (ND – NA ) ne – ni² = 0
उपर्युक्त समीकरण (ne) में द्विघात है।

(ND – NA) की अपेक्षा बहुत छोटा है अतः और भी छोटा होगा। अतः इसको छोड़ा जा सकता है।
= 1/2 [4.95 × 10²² + 4.95 × 10²²]
ne = 4.95 x 10²²
और
nh = ni²/ne
= \(\frac{2.25 \times 10^{32}}{4.95 \times 10^{22}}\)
nh = 4.55 x 10⁹
चूँकि ne >> nh, इसलिए दिया गया पदार्थ n – प्रकार का है।

प्रश्न 14.9.
किसी नैज अर्धचालक में ऊर्जा अंतराल Eg का मान 1.2ev है। इसकी होल गतिशीलता इलेक्ट्रॉन गतिशीलता की तुलना में काफी कम है तथा ताप पर निर्भर नहीं है। तथा 300 K पर चालकताओं का क्या अनुपात है? नैज वाहक सांद्रता की ताप निर्भरता इस प्रकार इसकी 600 K यह मानिए कि व्यक्त होती है:
ni = noexp(-E/2KBT)
जहाँ no एक स्थिरांक है।
उत्तर:
दिया गया है:
नैज अर्धचालक का ऊर्जा अन्तराल =
Eg = 1.2 ev
T = 600 K
T2 = 300 K
माना अर्धचालक T1 व T2 की चालकतायें क्रमशः σ1 व σ2
σ1/σ2 = ?
हम जानते हैं:
σ = 1/P
= e(neμe + nnμn) ………….(1)
नैज अर्धचालक के लिए
∴ समीकरण (1) से
σ = e niμe …………. (2)
यह भी दिया गया है कि
nj = nge Eg/2KAT …………… (3)
समीकरण (2) व (3) से हम
σ = e n0μ0 e-Eg/2KAT
σ = e-Eg/2KAT ………….(4)
जहाँ पर
K = 1.38 x 10^-23 JK^-1
= 8.62 x 10^-5 eVK^-1

= exp[11.600928] = e11.600928
σ1/σ2 = e11.6
दोनों तरफ log लेने पर
loge(σ1/σ2) = 11.6 loge
2.303log(σ1/σ2) = 11.6
log(σ1/σ2) = 11.6/2.303 = 5.3069 = 5.307
σ1/σ2 = Antilog(5.3037) = 1.1 x 10⁵
इससे हम यह निष्कर्ष निकालते हैं कि नैज अर्धचालक की चालकता ताप से बहुत प्रभावित होती है।

प्रश्न 14.10.
किसी p-n संधि डायोड में धारा I को इस प्रकार व्यक्त किया जा सकता है:
I = Io exp(ev/2kT – 1)
जहाँ Io को उत्क्रमित संतृप्त धारा कहते हैं, V डायोड के सिरों पर वोल्टता है तथा यह अग्रदिशिक बायस के लिए धनात्मक तथा पश्चदिशिक बायस के लिए ऋणात्मक है। I डायोड से प्रवाहित धारा है, kp बोल्ट्जमान नियतांक ( 8.6 x 10^-5 eV/K) है तथा T परम ताप है। यदि किसी दिए गए डायोड के लिए I = 5 x 10^-12 A तथा T = 300 K है, तब
(a) 0.6 V अग्रदिशिक वोल्टता के लिए अग्रदिशिक धारा क्या होगी?
(b) यदि डायोड के सिरों पर वोल्टता को बढ़ाकर 0.7 V कर दें तो धारा में कितनी वृद्धि हो जाएगी?
(c) गतिक प्रतिरोध कितना है?
(d) यदि पश्चदिशिक वोल्टता को 1 V से 2 V कर दें तो धारा का मान क्या होगा?
उत्तर:
(a)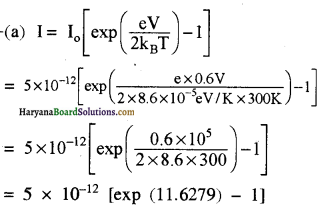
= 5 × 10^-12 [exp (11.6279 ) – 1]
= 5 x 10^-12 [1.119 × 10⁵ – 1]
(11.6279) 1.119 x 10⁵
= 5 x 10^-12 x 1.119 x 10⁵
= 5.595 x 10^-7
= 0.5595 μA
= 0.6 μA

(b) प्रश्नानुसार V = 0.7 वोल्ट

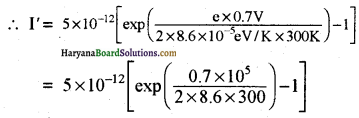
= 5 x 10^-2 [exp (13.5658) – 1]
= 5 x 10² [7.811 x 10⁵ – 1]
= 5 x 10² x 7.811 × 10⁵
∵exp (13.5658) = 7.811 x 10⁵
= 39.055 x 10⁷
= 3.9055 μA
∵ धारा में वृद्धि∆l = I – I
= (3.9055 – 0.5595) μA
= 3.3460 PA
= 3.3460 x 10^-6A

(c) गतिक प्रतिरोध
R = ∆V/∆I = \(\frac{0.7-0.6}{3.3460 \times 10^{-6}}\)
= \(\frac{0.1}{3.3460 \times 10^{-6}}\)
= 0.2988 × 10⁵ ओम
= 0.3 x 10⁵ ओम

(d) पश्च बायस में V ऋणात्मक तथा उच्च होने से
exp(ev/2KT – 1)
जिससे धारा सम्बन्ध ऋणात्मक हो जाता है।
अतः 1 वोल्ट या 2 वोल्ट के पश्च विभव के लिए धारा 1 का मान I के बराबर होगा, जिससे
R = \(\frac{2-1}{5 \times 10^{-12}-5 \times 10^{-12}}\)
अर्थात् गतिक प्रतिरोध अनन्त हो जाएगा।

प्रश्न 14.11.
आपको चित्र में दो परिपथ दिए गए हैं। यह दर्शाइए कि परिपथ (a) OR गेट की भाँति व्यवहार करता है जबकि परिपथ (b) AND गेट की भाँति कार्य करता है।

उत्तर:

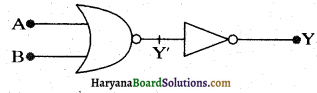
A	B	Y = \(\overline{A+B}\)	Y = \(\overline{\mathrm{A}+\mathrm{B}}\)
0	0	1	0
0	1	0	1
1	0	0	1
1	1	0	1

अतः परिपथ OR गेट की भाँति कार्य करता है।

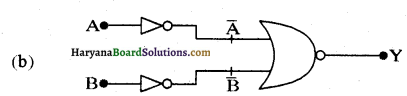
A	B	A	B	Y
0	0	1	0	0
0	1	0	1	0
1	0	0	1	0
1	1	0	1	1

अतः परिपथ AND गेट की भाँति कार्य करता है।

प्रश्न 14.12.
नीचे दिए गए चित्र में संयोजित NAND गेट. संयोजित परिपथ की सत्यमान सारणी बनाइए।

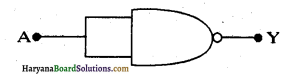
अतः इस परिपथ द्वारा की जाने वाली यथार्थ तर्क संक्रिया का अभिनिर्धारण कीजिए ।
उत्तर:
दिये गये NAND द्वार के दोनों निवेशी समान हैं अर्थात् A हैं अतः निर्गत
Y = A.B = A.A = A
(∵ A.A = A )
अतः सत्यता सारणी

निवेशी A	निर्गत Y = A
0	1
1	0

इस प्रकार यह परिपथ एक NOT द्वार का कार्य करता है।

प्रश्न 14.13.
आपको निम्न चित्र में दर्शाए अनुसार परिपथ दिए गए हैं जिनमें NAND गेट जुड़े हैं। इन दोनों परिपथों द्वारा की जाने वाली तर्क संक्रियाओं का अभिनिर्धारण कीजिए।

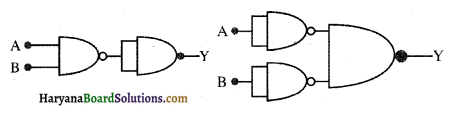
उत्तर:

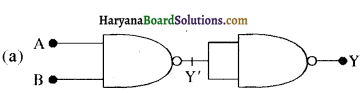
A	B	Y	Y	Y
0	0	1	1	0
0	1	1	0	1
1	0	0	1	1
1	1	0	0	1

अतः परिपथ AND संक्रिया को प्रस्तुत करता है।

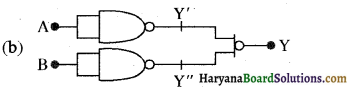
A	B	Y	Y
0	0	1	0
0	1	1	0
1	0	1	0
1	1	0	1

अतः परिपथ OR संक्रिया प्रस्तुत करता है।

प्रश्न 14.14.
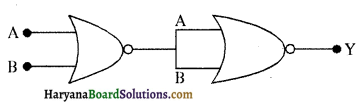
चित्र में दिए गए NOR गेट युक्त परिपथ की सत्यमान सारणी लिखिए और इस परिपथ द्वारा अनुपालित तर्क संक्रियाओं (OR, AND NOT) को अभिनिर्धारित कीजिए।
(संकेत – A = 0, B = 1 तब दूसरे NOR गेट के निवेश A और B 0 होंगे और इस प्रकार Y = 1 होगा। इसी प्रकार A और B के दूसरे संयोजनों के लिए Y के मान प्राप्त कीजिए । OR, AND, NOT द्वारों की सत्यमान सारणी से तुलना कीजिए और सही विकल्प प्राप्त कीजिए।)

उत्तर:
यहाँ उपर्युक्त चित्र एक NOT द्वारा अनुसरित NOR द्वार दर्शाता है जो NOR द्वार से ( NOT द्वार) प्राप्त किया गया है। इस प्रकार निर्गम Y NOR द्वार का निर्गम दर्शाता है।

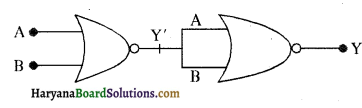
जिसे NOT द्वार को पुष्ट करने के काम लाया जाता है। इस प्रकार हम एक OR द्वार प्राप्त करते हैं जैसा कि सत्य तालिका में दर्शाया गया है तथा बुलियन संक्रिया भी यहाँ दर्शाई गई है, जो इन पर की
गई है।

A	B	Y = \(\overline{\mathrm{A}+\mathrm{B}}\)	Y = \(\overline{\mathrm{A}+\mathrm{B}}\)
0	0	1	0
0	1	0	1
1	0	0	1
1	1	0	1

इस प्रकार A, B और Y OR द्वार की तालिका दर्शाते हैं अतः यह परिपथ OR द्वार के तुल्य है अर्थात् जब A = B = O तब Y’ उच्च होगा क्योंकि NOR द्वार संक्रिया में यदि दोनों निवेश निम्न हैं तो निर्गम उच्च होगा और निर्गम निम्न होगा। यदि एक या दोनों निवेश उच्च हों
इसी प्रकार जब
A = 0, B = 1 Y = 0
A = 1, B = 0, Y = 0
A = B = 1, Y’ = 0

प्रश्न 14.15.
चित्र में दर्शाए गए केवल NOR गेटों से बने परिपथ की सत्यमान सारणी बनाइए। दोनों परिपथों द्वारा अनुपालित तर्क संक्रियाओं (OR, AND NOT) को अभिनिर्धारित कीजिए।

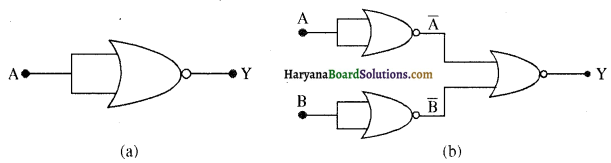
उत्तर:
(a) NOR गेट की सत्य सारणी नीचे दी गई है:

A	B	Y
0	0	1
0	1	0
1	0	0
1	1	0

दिए गए परिपथ में दो इनपुटों को साथ-साथ जोड़ा गया है। NOR द्वार के लिए यदि एक या दोनों निवेश उच्च हों तो निर्गम निम्न होगा और यदि दोनों निवेश निम्न हों तो निर्गम उच्च
(b)

A	B	A	B	Y
0	0	1	1	0
0	1	1	0	0
1	0	0	1	0
1	1	0	0	1

इस प्रकार निवेश A व B तथा निर्गम Y के साथ हटा AND द्वार की सत्य मान तालिका प्राप्त करते हैं।