Author name: Bhagya

Haryana State Board HBSE 9th Class Maths Notes Chapter 11 Constructions Notes.

Haryana Board 9th Class Maths Notes Chapter 11 Constructions

Introduction
In previous chapters, we have drawn rough diagrams to prove theorems or solving exercise. But sometimes we need to construct accurate figures. For example, to draw a map of building to be constructed, to design the parts of machine and tools etc. To draw such figures the following geometrical instruments are needed:
(i) A graduated scale, (ii) a pair of set squares, (iii) a pair of dividers, (iv) a pair of compasses, (v) a protractor (see in the figure below).

These instruments are used in drawing a geometrical figure, such as a triangle, quadrilateral, trapezium, circle etc. In this chapter we will learn about some simple and basic constructions such as bisector of a line segment, bisector of a given angle, constructions of some standard angle and some constructions of triangles with the help of graduated scale, compass and protractor.

Key Words
→ Geometrical Construction: A geometrical construction is the process of drawing a geometrical figure using only two instruments-an ungraduated ruler and compass.

→ Perpendicular bisector: A line which divides the given line in two equal parts and is perpendicular to the line segment is called the perpendicular bisector.

→ Corresponding: Angles, lines and points in one figure which bear a similar relationship, each to each, to angles, lines and points in another figure.

→ Triangle: A closed figure which bounded by three line segments is called a triangle.

→ Isosceles triangle: If at two sides of a triangle are equal, it is called an isosceles triangle.

→ Equilateral triangle: If all three sides of a triangle are equal, it is called an equilateral triangle.

→ Perimeter of a triangle: Sum of the all sides of a triangle is called the perimeter of a triangle.

→ Median: The median of a triangle, corresponding to any side, is the line joining the midpoint of that side with the opposite vertex.

→ Altitude: An altitude of a triangle, corresponding to any side, is the length of perpendicular drawn from the opposite vertex to that side.

Basic Concepts
Basic Constructions
(a) Construction 11.1: To construct the bisector of a given angle.
We have an ∠ABC, we need to construct its bisector.
Steps of construction:
Step – I: Taking B as centre and any suitable radius draw an arc cutting AB and BC at P and Q respectively.
Step – II: Taking P and Q as centres and radius more than \(\frac{1}{2}\)PQ, draw two arcs intersecting each other at R.
Step-III: Draw the ray BR. The ray BR is the required bisector of the angle ABC.

Justification: Join PR and QR.
In ΔBPR and ΔBQR, we have
PB = QB [Radii of the same arc]
PR = QR [Arcs of equal radii]
BR = BR [Common]
ΔBPR ≅ ΔBQR [By SSS congruence rule]
⇒ ∠PBR = ∠QBR [CPCT]
Hence, BR is the bisector of ∠ABC.

Construction 11.2:
To construct the perpendicular bisector of a given line segment.
We have a line segment AB, we need to construct its perpendicular bisector.
Steps of construction:
Step-I: Draw a line segment AB of given length.
Step-II: Taking A as centre and radius more than \(\frac{1}{2}\)AB, draw arcs one on each side of AB.
Step-III: Taking B as centre and the same radius as in Step (II), draw arcs intersecting previous arcs at P and Q.
Step-IV: Join PQ intersecting AB at M. Then line PQ is the perpendicular bisector of AB.
Justification: Join AP, BP, AQ and BQ.
In ΔPAQ and ΔPBQ, we have
AP = BP Arcs of equal radii]
AQ = BQ [Arcs of equal radii]
PQ = PQ [Common]
∴ ΔPAQ ≅ ΔPBQ [By SSS congruence rule]
⇒ ∠APQ ≅ ∠BPQ [CPCT]
⇒ ∠APM = ∠BPM ……(i)

In ΔPMA and ΔPMB, we have
PA = PB [Arcs of equal radii]
∠APM = ∠BPM [As proved in (i)]
PM = PM [Common]
ΔPMA ≅ ΔPMB (By SAS congruence rule)
⇒ AM = BM
and ∠PMA = ∠PMB (CPCT)
But, ∠PMA + ∠PMB = 180° [By linear pair axiom]
∠PMA + ∠PMA = 180°
2∠PMA = 180°
∠PMA = \(\frac{180^{\circ}}{2}\) = 90°
∠PMA = ∠PMB = 90°.
Hence, PM is the perpendicular bisector of AB.

Construction 11.3:
To construct an angle of 60° at the initial point of a given ray.
Let us take a ray AB with initial point A.
We need to construct a ray AC such that
∠CAB = 60°.

Steps of construction:
Step-I: Draw a ray AB with initial point A.
Step-II: Taking A as centre and suitable radius, draw an arc which intersects AB at P.
Step-III: Taking P as centre and same radius as before, draw an arc intersecting the previous are at point Q.
Step-IV: Draw a ray AC passing through Q. Then ∠CAB is the required angle of 60°.
Justification: Join PQ.
AP = PQ = AQ [By construction]
⇒ ΔPAQ is an equilateral triangle.
∴ ∠QAP = 60°
⇒ ∠CAB = 60°.

Some Constructions of Triangles:
Construction 11.4 To construct a triangle, given its base, a base angle and sum of other two sides.

Given: The base BC, a base angle, say ∠B and the sum AB + AC of the other two sides of a triangle ABC, we need to construct ΔABC.
Steps of construction:
Step-I: Draw the given base BC and the point B construct an angle ∠CBX equal to the given angle with BC.
Step-II: From the ray BX,
cut BD = AB + AC.
Step-III: Join DC and construct
∠DCY = ∠BDC.
Step-IV: Let CY intersects BX at A.
Then, ABC is the required triangle.
Justification: Since,
∠BDC = ∠DCY (By construction)
⇒ ∠ADC = ∠ACD
⇒ AD = AC
[Sides opp. to equal angles are equal]
Now, AB = BD – AD
⇒ AB = BD – AC [∵AD = AC]
⇒ AB + AC = BD
⇒ BD = AB + AC.
Alternative method

Steps of construction:

Step-I: Draw the given base BC and at the point B construct ∠CBX equal to the given angle with BC.
Step-II: From the ray BX, cut BD = AB + AC.
Step-III: Join DC and draw perpendicular bisector PY of CD intersecting BD at point A. Join AC.
Remarks: The construction of the trinagle is not possible if the sum AB + AC ≤ BC.

Construction 11.5: To construct a triangle given its base, a base angle and the difference of the other two sides.
Given: Base BC and a base angle, say ∠B and the difference of other two sides AB – AC or AC – AB. We need to construct AABC. There are following two cases arise:
Case I: If AB > AC that is AB – AC is given.

Steps of construction:
Step-I: Draw the given base BC. At the point B, construct ∠CBX equal to the given angle with BC.
Step-II: From ray BX, cut the line segment BD is equal to AB – AC.
Step-III Join DC and draw perpendicular bisector of CD intersecting BX at A.
Step-IV: Join AC. Then ABC is required triangle.
Justification: Since AP is the perpendicular to CD.
∴ AD = AC
So, BD = AB – AD
⇒ BD = AB – AC.
Case II: If AB < AC that is AC – AB is given.

Steps of construction:
Step-I: Draw the given base BC. At the point B, construct ∠CBX equal to the given angle with BC.
Step-II: Extend XB to D to the opposite side of BC such that
BD = AC – AB.
Step-III: Join CD and draw perpendicular bisector PQ of CD intersecting BX at A.
Step-IV: Join AC, then ABC is required triangle.
Justification: Since PQ is the perpendicular bisector of CD.
∴ AD = AC
Now, BD = AD – AB
⇒ BD = AC – AB.

Construction 11.6:
To construct a triangle, given its perimeter and its two base angles.
Given: Base angles ∠B and ∠C and perimeter of a triangle ABC (ie., BC + CA + AB) are given. We need to construct the triangle ABC.

Steps of construction:
Step – I: Draw a line segment XY equal to BC + CA + AB.
Step – II: Construct ∠LXY equal to ∠B and ∠MYX equal to ∠C with XY.
Step – III: Draw the bisectors of ∠LXY and ∠MYX intersecting at A.
Step – IV: Draw perpendicular bisectors PQ of AX and RS of AY.
Step – V: Let perpendicular bisectors PQ and RS intersect XY at B and C respectively.
Step – VI: Join AB and AC, then ABC is the required triangle.
Justification: Since PQ is the perpendicular bisector of AX.
∴ XB = AB …..(i)
Similarly, RS is the perpendicular bisector of AY.
∴ CY = AC ……(ii)
Now, XY = XB + BC + CY
XY = AB + BC + AC [Using (i) & (ii)]
Since, XB = AB
⇒ ∠AXB = ∠XAB ……(iii)
and CY = AC
⇒ ∠CAY = ∠CYA …..(iv)
∠ABC = ∠AXB + ∠XAB
[∵ Exterior angle is equal to its opp. two interior angles]
⇒ ∠ABC = ∠AXB + ∠AXB [Using (iii)]
⇒ ∠ABC = 2∠AXB
⇒ ∠ABC = ∠LXY
Similarly, ∠ACB = ∠MYX.

Haryana State Board HBSE 9th Class Maths Notes Chapter 10 Circles Notes.

Haryana Board 9th Class Maths Notes Chapter 10 Circles

Introduction
We used various objects in our daily life which are round in shape, such as coins of dimensions ₹ 1, ₹ 2 and ₹ 5, buttons of shirts, key rings, dials of clocks, wheels of vehicles etc. (see in figure 10.1). In a clock we have observed that the second’s hand goes round the dial of the clock rapidly and its tip moves round path. This path traced by the tip of the second’s hand is called a circle.

If we fix a pencil in compass and put its pointed leg on a point on a sheet of a paper, open the other leg to some distance. Keeping the pointed leg on the same point, rotate the other leg through one revolution we get a closed figure traced by the pencil on the paper which is known as the circle (see in figure 10.2). In this chapter we will study about circles, it’s related terms and some properties of a circle.

Key Words
→ Circle: A circle is a plane figure bounded by one curved line and is such that all straight lines drawn to this line from certain point within it are equal.

→ Radius: A line segment joining the centre and a point on the circle is called its radius.

→ Circular Region: The region consisting of all points which are either on the circle or lies inside the circle is called the circular region or circular disc.

→ Concentric Circles: The circles which have same centre and different radii are called concentric circles.

→ Centroid: The point of concurrency of the three medians of a triangle is called the centroid of the triangle.

→ Circumcentre: The point of concurrency of the perpendicular bisectors of the sides of a triangle is called the circumcentre of the triangle.

→ Circumcircle: The circumcentre O is equidistant from the three vertices of a triangle. A circle with centre O and radius OA is called the circumcircle of the triangle. It passes through all the three vertices.

→ Concyclic: A number of points are concyclic if there is a circle that passes through all of them.

Basic Concepts
Circles and Its Related Terms: A Review
(i) Circle: The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle.
(ii) Centre: The fixed point is called the centre of the circle. In the figure, O is the centre.

(iii) Radius: The constant distance from its centre is called the radius of the circle. The plural of radius is radii.
In the figure, OA, OB and OC are radii of the circle C(O, r).

(iv) Circumference: The length of the complete circle is called its circumference. The perimeter of a circle is also known as the circumference of the circle.

(v) Chord: A line segment joining any two points on the circle is known as the chord of the circle. In the figure, AB and CD are chords of a circle with centre O.

(vi) Diameter: The chord, which passes through the centre of the circle is called a diameter of the circle. A diameter is the longest chord and all diameters are equal in lengths. In the figure, AOB is the diameter.
Diameter = 2 × radius
A diameter divides the circle into two equal arcs. Each of these two arcs is called a semicircle. In the figure, \(\widehat{A P B}\) and \(\widehat{A Q B}\) are two semicircles. The degree measure of a semicircle is 180°.

(vii) Secant: A line which intersects a circle in two distinct points is called a secant of the cricle. In the figure, the line l cuts the circle in two points A and B. So, l is a secant of the circle.

(viii) Arc: A piece of a circle between two points is called an arc.

Let P and Q be two points on the circle. These points P and Q divide the circle into two pieces. Each piece is an arc. These arcs are denoted in anticlockwise direction from P to Q as PQ and from Q to Pas QP. The arc PQ is called the minor are and arc QRP is called the major arc,

where R is any point (figure 10.9) on the arc between P and Q. When arcs PQ and QRP are equal, then each is called a semicircle.

(ix) Interior and Exterior of a circle: A circle divides the plane on which it lies into three parts. They are:

(a) Inside the circle, which is also called the interior of the circle.
(b) Circle.
(c) Outside the circle, which is also called the exterior of the circle (see in figure).
The circle and its interior make up the circular region.
(x) Position of a point with respect to a circle:
(a) Point inside the circle: A point P is said to lie inside the circle C(O, r), if OP < r.

(b) Point on the circle: A point is said to lie on the circle C(O, r), if OP = r.

(c) Point outside the circle: A point is said to lie outside the circle C(O, r), if OP > r.

(xi) Segment of a circle: The region between a chord and either of its arcs is called a segment of the circular region or simply a segment of the circle.

The segment containing the minor area is called the minor segment. Thus APBA is the minor segment of the circle.
The segment containing the major arc is called the major segment. Thus ARBA is the major segment of the circle.
(xii) Sector of a circle: The region between an arc and the two radii, joining the centre to the end points of the arc is called a sector. The minor are corresponds to the minor sector and the major arc corresponds to the major sector. In the figure, the region OPQO is the minor. sector and remaining part of the circular region is the major sector.

(xiii) Quadrant of a circle: One fourth of a circle is called a quadrant of a circle. In the figure, OABO is the quadrant of the circle C(O, r).

(xiv) Central angle: Let C(O, r) be any circle, then any angle whose vertex is O, is called a central angle of the circle. In the figure, ∠AOB is a central angle of the circle C (O, r).

(xv) Degree measure of an arc: Degree measure of a minor arc is the measure of the central angle subtended by the arc. In the given figure 10.17, the measure of the minor are AB is 50° ie., m\(\widehat{A B}\) = 50°. The degree measure of the major are is 360° – 50° = 310°.
⇒ m\(\widehat{B A}\) = 310°
The degree measure of a circle is 360°.
∴ mC(O, r) = m arc AB + m arc BA
= 50° + 310° = 360°.

(xvi) Congruent circles: Two circles are said to be congruent, if and only if one of them can be superposed on the other so as to cover it exactly. This is possible only when the radii of the two circles are equal. Let C(O, r₁) and C(O’, r₂) be two circles such that C(O, r₁) is superposed on C(O’, r₂) so that O’ coincides with O. Then C(O, r₁) will cover C(O’, r₂) completely if and only if r₁ = r₂.

Thus two circles are congruent, if and only if, they have equal radii.

(xvii) Congruent arcs: Two arcs of a circle are said to be congruent if and only if they have the same degree measures.
If arc AB is congruent to arc CD. They are written as
AB = CD

In particular case, arcs of semicircles will be congruent because each has degree. measure = 180°.

Angle subtended by a chord at a point: The angle subtended by chord PQ at a point R (not on the chord PQ) on the circumference of the circle is ∠PRQ. And the angle subtended by chord PQ at the centre O is ∠POQ.

Theorem 10.1:
Equal chords of a circle subtend equal angles at the centre.
Given: Two equal chords AB and CD of a circle with centre O.

To prove: ∠AOB = ∠COD.
Proof: In ΔAOB and ΔCOD, we have
OA = OC (Equal radii of a circle)
OB = OD (Equal radii of a circle)
AB = CD (given)
∴ ΔAOB ≅ ΔCOD (By SSS congruence rule)
⇒ ∠AOB = ∠COD (CPCT)
Hence proved

Theorem 10.2: [Converse of theorem 10.1]
If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.

Given: Two chords AB and CD of a circle are such that
∠AOB = ∠COD.
To prove: AB = CD.
Proof: In ΔAOB and ΔCOD, we have
OA = OC [Equal radii of a circle]
∠AOB = ∠COD (given)
OB = OD [Equal radii of a circle]
∴ ΔAOB ≅ ΔCOD (By SAS congruence rule)
⇒ AB = CD (CPCT)
Hence proved

Perpendicular from the centre to a chord :
Theorem 10.3:
The perpendicular from the centre of a circle to a chord bisects the chord.

Given: A chord AB of a circle C(O, r) and OM ⊥ to the chord AB.
To prove: AM = MB.
Construction: Join OA and OB.
Proof: In the right ΔOMA and ΔOMB, we have
OA = OB (Equal radii of a circle)
∠OMA = ∠OMB (Each is 90°)
OM = OM (Common)
ΔΟΜΑ ≅ ΔΟΜΒ (By RHS congruence rule)
⇒ AM = MB (CPCT)
Hence proved

Theorem 10.4:
[Converse of theorem 10.3]
The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.

Given: A chord AB of a circle C(O, r) with mid point M.
To prove: OM ⊥ AB.
Construction: Join OA and OB.
Proof: In ΔOAM and ΔOBM, we have
OA = OB (Equal radii of a circle)
AM = BM
[∵ M is the mid point of AB]
OM = OM (common)
∴ ΔOAM ≅ ΔOBM (By SSS congruence rule)
⇒ ∠OMA = ∠OMB (CPCT) …..(i)
But ∠OMA + ∠OMB = 180° (Linear pair axiom)
⇒ ∠OMA + ∠OMA = 180° [using (i)]
⇒ ∠OMA = 180°
⇒ ∠OMA = \(\frac{180^{\circ}}{2}\) = 90°
∠OMA = ∠OMB = 90°
Hence OM ⊥ AB.
Hence proved

Circle Through Three Points: We take a point P on a paper. There are many circles passing through this point.
Take two points P and Q. There are many infinite number of circle passing through P and Q.
If you take three non-collinear points A, B and C. There is only one circle passing through these points (see in figure below).

Theorem 10.5:
There is one and only one circle passing through three given. noncollinear points.

Given: Three non-collinear points A, B and C.
To prove: There is one and only one circle passing through three points A, B and C.
Construction: Join AB and BC. Draw the 1 bisectors PQ and RS of AB and BC. Since A, B and C are non-collinear, PQ and RS are not parallel and will intersect, say the point O. Join OA, OB and OC.
Proof: Since, O lies on the perpendicular bisector of AB, we have
OA = OB …..(i)
Similarly, O lies on the perpendicular bisector of BC, we have
OC = OB …..(ii)
From (i) and (ii), we get
OA = OB = OC = r (say)
With O as the centre and r the radius, draw circle C(O, r) which will pass through A, B and C.
Hence, there is one and only one circle passing through three non-collinear points.
Remark: If ABC is a triangle, then by Theorem 10.5, there is a unique circle passing through the three vertices A, B and C of the triangle. This circle is called the circumcircle of the ΔABC. Its centre and radius are called respectively the circumcentre and the circumradius of the triangle.

Equal chords and their distances from the centre: Let AB be a line and P be a point (not on the line). There are many infinite number of points L₁, L₂, L₃, L₄, L₅ on the line. If we join these points to P, we will get many line segments PL₁, PL₂, PM, PL₃, PL₄, PL₅, where PM is the perpendicular from P to AB. On measuring these line segments PL₁, PL₂, PM, PL₃, PL₄, PL₅, we find that PM is the shortest line segment.

So, we conclude that the length of the perpendicular from a point to a line is the distance of the line from the point.

Note: If the point lies on the line, the distance of the line from the point is zero.

Theorem 10.6:
Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).

Given: A circle C(O, r) in which chord AB is equal to chord CD, OL ⊥ AB and OM ⊥ CD.
To prove: OL = OM.
Construction: Join OA and OC.
Proof: We have
AB = CD
\(\frac{1}{2}\)AB = \(\frac{1}{2}\)CD ……(i)
∵ OL ⊥ AB
∴ AL = LB = \(\frac{1}{2}\)AB
(By theorem 10.3)…(ii)
and OM ⊥ CD
∴ CM = MD = \(\frac{1}{2}\)CD
(By theorem 10.3)…(iii)
From (i), (ii) and (iii), we get
AL = CM
Now, right ΔOLA and ΔOMC, we have
Hyp. OA = Hyp. OC [Equal radii of a circle]
AL = CM (as proved above)
∠OLA = ∠OMC (Each is 90°)
ΔOLA ≅ ΔOMC (By RHS congruence rule)
⇒ OL = OM (CPCT)
Hence, equal chords of a circle are equidistant from the centre. Proved.

Theorem 10.7:
Chords equidistant from the centre of a circle are equal in length.

Given: Two chords AB and CD of a circle C(O, r) are such that OL = OM, OL ⊥ AB and OM ⊥ CD.
To prove: AB = CD.
Construction: Join OB and OD.
Proof: ∵ OL ⊥ AB and OM ⊥ CD
∴ LB = \(\frac{1}{2}\)AB and MD = \(\frac{1}{2}\)CD ……(i)
(By theorem 10.3)
Now, right ΔOLB and ΔOMD, we have
Hyp. OB = Hyp. OD [Equal radii of a circle]
∠OLB = ∠OMD (Each is 90°)
OL = OM (given)
∴ ΔΟLΒ ≅ ΔΟΜD (By RHS congruence rule)
⇒ LB = MD (CPCT)
⇒ 2LB = 2MD
⇒ AB = CD [using (i)]
Hence, chords of a circle, which are equidistant from the centre are equal.
Proved

Angle Subtended by an Arc of a Circle: If we cut two arcs corresponding to the equal chords AB and CD respectively. We observe that are AB superimpose the arc CD completely (see in figure). This shows that equal chords make congruent arcs and conversely congruent arcs make equal chords of a circle. You can state it as follows:

If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal.
In the given figure, minor are AB subtends ∠AOB at the centre O and major are BA subtends reflex ∠AOB at the centre.

In view of the property above and theorem 10.1, the following result is true:
Congruent ares (or equal arcs) of a circle subtend equal angles at the centre.

Theorem 10.8:
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Given: An arc PQ of a circle subtends ∠POQ at the centre and ∠PAQ at a point A on the remaining part of the circle.
To prove: ∠POQ = 2∠PAQ.
Construction: Join AO and produced it to B.

Proof : Consider three different cases as given in figures. In figure (i) \(\widehat{P Q}\) is minor arc, in (ii) \(\widehat{P Q}\) is a semi-circle and in (iii) \(\widehat{P Q}\) is major arc.
In figure (i) and (ii), In ΔAOP, we have
AO = OP [Equal radii of same circle]
⇒ ∠1 = ∠2 [Angles to the opposite sides are equal]
∠POB = ∠1 + ∠2
[Exterior angle is equal to sum of its two opposite interior angles]
⇒ ∠POB = ∠1 + ∠1
⇒ ∠POB = 2∠1 …..(i)
Similarly, In ΔAOQ, we have
∠3 = ∠4 [∵ AO = OQ]
∠QOB = ∠3 + ∠4
⇒ ∠QOB = ∠3 + ∠3
⇒ ∠QOB = 2∠3 ……(ii)
Adding (i) and (ii), we get
∠POB + ∠QOB = 2∠1 + 2∠3
⇒ ∠POQ = 2(∠1 + ∠3)
⇒ ∠POQ = 2∠PAQ
In figure (iii),
∠POB + ∠QOB = 2 (∠1 + ∠3)
⇒ Reflex ∠POQ = 2∠PAQ. Hence proved

Corollary: The angle in a semicircle is a right angle.
Given: In a circle C(O, r), AB is the diameter with centre O and ∠ACB is an angle in a semicircle.

To prove: ∠ACB = 90°,
Proof: ∠AOB = 2∠ACB (By theorem 10.8)
⇒ 180° = 2∠ACB (∵ AOB is a straight line)
∠ACB = \(\frac{180^{\circ}}{2}\)
∠ACB = 90°
Hence, angle in a semicircle is a right angle. Proved

Theorem 10.9:
Angles in the same segment of a circle are equal.
Given: A circle C(O, r) in which ∠ACB and ∠ADB are two angles made by arc AB in the same segment ACDB of the circle.
To prove: ∠ACB = ∠ADB.
Construction: Join OA and OB.

Proof: In figure (i), by theorem 10.8, we have
∠AOB = 2∠ACB…(i)
and ∠AOB = 2∠ADB…(ii)
From (i) and (ii), we get
2∠ACB = 2∠ADB
∠ACB = ∠ADB
In figure (ii), by theorem 10.8, we have
reflex ∠AOB = 2∠ACB…(iii)
and reflex ∠AOB = 2∠ADB…(iv)
From (iii) and (iv), we get
2∠ACB = 2∠ADB
∠ACB = ∠ADB
In both cases, ∠ACB = ∠ADB
Hence, angles in the same segment of a circle are equal. Hence proved

Theorem 10.10:
If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e., they are concyclic).

Given: AB is a line segment, which subtends equal angles at two points C and D, such that
∠ACB = ∠ADB.
To prove: The points A, B, C and D lie on a circle (i.e., they are concyclic).
Construction: Draw a circle through three non-collinear points A, B, C.
Proof: Suppose circle does not pass through D. Let it will intersect AD (or extended AD) at point, say E (or E’). If points A, C, E and B lie on a circle, then
∠ACB = ∠AEB …(i) (By theorem 10.9)
But, ∠ACB = ∠ADB (given)…(ii)
From (i) and (ii), we get
∠AEB = ∠ADB
This is not possible unless E coincides with D.
Therefore D lies on the circle passing through A, B, C.
Similarly, E’ should also coincide with D.
Hence, the points A, B, C and D are concylic. Hence Proved

Cyclic Quadrilaterals: A quadrilateral ABCD is called cyclic, if all the four vertices of it lie on a circle.
Theorem 10.11:
The sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
Or
The opposite angles of a cyclic quadrilateral are supplementary.

Given: A cyclic quadrilateral ABCD.
To prove: ∠A + ∠C = 180° and ∠B + ∠D = 180°.
Construction: Join AC and BD.
Proof: ∠ADB = ∠ACB [Angles in a same segment are equal]…(i)
∠ABD = ∠ACD [Angles in a same segment are equal]…(ii)
Adding (i) and (ii), we get
∠ADB + ∠ABD = ∠ACB + ∠ACD
⇒ ∠ADB + ∠ABD = ∠C
Adding ∠BAD on both sides, we get
∠ADB + ∠ABD + ∠BAD = ∠C + ∠BAD
⇒ 180° = ∠C + ∠A
[∵ Sum of angles of a ΔBAD is 180°]
∠A + ∠C = 180° …(iii)
But, we know that the sum of angles of a quadrilateral is 360°.
∴ ∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠B + ∠D + 180° = 360° [using (iii)]
⇒ ∠B + ∠D = 360° – 180° = 180°
Hence, ∠A + ∠C = 180° and
∠B + ∠D = 180°. Proved

Theorem 10.12:
If the sum of a pair of opposite angles of a quadrilateral is 180°, the quadrilateral is cyclic.
Given: A quadrilateral ABCD in which ∠A + ∠C = 180°.
To prove: ABCD is a cyclic quadrilateral.
Construction: If possible, let ABCD be not a cyclic quadrilateral. Draw a circle, passing through non-collinear points D, A, B. Let this circle meet DE or DE produced at C. Join EB.

Proof: ∠A + ∠C = 180° (given) …(i)
Now ABED is a cyclic quadrilateral.
∠A + ∠E = 180° ….(ii)
[∵ opposite angles of a cyclic quadrilateral is 180°]
From (i) and (ii), we get
∠A + ∠C = ∠A + ∠E
⇒ ∠C = ∠E
This is not possible, since an exterior angle of a triangle can never be equal to its interior opposite angle.
So, ∠C = ∠E is possible only when C coincides with E.
Hence, the circle passing through D, A, B must pass through C also.
Hence, ABCD is a cyclic quadrilateral.
Proved

Haryana State Board HBSE 9th Class Maths Notes Chapter 9 Areas of Parallelograms and Triangles Notes.

Haryana Board 9th Class Maths Notes Chapter 9 Areas of Parallelograms and Triangles

Introduction
In previous classes, we have studied the areas of plane figure such as, triangle, square, parallelogram, rhombus etc. We may recall that part of plane enclosed by a simple closed figure is called a planar region corresponding to that figure. The magnitude or measure of this planar region is called its area.

Area is always expressed with the help of a number such as 12 cm², 5 cm², 7 hectares etc. In this chapter, we will consolidate the knowledge about these formulae by studying some relationship between the areas of these geometric figures under the condition when they lie on the same base and between the same parallels.

Key Words
→ Base: In a geometry, a particular side or face of geometric figure, such as a triangle, parallelogram, cone etc.

→ Altitude: The perpendicular distance from a vertex to the opposite side is known as altitude.

→ Magnitude: Exter, size, bulk, amount, quantity, greateness. That which is extended in length, breadth and thickness. A thing which can be divided into parts.

→ Monotone: In one tone.

→ Planar region: Of, relating to or situated in a plane.
OR
Having a two dimensional characteristic.

→ Interior of a triangle: The part of the plane enclosed by a triangle is known as the interior of the triangle.

→ Area of a triangle = \(\frac{1}{2}\) × base × height

→ Area of a parallelogram = base × height

→ Area of a square = (side)² OR \(\frac{1}{2}\)d₁²,
[where d₁ is its diagonal]

→ Area of a rectangle = length × breadth

→ Area of a rhombus = base × height or \(\frac{1}{2}\)d₁ × d₂, [where d₁ and d₂ are its diagonals]

→ Area of a trapezium = \(\frac{1}{2}\)(sum of parallelside) × height

Basic Concepts
1. Polygonal Regions:
(a) Triangular region: The union of a triangle and its interior is called a triangular region. By the area of a triangle, we mean the area of its triangular region.

(b) Rectangular region: The part of the plane enclosed by a rectangle is called the interior of a rectangle and the union of a rectangle and its interior is a called a rectangular region. It can be represent as the union of two triangular regions.

(c) Polygonal region: A polygonal region is a plane figure that can be written as a union of a finite number of triangular regions, subject to a constraint. The constraint is that the triangular regions are non-over lapping. That means if two triangular region intersect then their intersetion is either vertex or edge of each of the triangular regions.

2. Area Axioms:
(a) Every polygonal region R has an area, measured in square units.
(b) (i) Congruent Area Axiom If two polygonal regions R₁ and R₂ are such that R₁ ≅ R₂, then
ar (R₁) = ar (R₂).
(ii) Area Monotone Axiom: If two polygonal regions are such that R₁ belongs to R₂ then
ar (R₁) ≤ ar (R₂).
(iii) Area Addition Axiom: If intersection of two polygonal regions R₁ and R₂, is a finite number of points and line segments such that R = R₁ ∪ R₂, then
ar (R) = ar (R₁) + ar (R₂).

(c) Rectangle Area Axiom: A rectangular region ABCD in which AB = a units and BC = b units then
ar (rectangle ABCD)= ab square units.

3. Figures on the Same Base and Between the Same Parallels:
Look at the following figures:

In figure 9.4 (i) parallelograms ABCD and ABQP have a common side AB. So we say that parallelogram ABCD and ABQP are on the same base AB. Similarly in figure 9.4 (ii) triangles ABC and DBC are on the same base BC, in figure 9.4 (iii) trapezium PQRS and parallelogram PQMN are on the same base PQ. In figure 9.4 (iv) parallelogram ABCD and triangle PDC are on the same base DC.

Now look at the figures (9.5):

We observe that in figure 9.5 (i) triangles CBA and DAB lie on the same base AB and, AB and CD are two parallel lines. In addition to the above, the vertex D of ADAB opposite to the base AB and vertex C of ACBA opposite to the base AB lie on a line CD parallel to the base AB. So we say that ADAB and ACBA are on the same base AB and between the same parallels CD and AB. Similarly in figure 9.5 (ii) trapezium ABCD and parallelogram ABPQ are on the same base AB between the same parallels AB and PD. In figure 9.5 (iii) trapezium ABCD and parallelogram ABFE are on the same base AB and between the same parallels AB and DF. In figure 9.5 (iv) parallelograms PQRS and PQMN are on the same base PQ and between the same parallels PQ and SM.

So, two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.

Now consider the following figures:


We observe that in figure 9.6 (i) triangles ABC and DBC are the same base BC but do not lie between the same parallels. In figure, 9.6 (ii) parallelogram ABCD and triangle PQR are lie between the same parallels AB and CD but they are not on the same base. In figure 9.6 (iii) the parallelograms ABCD and ABFE are on the same base AB but do not lie between the same parallels.

Parallelograms on the Same Base and Between the Same Parallels:
Theorem 9.1:
Parallelograms on the same base and between the same parallels are equal in area.

Given: Two parallelogram ABCD and ABFE are on the same base AB and are between the same parallels AB and DF.
To prove:
ar (||gm ABCD) = ar (||gm ABFE).
Proof: In ΔAED and ΔBFC, we have
AD = BC
[∵ AD and BC are the opposite sides of parallelogram ABCD]
∠DAE = ∠CBF
[∵ AD || BC and AE || BF,
∴ angle between AD and AE = angle between BC and BF]
and AE = BF
(∵ AE and BF are the opposite sides of the parallelogram ABFE)
ΔAED ≅ ΔBFC
(By SAS congruence rule)
⇒ ar (ΔAED) = ar (ΔBFC)
(By congruent area axiom) …(i)
Now
ar (||gm ABCD) = ar (☐ ABCE) + ar (ΔAED)
⇒ ar (||gm ABCD) = ar (☐ ABCE) + ar (ΔBFC) [using (i)]
⇒ ar (||gm ABCD) = ar (||gm ABFE)
Hence proved

Corollary 1: A parallelogram and a rectangle on the same base and between the same parallels are equal in area.
Corollary 2: If a triangle and a parallelogram are on the same base and between the same parallels, then area of the triangle is equal to half the area of the parallelogram.

Corollary 3: Area of parallelogram = base × height.
Given: A parallelogram ABCD in which AB is the base and AP is the corresponding height.
To prove : Area of parallelogram ABCD = AB × AP.
Construction: Draw BQ ⊥ CD so that rectangle ABQP is formed.

Proof: Since parallelogram ABCD and rectangle ABQP are on the same base AB and between the same parallels AB and PC.
∴ ar (||gm ABCD) = ar (rectangle ABQP)
⇒ ar (||gm ABCD) = AB × AP
[∵ area of rectangle = length × breadth]
⇒ ar (||gm ABCD) = base × height.

Triangles on the Same Base and Between the Same Parallels:
Theorem 9.2:
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.

Given: Two triangles ABC and PBC on the same base BC and between the same parallels BC and AP.
To prove : ar (ΔABC) = ar (ΔPBC).
Construction: Through B draw BD || CP, intersecting PA produced in D and through C, draw CQ || BA, intersecting AP produced in Q.
Proof: Since, BC || AP and AB || CQ.
∴ ABCQ is a parallelogram.
Again, BC || AP and BD || CP
∴ BCPD is a parallelogram.
Now, parallelograms ABCQ and DBCP are on the same base BC and between. the same parallels BC and DQ.
∴ ar (||gm ABCQ) = ar (||gm DBCP) …(i)
But, a diagonal of a parallelogram divides it into two triangles are of equal areas.
∴ ar (ΔABC) = ar (||gm ABCQ) …(ii)
Similarly, ar (ΔPBC) = \(\frac{1}{2}\)ar (||gm DBCP) …(iii)
From (i), (ii) and (iii), we get
ar (ΔABC) = ar (ΔPBC)
Hence proved

Corollory: Area of a triangle = \(\frac{1}{2}\)base × height.
Given: A ΔABC in which AP is the height to the side BC.
To prove: ar (ΔABC) = \(\frac{1}{2}\)BC × AP.

Construction: Through A and C, draw AD || BC and CD || BA, intersecting each other at D.
Proof : Since, AD || BC and CD || BA
∴ ABCD is a parallelogram.
AC is the diagonal of parallelogram ABCD. It divides the parallelogram ABCD into two triangles of equal areas.
∴ ar (ΔABC) = \(\frac{1}{2}\)ar (||gm ABCD)…(i)
Since BC is a side of ||gm ABCD and AP is its corresponding height.
ar (||gm ABCD) = BC × AP …..(ii)
From (i) and (ii), we get
ar(ΔABC) = \(\frac{1}{2}\)BC × AP.
Hence proved.

Corollary: Area of a trapezium = \(\frac{1}{2}\) × (sum of the parallel sides) × (distance between them)
Given: A trapezium ABCD in which AB || CD and CP ⊥ AB. Let CP = h.
To prove :
ar (trapezium) = \(\frac{1}{2}\)(AB + CD) × h.
Construction: Draw AQ ⊥ CQ, intersecting CD produced at Q. Join AC.

Proof: ar (trapezium ABCD) = ar (ΔABC) + ar (ΔACD)
= \(\frac{1}{2}\) × AB × CP + \(\frac{1}{2}\) × CD × AQ
= \(\frac{1}{2}\) × (AB + CD) × h, [∵ CP = AQ = h]
∴ Area of a trapezium = \(\frac{1}{2}\)(sum of the parallel sides) × (distance between them)

Theorem 9.3:
Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.
OR
If two triangles have equal areas and one side of the triangle is equal to one side of the other, then their corresponding altitudes are equal.
Given: Two triangles ABC and DEF are such that
ar (ΔABC) = ar (ΔDEF) and AB = DE and CM and FN are the altitudes corresponding to AB and DE respectively of the two triangles.
To prove: CM = FN.
Proof: In AABC, CM is the altitude to the corresponding side AB.

ar (ΔABC)= \(\frac{1}{2}\) × AB × CM …..(i)
[∵ ar (Δ) = \(\frac{1}{2}\) base × height]
Similarly,
ar (ΔDEF) = \(\frac{1}{2}\) × DE × FN …(ii)
But, ar (ΔABC) = ar (ΔDEF) (given)…(iii)
From (i), (ii) and (iii), we get
\(\frac{1}{2}\) × AB × CM = \(\frac{1}{2}\) × DE × FN
⇒ \(\frac{1}{2}\) × AB × CM = \(\frac{1}{2}\) × AB × FN
[given DE = AB]
⇒ CM = FN. Hence proved
As CM = FN (Proved above)
and CM ⊥ AB and FN ⊥ AB
∴ CF || AB

Hence, two triangles having the same base and equal area lie between the same parallels.

Haryana State Board HBSE 9th Class Maths Notes Chapter 8 Quadrilaterals Notes.

Haryana Board 9th Class Maths Notes Chapter 8 Quadrilaterals

Introduction
In previous chapters 6 and 7, we have studied about triangles and their properties. We know that figure obtained by joining three non-collinear points in pairs, is a triangle. If we have four points in a plane such that no three of them are collinear.

If we joined these points, we obtain a figure with four sides (see figure 8.1).

Key Words
→ Intercept: To cut off.

→ Internal bisector: Name sometimes given to the bisector of the interior angle of a triangle (or polygon).

→ External bisector: The bisector of the exterior angle of a triangle (or polygon) is sometimes called the external bisector of the angle of the triangle (or polygon).

Basic Concepts
1. Quadrilateral: A closed figure which bounded by four line segments is called quadrilateral. Figure 8.2 represents a quadrilateral with vertices A, B, C and D. It is denoted by the symbol quad. ABCD or ☐ABCD.

Four straight lines AB, BC, CD and DA are called the sides of the quadrilateral ABCD and ∠A, ∠B, ∠C and ∠D are the four angles of it.
The straight lines joining the opposite vertices of a quadrilateral are called its diagonals. Thus, a quadrilateral ABCD has two diagonals; namely AC and BD.

In a quadrilateral, we have the following definitions:
(a) Consecutive or adjacent sides: Two sides with common vertex are called the adjacent sides. In fig. 8.2 AB and BC, BC and CD, CD and DA and DA and AB are four adjacent sides of the quadrilateral ABCD.
(b) Opposite sides: Two sides of a quadrilateral having no common end point are called its opposite sides.
In fig. 8.2, AB and CD, AD and BC are two pairs of opposite sides of quad. ABCD.
(c) Consecutive angles: Two angles of a quadrilateral having a common side are called its consecutive angles.
In fig. 8.2, ∠A and ∠B, ∠B and ∠C, ∠C and ∠D and ∠D and ∠A are four pairs of consecutive angles of ☐ABCD.
(d) Opposite angles: Two angles of a quadrilateral having no common side are called its opposite angles.
In figure 8.2, ∠A and ∠C, ∠B and ∠D are two pairs of opposite angles of ☐ABCD.

2. Angle Sum Property of a Quadrilateral:
Let us now recall the angle sum property of a quadrilateral. The sum of the angles of a quadrilateral is 360°. This can be verified by drawing a diagonal and dividing the quadrilateral into two triangles.

Let ABCD be a quadrilateral and AC be a diagonal (see figure 8.3).
In ΔABC, we have
∠1 + ∠B + ∠2 = 180°…(1)
I. Sum of interior angles of a triangle 180°]
In ΔADC, we have
∠3 + ∠D + ∠4 = 180°…(ii)
Adding (i) and (ii), we get
∠1 + ∠3 + ∠B + ∠2 + ∠4 + ∠D = 180° + 180°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
[∵ ∠1 + ∠3 = ∠A and ∠2 + ∠4 = ∠C]
Hence, sum of angles of a quadrilateral is 360°.

3. Types of Quadrilaterals:
(i) Trapezium: A quadrilateral in which one pair of opposite sides is parallel but the other pair of opposite sides is non-parallel is called a trapezium.
The figure 8.4, represents a trapezium ABCD.

In which AB || CD and AD and BC are non-parallel sides. If the non-parallel sides AD and BC of the trapezium are equal, it is called an isosceles trapezium. In this case, ∠D = ∠C and ∠A = ∠B.

(ii) Parallelogram: A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram.

The figure 8.5, represents a parallelogram ABCD, since AD || BC and AB || CD.

(iii) Rectangle: A parallelogram in which each angle is a right angle is called a rectangle.

The figure 8.6, represents a rectangle ABCD in which ∠A = ∠B = ∠C = ∠D = 90°.

(iv) Square: A parallelogram in which all sides are equal and each angle is equal to 90° is called a square.

The figure 8.7, represents a square ABCD in which AB = BC = CD = DA and ∠A = ∠B = ∠C = ∠D = 90°.

(v) Rhombus: A parallelogram in which all sides are equal is called a rhombus.

The figure 8.8, represents a rhombus. ABCD in which AB = BC = CD = DA.

(vi) Kite: A quadrilateral in which both pairs of adjacent sides are equal is called a kite.

The figure 8.9, represents a kite ABCD in which AD = DC and AB = BC.

Note:
(i) Every parallelogram is a trapezium but every trapezium is not a parallelogram.
(ii) Every square is a rectangle and also a rhombus but every rectangle or rhombus is not a square.
(iii) A kite is not a parallelogram.
(iv) Every square, rectangle and rhombus are parallelograms.

4. Properties of a Parallelogram:
Theorem 8.1:
A diagonal of a parallelogram divides it into two congruent triangles.
Given: ABCD is a parallelogram and AC its diagonal.
To prove :
ΔABC ≅ ΔCDA.

Proof: ABCD and AC cuts them
∠BAC = ∠DCA …..(i)
(Alternate interior angles)
and BC || AD and AC cuts them.
∠BCA = ∠DAC (Alternate interior angles)
Now, in ΔABC and ΔCDA, we have
∠BAC = ∠DCA, [From (i)]
AC = AC, (Common)
and ∠BCA = ∠DAC, [From (ii)]
ΔABC ≅ ΔCDA [By ASA congruence rule]
Hence proved

Theorem 8.2:
In a parallelogram, opposite sides are equal.
Given: ABCD is a parallelogram.
To prove: AB = CD and AD = BC.
Construction: Join AC.

Proof: ABDC and AC cuts them.
∠BAC = ∠DCA …(i) (Alternate interior angles)
Again AD || BC and AC cuts them.
∠BCA = ∠DAC …(ii)
(Alternate interior angles).
Now, in AABC and ACDA, we have
∠BAC = ∠DCA, [From (i)]
AC = AC, [Common]
and ∠BCA = ∠DAC, [From (ii)]
ΔABC ≅ ΔCDA (By ASA congruence rule)
AB = CD and AD = BC, (CPCT)
Hence proved

Theorem 8.3:
If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Given: A quadrilateral ABCD in which AB = CD and BC = DA.
To prove: Quadrilateral ABCD is a parallelogram.

Construction: Join AC.
Proof: In ΔABC and ΔCDA, we have
AB = CD, (Given)
BC = AD, (Given)
and AC = AC, (Common)
ΔABC ≅ ΔCDA (By SSS congruence rule)
⇒ ∠BAC = ∠DCA, (CPCT)
⇒ AB || CD …..(i)
and ∠BCA = ∠DAC, (CPCT)
AD || BC …..(ii)
From (i) and (ii), we get
AB || CD and AD || BC
Hence, ABCD is a parallelogram. Hence Proved

Theorem 8.4:
In a parallelogram, opposite angles are equal.
Given: ABCD is a parallelogram.
To prove: ∠A = ∠C and ∠B = ∠D.
Proof : BC || AD and AB cuts them.

⇒ ∠A + ∠B = 180° …(1)
[Sum of co-interior angles is 180°]
Again, AB || CD and AD intersects them.
⇒ ∠A + ∠D = 180° …..(ii)
[Sum of co-interior angles is 180°]
From (i) and (ii), we get
∠A + ∠B = ∠A + ∠D
⇒ ∠B = ∠D
Similarly, ∠A = ∠C.
Hence proved

Theorem 8.5:
If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
Given: A quadrilateral ABCD in which ∠A = ∠C and ∠B = ∠D.
To prove: Quad. ABCD is a parallelogram.

Proof: We have
∠A = ∠C…(1)
and ∠B = ∠D…(ii)
Adding (i) and (ii), we have
∠A + ∠B = ∠C + ∠D…(iii)
In a quadrilateral ABCD, we have
∠A + ∠B + ∠C + ∠D = 360°,
[∵ Sum of angles of a quadrilateral is 360°]
⇒ ∠A + ∠B + ∠A + ∠B = 360°, [Using (iii)]
⇒ 2(∠A + ∠B) = 360°
⇒ ∠A + ∠B = \(\frac{360^{\circ}}{2}\) = 180°…(iv)
Now, line segments BC and AD cut by AB,
such that
∠A + ∠B = 180°
⇒ BC || AD
Again, ∠A + ∠B = 180°.
⇒ ∠C + ∠B = 180° [From (i) ∠A = ∠C]
Now, line segments AB and CD cut by BC,
∠B + ∠C = 180°
⇒ AB || CD
Thus, AB || CD and BC || AD.
Hence, ABCD is a parallelogram. Proved

Theorem 8.6:
The diagonals of a parallelogram bisect each other.
Given: A parallelogram ABCD such that its diagonals AC and BD intersect at O.
To prove: OA = OC and OB = OD.
Proof: Since ABCD is a parallelogram.

Therefore AB || CD and BC || AD.
Now, AB || CD and AC intersects.
∠BAC = ∠DCA, (Alternate interior angles)
∠BAO = ∠DCO …(1)
Again, AB || CD and BD intersects them.
∠ABD = ∠CDB, (Alternate interior angles)
⇒ ∠ABO = ∠CDO…(ii)
Now, in ΔAOB and ΔCOD, we have
∠BAO = ∠DCO, [From (i)]
AB = CD, (Opposite sides of parallelogram)
and ∠ABO = ∠CDO, [From (ii)]
∴ ΔAOB ≅ ΔCOD, (By ASA congruence rule)
⇒ OA = OC and OB = OD. Hence proved

Theorem 8.7:
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Given: ABCD is a quadrilateral in which the diagonals AC and BD bisect each other at O i.e., AO = OC and BO = OD.
To prove : Quadrilateral ABCD is a parallelogram.

Proof: In ΔAOB and ΔCOD, we have
AO = OC, (Given)
∠AOB = ∠COD, (vertically opposite angles)
and BO = OD, (Given)
∴ ΔAOB ≅ ΔCOD, (by SAS congruence rule)
⇒ ∠BAO = ∠DCO, (CPCT)
⇒ ∠BAC = ∠DCA
But these are alternate interior angles.
∴ AB || CD
and similarly, AD || BC
Hence, quad. ABCD is a parallelogram. Hence Proved

5. Another Conditions for a Quadrilateral to be a parallelogram:
In this chapter, we have studied many properties and verified that if in a quadrilateral any one of those properties is satisfied, then it will be a parallelogram. Now, we study a required condition for a quadrilateral to be a parallelogram. It is stated in the form of a theorem as given below.

Theorem 8.8:
A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.
Given: A quadrilateral ABCD in which AB = CD and AB || CD
To prove: Quadrilateral ABCD is a parallelogram.
Construction : Join AC.

Proof: We have
AB || CD and AC intersects them.
⇒ ∠BAC = ∠DCA …(i)
(Alternate interior angles)
In ΔABC and ∠CDA, we have
AB = CD, (Given)
∠BAC = ∠DCA, [From (i)]
and AC = AC, (Common)
∴ ΔABC ≅ ΔCDA (By SAS congruence rule)
⇒ ∠BCA = ∠DAC, (CPCT)
But these are alternate interios angles.
∴ AD || BC
and AB || CD, (Given)
Hence, quad. ABCD is a parallelogram.
Hence Proved

The Mid Point Theorem: In this section we shall discuss some more properties of a triangle using properties of a parallelogram which is related to the mid points of sides of a triangle.

Theorem 8.9:
The line segment joining the mid points of two sides of a triangle is parallel to the third side and equal to half of it.

Given: D and E are the mid points of the sides AB and AC of the triangle ABC.
To prove : (i) DE || BC, (ii) DE = \(\frac{1}{2}\)BC.
Construction: Produce DE to F, such that EF = DE and join CF.
Proof: In ΔAED and ΔCEF, we have
AE = CE, (∵ E is the mid point of AC)
∠AED = ∠CEF, (Vertically opposite angles)
and DE = EF, (By construction)
∴ ΔAED ≅ ΔCEF, (By SAS congruence rule)
⇒ ∠1 = ∠2, (CPCT)
But these are alternate interior angles.
AB || FC ⇒ BD || FC …(i)
and AD = FC (CPCT)
But AD = BD
(∵ D is the mid point of AB)
∴ BD = FC ……(ii)
From (i) and (ii), we get
BD || FC and BD = FC
∴ BCFD is a parallelogram. [By theorem 8.8]
⇒ DF || BC,
(∵ Opposite sides of a parallelogram)
⇒ DE || BC
and DF = BC,
(∵ Oppsite sides of a parallelogram)
⇒ 2DE = BC,
[∵ DE = EF ⇒ DF = DE + EF = 2DE]
⇒ DE = \(\frac{1}{2}\)BC
Hence, DE || BC and DE = BC. Proved

Theorem 8.10:
The line drawn through the mid point of one side of a triangle, parallel to another side bisects the third side.

Given: A ΔABC, D is the mid point of AB and line through D parallel to BC intersects AC in E.
To prove: E is the mid point of AC.
Construction: Draw CM || BA intersects line l in F.
Proof: Since, AB || CM (By construction)
∴ BD || CF
and DF || BC (Given)
∴ BDFC is a parallelogram.
⇒ BD = CF,
(Opposite sides of a parallelogram)
But, BD = AD,
(∵ D is the mid point of AB)
∴ AD = CF …..(i)
Now, AB || CM and AC intersects them.
∠1 = ∠2,
(Alternate interior angles) …(ii)
In ΔADE and ΔCFE, we have
∠1 = ∠2 [From (i)]
∠AED = ∠CEF
(Vertically opposite angles)
and AD = CF [From (i)]
∴ ΔADE ≅ ΔCFE
(By AAS congruence rule)
⇒ AE = EC
Hence, E is the mid point of AC. Proved

Haryana State Board HBSE 9th Class Maths Notes Chapter 7 Triangles Notes.

Haryana Board 9th Class Maths Notes Chapter 7 Triangles

Introduction
In previous classes, we have learnt about triangles and their various properties. Recall that, a closed figure formed by three line segments, is called a triangle. It is usually denoted by the greek letter Δ (delta).

The figure 7.1 shows a triangle ABC denoted as a ΔABC. A triangle has three sides namely AB, BC and CA, three vertices namely A, B and C and has three angles namely ∠A, ∠B and ∠C.

In this chapter we shall learn about the congruence of triangles, criteria for congruence of triangles, some more properties of triangles and inequalities in a triangle.

Key Words
→ Equalities: The logical relation expressing identity or sameness and denoted by the sign “=”.

→ Axiom: A statement whose truth is either to be taken as self evident or to be assumed.

→ Inequalities: Refers to a statement that a quantity is either greater than or less than but not equal to them.

→ Perimeter: The perimeter of a two dimensional region is the length of its boundary.

→ Concentrate: On one point, to pay attention upon.

→ Slides: A gliding seat or surface for sliding.

→ Swing: To move with to and fro motion.

→ Hexagon: It is a polygon bounded by six straight line. (six-sided figure).

Basic Concepts
1. (a) Definition of Congruence: If two geometrical figures coincide exactly, by placing one over the other, the figures are said to be congruent to each other.
(i) Two line segments are congruent if and only if their lengths are equal. (See fig. 7.2).

Two line segments AB and CD are congruent, if AB = CD.

(ii) Two angles are congruent if and only if their measures are equal. (See fig. 7-3)

Two angles ABC and PQR are congruent if m∠ABC = m∠PQR.

(iii) Two circles are congruent if and only if lengths of their radii are equal. (See fig. 7.4)

Two circles C and C2 are congruent, if r1 = r2.

(iv) Two squares are congruent if and only if they have equal sides in length. (See fig. 7.5)

Two squares ABCD and EFGH are congruent, if AB = BC = CD = DA = EF = FG = GH = HE.

(b) Congruence of Triangles: The three sides and three angles of a triangle are called its six parts or six elements. Two triangles are said to be congruent to each other, if on placing one over the other, they exactly coincide.

Let ΔABC is placed over ΔDEF, such that vertex A falls on vertex D and side AB falls on side DE, then if the two triangles coincide with each other in a such a way that B falls on E, C falls on F; side BC coincides with side EF and side AC coincides with side DF, then the two triangles are congruent to each other. (See fig. 7.6)

The symbol used for congruence is “≅”.
ΔABC is congruent to ΔDEF is written as:
ΔABC ≅ ΔDEF.
In case of congruent ΔABC and ΔDEF as given above, the sides of the two triangles, which coincide with each other are called corresponding sides. Thus the sides AB, BC and CA of AABC are corresponding to the side DE, EF and FD of ADEF respectively. In the same way, the angles of the two traingles which coincide with each other, are called corresponding angles. Thus three pairs of corresponding angles are ∠A and ∠D, ∠B and ∠E and ∠C and ∠F.

It follows from the above discussion that if ΔABC coincide ΔDEF exactly such that the vertices of ΔABC fall on the vertices of ΔDEF, in the order
A ↔ D, B ↔ E, C ↔ F.

Then we have the following six equalities:
(i) AB = DE, BC = EF and CA = FD i.e. corresponding sides are equal (congruent).
(ii) ∠A = ∠D, ∠B = ∠E and ∠C = ∠F i.e. corresponding angles are equal (congruent). Hence, following is the general condition for congruence of two triangles:
Two triangles are congruent if and only if there exists a correspondence between their sides and vertices such that the corresponding sides and the corresponding angles of two triangles are equal.

If ΔABC is congruent to ΔDEF and the correspondence ABC ↔ DEF makes the six pairs of corresponding parts of the two triangles congruent, then we write ΔABC ≅ ΔDEF.
But it will not be correct to write ΔCBA ≅ ΔDEF because corresponding parts of ΔCBA and ΔDEF will not be equal i.e., congruent.
Note: The corresponding parts of congruent triangles (abbreviated as CPCT).

(c) Congruence relation in the set of all triangles: From the definition of congruence triangles and notation above, we obtain the following results:
(i) ΔABC ≅ ΔABC
[Congruence relation is reflexive]
(ii) If ΔABC ≅ ΔDEF,
then ΔDEF ≅ ΔABC,
[Congruence relation is symmetric]
(iii) If ΔABC ≅ ΔDEF
and ΔDEF ≅ ΔKLM,
then ΔABC ≅ ΔKLM,
[Congruence relation is transitive]

2. Criteria for Congruence of Triangles:
Axiom 7.1 (SAS congruence rule): Two triangles are congruent if two sides and included angle of one triangle are equal to the two sides and the included angle of the other triangle.
Given: ΔABC and ΔDEF in which AB = DE, AC = DF and ∠A = ∠D. (See fig. 7.7).

To prove : ΔABC ≅ ΔDEF.
Proof: Place ΔABC over ΔDEF such that vertex A falls on vertex D and side AB falls on side DE. Since side AB side DE. Therefore vertex B falls on vertex E. Since ∠A = ∠D, therefore AC will fall on DF.
But AC = DF and A falls on D.
∴ C will fall on F.
Thus AC will coincide with DF.
Now B falls on E and C falls on F.
∴ BC will coincide with EF.
∴ ΔABC coincide with ΔDEF.
Hence, by definition of congruence ΔABC ≅ ΔDEF.
Note: (1) This axiom refers two sides and the angle between them so it is known as (side-angle-side) or the “SAS congruence axiom” or the “SAS” criteria

(2) SAS axiom is not applicable when two sides and one angle ‘not included between these sides’ of one triangle are equal to two sides and one angle of the other triangle.

Theorem 7.1 (ASA congruence rule):
Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.
Given: Two triangles ABC and DEF, such that
∠B = ∠E, ∠C = ∠F and BC = EF.
To prove : ΔABC ≅ ΔDEF.
Proof: For proving the congruence of the two triangles there are three cases arise:
Case I: Let AB = DE. (See figure 7.8)

In this case, we have
AB = DE, (Assumed)
∠B = ∠E, (Given)
and BC = EF, (Given)
So, ΔABC ≅ ΔDEF, (By SAS axiom)

Case II: Let if possible AB > DE, so we can take a point P on AB such that PB = DE. Now consider ΔPBC and ΔDEF.

In ΔPBC and ΔDEF, we have
PB = DE, (By construction)
∠B = ∠E, (Given)
and BC = EF, (Given)
So, ΔPBC ≅ ΔDEF,(By SAS axiom)
⇒ ∠PCB = ∠DFE, (CPCT)
But ∠ACB = ∠DFE, (Given)
∴ ∠ACB = ∠PCB
This is possible only when P coincide with A, therefore AB must be equal to DE.
Thus, in ΔABC and ΔDEF, we have
AB = DE, (As proved above)
∠B = ∠E, (Given)
and BC = EF, (Given)
So, ΔABC ≅ ΔDEF, (By SAS axiom)

Case III: If AB < DE, we can choose a point M on DE such that ME = AB and repeating the arguments as given in Case (II), we can conclude that AB = DE and so we can prove that

ΔABC ≅ ΔDEF
Hence, in all three cases, we have
ΔABC ≅ ΔDEF. Proved

Corollary (AAS congruence rule):
If any two angles and non-included side of one triangle are equal to the corresponding angles and side of another triangle, then two triangles are congruent.
Given: Two triangles ABC and DEF, such that
∠A = ∠D, ∠B = ∠E
and BC = EF.
To prove : ΔABC ≅ ΔDEF
Proof: Since, we know that sum of the interior angles of a triangle is 180°.

∴ ∠A + ∠B + ∠C = ∠D + ∠E + ∠F = 180°…(i)
But ∠A = ∠D and ∠B = ∠E, (given) …….(ii)
∠A + ∠B + ∠C = ∠A + ∠B + ∠F,
[From (i) and (ii)]
⇒ ∠C = ∠F
In ΔABC and ΔDEF, we have
∠B = ∠E, (Given)
∠C = ∠F, (As proved above)
and BC = EF, (Given)
So, ΔABC ≅ ΔDEF
(By ASA congruence rule)

Some Properties of a Triangle: In chapter 6 we have studied the triangle and their kinds. Recall that, if a triangle has two sides equal, then it is called an isosceles triangle. Now we shall study some results related to isosceles triangles.

Theorem 7.2:
Angles opposite to equal
Given: In ΔABC, AB = AC.
To prove: ∠B = ∠C. sides of an isosceles triangle are equal.

Construction: Draw AD, the bisector of ∠A which meets BC on D.
Proof: In ΔABD and ΔACD, we have
AB = AC, (Given)
∠BAD = ∠CAD, (By construction)
and AD = AD, (Common)
ΔABD ≅ ΔACD,
(By SAS congruence rule)
⇒ ∠B = ∠C. Hence proved.

Theorem 7.3:
[Converse of Theorem 7.2]: The sides opposite to equal angles of a triangle are equal.
Given: In ΔABC,
∠B = ∠C.
To prove: AB = AC.

Construction: Draw AD perpendicular to BC. It meets BC on D.
Proof: In ΔABD and ΔACD, we have
∠ABD = ∠ACD, (Given)
∠ADB = ∠ADC,
(By construction each = 90°)
and AD = AD, (Common)
∴ ΔABD ≅ ΔACD, (By AAS congruence rule)
⇒ AB = AC (CPCT)
Hence proved

Some More Criteria for Congruence of Triangles :
Theorem 7.4 (SSS congruence rule): If three sides of one triangle are equal to the three sides of another triangle, then two triangles are congruent.
Given: ΔABC and ΔPQR such that AB = PQ, BC = QR and AC = PR.
To prove : ΔABC = ΔPQR.

Construction: Suppose BC is the longest side of ΔABC. Draw QS and RS such that ∠SQR = ∠ABC and ∠SRQ = ∠ACB. Join P to S.
Proof: In ΔABC and ΔSQR, we have
BC = QR, (Given)
∠ABC = ∠SQR, (By construction)
and ∠ACB = ∠SRQ, (By construction)
∴ ΔABC ≅ ΔRQS,
(By ASA congruence rule)
⇒ ∠BAC = ∠QSR, (CPCT) …(i)
AB = QS, (CPCT)
and AC = SR, (CPCT)
Now AB = PQ (given)
and AC = PR (given) …(ii)
AB = QS
and AC = SR (as proved above)…(iii)
From (ii) and (iii), we get
PQ = QS and PR = SR
⇒ ∠QPS = ∠QSP…(iv)
and ∠RPS ∠RSP…(v)
Adding (iv) and (v), we get
∠QPS + ∠RPS = ∠QSP + ∠RSP
⇒ ∠QPR = ∠QSR
and ∠BAC = ∠QSR, [From (i)]
∴ ∠BAC = ∠QPR …(vi)
Now in ΔABC and ΔPQR, we have
AB = PQ, (Given)
∠BAC = ∠QPR, [From (vi)]
and AC = PR, (Given)
∴ ΔABC = ΔPQR (By SAS congruence rule).
Hence proved

Theorem 7.5.
[RHS congruence rule]: If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Given: In ΔABC and ΔDEF,
∠B = ∠E = 90°, AC = DF and BC = EF.
To prove: ΔABC ≅ ΔDEF.

Construction: Produce DE to G so that GE = AB. Join G to F.
Proof: In ΔABC and ΔGEF, we have
AB = GE, (by construction)
∠ABC = ∠GEF, [Each = 90°]
and BC = EF, (Given)
∴ ΔABC ≅ ΔGEF, (By SAS congruence rule)
⇒ ∠A = ∠G, (CPCT) …(i)
AC = GF, (CPCT) …(ii)
Now, AC = DF, (Given)
AC = GF, [from (ii)]
∴ DF = GF
⇒ ∠D = ∠G …(iii)
(Angles opposite to equal sides are equal)
From (i) and (iii), we get
∠A = ∠D…(iv)
In ΔABC and ΔDEF, we have
∠B = ∠E, (Each = 90°)
∠A = ∠D, [from (iv)]
∴ ∠C = ∠F …(v)
[third angles of the triangles]
Now in ΔABC and ΔDEF, we have
BC = EF, (Given)
∠C = ∠F, [From (v)]
and AC = DF, (Given)
∴ ΔABC = ΔDEF, (by SAS congruence rule)
Hence proved
Note: RHS stands for Right angle-Hypotenuse-Side.

Inequalities in a Triangle: In this section, we shall learn about some inequality relations among sides and angles of a triangle. Consider scalene triangle ΔABC such that AB = 7 cm, BC = 6 cm and AC = 5 cm. Now measure the three angles A, B and C with the help of protector, we observe that:

(i) AB > AC and ∠C > ∠B
i.e., the longer side has greater angle opposite to it.
(ii) AC < BC and ∠B < ∠A.
i.e., shorter side has smaller angle opposite to it.
(iii) AB > BC and ∠C > ∠A
i.e., angle opposite the larger side is greater.
Below we give some important results of inequalities in a triangle.
It is stated in the form of a theorem.

Theorem 7.6:
If two sides of a triangle are unequal, the angle opposite to the longer side is larger or (greater). (See fig. 7.62)

Given: A triangle ABC in which AB > AC.
To prove: ∠ACB > ∠ABC.
Construction: From AB, cut AD = AC.
Join C and D.
Proof: In ΔACD, we have
AC = AD, (By construction)
⇒ ∠ACD = ∠ADC …..(1)
(Angles opposite to equal sides are equal)
In ΔBDC, we have
Exterior ∠ADC > ∠B
(exterior angle of a triangle is always greater than each its opposite interior angle)
⇒ ∠ACD > ∠B, [From (i)]
⇒ ∠ACB > ∠B, [∵ ∠ACB > ∠ABC]
⇒ ∠ACB > ∠ABC

Theorem 7.7:
In any triangle, the side opposite to the larger (greater) angle is longer.
Given: A triangle ABC in which ∠ABC > ∠ACB.
To prove: AC > AB.

Proof: There are following possibilities.
(i) AC = AB
(ii) AC < AB
(iii) AC > AB
There is only one possibilities must be true.
(i) If AC = AB
⇒ ∠ABC = ∠ACB
[Angles opposite to equal sides are equal]
It is impossible, for it is given that
⇒ ∠ABC > ∠ACB
(ii) If AC < AB
⇒ AB>AC
⇒ ∠ACB > ∠ABC
This is also impossible, being contrary to hypothesis.
(iii) Since AC is neither less than nor equal to AB.
∴ AC must > AB.
Hence AC > AB. Proved.

Theorem 7.8:
The sum of any two sides of a triangle is greater than the third side. (See fig. 7.64).

Given: A triangle ΔABC.
To prove : (i) AB + AC > BC
(ii) AB + BC > AC
(iii) AC+ BC > AB.
Construction: Produce BA to D such that AD = AC. Join C to D

Proof: In ΔACD, we have
AD = AC (By construction)
⇒ ∠ADC = ∠ACD …..(i)
∠BCD > ∠ACD,
[∵ ∠BCD = ∠ACB + ∠ACD]
⇒ ∠BCD > ∠ADC, [from (i), ∠ACD = ∠ADC]
⇒ ∠BCD > ∠BDC
⇒ BD > BC (By theorem 7·7)
⇒ AB + AD > BC
⇒ AB + AC > BC (∵ AD = AC)
Similarly,
AB + BC > AC and AC + BC > AB.
Hence proved

Corollary 1.
The difference between the lengths of any two sides of a triangle is always less than the third side.

Haryana State Board HBSE 9th Class Maths Notes Chapter 6 Lines and Angles Notes.

Haryana Board 9th Class Maths Notes Chapter 6 Lines and Angles

Introduction
In previous chapter, we have already studied axioms, postulate and some terms allied to geometry. In this chapter, we shall study the angles and their properties and also the properties of the angles formed when a line intersects two or more parallel lines at distinct points.

An architect cannot draw the plan of the multistoried building without the knowledge of the properties of parallel lines, intersecting lines and angles.

In science, to study the refraction property of light when a ray enters from one medium to other medium, we use the properties of parallel lines and intersecting lines. We have to represent forces by direct line segments to study the net effect of the forces on the body.

Key Words
→ Architect: One who designs building and supervises their construction.

→ Congruent: Having the same size and shape.

→ Adjacent: Lying near to.

→ Intersect: Two geometrical figures or curves are said to intersect if they have at least one point in common.

→ Converse: The converse of an implication p ⇒ q is the implication q ⇒ p. If an implication is true, then its converse may or may not be true.

→ Concurrent: A number of lines are said to be concurrent, if there is a point through which they all pass.

→ Incident Ray: The incident ray is the ray of light that strikes the surface before reflection, transmission or absorption.

→ Reflected Ray: A ray extending outward from a point.

→ Angle of Incidence: The angle between the direction of an approaching emission and the normal to the surface upon which it is incident.

→ Angle of Reflection: The angle between the direction of propagation of a reflected emission and the normal to the reflecting surface.

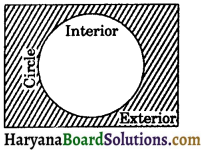
1. Basic Terms and Definitions : (a) Angle: An angle is formed when two rays or two line segments have a common end point. The two rays which form an angle are called the arms and the point at which they meet is called the vertex of the angle.

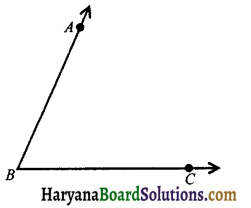
The adjacent figure represent an angle ABC or ∠ABC or ∠CBA or simply B. AB and BC are the arms of the angle and their common point B is the vertex.

∠ABC divides the plane containing it into two parts:
(i) Interior of an angle
(ii) Exterior of an angle.
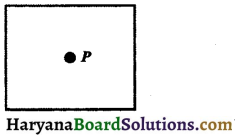
(i) Interior of an angle: The interior of an angle ABC is the set of all points in its plane, which lie on the same side of BC as A and also on the same side of AB as C. In the adjoining figure, P is a point in the interior of an angle ABC.

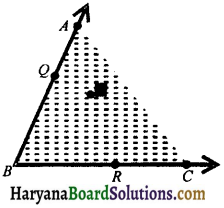
(ii) Exterior of an angle : The exterior of an ∠ABC is the set of all points in its plane, which do not lie on the angle or in its interior.
In the adjoining figure, the point Q is exterior of the ∠ABC.
Note: Point R lies on the angle ∠ABC.

(b) Measure of an angle: The amount of turning of a ray from the initial position of BC to BA is called the measure of ∠ABC which is written as m∠ABC. The unit of angle measure is a standard angle, called a degree.

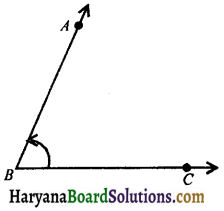
If the measure of an angle ABC is x degree, then we write
m∠ABC = x°.
Note: 1° = 60′ (i.e., 60 minutes),
1′ = 60″ (60 seconds)

(c) Congruent or equal angles: If the measures of the angles are same then they said to be equal or congruent.
For examples:
If m∠ABC = m∠PQR,
then ∠ABC ≅ ∠PQR
or if ∠ABC ≅ ∠DEF,
then m∠ABC = m∠DEF.

(d) Types of angles: (i) Right angle: The angle which measures equal to 90°, is called a right angle. In the figure 6.4, ∠PQR is a right angle.

(ii) Acute angle: The angle which measures less than one right angle (i.e., less than 90°) is called an acute angle.
In the figure 6.5, ∠PQR is an acute angle.

(iii) Obtuse angle: The angle which measures more than 90° and less than 180° is called an obtuse angle. In the figure 6.6, ∠PQR is an obtuse angle.

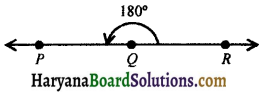
(iv) Straight angle: The angle which measures equal to two right angles (i.e., equal to 180°) is called a straight angle.
In the figure 6.7, ∠PQR is a straight angle.

(v) Reflex angle: The angle which measures more than 180° and less than 360° is called a reflex angle.
In the figure 6.8, ∠PQR is a reflex angle.

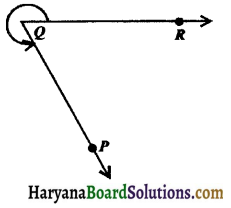
(vi) Complete angle: The angle which measures is 4 right angles (i.e., 360°) is called a complete angle.
In the figure 6.9, ∠QPR is a complete angle.

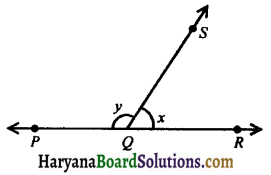
(vii) Complementary angles: If the sum of two angles is 90°, they are called complementary angles eg., if ∠a + ∠b= 90°, then ∠PQS and ∠RQS are complementary angles.

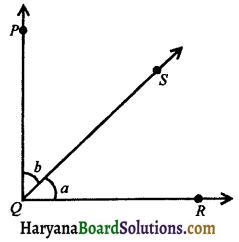
(viii)Supplementary angles: If the sum of two angles is 180°, they are called. supplimentary angles eg., if ∠x + ∠y = 180°, then ∠PQS and ∠RQS are supplementary angles.

(e) Bisetor of an angle: A ray is called the bisector of an angle if it divides the angle into two equal parts.

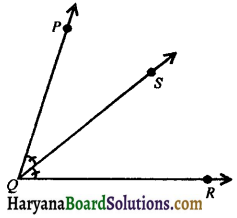
In the figure 6.12, ray QS is the bisector of ∠PQR, then
∠PQS = ∠RQS.

2. Pairs of Angles: (i) Adjacent angles: Two angles are called adjacent angles, if:
(i) they have the same vertex.
(ii) they have a common arm.
(iii) other arms of these angles are on opposite sides of the common arm.

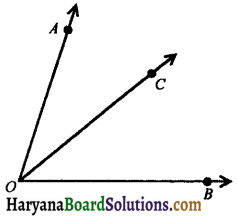
In the figure 6.13, ∠AOC and ∠BOC have the common vertex O and have a common arm OC and other arms OA and OB lie on the opposite sides of the common arm OC. Therefore, ∠AOC and ∠BOC are adjacent angles.

(ii) Linear pair angles: Two adjacent angles are said to form a linear pair of angles, if their non-common arms are two opposite rays.

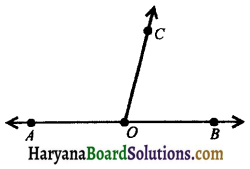
In the figure 6.14, ∠AOC and ∠BOC are two adjacent angles and OA and OB are two opposite rays. Therefore, ∠AOC and ∠BOC form a linear pair of angles.

Axiom 6.1: If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.
Recall that when the sum of two adjacent angle is 180°, then they are called a linear pair of angles.

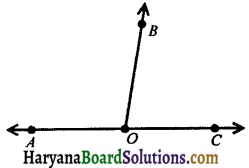
In the figure 6.15, ray OB stands on the line AC. It forms adjacent angles ∠AOB and ∠COB.
∵ ∠AOB + ∠COB = 180° and OA and OC are opposite rays. Thus, two angles form a linear pair of angles. The above axiom can be stated in the reverse ways as below:
Axiom 6.2: If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.

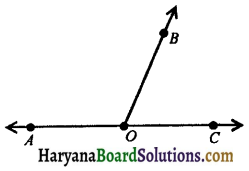
In the figure 6.16, ∠AOB and ∠COB are adjacent angles, such that
∠AOB + ∠COB = 180°
⇒ ∠AOC = 180°,
[∵ ∠AOC = ∠AOB + ∠COB]
⇒ ∠AOC is a straight line.
Hence, AOC is a straight line.
The two axioms above together is called the linear pair axiom.

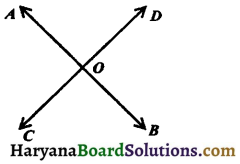
(iii) Vertically opposite angles: Two angles are called a pair of vertically opposite angles, if their arms form two pairs of opposite rays.

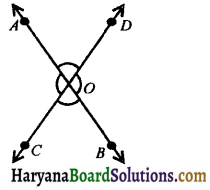
In the figure 6.17, two lines AB and CD intersect at O, then two pairs of vertically opposite angles are formed.
(i) ∠AOC and ∠BOD
(ii) ∠AOD and ∠BOC.

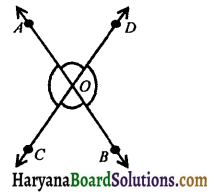
Theorem 6.18.
If two lines intersect each other, then the vertically opposite angles are equal.
Given: Two lines AB and CD intersect at a point O.
To prove : (i) ∠AOC = ∠BOD
(ii) ∠AOD = ∠BOC.
Proof. Since ray OA stands on line CD.
∴∠AOC + ∠AOD = 180°,
(Linear pair axiom) …….(i)
Ray OD stands on line AB.
∴ ∠AOD + ∠BOD = 180°,
(Linear pair axiom) …….(ii)
From (i) and (ii), we have
∠AOC + ∠AOD = ∠AOD + ∠BOD
⇒ ∠AOC = ∠BOD
Similarly, we can prove that
∠AOD = ∠BOC. Hence proved

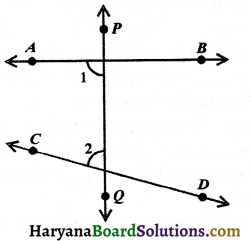
Parallel Lines and a Transversal: A line which intersects two or more given lines at distinct points is called a transversal of the given lines.

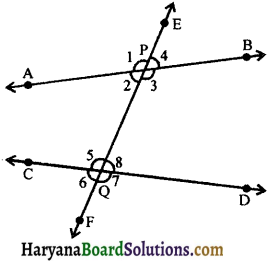
In the figure 6.32, AB and CD are two lines and a transversal EF intersects them at P and Q respectively. The three lines determine eight angles, four angles at P namely ∠1, ∠2, ∠3, ∠4 and remaining four angles at Q namely ∠5, ∠6, ∠7 and ∠8.

In the figure, ∠2, ∠3, ∠5 and ∠8 are called interior angles and ∠1, ∠4, ∠6 and ∠7 are called exterior angles. We classify these eight angles in the following groups:
(a) Corresponding angles: (i) ∠1 and ∠5, (ii) ∠4 and ∠8, (iii) ∠2 and ∠6, (iv) ∠3 and ∠7.
(b) Alternate interior angles: (i) ∠2 and ∠8, (ii) ∠3 and ∠5.
(c) Alternate Exterior angles: (i) ∠1 and ∠7, (ii) ∠4 and ∠6.
(d) Interior angles on the same side of the transversal: (i) ∠2 and ∠5, (ii) ∠3 and ∠8.
Interior angles on the same side of the transversal are also referred to as consecutive interior angles or allied angles or co-interior angles.

Some Important Relations
If AB || CD and transversal XY cuts them (see in the figure 6.33) then

(i) Corresponding angles are equal i.e., ∠1 = ∠5, ∠4 = ∠8, ∠2 = ∠6 and ∠3 = ∠7.
(ii) Alternate interior angles are equal i.e., ∠2 = ∠8 and ∠3 = ∠5.
(iii) Alternate exterior angles are equal i.e., ∠1 = ∠7 and ∠4 = ∠6.
(iv) Co-interior angles are supplementary i.e., ∠2 + ∠5 = 180° and ∠3 + ∠8 = 180°.
From this we conclude the following axioms:
Axiom 6.3: If a transversal intersects two parallel lines, then each pair of corresponding angles are equal. It is called corresponding angles axiom also.
Axiom 6.4: If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other. It is called converse of corresponding angles axiom.

Theorem 6.2:
If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
Given: A transversal line XY cuts the parallel lines AB and CD at P and Q respectively.

To prove : ∠2 = ∠8 and ∠3 = ∠5.
Proof :
∠4 = ∠2 ……(i)
(vertically opposite angles)
∠4 = ∠8 ……(ii)
(corresponding angles axiom)
From (i) and (ii), we get
∠2 = ∠8
Again, ∠1 = ∠3 ……(iii)
(vertically opposite angles)
∠1 = ∠5 ……(iv)
(corresponding angles axiom)
From (iii) and (iv), we get
∠3 = ∠5
Hence, ∠2 = ∠8 and ∠3 = ∠5.
Proved

Theorem 6.3:
(Converse of theorem 6.2) : If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.

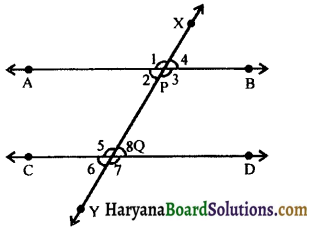
Given: A transversal line XY intersects two lines AB and CD at P and Q respectively such that ∠2 and ∠8 are a pair of alternate interior angles and ∠2 = ∠8.
To prove : AB || CD.
Proof :
∠2 = ∠8, (given) ……(i)
∠2 = ∠4 …….(ii)
(vertically opposite angles)
From (i) and (ii), we get
∠4 = ∠8
Thus, a pair of corresponding angles 24 and 28 are equal. Therefore, by converse of corresponding angle axiom, we have
AB || CD.
Hence proved

Theorem 6.4:
If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.

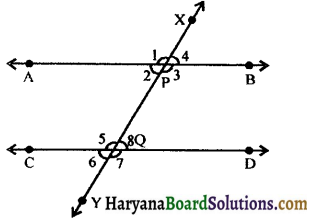
Given: A transversal line XY intersects two parallel lines AB at P and CD at Q making two pairs of consecutive interior angles ∠2, ∠5, ∠3 and ∠8.
To prove :
∠2 + ∠5 = 180° and ∠3 + ∠8 = 180°.
Proof: Ray PB stands on line XY.
∴ ∠3 + ∠4 = 180
(Linear pair axiom)
But ∠8 = ∠4
(corresponding angles axiom)
∴ ∠3 + ∠8 = 180° ……(i)
Now, ray QC stands on line XY.
∴ ∠5 + ∠6 = 180°,
(Linear pair axiom)
But ∠6 = ∠2,
(corresponding angles axiom)
∴ ∠5 + ∠2 = 180°
⇒ ∠2 + ∠5 = 180° ……(ii)
Hence, ∠2 + ∠5 = 180°
and ∠3 + ∠8 = 180°.
Proved.

Theorem 6.5.
(Converse of theorem 6.4): If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.

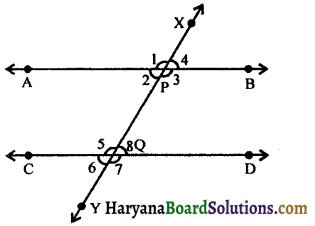
Given: A transversal line XY intersects two lines AB at P and CD at Q such that ∠2 and ∠5 are pair of consecutive interior angles and ∠2 + ∠5 = 180°.
To prove : AB || CD.
Proof: Since, Ray PA stands on line XY.
∴ ∠1 + ∠2 = 180°
(Linear pair axiom) …..(i)
∠2 + ∠5 = 180° (Given) …..(ii)
From (i) and (ii), we get
∠1 + ∠2 = ∠2 + ∠5
⇒ ∠1 = ∠5
Thus, a pair of corresponding angles ∠1 and ∠5 are equal.
Therefore, by converse of corresponding angles axiom, we have
AB || CD. Hence proved.

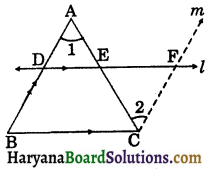
Lines Parallel to Same Line:
Theorem 6.6:
Lines which are parallel to the same line are parallel to each other.

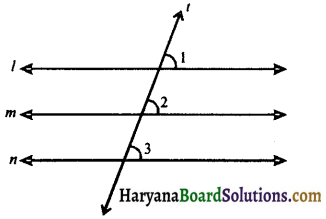
Given: l || m and n || m.
To prove : l || m
Construction: Draw a transversal lines t for the lines l, m and n.
Proof: Since, l || m (Given)
∠1 = ∠2 …….(i)
(Corresponding angles axiom)
Since, n || m (Given)
∠3 = ∠2 …….(ii)
(Corresponding angles axiom)
From (i) and (ii), we get
∠1 = ∠3
But these are corresponding angles.
⇒ l || n,
[By converse of corresponding angles]
Hence proved

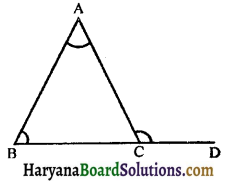
1. Triangle: A plane figure bounded by three straight lines, is called a triangle. It is usually denoted by the Greek letter Δ (delta).
The figure, given along side, shows a triangle ABC (ΔABC) bounded by three sides AB, BC and CA. Triangle ABC has three vertices, namely A, B and C and it has three angles, namely ∠A, ∠B and ∠C.
Note: If side BC of ΔABC is produced upto any point D, the angle ∠ACD so formed, is called exterior angle at C, where as the angles A and B are called its interior opposite angles.

2. Kinds of Triangles: (a) With regard to their sides:
(i) Equilateral triangle: If all the sides of a triangle are equal, it is called an equilateral triangle.
In the given figure, ΔABC is an equilateral triangle because AB = BC = CA. Also, all the angles of an equilateral triangle are equal to each other and so each angle = 60°.

(ii) Isosceles triangle: If at least two sides of a triangle are equal, it is called an isosceles triangle. In the given figure, ΔABC is an isosceles triangle, because AB = AC.

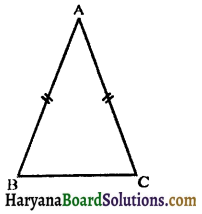
In an isosceles triangle, two angles of opposite equal side are also equal.

(iii) Scalene triangle: If all the sides of a triangle are unequal, it is called an scalene triangle.
The figure below shows a scalene triangle because AB ≠ BC ≠ AC.

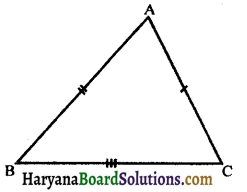
In a scalene triangle, all its angles are also unequal.

(b) With regard to their angles: (i) Acute angled triangle: When each angle of a triangle is acute (i.e., less than 90°), it is called an acute angled triangle.
The given figure 6.60, shows an acute angled triangle, because each angle of the triangle is less than 90°.

(ii) Right angled triangle: When one angle of a triangle is right angle (ie., equal to 90°), it is called right angled triangle, the side opposite to the right angle is called its hypotenuse and the remaining two sides are called its legs.

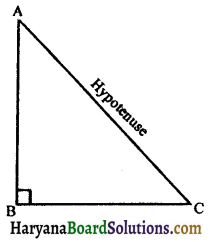
The given figure 6.61, shows a right angled triangle because ∠B = 90°. In triangle ABC, AC is hypotenuse and AB and BC are its legs. Each of the other two angles of the right triangle is acute.

(iii) Obtuse angled triangle: When one angle of a triangle is obtuse (i.e., greater than 90° but less than 180°), it is called an obtuse angled triangle. The given figure 6-62, shows an obtuse angled triangle, because B is obtuse.

In an obtuse angled triangle, each of the other two angles is acute.

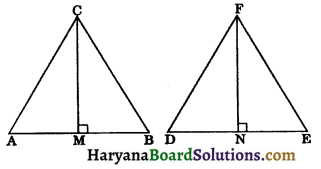
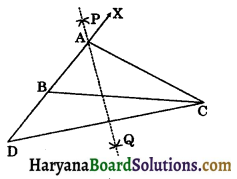
3. Some Important Terms Related to the Traingle: (i) Median : The median of a triangle, corresponding to any side, is the line joining the mid point of that side with the opposite vertex. e.g.,

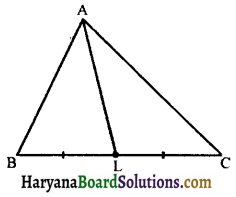
AL is the median corresponding to side BC

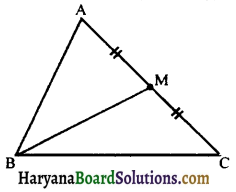
CN is the median corresponding to side AB

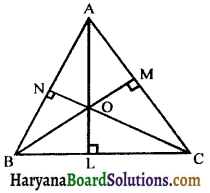
A triangle has three medians and all three medians are always concurrent i.e., they intersect each other at one point only.

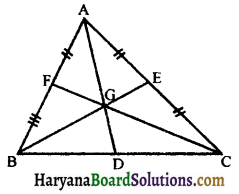
(ii) Centroid: The point of intersection of all the three medians of a triangle is called its centroid. In the given tigure 6-66, three medians AD, BE and CF intersect at the point G. Therefore, G is the centroid of the triangle ABC.

(iii) Altitude: An altitude of a triangle, corresponding to any side, is the length of perpendicular drawn from the opposite vertex to that side. e.g.,

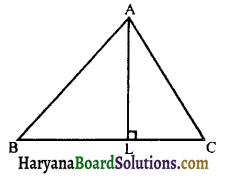
AL is the altitude corresponding to side BC

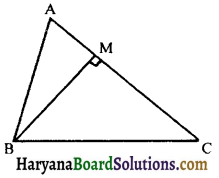
BM is the altitude corresponding to side AC

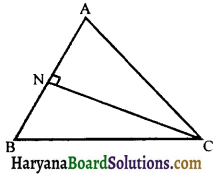
CN is the altitude co-rresponding to side AB A triangle has three altitudes and all three altitudes are always concurrent i.e., they intersect each other at one point only.

(iv) Ortho centre: The point of intersection of all the three altitudes of a triangle is called ortho centre.
In the given figure 6.69, O is the ortho centre of triangle ΔABC.

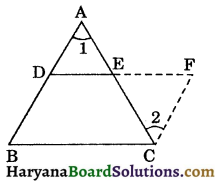
4. Angle sum property of a triangle: In previous classes, we have studied that sum of the angles of a triangle is 180°. We can prove this statement using the theorem related to parallel lines.

Theorem 6.7:
The sum of the angles of a triangle is 180°.

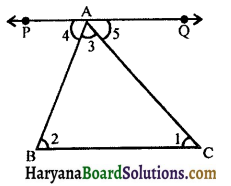
Given: A triangle ΔABC and ∠1 + ∠2 + ∠3 are its angles
To prove : ∠1 + ∠2 + ∠3 = 180°.
Construction: Through A, draw a line PQ parallel to BC.
Proof: PQ || BC and AB is the transversal.
∠2 = ∠4 ……(i)
(Alternate interior angles)
Again, PQ || BC and AC is the transversal.
∴ ∠1 = ∠5, ……(ii)
(Alternate interior angles)
Adding (i) and (ii), we get
∠2 + ∠1 = ∠4 + ∠5
⇒ ∠1 + ∠2 + ∠3 = ∠4 + ∠3 + ∠5,.
(Adding ∠3 on both sides)
But, ∠4 + ∠3 + ∠5 = 180°,
(Linear pair axiom)
∴ ∠1 + ∠2 + ∠3 = 180°
Hence, the sum of three angles of a triangle is 180°.
Hence Proved

Theorem 6.8:
If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.

Given: A ΔABC whose side BC has been produced to D such that ∠4 is its exterior angle.
To prove : ∠4 = ∠2 + ∠3.
Proof: We know that,
Sum of the angles of a triangle is 180°,
(By theorem 6.7)
⇒ ∠1 + ∠2 + ∠3 = 180°…(i)
∠1 + ∠4 = 180°…(ii)
(Linear pair axiom)
From (i) and (ii), we get
∠1 + ∠4 = ∠1 + ∠2 + ∠3
⇒ ∠4 = ∠2 + ∠3. Hence proved

Corollary: An exterior angle of a triangle is greater than either of its interior opposite angles.

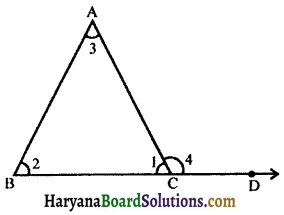
Proof: We know that an exterior angle of a triangle is equal to the sum of the interior opposite angles (By theorem 6.8)
∴ ∠4 = ∠2 + ∠3
∴ ∠4 > ∠2 and ∠4 > ∠3
Hence, an exterior angle of a triangle is greater than each interior opposite angle.

Haryana State Board HBSE 9th Class Maths Notes Chapter 5 Introduction to Euclid’s Geometry Notes.

Haryana Board 9th Class Maths Notes Chapter 5 Introduction to Euclid’s Geometry

Introduction
The word ‘geometry’ is derived from the Greek words ‘geo’, means the ‘earth’, and ‘metrein’, means ‘to measure’. So, it appears to have originated from the need for measuring land. Many ancient civilization of Egypt, Babylonia, India, Greece, China have studied the ‘geometry’ in various forms. They short out the several practical problems which required the development of geometry in various ways.

In Indus Valley Civilization, the ratio length : breadth : thickness of the bricks was taken as 4 : 2 : 1.

Construction of altars (or vedis) and fireplaces for performing Vedic rites were originated in Vedic period. Square and circular altars were used for household rituals, while shape of altars were the combination of rectangles, triangles and trapeziums. They are used for public worship. The ‘sriyantra’ consists of nine interwoven isosceles triangles which are arranged in such a way that they produce 43 subsidiary triangles. A Greek mathematician, Thales, (640 BC) gave the first known proof of the statement that a circle is bisected (cut into two equal parts) by its diameter.

Pythagoras (572 BC) was the most famous pupil of Thales discovered many geometric properties and developed the theory of geometry to a great extent. This process continued till 300 BC. His important theorem is; In right triangle, the square of hypotenuse is equal the sum of the square of base and square of perpendicular.

Euclid (300 BC) was a mathematics teacher who was born in Alexandria in Greece introduced the method of proving mathematical results by using deductive logical reasoning and the previously proved results. The geometry of plane figure is known as “Euclidean Geomery.”

The Indian Mathematician, Aryabhatta (born 476 AD) worked out the area of an isosceles triangle, the volume of a pyramid and approximate value of π.

Brahmagupta (born 598 AD) discovered the formula for finding the area of cyclic quadrilateral.

Bhaskara II (born 1114 AD) gave a dissection proof of Pythagoras’ theorem.

In this chapter, we shall study the Euclid’s approach to geometry.

Key Words
→ Version – Translation.

→ Altars – Raised plateform used for sacrifice or religious offering.

→ Rituals – Way of performing religious services.

→ Rite – Religious ceremony.

→ Subsidiary – Accessory.

→ Allied – Related.

→ Extent – Large space or tract size.

→ Volume – Space occupied, mass.

→ Cyclic Quadrilateral – A quadrilateral whose four vertices lie on a circle.

→ Proof – The course of reasoning which establishes the truth of a statement.

→ Logic – The science or art of reasoning.

→ Physical – Belonging to physics.

→ Universal – Belonging to all.

→ Fact – A thing known to be true.

→ Coincide – To occupy the same space.

→ Proposition – A statement of something to be done.

→ Interpreted – To exposed the meaning of.

→ Demonstrate – To prove with certainly.

→ Consequence – result.

→ Superposed – To put or place over or above.

→ Assumption – A supposition, thing assumed.

Basic Concepts
Euclid’s Definitions, Axioms and Postulates:
(a) Euclid summarised the work of ‘geometry’ as definitions. He listed 23 definitions in Book 1 of ‘Elements’. A few of them are given below:

• A point is that which has no part.
• A line is breadthless length.
• The ends of a line are points.
• A straight line is a line which lies evenly with the points on itself.
• A surface is that which has length and breadth only.
• The edges of surface are lines.
• A plane surface is a surface which lies evenly with the straight lines on itself.

In these definitions, we observe that, point, line, breadth, length, plane etc. are undefined terms. The only thing is that we can represent them intuitively or explain them with the help of ‘physical models.’

Starting with these definitions, Euclid assumed certain properties, which were not to be proved. These assumptions are actually “obvious universal truths”. He divided them into two types: axioms and postulates. He used term ‘postulate’ for the assumptions that were specific to geometry. Common notions (often called axioms), on the other hand, were. assumption used throughout mathematics and not specifically linked to geometry.

(b) Axioms: The basic facts which are taken for granted, without proof, are called axioms.
Some of the Euclid’s axioms (not in order) are given below:
(i) Things which are equal to the same thing are equal to one another.
i.e., If p = q and r = q, then p = r.
(ii) If equals are added to equals, the wholes are equal.
i.e., If p = q, then p + r = q + r.
(iii) If equals are subtracted from equals, the remainders are equal.
i.e., If p = q, then p – r = q – r.
(iv) Things which coincide with one. another are equal to one another.
(v) The whole is greater than the part ie., If p>q, then there exists r(r ≠ 0) such that
P = q + r.
(vi) Things which are double of the same things are equal to one another. i.e., If p = q, then 2p = 2q.
(vii) Things which are halves of the same things are equal to one another.
Le. If p = q, then \(\frac{p}{2}=\frac{q}{2}\)

(c) Postulate: A statement whose validity is accepted without proof, is called a postulate.
Euclid gave five postulates stated as below:
Postulate 1: A straight line may be drawn from any one point to any other point.
This postulate tells us that at least one straight line passes through two distinct points which is shown in the figure below:

Axiom 5.1. Given two distinct points, there is a unique line that passes through them.

In the given figure, P and Q are two distinct points. Out of all lines passing through the point P, there is exactly one line ‘l’ which also passes through Q. Also out of all lines passing through the point Q, there is exactly one line l which also passes through the point P. Hence, we find there is a unique line l which passes through the points P and Q.

Postulate 2: A terminated line can be produced indefinitely.

Postulate 3: A circle can be drawn with any centre and any radius.
Postulate 4: All right angles are equal to one another.
Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

For example, in the figure line PQ falls on the lines AB and CD such that ∠1 + ∠2 < 180° on the left side of PQ. Therefore, the lines AB and CD will eventually intersect on the left side of PQ.

(d) Statement: A sentence which can be judged either true or false is called a statement.
For example:
(i) The sum of the angles to a quadrilateral is 360°, is a true statement.
(ii) The sum of the angles of a triangle is 90°, is a false statement.
(iii) y + 5 > 9 is a sentence but not a statement.

Theorem: In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems and previously accepted statements, such as axioms. The derivation of a theorem is often interpreted as a proof of the truth of the resulting expression, but different deductive systems can yield other interpretations, depending on the meanings of the derivation rules. The proof of a mathematical theorem is logical argument demonstrating that the conclusion.

For example:
(i) The area of a triangle is equal to half its base, multiplied by its attitude.
(ii) An exterior angle of a triangle is equal to sum of its opposite interior angles.
Corollary: A proposition, whose truth can easily be deducted from a preceeding theorem, is called its corollary.

(e) Some terms allied to Geometry:
(i) Point: A point is a mark of position, which has no length, no breadth and no thickness. We represent a point by a capital letters A, B, C, P, Q etc., as shown in the figure.

(ii) Plane: A plane is a every surface such that point of the line joining any two points on it, lies on it.
The surface of the top of the table, surface of the smooth blackboard and surface of a sheet of paper are the some close examples of a plane surfaces are limited in extent but geometrical plane extends endlessly in all directions.

(iii) Line: A line has length but no breadth or thickness. A line has no ends points. A line has no definite length. It can be extended infinitely in both the directions. The given figure shows line \(\bar{AB}\).

Some times we shall denote lines by small letters such as l, m, n, p etc.

(iv) Ray: It is a straight line which starts from a fixed point and moves in the same direction. A ray has one endpoint and it has no definite length.
The given figure shows a ray \(\overrightarrow{A B}\).

(v) Line segment: It is a straight line with its both ends fixed. The given figure shows a line segment \(\bar{AB}\), with fixed ends A and B. A line has a definite length.

So, a line segment is the shortest distance between two fixed points.

(vi) Collinear points: Three or more than three points are said to be collinear, if they lie on the straight line.
The given figure shows the collinear points P, Q, R while A, B, C are non-collinear.

(vii) Parallel lines: The straight lines which lie in the same plane and do not meet at any point on producing on either side, are called parallel lines.
If l and m are parallel lines in a plane, we write l || m.

The distance between the two parallel lines always remains same.

(viii) Intersecting lines: Two lines having a common point are known as intersecting lines.
The common point (O, in figure 5.18) is known as the point of intersection.

(ix) Concurrent lines: In the figure 5.19, the lines pass through the same point. In this case, lines are called concurrent lines.

(x) Congruence of line segment: If the given two line segments are of the same size, they are said to be ‘congruent. Two lines AB and CD are congruent, if the trace copy of one can be superposed on the other so as to cover it completely and exactly.
Symbolically, \(\bar{AB}\) ≅ \(\bar{CD}\) or line segment AB ≅ line segment CD.

Congruence relation in the set of all line segments:
(i) AB ≅ AB
(ii) AB ≅ CD ⇒ CD ≅ AB
(iii) AB ≅ CD and CD ≅ EF, then AB ≅ EF.

Theorem 5.1.
Two distinct lines cannot have more than one point in common.
Proof. Here, we are given two lines I and m. We need to prove that they have only one point in common. If possible, let P and Q two points common to the given lines l and m. Then the line I passes through the points P and Q and line m passes through the points P and Q. But this assumption clashes with the axiom that one and only one line can pass through two distinct points. So, our supposition that two lines pass through two distinct points is wrong.
Hence, two distinct lines cannot have more than one point in common.

Equivalent Versions of Euclid’s Fifth Postulate:
There are several equivalent versions of fifth postulate of Euclid. One of them is ‘Playfair’s Axiom’ (given by Scottish mathematician John Playfair in 1729), as stated below:

Playfair’s Axiom: “For every line l and for every point P not lying on l, there exists a unique line m passing through P and parallel to l.”
From figure 5.52, we observe that all the lines passing through the point P, only line m is parallel to line l.

This result can also be stated as: Two distinct intersecting lines cannot be parallel to the same line.

Haryana State Board HBSE 9th Class Maths Notes Chapter 3 Coordinate Geometry Notes.

Haryana Board 9th Class Maths Notes Chapter 3 Coordinate Geometry

Introduction
In previous class, we have studied how to locate a point on a real number line. We also know how to describe the position of a point on the line.
In this chapter, we shall study to locate the coordinates of a point in a plane. We shall also learn about the plotting the points in the plane (Cartesian plane).

In the seventeenth century, French mathematician Rene Descartes developed the idea of describing the position of a point in a plane. His method was a development of the older idea of latitude and longitude. In honour of Descartes, the system used for describing the position of a point in a plane is also known as the cartesian system.

Key Words
→ Coordinates: A set of numbers which locate a point. In general, two numbers are needed to locate a point in a plane and is written as (x, y).

→ Quadrant : (\(\frac{1}{4}\))^th part of a plane divided by coordinate axes is known as a quadrant.

→ Abscissa: The first coordinate x, of a pair (x, y) of cartesian coordinates in the plane.

→ Ordinate: The second coordinate y, of a pair (x, y) of cartesian coordinates in the plane.

Basic Concepts
Cartesian System: We have studied the number line. On the number line, distance from a fixed point is marked in equal units positively in one direction and negatively in the other. The point from which the distances are marked is called the origin. A cartesian (or coordinate) plane consists of two mutually perpendicular number lines intersecting each other at their zeroes.

The adjoining figure shows a cartesian plane consisting of two mutually perpendicular number lines XOX’ and YOY’ intersecting each other at O.
1. The horizontal number line XOX’ is called the x-axis.
2. The vertical number line YOY’ is called the y-axis.
3. The point of intersection ‘O’ is called the origin which is zero for both the axes.

The system consisting of the x-axis, the y-axis and the origin is also called cartesian coordinate system. The x-axis and y-axis together are called coordinate axes.
(a) Coordinates of points in a plane: The position of each point in a coordinate plane is determined by means of an ordered pair (a pair of numbers) with reference of the coordinates axes; as stated below:
(i) The distance of the point along x-axis from the origin O is called x-coordinate or abscissa of the point.
(ii) The distance of the point along y-axis from the origin O is called y-coordinate or ordinate of the point.
Thus, coordinates of the point = Position of the point reference to coordinates axes = (abscissa, ordinate)
If the abscissa of a point is x and its ordinate is y, then its coordiantes = (x, y).

(b) Quadrants: The coordinate plane is divided by axes into four parts which are known as quadrants. Each point is located either in one of the quadrants or on one of the axes.
Starting from OX in the anticlockwise direction :
(i) XOY is called the first quadrant.
(ii) YOX’ is called the second quadrant.
(iii) X’OY’ is called the third quadrant.
(iv) Y’OX is called the fourth quadrant which are shown in the adjoining figure.

(c) Rules for signs of coordinates:
(i) In the first quadrant, the abscissa and ordinate both are positive.
(ii) In the second quadrant, the abscissa is negative and ordinate is positive.
(iii) In the third quadrant, the abscissa and ordinate both are negative.
(iv) In the fourth quadrant, the abscissa is positive and ordinate is negative.
Using the convention of signs, we have the signs of the coordinates in quadrants as given below :

(d) Coordinates of a point on the x-axis: The distance of every point on the x-axis from x-axis is 0 unit. So, its ordinate is 0.
So, the coordinates of a point on the x-axis is of the form (x, 0).
e.g., (5, 0), (3, 0), (-5, 0) etc.

(e) Coordinates of a point on the y-axis: The distance of every point on the y-axis from the y-axis is 0 unit. So, its abscissa is zero.
So, the coordinates of a point on the y-axis is of the form (0, y).
e.g., (0,5), (0, 2), (0, -7) etc.

(f) The coordinates of the origin are (0, 0).

Plotting of a point in the plane if its coordinates are given: In this section, we will learn about to locate a point in the cartesian plane if co-rdinates of the points are given. This process is known as the plotting of the point with given coordinates. In this process, we use a graph paper as the coordinates plane. We draw x-axis and y-axis on it which intersect each other at origin O. Any point P in the xy-plane can be located by using an ordered pair (x, y) of real numbers. Let x denote the signed distance of P from the y-axis (signed in the sence that, if x > 0, then P is to the right of the y-axis and if x < 0, then P is to the left of the y-axis); and let y denote the signed distance of P from the x-axis. The ordered pair (x, y) is called the coordinates of P, that gives us enough information to locate the point P in the cartesian plane.

If (a, b) are the coordinates of a point P, then ‘a’ is called the x-coordinate or abscissa of P and ‘b’ is called the y-coordinate or ordinate of P as shown in fig 3.11.

For example, to locate the point (-3, 5), go 3 units along x-axis to the left of O(origin) and then go up straight 5 units and to locate the point (5, -3), go 5 units along the x-axis to the right of O and then go down 3 units. We plot these points by placing a dot at this location. See figure 3.12 in which the points(-4, -7) and (2, 2) are also located.

Any point on the x-axis has coordinates of the form (x, 0) and any point on the y-axis has coordinates of the form (0, y).

Haryana State Board HBSE 9th Class Maths Notes Chapter 2 Polynomials Notes.

Haryana Board 9th Class Maths Notes Chapter 2 Polynomials

Introduction
In previous classes, we have learnt about algebraic expressions and various operations on them such as addition, subtraction, multiplication and division. We have also studied the factorization of algebraic expressions. In this chapter, we shall review these concepts and extent them to particular types of expressions known as polynomials. We shall also study the Remainder Theorem and Factor Theorem and their use in the factorization of polynomials.

Key Words
→ Polynomial: A polynomial is a algebraic expression in which the variables involved have only non negative integral powers.

→ TermEach individual part of an expression or sum which stands alone or is connected to other parts of an expression by a plus (+) or minus (-) sign e.g., in expression 3x² + 4x + 9, there are three terms, 3x², 4x and 9.

→ Coefficients of polynomial: Refers to a multiplying factor e.g., in 5x and 7xy; 5 and 7y are the coefficients of x.

→ Algebraic expression: An algebraic expression is a collection of one or more terms, which are seperated from each other by addition (+) or subtraction signs.

→ Standard form of a polynomial: A polynomial is said to be in standard form, if the powers of x are either in increasing or in decreasing order.

→ Remainder theorem: If p(x) is any polynomial of degree greater than or equal to 1 and p(x) is divided by the linear polynomial (x – a) then remainder is p(a).

→ Factor theorem: (x – a) is a factor of the polynomial p(x), if p(a) = 0.

→ Zero of a polynomial: A real number ‘a’ is a zero of a polynomial p(x), if p(a) = 0.

→ Algebraic equation: An algebraic equation is a statement which states that the two expressions are equal.

→ Factors of the polynomial: When a polynomial (an algebraic expression) is expressed as the product of two or more expressions, then each of these expressions is called a factor of the polynomial.

→ Linear factors: If a factors contains no higher power of the variable quantity than the first power is called linear factor e.g., 4x + 5 is a linear factor.

Basic Concepts
Polynomial in One Variable:
(a) Polynomial: An expression of the form a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + ….. + a₂xⁿ + a₁x + a₀ is called polynomial, where n is a whole number, a₀, a₁, a₂, a₃,…, a_n, are real numbers and coefficients of the polynomial.
e.g., (i) 4x³ + 9x² – 3x + 4 is a polynomial in one variable x.
(ii) y⁴ + 6y³ – 4y² + 2y + 7 is a polynomial in one variable y.

(b) Terms and their Coefficients: (i) The polynomial 5x³ + 9x² – 3x – 5 has four terms, namely 5x³, 9x², -3x and -5, and 5, 9, -3 are coefficients of x, x and x respectively.
(ii) The polynomial x² + 3x – 7 has three terms, namely x², 3x and -7 and 1, 3 are coefficients of x² and x respectively.

(c) Degree of a Polynomial: The highest power of the variable is called the degree of polynomial.
(i) f(x) = 3x³ + 4x² – 8x + 10.
Here, highest power term of given polynomial is 3x³, so it’s degree is 3.
(ii) g(x) = 5x² – 4x + 8.
Here, highest power term of given polynomial is 5x², so it’s degree is 2.

(d) Types of Polynomial (according to degree):
1. Constant Polynomial: A polynomial of degree zero is called a constant polynomial.
eg., 3, -7, \(\frac{5}{9}\), etc. are all constant polynomials.
2. Linear Polynomial: A polynomial of degree 1 is called a linear polynomial.
e.g., (i) 3x + 7 is a linear polynomial in one variable x.
(ii) 4y – 8 is a linear polynomial in one variable y.
(iii) ax + b, a ≠ 0 is a linear polynomial in one variable x.
3. Quadratic Polynomial: A polynomial of degree 2 is called a quadratic polynomial.
e.g., (i) 11x² + 6x – \(\frac{3}{2}\) is a quadratic polynomial in x.
(ii) y² + 6y – 8 is a quadratic polynomial in y.
(iii) ax² + bx + c, a ≠ 0 is a quadratic polynomial in x.

4. Cubic Polynomial: A polynomial of degree 3 is called a cubic polynomial.
e.g., (i) 7x³ + 5x² + 6 is a cubic polynomial in x.
(ii) 3x² – 4xy² + 7 is a cubic polynomial in x and y.
(iii) ax³ + bx² + cx + d, a ≠ 0 is a cubic polynomial in x.
5. Biquadratic Polynomial: A polynomial of degree 4 is called a biquadratic polynomial.
e.g., (i) x⁴ – 5x³ + 3x² – 6x + 4 is a biquadratic polynomial in x.
(ii) ax⁴ + bx³ + cx² + dx + e, a ≠ 0 is a biquadratic polynomial in x.

(e) Types of Polynomial (According to terms):
(i) Monomial: A polynomial having one term is called a monomial.
e.g., 5, 2x, 4xy, 3x² are all monomials.
(ii) Binomial: A polynomial having two terms is called a binomial.
eg., 4x + 3, 5x² + 9, 7x² + 7x are all binomials.
(iii) Trinomial: A polynomial having three terms is called a trinomial.
e.g., 7x³ + 4x² + 5, x² + 5x + 3 are all trinomials.
(iv) Zero Polynomial: A polynomial consisting of one term, namely zero only, is called a zero polynomial.
The degree of a zero polynomial is not defined.

Zeroes of a Polynomial: Consider the polynomial:
p(x) = 2x³ – 3x² + 4x + 5.
If we replace x by 1 everywhere in p(x), we get
p(1) = 2 × (1)³ – 3 × (1)² + 4 × 1 + 5
= 2 – 3 + 4 + 5
= 11 – 3 = 8.
So, we can say that the value of p(x) at x = 1 is 8.
Similarly,
P(0) = 2 × (0)³ – 3 × (0)² + 4 × 0 + 5
= 0 – 0 + 0 + 5 = 5.
So, we can say that the value of p(x) at x = 0 is 5 and
p(-2) = 2 × (-2)³ – 3 × (-2)² + 4 × (-2) + 5
= -16 – 12 – 8 + 5
= -31.
So, we can say that the value of p(x) at x = -2 is -31. Now, consider another polynomial
f(x) = x² – 4
f(2) = (2)² – 4 = 4 – 4 = 0
f(-2) = (-2)² – 4 = 4 – 4 = 0.
We can say, that 2 and -2 are the zeroes of the polynomial.
In general, a real number ‘a’ is said to be a zero of a polynomial p(x), if the value of the polynomial p(x) at x = a is 0 i.e., p(a) = 0.
Now, consider general linear polynomial p(x) = ax + b, a ≠ 0.
For zero of the polynomial p(x) = 0.
0 = ax + b
⇒ ax = -b
⇒ x = \(\frac{-b}{a}\)
∴ \(\frac{-b}{a}\) is the zero of the polynomial.
(v) A zero of polynomial need not to be zero.
(vi) Number of zeroes is equal to the degree of polynomial.

1. Remainder Theorem: Let p(x) be any polynomial of degree ≥ 1 and let a be any real number. If the polynomial p(x) is divided by linear polynomial (x – a), then the remainder is p(a).
Proof:
Suppose that when p(x) is divided by (x – a), then the quotient is q(x) and the remainder is r(x), then we have
p(x) = (x – a).q(x) + r(x)
where degree of r(x) < degree (x – a) or r(x) = 0. Since, degree of (x – a) = 1, degree of r(x) = 0 i.e., constant.
Let r(x) = r, then we have
p(x) = (x – a).q(x) + r ……..(i)
Putting x = a in (i), we get
p(a) = (a – a).q(a) + r
p(a) = 0·q(a) + r
p(a) = 0 + r
p(a) = r
Hence, the remainder is p(a) when p(x) is divided by (x – a).
Hence proved.

Corollary I. When a polynomial p(x) of degree ≥ 1 is divided by a linear polynomial ax + b, a ≠ 0, then remainder is equal to p\(\left(\frac{-b}{a}\right)\).
Corollary II. If a polynomial p(x) vanishes when x = a and also x = b, then p(x) is divisible by (x – a) (x – b).

2. Factor Theorem: If p(x) is a polynomial of degree ≥ 1 and a is any real number, then:
(i) (x – a) is a factor of p(x), if p(a) = 0 and
(ii) p(a) = 0, if (x – a) is a factor of p(x).
Proof:
When a polynomial p(x) is divided by (x – a), then
p(x) = (x – a).q(x) + r(x)…….(i)
where q(x) is the quotient and r(x) is the remainder.
By Remainder theorem, we have
remainder = p(a).
Putting r(x) = p(a) in (i), we get
p(x) = (x – a).q(x) + p(a).
(i) If p(a) = 0, then p(x) = (x – a).q(x)
⇒ (x – a) is a factor of p(x).
(ii) If (x – a) is a factor of p(x) (given), then p(x) = (x – a).g(x), for some polynomial g(x)
In this case, when p(x) is divided by (x – a), the remainder is
p(a) = (a – a).g(a)
⇒ p(a) = 0 × g(a)
⇒ p(a) = 0. Hence proved.

Factorisation of Polynomials:
(a) Factorisation of a quadratic polynomial by splitting the middle term : Quadratic polynomial ax² + bx + c, where a, b, c ≠ 0 divided into two classes:
(i) When a = 1 i.e., x² + bx + c.
(ii) When a ≠ 1 i.e., ax² + bx + c.
Resolution of x² + bx + c into two factors: Examine the following example:
(x + 3)(x + 4) = x² + (3 + 4)x + 3 × 4 = x² + 7x + 12
Here, we obtain product 12 by multiplying together 3 × 4 and 7 is obtain by adding together (+3) and (+4).
Hence, in order to find out factors of x² + 7x + 12, we must find two numbers whose product is 12 and sum is 7.
Since, (x + p) (x + q) = x² + (p + q)x + pq
∴ x² + (p + q)x + pq = (x + p) (x + q)
We observe that, the product pq is obtained by multiplying together p and q, and (p + q) is the sum of the coefficient of the two second terms. Conversely, to find the factors, we have to find two numbers whose sum is (p + q) and product is pq.
We have the following procedure for factorising the quadratic polynomial x² + bx +c:
Step 1: Rewrite the quadratic polynomial in standard form (x² + bx + c), if not already in this form.
Step 2: Factorise constant term e into two factors p and q such that p × q = c and p + q = b.
Step 3: Split the middle term i.e., the term x into two terms with the coefficients p and q.
Step 4: By using grouping factorisation method, factorise the obtained four terms.

(b) Factorisation of a quadratic polynomial by splitting the middle term (continued): For factors of the quadratic polynomial of the form ax² + bx + c, where a ≠ 1 and a, b, c ≠ 0. We have the following procedure for factorising the quadratic polynomial ax² + bx + c.
Step 1: Rewrite the quadratic polynomial in standard form (ax² + bx + c), if not already in this form.
Step 2: Find the product of constant term and the coefficient of x² i.e., a × c = ac.
Step 3: (i) Observe that, if ac is positive (+ve), then find two factors p and q of ac such that p + q = b.
(ii) If ac is negative (-ve), then find two factors p and q of ac such that p – q = b.
Step 4: Split the middle term into two terms with coefficients p and q.
Step 5: Factorize the four terms by grouping.

(c) Factorisation of cubic polynomials by factor theorem: In this section, we have studied how to factorize cubic polynomials. The idea is to find out a linear factor (x – a) of the given polynomial p(x) and write it as p(x) = (x – a).q(x).
The degree of q(x) is one less than that of p(x). Therefore, q(x) is a quadratic polynomial which can be factorised by the method of splitting the middle term or we may again try to find a linear factor (x – b) of q(x). Thus, we have p(x) = (x – a).(x – b) g(x).
Here, the degree of g(x) is one less than q(x) i.e., the degree of g(x) is 1. Thus p(x) = (x – a).(x – b) g(x), which is product of linear factors.

For example: Factorise x³ – 2x² – 5x + 6 by factor theorem.
Solution:
First Method: Let
p(x) = x³ – 2x² – 5x + 6.
Step 1. First check at which value, the given polynomial p(x) becomes zero. These values can be any one of the factors of constant term.
The factors of constant term (6) are ±1, ±2, ±3, ±6.
p(1) = p(1)³ – 2 × (1)² – 5 × 1 + 6
= 1 – 2 – 5 + 6
= 7 – 7 = 0.
∴ By factor theorem (x – 1) is a factor of p(x).
Step 2. Now, divide x³ – 2x² – 5x + 6 by x – 1

The other factor of p(x) is x² – x – 6.
Step 3. Now, p(x) = (x – 1) (x² – x – 6)
= (x – 1)[x² – (3 – 2)x – 6)
[∵ -6 = -(3 × 2), 3 – 2 = 1]
= (x – 1)[x² – 3x + 2x – 6[
= (x – 1)[x(x – 3) + 2(x – 3)]
= (x – 1)(x – 3)(x + 2)
Hence, x³ – 2x² – 5x + 6 = (x – 1)
(x – 3)(x + 2).

Second method: Let
p(x) = x³ – 2x² – 5x + 6
First check at which value, the given p(x) becomes zero. These values can be any one of the factors of constant term. Factors of constant term 6 are ±1, ± 2, ± 3, ±6.
Put x = 1,
p(1) = (1)³ – 2 × (1)² – 5 × 1 + 6
= 1 – 2 – 5 + 6
= 7 – 7 = 0
⇒ (x – 1) is a factor of x³ – 2x² – 5x + 6.
Put x = -2,
p(-2) = (-2)³ – 2 × (-2)² – 5 × (-2) + 6
= – 8 – 8 + 10 + 6
= -16 + 16 = 0
⇒ (x + 2) is a factor of p(x).
Put x = 3,
p(3) = (3)³ – 2 × (3)² – 5 × 3 + 6
= 27 – 18 – 15 + 6
= 33 – 33 = 0
⇒ (x – 3) is a factor of p(x).
Since, the given expression is a cubic polynomial.
So, it will have three factors of first degree.
∴ x³ – 2x² – 5x + 6 = k(x – 1)(x + 2)(x – 3) ……(i)
Here, k is the numerical coefficient yet to be found. Now putting x = 0 (value other than 1, 2, 3) on both sides of equation (i),
we get
6 = k(0 – 1) (0 + 2) (0 – 3)
⇒ 6 = 6k ⇒ k = \(\frac{6}{6}\) ⇒ k = 1
Putting the value of k in (i), we get
x³ – 2x² – 5x + 6 = (x – 1)(x + 2)(x – 3).

Algebraic Identities: In previous classes, we have learnt about some algebraic identities.
An algebraic identity is an algebraic equation that is true for all values of the variables present in the equation.
Identity I: (x + y)² = x² + 2xy + y².
Identity II: (x – y)² = x² – 2xy + y².
Identity III: x² – y² = (x + y) (x – y).
Identity IV: (x + a)(x + b) = x² + (a + b)x + ab.
(a) Algebraic Identities for Cubes of Binomials
Identity V: (x + y)³ = x³ + y³ + 3xy(x + y)
= x³ + y³ + 3x²y + 3xy².
Identity VI: (x – y)³ = x³ – y³ – 3xy(x – y)
= x³ – y³ – 3x²y + 3xy².

(b) Algebraic Identities Relating to Trinomials
Identity VII: (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx.
Identity VIII: x³ + y³ + z³ – 3xyz
= (x + y + z) (x² + y² + z² – xy – yz – zx)
Note: If x + y + z = 0, then
x³ + y³ + z³ – 3xyz = 0(x² + y² + z² – xy – yz – zx)
x³ + y³ + z³ – 3xyz = 0
x³ + y³ + z³ = 3xyz.

(c) Sum and Difference of Cubes
We will use the following identity for factorisation of sum and difference of two cubes.
Identity IX: x³ + y³ = (x + y)(x² – xy + y²).
Identity X: x³ – y³ = (x – y)(x² + xy + y²).

Haryana State Board HBSE 9th Class Maths Notes Chapter 1 Number Systems Notes.

Haryana Board 9th Class Maths Notes Chapter 1 Number Systems

Introduction
In our previous classes, we have learnt about various types of numbers such as natural numbers, whole numbers, integers, rational numbers etc. and their representation on the number line. In this chapter, we shall study rational numbers, irrational numbers and their representation on number line and laws of exponents for real numbers. Let us review the various types of numbers.
(a) Natural Numbers: The counting numbers 1, 2, 3, 4, 5, … are called natural numbers. The smallest natural number is 1 but there is no largest as it goes up to infinity. The set of natural numbers is denoted by N.
N = {1, 2, 3, 4, 5, ………}.
(b) Whole Numbers: In the set of natural numbers, if we include the number 0, the resulting set is known as the set of whole numbers. The set of whole numbers is denoted by W.
W = {0, 1, 2, 3, 4,……}.
(c) Integers: Natural numbers along with zero and their negative are called integers. The set of integers is denoted by Z.
Z = {…….., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ………}.
The set of integers contains negative numbers, zero and positive numbers. Z comes from the German word “Zahlen’ which means “to count”.

In order to represent integers on the number line we draw a straight line and mark origin (O) in the middle of the line. The numbers may be represented by dots along a straight line as shown in below figure. Positive numbers are represented on the right hand side of the origin and negative numbers are represented on the left hand side of the origin.

(d) Rational Numbers: A rational number is a number which can be expressed in the form of \(\frac{p}{q}\), where p and q are integers and q ≠ 0.
Thus, Q = {\(\frac{p}{q}\) : q ≠ 0, p, q ∈ Z}

A rational number may be positive, negative or zero. The rational number is positive if p and q have like signs and negative if p and q have unlike signs.
For example: 5 = \(\frac{5}{1}\), -11 = \(\frac{-11}{1}, \frac{-2}{3}, \frac{4}{7}, \frac{32}{96}, \frac{3}{-5}\)
In above examples 5, \(\frac{4}{7}\), \(\frac{32}{96}\), are positive rational numbers and -11, \(\frac{-2}{3}\), \(\frac{3}{-5}\) are negative rational numbers.
For representing rational numbers on the number line, we draw a line and mark origin (O) in the middle of line. Positive numbers are represented on the right hand side of the origin and negative numbers are represented on the left hand side of the origin. If we mark a point P on the line to the right of O to represent 1, then OP = 1 unit and mark a point Q on the line to the left of O to represent -1, then OQ = -1 unit.

For representing the rational numbers \(\frac{1}{3}\), \(\frac{2}{3}\) on the number line, we divide the segment OP into three equal parts such that OA = AB = BP = \(\frac{1}{3}\). So, A and B represent \(\frac{1}{3}\) and \(\frac{2}{3}\) respectively as shown in the figure 1.2.

For representing rational numbers \(\frac{1}{2}\) on the number line, we divide the segment OQ into four equal parts such that OR = RS = ST = TQ = \(\frac{1}{4}\). So R, S and T represent \(\frac{-1}{4}, \frac{-2}{4}\) and \(\frac{-3}{4}\) respectively.

(e) To find out rational numbers between two rationals: 1. If x and y are two rational numbers such that x < y.
Then a rational number lying between x and y is \(\left(\frac{x+y}{2}\right)\).

2. If a and b are two rational numbers, such that a < b.
Then a rational numbers lying between a and b are

Key Words
→ Numbers: The natural numbers or whole numbers are known as numbers. e.g., 0, 1, 2, 3,…, etc.

→ Even number: A number which is divisible by 2 is called an even number. e.g., 2, 4, 6, 8,…, etc.

→ Odd number: A number which cannot divisible by 2 is called an odd number. e.g., 1, 3, 5, 7,…, etc.

→ Prime number: A natural number which is divisible by 1 and itself, is called a prime number. e.g., 2, 3, 5, 7,…, etc.

→ Composite number: A whole number that can be divided evenly by numbers other than 1 or itself is called composite numbers e.g., 4, 6, 8, 9 …, etc.

→ Coprime numbers: Two numbers are said to be coprime, if their H.C.F. is 1. eg., (4, 5), (8, 9), (15, 16), etc.

→ Number line: Refers to a straight horizontal line on which each point represents a real number.

→ Terminating decimal: A number which divides completly in decimal or whole number is called terminating decimal.
e.g., \(\frac{3}{5}\) = 0.6, \(\frac{20}{4}\) = 5, etc.

→ Non terminating decimal: A number which cannot divide completly in decimal or whole number i.e., process of division will never end, is called non terminating decimal. eg., \(\frac{1}{11}\) = 0.090909…, \(\frac{1}{7}\) = 0.142857…, etc.

→ Recurring (or repeating) decimal: A non terminating decimal, in which a digit or set of digits repeats continually, is called a recurring or repeating decimal.
e.g., \(\frac{4}{9}\) = 0.444….., \(\frac{2}{11}\) = 0.181818…, \(\frac{1}{3}\) = 0.076923076923… etc.

→ Exponent or Index or Power: Suppose that ‘a’ is a real number, when the product a × a × a × a × a is written as a⁵, the number 5 is called the exponent of a.

Basic Concepts
1. Irrational Numbers: In previous section, we observe that some numbers are not rational. These numbers can not write in the form of \(\frac{p}{q}\), where p and q are intergers and q ≠ 0.
For example: 0.141441444…., 0.232332333…..
In 400 B.C., the famous Mathematician Pythagoras was the first to discover the number which were not rational. These numbers are called irrational numbers.
Let us define these numbers as an irrational is a non-terminating and non-recurring decimal, that is, it cannot be written in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.

Examples of Irrational Numbers:
(i) 0.2020020002……, 0.313311333111……., 0.535535553… are irrational numbers.
(ii) \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{5}\), \(\sqrt{6}\), \(\sqrt{7}\), \(\sqrt{10}\), \(\sqrt{11}\), \(\sqrt{12}\), \(\sqrt{15}\), \(\sqrt{16}\) etc. all are irrational numbers.
(iii) \(\sqrt[3]{2}, \sqrt[3]{3}, \sqrt[3]{4}, \sqrt[3]{5}, \sqrt[3]{6}, \sqrt[3]{7}, \sqrt[3]{9}, \sqrt[3]{10}\) etc. all are irrational numbers.
(iv) π is irrational, while \(\frac{22}{7}\) is rational.

2. Properties of Irrational Numbers:
A. (a) Sum of a rational number and an irrational number is an irrational number.
(b) Difference of a rational number and an irrational number is an irrational number.
(c) Product of a rational number and an irrational number is an irrational number.
(d) Quotient of a rational number and an irrational number is an irrational number.
For example: (5 + \(\sqrt{2}\)), (5 – \(\sqrt{3}\)), 3\(\sqrt{2}\) and \(\frac{7}{\sqrt{3}}\) all are irrational numbers.

B. (a) It is not necessary that sum of two irrational numbers may be an irrational number.
For example:(4 + \(\sqrt{5}\)) and (3 – \(\sqrt{5}\)) both are irrational number. But (4 + \(\sqrt{5}\))+(3 – \(\sqrt{5}\)) = 7, which is rational number.
(b) It is not necessary that difference of two irrational numbers may be an irrational number.
For example: (4 + \(\sqrt{3}\)) and (3 + \(\sqrt{3}\)) both are irrational numbers. But (4 + \(\sqrt{3}\)) – (3 + \(\sqrt{3}\)) = 1, which is rational number.

(c) It is not necessary that product of two irrational numbers may be an irrational number.
For example: \(\sqrt{2}\) is an irrational number. But \(\sqrt{2}\) × \(\sqrt{2}\) = 2, which is rational number.
(d) It is not necessary that quotient of two irrational numbers may be an irrational number.
For example: 6\(\sqrt{2}\) and 3\(\sqrt{2}\) both are irrational numbers. But \(\frac{6 \sqrt{2}}{3 \sqrt{2}}\) = 2, which is rational number.

3. Representation of Irrational Numbers on the Number Line: We show the representation of irrational numbers on the number line by help of some examples given below:

(a) Real Numbers: Rational numbers and irrational numbers form the collection of all real numbers.
Every real number is either rational or irrational number.
For example: -3\(\frac{1}{2}\), \(\sqrt{3}\), π, 1.596. etc.
(i) Rational Number: A number whose decimal expension is either terminating or non-terminating recurring is called a rational number.
For example: \(\frac{3}{4}\), 2.1, \(\frac{1}{3}\) etc.
(ii) Irrational Number: A number whose decimal expension is non-terminating non recurring is called an irrational number.
For example: \(\sqrt{2}\), \(\sqrt{3}\), 2010010001…., π, etc.

(b) Decimal Expansions of Rational Numbers: A rational number can be expressed as a decimal. For example, if we divide 3 by 5, we will get 0.6, a terminating decimal.

Similarly, if we divide 2 by 8, we will get 0.25, a terminating decimal.

Similarly,
\(\frac{3}{4}\) = 0.75
\(\frac{7}{16}\) = 0.4375
\(\frac{-2}{5}\) = -0.4 etc.
are rational numbers expressed as decimals. Now let us divide 3 by 11

We observe that the continued process of division by 11, in the quotient digits 2, 7 will repreat from the stage marked (→) onwards. Thus
\(\frac{3}{11}\) = 0.2727…..
= \(0 . \overline{27}\)
The process of division, in this case the decimal expressions are known as non-terminating repeating (recurring) decimals.
Similarly,

A repeating decimal such as 0.6666… is often written as \(0.\overline{6}\), where over bar indicates the number that repeats. Hence,
\(\frac{2}{3}\) = \(0.\overline{6}\)
So, we say that every terminating or repeating decimal represents a rational number.

Representing Real Numbers on the Number Line: In the previous section, we have learn about the decimal expansions of real numbers. This help us to represent it on the number line. In this section, we will learn how to visualise the position of real numbers in decimal form.

Suppose we want to visualise the representation of 2.665 on the number line. We observe that 2.665 is located between 2 and 3. So let us look closely at the portion of the number line 2 and 3. We divide it into 10 equal parts and mark each point of division as shown in figure 1.10. Then the first mark to the right of 2 will represent 2.1, the second 2.2 and so on. To see this clearly we may take a magnifying glass and look at the portion between 2 and 3. Now, we observe that 2.665 lies between 2.6 and 2.7. To get more accurate visualization of the representation, we divide this portion of real line into 10 equal parts. The first mark will represent 2.61, the second 2.62 and so on.

Again, 2.665 lies between 2.66 and 2.67, so let us focus on this portion of the number line. We magnify the portion of line between 2.66 and 2.67 and divide it into 10 equal parts. The first mark represents 2.661, the next one represents 2.662 and so on. So 2.665 is the 5th mark in these subdivisions. We call this process of visualisation of representation of numbers on the number line through a magnifying glass, as the process of successive magnification.

1. Operations on Real Numbers: In the previous classes, we have learnt about that rational numbers satisfied the associative, commutative and distributive properties for addition and multiplication. The sum, difference, product and quotient of two rational numbers will be a rational number. Irrational numbers also satisfied the commutative, associative and distributive properties for addition and multiplication. However the sum, difference, quotients and products of irrational numbers are not always irrational.

The facts related to operations on real numbers are given below:

• The sum or difference of a rational number and an irrational number is an irrational number.
• The product or quotient of a non-zero rational number with an irrational number is an irrational number.
• If we, add, subtract, multiply or divide two irrational numbers, the result may be a rational or irrational number.

2. Existence of Square Root of a given Positive Real Number:
To find \(\sqrt{x}\) geometrically, where x is any positive real number.
Construction: Draw a line AB of length x units extend AB to point C such that BC = 1 unit. Find the midpoint of AC and marked that point O. Draw a semicircle with centre O and radius OA. Draw a line perpendicular to AC passing through B and intersecting the semicircle at D, then BD = \(\sqrt{x}\).

Proof:
We have AB = x units, BC = 1 unit
⇒ AC = x + 1 units
OA = OD = OC = \(\frac{x+1}{2}\),
(∵ O is the mid-point of AC)
Now,
OB = x – \(\frac{(x+1)}{2}\)
⇒ OB = \(\frac{2 x-x-1}{2}=\frac{x-1}{2}\)
In right ΔOBD,
OD² = OB² + BD²,
(By Pythagoras theorem)
⇒ BD² = OD² – OB²
⇒ BD² = \(\left(\frac{x+1}{2}\right)^2-\left(\frac{x-1}{2}\right)^2\)
⇒ BD² = \(\frac{x^2+1+2 x}{4}-\frac{x^2+1-2 x}{4}\)
⇒ BD² = \(\frac{1}{4}\)[x² + 1 + 2x – x² – 1 + 2x]
⇒ BD² = \(\frac{1}{4}\) × 4x
⇒ BD² = x
⇒ BD = \(\sqrt{x}\)

3. Rationalisation of Irrational Number:
The process of multiplying a given irrational number by its rationalising factor to get a rational number as product is called rationalisation of the given irrational number.
When the product of two irrational numbers is a rational number, each is called the Rationalising Factors (R.F.) of the other.

For Example:
(i) Since 5\(\sqrt{2}\) × 3\(\sqrt{2}\) = 15 × 2 = 30; which is a rational number. Therefore, 5\(\sqrt{2}\) and 3\(\sqrt{2}\) are rationalising factors of each other.
(ii) (\(\sqrt{3}\) + \(\sqrt{2}\)) (\(\sqrt{3}\) – \(\sqrt{2}\)) = (\(\sqrt{3}\))² – (\(\sqrt{2}\))²
= 3 – 2 = 1
(\(\sqrt{3}\) + \(\sqrt{2}\)) and (\(\sqrt{3}\) – \(\sqrt{2}\)) are the
rationalising factors of each other.
(iii) (3 + \(\sqrt{5}\)) (3 – \(\sqrt{5}\)) = 3² – (\(\sqrt{5}\))²
= 9 – 5 = 4
(3 + \(\sqrt{5}\)) and (3 – \(\sqrt{5}\)) are rationalising factors of each other.

In the same way:
(i) R.F. of \(\sqrt{5}\) – 2 is \(\sqrt{5}\) + 2.
(ii) R.F. of 4 + 3\(\sqrt{5}\) is 4 – 3\(\sqrt{5}\).

Laws of Exponents for Real Numbers:
Let a be real number and m, n be rational numbers, then we have

Note: Here a is called base and m, n are called exponents.

Haryana State Board HBSE 9th Class Maths Notes Chapter 15 प्रायिकता Notes.

Haryana Board 9th Class Maths Notes Chapter 15 प्रायिकता

→ गणित की एक शाखा, जिसे ‘प्रायिकता का सिद्धांत’ (Theory of Probability) कहते हैं, में अनिश्चितता के मापन का प्रावधान है। इस सिद्धांत में हम ऐसी स्थितियों (या प्रयोगों या घटनाओं पर ध्यान देते हैं जिनमें कोई विशेष परिणाम निश्चित नहीं होता है, किंतु वह अनेक संभाव्य परिणामों में से एक हो सकता है।

→ किसी घटना E की प्रायिकता, जिसे P (E) से दर्शाते हैं, निम्न सूत्र से प्राप्त होती है :

→ किसी घटना के घटने की प्रायिकता 0 से 1 के बीच (जिसमें 0 व 1 सम्मिलित हैं) होती है।