Haryana State Board HBSE 9th Class Maths Notes Chapter 9 Areas of Parallelograms and Triangles Notes.
Haryana Board 9th Class Maths Notes Chapter 9 Areas of Parallelograms and Triangles
Introduction
In previous classes, we have studied the areas of plane figure such as, triangle, square, parallelogram, rhombus etc. We may recall that part of plane enclosed by a simple closed figure is called a planar region corresponding to that figure. The magnitude or measure of this planar region is called its area.
Area is always expressed with the help of a number such as 12 cm2, 5 cm2, 7 hectares etc. In this chapter, we will consolidate the knowledge about these formulae by studying some relationship between the areas of these geometric figures under the condition when they lie on the same base and between the same parallels.
Key Words
→ Base: In a geometry, a particular side or face of geometric figure, such as a triangle, parallelogram, cone etc.
→ Altitude: The perpendicular distance from a vertex to the opposite side is known as altitude.
→ Magnitude: Exter, size, bulk, amount, quantity, greateness. That which is extended in length, breadth and thickness. A thing which can be divided into parts.
→ Monotone: In one tone.
→ Planar region: Of, relating to or situated in a plane.
OR
Having a two dimensional characteristic.
→ Interior of a triangle: The part of the plane enclosed by a triangle is known as the interior of the triangle.
![]()
→ Area of a triangle = \(\frac{1}{2}\) × base × height
→ Area of a parallelogram = base × height
→ Area of a square = (side)2 OR \(\frac{1}{2}\)d12,
[where d1 is its diagonal]
→ Area of a rectangle = length × breadth
→ Area of a rhombus = base × height or \(\frac{1}{2}\)d1 × d2, [where d1 and d2 are its diagonals]
→ Area of a trapezium = \(\frac{1}{2}\)(sum of parallelside) × height
Basic Concepts
1. Polygonal Regions:
(a) Triangular region: The union of a triangle and its interior is called a triangular region. By the area of a triangle, we mean the area of its triangular region.

(b) Rectangular region: The part of the plane enclosed by a rectangle is called the interior of a rectangle and the union of a rectangle and its interior is a called a rectangular region. It can be represent as the union of two triangular regions.

(c) Polygonal region: A polygonal region is a plane figure that can be written as a union of a finite number of triangular regions, subject to a constraint. The constraint is that the triangular regions are non-over lapping. That means if two triangular region intersect then their intersetion is either vertex or edge of each of the triangular regions.
2. Area Axioms:
(a) Every polygonal region R has an area, measured in square units.
(b) (i) Congruent Area Axiom If two polygonal regions R1 and R2 are such that R1 ≅ R2, then
ar (R1) = ar (R2).
(ii) Area Monotone Axiom: If two polygonal regions are such that R1 belongs to R2 then
ar (R1) ≤ ar (R2).
(iii) Area Addition Axiom: If intersection of two polygonal regions R1 and R2, is a finite number of points and line segments such that R = R1 ∪ R2, then
ar (R) = ar (R1) + ar (R2).
(c) Rectangle Area Axiom: A rectangular region ABCD in which AB = a units and BC = b units then
ar (rectangle ABCD)= ab square units.
![]()
3. Figures on the Same Base and Between the Same Parallels:
Look at the following figures:

In figure 9.4 (i) parallelograms ABCD and ABQP have a common side AB. So we say that parallelogram ABCD and ABQP are on the same base AB. Similarly in figure 9.4 (ii) triangles ABC and DBC are on the same base BC, in figure 9.4 (iii) trapezium PQRS and parallelogram PQMN are on the same base PQ. In figure 9.4 (iv) parallelogram ABCD and triangle PDC are on the same base DC.
Now look at the figures (9.5):
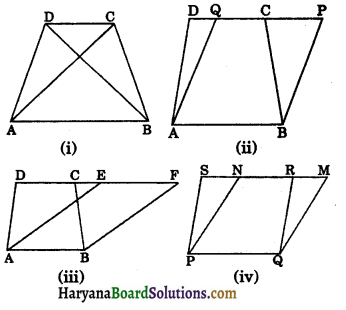
We observe that in figure 9.5 (i) triangles CBA and DAB lie on the same base AB and, AB and CD are two parallel lines. In addition to the above, the vertex D of ADAB opposite to the base AB and vertex C of ACBA opposite to the base AB lie on a line CD parallel to the base AB. So we say that ADAB and ACBA are on the same base AB and between the same parallels CD and AB. Similarly in figure 9.5 (ii) trapezium ABCD and parallelogram ABPQ are on the same base AB between the same parallels AB and PD. In figure 9.5 (iii) trapezium ABCD and parallelogram ABFE are on the same base AB and between the same parallels AB and DF. In figure 9.5 (iv) parallelograms PQRS and PQMN are on the same base PQ and between the same parallels PQ and SM.
So, two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.
Now consider the following figures:
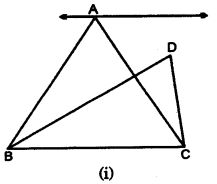
We observe that in figure 9.6 (i) triangles ABC and DBC are the same base BC but do not lie between the same parallels. In figure, 9.6 (ii) parallelogram ABCD and triangle PQR are lie between the same parallels AB and CD but they are not on the same base. In figure 9.6 (iii) the parallelograms ABCD and ABFE are on the same base AB but do not lie between the same parallels.
![]()
Parallelograms on the Same Base and Between the Same Parallels:
Theorem 9.1:
Parallelograms on the same base and between the same parallels are equal in area.
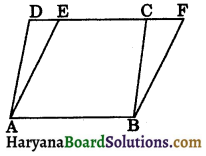
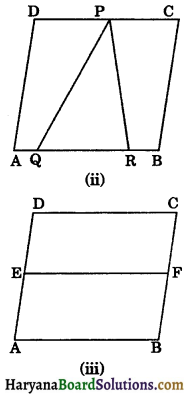
Given: Two parallelogram ABCD and ABFE are on the same base AB and are between the same parallels AB and DF.
To prove:
ar (||gm ABCD) = ar (||gm ABFE).
Proof: In ΔAED and ΔBFC, we have
AD = BC
[∵ AD and BC are the opposite sides of parallelogram ABCD]
∠DAE = ∠CBF
[∵ AD || BC and AE || BF,
∴ angle between AD and AE = angle between BC and BF]
and AE = BF
(∵ AE and BF are the opposite sides of the parallelogram ABFE)
ΔAED ≅ ΔBFC
(By SAS congruence rule)
⇒ ar (ΔAED) = ar (ΔBFC)
(By congruent area axiom) …(i)
Now
ar (||gm ABCD) = ar (☐ ABCE) + ar (ΔAED)
⇒ ar (||gm ABCD) = ar (☐ ABCE) + ar (ΔBFC) [using (i)]
⇒ ar (||gm ABCD) = ar (||gm ABFE)
Hence proved
Corollary 1: A parallelogram and a rectangle on the same base and between the same parallels are equal in area.
Corollary 2: If a triangle and a parallelogram are on the same base and between the same parallels, then area of the triangle is equal to half the area of the parallelogram.
Corollary 3: Area of parallelogram = base × height.
Given: A parallelogram ABCD in which AB is the base and AP is the corresponding height.
To prove : Area of parallelogram ABCD = AB × AP.
Construction: Draw BQ ⊥ CD so that rectangle ABQP is formed.
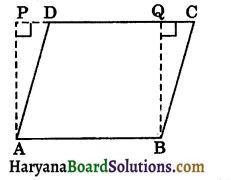
Proof: Since parallelogram ABCD and rectangle ABQP are on the same base AB and between the same parallels AB and PC.
∴ ar (||gm ABCD) = ar (rectangle ABQP)
⇒ ar (||gm ABCD) = AB × AP
[∵ area of rectangle = length × breadth]
⇒ ar (||gm ABCD) = base × height.
![]()
Triangles on the Same Base and Between the Same Parallels:
Theorem 9.2:
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.

Given: Two triangles ABC and PBC on the same base BC and between the same parallels BC and AP.
To prove : ar (ΔABC) = ar (ΔPBC).
Construction: Through B draw BD || CP, intersecting PA produced in D and through C, draw CQ || BA, intersecting AP produced in Q.
Proof: Since, BC || AP and AB || CQ.
∴ ABCQ is a parallelogram.
Again, BC || AP and BD || CP
∴ BCPD is a parallelogram.
Now, parallelograms ABCQ and DBCP are on the same base BC and between. the same parallels BC and DQ.
∴ ar (||gm ABCQ) = ar (||gm DBCP) …(i)
But, a diagonal of a parallelogram divides it into two triangles are of equal areas.
∴ ar (ΔABC) = ar (||gm ABCQ) …(ii)
Similarly, ar (ΔPBC) = \(\frac{1}{2}\)ar (||gm DBCP) …(iii)
From (i), (ii) and (iii), we get
ar (ΔABC) = ar (ΔPBC)
Hence proved
Corollory: Area of a triangle = \(\frac{1}{2}\)base × height.
Given: A ΔABC in which AP is the height to the side BC.
To prove: ar (ΔABC) = \(\frac{1}{2}\)BC × AP.
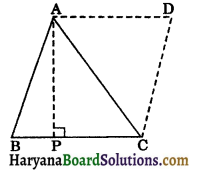
Construction: Through A and C, draw AD || BC and CD || BA, intersecting each other at D.
Proof : Since, AD || BC and CD || BA
∴ ABCD is a parallelogram.
AC is the diagonal of parallelogram ABCD. It divides the parallelogram ABCD into two triangles of equal areas.
∴ ar (ΔABC) = \(\frac{1}{2}\)ar (||gm ABCD)…(i)
Since BC is a side of ||gm ABCD and AP is its corresponding height.
ar (||gm ABCD) = BC × AP …..(ii)
From (i) and (ii), we get
ar(ΔABC) = \(\frac{1}{2}\)BC × AP.
Hence proved.
Corollary: Area of a trapezium = \(\frac{1}{2}\) × (sum of the parallel sides) × (distance between them)
Given: A trapezium ABCD in which AB || CD and CP ⊥ AB. Let CP = h.
To prove :
ar (trapezium) = \(\frac{1}{2}\)(AB + CD) × h.
Construction: Draw AQ ⊥ CQ, intersecting CD produced at Q. Join AC.
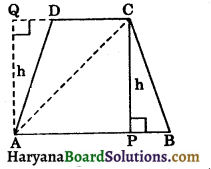
Proof: ar (trapezium ABCD) = ar (ΔABC) + ar (ΔACD)
= \(\frac{1}{2}\) × AB × CP + \(\frac{1}{2}\) × CD × AQ
= \(\frac{1}{2}\) × (AB + CD) × h, [∵ CP = AQ = h]
∴ Area of a trapezium = \(\frac{1}{2}\)(sum of the parallel sides) × (distance between them)
![]()
Theorem 9.3:
Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.
OR
If two triangles have equal areas and one side of the triangle is equal to one side of the other, then their corresponding altitudes are equal.
Given: Two triangles ABC and DEF are such that
ar (ΔABC) = ar (ΔDEF) and AB = DE and CM and FN are the altitudes corresponding to AB and DE respectively of the two triangles.
To prove: CM = FN.
Proof: In AABC, CM is the altitude to the corresponding side AB.
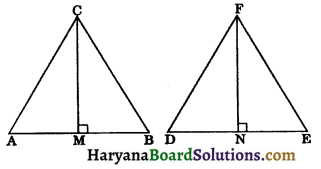
ar (ΔABC)= \(\frac{1}{2}\) × AB × CM …..(i)
[∵ ar (Δ) = \(\frac{1}{2}\) base × height]
Similarly,
ar (ΔDEF) = \(\frac{1}{2}\) × DE × FN …(ii)
But, ar (ΔABC) = ar (ΔDEF) (given)…(iii)
From (i), (ii) and (iii), we get
\(\frac{1}{2}\) × AB × CM = \(\frac{1}{2}\) × DE × FN
⇒ \(\frac{1}{2}\) × AB × CM = \(\frac{1}{2}\) × AB × FN
[given DE = AB]
⇒ CM = FN. Hence proved
As CM = FN (Proved above)
and CM ⊥ AB and FN ⊥ AB
∴ CF || AB

Hence, two triangles having the same base and equal area lie between the same parallels.