Haryana State Board HBSE 9th Class Maths Notes Chapter 7 Triangles Notes.
Haryana Board 9th Class Maths Notes Chapter 7 Triangles
Introduction
In previous classes, we have learnt about triangles and their various properties. Recall that, a closed figure formed by three line segments, is called a triangle. It is usually denoted by the greek letter Δ (delta).
The figure 7.1 shows a triangle ABC denoted as a ΔABC. A triangle has three sides namely AB, BC and CA, three vertices namely A, B and C and has three angles namely ∠A, ∠B and ∠C.
In this chapter we shall learn about the congruence of triangles, criteria for congruence of triangles, some more properties of triangles and inequalities in a triangle.
Key Words
→ Equalities: The logical relation expressing identity or sameness and denoted by the sign “=”.
→ Axiom: A statement whose truth is either to be taken as self evident or to be assumed.
→ Inequalities: Refers to a statement that a quantity is either greater than or less than but not equal to them.
→ Perimeter: The perimeter of a two dimensional region is the length of its boundary.
→ Concentrate: On one point, to pay attention upon.
→ Slides: A gliding seat or surface for sliding.
→ Swing: To move with to and fro motion.
→ Hexagon: It is a polygon bounded by six straight line. (six-sided figure).
![]()
Basic Concepts
1. (a) Definition of Congruence: If two geometrical figures coincide exactly, by placing one over the other, the figures are said to be congruent to each other.
(i) Two line segments are congruent if and only if their lengths are equal. (See fig. 7.2).

Two line segments AB and CD are congruent, if AB = CD.
(ii) Two angles are congruent if and only if their measures are equal. (See fig. 7-3)
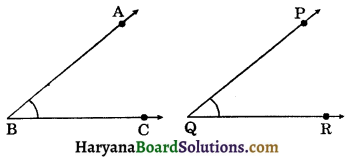
Two angles ABC and PQR are congruent if m∠ABC = m∠PQR.
(iii) Two circles are congruent if and only if lengths of their radii are equal. (See fig. 7.4)
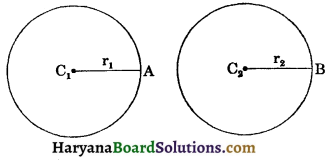
Two circles C and C2 are congruent, if r1 = r2.
(iv) Two squares are congruent if and only if they have equal sides in length. (See fig. 7.5)

Two squares ABCD and EFGH are congruent, if AB = BC = CD = DA = EF = FG = GH = HE.
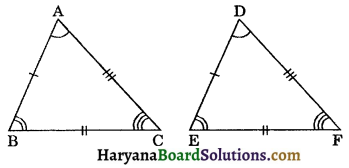
(b) Congruence of Triangles: The three sides and three angles of a triangle are called its six parts or six elements. Two triangles are said to be congruent to each other, if on placing one over the other, they exactly coincide.
Let ΔABC is placed over ΔDEF, such that vertex A falls on vertex D and side AB falls on side DE, then if the two triangles coincide with each other in a such a way that B falls on E, C falls on F; side BC coincides with side EF and side AC coincides with side DF, then the two triangles are congruent to each other. (See fig. 7.6)
The symbol used for congruence is “≅”.
ΔABC is congruent to ΔDEF is written as:
ΔABC ≅ ΔDEF.
In case of congruent ΔABC and ΔDEF as given above, the sides of the two triangles, which coincide with each other are called corresponding sides. Thus the sides AB, BC and CA of AABC are corresponding to the side DE, EF and FD of ADEF respectively. In the same way, the angles of the two traingles which coincide with each other, are called corresponding angles. Thus three pairs of corresponding angles are ∠A and ∠D, ∠B and ∠E and ∠C and ∠F.
It follows from the above discussion that if ΔABC coincide ΔDEF exactly such that the vertices of ΔABC fall on the vertices of ΔDEF, in the order
A ↔ D, B ↔ E, C ↔ F.
Then we have the following six equalities:
(i) AB = DE, BC = EF and CA = FD i.e. corresponding sides are equal (congruent).
(ii) ∠A = ∠D, ∠B = ∠E and ∠C = ∠F i.e. corresponding angles are equal (congruent). Hence, following is the general condition for congruence of two triangles:
Two triangles are congruent if and only if there exists a correspondence between their sides and vertices such that the corresponding sides and the corresponding angles of two triangles are equal.
If ΔABC is congruent to ΔDEF and the correspondence ABC ↔ DEF makes the six pairs of corresponding parts of the two triangles congruent, then we write ΔABC ≅ ΔDEF.
But it will not be correct to write ΔCBA ≅ ΔDEF because corresponding parts of ΔCBA and ΔDEF will not be equal i.e., congruent.
Note: The corresponding parts of congruent triangles (abbreviated as CPCT).
(c) Congruence relation in the set of all triangles: From the definition of congruence triangles and notation above, we obtain the following results:
(i) ΔABC ≅ ΔABC
[Congruence relation is reflexive]
(ii) If ΔABC ≅ ΔDEF,
then ΔDEF ≅ ΔABC,
[Congruence relation is symmetric]
(iii) If ΔABC ≅ ΔDEF
and ΔDEF ≅ ΔKLM,
then ΔABC ≅ ΔKLM,
[Congruence relation is transitive]
![]()
2. Criteria for Congruence of Triangles:
Axiom 7.1 (SAS congruence rule): Two triangles are congruent if two sides and included angle of one triangle are equal to the two sides and the included angle of the other triangle.
Given: ΔABC and ΔDEF in which AB = DE, AC = DF and ∠A = ∠D. (See fig. 7.7).
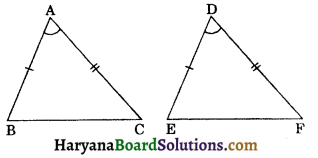
To prove : ΔABC ≅ ΔDEF.
Proof: Place ΔABC over ΔDEF such that vertex A falls on vertex D and side AB falls on side DE. Since side AB side DE. Therefore vertex B falls on vertex E. Since ∠A = ∠D, therefore AC will fall on DF.
But AC = DF and A falls on D.
∴ C will fall on F.
Thus AC will coincide with DF.
Now B falls on E and C falls on F.
∴ BC will coincide with EF.
∴ ΔABC coincide with ΔDEF.
Hence, by definition of congruence ΔABC ≅ ΔDEF.
Note: (1) This axiom refers two sides and the angle between them so it is known as (side-angle-side) or the “SAS congruence axiom” or the “SAS” criteria
(2) SAS axiom is not applicable when two sides and one angle ‘not included between these sides’ of one triangle are equal to two sides and one angle of the other triangle.
![]()
Theorem 7.1 (ASA congruence rule):
Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.
Given: Two triangles ABC and DEF, such that
∠B = ∠E, ∠C = ∠F and BC = EF.
To prove : ΔABC ≅ ΔDEF.
Proof: For proving the congruence of the two triangles there are three cases arise:
Case I: Let AB = DE. (See figure 7.8)
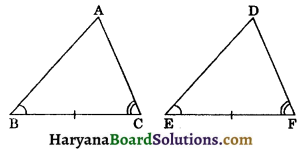
In this case, we have
AB = DE, (Assumed)
∠B = ∠E, (Given)
and BC = EF, (Given)
So, ΔABC ≅ ΔDEF, (By SAS axiom)
Case II: Let if possible AB > DE, so we can take a point P on AB such that PB = DE. Now consider ΔPBC and ΔDEF.
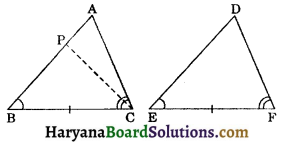
In ΔPBC and ΔDEF, we have
PB = DE, (By construction)
∠B = ∠E, (Given)
and BC = EF, (Given)
So, ΔPBC ≅ ΔDEF,(By SAS axiom)
⇒ ∠PCB = ∠DFE, (CPCT)
But ∠ACB = ∠DFE, (Given)
∴ ∠ACB = ∠PCB
This is possible only when P coincide with A, therefore AB must be equal to DE.
Thus, in ΔABC and ΔDEF, we have
AB = DE, (As proved above)
∠B = ∠E, (Given)
and BC = EF, (Given)
So, ΔABC ≅ ΔDEF, (By SAS axiom)
Case III: If AB < DE, we can choose a point M on DE such that ME = AB and repeating the arguments as given in Case (II), we can conclude that AB = DE and so we can prove that
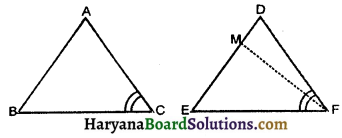
ΔABC ≅ ΔDEF
Hence, in all three cases, we have
ΔABC ≅ ΔDEF. Proved
![]()
Corollary (AAS congruence rule):
If any two angles and non-included side of one triangle are equal to the corresponding angles and side of another triangle, then two triangles are congruent.
Given: Two triangles ABC and DEF, such that
∠A = ∠D, ∠B = ∠E
and BC = EF.
To prove : ΔABC ≅ ΔDEF
Proof: Since, we know that sum of the interior angles of a triangle is 180°.
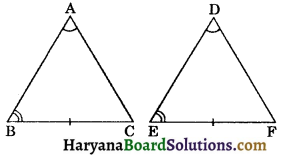
∴ ∠A + ∠B + ∠C = ∠D + ∠E + ∠F = 180°…(i)
But ∠A = ∠D and ∠B = ∠E, (given) …….(ii)
∠A + ∠B + ∠C = ∠A + ∠B + ∠F,
[From (i) and (ii)]
⇒ ∠C = ∠F
In ΔABC and ΔDEF, we have
∠B = ∠E, (Given)
∠C = ∠F, (As proved above)
and BC = EF, (Given)
So, ΔABC ≅ ΔDEF
(By ASA congruence rule)
Some Properties of a Triangle: In chapter 6 we have studied the triangle and their kinds. Recall that, if a triangle has two sides equal, then it is called an isosceles triangle. Now we shall study some results related to isosceles triangles.
![]()
Theorem 7.2:
Angles opposite to equal
Given: In ΔABC, AB = AC.
To prove: ∠B = ∠C. sides of an isosceles triangle are equal.

Construction: Draw AD, the bisector of ∠A which meets BC on D.
Proof: In ΔABD and ΔACD, we have
AB = AC, (Given)
∠BAD = ∠CAD, (By construction)
and AD = AD, (Common)
ΔABD ≅ ΔACD,
(By SAS congruence rule)
⇒ ∠B = ∠C. Hence proved.
Theorem 7.3:
[Converse of Theorem 7.2]: The sides opposite to equal angles of a triangle are equal.
Given: In ΔABC,
∠B = ∠C.
To prove: AB = AC.
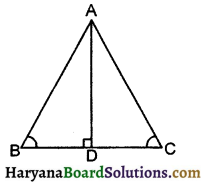
Construction: Draw AD perpendicular to BC. It meets BC on D.
Proof: In ΔABD and ΔACD, we have
∠ABD = ∠ACD, (Given)
∠ADB = ∠ADC,
(By construction each = 90°)
and AD = AD, (Common)
∴ ΔABD ≅ ΔACD, (By AAS congruence rule)
⇒ AB = AC (CPCT)
Hence proved
![]()
Some More Criteria for Congruence of Triangles :
Theorem 7.4 (SSS congruence rule): If three sides of one triangle are equal to the three sides of another triangle, then two triangles are congruent.
Given: ΔABC and ΔPQR such that AB = PQ, BC = QR and AC = PR.
To prove : ΔABC = ΔPQR.
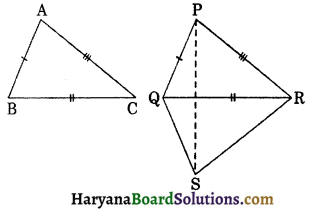
Construction: Suppose BC is the longest side of ΔABC. Draw QS and RS such that ∠SQR = ∠ABC and ∠SRQ = ∠ACB. Join P to S.
Proof: In ΔABC and ΔSQR, we have
BC = QR, (Given)
∠ABC = ∠SQR, (By construction)
and ∠ACB = ∠SRQ, (By construction)
∴ ΔABC ≅ ΔRQS,
(By ASA congruence rule)
⇒ ∠BAC = ∠QSR, (CPCT) …(i)
AB = QS, (CPCT)
and AC = SR, (CPCT)
Now AB = PQ (given)
and AC = PR (given) …(ii)
AB = QS
and AC = SR (as proved above)…(iii)
From (ii) and (iii), we get
PQ = QS and PR = SR
⇒ ∠QPS = ∠QSP…(iv)
and ∠RPS ∠RSP…(v)
Adding (iv) and (v), we get
∠QPS + ∠RPS = ∠QSP + ∠RSP
⇒ ∠QPR = ∠QSR
and ∠BAC = ∠QSR, [From (i)]
∴ ∠BAC = ∠QPR …(vi)
Now in ΔABC and ΔPQR, we have
AB = PQ, (Given)
∠BAC = ∠QPR, [From (vi)]
and AC = PR, (Given)
∴ ΔABC = ΔPQR (By SAS congruence rule).
Hence proved
Theorem 7.5.
[RHS congruence rule]: If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Given: In ΔABC and ΔDEF,
∠B = ∠E = 90°, AC = DF and BC = EF.
To prove: ΔABC ≅ ΔDEF.
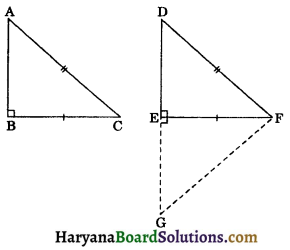
Construction: Produce DE to G so that GE = AB. Join G to F.
Proof: In ΔABC and ΔGEF, we have
AB = GE, (by construction)
∠ABC = ∠GEF, [Each = 90°]
and BC = EF, (Given)
∴ ΔABC ≅ ΔGEF, (By SAS congruence rule)
⇒ ∠A = ∠G, (CPCT) …(i)
AC = GF, (CPCT) …(ii)
Now, AC = DF, (Given)
AC = GF, [from (ii)]
∴ DF = GF
⇒ ∠D = ∠G …(iii)
(Angles opposite to equal sides are equal)
From (i) and (iii), we get
∠A = ∠D…(iv)
In ΔABC and ΔDEF, we have
∠B = ∠E, (Each = 90°)
∠A = ∠D, [from (iv)]
∴ ∠C = ∠F …(v)
[third angles of the triangles]
Now in ΔABC and ΔDEF, we have
BC = EF, (Given)
∠C = ∠F, [From (v)]
and AC = DF, (Given)
∴ ΔABC = ΔDEF, (by SAS congruence rule)
Hence proved
Note: RHS stands for Right angle-Hypotenuse-Side.
![]()
Inequalities in a Triangle: In this section, we shall learn about some inequality relations among sides and angles of a triangle. Consider scalene triangle ΔABC such that AB = 7 cm, BC = 6 cm and AC = 5 cm. Now measure the three angles A, B and C with the help of protector, we observe that:
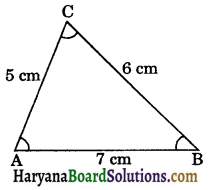
(i) AB > AC and ∠C > ∠B
i.e., the longer side has greater angle opposite to it.
(ii) AC < BC and ∠B < ∠A.
i.e., shorter side has smaller angle opposite to it.
(iii) AB > BC and ∠C > ∠A
i.e., angle opposite the larger side is greater.
Below we give some important results of inequalities in a triangle.
It is stated in the form of a theorem.
Theorem 7.6:
If two sides of a triangle are unequal, the angle opposite to the longer side is larger or (greater). (See fig. 7.62)
Given: A triangle ABC in which AB > AC.
To prove: ∠ACB > ∠ABC.
Construction: From AB, cut AD = AC.
Join C and D.
Proof: In ΔACD, we have
AC = AD, (By construction)
⇒ ∠ACD = ∠ADC …..(1)
(Angles opposite to equal sides are equal)
In ΔBDC, we have
Exterior ∠ADC > ∠B
(exterior angle of a triangle is always greater than each its opposite interior angle)
⇒ ∠ACD > ∠B, [From (i)]
⇒ ∠ACB > ∠B, [∵ ∠ACB > ∠ABC]
⇒ ∠ACB > ∠ABC
Theorem 7.7:
In any triangle, the side opposite to the larger (greater) angle is longer.
Given: A triangle ABC in which ∠ABC > ∠ACB.
To prove: AC > AB.
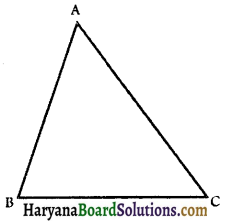
Proof: There are following possibilities.
(i) AC = AB
(ii) AC < AB
(iii) AC > AB
There is only one possibilities must be true.
(i) If AC = AB
⇒ ∠ABC = ∠ACB
[Angles opposite to equal sides are equal]
It is impossible, for it is given that
⇒ ∠ABC > ∠ACB
(ii) If AC < AB
⇒ AB>AC
⇒ ∠ACB > ∠ABC
This is also impossible, being contrary to hypothesis.
(iii) Since AC is neither less than nor equal to AB.
∴ AC must > AB.
Hence AC > AB. Proved.
![]()
Theorem 7.8:
The sum of any two sides of a triangle is greater than the third side. (See fig. 7.64).
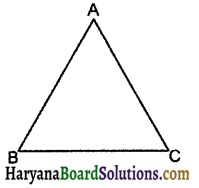
Given: A triangle ΔABC.
To prove : (i) AB + AC > BC
(ii) AB + BC > AC
(iii) AC+ BC > AB.
Construction: Produce BA to D such that AD = AC. Join C to D
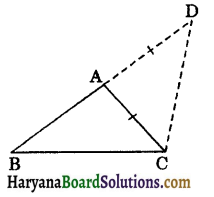
Proof: In ΔACD, we have
AD = AC (By construction)
⇒ ∠ADC = ∠ACD …..(i)
∠BCD > ∠ACD,
[∵ ∠BCD = ∠ACB + ∠ACD]
⇒ ∠BCD > ∠ADC, [from (i), ∠ACD = ∠ADC]
⇒ ∠BCD > ∠BDC
⇒ BD > BC (By theorem 7·7)
⇒ AB + AD > BC
⇒ AB + AC > BC (∵ AD = AC)
Similarly,
AB + BC > AC and AC + BC > AB.
Hence proved
Corollary 1.
The difference between the lengths of any two sides of a triangle is always less than the third side.