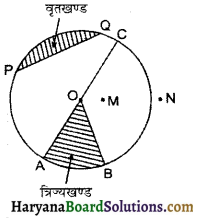
HBSE 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Ex 5.2
Haryana State Board HBSE 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Ex 5.2 Textbook Exercise Questions and Answers.
Haryana Board 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Exercise 5.2
प्रश्न 1.
घड़ी की घण्टे वाली सुई एक घूर्णन के कितनी भिन्न घूम जाती है, जब वह :
(a) 3 से 9 तक पहुँचती है ?
(b) 4 से 7 तक पहुँचती है ?
(c) 7 से 10 तक पहुँचती है ?
(d) 12 से 9 तक पहुँचती है?
(e) 1 से 10 तक पहुँचती है ?
(f) 6 से 3 तक पहुँचती है ?
हल :
(a) आधा घूर्णन
(b) एक-चौथाई घूर्णन
(c) एक-चौथाई घूर्णन
(d) तीन-चौथाई घूर्णन
(e) तीन-चौथाई घूर्णन
(f) तीन-चौथाई घूर्णन
![]()
प्रश्न 2.
एक घड़ी की सुई कहाँ रुक जाएगी, यदि वह:
(a) 12 से प्रारम्भ करे और घड़ी की दिशा में \(\frac {1}{2}\) घूर्णन करे ?
(b) 2 से प्रारम्भ करे और घड़ी की दिशा में \(\frac {1}{2}\) घूर्णन करे ?
(c) 5 से प्रारम्भ करे और घड़ी की दिशा में \(\frac {1}{2}\) घूर्णन करे
(d) 5 से प्रारम्भ करे और घड़ी की दिशा में \(\frac {1}{2}\) घूर्णन करे ?
हल :
(a) यदि घड़ी की सुई 12 से प्रारम्भ करे, तो \(\frac {1}{2}\) घूर्णन के बाद 6 पर पहुंचेगी।
(b) यदि घड़ी की सुई 2 से प्रारम्भ करे, तो \(\frac {1}{2}\) घूर्णन के बाद 8 पर पहुंचेगी।
(c) यदि घड़ी की सुई 5 से प्रारम्भ करें, तो \(\frac {1}{2}\) घूर्णन के बाद 8 पर पहुंचेगी।
(d) यदि घड़ी की सुई 5 से प्रारम्भ करे, तो \(\frac {1}{2}\) घूर्णन के बाद 2 पर पहुंचेगी।
प्रश्न 3.
आप किस दिशा में देख रहे होंगे यदि आप प्रारम्भ में:
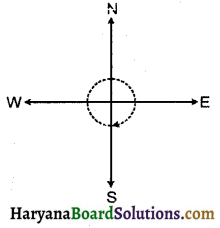
(a) पूर्व की ओर देख रहे हों और घड़ी की दिशा में \(\frac {1}{2}\) घूर्णन करें?
(b) पूर्व की ओर देख रहे हों और घड़ी की दिशा में 1\(\frac {1}{2}\) घूर्णन करें?
(c) पश्चिम की ओर देख रहे हों और घड़ी की विपरीत दिशा में \(\frac {3}{4}\) घूर्णन करें ?
(d) दक्षिण की ओर देख रहे हों और एक घूर्णन करें ? (क्या इस अंतिम प्रश्न के लिए, हमें घड़ी की दिशा या घड़ी की विपरीत दिशा की बात करनी चाहिए? क्यों नहीं ?)
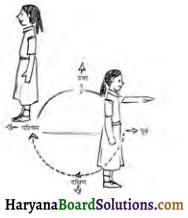
हल :
(a) पूर्व में देख रहे हों और घड़ी की दिशा में \(\frac {1}{2}\) घूर्णन करें, तो हम पश्चिम दिशा में देखेंगे।
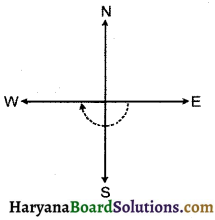
(b) पूर्व की ओर देख रहे हों और घड़ी की दिशा में 1\(\frac {1}{2}\) घूर्णन करें, तो हम पश्चिम दिशा में देखेंगे।
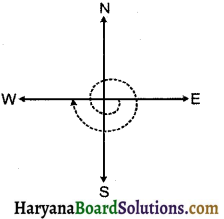
(c) पश्चिम की ओर देख रहे हों और घड़ी की विपरीत दिशा में \(\frac {3}{4}\) घूर्णन करें, तो हम उत्तर दिशा में देखेंगे।
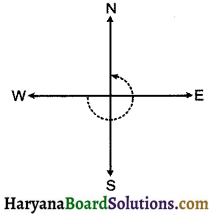
(d) दक्षिण की ओर देख, रहे हों और एक घूर्णन के बाद हम दक्षिण दिशा में देखेंगे।
(नोट : इस प्रश्न में घड़ी की दिशा अथवा विपरीत दिशा का महत्व नहीं है क्योंकि एक घूर्णन के बाद हम मूल स्थिति में वापस आ जाएँगे।)
![]()
प्रश्न 4.
आप एक घूर्णन को कितना भाग घूम जाएंगे, यदि आप:
(a) पूर्व की ओर मुख किए खड़े हों और घड़ी की दिशा में घूमकर उत्तर की ओर मुख कर लें?
(b) दक्षिण की ओर मुख किए खड़े हों और घड़ी की दिशा में घूमकर पूर्व की ओर मुख कर लें ?
(c) पश्चिम की ओर मुख किए खड़े हों और घड़ी . की दिशा में घूमकर पूर्व की ओर मुख कर लें ?
हल :
(a) \(\frac {3}{4}\) घूर्णन
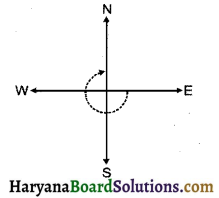
(b) \(\frac {3}{4}\) घूर्णन
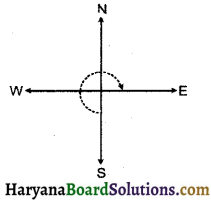
(c) \(\frac {1}{2}\) घूर्णन
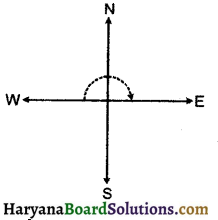
प्रश्न 5.
घड़ी की घण्टे की सुई द्वारा घूमे गए समकोणों की संख्या ज्ञात कीजिए, जब वह
(a) 3 से 6 तक पहुँचती है।
(b) 2 से 8 तक पहुँचती है।
(c) 5 से 11 तक पहुंचती है।
(d) 10 से 1 तक पहुंचती है।
(e) 12 से 9 तक पहुंचती है।
(f) 12 से 6 तक पहुँचती है।
हल:
∵ जब घड़ी की घण्टे की सुई 12 से चलना प्रारम्भ करके घूमती हुई पुनः 12 पर पहुँचने में 1 घूर्णन अथवा 4 समकोण बनाती है अर्थात्
∵ घण्टे की सुई 12 घण्टे में = 4 समकोण बनाती है।
∴ घण्टे की सुई 1 घण्टे में = \(\frac {4}{12}\) समकोण बनाती है।
(a) घड़ी की घण्टे की सुई को 3 से 6 तक पहुँचने में (3-4, 4-5, 5-6) 3 घण्टे लगते हैं।
∴ समकोणों की संख्या = \(\frac {4}{12}\) × 3
= 1 समकोण।
(b) घड़ी की घण्टे की सुई को 2 से 8 तक पहुँचने में (2-3, 3-4, 4-5, 5-6, 6-7, 7-8) 6 घण्टे लगते है।
∴ समकोणों की संख्या = \(\frac {4}{12}\) × 6 = 2 समकोण
(c) घड़ी को घण्टे की सुई को 5 से 11 तक पहुँचने में (5-6, 6-7, 7-8, 8-9, 9-10, 10-11) 6 घण्टे लगते हैं।
∴ समकोणों की संख्या = \(\frac {4}{12}\) × 6 = 2 समकोण।
(d) घड़ी के घण्टे की सुई को 10 से 1 तक पहुँचने में (10-11, 11-12, 12-1) 3 घण्टे लगते हैं।
∴ समकोणों की संख्या = \(\frac {4}{12}\) × 3 = 1 समकोण।
(e) घड़ी की घण्टे की सुई को 12 से 9 तक पहुँचने में (12-1, 1-2, 2-3, 3-4, 4-5, 5-6, 6-7, 8-9)9 घण्टे लगते हैं।
∴ समकोणों की संख्या = \(\frac {4}{12}\) × 9
= 3 समकोण।
(f) घड़ी की घण्टे की सुई को 12 से 6 तक पहुँचने में (12-1, 1-2, 2-3, 3-4, 4-5, 5-6) 6 घण्टे लगते हैं।
∴ समकोणों की संख्या = \(\frac {4}{12}\) × 6
= 2 समकोण।
![]()
प्रश्न 6.
आप कितने समकोण घूम जाएँगे, यदि आप प्रारम्भ में :
(a) दक्षिण की ओर देख रहे हों और घड़ी की दिशा में पश्चिम की ओर घम जाएँ ?
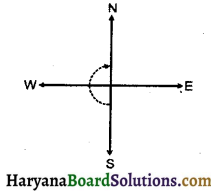
(b) उत्तर की ओर देख रहे हों और घड़ी की विपरीत (वामावर्त) दिशा में पूर्व की ओर घूम जाएँ ?
(c) पश्चिम की ओर देख रहे हों और पश्चिम की ओर घूम जाएँ ?
(d) दक्षिण की ओर देख रहे हों और उत्तर की ओर घूम जाएँ?
हल :
आकृतियों से स्पष्ट है कि कितने समकोण घूम जाएंगे यदि हम प्रारम्भ में :
(a) दक्षिण की ओर देख रहे हों और घड़ी की दिशा में पश्चिम की ओर घूम जाएँ, तो 1 समकोण घूम जाएँगे।
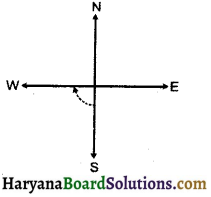
(b) उत्तर की ओर देख रहे हों और घड़ी की विपरीत (वामावर्त) दिशा में पूर्व की और घूम जाएँ, तो 3 समकोण घूम जाएंगे।
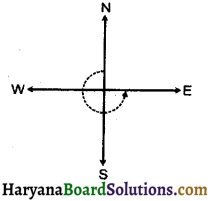
(c) पश्चिम की ओर देख रहे हों और पश्चिम की ओर घूम जाएँ, तो 4 समकोण घूम जाएँगे।
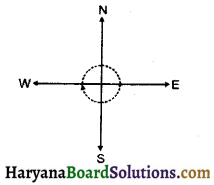
(d) दक्षिण की ओर देख रहे हों और उत्तर की ओर घूम जाएँ, तो 2 समकोण घूम जाएँगे।
प्रश्न 7.
घड़ी की घण्टे वाली सुई कहाँ रुकेगी, यदि वह प्रारम्भ करे:
(a) 6 से और 1 समकोण घूम जाए?
(b) 8 से और 2 समकोण घूम जाए ?
(c) 10 से और 3 समकोण घूम जाए ?
(d) 7 से और 2 ऋजुकोण घूम जाए ?
हल :
हम जानते हैं कि घड़ी की घण्टे की सुई 12 घण्टे में 4 समकोण घूर्णन करती है अर्थात् 3 घण्टे में एक समकोण घूर्णन करती है।
(a) यदि घड़ी की घण्टे की सुई 6 से प्रारम्भ होकर 1 समकोण चलती है, तो घण्टे की सुई (6 + 3 =) 9 पर रुकेगी।
(b) यदि घड़ी की घण्टे की सुई 8 से प्रारम्भ होती है और 2 समकोण चलती है, तो घण्टे की सुई (8 + 2 × 3 =) 14 अर्थात् 2 पर रुकेगी।
(c) यदि घड़ी की घण्टे की सुई 10 से प्रारम्भ होती है और 3 समकोण चलती है, तो घण्टे की सुई (10 + 3 × 3 =) 19 अर्थात् 7 पर रुकेगी।
(d) यदि घड़ी की घण्टे की सुई 7 से प्रारम्भ होती है और 2 ऋजुकोण (4 समकोण) चलती है तो घड़ी के घण्टे की सुई (7 + 4 × 3 =) 19 अर्थात् 7 पर रुकेगी।
HBSE 6th Class Maths Solutions Chapter 5 प्रारंभिक आकारों को समझना Ex 5.2 Read More »