Author name: Prasanna

Haryana State Board HBSE 12th Class Physics Solutions Chapter 10 तरंग-प्रकाशिकी Textbook Exercise Questions and Answers.

Haryana Board 12th Class Physics Solutions Chapter 10 तरंग-प्रकाशिकी

प्रश्न 1.
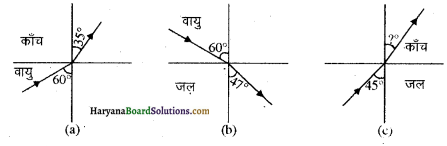
589 nm तरंगदैघ्र्य का एकवर्णिय प्रकाश वायु से जल की सतह पर आप्तित होता है।
(a) परावर्तित तथा
(b) अपरवार्तित प्रकाश की तरंगदैघ्र्य, आवृत्ति तथा चाल क्या होगी? जल का आवरत्नांक 1.33 है।
उत्तर:
दिया गया है:
एकवर्णीय प्रकाश का तरंगदैर्घ्य = 589nm
A = 589 × 10⁹ m
प्रकाश की चाल c = 3 x 10⁸ m/s,
वायु का अपवर्तनांक = n = 1

(a) परावर्तित प्रकाश के लिए:
परावर्तित प्रकाश का तरंगदैर्घ्य = 1
परावर्तित प्रकाश की आवृत्ति = v
परावर्तित प्रकाश की चाल = v
(i) चूँकि परावर्तित प्रकाश का तरंगदैर्घ्य अपरिवर्तित रहता है। चूँकि वायु का अपवर्तनांक 1 है इसलिए अपवर्तित प्रकाश की तरंगदैर्ध्य
चाल
λ1 = λ/n
= 589 × 10^-9/1
λ1 = 589 x 10^-9 m
(ii) चूँकि परावर्तन एक ही माध्यम में होता है अतः प्रकाश की
= v = c = 3 x 10⁸ m/s
(iii) अपवर्तित प्रकाश की आवृत्ति =0
आवृत्ति v = c/λ
= \(\frac{3 \times 10^8 \mathrm{~m} / \mathrm{s}}{589 \times 10^{-9} \mathrm{~m}}\)
= 5.09 × 10¹⁴ Hz

(b) अपवर्तित प्रकाश के लिए:
जल का अपवर्तनांक = 1.33
अपवर्तित प्रकाश की तरंगदैर्ध्य λ = λ/n
= \(\frac{589 \times 10^{-9}}{1.33}\)
= 442.857 nm
≈ 443 nm

अपवर्तित प्रकाश की आवृत्ति आपतित प्रकाश की आवृत्ति के समान होती है।
अतः आवृत्ति v’ = 0 = 5.09 × 10¹⁴ Hz
अपवर्तित प्रकाश की चाल (Vg) = c/n = \(\frac{3 \times 10^8}{1.33}\)
= 2.26 × 10⁸m/s

प्रश्न 10.2.
निम्नलिखित दशाओं में प्रत्येक तरंगाय की आकृति क्या है?
(a) किसी बिंदु स्रोत से अपसरित प्रकाश।
(b) उत्तल लेन्स से निर्गमित प्रकाश, जिसके फोकस बिंदु पर कोई बिंदु स्रोत रखा है।
(c) किसी दूरस्थ तारे से आने वाले प्रकाश तरंगाय का पृथ्वी द्वारा अवरोधित (intercepted) भाग।
उत्तर:
(a) तरंगाग्र गोलीय अभिसारी प्रकार का होता है।
(b) जब बिन्दु स्रोत को उत्तल लेंस के फोकस पर रखा जाता है तब लेंस से निर्गत प्रकाश किरणें एक-दूसरे के समान्तर होती हैं तथा तरंगाग्र समतल होगा।
(c) तरंगा की आवृत्ति लगभग समतल होती है क्योंकि प्रकाश स्रोत अर्थात् पृथ्वी से दूरस्थ है तारा। अतः बड़े गोले की सतह का एक छोटा क्षेत्र लगभग समतलीय होता है।

प्रश्न 10.3.
(a) काँच का अपवर्तनांक 1.5 है। काँच में प्रकाश की चाल क्या होगी ? (निर्वात में प्रकाश की चाल 3.0 x 10⁸ ms^-1 है।)
(b) क्या काँच में प्रकाश की चाल, प्रकाश के रंग पर निर्भर करती है? यदि हाँ, तो लाल तथा बैंगनी में से कौन-सा रंग काँच के प्रिज्म में धीमा चलता है?
उत्तर:
(a) दिया गया है:
काँच का अपवर्तनांक= 1.5
n = 1.5
निर्वात में प्रकाश की चाल = c = 3.0 x 10⁸ m/s
काँच में प्रकाश की
चाल = Vg (माना)
= \(\mathrm{v}_{\mathrm{g}}\) = \(\frac{\mathrm{c}}{\mathrm{n}}\) = \(\frac{3.0 \times 10^8}{1.5}\)
Vg = 2 × 10⁸ m/s.

(b) हाँ, काँच में प्रकाश की चाल इसके रंग से स्वतंत्र नहीं है। कोची सूत्र से अपवर्तनांक का मान रंग पर निर्भर करता है। अर्थात्
अपवर्तनांक (n) = a + b/ λ2 + c/λ4 + …………….
या c/vg = a + b/ λ2 + c/ λ4 + ……………..
यहाँ पर a, b तथा c स्थिरांक हैं।
∴ vg or λ2 स्पष्टतः है कि प्रकाश की चाल तरंगदैर्घ्य के वर्ग के अनुक्रमानुपाती है। हम जानते हैं कि
अर्थात् बैंगनी रंग का तरंगदैर्ध्य लाल रंग के तरंगदैर्ध्य से कम है। इसलिए काँच में से बैंगनी प्रकाश लाल रंग की अपेक्षा धीमे चलेगा।

प्रश्न 10.4.
यंग के द्विझिरी प्रयोग में झिरियों के बीच की दूरी 0.28mm है तथा परदा 1.4m की दूरी पर रखा गया है। केंद्रीय दीप्त फ्रिंज एवं चतुर्थ दीप्त फ्रिंज के बीच की दूरी 1.2cm मापी गई है। प्रयोग में उपयोग किए गए प्रकाश की तरंगदैर्ध्य ज्ञात कीजिए।
उत्तर:
दिया गया है:
झिरियों के बीच की दूरी = d = 0.28mm
d = 0.28 × 10³ m
झिरियों और पर्दे के बीच
दूरी = D= 1.4m
धारी की कोटि = n = 4
x = 1.2 cm = 1.2 x 10² m
सम्बन्ध सूत्र
x = nλD/d से हम प्राप्त करते हैं
या
λ = xd/nD
मान रखने पर

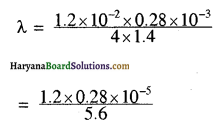
= 600 × 10⁹ m
= 6000 Å

प्रश्न 10.5.
यंग के द्विझिरी प्रयोग में, λ तरंगदैर्ध्य का एकवर्णीय प्रकाश उपयोग करने पर परदे के एक बिंदु पर जहाँ पथांतर λ है, प्रकाश की तीव्रता K इकाई है। उस बिंदु पर प्रकाश की तीव्रता कितनी होगी जहाँ पथांतर λ/3 है?
उत्तर:
एकवर्णीय प्रकाश के लिये
I1 = I2 = l0
तथा पथान्तर
∆ = λ
तब कलान्तर ¢ = 2π/λ .∆
¢ = 2π/λ .λ = 2π
परिणामी तीव्रता
= K
अतः
K = I1 + I2 + 2 √I1, √I2 cos ¢
= Io + I0 + 2√I0√I0 cos 2π
= 2I0 + 2I0 × 1 (∵ cos 2π = 1)
K = 4lo
⇒ Io = 1/4K
जब ∆ = λ/3
कलान्तर ¢ = 2π/λ × λ/3 = 2π/3
परिणामी तीव्रता I = – 1/4k + 1/4k + 2K/4 cos 2π/3
I = 1/2k + 1/2K(-1/2)
I = 1/4K

प्रश्न 10.6
यंग के द्विझिरी प्रयोग में व्यतिकरण फ्रिजों को प्राप्त करने के लिए 650 nm तथा 520 nm तरंगदैयों के प्रकाश-पुंज का उपयोग किया गया।
(a) 650nm तरंगदैर्घ्य के लिए परदे पर तीसरे दीप्त फ्रिज की केंद्रीय उच्चिष्ठ से दूरी ज्ञात कीजिए।
(b) केंद्रीय उच्चिष्ठ से उस न्यूनतम दूरी को ज्ञात कीजिए जहाँ दोनों तरंगदैघ्यों के कारण दीप्त फ्रिज संपाती (coincide) होते हैं।
दोनों झिरियों के बीच की दूरी 2 mm तथा झिरियों से पर्दे की दूरी 12m है।
उत्तर:
दिया गया है:
λ1 = 650 nm = 650 x 10⁹ m.
= 650 x 10⁷ cm.
= 65 × 10^-6 cm.
n = 3, D = 1.2 m = 120 cm.
d = 2 mm = 2 × 10^-1 cm.
λ2 = 520 nm
= 520 x 10^-9 m.
= 520 × 10^-7 cm.
= 52 × 10^-6 cm.

(a) केन्द्रीय फ्रिंज से nवीं दीप्त फ्रिंज की दूरी x = nλD/d
X = \(\frac{3 \times 65 \times 10^{-6} \times 120}{2 \times 10^{-1}}\)
∵ n = 3
= 117 × 10³ cm.
= 0.117 cm = 1.17 mm.

(b) प्रश्नानुसार न्यूनतम दूरी वह होगी, जहाँ पर एक तरंगदैर्घ्य के कारण वें क्रम की दीप्त फ्रिंज दूसरे तरंगदैर्घ्य के कारण (n + 1)d वें क्रम की दीप्त फ्रिज के सम्पाती होगी।
अतः
x = \(\frac{\mathrm{n} \lambda \mathrm{D}}{\mathrm{d}}\)
\(\frac{\mathrm{n} \lambda_1 \mathrm{D}}{\mathrm{d}}\) = \(\frac{(n+1) \lambda_2 D}{d}\)
nλ1 = (n + 1)λ2
या n × 65 × 10^-6 = (n + 1) × 52 × 10^-6
या 5n = (n + 1) × 4 = 4n + 4
या n = 4
अतः न्यूनतम दूरी x = \(\frac{\mathrm{n} \lambda_1 \mathrm{D}}{\mathrm{d}}\) = \(\frac{4 \times 65 \times 10^{-6} \times 120}{2 \times 10^{-1}}\)
x = 0.156 cm = 1.56mm.

प्रश्न 10.7.
एक द्विझिरी प्रयोग में एक मीटर दूर रखे परदे पर एक फ्रिज की कोणीय चौड़ाई 0.2° पाई गई। उपयोग किए गए प्रकाश की तरंगदैर्ध्य 600 nm है। यदि पूरा प्रायोगिक उपकरण जल में डुबो दिया जाए तो फ्रिज की कोणीय चौड़ाई क्या होगी? जल का अपवर्तनांक 4/3 लीजिए।
उत्तर:
कोणीय चौड़ाई θ = λ/d
या θ α λ
जहाँ
θ = 0.2°
nw = 4/3
\(\frac{\theta_w}{\theta}\) = \(\frac{\lambda_w}{\lambda}\)
∵ n = v1/v2 = λ1/λ2
अतः
nw = \(\frac{\lambda}{\lambda_w}\)
या = \(\frac{\lambda}{\mathrm{n}_{\mathrm{w}}}\)
\(\frac{\theta_w}{\theta}\) = \(\frac{\lambda}{\mathrm{n}_{\mathrm{w}} \lambda}\) = \(\frac{1}{\mathrm{n}_{\mathrm{w}}}\)
∴ θw = \(\frac{\theta}{n_w}\)
मान रखने पर
θ = \(\frac{0.2^{\circ}}{4 / 3}\) = \(\frac{0.2^{\circ} \times 3}{4}\)
θ = 0.15°

प्रश्न 10.8.
वायु से काँच में संक्रमण (transition ) के लिए ब्रूस्टर कोण क्या है? (काँच का अपवर्तनांक = 1.5 )।
उत्तर:
वायु से काँच में संक्रमण के लिए n = tan iB
यहाँ पर iB = ब्रूस्टर कोण है जिसे ध्रुवण कोण भी कहते हैं।
1.5 = tan iB
या
iB = tan^-1 (1.5)
= 56.3°

प्रश्न 10.9
5000 À तरंगदैर्घ्य का प्रकाश एक समतल परावर्तक सतह पर आपतित होता है। परावर्तित प्रकाश की तरंगदैर्ध्य एवं आवृत्ति क्या है? आपतन कोण के किस मान के लिए परावर्तित किरण आपतित किरण के लंबवत् होगी?
उत्तर:
दिया गया है
λ = 5000 A = 5000 x 10^-10m
λ = 5 x 10⁷ m
c = 3 × 10⁸ m/s.
∴ परावर्तित प्रकाश की तरंगदैर्घ्य = आपतित प्रकाश की तरंगदैर्ध्य
अतः परावर्तित प्रकाश की तरंगदैर्ध्य
= 5000 A
अब आवृत्ति v = c/λ से
= \(\frac{3 \times 10^8}{5 \times 10^{-7}}\) = \(\frac{3 \times 10^8}{5 \times 10^{-7}}\)
= 6 × 10¹⁴ Hz
अब परावर्तन के नियमानुसार i = r
अब i + r = 90°
∴ i + i = 90°
या 2i = 90°
या i = 45°

प्रश्न 10.10.
उस दूरी का आकलन कीजिए जिसके लिए किसी 4 mm के आकार के द्वारक तथा 400 nm तरंगदैर्ध्य के प्रकाश के लिए किरण प्रकाशिकी सन्निकट रूप से लागू होती है।
उत्तर:
दिया गया है:
प्रकाश का तरंगदैर्ध्य = λ = 400 nm
λ = 400 x 10^-9 m
= 4 × 10^-7 m
छिद्र के द्वारक का आकार a = 4 mm
= 4 × 10^-3 m
Zf = फ्रेनेल दूरी = वह दूरी जिसके लिए रेखा प्रकाशिकी एक अच्छा निकटतम है।
किरण प्रकाशिकी की वैधता
सूत्र
Zf = a2/λ से
= \(\frac{\left(4 \times 10^{-3}\right)^2}{4 \times 10^{-7}}\) = \(\frac{16 \times 10^{-6}}{4 \times 10^{-7}}\)
= 4 × 10 = 40m

अतिरिक्त अभ्यास प्रश्न (NCERT):

प्रश्न 10.11.
एक तारे में हाइड्रोजन से उत्सर्जित 6563 A की Hg लाइन में 15 का अभिरक्त विस्थापन ( red-shift) होता है। पृथ्वी से दूर जा रहे तारे की चाल का आकलन कीजिए।
उत्तर:
दिया गया है:
∆λ = 15 x 10^-10
m
λ = 6563
Å = 6563 x 10^-10 m
c = 3 × 10⁸ m/s.
हम जानते हैं λ – λ = vλ/c
या v = \(\frac{\left(\lambda^{\prime}-\lambda\right) \times c}{\lambda}\) = \(\frac{\Delta \lambda \times c}{\lambda}\)
= \(\frac{15 \times 10^{-10} \times 3 \times 10^8}{6563 \times 10^{-10}}\)
= \(\frac{15 \times 3 \times 10^8}{6563}\)
= 6.86 × 10⁵ m/s

प्रश्न 10.12.
किसी माध्यम (जैसे जल में प्रकाश की चाल निर्वात में प्रकाश की चाल से अधिक है। न्यूटन के कणिका सिद्धांत द्वारा इस आशय की भविष्यवाणी कैसे की गई? क्या जल में प्रकाश की चाल प्रयोग द्वारा ज्ञात करके इस भविष्यवाणी की पुष्टि हुई ? यदि नहीं, तो प्रकाश के चित्रण का कौन-सा विकल्प प्रयोगानुकूल है?
उत्तर:
न्यूटन के कणिका सिद्धान्त के अनुसार अपवर्तन में, विरल माध्यम से सघन माध्यम में प्रवेश करते समय आपतित कण सतह के लम्बवत् आकर्षण बल का अनुभव करता है। यह परिणाम वेग के अभिलम्ब घटक की वृद्धि में होगी लेकिन पृष्ठ के अनुदिश घटक अपरिवर्तित रहता है। इसका तात्पर्य
c sin i = v sin r
या v/c = sini/sinr
चूँकि n > 1 ∴ v > c
यह अवधारणा प्रायोगिक परिणाम के विरुद्ध है (v< c) प्रकाश का तरंग सिद्धान्त प्रयोग संगत है।

प्रश्न 10.13.
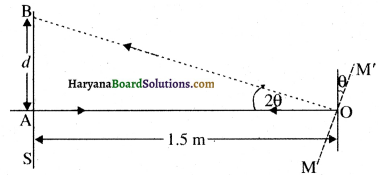
आप मूल पाठ में जान चुके हैं कि हाइगेंस का सिद्धांत परावर्तन और अपवर्तन के नियमों के लिए किस प्रकार मार्गदर्शक है। इसी सिद्धांत का उपयोग करके प्रत्यक्ष रीति से निगमन (deduce ) कीजिए कि समतल दर्पण के सामने रखी किसी वस्तु का प्रतिबिंब आभासी बनता है, जिसकी दर्पण से दूरी, बिंब से दर्पण की दूरी के बराबर होती है।
उत्तर:
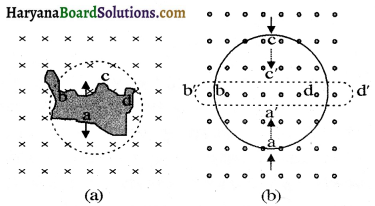
बिन्दु बिम्ब (वस्तु) को केन्द्र लेकर दर्पण को स्पर्श करते हुए एक वृत्त खींचिये यह गोलीय तरंगाग्र का बिम्ब से दर्पण पर पहुँचने वाला समतलीय भाग है। अब दर्पण की उपस्थिति एवं अनुपस्थिति में समय के बाद उसी तरंगाग्र की इन्हीं स्थितियों को आलेखित कीजिए। आप दर्पण के दोनों ओर स्थित दो एक जैसे चाप पायेंगे। सरल ज्यामिति के उपयोग से परावर्तित तरंगाग्र का केन्द्र ( वस्तु का प्रतिबिम्ब) दर्पण से वस्तु की बराबर दूरी पर दिखाई देगा।

प्रश्न 10.14
तरंग संचरण की चाल को प्रभावित कर सकने वाले कुछ संभावित कारकों की सूची है:
(i) स्रोत की प्रकृति,
(ii) संचरण की दिशा,
(iii) स्रोत और / या प्रेक्षक की गति,
(iv) तरंगदैर्घ्य, तथा
(v) तरंग की तीव्रता।
बताइए कि:
(a) निर्वात में प्रकाश की चाल,
(b) किसी माध्यम ( माना काँच या जल) में प्रकाश की चाल इनमें से किन कारकों पर निर्भर करती है?
उत्तर:
(a) निर्वात में प्रकाश की चाल एक सार्वभौमिक स्थिरांक है जो सूचीबद्ध कारकों में से किसी पर भी निर्भर नहीं है। यह स्रोत तथा प्रेक्षक की सापेक्ष गति पर भी निर्भर नहीं करता है। यह तथ्य आइंसटाइन के आपेक्षिकता के विशिष्ट सिद्धान्त का मूल अभिगृहीत है।

(b) माध्यम में प्रकाश की चाल की निर्भरता:
(i) माध्यम में प्रकाश की चाल स्रोतों की प्रकृति से स्वतंत्र है। प्रकाश की चाल का निर्धारण माध्यम के संचरण गुणों से है। यह तथ्य अन्य तरंगों के लिए भी सत्य है, जैसे ध्वनि तरंगों एवं जल तरंगों आदि के लिए।
(ii) समदैशिक माध्यम के लिए संचरण दिशा पर निर्भर नहीं है।
(iii) माध्यम की अपेक्षा स्रोत की चाल से उसमें प्रकाश की चाल स्वतंत्र है परन्तु माध्यम की अपेक्षा प्रेक्षक की चाल पर निर्भर है।
(iv) किसी माध्यम में प्रकाश की चाल तरंगाग्र पर निर्भर है। अर्थात् तरंगदैर्ध्य पर निर्भर करता है।
(v) किसी माध्यम में प्रकाश की चाल उसकी तीव्रता से स्वतंत्र है अर्थात् तीव्रता पर निर्भर नहीं करती (यद्यपि अधिक तीव्र किरण पुंज के लिए यह स्थिति अधिक जटिल है तथा यहाँ हमारे लिए यह महत्त्वपूर्ण नहीं है)।

प्रश्न 10.15
ध्वनि तरंगों में आवृत्ति विस्थापन के लिए डॉप्लर का सूत्र निम्नलिखित दो स्थितियों में थोड़ा-सा भिन्न है:
(i) स्रोत विरामावस्था में तथा प्रेक्षक गति में हो, तथा
(ii) स्रोत गति में परंतु प्रेक्षक विरामावस्था में हो जबकि प्रकाश के लिए डॉप्लर के सूत्र निश्चित रूप से निर्वात में इन दोनों स्थितियों में एकसमान हैं। ऐसा क्यों है? स्पष्ट कीजिए क्या आप समझते हैं कि ये सूत्र किसी माध्यम में प्रकाश गमन के लिए भी दोनों स्थितियों में पूर्णतः एकसमान होंगे?
उत्तर:
ध्वनि तरंगों के संचरण के लिए माध्यम आवश्यक है। यद्यपि (i) तथा (ii) स्थिति में संगत समान सापेक्ष गति (स्रोत तथा प्रेषक के मध्य) भौतिक रूप से समरूपी नहीं है क्योंकि माध्यम के सापेक्ष प्रेषक की गति इन दोनों स्थितियों में भिन्न है। अतः (i) तथा (ii) स्थितियों में हम ध्वनि के लिए डॉप्लर के सूत्रों की समानता की अपेक्षा नहीं कर सकते निर्वात में प्रकाश तरंगों के लिए स्पष्टतया (i) तथा (ii) स्थिति के बीच कोई भेद नहीं है। यहाँ मात्र स्रोत तथा प्रेक्षक की सापेक्ष गतियाँ ही अर्थ रखती हैं तथा आपेक्षिकीय डॉप्लर का सूत्र (i) तथा (ii) स्थिति के लिए समान है। माध्यम में प्रकाश संचरण के लिए पुनः ध्वनि तरंगों के समान दोनों स्थितियाँ समान नहीं हैं तथा (i) तथा (ii) स्थितियों के लिए हमें डॉप्लर के सूत्र के भिन्न होने की अपेक्षा रखनी चाहिए।

प्रश्न 10.16.
द्विझिरी प्रयोग में 600 nm तरंगदैर्घ्य का प्रकाश करने पर, एक दूरस्थ परदे पर बने फ्रिज की कोणीय चौड़ाई 0.1° है। दोनों झिरियों के बीच कितनी दूरी है?
उत्तर:
दिया गया है:
धारी की कोणीय
चौड़ाई = β = 0.1°
β = 0.1 x π/180 रेडियन
= π/1800 रेडियन
प्रकाश की तरंगदैर्ध्य
= λ = 600nm
λ = 600 x 10^-9 m
= 6 × 10^-7 m
झिरियों में दूरी = d = ?
∴ सूत्र β = λ/d का उपयोग करने पर
या
d = λ/β = \(\frac{6 \times 10^{-7} \times 1800}{\pi}\)
= \(\frac{108 \times 10^{-5}}{3.14}\)
= 3.44 x 10^-4 m

प्रश्न 10.17.
निम्नलिखित प्रश्नों के उत्तर दीजिए:
(a) एकल झिरी विवर्तन प्रयोग में झिरी की चौड़ाई मूल चौड़ाई से दोगुनी कर दी गई है। यह केंद्रीय विवर्तन बैंड के साइज तथा तीव्रता को कैसे प्रभावित करेगी?
(b) द्विझिरी प्रयोग में, प्रत्येक झिरी का विवर्तन, व्यतिकरण पैटर्न से किस प्रकार संबंधित है?
(c) सुदूर स्रोत से आने वाले प्रकाश के मार्ग में जब एक लघु वृत्ताकार वस्तु रखी जाती है तो वस्तु की छाया के मध्य एक प्रदीप्त बिंदु दिखाई देता है। स्पष्ट कीजिए क्यों?
(d) दो विद्यार्थी एक 10m ऊँची कक्ष विभाजक दीवार द्वारा 7m के अंतर पर हैं। यदि ध्वनि और प्रकाश दोनों प्रकार की तरंगें वस्तु के किनारों पर मुड़ सकती हैं तो फिर भी वे विद्यार्थी एक-दूसरे को देख नहीं पाते यद्यपि वे आपस में आसानी से वार्तालाप किस प्रकार कर पाते हैं?
(e) किरण प्रकाशिकी, प्रकाश के सीधी रेखा में गति करने की संकल्पना पर आधारित है। विवर्तन प्रभाव (जब प्रकाश का संचरण एक द्वारक / झिरी या वस्तु के चारों ओर प्रेक्षित किया जाए) इस संकल्पना को नकारता है तथापि किरण प्रकाशिकी की संकल्पना प्रकाशकीय यंत्रों में प्रतिबिंबों की स्थिति तथा उनके दूसरे अनेक गुणों को समझने के लिए सामान्यतः उपयोग में लाई जाती है। इसका क्या औचित्य है?
उत्तर:
(a) आकार – Md सूत्र के अनुसार, आकार आधा रह जाता है तीव्रता चार गुनी बढ़ जाती है।

(b) द्वि-झिरी समायोजन में व्यतिकरण फ्रिजों की तीव्रता प्रत्येक झिरी के विवर्तन पैटर्न द्वारा माडुलित (modulated) होती है।

(c) वृत्तीय अवरोध के किनारों से विवर्तित तरंगें छाया के केंद्र पर संपोषी व्यतिकरण द्वारा प्रदीप्त बिंदु उत्पन्न करती हैं। अतः छाया केंन्द्र पर चमकीला धब्बा दिखाई देता है।

(d) तरंगों के बड़े कोण पर विवर्तन अथवा मुड़ने के लिए अवरोधों / द्वारकों का आकार तरंग की तरंगदैर्घ्य के समकक्ष होना चाहिए। यदि अवरोध / द्वारक का आकार तरंगदैर्घ्य की तुलना में बहुत बड़ा है तो विवर्तन छोटे कोण से होगा। यहाँ आकार कुछ मीटरों की कोटि का होता है। प्रकाश की तरंगदैर्घ्य लगभग 5 x 10⁷m है, जबकि ध्वनि- तरंगों; जैसे lk Hz आवृत्ति वाली ध्वनि की तरंगदैर्घ्य लगभग 0.3m है। इस प्रकार ध्वनि तरंगें विभाजक के चारों ओर मुड़ सकती हैं जबकि प्रकाश तरंगें नहीं मुड़ सकतीं। अतः ध्वनि तरंगें विवर्तित हो जाती हैं जिससे दोनों विद्यार्थी एक-दूसरे की आवाज सुन लेते हैं।

(e) प्रकाशीय यन्त्रों में द्वारकों के आकार प्रकाश के तरंगदैर्ध्य की तुलना में बहुत बड़े होते हैं विवर्तन के लिये द्वारक के आकार को तरंगदैर्ध्य की कोटि का होना चाहिये। अतः विभिन्न प्रकाशीय यन्त्रों में बने प्रतिबिम्बों की स्थितियों और गुणों का अध्ययन करने के लिये ज्यामितीय प्रकाशिकी की परिकल्पना को ही प्रयुक्त करते हैं।

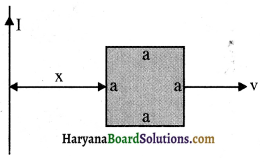
प्रश्न 10.18.
दो पहाड़ियों की चोटी पर दो मीनारें एक-दूसरे से 40km की दूरी पर हैं। इनको जोड़ने वाली रेखा मध्य में आने वाली किसी पहाड़ी के 50m ऊपर से होकर गुजरती है। उन रेडियो तरंगों की अधिकतम तरंगदैर्ध्य ज्ञात कीजिए, जो मीनारों के मध्य बिना पर्याप्त विवर्तन प्रभाव के भेजी जा सकें। हल दिया गया है:
a = 50m
Z_F = 40/2 = 20 km.
Z_F = 20 x 10³ = 2 x 10⁴m.
तरंगदैर्ध्य λ = ?
हम जानते हैं:
ZF = a²/λ से
या
λ_max = \(\frac{(50)^2}{2 \times 10^4}\) = \(\frac{(50)^2}{2 \times 10^4}\)
= \(\frac{50 \times 50}{2 \times 10^4}\)

प्रश्न 10.19.
500nm तरंगदैर्घ्य का एक समांतर प्रकाश-पुंज एक पतली झिरी पर गिरता है तथा 1m दूर परदे पर परिणामी विवर्तन पैटर्न देखा जाता है। यह देखा गया कि पहला निम्निष्ठ परदे के केंद्र से 2.5 mm कीजिए।
उत्तर:
दिया है:
दूरी पर है। झिरी की चौड़ाई ज्ञात
λ = 500nm
= 5 × 10⁷ m
D = 1 m, n = 1 x = 2.5 mm
= 2.5 × 10⁴ m
झिरी की चौड़ाई = ?
केन्द्रीय उच्चिष्ठ की चौड़ाई
2x = \(\frac{2 \mathrm{D} \lambda}{\mathrm{a}}\)
a = \(\frac{D \lambda}{x}\)
= \(\frac{1 \times 5 \times 10^{-7}}{25 \times 10^{-4}}\)
= 2 × 10⁴m
= 0.2 mm

प्रश्न 10.20.
निम्नलिखित प्रश्नों के उत्तर दीजिए:
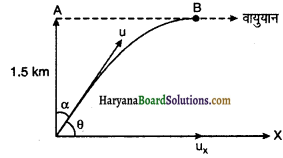
(a) जब कम ऊँचाई पर उड़ने वाला वायुयान ऊपर से गुजरता है तो हम कभी-कभी टेलीविजन के परदे पर चित्र को हिलते हुए पाते हैं। एक संभावित स्पष्टीकरण सुझाइए।
(b) जैसा कि आप मूल पाठ में जान चुके हैं कि विवर्तन तथा व्यतिकरण पैटर्न में तीव्रता का वितरण समझने का आधारभूत सिद्धांत तरंगों का रेखीय प्रत्यारोपण है। इस सिद्धांत की तर्कसंगति क्या है?
उत्तर:
(a) ऐंटीना द्वारा प्राप्त सीधे संकेत तथा गुजरने वाले वायुयान से परावर्तित संकेतों का व्यतिकरण के कारण होता है। अर्थात् कम ऊँचाई पर उड़ता हुआ वायुयान T.V. सिग्नल को परावर्तित कर देता है। सीधे आने वाले सिग्नल और परावर्तित सिग्नल में व्यतिकरण के कारण T.V. स्क्रीन पर चित्र कुछ हिलते हुए दिखाई देते हैं।

(b) अध्यारोपण का सिद्धांत तरंगगति को नियंत्रित करने वाली अवकल (differential) समीकरण के रेखीय चरित्र से प्रतिपादित है। यदि Y1 और Y2 इस समीकरण के हल हैं, तो Y1 और Y2 का रेखीय योग भी उनका हल होगा। जब आयाम बड़े हों (उदाहरण के लिए उच्च तीव्रता का लेजर किरण पुंज) तथा अरैखिक प्रभाव महत्वपूर्ण हो तो यह स्थिति और भी जटिल हो जाती है, जिसका समझना यहाँ आवश्यक नहीं है।

प्रश्न 10.21.
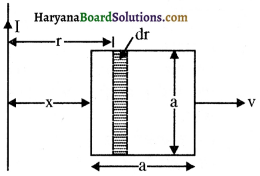
एकल झिरी विवर्तन पैटर्न की व्युत्पत्ति में कथित है कि n/a कोणों पर तीव्रता शून्य है। इस निरसन (cancellation) को, झिरी को उपयुक्त भागों में बाँटकर सत्यापित कीजिए।
उत्तर:
किसी एकल झिरी को n छोटी झिरियों में बाँटिए जिनमें प्रत्येक की चौड़ाई a = a/n है। कोण θ = nλ/a = λa प्रत्येक छोटी झिरी से कोण 6 की दिशा में तीव्रता शून्य है। इनका संयोजन भी शून्य तीव्रता प्रदान करता है।

Haryana State Board HBSE 11th Class Physics Solutions Chapter 5 गति के नियम Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 5 गति के नियम

प्रश्न 5.1.
निम्नलिखित पर कार्यरत् नेट बल का परिमाण व उसकी दिशा लिखिए:
(a) एकसमान चाल से नीचे गिरती वर्षा की कोई बूँद।
(b) जल में तैरता 10g संहति का कोई कॉर्क।
(c) कुशलता से आकाश में स्थिर रोकी गई कोई पतंग।
(d) 30kmh^-1 के एकसमान वेग से ऊबड़-खाबड़ सड़क पर गतिशील कोई कार
(e) सभी गुरुत्वीय पिण्डों से दूर तथा विद्युत और चुम्बकीय क्षेत्रों से मुक्त अन्तरिक्ष में तीव्र चाल वाला इलेक्ट्रॉन।
उत्तर:
(a) बूँद एकसमान चाल से नीचे गिर रही है, इसलिए त्वरण a = 0, अतः बल शून्य होगा।
(b) कॉर्क पानी में तैर रहा है तो कॉर्क का भार उत्पलावक बल के तुल्य है, अतः परिणामी बल शून्य होगा।
(c) पतंग स्थिर है तो न्यूटन के प्रथम नियम से परिणामी बल शून्य होगा।
(d) कार एकसमान वेग से गति कर रही है, इसलिए त्वरण a = 0, अतः बल शून्य होगा।
(e) इलेक्ट्रॉन पर गुरुत्वीय व विद्युत चुम्बकीय क्षेत्र कार्य नहीं कर रहे। हैं, अतः परिणामी बल शून्य होगा।

प्रश्न 5.2.
0.05 kg संहति का कोई कंकड़ ऊर्ध्वाधर ऊपर फेंका गया है। नीचे दी गई प्रत्येक परिस्थिति में कंकड़ पर लग रहे नेट बल का परिमाण व उसकी दिशा लिखिए-
(a) उपरिमुखी गति के समय
(b) अधोमुखी गति के समय
(c) उच्चतम बिन्दु जहाँ क्षण भर के लिए यह विराम में रहता है। यदि कंकड़ को क्षैतिज दिशा से 45° कोण पर फेंका जाये तो क्या आपके उत्तर में कोई परिवर्तन होगा?
वायु प्रतिरोध को उपेक्षणीय मानिए।
उत्तर:
(a) कंकड़ पर बल
= mg
= 0.05 × 10
= 0.5 N
कंकड़ का भार
गुरुत्वीय बल के कारण कंकड़ पर बल लम्बवत् नीचे की ओर कार्य करेगा।
(b) अधोमुखी गति में भी 0.5 N लम्बवत् नीचे को ओर कार्य करेगा।
(c) उच्चतम बिन्दु पर भी बल 0.5 N व दिशा लम्बवत् नीचे की ओर रहेगी।
कंकड़ को 45° कोण पर फेंकने पर भी बल 0.5 N ही लगेगा। उत्तर में कोई परिवर्तन नहीं होगा।

प्रश्न 5.3.
0.1 kg संहति के पत्थर पर कार्यरत् नेट बल का परिणाम व उसकी दिशा निम्नलिखित परिस्थितियों में ज्ञात कीजिए:
(a) पत्थर को स्थिर रेलगाड़ी की खिड़की से गिराने के तुरन्त पश्चात्।
(b) पत्थर को 36kmh^-1 के एकसमान वेग से गतिशील किसी रेलगाड़ी की खिड़की से गिराने के तुरन्त पश्चात।
(c) पत्थर को 1ms^-2 के त्वरण से गतिशील किसी रेलगाड़ी की खिड़की से गिराने के तुरन्त पश्चात्।
(d) पत्थर 1ms^-2 के त्वरण से गतिशील किसी रेलगाड़ी के फर्श पर पड़ा है तथा वह रेलगाड़ी के सापेक्ष विराम में है।
उपर्युक्त सभी स्थितियों में वायु का प्रतिरोध उपेक्षणीय मानिए।
उत्तर:
(a) पत्थर पर बल = पत्थर का भार
= mg
= 0.1 × 9.8
= 0.98N
(ऊर्ध्वाधर नीचे की ओर)
(b) पत्थर गाड़ी से गिरने के पश्चात् केवल पत्थर के भार के बराबर ही बल कार्य करेगा = 0.98 (ऊर्ध्वाधर नीचे की ओर )
(c) रेलगाड़ी से पत्थर गिरने के तुरन्त पश्चात् पूर्व त्वरण का प्रभाव नहीं रहता है।
∴ बल = 0.98N (ऊर्ध्वाधर नीचे की ओर)
(d) पत्थर, रेलगाड़ी के फर्श पर रखा है तो वह गाड़ी के त्वरण से ही गति करेगा। इसलिए पत्थर का त्वरण a = 1ms^-2
∴ पत्थर पर नेट बल
F = ma = 0.1 x 1 = 0.IN ( क्षैतिज दिशा में)
इस स्थिति में पत्थर का भार फर्श पर अभिलम्ब प्रतिक्रिया परस्पर सन्तुलित हो जाती है।

प्रश्न 5.4.
l लम्बाई की एक डोरी का एक सिरा m संहति के किसी कण से, दूसरा सिरा चिकनी क्षैतिज मेज पर लगी खूँटी से बँधा है। यदि कण चाल से वृत्त में गति करता है तो कण पर (केन्द्र की ओर निर्देशित) नेट बल है:
(i) T
(ii) T – \(\frac{m v^2}{l}\)
(iii) T + \(\frac{m v^2}{l}\)
(iv) 0
T डोरी में तनाव है। (सही विकल्प चुनिए)
उत्तर:
परिणामी बल T है क्योंकि वृत्तीय गति के लिए अभिकेन्द्र बल \(\frac{m v^2}{l}\) तनाव T से प्राप्त होता है।
∴ T = \(\frac{m v^2}{l}\)

प्रश्न 5.5.
15ms^-1 की आरम्भिक चाल से गतिशील 20 kg संहति के किसी पिण्ड पर 50 N का स्पर्श मंदन बल आरोपित किया गया है। पिण्ड को रुकने में कितना समय लगेगा?
उत्तर:
v0 = 15ms^-1 m = 20kg F = 50N
∵ F = ma से,
पिण्ड का मन्दन a = F/ma = \(-\frac{50}{20}\)
= – 2.5ms²
सूत्र v = v0 + at से, अन्तिम वेग v = 0
0 = vo + at से, अन्तिम वेग v = 0
0 = 15 – 2.5 x t
t = \(\frac{15}{2.5}\) = 6s

प्रश्न 5.6.
3.0 kg संहति के किसी पिण्ड पर आरोपित कोई बल 25s में उसकी चाल को 2.0ms^-1 से 3.5 ms^-1 कर देता है। पिण्ड की गति की दिशा अपरिवर्तित रहती है। बल का परिमाण व दिशा क्या है?
उत्तर:
m = 3.0kg; t = 25s; vo = 2.0ms^-1
v = 3.5 ms^-1
प्रथम समीकरण से, v = vo + at
a = \(\frac{v-v_0}{t}\)
= \(\frac{3.5-2.0}{25}\)
= 0.06ms^-2
पिण्ड पर लगा बल F = ma से,
F = 3 x 0.06
= 0.18 N
बल पिण्ड की गति की दिशा में लगेगा।

प्रश्न 5.7.
5.0 kg संहति के किसी पिण्ड पर 8 N व 6 N के दो लम्बवत् बल आरोपित हैं। पिण्ड के त्वरण का परिमाण व दिशा ज्ञात कीजिए।
उत्तर:
m = 5.0kg;
F₁ = 8N;
F₂ = 6N;

∴ परिणामी बल F = \(\sqrt{F_1^2+F_2^2+2 F_1 F_2 \cos 90^{\circ}}\)
= \(\sqrt{64+36}\)
F = 10N
∵ F = ma
त्वरण a = \(\frac{F}{m}=\frac{10}{5}\)
= 2 ms^-1
परिणामी बल द्वारा F₁ की दिशा से बनाया गया कोण
tan θ = \(\frac{F_2}{F_1}=\frac{6}{8}=\frac{3}{4}\)
θ = tan^-1 \(\frac{3}{4}\)
= 37°
यही त्वरण की दिशा होगी।

प्रश्न 5.8
36kmh^-1 की चाल से गतिमान किसी ऑटो रिक्शा का चालक सड़क के बीच एक बच्चे को खड़ा देखकर अपने वाहन को ठीक 4.0s में रोककर उस बच्चे को बचा लेता है। यदि ऑटो रिक्शा बच्चे के ठीक निकट रुकता है, तो वाहन पर लगा औसत मन्दन बल क्या है? ऑटो रिक्शा तथा चालक की संहतियाँ क्रमश: 400 kg और 65kg हैं।
उत्तर:
u0 = 36kmh^-1
= \(\frac{36 \times 1000}{60 \times 60}\) = 10ms^-1
t = 4.0s
अन्तिम वेग v = 0
कुल संहति m = 400+ 65 = 465kg
सूत्र v = u0 + at से,
a = \(\frac{v-u_0}{t}=\frac{0-10}{4}\) = – 2.5ms^-1
गति के द्वितीय नियम से,
त्वरण चिह्न मंदन को प्रदर्शित करता है।
औसत मन्दन बल F = ma
= 465 × 2.5
= 1162.5 N

प्रश्न 5.9.
20000 kg उत्थापन संहति के किसी रॉकेट में 5ms^-2 के आरम्भिक त्वरण के साथ ऊपर की ओर स्फोट किया जाता है। स्फोट का आरम्भिक प्रणोद (बल) परिकलित कीजिए।
उत्तर:
रॉकेट का द्रव्यमान
m= 20000kg
त्वरण = 5ms^-2
माना रॉकेट पर प्रणोद / ऊपर की ओर लगा रहा है जिससे रॉकेट a त्वरण से ऊपर की ओर गति कर रहा है।

बलों के सन्तुलन से,
F – mg = ma
∴ F = m(g + a)
= 20000(10 + 5) = 20000 × 15
∴ F = 3.0 × 10⁵ N

प्रश्न 5.10.
उत्तर की ओर 10ms^-1 की एकसमान आरम्भिक चाल से गतिमान 0.40 kg संहति के किसी पिण्ड पर दक्षिण दिशा के अनुदिश 8.0 N का स्थाई बल 30 के लिए आरोपित किया गया है। जिस क्षण बल आरोपित किया गया उसे t = 0 तथा उस समय पिण्ड की स्थिति x = 0 लीजिए। t = -5s: 25s; 100s पर इस कण की स्थिति क्या होगी?
उत्तर:
m = 0.40kg; vo = 10ms^-1 (उत्तर दिशा में);
F = -8N ( ∵ दिशा दक्षिण है इसलिए -ve चिह्न प्रयुक्त किया है।)
0 < t < 30
मन्दन a = \(\frac{F}{m}=\frac{-8}{0.40}\)
= 20 ms^-2
(i) = -5s अर्थात् बल लगाने से पूर्व की स्थिति है, जब त्वरण शून्य है।
x = Ut + \(\frac{1}{2}\) at^-2
= 10 x (-5) = -50m

(ii) t = 25s पर a = -20ms^-2 होगा
(iii) t = 100s, यहाँ t = 30s तक त्वरण -20ms^-2 होगा।
जबकि 30s से 100s = 70s तक त्वरण a = 0 होगा।
∴ x1 = ut + \(\frac{1}{2}\)at²
x1 = 10 x 30 + \(\frac{1}{2}\)(-20)(30)² = -8700m
30s के पश्चात् अन्तिम वेग v = uo + at
v = 10 – 20 x 30
= -590ms^-1
कुल दूरी x = x₁ + x₂
= -8700 + (-41300)
= -8700 – 41300
= -50000m
= – 50km

प्रश्न 5.11.
कोई ट्रक विरामावस्था से गति आरम्भ करके 2.0ms^-2 के समान त्वरण से गतिशील रहता है। t = 10s पर ट्रक के ऊपर खड़ा एक व्यक्ति धरती से 6m की ऊँचाई से कोई पत्थर बाहर गिराता है t = 11s पर पत्थर का (a) वेग, तथा (b) त्वरण क्या है? (वायु का प्रतिरोध उपेक्षणीय मानिए।)
उत्तर:
vo = 0; a = 2ms^-2; r = 10s
अन्तिम वेग v = vo + at
v = 0+ 2 × 10
= 20ms^-1
(a) x दिशा में त्वरण शून्य होता है अतः वेग का क्षैतिज घटक Vx = 20 ms^-1
y दिशा में त्वरण a = g = 10ms²
∴ vy = uy + at, t = 10s से पत्थर गिरता है।
t = 11s पर वेग ज्ञात करना है।

vy = 0 + 10 × 1 = 10ms^-1
क्योंकि
t = 11 – 10 = 1sec
परिणामी वेग
v = \(\sqrt{v_x^2+v_y^2}=\sqrt{(20)^2+(10)^2}\)
= \(\sqrt{500}\)
= 22.4ms^-1
यदि θ क्षैतिज दिशा में बना कोण हो, तो
tan θ = \(\frac{v_y}{v_x}=\frac{10}{20}=\frac{1}{2}\)
θ = tan^-1\(\frac{1}{2}\)
(b) पत्थर पर गुरुत्वीय त्वरण कार्य करता है। अतः t = 11s पर त्वरण a = 10ms^-2 होगा।

प्रश्न 5.12.
किसी कमरे की छत से 2m लम्बी डोरी द्वारा 0.1 kg संहति के गोलक को लटकाकर दोलन आरम्भ किये गये। अपनी माध्य स्थिति पर गोलक की चाल 1ms^-1 है। गोलक का प्रक्षेप पथ क्या होगा? यदि डोरी को उस समय काट दिया जाता है जब गोलक अपनी (a) चरम स्थितियों में से किसी एक पर है तथा (b) माध्य स्थिति पर है।
उत्तर:
(a) गोलक की चरम स्थिति में वेग शून्य होता है। अतः डोरी काट देने पर गोलक g के अधीन ऊर्ध्वाधर नीचे की ओर गिरेगा।
(b) माध्य स्थिति में गोलक के पास क्षैतिज दिशा में अधिकतम वेग होता है। अतः गोलक परवलय पथ पर गति करता हुआ नीचे गिरेगा।

प्रश्न 5.13.
किसी व्यक्ति की संहति 70 kg है। वह एक गतिमान लिफ्ट में तुला पर खड़ा है जो:
(a) 10 ms^-1 की एकसमान चाल से ऊपर जा रही है,
(b) 5 ms^-2 के एकसमान त्वरण से नीचे जा रही है,
(c) 5ms^-2 के एकसमान त्वरण से ऊपर जा रही है, तो प्रत्येक प्रकरण में तुला के पैमाने का पाठ्यांक क्या होगा?
(d) यदि लिफ्ट मशीन में खराबी आ जाये और वह गुरुत्वीय प्रभाव में मुक्त रूप से नीचे गिरे तो पाठ्यांक क्या होगा?
उत्तर:
(a) m = 70kg
लिफ्ट एकसमान वेग से गति कर रह है:
a = 0
∴ तुला का पाठ्यांक
R = mg = 70×10
= 700 N

(b) a = 5ms^-2 से नीचे
mg – R = ma
या
R = m (g – a )
∴ R = 70(10 – 5) …….(1)
= 350N

(c) a = 5ms^-2 ऊपर की ओर
R – mg = ma
या
R = m(g + a)
∴ R = 70 (10 + 5)
= 1050 N

(d) लिफ्ट गुरुत्वीय प्रभाव में मुक्त रूप से नीचे गिर रही है।
∴ a = g
समी० (1) से R = 0 यह भारहीनता की अवस्था है।

प्रथम 5.14.
चित्र में 4 kg संहति के किसी पिण्ड का स्थिति समय ग्राफ दर्शाया गया है-
(a) t < 0, r > 45, 0 < t < 4s के लिए पिण्ड पर आरोपित बल क्या है?
(b) t = 0 तथा t = 4s पर आवेग क्या है? (केवल एकविमीय गति पर विचार कीजिए।)

उत्तर:
(a) t < 0 पर ग्राफ A() स्थिति में होगा, यहाँ विस्थापन x = 0 अर्थात् पिण्ड विराम अवस्था में है। अतः आरोपित बल शून्य है। t > 4s पर पिण्ड 3m दूर स्थित है तथा विराम अवस्था में है। अतः आरोपित बल शून्य है।
0 < t < 4s पर पिण्ड नियत वेग से गति कर रहा है। अतः त्वरण शून्य होगा तथा आरोपित बल भी शून्य है। (b) t = 0 पर आवेग t = 0 पर वेग v₁ = 0 t > 0 पर वेग v₂ = tan θ = \(\frac{3}{4}\)
= 0.75ms-1
∴ आवेग l = mv₂ – mv₁
= m (V₂ – v₁)
= 4 (0.75 – 0) = 3kgms^-1

t = 4s पर आवेग
t < 4s पर वेग v₁ = 0.75 t > 4s पर v₂ = 0
आवेग l = mV₂ – mv₁ = m(V₂ – V₁)
= 4(0 – 0.75)
= -3 kg ms^-1

प्रश्न 5.15.
किसी घर्षण रहित मेज पर रखे 10 kg तथा 20 kg के दो पिण्ड किसी पतली डोरी द्वारा आपस में जुड़े हैं। 600N का कोई क्षैतिज बल (1) पर, (ii) B पर डोरी के अनुदिश लगाया जाता है। प्रत्येक स्थिति में डोरी में तनाव क्या है?
उत्तर:
F = 600 N

mA = 10kg;
mB = 20kg:
त्वरण a = \(\frac{F}{m_A+m_B}\)
\(\frac{600}{10+20}\) = 20ms^-2
(i) जब A ब्लॉक पर बल लगाया जाये, तो
T = mBa
क्योंकि B पर एकमात्र बल, डोरी का तनाव T आगे को ओर लगेगा
(ii) जब B पर बल लगाया जाये, तो
T = mAa
क्योंकि A पर एकमात्र बल, डोरी का तनाव T आगे को ओर लगेगा
T = 10 x 20 = 200N
Note: दो पिण्डों के इस प्रकार संयोजन में त्वरण समान रहता है परन्तु तनाव ज्ञात करने के लिए डोरी के अन्तिम सिरे पर ध्यान देते हैं।

प्रश्न 5.16.
8kg तथा 12kg के दो पिण्डों को किसी हल्की अवितान्य डोरी, जो घर्षणरहित पर चढ़ी है, के दो सिरों से बाँधा गया है। पिण्डों को मुक्त छोडने पर उनके त्वरण तथा डोरी में तनाव ज्ञात कीजिए।
उत्तर:
m₁ = 8 kg m₂ = 12kg

प्रश्न 5.17.
प्रयोगशाला के निर्देश फ्रेम में कोई नाभिक विराम में है। यदि यह नाभिक दो छोटे नाभिकों में विघटित हो जाता है, तो यह दर्शाडए कि उत्पाद विपरीत दिशाओं में गति करने चाहिए।
उत्तर:
माना m द्रव्यमान का नाभिक प्रारम्भ में विराम में है। यह m₁ व m₂ द्रव्यमान के दो नाभिकों में विघटित होता है, जिनके वेग क्रमशः v₁ व v₂ हैं।
∵ संवेग संरक्षण नियम से,
विघटन से पूर्व कुल संवेग = विघटन के बाद कुल संवेग
0 = \(m_1 \overrightarrow{v_1}+m_2 \overrightarrow{v_2}\)
∴ \(\overrightarrow{v_2}=\frac{-m_1}{m_2} \overrightarrow{v_1}\)
इस सूत्र में \(\overrightarrow{v_1}\) व \(\overrightarrow{v_2}\) परस्पर विपरीत हैं (क्योंकि-ve चिह्न है)। अत: नाभिक विपरीत दिशाओं में गति करेंगे।

प्रश्न 5.18.
दो बिलियर्ड गेंद जिनमें प्रत्येक की संहति 0.05 kg है, 6ms^-1 की चाल से विपरीत दिशाओं में गति करती हुई संघट्ट करती है और संघट्ट के पश्चात् उसी चाल से वापस लौटती हैं। प्रत्येक गेंद पर दूसरी गेंद कितना आवेग लगाती है?
उत्तर:
m₁ = m₂ = 005kg;
u₁ = 6ms^-1;
u₂ = -6ms^-1
(विपरीत दिशा),
v₁ = -6ms^-1
V₂ = 6ms^-1;

आवेग = संवेग में परिवर्तन टक्कर के पश्चात् दूसरी गेंद के कारण
प्रथम गेंद पर आवेग
= प्रथम गेंद के संवेग में परिवर्तन
= M₁V₁ – M₁u₁
= m₁(V₁ – u₁)
= 005 [-6 – 6]
= -0.60 kg-ms^-1
प्रथम गेंद के कारण दूसरी गेंद पर आवेग
= दूसरी गेंद के संवेग में परिवर्तन,
= M₂ (v₂ – u₂)
= 005[6 – (-6)]
= 005 × 12 = + 0.60kg ms^-1

प्रश्न 5.19.
100 kg संहति की किसी तोप द्वारा 0.020 kg का गोला दाग जाता है। यदि गोले की नालमुखी चाल 80ms^-1 है तो तोप की प्रतिक्षेप चाल क्या है?
उत्तर:
तोप का द्रव्यमान M = 100kg;
तोप की चाल V = ?;
गोले का द्रव्यमान m = 0.020kg:
गोले की नालमुखी चाल v=80ms^-1;
संवेग संरक्षण नियम से,
MV + mv = 0
या
= \(\frac{-0.020 \times 80}{100}\)
अर्थात् तोप 0.016ms^-1 की चाल से पीछे हटेगी।

प्रश्न 5.20.
कोई बल्लेबाज किसी गेंद को 45° के कोण पर विक्षेपित कर देता है। ऐसा करने में वह गेंद की आरम्भिक चाल जो 54 kmh^-1 है, में कोई परिवर्तन नहीं करता। गेंद को कितना आवेग दिया जाता है? गेंद की संहति 0.15 kg है।
उत्तर:
गेंद का द्रव्यमान m = 0.15mg
प्रारम्भिक वेग U = 54 kmh^-1
= 54 × \(\frac{1000}{3600}\) = 15ms^-1
अन्तिम वेग = 15ms (u1 से 45° कोण पर) चित्र में गेंद पर लगे संवेग को क्षैतिज व ऊर्ध्वाधर घटकों में वियोजित किया गया है। चित्र से स्पष्ट है कि क्षैतिज घटक में कोई परिवर्तन नहीं होता है, परन्तु उर्ध्वाधर घटकों में परिवर्तन होता है।

गेंद को दिया गया आवेग
= गेंद के संवेग में परिवर्तन
= अन्तिम संवेग – प्रारम्भिक संवेग
= mucosθ – (mucosθ)
= 2mucosθ
= 2 x 0.15 x 15 x cos22.50
= 4.5 × 0.9239
= 4.2kgms^-1
[∵ cos 22.5° = 0.9239]

प्रश्न 5.21.
किसी डोरी के एक सिरे से बँधा 0.25 kg संहति का कोई पत्थर क्षैतिज तल में 1.5 m त्रिज्या के वृत्त पर 40 rev /min की चाल से चक्कर लगाता है? डोरी में तनाव कितना है? यदि डोरी 200 N के अधिकतम तनाव को सहन कर सकती है तो वह अधिकतम चाल ज्ञात कीजिए जिससे पत्थर को घुमाया जा सकता है।
उत्तर:
पत्थर का द्रव्यमान m = 0.25kg R = 1.5m
घूर्णन आवृत्ति = 40 चक्कर / मिनट =
∴ ω = 2πn = 2 × 3.14 × \(\frac{2}{3}\)
पत्थर को वृत्तीय पथ पर घूमने के लिए अभिकेन्द्रय बल, तनाव T से मिलता है।

प्रश्न 5.22.
यदि प्रश्न 5.21 में पत्थर की चाल को अधिकतम निर्धारित सीमा से भी अधिक कर दिया जाये तथा डोरी यकायक टूट जाये, तो डोरी के टूटने के पश्चात् पत्थर के प्रक्षेप का सही वर्णन निम्नलिखित में से कौन करता है?
(a) वह पत्थर झटके के साथ त्रिज्यतः बाहर की ओर जाता है।
(b) डोरी टूटने के क्षण पत्थर स्पर्शरेखीय पथ पर उड़ जाता है।
(c) पत्थर स्पर्शी से किसी कोण पर, जिसका परिमाण पत्थर की चाल पर निर्भर करता है, उड़ जाता है।
उत्तर:
(b) डोरी टूटने के क्षण पत्थर स्पर्शरेखीय पथ पर उड़ जाता है (जड़त्व के दिशा नियम से)

प्रश्न 5.23.
स्पष्ट कीजिए कि क्यों?
(a) कोई घोड़ा रिक्त दिक् स्थान में किसी गाड़ी को खींचते हुए दौड़ नहीं सकता।
(b) किसी तीव्र गति से चल रही बस के यकायक रुकने पर यात्री आगे की ओर गिरते हैं।
(c) लॉन मूवर को धकेलने की तुलना में खींचना आसान होता है।
(d) क्रिकेट का खिलाड़ी गेंद को लपकते समय अपने हाथ गेंद के साथ पीछे को खींचता है।
उत्तर:
(a) जब घोड़ा गाड़ी खींचता है तो जमीन घोड़े के पैर पर प्रतिक्रिया बल लगाती है। यही बल गाड़ी को आगे बढ़ाता है, लेकिन रिक्त दिक् स्थान (empty space) में कोई प्रतिक्रिया बल प्राप्त नहीं होता। अतः गाड़ी गति नहीं करेगी।
(b) जड़त्व के नियम के कारण यात्री का फर्श के सम्पर्क में स्थित हिस्सा स्थिर अवस्था में आ जाता है, परन्तु शरीर के ऊपर का भाग गतिशील बना रहता है अतः यात्री आग की ओर गिर जाते हैं।
(c) लॉन मूवर को धकेलने पर, लॉन मूवर का प्रभावी भार अधिक हो जाता है, क्योंकि बल का ऊर्ध्वाधर घटक भार में जुड़ता है। (चित्र (a)) (Mg + F sinθ)
जबकि खींचने पर लॉन मूवर का प्रभावी भार कम हो जाता है क्योंकि बल का ऊर्ध्वाधर घटक भार में से घटता है। [ चित्र (b)]
(Mg – F sinθ)

(d) हाथ गेंद के साथ पीछे खींचने पर गेंद को विराम में आने तक पर्याप्त समय मिल जाता है जिससे हाथों पर लगने वाला बल घट जाता है। जिससे चोट लगने की सम्भावना कम हो जाती है।

अतिरिक्त अभ्यास (Additional Exercise):

प्रश्न 5.24.
चित्र में 0.04 kg संहति के किसी पिण्ड का स्थिति समय ग्राफ दर्शाया गया है। इस गति के लिए कोई उचित भौतिक सन्दर्भ प्रस्तावित कीजिए। पिण्ड द्वारा प्राप्त दो क्रमिक आवेगों के बीच समय-अन्तराल क्या है? प्रत्येक आवेग का परिमाण क्या है?

उत्तर:
यह दो समान्तर दीवारें जो परस्पर 2cm दूर स्थित हैं, के मध्य लगातार गेंद के टकराने की गति को प्रदर्शित करता है।
m = 0.04kg
प्रारम्भ 2s तक x = 0 से x = 2cm तक ग्राफ़ सीधी रेखा है।
∴ नियत चाल
V¹ = \(\frac{2-0}{2-0}\)
= 1cms^-1
= 0.01 ms^-1
पुनः t = 2sec पश्चात्
x = 2cm से x = 0 तक ग्राफ सीधी रेखा है।
नियत चाल
V² = \(\frac{0-2}{4-2}\)
= -1 cms^-1
= – 0.01ms^-1
आवेग का परिमाण = संवेग में परिवर्तन
= MV¹ – MV²
= m (V¹ – V² )
=0.04[(0.01) – (-0.01)]
= 0.04 × 0.02
= 8 × 10^-4 kgms^-1

प्रश्न 5.25.
चित्र में कोई व्यक्ति 1ms^-1 त्वरण से गतिशील क्षैतिज संवाहक पट्टे पर स्थिर खड़ा है। उस व्यक्ति पर आरोपित नेट बल क्या है? यदि व्यक्ति के जूतों और पट्टे के बीच स्थैतिक घर्षण गुणांक 0.2 है तो पट्टे के कितने त्वरण तक वह व्यक्ति उस पट्टे के सापेक्ष स्थिर रह सकता है? (व्यक्ति की संहति = 65 kg)

उत्तर:
(i) पट्टे का त्वरण a = 1ms^-2
व्यक्ति का द्रव्यमान = 65kg
व्यक्ति का त्वरण पट्टे का त्वरण = 1ms^-2
व्यक्ति पर आरोपित नेट बल
F = ma = 65 x 1 = 65N

(ii) μ^s= 0.2
F = μ^sR = μ^smg
यदि आदमी अधिकतम a त्वरण तक स्थिर रहता है, तो
ma = μ^smg
∴ a’ = μ^sg = 0.2 × 10 = 2ms^-2

प्रश्न 5.26.
संहति के पत्थर को किसी डोर के एक सिरे से बाँधकर R त्रिज्या के ऊर्ध्वाधर वृत्त में घुमाया जाता है। वृत्त के निम्नतम तथा उच्चतम बिन्दुओं पर ऊर्ध्वाधरतः अधोमुखी दिशा में नेट बल है (सह विकल्प चुनिए):

यहाँ T₁ तथा V₁ निम्नतम बिन्दु पर तनाव तथा चाल दर्शाते हैं। T₂ तथा V₂ इनके उच्चतम बिन्दु पर तदनुरूपी मान हैं।
उत्तर:
निम्नतम बिन्दु A पर तनाव T₁ ऊपर की ओर, भार mg नीचे की ओर
∴ अधोमुखी नेट बल = mg – T
उच्चतम बिन्दु B पर तनाव T₂ व भार mg दोनों नीचे की ओर लगेंगे।

∴ नेट अधोमुखी बल = mg + T₂
अतः विकल्प (i) सही है।
चित्र में बल प्रदर्शित है।

प्रश्न 5.27.
1000 kg संहति का कोई हेलीकॉप्टर 15 ms^-2 के ऊर्ध्वाधर त्वरण से ऊपर उठता है। चालक दल तथा यात्रियों की संहति 300 kg है। निम्नलिखित बलों का परिमाण व दिशा लिखिए:
(a) चालक दल तथा यात्रियों द्वारा फर्श पर आरोपित बल,
(b) चारों ओर की वायु पर हेलीकॉप्टर के रोटर की क्रिया, तथा
(c) चारों ओर की वायु के कारण हेलीकॉप्टर पर आरोपित बल।
उत्तर:
हेलीकॉप्टर का द्रव्यमान m₁ = 1000kg
चालक यात्रियों का द्रव्यमान m₂ = 300kg
हेलीकॉप्टर का ऊपर की ओर त्वरण a = 15ms ^-2
g = 10ms^-2
(a) (चालक + यात्रियों) पर दो बल कार्यरत हैं।
(i) प्रतिक्रिया R (ऊपर)
(ii) भार mg (नीचे)।
∴ ऊपर की ओर परिणामी बल
R – m₂g = m₂a
R = m₂(a + g)
= 300 x (15 + 10)
= 7500 N
(b) हेलीकॉप्टर पर दो बल कार्यरत हैं-
(i) वायु का उछाल बल R
(ii) भार ( m₁ + m₂) g

ऊपर की ओर परिणामी बल
F = R – (m₁ + m₂)g
या
(m₁ + m₂ )a = R – (m₁ + m₂) g
R’ = (m₁ + m₂ ) (a + g)
=(1000 + 300) (10 + 15)
= 1300 × 25 = 32500 N
यही वायु पर हेलीकॉप्टर के रोटर द्वारा क्रिया है (लम्बवत् नीचे की ओर)।
(c) न्यूटन के तृतीय नियम से यही वायु द्वारा हेलीकॉप्टर पर आरोपित बल है = 32500 N ( लम्बवत् ऊपर की ओर )।

प्रश्न 5.28.
15ms^-1 चाल से क्षैतिजतः प्रवाहित कोई जल धारा 10^-2m² अनुप्रस्थ काट की किसी नली से बाहर निकलती है तथा समीप की किसी ऊर्ध्वाधर दीवार से टकराती है। जल की टक्कर द्वारा, यह मानते हुए कि जल धारा टकराने पर वापस नहीं लौटती, दीवार पर आरोपित बल ज्ञात कीजिए।
उत्तर:
जल का वेग u = 15ms^-1
नली का अनुप्रस्थ क्षेत्रफल A = 10^-2m²
जल का घनत्व d = 10³ kgm^-3
प्रति सेकण्ड नली से निकले जल का आयतन = A x u = 10^-2 x 15m³s^-1
प्रति सेकण्ड नली में निकले जल का द्रव्यमान
m= आयतन x घनत्व
= 15 x 10^-2 × 10³ = 150kgs^-1
टकराने के बाद जल का वेग शून्य है,
v = 0
दीवार द्वारा जल पर आरोपित बल = आवेग परिवर्तन की दर
\(F=\frac{d p}{d t}=\frac{m(v-u)}{t}\)
∴ \(F=\frac{150 \times(0-15)}{1}\)
= – 2250 N
न्यूटन के तृतीय नियम से जल द्वारा दीवार पर आरोपित बल
= 2250N

प्रश्न 5.29.
किसी मेज पर एक-एक रुपये के दस सिक्कों को एक के ऊपर एक करके रखा गया है। प्रत्येक सिक्के की संहति है। निम्नलिखित प्रत्येक स्थिति में बल का परिमाण एवं दिशा लिखिए:
(a) सातवें सिक्के (नीचे से गिनने) पर उसके ऊपर रखे सभी सिक्कों के कारण बल।
(b) सातवें सिक्के पर आठवें सिक्के द्वारा आरोपित बल।
(c) छठे सिक्के की सातवें सिक्के पर प्रतिक्रिया।
उत्तर:
(a) सातवें सिक्के के ऊपर तीन सिक्के रखे हैं। अतः तीनों सिक्कों द्वारा आरोपित बल
= 3 x mg
= 3mgN ( लम्बवत् नीचे की ओर )
(b) सातवें सिक्के पर आठवें सिक्के द्वारा भी यही बल लगाया जायेगा।
= 3 mg ( लम्बवत् नीचे की ओर )
(c) छठे सिक्के के ऊपर चार और सिक्के हैं, अतः चारों सिक्कों द्वारा लगा बल
= 4 x mg
= 4mgN ( लम्बवत् ऊपर की ओर )

प्रश्न 5.30.
कोई वायुयान अपने पंखों को क्षैतिज से 15° के झुकाव पर रखते हुए 420 kmh^-1 की चाल से एक क्षैतिज लूप पूरा करता है। लूप की त्रिज्या क्या है?
उत्तर:
v = 720kmh^-1 = 720 x
= 200ms^-1
θ = 15° ∴ tan 15° = 0.27
tan θ = \(\frac{v^2}{g R}\) से,
R = \(\frac{v^2}{g \tan \theta}\)
= \(\frac{200 \times 200}{10 \times 0.27}\)
= 15km

प्रश्न 5.31.
कोई रेलगाड़ी बिना ढाल वाले 30m त्रिज्या के वृत्तीय मोड़ पर 54 kmh^-1 चाल से चलती है। रेलगाड़ी की संहति 10⁶ kg है। इस कार्य को करने के लिए आवश्यक अभिकेन्द्रीय बल कौन प्रदान करता है इंजन अथवा पटरियाँ ?
पटरियों को क्षतिग्रस्त होने से बचाने के लिए मोड़ का ढाल कोण कितना होना चाहिए?
उत्तर:
वृत्तीय पथ पर आवश्यक अभिकेन्द्रीय बल पटरियाँ प्रदान करती है।
यहाँ
v = 54 kmh^-1
= \(\frac{54 \times 1000}{60 \times 60}\)
= 15ms^-1
R = 30m
m = 10⁶ kg
ढाल कोण tan θ = \(\frac{v^2}{R g}=\frac{15 \times 15}{30 \times 10}=\frac{3}{4}\)
θ = 40°
अतः पटरियों का झुकाव कोण 40° होना चाहिए।

प्रश्न 5.32.
चित्र में दर्शाए अनुसार 50 kg संहति का कोई व्यक्ति 25kg संहति के किसी गुटके को दो भिन्न ढंग से उठाता है। दोनों स्थितियों में उस व्यक्ति द्वारा फर्श पर आरोपित क्रिया बल कितना है? यदि 700N अभिलम्बवत् बल से फर्श धँसने लगता है तो फर्श को धँसने से बचाने के लिए उस व्यक्ति को गुटके को उठाने के लिए कौन-सा ढंग अपनाना चाहिए?

उत्तर:
व्यक्ति का द्रव्यमान M = 50kg
व्यक्ति द्वारा भार के कारण लगा बल
W = Mg = 50× 10 = 500N
25kg भार को उठाने में लगाया गया बल
F = mg = 25×10 = 250N
(a) स्थिति में व्यक्ति 250N बल से गुटके को खींच रहा है तो प्रतिक्रिया स्वरूप रस्सी भी व्यक्ति पर नीचे की ओर 250N बल लगायेगी।
250 + 500 = 750N
∴ फर्श पर लगा परिणामी बल अतः इस स्थिति में फर्श धँस जायेगा।
(b) स्थिति में व्यक्ति 250 N बल नीचे की ओर लगाता है जिसकी प्रतिक्रिया स्वरूप रस्सी भी इतना बल व्यक्ति पर ऊपर की ओर लगाती है।
∴ परिणामी बल = 500 – 250
= 250N
अतः (b) ढंग से फर्श नहीं धँसेगा।

प्रश्न 5.33.
40 kg संहति का कोई बन्दर 600N का अधिकतम तनाव सह सकने योग्य किसी रस्सी पर चढ़ता है। नीचे दी गई स्थितियों में से किसमें रस्सी टूट जायेगी?
(a) बन्दर 6ms^-2 त्वरण से ऊपर चढ़ता है।
(b) बन्दर 4ms^-2 त्वरण से नीचे उतरता है।
(c) बन्दर 5ms^-1 की एकसमान चाल से ऊपर चढ़ता है।
(d) बन्दर लगभग मुक्त रूप से गुरुत्व बल के प्रभाव में रस्सी से गिरता है। (रस्सी की संहति उपेक्षणीय मानिए।)
उत्तर:

बन्दर का द्रव्यमान m = 40 kg
(a) बन्दर = 6ms^-2 त्वरण से ऊपर चढ़ता
∴ T – mg = ma
या
T = m(g + a)
= 40(10 + 6)
= 640N
∴ रस्सी अधिकतम 600N का तनाव सहन कर सकती है, अतः टूट जायेगी।

(b) बन्दर a = 4ms^-2 त्वरण से नीचे उतरता है
∴ mg – T = ma

या
T= m(g – a)
= 40(10 – 4)
= 240N
रस्सी नहीं टूटेगी।

(c) बन्दर एकसमान चाल से ऊपर चढ़ता है। अतः त्वरण

∴ a = 0
T = m(g – a)
= 40× 10 = 400N
रस्सी नहीं टूटेगी।

(d) मुक्त रूपसे गुरुत्व बल के प्रभाव में गिरने पर
a = g
T = m(g – a)
= m(g – g) = 0
अर्थात् रस्सी का तनाव शून्य है।
अतः केवल (a) स्थिति में ही रस्सी टूटेगी।

प्रश्न 5.34.
दो पिण्ड 4 तथा 8, जिनकी संहति क्रमश: 5 kg तथा 10kg है, एक-दूसरे के सम्पर्क में एक मेज पर किसी दृढ़, विभाजक दीवार के सामने विराम में रखे हैं। (चित्रानुसार) पिण्डों तथा मेज के बीच घर्षण गुणांक 0.15 है। 200 N का कोई बल क्षैतिजतः 4 पर आरोपित किया जाता है। (a) विभाजक दीवार की प्रतिक्रिया, तथा (b) 1 तथा B के बीच क्रिया-प्रतिक्रिया बल क्या हैं? विभाजक दीवार को हटाने पर क्या होता है? यदि पिण्ड गतिशील हैं तो क्या (b) का उत्तर बदल जायेगा? μ_s तथा μ_k के बीच अन्तर की उपेक्षा कीजिए।

उत्तर:
m_A = 5kg, m_B = 10kg
(a) A पर 200N बल लगाने पर विभाजक दीवार भी न्यूटन की तृतीय नियम से 200N का प्रतिक्रिया बल लगायेगी।
(b) 4 तथा B के बीच क्रिया-प्रतिक्रिया बल भी 200N है। जब विभाजक दीवार हटा लेते हैं तो गतिज घर्षण कार्य करेगा। घर्षण गति का विरोध करता है। घर्षण बल = μR
यहाँ
μ_K = μ_s = 0.15
परिणामी बल F = f – μ_KR
= f – μ_K (M_A + m_B) g
200 – 0.15(15 + 10) 10
= 200 – 22.5
= 177.5N
∴ त्वरण a = \(\frac{F}{\left(m_A+m_R\right)}\)
= \(\frac{177.5}{15}\)
= 11.8ms^-2
A पर लगा बल F1 = m_A a
= 5 × 11.8
= 59.1N

वस्तु A पर लगा घर्षण बल f₁ = μmAg
= 0.15 x 5 × 10
= 7.5N
∴ A पर B द्वारा लगा परिणामी बल
= 200 – 59.1 – 7.5
= 133.4N
= 1.3 × 10^-2 N
गति की विपरीत दिशा में)
एसी प्रकार पर 4 द्वारा लगा परिणामी बल भी 1.3 x 10^-2 N होगा गति की विष में)

प्रश्न 5.35.
15 kg संहति का कोई गुटका किसी लम्बी ट्रॉली पर रखा है। गुटके तथा ट्रॉली के बीच स्थैतिक घर्षण गुणांक 0.18 है। ट्रॉली विरामावस्था से 20s तक 0.5ms^-2 के त्वरण से त्वरित होकर एकसमान वेग से गति करने लगती है।
(a) धरती पर स्थिर खड़े किसी प्रेक्षक को तथा
(b) ट्रॉली के साथ गतिमान किसी अन्य प्रेक्षक को गुटके की गति कैसी प्रतीत होगी? इसकी विवेचना कीजिए।
उत्तर:
गुटके का द्रव्यमान
m = 15kg μ = 0.18 t = 20s के लिए
ट्रॉली पर त्वरण a = 0.5ms^-2 ट्रॉली के त्वरण के कारण गुटके पर
लगा काल्पनिक बल
F₁ = ma1 = 15 x 0.5
= 7.5N (पीछे की ओर)
परन्तु फर्श द्वारा गुटके पर आरोपित घर्षण बल
F₂ = μR = umg = 0.18 x 15 x 10
= 27N (आगे की ओर)।
अतः गुटका विक्षेप गति नहीं करेगा ट्रॉली के साथ गति करेगा, क्योंकि F₂ > F₁
एकसमान वेग से गति करने पर कोई घर्षण बल कार्य नहीं करता है।
(a) धरती पर खड़े प्रेक्षक को गुटका ट्रॉली के साथ गति करता प्रतीत होगा।
(b) ट्रॉली के साथ गतिमान प्रेक्षक को गुटका स्वयं के सापेक्ष स्थिर प्रतीत होगा।

प्रश्न 5.36.
चित्र में दर्शाए अनुसार किसी ट्रक का पिछला भाग खुला है तथा 40kg संहति का एक सन्दूक खुले सिरे से 5m दूरी पर रखा है। ट्रक के फर्श तथा सन्दूक के बीच घर्षण गुणांक 0.15 है। किसी सीधी सड़क पर ट्रक विरामावस्था से गति प्रारम्भ करके 2m^-2 से त्वरित होता है। आरम्भ बिन्दु से कितनी दूरी चलने पर वह सन्दूक ट्रक से नीचे गिर जायेगा? (सन्दूक के आमाप की उपेक्षा कीजिए।)

उत्तर:
सन्दूक का द्रव्यमान m = 40kg, μ = 0.15
ट्रक का त्वरण a₁ = 2ms^-2
∴ सन्दूक पर उत्पन्न छद्म त्वरण a₁ = 2ms^-2
घर्षण के कारण सन्दूक का त्वरण
a₂ = μg= 0.15 x 10 = 1.5ms^-2
∴ ट्रक के सापेक्ष सन्दूक का त्वरण
a = a₁ – a₂ = 2 – 1.5 = 0.5ms^-2
इसकी दिशा पीछे की ओर होगी।
∴ सन्दुक को 5m दूरी तक करने में t समय लगे, तो
x = u t + \(\frac{1}{2}\) a t²
5 = 0 + \(\frac{1}{2}\) a t²
t² = 20
∴ ट्रक का त्वरण गई दूरी S = ut + \(\frac{1}{2}\) a t²
= 0 + \(\frac{1}{2}\) x 2 x 20
= 20m

प्रश्न 5.37.
15cm त्रिज्या का कोई बड़ा ग्रामोफोन रिकॉर्ड 33 \(\frac{1}{3}\) rev/min की चाल से घूर्णन कर रहा है। रिकॉर्ड पर उसके केन्द्र से 4 cm तथा 14cm की दूरियों पर दो सिक्के रखे गये हैं। यदि सिक्के तथा रिकॉर्ड के बीच घर्षण गुणांक 0.15 है तो कौन-सा सिक्का रिकॉर्ड के साथ परिक्रमा करेगा?
उत्तर:
घूर्णन आवृत्ति
n = 33 \(\frac{1}{3}\) rev/min = \(\frac{100}{3 \times 60}\) rev/sec
μ = 0.15
ω = 2πn = 2π x \(\frac{100}{3 \times 60}\)
= \(\frac{10 \pi}{9}\) rad/s
= 3.49 rad/s
सिक्के द्वारा घूर्णन गति के लिए घर्षण बल, आवश्यक अभिकेन्द्रीय बल प्रदान करेगा।
इसलिए अभिकेन्द्रीय बल \(\frac{m v^2}{r}\) = mω²r
घर्षण बल μR= μmg
∴ mω²r < μmg

अतः 4cm दूर सिक्का गति करेगा जबकि 14cm दूर सिक्का गिर जायेगा।

प्रश्न 5.38.
आपने सरकस में मौत के कुएँ (एक खोखला जालयुक्त गोलीय चैम्बर ताकि उसके भीतर के क्रियाकलापों को दर्शक देख सकें) में मोटरसाइकिल सवार को ऊर्ध्वाधर लूप में मोटरसाइकिल चलाते हुए देखा होगा। स्पष्ट कीजिए कि वह मोटरसाइकिल सवार नीचे से कोई सहारा न होने पर भी गोले के उच्चतम बिन्दु से नीचे क्यों नहीं गिरता है? यदि चैम्बर की त्रिज्या 25 m है तो ऊर्ध्वाधर लूप को पूरा करने के लिए मोटरसाइकिल की न्यूनतम चाल कितनी होनी चाहिए?
उत्तर:
गोलीय चैम्बर के उच्चतम बिन्दु पर मोटरसाइकिल सवार चैम्बर को बाहर की ओर दबाता है और प्रतिक्रिया स्वरूप चैम्बर, सवार पर गोले के केन्द्र की ओर दिष्ट प्रतिक्रिया R लगाता है। सवार व मोटरसाइकिल का भार mg भी गोले के केन्द्र की ओर कार्य करता है। ये दोनों बल सावार को वृत्तीय गति करने के लिए आवश्यक अभिकेन्द्राय बल प्रदान करते हैं, जिसके कारण सवार नीचे नहीं गिर माता।

इस बिन्दु पर गति का समीकरण R+mg = \(\frac{m v^2}{r}\) जहाँ v सवार की चाल तथा R गोले की त्रिज्या है।
न्यूनतम चाल के लिए R = 0

= 15.8ms^-1
= 16ms^-1

प्रश्न 5.39.
70 kg संहति का कोई व्यक्ति अपने ऊर्ध्वाधर अक्ष पर 200 rev/min की चाल से घूर्णन करती 3m त्रिज्या की किसी बेलनाकार दीवार के साथ उसके सम्पर्क में खड़ा है। दीवार तथा उसके कपड़ों के बीच घर्षण गुणांक 0.15 है। दीवार की वह न्यूनतम घूर्णन चाल ज्ञात कीजिए, जिससे फर्श को यकायक हटा लेने पर भी वह व्यक्ति बिना गिरे दीवार से चिपका रह सके।
उत्तर:
दिया है:
m = 70kg:
v = 200 rev/min = \(\frac{200}{60}=\frac{10}{3}\)rev/s
त्रिज्या r = 3m μ = 0.15
माना दीवार की न्यूनतम घूर्णन चाल ω²r है।
व्यक्ति बिना गिरे दीवार से चिपका रहेगा यदि घर्षण बल, व्यक्ति के
भार को सन्तुलित कर ले तो mg < μN
∴ न्यूनतम कोणीय चाल पर μR = mg
यहाँ
R = अभिकेन्द्र बल = mω²r
μmω²_{यूनतम} r = mg
ω²_{यूनतम} = \(\frac{g}{\mu r}=\frac{10}{0.15 \times 3}\)
= 22.2
∴ω²_{यूनतम} = \(\sqrt{22.2}\) = 4.72 = 5 rad s^-1

प्रश्न 5.40.
R त्रिज्या का पतला वृत्तीय तार अपने ऊर्ध्वाधर व्यास के परितः कोणीय आवृत्ति ω से घूर्णन कर रहा है। यह दर्शाइए कि इस तार में डली कोई मणिका \(\omega \leq \sqrt{g / R}\) के लिए अपने निम्नतम 2g. बिन्दु पर रहती है। ω = \(\sqrt{\frac{2 g}{R}}\) के लिए, केन्द्र के मनके को जोड़ने वाला VR सदिश ऊर्ध्वाधर अधोमुखी दिशा में कितना कोण बनाता है?
उत्तर:
माना मणिका का द्रव्यमान m है। इस पर लगे बलों को चित्र में प्रदर्शित किया गया है।

Ncosθ = μg ………….(1) (ऊर्ध्वाधर घटक)
N sinθ = mrω²
(क्षैतिज घटक अभिकेन्द्र बल प्रदान करता है।)
या Nsinθ = m (Rsinθ)ω²
या mRω² = N …………(2)
चित्र में, sinθ = \(\frac{r}{R}\)
r = Rsinθ
समी० (1) से, cosθ = \(\frac{m g}{N}=\frac{m g}{m R \omega^2}\)
cosθ = \(\frac{g}{R \omega^2}\) ………(3)
cosθ < 1
∴ मणिका के न्यूनतम बिन्दु के लिए

यदि तो समी० (3) से,
cosθ = \(\frac{1}{2}\)
θ = 60°
अतः ऊर्ध्वाधर से अधोमुखी ( downward) दिशा से 60° कोण बनायेगी।

Haryana State Board HBSE 10th Class Science Solutions Chapter 3 Metals and Non-metals Textbook Exercise Questions and Answers.

Haryana Board 10th Class Science Solutions Chapter 3 Metals and Non-metals

HBSE 10th Class Science Metals and Non-metals Textbook Questions and Answers

Question 1.
Which of the following pairs will give displacement reactions?
(a) NaCI solution and copper metal
(b) MgCI₂ solution and aluminium metal
(C) FeSO₄ solution and silver metal
(d) AgNO₃ solution and copper metal
Answer:
(d) AgNO₃ solution and copper metal

Question 2.
Which of the following methods is suitable for preventing an iron frying pan from rusting?
(a) Applying grease
(b) Applying paint
(c) Applying a coating of zinc
(d) All of these
Answer:
(c) Applying a coating of zinc
Note: Although all options can be used to prevent rusting of an ordinary iron. But, the frying pan is used for cooking so the only best option is to coat it with zinc.

Question 3.
An element reacts with oxygen to give a compound with a high melting point. This compound is also soluble In water. The element is likely to be ……
(a) Calcium
(b) Carbon
(c) Silicon
(d) Iron
Answer:
(a) Calcium

Question  4.
Food cans are coated with tin and not with zinc because
(a) Zinc is costlier than tin.
(b) Zinc has a higher melting point than tin.
(c) Zinc Is more reactive than tin.
(d) Zinc is less reactive than tin.
Answer:
(c) Zinc Is more reactive than tin.

Question  5.
You are given a hammer, a battery, a bulb, wires and a switch.
(a) How could you use them to distinguish between samples of metals and non-metals?
(b) Assess the usefulness of these tests in distinguishing between metals and non-metals.
Answer:
1. (a) Take the given samples of metals and non-metals and strike them with the hammer. If a sample converts into a sheet, it is a metal and if not, it is non-metal. Metals are malleable, non-metals are not.

(b) If a sample produces sound when struck with the hammer, it is a metal. Metals are sonorous. But if it does not produce a round, it is non-metal.

(c) Now arranging the given objects to form an electric circuit. Insert any one sample between clips A and B, lithe bulb glows, it is a metal (good conductor of electricity). If the bulb does not glows, it is a non-metal.

2. From the above tests, it is clear that metals are generally malleable, sonorous and good conductors of electricity, while non-metals are generally non-malleable/brittle, non-sonorous and poor conductors of electricity.

Question 6.
What are amphoteric oxides? Give two examples of amphoteric oxides.
Answer:
Some metal oxides react with both acids and bases to produce salt and water. Such metal oxides are called amphoteric oxides.
Example:

Question 7.
Name two metals which will displace hydrogen from dilute acids, and two metals which will not.
Answer:
1. Sodium and magnesium will displace hydrogen from dilute acids because they lie above hydrogen in the activity series.

2. Metals such as copper and silver lie below hydrogen in the activity series and hence will not displace hydrogen from dilute acids.

Question 8.
In the electrolytic refining of a metal M, what would you take as the anode, the cathode and the electrolyte?
Answer:
(a) Cathode (negatively charged) — Pure metal M
(b) Anode (positively charged) — Impure metal M
(c) Electroyte — Aqueous solution of a salt of metal M

Question 9.
Pratyush took sulphur powder on a spatula and heated it. He collected the gas evolved by inverting a test tube over it, as shown in figure below.
(a) What will be the action of gas on  :
(i) Dry litmus paper?
(ii) Moist litmus paper?
(b) Write a balanced chemical equation for the reaction taking place.
Answer:
(a) (i) There will be no effect of gas on dry litmus paper. Hence, no change in colour will take place in case of dry litmus paper.
(ii) Moist blue litmus paper will turn red because sulphur is non-metal and non-metal oxides are acidic in nature.

(b) (i) S + O₂ → SO₂
(ii) SO₂ + H₂O → H₂SO₃

Question 10.
State two ways to prevent the rusting of iron.
Answer:
Two ways to prevent rusting of iron:
(1) Paint the iron articles.
(2) Galvanize iron article with the protective layer of zinc metal.

Question 11.
What type of oxides are formed when non-metals combine with oxygen?
Answer:
When non-metals combine with oxygen they form acidic oxides. SO₂, CO₂, etc. are some examples.

Question 12.
Give reasons
(a) Platinum, gold and silver are used to make jewellery.
(b) Sodium, potassium and lithium are stored under oil.
(c) Aluminium is a highly reactive metal, yet it Is used to make utensils for cooking.
(d) Carbonate and sulphide ores are usually converted into oxides during the process of extraction.
Answer:
(a) Metals such as gold, platinum and silver are rare as well as non-reactive metals.

These metals have very attractive luster and so catches the attention of people. Moreover, these metals are malleable and ductile and molded into desired shape and intricated into exquisite jewellery. Another major advantage is that these metals do not corrode when exposed to air. Hence, they can be kept and worn for years without fearing the loss of luster.

(b) 1. Sodium (and potassium) is a highly reactive metal. If kept open it reacts with oxygen at room temperature. The reaction is extremely exothermic i.e. a lot of heat is produced. This even causes burning and dangerous accidents.
2. Sodium does not react with kerosene and hence it is preserved in kerosene.

(c) Using metal vessels that can react with food can lead to severe harm to the body.

Although aluminium is quite reactive, if forms a protective layer of aluminium oxide on its surface. This protects it from getting corroded and hence reacting with food. Hence, even though aluminum is very reactive metal, it is used to make utensils for cooking.

(d) It is easier and a cheaper way to reduce metal oxide to metal. Hence, carbonate and sulphide ores are first converted into their oxides and then reduced into metals.

Question 13.
You must have seen tarnished copper vessels being cleaned with lemon or tamarind juice. Explain why these sour substances are effective in cleaning the vessels.
Answer:
1. On using copper metal, it gets corroded to form copper carbonate and get tarnished i.e. copper gets decoloured due to oxidation.

2. Copper carbonate dissolves in mild acids. Lemon or tamarind juice are mild acids which when rub on copper vessels dissolve copper carbonate and make copper vessels shiny again.

Question 14.
Differentiate between metal and non-metal on the basis of their chemical properties.
Answer:

Question 15.
A man went door to door posing as a goldsmith. He promised to bring back the glitter of old and dull gold ornaments. An unsuspecting lady gave a set of gold bangles to him which he dipped in a particular solution. The bangles sparkled like new but their weight was reduced drastically. The lady was upset but after a futile argument the man beat a hasty retreat. Can
you play the detective to find out the nature of the solution he had used?
Answer:
1. The crooked goldsmith fooled her by using a specific solution. The name of this solution is aqua regia.
2. This solution contains 1 part of concentrated nitric acid (HNO₃) and 3 parts of hydrochloric acid (HCl). On putting gold Ornaments in this solution, the solution dissolves gold.

Question 16.
Give reasons why copper is used to make hot water tanks and not steel (an alloy of Iron).
Answer:
1. The advantages of using copper over steel for making hot water tanks are many.
2. Copper does not react with any form of metal, not even steam.
3. Copper is cheap.
4. Copper is easily available and is also a good conductor of heat which enables heating water.

HBSE 10th Class Science Metals and Non-metals  InText Activity Questions and Answers

Textbook Page no – 40

Question 1.
Give an example of a metal which
(i) is a liquid at room temperature
(ii) can be easily cut with a knife
(iii) is the best conductor of heat
(iv) is a poor conductor of heat
Answer:
(i) Mercury
(ii) Sodium
(iii) Silver
(iv) Lead

Question 2.
Explain the meanings of malleable and ductile.
Answer:
1. Some metals can be hammered and turned into thin sheets. This property of the metals is known as malleability.

2. This property is specially found in metals like gold, silver and aluminium. Hence, thin strips can be prepared from gold and silver and very thin paper-like foil can be prepared from aluminium.

3. Some metals are ductile i.e. we can draw thin wires from them. For e.g. gold and silver.

4. For example, about 2 kilometer long wire can be drawn from one gram gold. Wires can also be prepared from metals like copper and aluminium, by drawing.

Textbook Page no – 46

Question 1.
Why Is sodium kept Immersed in kerosene oil?
Answer:
1. Sodium (and potassium) is a highly reactive metal. If kept open it reacts with oxygen at room temperature, The reaction is extremely exothermic i.e. a lot of heat is produced. This even causes burning and dangerous accidents.
2. Sodium does not react with kerosene and hence it is preserved in kerosene.

Question 2.
Write equations for the reactions of ……….
(i) Iron with steam,
(ii) Calcium and potassium with water
Answer:

Question 3.
Samples of four metals A, B, C and D were taken and added to the following solution one by one. The results obtained have been tabulated as follows.

Use the table above to answer the following questions about metals A, B, C and D.
(i) Which Is the most reactive metal?
(ii) What would you observe if B is added to a solution of copper (Il) sulphate?
(iii) Arrange the metals A, B, C and D in the order of decreasing reactivity.
Answer:
(i) B is the most reactive metal because it displaces iron from its salt solution.
(ii) On adding ‘B’ to copper sulphate solution, blue colour of copper sulphate solution disappears and reddish brown coloured copper metal gets deposited on metal B. This happens because B will displace Cu from CuSO₄.
(iii) The order of reactivity is B > A > C > D.

Question 4.
Which gas is produced when dilute hydrochloric acid is added to a reactive metal? Write the chemical reaction when iron reacts with dilute H₂SO₄ :
Answer:
Hydrogen gas is produced when dilute hydrochloride acid is added to a reactive metal.

Question 5.
What would you observe when zinc Is added to a solution of iron(lI) sulphate? Write the chemical reaction that takes place.
Answer:
Zinc is more reactive than iron. Hence, when zinc is added to iron (II) sulphate, zinc displaces iron metal and the colour of solution fades from green to colourless.

Textbook Page no – 49

(i) Write the electron-dot structures for sodium, oxygen and magnesium.
(ii) Show the formation of Na₂O and MgO by the transfer of electrons.
(iii) What are the ions present in these compounds?
Answer:

(iii) In Na₂O ions present are Na⁺ and O^2- — In MgO, ions present are Mg₂ and

Question 2.
Why do ionic compounds have high melting points?
Answer:
Melting point and boiling point :
In ionic compounds, positive and negative ions are joined strongly due to inter-ionic attraction. As a result, more energy is required to break such compounds and hence their melting and boiling points are high.

Textbook Page no – 53

Question 1.
Define the following terms.
(i) Mineral (ii) Ore (iii) Gangue
Answer:
(i) Mineral:
The elements or compounds that occur naturally in the earth’s crust are called minerals. Sea-water also contains salts of metals such as sodium chloride, magnesium chloride, etc.

(ii) Ores:
Those minerals from which the metals can be extracted, conveniently and profitably are called ores.

(Note: Although all minerals contain metals, they are not termed as ‘ores’. The reason behind this is that is not always practically possible to extract metals from these minerals. Hence, only those minerals in which metals is present in large quantity and from which metals can be extracted conveniently and reasonably are called ores.)

(iii) Gangue:
Impurities such as sand, mud, etc. present in the ore are called gangue.

Question 2.
Name two metals which are found in nature in the free state.
Answer:
Gold and silver.

Question 3.
What chemical process is used for obtaining a metal from 4ts oxide?
Answer:
Metal oxides can be converted to metal through the process of reduction using carbon (coke).
Example: Zinc oxide is reduced to obtain zinc metal by heating it with carbon.
ZnO_(s) + C_{(s) →} Zn_(s) + CO_(s)

Over and above carbon, highly reactive metals such as sodium, calcium, aluminium are also used as reducing agents.
Example: Fe₂O_3(s) + 2Al(s) → 2Fe₍₁₎ + Al₂O₃(s) + Heat

Textbook Page no – 55

Question 1.
Metallic oxides of zinc, magnesium and copper were heated with the following metals.

In which cases will you find displacement reactions taking place?
Answer:

Answer:
As per the reactivity series, magnesium is most reactive, then comes zinc and finally copper i.e. Mg > Zn > Cu. So, in the first column, zinc cannot displace itself. It also cannot displace magnesium because magnesium is more reactive than zinc. However, since zinc is more reactive than copper, it can displace copper. Similar events happen in the next two columns.

Question 2.
Which metals do not corrode easily?
Answer:
Gold and platinum

Question 3.
What are alloys?
Answer:
An alloy is a homogeneous mixture of two or more metals or metal and non-metal.

Activities

Activity 1.

Perform an activity to study that metals are lustrous.
Answer:
Take samples of iron, copper, aluminium and magnesium. Note the appearance of each sample.
1. Clean the surface of each sample by rubbing them with sand paper. Note their appearance again.
2. Initially the surface of these metals look dull. On rubbing with sand paper, the surface starts shinning This happened because pure metals have shiny surface.

Activity 2.

Perform an activity to study that metals are hard.
Answer.
1. Take small pieces of iron, copper, aluminium and magnesium. Try to cut these metals with a sharp knife. What do you observe?
2. Hold a piece of sodium metal with a pair of tongs. (Caution: Always handle sodium metal with care.) Dry it by pressing between the folds of a filter paper. Now, put it on a watch-glass and try to cut it with a knife. What do you observe?

Observation:
1. Pieces of iron, copper and aluminium are very hard and hence it is difficult to cut them with a knife. However, magnesium turned out to be soft and so could be cut
2. We can see that sodium metal gets cut easily with the knife.

Activity 3.

Perform an activity to study that metals are malleable.
1. Take pieces of iron, zinc, lead and copper.
2. Place any one metal on a block of iron and strike it four or five times with a hammer. What do you observe?
3. Repeat with other metals and record the change in the shape of these metals.
Answer:
1. On striking hammer, the metal becomes flat. This means metal is malleable on hammering.
2. Pieces of iron, zinc, lead and copper also become flat i.e. get converted into sheets on hammering.
3. This property of metals under which they can be hammered and made flat is called the property of malleability.

Activity 4.

Perform an activity to study that metals are ductile. Consider some metals such as iron, copper, aluminium, lead, etc. Which of these metals are also available in the form of wires?
Answer:
All the four metals mentioned here are available in the form of wire also. This property of metals where in they can be drawn into wires is called the property of ductility.

Activity 5.

Perform an activity to study that metals are good conductors of heat.
Answer:

1. Take an aluminium or copper wire. Clamp this wire on a stand, as shown in figure 1.
2. Fix a pin to the free end of the wire using wax.
3. Heat the wire with a spirit lamp, candle or a burner near the place where it is, clamped.

Activity (i).
What do you observe after sometime? Does the metal melt?
Answer:
1. On heating the wire on one end, soon the entire wire gets hot. The heat melts the wax and so the pin attached to it falls down. This means the heat given at one end of the metal got transferred to the entire metal wire. So, we conclude that aluminium and copper are good conductors of heat.
2. The heat melted the wax but not the metal wire because the temperature of the heat is not high enough.

Activity 6.

Perform an activity to study that metals are good conductors of electricity.
Set up an electric circuit as shown in figure.
Place the metal to be tested in the circuit between terminals A and B as shown. Does the bulb glow? What does this indicate?

Answer:
On joining the metal such as iron, aluminium or copper with two terminals namely A and B, the bulb starts glowing. This means that electricity flows through the metals. Hence, metals are good conductor of electricity.

Activity 7.

Aim: To study the properties of non-metals
Collect samples of carbon (coal or graphite), sulphur and iodine.

Question 1.
Carry out activities 1 to 6 with these non-metals and record your observations.
Answer:
Samples of carbon, sulphur and iodine do not show the properties of metals. However, carbon in the form of graphite is a good conductor of electricity and iodine has a shining surface.

Activity 8.

Perform an activity to study if the oxides of magnesium and sulphur are basic or acidic.
Answer:
Take a magnesium ribbon and some sulphur powder.
1. Burn the magnesium ribbon. Collect the ashes formed and dissolve them in water.
2. Test the resultant solution with both red and blue litmus paper. Is the product formed on burning magnesium acidic or basic?
3. Now burn sulphur powder. Place a test tube over the burning sulphur to collect the fumes produced. Add some water to the above test tube and shake. Test this solution with blue and red litmus paper.
Is the product formed on burning sulphur acidic or basic?

Q. Can you write equations for these reactions?
Answer:
On burning magnesium, magnesium oxide (MgO) is formed. The solution of magnesium oxide turns red litmus paper into blue. This means that magnesium oxide is basic.

1. When sulphur powder is burnt it produces sulphur dioxide (SO₂). Solution of SO₂ turns blue litmus into red. Hence, SO₂ is acidic.
The reactions of both these processes are as follows:
(i) 2Mg_(s)+ O_2(g) → 2MgO₍₅₎
(ii) S_(s) + O_2(g) →  SO_2(g)

Conclusion:
Oxide of magnesium is basic whereas oxide of sulphur is acidic.

Activity 9.

Aim: To study how metals burn in air
Caution: The following activity needs the teacher’s assistance. It would be better if students wear eye protection.
1. Collect samples of the following metals — Aluminium, copper, iron, lead magnesium, zinc and sodium.
2. Hold any of these samples with a pair of tongs and try burning over a flame. Repeat with the other metal samples.
3. Collect the product, if formed.
4. Let the products and the metal surface cool down.

Question 1.
Which metals burn easily?
Answer:
Sodium, potassium and magnesium burn easily.

Question 2.
What flame colour did you observe when the metal burnt?
Answer:
Refer table given below.

Question 3.
How does the metal surface appear after burning?
Answer:
Refer table given below.

Question 4.
Arrange the metals In the decreasing order of their reactivity towards oxygen.
Answer:
The reactivity of metals with oxygen decreasing order is –
Na > Ca > Mg > Al> Zn > Fe > Cu

Question 5.
Are the products soluble in water?
Answer:
Refer table given below.

Activity 10.

Aim: To study how metals react with water.
Answer:
Caution: This activity needs the teacher’s assistance.
1. Collect samples of the following metals — Aluminium, copper, iron, lead magnesium, zinc, calcium, sodium
and potassium.
2. Put small pieces of the samples separately in beakers half-filled with cold water.

Question 1.
Which metals reacted with cold water? Arrange them in the increasing order of their reactivity with cold water.
Answer:
Na, K and Ca reacted with cold water. The reactivity of metals with cold water in increasing order is: Mg < Ca < Na < K

Question 2.
Did any metal produce fire on water?
Answer:
Sodium (Na) and potassium (K) catch fire on water.

Question 3.
Does any metal start floating after some time?
Answer:
Calcium and magnesium start floating after some time.
1. Put the metals that did not react with cold water in beakers half-filled with hot water.
2. For the metals that did not react with hot water, arrange the apparatus as shown in the figure and observe their reaction with steam.

Question 4.
Which metals did not react even with steam?
Answer:
Metals namely copper, silver and gold did not react even with steam.

Question 5.
Arrange the metals, In the decreasing order of reactivity with water.
Answer:
Metals such as lead (Pb), copper (Cu), silver (Ag) and gold (Au) did not react with water. The reactivity of remaining metals with water in decreasing order is: K> Na > Ca > Mg > Al> Zn > Fe

Activity 11

Aim: To study how metals react with acids.
Answer:
Collect the sample of metal pieces such as magnesium, alumimnium, zinc, iron and copper. If the samples are tarnished, rub them clean with sand paper.

Caution: Do not take sodium and potassium as they react vigorously even with cold water.
1. Put the samples separately in test tubes containing dilute hydrochloric acid.
2. Suspend thermometers in the test tubes, so that their bulbs are dipped in the acid.

Question 1.
Observe the rate of formation of bubbles carefully.
Answer:
The rate of formation of bubbles is fastest in magnesium.

Question 2.
With which metal did you record the highest temperature?
Answer:
With magnesium (Mg).

Question 3.
Which metals reacted vigorously with dilute hydrochloric acid?
Answer:
Metals like Mg, Al, Zn and Fe react vigorously with dilute hydrochloric acid.

Question 4.
Arrange the metals in the decreasing order of reactivity with dilute acids.
Answer:
Mg > AI > Zn> Fe

Activity 12.

Aim: To study the reaction of metals with solution of other metals.
Answer:
1. Take a clean piece of copper wire of copper and an iron nail.
2. Put the copper wire in a solution of iron sulphate and the iron nail in a solution of copper sulphate taken in test tubes
3. Record your observations after 20 minutes.

Question 1.
In which test tube did you find that a reaction has occurred?
Answer:
The reaction took place in the test tube in which the iron nail is kept in copper sulphate (CuSO₄) solution.

Question 2.
On what basis can you say that a reaction has actually taken place?
Answer:
The blue colour of the copper sulphate solution starts fading. This assures occurrence of some chemical reaction.

Question 3.
Can you correlate your observations for activities 3.9, 3.10 and 3.11?
Answer:
This activity can be correlated with activities 3.9, 3.10 and 3.11 in the sense that all these activities affirm that iron (Fe) is more reactive than copper (Cu).

Question 4.
Write a balanced chemical equation for the reaction that has taken place.
Answer:
Chemical reaction:
Fe(s) + CUSO_4(aq) → CU(g) + FeSO_4(aq)

Question 5.
Name the type of reaction.
Answer:
The reaction is displacement reaction.

Activity 13.

Aim: To study the properties of ionic compounds.
Take samples of sodium chloride, potassium iodide, barium chloride or any other salt from the science laboratory.

1. What is the physical state of these salts?
Take a small amount of a sample on a metal spatula and heat directly on the flame. Repeat with other samples.

2. What did you observe? Did the samples impart any colour to the flame? Do these compounds melt?

3. Try to dissolve the samples in water, petrol and kerosene. Are they soluble?

4. Make a circuit as shown in figure and insert the electrodes into a solution of one salt. What did you observe? Test the other salt samples too in this manner.

5. What is your inference about the nature of these compounds?
Answer:
The answers of all these questions are tablulated below:

Activity 14.

Perform an activity to demonstrate that both air and water are needed for rusting of Iron.
Answer:
1. Take three test tubes and place clean iron nails in each of them.
2. Label these test tubes A, B and C.
3. Pour some water in test tube A and cork it. The nail should not completely submerge.
4. Pour boiled distilled water in test tube B, add about 1 mL of oil and cork it. The oil will float on water and prevent the air from dissolving in the water.
5. Put some anhydrous calcium chloride in test tube C and cork it. Anhydrous calcium chloride will absorb the moisture, if any, from the air. Leave these test tubes for a few days and then observe.

Observation:

• Nail in test tube A is in contact with water as well as air and so it will get rusted.
• Nail in test tube B is in contact with water but not air and so it will not rust.
• Nail in test tube C is in contact with air but not water and so it will not rust.

Conclusion :

• The nail in test-tube A got rusted due to oxidation reaction.
• The activity proves that rusting of iron can take place only if iron is in contact with (1) water as well as (2) air.

Haryana State Board HBSE 11th Class Physics Solutions Chapter 4 समतल में गति Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 4 समतल में गति

प्रश्न 4.1.
निम्नलिखित भौतिक राशियों में से बताइए कि कौन-सी सदिश हैं तथा कौन-सी अदिश?
आयतन, द्रव्यमान, चाल, त्वरण, घनत्व, मोल संख्या, वेग, कोणीय आवृत्ति, विस्थापन, कोणीय वेग।
उत्तर:
सदिश राशियाँ: त्वरण, वेग, विस्थापन तथा कोणीय वेग।
अदिश राशियाँ: आयतन द्रव्यमान, चाल, घनत्व, मोल संख्या तथा कोणीय आवृत्ति।

प्रश्न 4.2.
निम्नांकित सूची में से दो अदिश राशियों को छाँटिए:
बल, कोणीय संवेग, कार्य, धारा, रैखिक संवेग, विद्युत क्षेत्र, औसत वेग, चुम्बकीय आघूर्ण, आपेक्षिक वेग।
उत्तर:
दो अदिश राशियाँ कार्य तथा धारा हैं।

प्रश्न 4.3.
निम्नलिखित सूची में से एकमात्र सदिश राशि को छाँटिए:
ताप, दाब, आवेग, समय, शक्ति, दूरी, पथ लम्बाई, ऊर्जा, गुरुत्वीय विभव, घर्षण गुणांक, आवेश।
उत्तर:
एकमात्र सदिश राशि आवेग है।

प्रश्न 4.4.
कारण सहित बताइए कि सदिश तथा अदिश राशियों के साथ क्या निम्नलिखित बीजगणितीय संक्रियाएँ अर्थपूर्ण हैं?
(a) दो अदिशों को जोड़ना,
(b) एक ही विमाओं के एक अदिश व एक सदिश को जोड़ना,
(c) एक सदिश को एक अदिश से गुणा करना,
(d) दो अदिशों का गुणन,
(e) दो सदिशों को जोड़ना,
(f) एक सदिश के घटक को उसी सदिश से जोड़ना।
उत्तर:
(a) नहीं, दो अदिशों को जोड़ना केवल तभी अर्थपूर्ण हो सकता है. जबकि दोनों एक ही भौतिक राशि को प्रदर्शित करते हों।
(b) नहीं, सदिश को केवल सदिश के साथ तथा अदिश को केवल अदिश के साथ ही जोड़ा जा सकता है।
(c) अर्थपूर्ण है। जैसे – त्वरण सदिश को अदिश राशि द्रव्यमान गुणा करने पर बल प्राप्त होगा।
(d) अर्थपूर्ण है। जैसे – अदिश राशियाँ शक्ति P व समय को गुणा करने पर कार्य प्राप्त होगा।
(e) नहीं, केवल तभी अर्थपूर्ण होगा, जबकि दोनों एक ही भौतिक राशि को प्रदर्शित करते हों।
(f) चूँकि किसी सदिश का घटक एक सदिश होता है, जो मूल सदिश के समान भौतिक राशि को निरूपित करता है (जैसे-बल का घटक भी एक बल ही होता है)। अतः दोनों को जोड़ना अर्थपूर्ण है।

प्रश्न 4.5.
निम्नलिखित में से प्रत्येक कथन को ध्यानपूर्वक पढ़िए और कारण सहित बताइए कि यह सत्य है या असत्य
(a) किसी सदिश का परिमाण सदैव एक अदिश होता है।
(b) किसी सदिश का प्रत्येक घटक सदैव अदिश होता है।
(c) किसी कण द्वारा चली गई पथ की कुल लम्बाई सदैव विस्थापन सदिश के परिमाण के बराबर होती है।
(d) किसी कण की औसत चाल (पथ तय करने में लगे समय द्वारा विभाजित कुल पथ – लम्बाई) समय के समान अन्तराल में कण के औसत वेग के परिमाण से अधिक या उसके बराबर होती है।
(e) उन तीन सदिशों का योग जो एक समतल में नहीं हैं, कभी भी शून्य सदिश नहीं होता है।
उत्तर:
(a) सत्य, किसी भी भौतिक राशि का परिणाम एक धनात्मक संख्या है। जिसमें दिशा नहीं होती, अतः यह एक अदिश राशि है।
(b) असत्य, किसी सदिश का प्रत्येक घटक एक सदिश राशि होती
(c) असत्य, उदाहरण के लिए यदि कोई व्यक्ति R त्रिज्या के वृत्त की परिधि पर चलते हुए एक चक्कर पूर्ण करता है तो उसके द्वारा तय किए गये पथ की लम्बाई 2πR होगी, जबकि विस्थापन का परिमाण शून्य होगा।
(d) सत्य, क्योंकि औसत चाल पूर्ण पथ की लम्बाई पर तथा औसत वेग कुल विस्थापन पर निर्भर करता है, जबकि पूर्ण पथ की लम्बाई सदैव ही विस्थापन के परिमाण से अधिक अथवा बराबर होती है।
(e) सत्य, शून्य सदिश प्राप्त करने के लिए तीसरा सदिश पहले दो सदिशों के परिणामी के विपरीत दिशा में तथा परिमाण में उसके बराबर होना चाहिए। यह इस दशा में सम्भव नहीं है।

प्रश्न 4.6.
निम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिए:

इनमें समिका (समता) का चिह्न कब लागू होता है?
उत्तर:
माना OA = a, AB = b

(a)
\(\vec{a}+\vec{b}\) = OA + AB
= OB
∆OAB में तीसरी भुजा, सदैव शेष दो भुजाओं के योग से बड़ी नहीं हो सकती है।
अत:
OB < OA + AB यदि \(\vec{a}\) वह \(\vec{b}\) एक ही दिशा में हों तो समता का चिह्न लागू होगा। (b) ∆OAB में, तीसरी भुजा सदैव दो भुजाओं के अन्तर से बड़ी होती है। OB > OA – AB
\(|\vec{a}+\vec{b}| \geq|\vec{a}|-|\vec{b}|\) ………..(1)
या
OB > AB – OA
\(|\vec{a}+\vec{b}| \geq|\vec{b} \vdash| \vec{a} \mid\) …….(2)
∴ समी० (1) व (2) से,
\(|\vec{a}+\vec{b}| \geq \| \vec{a}-|\vec{b}| \mid\)
यदि \vec{a} व \vec{b} है विपरीत दिशाओं में हों, तो समता का चिह्न लागू होगा।

(c) \(-\vec{b}\) = AB
∴ \(\vec{a}-\vec{b}=\vec{a}+(-\vec{b})\)
= OA + AB = OB
अत:
\(|\vec{a}-\vec{b}|\) = OB
AOAB’ में,
\(|\vec{a}-\vec{b}| \leq|\vec{a}|+|-\vec{b}|\)
या
\(|\vec{a}-\vec{b}| \leq|\vec{a}|+|\vec{b}|\)

\(\vec{a}\) व \(\vec{b}\) है विपरीत दिशा में होने पर समता चिह्न लागू होगा।
(d) त्रिभुज OAB’ में, प्रत्येक भुजा शेष दो भुजाओं के अन्तर से चाहिए।
बड़ी होती है।
OB>OA-AB
\(|\vec{a}-\vec{b}| \geq|\vec{a}|-|\vec{b}|\) ……(1)
इसी प्रकार,
\(|\vec{a}-| \geq|\vec{b}|-|\vec{a}|\) ……..(2)
समी० (1) व (2) से,
\(|\vec{a}-\vec{b}| \geq|| \vec{a} \vdash|\vec{b}| \mid\)
\(\vec{a}\) व \(\vec{b}\) है एक ही दिशा में होने पर समता चिह्न लागू होगा। अर्थात् सभी में समिका चिह्न के लिए सदिश व संरखी होने

प्रश्न 4. 7.
दिया है a + b + c + d = 0, नीचे दिए गए कथनों में से कौन-सा सही है?
(a) \(\vec{a}, \vec{b}, \vec{c}\) तथा \(\overrightarrow{\boldsymbol{d}}\) में से प्रत्येक शून्य सदिश है।
(b) \((\vec{a}+\vec{c})\) का परिमाण \((\vec{b}+\vec{d})\) का परिमाण के बराबर है।
(c) \(\vec{a}\) का परिमाण \(\vec{b}, \vec{c}\) है, \(\vec{d}\) तथा के परिमाणों के योग से कभी भी अधिक नहीं हो सकता।
(d) यदि \(\vec{a}\) तथा \(\vec{d}\) संरेखीय नहीं हैं तो \((\vec{b}+\vec{C})\) अवश्य ही \(\vec{a}\) तथा \(\vec{d}\)
के समतल में होगा और यह \(\vec{a}\) तथा \(\vec{d}\) के अनुदिश होगा, यदि वे सरेखीय हैं।
उत्तर:

प्रश्न 4.8.
तीन लड़कियाँ 200m त्रिज्या वाली वृत्तीय बर्फीली सतह पर स्केटिंग कर रही हैं। वे सतह के किनारे के बिन्दु P से स्केटिंग शुरू करती हैं तथा P के व्यासीय विपरीत बिन्दु Q पर विभिन्न पथों से होकर पहुँचती हैं, जैसा कि चित्र में दिखाया गया है। प्रत्येक लड़की के विस्थापन सदिश का परिमाण कितना है? किस लड़की के लिए यह वास्तव में स्केट किए गए पथ की लम्बाई के बराबर है?

उत्तर:
∵ प्रत्येक लड़की का विस्थापन सदिश =
∴ विस्थापन सदिश का परिमाण
= व्यास PQ की लम्बाई
= 2R = 2 x 200m = 400m
∵ लड़की B द्वारा तय पथ (PQ) की लम्बाई
= 2R = 400m
∴ लड़की B के लिए विस्थापन सदिश का परिमाण वास्तव में स्केट किए गए पथ की लम्बाई के बराबर है।

प्रश्न 4.9.
कोई साइकिल सवार किसी वृत्तीय पार्क के केन्द्र 0 से चलना शुरू करता है तथा पार्क के किनारे P पर पहुँचता है। पुनः वह पार्क की परिधि के अनुदिश साइकिल चलाता हुआ 20 के रास्ते (जैसा कि चित्र में दिखाया गया है) केन्द्र पर वापस आ जाता है। पार्क की त्रिज्या 1km है। यदि पूरे चक्कर में 10 मिनट लगते हों तो साइकिल सवार का (a) कुल विस्थापन, (b) औसत वेग तथा (c) औसत चाल क्या होगी?

उत्तर:
(a) साइकिल सवार केन्द्र O से चलकर अन्त में पुनः केन्द्र O
पर पहुँच जाता है अतः
कुल विस्थापन = O
(b) औसत वेग
(c) कुल दूरी = त्रिज्या OP + परिधि भाग PQ + त्रिज्या QO
= 1 km + \(\frac{1}{4}\) x 2πR + 1km
= 2 + \(\frac{1}{2}\) × 3.14 × 1
= 3.57 km
समय = 10 मिनट
औसत चाल =
= 0.357 km / min

प्रश्न 4.10.
किसी खुले मैदान में कोई मोटर चालक एक ऐसा रास्ता अपनाता है जो प्रत्येक 500m के बाद उसके बाईं ओर 60° के कोण पर मुड़ जाता है। किसी दिए मोड़ से शुरू होकर मोटर चालक का तीसरे, छठे व आठवें मोड़ पर विस्थापन बताइए। प्रत्येक स्थिति में मोटर चालक द्वारा इन मोड़ों पर तय की गई कुल पथ लम्बाई के साथ विस्थापन के परिमाण की तुलना कीजिए।
उत्तर:
मोटर चालक द्वारा अपनाया गया मार्ग चित्रानुसार समषटभुज आकार का होगा।
(a) मोटर चालक 4 से प्रारम्भ कर तीसरे मोड़ पर बिन्दु D पर पहुँचता है।
विस्थापन = AD = 2AO
= 2AB
अतः

= 2x 500
= 1000m
= 1 km
कुल पथ की लम्बाई = AB + BC + CD
= 500 + 500 + 500 = 1.5 km

(b) मोटर चालक छठे मोड़ पर वापस शीर्ष 4 पर पहुँच जायेगा।
अतः विस्थापन = शून्य।
कुल पथ की लम्बाई = 6 × AB
= 6× 500
= 3000m = 3 km

(c) आठवें मोड़ शीर्ष C पर विस्थापन
अतः विस्थापन

कुल पथ लम्बाई = 8 x AB
= 8 × 500 = 4 km
अतः विस्थापन पथ लम्बाई = \(\frac{\sqrt{3}}{2}\) : 4
= √3 : 8

प्रश्न 4.11.
कोई यात्री किसी नए शहर में आया है और वह स्टेशन से किसी सीधी सड़क पर स्थित किसी होटल तक जो 10 किसी दूरी है, जाना चाहता है। कोई बेईमान टैक्सी चालक 23 किमी के चक्करदार रास्ते से उसे ले जाता है और 28 मिनट में होटल पहुँचता है।
(a) टैक्सी की औसत चाल और
(b) औसत वेग का परिमाण क्या होगा? क्या वे बराबर हैं?
उत्तर:
(a) टैक्सी द्वारा तय की गई कुल दूरी = 23km
समय = 28 मिनट

= 49.3 km h^-1

(b) टैक्सी का विस्थापन = 10km
समय = 28min
औसत वेग = \(\frac{10}{28}\) km/min = \(\frac{10}{28}\) × 60
= 21.4 km h^-1
औसत चाल व औसत वेग बराबर नहीं है। केवल सीधे पथों के लिए ही ये बराबर होते हैं।

प्रश्न 4.12.
वर्षा का पानी 30 ms^-1 की चाल से ऊर्ध्वाधर नीचे गिर रहा है। कोई महिला उत्तर से दक्षिण की ओर 10ms^-1 की चाल से साइकिल चला रही है। उसे अपना छाता किस दिशा में रखना चाहिए?
उत्तर:
वर्षा ऊर्ध्वाधर OA दिशा में, = 30ms^-1 वेग से गिर रही है। महिला OS दिशा में V = 10ms^-1 वेग से गति कर रही है। महिला वर्षा से बचने के लिए अपना छाता अपने सापेक्ष वर्षा के वेग की दिशा में

रखेगी।
वर्षा का महिला के सापेक्ष वेग
Vrw = Vr – Vw
इसलिए 10ms^-1 वेग को ऋणात्मक चिह्न में रखने पर यह ON दिशा में होगा।
∴ समान्तर चतुर्भुज OADC में,
tan θ = \(\frac{v_w}{v_r}=\frac{10}{30}=\frac{1}{3}\) = 0.33
या
θ = tan^-1 0.33
∴ θ = 18°
अतः महिला अपना छाता ऊर्ध्वाधर में 18° दक्षिण दिशा में रखेगा।

प्रश्न 4.13.
कोई व्यक्ति स्थिर जल में 4.0 km/h की चाल से तैर सकता है। उसे 1.0 km चौड़ी नदी को पार करने में कितना समय लगेगा? यदि नदी 3.0km/h की स्थिर चाल से बह रही है और वह नदी के बहाव के लम्ब दिशा में तैर रहा हो। जब वह नदी के दूसरे किनारे पर पहुँचता है तो वह नदी के बहाव की ओर कितनी दूर पहुँचेगा?
उत्तर:
बहाव का वेग Vr = 3.0 km/h
तैराक का वेग Vm = 4.0km/h
नदी को पार करने के लिए नदी के लम्ब दिशा में तय दूरी = 1 km

∴ नदी को पार करने में लगा समय
t =
h = 15 min
समय t में व्यक्ति नदी के बहाव की ओर BC दूरी तय कर चुका है।
अतः तय दूरी BC = बहाव का वेग x लगा समय
= 30 x \(\frac{1}{4}\) km
= 0.75 km = 750m

प्रश्न 4.14.
किसी बन्दरगाह में 72 km/h की चाल से हवा चल रही है और बन्दरगाह में खड़ी किसी नौका के ऊपर लगा झण्डा N-E दिशा में लहरा रहा है। यदि यह नौका उत्तर की ओर 51 km/h की चाल से गति करना प्रारम्भ कर दे तो नौका पर लगा झण्डा किस दिशा में लहराएगा?
उत्तर:
वायु का वेग = \(\overrightarrow{v_a}\)
नौका का वेग = \(\overrightarrow{v_b}\)
\(\overrightarrow{v_a}\) = 72 km/h (N-E) दिशा में,
\(\overrightarrow{v_b}\) = 51 km/h (N) दिशा में,
∴ वायु का नौका के सापेक्ष वेग \(\overrightarrow{v_{a b}}=\overrightarrow{v_a}-\overrightarrow{v_b}\)
झण्डा चित्रानुसार \(\overrightarrow{v_{a b}}\) दिशा में ही लहराएगा।

माना Vab वेग Va से \(\phi\) कोण बनाता है जबकि वेगों \(\overrightarrow{v_a}\) तथा \(\overrightarrow{v_b}\)
के बीच का कोण θ = 135° है।
∴ tan Φ = \(\frac{B \sin \theta}{A+B \cos \theta}\) सूत्र से,
∵ tan Φ = \(\frac{v_b \sin 135^{\circ}}{v_a+v_b \cos 135^{\circ}}\)
या
tan Φ = \(\frac{51 \times \frac{1}{\sqrt{2}}}{72+51 \times\left(-\frac{1}{\sqrt{2}}\right)}\)
= \(\frac{51}{72 \sqrt{2}-51} \approx 1\)
∴ Φ = 45° (लगभग)
∴ Vab द्वारा पूर्व दिशा में बनाया गया कोण
= Φ – 45°
= 45° – 45°
= 0°
अतः झण्डा लगभग पूर्व दिशा में लहरायेगा।

प्रश्न 4.15.
किसी लम्बे हाल की छत 25 m ऊँची है। वह अधिकतम क्षैतिज दूरी कितनी होगी जिसमें 40ms^-1 की चाल से फेंकी गई कोई गेंद छत से टकराये बिना गुजर जाए?
उत्तर:
अधिकतम ऊँचाई H = 25m,
वेग Vo = 40ms^-1
यदि गेंद को θ कोण पर फेंका जाये, तो
अधिकतम ऊँचाई H = \(\frac{u^2 \sin ^2 \theta}{2 g}\)
या
sin² θ = \(\frac{2 g H}{u^2}=\frac{2 \times 9.8 \times 25}{(40)^2}\)
या
sin² θ = \(\frac{49 \times 10}{(40)^2}\)
या
sin² θ = 0.30625
या
∴ sin θ = 0.553
cosθ = \(\sqrt{1-\sin ^2 \theta}\)
= \(\sqrt{1-(0.553)^2}\)
= \(\sqrt{1-0.306}\)
= \(\sqrt{0.694}\)
= 0.833
∴ अधिकतम क्षैतिज दूरी

= 150.5m

प्रश्न 4.16.
क्रिकेट का कोई खिलाड़ी किसी गेंद को 100 मीटर की अधिकतम क्षैतिज दूरी तक फेंक सकता है। वह खिलाड़ी उसी गेंद को जमीन से ऊपर कितनी ऊँचाई तक फेंक सकता है?
उत्तर:
R_max = 100m, R = \(\frac{u^2 \sin 2 \theta}{g}\)
या
R_max = \(\frac{u^2}{g}\)
या
u² = R_max x g
= 100 × 10 = 1000(ms^-1)²
∴ a = \(14 \sqrt{5}\) ms^-1
गेंद को महत्तम ऊंचाई तक फेंकने के लिए θ° = 90° होना चाहिए।

प्रश्न 4.17.
80cm लम्बे धागे के एक सिरे पर एक पत्थर बाँधा गया है और इसे किसी एक समान चाल के साथ किसी क्षैतिज वृत्त में घुमाया जाता है। यदि पत्थर 25s में 14 चक्कर लगाता है तो पत्थर के त्वरण का परिमाण और उसकी दिशा क्या होगी?
उत्तर:
R = 80cm = 0.80m
पत्थर द्वारा 1 सेकण्ड में चक्करों की संख्या

कोणीय आवृत्ति ω = 2πn = 2π x \(\frac{14}{25}\)
अभिकेन्द्रीय त्वरण
ac = ω²R
=(2 x 3.14 x 14) x 0.80
= 9.8 ms^-2
त्वरण की दिशा वृत्त के केन्द्र की ओर होगी।

प्रश्न 4.18.
कोई वायुयान 900 kmh की एक समान चाल से उड़ रहा है और 1.00 km त्रिज्या का कोई क्षैतिज लूप बनाता है। इसके अभिकेन्द्रीय त्वरण की गुरुत्वीय त्वरण के साथ तुलना कीजिए।
उत्तर:
वायुयान की चाल = 900kmh^-1
= 900 x \(\frac{1000}{60 \times 60}\)
= 250ms^-1
त्रिज्या R = 1.00km = 1000m
अभिकेन्द्रीय त्वरण ac = \(\frac{v^2}{R}=\frac{(250)^2}{1000}\)
∴ ac = 62.5ms^-2
∴
∴ अभिकेन्द्रीय त्वरण = 6.4 x गुरुत्वीय त्वरण
अतः वायुयान का त्वरण, गुरुत्वीय त्वरण का 6.4 गुना है।

प्रश्न 4.19.
नीचे दिये गये कथनों को ध्यानपूर्वक पढ़िए और कारण देकर बताइए कि वे सत्य हैं या असत्य:
(a) वृत्तीय गति में किसी कण का नेट त्वरण हमेशा वृत्त की त्रिज्या के अनुदिश केन्द्र की ओर होता है।
(b) किसी बिन्दु पर किसी कण का वेग सदिश सदैव उस बिन्दु पर कण के पथ की स्पर्श रेखा के अनुदिश होता है।
(c) किसी कण का एकसमान वृत्तीय गति में एक चक्र में लिया गया औसत त्वरण सदिश एक शून्य सदिश होता है।
उत्तर:
(a) असत्य यह कथन एक समान वृत्तीय गति के लिए ही सत्य है।
(b) सत्य है, वेग की दिशा स्पर्श रेखीय होती है।
(c) सत्य है, क्योंकि परिणामी विस्थापन शून्य है।

प्रश्न 4.20.
किसी कण का स्थिति सदिश निम्नलिखित है:
\(\vec{r}=\left(3.0 t \hat{i}-2.0 t^2 \hat{j}+4.0 \hat{k}\right)\) m
समय t सेकण्ड में है तथा सभी गुणांकों के मात्रक इस प्रकार हैं कि \overrightarrow{\boldsymbol{r}} मीटर में व्यक्त हो जाए।
(a) कण का वेग \(\overrightarrow{\boldsymbol{v}}\) तथा \(\overrightarrow{\boldsymbol{a}}\) निकालिए।
(b) t = 2.0 पर कण के वेग का परिणाम तथा दिशा कितनी होगी?
उत्तर:

प्रश्न 4.21.
कोई कण t = 0 क्षण पर मूलबिन्दु से 10 \(\hat{j}\) ms^-1 के वेग से चलना प्रारम्भ करता है तथा x-y समतल में एकसमान त्वरण \((8.0 \hat{i}+2.0 \hat{j})\) ms^-1 से गति करता है।
(a) किस क्षण कण का x- निर्देशांक 16m होगा? इसी समय इसका y-निर्देशांक कितना होगा?
(b) इस क्षण कण की चाल कितनी होगी?
उत्तर:

प्रश्न 4.22.
\(\hat{i}\) तथा \(\hat{i}\) क्रमश: x व y- अक्षों के अनुदिश एकांक सदिश हैं। सदिशों \(\hat{i}+\hat{j}\) तथा \(\hat{i}-\hat{j}\) का परिमाण तथा दिशाएँ क्या होंगी? सदिशों \(\vec{A}=2 \hat{i}+3 \hat{j}\) के \(\hat{i}+\hat{j}\) व \(\hat{i}-\hat{j}\) की दिशाओं के अनुदिश घटक निकालिए।
(आप ग्राफीय विधि का उपयोग कर सकते हैं।)
उत्तर:
सदिश \(\hat{i}+\hat{j}\) का परिमाण

प्रश्न 4.23.
किसी दिक्स्थान पर एक स्वैच्छ गति के लिए निम्नलिखित सम्बन्धों में से कौन-सा कथन सत्य है?

यहाँ औसत का आशय समयान्तराल t2 व t1 से सम्बन्धित भौतिक राशि के औसत मान से है।
उत्तर:
(a) असत्य,
(b) सत्य,
(c) असत्य,
(d) असत्य,
(e) सत्य।
(a), (c) व (d) केवल सम त्वरित गति में लागू होते हैं।

प्रश्न 4.24.
निम्नलिखित में से प्रत्येक फलन को ध्यानपूर्वक पढ़िए तथा कारण एवं उदाहरण सहित बताइए कि क्या यह सत्य है या
असत्य:
अदिश वह राशि है, जो:
(a) किसी प्रक्रिया में संरक्षित रहती है।
(b) कभी ऋणात्मक नहीं होती।
(e) विमाहीन होती है।
(d) किसी स्थान पर एक बिन्दु से दूसरे बिन्दु के बीच नहीं बदलती।
(e) उन सभी दर्शकों के लिए एक ही मान रखती है चाहे अक्षों से उनके अभिविन्यास भिन्न-भिन्न क्यों न हों?
उत्तर:
(a) असत्य, जैसे गतिज ऊर्जा अदिश राशि है परन्तु यह संरक्षित नहीं रहती है।
(b) असत्य, जैसे ताप अदिश राशि है जो धनात्मक, शून्य या ऋणात्मक हो सकता है।
(c) असत्य, उदाहरण के लिए, किसी वस्तु का द्रव्यमान अदिश राशि है परन्तु इसकी विमा [M] है
(d) असत्य, उदाहरण के लिए, ताप एक अदिश राशि है, किसी छड़ में ऊष्मा के एकविमीय प्रवाह में, प्रवाह की दिशा में ताप बदलता जाता है।
(e) सत्य, क्योंकि अदिश राशि में दिशा नहीं होती, अतः यह प्रत्येक विन्यास में स्थित दर्शक के लिए समान मान रखती है। उदाहरण के लिए, किसी वस्तु के द्रव्यमान का मान प्रत्येक दर्शक के लिए समान होगा।

प्रश्न 4.25.
कोई वायुयान पृथ्वी से 3400m की ऊँचाई पर उड़ रहा है। यदि पृथ्वी पर किसी अवलोकन बिन्दु पर वायुयान की 10.05 की दूरी की स्थितियाँ 30° का कोण बनाती हैं, तो वायुयान की चाल क्या होगी?
उत्तर:
माना 10s के अन्तराल पर वायुयान की दो स्थितियाँ P तथा Q हैं, जबकि O प्रेक्षण बिन्दु है।
बिन्दु O से PO पर लम्ब OA डाला।
प्रश्नानुसार, OA = 3400m
तथा
∴∠POQ = 30°
∴ ∠POA = ∠QOA = 15°
tan 15° = \(\frac{A Q}{O A}\)
या
AQ = OA tan 15°

∴10s में तय दूर PQ = 24Q
= 2AO tan 15°
[ tan 15° 0.268]
= 2 x 3400m x 0.268
= 1822.4 m

= 182.22 ms^-1

अतिरिक्त अभ्यास (Additional Exercise):

प्रश्न 4.26.
किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या दिस्थान में इसकी कोई स्थिति होती है? क्या यह समय के साथ परिवर्तित हो सकता है? क्या दिक्स्थान में भिन्न स्थानों पर दो बराबर सदिशों व का समान भौतिक प्रभाव अवश्य पड़ेगा? अपने उत्तर के समर्थन में उदाहरण दीजिए।
उत्तर:
सभी संदिशों की स्थिति नहीं होती, किसी बिन्दु के स्थिति सदिश के समान कुछ सदिशों की स्थिति होती है, जबकि वेग सदिश के 5 समान कुछ सदिशों की कोई स्थिति नहीं होती है। हाँ, कोई सदिश समय के 5 साथ परिवर्तित हो सकता है। जैसे त्वरित कण का वेग सदिश समय के साथ परिवर्तित हो सकता है। आवश्यक नहीं है, उदाहरण के लिए, दो अलग-अलग बिन्दुओं पर लगे बराबर बल अलग-अलग आघूर्ण उत्पन्न करेंगे।

प्रश्न 4.27.
किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या इसका यह अर्थ है कि कोई राशि जिसका परिमाण व दिशा हो, वह अवश्य ही सदिश होगी ? किसी वस्तु के घूर्णन की व्याख्या घूर्णन अक्ष की दिशा और अक्ष के परितः घूर्णन कोण द्वारा की जा सकती है। क्या इसका यह अर्थ है कि कोई भी घूर्णन एक सदिश है?
उत्तर:
किसी राशि में परिमाण तथा दिशा होने पर उसका सदिश होना आवश्यक नहीं है। उदाहरण के लिए, प्रत्येक घूर्णन कोण एक सदिश राशि नहीं हो सकता केवल सूक्ष्म घूर्णन को ही सदिश राशि माना जा सकता है।

प्रश्न 4.28.
क्या आप निम्नलिखित के साथ कोई सदिश सम्बद्ध कर सकते हैं:
(a) किसी लूप में मोड़ी गई तार की लम्बाई,
(b) किसी समतल क्षेत्र,
(c) किसी गोले के साथ? व्याख्या कीजिए।
उत्तर:
(a) नहीं, क्योंकि वृत्तीय लूप में मोड़े गए तार की कोई निश्चित दिशा नहीं होती।
(b) दिए गए समतल पर एक निश्चित अभिलम्ब खींचा जा सकता है, अत: समतल क्षेत्र के साथ एक सदिश सम्बद्ध किया जा सकता है, जिसकी दिशा समतल पर अभिलम्ब के अनुदिश हो सकती है।
(c) नहीं, क्योंकि किसी गोले का आयतन किसी विशेष दिशा के साथ सम्बद्ध नहीं किया जा सकता।

प्रश्न 4.29.
कोई गोली क्षैतिज से 30° के कोण पर दागी गई है। और वह धरातल पर 3.0 km दूरी गिरती है। इसके प्रक्षेप्य के कोण का समायोजन करके क्या 5.0 km दूर स्थित किसी लक्ष्य का भेद किया जा सकता है? गोली की नालमुख चाल को नियत तथा वायु के प्रतिरोध को नगण्य मानिए।
उत्तर:
परास R = \(\frac{u^2 \sin 2 \theta}{g}\)
∴ R = 3km = 3000m, u = ?, θ = 30°
∴ 3000 = \(\frac{u^2 \sin 2 \theta}{g}\)
∴ u² = 2000/3g
∴ गोली की अधिकतम परास
R = \(\frac{u^2}{g}=\frac{2000 \sqrt{3} g}{g}\)
= 2000\(\sqrt{3}\)m = 3.464 km
अधिकतम परास 3.4 km है, अत: गोली 5 km दूरी पर स्थित लक्ष्य को नहीं भेद सकेगी।

प्रश्न 4.30.
कोई लड़ाकू जहाज 1.5 km की ऊँचाई पर 720 km/h की चाल से क्षैतिज दिशा में उड़ रहा है और किसी वायुयान भेदी तोप के ठीक ऊपर से गुजरता है। ऊर्ध्वाधर से तोप की नाल का क्या कोण हो जिससे 600 ms-1 की चाल से दागा गया गोला वायुयान पर वार कर सके ? वायुयान के चालक को किस न्यूनतम ऊँचाई पर जहाज को उड़ाना चाहिए, जिससे गोला लगने से बच सके? (g = 10ms²)
उत्तर:
वायुयान की ऊँचाई 1.5 km = 1500m
चाल = 720 km/h
= 720 x \(\frac{1000}{60 \times 60}\)
= 200 ms^-1
गोले की चाल = 600ms^-1
माना जिस क्षण वायुयान B बिन्दु पर पहुँचेगा तो वह गोले से टकरायेगा।

गोले के वेग का क्षैतिज घटक
u_x = ucosθ (θ = 90° – α)
या
u_x = 600cos (90° – α)
या
u_x = 600 sin α
t समय बाद गोले की क्षैतिज दूरी
x = u_xt = 600sinαt ………..(1)
समय बाद वायुयान की दूरी
x = vt = 200t ………..(2)
∴ समी० (1) व (2) से,
600sin αt = 200
sin α = \(\frac{200}{600}=\frac{1}{3}\) = 0.33
∴ α = 19.5° (ऊर्ध्वाधर से)
तोप के गोले की अधिकतम ऊँचाई

प्रश्न 4.31.
एक साइकिल सवार 27 km/h की चाल से साइकिल चला रहा है। जैसे ही सड़क पर वह 80 m त्रिज्या के वृत्तीय मोड़ पर पहुँचता है। वह ब्रेक लगाता है और अपनी चाल को 0.5m/s की एकसमान दर से कम कर लेता है। वृत्तीय मोड़ पर साइकिल सवार के नेट त्वरण का परिमाण और उसकी दिशा निकालिए।
उत्तर:
साइकिल सवार की चाल
v = 27 km/h
= 27 x \(\frac{1000}{60 \times 60}\) = 7.5ms^-1
त्रिज्या R = 80m

अभिकेन्द्रीय त्वरण
\(a_c=\frac{v^2}{R}=\frac{7.5 \times 7.5}{80}\)
= 0.703 ms^-2
ब्रेक लगाने पर स्पर्श रेखीय मन्दन ar = 0.5ms 2
परिणामी त्वरण
a= \(\sqrt{a_c^2+a_r^2}\)
= \(\sqrt{(0.7)^2+(0.5)^2}\)
= 0.86 ms^-2
tan θ = \(\frac{a_c}{a_T}=\frac{0.7}{0.5}\)
= 1.4 या θ = tan^-1(1.4)
∴ θ = 54.5°

प्रश्न 4.32.
(a) सिद्ध कीजिए कि किसी प्रक्षेप्य के x- अक्ष तथा उसके वेग के बीच के कोण को समय के फलन के रूप में निम्न प्रकार से व्यक्त कर सकते हैं:
θ(t) = tan^-1 \(\left(\frac{u_y-g t}{u_x}\right)\)
(b) सिद्ध कीजिए कि मूलबिन्दु से फेंके गए प्रक्षेप्य कोण का मान θ = tan^-1\(\left(\frac{4 h_m}{R}\right)\) होगा। यहाँ प्रयुक्त प्रतीकों के अर्थ सामान्य हैं।
उत्तर:
(a) माना प्रक्षेप्य के x- अक्ष तथा y-अक्ष की दिशाओं में वियोजित घटक क्रमश: ux व uy हैं।
अतः गति के समी० (1) को द्विविमीय वियोजित करने पर,

(vt = uo + at)
v_x = u_ox + a_oxt
∵ a_ox = 0
∴ v_x = u_ox
v_y = u_oy + a_oyt
∵ a_oy = -g
∴ v_y = u_oy – gt
x- अक्ष से बनाया गया कोण

Haryana State Board HBSE 12th Class Physics Solutions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्र Textbook Exercise Questions and Answers.

Haryana Board 12th Class Physics Solutions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्र

प्रश्न 9.1.
2.5 cm साइज की कोई छोटी मोमबत्ती 36 cm वक्रता त्रिज्या के किसी अवतल दर्पण से 27 cm दूरी पर रखी है। दर्पण से किसी परदे को कितनी दूरी पर रखा जाए कि उसका सुस्पष्ट प्रतिबिंब परदे पर बने वर्णन कीजिए। यदि मोमबत्ती को को किस ओर हटाना पड़ेगा?
उत्तर:
दिया गया है
प्रतिबिंब की प्रकृति और साइज का दर्पण की ओर ले जाएँ, तो परदे
h= वस्तु का आकार = 2.5 cm
अवतल दर्पण से वस्तु की दूरी u = -27cm
अवतल दर्पण से वक्रता त्रिज्या = R = -36 cm
∴ अवतल दर्पण की फोकस दूरी f = 1⁄2R
=> R = -36/2 = -18cm
(i) दर्पण से प्रतिबिम्ब की दूरी = v = ?
सूत्र 1/u + 1/v = 1/f का उपयोग करने पर
1/v = 1/f – 1/u
1/v = 1/-18 – 1/-27
= -1/18 + 1/27 = -3+2/54
1/v = -1/54
∴ v = -54 cm
ऋण चिन्ह दर्शाता है कि प्रतिबिम्ब दर्पण के सामने बना है और उसी तरफ बना है जिस तरफ वस्तु रखी है। अतः पर्दा दर्पण के सामने 54 cm की दूरी पर रखा जाना चाहिए।
(ii) प्रतिबिम्ब की प्रकृति और आकार ज्ञात करना है।
m =
= -v/u का उपयोग करने पर
या
\(\frac{h^{\prime}}{2.5}\)=\(-\left(\frac{-54}{-27}\right)\) =\(\frac{-2}{1}\)
h’= – 2.5 x 2 = – 5 cm
इससे स्पष्ट होता है कि प्रतिबिम्ब वास्तविक, उल्टा व बड़ा और आवर्धित है।
(iii) यदि मोमबत्ती को दर्पण के पास लाया जाये तब पर्दे को दूर और अधिक दूर चलाना होगा अर्थात् पर्दा अनन्त पर रखना होगा। परन्तु जब मोमबत्ती की दूरी, दर्पण की फोकस दूरी से कम हो जैसे u → f, v →∞, u < f के लिए, उस स्थिति में प्रतिबिम्ब काल्पनिक (आभासी) होगा।

प्रश्न 9.2.
4.5 cm साइज की कोई सुई 15 cm फोकस दूरी के किसी उत्तल दर्पण से 12cm दूर रखी है। प्रतिबिंब की स्थिति तथा आवर्धन लिखिए क्या होता है जब सुई को दर्पण से दूर ले जाते हैं? वर्णन कीजिए।
उत्तर:
दिया गया है:
उत्तल दर्पण से वस्तु की दूरी (नीडिल) u = – 12 cm
उत्तल दर्पण की फोकस दूरी f = + 15 cm
वस्तु का आकार h = 4.5 cm
प्रतिबिम्ब की स्थिति = V = ?
सूत्र
\(\frac{1}{\mathrm{f}}\)=\(\frac{1}{\mathrm{u}}\) + \(\frac{1}{\mathrm{v}}\) का उपयोग करने पर
या
\(\frac{1}{v}\)= \(\frac{1}{f}\) – \(\frac{1}{u}\)
=\(\frac{1}{15}\) – \(\left(-\frac{1}{12}\right)\)
=\(\frac{1}{15}\) + \(\frac{1}{12}\) = \(\frac{4+5}{60}\)
\(\frac{1}{v}\) = \(\frac{9}{60}\) = \(\frac{3}{20}\)
V = 20/3cm = 6.67cm = 6.7.cm
v का मान यहाँ पर धनात्मक है। इससे ज्ञात होता है कि प्रतिबिम्ब दर्पण के पीछे बना है।
और प्रतिबिम्ब आभासी छोटा व सीधा बनेगा।
\(\mathrm{m}\) = \(-\frac{\mathrm{v}}{\mathrm{u}}\) = \(\frac{\mathrm{h}^{\prime}}{\mathrm{h}}\) का उपयोग करने पर
∴ \(h^{\prime}\) = \(\left(-\frac{v}{u}\right) \times h\)
अब आवर्धन \(\mathrm{h}^{\prime}\) = \(\left(-\frac{20 / 3}{-12}\right) \times 4.5\)

मान रखने पर = \(\frac{20}{3}\) \(\times\) \( \frac{1}{12}\) \(\times\)  \(\frac{9}{2}\)= \(+2.5 \mathrm{~cm}\)
= \(\frac{20}{3}\) \(\times\) \(\frac{1}{12}\) \(\times\) \( \frac{9}{2}\) = \(+2.5 \mathrm{~cm}\)
अतः प्रतिबिम्ब की साइज h’ = + 2.5 cm
आवर्धन
\(\mathrm{m}\) = \(\frac{\mathrm{h}^{\prime}}{\mathrm{h}}\) = \(\frac{2.5}{4.5}\) = \(\frac{5}{9}\)
जब सुई को दर्पण से दूर ले जाते हैं तब प्रतिबिम्ब फोकस की ओर पास आता है, लेकिन फोकस तक और आकार में छोटा और छोटा होता जाता है। अर्थात् जैसे u → ∞ v → f (परन्तु फोकस से आगे कभी नहीं बढ़ता) जबकि m → 0

प्रश्न 9.3.
कोई टैंक 12.5 cm ऊँचाई तक जल से भरा है। किसी सूक्ष्मदर्शी द्वारा बीकर की तली पर पड़ी किसी सुई की आभासी गहराई 9.4 cm मापी जाती है। जल का अपवर्तनांक क्या है? बीकर में उसी ऊँचाई तक जल के स्थान पर किसी 1.63 अपवर्तनांक के अन्य द्रव से प्रतिस्थापन करने पर सुई को पुनः फोकसित करने के लिए सूक्ष्मदर्शी को कितना ऊपर / नीचे ले जाना होगा?
उत्तर:
स्थिति I. जब टैंक पानी से भरा हो:
वास्तविक गहराई = 12.5 cm
आभासी गहराई = 9.4 cm
पानी का अपवर्तनांक= n = ?

= \(\frac{12.5}{9.4}\) = \(1.33\)
स्थिति II. जब टैंक को द्रव से भरा जाता है:
द्रव का अपवर्तनांक= n = 1.63
वास्तविक गहराई = 12.5 cm
आभासी गहराई = ?
∴ द्रव का अपवर्तनांक = 1.63

∴ आभासी गहराई = \(\frac{12.5}{1.63}\) = 7.67cm
अतः वह दूरी जिससे सूक्ष्मदर्शी को ऊपर चलाना है,
= 9.4 – 7.67
= 1.73 cm
= 1.70 cm

प्रश्न 9.4.
चित्र (a) तथा (b) में किसी आपतित किरण का अपवर्तन दर्शाया गया है जो वायु में क्रमशः काँच वायु तथा जल-वायु अंतरापृष्ठ के अभिलंब से 60° का कोण बनाती है। उस आपतित किरण का अपवर्तन कोण ज्ञात कीजिए, जो जल में जल-काँच अंतरापृष्ठ के अभिलंब से 45° का कोण बनाती है [ चित्र (c ) ] |

उत्तर:
चित्र (a) से:
आपतन कोण = i = 60°
अपवर्तन कोण= r = 35°
ang = वायु की अपेक्षा काँच का अपवर्तनांक = ?
सम्बन्ध
\({ }_{\mathrm{a}} \mathrm{n}_{\mathrm{g}}\)= \(\frac{\sin i}{\sin r}\) = \(\frac{\sin 60^{\circ}}{\sin 35^{\circ}}\)
\(\frac{0.8660}{0.5736}\) = \(1.51\)
चित्र (b) से:
हम जानते हैं:
i = 60°, r = 47°
anw = वायु की अपेक्षा पानी का अपवर्तनांक = ?
हम जानते हैं-

चित्र (c) से:
आपतन कोण = i = 45°
अपवर्तन कोण = r = ?
wng = पानी की अपेक्षा काँच का अपवर्तनांक
हम जानते हैं:

प्रश्न 9.5.
जल से भरे 80 cm गहराई के किसी टैंक की तली पर कोई छोटा बल्ब रखा गया है। जल के पृष्ठ का वह क्षेत्र ज्ञात कीजिए जिससे बल्ब का प्रकाश निर्गत हो सकता है जल का अपवर्तनांक 1.33 है। (बल्ब को बिंदु प्रकाश स्रोत मानिए । )
उत्तर:
माना प्रकाश स्रोत 0 पानी के पृष्ठ से 80 cm नीचे है। अर्थात् चित्र
\(\mathrm{OA}\) = \(80 \mathrm{~cm}\) = \(\frac{80}{100} \mathrm{~m}\)
anw = 1.33
O से उत्सर्जित प्रकाश किरण केवल वायु में अपवर्तित होती है, यदि आपतन कोण क्रान्तिक Ic से छोटा है, तब प्रकाश पानी के पृष्ठ के साथ वायु में अपवर्तित नहीं होगा, परन्तु यह वायु-पानी के अन्तरापृष्ठ पर संस्पर्श करेगा। इस प्रकार प्रकाश शंकु के शिरोबिन्दु कोण, जो 2Ic है, से आता प्रतीत होगा। यदि पानी वायु अन्तरापृष्ठ पर आपतन कोण Ic से अधिक है, तब प्रकाश किरण पूर्ण आन्तरिक परावर्तित होगी।

हम जानते हैं:
\(\sin \mathbf{I}_{\mathrm{C}}\) = \( \frac{1}{{ }_a n_w} \)
⇒ \(\sin \mathbf{I}_{\mathrm{C}}\) = \(\frac{1}{{ }_a n_w}\)
\(\sin \mathbf{I}_{\mathrm{C}}\) = \(\sin ^{-1}\left(\frac{1}{1.33}\right)\) =\(\sin ^{-1}(0.75)\)
Ic = 48.6°
अब
tan Ic = \(\frac{\mathrm{AB}}{\mathrm{OA}}\)
या
AB = OA tan Ic
\(\frac{80}{100}\) \(\times\) \(\tan 48.6^{\circ}\) = \(\frac{80}{100}\) \(\times\) 1.1345
= 0.907m = 90.7 cm
∴ पानी के उस पृष्ठ का क्षेत्रफल जिसमें से प्रकाश निकलेगा
= πr² = 3.14 x (0.907)²
= 3.14 x 0.823
= 2.584m² = 2.6m²

प्रश्न 9.6.
कोई प्रिज्म अज्ञात अपवर्तनांक के कांच का बना है। कोई समांतर प्रकाश-पुंज इस प्रिज्म के किसी फलक पर आपतित होता है। प्रिज्म का न्यूनतम विचलन कोण 40° मापा गया। प्रिज्म के पदार्थ का अपवर्तनांक क्या है? प्रिज्म का अपवर्तन कोण 60° है। यदि प्रिज्म को जल (अपवर्तनांक 1.33) में रख दिया जाए तो प्रकाश के समांतर पुंज के लिए नए न्यूनतम विचलन कोण का परिकलन कीजिए।
उत्तर:
दिया गया है:

प्रश्न 9.7.
अपवर्तनांक 1.55 के काँच से दोनों फलकों की समान वक्रता त्रिज्या के उभयोत्तल लेन्स निर्मित करने हैं। यदि 20 cm फोकस दूरी के लेन्स निर्मित करने हैं तो अपेक्षित वक्रता त्रिज्या क्या होगी?
उत्तर:
दिया गया है:
n = 1.55, R1 = R और R2 = R (उभयोत्तल के लिए)
f = + 20 cm
हम जानते हैं:
\( \frac{1}{f}\) = \( (\mathrm{n}-1)\) \(\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
⇒ \( \frac{1}{20}\) = \( (\mathrm{5}-1)\) \( \left(\frac{1}{R}+\frac{1}{R}\right)\)
⇒ \(\frac{1}{20}\) = \(0.55\) × \( \frac{2}{R}\)
⇒ R = 0.55 x 2 x 20
= 0.55 x 40
∴ R = 22 cm
∴ अपेक्षित वक्रता त्रिज्या R = 22cm

प्रश्न 9.8.
कोई प्रकाश-पुंज किसी बिंदु P पर अभिसरित होता है। कोई लेन्स इस अभिसारी पुंज के पथ में बिंदु P से 12 cm दूर रखा जाता है। यदि यह (a) 20 cm फोकस दूरी का उत्तल लेन्स है, (b) 16 cm फोकस दूरी का अवतल लेन्स है, तो प्रकाश-पुंज किस बिंदु पर अभिसरित होगा?
उत्तर:
इस समस्या में लेन्स के RHS की ओर बिन्दु एक काल्पनिक वस्तु की तरह कार्य करता है।
u = + 12 cm, v = ?
(a) उत्तल लेन्स के लिए:
f = + 20 cm

सूत्र \(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{v}}\) – \(\frac{1}{\mathrm{u}}\) का उपयोग करने पर
या
\(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\) + \(\frac{1}{\mathrm{u}}\)
मान रखने पर
\(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{20}}\) + \(\frac{1}{\mathrm{12}}\) = \(\frac{3+5}{60}\)
⇒ \(\frac{1}{\mathrm{v}}\) = \(\frac{8}{\mathrm{60}}\) = \(\frac{2}{\mathrm{15}}\)
या V = 15/2
= 7.5 cm

प्रतिबिम्ब वास्तविक है और लेन्स से R.HS की तरफ 7.5 cm पर स्थित है।
(b) अवतल लेन्स के लिए:
f= – 16 cm, u = + 12 cm
V = ?

सूत्र \(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{v}}\) – \(\frac{1}{\mathrm{u}}\) का उपयोग करके,
हम \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\) + \(\frac{1}{\mathrm{u}}\)
या \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{16}}\) + \(\frac{1}{\mathrm{12}}\) = \(\frac{-3+4}{48}\)
या \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{48}}\)
प्रतिबिम्ब वास्तविक बनेगा जो कि लेन्स के दाहिनी तरफ 48 cm दूरी पर बनेगा।

प्रश्न 9.9.
3.0 cm ऊँची कोई बिंब 21 cm फोकस दूरी के अवतल लेन्स के सामने 14 cm दूरी पर रखी है लेन्स द्वारा निर्मित प्रतिबिंब का वर्णन कीजिए क्या होता है जब बिंब लेन्स से दूर हटती जाती है?
उत्तर:
दिया गया है:
वस्तु का आकार = h = 3.0cm
अवतल लेन्स वस्तु की दूरी = u = – 14 cm
अवतल लेन्स की फोकस दूरी = f =
प्रतिबिम्ब की दूरी = ?
प्रतिबिम्ब का आकार = h’ = ?
(i) सम्बन्ध = का उपयोग करने पर

प्रतिबिम्ब काल्पनिक और सीधा बनेगा और लेन्स से 8.4 cm की दूरी पर वस्तु की तरफ ही बनेगा।
हम जानते हैं:
आवर्धन
लेकिन

अतः प्रतिबिम्ब आकार में छोटा आभासी व सीधा बनेगा।

(ii) जब u → ∞ तब v = f लेकिन f से आगे नहीं जाता जबकि
m = v/u = 0
जब बिम्ब (वस्तु) लेन्स से दूर हटता है।
माना u = f = -21 cm
तब \(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{v}}\) – \(\frac{1}{\mathrm{u}}\)
या \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\) + \(\frac{1}{\mathrm{u}}\)
\(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{21}}\) – \(\frac{1}{\mathrm{21}}\) = \(\frac{-2}{\mathrm{21}}\)
तब v = \(\frac{-21}{\mathrm{2}}\) = -10.5 cm
परन्तु अनन्त पर नहीं बनेगा।

प्रश्न 9.10.
किसी 30 cm फोकस दूरी के उत्तल लेन्स के संपर्क में रखे 20 cm फोकस दूरी के अवतल लेन्स के संयोजन से बने संयुक्त लेन्स (निकाय) की फोकस दूरी क्या है? यह तंत्र अभिसारी लेन्स है अथवा अपसारी? लेन्सों की मोटाई की उपेक्षा कीजिए।
उत्तर:
दिया गया है:
उत्तल लेन्स की फोकस दूरी = f = + 30 cm
अवतल लेन्स की फोकस दूरी = f2 = – 20cm
माना दोनों लेन्सों के संयोजन की फोकस दूरी = f = ?
हम जानते हैं:
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{f1}}\) + \(\frac{1}{\mathrm{f2}}\)
= \(\frac{1}{\mathrm{30}}\) + \(\frac{1}{\mathrm{-20}}\)
= \(\frac{1}{\mathrm{30}}\) – \(\frac{1}{\mathrm{20}}\) = \(\frac{2-3}{60}\)
\(\frac{1}{\mathrm{f}}\) = \(\frac{-1}{\mathrm{60}}\)
या
= – 60 cm
चूँकि दोनों लेन्सों के संयोजन की फोकस दूरी ऋणात्मक है। अतः संयोजन एक अपसारी लेन्स की तरह व्यवहार करता है अर्थात् अवतल लेन्स की तरह व्यवहार करता है।

प्रश्न 9.11.
किसी संयुक्त सूक्ष्मदर्शी में 2.0cm फोकस दूरी का अभिदृश्यक लेन्स तथा 6.25 cm फोकस दूरी का नेत्रिका लेन्स एक-दूसरे से 15 cm दूरी पर लगे हैं। किसी बिंब को अभिदृश्यक से कितनी दूरी पर रखा जाए कि अंतिम प्रतिबिंब (a) स्पष्ट दर्शन की अल्पतम दूरी (25 cm) तथा (b) अनंत पर बने? दोनों स्थितियों में सूक्ष्मदर्शी की आवर्धन क्षमता ज्ञात कीजिए।

हल दिया गया है:
fo = 2 cm, fc = 6.25 cm
L = 15 cm, D = 25 cm
(a) vc = – 25 cm, uc = ?
लेन्स सूत्र से

(b) जब अन्तिम प्रतिबिम्ब अनन्त पर बनता है:
यहाँ
L = Vo + fe
ue = fe
Vo = L – fe
= 15 – 6.25
Ve = ∞
Vo = + 8.75 cm
\(\frac{1}{f_0}\) = \(\frac{1}{v_o}\) – \(\frac{1}{u_o}\)
\(\frac{1}{u_o}\) = \(\frac{1}{v_o}\) – \(\frac{1}{f_o}\) = \(\frac{1}{8.75}\) – \(\frac{1}{2}\) = \(\frac{100}{875}\) – \(\frac{1}{2}\)
\(\frac{1}{u_o}\) = \(\frac{200-875}{1750}\) = \(\frac{-675}{1750}\)
\(\frac{-1750}{675}\) = – 2.59cm
∴ u0 = 2.59 cm
आवर्धन क्षमता m = \(\frac{-v_0}{u_o}\) \(\left[\frac{D}{f_e}\right]\)
= \(\frac{-8.75}{2.59}\) x \(\frac{25}{6.25}\) = \(\frac{-875}{259}\) x 4
m = – 13.5 = | 13.5 |
= 13.5

प्रश्न 9.12.
25 cm के सामान्य निकट बिंदु का कोई व्यक्ति ऐसे संयुक्त सूक्ष्मदर्शी जिसका अभिदृश्यक 8.0mm फोकस दूरी तथा नेत्रिका 2.5 cm फोकस दूरी की है, का उपयोग करके अभिदृश्य से 9.0mm दूरी पर रखे बिंब को सुस्पष्ट फोकसित कर लेता है। दोनों लेन्सों के बीच पृथक्कन दूरी क्या है? सूक्ष्मदर्शी की आवर्धन क्षमता क्या है?
उत्तर:
दिया गया है:
D = 25 cm
अभिदृश्यक लेन्स की फोकस दूरी = f = 8.0mm
∴ fo = 0.8cm
नेत्रक की फोकस दूरी fc = 2.5 cm
u0 = – 9.0mm = – 0.9cm
दोनों लेन्सों के बीच की दूरी = L = ?
m = ?
नेत्रक के लिए लेन्स सूत्र:

प्रश्न 9.13.
किसी छोटी दूरबीन के अभिदृश्यक की फोकस दूरी 144 cm तथा नेत्रिका की फोकस दूरी 6.0 cm है। दूरबीन की आवर्धन क्षमता कितनी है? अभिदृश्यक तथा नेत्रिका के बीच पृथक्कन दूरी क्या है?
उत्तर:
दिया गया है:
दूरदर्शी के अभिदृश्यक की फोकस दूरी = fo
∴fo = 144 cm.
दूरदर्शी के नेत्रक की फोकस दूरी fc = 2.5 cm
u0 = – 9.0 mm = – 0.9 cm
दूरदर्शी की आवर्धन क्षमता = m = ?
अभिदृश्यक और नेत्रक की बीच की दूरी = L = ?
हम जानते हैं:
दूरबीन की आवर्धन क्षमता = m = -f0/fc
m = – 144/6
= -24
= L = f0 + fc
= 144 + 6 = 150 cm

प्रश्न 9.14.
(a) किसी वेधशाला की विशाल दूरबीन के अभिदृश्यक की फोकस दूरी 15m है। यदि 1.0cm फोकस दूरी की नेत्रिका प्रयुक्त की गयी है, तो दूरबीन का कोणीय आवर्धन क्या है?
(b) यदि इस दूरबीन का उपयोग चन्द्रमां का अवलोकन करने में किया जाए तो अभिदृश्यक लेन्स द्वारा निर्मित चन्द्रमा के प्रतिबिंब का व्यास क्या है? चन्द्रमा का व्यास 3.48 x 10⁶m तथा चन्द्रमा की कक्षा की त्रिज्या 3.8 x 10⁸ m है।
उत्तर:
दिया गया है:
दूरदर्शक के अभिदृश्यक की फोकस दूरी = fo = 15 m
नेत्रक की फोकस दूरी = fc = 1.0cm
= 10² m

प्रश्न 9.15.
दर्पण- सूत्र का उपयोग यह व्युत्पन्न करने के लिए कीजिए कि
(a) किसी अवतल दर्पण के f तथा 25 के बीच रखे बिंब का वास्तविक प्रतिबिंब 25 से दूर बनता है।
(b) उत्तल दर्पण द्वारा सदैव आभासी प्रतिबिंब बनता है जो बिंब की स्थिति पर निर्भर नहीं करता ।
(c) उत्तल दर्पण द्वारा सदैव आकार में छोटा प्रतिबिंब, दर्पण के ध्रुव व फोकस के बीच बनता है।
(d) अवतल दर्पण के ध्रुव तथा फोकस के बीच रखे बिंब का आभासी तथा बड़ा प्रतिबिंब बनता है।
(नोट: यह अभ्यास आपकी बीजगणितीय विधि द्वारा उन प्रतिबिंबों के गुण व्युत्पन्न करने में सहायता करेगा जिन्हें हम किरण आरेखों द्वारा प्राप्त करते हैं।)
उत्तर:
(a)
\(\frac{1}{v}\) + \(\frac{1}{u}\) = \(\frac{1}{f}\)(अवतल दर्पण के सूत्र से )
या
\(\frac{1}{v}\) = \(\frac{1}{f}\) – \(\frac{1}{u}\)
f < 0 ( अवतल दर्पण)
u < 0 (वस्तु बायीं तरफ रखी है)
2f < u< f के लिए या \(\frac{1}{2 f}\) > \(\frac{1}{u}\) > \(\frac{1}{f}\)
या \(\frac{-1}{2f}\) < \(\frac{-1}{u}\) < \(\frac{-1}{f}\)
या \(\frac{1}{f}\) – \(\frac{-1}{2f}\) < \(\frac{1}{f}\) – \(\frac{1}{u}\) < \(\frac{1}{f}\) – \(\frac{1}{f}\)
जिससे \(\frac{1}{2f}\) < \(\frac{1}{v}\) > 0
अर्थात् v ऋणात्मक होगा तथा प्रतिबिम्ब वास्तविक व 2f से आगे बनेगा।
(b) उत्तल दर्पण के दर्पण सूत्र से
\(\frac{1}{u}\) + \(\frac{1}{v}\) = \(\frac{1}{f}\)
यहाँ u < 0 तथा f > 0
अर्थात् सदैव कम होने से प्रतिबिम्ब दर्पण के दाईं ओर व आभासी होगा।

(c) ∵ आवर्धन m = \(\frac{f}{f-u}\)
∵ उत्तल दर्पण के लिए u < 0 तथा f < 0 अतः f – u > f
जिससे m < 1 अर्थात् प्रतिबिम्ब वस्तु से छोटा होगा।

(d) अवतल दर्पण के लिए u < 0 तथा f < 0 प्रश्नानुसार
f < u < 0 = \(\frac{1}{f}\) – \(\frac{1}{u}\) > 0
लेकिन दर्पण सूत्र \(\frac{1}{v}\) = \(\frac{1}{f}\) – \(\frac{1}{u}\) से
\(\frac{1}{v}\) > 0, जिसमें v धनात्मक तथा ध्रुव के दाईं ओर स्थित है।
प्रतिबिम्ब आभासी है और आवर्धन
m = \(\frac{-v}{u}\) = \(\frac{v}{| u |}\)
परन्तु \(\frac{1}{v}\) < \(\frac{1}{| u |}\) या v > | u |
अर्थात् धनात्मक है तथा m > 1 जिससे प्रतिबिम्ब बड़ा बनता है।

प्रश्न 9.16.
किसी मेज के ऊपरी पृष्ठ पर जड़ी एक छोटी पिन को 50 cm ऊँचाई से देखा जाता है। 15 cm मोटे आयताकार काँच के गुटके को मेज के पृष्ठ के समांतर पिन व नेत्र के बीच रखकर उसी बिंदु से देखने पर पिन नेत्र से कितनी दूर दिखाई देगी? काँच का अपवर्तनांक 1.5 है। क्या उत्तर गुटके की अवस्थिति पर निर्भर करता है?
उत्तर:
दिया गया है:
काँच की पट्टी की मोटाई = t = 15 cm
काँच का अपवर्तनांक = n = 1.5
पिन की स्थिति में नॉरमल बदलाव = d
d = 1(1 – 1/n) से दिया जाता है।
यहाँ पर t = पिन की वास्तविक गहराई पट्टी की मोटाई
माना पिन की आभासी गहराई = y
अभिलम्ब बदलाव (विस्थापन का मान )t – y = ? = d
n = t/y या y = t/n
∴ d = अभिलम्ब विस्थापन = t – t/n
= t(1 – 1/n)
= 15(1 – 1/1.5) = 15(1 – 2/3)
= 15 × 1/3 = 5cm
अर्थात् पिन 5 cm उठा हुआ प्रतीत होगा।
नहीं, छोटे आपतन कोणों के लिए उत्तर काँच के गुटके की स्थिति पर निर्भर नहीं है।

प्रश्न 9.17.
निम्नलिखित प्रश्नों के उत्तर लिखिए:
(a) निम्न चित्र में अपवर्तनांक 1.68 तंतु काँच से बनी किसी ‘प्रकाश नलिका’ (लाइट पाइप) का अनुप्रस्थ परिच्छेद दर्शाया गया है। नलिका का बाह्य आवरण 1.44 अपवर्तनांक के पदार्थ का बना है। नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण परावर्तन होते हैं, ज्ञात कीजिए।

(b) यदि पाइप पर बाह्य आवरण न हो तो क्या उत्तर होगा?
उत्तर:
(a) sin Ic = n = \(\frac{\sin I}{\sin r}\) = \(\frac{1.44}{1.68}\)
= 0.8571
∴ Ic = sin-1 (0.8571) = 59°
Ic = 590
जब I > Ic अर्थात् I > 59 चूँकि I का मान 590 से 90° के बीच में है। यहाँ पर पूर्ण आन्तरिक परावर्तन होगा और कोण का मान 0° से 31° के बीच में होगा।
∴ rmax = 31°
अब वायु की अपेक्षा काँच तन्तु का अपवर्तनांक sin Imax स्नेल नियम से

या
n = \(\frac{\sin I_{\max }}{\sin r_{\max }}\) = स्नेल नियम से
⇒ 1.68 = \(\frac{\sin I_{\max }}{\sin 31^{\circ}}\)
⇒ sin Imax = 1.68 sin 31°
= 1.68 x 0.515 = 0.8652
Imax = sin-1 (0.8652 ) = 59.9°= 60°
अतः 0 < I < 60° परास में आपतित सभी किरणें पाइप में पूर्ण आन्तरिक परावर्तन में होंगी। (b) यदि पाइप पर कोई बाह्य लेपन नहीं है, तब पाइप के अन्दर अपवर्तन काँच से वायु में होगा- ∴ sinIc = 1/1.68= 0.5952 ∴ Ic = sin-1 (0.5952) Ic = 36.5° अतः पूर्ण आन्तरिक परावर्तन के लिए I > 36.5° होना चाहिए।
अब
I = 90° से r = 36.5° होगा।
∴ sinI/sinr = n = 1.68
∴ rmax = 90° – 36.5° = 53.5°
जो कि Ic से अधिक हैं।
∴ अक्ष 0 से 90° के परास में आपतित सभी किरणें पाइप के अन्दर से पूर्ण आन्तरिक में होंगी।

प्रश्न 9.18.
निम्नलिखित प्रश्नों के उत्तर लिखिए:
(a) आपने सीखा है कि समतल तथा उत्तल दर्पण सदैव आभासी प्रतिबिंब बनाते हैं। क्या ये दर्पण किन्हीं परिस्थितियों में वास्तविक प्रतिबिंब बना सकते हैं? स्पष्ट कीजिए।
(b) हम सदैव कहते हैं कि आभासी प्रतिबिंब को परदे पर केंद्रित नहीं किया जा सकता। यद्यपि जब हम किसी आभासी प्रतिबिंब को देखते हैं तो हम इसे स्वाभाविक रूप में अपनी आँख की स्क्रीन ( अर्थात् रेटिना) पर लाते हैं क्या इसमें कोई विरोधाभास है?
(c) किसी झील के तट पर खड़ा मछुआरा झील के भीतर किसी गोताखोर द्वारा तिरछा देखने पर अपनी वास्तविक लंबाई की तुलना में कैसा प्रतीत होगा-छोटा अथवा लंबा?
(d) क्या तिरछा देखने पर किसी जल के टैंक की आभासी गहराई परिवर्तित हो जाती है? यदि हाँ, तो आभासी गहराई घटती है अथवा बढ़ जाती है?
(e) सामान्य काँच की तुलना में हीरे का अपवर्तनांक काफी अधिक होता है? क्या हीरे को तराशने वालों के लिए इस तथ्य का कोई उपयोग होता है?
उत्तर:
(a) हाँ, किसी समतल अथवा उत्तल दर्पण के पीछे’ किसी बिन्दु पर अभिसरित किरणें दर्पण के सामने परदे पर किसी बिन्दु पर परावर्तित हो जाती हैं। दूसरे शब्दों में कोई समतल दर्पण अथवा उत्तल दर्पण आभासी बिंब के लिए वास्तविक प्रतिबिंब उत्पन्न कर सकता है।

(b) नहीं, कोई विरोधाभास नहीं है। यह इस सत्य के कारण है। कि जब परावर्तित अथवा अपवर्तित किरणें अपसारी होती हैं तो प्रतिबिंब आभासी होता है। अपसारी किरणों को उचित अभिसारी लेन्स की सहायता से परदे पर अभिसरित किया जा सकता है। नेत्र का आभासी लेन्स ठीक यही करता है। यहाँ आभासी प्रतिबिंब लेन्स के लिए बिंब की भाँति कार्य करता है और वास्तविक प्रतिबिंब बनता है।

(c) गोताखोर को, व्यक्ति जो है उससे लम्बा प्रतीत होगा क्योंकि व्यक्ति वायु में है, अतः प्रकाश विरल से सघन माध्यम में चलता है और लम्ब की ओर झुक जाता है जैसा चित्र में दिखाया गया है। अधिक दूरी आता प्रतीत होता है। मछुआरे AB के सिरे B से प्रकाश का आकार BP और BQ पानी वायु अन्तरापृष्ठ से अपवर्तन के पश्चात् अभिलम्ब की और बिन्दु P तथा Q पर झुकने के बाद चालक के B’ से आता प्रतीत होता है। स्पष्टत: AB’ > AB जहां AB’ मछुआरे AB का प्रतिबिम्ब है।

(d) यदि हम पानी से भरे हुए टैंक को तिरछा देखते हैं तो उसकी आभासी गहराई परिवर्तित होगी, इसकी आभासी गहराई वास्तविक गहराई से कम दिखेगी क्योंकि अपवर्तन के कारण उसका पैदा ऊपर उठता हुआ प्रतीत होता है।

(e) हाँ, हीरे का अपवर्तनांक लगभग 2.42 होता है, जो सामान्य काँच के अपवर्तनांक (n = 1.5) से काफी क्रान्तिक कोण लगभग 24 है जो काँच के अधिक होता है हीरे का क्रान्तिक कोण की अपेक्षा काफी कम है। एक हीरे को तराशने वाला इसके ऊपर अधिक परास के आपतन कोण 24° से 90° का लाभ उठाता है। यह सुनिश्चित करने के लिए कि प्रकाश हीरे के पटल पर 24° से अधिक कोण पर आपतित हो. यह पूर्ण आन्तरिक परावर्तन इसके बहुत से पटलों से निकलने से पहले भुगतता है। इससे हीरे में चमकने का प्रभाव उत्पन्न होता है।

प्रश्न 9.19.
किसी कमरे की एक दीवार पर लगे विद्युत बल्ब का किसी बड़े आकार के उत्तल लेन्स द्वारा 3m दूरी पर स्थित सामने की दीवार पर प्रतिबिंब प्राप्त करना है। इसके लिए उत्तल लेन्स की अधिकतम फोकस दूरी क्या होनी चाहिए?
उत्तर:
लेन्स के सूत्र से
\(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\) …………. (I)
दिया गया है:
– u + v = 3 चिन्ह परिपाटी के अनुसार
∴ v = 3 + u …..(ii)
समीकरण (i) से
\(\frac{1}{3+u}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\)
या \(\frac{u-3-u}{(3+u)(u)}\) = \(\frac{1}{f}\)
या f = \(\frac{u^2+3 u}{-3}\)
f के अधिकतम के लिए df/du = 0
∴
या -1/3(u2+3) = 0
या (2u+3) = 0
या u = -3/2
समीकरण (ii) से v = 3 – 3/2 = 3/2
u तथा v का मान समीकरण (i) में रखने पर

∴ इस कार्य के लिए लेन्स की वांछित अधिकतम फोकस दूरी 3/4m अर्थात् fmax = 0.75m
द्वितीय विधि; माना लेन्स की फोकस दूरी है, तो
f = a2-b2/4a
जहाँ पर a = v + u (वस्तु और प्रतिबिम्ब की बीच की दूरी)
b = (v – u) (लेन्स की दोनों स्थितियों के मध्य दूरी)
अधिकतम फोकस दूरी के लिए
∴ fmax = \(\frac{\mathrm{a}^2-0}{4 \mathrm{a}}\) = \(\frac{a^2}{4 a}\) = \(\frac{a}{4}\)
fmax = \(\frac{3}{4}\) = 0.75m
या fmax = 0.75m

प्रश्न 9.20.
किसी परदे को बिंब से 90 cm दूर रखा गया है। परदे पर किसी उत्तल लेन्स द्वारा उसे एक-दूसरे से 20 cm दूर स्थितियों पर रखकर दो प्रतिबिंब बनाए जाते हैं। लेन्स की फोकस दूरी ज्ञात कीजिए।
उत्तर:
दिया गया है:
– u + v = 90
=> v = 90 + u
चिन्ह परिपाटी के अनुसार …..(i)
लेन्स का सूत्र
\(\frac{1}{\mathrm{v}}\) – \(\frac{1}{\mathrm{u}}\) = \(\frac{1}{\mathrm{f}}\)
समीकरण (i) तथा (ii) से

या – 90f = 90u + u
या u2 + 90u + 90f = 0 ……… (iii)
समीकरण (iii) u में द्विघात समीकरण है। माना इस समीकरण के मूल u1 तथा u2 है।
∴ मूलों का योग
u1 + u2 = – 90 …..(iv)
मूलों का गुणनफल
u1u2 = 90f ……(V)
दिया गया है:
U1 – U2 = 20 …..(vi)
समीकरण (iv) तथा (vi) को हल करने पर (जोड़ने पर)
2u1 = – 90 + 20 = -70
⇒ u1 = -70/2 = -35 cm
घटाने पर
2u2 = – 90 – 20 = – 110
या
U2 = -110/2 = -55cm
अब
u1u2 = 90f
(-35) × (-55 ) = 90f
या
f = \(\frac{35 \times 55}{90}\) = 21.4cm
अतः लेन्स की फोकस दूरी 21.4 cm
द्वितीय विधि:
दिया है:
a = 90cm, b = 20

अतः फोकस दूरी f = 21.4 cm

प्रश्न 9.21.
(a) प्रश्न 9.10 के दो लेन्सों के संयोजन की प्रभावी फोकस दूरी उस स्थिति में ज्ञात कीजिए जब उनके मुख्य अक्ष संपाती हैं, तथा ये एक-दूसरे से 8 cm दूरी पर रखे हैं क्या उत्तर आपतित समांतर प्रकाश पुंज की दिशा पर निर्भर करेगा ? क्या इस तंत्र के लिए प्रभावी फोकस दूरी किसी भी रूप में उपयोगी है?
(b) उपरोक्त व्यवस्था (a) में 1.5 cm ऊँचा कोई बिंब उत्तल लेन्स की ओर रखा है। बिंब की उत्तल लेन्स से दूरी 40 cm है। दो लेन्सों के तंत्र द्वारा उत्पन्न आवर्धन तथा प्रतिबिंब का आकार ज्ञात कीजिए।
उत्तर:
(a) (i) माना कि कोई समान्तर प्रकाश पुंज बायीं ओर से पहले उत्तल लेन्स पर आपतित होता है। तब

तथा समान्तर प्रकाश पुंज दो बायीं ओर से (420 – 4 = 416 cm) प्रतीत होता है।
लेन्सों में तंत्र के मध्य बिन्दु की दूर स्थित बिन्दु से अपसरित होता इस प्रकार हम निष्कर्ष निकालते हैं कि उत्तर इस बात पर निर्भर है कि समान्तर किरण पुंज किस दिशा में आपतित है; क्योंकि दोनों स्थितियों में दूरियाँ भिन्न हैं। इस स्थिति में प्रभावी फोकस दूरी का विचार भी उपयोगी नहीं है।

प्रश्न 9.22.
60° अपवर्तन कोण के प्रिज्म के फलक पर किसी प्रकाश किरण को किस कोण पर आपतित कराया जाए कि इसका दूसरे फलक से केवल पूर्ण आंतरिक परावर्तन ही हो? प्रिज्म के पदार्थ का अपवर्तनांक 1.524 है।
उत्तर:
दिया गया है:
प्रिज्म का कोण = A = 60°
प्रिज्म के द्रव्य का अपवर्तनांक= n = 1.524

जब प्रकाश किरण PQ फलक AB पर आपतित होती है तो यह फलक AC पर पूर्ण आन्तरिक परावर्तन होता है और फलक AC पर कोण पर आपतित होगी जो प्रिज्म के पदार्थ के क्रान्तिक कोण के तुल्य है।
अब 60° + 90° – r + 90° i = 180°
या 240° – r – ic = 180°
या r = 60° – ic
अब
sin ic = 1/n = 1/1.524
ic = sin-1(1/1524) = sin-1(0.6562) = 41°
r = 60° – 41° = 19°
स्नेल नियम का प्रयोग करने
n = sini/sinr
∴ sin i = sin 19° x 1.524
= 0.3256 x 1.524
= 0.4962
या i = sin-1 (0.4962 ) = 29.75°
∴ i = 30°

प्रश्न 9.23.
कोई कार्ड शीट जिसे 1mm साइज के वर्गों में विभाजित किया गया है, को 9 cm दूरी पर रखकर किसी आवर्धक लेन्स (9 cm फोकस दूरी का अभिसारी लेन्स) द्वारा उसे नेत्र के निकट रखकर देखा जाता है।
(a) लेन्स द्वारा उत्पन्न आवर्धन (प्रतिबिंब – साइज / वस्तु-साइज) क्या है? आभासी प्रतिबिंब में प्रत्येक वर्ग का क्षेत्रफल क्या है?
(b) लेन्स का कोणीय आवर्धन (आवर्धन क्षमता) क्या है?
(c) क्या (a) में आवर्धन क्षमता (b) में आवर्धन के बराबर है? स्पष्ट कीजिए।
उत्तर:
(a) दिया गया है:
u = – 9 cm.
v = ?
f= 10cm.
लेन्स सूत्र से \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\)से
या \(\frac{1}{v}\) – \(\frac{1}{-9}\) = \(\frac{1}{10}\)
या \(\frac{1}{v}\) + \(\frac{1}{9}\) = \(\frac{1}{10}\)
या \(\frac{1}{v}\) = \(\frac{1}{10}\) – \(\frac{1}{9}\) = \(\frac{9-10}{10 \times 9}\) = \(\frac{-1}{90}\)
या v = – 90cm.
लेन्स में उत्पन्न आवर्धन m = v/-u = -90/90
m = + 10 आभासी प्रतिबिम्ब
आभासी प्रतिबिम्ब में प्रत्येक वर्ग का क्षेत्रफल = 1mm²
अर्थात्
1mm x 1 mm.
चूँकि लेन्स 10 का रैखिक आवर्धन उत्पन्न करता है, अतएव काल्पनिक प्रतिबिम्ब में प्रत्येक वर्ग का आकार (10 x 1 mm) x (10 x 1 mm) प्रतीक होगा।
या A = 100mm 2 = 1 cm2
(b) सुस्पष्ट दृष्टि की न्यूनतम दूरी D = -25cm
∴ m = कोणीय आवर्धन = आवर्धन क्षमता
∴ आवर्धन क्षमता = D/u = -25/-9
= 25/9 = 2.8

(c) नहीं, किसी लेन्स द्वारा आवर्धन तथा किसी प्रकाशिक यंत्र की ..कोणीय आवर्धन (अथवा आवर्धन क्षमता) दो भिन्न अभिधारणाएँ हैं। कोणीय आवर्धन वस्तु के कोणीय आकार (जो कि प्रतिबिम्ब के आवर्धित होने पर प्रतिबिम्ब के कोणीय आकार के बराबर होता है) तथा उस स्थिति में वस्तु के कोणीय आकार ( जबकि उसे निकट बिन्दु 25 cm पर रखा जाता है) का अनुपात होता है, इस प्रकार, आवर्धन का परिमाण होता है तथा आवर्धन क्षमता (v/u) होती है। केवल तब जब प्रतिबिम्ब निकट बिन्दु पर (25/u) = 25 cm पर है तो केवल तभी दोनों राशियाँ समान होती हैं।

प्रश्न 9.24.
(a) अभ्यास 9.23 में लेन्स को चित्र से कितनी दूरी पर रखा जाए ताकि वर्गों को अधिकतम संभव आवर्धन क्षमता के साथ सुस्पष्ट देखा जा सके?
(b) इस उदाहरण में आवर्धन ( प्रतिबिंब साइज / वस्तु-साइज) क्या है?
(c) क्या इस प्रक्रम में आवर्धन, आवर्धन क्षमता के बराबर है? स्पष्ट कीजिए।
उत्तर:
(a) यहाँ, जब काल्पनिक प्रतिबिम्ब सुस्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है तब अधिकतम आवर्धन क्षमता प्राप्त की जा सकती है।
v = – 25 cm, f = + 10cm, u = ?
लेन्स सूत्र से \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\) से
\(\frac{1}{25}\) – \(\frac{1}{u}\) = \(\frac{1}{10}\)
या \(\frac{1}{25}\) – \(\frac{1}{10}\) = \(\frac{1}{u}\)
या \(\frac{-2-5}{50}\) = \(\frac{1}{u}\)
या u = -50/7 = -7.14cm = |7.14| cm

(b) आवर्धन m = v/u = ?
सूत्र m = v/u का उपयोग करने पर
m = v/u
= \(\frac{-25}{-50 / 7}\) = \(\frac{25 \times 7}{50}\) = \(\frac{7}{2}\)
या m = 3.5

(c) आवर्धन क्षमता M = ?
जब वस्तु को इस प्रकार रखा जाये कि प्रतिबिम्ब सुस्पष्ट दृष्टि की न्यूनतम दूरी पर बने
m = 1 + D/f द्वारा दिया जाता है।
m = 1 + 25/10 = 1 + 25 = 3.5
m = \(\frac{D}{|\mathrm{u}|}\) = \(\frac{25}{50 / 7}\) = \(\frac{25 \times 7}{50}\)
m = 3.5
हाँ, इस स्थिति में आवर्धन, आवर्धन क्षमता के तुल्य है, क्योंकि- प्रतिबिम्ब सुस्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है।

प्रश्न 9.25.
अभ्यास 9.24 में वस्तु तथा आवर्धक लेन्स के बीच. कितनी दूरी होनी चाहिए ताकि आभासी प्रतिबिंब में प्रत्येक वर्ग 6.25 mm 2 क्षेत्रफल का प्रतीत हो? क्या आप आवर्धक लेन्स को नेत्र के अत्यधिक निकट रखकर इन वर्गों को सुस्पष्ट देख सकेंगे?
[नोट- अभ्यास 9.23 से 9.25 आपको निरपेक्ष साइज में आवर्धन तथा किसी यंत्र की आवर्धन क्षमता (कोणीय आवर्धन) के बीच अंतर को स्पष्टतः समझने में सहायता करेंगे।]
हल
दिया गया है:
वस्तु का क्षेत्रफल = 1mm²
∴ h = वस्तु का आकार = 1mm
प्रतिबिम्ब का क्षेत्रफल = 6.25 mm²
∴ h’ = प्रतिबिम्ब का आकार
= √6.25 = 2.5mm

लेकिन 2v = 5u
∴ 2v = 5 × (-6)
v = -30/2 = -15 cm
आभासी प्रतिबिम्ब सामान्य निकट बिन्दु (25 cm) से भी पास बनता है तथा इसे नेत्र स्पष्ट नहीं देख सकता।

प्रश्न 9.26.
निम्नलिखित प्रश्नों के उत्तर दीजिए:
(a) किसी वस्तु द्वारा नेत्र पर अंतरित कोण आवर्धक लेन्स द्वारा उत्पन्न आभासी प्रतिबिंब द्वारा नेत्र पर अंतरित कोण के बराबर होता है। तब फिर किन अर्थों में कोई आवर्धक लेन्स कोणीय आवर्धन प्रदान करता है?
(b) किसी आवर्धक लेन्स से देखते समय प्रेक्षक अपने नेत्र को लेन्स से अत्यधिक सटाकर रखता है। यदि प्रेक्षक अपने नेत्र को पीछे ले जाए तो क्या कोणीय आवर्धन परिवर्तित हो जाएगा ?
(c) किसी सरल सूक्ष्मदर्शी की आवर्धन क्षमता उसकी फोकस दूरी के व्युत्क्रमानुपाती होती है तब हमें अधिकाधिक आवर्धन क्षमता प्राप्त करने के लिए कम से कम फोकस दूरी के उत्तल लेन्स का उपयोग करने से कौन रोकता है?
(d) किसी संयुक्त सूक्ष्मदर्शी के अभिदृश्यक लेन्स तथा नेत्रिका लेन्स दोनों ही की फोकस दूरी कम क्यों होनी चाहिए ?
(e) संयुक्त सूक्ष्मदर्शी द्वारा देखते समय सर्वोत्तम दर्शन के लिए हमारे नेत्र, नेत्रिका पर स्थित न होकर उससे कुछ दूरी पर होने चाहिए। क्यों ? नेत्र तथा नेत्रिका के बीच की यह अल्प दूरी कितनी होनी चाहिए?
उत्तर:
(a) यदि प्रतिबिंब का निरपेक्ष आकार वस्तु के आकार से बड़ा भी है, तो भी प्रतिबिंब का कोणीय आकार वस्तु के कोणीय आकार के समान होता है। कोई आवर्धक लेन्स हमारी इस रूप में सहायता करता है : यदि आवर्धक लेन्स नहीं है तो वस्तु 25 cm से कम दूरी पर नहीं रखी जा सकती; आवर्धक लेन्स होने पर हम वस्तु को अपेक्षाकृत बहुत निकट रख सकते हैं। वस्तु निकट हो तो उसका कोणीय आकार 25 cm दूर रखने की तुलना में कहीं अधिक होता है। हमारे कोणीय आवर्धन पाने या उपलब्ध करने का यही अर्थ है।

(b) हाँ, यह थोड़ा कम होता है, क्योंकि नेत्र पर अंतरित कोण लेन्स पर अंतरित कोण से थोड़ा छोटा होता है। यदि प्रतिबिंब बहुत दूर हो तो यह प्रभाव नगण्य होता है (जब नेत्र को लेन्स से पृथक् रखते हैं, तो प्रथम वस्तु द्वारा नेत्र पर अंतरित कोण तथा इसके प्रतिबिंब द्वारा नेत्र पर अंतरित कोण समान नहीं होते।)

(c) प्रथम, अत्यंत छोटे फोकस दूरी के लेन्सों की घिसाई आसान नहीं है। इससे अधिक महत्त्वपूर्ण बात है कि यदि आप फोकस दूरी कम करते हैं तो इससे विपथन ( गोलीय तथा वर्ण) बढ़ जाता है। अतः व्यवहार में, आप किसी सरल उत्तल लेन्स से 3 या अधिक की आवर्धन क्षमता नहीं प्राप्त कर सकते हैं। तथापि, किसी विपथन संशोधित लेन्स प्रणाली के उपयोग से इस सीमा को 10 या इसके सन्निकट कारक से बढ़ा सकते हैं।

(d) किसी नेत्रिका का कोणीय आवर्धन [ (25/fc) +1] (fecm में) होता है जिसके मान में के घटने पर वृद्धि होती है। पुनः अभिदृश्यक का आवर्धन से प्राप्त होता है जो अधिक होता है यदि |u0||f0| से कुछ अधिक हो सूक्ष्मदर्शी का उपयोग अति निकट की वस्तुओं को देखने के लिए किया जाता है। अतः |u0| कम होता है और तदनुसार भी

(e) नेत्रिका के अभिदृश्यक के प्रतिबिंब को निर्गम द्वारक’ कहते हैं। वस्तु से आने वाली सभी किरणें अभिदृश्यक से अपवर्तन के पश्चात् निर्गम द्वारक से गुजरती हैं। अतः हमारे नेत्र से देखने के लिए यह एक आदर्श स्थिति है। यदि हम अपने नेत्र को नेत्रिका के बहुत ही निकट रखें तो त्रिका बहुत अधिक प्रकाश का अधिग्रहण नहीं कर पाएगी तथा दृष्टि- क्षेत्र भी घट जाएगा। यदि हम अपने नेत्र को निर्गम द्वारक पर रखें तथा हमारे नेत्र की पुतली का क्षेत्रफल निर्गम द्वारक के क्षेत्रफल से अधिक या समान हो तो हमारे नेत्र अभिदृश्यक से अपवर्तित सभी किरणों को अभिगृहीत कर लेंगे। निर्गम द्वारक का सटीक स्थान सामान्यतः अभिदृश्यक एवं नेत्रिका के अंतराल पर निर्भर करता है जब हम किसी सूक्ष्मदर्शी से, इसके एक सिरे पर अपने नेत्र को लगाकर देखते हैं तो नेत्र एवं नेत्रिका के मध्य आदर्श दूरी यंत्र के डिजाइन में अंतर्निहित होती है।

प्रश्न 9.27.
1.25 cm फोकस दूरी का अभिदृश्यक तथा 5 cm फोकस दूरी की नेत्रिका का उपयोग करके वांछित कोणीय आवर्धन (आवर्धन क्षमता ) 30 X होता है। आप संयुक्त सूक्ष्मदर्शी का समायोजन कैसे करेंगे?
उत्तर:
दिया गया है:
अभिदृश्यक की फोकस दूरी f0 = 1.25cm
नेत्रिका की फोकस दूरी = fc = 5 cm
कोणीय आवर्धन ( आवर्धन क्षमता) = m = 30
मान लीजिए कि सूक्ष्मदर्शी सामान्य उपयोग में है अर्थात् प्रतिबिम्ब 25 cm पर है। नेत्रिका का कोणीय आवर्धन
(m) = (1 + D/fe) = (1 + 25) = 6
माना अभिदृश्यक का कोणीय आवर्धन = mo
∴ m = m x me
m0 = m/me = 30/6 = 5
∴ mo = \(\frac{v_0}{-u_0}\)
5 = \(\frac{v_0}{-u_0}\)
या
Vo = – 5 uo
अभिदृश्यक के लिए लेन्स सूत्र का उपयोग करने पर
\(\frac{1}{v_0}\) – \(\frac{1}{u_o}\) = \(\frac{1}{f_o}\)
\(-\frac{1}{5 u_o}\) – \(\frac{1}{u_0}\) = \(\frac{1}{1.25}\)
या \(-\frac{6}{5 u_o}\) = \(\frac{100}{125}\) = \(\frac{4}{5}\)
या \(-\frac{30}{20}\) = -1.5cm
अर्थात् बिम्ब को अभिदृश्यक के सामने 1.5 cm दूरी पर रखना चाहिए।
∵ Vo = – 5 uo
= – 5 (- 1.5) = 7.5 cm
नेत्रक के लिए लेन्स सूत्र:
ve = – 25 cm, f = 5 cm
\(\frac{1}{v_e}\) – \(\frac{1}{u_e}\) = \(\frac{1}{f_c}\)
या \(\frac{1}{u_e}\) = \(\frac{1}{v_e}\) – \(\frac{1}{f_c}\)
= \(-\frac{1}{25}\) – \(-\frac{1}{5}\) = \(-\frac{6}{25}\)
∴ uc = \(-\frac{6}{25}\)
= -4.17 cm
∴ यौगिक सूक्ष्मदर्शी को इस प्रकार व्यवस्थित करना चाहिए कि अभिदृश्यक और नेत्र के बीच की दूरी
= |Vo| + |ue |
= 7.5 + 4.17
= 11.67 cm
अभिदृश्यक एवं नेत्रिका के बीच दूरी 11.67 cm होनी चाहिए। अपेक्षित आवर्धन प्राप्त करने के लिए वस्तु को अभिदृश्यक से 1.5 cm दूर रखना होगा।

प्रश्न 9.28.
किसी दूरबीन के अभिदृश्यक की फोकस दूरी 140 cm तथा नेत्रिका की फोकस दूरी 5.0 cm है। दूर की वस्तुओं को देखने के लिए दूरबीन की आवर्धन क्षमता क्या होगी जब:
(a) दूरबीन का समायोजन सामान्य है (अर्थात् अंतिम प्रतिबिंब अनंत पर बनता है)।
(b) अंतिम प्रतिबिंब स्पष्ट दर्शन की अल्पतम दूरी (25 cm) पर बनता है।
उत्तर:
दिया गया है:
अभिदृश्यक की फोकस दूरी = fo
∴ fo = 140cm
नेत्रिका की फोकस दूरी = fc
∴ fc = 5.0cm
(a) आवर्धन क्षमता का मान दूरदर्शी की सामान्य अवस्था में अर्थात् अन्तिम प्रतिबिम्ब अनन्त पर बनता है।
m = fo/|fc| – 140 = 28
(b) जब प्रतिबिम्ब सुस्पष्ट दर्शन की अल्पतम दूरी पर बनता है। तब आवर्धन क्षमता का मान
m = \(\frac{f_o}{\left|f_e\right|}\) = \(\left(1+\frac{f_e}{D}\right)\)
= \(\frac{140}{5}\) \(\left(1+\frac{5}{25}\right)\)
28 × 6/5 = 33.6

प्रश्न 9.29.
(a) अभ्यास 9.28 ( a) में वर्णित दूरबीन के लिए अभिदृश्यकलेन्स तथा नेत्रिका के बीच पृथक्कन दूरी क्या है?
(b) यदि इस दूरबीन का उपयोग 3 km दूर स्थित 100m ऊँची मीनार को देखने के लिए किया जाता है तो अभिदृश्यक द्वारा बने मीनार के प्रतिबिंब की ऊँचाई क्या है?
(c) यदि अंतिम प्रतिबिंब 25 cm दूर बनता है तो अंतिम प्रतिबिंब में मीनार की ऊँचाई क्या है?
उत्तर:
(a) अभिदृश्यकलेन्स तथा नेत्रिका के बीच पृथक्कन दूरी
L = fc + fe
= 140 + 5 = 145 cm
(b) माना कि 100 in ऊँची मीनार AB द्वारा प्रेक्षण बिन्दु o पर बनाया गया कोण θ है।

h = 100m
b = 3 km = 3,000m
θ = h/b सम्बन्ध को प्रयोग करने पर
θ = 100/3,000 = 1/30 रेडियन ……………. (i)
माना अभिदृश्यक द्वारा निर्मित प्रतिबिम्ब की ऊँचाई x है।
∴ अभिदृश्यक द्वारा निर्मित प्रतिबिम्ब से बनाया कोण
= x/fo
= -x/140 ……………. (ii)
समीकरण (i) व (ii) को बराबर करने पर
1/30 = x/140
⇒ x = 140/30 = 14/3cm = 4.7cm
(c) नेत्रिका का आवर्धन me है।
me= 1 + D/fe
= 1 + 25/5 = 1 + 5 = 6
हम जानते हैं:
me = h/h =
∴ अन्तिम प्रतिबिम्ब की ऊँचाई = mc x x
= 6 x 14/3 = 28 cm

प्रश्न 9.30.
किसी कैसेग्रेन दूरबीन में चित्र में दर्शाए अनुसार दो दर्पणों का प्रयोग किया गया है। इस दूरबीन में दोनों दर्पण एक-दूसरे से 20mm दूर रखे गए हैं। यदि बड़े दर्पण की वक्रता त्रिज्या 220 mm हो तथा छोटे दर्पण की वक्रता त्रिज्या 140mm हो तो अनंत पर रखे किसी बिंब का अंतिम प्रतिबिंब कहाँ बनेगा?

उत्तर:
अवतल दर्पण की वक्रता त्रिज्या (अर्थात् बड़े दर्पण की) = R1
∴ R1 = – 220mm = -22cm
उत्तल दर्पण की वक्रता त्रिज्या (अर्थात् छोटे दर्पण की) = R2
∴ R2 = 140mm = 14 cm
यदि बड़े और छोटे दर्पणों की फोकस दूरी क्रमशः f1 तथा f2 हो तब
f1 = R1/2 = -22/2 = -11cm
और
f2 = R2/2 = 14/2 = 7cm.
बड़े दर्पण द्वारा बनाया गया प्रतिबिम्ब छोटे दर्पण के लिए आभासी बिम्ब का कार्य करता है।
दर्पणों के बीच पृथक्कीकरण d = 20 mm
= 2 cm.
चिन्ह परिपाटी के अनुसार यहाँ पर f1, R को vc लिया गया है।
∵ वस्तु अनन्त पर है ∴ u = ∞
जैसा कि रेखाचित्र में दिखाया गया है। वस्तु का अन्तिम प्रतिबिम्ब अभिदृश्यक दर्पण के पीछे बनता है, जिसे हम नेत्रक में से देखते हैं। अनन्त पर स्थित वस्तु से आती किरणें अभिदृश्यक के मुख्य फोकस पर मिलने को होती हैं, लेकिन इससे पहले ही कम फोकस दूरी का अवतल दर्पण बीच में आ जाता है।
अभिदृश्यक के लिए:
u = – ∞
फोकस दूरी f1 = 11 cm
v = ?
दर्पण समीकरण से
या \(\frac{1}{\mathrm{u}}\) + \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\)
\(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\) – \(\frac{1}{\mathrm{u}}\)
= \(-\frac{1}{11}\) – \(\frac{1}{∞}\) = \(-\frac{1}{11}\) + \(-\frac{1}{∞}\)
= \(-\frac{1}{11}\) + 0 = –\(-\frac{1}{11}\)
या v = – 11 cm = अभिदृश्यक से दूरी
उत्तल दर्पण से दूरी
= – (v + d)
= – (- 11 + 2) = + 9 cm.
यह उत्तल दर्पण के लिए काल्पनिक वस्तु का कार्य करता है।
अर्थात्
u’= 9cm.
f’ = 7 cm.
v’= ?
\(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\) – \(\frac{1}{\mathrm{u}}\)
= \(\frac{1}{7}\) – \(=\frac{1}{9}\) = \(\frac{9-7}{63}\) =2/63
v’= 63/2 = 31.5 cm.
अर्थात् प्रतिबिम्ब 31.5 cm उत्तल दर्पण (छोटे वाले से) दूर बनता है।

प्रश्न 9.31.
किसी गैल्वेनोमीटर की कुंडली से जुड़े समतल दर्पण पर लंबवत् आपतित प्रकाश (चित्र), दर्पण से टकराकर अपना पथ पुनः अनुरेखित करता है। गैल्वेनोमीटर की कुंडली में प्रवाहित कोई धारा दर्पण में 3.5° का परिक्षेपण उत्पन्न करती है। दर्पण के सामने 1.5m दूरी पर रखे परदे पर प्रकाश के परावर्ती चिन्ह में कितना विस्थापन होगा?

उत्तर:
यहाँ पर हम जानते हैं कि परावर्तित किरणें दर्पण के घूर्णन कोण से दुगुने कोण पर विक्षेपित होती हैं। चित्र से हम देखते हैं कि जब दर्पण M से M’ स्थिति पर θ = 3.5° कोण से मोड़ा जाता है। परावर्तित किरण OB

∠2θ = 2 × 3.5° = 7° = ∠AOB से मुड़ जाती है।
समकोण त्रिभुज AOB में
tan 2θ = AB/AO
या tan 7° = d/1.5
या d = 1.5 × tan 7°
= 1.5 x 0.1228
= 0.1842 m
= 18.42 cm.

प्रश्न 9.32.
चित्र में कोई समोत्तल लेन्स (अपवर्तनांक 1.50) किसी समतल दर्पण के फलक पर किसी द्रव की परत के संपर्क में दर्शाया गया है। कोई छोटी सुई जिसकी नोक मुख्य अक्ष पर है, अक्ष के अनुदिश ऊपर-नीचे गति करादर इस प्रकार समायोजित की जाती है कि सुई की नोक का उलटा प्रतिबिंब सुई की स्थिति पर ही बने। इस स्थिति में सुई की लेन्स से दूरी 45.0 cm है। द्रव को हटाकर प्रयोग को दोहराया जाता है। नयी दूरी 30.0 cm मापी जाती है। द्रव का अपवर्तनांक क्या है?

उत्तर:
दिया गया है कि
द्विउत्तल लेन्स की फोकस दूरी L1 f1 = 30 cm.
द्वि- उत्तल लेन्सों के संयोजन और समतल उत्तल द्रव लेन्स की
फोकस दूरी L2 F = 45 cm.
यदि L2 की फोकस दूरी f2 है तब
\(\frac{1}{f2}\) = \(-\frac{1}{F}\) – \(-\frac{1}{f1}\)
= \(\frac{1}{45}\) – \(\frac{1}{30}\) = \(\frac{2-3}{90}\) = \(-\frac{1}{90}\)
या f2 = – 90cm.
L1 लेन्स के लिए (काँच के लेन्स के लिए) R1 = R तथा R2
\(\frac{1}{30}\) = (15 – 1) \(\left(\frac{1}{R}-\frac{1}{-R}\right)\)
\(\frac{1}{30}\) = 0.5 x \(\frac{2}{R}\) = \(\frac{1}{R}\)
R = 30cm.
L2 लेन्स के लिए (द्रव लेन्स के लिए)
R1 = – R = – 30 cm
R2 = ∞
\(-\frac{1}{90}\) = (n – 1) \(\left(\frac{1}{-30}-\frac{1}{\infty}\right)\)
\(-\frac{1}{90}\) = (n – 1) \(\left(\frac{1}{-30}-0\right)\) = \(\frac{-(n-1)}{30}\)
⇒ 30/90 = n – 1
⇒ 1/3 = n – 1
⇒ 1/3 + 1 = n
⇒ 0.33 + 1 = n
n = 1.33

Haryana State Board HBSE 11th Class Physics Solutions Chapter 3 सरल रेखा में गति Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 3 सरल रेखा में गति

प्रश्न 3.1.
नीचे दिये गये गति के कौन-कौन से उदाहरणो मे वस्तु को लगभग बिन्दु वस्तु माना जा सकता है?
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बन्दर।
(c) जमीन से टकराकर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद।
(d) किसी मेज के किनारे से फिसलकर गिरा कोई बीकर।
उत्तर:
(a) दो स्टेशनों के बीच की दूरी, रेलगाड़ी की लम्बाई की तुलना में अधिक है। अत: रेलगाड़ी को वस्तु बिन्दु माना जा सकता है।
(b) बन्दर द्वारा तय की गई दूरी अधिक है। अत: बन्दर को वस्तु बिन्दु माना जा सकता है।
(c) क्रिकेट की फिरकती गेंद द्वारा तय की गई दूरी कम होती है। अतः गेंद को वस्तु बिन्दु नहीं माना जा सकता।
(d) बीकर की मेज से नीचे गिरने की दूरी अधिक नहीं है। इसलिए इसे वस्तु बिन्दु नहीं माना जा सकता।

प्रश्न 3.2.
दो बच्चे A व B अपने विद्यालय 0 से लौटकर अपने-अपने घर क्रमश: P तथा Q को जा रहे हैं। उनके स्थिति समय (x – t) ग्राफ चित्र में दिखाये गये हैं।
नीचे लिखे कोष्ठकों में सही प्रविष्टियों को चुनिए:
(a) \(\frac{B}{A}\) की तुलना में \(\frac{A}{B}\) विद्यालय से निकट रहता है।
(b) \(\frac{B}{A}\) की तुलना में \(\frac{A}{B}\) विद्यालय से पहले चलता है।

(c) \(\frac{B}{A}\) की तुलना में \(\frac{A}{B}\) तेज चलता है।
(d) A और B घर (एक ही / भिन्न) समय पर पहुँचते हैं।
(e) \(\frac{A}{B}\) सड़क पर \(\frac{B}{A}\) से (एक बार / दो बार ) आगे हो जाते हैं।
उत्तर:
∵ OP < OQ, अत: A बच्चा, B की तुलना में विद्यालय के निकट रहता है।
(b) A मूलबिन्दु O से t = 0 पर गति प्रारम्भ करता है जबकि B, कुछ समय / पश्चात् गति प्रारम्भ करता है अतः A, B की तुलना में पहले चलता है।
(c) x – t वक्र की ढाल वेग के तुल्य होती है। अतः B, A की तुलना में तेज चलता है।
(d) A व B दोनों एक समय t पर घर पहुंचते हैं क्योंकि P व Q से ग्राफ पर खींचे गये लम्ब t समय पर मिलते हैं।
(e) B तेज चल रहा है अतः उभयनिष्ठ बिन्दु पर B एक बार A से आगे निकल जाता है।

प्रश्न 3.3.
एक महिला अपने घर से प्रातः 9.00 बजे 2.5 km दूर अपने कार्यालय के लिए सीधी सड़क पर 5 kmh^-1 चाल से चलती है। वहाँ वह सायं 5.00 बजे तक रहती है और 25 kmh^-1 की चाल से चल रही किसी ऑटो रिक्शा द्वारा अपने घर लौट आती है। उपयुक्त पैमाना चुनिये तथा उसकी गति का x – t ग्राफ भी खींचिए।
उत्तर:
घर से चलने पर तय की गई दूरी = 2.5km
चाल = 5km h^-1
कार्यालय पहुंचने में लगा समय = imm
यदि बिन्दु O को मूलबिन्दु माना जाये तब t = 9.00am पर x = 0 तथा = 9.30am पर x 2.5km, OA गति का x – t महिला अपने घर से कार्यालय के लिए चलती है।

महिला कार्यालय में 9.30am से 5.00pm तक रहती है।
अब वापस घर पहुँचने में लगा समय
= \(\frac{2.5}{25}\) = \(\frac{1}{10}h\) = 6 min
अत: 5.06p.m पर x = 2.5 km
इसे चित्र में BC रेखा द्वारा प्रदर्शित किया गया है।

प्रश्न 3.4.
कोई शराबी किसी तंग गली में 5 कदम आगे बढ़ता है। और 3 कदम पीछे आता है, उसके बाद फिर 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, और इसी तरह वह चलता रहता है। उसका हर कदम 1m लम्बा है और 1s समय लगता है। उसकी गति का x ग्राफ खींचिए ग्राफ से तथा किसी अन्य विधि से यह ज्ञात कीजिए कि वह जहाँ से चलना प्रारम्भ करता है वहाँ से 13m दूर किसी गड्ढे में कितने समय पश्चात् गिरता है?
उत्तर:
शराबी की गति का x-t ग्राफ चित्र में प्रदर्शित है।
प्रारम्भ में गड्ढे की दूरी = 13 मी
पहले 5 मी चलने में लगा समय = 5s

5 कदम आगे तथा 3 कदम पीछे चलने से तात्पर्य है कि चली गई कुल दूरी
= 5 – 3 = 2m
इस प्रक्रिया के पूरा होने में लगा समय
= 5 + 3 = 8s
अत: 8m चलने में लगा समय
= \(\frac{8 \times 8}{2}\) = 32s
अतः गड्डे तक शेष दूरी = 13 – 8 = 5m
अर्थात् शराबी अगले 5 कदमों में गड्ढे में गिर जायेगा जिसमें उसे 5s का समय और लगेगा।
अतः कुल समय 32 + 5 = 37s

प्रश्न 3.5.
कोई जेट वायुयान 500kmh^-1 की चाल से चल रहा है और यह जेट यान के सापेक्ष 1500 kmh^-1 की चाल से अपने दहन उत्पादों को बाहर निकालता है। जमीन पर खड़े किसी प्रेक्षक के सापेक्ष इन दहन उत्पादों की चाल क्या होगी?
उत्तर:
+x दिशा में जेट वायुयान का वेग
VA = 500km h^-1
दहन उत्पादों का सापेक्ष वेग (जेट वायुयान के सापेक्ष) VPA = -1500 kmh^-1
दहन उत्पादों का जेट वायुयान के सापेक्ष वेग
∵ VPA =Vp – VA
Vp = VA – 1500
= 500 – 1500 = 1000kmh^-1
यहाँ (-) चिह्न प्रदर्शित करता है कि दहन का वेग, जेट वायुयान की विपरीत दिशा में है।
∴ आपेक्षिक वेग का परिमाण = 1000kmh^-1

प्रश्न 3.6.
सीधे राजमार्ग पर कोई कार 126 kmh^-1 की चाल से चल रही है। इसे 200m की दूरी पर रोक दिया जाता है। कार के मंदन को एकसमान मानिए और इसका मान निकालिए। कार को रुकने में कितना समय लगेगा?
उत्तर:
u = 126km/h = \(\frac{126 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\)
= 35m/s
s = 200m, v = 0
गति के तीसरे समीकरण से,
v² = u² + 2as
या
a = \(\frac{v^2-u^2}{2 s}\) = \(\frac{0-(35)^2}{2 \times 200}\)
∴ a = – 3.06 ms^-2
-ve चिह्न मन्दन को प्रदर्शित करता है।
समीकरण v = u + at से,
या t = \(\frac{v-u}{a}\)
∴ t = \(\frac{0-35}{-3.06}\)
= 11.4s

प्रश्न 3.7.
दो रेलगाड़ियाँ A व B दो समान्तर पटरियों पर 72 km/h की एकसमान चाल से एक ही दिशा में चल रही है। प्रत्येक गाड़ी 400m लम्बी है और गाड़ी 4 गाड़ी B से आगे है। B का चालक 4 के आगे निकलना चाहता है तथा 1 ms^-2 से इसे त्वरित करता है। यदि 50 see के बाद B का गार्ड के चालक से आगे हो जाता है, तो दोनों के बीच आरम्भिक दूरी कितनी थी?
उत्तर:
यहाँ
u_A = 72 km/h
= 72 × \(\frac{1000}{60 \times 60}\) = 20m/s
t = 50s
S_A = u_At + \(\frac{1}{2}\) at²
= 20 x 50 + 0 = 1000m
तथा u_b = 72 km/s = 72 x \(\frac{5}{18}\) = 20m/s

a = 1 m/s²
तथा t = 50s
S_b = u_bt + \(\frac{1}{2}\) at² से,
sB = 20 x 50 + \(\frac{1}{2}\) x 1 x (50)²
= 2250m
∴ रेलगाड़ियों के बीच आरम्भिक दूरी
=2250 – 1000 = 1250 m

प्रश्न 3.8.
दो लेन वाली किसी सड़क पर कार 436kmh^-1 की चाल से चल रही है। एक-दूसरे की विपरीत दिशाओं में चलती दो कारें BTC जिनमें से प्रत्येक की चाल 54 km h^-1 है, कार 4 तक पहुँचना चाहती हैं। किसी क्षण जब दूरी AB दूरी AC के बराबर है तथा दोनों km है, कार B का चालक यह निर्णय करता है कि कार C के कार 4 तक पहुँचने के पहले ही वह कार 4 से आगे निकल जाए। किसी दुर्घटना से बचने के लिए कार B का कितना न्यूनतम त्वरण जरूरी है?
उत्तर:
कार A की चाल,
V_A = 36kmh^-1
= 36 x \(\frac{5}{18}\)
= 10ms^-1
कार B की चाल, VB = 54 kmh^-1
= 54 x \(\frac{5}{18}\) = 15ms^-1
इसी प्रकार, कार C की चाल VC = 15ms^-1

कार A के सापेक्ष कार C की आपेक्षिक चाल
= V_CA = 15 – (-10) = 25ms^-1
कार A के सापेक्ष कार B की आपेक्षिक चाल
= V_BA = 15 – 10 = 5ms^-1
∵ कार A तथा C नियत वेग से गतिमान हैं, अतः कार C का के सापेक्ष त्वरण शून्य है, а_CA =0
AB = AC = 1 km = 1000m
AC दूरी को तय करने में कार C को लगने वाला सम,
t = \(\frac{1000}{v_{A C}}\) = \(\frac{1000}{25}\)
= 40s
यदि कार B का त्वरण a है, तब चूँकि कार A का त्वरण शून्य है, अत: कार B का A के सापेक्ष त्वरण a_BA = a होगा।
कार B, कार C के कार A तक पहुँचने से पूर्व ही कार A तक पहुँच जायेगी यदि कार B, t = 40s कार A के सापेक्ष 1 km = 1000m की दूरी तय कर ले।
∴ S = ut + \(\frac{1}{2}\)at²
1000 = 5 x 40 + \(\frac{1}{2}\)a x (40)²
∴ कार B का न्यूनतम त्वरण
a = \(\frac{1000-200}{800}\)
= 1 ms^-2

प्रश्न 3.9.
दो नगर A व B नियमित बस सेवा द्वारा एक-दूसरे जुड़े हैं और प्रत्येक T मिनट के बाद दोनों तरफ बसें चलती हैं। कोई व्यक्ति साइकिल से 20 kmh^-1 की चाल से A से B की तरफ जा रहा है और यह नोट करता है कि प्रत्येक 18 मिनट के बाद एक बस उसकी गति की दिशा में तथा प्रत्येक 6 मिनट बाद उसके विपरीत दिशा में गुजरती है। बस सेवाकाल 7 कितना है और बसें सड़क पर किस चाल (स्थिर मानिए) से चलती हैं?
उत्तर:
माना प्रत्येक बस की चाल v_B तथा साइकिल सवार की चाल V_c है।
∴ साइकिल सवार की गति की दिशा में चल रही बसों की आपेक्षिक चाल = V_B – V_c
बस के गुजरने का समय = 18 मिनट = \(\frac{18}{60}\) घण्टा
∴ साइकिल सवार द्वारा पार की गयी दूरी
= आपेक्षिक चाल x समय
= (V_B – V_c) × \(\frac{18}{60}\)
चूँकि बसें प्रत्येक 7 मिनट बाद चलती हैं इसलिए दूरी V_B × \(\frac{T}{60}\) होगी।
अतः (V_B – V_c) × \(\frac{18}{60}\) = V_B × \(\frac{T}{60}\) ………..(1)
साइकिल सवार से विपरीत दिशा में प्रत्येक 6 मिनट के बाद गुजरने
वाली बसों का आपेक्षिक वेग = V_B + V_Cहै।
∴ चली गई दूरी = (V_B + V_C) × \(\frac{6}{60}\)
∴ (V_B + V_C)\(\frac{6}{60}\) = V_B × \(\frac{T}{60}\)
∴ समी० (1) से समी० (2) का भाग देने पर,
V_B = 2V_C
∵ V_C = 20 km h^-1
∴ V_B = 40 kmh^-1
समी० (1) से, [40 – 20] x \(\frac{18}{60}\) = 40 x \(\frac{T}{60}\)
T = 9 मिनट

प्रश्न 3.10.
कोई खिलाड़ी एक गेंद को ऊपर की ओर आरम्भिक चाल 29ms^-1 से फेंकता है।
(i) गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी?
(ii) इसकी गति के उच्चतम बिन्दु पर स्थान व समय को x = 0 व t = 0 चुनिये, ऊर्ध्वाधर नीचे की ओर की दिशा को X- अक्ष की धनात्मक दिशा मानिये। गेंद की ऊपर व नीचे की ओर गति के दौरान स्थिति, वेग व त्वरण के चिन्ह बताइए।
(iii) ज्ञात कीजिए कि किस ऊँचाई तक गेंद ऊपर जाती है और कितनी देर के बाद गेंद खिलाड़ी के हाथों में आ जाती है।
(g = 9.8ms^-2 तथा वायु का प्रतिरोध नगण्य है)
उत्तर:
(i) गुरुत्व के कारण त्वरण सदैव ऊर्ध्वाधर नीचे की ओर लगता है।
(ii) x = 0 व t = 0 को उच्चतम बिन्दु माना है जहाँ वेग शून्य होगा। उच्चतम बिन्दु पर त्वरण g = 9.8 m/s² (ऊर्ध्वाधर नीचे की ओर) ऊपर की ओर गति में,
स्थिति → धनात्मक (x > 0 )
वेग → ऋणात्मक (v < 0),

त्वरण → धनात्मक (∵ त्वरण 4 नीचे की ओर हैं) (a > 0)
नीचे की ओर गति में
स्थिति → धनात्मक (x > 0)
वेग → धनात्मक (v > 0)
त्वरण → धनात्मक (∵ त्वरण नीचे की ओर है) (a > 0)
(iii) ऊपर की गति के दौरान
u = – 29 m/s, a = 9.8 m/s², v =0
∴ v² = u² + 2as
0 = (-29)² + 2 × 9.8 × 8s
∴ S = \(\frac{-(-29)^2}{2 \times 9.8}\)
= -42.91m
अतः गेंद 42.91m ऊँचाई तक ऊपर जायेगी।
पुन: v = u + at से,
0 = (-29) + 9.8t
∴ t = \(\frac{29}{9.8}\) = 2.96 sec
कुल समय = 2.96 + 2.96 = 5.92 sec
(∵ जितना समय ऊपर जाने में लगता है उतना ही समय नीचे आने में लगता है।)

प्रश्न 3. 11.
नीचे दिये गये कथनों को ध्यान से पढ़िये और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य हैं या असत्य। एक विमीय गति में किसी कण की-
(a) किसी क्षण चाल शून्य होने पर उसका त्वरण अशून्य हो सकता है।
(b) चाल शून्य होने पर भी उसका वेग अशून्य हो सकता है।
(c) चाल स्थिर हो तो त्वरण अवश्य ही शून्य होना चाहिए।
(d) चाल अवश्य ही बढ़ती रहेगी, यदि उसका त्वरण धनात्मक
उत्तर:
(a) सत्य, कण की उच्चतम स्थिति में चाल शून्य होती है परन्तु त्वरण g होता है।
(b) असत्य, चाल शून्य है तो वेग का परिमाण शून्य है।
(c) असत्य, एकसमान वृत्तीय गति में चाल स्थिर रहने पर भी गति की दिशा बदलने के कारण त्वरण होता है।
(d) असत्य, जब दिशा धनात्मक होती है तो ही यह सत्य है।
वस्तु को ऊपर की ओर फेंकने पर त्वरण धनात्मक है परन्तु चाल घटती है।

प्रश्न 3.12.
किसी गेंद को 90m की ऊँचाई से फर्श पर गिराया जाता है। फर्श के साथ प्रत्येक टक्कर में गेंद की चाल \(1/10\) कम हो जाती है। इसकी गति का t = 0 से 125 के बीच चाल समय ग्राफ खींचिए।
उत्तर:
u1 = 0, s1 = 90m, a1 = 9.8 m/s²
v₁² = u₁² + 2a₁s₁
= 0 + 2 × 9.8 × 90
v₁² = 1764 → v₁ = 42m/s

∵ v₁ = u₁ + a₁t₁
42 = 0 + 9.8t₁
∴ t₁ = \(\frac{42}{9.8}\) = 4.2s
अर्थात् गेंद 4.2 sec तक नीचे आयेगी तो उसकी चाल सतत रूप से बढ़ेगी।
अतः ग्राफ सरल रेखा में होगा। इस स्थिति में अन्तिम वेग 42m/s होगा।
पुनः चाल \(\frac{1}{10}\) कम हो जाती है।
अतः
कमी = 42 x \(\frac{1}{10}\) = 4.2
∴ टकराने के पश्चात् चाल u2 = 42 – 4.2
= 37.8m/s
∵ v₂ = 0 ( उच्चतम बिन्दु पर ),
a₂ = -9.8m/s²
∴ v₂ = u₂ + a₂t₂
0 = 37.8 – 9.8 × t₂
∴ t₂ = \(\frac{37.8}{9.8}\) = 3.9 sec
कुल समय
t = t₁ + t₂ = 4.2 + 3.9 = 8.1 sec
अत: 8.1 sec पश्चात् चाल शून्य हो जायेगी।
∵ ऊपर जाने का समय = नीचे आने का समय
= 3.9 sec
t₃ = 3.9 sec, u₃ = 37.8m/s
अतः कुल समय
t = 8.1 + 3.9 = 12 sec पर चाल
= 37.8m/s

प्रश्न 3.13.
उदाहरण सहित निम्नलिखित के बीच के अन्तर को स्पष्ट कीजिए:
(a) किसी समय अन्तराल में विस्थापन के परिमाण (जिसे कभी-कभी दूरी कहा जाता है) और किसी कण द्वारा उसी अन्तराल के दौरान तय किए गए पथ की कुल लम्बाई।
(b) किसी समय अन्तराल में औसत वेग के परिमाण और उसी अन्तराल में औसत चाल (किसी समय अन्तराल में किसी कण की औसत चाल को समय अन्तराल द्वारा विभाजित की गई कुल पथ लम्बाई के रूप में परिभाषित किया जाता है)। प्रदर्शित कीजिए कि (a) व (b) दोनों में ही दूसरी राशि पहली राशि से अधिक या उसके बराबर हैं। समता का चिह्न कब सत्य होता है? (सरलता के लिए केवल एकविमीय गति पर विचार कीजिए।)
उत्तर:
(a) जब कोई वस्तु वृत्त का एक चक्कर पूर्ण करेगी तो विस्थापन शून्य होगा जबकि पथ की लम्बाई 2πr होगी।
(b) औसत चाल =
जबकि औसत वेग =
औसत चाल ≥ औसत वेग
यदि वस्तु सरल रेखा में गति करे तो औसत चाल, औसत वेग के समान होगी, तब समता का चिन्ह लगेगा।

प्रश्न 3.14.
कोई व्यक्ति अपने घर से सीधी सड़क पर 5kmh^-1 की चाल से 2.5 km दूर बाजार तक पैदल चलता है, परन्तु बाजार बन्द देखकर वह उसी क्षण वापस मुड़ जाता है तथा 7.5 kmh^-1 की चाल से घर लौट आता है।
समय अन्तराल (i) 0 – 30 मिनट, (ii) 0 – 50 मिनट, (iii) 0 – 40 मिनट की अवधि में उस व्यक्ति (a) के माध्य वेग का परिमाण तथा (b) का माध्य चाल क्या है?
उत्तर:
व्यक्ति के घर से बाजार की दूरी = 2.5 km
चाल V₁ = km/h
बाजार पहुँचने में लगा समय t₁ =
= 0.5 घण्टा = 30 मिनट
व्यक्ति की वापसी में चाल

∴ वापस आने में लगा समय, t₂ = \(\frac{2.5}{7.5}\) = 0.33h
= 0.33 × 60 = 19.8 20 मिनट
(i) 0 – 30 मिनट के अन्तराल में वस्तु द्वारा तय की गई दूरी
∆x = 2.5 km विस्थापन
अतः इस अन्तराल में औसत वेग का परिमाण, औसत चाल के तुल्य है।

(ii) 0 – 50 मिनट के अन्तराल में इस स्थिति में विस्थापन = 0
अतः
माध्य वेग = 0
कुल दूरी = 2.5 + 2.5 = 5km
कुल समय = 50 मिनट = \(\frac{50}{60}\) घण्टा
औसत चाल = \(\frac{5}{(50 / 60)}\) = \(\frac{5 \times 60}{50}\) = 6km/h
अतः यहाँ औसत वेग शून्य है जबकि औसत चाल 6km/h है।
(iii) 0 – 40 मिनट
= 30 मिनट जाने में + 10 मिनट वापस आने में व्यक्ति द्वारा 10 मिनट में तय की गई वापस दूरी
= 75 × \(\frac{10}{60}\)
= 1.25 km
∴ व्यक्ति का विस्थापन (AC)
= 2.5 km – 1.25m = 1.25km
समय = \(\frac{40}{60}\) घण्टा
∴ औसत वेग = \(\frac{1.25 \times 60}{40}\)
= 1.875 km/h
कुल तय की गई दूरी 2.5 + 1.25
AB + BC = 3.75km
∴ औसत चाल = \(\frac{3.75}{40}\) × 60
= 5.625km/h
अतः यहाँ भी औसत वेग, औसत चाल के बराबर नहीं है।

प्रश्न 3.15.
हमने अभ्यास प्रश्न 3.13 तथा 3.14 में औसत वेग के परिमाण के बीच के अन्तर को स्पष्ट किया है। यदि हम तात्क्षणिक चाल व वेग के परिमाण पर विचार करते हैं तो इस तरह का उत्तर करना आवश्यक नहीं होता। तात्क्षणिक चाल हमेशा तात्क्षणिक वेग के बराबर होती है, क्यों?
उत्तर:
हम जानते हैं कि तात्क्षणिक वेग
तात्क्षणिक चाल
अत्यन्त लघु समय अन्तरालों ∆t → 0 में वस्तु की गति की दिशा में कोई परिवर्तन नहीं माना जाता। अतः दूरी तथा विस्थापन के परिमाण में कोई अन्तर नहीं होता। एक प्रकार तात्क्षणिक चाल, सदैव तात्क्षणिक वेग के परिमाण के तुल्य होती है।

प्रश्न 3.16.
चित्र में (a) से (d) तक के ग्राफों को ध्यान से देखिए और देखकर बताइए कि इनमें से कौन-सा ग्राफ एकविमीय गति को सम्भवतः नहीं दर्शा सकता।

उत्तर:
(a) यह ग्राफ एकविमीय गति प्रदर्शित नहीं करता, क्योंकि किसी क्षण पर कण की दो स्थितियाँ होंगी, जो एकविमीय गति में सम्भव नहीं होतीं।
(b) यह ग्राफ एकविमीय गति प्रदर्शित नहीं करता, क्योंकि किसी क्षण पर कण का वेग धनात्मक तथा ऋणात्मक दोनों दिशाओं में, जो एकविमीय गति में सम्भव नहीं है।
(c) यह ग्राफ भी एकविमीय गति प्रदर्शित नहीं करता, क्योंकि यह ग्राफ कण की ऋणात्मक चाल व्यक्त कर रहा है तथा कण की चाल ऋणात्मक नहीं हो सकती।
(d) यह ग्राफ भी एकविमीय गति प्रदर्शित नहीं करता, क्योंकि यह प्रदर्शित कर रहा है कि कुल पथ की लम्बाई एक निश्चित समय के पश्चात् घट रही है, परन्तु गतिमान कण की कुल पथ- लम्बाई कभी भी समय के साथ नहीं घटती।

प्रश्न 3.17.
चित्र में किसी कण की एकविमीय गति का x – t ग्राफ दिखाया गया है। ग्राफ देखकर क्या यह कहना ठीक होगा कि यह कण t < 0 के लिए किसी सरल रेखा में और t > 0 के लिए किसी परवलीय पथ में गति करता है। यदि नहीं, तो ग्राफ के संगत किसी उचित भौतिक सन्दर्भ का सुझाव दीजिए।
उत्तर:

यह कहना ठीक नहीं होगा कि यह कण t < 0 के लिए किसी सरल रेखा में और t > 0 के लिए किसी परवलीय पक्ष में गति करता हैं, क्योंकि x- ग्राफ कण का पथ प्रदर्शित कर सकता है।
ग्राफ द्वारा t = 0 पर x = 0 प्रदर्शित है; अतः ग्राफ गुरुत्व के अन्तर्गत ऊँचाई से गिरती हुई किसी वस्तु की गति प्रदर्शित कर सकता है।

प्रश्न 3.18.
किसी राजमार्ग पर पुलिस की कोई गाड़ी 30km/h की चाल से चल रही है और यह उसी दिशा में 192 km/h की चाल से जा रही किसी चोर की कार पर गोली चलाती है। यदि गोली की नामुखी चाल 150ms^-1 है तो चोर की कार को गोली किस चाल के साथ आघात करेगी? (नोट- -उस चाल को ज्ञात कीजिए जो चोर की कार को हानि पहुँचाने में प्रासंगिक हो।)
उत्तर:
पुलिस की गाड़ी की चाल
Vp = 30km/h = 30 x \(\frac{5}{18}\) = \(\frac{25}{3}\) m/s
चोर की कार की चाल
Vt = 192km/h = 192 x \(\frac{5}{18}\) = \(\frac{160}{3}\) m/s
गोली की चाल = पुलिस की गाड़ी की चाल + गोली की नालमुखी चाल (Muzzle speed)
= (\(\frac{5}{18}\) + 150) = \(\frac{475}{3}\)m/s
∴ चोर की गाड़ी के सापेक्ष गोली का आपेक्षिक वेग
V_bt = V_b – V_t = \(\frac{475}{3}\) – \(\frac{160}{3}\) = \(\frac{315}{3}\) = 105m/s

प्रश्न 3.19.
चित्र में दिखाये गये प्रत्येक ग्राफ के लिए किसी उचित भौतिक स्थिति का सुझाव दीजिए।

उत्तर:
(a) x – t ग्राफ प्रदर्शित कर रहा है कि प्रारम्भ में x शून्य है, फिर यह एक स्थिर मान प्राप्त करता है, पुन: यह शून्य हो जाता है तथा फिर यह विपरीत दिशा में बढ़कर अन्त में एक स्थिर मान (विरामावस्था) प्राप्त कर लेता है। अतः यह ग्राफ इस प्रकार की भौतिक स्थिति व्यक्त कर सकता है जैसे एक गेंद को विरामावस्था से फेंका जाता है। वह दीवार से टकराकर लौटती है तथा कम चाल से उछलती है तथा यह क्रम इसके विराम में पहुँचने तक चलता रहता है।
(b) यह ग्राफ प्रदर्शित कर रहा है कि वेग समय के प्रत्येक अन्तराल के साथ परिवर्तित हो रहा है तथा प्रत्येक बार इसका वेग कम हो रहा है। इसलिए यह ग्राफ एक ऐसी भौतिक स्थिति को व्यक्त कर सकता है। जिसमें एक स्वतन्त्रतापूर्वक गिरती हुई गेंद (फेंके जाने पर) धरती से टकराकर कम चाल से पुन: उछलती है तथा प्रत्येक बार धरती से टकराने पर इसकी चाल कम होती जाती है।
(c) यह ग्राफ प्रदर्शित करता है कि वस्तु अल्प समय में ही त्वरित हो जाती है, अत: यह ग्राफ एक ऐसी भौतिक स्थिति को व्यक्त कर सकता है। जिसमें एकसमान चाल से चलती हुई गेंद को अत्यल्प समयान्तराल में बल्ले द्वारा टकराया जाता है।

प्रश्न 3.20.
चित्र में किसी कण की एक विमीय सरल आवर्ती गति के लिए x – t ग्राफ दिखाया गया है। समय t = 0.3s, 1.2s, -1.2s पर कण की स्थिति, वेग व त्वरण के चिन्ह क्या होंगे?

उत्तर:
(i) t = 0.3s पर ऋणात्मक, x – t वक्र की ढाल ऋणात्मक है। अतः स्थिति व वेग ऋणात्मक हैं। त्वरण a = -ω²x, अतः त्वरण धनात्मक है।
(ii) t = 1.2 s पर x स्थिति व वेग धनात्मक हैं। ऋणात्मक x-t वक्र की ढाल धनात्मक है। a = -ω²x से त्वरण धनात्मक है।
(iii) t = – 1.2 sec पर x ऋणात्मक x-t वक्र की ढाल धनात्मक है। अतः a = -ω²x से त्वरण ऋणात्मक है।

प्रश्न 3.21.
प्रस्तुत चित्र में किसी कण की एक विमीय गति का A ग्राफ दर्शाया गया। इसमें तीन समान अन्तराल दिखाए गए हैं। किस अन्तराल में औसत चाल अधिकतम है और किसमें न्यूनतम है? प्रत्येक अन्तराल के लिए औसत वेग का चिन्ह बताइए।

उत्तर:
(a) x-t वक्र की ढाल, औसत चाल व्यक्त करती है।
∴ अन्तराल (3) में ग्राफ की ढाल अधिकतम है तथा अन्तराल (2) में न्यूनतम होगी।
(c) (1) व (2) में ढाल धनात्मक है तथा अन्तराल (3) में ऋणात्मक ढाल है। अत: (1) व (2) में औसत वेग धनात्मक है परन्तु अन्तराल (3) है ऋणात्मक होगा।

प्रश्न 3.22.
चित्र में किसी नियत (स्थिर) दिशा के अनुदिश चल रहे कण का चाल – समय ग्राफ दिखाया गया है। इसमें तीन समान समय अन्तराल दिखाये गये हैं। किस अन्तराल में औसत त्वरण का परिमाण अधिकतम होगा? किस अन्तराल में औसत चाल अधिकतम होगी? धनात्मक दिशा को गति की स्थिर दिशा चुनते हुए तीनों अन्तराल में ” तथा के चिन्ह बताइए। A, B, C तथा D बिन्दुओं पर त्वरण क्या होंगे?

उत्तर:
(i) कण v-t वक्र की ढाल, औसत त्वरण प्रदर्शित करता है। ढाल (2) में अधिकतम है। अतः औसत त्वरण का परिमाण (2) में अधिकतम होगा। (3) में त्वरण का परिमाण न्यूनतम है।
(ii) औसत चाल (3) में अधिकतम तथा (1) में न्यूनतम है।
(iii) तीनों अन्तराल में धनात्मक है। (1) में त्वरण धनात्मक, (2) में त्वरण ऋणात्मक तथा (3) में त्वरण शून्य होगा क्योंकि इन बिन्दुओं पर स्पर्श रेखा समय अक्ष के समान्तर है।

अतिरिक्त अभ्यास (Additional Exercise):

प्रश्न 3.23.
कोई तीन पहिये वाला स्कूटर अपनी विरामावस्था में गति करता है। फिर 10 तक किसी सीधी सड़क पर 1ms^-2 के एकसमान त्वरण से चलता है। इसके बाद वह एक समान वेग से चलता है। स्कूटर द्वारा सेकण्ड (n = 1, 2, 3) में तय की गई दूरी को के सापेक्ष आलेखित कीजिए। आप क्या आशा करते हैं कि त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा?
उत्तर:
हम जानते हैं कि n वें Sec में तय की गई दूरी
S = u + \(\frac{a}{2}\)(2n – 1)

u = 0,a = 1
∴ n = 1
s₁ = 0 + \(\frac{1}{2}\)(2 × 1 – 1) = 0.5m
s₂ = \(\frac{1}{2}\)(2 x 2 – 1) = 1.5m
s₃ = \(\frac{1}{2}\)(2 x 3 – 1) = 2.5m
s₁₀ = \(\frac{1}{2}\)(2 × 10 – 1) = 9.5m
अतः ग्राफ से स्पष्ट है कि त्वरित गति के दौरान सरल रेखा प्राप्त होगी।

प्रश्न 3.24.
किसी स्थिर लिफ्ट में (जो ऊपर से खुली है ) कोई बालक खड़ा है। वह अपने पूरे जोर से एक गेंद ऊपर की ओर फेंकता है जिसकी प्रारम्भिक चाल 49 ms^-1 है। उसके हाथों में गेंद के वापस आने में कितना समय लगेगा? यदि लिफ्ट ऊपर की ओर 5m/s की एकसमान चाल से गति करना प्रारम्भ कर दे और वह बालक फिर गेंद को अपने जोर से फेंकता है तो कितनी देर में गेंद उसके हाथों में लौट आयेगी?
उत्तर:
यदि लिफ्ट स्थिर है, तब
h = 49m/s, a = -9.8m/s²
v = u + at
0 = 49 – 9.8t
∴ t = \(\frac{49}{9.8}\) = 5s
अतः गेंद को ऊपर जाने में 5s लगेंगे तथा 55 ही वापस आने में लगेंगे। अतः कुल समय 5 + 5 = 10s
जब लिफ्ट ऊपर की ओर एकसमान वेग से चलती है तो लिफ्ट के सापेक्ष गेंद का प्रारम्भिक वेग 49 m/s ही रहेगा। गेंद को बालक के हाथों में आने में 10s का ही समय लगेगा।

प्रश्न 3.25.
क्षैतिज में गतिमान कोई लम्बा पट्टा 4 km/h की चाल से चल रहा है। एक बालक इस पर (पट्टे के सापेक्ष) 9 km/h की चाल से कभी आगे कभी पीछे अपने माता-पिता के बीच दौड़ रहा है। माता व पिता के बीच 50m की दूरी है। बाहर किसी स्थिर प्लेटफार्म पर खड़े एक प्रेक्षक के लिए, निम्नलिखित का मान प्राप्त कीजिए।

(a) पट्टे की गति की दिशा में दौड़ रहे बालक की चाल,
(b) पट्टे की गति की दिशा के विपरीत दौड़ रहे बालक की चाल,
(c) बच्चे द्वारा (a) व (b) में लिया गया समय यदि बालक की गति का प्रेक्षण उसके माता या पिता करें तो कौन-सा उत्तर बदल जायेगा?
उत्तर:
माना \(\overrightarrow{v_B}\) = पट्टे का वेग = 4 km/h
\(\overrightarrow{v_{C B}}\) = पट्टे के सापेक्ष बालक का वेग
(a) जब बालक पट्टे की गति की दिशा में दौड़ता है:
पट्टे के सापेक्ष बालक का वेग = 9 km/h (बाएँ से दाएँ)
यदि बालक का वेग, प्लेटफार्म पर खड़े किसी प्रेक्षक के सापेक्ष \(\overrightarrow{v_C}\)
है, तो
\(\overrightarrow{v_{C B}}=\overrightarrow{v_C}-\overrightarrow{v_B}\)
VC = VC8+vg = 9+ 4 = 13km/h (बाएँ से दाएँ)
\(\overrightarrow{v_C}=\overrightarrow{v_{C B}}+\overrightarrow{v_B}\)

(b) जब बालक पट्टे की गति की दिशा के विपरीत दौड़ता है:
\(\overrightarrow{v_{C B}}\) = 9km/h (बाएँ से दाएँ)
यदि बालक का वेग किसी स्थिर प्रेक्षक के सापेक्ष \(\overrightarrow{v_C}\) है, तो
\(\overrightarrow{v_{C D}}=\overrightarrow{v_C}-\overrightarrow{v_B}\)
∴ \(\overrightarrow{v_C}=\overrightarrow{v_{C B}}+\overrightarrow{v_B}\)
= – 9+ 4 = -5km/h ( दाएँ से बाएँ)

(c) (a) अथवा (b) में लगने वाला समय

समय 20s रह जायेगा यदि माता या पिता बालक की गति का प्रेक्षण करते हैं।
माता/पिता समान बेल्ट पर हैं इसलिए उत्तर अपरिवर्तित रहेगा।

प्रश्न 3.26.
किसी 200m ऊँची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओर 15ms^-1 तथा 30ms^-1 की प्रारम्भिक चाल से फेंका जाता है। इसका सत्यापन कीजिए कि संलग्न ग्राफ पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है। वायु के प्रतिरोध को नगण्य मानिये और यह मानिये कि जमीन से टकराने के बाद पत्थर ऊपर की ओर उछलते नहीं। मान लीजिए g 10ms^-2 ग्राफ के रेखीय व वक्रीय भागों के लिए समीकरण लिखिए।

उत्तर:
पहले पत्थर के लिए,
x (0) = 200m,
v(0) = 15m/s,
a = -10m/s²
x₁(t) = x (0) + v (0)t + \(\frac{1}{2}\) at²
x₁(t) = 200 + 15t – 5t² …(1)
जब पहला पत्थर जमीन से टकराता है।
तो x₁(t) = 0
या -5t² + 15t + 2000 …….(2)
इसी प्रकार दूसरे पत्थर के लिए
x (0) = 200m, v(0) = 30m/s, a = – 10m/s²
X2(t) = 200 + 30t – 5t²
समी० (1) व समी० (2) से,
X2(t) – X1(t) = 15t
∴ x = 15t
∴ x ∝ t अर्थात् जब तक दोनों पत्थर गति करते रहेंगे उनके बीच की दूरी बढ़ती जायेगी।
∵ x व t समानुपाती हैं, अतः दोनों के मध्य ग्राफ सीधी रेखा में प्राप्त होगा।
समी० (2) से,
-5t² + 15t + 200 = 0
या 5t² – 15t – 200 = 0
या t²– 3t – 40 = 0
या t² – 8t + 5t – 40 = 0
या (t – 8) (t + 5) = 0
∴ t = 8 sec
अर्थात् 8s पश्चात् पहला पत्थर पृथ्वी पर गिर जायेगा। इसके पश्चात् एक ही पत्थर गति की अवस्था में होगा। अतः 8see पर दोनों के बीच दूरी अधिकतम होगी।
समी० (3) के अनुसार, समीकरण द्विघाती है अतः ग्राफ परवलयाकार होगा।

प्रश्न 3.27.
किसी निश्चित दिशा के अनुदिश चल रहे किसी कण का चाल-समय ग्राफ चित्र में दिखाया गया है। कण द्वारा (a) = 05 से t = 10s, (b) t = + 2s से 6s के बीच तय की गई दूरी ज्ञात कीजिए।
(a) तथा (b) में दिये गये अन्तरालों की अवधि में कण की औसत चाल क्या है?

उत्तर:
(a) t = 0 से t = 10 sec तक चली गई दूरी
= चाल-समय ग्राफ का समय अक्ष के साथ बनाया गया क्षेत्रफल
= \(\frac{1}{2}\) OC x AB
दूरी = \(\frac{1}{2}\) x 10 x 12 = 60m
औसत चाल = imm = 6m/s

(b) t = 2 sec से t = 6sec तक चली गई दूरी ज्ञात करने के लिए सर्वप्रथम t = 2 से t = 5 sec तक की दूरी ज्ञात करेंगे। इसके पश्चात् t = 5 से t = 6 sec की दूरी ज्ञात करेंगे।
∴ t = 2 से t = 5 sec के मध्य त्वरण
a = \(\frac{v-u}{t}\) = \(\\frac{12-0}{5}\)
= 2.4 m/s²
v = u + at से
u₀ = 12m/s², t = 1 sec
x = 12 × 1 – \(\frac{1}{2}\) × 24 × (1)²
= 12 – 1.2 = 10.8m
कुल दूरी = 25.2 + 10.8 = 36 m
औसत चाल = \(\frac{36}{4}\) = 9 m/s² 

प्रश्न 3.28.
एकविमीय गति में किसी कण का वेग समय ग्रांप चित्र में दिखाया गया है-नीचे दिये सूत्रों में से 12 तक के समय अन्तराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही हैं-
(i) x(t₂) = x(t₁) + v(t₁)(t₂ – t₁) + a(t₂ – t₁)²
(ii) v(t₂) = v(t₁) + a(t₂ -t₁)
(iii) aaverage = [x(t₂) – x(t₁)]\(t₂ – t₁)
(iv) aaverage = [v(t₂) – v(t₁)]\(t₂ -t₁)
(v) x(t₂) = x(t₁) + vaverage(t₂ – t₁) + aaverage(t₂ – t₁)²
(vi) x (t₂) – x (t₁) = t-अक्ष तथा दिखाई गई बिन्दुकित रेखा के बीच दर्शाए गए वक्र के अन्तर्गत आने वाला क्षेत्रफल

उत्तर:
(i) सही नहीं है, क्योंकि a का मान है t₁ तथा t₂ नियत नहीं है।
(ii) सही नहीं है, क्योंकि स्थिर नहीं है।
(iii) सही है। (iv) सही है।
(v) सही नहीं है, इसमें औसत त्वरण प्रयुक्त नहीं कर सकते हैं।
(vi) सही है।

Haryana State Board HBSE 12th Class Physics Solutions Chapter 8 वैद्युतचुंबकीय तरंगें Textbook Exercise Questions and Answers.

Haryana Board 12th Class Physics Solutions Chapter 8 वैद्युतचुंबकीय तरंगें

प्रश्न 8.1.
चित्र में एक संधारित्र दर्शाया गया है जो 12 cm त्रिज्या की दो वृत्ताकार प्लेटों को 5.0 cm की दूरी पर रखकर बनाया गया है। संधारित्र को एक बाह्य स्रोत (जो चित्र में नहीं दर्शाया गया है) द्वारा आवेशित किया जा रहा है। आवेशकारी धारा नियत है और इसका मान 0.15A है।
(a) धारिता एवं प्लेटों के बीच विभवान्तर परिवर्तन की दर का परिकलन कीजिए।
(b) प्लेटों के बीच विस्थापन धारा ज्ञात कीजिए।
(c) क्या किरखोफ का प्रथम नियम संधारित्र की प्रत्येक प्लेट पर लागू होता है? स्पष्ट कीजिए।

उत्तर:
संधारित्र की वृत्तीय प्लेट की त्रिज्या
r = 12 cm
= 12 × 10² m
प्लेटों के बीच की दूरी d = 5 cm
= 5 × 10² m
आवेशकारी धारा
I = 0.15 A
∴ प्लेट का क्षेत्रफल
A = πr²
A = π × (12 × 10²)²
= 144 x × 10^-4 m²
(a) समान्तर प्लेट संधारित्र के लिए
C = ∈A/d
मान रखने पर
= \(\frac{8.85 \times 10^{-12} \times 144 \pi \times 10^{-4}}{5 \times 10^{-2}}\)
= \(\frac{8.85 \times 144 \times 3.14 \times 10^{-14}}{5}\)
= 80.03 × 10^-13 F
= 8.01 × 10^-12F
= 8.01 pF
हम जानते हैं:
Q = CV
∴ dQ/dt = Cdv/dt
या
I = C dV/dt
या
dV/dt = I/C
मान रखने पर:
dV/dt = \(\frac{0.15}{8.01 \times 10^{-12}}\)
= 1.87 × 10¹⁰ V/s

(b) प्लेटों पर विस्थापन धारा = ID = ?
हमें ज्ञात है कि
ID = d/dt (∈0 Φ)
= \(\epsilon_0 \frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\)
जहाँ ΦE = लूप पर विद्युत अभिवाह है
= EA = q/∈0
∴ ID = ∈0d/dt (q/∈0)
= 0.15 A
अर्थात्
विस्थापन धारा = चालन धारा
(c) हाँ. संधारित्र की प्रत्येक प्लेट पर किरखोफ का पहला नियम सत्य है। धारा, चालन धारा और विस्थापन धारा के योग के बराबर है।

प्रश्न 8.2.
एक समान्तर प्लेट संधारित्र (चित्र) R = 6.0 cm त्रिज्या की दो वृत्ताकार प्लेटों से बना है और इसकी धारिता C = 100 pF है। संधारित्र को 230 V, 300 rad s^-1 की (कोणीय) आवृत्ति के किसी स्रोत से जोड़ा गया है।
(a) चालन धारा का rms मान क्या है?
(b) क्या चालन धारा विस्थापन धारा के बराबर है?
(c) प्लेटों के बीच अक्ष से 3.0 cm की दूरी पर स्थित बिन्दु पर B का आयाम ज्ञात कीजिए।
उत्तर:
दिया गया है:

R = 6.0cm = 6 x 10² m F
C = 100 pF = 100 x 10^-12
Vrms = 230 V
= 300 rad s^-1
(a) चालन धारा का rms मान= Irms = ?
हम जानते हैं
Irms = Vrms/XC
या
मान रखने पर
Irms = 230 x 300 × 100 x 10^-12
= 69 × ⁷
= 6.9 × 10^-6 A
Irms = 6.9 A

(b) हाँ, एक समान्तर संधारित्र के लिए सदैव I= ID चाहे I (d.c.) या a.c. (समय में दोलनी) हो जिसे निम्न प्रकार से सिद्ध किया जा सकता है
ID = ∈0 d/dt (ΦE)
∈0 d/dt (ΦE)
या
ID = ∈0 dE/dt
= ∈0 d/dt(Q/∈0)
∵E = σ/∈0 = Q/∈0A
या ID = ∈0A × 1/∈0A dQ/dt = dQ/dt = I

(c) हम जानते हैं B = μ/2π r/R² × ID
यदि
I = ID तब B = μ/2π r/R²I
यदि I = I0 = धारा का शीर्ष मान है, तब
B का आयाम = B का अधिकतम मान
B = μ/2π r/R² × I0 = μ/2π r/R² × √2 Irms
∵ Io = √2 Irms
यहाँ पर
Irms = 6.9 x 10⁶ A
r = प्लेटों के बीच अक्ष से बिन्दु की दूरी = 3.0 cm = 3 × 10² m
मान रखने पर B = \(\frac{4 \pi \times 10^{-7} \times 1.414 \times 6.9 \times 10^{-6} \times 3 \times 10^{-2}}{2 \times 3.14 \times\left(6 \times 10^{-2}\right)^2}\)
= 1.63 x 10^-11 T

प्रश्न 8.3.
10^-10m तरंगदैर्घ्य की X- किरणों, 6800 Å तरंगदैर्ध्य के प्रकाश तथा 500 m की रेडियो तरंगों के लिए किस भौतिक राशि का मान समान होगा?
उत्तर:
तीनों ही विद्युत चुम्बकीय तरंगें हैं। निर्वात में इनका वेग एक समान होगा तथा यह प्रकाश के वेग c = 3 x 10⁸ m/s मी./से. होगा।

प्रश्न 8.4.
एक समतल वैद्युतचुम्बकीय तरंग निर्वात में 2-अक्ष के अनुदिश चल रही है। इसके विद्युत तथा चुम्बकीय क्षेत्रों के सदिशों की दिशा के बारे में आप क्या कहेंगे? यदि तरंग की आवृत्ति 30 MHz हो, तो उसकी तरंगदैर्ध्य कितनी होगी?
उत्तर:
हम जानते हैं कि विद्युत चुम्बकीय तरंगें प्रकृति में अनुप्रस्थ होती हैं। यहाँ पर E है और Bxy तल में स्थित है और आपस में लम्बवत् है।
दिया है- तरंग की आवृत्ति
V = 30MHz
= 30 × 10⁶ Hz
तरंग का वेग = c = 3 x 10⁸ m/s
λ = ?
हम जानते हैं

अतः तरंगदैर्घ्य का मान = 10m

प्रश्न 8.5.
एक रेडियो 7.5 MHz से 12 MHz बैंड के किसी स्टेशन से समस्वरित हो सकता है। संगत तरंगदैर्ध्य बैंड क्या होगा?
उत्तर:
दिया गया है – आवृत्ति v1 = 7.5 MHZ
= 7.5 × 10⁶ Hz
V2 = 12 MHz
= 12 × 10⁶ Hz
तरंग का वेग c = 3 x 10⁸ m/s
माना संगत तरंगदैर्ध्य λ1 व λ2 है।
∴ λ1 = c/v1 = \(\frac{3 \times 10^8}{7.5 \times 10^6}\) =40 m
इसी तरह से
λ2 = c/v2 = \(\frac{3 \times 10^8}{12 \times 10^6}\) = 25cm
अतः तरंगदैर्घ्य बैंड स्टेशन 25m से 40m बैंड में है।

प्रश्न 8.6.
एक आवेशित कण अपनी माध्य साम्यावस्था के दोनों ओर 10⁹ Hz आवृत्ति से दोलन करता है। दोलक द्वारा जनित वैद्युत चुम्बकीय तरंगों की आवृत्ति कितनी है?
उत्तर:
हम जानते हैं कि एक त्वरित कण वैद्युत चुम्बकीय तरंगें उत्सर्जित करता है। एक निश्चित कम्पन आवृत्ति से कम्पित आवेशित कण (त्वरित आवेश) कम्पनी विद्युत क्षेत्र उत्पन्न करता है जो कम्पनशील चुम्बकीय क्षेत्र उत्पन्न करता है। यह दोनों कम्पनशील क्षेत्र एक-दूसरे को उत्पन्न करते हैं। वैद्युत चुम्बकीय तरंगों की आवृत्ति कम्पनशील आवेशित कण की आवृत्ति के बराबर है जिसका मान 10⁹ Hz है।

प्रश्न 8.7.
निर्वात में एक आवर्त वैद्युत चुम्बकीय तरंग के चुम्बकीय क्षेत्र वाले भाग का आयाम Bg = 510 nT है विद्युत क्षेत्र वाले भाग का आयाम क्या है?
उत्तर:
दिया गया है:
Bo = 510nT निर्वात में चुम्बकीय क्षेत्र वाले भाग का आयाम
= 510 × 10⁹ T
निर्वात में तरंग का वेग = c = 3 x 10⁸ m/s
निर्वात में तरंग के विद्युत क्षेत्र वाले भाग का आयाम = E0 = ?
हम जानते हैं कि वैद्युत चुम्बकीय तरंगों के लिए
c = E0/B0
या
मान रखने पर
Eg c= Bo
Eg = cBo
Eg = 3 x 10⁸ x 510 x 10^-9
= 153 V/m

प्रश्न 8.8.
कल्पना कीजिए कि एक वैद्युतचुम्बकीय तरंग के विद्युत क्षेत्र का आयाम E = 120 N/C है तथा इसकी आवृत्ति v = 50.0 MHz है। (a) Boo, k तथा 2 ज्ञात कीजिए (b) E तथा B के लिए व्यंजक प्राप्त कीजिए।
उत्तर:
दिया गया है:
विद्युत क्षेत्र का आयाम
= Eg = 120N/C
आवृत्ति v = 500MHz
= 50 × 10⁶ Hz
तरंग का वेग = c = 3 x 10⁸ m/s

(a) B0. ω k तथा λ का मान
(i) B0 का मान
c = E0/B0
∴ B0 = E0/c
मान रखने पर
B0 = \(\frac{120}{3 \times 10^8}\)
B0 = 4 x 10^-7 T
= 400 x 10⁹ T
= 400 nT

(ii) का मान
ω = 2πv
= 2π x 50 x 10⁶
= 3.14 x 10⁸ रेडियन / से.

(iii) k का मान
k = 2π/λ = 2πv/vλ = 2πv/c = ω/c
k = \(\frac{3.14 \times 10^8}{3 \times 10^8}\)
= 1.05 रेडियन / मी.

(iv) λ का मान
c = vλ
λ = c/v = \(\frac{3 \times 10^8}{50 \times 10^6}\) = 300/50m
λ = 6m

(b) माना वैद्युत चुम्बकीय तरंग x अक्ष की ओर गति करती है और है E और B y-अक्ष तथा 2-अक्ष की तरफ है। तब
E = Eosin(kx – ωt)j
= 120sin(1.05x – 3.14 x 10⁸)j N / C
Bz = B0sin (kx – ωt)K
= 4 × 10⁷ sin (1.05x – 3.14 x 10⁸)t) KT

प्रश्न 8.9.
वैद्युतचुम्बकीय स्पेक्ट्रम के विभिन्न भागों की पारिभाषिकी पाठ्यपुस्तक में दी गई है। सूत्र E = hv ( विकिरण के एक क्वांटम की ऊर्जा के लिए फोटॉन) का उपयोग कीजिए तथा em वर्णक्रम के विभिन्न भागों के लिए eV के मात्रक में फोटॉन की ऊर्जा निकालिए। फोटॉन ऊर्जा के जो विभिन्न परिमाण आप पाते हैं वे वैद्युतचुम्बकीय विकिरण के स्रोतों से किस प्रकार संबंधित हैं?
उत्तर:
सूत्र E = hv
उपर्युक्त सूत्र से फोटॉन की ऊर्जा ज्ञात करते हैं।
या
E = hc/λ
∴ आवृत्ति v = c/λ
फोटॉन ऊर्जा (λ = 1m के लिए)
E = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{1 \times 1.6 \times 10^{-19}} \mathrm{eV}\)
E = 1.243 x 10^-6 ev
λ के अन्य मानों के लिए
E = \(\frac{1.243 \times 10^{-6}}{\lambda} \mathrm{eV}\)

(a) γ-किरणों के लिए
λ → 10^-12 m
∴ E = \(\frac{1.243 \times 10^{-6}}{10^{-12}} \mathrm{eV}\)
E= 1.243 × 10^-6
= 1.243 Mev

(b) X-किरणों के लिए λ → 10^-9 m
∴ E = \(\frac{1.243 \times 10^{-6}}{10^{-9}} \mathrm{eV}\)
eV = 1.243 Kev

(c) दृश्य तरंगों के लिए
λ = 0.5 pum(5 x 10^-7 m )
∴ E = \(\frac{1.243 \times 10^{-6}}{5 \times 10^{-7}}\)
= 2.48 ev

(d) सूक्ष्म तरंगों के लिए λ → 1 cm = (10^-2m)
∴ E = \(\frac{1.243 \times 10^{-6}}{10^{-2}}\)
= 1.243 × 10^-4 ev

(e) रेडियो तरंगों के लिए λ → 100
∴ E = 1.243 x 10^-8 ev
y – किरणों का उत्सर्जन नाभिकीय अभिक्रियाओं में होता है अतः नाभिकीय ऊर्जा स्तरों में अन्तराल 1 MeV की कोटि का होता है। X-किरणें व दृश्य किरणें परमाणुओं में इलेक्ट्रॉनों के विभिन्न स्तरों में संक्रमण से उत्पन्न होती हैं। X किरणों के लिए संक्रमण भारी परमाणुओं के बाह्य ऊर्जा स्तरों से आन्तरिक ऊर्जा स्तरों में होता है जिनमें ऊर्जा अन्तराल 1 keV की कोटि का होता है। दृश्य तरंगों के लिए संक्रमण 2.5 eV ऊर्जा अन्तराल के स्तरों के मध्य होता है।

प्रश्न 8.10.
एक समतल em तरंग में विद्युत क्षेत्र 2.0 x 10¹⁰ Hz आवृत्ति तथा 48 Vm 1 आयाम से ज्यावक्रीय रूप में दोलन करता है।
(a) तरंग की तरंगदैर्ध्य कितनी है?
(b) दोलनशील चुम्बकीय क्षेत्र का आयाम क्या है ?
(c) यह दर्शाइए कि E क्षेत्र का औसत ऊर्जा घनत्व, B क्षेत्र के औसत ऊर्जा घनत्व के बराबर है।
[c = 3 x 10⁸ m s^-1]
उत्तर:
दिया गया है:
आवृत्ति v = 20 x 10¹⁰ Hz
E0 = 48V/m
λ = ?
Bo = ? और
c = 3 x 10⁸ m/s
(a) तरंगदैर्ध्य
λ = c/v
= \(\frac{3 \times 10^8}{2 \times 10^{10}}\)
= 1.5 x 10^-2m

(b)
Bo = E0/c
मान रखने पर Bo = \(\frac{48}{3 \times 10^8}T\)
B0 = 16 × 10⁸ T = 1.6 x 10⁷ T

(c) वैद्युत क्षेत्र में ऊर्जा घनत्व UE = 1/2∈0E²
चुम्बकीय क्षेत्र में ऊर्जा घनत्व UB = 1/2μ0 B²
ऊर्जा घनत्व UE = 1⁄2 ∈0 (CB)²
UE = 1⁄2∈0c²B² = c²(1/2∈0B²)
लेकिन
c = \(\frac{1}{\sqrt{\mu_0 \epsilon_0}}\)
c² = 1/μ0∈0
∴ UE = 1/μ0∈0 ((1/2∈0B²)
= 1/2μ0B² = UB
∴ UE = UB
अतः E क्षेत्र का औसत ऊर्जा घनत्व B क्षेत्र के औसत ऊर्जा घनत्व के बराबर है।

अतिरिक्त अभ्यास प्रश्न (NCERT):

प्रश्न 8.11.
कल्पना कीजिए कि निर्वात में एक वैद्युतचुम्बकीय तरंग का विद्युत क्षेत्र
E = { ( 3.1 N/C) cos [ ( 1.8rad/m) y + (5.4 x 10⁶ rad/s) t]}} i है।
(a) तरंग संचरण की दिशा क्या है?
(b) तरंगदैर्घ्य λ कितनी है?
(c) आवृत्ति v कितनी है?
(d) तरंग के चुम्बकीय क्षेत्र सदिश का आयाम कितना है?
(e) तरंग के चुम्बकीय क्षेत्र के लिए व्यंजक लिखिए।
उत्तर:
(a) निर्वात में एक वैद्युत चुम्बकीय तरंग का विद्युत क्षेत्र
E = {(3.1 N/C) cos [ ( 1.8 rad/m) y + (5.4 x 10⁶ rad/s) × t]} i
E के लिए यह व्यंजक है जिसका प्रकार
E = E0 cos (ky + ωt)i प्रकार का है।
जहाँ वैद्युत क्षेत्र i के अनुदिश है अर्थात् x अक्ष के अनुदिश है। E की समीकरण में cos कारक के अन्दर (ky + ωt) का प्रकार है
जो कि तरंग संचरण, ऋणात्मक y-अक्ष के अनुदिश प्रदर्शित करता है।
अर्थात् – j

(b) É = E0 cos (ky + ω t) i से दिए गए समीकरण की तुलना करने पर
E0 = 3.1 N/C, k = 1.8rad/m
ω = 5.4 × 10⁶ rad/s
k = 2π/λ , λ = 2π/k
= 2 x 3314/18
λ = 3.5 m

(c) आवृत्ति v = ω/2π = \(\frac{5.4 \times 10^6}{2 \times 3.14}\)Hz
= 859.87 kHz = 860 kHz

(d) B0 = E0/C = \(\frac{3.1}{3 \times 10^8}\) = 1.03 × 10T

(e) B = Bo cos (ky + ωt) k
B = 10.3 × 10⁹ cos (1.8y + 54 x 10⁶t) T

प्रश्न 8.12.
100 W विद्युत बल्ब की शक्ति का लगभग 5% दृश्य विकिरण में बदल जाता है।
(a) बल्ब से 1m की दूरी पर,
(b) 10m की दूरी पर दृश्य विकिरण की औसत तीव्रता कितनी है?
यह मानिए कि विकिरण समदैशिकतः उत्सर्जित होता है और परावर्तन की उपेक्षा कीजिए।
उत्तर:
विद्युत शक्ति दृश्य विकिरण में बदलती है
शक्ति = P = 5/100 × 100 W = 5W

तीव्रता = p/4πr²
(a) तीव्रता = \(\frac{5}{4 \times 3.14 \times 1 \times 1}\)
= 0.4Wm^-2
(b) तीव्रता = \(\frac{5}{4 \times 3.14 \times 10 \times 10}\) Wm^-2
= 0.004 Wm^-2

प्रश्न 8. 13.
em वर्णक्रम के विभिन्न भागों के लिए लाक्षणिक ताप परिसरों को ज्ञात करने के लिए T = 0.29cm K सूत्र का उपयोग कीजिए जो संख्याएँ आपको मिलती हैं, वे क्या बताती हैं? हल- हम जानते हैं कि प्रत्येक वस्तु किसी क्षेत्र में T ताप पर सभी तरंगदैर्घ्य के विकिरण उत्सर्जित करती है। इस प्रकार से कहा जा सकता है कि यह तरंगदैयों का सतत स्पेक्ट्रम उत्पन्न करती है।
हल:
हम जानते हैं कि प्रत्येक वस्तु किसी क्षेत्र में T ताप पर सभी तरंगदैर्घ्य के विकिरण उत्सर्जित करती है। इस प्रकार से कहा जा सकता है कि यह तरंगदैर्घ्यों का सतत स्पेक्ट्रम उत्पन्न करती है। एक कृष्णिका के लिए तीन विस्थापन नियमानुसार दिए गए ताप T विकिरण की अधिकतम तीव्रता के संगत तरंगदैर्घ्य
एक कृष्णिका के लिए तीन विस्थापन नियमानुसार दिए गए ताप T विकिरण की अधिकतम तीव्रता के संगत तरंगदैर्ध्य
λm T = 0.29 cm K से दी जाती है।
या
T = 0.29/λ
यहाँ पर λm सेमी. में है।
λm = 1 μm = 10^-6 m = 10^-4 cm के लिए T
T = 0.29/10^-4 2900K द्वारा दिया जाता है।
इसी प्रकार से दूसरी तरंगदैर्घ्य के लिए ताप को ज्ञात कर सकते हैं।
माना
λ = 5000 Å = 5000 × 10^-10 m
= 5 x 10^-5 cm तरंगदैर्घ्य के लिए
T = \(\frac{0.29}{5 \times 10^{-5}}\) = 29/5 × 1000
= 5800 K होना चाहिए।
नोट- पिण्ड कम ताप पर भी यह तरंगदैर्ध्य उत्पन्न करेगा परन्तु अधिकतम तीव्रता की नहीं।

प्रश्न 8. 14.
वैद्युतचुम्बकीय विकिरण से सम्बन्धित नीचे कुछ प्रसिद्ध अंक, भौतिकी में किसी अन्य प्रसंग में वैद्युतचुम्बकीय दिए गए हैं। स्पेक्ट्रम के उस भाग का उल्लेख कीजिए जिससे इनमें से प्रत्येक सम्बन्धित है।
(a) 21 cm (अंतरातारकीय आकाश में परमाण्वीय हाइड्रोजन द्वारा उत्सर्जित तरंगदैर्ध्य )
(b) 1057 MHz (लैंब – विचलन नाम से प्रसिद्ध, हाइड्रोजन में, पास जाने वाले दो समीपस्थ ऊर्जा स्तरों से उत्पन्न विकिरण की आवृत्ति)
(c) 2.7K [ सम्पूर्ण अन्तरिक्ष को भरने वाले समदैशिक विकिरण से सम्बन्धित ताप ऐसा विचार जो विश्व में बड़े धमाके ‘बिग बैंग’ के उद्भव का अवशेष माना जाता है ]।
(d) 5890 – 5896 À (सोडियम की द्विक् रेखाएँ)
(e) 14.4 kev [₅Fe नाभिक के एक विशिष्ट संक्रमण की ऊर्जा जो प्रसिद्ध उच्च विभेदन की स्पेक्ट्रमी विधि से संबंधित है ( मॉसबौर स्पेक्ट्रोस्कॉपी)]।
उत्तर:
(a) दिया गया है:
λ = 21 cm
वैद्युत चुम्बकीय तरंगों का यह तरंगदैर्घ्य रेडियो तरंगों के संगत है (जो कि कम तरंगदैर्घ्य अथवा उच्च आवृत्ति सिरे की ओर है ।) (b) दिया गया है
आवृत्ति v = 1057 MHz
v = 1057 × 10⁶ Hz
अतः संगत तरंगदैर्ध्य
λ = c/v = \(\frac{3 \times 10^{10} \mathrm{~cm} / \mathrm{s}}{1057 \times 10^6 \mathrm{~Hz}}\)
λ = 28.4cm
अतः संगत तरंगदैर्घ्य λ = 28.4 cm से दी जाती है।
(c) T = 2.7 K
∴ वीन के विस्थापन के नियम
λmT = 0.29cm K
λm = 0.29/T = 0.29/2.7
λm = 0.11 cm.
यह क्षेत्र वैद्युत चुम्बकीय स्पेक्ट्रम की सूक्ष्म तरंग के संगत है।

(d) दिया गया है λ = 5890A – 5896 À जो सोडियम प्रकाश की द्विक् रेखाएँ हैं और यह दृश्य विकिरण (पीला) प्रकाश क्षेत्र में है।

(e) E = 14.4 Kev
= 14.4 × 10³ ev
= 14.4 × 10³ × 1.6 x 10^-19J
1 eV = 1.6 × 10^-19 J
हम जानते हैं:
E = hv
आवृत्ति v = E/h
मान रखने पर V = \(\frac{14.4 \times 1.6 \times 10^3 \times 10^{-19}}{6.62 \times 10^{-34}}\)
v = 3 x 10¹⁷ Hz
= 3 x 10¹¹ MHz
यह आवृत्ति जो कि X – किरणों की कोटि की है (अथवा सॉफ्ट Y-किरण) क्षेत्र

प्रश्न 8. 15.
निम्नलिखित प्रश्नों का उत्तर दीजिए:
(a) लम्बी दूरी के रेडियो प्रेषित्र लघु-तरंग बैंड का उपयोग करते हैं। क्यों?
(b) लम्बी दूरी के TV प्रेषण के लिए उपग्रहों का उपयोग आवश्यक है क्यों?
(c) प्रकाशीय तथा रेडियो दूरदर्शी पृथ्वी पर निर्मित किए जाते हैं किन्तु X- किरण खगोलविज्ञान का अध्ययन पृथ्वी का परिभ्रमण कर रहे उपग्रहों द्वारा ही संभव है। क्यों?
(d) समतापमंडल के ऊपरी छोर पर छोटी-सी ओजोन की परत मानव जीवन के लिए निर्णायक है। क्यों?
(e) यदि पृथ्वी पर वायुमंडल नहीं होता तो उसके धरातल का औसत ताप वर्तमान ताप से अधिक होता या कम?
(f) कुछ वैज्ञानिकों ने भविष्यवाणी की है कि पृथ्वी पर नाभिकीय विश्व युद्ध के बाद ‘प्रचण्ड नाभिकीय शीतकाल’ होगा जिसका पृथ्वी के जीवों पर विध्वंसकारी प्रभाव पड़ेगा। इस भविष्यवाणी का क्या आधार होगा ?
उत्तर:
(a) लम्बी दूरी के रेडियो प्रेषित्र लघु तरंग बैंड का उपयोग इसलिए करते हैं चूँकि आयनमण्डल इन बैंडों की तरंगें परावर्तित करता है।
(b) लम्बी दूरी के TV प्रेषण के लिए उपग्रहों का उपयोग आवश्यक है क्योंकि दूरदर्शन संकेत आयन मण्डल द्वारा समुचित रूप से परावर्तित नहीं होते हैं, अतः परावर्तन उपग्रहों द्वारा किया जाता है।
(c) प्रकाशीय तथा रेडियो दूरदर्शी पृथ्वी पर निर्मित किए जाते हैं, किन्तु X – किरण खगोल विज्ञान का अध्ययन पृथ्वी का परिभ्रमण कर रहे उपग्रहों द्वारा ही संभव है क्योंकि वायुमंडल X-किरणों को अवशोषित करता है जबकि दृश्य और रेडियो तरंगें इन्हें बेध सकती हैं।
(d) समतापमण्डल के ऊपरी छोर पर छोटी-सी ओजोन की परत मानव जीवन के लिए निर्णायक है क्योंकि यह सूर्य से उत्सर्जित पराबैंगनी विकिरणों को अवशोषित कर लेती है और पृथ्वी के पृष्ठ पर पहुँचने से रोकती है और जीवन को नष्ट होने से बचाती है।

Haryana State Board HBSE 11th Class Physics Solutions Chapter 2 मात्रक और मापन Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 2 मात्रक और मापन

प्रश्न 2.1.
रिक्त स्थान भरिए:
(a) किसी 1 cm भुजा वाले घन का आयतन …………….. m³ के बराबर है।
उत्तर:
10⁶
[संकेत: घन की भुजा L = 1 cm = \(\frac{1}{100}\) m = 10^-2 m
घन का आयतन L³ = (10²m)³ = 10⁶ m³]

(b) किसी 2 cm त्रिज्या व 10 cm ऊँचाई वाले सिलेण्डर का पृष्ठ क्षेत्रफल (mm)² के बराबर है।
उत्तर:
15 x 10⁴
[संकेत: सिलेण्डर का पृष्ठ क्षेत्रफल
= 2πr (r + h)
यहाँ,
त्रिज्या r=2cm
ऊंचाई h = 10cm
= 2 × 3.14 × 2 (2 + 10)
= 12.56 × 12
= 150.72 cm²
= 1.5 × 10⁴ mm²
[दो अंकों तक पूर्णांकित करने पर]

(c) कोई गाड़ी 18 km/h की चाल से चल रही है तो वह 1 s में …………….. m चलती है।
उत्तर:
[संकेत:
दूरी = चाल x समय
= 5 × 1 = 5m
क्योंकि
चाल = 18 km/h
= \(\frac{18 \times 1000}{3600}\) m/s = 5m/s
और
समय = 1 (सेकण्ड)]

(d) सीसे का आपेक्षिक घनत्व 11.3 है। इसका घनत्व ………….. g.cm^-3……………. kg m^-3 है।
उत्तर:
11.3, 11.3 x 10^-3
[संकेत : सीसे का घनत्व
= आपेक्षिक घनत्व x जल का घनत्व
= 11.3 x 1 = 11.3 g cm^-3
(∵ जल का घनत्व = gm cm^-3)
= 11.3 x \(\frac{10^{-3}}{\left(10^{-2}\right)^3}\) kg m^-3
= 11.3 × 10³ kgm^-3

प्रश्न 2.2.
रिक्त स्थानों को मात्रकों के उचित परिवर्तन द्वारा भरिए:
(a) 1 kgm²s^-2 = ……………… gcm²S^-2
(b) 1 m = ……………… ly
(c) 3.0 ms^-2 = ………….. km h^-2
(d) G = 6.67 × 10^-11 Nm² kg^-2
उत्तर:
(a) 10⁷
(b) 1.06 x 10¹⁶
(c) 3.9 × 10^-4
(d) 667 x 10^-8
[संकेत: (a) 1 kg m² s^-2
= 1000 gx (100 cm)² x 1s^-2
= 10⁷ g cm² s^-2

(b) 1 ly = 9.46 x 10¹⁵ m
1 m = \(\frac{1}{9.46 \times 10^{15}}\)
= 1.06 × 10^-16 ly

(c) 3.0 ms^-2 = \(\frac{3.0}{1000}\) km x (60 x 60)² h^-2
= 3.9 × 10⁴ km h^-2

(d) G = 6.67 x 10^-11 Nm²kg^-2
(∵ IN = 1kg m/s²)
= 6.67 × 10^-11 1 x m² kg^-2
= 6.67 x 10^-11 m³ s^-2 kg^-1
= 6.67 × 10^-11 x (100)³ cm³ s^-2 x \(\left(\frac{1}{1000}\right)\) g^-1
= 6.67 x 10⁸ cm³ s^-2 g^-1

प्रश्न 2.3.
ऊष्मा (परागमन में ऊर्जा) का मात्रक कैलोरी है और यह लगभग 4.2 J के बराबर है, जहाँ 1J = 1kgm² s^-2। मान लीजिए कि हम मात्रकों की कोई ऐसी प्रणाली उपप्रयोग करते हैं, जिसमें द्रव्यमान का मात्रक α kg के बराबर है, लम्बाई का मात्रक βm के बराबर है। समय का मात्रक γ s के बराबर है तो यह प्रदर्शित कीजिए कि नये मात्रकों के पदों में कैलोरी का परिमाण 4.2 α^-1 β^-2 γ² है।
उत्तर:
1 cal = 4.2 J = 4.2 kg m² s^-2
ऊर्जा का विमीय सूत्र = [ML² T ^-2]
यहाँ
m₂ =α kg, L₂ = βm, T₂ = γs
सूत्र:
n₁u₁ = n₂u₂
n₂ = n₁
= 4.2 \(\left[\frac{\mathrm{M}_1}{\mathrm{M}_2}\right]^1 \) \(\left[\frac{\mathrm{L}_1}{\mathrm{L}_2}\right]^1 \) \(\left[\frac{\mathrm{T}_1}{\mathrm{T}_2}\right]^1 \)
= 4.2 \(\left[\frac{1 \mathrm{~kg}}{\alpha \mathrm{kg}}\right]^1\) \(\left[\frac{1 \mathrm{~m}}{\beta \mathrm{m}}\right]^2\) \(\left[\frac{1 s}{\gamma s}\right]^{-2}\)
= 4.2 α^-1 β^-2 γ²
1 cal = 4.2 α^-1 β^-2 γ²
यही सिद्ध करना है

प्रश्न 2.4.
इस कथन की स्पष्ट व्याख्या कीजिए तुलना के मात्रक का विशेष उल्लेख किये बिना “किसी विमीय राशि को ‘बड़ा’ या ‘छोटा’ कहना अर्थहीन है।” इसे ध्यान में रखते हुए नीचे दिये गये कथनों को जहाँ कहीं भी आवश्यक हो, दूसरे शब्दों में व्यक्त कीजिए:
(a) परमाणु बहुत छोटे पिण्ड होते हैं।
(b) जेट वायुयान अत्यधिक गति से चलता है।
(c) बृहस्पति का द्रव्यमान बहुत ही अधिक है।
(d) इस कमरे के अन्दर वायु में अणुओं की संख्या बहुत अधिक
(e) इलेक्ट्रॉन, प्रोटॉन से बहुत भारी होता है।
(f) ध्वनि की गति प्रकाश की गति से बहुत ही कम होती है।
उत्तर:
किसी विमीय राशि को छोटा या बड़ा तुलना के आधार पर ही कहा जा सकता है। जैसे हम कह सकते हैं कि टेनिस की गेंद फुटबाल से छोटी होती है परन्तु कंचे की गोली की तुलना में बड़ी है।
(a) बाजरे के दाने की तुलना में परमाणु बहुत छोटे पिण्ड हैं।
(b) जेट वायुयान, कार की तुलना में अत्यधिक तेज चलता है।
(c) बृहस्पति का द्रव्यमान, पृथ्वी के द्रव्यमान की तुलना में बहुत अधिक है।
(d) कमरे के अन्दर वायु में अणुओं की संख्या 1 ग्राम गैस में उपस्थित अणुओं की संख्या से बहुत अधिक है।
(e) व (1) में तुलना पाठ्य पुस्तक में दी गयी है।

प्रश्न 2.5.
लम्बाई का कोई ऐसा नया मात्रक चुना गया है, जिसके अनुसार निर्वात् में प्रकाश की चाल 1 है। लम्बाई के नये मात्रक के पदों में सूर्य तथा पृथ्वी के बीच की दूरी कितनी है, प्रकाश इस दूरी को तय करने में 8 min और 20s लगाता है।
उत्तर:

समय t = 8 min 20s = 8 x 60 + 20 = 500s
∴ सूर्य तथा पृथ्वी के बीच की दूरी
= चाल x समय
= 1 x 500 = 500 मात्रक

प्रश्न 2.6.
लम्बाई मापने के लिए निम्नलिखित में से कौन-सा सबसे परिशुद्ध यन्त्र है:
(a) एक वर्नियर कैलिपर्स जिसके वर्नियर पैमाने पर 20 विभाजन
(b) एक स्क्रूगेज जिसका चूड़ी अन्तराल 1 mm और वृत्तीय पैमाने पर 100 विभाजन हैं।
(c) कोई प्रकाशिक यन्त्र जो प्रकाश की तरंगदैर्ध्य की सीमा के अन्दर लम्बाई माप सकता है।
उत्तर:
(a) यहाँ वर्नियर कैलिपर्स का अल्पतमांक

= \(\frac{0.1}{20}\)
= 0.005 cm

(b) स्क्रूगेज का अल्पतमांक

= \(\frac{0.1}{100}\)
= 0.001 cm

(c) प्रकाश की तरंगदैर्ध्य कोटि = 10^-7 m
= 10^-5 cm
अत: (a), (b) तथा (c) से स्पष्ट है कि प्रकाशिक यन्त्र की अल्पतमांक सबसे कम है। अतः यह सर्वाधिक परिशुद्ध यन्त्र है।

प्रश्न 2.7.
कोई छात्र 100 आवर्धन के एक सूक्ष्मदर्शी के द्वारा देखकर मनुष्य के बाल की मोटाई मापता है। वह 20 बार प्रेक्षण करता है और उसे ज्ञात होता है कि सूक्ष्मदर्शी के दृश्य क्षेत्र में बाल की औसत मोटाई 3.5mm है। बाल की मोटाई का अनुमान क्या है?
उत्तर:
सूक्ष्मदर्शी का आवर्धन

अतः बाल की मोटाई का अनुमान = 0.035mm

प्रश्न 2.8.
निम्नलिखित के उत्तर दीजिए:
(a) आपको एक धागा और मीटर पैमाना दिया जाता है। आप धागे के व्यास का अनुमान किस प्रकार लगायेंगे?
(b) एक स्क्रूगेज का चूड़ी अन्तराल 1.0 mm है और उसके वृत्तीय पैमाने पर 200 विभाजन हैं। क्या आप यह सोचते हैं कि वृत्तीय पैमाने पर विभाजनों की संख्या स्वेच्छा से बढ़ा देने पर स्क्रूगेज की यथार्थता में वृद्धि करना सम्भव है?
(c) वर्नियर कैलिपर्स द्वारा पीतल की किसी पतली छड़ का माध्य व्यास मापा जाना है। केवल 5 मापनों के समुच्चय की तुलना में व्यास के 100 मापनों के समुच्चय के द्वारा अधिक विश्वसनीय अनुमान प्राप्त होने की सम्भावना क्यों है?
उत्तर:
(a) सर्वप्रथम एक मीटर पैमाना लेंगे, उसके ऊपर धागे को इस प्रकार लपेटेंगे कि एक-दूसरे से सटे रहें। फेरों की संख्या l तब पैमाने की लम्बाई को नाप लेते हैं।
∴ धागे का व्यास =
इस सूत्र द्वारा धागे का व्यास ज्ञात कर लेते हैं।

(b) ∵ स्क्रूगेज का अल्पतमांक

सूत्र से स्पष्ट है कि वृत्तीय पैमाने पर कुल भाग बढ़ाने पर अल्पतमाांक कम होगा। अतः यथार्थता बढ़ेगी परन्तु व्यावहारिकता में आँखों की विभेदन क्षमता के कारण पाठ्यांक लेना कठिन होगा।

(c) ∵ प्रेक्षणों की संख्या 5 गुना करने पर त्रुटि \(\frac{1}{n}\) रह जाती है।
अतः 5 मापन से 100 मापन करने पर 20 गुना प्रेक्षण बढ़ने से त्रुटि \(\frac{1}{20}\) रह जायेगी। अतः विश्वसनीयता बढ़ जायेगी।

प्रश्न 2.9.
किसी मकान का फोटोग्राफ 35 mm स्लाइड पर 1.75 cm² क्षेत्र घेरता है। स्लाइड को किसी स्क्रीन पर प्रक्षेपित किया जाता है और स्क्रीन पर मकान का क्षेत्रफल 1.55 m² है। प्रक्षेपित पर्दा व्यवस्था का रेखीय आवर्धन क्या है?
उत्तर:
स्लाइड पर मकान का क्षेत्रफल = 1.75 cm²
स्क्रीन पर मकान का क्षेत्रफल = 1.55m²

प्रश्न 2.10.
निम्नलिखित में सार्थक अंकों की संख्या लिखिए:
(a) 0.007m²
(b) 2.64 × 10²⁴ kg
(c) 0.2370g cm^-3
(d) 6.320 J
(e) 6.032Nm^-2
(f) 0.0006032 m²
उत्तर:
( a ) 1
(b) 3
(c) 4
(d) 4
(e) 4
(f) 4

प्रश्न 2.11.
धातु की किसी आयताकार शीट की लम्बाई, चौड़ाई व मोटाई क्रमशः 4.234m 1.005m व 2.01 cm है। उचित सार्थक अंकों तक इस शीट का पृष्ठीय क्षेत्रफल व आयतन ज्ञात कीजिए।
उत्तर:
लम्बाई L = 4.234m, चौड़ाई B = 1.005m मोटाई W = 2.01 cm = 0.0201 m
∴ शीट का पृष्ठीय क्षेत्रफल
= 2 x (LB + BW + WL )
= 2 [4.234 x 1.005 + 1.005 x 0.0201 + 0.0201 × 4.234] m²
= [4.25517 + 0.0202005 + 0.0851034] m²
= 2 x 4.3604739m²
= 8.7209478 m² = 8.72 m²
(∵ मोटाई में अधिकतम सार्थक अंक तीन हैं अतः 3 अंकों तक पूर्णाकित करने पर)
आयतन = L x B x W
= 4.234 ×1.005 × 0.0201m³
=0.08552
= 0.0855 m³
(अधिकतम तीन अंकों तक पूर्णाकित करने पर)

प्रश्न 2.12.
पंसारी की तुला द्वारा मापे गये डिब्बे का द्रव्यमान 2.30 kg है। सोने के दो टुकड़े जिनके द्रव्यमान क्रमशः 20.15 g व 20.17g हैं, डिब्बे में रखे जाते हैं।
(a) डिब्बे का कुल द्रव्यमान कितना है?
(b) उचित सार्थक अंकों तक टुकड़ों के द्रव्यमान में कितना अन्तर है?
उत्तर:
डिब्बे का द्रव्यमान = 2.300kg
पहले टुकड़े का द्रव्यमान 20.15g = 0.02015 kg
दूसरे टुकड़े का द्रव्यमान = 20.17g = 0.02017 kg
∴ टुकड़े रखने के बाद डिब्बे का कुल द्रव्यमान
= 2.300 + 0.02015 + 0.02017
= 2.34032 kg
डिब्बे के द्रव्यमान में सबसे कम दशमलव के पश्चात् तीन अंक हैं। अतः तीन अंकों तक पूर्णांकित करने पर कुल द्रव्यमान = 2.340 kg

(b) ∵ सोने के टुकड़ों के द्रव्यमान में दशमलव के पश्चात् दो अंक हैं। अतः अन्तर में भी दशमलव के पश्चात् दो ही अंक तक पूर्णांकित करेंगे।
∴ टुकड़ों के द्रव्यमानों का अन्तर
= (20.17 – 20.15) g
= 0.02g

प्रश्न 2.13.
कोई भौतिक राशि P, चार प्रेक्षण योग्य राशियों a, b, c तथा से निम्न प्रकार सम्बन्धित है:
P = \(\frac{a^3 b^2}{\sqrt{c} d}\)
ab, c तथा d के मापने में प्रतिशत त्रुटियाँ क्रमशः 1%, 3%, 4% तथा 2% हैं। राशि में प्रतिशत त्रुटि कितनी है? यदि उपर्युक्त सम्बन्ध का उपयोग करके P का परिकलित मान 3.763 आता है तो आप परिणाम का किस मान तक निकटन करेंगे?
उत्तर:
P = \(\frac{a^3 b^2}{\sqrt{c} d}\)
∴ P के मान में प्रतिशत त्रुटि
= \(\frac{\Delta P \times 100}{P}\)
= 3 x \(\frac{\Delta a}{a}\) x 100% + 2 x \(\frac{\Delta b}{b}\) x 100% + \(\frac{1}{2}\) \(\frac{\Delta c}{c}\) × 100% + \(\frac{\Delta d}{d}\) x 100%
= 3 x 1% + 2 x 3% + \(\frac{1}{2}\) × 4% + 2%
= 13%
P का परिकलित मान 3.763
∵ P की % त्रुटि में दो सार्थक अंक हैं। अतः इसे दो अंकों तक पूर्णांकित करने पर P का निकटतम मान = 3.8

प्रश्न 2.14.
किसी पुस्तक में, जिसमें छपाई की अनेक त्रुटियाँ हैं, आवर्त गति कर रहे किसी कण के विस्थापन के चार भिन्न सूत्र दिये गये हैं:
(a) y = a sin \(\frac{2 \pi t}{T}\)
(b) y = asin vt
(c) y = \(\left(\frac{a}{T}\right) sin \frac{t}{a}\)
(d) y = (a√2) (sin 2πtT + cos 2πt / T)
( a = कण का अधिकतम विस्थापन, कण की चाल, 7 = गति का आवर्तकाल ) विमीय आधारों पर गलत सूत्रों को निकाल दीजिए।
उत्तर:
∵ कोण विमाहीन राशि है। अतः इस आधार पर

अतः (ii) व (iii) दोनों गलत हैं।

प्रश्न 2.15.
भौतिकी का एक प्रसिद्ध सम्बंध किसी कण के ‘चल द्रव्यमान (moving mass) ‘ m ‘विराम द्रव्यमान (rest mass) ‘ mo इसकी चाल और प्रकाश की चाल के बीच है । (यह सम्बन्ध सबसे पहले अल्बर्ट आइंस्टीन के विशेष आपेक्षिकता सिद्धान्त के परिणामस्वरूप उत्पन्न हुआ था।) कोई छात्र इस सम्बन्ध को लगभग सही याद करता है लेकिन स्थिरांक को लगाना भूल जाता है। वह लिखता है:
m = \(\frac{m_0}{\left(1-v^2\right)^{1 / 2}}\)
अनुमान लगाइए कि कहाँ लगेगा?
उत्तर:
दिया गया सम्बन्ध है:
m = \(\frac{m_0}{\left(1-v^2\right)^{1 / 2}}\)
या
(1 – v²)^1/2 = Mo/m
इस सम्बन्ध का दायाँ पक्ष विमाहीन है। अतः L. H.S. भी विमाहीन होना चाहिए।
∴ (1 – v²)^1/2 = [ M°L°T° ]
∵ L.H.S. में 1 तो विमाहीन है परन्तु v² को विमाहीन करने के लिए v² में c² का भाग देने पर \(\frac{v^2}{c^2}\) विमाहीन राशि प्राप्त होगी।
अतः
सही सूत्र m = \(\frac{m_0}{\left(1-\frac{v^2}{c^2}\right)^{1 / 2}}\)

प्रश्न 2.16.
परमाण्विक पैमाने पर लम्बाई का सुविधाजनक मात्रक एंग्स्ट्रॉम है और इसे A ( 1A = 10_-10m) द्वारा निर्दिष्ट किया जाता है। हाइड्रोजन के परमाणु का आमाप लगभग 0.54 है। हाइड्रोजन परमाणुओं के एक मोल का m’ में कुल आण्विक आयतन कितना होगा?
उत्तर:
हाइड्रोजन अणु की त्रिज्या
r = 0.5 A = 0.5 × 10^-10 m
हाइड्रोजन का अध्ययन
\(\frac{4}{3}\) πr³ = \(\frac{4}{3}\) × 3.14 × (0.5 × 10^-10)³
= 5.23 × 10^-311 m³
1 मोल हाइड्रोजन गैस में अणुओं की संख्या = 6.023 x 10²³ होती है।
∵ 1 मोल गैस का आण्विक आयतन
= अणुओं की संख्या x एक अणु का आयतन
= 6,023 × 10²³ x 5.23 x 10^-31
= 3.15 × 10⁷ m³

प्रश्न 2.17.
किसी आदर्श गैस का एक मोल (ग्राम अणुक ) मानक ताप व दाब पर 22.4 L आयतन (ग्राम अणुक आयतन) घेरता है। हाइड्रोजन के ग्राम अणुक आयतन तथा उसके मोल के परमाण्विक आयतन का अनुपात क्या है? (हाइड्रोजन के अणु की आमाप लगभग 1 A मानिए)। यह अनुपात इतना अधिक क्यों है?
उत्तर:
1 मोल हाइड्रोजन गैस का आयतन
= 22.4 L = 22.4 × 10^-3 m³
हाइड्रोजन अणु की त्रिज्या
r = 0.5 A = 0.5 × 10^-10 m
हाइड्रोजन का अध्ययन
\(\frac{4}{3}\) πr³ = \(\frac{4}{3}\) × 3.14 × (0.5 × 10^-10)³
= 5.23 × 10^-311 m³
1 मोल हाइड्रोजन गैस में अणुओं की संख्या = 6.023 x 10²³ होती है।
∵ 1 मोल गैस का आण्विक आयतन
= अणुओं की संख्या x एक अणु का आयतन
= 6,023 × 10²³ x 5.23 x 10^-31
= 3.15 × 10⁷ m³
1 मोल हाइड्रोजन गैस आण्विक आयतन = 3.15 × 10⁷ m³

∴ अभीष्ट अनुपात 7.11 x 10⁴ : 1
इसका मान अधिक इसलिए है कि गैस का आयतन उसमें उपस्थित अणुओं के वास्तविक आयतन की तुलना में बहुत अधिक होता है। इसका अर्थ है कि गैस के अणुओं के बीच बहुत अधिक खाली स्थान होता है।

प्रश्न 2.18.
इस सामान्य प्रेक्षण की स्पष्ट व्याख्या कीजिए:
यदि आप तीव्र गति से गतिमान किसी रेलगाड़ी की खिड़की से बाहर देखें तो समीप के पेड़, मकान आदि रेलगाड़ी की गति के विपरीत दिशा में तेजी से गति करते प्रतीत होते हैं, परन्तु दूरस्थ पिण्ड (पहाड़ियाँ, तारे आदि) स्थिर प्रतीत होते हैं। (वास्तव में क्योंकि आपको ज्ञात है कि आप चल रहे हैं, इसलिए ये दूरस्थ वस्तुएँ आपको अपने साथ चलती हुई प्रतीत होती हैं।)
उत्तर:
प्रेक्षक की आँखों पर समीप की वस्तु, दूर की वस्तु की तुलना में अधिक कोण बनाती है। जब प्रेक्षक गति करेगा तो समीप की वस्तु की अपेक्षा दूर की वस्तु द्वारा बने कोण में परिवर्तन कम होता है। अतः दूरस्थ वस्तु आपके साथ गतिमय प्रतीत होती है जबकि समीपस्थ वस्तु विपरीत दिशा में गतिमय प्रतीत होती है।

प्रश्न 2.19.
समीपी तारों की दूरियाँ ज्ञात करने के लिए लम्बन के सिद्धान्त का प्रयोग किया जाता है। सूर्य के परित: अपनी कक्षा में छह महीनों के अन्तराल पर पृथ्वी की अपनी दो स्थानों को मिलाने वाली, आधार रेखा AB है अर्थात् आधार रेखा पृथ्वी की कक्षा के व्यास = 3 x 10¹¹ m के लगभग बराबर है। लेकिन चूँकि निकटतम तारे भी इतने अधिक दूर हैं कि इतनी लम्बी आधार रेखा होने पर भी वे चाप के केवल 1″ ( सेकण्ड चाप का) की कोटि का लम्बन प्रदर्शित करते हैं। खगोलीय पैमाने पर लम्बाई का सुविधाजनक मात्रक पारसेक है। यह किसी पिण्ड की वह दूरी है, जो पृथ्वी से सूर्य तक की दूरी के बराबर आधार रेखा के दो विपरीत किनारों से चाप के 1″ का लम्बन प्रदर्शित करती है। मीटरों में एक पारसेक कितना होता है?
उत्तर:
चित्र में S सूर्य तथा E₁ व E₂ पृथ्वी की छ: माह के अन्तराल में स्थिति है।
बिन्दु O की पृथ्वी से दूरी 1 पारसेक है।
पृथ्वी की कक्षा का व्यास = 3 x 10¹¹ m
चाप SE1 = \(\frac{3 \times 10^{11}}{2}\) = 1.5 x 10¹¹ m
रेखाखण्ड SE बिन्दु O पर 1″ (चाप का) कोण अन्तरित करता

प्रश्न 2.20.
हमारे सौर परिवार से निकटतम तारा 4.29 प्रकाश वर्ष दूर है। पारसेक में यह दूरी कितनी है? यह तारा (ऐल्फा सेंटौरी नामक) तब कितना लम्बन प्रदर्शित करेगा। जब इसे सूर्य के परितः ‘ अपनी कक्षा में पृथ्वी के दो स्थानों से जो छः महीने के अन्तराल पर है, देखा जायेगा?
उत्तर:
तारे की सौर परिवार से दूरी
= 4.29 प्रकाश वर्ष (ly)
= 4.29 x 9.46 x 10¹⁵m
[∵ 1ly = 9.46 x 10¹⁵ m]
= \(\frac{4.29 \times 9.46 \times 10^{15}}{3 \times 10^{16}}\) पारसेक
[∵ 1 पारसेक = 3 x 10¹⁶m]
= 1.35 पारसेक

छः महीने के अन्तराल पर पृथ्वी अपनी कक्षा के व्यासत: विपरीत सिरों पर होगी।
∵ पृथ्वी का विस्थापन d = कक्षा का व्यास
= 3 x 10¹¹ m
∵ तारे की सौरमण्डल के केन्द्र सूर्य से दूरी
r = 4.29 x 9.46 x 10¹⁵ m
∴ तारे द्वारा प्रदर्शित लम्बन
θ = \(\frac{d}{r}\) = \(\frac{3 \times 10^{11}}{4.29 \times 9.46 \times 10^{15}}\)rad
= 0.0739 × 10^-4 rad
= 0.0739 × 10^-4 x \(\frac{180}{\pi}\) x 60 x 60 सेकण्ड
∴ θ = \(\frac{4.79}{3.14}\) = 1.52

प्रश्न 2.21.
भौतिक राशियों का परिशुद्ध मापन विज्ञान की आवश्यकताएँ हैं। उदाहरण के लिए, किसी शत्रु के लड़ाकू जहाज की चाल सुनिश्चित करने के लिए बहुत ही छोटे समयान्तरालों पर इसकी स्थिति का पता लगाने की कोई यथार्थ विधि होनी चाहिए। द्वितीय विश्वयुद्ध में रडार की खोज के पीछे वास्तविक प्रयोजन यही था। आधुनिक विज्ञान के उन भिन्न उदाहरणों को सोचिए जिनमें लम्बाई, समय, द्रव्यमान आदि के परिशुद्ध मापन की आवश्यकता होती है।
अन्य जिस किसी विषय में भी आप बता सकते हैं, परिशुद्धता की मात्रात्मक धारणा दीजिए।
उत्तर:
लम्बाई का मापन: विभिन्न यौगिकों के क्रिस्टलों में परमाणुओं के बीच की दूरी का मापन करते समय लम्बाई के परिशुद्ध मापन की आवश्यकता होती है।
समय का मापन: फेको की विधि द्वारा किसी माध्यम में प्रकाश की चाल ज्ञात करने के प्रयोग में समय के परिशुद्ध मापन की आवश्यकता होती है। उपग्रह प्रक्षेपण में समय का मापन परिशुद्धता से किया जाता है।
द्रव्यमान का मापन: द्रव्यमान स्पेक्ट्रमलेखी में परमाणुओं के द्रव्यमान का परिशुद्ध मापन किया जाता है। दवाइयाँ बनाने में विभिन्न साल्ट मिलाये जाते हैं, जिनका द्रव्यमान परिशुद्धता से मापन करते हैं।

प्रश्न 2.22.
जिस प्रकार विज्ञान में परिशुद्ध मापन आवश्यक है, उसी प्रकार अल्पविकसित विचारों तथा सामान्य प्रेक्षणों को उपयोग करने वाली राशियों के स्थूल आकलन कर सकना भी उतना ही महत्वपूर्ण है। उन उपायों को सोचिए जिनके द्वारा आप निम्नलिखित का अनुमान लगा सकते हैं (जहाँ अनुमान लगाना कठिन है वहाँ राशि की उपरिसीमा पता लगाने का प्रयास कीजिए)
(a) मानसून की अवधि में भारत के ऊपर वर्षांधारी मेघों का कुल द्रव्यमान।
(b) किसी हाथी का द्रव्यमान।
(c) किसी तूफान की अवधि में वायु की चाल।
(d) आपके सिर के बालों की संख्या।
(e) आपकी कक्षा के कमरे में वायु के अणुओं की संख्या।
उत्तर:
(a) सर्वप्रथम मौसम विभाग से पूरे भारत में हुई कुल वर्षा की माप की जानकारी लेंगे और वर्षा जल के आयतन को जल के घनत्व से गुणा करके वर्षा जल के द्रव्यमान की गणना कर लेंगे। इससे मेघों का द्रव्यमान ज्ञात हो जायेगा।
जैसे: बादल का द्रव्यमान
= औसत वर्षा x भारत का क्षेत्रफल पानी का घनत्व
= 1 x 3.3 x 1012 × 103 kg
= 3.3 × 1015 kg
(b) हाथी का द्रव्यमान काँटे पर भी लीवर सिद्धान्त से ज्ञात कर सकते हैं।
(c) इसके लिए एक गैस का गुब्बारा लेते हैं तथा उसे ऊपर की ओर छोड़ते हैं तथा। सेकण्ड पश्चात् उसकी स्थिति ज्ञात कर कोण θ का मापन करते हैं।

चित्र में गुब्बारा बिन्दु 0 से छोड़ा गया है, जो 1 सेकण्ड पश्चात् बिन्दु B पर पहुँचता है। गुब्बारे की ऊँचाई / ज्ञात कर विस्थापन ज्ञात करते हैं। यही विस्थापन AB = dh= θ ही तूफान में हवा की चाल होगी।
(d) मनुष्य के बालों की संख्या =
जैसे: सिर की औसत त्रिज्या R = 8cm हो, तो
सिर का क्षेत्रफल = πR² = π(8)² = 64πcm²
बाल का व्यास पेचमापी से ज्ञात करते हैं जो लगभग 5 x 10^-3cm
∴ त्रिज्या r = \(\frac{5}{2}\) x 10^-3 cm
अत; एक बाल का क्षेत्रफल = πR²
= π × \(\left(\frac{5}{2} \times 10^{-3}\right)^2\)
= π × \(\frac{25}{4}\) × 10^-6 cm²
∴ बालों की संख्या = \(\frac{64 \pi}{\pi \times \frac{25}{4} \times 10^{-6}}\)
= 10⁷

(e) ∵ NTP पर 22.4 L = 22.4 x 10^-3 m³ में अणुओं की संख्या 6.02 × 10²³ होती है।
∴ कमरे के आयतन में अणुओं की संख्या
= \(\frac{6.02 \times 10^{23}}{22.4 \times 10^{-3}}\)
यदि कमरे का आकार 5 x 4 x 3m³ = 60m³ माने तो अणुओं की संख्या 10²⁷ कोटि की प्राप्त होगी।

प्रश्न 2.23.
सूर्य एक ऊष्मा प्लाज्मा (आयनीकृत पदार्थ) है, जिसके आन्तरिक क्रोड का ताप 10⁷ K से अधिक और बाह्य पृष्ठ का ताप लगभग 6000K है। इतने अधिक ताप पर कोई भी पदार्थ ठोस या तरल प्रावस्था में नहीं रह सकता। आपको सूर्य का द्रव्यमान घनत्व किस परिसर में होने की आशा है? क्या यह ठोसों, तरलों या गैसों के घनत्वों के परिसर में है? क्या आपका अनुमान सही है, इसकी जाँच आप निम्नलिखित आँकड़ों के आधार पर कर सकते हैं? सूर्य का द्रव्यमान = 2 x 10³⁰ kg, सूर्य की त्रिज्या = 7.0 x 10⁸ m
उत्तर:
सूर्य का घनत्व
d =
= \(\frac{M}{\frac{4}{3} \pi r^3}\)
यहाँ M = 2 x 10³⁰ kg, r = 7.0 x 10⁸ m
∴ d = \(\frac{3 \times 2 \times 10^{30}}{4 \times 3.14 \times\left(7.0 \times 10^8\right)^3}\)
= 1.4 x 10³ kg/m³
सूर्य का घनत्व द्रव / ठोस के घनत्व के परिसर में होता है। यह गैसों के परिसर में नहीं होता है क्योंकि सूर्य की भीतरी परतों के कारण बाहरी परतों पर गुरुत्वाकर्षण बल के कारण प्लाज्मा का घनत्व उच्च होता है।

प्रश्न 2.24.
जब बृहस्पति ग्रह पृथ्वी से 8247 लाख किलोमीटर दूर होता है तो इसके व्यास की कोणीय माप 35.72″ का चाप है। बृहस्पति का व्यास परिकलित कीजिए।
उत्तर:
कोणीय व्यास θ =
∴ व्यास d = θ x α
कोणीय माप θ = 35.72″ = \(\frac{35.72}{60 \times 60}\) डिग्री
= \(\frac{35.72}{60 \times 60}\) x \(\frac{\pi}{180}\) rad
दूरी α = 8247 लाख किलोमीटर
= 8247 × 10⁵ km
= 8247 x 10⁸ m
∴ d = \(\frac{35.72}{60 \times 60}\) x \(\frac{3.14}{180}\) x 8247 x 10⁸ m
= 1.427 x 10⁸ m
= 1.427 x 10⁵ km

अतिरिक्त अभ्यास (Additional Exercise):

प्रश्न 2.25.
वर्षा के समय में कोई व्यक्ति चाल के साथ तेजी से चला जा रहा है। उसे अपने छाते को टेढ़ा करके ऊर्ध्वं के साथ θ कोण बनाना पड़ता है। कोई विद्यार्थी कोण 9 व ” के बीच निम्नलिखित सम्बन्ध व्युत्पन्न करता है:
tan θ = v
और वह इस सम्बन्ध के औचित्य की सीमा का पता लगाता है जैसी कि आशा की जाती है यदि। v → θ तो θ → 01 ( हम यह मान रहे हैं कि तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा ऊर्ध्वाधरत पड़ रही है।) क्या आप सोचते हैं कि यह सम्बन्ध सही हो सकता है? यदि ऐसा नहीं है तो सही सम्बन्ध का अनुमान लगाइए।
उत्तर:
दिये गये सम्बन्ध में,
बाएँ पक्ष की विमाएँ = [M°L°T° ]

जबकि दाएँ पक्ष की विमाएँ = [M°L¹T^-1]
∵ दोनों पक्षों की विमाएँ परस्पर समान नहीं हैं, अतः यह सम्बन्ध
सही नहीं हो सकता। स्पष्ट है कि सही सम्बन्ध में दाएँ पक्ष की विमाएँ भी [M°L°T° ] होनी चाहिए।
सही सम्बन्ध tan θ = v²/ rg

प्रश्न 2.26.
यह दावा किया जाता है कि यदि बिना किसी बाधा के 100 वर्षों तक दो सीजियम घड़ियों को चलने दिया जाये तो उनके समयों में केवल 0.02 (s) का अन्तर हो सकता है, मानक सीजियम घड़ी द्वारा 1 (s) के समय अन्तराल को मापने में यथार्थता के लिए इसका क्या अभिप्राय है?
उत्तर:
समय T = 100 वर्ष
= 100 x 365 x 24 x 60 x 60
त्रुटि ΔΤ = 0.02 sec
∴ 1(s) के मापन में त्रुटि
= \(\frac{\Delta T}{T} = [latex]\frac{0.02}{100 \times 365 \times 24 \times 60 \times 60}
= 6.34 × 10^-12
= 10 x 10^-12 (पूर्णांकित करने पर)
= 10^-11 = [latex]\frac{1}{10^{11}}\)
अतः सीजियम घड़ी द्वारा 1s के मापन में 10¹¹ में से 1 भाग की परिशुद्धता है।

प्रश्न 2.27.
एक सोडियम परमाणु की आमाप लगभग 2.5 A° मानते हुए उसके माध्य द्रव्यमान घनत्व का अनुमान लगाइए। (सोडियम के परमाण्वीय द्रव्यमान तथा आवोगाद्रो संख्या के ज्ञात मान का प्रयोग कीजिए।)
इस घनत्व की क्रिस्टलीय प्रावस्था में सोडियम के घनत्व 970 kg m^-3 के साथ तुलना कीजिए। क्या इन दोनों घनत्वों के परिमाण की कोटि समान है। यदि हाँ, तो क्यों?
उत्तर:
सोडियम परमाणु की आमाप 2.5 A
∴ त्रिज्या R = \(\frac{2.5}{2}\)
= 1.25 A
= 1.25 x 10^-10 m
सोडियम का ग्राम परमाणु भार
= 23g = 23 x 10^-3 kg
1 ग्राम परमाणु में परमाणुओं की संख्या = 6,023 × 10²³
∴ सोडियम के एक परमाणु का द्रव्यमान
= 3.82 × 10^-26 kg
1 परमाणु का आयतन = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) × 3.14 × (1.25 × 10^-10)³
= 8.18 × 10³⁰ m³
∴ सोडियम परमाणु का माध्य द्रव्यमान घनत्व

= 4670 kg/m³
= 4.670 × 10³ kgm
क्रिस्टलीय अवस्था में सोडियम का घनत्व = 970kgm^-3
= 0.970 × 10³ kg/m³
∴ दोनों के घनत्व की कोटि (10³) लगभग समान है क्योंकि ठोस अवस्था में परमाणु दृढ़तापूर्वक संकुचित होते हैं। अतः परमाणु द्रव्यमान घनत्व ठोस के द्रव्यमान घनत्व के लगभग बराबर होता है।

प्रश्न 2.28.
नाभिकीय पैमाने पर लम्बाई का सुविधाजनक मात्रक फर्मी (1 fm = 10^-15 m) है। नाभिकीय आमाप लगभग निम्नलिखित आनुभविक सम्बन्ध का पालन करते हैं:
r = r0A^1/3
जहाँ नाभिक की त्रिज्या, 4 इसकी द्रव्यमान संख्या और ro कोई स्थिरांक है, जो लगभग 1.2 fm के बराबर है। यह प्रदर्शित कीजिए कि इस नियम का अर्थ है कि विभिन्न नाभिकों के लिए नाभिकीय द्रव्यमान घनत्व लगभग स्थिर है। सोडियम नाभिक के द्रव्यमान घनत्व का आकलन कीजिए। प्रश्न 27 में ज्ञात किये गये सोडियम परमाणु के माध्य द्रव्यमान घनत्व के साथ इसकी तुलना कीजिए।
उत्तर:
नाभिक की त्रिज्या r = r0A^1/3
∴ नाभिक का आयतन v = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\)π(r0A^1/3)³
V = \(\frac{4}{3}\) πr³0A
माना न्यूक्लिऑन (न्यूट्रॉनों प्रोटॉनों) का द्रव्यमान m (m = 1.66 x 10^-27 kg) है।
∴ नाभिक का कुल द्रव्यमान = mA
∴ नाभिक का द्रव्यमान घनत्व =
= \(\frac{m A}{\frac{4}{3} \pi r_0^3 A}\)
= \(\frac{3 m}{4 \pi r_0^3}\)
उपर्युक्त सूत्र में द्रव्यमान संख्या नहीं है अर्थात् नाभिकीय द्रव्यमान घनत्व स्थिर है।
(b) सोडियम नाभिक का द्रव्यमान घनत्व

∵ r0 = 1.2fm
= 1.2 x 10^-15 m
m = 1.66 x 10^-27 kg
= \(\frac{3 \times 1.66 \times 10^{-27}}{4 \times 3.14 \times\left(1.2 \times 10^{-15}\right)^3}\)
= 0.3 × 10¹⁸ kg/m³

(c) क्रिस्टलीय अवस्था में सोडियम का घनत्व = 970kgm^-3
= 0.970 × 10³ kg/m³
∴ दोनों के घनत्व की कोटि (10³) लगभग समान है क्योंकि ठोस अवस्था में परमाणु दृढ़तापूर्वक संकुचित होते हैं। अतः परमाणु द्रव्यमान घनत्व ठोस के द्रव्यमान घनत्व के लगभग बराबर होता है।,
सोडियम परमाणु का माध्य घनत्व = 4.6 x 10³ kg/m³

अर्थात् सोडियम नाभिक का घनत्व, उसके परमाणु के घनत्व से 10¹⁵ गुना अधिक है। इसका अर्थ है कि परमाणु का अधिकांश भाग खोखला होता है तथा उसका अधिकांश द्रव्यमान उसके नाभिक में केन्द्रित होता है।

प्रश्न 2.29.
लेसर (Laser), प्रकाश के अत्यधिक तीव्र, एकवर्णी तथा एकदिश किरण पुंज का स्रोत है। लेसर के इन गुणों का लम्बी दूरियाँ मापने में उपयोग किया जाता है। लेसर को प्रकाश के स्रोत के रूप में उपयोग करते हुए पहले ही चन्द्रमा की पृथ्वी से दूरी परिशुद्धता के साथ ज्ञात की जा चुकी है। कोई लेसर प्रकाश किरण-पुंज चन्द्रमा के पृष्ठ से परावर्तित होकर 2.565 में वापस आ जाता है। पृथ्वी के परितः चन्द्रमा की कक्षा की त्रिज्या कितनी है?
उत्तर:
माना चन्द्रमा की कक्षा की त्रिज्या = r
∴ लेसर प्रकाश द्वारा तय की गई कुल दूरी = 2r
∴ समय t = 2.56(s)
∴ दूरी 2r = चाल (c) x समय (t)
∴ त्रिज्या r = \(\frac{c \times t}{2}\)
= \(\frac{3 \times 10^8 \times 2.56}{2}\)
= 3.84 × 10⁸ m

प्रश्न 2.30.
जल के नीचे वस्तुओं को ढूँढ़ने व उनके स्थान का पता लगाने के लिए सोनार (SONAR) में पराश्रव्य तरंगों का प्रयोग होता है। कोई पनडुब्बी सोनार से सुसज्जित है। इसके द्वारा जनित अन्वेषी तरंग और शत्रु की पनडुब्बी से परावर्तित इसकी प्रतिध्वनि की प्राप्ति के बीच काल विलम्ब 77.0 (s) है। शत्रु की पनडुब्बी कितनी दूर है? (जल में ध्वनि की चाल = 1450ms^-1)
उत्तर:
माना शत्रु की पनडुब्बी की सोनार स्टेशन से दूरी = d
∴ तरंगों द्वारा तय की गई कुल दूरी 2d
∴ दूरी 2d = चाल v x समय t
d = \(\frac{v \times t}{2}\)
= 55825 m
∴ d = 55.825 km

प्रश्न 2.31.
हमारे विभ्व में आधुनिक खगोलविदों द्वारा खोजे गये सर्वाधिक दूरस्थ पिण्ड इतनी दूर हैं कि उनके द्वारा उत्सर्जित प्रकाश को पृथ्वी तक पहुँचने में अरबों वर्ष लगते हैं। इन पिण्डों (जिन्हें क्वासर ‘Quasar’ कहा जाता है) के कई रहस्यमय लक्षण हैं। जिनकी अभी तक सन्तोषजनक व्याख्या नहीं की जा सकी है। किसी ऐसे क्वासर की km में दूरी ज्ञात कीजिए, जिससे उत्सर्जित प्रकाश को हम तक पहुँचने में 300 करोड़ वर्ष लगते हों।
उत्तर:
प्रकाश को पहुँचने में लगा समय
= 300 करोड़ वर्ष = 300 x 10⁷ वर्ष
∴ दूरी = 300 x 10⁷ प्रकाश वर्ष
प्रकाश द्वारा 1 वर्ष में तय की गई दूरी
= 9.46 x 10¹⁵ m
∴ क्वासर की दूरी = 300 x 10⁷ x 9.46 x 10¹⁵
= 28.4 × 10²⁴m = 2.84 x 10²² km 

प्रश्न 2.32.
यह एक विख्यात तथ्य है कि पूर्ण सूर्यग्रहण की अवधि में चन्द्रमा की चक्रिका सूर्य की चक्रिका को पूरी तरह ढक लेती है । चन्द्रमा का लगभग व्यास ज्ञात कीजिए। (उदाहरण 2.3 व 2.4 की सूचनाओं को प्रयुक्त कीजिए। )
उत्तर:
चन्द्रमा का कोणीय व्यास

d = \(\frac{d}{3.84 \times 10^8}\) × \(\frac{180}{\pi}\) डिग्री
d = \(\frac{d}{3.84 \times 10^8}\) × \(\frac{180}{\pi}\) × 60 × 60(s)
यहाँ चन्द्रमा की पृथ्वी से दूरी
α = 3.84 x 108 m है।
∵ चन्द्रमा की चक्रिका, सूर्य की चक्रिका को पूरी तरह ढक लेती है। अतः चन्द्रमा तथा सूर्य दोनों के कोणीय व्यास बराबर होंगे।
∴d = \(\frac{d}{3.84 \times 10^8}\) × \(\frac{180}{\pi}\) × 60 × 60 = 1920
( ∵ सूर्य का कोणीय व्यास = 1920)
d = \(\frac{1920 \times 3.84 \times 10^8 \times \pi}{180 \times 60 \times 60}\)
= 3.576 × 10⁶ m
∵ चन्द्रमा का व्यास
= 3.576 × 10³ km = 3576 km

प्रश्न 2.33.
इस शताब्दी के एक महान भौतिकविद (पी.ए.एम. डिरैक) प्रकृति के मूल स्थिरांकों (नियतांकों) के आंकिक मानों के साथ क्रीड़ा में आनन्द लेते थे। इससे उन्होंने एक बहुत ही रोचक प्रेक्षण किया । परमाण्वीय भौतिकी के मूल नियतांकों (जैसे इलेक्ट्रॉन का द्रव्यमान, प्रोटॉन का द्रव्यमान तथा गुरुत्वीय नियतांक 6) से उन्हें पता लगा कि वे एक ऐसी संख्या पर पहुँच गये हैं, जिसकी विमा समय की विमा है। साथ ही यह एक बहुत ही बड़ी संख्या थी और इसका परिमाण विश्व की वर्तमान आकलित आयु – 1500 करोड़ वर्ष) के करीब है। इस पुस्तक में दी गई मूल नियतांकों की सारणी के आधार पर यह देखने का प्रयास कीजिए कि क्या आप भी यह संख्या बना सकते हैं? यदि विश्व की आयु तथा इस संख्या में समानता महत्वपूर्ण है तो मूल नियतांकों की स्थिरता किस प्रकार प्रभावित होगी?
उत्तर:
समय की विमा t = \(\left(\frac{e^2}{4 \pi \varepsilon_0}\right) \times \frac{1}{m_p m_e^2 c^3 G}\)
∵ e = 1.6 x 10^-19C,
\(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹
c = 3 x 10⁸ m/s,
G = 6.67 × 10^-11 Nm² kg²,
mp = 1.67 x 10^-27 kg.
mg = 9 x 10^-31 kg.
मान रखने पर,
t = (1.6 × 10^-19)⁴ × (9 × 10⁹ )² × \(\frac{1}{1.67 \times 10^{-27} \times\left(9 \times 10^{-31}\right)^2}\) x (3 x 10⁸) 3 x 6.67 x 10^-11
t = 2.18 x 10¹⁶ sec
∴ यह समय ब्रह्माण्ड की आयु की कोटि का है।

Haryana State Board HBSE 12th Class Physics Solutions Chapter 7 प्रत्यावर्ती धारा Textbook Exercise Questions and Answers.

Haryana Board 12th Class Physics Solutions Chapter 7 प्रत्यावर्ती धारा

प्रश्न 7.1.
एक 100 52 का प्रतिरोधक 220 V 50Hz आपूर्ति से संयोजित है।
(a) परिपथ में धारा का rms मान कितना है?
(b) एक पूरे चक्र में कितनी नेट शक्ति व्यय होती है?
उत्तर:
हल दिया गया है-
R = 10052
E_rms = 220 V
आवृत्ति f = 50 Hz
(a) परिपथ में धारा का mms मान होगा
I_rms = \(\frac{E_{\text {mws }}}{R}\)
= \(\frac{220}{100}\) = 2. 2A

(b) शक्ति व्यय (P) हुई = ?
P= I_rms × E_rms
= 2.2 x 220
= 484 W प्रति चक्र

प्रश्न 7.2.
(a) ac आपूर्ति का शिखर मान 300v है। rms वोल्टता कितनी है?
(b) ac परिपथ में धारा का rms मान 10 A है शिखर धारा कितनी है?
उत्तर:
हल दिया गया है- E₀ = 300 V
E_rms = ?
I_rms= 10 A
I₀ = ?

(a) हम जानते हैं – E_rms = \(\frac{E_0}{\sqrt{2}}\)
= 0.707 × 300
= 212.100
= 212.1 V प्राप्त करते हैं।

(b) I_rms = \(\frac{\mathrm{I}_0}{\sqrt{2}}\)
∴ I₀ = \(\sqrt{2} I_{\mathrm{rms}}\)
= √2 × 10
= 1.414 × 10 = 14.14 A

प्रश्न 7.3.
एक 44 mH की प्रेरक कुण्डली को 220 V, 50 परिपथ में धारा के rms मान को ज्ञात कीजिए।
उत्तर:
हल दिया गया है-
L = 44 mH = 44 x 10^-3 H
E_rms = 220 V
f = 50 Hz
I_rms = ?
X_L = Lω
= L × 2πf
X_L = 44 × 10^-3 × 2 × \(\frac{22}{7}\) × 50Ω

प्रश्न 7.4.
एक 60 µF का संधारित्र 110 V, 60 Hz ac आपूर्ति से जोड़ा गया है। परिपथ में धारा के rms मान को ज्ञात कीजिए।
उत्तर:
हल दिया गया है-
C = 60 µF = 60 × 10^-6 F
E_rms = 110 V
f = 60 Hz
I_rms = ?
\(I_{\mathrm{rms}}=\frac{\mathrm{E}_{\mathrm{rms}}}{X_{\mathrm{C}}}=\omega C \mathrm{E}_{\mathrm{rms}}\)
I_rms = 2πfC E_rms
= 2 × 3.14 × 60 x 60 x 10 x 110
= 2.49 A

प्रश्न 7.5
प्रश्न 7.3 व 7.4 में एक पूरे चक्र की अवधि में प्रत्येक परिपथ में कितनी नेट शक्ति अवशोषित होती है? अपने उत्तर का विवरण दीजिए।
उत्तर:
हल – संधारित्र एवं प्रेरण कुण्डली के लिये वोल्टता और धारा के
मध्य कलान्तर Φ = ± \(\frac{\pi}{2}\) अतः एक पूरे चक्र में शक्ति व्यय
P = E_rms I_rms cos Φ
P = E_rms I_rms cos \(\left( \pm \frac{\pi}{2}\right)\) = 0
यहाँ पर Φ = \(\frac{\pi}{2}\)
∴ cos Φ = cos \(\frac{\pi}{2}\) = 0
∴ P_av = 0 प्रत्येक स्थिति के लिए

प्रश्न 7.6.
एक LCR परिपथ की, जिसमें L=2.0 H, C = 32 µF तथा R = 10 Ω अनुनाद आवृत्ति ω_r परिकलित कीजिए। इस परिपथ के लिए Q का क्या मान है?
उत्तर:
हल-दिया गया है-
L = 2.0 H
C = 32 µF = 32 × 10^-6F
तथा R = 10 Ω
अनुनाद आवृत्ति ω^r = ?
इस परिपथ के लिए आवेश = Q = ?

प्रश्न 7.7.
30 µF का एक आवेशित संधारित्र 27 mH की प्रेरण कुण्डली से जोड़ा गया है। परिपथ के मुक्त दोलनों की कोणीय आवृत्ति कितनी है?
उत्तर:
हल-दिया गया है-
c = 30 µF = 30 × 10^-6F
L = 27 mH = 27 × 10^-3 H
हम जानते हैं-

प्रश्न 7.8.
कल्पना कीजिए कि अभ्यास 7.7 में संधारित्र पर प्रारम्भिक आवेश 6 mC है। प्रारम्भ में परिपथ में कुल कितनी ऊर्जा संचित होगी? बाद में कुल ऊर्जा कितनी होगी?
उत्तर:
हल-दिया गया है-
q = 6 mC = 6 × 10^-3C
C = 30 µF = 30 × 10^-6F
फुल ऊर्जा संचित U_E = ?
अतः प्रारम्भ में संचित ऊर्जा U_E = [/latex]\frac{\mathrm{q}^2}{2 \mathrm{C}}[/latex]
मान रखने पर U_E = \(\frac{1}{2}\left(\frac{\left(6 \times 10^{-3}\right)^2}{30 \times 10^{-6}}\right)\)
= \(\frac{36}{2 \times 30}=\frac{6}{10}\)
U_E = 0.6 J
यदि हम परिपथ में ऊर्जा हास को शून्य मानें तो यह ऊर्जा बाद में प्रेरकत्व एवं संधारित्र में संचित ऊर्जाओं में विभक्त हो जायेगी, जिसका कुल मान एक समान रहेगा अर्थात् 0.6 जूल ही रहेगा।

प्रश्न 7.9.
एक श्रेणीबद्ध LCR परिपथ को, जिसमें R = 20 Ω, L=1.5 H तथा C = 35 µF, एक परिवर्ती आवृत्ति की 200 V ac आपूर्ति से जोड़ा गया है। जब आपूर्ति की आवृत्ति परिपथ की मूल आवृत्ति के बराबर होती है, तो एक पूरे चक्र में परिपथ को सथानान्तरित की गई माध्य शक्ति कितनी होगी?
उत्तर:
हल-दिया गया है
R = 20 Ω,
L = 1.5 H
C = 35 µF = 35 × 10^-6 F
E_rms = 200 V
आवृत्ति f = परिवर्ती
जब आपूर्ति की आवृत्ति परिपथ की प्राकृतिक आवृत्ति के बराबर होती है तब अनुनाद होता है और उस स्थिति में X_L =X_C इस स्थिति में Z= R = 20 ओम होगा और Φ = 0°
चूँकि Z = \(\sqrt{R^2+\left(X_L-X_C\right)^2}\) होता है।
I_r.m.s = \(\frac{E_{\text {sms }}}{Z}=\frac{200}{20}\) = 10 A
एक पूरे चक्र में शक्ति स्थानान्तरित की गई है
= E_rms × I_rms
P = 200 V × 10 A
= 2000 W = 2 kW

प्रश्न 7.10.
एक रेडियो को MW प्रसारण बैंड के एक खण्ड के आवृत्ति परास के एक ओर से दूसरी ओर (800 kHz से 1200 kHz) तक समस्वरित किया जा सकता है। यदि इसके LC परिपथ का प्रभावकारी प्रेरकत्व 200 µH हो, तो उसके परिवर्ती संधारित्र की परास कितनी होनी चाहिए? (संकेत-समस्वरित करने के लिए मूल आवृत्ति अर्थात् LC परिपथ के मुक्त दोलनों की आवृत्ति रेडियो तरंग की आवृत्ति के समान होनी चाहिए।)
उत्तर:
हल-दिया गया है-
आवृत्ति f₁ = 800 kHz
= 8 × 10^-5
आवृत्ति f₂ = 1200 kz
= 12 × 10⁵ Hz
L = 200 μH = 200 × 10^-6H
= 2 × 10^-4H, C = ?
हम जानते हैं कि अनुनाद की आवृत्ति

प्रश्न 7.11.
चित्र में एक श्रेणीबद्ध LCR परिपथ दिखाया गया है जिसे परिवर्ती आवृत्ति के 230 V के स्रोत से जोड़ा गया है। L = 5.0 H, C = 80 μF, R = 40 Ω
(a) ख्रोत की आवृत्ति निकालिए जो परिफ्थ में अनुनाद उत्पन्न करे।
(b) परिपथ की प्रतिबाधा ε तथा अनुनादी आवृत्ति पर धारा का आयाम निकालिए।
(c) परिपथ के तीनों चित्र अवयवों के सिरों पर विभवपात के rms मानों को निकालिए। दिखलाइए कि अनुनादी आवृत्ति पर LC संयोग के सिरों पर विभवपात शन्य है।

उत्तर:
हल-दिया गया है L = 50. H
C = 80 μF = 80 × 10^-6F
R = 40 Ω
E_rms = 230 V
(a) स्रोत की आवृत्ति f जो परिपथ में अनुनाद f_r उत्पन्न करे

(b) माना अनुनाद पर परिपथ प्रतिबाधा Z है और I_m धारा का आयाम = धारा का शीर्षमान तब

∴ I₀ = I_rms√2
= 5.75 × √2A
= 8. 13 A = 8.1 A
(c) प्रतिरोध के सिरों पर विभवपात का मान होगा
V_R = I_rms R
= 5. 75 × 50 × 5.0
V_rms 1437.5 V
इसी तरह से C के सिरों पर विभवपात का मान निकालने पर

C के सिरों पर विभवपात = L के सिरों पर विभवपात E_L, E_C के बराबर व विपरीत है। अतः अनुनादी आवृत्ति पर LC संयोग के सिरों पर विभवान्तर का मान शून्य होता है।

अतिरिक्त अभ्यास प्रश्न (NCERT)

प्रश्न 7.12
किसी LC परिपथ में 20 mH का एक प्रेरक तथा 50 μF का एक संधारित्र है जिस पर प्रारम्भिक आवेश 10 mC है। परिपथ का प्रतिरोध नगण्य है। मान लीजिए कि वह क्षण जिस पर परिपथ बन्द किया जाता है t = 0 है।
(a) प्रारम्भ में कुल कितनी ऊर्जा संचित है? क्या यह LC दोलनों की अवधि में संरक्षित है?
(b) परिपथ की मूल आवृत्ति क्या है?
(c) किस समय पर संचित ऊर्जा
(i) पूरी तरह से वैद्युत है (अर्थात् वह संधारित्र में संचित है?
(ii) पूरी तरह से चुंबकीय है (अर्थात् प्रेरक में संचित है?
(d) किन समयों पर सम्पूर्ण ऊर्जा प्रेरक एवं संधारित्र के मध्य समान रूप से विभाजित है?
(e) यदि एक प्रतिरोधक को परिपथ में लगाया जाए तो कितनी ऊर्जा अंततः ऊष्मा के रूप में क्षयित होगी?
उत्तर:
हल-दिया गया है
L = 20 mH = 20 × 10^-3 H
C = 50 μF = 50 × 10^-6 F
q₀ = 10 mC = 10 × 10^-3 C
t = 0 पर q = q₀
q₀ = 10 × 10^-3 C (प्रारम्भिक आवेश है)
तथा q = q₀ cos ωt
(a) प्रारम्भ में कुल ऊर्जा का मान

हाँ L तथा C में संचित ऊर्जाओं का योग संरक्षित है यदि R = 0

(c) किसी भी क्षण, धारित्र पर आवेश
q = q₀ cos ωt
= q₀ cos \(\left(\frac{2 \pi}{T} \cdot t\right)\) से व्यक्त किया जाता है।

(i) t = 0, \(\frac{\Gamma}{2}\), T, \(\frac{3 \mathrm{~T}}{2}\) समयों पर
q = q₀ (आरम्भ में दत्त अधिकतम आवेश)
∴ ऊर्जा धारित्र में संचित होती है। अतः यह पूर्णरूपेण वैद्युत ऊर्जा है क्योंकि इसका अधिकतम मान इन्हीं समयों पर होता है जहाँ
T = \(\frac{1}{\mathrm{f}}\) = 6. 28 × 10^-3 s
= 6. 28 ms

(ii) L में संचित ऊर्जा उस समय अधिकतम होगी जब C में वैद्युत ऊर्जा शून्य होगी।
अर्थात् q = 0
q उस समय शून्य होगा जब
cos ωt = cos \(\frac{\pi}{2}\) = 0
∴ t = \(\frac{T}{4}, \frac{3 \mathrm{~T}}{4}, \frac{5 \mathrm{~T}}{4}\) ……………… आदि समय पर q शून्य है।
अतः संचित ऊर्जा पूर्णरूपेण चुम्बकीय ऊर्जा है।

(e) यदि एक प्रतिरोधक को परिपथ में लगाया जाये तो LC दोलनों को अवमंदित कर देता है। उनका आयाम कम हो जाता है और अन्त में मर जाते हैं। इस स्तर पर कुल प्रारम्भिक ऊर्जा = 1.0 J ऊष्मा के रूप में क्षयित हो जाती है।

प्रश्न 7.13.
एक कुण्डली को जिसका प्रेरण 0.50 H तथा प्रतिरोध 100 Ω है, 240 V व 50 Hz की एक आपूर्ति से जोड़ा गया है।
(a) कुण्डली में अधिकतम धारा कितनी है?
(b) वोल्टेज शीर्ष व धारा शीर्ष के बीच समय-पश्चता (time lag) कितनी है?
उत्तर:
हल-दिया गया है-
L = 0.50 H
R = 100 Ω
a.c. आपूर्ति की आवृत्ति f = 50 Hz
a.c. आपूर्ति का rms का मान = E_rms = 240 V
∴ कोणीय आवृत्ति = ω = 2πf
= 2π × 50
= 100 π rad s^-1
और E₀ = √2E_rms
= √2 × 240 V
(a) कुण्डली में अधिकतम धारा = I₀ = ?

(b) LR परिपथ के लिए
यदि E = E₀ cos ωt
तब I = I₀ cos ( ωt – Φ)
स्पष्ट है कि E अधिकतम t = 0 पर होगा और I अधिकतम ωt = Φ पर होगा

प्रश्न 7.14.
यदि परिपथ को उच्च आवृत्ति की आपूर्ति ( 240 V, 10 kHz ) से जोड़ा जाता है तो अभ्यास 7.13 (a) तथा (b) के उत्तर निकालिए। इससे इस कथन की व्याख्या कीजिए कि अति उच्च आवृत्ति पर किसी परिपथ में प्रेरक लगभग खुले परिपथ के तुल्य होता है। स्थिर अवस्था के पश्चात् किसी dc परिपथ में प्रेरक किस प्रकार का व्यवहार करता है?
उत्तर:
हल-दिया गया है-
E_rms = 240 V
a. c. की आवृत्ति = f = 10 kHz
f = 10 × 10₃ Hz
f = 10⁴ Hz
∴ ω = 2πf
= 2π × 10⁴ rad s^-1
और E₀ = √2E_rms
= √2 × 240V
L = 0.50 H, R = 100 Ω
∴ LR परिपथ की प्रतिबाधा.

स्पष्टतः उच्च आवृत्ति पर प्रेरणिक प्रतिघात X_L = ωL अत्यधिक हो जाता है जिससे परिपथ में अत्यल्प मान की धारा प्रवाहित होती है तथा परिपथ लगभग खुले परिपथ के तुल्य होता है। dc परिपथ में ω = 0 अतः X_L = 0 अतः प्रेरक एक शुद्ध चालक की तरह व्यवहार करता  है।

प्रश्न 7.15.
40 Ω प्रतिरोध के श्रेणीक्रम में एक 100 µF के संधारित्र को 110 V, 60 Hz की आपूर्ति से जोड़ा गया है।
(a) परिपथ में अधिकतम धारा कितनी होगी?
(b) धारा शीर्ष व वोल्टेज शीर्ष के बीच समय-पश्चता कितनी होगी?
उत्तर:
हल-CR परिपथ के लिए यदि E = E₀ cos ωt तब
I = I₀ cos (ωt – Φ)
जहाँ पर I₀ = \(\frac{E_0}{\sqrt{R^2+\frac{1}{\omega^2 C^2}}}\)
और tan Φ = \(\frac{1}{\omega C R}\)
(a) दिया गया है – R = 40 Ω
C = 100 μF = 100 × 10^-6 F
C = 10^-4 F
E_rms = 110 V, f = 60 Hz
ω = 2πf
= 2π × 60 = 120 π rad s^-1

प्रश्न 7.16.
यदि परिपथ को 110 V, 12 kHz आपूर्ति से जोड़ा जाए तो प्रश्न. 7.15 (a) और (b) का उत्तर निकालिए। इससे इस कथन की व्याख्या कीजिए कि अति उच्च आवृत्तियों पर एक संधारित्र चालक होता है। इसकी तुलना उस व्यवहार से कीजिए जो किसी dc परिपथ में एक संधारित्र प्रदर्शित करता है।
उत्तर:
हल-दिया गया है-
E_rms = 110V, R = 40 Ω
C = 100 μF = 100 × 10^-6 F = 10^-4 F
f = 12 kHz = 12 × 10³ Hz
∴ ω = 2πf
= 2π × 12 × 10³ rad s^-1
= 24π × 10³ rad s^-1
E₀ = √2E_rms
= √2 × 110V
(a) अधिकतम धारा I₀
I₀ = [/latex]\frac{E_0}{Z}[/latex] द्वारा दी जाती है।
यहाँ पर CR परिपथ के लिए Z का मान होगा-

(b) एक RC परिपथ में वोल्टता की कला, धारा की कला से Φ कोण से पीछे होती है

स्पष्टतः उच्च आवृत्ति पर संधारित्र एक चालक की तरह व्यवहार करता है जबकि दिष्ट धारा के लिये ω = 0 होने के कारण X_C = \(\frac{1}{\omega C}\) = ∞ तथा दिष्ट धारा के लिये संधारित्र युक्त परिपथ एक खुला परिपथ होता है।

प्रश्न 7.17.
र्रोत की आवृत्ति को एक श्रेणीबद्ध LCR परिपथ के अनुनादी आवृत्ति के बराबर रखते हुए तीन अवयवो L,C तथा R को समान्तर क्रम में लगाते हैं। यह दर्शाइए कि समान्तर LCR परिपथ में इस आवृत्ति पर कुल धारा न्यूनतम है। इस आवृत्ति के लिए अभ्यास 7.11 में निर्दिष्ट र्रोत तथा अवयवों के लिए परिपथ की हर शाखा में धारा के rms मान को परिकलित कीजिए।
उत्तर:
हल-दिया गया है L = 5.0 H
C = 80 μF = 80 × 10^-6 F
= 8 × 10^-5 F
R = 40 Ω
समान्तर LCR परिपथ की प्रभावी प्रतिबाधा
\(\frac{1}{\mathrm{Z}}=\sqrt{\frac{1}{\mathrm{R}^2}+\left(\omega \mathrm{C}-\frac{1}{\omega \mathrm{L}}\right)^2}\) से प्रदर्शित करते हैं
जो कि ω = ω₀ = \(\frac{1}{\sqrt{\mathrm{LC}}}\) पर न्यूनतम होगी
∴ω = ω_r पर |Z| अधिकतम होगा। इसलिए कुल धारा का आयाम न्यूनतम होगा ।
समान्तर LCR परिपथ में I धारा I_L, I_C व I_Rके योग के बराबर होगी।

प्रश्न 7.18.
एक परिपथ को जिसमें 80 mH का एक प्रेरक तथा 60 μF का संधारित्र श्रेणीक्रम में है, 230 V, 50 Hz की आपूर्ति से जोड़ा गया है। परिपथ का प्रतिरोध नगण्य है।
(a) धारा का आयाम तथा rms मानों को निकालिए।
(b) हर अवयव के सिरों पर विभवपात के rms मानों को निकालिए।
(c) प्रेरक में स्थानान्तरित माध्य शक्ति कितनी है?
(d) संधारित्र में स्थानान्तरित माध्य शक्ति कितनी है?
(e) परिपथ द्वारा अवशोषित कुल माध्य शक्ति कितनी है?
(‘माध्य में यह समाविष्ट है’ कि इसे ‘पूरे चक्र’ के लिए लिया गया है।)
उत्तर:
हल-दिया गया है-
L = 80 mH = 80 × 10^-3 H
= 8 × 10^-2 H
C = 60 μF = 60 × 10^-6 F
= 6 × 10^-5 F
E_rms = 230 V, f = 50 Hz

(b) L के सिरों पर E_rms = I_rms × ωL
= 8. 24 × 25. 14
= 207 V
C के सिरों पर E_rms = I_rms × \(\frac{1}{\omega C}\)
= 8. 24 × 53. 03
= 436.8 V
= 437 V
(c) L में धारा I चाहे कुछ भी हो, वास्तविक वोल्टता धारा से \(\frac{\pi}{2}\) अग्र है अतः C द्वारा उपभुक्त माध्य शक्ति शून्य है।
(d) C हेतु वोल्टता धारा के \(\frac{\pi}{2}\) पश्च है। पुनः C द्वारा उपभुक्त माध्य शक्ति शून्य है।

(e) चूँकि परिपथ का प्रतिरोध नगण्य है। कुल औसत उपभुक्त
शक्ति =L द्वारा उपभुक्त माध्य शक्ति +C द्वारा उपभुक्त माध्य शक्ति = 0 शुन्य

प्रश्न 7.19.
कल्पना कीजिए कि अभ्यास 7.18 में प्रतिरोध 15 Ω है। परिपथ के हर अवयव को स्थानान्तरित माध्य शक्ति तथा सम्पूर्ण अवशोषित शक्ति को परिकलित कीजिए।
उत्तर:
हल-दिया गया है-R = 15 Ω
L = 80 mH = 8 × 10^-2 H
C = 60 μF = 6 × ^-5 F
E_rms = 230 V
f = 50 Hz
∴ ω 2πf = 2π × 50 = 100 π
∴LCR परिपथ की प्रतिबाधा = Z

प्रश्न 7.20. एक श्रेणीबद्ध LCR परिपथ को जिसमें
L = 0.12 H, C = 480 nF, R = 23 Ω, 230 V परिवर्ती आवृत्ति वाले स्रोत से जोड़ा गया है।
(a) र्रोत की वह आवृत्ति कितनी है जिस पर धारा आयाम अधिकतम है। इस अधिकतम मान को निकालिए।
(b) स्रोत की वह आवृत्ति कितनी है जिसके लिए परिपथ द्वारा अवशोषित माध्य शक्ति अधिकतम है।
(c) स्रोत की किस आवृत्ति के लिए परिपथ को स्थानान्तरित शक्ति अनुनादी आवृत्ति की शक्ति की आधी है?
उत्तर:
(d) दिए गए परिपथ के लिए Q कारक कितना है?
हल-दिया गया है- L = 0.12 H
C = 480 nF = 480 × 10^-9 F
R = 23 Ω
E_rms = 230 V
(a) जब धारा आयाम अधिकतम है, स्रोत आवृत्ति, अनुनादी आवृत्ति के बराबर होती है = ?

(b) जब आवृत्ति अनुनादी आवृत्ति के बराबर है परिपथ द्वारा अवशोषित माध्य शक्ति अधिकतम है और दी जाती है।
\(\mathrm{P}_{\max }=\frac{1}{2} \mathrm{I}_0^2 \mathrm{R}\)
= \(\frac{1}{2}\) × (14.14)² × 23
= 2300 वाट (लगभग)
(c) ω = ω_r + ∆ω
अवशोषित ऊर्जा, [/latex]\frac{1}{2}[/latex] शिखर मान के बराबर है अर्थात् 663 Hz पर ।
हम यह सिद्ध कर सकते हैं।

प्रश्न 7.21.
एक श्रेणीबद्ध LCR परिपथ के लिए जिसमें L = 3.0 H, C = 27 μF तथा R = 7.4 Ω अनुनादी आवृत्ति तथा Q कारक निकालिए। परिपथ के अनुनाद की तीक्ष्णता को सुधारने की इच्छा से ‘अर्द्ध उच्चिष्ठ पर पूर्ण चौड़ाई’ को 2 गुणक द्वारा घटा दिया जाता है। इसके लिए उचित उपाय सुझाइए।
उत्तर:
हल-दिया गया है- L = 3.0 H
C = 27 μF = 27 × 10^-6 F
R = 7.4 Ω
आवृत्ति f_r = ?, Q = ?
आवृत्ति f_r = \(\frac{1}{2 \pi \sqrt{\mathrm{LC}}}\)

प्रश्न 7.22.
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(a) क्या किसी ac परिपथ में प्रयुक्त तात्क्षणिक वोल्टता परिपथ में श्रेणीक्रम में जोड़े गए अवयवों के सिरों पर तात्क्षणिक वोल्टताओं के बीजगणितीय योग के बराबर होता है? क्या यही बात rms वोल्टताओं में भी लागू होती है?
(b) प्रेरण कुण्डली के प्राथमिक परिपथ में एक संधारित्र का उपयोग करते हैं।
(c) एक प्रयुक्त वोल्टता संकेत एक de वोल्टता तथा उच्च आवृत्ति के एक ac वोल्टता के अध्यारोपण से निर्मित है। परिपथ एक श्रेणीबद्ध प्रेरक तथा संधारित्र से निर्मित है। दर्शाइए कि dc संकेत C तथा ac संकेत L के सिरे पर प्रकट होगा ।
(d) एक लैंप से श्रेणीक्रम में जुड़ी चोक को एक de लाइन से जोड़ा गया है। लैंप तेजी से चमकता है। चोक में लोहे के क्रोड को प्रवेश कराने पर लैंप की दीप्ति में कोई अन्तर नहीं पड़ता है। यदि एक ac लाइन से लैंप का संयोजन किया जाए तो तदनुसार प्रेक्षणों की प्रामुक्ति कीजिए ।
(e) ac मेंस के साथ कार्य करने वाली फ्लोरोसेंट ट्यूब में प्रयुक्त चोक कुण्डली की आवश्यकता क्यों होती है? चोक कुण्डली के स्थान पर सामान्य प्रतिरोधक का उपयोग क्यों नहीं होता है?
उत्तर:
(a) हाँ, यह rs वोल्टता के लिए सत्य नहीं है। चूँकि विभिन्न अवयवों के सिरों पर वोल्टता का मान समान कला में नहीं हो सकता है।
(b) जब परिपथ खण्डित किया जाता है तो उच्च प्रेरित धारा संधारित्र को आवेशित करने के लिए प्रयुक्त की जाती है जो चिंगारी (स्पार्क) का परिवर्जन करती है।
(c) दिष्ट धारा के लिए L की प्रतिबाधा उपेक्षणीय है और C की प्रतिबाधा बहुत अधिक (अनन्त) है। अतः दिष्ट धारा C के सिरे पर होती है। उच्च आवृत्ति प्रत्यावर्ती धारा के लिए L की प्रतिबाधा उच्च हो और C की बहुत कम अतः प्रत्यावर्ती धारा संकेत L के सिरे पर होता है।
(d) स्थायी अवस्था दिष्ट धारा के लिए L का कोई प्रभाव नहीं है, चाहे इसे लौह क्रोड के प्रयोग से क्यों न बढ़ाया जाए। प्रत्यावर्ती धारा के लिए लैम्प चोक की अतिरिक्त प्रतिबाधा के कारण धूमिल दिखाई पड़ेगा। यहाँ लौह क्रोड के विवेशन से चोक की प्रतिबाधा में वृद्धि होगी जिसके कारण बल्ब और अधिक धूमिल हो जाएगा।
(e) शक्ति का क्षय किए बिना एक चोक कुण्डली ट्यूब के परितः वोल्टेज को कम करता है। प्रतिरोधक ऊष्मा के रूप में शक्ति का क्षय करता है।

प्रश्न 7.23.
एक शक्ति संप्रेषण लाइन अपचयी ट्रांसफार्मर में जिसकी प्राथमिक कुण्डली में 4000 फेरे हैं, 2300 वोल्ट पर शक्ति निवेशित करती है। 230 V की निर्गत शक्ति प्राप्त करने के लिए द्वितीयक में कितने फेरे होने चाहिए?
उत्तर:
हल- V_p = V निवेशित = 2300 V
N_p =4000
V_s = 230 V
N_s = ?
हम जानते हैं- \(\frac{V_s}{V_p}=\frac{N_s}{N_p}\)
या N_s = \(\frac{V_S N_P}{V_P}\)
मान रखने पर- N_s = [/latex]\frac{230 \times 4000}{2300}[/latex] = 400
अतः द्वितीयक कुण्डली में फेरों की संख्या = 400

प्रश्न 7.24.
एक जल विद्युत शक्ति संयंत्र में जल दाब शीर्ष 300 m की ऊँचाई पर है तथा उपलब्ध जल प्रवाह 100 mg है। यदि टर्बाइन जनित्र की दक्षता 60% हो, तो संयंत्र से उपलब्ध विद्युत शक्ति का आकलन कीजिए, g= 9.8 m s^-2
उत्तर:
हल दिया गया है-
दाब शीर्ष (h) = 300m
दक्षता η = 60%
प्रवाहित जल का आयतन प्रति सेकण्ड = 100 m³ s^-1
अर्थात् v = 100 m³/s
8 = 9.8 m/s²
जल का घनत्व = 1000 kg/m³
प्रति सेकण्ड प्रवाहित जल का द्रव्यमान
m = आयतन x घनत्व
= 100 × 1000
= 10⁵ kg/s
जल की स्थितिज ऊर्जा (p.E) = mgh
जहाँ पर m = 10⁵ kg/s
P.E = 10⁵ × 9.8 × 300
= 29.4 × 10⁷ Js^-1 या वाट
η = 60%
संयंत्र से उपलब्ध विद्युत शक्ति = 29.4 × 10⁷ × \(\frac{60}{100}\)
= 17.64 × 10⁷ वाट
= 176.4 MW

प्रश्न 7.25.
440 V पर शक्ति उत्पादन करने वाले किसी विद्युत संयंत्र से 15 km दूर स्थित एक छोटे से कस्बे में 220 V पर 800 kW शक्ति की आवश्यकता है। विद्युत शक्ति ले जाने वाली दोनों तार की लाइनों का प्रतिरोध 0.5 Ω प्रति किलोमीटर है। कस्बे को उप-स्टेशन में लगे 4000 – 220 V अपचयी ट्रांसफार्मर से लाइन द्वारा शक्ति पहँचती है।
(a) ऊष्मा के रूप में लाइन से होने वाली शक्ति के क्षय का आकलन कीजिए।
(b) संयंत्र से कितनी शक्ति की आपूर्ति की जानी चाहिए, यदि क्षरण द्वारा शक्ति का क्षय नगण्य है।
(c) संयंत्र के उच्चायी ट्रांसफार्मर की विशेषता बताइए। हल-दिया गया है- दो तारों की लाइन की लम्बाई
उत्तर:
हल-दिया गया है- दो तारों की लाइन की लम्बाई = l = 15 × 2
l = 30 km.
तार की लाइन की इकाई लम्बाई का प्रतिरोध = 0.5 Ω/km.
दो तारों वाली लाइन का प्रतिरोध = R
R = 30 × 0.5
= 15 Ω
p = 800 kW
= 8 × 10⁵ W
चूँकि 4000-220 V अपचायी परिणामित्र से शक्ति प्रदत्त है।
E_rms = 4000 V = लाइन की प्राप्ति सिरे पर वोल्टता
माना लाइन धारा का मान = I_rms = ?
p = E_rms × I_rms
⇒ I_rms = \(\frac{\mathrm{P}}{\mathrm{E}_{\mathrm{rms}}}=\frac{8 \times 10^5}{4000}\)
⇒ I_rms = 200 A
(a) लाइन में शक्ति हानि = \(\mathrm{I}_{\mathrm{rms}}^2 \mathrm{R}\)
= (200)² × 15
= 40000 × 15
= 60 × 10⁴ = 6 × 10⁵
= 600 kW

(b) प्लान्ट द्वारा प्रदत्त शक्ति जबकि क्षरण के कारण कोई हानि नहीं है
= p + शक्ति हानि
= [ 800 + 600] × 10³
= 1400 kW

(c) लाइन में वोल्टता-पात = I_rms × R
= 20 × 15 = 300 V
∴ संयंत्र द्वारा विद्युत प्रदाय = प्राप्ति सिरे पर वोल्टता + लाइन में विभवपात
= 40000 + 300
= 7000 V

प्लान्ट 440 V पर शक्ति जनित करता है और इसे उपचायी भी करनी है जिससे लाइन में 3000 V पात के बाद भी शहर के विद्युत उपकेन्द्र में शक्ति 4000 V पर प्राप्त की जा सके।
∴ प्लान्ट पर उच्चायी परिणामित्र 440 V – 7000 V तक का उपलब्ध होना चाहिए।

प्रश्न 7.26.
ऊपर किए गए अभ्यास को पुन: कीजिए। इसमें पहले के ट्रांसफार्मर के स्थान पर 40,000-220 V का अपचयी ट्रांसफार्मर है। [पूर्व की भाँति क्षरण के कारण हानियों को नगण्य मानिए। यद्यपि अब यह सन्निकटन उचित नहीं है क्योंकि इसमें उच्च वोल्टता का संप्रेषण होता है]। अतः समझाइए कि क्यों उच्च वोल्टता संप्रेषण अधिक वरीय है?
हल-दिया गया है
E_rms = 40000 V = 4 × 10⁴ V
लाइन धारा = I_rms = ?
शक्ति p = 800 kW = 8 × 10⁵ W
∴I_rms = \( \frac{P}{E_{\mathrm{rms}}}=\frac{8 \times 10^5}{4 \times 10^4}=20 \mathrm{~A}\)
(a) ऊष्मा के रूप में लाइन से होने वाली शक्ति का क्षय
= \(I_{\mathrm{rms}}^2 \times R\)
= (20)² × 15
= 400 × 15 = 6000 w
= 6 kW
(b) संयंत्र द्वारा विद्युत प्रदाय = आवश्यक शक्ति + लाइन में शक्ति हानि
= 800 + 6 = 806 kW
(c) लाइन में विभवपात = I_rms × R
= 20 × 15 = 300 V
प्रसारण के लिए वोल्टता = प्राप्ति सिरे पर वोल्टता + लाइन में विभवपात
= 40000 + 300
= 40300 V
संयंत्र के लिए उच्चायी ट्रांसफार्मर चाहिए 440 – 40300 V
स्पष्टीकरण-उच्च विभव पर \% शक्ति क्षय

स्पष्टतः उच्च वोल्टता पर संचरण से शक्ति क्षय कम होती है अतः संप्रेषण में उच्च वोल्टता संप्रेषण को वरीयता दी जाती है।

Haryana State Board HBSE 11th Class Physics Solutions Chapter 1 भौतिक जगत Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 1 भौतिक जगत

प्रश्न 1.1.
विज्ञान की प्रकृति से सम्बन्धित कुछ अत्यन्त पारंगत प्रकथन आज तक के महानतम् वैज्ञानिकों में से एक अल्बर्ट आइंस्टीन द्वारा प्रदान किये गये हैं। आपके विचार से आइंस्टीन का उस समय क्या तात्पर्य था, जब उन्होंने कहा था “संसार के बारे में सबसे अधिक अबोधगम्य विषय यह है कि यह बोधगम्य है?
उत्तर:
जब कोई घटना पहली बार देखी जाती है तो यह अबोधगम्य होती है परन्तु जब हम उस घटना से सम्बन्धित सिद्धान्त, नियम एवं तथ्यों का गहन विश्लेषण करते हैं तो वह हमारे लिए बोधगम्य हो जाती है। दूसरे शब्दों में, भौतिक जगत की जटिल प्रकृति कुछ मूलभूत नियमों के पदों में समझी जा सकती हैं। अत: आइंस्टाइन का यह कथन तर्कसंगत है।

प्रश्न 1.2.
“प्रत्येक महान भौतिक सिद्धान्त अपसिद्धान्त से आरम्भ होकर धर्म सिद्धान्त के रूप में समाप्त होता है।” इस तीक्ष्ण टिप्पणी की वैधता के लिए विज्ञान के इतिहास से कुछ उदाहरण लिखिए।
उत्तर:
समाज में स्थापित विश्वास और धर्म सिद्धान्त वैज्ञानिक सिद्धान्तों एवं प्रबुद्ध व्यक्तियों के विचारों से कई बार भिन्न होते हैं। ऐसे कुछ प्रमुख उदाहरण निम्नलिखित हैं-
1. प्राचीन काल में टॉलमी ने भूकेन्द्रीय सिद्धान्त का प्रतिपादन किया जिसके अनुसार पृथ्वी को स्थिर माना गया तथा सभी आकाशीय पिण्ड पृथ्वी के चारों और चक्कर लगाते थे। बाद में इटली के वैज्ञानिक गैलीलियो ने माना कि पृथ्वी नहीं सूर्य स्थिर है तथा पृथ्वी सहित सभी प्रह सूर्य की परिक्रमा करते हैं। तत्कालीन शासकों द्वारा गैलीलियों की संकल्पना को गलत कहा गया और इसके लिये उन्हें दण्डित भी किया गया।
2. आइंस्टीन से पहले चह माना जाता था कि द्रव्य तथा ऊर्जा अविनाशी होते हैं तथा दोनों में कुछ भी सम्बन्ध नहीं होता है। अत: दोनों ही राशियों के संरक्षण के स्वतंत्र नियम थे। आइंस्टीन ने इन दोनों स्वतंत्र नियमों के स्थान पर द्रव्यमान-ऊर्जा का संरक्षण नियम प्रस्तुत करते हुए द्रव्यमान-ऊर्जा तुल्यता समीकरण E=mc² दिया।

प्रश्न 1.3.
“सम्भव की कला ही राजनीति है।” इसी प्रकार “समाधान की कला ही विज्ञान है।” विज्ञान की प्रकृति तथा व्यवह्हार पर इस सुन्दर सूक्ति की व्याख्या कीजिए।
उत्तर:
राजनीतिज्ञ यह मानते हुए भी कि उनके द्वारा किये गये वायदों की घोषणाओं का पूरा कर पाना उनके लिए असम्भव है, बहुत से कार्यों को पूरा करने के बारे में वे स्वयं अनिश्चित होते है, लेकिन फिर भी वे उन्हे संभव करने का प्रयास करते हैं तथा प्रतिकूल परिस्थितियों को अनुकूल बनाने की संभावना निरन्तर तलाशते रहते हैं। इस प्रकार स्पष्ट है कि “संभव की कला ही राजनीति है।”
वहीं वैज्ञानिक किसी समस्या के समाधान के लिये धैर्यपूर्वक निरन्तर प्रेक्षण लेते हैं और उनके विश्लेषण से कुछ नियमों का प्रतिपादन करते हैं। उदाहरण के लिए टाइको ब्राहे ने लगभग 20 वर्षों तक ग्रहों की गति का अध्ययन किया। फैराडे ने लगभग 18 वर्षों तक चुम्बकीय क्षेत्र द्वारा विद्युत् धारा उत्पन्न करने के लिए धैर्यपूर्वक प्रयोग किये तथा इसके फलस्वरूप उन्होंने विद्युत् चुम्बकीय प्रेरण की घटना का आविष्कार किया।

प्रश्न 1.4.
यद्यषि अब भारत में विज्ञान तथा प्रौद्योगिकी का विस्तृत आधार है तथा यह तीव्रता से फैल भी रहा है, परन्तु फिर भी इसे विज्ञान के क्षेत्र में विश्ष नेता बनने की अपनी क्षमता को कायान्वित करने में काफी दूरी तय करनी है। ऐसे कुछ महत्वपूर्ण कारक लिखिए जो आपके विचार से भारत में विज्ञान के विकास में बाधक रहे हैं।
उत्तर:
भारत में विज्ञान के विकास में कई महत्वपूर्ण कारक बाधक रहे हैं। इनमें से प्रमुख बाधाएँ निम्नलिखित हैं-
1. भारत में वैज्ञानिकों को शैक्षणिक स्वतंत्रता प्राप्त नहीं है।
2. प्रारम्भिक अनुसंधान के सरकारी सुविधाओं एवं सहयोग की कमी।
3. प्रश्शिक्षित वैज्ञानिकों का देश से पलायन।
4. विज्ञान प्रबंधन पर अवैज्ञानिक और संकुचित विचारधारा वाले नौकरशाहों, राजनेताओं एवं धार्मिक संस्थानों का नियंत्रण।
5. अनुसंधान तथा प्रौद्योगिंकी में सामंजस्य का अभाव।
6. स्कूल तथा कॉलेज स्तर पर विज्ञान की शिक्षा का सही रूप में न होना।

प्रश्न 1.5.
किसी भी भौतिक विज्ञानी ने इलेक्ट्रॉन के कभी भी दर्शन नहीं किये हैं, परन्तु फिर भी सभी भौतिक विज्ञानियों का इलेक्ट्रॉन के अस्तित्व में विभ्वास है। कोई बुद्धिमान, परन्तु अन्धविश्वासी व्यक्ति इसी तुल्यस्ूपता को इस तर्क के साथ आगे बढ़ाता है कि यद्यपि किसी ने ‘ देखा ‘ नहीं है, परन्तु 4 भूतों ‘ का अस्तित्व है। आप इस तर्क का खण्डन किस प्रकार करेंगे?
उत्तर:
भातिक विज्ञानियों का इलेक्ट्रॉन के अस्तित्व में विश्वास का कारण उसकी प्रायोगिक पुष्टि जैसे, अणुओं की विभिन्न आकृतियाँ, विद्युत् धारा का प्रवाह इत्यादि है परन्तु भूतों का कोई प्रायोगिक प्रमाण नहीं है। अत: दोनों की तुलना निरर्थक है।

प्रश्न 1.6.
जापान के एक विशेष समुद्रतटीय क्षेत्र में पाये जाने वाले केकड़े के कवचों (खोल ) में से अधिकांश समुरई के अनुभुत चेहरे से मिलते-जुलते प्रतीत होते हैं। नीचे इस प्रेक्षित तथ्य की दो व्याख्याएँ दी गई हैं। इनमें से आपको कौन-सा वैज्ञानिक स्पष्टीकरण लगता है?
(i) कई शताब्दियों पूर्व किसी भयानक समुद्री दुर्घटना में एकयुवा समुरई डूब गया। उसकी बहादुरी के लिए शब्द्धांजलि के रूप में प्रकृति ने अबोधगम्य बंगों द्वारा उसके चेहरे को केकड़े के कवचों पर अंकित करके उसे उस क्षेत्र में अमर बना दिया।
(ii) समुद्री दुर्घटना के पश्शात् उस क्षेत्र के मछुआरे अपने मृत नेता के सम्मान में सद्भावना प्रदर्शन के लिए, उस हर केकड़े के कवच को जिसकी आकृति संयोगवश समुरई से मिलती-जुलती प्रतीत होती थी, उसे वापस समुब्र में फेंक देते थे। परिणामस्वरूप केकड़े के कवचों की इस प्रकार की विशेष आकृतियाँ अधिक समय तक विद्यमान रहीं और इसीलिए कालान्तर में इसी आकृति का आनुवंशतः जनन हुआ। यह कृत्रिम वरण द्वारा विकास का एक उदाहरण है।
उत्तर:
कथन (ii) वैज्ञानिक स्पष्टीकरण देने में पर्याप्त रूप समंथ है।

प्रश्न 1.7.
दो शताब्दियों से भी अधिक समय पूर्व इंग्लैण्ड तथा पश्चिमी यूरोष में जो औद्योगिक कान्ति हुई थी। उसकी चिंगारी का कारण कुछ प्रमुख वैज्ञानिक तथा प्रौद्योगिक उपलव्धियां थीं। ये उपलब्बियों क्या थीं?
उत्तर:
औद्योगिक क्रान्ति की कुछ प्रमुख वैज्ञानिक तथा प्रौद्योगिक उपलविधियाँ निम्न थी-
1. भाप इजन-इसका आविष्कार जेम्स वाट द्वारा किया गया। इसकी सहायता से औद्योगिक इकाइयों को देश के भीतरी भागों में समुद्री किनारों से दूर स्थान प्राप्त हो सका।
2. पावर लूम-इसके खोजकर्ता कार्लराइट (1785) है। इसकी सहायता से कपड़ों की बुनाई का कार्य किया जाता है।
3. वात्या भट्टी-इसकी सहायता से स्ट्रोल (इस्पात) क्षेत्र में प्रगति हुई है।
4. सेफ्टी पिन-इसका आविष्कार सर हम्फ्री डेवी ने किा इसका उपयोग कोयला खदानों में किया जाता है।
5. स्पिनिंग जिन-इसकी खोज 1765 A.D. में हारग्रीब्ज द्वारा की गयी थी। स्पिनिंग जिन ने सूत कातने का काम तेज कर दिया।

प्रश्न 1.8.
प्रायः यह कहा जाता है कि संसार अब दूसरी औद्योगिक क्रान्ति के दैर से गुजर रहा है, जो समाज में पहली क्रान्ति की भांति आमूलचूल परिवर्तन ला देगी। विज्ञान तथा प्रौद्योगिकी के उन प्रमुख समकालीन क्षेत्रों की सूची बनाइए, जो इस क्रान्ति के लिए उत्तरदायी है।
उत्तर:
दूसरी औद्योगिक क्रान्ति के लिए उत्तरदायी विज्ञान के प्रमुख क्षेत्र निम्नवत् हैं
(i) कृषि क्षेत्र में विकास,
(ii) प्रकाश विद्युत् प्रभाव,
(iii) नाभिकीय ऊर्जा का उत्पादन,
(iv) प्लाज्मा का चुम्बकीय परिरोध,
(v) कमरे के ताप पर अतिचालक पदार्थों का विकास,
(vi) प्रकाशिक रेशे,
(vii) लेसर पुंजों तथा चुम्बकीय क्षेत्रों द्वारा परमाणुओं का परिग्रहण तथा शीतलन,
(viii) अवरक्त संसूचकों का विकास,
(ix) सेटेलाइट के उपयोग एवं अंतरिक्ष विज्ञान का विकास।

प्रश्न 1.9.
बाईसवीं शताब्दी के विज्ञान तथा प्रौद्योगिकी पर अपनी निराधार कल्पनाओं को आधार मानकर लगभग 1000 शब्दों में कोई कथा लिखिए।
उत्तर:
मैं सुबह 6 बजे व्यायाम कर रहा था कि उसी समय बंगलौर से मेरे वैज्ञानिक मित्र का फोन आ गया। उसने कहा कि अनुसंधान कार्य के लिए 10 बजे तक बंगलौर आना है। मैं जल्दी से तैयार होने लगा। खाने बनाने वाली 8 बजे आती है। इसीलिए मैंने रोबोट को कमांड दी कि वह नाश्ता तैयार करे। रोबोट ने अगले 20 मिनट में नाश्ते में स्वादिष्ट पराठे तैयार कर मेरे सामने परोस दिए। में नाश्ता कर सीधे नई दिल्ली रेलवे स्टेशन कार द्वारा पहुँचा। वहाँ से 7 बजे सुपर बुलेट ट्रेन में सवार हो गया। 9 : 35 मिनट पर बुलेट ट्रेन बंगलौर पहुँच गई। जहाँ से हमें अंतरिक्ष स्टेशन पहुँचना था। वहाँ स्टेशन पर खड़ी डूाइवरलैस वायु कार के की-बोर्ड पर गन्तव्य स्थान का कोड निवेशित किया और कार का दरवाजा खुला। मैं कार में बैठ गया। कार में बैठते ही सीट बैल्ट कस गई और कार का दरवाजा बन्द हो गया। कार ने भारी ट्रैफिक होने के बावजूद मुझे ठीक समय पर अंतरिक्ष स्टेशन पहुँचा दिया। अंतरिक्ष स्टेशन पर सुरक्षा रोबोट तैनात थे। द्वार पर लगे संवेदी स्क्रीन पर हाथ रखने पर सम्बद्ध कम्य्यूटर ने मेरी पहचान की और मेरे आने की जानकारी मेंरे मित्र के मोबाइल पर पहुँच गई। मेरे मित्र ने मिलने की अनुमति दे दी। जिसका मैसेज मोबाइल से दरवाजे के संवेदी कम्प्यूटर तक पहुँचते ही दरवाजा खुल गया। अन्दर प्रवेश करते ही एक रोबोट ने हाथ मिलाकर मेरा स्वागत किया और मेरे मित्र के पास ले गया।

मेरे मित्र ने जानकारी दी कि मुझे उसके साथ मंगल ग्रह पर पिकनिक मनाने जाना है। पृथ्वी से मंगल तक यात्रा में 72 घण्टे लगना था तथा मंगलयान से अगली सुबह 7 बजे उड़ान भरनी थी। इससे पूर्व रोबोट चिकित्सकों ने हमारी चिकित्सकीय जाँच की। इस यात्रा के लिए आवश्यक सामम्मी जसे-यात्रा में पहने जाने वाले विशेष वस्त, ऑक्सीजन मॉस्क, भोजन की ट्यूब तथा कैप्सूल, पानी की ट्यूब आदि चन्द्र यात्रा का प्रबंध करने वाली एजेन्सी ने ही उपलख्ध कराये। हमें व्यक्तिगत सुरक्षा के लिए लेसरगन तथा न्यूट्रॉन गन भी उपलब्ध करायी गई।

ठीक समय पर हमने मंगलयान से उड्ान भरी और हम अन्य तीन रोबोट के साथ मंगल की सतह पर पहुँच गये। वहॉ कैम्प एक झील के किनारे प्लास्टिक की शीट से बना था, जो अति उच्च दाब सहन कर सकती थी। इसके अन्दर वायुदाब पृथ्वी के वायुदाब के बराबर रखा गया था। कैप्य अतिचालक तारों की सहायता से उत्पन्न अति उच्च तीव्रता के विद्युत् चुम्बकीय बल क्षेत्र से घिरा था, ताकि वह उल्का पिण्डों तथा शत्रु के आक्रमणों से सुरक्षित रहे। मंगलयान पर दो दिन रहने के बाद मैं दिल्ली लौट आया।

प्रश्न 1.10.
‘विज्ञान के व्यवहार’ पर अपने ‘नैतिक’ दृष्टिकोणों को रचने का प्रयास कीजिए। कल्पना कीजिए कि आप स्वयं किसी संयोगवश ऐसी खोज में लगे हैं, जो शैक्षिक दृष्टि से रोचक है परन्तु उसके परिणाम निश्चित रूप से मानव समाज के लिए भयंकर होने के अतिरिक्त कुछ नहीं होंगे। फिर भी यदि ऐसा है तो आप इस दुविधा के हल के लिए क्या करेंगे?
उत्तर:
सर्वप्रथम वैज्ञानिक खोज के गलत प्रयोग के सम्बन्ध में लोक विचार प्राप्त किये जायें। यदि समाज इसे हानिकारक मानता है तो इस प्रकार के प्रयोग रोक देने चाहिये। यदि उस प्रयोग से कुछ लाभ हो सकता है तो ही उसे आगे बढ़ाना चाहिये।

प्रश्न 1.11.
किसी भी ज्ञान की भाँति विज्ञान का उपयोग भी, उपयोग करने वाले पर निर्भर करते हुए, अच्छा अथवा बुरा हो सकता है। नीचे विज्ञान के कुछ अनुप्रयोग दिये गये हैं। विशेषकर कौन-सा अनुप्रयोग अच्छा है, बुरा है अथवा ऐसा है कि जिसे स्पष्ट रूप से वर्गबद्ध नहीं किया जा सकता। इसके बारे में अपने दृष्टिकोणों को सूचीबद्ध कीजिए:
(i) आम जनता को चेचक के टीके लगाकर इस रोग को दबाना और अन्तत: इस रोग से जनता को मुक्ति दिलाना।
(ii) निरक्षरता का विनाश करने तथा समाचारों एवं धारणाओं के जनसंचार के लिए टेलीविजन।
(iii) जन्म से पूर्व लिंग निर्धारण।
(iv) कार्यदक्षता में वृद्धि के लिए कम्प्यूटर।
(vi) पृथ्वी के परितः कक्षाओं में मानव-निर्मित उपग्रहों की स्थापना।
(vii) रासायनिक तथा जैव युद्ध की नवीन तथा शक्तिशाली तकनीकों का विकास।
(viii) पीने के लिए जल का शोधन।
(ix) प्लास्टिक शल्यक्रिया।
(x) क्लोनिंग।
उत्तर:
(i) अच्छा, क्योकि इससे जनता को चेचक के रोग से मुक्ति मिल गई।
(ii) अच्छा, टेलींविजन द्वारा अपनी बात प्रभावी रूप से सम्रेषित की जा सकती है।
(iii) बुरा, इससे लड़कियों की संख्या में गिरावट आ रही है, जिससे सामाजिक असंतुलन उत्पन्न हो रहा है।
(iv) अच्छा, कम्प्यूटर से दक्षता में वृद्धि हुई है।
(v) अच्छा, इससे संचार, अनुसंधान, मौसम का पूर्वानुमान आदि में लाभ हुआ है।
(vi) बुरा, इससे मानव-जाति के महाविनाश की स्थिति बन सकती है।
(vii) बुरा, इससे भी मानव जाति नष्ट हो सकती है।
(viii) अच्छा, इससे प्रचुर मात्रा में पीने योग्य जल उपलब्ध होगा।
(ix) अच्छा, इससे व्यक्ति की दुर्घटना आदि से उत्पन्न कुरुपता को हटाया जा सकता है।
(x) अच्छा, इसका प्रयोग अत्यन्त सावधानी से किया जाना चाहिए क्योंकि इसके उचित प्रयोग से भावी पीड़ी का सवास्थ्य बेहतर हो सकता है जबकि अनुचित प्रयोग से नुकसान भी हो सकता है।

प्रश्न 1.12.
भारत में गणित, खगोलिकी, भाषा विज्ञान, तर्क तथा नैतिकता में महान विद्वता की एक लम्बी एवं अटूट परम्परा रही है। फिर भी इसके साथ एवं समान्तर हमारे समाज में बहुत-से अन्धविश्वास तथा रूढ़िवादी दृष्टिकोण व परम्पराएँ फली फूली हैं और दुर्भाग्यवश ऐसा अभी भी हो रहा है और बहुत से शिक्षित लोगों में व्याप्त है। इन दृष्टिकोणों का विरोध करने के लिए अपनी रणनीति बनाने में आप अपने विज्ञान के ज्ञान का प्रयोग किस प्रकार करेंगे?
उत्तर:
(i) विद्यालयों में ऐसे कार्यक्रम दिखाये जायें, जिनसे छात्रों में अन्धविश्वास दूर हो सके। जैसे- सोडियम पर पानी डालकर आग उत्पन्न
करना।
(ii) वैज्ञानिक, डॉक्टर्स, शिक्षाविदों द्वारा विभिन्न घटनाओं के वास्तविक कारण व अन्धविश्वास को सही रूप से समझाएँ। जैसे – मानसिक बीमारियों के लिए जादू-टोने के इस्तेमाल को रोकना।
(iii) रेडियो, टेलीविजन, समाचार पत्र, इंटरनेट आदि जनसंचार माध्यमों का प्रयोग लोगों में व्याप्त अन्धविश्वास को दूर कर सकता है।

प्रश्न 1.13.
यद्यपि भारत में स्त्री तथा पुरुषों को समान अधिकार प्राप्त हैं, फिर भी बहुत से लोग महिलाओं की स्वाभाविक प्रकृति, क्षमता, बुद्धिमत्ता के बारे में अवैज्ञानिक विचार रखते हैं तथा व्यवहार में उन्हें गौण महत्व तथा भूमिका देते हैं। वैज्ञानिक तर्कों तथा विज्ञान एवं अन्य क्षेत्रों में महान महिलाओं का उदाहरण देकर इन विचारों को धराशायी कीजिए तथा अपने को स्वयं तथा दूसरों को भी समझाइए कि समान अवसर दिये जाने पर महिलाएँ पुरुषों के समकक्ष होती हैं।
उत्तर:
महिलाएँ भी किसी भी क्षेत्र में पुरुषों से कम नहीं हैं। मैडम क्यूरी ऐसी महिला थीं, जिन्होंने भौतिक व रसायन विज्ञान दोनों में नोबेल पुरस्कार प्राप्त किया। अन्य क्षेत्रों में भी महिलाओं ने बहुत योगदान किया। जैसे – कल्पना चावला, इन्दिरा गाँधी, बछेन्द्री पाल, लक्ष्मीबाई इत्यादि जिन्होंने अपने क्षेत्रों में असाधारण योगदान दिया। अतः महिलाएँ किसी भी क्षेत्र में पुरुषों से कम नहीं हैं।

प्रश्न 1.14.
“भौतिकी के समीकरणों में सुन्दरता होना उनका प्रयोगों के साथ सहमत होने की अपेक्षा अधिक महत्वपूर्ण है।” यह मत महान ब्रिटिश वैज्ञानिक पी०ए०एम० डिरैक का था। इस दृष्टिकोण की समीक्षा कीजिए। इस पुस्तक में ऐसे सम्बन्धों तथा समीकरणों को खोजिए जो आपको सुन्दर लगते हैं।
उत्तर:
भौतिकी में समीकरणों की सुन्दरता होना भी महत्वपूर्ण है क्योंकि समीकरण यदि सुन्दर है तो वह सरल व बोधगम्य भी होगा। जैसे – E = mc² एक सुन्दर समीकरण है, जो ऊर्जा व द्रव्यमान में सम्बन्ध बताता है।

प्रश्न 1.15.
यद्यपि उपर्युक्त प्रकथन विवादास्पद हो सकता है परन्तु अधिकांश भौतिक विज्ञानियों का यह मत है कि भौतिकी के महान नियम एक ही साथ सरल एवं सुन्दर होते हैं। डिरैक के अतिरिक्त जिन सुप्रसिद्ध भौतिक विज्ञानियों ने ऐसा अनुभव किया उनमें से कुछ के नाम इस प्रकार हैं-आइंस्टीन, बोर, हाइजेनबर्ग, चन्द्रशेखर तथा फाइनमैन। आपसे अनुरोध है कि आप भौतिकी के इन विद्वानों तथा अन्य महानायकों द्वारा रचित सामान्य पुस्तकों एवं लेखों तक पहुँचने के लिए विशेष प्रयास अवश्य करें। (पाठ्य पुस्तक के अन्त में दी गई ग्रन्थ सूची देखिए।) इनके लेख सचमुच प्रेरक हैं।
उत्तर:
भौतिकी के अति महत्वपूर्ण नियम एवं समीकरण एक साथ ही सरल तथा सुन्दर हैं। इनमें से कुछ निम्नलिखित हैं-
1. भारतीय मूल के वैज्ञानिक एस० चन्द्रशेखर ने खगोलीय पिण्डों के लिए ‘ब्लैक होल’ का सिद्धान्त देकर विश्व के सामने अनबूझे आकाशीय पिण्डों का रहस्य पता करके अपने सिद्धान्त को सरल रूप में प्रस्तुत किया।
2. इसी प्रकार फाइनमैन जिसे भौतिकी की गीता का प्रणेता कहा जाता है, ने लेजर की शक्ति का सरल, सुन्दर तथा सुग्राही भाषा में प्रतिपादन किया।
3. न्यूटन का गति विषयक द्वितीय नियम F = \(\frac{d}{d t}\)(mu) केप्लर का खगोलीय पिण्डों की गति का तीसरा नियम T² ∝ r³ भी कुछ सरल, सुन्दर तथा महत्वपूर्ण समीकरण है।
4. नील्स बोर ने परमाणु के कोणीय संवेग को छोटे से सुन्दर समीकरण L = n \(\frac{h}{2 \pi}\) द्वारा दर्शाकर एक विकट समस्या का सरल समाधान प्रस्तुत किया।
5. आइंस्टीन का द्रव्यमान ऊर्जा E = mc² अत्यन्त सरल, गूढ़ सुन्दर एवं आसानी से याद रखने वाला है।
6. डी- ब्रॉग्ली का द्रव्य तरंग के लिए सम्बन्ध λ = \(\frac{h}{p}\) = \(\frac{h}{m u}\) न केवल सरल एवं सुन्दर है, अपितु एक अत्यन्त गूढ़ तथ्य को उजागर करता है कि कण की प्रकृति द्वैती होती है।

प्रश्न 1.16.
विज्ञान की पाठ्य पुस्तकें आपके मन में यह गलत धारणा उत्पन्न कर सकती हैं कि विज्ञान पढ़ना शुष्क तथा पूर्णतः अत्यन्त गंभीर है एवं वैज्ञानिक अन्तर्मुखी, भुलक्कड़ व कभी न हँसने वाले अथवा खीसें निकालने वाले व्यक्ति होते हैं। विज्ञान एवं वैज्ञानिकों का यह चित्रण पूर्णतः आधारहीन है। अन्य समुदाय के मनुष्यों की भाँति ही वैज्ञानिक भी विनोदी होते हैं तथा बहुत से वैज्ञानिकों ने तो वैज्ञानिक कार्यों को गम्भीरता से पूरा करते हुए अत्यन्त विनोदी प्रकृति तथा साहसिक कार्य करके अपना जीवन व्यतीत किया है। गैमो तथा फाइनमैन इसी श्रेणी के दो भौतिकविद हैं। ग्रन्थ सूची में इनके द्वारा रचित पुस्तकें पढ़ने से आपको आनन्द प्राप्त होगा।
उत्तर:
समाज के अन्य व्यक्तियों की भाँति ही वैज्ञानिक भी विनोदी स्वभाव के हँसमुख व्यक्ति होते हैं तथा विज्ञान शुष्क तथा नीरस विषय नहीं है। कुछ विनोदी स्वभाव के भारतीय वैज्ञानिक हैं- होमी जहाँगीर भाभा, डी० एस० कोठारी, सी०वी० रमन, एम०एम० जोशी, ए०पी० जे० अब्दुल कलाम आदि।

Haryana State Board HBSE 12th Class Physics Solutions Chapter 6 वैद्युत चुंबकीय प्रेरण Textbook Exercise Questions and Answers.

Haryana Board 12th Class Physics Solutions Chapter 6 वैद्युत चुंबकीय प्रेरण

प्रश्न 6.1.
चित्र (a) से (f) में वर्णित स्थितियों के लिए प्रेरित धारा की दिशा की प्रागुक्ति (Predict) कीजिए।

उत्तर:
(a) जैसे-जैसे चुम्बक परिनालिका की तरफ आती है, तो परिनालिका से सम्बद्ध चुम्बकीय क्षेत्र बढ़ता जाता है। लेंज के नियम से परिनालिका में प्रेरित चुम्बकीय क्षेत्र (विद्युत वाहक बल) इसके उत्पन्न करने वाले कारण पर ही कुठाराघात करता है अर्थात् यह चुम्बक की गति का विरोध करता है अतः इसका आनन q दक्षिणी ध्रुव व p उत्तरी ध्रुव बन जाते हैं। अतएव कुण्डली में धारा pq के अनुदिश प्रवाहित होगी अर्थात् qrpq$ के अनुदिश जैसा चित्र में दिखाया गया है अर्थात् जब चुम्बक की ओर से देखी जाएगी, तो दक्षिणावर्ती घड़ी के नियमानुसार।
(b) जैसे-जैसे कुण्डली x y से उत्तरी ध्रुव दूर होता जाता है, कुण्डली से सम्बद्ध चुम्बकीय अभिवाह भी कम होता जाता है। इस प्रकार लेंज के नियमानुसार कुण्डली में प्रेरित विद्युत वाहक बल चुम्बक की गति का विरोध करेगा। अतएव फलक X, S ध्रुव बन जाता है अतः धारा दक्षिणावर्ती होगी अर्थात् कोण में yzx के अनुदिश pq कुण्डली के लिए दक्षिणी ध्रुव q सिरे की ओर अग्रसर है और इस प्रकार यह सिरा दक्षिणी ध्रुवता धारण करेगा जिससे यह चुम्बक की गति का विरोध कर सके अतः कुण्डली में धारा prq के अनुदिश प्रवाहित होगी।
(c) प्रेरित धारा वामावर्ती दिशा में होगी अर्थात् yzx के अनुदिश।
(d) प्रेरित धारा दक्षिणावर्ती दिशा में होगी अर्थात् zyx के
(e) बायीं कुण्डली में बैटरी की धारा दाहिनी से बायीं ओर होगी। इसलिए अन्योन्य प्रेरण से दाहिनी कुण्डली में प्रेरित धारा विपरीत दिशा में होगी अर्थात् बायीं से दाहिनी ओर अथवा xry के अनुदिश।
(f) कोई प्रेरित धारा नहीं क्योंकि क्षेत्र रेखाएँ लूप तल में स्थित हैं।

प्रश्न 6.2.
चित्र में वर्णित स्थितियों के लिए लेंज के नियम का उपयोग करते हुए प्रेरित विद्युत धारा की दिशा ज्ञात कीजिए।
(a) जब अनियमित आकार का तार वृत्ताकार लूप में बदल रहा हो;
(b) जब एक वृत्ताकार लूप एक सीधे बारीक तार में विरूपित किया जा रहा हो।

उत्तर:
(a) adcb के अनुदिश आकार परिवर्तन के समय पृष्ठ से गुजरने वाला फ्लक्स बढ़ता है, अतः प्रेरित धारा विरोधी फ्लक्स उत्पन्न करती है।
(b) a’b’c’d’ अनुदिश (इस प्रक्रम में फ्लक्स घटता है)।

प्रश्न 6.3.
एक लम्बी परिनालिका के इकाई सेंटीमीटर लम्बाई में 15 फेरे हैं। उसके अन्दर 2.0 cm² का एक छोटा-सा लूप परिनालिका की अक्ष के लम्बवत् रखा गया है। यदि परिनालिका में बहने वाली धारा का मान 2.0 A में 4.0 A से 0 .1 s कर दिया जाए, तो धारा परिवर्तन के समय प्रेरित विद्युत वाहक बल कितना होगा?
उत्तर:
हल-दिया गया है-
इकाई सेंटीमीटर लम्बाई में फेरे = 15
∴ इकाई मीटर लम्बाई में फेरे = 1500
n = 1500 फेरे / मीटर
A = 2.0 cm²
= 2 × 10^-4 m²
I₁ = 2.0 A, I₂ = 4.0 A
dI = I₂ – I₁ = 4 – 2 = 2A
dt = 0.1 s,
∴ \(\frac{\mathrm{dI}}{\mathrm{dt}}=\frac{2}{0.1}=20 \mathrm{As}^{-1}\)
ε = लूप में प्रेरित विद्युत वाहक बल
परिनालिका के अन्दर उत्पन्न चुम्बकीय क्षेत्र
B = µ₀nI
हम जानते हैं- Φ_B = BA = µ₀nIA
∴ सम्बन्ध ε = \( -\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) का उपयोग करने पर
ε = \( -\frac{\mathrm{d}}{\mathrm{dt}} \phi_{\mathrm{B}}\)

प्रश्न 6.4.
एक आयताकार लूप जिसकी भुजाएँ 8 cm एवं 2 cm हैं, एक स्थान पर थोड़ा कटा हुआ है। यह लूप अपने तल के अभिलम्बवत् 0.3 T के एकसमान चुम्बकीय क्षेत्र से बाहर की ओर निकल रहा है। यदि लूप के बाहर निकलने का वेग 1 cm s^-1 है तो कटे भाग के सिरों पर उत्पन्न विद्युत वाहक बल कितना होगा, जब लूप की गति अभिलम्बवत् हो (a) लूप की लम्बी भुजा के (b) लूप की छोटी भुजा के। प्रत्येक स्थिति में उत्पन्न प्रेरित वोल्टता कितने समय तक टिकेगी?
उत्तर:
उत्तर-दिया गया है-
लूप की लम्बाई = l = 8 cm = 8 × 10^-2 m
लूप की चौड़ाई = b = 2 cm = 2 × 10^-2 m
चुम्बकीय क्षेत्र = B = 0.3 T
लूप का वेग = v = 1 cm s^-1 = 10^-2 ms^-1
∴ लूप का क्षेत्रफल = A = l × b
A = 8 × 2 × 10^-4 m²
A = 16 × 10^-4 m²
प्रेरित विद्युत वाहक बल = ε = ?
लूप में रहने वाले प्रत्येक विद्युत वाहक बल का समय = t =?
(a) जब वेग लम्बी भुजा के अभिलम्ब है।
ε = Blv
= 0.3 × 8 × 10^-2× 10^-2
= 2.4 × 10^-4v
= 2.4 × 10^-4v
लूप में विद्युत वाहक बल तब तक रहेगा जब तक कि लूप चुम्बकीय क्षेत्र से बाहर नहीं हो जाता अर्थात् उस समय तक जब तक कि लूप की छोटी भुजा के तुल्य लम्बाई के बराबर दूरी तय करने में लूप द्वारा लिए गए समय के बराबर

t = \(\frac{2 \times 10^{-2}}{10^{-2}}\) = 2s
अतः 2.4 × 10^-4V, जो 2 सेकण्ड तक बना रहेगा।
(b) जब वेग छोटी भुजा के लम्बवत् है।
चौड़ाई = b = 2 × 10^-2m
ε = Blv से
ε = Bbv ∵ यहाँ पर l = b लेना है।
= 0.3 × 2 × 10^-2 × 10^-2
= 0.6 × 10^-4 = 6 × 10^-5
= 0.6 × 10^-4 v,
t = \(
समय (t) = [latex]\frac{8 \times 10^{-2}}{10^{-2}}\) = 8 सेकण्ड
अत: 0.6 × 10^-4 V, जो 8 सेकण्ड तक बना रहेगा।

प्रश्न 6.5.
1.0 m लम्बी धातु की छड़ उसके एक सिरे से जाने वाले अभिलम्बवत् अक्ष के परितः 400 rad s^-1 की कोणीय आवृत्ति से घूर्णन कर रही है। छड़ का दूसरा सिरा एक धात्विक वलय से संपर्कित है। अक्ष के अनुदिश सभी जगह 0.5 T का एकसमान चुम्बकीय क्षेत्र उपस्थित है। वलय तथा अक्ष के बीच स्थापित विद्युत वाहक बल की गणना कीजिए।
उत्तर:
हल-दिया गया है-
l = 1.0 m
ω = 400 rad/s
B = 0.5 T
माना वलय तथा अक्ष के बीच स्थापित विद्युत वाहक बल = ε = ?
सम्बन्ध ε = \(\frac{1}{2}\) Bl²ω का उपयोग करने पर
मान रखने पर ε = \(\frac{1}{2}\) × 0.5 × (1)² × 400
= 0.5 × 200 = 100. 0 V
अतः केन्द्र तथा वलय के बीच प्रेरित विद्युत वाहक बल
ε = 100 .0 volt

प्रश्न 6.6.
एक वृत्ताकार कुण्डली जिसकी त्रिज्या 8.0 cm तथा फेरों की संख्या 20 है अपने ऊर्ष्वाषर व्यास के परित: 50 rad s^-1 की कोणीय आवृत्ति से 3.0 × 10^-2 T के एकसमान चुम्बकीय क्षेत्र में घूम रही है। कुण्डली में उत्पन्न अधिकतम तथा औसत प्रेरित विद्युत वाहक बल का मान ज्ञात कीजिए। यदि कुण्डली 10 Ω प्रतिरोध का एक बन्द लूप बनाए तो कुण्डली में धारा के अधिकतम मान की गणना कीजिए। जूल ऊष्मन के कारण क्षयित औसत शक्ति की गणना कीजिए। यह शक्ति कहाँ से प्राप्त होती है?
उत्तर:
हल-दिया गया है-
r = 8.0 cm = 8 × 10^-2m
N = 20
ω = 50 rad ^-1
B = 3.0 × 10^-2 T
कुण्डली में उत्पन्न अधिकतम विद्युत वाहक बल = ε_max = ?
∴ ε_max = NBAω = NBπr²ω
ε_max = 20 × 3 × 10^-2 × 3.14 × (8 × 10^-2) × 50
= 60 × 3.14 × 64 × 50 × 10^-2 × 10^-4
= 3000 × 3.14 × 64 × 10^-6
= 603 × 10^-3 Volt = 0.603 V = 0.6 V
वि.वा. बल सरल आवर्ती रूप से समय के साथ परिवर्तित होता है। अतः प्रतिचक्र औसत मान शून्य होगा।
परिपथ का प्रतिरोध R = 10Ω
I_max = \(\frac{\varepsilon_{\max }}{\mathrm{R}}=\frac{0.6}{10} \mathrm{~A}\)
= 0.06 A
शक्ति में क्षय (p)_av = \(\frac{1}{2}\)ε_max.I_max
(p)_av = \(\frac{1}{2}\) × 0.6 ×0.06W
= 0. 018 W
प्रेरण धारा कुण्डली के घूमने की विपरीत दिशा में बल आघूर्ण उत्पन्न करती है। कुण्डली को एकसमान रूप से घूमते रखने के लिए बाह्य स्रोत से ऐंठन देनी पड़ेगी और ऐसा करने के लिए कार्य भी करना होगा। अतः शक्ति का स्रोत ऊष्मीय ऊर्जा को कुण्डली में बाह्य स्रोत की उपस्थिति में क्षयित करता है अर्थात् घूर्णक (रोटर) देता है।

प्रश्न 6.7.
पूर्व से पश्चिम दिशा में विस्तृत एक 10 m लम्बा क्षैतिज सीधा तार 0.30 × 10^-4 Wb m^-2 तीव्रता वाले पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज घटक से लम्बवत् 5.0 ms^-1 की चाल से गिर रहा है।
(a) तार में प्रेरित विद्युत वाहक बल का तात्क्षणिक मान क्या होगा?
(b) विद्युत वाहक बल की दिशा क्या है?
(c) तार का कौनसा सिरा उच्च विद्युत विभव पर है?
उत्तर:
दिया गया है-
l = 10 m
B^E = 0.30 × 10^-4 Wb m^-2
v = 5.0 m/s
(a) माना तार में प्रेरित तात्क्षणिक विद्युत वाहक बल का मान = ε = ?
सूत्र ε = Blv का उपयोग करने पर
∴ ε = B^Elv
∵ क्षैतिज घटक है।
मान रखने पर- = (0. 30 × 10) × (10) × (5)
= 1.5 × 10^-3V = 1.5 mV
(b) प्रेरित विद्युत वाहक बल की दिशा पश्चिम से पूर्व की ओर होगी। यह हम फ्लेमिंग के दायें हाथ के नियम से प्राप्त कर सकते हैं।
(c) चूँकि प्रेरित विद्युत वाहक बल इसके कारण का विरोध करता है अर्थात् यह कम से अधिक विभव सिरे की ओर स्थित होता है। अतः पूर्वी सिरा अधिक विभव पर होगा क्योंकि प्रेरित विद्युत वाहक बल पश्चिम से पूर्व की ओर कार्य करता है।

प्रश्न 6.8.
किसी परिपथ में 0.1 s में धारा 5.0 A से 0.0 A तक गिरती है। यदि औसत प्रेरित विद्युत वाहक बल 200 V है, तो परिपथ में स्वप्रेरकत्व का आकलन कीजिए।
उत्तर:
हल-दिया गया है-
I₁ = 5. 0 A
I₂ = 0.0 A
धारा में परिवर्तन = dI = I² – I¹ = 0.0 A – 5.0 A
dI = – 5A
वह समय जिसमें धारा परिवर्तित होती है = dt = 0. 1 s
औसत प्रेरित विद्युत वाहक बल = ε = 200 V
माना परिपथ का स्वप्रेरकत्व = L = ?
हम जानते हैं-सूत्र ε = -L \(\frac{\mathrm{dI}}{\mathrm{dt}}\)
मान रखने पर- 200 = -L\(\left(\frac{-5}{0.1}\right)\) = 50L
∴ L = \(\frac{200}{50}\) = 4 हेनरी
L = 4 H

प्रश्न 6.9.
पास-पास रखे कुण्डलियों के एक युग्म का अन्योन्य प्रेरकत्व 1.5 H है। यदि एक कुण्डली में 0.5 s में धारा 0 से 20 A तक परिवर्तित हो, तो दूसरी कुण्डली की फ्लक्स बंधता में कितना परिवर्तन होगा?
उत्तर:
हल-दिया गया है-
कुण्डलियों के एक युग्म का अन्योन्य प्रेरकत्व = M = 1.5 H
धारा परिवर्तन = dI = I₂ – I₁
= 20 – 0
= 20 A
वह समय जिसमें धारा परिवर्तन होता है = dt
= 0.5 s
माना दूसरी कुण्डली की फ्लक्स बंधता का मान = d Φ_b = ?
यदि दूसरी कुण्डली में प्रेरित विद्युत वाहक बल का मान ε है तब
सूत्र ε = – M\(\frac{\mathrm{dI}}{\mathrm{dt}}\) से
मान रखने पर = -1.5 × \(\frac{20}{0.5}\) = -60V
हम यह भी जानते हैं ε = \(-\frac{\mathrm{d} \phi}{\mathrm{dt}}\)
∴ dΦ = -ε × dt = -(- 60) × (0.5)
dΦ = 30 Wb

प्रश्न 6.10.
एक जेट प्लेन पश्चिम की ओर 1800 km/h वेग से गतिमान है। प्लेन के पंख 25 m लम्बे हैं। इनके सिरे पर कितना विभवान्तर उत्पन्न होगा? पृथ्वी के चुम्बकीय क्षेत्र का मान उस स्थान पर 5 × 10^-4T तथा नति कोण 30° है।
उत्तर:
हल-दिया गया है-
वेग v = 1800 Km/h
∴ v = 1800 × \(\times \frac{5}{18}\) m/s
= 500 m/s पश्चिम की ओर
l = 25 m
नति कोण (I) = 30° और B_E = 5 × 10^-4T
चम्बकीय क्षेत्र के ऊर्ध्वाधर घटक का मान होगा
Z_E = B_E sin I
Z_E = B_E sin 30°
= 5.0 × 10^-4 × \(\frac{1}{2}\)T
Z_E = 2.5 × 10^-4T
Z_E सिरों और वायु दिशा दोनों के अभिलम्बवत् है।
अतः यदि उत्पन्न प्रेरक विद्युत वाहक बल = पंखों के सिरों के बीच उत्पन्न विभवान्तर
तब ε = Z_Elv से
मान रखने पर = 2.5 × 10^-4 × 25 × 500
= 25 × 25 × 500 × 10^-5
= 312500 × 10^-5
= 3. 125 = 3.1 volt
इस उत्तर के लिए पंखों की दिशा महत्वहीन है जब तक वह क्षैतिज है।

अतिरिक्त अभ्यास प्रश्न (NCERT)

प्रश्न 6.11.
मान लीजिए कि अभ्यास 6.4 में उउल्लिखित लूप स्थिर है किन्तु चुम्बकीय क्षेत्र उत्पन्न करने वाले विद्युत चुम्बक में धारा का मान कम किया जाता है जिससे चुम्बकीय क्षेत्र का मान अपने प्रारम्भिक मान 0.3 T से 0.02 T s^-1 की दर से घटता है। अब यदि लूप का कटा भाग जोड़ दें जिससे प्राप्त बन्द लूप का प्रतिरोध 1.6 Ω हो, तो इस लूप में ऊष्मन के रूप में शक्ति हास क्या है? इस शक्ति का रत्रोत क्या है?
उत्तर:
हल-दिया गया है-
लूप की लम्बाई (l) = 8 cm = 8 × 10^-2m
लूप की चौड़ाई (b) = 2 cm = 2 × 10^-2m
∴ क्षेत्रफल (A) = 8 × 10^-2 × 2 × 10^-2
= 16 × 10^-4m²
चुम्बकीय क्षेत्र का प्रारम्भिक मान = B = 0.3 T
\(\frac{\mathrm{dB}}{\mathrm{dt}}\) = चुम्बकीय क्षेत्र की कम होने की दर
∴ \( \frac{\mathrm{dB}}{\mathrm{dt}}\) = 0. 02 T s^-1
प्राप्त बन्द लूप का प्रतिरोध R = 1.6 Ω
शक्ति हास = p = ?
हम जानते हैं-

इस शक्ति का स्रोत समय के साथ चुम्बकीय क्षेत्र में परिवर्तन करने वाला बाह्य कारक है।

प्रश्न 6.12.
12 cm भुजा वाला वर्गाकार लूप जिसकी भुजाएँ X एवं Y अक्षों के समान्तर हैं, x-दिशा में 8 cm s^-1 की गति से चलाया जा रहा है। लूप तथा उसकी गति का परिवेश धनात्मक z-दिशा के चुम्बकीय क्षेत्र का है। चुम्बकीय क्षेत्र न तो एकसमान है और न ही समय के साथ नियत है। इस क्षेत्र की ऋणात्मक दिशा में प्रवणता 10^-3 T cm ^-1 है (अर्थात् ऋणात्मक x-अक्ष की दिशा में इकाई सेंटीमीटर दूरी पर क्षेत्र के मान में 10^-3T cm^-1 की वृद्धि होती है), तथा क्षेत्र के मान में 10^-3 T cm^-1 की दर से कमी भी हो रही है। यदि कुण्डली का प्रतिरोध 4.50 m} Ω हो तो प्रेरित धारा का परिमाण एवं दिशा ज्ञात कीजिए।
उत्तर:
हल-दिया गया है-
l = 12 cm = 12 × 10^-2m
v = 8 cm/s = 8 × 10^-2 m/s
\(\frac{\mathrm{dB}}{\mathrm{dx}}\) = – 10^-2 m
v = 8 cm/s = 8 × 10^-2 m/s
\(\frac{\mathrm{dB}}{\mathrm{dx}}\) = – 10^-3 T/cm
= -10^-1 T/m
= -0.1 T/m
\(\frac{\mathrm{dB}}{\mathrm{dt}}\) = -10^-3 T/s और R = 4. 50 mΩ
R = 4.5 × 10^-3Ω
R = 4.5 × 10^-3Ω
समय पर निर्भर B के कारण फ्लक्स में परिवर्तन की दर
ε = \(\frac{\mathrm{d}}{\mathrm{dt}}\left(\phi_{\mathrm{B}}\right)=\frac{\mathrm{d}}{\mathrm{dt}}(\mathrm{BA})=\mathrm{A} \frac{\mathrm{dB}}{\mathrm{dt}}\)
ε = (12 × 10^-2)^-2 × (- 10^-3)
= – 144 × 10^-4 × 10^-3
= – 144 × 10^-7 Wb s^-1
स्थिति पर निर्भर B के कारण फ्लक्स में परिवर्तन की दर
ε = \(\frac{\mathrm{d}}{\mathrm{dt}}\left(\phi_{\mathrm{B}}\right)=\frac{\mathrm{d}}{\mathrm{dt}}(\mathrm{BA})=\mathrm{A} \frac{\mathrm{dB}}{\mathrm{dt}}\)
= \(\mathrm{A} \frac{\mathrm{dB}}{\mathrm{dt}} \cdot \frac{\mathrm{dx}}{\mathrm{dt}}=\mathrm{A} v \frac{\mathrm{dB}}{\mathrm{dx}}\)
मान रखने पर = (12 × 10^-2)^-2 × 8 × 10^-2 × (-0.1)
= -144 × 10^-4 × 8 × 10^-3
= -1152 × 10^-7 Wb s^-1
क्योंकि दोनों ही धनात्मक z-दिशा के अनुदिश फ्लक्स को कम करते हैं। अतः दोनों प्रभाव जुड़ जाते हैं।
= – 144 × 10^-7 – 1152 × 10^-7 Wb s^-1
= – 1296 × 10^-7 Wb s^-1
= -12.96 × 10^-7V
प्रेरित धारा का मान (I) = \(\frac{चुम्बकीय फ्लक्स में परिवर्तन की दर}{\mathrm{प्रतिरोध}}\)
= \(\frac{12.96 \times 10^{-5}}{4.5 \times 10^{-3}}\)A
I = 2.88 × 10^-2A
प्रेरित धारा की दिशा वह होगी जो लूप में से धनात्मक z-दिशा के फ्लक्स को बढ़ाए, यदि किसी प्रेक्षक हेतु लूप दाहिनी ओर गतिमान है, तो लूप में धारा घड़ी की सुई के घूमने की दिशा के विपरीत होगी।

प्रश्न 6.13.
एक शक्तिशाली लाउडस्पीकर के चुम्बक के ध्रुवो के बीच चुम्बकीय क्षेत्र की तीव्रता के परिमाण का मापन किया जान है। इस हेतु एक छोटी चपटी 2 cm^-2 क्षेत्रफल की अन्वेषी कुण्डली (search coil) का प्रयोग किया गया है। इस कुण्डली में पास-पास लिपटे 25 फेरे हैं तथा इसे चुम्बकीय क्षेत्र के लम्बवत् व्यवस्थित किया गया है और तब इसे दुत गति से क्षेत्र के बाहर निकाला जाता है। तुल्यतः एक अन्य विधि में अन्वेषी कुण्डली को 90° से तेजी से घुमा देते हैं जिससे कुण्डली का तल चुम्बकीय क्षेत्र के समान्तर हो जाए। इन दोनों घटनाओं में कुल 7.5 mC आवेश का प्रवाह होता है (जिसे परिपथ में प्रक्षेप धारामापी (ballistic galvanometer) लगाकर ज्ञात किया जा सकता है)। कुण्डली तथा धारामापी का संयुक्त प्रतिरोध 0.50 Ω है। चुम्बक की क्षेत्र तीव्रता का आकलन कीजिए।
उत्तर:
हल-दिया गया है-
A = 2.0 cm² = 2.0 × 10^-4m²
फेरों की संख्या (N) = 25
आवेश q = 7.5 mC
= 7.5 × 10^-3C
R = 0.50 Ω
B = ?
विद्युत वाहक बल ε = \( -\frac{d \phi_{\mathrm{B}}}{\mathrm{dt}}\)

प्रश्न 6.14.
चित्र में एक धातु की छड़ PQ को दर्शाया गया है जो पटरियों AB पर रखी है तथा एक स्थायी चुम्बक के ध्रुवों के मध्य स्थित है। पटरियाँ, छड़ एवं चुम्बकीय क्षेत्र परस्पर अभिलम्बवत् दिशाओं में हैं। एक गैल्वेनोमीटर (धारामापी) G को पटरियों से एक स्वि K की सहायता से संयोजित किया गया है। छड़ की लम्बाई = 15 cm, B = 0.50 T तथा पटरियों, छड़ तथा धारामापी से बने बन्द लूप का प्रतिरोध = 9.0 mΩ है। क्षेत्र को एकसमान मान लें।
(a) माना कुंजी K खुली (open) है तथा छड़ 12 cm s^-1 की चाल से दर्शायी गई दिशा में गतिमान है। प्रेरित विद्युत वाहक बल का मान एवं धुवणता (polarity) बताइए।

(b) क्या कुंजी K खुली होने पर छड़ के सिरों पर आवेश का आधिक्य हो जाएगा? क्या होगा यदि कुंजी K बन्द (close) कर दी जाए?
(c) जब कुंजी K खुली हो तथा छड़ एकसमान वेग से गति में हो तब भी इलेक्ट्रॉनों पर कोई परिणामी बल कार्य नहीं करता यद्यपि उन पर छड़ की गति के कारण चुम्बकीय बल कार्य करता है। कारण स्पष्ट कीजिए।
(d) कुंजी बन्द होने की स्थिति में छड़ पर लगने वाले अवमंदन बल का मान क्या होगा?
(e) कुंजी बन्द होने की स्थिति में छड़ को उसी चाल = 12 cm s^-1 से चलाने हेतु कितनी शक्ति (बाह्य कारक के लिए) की आवश्यकता होगी?
(f) बंद परिपथ में कितनी शक्ति का ऊष्मा के रूप में क्षय होगा? इस शक्ति का र्रोत क्या है?
(g) गतिमान छड़ में उत्पन्न विद्युत वाहक बल का मान क्या होगा यदि चुम्बकीय क्षेत्र की दिशा पटरियों के लम्बवत् होने के बजाय उनके समान्तर हो?
उत्तर:
हल-दिया गया है-
l = 15 cm = 15 × 10^-2m
(A और B पटरियों के बीच)
B =0.50 T,
v = 12 cm/s = 12 × 10^-2 m/s
R = 9.0 mΩ = 9 × 10^-3 Ω
(a) छड़ द्वारा इकाई सेकण्ड में तय किया गया क्षेत्रफल
A = lv
छड़ द्वारा इकाई सेकण्ड में काटा गया चुम्बकीय फ्लक्स का मान होगा
Φ_B = BA = Blv
अर्थात् \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) = Blv
प्रेरित विद्युत वाहक बल ε = \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\) = Blv
मान रखने पर ε = 0.5 × 15 × 10^-2× 1.2 × 10^-2
= 90 × 10^-4 = 9.0 × 10^-3 V
= 9.0 mV
फ्लेमिंग के बायें हाथ नियम से छड़ PQ के मुक्त इलेक्ट्रॉनों पर बल Q सिरे की ओर होगा अतः सिरा P धनात्मक ध्रुव तथा सिरा Q ऋणात्मक़ ध्रुव होगा।
(b) जब कुंजी K खुली है, प्रेरित विद्युत वाहक बल, P पर आधिक्य धनात्मक आवेश उत्पन्न करेगा तथा Q पर आधिक्य ऋणात्मक आवेश। जब कुंजी बन्द कर दी जाए, तो धारा के सतह प्रवाह के कारण आवेश का आधिक्य होता है।
(c) छड़ के सिरों पर विपरीत चिह्न युक्त आवेश आधिक्य के कारण स्थापित विद्युत क्षेत्र द्वारा चुम्बकीय बल निरस्त हो जाता है।
(d) छड़ में प्रेरित धारा I = \(\frac{\varepsilon}{\mathrm{R}}\)
= \(\frac{9 \times 10^{-3}}{9 \times 10^{-3}}\) = 1 A
अतः छड़ पर अवमन्दन बल
F = I l B
= 1 × 15 × 10^-2 × 0. 50
= 7.5 × 10^-2 N
(e) बाह्य कारक द्वारा उक्त अवमंदन बल के विरुद्ध छड़ को 12 × 10^-2 m/s की एकसमान गति से चलाने हेतु शक्ति का व्यय = 75 × 10^-3 × 12 × 10^-2
∵ p = Fv होता है।
= 9.0 × 10^-3 W
कुंजी K खुली हो, तो कोई शक्ति खर्च नहीं होगी।
(f) शक्ति का ऊष्मा के रूप में क्षय = I^-2R
= 1 × 1 × 9 × 10^-3
= 9.0 × 10^-3 W
प्रयुक्त शक्ति का स्रोत बाह्य कारक है जिसका परिकलन ऊपर भाग (e) में किया गया है।
(g) पटरियों के समान्तर चुम्बकीय क्षेत्र चालक छड़ PQ की
गति के समान्तर होगा अर्थात् \(\overrightarrow{\mathrm{B}} \| \vec{v}\) अतः इस स्थिति में प्रेरित विद्युत वाहक बल शून्य होगा।

प्रश्न 6.15.
वायु के क्रोड वाली एक परिनालिका में जिसकी लम्बाई 30 cm तथा अनुप्रस्थ काट का क्षेत्रफल 25 cm^-2 तथा कुल फेरे 500 हैं, 2.5 A धारा प्रवाहित हो रही है। धारा को 10^-3 के अल्पकाल में अचानक बन्द कर दिया जाता है। परिपथ में स्विच के खुले सिरों के बीच उत्पन्न औसत विद्युत वाहक बल का मान क्या होगा? परिनालिका के सिरों पर चुम्बकीय क्षेत्र के परिवर्तन की उपेक्षा कर सकते हैं।
उत्तर:
हल-दिया गया है-
l = 30 cm 30 × 10^-2m
A = 25 cm^-2 = 25 × 10^-4 m²
फेरों की कुल संख्या = N = 500
धरा I = 2.5 A
समय अन्तराल (dt) = 10^-3s
माना परिनालिका में प्रेरित औसत विरोधी विद्युत वाहक बल = ε
परिनालिका के अन्दर चुम्बकीय क्षेत्र का मान
B = \(\frac{\mu_0 \mathrm{NI}}{l}\)
हम जानते हैं-
Φ_B = BA
∴ Φ_B = \(\frac{\mu_0 \mathrm{NI}}{l}\).A

प्रश्न 6.16.
(a) चित्र में दर्शाए अनुसार एक लम्बे, सीधे तार तथा एक वर्गाकार लूप जिसकी एक भुजा की लम्बाई a है, के लिए अन्योन्य प्रेरकत्व का व्यंजक प्राप्त कीजिए।

(b) अब मान लीजिए कि सीधे तार में 50 A की धारा प्रवाहित हो रही है तथा लूप एक स्थिर वेग v = 10 m/s से दार्यी ओर को गति कर रहा है। लूप में प्रेरित विद्युत वाहक बल का परिकलन उस क्षण पर कीजिए जब x = 0.2 m हो। लूप के लिएa a = 0.1 m लीजिए तथा यह मान लीजिए कि उसका प्रतिरोध बहुत अधिक है।
उत्तर:
हल-
(a) dr चौड़ाई की एक स्ट्रिप पर विचार कीजिए जो कि तार से r दूरी पर स्थित चित्र में स्ट्रिप को दिखाया गया है। एक लम्बे, सीधे चालक से r दूरी पर चुम्बकीय क्षेत्र का मान होगा

B = \(\frac{\mu_0 \mathrm{I}}{2 \pi \mathrm{r}}\)
यहाँ पर यह कल्पना की गई है कि दूरी dr में एकसमान चुम्बकीय क्षेत्र है।
स्ट्रिप का क्षेत्रफल = लम्बाई × चौड़ाई
= a × dr = adr
स्ट्रिप से जुड़ा चुम्बकीय फ्लक्स का मान
dΦ_B = B × स्ट्रिप का क्षेत्रफल

यहाँ पर M अन्योन्य प्रेरकत्व गुणांक है जो कि तार और वर्गाकार लूप के बीच में है तब चुम्बकीय फ्लक्स का मान निम्न सूत्र से ज्ञात करते हैं-

प्रश्न 6.17.
किसी M द्रव्यमान तथा R त्रिज्या वाले एक पहिए के किनारे (rim) पर एक रैखिक आवेश स्थापित किया गया है जिसकी प्रति इकाई लम्बाई पर आवेश का मान λ है। पहिए के स्पोक (spoke) हल्के और कुचालक हैं तथा वह अपनी अक्ष के परितः घर्षण रहित घूर्णन हेतु स्वतन्त्र है जैसा कि चित्र में दर्शाया गया है। पहिए के वृत्तीय भाग पर रिम के अन्दर एकसमान चुम्बकीय क्षेत्र विस्तरित है। इसे इस प्रकार परिभाषित किया गया है,
B = – B₀K (r≤a; a<R)
= 0
चुम्बकीय क्षेत्र को अचानक ‘ऑफ’ (switched off) करने के पश्चात् पहिए का कोणीय वेग ज्ञात कीजिए।

उत्तर:
हल-M द्रव्यमान तथा R त्रिज्या के चक्र की कोणीय चाल माना ω है।
माना उत्पन्न प्रेरण वि.वा. बल = ε
घूर्णित चक्र की घूर्णन गतिज ऊर्जा (K.E) = \(\frac{1}{2}\) Iω² ………….(1)
जहाँ पर I = चक्र का जड़त्व आघूर्ण है।
I = \(\frac{1}{2}\)MR² ………………(2)
किया गया कार्य W = (वि.वा. बल) × आवेश
कार्य ऊर्जा सिद्धान्त को लगाने पर-
घूर्णन गतिज ऊर्जा (K.E.) = किया गया कार्य
K.E. = Q × ε …………..(3)
हम जानते हैं कि एकसमान चुम्बकीय क्षेत्र में घूर्णन करती छड़
वि.वा. बल = \(\frac{1}{2}\)Bωa² द्वारा दिया जाता है। चूँकि यहाँ चुम्बकीय
क्षेत्र परिवर्तनशील है, इस कारण से वि.वा. बल का औसत मान
\(\frac{1}{2}\left(\frac{1}{2} \mathrm{~B} \omega \mathrm{a}^2\right)=\frac{1}{4}{\mathrm{~B} \omega \mathrm{a}^2}^2\) द्वारा दिया जाता है।
= \(\frac{1}{4}\)Bωa² ……………..(4)
अब आवेश Q = λ . 2πR
Q = 2πRλ …………………. (5)
अतः समीकरण 1 व 3 से Q × ε = \(\frac{1}{2}\)Iω²
सभी का मान उपरोक्त समीकरणों से रखने पर