HBSE 12th Class Physics Solutions Chapter 8 वैद्युतचुंबकीय तरंगें

Haryana State Board HBSE 12th Class Physics Solutions Chapter 8 वैद्युतचुंबकीय तरंगें Textbook Exercise Questions and Answers.

Haryana Board 12th Class Physics Solutions Chapter 8 वैद्युतचुंबकीय तरंगें

प्रश्न 8.1.
चित्र में एक संधारित्र दर्शाया गया है जो 12 cm त्रिज्या की दो वृत्ताकार प्लेटों को 5.0 cm की दूरी पर रखकर बनाया गया है। संधारित्र को एक बाह्य स्रोत (जो चित्र में नहीं दर्शाया गया है) द्वारा आवेशित किया जा रहा है। आवेशकारी धारा नियत है और इसका मान 0.15A है।
(a) धारिता एवं प्लेटों के बीच विभवान्तर परिवर्तन की दर का परिकलन कीजिए।
(b) प्लेटों के बीच विस्थापन धारा ज्ञात कीजिए।
(c) क्या किरखोफ का प्रथम नियम संधारित्र की प्रत्येक प्लेट पर लागू होता है? स्पष्ट कीजिए।

उत्तर:
संधारित्र की वृत्तीय प्लेट की त्रिज्या
r = 12 cm
= 12 × 10² m
प्लेटों के बीच की दूरी d = 5 cm
= 5 × 10² m
आवेशकारी धारा
I = 0.15 A
∴ प्लेट का क्षेत्रफल
A = πr²
A = π × (12 × 10²)²
= 144 x × 10^-4 m²
(a) समान्तर प्लेट संधारित्र के लिए
C = ∈A/d
मान रखने पर
= \(\frac{8.85 \times 10^{-12} \times 144 \pi \times 10^{-4}}{5 \times 10^{-2}}\)
= \(\frac{8.85 \times 144 \times 3.14 \times 10^{-14}}{5}\)
= 80.03 × 10^-13 F
= 8.01 × 10^-12F
= 8.01 pF
हम जानते हैं:
Q = CV
∴ dQ/dt = Cdv/dt
या
I = C dV/dt
या
dV/dt = I/C
मान रखने पर:
dV/dt = \(\frac{0.15}{8.01 \times 10^{-12}}\)
= 1.87 × 10¹⁰ V/s

(b) प्लेटों पर विस्थापन धारा = ID = ?
हमें ज्ञात है कि
ID = d/dt (∈0 Φ)
= \(\epsilon_0 \frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\)
जहाँ ΦE = लूप पर विद्युत अभिवाह है
= EA = q/∈0
∴ ID = ∈0d/dt (q/∈0)
= 0.15 A
अर्थात्
विस्थापन धारा = चालन धारा
(c) हाँ. संधारित्र की प्रत्येक प्लेट पर किरखोफ का पहला नियम सत्य है। धारा, चालन धारा और विस्थापन धारा के योग के बराबर है।

प्रश्न 8.2.
एक समान्तर प्लेट संधारित्र (चित्र) R = 6.0 cm त्रिज्या की दो वृत्ताकार प्लेटों से बना है और इसकी धारिता C = 100 pF है। संधारित्र को 230 V, 300 rad s^-1 की (कोणीय) आवृत्ति के किसी स्रोत से जोड़ा गया है।
(a) चालन धारा का rms मान क्या है?
(b) क्या चालन धारा विस्थापन धारा के बराबर है?
(c) प्लेटों के बीच अक्ष से 3.0 cm की दूरी पर स्थित बिन्दु पर B का आयाम ज्ञात कीजिए।
उत्तर:
दिया गया है:

R = 6.0cm = 6 x 10² m F
C = 100 pF = 100 x 10^-12
Vrms = 230 V
= 300 rad s^-1
(a) चालन धारा का rms मान= Irms = ?
हम जानते हैं
Irms = Vrms/XC
या
मान रखने पर
Irms = 230 x 300 × 100 x 10^-12
= 69 × ⁷
= 6.9 × 10^-6 A
Irms = 6.9 A

(b) हाँ, एक समान्तर संधारित्र के लिए सदैव I= ID चाहे I (d.c.) या a.c. (समय में दोलनी) हो जिसे निम्न प्रकार से सिद्ध किया जा सकता है
ID = ∈0 d/dt (ΦE)
∈0 d/dt (ΦE)
या
ID = ∈0 dE/dt
= ∈0 d/dt(Q/∈0)
∵E = σ/∈0 = Q/∈0A
या ID = ∈0A × 1/∈0A dQ/dt = dQ/dt = I

(c) हम जानते हैं B = μ/2π r/R² × ID
यदि
I = ID तब B = μ/2π r/R²I
यदि I = I0 = धारा का शीर्ष मान है, तब
B का आयाम = B का अधिकतम मान
B = μ/2π r/R² × I0 = μ/2π r/R² × √2 Irms
∵ Io = √2 Irms
यहाँ पर
Irms = 6.9 x 10⁶ A
r = प्लेटों के बीच अक्ष से बिन्दु की दूरी = 3.0 cm = 3 × 10² m
मान रखने पर B = \(\frac{4 \pi \times 10^{-7} \times 1.414 \times 6.9 \times 10^{-6} \times 3 \times 10^{-2}}{2 \times 3.14 \times\left(6 \times 10^{-2}\right)^2}\)
= 1.63 x 10^-11 T

प्रश्न 8.3.
10^-10m तरंगदैर्घ्य की X- किरणों, 6800 Å तरंगदैर्ध्य के प्रकाश तथा 500 m की रेडियो तरंगों के लिए किस भौतिक राशि का मान समान होगा?
उत्तर:
तीनों ही विद्युत चुम्बकीय तरंगें हैं। निर्वात में इनका वेग एक समान होगा तथा यह प्रकाश के वेग c = 3 x 10⁸ m/s मी./से. होगा।

प्रश्न 8.4.
एक समतल वैद्युतचुम्बकीय तरंग निर्वात में 2-अक्ष के अनुदिश चल रही है। इसके विद्युत तथा चुम्बकीय क्षेत्रों के सदिशों की दिशा के बारे में आप क्या कहेंगे? यदि तरंग की आवृत्ति 30 MHz हो, तो उसकी तरंगदैर्ध्य कितनी होगी?
उत्तर:
हम जानते हैं कि विद्युत चुम्बकीय तरंगें प्रकृति में अनुप्रस्थ होती हैं। यहाँ पर E है और Bxy तल में स्थित है और आपस में लम्बवत् है।
दिया है- तरंग की आवृत्ति
V = 30MHz
= 30 × 10⁶ Hz
तरंग का वेग = c = 3 x 10⁸ m/s
λ = ?
हम जानते हैं

अतः तरंगदैर्घ्य का मान = 10m

प्रश्न 8.5.
एक रेडियो 7.5 MHz से 12 MHz बैंड के किसी स्टेशन से समस्वरित हो सकता है। संगत तरंगदैर्ध्य बैंड क्या होगा?
उत्तर:
दिया गया है – आवृत्ति v1 = 7.5 MHZ
= 7.5 × 10⁶ Hz
V2 = 12 MHz
= 12 × 10⁶ Hz
तरंग का वेग c = 3 x 10⁸ m/s
माना संगत तरंगदैर्ध्य λ1 व λ2 है।
∴ λ1 = c/v1 = \(\frac{3 \times 10^8}{7.5 \times 10^6}\) =40 m
इसी तरह से
λ2 = c/v2 = \(\frac{3 \times 10^8}{12 \times 10^6}\) = 25cm
अतः तरंगदैर्घ्य बैंड स्टेशन 25m से 40m बैंड में है।

प्रश्न 8.6.
एक आवेशित कण अपनी माध्य साम्यावस्था के दोनों ओर 10⁹ Hz आवृत्ति से दोलन करता है। दोलक द्वारा जनित वैद्युत चुम्बकीय तरंगों की आवृत्ति कितनी है?
उत्तर:
हम जानते हैं कि एक त्वरित कण वैद्युत चुम्बकीय तरंगें उत्सर्जित करता है। एक निश्चित कम्पन आवृत्ति से कम्पित आवेशित कण (त्वरित आवेश) कम्पनी विद्युत क्षेत्र उत्पन्न करता है जो कम्पनशील चुम्बकीय क्षेत्र उत्पन्न करता है। यह दोनों कम्पनशील क्षेत्र एक-दूसरे को उत्पन्न करते हैं। वैद्युत चुम्बकीय तरंगों की आवृत्ति कम्पनशील आवेशित कण की आवृत्ति के बराबर है जिसका मान 10⁹ Hz है।

प्रश्न 8.7.
निर्वात में एक आवर्त वैद्युत चुम्बकीय तरंग के चुम्बकीय क्षेत्र वाले भाग का आयाम Bg = 510 nT है विद्युत क्षेत्र वाले भाग का आयाम क्या है?
उत्तर:
दिया गया है:
Bo = 510nT निर्वात में चुम्बकीय क्षेत्र वाले भाग का आयाम
= 510 × 10⁹ T
निर्वात में तरंग का वेग = c = 3 x 10⁸ m/s
निर्वात में तरंग के विद्युत क्षेत्र वाले भाग का आयाम = E0 = ?
हम जानते हैं कि वैद्युत चुम्बकीय तरंगों के लिए
c = E0/B0
या
मान रखने पर
Eg c= Bo
Eg = cBo
Eg = 3 x 10⁸ x 510 x 10^-9
= 153 V/m

प्रश्न 8.8.
कल्पना कीजिए कि एक वैद्युतचुम्बकीय तरंग के विद्युत क्षेत्र का आयाम E = 120 N/C है तथा इसकी आवृत्ति v = 50.0 MHz है। (a) Boo, k तथा 2 ज्ञात कीजिए (b) E तथा B के लिए व्यंजक प्राप्त कीजिए।
उत्तर:
दिया गया है:
विद्युत क्षेत्र का आयाम
= Eg = 120N/C
आवृत्ति v = 500MHz
= 50 × 10⁶ Hz
तरंग का वेग = c = 3 x 10⁸ m/s

(a) B0. ω k तथा λ का मान
(i) B0 का मान
c = E0/B0
∴ B0 = E0/c
मान रखने पर
B0 = \(\frac{120}{3 \times 10^8}\)
B0 = 4 x 10^-7 T
= 400 x 10⁹ T
= 400 nT

(ii) का मान
ω = 2πv
= 2π x 50 x 10⁶
= 3.14 x 10⁸ रेडियन / से.

(iii) k का मान
k = 2π/λ = 2πv/vλ = 2πv/c = ω/c
k = \(\frac{3.14 \times 10^8}{3 \times 10^8}\)
= 1.05 रेडियन / मी.

(iv) λ का मान
c = vλ
λ = c/v = \(\frac{3 \times 10^8}{50 \times 10^6}\) = 300/50m
λ = 6m

(b) माना वैद्युत चुम्बकीय तरंग x अक्ष की ओर गति करती है और है E और B y-अक्ष तथा 2-अक्ष की तरफ है। तब
E = Eosin(kx – ωt)j
= 120sin(1.05x – 3.14 x 10⁸)j N / C
Bz = B0sin (kx – ωt)K
= 4 × 10⁷ sin (1.05x – 3.14 x 10⁸)t) KT

प्रश्न 8.9.
वैद्युतचुम्बकीय स्पेक्ट्रम के विभिन्न भागों की पारिभाषिकी पाठ्यपुस्तक में दी गई है। सूत्र E = hv ( विकिरण के एक क्वांटम की ऊर्जा के लिए फोटॉन) का उपयोग कीजिए तथा em वर्णक्रम के विभिन्न भागों के लिए eV के मात्रक में फोटॉन की ऊर्जा निकालिए। फोटॉन ऊर्जा के जो विभिन्न परिमाण आप पाते हैं वे वैद्युतचुम्बकीय विकिरण के स्रोतों से किस प्रकार संबंधित हैं?
उत्तर:
सूत्र E = hv
उपर्युक्त सूत्र से फोटॉन की ऊर्जा ज्ञात करते हैं।
या
E = hc/λ
∴ आवृत्ति v = c/λ
फोटॉन ऊर्जा (λ = 1m के लिए)
E = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{1 \times 1.6 \times 10^{-19}} \mathrm{eV}\)
E = 1.243 x 10^-6 ev
λ के अन्य मानों के लिए
E = \(\frac{1.243 \times 10^{-6}}{\lambda} \mathrm{eV}\)

(a) γ-किरणों के लिए
λ → 10^-12 m
∴ E = \(\frac{1.243 \times 10^{-6}}{10^{-12}} \mathrm{eV}\)
E= 1.243 × 10^-6
= 1.243 Mev

(b) X-किरणों के लिए λ → 10^-9 m
∴ E = \(\frac{1.243 \times 10^{-6}}{10^{-9}} \mathrm{eV}\)
eV = 1.243 Kev

(c) दृश्य तरंगों के लिए
λ = 0.5 pum(5 x 10^-7 m )
∴ E = \(\frac{1.243 \times 10^{-6}}{5 \times 10^{-7}}\)
= 2.48 ev

(d) सूक्ष्म तरंगों के लिए λ → 1 cm = (10^-2m)
∴ E = \(\frac{1.243 \times 10^{-6}}{10^{-2}}\)
= 1.243 × 10^-4 ev

(e) रेडियो तरंगों के लिए λ → 100
∴ E = 1.243 x 10^-8 ev
y – किरणों का उत्सर्जन नाभिकीय अभिक्रियाओं में होता है अतः नाभिकीय ऊर्जा स्तरों में अन्तराल 1 MeV की कोटि का होता है। X-किरणें व दृश्य किरणें परमाणुओं में इलेक्ट्रॉनों के विभिन्न स्तरों में संक्रमण से उत्पन्न होती हैं। X किरणों के लिए संक्रमण भारी परमाणुओं के बाह्य ऊर्जा स्तरों से आन्तरिक ऊर्जा स्तरों में होता है जिनमें ऊर्जा अन्तराल 1 keV की कोटि का होता है। दृश्य तरंगों के लिए संक्रमण 2.5 eV ऊर्जा अन्तराल के स्तरों के मध्य होता है।

प्रश्न 8.10.
एक समतल em तरंग में विद्युत क्षेत्र 2.0 x 10¹⁰ Hz आवृत्ति तथा 48 Vm 1 आयाम से ज्यावक्रीय रूप में दोलन करता है।
(a) तरंग की तरंगदैर्ध्य कितनी है?
(b) दोलनशील चुम्बकीय क्षेत्र का आयाम क्या है ?
(c) यह दर्शाइए कि E क्षेत्र का औसत ऊर्जा घनत्व, B क्षेत्र के औसत ऊर्जा घनत्व के बराबर है।
[c = 3 x 10⁸ m s^-1]
उत्तर:
दिया गया है:
आवृत्ति v = 20 x 10¹⁰ Hz
E0 = 48V/m
λ = ?
Bo = ? और
c = 3 x 10⁸ m/s
(a) तरंगदैर्ध्य
λ = c/v
= \(\frac{3 \times 10^8}{2 \times 10^{10}}\)
= 1.5 x 10^-2m

(b)
Bo = E0/c
मान रखने पर Bo = \(\frac{48}{3 \times 10^8}T\)
B0 = 16 × 10⁸ T = 1.6 x 10⁷ T

(c) वैद्युत क्षेत्र में ऊर्जा घनत्व UE = 1/2∈0E²
चुम्बकीय क्षेत्र में ऊर्जा घनत्व UB = 1/2μ0 B²
ऊर्जा घनत्व UE = 1⁄2 ∈0 (CB)²
UE = 1⁄2∈0c²B² = c²(1/2∈0B²)
लेकिन
c = \(\frac{1}{\sqrt{\mu_0 \epsilon_0}}\)
c² = 1/μ0∈0
∴ UE = 1/μ0∈0 ((1/2∈0B²)
= 1/2μ0B² = UB
∴ UE = UB
अतः E क्षेत्र का औसत ऊर्जा घनत्व B क्षेत्र के औसत ऊर्जा घनत्व के बराबर है।

अतिरिक्त अभ्यास प्रश्न (NCERT):

प्रश्न 8.11.
कल्पना कीजिए कि निर्वात में एक वैद्युतचुम्बकीय तरंग का विद्युत क्षेत्र
E = { ( 3.1 N/C) cos [ ( 1.8rad/m) y + (5.4 x 10⁶ rad/s) t]}} i है।
(a) तरंग संचरण की दिशा क्या है?
(b) तरंगदैर्घ्य λ कितनी है?
(c) आवृत्ति v कितनी है?
(d) तरंग के चुम्बकीय क्षेत्र सदिश का आयाम कितना है?
(e) तरंग के चुम्बकीय क्षेत्र के लिए व्यंजक लिखिए।
उत्तर:
(a) निर्वात में एक वैद्युत चुम्बकीय तरंग का विद्युत क्षेत्र
E = {(3.1 N/C) cos [ ( 1.8 rad/m) y + (5.4 x 10⁶ rad/s) × t]} i
E के लिए यह व्यंजक है जिसका प्रकार
E = E0 cos (ky + ωt)i प्रकार का है।
जहाँ वैद्युत क्षेत्र i के अनुदिश है अर्थात् x अक्ष के अनुदिश है। E की समीकरण में cos कारक के अन्दर (ky + ωt) का प्रकार है
जो कि तरंग संचरण, ऋणात्मक y-अक्ष के अनुदिश प्रदर्शित करता है।
अर्थात् – j

(b) É = E0 cos (ky + ω t) i से दिए गए समीकरण की तुलना करने पर
E0 = 3.1 N/C, k = 1.8rad/m
ω = 5.4 × 10⁶ rad/s
k = 2π/λ , λ = 2π/k
= 2 x 3314/18
λ = 3.5 m

(c) आवृत्ति v = ω/2π = \(\frac{5.4 \times 10^6}{2 \times 3.14}\)Hz
= 859.87 kHz = 860 kHz

(d) B0 = E0/C = \(\frac{3.1}{3 \times 10^8}\) = 1.03 × 10T

(e) B = Bo cos (ky + ωt) k
B = 10.3 × 10⁹ cos (1.8y + 54 x 10⁶t) T

प्रश्न 8.12.
100 W विद्युत बल्ब की शक्ति का लगभग 5% दृश्य विकिरण में बदल जाता है।
(a) बल्ब से 1m की दूरी पर,
(b) 10m की दूरी पर दृश्य विकिरण की औसत तीव्रता कितनी है?
यह मानिए कि विकिरण समदैशिकतः उत्सर्जित होता है और परावर्तन की उपेक्षा कीजिए।
उत्तर:
विद्युत शक्ति दृश्य विकिरण में बदलती है
शक्ति = P = 5/100 × 100 W = 5W

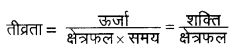
तीव्रता = p/4πr²
(a) तीव्रता = \(\frac{5}{4 \times 3.14 \times 1 \times 1}\)
= 0.4Wm^-2
(b) तीव्रता = \(\frac{5}{4 \times 3.14 \times 10 \times 10}\) Wm^-2
= 0.004 Wm^-2

प्रश्न 8. 13.
em वर्णक्रम के विभिन्न भागों के लिए लाक्षणिक ताप परिसरों को ज्ञात करने के लिए T = 0.29cm K सूत्र का उपयोग कीजिए जो संख्याएँ आपको मिलती हैं, वे क्या बताती हैं? हल- हम जानते हैं कि प्रत्येक वस्तु किसी क्षेत्र में T ताप पर सभी तरंगदैर्घ्य के विकिरण उत्सर्जित करती है। इस प्रकार से कहा जा सकता है कि यह तरंगदैयों का सतत स्पेक्ट्रम उत्पन्न करती है।
हल:
हम जानते हैं कि प्रत्येक वस्तु किसी क्षेत्र में T ताप पर सभी तरंगदैर्घ्य के विकिरण उत्सर्जित करती है। इस प्रकार से कहा जा सकता है कि यह तरंगदैर्घ्यों का सतत स्पेक्ट्रम उत्पन्न करती है। एक कृष्णिका के लिए तीन विस्थापन नियमानुसार दिए गए ताप T विकिरण की अधिकतम तीव्रता के संगत तरंगदैर्घ्य
एक कृष्णिका के लिए तीन विस्थापन नियमानुसार दिए गए ताप T विकिरण की अधिकतम तीव्रता के संगत तरंगदैर्ध्य
λm T = 0.29 cm K से दी जाती है।
या
T = 0.29/λ
यहाँ पर λm सेमी. में है।
λm = 1 μm = 10^-6 m = 10^-4 cm के लिए T
T = 0.29/10^-4 2900K द्वारा दिया जाता है।
इसी प्रकार से दूसरी तरंगदैर्घ्य के लिए ताप को ज्ञात कर सकते हैं।
माना
λ = 5000 Å = 5000 × 10^-10 m
= 5 x 10^-5 cm तरंगदैर्घ्य के लिए
T = \(\frac{0.29}{5 \times 10^{-5}}\) = 29/5 × 1000
= 5800 K होना चाहिए।
नोट- पिण्ड कम ताप पर भी यह तरंगदैर्ध्य उत्पन्न करेगा परन्तु अधिकतम तीव्रता की नहीं।

प्रश्न 8. 14.
वैद्युतचुम्बकीय विकिरण से सम्बन्धित नीचे कुछ प्रसिद्ध अंक, भौतिकी में किसी अन्य प्रसंग में वैद्युतचुम्बकीय दिए गए हैं। स्पेक्ट्रम के उस भाग का उल्लेख कीजिए जिससे इनमें से प्रत्येक सम्बन्धित है।
(a) 21 cm (अंतरातारकीय आकाश में परमाण्वीय हाइड्रोजन द्वारा उत्सर्जित तरंगदैर्ध्य )
(b) 1057 MHz (लैंब – विचलन नाम से प्रसिद्ध, हाइड्रोजन में, पास जाने वाले दो समीपस्थ ऊर्जा स्तरों से उत्पन्न विकिरण की आवृत्ति)
(c) 2.7K [ सम्पूर्ण अन्तरिक्ष को भरने वाले समदैशिक विकिरण से सम्बन्धित ताप ऐसा विचार जो विश्व में बड़े धमाके ‘बिग बैंग’ के उद्भव का अवशेष माना जाता है ]।
(d) 5890 – 5896 À (सोडियम की द्विक् रेखाएँ)
(e) 14.4 kev [₅Fe नाभिक के एक विशिष्ट संक्रमण की ऊर्जा जो प्रसिद्ध उच्च विभेदन की स्पेक्ट्रमी विधि से संबंधित है ( मॉसबौर स्पेक्ट्रोस्कॉपी)]।
उत्तर:
(a) दिया गया है:
λ = 21 cm
वैद्युत चुम्बकीय तरंगों का यह तरंगदैर्घ्य रेडियो तरंगों के संगत है (जो कि कम तरंगदैर्घ्य अथवा उच्च आवृत्ति सिरे की ओर है ।) (b) दिया गया है
आवृत्ति v = 1057 MHz
v = 1057 × 10⁶ Hz
अतः संगत तरंगदैर्ध्य
λ = c/v = \(\frac{3 \times 10^{10} \mathrm{~cm} / \mathrm{s}}{1057 \times 10^6 \mathrm{~Hz}}\)
λ = 28.4cm
अतः संगत तरंगदैर्घ्य λ = 28.4 cm से दी जाती है।
(c) T = 2.7 K
∴ वीन के विस्थापन के नियम
λmT = 0.29cm K
λm = 0.29/T = 0.29/2.7
λm = 0.11 cm.
यह क्षेत्र वैद्युत चुम्बकीय स्पेक्ट्रम की सूक्ष्म तरंग के संगत है।

(d) दिया गया है λ = 5890A – 5896 À जो सोडियम प्रकाश की द्विक् रेखाएँ हैं और यह दृश्य विकिरण (पीला) प्रकाश क्षेत्र में है।

(e) E = 14.4 Kev
= 14.4 × 10³ ev
= 14.4 × 10³ × 1.6 x 10^-19J
1 eV = 1.6 × 10^-19 J
हम जानते हैं:
E = hv
आवृत्ति v = E/h
मान रखने पर V = \(\frac{14.4 \times 1.6 \times 10^3 \times 10^{-19}}{6.62 \times 10^{-34}}\)
v = 3 x 10¹⁷ Hz
= 3 x 10¹¹ MHz
यह आवृत्ति जो कि X – किरणों की कोटि की है (अथवा सॉफ्ट Y-किरण) क्षेत्र

प्रश्न 8. 15.
निम्नलिखित प्रश्नों का उत्तर दीजिए:
(a) लम्बी दूरी के रेडियो प्रेषित्र लघु-तरंग बैंड का उपयोग करते हैं। क्यों?
(b) लम्बी दूरी के TV प्रेषण के लिए उपग्रहों का उपयोग आवश्यक है क्यों?
(c) प्रकाशीय तथा रेडियो दूरदर्शी पृथ्वी पर निर्मित किए जाते हैं किन्तु X- किरण खगोलविज्ञान का अध्ययन पृथ्वी का परिभ्रमण कर रहे उपग्रहों द्वारा ही संभव है। क्यों?
(d) समतापमंडल के ऊपरी छोर पर छोटी-सी ओजोन की परत मानव जीवन के लिए निर्णायक है। क्यों?
(e) यदि पृथ्वी पर वायुमंडल नहीं होता तो उसके धरातल का औसत ताप वर्तमान ताप से अधिक होता या कम?
(f) कुछ वैज्ञानिकों ने भविष्यवाणी की है कि पृथ्वी पर नाभिकीय विश्व युद्ध के बाद ‘प्रचण्ड नाभिकीय शीतकाल’ होगा जिसका पृथ्वी के जीवों पर विध्वंसकारी प्रभाव पड़ेगा। इस भविष्यवाणी का क्या आधार होगा ?
उत्तर:
(a) लम्बी दूरी के रेडियो प्रेषित्र लघु तरंग बैंड का उपयोग इसलिए करते हैं चूँकि आयनमण्डल इन बैंडों की तरंगें परावर्तित करता है।
(b) लम्बी दूरी के TV प्रेषण के लिए उपग्रहों का उपयोग आवश्यक है क्योंकि दूरदर्शन संकेत आयन मण्डल द्वारा समुचित रूप से परावर्तित नहीं होते हैं, अतः परावर्तन उपग्रहों द्वारा किया जाता है।
(c) प्रकाशीय तथा रेडियो दूरदर्शी पृथ्वी पर निर्मित किए जाते हैं, किन्तु X – किरण खगोल विज्ञान का अध्ययन पृथ्वी का परिभ्रमण कर रहे उपग्रहों द्वारा ही संभव है क्योंकि वायुमंडल X-किरणों को अवशोषित करता है जबकि दृश्य और रेडियो तरंगें इन्हें बेध सकती हैं।
(d) समतापमण्डल के ऊपरी छोर पर छोटी-सी ओजोन की परत मानव जीवन के लिए निर्णायक है क्योंकि यह सूर्य से उत्सर्जित पराबैंगनी विकिरणों को अवशोषित कर लेती है और पृथ्वी के पृष्ठ पर पहुँचने से रोकती है और जीवन को नष्ट होने से बचाती है।