HBSE 12th Class Physics Solutions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्र

Haryana State Board HBSE 12th Class Physics Solutions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्र Textbook Exercise Questions and Answers.

Haryana Board 12th Class Physics Solutions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्र

प्रश्न 9.1.
2.5 cm साइज की कोई छोटी मोमबत्ती 36 cm वक्रता त्रिज्या के किसी अवतल दर्पण से 27 cm दूरी पर रखी है। दर्पण से किसी परदे को कितनी दूरी पर रखा जाए कि उसका सुस्पष्ट प्रतिबिंब परदे पर बने वर्णन कीजिए। यदि मोमबत्ती को को किस ओर हटाना पड़ेगा?
उत्तर:
दिया गया है
प्रतिबिंब की प्रकृति और साइज का दर्पण की ओर ले जाएँ, तो परदे
h= वस्तु का आकार = 2.5 cm
अवतल दर्पण से वस्तु की दूरी u = -27cm
अवतल दर्पण से वक्रता त्रिज्या = R = -36 cm
∴ अवतल दर्पण की फोकस दूरी f = 1⁄2R
=> R = -36/2 = -18cm
(i) दर्पण से प्रतिबिम्ब की दूरी = v = ?
सूत्र 1/u + 1/v = 1/f का उपयोग करने पर
1/v = 1/f – 1/u
1/v = 1/-18 – 1/-27
= -1/18 + 1/27 = -3+2/54
1/v = -1/54
∴ v = -54 cm
ऋण चिन्ह दर्शाता है कि प्रतिबिम्ब दर्पण के सामने बना है और उसी तरफ बना है जिस तरफ वस्तु रखी है। अतः पर्दा दर्पण के सामने 54 cm की दूरी पर रखा जाना चाहिए।
(ii) प्रतिबिम्ब की प्रकृति और आकार ज्ञात करना है।
m =
= -v/u का उपयोग करने पर
या
\(\frac{h^{\prime}}{2.5}\)=\(-\left(\frac{-54}{-27}\right)\) =\(\frac{-2}{1}\)
h’= – 2.5 x 2 = – 5 cm
इससे स्पष्ट होता है कि प्रतिबिम्ब वास्तविक, उल्टा व बड़ा और आवर्धित है।
(iii) यदि मोमबत्ती को दर्पण के पास लाया जाये तब पर्दे को दूर और अधिक दूर चलाना होगा अर्थात् पर्दा अनन्त पर रखना होगा। परन्तु जब मोमबत्ती की दूरी, दर्पण की फोकस दूरी से कम हो जैसे u → f, v →∞, u < f के लिए, उस स्थिति में प्रतिबिम्ब काल्पनिक (आभासी) होगा।

प्रश्न 9.2.
4.5 cm साइज की कोई सुई 15 cm फोकस दूरी के किसी उत्तल दर्पण से 12cm दूर रखी है। प्रतिबिंब की स्थिति तथा आवर्धन लिखिए क्या होता है जब सुई को दर्पण से दूर ले जाते हैं? वर्णन कीजिए।
उत्तर:
दिया गया है:
उत्तल दर्पण से वस्तु की दूरी (नीडिल) u = – 12 cm
उत्तल दर्पण की फोकस दूरी f = + 15 cm
वस्तु का आकार h = 4.5 cm
प्रतिबिम्ब की स्थिति = V = ?
सूत्र
\(\frac{1}{\mathrm{f}}\)=\(\frac{1}{\mathrm{u}}\) + \(\frac{1}{\mathrm{v}}\) का उपयोग करने पर
या
\(\frac{1}{v}\)= \(\frac{1}{f}\) – \(\frac{1}{u}\)
=\(\frac{1}{15}\) – \(\left(-\frac{1}{12}\right)\)
=\(\frac{1}{15}\) + \(\frac{1}{12}\) = \(\frac{4+5}{60}\)
\(\frac{1}{v}\) = \(\frac{9}{60}\) = \(\frac{3}{20}\)
V = 20/3cm = 6.67cm = 6.7.cm
v का मान यहाँ पर धनात्मक है। इससे ज्ञात होता है कि प्रतिबिम्ब दर्पण के पीछे बना है।
और प्रतिबिम्ब आभासी छोटा व सीधा बनेगा।
\(\mathrm{m}\) = \(-\frac{\mathrm{v}}{\mathrm{u}}\) = \(\frac{\mathrm{h}^{\prime}}{\mathrm{h}}\) का उपयोग करने पर
∴ \(h^{\prime}\) = \(\left(-\frac{v}{u}\right) \times h\)
अब आवर्धन \(\mathrm{h}^{\prime}\) = \(\left(-\frac{20 / 3}{-12}\right) \times 4.5\)

मान रखने पर = \(\frac{20}{3}\) \(\times\) \( \frac{1}{12}\) \(\times\)  \(\frac{9}{2}\)= \(+2.5 \mathrm{~cm}\)
= \(\frac{20}{3}\) \(\times\) \(\frac{1}{12}\) \(\times\) \( \frac{9}{2}\) = \(+2.5 \mathrm{~cm}\)
अतः प्रतिबिम्ब की साइज h’ = + 2.5 cm
आवर्धन
\(\mathrm{m}\) = \(\frac{\mathrm{h}^{\prime}}{\mathrm{h}}\) = \(\frac{2.5}{4.5}\) = \(\frac{5}{9}\)
जब सुई को दर्पण से दूर ले जाते हैं तब प्रतिबिम्ब फोकस की ओर पास आता है, लेकिन फोकस तक और आकार में छोटा और छोटा होता जाता है। अर्थात् जैसे u → ∞ v → f (परन्तु फोकस से आगे कभी नहीं बढ़ता) जबकि m → 0

प्रश्न 9.3.
कोई टैंक 12.5 cm ऊँचाई तक जल से भरा है। किसी सूक्ष्मदर्शी द्वारा बीकर की तली पर पड़ी किसी सुई की आभासी गहराई 9.4 cm मापी जाती है। जल का अपवर्तनांक क्या है? बीकर में उसी ऊँचाई तक जल के स्थान पर किसी 1.63 अपवर्तनांक के अन्य द्रव से प्रतिस्थापन करने पर सुई को पुनः फोकसित करने के लिए सूक्ष्मदर्शी को कितना ऊपर / नीचे ले जाना होगा?
उत्तर:
स्थिति I. जब टैंक पानी से भरा हो:
वास्तविक गहराई = 12.5 cm
आभासी गहराई = 9.4 cm
पानी का अपवर्तनांक= n = ?

= \(\frac{12.5}{9.4}\) = \(1.33\)
स्थिति II. जब टैंक को द्रव से भरा जाता है:
द्रव का अपवर्तनांक= n = 1.63
वास्तविक गहराई = 12.5 cm
आभासी गहराई = ?
∴ द्रव का अपवर्तनांक = 1.63

∴ आभासी गहराई = \(\frac{12.5}{1.63}\) = 7.67cm
अतः वह दूरी जिससे सूक्ष्मदर्शी को ऊपर चलाना है,
= 9.4 – 7.67
= 1.73 cm
= 1.70 cm

प्रश्न 9.4.
चित्र (a) तथा (b) में किसी आपतित किरण का अपवर्तन दर्शाया गया है जो वायु में क्रमशः काँच वायु तथा जल-वायु अंतरापृष्ठ के अभिलंब से 60° का कोण बनाती है। उस आपतित किरण का अपवर्तन कोण ज्ञात कीजिए, जो जल में जल-काँच अंतरापृष्ठ के अभिलंब से 45° का कोण बनाती है [ चित्र (c ) ] |

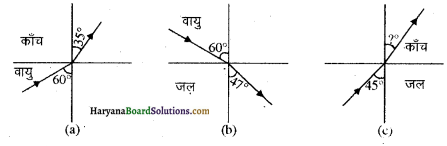
उत्तर:
चित्र (a) से:
आपतन कोण = i = 60°
अपवर्तन कोण= r = 35°
ang = वायु की अपेक्षा काँच का अपवर्तनांक = ?
सम्बन्ध
\({ }_{\mathrm{a}} \mathrm{n}_{\mathrm{g}}\)= \(\frac{\sin i}{\sin r}\) = \(\frac{\sin 60^{\circ}}{\sin 35^{\circ}}\)
\(\frac{0.8660}{0.5736}\) = \(1.51\)
चित्र (b) से:
हम जानते हैं:
i = 60°, r = 47°
anw = वायु की अपेक्षा पानी का अपवर्तनांक = ?
हम जानते हैं-

चित्र (c) से:
आपतन कोण = i = 45°
अपवर्तन कोण = r = ?
wng = पानी की अपेक्षा काँच का अपवर्तनांक
हम जानते हैं:

प्रश्न 9.5.
जल से भरे 80 cm गहराई के किसी टैंक की तली पर कोई छोटा बल्ब रखा गया है। जल के पृष्ठ का वह क्षेत्र ज्ञात कीजिए जिससे बल्ब का प्रकाश निर्गत हो सकता है जल का अपवर्तनांक 1.33 है। (बल्ब को बिंदु प्रकाश स्रोत मानिए । )
उत्तर:
माना प्रकाश स्रोत 0 पानी के पृष्ठ से 80 cm नीचे है। अर्थात् चित्र
\(\mathrm{OA}\) = \(80 \mathrm{~cm}\) = \(\frac{80}{100} \mathrm{~m}\)
anw = 1.33
O से उत्सर्जित प्रकाश किरण केवल वायु में अपवर्तित होती है, यदि आपतन कोण क्रान्तिक Ic से छोटा है, तब प्रकाश पानी के पृष्ठ के साथ वायु में अपवर्तित नहीं होगा, परन्तु यह वायु-पानी के अन्तरापृष्ठ पर संस्पर्श करेगा। इस प्रकार प्रकाश शंकु के शिरोबिन्दु कोण, जो 2Ic है, से आता प्रतीत होगा। यदि पानी वायु अन्तरापृष्ठ पर आपतन कोण Ic से अधिक है, तब प्रकाश किरण पूर्ण आन्तरिक परावर्तित होगी।

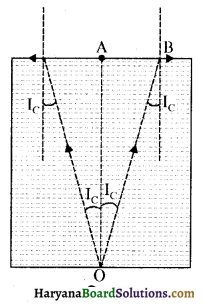
हम जानते हैं:
\(\sin \mathbf{I}_{\mathrm{C}}\) = \( \frac{1}{{ }_a n_w} \)
⇒ \(\sin \mathbf{I}_{\mathrm{C}}\) = \(\frac{1}{{ }_a n_w}\)
\(\sin \mathbf{I}_{\mathrm{C}}\) = \(\sin ^{-1}\left(\frac{1}{1.33}\right)\) =\(\sin ^{-1}(0.75)\)
Ic = 48.6°
अब
tan Ic = \(\frac{\mathrm{AB}}{\mathrm{OA}}\)
या
AB = OA tan Ic
\(\frac{80}{100}\) \(\times\) \(\tan 48.6^{\circ}\) = \(\frac{80}{100}\) \(\times\) 1.1345
= 0.907m = 90.7 cm
∴ पानी के उस पृष्ठ का क्षेत्रफल जिसमें से प्रकाश निकलेगा
= πr² = 3.14 x (0.907)²
= 3.14 x 0.823
= 2.584m² = 2.6m²

प्रश्न 9.6.
कोई प्रिज्म अज्ञात अपवर्तनांक के कांच का बना है। कोई समांतर प्रकाश-पुंज इस प्रिज्म के किसी फलक पर आपतित होता है। प्रिज्म का न्यूनतम विचलन कोण 40° मापा गया। प्रिज्म के पदार्थ का अपवर्तनांक क्या है? प्रिज्म का अपवर्तन कोण 60° है। यदि प्रिज्म को जल (अपवर्तनांक 1.33) में रख दिया जाए तो प्रकाश के समांतर पुंज के लिए नए न्यूनतम विचलन कोण का परिकलन कीजिए।
उत्तर:
दिया गया है:

प्रश्न 9.7.
अपवर्तनांक 1.55 के काँच से दोनों फलकों की समान वक्रता त्रिज्या के उभयोत्तल लेन्स निर्मित करने हैं। यदि 20 cm फोकस दूरी के लेन्स निर्मित करने हैं तो अपेक्षित वक्रता त्रिज्या क्या होगी?
उत्तर:
दिया गया है:
n = 1.55, R1 = R और R2 = R (उभयोत्तल के लिए)
f = + 20 cm
हम जानते हैं:
\( \frac{1}{f}\) = \( (\mathrm{n}-1)\) \(\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
⇒ \( \frac{1}{20}\) = \( (\mathrm{5}-1)\) \( \left(\frac{1}{R}+\frac{1}{R}\right)\)
⇒ \(\frac{1}{20}\) = \(0.55\) × \( \frac{2}{R}\)
⇒ R = 0.55 x 2 x 20
= 0.55 x 40
∴ R = 22 cm
∴ अपेक्षित वक्रता त्रिज्या R = 22cm

प्रश्न 9.8.
कोई प्रकाश-पुंज किसी बिंदु P पर अभिसरित होता है। कोई लेन्स इस अभिसारी पुंज के पथ में बिंदु P से 12 cm दूर रखा जाता है। यदि यह (a) 20 cm फोकस दूरी का उत्तल लेन्स है, (b) 16 cm फोकस दूरी का अवतल लेन्स है, तो प्रकाश-पुंज किस बिंदु पर अभिसरित होगा?
उत्तर:
इस समस्या में लेन्स के RHS की ओर बिन्दु एक काल्पनिक वस्तु की तरह कार्य करता है।
u = + 12 cm, v = ?
(a) उत्तल लेन्स के लिए:
f = + 20 cm

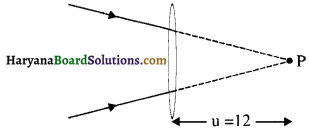
सूत्र \(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{v}}\) – \(\frac{1}{\mathrm{u}}\) का उपयोग करने पर
या
\(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\) + \(\frac{1}{\mathrm{u}}\)
मान रखने पर
\(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{20}}\) + \(\frac{1}{\mathrm{12}}\) = \(\frac{3+5}{60}\)
⇒ \(\frac{1}{\mathrm{v}}\) = \(\frac{8}{\mathrm{60}}\) = \(\frac{2}{\mathrm{15}}\)
या V = 15/2
= 7.5 cm

प्रतिबिम्ब वास्तविक है और लेन्स से R.HS की तरफ 7.5 cm पर स्थित है।
(b) अवतल लेन्स के लिए:
f= – 16 cm, u = + 12 cm
V = ?

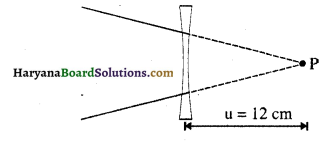
सूत्र \(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{v}}\) – \(\frac{1}{\mathrm{u}}\) का उपयोग करके,
हम \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\) + \(\frac{1}{\mathrm{u}}\)
या \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{16}}\) + \(\frac{1}{\mathrm{12}}\) = \(\frac{-3+4}{48}\)
या \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{48}}\)
प्रतिबिम्ब वास्तविक बनेगा जो कि लेन्स के दाहिनी तरफ 48 cm दूरी पर बनेगा।

प्रश्न 9.9.
3.0 cm ऊँची कोई बिंब 21 cm फोकस दूरी के अवतल लेन्स के सामने 14 cm दूरी पर रखी है लेन्स द्वारा निर्मित प्रतिबिंब का वर्णन कीजिए क्या होता है जब बिंब लेन्स से दूर हटती जाती है?
उत्तर:
दिया गया है:
वस्तु का आकार = h = 3.0cm
अवतल लेन्स वस्तु की दूरी = u = – 14 cm
अवतल लेन्स की फोकस दूरी = f =
प्रतिबिम्ब की दूरी = ?
प्रतिबिम्ब का आकार = h’ = ?
(i) सम्बन्ध = का उपयोग करने पर

प्रतिबिम्ब काल्पनिक और सीधा बनेगा और लेन्स से 8.4 cm की दूरी पर वस्तु की तरफ ही बनेगा।
हम जानते हैं:
आवर्धन
लेकिन

अतः प्रतिबिम्ब आकार में छोटा आभासी व सीधा बनेगा।

(ii) जब u → ∞ तब v = f लेकिन f से आगे नहीं जाता जबकि
m = v/u = 0
जब बिम्ब (वस्तु) लेन्स से दूर हटता है।
माना u = f = -21 cm
तब \(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{v}}\) – \(\frac{1}{\mathrm{u}}\)
या \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\) + \(\frac{1}{\mathrm{u}}\)
\(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{21}}\) – \(\frac{1}{\mathrm{21}}\) = \(\frac{-2}{\mathrm{21}}\)
तब v = \(\frac{-21}{\mathrm{2}}\) = -10.5 cm
परन्तु अनन्त पर नहीं बनेगा।

प्रश्न 9.10.
किसी 30 cm फोकस दूरी के उत्तल लेन्स के संपर्क में रखे 20 cm फोकस दूरी के अवतल लेन्स के संयोजन से बने संयुक्त लेन्स (निकाय) की फोकस दूरी क्या है? यह तंत्र अभिसारी लेन्स है अथवा अपसारी? लेन्सों की मोटाई की उपेक्षा कीजिए।
उत्तर:
दिया गया है:
उत्तल लेन्स की फोकस दूरी = f = + 30 cm
अवतल लेन्स की फोकस दूरी = f2 = – 20cm
माना दोनों लेन्सों के संयोजन की फोकस दूरी = f = ?
हम जानते हैं:
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{f1}}\) + \(\frac{1}{\mathrm{f2}}\)
= \(\frac{1}{\mathrm{30}}\) + \(\frac{1}{\mathrm{-20}}\)
= \(\frac{1}{\mathrm{30}}\) – \(\frac{1}{\mathrm{20}}\) = \(\frac{2-3}{60}\)
\(\frac{1}{\mathrm{f}}\) = \(\frac{-1}{\mathrm{60}}\)
या
= – 60 cm
चूँकि दोनों लेन्सों के संयोजन की फोकस दूरी ऋणात्मक है। अतः संयोजन एक अपसारी लेन्स की तरह व्यवहार करता है अर्थात् अवतल लेन्स की तरह व्यवहार करता है।

प्रश्न 9.11.
किसी संयुक्त सूक्ष्मदर्शी में 2.0cm फोकस दूरी का अभिदृश्यक लेन्स तथा 6.25 cm फोकस दूरी का नेत्रिका लेन्स एक-दूसरे से 15 cm दूरी पर लगे हैं। किसी बिंब को अभिदृश्यक से कितनी दूरी पर रखा जाए कि अंतिम प्रतिबिंब (a) स्पष्ट दर्शन की अल्पतम दूरी (25 cm) तथा (b) अनंत पर बने? दोनों स्थितियों में सूक्ष्मदर्शी की आवर्धन क्षमता ज्ञात कीजिए।

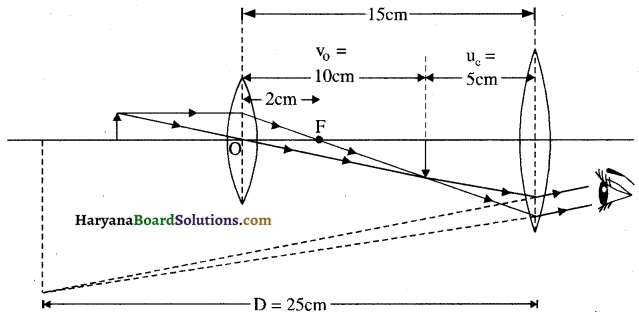
हल दिया गया है:
fo = 2 cm, fc = 6.25 cm
L = 15 cm, D = 25 cm
(a) vc = – 25 cm, uc = ?
लेन्स सूत्र से

(b) जब अन्तिम प्रतिबिम्ब अनन्त पर बनता है:
यहाँ
L = Vo + fe
ue = fe
Vo = L – fe
= 15 – 6.25
Ve = ∞
Vo = + 8.75 cm
\(\frac{1}{f_0}\) = \(\frac{1}{v_o}\) – \(\frac{1}{u_o}\)
\(\frac{1}{u_o}\) = \(\frac{1}{v_o}\) – \(\frac{1}{f_o}\) = \(\frac{1}{8.75}\) – \(\frac{1}{2}\) = \(\frac{100}{875}\) – \(\frac{1}{2}\)
\(\frac{1}{u_o}\) = \(\frac{200-875}{1750}\) = \(\frac{-675}{1750}\)
\(\frac{-1750}{675}\) = – 2.59cm
∴ u0 = 2.59 cm
आवर्धन क्षमता m = \(\frac{-v_0}{u_o}\) \(\left[\frac{D}{f_e}\right]\)
= \(\frac{-8.75}{2.59}\) x \(\frac{25}{6.25}\) = \(\frac{-875}{259}\) x 4
m = – 13.5 = | 13.5 |
= 13.5

प्रश्न 9.12.
25 cm के सामान्य निकट बिंदु का कोई व्यक्ति ऐसे संयुक्त सूक्ष्मदर्शी जिसका अभिदृश्यक 8.0mm फोकस दूरी तथा नेत्रिका 2.5 cm फोकस दूरी की है, का उपयोग करके अभिदृश्य से 9.0mm दूरी पर रखे बिंब को सुस्पष्ट फोकसित कर लेता है। दोनों लेन्सों के बीच पृथक्कन दूरी क्या है? सूक्ष्मदर्शी की आवर्धन क्षमता क्या है?
उत्तर:
दिया गया है:
D = 25 cm
अभिदृश्यक लेन्स की फोकस दूरी = f = 8.0mm
∴ fo = 0.8cm
नेत्रक की फोकस दूरी fc = 2.5 cm
u0 = – 9.0mm = – 0.9cm
दोनों लेन्सों के बीच की दूरी = L = ?
m = ?
नेत्रक के लिए लेन्स सूत्र:

प्रश्न 9.13.
किसी छोटी दूरबीन के अभिदृश्यक की फोकस दूरी 144 cm तथा नेत्रिका की फोकस दूरी 6.0 cm है। दूरबीन की आवर्धन क्षमता कितनी है? अभिदृश्यक तथा नेत्रिका के बीच पृथक्कन दूरी क्या है?
उत्तर:
दिया गया है:
दूरदर्शी के अभिदृश्यक की फोकस दूरी = fo
∴fo = 144 cm.
दूरदर्शी के नेत्रक की फोकस दूरी fc = 2.5 cm
u0 = – 9.0 mm = – 0.9 cm
दूरदर्शी की आवर्धन क्षमता = m = ?
अभिदृश्यक और नेत्रक की बीच की दूरी = L = ?
हम जानते हैं:
दूरबीन की आवर्धन क्षमता = m = -f0/fc
m = – 144/6
= -24
= L = f0 + fc
= 144 + 6 = 150 cm

प्रश्न 9.14.
(a) किसी वेधशाला की विशाल दूरबीन के अभिदृश्यक की फोकस दूरी 15m है। यदि 1.0cm फोकस दूरी की नेत्रिका प्रयुक्त की गयी है, तो दूरबीन का कोणीय आवर्धन क्या है?
(b) यदि इस दूरबीन का उपयोग चन्द्रमां का अवलोकन करने में किया जाए तो अभिदृश्यक लेन्स द्वारा निर्मित चन्द्रमा के प्रतिबिंब का व्यास क्या है? चन्द्रमा का व्यास 3.48 x 10⁶m तथा चन्द्रमा की कक्षा की त्रिज्या 3.8 x 10⁸ m है।
उत्तर:
दिया गया है:
दूरदर्शक के अभिदृश्यक की फोकस दूरी = fo = 15 m
नेत्रक की फोकस दूरी = fc = 1.0cm
= 10² m

प्रश्न 9.15.
दर्पण- सूत्र का उपयोग यह व्युत्पन्न करने के लिए कीजिए कि
(a) किसी अवतल दर्पण के f तथा 25 के बीच रखे बिंब का वास्तविक प्रतिबिंब 25 से दूर बनता है।
(b) उत्तल दर्पण द्वारा सदैव आभासी प्रतिबिंब बनता है जो बिंब की स्थिति पर निर्भर नहीं करता ।
(c) उत्तल दर्पण द्वारा सदैव आकार में छोटा प्रतिबिंब, दर्पण के ध्रुव व फोकस के बीच बनता है।
(d) अवतल दर्पण के ध्रुव तथा फोकस के बीच रखे बिंब का आभासी तथा बड़ा प्रतिबिंब बनता है।
(नोट: यह अभ्यास आपकी बीजगणितीय विधि द्वारा उन प्रतिबिंबों के गुण व्युत्पन्न करने में सहायता करेगा जिन्हें हम किरण आरेखों द्वारा प्राप्त करते हैं।)
उत्तर:
(a)
\(\frac{1}{v}\) + \(\frac{1}{u}\) = \(\frac{1}{f}\)(अवतल दर्पण के सूत्र से )
या
\(\frac{1}{v}\) = \(\frac{1}{f}\) – \(\frac{1}{u}\)
f < 0 ( अवतल दर्पण)
u < 0 (वस्तु बायीं तरफ रखी है)
2f < u< f के लिए या \(\frac{1}{2 f}\) > \(\frac{1}{u}\) > \(\frac{1}{f}\)
या \(\frac{-1}{2f}\) < \(\frac{-1}{u}\) < \(\frac{-1}{f}\)
या \(\frac{1}{f}\) – \(\frac{-1}{2f}\) < \(\frac{1}{f}\) – \(\frac{1}{u}\) < \(\frac{1}{f}\) – \(\frac{1}{f}\)
जिससे \(\frac{1}{2f}\) < \(\frac{1}{v}\) > 0
अर्थात् v ऋणात्मक होगा तथा प्रतिबिम्ब वास्तविक व 2f से आगे बनेगा।
(b) उत्तल दर्पण के दर्पण सूत्र से
\(\frac{1}{u}\) + \(\frac{1}{v}\) = \(\frac{1}{f}\)
यहाँ u < 0 तथा f > 0
अर्थात् सदैव कम होने से प्रतिबिम्ब दर्पण के दाईं ओर व आभासी होगा।

(c) ∵ आवर्धन m = \(\frac{f}{f-u}\)
∵ उत्तल दर्पण के लिए u < 0 तथा f < 0 अतः f – u > f
जिससे m < 1 अर्थात् प्रतिबिम्ब वस्तु से छोटा होगा।

(d) अवतल दर्पण के लिए u < 0 तथा f < 0 प्रश्नानुसार
f < u < 0 = \(\frac{1}{f}\) – \(\frac{1}{u}\) > 0
लेकिन दर्पण सूत्र \(\frac{1}{v}\) = \(\frac{1}{f}\) – \(\frac{1}{u}\) से
\(\frac{1}{v}\) > 0, जिसमें v धनात्मक तथा ध्रुव के दाईं ओर स्थित है।
प्रतिबिम्ब आभासी है और आवर्धन
m = \(\frac{-v}{u}\) = \(\frac{v}{| u |}\)
परन्तु \(\frac{1}{v}\) < \(\frac{1}{| u |}\) या v > | u |
अर्थात् धनात्मक है तथा m > 1 जिससे प्रतिबिम्ब बड़ा बनता है।

प्रश्न 9.16.
किसी मेज के ऊपरी पृष्ठ पर जड़ी एक छोटी पिन को 50 cm ऊँचाई से देखा जाता है। 15 cm मोटे आयताकार काँच के गुटके को मेज के पृष्ठ के समांतर पिन व नेत्र के बीच रखकर उसी बिंदु से देखने पर पिन नेत्र से कितनी दूर दिखाई देगी? काँच का अपवर्तनांक 1.5 है। क्या उत्तर गुटके की अवस्थिति पर निर्भर करता है?
उत्तर:
दिया गया है:
काँच की पट्टी की मोटाई = t = 15 cm
काँच का अपवर्तनांक = n = 1.5
पिन की स्थिति में नॉरमल बदलाव = d
d = 1(1 – 1/n) से दिया जाता है।
यहाँ पर t = पिन की वास्तविक गहराई पट्टी की मोटाई
माना पिन की आभासी गहराई = y
अभिलम्ब बदलाव (विस्थापन का मान )t – y = ? = d
n = t/y या y = t/n
∴ d = अभिलम्ब विस्थापन = t – t/n
= t(1 – 1/n)
= 15(1 – 1/1.5) = 15(1 – 2/3)
= 15 × 1/3 = 5cm
अर्थात् पिन 5 cm उठा हुआ प्रतीत होगा।
नहीं, छोटे आपतन कोणों के लिए उत्तर काँच के गुटके की स्थिति पर निर्भर नहीं है।

प्रश्न 9.17.
निम्नलिखित प्रश्नों के उत्तर लिखिए:
(a) निम्न चित्र में अपवर्तनांक 1.68 तंतु काँच से बनी किसी ‘प्रकाश नलिका’ (लाइट पाइप) का अनुप्रस्थ परिच्छेद दर्शाया गया है। नलिका का बाह्य आवरण 1.44 अपवर्तनांक के पदार्थ का बना है। नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण परावर्तन होते हैं, ज्ञात कीजिए।

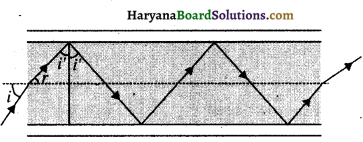
(b) यदि पाइप पर बाह्य आवरण न हो तो क्या उत्तर होगा?
उत्तर:
(a) sin Ic = n = \(\frac{\sin I}{\sin r}\) = \(\frac{1.44}{1.68}\)
= 0.8571
∴ Ic = sin-1 (0.8571) = 59°
Ic = 590
जब I > Ic अर्थात् I > 59 चूँकि I का मान 590 से 90° के बीच में है। यहाँ पर पूर्ण आन्तरिक परावर्तन होगा और कोण का मान 0° से 31° के बीच में होगा।
∴ rmax = 31°
अब वायु की अपेक्षा काँच तन्तु का अपवर्तनांक sin Imax स्नेल नियम से

या
n = \(\frac{\sin I_{\max }}{\sin r_{\max }}\) = स्नेल नियम से
⇒ 1.68 = \(\frac{\sin I_{\max }}{\sin 31^{\circ}}\)
⇒ sin Imax = 1.68 sin 31°
= 1.68 x 0.515 = 0.8652
Imax = sin-1 (0.8652 ) = 59.9°= 60°
अतः 0 < I < 60° परास में आपतित सभी किरणें पाइप में पूर्ण आन्तरिक परावर्तन में होंगी। (b) यदि पाइप पर कोई बाह्य लेपन नहीं है, तब पाइप के अन्दर अपवर्तन काँच से वायु में होगा- ∴ sinIc = 1/1.68= 0.5952 ∴ Ic = sin-1 (0.5952) Ic = 36.5° अतः पूर्ण आन्तरिक परावर्तन के लिए I > 36.5° होना चाहिए।
अब
I = 90° से r = 36.5° होगा।
∴ sinI/sinr = n = 1.68
∴ rmax = 90° – 36.5° = 53.5°
जो कि Ic से अधिक हैं।
∴ अक्ष 0 से 90° के परास में आपतित सभी किरणें पाइप के अन्दर से पूर्ण आन्तरिक में होंगी।

प्रश्न 9.18.
निम्नलिखित प्रश्नों के उत्तर लिखिए:
(a) आपने सीखा है कि समतल तथा उत्तल दर्पण सदैव आभासी प्रतिबिंब बनाते हैं। क्या ये दर्पण किन्हीं परिस्थितियों में वास्तविक प्रतिबिंब बना सकते हैं? स्पष्ट कीजिए।
(b) हम सदैव कहते हैं कि आभासी प्रतिबिंब को परदे पर केंद्रित नहीं किया जा सकता। यद्यपि जब हम किसी आभासी प्रतिबिंब को देखते हैं तो हम इसे स्वाभाविक रूप में अपनी आँख की स्क्रीन ( अर्थात् रेटिना) पर लाते हैं क्या इसमें कोई विरोधाभास है?
(c) किसी झील के तट पर खड़ा मछुआरा झील के भीतर किसी गोताखोर द्वारा तिरछा देखने पर अपनी वास्तविक लंबाई की तुलना में कैसा प्रतीत होगा-छोटा अथवा लंबा?
(d) क्या तिरछा देखने पर किसी जल के टैंक की आभासी गहराई परिवर्तित हो जाती है? यदि हाँ, तो आभासी गहराई घटती है अथवा बढ़ जाती है?
(e) सामान्य काँच की तुलना में हीरे का अपवर्तनांक काफी अधिक होता है? क्या हीरे को तराशने वालों के लिए इस तथ्य का कोई उपयोग होता है?
उत्तर:
(a) हाँ, किसी समतल अथवा उत्तल दर्पण के पीछे’ किसी बिन्दु पर अभिसरित किरणें दर्पण के सामने परदे पर किसी बिन्दु पर परावर्तित हो जाती हैं। दूसरे शब्दों में कोई समतल दर्पण अथवा उत्तल दर्पण आभासी बिंब के लिए वास्तविक प्रतिबिंब उत्पन्न कर सकता है।

(b) नहीं, कोई विरोधाभास नहीं है। यह इस सत्य के कारण है। कि जब परावर्तित अथवा अपवर्तित किरणें अपसारी होती हैं तो प्रतिबिंब आभासी होता है। अपसारी किरणों को उचित अभिसारी लेन्स की सहायता से परदे पर अभिसरित किया जा सकता है। नेत्र का आभासी लेन्स ठीक यही करता है। यहाँ आभासी प्रतिबिंब लेन्स के लिए बिंब की भाँति कार्य करता है और वास्तविक प्रतिबिंब बनता है।

(c) गोताखोर को, व्यक्ति जो है उससे लम्बा प्रतीत होगा क्योंकि व्यक्ति वायु में है, अतः प्रकाश विरल से सघन माध्यम में चलता है और लम्ब की ओर झुक जाता है जैसा चित्र में दिखाया गया है। अधिक दूरी आता प्रतीत होता है। मछुआरे AB के सिरे B से प्रकाश का आकार BP और BQ पानी वायु अन्तरापृष्ठ से अपवर्तन के पश्चात् अभिलम्ब की और बिन्दु P तथा Q पर झुकने के बाद चालक के B’ से आता प्रतीत होता है। स्पष्टत: AB’ > AB जहां AB’ मछुआरे AB का प्रतिबिम्ब है।

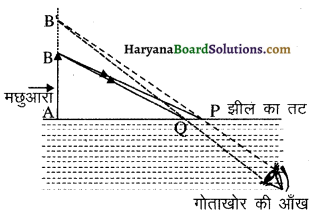
(d) यदि हम पानी से भरे हुए टैंक को तिरछा देखते हैं तो उसकी आभासी गहराई परिवर्तित होगी, इसकी आभासी गहराई वास्तविक गहराई से कम दिखेगी क्योंकि अपवर्तन के कारण उसका पैदा ऊपर उठता हुआ प्रतीत होता है।

(e) हाँ, हीरे का अपवर्तनांक लगभग 2.42 होता है, जो सामान्य काँच के अपवर्तनांक (n = 1.5) से काफी क्रान्तिक कोण लगभग 24 है जो काँच के अधिक होता है हीरे का क्रान्तिक कोण की अपेक्षा काफी कम है। एक हीरे को तराशने वाला इसके ऊपर अधिक परास के आपतन कोण 24° से 90° का लाभ उठाता है। यह सुनिश्चित करने के लिए कि प्रकाश हीरे के पटल पर 24° से अधिक कोण पर आपतित हो. यह पूर्ण आन्तरिक परावर्तन इसके बहुत से पटलों से निकलने से पहले भुगतता है। इससे हीरे में चमकने का प्रभाव उत्पन्न होता है।

प्रश्न 9.19.
किसी कमरे की एक दीवार पर लगे विद्युत बल्ब का किसी बड़े आकार के उत्तल लेन्स द्वारा 3m दूरी पर स्थित सामने की दीवार पर प्रतिबिंब प्राप्त करना है। इसके लिए उत्तल लेन्स की अधिकतम फोकस दूरी क्या होनी चाहिए?
उत्तर:
लेन्स के सूत्र से
\(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\) …………. (I)
दिया गया है:
– u + v = 3 चिन्ह परिपाटी के अनुसार
∴ v = 3 + u …..(ii)
समीकरण (i) से
\(\frac{1}{3+u}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\)
या \(\frac{u-3-u}{(3+u)(u)}\) = \(\frac{1}{f}\)
या f = \(\frac{u^2+3 u}{-3}\)
f के अधिकतम के लिए df/du = 0
∴
या -1/3(u2+3) = 0
या (2u+3) = 0
या u = -3/2
समीकरण (ii) से v = 3 – 3/2 = 3/2
u तथा v का मान समीकरण (i) में रखने पर

∴ इस कार्य के लिए लेन्स की वांछित अधिकतम फोकस दूरी 3/4m अर्थात् fmax = 0.75m
द्वितीय विधि; माना लेन्स की फोकस दूरी है, तो
f = a2-b2/4a
जहाँ पर a = v + u (वस्तु और प्रतिबिम्ब की बीच की दूरी)
b = (v – u) (लेन्स की दोनों स्थितियों के मध्य दूरी)
अधिकतम फोकस दूरी के लिए
∴ fmax = \(\frac{\mathrm{a}^2-0}{4 \mathrm{a}}\) = \(\frac{a^2}{4 a}\) = \(\frac{a}{4}\)
fmax = \(\frac{3}{4}\) = 0.75m
या fmax = 0.75m

प्रश्न 9.20.
किसी परदे को बिंब से 90 cm दूर रखा गया है। परदे पर किसी उत्तल लेन्स द्वारा उसे एक-दूसरे से 20 cm दूर स्थितियों पर रखकर दो प्रतिबिंब बनाए जाते हैं। लेन्स की फोकस दूरी ज्ञात कीजिए।
उत्तर:
दिया गया है:
– u + v = 90
=> v = 90 + u
चिन्ह परिपाटी के अनुसार …..(i)
लेन्स का सूत्र
\(\frac{1}{\mathrm{v}}\) – \(\frac{1}{\mathrm{u}}\) = \(\frac{1}{\mathrm{f}}\)
समीकरण (i) तथा (ii) से

या – 90f = 90u + u
या u2 + 90u + 90f = 0 ……… (iii)
समीकरण (iii) u में द्विघात समीकरण है। माना इस समीकरण के मूल u1 तथा u2 है।
∴ मूलों का योग
u1 + u2 = – 90 …..(iv)
मूलों का गुणनफल
u1u2 = 90f ……(V)
दिया गया है:
U1 – U2 = 20 …..(vi)
समीकरण (iv) तथा (vi) को हल करने पर (जोड़ने पर)
2u1 = – 90 + 20 = -70
⇒ u1 = -70/2 = -35 cm
घटाने पर
2u2 = – 90 – 20 = – 110
या
U2 = -110/2 = -55cm
अब
u1u2 = 90f
(-35) × (-55 ) = 90f
या
f = \(\frac{35 \times 55}{90}\) = 21.4cm
अतः लेन्स की फोकस दूरी 21.4 cm
द्वितीय विधि:
दिया है:
a = 90cm, b = 20

अतः फोकस दूरी f = 21.4 cm

प्रश्न 9.21.
(a) प्रश्न 9.10 के दो लेन्सों के संयोजन की प्रभावी फोकस दूरी उस स्थिति में ज्ञात कीजिए जब उनके मुख्य अक्ष संपाती हैं, तथा ये एक-दूसरे से 8 cm दूरी पर रखे हैं क्या उत्तर आपतित समांतर प्रकाश पुंज की दिशा पर निर्भर करेगा ? क्या इस तंत्र के लिए प्रभावी फोकस दूरी किसी भी रूप में उपयोगी है?
(b) उपरोक्त व्यवस्था (a) में 1.5 cm ऊँचा कोई बिंब उत्तल लेन्स की ओर रखा है। बिंब की उत्तल लेन्स से दूरी 40 cm है। दो लेन्सों के तंत्र द्वारा उत्पन्न आवर्धन तथा प्रतिबिंब का आकार ज्ञात कीजिए।
उत्तर:
(a) (i) माना कि कोई समान्तर प्रकाश पुंज बायीं ओर से पहले उत्तल लेन्स पर आपतित होता है। तब

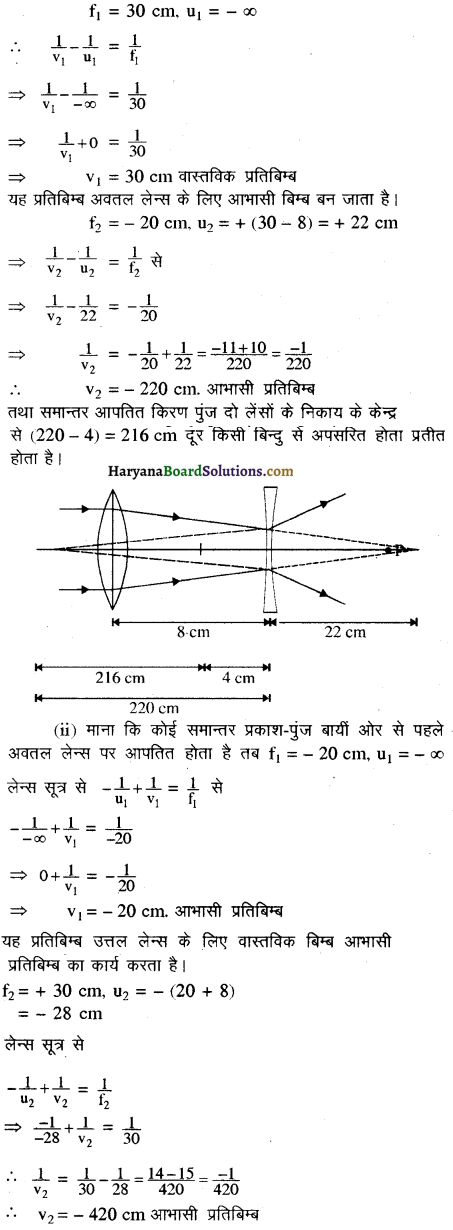
तथा समान्तर प्रकाश पुंज दो बायीं ओर से (420 – 4 = 416 cm) प्रतीत होता है।
लेन्सों में तंत्र के मध्य बिन्दु की दूर स्थित बिन्दु से अपसरित होता इस प्रकार हम निष्कर्ष निकालते हैं कि उत्तर इस बात पर निर्भर है कि समान्तर किरण पुंज किस दिशा में आपतित है; क्योंकि दोनों स्थितियों में दूरियाँ भिन्न हैं। इस स्थिति में प्रभावी फोकस दूरी का विचार भी उपयोगी नहीं है।

प्रश्न 9.22.
60° अपवर्तन कोण के प्रिज्म के फलक पर किसी प्रकाश किरण को किस कोण पर आपतित कराया जाए कि इसका दूसरे फलक से केवल पूर्ण आंतरिक परावर्तन ही हो? प्रिज्म के पदार्थ का अपवर्तनांक 1.524 है।
उत्तर:
दिया गया है:
प्रिज्म का कोण = A = 60°
प्रिज्म के द्रव्य का अपवर्तनांक= n = 1.524

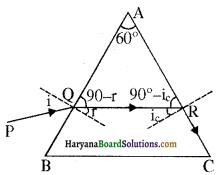
जब प्रकाश किरण PQ फलक AB पर आपतित होती है तो यह फलक AC पर पूर्ण आन्तरिक परावर्तन होता है और फलक AC पर कोण पर आपतित होगी जो प्रिज्म के पदार्थ के क्रान्तिक कोण के तुल्य है।
अब 60° + 90° – r + 90° i = 180°
या 240° – r – ic = 180°
या r = 60° – ic
अब
sin ic = 1/n = 1/1.524
ic = sin-1(1/1524) = sin-1(0.6562) = 41°
r = 60° – 41° = 19°
स्नेल नियम का प्रयोग करने
n = sini/sinr
∴ sin i = sin 19° x 1.524
= 0.3256 x 1.524
= 0.4962
या i = sin-1 (0.4962 ) = 29.75°
∴ i = 30°

प्रश्न 9.23.
कोई कार्ड शीट जिसे 1mm साइज के वर्गों में विभाजित किया गया है, को 9 cm दूरी पर रखकर किसी आवर्धक लेन्स (9 cm फोकस दूरी का अभिसारी लेन्स) द्वारा उसे नेत्र के निकट रखकर देखा जाता है।
(a) लेन्स द्वारा उत्पन्न आवर्धन (प्रतिबिंब – साइज / वस्तु-साइज) क्या है? आभासी प्रतिबिंब में प्रत्येक वर्ग का क्षेत्रफल क्या है?
(b) लेन्स का कोणीय आवर्धन (आवर्धन क्षमता) क्या है?
(c) क्या (a) में आवर्धन क्षमता (b) में आवर्धन के बराबर है? स्पष्ट कीजिए।
उत्तर:
(a) दिया गया है:
u = – 9 cm.
v = ?
f= 10cm.
लेन्स सूत्र से \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\)से
या \(\frac{1}{v}\) – \(\frac{1}{-9}\) = \(\frac{1}{10}\)
या \(\frac{1}{v}\) + \(\frac{1}{9}\) = \(\frac{1}{10}\)
या \(\frac{1}{v}\) = \(\frac{1}{10}\) – \(\frac{1}{9}\) = \(\frac{9-10}{10 \times 9}\) = \(\frac{-1}{90}\)
या v = – 90cm.
लेन्स में उत्पन्न आवर्धन m = v/-u = -90/90
m = + 10 आभासी प्रतिबिम्ब
आभासी प्रतिबिम्ब में प्रत्येक वर्ग का क्षेत्रफल = 1mm²
अर्थात्
1mm x 1 mm.
चूँकि लेन्स 10 का रैखिक आवर्धन उत्पन्न करता है, अतएव काल्पनिक प्रतिबिम्ब में प्रत्येक वर्ग का आकार (10 x 1 mm) x (10 x 1 mm) प्रतीक होगा।
या A = 100mm 2 = 1 cm2
(b) सुस्पष्ट दृष्टि की न्यूनतम दूरी D = -25cm
∴ m = कोणीय आवर्धन = आवर्धन क्षमता
∴ आवर्धन क्षमता = D/u = -25/-9
= 25/9 = 2.8

(c) नहीं, किसी लेन्स द्वारा आवर्धन तथा किसी प्रकाशिक यंत्र की ..कोणीय आवर्धन (अथवा आवर्धन क्षमता) दो भिन्न अभिधारणाएँ हैं। कोणीय आवर्धन वस्तु के कोणीय आकार (जो कि प्रतिबिम्ब के आवर्धित होने पर प्रतिबिम्ब के कोणीय आकार के बराबर होता है) तथा उस स्थिति में वस्तु के कोणीय आकार ( जबकि उसे निकट बिन्दु 25 cm पर रखा जाता है) का अनुपात होता है, इस प्रकार, आवर्धन का परिमाण होता है तथा आवर्धन क्षमता (v/u) होती है। केवल तब जब प्रतिबिम्ब निकट बिन्दु पर (25/u) = 25 cm पर है तो केवल तभी दोनों राशियाँ समान होती हैं।

प्रश्न 9.24.
(a) अभ्यास 9.23 में लेन्स को चित्र से कितनी दूरी पर रखा जाए ताकि वर्गों को अधिकतम संभव आवर्धन क्षमता के साथ सुस्पष्ट देखा जा सके?
(b) इस उदाहरण में आवर्धन ( प्रतिबिंब साइज / वस्तु-साइज) क्या है?
(c) क्या इस प्रक्रम में आवर्धन, आवर्धन क्षमता के बराबर है? स्पष्ट कीजिए।
उत्तर:
(a) यहाँ, जब काल्पनिक प्रतिबिम्ब सुस्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है तब अधिकतम आवर्धन क्षमता प्राप्त की जा सकती है।
v = – 25 cm, f = + 10cm, u = ?
लेन्स सूत्र से \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\) से
\(\frac{1}{25}\) – \(\frac{1}{u}\) = \(\frac{1}{10}\)
या \(\frac{1}{25}\) – \(\frac{1}{10}\) = \(\frac{1}{u}\)
या \(\frac{-2-5}{50}\) = \(\frac{1}{u}\)
या u = -50/7 = -7.14cm = |7.14| cm

(b) आवर्धन m = v/u = ?
सूत्र m = v/u का उपयोग करने पर
m = v/u
= \(\frac{-25}{-50 / 7}\) = \(\frac{25 \times 7}{50}\) = \(\frac{7}{2}\)
या m = 3.5

(c) आवर्धन क्षमता M = ?
जब वस्तु को इस प्रकार रखा जाये कि प्रतिबिम्ब सुस्पष्ट दृष्टि की न्यूनतम दूरी पर बने
m = 1 + D/f द्वारा दिया जाता है।
m = 1 + 25/10 = 1 + 25 = 3.5
m = \(\frac{D}{|\mathrm{u}|}\) = \(\frac{25}{50 / 7}\) = \(\frac{25 \times 7}{50}\)
m = 3.5
हाँ, इस स्थिति में आवर्धन, आवर्धन क्षमता के तुल्य है, क्योंकि- प्रतिबिम्ब सुस्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है।

प्रश्न 9.25.
अभ्यास 9.24 में वस्तु तथा आवर्धक लेन्स के बीच. कितनी दूरी होनी चाहिए ताकि आभासी प्रतिबिंब में प्रत्येक वर्ग 6.25 mm 2 क्षेत्रफल का प्रतीत हो? क्या आप आवर्धक लेन्स को नेत्र के अत्यधिक निकट रखकर इन वर्गों को सुस्पष्ट देख सकेंगे?
[नोट- अभ्यास 9.23 से 9.25 आपको निरपेक्ष साइज में आवर्धन तथा किसी यंत्र की आवर्धन क्षमता (कोणीय आवर्धन) के बीच अंतर को स्पष्टतः समझने में सहायता करेंगे।]
हल
दिया गया है:
वस्तु का क्षेत्रफल = 1mm²
∴ h = वस्तु का आकार = 1mm
प्रतिबिम्ब का क्षेत्रफल = 6.25 mm²
∴ h’ = प्रतिबिम्ब का आकार
= √6.25 = 2.5mm

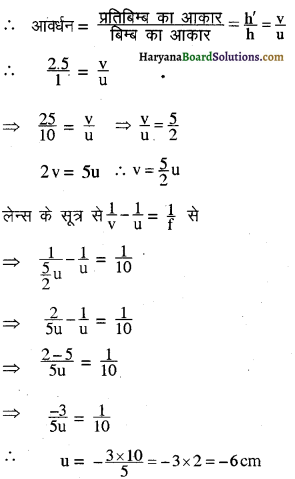
लेकिन 2v = 5u
∴ 2v = 5 × (-6)
v = -30/2 = -15 cm
आभासी प्रतिबिम्ब सामान्य निकट बिन्दु (25 cm) से भी पास बनता है तथा इसे नेत्र स्पष्ट नहीं देख सकता।

प्रश्न 9.26.
निम्नलिखित प्रश्नों के उत्तर दीजिए:
(a) किसी वस्तु द्वारा नेत्र पर अंतरित कोण आवर्धक लेन्स द्वारा उत्पन्न आभासी प्रतिबिंब द्वारा नेत्र पर अंतरित कोण के बराबर होता है। तब फिर किन अर्थों में कोई आवर्धक लेन्स कोणीय आवर्धन प्रदान करता है?
(b) किसी आवर्धक लेन्स से देखते समय प्रेक्षक अपने नेत्र को लेन्स से अत्यधिक सटाकर रखता है। यदि प्रेक्षक अपने नेत्र को पीछे ले जाए तो क्या कोणीय आवर्धन परिवर्तित हो जाएगा ?
(c) किसी सरल सूक्ष्मदर्शी की आवर्धन क्षमता उसकी फोकस दूरी के व्युत्क्रमानुपाती होती है तब हमें अधिकाधिक आवर्धन क्षमता प्राप्त करने के लिए कम से कम फोकस दूरी के उत्तल लेन्स का उपयोग करने से कौन रोकता है?
(d) किसी संयुक्त सूक्ष्मदर्शी के अभिदृश्यक लेन्स तथा नेत्रिका लेन्स दोनों ही की फोकस दूरी कम क्यों होनी चाहिए ?
(e) संयुक्त सूक्ष्मदर्शी द्वारा देखते समय सर्वोत्तम दर्शन के लिए हमारे नेत्र, नेत्रिका पर स्थित न होकर उससे कुछ दूरी पर होने चाहिए। क्यों ? नेत्र तथा नेत्रिका के बीच की यह अल्प दूरी कितनी होनी चाहिए?
उत्तर:
(a) यदि प्रतिबिंब का निरपेक्ष आकार वस्तु के आकार से बड़ा भी है, तो भी प्रतिबिंब का कोणीय आकार वस्तु के कोणीय आकार के समान होता है। कोई आवर्धक लेन्स हमारी इस रूप में सहायता करता है : यदि आवर्धक लेन्स नहीं है तो वस्तु 25 cm से कम दूरी पर नहीं रखी जा सकती; आवर्धक लेन्स होने पर हम वस्तु को अपेक्षाकृत बहुत निकट रख सकते हैं। वस्तु निकट हो तो उसका कोणीय आकार 25 cm दूर रखने की तुलना में कहीं अधिक होता है। हमारे कोणीय आवर्धन पाने या उपलब्ध करने का यही अर्थ है।

(b) हाँ, यह थोड़ा कम होता है, क्योंकि नेत्र पर अंतरित कोण लेन्स पर अंतरित कोण से थोड़ा छोटा होता है। यदि प्रतिबिंब बहुत दूर हो तो यह प्रभाव नगण्य होता है (जब नेत्र को लेन्स से पृथक् रखते हैं, तो प्रथम वस्तु द्वारा नेत्र पर अंतरित कोण तथा इसके प्रतिबिंब द्वारा नेत्र पर अंतरित कोण समान नहीं होते।)

(c) प्रथम, अत्यंत छोटे फोकस दूरी के लेन्सों की घिसाई आसान नहीं है। इससे अधिक महत्त्वपूर्ण बात है कि यदि आप फोकस दूरी कम करते हैं तो इससे विपथन ( गोलीय तथा वर्ण) बढ़ जाता है। अतः व्यवहार में, आप किसी सरल उत्तल लेन्स से 3 या अधिक की आवर्धन क्षमता नहीं प्राप्त कर सकते हैं। तथापि, किसी विपथन संशोधित लेन्स प्रणाली के उपयोग से इस सीमा को 10 या इसके सन्निकट कारक से बढ़ा सकते हैं।

(d) किसी नेत्रिका का कोणीय आवर्धन [ (25/fc) +1] (fecm में) होता है जिसके मान में के घटने पर वृद्धि होती है। पुनः अभिदृश्यक का आवर्धन से प्राप्त होता है जो अधिक होता है यदि |u0||f0| से कुछ अधिक हो सूक्ष्मदर्शी का उपयोग अति निकट की वस्तुओं को देखने के लिए किया जाता है। अतः |u0| कम होता है और तदनुसार भी

(e) नेत्रिका के अभिदृश्यक के प्रतिबिंब को निर्गम द्वारक’ कहते हैं। वस्तु से आने वाली सभी किरणें अभिदृश्यक से अपवर्तन के पश्चात् निर्गम द्वारक से गुजरती हैं। अतः हमारे नेत्र से देखने के लिए यह एक आदर्श स्थिति है। यदि हम अपने नेत्र को नेत्रिका के बहुत ही निकट रखें तो त्रिका बहुत अधिक प्रकाश का अधिग्रहण नहीं कर पाएगी तथा दृष्टि- क्षेत्र भी घट जाएगा। यदि हम अपने नेत्र को निर्गम द्वारक पर रखें तथा हमारे नेत्र की पुतली का क्षेत्रफल निर्गम द्वारक के क्षेत्रफल से अधिक या समान हो तो हमारे नेत्र अभिदृश्यक से अपवर्तित सभी किरणों को अभिगृहीत कर लेंगे। निर्गम द्वारक का सटीक स्थान सामान्यतः अभिदृश्यक एवं नेत्रिका के अंतराल पर निर्भर करता है जब हम किसी सूक्ष्मदर्शी से, इसके एक सिरे पर अपने नेत्र को लगाकर देखते हैं तो नेत्र एवं नेत्रिका के मध्य आदर्श दूरी यंत्र के डिजाइन में अंतर्निहित होती है।

प्रश्न 9.27.
1.25 cm फोकस दूरी का अभिदृश्यक तथा 5 cm फोकस दूरी की नेत्रिका का उपयोग करके वांछित कोणीय आवर्धन (आवर्धन क्षमता ) 30 X होता है। आप संयुक्त सूक्ष्मदर्शी का समायोजन कैसे करेंगे?
उत्तर:
दिया गया है:
अभिदृश्यक की फोकस दूरी f0 = 1.25cm
नेत्रिका की फोकस दूरी = fc = 5 cm
कोणीय आवर्धन ( आवर्धन क्षमता) = m = 30
मान लीजिए कि सूक्ष्मदर्शी सामान्य उपयोग में है अर्थात् प्रतिबिम्ब 25 cm पर है। नेत्रिका का कोणीय आवर्धन
(m) = (1 + D/fe) = (1 + 25) = 6
माना अभिदृश्यक का कोणीय आवर्धन = mo
∴ m = m x me
m0 = m/me = 30/6 = 5
∴ mo = \(\frac{v_0}{-u_0}\)
5 = \(\frac{v_0}{-u_0}\)
या
Vo = – 5 uo
अभिदृश्यक के लिए लेन्स सूत्र का उपयोग करने पर
\(\frac{1}{v_0}\) – \(\frac{1}{u_o}\) = \(\frac{1}{f_o}\)
\(-\frac{1}{5 u_o}\) – \(\frac{1}{u_0}\) = \(\frac{1}{1.25}\)
या \(-\frac{6}{5 u_o}\) = \(\frac{100}{125}\) = \(\frac{4}{5}\)
या \(-\frac{30}{20}\) = -1.5cm
अर्थात् बिम्ब को अभिदृश्यक के सामने 1.5 cm दूरी पर रखना चाहिए।
∵ Vo = – 5 uo
= – 5 (- 1.5) = 7.5 cm
नेत्रक के लिए लेन्स सूत्र:
ve = – 25 cm, f = 5 cm
\(\frac{1}{v_e}\) – \(\frac{1}{u_e}\) = \(\frac{1}{f_c}\)
या \(\frac{1}{u_e}\) = \(\frac{1}{v_e}\) – \(\frac{1}{f_c}\)
= \(-\frac{1}{25}\) – \(-\frac{1}{5}\) = \(-\frac{6}{25}\)
∴ uc = \(-\frac{6}{25}\)
= -4.17 cm
∴ यौगिक सूक्ष्मदर्शी को इस प्रकार व्यवस्थित करना चाहिए कि अभिदृश्यक और नेत्र के बीच की दूरी
= |Vo| + |ue |
= 7.5 + 4.17
= 11.67 cm
अभिदृश्यक एवं नेत्रिका के बीच दूरी 11.67 cm होनी चाहिए। अपेक्षित आवर्धन प्राप्त करने के लिए वस्तु को अभिदृश्यक से 1.5 cm दूर रखना होगा।

प्रश्न 9.28.
किसी दूरबीन के अभिदृश्यक की फोकस दूरी 140 cm तथा नेत्रिका की फोकस दूरी 5.0 cm है। दूर की वस्तुओं को देखने के लिए दूरबीन की आवर्धन क्षमता क्या होगी जब:
(a) दूरबीन का समायोजन सामान्य है (अर्थात् अंतिम प्रतिबिंब अनंत पर बनता है)।
(b) अंतिम प्रतिबिंब स्पष्ट दर्शन की अल्पतम दूरी (25 cm) पर बनता है।
उत्तर:
दिया गया है:
अभिदृश्यक की फोकस दूरी = fo
∴ fo = 140cm
नेत्रिका की फोकस दूरी = fc
∴ fc = 5.0cm
(a) आवर्धन क्षमता का मान दूरदर्शी की सामान्य अवस्था में अर्थात् अन्तिम प्रतिबिम्ब अनन्त पर बनता है।
m = fo/|fc| – 140 = 28
(b) जब प्रतिबिम्ब सुस्पष्ट दर्शन की अल्पतम दूरी पर बनता है। तब आवर्धन क्षमता का मान
m = \(\frac{f_o}{\left|f_e\right|}\) = \(\left(1+\frac{f_e}{D}\right)\)
= \(\frac{140}{5}\) \(\left(1+\frac{5}{25}\right)\)
28 × 6/5 = 33.6

प्रश्न 9.29.
(a) अभ्यास 9.28 ( a) में वर्णित दूरबीन के लिए अभिदृश्यकलेन्स तथा नेत्रिका के बीच पृथक्कन दूरी क्या है?
(b) यदि इस दूरबीन का उपयोग 3 km दूर स्थित 100m ऊँची मीनार को देखने के लिए किया जाता है तो अभिदृश्यक द्वारा बने मीनार के प्रतिबिंब की ऊँचाई क्या है?
(c) यदि अंतिम प्रतिबिंब 25 cm दूर बनता है तो अंतिम प्रतिबिंब में मीनार की ऊँचाई क्या है?
उत्तर:
(a) अभिदृश्यकलेन्स तथा नेत्रिका के बीच पृथक्कन दूरी
L = fc + fe
= 140 + 5 = 145 cm
(b) माना कि 100 in ऊँची मीनार AB द्वारा प्रेक्षण बिन्दु o पर बनाया गया कोण θ है।

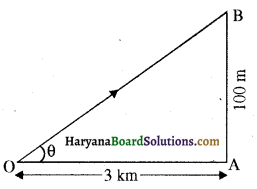
h = 100m
b = 3 km = 3,000m
θ = h/b सम्बन्ध को प्रयोग करने पर
θ = 100/3,000 = 1/30 रेडियन ……………. (i)
माना अभिदृश्यक द्वारा निर्मित प्रतिबिम्ब की ऊँचाई x है।
∴ अभिदृश्यक द्वारा निर्मित प्रतिबिम्ब से बनाया कोण
= x/fo
= -x/140 ……………. (ii)
समीकरण (i) व (ii) को बराबर करने पर
1/30 = x/140
⇒ x = 140/30 = 14/3cm = 4.7cm
(c) नेत्रिका का आवर्धन me है।
me= 1 + D/fe
= 1 + 25/5 = 1 + 5 = 6
हम जानते हैं:
me = h/h =
∴ अन्तिम प्रतिबिम्ब की ऊँचाई = mc x x
= 6 x 14/3 = 28 cm

प्रश्न 9.30.
किसी कैसेग्रेन दूरबीन में चित्र में दर्शाए अनुसार दो दर्पणों का प्रयोग किया गया है। इस दूरबीन में दोनों दर्पण एक-दूसरे से 20mm दूर रखे गए हैं। यदि बड़े दर्पण की वक्रता त्रिज्या 220 mm हो तथा छोटे दर्पण की वक्रता त्रिज्या 140mm हो तो अनंत पर रखे किसी बिंब का अंतिम प्रतिबिंब कहाँ बनेगा?

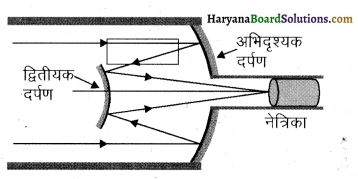
उत्तर:
अवतल दर्पण की वक्रता त्रिज्या (अर्थात् बड़े दर्पण की) = R1
∴ R1 = – 220mm = -22cm
उत्तल दर्पण की वक्रता त्रिज्या (अर्थात् छोटे दर्पण की) = R2
∴ R2 = 140mm = 14 cm
यदि बड़े और छोटे दर्पणों की फोकस दूरी क्रमशः f1 तथा f2 हो तब
f1 = R1/2 = -22/2 = -11cm
और
f2 = R2/2 = 14/2 = 7cm.
बड़े दर्पण द्वारा बनाया गया प्रतिबिम्ब छोटे दर्पण के लिए आभासी बिम्ब का कार्य करता है।
दर्पणों के बीच पृथक्कीकरण d = 20 mm
= 2 cm.
चिन्ह परिपाटी के अनुसार यहाँ पर f1, R को vc लिया गया है।
∵ वस्तु अनन्त पर है ∴ u = ∞
जैसा कि रेखाचित्र में दिखाया गया है। वस्तु का अन्तिम प्रतिबिम्ब अभिदृश्यक दर्पण के पीछे बनता है, जिसे हम नेत्रक में से देखते हैं। अनन्त पर स्थित वस्तु से आती किरणें अभिदृश्यक के मुख्य फोकस पर मिलने को होती हैं, लेकिन इससे पहले ही कम फोकस दूरी का अवतल दर्पण बीच में आ जाता है।
अभिदृश्यक के लिए:
u = – ∞
फोकस दूरी f1 = 11 cm
v = ?
दर्पण समीकरण से
या \(\frac{1}{\mathrm{u}}\) + \(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\)
\(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\) – \(\frac{1}{\mathrm{u}}\)
= \(-\frac{1}{11}\) – \(\frac{1}{∞}\) = \(-\frac{1}{11}\) + \(-\frac{1}{∞}\)
= \(-\frac{1}{11}\) + 0 = –\(-\frac{1}{11}\)
या v = – 11 cm = अभिदृश्यक से दूरी
उत्तल दर्पण से दूरी
= – (v + d)
= – (- 11 + 2) = + 9 cm.
यह उत्तल दर्पण के लिए काल्पनिक वस्तु का कार्य करता है।
अर्थात्
u’= 9cm.
f’ = 7 cm.
v’= ?
\(\frac{1}{\mathrm{v}}\) = \(\frac{1}{\mathrm{f}}\) – \(\frac{1}{\mathrm{u}}\)
= \(\frac{1}{7}\) – \(=\frac{1}{9}\) = \(\frac{9-7}{63}\) =2/63
v’= 63/2 = 31.5 cm.
अर्थात् प्रतिबिम्ब 31.5 cm उत्तल दर्पण (छोटे वाले से) दूर बनता है।

प्रश्न 9.31.
किसी गैल्वेनोमीटर की कुंडली से जुड़े समतल दर्पण पर लंबवत् आपतित प्रकाश (चित्र), दर्पण से टकराकर अपना पथ पुनः अनुरेखित करता है। गैल्वेनोमीटर की कुंडली में प्रवाहित कोई धारा दर्पण में 3.5° का परिक्षेपण उत्पन्न करती है। दर्पण के सामने 1.5m दूरी पर रखे परदे पर प्रकाश के परावर्ती चिन्ह में कितना विस्थापन होगा?

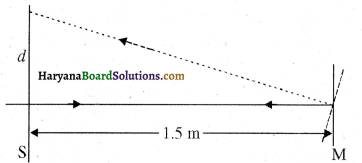
उत्तर:
यहाँ पर हम जानते हैं कि परावर्तित किरणें दर्पण के घूर्णन कोण से दुगुने कोण पर विक्षेपित होती हैं। चित्र से हम देखते हैं कि जब दर्पण M से M’ स्थिति पर θ = 3.5° कोण से मोड़ा जाता है। परावर्तित किरण OB

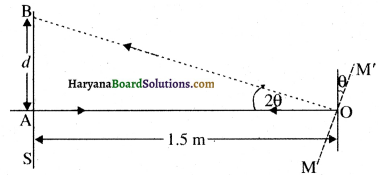
∠2θ = 2 × 3.5° = 7° = ∠AOB से मुड़ जाती है।
समकोण त्रिभुज AOB में
tan 2θ = AB/AO
या tan 7° = d/1.5
या d = 1.5 × tan 7°
= 1.5 x 0.1228
= 0.1842 m
= 18.42 cm.

प्रश्न 9.32.
चित्र में कोई समोत्तल लेन्स (अपवर्तनांक 1.50) किसी समतल दर्पण के फलक पर किसी द्रव की परत के संपर्क में दर्शाया गया है। कोई छोटी सुई जिसकी नोक मुख्य अक्ष पर है, अक्ष के अनुदिश ऊपर-नीचे गति करादर इस प्रकार समायोजित की जाती है कि सुई की नोक का उलटा प्रतिबिंब सुई की स्थिति पर ही बने। इस स्थिति में सुई की लेन्स से दूरी 45.0 cm है। द्रव को हटाकर प्रयोग को दोहराया जाता है। नयी दूरी 30.0 cm मापी जाती है। द्रव का अपवर्तनांक क्या है?

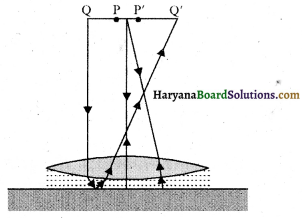
उत्तर:
दिया गया है कि
द्विउत्तल लेन्स की फोकस दूरी L1 f1 = 30 cm.
द्वि- उत्तल लेन्सों के संयोजन और समतल उत्तल द्रव लेन्स की
फोकस दूरी L2 F = 45 cm.
यदि L2 की फोकस दूरी f2 है तब
\(\frac{1}{f2}\) = \(-\frac{1}{F}\) – \(-\frac{1}{f1}\)
= \(\frac{1}{45}\) – \(\frac{1}{30}\) = \(\frac{2-3}{90}\) = \(-\frac{1}{90}\)
या f2 = – 90cm.
L1 लेन्स के लिए (काँच के लेन्स के लिए) R1 = R तथा R2
\(\frac{1}{30}\) = (15 – 1) \(\left(\frac{1}{R}-\frac{1}{-R}\right)\)
\(\frac{1}{30}\) = 0.5 x \(\frac{2}{R}\) = \(\frac{1}{R}\)
R = 30cm.
L2 लेन्स के लिए (द्रव लेन्स के लिए)
R1 = – R = – 30 cm
R2 = ∞
\(-\frac{1}{90}\) = (n – 1) \(\left(\frac{1}{-30}-\frac{1}{\infty}\right)\)
\(-\frac{1}{90}\) = (n – 1) \(\left(\frac{1}{-30}-0\right)\) = \(\frac{-(n-1)}{30}\)
⇒ 30/90 = n – 1
⇒ 1/3 = n – 1
⇒ 1/3 + 1 = n
⇒ 0.33 + 1 = n
n = 1.33