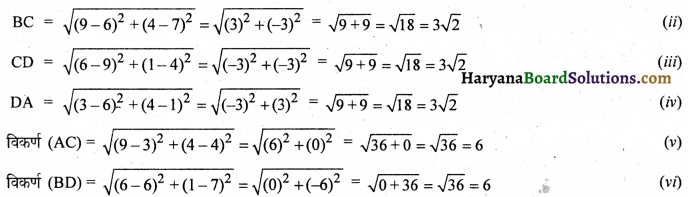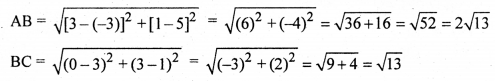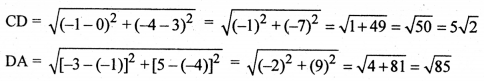Author name: Prasanna

Haryana State Board HBSE 12th Class Hindi Solutions नए और अप्रत्याशित विषयों पर लेखन Questions and Answers, Notes.

Haryana Board 12th Class Hindi नए और अप्रत्याशित विषयों पर लेखन

प्रश्न 1.
नए और अप्रत्याशित विषयों पर लेखन का क्या अर्थ है ? स्पष्ट करें।
उत्तर:
प्रायः किसी एक विचार या भाव पर निबंध लिखा जाता है। परंतु कभी-कभी लेखक नए और अप्रत्याशित विषयों पर अपने विचार प्रस्तुत करता है। यदि लेखक सर्वथा नवीन और सामान्य विषयों से हटकर किसी विषय पर लेख लिखता है, तो उसे हम अप्रत्याशित विषय कह सकते हैं। अपने विचारों को व्यक्त करना बड़ा सरल है, परंतु लिखकर अभिव्यक्त करना बड़ा कठिन है। इसका प्रमुख कारण यह है कि प्रायः लोगों को सुनियोजित ढंग से लिखने का अभ्यास नहीं होता। प्रायः विद्यार्थी दूसरों के द्वारा लिखे निबंधों को पढ़कर ज्यों-का-त्यों प्रस्तुत कर देते हैं। कभी-कभी वे मौखिक ढंग से भी अपने विचार प्रकट कर देते हैं, परंतु उन्हें लिखित रूप देना कठिन होता है।

उदाहरण के रूप में, यदि किसी व्यक्ति ने रेल यात्रा की है, तो वह अपने अनुभवों को बड़ी आसानी से सुना सकता है। कैसे उसने लाइन में लगकर टिकट ली, कैसे सामान के साथ स्टेशन पर प्रतीक्षा की और कैसे गाड़ी आने पर भीड़ में से गुजरकर ट्रेन पर सवार हुआ आदि इन सबका विवरण वह बता सकता है, परंतु अपने अनुभवों को सुनियोजित ढंग से लिखना एक चुनौतीपूर्ण कार्य है। अतः नए और अप्रत्याशित विषयों पर लिखना कोई सहज कार्य नहीं है। फिर भी यदि कोई विद्यार्थी प्रयास करे, तो यह इतना कठिन भी नहीं है। दो-चार बार लिखने के बाद वह स्वयं इस कार्य में पारंगत हो सकता है।

प्रश्न 2.
नए और अप्रत्याशित विषयों पर लेखन में कौन-कौन सी कठिनाइयाँ आती हैं? स्पष्ट करें।
उत्तर:
लेखन का अर्थ है-भाषा के माध्यम से किसी विषय पर अपने विचारों को लिपिबद्ध करना। वस्तुतः भाव और भाषा को समन्वित रूप में अभिव्यक्त करना ही लेखन कहलाता है। यदि एक व्यक्ति के पास मौलिक विचार हैं, परंतु भाषा पर उसका मौलिक अधिकार नहीं है, तो वह अप्रत्याशित विषय पर लेख नहीं लिख सकता। इस प्रकार मौलिक विचार भी कुछ नया सोचने तथा चिंतन करने से बनते हैं। पिछले लंबे समय से विद्यार्थियों तथा शिक्षकों को तैयार सामग्री उपलब्ध होती आ रही है। इसलिए न तो कोई शिक्षक नया सोचता है, न ही लिखने का प्रयास करता है। शिक्षकों की यही मानसिकता विद्यार्थियों को प्रभावित करती है।

जब भी किसी विद्यार्थी को नए विषय पर लिखने के लिए कहा जाता है, तो वह लिख नहीं पाता। नए और अप्रत्याशित विषयों पर लेखन के लिए विद्यार्थियों को कुछ नया सोचने की प्रेरणा दी जानी चाहिए, साथ ही उन्हें लिखने का अभ्यास भी करवाया जाना चाहिए। सबसे पहली शर्त है कि विद्यार्थियों को नए-नए विषयों के बारे में सोचने के लिए कहा जाए। ये नए विषय परंपरागत विषयों से अलग प्रकार के होने चाहिएँ। दूसरा विद्यार्थियों को शुद्ध भाषा लिखने का अभ्यास करवाया जाना चाहिए। यदि विद्यार्थियों की भाषा व्याकरण-सम्मत होगी, तो वे निश्चय से अपने मौलिक विचारों को सफलतापूर्वक प्रस्तुत कर पाएंगे। नया सोचना और नया लिखना ही विद्यार्थी को अभिव्यक्ति कौशल प्रदान करता है।

प्रश्न 3.
कहा जाता है कि नए और अप्रत्याशित विषयों पर लिखना कठिन है। कौन-कौन से उपाय अपनाकर इसे सरल बना सकते हैं?
अथवा
नए और अप्रत्याशित विषयों पर लेखन में कौन-कौन-सी बातों को ध्यान में रखना आवश्यक है?
उत्तर:
नए और अप्रत्याशित विषयों पर लेखन को सरल बनाने के लिए निम्नलिखित उपाय अपनाए जा सकते हैं
(1) किसी भी नए और अप्रत्याशित विषय पर लेख लिखने से पहले उसके बारे में सोच-विचार करना चाहिए और मन में उसकी एक रूपरेखा बना लेनी चाहिए। तत्पश्चात उसे लिखना चाहिए।

(2) जिस विषय पर भी लेख लिखा जाना है, उस विषय की लेखक को समुचित जानकारी होनी चाहिए। विषय से संबंधित सभी विचारों को सुसंबद्धता के साथ प्रस्तुत करना चाहिए।

(3) नए और अप्रत्याशित विषय से जुड़ी सभी बातों को सुनियोजित ढंग से प्रस्तुत करना चाहिए। ऐसा न हो कि पहले कही जाने वाली बात बाद में आ जाए और बाद में कही जाने वाली बात पहले आ जाए। यदि हम रोहतक से दिल्ली तक की रेल यात्रा का वर्णन करना चाहते हैं, तो हमें स्टेशन पहुँचने, टिकट खरीदने तथा रेल में चढ़ने की सभी बातों को क्रमबद्ध तरीके से प्रस्तुत करना चाहिए। तभी
हमारा लिखना सार्थक होगा।

(4) नए और अप्रत्याशित विषयों के लिए आत्मपरक (मैं) शैली का प्रयोग किया जाना चाहिए। निबंधों के लिए यह शैली वर्जित है, लेकिन नए विषयों के लिए यह शैली अत्यधिक उपयोगी मानी गई है।

(5) नए और अप्रत्याशित लेखों की भाषा सहज, सरल तथा बोधगम्य होनी चाहिएँ। इसके वाक्य अधिक लंबे नहीं होने चाहिएँ। शब्द-प्रयोग तथा वाक्य-विन्यास सर्वथा भावानुकूल तथा विषयानुकूल होना चाहिए।

प्रश्न 4.
“अब पछताए होत क्या, जब चिड़िया चुग गई खेत” पर संक्षिप्त लेख लिखिए।
उत्तर:
अकसर देखने में आया है कि लोग कोई दुर्घटना अथवा हानि होने के पश्चात पश्चात्ताप करने लगते हैं। यह तो वही हुआ कि “साँप निकल गया, अब बैठकर लकीर को पीटो।” जो हो चुका है, उसके बारे में सोचना अथवा पश्चात्ताप करना सबसे बड़ी मूर्खता है। कहा भी गया है कि मूर्ख लोग बीती बातों के बारे में अधिक सोचते हैं। इसका दुष्परिणाम यह होता है कि हम बीती हुई बातों पर व्यर्थ में ही सोच-सोचकर अपने समय को नष्ट करते हैं और अपने मन में अशांति उत्पन्न करते हैं कि “यदि मैं ऐसा न करता तो मेरे साथ ऐसा न होता।” इस प्रकार की सोच हमें नुकसान ही पहुँचाती है। हमें बीती बातों को भूलकर आगे के लिए सोचना चाहिए। यदि हम एक बार परीक्षा में असफल हो जाते हैं, तो उसके लिए रोना-धोना तथा पश्चात्ताप करना व्यर्थ है। बल्कि हमें फिर से एक नई योजना बनाकर अपनी पढ़ाई को आरंभ करना चाहिए। जो गलतियाँ हमने पिछली बार की थीं, उन्हें पुनः नहीं दोहराना चाहिए।

कहा भी तो गया है-“बीती ताहि बिसार के आगे की सुध ले।” – हमारे जीवन में सुख-दुख, सफलता-असफलता आदि का भी महत्त्व है। पुरानी गलतियों से हम बहुत कुछ सीखते हैं, परंतु पुरानी गलतियों को फिर से करना सबसे बड़ी मूर्खता है। जीवन की प्रक्रिया तो निरंतर चलती रहती है। हमें कदम-कदम पर अनेक बाधाओं का सामना करना पड़ता है। हमारा कर्तव्य है कि उन बाधाओं को दूर करना और निरंतर आगे बढ़ना। जो हो चुका है, उसे भूल जाओ और आगे बढ़ो, संघर्ष करो। निश्चय से आपको सफलता मिलेगी। इसलिए किसी ने ठीक ही कहा है-“अब पछताए होत क्या, जब चिड़िया चुग गई खेत।”

प्रश्न 5.
क्या नए और अप्रत्याशित विषयों का लेखन अभिव्यक्ति कौशल में सहायक है? स्पष्ट करें।
उत्तर:
निबंध गद्य लेखन की एक महत्त्वपूर्ण विधा है। निबंधकार इस विधा द्वारा अपने विचारों को व्यक्त करता है। निबंध लिखने की यह विधा बहुत पुरानी है। प्रायः कुछ परंपरागत विषयों पर निबंध लिखे जाते हैं। पुराने विषयों पर तैयार सामग्री हमें पर्याप्त मात्रा में मिल जाती है। इसका दुष्परिणाम यह होता है कि न हम कुछ नया सोच पाते हैं, न ही किसी नए विषय पर लिख पाते हैं। हमारे अंदर अभिव्यक्ति की क्षमता अवरुद्ध हो जाती है। न निबंधकार की सोच आगे बढ़ पाती है, न ही विद्यार्थियों की।

उदाहरण के रूप में, मेरा प्रिय साहित्यकार, दीवाली, ग्रीष्म ऋतु, बेरोज़गारी की समस्या, आतंकवाद आदि विषयों पर लिखे-लिखाए निबंध मिल जाते हैं। न ही हम परंपरागत और बासी विषयों को छोड़ पाते हैं, न ही नए विषयों के बारे में सोच पाते हैं। इसके फलस्वरूप हम मौलिक अभिव्यक्ति से वंचित हो जाते हैं। सभी को अभिव्यक्ति का अधिकार प्राप्त है। यदि नए विषयों के लेखन में इस अधिकार का प्रयोग किया जाए, तो निश्चय से विद्यार्थियों के अभिव्यक्ति कौशल में आशातीत उन्नति होगी। इससे विद्यार्थी न केवल नए विषयों के बारे में चिंतन करेगा, बल्कि अपनी भाषा को भी समृद्ध कर सकेगा।

प्रश्न 6.
रटंत का क्या अर्थ है? क्या यह बुरी लत है? स्पष्ट करो।
उत्तर:
रटंत का अर्थ है किसी के द्वारा लिखी गई पठनीय सामग्री को रटा लगाकर ज्यों-का-त्यों प्रस्तुत करना। इसको बुरी लत भी कहा गया है। हमारे आज के अधिकांश विद्यार्थियों में तोता-रटंत प्रवृत्ति है। शिक्षक कक्षा में उन्हें जो कुछ पढ़ाता है, वे रटा लगाकर याद कर लेते हैं और ज्यों-का-त्यों परीक्षा में लिख आते हैं। इसका दुष्परिणाम यह होता है कि वे हमेशा दूसरों के लिखे पर ही निर्भर रहते हैं। उनमें कुछ मौलिक सोचने की क्षमता विकसित नहीं हो पाती। यही प्रवृत्ति आगे चलकर घातक सिद्ध होती है। लिखना एक कला है। इस कला का विकास तभी हो सकता है, जब वे रटंत प्रवृत्ति पर निर्भर न रहें, वह स्वयं सोचकर लिखें। इसके लिए अभ्यास की आवश्यकता पड़ती है। अतः जो विद्यार्थी बार-बार सोचकर लिखने का प्रयास करेंगे, उनमें निश्चित ही मौलिक प्रतिभा का विकास होगा। किसी प्रसिद्ध व्यक्ति ने कहा है

“करत-करत अभ्यास से जड़मति होत सुजान रसरी आवतु जात ते सिल पर पड़त निशान”
इसलिए विद्यार्थियों तथा लेखकों को रटंत प्रवृत्ति को छोड़कर मौलिक लेखन की ओर ध्यान देना चाहिए। ऐसा करने से ही वे नए और अप्रत्याशित विषयों के लेखन में पारंगत हो सकेंगे।

पाठ से संवाद

प्रश्न 1.
अधूरे वाक्यों को अपने शब्दों में पूरा करें–

1. हम नया सोचने-लिखने का प्रयास नहीं करते क्योंकि ………
2. लिखित अभिव्यक्ति की क्षमता का विकास नहीं होता क्योंकि ………..
3. हमें विचार-प्रवाह को थोड़ा नियंत्रित रखना पड़ता है क्योंकि ….
4. लेखन के लिए पहले उसकी रूपरेखा स्पष्ट होनी चाहिए क्योंकि .
5. लेख में ‘मैं’ शैली का प्रयोग होता है क्योंकि ……….

अभिव्यक्ति और माध्यम (नए और अप्रत्याशित विषयों पर लेखन)
उत्तर:

1. हम नया सोचने-लिखने का प्रयास नहीं करते क्योंकि हमें स्वयं लिखने और अपने भावों को अभिव्यक्त करने का अभ्यास नहीं होता। हम किसी दूसरे द्वारा लिखित पठनीय सामग्री को ज्यों-का-त्यों प्रस्तुत कर देते हैं।
2. लिखित अभिव्यक्ति की क्षमता का विकास नहीं होता क्योंकि हम कुछ नया सोचने या लिखने की कोशिश नहीं करते, बल्कि हम पहले से ही किसी विषय पर लिखी हुई सामग्री का प्रयोग करते हैं।
3. हमें विचार-प्रवाह को थोड़ा नियंत्रित रखना पड़ता है क्योंकि यदि हम अपने विचारों को नियंत्रित करके किसी एक विषय पर लिखने का प्रयास करेंगे, तो हम उस विषय का सही विवेचन कर सकेंगे।
4. लेखन के लिए पहले उसकी रूपरेखा स्पष्ट होनी चाहिए क्योंकि जब तक हमें यह स्पष्ट नहीं होगा कि हमें क्या और कैसे लिखना है, तब तक हम उस विषय को सुनियोजित ढंग से प्रस्तुत नहीं कर पाएंगे।
5. लेख में ‘मैं’ शैली का प्रयोग होता है क्योंकि लेख में लेखक अपने ही विचार प्रस्तुत करता है और लेखन में उसका व्यक्तित्व झलकता है, इसलिए लिखते समय वह कहता है-‘मेरे विचारानुसार’ अथवा ‘मैं ये कह रहा था।

प्रश्न 2.
निम्नलिखित विषयों पर दो से तीन सौ शब्दों में लेख लिखिए
→ बाढ़ का प्रकोप
→ सावन की पहली झड़ी
→ अच्छे दिन
→ दीया और तूफान
→ इम्तहान के दिन
→ मेरा प्रिय टाइमपास
→ मेरे मुहल्ले का चौराहा
→ एक कामकाज़ी औरत की शाम [
उत्तर:
1. बाढ़ का प्रकोप–सूर्य देवता की प्रचण्ड किरणों के ताप से सभी जीव-जन्तु व्याकुल थे। इन्द्र देवता की कृपा-दृष्टि से आकाश में काले बादल छा गए। ठण्डी हवा के साथ ही मूसलाधार वर्षा होने लगी। चारों ओर उल्लास छा गया। लेकिन जब तीन दिन तक वर्षा नहीं रुकी तो लोग घबराने लगे। शीघ्र ही आशंका और भय का वातावरण छा गया। पर्वतीय क्षेत्रों में भारी वर्षा के कारण नदी में बाढ़ आ गई। बाढ़ का पानी अनेक गाँवों को तहस-नहस करता हुआ शहर की ओर बढ़ने लगा। दूर-दूर तक एक विशाल सागर-सा दिखाई दे रहा था। घर, मकान, झोंपड़ियाँ और फसलें सभी कुछ जल-मग्न हो गया। शीघ्र ही पानी ने नगर को चारों ओर से घेर लिया। नगर के चारों ओर बाँध बनाया जाने लगा। रेलवे लाइन पानी में डूब गयी। नौकाओं द्वारा लोगों को सुरक्षित स्थानों पर पहुँचाया जाने लगा। बाढ़ग्रस्त क्षेत्रों में विद्यार्थी, सामाजिक कार्यकर्ता और सरकारी कर्मचारी राहत कार्य के लिए जाने लगे। केन्द्रीय सरकार ने हैलीकॉप्टरों द्वारा खाने की वस्तुएँ और दवाइयाँ पहुचाने का कार्य आरम्भ कर दिया। प्रत्येक मकान में बाढ़ का पानी प्रवेश कर गया। लोग छतों पर बैठे पानी के उतरने की प्रतीक्षा करने लगे। असंख्य लोग तथा पशु इस विनाशकारी बाढ़ के शिकार बन गए। लोगों के घर और खेत बर्बाद हो गए।

2. अच्छे दिन-‘अच्छे दिन’ का अर्थ है जीवन में खुशहाली का आना। सभी प्रकार की उन्नति के साधनों का उपलब्ध होना ही अच्छे दिनों का आना है। किन्तु क्या कभी ऐसा होना सम्भव है? जीवन में यदि एक आवश्यकता पूरी होती है तो तत्काल दूसरी कामना का जन्म हो जाता है। उसके पूरा न होने पर अच्छे दिन होने की कल्पना गायब हो जाती है। आज के समय में ‘अच्छे दिन’ का अर्थ कुछ बदला हुआ रूप लेकर हमारे सामने आया है। इसका अर्थ है कि गरीबी न हो, महँगाई पर पूरा नियन्त्रण हो, दैनिक जीवन के प्रयोग की सभी वस्तुएँ सही कीमत पर उपलब्ध हों आदि। प्रश्न उठता है कि क्या यह सब सम्भव है। यदि सम्भव नहीं है तो अच्छे दिनों का यह नारा व्यर्थ सिद्ध होता है। अच्छे दिन किसी सरकार द्वारा नहीं लाए जा सकते। इन्हें लाने के लिए तो हम सबको मिलकर सहयोग करना पड़ेगा। इसके लिए चोर बाजारी, भ्रष्टाचार आदि को दूर करना होगा। अपनी आवश्यकताओं पर नियन्त्रण रखना होगा। जमाखोरी की भावना को त्यागना होगा। हर कार्य को ईमानदारी से करना होगा। तभी अच्छे दिन आने की सम्भावना बन सकती है।

3. सावन की पहली झड़ी-जेठ और आषाढ़ की भयंकर गर्मी से पूरा संसार तप रहा है। भयंकर लू के कारण पल-भर भी चैन नहीं मिलता। बिजली हर समय नदारद रहती है। जब हवा का चलना बंद हो जाता है, तो घुटन-सी होने लगती है। पसीने से सारा शरीर तर-बतर हो जाता है। न रात को चैन है, न दिन को। घर के सभी प्राणी बिस्तर पर करवटें लेते-लेते कब सो जाते हैं, पता ही नहीं चलता। सभी लोग भगवान से वर्षा के लिए प्रार्थना करते हैं। अब तो सावन का महीना भी लग गया है, लेकिन वर्षा का दूर-दूर तक नामोनिशान नहीं है, केवल गर्मी-ही-गर्मी है। लेकिन आज सुबह जब आँखें खुलीं, तो ऐसा महसूस हुआ कि ठंडी-ठंडी हवा चल रही हो। मैं शीघ्र ही बिस्तर से उठकर बाहर गया। देखा तो आकाश में घने काले बदल छाए हुए थे। सूर्य देवता कहीं नज़र नहीं आ रहा था। ठंडी-ठंडी बयार चल रही थी और नीले-काले बादलों से गड़-गड़ की आवाज़ आ रही थी। थोड़ी देर में हल्की-हल्की बूंदा-बाँदी होने लगी। मेरा मन खुशी से झूम उठा। अचानक हवा चलनी बंद हो गई। मस्त हाथियों जैसे काले-काले बादल ज़ोर-ज़ोर से गरजने लगे। वर्षा की मोटी-मोटी बूंदें टपकने लगीं। इससे पहले कि घर के बाहर बिखरा हुआ सामान भीतर रख पाते, मूसलाधार बारिश शुरू हो गई।

महीनों से प्यासी धरती की प्यास बुझने लगी। पेड़-पौधों के पत्ते धुल रहे थे और उनकी हरी-भरी कांति फिर से दिखाई देने लगी। पक्षी चहचहाने लगे और पानी में नहाने लगे। बच्चे घरों से बाहर आ गए और बारिश के पानी में उछलते-कूदते नहाने लगे। यह सावन की पहली झड़ी थी। थोड़ी देर में, सड़कों तथा गलियों में पानी की नदी-सी बहने लगी। इस बार की सावन की पहली झड़ी बड़ी खुशनुमा लग रही थी। मूसलाधार वर्षा सात-आठ घंटे से लगातार हो रही थी। कुछ लोग तो घबरा गए थे कि पता नहीं ये बरसात क्या करेगी? परंतु कुछ देर के लिए बरसात रुक गई। लोग घरों से बाहर आकर बिखरा सामान समेटने लगे। लगभग एक घंटे बाद फिर से रिमझिम बारिश शुरू हो गई। छत्तों के परनालों से पानी बहना फिर से शुरू हो गया था। अब यह बारिश रुकने का नाम नहीं ले रही थी। मेरे पिता जी ने कहा कि यह शनिवार की झड़ी है अब तो एक सप्ताह बाद ही रुकेगी। मैं मन-ही-मन कामना करने लगा कि भगवान करे ऐसा ही हो। यदि सावन की पहली झड़ी लंबी होगी, तो सूखे खेत फिर से लहलहाने लगेंगे और भरपूर फसल से किसान खुशहाल हो जाएँगे।

4. इम्तहान के दिन इम्तहान के दिन भी क्या दिन हैं। बड़े-बड़े लोग इम्तहान का नाम सुनते ही काँप पड़ते हैं। हर एक के मन में यह डर लगा रहता है कि वह इम्तहान में पास होगा कि फेल होगा? मेरी बारहवीं की परीक्षा के दिन नज़दीक आ चुके हैं। स्कूल में पढ़ते समय बार-बार परीक्षा का डर दिखाया जाता है। घर के लोग भी बार-बार यही याद दिलाते हैं कि भई इम्तहान सिर पर आ चुका है। अब तो मन लगाकर पढ़ लो। यदि पास न हुए तो साल भर का परिश्रम बर्बाद हो जाएगा। भले ही मैंने सारा साल अच्छी तरह से पढ़ाई की हो और टेस्ट भी दिए हो, परंतु इम्तहान का भूत तो हमेशा डराता ही रहता था। पिता जी ने मेरी घबराहट देखकर टयूशन भी लगवा दी, परंतु इम्तहान का डर मन से निकलता नहीं था। आखिर इम्तहान का दिन नज़दीक आ गया। अगले दिन मेरा गणित का पेपर था, मैं रात-भर सो नहीं पाया। सुबह तीन बजे मैंने भगवान से प्रार्थना की कि मेरा बेड़ा पार लगा दो।

यदि मेरा पेपर आज ठीक हो जाए, तो मैं मंदिर में प्रसाद चढ़ाने आऊँगा। यही सोचते-सोचते मेरी आँख लग गई और मुझे नींद आ गई। लगभग सात बजे पिता जी ने आकर उठाया और कहा कि अरे, तुम्हारा तो आज गणित का पेपर है, तुम घोड़े बेचकर सो रहे हो। मैं घबराकर जाग गया। गहरी नींद आने से अब मेरा मन शांत था। ऐसा लगा कि मन की चिंता अब दूर हो गई है। मैंने नहा-धोकर प्रभु का नाम लिया और हल्का-सा भोजन करके इम्तहान देने चला गया। परीक्षा में बैठते ही मैं गणित के प्रश्नों का हल निकालने लगा। पता ही नहीं चला कि कब तीन घंटे बीत गए। मेरा सारा पेपर बड़े संतोषपूर्वक ढंग से हुआ था। कमरे से बाहर आया, तो मन प्रसन्न था। दोस्तों से बातचीत करते हुए मैं घर पहुंचा। अगला पेपर हिंदी का था। उसकी मुझे कोई चिंता नहीं थी। धीरे-धीरे एक के बाद एक सभी पेपर खत्म हो गए। मुझे आशा थी कि मैं अच्छे अंक लेकर उत्तीर्ण हो जाऊँगा। परंतु इन पंद्रह दिनों में यह अनुभव हुआ कि इम्तहान के दिन बड़े तनाव के दिन होते हैं। इन दिनों न ठीक से भूख लगती है, न खेलने को मन करता है। हर वक्त इम्तहान की चिंता लगी रहती है।

5. दीया और तूफान-मिट्टी से बना छोटा-सा दीपक जल रहा है। हवा का झोंका उसे बुझाना चाहता है, परंतु वह अधंकार को दूर भगाने के लिए संघर्ष कर रहा है। उसके द्वारा उत्पन्न किया गया हल्का-सा उजाला आस-पास के वातावरण में आशा की किरण जगाता है। इस घने-काले अंधकार में वह अपने मंद-मंद प्रकाश से लोगों को रास्ता दिखाता है। जैसे ही कोई हवा का झोंका आता है, तो दीये की लौ काँप उठती है। ऐसा लगता है कि यह लौ अंधकार में लीन हो जाएगी। फिर वह दीया टिमटिमाता हुआ पुनः प्रकाश की किरणें बिखेरने लग जाता है। सामने से आता हआ तूफान भी दीपक की लौ को बुझा नहीं पाता।

लगभग यही स्थिति मानव की है। उसके जीवन में अनेक बाधाएँ उत्पन्न होती रहती हैं। दीये के समान वह भी उन बाधाओं का सामना करता हुआ निरंतर आगे बढ़ता रहता है। जो लोग बाधाओं से घबराकर संघर्ष करना छोड़ देते हैं, वे नष्ट हो जाते हैं। परंतु जो निरंतर संघर्ष करते रहते हैं, वे निश्चय से ही अपना लक्ष्य प्राप्त कर लेते हैं। उनकी स्थिति तूफान में दिये के समान होती है। मानव को जीवन की कठिनाइयों से कभी घबराना नहीं चाहिए, बल्कि उनका डटकर सामना करना चाहिए। यदि एक नन्हा-सा दीपक तूफान का सामना कर सकता है, तो फिर मनुष्य क्यों नहीं कठिनाइयों का सामना कर सकता। जो लोग बाधाओं का सामना करके सफलता प्राप्त करते हैं, वे आग में तपे हुए सोने के समान शुद्ध होते हैं। वही समाज के लिए उपयोगी होते हैं। ऐसे लोग न केवल अपना निर्वाण करते हैं, बल्कि समाज के विकास में भी महत्त्वपूर्ण योगदान देते हैं।

6. मेरे मुहल्ले का चौराहा मेरे घर के पास ही चौराहा है। कॉलोनी की चार मुख्य सड़कें इसके आर-पार से गुजरती हैं। कोने पर एक छोटा-सा पार्क है। मुहल्ले के चौराहे पर पीपल का एक विशाल पेड़ है जिसके नीचे मुहल्ले के लोगों ने एक छोटा-सा मंदिर बना रखा है। इस चौराहे पर हर समय हलचल बनी रहती है। पुल से आने वाली कार या रिक्शा इसी चौराहे से गुज प्रकार उत्तर दिशा के वाहन भी इस चौराहे से होकर दक्षिण दिशा में जाते हैं। लोगों के घरों में काम करने वाली औरतें प्रायः इसी पीपल के पेड़ के नीचे बैठी रहती हैं। कुछ मनचले युवक भी यहाँ खड़े दिखाई देते हैं। चौराहे पर खड़ा होकर कोई भी व्यक्ति चारों ओर का नज़ारा देख सकता है। सब्जी और फलों की रेहड़ी वाले यहीं से होकर गुज़रते हैं तथा सांयकाल को यहाँ अपनी रेहड़ियाँ लगा लेते हैं। कॉलोनी की औरतें प्रायः उन्हीं से ही फल और सब्जियाँ खरीदती हैं। सुबह-सवेरे बच्चों की बसें और रिक्शा भी यहीं से निकलती हैं।

कभी-कभी रिक्शा में बैठे छोटे-छोटे बच्चे रोते हुए यहाँ से गुजरते हैं। उनकी ओर कोई ध्यान नहीं देता। क्योंकि वे स्कूल नहीं जाना चाहते। हमारे मुहल्ले का चौराहा बहुत व्यस्त रहता है। कभी-कभी यहाँ आवारा युवक भी खड़े हो जाते हैं तथा आने-जाने वाली लड़कियों तथा युवतियों पर तानाकशी करते हैं। कई बार कॉलोनी के लोगों ने उन्हें समझाया भी पर वे बाज नहीं आए। आखिर एक दिन हमारे मुहल्ले के सूरी साहब ने कुछ पुलिस वालों को वहाँ बुला लिया। चार-पाँच युवक पुलिस की पकड़ में आ गए। उनकी जमकर पिटाई हुई। उसके बाद वे आवारा लड़के चौराहे पर नज़र नहीं आए। फिर भी हमारे मुहल्ले का चौराहा सारी कॉलोनी में प्रसिद्ध है। यहाँ का वातावरण आपेक्षक शांत है। पार्क में अनेक पेड़ लगे हुए हैं। पीपल के पेड़ की छाया तो बड़ी सुखद लगती है। मैं कभी-कभी सांयकाल को इस पेड़ के नीचे जाकर बैठ जाता हूँ।

7. मेरा प्रिय टाइमपास-आज के भौतिकवादी युग में लोग अपने-अपने कामों में व्यस्त हैं। किसी के पास भी इतना समय नहीं है कि वह अपने सगे-संबंधियों के सुख-दुख में भाग ले सके अथवा उनकी सहायता कर सके। कभी-कभी वे अपने दायित्व को पूरा नहीं कर पाते। महानगरों के लोगों की निरंतर भाग-दौड़ लगी रहती है। मैं हरियाणा के नगर में रहता हूँ। प्रातः उठकर मैं नहा-धोकर कलेवा करने के बाद अपने दफ्तर जाता हूँ। दफ्तर में दिन-भर काम का बड़ा बोझ रहता है। कभी-कभी दोपहर का भोजन भी नहीं कर पाता। शाम को लौटकर घर के छोटे-मोटे काम करने पड़ते हैं। फिर भी मैं सात बजे के बाद कुछ समय के लिए खाली हो जाता हूँ। लगभग दो घंटे का समय काटे नहीं कटता। न मुझे टी०वी० देखना अच्छा लगता है, न ही सिनेमा, इसलिए मैंने अपने घर के एक छोटे-से कमरे में पुस्तकालय बना रखा है, जिसमें अंग्रेज़ी, हिंदी, पंजाबी की कुछ पुस्तकें हैं। मैं समय-समय पर नई पुस्तकें भी खरीदता रहता हूँ। टाइमपास करने का मेरा यह तरीका है साहित्यिक पुस्तकें पढ़ना। कभी-कभी तो पढ़ते-पढ़ते मैं इतना मग्न हो जाता हूँ कि मुझे ध्यान ही नहीं रहता कि मैंने रात का भोजन भी करना है। अन्ततः मेरी माँ मुझे आकर डाँटती है और भोजन करने के लिए कहती है।

के टाइमपास करने का सबसे बढ़िया तरीका पस्तकें पढना है, क्योंकि पस्तकें ज्ञान का भंडार होती हैं। दिन-प्रतिदिन नई-नई पुस्तकें पढ़ने से जहाँ ज्ञान की वृद्धि होती है, वहाँ जीवन जीने के ढंग भी सीखने को मिलते हैं। मुंशी प्रेमचंद मेरा प्रिय साहित्यकार है। मैंने उनके उपन्यासों और कहानियों को अनेक बार पढ़ा है। ‘गोदान’ जैसे उपन्यास को तो बार-बार पढ़ने का मन करता है। शनिवार और रविवार को हमारा कार्यालय बंद होता है। इन दो दिनों में मैं खूब पुस्तकें पढ़ता हूँ। यद्यपि लोग टी०वी० देखकर अपना टाइमपास करते हैं, या इंटरनेट, कंप्यूटर पर बैठे हुए अपना समय व्यतीत करते हैं परंतु मैं समझता हूँ कि पुस्तकें पढ़ने से टाइमपास करने का ओर कोई बढ़िया तरीका नहीं हो सकता। इससे हमारे मन तथा मस्तिष्क की थकान खत्म होती है, परिश्रम करने की प्रेरणा मिलती है और समाज को समझने और जाँचने का संदेश मिलता है। टाइमपास करने का ऐसा ढंग होना चाहिए कि जिससे हमारा टाइम बर्बाद न हो क्योंकि समय सर्वाधिक मूल्यवान होता है। इसे व्यर्थ नहीं गँवाना चाहिए, बल्कि समय को किसी सार्थक काम में काम लगाना चाहिए। पुस्तकें हमारे जीवन की साथी होती हैं। इन्हें पढ़ने से जहाँ ज्ञान की प्राप्ति होती है, वहाँ हमें जीवन के लिए संदेश भी मिलता है।

8. एक कामकाजी औरत की शाम-हमारे देश के मध्यवर्गीय परिवारों में पति-पत्नी दोनों को ही धन कमाने के लिए काम करना पड़ता है। एक ज़माना था, जब एक कमाता था, दस लोग खाते थे। परंतु आज वह ज़माना नहीं रहा। महँगाई के कारण सुख से जीना बड़ा कठिन हो गया है। इसलिए पति के साथ-साथ पत्नी भी कोई-न-कोई काम कर रही है। परंतु कामकाजी औरतों का जीवन पुरुषों की अपेक्षा बड़ा कठिन है। वह घर के साथ-साथ बाहर के कामों को भी सँभालती है। दफ़्तर से छुट्टी मिलने के बाद ही उसकी शाम शुरू हो जाती है। हमारे पड़ोस में राधेश्याम की पत्नी सरकारी दफ्तर में नौकरी करती है। छुट्टी मिलते ही वह रास्ते से फल और सब्जियाँ लेकर घर लौटती है। कभी-कभी उसे करियाने का सामान भी खरीदना होता है। उसके आने से पहले पति और बच्चे घर आ जाते हैं। वह भी दिन-भर की थकी-हारी होती है और कुछ आराम करना चाहती है, परंतु उसके भाग्य में आराम कहाँ? वह पति और अपने लिए चाय बनाती है और बच्चों के लिए कुछ पकाती है।

चाय पीते समय ही वह पति और बच्चों का हाल-चाल पूछती है। पति महोदय तो चाय पीकर घूमने के लिए बाहर निकल जाते हैं लेकिन वह बेचारी घर के काम-काज में व्यस्त हो जाती है। काम करते-करते शाम के सात बज जाते हैं। इसके बाद वह एक घंटे के लिए बच्चों की होमवर्क करने में सहायता करती है। इसी बीच उसे आस-पड़ोस के घरों में आना-जाना पड़ता है। इसके बाद वह रात का खाना तैयार करती है। उसका भी मन करता है कि वह टी०वी० के सीरियल देखे और अपना मनोरंजन करे, लेकिन कामकाजी औरत होने के कारण उसके पास खाली समय नहीं है। कभी वह पति की फरमाइश को पूरा करती है, कभी बच्चों की फरमाइश को। लगता है कामकाजी औरत की शाम दिन से अधिक कठिन है। उसका जीवन घड़ी की सुई के समान निरंतर गतिशील रहता है। मैं सोचता हूँ कि विधाता ने कामकाजी औरत के जीवन में सुख लिखा ही नहीं।

प्रश्न 3.
घर से स्कूल तक के सफर में आज आपने क्या-क्या देखा और अनुभव किया? लिखें और अपने लेख को एक अच्छा-सा शीर्षक भी दें।
उत्तर:
घर से स्कूल तक सफर
मेरा विद्यालय मेरे घर से लगभग 4 किलोमीटर दूर है। मैं प्रातःकाल साइकिल पर सवार होकर घर से स्कूल के लिए चल पड़ता हूँ, क्योंकि मेरे गाँव में केवल एक ही प्राइमरी स्कूल है। बड़ी कक्षाओं के लिए पास के गाँव में जाना पड़ता है जहाँ पर एक उच्चतर माध्यमिक विद्यालय है। गाँव की सड़क बड़ी ही ऊबड़-खाबड़ है। लगभग 4 वर्ष पहले इस सड़क का निर्माण हुआ था। इस पर अब ट्रैक्टर, ट्रालियाँ, बसें, कारें, ट्रक भी चलते रहते हैं। हमारे गाँव की सड़क मुख्य सड़क से जुड़ी है। सड़क पर जगह-जगह गड्ढे हैं। गाँव से बाहर निकलते ही मेरा सामना सामने हरे-भरे खेतों से होता है। सड़क के दोनों ओर वृक्ष लगे हैं। खेतों में स्त्री-पुरुष काम करते दिखाई देते हैं। कुछ किसान खेतों में ट्रैक्टर द्वारा हल चलाते देखे जा सकते हैं। प्रायः ग्रामीण स्त्रियाँ पशुओं के लिए चारा काटती हैं। यहाँ-वहाँ ट्यूबवैल भी लगे हैं। हम अपनी प्यास बुझाने के लिए यहीं का पानी पीते हैं। रास्ते में आते-जाते वाहन मिलते रहते हैं। मैं सावधान होकर साइकिल चलाता हूँ क्योंकि पिछले दिनों मेरा साथी मोटरसाइकिल से टकरा गया था जिससे उसको चोटें लगी थीं। कभी-कभी रास्ते में बस भी मिल जाती है जिसमें यात्री खचाखच भरे होते हैं। कुछ यात्री तो बस क ते हैं। इस सड़क पर थ्री-विलर और जीपें भी चलती हैं। ये वाहन लोगों को नगर तक पहँचाते हैं। जिन दिनों फसल पक कर तैयार हो जाती है, तब किसान उस फसल को ट्रालियों में भरकर बाहर की मंडी में ले जाते हैं। सड़क पर मैं तेज साइकिल नहीं चला सकता क्योंकि सड़क पर अनके गड्ढे हैं और हमेशा गिरने का भय लगा रहता है।

गाँव की पंचायत अनेक बार सरकार को पत्र लिख चुकी है कि वह इस सड़क की मरम्मत करा दे। परंतु अधिकारियों के कान पर जूं नहीं रेंगती। चुनाव के दिनों में यहाँ-वहाँ मरम्मत कर दी जाती है। चुनाव खत्म होते ही सड़कों का हुलिया फिर से बिगड़ जाता है। किंतु मुझे यह सड़क बहुत अच्छी लगती है। क्योंकि यहाँ खुली हवा है और प्रदूषण न के बराबर है। जिस बड़े गाँव में मेरा स्कूल है, वहाँ काफी भीड़ रहती है। आसपास कई दुकानें हैं, परंतु मैं इन सबसे बचते-बचाते स्कल पहँच जाता हूँ। मैं कई बार कि क्या ऐसी सरकार भी आएगी जो गाँवों की बिगड़ी हालत को सुधारने का काम करेगी।

प्रश्न 4.
आपने आसपास की किसी ऐसी चीज पर एक लेख लिखें, जो आपको किसी वजह से वर्णनीय प्रतीत होती हो। वह कोई चाय की दुकान हो सकती है, कोई सैलून हो सकता है, कोई खोमचेवाला हो सकता है या किसी खास दिन पर लगनेवाला हाट-बाज़ार हो सकता है। विषय का सही अंदाज़ा देनेवाला शीर्षक अवश्य दें।
उत्तर:
संडे बाजार अथवा ‘रविवारीय हाट-बाज़ार’
हमारे नगर में सार्वजनिक पार्क के पास एक बहुत बड़ा मैदान खाली पड़ा है। जिले के उपायुक्त ने हर रविवार को वहाँ मंडी आरंभ करने का निर्णय किया था। इस मंडी में प्रत्येक रविवार को गाँव के किसान अपने खेतों की ताजी सब्जियाँ सस्ते दामों पर बेचने आते थे। साँयकाल 4 बजे किसान लोग ट्रैक्टर-ट्रालियों में भरकर सब्जी यहाँ लाते थे और स्वयं उसे बेचते थे। था-बिचौलियों की मुनाफाखोरी को समाप्त करना। वस्तुतः उपायुक्त महोदय की अच्छी सोच थी जो कि नगर के लोगों को काफी पसंद आई, लेकिन धीरे-धीरे यह मंडी संडे बाज़ार का रूप धारण करने लगी। अब यहाँ मुख्य सड़क के दोनों ओर व्यापारी रेडिमेड गारमेन्टस और प्रतिदिन के प्रयोग की वस्तुएँ बेचने के लिए प्रातःकाल ही अपनी दुकानें सजा लेते हैं। वस्तुतः ये दुकानदार बड़ी दुकानों के एजेंट होते हैं और वे बाज़ार की वस्तुएँ यहाँ पर बेचते हैं।

संडे बाज़ार से आप सस्ते कपड़े, जूते, चाय, चीनी, मोजे, बर्तन आदि सब कुछ खरीद सकते हैं। संडे बाज़ार में काफी चहल-पहल होती है। यहाँ-वहाँ खोमचे वाले खड़े होते हैं। चाय की भी दुकानें हैं और हलवाई की दुकानें भी हैं। सस्ते मोबाइल, रेडियो आदि इलैक्ट्रॉनिक चीजें भी यहाँ उपलब्ध हो जाती हैं। यहाँ दिन भर काफी भीड़ लगी रहती है। नगर भर के लोग यहाँ सस्ता सामान खरीदने आते हैं। अनजान व्यक्ति तो यहाँ धोखा खा जाता है। इस मंडी में अनेक बार लोगों की जेबें भी कट जाती हैं पुलिस का कोई बंदोबस्त नहीं है। दुकानदार ऊँची आवाज़ में ग्राहक को आवाजें देते हैं। जो समझदार ग्राहक होते हैं वही उचित मूल्य पर वस्तुएँ खरीद सकते हैं। साथ ही दुकानदार कह देते हैं कि बिका हुआ माल वापिस नहीं होगा।

पास में सब्जी और फलों की दुकानें भी हैं। इसी को लोग अपनी मंडी कहते हैं, परंतु यहाँ मुख्य मंडी के दुकानदार ही सब्जी बेचने आते हैं। वे मनमाने दामों पर सब्जियाँ बेचते हैं। लगभग चार बजे गाँव के कुछ किसान भी सब्जियाँ लेकर यहाँ पहुँच जाते हैं। गोभी, पालक, बैंगन, मूली, गाजर, टमाटर आदि हरी सब्जियाँ यहाँ उपलब्ध हो जाती हैं। उनके दाम भी सही होते हैं। जो ग्राहक संडे बाजार को अच्छी तरह समझते हैं, वे इन्हीं किसानों से सब्जी खरीदते हैं। यह बाज़ार सुबह 10 बजे खुलता है तथा रात 9 बजे तक खुला रहता है। यहाँ सरकार द्वारा बिजली का प्रबंध तो है, परंतु कोई शैड नहीं बना। इसलिए दुकानदार स्वयं ही कोई तरपाल या शामियाना लगाकर सामान बेचते रहते हैं। मैं समझता हूँ कि यह संडे बाज़ार गरीब ग्राहकों का अच्छा सहारा है क्योंकि यहाँ पर मुख्य बाज़ार की अपेक्षा सस्ती वस्तुएँ मिल जाती हैं।

Haryana State Board HBSE 7th Class Maths Solutions Chapter 2 भिन्न एवं दशमलव Ex 2.5 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 2 भिन्न एवं दशमलव Ex 2.5

प्रश्न 1.
कौन बड़ा है ?
(i) 0.5 अथवा 0.05
(ii) 0.7 अथवा 0.5
(iii) 7 अथवा 0.7
(iv) 1.37 अथवा 1.49
(v) 2.03 अथवा 2.30
(vi) 0.8 अथवा 0.88.
हल :
(i) 0.5 अथवा 0.05 की तुलना :
दोनों दशमलव संख्याओं में पूर्णांक शून्य है। अत: दोनों पूर्णांक बराबर हैं। अब दशमलव के बाद दाईं ओर की संख्याओं को देखते हैं। पहली संख्या में पहला अंक 5 तथा दूसरी संख्या में अंक 0 है।
∴ 5 > 0
अतः 0.5 > 0.05

(ii) 0.7 अथवा 0.5 की तुलना :
दोनों दशमलव संख्याओं में पूर्णाक शून्य समान है तथा दशमलव के बाद दाईं ओर पहली संख्या में 7 तथा दूसरी संख्या में 5 है।
∴ 7 > 5
अत: 0.7 > 0.5

(iii) 7 और 0.7 की तुलना:
पहली संख्या में पूर्णांक 7 तथा दूसरी संख्या में पूर्णांक 0 है।
∴ 7 > 0
अत: 7 > 0.7

(iv) 1.37 और 1.49 की तुलना :
दोनों दशमलव संख्याओं के पूर्णांक 1, 1 हैं। अत: ये समान हैं। अब दशमलव के बाद सबसे पहले दाईं ओर वाले अंक 3 व 4 हैं।
3 < 4
अत: 1.37 < 1.49

(v) 2.03 तथा 2.30 की तुलना :
यहाँ पूर्णांक वाले भाग समान हैं। अत: दशमलव के बाद सबसे पहले दाईं ओर वाले अंक 0 व 3 हैं। 0 < 3 अर्थात् 3 > 0
अत: 2.30 > 2.03

(vi) 0.8 और 0.88 की तुलना :
दोनों संख्याओं के पूर्णांक 0 हैं। अतः ये समान हैं और दशमलव के बाद सबसे पहले दाई ओर वाले अंक 8, 8 भी समान हैं। अत: दुसरे अगले अंक में 0 तथा 8 हैं।
∴ 8 > 0
अत: 0.88 > 0.8

प्रश्न 2.
दशमलव का उपयोग करते हुए निम्नलिखित को रुपये के रूप में व्यक्त कीजिए:
(i) 7 पैसे
(ii) 7 रुपये 7 पैसे
(iii) 77 रुपये 77 पैसे
(iv) 50 पैसे
(v) 235 पैसे
हल :
(i) 7 पैसे = \(\frac {7}{100}\)रु. = 0.07 रु.
(∵ 100 पैसे = 1 रुपया)

(ii) 7 रु. 7 पैसे = 7 रु. + \(\frac {7}{100}\)रु.
(∵ 100 पैसे – 1 रु.)
= 7 रु. + 0.07 रु. = 7.07 रु.

(iii) 77 रु. 77 पैसे = 77 रु. + \(\frac {77}{100}\)रु.
(∵ 100 पैसे = 1 रु.)
= 77 रु. + 0.77 रु. = 77.77 रु.

(iv) 50 पैसे = \(\frac {50}{100}\) रु. (∵ 100 पैसे = 1 रु.)
= 0.50 रु.

(v) 235 पैसे = \(\frac {235}{100}\)रु. (∵ 100 पैसे = 1 रु.)
= 2.35 रु.

प्रश्न 3.
(i) 5 सेमी को मीटर एवं किमी में व्यक्त कीजिए।
(ii) 35 मिमी को सेमी,मीटर एवं किमी में व्यक्त कीजिए।
हल :
(i) 5 सेमी = \(\frac {5}{100}\) मीटर = 0.05 मीटर
(∵ 1 मीटर = 100 सेमी)
5 सेमी = \(\frac{5}{100 \times 1000}\) किमी,
(∵ 1000 मीटर =1 किमी) (1000 × 100 सेमी = 1 किमी )
= \(\frac {5}{100000}\)
= 0.00005 किमी।

(ii) 35 मिमी = \(\frac {35}{10}\) सेमी = 3.5 सेमी
35 मिमी = \(\frac{35}{10 \times 100}\) मीटर = \(\frac {35}{1000}\) मीटर
= 0.035 मीटर
35 मिमी = \(\frac{35}{10 \times 100 \times 1000}\) किमी
= \(\frac{35}{1000000}\) किमी
= 0.000035 किमी।

प्रश्न 4.
निम्नलिखित को किग्रा में व्यक्त कीजिए :
(i) 200 ग्राम
(ii) 3470 ग्राम
(iii) 4 किग्रा 8 ग्राम
हल :
(i) 200 ग्राम = \(\frac {200}{1000}\) किग्रा
(∵ 1000 ग्राम = 1 किग्रा)
= \(\frac {2}{10}\) किग्रा।

(ii) 3470 ग्राम = \(\frac {3470}{1000}\) किग्रा
(∵ 1000 ग्राम = 1 किग्रा)
= 3.47 किग्रा।

(iii) 4 किग्रा 8 ग्राम = 4 किग्रा +8 ग्राम
= 4 किग्रा + \(\frac {8}{1000}\)किग्रा
(∵ 1000 ग्राम = 1 किग्रा)
= 4 किग्ना + 0.008 किग्ना
= 4.008 किया।

प्रश्न 5.
निम्नलिखित दशमलव संख्याओं को विस्तारित रूप में लिखिए :
(i) 20.03
(ii) 2.03
(iii) 200.03
(iv) 2.034
हल :

प्रश्न 6.
निम्नलिखित दशमलव संख्याओं में 2 का स्थानीय मान लिखिए :
(i) 2.56
(ii) 21.37
(iii) 10.25
(iv) 9.42
(v) 63.352
हल :
(i) 2 का स्थानीय मान संख्या 2.56 में 2 इकाई है।
(ii) 2 का स्थानीय मान संख्या 21.37 में 2 दहाई है।
(iii) 2 का स्थानीय मान संख्या 10.25 में 2 दसवाँ भाग है।
(iv) 2 का स्थानीय मान संख्या 9.42 में 2 सौवाँ भाग
(v) 2 का स्थानीय मान संख्या 63.352 में 2 हजारवाँ भाग है।

प्रश्न 7.
दिनेश स्थान A से स्थान B तक गया और वहाँ से स्थान C तक गया। 4 से B की दूरी 7.5 किमी और B से C की दूरी 12.7 किमी है। अयूब स्थान 4 से स्थान D तक गया और वहाँ से वह स्थान C को गया। 4 से 7 की दूरी 9.3 किमी और D से C की दूरी 11.8 किमी है। किसने ज्यादा दूरी तय की और वह दूरी कितनी अधिक थी ?

हल :
दिनेश द्वारा तय की गई दूरी
= AB + BC
= 7.5 किमी + 12.7 किमी
= 20.2 किमी
अयूब द्वारा तय की गई दूरी
= AD + DC
= 9.3 किमी + 11.8 किमी
= 21.1 किमी
स्पष्ट है, 20.2 < 21.1 अतः अयूब ने अधिक दूरी तय की = 21.1 किमी – 20.2 किमी = 0.9 किमी। उत्तर प्रश्न 8. श्यामा ने 5 किग्रा 300 ग्राम सेब और 3 किग्रा 250 ग्राम आम खरीदे। सरला ने 4 किग्रा 800 ग्राम संतरे और 4 किग्रा 150 ग्राम केले खरीदे। किसने अधिक फल खरीदे? हल : श्यामा ने फल खरीदे = 5 किग्रा 300 ग्राम सेब +3 किग्रा 250 ग्राम आम = 8 किग्रा 550 ग्राम = 8.550 किग्रा और सरला ने फल खरीदे = 4 किग्रा 800 ग्राम संतरे + 4 किग्ना 150 ग्राम केले = 8 किग्रा 950 ग्राम । = 8.950 किग्रा स्पष्ट है, 8.950 > 8.550,
अतः सरला ने अधिक फल खरीदे।

प्रश्न 9.
28 किमी, 42.6 किमी से कितना कम है ?
हल:
अन्तर = 42.6 किमी. – 28.0 किमी
= 14.6 किमी
अत: 28 किमी, 42.6 से 14.6 किमी कम है। उत्तर

Haryana State Board HBSE 7th Class Maths Solutions Chapter 14 सममिति InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 14 सममिति InText Questions

प्रयास कीजिए (पृष्ठ सं. 288)

प्रश्न 1.
(a) क्या अब आप एक समबाहु त्रिभुज के लिए, घूर्णन सममिति के क्रम को बता सकते हैं ?

(b) जब उपरोक्त त्रिभुज को उसके केन्द्र के परित : (चारों ओर) 120° के कोण पर घुमाया जाता है, तो कितनी स्थितियों में त्रिभुज (स्थिति के अनुसार) पहले जैसा ही लगता है ?
हल :
(a) पूरे चक्र की तीन स्थितियों में कोण 120°, 240° और 360° के घूर्णन पर त्रिभुज पहले जैसा दिखाई देगा, अतः हम कह सकते हैं कि इसमें क्रम 3 की घूर्णन सममिति होगी।

(b) यहाँ केवल एक ही स्थिति है जहाँ त्रिभुज पहले जैसा दिखाई देगा, जब इसको केन्द्र के परित घुमाया जाएगा।

प्रश्न 2.
निम्नलिखित में से कौन-से आकारों में अंकित बिन्दु के परित : (चारों ओर) घूर्णन सममिति है ?

हल :
हम जानते हैं कि जब कोई आकृति एक कोण के द्वारा एक बिन्दु पर घूर्णन करती है और पहले जैसा दिखाई देती है तो इसे घूर्णन समिमित कहते हैं।
आकृति (i), (ii), (iii) और (iv) में घूर्णन सममिति है।

पृष्ठ सं. 289

प्रश्न 1.
दी हुई आकृतियों के लिए × से अंकित बिंदु के परित घूर्णन सममिति का क्रम बताइए।

हल :
(i) आकृतियों के लिए × से अंकित बिन्दु से परित घूर्णन सममिति क्रम है,

माना आयत को ऊर्ध्वाधर सिरे पर A लगाते हैं। हम देखते हैं कि पहले जैसा दिखने के लिए (×) के परितः 90° के चार घूर्णनों की आवश्यकता होगी।
अतः आकृति में क्रम 4 की घूर्णन सममिति होगी।

(ii) आकृति के संदर्भ में घूर्णन क्रम ज्ञात करना-

स्पष्ट है आकृति को 120° के कोण की तीन घूर्णनों की (×) के परितः आवश्यकता होगी जिसमें यह पहले वाली स्थिति में होगा। अत: इसमें क्रम 3 की घूर्णन सममिति होगी।

(iii) आकृति के संदर्भ में घूर्णन क्रम ज्ञात करना-

स्पष्ट है कि इसको पहले जैसा दिखने के लिए (×) के परित : 90° के कोण की चार घूर्णनों की आवश्यकता होगी। अतः इसमें क्रम 4 की घूर्णन सममिति होगी।

इन्हें कीजिए (पृष्ठ सं. 291)

प्रश्न 1.
अंग्रेजी वर्णमाला के कुछ अक्षरों में अद्भुत एवं आकर्षक सममितीय संरचनाएँ (structures) हैं। किन बड़े अक्षरों में केवल एक ही सममित रेखा है (जैसे E) ? किन बड़े अक्षरों में क्रम 2 की घूर्णन सममिति है (जैसेI)?
उपरोक्त प्रकार से सोचते हुए, आप निम्नलिखित सारणी को भरने में समर्थ हो पाएँगे।

हल :
दी गई सारणी को भरने पर-

Haryana State Board HBSE 10th Class Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.4 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 7 निर्देशांक ज्यामिति Exercise 7.4

प्रश्न 1.
बिंदुओं A(2,-2) और B(3, 7) को जोड़ने वाले रेखाखंड को रेखा 2x +y-4 = 0 जिस अनुपात में विभाजित करती है उसे ज्ञात कीजिए।
हल :
माना रेखा 2x + y – 43 = 0 बिंदुओं A (2,-2) और B (3,7) को जोड़ने वाले रेखाखंड को बिंदु P पर k:1 के अनुपात में विभाजित करती है, तो

या 2 (3k + 2) + (7k-2)-4 (k+ 1) = 0
या 6k + 4 + 7k – 2 – 4k – 4 = 0
या 9k – 2 = 0
या 9k = 2
या k = \(\frac{2}{9}\)
अतः वांछित अनुपात = 2 : 9

प्रश्न 2.
x और ” में एक संबंध ज्ञात कीजिए, यदि बिंदु (x,y), (1, 2) और (7,0) सरेखी हैं।
हल :
A(x,y), B(1,2) और (7,0) संरेखी बिंदु तभी होंगे जब इनसे बनने वाले त्रिभुज का क्षेत्रफल शून्य होगा।
\(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
या \(\frac{1}{2}\)[x(2 – 0)+1(0 – y)+7(y -2)] = 0
या \(\frac{1}{2}\)[2x – 1(y – y) + 7y – 14] = 0
या \(\frac{1}{2}\)[[2x + 6y – 14] = 0
x + 3y – 7 = 0

प्रश्न 3.
बिंदुओं (6,-6), (3,-7) और (3, 3) से होकर जाने वाले वृत्त का केंद्र ज्ञात कीजिए।
हल :

माना O(x, y) उस वृत्त का केंद्र है जो बिंदुओं
A (6-6), B (3-7) तथा C (3, 3), A (6,-6) से होकर जाता है, तो OA = OB = OC (वृत्त की त्रिज्याएँ)
(OA)² = (OB)² = (OC)²
(OA)² = (OB)²
(x-6)² + (y + 6)² = (x – 3)²+ (y + 7)²
x² + 36 – 12x + 12 + 36 + 12 = x² + y² + 9 – 6x + y² + 49 + 14y
x² + y² + 12y – 12x + 72 = x² + y² – 6x + 14y + 58
12y- 12x + 6x – 14y = 58 – 72
-6x – 2y= – 14
3x + y = 7 (दोनों ओर – 2 भाग करने पर)
इसी प्रकार (OB)² = (OC)²
(x -3)² + (y+ 7)² = (x – 3)² + (y – 3)²
या y² + 49 + 14y = y² + 9 – 6y
या 14y + 6y = 9-49
या 20y = – 40
या y = -40/20 = -2
y का मान समीकरण (i) में रखने पर
3x – 2 = 7
या 3x = 7 + 2
x = \(\frac{9}{3}\) = 3
अतः वृत्त का केंद्र 0 (3, -2) है।

प्रश्न 4.
किसी वर्ग के दो सम्मुख शीर्ष (-1, 2) और (3, 2) हैं। वर्ग के अन्य दोनों शीर्ष ज्ञात कीजिए।
हल :

माना A(-1, 2) तथा C (3, 2) दिए गए वर्ग ABCD के दो सम्मुख शीर्ष हैं तथा B (x, y) एक अज्ञात शीर्ष है, तो
AB = BC
AB² = BC²
(x + 1)² + (y – 2)² = (x – 3)² + (y – 2)²
x² + 1 + 2x + y² + 4 – 4y = x² + 9 – 6x + y² + 4 – 4y
2x – 4y + 6x + 4y = 13 -5
8x = 8
x = \(\frac{8}{8}\) = 1

इसी प्रकार AB² + BC² = AC² [:: ZB = 90°]
(x + 1)² + (y – 2)² + (x – 3)² + (y – 2)² = (3 + 1)² + (2 – 2)²
x² + 1 + 2x + y² + 4 – 4y + x² + 9 – 6x + y² + 4 – 4y = 16
2x² + 2y² – 4x – 8y = 16 – 18
2x² + 2y² – 4x – 8y = -2
x² + y² – 2x – 4y = – 1 (दोनों ओर 2 से भाग करने पर)
x = 1 प्रतिस्थापित करने पर
(1)² + y² – 2 (1) – 4y = -1
1 + y² – 2 – 4y + 1 = 0
y² – 4y = 0
y(y – 4)= 0
y = 0 या y -4 = 0
y = 0 या y = 4
अतः वर्ग के अन्य शीर्ष (1,0) व (1, 4) हैं।

प्रश्न 5.
कृष्णानगर के एक सेकेंडरी स्कूल के कक्षा X के विद्यार्थियों को उनके बागवानी क्रियाकलाप के लिए, एक आयताकार भूखंड दिया गया है। गुलमोहर की पौध (sapling) को परस्पर 1 m की दूरी पर इस भूखंड की परिसीमा (boundary) पर लगाया जाता है। इस भूखंड के अंदर एक त्रिभुजाकार घास लगा हुआ लॉन (Lawn) है, जैसाकि संलग्नआकृति में दर्शाया गया है। विद्यार्थियों को भूखंड के शेष भाग में फूलों के पौधे के बीज बोने हैं।
(i) A को मूलबिंदु मानते हुए, त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए।
(ii) यदि मूलबिंदु C हो, तो APQR के शीर्षों के निर्देशांक क्या होंगे? . साथ ही, उपरोक्त दोनों स्थितियों में, त्रिभुजों के क्षेत्रफल ज्ञात कीजिए। आप क्या सोचते हैं?

हल :
(i) प्रश्नानुसार A मूलबिंदु तथा AD को x-अक्ष व AB को y-अक्ष मानते हुए त्रिभुज PQR के शीर्षों के निर्देशांक होंगे- P(4, 6), Q (3, 2) व R (6, 5)
यहाँ पर x₁ = 4, y₁ = 6, x₂ = 3, y₂ = 2, x₃ = 6, y₃ = 5
∆POR का क्षेत्रफल = \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[4(2- 5)+3(5-6)+6(6-2)]
= \(\frac{1}{2}\)[(4) (-3) + (3)(-1)+6 (4)]
= \(\frac{1}{2}\)[-12 – 3 + 24]
=\(\frac{1}{2}\) x 9 = 4.5 वर्ग मात्रक

(ii) यदि C को मूलबिंदु तथा CB तथा CD को x-अक्ष व y-अक्ष मानें तो∆PQR के शीर्षों के निर्देशांक होंगे P(1, 2, 2), Q (13, 6) व R (10, 3)
यहाँ पर x₁ = 12, y₁ = 2, x₂ = 13, y₂ = 6, x₃ = 10,y₃ = 3
∆PQR का क्षेत्रफल =\(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[12(6-3)+13(3-2)+10 (2-6)]
= \(\frac{1}{2}\)[12 x 3 + 13 x 1 + 10(-4)]
= \(\frac{1}{2}\)[36 + 13 -40]
= \(\frac{1}{2}\) x 9 = 9/2 = 4.5 वर्ग मात्रक
अतः दोनों अवस्थाओं में त्रिभुज का क्षेत्रफल समान है।

प्रश्न 6.
एक त्रिभुज ABC के शीर्ष A(4, 6), B(1, 5) और C(7, 2) हैं। भुजाओं AB और AC को क्रमशः D और E पर प्रतिच्छेद करते हुए एक रेखा इस प्रकार खींची गई है कि \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{1}{4}\) है। ∆ADE का क्षेत्रफल परिकलित कीजिए और इसकी तुलना AABC के क्षेत्रफल से कीजिए।(प्रमेय 6.2 और प्रमेय 6.6 का स्मरण कीजिए।)
हल :

प्रश्नानुसार

अतः D और E, क्रमशः AB और AC को 1 : 3 के अनुपात में विभाजित करते हैं।
D के निर्देशांक

अब ΔADB के क्षेत्रफल के लिए
x₁ = 4, y₁ = 6, x₂ = 13/4, y₂ = 23/4 x₃ = 19/4 y₃ = 5
∴ ΔADE का क्षेत्रफल = \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

ΔABC का क्षेत्रफल के लिए-
x₁ = 4, y₁ = 6, x₂ = 1, y₂ = 5 x₃ = 7 y₃ = 2
ΔABC का क्षेत्रफल = \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\) [4(5 – 2) + 1(2-6) + 7(6-5)]
= \(\frac{1}{2}\)[12-4+7]
= \(\frac{1}{2}\) – 15 = 15/2 वर्ग मात्रक

ΔADE का क्षेत्रफल : ΔABC का क्षेत्रफल = 1 : 16

प्रश्न 7.
मान लीजिए A(4, 2), B(6, 5) और C(1, 4) एक त्रिभुज ABC के शीर्ष हैं।
(i) A से होकर जाने वाली माध्यिका BC से D पर मिलती है। बिंदु D के निर्देशांक ज्ञात कीजिए।
(ii)AD पर स्थित ऐसे बिंदु Pके निर्देशांक ज्ञात कीजिए कि AP : PD = 2 : 1 हो।
(iii) माध्यिकाओं BE और CF पर ऐसे बिंदुओ Q और R के निर्देशांक ज्ञात कीजिए कि BQ : OE = 2:1 हो और CR : RF = 2 : 1 हो।
(iv) आप क्या देखते हैं?
[नोट : वह बिंदु जो तीनों माध्यिकाओं में सार्वनिष्ठ हो, उस त्रिभुज का केंद्रक (centroid) कहलाता है और वह प्रत्येक माध्यिका को 2 :1 के अनुपात में विभाजित करता है।
(v) यदि A(x₁, y₁), B(x<sub<2, y₂) और C(x₃, y₃) त्रिभुज ABC के शीर्ष हैं, तो इस त्रिभुज के केंद्रक के निर्देशांक ज्ञात कीजिए।
हल :
(i) क्योंकि A से होकर जाने वाली माध्यिका AD भुजा BC को D पर मिलती है इससे पता चलता है कि D, BC का मध्य-बिंदु है।

(ii) प्रश्नानुसार, AP : PD = 2 : 1

(iii) क्योंकि BE शीर्ष B से माध्यिका है इसलिए E, AC का मध्य-बिंदु होगा।


(iv) हम देखते हैं कि P, Q तथा R के निर्देशांक समान हैं। इसलिए P, Q तथा R एक ही बिंदु है। इसे त्रिभुज का केंद्रक कहते हैं।
(v) हम जानते हैं कि त्रिभुज का केंद्रक प्रत्येक माध्यिका को शीर्ष से 2 : 1 के अनुपात में विभाजित करता है। माना D, BC
का मध्य-बिंदु है, तो D\(\mathrm{D}\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)\)
माना G(x,y) त्रिभुज ABC का केंद्रक है तो AG : GD = 2 : 1

प्रश्न 8.
बिंदुओं A(-1,-1), B(-1, 4), C(5, 4) और D(5,-1) से एक आयत ABCD बनता है। P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। क्या चतुर्भुज PQRS एक वर्ग है? क्या यह एक आयत है? क्या यह एक समचतुर्भुज है? सकारण उत्तर दीजिए।
हल :
यहाँ पर आयत ABCD के शीर्ष A(-1,-1), B(-1, 4), C(5,4) तथा D(5,-1) हैं। क्योंकि P, Q, R तथा S क्रमशः AB, BC, CD तथा DA के मध्य-बिंदु हैं इसलिए इनके निर्देशांक होंगे-


अब क्योंकि PQ = QR = RS = SP
परंतु PR ≠ Qs
∴ PQRS एक समचतुर्भुज है।

Haryana State Board HBSE 7th Class Maths Solutions Chapter 3 आँकड़ो का प्रबंधन Ex 3.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 3 आँकड़ो का प्रबंधन Ex 3.1

प्रश्न 1.
अपनी कक्षा के किन्हीं दस (10) विद्यार्थियों की ऊँचाइयों का परिसर ज्ञात कीजिए।
हल :
माना कक्षा के किन्हीं दस (10) विद्यार्थियों की ऊँचाई (सेमी में)
148, 150, 146, 152, 155, 140, 160, 158, 147 और 142 है।
आरोही क्रम में व्यवस्थित करने पर
140, 142, 146, 147, 148, 150, 152, 155, 158 और 160
विद्यार्थियों की ऊँचाइयों का परिसर
= 160 – 140 = 20 सेमी।

प्रश्न 2.
कक्षा के एक मूल्यांकन में प्राप्त किए गए निम्नलिखित अंकों को एक सारणीबद्ध रूप में संगठित कीजिए :
4, 6, 7, 5, 3, 5, 4, 5, 2, 6
2, 5, 1, 9, 6, 5, 8, 4, 6, 7
(i) सबसे बड़ा अंक कौन-सा है?
(ii) सबसे छोटा अंक कौन-सा है?
(iii) इन आँकड़ों का परिसर क्या है ?
(iv) अंकगणितीय माध्य ज्ञात कीजिए।
हल :
अंकों को सारणीबद्ध रूप में लिखने पर,

(i) सबसे बड़ा अंक = 9
(ii) सबसे छोटा अंक = 1
(iii) परिसर = 9 – 1 = 8
(iv) माध्य = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}=\frac{100}{20}\) = 5

प्रश्न 3.
प्रथम 5 पूर्ण संख्याओं का माध्य ज्ञात कीजिए।
हल :
प्रथम 5 पूर्ण संख्याएँ 0, 1, 2, 3 और 4 हैं।
माध्य = \(\frac{0+1+2+3+4}{5}=\frac{10}{2}\) = 5 उत्तर

प्रश्न 4.
एक क्रिकेट खिलाड़ी ने 8 पारियों में निम्नलिखित रन बनाए :
58, 76, 40, 35, 46, 50, 0, 100
उनका माध्य स्कोर या रन ज्ञात कीजिए।
हल:
कुल स्कोर = 58 + 76 + 40 + 35 + 46 + 50 + 0 + 100
= 405
प्रेक्षणों की संख्या – 8
माध्य = \(\frac {1}{2}\) उत्तर

प्रश्न 5.
निम्नलिखित सारणी प्रत्येक खिलाड़ी द्वारा चार खेलों में अर्जित किए गए अंकों को दर्शाती है:

अब निम्नलिखित प्रश्नों के उत्तर दीजिए :
(i) प्रत्येक खेल में 4 द्वारा अर्जित औसत अंक ज्ञात करने के लिए माध्य ज्ञात कीजिए।
(ii) प्रत्येक खेल में C द्वारा अर्जित माध्य अंक ज्ञात करने के लिए आप कल अंकों को 3 से भाग देंगे या 4 से? क्यों ?
(iii) B ने सभी चार खेलों में भाग लिया है। आप उसके अंकों का माध्य किस प्रकार ज्ञात करेंगे?
(iv) किसका प्रदर्शन सबसे अच्छा है?
हल :
(i) A के प्रत्येक खेल के लिए माध्य
= \(\frac{14+16+10+10}{4}=\frac{50}{4}\) = 12.5

(ii) C के प्रत्येक खेल के लिए माध्य अंक
= \(\frac{8+11+0+13}{4}=\frac{32}{4}\) = 8
हम स्थिति की तुलना कर रहे हैं। इसलिए, C का माध्य ज्ञात करने के लिए 4 से भाग देंगे।

(iii) B के प्रत्येक खेल के लिए माध्य अंक
= \(\frac{0+8+6+4}{4}=\frac{18}{4}\) = 4.5

(iv) इसलिए 12.5 > 8 > 4.5
∴ A का प्रदर्शन सबसे अच्छा है।

प्रश्न 6.
विज्ञान की एक परीक्षा में, विद्यार्थियों के एक समूह द्वारा (100 में से) प्राप्त किए गए अंक 85, 76, 90, 85, 39, 48, 56, 95, 81 और 75 हैं। ज्ञात कीजिए :
(i) विद्यार्थियों द्वारा प्राप्त सबसे अधिक अंक और सबसे कम अंक।
(ii) प्राप्त अंकों का परिसर,
(iii) समूह द्वारा प्राप्त माध्य अंक।
हल :
विद्यार्थियों के एक समूह द्वारा प्राप्त किए अंकों को आरोही क्रम में व्यवस्थित करने पर,
39, 48, 56, 75, 76, 81, 85, 85, 90 और 95
(i) सबसे अधिक अंक = 95 और सबसे कम अंक = 39
(ii) प्राप्त अंकों का परिसर = 95 – 39 = 56
(iii) माध्य अंक = \(\frac{39+48+56+75+76+81+85+85+90+95}{10}\)
= \(\frac {730}{10}\) = 73 उत्तर

प्रश्न 7.
छः क्रमागत वर्षों में एक स्कूल में विद्यार्थियों की संख्या निम्नलिखित थी:
1555, 1670, 1750, 2013, 2540, 2820
इस समय-काल में स्कूल के विद्यार्थियों की माध्य संख्या ज्ञात कीजिए।
हल :
छः क्रमागत वर्षों में विद्यार्थियों की संख्या का योग = 1555 + 1670 + 1750 + 2013 + 2540 + 2820
= 12348
माध्य = \(\frac {12348}{6}\) = 2058. उत्तर

प्रश्न 8.
एक नगर में किसी विशेष सप्ताहके 7 दिनों में हुई वर्धा (मिमी में) निम्नलिखित रूप से रिकॉर्ड की गई:

(i) उपरोक्त आँकड़ों से वर्षा का परिसर ज्ञात कीजिए।
(ii) इस सप्ताह की माध्य वर्षा ज्ञात कीजिए।
(iii) कितने दिन वर्षा, माध्य वर्षा से कम रही ?
हल :
(i) 7 दिनों में हुई वर्षा को आरोही क्रम में रखने पर,
0.0, 0.0, 1.0, 2.1, 5.5, 12.2, 20.5
परिसर = 20.5 – 0.0 = 20.5

(ii) 7 दिनों की वर्षा का योग = 0.0 + 0.0 + 1.0 + 2.1 +5.5 + 12.2 + 20.5 = 41.3
माध्य = \(\frac {41.3}{7}\) = 5.9 मिमी

(iii) पाँच दिन वर्षा, माध्य वर्षा से कम रही।

प्रश्न 9.
10 लड़कियों की ऊँचाइयाँ सेमी में मापी गई और निम्नलिखित परिणाम प्राप्त हुए।
135, 150, 139, 128, 151, 132, 146, 149, 143, 141
(i) सबसे लम्बी लड़की की लम्बाई क्या है?
(ii) सबसे छोटी लड़की की लम्बाई क्या है ?
(iii) इन आंकड़ों का परिसर क्या है ?
(iv) लड़कियों की माध्य ऊँचाई (लम्बाई) क्या है?
(v) कितनी लड़कियों की लम्बाई, माध्य लम्बाई से अधिक है?
हल :
ऊँचाइयों को आरोही क्रम में व्यवस्थित करने पर,
128, 132, 135, 139, 141, 143, 146, 149, 150, 151
(i) सबसे लम्बी लड़की की ऊँचाई = 151 सेमी
(ii) सबसे छोटी लड़की की ऊँचाई = 128 सेमी
(iii) परिसर = (151 – 128) सेमी = 23 सेमी
(iv) माध्य ऊँचाई = \(\frac {कुल ऊँचाइयों का योग}{लड़कियों की संख्या}\)
= \(\frac{128+132+135+139+141+143+146+149+150+151}{10}\)
= \(\frac {1414}{10}\) = 141.4 सेमी।
(v) पाँच लड़कियों की लम्बाई माध्य लम्बाई से अधिक है।

Haryana State Board HBSE 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक InText Questions

प्रयास कीजिए (पृष्ठ सं. 246)

प्रश्न 1.
बताइए कि निम्नलिखित व्यंजक किस प्रकार प्राप्त किए जाते हैं :
7xy + 5, x²y, 4x² – 5x
हल :
7xy + 5 में, पहले हमें xy प्राप्त होता है। इसको 7 से गुणा करने पर 7xy प्राप्त होता है और 7xy में 5 जोड़ने पर 7xy + 5 प्राप्त होता है।
x²y में, पहले हमें x2 प्राप्त होता है। इसमें का गुणा करने पर x²y प्राप्त होता है।
4x² – 5y में, पहले हमें x2 प्राप्त होता है और इसे 4 से गुणा करने पर 4x² प्राप्त होता है और दूसरे पद को प्राप्त करने के लिए y को 5 से गुणा करके 4x² में से घटाने पर 4x² – 5y प्राप्त होता है।

पृष्ठ सं. 247

प्रश्न 1.
निम्नलिखित व्यंजकों में कौन-कौन से पद हैं ? दर्शाइए कि ये व्यंजक कैसे बनाए जाते हैं। प्रत्येक व्यंजक के लिए एक पेड़ आरेख भी खींचिए-
8y + 3x², 7mn – 4, 2x²y
हल :
8y + 3x² में 8y और 3x² पद हैं।
पद 8y, स्थिरांक 8 और y गुणा करने से प्राप्त होता है।
पद 3x², 3, x और x को गुणा करने से प्राप्त होता है।
इसका पेड़ आरेख निम्न है-

7mn – 4 में, 7mn और (-4) पद हैं।
7mn प्राप्त करने के लिए हम चर m, n को 7 से गुणा करते हैं।
(-4) प्राप्त करने के लिए पूर्णांक (-4) लेंगे।
इसका पेड़ आरेख निम्न है-

2x²y में, एक ही पद 2x²y है।
2x²y में, पहले हम x² प्राप्त करते हैं। इसको y से गुणा करके x²y प्राप्त करते हैं। इसे 2 से गुणा करने पर 2x²y प्राप्त होता है।
इसका पेड़ आरेख निम्न है-

प्रश्न 2.
ऐसे तीन व्यंजक लिखिए, जिनमें से प्रत्येक में चार पद हों।
हल :
चार पदों वाले तीन व्यंजक
3x + 2y + z – 7, 2x² – 5y³ + z + 2, xy + yz + zx + 5

पृष्ठ सं. 248

प्रश्न 1.
निम्नलिखित व्यंजकों के पदों के गुणांकों की पहचान कीजिए :
4x – 3y, a + b + 5, 2y + 5, 2xy.
हल :
4x – 3y में,
4x में x का गुणांक 4 है।
-3y में का गुणांक – 3 है।

a + b + 5 में,
a का गुणांक 1 है।
b का गुणांक 1 है।

2y + 5 में,
2y में y का गुणांक 2 है।

2xy में,
2xy में xy का गुणांक 2 है।
2xy में y का गुणांक 2x है।
2xy में x का गुणांक 2y है।

पृष्ठ सं. 249

प्रश्न 1.
निम्नलिखित में, समान पदों के समूह बनाइए :
12x, 12, – 25x, – 25, – 25y, 1, x, 12y, y.
हल :
समान पदों के समूह :
12x, – 25x, x; 12, – 25, 1; -25y, 12y, y.

पृष्ठ सं. 250

प्रश्न 1.
निम्नलिखित व्यंजकों को एकपदी, द्विपद और त्रिपद के रूप में वर्गीकृत कीजिए :
a, a + b, ab + a + b, ab + a + b – 5, xy, xy + 5, 5x² – x + 2, 4pq – 3q + 5p, 7, 4m – 7n + 10, 4mn +7.
हल :
एक पदी : a, xy और 7.
द्विपद : a + b, xy + 5 और 4mn + 7
त्रिपद : ab + a + b, 5x² – x + 2, 4pq – 3q + 5p और 4m – 7n + 10.

पृष्ठ सं. 253

प्रश्न 1.
कम-से-कम ऐसी दो स्थितियों के बारे में सोचिए जिनमें से प्रत्येक में आपको दो बीजीय व्यंजकों को बनाने की आवश्यकता पड़े और उन्हेंजोड़ना या घटाना पड़े।
हल :
प्रथम स्थिति : A व्यक्ति के पिता का भार, A के भार से 3 गुना है।
A व्यक्ति के नाना का भार A के भार और A के पिता के भार के योग से 5 किग्रा अधिक है। आप A व्यक्ति के नाना का भार कैसे ज्ञात करोगे?

द्वितीय स्थिति : दो ट्रेन एक ही स्टेशन से विपरीत दिशाओं में चलना प्रारम्भ करती है। एक को औसत चाल दूसरी ट्रेन की औसत चाल से 15 किमी प्रति घंटा कम है। यदि 3 घण्टे बाद उनके बीच की दूरी 1800 किमी हो तो आप उनकी औसत चाल कैसे ज्ञात करोगे ?

पृष्ठ सं. 255

प्रश्न 1.
जोड़िए और घटाइए :
(i) m – n, m + n
(ii) mn + 5 – 2, mn + 3
हल :
(i) (m – n) + (m + n)
= m – n + m + n
= m + m – n + n
= (1 + 1)m + (-1 + 1)n
= 2m + 0n
= 2m + 0 = 2m
और (m – n) – (m + n) = m – n – m – n
= m – m – n – n
= (1 – 1)m + (- 1 – 1)n
= 0m + (-2)n
= 0 – 2n = – 2n

(ii) (mn + 5 – 2) + (mn + 3)
= (mn + 3) + (mn + 3)
= 2mn + 6
(mn + 5 – 2) – (mn + 3)
= (mn + 3) – (mn + 3) = 0

पृष्ठ सं. 261

प्रश्न 1.
दर्शाए गए आधारभूत आकारों को लेकर उपर्युक्त प्रकार के पैटर्न बनाइए:

[आकारों को बनाने के लिए आवश्यक रेखाखण्डों की संख्या दाईं ओर लिखी हुई है। साथ ही n आकारों को बनाने के लिए आवश्यक रेखाखण्डों के दर्शाने वाला व्यंजक भी दाईं ओर दिया हुआ है।]
आगे बढ़िए और ऐसी ही और पैटनों की खोज कीजिए।
हल :
आगे के पैटर्न इस प्रकार होंगे-

Haryana State Board HBSE 10th Class Maths Solutions Chapter 7 निर्देशांक ज्यामिति Ex 7.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 7 निर्देशांक ज्यामिति Exercise 7.1

प्रश्न 1.
बिंदुओं के निम्नलिखित युग्मों के बीच की दूरियाँ ज्ञात कीजिए-
(i) (2,3), (4,1)
(ii) (-5, 7), (-1,3)
(iii) (a, b), (-a,-b)
हल :
(i) माना A(2, 3) व B(4, 1) है।
हम जानते हैं कि दो बिंदुओं के बीच की दूरी

(ii) माना A(-5, 7) व B(-1, 3) है।
हम जानते हैं कि दो बिंदुओं के बीच की दूरी

(iii) माना A(a, b) व B(-a,-b) है।
हम जानते हैं कि दो बिंदुओं के बीच की दूरी

प्रश्न 2.
बिंदुओं (0, 0) और (36, 15) के बीच की दूरी ज्ञात कीजिए। क्या अब आप अनुच्छेद 7.2 में दिए दोनों शहरों A और B के बीच की दूरी ज्ञात कर सकते हैं ?
[अनुच्छेद 7.2 एक शहर B एक अन्य शहर A से 36 km पूर्व और 15 km उत्तर की ओर है तो शहर B की शहर A से दूरी ज्ञात कीजिए]
हल :

माना P (0, 0) व Q(36, 15) है।
हम जानते हैं कि दो बिंदुओं के बीच की दूरी

अनुच्छेद 7.2 के अनुसार शहर B की शहर A से दूरी = 39 km

प्रश्न 3.
निर्धारित कीजिए कि क्या बिंदु (1,5), (2, 3) और (-2,-11) सरेखी हैं।
हल :
माना तीनों बिंदु A(1, 5), B(2, 3) और C (-2, -11) हैं। ये बिंदु तभी संरेखी हो सकते हैं, जब दो रेखाखंडों की लंबाई का योग तीसरे रेखाखंड की लंबाई के समान हो।
अब दूरी सूत्र द्वारा,

समीकरण (i), (ii) व (iii) से स्पष्ट है कि किन्हीं दो रेखाखंडों का योग तीसरे रेखाखंड के समान नहीं है। अतः बिंदु (1, 5), (2, 3) व (-2, -11) संरेखी नहीं हैं।

प्रश्न 4.
जाँच कीजिए कि क्या बिंदु (5,-2), (6, 4) और (7,-2) एक समद्विबाहु त्रिभुज के शीर्ष हैं।
हल :
माना तीन बिंदु A(5,-2), B(6, 4) और C (7,-2) हैं। ये बिंदु तभी समद्विबाहु त्रिभुज के शीर्ष होंगे, यदि किन्हीं दो रेखाखंडों की लंबाई समान होगी।
अतः दूरी सूत्र द्वारा,

समीकरण (i) व (ii) से स्पष्ट है कि AB = BC
अतः बिंदु (5, -2), (6, 4) व (7,-2) एक समद्विबाहु त्रिभुज के शीर्ष हैं।

प्रश्न 5.
किसी कक्षा में, चार मित्र बिंदुओं A, B, C और
D पर बैठे हुए हैं, जैसाकि संलग्न आकृति में दर्शाया गया है। चंपा और चमेली कक्षा के अंदर आती हैं और कुछ मिनट तक देखने के बाद, चंपा चमेली से पूछती है, ‘क्या तुम नहीं सोचती हो कि ABCD एक वर्ग है?’ चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके, बताइए कि इनमें से कौन सा सही है।

हल :
यहाँ पर आकृति अनुसार, A(3, 4), B(6, 7), C(9, 4) व D(6, 1) हैं।
अब दूरी सूत्र से,


समीकरण (i), (ii), (iii), (iv), (v) व (vi)
भुजा AB = भुजा BC = भुजा CD = भुजा DA
तथा विकर्ण AC = विकर्ण BD
अतः बिंदु A, B, C व D एक वर्ग है, जिससे पता चलता है कि चंपा सही है।

प्रश्न 6.
निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए
(i) (-1, -2), (1,0), (-1, 2), (-3,0)
(ii) (-3,5), (3, 1), (0, 3), (-1,-4)
(iii) (4, 5), (7,6), (4,3), (1, 2)
हल :
(i) माना दिए गए बिंदु A(-1,-2), B(1, 0), C(-1, 2), व D(-3, 0) हैं।
अब दूरी सूत्र से,

अतः AC = BD
क्योंकि चतुर्भुज की सभी भुजाएँ व विकर्ण समान हैं इसलिए ये बिंदु एक वर्ग के हैं।

(ii) माना दिए गए बिंदु A(-3, 5), B(3, 1), C(0, 3), व D(-1,-4) हैं।
अब दूरी सूत्र से,


भुजाओं के माप से पता चलता है कि ABCD चतुर्भुज संभव नहीं है।

(iii) माना दिए गए बिंदु A(4, 5), B(7, 6), C(4, 3), व D(1, 2) हैं।
अब दूरी सूत्र से,

क्योंकि AB = CD = \(\sqrt{10}\)
तथा BC = DA = \(\sqrt{18}\)
चतुर्भुज की सम्मुख भुजाएँ बराबर हैं।

क्योंकि AC ≠ BD
अतः ABCD एक समांतर चतुर्भुज है।

प्रश्न 7.
x-अक्ष पर वह बिंदु ज्ञात कीजिए जो (2,-5) और (-2, 9) से समदूरस्थ हैं।
हल :
माना x-अक्ष पर बिंदु A(x, 0) है जो B(2,-5) तथा C(-2, 9) से समदूरस्थ हैं।
AB = AC
AB² = AC²
(2-x)² + (-5-0)² = (-2-x)² + (9-0)²
4 + x² – 4x + 25 = 4 + x² + 4x + 81
29 – 85 = 4x + 4x
-56 = 8x
x = -56/8 =-7
अतः x-अक्ष पर वांछित बिंदु = (-7, 0)

प्रश्न 8.
y का वह मान ज्ञात कीजिए, जिसके लिए बिंदु P(2,-3) और Q(10,y) के बीच की दूरी 10 मात्रक है।
हल :
प्रश्नानुसार, P(2,-3), Q(10, y) तथा PQ = 10 मात्रक अब
PQ = 10
(PQ)² = 100
(10-2)² + (y + 3)² = 100
64 + y² +9+ 6y = 100
y² + 6y + 73 – 100 = 0
y² + 6y – 27 = 0
y + 9y – 3y – 27 = 0
y(y +9)-3(+ 9) = 0
(y + 9) (y – 3) = 0
y + 9 = 0 या y – 3 = 0
y = -9 या y = 3
अतः y का वांछित मान =-9 व 3 है।

प्रश्न 9.
यदि Q(0, 1) बिंदुओं P(5,-3) और Rx, 6) से समदूरस्थ है, तो x के मान ज्ञात कीजिए। दूरियाँ QR और PR भी ज्ञात कीजिए।
हल :
क्योंकि बिंदु Q(0, 1) बिंदुओं P(5,-3) व R(x, 6) से समदूरस्थ है।
PQ = RQ
PQ² = RQ²
(0-5)² + [1 – (-3)]² = (0 –x)² + (1 – 6)²
(-5) + (4)² = (-x) + (-5)²
25 + 16 = x² + 25
x² = 16
x = ±4
अतः R के निर्देशांक (±4, 6) हैं। .

प्रश्न 10.
x और ” में एक ऐसा संबंध ज्ञात कीजिए कि बिंदु (x,y) बिंदुओं (3, 6) और (-3, 4) से समदूरस्थ हो।
हल :
माना बिंदु P(x, y) बिंदुओं A(3, 6) व B(-3, 4) से समदूरस्थ है तो
AP = BP
AP² = BP²
(x-3)² + (y-6)² = [x – (-3)]² + (y-4)²
या x² + 9 – 6x + y² + 36 – 12y = x² + 9 + 6x + y² + 16 – 8y
या x² +y² – 6x – 12y + 45 = x² + y² + 6x – 8y + 25
या 6x + 6x – 8y + 12y + 25 – 45 = 0
या 12x + 4y – 20 = 0
या 3x + y – 5 = 0

Haryana State Board HBSE 7th Class Maths Solutions Chapter 2 भिन्न एवं दशमलव InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 2 भिन्न एवं दशमलव InText Questions

प्रयास कीजिए (पृष्ठ सं. 34)

प्रश्न 1.
हल कीजिए : 3 × \(\frac {8}{7}\) = ?, 4 × \(\frac {7}{5}\) = ?
हल:
3 × \(\frac{8}{7}=\frac{3 \times 8}{7}=\frac{24}{7}\)
4 × \(\frac{7}{5}=\frac{4 \times 7}{5}=\frac{28}{5}\)

पृष्ठ सं. 34

प्रश्न 2.
ज्ञात कीजिए:
(a) \(\frac {2}{7}\) × 3
(b) \(\frac {9}{7}\) × 6
(c) 3 × \(\frac {1}{8}\)
(d) \(\frac {13}{11}\) × 6
यदि गुणनफल एक विषम भिन्न है, तो इसे मिश्रित भिन्न के रूप में व्यक्त कीजिए।
हल :

प्रश्न 3.
2 × \(\frac{2}{5}=\frac{4}{5}\) = को सचित्र निरूपित कीजिए।
हल :
2 × \(\frac{2}{5}=\frac{4}{5}\) को निम्न प्रकार चित्र द्वारा व्यक्त कर सकते हैं :

पृष्ठ सं. 34

प्रश्न 4.
ज्ञात कीजिए :
(i) 5 × 2 \(\frac {3}{7}\)
(ii) 1\(\frac {4}{9}\) × 6
हल :

पृष्ठ सं. 35

प्रश्न 1.
क्या आप बता सकते हैं कि:
(i) 10 का \(\frac {1}{2}\)
(ii) 16 का \(\frac {1}{4}\)
(iii) 25 का \(\frac {2}{5}\) क्या है?
हल :

पृष्ठ सं. 39

प्रश्न 1.
निम्नलिखित बक्सों को भरिए।
हल :

पृष्ठ सं. 40

प्रश्न 1.
ज्ञात कीजिए :
\(\frac{2}{3} \times \frac{4}{5}\), \(\frac{2}{3} \times \frac{1}{5}\)
हल :
\(\frac{2}{3} \times \frac{4}{5}=\frac{2 \times 4}{3 \times 5}=\frac{8}{15}\)
\(\frac{2}{3} \times \frac{1}{5}=\frac{2 \times 1}{3 \times 5}=\frac{2}{15}\)

प्रश्न 2.
ज्ञात कीजिए :
\(\frac{8}{3} \times \frac{4}{7} ; \frac{3}{4} \times \frac{2}{3}\)
हल:
\(\frac{8}{3} \times \frac{4}{7}=\frac{8 \times 4}{3 \times 7}=\frac{32}{21}\)
\(\frac{3}{4} \times \frac{2}{3}=\frac{3 \times 2}{4 \times 3}=\frac{6}{12}\)

पृष्ठ सं. 45

प्रश्न 1.
ज्ञात कीजिए :
(i) 7 ÷ \(\frac {2}{5}\)
(ii) 6 ÷ \(\frac {4}{7}\)
(iii) 2 ÷ \(\frac {8}{9}\)
हल :
हम जानते हैं कि किसी पूर्ण संख्या को एक भिन्न से भाग करने के लिए उस पूर्ण संख्या को उस भिन्न के व्युत्क्रम से गुणा करते हैं।

प्रश्न 2.
ज्ञात कीजिए:
(i) 6 ÷ 5\(\frac {1}{3}\)
(ii) 7 ÷ 2\(\frac {4}{7}\)
हल :

पृष्ठ सं. 46

प्रश्न 1.
ज्ञात कीजिए:
(i) \(\frac{3}{5} \div \frac{1}{2}\)
(ii) \(\frac{1}{2} \div \frac{3}{5}\)
(iii) 2\(\frac{1}{2} \div \frac{3}{5}\)
(iv) 5\(\frac{1}{6} \div \frac{9}{2}\)
हल :

पृष्ठ सं. 51

प्रश्न 1.
ज्ञात कीजिए:
(i) 2.7 × 4
(ii) 1.8 × 1.2
(iii) 2.3 × 4.35
हल :
(i) 27 × 4 = 108
अतः 2.7 × 4 = 10.8
(ii) 18 × 12 =216
अत: 1.8 × 1.2 = 2.16
(iii) 23 × 435 = 10005
अत: 2.3 × 4.35 = 10.005

प्रश्न 2.
प्रश्न 1 में प्राप्त गुणनफलों को अवरोही क्रम में क्रमबद्ध कीजिए।
हल :
10.8, 2.16 और 10.005 को अवरोही क्रम में लिखने पर,
10.005 > 2.16 (∵ 10 > 2)
10.8 और 10.005 में,
10.8 > 10.005, (∵ 0.8 > 0.005)
अतः 10.8 > 10.005 > 2.16.

पृष्ठ सं. 52

प्रश्न 1.
ज्ञात कीजिए:
(i) 0.3 × 10
(ii) 1.2 × 100
(iii) 56.3 × 1000
हल :
(i) 0.3 × 10 = 3
(ii) 1.2 × 100 = 120
(iii) 56.3 × 1000 = 56300

पृष्ठ सं. 53

प्रश्न 1.
ज्ञात कीजिए:
(i) 235.4 ÷ 10
(ii) 235.4 ÷ 100
(iii) 235.4 ÷ 1000
हल :
(i) 235.4 ÷ 10 = 23.54
(ii) 235.4 ÷ 100 = 2.354
(iii) 235.4 ÷ 1000 = 0.2354

पृष्ठ सं. 54

प्रश्न 1.
(i) 35.7 ÷ 3 = ?
(ii) 25.5 ÷ 3 = ?
हल :

प्रश्न 2.
(i) 43.15 ÷ 5 = ?
(ii) 82.44 ÷ 6 = ?
हल:

पृष्ठ सं. 55

प्रश्न 1.
(i) 15.5 ÷ 5 = ?
(ii) 126.35 ÷ 7 = ?
हल :

पृष्ठ सं. 56

प्रश्न 1.
ज्ञात कीजिए:
(i) \(\frac{7.75}{0.25}\)
(ii) \(\frac{42.8}{0.02}\)
(iii) \(\frac{5.6}{1.4}\)
हल :

Haryana State Board HBSE 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Ex 13.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल और आयतन Exercise 13.1

(जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}[/ltaex] लीजिए।)

प्रश्न 1.
दो घनों, जिनमें से प्रत्येक का आयतन 64 cm है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

माना दिए गए प्रत्येक घन की भुजा = a cm
प्रश्नानुसार,
दिए गए प्रत्येक घन का आयतन = 64 cm³
a³ = 64
(a)³ = (4)³
a = 4
अब दो घनों को मिलाकर रखने से बने घनाभ के लिए
लंबाई (l) = (4 +4) cm = 8 cm
चौड़ाई (b) = 4 cm
ऊँचाई (h) = 4 cm
घनाभ का पृष्ठीय क्षेत्रफल = 2 (लं० × चौ० + चौ० × ॐ + ऊँ० × लं०)
= 2 (8 × 4+4 × 4 +4 × 8) cm²
= 2 (32 + 16 + 32) cm²
= 2 × 80 cm² = 160 cm²

प्रश्न 2.
कोई बर्तन एक खोखले अर्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्धगोले का व्यास 14 cm है और इस बर्तन (पात्र) की कुल ऊँचाई 13 cm है। इस बर्तन का आंतरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

यहाँ पर, बर्तन के अर्धगोले का व्यास = 14 cm
बर्तन के अर्धगोले की त्रिज्या (r) = [latex]\frac{14}{2}\) cm = 7 cm
बर्तन के अर्धगोले का पृष्ठीय क्षेत्रफल = 2πr²
= 2 × \(\) × 7 × 7 cm²
= 308 cm²

बर्तन के बेलनाकार भाग की त्रिज्या (r) = \(\frac{14}{2}\) cm cm = 7 cm
बर्तन के बेलनाकार भाग की ऊँचाई (h) = (13 – 7) cm = 6 cm
बर्तन के बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × 7 × 6 cm²
= 264 cm²
अतः बर्तन का आंतरिक पृष्ठीय क्षेत्रफल = (308 + 264) cm²
= 572 cm²

प्रश्न 3.
एक खिलौना त्रिज्या 3.5 cm वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की संपूर्ण ऊँचाई 15.5 cm है। इस खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

यहाँ पर,
खिलौने के अर्धगोलाकार भाग की त्रिज्या (r) = 3.5 cm
खिलौने के अर्धगोलाकार भाग का पृष्ठीय क्षेत्रफल = 2πr²
= 2 × \(\frac{22}{7}\) × 3.5 × 3.5 cm²
= 77 cm²
खिलौने के शंकु वाले भाग की त्रिज्या (r= 3.5 cm
खिलौने के शंकु वाले भाग की ऊँचाई (h) = (15.5-3.5) cm = 12 cm

खिलौने के शंकु वाले भाग का पृष्ठीय क्षेत्रफल = πrl
= \(\frac{22}{7}\) × 3.5 × 12.5 cm²
= 137.5 cm²
अतः खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल = (अर्धगोलाकार + शंकु वाले भाग का पृष्ठीय क्षेत्रफल)
= (77 + 137.5) cm² = 214.5 cm²

प्रश्न 4.
भुजा 7 cm वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

यहाँ पर,
घनाकार ब्लॉक की भुजा = 7 cm
प्रश्नानुसार अर्धगोले का अधिकतम व्यास = घनाकार ब्लॉक की भुजा
अर्धगोले का अधिकतम व्यास = 7 cm
अर्धगोले की त्रिज्या (r) = \(\frac{7}{2}\) cm
घनाकार ब्लॉक का पृष्ठीय क्षेत्रफल = 6 (भुजा)²
= 6 × 7 × 7 cm²
= 294 cm²
अर्धगोले का पृष्ठीय क्षेत्रफल = 2 πr² – πr² = πr²
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) cm²
= \(\frac{77}{2}\) cm² = 38.5 cm²
अतः पूर्ण ठोस का पृष्ठीय क्षेत्रफल = (294 + 38.5) cm²
= 332.5 cm²

प्रश्न 5.
एक घनाकार ब्लॉक के एक फलक को अंदर की ओर से काटकर एक अर्धगोलाकार गड्ढा इस प्रकार बनाया गया है कि अर्धगोले का व्यास l घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
यहाँ पर, घनाकार ब्लॉक की भुजा = l मात्रक
घनाकार ब्लॉक का पृष्ठीय क्षेत्रफल = 6 (भुजा)²
= 6l² वर्ग मात्रक
अर्धगोले का व्यास = l मात्रक
अर्धगोले की त्रिज्या (r) = \(\frac{l}{2}\) मात्रक
अर्धगोले का पृष्ठीय क्षेत्रफल – 2 πr² – πr²
= πr²
= \(\pi\left(\frac{l}{2}\right)^{2}=\frac{\pi l^{2}}{4}\) = वर्ग मात्रक
अतः शेष बचे ठोस का पृष्ठीय क्षेत्रफल = 6l² + \(\frac{\pi l^{2}}{4}\)
= \(\frac{l^{2}}{4}\) [π + 24] वर्ग मात्रक उत्तर

प्रश्न 6.
दवा का एक कैप्सूल (capsule) एक बेलन के आकार का है जिसके दोनों सिरों पर एक-एक अर्धगोला लगा हुआ है (देखिए संलग्न आकृति)। पूरे कैप्सूल की लंबाई 14 mm है और उसका व्यास 5 mm है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

यहाँ पर, कैप्सूल के बेलनाकार भाग का व्यास = 5 mm
कैप्सूल के बेलनाकार भाग की त्रिज्या (r) = \(\frac{5}{2}\)mm
कैप्सूल के बेलनाकार भाग की ऊँचाई (h) = (14 – \(\frac{5}{2}-\frac{5}{2}\) ) mm = 9 mm
कैप्सूल के बेलनाकार भाग का पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7} \times \frac{5}{2}\) × 9mm²
= \(\frac{990}{7}\) mm²
कैप्सूल के दोनों अर्धवृत्ताकार सिरों की त्रिज्या (r) = \(\frac{5}{2}\) mm
कैप्सूल के दोनों अर्धवृत्ताकार सिरों का पृष्ठीय क्षेत्रफल = 2 [2πr²]

प्रश्न 7.
कोई तंबू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमशः 2.1 m और 4 m हैं तथा शंकु की तिर्यक ऊँचाई 2.8 m है तो इस तंबू को बनाने में प्रयुक्त कैनवस (canvas) का क्षेत्रफल ज्ञात कीजिए। साथ ही, 500 रु० प्रति m² की दर से इसमें प्रयुक्त कैनवस की लागत ज्ञात कीजिए। (ध्यान दीजिए कि तंबू के आधार को कैनवस से नहीं ढका जाता है।)
हल :

यहाँ पर, तंबू के बेलनाकार भाग का व्यास = 4 m
तंबू के बेलनाकार भाग की त्रिज्या (r) = \(\frac{4}{2}\)m = 2 m
तंबू के बेलनाकार भाग की ऊँचाई (h) = 2.1 m
तंबू के बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\)x 2 × 2.1 m²
= 26.4 m²
तंबू के शंकु वाले भाग की त्रिज्या (r) = \(\frac{4}{2}\)m = 2 m
तंबू के शंकु वाले भाग की तिर्यक ऊँचाई (l) = 2.8 m
→ तंबू के शंकु वाले भाग का वक्र पृष्ठीय क्षेत्रफल = πrl
= \(\frac{22}{7}\) × 2 × 2.8 m²
= 17.6 m²
अतः तंबू बनाने के लिए आवश्यक कैनवस का क्षेत्रफल = (26.4 + 17.6) m² = 44 m²
1 m² कैनवस की लागत = 500 रु०
44 m² कैनवस की लागत = 44 × 500 रु० = 22000 रु०

प्रश्न 8.
ऊँचाई 2.4 cm और व्यास 1.4 cm वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल (cavity) काट लिया जाता है। शेष बचे ठोस का निकटतम वर्ग सेंटीमीटर तक पृष्टीय क्षेत्रफल ज्ञात कीजिए।
हल :

यहाँ पर, बेलनाकार ठोस का व्यास = 1.4 cm
बेलनाकार ठोस की त्रिज्या (r₁) = \(\frac{1.4}{2}\) cm = 0.7 cm
बेलनाकार ठोस की ऊँचाई (h₁) = 2.4 cm
बेलनाकार ठोस का वक्र पृष्ठीय क्षेत्रफल (A₁) = 2πr₁h₁
= 2 × \(\frac{22}{7}\) × 0.7 × 2.4 cm² = 10.56 cm²
तथा बेलनाकार ठोस के आधार का क्षेत्रफल (A₂) = πr₁² = \(\frac{22}{7}\) × 0.7 × 0.7 cm²
= 1.54 cm²
काटे गए शंक्वाकार खोल की तिर्यक ऊँचाई (l₁) = \(\sqrt{r_{1}^{2}+h_{1}^{2}}\)
= \(\sqrt{(0.7)^{2}+(2.4)^{2}}\) cm
= \(\sqrt{(0.49+5.76)}\) cm
= \(\sqrt{6.25}\) cm
= (0.7) + (2.4) cm = 2.5 cm
काटे गए शंक्वाकार खोल का वक्र पृष्ठीय क्षेत्रफल (A₃) = πr₁l₁
= \(\frac{22}{7}\) × 0.7 × 2.5 cm²
= 5.5 cm²
अतः शेष बचे ठोस का पृष्ठीय क्षेत्रफल = A₁ + A₂ + A₃
= [10.56 + 1.54 + 5.5) cm²
= 17.6 cm² ≅ 18 cm²

प्रश्न 9.
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसा कि आकृति में दर्शाया गया है। यदि बेलन की ऊँचाई 10 cm है और आधार की त्रिज्या 3.5 cm है तो इस वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

यहाँ पर, दिए गए ठोस बेलन के
आधार की त्रिज्या (r) = 3.5 cm
दिए गए ठोस बेलन की ऊँचाई (h) = 10 cm
दिए गए ठोस बेलन का वक्र पृष्ठीय क्षेत्रफल (A₁) = 2πrh
= 2 × \(\frac{22}{7}\) × 3.5 × 10 cm² = 220 cm²
निकाले गए प्रत्येक अर्धगोले की त्रिज्या (r)= 3.5 cm
निकाले गए दोनों अर्धगोलों का पृष्ठीय क्षेत्रफल (A₂) = 2 (2πr²)
= 4 × \(\frac{22}{7}\) × 3.5 × 3.5 cm²
= 154 cm²
अतः दी गई वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल = A₁ + A₂
= (220 + 154) cm²
= 374 cm²

Haryana State Board HBSE 7th Class Maths Solutions Chapter 14 सममिति Ex 14.3 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 14 सममिति Ex 14.3

प्रश्न 1.
किन्हीं दो आकृतियों के नाम बताइए, जिनमें रैखिक सममिति और क्रम 1 से अधिक की घूर्णन सममिति दोनों ही हों।
हल :
दो आकृतियाँ निम्न होंगी-

1. समबाहु त्रिभुज
2. एक वृत्त।

प्रश्न 2.
जहाँ सम्भव हो, निम्नलिखित की एक रफ आकृति खींचिए :
(i) एक त्रिभज, जिसमें रैखिक सममिति और क्रम 1 से अधिक की घूर्णन सममिति दोनों ही हों।
(ii) एक त्रिभुज, जिसमें केवल रैखिक सममिति और क्रम 1 से अधिक की घूर्णन सममिति न हो।
(iii) एक चतुर्भुज जिसमें क्रम 1 से अधिक की घूर्णन सममिति हो, परन्तु रैखिक सममिति न हो।
(iv) एक चतुर्भुज जिसमें केवल रैखिक सममिति हो और क्रम 1 से अधिक की घूर्णन सममिति न हो।
हल :
प्रत्येक स्थिति की एक आकृति निम्न है-
(i)

तीन रैखिक सममिति

(ii) एक रैखिक सममिति लेकिन कोई भी घूर्णन सममिति क्रम 1 से अधिक नहीं।

(iii) कोई रैखिक सममिति नहीं लेकिन क्रम 2 की घूर्णन सममिति।

(iv) एक रैखिक सममिति लेकिन कोई घूर्णन सममिति नहीं।

प्रश्न 3.
यदि किसी आकृति की दो या अधिक सममित रेखाएँ हों, तो क्या यह आवश्यक है कि उसमें क्रम 1 से अधिक की घूर्णन सममिति होगी ?
हल :
जब किसी आकृति की दो या अधिक रैखिक सममिति होती हैं तो आकृति में क्रम 1 से अधिक घूर्णन सममिति होती है।

प्रश्न 4.
रिक्त स्थानों को भरिए :

हल :
रिक्त स्थानों की पूर्ति करने पर,

प्रश्न 5.
ऐसे चतुर्भुजों के नाम बताइए, जिसमें रैखिक सममिति और क्रम 1 से अधिक की घूर्णन सममिति दोनों ही हों।
हल :
ऐसे चतुर्भुजों जिनमें रैखिक सममिति और क्रम 1 से अधिक घूर्णन सममिति दोनों ही हों, वह वर्ग होगा।

प्रश्न 6.
किसी आकृति को उसके केन्द्र के परितः 60° के कोण पर घुमाने पर, वह उसकी प्रारम्भिक स्थिति जैसी ही दिखाई देती है। इस आकृति के लिए ऐसे कौन-से अन्य कोणों के लिए भी हो सकता है ?
हल :
अन्य कोण निम्न होंगे :
120°, 180°, 240°, 300°, 360°.

प्रश्न 7.
क्या हमें कोई ऐसी क्रम 1 से अधिक की घूर्णन सममिति प्राप्त हो सकती है, जिसके घूर्णन के कोण निम्नलिखित हों ?
(i) 45°
(ii) 17°
हल :
(i) हाँ
(ii) नहीं।

Haryana State Board HBSE 12th Class Economics Solutions Chapter 5 बाज़ार संतुलन Textbook Exercise Questions and Answers.

Haryana Board 12th Class Economics Solutions Chapter 5 बाज़ार संतुलन

पाठ्यपुस्तक के प्रश्न

प्रश्न 1.
बाज़ार संतुलन की व्याख्या कीजिए।
उत्तर:
बाज़ार संतुलन से अभिप्राय उस स्थिति से है, जहाँ बाज़ार माँग और बाज़ार पूर्ति एक-दूसरे के बराबर होती हैं।
बाज़ार संतुलन : बाज़ार माँग = बाज़ार पूर्ति

प्रश्न 2.
हम कब कहते हैं कि बाज़ार में किसी वस्तु के लिए अधिमाँग है?
उत्तर:
बाज़ार में अधिमाँग के होने की स्थिति उस समय होती है, जब वस्तु की बाज़ार माँग वस्तु की बाज़ार पूर्ति से अधिक है।
अधिमाँग = बाज़ार माँग > बाज़ार पूर्ति अथवा अतिरिक्त माँग = बाज़ार माँग – बाज़ार पूर्ति

प्रश्न 3.
हम कब कहते हैं कि बाज़ार में किसी वस्तु के लिए अधिपूर्ति है?
उत्तर:
बाज़ार में अधिपूर्ति के होने की स्थिति उस समय होती है, जब वस्तु की बाज़ार पूर्ति वस्तु की बाज़ार माँग से अधिक है।
अधिपूर्ति = बाज़ार पूर्ति > बाज़ार माँग अथवा अतिरिक्त पूर्ति = बाज़ार पूर्ति – बाज़ार माँग

प्रश्न 4.
क्या होगा यदि बाज़ार में प्रचलित मूल्य (a) संतुलन कीपत से अधिक है? (b) संतुलन कीमत से कम है?
उत्तर:
(a) यदि बाज़ार में प्रचलित मूल्य संतुलन कीमत से अधिक है तो अधिपूर्ति की स्थिति होगी अर्थात् बाज़ार पूर्ति बाज़ार माँग से अधिक होगी।(b) यदि बाज़ार में प्रचलित मूल्य संतुलन कीमत से कम है तो अधिमाँग की स्थिति होगी अर्थात् बाज़ार माँग बाज़ार पूर्ति . से अधिक होगी।

प्रश्न 5.
फर्मों की एक स्थिर संख्या के होने पर पूर्ण प्रतिस्पर्धी बाज़ार में कीमत का निर्धारण किस प्रकार होता है? व्याख्या कीजिए।
उत्तर:
फर्मों की संख्या स्थिर होने पर संतुलन कीमत बाज़ार माँग और बाज़ार पूर्ति के वक्रों के परस्पर प्रतिच्छेदन बिंदु पर निर्धारित होती है। इसे संलग्न रेखाचित्र के द्वारा दर्शाया जा सकता है।

संलग्न रेखाचित्र में वस्तु का पूर्ति वक्र SS वस्तु के माँग वक्र DD को E बिंदु पर काटता है। परिणामस्वरूप OP बाज़ार कीमत का निर्धारण होता है। OP कीमत से अधिक कोई भी कीमत जैसे OP₁ बाज़ार में अधिपूर्ति की स्थिति उत्पन्न करेगी। इसी प्रकार OP कीमत से कम कोई भी कीमत जैसे OP₂ बाज़ार में अधिमाँग की स्थिति उत्पन्न करेगी।

प्रश्न 6.
मान लीजिए कि अभ्यास 5 में संतुलन कीमत बाज़ार में फर्मों की न्यूनतम औसत लागत से अधिक है। अब यदि हम फर्मों के निर्बाध प्रवेश तथा बहिर्गमन की अनुमति दे दें, तो बाज़ार कीमत इसके साथ किस प्रकार समायोजन करेगी?
उत्तर:
यदि बाज़ार में फर्मों का निर्बाध प्रवेश तथा बहिर्गमन है तो संतुलन कीमत सदैव फर्मों की न्यूनतम औसत लागत के समान होगी। यदि बाज़ार कीमत को न्यूनतम औसत लागत से ऊँचा रखा जाता है तो इसका अर्थ यह होगा कि कुछ फर्मों को असामान्य लाभ हो रहा है। इस स्थिति में नई फ बाज़ार में प्रवेश करेंगी और अंततः बाज़ार कीमत घटकर न्यूनतम औसत लागत पर आ जाएगी। यदि बाज़ार कीमत को न्यूनतम औसत लागत से नीचा रखा जाता है तो इसका अर्थ यह होगा कि कुछ फर्मों को असामान्य हानि हो रही है। इस स्थिति में कुछ फर्मे बाज़ार से बाहर चली जाएँगी और अंततः बाज़ार कीमत बढ़कर न्यूनतम औसत लागत पर आ जाएगी। इस प्रकार बाज़ार कीमत प्रत्येक स्थिति में न्यूनतम औसत लागत के समान होगी।

प्रश्न 7.
जब बाज़ार में निर्बाध प्रवेश तथा बहिर्गमन की अनुमति है, तो फर्मे पूर्ण प्रतिस्पर्धी बाज़ार में कीमत के किस स्तर पर पूर्ति करती हैं? ऐसे बाज़ार में संतुलन मात्रा किस प्रकार निर्धारित होती है?
उत्तर:
जब बाज़ार में निर्बाध प्रवेश तथा बहिर्गमन की अनुमति है तो फर्म की बाज़ार कीमत, कीमत के उस स्तर पर होती है जहाँ वह न्यूनतम औसत लागत के बराबर होती है। फलस्वरूप बाज़ार पूर्ति वक्र पूर्णतया लोचदार वक्र होगा जो X-अक्ष के समानांतर होगा।

ऐसी स्थिति में संतुलन मात्रा उस बिंदु पर निर्धारित होगी जहाँ पूर्ति की गई मात्रा माँगी गई मात्रा के बराबर हो। माँग के बढ़ने या घटने से बाज़ार की कीमत पर कोई प्रभाव नहीं पड़ता, परंतु संतुलन मात्रा में परिवर्तन होता है। इसे हम संलग्न रेखाचित्र द्वारा दर्शा सकते हैं।

संलग्न रेखाचित्र में PP कीमत रेखा तथा पूर्ति वक्र है तथा प्रारंभिक माँग वक्र DD है। ये दोनों वक्र एक-दूसरे को E बिंदु पर स्पर्श करते हैं जहाँ संतुलन कीमत OP और संतुलन मात्रा OQ है। जब वस्तु की माँग बढ़कर D₁D₁ हो जाती है तो संतुलन बिंदु E₁ तथा संतुलन मात्रा OQ₁ हो जाएगी।

प्रश्न 8.
एक बाज़ार में फर्मों की संतुलन संख्या किस प्रकार निर्धारित होती है, जब उन्हें निर्बाध प्रवेश तथा बहिर्गमन की अनुमति हो?
उत्तर:
जब फर्मों को बाज़ार में निर्बाध प्रवेश तथा बहिर्गमन की अनुमति हो तो प्रत्येक फर्म की पूर्ति एक समान (q_0f) होगी। इस प्रकार बाज़ार में फर्मों की संतुलन संख्या फर्मों की उस संख्या के बराबर होगी जो P₀ निर्गत पर q₀ पूर्ति के लिए आवश्यक है। प्रत्येक फर्म इस कीमत पर q_0f मात्रा की पूर्ति करेगी। इस प्रकार

प्रश्न 9.
संतुलन कीमत तथा मात्रा किस प्रकार प्रभावित होती है, जब उपभोक्ताओं की आय में
(a) वृद्धि होती है।
(b) कमी होती है।
उत्तर:
(a) जब उपभोक्ताओं की आय में वृद्धि होती है तो उपभोक्ता की क्रय करने की शक्ति में भी वृद्धि होती है। फलस्वरूप (घटिया वस्तुओं को छोड़कर) सभी वस्तुओं की माँग में वृद्धि होगी, जिसके परिणामस्वरूप वस्तु का माँग वक्र दाईं ओर खिसक जाएगा। माँग वक्र में इस परिवर्तन के कारण संतुलन कीमत और संतुलन मात्रा दोनों में वृद्धि होगी। इसे हम संलग्न रेखाचित्र द्वारा दिखा सकते हैं।

संलग्न रेखाचित्र में प्रारंभिक माँग वक्र DD है जो पूर्ति वक्र SS को E बिंदु पर काटता है। यहाँ संतुलन कीमत OP और मात्रा OQ है। जब माँग वक्र DD से बढ़कर D₁D₁ हो जाता है तो संतुलन बिंदु E₁ हो जाता है और संतुलन कीमत OP से बढ़कर OP₁ तथा मात्रा OQ₁ से बढ़कर OQ₁ हो जाती है।

(b) जब उपभोक्ताओं की आय में कमी होती है तो उपभोक्ताओं की क्रय करने की शक्ति में भी कमी होती है। परिणामस्वरूप (घटिया वस्तुओं को छोड़कर) सभी वस्तुओं की माँग में कमी आएगी, जिसके फलस्वरूप वस्तु का माँग वक्र बाईं ओर खिसक जाएगा। माँग वक्र में इस परिवर्तन के कारण संतुलन कीमत और संतुलन मात्रा दोनों में कमी होगी। इसे हम संलग्न रेखाचित्र द्वारा दिखा सकते हैं।

संलग्न रेखाचित्र में प्रारंभिक माँग वक्र DD है जो पूर्ति वक्र SS को E बिंदु पर काटता है। यहाँ संतुलन कीमत OP और मात्रा OQ है। जब माँग वक्र D₁D₁ से कम होकर D₁D₁ हो जाता है तो संतुलन बिंदु E₁ हो जाता है और संतुलन कीमत OP से घटकर OP₁ तथा मात्रा OQ से घटकर OQ₁ हो जाती है।

प्रश्न 10.
पूर्ति तथा माँग वक्रों का उपयोग करते हुए दर्शाइए कि जूतों की कीमतों में वृद्धि, खरीदी व बेची जानी वाली मोजों की जोड़ी की कीमतों को तथा संख्या को किस प्रकार प्रभावित करती है?
उत्तर:
जूते और मोजों की जोड़ी पूरक वस्तुएँ हैं जिनका उपयोग साथ-साथ किया जाता है। पूरक वस्तुओं की स्थिति में, जूतों की कीमतों में कमी से दूसरी वस्तु, मोजों की जोड़ी की माँग में वृद्धि होगी और जूतों की कीमतों में वृद्धि से दूसरी वस्तु मोजों की जोड़ी की माँग में कमी होगी। इस प्रकार जूतों की कीमतों में वृद्धि से मोजों की जोड़ी का माँग वक्र बाईं ओर खिसक जाता है। फलस्वरूप मोजों की जोड़ी की कीमत व मात्रा दोनों में कमी होगी। इसे हम संलग्न रेखाचित्र द्वारा दिखा सकते हैं।

संलग्न रेखाचित्र में मोजों की जोड़ी का प्रारंभिक माँग वक्र DD है जो पूर्ति वक्र ss को E बिंदु पर काटता है। यहाँ संतुलन कीमत OP और मात्रा OQ है। जब माँग वक्र DD से घटकर D₁D₁ हो जाता है तो संतुलन बिंदु E₁ हो जाता है और संतुलन कीमत OP से घटकर OP₁ तथा मात्रा OQ से घटकर OQ₁ हो जाती है।

प्रश्न 11.
कॉफी की कीमत में परिवर्तन, चाय की संतुलन कीमत को किस प्रकार प्रभावित करेगा? एक आरेख द्वारा संतलन मात्रा पर प्रभाव को भी समझाइए।
उत्तर:
कॉफ़ी और चाय स्थानापन्न वस्तुएँ हैं। स्थानापन्न वस्तुओं की स्थिति में एक उपभोक्ता इन वस्तुओं का उपभोग एक-दूसरे के स्थान पर सुगमतापूर्वक कर सकता है। कॉफ़ी की कीमत में वृद्धि से कॉफी की माँग कम हो जाएगी और चाय की माँग बढ़ जाएगी। कॉफ़ी की कीमत में कमी से कॉफ़ी की माँग बढ़ जाएगी और चाय की माँग में कमी होगी। इस प्रकार कॉफ़ी की कीमत में परिवर्तन चाय की संतुलन कीमत और संतुलन मात्रा दोनों को प्रभावित करेगा। इसे हम संलग्न रेखाचित्र द्वारा दिखा सकते हैं।

संलग्न रेखाचित्र में DD चाय का प्रारंभिक माँग वक्र है और SS पूर्ति वक्र है। ये दोनों वक्र एक-दूसरे को E बिंदु पर काटते हैं जहाँ संतुलन कीमत OP और संतुलन मात्रा OQ है। जब कीमत में बढ़ोतरी से चाय की माँग बढ़ जाती है तो माँग वक्र दाईं ओर खिसककर D₁D₁ हो जाता है। इससे संतुलन बिंदु E₁ हो जाता है जहाँ संतुलन कीमत OP, और संतुलन मात्रा OQ₁ हो जाएगी। जब कीमत में कमी से चाय की माँग कम हो जाती है तो माँग वक्र बाईं ओर खिसककर D₁D₁ हो जाता है। इससे संतुलन बिंदु हो जाता है। जहाँ संतुलन कीमत OP₂ और संतुलन मात्रा OQ₂ हो जाएगी।

प्रश्न 12.
जब उत्पादन में प्रयुक्त आगतों की कीमतों में परिवर्तन होता है, तो किसी वस्तु की संतुलन कीमत तथा मात्रा किस प्रकार परिवर्तित होती है?
उत्तर:
जब उत्पादन में प्रयुक्त आगतों (Inputs) की कीमतों में परिवर्तन होता है तो उस वस्तु की पूर्ति में परिवर्तन होगा। उत्पादन में प्रयुक्त आगतों की कीमतों में कमी से उत्पादन लागत में कमी आएगी और उस वस्त की पर्ति बढ जाएगी। परिणामस्वरूप पूर्ति वक्र दाईं ओर खिसक जाएगा। उत्पादन में प्रयुक्त आगतों की कीमतों में वृद्धि से उत्पादन लागत में वृद्धि होगी और उस वस्तु की पूर्ति कम हो जाएगी। फलस्वरूप पूर्ति वक्र बाईं ओर खिसक जाएगा। पूर्ति वक्र में परिवर्तन से संतुलन कीमत और मात्रा में भी परिवर्तन होगा, जिसे संलग्न रेखाचित्र द्वारा दर्शाया गया है।

संलग्न रेखाचित्र में SS वस्तु का प्रारंभिक पूर्ति वक्र है जो माँग वक्र DD को E बिंदु पर काटता है जहाँ संतुलन कीमत OP और संतुलन मात्रा OQ है। जब प्रयुक्त आगतों की कीमतों में कमी से पूर्ति वक्र S₁S₁ हो जाता है तो नया संतुलन बिंदु E₁ हो जाएगा। जहाँ वस्तु की कीमत OP₁ तथा वस्तु की मात्रा OQ₁ होगी। जब प्रयुक्त आगतों की कीमतों में वृद्धि से पूर्ति वक्र S₂S₂ हो जाता है तो नया संतुलन बिंदु E₂ हो जाएगा। जहाँ वस्तु की कीमत OP₂ तथा वस्तु की मात्रा OQ₂ होगी।

प्रश्न 13.
यदि वस्तु X की स्थानापन्न वस्तु Y की कीमत में वृद्धि होती है, तो वस्तु X की संतुलन कीमत तथा मात्रा पर इसका क्या प्रभाव होता है?
उत्तर:
जब X की स्थानापन्न वस्तु Y की कीमत में वृद्धि होती है तो X-वस्तु की माँग। में वृद्धि हो जाएगी क्योंकि उपभोक्ता Y-वस्तु के बदले X-वस्तु की ओर आकर्षित होगा। परिणामस्वरूप X-वस्तु का माँग वक्र दाईं ओर खिसक जाएगा, जिससे संतुलन कीमत और संतुलन मात्रा दोनों में वृद्धि होगी। इसे हम संलग्न रेखाचित्र द्वारा दिखा सकते हैं।

संलग्न रेखाचित्र में DD, X-वस्तु का प्रारंभिक माँग वक्र है जो पूर्ति वक्र SS को E बिंदु पर काटता है जिससे संतुलन कीमत OP और संतुलन मात्रा OQ निर्धारित होती। है। X-वस्तु के माँग वक्र के दाईं ओर खिसकने से नई माँग D₁D₁ हो जाती है जो पूर्ति वक्र को E₁ बिंदु पर काटती है। इस बिंदु पर संतुलन कीमत OP से बढ़कर OP₁ हो जाती है और संतुलन मात्रा OQ से बढ़कर OQ₁ हो जाती है।

प्रश्न 14.
बाज़ार फर्मों की संख्या स्थिर होने पर तथा निर्बाध प्रवेश तथा बहिर्गमन की स्थिति में, माँग वक्र के स्थानांतरण का संतुलन पर प्रभाव की तुलना कीजिए।
उत्तर:
जब बाज़ार में फर्मों की संख्या स्थिर होती है, संतुलन स्थिति (संतुलन कीमत और संतुलन मात्रा) बाज़ार माँग और बाज़ार पूर्ति वक्रों के प्रतिच्छेदन बिंदु पर निर्धारित होती है। जब माँग वक्र का स्थानांतरण होता है तो संतुलन स्थिति में भी परिवर्तन होता है। इसे संलग्न रेखाचित्र द्वारा दर्शाया गया है।

संलग्न रेखाचित्र में, DD वस्तु का प्रारंभिक माँग वक्र है जो पूर्ति वक्र ss को E बिंदु पर काटता है जहाँ संतुलन कीमत OP और संतुलन मात्रा OQ है। जब माँग वक्र में दाईं ओर खिसकाव होता है तो माँग वक्र D₁D₁ हो जाता है जिससे कीमत OP से बढ़कर OP₁ और संतुलन मात्रा OQ₁ से OQ हो जाती है। जब माँग वक्र में बाईं वस्तु की मात्रा ओर खिसकाव होता है तो माँग वक्र D₁D₁ हो जाता है जिससे कीमत OP से कम होकर OP₂ तथा संतुलन मात्रा OQ से कम होकर OQ₂ हो जाती है।

जंब बाज़ार में फर्मों के निर्बाध प्रवेश तथा बहिर्गमन की स्थिति पाई जाती है तो संतुलन कीमत फर्म की न्यूनतम औसत लागत के बराबर होती है। बाज़ार पूर्ति वक्र पूर्णतया लोचदार वक्र होगा, जो X-अक्ष के समानांतर होगा। ऐसी स्थिति में बाज़ार की संतुलन कीमत में कोई परिवर्तन नहीं होता। ऐसी स्थिति में संतुलन मात्रा उस बिंदु पर निर्धारित होगी जहाँ पूर्ति की गई मात्रा माँगी गई मात्रा के बराबर हो। माँग के बढ़ने या घटने से संतुलन मात्रा में भी परिवर्तन होता है। इसे संलग्न रेखाचित्र द्वारा दर्शाया गया है। संलग्न रेखाचित्र में, संतुलन बिंदु E है जहाँ संतुलन कीमत OP और संतुलन मात्रा OQ है। जब माँग वक्र D₁D₁ हो जाता है तो संतुलन मात्रा OQ₁ हो जाएगी। जब माँग वक्र D₂D₂ हो जाता है तो संतुलन मात्रा OQ₂ हो जाएगी।

प्रश्न 15.
माँग तथा पूर्ति वक्र दोनों के दाईं ओर शिफ्ट का, संतुलन कीमत तथा मात्रा पर प्रभाव को एक आरेख द्वारा समझाइए।
उत्तर:
जब किसी वस्तु की माँग और पूर्ति वक्र दोनों ही दाईं ओर शिफ्ट होते (खिसकते) हैं तो इसका अर्थ है-दोनों में वृद्धि होना। इस संबंध में तीन परिस्थितियाँ हो सकती हैं
1. जब माँग और पूर्ति दोनों में समान वृद्धि हो-इस स्थिति में संतुलन कीमत पर कोई प्रभाव नहीं पड़ेगा जबकि मात्रा बढ़ जाएगी, जैसाकि निम्न रेखाचित्र (i) से स्पष्ट है। संतुलन कीमत पूर्ववत् OP बनी रहती है, जबकि संतुलन मात्रा OQ से बढ़कर OQ₁ हो जाती है।

2. जब माँग में वृद्धि, पूर्ति में वृद्धि की अपेक्षा अधिक हो इस स्थिति में संतुलन कीमत व मात्रा दोनों में वृद्धि होगी, जैसाकि निम्न रेखाचित्र (ii) से स्पष्ट है, संतुलन कीमत OP से बढ़कर OP₁ हो जाती है तथा संतुलन मात्रा OQ से बढ़कर OQ₁ हो जाती है।

3. जब माँग में वृद्धि, पूर्ति में वृद्धि की अपेक्षा कम हो इस स्थिति में नई संतुलन कीमत आरंभिक कीमत की अपेक्षा कम होगी, जैसाकि निम्न रेखाचित्र (ii) से स्पष्ट है, संतुलन कीमत OP से गिरकर OP₁ हो जाती है और संतुलन मात्रा OQ से बढ़कर OQ₁ हो जाती है।

प्रश्न 16.
संतुलन कीमत तथा मात्रा किस प्रकार प्रभावित होते हैं जब (a) माँग तथा पूर्ति वक्र दोनों, समान दिशा में शिफ्ट होते हैं? (b) माँग तथा पूर्ति वक्र विपरीत दिशा में शिफ्ट होते हैं?
उत्तर:
(a) माँग तथा पूर्ति वक्र दोनों, समान दिशा में शिफ्ट होते हैं जब माँग तथा पूर्ति वक्र दोनों समान (एक) दिशा में शिफ्ट होते हैं तो संतुलन कीमत व संतुलन मात्रा में परिवर्तन इस बात पर निर्भर करता है कि दोनों में परिवर्तन की मात्रा कितनी है? इस संबंध में निम्नलिखित स्थितियाँ हो सकती हैं
(i) यदि माँग और पर्ति दोनों वक्र बाईं ओर शिफ्ट होते हैं तो संतलन मात्रा में कमी आएगी. परंत संतलन कीमत में परिवर्तन नहीं भी। जब माँग और पूर्ति में कमी समान दर से होती है तो संतुलन कीमत में कोई परिवर्तन नहीं आता। जब माँग में कमी पूर्ति में कमी की अपेक्षा कम होती है तो कीमत में वृद्धि हो जाती है। जब माँग में कमी पूर्ति में कमी की अपेक्षा अधिक होती है तो कीमत में गिरावट आ जाती है।

(ii) यदि माँग और पूर्ति दोनों वक्र दाईं ओर शिफ्ट होते हैं तो संतुलन मात्रा में वृद्धि होगी, परंतु संतुलन कीमत में परिवर्तन आ भी सकता है और नहीं भी। जब माँग और पूर्ति में वृद्धि एक-समान दर से होती है तो संतुलन कीमत में कोई परिवर्तन नहीं होता। जब माँग में वृद्धि पूर्ति की वृद्धि की अपेक्षा कम होती है तो कीमत में कमी हो जाती है। जब माँग में वृद्धि पूर्ति की वृद्धि की अपेक्षा अधिक होती है तो कीमत में वृद्धि हो जाती है।

(b) माँग तथा पूर्ति वक्र विपरीत दिशा में शिफ्ट होते हैं जब माँग और पूर्ति वक्र दोनों विपरीत दिशा में शिफ्ट होते हैं तो संतुलन कीमत व मात्रा में परिवर्तन इस बात पर निर्भर करते हैं कि दोनों में शिफ्ट की मात्रा कितनी है? यदि माँग वक्र बाईं ओर तथा पूर्ति वक्र दाईं ओरं शिफ्ट होते हैं तो संतुलन कीमत में कमी आएगी, लेकिन संतुलन मात्रा में परिवर्तन हो भी सकता है और नहीं भी। यदि माँग वक्र का बायाँ शिफ्ट पूर्ति वक्र के दाएँ शिफ्ट के अनुपात में बराबर है तो संतुलन मात्रा में कोई परिवर्तन नहीं होगा। यदि माँग वक्र का बायाँ शिफ्ट पूर्ति वक्र के दाएँ शिफ्ट के अनुपात से अधिक है तो संतुलन मात्रा में कमी आएगी। यदि माँग वक्र का बायाँ शिफ्ट पूर्ति वक्र के दाएँ शिफ्ट के अनुपात से कम है तो संतुलन मात्रा में वृद्धि होगी।

यदि माँग वक्र दाईं ओर तथा पूर्ति वक्र बाईं ओर शिफ्ट होता है तो संतुलन कीमत में वृद्धि होगी, लेकिन संतुलन मात्रा में परिवर्तन हो भी सकता है और नहीं भी। यदि माँग वक्र का दायाँ शिफ्ट पूर्ति वक्र के बाएँ शिफ्ट के अनुपात के बराबर है तो संतुलन मात्रा में कोई परिवर्तन नहीं होगा। यदि माँग वक्र का दायाँ शिफ्ट पूर्ति वक्र के बाएँ शिफ्ट के अनुपात से अधिक है तो संतुलन मात्रा में वृद्धि होगी। यदि माँग वक्र का दायाँ शिफ्ट पूर्ति वक्र के बाएँ शिफ्ट के अनुपात से कम है तो संतुलन मात्रा में कमी होगी।

प्रश्न 17.
वस्तु बाज़ार में तथा श्रम बाज़ार में माँग तथा पूर्ति वक्र किस प्रकार भिन्न होते हैं?
उत्तर:
वस्तु बाज़ार और श्रम बाज़ार में माँग और पूर्ति के स्रोत में अंतर होता है। श्रम बाज़ार में श्रम की माँग फर्मों से आती है जबकि वस्तु बाज़ार में वस्तुओं की माँग घर-परिवार से आती है। श्रम बाज़ार में श्रम की पूर्ति घर-परिवार द्वारा होती है और वस्तु बाज़ार में वस्तुओं की पूर्ति फर्मों द्वारा की जाती है। श्रम बाज़ार में श्रम की माँग व्युत्पन्न (अप्रत्यक्ष) माँग है जबकि वस्तु बाज़ार में वस्तु की माँग प्रत्यक्ष है। श्रम की माँग श्रम की उत्पादकता से प्रभावित होती है। श्रम की माँग स्थानापन्न साधन अर्थात् पूँजी की कीमत पर निर्भर होगी। यदि पूँजी की कीमत कम हो तो श्रम की माँग कम होगी। श्रम की पूर्ति वस्तु की पूर्ति से निम्नलिखित संदर्भो में होती है
(i) श्रम वस्तु की तुलना में कम गतिशील होता है।

(ii) श्रम का पूर्ति वक्र पीछे की ओर मुड़ता हुआ होता है जो यह दिखाता है कि एक सीमा के पश्चात् मजदूरी दर के बढ़ने पर श्रम की पूर्ति कम होने कार्य के घंटे+ लगती है क्योंकि मजदूरी के एक उच्च स्तर पर श्रमिक काम की तुलना में अवकाश अधिक पसंद करने लगते हैं। इसे हम संलग्न रेखाचित्र द्वारा दिखा सकते हैं।

संलग्न रेखाचित्र से स्पष्ट है कि M बिंदु तक मजदूरी के बढ़ने से श्रम की पूर्ति बढ़ती है परंतु उसके बाद जब मज़दूरी ow, से बढ़कर ow, हो जाती है तो श्रम की पूर्ति OL₂ से घटकर OL₁ रह जाती है।

प्रश्न 18.
एक पूर्ण प्रतिस्पर्धी बाज़ार में श्रम की इष्टतम मात्रा किस प्रकार निर्धारित होती है?
उत्तर:
एक पूर्ण प्रतिस्पर्धी बाज़ार में श्रम की इष्टतम मात्रा का निर्धारण उस बिंदु पर होता है जहाँ मज़दूरी दर श्रम की सीमांत उत्पादकता के बराबर होती है अर्थात्
W = MP_L
अथवा
मज़दूरी की दर = श्रम की सीमांत उत्पादकता

प्रश्न 19.
एक पूर्ण प्रतिस्पर्धी श्रम बाज़ार में मजदूरी दर किस प्रकार निर्धारित होती है?
उत्तर:
एक पूर्ण प्रतिस्पर्धी बाजार में मजदूरी दर का निर्धारण उस बिंद पर होता है जहाँ श्रम की माँग श्रम की पूर्ति के बराबर हो। इसे संलग्न रेखाचित्र द्वारा दर्शाया गया है।

इस रेखाचित्र में D_LD_L श्रम का माँग वक्र है जो श्रम की पूर्ति वक्र S_LS_L को E बिंदु पर काटता है। इस प्रकार E संतुलन बिंदु है जहाँ मजदूरी दर OW निर्धारित होती है। यदि मज़दूरी दर OW से अधिक (अर्थात् OW₁) है तो श्रम की अधिमाँग पूर्ति श्रम की माँग से अधिक होगी। यदि मज़दूरी दर OW से कम (अर्थात् ow₂) है तो श्रम की माँग श्रम की पूर्ति से अधिक होगी। इस प्रकार OW मज़दूरी दर ही संतुलित मजदूरी दर है जहाँ श्रम की माँग व पूर्ति बराबर है।

प्रश्न 20.
क्या आप किसी ऐसी वस्तु के विषय में सोच सकते हैं, जिस पर भारत में कीमत की उच्चतम निर्धारित कीमत लागू है? निर्धारित उच्चतम कीमत सीमा के क्या परिणाम हो सकते हैं?
उत्तर:
भारत में पेट्रोल, अनाज आदि पर उच्चतम निर्धारित कीमत लागू है। कीमत नियंत्रण का उद्देश्य गरीब जन-समुदाय को अति आवश्यक वस्तुओं; जैसे खाद्यान्नों आदि को उचित कीमत पर उपलब्ध कराना है। नियंत्रित कीमत संतुलन कीमत से कम होती है। इसे हम संलग्न रेखाचित्र द्वारा दिखा सकते हैं।

संलग्न रेखाचित्र में OP संतुलन कीमत है जिस पर OQ मात्रा का विनिमय किया जाता है। सरकार OP₁ नियंत्रित कीमत निर्धारित करती है जिससे MN अर्थात् RT मात्रा में वस्तु की कमी उत्पन्न हो जाएगी। इस कमी को पूरा करने के लिए सरकार को राशनिंग की नीति अपनानी चाहिए। राशनिंग का अर्थ है-एक व्यक्ति के लिए वस्तु के क्रय की उच्चतम सीमा निर्धारित करना। राशनिंग व्यवस्था के अंतर्गत निम्नलिखित दोष होते हैं
(i) प्रत्येक उपभोक्ता को राशन की दुकानों से वस्तुओं को खरीदने के लिए लंबी कतारों में खड़ा रहना पड़ता है।
वस्तु की मात्रा

(ii) क्योंकि सभी उपभोक्ता उचित कीमत की दुकानों से प्राप्त वस्तुओं की मात्रा से संतुष्ट नहीं होंगे, उनमें से कुछ अधिक कीमत देने के लिए तत्पर होंगे। इससे कालाबाजारी की स्थिति उत्पन्न हो सकती है।

प्रश्न 21.
माँग वक्र में शिफ्ट का कीमत पर अधिक तथा मात्रा पर कम प्रभाव होता है, जबकि फर्मों की संख्या स्थिर रहती है। स्थितियों की तुलना करें जब निर्बाध प्रवेश तथा बहिर्गमन की अनुमति हो। व्याख्या करें।
उत्तर:
जब फर्मों की संख्या स्थिर रहती है तो माँग वक्र में शिफ्ट का संतुलन कीमत पर अधिक तथा मात्रा पर कम प्रभाव पड़ता है, क्योंकि माँग में परिवर्तन कीमत में परिवर्तन करते हैं। यदि माँग वक्र दाईं ओर शिफ्ट होता है तो कीमत में वृद्धि होती है और यदि माँग वक्र बाईं ओर शिफ्ट करता है. तो कीमत में कमी होती है।

जब बाज़ार में निर्बाध प्रवेश तथा बहिर्गमन की अनुमति हो तो माँग वक्र में शिफ्ट का संतुलन कीमत पर कोई प्रभाव नहीं पड़ेगा, लेकिन संतुलन मात्रा में परिवर्तन होगा। यदि माँग वक्र दाईं ओर शिफ्ट होता है तो संतुलन मात्रा में वृद्धि होती है। यदि माँग वक्र बाईं ओर शिफ्ट होता है तो संतुलन मात्रा में कमी होती है।

प्रश्न 22.
मान लीजिए, एक पूर्ण प्रतिस्पर्धी बाज़ार में वस्तु X की माँग तथा पूर्ति वक्र निम्नलिखित प्रकार दिए गए है q^d = 700 – p
q^s = 500 + 3p क्योंकि p ≥ 15
= 0 क्योंकि ≤ 0 p ≤ 15
मान लीजिए कि बाज़ार में समरूपी फर्मे हैं। 15 रुपए से कम, किसी भी कीमत पर वस्तु X की बाज़ार पूर्ति के शून्य होने के कारण की पहचान कीजिए। इस वस्तु के लिए संतुलन कीमत क्या होगी? संतुलन की स्थिति में x की कितनी मात्रा का उत्पादन होगा?
हल:
वस्तु का बाज़ार माँग वक्र q^d = 700 – p
वस्तु का बाज़ार पूर्ति वक्र-
q^d = 500 + 3p क्योंकि p ≥ 15
= 0 क्योंकि 0 ≤ p ≤ 15
वस्तु X की बाज़ार पूर्ति 15 रुपए से कम किसी भी कीमत पर शून्य होगी क्योंकि यह वस्तु X को उत्पादित करने की न्यूनतम औसत लागत है। यदि एक फर्म 15 रुपए से कम कीमत पर वस्तु की पूर्ति करती है तो फर्म को हानि सहन करनी होगी। इस प्रकार पूर्ति वक्र का प्रारंभिक बिंदु 15 रुपए की कीमत होगा।

संतुलन बिंदु पर-
q^d = q^s
700 – p = 500 + 3p
4p = 200
p = 50
इस प्रकार 50 रुपए संतुलन बिंदु है। संतुलन मात्रा की गणना निम्नलिखित प्रकार से होगी-
संतुलन मात्रा = 700 – p
= 700 – 50
= 650 उत्तर

प्रश्न 23.
अभ्यास 22 में दिए गए समान माँग वक्र को लेते हुए, आइए, फर्मों को वस्तु X का उत्पादन करने के निर्बाध प्रवेश तथा बहिर्गमन की अनुमति देते हैं। यह भी मान लीजिए कि बाज़ार समानरूपी फर्मों से बना है जो वस्तु x का उत्पादन करती है। एक अकेली फर्म का पूर्ति वक्र निम्नलिखित प्रकार से है-
q^s_f = 8+ 3p क्योंकि p ≥ 20
= 0 क्योंकि 0 ≤ p < 20
(a) p = 20 का क्या महत्त्व है?
(b) बाज़ार में x के लिए किस कीमत पर संतुलन होगा? अपने उत्तर का कारण बताइए।
(c) संतुलन मात्रा तथा फर्मों की संख्या का परिकलन कीजिए।
हल:
एक वस्तु का माँग वक्र निम्नलिखित है-
q^d = 700 – p (अभ्यास 22 में दिया गया है)
एक एकल फर्म का पूर्ति वक्र निम्नलिखित है-
q^s_f = 8 + 3p क्योंकि p ≥ 0
= 0 क्योंकि 0 ≤ P< 20
(a) p = 20 का महत्त्व यह है कि यह फर्मों की न्यूनतम औसत लागत है। इस कीमत स्तर से नीचे एक फर्म वस्तु की पूर्ति के लिए इच्छुक नहीं होगी।

(b) X के लिए बाज़ार में संतुलन 20 रुपए की कीमत पर होगा। जब बाज़ार में फर्मों का प्रवेश और बहिर्गमन निर्बाध रूप से होता है तो बाजार का संतुलन उस कीमत पर होगा जो फर्मों की न्यूनतम औसत लागत के बराबर हो। इसी कीमत पर बाजार की माँग और पूर्ति बराबर होगी।

(c) माँग वक्र से हम संतुलन मात्रा का परिकलन कर सकते हैं-
q₀ = 700 – 20
= 680
P₀ = 20 पर प्रत्येक फर्म की पूर्ति है-
q^s_f = 8 + 3p
= 8 + (3 x 20)
= 68
फर्मों की संख्या (n₀) = \(\frac{q_{0}}{q_{0 f}}\)
= \(\frac { 680 }{ 68 }\)
= 10 उत्तर

प्रश्न 24.
मान लीजिए कि नमक की माँग तथा पूर्ति वक्र को इस प्रकार दिया गया है-
q^d = 1000 – p
q^s = 700 + 2P
(a) संतुलन कीमत तथा मात्रा ज्ञात कीजिए।
(b) अब मान लीजिए कि नमक के उत्पादन के लिए प्रयुक्त एक आगत की कीमत में वृद्धि हो जाती है और नया पूर्ति वक्र है
q^s = 400 + 2p
संतुलन कीमत तथा मात्रा किस प्रकार परिवर्तित होती है? क्या परिवर्तन आपकी अपेक्षा के अनुकूल है?
(c) मान लीजिए, सरकार नमक की बिक्री पर 3 रुपए प्रति इकाई कर लगा देती है। यह संतुलन कीमत तथा मात्रा को किस प्रकार प्रभावित करेगा?
हल:
नमक का माँग वक्र निम्नलिखित है-
q^d = 1000 – p
नमक का पूर्ति वक्र निम्नलिखित है–
q^s = 700 + 2p
(a) संतुलन पर नमक की माँग और नमक की पूर्ति बराबर होंगे-
q^d = q^s
1000 – p = 700 + 2p
– 3p = 700 – 1000
– 3p = – 300
3p = 300
p = 100
संतुलन कीमत = 100
संतुलन मात्रा = 1000 – p
= 1000 – 100
= 900 उत्तर

(b) नमक का माँग वक्र है
q^d = 100 – p
नमक की नई पूर्ति वक्र है-
q^s = 400 – 2p
नए संतुलन के लिए भी q^d = q^s की शर्त का लागू होना आवश्यक है।
इसलिए
q^d = q^s
1000 – p = 400 + 2 p
– 3p = 400 – 1000
3p = 600
p = 200
नई संतुलन कीमत = 200
संतुलन मात्रा = 1000 – p
= 1000 – 200 = 800
संतुलन मात्रा में कमी = 900 – 800
= 100
संतुलन कीमत में वृद्धि = 200 – 100
= 100 उत्तर
ये परिवर्तन हमारी अपेक्षा के अनुकूल हैं। जब नमक के उत्पादन के लिए प्रयुक्त एक आगत की कीमत में वृद्धि हो जाती है तो वस्तु की लागत में वृद्धि होगी। फलस्वरूप संतुलन कीमत में वृद्धि तथा संतुलन मात्रा में कमी होना स्वाभाविक है।

(c) नमक पर बिक्री कर = 3 रुपए
कर पूर्व माँग वक्र है = 1000 – p
कर पश्चात् माँग वक्र होगा = 1000 – 3 – p
= 997 – p
कर पूर्व पूर्ति वक्र है = 700 + 2p
कर पश्चात् पूर्ति वक्र होगा = 700 + 2 (p – 3)
= 700 + 2p – 6
= 694 + 2p
संतुलन स्थिति है- q^d = q^s
997 – p = 694 + 2p
3p = 303
p = \(\frac { 303 }{ 3 }\)
p = 101 रुपए
संतुलन कीमत = 101 रुपए
संतुलन मात्रा = 997 – p
= 997 -101
= 896 उत्तर
इस प्रकार 3 रुपए प्रति इकाई के कर के परिणामस्वरूप संतुलन कीमत 100 रुपए से बढ़कर 101 रुपए हो गई है और संतुलन मात्रा 900 से 896 तक घट गई है।

प्रश्न 25.
मान लीजिए कि एपार्टमेंटों के लिए बाज़ार-निर्धारित किराया इतना अधिक है कि सामान्य लोगों द्वारा वहन नहीं किया जा सकता, यदि सरकार किराए पर एपार्टमेंट लेने वालों की मदद करने के लिए किराया नियंत्रण लागू करती है, तो इसका एपार्टमेंटों के बाज़ार पर क्या प्रभाव पड़ेगा?
उत्तर:
यदि सरकार किराए पर एपार्टमेंट लेने वालों की मदद करने के लिए किराया नियंत्रण लागू करती है तो इसका अर्थ यह होगा कि सरकार द्वारा निर्धारित किया हआ किराया बाजार द्वारा निर्धारित (संतलन) किराए से कम होगा। इसके परिणामस्वस एपार्टमेंट की पूर्ति उसकी माँग से कम हो जाएगी। इस प्रकार एपार्टमेंट की माँग की तुलना में पूर्ति कम होगी। इस कमी को पूरा करने के लिए सरकार को नियंत्रित किराए पर एपार्टमेंट की पूर्ति स्वयं बढ़ानी होगी। यदि सरकार किसी भी कारणवश ऐसा नहीं कर पाती है तो बाज़ार में कालाबाज़ारी का बोलबाला हो जाएगा।

बाज़ार संतुलन HBSE 12th Class Economics Notes

→ संतुलन वह स्थिति है, जहाँ किसी परिवर्तन की कोई प्रवृत्ति नहीं होती।

→ एक पूर्ण प्रतिस्पर्धी बाज़ार में संतुलन वहाँ होता है, जहाँ बाज़ार माँग तथा बाज़ार पूर्ति बराबर होती है।
बाज़ार संतुलन : बाज़ार माँग = बाज़ार पूर्ति ।

→ फर्मों की संख्या स्थिर होने पर संतुलन कीमत तथा मात्रा, बाज़ार माँग तथा बाज़ार पूर्ति वक्रों के परस्पर प्रतिच्छेदन बिंदु पर निर्धारित होती है।

→ प्रत्येक फर्म श्रम का उपयोग उस बिंदु तक करती है, जहाँ श्रम का सीमांत संप्राप्ति (आगम) उत्पाद, मजदूरी दर के बराबर होता है। यही बिंदु श्रम की इष्टतम मात्रा का बिंदु होता है।

→ पर्ति वक्र के अपरिवर्तित रहने पर जब माँग वक्र दायीं (बायीं ओर शिफ्ट होता है, तो फर्मों की स्थिर संख्या होने पर संतुलन मात्रा में वृद्धि (गिरावट) होती है।

→ माँग वक्र के अपरिवर्तित रहने पर जब पूर्ति वक्र दायीं (बायीं) ओर शिफ्ट होता है, तो फर्मों की स्थिर संख्या होने पर संतुलन मात्रा में वृद्धि (गिरावट) होती है तथा संतुलन कीमत में गिरावट (घृद्धि) होती है।

→ जब माँग तथा पूर्ति दोनों वक्र समान दिशा में शिफ्ट होते हैं, तो संतलन मात्रा पर इसका प्रभाव सस्पष्ट रूप से निर्धारित किया जा सकता है, जबकि संतुलम कीमत पर इसका प्रभाव शिफ्ट के परिमाण पर निर्भर करता है।

→ जब माँग तथा पूर्ति वक्र, दोनों का दायीं ओर शिफ्ट होता है, तो संतलन मात्रा में बद्धि होती है जबकि संतलन कीमत में वृद्धि, कमी हो सकती है अथवा अपरिवर्तित भी रह सकती है। यह माँग और पूर्ति चक्रों में शिफ्ट के परिमाण पर निर्भर करता है।

→ जब माँग तथा पूर्ति वक्र विपरीत दिशाओं में शिफ्ट होते हैं, तो संतुलन कीमत पर इसका प्रभाव सुस्पष्ट रूप से निर्धारित किया जा सकता है, जबकि संतुलन मात्रा पर प्रभाव शिफ्ट के परिमाण पर निर्भर करता है।

→ जब माँग तथा पूर्ति वक्र दोनों का बायीं ओर शिफ्ट होना है, तो संतुलन मात्रा में कमी होती है, जबकि संतुलन कीमत ‘ में वृद्धि कमी अथवा अपरिवर्तित हो सकती है। यह माँग और पूर्ति वक्रों में शिफ्ट के परिमाण पर निर्भर करता है।

→ संतुलन कीमत से कम कीमत का उच्चतम निर्धारित कीमत निर्धारण से अधिमाँग उत्पन्न होती है।

→ संतुलन कीमत से अधिक कीमत की निम्नतम निर्धारित कीमत निर्धारण से अधिपूर्ति उत्पन्न होती है।

→ एक पूर्ण प्रतिस्पर्धी बाज़ार में समरूपी के साथ यदि फर्मे बाज़ार में निर्बाध प्रवेश तथा बहिर्गमन कर सकती है, तो संतुलन कीमत सदैव फर्मों की न्यूनतम औसत लागत के ही बराबर होती है अर्थात् P = न्यूनतम औसत लागत।

→ नर्बाध प्रवेश तथा बहिर्गमन होने पर माँग में शिफ्ट का संतुलन कीमत पर कोई प्रभाव नहीं होता, परंतु संतुलन मात्रा तथा फर्मों की संख्या में परिवर्तन माँग की दिशा में परिवर्तन के समान होता है।

→ फर्मों की स्थिर संख्या वाले बाज़ार की तुलना में निर्बाध प्रवेश तथा बहिर्गमन वाले बाज़ार में माँग वक्र के शिफ्ट का संतुलन मात्रा पर प्रभाव अधिक प्रबल होगा।