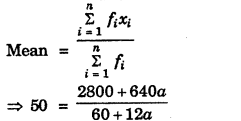Author name: Bhagya

Haryana State Board HBSE 9th Class Science Important Questions Chapter 8 गति Important Questions and Answers.

Haryana Board 9th Class Science Important Questions Chapter 8 गति

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
विरामावस्था से क्या अभिप्राय है?
उत्तर:
यदि कोई वस्तु अपनी आस-पास की वस्तुओं की अपेक्षा अपनी स्थिति नहीं बदलती, तो उस वस्तु को विरामावस्था में कहा जाता है।

प्रश्न 2.
गति अवस्था से क्या अभिप्राय है?
उत्तर:
यदि कोई वस्तु किसी अन्य वस्तु की तुलना में अपनी स्थिति निरंतर बदलती रहती हो, तो वह वस्तु गति अवस्था में कहलाती है।

प्रश्न 3.
सापेक्षिक गति से क्या अभिप्राय है?
उत्तर:
दो गतिशील वस्तुओं के बीच दूरी का घटना या बढ़ना सापेक्षिक गति कहलाता है।

प्रश्न 4.
वायु की गतिशीलता को कैसे जाना जा सकता है?
उत्तर:
वायु की गतिशीलता को उसके प्रभाव द्वारा जाना जा सकता है।

प्रश्न 5.
एक रेलगाड़ी चल रही है। उसमें यात्री बैठे हैं। बताओ ये यात्री किस-किस वस्तु की अपेक्षा स्थिर हैं और किस-किस वस्तु की अपेक्षा गति में हैं?
उत्तर:
चलती हुई रेलगाड़ी में बैठा हुआ एक यात्री अन्य यात्रियों और गाड़ी में रखे सामान के सापेक्ष विरामावस्था में होता है, परंतु वही यात्री बाहर के वृक्षों और भवनों की अपेक्षा गति में होता है।

प्रश्न 6.
सजीवों व निर्जीवों की गति में एक अंतर बताओ।
उत्तर:
सजीवों में गति स्वेच्छा से होती है, जबकि निर्जीवों में गति के लिए बाह्य कारक की आवश्यकता होती है। प्रश्न 7. दूरी क्या है? उत्तर:किसी वस्तु द्वारा प्रारंभिक व अंतिम बिंदुओं के बीच तय किया गया कुल पथ, दूरी कहलाता है।

प्रश्न 8.
विस्थापन किसे कहते हैं?
उत्तर:
किसी वस्तु द्वारा किसी विशेष दिशा में तय की गई दूरी विस्थापन कहलाती है अर्थात् यह अंतिम व प्रारंभिक स्थिति के बीच की न्यूनतम दूरी है।

प्रश्न 9.
दूरी व विस्थापन का SI मात्रक क्या है?
उत्तर:
दूरी व विस्थापन का SI मात्रक मीटर है।

प्रश्न 10.
निर्देश-बिंदु या मूल-बिंदु से क्या अभिप्राय है?
उत्तर:
वह बिंदु जिससे किसी गतिमान वस्तु द्वारा तय की गई दूरी मापी जाती है, निर्देश-बिंदु या मूल-बिंदु कहलाता है।

प्रश्न 11.
जिन राशियों को पूर्ण रूप से व्यक्त करने के लिए परिमाण तथा दिशा दोनों की आवश्यकता होती है, उन्हें क्या कहते हैं?
उत्तर:
जिन राशियों को पूर्ण रूप से व्यक्त करने के लिए परिमाण तथा दिशा दोनों की आवश्यकता होती है, उन्हें सदिश राशियाँ कहते हैं।

प्रश्न 12.
किन राशियों को केवल परिमाण द्वारा व्यक्त किया जाता है?
उत्तर:
अदिश राशियों को केवल परिमाण द्वारा व्यक्त किया जाता है।

प्रश्न 13.
सदिश तथा अदिश राशियों के दो-दो उदाहरण लिखें।
उत्तर:
सदिश राशियाँ वेग तथा विस्थापन। अदिश राशियाँ-दरी तथा चाल।

प्रश्न 14.
जब कोई वस्तु समान समयांतरालों में समान दूरी तय करे तो उस वस्तु की चाल को क्या कहते हैं?
उत्तर:
समान समयांतरालों में समान दूरी तय करने की चाल को समान चाल कहते हैं।

प्रश्न 15.
समान चाल के दो उदाहरण दीजिए।
उत्तर:

1. पृथ्वी की गति
2. घड़ी के पेंडुलम की गति।

प्रश्न 16.
जब कोई वस्तु समान समयांतरालों में असमान दूरी तय करे तो उस वस्तु की चाल को क्या कहते हैं?
उत्तर:
समान समयांतरालों में असमान दूरी तय करने की चाल को असमान चाल कहते हैं।

प्रश्न 17.
असमान चाल के दो उदाहरण लिखो।
उत्तर:

1. स्टेशन से छूटती रेलगाड़ी।
2. आकाश में उड़ते पक्षी।

प्रश्न 18.
किसी गतिशील पिंड की औसत चाल ज्ञात करने का सूत्र लिखें।
उत्तर:
किसी वस्तु द्वारा इकाई समय में तय की गई दूरी को औसत चाल कहते हैं।

प्रश्न 19.
वेग किसे कहते हैं?
उत्तर:
किसी गतिशील वस्तु द्वारा निश्चित दिशा में एक सेकंड में तय की गई दूरी वस्तु का वेग कहलाती है।

प्रश्न 20.
वेग का मानक मात्रक क्या है?
उत्तर:
वेग का मानक मात्रक मीटर/सेकंड (m/s) है।

प्रश्न 21.
दूरी, चाल तथा समय में क्या संबंध है?
उत्तर:
दूरी = चाल x समय।

प्रश्न 22.
यदि कोई धावक 100 मीटर की दूरी को 10 सेकंड में पूरा करे तो उसका वेग क्या होगा?
उत्तर:

प्रश्न 23.
त्वरण से क्या अभिप्राय है?
उत्तर:
किसी वस्तु के वेग में परिवर्तन की दर को त्वरण कहते हैं अर्थात् a = \(\frac { v-u }{ t }\)

प्रश्न 24.
मंदन से क्या अभिप्राय है?
उत्तर:
किसी विशेष दिशा में वेग की कमी की दर को मंदन कहते हैं अर्थात् ऋणात्मक त्वरण मंदन कहलाता है।

प्रश्न 25.
त्वरण का SI मात्रक क्या है?
उत्तर:
त्वरण का SI मात्रक मीटर/सेकंड² या m/s² है।

प्रश्न 26.
त्वरित गति का उदाहरण लिखें।
उत्तर:
वृत्त में एकसमान चाल से चल रही वस्तु त्वरित गति का उदाहरण है।

प्रश्न 27.
निम्नलिखित में से अदिश तथा सदिश चुनें-

1. मुंबई से दिल्ली 1450 कि०मी० दूर है।
2. मुंबई से दिल्ली 1450 कि०मी० दूर उत्तर में है।

उत्तर:

1. यह अदिश राशि का उदाहरण है।
2. यह सदिश राशि का उदाहरण है।

प्रश्न 28.
कोई वस्तु एकसमान त्वरण से कब गतिशील कही जाती है?
उत्तर:
यदि समान अंतराल में किसी वस्तु के वेग में समान परिवर्तन हो तो हम कह सकते हैं कि वस्तु एकसमान त्वरण से गतिशील है।

प्रश्न 29.
एकसमान वृत्तीय गति को परिभाषित करें।
उत्तर:
जब कोई कण किसी निश्चित बिंदु को केंद्र मानकर उसके चारों ओर एक वृत्त की परिधि पर एकसमान चाल से चलता है, तो उसकी गति को एकसमान वृत्तीय गति कहते हैं।

प्रश्न 30.
यदि चाल-समय ग्राफ एक सरल रेखा हो तो वह किस प्रकार की गति को प्रदर्शित करता है?
उत्तर:
एकसमान त्वरित गति को प्रदर्शित करता है।

प्रश्न 31.
यदि चाल-समय ग्राफ समय अक्ष के समानांतर हो तो वस्तु का त्वरण क्या होगा?
उत्तर:
वस्तु की चाल एकसमान होगी, अतः त्वरण शून्य होगा।

प्रश्न 32.
वस्तु के चाल-समय ग्राफ का ढाल क्या प्रदर्शित करता है?
उत्तर:
वस्तु का त्वरण।

प्रश्न 33.
किसी गतिमान वस्तु के चाल-समय ग्राफ के नीचे तथा अंतरालों के बीच का क्षेत्रफल क्या दर्शाता है?
उत्तर:
वस्तु द्वारा उस समयांतराल में तय दूरी।

प्रश्न 34.
यदि दूरी-समय ग्राफ एक समय-अक्ष के समांतर ग्राफ एक सरल रेखा हो तो भिन्न-भिन्न अंतरालों में औसत चाल भिन्न-भिन्न होगी या बराबर?
उत्तर:
बराबर।

प्रश्न 35.
यदि किसी वस्तु की चाल का दूरी-समय ग्राफ एक सरल रेखा है तो उस वस्तु की गति के विषय में आप क्या कहेंगे?
उत्तर:
वस्तु स्थिर अवस्था में होगी।

प्रश्न 36.
यदि किसी वस्तु की चाल का दूरी-समय ग्राफ एक वक्र रेखा हो तो भिन्न-भिन्न अंतरालों में उसकी औसत चाल भिन्न-भिन्न होगी या एकसमान?
उत्तर:
भिन्न-भिन्न अंतरालों में औसत चाल भिन्न-भिन्न होगी।

प्रश्न 37.
यदि किसी गतिमान वस्तु की चाल 2 घंटे में 0 से 30 km/h हो जाती है तो उसका त्वरण कितना होगा?
उत्तर:
त्वरण = \(\frac{(30-0) \mathrm{km} / \mathrm{h}}{2 \mathrm{~h}}\) 15km/h²

प्रश्न 38.
यदि कोई वस्तु एक वृत्तीय पथ पर एकसमान चाल से गति कर रही हो तो उसकी गति किस प्रकार की होगी?
उत्तर:
एक असमान तथा त्वरित गति।

प्रश्न 39.
प्रकाश की चाल 3 x 10⁸ m/s है। इसकी चाल km/h में कितनी होगी?
उत्तर:
प्रकाश की चाल = 3 x 10⁸ m/s = \(\frac{3 \times 10^8 \times 3600}{1000}\)
= 1.08 x 10⁹ km/h

प्रश्न 40.
राजधानी एक्सप्रेस 1384 km की दूरी 17 घंटे में तय करती है। इसकी औसत चाल क्या होगी?
उत्तर:

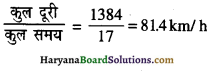
प्रश्न 41.
यदि कोई कार दो घटे में 80 km की दूरी तय करे तो उसकी औसत चाल क्या होगी?
उत्तर:
औसत चाल = \(\frac { 80 }{ 2 }\) = 40km/h

प्रश्न 42.
वृत्तीय गति किसे कहते हैं?
उत्तर:
जब कोई वस्तु वृत्ताकार पथ पर गति करती है तो उसकी गति को वृत्तीय गति कहते हैं।

प्रश्न 43.
वृत्तीय गति के दो उदाहरण दीजिए।
उत्तर:

1. किसी वाहन के पहिए की गति।
2. रस्सी के सिरे पर बंधा पत्थर जो समतल वृत्त में गतिमान हो।

प्रश्न 44.
ग्राफ किसे कहते हैं?
उत्तर:
किसी सूचना का चित्र प्रदर्शन ग्राफ कहलाता है।

प्रश्न 45.
मुक्त रूप से गिरता हुआ पिंड किस प्रकार की गति प्रदर्शित करता है?
उत्तर:
यह एकसमान त्वरित गति प्रदर्शित करता है।

प्रश्न 46.
एक पत्थर ऊर्ध्वाधर दिशा में फेंका जाता है, इसका वेग लगातार कम होता जाता है, क्यों?
उत्तर:
जब कोई पत्थर ऊर्ध्वाधर ऊपर फेंका जाता है तो उसका वेग लगातार कम होता जाता है क्योंकि गुरुत्वीय त्वरण सदैव पृथ्वी के केंद्र की तरफ आरोपित होता है।

प्रश्न 47.
आप सुबह 8.00 बजे स्कूल गए और दोपहर बाद 2.00 बजे घर वापस लौट आए। आपका विस्थापन क्या होगा?
उत्तर:
शून्य।

प्रश्न 48.
पृथ्वी तल से ऊर्ध्वाधर ऊपर की ओर फेंका गया पिंड जब अधिकतम ऊँचाई पर होता है तो उसका वेग क्या होता है?
उत्तर:
शून्य।

प्रश्न 49.
s, u, a तथा t में क्या संबंध है?
उत्तर:
s = ut + \(\frac { 1 }{ 2 }\) at²।

प्रश्न 50.
V, u, a तथा t में क्या संबंध है?
उत्तर:
v = u + at।

प्रश्न 51.
v, u, a तथा s में क्या संबंध है?
उत्तर:
v² – u² = 2as।

प्रश्न 52.
यदि कोई एथलीट : त्रिज्या वाले किसी वृत्ताकार पथ पर t सेकंड में एक चक्कर पूरा करता हो तो उसकी चाल क्या होगी?
उत्तर:
चाल (v) = \(\frac { 2πr }{ t }\)

प्रश्न 53.
जब आसमान में बादल होते हैं, तो बिजली के चमकने और बादलों के गरजने की क्रिया एक ही समय होती है। पहले बिजली की चमक दिखाई देती है। उसके कुछ समय पश्चात् बादलों के गरजने की ध्वनि आप तक पहुँचती है। क्या बता सकेंगे, ऐसा क्यों होता है?
उत्तर:
क्योंकि प्रकाश का वेग (3 x 10⁸ m/s), ध्वनि के वेग (346 m/s) से बहुत अधिक होता है।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
विरामावस्था तथा गति अवस्था में क्या अंतर है?
उत्तर:
यदि किसी वस्तु की स्थिति एक स्थिर बिंदु के सापेक्ष परिवर्तित नहीं होती तो वस्तु विरामावस्था में कहलाती है; जैसे मेज पर पड़ी पुस्तक, फर्श पर पड़ा हुआ पत्थर आदि। जब वस्तु की स्थिति एक स्थिर बिंदु के सापेक्ष परिवर्तित होती रहती है तो वस्तु गति अवस्था में कहलाती है; जैसे चलती हुई कार, भागता हुआ घोड़ा आदि।

प्रश्न 2.
विस्थापन से क्या अभिप्राय है? यह धनात्मक और ऋणात्मक कब होता है?
उत्तर:
किसी निश्चित दिशा में वस्तु की स्थिति में परिवर्तन को विस्थापन कहते हैं।
यदि किसी वस्तु की स्थिति x₁ से x₂ तक परिवर्तित होती है तो विस्थापन (d) को निम्नलिखित प्रकार से लिखा जाता है-
d = (x₂ – x₁) विस्थापन का चिह्न धनात्मक (+) या ऋणात्मक (-) वस्तु की स्थिति में परिवर्तन की दिशा बतलाता है। यदि विस्थापन धनात्मक हो तो वस्तु बाईं से दाईं ओर चलती है। यदि विस्थापन ऋणात्मक हो तो वस्तु दाईं से बाईं ओर चलती है। विस्थापन एक वैक्टर (सदिश) राशि है।

प्रश्न 3.
चाल किसे कहते हैं? इसका मात्रक लिखें।
उत्तर:
किसी वस्तु द्वारा इकाई समय में किसी भी दिशा में तय की गई दूरी को चाल कहते हैं।

लिया गया समय माना एक वस्तु ‘t’ समय में ‘s’ दूरी तय करती है तो इसकी चाल v = \(\frac { s }{ t }\) = चाल का मात्रक मीटर/सेकंड (m/s) है।

प्रश्न 4.
असमान गति किसे कहते हैं? असमान गति के लिए एक समय-दूरी ग्राफ खींचो।
उत्तर:
यदि कोई गतिमान पिंड समान समयांतरालों में असमान दूरी तय करे तो पिंड की उस गति को असमान गति कहते हैं। जैसे-सड़क पर चलती हुई कार की गति असमान गति का उदाहरण है, क्योंकि उसकी चाल बदलती रहती है। इसी प्रकार किसी रेलगाड़ी की गति असमान गति का उदाहरण है, क्योंकि रेलगाड़ी एक सेकंड में भिन्न-भिन्न दूरी तय करती है। रेलगाड़ी की गति को स्पष्ट करने के लिए दूरी-समय ग्राफ दर्शाया गया है।

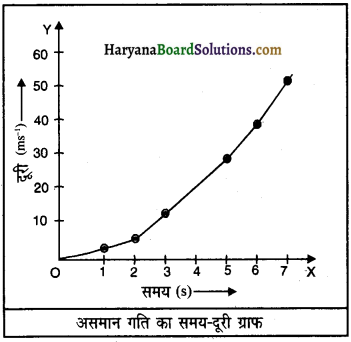
चित्र में स्पष्ट है कि चाल, समय के साथ बदलती रहती है और दूरी-समय सरल रेखीय नहीं है। यह असमान गति का एक उदाहरण है।

प्रश्न 5.
किसी सदिश को कैसे निरूपित किया जाता है?
उत्तर:
किसी सदिश को एक ऐसी सरल रेखा द्वारा निरूपित किया जाता है जिसके आगे एक तीर का चिह्न हो। इस सरल रेखा की लंबाई सदिश के परिमाण के समानुपाती होती है और तीर का शीर्ष दिशा को दर्शाता है जो सदिश का शीर्ष’ कहलाता है तथा दूसरा सिरा सदिश की ‘पूछ’ कहलाता है।

उदाहरण के लिए 30 m/s, 30° दक्षिण-पश्चिम की वेग को चित्र में तीर द्वारा दर्शाया गया है।

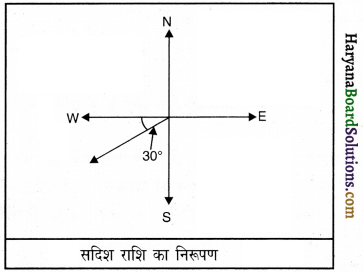
प्रश्न 6.
दो विपरीत दिशाओं में गतिमान कारें, एक घंटे में बराबर दूरी d तय करती हैं। यदि क्रमशः उत्तर व दक्षिण दिशा में गतिमान हों तो एक घंटे के पश्चात् प्रत्येक का विस्थापन कितना होगा?
हल:
माना O दोनों कारों का निर्देश बिंदु है।

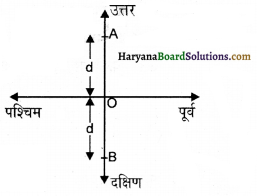
कार A द्वारा निर्देश बिंदु 0 से 1 घंटे में उत्तर दिशा में चली गई दूरी = d
अतः विस्थापन OA = d
कार B द्वारा निर्देश बिंदु 0 से 1 घंटे में दक्षिण दिशा में चली गई दूरी = d
अतः विस्थापन OB = d
दोनों कारों का कुल विस्थापन AB = d + d
= 2d उत्तर

प्रश्न 7.
ग्राफ से क्या अभिप्राय है तथा इसके क्या उपयोग हैं?
उत्तर:
एक भौतिक राशि के दूसरी भौतिक राशि के सापेक्ष परिवर्तन को दो विभिन्न अक्षों पर चित्रित करना ग्राफ कहलाता है।

ग्राफ के उपयोग निम्नलिखित हैं-

• विभिन्न राशियों के संबंध का सरलता से अध्ययन किया जा सकता है।
• दो या दो से अधिक राशियों की तालिका की तुलना आसानी से की जा सकती है।
• राशि का वर्णन करने में ग्राफ तालिका की अपेक्षा अधिक सरल है।
• तालिका में आँकड़े प्रस्तुत करने में लंबा स्थान घेरने की अपेक्षा ग्राफ थोड़े स्थान में आँकड़े पेश करता है।
• ग्राफ की ढाल से संबंधित राशि ज्ञात की जा सकती है।

प्रश्न 8.
दूरी-समय ग्राफ क्या होता है? एक बस द्वारा विभिन्न समयांतरालों में तय की गई दूरी निम्नलिखित तालिका में दी गई है। इसकी सहायता से समय-दूरी ग्राफ खींचो।

उत्तर:
ऐसा सरल और क्रमबद्ध तरीका जिसमें गतिमान वस्तु की विभिन्न समय पर विभिन्न दूरियों को दर्शाया जाता है, उसे दूरी-समय ग्राफ कहते हैं। बस द्वारा विभिन्न समयांतरालों में तय की गई दूरी का दूरी-समय ग्राफ चित्र में दर्शाया गया है।

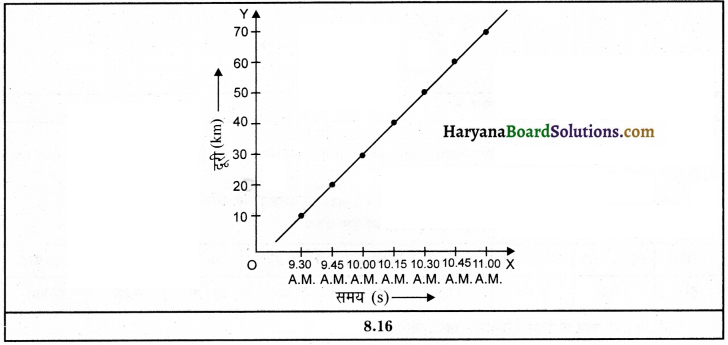
प्रश्न 9.
4 m/s तथा 7 m/s की एकसमान चाल से गतिशील वस्तुओं के लिए दूरी-समय ग्राफ खींचकर इनकी तुलना करो।
उत्तर:
हम जानते हैं कि दूरी = चाल – समय
(1) 4 m/s की एकसमान चाल से गतिशील वस्तु के लिए दूरी-समय ग्राफ-

इन मानों को ग्राफ पेपर पर अंकित करने से हम देखते हैं कि दी गई वस्तु का दूरी-समय ग्राफ संलग्नानुसार होगा-

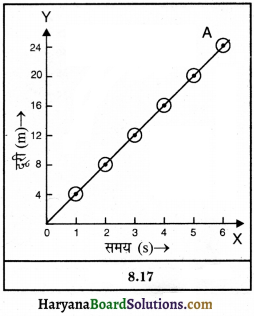
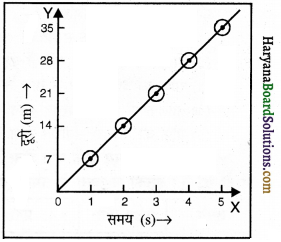
(2) 7 m/s की एकसमान चाल से गतिशील वस्तु के लिए दूरी-समय ग्राफ-

ग्राफों की तुलना (Comparison of Graphs)-7 m/s की एकसमान चाल से गतिशील वस्तु की ढलान 4 m/s की एकसमान चाल से गतिशील वस्तु से अधिक है।

प्रश्न 10.
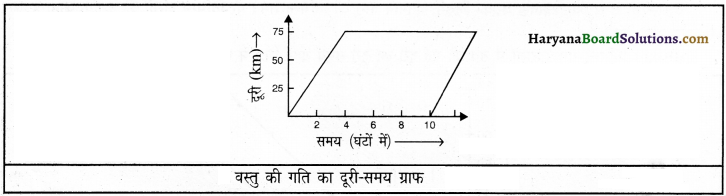
चित्र में किसी वस्तु की गति का दूरी-समय ग्राफ दिया गया है। क्या वह वास्तविक परिस्थिति का ग्राफ है? कारण बताइए।

उत्तर:
नहीं, यह वास्तविक परिस्थिति का ग्राफ नहीं है। इसके निम्नलिखित कारण हैं-

• समय-दूरी ग्राफ के अनुसार जिस बिंदु से उसने अपनी यात्रा प्रारंभ की थी, उस बिंदु तक पहुँचने के लिए लगा समय उसके द्वारा यात्रा पूरी करने के लिए लगे समय से कम है।
• समय (t) एक ऐसी राशि है जो निरंतर बढ़ रही है। t = 14 के पश्चात् यह अधिक हुई होगी।

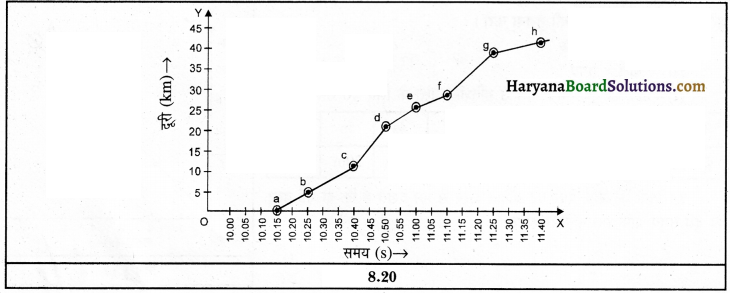
प्रश्न 11.
किसी गतिशील कार की दूरी-समय तालिका इस प्रकार है-

ग्राफ पेपर में कार के लिए दूरी-समय ग्राफ खींचिए।
उत्तर:
कार के लिए दूरी-समय ग्राफ-

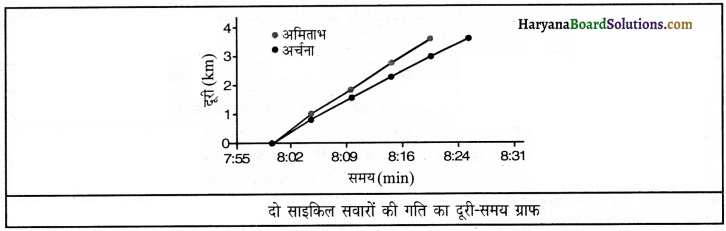
प्रश्न 12.
अमिताभ व अर्चना द्वारा अपनी साइकिलों से भिन्न-भिन्न समयों पर तय की गई दूरियाँसमय (पूर्वाह्न)

उत्तर:
दोनों दूरी-समय को एक ग्राफ द्वारा दर्शाइए।

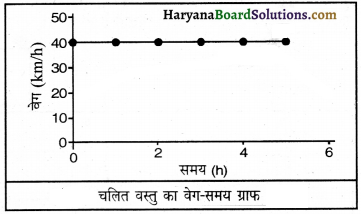
प्रश्न 13.
40 km/h के स्थिर वेग से चलित वस्तु का वेग-समय ग्राफ खींचिए।
उत्तर:
40 km/h के स्थिर वेग से गतिशील किसी कार का वेग-समय ग्राफ बनाना है। इसका तात्पर्य है कि कार 1 घंटे में 40 km की दूरी तय करती है, 2 घंटे में 80 km, 3 घंटे में 120 km और इसी प्रकार आगे दूरी तय करती रहेगी। चित्र में यह देखा जा सकता है कि इसका वेग-समय ग्राफ सरल रेखा है और समय-अक्ष के समांतर है। यह सभी वेग-समय ग्राफों के लिए सत्य है, जबकि गति एकसमान हो।

प्रश्न 14.
किसी वस्तु के वेग-समय ग्राफ से हम वस्तु द्वारा किसी दिए गए समय में तय की गई दूरी की गणना कैसे करते हैं?
उत्तर:
माना 40 km/h की चाल से चलित किसी कार का वेग-समय ग्राफ चित्र के अनुसार है। मान लीजिए, हमें कार द्वारा t₁ व t₂ समय के बीच तय की गई दूरी ज्ञात करनी है। इसके लिए समय-अक्ष पर t₁ व t₂ संगत बिंदुओं से ग्राफ पर अभिलंब खींचते हैं जैसा कि चित्र में दिखाया गया है।

इन दो अभिलंबों से ग्राफ व X-अक्ष के बीच एक आयत ABCD बनता है। इस आयत में भुजा AD और BC बराबर है तथा (t₂-t₁) के तुल्य हैं, जबकि भुजा AB व CD बराबर हैं जो 40 km/h के तुल्य हैं। हम जानते हैं कि v वेग से चलती हुई वस्तु द्वारा t समय में चली गई दूरी s हो तो-
s = vt
अतः कार द्वारा (t₂-t₁) समय में तय की गई दूरी = [(40 km/h) (t₂-t₁)h]
= 40(t₂-t₁) km
= आयत ABCD का क्षेत्रफल।

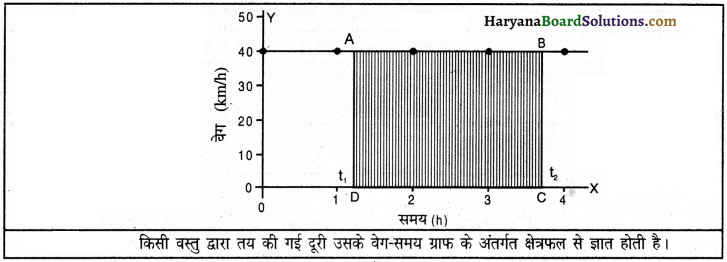
अर्थात् वेग-समय ग्राफ के अंतर्गत क्षेत्रफल, कार द्वारा चली गई दूरी को प्रदर्शित करता है। यह किसी भी वेग-समय ग्राफ के लिए सत्य है, भले ही वेग एकसमान हो या असमान।

प्रश्न 15.
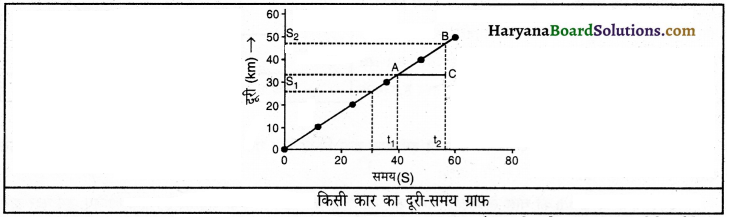
सरल रेखीय दूरी-समय ग्राफ की सहायता से वेग की गणना कैसे की जाती है? समझाइए।
उत्तर:
किसी कार के दूरी – समय ग्राफ से हम कार के वेग की गणना भी कर सकते हैं। चित्र में कार की गति के दूरी – समय ग्राफ के एक छोटे से भाग AB पर विचार कीजिए। कार का वेग ज्ञात करने के लिए हम बिंदु A से X- अक्ष के समांतर एक सरल रेखा खींचते हैं और बिंदु B से Y-अक्ष के समांतर दूसरी सरल रेखा खींचते हैं। ये दोनों सरल रेखाएँ बिंदु C पर मिलकर एक त्रिभुज ABC बनाती हैं। अब ग्राफ पर AC समय अंतराल (t₂ – t₁) को प्रकट करता है, जबकि BC दूरी (s₂ – s₁ ) के संगत है। ग्राफ से यह देखा जा सकता है कि जब कार A से B तक चलती है तो वह (t₂ – t₁) समय में (s₂ – s₁ ) दूरी तय करती है। अतः कार का वेग-
v = \(\frac{\mathrm{S}_2-\mathrm{S}_1}{\mathrm{t}_2-\mathrm{t}_1}\)

प्रश्न 16.
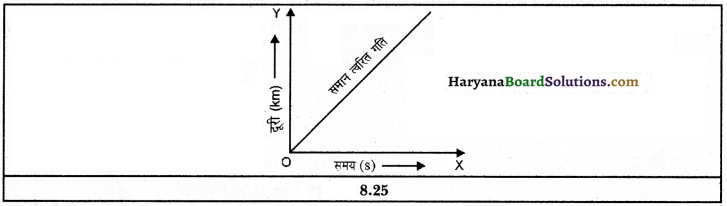
एकसमान त्वरित गति, एक असमान त्वरित गति तथा एकसमान मंदन गति को ग्राफ द्वारा प्रदर्शित कीजिए।
उत्तर:
(1) एकसमान त्वरित गति – एकसमान त्वरित गति में चाल – समय ग्राफ एक सरल रेखीय होता है।

(2) एक असमान त्वरित गति-एक असमान त्वरित गति में चाल-समय ग्राफ एक वक्र (Curve) रेखीय होता है।

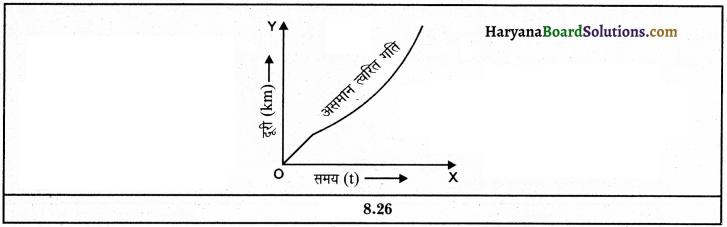
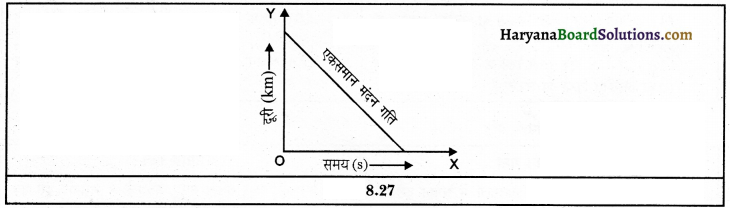
(3) एकसमान मंदन गति ग्राफ-एकसमान मंदन की स्थिति में त्वरण ऋणात्मक (-) होता है तथा वेग-समय ग्राफ एक सरल रेखीय होता है।

प्रश्न 17.
एक सरल रेखा में गमन करने वाली वस्तु का चाल-समय ग्राफ खींचिए। इस सरल रेखा की ढाल क्या व्यक्त करती है?
उत्तर:
यदि बराबर समय अंतराल में किसी वस्तु के वेग में बराबर परिवर्तन हो तो हम कह सकते हैं कि वस्तु एकसमान त्वरण से गतिशील है।

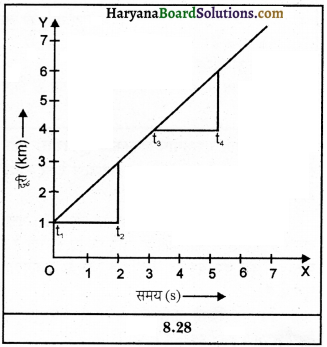
किसी सरल रेखा में गतिशील वस्तु का चाल-समय ग्राफ चित्र में दिखाया गया है। यदि t₁ समय पर वस्तु की चाल v₁ और t₂ समय में वस्तु की चाल v₂ हो तो
वस्तु का त्वरण = \(\frac{\mathrm{S}_2-\mathrm{S}_1}{\mathrm{t}_2-\mathrm{t}_1}\)
इस ग्राफ में दिखाए गए समय अंतराल t₂-t₁ और t₄-t₃ बराबर है, क्योंकि चाल परिवर्तन की ऊँचाइयाँ भी बराबर हैं, इसलिए यह ग्राफ किसी ऐसी वस्तु की गति को दर्शाता है जो एकसमान त्वरण से गतिशील है। एकसमान त्वरित वस्तु की चाल-समय ग्राफ कोई सरल रेखा होता है। ऐसी वस्तु का त्वरण इस सरल रेखा का ढाल होता है।

प्रश्न 18.
तुम कैसे सिद्ध करोगे कि गति सापेक्षी होती है?
उत्तर:
गति को सापेक्षी सिद्ध करने के लिए हम किसी चलती हुई बस या रेलगाड़ी में बैठे हुए व्यक्तियों की तुलना सड़क या पटरी के किनारे खड़े हुए पेड़, वाहन या व्यक्तियों से कर सकते हैं; जैसे बस व रेलगाड़ी में बैठे हुए यात्री बस व रेलगाड़ी के अंदर के सामान की अपेक्षा स्थिर अवस्था में होते हैं, परंतु बाह्य वस्तुओं की अपेक्षा गति में होते हैं।

प्रश्न 19.
इनमें अंतर लिखो-
(1) सदिश तथा अदिश।।
(2) एकसमान तथा असमान गति।
(3) दूरी तथा विस्थापन।
उत्तर:
(1) सदिश तथा अदिश में अंतर

(2) एकसमान तथा असमान गति में अंतर-

(3) दूरी तथा विस्थापन में अंतर-

प्रश्न 20.
एकसमान चक्राकार (वृत्ताकार) गति से क्या अभिप्राय है? अपना उत्तर उदाहरण देकर स्पष्ट करो।
उत्तर:
जब कोई वस्तु वृत्ताकार मार्ग पर गति करती है तो वह अपनी दिशा हर बिंदु पर बदल लेती है। वास्तव में वृत्त एक बहुभुज आकृति है जिसकी अनगिनत भुजाएँ हैं।

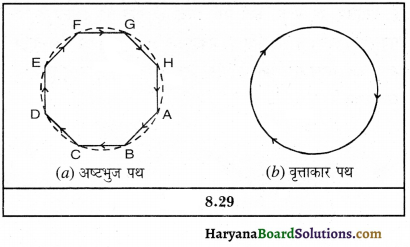
चित्र में किसी गोलाकार पथ को अंतःभुजाओं वाला बहुभुज कह सकते हैं। इसलिए वृत्त में एकसमान चाल से चल रही वस्तु त्वरित गति का उदाहरण है। यद्यपि वस्तु की चाल में कोई परिवर्तन नहीं होता, परंतु वस्तु की गति की दिशा लगातार बदलती रहती है।

उदाहरण-धागे का एक टुकड़ा लीजिए और उसके एक सिरे पर पत्थर बाँधकर घुमाइए, तो यह गति वृत्ताकार गति होगी।

गणनात्मक प्रश्न

महत्त्वपूर्ण सूत्र एवं तथ्य:
(1) दूरी (s) = वेग (v) x समय (t)

(5) यदि आरंभिक वेग = u, अंतिम वेग = v, समय =t, त्वरण = a, दूरी = s हो तो इनमें निम्नलिखित संबंध होता है-

• v = u + at
• s = ut + \(\frac { 1 }{ 2 }\) at²
• v² – u² = 2as

(6) r त्रिज्या वाले वृत्ताकार पथ पर 1 सेकंड में चक्कर पूरा करने पर चाल = \(\frac { 2πr }{ t }\)

प्रश्न 1.
किसी लड़के के घर से विद्यालय तक की दूरी 1.8 कि०मी० है। यदि वह साइकिल द्वारा विद्यालय पहुँचने में 5 मिनट लेता है तो उसकी चाल का परिकलन मीटर/सेकंड में कीजिए।
हल:
दूरी (s) = 1.8 कि०मी०
= 1.8 x 1000 मीटर
= 1800 मीटर
लिया गया समय (t) = 5 मिनट
= 5 x 60 सेकंड
= 300 सेकंड

= 6 m/s उत्तर

प्रश्न 2.
एक व्यक्ति को अपने घर से दफ्तर पहुँचने में 10 मिनट लगते हैं। यदि दफ्तर घर से 3.6 कि०मी० की दूरी पर हो तो व्यक्ति की औसत चाल ज्ञात करो।
हल:
कुल दूरी = 3.6 कि०मी० = 3.6 x 1000 मीटर
= 3600 मीटर
कुल समय = 10 मिनट = 10 x 60 सेकंड
= 600 सेकंड

= 6 m/s उत्तर

प्रश्न 3.
त्रिवेंद्रम एक्सप्रेस गुवाहाटी से सोमवार 23.30 पर चलती है और 3574 कि०मी० की दूरी तय करके वीरवार को 22.30 पर त्रिवेंद्रम पहुँचती है। इस रेलगाड़ी की औसत चाल ज्ञात कीजिए।
हल:
गाड़ी द्वारा चली गई कुल दूरी = 3574 कि०मी०
सोमवार 23.30 से वीरवार 22.30 के बीच कुल समय = 24 + 24 + 23 = 71 घंटे

= 50.34 km/hr. उत्तर

प्रश्न 4.
एक कार विरामावस्था से गतिमान होकर 10 सेकंड में 36 km/hr. का वेग प्राप्त कर लेती है। कार का त्वरण (प्रवेग) ज्ञात करो।
हल:
कार विरामावस्था से गतिमान हुई है-
∴ आरंभिक वेग (u) = 0
अंतिम वेग (v) = 36 km/h = 36 x \(\frac { 5 }{ 18 }\) = 10 m/sec
समय (t) = 10 sec
हम जानते हैं कि v = u+ at
10 = 0 + ax 10
10 = 10 a
a = \(\frac { 10 }{ 10 }\) = 1ms^-2 उत्तर

प्रश्न 5.
3 मीटर प्रति सेकंड के वेग से गतिमान किसी साइकिल की गति 0.5 m/s² के त्वरण से बढ़ती है। उसका वेग 5 सेकंड के बाद कितना होगा तथा इस समय में वह कितनी दूरी चलेगी?
हल:
यहाँ पर
आरंभिक वेग (u) = 3 m/s
त्वरण (a) = 0.5 m/s²
समय (t) = 5 sec
अंतिम वेग (v) = ?
दूरी (s) = ?
हम जानते हैं कि
(1) V = u + at
= 3 + 0.5 x 5
= 3 + 2.5 = 5.5 m/s उत्तर

(2) s = u x t + \(\frac { 1 }{ 2 }\) at²
= 3 x 5 + \(\frac { 1 }{ 2 }\) x 0.5 x 5 x 5
= 15 + 6.25 = 21.25 m उत्तर

प्रश्न 6.
किसी स्कूटर का एकसमान त्वरण 4 m/sec² है। स्कूटर गतिमान होने के बाद वह 10 sec में कितनी दूरी तय करेगा। 10 sec के बाद उसका वेग क्या होगा?
हल:
यहाँ पर स्कूटर का आरंभिक वेग (u) = 0
त्वरण (a) = 4 m/sec²
समय (t) = 10 sec
दूरी (s) = ?
अंतिम वेग (v) = ?
हम जानते हैं कि
(1) s = ut + \(\frac { 1 }{ 2 }\) = at²
s = 0 x 10 + \(\frac { 1 }{ 2 }\) x 4 (10)²
s = 0 + \(\frac { 1 }{ 2 }\) x 4 x 100
= 200 m उत्तर

(2) v = u + at = 0 + 4 x 10 = 40 m/s उत्तर

प्रश्न 7.
एक साइकिल 10 m/s की चाल से चल रही है, उसे ब्रेक लगाकर रोकने पर उसमें 0.5 m/s² का मंदन उत्पन्न हो जाता है। साइकिल विरामावस्था में आने से पहले कितनी दूरी तय करेगी?
हल:
साइकिल का आरंभिक वेग (u) = 10 m/s
साइकिल का अंतिम वेग (v) = 0
मंदन (a) = 0.5 m/s²
हम जानते हैं कि v² – u² = 2as
या (0)² – (10)² = 2 (-0.5) xs या
या – 100 = – 1s
या s = 100 m उत्तर

प्रश्न 8.
एक कार 5s के लिए 20 m/s के समान वेग से चलती है। तब ब्रेक लगाने पर कार एकसमान मंदन से 8s में विरामावस्था में आ जाती है। वेग और समय का ग्राफ खींचो। ब्रेकें लगाने के बाद कार कितनी दूरी तक जाएगी?
हल:
समय और वेग में ग्राफ चित्र में प्रदर्शित है। ब्रेकें लगाने के बाद कार द्वारा तय की गई दूरी-

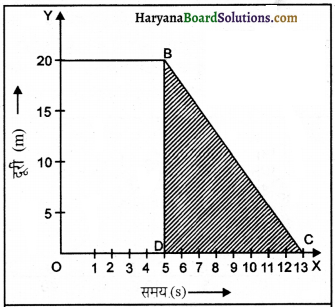
= ∆BDC का क्षेत्रफल
= \(\frac { 1 }{ 2 }\) x DC x DB [\(\frac { 1 }{ 2 }\) x आधार x लंब]
= \(\frac { 1 }{ 2 }\) x (13 – 5) x 20
= \(\frac { 1 }{ 2 }\) x 8 x 20 = 80 m उत्तर

प्रश्न 9.
किसी लंबी दौड़ में धावकों को दौड़-पथ के 4 चक्कर लगाने हैं और दौड़ का प्रारंभ व अंत एक ही स्थान पर होना है। यदि एक चक्कर की लंबाई 200 m हो तो-
(क) धावकों को कुल कितनी दूरी तय करनी है?
(ख) जब धावक दौड़ पूरी कर लेते हैं तो उनका कुल विस्थापन कितना होगा?
(ग) धावकों की गति एकसमान है या असमान?
(घ) क्या दौड़ की समाप्ति पर धावकों द्वारा तय की दूरी व उनके विस्थापन बराबर हैं?
उत्तर:
(क) धावकों द्वारा तय की जाने वाली कुल दूरी = 200 x 4 = 800 मीटर।
(ख) क्योंकि दौड़-पथ के प्रारंभिक व अंतिम स्थान एक ही जगह पर हैं इसलिए धावकों का कुल विस्थापन = शून्य।
(ग) धावकों की गति असमान गति है।
(घ) दौड़ की समाप्ति पर धावकों द्वारा तय की गई दूरी व विस्थापन बराबर नहीं है। क्योंकि
दूरी = 800 मी०
विस्थापन = शून्य

प्रश्न 10.
निम्नलिखित वस्तुओं की चाल को घटते क्रम में लिखिए-
(1) 18 km/h की चाल से चलती बाइसाइकिल।
(2) 7 m/s की चाल से दौड़ता हुआ कोई धावक।
(3) 2000 m/min की चाल से चलती हुई कोई कार।
उत्तर:
हम जानते हैं कि-
(1) 18 km/h = \(\frac { 1800 }{ 3600 }\) m/s = 5 m/s
(2) 7 m/s
(3) 2000 m/ min = \(\frac { 2000 }{ 60 }\) m/s = 33.33 m/s

अतः वस्तुओं की चाल का घटता क्रम निम्नलिखित है-
(1) 2000 m/min की चाल से चलती हुई कोई कार।
(2) 7 m/s की चाल से दौड़ता हुआ कोई धावक।
(3) 18 km/h की चाल से चलती हुई बाइसाइकिल।

प्रश्न 11.
कोई वस्तु 2 m/s के वेग से 5 s तक चलती है। अगले 5 s में एकसमान त्वरण के कारण इसका वेग बढ़कर 10 m/s हो जाता है। इसके बाद इस वस्तु का वेग एकसमान रूप से कम होता है और वस्तु 10 s में विराम की अवस्था में आ जाती है, तो
(a) इस वस्तु की गति के लिए वेग-समय तथा दूरी-समय ग्राफ खींचिए।
(b) ग्राफ में वह भाग दिखाइए जहाँ गति एकसमान है तथा जहाँ गति असमान है।
(c) ग्राफ से वस्तु द्वारा प्रारंभ से 25 तथा 12s बाद तथा अंतिम 10s में तय की गई दूरी ज्ञात कीजिए।
उत्तर:
(a) वेग-समय ग्राफ-पहले 5 सेकंड तक वस्तु का वेग 2 m/s रहता है जोकि ग्राफ में AB द्वारा दर्शाया गया है। इसके बाद दूसरे 5 सेकंड में (5 से 10 सेकंड के बीच) यह बढ़कर 10 m/s हो जाता है जोकि ग्राफ में BC द्वारा दर्शाया गया है। इसके बाद अगले 10 सेकंड में वस्तु विरामावस्था में आ जाती है जोकि ग्राफ में CD द्वारा दर्शाया गया है।

दूरी-समय ग्राफ क्योंकि वस्तु की चाल समान नहीं है, इसलिए दूरी-समय ग्राफ सरल रेखा न होकर चित्र में दिखाए अनुसार होगा।

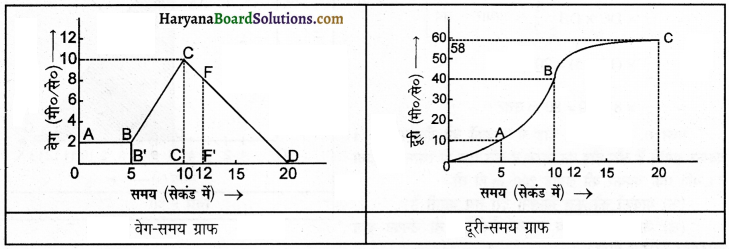
(b) वेग-समय ग्राफ को देखने से पता चलता है AB भाग में वस्तु की गति समान रहती है, जबकि भाग BC तथा भाग CD में गति असमान रहती है।

(c) (1) 2 सेकंड में वस्तु द्वारा तय दूरी = 2 x 2 = 4 मी०

(2) 12 सेकंड में वस्तु द्वारा तय दूरी = (OB’BA + BB’C’C + CC’FF’) का क्षेत्रफल
अब आयत OB’BA का क्षेत्रफल = 2 x 5 = 10
समलंब BB’C’C का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x (BB’ + CC’) x B’C’
= \(\frac { 1 }{ 2 }\) (2 + 10) x 5
= \(\frac { 1 }{ 2 }\) x 12 x 5 = 30
समलंब CCFF’ का क्षेत्रफल = \(\frac { 1 }{ 2 }\) (CC’ + FF’) x CF’
= \(\frac { 1 }{ 2 }\) x (10 + 8) x 2
= \(\frac { 1 }{ 2 }\) x 18 x 2 = 18
अतः 12 सेकंड में वस्तु द्वारा तय दूरी = 10 + 30 + 18 = 58 मी०

(3) अंतिम 10 सेकंड में वस्तु की तय दूरी = (समलंब CC’F’F + समकोण AFF’D) का क्षेत्रफल
अब समलंब CCFF का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x (CC’ + FF’) x CF
= \(\frac { 1 }{ 2 }\) x (10 + 8) x 2
= \(\frac { 1 }{ 2 }\) x 18 x 2 = 18
समकोण ∆FF’D का क्षेत्रफल =\(\frac { 1 }{ 2 }\) x F’D x F’F
= \(\frac { 1 }{ 2 }\) x 8 x 8 = 32
अतः अंतिम 10 सेकंड में वस्तु द्वारा तय दूरी = 18 + 32 = 50 मी० उत्तर

निबंधात्मक प्रश्न

प्रश्न 1.
निम्नलिखित समीकरण सिद्ध करो-
(1) v = u + at, (2) s = ut +1/2at² (3) v² – u² = 2as
उत्तर:
(1) माना वस्तु का प्रारंभिक वेग = u
समय = t
अंतिम वेग = v
वेग में परिवर्तन = v – u
वेग में परिवर्तन की दर (त्वरण) a = \(\frac { v-u }{ t }\)
या at = V – u
या at + u = v
या v = u + at

(2) माना किसी वस्तु का प्रारंभिक वेग u, त्वरण a और 1 सेकंड के पश्चात् अंतिम वेग v है। यदि t सेकंड बाद दूरी s हो तो
दूरी (s) = औसत वेग x समय
परंतु औसत वेग =\(\frac { u+v }{ 2 }\)
∴ दूरी (s) = (\(\frac { u+v }{ 2 }\)) x t
या s = (\(\frac { u+u+at }{ 2 }\)) x t (∵ v = u + at)
या s = (\(\frac { 2u+at }{ 2 }\)) x t
या s = \(\left(\frac{2 u t+a t^2}{2}\right)=\frac{2 u t}{2}+\frac{{a t^2}^2}{2}\)
या s = ut + \(\frac { 1 }{ 2 }\) at²

(3) हम जानते हैं कि v = u + at
दोनों तरफ वर्ग करने पर
(v)² = (u² + a²t²)
v² = u² + a²t² + 2 uat
v² – u² = a²t² + 2 uat
v² – u² = 2 uat + a² t²
v² – u² = 2a (ut + \(\frac { 1 }{ 2 }\) at²)
∴ v² – u² = 2as [∵ s = ut + \(\frac { 1 }{ 2 }\)at²]

प्रयोगात्मक कार्य

क्रियाकलाप 1.
दूरी और विस्थापन में अंतर के लिए एक क्रियाकलाप का वर्णन करें।

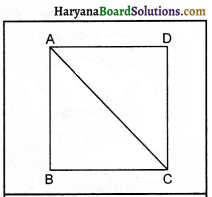
कार्य-विधि-एक मीटर स्केल और एक लंबी रस्सी लीजिए। आप बॉस्केट बॉल कोर्ट के एक कोने से दूसरे कोने तक उसके किनारे से होते हुए जाएँ। इस रास्ते के साथ-साथ रस्सी रखें तथा इसे स्केल की सहायता से मा। यह आप द्वारा तय की गई दूरी होगी जबकि एक कोने से दूसरे कोने तक सीधी रस्सी रखने पर मापने पर प्राप्त राशि विस्थापन होगी। माना ABCD बॉस्केट बॉल कोर्ट है। A से C तक जाने में दूरी = AB+ BC जबकि विस्थापन = AC होगा।

क्रियाकलाप 2.
एक क्रियाकलाप द्वारा समझाएँ कि वृत्तीय पथ पर प्रत्येक बिंदु पर गति की दिशा परिवर्तित होती है।
कार्य-विधि-एक धागे का टुकड़ा लें और उसके एक छोर पर एक छोटे पत्थर को बाँध दें। धागे के दूसरे छोर को पकड़कर पत्थर को वृत्तीय पथ पर नियंत चाल से घुमाएँ जैसा कि चित्र में दिखाया गया है। अब पत्थर सहित धागे को छोड़ दें तथा उसके गिरने की दिशा नोट करें। इस क्रिया को बार-बार दोहराएँ और वृत्तीय पथ के अलग-अलग जगहों से पत्थर को छोड़ें और यह देखें कि पत्थर के गति करने। की दिशा समान है या नहीं।

ध्यानपूर्वक देखने पर आप पाएँगे कि पत्थर वृत्तीय रेखा के स्पर्शरेखीय सीधी रेखा के साथ गति करता है। ऐसा इसलिए क्योंकि जब पत्थर को छोड़ा जाता है तो वह उसी दिशा| में गति जारी रखता है जिस दिशा में उस क्षण वह गति कर रहा है। इससे पता चलता है कि जब किसी पत्थर को वृत्तीय पथ पर घुमाया जाता है तो उसकी गति की दिशा प्रत्येक बिंदु पर परिवर्तित होती है।

अध्याय का तीव्र अध्ययन

1. अगर कोई वस्तु वृत्तीय पथ पर एकसमान चाल से चलती है तो उसकी गति कहलाती है-
(A) एकसमान वृत्तीय गति
(B) असमान वृत्तीय गति
(C) एकसमान वक्र गति
(D) असमान वक्र गति
उत्तर:
(A) एकसमान वृत्तीय गति

2. यदि कोई वस्तु किसी अन्य वस्तु की तुलना में अपनी स्थिति निरंतर बदलती रहती हो तो उस वस्तु को …………………. कहा जाता है।
(A) गति अवस्था में
(B) स्थिर अवस्था में
(C) विरामावस्था में
(D) इनमें से कोई नहीं
उत्तर:
(A) गति अवस्था में

3. निम्नलिखित में से किनमें स्वेच्छा से गति होती है?
(A) सजीवों में
(B) निर्जीवों में
(C) सजीव व निर्जीव दोनों में
(D) सजीव व निर्जीव दोनों में नहीं
उत्तर:
(A) सजीवों में

4. किसी वस्तु द्वारा अंतिम व प्रारंभिक स्थिति के बीच की न्यूनतम दूरी कहलाती है-
(A) विस्थापन
(B) चाल
(C) दूरी
(D) द्रव्यमान
उत्तर:
(A) विस्थापन

5. जिन राशियों को केवल परिमाण द्वारा व्यक्त किया जा सकता है, उन्हें कहा जाता है…
(A) सदिश राशियाँ
(B) अदिश राशियाँ
(C) स्थिर राशियाँ
(D) इनमें से कोई नहीं
उत्तर:
(B) अदिश राशियाँ

6. दूरी का SI मात्रक है-
(A) km
(B) m
(C) cm
(D) mm
उत्तर:
(B) m

7. निम्नलिखित में से कौन-सी राशि सदिश नहीं है?
(A) त्वरण
(B) वेग
(C) घनत्व
(D) विस्थापन
उत्तर:
(C) घनत्व

8. निम्नलिखित में से कौन-सी सदिश राशि है?
(A) दूरी
(B) त्वरण
(C) चाल
(D) घनत्व
उत्तर:
(B) त्वरण

9. जब कोई वस्तु समान समयांतरालों में असमान दूरी तय करे तो उस वस्तु की चाल को कहा जाता है
(A) समान चाल
(B) औसत चाल
(C) असमान चाल
(D) वृत्तीय चाल
उत्तर:
(C) असमान चाल

10. निम्नलिखित में से कौन-सी असमान चाल है?
(A) पृथ्वी की गति
(B) घड़ी के पेंडुलम की गति
(C) चंद्रमा की गति
(D) स्टेशन से छूटती रेलगाड़ी की गति
उत्तर:
(D) स्टेशन से छूटती रेलगाड़ी की गति

11. यदि त्वरण वेग की दिशा में हो तो उसे क्या कहा जाता है?
(A) ऋणात्मक त्वरण
(B) शून्य त्वरण
(C) धनात्मक त्वरण
(D) इनमें से कोई भी नहीं
उत्तर:
(C) धनात्मक त्वरण

12. यदि त्वरण वेग की दिशा के विपरीत हो तो उसे क्या कहा जाता है?
(A) ऋणात्मक त्वरण
(B) शून्य त्वरण
(C) धनात्मक त्वरण
(D) इनमें से कोई भी नहीं
उत्तर:
(A) ऋणात्मक त्वरण

13. वेग में परिवर्तन की दर को कहा जाता है-
(A) चाल
(B) वेग
(C) त्वरण
(D) इनमें से कोई भी नहीं
उत्तर:
(C) त्वरण

14. चाल का SI मात्रक है-
(A) m/s²
(B) m/s
(C) km/h
(D) km/s
उत्तर:
(B) m/s

15. दूरी, चाल तथा समय में कौन-सा संबंध होता है?
(A) दूरी x चाल = समय
(B) समय x दूरी = चाल
(C) दूरी = चाल – समय
(D) इनमें से कोई भी नहीं
उत्तर:
(C) दूरी = चाल x समय

16. किसी विशेष दिशा में वेग की कमी दर कहलाती है-
(A) धनात्मक त्वरण
(B) ऋणात्मक त्वरण
(C) धनात्मक व ऋणात्मक त्वरण
(D) इनमें से कोई भी नहीं
उत्तर:
(B) ऋणात्मक त्वरण

17. यदि किसी वस्तु का चाल-समय ग्राफ समय अक्ष के समांतर हो तो वस्तु में त्वरण होगा-
(A) समान
(B) असमान
(C) शून्य
(D) इनमें से कोई भी नहीं
उत्तर:
(C) शून्य

18. कोई वस्तु वृत्ताकार पथ पर निश्चित चाल से चल रही है। उसकी गति होगी-
(A) समान
(B) त्वरित
(C) मंदित
(D) इनमें से कोई भी नहीं
उत्तर:
(B) त्वरित

19. नीचे की ओर ढाल वाला वेग-समय ग्राफ प्रदर्शित करता है-
(A) त्वरित गति को
(B) समान गति को
(C) मंदन गति को
(D) इनमें से कोई भी नहीं
उत्तर:
(C) मंदन गति को

20. यदि कोई कार 2 घंटे में 80km की दूरी तय करे तो उसकी औसत चाल होगी-
(A) 40 km/h
(B) 40 km/s
(C) 40 m/s
(D) 40 m/h
उत्तर:
(A) 40 km/h

21. किसी वस्तु का दूरी-समय ग्राफ X-अक्ष के समांतर है। यह प्रदर्शित करता है कि-
(A) वस्तु असमान गति से चल रही है
(B) वस्तु त्वरित गति से चल रही है
(C) वस्तु विरामावस्था में है
(D) वस्तु समान गति से चल रही है
उत्तर:
(C) वस्तु विरामावस्था में है

22. m/s² किसका SI मात्रक है?
(A) चाल का
(B) वेग का
(C) विस्थापन का
(D) त्वरण का
उत्तर:
(D) त्वरण का

23. आपका स्कूल आपके घर से 5km दूर है। आप सुबह 8.00 बजे स्कूल गए और दोपहर बाद 2.00 बजे घर वापस लौट आए। आपका विस्थापन होगा-
(A) 5 km
(B) 10 km
(C) शून्य
(D) इनमें से कोई भी नहीं
उत्तर:
(C) शून्य

24. निर्वात में प्रकाश की चाल कितनी होती है-
(A) 3 x 10¹⁰ m/s
(B) 3 x 10⁵ m/s
(C) 3 x 10⁸ m/s
(D) 3 x 10⁷ m/s
उत्तर:
(C) 3 x 10⁸ m/s

25. कोई बस विरामावस्था से चलना प्रारंभ करती है तथा 2 मिनट तक 0.1 m/s² का एकसमान त्वरण प्राप्त करती हो तो वस्तु की चाल होगी-
(A) 12 m/h
(B) 12 km/h
(C) 12 km/s
(D) 12 m/s
उत्तर:
(D) 12 m/s

26. कोई रेलगाड़ी 90 km/h की चाल से चल रही है। ब्रेक लगाए जाने पर वह – 0.5 m/s² का एकसमान त्वरण उत्पन्न करती है। रेलगाड़ी विरामावस्था में आने से पहले कितनी दूरी तय करेगी? (A) 62.5 m
(B) 6.25 m
(C) 625 m
(D) 625 km
उत्तर:
(C) 625 m

27. एक रेसिंग कार का एकसमान त्वरण 4 m/s² है। गति प्रारंभ करने के 10s के पश्चात् वह कितनी दूरी तय करेगी?
(A) 20 m
(B) 200 m
(C) 2000 m
(D) 2 m
उत्तर:
(B) 200 m

28. कोई मोटरबोट झील में विरामावस्था से सरल रेखीय पथ पर 3.0 m/s² के नियत त्वरण से 8s तक चलती है। इस समयांतराल में बोट द्वारा तय दूरी होगी-
(A) 96 m
(B) 9.6 m
(C) 24 m
(D) 2.4 m
उत्तर:
(A) 96 m

29. v, u, a तथा 5 में उचित संबंध होता है-
(A) v² = u² – 2as
(B) v² = 2as – u²
(C) v² – u² = 2as
(D) v² + u² = 2as
उत्तर:
(C) v² – u² = 2as

30. एक कार विरामावस्था से गतिमान होकर 10s में 36 km/h का वेग प्राप्त कर लेती है। कार का त्वरण होगा-
(A) 1m/s²
(B) 1 m/s
(C) 2 m/s²
(D) 2 m/s
उत्तर:
(A) 1 m/s²

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 14 Statistics Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 14 Statistics

Very Short Answer Type Questions

Question 1.
A cumulative frequency distribution is given below. Convert it into a frequency distribution table :

Solution:
To convert less than cumulative frequency distribution into frequency distribution, we subtract the cumulative frequency of preceding class from the cumulative frequency of each class.

Frequency distribution table

Question 2.
A cumulative frequency table is given below. Convert it into a frequency distribution table :

Solution:
Frequency distribution table

Question 3.
The mean of ages of 5 students is 15 years. If the individual ages of four of them are 14 years, 15 years, 16 years and 17 years, find the age of fifth student.
Solution:
Mean age of 5 students = 15 years
Sum of ages of 5 students = 15 × 5 = 75 years
Sum of ages of 4 students = 14 + 15 + 16 + 17 = 62 years
Age of fifth student = Sum of ages of 5 students – Sum of ages of 4 students
= 75 – 62
= 13 yeras
Hence, age of fifth student = 13 years.

Question 4.
If the mean of 10 observations is 18 and that of another 15 observations is 16, find the mean of all 25 observations.
Solution:
Mean of 10 observations = 18
∴ Sum of 10 observations = 18 × 10 = 180
and mean of 15 observations = 16
∴ Sum of 15 observations: 16 × 15 = 240
Sum of (10 + 15 = 25) observations
= 180 + 240 = 420
Mean of 25 observations
= \(\frac{\text { Sum of } 25 \text { observations }}{\text { Total no. of observations }}\)
= \(\frac{420}{25}\) = 16.8
Hence, mean of 25 observations = 16.8.

Question 5.
The mean of 13 results is 20. If the mean of first 7 results is 16 and that of the last 7 results is 25, find the 7th result.
Solution:
Mean of 13 results = 20
Sum of 13 results = 20 × 13 = 260
Mean of first 7 results = 16
Sum of first 7 results = 16 × 7 = 112
and mean of last 7 results = 25
∴ Sum of last 7 results = 25 × 7 = 175
7th result = Sum of first 7 results + Sum of last 7 results – Sum of 13 results
= 112 + 175 – 260 = 27
Hence, 7th result = 27.

Question 6.
Mean weight of 14 members of a group is 60 kg. One more member whose weight is 45 kg has joined the group. Find the mean weight of 15 members of the group.
Solution:
Mean weight of 14 members = 60 kg
∴ Sum of weight of 14 members = 60 × 14 = 840 kg
∵ One member whose weight 45 kg is joined the group.
∴ Sum of weight of 15 (14 + 1) members = 840 + 45 = 885 kg
Mean weight of 15 members = \(\frac{885}{15}\)
= 59 kg
Hence,mean weight of 15 members = 59 kg.

Question 7.
The mean weight of 50 students of a class is 42 kg. If the weight of a teacher be included, the mean rises 1 kg. Find the weight of the teacher.
Solution:
Mean weight of 50 students = 42 kg
Sum of weight of 50 students = 42 × 50 = 2100 kg
If weight of 1 teacher included mean rises 1 kg i.e.,
Mean weight of (50 students + 1 teacher) = 43 kg
Sum of weight of (50 students + 1 teacher) = 43 × 51 = 2193 kg
Weight of teacher= Sum of weight of (50 students + 1 teacher) – Sum of weight of 50 students
= 2193 – 2100 = 93 kg
Hence,weight of teacher = 93 kg.

Question 8.
Mean of 50 observations was found to be 804. But later on, it was discovered that 96 was misread as 69 at one place. Find the correct mean.
Solution:
Mean of 50 observations = 80.4
Incorrect sum of 50 observations = 80.4 × 50
= 4020.
Correct sum of 50 observations = sum of incorrect 50 observations – incorrect observation + correct observation
= 4020 – 69 + 96 = 4047
∴ correct mean = \(\frac{4047}{50}\) = 80.94
Hence, correct mean = 80.94.

Short Answer Type Questions

Question 1.
The class marks of a distribution are 42, 47, 52, 57, 62, 67, 72, 77, 82, 87, 92, 97. Determine the class size, the class limits and true class limits.
Solution:
Since class marks are uniformly space.
∴ Class size is the difference between any two consecutive class marks.
Class size (h) = 47 – 42 = 5
Half of the class size \(\left(\frac{h}{2}\right)=\frac{5}{2}\) = 2.5
To obtain lower class limit, we substract 2.5 from each class mark and to obtain upper class limit, we add 2.5 to each the class mark.
Class mark of the first class = 42
∴ Corresponding class limits are 42 – 2.5 and 42 + 2.5.
i.e., 39.5 – 44.5
Similarly, we get the following class limits :

Since, the classes are exclusive, true class limits are the same as the class limits.

Question 2.
The ages (in years) of 70 patients getting medical treatment in a hospital are:
10, 13, 11, 15, 12, 14, 18, 16, 54, 51, 32, 35, 25, 22, 18, 13, 28, 29, 20, 52, 53, 66, 33, 37, 67, 68, 57, 42, 45, 24, 26, 23, 55, 60, 31, 33, 38, 37, 63, 60, 35, 38, 27, 21, 39, 39, 61, 40, 48, 62, 42, 43, 22, 45, 68, 41, 49, 46, 58, 42, 50, 59, 40, 25, 44, 24, 56, 18, 46, 47
Construct a cumulative frequency (distribution) table.
Solution:
Maximum age = 68 years
Minimum age = 10 years
Range = 68 – 10 = 58 years
Let the class size be 10.
Number of classes = \(\frac{58}{10}\)
= 5.8 = 6, (say)
So, class intervals are 10 – 20, 20 – 30, 30 – 40, 40 – 50, 50 – 60 and 60 – 70
The cumulative frequency distribution table is given below :
Cumulative frequency distribution of ages of patients

Question 3.
Following are the weights (in gm) of 100 apples picked at random from a basket :

Construct the cumulative frequency table (less than type and more than type) for the above data.
Solution:
Less than cumulative frequency table

More than cumulative frequency table

Question 4.
The following frequency distribution table gives the production yield per hectare of wheat of 100 farms of a village. Find the unknown values (p, q, r, x, y, z).

Solution:
Since the given frequency distribution is the frequency distribution of production yield of 100 farms. Therefore z = 100.

From the table, we get
p = 2
2 + g = 10
⇒ q = 10 – 2 = 8
r = 10 + 12 = 22
12 + 10 + x = 46
⇒ 22 + x = 46
⇒ x = 46 – 22
⇒ x = 24
y = 46 + 38
⇒ y = 84
and z = 100
Hence, p = 2, q = 8, r = 22, x = 24, y = 84 and z = 100.

Question 5.
The income and expenditure for 5 years of a family is given in the following data :

Draw a bar graph to represent the above data.
Solution:
We draw the bar graph of this data in the following steps :
(i) We draw a horizontal and vertical line.
(ii) We represent the years on horizontal axis on a suitable scale. We take equal widths for all bars and maintain equal gaps in between. Let one head be represented by one unit.
(iii) We represent income (in thousands) and expenditure (in thousands) along vertical axis. Let 1 unit = Rs. 20 thousands.
(iv) To represent first head, we draw a rectangular bars with width 1 unit and heights 6 units and 3.5 units.
(v) Similarly, other heads are represented leaving gap of 2 units in between two consecutive bars.

Question 6.
If \(\bar{x}\) is the mean of n observations x₁, x₂, …, x_n, then show \(\sum_{i=1}^n\left(x_i-\bar{x}\right)=0\)
Solution:
Since \(\bar{x}\) is the mean of n observations x₁, x₂, ……., x_n.
∴ \(\bar{x}\) = \(\frac{x_1+x_2+\ldots+x_n}{n}\)
⇒ n\(\bar{x}\) = x₁ + x₂ + … + x_n …(1)
Now, = (x₁ – \(\bar{x}\)) + (x₂ – \(\bar{x}\))+…+(x_n – \(\bar{x}\))
= (x₁ + x₂ + …… + x_n) – n\(\bar{x}\)
= n\(\bar{x}\) – n\(\bar{x}\), [Using (1)]
= 0
Hence, \(\sum_{i=1}^n\left(x_i-\bar{x}\right)=0\) Hence Proved.

Question 7.
The mean of n observations x₁, x₂, …, x_n is \(\bar{x}\). If a is added to each of the observations, show that mean of new set of observations is \(\bar{x}\) + a.
Solution:
Since \(\bar{x}\) is the mean of n observations x₁, x₂, …, x_n.
∴ \(\bar{x}\) = \(\frac{x_1+x_2+\ldots+x_n}{n}\)
⇒ n\(\bar{x}\) = x₁ + x₂ + … + x_n … (1)
If a is added to each observation. Sum of observations of new set
= (x₁ + a) + (x₂ + a) + ……. + (x_n + a)
Mean of observations of new set

Hence, mean of observations of new set = \(\bar{x}\) + a.
Proved.

Question 8.
The mean of 18 members is 5. If 2 is added to every number, find the new mean.
Solution:
Here, n = 18, \(\bar{x}\) = 5
We know that
∴ \(\bar{x}\) = \(\frac{x_1+x_2+\ldots+x_n}{n}\)
⇒ 5 = \(\frac{x_1+x_2+\ldots+x_{18}}{18}\)
⇒ 90 = x₁ + x₂ + … + x₁₈ …(i)
Since, 2 is added to every number, then new numbers are (x₁ + 2), (x₂ + 2), …, (x₁₈ + 2).
Then,mean of new numbers

Hence, new mean = 7.

Question 9.
The mean of n observations x₁, x₂, …, x_n is \(\bar{x}\). If each observation is multiplied by non-zero number a, then show that mean of new observations is a\(\bar{x}\).
Solution:
Since mean of n observations x₁, x₂, …, x_n is \(\bar{x}\).
∴ \(\bar{x}\) = \(\frac{x_1+x_2+\ldots+x_n}{n}\)
n\(\bar{x}\) = x₁ + x₂ + … + x_n …(1)
If each observation is multiplied by a, then new observations are ax₁, ax₂, …, ax_n.
Sum of new observations
= ax₁ + ax₂ + … + ax_n
Mean of new observations
= \(\frac{a x_1+a x_2+\ldots+a x_n}{n}\)
= \(\frac{a\left(x_1+x_2+\ldots+x_n\right)}{n}\)
= \(\frac{a \times n \bar{x}}{n}\)
= a\(\bar{x}\)
Hence,mean of new observations = a\(\bar{x}\).
Proved

Question 10.
Mean of 12 numbers is 20. If each number is multiplied by 3, what will be the new mean.
Solution:
Here, n = 12, \(\bar{x}\) = 20
We know that
\(\bar{x}\) = \(\frac{x_1+x_2+\ldots+x_n}{n}\)
⇒ 20 = \(\frac{x_1+x_2+\ldots+x_{12}}{12}\)
⇒ x₁ + x₂ + … + x₁₂ = 20 × 12 = 240 …..(1)
Since, each number is multiplied by 3, then new numbers are 3x₁, 3x₂, …, 3x₁₂.
Sum of new numbers = 3x₁ + 3x₂ +…+ 3x₁₂
Mean of new numbers
= \(\frac{3 x_1+3 x_2+\ldots+3 x_{12}}{12}\)
= \(\frac{3\left(x_1+x_2+\ldots+x_12\right)}{12}\)
= \(\frac{3 \times 240}{12}\), [Using (1)]
= 60
Hence, new mean = 60.

Question 11.
The mean weight of the students of a class is 40 kg. The mean weight of the boys is 45 kg and that of girls is 36 kg. Find the ratio of the number of boys to number of girls.
Solution:
Let the number of boys be n₁ and number of girls be n₂, then
Mean of n₁ boys (\(\bar{x}_1\)) = 45 kg
Mean of n₂ girls (\(\bar{x}_2\)) = 36 kg
and mean of (n₁ + n₂) students (\(\bar{x}[/katex]) = 40 kg
We know that, ([latex]\bar{x}\)) = \(\frac{n_1 \bar{x}_1+n_2 \bar{x}_2}{n_1+n_2}\)
⇒ 40 = \(\frac{n_1 \times 45+n_2 \times 36}{n_1+n_2}\)
⇒ 40n₁ + 40n₂ = 45n₁ + 36n₂
= 40n₂ – 36n₂ = 45n₁ – 40n₁
⇒ 4n₂ = 5n₁
⇒ \(\frac{n_1}{n_2}=\frac{4}{5}\)
⇒ n₁ : n₂ = 4 : 5
Hence,number of boys : number of girls = 4 : 5.

Question 12.
The mean marks of 150 students in an examination was 60. The mean marks of boys was found to be 70 and that of the girls was 55. Find the number of boys and number of girls in the class.
Solution:
Let the number of boys be n₁ and number of girls be n₂, then
n₁ + n₂ = 150 ……(1)
Mean marks of 150 students (\(\bar{x}\)) = 60
Mean marks of n₁ boys (\(\bar{x}\)) = 70
and mean marks of n₂ girls (\(\bar{x}\)) = 55
We know that, (\(\bar{x}\)) = \(\frac{n_1 \bar{x}_1+n_2 \bar{x}_2}{n_1+n_2}\)
⇒ 60 = \(\frac{n_1 \times 70+n_2 \times 55}{150}\)
[Using (1)]
⇒ 60 × 150 = 70n₁ + 55n₂
⇒ 150 × 12 = 14n₁ + 11n₂
⇒ 14n₁ + 11n₂ = 1800 ……(2)
Multiplying equation (1) by 14 and subtracting equation (2) from (1), we get

Putting the value of n₂ in equation (1), we get
n₁ + 100 = 150
⇒ n₁ = 150 – 100 = 50
Hence, number of boys = 50 and number of girls = 100.

Question 13.
The following observations have been arranged in ascending order. If median of data is 39, then find the value of x:
18, 24, 26, 29, x, x + 4, 45, 57, 59, 63.
Solution:
Here, median = 39
n = 10, which is even

⇒ 78 = 5th term + 6th term
⇒ 78 = x + x + 4
⇒ 78 = 2x + 4
2x = 78 – 4 = 74
⇒ x = \(\frac{74}{2}\) = 37
Hence, x = 37.

Question 14.
Find the median of the following observations:
33, 68, 55, 72, 44, 63, 74, 85, 52, 40, 45
If 44 is replaced by 64 and 74 by 58 in the above data, then find the new median.
Solution:
We arrange the data in ascending order :
33, 40, 44, 45, 52, 55, 63, 68, 72, 74, 85
Here, n = 11, which is odd
∴ Median = \(\left(\frac{n+1}{2}\right)^{\mathrm{th}}\) term
= \(\left(\frac{11+1}{2}\right)^{\mathrm{th}}\) term
= 6th term
= 55
If 44 is replaced by 64 and 74 by 58, then we obtain new data of observations in ascending order as follow :
33, 40, 45, 52, 55, 58, 63, 64, 68, 72, 85
Here, n = 11
∴ Median = 6th term
= 58.
Hence, median = 55 and new median = 58

Long Answer Type Questions

Question 1.
The following are the marks (out of 100) of 60 students in mathematics
16, 15, 5, 80, 86, 7, 51, 48, 24, 56, 70, 19, 61, 17, 16, 36, 34, 42, 35, 72, 55, 75, 31, 52, 28, 72, 97, 74, 45, 62, 68, 86, 35, 85, 36, 81, 75, 55, 26, 95, 31, 7, 78, 92, 62, 52, 56, 15, 63, 25, 36, 54, 44, 47, 27, 72, 17, 4, 30, 34
(i) construct a grouped frequency distribution table with width 10 of each class starting from 0 – 9, 10 – 19, itc, (i.e., inclusive form)
(ii) Construct a grouped frequency distribution table with width 10 of each class, in such a way that one of the classes is 10 – 20 (20 is not included) i.e., exclusive form.
Solution:
Highest marks = 97
Lowest maks = 4
Range = 97 – 4 = 93
Width of class = 10
No. of classes = \(\frac{93}{10}\) = 9.3 = 10 (say)
(i) For inclusive from :
The class intervals of the data are :
0 – 9, 10 – 19, 20 – 29, 30 – 39, 40 – 49, 50 – 59, 60 – 69, 70 – 79, 80 – 89, 90 – 99
Frequency distribution of marks

For exclusive form :
The class intervals of the data are :
0 – 10, 10 – 20, 20 – 30, 30 – 40, 40 – 50, 50 – 60, 60 – 70, 70 – 80, 80 – 90, 90 – 100
Frequency distribution of marks

Question 2.
For the following data of daily wages (in Rs.) received by 30 labourers in a certain factory, construct a grouped frequency distribution table by dividing the range into class interval of equal width, each corresponding to Rs. 2, in such a way that the mid value of the first class interval corresponds to Rs. 12.
11, 22, 24, 16, 15, 17, 23, 20, 17, 18, 19, 23, 18, 12, 11, 12, 13, 13, 14, 15, 16, 20, 19, 19, 20, 22, 22, 21, 24, 23.
Solution:
Maximum daily wage = Rs. 24
Minimum daily wage = Rs. 11
Range = Rs. 24 – Rs. 11 = Rs. 13
Size of the class interval = Rs. 2
∴Number of class intervals = \(\frac{13}{2}\) = 6.5
= 7 (say)
∵Mid value of first class interval = 12
and size of class interval = 2
Let the lower limit of first class interval be x, then its upper limit = x + 2
Mid value of class interval = \(\frac{\text { lower limit + upper limit }}{2}\)
⇒ 12 = \(\frac{x+x+2}{2}\)
⇒ 24 = 2x + 2
⇒2x = 24 – 2 = 22
⇒ x = \(\frac{22}{2}\) = 11
∴The first class interval is 11 – 13 and other class intervals are :
13 – 15, 15 – 17, 17 – 19, 19 – 21, 21 – 23, 23 – 25
∴Frequency distribution table is given below :
Frequency distribution of wages of 30 labourers

Question 3.
The following table shows the number of females in the group (10 – 70) in a town:

Draw a histogram to represent the above data.
Solution:
Here the class intervals are discontinuous. So, we convert it into continuous class intervals. For this we subtract \(\frac{h}{2}=\frac{1}{2}\) = 0.5 from each of lower limit and add 0.5 to each upper limit. So, continuous class intervals obtained as follows:

We represent the age group (in years) along x-axis on a suitable scale and corresponding frequencies along y-axis on a suitable scale.

We construct rectangles with class intervals as bases and the corresponding frequencies as heights.
Thus, we obtain a histogram as shown below :

Question 4.
The daily pocket expense (in Rs.) of 200 students in a school are given below :

Pocket expense (mid value)
Draw a histogram to represent the above data.
Solution:
Since class marks are uniformly space.
∴ Class size is the difference between any two consecutive class marks.
Class size (h) = 7.5 – 2.5 = 5
Half of the class size \(\left(\frac{h}{2}\right)=\frac{5}{2}\) = 2.5
To obtain lower class limit, we substract 2.5 from each class mark and to obtain upper class limit, we add 2.5 to the class mark. Class mark of the first class = 2:5
∴ Corresponding class limits are
2.5 – 2.5 and 2.5 + 2.5 i.e., 0 – 5
Similarly, we obtain the other classes as under:

We represent the pocket expense (in Rs.) along x-axis on a suitable scale and corresponding frequencies along y-axis. We construct rectangles class intervals as bases and corresponding frequencies as heights. Thus we obtain a histogram as shown below :

Question 5.
Construct a histogram and a frequency polygon for the following data :

Solution:
Here the class intervals are in inclusive form. For coverting it into exclusive form, we subtract \(\frac{h}{2}=\frac{1}{2}\) = 0.5 from each of lower limit and add 0.5 to each upper limit. So, exclusive form of distribution table obtained as follows :

Let us first draw a histogram for this data and mark the mid points of the tops of the rectangles as B, C, D, E, F, G, H respectively. Here, the first class is 19.5 – 24.5, so to find the class preceeding 19.5 – 24.5 and find the mid point of the imaginary class interval (14.5 – 19.5). The first end point i.e., B is joined with the mid point of the imaginary class interval (14.5 – 19.5) and it is marked as A. Let I be mid point of the class succeeding the last class of the given data. Then ABCDEFGHI is the frequency polygon, which is shown below figure

Question 6.
The mean of the following distribution is 50.

Find the value of a and hence the frequencies of 30 and 70.
Solution:
For calculating the mean, we prepare the following table

From table, we have
\(\sum_{i=1}^n f_i\) = 60 + 120 and \(\sum_{i=1}^n f_i x_i\) = 2800 + 640a
Mean of distribution = 50 (given)

⇒ 3000 + 600a = 2800 + 640a
⇒ 3000 – 2800 = 640a – 600a
⇒ 40a = 200
⇒ a = \(\frac{200}{40}\) = 5
Frequency of 30 = 5a + 3 = 5 × 5 + 3 = 28
Frequency of 70 = 7a – 11 = 7 × 5 – 11 = 24
Hence, a = 5, frequencies of 30 and 70 are 28 and 24 respectively.

Question 7.
Find the missing frequencies, if mean of the following distribution is 18.

Solution:
For calculating the mean, we prepare the following table :

From the table, we get
\(\sum_{i=1}^n f_i\) = 40 or 20 + f₁ + f₂ = 40
⇒ f₁ + f₂ = 20 …..(1)
and \(\sum_{i=1}^n f_i x_i\) = 280 + 20f₁ + 25f₂, mean = 18
We know that, mean = \(\sum_{i=1}^n f_i x_i\)

⇒ 720 = 280 + 20f₁ + 25f₂
⇒ 20f₁ + 25f₂ = 720 – 280
⇒ 20f₁ + 25f₂ = 440 …….(2)
Multiplying the equation (1) by 20 and substracting from equation (2), we get

Putting the value of f₂ in equation (1), we get
f₁ + 8 = 20
⇒ f₁ = 20 – 8 = 12
Hence, f₁ = 12 and f₂ = 8.

Multiple Choice Questions

Choose the correct answer in each of the following:

Question 1.
The class mark of the class 20 – 30 is:
(a) 20
(b) 25
(c) 30
(d) 35
Answer:
(c) 30

Question 2.
The range of the data of observations is :
33, 56, 17, 44, 26, 47, 58, 40, 67, 54, 37, 22, 35, 52, 63
(a) 46
(b) 41
(c) 50
(d) 67
Answer:
(c) 50

Question 3.
In the class intervals 10 – 20, 20 – 30, the number 20 is included in :
(a) 10 – 20
(b) 20 – 30
(c) both the intervals
(d) none of these intervals
Answer:
(d) none of these intervals

Question 4.
In a frequency distribution, the mid value of a class is 10 and the width of the class is 6. The lower limit of the class is:
(a) 6
(b) 7
(c) 8
(d) 12
Answer:
(b) 7

Question 5.
The mid value of a class interval is 32. If the class size is 10, then the class interval is :
(a) 27.5 – 37.5
(b) 37.5 – 27.5
(c) 22 – 42
(d) 27 – 37
Answer:
(c) 22 – 42

Question 6.
The class marks of a frequency distribution are 5, 10, 15, 20, ……..
The class corresponding to the class mark 15 is :
(a) 7.5 – 12:5
(b) 12.5 – 17.5
(c) 17.5 – 22.5
(d) 22.5 – 27.5
Answer:
(d) 22.5 – 27.5

Question 7.
The tabular arrangement of data, showing the frequency of each observation is called:
(a) frequency
(b) cumulative frequency
(c) frequency distribution
(d) none of these
Answer:
(d) none of these

Question 8.
The difference between the true upper limit and the true lower limit of a class is called its :
(a) class size
(b) class mark
(c) range
(d) none of these
Answer:
(c) range

Question 9.
The number of times a particular item occurs in a class interval is called its :
(a) Frequency distribution
(b) Variation
(c) Frequency
(d) Cumulative frequency
Answer:
(d) Cumulative frequency

Question 10.
In a histogram the area of each rectangle is proportional to :
(a) The class size of the corresponding class interval
(b) The class mark of the corresponding class interval
(c) Cumulative frequency of the corresponding class interval
(d) Frequency of the corresponding class interval.
Answer:
(a) The class size of the corresponding class interval

Haryana State Board HBSE 9th Class Science Important Questions Chapter 7 जीवों में विविधता Important Questions and Answers.

Haryana Board 9th Class Science Important Questions Chapter 7 जीवों में विविधता

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
वर्गिकी किसे कहते हैं?
उत्तर:
जीवों का वर्गीकरण करने वाली विज्ञान की शाखा. वर्गिकी कहलाती है।

प्रश्न 2.
किस व्यक्ति ने जीवों का वर्गीकरण उनके आवास के आधार पर किया?
उत्तर:
यूनानी विचारक एरिस्टोटल ने।

प्रश्न 3.
किन कोशिकाओं में केंद्रक, कोशिकांग और झिल्ली पाई जाती है?
उत्तर:
यूकैरियोटिक कोशिकाओं में।

प्रश्न 4.
किन कोशिकाओं में बहुकोशिकीय जीव के निर्माण की क्षमता होती है?
उत्तर:
केंद्रक युक्त कोशिकाओं में।

प्रश्न 5.
जो कोशिकाएँ समूह बनाकर किसी जीव का निर्माण करती हैं, उनमें पाए जाने वाले एक गुण के बारे में लिखो।
उत्तर:
श्रम विभाजन का गुण।

प्रश्न 6.
पौधे किन्हें कहते हैं?
उत्तर:
जिन जीवों में प्रकाशसंश्लेषण प्रक्रिया द्वारा भोजन बनाने की क्षमता हो, उन्हें पौधे कहते हैं।

प्रश्न 7.
जंतु किन्हें कहते हैं?
उत्तर:
जो जीव अपना भोजन बाहर से ग्रहण करें, उन जीवों को जंतु कहते हैं।

प्रश्न 8.
जैव विकास की अवधारणा किस वैज्ञानिक ने दी?
उत्तर:
चार्ल्स डार्विन ने 1859 में अपनी पुस्तक ‘दि ओरिजिन ऑफ स्पीशीज़’ में।

प्रश्न 9.
आदिम या निम्न जीव किन्हें कहते हैं?
उत्तर:
पृथ्वी पर पहले प्रकार के जीव आदिम जीव या निम्न जीव कहलाते हैं।

प्रश्न 10.
उन्नत या उच्च जीव किसे कहते हैं?
उत्तर:
आदिम जीवों में आई जटिलताओं से बने जीवों को उन्नत या उच्च जीव कहते हैं।

प्रश्न 11.
जीवों का किंगडम नामक बड़े वर्ग में विभाजित करने का प्रयास किन जैव वैज्ञानिकों ने किया?
उत्तर:
अन्सर्ट हेकेल (1894), राबर्ट व्हिटेकर (1959) और कार्ल वोस (1977) ने।

प्रश्न 12.
व्हिटेकर द्वारा प्रस्तावित वर्गीकरण का नाम क्या है?
उत्तर:
पाँच-किंगडम।

प्रश्न 13.
मोनेरा किंगडम को किस जैव वैज्ञानिक ने आर्कीबैक्टीरिया और यूबैक्टेरिया में बाँटा?
उत्तर:
कार्ल वोस ने।

प्रश्न 14.
स्पीशीज किसे कहते हैं?
उत्तर:
जीवों का समूह जिसकी प्रजाति परस्पर संकरण कर सकती है। यह वर्गीकरण की सबसे छोटी इकाई है।

प्रश्न 15.
वर्गीकरण की आधारभूत इकाई क्या है?
उत्तर:
जाति।

प्रश्न 16.
नामकरण किसे कहते हैं?
उत्तर:
ऐसी पद्धति जिसमें जीव-जंतुओं और पौधों की प्रत्येक जाति का नामकरण किया जाता है।

प्रश्न 17.
वर्गिकी के जनक कौन हैं?
उत्तर:
केरोलस लिनियस।

प्रश्न 18.
वैज्ञानिक नाम लिखने की पद्धति को द्विनाम पद्धति क्यों कहते हैं?
उत्तर:
इस पद्धति में किसी भी जीव के दो नाम लिखे जाते हैं-पहला नाम जेनेटिक और दूसरा स्पीशीज़ (प्रजाति) का।

प्रश्न 19.
मनुष्य का वैज्ञानिक नाम क्या है?
उत्तर:
होमो सेपिएंस।

प्रश्न 20.
नामकरण की अंतर्राष्ट्रीय नाम पद्धति कौन-सी है?
उत्तर:
द्विनाम पद्धति।

प्रश्न 21.
वर्गीकरण की विभिन्न इकाइयाँ क्या हैं?
उत्तर:
जाति, वंश, गण, वर्ग, संघ तथा जगत।

प्रश्न 22.
जीनस (Genus) क्या है?
उत्तर:
समान जातियाँ मिलकर वंश या जीनस बनाती हैं।

प्रश्न 23.
पुराने तंत्र के अनुसार संसार को कितने जगतों में बाँटा गया है?
उत्तर:
दो जगतों में-

• पादप जगत
• जंतु जगत।

प्रश्न 24.
वर्गीकरण किसे कहते हैं?
उत्तर:
जीवों में समानता, विभिन्नता तथा इनके आपसी संबंधों के आधार पर समूहों या वर्गों में बाँटना वर्गीकरण कहलाता है।

प्रश्न 25.
वर्गीकरण का एक महत्त्व लिखो।
उत्तर:
जीवों का अध्ययन सरल हो गया है।

प्रश्न 26.
संसार के समूचे जीवों को वनस्पति व जंतु जगत में किस वैज्ञानिक ने बाँटा?
उत्तर:
केरोलस लिनियस ने सन् 1758 में।

प्रश्न 27.
प्रोटिस्टा (तीसरा श्रेणी जगत) किसकी देन है?
उत्तर:
ई०एच० हेकेल (1866) की।

प्रश्न 28.
चौथा श्रेणी जगत मोनेरा और पांचवाँ श्रेणी जगत फेजार्ड किसने बनाए?
उत्तर:
राबर्ट व्हिटेकर (1959) ने।

प्रश्न 29.
किन जीवों में वृद्धि जीवन-भर होती रहती है?
उत्तर:
पौधों में।

प्रश्न 30.
आइशलर (1883) ने वनस्पति जगत को कितने उपजगतों में बाँटा?
उत्तर:
दो-क्रिप्टोगैमी व फैनरोगैमी।

प्रश्न 31.
कवक अपना भोजन स्वयं क्यों नहीं बना सकते?
उत्तर:
क्योंकि कवक में पर्णहरिम नहीं पाया जाता।

प्रश्न 32.
आवृतबीजी पौधे कितने प्रकार के होते हैं?
उत्तर:
दो प्रकार के-

• द्विबीजपत्री तथा
• एकबीजपत्री।

प्रश्न 33.
अनावृतबीजी पौधों के दो उदाहरण दो।
उत्तर:
साइकस व चीड़।

प्रश्न 34.
शैवाल और कवक में एक अंतर बताओ।
उत्तर:
शैवाल में पर्णहरितम पाया जाता है, जबकि कवक में नहीं।

प्रश्न 35.
लाइकेन क्या है?
उत्तर:
कवक और शैवाल के सहजीवी लाइकेन कहलाते हैं।

प्रश्न 36.
क्रिप्टोगैमी का कौन-सा विभाजक कवक से संबंधित है?
उत्तर:
थैलोफाइटा।

प्रश्न 37.
ब्रायोफाइटा का एक उदाहरण दो।
उत्तर:
मॉस (फ्यूनेरिया)।

प्रश्न 38.
टेरिडोफाइटा का एक उदाहरण दो।
उत्तर:
फर्नस, मार्सीलिया।

प्रश्न 39.
क्रिप्टोगैम्स किसे कहते हैं?
उत्तर:
जिन पौधों में बीज उत्पन्न करने की क्षमता न हो और इनमें अप्रत्यक्ष जननांग स्पोर पाए जाते हैं।

प्रश्न 40.
फैनरोगैम्स किसे कहते हैं?
उत्तर:
जिन पौधों में जनन प्रक्रिया के पश्चात् बीज उत्पन्न हो।

प्रश्न 41.
जिम्नोस्पर्म किसे कहते हैं?
उत्तर:
नग्न बीज उत्पन्न करने वाले पौधों को जिम्नोस्पर्म कहते हैं।

प्रश्न 42.
एंजियोस्पर्म किसे कहते हैं?
उत्तर:
फल के अंदर बीज उत्पन्न करने वाले पौधों को एंजियोस्पर्म कहते हैं।

प्रश्न 43.
प्लांटी का प्रमुख गुण क्या है?
उत्तर:
स्वपोषण।

प्रश्न 44.
एनिमेलिया का प्रमुख गुण क्या है?
उत्तर:
परपोषण।

प्रश्न 45.
पोरीफेरा किसे कहते हैं?
उत्तर:
जिन जीवों के शरीर पर अनेकों छिद्र पाए जाते हैं।

प्रश्न 46.
सीलेंटरेटा के दो उदाहरण दो।
उत्तर:
हाइड्रा, समुद्री एनीमोन।

प्रश्न 47.
चपटे कृमि वर्ग का नाम क्या है?
उत्तर:
प्लेटीहेल्मिन्थीज।

प्रश्न 48.
फीताकृमि का वैज्ञानिक नाम लिखो।
उत्तर:
टिनिया सोलियम।

प्रश्न 49.
किस वर्ग के अधिकतर जीव परजीवी हैं?
उत्तर:
निमेटोडा के।

प्रश्न 50.
एनीलिडा का एक उदाहरण दो।
उत्तर:
केंचुआ, जोंक।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
वर्गिकी अथवा वर्गीकरण विज्ञान क्या है?
उत्तर:
वर्गिकी-जीव विज्ञान की वह शाखा जिसमें जीवों का वर्गीकरण किया जाता है, वर्गिकी कहलाती है। सबसे पहले डी० केंडोली ने इस शब्द का उपयोग किया। वर्गिकी द्वारा जीवों की पहचान, वर्गीकरण, नामकरण आदि किया जाता है।

वर्गीकरण-यह जीवों को उनके संबंधों के आधार पर समूहों में व्यवस्थित करता है। जंतु तथा पौधों को विभिन्न श्रेणियों; जैसे फाइलम, वर्ग, आर्डर, कुल, जीनस तथा जाति में विकास के क्रम में रखा गया है। केरोलस लिनियस (1707-1778) ने सर्वप्रथम अपनी पुस्तक Systema Naturae में इस बारे में जानकारी दी। इसीलिए केरोलस लिनीयस को जीव वर्गिकी का जनक कहा जाता है।

प्रश्न 2.
जीवों को वर्गीकृत करना क्यों आवश्यक है? अपने शब्दों में बताओ।
उत्तर:
संसार में जीवों की संख्या अत्यधिक है। इन जीवों में कुछ समानताएँ हैं तो कुछ विभिन्नताएँ पाई जाती हैं। इन जीवों की संरचना कुछ की सरल तो कुछ की जटिल है। इन जीवों की रचना, स्वभाव, जीवन-चक्र, पोषण, श्वसन, जनन आदि करने में भारी भिन्नताएँ पाई जाती हैं। अतः इन जीवों का अध्ययन करने के लिए वर्गीकृत करना आवश्यक है। जीवों को इनकी समानताओं और असमानताओं के आधार पर वर्गीकृत किया जाता है। वर्गीकरण जीव विज्ञान की विभिन्न शाखाओं के लिए आधार का कार्य करता है।

प्रश्न 3.
वर्गीकरण क्या है? इसका महत्त्व बताइए।
उत्तर:
जीवों को इनकी समानताओं, विभिन्नताओं तथा आपसी संबंधों के आधार पर वर्गीकृत करना ‘वर्गीकरण’ कहलाता है। महत्त्व-वर्गीकरण का महत्त्व निम्नलिखित है-

• वर्गीकरण अन्य जीव विज्ञान की शाखाओं को आधार प्रदान करता है।
• वर्गीकरण से जीवों का अध्ययन करना सरल और आसान हो जाता है।
• वर्गीकरण सभी जीवों की एकदम स्पष्ट तस्वीर प्रदान करता है।
• इससे विभिन्न जीवों के समूहों के बीच आपसी संबंधों के बारे में जानकारी मिलती है।
• भूगोल का अध्ययन पूर्णतया पौधों तथा जंतुओं के वर्गीकरण पर आधारित है।
• जीवों का वर्गीकरण अन्य विषयों में से अधिकतर ज्ञान विकास में काफी सीमा तक योगदान करता है।
• पारिस्थितिकी कोशिका विज्ञान, कायिकी आदि जीव विज्ञान की शाखाएँ वर्गीकरण के कारण विकसित हो पाई हैं।

प्रश्न 4.
द्विपद नाम पद्धति क्या है? एक उदाहरण देकर स्पष्ट करो।
उत्तर:
द्विपद नाम पद्धति (Binomial Nomenclature) यह पद्धति केरोलस लिनियस की देन है। इस पद्धति में जंतुओं की 4200 जातियों का नामकरण सन् 1758 में सिस्टेमा नेचुरी नामक पुस्तक में किया गया। इस पद्धति में प्रत्येक पौधे व जंतु को दो नाम दिए जाते हैं। पहला नाम जेनेटिक तथा दूसरा नाम स्पीशीज अर्थात जीव के वंश का नाम होता है। लिनियस को द्विनाम पद्धति का जनक माना गया है।

उदाहरणार्थ-आम (Mango) का वैज्ञानिक नाम मेंगिफेरा इंडिका (Mangifere Indica), सरसों का नाम ब्रेसिका कंपेस्ट्रिस (Brassica Compertis) और मनुष्य का नाम होमो सेपिएंस (Homo Sapiens) है। इन सभी में पहला नाम जेनेटिक और दूसरा स्पीशीज़ है और ये नाम पूरे संसार में एक समान अर्थात् उक्त नाम ही प्रचलित हैं।

प्रश्न 5.
वर्गीकरण की द्वि-जगतीय प्रणाली की प्रमुख विशेषताएँ क्या हैं? बैक्टीरिया और कवक को पौधों के साथ वर्गीकृत क्यों किया गया है?
उत्तर:
संसार के सभी जीवों को दो मुख्य जगतों में बाँटा गया है-

• जंतु जगत (Animals) तथा
• पादप जगत (Plants)।

इन दोनों जगत के जीवों में जीवों के मुख्य लक्षण तो एक समान हैं परंतु कुछ लक्षणों के कारण भिन्न होते हैं। जंतु जगत के जीव प्रायः एक स्थान पर नहीं रहते हैं। ये अपना भोजन स्वयं तैयार नहीं कर सकते, क्योंकि इनमें हरे रंग का पदार्थ पर्णहरिम अर्थात् क्लोरोफिल नहीं पाया जाता, जबकि पादप जगत के जीव प्रायः स्वपोषी होते हैं। ये प्रायः एक स्थान पर रहते हैं। इनकी कोशिका . भित्ति सैल्यूलोज की बनी होती है। इन जीवों में पर्णहरिम अर्थात् क्लोरोफिल पाया जाता है।

बैक्टीरिया और कवक में हरे रंग का पदार्थ पर्णहरिम नहीं पाया जाता और न ही ये स्वपोषी होते हैं। ये अपना भोजन मृत अथवा जीवित जीवों से प्राप्त करते हैं। फिर भी इन्हें निम्नलिखित कारणों से पादप जगत में रखा गया है-

• इनकी कोशिका भित्ति सैल्यूलोज की बनी होती है।
• यह अपना भोजन पौधों की तरह घोल अवस्था में ही प्राप्त करते हैं।

प्रश्न 6.
वर्गीकरण की विभिन्न श्रेणियों का वर्णन कीजिए।
उत्तर:
वर्गीकरण की निम्नलिखित श्रेणियाँ हैं-

• जाति-यह जीवों की निम्नतम श्रेणी है।
• जीनस-जातियाँ मिलकर जीनस बनाती हैं।
• कुल-जीनस से उच्चतम श्रेणी कुल है।
• आर्डर-कुल मिलकर आर्डर बनाते हैं।
• वर्ग-आर्डर मिलकर वर्ग बनाते हैं।
• फाइलम-वर्ग से उच्चतम तथा वर्गों से मिलकर फाइलम बनता है।

प्रश्न 7.
क्रिप्टोगैमी और फैनरोगेमी किसे कहते हैं?
उत्तर:

• क्रिप्टोगैमी-ये निम्नकोटि के पौधे होते हैं। इनमें फूल, फल व बीजों का अभाव होता है। इनमें गुप्त जननांग होते हैं। स्पोर के द्वारा जनन करते हैं।
• फैनरोगैमी-ये उच्च-कोटि के पौधे होते हैं। इनमें जड़, तना, पत्ते, फूल, फल व बीज पाए जाते हैं। इनमें जनन प्रक्रिया के पश्चात बीज बनता है। बीज में भ्रूण और संचित खाद्य पदार्थ होता है।

प्रश्न 8.
क्रिप्टोगैमी का वर्गीकरण कैसे किया गया है?
उत्तर:
क्रिप्टोगैमी-ये सभी अपुष्पी पौधे होते हैं। इनमें जनन अंग छुपे हुए होते हैं। इनमें बाहरी फूल व बीज नहीं पाए जाते। लिंडले और आइशलर के वर्गीकरण अनुसार क्रिप्टोगैमी को तीन फाइलमों (संघों) में विभाजित किया गया है-

• थैलोफाइटा; जैसे यूलोथ्रिक्स, पेनिसिलियम, लाइकेन आदि।
• ब्रायोफाइटा; जैसे फ्यूनेरिया, मार्केशिया आदि।
• टेरिडोफाइटा; जैसे फर्नस, सिलैजीनैला आदि।

प्रश्न 9.
एकबीजपत्री और द्विबीजपत्री पौधों में अंतर स्पष्ट करो।
उत्तर:
एकबीजपत्री और द्विबीजपत्री पौधों में निम्नलिखित अंतर हैं-

प्रश्न 10.
एनिमेलिया किसे कहते हैं? इस वर्ग की प्रमुख विशेषताएँ और इनके प्रमुख फाइलम के नाम लिखो।
उत्तर:
एनिमेलिया-ऐसे बहुकोशीय जीव जिनमें कोशिका भित्ति का अभाव होता है, एनिमेलिया कहलाते हैं। इनकी प्रमुख विशेषताएँ निम्नलिखित हैं-

• ये सभी जीव विषमपोषी और परपोषी होते हैं।
• ये एक निश्चित आकृति प्राप्त कर देहवृद्धि रोकने वाले जीव होते हैं।
• अधिकतर जीव जंगम (चल) होते हैं।

इनका वर्गीकरण निम्नलिखित प्रकार से किया जा सकता है-

• पोरीफेरा
• सीलेंटरेटा
• प्लेटीहेल्मिन्थीज
• निमेटोडा
• एनीलिडा
• आर्थोपोडा
• मोलस्का
• इकाइनोडर्मेटा
• प्रोटोकॉर्डेटा
• वर्टीब्रेटा।

प्रश्न 11.
पोरीफेरा फाइलम (संघ) की विशेषताएँ बताइए।
उत्तर:
पोरीफेरा की विशेषताएँ निम्नलिखित हैं-

• ये अधिकतर लवणीय होते हैं, जबकि कुछ अलवण जल (ताजे जल) में भी पाए जाते हैं।
• ये बहुकोशिक होते हैं।
• उनकी देहाभित्ति दो स्तरों की बनी होती है।
• इनमें तंत्रिका तंत्र व कंकाल-तंत्र नहीं पाया जाता।
• देहाकृति क्लश या थैलीनुमा गोलाकार या शाखित होती है।
• सारे शरीर में छिद्र (Ostia) पाए जाते हैं, जबकि शिखर पर एक बड़ा मुख ऑसकुलम (Osculum) पाया जाता है।
• इनमें नाल तंत्र पाया जाता है।
• जनन लैंगिक (निषेचन) तथा अलैंगिक (मुकुलन) द्वारा होता है। उदाहरण-साइकॉन, यूप्लेक्टेला, स्पांजिला आदि।

प्रश्न 12.
सीलेंटरेटा फाइलम (गुहांत्र जीव) के मुख्य लक्षण बताइए।
उत्तर:
सीलेंटरेटा (गुहांत्र) के मुख्य लक्षण निम्नलिखित हैं-

• ये समुद्र में एकल या कॉलोनी के रूप में पाए जाते हैं।
• इनमें सत्य गुहा नहीं होती।
• अरीय सममित होती है।
• इनमें सीलेंटट्रोन उपस्थित होता है।
• दंश कोशीय टेंटाकलस पर पाई जाती हैं।
• इनमें स्टिगिंग कोशिकाएँ पाई जाती हैं, जिन्हें निडोब्लास्ट कहते हैं।
• निवाही जीवों में (पॉलिप व मेडूसा) जीवन-चक्र में बारी-बारी से आते हैं अर्थात् पीढ़ी एकांतरण पाया जाता है।
• जनन प्रायः पॉलिप में अलैंगिक और मेडूसा में लैंगिक होता है। उदाहरण-हाइड्रा, ओबीलिया, समुद्री एनीमोन, मूंगा आदि।

प्रश्न 13.
प्लेटीहेल्मिन्थीज फाइलम (चपटे कृमि) की विशेषताएँ बताओ।
उत्तर:
प्लेटीहेल्मिन्थीज की विशेषताएँ निम्नलिखित हैं-

• ये प्रायः चपटे कृमि होते हैं
• ये अधिकतर परजीवी होते हैं, कुछ मुक्तजीवी भी हैं
• इनका शरीर तीन स्तरों (layers) का बना होता है
• शरीर द्विपार्श्व (Bilateral) होता है
• ये उभयलिंगी होते हैं
• आहार नाल में केवल एक मुँह छिद्र होता है
• इनका शरीर यकृत पर्णाभ पृष्ठधारीय, चपटा और पत्ते जैसा या रिबॅननुमा होता है।

उदाहरण-फीताकृमि, प्लेनेरिया, लिवरफ्लूक आदि। ।

प्रश्न 14.
निमेटोडा फाइलम (गोल कृमि) की विशेषताएँ लिखें।
उत्तर:
निमेटोडा फाइलम की विशेषताओं का वर्णन निम्नलिखित है-

• ये परजीवी या मुक्तजीवी हैं।
• इनकी द्विपार्श्व सममित होती है।
• उनकी आहार नाल पूर्ण होती है।
• देहगुहा असली नहीं है, उसे कूटसीलोम कहते हैं।
• ये एकलिंगी होते हैं।
• शरीर त्रिस्तरीय और अखंडित होता है।
• शरीर का आकार सूक्ष्मदर्शी से लेकर कुछ सेंटीमीटर तक होता है।

उदाहरण-एस्केरिस, पिन कृमि, गोल कृमि आदि।

प्रश्न 15.
ऐनीलिडा फाइलम (सखंड कमि) की विशेषताएँ लिखें।
उत्तर:
ऐनीलिडा फाइलम की विशेषताएँ निम्नलिखित हैं-

• ये गीली मिट्टी, अलवण व लवण जल में पाए जाते हैं।
•  ये लंबे व सखंड शरीर वाले होते हैं।
• ये असली देहगुहा वाले प्रथम प्राणी हैं।
• इनमें उत्सर्जन के लिए नेफेरिया नामक अंग पाए जाते हैं।
• द्विपार्श्व सममित शरीर होता है।
• कुछ जीव द्विलिंगी होते हुए भी जनन लैंगिक करते हैं; जैसे जनन लैंगिक व अलैंगिक दोनों प्रकार का होता है।
• इनमें गति के लिए काइटिन युक्त शुकमय तथा पैरापोडियम के रूप में पार्श्व उपांग होते हैं।

उदाहरण-केंचुआ, जोंक, नेरीस, समुद्री चूहा आदि।

प्रश्न 16.
आर्थोपोडा फाइलम की विशेषताएँ क्या-क्या हैं?
उत्तर:
आर्थोपोडा फाइलम (संधित उपांग वाले जीव) की विशेषताओं का वर्णन इस प्रकार है-

• ये ज़मीन पर, मिट्टी में, अलवण व लवण जल में सभी जगह पाए जाते हैं।
• ये परजीवी के रूप में भी पाए जाते हैं।
• इनके पाँव सखंड होते हैं।
• इनका शरीर भी सखंड है। पूरा शरीर तीन भागों-सिर, वृक्ष व उदर में समूहित होता है।
• शरीर का अग्रभाग मस्तिष्क व संवेदी अंगों के लिए एक पृथक् सिर बनाता है।
• शरीर पर काईटिननी का बना निर्जीव बाहरी कंकाल पाया जाता है।
• परिवहन तंत्र खुले प्रकार का होता है।
• इनमें शरीर गुहा (Haemocoel) होती है।
• नर व मादा जननांग अलग-अलग होते हैं।

उदाहरण-कॉकरोच, केकड़ा, बिच्छू, मक्खी, तितली, मच्छर आदि।

प्रश्न 17.
मोलस्का फाइलम (नरम देह वाले कवची जीव) के जीवों की विशेषताएँ बताइए।
उत्तर:
मोलस्का फाइलम की विशेषताएँ निम्नलिखित हैं-

• ये नरम शरीर वाले कवची जीव होते हैं।
• ये जलचर होते हैं।
• इनका आकार सूक्ष्म से लेकर भीमकाय (ऑक्टोपस 50 फुट) तक होता है।
• इनका शरीर अखंड व उपांगरहित होता है।
• श्वसन गिल या कंकत्वक्लोम (Ctenidia) द्वारा होती है।
• ये एकलिंगी होते हैं।
• इनमें सत्य देह गुहिका पाई जाती है।
• इनमें प्रचलन पाद द्वारा होता है।

उदाहरण-पाइला, यूनियो, ऑक्टोपस, काइटॉन।

प्रश्न 18.
हेमीकॉर्डेटा फाइलम की विशेषताएँ लिखो।
उत्तर:
हेमीकॉर्डेटा फाइलम की विशेषताएँ निम्नलिखित हैं-

• ये कृमिनुमा अखंड जीव होते हैं,
• ये सभी जीव समुद्र के निवासी हैं
• इनमें कशेरुकी व अकशेरुकी दोनों के गुण पाए जाते हैं
• इनका शरीर शुंड (Proboscis), कॉलर व धड़ में बँटा होता है
• ये सममिति द्विपार्शिव होते हैं
• इनमें श्वसन गिल स्लिट (कलोम छिद्र) द्वारा होता है
• ये एकलिंगी होते हैं।

उदाहरण बैलैनाग्लोसस, सेफैलोडिस्कस आदि।

प्रश्न 19.
नानकॉर्डेटा और कॉर्डेटा जंतुओं में मुख्य अंतर लिखो।
उत्तर:
नानकॉर्डेटा और कॉर्डेटा में मुख्य अंतर निम्नलिखित हैं-

निबंधात्मक प्रश्न

प्रश्न 1.
क्रिप्टोगैमी के वर्गीकरण का वर्णन करो।
उत्तर:
क्रिप्टोगैमी-ये पौधे पुष्पविहीन व फलविहीन होते हैं। इनमें जनन अंग छुपे हुए होते हैं। इनमें बाहरी फूल व बीज नहीं पाए जाते। इन्हें तीन वर्गों में बाँटा गया है-
1. थैलोफाइटा-पादप शरीर तना, जड़ व पत्तियों में विभाजित नहीं होता, अपितु एक समरूप थैलस के रूप में होता है। इनमें कोई संवहन तंत्र नहीं होता। उनके जननांग एककोशी होते हैं। इस डिवीज़न में पौधों के तीन स्पष्ट समूह हैं-

• शैवाल; जैसे यूलोथ्रिक्स, क्लैडोफोरा, अल्वा।
• कवक; जैसे ऐस्पर्जिलस, पेनिसिलियम, ऐगैरिकस।
• लाइकेन; जैसे लाइकेन पर्णिल, फ्रुटिकोज लाइकेन (सहजीवी)।

2. ब्रायोफाइटा-इन पौधों का शरीर जड़, तना व पत्तों जैसी संरचनाओं में बंटा होता है। ये नमी वाले छायादार स्थानों पर उगते हैं। इनमें भी संवहन तंत्र अनुपस्थित होता है। जननांग बहुकोशीय होते हैं। इनमें निषेचन के बाद भ्रूण बनता है; जैसे रिक्सिया, फ्यूनेरिया, मार्केशिया आदि।

3. टेरिडोफाइटा-इनका शरीर जड़, तना, पत्तों में विभाजित होता है। इनमें संवहन तंत्र विद्यमान होता है। इनके जननांग बहुकोशिक होते हैं। इनमें निषेचन के बाद भ्रूण बनता है; जैसे फर्नस (टेरिस, सिलैजीनैला)।

प्रश्न 2.
प्रत्येक की एक या दो विशेषताओं व उदाहरण सहित प्राणियों के मुख्य फाइलम के नाम दीजिए।
उत्तर:
जंतुओं के प्रमुख फाइलम व उनकी विशेषताएँ व उदाहरण निम्नलिखित प्रकार से हैं-

प्रयोगात्मक कार्य

क्रियाकलाप 1.
एकबीजपत्री और द्विबीजपत्री में अंतर करना।
कार्य-विधि-गेहूँ, चना, मटर, मक्का, धान, इमली आदि के बीज लेकर इन्हें पानी में भिगोओ। जब अच्छी तरह फूल जाए
इनका वर्गीकरण उतारकर अवलोकन करो। जिनमें एकबीजपत्र (गेहूँ, मक्का, धान) हो एकबीजपत्री और जिनमें द्विबीजपत्र (चना, मटर, इमली) हो द्विबीजपत्री होता है। इन पौधों में अन्य अंतर देखने के लिए तालिका बनाओ-
तालिका

अध्याय का तीव्र अध्ययन

1. ‘वर्गिकी’ शब्द के जनक हैं-
(A) एरिस्टोटल
(B) राबर्ट हुक
(C) डी. केंडोली
(D) केरोलस लिनियस
उत्तर:
(D) केरोलस लिनियस

2. मोनेरा जैसे जीवों के वर्गीकरण का आधार नहीं है-
(A) कोशिकीय संरचना
(B) पोषण
(C) शारीरिक संगठन
(D) निवास
उत्तर:
(D) निवास

3. पर्णहरित नहीं पाया जाता-
(A) मोनेरा में
(B) प्रोटिस्टा में
(C) फंजाई में
(D) प्लांटी में
उत्तर:
(C) फंजाई में

4. मत्स्य का लक्षण नहीं है-
(A) धारारेखीय शरीर
(B) श्वसन गलफड़ों द्वारा
(C) हृदय तीन कक्षीय
(D) शरीर पर शल्क पाए जाते हैं।
उत्तर:
(C) हृदय तीन कक्षीय

5. उभयचर प्राणी नहीं है
(A) ड्रैको
(B) हाइला
(C) टोड
(D) मेंढक
उत्तर:
(A) ड्रैको

6. कंकाल खोखला होता है
(A) मत्स्य में
(B) उभयचर में
(C) सरीसृप में
(D) एवीज़ में
उत्तर:
(D) एवीज़ में

7. जीवों को किंगडम नामक बड़े वर्ग में विभाजित करने में योगदान नहीं था-
(A) अन्सर्ट हेकेल का
(B) राबर्ट व्हिटेकर का
(C) कार्ल वोस का
(D) डार्विन का
उत्तर:
(D) डार्विन का

8. निम्नलिखित में से कौन-सा जीव अंडे देता है, परंतु स्तनों से बच्चों को दूध पिलाता है?
(A) मनुष्य
(B) हाथी
(C) कंगारू
(D) डकबिल प्लेटीपस
उत्तर:
(D) डकबिल प्लेटीपस

9. निम्नलिखित में से जीनस है-
(A) समान आर्डर का समूह
(B) समान जातियों का समूह
(C) समान गणों का समूह
(D) समान कुलों का समूह
उत्तर:
(B) समान जातियों का समूह

10. आइशलर ने वनस्पति जगत को दो उपजगतों में बाँटा, उनके नाम हैं-
(A) क्रिप्टोगैमी व फैनरोगैमी
(B) जिम्नोस्पर्मी व एंजियोस्पर्मी
(C) ब्रायोफाइटा व टेरिडोफाइटा
(D) मोनेरा व प्रोटिस्टा
उत्तर:
(A) क्रिप्टोगैमी व फैनरोगैमी

11. अनावृतबीजी का उदाहरण है-
(A) फर्नस
(B) मार्सीलिया
(C) साइकस
(D) मॉस
उत्तर:
(C) साइकस

12. थैलस पाया जाता है-
(A) थैलोफाइटा में
(B) ब्रायोफाइटा में
(C) टेरिडोफाइटा में
(D) इनमें से किसी में भी नहीं
उत्तर:
(A) थैलोफाइटा में

13. फैनरोगैम्स वे होते हैं जिनमें बीज-
(A) होते हैं।
(B) नहीं होते
(C) नग्न होते हैं
(D) ढके होते हैं
उत्तर:
(A) होते हैं

14. जीव विज्ञान का जनक है-
(A) कार्ल वोस
(B) केरोलस
(C) डार्विन
(D) थियोफ्रेस्टस
उत्तर:
(D) थियोफ्रेस्टस

15. सहजीविता का गुण निम्नलिखित में से किसमें पाया जाता है?
(A) मोनेरा में
(B) लाइकेन में
(C) प्रोटिस्टा में
(D) इनमें से किसी में भी नहीं
उत्तर:
(B) लाइकेन में

16. निम्नलिखित में से जिम्नोस्पर्म का पादप कौन-सा है?
(A) आम
(B) मटर
(C) साइकस
(D) अमरूद
उत्तर:
(C) साइकस

17. निम्नलिखित में से किसमें बाह्य कवच पाया जाता है?
(A) यूनियो में
(B) घोंघा में
(C) काइटॉन में
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

18. निम्नलिखित में से किस वर्ग में दुग्ध ग्रंथियाँ पाई जाती हैं?
(A) पक्षियों में
(B) स्तनधारियों में
(C) सरीसृप में
(D) इनमें से किसी में भी नहीं
उत्तर:
(B) स्तनधारियों में

19. किस संघ के जंतु का शरीर छिद्रमय होता है?
(A) मोलस्का
(B) सरीसृप
(C) स्पंज
(D) प्रोटोजोआ
उत्तर:
(C) स्पंज

20. रेशेदार जड़ तंत्र पाया जाता है-
(A) सरसों में
(B) मूली में
(C) गेहूँ में
(D) गाजर में
उत्तर:
(C) गेहूँ में

21. किस संघ के जीव उभयलिंगी होते हैं?
(A) प्लेटीहेल्मिन्थीज़
(B) सीलेंटरेटा
(C) पोरीफेरा
(D) मोलस्का
उत्तर:
(A) प्लेटीहेल्मिन्थीज़

22. किन जीवों का शरीर सिर, वक्ष व उदर में बंटा होता है?
(A) एनीलिड़ा
(B) प्लेटीहेल्मिन्थीज
(C) निमेटोडा
(D) आर्थोपोडा
उत्तर:
(D) आर्थोपोडा

23. काइटन किस फाइलम से संबंधित है?
(A) आर्थोपोडा
(B) मोलस्का
(C) नेमेटोडा
(D) एनीलीडा
उत्तर:
(B) मोलस्का

24. किस फाइलम में कशेरुकी और अकशेरुकी दोनों के गुण पाए जाते हैं?
(A) यूरोकॉर्डेटा
(B) सेफैलोकॉर्डेटा
(C) हेमीकॉर्डेटा
(D) वर्टीब्रेटा
उत्तर:
(C) हेमीकॉर्डेटा

25. पादप जगत का उभयचर है-
(A) थैलोफाइटा
(B) ब्रायोफाइटा
(C) टेरिडोफाइटा
(D) इनमें से कोई नहीं
उत्तर:
(B) ब्रायोफाइटा

26. हाइड्रा, आबीलिया, ओरेलिया का फाइलम कौन-सा है?
(A) पोरीफेरा
(B) सीलेंटरेटा
(C) प्लेटीहेल्मिन्थीज
(D) इनमें से कोई नहीं
उत्तर:
(B) सीलेंटरेटा

27. यूनियो, घोंघा, ऑक्टोपस का फाइलम कौन-सा है?
(A) आर्थोपोडा
(B) एनीलिडा
(C) मोलस्का
(D) इकाइनोडर्मेटा
उत्तर:
(C) मोलस्का

28. आर्थोपोडा का सबसे मुख्य लक्षण है-
(A) जोड़ीदार टांगें
(B) बाह्य कंकाल
(C) श्वसन ट्रेकिया
(D) एंटीना
उत्तर:
(A) जोड़ीदार टांगें

29. स्टारफिश पाए जाते हैं-
(A) वायु में
(B) स्थल में
(C) समुद्र में
(D) पहाड़ों में
उत्तर:
(C) समुद्र में

30. जीवों के स्तर में सबसे ऊपर का स्तर है-
(A) वर्ग
(B) जाति
(C) गण
(D) जगत
उत्तर:
(D) जगत

31. चार्ल्स डार्विन ने जैव विकास की अवधारणा को कब जन्म दिया?
(A) सन् 1857 में
(B) सन् 1858 में
(C) सन् 1859 में
(D) सन् 1860 में
उत्तर:
(C) सन् 1859 में

32. प्रकाशसंश्लेषण प्रक्रिया द्वारा अपना भोजन बनाते हैं-
(A) पक्षी
(B) पशु
(C) हरे पौधे
(D) मछलियाँ
उत्तर:
(C) हरे पौधे

33. निम्नलिखित में त्रिकोरक का उदाहरण कौन-सा है?
(A) स्पांजिला
(B) हाइड्रा
(C) यूग्लीना
(D) फीता कृमि
उत्तर:
(D) फीता कृमि

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 14 सांख्यिकी Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 14 सांख्यिकी

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
वन महोत्सव के दौरान 100 विद्यालयों में से प्रत्येक में 100 पौधे लगाए गए। एक महीने बाद लगाए गए पौधों में से बच गए पौधों की संख्याएं निम्न थीं:
हल :
95 67 28 32 65 65 69 33 98 96
76 42 32 38 42 40 40 69 95 92
75 83 76 83 85 62. 37 65 63 42
89 65 73 81 49 52 64 76 83 92
93 68 52 79 81 83 59 82 75 82
86 90 44 62 31 36 38 42 39 83
87 56 58 23 35 76 83 85 30 68
69 83 86 43 45 39 83 75 66 83
92 75 89 66 9 1 27 88 89 93 42
53 69 90 55 66 49 52 83 34 36
इन आंकड़ों से वर्ग अंतराल 20-29 लेकर एक वर्गीकृत बारंबारता सारणी बनाइए।
हल :
दिए गए वर्ग अंतराल के अनुसार दिए गए आंकड़ों की बारंबारता सारणी निम्न होगी-

बचे हुए पौधों की संख्या मिलान चिह्न विद्यालयों की संख्या.

प्रश्न 2.
निम्नलिखित आंकड़ों का दंड आलेख खींचिए-

हल :
दिए गए आंकड़ों का दंड आलेख निम्न है-

प्रश्न 3.
एक परिवार द्वारा भिन्न-भिन्न मदों पर किया गया मासिक खर्च निम्न अनुसार है। इनको दर्शाने के लिए एक दंड आलेख (Bar-graph) बनाइए-

हल :
दिए गए आंकड़ों का दंड आलेख निम्न होगा –

प्रश्न 4.
निम्नलिखित आंकड़ों के लिए एक ही आलेख पर आयतचित्र तथा बारंबारता बहुभुज बनाएं-

हल :
30 विद्यार्थियों के अंकों की बंटन सारणी को दर्शाने के लिए आयतचित्र तथा बारंबारता बहुभुज अग्रांकित होगा-

प्रश्न 5.
एक क्रिकेट टीम ने पहले 10 ओवर्स में जो रन बनाए वह निम्न अनुसार हैं। इनके लिए एक आलेख बनाएं।

हल :
दिए गए आंकड़ों का आलेख संलग्न है-

प्रश्न 6.
यदि प्रेक्षणों 9, 13, 18, 15, p तथा 17 का मध्यमान 15 हो तो p का मान ज्ञात करें।
हल :
मध्यमान = \(\frac{9+13+18+15+p+17}{6}\)
⇒ 15 = \(\frac{72+p}{6}\)
15 × 6 = 72 + p
90 = 72 + p
p = 90 – 72 = 18

प्रश्न 7.
निम्नलिखित आंकड़ों का बहुलक ज्ञात करें।
30, 50, 35, 30, 42, 70, 55, 50, 60, 65, 61, 60, 60, 50, 50, 55
हल :
उपरोक्त आंकड़ों से निम्नलिखित सारणी बनती हैं-

यहां हम देखते हैं कि प्रेक्षण 50 की बारंबारता (4) सबसे अधिक है। इसलिए बहुलक (mode) = 50 है।

प्रश्न 8.
हॉकी की एक टीम द्वारा अनेक मैचों में प्राप्त किए गए अंक ये हैं-
24, 10, 8, 14, 5, 48, 10, 8, 7, 18, 28, 15, 27, 10, 2, 7
टीम द्वारा प्राप्त किए गए अंकों का माध्य, माध्यक व बहुलक ज्ञात कीजिए।
हल :
(i) माध्य \((\bar{x})=\frac{24+10+8+14+5+48+10+8+7+18+28+15+27+10+2+7}{16}\)
= \(\frac{241}{16}\)
= 15.06

(ii) आंकड़ों का आरोही क्रम = 2, 5, 7, 7, 8, 8, 10, 10, 10, 14, 15, 18, 24, 27, 28, 48
माध्यक = (आठवां आंकड़ा + नौवां आंकड़ा) / 2
= \(\frac{10+10}{2}=\frac{20}{2}\) = 10

(iii) बहुलक = 10 [∵ 10 सबसे अधिक बार आता है।]

Multiple Choice Questions with Answers:

प्रश्न 1.
अध्ययन का वह क्षेत्र जिसमें आँकड़ों के प्रस्तुतिकरण, विश्लेषण तथा निर्वचन पर विचार किया जाता है, उसे कहा जाता है-
(A) सांख्यिकी
(B) क्षेत्रमिति
(C) त्रिकोणमिति
(D) ज्यामिति
उत्तर-
(A) सांख्यिकी

प्रश्न 2.
अन्वेषक द्वारा स्वयं एकत्रित किए गए आँकड़ों को कहा जाता है-
(A) गौण आँकड़े
(B) प्राथमिक आँकड़े
(C) द्वितीयक आँकड़े
(D) माध्यक आँकड़े
उत्तर-
(B) प्राथमिक आँकड़े

प्रश्न 3.
दिए गए आँकड़ों के अधिकतम और न्यूनतम मानों के अन्तर को आँकड़ों का कहा जाता है-
(A) माध्यक
(B) बहुलक
(C) परिसर
(D) माध्य
उत्तर-
(C) परिसर

प्रश्न 4.
गणित की परीक्षा में 10 विद्यार्थियों द्वारा प्राप्त किए गए निम्न अंकों का परिसर होगा-
18, 12, 36, 24, 40, 60, 23, 09, 70, 62
(A) 23
(B) 61
(C) 09
(D) 70
उत्तर-
(B) 61

प्रश्न 5.
सबसे अधिक बार आने वाले प्रेक्षण का मान कहलाता है-
(A) बहुलक
(B) माध्यक
(C) माध्य
(D) उपरोक्त में से कोई नहीं
उत्तर-
(A) बहुलक

प्रश्न 6.
रक्त समूह विद्यार्थियों की संख्या-

इस सारणी में सामान्य रक्त समूह हैं-
(A) AB
(B) A
(C) B
(D) 0
उत्तर-
(D) 0

प्रश्न 7.
प्रश्न नं0 6 की सारणी में विरलतम रक्त समूह है-
(A) A
(B) AB
(C) B
(D) 0
उत्तर-
(B) AB

प्रश्न 8.
प्रश्न नं० 6 की सारणी में कुल कितने विद्यार्थियों के रक्त की जाँच हुई ?
(A) 12
(B) 18
(C) 27
(D) 30
उत्तर-
(D) 30

प्रश्न 9.
प्रश्न नं० 6 की सारणी में 0 रक्त समूह वाले विद्यार्थियों की संख्या B रक्त समूह वाले विद्यार्थियों की संख्या से जितनी अधिक है-
(A) 6
(B) 3
(C) 9
(D) 12
उत्तर-
(A) 6

प्रश्न 10.

प्रत्येक वर्ग-अन्तराल की माप है-
(A) 10
(B) 5
(C) 35
(D) 12
उत्तर-
(B) 5

प्रश्न 11.
प्रश्न नं० 10 की सारणी में चौथे वर्ग-अन्तराल की निम्न वर्ग सीमा है-
(A) 15
(B) 20
(C) 17.5
(D) 8
उत्तर-
(A) 15

प्रश्न 12.
प्रश्न नं0 10 की सारणी में अन्तिम वर्ग-अन्तराल की उच्च वर्ग सीमा है-
(A) 30
(B) 32.5
(C) 35
(D) 2
उत्तर-
(C) 35

प्रश्न 13.
प्रश्न नं0 10 की सारणी में तीसरे वर्ग-अन्तराल का वर्ग-चिह्न है-
(A) 10
(B) 15
(C) 11
(D) 12.5
उत्तर-
(D) 12.5

प्रश्न 14.
प्रश्न नं0 10 की सारणी में अधिकतम बारम्बारता वाला वर्ग-अन्तराल है-
(A) 0 – 5
(B) 5 – 10
(C) 10 – 15
(D) 15 – 20
उत्तर-
(B) 5 – 10

प्रश्न 15.
नीचे की सारणी में 400 नियॉन लैंपों के जीवन काल दिए गए हैं :

उपरोक्त सारणी में 700 घण्टों से अधिक जीवन काल वाले लैंपों की संख्या है-
(A) 74
(B) 136
(C) 184
(D) 110
उत्तर-
(C) 184

प्रश्न 16.
प्रश्न नं० 15 की सारणी में 500 घण्टों से कम जीवन काल वाले लैंपों की संख्या है-
(A) 14
(B) 70
(C) 56
(D) 42
उत्तर-
(B) 70

प्रश्न 17.
प्रश्न नं 15 की सारणी में अधिकतम लैंपों का जीवन काल कितना है ?
(A) 700 – 800 घण्टे
(B) 800 – 900 घण्टे
(C) 500 – 600 घण्टे
(D) 600 – 700 घण्टे
उत्तर-
(D) 600 – 700 घण्टे

प्रश्न 18.
प्रश्न नं० 15 की सारणी में 800 घण्टों से अधिक जीवन काल वाले लैंपों की संख्या है-
(A) 74
(B) 136
(C) 184
(D) 110
उत्तर-
(D) 110

प्रश्न 19.
नौवीं कक्षा के 40 विद्यार्थियों से उनके जन्म का महीना बताने के लिए कहा गया। इस प्रकार प्राप्त आंकड़ों से निम्नलिखित आलेख बनाया गया-

उपरोक्त आलेख से बताइए कि नवम्बर के महीने में कितने विद्यार्थियों का जन्म हुआ ?
(A) 4
(B) 5
(C) 6
(D) 12
उत्तर-
(A) 4

प्रश्न 20.
प्रश्न नं0 19 के आलेख में किस महीने में सबसे अधिक विद्यार्थियों का जन्म हुआ ?
(A) फरवरी
(B) मई
(C) अगस्त
(D) अक्तूबर
उत्तर-
(C) अगस्त

प्रश्न 21.
प्रश्न नं० 19 के आलेख में किस महीने में सबसे कम विद्यार्थियों का जन्म हुआ ?
(A) मार्च
(B) अप्रैल
(C) सितम्बर
(D) जून
उत्तर-
(D) जून

प्रश्न 22.
प्रश्न नं० 19 के आलेख में जनवरी से अप्रैल के बीच कितने विद्यार्थियों का जन्म हुआ ?
(A) 11
(B) 9
(C) 7
(D) 16
उत्तर-
(A) 11

प्रश्न 23.
प्रश्न नं० 19 के आलेख में मई के महीने में कितने विद्यार्थियों का जन्म हुआ ?
(A) 4
(B) 5
(C) 6
(D) 3
उत्तर-
(B) 5

प्रश्न 24.
प्रश्न नं0 19 के आलेख में अक्तूबर से दिसम्बर के बीच कितने विद्यार्थियों का जन्म हुआ ?
(A) 4
(B) 8
(C) 12
(D) 16
उत्तर-
(C) 12

प्रश्न 25.
10, 7, 13, 20 और 15 का माध्य होगा-
(A) 13
(B) 13.5
(C) 14
(D) 14.5
उत्तर-
(A) 13

प्रश्न 26.
दिए गए सभी प्रेक्षणों के योग को प्रेक्षणों की कुल संख्या से भाग करने पर प्राप्त परिणाम को कहा जाता है-
(A) माध्यक
(B) बहुलक
(C) वर्ग-चिह्न
(D) माध्य
उत्तर-
(D) माध्य

प्रश्न 27.
आँकड़ों 2, 3, 4, 5, 0, 1, 3, 3, 4, 3 का माध्य होगा-
(A) 2.5
(B) 2.6
(C) 2.8
(D) 2.9
उत्तर-
(C) 2.8

प्रश्न 28.
प्रथम पाँच प्राकृतिक संख्याओं का माध्य होगा-
(A) 3.0
(B) 3.5
(C) 2.5
(D) 4.0
उत्तर-
(A) 3.0

प्रश्न 29.
15, 2, 7, 9, 3, 11, 12, 19 का माध्यक होगा-
(A) 9
(B) 10
(C) 11
(D) 19
उत्तर-
(B) 10

प्रश्न 30.
किसी वर्ग अन्तराल 150-160 का वर्ग-चिह्न होगा-
(A) 150
(B) 160
(C) 310
(D) 155
उत्तर-
(D) 155

प्रश्न 31.
प्रथम छः विषम संख्याओं का माध्य होगा-
(A) 4
(B) 5
(C) 5.5
(D) 6
उत्तर-
(D)6

प्रश्न 32.
एक कक्षा के 9 विद्यार्थियों की (सेंटीमीटरों में) लंबाइयाँ ये हैं-
155, 160 145 149 150 147 152 144 148 इन आँकड़ों का माध्यक होगा-
(A) 149
(B) 148.5
(C) 148
(D) 147
उत्तर-
(A) 149

प्रश्न 33.
कबड्डी की एक टीम द्वारा अनेक मैचों में प्राप्त किए गए अंक ये हैं- 17, 2, 7, 27, 15, 5, 14, 8, 10, 24, 48, 10, 8, 7, 18, 28 टीम द्वारा प्राप्त किए गए अंकों का माध्यक होगा-
(A) 10
(B) 12
(C) 14
(D) 13
उत्तर-
(B) 12

प्रश्न 34.
20 विद्यार्थियों द्वारा (10 में से) प्राप्त किए गए निम्नलिखित अंकों का बहुलक ज्ञात कीजिए-
4, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9
(A) 7
(B) 6
(C) 9
(D) 10
उत्तर-
(C) 9

प्रश्न 35.
निम्नलिखित आँकड़ों का बहुलक होगा-
5, 7, 19, 12, 12, 9, 17, 13, 12, 15, 15, 17, 13, 12, 9
(A) 12
(B) 15
(C) 9
(D) 17
उत्तर-
(A) 12

प्रश्न 36.
यदि प्रेक्षणों 9, 13, 18, 15, p तथा 17 का मध्यमान 15 हो तो p का मान होगा-
(A) 16
(B) 18
(C) 17
(D) 15
उत्तर-
(B) 18

प्रश्न 37.
निम्नलिखित आँकड़ों का माध्यक होगा-
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
(A) 48
(B) 50
(C) 52
(D) 53
उत्तर-
(C) 52

प्रश्न 38.
एक फैक्टरी की एक छोटी इकाई लीजिए जहाँ 5 व्यक्ति काम करते हैं, जिनमें एक सुपरवाइजर है और चार मजदूर हैं। प्रत्येक मजदूर को प्रति माह ₹ 5000 वेतन मिलता है, जबकि सुपरवाइजर को प्रति माह ₹ 15000 वेतन मिलता है। फैक्टरी की इस इकाई के वेतनों का माध्य होगा-
(A) ₹ 5000
(B) ₹ 5500
(C) ₹ 6000
(D) ₹ 7000
उत्तर-
(D) ₹ 7000

Haryana State Board HBSE 9th Class Science Important Questions Chapter 6 ऊतक Important Questions and Answers.

Haryana Board 9th Class Science Important Questions Chapter 6 ऊतक

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
क्या पौधों और जन्तुओं में एक ही प्रकार के ऊतक होते हैं?
उत्तर:
नहीं अलग-अलग प्रकार के।

प्रश्न 2.
नई कोशिकाएँ कैसे बनती हैं?
उत्तर:
कोशिका विभाजन प्रक्रिया से।

प्रश्न 3.
एककोशी जीव किसे कहते हैं?
उत्तर:
जिन जीवों में सभी जैव प्रक्रियाएँ एक ही कोशिका के द्वारा संपन्न हों, उन्हें एककोशी जीव कहते हैं।

प्रश्न 4.
श्रम-विभाजन किन जीवों में मिलता है?
उत्तर:
बहुकोशी जीवों में।

प्रश्न 5.
पौधों में कितने प्रकार के ऊतक पाए जाते हैं?
उत्तर:
दो प्रकार के-

• विभज्योतक तथा
• स्थायी ऊतक।

प्रश्न 6.
विभज्योतक कहाँ पाए जाते हैं?
उत्तर:
पौधे के वृद्धि वाले भागों; जैसे प्ररोह की चोटी तथा जड़ की चोटी पर विभज्योतक पाए जाते हैं।

प्रश्न 7.
विभज्योतक का प्रमुख कार्य क्या है?
उत्तर:
नई कोशिकाओं का निर्माण करना।

प्रश्न 8.
क्या स्थायी ऊतकों में भी विभाजन की क्षमता पाई जाती है?
उत्तर:
नहीं।

प्रश्न 9.
पादप स्थायी ऊतक कितने प्रकार के होते हैं?
उत्तर:
दो प्रकार के-

• सरल ऊतक और
• जटिल ऊतक।

प्रश्न 10.
मृदु ऊतक क्या हैं?
उत्तर:
मृदु ऊतक कोशिकाएँ सजीव तथा अंडाकार, गोल, लंबी या बहुपृष्ठीय हो सकती हैं। इनकी कोशिका भित्ति पतली और कोशिकाएँ समव्यासी होती हैं।

प्रश्न 11.
स्थूलकोणक ऊतक क्या है?
उत्तर:
इन ऊतकों के कोने सैल्यूलोज और पेक्टिन जमा होने के कारण मोटे हो जाते हैं। इन ऊतकों में अंतर कोशिकीय स्थान नहीं होता।

प्रश्न 12.
दृढ़ोत्तक किसे कहते हैं?
उत्तर:
ये कोशिकाएँ मृत होती हैं। इन कोशिकाओं के बीच भी अंतर्कोशिकीय स्थान नहीं होता। ये पादप अंगों को दृढ़ता प्रदान करते हैं।

प्रश्न 13.
सरल स्थायी ऊतक क्या हैं?
उत्तर:
ये ऊतक मृदु ऊतक कोशिकाओं के बने होते हैं। इनकी उत्पत्ति, संरचना और कार्य एक-समान होते हैं।

प्रश्न 14.
मृदु ऊतक पौधे के किस भाग में पाए जाते हैं?
उत्तर:
पौधे के हरे भाग में।

प्रश्न 15.
रक्षी ऊतक कितने ऊतकों से बनते हैं?
उत्तर:
दृढ़ोत्तकों से।

प्रश्न 16.
रक्षी ऊतक पौधे के किन भागों में पाए जाते हैं?
उत्तर:
पत्तियों, फूलों, तनों व जड़ों में।

प्रश्न 17.
स्केलेरीडस का दूसरा नाम क्या है?
उत्तर:
पाषाण कोशिकाएँ।

प्रश्न 18.
जटिल ऊतक किसे कहते हैं?
उत्तर:
विभिन्न आकार व माप की कोशिकाएँ मिलकर एक ऐसा समूह बनाती हैं जो एक विशेष कार्य करता है, उसे जटिल ऊतक कहते हैं।

प्रश्न 19.
जटिल ऊतक कितने प्रकार के होते हैं?
उत्तर:
दो-

• फ़्लोएम व
• ज़ाइलम।

प्रश्न 20.
उस ऊतक का नाम बताएँ जो पौधों में भोजन का संवहन करता है।
उत्तर:
फ्लोएम (पोषवाह)।

प्रश्न 21.
जंतु ऊतक कितने प्रकार के होते हैं? नाम लिखो।
उत्तर:
चार प्रकार के-

• एपिथीलियमी ऊतक
• संयोजी ऊतक
• पेशीय ऊतक
• तंत्रिका ऊतक।

प्रश्न 22.
एपीथीलियमी ऊतक कहाँ पर पाए जाते हैं?
उत्तर:
जंतुओं के बाहरी तथा आंतरिक सतहों पर।

प्रश्न 23.
जंतुओं में ‘रक्षी अस्तर’ किस ऊतक को कहते हैं?
उत्तर:
एपीथीलियमी ऊतक।

प्रश्न 24.
प्राणियों में शुक्राणु और अंडाणु किस ऊतक के द्वारा बनाए जाते हैं?
उत्तर:
एपीथीलियमी ऊतक द्वारा।

प्रश्न 25.
पेशीय ऊतक कितने प्रकार के होते हैं?
उत्तर:
तीन प्रकार के-

• रेखित
• अरेखित व
• हृदय पेशी।

प्रश्न 26.
हमारी इच्छानुसार कौन-सी पेशियाँ कार्य करती हैं?
उत्तर:
ऐच्छिक पेशियाँ (रखित पेशियाँ)।

प्रश्न 27.
हृदय की पेशियाँ किस प्रकार की पेशियाँ होती हैं?
उत्तर:
अनैच्छिक पेशियाँ।

प्रश्न 28.
संयोजी ऊतक कितने प्रकार के होते हैं?
उत्तर:
तीन।

प्रश्न 29.
संयोजी ऊतकों के दो मुख्य कार्य लिखो।
उत्तर:
विभिन्न अंगों को जोड़ना व सुरक्षा प्रदान करना।

प्रश्न 30.
कंकाल संयोजी ऊतक कितने प्रकार के होते हैं?
उत्तर:
दो-

• अस्थि और
• उपास्थि।

प्रश्न 31.
अस्थि को अस्थि से जोड़ने का कार्य कौन-सा ऊतक करता है?
उत्तर:
स्नायु।

प्रश्न 32.
कंडरा ऊतक किसको जोड़ते हैं?
उत्तर:
पेशी को अस्थि से।

प्रश्न 33.
शरीर में पाए जाने वाले तरल ऊतक का नाम लिखो।
उत्तर:
रुधिर।

प्रश्न 34.
रुधिर में कितने प्रकार की कणिकाएँ पाई जाती हैं?
उत्तर:
तीन-

• लाल रुधिर कणिका
• श्वेत रुधिर कणिका तथा
• प्लेटलैटस।

प्रश्न 35.
रुधिर के तरल भाग को क्या कहते हैं?
उत्तर:
प्लाज्मा।

प्रश्न 36.
रुधिर में कितने प्रतिशत जल होता है?
उत्तर:
90%।

प्रश्न 37.
मस्तिष्क, मेरुरज्जु तथा तंत्रिकाएँ किस ऊतक से बनी होती हैं?
उत्तर:
तंत्रिका ऊतक से।

प्रश्न 38.
तंत्रिका ऊतक की कोशिका को क्या कहते हैं?
उत्तर:
न्यूरॉन।

प्रश्न 39.
न्यूरॉन का प्रमुख कार्य क्या है?
उत्तर:
संदेशवाहक का।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
एककोशी जीव की तुलना में बहुकोशी जीव श्रेष्ठ हैं, क्यों?
उत्तर:
एककोशी जीव कुछ ही कार्यों को संपन्न कर सकते हैं और उन कार्यों को करने में बहुकोशी जीवों की तुलना में ये इतने दक्ष भी नहीं होते। बहुकोशी जीवों में लाखों कोशिकाएँ समूह बनाकर न केवल उन्हीं कार्यों को, बल्कि और अधिक कार्यों को पूरी दक्षता के साथ कर सकते हैं क्योंकि इनमें श्रम विभाजन का गुण पाया जाता है।

प्रश्न 2.
क्या पौधों और जंतुओं के ऊतकों में कुछ अंतर हैं?
उत्तर:
पौधों के ऊतक सहारा देने का कार्य करते हैं। पौधों के अधिकांश ऊतक मृत होते हैं। मृत ऊतक जीवित ऊतक की तरह ही यांत्रिक मजबूती प्रदान करते हैं। इन्हें कम रख-रखाव की आवश्यकता होती है। जबकि जंतु साथी भोजन और आश्रय की खोज में इधर-उधर घूमते रहते हैं। ये पौधों की अपेक्षा ऊर्जा की अधिक खपत करते हैं। इनके अधिकांश ऊतक जीवित होते हैं। पौधों की वृद्धि कुछ भागों में ही सीमित रहती है जबकि जंतुओं में ऐसा नहीं होता।

प्रश्न 3.
पौधों में पाए जाने वाले विभिन्न प्रकार के ऊतक कौन-से हैं?
उत्तर:
पौधों में दो प्रकार के ऊतक पाए जाते हैं-
पादप ऊतक-

• विभज्योतक (Meristematic Tissue)
• स्थायी ऊतक (Permanent Tissue)

प्रश्न 4.
विभज्योतक की विशेषताएँ लिखें।
उत्तर:
विभज्योतक की विशेषताएँ निम्नलिखित हैं-

• विभज्योतक की कोशिकाएँ समान संरचना वाली हैं और इनकी कोशिका भित्ति पतली होती है।
• कोशिकाओं का आकार गोल, अंडाकार या बहुपृष्ठीय होता है।
• ये आपस में सघनता से जुड़ी रहती हैं और इसलिए इनके बीच में अंतर्कोशिकीय स्थान नहीं होता।
• इन कोशिकाओं में सघन अथवा पर्याप्त कोशिका द्रव्य (साइटोप्लाज्म) और एक बड़ा केंद्रक होता है।
• इनमें अपेक्षाकृत कम रिक्तिकाएँ होती हैं अथवा कोई रिक्तिका नहीं होती।

प्रश्न 5.
पौधों में विभज्योतक कहाँ-कहाँ होता है?
उत्तर:
विभज्योतक पौधों में केवल वृद्धि करने वाले भागों; जैसे प्ररोह की चोटी और कैंबियम (ऐसा क्षेत्र जो मोटाई में वृद्धि करता है) में पाए जाते हैं।

प्रश्न 6.
स्थायी ऊतकों की विशेषताएँ लिखें।
उत्तर:
स्थायी ऊतकों की विशेषताएँ निम्नलिखित हैं

• स्थायी ऊतक विभज्योतक से बनते हैं।
• इनकी कोशिकाओं में विभाजन की क्षमता नहीं होती।
• इनका आकार निश्चित होता है।
• इनकी भित्ति मृत, पतली या फिर मोटी हो सकती है।
• इनकी कोशिकाएँ बड़ी होती हैं तथा रिक्तिकामय कोशिका द्रव्य होता है।

प्रश्न 7.
विभज्योतक और स्थायी ऊतक में अंतर स्पष्ट करें।
उत्तर:
विभज्योतक और स्थायी ऊतक में निम्नलिखित अंतर हैं-

प्रश्न 8.
स्थायी ऊतक किन्हें कहते हैं?
उत्तर:
स्थायी ऊतक-स्थायी ऊतक विभज्योतकों से बनते हैं। इन ऊतकों में विभाजन क्षमता नहीं होती। इनका आकार व परिमाण निश्चित होता है। स्थायी ऊतक दो प्रकार के होते हैं-

• सरल ऊतक
• जटिल ऊतक।

प्रश्न 9.
पैरेन्काइमा (मृदु ऊतक) व कॉलेन्काइमा (स्थूलकोणक ऊतक) में अंतर स्पष्ट कीजिए।
उत्तर:
पैरेन्काइमा (मृदु ऊतक) और कॉलेन्काइमा (स्थूलकोणक ऊतक) में निम्नलिखित अंतर हैं-

मृदु ऊतक [Parenchyma]	स्थूलकोणक ऊतक [Collenchyma]
1. ये जड़, तने व पत्तों में पाए जाते हैं।	1. ये तने व पत्ती की मध्य शिरा में पाए जाते हैं।
2. इनकी भित्तियों पर स्थूलन नहीं होता।	2. इनकी भित्तियों पर स्थूतन होता है।
3. ये गोल व महीन कोशिका भित्ति वाली कोशिकाओं से बने होते हैं।	3. इनकी कोशिका भित्ति मोटी ब लंबी होती है।
4. इनकी कोशिका भित्ति पेक्टिन व सैल्यूलोज की बनी होती है।	4. इनकी कोशिका भित्ति पर पेक्टिन के स्थूलक पाए जाते हैं।
5. ये खाद्य भंडारण व यांत्रिक सहारा देने का कार्य करते हैं।	5. ये केवल यांत्रिक सहारा देने का कार्य करते हैं।
6. इनके बीच अंतर्कोशिकीय स्थान पाया जाता है।	6. इनमें यह अनुपस्थित होता है।

प्रश्न 10.
सरल स्थायी ऊतक के विभिन्न प्रकार बताइए और प्रत्येक का कार्य लिखिए।
उत्तर-
सरल स्थायी ऊतक तीन प्रकार के होते हैं-(क) पैरेन्काइमा (ख) कॉलेन्काइमा (ग) स्क्लेरेन्काइमा।
(क) पैरेन्काइमा के कार्य-

• भोजन का संचय और स्वांगीकरण करना।
• पादप भागों को दृढ़ता प्रदान करना।
• रेजिन, टैनिन, गोंद कण, अकार्बनिक व्यर्थ पदार्थों के रेजिन को संचित करना।
• इनमें पर्णहरिम पाए जाने पर ये भोजन बनाते हैं।

(ख) कॉलेन्काइमा के कार्य-

• यह पौधों को लचीलापन व दृढ़ता प्रदान करता है।
• पर्णहरिम पाए जाने पर ये शर्करा व मंड बनाते हैं।

(ग) स्क्लेरेन्काइमा के कार्य-

• ये कार्टेक्स, पिथ, कठोर बीजों को अधिक दृढ़ता प्रदान करता है।
• ये रक्षी ऊतकों में रूपांतरित होकर भीतरी अंगों की रक्षा करते हैं।

प्रश्न 11.
मूदु ऊतक, स्थूलकोणक ऊतक, दृढ़ोत्तक में अंतर स्पष्ट करें।
अथवा
कोशिका भित्ति के आधार पर पैरेन्काइमा, कॉलेन्काइमा और स्क्लेरेन्काइमा के बीच भेद स्पष्ट करें।
उत्तर
मृदु ऊतक, स्थूलकोणक ऊतक तथा दृढ़ोत्तक में निम्नलिखित अंतर हैं-

प्रश्न 12.
स्क्लेरेनकाइमेटस ऊतक का वर्णन कीजिए।
उत्तर
स्क्लेरेनकाइमेटस (Sclerenchyma) ऊतक पौधे को कठोर एवं मजबूत बनाता है। हमने नारियल के रेशेयुक्त छिलके को देखा है। यह स्क्लेरेनकाइमेटस ऊतक से बना होता है। इस ऊतक की कोशिकाएँ मृत होती हैं। ये लम्बी और पतली होती हैं, क्योंकि इस ऊतक की भित्ति लिग्निन के कारण मोटी होती है।

ये भित्तियाँ प्रायः इतनी मोटी होती हैं कि कोशिका के भीतर कोई आन्तरिक स्थान नहीं होता। यह ऊतक तने में संबहन बण्डल के समीप, पत्तों की शिराओं में तथा बीजों और फलों के कठोर छिलके में उपस्थित होता है। यह पौधों के भागों को मजबूती प्रदान करता है।

प्रश्न 13.
ज़ाइलम (दारू ऊतक) में पाए जाने वाले विभिन्न अवयवों के नाम लिखिए।
उत्तर
ज़ाइलम (Xylem) में पाए जाने वाले निम्नलिखित चार प्रकार के अवयव हैं-

• वाहिनीकाएँ (Trachieds)
• वाहिकाएँ (Vessels)
• दारू या काष्ठ मृदु ऊतक (Xylem or Wood Parenchyma)
• काष्ठ तंतु (Wood or Xylem Fibres)।

प्रश्न 14.
फ्लोएम (पोषवाह) की पौधे के लिए उपयोगिता बताइए।
उत्तर:
फ्लोएम की उपयोगिता-यह पादप संवहन ऊतक है। यह पौधे की पत्तियों में निर्मित मंड (भोजन) को पौधे के विभिन्न भागों तक पहुँचाने का कार्य करता है।

प्रश्न 15.
जाइलम (दारू ऊतक) के कार्य लिखिए।
उत्तर:
ज़ाइलम के कार्य-यह भी पादप संवहन ऊतक है। पौधे की जड़ों द्वारा अवशोषित जल व घुलित खनिज लवणों को जड़ से लेकर पौधे के पत्तों और शीर्ष तक पहुंचाने का कार्य करता है। यह पौधे को यांत्रिक शक्ति भी प्रदान करता है।

प्रश्न 16.
रक्षी ऊतक पर संक्षिप्त नोट लिखें।
उत्तर:
रक्षी ऊतक-पौधे के बाह्य भागों में पाए जाने वाले स्क्लेरेन्काइमा रक्षी ऊतकों में रूपांतरित हो जाते हैं। ये ऊतक पत्तों, तनों तथा जड़ों की बाह्य परत पर स्थित होते हैं। ये ऊतक पौधों के भीतरी ऊतकों की रक्षा करते हैं। ये ऊतक क्यूटिन द्वारा ढके होते हैं। कॉर्क की कोशिकाएँ मृत होती हैं। कॉर्क एक हल्का और सुरक्षात्मक ऊतक है, यह अधिक दाब वाला होता है और आग जल्दी नहीं पकड़ता।

प्रश्न 17.
स्टोमेटा क्या है? इसके कार्य लिखें।
उत्तर:
स्टोमेटा (Stomata)-पौधों की पत्तियों की निचली सतह पर बाह्य त्वचीय कोशिकाएँ (Epidermal Cells) पाई जाती हैं जिन्हें रंध्र छिद्र कहते हैं। रंध्र दो गार्ड कोशिकाओं के द्वारा सुरक्षित रहते हैं।

कार्य-

• स्टोमेटा पौधों के नाक होते हैं।
• स्टोमेटा पौधों के लिए गैसों का आदान-प्रदान करते हैं और इनके द्वारा पौधों में स्थित जल का ह्रास होता है।

प्रश्न 18.
जंतुओं में पाए जाने वाले विभिन्न ऊतकों के नाम लिखिए।
उत्तर:
जंतुओं के ऊतक-जंतुओं में निम्नलिखित चार प्रकार के ऊतक पाए जाते हैं-

• उपकला या एपिथीलियमी ऊतक (Epithelial Tissue)
• संयोजी ऊतक (Connective Tissue)
• पेशी ऊतक (Muscular Tissue)
• तंत्रिका ऊतक (Nervous Tissue)

प्रश्न 19.
जंतु ऊतकों के नाम और उनके प्रमुख कार्य लिखें।
उत्तर:
जंतु ऊतक (Animal Tissue)-

• एपीथीलियम ऊतक कार्य : ये अवशोषण, स्रावण, सुरक्षा, उत्सर्जन आदि कार्य करते हैं।
• संयोजी ऊतक कार्य : इस ऊतक का कार्य शरीर के विभिन्न अंगों को एक-दूसरे से जोड़ना, सहारा देना, बांधना, भंडारण, सुरक्षा और परिवहन हैं।
• पेशीय ऊतक-कार्य : पेशीय ऊतक गति, प्रचलन, संकुचन, संचलन आदि का कार्य करते हैं।
• तंत्रिका ऊतक-कार्य : ये ऊतक नियंत्रण और संचालन के प्रमुख कार्य करते हैं।

प्रश्न 20.
एपिथीलियम ऊतक पर टिप्पणी लिखें।
उत्तर:
यह जंतु के शरीर को ढांपने या बाहरी रक्षा करने वाला ऊतक है। शरीर के अंदर भी बहुत से अंगों और गुहिकाओं को ढांपने का काम करता है। त्वचा, मुँह, आहारनली, रक्तवाहिनी नली का अस्तर, फेफड़ों की कूपिका, वृक्क नली आदि सभी इसी ऊतक से बने होते हैं। इन कोशिकाओं के बीच बहुत कम जगह होती है अर्थात् कोशिकाएँ सटी हुई होती हैं।

प्रश्न 21.
एपिथीलियम ऊतक का वर्गीकरण करें।
उत्तर:
एपिथीलियम ऊतक की कोशिकाओं की आकृति एवं कार्य के आधार पर ये निम्नलिखित प्रकार की होती हैं-

• शल्की एपिथीलियम-ये चौड़ी व चपटी कोशिकाएँ शरीर के अंगों को ढकने व सुरक्षा प्रदान करने का कार्य करती हैं।
• घनाकार एपिथीलियम-ये घनाकार कोशिकाएँ लार ग्रंथि व वृक्क नलिकाओं में पाई जाती हैं।
• स्तंभाकार एपिथीलियम-आमाश्य व आंत की परत में स्तंभ के आकार व चौड़ाई वाली कोशिकाएँ पाई जाती हैं।
• सिलियरी एपिथीलियम-स्तंभाकार व घनाकार कोशिकाओं के सिरों से बाल जैसी संरचनाएँ रोम या सिलिया निकलती हैं।
• ग्रंथि एपिथीलियम ये कोशिकाएँ स्रावी ग्रंथियों में पाई जाती हैं।

प्रश्न 22.
एपिथीलियम ऊतक के कार्य लिखो।
उत्तर:
एपिथीलियम ऊतक के कार्य-

• यह अंगों की रक्षा व ढकने का कार्य करता है।
• यह स्रावण का कार्य करता है। (आमाशय व लार ग्रंथियों में)
• यह संवेदना उत्पन्न करता है। (आँख के रेटीना की कोशिकाएँ)
• यह शुक्राणु व अंडाणु का निर्माण करता है।
• ये पानी व अन्य लवणों को अवशोषित करती हैं।
• ये उत्सर्जन का कार्य भी करती हैं।

प्रश्न 23.
संयोजी ऊतकों के कार्य लिखें।
उत्तर:
संयोजी ऊतकों के कार्य-

• ये ऊतक शरीर के विभिन्न अंगों को एक-दूसरे से जोड़ने का कार्य करते हैं।
• ये ऊतकों को बांधने का कार्य करते हैं।
• ये ऊतक शरीर के अंगों को सहारा देते हैं।
• अस्थि और उपास्थि शरीर का कंकाल बनाते हैं जो शरीर के कोमल अंगों का सुरक्षा कवच होता है।
• वसा ऊतक वसा का भंडारण करते हैं।
• रुधिर परिवहन का कार्य करता है।
• रुधिर की श्वेत-कणिकाएँ रोगाणुओं से लड़ती हैं।
  

प्रश्न 24.
रुधिर क्या है?
उत्तर:
रुधिर (Blood)-रुधिर एक संयोजी तरल ऊतक है। इसके तरल भाग को प्लाज्मा कहते हैं। इस ऊतक की कोशिकाएँ तरल प्लाज्मा (मैट्रिक्स) में तैरती रहती हैं। रुधिर कोशिकाओं को रुधिर कणिकाएँ कहते हैं। ये तीन प्रकार की होती हैं-

• लाल रुधिर कणिकाएँ
• श्वेत रुधिर कणिकाएँ तथा
• प्लेटलैटस। रुधिर शरीर के प्रत्येक भाग में दौड़ता है और इस प्रकार यह सभी भागों को जोड़ता है।

प्रश्न 25.
रुधिर के क्या कार्य हैं? वर्णन करें।
उत्तर:
रुधिर के कार्य-

• रक्त की लाल कणिकाएँ फेफड़ों से ऑक्सीजन लेकर शरीर के विभिन्न भागों में पहुंचाती हैं।
• रक्त हार्मोंस ग्रंथियों से हार्मोन लेकर शरीर के विभिन्न भागों में पहुंचाता है।
• अपशिष्ट पदार्थों को शरीर से बाहर निकालने में सहायक है।
• रक्त की श्वेत कणिकाएँ रोगाणुओं से रक्षा करती हैं।
• रक्त शरीर के तापमान को नियंत्रित करता है।
• रक्त की प्लेटलैटस कणिकाएँ रक्त को जमाकर, अधिक रक्त निकलने से रोक देती हैं।

प्रश्न 26.
अस्थि क्या है? यह कितने प्रकार की होती है?
उत्तर:
अस्थि (Bone)-अस्थि ऊतक एक संयोजी ऊतक है। इस ऊतक में 1/3 भाग कार्बनिक पदार्थ तथा 2/3 भाग अकार्बनिक पदार्थ पाया जाता है। इसकी आधात्री में विशेष प्रकार की प्रोटीन ‘ओसीन’ होती है जो कोलेजन तंतुओं के रूप में होती है। अस्थि में आधात्री ओसटिओ, साइटस, तंतुओं तथा आधात्री पदार्थ में कैल्शियम फास्फेट, कैल्शियम कार्बोनेट व कैल्शियम फ्लोराइड पाया जाता है। यह अस्थि को मज़बूती प्रदान करते हैं।

प्रश्न 27.
संहत अस्थि क्या है?
उत्तर:
संहत अस्थि (Compact Bone) यह अस्थि सख्त और कठोर होती है। अस्थि के मैट्रिक्स में कैल्शियम लवण अस्थि को कठोरता प्रदान करता है। संहत अस्थि गोल तथा अनियमित अस्थियों की सघन परतों से बनी होती है। संहत अस्थि लंबी अस्थियों की शाफ्ट जैसे फीमर में पाई जाती है। इसमें हेवरसियन नलिकाएँ पाई जाती हैं।

प्रश्न 28.
अस्थि और उपास्थि में दो-दो अंतर लिखिए।
उत्तर:
अस्थि और उपास्थि में निम्नलिखित अंतर हैं-

प्रश्न 29.
कंडरा और स्नायु में अंतर लिखिए।
उत्तर:
कंडरा (Tendon) तथा स्नायु (Ligament) में निम्नलिखित अंतर हैं-

प्रश्न 30.
अस्थि, उपास्थि, कंडरा तथा स्नायु के कार्य लिखिए।
उत्तर:

• अस्थि-यह शरीर का ढाँचा बनाती है तथा कोमल अंगों की रक्षा करती है।
• उपास्थि यह कार्टेलेजिनश मछलियों का अंतः कंकाल बनाती है। हमारे शरीर में नाक की चोटी और बाह्य कान इसी का बना होता है।
• कंडरा-यह पेशी को अस्थि से जोड़ता है।
• स्नायु–यह अस्थि को अस्थि से जोड़ता है।

प्रश्न 31.
अस्थि ऊतक के कार्य लिखो।
उत्तर:
अस्थि ऊतक-अस्थि ऊतक दृढ़ होता है, अस्थि के मैट्रिक्स में प्रचुर मात्रा में कैल्शियम लवण पाए जाते हैं। अस्थि ऊतक के निम्नलिखित प्रमख कार्य हैं

• अस्थि ऊतक शरीर को आकृति प्रदान करता है।
• अस्थि ऊतक शरीर के कोमल अंगों की रक्षा करता है।
• अस्थि ऊतक पेशियों को जोड़ने में सहायता प्रदान करता है।
• यह ऊतक शरीर को गति प्रदान करता है।
• अस्थि ऊतक के केंद्रीय भाग में लाल रुधिर कणिकाओं का निर्माण होता है।
• यह पेशियों को संधि स्थान प्रदान करता है।

प्रश्न 32.
अंतरालिक ऊतक क्या है?
उत्तर:
अंतरालिक ऊतक (Areolar Tissue) यह ऊतक त्वचा के नीचे, पेशियों के बीच तथा रक्त वाहिकाओं के बीच व तंत्रिका ऊतक के चारों ओर पाया जाता है। इन कोशिकाओं में जैलीनुमा पारदर्शक तथा चिपचिपा आधात्री पाया जाता है। यह संयोजी ऊतक है। यह ऊतक शरीर गुहिका तथा अन्य अंगों को आपस में जोड़ता है।

प्रश्न 33.
पेशीय ऊतक क्या है? ये कितने प्रकार के होते हैं?
उत्तर:
पेशीय ऊतक-इन ऊतकों की कोशिकाएँ लंबी, बेलनाकार तथा अशाखित होती हैं। हृदय पेशियाँ शाखित होती हैं। पेशीय ऊतक विभिन्न मापों के होते हैं। पेशीय ऊतक शरीर के विभिन्न अंगों व भागों को गति प्रदान करते हैं। पेशीय ऊतक तीन प्रकार के होते हैं

• रेखित पेशी (कंकाल या ऐच्छिक पेशी)।
• अरेखित पेशी (चिकनी पेशी या अनैच्छिक पेशी)।
• हृदय पेशी।

प्रश्न 34.
रेखित पेशी और हृदय पेशी में अंतर स्पष्ट करो।
उत्तर:
रेखित पेशी और हृदय पेशी में निम्नलिखित अंतर है-

प्रश्न 35.
रेखित तथा अरेखित पेशी में अंतर स्पष्ट कीजिए।
उत्तर:

निबंधात्मक प्रश्न

प्रश्न 1.
ऊतक किसे कहते हैं? पादप ऊतक कितने प्रकार के होते हैं? विभज्योतक का वर्णन करो।
उत्तर:
ऊतक-एक समान उत्पत्ति, संरचना तथा कार्य करने वाली कोशिकाओं के समूह को ऊतक कहते हैं। पौधों में ऊतक दो प्रकार के होते हैं-
(1) विभज्योतक
(2) स्थायी ऊतक

विभज्योतक (Meristematic Tissue)-इन ऊतकों में कोशिकाओं का निरंतर विभाजन होता रहता है तथा विभाजन की क्षमता वाली ये कोशिकाएँ, नई कोशिकाओं को उत्पन्न करती रहती हैं। विभज्योतक, केवल वृद्धि करने वाले भागों; जैसे प्ररोह का शीर्ष और जड़ की चोटी और कैंबियम में ही पाया जाता है। इन ऊतकों के कारण ही पौधों की लंबाई और मोटाई बढ़ती है।

उत्पत्ति के आधार पर विभज्योतक दो प्रकार के होते हैं-

• प्राथमिक विभज्योतक
• द्वितीय विभज्योतक

स्थिति के आधार पर विभज्योतक तीन प्रकार के होते हैं-
(क) शीर्षस्थ विभज्योतक ये जड़, तना व शाखाओं के शीर्ष पर पाए जाते हैं। ये भी तीन प्रकार के होते हैं-

• त्वचाजन-ये ऊतक पौधे की बाह्य त्वचा बनाते हैं।
• बल्कुटजन-ये ऊतक भरण तंत्र का निर्माण करते हैं।
• रंभजन ये ऊतक संवहन ऊतकों, फ़्लोएम व जाइलम को बनाते हैं।

(ख) अंतर्वेशी विभज्योतक-यह ऊतक एक बीज पत्री तनों में पाया जाता है। इसकी सक्रियता के कारण लंबाई में वृद्धि होती है।

(ग) पार्श्व विभज्योतक-यह ऊतक द्विबीज पत्री, तनों व जड़ के पार्श्व भागों में पाया जाता है।

प्रश्न 2.
पौधे के साधारण ऊतक कितने प्रकार के हैं? उनका वर्णन करो।
उत्तर:
साधारण ऊतक (Simple Tissue)-जब विभज्योतकों में विभाजन की क्षमता नष्ट हो जाती है तो वे स्थायी ऊतकों में बदल जाते हैं। स्थायी ऊतक दो प्रकार के होते हैं-साधारण ऊतक व जटिल ऊतक।

साधारण ऊतक एक ही प्रकार की समान संरचना वाली कोशिकाओं से मिलकर बने होते हैं। इनका कार्य भी एक-समान होता है। संरचना के आधार पर ये ऊतक तीन प्रकार के होते हैं-
(1) मूदु ऊतक (Parenchyma)-ये ऊतक पौधों के प्ररोह तंत्र (तना, पत्तियां तथा फूल) तथा जड़ों में पाए जाते हैं। पौधे के हरे भाग में इनकी संख्या अधिक होती है। ये कोशिकाएँ गोल, लंबी या बहुपृष्ठीय आकार की हो सकती हैं। ये जीवित कोशिकाएँ होती हैं। इनकी कोशिका भित्ति महीन व सैल्यूलोज की बनी होती है। इन कोशिकाओं में जीवद्रव्य सघन होता है।

इन ऊतकों का प्रमुख कार्य भोजन का संचय, स्वांगीकरण करना, दृढ़ता प्रदान करना, रेजिन, टैनिन, गोंद का संचय करना और कई बार भोजन बनाना भी होता है।

(2) स्थूलकोणक (Collenchyma)-ये कोशिकाएँ भी जीवित होती हैं। ये बहुभुजी अंडाकार तथा गोल आकार की होती हैं। इनकी कोशिका भित्ति पतली होती है, परंतु कोशिका के कोनों पर सैल्यूलोज व पेक्टिन जमा होने के कारण स्थूल हो जाती हैं। इन कोशिकाओं में प्रायः कुछ क्लोरोप्लास्ट होते हैं।

यह ऊतक पौधों में लचीलापन व दृढ़ता प्रदान करता है तथा क्लोरोप्लास्ट पाए जाने पर स्टार्च व मंड बनाता है।

(3) दृढ़ोत्तक (Sclerenchyma)-ये कोशिकाएँ आकार में लंबी व पतली परंतु लिग्निनयुक्त होती हैं। ये कोशिकाएँ मृत होती हैं और ये एक-दूसरी से सटी होती हैं।

ये कोशिकाएँ दोनों सिरों पर नुकीली होती हैं। दो निकटवर्ती कोशिकाओं के बीच सुस्पष्ट मध्य पट्टिका होती है। कोशिकाओं में तिरछे क्षेत्र पाए जाते हैं जिन्हें गर्त कहते हैं। ये कोशिकाएँ पौधों के भागों को दृढ़ता प्रदान करती हैं।

प्रश्न 3.
जटिल ऊतक किसे कहते हैं? पौधों में ये कितने प्रकार के होते हैं? प्रत्येक का वर्णन करें।
उत्तर:
जटिल ऊतक (Complex Tissue)-जटिल ऊतक एक-से-अधिक प्रकार की कोशिकाओं का कांच प्लेट ऐसा समूह होता है जो एक विशेष कार्य करता है। जटिल ऊतक दो प्रकार के होते हैं-

1. दारू या जाइलम (Xylem)-ज़ाइलम एक संवहन ऊतक है। यह जल तथा उसमें घुले लवणों को जड़ से प्ररोह तंत्र के भाग पत्ते तक पहुँचाता है। इस ऊतक की सभी कोशिकाएँ मृत, मोटी भित्ति वाली तथा लिग्निन किरण युक्त होती हैं। यह ऊतक चार प्रकार की कोशिकाओं से कोशिका मिलकर बना होता है-

• वाहिनीकाएँ (Trachieds)
• वाहिकाएँ (Vessels)
• दारू या काष्ठ मृदु ऊतक (Xylem or Wood Parenchyma) तथा
• काष्ठ तंतु (Xylem Fibers)

2. पोषवाह या फ्लोएम (Phloem)-यह एक जीवित संवहन ऊतक है। प्रकाश-संश्लेषण क्रिया से तैयार मंड (स्टार्च) को यह पौधे के विभिन्न भागों तक पहुँचाता है। यह ऊतक भी चार प्रकार के अवयवों से मिलकर बना होता है-

• चालनी नलिकाएँ (Sieve Tube)
• सखी कोशिकाएँ (Companion Cells)
• फ़्लोएम मृदु ऊतक (Phloem Parenchyma) एवं
• फ़्लोएम तंतु (Phloem Fibers)

इनमें से सबसे प्रमुख चालनी नलिका है। इन चालनी नलिकाओं में छिद्रित भित्ति होती है जो पत्तियों से भोजन को पौधे के विभिन्न भागों तक पहुँचाती है।

प्रश्न 4.
तंत्रिका ऊतक किसे कहते हैं? यह कितने प्रकार की होती है?
अथवा
तंत्रिका ऊतक का सचित्र वर्णन करें।
उत्तर:
तंत्रिका कोशिका-यह विशेष रूप से लंबी कोशिका है जो संदेशों के संवहन की मूल इकाई है।

इस कोशिका में जीवद्रव्य से घिरा एक केंद्रक होता है। जीवद्रव्य से बहुत-सी छोटी-छोटी शाखाएँ निकलती हैं, जिन्हें डेंड्राइट कहते हैं। इनमें से एक शाखा बहुत लंबी होती है जिसे एक्सॉन कहते हैं। एक्सॉन संदेशों को कोशिका से दूर ले जाता है।

एक तन्त्रिका कोशिका सीधे ही दूसरे तंत्रिका कोशिका से नहीं जुड़ी होती। इनके बीच में कुछ खाली स्थान होता है जिसमें बहुत ही समीप का एक्सॉन संवहन होता है। इसे अंतर्ग्रथन (सिनेप्स) कहते हैं। यदि हमें हाथ में दर्द है तो यह सूचना हाथ में स्थित संवेदी तंत्रिका कोशिका के डेंड्राइट ग्रहण करते एक्साप्लाज्म हैं।

तंत्रिका कोशिका इसे विद्युत् सिग्नल (संकेत) में बदल देती है। यह संकेत तंत्रिकाक्ष द्वारा प्रवाहित होता है तथा अंतर्ग्रथन में होता हुआ मस्तिष्क तक पहुँचता है। मस्तिष्क संदेश को ग्रहण करके उस पर अनुक्रिया करता है। प्रेरक तंत्रिका इस अनुक्रिया को हाथ की पेशियों तक पहुँचाती है तथा हाथ की पेशियाँ उचित अनुक्रिया करती हैं।

इस प्रकार तंत्रिका कोशिका तीन प्रकार की होती हैं-

• संवेदी तंत्रिका कोशिका-यह शरीर के विभिन्न भागों में संवेदनाएँ मस्तिष्क की ओर ले जाती हैं।
• प्रेरक तंत्रिका कोशिका-यह मस्तिष्क से आदेश लेकर पेशियों तक पहुँचाती है।
• बहुध्रुवी तंत्रिका कोशिका-यह संवेदनाओं को मस्तिष्क की ओर तथा मस्तिष्क के आदेशों को पेशियों की ओर ले जाने के दोनों कार्य करती है।

प्रश्न 5.
रुधिर (मानव रुधिर) क्या है? इसके घटकों का वर्णन करो।
उत्तर:
रुधिर (Blood)-रुधिर लाल रंग का तरल संयोजी ऊतक है। रुधिर शरीर के भागों में दौड़ता है, इसलिए कह सकते हैं कि यह शरीर के सभी भागों को आपस में जोड़ता है। मानव रक्त के प्रमुख दो घटक हैं-
(क) प्लाज्मा-यह रुधिर का हल्के पीले (धानी) रंग का पदार्थ होता है। इसमें 90% जल होता है, शेष लवण, ग्लूकोज एमीनो अम्ल, प्रोटीन, हार्मोन, ऑक्सीजन, कार्बन-डाइऑक्साइड गैस तथा कुछ पचे-अनपचे पदार्थ होते हैं।

कार्य-इसमें फाइब्रोजीन नामक प्रोटीन होता है जो रुधिर को जमाने में काम आता है। इसमें प्रतिरक्षी (प्रतिजन) भी पाए जाते हैं जो बाह्य पदार्थों-जीवाण आदि को निष्क्रिय कर देते हैं।

(ख) रुधिर कणिकाएँ-रुधिर में तीन प्रकार की कणिकाएँ पाई जाती हैं जिनका वर्णन निम्नलिखित प्रकार से है
1. लाल रुधिर कणिकाएँ-ये गोलाकार होती हैं। प्रत्येक लाल कणिका का जीवन लगभग चार महीने का होता है। इनके अंदर हीमोग्लोबिन नामक एक पदार्थ होता है जो रुधिर को लाल रंग प्रदान करता है। ये आकार में गोल, चपटी तथा छोटी लाल कणिका होती हैं। इनमें केंद्रक नहीं होता। इनकी संख्या सबसे अधिक होती है (50 लाख प्रति घन मिलीलीटर)।

कार्य-

• लाल रुधिर कणिकाएँ रक्त को लाल रंग प्रदान करती हैं।
• इनका हीमोग्लोबिन सारे शरीर में ऑक्सीजन का वितरण करता है। ऑक्सीजन पाकर ये कणिकाएँ ऑक्सी हीमोग्लोबिन बन जाती हैं।

2. श्वेत रुधिर कणिकाएँ-श्वेत रुधिर कणिकाओं की संख्या लाल रुधिर कणिकाओं से कम होती है, परंतु माप में उनसे बड़ी होती हैं। इनका रंग सफेद होता है, क्योंकि इनमें हीमोग्लोबिन नहीं होता। अतः इनका आकार भी निश्चित नहीं होता। इनमें केंद्रक भी होता है। ये पाँच प्रकार की होती हैं।

कार्य-ये शरीर को नुकसान पहुंचाने वाले रोगाणुओं को मार देती हैं और उन्हें निगल जाती हैं। इस प्रकार ये रोगों से हमारी रक्षा करती हैं।

(ग) पट्टिकाणु या थ्रोम्बोसाइट या प्लेटलैटस-ये बीच में से मोटी और किनारे पर से पतली होती हैं। ये बहुत छोटी होती हैं। इनमें भी केंद्रक होता है।

कार्य-ये रक्त को जमने में सहायता करती हैं। चोट लगने पर जब रक्त बाहर निकलता है, तो ये कणिकाएँ चोट लगे हुए स्थान पर इकट्ठी हो जाती हैं और एक रासायनिक क्रिया द्वारा वहाँ जम जाती हैं, ताकि और अधिक रक्त न बह सके।

प्रश्न 6.
कंकाल और हृदय पेशियों की संरचना का वर्णन कीजिए।
उत्तर:
कंकाल पेशी (ऐच्छिक पेशी)-कुछ पेशियों की हम इच्छानुसार गति करा सकते हैं। हाथ और पैर में विद्यमान पेशियों को हम अपनी इच्छानुसार आवश्यकता पड़ने पर गति करा सकते हैं या उनकी गति को रोक सकते हैं। इस तरह की पेशियों को ऐच्छिक पेशी कहा जाता है।

इन पेशियों को कंकाल पेशी भी कहा जाता है क्योंकि ये अधिकतर हड्डियों से जुड़ी होती हैं तथा शारीरिक गति में सहायक होती हैं। सूक्ष्मदर्शी से देखने पर ये पेशियाँ हलके तथा गहरे रंगों में एक के बाद एक रेखाओं या धारियों की तरह प्रतीत होती हैं। इसी कारण इसे रेखित पेशी भी कहते हैं। इस ऊत्तक की कोशिकाएँ लम्बी, बेलनाकार, शाखा-रहित और बहुनाभीय होती हैं।

हृदय पेशी-हृदय की पेशियाँ जीवनभर लयबद्ध होकर प्रसार एवं संकुचन करती रहती हैं। इन अनैच्छिक पेशियों को कार्डिक (हृदयक) पेशी कहा जाता है जैसाकि चित्र में दर्शाया गया है। हृदय की पेशी कोशिकाएँ बेलनाकार, शाखाओं वाली और एक केन्द्रकीय होती हैं। ये हृदय की दीवारों में पाई जाती हैं।

प्रयोगात्मक कार्य

क्रियाकलाप 1.
तने की संरचना को एक अनुप्रस्थ काट के द्वारा देखना।
कार्य-विधि-
(1) एक पौधे के पतले व नर्म तने का पतला अनुप्रस्थ काटकर सेफेनिन घोल में डाल दो।

(2) एक अनुप्रस्थ काट को स्लाइड पर सावधानीपूर्वक रखो और उस पर ग्लिसरीन की एक बूंद डालकर कवर स्लिप से ढक दो।

(3) तैयार स्लाइड का सूक्ष्मदर्शी से निरीक्षण करो तथा दिखाई देने वाली कोशिकाओं के विन्यास का रेखाचित्र बनाओ।

अध्याय का तीव्र अध्ययन

1. रक्त का वहन करता है-
(A) ऑक्सीजन
(B) भोजन
(C) हार्मोन व अपशिष्ट पदार्थ
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

2. ………………….. के अधिकांश ऊतक मृत होते हैं।
(A) पौधों
(B) प्राणियों
(C) (A) और (B) दोनों
(D) मृतोपजीवियों
उत्तर:
(A) पौधों

3. पौधों में नई कोशिकाएँ ………………….. द्वारा बनती हैं।
(A) मृदु उतक
(B) स्थूलकोणक ऊतक
(C) विभज्योतक
(D) दृढ़ोतक
उत्तर:
(C) विभज्योतक

4. विभज्योतक का गुण नहीं है-
(A) अत्यधिक क्रियाशील
(B) अधिक कोशिका द्रव्य
(C) रसधानी विद्यमान
(D) स्पष्ट केंद्रक
उत्तर:
(C) रसधानी विद्यमान

5. जड़ व तने के अग्र भाग पर स्थित ऊतक है।
(A) पैरेन्काइमा
(B) विभज्योतक
(C) स्क्लेरेन्काइमा
(D) कॉलेन्काइमा
उत्तर:
(B) विभज्योतक

6. प्रकाश संश्लेषण में सहायक ऊतक है-
(A) पैरेन्काइमा
(B) कॉलेन्काइमा
(C) स्क्लेरेन्काइमा
(D) उपर्युक्त सभी
उत्तर:
(A) पैरेन्काइमा

7. ………………….. भंडारण का कार्य करने वाला ऊतक है।
(A) कॉलेन्काइमा
(B) पैरेन्काइमा
(C) स्क्लेरेन्काइमा
(D) विभज्योतक
उत्तर:
(B) पैरेन्काइमा

8. पौधे को कठोर व मजबूत बनाने वाला ऊतक होता है-
(A) क्लोरेन्काइमा
(B) स्क्लेरेन्काइमा
(C) पैरेन्काइमा
(D) दारू
उत्तर:
(B) स्क्लेरेन्काइमा

9. नारियल के रेशेयुक्त छिलके किस ऊतक से बने होते हैं?
(A) स्क्लेरेन्काइमा
(B) कॉलेन्काइमा
(C) पैरेन्काइमा
(D) पोषवाह
उत्तर:
(A) स्क्लेरेन्काइमा

10. स्क्लेरेन्काइमा पौधे के किस भाग में पाया जाता है?
(A) तने में
(B) संवहन बंडल के समीप
(C) पत्तों की शिराओं में व बीजों में
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

11. छिद्र पाए जाते हैं-
(A) पत्ती की सतह पर
(B) वाहिकाओं में
(C) जाइलम में
(D) फ्लोएम में
उत्तर:
(A) पत्ती की सतह पर

12. एपीडर्मिस का कार्य नहीं है-
(A) जल की हानि कम करती है
(B) जल हानि के विरुद्ध यांत्रिक आघात से रक्षा करती है
(C) परजीवी कवक के प्रवेश में सहायक है।
(D) उपर्युक्त सभी
उत्तर:
(C) परजीवी कवक के प्रवेश में सहायक है

13. स्टोमेटा में रक्षी कोशिकाओं की आकृति होती है-
(A) यकृत जैसी
(B) वृक्क जैसी
(C) सेम के बीज जैसी
(D) चने के बीज जैसी
उत्तर:
(B) वृक्क जैसी

14. स्टोमेटा का कार्य है-
(A) वाष्पोत्सर्जन
(B) ऑक्सीजन ग्रहण करना व निष्कासन
(C) कार्बन डाइऑक्साइड का ग्रहण व निष्कासन
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

15. जड़ों में जल अवशोषण की क्षमता बढ़ती है-
(A) जड़ का आकार बढ़ने से
(B) जड़ की लंबाई बढ़ने से
(C) जड़ पर स्थित मूल रोमों के कारण
(D) उपर्युक्त सभी
उत्तर:
(C) जड़ पर स्थित मूल रोमों के कारण

16. छाल को हवा व पानी के लिए अभेद्य बनाता है-
(A) मोमी आवरण
(B) छाल की मोटी सतह
(C) सुबरिन नामक रसायन
(D) उपर्युक्त सभी
उत्तर:
(C) सुबरिन नामक रसायन

17. जटिल ऊतक का उदाहरण है-
(A) जाइलम
(B) विभज्योतक
(C) फ्लोएम
(D) (A) और (C) दोनों
उत्तर:
(D) (A) और (C) दोनों

18. निम्नलिखित में से संवहन ऊतक है-
(A) जाइलम
(B) फ्लोएम
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों ही नहीं
उत्तर:
(C) (A) और (B) दोनों

19. जाइलम के भाग हैं-
(A) वाहिनिका
(B) वाहिका
(C) जाइलम पैरेन्काइमा व फाइबर
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

20. फ्लोएम के भाग हैं-
(A) चालनी नलिका
(B) साथी कोशिकाएँ
(C) फ्लोएम पैरेन्काइमा व रेशे
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

21. खनिज व जल वाहित किए जाते हैं-
(A) फ्लोएम से
(B) जाइलम से
(C) चालनी नलिका से
(D) साथी कोशिकाओं से
उत्तर:
(B) जाइलम से

22. फ्लोएम संवाहित करता है-
(A) संश्लेषित खाद्य
(B) खनिज लवण
(C) जल
(D) उपर्युक्त सभी
उत्तर:
(A) संश्लेषित खाद्य

23. कौन-सा ऊतक सरल ऊतक नहीं है?
(A) स्क्लेरेन्काइमा
(B) फ्लोएम
(C) पैरेन्काइमा
(D) कॉलेन्काइमा
उत्तर:
(B) फ्लोएम

24. कौन-सा ऊतक जंतु ऊतक नहीं है?
(A) एपीथिलियल
(B) एपीडर्मल
(C) संयोजी
(D) पेशीय
उत्तर:
(B) एपीडर्मल

25. शरीर को ढकने व शरीर के अंदर विभिन्न अंगों के आवरण बनाने का कार्य कौन-सा ऊतक करता है?
(A) एपिथीलियमी
(B) संयोजी
(C) तंत्रिका
(D) पेशीय
उत्तर:
(A) एपिथीलियमी

26. एपिथीलियमी ऊतक का प्रकार नहीं है-
(A) शल्की
(B) घनाकार
(C) गोलाकार
(D) स्तंभाकार व स्तरित शल्की
उत्तर:
(C) गोलाकार

27. आहारनली तथा मुँह का अंतर किस एपिथीलियमी ऊतक से बना होता है?
(A) ग्रंथिल
(B) शल्की
(C) स्तंभाकार
(D) घनाकार
उत्तर:
(B) शल्की

28. रक्त किस प्रकार का ऊतक है?
(A) एपिथीलियमी
(B) संयोजी
(C) पेशीय
(D) तंत्रिका
उत्तर:
(B) संयोजी

29. रक्त की कौन-सी कोशिकाएँ ऑक्सीजन ग्रहण करने का कार्य करती हैं?
(A) RBC
(B) WBC
(C) प्लेटलेट्स
(D) उपर्युक्त सभी
उत्तर:
(A) RBC

30. अस्थि किस प्रकार के ऊतक का उदाहरण है?
(A) एपिथीलियमी
(B) संयोजी
(C) पेशीय
(D) तंत्रिका
उत्तर:
(B) संयोजी

31. शरीर को गति प्रदान करने वाला ऊतक होता है-
(A) एपिथीलियमी
(B) संयोजी
(C) पेशीय
(D) उपर्युक्त सभी
उत्तर:
(C) पेशीय

32. ऐच्छिक पेशी का गुण है-
(A) आकार में लंबी
(B) बेलनाकार
(C) शाखारहित
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

33. अनैच्छिक पेशियाँ नहीं पाई जाती-
(A) अस्थियों में
(B) आँख की पलक में
(C) मूत्रवाहिनी में
(D) फेफड़ों की श्वसनी में
उत्तर:
(A) अस्थियों में

34. कौन-सी कोशिका सबसे लंबी हो सकती है?
(A) एपिथीलियमी
(B) तंत्रिका
(C) संयोजी
(D) पेशीय
उत्तर:
(B) तंत्रिका

35. हृदय में कौन-सा ऊतक होता है?
(A) पेशीय
(B) तंत्रिका
(C) एपिथीलियमी
(D) संयोजी
उत्तर:
(A) पेशीय

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 15 Probability Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 15 Probability

Very Short Answer Type Questions

Question 1.
Two coins are tossed simultaneously. What is the probability of getting at least one head?
Solution:
When two coins are tossed simultaneously all possible outcomes are HH, HT, TH, TT.
∴ Total number of possible outcomes = 4
Let E be the event of getting at least one head, then the favourable outcomes are HH, HT, TH.
Number of favourable outcomes = 3
∴ P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{3}{4}\)
Hence,
∴ P(E) = \(\frac{3}{4}\)

Question 2.
Three unbaised coins are tossed simultaneously. Find the probability of getting exactly (i) 2 tails, (ii) atmost 2 tails.
Solution:
When 3 coins are tossed simultaneously all possible outcomes are HHH, HHT, THH, HTH, THT, HTT, TTH, TTT
∴ Total number of possible outcomes = 8
(i) Let E₁ be the event of getting 2 tails, then favourable outcomes are
THT, HTT, TTH
∴ Number of favourable outcomes = 3
∴ P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{3}{8}\)

(ii) Let E₂ be the event of getting at most 2 tails, then E₂ = event of getting 0 or 1 or 2 tails
So, the favourable outcomes are HHH, HHT, THH, HTH, THT, HTT, TTH
∴ Number of favourable outcomes = 7
∴ P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{7}{8}\)
Hence, (i) P(E₁) = \(\frac{3}{8}\), (ii) P(E₂) = \(\frac{7}{8}\)

Question 3.
A dice is thrown once. What is probability that shows as:
(i) 3,
(ii) an even number,
(iii) greater than 4.
Solution:
When a dice thrown once, all possible outcomes are : 1, 2, 3, 4, 5, 6.
∴ total number of possible outcomes = 6
(i) Let E₁ be event of getting 3, then
∴ P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{1}{6}\)

(ii) Let E₂ be the event of getting an even number, then favourable outcomes are: 2, 4, 6.
∴ Number of favourable outcomes = 3
∴ P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{3}{6}\) = \(\frac{1}{2}\)

(iii) Let E₃ be the event of getting a number greater than 4, then favourable outcomes are : 5,6.
∴ Number of favourable outcomes = 2
∴ P(E₃) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{2}{6}\) = \(\frac{1}{3}\)
Hence, (i) P(E₁) = \(\frac{1}{6}\)
(ii) P(E₂) = \(\frac{1}{2}\)
(ii) P(E₃) = \(\frac{1}{3}\)

Long Answer Type Questions

Question 1.
Over the past 200 working days, the number of defective parts produced by a machine is given in the following table :

Determine the probability that tomorrow’s output will have
(i) no defective part
(ii) at least one defective part
(iii) not more than 5 defective parts
(iv) more than 13 defective parts.
Solution:
Total number of days = 200
∴ Total number of possible outcomes = 200
(i) Number of days having no defective parts = 50
∴ Favourable outcomes = 50
Let E₁ be the event of number of days having no defective part. Then
∴ P(E₁) = \(\frac{\text { Favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{50}{200}\) = 0.25

(ii) Number of days having at least one defective part
= 32 + 22 + 18 + 12 + 12 + 10 + 10 + 10 + 8 + 6 + 6 + 2 + 2
= 150
∴ Favourable outcomes = 150
Let E₂ be the event of number of days having at least one defective part. Then
∴ P(E₂) = \(\frac{\text { Favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{150}{200}\) = 0.75

(iii) Number of days having not more than 5 defective parts
= 50 + 32 + 22 + 18 + 12 + 12 = 146
∴ Favourable outcomes = 146.
Let E₃ be the event of number of days having not more than 5 defective parts. Then
∴ P(E₃) = \(\frac{\text { Favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{146}{200}\) = 0.73

(iv) Number of days having more than 13 defective parts = 0
∴ favourable outcomes = 0
Let E₄ be the event of number of days having more than 13 defective parts. Then
∴ P(E₄) = \(\frac{\text { Favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{0}{200}\) = 0.
Hence, (i) p(E₁) = 0·25 (ii) p(E₂) = 0.25 (iii) p(E₃) = 0.73 (iv) p(E₄) = 0.

Question 2.
Find the probability that a number selected at random from the numbers 1, 2, 3, …, 39, 40 is :
(i) a prime number less than 30.
(ii) a number which is a perfect square.
(iii) multiple of 2 or 5.
Solution:
Total number of possible outcomes = 40
(i) Out of the given numbers, prime numbers less than 30 are
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
∴ Number of favourable outcomes = 10
Let E₁ be the event of getting a prime number. Then,
∴ P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{10}{40}\) = \(\frac{1}{4}\)

(ii) Out of the given numbers, perfect square numbers are 1, 4, 9, 16, 25, 36,
∴ Number of favourable outcomes = 6
Let E₂ be the event of getting a perfect square number. Then,
∴ P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{6}{40}\) = \(\frac{3}{20}\)

(iii) Out of the given numbers, multiple of 2 are :
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40
Multiple of 5 are: 5, 10, 15, 20, 25, 30, 35, 40
Multiple of 2 and 5 both are: 10, 20, 30, 40.
∴ Number of favourable outcomes = 20 + 8 – 4 = 24
Let E₃ be the event of getting a multiple of 2 or 5, then
∴ P(E₃) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{24}{40}\) = \(\frac{3}{5}\)
Hence, (i) P(E₁) = \(\frac{1}{4}\) (ii) P(E₂) = \(\frac{3}{20}\) (ii) P(E₃) = \(\frac{3}{5}\)

Question 3.
A bag contains 4 white balls and some blue balls. If the probability of drawing a blue ball from the bag is thrice that a white ball. Find the number of blue balls in the bag.
Solution:
Let the number of blue balls be x, then
total number of balls = 4 + x
∴ Total number of possible outcomes = 4 + x
Number of white balls = 4
∴ Number of fovourable outcomes = 4
Let E₁ be event of getting a white ball,
∴ P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{4}{4+x}\)
Number of blue balls = x
∴ Number of favourable outcomes = x
Let E₂ be the event of getting a blue ball, then
∴ P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{x}{4+x}\)
According to the question
P(E₂) = 3 × P(E₁)
⇒ \(\frac{x}{4+x}=3 \times \frac{4}{4+x}\)
⇒ \(\frac{x}{4+x}=\frac{12}{4+x}\)
⇒ x = \(\frac{12(4+x)}{(4+x)}\)
⇒ x = 12
Hence, number of white balls = 12.

Multiple Choice Questions

Choose the correct answer in each of the following:

Question 1.
Which one of the following cannot be probability of an event?
(a) \(\frac{1}{3}\)
(b) 0.5
(c) \(\frac{-2}{3}\)
(d) \(\frac{3}{4}\)
Answer:
(c) \(\frac{-2}{3}\)

Question 2.
Which one of the following cannot be probability of an event?
(a) \(\frac{4}{3}\)
(b) 0
(d) 0.75
(d) \(\frac{2}{5}\)
Answer:
(a) \(\frac{4}{3}\)

Question 3.
The sum of all the elementary events of an experiment is :
(a) 0
(b) 13
(c) -1
(d) \(\frac{1}{2}\)
Answer:
(b) 13

Question 4.
It is given that probability of winning a game is 0.3, then probability of losing the game is :
(a) 0.03
(b) 0.3
(c) -0.3
(d) 0.7
Answer:
(d) 0.7

Question 5.
Sum of probability of happening and not happening of an event is :
(a) 0
(b) -1
(c) 1
(d) \(\frac{1}{2}\)
Answer:
(c) 1

Question 6.
A coin is tossed 40 times and the head appears 15 times, then probability of getting a tail is :
(a) \(\frac{3}{8}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{5}{8}\)
(d) \(\frac{2}{3}\)
Answer:
(c) \(\frac{5}{8}\)

Question 7.
Two coins are tossed simultaneously, Probability of getting atmost one tail is :
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{3}{4}\)
(d) 1
Answer:
(c) \(\frac{3}{4}\)

Question 8.
In 60 throws of a dice, the outcomes were noted as given below :

A dice is thrown at random. Probability of getting a not even number is :
(a) \(\frac{17}{30}\)
(b) \(\frac{13}{30}\)
(c) \(\frac{1}{5}\)
(d) \(\frac{4}{5}\)
Answer:
(a) \(\frac{17}{30}\)

Question 9.
In a family of two children, probability of at least one girl is :
(a) \(\frac{1}{4}\)
(b) \(\frac{3}{4}\)
(c) \(\frac{1}{2}\)
(d) none of these
Answer:
(b) \(\frac{3}{4}\)

Question 10.
A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. Probability that this bulb defective is :
(a) \(\frac{1}{5}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{4}{5}\)
(d) \(\frac{3}{4}\)
Answer:
(a) \(\frac{1}{5}\)

Haryana State Board HBSE 10th Class Maths Solutions Chapter 15 Probability Ex 15.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 15 Probability Ex 15.2

Question 1.
Two customers Shyam and Ekta are visiting a particular shop in the same week. (Tuesday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on :
(i) the same day ?
(ii) consecutive days
(iii) different days?
Solution:
Two customers can visit the shop on two days in 5 × 5 = 25 days
Total number of possible outcomes = 25
(i) Two customers can visit the shop on the same day in one of the following ways.
Tuesday, Wednesday, Thursday, Friday, Saturday
Number of favourable ways = 5
P(visit the shop on the same day) = \(\frac{5}{25}=\frac{1}{5}\).

(ii) Two customers can visit the shop on consecutive days in the following ways:
(Tue, Wed), (Wed, Tue), (Wed, Th), (Th, Wed), (Th, Fri) (Fri, Th), (Fri, Sat), (Sat, Fri)
∴ Number of favourable ways = 8
P (visit the shop on consecutive days) = \(\frac{8}{25}\).

(iii)P (visit the shop on different days) = 1 – P(visit the shop on same day)
= 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)

Hence, (i) P (visit the shop on the same day) = \(\frac{1}{5}\)
(ii) P (visit the shop on consecutive days) = \(\frac{8}{25}\).
(iii) P (visit the shop on different days) = \(\frac{4}{5}\).

Question 2.
A die is numbered in such a way that its faces shows the numbers 1, 2, 2, 3, 3, 6. It is thrown two times and the total score in two throws is noted. Complete the following table which gives a few values of the total score on the two throws:

What is the probability that the total score is
(i) even ?
(ii) 6 ?
(iii) at least 6 ?
Solution:
The complete table is given below

Total number of possible outcomes = 6 × 6 = 36.
(i) Let E₁ denote the event that total score is a even number
Then favourable outcomes are 2, 4, 4, 4, 4, 8, 4, 4, 8, 4, 6, 6, 4, 6, 6, 8, 8, and 12
The number of outcomes favourable to E₁ = 18.
∴ P(E₁) = \(\frac{18}{36}=\frac{1}{2}\).

(ii) Let E₂ denote the event that total score is 6.
Then favourable outcomes are 6, 6, 6 and 6
The number of outcomes favourable to
E₂ = 4
∴ P(E₂) = \(\frac{4}{36}=\frac{1}{9}\).

(iii) Let E₃ denote the event that total score is at least 6.
Then favourable outcomes are 7, 8, 8, 6, 6, 9, 6, 6, 9, 7, 8, 8, 9, 9 and 12
The number of outcomes favourable to
E₃ = 15
∴ P(E₃) = \(\frac{15}{36}=\frac{5}{12}\)

Hence, (i) P (E₁) = \(\frac{1}{2}\)
(ii) P (E₂) = \(\frac{1}{9}\)
(iii) P(E₃) = \(\frac{5}{12}\).

Question 3.
A bag contains 5 red balls andsome blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.
Solution:
Let the number of blue balls in the bag be x.
Then total number of balls = (5 + x)
∴ Total number of possible outcomes = (5 + x)
∴ P(a blue ball) = \(\frac{x}{(5+x)}\)
∴ P(a red ball) = \(\frac{5}{(5+x)}\)
According to question,
P (a blue ball) = 2 × P(a red ball)
⇒ \(\frac{x}{(5+x)}\) – 2 × \(\frac{5}{(5+x)}\)
⇒ x = 10.
Hence, number of blue ba1ls in the bag = 10.

Question 4.
A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball ?
If 6 more black balls are put in the boiie probability of drawing a black ball is now double of what it was before ? Find x.
Solution:
Total number of balls in the bag = 12
∴ Total number of possible outcomes = 12
There are x black balls
∴ Number of favourable outcomes = x
∴ P (getting a black ball) = \(\frac{x}{12}\)
If 6 more black balls are put in the box. Then
Total number of balls in the box = 12 + 6 = 18
∴ Total number of possible outcomes = 18
Number of black balls in the box = x + 6
∴ Number of favourable outcomes = x + 6
∴ P (getting a black ball) = \(\frac{x+6}{18}\)
According to question,
\(\frac{x+6}{18}=2 \times \frac{x}{12}\)
\(\frac{x+6}{18}=\frac{x}{6}\)
⇒ 18 x = 6x + 36
⇒ 18x – 6x = 36
⇒ 12x = 36
⇒ x = \(\frac{36}{12}\) = 3
Hence, P (getting a black ball) = \(\frac{x}{12}\) and x = 3.

Question 5.
A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green is \(\frac{2}{3}\). Find the number of blue marbles in the jar.
Solution:
Total marbles in the jar = 24
Let x be green marbles in the jar.
Then blue marbles in the jar = 24 – x
Total number of possible outcomes = 24
P (getting a green marble) = \(\frac{x}{24}\)
⇒ \(\frac{2}{3}=\frac{x}{24}\)
⇒ x = \(\frac{24 \times 2}{3}\) = 16
Number of blue marbles in jar = 24 – 16 = 8.
Hence, number of blue marbles in the jar = 8

Haryana State Board HBSE 10th Class Maths Solutions Chapter 15 Probability Ex 15.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 15 Probability Ex 15.1

Question 1.
Complete the following statements:
(i) ProbabilIty of an event E + Probability of the event ‘not E’ = ………………….
(ii) The probability of an event that cannot happen is …………………. . Such an event is called …………………. .
(iii) The probability of an event that is certain to happen is …………………. . Such an event is called …………………. .
(iv) The sum of the probabilities of all the elementry events of an experiment is …………………. .
(v) The probability of an event is greater than or equal to …………………. . and less than or equal to …………………. .
Solution:
(i) 1
(ii) 0, impossible event
(iii) 1, sure or certain event
(iv) 1
(v) 0, 1.

Question 2.
Which of the following experiments have equally likely outcomes ? Explain.
(i) A driver attempts to start a car. The car starts or does not start.
(ii) A player attempts to shoot a basket ball. She/he shoots or misses the shot.
(iii) A trial is made to answer a true-false question. The answer is right or wrong.
(iv) A bady is born. It is a boy or a girl.
Solution:
(i) The outcome is not equally, likely because when there is some defect the car does not start.
(ii) The outcome in this situation is not equally likely because the outcome depends on many factors such quality of the gun, training of the player etc.
(iii) The outcome in this situation are equally likely because out come in this trial the answer is right or wrong i.e., one out of the two and both have equal chances to happen.
(iv) The outcome in this situation are equally likely because a baby is bom can be either a boy or girl.

Question 3.
Why is tossing a coin considerd to be fair way of deciding which team should get the ball at the beginning of a football game ?
Solution:
When we toss a coin, the outcomes head and tail are equally likely. So the result of an individual coin toss is completely unpredictable.

Question 4.
Which of the following cannot be the probability of an event ?
(a) \(\frac{2}{3}\)
(b) – 1.5
(c) 15%
(d) 0.7
Solution:
The value of probability of an event cannot be negative or greater than 1.
So, the correct option is (B).

Question 5.
If P (E) = 0.05, what is the probability of “not E” ?
Solution:
We have,
P(E) = 0.05
P (not E) = 1- P(E)
= 1 – 0.05 = 0.95
Hence, P(not E) = 0.95.

Question 6.
A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out
(i) an orange flavoured candy?
(ii) a lemon flavoured candy?
Solution:
(i) Let E denote the event to get an orange flavoured candy.
There is no outcome favourable to the event E because all the candies are lemon flavoured.
So, P(E) = 0.
(ii) Let F denote the event to get a lemon flavoured candy.
All the outcomes favourable to event F because all the candies in the bag lemon flavoured.
So P(F) = 1.
Hence, (i) P(E) = 0
(ii) P(F) = 1.

Question 7.
It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
Solution:
Let E denote the event that two students out of three have same birthday.
P(not E) = 0.992 (given)
Then P(E) = 1 – P (not E)
= 1 – 0992
= 0008.
Hence, P(E) = 0.008.

Question 8.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is
(i) red ?
(ii) not red?
Solution:
Number of all possible out comes = 3 + 5 = 8
(i)Number of red balls = 3
Number of favourable outcomes = 3
∴ P(redball) = \(\frac{3}{8}\)

(ii)Number of not red balls = black balls = 5
Number of favourable outcomes = 5
P(not red ball) = \(\frac{5}{8}\)

Hence, (i) P(red ball) = \(\frac{3}{8}\),
(ii) P (not red ball) = \(\frac{5}{8}\).

Question 9.
A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be
(i) red?
(ii) white ?
(iii) not green ?
Solution:
Total number of possible out comes = 5 + 8 + 4 = 17
(i) Number of red marbles = 5
Number of favourable outcomes = 5
P(a red marble) = \(\frac{5}{17}\).

(ii) Number of white marbles = 8
Number of favourable outcomes = 8
P(a white marble) = \(\frac{8}{17}\).

(iii) Number of marbles which are not green = 5 + 8 = 13
Number of favourable outcomes = 13
∴ P(a marble not green) = \(\frac{13}{17}\).

Hence, (i) P(a red marble) = \(\frac{5}{17}\)
(ii) P(a white marble) = \(\frac{8}{17}\)
(iii) P(a marble not green) = \(\frac{13}{17}\).

Question 10.
A piggy bank contains hundred 50 P coins, fifty ₹ 1 coins, twenty ₹ 2 coins and ten ₹ 5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, what is the probability that the coin
(i) will be a 50 P coin ?
(ii) will not be a ₹ 5 coin?
Solution:
Total number of coins = 100 + 50 + 20 + 10 = 180
Total number of possible outcomes = 180
(i) Number of 50 paise coins = 100
Number of favourable outcomes = 100
∴ P(50 paise coins) = \(\frac{100}{180}=\frac{5}{9}\).

(ii) Number of coins other than 5 coins 100 + 50 + 20 = 170
Number of favourable outcomes = 170
P(will not be ₹ 5 coins) = \(\frac{170}{180}=\frac{17}{18}\)

Hence, (i) P (50 P coins) = \(\frac{5}{9}\)
(ii) P(will not be ₹ 5 coins) = \(\frac{17}{18}\).

Question 11.
Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish (see in figure). What is the probability that the fish taken out is a male fish?

Solution:
Total fish in the aquarium = 5 + 8 = 13
Total number of possible outcomes = 13
Number of male fish = 5
Number of favourable outcomes = 5
P(male fish) = \(\frac{5}{13}\)
Hence, P(male fish) = \(\frac{5}{13}\).

Question 12.
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2,3,4, 5,6, 7,8, (see in figure), and these are equally likely outcomes. What is the probability that it will point at [CBSE 2016]

(i) 8 ?
(ii) an odd number ?
(iii) a number greater than 2 ?
(iv) a number less than 9 ?
Solution:
Since arrow can come to rest at any one of the numbers 1, 2, 3, 4, 5, 6, 7, 8.
Total number of possible outcomes = 8
(i) Number of favourable outcomes = 1
∴ P(Arrow point at 8) = \(\frac{1}{8}\).

(ii) Odd numbers are 1, 3, 5, 7
Number of favourable outcomes = 4
∴ P(Arrow points at an odd number) = \(\frac{4}{8}=\frac{1}{2}\)

(iii) The numbers greater than 2 are 3, 4, 5, 6, 7 , 8
Number of favourable outcomes = 6
∴ P(Arrow points a number greater than 2 = \(\frac{6}{8}=\frac{3}{4}\).

(iv) The numbers less than 9 are 1, 2, 3, 4, 5, 6, 7, 8.
Number of favourable outcomes = 8.
∴ P(Arrow points at a number less than 9 = \(\frac{8}{8}\) = 1.

Hence, (i) P (Arrow point at 8) = \(\frac{1}{8}\)
(ii) P(Arrow points at an odd number) = \(\frac{1}{2}\)
(iii) P(Arrow points at a number greater them 2) = \(\frac{3}{4}\)
(iv) P(Arrow points at a number less than 9) = 1.

Question 13.
A die is thrown once. Find the probability of getting
(i) a Prime number
(ii) a number lying between 2 and 6
(iii) an odd number.
Solution:
In a single throw of a die, all possible out comes are 1, 2, 3, 4, 5, 6.
Total number of possible outcomes = 6
(i) Let E₁ be event of getting a prime number. Prime numbers are 2, 3, 5
Number of favourable outcomes = 3
∴ P (getting a prime number) = p(E₁) = \(\frac{3}{6}=\frac{1}{2}\).

(ii) Let E₂ be event of getting a number lying between 2 and 6
The numbers lying between 2 and 6 are 3, 4, 5.
Number of favourable outcomes = 3
P(E₂) = \(\frac{3}{6}=\frac{1}{2}\).

(iii) Let E₃ be event of getting an odd number The odd numbers are 1, 3, 5
Number of favourable outcomes = 3
P(E₃) = \(\frac{3}{6}=\frac{1}{2}\).

Hence, (i) P(E₁) = \(\frac{1}{2}\)
(ii) P(E₂) = \(\frac{1}{2}\)
(iii) P(E₃) = \(\frac{1}{2}\).

Question 14.
One card is drawn from a well- shuffled deck of 52 cards. Find the probability of getting of
(i) a king of red colour
(ii) a face card
(iii) a red face card,
(iv) the jack of hearts
(v) a spade
(vi) the queen of diamonds.
Solution:
Total number of all possible out comes = 52
(i) Number of king of red colour = 2
Number of favourable out comes = 2
P(getting a king of red colour) = \(\frac{2}{52}=\frac{1}{26}\).

(ii) We know that kings, queens and jacks are the face cards
Number of face cards = 12
Number of favourable outcomes = 12
P(getting a face card) = \(\frac{12}{52}=\frac{3}{13}\).

(iii) Number of red face cards = 6
Number of favourable outcomes = 6
P(getting a red face card) = \(\frac{6}{52}=\frac{3}{26}\).

(iv) Number of jack of hearts = 1
Number of favourable outcomes = 1
P(getting the jack of hearts) = \(\frac{1}{52}\)

(v) Number of spades = 13
Number of favourable outcomes = 13
P(getting a spade) = \(\frac{13}{52}=\frac{1}{4}\).

(vi) Number of queen of diamonds = 1
Number of favourable outcome = 1
P (getting the queen of diamonds) = \(\frac{1}{52}\)

Hence, (i) P(getting a king of red colour) = \(\frac{1}{26}\)
(ii) P (getting a face card) = \(\frac{3}{13}\)
(iii) PCgetting a red face card) = \(\frac{3}{26}\)
(iv) P(getting the jack of hearts) = \(\frac{1}{52}\)
(v) P(getting a spade) = \(\frac{1}{4}\)
(vi) P(getting the queen of diamonds) = \(\frac{1}{52}\).

Question 15.
Five cards the ten, jack, queen, king and ace of diamonds, are well- shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen ?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is
(a) an ace ?
(b) a queen ?
Solution:
(i) The total number of cards = 5
Total number of possible outcomes = 5
Out of these 5 cards only one is queen
Number of favourable outcomes = 1
∴ P(a queen) = \(\frac{1}{5}\)

(ii) After the queen has been drawn and put a side total number of cards = 5 – 1 = 4
Number of possible outcomes = 4
These four cards include one ace and no queen
P (an ace) = \(\frac{1}{4}\),
P (a queen) = 0.

Hence, (i) P(a queen) = \(\frac{1}{5}\)
(ii) (a) P(an ace) = \(\frac{1}{4}\)
(b) P(a queen) = 0.

Question 16.
12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Solution:
Number of total pens = 12 + 132 = 144
Total number of possible outcomes = 144
Number of good pens = 132
Number of favourable outcomes = 132
P(good pens) = \(\frac{132}{144}=\frac{11}{12}\)
Hence, P (good pens) = \(\frac{11}{12}\).

Question 17.
(i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
(ii) Suppose the bulb drawn in
(i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective ?
Solution:
(i) Total number of bulbs = 20
Total number of possible outcomes = 20
Number of bulbs defective in this lot = 4
Number of favourable outcomes = 4
P(a defective bulb) = \(\frac{4}{20}=\frac{1}{5}\)

(ii) According to question, the bulb drawn is not defective and it is not replaced.
Total number of bulbs contains the lot = 19
Total number of possible outcomes = 19
Number of good bulbs are = 19 – 4 = 15
Number of favourable outcomes = 15
∴ P(a non defective bulb) = \(\frac{15}{19}\)

Hence, (i) P (a defective bulb) = \(\frac{1}{5}\)
(ii) P(a non defective bulb) = \(\frac{15}{19}\).

Question 18.
A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears.
(i) a two-digit number
(ii) a perfect square number
(iii) a number divisible by 5.
Solution:
Total number of possible outcomes = 90
(i) Two digit numbers from 1 to 90 are 10, 11, 12, 13, ……………. 90
Total two digit numbers = 81
Number of favourable outcomes = 81
∴ P(a disc bearing a two digit number) = \(\frac{81}{90}=\frac{9}{10}\).

(ii) Perfect square numbers from 1 to 90 are 1, 4, 9, 16, 25, 36, 49, 64, 81.
Total perfect square numbers = 9
Number of favourable outcomes = 9
∴ P(a disc bearing a perfect square number) = \(\frac{9}{90}=\frac{1}{10}\).

(iii) The numbers divisible by 5 from 1 to 90 are 5, 10, 15, 20, ……………….. 90.
Total numbers divisible by 5 from 1 to 90 = 18
Number of favourable outcomes = 18
P(a disc bearing a number divisible by 5) = \(\frac{18}{90}=\frac{1}{5}\)

Hence, (i) P(a disc bearing a two digit number) = \(\frac{9}{10}\)
(ii) P(disc bearing a perfect square number) = \(\frac{1}{10}\)
(iii) P(a disc bearing a number divisible by 5) = \(\frac{1}{5}\).

Question 19.
A child has a die whose six faces shows the letters as given below :
A B C D E A
The die is thrown once. What is the probability of getting
(i) A ?
(ii) D ?
Solution:
In throwing the die any one of the six faces may come upward.
Total number of possible outcomes = 6
(i) Since there are two faces with letter A .
∴ Number of favourable outcomes = 2
∴ P(getting A) = \(\frac{2}{6}=\frac{1}{3}\)

(ii) There is one face with letter D
Number of favourable outcome = 1
P(gettings D) = \(\frac{1}{6}\)

Hence, (i) P(getting A) = \(\frac{1}{3}\)
(ii) P(getting D) = \(\frac{1}{6}\).

Question 20.
Suppose you drop a die at random on the rectangular region shown in figure. What is the probability that it will land inside the circle with diameter 1 m ?

Solution:
Total area of the rectangular region = l × b
= 3 × 2 = 6 m²
Area of the circular region = πr²
= π × \(\left(\frac{1}{2}\right)^2\) = \(\frac{\pi}{4}\) m².
P(the die lands inside the circle) = \(\frac{\text { Area of the circular region }}{\text { Total area of rectangular region }}\)
= \(\frac{\frac{\pi}{4}}{6}=\frac{\pi}{24}\)
Hence, P(the die lands inside the circle) = \(\frac{\pi}{24}\).

Question 21.
A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
(i) She will buy it ?
(ii) She will not buy it ?
Solution:
Total number of pens = 144
Total number of possible outcomes = 144
(i)Number of defective pens = 20
The number of good pens = 144 – 20 = 124
Number of favourable outcomes = 124
P (Nuri will buy good pen) = \(\frac{124}{144}=\frac{31}{36}\).

(ii) P (Nuri will not buy a good pen) = P
(selecting a defective pen) = \(\frac{20}{144}=\frac{5}{36}\)

Hence, (i) P (Nuri will buy a good pen) = \(\frac{31}{36}\)
(ii) P (Nuri will not buy a good pen) = \(\frac{5}{36}\).

Question 22.
Refer to example 25 of NCERT (i) complete the following table:

(ii) A student argues that ‘there are 11 possible out comes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12.
Therefore, each of them has a probability 1/11. Do you agree with this argument ? Justify your answer.
Solution:
Total number of possible outcomes of the toss of the pair of two dice = 36
(i) (1, 2), (2, 1), favour the event of the getting the sum 3
∴ P(getting the sum 3) = \(\frac{2}{36}\).

Cases (1, 3), (2, 2), (3, 1) favour the event of getting sum 4
∴ P(getting the sum 4) = \(\frac{3}{36}\).

Cases (1, 4), (2, 3), (3, 2), (4, 1) favour the event of getting the sum 5
∴ P(getting the sum 5) = \(\frac{4}{36}\)

Cases (1, 5), (2, 4), (3, 3), (4, 2), (5, 1) favour the event of getting the sum 6
∴ P(getting the sum 6) = \(\frac{5}{36}\)

Cases (1, 6), (2, 6), (3, 4), (4, 3), (6, 2), (6, 1) favour the event of getting the sum 7
∴ P(getting the sum 7) = \(\frac{6}{36}\)

Cases (2, 6), (3, 5), (4, 4), (5, 3), (6, 2) favour the event of getting the sum 8
∴ P(getting the sum 8) = \(\frac{5}{36}\)

Cases (3, 6), (4, 5), (5, 4), (6, 3) favour the event of getting the sum 9
∴ P(getting the sum 9) = \(\frac{4}{36}\)

Cases (4, 6), (5, 5), (6, 4) favour the event of getting the sum 10
∴ P(getting the sum 9) = \(\frac{3}{36}\)

Cases (5, 6), (6, 5), (6, 4) favour the event of getting the sum 11
∴ P(getting the sum 9) = \(\frac{2}{36}\)

(ii) No, as the eleven different outcomes are not equally likely.

Question 23.
A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hervitwins if all the tosses give the same result £evthfee heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Solution:
When a coin tossed three times, the possible outcomes are (H, H, H), (H, H, T), (H, T, T), (H, T, H), (T, H, H), (T, H, T), (T, T, H) and (T, T, T)
Total number of possible outcomes = 8
Number of cases when all the tosses give the same results are two i.e., (H, H, H) and (T, T, T).
It is given that Hanif wins when all the tosses give the same results,
Number of cases in which Hanif will lose the game = 8 – 2 = 6
Number of favorable outcomes = 6
∴ P (Hanif will lose the game) = \(\frac{6}{8}=\frac{3}{4}\).
Hence, P (Hanif will lose the game) =\(\frac{3}{4}\).

Question 24.
A die is thrown twice. What is the probability that
(i) 5 will not come up either time ?
(ii) 5 will come up at least once ?
[Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment.]
Solution:
A die is thrown twice Total number of possible outcomes = 36
(i) Out of these 36 outcomes, 5 comes at least once in the following cases :
(1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 6)
Total number of these cases = 11
∴ Number of cases when 5 will not come up either time = 36 – 11 = 25
Number of favourable outcomes = 25
∴ P(5 will not come up either time) = \(\frac{25}{36}\).

(ii) Number of cases when 5 comes up at least once = 11
Number of favourable outcomes = 11
∴ P (5 will come up at least once) = \(\frac{11}{36}\)

Hence, (i) P (5 will not come up either time) = \(\frac{25}{36}\)
(ii) P (5 will come up at least once) = \(\frac{11}{36}\).

Question 25.
Which of the following arguments are correct and which are not correct ? Give reasons for your answer.
(i) If two coins are tossed simultaneously there are three possible outcomes – two heads, two tails or one ofeach. Therefore, for each of these outcomes, the probability is 1/3.
(ii) If a die is thrown, there are two possible outcomes – an odd number or an even number. Therefore, the probability of getting an odd number is 1/2.
Solution:
When two coins are tossed.
(i) The possible outcomes are (H, H), (H, T), (T, H), (T, T)
Total number of possible outcomes = 4
P(H, H) = \(\frac{1}{4}\)
P(T, T) = \(\frac{1}{4}\)
P(H, T and T, H) = \(\frac{2}{4}=\frac{1}{2}\)
Hence, argument is incorrect.

(ii) When a die is thrown The possible outcomes are 1, 2, 3, 4, 5, 6
Total number of possible outcomes = 6
We have odd numbers or even numbers
Odd numbers are 1, 3, 5
Number of favourable outcomes = 3
Probability (getting an odd number) = \(\frac{3}{6}=\frac{1}{2}\)
Hence, argument is correct.

Haryana State Board HBSE 9th Class Maths Solutions Chapter 8 Quadrilaterals Ex 8.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 8 Quadrilaterals Exercise 8.2

Question 1.
ABCD is a quadrilateral in which P, Q, R and S are mid points of the sides AB, BC, CD and DA (see figure 8.29). AC is a diagonal. Show that:
(i) SR || AC and SR = \(\frac{1}{2}\)AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.

Solution:
Given : ABCD is a quadrilateral in which P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively. AC is a diagonal.
To prove : (i) SR || AC and SR = \(\frac{1}{2}\)AC,
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Proof : (i) In ΔACD, we have
∴ S and R are the mid points of AD and CD respectively.
∴ SR || AC and SR = \(\frac{1}{2}\)AC
(ii) In ΔABC, we have
∴ P and Q are the mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac{1}{2}\)AC,
[By theorem 8.9] …(ii)
From (i) and (i), we get
PQ || SR and PQ = SR.
(iii) ∵ PQ || SR and PQ = SR,
(As proved above)
∴ PQRS is a parallelogram.
Hence proved

Question 2.
ABCD is a rhombus and P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:

Given: A rhombus ABCD in which P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively.
To prove: Quadrilateral PQRS is a rectangle.
Construction: Join AC and BD.
Proof: In ΔADC, we have S and R are the mid points of AD and CD respectively.
∴ SR || AC and SR = \(\frac{1}{2}\)AC ……(1)
and in ΔABC, we have
P and Q are the mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac{1}{2}\)AC,
[By theorem 8.9] …….. (ii)
From (i) and (ii), we get
PQ || SR and PQ = SR
∴ PQRS is a parallelogram.
[By theorem 8.8]
Again in ΔDAB, we have
S and P are the mid points of AD and AB respectively.
SP || BD
⇒ SL || MO
and SR || AC [From (i)]
⇒ SM || LO
∴ SLOM is a parallelogram.
Since, diagonals of a rhombus bisect each other at 90°.
∴ ∠AOD = 90°
∠MOL = 90°
But, ∠LSM = ∠MOL,
(Opposite angles of a parallelogram)
⇒ ∠LSM = 90°
⇒ ∠PSR = 90°
Since, one angle of a parallelogram PQRS is 90°.
Therefore, quadrilateral PQRS is a rectangle.
Hence proved

Question 3.
ABCD is a rectangle and P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
Given: A rectangle ABCD in which P, Q, R and S are mid points of the sides AB, BC, CD and DA respectively.
To prove : Quadrilateral PQRS is a rhombus.

Construction: Join AC.
Proof: In ΔADC, S and R are the mid points of AD and CD respectively.
∴ SR || AC and SR = \(\frac{1}{2}\)AC …(i)
[By thoerem 8.9]
In ΔABC, P and Q are the mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac{1}{2}\)AC …..(ii)
From (i) and (ii), we get
PQ || SR and PQ = SR
∴ PQRS is a parallelogram.
[By theorem 8.8]
∵ ABCD is a rectangle.
∠A = ∠B = 90° …(ii)
and AD = BC, (Opposite sides of a rectangle)
⇒ \(\frac{1}{2}\)AD = \(\frac{1}{2}\)BC
⇒ AS = BQ,
[∵ S is the mid point of AD and Q is the mid point of BC]
∴ AS = \(\frac{1}{2}\)AD and BQ = \(\frac{1}{2}\)BC]
Now in ΔSAP and ΔQBP, we have
AS = BQ, [As proved above]
∠SAP = ∠QBP,
[From (iii), Each = 90°]
and AP = BP,
[∵ P is the mid point of AB]
∴ ΔSAP ≅ ΔQBP,
(By SAS congruence rule)
⇒ SP = PQ, (CPCT)
Thus, adjacent sides of a parallelogram PQRS are equal.
Therefore, PQRS is a rhombus.
Hence proved

Question 4.
ABCD is a trapezium in which AB || CD, BD is a diagonal and E is the mid point of AD. A line is drawn through E parallel to AB intersecting BC at F(see figure 8.30). Show that F is the mid point of BC.

Solution:
Given: ABCD is a trapezium in which AB || CD, EF || AB and E is the mid point of AD.
To prove: F is the mid point of BC.
Proof: Let line EF intersecting BD at G.
In ΔDAB, we have
EG || AB (∵ EF || AB)
and E is the mid point of AD.
∴ G is the mid point of BD.
Now, AB || CD and AB || EF, (Given)
⇒ EF || CD
⇒ GF || CD
and G is the mid point of BD. (As proved above)
∴ F is the mid point of BC.
Hence proved

Question 5.
In a parallelogram ABCD, E and Fare the mid points of sides AB and CD respectively (see figure 8.31). Show that the line segments AF and EC trisect the diagonal BD.

Solution:
Since, ABCD is a parallelogram.
∴ AB = CD,
(Opposite sides of parallelogram)
\(\frac{1}{2}\)AB = \(\frac{1}{2}\)CD
AE = FC,
[∵ E and F are mid points of AB and CD respectively
∴ AE = \(\frac{1}{2}\)AB and FC = \(\frac{1}{2}\)CD]
and AB || CD
⇒ AE || FC
∴ AECF is a parallelogram.
⇒ AF || EC …..(i)
In ΔABP, we have
E is the mid point of AB.
and EQ || AP [∵ AF || EC]
∴ Q is the mid point of BP
⇒ BQ = PQ …….(ii)
In ΔCQD, we have
F is the mid point of CD.
and PF || CQ [∵ AF || EC]
∴ P is the mid point of DQ.
⇒ DP = PQ ……..(iii)
From (ii) and (iii), we get
DP = PQ = BQ
Hence, line segments AF and EC trisect the diagonal BD.
Hence proved

Question 6.
Show that the line segments joining the mid points of the opposite sides of a quadrilateral bisect each other.
Solution:
Given: ABCD is a quadrilateral in which EG and FH are the line segments joining the mid points of opposite sides of a quadrilateral.
To prove: EG and FH bisect each other.

Construction: Join EF, FG, GH, HE and AC.
Proof: In ΔABC, E and F are mid points of AB and BC.
∴ EF || AC and EF = \(\frac{1}{2}\)AC
[By mid point theorem]
In ΔADC, H and G are mid points of AD and CD.
∴ HG || AC and HG = \(\frac{1}{2}\)AC ……(ii)
From (i), (ii), we get
EF || HG and EF = HG
∴ EFGH is a parallelogram. [By theorem 8.8]
We know that diagonals of a parallelogram bisect each other.
Therefore EG and FH bisect each other.
Hence proved

Question 7.
ABC is a triangle right angled at C. A line through the mid point M of hypotenuse AB and parallel to BC intersects AC at D. Show that:
(i) D is the mid point of AC,
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac{1}{2}\)AB.
Solution:
Given: A ΔABC in which ∠C = 90°,
M is the mid point of AB and MD || BC.
To prove : (i) D is the mid point of AC.
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac{1}{2}\)AB.

Proof: (i) In ΔABC, M is the mid point of AB.
and MD || BC, (Given)
∴ D is the mid point of AC.
(By theorem 8.10)
(ii) Since, MD || BC and ∠ACB = 90°
∴ ∠ADM = 90°
(Corresponding angles) …(i)
(iii) But, ∠DM + ∠CDM = 180°, (Linear pair)
⇒ 90° + ∠CDM = 180°, [Using (i)]
⇒ ∠CDM = 180° – 90° = 90° … (ii)
Now, ΔADM and ΔCDM, we have
AD = CD,
(As proved above, D is the mid point of AC)
∠ADM = ∠CDM, [From (i) and (ii), Each = 90°]
and MD = MD, (Common)
∴ ΔADM ≅ ΔCDM,
(By SAS congruence rule)
⇒ AM = CM, (CPCT)
But, AM = BM, (∵ M is the mid point of AB)
∴ AM = CM = \(\frac{1}{2}\)AB.
Hence proved

Haryana State Board HBSE 10th Class Maths Solutions Chapter 14 Statistics Ex 14.4 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 14 Statistics Ex 14.4

Question 1.
The following distribution gives the daily income of 50 workers of a factory.

Convert the distribution above to less than type cumulative frequency distribution, and draw its ogive.
Solution:
We prepare the cumulative frequency table by less than method as given :

We plot the points (120, 12), (140, 26), (160, 34), (180, 40), (200, 50) on the graph paper. Joining these points with a free hand to get less than curve as shown in graph.

Question 2.
During the medical check up of 35 students of a class, their weights were recorded as follows:

Draw a less than type give for the given data. Hence, obtain the median weight from the graph and verify the result by using the formula.
Solution:
We convert the cumulative frequency table into depicting class intervals with their respective frequencies as given below :

We plot the points (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32) and (52, 35) on the graph paper.
Joining these points with a free hand to get less than ogive curve as shown in ahead graph. .
We have, n = 35
⇒ \(\frac{n}{2}=\frac{35}{2}\) = 17.5
Take a point A (0, 17 5) on y-axis. Draw AP parallel to x-axis cutting the curve at point P. Draw PM perpendicular to OX intersecting OX at M.
OM = 46.5
Hence median = 46.5 kg.
Now, \(\frac{n}{2}\) = 17.5
But 17.5 comes under the cumulative frequency 28. The class interval against the cumulative frequency 17.5 is 46 – 48. So, it is the median class.
∴ l = 46, cf = 14, f = 14, and h = 2 .
Median = l + \(\left(\frac{\frac{n}{2}-c f}{f}\right)\)
46 + \(\left(\frac{17 \cdot 5-14}{14}\right)\) × h
= 46 + \(\frac{3.5}{7}\) × 2
= 46 + 0.5 = 46.5 kg.
Hence, median in both cases is 46.5 kg.

Question 3.
The following table gives production yeild per hectare of wheat of 100 farms of a village.

Change the distribution to a more than type distribution, and draw its give.
Solution:
We prepare the cumulative frequency table by more than type method as given :

We plot the points (50, 100), (55, 98), (60, 90), (65, 78), (70, 54) and (75, 16) on the graph paper.
Joining these points with free hand to obtain more than type give curve as shown below in graph.

Haryana State Board HBSE 10th Class Maths Solutions Chapter 14 Statistics Ex 14.3 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 14 Statistics Ex 14.3

Question 1.
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.

Solution:
For calculating the median we prepare cumulative frequency distribution table as given below :

n = 68
⇒ \(\frac{n}{2}=\frac{68}{2}\) = 34
But 34 comes under the cumulative frequency 42 and the class interval against the cumulative frequency 42 is 125 – 145. So, it is the median class.
∴ l = 125, cf = 22, f = 20 and h = 20
Median = l + \(\left(\frac{\frac{n}{2}-c f}{f}\right)\) × h
= 125 + \(\left(\frac{34-22}{20}\right)\) × 20
= 125 + 12 = 137.
For calculating mean, we prepare the table as given below :

From the table, we have
Σf_i = 68, Σf_iu_i = 7, a = 135, h = 20
Mean = a + \(\left(\frac{\Sigma f_i u_i}{\Sigma f_i}\right)\) × h
= 135 + \(\frac{7}{68}\) × 20
= 135 + \(\frac{140}{68}\)
= 135 + 2.05 = 137.05.
For calculating mode, the class 125 – 145 has maximum frequency. So, it is the modal class.
∴ l = 125, f₀ = 13, f₁ = 20, f₂ = 14, and h = 20
Mode = l + \(\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right)\) × h
= 125 + \(\left(\frac{20-13}{2 \times 20-13-14}\right)\) × 20
= 125 + \(\frac{7 \times 20}{13}\)
= 125 + \(\frac{140}{13}\)
= 125 + 10.76 = 135.76.
Hence, median, mean and mode are 137, 137.05 and 135.76 reapectively.
The three measures are approximately same in this case.

Question 2.
If the median of the distribution given below is 1. 285, find the values of x and y.

Solution:
For calculating the median, we prepare the cumulative frequency distribution table as given below :

n = 60
⇒ 45 + x + y = 60
⇒ x + y = 60 – 45
⇒ x + y = 15
Median is 28.5, which lies in the class 20 – 30.
So, it is the median class.
∴ l = 20, f = 20, cf = 5 + x and h = 10.
∴ Median = l + \(-\left(\frac{\frac{n}{2}-c f}{f}\right)\) × h
28.5 = 20 + \(\frac{\left[\frac{60}{2}-(5+x)\right]}{20}\) × 10
28.5 = 20 + \(\frac{(30-5-x)}{20}\) × 10
28.5 = 20 + \(\frac{(25-x)}{2}\)
28.5 – 20 = \(\frac{25-x}{2}\)
8.5 = \(\frac{25-x}{2}\)
⇒ 17 = 25 – x
⇒ x = 25 – 17
⇒ x = 8
Putting the value of x in equation (1), we get
8 + y = 15
⇒ y = 15 – 8 = 7.
Hence, x = 8, y = 7.

Question 3.
A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 year.

Solution:
Let us prepare the table depicting class intervals with their respective frequencies and cumulative frequencies from the given data as below:

n = 100
⇒ \(\frac{n}{2}=\frac{100}{2}\) = 50
But 50 comes under the cumulative frequency 78 and the class interval against the cumulative frequency 78 is 35 – 40. So, it is the median class.
∴ l = 35, cf = 45, f = 33 and h = 5
∴ Median = l + \(\left(\frac{\frac{n}{2}-c f}{f}\right)\) × h
= 35 + \(\left(\frac{50-45}{33}\right)\) × 5
= 35 + \(\frac{25}{33}\)
= 35 + 0.76
= 35.76
Hence, median age = 35.76 years.

Question 4.
The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and data obtained is represented in the following table :

Find the median length of the leaves.
Solution:
The series is in inclusive form. We convert it into exclusive form and prepare the cumulative frequency table as given below :

n = 40
⇒ \(\frac{n}{2}\) = 20
But 20 comes under the cumulative frequency 29 and the class interval against the cumulative frequency 29 is 144.5 – 153.5. So, it is the median class.
∴ l = 144.5, cf = 17, f = 12, and h = 9
Median = l + \(\left(\frac{\frac{n}{2}-c f}{f}\right)\) × h
= 144.5 + \(\left(\frac{20-17}{12}\right)\) × 9
= 144.5 + \(\frac{3 \times 9}{12}\)
= 144.5 + \(\frac{9}{4}\)
= 144.5 + 2.25
= 146.75 mm.
Hence, median length of leaves = 146.75 mm.

Question 5.
The following table gives the distribution of the life time of 400 neon lamps :

Find the median life time of a lamp.
Solution:
We prepare the cumulative frequency distribution table as given below:

n = 400
⇒ \(\frac{n}{2}=\frac{400}{2}\) = 200
But 200 comes under the cumulative frequency 216 and the class interval against the cumulative frequency 216 is 3000 – 3500. So, it is the median class.
∴ l = 3000, cf =130, f = 86, and h = 500
∴ Median = l + \(\left(\frac{\frac{n}{2}-c f}{f}\right)\) × h
= 3000 + \(\left(\frac{200-130}{86}\right)\) × 500
= 3000 + \(\frac{35000}{86}\)
= 3000 + 406.98 = 3406.98
Hence, median life time of a lamp = 3406.98 hours.

Question 6.
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows :

Determine the median number of letters in the surnames. Find the mean number of letters in the surnames ? Also, find the modal size of the surnames.
Solution:
For calculating the median, we prepare the cumulative frequency distribution table as given below :

Total n = 100
⇒ \(\frac{n}{2}=\frac{100}{2}\) = 50
But 50 comes under the cumulative frequency 76. The class interval against cumulative frequency 76 is 7 – 10.
So, it is the median class.
∴ l = 7, cf = 36, f = 40 and h = 3
∴ Median = l + \(\left(\frac{\frac{n}{2}-c f}{f}\right)\) × h
= 7 + \(\left(\frac{50-36}{40}\right)\) × 3
= 7 + \(\frac{14 \times 3}{40}\)
= 7 + \(\frac{42}{40}\)
= 7 + 1.05 = 8.05
For calculating the mean we prepare table as given below :

From the table, we have Σf_i = 100, Σf_id_i = – 18, a = 8.5
∴ Mean = a + \(\left(\frac{\Sigma f_i d_i}{\Sigma f_i}\right)\)
= 8.5 + \(\left(\frac{-18}{100}\right)\)
= 8.5 + \(\frac{18}{100}\)
= 8.5 – 0.18 = 8.32.
For calculating mode, the class 7 – 10 has maximum frequency.
So, it is the modal class.
∴ l = 7, f₁ = 40, f₀ = 30, f₂ = 16 and h = 3
Mode = l + \(\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right)\) × h
= 7 + \(\left(\frac{40-30}{2 \times 40-30-16}\right)\) × 3
= 7 + \(\frac{10 \times 3}{34}\)
= 7 + \(\frac{30}{34}\)
= 7 + 0.88 = 7.88
Hence, median = 8.05, Mean = 8.32 and modal size = 7.88.

Question 7.
The distribution below gives the weights of 30 students of a class. Find the median weight of the students. ’

Solution:
We prepare the cumulative frequency distribution table as given below.

n = 30
⇒ \(\frac{n}{2}=\frac{30}{2}\) = 15
But 15 comes under the cumulative frequency 19 and the class interval against the cumulative frequency 19 is 55 – 60. So, it is the median class.
∴ l = 55, cf = 13, f = 6 and h = 5
Median = 55 + \(\left(\frac{\frac{n}{2}-c f}{f}\right)\) × h
= 55 + \(\left(\frac{15-13}{6}\right)\) × 5
= 55 + \(\frac{10}{6}\)
= 55 + 1.67 = 56.67
Hence, median weight of the students = 56.67 kg.