Author name: Bhagya

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 वृत्त Ex 10.4 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 वृत्त Exercise 10.4

प्रश्न 1.
5 सें०मी० तथा 3 सें०मी० त्रिज्या वाले दो वृत्त दो बिंदुओं पर प्रतिच्छेद करते हैं तथा उनके केंद्रों के बीच की दूरी 4 सें०मी० है। उभयनिष्ठ जीवा की लंबाई ज्ञात कीजिए।
हल :

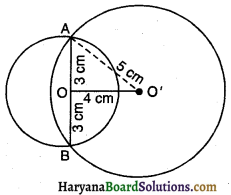
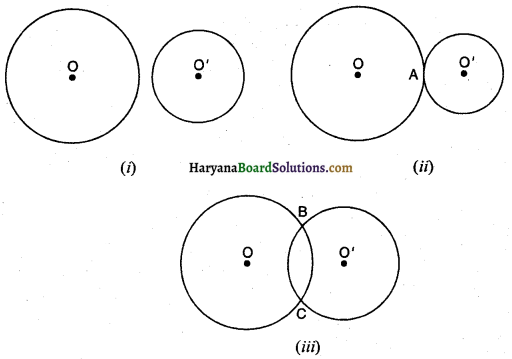
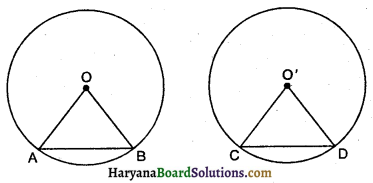
माना O व O’ केंद्र वाले दो वृत्त हैं जिनकी त्रिज्याएं क्रमशः 3 सें०मी० व 5 सें०मी० हैं।
∴ O’A = 5 सें०मी, OO’ = 4 सें०मी
समकोण त्रिभुज AOO’ में,
AO’² = AO² + OO’²
⇒ (5)² = AO² + (4)²
⇒ AO² = 25 – 16
⇒ AO² = 9
⇒ AO = 3
अतः उभयनिष्ठ जीवा AB है अर्थात 2AO या 2 × 3 = 6 सें०मी० उत्तर

प्रश्न 2.
यदि एक वृत्त की दो समान जीवाएं वृत्त के अंदर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खंड दूसरी जीवा के संगत खंडों के बराबर हैं।
हल :

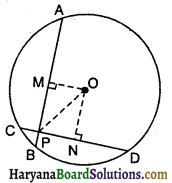
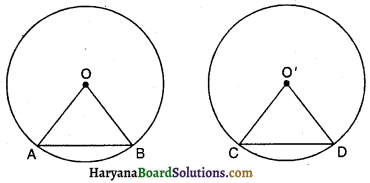
दिया है : AB तथा CD वृत्त की दो समान जीवाएं हैं, O वृत्त का केंद्र है। AB तथा CD, P पर प्रतिच्छेद करती हैं।
सिद्ध करना है:
(i) AP = PD
(ii) PB = CP
रचना : OM ⊥ AB, ON ⊥ CD खींचिए। OP को मिलाओ।
प्रमाण: AM = MB = \(\frac{1}{2}\) AB [∵ वृत्त के केंद्र से जीवा पर खींचा गया लंब जीवा को समद्विभाजित करता है]
इसी प्रकार CN = ND = \(\frac{1}{2}\)CD [वृत्त के केंद्र से जीवा पर खींचा गया लंब जीवा को समद्विभाजित करता है]
⇒ AM = ND तथा MB = CN …..(i) [∵ AB = CD दिया है]
अब ΔOMP तथा ΔONP में,
OM = ON [एक वृत्त की समान जीवाएं केंद्र से समान दूरी पर होती हैं।
∠OMP = ∠ONP [∵ प्रत्येक 90°]
OP = OP [उभयनिष्ठ]
∴ ΔΟΜΡ ≅ ΔΟΝΡ [समकोण-कर्ण-भुजा सर्वांगसमता]
⇒ MP = PN ….. (ii) [सर्वांगसम त्रिभुजों के संगत भाग]
समीकरण (i) तथा (ii) को जोड़ने पर,
AM + MP = ND + PN
⇒ AP = PD [इति सिद्धम]
समीकरण (i) में से समीकरण (ii) घटाने पर,
MB – MP = CN – PN
⇒ PB = CP [इति सिद्धम]

प्रश्न 3.
यदि एक वृत्त की दो समान जीवाएं वृत्त के अंदर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिंदु को केंद्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
हल :

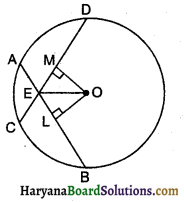
दिया है : केंद्र O वाले वृत्त की दो समान जीवाएं AB तथा CD वृत्त के अंदर परस्पर बिंदु E पर प्रतिच्छेदित होती हैं।
सिद्ध करना है : ∠OEB = ∠OED
रचना : O से OL ⊥ AB तथा OM ⊥ CD खींचिए।
प्रमाण : ∵ AB = CD [दिया है]
⇒ OL = OM [समान जीवाएं केंद्र से समान दूरी पर होती हैं]
ΔOEL तथा ΔOEM में,
OL = OM [प्रमाणित]
OE = OE [उभयनिष्ठ]
∠OLE = ∠OME [प्रत्येक = 90°]
∴ ΔOEL ≅ ΔOEM [समकोण-कर्ण-भुजा सर्वांगसमता]
∴ ∠OEL = ∠OEM [सर्वांगसम त्रिभुजों के संगत भाग]
या ∠OEB = ∠OED [इति सिद्धम]

प्रश्न 4.
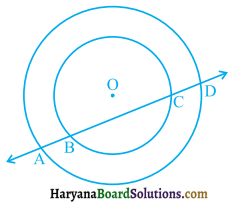
यदि एक रेखा दो संकेंद्री वृत्तों (एक ही केंद्र वाले वृत्त) को, जिनका केंद्र O है, A,B,C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB =CD है (आकृति अनुसार)।

हल :

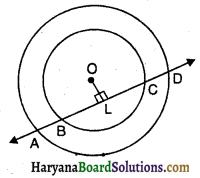
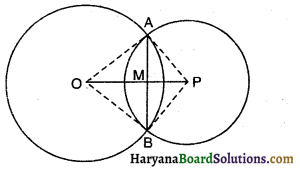
दिया है : दो संकेंद्री वृत्त जिनका केंद्र O है। एक रेखा इन्हें A, B, C तथा D बिंदुओं पर प्रतिच्छेद करती है।
सिद्ध करना है : AB = CD
रचना : O से OL ⊥ AD खींचिए।
प्रमाण : बड़े वृत्त में,
OL ⊥ AD
∴ AL = LD …(i) [∵ केंद्र से जीवा पर खींचा गया लंब उसे समद्विभाजित करता है]
इसी प्रकार छोटे वृत्त में,
OL ⊥ BC
∴ BL = LC …(ii) [∵ केंद्र से जीवा पर खींचा गया लंब उसे समद्विभाजित करता है]
समीकरण (ii) को (i) में से घटाने पर,
AL – BL = LD – LC
⇒ AB = CD [इति सिद्धम]

प्रश्न 5.
एक पार्क में बने 5 मी० त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियां रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 मी० हो, तो रेशमा और मनदीप के बीच की दूरी क्या है ?
हल :
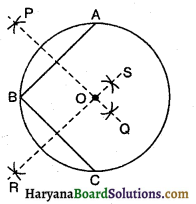
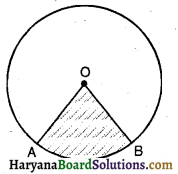
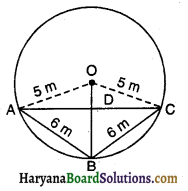
माना तीन लड़कियां रेशमा, सलमा तथा मनदीप एक वृत्त की परिधि पर क्रमशः बिंदु A, B तथा C पर खड़ी हैं। वृत्त की त्रिज्या 5 मी० है।
प्रश्नानुसार AB = BC = 6 मी०
AC = ? OA, OB तथा OC को मिलाओ।
AB = BC [दिया है]
∴ बिंदु B, AC के लंबार्धक पर स्थित है।
OA = OC [एक ही वृत्त की त्रिज्याएं]
∴ बिंदु O, AC के लंबार्धक पर स्थित है।
∴ OB, AC का लंबार्धक है जो AC को D बिंदु पर प्रतिच्छेदित करती है।
∴ AD = DC
∴ AC = 2 AD
माना OD = x मी०

तो DB = (5 – x) मी०
समकोण ΔOAD में,
AD² = OA² – OD²
= (5)² – (x)² …….(i)
समकोण ΔABD में,
AD² = AB² – DB²
= (6) – (5 – x)²
समीकरण (i) तथा (ii) की तुलना से,
(5)² – (x)² = (6)² – (5 – x)²
या 25 – x² = 36 – (25 + x² – 10x)
या 25 – x² = 36 – 25 – x² + 10x
या -10 x = 36 – 25 – 25
या -10x = -14
या x = \(\frac{14}{10}\) = 1.4 मी०
अतः OD = 1.4 मी०
अब AD² = (5)² – (x)²
= 25 – (1.4)²
= 25 – 1.96 = 23.04
AD = \(\sqrt{23.04}\) = 4.8 मी०
⇒ AC = 2AD = 2 × 4.8 = 9.6 मी०
अतः रेशमा व मनदीप के मध्य की दूरी = 9.6 मी० उत्तर

प्रश्न 6.
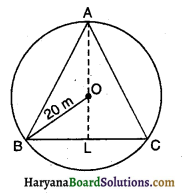
20 मी० त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लंबाई ज्ञात कीजिए।
हल :
माना तीन लड़के अंकुर, सैय्यद तथा डेविड वृत्त की परिधि पर एक-दूसरे से बराबर दूरी पर बिंदु A, B व C पर बैठे हैं। इसलिए ABC समबाहु त्रिभुज है। वृत्त की त्रिज्या 20 मी० है। A से AL ⊥ BCखींचिए। क्योंकि त्रिभुज समबाहु है इसलिए यह लंब केंद्र O में से भी गुजरता है।
माना समबाहु त्रिभुज की प्रत्येक भुजा = 2x मी० है
तो BL = \(\frac{\mathrm{BC}}{2}=\frac{2 x}{2}\) = x मी० [∵ OL ⊥ BC है]
समकोण ΔABL में

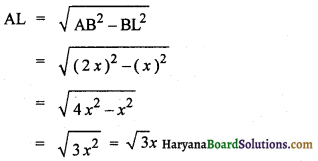
OL = AL – AO = (\(\sqrt{3}\)x – 20) मी०
समकोण ΔOBL में

OB² = OL² + BL²
(20)² = (\(\sqrt{3}\)x – 20) + (x)²
400 = 3x² + 400 – 40\(\sqrt{3}\)x + x²
4x² – 40\(\sqrt{3}\)x = 0
4x (x – 10\(\sqrt{3}\)) = 0
⇒ 4x = 0
⇒ x = \(\frac{0}{4}\) = 0 जो कि संभव नहीं है।
या x – 10\(\sqrt{3}\) = 0
x = 10\(\sqrt{3}\)
∴ BC = 2 BL = 2 × 10\(\sqrt{3}\) = 20\(\sqrt{3}\) मी०
अतः प्रत्येक फोन की डोरी की लंबाई = 20\(\sqrt{3}\) मी० उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 वृत्त Ex 10.3 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 वृत्त Exercise 10.3

प्रश्न 1.
वृत्तों के कई जोड़े (युग्म) खींचिए। प्रत्येक जोड़े में कितने बिंदु उभयनिष्ठ हैं ? उभयनिष्ठ बिंदुओं की अधिकतम संख्या क्या है ?
हल :

(1) स्थिति (i) में वृत्तों का कोई उभयनिष्ठ बिंदु नहीं है। इसलिए इस अवस्था में इनके उभयनिष्ठ बिंदु 0 हैं।
(2) स्थिति (ii) में वृत्तों का उभयनिष्ठ बिंदु A है। इसलिए इस अवस्था में इनके उभयनिष्ठ बिंदु 1 हैं।
(3) स्थिति (iii) में वृत्तों के उभयनिष्ठ बिंदु B और C हैं। इसलिए इस अवस्था में इनके उभयनिष्ठ बिंदु 2 हैं।
इसलिए वृत्तों के युग्म खींचने पर इनके अधिक से अधिक 2 उभयनिष्ठ बिंदु हो सकते हैं।

प्रश्न 2.
मान लीजिए आपको एक वृत्त दिया है। एक रचना इसके केंद्र को ज्ञात करने के लिए दीजिए।
हल :

रचना के चरण :

1. तीन बिंदु A, B तथा C वृत्त की परिधि पर लीजिए।
2. AB तथा BC को मिलाइए।
3. AB तथा BC के लंब समद्विभाजक PQ तथा RS खींचे, जो एक-दूसरे को O पर प्रतिच्छेद करते हैं। तब, O वृत्त का केंद्र है।

प्रश्न 3.
यदि दो वृत्त परस्पर दो बिंदुओं पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि उनके केंद्र उभयनिष्ठ जीवा के लंब समद्विभाजक पर स्थित हैं।
हल :

दिया है :
दो वृत्त जिनके केंद्र O तथा P हैं। एक-दूसरे को A व B बिंदुओं पर प्रतिच्छेदित करते हैं।
सिद्ध करना है : OP, AB का लंब समद्विभाजक है।
रचना : OA, OB, PA व PB को मिलाओ। माना OP, AB को M पर प्रतिच्छेदित करती है।
प्रमाण : ΔOAP और ΔOBP में,
OA = OB [एक ही वृत्त की त्रिज्याएं]
PA = PB [एक ही वृत्त की त्रिज्याएं]
OP = OP [उभयनिष्ठ]
∴ ΔOAP ≅ ΔOBP [भुजा-भुजा-भुजा सर्वांगसमता]
या ∠AOP = ∠BOP [सर्वांगसम त्रिभुजों के संगत भाग]
अर्थात ∠AOM = ∠BOM ………(i)
अब ΔAOM और ΔBOM में,
OA = OB [एक ही वृत्त की त्रिज्याएं]
∠AOM = ∠BOM [समीकरण (i) से]
और OM = OM [उभयनिष्ठ]
∴ ΔΑΟΜ ≅ ΔBOM [भुजा-कोण-भुजा सर्वांगसमता]
या AM = BM [सर्वांगसम त्रिभुजों के संगत भाग] …(ii)
तथा ∠AMO = ∠BMO [सर्वांगसम त्रिभुजों के संगत भाग] …(iii)
परंतु ∠AMO + ∠BMO = 180° [रैखिक युग्म]
∴ ∠AMO = ∠BMO = 90° ….(iv)
∴ OM अर्थात OP, AB का लंब समद्विभाजक है। [समीकरण (ii) और (iv) से]
[इति सिद्धम]

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.6 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.6

[नोट-जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।]

प्रश्न 1.
एक बेलनाकार बर्तन के आधार की परिधि 132 सें०मी० और उसकी ऊंचाई 25 सें०मी० है। इस बर्तन में कितने लीटर पानी आ सकता है ? (1000 सें०मी०³ = 1 लीटर)
हल :
यहां पर,
बेलनाकार बर्तन की ऊंचाई (h) = 25 सें०मी०
बेलनाकार बर्तन के आधार की परिधि = 132 सें०मी०
⇒ 2πr = 132
⇒ 2 × \(\frac{22}{7}\) × r = 132
या r = \(\frac{132 \times 7}{2 \times 22}\) = 21 सें०मी०
∴ बेलनाकार बर्तन का आयतन (V) = πr²h
= \(\frac{22}{7}\) × 21 × 21 × 25 सें०मी०³
= 34650 सें०मी०³
अतः बर्तन में जितने लीटर पानी आ सकता है = \(\frac{34650}{1000}\) लीटर
= 34.65 लीटर उत्तर

प्रश्न 2.
लकड़ी के एक बेलनाकार पाइप का आंतरिक व्यास 24 सें०मी० है और बाहरी व्यास 28 सें०मी० है। इस पाइप की लंबाई 35 सें०मी० है। इस पाइप का द्रव्यमान ज्ञात कीजिए, यदि 1 सें०मी०³ लकड़ी का द्रव्यमान 0.6 ग्राम है।
हल :
यहां पर,
बेलनाकार पाइप का अंतः व्यास (d) = 24 सें०मी०
बेलनाकार पाइप की अंतः त्रिज्या (r) = \(\frac{24}{2}\) = 12 सें०मी०
बेलनाकार पाइप का बाह्य व्यास (D) = 28 सें०मी०
बेलनाकार पाइप की बाह्य त्रिज्या (R) = \(\frac{28}{2}\) = 14 सें०मी०
बेलनाकार पाइप की लंबाई (h) = 35 सें०मी०
इस प्रकार पाइप में लगी लकड़ी का आयतन (V) =
बाह्य आयतन – आंतरिक आयतन = πh (R² – r²)
= \(\frac{22}{7}\) × 35 [(14)² – (12)²] सें०मी०³
= 110 [196 – 144] सें०मी०³
= 110 × 52 = 5720 सें०मी०³
1 सें०मी०³ लकड़ी का द्रव्यमान = 0.6 ग्राम
अतः 5720 सें०मी०³ पाइप का द्रव्यमान = 5720 × 0.6 ग्राम = 3432 ग्राम
= 3.432 किलोग्राम उत्तर

प्रश्न 3.
एक सोफ्ट ड्रिंक (soft drink) दो प्रकार के पैकों में उपलब्ध है : (i) लंबाई 5 सें०मी० और चौड़ाई 4 सें०मी० वाले एक आयताकार आधार का टिन का डिब्बा जिसकी ऊंचाई 15 सें०मी० है और (ii) व्यास 7 सें०मी० वाले वृत्तीय आधार और 10 सें०मी० ऊंचाई वाला एक प्लास्टिक का बेलनाकार डिब्बा। किस डिब्बे की धारिता अधिक है और कितनी अधिक है ?
हल :
यहां पर,
आयताकार आधार वाले डिब्बे की लंबाई (l) = 5 सें०मी०
आयताकार आधार वाले डिब्बे की चौड़ाई (b) = 4 सें०मी०
आयताकार आधार वाले डिब्बे की ऊंचाई (h) = 15 सें०मी०
∴ आयताकार आधार वाले डिब्बे का आयतन (V) = l × b × h = 5 × 4 × 15 = 300 सें०मी०³
बेलनाकार डिब्बे की ऊंचाई (h) = 10 सें०मी०
बेलनाकार डिब्बे के आधार का व्यास (d) = 7 सें०मी०
बेलनाकार डिब्बे के आधार की त्रिज्या (r) = \(\frac{7}{2}\) = सें०मी०
∴ बेलनाकार डिब्बे का आयतन (V) = πr²h
\(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 10 सें०मी०³
= 385 सें०मी०³
∵ 385 > 300 ∴ बेलनाकार डिब्बे की धारिता अधिक है।
अतः बेलनाकार डिब्बे की धारिता जितनी अधिक है = 385 – 300 सें०मी०³
= 85 से०मी०³ उत्तर

प्रश्न 4.
यदि एक बेलन का पार्श्व पृष्ठीय क्षेत्रफल 94.2 सें०मी०² है और उसकी ऊंचाई 5 सें०मी० है, तो ज्ञात कीजिए:
(i) आधार की त्रिज्या,
(ii) बेलन का आयतन (70 = 3.14 लीजिए)।
हल :
(i) यहां पर,
बेलन की ऊंचाई (h) = 5 सें०मी०
बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 94.2 सें०मी०²
⇒ 2πrh = \(\frac{942}{10}\) सें०मी०²
या 2 × 3.14 × r × 5 = \(\frac{942}{10}\)
या \(\frac{2 \times 314 \times r \times 5}{100}\) = \(\frac{942}{10}\)
या \(\frac{314 r}{10}\) = \(\frac{942}{10}\)
या r = \(\frac{942}{10} \times \frac{10}{314}\) = 3 सें०मी०
अतः बेलन के आधार की त्रिज्या (r) = 3 सें०मी० उत्तर

(ii) बेलन का आयतन = πr²h
= 3.14 × 3 × 3 × 5 सें०मी०³
= 3.14 × 45 = 141.3 सें०मी०³ उत्तर

प्रश्न 5.
10m गहरे एक बेलनाकार बर्तन की आंतरिक वक्र पृष्ठ को पेंट कराने का व्यय 2200 रुपए है। यदि पेंट कराने की दर ₹ 20 प्रति मी०² है, तो ज्ञात कीजिए :
(i) बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल,
(ii) आधार की त्रिज्या,
(iii) बर्तन की धारिता।
हल :
(i) बेलनाकार बर्तन के आंतरिक वक्र पृष्ठ पर पेंट कराने का व्यय = ₹ 2200
बेलनाकार बर्तन के आंतरिक वक्र पृष्ठ पर पेंट कराने की दर = ₹ 20 प्रति मी०²
अतः बेलनाकार बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल
= \(\frac{2200}{20}\) मी०²
= 110 मी०² उत्तर

(ii) बेलनाकार बर्तन की गहराई (h) = 10 मी०
बेलनाकार बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल = 110 मी०²
⇒ 2πrh = 110
या 2 × \(\frac{22}{7}\) × r × 10 = 110
या \(\frac{440}{7}\)r = 110
या r = \(\frac{110 \times 7}{440}=\frac{7}{4}\) मी० = 1.75 मी०
अतः बेलनाकार बर्तन के आधार की त्रिज्या (r) = 1.75 मी० उत्तर

(iii) बेलनाकार बर्तन का आयतन (V) = πr²h
= \(\frac{22}{7} \times \frac{7}{4} \times \frac{7}{4}\) × 10 मी०³ = 96.25 मी०³
अतः बेलनाकार बर्तन की धारिता = 96.25 किलोलीटर (∵ 1 मी०³ = 1 kl) उत्तर

प्रश्न 6.
ऊंचाई 1 मी० वाले एक बेलनाकार बर्तन की धारिता 15.4 लीटर है। इसको बनाने के लिए कितने वर्ग मीटर धातु की शीट की आवश्यकता होगी ? [B.S.E.H. March, 2020]
हल :
यहां पर,
बेलनाकार बर्तन की ऊंचाई (h) = 1 मी०
बेलनाकार बर्तन की धारिता = 15.4 लीटर
बेलनाकार बर्तन का आयतन (V) = \(\frac{154}{10 \times 1000}\)मी०³

प्रश्न 7.
सीसे की एक पेंसिल (lead pencil) लकड़ी के एक बेलन के अभ्यंतर में ग्रेफाइट (graphite) से बने ठोस बेलन को डालकर बनाई गई है। पेंसिल का व्यास 7 मि०मी० है और ग्रेफाइट का व्यास 1 मि०मी० है। यदि पेंसिल की लंबाई 14 सें०मी० है, तो लकड़ी का आयतन और ग्रेफाइट का आयतन ज्ञात कीजिए।
हल :
यहां पर,
पेंसिल का व्यास (d) = 7 मि०मी०
पेंसिल की त्रिज्या (r) = \(\frac{7}{2}\) मि०मी० = \(\frac{7}{20}\) सें०मी०
पेंसिल की लंबाई (h) = 14 सें०मी०
अतः पेंसिल का आयतन (V) = πr²h
= \(\frac{22}{7} \times \frac{7}{20} \times \frac{7}{20}\) × 14 सें०मी०³
= \(\frac{539}{100}\) सें०मी०³
= 5.39 सें०मी०³
ग्रेफाइट के सिक्के का व्यास (d) = 1 मि०मी०
ग्रेफाइट के सिक्के की त्रिज्या (r₁) = \(\frac{1}{2}\) मि०मी० = \(\frac{1}{20}\) सें०मी०
ग्रेफाइट के सिक्के का आयतन (V) = πr₁²h
= \(\frac{22}{7} \times \frac{1}{20} \times \frac{1}{20}\) × 14 सें०मी०³
= \(\frac{11}{100}\) सें०मी०³
= 0.11 सें०मी०³
इस प्रकार पेंसिल में लगी लकड़ी का आयतन = 5.39 – 0.11 = 5.28 सें०मी०³ उत्तर

प्रश्न 8.
एक अस्पताल (hospital) के एक रोगी को प्रतिदिन 7 सें०मी० व्यास वाले एक बेलनाकार कटोरे में सूप (soup) दिया जाता है। यदि यह कटोरा सूप से 4 सें०मी० ऊंचाई तक भरा जाता है, तो इस अस्पताल में 250 रोगियों के लिए प्रतिदिन कितना सूप तैयार किया जाता है ?
हल :
यहां पर,
बेलनाकार कटोरे का व्यास (d) = 7 सें०मी०
बेलनाकार कटोरे की त्रिज्या (r) = \(\frac{7}{2}\) सें०मी०
कटोरे में सूप की ऊंचाई (h) = 4 सें०मी०
कटोरे में सूप का आयतन = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 4
= 154 सें०मी०³
1 रोगी को दिया जाने वाला सूप = 154 सें०मी०³
250 रोगियों को दिया जाने वाला सूप = 154 × 250 सें०मी०³
= 38500 सें०मी०³
= \(\frac{38500}{1000}\) = 285 लीटर (∵ 1000 सें०मी०³ = 1 लीटर)
अतः अस्पताल में प्रतिदिन जितने लीटर सूप तैयार होता है = 38.5 लीटर उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 वृत्त Ex 10.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 वृत्त Exercise 10.2

प्रश्न 1.
याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएं बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएं उनके केंद्रों पर बराबर कोण अंतरित करती हैं।
हल :
दिया है : दो सर्वांगसम वृत्त जिनके केंद्र O तथा O’ हैं। AB व CD दो समान जीवाएं हैं।
सिद्ध करना है : ∠AOB = ∠CO’D

ΔAOB तथा ΔCO’D में,
OA = O’C [सर्वांगसम वृत्तों की त्रिज्याएं]
OB = O’D [सर्वांगसम वृत्तों की त्रिज्याएं]
AB = CD [दिया है]
ΔAOB ≅ ΔCO’D [भुजा-भुजा-भुजा सर्वांगसमता]
∠AOB = ∠CO’D [सर्वांगसम त्रिभुजों के संगत भाग]
[इति सिद्धम]

प्रश्न 2.
सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएं उनके केंद्रों पर बराबर कोण अंतरित करें, तो जीवाएं बराबर होती हैं।
हल :
दिया है : दो सर्वांगसम वृत्त जिनके केंद्र O तथा O’ हैं। दो जीवाएं AB और CD इस प्रकार हैं कि ∠AOB = ∠CO’D.
सिद्ध करना है : जीवा AB = जीवा CD.

ΔAOB तथा ΔCO’D में,
OA = O’C [सर्वांगसम वृत्तों की त्रिज्याएं]
OB = O’D [सर्वांगसम वृत्तों की त्रिज्याएं]
∠AOB ≅ ∠CO’D [दिया है]
∴ ΔAOB = ΔCO’D [भुजा-कोण-भुजा सर्वांगसमता]
∴ जीवा AB = जीवा CD [सर्वांगसम त्रिभुजों के संगत भाग]
[इति सिद्धम]

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 वृत्त Ex 10.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 वृत्त Exercise 10.1

प्रश्न 1.
खाली स्थान भरिए :
(i) वृत्त का केंद्र वृत्त के ………………….. में स्थित है।
(ii) एक बिंदु, जिसकी वृत्त के केंद्र से दूरी त्रिज्या से अधिक हो, वृत्त के ……………… में स्थित होता है।
(iii) वृत्त की सबसे बड़ी जीवा वृत्त का …………….. होता है।
(iv) एक चाप ……………………… होता है, जब इसके सिरे एक व्यास के सिरे हों।
(v) वृत्तखंड एक चाप तथा ……………………….. के बीच का भाग होता है।
(vi) एक वृत्त, जिस तल पर स्थित है, उसे …………….. भागों में विभाजित करता है।
उत्तर :
(i) अभ्यंतर
(ii) बहिर्भाग
(iii) व्यास
(iv) अर्द्धवृत्त
(v) जीवा
(vi) तीन।

प्रश्न 2.
लिखिए, सत्य या असत्य। अपने उत्तर के कारण दीजिए।
(i) केंद्र को वृत्त पर किसी बिंदु से मिलाने वाला रेखाखंड वृत्त की त्रिज्या होती है।
(ii) एक वृत्त में समान लंबाई की परिमित जीवाएं होती हैं।
(ii) यदि एक वृत्त को तीन बराबर चापों में बांट दिया जाए, तो प्रत्येक भाग दीर्घ चाप होता है।
(iv) वृत्त की एक जीवा, जिसकी लंबाई त्रिज्या से दोगुनी हो, वृत्त का व्यास है।
(v) त्रिज्यखंड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
(vi) वृत्त एक समतल आकृति है।
उत्तर :
(i) सत्य : क्योंकि वृत्त की परिधि पर स्थित सभी बिंदु केंद्र से समान दूरी पर होते हैं, जिसे वृत्त की त्रिज्या कहते हैं।
(ii) असत्य : क्योंकि वृत्त की परिधि पर अनेक बिंदु होते हैं जिन्हे मिलाने से अपरिमित जीवाएं प्राप्त की जा सकती हैं।
(iii) असत्य : क्योंकि एक वृत्त को तीन बराबर चापों में बांट देने पर प्रत्येक भाग समान चाप कहलाता है।
(iv) सत्य : क्योंकि व्यास सबसे बड़ी जीवा होती है, जिसकी लंबाई त्रिज्या से दोगुनी होती है।
(v) असत्य : क्योंकि चाप और दो त्रिज्याओं के बीच का क्षेत्र (केंद्र को चाप के बिंदु से मिलाने वाला) त्रिज्यखंड कहलाता है। आकृति में OAB त्रिज्यखंड है।

(vi) सत्य : क्योंकि वृत्त एक बिंदु का बिंदुपथ होता है, जो एक तल में स्थित होता है।

Haryana State Board HBSE 9th Class Maths Solutions Chapter 11 रचनाएँ Ex 11.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 11 रचनाएँ Exercise 11.2

प्रश्न 1.
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 7 cm, ∠B = 750 और AB + AC = 13 cm हो।
हल :
रचना के चरण-

1. एक किरण BX खींचिए तथा इसमें से एक रेखाखंड BC = 7 cm लीजिए।
2. बिंदु B पर ∠YBX = 75° बनाओ।
3. BY से BD = 13 cm काटो।
4. D को C से मिलाओ।
5. CD का लंब समद्विभाजक खींचिए जो BD को A पर प्रतिच्छेद करें।
6. A को C से मिलाइए।
7. इस प्रकार ABC अभीष्ट त्रिभुज है।

प्रश्न 2.
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 8 cm, ∠B = 45° और AB – AC = 3.5 cm हो। [B.S.E.H. 2017, 2018, 2020]
हल :
रचना के चरण-

1. एक किरण BX खींचिए तथा इसमें से एक रेखाखंड BC = 8 cm लीजिए।
2. अब बिंदु B पर ∠YBC = 45° बनाओ।
3. BY से BD = 3.5 cm काटो।
4. D को C से मिलाओ।
5. CD का लंब समद्विभाजक RS खींचो जो BY को A पर प्रतिच्छेद करता है।
6. A को C से मिलाइए।
7. इस प्रकार ABC अभीष्ट त्रिभुज है।

प्रश्न 3.
एक त्रिभुज PQR की रचना कीजिए, जिसमें QR = 6 cm, ∠Q = 60° और PR – PQ = 2 cm हो।
हल :
रचना के चरण-

1. एक किरण QX खींचिए तथा इसमें से एक रेखाखंड QR = 6 cm लीजिए।
2. बिंदु Q पर ∠YQX = 60° बनाओ।
3. YQ को Y’ तक आगे बढ़ाकर QY’ में से QS = 2 cm काटो।
4. R को S से मिलाओ।
5. RS का लंब समद्विभाजक AB खींचिए जो QY को P पर काटे।
6. P को R से मिलाइए।
7. इस प्रकार PQR अभीष्ट त्रिभुज है।

प्रश्न 4.
एक त्रिभुज XYZ की रचना कीजिए, जिसमें ∠Y =30°, ∠Z = 90° और XY + YZ + ZX = 11 cm हो।
हल :
रचना के चरण-

1. एक रेखाखंड PQ = 11 cm खींचिए।
2. P पर एक किरण PL खींचिए जिससे कि ∠LPQ = \(\frac{1}{2}\) × 30° = 150
3. Q पर, एक किरण QM खींचिए जिससे कि ∠MQP = \(\frac{1}{2}\) × 90° = 45० जो PL को X पर काटे।
4. PX का लंब समद्विभाजक AB खींचिए जो PQ को Y पर प्रतिच्छेद करे।
5. QX का लंब समद्विभाजक CD खींचिए जो PQ को Z पर प्रतिच्छेद करे।
6. XY तथा Xz को मिलाओ।
7. इस प्रकार XYZ अभीष्ट त्रिभुज है।

प्रश्न 5.
एक समकोण त्रिभुज की रचना कीजिए, जिसका आधार 12 cm और कर्ण तथा अन्य भुजा का योग 18 cm है।
हल :
रचना के चरण-

1. एक रेखाखंड BC = 12 cm खींचिए।
2. बिंदु B पर ∠YBC = 90° बनाओ तथा BD = 18 cm काटो।
3. DC को मिलाओ।
4. अब DC का लंबार्धक PQ खींचो जो DB को A पर प्रतिच्छेद करे।
5. AC को मिलाओ।
6. इस प्रकार ABC अभीष्ट त्रिभुज है।

Haryana State Board HBSE 9th Class Maths Solutions Chapter 11 रचनाएँ Ex 11.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 11 रचनाएँ Exercise 11.1

प्रश्न 1.
एक दी हुई किरण के प्रारंभिक बिंदु पर 90° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
हल :

रचना के चरण-

1. एक किरण AB खींचिए।
2. A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
3. परकार को इतना ही खुला रखकर D से चाप DE लगाओ। इसी प्रकार E से चाप EF लगाओ।
4. अब परकार कुछ अधिक खोलकर E तथा F से चापें लगाओ जो परस्पर K पर काटें।
5. अब K से गुजरती हुई एक किरण AC खींचिए।
6. ∠CAB, अभीष्ट कोण है जो 90° का है।

सत्यापन- रचना से EA = AD = ED
∴ AED एक समबाहु त्रिभुज है।
अतः ∠EAD = 60° …….(i)
इसी प्रकार, AE = EF = FA
⇒ AEF एक समबाहु त्रिभुज है।
∠EAF = 60°
क्योंकि AC, ∠EAF का समद्विभाजक है।
∴ ∠EAC = \(\frac{1}{2}\) × 60° = 30° …….(ii)
समीकरण (i) व (ii) से,
∠CAB = ∠EAC + ∠EAD
= 30° + 60° = 90°

प्रश्न 2.
एक दी हुई किरण के प्रारंभिक बिंदु पर 45° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
हल :

रचना के चरण-

1. एक किरण AB खींचिए।
2. A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
3. परकार को इतना ही खुला रखकर D से चाप DE लगाओ। इसी प्रकार E से चाप EF लगाओ। अब परकार कुछ अधिक खोलकर E तथा F से चापें लगाओ जो परस्पर K पर काटें।
4. अब K से गुजरती हुई एक किरण AL खींचो। ∠LAB का माप 90° होगा।
5. अब M तथा D से चापें लगाओ जो परस्पर N पर काटें।
6. अब N से गुजरती हुई एक किरण AC खींचिए।
7. ∠CAB, अभीष्ट कोण है जो 45° का है।

सत्यापन- रचना में ∠LAB = 90° है और AC, ∠LAB का समद्विभाजक है।
∠CAB = \(\frac{1}{2}\)∠LAB = \(\frac{1}{2}\) × 90° = 45°

प्रश्न 3.
निम्न मापों के कोणों की रचना कीजिए- [B.S:E.H. March, 2018]
(i) 30°
(ii) \(22 \frac{1^{\circ}}{2}\)
(iii) 15°
हल :
(i) रचना के चरण-

1. एक किरण AB खींचिए।
2. A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
3. परकार को इतना ही खुला रखकर D से DE चाप लगाओ।
4. अब परकार कुछ अधिक खोलकर D व E से चापें लगाओ जो परस्पर F पर काटें।
5. F में से गुजरती हुई एक किरण AC खींचिए।
6. ∠CAB, अभीष्ट कोण है जो 30° का है।

(ii) रचना के चरण- [B.S.E.H. March, 2019]

1. एक किरण AB खींचिए।
2. A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
3. परकार को इतना ही खुला रखकर D से DE चाप लगाओ।
4. अब परकार कुछ अधिक खोलकर D व E से चापें लगाओ जो परस्पर K पर काटें।
5. K से गुजरती हुई एक किरण AH खींचिए। इस प्रकार ∠HAB = 30° का होगा।
6. अब D व L से चापें लगाओ जो परस्पर M पर काटें।
7. M से गुजरती हुई किरण AF खींचिए। इस प्रकार ∠FAB = 15° का होगा।
8. अब N तथा L से चापें लगाओ जो परस्पर P पर काटें।
9. P में से गुजरती हुई किरण AC खींचिए।
10. ∠CAB, अभीष्ट कोण है जो \(22 \frac{1^{\circ}}{2}\) का है।

(iii) रचना के चरण-

1. एक किरण AB खींचिए।
2. A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
3. परकार को इतना ही खुला रखकर D से DE चाप लगाओ।
4. अब परकार कुछ अधिक खोलकर D व E से चापें लगाओ जो परस्पर K पर काटें।
5. K से गुजरती हुई एक किरण AH खींचिए। इस प्रकार ∠HAB = 30° का होगा।
6. अब F व D से चापें लगाओ जो परस्पर L पर काटें।
7. L में से गुजरती हुई एक किरण AC खींचिए।
8. ∠CAB, अभीष्ट कोण है जो 15° का है।

प्रश्न 4.
निम्न कोणों की रचना कीजिए और चाँदे द्वारा मापकर पुष्टि कीजिए-
(i) 750
(ii) 105° [March, 2020]
(iii) 135°
हल :
(i) रचना के चरण-

1. एक किरण AB खींचिए।
2. A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
3. परकार को इतना ही खुला रखकर D से DE चाप लगाओ। इसी प्रकार E से चाप EF लगाओ।
4. अब परकार कुछ अधिक खोलकर E व F से चापें लगाओ जो परस्पर K पर काटें।
5. K से गुजरती हुई एक किरण AH खींचिए।
6. बिंदु L व E से चापें लगाओ जो परस्पर N पर प्रतिच्छेद करें।
7. N से गुजरती हुई एक किरण AC खींचिए।
8. ∠CAB, अभीष्ट कोण है जो 75° का है।
9. ∠CAB को चाँदे से नापने पर पता चलता है कि यह 75° का है।

(ii) रचना के चरण-

1. एक किरण AB खींचिए।
2. A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
3. परकार को इतना ही खुला रखकर D से DE चाप लगाओ। इसी प्रकार E से चाप EF लगाओ।
4. अब परकार कुछ अधिक खोलकर E व F से चापें लगाओ जो परस्पर G पर काटें।
5. G से गुजरती हुई एक किरण AH खींचिए।
6. बिंदु F तथा L से चापें लगाओ जो परस्पर M पर काटें।
7. M से गुजरती हुई किरण AC खींचिए।
8. ∠CAB, अभीष्ट कोण है जो 105° का है।
9. इस कोण को चाँदे से नापने पर पता चलता है कि यह 105° का है।

(iii) रचना के चरण-

1. एक किरण AB खींचिए।
2. A को केंद्र मानकर तथा किसी त्रिज्या की परकार खोलकर एक चाप लगाओ जो किरण AB को D पर प्रतिच्छेद करे।
3. परकार को इतना ही खुला रखकर D से DE चाप लगाओ। इसी प्रकार E से EF तथा F से FG चाप लगाओ।
4. अब परकार को पहले से अधिक खोलकर E व F से चापें लगाओ जो परस्पर K पर काटें।
5. K में से गुजरती हुई एक किरण AH खींचिए।
6. बिंदु L तथा G से चापें लगाओ जो परस्पर M पर काटें।
7. अब M से गुजरती हुई एक किरण AC खींचिए।
8. ∠CAB, अभीष्ट कोण है जो 135° का है।
9. ∠CAB को चाँदे से नापने पर पता चलता है कि यह 135° का है।

प्रश्न 5.
एक समबाहु त्रिभुज की रचना कीजिए, जब इसकी भुजा दी हो तथा कारण सहित रचना कीजिए।
हल :
रचना के चरण-

1. एक रेखाखंड BC = 5.5 cm खींचिए।
2. B और C को केंद्र मानकर BC = 5.5 cm त्रिज्या की परकार खोलकर दो चापें लगाएँ जो परस्पर A पर प्रतिच्छेद करें।
3. A को B व C से मिलाओ।
4. इस प्रकार ABC अभीष्ट समबाहु त्रिभुज है।

सत्यापन-क्योंकि रचना द्वारा AB = BC = CA = 5.5 cm
⇒ ∠C = ∠B = ∠A = 60°
∴ ΔABC समबाहु त्रिभुज है।

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.8 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.8

[नोट-जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।]

प्रश्न 1.
उस गोले का आयतन ज्ञात कीजिए जिसकी त्रिज्या निम्न है :
(i) 7 सें०मी०
(ii) 0.63 मी०
हल :
(i) यहां पर,
गोले की त्रिज्या (r) = 7 सें०मी०
गोले का आयतन (V) = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7}\) 7 × 7 × 7 सें०मी०³
= \(\frac{4312}{3}\) सें०मी०³ = 1437\(\frac{1}{3}\)सें०मी०³ उत्तर

(ii) यहां पर,
गोले की त्रिज्या (r) = 0.63 मी० = \(\frac{63}{100}\) मी०
गोले का आयतन (V) = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times \frac{63}{100} \times \frac{63}{100} \times \frac{63}{100}\) मी०³
= \(\frac{1047816}{1000000}\) मी०³
= 1.05 मी०³ उत्तर

प्रश्न 2.
उस ठोस गोलाकार गेंद द्वारा हटाए गए (विस्थापित) पानी का आयतन ज्ञात कीजिए, जिसका व्यास निम्न है:
(i) 28 सें०मी०
(ii) 0.21 मी०
हल :
(i) यहां पर,
गोले का व्यास (d) = 28 सें०मी०
गोले की त्रिज्या (r) = \(\frac{28}{2}\) सें०मी० = 14 सें०मी०
गोले का आयतन (V) = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7}\) × 14 × 14 × 14 सें०मी०³
\(\frac{34496}{3}\) सें०मी०³ = 11498\(\frac{2}{3}\) सें०मी०³ उत्तर
अतः गोले द्वारा हटाए गए पानी का आयतन = 11498\(\frac{2}{3}\) सें०मी०³ उत्तर

(ii) यहां पर,
गोले का व्यास (d) = 0.21 मी० = \(\frac{21}{100}\) मी०
गोले की त्रिज्या (r) = \(\frac{21}{2 \times 100}\) = \(\frac{21}{100}\)
∴ गोले का आयतन (V) = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times \frac{21}{200} \times \frac{21}{200} \times \frac{21}{200}\) सें०मी०³
= \(\frac{4851}{1000000}\) सें०मी०³ = 0.004851 मी०³
अतः गोले द्वारा हटाए गए पानी का आयतन = 0.004851 मी०³ उत्तर

प्रश्न 3.
धातु की एक गेंद का व्यास 4.2 सें०मी० है। यदि इस धातु का घनत्व 8.9 ग्राम प्रति सें०मी०³ है, तो इस गेंद का द्रव्यमान ज्ञात कीजिए।
हल :
यहां पर,
धातु की गेंद का व्यास (d) = 4.2 सें०मी० = \(\frac{21}{100}\) सें०मी०
धातु की गेंद की त्रिज्या (r) = \(\frac{21}{100}\) सेंमी० = \(\frac{21}{100}\) सें०मी०
धातु की गेंद का आयतन (V) = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times \frac{21}{10} \times \frac{21}{10} \times \frac{21}{10}\) सें०मी०³
= \(\frac{38808}{1000}\) सें०मी०³
1 सें०मी० धातु का द्रव्यमान = 8.9 ग्राम
दी गई धातु की गेंद का द्रव्यमान = \(\frac{38808}{1000} \times \frac{89}{10}\) ग्राम
\(\frac{3453912}{10000}\) ग्राम = 345.3912 ग्राम
= 345.39 ग्राम उत्तर

प्रश्न 4.
चंद्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। चंद्रमा का आयतन पृथ्वी के आयतन की कौन-सी भिन्न है ?
हल :
माना पृथ्वी का व्यास (d) = 2x मी०
पृथ्वी की त्रिज्या (r₁) = \(\frac{2 x}{2}\)
पृथ्वी का आयतन (V) = \(\frac{4}{3}\)πr₁³
= \(\frac{4}{3}\)π × x × x × x मी०³
= \(\frac{4}{3}\)πx³
चंद्रमा का व्यास (d) = \(\frac{2 x}{4}\) मी०
चंद्रमा की त्रिच्या (r₂) = \(\frac{2 x}{2 \times 4}=\frac{x}{4}\) मी०
चंद्रमा का आयतन (V) = \(\frac{4}{3}\)πr₂³
= \(=\frac{4}{3} \pi \times \frac{x}{4} \times \frac{x}{4} \times \frac{x}{4}\) मी०³
= \(\frac{1}{48}\)πx³ मी०³
चंद्रमा का आयतन पृथ्वी के आयतन का जितना भाग है

प्रश्न 5.
व्यास 10.5 सें०मी० वाले एक अर्धगोलाकार कटोरे में कितने लीटर दूध आ सकता है ?
हल :
यहां पर,
अर्धगोलाकार कटोरे का व्यास (d) = 10.5 सें०मी० = \(\frac{105}{10}\) = \(\frac{21}{2}\) सें०मी०
अर्धगोलाकार कटोरे की त्रिज्या (r) = \(\frac{21}{2 \times 2}\) सें०मी० = \(\frac{21}{4}\) सें०मी०
∴ अर्धगोलाकार कटोरे का आयतन (V) = \(\frac{2}{3}\)πr³
= \(\frac{2}{3} \times \frac{22}{7} \times \frac{21}{4} \times \frac{21}{4} \times \frac{21}{4}\) सें०मी०³
= \(\frac{4851}{16}\) सें०मी०³
अतः अर्धगोलाकार कटोरे की धारिता = \(\frac{4851}{16 \times 1000} \ell\)
= \(\frac{4851}{16000} \ell\) = 0.303 l (लगभग) उत्तर

प्रश्न 6.
एक अर्धगोलाकार टंकी 1 सें०मी० मोटी एक लोहे की चादर (sheet) से बनी है। यदि इसकी आंतरिक त्रिज्या 1 मी० है, तो इस टंकी के बनाने में लगे लोहे का आयतन ज्ञात कीजिए।
हल :
यहां पर,
अर्धगोलाकार टंकी की अंतः त्रिज्या (r) = 1 मी० = 100 सें०मी०
अर्धगोलाकार टंकी की बाह्य त्रिज्या (R) = 100 + 1 = 101 सें०मी०
∴ टंकी में लगी लोहे की चादर का आयतन = बाह्य आयतन – आंतरिक आयतन

प्रश्न 7.
उस गोले का आयतन ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 सें०मी०² है।
हल :
यहां पर,
गोले का पृष्ठीय क्षेत्रफल = 154 सें०मी०²
⇒ 4πr² = 154
या 4 × \(\frac{22}{7}\) × r² = 154
या \(\frac{88}{7}\)r² = 154

प्रश्न 8.
किसी भवन का गुंबद एक अर्धगोले के आकार का है। अंदर से, इसमें सफेदी कराने में ₹ 4989.60 व्यय हुए। यदि सफेदी कराने की दर ₹ 20 प्रति वर्ग मीटर है, तो ज्ञात कीजिए :
(i) गुंबद का आंतरिक वक्र पृष्ठीय क्षेत्रफल,
(ii) गुंबद के अंदर की हवा का आयतन।
हल :
(i) गुंबद के अंतः तल पर सफेदी कराने का खर्च = ₹ 4989.60
सफेदी कराने की दर = ₹ 20 प्रति वर्ग मीटर
4989.60 इस प्रकार गुंबद के अंतः तल का क्षेत्रफल = \(\frac{4989.60}{2}\)
= 249.48 वर्ग मीटर उत्तर
(ii) 2πr² = 249.48

प्रश्न 9.
लोहे के 27 ठोस गोलों को पिघलाकर, जिनमें से प्रत्येक की त्रिज्या r है और पृष्ठीय क्षेत्रफल S है, एक बड़ा गोला बनाया जाता है जिसका पृष्ठीय क्षेत्रफल S’ है। ज्ञात कीजिए :
(1) नए गोले की त्रिज्या r’
(ii) S और S’ का अनुपात
हल :
(i) यहां पर,
गोले की त्रिज्या (r) = r
गोले का पृष्ठीय क्षेत्रफल (S) = 4πr²
गोले का आयतन (V) = \(\frac{4}{3}\)πr³
इस प्रकार 27 ठोस गोलों को पिघलाकर बने
गोले का आयतन (V) = 27 × \(\frac{4}{3}\)πr³ = 36πr³
नए गोले की त्रिज्या = r’
नए गोले का आयतन = \(\frac{4}{3}\)π(r’)³
प्रश्नानुसार \(\frac{4}{3}\)π(r’)³ = 36πr³
या (r’)³ = 36r³ × \(\frac{3}{4}\)
या (r’)³ = 27(r)³
या (r’)³ = (3r)³
⇒ r’ = 3r
नए गोले की त्रिज्या r’ = 3r उत्तर

(ii) यहां पर,
नए गोले का पृष्ठीय क्षेत्रफल (S’) = 4π(r’)²
= 4π(3r)²
= 4π(9r²)
S’ = 36πr²
S तथा S’ का अनुपात = 4πr² : 36πr²
= 1 : 9 उत्तर

प्रश्न 10.
दवाई का एक कैपसूल (capsule) 3.5 मि०मी० व्यास का एक गोला (गोली) है। इस कैपसूल को भरने के लिए कितनी दवाई (mm³ में) की आवश्यकता होगी ?
हल :
यहां पर,
कैपसूल का व्यास (d) = 3.5 मि०मी० = \(\frac{35}{10}=\frac{7}{2}\) मि०मी०
कैपसूल की त्रिज्या (r) = \(\frac{7}{2} \times \frac{1}{2}\) मि०मी० = \(\frac{7}{4}\) मि०मी०
कैपसूल का आयतन (V) = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times \frac{7}{4} \times \frac{7}{4} \times \frac{7}{4}\) मि०मी०
= \(\frac{539}{24}\) मि०मी०³ = 22.46 मि०मी०³ (लगभग)
इस प्रकार कैपसूल को भरने के लिए जितनी दवाई की आवश्यकता होगी।
= 22.46 मि०मी०³ उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.5

प्रश्न 1.
माचिस की डिब्बी के माप 4 सें०मी० × 2.5 सेंमी० × 1.5 सें०मी० हैं। ऐसी 12 डिब्बियों के एक पैकेट का आयतन क्या होगा ?
हल :
यहां पर,
माचिस की डिब्बी की लंबाई (l) = 4 सें०मी०
माचिस की डिब्बी की चौड़ाई (b) = 2.5 सें०मी०
माचिस की डिब्बी की ऊंचाई (h) = 1.5 सें०मी०
माचिस की 1 डिब्बी का आयतन (V) = l × b × h = 4 × 2.5 × 1.5 सें०मी०³
= 15 सें०मी०³
अतः माचिस की 12 डिब्बियों का आयतन = 15 × 12 = 180 सें०मी०³ उत्तर

प्रश्न 2.
एक घनाभाकार पानी की टंकी 6 मी० लंबी, 5 मी० चौड़ी और 4.5 मी० गहरी है। इसमें कितने लीटर पानी आ सकता है ? (1 मी०³ = 1000 l)
हल :
यहां पर,
घनाभाकार टंकी की लंबाई (l) = 6 मी०
घनाभाकार टंकी की चौड़ाई (b) = 5 मी०
घनाभाकार टंकी की गहराई (h) = 4.5 मी०
घनाभाकार टंकी का आयतन (V) = l × b × h= 6 × 5 × 4.5 मी०³
= 135 मी०³
1 मी०³ टंकी में पानी आ सकता है = 1000 l
135 मी०³ टंकी में पानी आ सकता है = 135 × 1000
= 135000 लीटर उत्तर

प्रश्न 3.
एक घनाभाकार बर्तन 10 मी० लंबा और 8 मी० चौड़ा है। इसको कितना ऊंचा बनाया जाए कि इसमें 380 घन मीटर द्रव आ सके ?
हल :
यहां पर,
घनाभाकार बर्तन की लंबाई (l) = 10 मी०
घनाभाकार बर्तन की चौड़ाई (b) = 8 मी०
घनाभाकार बर्तन की ऊंचाई (h) = ?
घनाभाकार बर्तन का आयतन (V) = 380 मी०³
⇒ l × b × h = 380
या 10 × 8 × h = 380
या 80h = 380
या h = \(\frac{380}{80}\) = 4.75 मी०
अतः घनाभाकार बर्तन की ऊंचाई (h) = 4.75 मी० उत्तर

प्रश्न 4.
8 मी० लंबा, 6 मी० चौड़ा और 3 मी० गहरा एक घनाभाकार गड्ढा खुदवाने में ₹ 30 प्रति मी०³ की दर से होने वाला व्यय ज्ञात कीजिए।
हल :
यहां पर,
घनाभाकार गड्ढे की लंबाई (l) = 8 मी०
घनाभाकार गड्ढे की चौड़ाई (b) = 6 मी०
घनाभाकार गड्ढे की गहराई (h) = 3 मी०
घनाभाकार गड्ढे का आयतन (V) = l × b × h = 8 × 6 × 3 मी०³
= 144 मी०³
अतः घनाभाकार गड्ढे को खुदवाने का व्यय = 144 × 30 = ₹ 4320 उत्तर

प्रश्न 5.
एक घनाभाकार टंकी की धारिता 50000 लीटर पानी की है। यदि इस टंकी की लंबाई और गहराई क्रमशः 2.5 मी० और 10 मी० हैं, तो इसकी चौड़ाई ज्ञात कीजिए।
हल :
यहां पर,
घनाभाकार टंकी का आयतन (V) = 50000 लीटर
= \(\frac{50000}{1000}\) मी०³
= 50 मी०³
घनाभाकार टंकी की लंबाई (l) = 2.5 मी०
घनाभाकार टंकी की चौड़ाई (b) = ?
घनाभाकार टंकी की गहराई (h) = 10 मी०
घनाभाकार टंकी का आयतन (V) = 50 मी०³
⇒ l × b × h = 50
या 2.5 × b × 10 = 50
या 25 b = 50
या b = \(\frac{50}{25}\) = 2 मी०
अतः घनाभाकार टंकी की चौड़ाई = 2 मी० उत्तर

प्रश्न 6.
एक गांव जिसकी जनसंख्या 4000 है, को प्रतिदिन प्रति व्यक्ति 150 लीटर पानी की आवश्यकता है। इस गांव में 20 मी० × 15 मी० × 6 मी० मापों वाली एक टंकी बनी हुई है। इस टंकी का पानी वहां कितने दिन के लिए पर्याप्त होगा ?
हल :
यहां पर, एक व्यक्ति को प्रतिदिन जितने पानी की आवश्यकता है = 150 लीटर
4000 व्यक्तियों को प्रतिदिन जितने पानी की आवश्यकता है = 4000 × 50 = 6,00,000 लीटर
दी गई टंकी की लंबाई (l) = 20 मी०
दी गई टंकी की चौड़ाई (b) = 15 मी०
दी गई टंकी की गहराई (h) = 6 मी०
दी गई टंकी में उपस्थित पानी का आयतन (V) = l × b × h = 20 × 15 × 6 = 1800 मी०³
= 1800 × 1000 लीटर
= 18,00,000 लीटर
अतः टंकी का पानी जितने दिन के लिए पर्याप्त है = \(\frac{1800000}{600000}\) = 3 दिन उत्तर

प्रश्न 7.
किसी गोदाम की माप 40 मी० × 25 मी० × 15 मी० हैं। इस गोदाम में 1.5 मी० × 1.25 मी० × 0.5 मी० की माप वाले लकड़ी के कितने अधिकतम क्रेट (crate) रखे जा सकते हैं ? [B.S.E.H. March, 2018]
हल :
यहां पर,
गोदाम का आयतन (V₁) = 40 × 25 × 15 = 15000 मी०³
1 क्रेट का आयतन (V₂) = 1.5 × 1.25 × 0.5 = 0.9375 मी०³

प्रश्न 8.
12 सें०मी० भुजा वाले एक ठोस धन को बराबर आयतन वाले 8 घनों में काटा जाता है। नए घन की क्या भुजा होगी? साथ ही, इन दोनों घनों के पृष्ठीय क्षेत्रफलों का अनुपात भी ज्ञात कीजिए।
हल :
यहां पर,
ठोस धन की भुजा = 12 सें०मी०
ठोस घन का आयतन = 12 × 12 × 12 = 1728 सें०मी०³
नए घन का आयतन = \(\frac{1728}{8}\) = 216 सें०मी०³
अतः नए घन की भुजा = \(\sqrt[3]{\text { आयतन }}=\sqrt[3]{216}=\sqrt[3]{6 \times 6 \times 6}\)
= 6 सें०मी० उत्तर
पहले घन का पृष्ठीय क्षेत्रफल = 6 × भुजा
= 6 × (12)² सें०मी०²
= 6 × 144 = 864 सें०मी०²
नए घन का पृष्ठीय क्षेत्रफल = 6 × भुजा²
= 6 × (6)2 सें०मी०²
= 6 × 36 = 216 सें०मी०²
दोनों घनों के पृष्ठीय क्षेत्रफलों का अनुपात = 864 : 216
= 4 : 1 उत्तर

प्रश्न 9.
3 मी० गहरी और 40 मी० चौड़ी एक नदी 2 km प्रति घंटा की चाल से बह कर समुद्र में गिरती है। एक मिनट में समुद्र में कितना पानी गिरेगा ?
हल :
यहां पर,
नदी की गहराई (h) = 3 मी०
नदी की चौड़ाई (b) = 40 मी०
1 घंटे में बहने वाले पानी की लंबाई (l) = 2 km = 2000 मी०
अतः 1 घंटे में बहने वाले पानी का आयतन (V) = l × b × h = 2000 × 40 × 3 मी०³
= 24,0000 मी०³
1 मिनट में बहने वाले पानी का आयतन = \(\frac{240000}{60}\) मी०³
= 4000 मी०³
अतः 1 मिनट में जितना पानी समुद्र में गिरेगा = 4000 मी०³ उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 14 सांख्यिकी Ex 14.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 14 सांख्यिकी Exercise 14.2

प्रश्न 1.
आठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह ये हैं :
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O
इन आंकड़ों को एक बारंबारता बंटन सारणी के रूप में प्रस्तुत कीजिए। बताइए कि इन विद्यार्थियों में कौन-सा रक्त समूह अधिक सामान्य है और कौन-सा रक्त समूह विरलतम रक्त समूह है।
हल :
आठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह की बारंबारता सारणी निम्न होगी-

विद्यार्थियों में सामान्य रक्त समूह = O
विद्यार्थियों में विरलतम रक्त समूह = AB उत्तर

प्रश्न 2.
40 इंजीनियरों की उनके आवास से कार्य-स्थल की (किलोमीटर में) दूरियां ये हैं :

0-5 को (जिसमें 5 सम्मिलित नहीं है) पहला अंतराल लेकर ऊपर दिए हुए आंकड़ों से वर्ग-माप 5 वाली एक वर्गीकृत बारंबारता बंटन सारणी बनाइए। इस सारणी बद्ध निरूपण में आपको कौन-से मुख्य लक्षण देखने को मिलते हैं?
हल :
आंकड़ों की वर्गीकृत बारंबारता सारणी अग्रांकित है-

मुख्य अभिलक्षण :
(1) 20 कि०मी० से कम दूरी तय करने वाले अभियन्ता = 5 + 11 + 11 + 9 = 36
(2) 20 कि०मी० से अधिक दूरी तय करने वाले अभियन्ता = 1 + 1 + 2 = 4

प्रश्न 3.
30 दिन वाले महीने में एक नगर की सापेक्ष आर्द्रता (% में) यह रही है :

(i) वर्ग 84-86, 86-88 आदि लेकर एक वर्गीकृत बारंबारता बंटन बनाइए।
(ii) क्या आप बता सकते हैं कि ये आंकड़े किस महीने या ऋतु से संबंधित हैं?
(iii) इन आंकड़ों का परिसर क्या है?
हल :
दिए गए आंकड़ों को दी गई वर्ग बारंबारता के अनुसार वर्गीकृत करने पर प्राप्त बारंबारता बंटन निम्न होगा-
(i)

(ii) ये आंकड़े वर्षा ऋतु में लिए हुए प्रतीत होते हैं क्योंकि सापेक्ष आर्द्रता बहुत अधिक है।
(iii) आंकड़ों का परिसर = 99.2 – 84.9 = 14.3 उत्तर

प्रश्न 4.
निकटतम सेंटीमीटरों में मापी गई 50 विद्यार्थियों की लंबाइयां ये हैं :

(i) 160-165, 165-170 आदि का वर्ग अंतराल लेकर ऊपर दिए गए आंकड़ों को एक वर्गीकृत बारंबारता बंटन सारणी के रूप में निरूपित कीजिए।
(ii) इस सारणी की सहायता से आप विद्यार्थियों की लंबाइयों के संबंध में क्या निष्कर्ष निकाल सकते हैं?
हल :
दिए गए आंकड़ों को दिए गए वर्ग अंतरालों के अनुसार बांटने पर निम्न बारंबारता बंटन सारणी प्राप्त होगी-
(i)

(ii) इन आंकड़ों से यह निष्कर्ष निकलता है कि 35 बच्चे ऐसे हैं जिनकी लंबाई 165 सें०मी० से कम है। अर्थात 70% विद्यार्थियों की लंबाई 165 सें०मी० से कम है।

प्रश्न 5.
एक नगर में वायु में सल्फर डाइ-ऑक्साइड का सांदण भाग प्रति मिलियन [parts per million (ppm)] में ज्ञात करने के लिए एक अध्ययन किया गया। 30 दिनों के प्राप्त किए गए आंकड़े ये हैं :

(i) 0.00-0.04, 0.04-0.08 आदि का वर्ग अंतराल लेकर इन आंकड़ों की एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
(ii) सल्फर डाइ-ऑक्साइड की सांद्रता कितने दिन 0.11 भाग प्रति मिलियन से अधिक रही?
हल :
दिए गए वर्ग अंतरालों के अनुसार दिए गए आंकड़ों की बारंबारता बंटन सारणी निम्न होगी-
(i)

(ii) जितने दिन सल्फर डाइ-ऑक्साइड की सांद्रता 0.11 भाग प्रति मिलियन से अधिक रही = 2 + 4 + 2 = 8 दिन

प्रश्न 6.
तीन सिक्कों को एक साथ 30 बार उछाला गया। प्रत्येक बार चित (Head) आने की संख्या निम्न है :

ऊपर दिए गए आंकड़ों के लिए एक बारंबारता बंटन सारणी बनाइए।
हल :
दिए गए आंकड़ों की बारंबारता बंटन सारणी निम्न है-

प्रश्न 7.
50 दशमलव स्थान तक शुद्ध π का मान नीचे दिया गया है : [B.S.E.H. March, 2019]
3.14159265358979323846264338327950288419716939937510
(i) दशमलव बिंद्र के बाद आने वाले 0 से 9 तक के अंकों का एक बारंबारता बंटन बनाइए।
(ii) सबसे अधिक बार और सबसे कम बार आने वाले अंक कौन-कौन से हैं?
हल :
दिए गए π के मान में 0 से 9 तक के अंकों की बारंबारता बंटन सारणी निम्न होगी-
(i)

(ii) सबसे अधिक बार आने वाले अंक = 3 व 9
सबसे कम बार आने वाले अंक = 0.

प्रश्न 8.
तीस बच्चों से यह पूछा गया कि पिछले सप्ताह उन्होंने कितने घंटों तक टी.वी. के प्रोग्राम देखे। प्राप्त परिणाम ये रहे हैं-

(i) वर्ग-चौड़ाई 5 लेकर और एक वर्ग अंतराल को 5-10 लेकर इन आंकड़ों की एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
(ii) कितने बच्चों ने सप्ताह में 15 या अधिक घंटों तक टेलीविजन देखा?
हल :
(i) दिए गए वर्ग-अंतरालों के अनुसार दिए गए आंकड़ों की बारंबारता सारणी अग्रांकित होगी-

(ii) जितने बच्चों ने सप्ताह में 15 घंटे या 15 घंटे से अधिक टेलीविजन देखा = 2

प्रश्न 9.
एक कंपनी एक विशेष प्रकार की कार-बैट्री बनाती है। इस प्रकार की 40 बैट्रियों के जीवन-काल (वर्षों में) ये रहे हैं :

0.5 माप के वर्ग-अंतराल लेकर तथा अंतराल 2-2.5 से प्रारंभ करके इन आंकड़ों की एक वर्गीकृत बारंबारता बंटन सारणी बनाइए।
हल :
दिए गए वर्ग-अंतरालों के अनुसार दिए गए आंकड़ों की बारंबारता बंटन सारणी निम्न होगी-

Haryana State Board HBSE 9th Class Maths Solutions Chapter 14 सांख्यिकी Ex 14.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 14 सांख्यिकी Exercise 14.1

प्रश्न 1.
उन आंकड़ों के पांच उदाहरण दीजिए जिन्हें आप अपने दैनिक जीवन से एकत्रित कर सकते हैं।
हल :
हमारे दैनिक जीवन में एकत्रित किए जाने वाले आंकड़ों के पांच उदाहरण निम्नलिखित हैं-

• अपनी कक्षा में छात्रों की संख्या।
• अपने विद्यालय में पंखों की संख्या।
• पिछले दो वर्षों के घर की बिजली का बिल।
• टेलीविजन या समाचार पत्रों से प्राप्त चुनाव के परिणाम।
• शैक्षिक सर्वेक्षण से प्राप्त साक्षरता दर के आंकड़े।

प्रश्न 2.
ऊपर दिए गए प्रश्न 1 के आंकड़ों को प्राथमिक आंकड़ों या गौण आंकड़ों में वर्गीकृत कीजिए।
हल :
1. प्राथमिक आंकड़े : अन्वेषक द्वारा स्वयं एकत्रित किए गए आंकड़े प्राथमिक आंकड़े (Primary Data) कहलाते हैं। इसलिए प्रश्न (1) में (i), (ii) व (iii) प्राथमिक आंकड़ें हैं।
2. गौण आंकड़े : किसी अन्य स्रोत से प्राप्त किए गए आंकड़े गौण आंकड़े (Secondary data) कहलाते हैं। इसलिए प्रश्न (1) में (iv) व (v) गौण आंकड़े हैं।