Class 9

Haryana State Board HBSE 9th Class Maths Solutions Chapter 8 चतुर्भुज Ex 8.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 8 चतुर्भुज Exercise 8.2

प्रश्न 1.
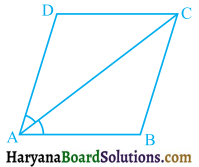
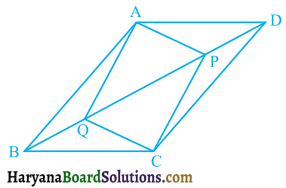
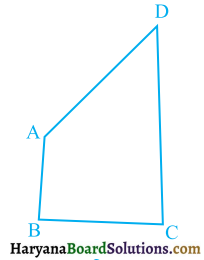
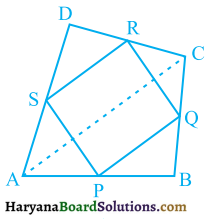
ABCD एक चतुर्भुज है जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं (देखिए आकृति)। AC उसका एक विकर्ण है। दर्शाइए कि :
(i) SR || AC और SR = \(\frac {1}{2}\)AC है।
(ii) PQ = SR है।
(iii) PQRS एक समांतर चतुर्भुज है।

हल :
दिया है : एक चतुर्भुज ABCD में, P, Q, R व S क्रमशः भुजाओं AB, BC, CD व DA के मध्य-बिंदु है। AC इसका विकर्ण है।
सिद्ध करना है : (i) SR || AC व SR = \(\frac {1}{2}\)AC (ii) PQ = SR (iii) PQRS एक समांतर चतुर्भुज है।
प्रमाण : (i) ΔACD में S व R क्रमशः AD ब CD के मध्य-बिंदु हैं।
∴ SR || AC [∵ त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने बाला रेखाखंड तीसरी भुजा के समांतर व उसका आधा होता है।]
व SR = \(\frac {1}{2}\)AC …(1) [इति सिद्धम]

(ii) ΔABC में P व Q क्रमशः AB ब BC के मध्य-बिंदु हैं।
∴ PQ || AC [∵ त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर व उसका आधा होता है।]
व PQ = \(\frac {1}{2}\)AC …(2)
समीकरण (1) व (2) की तुलना से, PQ = SR [इति सिद्धम]

(ii) समीकरण (1) व (2) की तुलना से,
SR || PQ
व SR = PQ
अर्थात सम्मुख भुजाओं का एक युग्म बराबर व समांतर है।
∴ PQRS एक समांतर चतुर्भुज है। [इति सिद्धम]

प्रश्न 2.
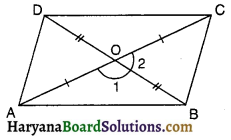
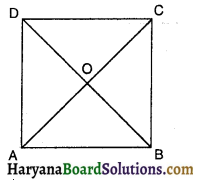
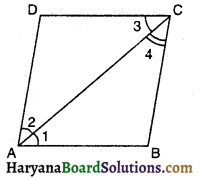
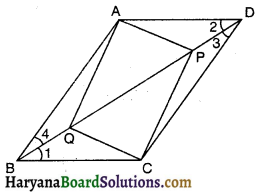
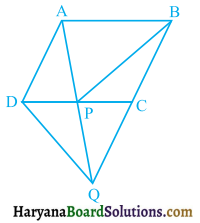
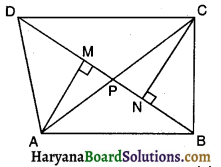
ABCD एक समचतुर्भुज है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। दर्शाइए कि चतुर्भुज PQRS एक आयत है।
हल :

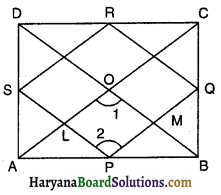
दिया है : एक समचतुर्भुज ABCD में P, Q, R व S क्रमशः भुजाओं AB, BC, CD व DA के मध्य-बिंदु है।
सिद्ध करना है : P, Q, R व 5 को मिलाने से बना चतुर्भुज PQRS एक आयत है।
रचना : AC व BD को मिलाओ।
प्रमाण : ΔACD में S व R क्रमशः AD a CD के मध्य-बिंदु हैं।
∴ SR || AC व SR = \(\frac {1}{2}\)AC
[∵ त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने बाला रेखाखंड तीसरी भुजा के समांतर व उसका आथा होता है।]
इसी प्रकार ΔABC में P व Q क्रमशः AB व BC के मध्य-बिंदु हैं।
∴ PQ || AC व PQ = \(\frac {1}{2}\)AC ….(ii)
[∵ त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर व उसका आधा होता है।]
समीकरण (i) व (ii) की तुलना से,
∴ SR || PQ व SR = PQ
अर्थात चतुर्भुज PQRS में सम्मुख भुजाओं का एक युग्म समांतर व बराबर है।
∴ PQRS एक समांतर चतुर्भुज है।
PM || LO [∵ PQ ||AC प्रमाणित] …(iii)
इसी प्रकार हम सिद्ध कर सकते हैं ।
PL || MO ……….(iv)
समीकरण (iii) व (iv) की तुलना से,
PMOL एक समांतर चतुर्भुज है। परंतु समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
∴ ∠1 = ∠2
परंतु ∠1 = 90° [∵ समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं।]
⇒ ∠2 = ∠P = 90°
∴ PQRS एक आयत है। [इति सिद्धम]

प्रश्न 3.
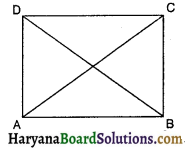
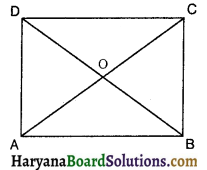
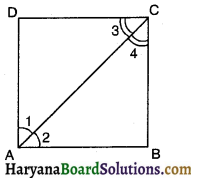
ABCD एक आयत है, जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
हल :

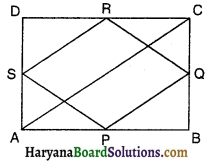
दिया है : ABCD एक आयत है, जिसमें P, Q, R व S क्रमशः
भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं।
सिद्ध करना है : P, Q, R व S को मिलाने से बना चतुर्भुज एक समचतुर्भुज है।
रचना : AC को मिलाओ।
प्रमाण : ΔADC में S व R क्रमशः AD तथा CD के मध्य-बिंदु हैं।
∴ SR || AC व SR = \(\frac {1}{2}\) AC
[∵ त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर व उसका आधा होता है]
इसी प्रकार, ΔABC में,
PQ || AC व PQ = \(\frac {1}{2}\)AC ………..(ii)
समीकरण (i) व (ii) की तुलना से,
SR || PQ व SR = PQ
क्योंकि चतुर्भुज PQRS की सम्मुख भुजाओं का एक युग्म बराबर व समांतर है।
∴ PQRS एक समांतर चतुर्भुज है।
अब ΔSAP तथा ΔQBP में,
SA = QB [समान भुजाओं के आधे खंड]
AP = PB [दिया है]
∠SAP = ∠QBP [प्रत्येक 90°]
∴ ΔSAP ≅ ΔQBP [भुजा-कोण-भुजा सर्वांगसमता]
⇒ SP = PQ [सांगसम त्रिभुजों के संगत भाग]
क्योंकि समांतर चतुर्भुज PQRS की दो आसन्न भुजाएं SP तथा PQ समान हैं।
∴ PQRS एक समचतुर्भुज है। [इति सिद्धम]

प्रश्न 4.
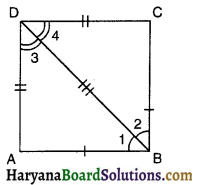
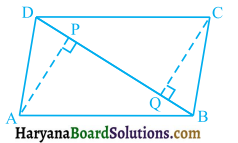
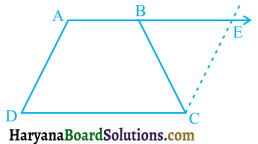
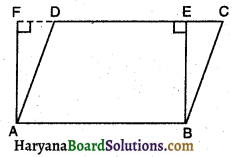
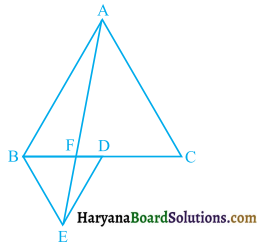
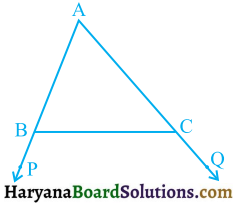
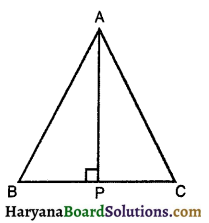
ABCD एक समलंब है, जिसमें AB || DC है। साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य-बिंदु है। Eसे होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है (देखिए आकृति) । दर्शाइए कि F भुजा BC का मध्य-बिंदु है।

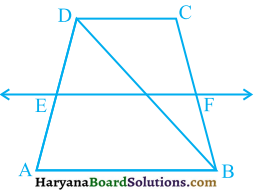
हल :
दिया है : समलंब ABCD में AB || DC तथा E, भुजा AD का मध्य-बिंदु है व EF || AB है। BD समलंब का विकर्ण है।
सिद्ध करना है : F, BC का मध्य-बिंदु है।
रचना : माना EF विकर्ण BD को G पर काटती है।
प्रमाण : ΔABD में,
E, AD का मध्य-बिंदु है तथा EG || AB (दिया है)
∴ G, BD का मध्य-बिंदु है।
अब, EF || AB [दिया है]
AB || CD [दिया है]
∴ EF || CD
ΔBCD में,
G, BD का मध्य-बिंदु है। [प्रमाणित]
GF || CD [प्रमाणित]
∴ F, BC का मध्य-बिंदु है। [इति सिद्धम]

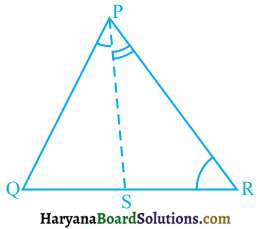
प्रश्न 5.
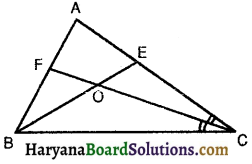
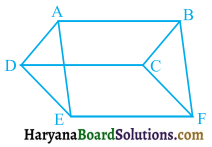
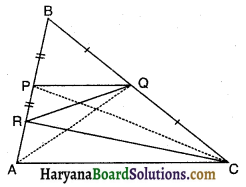
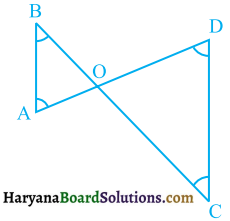
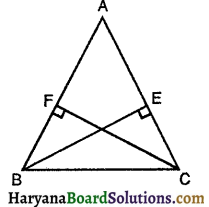
एक समांतर चतुर्भुज ABCD में E और F क्रमशः भुजाओं AB और CD के मध्य-बिंदु है (देखिए आकृति)। दर्शाइए कि रेखाखंड AF और EC विकर्ण BD को समत्रिभाजित करते हैं।

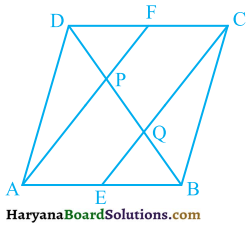
हल :
दिया है। समांतर चतुर्भुज ABCD में E व F क्रमशः भुजाओं AB तथा CD के मध्य-बिंदु हैं। AF व CE रेखाखंड विकर्ण BD को क्रमशः P व Q पर प्रतिच्छेदित करते हैं।
सिद्ध करना है : BQ = QP = PD
प्रमाण : समांतर चतुर्भुज ABCD में,
AB = CD [सम्मुख भुजाएं]
या \(\frac {1}{2}\)AB = \(\frac {1}{2}\)CD
⇒ AE = FC व AE || FC
अतः AECF एक समांतर चतुर्भुज है।
⇒ AF || CE [दिया है]
अब ΔCDQ में, F, CD का मध्य-बिंदु है।
तथा PF || CQ [प्रमाणित]
∴ DP = PQ ……..(i)
इसी प्रकार, ΔABP में,
PQ = BQ
समीकरण (i) व (ii) की तुलना से,
BQ = QP = PD [इति सिद्धम]

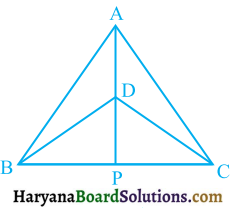
प्रश्न 6.
दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने वाले रेखाखंड परस्पर समद्विभाजित करते हैं।
हल :

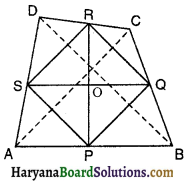
दिया है : एक चतुर्भुज ABCD में, P, Q, R और S क्रमशः भुजा AB, BC, CD और DA के मध्य-बिंदु हैं। PR और QS एक-दूसरे को O प्रतिच्छेदित करते हैं।
सिद्ध करना है : OP = OR, OQ = OS
रचना : PQ, QR, RS, SP, AC और BD को मिलाया।
प्रमाण : ΔABC में, P और Q क्रमशः AB और BC के मध्य-बिंदु हैं।
∴ PQ || AC व PQ = \(\frac {1}{2}\)AC
[∵ त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर व उसका आधा होता है।]
इसी प्रकार हम सिद्ध कर सकते हैं कि,
ΔADC में,
∴ RS || AC व RS = \(\frac {1}{2}\)AC …………..(ii)
समीकरण (i) व (ii) की तुलना में,
∴ PQ || SR व PQ = SR
अतः चतुर्भुज PQRS की सम्मुख भुजाओं का एक युग्म समांतर और बराबर है।
∴ चतुर्भुज PQRS एक समांतर चतुर्भुज है।
क्योंकि समांतर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
∴ समांतर चतुर्भुज PQRS के विकर्ण PR और QS एक दूसरे को समद्विभाजित करते हैं।
⇒ OP = OR व OQ = OS [इति सिद्धम]

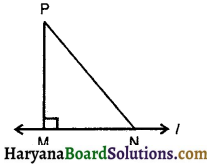
प्रश्न 7.
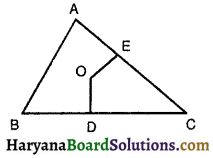
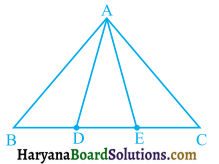
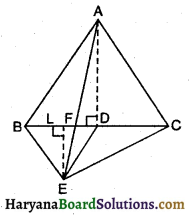
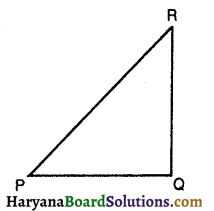
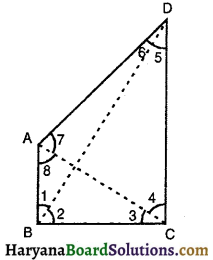
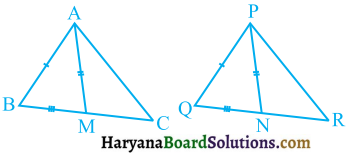
ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य-बिंद M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि :
(i) D भुजा AC का मध्य-बिंदु है।
(ii) MD ⊥ AC है।
(iii) CM = MA = \(\frac {1}{2}\)AB है।
हल :

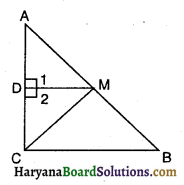
दिया है : त्रिभुज ABC में, ∠C = 90°। कर्ण AB के मध्य-बिंदु M से होकर BC || MD खींची गई है जो रेखा AC को D पर प्रतिच्छेदित करती है।
सिद्ध करना है : (i) D भुजा AC का मध्य-बिंदु है।
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac {1}{2}\)AB
रचना : MC को मिलाओ।
प्रमाण : (i) ΔABC में,
M, AB का मध्य-बिंदु है।
तथा MD || BC (दिया है)
∴ D, AC का मध्य-बिंदु है। [इति सिद्धम]

(ii) MD || BC [दिया है]
∴ ∠1 = ∠ACB [संगत कोण]
परंतु ∠ACB = 90° [दिया है]
⇒ ∠1 = 90°
∴ MD ⊥ AC [इति सिद्धम]

(iii) अब ∠1 + ∠2 = 180° [रैखिक युग्म]
या 90° + ∠2 = 180°
या ∠2 = 180° – 90° = 90°
ΔADM तथा ΔCDM में,
AD = DC [∵ D, AC का मध्य-बिंदु प्रमाणित]
DM = DM [उभयनिष्ठ]
∠1 = ∠2 [प्रत्येक 90°]
∴ ΔADM ≅ ΔCDM [भुजा-कोण-भुजा सर्वांगसमता]
∴ CM = MA [सर्वांगसम त्रिभुजों के संगत भाग] …(i)
परंतु MA = \(\frac {1}{2}\)AB [दिया है]…(ii)
समीकरण (i) व (ii) की तुलना से,
CM = MA = \(\frac {1}{2}\)AB [इति सिद्धम]

Haryana State Board HBSE 9th Class Maths Solutions Chapter 8 चतुर्भुज Ex 8.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 8 चतुर्भुज Exercise 8.1

प्रश्न 1.
एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
हल :
माना चतुर्भुज के कोण = (3x), (5x), (9x), (13x)
हम जानते हैं कि
चतुर्भुज के कोणों का योग = 360°
⇒ 3x + 5x + 9x + 13x = 360°
या 30x = 360°
या x = \(\frac{360^{\circ}}{30}\) = 12°
अतः चतुर्भुज के कोण = (3 × 12)°; (5 × 12)°, (9 × 12)°, (13 × 12)°
= 36°, 60°, 108°, 156° उत्तर

प्रश्न 2.
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दशाइए कि वह एक आयत है। [B.S.E.H. March, 2018]
हल :

दिया है : एक समांतर चतुर्भुज ABCD में AC = BD है।
सिद्ध करना है : ABCD एक आयत है।
प्रमाण : ΔABD और ΔABC में,
AB = AB [उभयनिष्ठ]
AD = BC [|| चतुर्भुज की सम्मुख भुजाएं]
BD = AC [दिया है]
∴ ΔABD ≅ ΔABC [भुजा-भुजा-भुजा सर्वांगसमता]
⇒ ∠DAB = ∠CBA [सर्वांगसम त्रिभुजों के संगत भाग]
परन्तु AD || BC [॥ चतुर्भुज की सम्मुख भुजाएं]
∴ ∠DAB + ∠CBA = 180° [एक ही ओर बने अंतः कोण]
अतः ∠DAB = ∠CBA = 90°
∴ ABCD एक आयत है। [इति सिद्धम]

प्रश्न 3.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।
हल :
दिया है : एक चतुर्भुज ABCD के विकर्ण AC और BD परस्पर समकोण पर समद्विभाजित करते हैं अर्थात OA = OC व OB = OD
सिद्ध करना है : ABCD एक समचतुर्भुज है।

प्रमाण : ΔAOB तथा ΔBOC में,
AO = OC [दिया है]
BO = BO [उभयनिष्ठ]
∠1 = ∠2 [प्रत्येक 90°]
∴ ΔAOB ≅ ΔBOC [भुजा-कोण-भुजा सर्वांगसमता]
अतः AB = BC [सर्वांगसम त्रिभुजों के संगत भाग]
इसी प्रकार हम सिद्ध कर सकते हैं,
BC = CD = DA
⇒ AB = BC = CD = DA
∴ ABCD एक समचतुर्भुज है।
[इति सिद्धम]

प्रश्न 4.
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
हल :

दिया है : एक वर्ग ABCD, जिसमें AC व BD विकर्ण हैं।
सिद्ध करना है : (i) विकर्ण AC = विकर्ण BD
(ii) AC व BD परस्पर समकोण पर समद्विभाजित करते हैं।
प्रमाण : (i) ΔABC और ΔABD में,
भुजा AB = भुजा AB [उभयनिष्ठ]
BC = AD [वर्ग की भुजाएं]
∠ABC = ∠BAD [प्रत्येक 90°]
∴ ΔABC ≅ ΔABD [भुजा-कोण-भुजा सर्वांगसमता]
⇒ AC = BD [सर्वांगसम त्रिभुजों की संगत भुजाएं]
अतः वर्ग के विकर्ण बराबर होते हैं। [इति सिद्धम]

(ii) ΔBOC और ΔAOD में,
BC = AD [वर्ग की भुजाएं]
∠OBC = ∠ODA [एकांतर कोण]
∠OCB = ∠OAD [एकांतर कोण]
∴ ΔBOC ≅ ΔAOD [कोण-भुजा-कोण सर्वांगसमता]
⇒ OB = OD व OC = OA [सर्वांगसम त्रिभुजों की संगत भुजाएं]
अब, ΔAOB और ΔBOC में,
OA = OC [प्रमाणित]
OB = OB [उभयनिष्ठ]
AB = BC [वर्ग की भुजाएं]
∴ ΔAOB ≅ ΔBOC [भुजा-भुजा-भुजा सर्वांगसमता]
⇒ ∠AOB = ∠BOC [सर्वांगसम त्रिभुजों के संगत कोण]
परन्तु ∠AOB + ∠BOC = 180° [रैखिक युग्म]
या ∠AOB + ∠AOB = 180°
या 2∠AOB = 180°
या ∠AOB = \(\frac{180^{\circ}}{2}\) = 90°
इसी प्रकार ∠BOC = ∠COD = ∠DOA = 90°
अतः विकर्ण AC व BD परस्पर बिंदु O पर समकोण पर समद्विभाजित करते हैं। [इति सिद्धम]

प्रश्न 5.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर समद्विभाजित करें, तो वह एक वर्ग होता है।
हल :

दिया है : एक चतुर्भुज ABCD के विकर्ण AC और विकर्ण BD बराबर हैं तथा परस्पर समकोण पर समद्विभाजित करते हैं। अर्थात OA = OC व OB = OD तथा AC ⊥ BD हैं।
सिद्ध करना है : चतुर्भुज ABCD एक वर्ग है।
प्रमाण : ΔAOB और ΔBOC में,
OA = OC [दिया है]
OB = OB [उभयनिष्ठ]
∠AOB = ∠BOC [प्रत्येक 90°]
∴ ΔAOB ≅ ΔBOC [भुजा-कोण-भुजा सर्वांगसमता]
⇒ AB = BC [सर्वांगसम त्रिभुजों के संगत भाग]
इसी प्रकार हम सिद्ध कर सकते हैं कि
BC = CD = DA
अतः AB = BC = CD = DA …….(i)
इससे पता चलता है कि ABCD एक समचतुर्भुज है।
अब ΔABC और ΔABD में,
AB = AB [उभयनिष्ठ]
AC = BD [दिया है]
BC = DA [प्रमाणित]
∴ ΔABC ≅ ΔABD [भुजा-भुजा-भुजा सर्वांगसमता]
⇒ ∠ABC = ∠BAD [सर्वांगसम त्रिभुजों के संगत भाग]
परंतु AD || BC (समचतुर्भुज की सम्मुख भुजाएं) व AB एक तिर्यक रेखा है।
∠ABC + ∠BAD = 180° [तिर्यक रेखा के एक ओर बने कोण]
⇒ ∠ABC + ∠ABC = 180°
या 2∠ABC = 180°
या ∠ABC = \(\frac{180^{\circ}}{2}\) = 90°
क्योंकि समचतुर्भुज ABCD का एक कोण 90° है। इसलिए ABCD एक वर्ग है। [इति सिद्धम]

प्रश्न 6.
समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति)। दर्शाइए कि :
(i) यह ∠C को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।

हल :

दिया है : समांतर चतुर्भुज ABCD में विकर्ण AC, ∠A को समद्विभाजित करता है अर्थात् ∠1 = ∠2
(i) सिद्ध करना है : विकर्ण AC, ∠C को समद्विभाजित करता है।
प्रमाण : क्योंकि ABCD एक समांतर चतुर्भुज है।
∴ AB || DC है तथा AC एक तिर्यक रेखा है।
∴ ∠1 = ∠3 [एकांतर कोण]…(i)
इसी प्रकार AD || BC तथा AC एक तिर्यक रेखा है।
∴ ∠2 = ∠4 [एकांतर कोण]…(ii)
परंतु ∠1 = ∠2 [दिया है]
अतः ∠3 = ∠4
इससे सिद्ध होता है कि AC, ∠C को समद्विभाजित करता है। [इति सिद्धम]

(ii) सिद्ध करना है : ABCD एक समचतुर्भुज है।
प्रमाण : ∵ ∠1 = ∠2 [दिया है]
तथा ∠1 = ∠3 [एकांतर कोण]
अतः ∠2 = ∠3
⇒ AD = DC
इसलिए समांतर चतुर्भुज ABCD की दो आसन्न भुजाएं बराबर हैं तो ABCD एक समचतुर्भुज है। [इति सिद्धम]

प्रश्न 7.
ABCD एक समचतुर्भुज है। दर्शाइए कि विकर्ण AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B और D दोनों को समद्विभाजित करता है।
हल :

दिया है : ABCD एक समचतुर्भुज है अर्थात AB = BC = CD = DA
सिद्ध करना है : (i) विकर्ण AC, ∠A और ∠C को समद्विभाजित करता है।
(ii) विकर्ण BD, ∠B और ∠D को समद्विभाजित करता है।
प्रमाण : ΔABC और ΔADC में,
AB = AD (समचतुर्भुज की भुजाएं)
AC = AC (उभयनिष्ठ)
BC = CD [समचतुर्भुज की भुजाएं]
∴ ΔABC ≅ ΔADC [भुजा-भुजा-भुजा सर्वांगसमता]
∴ ∠1 = ∠2 व ∠3 = ∠4 [सर्वांगसम त्रिभुजों के संगत कोण]
अतः विकर्ण AC, ∠A और ∠C को समद्विभाजित करता है।
इसी प्रकार हम सिद्ध कर सकते हैं कि विकर्ण BD, ∠B और ∠D को समद्विभाजित करता है।

प्रश्न 8.
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि (i) ABCD एक वर्ग है। (ii) विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
हल :

दिया है : ABCD एक आयत है। जिसमें विकर्ण AC, ∠A व ∠C को समद्विभाजित करता है। अर्थात ∠1 = ∠2 व ∠3 = ∠4
सिद्ध करना है : (i) ABCD एक वर्ग है।
(ii) विकर्ण BD, ∠B व ∠D को समद्विभाजित करता है।
प्रमाण : (i) ∵ AB || DC [आयत की सम्मुख भुजाएं]
∠1 = ∠4 [एकांतर कोण]
परंतु ∠1 = ∠2
अतः ∠2 = ∠4
⇒ AB = BC [समान कोणों की सम्मुख भुजाएं समान होती हैं।]
इस प्रकार आयत ABCD की दो आसन्न भुजाएं समान हैं। इसलिए ABCD एक वर्ग है। [इति सिद्धमा]

(ii) ΔABD तथा ΔBCD में,

AB = BC [वर्ग की भुजाएं]
AD = DC [वर्ग की भुजाएं]
BD = BD [उभयनिष्ठ]
∴ ΔABD ≅ ΔBCD [भुजा-भुजा-भुजा सर्वांगसमता]
∴ ∠1 = ∠2 तथा ∠3 = ∠4 [सर्वांगसम त्रिभुजों के संगत भाग]
अतः विकर्ण BD, ∠B तथा ∠D को समद्विभाजित करता है। [इति सिद्धम]

प्रश्न 9.
समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु Pऔर Q इस प्रकार स्थित हैं कि DP = BQ है (देखिए आकृति)। दर्शाइए कि:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ एक समांतर चतुर्भुज है।

हल :

दिया है : समांतर चतुर्भुज ABCD के विकर्ण BD पर बिंदु P व Q इस प्रकार हैं कि DP = BQ
सिद्ध करना है : (i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ एक समांतर चतुर्भुज है।
प्रमाण : (i) ΔAPD और ΔCQB में,
AD = BC [समांतर चतुर्भुज की सम्मुख भुजाएं]
DP = BQ [दिया है]
∠2 = ∠1 [एकांतर कोण]
∴ ΔAPD ≅ ΔCQB [भुजा-कोण-भुजा सर्वांगसमता] [इति सिद्धम]

(ii) क्योंकि ΔAPD ≅ ΔCQB [प्रमाणित]
AP = CQ [सर्वांगसम त्रिभुजों के संगत भाग] [इति सिद्धम]

(iii) ΔAQB तथा ΔCPD में,
AB = CD [समांतर चतुर्भुज की सम्मुख भुजाएं]
∠4 = ∠3 [एकांतर कोण]
BQ = DP [दिया है]
∴ ΔAQB ≅ ΔCPD [भुजा-कोण-भुजा सर्वांगसमता] [इति सिद्धम]

(iv) क्योंकि ΔAQB ≅ ΔCPD [प्रमाणित]
∴ AQ = CP [सर्वांगसम त्रिभुजों के संगत भाग]

(v) क्योंकि चतुर्भुज APCQ में AP = CQ [प्रमाणित]
तथा AQ = CP [प्रमाणित]
∴ APCQ समांतर चतुर्भुज है। [इति सिद्धम]

प्रश्न 10.
ABCD एक समांतर चतुर्भुज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लंब हैं (देखिए आकृति)। दर्शाइए कि:
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ

हल :
दिया है : एक समांतर चतुर्भुज ABCD में शीर्षों A व C से क्रमशः AP ⊥ BD व CQ ⊥ BD हैं।
सिद्ध करना है : (i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
प्रमाण : (i) ΔAPB और ΔCQD में,
AB = CD [समांतर चतुर्भुज की सम्मुख भुजाएं]
∠APB = ∠CQD [प्रत्येक 90°]
∠ABP = ∠CDQ [एकांतर कोण]
∴ ΔAPB ≅ ΔCQD [कोण-कोण-भुजा सर्वांगसमता] [इति सिद्धम]

(ii) क्योंकि ΔAPB ≅ ΔCQD [प्रमाणित]
∴ AP = CQ [सर्वांगसम त्रिभुजों के संगत भाग] [इति सिद्धम]

प्रश्न 11.
ΔABC और ΔDEF में, AB= DE, AB || DE, BC = EF और BC || EF है। शीर्षों A, B और C को क्रमशः शीर्षों D, E और F से जोड़ा जाता है (देखिए आकृति)। दर्शाइए कि :
(i) चतुर्भुज ABED एक समांतर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समांतर चतुर्भुज है।
(iii) AD || CF और AD = CF है।
(iv) चतुर्भुज ACFD एक समांतर चतुर्भुज है।
(v) AC = DF है।
(vi) ΔABC ≅ ΔDEF है।

हल :
दिया है : AABC और ADEF में, AB = DE और AB || DE तथा BC = EF व BC || EF है। शीर्षों A, B, व C को क्रमशः शीर्षों D, E व F से जोड़ा गया है।
सिद्ध करना है : (i) चतुर्भुज ABED एक समांतर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समांतर चतुर्भुज है।
(iii) AD||CF और AD = CF है।
(iv) चतुर्भुज ACFD एक समांतर चतुर्भुज है।
(v) AC = DF है।
(vi) ΔABC ≅ ΔDEF है।
प्रमाण : (i) क्योंकि चतुर्भुज ABED में,
AB = DE व AB || DE [दिया है]
∴ ABED एक समांतर चतुर्भुज है। [इति सिद्धम]
(ii) क्योंकि चतुर्भुज BEFC में,
BC = EF व BC || EF [दिया है]
∴ BEFC एक समांतर चतुर्भुज है। [इति सिद्धम]

(iii) समांतर चतुर्भुज ABED में,
AD = BE व AD || BE …(1)
समांतर चतुर्भुज BEFC में,
CF = BE व CF || BE …(2)
समीकरण (1) व (2) की तुलना से,
AD = CF व AD || CF [इति सिद्धम]
(iv) क्योंकि चतुर्भुज ACFD में,
AD = CF व AD || CF [प्रमाणित]
∴ ACFD एक समांतर चतुर्भुज है। [इति सिद्धम]
(v) समांतर चतुर्भुज ACFD में,
AC = DF …(3)
[समांतर चतुर्भुज की सम्मुख भुजाएं] [इति सिद्धम]
(vi) ΔABC और ΔDEF में,
AB = DE [दिया है]
AC = DF [प्रमाणित]
BC = EF [दिया है]
∴ ΔABC ≅ ΔDEF [भुजा-भुजा-भुजा सर्वांगसमता] [इति सिद्धम]

प्रश्न 12.
ABCD एक समलंब है, जिसमें AB || DC और AD = BC है (देखिए आकृति)। दर्शाइए कि :
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) विकर्ण AC = विकर्ण BD है।

हल :
दिया है : ABCD एक समलंब है, जिसमें AB || DC और AD = BC है।
सिद्ध करना है :
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) विकर्ण AC = विकर्ण BD
रचना : C से CE || AD खींचिए जो AB को बढ़ाने पर E पर प्रतिच्छेद करे। AC व BD को मिलाओ।
प्रमाण : (i) CE || AD [रचना से]
AE || DC [दिया है]
∴ ADCE एक समांतर चतुर्भुज है।
अतः AD = CE [समांतर चतुर्भुज की सम्मुख भुजाएं]…(1)
परंतु AD = BC [दिया है]…(2)
समीकरण (1) व (2) की तुलना से,
CE = BC
⇒ ∠1 = ∠2 [समान भुजाओं के सम्मुख कोण]
अब AD || CE और AE एक तिर्यक रेखा है।
∴ ∠A + ∠2 = 180° [एक ही ओर बने अंतः कोण] …(3)
∠1 + ∠B = 180° …(4)
समीकरण (3) व (4) से
∠A + ∠2 = ∠1 + ∠B
परंतु ∠1 = ∠2 [प्रमाणित]
∴ ∠A = ∠B [इति सिद्धम]
(ii) ∠D = ∠2 [समांतर चतुर्भुज के सम्मुख कोण]
परंतु ∠1 = ∠2 [प्रमाणित]
∴ ∠D = ∠1 ….(5)
परंतु ∠3 = ∠1 [एकांतर कोण]…(6)
समीकरण (5) व (6) से…
∠D = ∠3
या ∠D = ∠C [इति सिद्धमा

(iii) ΔABC और ΔBAD में,
AB = AB [उभयनिष्ठ]
BC = AD [दिया है]
∠ABC = ∠BAD [प्रमाणित]
∴ ΔABC ≅ ΔBAD [भुजा-कोण-भुजा सर्वांगसमता] [इति सिद्धम]

(iv) क्योंकि ΔABC ≅ ΔBAD [प्रमाणित]
AC = BD [सर्वांगसम त्रिभुजों के संगत भाग] [इति सिद्धम]

Haryana State Board HBSE 9th Class Science Notes Chapter 4 Structure of the Atom Notes.

Haryana Board 9th Class Science Notes Chapter 4 Structure of the Atom

→ Matter is composed of atoms and molecules together.

→ Electrons and protons were discovered by J.J. Thomson and E. Goldstein respectively.

→ J.J.Thomson proposed that electrons are struck into the +ve sphere.

→ The mass of proton is single unit and the charge is written as +1, whereas the mass of electron is negligible and the charge is taken as -1.

→ The defraction experiment of Rutherford’s alpha particles discovered the nucleus.

→ Rutherford’s atomic model proposed that atom has a very small nucleus in its centre and electrons revolve around the nucleus. The stability of atom cannot be described by this model.

→ According to Rutherford, the radius of nucleus is 105 times smaller than the radius of an atom.

→ The model presented by Neils Bohr was more successful. He proposed that electrons have been distributed around the nucleus in different shells with a definite energy. If the outermost shells of the atom gets accommodated, the atom will be most stable and will be less active. ’

→ J. Chadwick in 1932 discovered the existence of neutron in an atom.

→ The nucleus of hydrogen does not possess neutron.

→ Atom has three sub-atomic particles namely electron, proton and neutron.

→ According to Bohr and Bury’s law, the maximum number of electrons in an orbit cannot exceed 2n2. Here, n is the number of orbit or shell.

→ The orbits of an atom have been named as K, L, M, N, ……………..

→ The outermost shell of an atom can possess maximum electrons.

→ The elements whose outermost shells remain completely filled up, are chemically inactive.

→ Hydrogen has three isotopes protium (₁H¹), Deuterium (₁H²), and Tritium (₁H³).

→ Chlorine has two ₁₇Cl³⁵ and ₁₇Cl³⁷ isotopes.

→ Isotopes have same chemical properties and different physical properties.

→ The mass of an atom of a natural element is equal to the average mass of all existed natural forms of that element.

→ In nuclear plant, the isotopes of uranium are used up as a fuel.

→ The isotopes of cobalt are used in treatment of cancer.

→ The isotopes of iodine are used in treatment of goitre.

→ Calcium and argon are isobaric atoms.

→ Elements are defined according to the number of protons present in them.

→ Valence Electrons: Electrons present in the outermost shell of an atom are called valence electrons.

→ Valency: Valency is the combining capacity of an atom.

→ Non-reacting Elements: Elements which have complete valence shells are known as non-reacting elements.

→ Atomic Number: The total number of protons present in the nucleus of an atom is called its atomic number (Z).

→ Mass Number: The sum total of protons and neutrons present in the nucleus of an atom is known as mass number (A).

→ Nucleons: Protons and neutrons present in the nucleus of an atom are called nucleons.

→ Isotopes: Atoms of the same element whose atomic number is the same, but mass number is different are called isotopes of an element.

→ Isobars: Isobars are those atoms whose mass number is same, but atomic number is different.

Haryana State Board HBSE 9th Class Science Notes Chapter 3 Atoms and Molecules Notes.

Haryana Board 9th Class Science Notes Chapter 3 Atoms and Molecules

→ Any compound is composed of two or more than two elements.

→ In a compound of water, the ratio of masses of hydrogen and oxygen is always 1: 8, it does not concern whether which source does the water belong to.

→ In ammonia (NH₃), Nitrogen and Hydrogen always exist in the ratio of 14: 3 according to their masses.

→ John Dalton was bom in 1766 in England.

→ In a compound, the relative number of atoms and its type are definite.

→ The structural unit of all the fluids is atom.

→ The atomic radius is measured in nanometre (nm). (1nm = 10^-9m)

→ Nowadays the International Union of Pure and Applied Chemistry (IUPAC) approves names of elements.

→ Each element have a name and an unmatched chemical symbol.

→ Each element has a characteristic atomic mass.

→ We assume unit of atomic mass equal to that of the mass of a carbon atom.

→ Atomic masses of all the elements are obtained in relation to single atomic mass of isotope of carbon-12

→ Generally, a molecule is a group of two or more than two atoms which are interlinked by a chemical bond.

→ Molecules of an element are composed of only one kind of atoms.

→ Molecule with negative charge is called as electron and the molecule with positive charge is called as proton.

→ The chemical formulae of molecular compound are based on by means of combination of each element.

→ In ionic compounds, chemical formulae of compound are learnt by the number of electrons on each of the ions.

→ The number of particles (atoms, molecules or ions) in a mole of a substance is constant whose mass is 6.022 × 10²³.

→ Law of Conservation of Mass: According to the law of conservation of mass, in a chemical reaction mass can neither be created, nor destroyed.

→ Law of Constant Proportions: In a pure chemical compound, elements always exist in constant proportions of masses, it is called the law of constant proportions.

→ Atom: The smallest particle of an element is atom, which can exist independently and it exhibits all its chemical properties.

→ Molecule: Molecule is that minute particle of an element or compound which can remain in a free state in normal conditions. It exhibits all properties of matter.

→ Relative Atomic Mass Unit: 1/12th part of atomic mass of an atom of carbon-12 isotopes is taken to be the relative atomic mass unit.

→ Atomicity: The number of atoms being used in structural formation of any molecule is called atomicity of its molecule.

→ Ions: Compounds are composed of metals and non-metals contain charged particles. These charged particles are called as ions e.g. sodium, magnisium.

→ Polyatomic Ions: A group of atoms that behave as an ion are called polyatomic ions.

→ Chemical Formula: The chemical formula of a compound is a symbolic representation of its composition.

→ Valency: The combining power (or capacity) of an element is the valency of that element.

→ Binary Compounds: The simplest compounds formed by combination of two different elements are known as binary compounds.

→ Molecular Mass: Molecular mass is the sum total of masses of overall combined atoms of matter. It is expressed by atomic mass units (u).

→ Formula Unit Mass: Formula unit mass of a substance is a sum total of atomic masses of its whole combined atoms.

→ Mole: Mole is that quantity of a substance in which the number of particles (atom, ion, molecule or formula unit) is equal to the existing atoms in exactly 12g of carbon =12.

→ Molar Mass: Mass of molecules of a single mole of a substance is called its molar mass.

Haryana State Board HBSE 9th Class Science Notes Chapter 2 Is Matter Around Us Pure Notes.

Haryana Board 9th Class Science Notes Chapter 2 Is Matter Around Us Pure

→ A pure substance is composed of only one type of molecules.

→ Sodium chloride dissolved in water can be separated from water by evaporation or distillation method.

→ Mixture contains more than one substances. .

→ Copper sulphate forms homogeneous mixture in water.

→ The mixture of water and oil is heterogeneous.

→ Lemon water and soda water are examples of solution.

→ In the solution of sugar and water, sugar is solute and water is solvent.

→ Air is a homogeneous mixture of 21% of oxygen and 78% of nitrogen.

→ The molecules of a solution are even smaller than in diameter of 1nm (1 × 10^-9m).

→ Solution is a homogeneous mixture from which the molecules of solute cannot be separated by

→ Suspended particles are larger than 100 nm (10^-7m). These particles can be seen with eyes.

→ The molecules of colloid spread uniformly in solution.

→ Milk is a colloidal solution.

→ Divergence of sunrays by colloidal molecules is called Tyndall effect.

→ The size of the molecules of colloid is between 1 nm to 100 nm.

→ Different components of colloid can be separated through centrifugation process.

→ Two insoluble liquids can be separated by separating funnel.

→ Ammonium chloride, camphor, naphthalene and anthracene are volatile solid materials.

→ Amixture of two soluble liquids whose components have more difference in their boiling point can be separated through distillation process.

→ The process of crystallization is applied to refine the solid materials.

→ Chemical change brings about change in the chemical properties of matter.

→ On the basis of chemical composition, materials can either be classified into elements or compounds.

→ Elements can generally be divided into metals, non-metals and metalloids.

→ Two elements-mercury and bromine are in liquid state at room temperature.

→ The properties already present in the elements of the compounds are different from that of the properties of the compounds. Though, the elements and compounds present in mixture shows their own properties.

→ Pure Substance: A substance composed of only one type of molecules is called as pure substance.

→ Mixture: A substance composed with the combination of one or more than one pure elements or compounds is called as mixture.

→ Solution: Homogeneous mixture of two or more than two substances is called as solution.

→ Alloys: Those homogeneous mixtures of metals that cannot be isolated through physical processes from their components are called alloys.

→ Solvent: That molecule of solution (whose quantity is more than the other one) which mixes other molecules into solution is called solvent.

→ Solute: That component of solution which dissolved in solvent is called solute.

→ Saturated solution: At a given fixed temperature if in the solution, solute is not miscible, that is called saturated solution.

→ Solubility: That quantity of solute material which at a definite temperature is present in the saturated solution, is called as solubility.

→ Unsaturated Solution: If in any solution quantity of solute material remains little to saturation, then it is called as unsaturated solution.

→ Supersaturated Solution: If in any solution the concentration of Solute is more than that of the saturated concentration, that is called as supersaturated solution.

→ Strength of Solution: Quantity (volume) of solute material dissolved into solvent’s volume is called strength of solution.

→ Suspension: Suspension is an heterogeneous mixture, in which the solute particles do not dissolve rather keep suspending in the medium.

→ Principle of Centrifugation Method: In the centrifugation method, on rotating the mixture fastly the heavier particles settle down at the bottom and the lighter particles come upward.

→ Chromatography: Chromatography is such a process which is used to isolate those solute materials which are dissolved in just one type of solvent.

→ Crystallisation: Crystallisation is that process by which pure solid substance & separated from solution in the form of crystal.

→ Element: Element is that basic form of matter which cannot be further disintegrated into smaller pieces through chemical process.

→ Metalloids: The elements showing the properties in between metals and non-metals are called metalloids, e.g., boron and silicon.

→ Compound: The substance made up of combining chemically two or more than two elements together in the same ratio is called as compound.

Haryana State Board HBSE 9th Class Maths Solutions Chapter 7 त्रिभुज Ex 7.5 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 7 त्रिभुज Exercise 7.5

प्रश्न 1.
ABC एक त्रिभुज है। इसके अभ्यंतर में एक ऐसा बिंदु ज्ञात कीजिए, जो ΔABC के तीनों शीर्षों से समदूरस्थ है।
हल :

माना एक ΔABC में, OD तथा OE, क्रमशः भुजा BC तथा CA के लंब समद्विभाजक हैं।
O रेखाखंड BC के दोनों सिरों B तथा C से समान दूरी पर है, क्योंकि O, BC के
लंब समद्विभाजक पर स्थित है।
इसी प्रकार O, C तथा A से भी समान दूरी पर है, क्योंकि O, CA के लंब
समद्विभाजक पर स्थित है।
आकृति इसीलिए, भुजा BC, CA तथा AB के लंब समद्विभाजकों प्रतिच्छेदन बिंदु O, आवश्यक बिंदु है जो ΔABC के शीर्षों से समदूरस्थ है। [इति सिद्धम]

प्रश्न 2.
किसी त्रिभुज के अभ्यंतर में एक ऐसा बिंदु ज्ञात कीजिए, जो त्रिभुज की सभी भुजाओं से समदूरस्थ है।
हल :

माना BE और CF क्रमशः ∠ABC तथा ∠ACB के कोण समद्विभाजक हैं। ये AC तथा AB को क्रमशः E तथा F पर काटते हैं।
क्योंकि O, ∠ABC के कोण समद्विभाजक BE पर स्थित है।
इसलिए O, AB तथा BC से समान दूरी पर है।
इसी प्रकार O, ∠ACB के कोण समद्विभाजक पर स्थित हैं। इसलिए O, BC और CA से समान दूरी पर है। इस प्रकार ΔABC के कोणों का समद्विभाजक अभीष्ट बिंदु है। [इति सिद्धम]

प्रश्न 3.
एक बड़े पार्क में, लोग तीन बिंदुओं (स्थानों) पर केंद्रित हैं। (देखिए आकृति)
A : जहाँ बच्चों के लिए फिसल पट्टी और झूले हैं।
B : जिसके पास मानव-निर्मित एक झील है।
C : जो एक बड़े पार्किंग स्थल और बाहर निकलने के रास्ते के निकट है।
एक आइसक्रीम का स्टॉल कहाँ लगाना चाहिए, ताकि वहाँ लोगों की अधिकतम संख्या पहुंच सके ?
हल :

आइसक्रीम का स्टॉल A, B और C से समान दूरी पर होना चाहिए, जिसके लिए AB और BC का समद्विभाजक करना पड़ेगा, जोकि O पर मिलेंगे।
इसीलिए O आवश्यक बिंदु है जोकि A, B तथा C से समान दूरी पर है,
जहाँ पर आइसक्रीम का स्टॉल स्थापित किया जा सकता है।

प्रश्न 4.
षडभुजीय और तारे के आकार की रंगोलियों [देखिए आकृति (i) और (ii)] को 1 cm भुजा वाले समबाहु त्रिभुजों से भर कर पूरा कीजिए। प्रत्येक स्थिति में, त्रिभुजों की संख्या गिनिए। किसमें अधिक त्रिभुज हैं ?

हल :

प्रत्येक आकृति को 1 cm के समबाहु त्रिभुजों के साथ भरने पर हमें प्राप्त हुआ कि आकृति
(i) में इस प्रकार के त्रिभुजों की संख्या = 150 तथा आकृति
(ii) में इस प्रकार के त्रिभुजों की संख्या 300 है।
अतः तार के आकार की रंगोलियों में त्रिभुजों की संख्या अधिक है।

Haryana State Board HBSE 9th Class Science Notes Chapter 1 Matter in Our Surroundings Notes.

Haryana Board 9th Class Science Notes Chapter 1 Matter in Our Surroundings

→ Materials found around us have different sizes, shapes and forms.

→ Matter is a substance that possesses mass and occupies space.

→ The ancient philosophers of India have classified matter mainly into five basic elements viz. air, earth, fire, water and sky (which are said to be ‘Panch Tatvas’).

→ The modem scientists have classified matter on the basis of its physical properties and chemical nature.

→ The particles of a matter have presumably sufficient space in them.

→ The purity of honey can be tested merely by pouring down just a drop of it into a glass of water as if honey falls in form of a colour line, then it is supposed to be pure.

→ The particles in the matter do always remain in motion continuously i.e., they do have kinetic energy in them.

→ The kinetic energy of the particles speeds up with the increase in temperature.

→ The particles of matter attract one another, but the capability of force of cohesion is different in every material.

→ Matter exists in three different states namely solid, liquid and gas.

→ Solids are fully incompressible, of definite shapes and fixed volume.

→ The particles of solids have the ability to rotate about accordingly to their mean positions.

→ The solids do not have the property to lose their indentity while intermixing into other solid materials.

→ Liquids are comparatively compressible to solids. They have fixed volume, but no definite shape.

→ Gases diffuse up and dissolve into water. Due to this property of them the aquatic plants and animals sustain life in water.

→ The aquatic living beings are able to breathe in water because of the dissolved oxygen in water.

→ In liquids, there is complete possibility of solubility of solids, liquids and gases.

→ There is comparatively more mixing-rate in liquids than that of solids, since in liquid state the particles have maximum space in them and they can freely move about.

→ In comparison to solids and liquids, gases are more compressible.

→ Due to random speed and maximum space, gases mix up with other gases more quickly.

→ In order to convert the degree of temperature from kelvin into Celsius, 273 should be subtracted from the given temperature and to convert from Celsius into kelvin the given temperature should be added to 273.

→ The melting point of a solid indicates the ability of force of cohesion between its particles.

→ At 0°C, the energy of the particles of water use to be more at the similar temperature than that of the energy of the particles of ice.

→ The boiling point of water is 373 K (100°C).

→ By changing in temperature we can convert matter from one state into another.

→ With the increase in pressure and decrease in temperature, gas can be converted into liquid.

→ Camphor and ammonium chloride are volatile substances.

→ Increase in the level-region, increases the rate of vaporisation.

→ With an increase in temperature, the rate of vaporisation rises.

→ Due to vaporisation, cooling occurs.

→ Diffusion: Intermixing of particles of two different materials by themselves is called diffusion.

→ LPG: By compressing butane at high pressure the fuel-gas used in the kitchen to cook is called Liquefied Petroleum Gas (LPG).

→ CNG: The natural gas after treating it with high pressure and such treated gas which is used in vehicles in the form of fuel is called as Compressed Natural Gas (CNG).

→ Density: The mass per unit volume of a substance is called density. i.e„
Density = \(\frac{\text { Mass of the substance }}{\text { Volume of the substance }}\)
or
D = \(\frac{M}{V}\)

→ Thermometer: The device used to measure temperature is called thermometer.

→ Melting Point: That fixed temperature at which a solid converts into a liquid is called melting point.

→ Melting: The process of melting or changing of a solid into liquid state is known as melting.

→ Dormant (Hidden) Heat of Melting: The heat energy that is required to convert 1 kg of a solid at atmospheric pressure at its melting point into liquid is called dormant heat of melting.

→ Boiling Point: That temperature at a certain atmospheric pressure at which a liquid starts boiling is said to be boiling point.

→ Unexposed Heat of Vaporisation: The amount of heat energy that is required to convert 1 kg of liquid at a certain atmospheric pressure at its boiling point is called as dormant/unexposed heat of vaporisation.

→ Sublimation: The process by means of which a substance converts into gaseous state directly from solid state without changing into liauid is called sublimation.

→ Dry Ice: Solid carbon dioxide is called dry ice.

→ Thawing: Changing of a liquid in solid state is called thawing.

→ Freezing Point: That fixed degree of temperature at which some liquid stmts converting into solid state is called freezing point.

→ Vaporisation: The process where a liquid changes into vapour state below the temperature of its boiling point is called vaporisation.

→ Humidity: The quantity of water vapours present in the air is called humidity.

Haryana State Board HBSE 9th Class Science Solutions Chapter 1 हमारे आस-पास के पदार्थ Textbook Exercise Questions and Answers.

Haryana Board 9th Class Science Solutions Chapter 1 हमारे आस-पास के पदार्थ

HBSE 9th Class Science हमारे आस-पास के पदार्थ Intext Questions and Answers

(पृष्ठ संख्या -4)
प्रश्न 1.
निम्नलिखित में से कौन-से पदार्थ हैं कुर्सी, वायु, स्नेह, गंध, घृणा, बादाम, विचार, शीत, नींबू पानी, इत्र की सुगंध।
उत्तर:
कुर्सी, वायु, बादाम व नींबू पानी, पदार्थ हैं क्योंकि ये स्थान घेरते हैं तथा द्रव्यमान रखते हैं।

प्रश्न 2.
निम्नलिखित प्रेक्षण के कारण बताएँ गर्मा-गरम खाने की गंध कई मीटर दूर से ही आपके पास पहुँच जाती है लेकिन ठडे खाने की महक लेने के लिए आपको उसके पास जाना पड़ता है।
उत्तर:
क्योंकि तापमान बढ़ने से विसरण तेज हो जाता है। इसी कारण गर्मा-गरम खाने की गंध कई मीटर से ही हमारे पास पहुँच जाती है, जबकि ठंडे खाने की महक लेने के लिए हमें उसके पास जाना पड़ता है।

प्रश्न 3.
स्वीमिंग पूल में गोताखोर पानी काट पाता है। इससे पदार्थ का कौन-सा गुण प्रेक्षित होता है?
उत्तर:
जल के कणों के बीच दूरी अपेक्षाकृत अधिक होने के कारण इसमें संपीडय का गुण पाया जाता है इसी कारण स्वीमिंग पूल में गोताखोर पानी (जल) को काट पाता है।

प्रश्न 4.
पदार्थ के कणों की क्या विशेषताएँ होती हैं? ।
उत्तर:
पदार्थ के कणों की निम्नलिखित विशेषताएँ होती हैं

1. पदार्थ के कणों के बीच रिक्त स्थान होता है।
2. पदार्थ के कण निरंतर गतिशील होते हैं अर्थात् उनमें गतिज ऊर्जा होती है।
3. तापमान बढ़ने से पदार्थ के कणों की गतिज ऊर्जा बढ़ जाती है।
4. पदार्थ के कण अपने आप अंतः मिश्रित हो जाते हैं।
5. पदार्थ के कण एक-दूसरे को आकर्षित करते हैं।

(पृष्ठ संख्या -6)

प्रश्न 1.
किसी तत्त्व के द्रव्यमान प्रति इकाई आयतन को घनत्व कहते हैं। (घनत्व = द्रव्यमान/आयतन)। बढ़ते हुए घनत्व के क्रम में निम्नलिखित को व्यवस्थित करें-वायु, चिमनी का धुआँ, शहद, जल, चॉक, रुई और लोहा।
उत्तर:
दिए गए तत्त्वों को घनत्व बढ़ने के साथ आरोही क्रम में लिखने पर निम्नलिखित क्रम प्राप्त होगाचिमनी का धुआँ, वायु, रुई, चॉक, जल, शहद व लोहा।

प्रश्न 2.
(a) पदार्थ की विभिन्न अवस्थाओं के गुणों में होने वाले अंतर को सारणीबद्ध कीजिए।
(b) निम्नलिखित पर टिप्पणी कीजिए-दृढ़ता, संपीडयता, तरलता, बर्तन में गैस का भरना, आकार, गतिज ऊर्जा एवं घनत्व।
उत्तर:
(a) पदार्थ की विभिन्न अवस्थाओं के गुणों में निम्नलिखित अंतर पाए जाते हैं

(b) दृढ़ता-पदार्थ के कणों के बीच लगने वाला आकर्षण बल पदार्थ की दृढ़ता निश्चित करता है। ठोसों में आकर्षण बल अधिक होने के कारण दृढ़ता अधिक होती है। द्रवों में उससे कम तथा गैसों में सबसे कम दृढ़ता होती है।

संपीडयता – किसी पदार्थ पर बल लगाकर उसके कणों की बीच की दूरी को कम करना संपीडयता कहलाता है। गैसों में संपीडयता का गुण पाया जाता है।

तरलता – जिन पदार्थों में बहने का गुण पाया जाता है, उन्हें तरल पदार्थ कहते हैं। द्रवों में तरलता का गुण पाया जाता है।

बर्तन में गैस का भरना-किसी बर्तन में गैस कणों में अंतराणुक बल क्षीण होने के कारण गैस सारे उपलब्ध स्थान को घेर लेती है। अर्थात् गैसों का आयतन निश्चित नहीं होता। इन्हें बर्तन में उच्च दाब पर भरा जाता है।

आकार-ठोस के कण अधिक अंतराणुक बल के साथ जुड़े होने के कारण ठोस को निश्चित आकार प्रदान करते हैं, जबकि द्रवों में यह अंतराणुक बल कम होता है जिस कारण इनका आकार निश्चित नहीं होता। गैसों में भी ऐसा होता है।

गतिज ऊर्जा-कणों की गति के कारण उत्पन्न ऊर्जा को गतिज ऊर्जा कहा जाता है। तापमान बढ़ाने से कणों की गतिज ऊर्जा बढ़ जाती है। ठोस में अधिक गतिज ऊर्जा नहीं होती, द्रव में कुछ गतिज ऊर्जा होती है जबकि गैसों में उच्च गतिज ऊर्जा होती है।

घनत्व-किसी तत्त्व के द्रव्यमान प्रति इकाई आयतन को घनत्व कहते हैं अर्थात् घनत्व = द्रव्यमान । ठोस पदार्थों का घनत्व उच्च होता है, द्रव में निम्न जबकि गैसों में नगण्य होता है।

प्रश्न 3.
कारण बताएँ
(a) गैस पूरी तरह उस बर्तन को भर देती है, जिसमें इसे रखते हैं।
(b) गैस बर्तन की दीवारों पर दबाव डालती है।
(c) लकड़ी की मेज़ ठोस कहलाती है।
(d) हवा में हम आसानी से अपना हाथ चला सकते हैं, लेकिन एक ठोस लकड़ी के टुकड़े से हाथ चलाने के लिए हमें कराटे में दक्ष होना पड़ेगा।
उत्तर:
(a) गैस का आयतन निश्चित न होने के कारण गैस पूरी तरह उस बर्तन को भर देती है जिसमें इसे रखा जाता है।
(b) गैसीय अवस्था में कणों की गति अनियमित और अत्यधिक तीव्र होती है। इस अनियमित गति के कारण गैस के कण आपस में एवं बर्तन की दीवारों से टकराते हैं। बर्तन की दीवार पर गैस कणों द्वारा प्रति इकाई क्षेत्र पर लगे बल के कारण गैस का दबाव बनता है।
(c) लकड़ी की मेज का निश्चित आकार, निश्चित आयतन तथा असंपीडय होने के कारण ठोस कहलाती है।
(d) हवा के कणों के बीच अधिक दूरी होने के कारण हवा में हम हाथ को आसानी से चला सकते हैं, जबकि ठोस लकड़ी के टुकड़े के कणों के बीच की दूरी कम होने के कारण हमें हाथ चलाने के लिए कराटे में दक्ष होना पड़ेगा।

प्रश्न 4.
सामान्यतया ठोस पदार्थों की अपेक्षा द्रवों का घनत्व कम होता है, लेकिन आपने बर्फ के टुकड़े को जल में तैरते हुए देखा होगा। पता लगाइए, ऐसा क्यों होता है?
उत्तर:
सामान्यतया ठोस पदार्थों की अपेक्षा द्रवों का घनत्व कम होता है परंतु जल का घनत्व 4°C पर अधिकतम होता है। जब इसे 4°C से नीचे ठंडा किया जाता है तो 0°C पर बर्फ जम जाती है जिसका घनत्व जल के घनत्व से कम होता है इसी कारण बर्फ जल में तैरती है।

(पृष्ठ संख्या-9)

प्रश्न 1.
निम्नलिखित तापमान को सेल्सियस में बदलें
(a) 300K
(b) 573K
उत्तर:
(a) 300K = (300 – 273)°C = 27°C
(b) 573K = (573 – 273)°C = 300°C

प्रश्न 2.
निम्नलिखित तापमान पर जल की भौतिक अवस्था क्या होगी?
(a) 250°C
(b) 100°C
उत्तर:
(a) 250°C तापमान पर समस्त जल भाप बनकर उड़ जाएगा।
(b) 100°C पर जल उबलना शुरू कर देगा क्योंकि यह जल का क्वथनांक है।

प्रश्न 3.
किसी भी पदार्थ की अवस्था परिवर्तन के दौरान तापमान स्थिर क्यों रहता है?
उत्तर:
किसी भी पदार्थ की अवस्था परिवर्तन के दौरान तापमान स्थिर रहता है क्योंकि अवस्था परिवर्तन के समय पदार्थ को दी जाने वाली समस्त ऊष्मा कणों के पारस्परिक आकर्षण बल को वशीभूत करके पदार्थ की अवस्था को बदलने में उपयोग हो जाती है।

प्रश्न 4.
वायुमंडलीय गैसों को द्रव में परिवर्तन करने के लिए कोई विधि सुझाइए।
उत्तर:
वायुमंडलीय गैसों को किसी बंद बर्तन में बंद करके तथा दाब बढ़ाकर व तापमान घटाकर द्रव में परिवर्तित किया जा सकता है।

(पृष्ठ संख्या-11)

प्रश्न 1.
गर्म, शुष्क दिन में कूलर कमरे को अधिक ठंडा क्यों करता है?
उत्तर:
गर्म, शुष्क दिन में आर्द्रता कम होने के कारण वायु शुष्क होती है जब यह वायु कूलर के पंखे द्वारा खींची जाती है तो कूलर में मैट पर टपकता हुआ जल वाष्पीकृत होकर गर्म व शुष्क वायु की गर्मी को अवशोषित कर लेता है जिसके परिणामस्वरूप वायु ठंडी हो जाती है। यह ठंडी वायु कमरे को ठंडा कर देती है।

प्रश्न 2.
गर्मियों में घड़े का जल ठंडा क्यों होता है?
उत्तर:
घड़े में छोटे-छोटे छिद्र होते हैं जिनके माध्यम से गर्मियों में जल रिसकर वाष्पीकृत होता रहता है तथा वाष्पन के लिए वह ऊष्मा जल से ही लेता है जिस कारण घड़े में रखा जल ठंडा हो जाता है।

प्रश्न 3.
एसीटोन/पेट्रोल या इत्र डालने पर हमारी हथेली ठंडी क्यों हो जाती है?
उत्तर:
एसीटोन पेट्रोल या इत्र को हथेली पर डालने से इसके कण हथेली से ऊर्जा प्राप्त कर वाष्पीकृत हो जाते हैं जिससे हथेली ठंडी हो जाती है।

प्रश्न 4.
कप की अपेक्षा प्लेट से हम गर्म दूध या चाय जल्दी क्यों पी लेते हैं?
उत्तर:
प्लेट की सतह का क्षेत्रफल कप की सतह की अपेक्षा अधिक होता है जिस कारण प्लेट की सतह से वाष्पीकरण अधिक होने के कारण गर्म दूध या चाय जल्दी ठंडी हो जाती है तथा ठंडी होने के कारण जल्दी पी जाती है।

प्रश्न 5.
गर्मियों में हमें किस तरह के कपड़े पहनने चाहिएँ?
उत्तर:
गर्मियों में हमें सूती कपड़े पहनने चाहिएँ क्योंकि गर्मियों में शारीरिक प्रक्रिया के कारण अधिक पसीना आता है, जिससे हमें ठंडक मिलती है जैसा कि हम जानते हैं कि वाष्पीकरण के दौरान द्रव की सतह के कण हमारे शरीर से ऊर्जा प्राप्त करके वाष्प में बदल जाते हैं। वाष्पीकरण की प्रसुप्त ऊष्मा के बराबर ऊष्मीय ऊर्जा हमारे शरीर से अवशोषित हो जाती है, जिससे शरीर शीतल हो जाता है। सूती कपड़े पहनने से जल का अवशोषण अधिक होता है, जिस कारण पसीना इसमें अवशोषित होकर वायुमंडल में आसानी से वाष्पीकृत हो जाता है।

HBSE 9th Class Science हमारे आस-पास के पदार्थ Textbook Questions and Answers

प्रश्न 1.
निम्नलिखित तापमानों को सेल्सियस इकाई में परिवर्तित करें
(a) 300K
(b) 573K
उत्तर:
(a) 300K = (300 – 273)° = 27°C
(b) 573K = (573 — 273)°C = 300°C

प्रश्न 2.
निम्नलिखित तापमानों को केल्विन इकाई में परिवर्तित करें
(a) 25°C
(b) 373°C
उत्तर:
(a) 25°C = (25 + 273)K 298K
(b) 373°C = (373 + 273)K = 646K

प्रश्न 3.
निम्नलिखित अवलोकनों हेतु कारण लिखें
(a) नैफ्थलीन को रखा रहने देने पर यह समय के साथ कुछ भी ठोस पदार्थ छोड़े बिना अदृश्य हो जाती है।
(b) हमें इत्र की गंध बहुत दूर बैठे हुए भी पहुँच जाती है।
उत्तर:
(a) नैफ्थलीन को रखा रहने देने पर यह समय के साथ कुछ भी ठोस पदार्थ छोड़े बिना अदृश्य हो जाती है क्योंकि नैफ्थलीन एक ऊर्ध्वापातित पदार्थ है जो ठोस से सीधा ही गैसीय अवस्था में परिवर्तित हो जाता है।
(b) हमें इत्र की गंध बहुत दूर बैठे हुए भी पहुँच जाती है क्योंकि इत्र वायु में विसरित होने का गुण रखता है।

प्रश्न 4.
निम्नलिखित पदार्थों को उनके कणों के बीच बढ़ते आकर्षण के अनुसार व्यवस्थित करें
(a) जल,
(b) चीनी,
(c) ऑक्सीजन।
उत्तर:
कणों के बीच बढ़ते आकर्षण के अनुसार पदार्थों का व्यवस्थित रूप निम्नलिखित है-
ऑक्सीजन < जल < चीनी

प्रश्न 5.
निम्नलिखित तापमानों पर जल की भौतिक अवस्था क्या है
(a) 25°C,
(b) 0°C,
(c) 100°C
उत्तर:
(a) 25°C पर जल द्रव अवस्था में होगा।
(b) 0°C पर जल ठोस (बफ) अवस्था में होगा।
(c) 100°C पर जल क्वथित अवस्था (भाप) में होगा।

प्रश्न 6.
पुष्टि हेतु कारण दें
(a) जल कमरे के ताप पर द्रव है।
(b) लोहे की अलमारी कमरे के ताप पर ठोस है।
उत्तर:
(a) जल कमरे के ताप पर द्रव है, क्योंकि

1. इस ताप पर इसके अणुओं के बीच लगने वाला आकर्षण बल सामान्य होता है।
2. इसके अणुओं की गतिज सामान्य होती है।

(b) लोहे की अलमारी कमरे के ताप पर ठोस है क्योंकि

1. लोहे के अणुओं के बीच लगने वाला आकर्षण बल काफी अधिक होता है।
2. लोहे के अणुओं के बीच दूरी नगण्य होती है जिस कारण वे निश्चित दूरी तक घूम सकते हैं।

प्रश्न 7.
273K पर बर्फ को ठंडा करने पर तथा जल को इसी तापमान पर ठंडा करने पर शीतलता का प्रभाव अधिक क्यों होता है?
उत्तर:
273K तापमान पर बर्फ को ठंडा करने पर तथा जल को इसी तापमान पर ठंडा करने पर शीतलता का प्रभाव अधिक होता है, क्योंकि बर्फ में संगलन गुप्त ऊष्मा अधिक होती है।

प्रश्न 8.
उबलते हुए जल अथवा भाप में से जलने की तीव्रता किसमें अधिक महसूस होती है?
उत्तर:
उबलते हुए जल अथवा भाप में से जलने की तीव्रता भाप में अधिक महसूस होती है क्योंकि भाप में अतिरिक्त ऊष्मा होती है जिसे वाष्पन की गुप्त ऊष्मा कहते हैं।

प्रश्न 9.
निम्नांकित चित्र के लिए A, B, C, D, E तथा F की अवस्था परिवर्तन को नामांकित करें

उत्तर:
(A) संगलन,
(B) वाष्पन,
(C) संघनन,
(D) जमना,
(E) ऊर्ध्वपातन,
(F) ऊर्ध्वपातन।

Haryana State Board HBSE 9th Class Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.4 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Exercise 9.4

प्रश्न 1.
समांतर. चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए कि समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
हल :

दिया है : एक समांतर चतुर्भुज ABCD और एक आयत ABEF एक ही आधार AB पर स्थित हैं और उनके क्षेत्रफल भी समान हैं।
सिद्ध करना है : समांतर चतुर्भुज ABCD का परिमाप > आयत ABEF का परिमाप।
प्रमाण : क्योंकि समांतर चतुर्भुज और आयत की सम्मुख भुजाएँ बराबर होती हैं।
∴ AB = DC [∵ ABCD एक समांतर चतुर्भुज है।]
और AB = EF [∵ ABEF एक आयत है।]
⇒ DC = EF ……(i)
या AB + DC = AB + EF ……(ii)
क्योंकि दी गई रेखा के किसी बिंदु से खींचे जा सकने वाले सभी खंड इस पर स्थित नहीं हैं, अतः लंब खंड सबसे छोटा है।
∴ BE < BC व AF < AD
या BC > BE व AD > AF
या BC + AD > BE + AF ……(iii)
समीकरण (ii) व (iii) को जोड़ने पर,
AB + DC + BC + AD > AB + EF + BE + AF
या AB + BC + CD + DA > AB + BE + EF + FA
अतः समांतर चतुर्भुज ABCD का परिमाप > आयत ABEF का परिमाप। [इति सिद्धम]

प्रश्न 2.
आकृति में, भुजा BC पर दो बिंदु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
क्या आप अब उस प्रश्न का उत्तर दे सकते हैं, जो आपने इस अध्याय की ‘भूमिका’ में छोड़ दिया था कि “क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया है”?

हल :
दिया है : ΔABC की भुजा BC पर दो बिंदु D व E इस प्रकार हैं कि BD = DE = EC
सिद्ध करना है : ar (ΔABD) = ar (ΔADE) = ar (ΔAEC)
रचना : A से AL ⊥ BC खींचो।
प्रमाण : आकृति अनुसार, AL, ΔABD, ΔADE व ΔAEC का शीर्षलंब है।
ar (ΔABD) = \(\frac{1}{2}\) × BD × AL …..(i)
ar (ΔADE) = \(\frac{1}{2}\) × DE × AL …(ii)
ar (ΔAEC) = \(\frac{1}{2}\) × EC × AL …(iii)
परंतु BD = DE = EC (दिया है)…(iv)
समीकरण (i), (ii), (iii) व (iv) की तुलना करने पर,
ar (ΔABD) = ar (ΔADE) = ar (ΔAEC)
हां सभी त्रिभुजों के शीर्षलंब समान हैं। बुधिया इस प्रश्न के उत्तर द्वारा अपने खेत तीन समान भागों में बांट सकती है।

प्रश्न 3.
आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।

हल :
दिया है : आकृति में ABCD, DCFE व ABFE तीन समांतर चतुर्भुज हैं।
सिद्ध करना है : ar (ΔADE) = ar (ΔBCF)
प्रमाण : क्योंकि समांतर चतुर्भुजों की सम्मुख भुजाएं बराबर होती हैं।
∴ AD = BC [|| चतुर्भुज ABCD की भुजाएं]
DE = CF [|| चतुर्भुज DCFE की भुजाएं]
AE = BF [|| चतुर्भुज ABFE की भुजाएं]
अब ΔADE और ΔBCF में,
AD = BC [प्रमाणित]
DE = CF [प्रमाणित]
AE = BF [प्रमाणित]
∴ ΔADE ≅ ΔBCF [भुजा-भुजा-भुजा सर्वांगसमता]
अतः ar (ΔADE) = ar (ΔBCF) [इति सिद्धम]

प्रश्न 4.
आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है, तो दर्शाइए कि ar (BPC) = ar (DPO) है।

हल :
दिया है : एक समांतर चतुर्भुज ABCD की भुजा BC को Q तक इस प्रकार बढ़ाया गया है कि AD = CQ, AQ भुजा DC को P पर प्रतिच्छेद करती है।
सिद्ध करना है : ar (ΔBPC) = ar (ΔDPQ)
रचना : A व C को मिलाओ।
प्रमाण : क्योंकि ΔADC और ΔADQ एक ही आधार AD और एक ही समांतर रेखाओं AD व CQ के मध्य स्थित है।
∴ ar (ΔADC) = ar (ΔADQ)
दोनों ओर से ΔADP का क्षेत्रफल घटाने पर,
ar (ΔADC) – ar (ΔADP) = ar (ΔADQ) – ar (ΔADP)
⇒ ar (ΔAPC) = ar (ΔDPQ) …(i)
इसी प्रकार ΔAPC और ΔPCB एक ही आधार PC तथा एक ही समांतर रेखाओं PC व AB के मध्य स्थित हैं।
∴ ar (ΔAPC) = ar (ΔPCB)
समीकरण (i) व (ii) की तुलना से,
ar (ΔPCB) = ar (ΔDPQ)
या ar (ΔBPC) = ar (ΔDPQ) [इति सिद्धम]

प्रश्न 5.
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि
(i) ar (BDE) = \(\frac{1}{4}\)ar (ABC)
(ii) ar (BDE) = \(\frac{1}{2}\)ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = \(\frac{1}{8}\)ar (AFC)

हल :
दिया है : ΔABC और ΔBDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। AE भुजा BC को F पर प्रतिच्छेद करती है।

सिद्ध करना है : (i) ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC)
(ii) ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBAE)
(iii) ar (ΔABC) = 2 ar (ΔBEC)
(iv) ar (ΔBEF) = ar (ΔAFD)
(v) ar (ΔBFE) = 2 ar (ΔFED)
(vi) ar (ΔFED) = \(\frac{1}{8}\)ar (ΔAFC)
रचना : EC व AD को मिलाओं तथा EL ⊥ BC खींचो।
प्रमाण : माना समबाहु ΔABC की प्रत्येक भुजा = a मात्रक
(i) ar (ΔABC) = \(\frac{\sqrt{3}}{4}\)a² …(1) [∵ समबाहु त्रिभुज का क्षेत्रफल = \(\frac{\sqrt{3}}{4}\)(भुजा)²]
ar (ΔBDE) = \(\frac{\sqrt{3}}{4}\left(\frac{a}{2}\right)^2\)
= \(\frac{\sqrt{3}}{4}\left(\frac{a^2}{4}\right)=\frac{\sqrt{3} a^2}{16}\)
= \(\frac{1}{4} \times \frac{\sqrt{3}}{4} a^2\)
= \(\frac{1}{4}\)ar (ΔABC) [समीकरण (1) से]
अतः ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC) [इति सिद्धम]

(ii) ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBEC) …..(2)
[∵ ED, ΔBEC की माध्यिका है तथा माध्यिका A के दो समान भाग करती है।]
अब ∠EBC = ∠ACB [प्रत्येक = 60%]
परंतु यह एकांतर कोण हैं।
∴ BE || AC
ΔBEC तथा ΔBEA एक ही आधार BE तथा एक ही समांतर रेखाओं BE व AC के मध्य स्थित हैं।
∴ ar (ΔBEC) = ar (ΔBEA) …..(3)
\(\frac{1}{2}\)ar (ΔBEC) = \(\frac{1}{2}\)ar (ΔBEA) …..(3)
समीकरण (2) व (3) की तुलना से,
ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBAE) [इति सिद्धम]

(iii) ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC) ….(4) [प्रमाणित]
ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBEC) ….(5) [प्रमाणित]
समीकरण (4) तथा (5) की तुलना से,
\(\frac{1}{4}\)ar (ΔABC) = \(\frac{1}{2}\)ar (ΔBEC)
ar (ΔABC) = 2 ar (ΔBEC) [इति सिद्धम]

(iv) ∠ABD = ∠BDE [प्रत्येक = 60%]
परन्तु यह एकांतर कोण हैं।
∴ AB || DE
अब ΔBED व ΔAED एक ही आधार ED तथा एक ही समांतर रेखाओं ED और AB के मध्य स्थित हैं।
∴ ar (ΔBED) = ar (ΔAED)
दोनों ओर से ΔEDF का क्षेत्रफल घटाने पर,
ar (ΔBED) – ar (ΔEDF) = ar (ΔAED) – ar (ΔEDF)
∴ ar (ΔBFE) = ar (ΔAFD) …..(6) [इति सिद्धम]

(v) ΔABD में,
AD² = AB² – BD²
= (a²) – (\(\frac{a}{2}\))²
= \(a^2-\frac{a^2}{4}=\frac{3 a^2}{4}\)
AD = \(\frac{\sqrt{3} a}{2}\)
ΔLED में,
EL² = DE² – DL²

समीकरण (7) व (8) से,
ar (ΔAFD) = 2 ar (ΔEFD)
समीकरण (6) व (9) से,
ar (ΔBEF) = 2 ar (ΔEFD)

(vi) अब ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC) [प्रमाणित]
ar (ΔBEF) + ar (ΔFED) = \(\frac{1}{4}\) × 2 ar (ΔADC)
2 ar (ΔFED) + ar (ΔFED) = \(\frac{1}{2}\)ar (ΔADC) {∵ ar (ΔBEF) = 2ar (ΔFED) प्रमाणित}
3 ar (ΔFED) = \(\frac{1}{2}\)[ar (ΔAFC) – ar (ΔAFD)]
3 ar (ΔFED) = \(\frac{1}{2}\)ar (ΔAFC) – \(\frac{1}{2}\) × 2ar (ΔFED)
{∵ ar (ΔAFD) = 2 ar (ΔFED) प्रमाणित}
4 ar (ΔFED) = \(\frac{1}{2}\)ar (ΔAFC)
ar (ΔFED) = \(\frac{1}{8}\)ar (ΔAFC) [इति सिद्धम]

प्रश्न 6.
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु P पर प्रतिच्छेद D करते हैं। दर्शाइए कि ar (APB) × ar (CPD) = ar (APD) × ar (BPC) है।
हल :

दिया है : चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु P पर प्रतिच्छेद करते हैं।
सिद्ध करना है : ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC)
रचना : AM ⊥ BD व CN ⊥ BD खींचिए।
प्रमाण: ar (ΔAPB) = \(\frac{1}{2}\) × PB × AM …(i)
ar (ΔCPD) = \(\frac{1}{2}\) × DP × CN …(ii)
ar (ΔAPD) = \(\frac{1}{2}\) × DP × AM….(iii)
ar (ΔBPC) = \(\frac{1}{2}\) × PB × CN …(iv)
समीकरण (i) व (ii) से,
ar (ΔAPB) × ar (ΔCPD) = \(\frac{1}{2}\) × PB × AM × \(\frac{1}{2}\) × DP × CN …(v)
समीकरण (iii) व (iv) से,
ar (ΔAPD) × ar (ΔBPC) = \(\frac{1}{2}\) × DP × AM × \(\frac{1}{2}\) × PB × CN …(vi)
समीकरण (v) व (vi) से,
ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC) [इति सिद्धम]

प्रश्न 7.
Pऔर Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिंदु हैं तथा R रेखाखंड AP का मध्य-बिंदु है। दर्शाइए कि:
(i) ar (PRQ) = \(\frac{1}{2}\)ar (ARC)
(ii) ar (RQC) = \(\frac{3}{8}\)ar (ABC)
(iii) ar (PBQ)= ar (ARC)
हल :
दिया है : ΔABC की भुजाओं AB और BC के मध्य-बिंदु क्रमशः P व Q है। R रेखाखंड AP का मध्य-बिंदु है।
सिद्ध करना है :
(i) ar (ΔPRQ) = \(\frac{1}{2}\)ar (ΔARC)
(ii) ar (ΔRQC) = \(\frac{3}{8}\)ar (ΔABC)
(iii) ar (ΔPBQ) = ar (ΔARC)
रचना : AQ तथा PC को मिलाओ।

प्रमाण : (i) ∵ ar (ΔPQR) = \(\frac{1}{2}\)ar (ΔAPQ) [∵ QR त्रिभुज APQ की माध्यिका है जो त्रिभुज को दो समान क्षेत्रफलों वाले त्रिभुजों में बांटती है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔABQ) [∵ QP त्रिभुज ABQ की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔABQ)
= \(\frac{1}{4} \times \frac{1}{2}\)ar (ΔABC) [∵ AQ त्रिभुज ABC की माध्यिका है।]
= \(\frac{1}{8}\)ar (ΔABC) …..(i)
अब ar (ΔARC) = \(\frac{1}{2}\)ar (ΔAPC) [∵ CR त्रिभुज APC की माध्यिका है।]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔABC) [∵ CP त्रिभुज ABC की माध्यिका है।]
= \(\frac{1}{4}\)ar (ΔABC) ……(ii)
समीकरण (i) व (ii) की तुलना से,
ar (ΔPQR) = \(\frac{1}{8}\)ar (ΔABC)
= \(\frac{1}{2} \times \frac{1}{4}\)ar (ΔABC)
= \(\frac{1}{2}\)ar (ΔARC) [इति सिद्धम]

(ii) ar (ΔRQC) = ar (ΔRQA) + ar (ΔAQC) – ar (ΔARC) ….(iii)
अब ar (ΔRQA) = \(\frac{1}{2}\)ar (ΔPQA) [∵ RQ, ΔPQA की माध्यिका है।]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (AQB) [∵ PQ, ΔAQB की माध्यिका है।]
= \(\frac{1}{4}\)ar (AQB)
= \(\frac{1}{4} \times \frac{1}{2}\)ar(ABC) [∵ AQ, ΔABC की माध्यिका है।]
= \(\frac{1}{8}\)ar (ΔABC) …..(iv)
अतः ar (ΔAQC) = \(\frac{1}{2}\)ar (ΔABC) …..(v)
[∵ AQ, ΔABC की माध्यिका है।]
या ar (ΔARC) = \(\frac{1}{2}\)ar(ΔAPC) [∵ CR, ΔAPC की माध्यिका है।]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔABC) [∵ CP, ΔABC की माध्यिका है।
= \(\frac{1}{4}\)ar (ΔABC) …..(vi)
समीकरण (iii), (iv), (v) व (vi) की तुलना से,
ar (ΔRQC) = \(\frac{1}{8}\)ar (ΔABC) + \(\frac{1}{2}\)ar(ΔABC) – \(\frac{1}{4}\)ar(ΔABC)
= \(\frac{3}{8}\)ar (ΔABC) [इति सिद्धम]

(iii) ∵ ar (ΔPBQ) = \(\frac{1}{2}\)ar (ΔABQ) [∵ PQ, ΔABQ की माध्यिका है।]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔABC) [∵ AQ, ΔABC की माध्यिका है।]
= \(\frac{1}{4}\)ar (ΔABC)
= ar (ΔARC) [समीकरण (iv) से]
[इति सिद्धम]

प्रश्न 8.
आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड AX ⊥ DE भुजा BC को बिंदु Y पर मिलता है। दर्शाइए किः

(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
हल :
दिया है : समकोण ΔABC में ∠A समकोण है। BCED, ACFG व ABMN क्रमशः भुजाओं BC, CA व AB बने तीन वर्ग हैं। रेखाखंड AX ⊥ DE भुजा BC को बिंदु Y पर मिलता है।
सिद्ध करना है :
(i) ΔMBC ≅ ΔABD
(ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
प्रमाण : (i) ∠BAC + ∠CAG = 180° (प्रत्येक = 90°)
∴ BAG एक सरल रेखा है।
इसी प्रकार CAN एक सरल रेखा है।
∠MBA = ∠CBD (प्रत्येक = 90°)
दोनों ओर ∠ABC जोड़ने पर,
∠MBA + ∠ABC = ∠CBD + ∠ABC
⇒ ∠MBC = ∠ABD
ΔMBC तथा ΔABD में,
BC = BD [वर्ग BCDE की भुजाएं]
MB = AB [वर्ग ABMN की भुजाएं]
∠MBC = ∠ABD [प्रमाणित]
∴ ΔMBC ≅ ΔABD [भुजा-कोण-भुजा सर्वांगसमता]
[इति सिद्धम]

(ii) ΔABD तथा आयत BYXD एक ही आधार BD तथा एक ही समांतर रेखाओं BD एवं AX के मध्य स्थित हैं।
∴ ar (आयत BYXD) = 2 ar (ΔABD)
∴ ar (आयत BYXD) = 2 ar (ΔMBC) …..(i)
[∵ ΔABD = ΔMBC प्रमाणित] [इति सिद्धम]

(iii) ΔMBC तथा वर्ग ABMN एक ही आधार MB तथा एक ही समांतर रेखाओं MB तथा NC के मध्य स्थित हैं।
∴ ar (वर्ग ABMN) = 2 (ar AMBC) …..(ii)
समीकरण (i) व (ii) से,
ar (आयत BYXD) = ar (वर्ग ABMN) [इति सिद्धम]

(iv) ΔFCB तथा ΔACE में,
CB = CE [वर्ग BCED की भुजाएं]
FC = AC [वर्ग ACFG की भुजाएं]
∠FCB = ∠ACE [प्रत्येक = ∠ACB+ 90°]
∴ ΔFCB ≅ ΔACE [भुजा-कोण-भुजा सर्वांगसमता] [इति सिद्धम]

(v) ΔACE तथा आयत CYXE एक ही आधार CE तथा एक ही समांतर रेखाओं के मध्य स्थित हैं।
∴ ar (आयत CYXE) = 2 ar (ΔACE)
∴ ar (आयत CYXE) = 2 ar (ΔFCB) ….(iii) [इति सिद्धम]
[∵ ΔACE ≅ ΔFCB प्रमाणित] [इति सिद्धम]

(vi) ΔFCB तथा वर्ग ΔCFG एक ही आधार CF तथा एक ही समांतर रेखाओं के मध्य स्थित हैं।
∴ ar (वर्ग ΔCFG) = 2 ar (ΔFCB) ….(iv)
समीकरण (iii) व (iv) की तुलना से,
ar (आयत CYXE) = ar (वर्ग ACFG)

(vii) ar (वर्ग BCED) = ar (आयत BYXD) + ar (आयत CYXE)
⇒ ar (वर्ग BCED) = ar (वर्ग ABMN) + ar (वर्ग ACFG)
{∵ ar (आयत BYXD) = ar (वर्ग ABMN) तथा ar (आयत CYXE) = ar (वर्ग ACFG)}
[इति सिद्धम]

Haryana State Board HBSE 9th Class Maths Solutions Chapter 7 त्रिभुज Ex 7.4 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 7 त्रिभुज Exercise 7.4

प्रश्न 1.
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है।
हल :

माना ΔPQR एक समकोण त्रिभुज है जिसमें,
∠PQR = 90°
हम जानते हैं कि ΔPQR में,
∠PQR + ∠QRP + ∠RPQ = 180°
या 90° + ∠QRP + ∠RPQ = 180°
या ∠QRP + ∠RPQ = 180° – 90° = 90°
⇒ ∠QRP = ∠RPQ = न्यून कोण
अतः ∠QRP < 90° तथा ∠RPQ < 90°
इस प्रकार ΔPQR में ∠PQR सबसे बड़ा कोण है तथा सबसे बड़े कोण के सामने की भुजा सबसे बड़ी होती है।
∴ PR सबसे बड़ी भुजा है।
अतः समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है। [इति सिद्धम]

प्रश्न 2.
आकृति में, ΔABC की भुजाओं AB और AC को क्रमशः बिंदुओं Pऔर Q तक बढ़ाया गया है। साथ ही, ∠PRC < ∠QCB है। दर्शाइए कि AC > AB है।

हल :
यहाँ पर दिया गया है,
∠PBC < ∠QCB या – ∠PBC > – ∠QCB
या 180° – ∠PBC > 180° – ∠QCB
या ∠ABC > ∠ACB
या AC > AB [∵ बड़े कोण की सम्मुख भुजा बड़ी होती है।] [इति सिद्धम]

प्रश्न 3.
आकृति में, ∠B < ∠A और ∠C < ∠D है। दर्शाइए कि AD < BC है।

हल :
यहाँ पर दिया गया है,
∠B < ∠A और ∠C < ∠D
⇒ AO < BO तथा OD < OC [∵ बड़े कोण की सम्मुख भुजा बड़ी होती है]
दोनों को जोड़ने पर,
AO + OD < BO + OC
⇒ AD < BC [इति सिद्धम]

प्रश्न 4.
AB और CD क्रमशः एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएं हैं (देखिए आकृति)। दर्शाइए कि ∠A > ∠C और ∠B > ∠D है।

हल :
यहाँ पर, ABCD एक चतुर्भुज है, जिसमें AB सबसे छोटी भुजा है और CD सबसे बड़ी भुजा है।
AC तथा BD को मिलाया।
क्योंकि AB, चतुर्भुज ABCD की सबसे छोटी भुजा है।
∴ ΔABC में, BC > AB
∠8 > ∠3 ………..(i)
[∵ बड़ी भुजा के सामने का कोण बड़ा होता है]
इसी प्रकार CD चतुर्भुज ABCD की सबसे बड़ी भुजा है।
∴ ΔACD में,
CD > AD
∠7 > ∠4 …..(ii) [∵ बड़ी भुजा के सामने का कोण बड़ा होता है]

समीकरण (i) व (ii) से,
∠8 + ∠7 > ∠3 + ∠4
या ∠A > ∠C [इति सिद्धम]
अब ΔABD में,
AD > AB [∵ AB सबसे छोटी भुजा है]
या ∠1 > ∠6 ….(iii)
ΔBDC में,
CD > BC [∵ CD सबसे बड़ी भुजा है]
∴ ∠2 > ∠5 ……..(iv)
समीकरण (iii) व (iv) से
∠1 + ∠2 > ∠5 + ∠6
या ∠B > ∠D [इति सिद्धम]

प्रश्न 5.
आकृति में, PR > PQ है और PS कोण OPR को समद्विभाजित करता है। सिद्ध कीजिए कि ∠PSR > ∠PSQहै।
हल :

यहाँ पर ΔPQR में, PR > PQ [दिया है]
⇒ ∠PQR > ∠PRQ [∵ बड़ी भुजा के सामने का कोण बड़ा होता है]
दोनों ओर ∠1 जोड़ने पर,
∠PQR + ∠1 > ∠PRQ + ∠1
या ∠PQR + ∠1 > ∠PRQ + ∠2 ……..(i)
[∵ PS, ∠P का कोण समद्विभाजक है, ∴ ∠1 = ∠2]
अब ΔPQS में,
∠PQR + ∠1 + ∠PSQ = 180°
∠PQR + ∠1 = 180° – ∠PSQ …(ii)
इसी प्रकार ΔPSR में, ∠PRQ + ∠2 = 180° – ∠PSR ……(iii)
समीकरण (i), (ii) व (iii) से,
∴ 180° – ∠PSQ > 180° – ∠PSR
या – ∠PSQ > -∠PSR
या ∠PSQ < ∠PSR अर्थात ∠PSR > ∠PSQ [इति सिद्धम]

प्रश्न 6.
दर्शाइए कि एक रेखा पर एक दिए हुए बिंदु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखंड खींचे जा सकते हैं, उनमें लंब रेखाखंड सबसे छोटा होता है।

हल :
माना P कोई एक बिंदु है, जो रेखा l पर नहीं है,
तथा PM ⊥ l,M के अतिरिक्त रेखा l पर N कोई बिंदु है।
अब ΔPMN में,
∠M = 90°
⇒ ∠N < 90° [∵ ∠MPN + ∠PNM = 90° ⇒ ∠N < 90°]
या ∠N < ∠M
या PM < PN [∵ बड़े कोण के सामने की भुजा बड़ी होती है]
अतः P से l तक रेखाखंडों में से PM लंब सबसे छोटा रेखाखंड है। [इति सिद्धम]

Haryana State Board HBSE 9th Class Maths Solutions Chapter 7 त्रिभुज Ex 7.3 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 7 त्रिभुज Exercise 7.3

प्रश्न 1.
ΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)।
यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखंड BC का लंब समद्विभाजक है।

हल :
(i) ΔABD और ΔACD में,
AB = AC [दिया है]
BD = DC [दिया है]
तथा AD = AD [उभयनिष्ठ]
∴ ΔABD = ΔACD [भुजा-भुजा-भुजा सर्वांगसमता]

(ii) ΔABP और ΔACP में,
AB = AC [दिया है]
∠BAP = ∠CAP [सर्वांगसम ΔABD और ΔACD के संगत भाग]
AP = AP [उभयनिष्ठ]
∴ ΔABP ≅ ΔACP [भुजा-कोण-भुजा सर्वांगसमता]

(iii) क्योंकि ΔABD ≅ ΔACD [प्रमाणित]
∴ ∠BAD = ∠CAD
अर्थात AD, ∠A को समद्विभाजित करता है।
अतः AP, ∠A को समद्विभाजित करता है।
अब ΔBDP और ΔCDP में,
BD = CD [दिया है]
BP = CP [सर्वागसम ΔABP और ΔACP के संगत भाग]
DP = DP [उभयनिष्ठ]
∴ ΔBDP ≅ ΔCPD [भुजा-भुजा-भुजा सर्वांगसमता]
⇒ ∠BDP = ∠CDP [सर्वांगसम त्रिभुजों के संगत भाग]
अर्थात DP, ∠D को समद्विभाजित करता है।
या AP, ∠D को समद्विभाजित करता है। ……….(ii)
समीकरण (i) व (ii) से,
AP, ∠A व ∠D को समद्विभाजित करता है। [इति सिद्धम]

(iv) क्योंकि AP भुजा BC पर स्थित है।
∴ ∠APB + ∠APC = 180°
ΔBAP ≅ ΔCAP [प्रमाणित]
∠APB = ∠APC [सर्वांगसम त्रिभुजों के संगत भाग]
अतः ∠APB + ∠APB = 180° [∵ ∠APB = ∠APC]
या 2∠APB = 180°
या ∠APB = \(\frac {180°}{2}\) = 90°
अतः ∠APB = ∠APC = 90° तथा BP = PC [प्रमाणित]
इस प्रकार AP रेखाखंड BC का लंब समद्विभाजक है। [इति सिद्धम]

प्रश्न 2.
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलंब है, जिसमें AB = AC है। दर्शाइए कि-
(i) AD रेखाखंड BC को समद्विभाजित करता है।
(ii) AD कोण A को समद्विभाजित करता है।

हल :
यहाँ पर दिया गया है, AD, शीर्ष A से डाला हुआ लंब है, जोकि समद्विबाहु ΔABC के आधार BC के सम्मुख है। AB = AC, ∠ADC = ∠ADB = 90°
अब ΔADB और ΔADC में,
कर्ण AB = कर्ण AC [दिया है]
AD = AD
∠ADC = ∠ADB [∵ प्रत्येक = 90°]
∴ ΔADB ≅ ΔADC [समकोण-कर्ण-भुजा सर्वांगसमता]
⇒ BD = DC तथा ∠BAD = ∠DAC [सर्वांगसमता त्रिभुजों के संगत भाग]
अतः (i) AD, BC को समद्विभाजित करता है। [इति सिद्धम]
तथा (ii) AD, ∠A को समद्विभाजित करता है। [इति सिद्धमा]

प्रश्न 3.
एक त्रिभुज ABC की दो भुजाएं AB और BC तथा माध्यिका AM क्रमशः एक-दूसरे त्रिभुज की भुजाओं PQ और QR तथा माध्यिका PN के बराबर हैं (देखिए आकृति) दर्शाइए कि
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR

हल :
(i) यहाँ पर दिया गया है, ΔABC और ΔPQR में,
AB = PQ
BC = QR
तथा AM = PN
क्योंकि AM तथा PN क्रमशः ΔARC तथा ΔPQR की माध्यिकाएँ हैं।
अब BC = QR [दिया है]
या \(\frac {1}{2}\)BC = \(\frac {1}{2}\)QR
या BM = QN
अब, ΔABM तथा ΔPQN में,
AB = PQ [दिया है]
BM = QN [प्रमाणित]
तथा AM = PN [दिया है]
∴ ΔΑΒΜ ≅ ΔΡQΝ [भुजा-भुजा-भुजा सर्वांगसमता] [इति सिद्धम]

(ii) ∠B = ∠Q
सर्वांगसम त्रिभुजों के संगत भाग
अब ΔABC तथा ΔPQR में,
AB = PQ [दिया है]
∠B = ∠Q [प्रमाणित]
BC = QR [दिया है]
∴ ΔABC ≅ ΔPQR [भुजा-कोण-भुजा सर्वांगसमता] [इति सिद्धम]

प्रश्न 4.
BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलंब हैं। RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है।
हल :

ΔBCF और ΔCBE में,
∠BFC = ∠CEB [प्रत्येक = 90°]
कर्ण BC = कर्ण BC [उभयनिष्ठ]
FC = EB [दिया है]
ΔBCF ≅ ΔCBE [समकोण-कर्ण-भुजा सर्वांगसमता]
⇒ ∠FBC = ∠ECB [सर्वागसम त्रिभुजों के संगत भाग]
अतः ΔABC एक समद्विबाहु त्रिभुज है। [इति सिद्धम]

प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। AP ⊥ BC खींचकर दर्शाइए कि ∠B = ∠C है।
हल :

यहाँ पर, ΔABP और ΔACP में,
AB = AC [दिया है]
AP = AP [उभयनिष्ठ]
तथा ∠APB = ∠APC [प्रत्येक = 90°]
∴ ΔABP ≅ ΔACP [समकोण-कर्ण-भुजा सर्वांगसमता]
⇒ ∠B = ∠C [सर्वांगसम त्रिभुजों के संगत भाग] [इति सिद्धम|