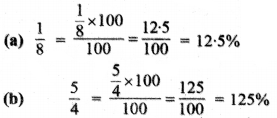Class 7

Haryana State Board HBSE 7th Class Maths Solutions Chapter 8 राशियों की तुलना Ex 8.3 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 8 राशियों की तुलना Ex 8.3

प्रश्न 1.
क्रय-विक्रय के निम्न सौदों में हानि या लाभ ज्ञात कीजिए। प्रत्येक दशा में प्रतिशत हानि या प्रतिशत लाभ भी ज्ञात कीजिए।
(a) बगीचे में काम आने वाली कैंची ₹ 250 में खरीदी गई तथा ₹ 325 में बेची गई।
(b) एक रेफ्रीजरेटर ₹ 12000 में खरीदा गया और ₹ 13500 में बेचा गया।
(c) एक अलमारी ₹ 2500 में खरीदी गई और ₹ 3000 में बेची गई।
(d) एक स्कर्ट ₹ 250 में खरीद कर ₹ 150 में बेची गई।
हल :
(a) क्र. मू. (C.P.) = ₹ 250 और वि. मू. (S.P.) = ₹ 325
∵ S.P. > C.P.
अत: लाभ होगा।
लाभ = वि. म. – क्र. मू.
= ₹ (325 – 250) = ₹75
लाभ % = (लाभ / क्र. मू. × 100%) %
= (\(\frac {75}{250}\) × 100)% = 30% उत्तर

(b) क्र. मू. (C.P.) = ₹ 12000 और वि. मू. (S.P.) = ₹ 13500
∵ वि. मू. > क्र. मू.
∴ लाभ = ₹(13500 – 12000) = 1500
लाभ % = (लाभ / क्र. मू. × 100)%
= (\(\frac {1500}{12000}\) × 100)% = 12.5% उत्तर

(c) क्र. मू. (C.P.) = ₹ 2500
तथा वि. मू. (S.P.) = ₹ 3000
∵ S.P. > C.P.
अत: लाभ होगा।
लाभ = S.P. – C.P. = ₹(3000 – 2500) = ₹ 500
लाभ लाभ % = (लाभ / क्र. मू. × 100) %
= (\(\frac {500}{2500}\) × 100)% = 20% उत्तर

(d) क्र. मू. (C.P.) = ₹ 250
और वि. मू. (S.P.) = ₹ 150
∵ लाभ S.P. < C.P.
अतः हानि होगी।
हानि = क्र. मू. – वि. मू.
= ₹ (250 – 150) = ₹ 100
हानि % = (लाभ / क्र. मू. × 100)%
= (\(\frac {100}{250}\) × 100) % = 40% उत्तर

प्रश्न 2.
दिए गए प्रत्येक अनुपात के दोनों पदों को प्रतिशत में बदलिए:
(a) 3 : 1
(b) 2 : 3 : 5
(c) 1 : 4
(d) 1 : 2 : 5
हल :
(a) दिया है, 3 : 1
कुल भाग = 3 + 1 = 4
इसका अर्थ है \(\frac {3}{4}\) और \(\frac {1}{4}\)
इनका प्रतिशत (\(\frac {3}{4}\) × 100)% = 75%
और (\(\frac {1}{4}\) × 100)% = 25% उत्तर

(b) दिया अनुपात = 2 : 3 : 5
कुल भाग = 2 + 3 + 5 = 10
इसक अर्थ है \(\frac {2}{10}\), \(\frac {3}{10}\) और \(\frac {5}{10}\)
अब इनकी प्रतिशतता क्रमशः (\(\frac {2}{10}\) × 100)% = 20%,
(\(\frac {3}{10}\) × 100)% = 30% और (\(\frac {5}{10}\) × 100)% = 50% है। उत्तर

(c) दिया है, 1 : 4
कुल भाग = 1 + 4 = 5
इसका अर्थ है \(\frac {1}{5}\), और \(\frac {4}{5}\)
इनका प्रतिशत क्रमशः (\(\frac {1}{5}\) × 100) % = 20% और
(\(\frac {4}{5}\) × 100)% = 80% है। उत्तर

(d) दिया है, 1 : 2 : 5
कुल भाग = 1 + 2 + 5 = 8
इसका अर्थ है \(\frac {1}{8}\), \(\frac {2}{8}\) और \(\frac {5}{8}\)
इनकी प्रतिशतता
\(\frac {1}{8}\) × 100 = 12.5%
\(\frac {2}{8}\) × 100 = 25% और
\(\frac {5}{8}\) × 100 = 62.5% उत्तर

प्रश्न 3.
एक नगर की जनसंख्या 25000 से घटकर 24500 रह गई। घटाने का प्रतिशत ज्ञात कीजिए।
हल:
नगर की जनसंख्या = 25000
नयी जनसंख्या = 24500
जनसंख्या में कमी = 25000 – 24500 = 500
प्रतिशत कमी = (\(\frac {500}{25000}\) × 100) %
= 2%.

प्रश्न 4.
अरुण ने एक कार ₹ 3,50,000 में खरीदी। अगले वर्ष उसका मूल्य बढ़कर ₹ 3,70,000 हो गया। कार के मूल्य की प्रतिशत वृद्धि ज्ञात कीजिए।
हल :
कार का वास्तविक मूल्य = ₹ 3,50,000
कार का बड़ा मूल्य = ₹ 3,70,000
मूल्य में वृद्धि = ₹ (3,70,000 – 3,50,000)
= ₹ 20,000
वृद्धि प्रतिशत = (\(\frac {20000}{350000}\) × 100)%
= \(\frac {40}{7}\) % = 5\(\frac {5}{7}\)%. उत्तर

प्रश्न 5.
मैंने एक टी.वी. ₹ 10,000 रु. में खरीद कर 20 प्रतिशत लाभ पर बेच दिया। मुझे बेचने पर कितना धन प्राप्त हुआ ?
हल :
क्रय मूल्य (C.P) = ₹ 10,000 और लाभ = 20%
अब विक्रय मूल्य = (100 + लाभ %) × C.P. / 100
= ₹ \(\left[\frac{(100+20) \times 10000}{100}\right]\)
= ₹(120 × 100) = ₹ 12,000
अत: टी.वी. का विक्रय मूल्य = ₹ 12,000 उत्तर

प्रश्न 6.
जही एक वाशिंग मशीन ₹ 13,500 में बेचने पर 20 प्रतिशत की हानि उठाती है। उसने वह मशीन कितने में खरीदी थी ?
हल:
वि. मू. (S.P.) = ₹ 13,500 और हानि = 20%
अब क्र. मू. (C.P.) = 100 × S.P. / 100 – हानि %
क्र. मू. (C.P) = ₹ \(\frac{100 \times 13500}{100-20}\)
= ₹ \(\frac{100 \times 13500}{80}\)
= ₹ 16,875
अत: वाशिंग मशीन का क्रय मूल्य = ₹ 16,875 उत्तर

प्रश्न 7.
(i) चाक-पाउडर में कैल्शियम, कार्बन तथा ऑक्सीजन का अनुपात 10 : 3 : 12 होता है। इसमें कार्बन की प्रतिशत मात्रा ज्ञात कीजिए।
(ii) चाक की एक छड़ी में यदि कार्बन की मात्रा 3 ग्राम है, तब उसका कुल भार कितना होगा?
हल :
(i) कोल्शयम : काबन : आक्साजन
10 : 3 : 12
अनुपातों का योग = 10 + 3 + 12 = 25
चाक में कार्बन का भाग = \(\frac {3}{25}\)
∴ कार्बन का प्रतिशत = (\(\frac {3}{25}\) × 100) %
= (3 × 4)% = 12% उत्तर

(ii) चूंकि चाक में कैल्सियम, कार्बन और ऑक्सीजन का अनुपात 10 : 3 : 12 है।
अनुपातों का योग = 10 + 3 + 12 = 25
स्पष्ट है कि यदि कार्बन का भार 3 ग्राम होगा, तो चाक का भार = 25 ग्राम होगा। उत्तर

प्रश्न 8.
अमीना एक पुस्तक ₹275 में खरीद कर उसे 15 प्रतिशत हानि पर बेचती है। पुस्तक का विक्रय मूल्य ज्ञात कीजिए।
हल:
पुस्तक का क्रय मूल्य (C.P) = ₹275 और
हानि = 15%
विक्रय मूल्य (S.P.) = (100 – हानि %) × क्र. मू. / 100}[/latex]
= \(\frac{(100-15) \times 275}{100}\)
= \(\frac{85 \times 275}{100}\) = 85 × 2.75
= ₹ 233.75
अत: पुस्तक का विक्रय मूल्य = ₹ 233.75 उत्तर

प्रश्न 9.
प्रत्येक दशा में 3 वर्ष बाद कितना मिश्रधन देय होगा?
(a) मूलधन = 1200 रु., दर 12% वार्षिक
(b) मूलधन = 7500 रु., दर 5% वार्षिक
हल :
(a) P= 1200 रु., R= 12% और T = 3 वर्ष
साधारण ब्याज (S.I) = \(\frac{P \times R \times T}{100}\)
= ₹ \(\frac{1200 \times 12 \times 3}{100}\)
= ₹ 432
अब, मिश्रधन- मूलधन (P) + साधारण ब्याज (S.I.)
= ₹(1200 + 432)
= ₹ 1632 उत्तर

(b) P = ₹ 7500, R = 5% और T= 3 वर्ष
साधारण ब्याज (S.I.) = \(\frac{P \times R \times T}{100}\)
= ₹ \(\frac{7500 \times 5 \times 3}{100}\)
= ₹ 1125
अब, मिश्रधन = मूलधन (P)+ साधारण ब्याज (S.I.)
= ₹(7500 + 1125)
= ₹ 8625 उत्तर

प्रश्न 10.
₹ 56000 पर, 2 वर्ष पश्चात् किस दर से 280 रु. साधारण व्याज देय होगा?
हल :
P = ₹ 56000, S.I = ₹ 280, T= 2 वर्ष
दर (R) = \(\frac{\text { S.I } \times 100}{P \times T}\)
= (\(\frac{280 \times 100}{56000 \times 2}\)) = 0.25%
अतः, ब्याज की दर = 0.25% प्रति वर्ष। उत्तर

प्रश्न 11.
मीना ने 9 प्रतिशत वार्षिक दर से, 1 वर्ष पश्चात् ₹ 45 व्याज के रूप में लिए। उसने कितना धन उधार लिया था ?
हुल :
साधारण ब्याज (S.I.) = ₹ 45
दर (R) = 9%
समय (T) = 1 वर्ष
मूलधन (P) = \(\frac{\text { S.I. } \times 100}{R \times T}=\frac{45 \times 100}{9 \times 1}\)
= 5 × 100 = ₹ 500
अत: उधार लिया गया धन = ₹ 500 उत्तर

Haryana State Board HBSE 7th Class Maths Solutions Chapter 9 परिमेय संख्याएँ Ex 9.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 9 परिमेय संख्याएँ Ex 9.1

प्रश्न 1.
निम्नलिखित परिमेय संख्याओं के बीच में पाँच परिमेय संख्याएँ लिखिए :
(i) – 1 और 0
(ii) – 2 और -1
(iii) \(\frac{-4}{5}\) और \(\frac{-2}{3}\)
(iv) –\(\frac{1}{2}\) और \(\frac{2}{3}\)
हल :
(i) हम जानते हैं कि

(ii) हम जानते हैं कि

प्रश्न 2.
निम्नलिखित प्रतिरूपों में से प्रत्येक में चार और परिमेय संख्याएँ लिखिए :
(i) \(\frac{-3}{5}, \frac{-6}{10}, \frac{-9}{15}, \frac{-12}{20}, \ldots \ldots\)
(ii) \(\frac{-1}{4}, \frac{-2}{8}, \frac{-3}{12}, \ldots .\)
(iii) \(\frac{-1}{6}, \frac{2}{-12}, \frac{3}{-18}, \frac{4}{-24}, \ldots . .\)
(iv) \(\frac{-2}{3}, \frac{2}{-3}, \frac{4}{-6}, \frac{6}{-9}, \ldots \ldots\)
हल :

प्रश्न 3.
निम्नलिखित के समतुल्य चार परिमेय संख्याएँ लिखिए :
(i) \(\frac{-2}{7}\)
(ii) \(\frac{5}{-3}\)
(iii) \(\frac{4}{9}\)
हल :

प्रश्न 4.
एक संख्या रेखा खींचिए और उस पर निम्नलिखित परिमेय संख्याओं को निरूपित कीजिए :
(i) \(\frac{3}{4}\)
(ii) \(\frac{-5}{8}\)
(iii) \(\frac{-7}{4}\)
(iv) \(\frac{7}{8}\)
हल :
(i) \(\frac{3}{4}\) को संख्या रेखा पर व्यक्त करने के लिए हम एक संख्या रेखा खींचते है। रेखा पर एक बिन्दु O लेते हैं जो शून्य को व्यक्त करता है। अब संख्या 3 को व्यक्त करने के लिए बिन्दु P अंकित करते हैं।

रेखाखण्ड OP को 4 समान भागों (OA = AB = BC = CP) में विभाजित करते हैं। बिन्दु A, \(\frac{3}{4}\) भाग को निरूपित करता है।

(ii) \(\frac{-5}{8}\) को संख्या रेखा पर व्यक्त करने के लिए हम संख्या रेखा खींचते हैं जिस पर एक बिन्दु O लेते हैं जो शून्य को प्रदर्शित करता है। अब बिन्दु P लेंगे जो -5 को प्रदर्शित करता है, अब रेखाखण्ड OP को 8 भागों में बाँटते हैं, माना OA = AB = BC = CD = DE = EF = FG = GP । रचना से OA = \(\frac{1}{8}\) भाग है। इसलिए A, OP के \(\frac{-5}{8}\) भाग को प्रदर्शित करता है।

(iii) \(\frac{-7}{4}\) को संख्या रेखा पर व्यक्त करने के लिए हम एक संख्या रेखा खींचते हैं जिस पर एक बिन्दु O लेते हैं जो शून्य को प्रदर्शित करता है। अब संख्या -7 को व्यक्त करने के लिए शून्य के बाईं ओर बिन्दु P अंकित करते हैं।

अब रेखाखण्ड OP को चार बराबर भागों (OA = AB = BC = CP) में विभाजित करते हैं।
रचना से OA, OP का \(\frac{1}{4}\) भाग है।
∴ बिन्दु A परिमेय संख्या \(\frac{-7}{4}\) को व्यक्त करता है।

(iv) \(\frac{7}{8}\) को संख्या रेखा पर व्यक्त करने के लिए हम एक संख्या रेखा खींचते हैं जिस पर एक बिन्दु O लेते हैं जो शून्य को व्यक्त करता है। अब संख्या 7 को व्यक्त करने के लिए O के दाईं ओर बिन्दु P अंकित करते हैं।

अब OP रेखाखण्ड को 8 समान भागों (OA = AB = BC = CD = DE = EF = FG = GP) में विभाजित करते हैं। रचना से OA, OP का \(\frac{1}{8}\) भाग है।
∴ बिन्दु A, OP के \(\frac{7}{8}\) भाग को व्यक्त करता है।

प्रश्न 5.
एक संख्या रेखा पर बिन्दु P, Q, R, S, T, U, A और B इस प्रकार हैं कि TR = RS = SU तथा AP = PQ = OB है। P, Q, R और S से निरूपित परिमेय संख्याओं को लिखिए।

हल :
संख्या रेखा से स्पष्ट है
बिन्दु P, 2\(\frac{1}{3}\) को प्रदर्शित करता है = \(\frac{2 \times 3+1}{3}\)
= \(\frac{6+1}{3}=\frac{7}{3}\)

बिन्दु Q, 2\(\frac{2}{3}\) को व्यक्त करता है = \(\frac{2 \times 3+2}{3}\)
= \(=\frac{6+2}{3}=\frac{8}{3}\)

बिन्दु R, -1\(\frac{1}{3}\) को व्यक्त करता है = \(-\frac{1 \times 3+1}{3}\)
= \(-\frac{3+1}{3}=\frac{-4}{3}\)
और बिन्दु S, -1\(\frac{2}{3}\) को व्यक्त करता है।
\(-\frac{1 \times 3+2}{3}\)
= \(-\frac{3+2}{3}=\frac{-5}{3}\)

प्रश्न 6.
निम्नलिखित में से कौन-से युग्म एक ही परिमेय संख्या को निरूपित करते हैं ?

हल :
(i) दी गई परिमेय संख्याओं को मानक रूप में व्यक्त करने पर,
\(\frac{-7}{21}=\frac{-7 \div 7}{21 \div 7}=\frac{-1}{3}\)
और \(\frac{3}{9}=\frac{3 \div 3}{9 \div 3}=\frac{1}{3}\)
दी गई परिमेय संख्याओं का मानक रूप समान नहीं है।
∴ \(\frac{-7}{21} \neq \frac{3}{9}\)

(ii) दी गई परिमेय संख्या को मानक रूप में व्यक्त करने पर,

(iii) दी गई परिमेय संख्या को मानक रूप में व्यक्त करने पर,

(v) दी गई परिमेय संख्याओं को मानक रूप में व्यक्त करने पर,

(vi) दी गई परिमेय संख्याओं को मानक रूप में व्यक्त करने पर,
\(\frac{1}{3}\) = \(\frac{1}{3}\)

प्रश्न 7.
निम्नलिखित परिमेय संख्याओं को उनके सरलतम रूप में लिखिए :
(i) \(\frac{-8}{6}\)
(ii) \(\frac{25}{45}\)
(iii) \(\frac{-44}{72}\)
(iv) \(\frac{-8}{10}\)
हल :
(i) 8 और 6 का म. स. = 2
∴ \(\frac{-8}{6}\) के अंश व हर को 2 से भाग देने पर,
\(\frac{-8}{6}=\frac{(-8) \div 2}{6 \div 2}=\frac{-4}{3}\)
इसलिए \(\frac{-8}{6}\) का सरलतम रूप में है।

(ii) 25 और 45 का म. स. = 5
\(\frac{25}{45}\) के अंश व हर को 5 से भाग देने पर,
\(\frac{25}{45}=\frac{25 \div 5}{45 \div 5}=\frac{5}{9}\)
\(\frac{25}{45}\) का सरलतम रूप \(\frac{5}{9}\) है।

(iii) 44 और 72 का म.स. = 4
\(\frac{-44}{72}\) के अंश व हर को 4 से भाग देने पर,
\(\frac{-44}{72}=\frac{(-44) \div 4}{72 \div 4}=\frac{-11}{18}\)
\(\frac{-44}{72}\) का सरलतम रूप \(\frac{-11}{18}\) है।

(iv) 8 और 10 का म.स. = 2
\(\frac{-8}{10}\) को 2 से भाग देने पर
\(\frac{-8}{10}=\frac{(-8) \div 2}{10 \div 2}=\frac{-4}{5}\)
\(\frac{-8}{10}\) का सरलतम रूप \(\frac{-4}{5}\) है।

प्रश्न 8.
संकेतों >, < और = में से सही संकेत चुन कर रिक्त स्थानों को भरिए :

हल :
(i) हम जानते हैं कि ऋणात्मक परिमेय संख्या, धनात्मक परिमेय संख्या से छोटी होती है।
∴ \(\frac{-5}{7}\) < \(\frac{2}{3}\)

(ii) दी गई परिमेय संख्याओं का हर 5 व 7 है और उनका म.स. 35 है।

(iii) प्रत्येक परिमेय संख्याओं को धनात्मक हर के रूप में लिखने पर स्पष्ट है \(\frac{-7}{8}\) हर का धनात्मक, \(\frac{14}{-16}\) का हर ऋणात्मक है। इसको भी धनात्मक रूप में व्यक्त करने पर,

(iv) परिमेय संख्याओं का धनात्मक हर 5 व 4 है।
उनका ल.स. = 20 होगा। प्रत्येक परिमेय को सर्वनिष्ठ 20 के हर में व्यक्त करने पर,

(v) प्रत्येक परिमेय संख्या के हर को धनात्मक रूप में व्यक्त करने पर,
\(\frac{1}{-3}=\frac{1 \times(-1)}{(-3) \times(-1)}=\frac{-1}{3}\)
और \(\frac{-1}{4}\) का हर धनात्मक है।
अब 3 व 4 का ल.स. 12 है।

(vi) दी गई ऋणात्मक परिमेय संख्या के हर को धनात्मक हर में व्यक्त करने पर,

(vii) हम जानते हैं कि प्रत्येक परिमेय संख्या शून्य से छोटी होती है।
0 > \(\frac{-7}{6}\)

प्रश्न 9.
निम्नलिखित में प्रत्येक में से कौन-सी संख्या बड़ी है ?
(i) \(\frac{2}{3}\), \(\frac{5}{2}\)
(ii) \(\frac{-5}{6}\), \(\frac{-4}{3}\)
(iii) \(\frac{-3}{4}\), \(\frac{2}{-3}\)
(iv) \(\frac{-1}{4}\), \(\frac{1}{4}\)
(v) -3\(\frac{2}{7}\), -3\(\frac{4}{5}\)
हल :
(i) 3 और 2 का ल.स. = 6

(iii) पहले परिमेय संख्याओं को धनात्मक हर में बदलने पर,

(iv) प्रत्येक ऋणात्मक परिमेय संख्या, प्रत्येक धनात्मक परिमेय संख्या से छोटी होती है।
∴ \(\frac{-1}{4}\) < \(\frac{1}{4}\)

(v) 7 और 5 का ल.स. = 35

प्रश्न 10.
निम्नलिखित परिमेय संख्याओं को आरोही क्रम में लिखिए :
(i) \(\frac{-3}{5}, \frac{-2}{5}, \frac{-1}{5}\)
(ii) \(\frac{1}{3}, \frac{-2}{9}, \frac{-4}{3}\)
(iii) \(\frac{-3}{7}, \frac{-3}{2}, \frac{-3}{4}\)
हल :
(i) दी गई परिमेय संख्याओं का प्रत्येक हर धनात्मक और सर्वनिष्ठ है।
आरोही क्रम में व्यवस्थित करने पर,

(ii) दी गई परिमेय संख्याओं के हर धनात्मक हैं।
3, 9 और 3 का ल.स. = 9
दी गई परिमेय संख्याओं के हर को 9 लिखने पर,

(iii) दी गई परिमेय संख्याओं के अंश धनात्मक हैं। हर 7, 2,4 हैं। उनका ल.स. = 28 है।
संख्याओं को सर्वनिष्ठ हर 28 के साथ लिखने पर,
\(\frac{-3}{7}=\frac{-3 \times 4}{7 \times 4}=\frac{-12}{28}\)

Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 प्रायोगिक ज्यामिती Ex 10.5 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 10 प्रायोगिक ज्यामिती Ex 10.5

प्रश्न 1.
समकोण ΔPQR की रचना कीजिए, जहाँ m∠Q= 90°, QR = 8 सेमी और PR = 10 सेमी है।
हल :
रचना के पद :

1. एक रेखाखण्ड QR = 8 सेमी खींचा।
2. बिन्दु Q पर ∠XQR = 90° बनाया।
3. अब बिन्दु R को केन्द्र मानकर 10 सेमी की त्रिज्या का चाप खींचा जो QX को बिन्दु P पर काटता है।
4. RP को मिलाया।
इस प्रकार अभीष्ट ΔPQR प्राप्त हुआ।

प्रश्न 2.
एक समकोण त्रिभुज की रचना कीजिए, जिसका कर्ण 6 सेमी लम्बा है और एक पाद 4 सेमी लंबा है।
हल :
रचना के पद :

1. एक रेखाखण्ड QR = 4 सेमी खींचा।
2. बिन्दु Q पर ∠XQR = 90° का बनाया।
3. बिन्दु R को केन्द्र मानकर कर्ण 6 सेमी की त्रिज्या का एक चाप लगाया जो QX को बिन्दु P पर काटता है।
4. RP को मिलाया।
इस प्रकार अभीष्ट ΔPQR प्राप्त होगा।

प्रश्न 3.
एक समद्विबाहु समकोण त्रिभुज ABC की रचना कीजिए, जहाँ m∠ACB = 90° है और AC = 6 सेमी है।
हल :
रचना के पद :

1. रेखाखण्ड AC = 6 सेमी खींचा।
2. बिन्दु C पर ∠ACX = 90° बनाया।
3. बिन्दु C से परकार में 6 सेमी की त्रिज्या का चाप लेकर खींचा, जो CX को बिन्दु B पर काटता है।
4. BA को मिलाया।
इस प्रकार अभीष्ट ΔABC प्राप्त होगा।

Haryana State Board HBSE 7th Class Maths Solutions Chapter 8 राशियों की तुलना Ex 8.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 8 राशियों की तुलना Ex 8.2

प्रश्न 1.
दी गई भिन्न संख्याओं को प्रतिशत में बदलो :
(i) \(\frac {1}{8}\)
(ii) \(\frac {5}{4}\)
(iii) \(\frac {3}{40}\)
(iv) \(\frac {2}{7}\)
हल :

प्रश्न 2.
दी गई दशमलव भिन्नों को प्रतिशत में बदलो
(a) 0.65
(b) 2.1
(c) 0.02
(d) 12.35
हल :
(a) 0.65 = \(\frac{0 \cdot 65 \times 100}{100}=\frac{65}{100}\) = 65%
(b) 2.1 = \(\frac{2.1 \times 100}{100}=\frac{210}{100}\) = 210%
(c) 0.02 = \(\frac{0.02 \times 100}{100}=\frac{2}{100}\) = 2%
(d) 12.35 = \(\frac{12.35 \times 100}{100}=\frac{1235}{100}\) = 1235%.

प्रश्न 3.
अनुमान लगाइए कि आकृति का कितना भाग रंग दिया गया है और इस प्रकार ज्ञात कीजिए कि कितने प्रतिशत रंगीन है:

हल :
(i) \(\frac {1}{4}\) भाग रंगा है।
रंगे भाग का प्रतिशत = (\(\frac {1}{4}\) × 100)% = 25%.

(ii) \(\frac {3}{5}\) भाग रंगा है।
रंगे भाग का प्रतिशत = (\(\frac {3}{5}\) × 100)%
= (3 × 20)% = 60%

(iii) \(\frac {3}{8}\) भाग रंगा है।
रंगे भाग का प्रतिशत = (\(\frac {3}{8}\) × 100)%
= (\(\frac {3}{2}\) × 25)% = \(\frac {75}{2}\)%
= 37.5%.

प्रश्न 4.
ज्ञात कीजिए
(a) 250 का 15%
(b) 1 घंटे का 1%
(c) 2500 का 20%
(d) 1 किग्रा का 75%
हल :

प्रश्न 5.
संपूर्ण राशि ज्ञात कीजिए, यदि :
(a) इसका 5%, 600 है।
(b) इसका 12%, 1080 है।
(c) इसका 40%, 500 किमी है।
(d) इसका 70%, 14 मिनट है।
(e) इसका 8%, 40 लीटर है।
हल :
(a) माना सम्पूर्ण राशि x है, तो
x का 5% = 600
⇒ \(\frac {5}{100}\) × x = 600
⇒ x = \(\frac{600 \times 100}{5}\)
= 600 × 20 = ₹ 12000
अतः सम्पूर्ण राशि ₹ 12000 है।

(b) माना सम्पूर्ण राशि x है, तो
x का 12% = 1080
⇒ x × \(\frac {12}{100}\) = 1080
⇒ x = \(\frac{1080 \times 100}{12}\)
= 90 × 100 = ₹ 9000
अतः सम्पूर्ण राशि ₹ 9000 है।

(c) माना संपूर्ण राशि x है, तो
x का 40% = 500 किमी
⇒ \(\frac {40}{100}\) × x = 500 किमी
⇒ x = (500 × \(\frac {100}{40}\)) किमी
⇒ x = 25 × 50 = 1250 किमी
अत: संपूर्ण राशि 1250 किमी है!

(d) माना संपूर्ण राशि x है, तो
x का 70% = 14 मिनट
⇒ \(\frac {70}{100}\) × x = 14 मिनट
⇒ x = (14 × \(\frac {10}{7}\)) मिनट
⇒ x = (2 × 10) मिनट
⇒ x = 20 मिनट
अत: संपूर्ण राशि 20 मिनट है।

(e) माना संपूर्ण राशि x है, तो
x का 8% = 40 लीटर
⇒ \(\frac {8}{100}\) × x = 40 लीटर
⇒ x = \(\frac{40 \times 100}{8}\)
⇒ = 500 लीटर।
अतः सम्पूर्ण राशि 500 लीटर है।

प्रश्न 6.
दिए गए प्रतिशतों को साधारण व दशमलव भिन्नों में बदलो और अपने उत्तर को सरलतम रूप में लिखो
(a) 25%
(b) 150%
(c) 20%
(d) 5%
हल :
(a) 25% = \(\frac{25}{100}=\frac{1}{4}\) = 0.25
(b) 150% = \(\frac{150}{100}=\frac{3}{2}\) = 1:50
(c) 20% = \(\frac{20}{100}=\frac{1}{5}\) = 0.20
(d) 5% = \(\frac{5}{100}=\frac{1}{20}\) = 0.05

प्रश्न 7.
एक नगर में 30% महिलाएँ, 40% पुरुष तथा शेष बच्चे हैं। बच्चों का प्रतिशत कितना है ?
हल :
एक नगर में महिलाओं का प्रतिशत = 30%
पुरुषों का प्रतिशत = 40%
शेष बच्चों का प्रतिशत = (100 – 30 – 40)%
= (100 – 70)%
= 30%.

प्रश्न 8.
किसी क्षेत्र के 15,000 मतदाताओं में से 60% ने मतदान में भाग लिया। ज्ञात कीजिए कि कितने प्रतिशत ने मतदान में भाग नहीं लिया। क्या अब ज्ञात कर सकते हैं कि वास्तव में कितने मतदाताओं ने मतदान नहीं किया ?
हल :
∵ मतदान करने वाले मतदाताओं का प्रतिशत = 60%
∴ मतदान न करने वाले मतदाताओं का प्रतिशत = (100 – 60)% = 40%
कुल मतदाताओं की संख्या = 15000
ऐसे मतदाता जिन्होंने मतदान में भाग नहीं लिया = 40%
∴ 15000 का 40% = \(\frac {40}{100}\) × 15000
= 6000
अत: मतदान में भाग नहीं लेने वाले मतदाताओं की संख्या = 6000.

प्रश्न 9.
मीता अपने वेतन में से ₹400 रु बचाती है। यदि यह उसके वेतन का 10% है, तब उसका वेतन कितना है?
हल :
मीता का वेतन = ₹ a तो
a का 10% = ₹ 400
⇒ \(\frac {10}{100}\) × a = 400
⇒ \(\frac {1}{100}\) × a = 400
⇒ a= (10 × 400) = ₹ 4000
अतः मीता का वेतन = ₹ 4000। उत्तर

प्रश्न 10.
एक स्थानीय क्रिकेट टीम ने एक सत्र (season) में 20 मैच खेले। इनमें से उस टीम ने 25% मैच जीते। जीते गए मैचों की संख्या कितनी थी?
हल :
100 मैचों में से 25% मैच जीते, तो
20 मैचों में से मैच जीते = \(\frac {25}{100}\) × 20 = \(\frac {1}{4}\) × 20 = 5. उत्तर

Haryana State Board HBSE 7th Class Maths Solutions Chapter 10 प्रायोगिक ज्यामिती Ex 10.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 10 प्रायोगिक ज्यामिती Ex 10.1

प्रश्न 1.
एक रेखा (मान लीजिए AB) खींचिए और इसके बाहर स्थित कोई बिन्दु C लीजिए। केवल पैमाना (रूलर) और परकार का प्रयोग करते हुए, C से होकर AB के समान्तर एक रेखा खींचिए।
हल :
रचना के पद :

1. रेखा AB पर कोई बिन्दु P लेते हैं।
2. AB के बाहर कोई बिन्दु C लिया और CP को मिलाया।
3. P को केन्द्र मानकर एक चाप खींचा जो AB और PC को क्रमशः X और Y पर काटते हैं।
4. केन्द्र C को और तीसरे चरण की त्रिज्या के बराबर एक चाप खींचा जो PC को Q पर काटता है।
5. केन्द्र Q से XY के बराबर त्रिज्या से एक चाप खींचा जो चरण 4 में R पर काटता हैं।
6. CR को मिलाया और इसको दोनों दिशाओं में बढ़ाने पर अभीष्ट रेखा प्राप्त होगी।
∴ ∠RCQ = ∠XPY (एकान्तर कोण)
∴ AB || CR.

प्रश्न 2.
एक रेखा l खींचिए और l पर स्थित किसी भी बिन्दु पर l पर लम्ब खींचिए। इस लम्ब रेखा पर एक बिंदु x लीजिए जो l से 4 सेमी की दूरी पर हो। Xसे होकर l के समान्तर एक रेखा m खींचिए।
हल :
रचना के पद :

1. एक रेखा l खींचते हैं और उस पर कोई बिन्दु P लेते हैं।
2. P को केन्द्र मानकर उचित त्रिज्या का एक चाप खींचते हैं जो l को A व B बिन्दु पर काटता है।
3. A को केन्द्र मानकर AP त्रिज्या से अधिक त्रिज्या लेकर ऊपर की ओर चाप खींचते हैं।
4. अब B को केन्द्र मानकर चरण 3 के बराबर त्रिज्या का चाप खींचते हैं जो पहले चाप को C बिन्दु पर काटता है।
5. PC को मिलाते हुए आगे Q तक बढ़ाया। तब PQ⊥l.
6. P को केन्द्र मानकर 4 सेमी की त्रिज्या लेकर एक चाप खींचते हैं जो PQ को N पर काटता है। तब
PN = 4 सेमी।
7. बिन्दु N पर ∠RNP = ∠BPN बनाया।
8. NR को मिलाते हुए आगे बढ़ाया। इस प्रकार l के समान्तर m रेखा प्राप्त होगी।
∠RNP = ∠BPN (एकान्तर कोण)
∴ NR || l
⇒ m || l.

प्रश्न 3.
मान लीजिए l एक रेखा है और P एक बिन्दु है जो l पर स्थित नहीं है। Pसे होकर l के समान्तर एक रेखा m खींचिए। अब Pको के किसी बिंदुए से जोडिए। m पर कोई अन्य बिन्दु R चुनिए। R से होकर, PQ के समान्तर एक रेखा खींचिए। मान लीजिए यह रेखा, रेखा l से बिंदु S पर मिलती है। समान्तर रेखाओं के इन दोनों युग्मों से क्या आकृति बनती है ?
हल :
रचना के पद :

1. एक रेखा l खींचते हैं। इसके बाहर कोई बिन्दु P लेते हैं।
2. रेखा l पर दूसरा बिन्दु 0 लेते हैं।
3. PQ को मिलाया।
4. Q को केन्द्र मानकर एक चाप खींचते हैं जो l को क्रमशः C और D बिन्दु पर काटता है।
5. P को केन्द्र मानकर चरण 4 की त्रिज्या का चाप खींचते हैं जो PQ को E बिन्दु पर काटता है।
6. अब E बिन्दु को केन्द्र मानकर CD त्रिज्या के बराबर एक चाप खींचते हैं जो पहले चाप को F बिन्दु पर काटता है।
7. PF को मिलाते हुए दोनों दिशाओं में आगे बढ़ाया।
8. इस प्रकार एक अभीष्ट रेखा m प्राप्त होगी।
9. रेखा m पर कोई बिन्दु R लिया।
10. R से PQ के समान्तर RS रेखा खींची।
इस प्रकार प्राप्त आकृति PQRS एक समान्तर चतुर्भुज होगा।

Haryana State Board HBSE 7th Class Maths Solutions Chapter 8 राशियों की तुलना Ex 8.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 8 राशियों की तुलना Ex 8.1

प्रश्न 1.
अनुपात ज्ञात कीजिए :
(a) ₹ 5 रु. का 50 पैसे से
(b) 15 किग्रा का 210 ग्राम से
(c)9 मीटर का 27 सेमी से
(d) 30 दिनों का 36 घण्टों से
हल :
(a) ₹ 5 का 50 पैसे से
= 5 × 100 पैसे : 50 पैसे,
[∵ ₹ 1 = 100 पैसे]
= 500 पैसे : 50 पैसे,
दोनों पदों के H.C.F. = 50 से भाग देने पर]
= 10 : 1

(b) 15 किग्रा का 210 ग्राम से
= 15 × 1000 ग्राम : 210 ग्राम,
[∵ 1 किग्रा = 1000 ग्राम]
= 15000 : 210, [दोनों पदों के H.C.E. = 30 से भाग देने पर]
= 500 : 7

(c) मीटर का 27 सेमी से।
= 9 × 100 सेमी : 27 सेमी,
[∵ 1 मीटर = 100 सेमी]
= 900 : 27,
[दोनों पदों के H.C.F = 9 से भाग देने पर]
= 100 : 3

(d) 30 दिनों का 36 घण्टों से
= 30 × 24 घण्टे : 36 घण्टे,
[∵ 1 दिन = 24 घण्टे]
= 720 : 36, [दोनों पदों के H.C.E = 36 से भाग देने पर]
= 20 : 1

प्रश्न 2.
एक कम्प्यूटर प्रयोगशाला में 6 विद्यार्थियों के लिए 3 कम्प्यूटर झेने चाहिए। ज्ञात कीजिए कि 34 विद्यार्थियों के लिए कितने कम्प्यूटर की आवश्यकता होगी?
हल :
कम्प्यूटर प्रयोगशाला में,
∵ 6 विद्यार्थियों के लिए कम्प्यूटर = 3
∴ 1 विद्यार्थी के लिए कम्प्यूटर = \(\frac {3}{6}\)
∴ 24 विद्यार्थियों के लिए कम्प्यूटर = \(\frac {3}{6}\) × 24
= 3 × 4
= 12 उत्तर

प्रश्न 3.
राजस्थान की जनसंख्या = 570 लाख और उत्तर प्रदेश की जनसंख्या = 1660 लाख तथा राजस्थान का क्षेत्रफल = 3 लाख किमी² और उत्तर प्रदेश का क्षेत्रफल = 2 लाख किमी²। ज्ञात कीजिए :
(i) इन दोनों राज्यों में प्रति किमी² कितने व्यक्ति हैं?
(ii) किस राज्य की जनसंख्या कम घनी है?
हल :
(i) राजस्थान की जनसंख्या = 570 लाख
राजस्थान का क्षेत्रफल = 3 लाख किमी²
∴ प्रति वर्ग किमी में लोगों की संख्या = \(\frac {570}{3}\)
= 190
उत्तर प्रदेश की जनसंख्या = 1660 लाख
उत्तर प्रदेश का क्षेत्रफल = 2 लाख किमी²
∴ प्रति वर्ग किमी में लोगों की संख्या = \(\frac {1660}{2}\)
= 830

(ii) क्योंकि राजस्थान की प्रति वर्ग किमी जनसंख्या उत्तर प्रदेश की प्रति वर्ग किमी जनसंख्या से कम है।
अत: राजस्थान की जनसंख्या कम घनी है। उत्तर

Haryana State Board HBSE 7th Class Maths Solutions Chapter 7 त्रिभुजों की सर्वांगसमता InText Questions and Answers.

Haryana Board 7th Class  Maths Solutions Chapter 7 त्रिभुजों की सर्वांगसमता InText Questions

पृष्ठ सं. 152-153

प्रश्न 1.
आकृतियों में त्रिभुजों की भुजाओं की लम्बाइयाँ दर्शाई गई हैं। S.S.S. सर्वांगसमता प्रतिबंध का प्रयोग करके बताइए कि कौन-कौन से त्रिभुज-युग्म सर्वांगसम हैं। सर्वागसमता की स्थिति में, उत्तर को सांकेतिक रूप में लिखिए :


हल :
(i) ΔABC और ΔPQR में,
AB = PQ = 15 सेमी
BC = QR = 2.5 सेमी
CA = RP = 2.2 सेमी
S.S.S. सर्वांगसमता से,
ΔABC ≅ ΔPQR

(ii) ΔDEF और ΔLMN में,
EF ≠ MN
अत: ये त्रिभुज सर्वांगसम नहीं हैं।

(iii) ΔABC और ΔPQR में
BC ≠ QR
अत: ये त्रिभुज सर्वांगसम नहीं हैं।

(iv) ΔADB और Δ ADC में,
AD = AD (उभयनिष्ठ)
DB = DC = 2.5 सेमी और
BA = CA = 3.5 सेमी
∴ S.S.S. सर्वांगसमता से,
ΔADB ≅ ΔADC.

प्रश्न 2.
आकृति में, AB = AC और D, \(\overline{B C}\) का मध्य बिंदु है।
(i) ΔADB और ΔADC में बराबर भागों के तीन युग्म बताइए।
(ii) क्या ΔADB ≅ ΔADC है? कारण दीजिए।
(iii) क्या ∠B = ∠C है? क्यों?

हल :
(i) ΔADB और ΔADC में,
AD = AD, (उभयनिष्ठ)
AB = AC, (दिया है)
और DB = DC,
[∵ D, \(\overline{B C}\) का मध्य बिन्दु है]

(ii) S.S.S. सर्वांगसमता प्रतिबन्ध से ।
ΔADB ≅ ΔADC

(iii) ∠B = ∠C है।
क्योंकि सर्वांगसम त्रिभुजों के संगत कोण समान होते हैं।

प्रश्न 3.
आकृति में, AC = BD और AD = BCहै। निम्नलिखित कथनों में कौन-सा कथन सत्य है?
(i) ΔABC ≅ ΔABD
(ii) ΔABC ≅ ΔBAD

हल :
(i) ΔABC ≅ ΔABD नहीं लिख सकते
AB = AB [सही है]
BC = BD, [सही नहीं है।
और CA = DA, [सही नहीं है]

(ii) ΔABC ≅ ΔBAD लिख सकते हैं।
AB = AB [उभयनिष्ठ]
BC = AD [दिया है]
और CA = DB, [दिया है]

पृष्ठ सं. 156 (इन्हें कीजिए)

प्रश्न 1.
ΔDEF की भुजाओं \(\overline{D E}\) और \(\overline{E F}\) का अंतर्गत कोण कौन-सा है?

हल :
ΔDEF को भुजाओं \(\overline{D E}\) और \(\overline{E F}\) का अंतर्गत कोण ∠DEF है।

प्रश्न 2.
S.A.S. सर्वांगसमता प्रतिबंध का उपयोग करके आप ΔPQR ≅ ΔFED स्थापित करना चाहते हैं। यह दिया गया है कि PQ = FE और RP = DF है। सर्वांगसमता को स्थापित करने के लिए अन्य किस तथ्य या सूचना की आवश्यकता होगी?
हल :
ΔPQR ≅ ΔFED को स्थापित करने के लिए अन्य तथ्य ∠P = ∠F की आवश्यकता होगी।

प्रश्न 3.
आकृति में, त्रिभुजों के युग्मों में कुछ भागों की माप अंकित की गई है। S.A.S. सर्वांगसमता प्रतिबंध का उपयोग करके, इनमें वेयुग्म छाँटिए जोसर्वांगसम हैं। सर्वांगसम त्रिभुजों की स्थिति में उन्हें सांकेतिक रूप में भी लिखिए।

हल :
(i) ΔABC और ΔDEF में,
∠A ≠ ∠D
अतः ये दोनों Δ सर्वांगसम नहीं हैं।

(ii) ΔACB और ΔRPQ में,
AC = RP = 2.5 सेमी
∠C = ∠P = 35° और
CB = PQ = 3 सेमी
∴ S.A.S. सर्वांगसमता से,
ΔACB ≅ ΔRPQ

(iii) ΔDEF और ΔPQR में,
DE = PQ = 3.5 सेमी
∠F = ∠Q = 40°
सेमी EF = RQ = 3 सेमी
∴ SAS सर्वांगसमता से,
ΔDFE ≅ ΔPQR

(iv) ΔRSP और ΔPQR में,
RS = PQ = 3.5 सेमी
∠PRS = ∠RPQ = 30°
और RP = PR
∴ S.A.S. सर्वांगसमता से,
ΔRSP ≅ ΔPQR.

प्रश्न 4.
आकृति में, \(\overline{A B}\) और \(\overline{C D}\) एक-दूसरे को O पर समद्विभाजित करती हैं।

(i) दोनों त्रिभुजों AOC और BOD में बराबर भागों के तीन युग्मों को बताइए।
(ii) निम्न कथनों में से कौन-से कथन सत्य हैं ?
(a) ΔAOC ≅ ΔDOB
(b) ΔAOC ≅ ΔBOD
हल :
(i) ΔAOC और ΔBOD के बराबर भागों के तीन युग्म निम्न हैं:
OA = OB
OC = OD और
∠AOC = ∠BOD

(ii) सही विकल्प (b) है।

पृष्ठ सं. 158

प्रश्न 1.
ΔMNP में कोणों, M तथा Nके अंतर्गत भुजा क्या है ?
हल :
ΔMNP में कोणों M तथा N के अंतर्गत भुजा MN है।

प्रश्न 2.
A.S.A. सर्वांगसमता प्रतिबंध का उपयोग करके आप ΔDEF ≅ ΔMNP स्थापित करना चाहते हैं। आपको दिया गया है कि ∠D = ∠M और ∠F = ∠P इस सर्वांगसमता को स्थापित करने के लिए और कौन-से तथ्य की आवश्यकता है ? (खाका आकृति बनाकर कोशिश कीजिए।
हल:
ΔDEF ≅ ΔMNP

स्थापित करने के लिए दिए गए प्रतिबन्धों के अतिरिक्त भुजा DF = भुजा MP की आवश्यकता होगी।

प्रश्न 3.
निम्न आकृतियों में, त्रिभुजों के कुछ भागों की माप अंकित की गई है। A.S.A. सांगसमता प्रतिबंध का उपयोग करके बताइए कौन-से त्रिभुजों के युग्म सर्वांगसम हैं। सांगसमता की स्थिति में, उत्तर को सांकेतिक रूप में लिखिए।

हल :
(i) ΔABC और ΔFED में,
∠A = ∠F = 40°
AB = FE = 3.5 सेमी
और
∠B = ∠E = 60°
∴ A.S.A. सर्वांगसमता से,
ΔABC ≅ ΔFED

(ii) ΔPQR और ΔEDF में,
PR ≠ EF
∴ A.S.A. सर्वांगसमता से,
अतः ये त्रिभुज सर्वांगसम नहीं है।

(iii) ΔPQR और MNL में,
∠R = ∠L = 60°
QR = NL = 6 सेमी और
∠Q = ∠N = 30°
∴ A.S.A. सर्वांगसमता से,
ΔPQR ≅ ΔMNL

(iv) ΔABC और ΔBAD में,
∠CAB = ∠DBA = 30°
AB = BA और
∠ABC = ∠BAD = 75°,
(∵ 30° + 45° = 75°)
∴ A.S.A. सर्वांगसमता से,
ΔABC ≅ ΔBAD

प्रश्न 4.
दो त्रिभुजों के कुछ भागों की माप नीचे दी गई हैं। A.S.A. सर्वांगसमता प्रतिबंध का उपयोग करके जाँचिए कि क्या ये दोनों त्रिभुज सर्वांगसम हैं या नहीं। सर्वांगसमता की स्थिति में उत्तर को सांकेतिक रूप में भी लिखिए :

हल :
(i) ΔDEF और ΔQPR में,
∠D = ∠Q
DF = QR और
∠F = ∠R = 80°

∴ A.S.A. सर्वांगसमता से,
ΔDEF ≅ ΔQPR

(ii) ∵ समान कोणों के बीच समान भुजा नहीं है।
∴ ये त्रिभुज सर्वांगसम नहीं हैं।

(iii) ΔDEF और ΔQPR में,
∠E = ∠P = 80°

EF = PR = 5 सेमी और
∠F = ∠R = 30°
∴ A.S.A. सर्वांगसमता से,
ΔDEF ≅ ΔQPR.

प्रश्न 5.
आकृति में, किरण AZ, ∠DAB तथा ∠DCB को समद्विभाजित करती है।

(i) त्रिभुजों BAC और DAC में बराबर भागों के तीन युग्म बताइए।
(ii) क्या ΔBAC ≅ ΔDAC हैं ? कारण दीजिए।
(iii) क्या AB = AD है ? अपने उत्तर का उचित कारण दीजिए।
(iv) क्या CD = CBहै? कारण दीजिए।
हल :
(i) ΔBAC तथा ΔDAC में तीन समान युग्म हैं।
∠BAC = ∠DAC, AC = AC और ∠BCA = ∠DCA.

(ii) हाँ, A.S.A. सर्वांगसमता से,
ΔBAC ≅ ΔDAC.

(iii) हाँ, AB = AD [∵ सर्वांगसम त्रिभुजों में संगत भुजाएँ समान होती हैं]

(iv) हाँ, CD = CB, [∵ सर्वांगसम त्रिभुजों में संगत भुजाएँ समान होती हैं]

पृष्ठ सं. 160 – 161

प्रश्न 1.
आकृतियों में, त्रिभुजों के कुछ भागों की माप दी गई हैं। R.H.S. सर्वांगसमता प्रतिबंध का उपयोग करके बताइए कि कौन-कौन से त्रिभुज युग्म सर्वांगसम हैं ? सर्वांगसम त्रिभुजों की स्थिति में, उन्हें सांकेतिक रूप में लिखिए।

हल :
(i) ΔPQR और ΔDEF में,
PQ ≠ DE
अतः ये त्रिभुज सांगसम नहीं हैं।

(ii) ΔCAB और ΔDBA में,
∠C = ∠D = 90°
AB = BA = 3.5 सेमी और
CA = DB = 2 सेमी
∴ R.H.S. सर्वांगसमता से,
ΔCAB ≅ ΔDBA.

(iii) ΔABC और ΔADC में,
∠B = ∠D = 90°
कर्ण AC = कर्ण AC और
AB = AD = 3.6 सेमी
∴ R.H.S. सर्वांगसमता से,
ΔABC ≅ ΔADC

(iv) ΔPSQ और ΔPSR में,
∠PSQ = ∠PSR = 90°
कर्ण PQ = कर्ण PR = 3 सेमी
और PS = PS
∴ R.H.S. सांगसमता से,
ΔPSQ ≅ ΔPSR.

प्रश्न 2.
R.H.S. सर्वांगसमता प्रतिबंध से ΔABC ≅ ΔRPQ स्थापित करना है। यदि यह दिया गया हो कि ∠B = ∠P= 90° और AB = RP है, तो अन्य किस और सूचना की आवश्यकता है?
हल :
R.H.S. सर्वांगसमता प्रतिबन्ध से ΔABC ≅ ΔRPQ स्थापित करने के लिए दिए गए प्रतिबन्धों के अतिरिक्त हमें कर्ण AC = कर्ण AC को समान करने की आवश्यकता है।

प्रश्न 3.
आकृति में, BD और CE, ΔABC के शीर्ष लंब हैं और BD = CE.
(i) ΔCBD और ΔBCE में, बराबर भागों के तीन बुग्म बताइए।
(ii) क्या ΔCBD ≅ ΔBCE है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∠DCB = ∠EBC है ? क्यों या क्यों नहीं ?

हल :
(i) ΔCBD और ΔBCE में बराबर भागों के तीन युग्म हैं :
CB = BC
∠CDB = ∠BEC
और BD = CE

(ii) R.H.S. सर्वांगसमता से,
ΔCED ≅ ΔBCE.

(iii) हाँ, ∠DCB = ∠EBC, (∵ सर्वांगसम त्रिभुजों के संगत कोण समान होते हैं)

प्रश्न 4.
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC और AD इसका एक शीर्षलंब है।
(i) ΔADB और ΔADC में, बराबर भागों में तीन युग्म बताइए।
(ii) क्या ΔADB ≅ ΔADC है ? क्यों अथवा क्यों नहीं ?
(iii) क्या ∠B = ∠C है? क्यों या क्यों नहीं ?
(iv) क्या BD = CD है ? क्यों या क्यों नहीं ?

हल :
(i) ΔADB और ΔADC में, बराबर भागों के तीन युग्म निम्न हैं:
AD = AD
∠ADB = ∠ADC
और AB = AC.

(ii) R.H.S. सर्वांगसमता से,
ΔADB ≅ ΔADC.

(iii) हाँ, ∠B = ∠C
(∵ सर्वांगसम त्रिभु के संगत कोण समान होते हैं)

(iv) हाँ, BD = CD, (∵ सर्वांगसम त्रिभुजों की संगत भुजाएँ समान होती हैं)

Haryana State Board HBSE 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल InText Questions

इन्हें कीजिए (पृष्ठ सं. 221-222)

प्रश्न 1.
नीचे दिए गए प्रश्नों के उत्तर देने के लिए आपको क्षेत्रफल या परिमाप में से किसको ज्ञात करने की आवश्यकता होगी।
1. एक श्यामपट कितनी जगह घेरता है ?
2. एक आयताकार फूलों की क्यारी के चारों ओर बाड़ लगाने के लिए आवश्यक तार की लम्बाई क्या है ?\
3. एक तिकोने पार्क के चारों ओर दो बार चक्कर लगाने पर आप कितनी दरी तय करेंगे ?
4. एक आयताकार स्वीमिंग पूल को ढकने के लिए आपको कितनी प्लास्टिक शीट की आवश्यकता होगी ?
हल :
1. श्यामपट द्वारा घेरे गए क्षेत्र/स्थान के लिए श्यामपट का क्षेत्रफल ज्ञात करना होगा।
क्षेत्रफल = लम्बाई × चौड़ाई
2. आयताकार फूलों की क्यारी के चारों ओर बाड़ लगाने के लिए फूलों की क्यारी का परिमाप ज्ञात करना होगा।
परिमाप = 2 × (लम्बाई + चौड़ाई)
3. तिकोने पार्क के चारों ओर दो बार चक्कर लगाने की दूरी = 2 × पार्क का परिमाप।
4. आयताकार स्वीमिंग पुल को ढकने के लिए प्लास्टिक शीट की आवश्यकता = तालाब का क्षेत्रफल।

पृष्ठ सं. 222

प्रश्न 1.
छात्र स्वयं करें।

प्रश्न 2.
दो ऐसे उदाहरण दीजिए जहाँ परिमाप के बढ़ने पर उसका क्षेत्रफल भी बढ़ जाए।
हल :
(i) माना एक आयत ABCD है।

क्षेत्रफल (ABCD) = A₁ = 9 × 3 वर्ग सेमी
= 27 वर्ग सेमी
परिमाप (ABCD) = P₁ = 2(9 + 3) सेमी
= 24 सेमी
दूसरा आयत ABEF मानते हैं।

क्षेत्रफल (ABEF) = A₂ = 10 × 3 वर्ग सेमी
= 30 वर्ग सेमी
परिमाप (ABEF) = P₂ = 2(10 + 3) सेमी
= 26 सेमी
A₂ > A₁ ⇒ P₂ > P₁ अर्थात् जब क्षेत्रफल बढ़ता है, परिमाप बढ़ता है।

(ii) एक वर्ग ABCD मानते हैं।
क्षेत्रफल (ABCD) = 4 × 4 वर्ग सेमी
= 16 वर्ग सेमी
परिमाप (ABCD) = 2 × (4 + 4) सेमी
= 2 × 8 = 16 सेमी

आयत ABFE मानते हैं।
क्षेत्रफल (ABFE) = 4 × 5 वर्ग सेमी
= 20 वर्ग सेमी

परिमाप (ABFE) = 2 × (4 + 5) सेमी
= 2 × 9 = 18 सेमी
अतः क्षेत्रफल बढ़ता है तो परिमाप बढ़ता है।

प्रश्न 3.
ऐसे दो उदाहरण दीजिए, जहाँ परिमाप के बढ़ने पर उसके क्षेत्रफल में बढ़ोत्तरी न हो।
हल :
(i) आयत ABCD में,
क्षेत्रफल (ABCD) = A₁ = 8 × 10 सेमी²
= 80 सेमी²

परिमाप (ABCD) = P₁ = 2 × (8 + 10) सेमी
= 2 × 18 = 36 सेमी
अब आयत ABCD में से एक त्रिभुज काटते हैं।
इसी आकृति का क्षेत्रफल (A₂)
= [8 × 10 – \(\frac{1}{2}\) × 3 × 4] सेमी²

= (80 – 6) सेमी
= 74 सेमी²
इसका परिमाप (P₂)
= (8 + 10 + 8 + 3 + 3 + 5 + 3) सेमी
= 40 सेमी
स्पष्ट है कि A₁ < A₂ क्षेत्रफल घटता है।
परन्तु P₂ > P₁ परिमाप बढ़ता है।

(ii) उपर्युक्त आकृति में से एक कट और करने पर, इस आकृति का क्षेत्रफल (A₃)
= (A₂ – 4 × 3) सेमी²
= (74 – 12) सेमी²
= 62 सेमी²

सेमी इस आकृति का परिमाप (P₃)
= (2 + 3 +4+ 3 + 2 + 10 + 8 + 3 + 3 + 5 + 3) सेमी
= 46 सेमी
स्पष्ट है कि A₃ < A₂ क्षेत्रफल घटता है।
परन्तु P₃ > P₂ परिमाप बढ़ता है।

पृष्ठ सं. 226

प्रश्न 1.
नीचे दिए गए प्रत्येक आयत जिसकी लम्बाई 6 सेमी और चौड़ाई 4 सेमी है, सर्वांगसम बहुभुजों से मिलकर बने हैं। प्रत्येक बहुभुज का क्षेत्रफल ज्ञात कीजिए।

हल:
लम्बाई = 6 सेमी
चौड़ाई = 4 सेमी
प्रत्येक बहुभुज का क्षेत्रफल = आयत का क्षेत्रफल
= लम्बाई × चौड़ाई
= (6 × 4) सेमी
= 24 सेमी²।

पृष्ठ सं. 229

प्रश्न 1.
निम्न समांतर चतुर्भुजों के क्षेत्रफल ज्ञात कीजिए :

(iii) समान्तर चतुर्भुज ABCD में, AB = 7.2 सेमी और C से AB पर लम्ब 4.5 सेमी है।
हल :
(i) समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= 8 × 3.5 = 28 सेमी²

(ii) समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
= 8 × 2.5 = 20 सेमी²

(iii) समान्तर चतुर्भुज ABCD का क्षेत्रफल
= AB × C से AB पर लम्ब की लम्बाई
= 7.2 × 4.5 = 32.4 सेमी²।

पृष्ठ सं. 230

प्रश्न 1.
ऊपर दिए गए क्रियाकलापों को अलग-अलग प्रकार के त्रिभुज लेकर कीजिए।
हल :
एक त्रिभुज ABC दिया है। सर्वांगसम त्रिभुज ACP है। दोनों मिलाने पर ABCP समान्तर चतुर्भुज जैसी आकृति प्राप्त होती है।

प्रश्न 2.
अलग-अलग प्रकार के समांतर चतुर्भुज लीजिए। प्रत्येक समान्तर चतुर्भुज को दो त्रिभुजों में एक विकर्ण के अनुदिश काटिए। क्या ये त्रिभुज सर्वांगसम हैं ?
हल :
ABCD एक समान्तर चतुर्भुज है (दिया है)। प्रत्येक समान्तर चतुर्भुज को विकर्ण AC अथवा BD के अनुदिश काटने पर। दो त्रिभुजों में विभाजित होता है।

ये दोनों त्रिभुज आपस में सर्वांगसम होंगे।

पृष्ठ सं. 235

प्रश्न 1.
एक बोतल का ढक्कन एक चूड़ी या कोई अन्य वृत्ताकार वस्तु लीजिए और उसकी परिधि ज्ञात कीजिए।
हल :
छात्र स्वयं करें।

पृष्ठ सं. 236

प्रश्न 1.
आकृति में :
(a) किस वर्ग का परिमाप अधिक है?
(b) कौन-सा अधिक है, छोटे वर्ग का परिमाप या वृत्त की परिधि ?

हल :
(a) बाहरी वर्ग का परिमाप सबसे अधिक होगा।
(b) छोटे वर्ग के परिमाप से वृत्त की परिधि अधिक होगी।

पृष्ठ सं. 239

प्रश्न 1.
ग्राफ पेपर पर अलग-अलग त्रिज्याओं के वृत्तों को बनाइए। वर्गों की संख्या को गिनकर क्षेत्रफल ज्ञात कीजिए। सूत्र का प्रयोग करके भी क्षेत्रफल ज्ञात कीजिए। दोनों उत्तरों की तुलना कीजिए।
हल :
1 वर्ग सेमी के ग्राफ पर 1 सेमी और 2 सेमी त्रिज्या के दो वृत्त खींचने पर,

ग्राफ पेपर पर प्रयोग करने पर, हमें दोनों वृत्तों का क्षेत्रफल क्रमशः 4 सेमी2 और 12 सेमी2 प्राप्त होता है।
सूत्र का प्रयोग करके हम उनका क्रमशः क्षेत्रफल
πr₁² = (\(\frac{22}{7}\) × 12 ) सेमी² = 3.14 सेमी² (लगभग)
और πr₂² = (\(\frac{22}{7}\) × 22 ) सेमी² = (\(\frac{22}{7}\) × 4) सेमी²
= 12.57 सेमी² (लगभग)
हम देखते हैं कि दोनों मान भिन्न हैं।

पृष्ठ सं. 241

प्रश्न 1.
निम्न को बदलिए :
(i) 50 सेमी² को मिमी² में
(ii) 2 हेक्टेअर को मीटर² में
(iii) 10 मीटर² को सेमी² में
(iv) 1000 सेमी² को मिमी²
हल :
(i) 1 सेमी² = 1 सेमी × 1 सेमी
= 10 मिमी × 10 मिमी
= 100 मिमी²
∴ 50 सेमी² = (50 × 100) मिमी²
= 5000 मिमी²।

(ii) 1 हेक्टेअर = 100 मीटर भुजा वाले वर्ग का क्षेत्रफल
= 100 मीटर × 100 मीटर
= 10000 मीटर²
हेक्टेअर = 20000 मीटर²।

(iii) 1 मीटर² = 1 मीटर × 1 मीटर
= 100 सेमी × 100 सेमी
= 10000 सेमी²
∴ 10 मीटर² = 10 × 10000 सेमी²
= 100000 सेमी²

(iv) 1 सेमी² = 100 मिमी²
1000 सेमी² = 100 × 1000 मिमी
= 100000 मिमी²।

Haryana State Board HBSE 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.4 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.4

प्रश्न 1.
एक बगीचा 90 मीटर लम्बा और 75 मीटर चौड़ा है। इसके बाहर, चारों ओर एक 5 मीटर चौड़ा पथ बनाना है। पथ का क्षेत्रफल ज्ञात कीजिए। बगीचे का क्षेत्रफल हेक्टेअर में भी ज्ञात कीजिए।
हल :
माना ABCD एक बगीचा है और माना PQRS पथ की बाहरी चारदीवारी है।

DC = 90 मीटर
AD = 75 मीटर
PQ = (90 + 5 + 5) मीटर = 100 मीटर
और QR = (75 + 5 + 5) = 85 मीटर
अब पथ का क्षेत्रफल = PQRS का क्षेत्रफल – ABCD का क्षेत्रफल
= (100 × 85 – 90 × 75) मीटर²
= (8500 – 6750) मीटर²
= 1750 मीटर²
बगीचे का क्षेत्रफल = ABCD का क्षेत्रफल
= (90 × 75) मीटर² = 6750 मीटर²
[∵ 1 हेक्टेअर = 10,000 मीटर²]
= \(\frac{6750}{10000}\) हेक्टेअर
= 0.675 हेक्टेअर। उत्तर

प्रश्न 2.
125 मीटर लम्बाई और 65 चौड़ाई वाले एक आयताकार पार्क के चारों ओर बाहर एक 3 मीटर चौड़ा पथ बना हुआ है। पथ का क्षेत्रफल ज्ञात कीजिए।
हल :
माना ABCD एक आयताकार पार्क है और PQRS बाहरी पथ की चार दीवारी है।

AB = 125 मीटर
AD = 65 मीटर
PQ = (125 + 3 + 3) मीटर
= 131 मीटर
और QR = (65 + 3 + 3) मीटर = 71 मीटर
पथ का क्षेत्रफल = PQRS का क्षेत्रफल – ABCD का क्षेत्रफल
= (131 × 71 – 125 × 65) मीटर²
= (9301 – 8125) मीटर²
= 1176 मीटर। उत्तर

प्रश्न 3.
8 सेमी लम्बे और 5 सेमी चौड़े एक गत्ते पर एक चित्र की पेंटिंग इस प्रकार बनाई गई है कि इसकी प्रत्येक भुजाओं के अनुदिश 1.5 सेमी चौड़ा हाशिया (margin) छोड़ा गया है। हाशिये का कुल क्षेत्रफल ज्ञात कीजिए।

हल :
PQ = 8 सेमी
QR = 5 सेमी
AB = (8 – 1.5 – 1.5) सेमी = 5 सेमी
AD = (5 – 1.5 – 1.5) सेमी = 2 सेमी
हाशिये का क्षेत्रफल = PQRS का क्षेत्रफल – ABCD का क्षेत्रफल
= (8 × 5 – 5 × 2) सेमी²
= (40 – 10) सेमी² = 30 सेमी²। उत्तर

प्रश्न 4.
5.5 मीटर लम्बे और 4 मीटर चौड़े कमरे के चारों ओर बाहर 2.25 मीटर चौड़ा बरामदा बनाया गया है। ज्ञात कीजिए:
(i) बरामदे का क्षेत्रफल
(ii) ₹ 200 प्रति मीटर की दर से बरामदे के फर्श पर सीमेन्ट कराने का व्यय।

हल :
माना ABCD का कमरा है और माना PQRS बाहरी बरामदे की चार दीवारें हैं।
हम जानते हैं, AB = 5.5 मीटर
AD = 4 मीटर
PQ = (5.5 + 2.25 + 2.25) मीटर
= 10 मीटर
और QR = (4 + 2.25 + 2.25) मीटर
= 8.5 मीटर

(i) बरामदे का क्षेत्रफल = PQRS का क्षेत्रफल – ABCD का क्षेत्रफल
= (10 × 8.5 – 5.5 × 4) मीटर²
= (85 – 22) मीटर²
= 63 मीटर। उत्तर

(ii) ₹ 200 प्रति मीटर की दर से बरामदे के फर्श पर सीमेन्ट कराने का व्यय
= ₹ (200 × 63)
= ₹ 12600

प्रश्न 5.
30 मीटर भुजा वाले एक वर्गाकार बगीचे की परिसीमा से लगा भीतर की ओर 1 मीटर चौड़ा पथ बना हुआ है। ज्ञात कीजिए:
(i) पथ का क्षेत्रफल
(ii) ₹40 प्रति मीटर² की दर से बगीचे के शेष भाग II पर घास लगवाने का व्यय।

हल :
माना ABCD एक वर्याकार बगीचा है। माना PQRS रास्ते की आन्तरिक दीवार है।
AB = 30 मीटर
और PQ = (30 – 1 – 1) मीटर
= 28 मीटर

(i) रास्ते का क्षेत्रफल = ABCD का क्षेत्रफल – PQRS का क्षेत्रफल
(30 × 30 – 28 × 28) मीटर²
= (900 – 784) मीटर²
= 116 मीटर²। उत्तर

(ii) बगीचे के शेष भाग का क्षेत्रफल
= PQRS का क्षेत्रफल
= (28 × 28) मीटर²
= 784 मीटर²
₹ 40 प्रति मीटर² की दर से घास लगाने का व्यय
= ₹ 40 × 784
= ₹ 31,360। उत्तर

प्रश्न 6.
700 मीटर लम्बे और 300 मीटर चौड़े एक आयताकार पार्क के मध्य से होकर जाते 10 मीटर चौड़े दो पथ बने हुए हैं जो एक-दूसरे पर परस्पर लम्ब और चौपड़ के आकार के हैं। इनमें से प्रत्येक पथ का क्षेत्रफल ज्ञात कीजिए तथा पार्क की भुजाओं को छोड़कर पार्क के शेष भाग का भी क्षेत्रफल ज्ञात कीजिए। उत्तर को हेक्टेअर में दीजिए।
हल :
माना ABCD और EFGH पार्क के मध्य दो पथ हैं।

AB = 700 मीटर
BC = 10 मीटर
∴ ABCD पथ का क्षेत्रफल = AB × BC
= (700 × 10) मीटर² = 7000 मीटर²
पुनः EF = 300 मीटर
FG = 10 मीटर
∴ EFGH पथ का क्षेत्रफल = EF × FG
= (300 × 10) मीटर²
= 3000 मीटर² उत्तर
∵ MNOP क्षेत्र दोनों पथों में उभयनिष्ठ है।
∴ MNOP क्षेत्र का क्षेत्रफल = ( 10 × 10) मीटर²
= 100 मीटर²
पथों का कुल क्षेत्रफल = पथ ABCD का क्षेत्रफल + पथ EFGH का क्षेत्रफल – MNOP का क्षेत्रफल
= (7000 + 3000 – 100) मीटर²
= 9900 मीटर2 = \(\frac{9900}{10000}\) हेक्टेअर
[∵ 1 हेक्टेअर = 10.000 वर्ग मीटर²]
= 0.99 हेक्टेअर
चौपड़ पथ को छोड़ कर पार्क का क्षेत्रफल = आयताकार पार्क का क्षेत्रफल – सड़कों का क्षेत्रफल
= (700 × 300 – 9900) मीटर²
= (210000 – 9900) मीटर²
= 200100 मीटर²
[∵ 1 हेक्टेअर = 10,000 वर्ग मीटर²]
= \(\frac{200100}{10000}\) हेक्टेअर
= 20.01 हेक्टेअर। उत्तर

प्रश्न 7.
90 मीटर लम्बाई और 60 मीटर चौड़ाई वाले एक आयताकार मैदान में दो पथ बनाए गए हैं, जो भुजाओं के समान्तर हैं, एक-दूसरे को लम्बवत् काटते हैं और मैदान के मध्य से होकर निकलते हैं। यदि प्रत्येक पथ की चौड़ाई 3 मीटर हो, तो ज्ञात कीजिए :

(i) पथों का आच्छादित क्षेत्रफल
(ii) ₹ 110 प्रति मीटर2 की दर से पथ बनाने का व्यय।
हल :
(i) माना ABCD और EFGH लम्बवत् पथ हैं।
AB = 90 मीटर
और BC = 3 मीटर
∴ ABCD पथ का क्षेत्रफल = (90 × 3) मीटर²
= 270 मीटर²
पुनः EF = 60 मीटर
FG = 3 मीटर
∴ EFGH का क्षेत्रफल = (60 × 3) मीटर²
= 180 मीटर²
दोनों पथों में PQRS उभयनिष्ठ क्षेत्र है।
∴ PQRS का क्षेत्रफल = (3 × 3) मीटर²
= 9 मीटर²
पथ का क्षेत्रफल = ABCD पथ का क्षेत्रफल + EFGH पथ का क्षेत्रफल – PORS का क्षेत्रफल
= (270 + 180 – 9) मीटर²
= 441 मीटर2

(ii) ₹ 110 प्रति मी² की दर से पथ बनाने का खर्चा
= ₹ (110 × 441)
=₹ 48.510 उत्तर

प्रश्न 8.
प्रज्ञा 4 सेमी त्रिज्या एक वृत्ताकार पाइप के चारों ओर एक रस्सी लपेटती है (जैसा दिखाया गया है) और रस्सी की आवश्यक लम्बाई को काट लेती है। इसके बाद वह उसे 4 सेमी भुजा वाले एक वर्गाकार बॉक्स के चारों ओर लपेटती है (दिखाया गया है)। क्या उसके पास कुछ और रस्सी बचेगी ? (π = 3.14 लीजिए)

हल :
वृत्ताकार पाइप के चारों ओर लपेटी गई रस्सी की लम्बाई
= पाइप की परिधि
= 2πr = (2 × 3.14 × 4) सेमी
= 25.12 सेमी
वर्गाकार बॉक्स के चारों ओर लपेटी गई रस्सी की लम्बाई
= वर्ग का परिमाप
= 4 × भुजा = (4 × 4) सेमी = 16 सेमी
अतः 25.12 सेमी > 16 सेमी
हाँ, (25.12 – 16) सेमी = 9.12 सेमी
अतः प्रज्ञा के पास 9.12 सेमी बचती है। उत्तर

प्रश्न 9.
संलग्न आकृति एक आयताकार पार्क के मध्य में एक वृत्ताकार फूलों की क्यारी को दर्शाती है। ज्ञात कीजिए:
(i) पूरे पार्क का क्षेत्रफल
(ii) फूलों की क्यारी का क्षेत्रफल
(iii) फूलों की क्यारी को छोड़कर, पार्क के शेष भाग का क्षेत्रफल
(iv) क्यारी की परिधि।

हल :
(i) पूरे पार्क का क्षेत्रफल = लम्बाई × चौड़ाई
= (10 × 5) मीटर²
= 50 मीटर। उत्तर

(ii) फूलों की क्यारी का क्षेत्रफल = πr²
= (3.14 × 2 × 2) मीटर²
= 12:56 मीटर²।

(ii) शेष भाग का क्षेत्रफल = पूरे पार्क का क्षेत्रफल – फूलों की क्यारी का क्षेत्रफल
= (50 – 12.56) मीटर²
= 37:44 मीटर²। उत्तर

(iv) फूलों की क्यारी की परिधि
= 2πr = (2 × 3.14 × 2) मीटर
= 12.56 मीटर। उत्तर

प्रश्न 10.
दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए:

हल :
(i) छायांकित भाग DCEFD का क्षेत्रफल = आयत ABCD का क्षेत्रफल – ΔEAF का क्षेत्रफल – ΔEBC का क्षेत्रफल
= (AB × BC) – (\(\frac{1}{2}\) × AE × AF) – (\(\frac{1}{2}\) × EB × BC)
= (18 × 10) – (\(\frac{1}{2}\) × 10 × 6) – (\(\frac{1}{2}\) × 8 × 10)
= 180 – 30 – 40 = 180 – 70 = 110 सेमी²। उत्तर

(ii) छायांकित भाग TUQ का क्षेत्रफल = वर्ग PORS का क्षेत्रफल – ΔTSU का क्षेत्रफल – ΔURQ का क्षेत्रफल – ΔTPQ का क्षेत्रफल
= (PQ)² – (\(\frac{1}{2}\) × TS × SU) – (\(\frac{1}{2}\) × UR × QR) – (\(\frac{1}{2}\) × PQ × TP)
= (20)² – (\(\frac{1}{2}\) × 10 × 10) – (\(\frac{1}{2}\) × 10 × 20) -(\(\frac{1}{2}\) × 20 × 10)
= 400 – 50 – 100 – 100
= 400 – 250 = 150 सेमी²। उत्तर

प्रश्न 11.
चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए, जहाँ AC = 22 सेमी, BM = 3 सेमी, DN = 3 सेमी और BM⊥AC, DN⊥AC.

हल :
चतुर्भुज ABCD का क्षेत्रफल = ΔABC का क्षेत्रफल + ΔACD का क्षेत्रफल
= \(\frac{1}{2}\) × AC × BM + \(\frac{1}{2}\) × AC × ND
= (\(\frac{1}{2}\) × 22 × 3 + \(\frac{1}{2}\) × 22 × 3) सेमी²
= (33 + 33) सेमी²
= 66 सेमी²। उत्तर

Haryana State Board HBSE 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.3 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.3

प्रश्न 1.
निम्न त्रिज्याओं वाले वृत्तों की परिधि ज्ञात कीजिए :
(a) 14 सेमी
(b) 28 मिमी
(c) 21 सेमी
हल :
हम जानते हैं कि वृत्त की परिधि = 2πr
(i) त्रिज्या (r) = 14 सेमी
∴ परिधि = 2πr = 2 × \(\frac{22}{7}\) × 14
= 88 सेमी। उत्तर

(ii) त्रिज्या (r) = 28 मिमी
परिधि = 2πr = 2 × \(\frac{22}{7}\) × 28
= 2 × 22 × 4 = 176 मिमी। उत्तर

(iii) त्रिज्या (r) = 21 सेमी
परिधि = 2πr = 2 × \(\frac{22}{7}\) × 21
= 2 × 22 × 3 = 132 सेमी। उत्तर

प्रश्न 2.
निम्न वृत्तों का क्षेत्रफल ज्ञात कीजिए। दिया गया है :
(a) त्रिज्या = 14 मिमी [π = \(\frac{22}{7}\) लीजिए]
(b) व्यास = 49 मीटर
(c) त्रिज्या = 5 सेमी
हल :
(a) r = 14 मिमी
वृत्त का क्षेत्रफल = πr² = (\(\frac{22}{7}\) × 142 ) मिमी²
= (\(\frac{22}{7}\) × 14 × 14) मिमी²
= (22 × 14 × 2) मिमी² = 616 मिमी²। उत्तर

(b) व्यास = 49 मीटर
r = \(\frac{49}{2}\) मीटर
वृत्त का क्षेत्रफल = πr²
= \(\frac{22}{7}\) मीटर²
= \(\frac{22}{7}\) मीटर²
= \(\frac{22}{7}\) मीटर²
= 1886.5 मीटर²। उत्तर

(c) r = 5 सेमी
वृत्त का क्षेत्रफल = πr² = (\(\frac{22}{7}\) × 5 × 5) सेमी²
= \(\frac{550}{7}\) सेमी²। उत्तर

प्रश्न 3.
यदि एक वृत्ताकार शीट की परिधि 154 मीटर हो तो इसकी त्रिज्या ज्ञात कीजिए। शीट का क्षेत्रफल भी ज्ञात कीजिए। (π = \(\frac{22}{7}\) लीजिए)
हल :
माना वृत्त की त्रिज्या है।
परिधि = 154 मीटर
⇒ 2πr = 154
⇒ 2 × \(\frac{22}{7}\) × r = 154
⇒ r = 154 × \(\frac{7}{44}\)
= \(\frac{49}{2}\) मीटर = 24.5 मीटर उत्तर

वृत्त का क्षेत्रफल = πr²
= \(\left(\frac{22}{7} \times \frac{49}{2} \times \frac{49}{2}\right)\) मीटर²
= \(\left(\frac{11}{1} \times 7 \times \frac{49}{2}\right)\)मीटर² = \(\frac{3773}{2}\) मीटर²
= 1886.5 मीटर²। उत्तर

प्रश्न 4.
21 मीटर व्यास वाले एक वृत्ताकार बगीचे के चारों ओर माली बाड़ लगाना चाहता है। खरीदे जाने वाले आवश्यक रस्से की लम्बाई ज्ञात कीजिए, यदि वह 2 पूरे चक्कर की बाड़ बनाना चाहता है। ₹ 4 प्रति मीटर की दर से रस्से पर व्यय ज्ञात कीजिए। (π = \(\frac{22}{7}\) लीजिए)
हल :
व्यास = 21 मीटर
त्रिज्या (r) = \(\frac{21}{2}\) मीटर
वृत्ताकार बगीचे की परिधि = 2πr
= (2 × \(\frac{22}{7} \times \frac{21}{2}\)) मीटर
= (22 × 3) मीटर = 66 मीटर
∵ 1 चक्कर लगाने के लिए रस्सी की आवश्यकता
= 66 मीटर
∴ 2 चक्कर लगाने के लिए रस्सी की आवश्यकता
= 2 × 66 मीटर = 132 मीटर
₹4 प्रति मीटर की दर से रस्सी की कीमत
= ₹4 × 132 = ₹ 528। उत्तर

प्रश्न 5.
4 सेमी त्रिज्या वाली एक वृत्ताकार शीट में से 3 सेमी त्रिज्या वाले एक वृत्त को निकाल दिया जाता है। शीट के शेष भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)
हल:
बाहरी त्रिज्या (R) = 4 सेमी
भीतरी त्रिज्या (r) = 3 सेमी
शेष शीट का क्षेत्रफल = बाहरी क्षेत्रफल – भीतरी क्षेत्रफल
= π(R² – r²)
= 3.14(4² – 3²) सेमी²
= 3.14(16 – 9) सेमी²
= 3.14 × 7 सेमी²
= 21.98 सेमी²। उत्तर

प्रश्न 6.
साइमा 1.5 मीटर व्यास वाले एक वृत्ताकार टेबल कवर के चारों ओर किनारी लगाना चाहती है। आवश्यक किनारी की लम्बाई ज्ञात कीजिए और ₹ 15 प्रति मीटर की दर से किनारी लगाने का व्यय ज्ञात कीजिए। (π = 3.14 लीजिए)।
हल :
आवश्यक किनारी की लम्बाई = वृत्ताकार टेबल की परिधि
= 2πr (∵ r = \(\frac{1.5}{2}\) = 0.75 मीटर)
= (2 × 3.14 × 0.75) मीटर = 4.71 मीटर
∵ 1 मीटर किनारी लगाने का व्यय = ₹ 15
∴ 4.71 मीटर किनारी लगाने का व्यय
= ₹ 15 × 4.71 = ₹ 70.65। उत्तर

प्रश्न 7.
दी गई आकृति, व्यास के साथ एक अर्धवृत्त है। उसका परिमाप ज्ञात कीजिए।

हल :
दी गई आकृति का परिमाप


= \(\frac{180}{7}\) सेमी = 25.7 सेमी (लगभग)। उत्तर

प्रश्न 8.
₹ 15 प्रति वर्ग मीटर की दर से, 1.6 मीटर व्यास वाले एक वृत्ताकार टेबल की ऊपरी सतह पर पॉलिश कराने का व्यय ज्ञात कीजिए। (r = 3.14 लीजिए)
हल :
वृत्ताकार टेबल की ऊपरी सतह का क्षेत्रफल = πr²
दिया है : r = मीटर = 0.8 मीटर
∴ क्षेत्रफल = (3.14 × 0.8 × 0.8) मीटर²
= 2:0096 मीटर²
∵ 1 मीटर² वृत्ताकार टेबल पर पॉलिश कराने का व्यय = ₹ 15
∴ 2.0096 मीटर² वृत्ताकार टेबल पर पॉलिश कराने का व्यय = ₹ (15 × 2.0096)
=₹ 30.14। उत्तर

प्रश्न 9.
शाझली 44 सेमी लम्बाई वाली एक तार लेती है और उसे एक वृत्त के आकार में मोड़ देती है। उस वृत्त की त्रिज्या ज्ञात कीजिए। इसका क्षेत्रफल भी ज्ञात कीजिए। यदि इसी तार को दुबारा एक वर्ग के आकार में मोड़ा जाता है, तो इसकी प्रत्येक भुजा की लम्बाई क्या होगी ? कौन-सी आकृति अधिक क्षेत्रफल घेरती है वृत्त या वर्ग ? (π = \(\frac{22}{7}\) लीजिए)
हल :
माना वृत्त की त्रिज्या r है।
परिधि = 2πr
परिधि = तार की लम्बाई
2πr = 44
⇒ 2 × \(\frac{22}{7}\) × r = 44
r = \(\frac{44 \times 7}{2 \times 22}\) = 7 सेमी उत्तर
तब वृत्त का क्षेत्रफल = πr²
\(\frac{22}{7}\) × 7 × 7 सेमी²
= 154 सेमी² उत्तर
माना वर्ग की भुजा = x सेमी है।
वर्ग का परिमाप = तार की लम्बाई
4 × x = 44
⇒ x = \(\frac{44}{4}\) = 11 सेमी
∴ वर्ग का क्षेत्रफल = (भुजा)²
= (11 सेमी)² = 121 सेमी²
अतः वृत्त, वर्ग से अधिक क्षेत्रफल घेरता है। उत्तर

प्रश्न 10.
14 सेमी त्रिज्या वाली एक वृत्ताकार गत्ते की शीट में से, 3.5 सेमी त्रिज्या वाले दो वृत्तों को और 3 सेमी लम्बाई तथा 1 सेमी चौड़ाई वाले एक आयत को निकाल दिया जाता है (जैसा कि आकृति में दिखाया गया है)। शीट के शेष भाग का क्षेत्रफल ज्ञात कीजिए। (π = \(\frac{22}{7}\) लीजिए)

हल :
शेष शीट का क्षेत्रफल = वृत्ताकार गत्ते का क्षेत्रफल – 2 × छोटे वृत्त का क्षेत्रफल – आयत का क्षेत्रफल
= (\(\frac{22}{7}\) × 14 × 14 – 2 × \(\frac{22}{7}\) × 3.5 × 3.5 – 3 × 1) सेमी²
= (44 × 14 – 44 × 0.5 × 3.5 – 3) सेमी²
= (616 – 77 – 3) सेमी² = 536 सेमी²। उत्तर

प्रश्न 11.
6 सेमी भुजा वाले एक वर्गाकार एल्युमिनियम शीट के टुकड़े में से 2 सेमी त्रिज्या वाले एक वृत्त को काट दिया जाता है। शीट के शेष भागका क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)
हल :
वर्गाकार एल्युमिनियम शीट का क्षेत्रफल = भुजा² = (6)² सेमी² = 36 सेमी²
वृत्ताकार काटी गई शीट का क्षेत्रफल = πr² = 3.14 × 2 × 2 सेमी²
= 12.56 सेमी²
शेष शीट का क्षेत्रफल = वर्गाकार शीट का क्षेत्रफल – काटी गई शीट का क्षेत्रफल
= (36 – 12.56) सेमी²
= 23.44 सेमी²। उत्तर

प्रश्न 12.
एक वृत्त की परिधि 31.4 सेमी है। वृत्त की त्रिज्या और क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)
हल :
माना वृत्त की त्रिज्या = r सेमी है।
परिधि = 31.4 सेमी
2πr = 31.4
2 × 3.14 × r = 31.4
∴ r = \(\frac{31.4}{2 \times 3.14}\)
= 5 सेमी उत्तर
∴ वृत्त का क्षेत्रफल = πr² = 3.14 × 5²
= 3.14 × 25
= 78.5 सेमी²। उत्तर

प्रश्न 13.
एक वृत्ताकार फूलों की क्यारी के चारों ओर 4 मीटर चौड़ा पथ हैतथा फूलों की क्यारी का व्यास 66 मीटर है। इस पथ का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)

हल :
व्यास = 66 मीटर
त्रिज्या = \(\frac{66}{2}\) मीटर = 33 मीटर
पथ सहित क्यारी की त्रिज्या = (33 + 4) मीटर = 37 मीटर
पथ का क्षेत्रफल = [π(37)² – π(33)²] मीटर²
= π(37² – 33²) मीटर²
= π(37 + 33) (37 – 33) मीटर²
= (3.14 × 70 × 4) मीटर²
= 879.20 मीटर²। उत्तर

प्रश्न 14.
एक वृत्ताकार फूलों के बगीचे का क्षेत्रफल 314 मीटर² है। बगीचे के केन्द्र में एक घूमने वाला फव्वारा (sprinkler) लगाया जाता है, जो अपने चारों ओर 12 मीटर त्रिज्या के क्षेत्रफल में पानी का छिड़काव करता है। क्या फव्वारा पूरे बगीचे में पानी का छिड़काव कर सकेगा ? (π = 3.14 लीजिए)
हल :
माना फूलों के बगीचे की त्रिज्या r मीटर है।
क्षेत्रफल = 314 मीटर²
πr² = 314
3.14 × r² = 314
r² = \(\left(\frac{314}{3.14}\right)\)
r² = 100
r = 10 मीटर
फव्वारे द्वारा घेरे गए क्षेत्रफल की त्रिज्या से बगीचे की त्रिज्या कम है। अतः फव्वारा पूरे बगीचे में छिड़काव कर सकेगा। उत्तर

प्रश्न 15.
आकृति में, अन्तः और बाह्य वृत्तों की परिधि ज्ञात कीजिए। (π = 3.14 लीजिए)

हल :
बाहरी त्रिज्या R = 19 मीटर
और भीतरी त्रिज्या, r = (19 – 10) मीटर = 9 मीटर
भीतरी वृत्त की परिधि = 2πr
= (2 × 3.14 × 9) मीटर
= 56.52 मीटर उत्तर
बाहरी वृत्त की परिधि = 2πR
= (2 × 3.14 × 19) मीटर
= 119.32 मीटर।

प्रश्न 16.
28 सेमी त्रिज्या वाले एक पहिए को 352 मीटर दूरी तय करने के लिए कितनी बार घुमाना पड़ेगा ? (π = \(\frac{22}{7}\) लीजिए)
हल :
पहिए द्वारा 1 चक्कर में तय की गई दूरी
= 2πr = (2 × \(\frac{22}{7}\) × 28 ) मीटर
= 176 मीटर
352 मीटर तय करने में चक्करों की संख्या
= \(\frac{352 \times 100}{176}\) = 200 उत्तर

प्रश्न 17.
एक वृत्ताकार घड़ी की मिनट की सुई की लम्बाई 15 सेमी है। मिनट की सुई की नोक 1 घण्टे में कितनी दूरी तय करती है। (π = 3.14 लीजिए)
हल :
हम जानते हैं कि मिनट की सुई एक पूरे चक्कर में एक घण्टा तय करती है।
r = 15 सेमी
तय की गई दूरी = परिधि = 2πr
= (2 × 3.14 × 15) सेमी
= 94.2 सेमी।

Haryana State Board HBSE 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.2

प्रश्न 1.
निम्न में से प्रत्येक समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए :

हल :
(a) समांतर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= (7 × 4) सेमी² = 28 सेमी2। उत्तर

(b) समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= (5 × 3) सेमी² = 15 सेमी। उत्तर

(c) समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= (2.5 × 3.5) सेमी² = 8.75 सेमी। उत्तर

(d) समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= (5 × 4.8) सेमी² = 24 सेमी2 उत्तर

(e) समांतर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
= (2 × 4.4) सेमी² = 8.8 सेमी। उत्तर

प्रश्न 2.
निम्न में प्रत्येक त्रिभुज का क्षेत्रफल ज्ञात कीजिए:

हल :
(a) त्रिभुज का क्षेत्रफल
= \(\frac{1}{2}\) × आधार × ऊँचाई
= \(\frac{1}{2}\) × 4 × 3
= \(\frac{12}{2}\) = 6 सेमी²। उत्तर

(b) त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई
= \(\frac{1}{2}\) × 5 × 3.2
= 5 × 1.6
= 8 सेमी²। उत्तर

(c) त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई
= \(\frac{1}{2}\) × 3 × 4
= \(\frac{12}{2}\) = 6 सेमी²। उत्तर

(d) त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई
= \(\frac{1}{2}\) × 3 × 2
= 3 × 1 = 3 सेमी²। उत्तर

प्रश्न 3.
रिक्त स्थान का मान ज्ञात कीजिए :

हल :
हम जानते हैं कि
समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
इसलिए रिक्त स्थान की गणना निम्न प्रकार है-

प्रश्न 4.
रिक्त स्थानों के मान ज्ञात कीजिए :

हल :
हम जानते हैं कि
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई

रिक्त स्थान की पूर्ति निम्न प्रकार करते हैं-

प्रश्न 5.
PQRS एक समान्तर चतुर्भुज है (आकृति देखें)। QM शीर्ष Q से SR तक P की ऊँचाई तथा ON शीर्ष Q से PS तक की ऊँचाई है। यदि SR = 12 सेमी और QM = 7.6 सेमी तो ज्ञात कीजिए :
(a) समान्तर चतुर्भुज PQRS का क्षेत्रफल
(b) QN, यदि PS = 8 सेमी

हल :
(a) PQRS समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई = SR × QM
= (12 × 7.6) सेमी² = 91.2 सेमी। उत्तर

(b) समान्तर चतुर्भुज PQRS का क्षेत्रफल
= आधार × ऊँचाई
⇒ PS × QN = स. मा. चतुर्भुज PQRS का क्षेत्रफल
⇒ 8 × QN = 91.2
⇒ QN = \(\frac{91.2}{8}\) = 11.4 सेमी। उत्तर

प्रश्न 6.
DL और BM समान्तर चतुर्भुज ABCD की क्रमशः भुजाएँ AB और AD पर लम्ब हैं (आकृति देखें)। यदि समान्तर चतुर्भुज का P {l∈Qy 1470 सेमी² है, AB = 35 सेमी और AD = 49 सेम है, तो BM तथा DL की लम्बाई ज्ञात कीजिए।

हल :
ABCD चतुर्भुज का क्षेत्रफल = 1470 सेमी²
AB = 35 सेमी और AD = 49 सेमी
ABCD का क्षेत्रफल = AD × BM
⇒ 1470 = 49 × BM
∴ BM = \(\frac{1470}{49}\) = 30 सेमी। उत्तर
ABCD का क्षेत्रफल = AB × DL
⇒ 1470 = 35 × DL
∴ DL = \(\frac{1470}{35}\) = 42 सेमी। उत्तर

प्रश्न 7.
त्रिभुज ABC, A पर समकोण है (आकृति देखें) और AD भुजा BC पर लम्ब है। यदि AB = 5 सेमी, BC = 13 सेमी और AC = 12 सेमी है, तो ΔABC का क्षेत्रफल ज्ञात कीजिए। AD की लम्बाई भी ज्ञात कीजिए।

हल :
ΔABC में, AD, BC पर लम्ब है।
∴ ΔABC का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई
= \(\frac{1}{2}\) × AB × AC = \(\frac{1}{2}\) × 5 × 12
= \(\frac{1}{2}\) × 60 = 30 सेमी²। उत्तर
पुनः ΔABC का क्षेत्रफल = \(\frac{1}{2}\) × BC × AD
30 = \(\frac{1}{2}\) × 13 × AD
AD = \(\frac{30 \times 2}{13}=\frac{60}{13}\) सेमी। उत्तर

प्रश्न 8.
ΔABC समद्विबाहु त्रिभुज है जिनमें AB = AC = 7.5 सेमी और BC = 9 सेमी है(आकृति देखें)। A से BC तक की ऊँचाई AD, 6 सेमी है। ΔABC का क्षेत्रफल ज्ञात कीजिए। C से AB तक की ऊँचाई अर्थात् CE क्या होगी?

हल :
ΔABC का क्षेत्रफल = \(\frac{1}{2}\) × BC × AD
= \(\frac{1}{2}\) × 9 × 6
= \(\frac{54}{2}\) = 27 सेमी² उत्तर
पुनः ΔABC का क्षेत्रफल = \(\frac{1}{2}\) × AB × ऊँचाई
27 = \(\frac{1}{2}\) × 7.5 × CE
ऊँचाई (CE) = \(\frac{27 \times 2}{7.5}\) = 7.2 सेमी। उत्तर