Haryana State Board HBSE 7th Class Maths Solutions Chapter 4 सरल समीकरण Ex 4.1 Textbook Exercise Questions and Answers.
Haryana Board 7th Class Maths Solutions Chapter 4 सरल समीकरण Ex 4.1
प्रश्न 1.
निम्नलिखित सारणी के अंतिम स्तंभ को पूरा कीजिए :
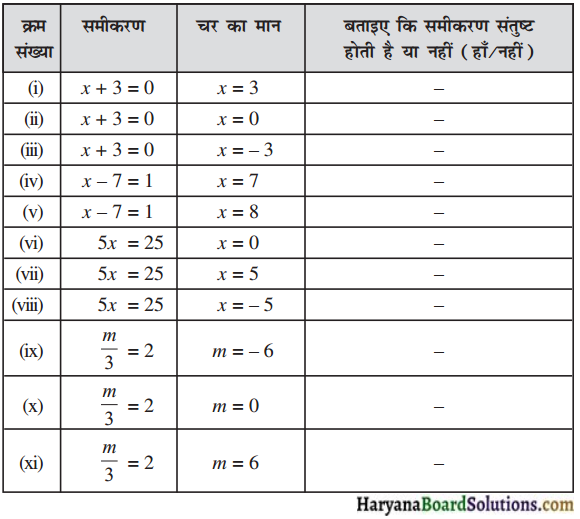
हल:
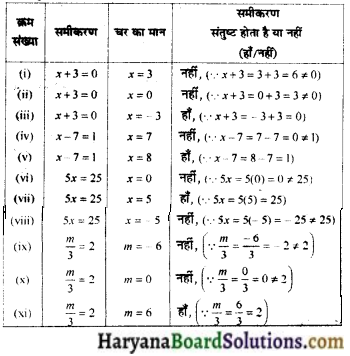
![]()
प्रश्न 2.
जाँच कीजिए कि कोष्ठकों में दिये हुए मान, दिए गए संगत समीकरणों के हल हैं या नहीं:
(a) n + 5 = 19,(n = 1)
(b) 7n + 5 = 19, (n = – 2)
(c) 7n + 5 = 19, (n = 2)
(d) 4p – 3 = 13, (p = 1)
(e) 4p – 3 = 13, (p = – 4)
(f) 4p – 3 = 13, (p = 0)
हल :
(a) जब 13 1 हो, तब
n + 5 = 1 + 5 = 6
= 6 ≠ 19
∴ n = 1 समीकरण का हल नहीं है।
(b) जब n = – 2 हो, तब
7n + 5 = 7(-2) + 5 + 5
= – 9 ≠ 19
∴ n = -2 समीकरण का हल नहीं है।
(c) जब n = 2 हो, तब
7n + 5 = 7 × 2 + 5
= 14 + 5 = 19
∴ n = 2 समीकरण का हल है।
(d) जब p = 1 हो, तब
4p – 3 = 4 × 1 – 3
= 4 – 3
= 1 ≠ 13
∴ p = 1 समीकरण का हल नहीं है।
(e) जब p = -4 हो, सब
4p – 3 = 4 × (-4) – 3
= – 16 – 3
= – 19 ≠ 13
∴ p = – 4 समीकरण का हल नहीं है।
(f) जब p = 0 हो, तब
4p – 3 = 4(0) – 3
= 0 – 3
= – 3 ≠ 13
∴ p = 0 समीकरण का हल नहीं है।
प्रश्न 3.
प्रयत्न और भूल विधि से निम्नलिखित समीकरणों को हल कीजिए:
(i) 5p + 2 = 17
(ii) 3m – 14 = 4
हल :
(i) हम समीकरण के बायें पक्ष में p का मान 1, 2, 3, …….. रखकर हल करते हैं जब तक दायाँ पक्ष बायें पक्ष के बराबर न हो जाए।
दिया गया समीकरण 5p + 2 = 17
बायाँ पक्ष = 5p + 2 और दायाँ पक्ष = 17
| p | बायाँ पक्ष | दायाँ पक्ष | क्या बायाँ पक्ष = दायाँ पक्ष? |
| 1 | 5 × 1 + 2 = 5 + 2 = 7 | 17 | नहीं |
| 2 | 5 × 2 + 2 = 10 + 2 = 12 | 17 | नहीं |
| 3 | 5 × 3 + 2 = 15 + 2 = 17 | 17 | नहीं |
स्पष्ट है, दायाँ पक्ष = बायाँ पक्ष ।
इसलिए, p = 3 दिये गये समीकरण का हल है।
(ii) हम बाएँ पक्ष को m के कुछ मानों के लिए हल करते हैं और m के मान रखते चलते हैं, जब तक दायाँ पक्ष बाएँ पक्ष के बराबर न हो जाए।
दिया गया समीकरण 3m – 14 = 4 है।
अत: बायाँ पक्ष = 3m -14 और दायाँ पक्ष = 4
| m | बायाँ पक्ष | दायाँ पक्ष | क्या बायाँ पक्ष = दायाँ पक्ष? |
| 5 | 3 × 5 – 14 = 15 – 14 = 1 | 4 | नहीं |
| 6 | 3 × 6 – 14 = 18 – 14 = 4 | 4 | हाँ |
स्पष्ट है, m = 6 के लिए, दायाँ पक्ष = बायाँ पक्ष।
अत: m = 6 दिए गए समीकरण का हल है।
![]()
प्रश्न 4.
निम्नलिखित कथनों के लिए समीकरण दीजिए :
(i) संख्याओं x और 4 का योग है।
(ii) y में से 2 घटाने पर 8 प्राप्त होते हैं।
(iii) a का 10 गुना 70 है।
(iv) संख्या 6 को 5 से भाग देने पर 6 प्राप्त होता है।
(v) t का तीन-चौथाई 15 है।
(vi) m का 7 गुना और 7 का योगफल आपको 77 देता है।
(vii) एक संख्या x की चौथाई ऋण 4 आपको 4 देता
(viii) यदि आपy के 6 गुने में से 6 घटाएँ, तो आपको 60 प्राप्त होता है।
(ix) यदि आप: z के एक-तिहाई में 3 जोड़ें, तो आपको 30 प्राप्त होता है।
हल :
दिए गए कथनों के समीकरण निम्न प्रकार हैं :
(i) x + 4 = 9
(ii) y – 2 = 8
(iii) 10a = 70
(iv) b ÷ 5 = 6
(v) \(\frac {3}{4}\) × t = 15
(vi) 7m + 7 = 77
(vii) \(\frac {1}{4}\) × x – 4 = 4 जहाँ x एक संख्या है
(viii) 6y – 6 = 60
(ix) \(\frac {1}{3}\) × z + 3 = 30
प्रश्न 5.
निम्नलिखित समीकरणों को सामान्य कथनों के रूप में लिखिए :
(i) p + 4 = 15
(ii) m – 7= 3
(iii) 2m = 7
(iv) \(\frac {m}{5}\) = 3
(v) \(\frac {3m}{5}\) = 6
(vi) 3p + 4 = 25
(vii) 4p – 2 = 18
(viii) \(\frac {p}{2}\) + 2 = 8
हल :
दिये गये समी करणों के कथन निम्न प्रकार हैं :
(i) p और 4 योग 15 है।
(ii) m और 7 का अन्तर 3 है।
(iii) m का दुगुना 7 है।
(iv) m को 5 से भाग देने पर 3 आता है।
(v) m के तीन गुने को 5 से भाग देने पर 6 आता है।
(vi) p के तीन गुने में 4 जोड़ने पर 25 आता है।
(vii) p के 4 गुने में से 2 घटाने पर 18 आता है।
(viii) p में 2 का भाग दिया जाए और 2 जोड़ने पर 8 आता है।
![]()
प्रश्न 6.
निम्नलिखित स्थितियों में समीकरण बनाइए:
(i) इरफान कहता है कि उसके पास, परमीत के पास जितने कंचे हैं उनके पाँच गुने से 7 अधिक कैचे हैं। इरफान के पास 37 कंचे हैं। (परमीत के कंचों की संख्या को m लीजिए।)
(ii) लक्ष्मी के पिता की आयु 49 वर्ष है। उनकी आयु, लड़की की आयु के तीन गुने से 4 वर्ष अधिक है। (लक्ष्मी की आयु को। वर्ष लीजिए।)
(iii) अध्यापिका बताती हैं कि उनकी कक्षा में एक विद्यार्थी द्वारा प्राप्त किए गए अधिकतम अंक, प्राप्त किए न्यूनतम अंक का दुगुना धन 7 हैं। प्राप्त किए गए अधिकतम अंक 87 हैं। (न्यूनतम प्राप्त किए गए अंकों को l लीजिए।)
(iv) एक समद्विबाहु त्रिभुज में शीर्ष कोण प्रत्येक आधार कोण का दुगुना है। (मान लीजिए प्रत्येक आधार कोण b डिग्री है। याद रखिए कि त्रिभुज के तीनों कोणों का योग 180 डिग्री होता है।)
हल :
(i) माना परमीत के पास कंचेm हैं।
m के पाँच गुने में 7 जोड़ा जाता है, तब 5m + 7
5 गुने से 7 अधिक कंचे = 37
∴ समीकरण 5m + 7 = 37 होगा। उत्तर
(ii) माना लक्ष्मी की आयु वर्ष है।
y के तीन गुने में 4 जोड़ा जाता हैं 3y + 4
उसके पिता की आयु 49 वर्ष है।
∴ समीकरण 3y + 4 = 49 होगा। उत्तर
(iii) माना न्यूनतम अंक l हैं।
तब न्यूनतम अंकों के दुगुने में 7 जोड़ने पर 87 अंक प्राप्त होते हैं।
∴ समीकरण 2l + 7 = 87 है। उत्तर
(iv) माना आधार कोण b° है तब शीर्ष कोण = 2b°
त्रिभुज के तीनों कोणों का योग = 180°
∴ b° + b° + 2b° = 180°
4b° = 180°
अभीष्ट समीकरण है। उत्तर