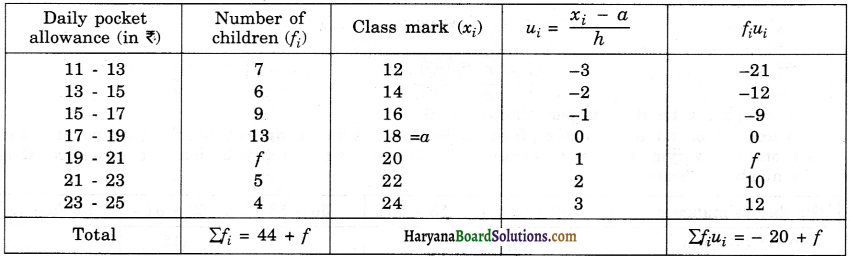
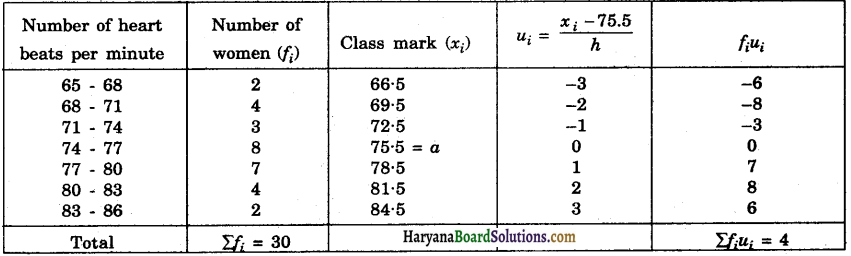
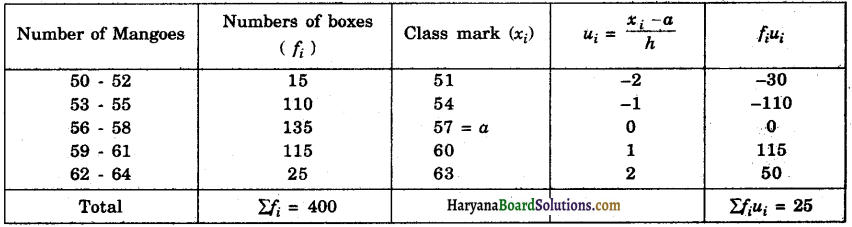
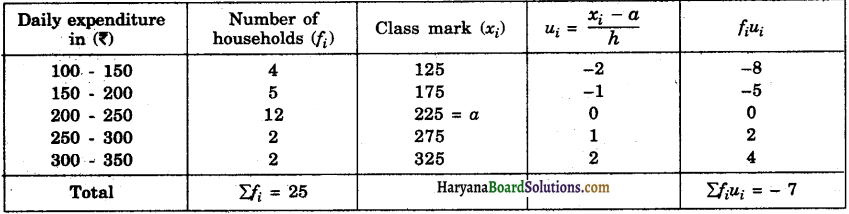
Haryana State Board HBSE 9th Class Hindi Solutions Kshitij Chapter 2 ल्हासा की ओर Textbook Exercise Questions and Answers.
Haryana Board 9th Class Hindi Solutions Kshitij Chapter 2 ल्हासा की ओर
HBSE 9th Class Hindi ल्हासा की ओर Textbook Questions and Answers
ल्हासा की ओर पाठ के प्रश्न उत्तर HBSE 9th Class Hindi प्रश्न 1.
थोङ्ला के पहले के आखिरी गाँव पहुँचने पर भिखमंगे के वेश में होने के बावजूद लेखक को ठहरने के लिए उचित स्थान मिला जबकि दूसरी यात्रा के समय भद्रवेश भी उन्हें उचित स्थान नहीं दिला सका। क्यों ?
उत्तर-
लेखक जब पहली बार तिब्बत की यात्रा पर गया तो एक भिखारी के वेश में था। यात्रा के समय मार्ग में उसकी मुलाकात मंगोल जाति के बौद्ध भिक्षु से हुई थी, जिसे लेखक ने सुमति का नाम दिया। सुमति की तिब्बत के गाँवों में बहुत जान-पहचान थी। वहाँ के लोग उसका बहुत सम्मान करते थे। उसके साथ होने के कारण ही लेखक को भिखारी के वेश में भी ठहरने का उचित स्थान मिला था। किन्तु दूसरी बार वह एक सम्मानित यात्री के रूप में संध्या के समय तिब्बत पहुंचा था। उस समय वहाँ के लोग नशीला पदार्थ पीने के कारण नशे की अवस्था में थे। इसलिए उसे ठहरने के लिए कोई उचित स्थान नहीं मिला था।
ल्हासा की ओर HBSE 9th Class Hindi प्रश्न 2.
उस समय के तिब्बत में हथियार का कानून न रहने के कारण यात्रियों को किस प्रकार का भय बना रहता था ?
उत्तर-
उस समय जब लेखक ने तिब्बत की यात्रा की थी तब वहाँ हथियार का कानून न होने के कारण लोग लाठियों की भाँति पिस्तौल और बंदूक उठाए फिरते थे। उस समय एकांत मार्ग पर चलते समय डाकुओं का भय सदा बना रहता था कि कहीं कोई डाकू उनका खून न कर डाले। कहने का भाव है कि यात्रियों के साथ लूटपाट व उनकी हत्या होने का भय बना रहता था।
ल्हासा की ओर प्रश्न उत्तर HBSE 9th Class Hindi प्रश्न 3.
लेखक लड़कोर के मार्ग में अपने साथियों से किस कारण पिछड़ गया था ?
उत्तर-
लेखक के अपने साथियों से पिछड़ने के मुख्यतः दो कारण थे-
- उसका घोड़ा बहुत धीमी चाल से चल रहा था।
- दूसरा कारण था कि लेखक रास्ता भूल गया था। उसे एक-डेढ़ मील चलने पर पता चला था कि वह गलत मार्ग पर जा रहा है। वहाँ से लौटने में भी उसे देरी हो गई थी।
Lhasa Ki Aur Summary In Hindi HBSE 9th Class प्रश्न 4.
लेखक ने शेकर विहार में सुमति को उनके यजमानों के पास जाने से रोका, परन्तु दूसरी बार रोकने का प्रयास क्यों नहीं किया ?
उत्तर-
शेकर विहार में लेखक का मित्र सुमति अपने यजमानों को, जो आसपास के गाँवों में रहते थे, मिलना चाहता था। लेखक ने उसे इसलिए रोका क्योंकि वह अपने यजमानों से मिलने में कई दिन लगा देता और यात्रा में और भी विलंब हो जाता। दूसरी बार लेखक ने सुमति को यजमानों से मिलने के लिए इसलिए नहीं रोका क्योंकि लेखक मंदिर में रखी हस्तलिखित कन्जुर (बुद्धवचन-अनुवाद) की पोथियों को पढ़ना चाहता था। उसके जाने पर उसे उन पोथियों को पढ़ने का समय मिल जाता।

Lhasa Ki Aur Class 9 HBSE Hindi प्रश्न 5.
अपनी यात्रा के दौरान लेखक को किन कठिनाइयों का सामना करना पड़ा ? [H.B.S.E. March, 2017]
उत्तर-
लेखक को पहाड़ों पर पैदल चलना पड़ा था। इसके साथ ही लेखक को अपना सामान भी स्वयं उठाना पड़ा था। दूसरी बड़ी कठिनाई यह रही कि लेखक साधारण यात्री के वेश में नहीं था। उसने भिखमंगे का रूप धारण किया हुआ था जबकि तिब्बत में भिखमंगों के प्रति आदर का भाव नहीं रखा जाता था। इसलिए लेखक को कदम-कदम पर संदेह की दृष्टि से देखा जाता था। लेखक को भार ढोने वाला व्यक्ति न मिलने पर भी यात्रा में कठिनाई का सामना करना पड़ा। एक स्थान पर जब लेखक ने भार उठाने और सवार होने के लिए घोड़ा लिया तो वह बहुत ही धीमी गति से चला, फलस्वरूप लेखक अपने अन्य साथियों से पिछड़ गया। निर्जन मार्ग पर चलते समय डाकुओं द्वारा लूटने व हत्या होने का भय भी लेखक के मन में था।
ल्हासा की ओर पाठ 2 के प्रश्न उत्तर HBSE 9th Class Hindi प्रश्न 6.
प्रस्तुत यात्रा-वृत्तांत के आधार पर बताइए कि उस समय का तिब्बती समाज कैसा था ?
उत्तर-
जिस समय लेखक ने तिब्बत की यात्रा की थी, उस समय तिब्बत का सामाजिक ढाँचा व्यवस्थित था। वहाँ पर जातिगत भेदभाव नहीं किया जाता था। सब एक-दूसरे को समान समझते थे। स्त्रियाँ भी परदा नहीं करती थीं। भिखमंगों को छोड़कर सभी का आदर या सम्मान किया जाता था। किन्तु हथियार रखने का कानून न होने के कारण वहाँ प्रत्येक व्यक्ति लाठी की भाँति हथियार (पिस्तौल व बंदूक) उठाए फिरता था। निर्जन मार्ग में डाकुओं का भय भी था। तिब्बत में जागीरदारी व्यवस्था थी। वहाँ छोटे-बड़े सभी प्रकार के जागीरदार थे, किन्तु अधिकाँश जागीरें बौद्ध विहारों के पास थीं। खेतों में काम करने वाले मजदूरों का शोषण किया जाता था। जागीरों में बौद्ध भिक्षुओं को राजा के समान आदर दिया जाता था।
प्रश्न 7.
‘मैं अब पुस्तकों के भीतर था। नीचे दिए गए विकल्पों में से कौन-सा इस वाक्य का अर्थ बतलाता है-
(क) लेखक पुस्तकें पढ़ने में रम गया।
(ख) लेखक पुस्तकों की शैल्फ के भीतर चला गया।
(ग) लेखक के चारों ओर पुस्तकें ही थीं।
(घ) पुस्तक में लेखक का परिचय और चित्र छपा था।
उत्तर-
(क) लेखक पुस्तकें पढ़ने में रम गया।
रचना और अभिव्यक्ति
प्रश्न 8.
सुमति के यजमान और अन्य परिचित लोग लगभग हर गाँव में मिले। इस आधार पर आप सुमति के व्यक्तित्व की किन विशेषताओं का चित्रण कर सकते हैं ?
उत्तर-
सुमति के यजमान और अन्य परिचितों का हर गाँव में मिलने से पता चलता है कि वह बहुत ही मिलनसार व्यक्ति है। वह सबके भले की कामना करता है, तभी उसे हर गाँव में सम्मान दिया जाता है। वह परोपकारी व्यक्ति है। वह हमारे लेखक के लिए तिब्बत में प्रवेश की राहदारी बनवाता है और अपने परिचितों के यहाँ ठहराता है। वह थोड़ा-सा लालची प्रवृत्ति का भी है क्योंकि वह हर गाँव में अपने यजमानों को गंडे देना चाहता है क्योंकि उसके बदले में यजमान उसे दान-दक्षिणा अवश्य देते हैं।
प्रश्न 9.
‘हालाँकि उस वक्त मेरा भेष ऐसा नहीं था कि उन्हें कुछ भी खयाल करना चाहिए था’-उक्त कथन के अनुसार हमारे आचार-व्यवहार के तरीके वेशभूषा के आधार पर तय होते हैं। आपकी समझ से यह उचित है अथवा अनुचित, विचार व्यक्त करें।
उत्तर-
हमारे आचार-व्यवहार के तरीकों का वेशभूषा के आधार पर तय होना उचित नहीं है क्योंकि किसी भी व्यक्ति की वेशभूषा को देखकर उसके अच्छे-बुरे का निर्णय करना अथवा उसके साथ कैसा व्यवहार करना चाहिए इसका अंदाजा लगाना उचित नहीं है। अतः हमें किसी की वेशभूषा की अपेक्षा व्यक्ति के गुणों को देखकर ही उसके साथ व्यवहार करना चाहिए।
प्रश्न 10.
यात्रा-वृत्तांत के आधार पर तिब्बत की भौगोलिक स्थिति का शब्द-चित्र प्रस्तुत करें। वहाँ की स्थिति आपके राज्य/शहर से किस प्रकार भिन्न है ?
उत्तर-
तिब्बत पहाड़ों में बसा एक देश है। वहाँ ऊँचे-ऊँचे पर्वत हैं तथा उनको काटती हुई अनेक जल की धाराएँ बहती हैं। वहाँ के कुछ पहाड़ों पर कुछ हरे-भरे वृक्ष बर्फ से ढके हुए हैं तो कुछ बिल्कुल नंगे हैं। कहीं-कहीं थोड़ी-बहुत समतल भूमि भी है कहीं-कहीं तो पहाड़ों से घिरा हुआ टापू-सा लगता है। कहीं-कहीं पहाड़ों की ढलानों पर छोटे-छोटे गाँव बसे हुए हैं। पहाड़ों को काटकर छोटे-छोटे मार्ग व सड़कें बनाई हुई हैं। पहाड़ी की चढ़ाई कहीं-कहीं सरल है तो कहीं-कहीं अत्यंत सीधी और कठिन है। हमारे हरियाणा राज्य से तिब्बत की भौगोलिक स्थिति पूर्णतः भिन्न है। यहाँ की भूमि सर्वत्र समतल है और चारों ओर हरे-भरे खेत लहराते हैं। सिंचाई के अनेक साधन हैं। आवागमन के लिए सड़कों व रेल की पटरियों का जाल बिछा हुआ है।
प्रश्न 11.
आपने भी किसी स्थान की यात्रा अवश्य की होगी, यात्रा के दौरान हुए अनुभवों को लिखकर प्रस्तुत करें।
उत्तर-
मैंने छोटी-छोटी कई यात्राएँ की हैं। उनमें से एक यात्रा के दौरान हुए अनुभवों का वर्णन इस प्रकार है। मैं अपने स्कूल के बच्चों के साथ गर्मियों के अवकाश में कुल्लू-मनाली गया था। स्कूल की ओर से एक प्राइवेट बस का प्रबंध किया गया। हम लगभग 40 विद्यार्थी और दो अध्यापक उस यात्रा में थे। सबसे रोचक अनुभव मेरे लिए यह रहा कि मैंने प्रथम बार रात को यात्रा की थी। प्रातः होते ही हम कुल्लू पहुँच गए थे। वहाँ से नाश्ता करने के पश्चात् हमारी बस मनाली के लिए चल पड़ी। मार्ग में घुमावदार पहाड़ी सड़कों से जाते पहाड़ों एवं नदी-नालों के दृश्य देखते ही बनते हैं। मनाली हिमाचल प्रदेश का सबसे सुंदर पर्यटन स्थल है। वहाँ हम एक दिन ठहरे तथा आस-पास के सुंदर स्थान एवं प्राकृतिक दृश्य देखे। अगले दिन हमने रोहतांग दर्रा देखने का निश्चय किया और कई छोटी बसें किराए पर कीं। आस-पास के पूरे क्षेत्र में बर्फ दिखाई दे रही थी। वहाँ का तापमान बहुत कम था। वहाँ पर अनेक विदेशी पर्यटक भी घूमने के लिए आए हुए थे। कुछ ही दूरी पर चीन का बार्डर दिखाई दे रहा था। हम रोहतांग दर्रा देखकर लौट रहे थे कि एक बर्फीला तूफान आ गया। पहले तो मैं घबरा गया कि हम अपने ठहरने के स्थान पर कैसे पहुंचेंगे। किन्तु बस के ड्राइवर ने हमें साहस दिलाया और कहा कि यह तूफान थोड़ी देर में निकल जाएगा। तूफान खत्म होने पर हम फिर चल पड़े और सूर्य छिपते-छिपते हम मनाली लौट आए। अगले दिन प्रातः वहाँ से वापस चल पड़े और अपनी यात्रा के खट्टे-मीठे अनुभवों के साथ घर पहुँच गए।।

प्रश्न 12.
यात्रा-वृत्तांत गद्य साहित्य की एक विधा है। आपकी इस पाठ्यपुस्तक में कौन-कौन सी विधाएँ हैं ? प्रस्तुत विधा उनसे किन मायनों में अलग है ?
उत्तर-
हमारी पाठ्यपुस्तक में कहानी, निबंध, यात्रा, संस्मरण, रिपोर्ताज, व्यंग्य आदि गद्य साहित्यिक विधाएँ संकलित हैं। प्रत्येक विधा का अपना-अपना महत्त्व है। ‘यात्रा’ विधा इन सभी विधाओं से अलग है। कहानी में कथानक, पात्र, संवाद, देशकाल और वातावरण प्रमुख होता है। निबंध विचारों का गुंफन होता है और संस्मरण में पूर्व जीवन में बीती बातों को अनुभव के साथ लपेटकर प्रस्तुत किया जाता है तो व्यंग्य में किसी प्रवृत्ति पर करारा व्यंग्य करके उसकी वास्तविकता को नंगा करने का प्रयास किया जाता है। किन्तु यात्रा में यह सब कुछ नहीं होता। यात्रा में देखी और अनुभव की हुई बातों के साथ प्राकृतिक दृश्यों, स्थान-विशेष की भौगोलिक स्थितियों, वहाँ की संस्कृति, सामाजिक जीवन, रीति-रिवाजों आदि को यथार्थ रूप से साहित्यिक भाषा में प्रस्तुत किया जाता है। यह कल्पना की अपेक्षा तथ्यों पर आधारित होती है। रोचकता का तत्त्व इसमें आदि से अंत तक बना रहता है। अतः स्पष्ट है कि यात्रा-वृत्तांत गद्य साहित्य की एक स्वतंत्र विधा है।
भाषा-अध्ययन
प्रश्न 13.
किसी भी बात को अनेक प्रकार से कहा जा सकता है, जैसे–
सुबह होने से पहले हम गाँव में थे।
पौ फटने वाली थी कि हम गाँव में थे।
तारों की छाँव रहते-रहते हम गाँव पहुँच गए।
नीचे दिए गए वाक्य को अलग-अलग तरीके से लिखिए
‘जान नहीं पड़ता था कि घोड़ा आगे जा रहा है या पीछे।’
उत्तर-
(1) घोड़ा अत्यंत मरियल चाल से चल रहा था।
(2) जान नहीं पड़ता था कि घोड़ा चल भी रहा है कि नहीं।
(3) घोड़े की चाल से पता चलता था कि मैं अपने लक्ष्य स्थान पर कभी नहीं पहुँच पाऊँगा।
प्रश्न 14.
ऐसे शब्द जो किसी ‘अँचल’ यानी क्षेत्र विशेष में प्रयुक्त होते हैं उन्हें आँचलिक शब्द कहा जाता है। प्रस्तुत पाठ में से आंचलिक शब्द ढूँढकर लिखिए।
उत्तर-
बसेरा, चोभी, टोटीदार, छङ्, डाँडा, गिराँव, कुची-कुची, भीटे, गंडे, कंडे, थुक्पा आदि।
प्रश्न 15.
पाठ में कागज, अक्षर, मैदान के आगे क्रमशः मोटे, अच्छे और विशाल शब्दों का प्रयोग हुआ है। इन शब्दों से उनकी विशेषता उभरकर आती है। पाठ में से कुछ ऐसे ही और शब्द छाँटिए जो किसी की विशेषता बता रहे हों।
उत्तर-
मुख्य) परित्यक्त, आखिरी, अच्छी, निर्जन, उतना, सर्वोच्च, बराबर, थोड़ी, सुस्त, जल्दी आदि।
पाठेतर सक्रियता
प्रश्न 1.
यह यात्रा राहुल जी ने 1930 में की थी। आज के समय यदि तिब्बत की यात्रा की जाए तो राहुल जी की यात्रा से कैसे भिन्न होगी ?
उत्तर-
जब राहुल जी ने यह यात्रा की थी तब आवागमन के साधन नहीं थे और न ही तिब्बत जाने वाला मार्ग ‘फरी-कलिङ्पोङ् खुला था। इसलिए उस समय की यात्रा और आज की जाने वाली यात्रा में निश्चित रूप से अंतर होगा। उस समय कोई मोटरगाड़ी आदि वहाँ नहीं चलती थी। इसलिए उन्हें यात्रा पैदल व घोड़ों पर करनी पड़ी थी। मार्ग में चोर-डाकुओं का भी डर निरंतर बना रहता था, किन्तु आजकल तिब्बत में आने-जाने के साधन उपलब्ध हैं। चोर-डाकुओं का भी कोई डर नहीं है। कहने का तात्पर्य है कि आज की तिब्बत यात्रा राहुल जी की 1930 में की गई यात्रा से अत्यंत सरल एवं आरामदायक होगी।
प्रश्न 2.
क्या आपके किसी परिचित को घुमक्कड़ी/यायावरी का शौक है ? उसके इस शौक का उसकी पढ़ाई/काम आदि पर क्या प्रभाव पड़ता होगा, लिखें।
उत्तर-
निश्चय ही घुमक्कड़ी या यायावरी से किसी भी व्यक्ति की पढ़ाई या काम पर प्रभाव अवश्य पड़ेगा क्योंकि प्रत्येक काम को करने का एक निश्चित समय होता है। यदि उस काम को समय पर न किया गया तो उसमें सफलता नहीं मिलेगी। मेरे एक संबंधी घुमक्कड़ प्रवृत्ति के व्यक्ति हैं। वे अच्छे इंसान हैं। वे साहसी भी हैं, किन्तु अपनी घुमक्कड़ी प्रवृत्ति के कारण गृहस्थ जीवन की जिम्मेवारियों को पूर्ण करने में सफल नहीं हो सके। यदि वे अपनी यात्राओं को योजनाबद्ध करके करते तो शायद उनका उनके कार्यों पर बुरा प्रभाव न पड़ता।
प्रश्न 3.
अपठित गद्यांश को पढ़कर दिए गए प्रश्नों के उत्तर दीजिए-
आम दिनों में समुद्र किनारे के इलाके बेहद खूबसूरत लगते हैं। समुद्र लाखों लोगों को भोजन देता है और लाखों उससे जुड़े दूसरे कारोबारों में लगे हैं। दिसंबर 2004 को सुनामी या समुद्री भूकंप से उठने वाली तूफानी लहरों के प्रकोप ने एक बार फिर साबित कर दिया है कि कुदरत की यह देन सबसे बड़े विनाश का कारण बन सकती है।
प्रकृति कब अपने ही ताने-बाने को उलटकर रख देगी, कहना मुश्किल है। हम उसके बदलते मिजाज को उसका कोप कह लें या कुछ और मगर यह अबूझ पहेली अकसर हमारे विश्वास के चीथड़े कर देती है और हमें यह अहसास करा जाती है कि हम एक कदम आगे नहीं, चार कदम पीछे हैं। एशिया के एक बड़े हिस्से में आने वाले उस भूकंप ने कई द्वीपों को इधर-उधर खिसकाकर एशिया का नक्शा ही बदल डाला। प्रकृति ने पहले भी अपनी ही दी हुई कई अद्भुत चीजें इंसान से वापस ले ली हैं जिसकी कसक अभी तक है।
दुख जीवन को माँजता है, उसे आगे बढ़ने का हुनर सिखाता है। वह हमारे जीवन में ग्रहण लाता है, ताकि हम पूरे प्रकाश की अहमियत जान सकें और रोशनी को बचाए रखने के लिए जतन करें। इस जतन से सभ्यता और संस्कृति का निर्माण होता है। सुनामी के कारण दक्षिण भारत और विश्व के अन्य देशों में जो पीड़ा हम देख रहे हैं, उसे निराशा के चश्मे से न देखें। ऐसे समय में भी मेघना, अरुण और मैगी जैसे बच्चे हमारे जीवन में जोश, उत्साह और शक्ति भर देते हैं। 13 वर्षीय मेघना और अरुण दो दिन अकेले खारे समुद्र में तैरते हुए जीव-जंतुओं से मुकाबला करते हुए किनारे आ लगे। इंडोनेशिया की रिजा पड़ोसी के दो बच्चों को पीठ पर लादकर पानी के बीच तैर रही थी कि वह विशालकाय साँप ने उसे किनारे का रास्ता दिखाया। मछुआरे की बेटी मैगी ने रविवार को समुद्र का भयंकर शोर सुना, उसकी शरारत को समझा, तुरंत अपना बेड़ा उठाया और अपने परिजनों को उस पर बिठा उतर आई समुद्र में, 41 लोगों को लेकर। महज 18 साल की यह जलपरी चल पड़ी पगलाए सागर से दो-दो हाथ करने। दस मीटर से ज्यादा ऊँची सुनामी लहरें जो कोई बाधा, रुकावट मानने को तैयार नहीं थीं, इस लड़की के बुलंद इरादों के सामने बौनी ही साबित
जिस प्रकृति ने हमारे सामने भारी तबाही मचाई है, उसी ने हमें ऐसी ताकत और सूझ दे रखी है कि हम फिर से खड़े होते हैं और चुनौतियों से लड़ने का एक रास्ता ढूँढ निकालते हैं। इस त्रासदी से पीड़ित लोगों की सहायता के लिए जिस तरह पूरी दुनिया एकजुट हुई है, वह इस बात का सबूत है कि मानवता हार नहीं मानती।
(1) कौन-सी आपदा को सुनामी कहा जाता है ? ।
(2) ‘दुख जीवन को माँजता है, उसे आगे बढ़ने का हुनर सिखाता है’-आशय स्पष्ट कीजिए।
(3) मैगी, मेघना और अरुण ने सुनामी जैसी आपदा का सामना किस प्रकार किया ?
(4) प्रस्तुत गद्यांश में ‘दृढ़-निश्चय’ और ‘महत्त्व’ के लिए किन शब्दों का प्रयोग हुआ है ?
(5) इस गद्यांश के लिए एक शीर्षक ‘नाराज समुद्र’ हो सकता है।
आप कोई अन्य शीर्षक दीजिए।
उत्तर-
(1) समुद्री भूकंप से उठने वाली तूफानी लहरों को सुनामी कहा जाता है।
(2) जीवन में आने वाले दुख व संकट का सामना करने से मनुष्य के जीवन में साहस और हिम्मत उत्पन्न होती है। उसी साहस और हिम्मत के बल पर हम जीवन को और भली-भाँति जीने का प्रयास करते हैं। अतः यह कहना ठीक है कि दुख जीवन को माँजता है और उसे आगे बढ़ने का हुनर सिखाता हैं। दुख न हो तो मनुष्य साहसी नहीं बन सकता।
(3) मैगी ने अपने बेड़े पर अपने परिवार के अतिरिक्त 41 लोगों की जानें बचाई थीं। उसने समुद्र की भयंकर लहरों का सामना करके साहसी कार्य किया था।
मेघना-13 वर्षीय मेघना दो दिन अकेली समुद्र के खारे पानी में तैरती हुई और समुद्री जीव-जंतुओं का मुकाबला करती हुई समुद्र के किनारे आ लगी।
अरुणा-अरुणा दो दिनों तक समुद्र की लहरों का मुकाबला करती हुई किनारे पर आ पहुँची थी। उसके साहस को देखकर अच्छे-अच्छे तैराक भी अवाक् रह गए थे।
(4) दृढ़ निश्चय और महत्त्व के लिए क्रमशः ‘बुलंद इरादों’ और ‘अहमियत’ का प्रयोग किया गया है। (5) इस गद्यांश का शीर्षक ‘नाराज समुद्र’ के अतिरिक्त ‘समुद्री प्रकोप’ भी हो सकता है।

HBSE 9th Class Hindi ल्हासा की ओर Important Questions and Answers
प्रश्न 1.
‘लहासा की ओर’ पाठ का उद्देश्य स्पष्ट कीजिए।
उत्तर-
‘लहासा की ओर’ एक यात्रावृत्त है। इसमें श्री राहुल सांकृत्यायन ने अपनी तिब्बत यात्रा का अत्यन्त सुन्दर वर्णन किया है। लेखक ने यह यात्रा नियमानुकूल नहीं की अपितु छद्मवेश में की है क्योंकि उस समय भारतीयों को तिब्बत यात्रा की अनुमति नहीं थी। इस यात्रावृत्त के लेखन का प्रमुख उद्देश्य तिब्बत के लोगों के जीवन का वर्णन करना है। साथ ही तिब्बत एक पहाड़ी क्षेत्र हैं वहाँ की प्राकृतिक छटा को दर्शाना भी लेखक के लिए मुख्य बात थी। भारत से तिब्बत तक की यात्रा करने में कैसी-कैसी कठिनाइयाँ आती हैं, दर्शाना भी यात्रावृत्त का लक्ष्य है। तिब्बत में लोगों का जीवन कैसा है, उनके व्यवसाय, समाज, संस्कृति अर्थिक व्यवस्था आदि सभी का एक साथ वर्णन करना भी महत्त्वपूर्ण लक्ष्य रहा है।
प्रश्न 2.
पठित पाठ के आधार पर सिद्ध कीजिए कि भारतीय महिलाओं की अपेक्षा तिब्बती महिलाओं की स्थिति अधिक सुरक्षित है।
उत्तर-
भारत में महिलाओं को पुरुषों से परदा करना पड़ता है, जबकि तिब्बत में ऐसी कोई प्रथा नहीं है। भारत में महिलाएँ अपरिचित व्यक्ति को घर में नहीं घुसने नहीं देतीं। उनके घर के अन्दर तक जाना तो और भी कठिन है। इसका कारण है कि वे असुरक्षित अनुभव करती हैं। तिब्बती महिलाएँ न तो परदा करती हैं और न ही किसी अपरिचित से भयभीत ही होती हैं, अपितु वे अपरिचितों पर सहज विश्वास करके उनका स्वागत करती हैं और मुसीबत में अपनी सुरक्षा स्वयं कर लेती हैं।
प्रश्न 3.
पठित पाठ के आधार पर नम्से का परिचय देते हुए उसके जीवन की विशेषताओं का उल्लेख कीजिए।
उत्तर-
नम्से एक बौद्ध भिक्षु था। वह तिब्बत में शेकर बिहार नामक जागीर का प्रमुख बौद्ध भिक्षु था। उस जागीर में उसका खूब मान-सम्मान था। वह अत्यन्त ही भला व्यक्ति था। अहंकार तो उसे छूता भी नहीं था। वह लेखक से अत्यन्त प्रेम एवं सम्मानपूर्वक मिला। यद्यपि उस समय लेखक भिखारी की वेशभूषा में था, किन्तु नम्से ने इस ओर ध्यान न देकर उसका हार्दिक स्वागत किया।
प्रश्न 4.
लेखक को भिखारी के वेश में तिब्बत की यात्रा क्यों करनी पड़ी ? [H.B.S.E. March, 2020]
उत्तर-
पाठ में बताया गया है कि तिब्बत के पहाड़ों में निर्जन स्थान अधिक है। वहाँ लूटपाट व हत्या का भय बना रहता है। वहाँ ज्यादातर हत्याएँ धन व रुपए-पैसे लूटने के लिए की जाती हैं। लेखक ने डाकुओं से बचने के लिए यह वेश धारण किया था। जब भी लेखक के सामने कोई भयानक दिखने वाला व्यक्ति आता तो वह कुची-कुची (दया-दया) ‘एक पैसा’ कहकर भीख माँगने लगता। अतः स्पष्ट है कि लेखक ने अपने जान-माल की सुरक्षा हेतु यह उपाय किया था।
प्रश्न 5.
लेखक सुमति को उसके यजमानों से मिलने को क्यों मना करता था ?
उत्तर-
सुमति का स्वभाव थोड़ा लालची था। वह यजमानों के पास जाकर हफ्ता-हफ्ता आने का नाम नहीं लेता था। इतने दिनों तक लेखक को उसकी प्रतीक्षा में एक ही स्थान पर ठहरना पड़ता था। इससे उसकी यात्रा में बाधा पड़ती थी। इसलिए लेखक सुमति को उसके यजमानों से मिलने से मना करता था।
प्रश्न 6.
पाठ में वर्णित ‘थोङ्ला के जंगल’ का उल्लेख सार रूप में कीजिए।
उत्तर-
डाँडा थोङ्ला का जंगल तिब्बत का खतरनाक स्थान माना जाता है। यह जंगल सोलह-सत्रह हजार फीट की ऊँचाई पर स्थित है। इन जंगलों के आस-पास कोई गाँव व बस्ती नहीं है। नदियों के मोड़ों व पहाड़ों के कारण यहाँ कोई आदमी दिखाई नहीं देता। ये जंगल डाकुओं के लिए सुरक्षित स्थल हैं। यहाँ सरकार पुलिस पर अधिक धन खर्च नहीं करती। इसलिए यहाँ आदमी की हत्या करना बहुत सरल है। डाकू पहले आदमी को मार डालते हैं फिर उसका माल लूटते हैं। यही कारण है कि लोग यहाँ अपनी सुरक्षा के लिए लाठी की अपेक्षा बंदूक व पिस्तौल लिए फिरते हैं।
बहुविकल्पीय प्रश्नोत्तर
प्रश्न 1.
‘ल्हासा की ओर’ नामक पाठ के लेखक का नाम क्या है ?
(A) राहुल सांकृत्यायन
(B) प्रेमचंद
(C) हजारीप्रसाद द्विवेदी
(D) श्यामाचरण दुबे
उत्तर-
(A) राहुल सांकृत्यायन
प्रश्न 2.
‘ल्हासा की ओर’ पाठ हिंदी साहित्य की किस विधा के अंतर्गत आता है ?
(A) कहानी
(B) यात्रा-वृत्तांत
(C) एकांकी
(D) निबंध
उत्तर-
(B) यात्रा-वृत्तांत
प्रश्न 3.
ल्हासा किस देश में स्थित है ?
(A) चीन
(B) बर्मा
(C) भारत
(D) तिब्बत
उत्तर-
(D) तिब्बत

प्रश्न 4.
राहुल सांकृत्यायन कहाँ के रहने वाले थे ?
(A) हरियाणा
(B) पंजाब
(C) मध्य प्रदेश
(D) उत्तर प्रदेश
उत्तर-
(D) उत्तर प्रदेश
प्रश्न 5.
लेखक ने अपना नाम परिवर्तन कब किया था ?
(A) तिब्बत जाने पर
(B) विवाह करने पर
(C) बौद्ध धर्म ग्रहण करने पर
(D) चीन जाने पर
उत्तर-
(C) बौद्ध धर्म ग्रहण करने पर
प्रश्न 6.
राहुल सांकृत्यायन ने बौद्ध धर्म कब ग्रहण किया था ?
(A) सन् 1925 में
(B) सन् 1930 में
(C) सन् 1935 में
(D) सन् 1940 में
उत्तर-
(B) सन् 1930 में
प्रश्न 7.
राहुल जी ने किस शास्त्र की रचना की है ?
(A) कामशास्त्र
(B) राजनीतिशास्त्र
(C) घुमक्कड़ी शास्त्र
(D) अर्थशास्त्र
उत्तर-
(C) घुमक्कड़ी शास्त्र
प्रश्न 8.
श्री राहुल सांकृत्यायन प्रथम बार तिब्बत किस रास्ते से गए थे ?
(A) नेपाल
(B) फरी-कलिङ्पोङ्
(C) बर्मा
(D) चीन
उत्तर-
(A) नेपाल
प्रश्न 9.
लेखक, ने तिब्बत के किस स्थान की यात्रा को खतरनाक बताया है ?
(A) थोङ्ला
(B) ल्हासा
(C) डाँडा
(D) लङ्कोर
उत्तर-
(C) डाँडा
प्रश्न 10.
तिब्बत में डाकुओं के लिए कौन-सा स्थान अच्छा माना गया है ?
(A) डाँडा
(B) ल्हासा
(C) लङ्कोर
(D) थोङ्ला
उत्तर-
(A) डाँडा
प्रश्न 11.
कुची-कुची का क्या अर्थ है?
(A) धीरे-धीरे
(B) कुछ-कुछ
(C) दया-दया
(D) परे-परे
उत्तर-
(C) दया-दया
प्रश्न 12.
डाँड़े की समुद्रतल से कितनी ऊँचाई है ?
(A) 15-16 हजार फीट
(B) 16-17 हजार फीट
(C) 17-18 हजार फीट
(D) 20-22 हजार फीट
उत्तर-
(C) 17-18 हजार फीट

प्रश्न 13.
रात को लेखक और उसका मित्र किस स्थान पर ठहरे थे ?
(A) लङ्कोर
(B) तिकी
(C) डाँड़े
(D) थोङ्ला
उत्तर-
(A) लङ्कोर
प्रश्न 14.
लेखक लङ्कोर के मार्ग में अपने साथियों से क्यों पिछड़ गया था ?
(A) आराम करने के कारण
(B) चाय पीने के कारण
(C) मार्ग भूल जाने के कारण
(D) घोड़े से गिर जाने के कारण
उत्तर-
(C) मार्ग भूल जाने के कारण
प्रश्न 15.
तिकी का मैदान कैसा था ?
(A) पहाड़ों से घिरा हुआ
(B) नदियों से घिरा हुआ
(C) बर्फ से ढका हुआ
(D) फसलों से भरा हुआ
उत्तर-
(A) पहाड़ों से घिरा हुआ
प्रश्न 16.
‘तिकी-समाधि-गिरि’ किसका नाम है ?
(A) मैदान का
(B) छोटी-सी पहाड़ी का
(C) मंदिर का
(D) गाँव का
उत्तर-
(B) छोटी-सी पहाड़ी का
प्रश्न 17.
राहुल सांकृत्यायन एवं उसका साथी तिभी से कितने बजे चले थे ?
(A) 8 बजे (प्रातः)
(B) 10-11 बजे
(C) 12 बजे
(D) दोपहर 2 बजे
उत्तर-
(B) 10-11 बजे
प्रश्न 18.
तिब्बत में जागीरों का बड़ा भाग किनके हाथों में है ?
(A) राजाओं के
(B) मठों के
(C) भिक्षुओं के
(D) किसानों के
उत्तर-
(B) मठों के
प्रश्न 19.
शेकर के मंदिर में रखी बुद्धवचन की हस्तलिखित पोथियों को क्या कहा जाता है ?
(A) कंजुर
(B) बुद्ध ग्रंथ
(C) हस्तलिखित बुद्ध ग्रंथ
(D) काव्य ग्रंथ
उत्तर-
(A) कंजुर
प्रश्न 20.
एक कंजुर का वजन अनुमानतः कितना-कितना बताया गया है ?
(A) 8-10 सेर
(B) 12-12 सेर
(C) 15-15 सेर
(D) 20-20 सेर
उत्तर-
(C) 15-15 सेर
प्रश्न 21.
सुमति कौन था ?
(A) लेखक का नौकर
(B) मंगोल भिक्षु
(C) लेखक का गुरु
(D) लेखक का संबंधी
उत्तर-
(B) मंगोल भिक्षु
प्रश्न 22.
मंगोल भिक्षु का नाम लोब्ज था। लोज़ का सामान्य अर्थ है-
(A) सुबुद्धि .
(B) प्रज्ञ
(C) सुमति
(D) सुविचार
उत्तर-
(C) सुमति

प्रश्न 23.
तिब्बत में किस धर्म के अनुयायी रहते हैं ?
(A) हिंदू धर्म
(B) सिक्ख धर्म
(C) बौद्ध धर्म
(D) जैन धर्म
उत्तर-
(C) बौद्ध धर्म

ल्हासा की ओर प्रमुख गद्यांशों की सप्रसंग व्याख्या/भाव ग्रहण
1. वह नेपाल से तिब्बत जाने का मुख्य रास्ता है। फरी-कलिङ्पोङ् का रास्ता जब नहीं खुला था, तो नेपाल ही नहीं हिंदुस्तान की भी चीजें इसी रास्ते तिब्बत जाया करती थीं। यह व्यापारिक ही नहीं सैनिक रास्ता भी था, इसलिए जगह-जगह फौजी चौकियाँ और किले बने हुए हैं, जिनमें कभी चीनी पलटन रहा करती थी। आजकल बहुत से फौजी मकान गिर चुके हैं। दुर्ग के किसी भाग में, जहाँ किसानों ने अपना बसेरा बना लिया है, वहाँ घर कुछ आबाद दिखाई पड़ते हैं। [पृष्ठ 25]
शब्दार्थ-फरी-कलिङपोङ् = तिब्बती सीमावर्ती स्थान का नाम। व्यापारिक = व्यापार से संबंधित। फौजी चौकियाँ = सेना की एक टुकड़ी के ठहरने का स्थान। पलटन = सेना। दुर्ग = किला। बसेरा = घर। आबाद = बसे हुए।
प्रसंग-प्रस्तुत गद्यांश हिन्दी की पाठ्यपुस्तक ‘क्षितिज’ भाग-1 में संकलित ‘ल्हासा की ओर’ शीर्षक यात्रावृत्त से लिया गया है। इसके लेखक श्री राहुल सांकृत्यायन हैं। इस पाठ में लेखक ने अपनी तिब्बत की राजधानी ल्हासा की यात्रा का वर्णन किया है। इन पंक्तियों में लेखक ने भारत की स्वतंत्रता से पूर्व के समय के तिब्बत जाने वाले मार्ग एवं वहाँ के लोगों की स्थितियों का वर्णन किया है।
व्याख्या/भाव ग्रहण-लेखक का कथन है कि जब उसने तिब्बत की यात्रा की थी, उस समय भारत का प्रत्येक यात्री तथा व्यापारिक वस्तुएँ भी नेपाल से होकर तिब्बत पहुँचती थीं। लेखक भी उसी प्रमुख रास्ते से तिब्बत गया था, क्योंकि उस समय फरी-कलिङपोङ् का रास्ता नहीं खुला था। नेपाल की ही नहीं, भारतवर्ष की वस्तुएँ भी इसी मार्ग से तिब्बत ले जाई जाती थीं। यह केवल व्यापार करने का ही रास्ता नहीं था, अपितु सैनिक रास्ता भी था। सेना भी इसी मार्ग से होकर जाती थी। इसलिए स्थान-स्थान पर सेना के ठहरने के लिए चौकियाँ (अस्थाई व्यवस्था) और किले (सेना के ठहरने के बड़े-बड़े भवन) बनाए हुए थे। इनमें चीनी सेनाएँ रहा करती थीं। आजकल (जब लेखक ने यात्रा की थी) बहुत-से फौजी मकान गिर चुके थे। दुर्ग के किसी-किसी भाग में जहाँ किसानों ने अपना घर बना लिया था वह भाग ही आबाद दिखाई पड़ता था अन्यथा शेष भाग गिर चुके थे। अतः स्पष्ट है कि लेखक ने तत्कालीन नेपाल से तिब्बत जाने के मार्ग का यथार्थ चित्र अंकित किया है।
विशेष-
- तत्कालीन तिब्बत जाने वाले मार्ग की दशा और उससे भी पूर्व उस मार्ग पर बनाई चीनी सैनिक व्यवस्था की ओर भी संकेत किया गया है।
- लेखक ने तथ्य एवं घटना को आधार बनाकर सुंदर एवं रोचक वर्णन किया है।
- भाषा सरल, सहज एवं व्यावहारिक है जिसमें तत्सम शब्दों के साथ-साथ उर्दू-फारसी शब्दों का भी सफल प्रयोग किया गया है।
उपर्युक्त गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्नोत्तर
प्रश्न-
(1) पहले तिब्बत जाने के लिए कौन-सा रास्ता प्रयोग में लाया जाता था ?
(2) इस मार्ग में स्थान-स्थान पर क्या बना हुआ है ? उनका क्या प्रयोग होता था ?
(3) बाद में भारत से तिब्बत जाने का कौन-सा मार्ग खुला था ?
(4) तिब्बत में भिखमंगों की कैसी स्थिति थी ?
उत्तर-
(1) आरंभ में भारत से तिब्बत जाने के लिए नेपाल के मार्ग से जाना पड़ता था। उस समय कोई अन्य मार्ग नहीं बना था।
(2) नेपाल से तिब्बत के मार्ग पर स्थान-स्थान पर. फौजी चौंकियाँ बनी हुई थीं। मार्ग में अनेक किले भी बने हुए थे। इनमें कभी चीन की सेनाएँ रहती थीं। अब इनमें से बहुत-सी चौकियाँ व दुर्ग गिर चुके थे।
(3) बाद में भारत से तिब्बत जाने के लिए ‘फरी-कलिङ्पोङ्’ नामक मार्ग बना दिया गया था। इसके बनने से तिब्बत जाने के लिए नेपाल नहीं जाना पड़ता था।
(4) तिब्बत में भिखमंगों की स्थिति अच्छी नहीं थी। लोग चोरी के डर के कारण उन्हें अपने घरों में घुसने नहीं देते थे।
2. वहाँ जाति-पाँति, छुआछूत का सवाल ही नहीं है और न औरतें परदा ही करती हैं। बहुत निम्न श्रेणी के भिखमंगों को लोग चोरी के डर से घर के भीतर नहीं आने देते; नहीं तो आप बिलकुल घर के भीतर चले जा सकते हैं। चाहे आप बिलकुल अपरिचित हों, तब भी घर की बहू या सासु को अपनी झोली में से चाय दे सकते हैं। वह आपके लिए उसे पका देगी। [पृष्ठ 25]
शब्दार्थ-छुआछूत = छोटे-बड़े के भेदभाव की भावना। सवाल = प्रश्न। निम्न श्रेणी = तुच्छ। भिखमंगों = भिखारी, भीख माँगने वाले। अपरिचित = अनजान।
प्रसंग-प्रस्तुत गद्यांश हिन्दी की पाठ्यपुस्तक ‘क्षितिज’ भाग-1 में संकलित ‘ल्हासा की ओर’ शीर्षक पाठ से अवतरित है। इस पाठ के रचयिता श्री राहुल सांकृत्यायन हैं। इसमें लेखक ने अपनी तिब्बत यात्रा का वर्णन किया है, साथ ही वहाँ के लोगों की चारित्रिक विशेषताओं का भी उल्लेख किया है।
व्याख्या/भाव ग्रहण-लेखक का कथन है कि तिब्बत में जातिगत भेदभाव नहीं किया जाता। विभिन्न जातियों के लोग आपस में मिलजुल कर रहते हैं। वहाँ छुआछूत की भावना भी नहीं है। वे सबको एक समान समझते हैं। वहाँ स्त्रियाँ भी परदा नहीं करतीं। कहने का तात्पर्य है कि स्त्रियाँ पुरुषों के समान स्वतंत्रतापूर्वक काम करती हैं। किन्तु वहाँ घटिया किस्म के भीख माँगने वालों को घर में घुसने नहीं दिया जाता क्योंकि उनके द्वारा चोरी करने का संदेह होता है। अन्यथा सामान्य व्यक्ति उनके घरों में आ-जा सकता है। चाहे आप उनसे अनजान भी हों तो भी आप उनके घरों में बेरोक-टोक जा सकते हैं। आप अनजान होने पर भी उनके घर की बहू या सास को अपनी झोली में से चाय निकालकर दे सकते हैं। वे आपको पकाकर दे देंगी। कहने का अभिप्राय है कि तिब्बत में स्त्रियाँ अधिक स्वतंत्र हैं। उन पर विश्वास किया जाता है।
विशेष-
- लेखक ने तिब्बती समाज की सामाजिक दशा और स्त्रियों के जीवन के विषय में बताया है।
- तिब्बत में भिखारियों को अच्छी दृष्टि से नहीं देखा जाता।
- भाषा सरल, सहज एवं भावानुकूल है।
उपर्युक्त गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्नोत्तर
प्रश्न-
(1) तिब्बत में जातिगत स्थिति कैसी है ?
(2) क्या तिब्बत में परदा प्रथा है ?
(3) तिब्बत में भिखारियों को घर में क्यों नहीं आने देते ? (4) आम लोगों के प्रति तिब्बत की औरतों का व्यवहार कैसा है ? उत्तर-(1) तिब्बत में जातिगत भेदभाव नहीं किया जाता। वहाँ जातिगत दृष्टि से सबको समान देखा जाता है। (2) तिब्बत में नारियाँ परदा नहीं करतीं। वे पुरुषों के समान काम करती हैं। (3) तिब्बत में निम्न स्तर के भिखारियों को घरों में चोरी के भय के कारण नहीं आने दिया जाता।
(4) आम लोगों के प्रति तिब्बती नारियों का व्यवहार सम्मानजनक होता है। आप सीधे उनके घरों में जा सकते हो। वे आपको चाय आदि भी बनाकर दे देंगी।
{3} नदियों के मोड़ और पहाड़ों के कोनों के कारण बहुत दूर तक आदमी को देखा नहीं जा सकता। डाकुओं के लिए यही सबसे अच्छी जगह है। तिब्बत में गाँव में आकर खून हो जाए, तब तो खूनी को सज़ा भी मिल सकती है, लेकिन इन निर्जन स्थानों में मरे हुए आदमियों के लिए कोई परवाह नहीं करता। [पृष्ठ 26]
शब्दार्थ-कोनों = किनारों। खून होना = मार देना। खूनी = मारने वाला। निर्जन = एकांत स्थान।
प्रसंग-प्रस्तुत गद्यावतरण हिन्दी की पाठ्यपुस्तक ‘क्षितिज’ भाग-1 में संकलित ‘ल्हासा की ओर’ शीर्षक पाठ से उद्धृत है। इसके लेखक श्री राहुल सांकृत्यायन हैं। इस गद्यांश में लेखक ने तिब्बत के निर्जन स्थानों पर डाकुओं के डर की ओर संकेत किया है।
व्याख्या/भाव ग्रहण-लेखक जब तिब्बत-यात्रा पर था तो उसके मार्ग में ‘डाँडा थोङ्ला’ एक ऐसा स्थान आया, जो बिल्कुल सुनसान था। सोलह-सत्रह हजार फुट की ऊँचाई होने के कारण वहाँ मार्ग के दोनों ओर कोई गाँव या थोड़ी-बहुत आबादी नहीं थी। यहाँ तक कि नदियों के मोड़ और पहाड़ों के कोनों के कारण वहाँ मीलों तक कोई आदमी दिखाई नहीं देता। यह उस यात्रा का सबसे खतरनाक स्थल था, क्योंकि डाकुओं के लिए डाका डालने के लिए यही सबसे अच्छा स्थान है। यहाँ डाकू अपनी मनमानी करते हैं। तिब्बत में यदि किसी गाँव में किसी का खून हो जाए तो खूनी को सजा होती है, किन्तु एकांत स्थान पर यदि किसी का खून हो
विरुद्ध किसी प्रमाण का न मिलना ही है।

विशेष-
- लेखक ने तिब्बत यात्रा के समय विशेषकर ‘डाँड़े थोङ्ला’ स्थान को पार करने में होने वाले खतरे का उल्लेख किया है।
- तिब्बत में कानून की डुलमुल स्थिति की ओर भी संकेत किया गया है।
- भाषा सरल, सहज एवं व्यावहारिक है।
उपर्युक्त गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्नोत्तर
प्रश्न-
(1) उक्त गद्यांश के पाठ एवं लेखक का नाम बताइए।
(2) तिब्बत की सड़कों पर बहुत दूर तक आदमी क्यों नहीं दिखाई देते थे ?
(3) डाकुओं के लिए कौन-सी जगह सबसे अच्छी थी ?
(4) कहाँ खून करने पर खूनी को सजा मिल सकती है ?
(5) निर्जन स्थानों से लेखक का क्या तात्पर्य है?
उत्तर-
(1) पाठ का नाम ल्हासा की ओर लेखक का नाम-राहुल सांकृत्यायन।
(2) तिब्बत एक पहाड़ी क्षेत्र है। यहाँ गाँव बहुत दूर-दूर बसे हुए हैं। नदियों के मोड़ और पहाड़ों के कोनों के कारण दूर-दूर तक आदमी दिखाई नहीं देता।
(3) डाकुओं के लिए नदियों के मोड़ व पहाड़ों के कोनों वाला स्थान ही अधिक अच्छे होते हैं क्योंकि ऐसे स्थानों पर दूर-दूर तक आदमी दिखाई नहीं देते और उन्हें लूटमार करने का अवसर मिल जाता है।
(4) तिब्बत में गाँव में किए गए खून के कारण सजा मिल सकती है। गाँव के बाहरी क्षेत्रों में किए गए खून के लिए कोई सजा नहीं दी जाती।
(5) निर्जन स्थानों से तात्पर्य है-एकांत व शांत स्थान जहाँ दूर-दूर तक कोई आदमी दिखाई नहीं देता।
4. सरकार खुफिया विभाग और पुलिस पर उतना खर्च नहीं करती और वहाँ गवाह भी तो कोई नहीं मिल सकता। डकैत पहिले आदमी को मार डालते हैं, उसके बाद देखते हैं कि कुछ पैसा है कि नहीं। हथियार का कानून न रहने के कारण यहाँ लाठी की तरह लोग पिस्तौल, बंदूक लिए फिरते हैं। डाकू यदि जान से न मारे तो खुद उसे अपने प्राणों का खतरा है। [पृष्ठ 26]
शब्दार्थ-खुफिया-विभाग = गुप्त-विभाग। गवाह = साक्षी। डकैत = डाका डालने वाले। हथियार का कानून = हथियार रखने का नियम।
प्रसंग-ये गद्य-पंक्तियाँ हिन्दी की पाठ्यपुस्तक ‘क्षितिज’ भाग-1 में संकलित श्री राहुल सांकृत्यायन की प्रमुख रचना ‘ल्हासा की ओर’ से उद्धृत हैं। इन पंक्तियों में उन्होंने तिब्बत की कानून-व्यवस्था का उल्लेख किया है।
व्याख्या/भाव ग्रहण-लेखक ने अपनी तिब्बत-यात्रा के समय वहाँ की सामाजिक व्यवस्था को ध्यानपूर्वक देखा तो उन्हें पता चला कि वहाँ की सरकार खुफ़िया-विभाग (गुप्त रूप से सरकार को सूचनाएँ देने वाला विभाग) और पुलिस पर बहुत कम व्यय करती है, इसीलिए वहाँ का गुप्त-विभाग अधिक सक्रिय एवं सतर्क नहीं है। किसी हत्यारे के विरुद्ध कोई कार्रवाई इसलिए भी नहीं की जा सकती क्योंकि वहाँ उसके विरुद्ध कोई गवाही भी नहीं देता। वहाँ डाकू भी अत्यंत निर्दयी एवं हृदयहीन होते हैं। वे पहले व्यक्ति को मारते हैं फिर देखते हैं कि उसके पास पैसा है भी या नहीं। ऐसा शायद वे इसलिए करते हैं कि यदि वे उसकी हत्या नहीं करते तो कहीं वह उन्हें मार न डालें या उनके विरुद्ध गवाही देकर उन्हें पुलिस के हवाले न कर दे। तिब्बत में हथियार रखने का कोई कानून नहीं है। यही कारण है कि वहाँ लोग लाठी की भाँति ही पिस्तौल व बंदूक लिए घूमते हैं। कहने का तात्पर्य है कि तिब्बत में हथियार रखने पर सरकार की ओर से कोई पाबंदी नहीं है। इसलिए कानून-व्यवस्था ठीक नहीं है। हर कोई हथियार रख सकता है। डाकू भी इसलिए डरते हैं कि कहीं कोई उन पर पहले वार करके उन्हें न मार डाले।
विशेष-
- तिब्बत की कानून-व्यवस्था का यथार्थ चित्रण किया गया है।
- तिब्बत में हथियार रखने का कोई नियम नहीं है, जिससे वहाँ की सरकार की कमजोरी का कोई भी नाजायज फायदा उठा सकता है।
उपर्युक्त गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्नोत्तर
प्रश्न-
(1) तिब्बत में लोगों की सुरक्षा का क्या प्रबंध है ?
(2) तिब्बत में लोग लाठी की बजाए पिस्तौल या बंदूक क्यों रखते हैं ?
(3) डकैत आदमी को लूटने से पहले क्यों मार देते हैं ?
(4) प्रस्तुत गद्यांश के आशय पर प्रकाश डालिए। .
उत्तर-
(1) तिब्बत में लोगों की सुरक्षा के लिए उचित प्रबंध नहीं है। यहाँ की सरकार खुफिया विभाग तथा पुलिस पर अधिक खर्च नहीं करती। यहाँ कोई किसी की गवाही भी नहीं देता।

(2) तिब्बत में हथियार रखने या न रखने का कोई कानून नहीं है। वहाँ कोई भी नागरिक अपनी इच्छानुसार हथियार रख . सकता है। यही कारण है कि यहाँ लोग अपनी सुरक्षा के लिए लाठी की अपेक्षा पिस्तौल या बंदूक रखते हैं।
(3) डकैत जानते हैं कि यहाँ लोग अपनी सुरक्षा के लिए पिस्तौल या बंदूक रखते हैं। इसलिए उन्हें अपनी जान का खतरा रहता है। यही कारण है कि वे आदमी को मारते पहले हैं और उसका धन बाद में लूटते हैं।
(4) प्रस्तुत गद्यांश में बताया है कि तिब्बत में कानून-व्यवस्था उचित नहीं है। यहाँ डाकुओं के लिए लूटमार करके या खून करके बच निकलना बहुत आसान है। निर्जन स्थान होने के कारण कोई गवाह भी नहीं मिलता। सरकार भी इस ओर कोई विशेष ध्यान नहीं देती।
5.तिब्बत की ज़मीन बहुत अधिक छोटे-बड़े जागीरदारों में बँटी है। इन जागीरों का बहुत ज्यादा हिस्सा मठों (विहारों) के हाथ में है। अपनी-अपनी जागीर में हरेक जागीरदार कुछ खेती खुद भी कराता है, जिसके लिए मज़दूर बेगार में मिल जाते हैं। खेती का इंतजाम देखने के लिए वहाँ कोई भिक्षु भेजा जाता है, जो जागीर के आदमियों के लिए राजा से कम नहीं होता। [पृष्ठ 28]
शब्दार्थ-जागीरदार = बहुत बड़े भू-भाग के स्वामी। हिस्सा = भाग। बेगार = बिना मजदूरी दिए काम करवाना। इंतजाम = प्रबंध। भिक्षु = बौद्ध धर्म का अनुयायी।
प्रसंग-प्रस्तुत गद्यांश हिन्दी की पाठ्यपुस्तक ‘क्षितिज’ भाग-1 में संकलित ‘ल्हासा की ओर’ यात्रावृत्त से लिया गया है। इस पाठ के लेखक श्री राहुल सांकृत्यायन हैं। इसमें उन्होंने अपनी तिब्बत यात्रा का वर्णन किया है। इन पंक्तियों में उन्होंने तिब्बत की भूमि-विभाजन अथवा जागीरदारी व्यवस्था का वर्णन किया है।
व्याख्या/भाव ग्रहण-लेखक ने अपनी तिब्बत यात्रा के समय देखा कि तिब्बत की जमीन बहुत-सी छोटी-बड़ी जागीरों में बँटी हुई है। इनके स्वामी जागीरदार हैं। तिब्बत की अधिकांश जागीरें वहाँ के बौद्ध धर्म के मठों व विहारों के अधीन हैं। कहने का तात्पर्य है कि वहाँ के सामाजिक एवं आर्थिक जीवन पर बौद्ध धर्म का अत्यधिक प्रभाव है। इन जागीरों के स्वामी अपनी-अपनी जागीरों में कुछ खेती स्वयं करवाते हैं क्योंकि वहाँ मजदूरों की कमी नहीं है। वहाँ बहुत कम मजदूरी पर मजदूर उपलब्ध हो जाते हैं। विहारों की जागीरों का प्रबंध करने के लिए किसी बौद्ध भिक्षु को भेजा जाता है। वहाँ उस बौद्ध भिक्षु की स्थिति किसी राजा से कम नहीं होती। जागीरों में काम करने वाले आदमी भिक्षु को राजा के समान आदर-सत्कार देते हैं।
विशेष-
- लेखक ने तिब्बत में प्रचलित जागीरदारी व्यवस्था का विस्तारपूर्वक उल्लेख किया है।
- जागीरदारी व्यवस्था में होने वाले मजदूरों के शोषण की ओर भी संकेत किया गया है।
- लेखक ने भिक्षु की स्थिति राजा के समान बताकर वहाँ की व्यवस्था पर व्यंग्य किया है।
उपर्युक्त गद्यांश पर आधारित अर्थग्रहण संबंधी प्रश्नोत्तर
प्रश्न-
(1) तिब्बत की जागीर व्यवस्था पर प्रकाश डालिए।
(2) तिब्बत में खेती का प्रबंध करने वाले भिक्षुओं की स्थिति कैसी है ?
(3) तिब्बत में खेती मजदूरों की दशा कैसी है ?
(4) जागीरों का बड़ा हिस्सा किसके हाथ में है ?
उत्तर-
(1) तिब्बत में सारी जमीन छोटे-बड़े जागीरदारों में विभाजित है। इन जागीरों में अधिक जागीरें बौद्ध मठों व विहारों के अधीन हैं। बौद्ध भिक्षु ही वहाँ जागीरों में खेती-बाड़ी का काम देखते हैं। इन भिक्षुओं को अत्यधिक महत्त्व दिया जाता है।
(2) खेती का प्रबंध करने वाले भिक्षुओं की स्थिति एक राजा जैसी होती है। वहाँ के लोग भिक्षु को राजा जैसा सम्मान देते हैं।
(3) तिब्बत में खेती मज़दूरों की दशा दयनीय है। वहाँ खेती मज़दूरों को बहुत कम मजदूरी दी जाती है।
(4) जागीरों का बड़ा हिस्सा विहारों व मठों के हाथ में है।
ल्हासा की ओर Summary in Hindi
ल्हासा की ओर लेखक-परिचय
प्रश्न-
श्री राहुल सांकृत्यायन का संक्षिप्त जीवन-परिचय देते हुए उनके साहित्य की प्रमुख विशेषताओं पर प्रकाश डालिए।
अथवा
श्री राहुल सांकृत्यायन का साहित्यिक परिचय दीजिए।
उत्तर-
1. जीवन-परिचय श्री राहुल सांकृत्यायन का नाम आधुनिक हिंदी साहित्यकारों में बड़े आदर के साथ लिया जाता है। वे घुमक्कड़ प्रवृत्ति वाले थे। उन्होंने अपनी इसी प्रवृत्ति के कारण हिंदी साहित्य को समृद्ध किया है। श्री राहुल सांकृत्यायन का जन्म सन् 1893 में गाँव पंदहा, जिला आज़मगढ़ (उत्तर प्रदेश) में हुआ। उनका असली नाम केदार पांडेय था। उन्होंने अपनी आरंभिक शिक्षा गाँव की पाठशाला में प्राप्त की। तत्पश्चात् काशी, आगरा और लाहौर में उच्च शिक्षा ग्रहण की। सन् 1930 में उन्होंने श्रीलंका जाकर बौद्ध धर्म ग्रहण कर लिया था। तब से ही ये केदार पांडेय से राहुल सांकृत्यायन बन गए थे। उन्होंने हिंदी के अतिरिक्त पालि, प्राकृत, अपभ्रंश, तिब्बती, चीनी, जापानी, रूसी, अंग्रेज़ी, संस्कृत, उर्दू, फारसी आदि अनेक भाषाओं का ज्ञान प्राप्त किया। इसीलिए उन्हें ‘महापंडित’ कहा जाता था। माँ भारती के इस सपूत की मृत्यु सन् 1963 में हुई थी। उन्होंने आजीवन साहित्य की रचना की।
2. प्रमुख रचनाएँ-श्री राहुल सांकृत्यायन ने एक सफल साहित्यकार की भाँति अनेक विधाओं पर अपनी लेखनी साधिकार चलाई। उन्होंने उपन्यास, कहानी, आत्मकथा, यात्रावृत्त, जीवनी, आलोचना, शोध आदि अनेक साहित्यिक विधाओं की रचना की है। इतना ही नहीं, उन्होंने अनेक ग्रंथों का हिंदी अनुवाद भी किया है। ‘मेरी जीवन यात्रा’ (छह भाग), ‘दर्शन-दिग्दर्शन’, ‘बाइसवीं सदी’, ‘वोल्गा से गंगा’, ‘भागो नहीं दुनिया को बदलो’, ‘दिमागी गुलामी’, ‘घुमक्कड़ शास्त्र’ आदि उनकी प्रमुख रचनाएँ हैं। साहित्य के अतिरिक्त दर्शन, राजनीति, धर्म, इतिहास, विज्ञान आदि विभिन्न विषयों पर भी उनकी लगभग 150 रचनाएँ उपलब्ध हैं। राहुल सांकृत्यायन ने हिंदी साहित्य की छुपी हुई सामग्री को ढूँढ़कर साहित्य का उद्धार कर अत्यंत महत्त्वपूर्ण कार्य किया है।
3. साहित्यिक विशेषताएँ-यात्रावृत्त लेखन-कार्य में राहुल सांकृत्यायन जी का महत्त्वपूर्ण योगदान रहा है। उन्होंने घुमक्कड़ी शास्त्र की रचना की। इसमें उन्होंने घुमक्कड़ी से होने वाले लाभों का सविस्तार वर्णन किया है। उन्होंने यात्रावृत्त पर प्रकाश डालते हुए मंजिल के स्थान पर यात्रा को ही घुमक्कड़ का उद्देश्य बताया है। कहने का भाव है कि मंजिल पर पहुंचने से पहले यात्रा करते समय जो अनुभव होते हैं, वे अत्यंत महत्त्वपूर्ण होते हैं। घुमक्कड़ी में मनोरंजन, ज्ञानवर्धन एवं अज्ञात स्थानों की जानकारी के साथ-साथ भाषा एवं संस्कृति का भी आदान-प्रदान होता है। घुमक्कड़ी से मनुष्य साहसी और संघर्षशील भी बनता है। राहुल जी ने विभिन्न स्थानों के भौगोलिक वर्णन के अतिरिक्त वहाँ के जन-जीवन का सुंदर एवं सजीव चित्रण किया है। इसे ही यदि राहुल जी के यात्रावृत्तों की महत्त्वपूर्ण विशेषता कहें तो कोई अतिशयोक्ति नहीं होगी।
4. भाषा-शैली-राहुल जी को विभिन्न भाषाओं का गहन ज्ञान था। हिंदी के प्रति उनका विशेष लगाव था। उन्होंने अपनी रचनाओं में शुद्ध साहित्यिक हिंदी का प्रयोग किया है, किन्तु यात्रावृत्तों में विभिन्न-विभिन्न स्थानों की बोलियों एवं भाषाओं के शब्दों का प्रयोग प्रसंगानुकूल किया है। इससे भाषा में व्यावहारिकता एवं रोचकता का समावेश हुआ है। लोक-प्रचलित मुहावरों का प्रयोग करके भाषा को सारगर्भित रूप भी प्रदान किया है। सुगठित वाक्य-रचना के कारण भाषा प्रभावशाली बन पड़ी है। गंभीर भावों व विचारों को सरलतम भाषा में व्यक्त करना श्री राहुल जी की भाषा-शैली की प्रमुख विशेषता है।

ल्हासा की ओर पाठ-सार/गद्य-परिचय
प्रश्न-
‘ल्हासा की ओर’ शीर्षक यात्रावृत्त का सार/गद्य-परिचय अपने शब्दों में लिखिए।
उत्तर-
‘ल्हासा की ओर’ श्री राहुल सांकृत्यायन की प्रथम तिब्बत यात्रा है जो उन्होंने 1929-30 में नेपाल के रास्ते से की थी। उस समय भारतीयों को तिब्बत यात्रा की अनुमति नहीं थी। इसलिए राहुल जी ने यह यात्रा भिखमंगे के छद्मवेश में की थी।
इसमें उन्होंने तिब्बत की राजधानी ‘ल्हासा’ की ओर जाने वाले दुर्गम रास्तों का वर्णन अत्यंत रोचकतापूर्ण किया है। जब राहुल जी ने यह यात्रा की थी, तब फरी-कलिङपोङ्ग का मार्ग नहीं खोला गया था। इसलिए भारत की वस्तुएँ नेपाल होकर ही तिब्बत जाती थीं। इसे सैनिक व व्यापारिक रास्ता भी कहा जाता था। मार्ग में स्थान-स्थान पर चीनी सेना की चौकियाँ और किले बने हुए थे जिनमें चीनी पलटन के सैनिक रहते थे। किन्तु आजकल वे दुर्ग गिर चुके हैं और उनमें किसान रहते हैं। मार्ग में अनेक कठिनाइयों का सामना करना पड़ता है। वहाँ जातिगत भेदभाव नहीं हैं और न ही स्त्रियाँ वहाँ परदा करती हैं। वे आपके लिए निःसंकोच खाना पका देंगी व चाय बना देंगी। वे यात्रियों की खूब सेवा करती हैं।
परित्यक्त चीनी किले से चाय पीने के पश्चात् जब लेखक आगे बढ़ा तो उन्हें राहदारी देनी पड़ी। उसी दिन वे थोङ्ला के पहले के अंतिम गाँव में पहुंच गए। वहाँ उनके सहायक सुमति के जान-पहचान के आदमी थे। भिखमंगे के वेश में होने पर भी उन्हें रहने के लिए अच्छी जगह मिली। लेखक पाँच वर्ष पश्चात् एक यात्री के रूप में इस स्थान से गुजरा था, किन्तु तब उसे किसी ने अच्छी जगह नहीं दी थी। यह वहाँ के लोगों की मनोवृत्ति पर निर्भर करता है।
लेखक को अब सबसे खतरनाक मार्ग डाँड़ा थोङ्ला पार करना था। तिब्बत में सबसे खतरनाक स्थान डाँड़े है। यहाँ दूर-दूर तक मार्ग के दोनों ओर कोई गाँव नहीं है। डाकुओं के लिए यह सबसे अच्छी जगह है। ऐसे स्थान पर हुए खून की वहाँ परवाह नहीं की जाती और न ही सरकार इस ओर कोई ध्यान देती है। हथियार का कानून न होने के कारण वहाँ लाठी की भाँति लोग पिस्तौल व बंदूक रखते हैं। इस मार्ग पर अनेक खून हो चुके थे, किन्तु लेखक को खून की कोई परवाह नहीं थी क्योंकि वह भिखमंगे के वेश में था। पहाड़ की ऊँची चढ़ाई और पीठ पर सामान लदा हुआ था। अगला पड़ाव भी 16-17 मील की दूरी पर था। लेखक के सहायक ने दो घोड़े लेने की सलाह दी।
अगले दिन वे घोड़ों पर सवार होकर चले और दोपहर तक डाँड़े से ऊपर जा पहुँचे। वहाँ हजारों मील तक पहाड़-ही-पहाड़ थे। भीटे की ओर दिखाई देने वाले पहाड़ तो बिल्कुल नंगे थे। डाँड़े के सबसे ऊँचे स्थान पर वहाँ के देवता का स्थान था, जो पत्थरों के ढेर, जानवरों के सींगों और रंग-बिरंगे कपड़ों की झाड़ियों से सजाया हुआ था। लेखक के साथ कुछ और घुड़सवार भी चल रहे थे। अब चढ़ाई कम थी, किन्तु उतराई अधिक थी। लेखक का घोड़ा बहुत सुस्त पड़ गया था। इसलिए लेखक अन्य सवारों से पिछड़ गया था। आगे चलकर दो मार्ग फूट रहे थे। लेखक गलत मार्ग पर चल पड़ा। एक डेढ़-मील चलकर पता चला कि वह गलत मार्ग पर जा रहा है। उसने लौटकर सही मार्ग पकड़ा। गाँव से मील भर की दूरी पर लेखक सुमति से सांय के चार-पाँच बजे मिला। वह उस पर लाल-पीला हो उठा। किन्तु लेखक ने घोड़े की धीमी गति का बहाना बताकर उसे शांत कर दिया। लङ्कोर में वे एक अच्छी जगह पर ठहरे थे। पहले उन्होंने चाय-सत्तू खाया और रात को गरमागरम थुक्पा मिला।
अंततः लेखक तिकी के विशाल मैदान में पहुँच गया जो पहाड़ों से घिरा टापू-सा लगता था। उसमें एक छोटी-सी पहाड़ी दिखाई देती थी। उसी पहाड़ी का नाम ‘तिश्री-समाधि-गिरि’ था। वहाँ सुमति के अनेक यजमान थे जिनके पास वह जाना चाहता था। किन्तु लेखक ने उसे जाने की आज्ञा नहीं दी। हाँ, इतना अवश्य कहा कि जिस गाँव में वे रुके थे, उसी गाँव के यजमानों में वह गंडे बाँट सकता है। सुमति ने यह बात स्वीकार कर ली। दूसरे दिन उन्हें कोई भरिया नहीं मिला। वे सुबह ही आगे चल दिए। तिब्बत में 10-11 बजे तक धूप बहुत तेज हो जाती है। वे दो बजे तक सूरज की ओर मुँह करके चलते रहे। ललाट धूप से जलता रहा। तिब्बत की जमीन बहुत-से छोटे-बड़े ज़मींदारों में बँटी हुई है। प्रत्येक ज़मींदार अपनी-अपनी जमीन पर खेती स्वयं कराते हैं, जिसके लिए मजदूर बेगार में मिल जाते हैं। खेती का प्रबंध देखने के लिए किसी भिक्षु को भेज दिया जाता है। वह किसी राजा से कम नहीं होता। सुमति के यजमान शेकर की खेती का मुखिया भिक्षु बहुत अच्छा व्यक्ति था। वह लेखक के भिखारी के वेश में होने पर भी बहुत प्रेम से मिला। वहाँ उन्हें एक मंदिर में ठहराया गया। इस मंदिर में कन्जुर (बुद्धवचन अनुवाद) की हस्तलिखित 103 पोथियाँ रखी हुई थीं। वे मोटे और अच्छे कागज पर लिखित थीं। एक-एक पोथी का बोझ 15-15 सेर से कम न था। लेखक उनमें रम गया तथा सुमति दूसरे दिन तक अपने यजमानों से मिलकर लौट आया। तिकी गाँव वहाँ से दूर नहीं था। उन्होंने अपना-अपना सामान पीठ पर लादा और अपने मार्ग पर चल दिए।
कठिन शब्दों के अर्थ
(पृष्ठ-25) : व्यापारिक = व्यापार से संबंधित। सैनिक = सेना के लिए। पलटन = सेना का भाग। दुर्ग = किला। बसेरा = रहने के लिए घर। आबाद = बसे हुए। परित्यक्त = छोड़ा हुआ। तकलीफें = कठिनाइयाँ। औरतें = नारियाँ । अपरिचित = अनजान।
(पृष्ठ-26) : राहदारी = जेनम् गाँव के पास पुल से नदी पार करने के लिए जोपोन (मजिस्ट्रेट) के हाथ की लिखी लमयिक् (राहदारी) जो लेखक ने अपने मंगोल दोस्त के माध्यम से प्राप्त की (पहचान के लिए दी गई चिट्ठी)। थोङ्ला = तिब्बती सीमा का एक स्थान। भद्र = सज्जन। छङ् = नशीला पदार्थ । दुरुस्त = स्वस्थ, सही। डाँडा = ऊँची जमीन। गाँव-गिराँव = गाँव या बस्ती। निर्जन = एकांत। डकैत = डाकू। पड़ाव = ठहरने का स्थान।
(पृष्ठ-27) : श्वेत = सफेद। शिखर = चोटियाँ। सर्वोच्च = सबसे ऊँचा। दोन्क्विक्स्तो = स्पेनिश उपन्यासकार सार्वेतेज (17 वीं शताब्दी) के उपन्यास ‘डॉन क्विक्ज़ोट’ का नायक, जो घोड़े पर चलता था। सुमति = लेखक को यात्रा के दौरान मिला मंगोल भिक्षु जिसका नाम लोब्जङ् शेख था। इसका अर्थ है-सुमति प्रज्ञ। अतः सुविधा के लिए लेखक ने उसे सुमति नाम से पुकारा है। इंतजार = प्रतीक्षा। सत्तू = भूने हुए अन्न (जौ, चना) का आटा। थुक्पा = सत्तू या चावल के साथ मूली, हड्डी और माँस के साथ।

(पृष्ठ-28-29) : तिकी = तिब्बत के महत्त्वपूर्ण स्थान का नाम। गडे = मंत्र पढ़कर गाँठ लगाए हुए धागे व वस्त्र। चिरी = फाड़ी हुई। भरिया = भारवाहक। ललाट = माथा। बेगार = बिना मजदूरी या कम मजदूरी पर। इंतजाम = व्यवस्था। पुस्तकों के भीतर = पुस्तकें पढ़ने में लीन।
![]()

![]()
![]()
![]()