HBSE 10th Class Social Science Important Questions Geography Chapter 7 राष्ट्रीय अर्थव्यवस्था की जीवन रेखाएँ
Haryana State Board HBSE 10th Class Social Science Important Questions Geography Chapter 7 राष्ट्रीय अर्थव्यवस्था की जीवन रेखाएँ Important Questions and Answers.
Haryana Board 10th Class Social Science Important Questions Geography Chapter 7 राष्ट्रीय अर्थव्यवस्था की जीवन रेखाएँ
राष्ट्रीय अर्थव्यवस्था की जीवन रेखाएँ Important Questions Geography HBSE 10th Class प्रश्न 1.
परिवहन क्यों आवश्यक है?
उत्तर-
परिवहन की आवश्यकता मुख्यतः दो कारणों से है-
- मनुष्यों के एक स्थान से दूसरे स्थान पर सुगमतापूर्वक यातायात हेतु।
- मालों को एक स्थान दो दूसरे स्थान पर सहजता से ले जाने हेतु।
HBSE 10th Class राष्ट्रीय अर्थव्यवस्था की जीवन रेखाएँ Important Questions Geography प्रश्न 2.
परिवहन के पाँच साधनों के नाम बताइए।
उत्तर-
- सड़क मार्ग,
- रेलमार्ग,
- पाइप लाइन,
- जलमार्ग,
- वायुमार्ग।
Chapter 7 राष्ट्रीय अर्थव्यवस्था की जीवन रेखाएँ Important Questions HBSE 10th Class प्रश्न 3.
जीवन के लिए संचार साधन क्यों आवश्यक हैं?
उत्तर-
संचार साधनों की आवश्यकता दूसरे लोगों के साथ संपर्क बनाये रखने के लिए आवश्यक है। आज संचार साधनों के विकसित रूप ने ही सुविधा प्रदान की है कि सात समुद्र पार स्थित अपने प्रियजनों से पलभर में संपर्क स्थापित किया जा सकता है। वस्तुत: वह संचार साधनों का ही श्रेय है कि आज सारा विश्व सिमटकर एक गाँव जैसा बन गया है।
![]()
प्रश्न 4.
संचार के चार साधनों के नाम बताइये।
उत्तर-
संचार के चार साधन हैं-
- डाक तार,
- टेलिफोन,
- रेडियो,
- समाचार-पत्र।
प्रश्न 5.
जनसंचार क्या है?
उत्तर-
जनसंचार संचार का वह माध्यम है जिसके द्वारा बहुत से लोगों तक एक साथ सूचना या जानकरी दी जा सके। जनसंचार के माध्यम से लोगों तक मनोरंजन भी पहुँचाया जा सकता है।
टाटा-तमीणबाटणटावा जनसंचार के दो स्वरूप हैं-1. प्रिटमीडिया, 2. इलैक्ट्रोनिक मीडिया।
प्रश्न 6.
भारत के दो अंतःस्थलीय जलमार्गों के नाम बताइए।
उत्तर-
भारत के दो अंत:स्थलीय जलमार्गों के नाम निम्नवत् हैं
- गंगानदी जलमार्ग-इलाहाबाद से हल्दिया के मध्य।
- ब्रह्मपुत्र नदी जलमार्ग-सदिया से धुबरी के मध्य। ‘
प्रश्न 7.
भारत के पूर्वी तट पर स्थित प्रमुख पत्तनों के नाम बताइए।
उत्तर-
- कोलकाता,
- हल्दिया.
- पारादीप,
- विशाखापट्टनम,
- इन्नौर,
- चेन्नई,
- तुतीकोरिन।
प्रश्न 8.
उन राज्यों के नाम बताइए, जिनमें मुरमूर्गों व न्यू मंगलौर, पारीदीप और तुतिकारिन पत्तन स्थित हैं?
उत्तर-
पत्तन — राज्य
1. मूरमूगाँव — गोवा
2. न्यू मंगलौर — कर्नाटक
3. पारादीप — उड़ीसा
4. तूतीकोरिन — तमिलनाडु।
प्रश्न 9.
अनुकूल व्यापार संतुलन का अर्थ समझाइये। भारत के विदेशी व्यापार का संतुलन कैसा है?
उत्तर-
अनुकूल व्यापार संतुलन का अर्थ विदेश व्यापार की उस स्थिति से है जहाँ आयात कम और निर्यात अधिक हो। वर्तमान में भारत में आयात की अपेक्षा निर्यात कम है अत: वर्तमान समय में भारत का विदेशी व्यापार संतुलन प्रतिकूल अवस्था में है।
प्रश्न 10.
सड़के किस प्रकार के परिवहन के लिए उत्तम हैं,
उत्तर-
सड़कें छोटी और मध्यम दूरी की यात्रा और माल परिवहन के लिए बहुत उत्तम साधन हैं।
प्रश्न 11.
चार महानगरों को जोड़ने वाले एक्सप्रेस महामार्ग का क्या नाम रखा गया है।
उत्तर-
स्वर्णिम चतुष्कोण।
प्रश्न 12.
पूर्व-पश्चिम गलियारा पोरबंदर से किस नगर को जोड़ेगा?
उत्तर-
पूर्व-पश्चिम गलियारा पोरबंदर से सिलचर को जोड़गा।
प्रश्न 13.
भारतीय रेलवे का एशिया में कौन-सा स्थान
उत्तर-
भारतीय रेलवे का एशिया में दूसरा स्थान है।
प्रश्न 14.
भारत में सार्वजनिक क्षेत्र का सबसे बड़ा उपक्रम कौन-सा है?
उत्तर-
भारत में सार्वजनिक क्षेत्र का सबसे बड़ा उपक्रम भारतीय रेल है।
प्रश्न 15.
भारत में कितने रेलवे स्टेशन हैं?
उत्तर-
भारत में इस समय 7031 रेलवे स्टेशन हैं।
प्रश्न 16.
भारत में रेलमार्गों को कितना भाग विद्युतीकृत हो चुका है?
उत्तर-
भारत में रेलमार्गो की लगभग 23% भाग विद्युतीकृत किया जा चुका है।
प्रश्न 17.
छोटी लाइनों को बड़ी लाइनों में बदले जाने के पीछे क्या कारण है?
उत्तर-
छोटी लाइनों को बड़ी लाइनों में बदलने से रेलवे की पटरियों के बीच एक जैसी दूरी हो जायेगी जिससे परिवहन क्षमता तो बढ़ेगी ही, साथ ही गति भी बढ़ेगी।
प्रश्न 18.
भारत में इस समय कितने राष्ट्रीय जलमार्ग हैं?
उत्तर-
पाँच। प्रश्न-उद्योग मंडल नहर किस राज्य में है? उत्तर-उद्योग मंडल नहर केरल राज्य में हैं।
![]()
प्रश्न 19.
वायु परिवहन का राष्ट्रीयकरण कब किया गया था?
उत्तर-
वायु परिवहन का राष्ट्रीयकरण सन् 1953 में किया गया था।
प्रश्न 20.
मुंबई को भारत का द्वारा क्यों कहा जाता है?
उत्तर-
वायु परिवहन की दृष्टि से मुंबई भारत से सबसे बड़ा पत्तन है। इसी कारण से इसे भारत के द्वारा की संज्ञा की गई है।
प्रश्न 21.
भारतीय पत्तनों के माध्यम से आयात और निर्यात में से कौन-सा अधिक होता है?
उत्तर-
भारतीय पत्तनों से आयात अधिक होता है और निर्यात कम।
प्रश्न 22.
आकाशवाणी के पास इस समय कितने रेडियों स्टेशन और ट्रांसमीटर्स है?
उत्तर-
आकाशवाणी के पास इस समय 200 रेडियो स्टेशन और 327 ट्रांसमीटर्स हैं।
प्रश्न 23.
समाचर-पत्र किस प्रकार की डाक सेवा के अंतर्गत शामिल किये जाते हैं?
उत्तर-
समाचार-पत्र दूसरे दर्जे की डाक सेवा के अंतर्गत शामिल किये जाते हैं।
प्रश्न 24.
डाक को जल्दी पहुँचने के लिए कौन-कौन से नए चैनल प्रारंभ किये जाते हैं?
उत्तर-
डाक व्यवस्था को तीव्रगति देने के लिए निम्नलिखित छः चैनल आरंभ किए गये हैं-
- राजधानी चैनल,
- मैट्रो चैनल,
- ग्रीन चैनल,
- व्यापार चैनल,
- भारी डाक चैनल,
- पत्र-पत्रिका चैनल।
प्रश्न 25.
भारत में सबसे अधिक किस वस्तु का आयात किया जाता है?
उत्तर-
भारत में सबसे अधिक पेट्रोलियम का आयात होता
प्रश्न 26.
भारत में प्रतिवर्ष लगभग कितने विदेशी पर्यटक आते हैं?
उत्तर-
भारत में प्रतिवर्ष 26 लाख विदेशी पर्यटक आते है।
प्रश्न 27.
भारत में सबसे अधिक दैनिक समाचार-पत्र किस भाषा में प्रकाशित होते हैं?
उत्तर-
हिंदी में।
प्रश्न 28.
वर्ष 2005 तक भारत की निर्यात वृद्धि वाली वस्तुओं की सूची बनाइए।
उत्तर-
पिछले कुछ वर्षों से वर्ष 2005-2004 तक, निर्यात वृद्धि वाली, वस्तुएँ थीं कृषि वर्गों से संबंधित उत्पाद (वृद्धि 2.53),खनिज व अयस्क (9.21%), रत्न व जवाहरात (26.75%), रसायन व संबंधित उत्पाद (24.45%) तथा पेट्रोलियम उत्पाद (कोयला सहित) (86.12%) आदि।
प्रश्न 29.
भारत में आयातित वस्तुओं की एक सूची बनाइए।
उत्तर-
भारत में आयातित वस्तुओं में पेट्रोलियम तथापेट्रोलियम उत्पाद (वृद्धि 28.6%), मोती व बहुमूल्य रत्न (9.4%), कोयला, कोक तथा कोयले का गोला (briquettes) (2.7%), मशीनरी (12.56%) आदि शामिल थे। एक समूह के रूप में भारी वस्तुओं के आयात में 28.2% प्रतिशत (कुल आयात का) वृद्धि हुई है। इस समूह में उर्वरक (3.4%), खाद्यान्न (14. 3%), वनस्पति तेल (17.4%) व न्यूज प्रिंट (40.3%) छपाई मशीनें भी शामिल हैं। अंतर्राष्ट्रीय व्यापार में पिछले 15 वर्षों में भारी बदलाव आया है। वस्तुओं के आदान-प्रदान की अपेक्षा सूचनाओं, ज्ञान तथा प्रौद्योगिकी का आदान-प्रदान बढ़ा है।
प्रश्न 30.
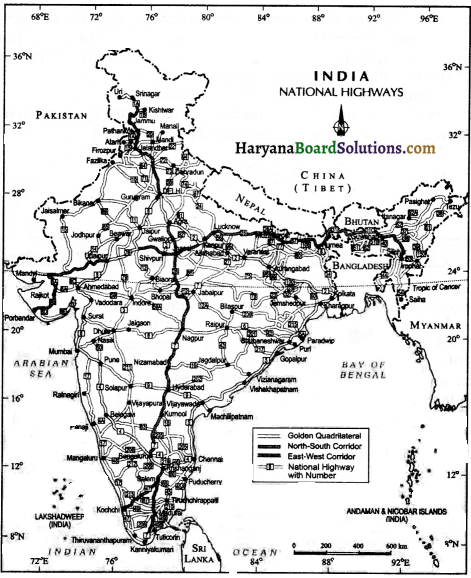
राष्ट्रीय महामार्ग क्या हैं?
उत्तर-
राष्ट्रीय महामार्ग का तात्पर्य उन सड़को से जो राष्ट्रीय महत्त्व की है। ये महामार्ग एक राज्य को दूसरे राज्य से जोड़ते हैं। इन राष्ट्रीय महामार्गों का निर्माण कार्य तथा रखरखाव केंद्र सरकार द्वारा करवाया जाता है। वर्तमान समय में भारत में राष्ट्रीय महामार्गों की कुल लंबाई लगभग 52,000 किमी. है। परंतु भारत की कुल सड़कों की लंबाई में इनका हिस्सा केवल 2% ही है। देश में 1991-2007 के मध्य लगभग 14,856 किमी. लंबा राष्ट्रीय महामार्ग बनाये जाने का प्रस्ताव है। ये राष्ट्रीय महामार्ग 4-6 लेन वाले होंगे। इनके निर्माण में आने वाले विशाल खर्च को संतुलित करने हेतु सरकार ने “बनाओ, चलाओं, और सौंपों। की नीति निर्धारित की है।
![]()
प्रश्न 31.
पेट्रोलियम और प्राकृतिक गैस के परिवहन में पाइपलाइनों के लाभ बताइए।
उत्तर-
पहले समय में पाइपलाइनों का उपयोग नगरों तथा उद्योगों तक पानी पहुंचाने में ही होता था। परंतु आज इन पाइप लाइनों के माध्यम से कच्चा तेल और प्राकृतिक गैस को उत्पादन क्षेत्रों से परिष्करण शालाओं तक पहुंचाया जाता है। इससे सबसे बड़ा लाभ यह है कि इस प्रकार के ताप केंद्रों को बहुत थोड़े समय में ही मांग क्षेत्रों के निकट स्थापित किया जा सकता है। वर्तमान में देश में देश में तीन पाइपलाइनों के परिवहन जाल फैले हुए हैं। इनके प्रमुख लाभ निम्नवत हैं
- पाइप लाइन के रखरखाव में अत्यधिक खर्च नहीं आता।
- भूमिगत पाइपलाइन से प्रदुषण भी नहीं फैलता। 3. यह साधन सुविधाजनक होने के साथ-साथ सस्ता भी
प्रश्न 32.
एक्सप्रेस राष्ट्रीय महामार्ग किसे कहते हैं?
उत्तर-
एक्सप्रेस राष्ट्रीय महामार्ग का तात्पर्य उन मार्गों से है जिनका निर्माण देश में तीव्रगमी परिवहन की आवश्यकता की पूर्ति के लिए किया जा रहा है। 1999-2007 के मध्य इस प्रकार के 14,846 किमी. लंबे महामार्ग निर्माण की योजना है। इसमें आने वाले खर्च की भरपाई करने हेतु सरकार ने “बनाओं, चलाओ , और सौंपो” की नीति निर्धारित की है। एक्सप्रेस राष्ट्रीय महामार्गों का 4-6 लेन वाला होना निर्धारित है।
इस एक्सप्रेस राष्ट्रीय महामार्गों के नाम निम्नवत हैं-
- स्वर्णिम चतुष्कोण-यह चारों महानगरों को जोड़ने वाला महामार्ग है। इसकी प्रस्तावित लंबाई 5846 किमी. है।?
- उत्तर-दक्षिण तथा पूर्व-पश्चिम गलियारे-ये महामार्ग जहाँ एक ओर श्रीनगर को कन्याकुमारी से जोड़ेगें वही दूसरी ओर पोरबंदर को सिलचर से जोडेंगे। इनकी कुल प्रस्तावित लंबाई 7300 किमी. है।
- स्वर्णिम चतुष्कोण तथा गलियारों को 10 प्रमुख पत्तनों से जोड़ने वाले महामार्ग-इन महामार्गों की प्रस्तावित लंबाई 363 किमी. है। ये मार्ग कांडला, न्हावशेवा, मूरमूगाँव, तूतीकोरिन, चेन्नई, विशाखापट्टनम, पारादीप आदि पत्तनों को जोडेंगे।
प्रश्न 33.
स्वर्णिम चतुष्कोण एक्सप्रेस महामार्ग से जोड़ने वाले नगरों के नाम बताइए।
उत्तर-
स्वर्णिम चतुष्कोण एक्सप्रेस महामार्ग से जोडे जाने वाले नगरों के नाम हैं
- दिल्ली,
- मुंबई,
- कोलकाता,
- चेन्नई।
प्रश्न 34.
अंतर स्पष्ट कीजिए।
(क) व्यक्तिगत संचार साधन और जनसंचार के साधन
उत्तर-
व्यक्तिगत संचार साधन
- इसका तात्पर्य संचार के उन साधनों से है जिनका प्रयोग व्यक्तिगत तौर पर किया जाता है।
- इनके माध्यम से एक साथ सामान्यतः एक ही व्यक्ति से संपर्क किया जा सकता है।
- इसमें पत्र, टेलिफोन इंटरनेट, ई-मेल आदि सम्मिलित हैं
जनसंचार के साधन ।
- इनका प्रयोग मुख्यतः सार्वजनिक तौर पर किया जाता है।
- इनके माध्यम से एक साथ एक से अधिक व्यक्तियों से संपर्क किया जा सकता है।
- इसमें समाचार-पत्र, रेडियो, टी.वी., तथा चलचित्र आदि सम्मिलित है।
(ख) परिवहन और संचार
उत्तर-
परिवहन
- ये वे साधन है जिनके माध्यम से एक स्थान से दूसरे स्थान पर आवागमन कर सकते है।
- इनके माध्यम से वस्तुओं को भिन्न-भिन्न स्थानों पर ले जाया जा सकता है।
- परिवहन साधन मुख्यतः तीन वर्गों में विभक्त हैं-1. जल, 2. स्थल, 3. वायु परिवहन।
संचार:
- इनके माध्यम से व्यक्ति एक दूसरे के साथ संपर्क स्थापित कर सकते हैं।
- इनके माध्यम से विचारों का आदान-प्रदान हो सकता
- संचार माध्यम मुख्यत5 दो भागों में विभक्त हैं- 1. व्यक्ति गत 2. जनसंचार।
प्रश्न 35.
भारतीय रेलों के सामने बढ़ते हुए दबावों को आप कैसे कम करेंगे।
अथवा
भारतीय रेल के बढ़ते दबावों को कम करने के कुछ उपाय सुझाइए।
उत्तर-
भारतीय रेल के बढ़ते दबावों को कम करने के लिए निम्नलिखित उपाय अपनाये जा सकते हैं
- अधिक-से अधिक रेलमार्गों का विद्युतीकरण कर दिया जाए ताकि परिवहन में और भी अधिक शीघ्रता आ सके।
- रेल दुर्घटनाओं को रोकने के पुख्ता बंदोबस्त किए जायें।
- रेल दुर्घटनाओं के लिए जिम्मेदार लोगों को कठिन-से-कठिन और कठोरतम सजा दी जाये।
- रेलवे के साथ-साथ भारी मालों की ढुलाई के लिए अन्य परिवहन साधनों का भी प्रयोग किया जाये।
- प्राकृतिक गैस तथा पेट्रोलियम पदार्थो की ढुलाई के लिए पाइप लाइनों का प्रयोग अधिकाधिक किया जाये।
- थोड़ी दूरी के लिए बस ट्रक सेवाओं का प्रयोग अधि क किया जाये।
प्रश्न 36.
क्या आप इस कथन से सहमत हैं कि यदि सीमा सड़क संगठन सीमावर्ती क्षेत्रों में सड़क बनाने में सफल नहीं होता तो देश की सुरक्षा के लिए खतरा उत्पन्न हो सकता था?
उत्तर-
भारत के अधिकांश उत्तरी राज्य सीमा पर विदेशी के साथ जुड़े हुए हैं। ऐसे में इन सीमावर्ती इलाकों की सुरक्षा
एक नाजुक विषय है क्योंकि एक ओर तो यहाँ से शत्रु देशों से आक्रमण का भय बना रहता है दूसरी और घुसपैठियों भी इन्हीं मार्गों से आते हैं। इस संवेदनशील को देखते हुए ही सीमा क्षेत्रों में पुरानी सड़कों की देखभाल और नई सड़कों को बनाने के उद्देश्य से केंद्र सरकार ने सीमा सड़क संगठन की स्थापना की। इस संगठन ने सफलता पूर्वक सीमाक्षेत्र में सड़कों का विकास किया। इससे जहाँ देश की सुरक्षा के पुख्ता बंदोबस्त किये जा सके है। वहीं दुर्गम इलाकों पर तैनात सैनिकों तक रक्षा उपकरण तथा आवश्यक साजो-सामान सहजता से पहुँचाया जाना संभव हो पाया है। इससे देश को स्थायी सुरक्षा बंदोबस्त प्राप्त हो सका है। अत: यह स्पष्ट है कि सीमा सड़क संगठन द्वारा सीमावर्ती क्षेत्रों में सड़क बनाने में सफलता न मिलने पर देश की सुरक्षा के लिए खतरा उत्पन्न हो सकता था।
![]()
प्रश्न 37.
निम्नलिखित पर संक्षिप्त टिप्पणी करें।
अंतर्राष्ट्रीय महामार्ग।
उत्तर-
अंतर्राष्ट्रीय महामार्ग-ये वे महामार्ग हैं जो देश को दूसरे देश के साथ जोड़ते हैं जैसे-ये महामार्ग भिन्न-भिन्न देशों से होकर गुजरते हैं। इन महामार्गों की देखरेख तथा सुरक्षा का दायित्व उस देश पर होता है। जिससे होकर ये मार्ग गुजरते
प्रश्न 38.
हुगली नदी को नाव्य बनाए रखने के लिए कौन-कौन से प्रयास किए गये हैं?
उत्तर-
हुगली नदी को नाव्य बनाए रखने के लिए निम्नलिखित प्रयास किये गये हैं
- फरक्का बांध बनाकर पानी को स्तर को ऊँचा किया गया। जिससे नावों के चलने में आसानी हों
- फरक्का बांध की भांति और अधिक बांध बनाकर इसे इलाबाद तक नाव्य बनाये जाने की योजना बनाई जा रही है।
प्रश्न 39.
सघन व सक्षम परिवहन का जाल तथा संचार के साधन आज विश्व, राष्ट्र व स्थानीय व्यापार हेतु पूर्व-अपेक्षित है। समीक्षा कीजिए।
उत्तर-
- आज भारत अपने विशाल आकार, विविधताओं भाषाई तथा सामाजिक व सांस्कृतिक बहुलताओं के बावजूद संसार के सभी क्षेत्रों से सुचारू रूप से जुड़ा हुआ है।
- रेल, वायु, एवं जल परिवहन, समाचार-पत्र, रेडियो, दूरदर्शन सिनेमा तथा इंटरनेट आदि इसके सामाजिक-आर्थिक विकास में अनेक प्रकार से सहायक है।
- स्थानिक से अंतर्राष्ट्रीय स्तरीय व्यापार ने अर्थव्यवस्था को जीवन शक्ति दी है। इसने हमारे जीवन को समृद्ध किया है तथा आरामदायक जीवन के लिए सुविधाओं व साधनों में बढ़ोतरी की है।
- आधुनिक संचार तथा परिवहन के साधन हमारे देश है और इसकी आधुनिक अर्थव्यवस्था को संचालित करते हैं। अतः यह स्पष्ट है कि सघन व सक्षम परिवहन का जाल तथा संचार के साधन आज विश्व, राष्ट्र व स्थानीय व्यापार हेतु पूर्व-अपेक्षित हैं।
प्रश्न 40.
परिवहन के विभिन्न साधनों को एक रेखाचित्र के माध्यम से दर्शाइए।
उत्तर-
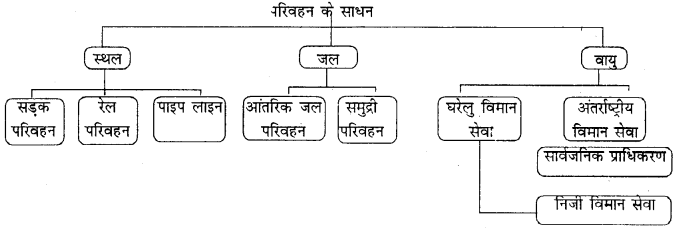
प्रश्न 41.
भारत में सड़क परिवहन को किन समस्याओं से जूझना पड़ रहा है?
उत्तर-
- भारत में सड़क परिहवन अनेक समस्याओं से जूझ रहा है। यातायात व यात्रियों की संख्या को देखते हुए सड़कों. को जाल अपर्याप्त है।
- लगभग आधी सड़के कच्ची है तथा वर्षा ऋतु को दौरान इनका उपयोग सीमित हो जाता है।
- राष्ट्रीय राजमार्ग भी अपर्याप्त है।
- इसके साथ ही शहरों में भी सड़के अत्यंत तंग तथा भीड़ भरी है तथा इन पर बने पुल व पुलिया पुराने तथा तंग है।
प्रश्न 42.
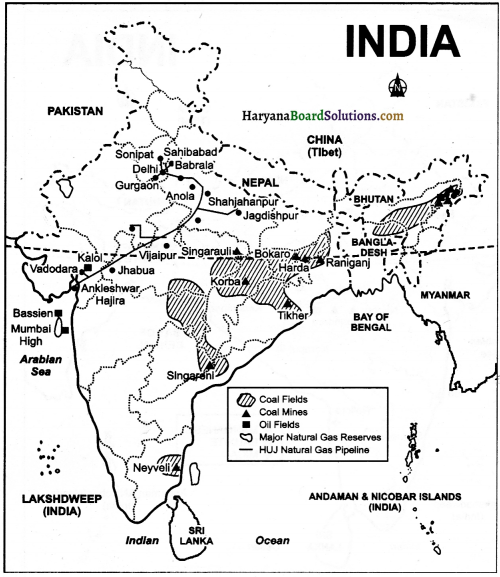
देश में फैले पाइपलाइन परिवहन के जालों की व्याख्या करें।
उत्तर-
देश में पाइपलाइन परिवहन के तीन प्रमुख जाल हैं
- ऊपरी असम के तेल क्षेत्रों से गुवाहाटी, बरौनी, इलाहाबाद, के रास्ते कानपुर (उत्तर प्रदेश) तक। इसकी एक शाखा बरौनी से राजबंध होकर हल्दिया तक है; दूसरी राजबंध से मौरी ग्राम तक तथा गुवाहाटी से सिलिगुडी तक है।
- गुजरात में सलाया से वीरमगाव, मथुरा, दिल्ली व सोनीपत के रास्ते पंजाब में जालंधर तक। इसकी अन्य शाखा वडोदरा के निकट कोयली को चक्शु व अन्य स्थानों से जोड़ती है।
- गैस पाइपलाइन गुजरात में हजीरा को उत्तर प्रदेश में जगदीशपुर से मिलाती है। यह मध्यप्रदेश के विजयपुर के रास्ते होकर जाती है। इसकी शाखाएं राजस्थान में कोटा, तथा उत्तरप्रदेश के शाहजहाँपुर, बबराला, व अन्य स्थानों पर हैं।
प्रश्न 43.
भारत सरकार द्वारा घोषित राष्ट्रीय जलमार्गों की जानकरी दीजिए।
उत्तर-
निम्न जलमार्गों को भारत सरकार द्वारा राष्ट्रीय जलमार्ग घोषित किया गया है
- हल्दिया तथा इलाहाबाद के मध्य गंगा जलमार्ग जो 1620 किमी. लंबा है- नौगम्य जलमार्ग संख्या-1।
- सदिया व धुबरी के मध्य 891 किमी. लंबा ब्रह्मपुत्र नदी जलमार्ग-नौगम्य जलमार्ग संख्या-21
- केरल में पश्चिम-तटीय नहर (कोट्टमपुरम से कोम्मान तक, उद्योगमंडल तथा चंपक्कारा नहरें-205 किमी.) नौगम्य जलमार्ग संख्या-3 ।
प्रश्न 44.
आजकल रेल परिवहन की अपेक्षा सड़क परिवहन महत्त्व क्यों बढ़ रहा है? ।
उत्तर-
भारत विश्व के सर्वाधिक सड़क जाल वाले देशों में से एक हैं यह सड़क जाल लगभग 23 लाख किमी. है। भारत में सड़क परिवहन, रेल परिहवन से पहले प्रारंभ हुआ। निर्माण तथा व्यवस्था में सड़क परिवहन, रेल परिवहन की अपेक्षा अधिक सुविधाजनक है। रेल परिवहन की अपेक्षा सड़क परिवहन की बढ़ती महता निम्न कारणों से है-
- रेलवे लाइन की अपेक्षा सड़कों की निर्माण लागत बहुत कम है।
- अधिक ढाल प्रवणता तथा पहाड़ी क्षेत्रों में भी सड़कें निर्मित की जा सकती है।
- अपेक्षाकृत ऊबड़-खाबड व विच्छिन्न भू-भागों पर सड़कें बनाई जा सकती है।
- अपेक्षाकृत कम व्यक्तियों कम दूरी व कम वस्तुओं के परिवहन में सड़क मितव्ययी है।
- यह घर-घर सेवाएं उपलब्ध करवाता है तथा सामान चढ़ाने व उतारने की लागत भी अपेक्षाकृत कम है।
- सड़क परिवहन अन्य परिवहन साधनों के उपयोग में एक कड़ी के रूप में भी कार्य करता है, जैसे सड़कें, रेलवे स्टेशन, वायु व समुद्री पत्तनों को जोड़ती है।
प्रश्न 45.
भारतीय रेलों के आधुनिकीकरण हेतु आप क्या सुझाव देंगे?
अथवा
भारतीय रेल द्वारा उपलब्ध कारायी जा रही सुविध ाओं के बारे में आप क्या जानते हैं? आप इन सुविधाओं के विस्तार हेतु क्या सुझाव देंगे। .
उत्तर-
भारतीय रेल देश में सबसे बड़ा सार्वजनिक उपक्रम है। यह एशिया का दूसरा सबसे बड़ा रेल तंत्र है। भारतीय रेल के आधुनिकीकरण हेतु तथा यात्रियों को अधिकाधिक सुविधा उलब्ध कराने हेतु समय-समय पर अनेकानेक कदम उठाये जाते रहे हैं। इनका बिंदुवत उल्लेख निम्न प्रकार से किया जा सकता है-
- रेलमार्गों को अधिक-से-अधिक विद्युतीकरण किया जा रहा है। ताकि विद्युत इंजनों का अधिक प्रयोग हो सके, जिससे प्रदुषण की समस्या का अंत तो होगा ही साथ; परिवहन अधिक सुविधाजनक तथा तीव्रगामी हो सकेगां विद्युतीकरण की दिशा में और भी त्वरित प्रगति की जाय।
- रेल पटरियों की संख्या में प्रचुर इजाफा किया गया है। इससे अधिकाधिक रेलों को एक समय पर चला पाना संभव हो रहा है। फिर भी यात्रियों की भीड़ को देखते हुए मार्गों के और भी विस्तार की आवश्यकता है।
- सभी रेल लाइनों को शीघ्रतिशीघ्र बड़ी लाइन में बदल दिया जाये।
- जिन गाड़ियों में यात्रियों की संख्या कम होती है उनमें सवारी डिब्बों की संख्या कम की जाये और उन गाड़ियों में डिब्बों की संख्या बढ़ाई जो जिनमें यात्रियों की संख्या अधिक होती है।
- रेलवे में परोसे जाने वाले भोजन तथा पीने के पानी की गुणवता पर पुरा ध्यानि दिया जाये।
- रेलवे द्वारा कुलियों का शुल्क निर्धारित किया जाये।
प्रश्न 46.
‘भारतीय पर्यटन-ए व्यापार के रूप में’ विषय पर एक निबंध लिखिए।
उत्तर-
पिछले तीन दशकों में भारत में पर्यटन उद्योग में महत्त्वपूर्ण वृद्धि हुई है। वर्ष 2003 की अपेक्षा 2004 के दौरान देश में विदेशी पर्यटकों के आगमन में 23.5% वृद्धि दर्ज की गई जिसे 21,828 करोड़ विदेशी मुद्रा प्राप्त हुई। । प्रत्येक वर्ष, भारत में 26 लाख से अधिक विदेशी पर्यटक आते हैं। 150 लाख से अधिक व्यक्ति पर्यटन उद्योग में प्रत्यक्ष रूप से संलगन हैं। पर्यटन राष्ट्रीय एकता को प्रोत्साहित करता है। तथा स्थानीय हस्तकला व सांस्कृतिक उद्यमों को प्रश्रय देता है। अंतर्राष्ट्रीय स्तर पर यह में संस्कृतिक तथा विरासत कीसमझ विकसित करने में सहायक है। विदेशी पर्यटक भारत में विरासत पर्यटन, पारि-पर्यटन रोमांचकारी पर्यटन, सांस्कृतिक पर्यटन, चिकित्सा पर्यटन तथा व्यापारिक पर्यटन के लिए आते हैं।
भारत में विदेशी पर्यटकों के लिए राजस्थान, गोवा, जम्मू व कश्मीर तथा दक्षिण भारत के मंदिरों के नगर प्रमुख दर्शनीय स्थल है। उत्तर-पूर्वी भारत व हिमालय के अंदरूनी भाग संभव्य पर्यटन विकास स्थल है, लेकिन सामरिक कारणों से इनके विकास को अब तक प्रोत्साहित नहीं किया गया है। यद्यपि पर्यटन उद्योग विकास का एक उज्ज्वल भविष्य है।
![]()
प्रश्न 47.
जनसंचार मानव को मनोरंजन के साथ-साथ बहुत से राष्ट्रीय कार्यक्रमों व नीतियों के विषय में जागरूक करता है। विवेचना कीजिए।
उत्तर-
जन-संचार, मानव को मनोरंजन के साथ बहुत से राष्ट्रीय कार्यक्रमों व नीतियों के विषय में जारूकता करता है। इसमें रेडियों, दूरदर्शन, समाचार-पत्र, पत्रिकाएं किताबें तथा चलचित्र सम्मिलित है। आकाशवाणी (ऑल इंडिया रेडियो) राष्ट्रीय, क्षेत्रीय तथा स्थानीय भाषा में देश के विभिन्न भागों में अनके वर्गों के व्यक्तियों के लिए विविध कार्यक्रम प्रसारित करता है। दूरदर्शन देश का राष्ट्रीय समाचार व संदेश माध्यम है तथा विश्व के वृहत्तम संचार-तंत्र में एक है। यह विभिन्न आयु वर्ग के व्यक्तियों हेतु मनोरंजक ज्ञानावर्धक, व ,खेल-जगत संबंधी कार्यक्रम प्रसारित करता है।
भारत में वर्षभर अनेक समाचार-पत्र तथा सामायिक पत्रिकाएं प्रकाशित की जाती है। ये पत्रिकाएं सामयिक होने के नाते (जैसे-मासि, साप्ताहिक आदि) कई प्रकार की है। समाचार-पत्र लगभग आते हैं। भारत विश्व में सर्वाधिक चलचित्रों का उत्पादक भी है। यह कम अवधि वाली , फिल्में वीडियों फीचर फिल्म तथा छोटी वीडियों फिल्में बनाता है। भारतीय व विदेशी सभी फिल्मों को प्रमाणित करने का अधिकार केंद्रीय फिल्म प्रमाणन बोर्ड को है।
प्रश्न 48.
रेलवे की समस्याओं का वर्णन कीजिए।
उत्तर-
- रेलवे की सबसे बड़ी समस्या आये दिन होने वाली दुर्घटनाएं हैं। इन दुर्घटनओं का कारण जहाँ एक ओर मानवीय भूल होती है तो दूसरी ओर तकनीकी खरीबी या असामाजिक तत्वों का उपद्रव। कारण जो भी हो इस समस्या से निजात पाना भारतीय रेलवे के लिए अत्यंत आवश्यक है।
- भारत में बड़ी संख्या में बिना टिकट यात्रा करते हैं इससे रेलवे को करोड़ों रूपये की हानि सहनी पड़ती है। साथ ही इसका विकास भी प्रस्तावित होता है।
- रेलवे के मालों की चोरी एक आम समस्या है। रेलवे __ अभी तक इस समस्या से निजात पाने का कोई प्रभावी कदम नहीं ढूंढ पाया है।
- यात्री समय-असमय व्यर्थ ही गाड़ी की चैन खींच देते हैं।
- असामाजिक तत्व जनता को तथा सरकार को परेशान करने के उद्देश्य से रेलवे को अपना निशाना बनाते हैं। वे कहीं रेलवे की पटरियों उखाड़ देते हैं। तो कहीं तोड़फोड़ और आगजनी तक कर बैठते हैं। इससे रेलयात्रा की सुरक्षा पर प्रश्न-चिह्न लग जाता है।
- भारतीय रेल की कई पटरियाँ, स्लीपर, तथा नदियों पर बनाये गये पुल पुराने हो चुके हैं। जिनके कारण दुर्घटना का व्यपाक भय बना रहता है।
प्रश्न 49.
स्वतंत्रता प्राप्ति के बाद भारत के अंतर्राष्ट्रीय व्यापार की प्रकृति में क्या परिवर्तन आया है।
उत्तर-
स्वतंत्रता से पहले जहाँ भारत का विदेश व्यापार भारत से अधिक इंग्लैण्ड को लाभ पहुंचाता था वहीं स्वतंत्रता के बाद भारत का अंतर्राष्ट्रीय व्यापार पूर्णत: भारत के हितों की पूर्ति करता है। स्वतंत्रता के बाद भारत के विदेश व्यापार के क्षेत्र में मुख्यतः निम्नलिखित अंतर आये हैं
- स्वतंत्रता के बाद भारत के विदेशी व्यापार की मात्रा में अभूतपूर्व वृद्धि हुई है।
- स्वतंत्रता के बाद का विदेश व्यापार भारत को अधि क-से-अधिक मूल्य उपलब्ध करा रहा हैं
- स्वतंत्रता प्राप्ति के बाद भारत का विदेश व्यापार मात्र इंग्लैण्ड या राष्ट्रमण्डल के देशों तक ही सीमित नहीं है। वरन् यह विश्वभर में फैल गया है।
- आज भारत कच्चे माल का निर्यात नक करके तैयार माल का निर्यात करता है। इससे अधिकतम लाभ अर्जित कर पाना संभव होता है।
- आज भारत कई ऐसी वस्तुओं का आयात भीकरता है जिन्हें पुनः उत्पादित करके वह निर्यात कर सकता है। और अधिक मुनाफा कमा सकता है।
- भारत का विदेशी व्यापार अब इंग्लैण्ड को अपेक्षा यूरोप के अन्य देशों पोलैण्ड जर्मनी आदि के साथ अधिक हो रहा है।
- स्वतंत्रता के बाद का भारतीय विदेश व्यापार भारत की आय तथा आर्थिक समृद्धि को बढ़ा रहा है।
इस प्रकार स्वतंत्रता के बाद भारत के विदेश व्यापार की प्रकृति में न केवल रूख में परिवर्तन आया है बल्कि यह अधि क-से अधिक देश तथा जनता का हित साधने वाला हो गया है।
प्रश्न 50.
भारत का सबसे महत्त्वपूर्ण बंदरगाह कौनसा है?
अथवा
क्या कारण है कि मुंबई को भारत का सबसे महत्त्वपूर्ण बंदरगाह माना जाता है? ..
उत्तर-
भारत का सबसे महत्त्वपूर्ण बंदरगाह मुंबई कहा जाता है। इसके प्रमुख कारण निम्नलिखित हैं
- मुंबई बंदरगाह भारत से होने वाले विदेश व्यापार को बड़ी मात्रा में संचालित करता है।
- यात्रियों का आवागमन सबसे अधिक मुंबई बंदरगाह द्वारा ही होता है।
- चूंकि भारत का विदेश व्यापार मुख्यतः यूरोपीय दक्षिण पश्चिमी एशियाई तथा अफ्रीकी देशों के साथ है; अत: व्यापार का केंद्रबिंदु यही बंदरगाह है।
प्रश्न 51.
भारत में वायु परिवहन पर संक्षिप्त टिप्पणी करें।
उत्तर-
वायु, परिवहन, परिवहन का आधुनिकतम रूप मो है ही, साथ ही सबसे मंहगा साधन भी है। लेकिन परिवहन साधनों में सबसे तेज साधन भी वायु परिवहन ही है। वायु परिवहन का आज के समय में बहुत अधिकक महत्त्व है। विशेष कर विशाल आकार और नियोजित आर्थिक विकास के कारण परिवहन का यह साधन भारत के लिए बहुत महत्त्वपूर्ण बन गया है। बड़े-बड़े औद्योगिक व व्यापारिक केन्द्र इसी माध्यम से आपस में संपर्क स्थापित करते हैं। भारत की वायु सीमा में सुरक्षित व सक्षम वायु यातायात व वैमानिक संचार सेवा प्रदान करने का दायित्व भारतीय विमानन प्राधिकरण का है। यह प्राधिकरण का है। यह प्राधिकरण वर्तमान समय में 11 अंतर्राष्ट्रीय विमान पत्तनों, 112 घरेलू विमानों पत्तनों तथा 28 सैनिक विमान टर्मिनलों का प्रबंध कर रहा है।
भारत में बायुपरिवहन मुख्य रूप से दो प्रकारों में उपलब्ध है-
1. अंतर्राष्ट्रीय वायु परिवहन सेवा-यात्रियों तथा माल परिवहन के लिए भारत में अंतर्राष्ट्रीय वायु सेवा एयर इंडिया द्वारा प्रदान की जाती है। एयर इंडिया के माध्यम से चार प्रमुख विमान पत्तनों-1. दिल्ली, 2. मुंबई, 3. चेन्नई, 4. कोलकाता से 35 देशों के लिए विमान सेवा उपलब्ध कराई जाती है। वर्ष 2000-01 में एयर इंडिया ने 38.3 लाख यात्रियों को सेवा प्रदान की।
भारत के प्रमुख अंतर्राष्ट्रीय वायु मार्ग हैं- 1. दिल्ली-रोम-फैकफुर्ट, 2. दिल्ली-मास्को, 3. कोलकाता-टोकियों, 4. कोलकाता-पर्थ, 5. मुंबई-लंदन-न्यूयार्क।
एयर इंडिया के अतिरिक्त कुछ विदेशी विमान कंपनियों भी भारत से विदेशों के लिए वायु सेवा प्रदान करती हैं।
2. घरेलू वायु परिवहन सेवा-भारत में घरेलू वायु परिवहन सेवा इंडियन एयर लाइंस अलांयस एअर और कुछ निजी वायु सेवा कंपनियों द्वारा तथा एयर टैक्सियों द्वारा प्रदान की जाती है। – इंडियन एयरलाइस दक्षिण-पूर्व-एशिया और पश्चिम एशिया के पड़ोसी देशों को भी वायु सेवा प्रदान की जा रही है, जबकि 38 निजी कंपनियों के पास अनियमित एयर टैक्सी चलाने का परमिट है।
निजी वायु सेवा कंपनियों की घरेलू वायु याततायात में इस समय 52.8% की भागीदारी है।
प्रश्न 52.
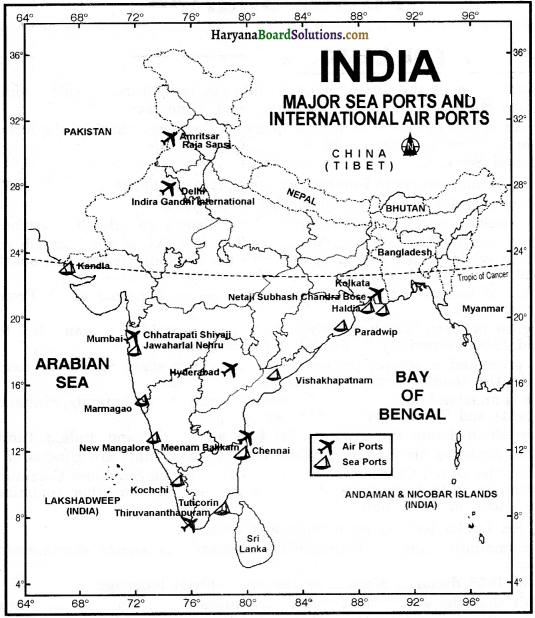
भारत के प्रमुख पत्तनों का संक्षिप्त परिचय दें
उत्तर-
- मुंबई-यह प्राकृतिक बंदरगाह है और देश का सबसे बड़ा पत्तन है।
- न्हावाशेवा-यह स्थान मुंबई में पास है। इसका विकास मुंबई बंदरगाह पर दबाव कम करने के लिए किया गया है।
- कांडला-स्वतंत्रता के समय कराची बंदरगाह के पाकिस्तान में चले जाने के बाद देश के उत्तर-पश्चिम भाग की आवश्यकतों को पूरा करने के लिए इस बंदरगाह काविकास किया गया है।
- मुरमूगांव-यह पोताश्रय गोवा में स्थित है। यहाँ से मुख्यतः लौह-अयस्क, मछलियों के उत्पादों, नारियल, और मसालों का निर्यात किया जाता है।
- न्यू मंगलौर-यह कर्नाटक में अवस्थित है और कुद्रेमुख के लौह अयस्क तथा लौह सान्द्र का निर्यात करता है।
- कोचीन-यह केरल में स्थित है। यह केरल, दक्षिण कर्नाटक और दक्षिणी-पश्चिमी तमिलनाडु की आवश्यकतों को पूरा करता है।
- कोलकता-यह हुगली नदी पर स्थित एक नदीय पत्तन है। यह बंगाल की खाड़ी से 128 किमी. दूर अंदर की ओर स्थित है। इस पत्तन का विकास ब्रिटिश भारत में ही हो गया था। यह एक ज्वारीय पत्तन है।
- हल्दिया-यह कोलकता से लगभग 105 किमी. दूर है और इसका विकास कोलकाता बंदरगाह के दबाव को कम करने के लिए किया गया है।
- पारीदीप-उड़ीसा के तट पर स्थित यह पत्तन मुख्य रूप से लौह अयस्क तथा कोयले का व्यापार करता है।
- विशाखापट्टनम-यह आंध्र प्रदेश के तट पर स्थित हैं यह सबसे गहरा और स्थल रूद्ध पत्तन है। इसे सबसे अधि क सुरक्षित पत्तन भी माना जाता है।
- चेन्नई-इसका विकास भी ब्रिटिश शासन में हो चुका __ था यह एक कृत्रिम पत्तन है। तट के निकट जल की कम गहराई के कारण इसमें बड़े जहाज नहीं आ पाते।
- इन्नौर-इसे एण्णर भी कहा कहा जाता है। यह एक नया पतन है। ये चेन्नई पत्तन दबाव कम करने के उद्देश्य से विकसित किया गया है।
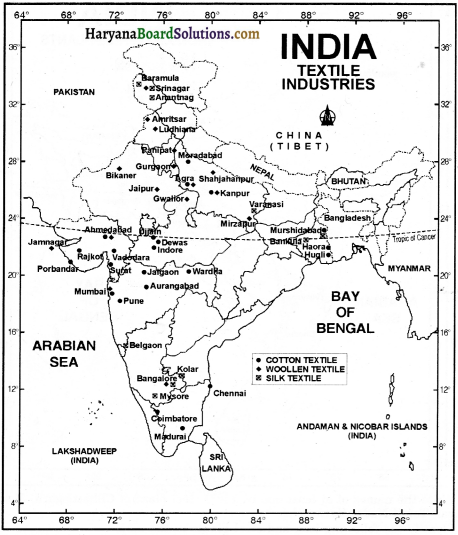
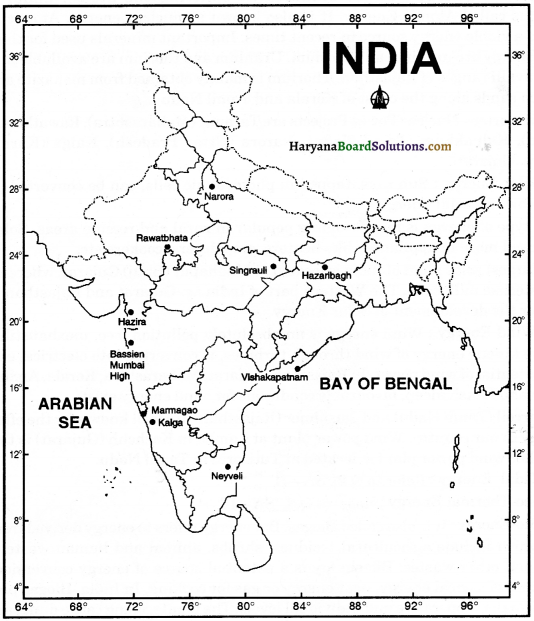
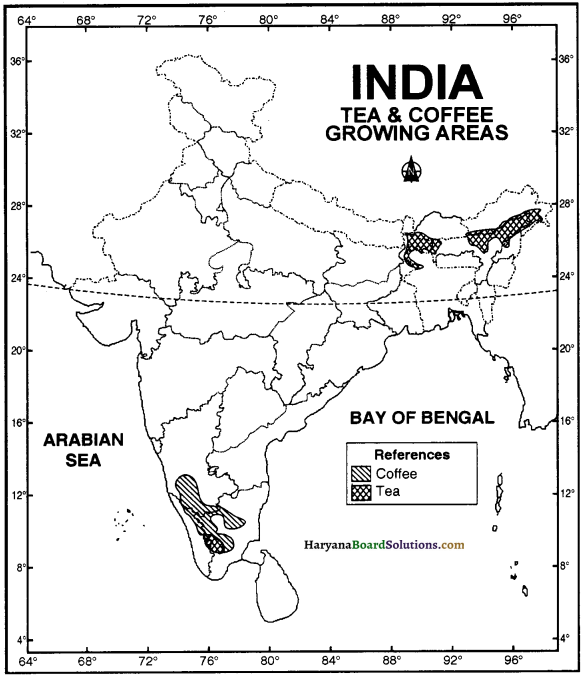
मानचित्र
प्रश्न-
भारत के मानचित्र पर पाँच प्रमुख पत्तन तथा पाँच प्रमुख हवाई पत्तन को दर्शाइए।
उत्तर-
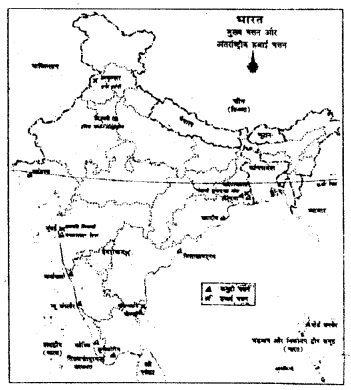
वस्तुनिष्ठ प्रश्न
1. सही उत्तर का चयन कीजिए।
प्रश्न 1.
भारत में सड़कों का जाल कितना लंबा है?
(क) 15 लाख किमी.
(ख) 18 लाख किमी.
(ग) 25 लाख किमी.
(घ) 23 लाख किमी.
उत्तर-
(घ) 23 लाख किमी.
प्रश्न 2.
स्वर्णिम चतुर्भूज महा मार्ग किस संस्था के अधि कार क्षेत्र में है?
(क) राष्ट्रीय राजमार्ग प्राधिकरण
(ख) सीमा सड़क संगठन
(ग) सी.पी. डब्ल्यू. डी.
(घ) इनमें कोई नहीं
उत्तर-
(क) राष्ट्रीय राजमार्ग प्राधिकरण
![]()
प्रश्न 3.
जिला मार्गों की व्यवस्था का दायित्व किस संस्था का होता है?
(क) सी.पी.डब्ल्यू.डी
(ख) पी.डब्ल्यू. डी.
(ग) जिला परिषद्
(घ) एन.एच.ए.आई
उत्तर-
(ग) जिला परिषद्
प्रश्न 4.
सीमा सड़क संगठन की स्थापना कब हुई थीं?
(क) 1947
(ख) 1952
(ग) 1960
(घ) 1971
उत्तर-
(ग) 1960
प्रश्न 5.
सड़कों का औसत राष्ट्रीय घनत्व कितना है।
(क) 50 किमी. प्रति सौ वर्ग किमी.
(ख) 75 किमी. प्रति सौ वर्ग किमी.
(ग) 95 किमी. प्रति सौ वर्ग किमी.
(घ) 105 किमी. प्रति सौ वर्ग किमी.
उत्तर-
(ख) 75 किमी. प्रति सौ वर्ग किमी.
प्रश्न 6.
2004 ई. में भारतीय रेल की मार्गीय लंबाई क्या थी?
(क) 63,221 किमी
(ख) 50522 किमी
(ग) 63,729 किमी
(घ) 85,005 किमी
उत्तर-
(क) 63,221 किमी
प्रश्न 7.
भारत में पहली बार रेल कब चलाई गई थीं?
(क) 1848
(ख) 1851
(ग) 1853
(घ) 1858
उत्तर-
(ग) 1853
प्रश्न 8.
भारतीय रेल को कितने प्रखंडों में संकलित किया गया है?
(क) 9
(ख) 13
(ग) 18
(घ) 16
उत्तर-
(घ) 16
प्रश्न 9.
भारत में अंतः स्थलीय नौसंचालन जलमार्ग कितना किलोमीटर लंबा है?
(क) 14,500
(ख) 18500
(ग) 17,800
(घ) 21,523
उत्तर-
(क) 14,500
प्रश्न 10.
नौगम्य जलमार्ग संख्या-
1 की कुल लंबाई कितनी
(क) 14,500 किमी
(ख) 1620 किमी
(ग) 3700 किमी
(ग) 891 किमी
उत्तर-
(ख) 1620 किमी
प्रश्न 11.
देश का कितना प्रतिशत व्यापार समुद्र द्वारा होता है?
(क) 60%
(ख) 75%
(ग) 95%
(ग) 99%
उत्तर-
(ग) 95%
प्रश्न 12.
भारत की समुद्री तटरेखा कितनी लंबी हैं?
(क) 7,516.6 किमी.
(ख) 8,5116.6 किमी.
(ग) 95,16.6 किमी.
(घ) 5,516.6 किमी.
उत्तर-
(क) 7,516.6 किमी.
प्रश्न 13.
भारत में कितने बड़े पत्तन हैं?
(क) 5
(ख) 7
(ग) 9
(घ) 12
उत्तर-
(घ) 12
![]()
प्रश्न 14.
भारत का पहला पत्तन कौन है? ।
(क) हल्दिया
(ख) कांडला
(ग) पारादीप
(घ) मुंबई
उत्तर-
(ख) कांडला
प्रश्न 15.
मारमागाओं पत्तन से कितना लौह-अयस्क निर्यात किया जाता है?
(क) 25%
(ख) 50%
(ग) 70%
(घ) 80%
उत्तर-
(ख) 50%
प्रश्न 16.
हमारे देश का प्राचीनतम कृत्रिम पत्तन का क्या नाम है?
(क) मुंबई
(ख) कोची
(ग) कांडला
(घ) चेन्नई
उत्तर-
(घ) चेन्नई
प्रश्न 17.
वायु परिवहन का राष्ट्रीयकरण कब किया गया था?
(क) 1953
(ख) 1954
(ग) 1955
(घ) 1956
उत्तर-
(क) 1953
प्रश्न 18.
भारत में अंतर्राष्ट्रीय वायुसेवा प्रदान करने वाली कंपनी का नाम बताइए।
(क) इंडियन एयरलाइस
(ख) जेट एयरवेज
(ग) एयर इंडिया
(घ) एलाइस एयर
उत्तर-
(ग) एयर इंडिया
प्रश्न 19.
किस देश का डाक-संचार तंत्र विश्व का वृहत्तम है?
(क) भारत
(ख) अमेरिका
(ग) फ्रांस
(घ) रूस
उत्तर-
(क) भारत
प्रश्न 20.
हमारे देश में सर्वाधिक समाचार-पत्र किस भाषा में प्रकाशित होता है?
(क) अंग्रेजी
(ख) बंगला
(ग) हिंदी
(घ) मलयालम
उत्तर-
(ग) हिंदी
प्रश्न 21.
बड़े शहरों व नगरों में डाक-संचार में शीघ्रता हेतु कितने डाकमार्ग बनाए गए हैं?
(क) 4
(ख) 6
(ग) 8
(घ) 11
उत्तर-
(ख) 6
2. निम्नलिखित सूचियों का सही मिलान कीजिए-
सूची (अ) — सूची (ब)
(क) एशिया ओशनिया — (अ) वायु परिवहन का राष्ट्रीयकरण
(ख) केरल — (ब) सर्वाधिक निर्यात
(ग) 1953 — (स) आंध्रप्रदेश
(घ) जवाहर लाल नेहरू पत्तन — (द) न्हावाशेवा
(ङ) वारंगल — (य) चंपाकर नहर
उत्तर-
(क) – ब,
(ख) – य,
(ग) – अ,
(घ) -घ,
(ङ) – स
3. निम्नलिखित सूचियों का सही मिलान कीजिए-
सूची (अ) — सूची (ब)
(क) 63,000 किमी — (अ) भारत की तटरेखा
(ख) 6867 — (ब) भारत में रेल मार्गों की कुल लंबाई
(ग) 5846 किमी. — (स) भारत में रेलवे स्टेशनों की संख्या
(घ) 7500 किमी. — (द) स्वर्णिम चतुष्कोण की लंबाई
(ङ) 32,000 — (य) भारत में टेलिफोन एक्सचेंजों
(च) 14 किमी. — (र) चम्पाकर नहर।
उत्तर-
(क) – ब,
(ख) – स,
(ग) – द,
(घ) – अ,
(ङ) – य
(च) – (र)