Class 10

Haryana State Board HBSE 10th Class Maths Solutions Chapter 6 Triangles Ex 6.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 6 Triangles Ex 6.2

Question 1.
In given figure (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).

Solution :
(i) we have, AD = 1.5 cm, AE = 1 cm, DB = 3 cm
DE || BC
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
[By theorem 6.1 (BPT)]
\(\frac{1 \cdot 5}{3 \cdot 0}=\frac{1}{\mathrm{EC}}\) = 2
EC = \(\frac{3.0}{1.5}\) = 2
Hence, EC = 2 cm.

(ii) We have, DB = 7.2 cm, AE = 1.8 cm, EC = 5.4 cm and DE || BC
∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) [By Theorem 6.1 (BPT)]
\(\frac{\mathrm{AD}}{7 \cdot 2}=\frac{1 \cdot 8}{5 \cdot 4}\)
AD = \(\frac{7.2 \times 1.8}{5.4}\) = 2.4
Hence, AD = 2.4 cm.

Question 2.
E and F are points on the sides PQ and PR respectively of a APQR. For each of the following cases, state whether EF || QR :
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm.
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm.
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 018 cm and PF = 0.36 cm.

Solution :
(i) we have PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
Now, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{3.9}{3.0}\) = 1.3
and \(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{3 \cdot 6}{2 \cdot 4}\) = 1.5
∵ \(\frac{\mathrm{PE}}{\mathrm{EQ}} \neq \frac{\mathrm{PF}}{\mathrm{FR}}\)
∴ EF is not parallel to QR.

(ii) We have,
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
Now, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{4}{4 \cdot 5}=\frac{8}{9}\) and
\(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{8}{9}\)
∵ \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}\)
∴ EF || QR

(iii) We have,
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm,
EQ = PQ – PE = 1.28 – 0.18 = 11 cm,
PR = PF = 2.56 – 0.36 = 2.2 cm.
Now, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{0 \cdot 18}{1 \cdot 1}=\frac{9}{55}\)
and \(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{0.36}{2 \cdot 2}=\frac{9}{55}\)
∵ \(\frac{P E}{E Q}=\frac{P F}{F R}\)
∴ EF || QR

Question 3.
In given figure, if LM || CB and LN || CD, prove that \(\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AD}}\).

Solution:
Given: In □ABCD, LM || CB and LN || CD
To Prove: \(\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AD}}\)
Solution: In ∆ABC LM || CB (given)

Question 4.
In given figure DE || AC and DF || AE. Prove that \(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BE}}{\mathrm{EC}}\).

Solution:
Given : In ∆ABC DE || AC and DF || AE
To prove: \(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BE}}{\mathrm{EC}}\).
Proof: In ∆BAE,
DF || AE (given)
∴ \(\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{\mathrm{BF}}{\mathrm{FE}}\) ………………..(1)
[By Theorem 6.1 (BPT)]
In ∆ABC, DE || AC (given)
∴ \(\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{\mathrm{BE}}{\mathrm{EC}}\) [By Theorem 6.1 (BPT)]
From(1) and (2) we get
\(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BE}}{\mathrm{EC}}\)
Hence Proved.

Question 5.
In given figure DE || OQ and DF || OR. Show that EF || QR.

Solution:
Given: In ∆POQ, DE || OQ and in POR, DF || OR
To prove: EF || QR
Proof: In ∆POQ DE || OQ (given)
∴ \(\frac{\mathrm{PD}}{\mathrm{DO}}=\frac{\mathrm{PE}}{\mathbf{E Q}}\) ……………..(1)
[By Theorem 6.1 (BPT)]
In ∆POR DF || OR
∴ \(\frac{\mathrm{PD}}{\mathrm{DO}}=\frac{\mathrm{PF}}{\mathrm{FR}}\) ……………..(2)
[By Theorem 6.1 (BPT)]
From (1) and (2), we get
\(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}\)
∴ EF | | QR [By converse of BPT]

Question 6.
In given figure, A. B, and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Solution:
Given: In figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR.
To prove: BC || QR
Proof: In ∆OPQ
AB || PQ (given)
\(\frac{O A}{A P}=\frac{O B}{B Q}\) …………………(1)
[By theorem 6.1 (BPT)]
In ∆OPR, AC || PR (given)
\(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OC}}{\mathrm{CR}}\) …………….(2)
[By theorem 6.1 (BPT)]
From (1) and (2) we get
\(\frac{\mathrm{OB}}{\mathrm{BQ}}=\frac{\mathrm{OC}}{\mathrm{CR}}\)
Thus B and C are respectively points on sides OQ and OR of ∆OQR, such that \(\frac{\mathrm{OB}}{\mathrm{BQ}}=\frac{\mathrm{OC}}{\mathrm{CR}}\).
⇒ BC || QR [By converse of BPT]
Hence Proved.

Question 7.
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in class IX).
Solution:
Given : A ∆ABC in which D is the mid-point of AB and DE || BC and meeting AC at E.

To Prove : AE = EC
Proof : Since, DE || BC
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) ……………..(1)
[By Theorem 6.1 (BPT)]
But AD = DB
[∵ D is the mid point of AB]
∴ \(\frac{\mathrm{AD}}{\mathrm{AD}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) ………………(2)
⇒ \(\frac{\mathrm{AE}}{\mathrm{EC}}\) = 1
⇒ AE = EC.

Question 8.
Using theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in class IX).
Solution:
Given : A ∆ABC in which D is the mid-point of AB and E is the mid-point of AC
To prove : DE || BC
Proof : Since D and E are the mid-points of AB and AC respectively
AD = DB
⇒ \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = 1
and AE = EC
⇒ \(\frac{\mathrm{AE}}{\mathrm{EC}}\) = 1

∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
⇒ DE || BC
[By Theorem of 6.2 (converse of BPT)]
Hence Proved.

Question 9.
ABCD is a trapezium in which AB | DC and its diagonals intersect each other at the point O. Show that \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\).
OR
PQRS is a trapezum in which PQ || RS and its diagonals intersect each other at the point O. Prove \(\frac{\mathrm{PO}}{\mathrm{QO}}=\frac{\mathrm{RO}}{\mathrm{SO}}\)
Solution:
Given : A trapezium ABCD in which AB || CD and its diagonals AC and BD intersect at O.

To Prove: \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
Construction: Draw OE || AB through O, which meets AD at E.
Proof : We have,
EO || AB (By construction) …………(1)
DC || AB (given) …………(2)
From (1) and (2), we get
EO || DC
∴ \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{AO}}{\mathrm{OC}}\) ………………..(3)
[By Theorem 6.1 (BPT)]
In ∆ DAB EO || AB
\(\frac{\mathrm{DE}}{\mathrm{EA}}=\frac{\mathrm{DO}}{\mathrm{OB}}\)
∴ \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{BO}}{\mathrm{OD}}\) ………………(4)
[By Theorem 6.1 (BPT)]
From (3), (4), we get
\(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{BO}}{\mathrm{OD}}\)
⇒ \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
Hence Proved.

Question 10.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\). Show that ABCD is a trapezium.
OR
The diagonals of a quadrilateral PQRS intersect each other at the point O, such that \(\frac{\mathrm{PO}}{\mathrm{QO}}=\frac{\mathrm{RO}}{\mathrm{SO}}\). Show that PQRS is a trapezium.
Solution:
Given : A quadrilateral ABCD whose diagonals AC and BD intersect at a point O such that

\(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
To Prove : ABCD is a trapezium i.e. AB || DC.
Construction : Draw OE || DC which meets AD at E.
Proof: In ∆ACD,
0E || DC (By construction)
∴ \(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{AE}}{\mathrm{ED}}\) ……………..(1)
[By Theorem 6.1 (BPT)]
But, \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) (given)
⇒ \(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{BO}}{\mathrm{DO}}\) ………………..(2)
From (1) and (2), we get
\(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{BO}}{\mathrm{DO}}\)
⇒ EO || AB
[By Theorem 6.2 (converse of BPT)1
But, OE || DC (By construction)
From (3) and (4), we get
AB || CD
Hence, ABCD is a trapezium. Hence Proved.

Haryana State Board HBSE 10th Class Maths Solutions Chapter 7 Coordinate Geometry Ex 7.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 7 Coordinate Geometry Ex 7.1

Question 1.
Find the distance between the following pairs of points :
(i) (2, 3), (4, 1)
(ii) (- 5, 7), (- 1, 3)
(iii) (a, 6), (- a, – b)
Solution :
(i) Let the given points be A(2, 3) and B(4, 1), then
AB = \(\sqrt{(4-2)^2+(1-3)^2}\)
⇒ AB = \(\sqrt{(2)^2+(-2)^2}\)
⇒ AB = \(\sqrt{4+4}\)
⇒ AB = √8
⇒ AB = \(\sqrt{2 \times 2 \times 2}\)
⇒ AB = 2√2
Hence, distance (AB) = 2√2.

(ii) Let the given points be P(- 5, 7) and Q(- 1, 3), then
PQ = \(\sqrt{(-1+5)^2+(3-7)^2}\)
PQ = \(\sqrt{(4)^2+(-4)^2}\)
⇒ PQ = \(\sqrt{16+16}\)
⇒ PQ = √32
⇒ PQ = \(\sqrt{4 \times 4 \times 2}\)
⇒ PQ = 4√2
Hence, distance (PQ) = 4√2

(iii) Let the given points be P(a, b) and Q(- a, – 6), then
PQ = \(\sqrt{(-a-a)^2+(-b-b)^2}\)
⇒ PQ = \(\sqrt{(-2 a)^2+(-2 b)^2}\)
⇒ PQ = \(\sqrt{4 a^2+4 b^2}\)
⇒ PQ = \(\sqrt{4\left(a^2+b^2\right)}\)
⇒ PQ = 2\(\sqrt{a^2+b^2}\)
Hence, the distance (PQ) = 2\(\sqrt{a^2+b^2}\).

Question 2.
Find the distance between the points (0,0) and (36,15). Can you now find the distance between the two towns A and B.

Solution:
Let the given points be A(0,0) and B(36, 15) then
AB = \(\sqrt{(36-0)^2+(15-0)^2}\)
⇒ AB = \(\sqrt{(36)^2+(15)^2}\)
⇒ AB = \(\sqrt{1296+225}\)
⇒ AB = \(\sqrt{1521}\)
⇒ AB = 39
Hence, distance between two towns = 39 km.

Question 3.
Determine if the points (1, 5), (2, 3) and (- 2, – 11) are collinear.
Solution:
Let the given points be A(1, 5), B(2, 3) and C(- 2, – 11). Then,

⇒ AC = √256 = 16.28 (approx)
Now,AB + BC = 2.24 + 14.56 = 16.8
AC = 16.28
∴ AB + BC ≠ AC
Hence, the given points (1, 5), (2, 3) and (- 2, – 11) are not collinear.

Question 4.
Check whether (5, – 2), (6,4) and (7, – 2) are the vertices of an isosceles triangle.
Solution :
Let the given points be A(5, – 2), B(6, 4) and C(7, – 2), then
AB = \(\sqrt{(6-5)^2+(4+2)^2}\)
= \(\sqrt{(1)^2+(6)^2}\)
= \(\sqrt{37}\)

BC = \(\sqrt{(7-6)^2+(-2-4)^2}\)
= \(\sqrt{(1)^2+(-6)^2}\)
= \(\sqrt{37}\)
Since, AB = BC
Therefore, the given joints are the vertices of an isosceles triangle.

Question 5.
In a class room, 4 friends are seated at the points A, B, C and D as shown in figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square ?” Chameli disagrees. Using distance formula, find which of them is correct ?

Solution:
From the figure, coordinates of A, B, C, D, are respectively (3, 4), (6, 7), (9, 4), (6, 1)

⇒ BD = √36
⇒ BD = 6.
Since, AB = BC = CD = DA and diagonal AC = diagonal BD.
Therefore, ABCD is a square.
Hence, Champa is correct.

Question 6.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer :
(i) (- 1, – 2), (1, 0), (- 1, 2), (- 3, 0)
(ii) (- 3, 5), (3, 1), (0, 3), (-1, – 4)
(iii) (4, 6), (7, 6), (4, 3), (1, 2)
Solution :
(i) Let the given points of the quadrilateral be A(- 1, – 2), B(1, 0), C(- 1, 2) and D(- 3, 0).
Join AC and BD

Since, AB = BC = CA = DA and diagonal AC = diagonal BD
Therefore, given points form a square.

(ii) Let the given points of the quadrilateral be A(- 3, 5), B(3, 1), C(0, 3) and D(- 1, – 4).
Join AC and BD

Now,
AC + BC = √13 + √13 = 2√13
AB = 2√13
Since, AC + BC = AB.
Therefore, A, B, C are collinear. So, the given points do not form any quadrilateral.

(iii) The given points of a quadrilateral be A(4, 5), B(7, 6), C(4, 3) and D(l, 2). Join AC and

Diagonal AC ≠ diagonal BD.
Since, opposite sides are equal but diagonals are not equal.
Therefore, the given points form a parallelogram.

Question 7.
Find the point on the x-axis which is equidistant from (2, – 5) and (- 2, 9).
Solution :
Let the given points be A(2, – 5) and B(- 2, 9) and let the required point be POc, 0), then
PA = PB
⇒ PA² = PB²
⇒ (x – 2)² + (0 + 5)² = (x + 2)² + (0 – 9)²
⇒ x² + 4 – 4x + 25 = x² + 4 + 4x + 81
⇒ x² – 4x + 29 = x² + 4x + 85
⇒ x² – 4x – x² – 4x = 85 – 29
⇒ – 8x = 56.
⇒ x = \(\frac{56}{-8}\)
x = – 7
Hence, the required point = (- 7, 0)

Question 8.
Find the values ofy for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.
Solution :
The given points are P(2, – 3) and Q(dfgvbtyh10, y)
and PQ = 10 units
∴ PQ = \(\sqrt{(10-2)^2+(y+3)^2}\)
10 = \(\sqrt{(8)^2+y^2+9+6 y}\)
10 = \(\sqrt{64+y^2+9+6 y}\)
10 = \(\sqrt{73+y^2+6 y}\)
100 = 73 + y² + 6y (squaring both sides)
y² + 6y + 73 – 100 = 0
y² + 6y – 27 = 0
y² + (9 – 3)y – 27 = 0
y² + 9y – 3y – 27 = 0
[∵ 1 × – 27 = – 27
9 × – 3 = – 27
9 – 3 = 6]
⇒ y(y + 9) – 3(y + 9) = 0
⇒ (y + 9) (y – 3) = 0
⇒ y + 9 = 0 or y – 3 = 0
⇒ y = – 9 or y = 3.
Hence, y = – 9 or 3.

Question 9.
If Q(0, 1) is equidistant from P(5, – 3) and R(x, 6), find the values of x. Also find the distances QR and PR.
Solution:
The given points are P(5, -3), Q(0, 1) and R(x, 6)
∵ Q is the equidistant from P and R.
∴ PQ = RQ
⇒ PQ² = RQ²
⇒ (0 – 5)² + (1 + 3)² = (0 – x)² + (1 – 6)²
⇒ (- 5)² + (4)² = (- x)² + (- 5)²
⇒ 25 + 16 = x² + 25
⇒ 25 – 25 + 16 = x²
⇒ x² = 16
⇒ x = ± 4

Case II: x = 4

PR = \(\sqrt{(-1)^2+81}\)
PR = \(\sqrt{1+81}=\sqrt{82}\)

Case II: If x = – 4

Hence, x = ± 4, QR = √41 and PR = √82 or 9√2.

Question 10.
Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (-. 3, 4).
Solution:
Let P(x, y) be the equidistant from the points M(3, 6) and B(- 3, 4), then
PA = PB
PA² = PB² .
⇒ (3 – x)² + (6 – y)²
⇒ (- 3 – x)² + (4 – y)²
⇒ 9 + x² – 6x + 36 + y² – 12y = 9 + x² + 6x + 16 + y² – 8y
⇒ x² + y² + 6x – 8y + 6x + 12y – x² -y² = 45 – 25
⇒ 12x + 4y = 20
⇒ 3x + y = 5
⇒ 3x + y – 5 = 0
Hence, the required relation is 3x + y – 5 = 0

Haryana State Board HBSE 10th Class Maths Solutions Chapter 6 Triangles Ex 6.6 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 6 Triangles Ex 6.6

Question 1.
In the given figure, PS is the bisector of ∠QPR of ∆PQR. Prove that \(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{PQ}}{\mathrm{PR}}\).

Solution :
Given : A ∆PQR in which PS is the bisector of ∠QPR
To Prove: \(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{PQ}}{\mathrm{PR}}\)
Construction : Draw RT || PS to meet QP produced at T.
Proof : Since RT || SP and PR is the trans-versal :
∠2 = ∠3 ……………..(1) [alternate interior ∠s]
∠1 = ∠4 ……………..(2) [Corresponding ∠s]
∠1 = ∠2 ……………..(3) [PS is the bisector of ∠QPR]
From (1), (2) and (3) we get

∠3 = ∠4
∴ PR = PT
Now in ∆QRT, PS || TR
⇒ \(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{PQ}}{\mathrm{PT}}\) [By BPT]
⇒ \(\frac{\mathrm{QS}}{\mathrm{SR}}=\frac{\mathrm{PQ}}{\mathrm{PR}}\) [∵ PT = PR]
Hence Proved.

Question 2.
In the given figure D is a point on hypotenuse AC of ∆ABC, such that BD ⊥ AC, DM ⊥ BC and DN ⊥ AB. Prove that:
(i) DM² = DN.MC
(ii) DN² = DM.AN

Solution :
Given : D is a point on AC such that BD ⊥ AC, DM ⊥ BC and DN ⊥ AB.
To Prove :
(i) DM² = DN.MC
(ii) DN² = DM.AN
Proof: ∠ABC = 90° [∵ AC is hypotenuse of right ∆ABC]
∠DMB = 90° [∵ DM ⊥ BC]
∠DNB = 90° [∵ DN ⊥ AB]
∠MDN = 90° [Fourth ∠ of a quadrilateral]
Therefore, quadrilateral BMDN is a rectangle, (i) In ABMDZ1 + Z2 + ZDMB = 180°
⇒ ∠1 + ∠2 + 90° = 180°
⇒ ∠1 + ∠2 = 180° – 90°
⇒ ∠1 + ∠2 = 90° ………………..(1)
In ∆CMD
∠3 + ∠4 + ∠CMD = 180°
⇒ ∠3 + ∠4 + 90° = 180°
⇒ ∠3 + ∠4 = 180° – 90°
⇒ ∠3 + ∠4 = 90° ……………….(2)
BD ⊥ AC
∴ ∠1 + ∠3 = 90° ……………….(3)
From (1) and (3), we get
∠1 + ∠2 = ∠1 + ∠3
⇒ ∠2 = ∠3 ……………….(4)
From (2), and (3), we get
∠3 + ∠4 = ∠1 + ∠3
⇒ ∠1 = ∠4 …………….(5)
Now in ∆BMD and ∆DMC,
∠2 = ∠3 [from (4)]
∠1 = ∠4 [from (5)]
∆BMD ~ ∆DMC [By AA similarity criterion]
⇒ \(\frac{B M}{D M}=\frac{M D}{M C}\)
⇒ \(\frac{D N}{D M}=\frac{D M}{M C}\) [∵ BM = DN]
⇒ DM² = DN.MC.
Hence Proved.

(ii) Similarly, ∆BND ~ ∆DNA
⇒ \(\frac{B N}{D N}=\frac{N D}{N A}\)
⇒ \(\frac{\mathrm{DM}}{\mathrm{DN}}=\frac{\mathrm{DN}}{\mathrm{AN}}\)
DN² = DM.AN
Hence Proved.

Question 3.
In the given figure, ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that :
AC² = AB² + BC² + 2BC.BD.

Solution:
See this proof in result (1) of some results related to Pythagoras theorem.

Question 4.
In figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC² = AB² + BC² – 2BC.BD.

Solution:
See this prove in result (2) of some results related to Pythagoras theorem.

Question 5.
In given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that
(i) AC² = AD² + BC.DM + \(\left(\frac{\mathrm{BC}}{2}\right)^2\)
(ii) AB² = AD² – BC.DM + \(\left(\frac{\mathrm{BC}}{2}\right)^2\)
(iii) AC² + AB² = 2AD² + \(\frac{1}{2}\) BC²

Solution:
See this proof in result (3) of some results related to Pythagoras theorem.

Question 6.
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Solution :
Given : A parallelogram ABCD with diagonals AC and BD.

To Prove: Sum of the squares of the diagonals of ||gm is equal to sum of the squares of its sides. i.e., AC² + BD² = AB² + BC² + CD² + AD²
Construction :
Draw AM ⊥ DC and BN ⊥ DC [Produced].
Proof : In right triangles AMD and BNC. AD = BC [Opposite sides of ]|gm]
AM = BN
[Perpendiculars between two || lines are same]
∠AMD = ∠BNC [Each is 90°]
∆AMD ≅ ∆BNC [By RHS congruence]
MD = NC [CPCT]
Now, in right ∆BND,
BD² = BN² + DN² [By Pythagoras theorem]
⇒ BD² = BN² + (DC + CN)²
⇒ BD² = BN² + DC² + CN² + 2DC.CN
⇒ BD² = (BN² + CN²) + DC² + 2DC.CN
⇒ BD² = BC² + DC² + 2DC.CN …………………….(1)
[∵ In right ∆BNC, BC² = BN² + CN²]
In right ∆AMC, AC² = AM² + MC²
[By Pythagoras theorem]
AC² = AM² + (DC – DM)²
AC² = AM² + DC² + DM² – 2DC.DM
AC² = (AM² + DM²) + DC² – 2DC.DM
AC² = AD² + DC² – 2DC.DM
[∵ In right ∆AMD AD² = AM² + MD²]
AC² = AD² + AB² – 2DC.CN ………………….(2)
[DC = AB and DM = CN]
Adding (1) and (2), we get
BD² + AC² = BC² + DC² + 2DC.CN + AD² + AB² – 2DC.CN
⇒ AC² + BD² = AB² + BC² + CD² + AD²
Hence, sum of square of diagonals is equal to sum of square of its sides.
Hence Proved.

Question 7.
In given figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ∆APC ~ ∆DPB
(ii) AP.PB = CP.DP

Solution :
Given : Two chords AB and CD in-tersect each other at point P.
To Prove :
(i) ∆APC ~ ∆DPB
(ii) AP.PB = CP.DP.
Proof :
(i) In ∆APC and ∆DPB,
∠CAB = ∠BDC
[Angles in the same segment are equal]
⇒ ∠CAP = ∠BDP
and ∠APC = ∠BPD [Vertically opposite angles]
∴ ∆APC ~ ∆DPB [By AA similarity criterion]
Hence Proved.

(ii) ∆APC ~ ∆DPB (Proved above)
\(\)
[Corresponding sides of similar triangles are proportional]
⇒ AP.PB = CP.DP.
Hence proved.

Question 8.
In given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that :

To Prove :
(i) ∆PAC ~ ∆PDB
(ii) PA.PB = PC.PD
Proof : (i) In ∆PAC and ∆PDB
∠ACP = ∠PBD [Exterior angle of the cyclic quadrilateral is equal to its interior opposite angle] ZP = ZP [Common]
∴ ∆PAC ~ ∆PDB [By AA similarity criterion]
Hence proved.

(ii) ∆PAC ~ ∆PDB (Proved above)
\(\frac{P A}{P D}=\frac{P C}{P B}\)
⇒ PA.PB = PC.PD.
Hence proved.

Question 9.
In given figure, D is a point on side BC of ∆ABC such that \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AC}}\). Prove that AD is the bisector of ∠BAC.

Solution :
Given : A triangle ABC such that \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AC}}\).
To Prove : AD is the bisector of ∠BAC.
Construction : Produce BA to E such that AE = AC and join CE.

Proof: In ∆ABC AE = AC (By Construction)
∴ ∠1 = ∠2 ……………(1)
Now, \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AC}}\) (Given)
⇒ \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AE}}\) [∵ AC = AE]
∴ In ∆BCE
⇒ \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{AB}}{\mathrm{AE}}\)
⇒ AD || CE [By the converse of BPT]
∠1 = ∠4 [Alternate interior angles] ……………(2)
∠3 = ∠2 [Corresponding angles] …………….(3)
From (1), (2) and (3), we get
∠3 = ∠4
Hence, AD is the bisector of ∠BAC.
Hence proved.

Question 10.
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

Solution:
Let AB be the distance from a point directly under the tip of the rod and BC be the tip of her fishing rod and AC be the length of string.
Now, in right ∆ABC,

AC² = AB² + BC² [By Pythagoras theorem]
AC² = (2.4)² + (1.8)²
AC² = 5.76 + 3.24
AC² = 9
AC = 3 m.
The length of string pulls in 12 seconds = 12 × 5 = 60 cm = 0.6 m.
Length of remaining string = 3 – 0.6 = 2.4 m.
In 2nd position,
String length (CD) = 2.4 m.

Tip of her fishing rod (BC) = 1.8 m
Now In right ∆CBD,
CD² = BD² + BC²
⇒ 2.4² = BD² + (1.8)²
⇒ 5.76 = BD² + 3.24
⇒ BD² = 5.76 – 3.24
⇒ BD² = 2.52
⇒ BD = 1.59 (Approx)
So, horizontal distance of the fly from Nazima after 12 seconds = 1.59 + 1.2 = 2.79m. (Approx.)
Hence, Length of string = 3.0 m and
Horizontal distance of fly from Nazima = 2.79 m (Approx.)

Haryana State Board HBSE 10th Class Maths Solutions Chapter 6 Triangles Ex 6.5 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 6 Triangles Ex 6.5

Question 1.
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 26 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm.
Solution:
(i) The given sides of the triangle are 7 cm, 24 cm, 25 cm,
The longest side = 25cm.
The triangle is right angled if
(the longest side)² = (sum of squares of other two sides) (by Pythagoras theorem)
(25)² = (7)² + (24)²
625 = 49 + 576
625 = 625
The given sides make a right triangle and length of hypotenuse = 25cm.

(ii) The given sides of the triangle are 3cm, 8 cm, 6 cm.
The longest side = 8 cm
(the longest side)² = (sum of the squares of other two sides) (by Pythagoras theorem)
(8)² = (3)² + (6)²
64 = 9 + 36
But 64 ≠ 45
The given sides do not make a right triangle.

(iii) The given sides of the triangle Eire 50 cm, 80 cm, 100 cm.
The longest side = 100 cm,
(the longest side)² = (sum of the squares of other two sides) (by Pythagoras theorem)
(100)² = (50)² + (80)²
10000 = 2500 + 6400
But 10000 ≠ 8900
∴ The given sides do not mEike a right triangle.

(iv) The given sides of the triangle are 13 cm, 12 cm, 5 cm.
The longest side = 13 cm.
(the longest side)² = (sum of the squares of other two sides) (by Pythagoras theorem)
(13)² = (12)² + (5)²
169 = 144 + 25
169 = 169
∴ The given sides make a right triangle and length of hypotenuse = 13 cm.

Question 2.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM.MR.

Solution:
Given : A right ∆PQR in which ∠P = 90° and PM ⊥ QR.
To Prove : PM² = QM.MR
Proof : In right ∆QPR, PM ⊥ QR.
∆RPM ~ ∆PQM [By theorem 6.7]
⇒ \(\frac{\mathrm{MR}}{\mathrm{PM}}=\frac{\mathrm{PM}}{\mathrm{QM}}\)
[Corresponding sides of similar triangles sere proportional]
⇒ PM² = QM × MR
Hence Proved.

Question 3.
In given figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that
(i) AB² = BC.BD
(ii) AC² = BC.DC
(iii) AD² = BD.CD

Solution:
Given : A right triangle in which ∠A = 90° sind AC ⊥ BD.
To Prove :
(i) AB² = BC.BD
(ii) AC² = BC.DC
(iii) AD² = BD.CD
Proof :
(i) In right ∆BAC, AC ⊥ BD.
∆BAC ~ ∆BDA [By theorem 6.7]
⇒ \(\frac{\mathrm{AB}}{\mathrm{BD}}=\frac{\mathrm{BC}}{\mathrm{AB}}\)
[Corresponding sides of similar triEingles are proportional]
⇒ AB² = BC.BD
Hence Proved.

(ii) Similsirly, ∆ABC~ ∆DAC [By theorem 6.7]
\(\frac{\mathrm{AC}}{\mathrm{DC}}=\frac{\mathrm{BC}}{\mathrm{AC}}\)
[Corresponding sides of similar triEingles Eire proportional]
⇒ AC² = BC.CD
Hence Proved.

(iii) Similarly, ∆DAC ~ ∆DBA [By theorem 6.7]
\(\frac{\mathrm{CD}}{\mathrm{AD}}=\frac{\mathrm{AD}}{\mathrm{BD}}\)
[Corresponding sides of similar triangles are proportional]
⇒ AD² = BD.CD
Hence Proved.

Question 4.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².
Solution:
Given : ∆ABC is an isosceles triangle right angled at C.
i.e., AC = BC
To Prove : AB² = 2AC²
Proof : In right ∆ACB

AB² = BC² + AC² [By Pythagoras theorem]
⇒ AB² = AC² + AC² [∵ BC = AC]
⇒ AB² = 2AC².
Hence Proved.

Question 5.
ABC is an isosceles triangle with AC = BC. If AB² = 2AC², prove that ABC is a right triangle.
Solution:
Given: ∆ABC is an isosceles triangle in which AC = BC and AB² = 2AC²
To Prove : ∆ABC is a right triangle.

Proof : In ∆ABC, AC = BC and AB² = 2AC²
⇒ AB² = AC² + AC²
⇒ AB² = BC² + AC² [v AC = BC]
⇒ ABC is right angle triangle.
[By converse of Pythagoras theorem]
Hence Proved.

Question 6.
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution :
Side of equilateral ∆ = 2a.
And AD is its altitude. We know that altitude bisects its corresponding side.
i.e., BD = CD = a

Now right triangle ∆ADC.
AC² = AD² + CD² [By Pythagoras theorem]
⇒ (2a)² = AD² + a²
⇒ 4a² = AD² + a²
⇒ AD² = 4a² – a² = 3a²
⇒ AD = √3a
Hence, Altitude = √3a.

Question 7.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Given : ABCD is a rhombus

Proof: We know that diagonals of a rhombus bisect each other at right angle
∴ ∠AOB = ∠BOC = ∠COD = ∠AOD = 90° and AO = CO, OD = BO.
In right ∆AOB, AB² = OA² + OB² [By Pythagoras theorem]
AB² = (\(\frac{1}{2}\) AC)² + (\(\frac{1}{2}\) BD)²
[∵ OA = OC and OB = OD]
⇒ AB² = 7 AC² + 7BD²
⇒ 4AB² = AC² + BD² ……………(1)
Similarly, we have
4BC² = AC² + BD² ……………….(2)
4CD² = AC² + BD² ……………….(3)
4AD² = AC² + BD² ……………….(4)
Adding (1), (2), (3) and (4), we get
4(AB² + BC² + CD² + AD²) = 4(AC² + BD²)
⇒ AB² + BC² + CD² + AD² = AC² + BD²
Hence Proved.

Question 8.
In given figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF².

Solution: Given: A ∆ABC in which OD ⊥BC, OE ⊥ AC, OF ⊥ AB.
To Prove :
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF²
Construction : Join OB, OC and OA.

Proof :
(i) By Pythagoras theorem for each of the right triangles namely ∆OFA, ∆ODB, and ∆OEC, we get
OA² = OF² + AF² …………….(1)
OB² = OD² + BD² ……………(2)
OC² = OE² + CE² ……………..(3)
Adding (1), (2) and (3), we get
OA² + OB² + OC² = OF² + AF² + OD² + BD² + OE² + CE² = AF² + BD² + CE²
⇒ OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
Hence Proved.

(ii) In right triangles ODB and ODC, we have
OB² = OD² + BD² …………….(4) [By Pythagoras theorem]
OC² = OD² + CD² ……………..(5)
Subtracting (5) from (4), we get
OB² – OC² = BD² – CD² ………….(6)
Similarly OC² – OA² = CE² – AE² ……………(7)
and OA² – OB² = AF² – BF² ……………(8)
Adding (6), (7) and (8), we get
OB² – OC² + OC² – OA² + OA² – OB² = BD² – CD² + CE² – AE² + AF² – BF²
⇒ 0 = BD² – CD² + CE² – AE² + AF² – BF²
⇒ AF² + BD² + CE² = AE² + CD² + BF²
Hence Proved.

Question 9.
A ladder 10 m long reaches a window 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
Solution :
Let AC be ladder and AB be wall and BC be the distance of the ladder from wall.

∴ AB = 8 m
AC = 10 m
In right ∆ABC, AC² = BC² + AB²
⇒ 10² = BC² + 8²
⇒ 100 = BC² + 64
⇒ BC² = 100 – 64
⇒ BC² = 36
⇒ BC = 6m.
Hence, distance of the foot of the ladder from base of the wall = 6m.

Question 10.
A guy wire attached to a vertical pole of height 18m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut ?
Solution :
Let AC be guy wire and AB be vertical pole and BC be distance of the stake from the base of the pole.
∴ AB = 18m, AC = 24m,
In right ∆ABC,
AC² = BC² + AB² [By Pythagoras theorem]
⇒ (24)² = BC² + (18)²
⇒ 576 = BC² + 324
⇒ BC² = 576 – 324

⇒ BC² = 252
⇒ BC = √252
⇒ BC = 6√7 m
Hence, distance of stake from the base of the pole = 6√7 m.

Question 11.
An aeroplane leaves an airport and flies due north at a speed of 1000 km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1\(\frac{1}{2}\)hours?
Solution:
Let point B represents the position of airport. Then distance covered by first plane in the north direction (AB) = Speed × Time
= 1000 × 1\(\frac{1}{2}\)
= 1000 × \(\frac{3}{2}\)
= 1500 km

and distance covered by second plane in the west direction (BC) = Speed × Time
= 1200 × \(\frac{1}{2}\)
= 1200 × \(\frac{3}{2}\) = 1800 km.

Now, in right ∆ABC,
AC² = BC² + AB²
[By Pythagoras theorem]
⇒ AC² = (1800)² + (1500)²
⇒ AC² = 3240000 + 2250000
⇒ AC² = 5490000
⇒ AC = \(\sqrt{5490000}\)
⇒ AC = 300√61 km
Hence, distance between two planes = 300√61 km.

Question 12.
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution:
Let AB and CD be two poles, BD be distance between the feet of two poles and AC be distance between their tops.
∴ AB = 11 m, BD = 12 m, CD = 6 m
∠B = ∠D = 90°
CE || BD
∠AEC = 90°, CE = 12m, AE = 11 – 6 = 5 m
Now, in right ∆AEC,
∴ AC² = CE² + AE² [By Pythagoras theorem]

⇒ AC² = 12² + 5²
⇒ AC² = 144 + 25
⇒ AC² = 169
⇒ AC = √169
⇒ AC = 13 m.
Hence, distance between tops of two poles = 13 m.

Question 13.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE².
Solution :
Given : A triangle ABC in which ∠C = 90°, D and E are points on the sides CA and CB respectively.
To Prove : AE² + BD² = AB² + DE²
Proof: In right ∆ACE,
AE² = AC² + CE² ………………(1)
[By Pythagoras theorem]
In right ∆DCB,
BD² = BC² + DC² ………………(2)
In right ∆ABC,
AB² = BC² + AC² ……………….(3)
In right ∆DCE,
DE² = EC² + CD² ………………..(4)
Adding (1) and (2), we get

AE² + BD² = AC² + BC² + CE² + CD²
AE² + BD² = AB² + DE² [Using (3) and (4)]
Hence Proved.

Question 14.
The perpendicular from A on side BC of a ∆ABC intersects BC at D such that DB = 3CD (see figure). Prove that 2AB² = 2AC² + BC².

Solution :
Given : A ∆ABC such that AD ⊥ BC and DB = 3CD
To Prove: 2AB² = 2AC² + BC²
Proof: DB = 3CD (given)
Now BC = DB + CD
⇒ BC = 3CD + CD [. DB = 3CD]
⇒ BC = 4CD
⇒ CD = \(\frac{1}{4}\)BC
⇒ and BD = 3CD = \(\frac{3}{4}\)BC
In right ∆ADB ,
AB² = BD² + AD² ………………..(1)
In right ∆ADC,
AC² = CD² + AD² …………………(2)
Subtracting (2) from (1), we get
AB² – AC² = BD² + AD² – CD² – AD²
⇒ AB² – AC² = (\(\frac{3}{4}\)BC)² – (\(\frac{1}{4}\)BC)²
[∵ BD = \(\frac{3}{4}\)BC and CD = \(\frac{1}{4}\)BC]
⇒ AB² – AC² = \(\frac{9}{16}\) BC² – \(\frac{9}{16}\) BC²
⇒ AB² – AC² = \(\frac{8}{16}\)BC²
⇒ AB² – AC² = \(\frac{1}{2}\)BC²
⇒ 2AB² – 2AC² = BC²
⇒ 2AB² = 2AC² + BC²
Hence Proved.

Question 15.
In an equilateral triangle ABC, D is a point on side BC such that BD = \(\frac{1}{3}\)BC. Prove that 9AD² = 7AB².
Solution :
Given : An equilateral ∆ABC such that BD = \(\frac{1}{3}\)BC.
To Prove: 9AD² = 7AB²
Construction : Draw AE ⊥ BC and Join AD.
Proof: Let each side of equilateral triangle be x units.

BD = \(\frac{1}{3}\)BC
⇒ BD = \(\frac{x}{3}\)
We know that in equi1ateral perpendicular bisects its corresponding opposite side
BE = EC = \(\frac{x}{2}\)
DE = BE – BD
DE = \(\frac{x}{2}\) – \(\frac{x}{3}\)
DE = \(\frac{x}{6}\)
In right ∆AED, AD² = AE² + DE² ……………..(1)
[By Pythagoras theorem]
In right ∆AEB, AB² = BE² + AE²
[By Pythagoras theorem]
AE² = AB² – BE²
Put AE² = AB² – BE² in (1), we get
AD² = 2 BE² + DE²
AD² = x² – (\(\frac{x}{2}\))² + (\(\frac{x}{6}\))²
⇒ AD² = x² – \(\frac{x^2}{4}+\frac{x^2}{36}\)
⇒ AD² = \(\frac{36 x^2-9 x^2+x^2}{36}\)
⇒ AD² = \(\frac{28 x^2}{36}\)
⇒ AD² = \(\frac{7}{9}\) x²
⇒ AD² = \(\frac{7}{9}\) AB²
⇒ 9AD² = 7AB²
Hence Proved.

Question 16.
In an equilateral triangle prove that three times the square of one side is equal to four times the square of one of its aftitudes.
Solution :
Given : A triangle ABC in which AB = BC = CA and AD ⊥ BC.
To Prove: 3AB² = 4AD²
Proof: In right ∆ADB and right ∆ADC.
AB = AC (Given)
∠ADB = ∠ADC (Each is 90°)

AD = AD (Common)
∴ ∆ADB ≅ ∆ADC (By RHS congruence criterion)
⇒ BD = CD (CPCT)
In right ∆ADB, AB² = AD² + BD² [By Pythagoras theorem]
⇒ AB² = AD² + (\(\frac{1}{2}\)AB)²
[∵ BD = CD
∴ BD = \(\frac{1}{2}\)AB]
⇒ AB² = 4AD² + \(\frac{1}{4}\)AB²
⇒ 4AB² = 4AD² + AB²
⇒ 3AB² = 4 AD²
Hence Proved.

Question 17.
Tick the correct answer and justify. In ∆ABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm. The angle B is :
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Solution :
In ∆ABC,
AC² = 12²
⇒ AC² = 144
BC² + AB² = (6)² + (6√3)²
⇒ BC² + AB² = 36 + 108
⇒ BC² + AB² = 144
∴ AC² = BC² + AB²

By converse of Pythagoras theorem,
∠B = 90°
Correct answer = (C)
Solution is also justified.

Haryana State Board HBSE 10th Class Maths Solutions Chapter 6 Triangles Ex 6.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 6 Triangles Ex 6.1

Question 1.
Fill in the blanks using the correct word given in the brackets :
(i) All circles are ……………… (congruent, similar)
(ii) All squares are …………….. (similar, congruent)
(iii) All triangles are similar (isosceles, equilateral)
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are ………………. and (b) their corresponding sides are ………………… (equal, proportional)
Solution:
(i) All circles are similar.
(ii) All squares are similar.
(iii) All equilateral triangles are similar.
(iv) Two polygons of the same number of sides are similar if (a) their corresponding angles are equal and (b) their corresponding sides are proportional.

Question 2.
Give two different examples of pair of :
(i) Similar figures
(ii) non-similar figures
Solution:
(i) (a) Pair of equilateral triangles are similar figures.
(b) Pair of circles are similar figures.

(ii) (a) A pair of a triangle and a square are non-similar figures.
(b) A pair of a square and a rectangle are non-similar figures.

Question 3.
State whether the following quadrilaterals are similar or not.

Solution:
The two quadrilaterals PQRS and ABCD are not similar because their corresponding angles are not equal.

Haryana State Board HBSE 10th Class Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.4 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.4

Question 1.
Which term of the AP: 121, 117, 113, ……………… is its first negative term?
Solution:
The given sequence of AP is 121, 117, 113, ……………
Here a = 121
d = a₂ – a₁
= 117 – 121 = – 4
Let nth term of AP be the first negative term,
a_n = a + (n – 1)d < 0
a + (n – 1)d < 0
= 121 + (n – 1) × (- 4) < 0
= 121 – 4n + 4 < 0
125 – 4n < 0
125 < 4n 4n > 125
⇒ n > \(\frac{125}{4}\)
⇒ n > 31.26
Hence, 32th term of the AP is the first negative term.

Question 2.
The sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.
Solution :
Let a be the first term and d be the common difference of AP. Then,
According to question :
a₃ + a₇ = 6
⇒ a + (3 – 1)d + a + (7 – 1)d = 6
⇒ a + 2d + a + 6d = 6
⇒ 2a + 8d = 6
⇒ a + 4d = 3
⇒ a = 3 – 4d ……………..(1)
And a₃ × a₇ = 8
⇒ (a + 2d)(a + 6d) = 8
⇒(3 – 4d+ 2d)(3 – 4d + 6d) = 8
[From equation (1) put a = 3 – 4d]
⇒ (3 – 2d) (3 + 2d) = 8
⇒ 9 – 4d² = 8
⇒ 4d² = 9 – 8
⇒ 4d² = 1
⇒ d² = \(\frac{1}{4}\)
d = ± \(\frac{1}{2}\)

Case I:
If d = \(\frac{1}{2}\)
Putting the value of d in equation (1), we get
a = 3 – 4 × \(\frac{1}{2}\)
a = 3 – 2 = 1
a = 1
Now S₁₆ = \(\frac{16}{2}\) [2 × 1 + (16 – 1) × \(\frac{1}{2}\)]
S₁₆ = 8[2 + \(\frac{15}{2}\)]
S₁₆ = 8 × \(\frac{19}{2}\)
⇒ S₁₆ = 76.

Case II:
If d = – \(\frac{1}{2}\)
Putting the value of d in equation (1), we get
a = 3 – 4 × (- \(\frac{1}{2}\))
⇒ a = 3 + 2 = 5
Now, S₁₆ = \(\frac{16}{2}\) [2 × 5 + (16 – 1) ×(- \(\frac{1}{2}\))]
⇒ S₁₆ = 8 [10 – \(\frac{15}{2}\)]
S₁₆ = 8 × \(\frac{5}{2}\)
⇒ S₁₆ = 20
Hence, S₁₆ = 76 or S₁₆ = 20.

Question 3.
A ladder has rungs 25 cm apart (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and the bottom rungs are 2 \(\frac{1}{2}\) m apart, what is the length of the wood required for the rungs?

Solution:
We have,
Gap between two consecutive rungs = 25 cm
Distance between bottom and top rungs = 2\(\frac{1}{2}\) m = 250 cm
Number of rungs = \(\frac{250}{25}\) + 1 = 11
Since, rungs are decreasing uniformly in length from 45 cm at the bottom to 25 cm at the top.
Therefore, the lengths of rungs form an AP in which a = 45, a₁₁ = 25
Required length of wood for rungs = S₁₁
= \(\frac{11}{2}\) (45 + 25)
[∵ S_n = \(\frac{n}{2}\) (a + l)]
= \(\frac{11}{2}\) × 70
= 385 cm
or = 3.85 m
Hence, required length of wood for rungs = 3.85 m.

Question 4.
The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to sum of numbers of the houses following it. Find this value of x.
Solution:
Let there be a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the num¬bers of the houses following it i.e. :
House No. 1, 2, 3, …………….., (x – 1), x, (x + 1), ……………, 49.
Now, S_{x – 1} = S₄₉ – S_x

x² = 1225
x = √ 1225
x = ± 35.
Since, x can’t be negative. Therefore, x = 35.

Question 5.
A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of \(\frac{1}{4}\) m and a tread of \(\frac{1}{2}\) m (see figure). Calculate the total volume of concrete required to build the terrace.

Solution:
We have, Length and breadth of each step are 50 m and \(\frac{1}{2}\) m respectively.
Height of first step = \(\frac{1}{4}\) m
Height of second step = \(\frac{1}{4}+\frac{1}{4}=\frac{2}{4}\) m
Height of third step = \(\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=\frac{3}{4}\) m
and so on.
Volume of concrete to build the first step = 50 × \(\frac{1}{2} \times \frac{1}{4}=\frac{25}{4}\) m³
[∵ Volume of cuboidal step = L × B × H]
Volume of concrete to build the second step = 50 × \(\frac{1}{2} \times \frac{1}{4}=\frac{50}{4}\) = m³
Volume of concrete to build the third step = 50 × \(\frac{1}{2} \times \frac{3}{4}=\frac{75}{4}\) m³
and so on.
The sequence of volume of concrete 0f steps are: \(\frac{25}{4}, \frac{50}{4}, \frac{75}{4}, \ldots\)
a₂ – a₁ = \(\frac{50}{4}-\frac{25}{4}=\frac{25}{4}\)
a₃ – a₂ = \(\frac{75}{4}-\frac{50}{4}=\frac{25}{4}\)
∵ a₂ – a₁ = a₃ – a₂
∴ The sequence forms an AP in which a = \(\frac{25}{4}\) and d = \(\frac{25}{4}\).
Now, total volume of concrete = Sum of volumes of concrete ta build 15 steps
= S₁₅
= \(\frac{15}{2}\left[2 \times \frac{25}{4}+(15-1) \times \frac{25}{4}\right]\)
= \(\frac{15}{2}\left[\frac{25}{2}+14 \times \frac{25}{4}\right]\)
= \(\frac{15}{2}\left[\frac{25}{2}+\frac{175}{2}\right]\)
= \(\frac{15}{2} \times \frac{200}{2}\)
= 15 × 50
= 750 m³
Hence, the total volume of concrete = 750 m³.

Haryana State Board HBSE 10th Class Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.3 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.3

Question 1.
Find the sum of the following APs :
(i) 2, 7, 12, ………….., to 10 terms.
(ii) – 37, – 33, – 29, ………….., to 12 terms.
(iii) 0.6, 1.7, 2.8, …………., to 100 terms.
(iv) \(\frac{1}{15}, \frac{1}{12}, \frac{1}{10}, \ldots\) to 11 terms.
Solution :
(i) The given sequence of AP is : 2, 7, 12, …………….., to 10 terms
Here, a = 2
d = a₂ – a₁
=7 – 2 = 5 and n = 10
We know that
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
⇒ S₁₀ = \(\frac{10}{2}\) [2 × 2 + (10 – 1) × 5]
⇒ S₁₀ = 5[4 + 9 × 5]
⇒ S₁₀ = 5 [4 + 45]
⇒ S₁₀ = 5 × 49 = 245
Hence, the sum of 10 terms of given AP = 245.

(ii) The given sequence of AP is : – 37, – 33, – 29, …………., to 12 terms
Here, a = – 37
d = a₂ – a₁
= – 33 – (- 37)
= – 33 + 37 = 4
and n = 12
We know that
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
⇒ S₁₂ = \(\frac{n}{2}\) [2 × (- 37) + (12 – 1) × 4]
⇒ S₁₂ = 6[- 74 + 11 × 4]
⇒ S₁₂ = 6[- 74 + 44]
⇒ S₁₂ = 6 × (- 30) = – 180
Hence, the sum of 12 terms of given AP = – 180.

(iii) The given sequence of AP is : 0.6, 1.7, 2.8, …………., to 100 terms.
Here, a = 0.6
d = a₂ – a₁
= 1.7 – 0.6 = 1.1 and n = 100
We know that
S_n = \(\frac{n}{2}\) [2a + (n – l)d]
⇒ S₁₀₀ = \(\frac{100}{2}\) [2 × 0.6 + (100 – 1) × 1.1]
⇒ S₁₀₀ = 50 [1.2 + 99 × 1.1]
⇒ S₁₀₀ = 50[1.2 + 108.9]
⇒ S₁₀₀ = 50 × 110.1 = 5505
Hence, the sum of 100 terms of given AP = 5505.

(iv) The given sequence of AP is : \(\frac{1}{15}, \frac{1}{12}, \frac{1}{10}, \ldots\) to 11 terms

Hence, the sum of 11 terms of given AP = \(\frac{33}{20}\).

Question 2.
Find the sum of the following APs given below :
(i) 7 + 10\(\frac{1}{2}\) + 14 + …………. + 84
(ii) 34 + 32 + 30 + …………. + 10
(iii) – 5 + (- 8) + (- 11) + …………. + (- 230)
Solution:
(i)Wehave, 7 + 10\(\frac{1}{2}\) + 14 + …………. + 84
It is an AP.
Here, a = 7
d = a₂ – a₁
d = 10\(\frac{1}{2}\) – 1
d = \(\frac{21-14}{2}\) = \(\frac{7}{2}\)
and l = a_n = 84
⇒ a + (n – 1)d = 84
⇒ 7 + (n – 1) × \(\frac{7}{2}\) = 84
\(\frac{7}{2}\) n – \(\frac{7}{2}\) = 84 – 7
\(\frac{7}{2}\) n – \(\frac{7}{2}\) = 77
\(\frac{7}{2}\) n = 77 + \(\frac{7}{2}\)
\(\frac{7}{2}\) n = \(\frac{154+77}{2}\)
⇒ n = \(\frac{161}{7}\) = 23
We know that
S_n = \(\frac{n}{2}\) [a + l]
S_n = \(\frac{23}{2}\) [7 + 84]
S₂₃ = \(\frac{23}{2}\) × 91
S₂₃ = 1046\(\frac{1}{2}\)
Hence, S₂₃ = 1046\(\frac{1}{2}\)

(ii) We have, 34 + 32 + 30 + …………….. + 10.
It is an AP.
Here, a = 34
d = a₂ – a₁
= 32 – 34 = – 2 and
l = a_n = 10
⇒ a + ( n – 1 )d = 10
⇒ 34 + (n – 1) × (- 2) = 10
⇒ – 2n + 2 = 10 – 34
⇒ – 2n + 2 = – 24
⇒ – 2n = – 24 – 2
⇒ – 2n = – 26
⇒ n = \(\frac{-26}{-2}\) = 13
We know that
S_n = \(\frac{n}{2}\) [a + l]
S₁₃ = \(\frac{13}{2}\) [34 + 10]
= \(\frac{13}{2}\) × 44
S₁₃ = 286
Hence S₁₃ = 286.

(ill) Wehave, – 5 + (- 8) + (- 11) + …………… + (- 230)
It is an AP.
Here, a = – 5
d = a₂ – a₁
= (- 8) – (- 5)
and l = a_n = – 230
⇒ a + (n – 1) d = – 230
⇒ – 5 + (n – 1) × (- 3) = – 230
⇒ – 3n + 3 = – 230 + 5
⇒ – 3n + 3 = – 225
⇒ – 3n = – 225 – 3
⇒ – 3n = – 228
⇒ n = \(\frac{-228}{-3}\) = 76
We know that S_n = \(\frac{n}{2}\) [a + l]
S₇₆ = \(\frac{76}{2}\) [- 5 – 230] = 38 × (- 235)
S₇₆ = – 8930
Hence, S₇₆ = – 8930.

Question 3.
In an AP :
(i) given a = 5, d = 3, a_n = 50, find n and S_n.
(ii) given a = 7, a₁₃ = 35, find d and S₁₃.
(iii) given a₁₂ = 37, d = 3, find a and S₁₂.
(iv) given a₃ = 15, S₁₀ = 125, find d and a₁₀.
(v) given d = 5, S₉ = 75, find a and a₉.
(vi) given a = 2, d = 8, S_n = 90, find n and a_n.
(vii) given a = 8, a_n = 62, S_n = 210, find n and d.
(viii) given a_n = 4, d = 2, S_n = – 14, find n and a.
(ix) given a = 3, n = 8, S_n = 192, find d.
(x) given l = 28, S_n = 144, and there are total 9 terms. Find a.
Solution :
(i) We have, a = 5, d = 3, a_n = 50
We know that
a + (n – l)d = a_n
⇒ 5 + (n – 1) × 3 = 50
⇒ 5 + 3n – 3 = 50
⇒ 2 + 3n – 50
⇒ 3n = 50 – 2 = 48
⇒ n = \(\frac{48}{3}\) = 16
We know that
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₁₆ = \(\frac{16}{2}\) [2 × 5 + (16 – 1) × 3]
S₁₆ = 8 [10 + 15 × 3]
= 8 [10 + 45]
S₁₆ = 8 × 55 = 440
Hence, n = 16, S₁₆ = 440.

(ii) We have, a = 7, a₁₃ = 35
We know that
a + (n – 1) d = a_n
7 + (13 – 1) d = 35
7 + 12d = 35
12d = 35 – 7 = 28
d = \(\frac{28}{12}=\frac{7}{3}\)
We know that
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
[ l = a₁₃ = 35]
S₁₃ = \(\frac{13}{2}\) [7 + 35]
= \(\frac{13}{2}\) × 42 = 273
Hence d = \(\frac{7}{3}\), S₁₃ = 273.

(iii) We have, d = 3, a₁₂ = 37
We know that
a + (n – 1 )d = a_n
⇒ o + (12 – 1) × 3 = 37
⇒ a + 11 × 3 = 37
⇒ a + 33 = 37
⇒ a = 37 – 33 = 4
We know that
S_n = \(\frac{n}{2}\) [a + l]
S₁₂ = \(\frac{12}{2}\) [4 + 37] = 6 × 41
[∵ l = a₁₂ = 37]
S₁₂ = 246.
Hence, a = 4, a₁₂ = 246.

(iv) We have, a₃ = 15, S₁₀ = 126
Now, a₃ – 15
a + (3 – 1) d = 15
[∵ a_n = a + (n – 1)d]
a + 2d = 15 ……………(1)
and S₁₀ = 125
\(\frac{n}{2}\) [2a + (10- 1)d] = 125
[∵ S_n = \(\frac{n}{2}\) (2a +(n – 1)d)]
5 [2a + 9d] = 125
2a + 9d = \(\frac{125}{5}\)
2a + 9d = 25 ………………(2)
Multiplying equation (1) by 2 and subtracting (2) from it, we get

Putting the value of d in equation (1), we get
a + 2 × (- 1) = 16
a – 2 = 15
a = 15 + 2
a = 17
Now, a₁₀ = 17 + (10 – 1) × (- 1)
a₁₀ = 17 + 9 × (- 1)
a₁₀ = 17 – 9
a₁₀ = 8
Hence, d = – 1 and a₁₀ = 8.

(v) We have, d = 5, S₉ = 75
⇒ \(\frac{9}{2}\) [2a + (9 – 1) × 5] = 75
[∵ S_n = \(\frac{n}{2}\) [2a + (n – 1)d]]
⇒ \(\frac{9}{2}\) [2a + 8 × 5] = 75

(vi) We have, a = 2, d = 8, S_n = 90
⇒ \(\frac{n}{2}\) [2a + (n – 1) d] = 90
[∵ S_n = \(\frac{n}{2}\) [2a + (n – 1)d]]
\(\frac{n}{2}\) [2 × 2 + (n – 1)d] = 90
[∵ S_n = \(\frac{n}{2}\) [2a + (n – 1)d]]
⇒ \(\frac{n}{2}\) [2 × 2 + (n – 1) × 8] =90
⇒ \(\frac{n}{2}\) [4 + 8n – 8] = 90
⇒ \(\frac{n}{2}\) [8n – 4] = 90 × 2
⇒ 8n² – 4n = 180
⇒ 2n² – n = 45
⇒ 2n² – n – 45 = 0
⇒ 2n² – (10 – 9)n – 45 = 0
⇒ 2n² – 10n + 9n – 45 =0
⇒ 2n(n – 5) + 9(n – 5) = 0
[∵ 2 × – 45 = – 90
10 × – 9 = – 90
10 – 9 = 1]
⇒ (n – 5) (2n + 9) = 0
n – 5 = 0 or 2n + 9 = 0
n = 5 or n = – \(\frac{9}{2}\)
Reject n = – \(\frac{9}{2}\) [∵ n ≠ – \(\frac{9}{2}\)]
So, n = 5
Now, a_n = a + (n – 1)d
⇒ a₅ = 2 + (5 – 1) × 8
⇒ a₅ = 2 + 4 × 8
⇒ a₅ = 2 + 32
⇒ a₅ = 34
Hence, n = 5 and a₅ = 34.

(vii) We have, a = 8, a_n = 62, S_n = 210
Now, S_n = 210
\(\frac{9}{2}\) [a + l] = 210
\(\frac{9}{2}\) [8 + 62] = 210 [∵ l = a_n = 62]
\(\frac{n}{2}\) × 70 = 210
35n = 210
n = \(\frac{210}{35}\) = 6
Now, a_n = 62
⇒ 8 + (6 – 1) d = 62
⇒ [a_n = a + (n – 1)d]
⇒ 8 + 5d = 62
⇒ 5d = 62 – 8
⇒ 5d = 54
⇒ d = – \(\frac{54}{5}\)
Hence, n = 6, d = \(\frac{54}{5}\).

(viii) We have, d = 2, S_n = – 14, a_n = 4
⇒ a + (n – 1) × 2 = 4[∵ a_n = a + (n – 1) d]
⇒ a + 2n – 2 = 4
⇒ a + 2n = 4 + 2
⇒ a + 2n = 6
⇒ a = 6 – 2n ……………….(i)
Now, S_n = – 14
⇒ \(\frac{n}{2}\) [a + l] = – 14
⇒ n[6 – 2n + 4] = – 14 × 2
[From (1) Put a = 6 – 2n]
⇒ n [10 – 2n] = – 28 [∵ l = a_n = 4]
⇒ 10n – 2n² = – 28
⇒ 2n² – 10n – 28 = 0
⇒ n² – 5n – 14 = 0
⇒ n² – (7 – 2)n – 14 = 0
⇒ n² – 7n + 2n – 14 = 0
[∵ 1 × – 14 = – 14
7 × – 2 = – 14
7 – 2 = 5]
⇒ n(n – 7) + 2(n – 7) = 0
⇒ (n – 7)(n + 2) = 0
⇒ n – 7 = 0 or n + 2 = 0
⇒ n = 7 or n = – 2
Reject n = – 2 [∵ n ≠ – 2]
So, n = 7
Substituting the value of n in equation (1), we
a = 6 – 2 × 7
⇒ a = 6 – 14
⇒ a = – 8.
Hence, n = 7, a = – 8.

(ix) We have, a = 3, n = 8, S_n = 192
i.e. S₈ = 192
⇒ \(\frac{8}{2}\) [2 × 3 + (8 – 1) d] = 192
[∵ S_n = \(\frac{n}{2}\) (2a + (n – 1) d)]
⇒ 4 [6 + 7d] = 192
⇒ 6 + 7d = 48
⇒ 7d = 48 – 6
⇒ 7d = 42
⇒ d = \(\frac{42}{7}\) = 6
Hence, d = 6.

(x) We have, n = 9, l = 28, S_n = 144
\(\frac{n}{2}\) [a + l] = 144
\(\frac{9}{2}\) [a + 28] = 144
a + 28 = \(\frac{144 \times 2}{9}\)
a + 28 = 32
a = 32 – 28 = 4
Hence, a = 4.

Question 4.
How many terms of the AP: 9, 17, 25, ………. must be taken to give a sum of 636?
Solution:
The given sequence of AP is: 9, 17, 25, ………….
Here, a = 9
d = a₂ – a₁
= 17 – 9 = 8
and S_n = 636 (Given)
\(\frac{n}{2}\) [2a + (n – 1)d] = 636
\(\frac{n}{2}\) [2 × 9 + (n – 1) × 8] = 636
n [18 + 8n – 8] = 636 × 2
n [10 + 8n] = 1272
10n + 8n² = 1272
8n² + 10n – 1272 = 0
4n² + 5n – 636 = 0
4n² + (53 – 48)n – 636 = 0
[∵ – 636 × 4 = – 2544
53 × – 48 = – 2544
53 – 48 = 5]
4n² + 53n – 48n – 636 = 0
n(4n + 53) – 12(4n + 53) = 0
(4n + 53)(n – 12) = 0
4n + 53 = 0 or n – 12 = 0
n = – \(\frac{53}{4}\) or n = 12
Reject, n = – \(\frac{53}{4}\)
[∵ n cannot be fraction]
So, n = 12.
Hence, 12 terms of the given AP must be taken to give a sum of 636.

Question 5.
The first term of an AP is 5, the last term 1845 and the sum is 400. Find the number of terms and the common difference.
Solution :
We have, a = 5, l = a_n = 45, S_n = 400
\(\frac{n}{2}\) [a + l] = 400
\(\frac{n}{2}\) [15 + 45] = 400
n × 50 = 400 × 2
50n = 800
n = \(\frac{800}{50}\)
n = 16
Now, a_n = 45
a + (n – 1) d = 45
5 + (16 – 1)d = 45
5 + 15d = 45
15d = 45 – 5
15d = 40
d = \(\frac{40}{15}\)
d = \(\frac{8}{3}\)
Hence, n = 16, d = \(\frac{8}{3}\).

Question 6.
The first and last terms of an AP are 17 and 350 respectively. 1f the common difference is 9, how many terms are there and what is their sum?
Solution:
We have, a = 17, d = 9, l = a_n = 350
a + (n – 1)d = 350
17 + (n – 1)9 = 350
17 + 9n – 9 = 350
8 + 9n = 350
9n = 350 -8
9n = 342
n = \(\frac{342}{9}\) = 38
Now, S_n = \(\frac{n}{2}\) [a + l]
S₃₈ = \(\frac{38}{2}\) [17 + 350]
S₃₈ = 19 × 367
S₃₈ = 6973
Hence, the number of terms = 38
and their sum = 6973.

Question 7.
Find the sum of first 22 terms of an AP in which d = 7 and 22nd term is 149.
Solution :
We have, d = 7, n = 22, a₂₂ = 149
a + (22 – 1) × 7 = 149
[∵ a_n = a + (n – 1)d]
a + 21 × 7 = 149
a + 147 = 149
a = 149 – 147
a = 2
Now, S_n = \(\frac{n}{2}\) [a + l]
S₂₂ = \(\frac{22}{2}\) [2 + 149]
[∵ l = a_n = 149]
S₂₂ = 11 × 151
S₂₂ = 1661
Hence, S₂₂ = 1661.

Question 8.
Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.
Solution :
We have, n = 51, a₂ = 14, a₃ = 18
d = a₂ – a₁
⇒ d = 18 – 14
d = 4
Therefore, a₃ = a – d
= 14 – 4 = 10
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₅₁ = \(\frac{51}{2}\) [2 × 10 + (51 – 1) × 4]
S₅₁ = \(\frac{51}{2}\) [20 + 50 × 4]
⇒ S₅₁ = \(\frac{51}{2}\) [20 + 200]
⇒ S₅₁ = \(\frac{51}{2}\) [220]
⇒ S₅₁ = 51 × 110
⇒ S₅₁ = 5610
Hence, S₅₁ = 5610.

Question 9.
If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289. Find the sum of first n terms.
Solution :
We have, S₇ = 49
⇒ \(\frac{7}{2}\) [2a + (7 – 1)5] = 49
[∵ S_n = \(\frac{n}{2}\) [2a + (n – 1)d]]
2a + 6d = \(\frac{49 \times 2}{7}\)
2a + 6d = 14
a + 35 = 7 ……………..(1)
S₁₇ = 289
\(\frac{17}{2}\) [2a + (17 – 1) 5] = 289
2a + 16d = \(\frac{289 \times 2}{17}\)
2a + 16d = 34
a + 8d = 17
Subtracting equation (2) from equation (1), we get

Putting the value of 5 in equation (1), we get
a + 3 × 2 = 7
⇒ a + 6 = 7
⇒ a = 7 – 6
⇒ a = 1
Now, S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
⇒ S_n = \(\frac{n}{2}\) [2 x 1 + (n – 1) x 2]
⇒ S_n = \(\frac{n}{2}\) [2 + 2n – 2]
⇒ S_n = \(\frac{n}{2}\) [2n]
⇒ S_n = n²
Hence S_n = n².

Question 10.
Show that a₁, a₂, …………., a_n form an AP, where a_n is defined as below :
(i) a_n = 3 + 4n
(ii) a_n = 9 – 5n.
Also find the sum of the first 15 terms in each case.
Solution :
(i) We have, a_n = 3 + 4n
Putting n = 1, 2, 3, 4,…………. in this equation, we get
a₁ = 3 + 4 × 1
⇒ a₁ = 7
a₂ = 3 + 4 × 2
⇒ a₂ = 3 + 8
⇒ a = 11
a₃ = 3 + 4 × 3
⇒ a₃ = 3 + 12
a₃ = 15
a₄ = 3 + 4 × 4
⇒ a₄ = 3 + 16
⇒ a₄ = 19 …………… and so on.
Therefore, the sequence is : 7, 11, 15, 19, …………..
a₂ – a₁ = 11 – 7 = 4
a₃ – a₂ = 15 – 11 = 4
a₄ – a₃ = 19 – 15 = 4
∵ a₂ – a₁ = a₃ – a₂ = a₄ – a₃
The given sequence forms an AP Proved.
Here a = 7, d = a₂ – a₁ = 11 – 7 = 4, n = 15
Now, S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
⇒ S₁₅ = \(\frac{15}{2}\) [2 × 7 + (15 – 1)
⇒ S₁₅ = \(\frac{15}{2}\) [14 + 14 × 4]
⇒ S₁₅ = \(\frac{15}{2}\) [14 + 56]
⇒ S₁₅ = \(\frac{15}{2}\) × 70
S₁₅ = 15 × 35
S₁₅ = 525
Hence, S₁₅ = 525.

(ii) We have, a_n = 9 – 5n
Putting n = 1, 2, 3, 4, …………. in this equation,
a₁ = 9 – 5 × 1
a₁ = 9 – 5
⇒ a₁ = 4
a₂ = 9 – 5 × 2
⇒ a₂ = 9 – 10
⇒ a₂ = -1
a₃ = 9 – 5 × 3
⇒ a₃ = 9 – 15
a₃ = – 6
a₄ = 9 – 5 × 4
⇒ a₄ = 9 – 20
⇒ a₄ = – 11
Therefore, the sequence is : 4, – 1, – 6, – 11,…………..
a₂ – a₁ = -1 – 4 = – 5
a₃ – a₂ = – 6 – (- 1)
= – 6 + 1 = – 5
a₄ – a₃ = – 11 – (- 6)
= – 11 + 6 = – 5
∵ a₂ – a₁ = a₃ – a₂ = a₄ – a₃
∴ The given sequence forms an AP. Proved
Here, a = 4, d = a₂ – a₂ = – 1 – 4 = – 5, n = 15
Now, S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
⇒ S₁₅ = \(\frac{15}{2}\) [2 × 4 + (15 – 1) (- 15)]
⇒ S₁₅ = \(\frac{15}{2}\) [8 + 14 × (- 5)]
⇒ S₁₅ = \(\frac{15}{2}\) [8 – 70]
⇒ S₁₅ = \(\frac{15}{2}\) × (- 62)
⇒ S₁₅ = 15 × (- 31)
⇒ S₁₅ = – 465
Hence, S₁₅ = – 465.

Question 11.
If the sum of the first n terms of an AP is 4n – n², what is the first term (i.e., S4)? What is the sum of first two terms? What is the second term? Similarly, find the 3rd, the 10th and 71th terms.
Solution :
We have, S_n = 4n – n²
Putting n = 1, We get
S₁ = 4 × 1 – (1)²
⇒ S₁ = 4 – 1
⇒ S₁ = 3
⇒ a₁ = 3
Putting n = 2, we get
S₂ = 4 × 2 – (2)²
⇒ S₂ = 8 – 4
⇒ S₂ = 4
⇒ a₄ + a₂ = 4
⇒ 3 + a₂ = 4
⇒ a₂ = 4 – 3
⇒ a₂ = 1
Now, d = a₂ – a₁
= 1 – 3 = – 2
a₃ = 3 + (3 – 1) × (- 2)
[∵ a_n = a + (n – 1)d]
a₃ = 3 + 2 × (- 2)
a₃ = 3 – 4
a₃ = – 1
a₁₀ = 3 + (10 – 1) × (- 2)
a₁₀ = 3 + 9 × (- 2)
a₁₀ = 3 – 18 = -15
And a_n = 3 + (n – 1) × (- 2)
a_n = 3 – 2n + 2
a_n = 5 – 2n
Hence a₁ = 3, S₂ = 4, a₂ = 1, a₃ = – 1, a₁₀ = – 15, a_n = 56 – 2n.

Question 12.
Find the sum of the first 40 positive integers divisible by 6.
Solution:
The first 40 positive integers divisible by 6 are : 6, 12, 18, 24, …, 240.
Since, each number is divisible by 6.
So it is an AP in which
a = 6,
d = a₂ – a₁
= 12 – 6 = 6,
n = 40 and l = 240
Now, S₄₀ = [16 + 240]
[∵ S_n = (a + l)]
S₄₀ = 20 × 246
S₄₀ = 4920
Hence, the sum of the first 40 positive integers divisible by 6 = 4920.

Question 13.
Find the sum of the first 15 multiples of 8.
Solution :
The first 15 multiples of 8 are 8, 16, 24, 32, …, 120.
Since each number is multiple of 8, So, it is an AP in which
a = 8,d = a₂ – a₁ = 16 – 8 = 8, n = 5 and l = 120
Now, S₁₅ – a₁ = \(\frac{15}{2}\) [8 + 120]
[∵ S_n = \(\frac{n}{2}\) (a + l)]
S₁₅ = \(\frac{15}{2}\) × 128
S₁₅ = 15 × 64
S₁₅ = 960
Hence, the sum of the first 15 multiples of 8 = 960.

Question 14.
Find the sum of the odd numbers between 0 and 50.
Solution :
The odd numbers between 0 and 50 are : 1, 3, 5, 7, ………….., 49.
Since, difference between each two consecutive odd numbers is 2. So it is an AP.
In which a = 1, d = a₂ – a₁ = 3 – 1 = 2, l = a_n =49
a + (n – 1)d = 49[∵ a + (n – 1) d = a_n]
1 + (n – 1) × 2 = 49
1 + 2n – 2 = 49
2n – 1 = 49
2n = 49 + 1
2n = 50
n = \(\frac{50}{2}\)
n = 25
Now, S_n = \(\frac{n}{2}\) [a + l]
S₂₅ = \(\frac{25}{2}\) [1 + 49]
S₂₅ = \(\frac{25}{2}\) × 50
S₂₅ = 25 × 25
S₂₅ = 625
Hence, the sum of odd numbers between 0 and 50 = 625.

Question 15.
A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: ₹ 200 for the first day, ₹ 250 for the second day, ₹ 300 for the third day, etc …, the penalty for each succeeding day being ₹ 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by 30 days?
Solution :
We have,
Penalty for the first day = ₹ 200
Penalty for the second day = ₹ 250
Penalty for the third day = ₹ 300
So, the sequence of penalty is :200, 250, 300, …………..
Here, a = 200
The penalty for each succeeding day is ₹ 50
more than for each the preceding day.
So, d = 250 – 200 = 50
and n = 30
Now, S₃₀ = \(\frac{30}{2}\) [2 × 200 + (30 – 1) x50]
[∵ S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₃₀ = 15[400 + 29 × 50]
S₃₀ = 15 [400 + 1450]
S₃₀ =15 × 1850
S₃₀ = 27750
Hence, the penalty paid for 30 days = ₹ 27750.

Question 16.
A sum of ₹ 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is ₹ 20 less than its preceding prize, find the value of each of the prizes.
Solution :
Let Ist Prize be ₹ a
Then 2nd prize = ₹ (a – 20)
3rd prize = ₹ (a – 20 – 20) = (a – 40)
Thus, the seven prize are a,
(a – 20), (a – 40), …………….., (a – 120)
Since, each prize is Rs. 20 less than its pre ceding prize. So it is an AP.
Here first term (a) = a
Common difference (d)
= a₂ – a₁
= a – 20 – a = – 20
Number of prizes (n)= 7 and
a_n = l = a – 120
Sum of prizes (S_n) = 700
Now, S₇ = 700
⇒ l [a + a – 120] = 700
[∵ S_n = \(\frac{n}{2}\) [a + l]
[2a – 120] = \(\frac{700 \times 2}{7}\)
⇒ 2a – 120 = 200
⇒ 2a = 200 + 120 = 320
⇒ a = \(\frac{320}{2}\)
⇒ a = 160
So, given prizes are 160, 160 – 20, 160 – 40, 160 – 60, 160 – 80, 160 – 100, 160 – 120,
i.e. 160, 140, 120, 100, 80, 60, 40.
Hence, seven prizes are ₹ 160, ₹ 140, ₹ 120, ₹ 100, ₹ 80, ₹ 60, ₹ 40.

Question 17.
In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g. a section of class I will plant 1 tree, a section of class II will plant 2 trees and so on till class XII. There are three sections of each class. How many trees will be planted by the students?
Solution :
Trees planted by three sections of class I = 3 × 1 = 3
Trees planted by three sections of Class II = 3 × 2 = 6
Trees planted by three sections of Class III = 3× 3 = 9
Trees planted by three sections of class IV = 3 × 4 = 12
Trees planted by three section of class XII = 3 × 12 = 36
. .
. .
. .
. .
. .
∴ The sequence of trees is : 3, 6, 9, 12, …, 36
a₂ – a₁ = 6 – 3 = 3
a₃ – a₂ = 9 – 6 = 3
a₄ – a₃ = 1293
∵ a₂ – a₁ = a₃ – a₂ = a₄ – a₃
The given sequence of trees forms an AP.
Here a = 3, d = a₂ – a₁ = 6 – 3 = 3,
a_n = l = 36, n = 12
Total number of trees will be planted = S_n
= \(\frac{n}{2}\) [a + l]
= \(\frac{12}{2}\) [3 + 36]
= 6 × 39 = 234
Hence, the total number of trees will be planted = 234.

Question 18.
A spiral is made up of succes¬sive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm … as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take π = \(\frac{22}{7}\))

Solution:
Let l₁, l₂, l₃, l₄, ……………….., l₁₃ be the lengths (Circumferences) of semicircles of radii r₁ = 0.5 cm, r₂ = 1.0 cm, r₃ = 1.5 cm, r₄ = 2.0 cm,… respectively.
Then
l₁ = πr₁
= π × 0.5
= \(\frac{\pi}{2} \mathrm{~cm}=\frac{22}{14} \mathrm{~cm}=\frac{11}{7}\) cm

l₂ = πr₂
= π × 1.0
= π cm = \(\frac{22}{7}\) cm

l₃ = πr₃
= π × 1.5
= 1.5π cm = 1.5 × \(\frac{22}{7}\) = \(\frac{33}{7}\) cm

l₄ = πr₄
= π × 2.0
= 2π cm = \(\frac{44}{7}\) cm
. .
. .
. .
. .
. .
l₁₃ = πr₁₃
= π × 6.5
= 6.5π = 6.5 × \(\frac{22}{7}\)
= \(\frac{143}{7}\)
The sequence of length of spiral is \(\frac{11}{7}, \frac{22}{7}, \frac{33}{7}, \frac{44}{7}, \ldots, \frac{143}{7}\).
a₂ – a₁ = \(\frac{22}{7}-\frac{11}{7}=\frac{11}{7}\)
a₃ – a₂ = \(\frac{33}{7}-\frac{22}{7}=\frac{11}{7}\)
a₄ – a₃ = \(\frac{44}{7}-\frac{33}{7}=\frac{11}{7}\)
∵ a₂ – a₁ = a₃ – a₂ = a₄ – a₃ =
The sequence of length of spiral forms an
Here a = \(\frac{11}{7}\)
d = a₂ – a₁
= \(\frac{22}{7}-\frac{11}{7}=\frac{11}{7}\)
l = \(\frac{143}{7}\),
and n = 13
Now, the length of such a spiral made up of thirteen consecutive semicircles = S₁₃
S₁₃ = \(\frac{13}{2}\left[\frac{11}{7}+\frac{143}{7}\right]\)
[∵ S_n = \(\frac{n}{2}\) [a + l]]
⇒ S₁₃ = \(\frac{13}{2}\left[\frac{154}{7}\right]\)
⇒ S₁₃ = \(\frac{13}{2}\) × 22
⇒ S₁₃ = 13 × 11
⇒ S₁₃ = 143.
Hence, the length of a spiral made up of thir¬teen consecutive semicircles = 143 cm.

Question 19.
200 logs are stacked in the following manner : 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on (see in figure). In how many rows are the 200 logs placed and how many logs are in the top row?

Solution :
Sequence of logs row-wise is as follows :
20, 19, 18, 17, ………………
a₂ – a₁ = 19 – 20 = – 1
a₃ – a₂ = 18 – 19 = – 1
a₄ – a₃ = 17 – 18 = – 1
∵ a₂ – a₁ = a₃ – a₂ = a₄ – a₃
∴ Sequence of logs row-wise forms an AP.
Here, a = 20, d = a₂ – a₁ = 19 – 20 = – 1, S_n = 200
\(\frac{n}{2}\) [2a + (n – 1)d] = 200
n[2 × 20 + (n – 1) × (- 1)] = 200 × 2
n[40 – n + 1] = 400
n [41 – n] = 400
41n – n² = 400
n² – 41n + 400 = 0
n² – (25 + 16)n + 400 = 0
[1 × 400 = 400
25 × 16 = 400
25 + 16 = 41]
n² – 25n – 16n + 400 = 0
⇒ n(n – 25) – 16(n – 25) = 0
⇒(n – 25) (n – 16) = 0
⇒ n – 25 = 0 or n – 16 = 0
⇒ n = 25 or n = 16
If n = 25
Number of logs in top row = a₂₅
= 20 + (25 – 1) × (- 1) [∵ a_n = a + (n – 1)d]
= 20 – 24 = – 4
– 4 is not meaningful
So, we reject n = 25.
∴ n = 16
∴ Number of logs in top row = a₁₆
= 20 + (16 – 1) × (- 1)
= 20 – 15 = 5
Hence, the number of rows = 16 and
the number of logs in top row = 5.

Question 20.
In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see figure).

A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are draped in the bucket. What is the total distance the competitor has to run ?
Solution :
Distance run to pick up the 1st potato = 2 × 5 = 10 m
Distance run to pick up the 2nd potato = 2 × (5 + 3) = 16 m
Distance run to pick up the 3rd potato = 2 × (5 + 3 + 3) = 22 m
Distance run to pick up the 4th potato = 2 × (5 + 3 + 3 + 3) = 28 m
The sequence of distances is 10, 16, 22, 28.
a₂ – a₁ = 16 – 10 = 6
a₃ – a₂ – 22 – 16 = 6
a₄ – a₃ = 28 – 22 = 6
∵ a₂ – a₁ = a₃ – a₂ = a₄ – a₃
The sequence forms an AP.
Here, a = 10, d = a₂ – a₁ = 16 – 10 = 6, n = 10
Now, total distance run by a competitor = S₁₀
= \(\frac{10}{2}\) [2 × 10 + (10 – 1) × 61]
[∵ S_n = \(\frac{n}{2}\) [2a + (n – 1)d)]]
= 5 [20 + 9 × 6]
= 5 [20 + 54]
= 5[74] = 370 m
Hence, the total distance run by competitor = 370 m.

Haryana State Board HBSE 10th Class Social Science Notes Civics Chapter 8 लोकतंत्र की चुनौतियाँ Notes.

Haryana Board 10th Class Social Science Notes Civics Chapter 8 लोकतंत्र की चुनौतियाँ

लोकतंत्र की चुनौतियाँ Class 10 Notes HBSE

→ लोकतांत्रिक व्यवस्था में बनी सरकार एक मुश्किल प्रकार कीसरकार होती है। ऐसी सरकार अन्य प्रकार की सरकारों से बेहतर अवश्य होती है। परंतु इस प्रकार की अपनी ही विशेष प्रकार की चुनौतियाँ होती है

→ लोकतांत्रिक युग होने के बावजूद भी आज संसार में एक-चौथाई भाग में लोकतांत्रिक नहीं है। ऐसे भाग में चुनौतियाँ उस भाग से जहाँ लोकतंत्र है की चुनौतियाँ से अलग है। कुल मिलाकर लोकतंत्र के समक्ष की चुनौतयों को तीन श्रेणियों में बाँटा जा सकता है।

→ जिन देशों में लोकतंत्र नहीं है, उन देशों में लोकतांत्रिक सरकरों का गठन करने हेतु बुनियादी आधार तैयार करने की चुनौतियाँ है। इन देशों में गैर-लोकतांत्रिक शासकीय व्यवस्था को मिटाना, सेना शासन का अंत करना तथा लोक संप्रभुता का निर्माण करना।

लोकतंत्र की चुनौतियाँ Class 10 Notes In Hindi HBSE

→ जहाँ लोकतंत्र विद्यमान है, उस भाग में लोकतंत्र का विस्तार करना; लोकतांत्रिक संस्थाओं को अधिक अधिकार संपन्न बनाना, स्थानीय इकाइयों को सुदृढ़ करना, महिलाओं व अल्पसंख्यक वर्गों की भागीदारी बढ़ाना।

→ लोकतंत्र को मजबूत करना; लोकतांत्रिक मूल्यों में वृद्धि लोकतांत्रिक आकांक्षाओं की पूर्ति तथा जनमानस का लोकतंत्र में विश्वास बढ़ाना; लोकतंत्र की कार्यविधि में सुधार करना।

→ लोकतंत्र एक कठिन प्रकार की शासन प्रणाली है। इसे शत्रुओं से बचाना तथा इसकी मान-मर्यादा को, मजबूत करना इसे बनाए रखने के लिए जरूरी साधन है।

→ प्रत्येक प्रकार का लोकतंत्र अलग-अगल है, उसके संदर्भ भी अलग-अलग है तथा उसकी चुनौतियाँ भी अलग-अलग। अतः लोकतंत्रीय व्यवस्था में लगातार राजनीतिक सुधार किए जाने चाहिए।

→ उनमें जो लोकतंत्र का प्रयोग करते हैं तथा उनमें जिन पर लोकतंत्र लागू होता है तथा उन सभी संस्थाओं, प्रक्रियाओं व परिस्थितियों में जिनमें लोकतंत्र का संचालन होता है।

→ बुनियादी आधार : वह जिसका संबंध नींव से हो, वास्तविकता से जुड़ी ज़मीनी वास्तविकता।

→ कुछ महत्त्वपूर्ण चुनौतियाँ : स्थानीय संस्थाओं को संपन्न बनाना, महिलाओं व अल्पसंख्यकों के समूहों की पर्याप्त भागीदार, राजनीतिक जागरूकता आदि।

→ लोकतंत्रीय मूल्य : वह मूल्य जो लोकतंत्र की मजबूत कर सकते हैं। लोकतांत्रिक संस्थाएँ जितनी अधिक लागू दी जाएंगी उनकी मुश्किलों को उतनी अधिक सुलझाने के प्रयास किए जाएंगे।

→ नागरिक नियंत्रण : शासकीय संस्थाओं की कार्यवाही में नागरिकों द्वारा नियंत्रण

→ संविधानवाद : संविधान के उपबन्धों द्वारा किया गया शासन

→ लोकतांत्रिक अधिकार : लोकतांत्रिक व्यवस्था में सभी नागरिकों को एक समान अधिकारों की उपलब्धि

→ निर्वाचन : प्रतिनिधियों व शासकीय अधिकारियों का चुना जाना।

→ संघवाद : संघीय व उसके चारों ओर का इकाइयों की सरकारों की व्यवस्था। यह शासन का एक रूप है।

Haryana State Board HBSE 10th Class Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.2

Question 1.
Fill in the blanks in the following table, given that a is the first term, d the common difference and a„ the 71th term of the AP :

Solution :
(i) We have, a = 7, d = 3, n = 8, an = ?
We know that 71th term of an AP is : a_n = a + (n – 1)d
⇒ a₈ = 7 + (8 – 1) × 3
⇒ a₈ = 7 + 7 × 3
⇒ a₈= 7 + 21
⇒ a₈ = 28
Hence, a₈ = 28.

(ii) We have, a = – 18, n = 10, a_n = 0, d = ?
We know that 7th term of an AP is a_n = a + (n – 1) d
⇒ 0 = – 18 + (10 – 1) × d
⇒ 0 = – 18 + 9d
⇒ 9d = 18
⇒ d = \(\frac{18}{9}\) = 2
Hence, d = 2.

(iii) We have, d = – 3, n = 18, a_n = – 5, a = ?
We know that n term of an AP is
a_n = a + (n – 1)d
⇒ – 5 = a + (18 – 1) × (- 3)
⇒ – 5 = a + 17 × (- 3)
⇒ – 5 = a – 51
⇒ a = 51 – 5 = 46
Hence, a = 46.

(iv) We have, a = – 18.9, d = 2.5, n = ?, a_n = 3.6.
We know that 71th term of an AP is
a_n = a + (n – 1) d
⇒ 3.6 = – 18.9 + (n – 1) × 2.5
⇒ 3.6 = – 18.9 + 2.5n – 2-5
⇒ 3.6 = – 21.4 + 2.5n
⇒ 2.5n = 3.6 + 21.4
⇒ 2.5n = 25
⇒ n = \(\frac{25}{2.5}\)
⇒ n = 10
Hence, n = 10.

(v) We have, a = 3.5, d = 0, n = 105, a_n = ?
We know that nth term of an AP is
a_n = a + (n – 1) d
⇒ a₁₀₅ = 3.5 + (105 – 1) × 0
⇒ a₁₀₅ = 3.5 + 0
⇒ a₁₀₅ = 3.5
Hence, a₁₀₅ = 3.5.

Question 2.
Choose the correct choice in the following and justify :
(i) 30th term of the AP : 10, 7, 4, … is
(A) 97
(B) 77
(C) – 77
(D) – 87

(ii) 11th term of the AP : – 3, – \(\frac{1}{2}\), 2, ……………… is
(A) 28
(B) 22
(C) – 38
(D) – 48 \(\frac{1}{2}\)
Solution :
(i) The given sequence of AP is : 10, 7, 4, …
Here a = 10, d = 7 – 10 = – 3, n = 30
We know that 77th term of an AP is a_n = a + (n – 1) d
⇒ a₃₀ = 10 + (30 – 1) × (- 3)
⇒ a₃₀ = 10 + 29 × (- 3)
⇒ a₃₀ = 10 – 87
a₃₀ = – 77
Hence, the correct option is (C).

(ii) The given sequence is : – 3, – \(\frac{1}{2}\), 2, ………………..
Here a = – 3,
d = – \(\frac{1}{2}\) – (- 3)
= – \(\frac{1}{2}\) + 3
= \(\frac{-1+6}{2}=\frac{5}{2}\)
and n= 11
We know that nth term of an AP is a_n = a + (n – 1) d
⇒ a₁₁ = – 3 + (11 – 1) × \(\frac{5}{2}\)
⇒ a₁₁ = – 3 + 10 × \(\frac{5}{2}\)
⇒ a₁₁ = – 3 + 25
⇒ a₁₁ = 22.
Hence, the correct option is (B).

Question 3.
In the following APs, find the missing terms in the boxes.
(i) 2, ___, 26
(ii) ___, 13, ___, 3
(iii) 5, ___, ___, 91
(iv) – 4, ___, ___, ___, ___, 6
(v) ___, 38, ___, ___, ___, – 22.
Solution :
(i) We have, a = 2, a₃ = 26
Now, a₃ = 26
⇒ a + (3 – 1)d = 26
⇒ a + 2d = 26
⇒ 2 + 2d = 26 [∵ a = 2]
⇒ 2d = 26 – 2
⇒ d = \(\frac{24}{2}\) = 12.
Then missing term = a₂ = a + d = 2 + 12 = 14
Hence, the missing term = 14.

(ii) We have, a₂ = 13
⇒ a + d = 13 …(1)
and a₄ = 3.
⇒ a + (4 – 1)d = 3
⇒ a + 3d = 3 ……………..(2)
Subtracting equation (2) from equation (1), we get

Putting the value of d in equation (1), we get
a – 5 = 13
a = 13 + 5
⇒ a = 18
⇒ 3rd missing term (a₃) = a + 2d
⇒ a₃ = 18 + 2 × (- 5)
⇒ a₃ = 18 – 10
⇒ a₃ = 8.
Hence, 1st and 3rd missing terms are 18, 8.

(iii) We have, a = 5
a₄ = 9\(\frac{1}{2}\)
a +(4 – 1) d = \(\frac{19}{2}\)
a + 3d = \(\frac{19}{2}\) …………..(1)
5 + 3d = \(\frac{19}{2}\) [∵ a = 5]
3d = \(\frac{19}{2}\) – 5
3d = \(\frac{19-10}{2}\)
d = \(\frac{9}{2 \times 3}\)
d = \(\frac{3}{2}\)
So, 2nd missing term (a₂) = a + d
⇒ a₂ = 5 + \(\frac{3}{2}\)
⇒ a₂ = \(\frac{13}{2}\)
⇒ a₂ = 6\(\frac{1}{2}\)
and 3rd missing term (a₃) = a + 2d
⇒ a₃ = 5 + 2 × \(\frac{3}{2}\)
a₃ = 5 + 3
a₃ = 8
Hence, 2nd and 3rd missing terms are 6 \(\frac{1}{2}\), 8.

(iv) We have a = – 4 and a₆ = 6
a + (6 – 1)d = 6
a + 5d = 6
– 4 + 5d = 6 [:a = – 4]
5d = 6 + 4
5d = 10
d = \(\frac{10}{2}\) = 2
d = 2

2nd missing term (a₂) = a + d
a₂ = – 4 + 2
a₂ = – 2

3rd missing term (a₃) = a + 2d
a₃ = – 4 + 2 × 2
a₃ = – 4 + 4
a₃ = 0

4th missing term (a₄) = a + 3d
a₄ = – 4 + 3 × 2
a₄ = – 4 + 6
a₄ = 2

5th missing term (a₅) = a + 4d
⇒ a₅ = -4 + 4 × 2
⇒ a₅ = – 4 + 8
⇒ a₅ =4
Henae, 2nd, 3rd, 4th, 5th missing terms are – 2, 0, 2, 4.

(v) We have, a₂ = 38
⇒ a + d = 38 ……………(1)
and a₆ = – 22
⇒ a + (6 – 1)d = – 22
⇒ a + 5d = – 22 …………..(2)
Subtracting equation (2) from (1), we get

⇒ d = – 15
Substituting the value of d in equation (1), we
a – 15 = 38
⇒ a = 38 + 15
⇒ a = 53
So, 1st missing term = 53

3rd missing term (a₃) = a + 2d
⇒ a₃ = 53 + 2 × (- 15)
⇒ a₃ = 53 – 30
⇒ a₃ = 23

4th missing term (a₄) = a + 3d
⇒ a₄ = 53 + 3 × (- 15)
⇒ a₄ = 53 – 45
⇒ a₄ = 8

5th missing term (a₅) = a + 4d
⇒ a₅ = 53 + 4 × (- 15)
⇒ a₅ = 53 – 60
⇒ a₅= – 7
Hence, 1st, 3rd, 4th, 5th missing terms are: 53, 23, 8, – 7.

Question 4.
Which term of the AP : 3, 8, 13, 18, … is 78 ?
Solution :
The given sequence of AP is : 3, 8, 13, 18, …
Here, a = 3, d = a₂ – a₁ = 8 – 3 = 5, a_n = 78
We know that nth term of AP is
a_n = a + (n – 1 )d.
⇒ 78 = 3 + (n – 1) × 5
⇒ 78 = 3 + 5n – 5
⇒ 78 = – 2 + 5n
⇒ 78 + 2 = 5 n
⇒ 5n = 80
⇒ n = \(\frac{80}{2}\) = 16
Hence, 16th term of the given AP is 78.

Question 5.
Find the number of terms in each of the following APs :
(i) 7, 13, 19, ………., 205
(ii) 18, 15\(\frac{1}{2}\), 13, ………….., – 47
Solution :
(i) The given sequence of AP is : 7, 13, 19, …, 205
Here, a = 7, d = a₂ – a₁ = – 13 – 7 = 6, a_n = 205
We know that term of AP is
a_n = a + (n – 1) d
⇒ 205 = 7 + (n – 1) × 6
⇒ 205 = 7 + 6n – 6
⇒ 205 = 1 + 6n
⇒ 6n = 205 – 1
⇒ 6n = 204
n = \(\frac{204}{6}\) = 34
Hence, the number of terms = 34.

(ii) The given sequence of AP is 18, 15\(\frac{1}{2}\), 13, ……….. – 47
Here, a = 18, d = a₂ – a₁
= 15\(\frac{1}{2}\) – 18
= \(\frac{31}{2}\) – 18
= \(\frac{31-36}{2}=-\frac{5}{2}\)
d = – \(\frac{5}{2}\)
and a_n = – 47
We know that nth term of AP is a_n = a + (n – 1)d

\(-\frac{135}{2}=-\frac{5}{2} n\)
n = \(-\frac{135}{2} \times \frac{2}{-5}\) = 27
Hence, the number of terms = 27.

Question 6.
Check whether – 150 is a term of the AP : 11, 8, 5, 2, …………….
Solution :
The given sequence of AP is : 11, 8, 5, 2,…
Here, a = 11
d = a₂ – a₁
= 8 – 11 = – 3 and
a_n = – 150
We know that nth term of AP is
a_n = a + (n – 1) d
– 150 = 11 + (n – 1) x (- 3)
– 15o = 11 – 3n + 3
– 150 = 14 – 3n
150 – 14 = – 3n
– 3n = – 164
n = \(\frac{-164}{-3}=54 \frac{2}{3}\)
∵ n is a natural number, so it is not possible.
Hence, – 150 is not a term of given AP.

Question 7.
Find the 31st term of an AP whose 11th term is 38 and the 16th term is 73.
Solution :
We have,
a₁₁ = 38
⇒ a + (11 – 1)d = 38
⇒ a + 10d = 38 ……………(1)
and a₁₆ = 73
⇒ a + (16 – 1)d = 73
⇒ a + 15d = 73 ……………(2)
Subtracting equation (2) from equation (1), we get

Putting the value of d in equation (1), we get
a + 10 × 7 = 38
⇒ a + 70 = 38
⇒ a = 38 – 70 = – 32
We know that nth term of AP is :
a_n = a + (n – 1 )d
⇒ a₃₃₁ = – 32 + (31 – 1) × 7
⇒ a₃₁ = – 32 + 30 × 7
⇒ a₃₁ = – 32 + 210
⇒ a₃₁ = 178
Hence, 31st term of AP = 178.

Question 8.
An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.
Solution :
We have,
n = 50
a₃ = 12
⇒ a+ (3 – 1)d = 12
⇒ a + 2d = 12 ………….(1)
and last term (a₅₀) = 106
⇒ a + (50 – 1 )d = 106
⇒ a + 49d = 106 ……………(2)
Subtracting equation (2) from equation (1), we get

Putting the value of d in equation (1), we get
a + 2 × 2 = 12
⇒ a + 4 = 12
⇒ a = 12 – 4
⇒ a = 8
We know that nth term of AP is a_n = a + (n – 1 )d
a₂₉ = 8 + (29 – 1) × 2
a₂₉ = 8 + 28 × 2
a₂₉ = 8 + 56
a₂₉ = 64.
Hence, 29th term of AP = 64.

Question 9.
If the 3rd term and 9th term of an AP are 4 and – 8 respectively, which term of this AP is zero?
Solution :
We have, a₃ = 4
⇒ a + (3 – 1)d = 4
⇒ a + 2d = 4 ………….(1)
and a₉ = – 8
⇒ a + (9 – 1)d = – 8
⇒ a + 8d = – 8 ………….(2)
Subtracting equation (2) from equation (1), we get

putting the value of d in equation (1), we get
a + 2 × (- 2) = 4
⇒ a – 4 = 4
so a = 4 + 4
⇒ a = 8
We know that nth term of AP is :
a_n = a + (n – 1)d
0 = 8 + (n – 1) × (- 2)
[∵ given that a_n = 0]
⇒ 0 = 8 – 2n + 2
0 = 10 – 2n
⇒ 2n = 10
n = \(\frac{10}{2}\) = 5
Hence, 5th term of AP is zero.

Question 10.
The 17th term of an AP exceeds its 10th term by 7. Find the common difference.
Solution :
We have,
a₁₇ – a₁₀ = 7
⇒ a + (17 – 1)d – [a + (10 – 1)d] = 7
⇒ a + 16d – a – 9d = 7
⇒ 7d = 7
⇒ d = \(\frac{7}{7}\)
⇒ d = 1
Hence, common difference = 1.

Question 11.
Which term of the AP : 3, 15, 27, 39, … will be 132 more than its 54th, term?
Solution:
The given sequence of AP is: 3, 15, 27, 39, ……………
Here, a = 3
d = a₂ – a₁ = 15 – 3 = 12
Let nth term of given AP be 132 more than its 54th term
i. e. a_n = a₅₄ + 132
⇒ a + (n – 1 )d = 3 + (54 – 1) × 12 + 132
3 + (n – 1) × 12 = 3 + 53 × 12 + 132
3 + (n – 1) × 12 = 3 + 636 + 132
⇒ 3 + 12n – 12 = 771
⇒ 12n – 9 = 771
⇒ 12n = 771 + 9
⇒ 12n = 780
⇒ n = \(\frac{780}{12}\)
⇒ n = 65
Hence 65th term is 132 more than 54th term.

Question 12.
Two AP’s have the same common difference. The difference between their 100th terms is 100, what is the difference between their 1000th terms?
Solution :
Let the two APs, with same common difference d be
a, a + d, a + 2d, a + 3d, …
and b, b + d, b + 2d, b + 3d, …
According to question,
a₁₀₀ – b₁₀₀ = 100
⇒ a + (100 – 1)d – [b + (100 – 1)d] = 100
⇒ a + 99d – b – 99d = 100
⇒ a – b = 100 ……………..(1)
Now, a₁₀₀₀ – b₁₀₀₀ = a + (1000 – 1)d – [b + (1000 – 1)d]
⇒ a₁₀₀₀ – b₁₀₀₀ = a + 999d – b – 999d
⇒ a₁₀₀₀ – b₁₀₀₀ = a – b
⇒ a₁₀₀₀ – b₁₀₀₀ = 100
[From equation (1) a – b = 100]
Hence, the difference between 1000th terms = 100.

Question 13.
How many three-digit numbers are divisible by 7?
Solution :
The list of three digit numbers which are divisible by 7 is : 105, 112, 119, 126,…, 994.
Let n numbers be divisible by 7.
It is an AP with a = 105, d = 7, a_n = 994.
We know that nth term of AP is
a_n = a + (n – 1 )d
⇒ 994 = 105 + (n – 1) × 7
⇒ 994 = 105 + 7n – 7
⇒ 994 = 98 + 7n
⇒ 7n = 994 – 98
⇒ 7n = 896
n = \(\frac{896}{7}\) = 128
Hence, 128 numbers are divisble by 7.

Question 14.
How many multiples of 4 lie between 10 and 250?
Solution :
Let the multiples of 4 lying between 10 and 250 are : 12, 16, 20, …………… 248.
Let the multiples of 4 between 10 and 250 be n.
It is an AP with a = 12, d = 4, a_n = 248.
We know that nth term of AP is
a_n = a + (n – 1)d
248 = 12 + (n – 1) × 4
248 = 12 + 4n – 4
248 = 8 + 4n
248 = 4n
4n = 240
n = \(\frac{240}{4}\) = 60
Hence, 60 multiples of 4 lie between 10 and 250.

Question 15.
For what value of n, are the /ith terms of two APs : 63, 65, 67, ……….. and 3, 10, 17, ………… equal ?
Solution:
The first given AP is : 63, 65, 67, …………..
Here, a = 63
d = a₂ – a₁
= 65 – 63 = 2
Let nth terms of given two APs are equal
a_n = a + (n – 1)d
⇒ a_n = 63 + (n – 1) × 2
⇒ a_n = 63 + 2n – 2
a_n = 61 + 2n …………….(1)

The second given AP is : 3, 10, 17, …………..
Here a = 3
d = a₂ – a₁ = 10 – 3 = 7
a_n = a + (n- 1 )d
⇒ a_n = 3 + (n – 1) × 7
⇒ a_n = 3 + 7n – 7
⇒ a_n = – 4 + 7n …………(2)
Since, /ith terms of given two APs are equal, from equations (1) and (2), we get
61 + 2n = – 4 + 7n
⇒ 7n – 2n = 61 + 4
⇒ 5n = 65
⇒ n = \(\frac{65}{5}\)
⇒ n = 13
Hence, 13th terms of given two APs are equal.

Question 16.
Determine the AP whose third term is 16 and the 7th term exceeds the 5th term by 12.
Solution :
We have,
a₃ = 16
a + (3 – 1 )d = 16
⇒ a + 2d = 16 …………..(1)
and given, 7th term – 5th term = 12
⇒ a₇ – a₅ = 12
⇒ a + (7 – 1 )d – [a + (5 – 1) d] = 12
⇒ a + 6d – a – 4d = 12
⇒ 2d = 12
⇒ d = \(\frac{12}{2}\) = 6
Putting the value of d in equation (1), we get
a + 2 × 6 = 16
⇒ a + 12 = 16
⇒ a = 16 – 12
⇒ a = 4
So, the AP is : a, a + d, a + 2d, a + 3d, ………..
i.e. 4, 4 + 6, 4 + 2 × 6, 4 + 3 × 6, ……………….
i.e. 4, 10, 16, 22, …………..
Hence, AP is 4, 10, 16, 22, ……………..

Question 17.
Find the 20th term from the last term of the AP : 3, 8, 13, ……………. 253.
Solution:
For finding the 20th term from the last term of AP.
We write the given AP in reverse order as follows : 253, …………….. 13, 8, 3.
Here, a = 253
d= 3 – 8 = – 5
We know that nth term of AP is :
a_n = a + (n – 1) d
⇒ a₂₀ = 253 + (20 – 1) × (- 5)
⇒ a₂₀ = 253 + 19 × (- 5)
⇒ a₂₀ = 253 – 95
⇒ a₂₀ = 158
Hence, 20th term from the last term of given AP = 158.

Question 18.
The sum of the 4th and 8th terms of an AP is 24 and the sum of 6th and 10th terms is 44. Find the first three terms of the AP.
Solution:
We have,
a₄ + a₈ = 24
⇒ a + (4 – 1 )d + a + (8 – 1 )d = 24
⇒ o + 3d + o + 7d = 24
⇒ 2a + 10d= 24 …………..(1)
⇒ a + 5d = 12
and a₆ + a₁₀ = 44
⇒ a + (6 – 1)d + a + (10 – 1)d = 44
⇒ a + 5d + a + 9d = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22 …………….(2)
Subtracting equation (2) from equation (1), we get

Putting the value of d in equation (1), we get
a + 5 × 5 = 12
⇒ a + 25 = 12
⇒ a = 12 – 25
⇒ a = – 13
So, the first three terms of AP are : a, a + d, a + 2d.
i.e. – 13, – 13 + 5, – 13 + 2 × 5
i.e. – 13, – 8, – 3.
Hence, the first three terms of AP are – 13, – 8, – 3.

Question 19.
Subba Rao started work in 1995 at an annual salary of ₹ 5000 and received an increment of ₹ 200 each year. In which year did his income reach ₹ 7000?
Solution :
We have,
Increment of each year = ₹ 200
Income in 1995 = ₹ 5000
Income in 1996 = 5000 + 200 = ₹ 5200
Income in 1997 = 5200 + 200
= ₹ 5400 and so on.
Sequence of salary of Subba Rao is : 5000, 5200, 5400, ………….., 7000
a₂ – a₁= 5200 – 5000 = 200
a₃ – a₂ = 5400 – 5200 = 200
a₂ – a₁ = a₃ – a₂
∴ The given sequence of salary forms an AP.
Here a = 5000
d= 5200 – 5000 = 200 and a_n = 7000
We know that nth term of AP is
a_n = a + (n – 1) d
7000= 5000 + (n – 1) × 200
7000 = 5000 + 200n – 200
7000 = 4800 + 200n
200n = 7000 – 4800
200n = 2200
n = \(\frac{2200}{200}\)
n = 11
Hence, in 11th year Subba Rao’s income reached ₹ 7000.

Question 20.
Reunkali saved ₹ 5 in the first week of a year and then increased her weekly savings by ₹ 1.75. If in the nth week, her weekly savings become ₹ 20.75, Find n.
Solution:
We have weekly increment = ₹ 1.75
Saving in first week = ₹ 5.00
Saving in second week = ₹ 5.00 + ₹ 1.75 = ₹ 6.75
Saving in third week= 6.75 + 1.75
= Rs. 8.50 … and so on.
Sequence of savings of Ramkali is : 5.00, 6.75, 8.50, ……………. 20.75.
a₂ – a₁ = 6.75 – 5.00 = 1.75
a₃ – a₂ = 8.50 – 6.75 = 1.75
a₂ – a₁ = a₃ – a₂
∴ The sequence of savings of Ramkali forms an AP
Here, a = 5.00
d= 6.75 – 5.00 = 1.75
a_n = 20.75
We know that nth term of AP is
a_n = a + (n – 1 )d
⇒ 20.75 = 5 + (n – 1) × 1.75
⇒ 20.75 = 5 + 1.75n – 1.75
⇒ 20.75 = 3.25 + 1.75n
⇒ 1.75n = 20.75 – 3.25
⇒ 1.75n = 17.50
⇒ n = \(\frac{17.50}{1.75}\)
⇒ n = \(\frac{1750}{175}\)
Hence, in 10th week Ramkali’s savings become ₹ 20.75.

Haryana State Board HBSE 10th Class Social Science Important Questions History Chapter 5 Print Culture and the Modern World Important Questions and Answers.

Haryana Board 10th Class Social Science Important Questions History Chapter 5 Print Culture and the Modern World

Multiple Choice Questions

Important Questions On Print Culture and the Modern World HBSE 10th Class Question 1.
In which of the following countries was print technology first developed ?
(a) India
(b) China
(c) Germany
(d) France.
Answer:
(b) China

Important Question On Print Culture and the Modern World HBSE 10th Class Question 2.
When was hand-printing technology introduced in Japan ?
(a) 1002-1008
(b) 768-770
(c) 1008-1012
(d)1012-1014
Answer:
(b) 768-770

Print Culture and the Modern World Map Based Questions HBSE 10th Class Question 3.
Who was Marco Polo?
(a) An explorer
(b) A scientist
(c) A writer
(d) A publisher
Answer:
(a) An explorer

Important Questions Of Print Culture and the Modern World HBSE 10th Class Question 4.
The first book printed in Europe by Johann Gutenberg was
(a) Ramcharitmanas
(b) Bible
(c) Ramayan
(d) Quran.
Answer:
(b) Bible

Important Questions In Print Culture and the Modern World HBSE 10th Class Question 5.
Who wrote Ninety Five Thesis, criticising the practices and rituals of Roman Catholic Church?
(a) Erasmus
(b) Louise Sebastien
(c) James Augustus
(d) Martin Luther.
Answer:
(d) Martin Luther.

Question 6.
What were the cheap books known in England ?
(a) Chapbooks
(b) Biliotheque Bleue
(c) Handbooks
(d) Textbooks.
Answer:
(a) Chapbooks

Question 7.
What were low-priced small books in France called ?
(a) Penny chapbooks
(b) Biliotheque Bleue
(c) Alamnacs
(d) Journals.
Answer:
(b) Biliotheque Bleue

Question 8.
What was the Shilling Series ?
(a) A famous newspaper series of 1920s.
(b) A serialisation of a long story
(c) A cheap series of popular books in England
(d) All of the above.
Answer:
(c) A cheap series of popular books in England

Question 9.
Who printed the first Tamil book ?
(a) The Protestant priests
(b) Ulamas
(c) The Catholic priests
(d) All of these.
Answer:
(c) The Catholic priests

Question 10.
Which of the following was the weekly newspaper published by Gangadhar Bhattacharya ?
(a) Bengal Samachar
(b) Bengal Gazette
(c) Bengal Kesari
(d) Bengal Weekly.
Answer:
(b) Bengal Gazette

Question 11.
Which weekly newspaper was published by Raja Rammohan Roy ?
(a) Sambad Kaumudi
(b) The Bengal Gazette
(c) The Hindu Patrika
(d) The Kesari.
Answer:
(a) Sambad Kaumudi

Question 12.
Who was Raja Ravi Verma ?
(a) A painter
(b) A novelist
(c) A writer
(d) A publisher.
Answer:
(a) A painter

Question 13.
Who was the writer of the first full-length autobiography ‘Amar Jiban’ published in Bengali language ?
(a) Kailashbashini Debi
(b) Rashsundari Debi
(c) Begum
(d) Suhashini Chaudhary.
Answer:
(b) Rashsundari Debi

Question 14.
Who was the author of ‘Gulamgiri’ ?
(a) Dr. B.R. Ambedkar
(b) Jyotiba Phule
(c) E.V. Ramaswamy Naicker
(d) Rammohan Roy.
Answer:
(b) Jyotiba Phule

Question 15.
When was the Vernacular Press Act passed ? ‘
(a) 1878
(b) 1879
(c) 1880
(d) 1881.
Answer:
(a) 1878

Fill in the blanks

1. The earliest kind of …………. technology was developed in
Answer:
printing, China.

2. The first book to be printed by Johann Gutenberg was the …………..
Answer:
Bible.

3. There were …………… or ritual calandars, along with ballads and folk-tales.
Answer:
Almanacs.

4. Lending libraries had been in existence from the …………… century onwards.
Answer:
seventeenth.

5. Manuscripts were copied on ………… leaves or on ………… paper.
Answer:
palm, hand-made.

6. In ………… the Vernacular Press Act was passed.
Answer:
1878.

7. Despite repressive measures ……………. newspapers grew in numbers in all parts of …………..
Answer:
nationalist, India.

8. Balgangadhar Tilak wrote with great sympathy about Punjab deportees in his ………….
Answer:
Kesari.

Very Short Answer Type Questions

Question 1.
Where did the earliest kind of print technology develop ?
Answer:
The earliest kind of print technology was developed in China, Japan and Korea.

Question 2.
What is Calligraphy ?
Answer:
The art of beautiful and stylish handwriting is known as Calligraphy.

Question 3.
Who was the leading producer of printed material in China ?
Answer:
The imperial state of China.

Question 4.
For what purpose were the earliest textbooks printed in China?
Answer:
To recruit the civil servants through written examination.

Question 5.
Who introduced the hand-printing technology in oapan ? (CBS! 2019
Answer:
Buddhist missionaries from China introduced the hand-printing technology in Japan around 768-770 CE.

Question 6.
Which was the oldest book to be printed in Japan ?
Answer:
Diamond Sutra.

Question 7.
Name the things that had printed pictures on them, in Japan ?
Answer:
Playing cards, textiles and paper money.

Question 8.
Who contributed to an art form called Ukiyo?
Answer:
Kitagawa Utamaro.

Question 9.
Who developed the first printing press ?
Answer:
Johann Gutenberg (Germany) developed the first printing press in 1448.

Question 10.
What was the main cause of print revolution?
Answer:
Invention of printing press.

Question 11.
Who was the writer of the Ninety Five Theses ?
Answer:
Martin Luther.

Question 12.
Who said “Printing is the ultimate gift of God and the greatest one?”
Answer:
Martin Luther.

Question 13.
What is an Inquisition?
Answer:
A former Roman Catholic court for identifying and punishing heretics is known as an Inquisition.

Question 14.
Who was Erasmus ?
Answer:
Erasmus was a Latin scholar and a Catholic reformer.

Question 15.
What were the names given to the books in France and England?
Answer:
France – Bilotheque Bleue England – Chap Book.

Question 16.
What is Despotism?
Answer:
A system of governance, in which absolute power is exercised by an individual, unregulated by legal and constitutional checks, is known as despotism.

Question 17.
“The printing press is the most powerful engine of progress and public opinion is the force that will sweep despotism away.” Who said these words ?
Answer:
Louise-Sebastien Mercier, a French novelist.

Question 18.
Where was Penny Magazine first published ?
Answer:
Penny Magazine was published between 1832 and 1835 in England by the Society for the Diffusion of Useful Knowledge.

Question 19.
Which class was the Penny Magazine published for ?
Answer:
It aimed primarily at the working class.

Question 20.
Name any four languages in which Indian manuscripts were prepared before the age of print.
Answer:
(i) Sanskrit
(ii) Arabic
(iii) Persian
(iv) Bengali.

Question 21.
Who wrote Gita Govinda?
Answer:
Jayadeva.

Question 22.
When did the first printing press come to India?
Answer:
The first printing press came to Goa (India) with the Portuguese missionaries in the mid-sixteenth century.

Question 23.
When and who began to edit the Bengal Gazette?
Answer:
In 1780, James Augustus Hickey began to edit the Bengal Gazette.

Question 24.
Punjab Keshari was published by
Answer:
Bal Gangadhar Tilak.

Question 25.
By whom and when was the first Indian Newspaper published in India?
Answer:
Gangadhar Bhattacharya published the first Indian newspaper ‘Bengal Gazette’ in 1821.

Question 26.
Give the names of two Persian newspapers published in India in the early nineteenth century.
Answer:
(i) Jan-i-Jahan Nama, (ii) Shamsul Akhbar.

Question 27.
Name the first printed edition of Tulsidas (a sixteenth century text), published in 1810.
Answer:
Ramcharitmanas.

Question 28.
Who was the author of Amar Jiban?
Answer:
Rashsundari Debi.

Question 29.
Who wrote Istri Dharm Vichar?
Answer:
Ram Chaddha.

Question 30.
Who was known as ‘Maratha Pioneer’ of low caste?
Answer:
Jyotiba Phule.

Question 31.
Name the book written by Jyotiba Phule.
Answer:
Gulamgiri.

Question 32.
Why was Gulamgiri book written by Jyotiba Phule in 1871?
Answer:
In Gulamgiri, Jyotiba Phule wrote about the injustices of the caste system in India.

Question 33.
Who is known as Periyar ?
Answer:
E.V. Ramaswami Naicker.

Question 34.
Name the paper started by Bal Gangadhar Tilak?
Answer:
Kesari.

Question 35.
What are Seditions ?
Answer:
Seditions are actions, speech or writings which are presumed as against the government.

Question 36.
Name the official language of China.
Answer:
Mandarin.

Question 37.
What is Vellum ?
Answer:
A parchment made from the skin of animals.

Short Answer Type Questions-I

Question 1.
What were the two demerits in copying manuscripts ?
Answer:
The two demerits in copying manuscripts were the following :
(i) Copying manuscripts was an expensive, laborious and time consuming business.
(ii) Manuscripts were .fragile, difficult to handle and could not be carried away easily.

Question 2.
Who was Kitagawa Utamaro ? What was his contribution in printing?
Answer:
Kitagawa Utamaro was a painter, born in Edo in 1753. He was widely known for his contributions to an.art form called ukiya (pictures of the floating world), or depiction, of ordinary human experiences, especially urban ones. This art influenced arfists like Manet, Monet and Van Gogh.

Question 3.
Who was Marco Polo? What was his contribution in printing ?
Answer:
Marco Polo was a great Italian explorer who visited China in the thirteenth century. When he returned to Italy in 1295, he brought back the technology of woodblock printing, which he had learnt in China. ’

Question 4.
What did the earlier printed books look like ?
Answer:
(i) Printed books, at first, closely resembled the written manuscripts, in appearance and layout. The metal letters imitated the ornamental hand-written styles.
(ii) Borders were illuminated by hand, with foliage and other patterns, and illustrations were painted.
(iii) Space for decoration was left blank on the printed page.

Question 5.
How did printing bring the people close to one another ?
Answer:
Publishers began to print popular ballads and folktales, with beautiful illustrations and pictures.

These could be sung and recited at gatherings in villages, and in taverns in towns.

Oral cultures, thus, entered the printed material, orally transmitted. In this way, printing brought common people close to one another.

Question 6.
How did the print relate scientists and philosophers to the common people ?
Answer:

Due to print, the ideas of scientists and philosophers now became more accessible to the common people.

Ancient and medieval scientific texts were compiled and published, and maps and scientific diagrams were widely printed.

When scientists, like Issac Newton, began to publish their discoveries, they could influence a much wider circle of scientifically minded readers.

Question 7.
What do you understand by the Shilling Series ?
Answer:
Nineteenth-century periodicals serialised important novels which gave birth to a particular way of writing novels. In the 1920s in England, popular works were sold in cheap series, called the Shilling Series.

Question 8.
Who invented the power driven cylindrical press ? What were its advantages?
Answer:
Richard M. Hoe of New York invented the power-driven cylindrical press.
Advantages:

• The press was capable of printing about 8,000 sheets per hour.
• The press was useful for printing newspapers.

Question 9.
Who were Ulama? Why were they deeply anxious about the collapse of Muslim dynasties ?
Answer:
Legal scholars of Islam and the Sharia were called Ulama. They feared that British colonial rulers would encourage conversion and change the Muslim personal laws. To counter this, they used cheap lithographic presses, which published Urdu and Persian translations of holy scriptures and printed religious newspapers and tracts.

Question 10.
What do you know about Rashsundari Debi ?
Answer:
Rashsundari Debi lived in East Bengal. In the early 19th century, she was a young married girl in a very orthodox household. She learned to read secretly in her kitchen. She wrote her autobiography ‘Amar Jiban’, which was published in the year 1876. This was the first full-length autobiography published in the Bengali language.

Question 11.
How did Begum Rokeya Sakhawat Hossein react against withholding women from education in the name of religion?
Answer:
Begum Rokeya Sakhawat Hossein was a famous educationist and literary figure. In 1926, she strongly condemned men for withholding education from women in the name of religion, as she addressed the Bengal Women’s Education Conference: “The opponents of female education call themselves Muslims and yet go against the basic tenet of Islam which gives women an equal right to education. If men are not led astray once educated, why should women ?” In this way, she reacted against them.

Short Type Questions – II

Question 1.
Trace the development of print in Japan. ( HSI: 2019
Answer:

Buddhist missionaries from China introduced hand-printing technology into Japan in around 768-770 CE.
The oldest Japanese book, printed in 868 CE, is the Buddhist Diamond Sutra containing six sheets of text and woodcut illustrations.
Playing cards, paper money and textile products were used for printing pictures on them.
In medieval Japan, the works of poets and prose writers were regularly published and books were cheap and abundant.
In the late 18th century, in the flourishing urban circles at Edo (later to be known as Tokyo), illustrated collections of paintings depicting an elegant urban culture were popular among the artists, courtesans and teahouse gatherings.

Question 2.
What is a manuscript? Why were they not used widely ?
OR
Why was reading of manuscript not easy in India ? > u- F nc h n,<ard 2020
Answer:
Manuscript: Book or document written by hand is called manuscript. It is an author’s original copy, handwritten or typed, but not printed.
They were not used widely because :

• These were fragile, difficult to handle and could not be carried away easily.
• Highly expensive.
• Could not be read easily, as the script was written in different styles.
• They were limited in numbers.
• Style of writing of every individual manuscript differs.

Question 3.
Who was Gutenberg ? How did he get the idea of a printing press ?
Answer:

• Johann Gutenberg was a German goldsmith and inventor related with the invention of the movable type printing in Europe.
• He had seen wine and olive presses since his childhood because his father had a large agricultural estate.
• It is said that the olive press provided the model for the printing press and moulds were used for casting
• the metal types for the letters of the alphabet.
• The first book printed by him was the Bible. About 180 copies were printed in three years.

Question 4.
Describe some of the new printed books which were sold by the peddlers in villages in the eighteenth century.
Answer:

• They were almanacs (ritual calendars), alongwith ballads and folktales. In England, penny chapbooks were carried by petty peddlers, known as chapmen, and sold for a penny.
• ‘Biliotheque Bleue’ were low-priced small books that were sold in France. These could be bought even by the poor.
• Then, there were the romances, printed on four to six pages and the more substantial ‘histories’, which were
• stories about the past. Books were of various sizes and served different purposes and interests.

Question 5.
“With the inducement of the printing press, a new reading public emerged”. Explain the statement.
OR
How did the invention of the printing press influence the reading culture ?
Answer:
The invention of the printing press had the following influences on the reading culture :

• Printing reduced the cost of books. The time and labour required to produce each book came down, and multiple copies could be produced with greater ease.
• Books flooded the market, reaching out to an ever-growing readership.
• Access to books created a new culture of reading. If earlier, there was the public to listen, now, a reading public came into being.
• Printers began publishing popular ballads and folktales, and such books would be profusely illustrated with pictures, for those, who did not read.

Question 6.
The shift from hand-printing to mechanical printing led to the print revolution. Explain.
Answer:

• In the hundred years between 1450 and 1550, the printing presses were set up in most of the countries of Europe.
• Printers from Germany travelled to other countries, seeking work -and helping to start new presses. As the number of printing presses grew, books’ production boomed.
• The second half of the fifteenth century, saw around 20 million copies of printed books, flooding the markets in Europe. The number went up in the sixteenth century to about 200 million copies.
• It influenced popular perceptions and opened up new ways of looking at things.

Question 7.
“Print popularised the ideas of the enlightened thinkers”. Explain.
Answer:

• Collectively, the writings of thinkers provided a critical commentary on tradition, superstition and despotism.
• They attacked the sacred authority of the Church and the despotic power of the state, thus eroding the legitimacy of a social order, based on tradition.
• They argued for the rule of reason, rather than custom, and demanded that everything should be judged through the application of reason and rationality.
• The writings of Voltaire, Rousseau were read widely and those, who read these books, saw the world through new eyes, eyes that were questioning, critical and rational.

Question 8.
What innovations happened after the seventeenth century, which improved the printing technology ?
Answer:

• In the late eighteenth century, the press came to be made out of metal.
• Richard M. Hoe, an American inventor, designed an improved printing press which was known as the rotatory printing press. This new press could print about 8,000 sheets per hour.
• In the late nineteenth century, the offset press was developed, which could print up to six colours at a time.
  From the beginning of the twentieth century, electrically operated presses accelerated printing operations.
• A series of many other developments followed. Methods of feeding paper improved, the quality of plates became better, automatic paper reels and photoelectric controls of the colour register were introduced.

Question 9.
Explain the main features of handwritten manuscripts before the age of print in India.
Answer:

• India had a very rich and old tradition of handwritten manuscripts in Sanskrit Arabic, Persian, as well as in various vernacular languages.
• Manuscripts were copied on palm leaves or on handmade paper. Papers were sometimes beautifully illustrated.
• They would be either pressed between wooden covers or sewn together to ensure preservation.
• They were highly expensive and fragile.
• They had to be handled carefully and could not be read easily, as the script was written in different styles.

Question 10.
Trace the development of print in India.
Answer:

• The printing press first came to Goa with Portuguese missionaries in the mid-sixteenth century,
• Jesuit priests learnt Konkani and printed several tracts. By 1674, about 50 books had been printed in the Konkani and Kanara languages.
• Catholic priests printed the first Tamil book in 1579 at Cochin, and in 1713, the first Malayalam book was printed by them.
• The English East India Company began to import presses from the late seventeenth century.
• From 1780, James Augustus Hickey began to edit the Bengal Gazette, a weekly magazine.
• By the close of the eighteenth century, a number of newspapers and journals appeared in print.

Question 11.
What do you know about visual culture and its role in printing in India?
Answer:
By the end of 19th century, a new visual culture started taking shape. An increasing number of printing presses helped in the production of visual images and reproduced them in multiple copies. Famous Indian painters, like Raja Ravi Verma, produced images for mass circulation. Cheap prints and calendars were easily available in the markets and could be bought even by the poor to decorate the walls of their workplaces and homes. These prints and calendars helped in developing popular ideas about modernity and tradition, religion, society, culture and politics.

Question 12.
Explain the impact of print culture on Indian women. <Raj. Board 2015′
Answer:
The impact of print culture on Indian women was following :

• Writers started writing about the lives and feelings of women, and this increased the number of women readers enormously in middle-class homes.
• Liberal husbands and fathers began educating their womenfolk at home and sent them to schools when women’s schools were set-up after the mid-nineteenth century.
• Many journals, carrying writings by women and explaining why women should be educated, were published.
• Many women writers, like Rashsundari Debi, Begum Rokeya Sakhawat Hossein, Kailashbashini Debi, Tarabai Shinde and Pandita Ramabai wrote books, highlighting the experiences of women.
• In the early twentieth century, journals written for and sometimes edited by women, discussed issues, like women’s education, widowhood, widow remarriage and the national movement.

Question 13.
What was the role of nationalist newspapers in spreading national feelings among the Indian people in the early 20th century ?
Answer:
The role of nationalist newspapers in spreading national feelings among the people in the early 20th century was the following :

• Nationalist newspaper grew in numbers in all parts of India.
• They reported on colonial misrule and encouraged nationalist activities.
• The newspaper attempted to throttle nationalist criticism and provoked militant protest.
• When Punjab revolutionaries were deported in the year 1907, Lokmanya Bal Gangadhar Tilak wrote with
• great sympathy about them in his ‘Kesari’ newspaper. This led to his imprisonment in the year 1908.

Long Answer Type Questions

Question 1.
Describe in detail the earliest developments in printing technology.
Answer:
The earliest developments in printing technology can be explained through the following points :«
(i) The earliest kind of print technology developed in China, Japan and Korea. In China, since 594 CE, woodblocks were used for hand-printing. As both sides of the thin and porous sheet could not be printed, the traditional Chinese ‘accordion book’ was folded and stitched at the side. Superbly skilled craftsmen could duplicate it with remarkable accuracy, and the beauty of calligraphy. After the seventeenth century, the merchants, along with the reading public began to use print in their everyday life, whereas print was the preserve of scholar-officials, earlier.

(ii) Buddhist missionaries from China introduced hand-printing technology into Japan around 768-770 CE. The oldest Japanese book, printed in 868 AD, is the Buddhist Diamond Sutra, containing six sheets of text and woodcut illustrations. ^

(iii) Paper reached Europe from China through the silk route in the eleventh century. With this, the production of manuscripts written by scribes became a regular feature. Marco Polo, a great explorer, returned to Italy after several years of exploration in China. In the year 1295, he brought back with him the technology of woodblock printing. Thus, woodblock printing came to Europe around the year 1295.

(iv) The invention of the printing press proved a great miracle in spreading knowledge. The first printing press was developed by Johann Gutenberg in Germany in the year 1448, which greatly facilitated the printing of books in large numbers. He developed metal types and developed a way of moving them around, so as to compose different words of the text. The first book printed by Gutenberg was the Bible, of which about 180 copies were printed in the three years. His novel printing machine dominated the printing world for the next 300 years.

(v) Between the year 1450 and 1550, printing presses were set-up in most of the European countries. Printers from Germany travelled to other countries, seeking work and thus helping to start new presses. As the number of printing presses grew, book production also vastly increased. This shift from hand-printing to mechanical printing led to the print revolution.

Question 2.
Trace the history of print in China.
Answer:
The history of print in China can be depicted as follows:

• The earliest kind of print technology was developed in China. This was a system of hand-printing.
• From 594 CE onwards, books in China were printed by rubbing paper against the inked surface of wood blocks.
• As both sides of the thin and porous sheet could not be printed, the traditional Chinese ‘accordion book’ was folded and stitched at the side.
• Superbly skilled craftsmen could duplicate it with remarkable accuracy, and the beauty of calligraphy.
• The imperial state in China was, for a long time, a major producer of printed material. China possessed a huge bureaucratic system, which recruited its personnel through civil service examinations.

Question 4.
What do you understand by Print Revolution? Explain its impacts.
Answer:
Print Revolution: With the invention of printing press, the printing of books started at a large scale. Printing reduced the cast. The time and labour, required to produce each book, came down. Books flooded the market and reached out to an evergrowing
readership.

Impacts of Print Revolution: The impact of Print Revolution can be explained through the following points

(i) Emergence of new reading public:
Access to books created a new culture of reading. Earlier, common people lived in a world of oral culture. Knowledge was transferred orally. Now, the books could be made easily available to the wider sections of people. Earlier, there was public only to listen, now, a reading public came into being.

(ii) Wide Circulation of Ideas:
With the invention of printing press, circulation of ideas of people and discussion on various subjects started taking place. Now, people could debate and discuss different topics. Even those, who dis-agreed with established authorities, could now print and circulate their ideas. Through a printed message, they could persuade people to think in different ways. Religious reformer Martin Luther praised the print revolution and said, “printing is the ultimate gift of God and the greatest one”. According to many historions, printing created a new intellectual atmosphere and helped to spread new ideas that led to the Reformation.

(iii) Introduction with the different Explanations of Religion:
Print and popular religious literature stimulated many distinctive interpretations of faith, even among little educated working people. Many people started to reinterpret the message of the Bible and form new ideas about God and His creation.

Question 5.
“After print revolution, as literacy and schools spread in European countries, there was a virtual reading mania.” Explain the statement.
Answer:
The above-mentioned statement can be explained as given below:

(i) The extension of schools and literacy:
During the seventeenth and by the end of the eighteenth century, in many countries of the European continent, the literacy rate increased by sixty to seventy percent. Churches of different denominations opened schools in villages, carrying literacy to peasants and artis: As literacy and schools spread in European countries, there was a virtual reading mania. There was a great demand of books, and the publishers began to print books in large numbers.

(ii) Printing of various types of literature:
New forms of literature appeared in print, targeting new readers in Europe. Booksellers employed peddlers, who roamed around villages, carrying little books for sale. There were almanacs (ritual calendars), alongwith ballads and folktales.

(iii) Printing of Entertainment-based Literature:
Targeting the interest of hew readers, the printing of entertainment-based literature also started in Europe. Such books were very cheap and could be read even by the poor. In those books, Penny Chapbooks of England and Biliotheque Bleue of France, etc. were prominent.

(iv) Printing of Romantic as well as Historical books:
Apart from the amusement- based books, books on romances were also printed on four to six pages by European publishers. There were some substantial books written on ‘histories’, which were stories about the past.

(v) Printing of Journals:
In the beginning of eighteenth century, the publication of journals started in Europe.

(vi) Printing of books related to science and philosophy:
The ideas of scientists and philosophers now became more popular among the common people. Ancient and medieval scientific texts were compiled and published, maps and scientific diagrams were widely printed. The writings of scientists and thinkers like, Issac Newton, Thomas Paine, Voltaire and Rousseau, were widely printed and read.

Question 6.
Many historians argued that print culture created the conditions within which French Revolution occurred. Cm we make such a connection?
Answer:
Many historians argued, that the print culture created the conditions which were responsible for the French Revolution. The following reasons can be presented to support this view:

(i) Print popularised the ideas of the Enlightened thinkers:
Due to print culture, the ideas of the Enlightened thinkers were popularized. They criticised traditions, superstitions and despotism through their writings. They agreed for the rule of reason, rather than custom, and demanded that everything be judged through the application of reason and rationality. Consequently, many thinkers began to attack the sacred authority of the Church and despotic power of the state.

(ii) Print created a new culture of debate and dialogue:
All existing ideas and beliefs began to be questioned by the public. Such things created the ground for social revolution.

(iii) Publication of Literature that mocked the royalty:
By the decade of 1780, there was an outpouring of literature, that mocked the royalty and criticised their morality. In the process, it raised questions about the existing social order. This process led to the growth of hostile sentiments against the rulers.

Question 7.
How was the print culture used to spread the religious texts by various communities? Explain with examples.
Answer:
Print culture was used to spread the religious texts by various communities as following:

Print and the Muslims:
In north India, the Ulamas (the religious heads of Muslims) were deeply worried about the collapse of the Muslim dynasties. To counter their fear they used cheap lithographic presses which published Persian and Urdu translations of the holy scriptures, and printed religious newspapers and tracts. The Deoband Seminary, which was founded in the year 1867, published many fatwas, making muslim readers aware of the code of conduct to be followed in their everyday lives and explained the meanings of Islamic doctrines.

Print and the Hindus:
Among Hindus, too, print culture encouraged the readings of religious texts especially in the vernacular languages. The first printed edition of the Ramcharitmanas of Tulsidas, came out from Calcutta (Kolkata) in 1810. From the 1880s, the Naval Kishore Press at Lucknow and the Shri Venkateshwar Press in Bombay published many religious texts and books, reaching a very wide circle of people, encouraging debates and controversies within and among different religions.

Haryana State Board HBSE 10th Class Social Science Important Questions History Chapter 3 The Making of a Global World Important Questions and Answers.

Haryana Board 10th Class Social Science Important Questions History Chapter 3 The Making of a Global World

Multiple Choice Questions

Important Questions On The Making of a Global World HBSE 10th Class Question 1.
The routes which knitted together, vast regions of Asia and linked Asia with Europe and Northern Africa:
(a) Silk routes
(b) Royal routes
(c) Golden quadrilateral
(d) None of these.
Answer:
(a) Silk routes

Important Question On The Making of a Global World HBSE 10th Class Question 2.
From which country did noodles travel to the west?
(a) India
(b) Pakistan
(c) China
(d) Sri Lanka.
Answer:
(c) China

The Making of a Global World Map Based Questions HBSE 10th Class Question 3.
What were the most powerful weapons used by the Spanish conquerors to colonise America?
(a) Chemical agents
(b) Traditional arms and ammunitions
(c) Germs
(d) All of these.
Answer:
(c) Germs

Important Questions Of The Making of a Global World HBSE 10th Class Question 4.
Which of the following continent’s original inhabitants had no immunity against diseases due to their long isolation?
(a) America
(b) Africa
(c) Asia
(d) Europe.
Answer:
(a) America

Important Questions In The Making of a Global World HBSE 10th Class Question 5.
Which of the following diseases was spread in America by the Spanish soldiers?
(a) Plague
(b) Small pox
(c) Malaria
(d) Polio.
Answer:
(b) Small pox

Important Questions For The Making of a Global World HBSE 10th Class Question 6.
Which of the following laws allowed the British Government to restrict the import of com?
(a) Com Laws
(b) Corn Act
(c) Food Act
(d) Import Laws.
Answer:
(a) Com Laws

Important Question The Making of a Global World HBSE 10th Class Question 7.
Which of the following technology enabled the transportation of perishable foods over long distances?
(a) Refrigerated ships
(b) Introduction of lighter wagons
(c) Faster railways
(d) None of these.
Answer:
(a) Refrigerated ships

Question 8.
In which of the following continents did the Rinderpest spread?
(a) Europe
(b) Asia
(c) Africa
(d) America.
Answer:
(c) Africa

Question 9.
Who was a well known pioneer of mass production?
(a) Abraham Lincoln
(b) Henry Ford
(c) Michele Johnes
(d) All of these.
Answer:
(b) Henry Ford

Question 10.
The time period of the Great Depression was:
(a) 1929-1930s
(b) 1930-1940s
(c) 1940-1950s
(d) 1950-1960s.
Answer:
(a) 1929-1930s

Question 11.
The Second World War was fought between:
(a) The Axis powers and the Central powers
(b) The Axis Powers and the Allies
(c) The Central powers and the Allies
(d) None of these.
Answer:
(b) The Axis Powers and the Allies

Question 12.
Which countries organised a group called G-77 ?
(a) Developing Countries
(b) Developed Countries
(c) Undeveloped Countries
(d) All of these.
Answer:
(a) Developing Countries

Fill in the blanks

1. Human societies have become steadily more ………….
Answer:
interlinked.

2. The long distance spread of ………….. germs may be trace as far back as the seventh century CE.
Answer:
disease-carrying.

3. European conquest was not just a result of superior ………….
Answer:
firepower.

4. Europe now emerged as the centre of ………….
Answer:
world trade.

5. Trade …………. and markets expanded in the late nineteenth century.
Answer:
flourished.

6. ……………. arrived in Africa in the late
Answer:
Rinderpest, 1880s.

7. Indian traders and …………. also followed European ………….. into Africa.
Answer:
moneylenders, colonisers.

8. The …………… and the World Bank were designed to meet the ………….. needs of the industrial countries.
Answer:
IMF, financial.

Very Short Answer Type Questions

Question 1.
What is globalisation?
Answer:
Movement of people, goods and services across the nations has been termed as globalisation.

Question 2.
Name the elements that helped to create the globalised world.
AnsweR:
(i) Trade
(ii) Migration of people from one place to another in search of work,
(iii) Capital
(iv) Global exchange of goods.

Question 3.
Who interlinked human societies more steadily from ancient times?
Answer:
Since ancient times, travellers, traders, priests and pilgrims travelled to interlink human societies more steadily.

Question 4.
Name the common foods which were not known to our ancestors until about five centuries ago.
Answer:
Potatoes, soya, groundnuts, maize, tomatoes, chillies, sweet potatoes, etc.

Question 5.
Where was spaghetti bom?
Answer:
It is believed that noodles travelled to the west from China to become spaghetti.

Question 6.
What does the word ‘America’ describe?
Answer:
The word America describes the collective group of North America, South America and the Caribbean islands.

Question 7.
In which century did the European sailors find a sea route to Asia?
Answer:
In the sixteenth century.

Question 8.
Which was the fabled city of gold?
Answer:
The El Dorado.

Question 9.
What was the impact of germs on the original inhabitants of America?
Answer:
The germs killed and decimated entire communities due to a lack of immunity.

Question 10.
In which continent, poverty and hunger was common until the nineteenth century?
Answer:
Europe.

Question 11.
Which countries were among the world’s richest countries until the eighteenth century?
Answer:
India and China.

Question 12.
Give the three types of flows within the international economic exchanges.
Answer:

• Flow of trade
• Flow of labour
• Flow of capital.

Question 13.
To which continents did the European people flee, by the end of the nineteenth century?
Answer:
America and Australia.

Question 14.
What steps were taken by the British government to improve agriculture in West Punjab?
Answer:
(i) To improve agriculture, a network of irrigation canals was built.
(ii) Canal colonies were established by peasants who came from other parts of Punjab.

Question 15.
What were canal colonies?
Answer:
The semi-desert waste areas of Punjab, after being irrigated by the new canals, began to be called as canal colonies. They were created to grow wheat and cotton for export.

Question 16.
Why did most of the borders of African countries run straight?
Answer:
Most of the borders of African countries ran straight because Africa was divided on paper by the rival European powers in the conference hall in Berlin.

Question 17.
What was Rinderpest?
Answer:
Rinderpest was a cattle plague. It was a fast-spreading disease among cattle.

Question 18.
Explain the term ‘Indentured Labour’.
Answer:
A bonded labourer, under contract to work for an employer for a specific period, is known as an indentured labourer.

Question 19.
Name any four states of India from where the indentured labour migrated.
Answer:

• Uttar Pradesh
• Bihar
• Tamil Nadu
• Madhya Pradesh.

Question 20.
Where did indentured labour migrate from India?
Answer:
The Indian indentured labour migrated to the Caribbean islands (mainly Trinidad, Guyana and Surinam), Mauritius and Fiji.

Question 21.
What was ‘Hosay’?
Answer:
In Trinidad, the annual ‘Muharram’ procession was transformed into a riotous carnival called ‘Hosay’. It was one of the ways to preserve the culture of indentured labourers.

Question 22.
Where was the ‘Chutney music’ popular?
Answer:
The ‘Chutney music was popular in the American states of Trinidad and Guyana.

Question 23.
Who was V. S. Naipaul?
Answer:
He was the Nobel Prize-winning writer, whose forefathers migrated as indentured workers.

Question 24.
What is common among V.S. Naipaul, Shivnarain Chandrapaul and Ramnaresh Sarwan?
Answer:
They all have descended from indentured labour migrants from India.

Question 25.
Explain the term Trade Surplus’.
Answer:
The trade surplus is a situation under which the value of exports is more than imports.

Question 26.
Name the countries comprising the Allied powers in the First World War.
Answer:
Britain, France and Russia (Later joined by the US.)

Question 27.
Name the countries comprising the Central powers.
Answer:
Germany, Austria-Hungary and Ottoman Turkey.

Question 28.
Who was the biggest international creditor after the First World War?
Answer:
The United States of America.

Question 29.
Write the name of the world’s first mass-produced car.
Answer:
T-model Ford.

Question 30.
When did the great economic depression begin?
Answer:
In 1929.

Question 31.
Name the countries comprising the Axis powers in the Second World War.
Answer:
Germany, Japan and Italy.

Question 32.
Name the countries comprising the Allied powers in the Second World War.
Answer:
Britain, France, the Soviet Union and the US.

Question 33.
What is the full form of IMF?
Answer:
International Monetary Fund.

Question 34.
Name the two institutions which were established under the Bretton Woods Agreement.
Answer:

• International Monetary Fund (IMF).
• International Bank for Reconstruction and Development (popularly known as World Bank.)

Question 35.
In which year did the IMF and the World Bank commence financial operations?
Answer:
In 1947.

Question 36.
What is the difference between the International Monetary System and the Bretton Woods System?
Answer:
The International Monetary System is the system linking national currencies and the monetary system, whereas the Bretton Woods System was based on fixed exchange rates.

Question 37.
What is NIEO?
Answer:
New International Economic Order (NIEO) is demanded by G-77, which meant a system, that would give the developing countries control over their natural resources, more developmental assistance, fair prices for raw materials, and better access for their manufactured goods in the markets of developed countries.

Question 38.
What do you mean by G-77?
Answer:
G-77 was a group of 77 developing countries which did not benefit from the fast growth, which the western economies experienced in the 1950s.

Question 39.
Give the two types of exchange rates.
Answer:
(i) Fixed exchange rate
(ii) Floating exchange rate.

Question 40.
Which person is called a Dissenter?
Answer:
A dissenter is a person who refuses to accept established beliefs and practices.

Question 41.
Name any two primary agricultural products and one primary mineral product.
Answer:
(i) Agricultural products: Wheat, Cotton
(ii) Mineral product: Coal

Question 42.
What has been described as a ‘new system of slavery?
Answer:
Nineteenth-century indenture has been described as a ‘new system of slavery.

Short Answer Type Questions – I

Question 1.
What were the silk routes ?
Answer:
These were the routes that knitted together vast regions of Asia and linked Asia with Europe and northern Africa. The name ‘silk routes’ points to the importance of Westbound Chinese silk cargoes along this route. These routes are known to have existed since before the
Christian Era and thrived almost till the fifteenth century.

Question 2.
“The pre-modern world shrank greatly in the sixteenth century”. Explain.
Answer:
The pre-modem world shrank greatly in the sixteenth century because :
(i) European sailors found a sea route to Asia and also successfully crossed the western ocean to reach America.
(ii) The Portuguese and Spanish conquest and colonisation of America was decisively underway by the mid-sixteenth century.

Question 3.
(i) When and where did the Irish potato famine take place? What was its impact?
(ii) “Till the 1870s, meat was an expensive luxury beyond the reach of the European poor”. Give reasons.
Answer:
(i) The Irish potato famine took place between 1845 to 1849 iir Ireland. The potato was the main food of poor Irish peasants. When a disease destroyed the potato crop in the mid-1840s, hundreds of thousands died of starvation in Ireland and double the number, emigrated in search of work.

(ii) Till the 1870s, animals were shipped live from America to Europe and slaughtered when they arrived there. But, live animals took up a lot of ship space. Many also died in the voyage, fell ill, lost weight or became unfit to eat. Thus, meat was an expensive luxury, beyond the reach of the European poor.

Question 4.
(i) what were Com Laws? Why were these laws abolished?
(ii) How was the food problem of Britain solved after the scrapping of the Com Laws?
Answer:
(i) Under pressure from landed groups, the British government restricted the import of com. These laws were popularly known as the Com Laws. Unhappy with high food prices, industrialists and urban dwellers forced the abolition of the Com Laws.

(ii) After the Com Laws were scrapped, food could be imported to Britain. As food prices fell, consumption in Britain rose. Faster industrial growth in Britain also led to higher incomes, and therefore more food imports.

Question 5.
Why did thousands of people flee from Europe to America in the nineteenth century?
Answer:
Thousands of people fled from Europe to America because of the following reasons:

• Until the nineteenth century, poverty and hunger were common in Europe.
• Cities were crowded and deadly diseases were widespread.
• Religious conflicts were common and religious dissenters were persecuted.

Therefore, people migrated from Europe to America.

Question 6.
Write in brief about the transport of gold by the Europeans from Transvaal gold mines.
Answer:
After the discovery of gold in Witwatersrand, Europeans rushed to the region, despite their fear of disease and death and the difficulties of the journey. Crossing the Wilge river was the quickest method of travel to the gold fields of Transvaal. By the 1890s, South Africa contributed over 20 per cent of the world’s gold production.

Question 7.
What was Rinderpest? How did it affect the lives of Africans?
Answer:
Rinderpest was a devastating cattle disease which arrived in Africa in the late 1880s. It was carried by infected cattle imported from British Asia, to feed the Italian soldiers invading Eritrea in East Africa. Rinderpest killed 90 per cent of the cattle. The loss of cattle destroyed African livelihoods. Planters, mine owners and colonial governments now successfully monopolised what scarce cattle resources remained, to strengthen their power and to force Africans into the labour market. Control over the scarce resource of cattle enabled European colonisers to conquer and subdue Africa.

Question 8.
Why was the indentured labour of the nineteenth century described as “New System of Slavery” ? How were the indentured workers exploited by the recruiting agents?
Answer:
Indentured labour of the nineteenth century had been described as a ‘New System of Slavery1 because, on arrival at the plantations, labourers found that living and working conditions were very harsh, and there were few legal rights. Many workers escaped into the wilds though, and if caught, faced severe punishment. Agents tempted the prospective migrants by providing false information about final destinations, modes of travel, the nature of the work and living and working conditions. Often, migrants were not even told that they were to embark on a long sea voyage. Sometimes, agents even forcibly abducted less willing migrants.

Question 9.
Mention any four factors responsible for indentured labour.
Answer:
Four factors responsible for indentured labour were:

• Decline of cottage industry in India.
• Increase in land rents.
• Loss of cattle due to Rinderpest in Africa.
• Unemployment and poverty.

Question 10.
‘India played a crucial role in the late nineteenth-century world economy. Explain.
Answer:
India was a British colony. Britain had a ‘trade surplus with India. Britain used this surplus to balance its trade deficits with other countries, that is, with countries from which Britain was importing more than it was selling to. Thus, we can say that, by helping Britain in balancing its deficit, India played an important role in the world economy in the late nineteenth century.

Question 11.
(i) What was the main aim of the post-war international economic system? Which institutions were established to achieve this aim?
(ii) What were the limitations of the IMF and the World Bank?
Answer:
(i) The main aim of the post-war international economic system was to preserve economic stability and full employment in the industrial world. To achieve this aim, the International Monetary Fund and the World Bank were formed through the Bretton Woods Conference.

(ii) (a) The IMF and the World Bank were not equipped to cope with the challenges of poverty and lack of development in the former colonies.
(b) They were controlled by the United States of America, as it had veto power.

Question 12.
Why did the countries of G-77 demand a new international economic order?
Answer:
The countries of G-77 demanded a new international economic order because of the following reasons :
(i) The developing countries wanted a system which provided them loan on their resources but did not exploit those resources.
Social Science

(ii) They wanted fairer prices for raw materials and better access for their manufactured goods in the markets of developed countries.

Question 13.
Why did the inflow of fine Indian cotton begin to decline in Britain?
Answer:
Earlier, fine cotton, produced in India was exported to Europe. With industrialisation, British cotton manufacturing started to expand, and the industrialists pressurised the Government to stop cotton imports and protect local industries. As a result, the inflow of fine Indian cotton started to decline.

Long Answer Type Questions

Question 1.
How did human societies become inter-connected in the pre-modem era?
Answer:

• All through history, human societies have become steadily more interlinked.
• Since ancient times, travellers, traders, priests and pilgrims travelled long distances for knowledge, opportunity and spiritual fulfilment, or to escape persecution. ,
• They carried goods, money, skills, ideas, values, inventions, and even, germs and diseases.
• As early as 3000 BCE, an active coastal trade linked the Indus valley civilisation with present-day West Asia.
• For more than a millennia, cowries used as a form of currency from the Maldives found their way to China and East Africa.

Question 2.
‘By 1890, a global agricultural economy had taken shape.’ Support this statement by giving examples.
Answer:
By 1890, a global agricultural economy had taken shape. There were many changes in labour movement patterns, capital flows, ecologies and technology. Food no longer came from a nearby village or town, but from thousands of miles away. It was not grown by a peasant tilling his own land, but by an agricultural worker, who was now working on a large farm, that only a generation ago, had most likely, been a forest.

It was transported by railway and by ships, which were increasingly manned in these decades by low-paid workers from Southern Europe, Asia, Africa and the Caribbean. The world trade is estimated to have multiplied 25 to 40 times, between 1820 and 1914. Nearly 60 per cent of this trade comprised ‘Primary products’, that is, agricultural products such as wheat and cotton, and minerals such as coal.

Question 3.
What were the advantages of the invention of refrigerated ships?
Answer:
The advantages of the invention of refrigerated ships were the following:

• Now, animals were transported as frozen meat. This reduced shipping costs and lowered meat prices in Europe.
• The poor in Europe could now consume a more varied diet.
• To the earlier monotony of bread and potatoes many, though not all, could now add meat, butter and eggs, in their diet.
• Better living conditions promoted social peace within the country and support for imperialism abroad.

Question 4.
What were the main sources of attraction for Europeans to come to Africa in the late nineteenth century?
Answer:

• Historically, Africa had abundant land and a relatively small population. Europeans were attracted to Africa due to its vast resources of land and minerals.
• They came to Africa, hoping to establish plantations and mines to produce crops and minerals for export to Europe.
• Europeans divided different regions of Africa among themselves.

Question 5.
“The journey of Stanley was inspired by the imperialistic aims”. Explain the statement.
Answer:
Sir Henry Morton Stanley was a journalist and an explorer. He was sent by the New York Herald in 1871 to find Livingston, a missionary and explorer, who had been in Africa for several years. Like other American and European explorers of that time, Stanley went with arms, and mobilised local hunters, warriors and labourers to help him. He fought with local tribes, investigated African terrains, and mapped different regions. These explorations helped the conquest of Africa. These type of geographical explorations were not driven by an innocent search for scientific information. They were directly linked to imperial projects.

Question 6.
What methods were used by European employers to recruit and retain African labourers?
Answer:

• Heavy taxes were imposed, which could be paid only by working for wages on plantations and mines.
• Inheritance laws were changed, so that peasants were displaced from land; only one member of a family was allowed to inherit land, others were pushed into the labour market.
• Mine workers were also enclosed in compounds, and not allowed to move freely.

Question 7.
What was the impact of industrialisation in Britain on Indian economy?
Answer:
(i) With industrialisation, British cotton manufacturers began to expand and industrialists pressurised the government to restrict cotton imports and protect local industries. Tariffs were imposed on cloth imports to Britain. As a result, the inflow of fine Indian cotton began to decline.

(ii) From the early nineteenth century, British manufacturers also began to search the overseas markets for their cloths. The British machines made textile products which started giving a tough competition to the Indian textile industry at home. So, there was a decline in the share of cotton textiles, from some 30 per cent around 1800, to 15 per cent by 1815. By the 1870s, the proportion had dropped to below 3 per cent.

Question 8.
The First World War was a modern industrial war. Explain.
Answer:
The First World War saw the use of machine guns, tanks, aircrafts, chemical weapons, etc. on a massive scale. These all were developing products of modem large- scale industries. To fight the war, millions of soldiers had to be recruited from around the world and moved to the frontlines on large ships and trains. The scale of death and destruction 9 million dead and 20 million injured was unthinkable before the industrial age without the use of industrial arms.

Question 9.
Explain the exchange rates.
Answer:
Exchange rates link national currencies for the purpose of International trade.

There are two types of exchange rates:
(i) Fixed exchange rate, and (ii) Flexible or floating exchange rate.
(i) Fixed Exchange rate : When exchange rates are fixed and governments intervene to prevent sudden fluctuation in them, they are known as fixed exchange rate.
(ii) Flexible or Floating Exchange rates : When exchange rates are determined by demand and supply forces of the open market without any interference by government, they are known as flexible or floating exchange rates.

Long Answer Type Question

Question 1.
How did the Silk Routes link the world?
Answer:

• The silk routes are a good example of vibrant pre-modem trade and cultural links between distant parts of the world.
• The silk route was used by the Chinese traders to export silk to other countries.
• These routes were used by traders to trade goods and exchange culture from one country to another.
• Trade and cultural exchange always went hand in hand. Early Christian missionaries, almost certainly travelled through this route to Asia, as did early Muslim preachers, a few centuries later.
• These routes were also used to spread religions. Buddhism emerged from eastern India and spread in several directions through intersecting points on the silk routes.

Question 2.
How did the US economy resume its strong growth in the 1920s?
Answer:
(i) One important feature of the US economy of the 1920s was mass production. The move toward mass production had begun in the late nineteenth century, but in the 1920s, it became a characteristic feature of industrial production in the US.

(ii) A well-known pioneer of mass production was the car manufacturer- Henry Ford. He adapted the assembly line of a Chicago slaughterhouse to his new car plant in Detroit (USA). He realised, that the ‘assembly line’ method would allow a faster and cheaper way of producing vehicles.

(iii) Ford’s industrial practices soon spread in the US. They were also widely copied in Europe in the 1920s. Due to higher wages, more workers could now afford to purchase durable consumer goods, such as cars. Car production in the US rose from 2 million in 1919, to more than 5 million in the year 1929. Similarly, there was a spurt in the purchase of refrigerators, washing machines, radios, gramophone players, all through a system of “hire purchase’, that means on credit, repaid in weekly or monthly instalments.

(iv) The demand for refrigerators, washing machines, etc. was also fuelled by a boom in house construction and home ownership, financed once again by loans.

(v) The housing and consumer boom, of the 1920s created the basis of prosperity in the US. Large investments in housing and household goods seemed to create a cycle of higher employment and incomes, rising consumption demand, more investment, and yet more employment and incomes.

(vi) In 1923, the US resumed exporting capital to the rest of the world and became the largest overseas lender.

Question 3.
What do you know about the Great Depression? Discuss its effects also.
Answer:
An economic depression means when a country records an immense increase in production, the purchasing power of the masses records a steep fall and the face value of the currency decreases. This state of economic depression set in the United States of America (USA) in 1929 and engulfed the whole world. That’s why it is known as the Great Depression.

Effects of the Great Depression:
(i) The US was the industrial country, most severely affected by the depression. With the fall in prices and the prospect of a depression, US banks had also slashed domestic lending and called back loans.

(ii) Farmers could not sell their harvests, households were ruined and businesses collapsed.

(iii) Faced with falling incomes, many households in the US could not repay what they had borrowed and were forced to give up their homes, cars and other consumer durables.

(iv) The consumerist prosperity of the 1920s now disappeared in a puff of dust.

(v) As unemployment soared, people trudged long distances, looking for any work they could find.

(vi) Ultimately, the US banking system itself collapsed. Unable to recover investments, collect loans and repay depositors, thousands of banks went bankrupt and were forced to close. The numbers were phenomenal by 1933, over 4,000 banks had closed, and between 1929 and 1932, about 110,000 companies had collapsed.

Question 4.
What were the factors responsible for the end of the Bretton Woods System ?
Answer:
The factors responsible for the end of the Bretton Woods system were as follows:

(i) The Decline of US Currency:
After 1960s, the US was no longer a dominant economic power, as it had been, for more than two decades. The US dollar now no longer commanded confidence as the world’s principal currency. The dollar could not maintain its value in relation to gold.

(ii) Rise of Western Commercial Banks:
From the mid 1970s, the international financial system also changed in important ways. Earlier, developing countries could turn to international institutions for loans and development assistance. But now, they were forced to borrow from Western Commercial banks and private lending institutions. This led to periodic debt crisis in the developing world, and lower incomes and increased poverty, especially in Africa and Latin America.

(iii) Problem of Unemployment:
The industrial world was also hit by unemployment, that began rising from the mid-1970s, and remained high until the early 1990s. From the late 1970s, MNCs also began to shift production operations to low-wage Asian countries.

(iv) Low Cost Structure in China:
The Chinese economy came out as a new super power, due to low cost structure. Wages were relatively low in countries like China. In this way, they became attractive destinations for investment by foreign MNCs, competing to capture the world markets.

(v) Relocation of Industry:
The relocation of industry to low-wage countries stimulated world trade and capital flows. In the last two decades, the world’s economic geography had been transformed by countries such as India, China and Brazil which had undergone rapid economic transformation.

Map Work

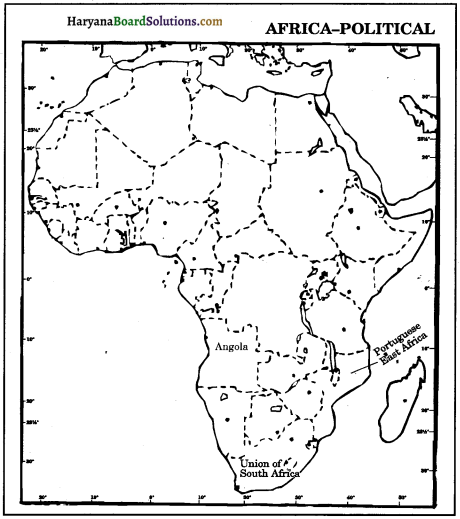
Question 1.
Mark and locate any three 19th Century British colonies on the given outline map of Africa.
Answer:
Africa-Political

Question 2.
On an outline map of Africa locate and label the two colonies of Spain, Germany and France at the end of the 19th century :
Answer:
(a) Spanish Colonies:
(i) Spanish Sahara
(ii) Spanish Morocco.

(b) German Colonies:
(i) German South West Africa
(ii) German East Africa.

(c) French Colonies:
(i) Algeria
(ii) Middle Congo.

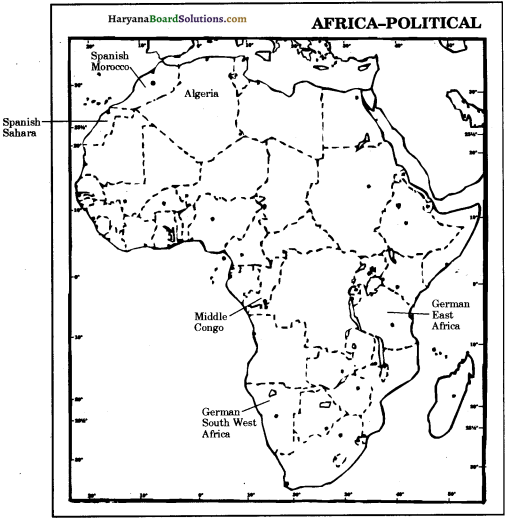
Question 3.
An outline map of Africa show the following:
(i) British Dominion (19th Century)
(ii) Two Portuguese Colonies (19th Century)
Answer:
(i) British Dominion: Union of South Africa.
(ii) Portuguese Colonies: Angola