Haryana State Board HBSE 10th Class Maths Solutions Chapter 6 Triangles Ex 6.2 Textbook Exercise Questions and Answers.
Haryana Board 10th Class Maths Solutions Chapter 6 Triangles Ex 6.2
Question 1.
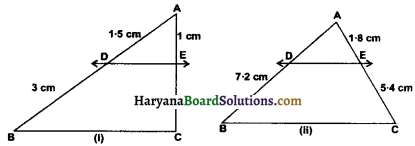
In given figure (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
Solution :
(i) we have, AD = 1.5 cm, AE = 1 cm, DB = 3 cm
DE || BC
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
[By theorem 6.1 (BPT)]
\(\frac{1 \cdot 5}{3 \cdot 0}=\frac{1}{\mathrm{EC}}\) = 2
EC = \(\frac{3.0}{1.5}\) = 2
Hence, EC = 2 cm.
(ii) We have, DB = 7.2 cm, AE = 1.8 cm, EC = 5.4 cm and DE || BC
∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) [By Theorem 6.1 (BPT)]
\(\frac{\mathrm{AD}}{7 \cdot 2}=\frac{1 \cdot 8}{5 \cdot 4}\)
AD = \(\frac{7.2 \times 1.8}{5.4}\) = 2.4
Hence, AD = 2.4 cm.
![]()
Question 2.
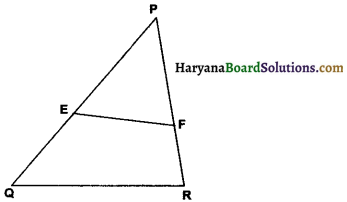
E and F are points on the sides PQ and PR respectively of a APQR. For each of the following cases, state whether EF || QR :
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm.
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm.
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 018 cm and PF = 0.36 cm.
Solution :
(i) we have PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
Now, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{3.9}{3.0}\) = 1.3
and \(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{3 \cdot 6}{2 \cdot 4}\) = 1.5
∵ \(\frac{\mathrm{PE}}{\mathrm{EQ}} \neq \frac{\mathrm{PF}}{\mathrm{FR}}\)
∴ EF is not parallel to QR.
(ii) We have,
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
Now, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{4}{4 \cdot 5}=\frac{8}{9}\) and
\(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{8}{9}\)
∵ \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}\)
∴ EF || QR
(iii) We have,
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm,
EQ = PQ – PE = 1.28 – 0.18 = 11 cm,
PR = PF = 2.56 – 0.36 = 2.2 cm.
Now, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{0 \cdot 18}{1 \cdot 1}=\frac{9}{55}\)
and \(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{0.36}{2 \cdot 2}=\frac{9}{55}\)
∵ \(\frac{P E}{E Q}=\frac{P F}{F R}\)
∴ EF || QR
Question 3.
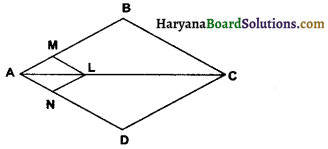
In given figure, if LM || CB and LN || CD, prove that \(\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AD}}\).
Solution:
Given: In □ABCD, LM || CB and LN || CD
To Prove: \(\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AD}}\)
Solution: In ∆ABC LM || CB (given)

![]()
Question 4.
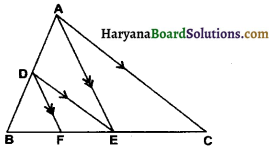
In given figure DE || AC and DF || AE. Prove that \(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BE}}{\mathrm{EC}}\).
Solution:
Given : In ∆ABC DE || AC and DF || AE
To prove: \(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BE}}{\mathrm{EC}}\).
Proof: In ∆BAE,
DF || AE (given)
∴ \(\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{\mathrm{BF}}{\mathrm{FE}}\) ………………..(1)
[By Theorem 6.1 (BPT)]
In ∆ABC, DE || AC (given)
∴ \(\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{\mathrm{BE}}{\mathrm{EC}}\) [By Theorem 6.1 (BPT)]
From(1) and (2) we get
\(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BE}}{\mathrm{EC}}\)
Hence Proved.
Question 5.
In given figure DE || OQ and DF || OR. Show that EF || QR.
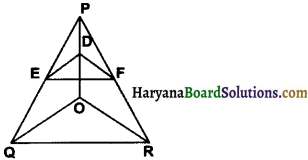
Solution:
Given: In ∆POQ, DE || OQ and in POR, DF || OR
To prove: EF || QR
Proof: In ∆POQ DE || OQ (given)
∴ \(\frac{\mathrm{PD}}{\mathrm{DO}}=\frac{\mathrm{PE}}{\mathbf{E Q}}\) ……………..(1)
[By Theorem 6.1 (BPT)]
In ∆POR DF || OR
∴ \(\frac{\mathrm{PD}}{\mathrm{DO}}=\frac{\mathrm{PF}}{\mathrm{FR}}\) ……………..(2)
[By Theorem 6.1 (BPT)]
From (1) and (2), we get
\(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}\)
∴ EF | | QR [By converse of BPT]
![]()
Question 6.
In given figure, A. B, and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
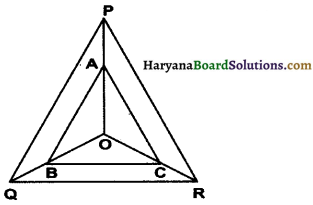
Solution:
Given: In figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR.
To prove: BC || QR
Proof: In ∆OPQ
AB || PQ (given)
\(\frac{O A}{A P}=\frac{O B}{B Q}\) …………………(1)
[By theorem 6.1 (BPT)]
In ∆OPR, AC || PR (given)
\(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OC}}{\mathrm{CR}}\) …………….(2)
[By theorem 6.1 (BPT)]
From (1) and (2) we get
\(\frac{\mathrm{OB}}{\mathrm{BQ}}=\frac{\mathrm{OC}}{\mathrm{CR}}\)
Thus B and C are respectively points on sides OQ and OR of ∆OQR, such that \(\frac{\mathrm{OB}}{\mathrm{BQ}}=\frac{\mathrm{OC}}{\mathrm{CR}}\).
⇒ BC || QR [By converse of BPT]
Hence Proved.
Question 7.
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in class IX).
Solution:
Given : A ∆ABC in which D is the mid-point of AB and DE || BC and meeting AC at E.
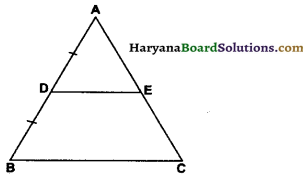
To Prove : AE = EC
Proof : Since, DE || BC
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) ……………..(1)
[By Theorem 6.1 (BPT)]
But AD = DB
[∵ D is the mid point of AB]
∴ \(\frac{\mathrm{AD}}{\mathrm{AD}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) ………………(2)
⇒ \(\frac{\mathrm{AE}}{\mathrm{EC}}\) = 1
⇒ AE = EC.
![]()
Question 8.
Using theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in class IX).
Solution:
Given : A ∆ABC in which D is the mid-point of AB and E is the mid-point of AC
To prove : DE || BC
Proof : Since D and E are the mid-points of AB and AC respectively
AD = DB
⇒ \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = 1
and AE = EC
⇒ \(\frac{\mathrm{AE}}{\mathrm{EC}}\) = 1
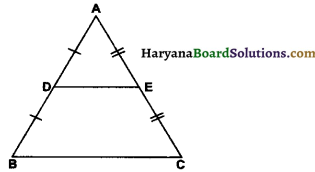
∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
⇒ DE || BC
[By Theorem of 6.2 (converse of BPT)]
Hence Proved.
Question 9.
ABCD is a trapezium in which AB | DC and its diagonals intersect each other at the point O. Show that \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\).
OR
PQRS is a trapezum in which PQ || RS and its diagonals intersect each other at the point O. Prove \(\frac{\mathrm{PO}}{\mathrm{QO}}=\frac{\mathrm{RO}}{\mathrm{SO}}\)
Solution:
Given : A trapezium ABCD in which AB || CD and its diagonals AC and BD intersect at O.
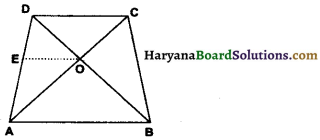
To Prove: \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
Construction: Draw OE || AB through O, which meets AD at E.
Proof : We have,
EO || AB (By construction) …………(1)
DC || AB (given) …………(2)
From (1) and (2), we get
EO || DC
∴ \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{AO}}{\mathrm{OC}}\) ………………..(3)
[By Theorem 6.1 (BPT)]
In ∆ DAB EO || AB
\(\frac{\mathrm{DE}}{\mathrm{EA}}=\frac{\mathrm{DO}}{\mathrm{OB}}\)
∴ \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{BO}}{\mathrm{OD}}\) ………………(4)
[By Theorem 6.1 (BPT)]
From (3), (4), we get
\(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{BO}}{\mathrm{OD}}\)
⇒ \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
Hence Proved.
![]()
Question 10.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\). Show that ABCD is a trapezium.
OR
The diagonals of a quadrilateral PQRS intersect each other at the point O, such that \(\frac{\mathrm{PO}}{\mathrm{QO}}=\frac{\mathrm{RO}}{\mathrm{SO}}\). Show that PQRS is a trapezium.
Solution:
Given : A quadrilateral ABCD whose diagonals AC and BD intersect at a point O such that
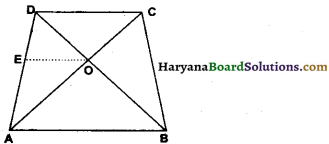
\(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
To Prove : ABCD is a trapezium i.e. AB || DC.
Construction : Draw OE || DC which meets AD at E.
Proof: In ∆ACD,
0E || DC (By construction)
∴ \(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{AE}}{\mathrm{ED}}\) ……………..(1)
[By Theorem 6.1 (BPT)]
But, \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) (given)
⇒ \(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{BO}}{\mathrm{DO}}\) ………………..(2)
From (1) and (2), we get
\(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{BO}}{\mathrm{DO}}\)
⇒ EO || AB
[By Theorem 6.2 (converse of BPT)1
But, OE || DC (By construction)
From (3) and (4), we get
AB || CD
Hence, ABCD is a trapezium. Hence Proved.