Author name: Bhagya

Haryana State Board HBSE 9th Class Science Notes Chapter 8 गति Notes.

Haryana Board 9th Class Science Notes Chapter 8 गति

→ स्थिति में परिवर्तन एक गति है।

→ गति की व्याख्या तय की गई दूरी या विस्थापन के रूप में की जा सकती है।

→ सभी सजीव वस्तुएँ चाहे वे पौधे हों या जंतु, किसी-न-किसी प्रकार की गति करती हैं।

→ पौधों की तुलना में जंतुओं की गति का प्रेक्षण करना आसान होता है।

→ निर्जीव वस्तुओं को गति में लाने के लिए किसी बाहरी कारक की आवश्यकता होती है।

→ दूरी एक अदिश राशि है।

→ विस्थापन एक सदिश राशि है।

→ चाल का SI मात्रक मीटर प्रति सेकंड (ms^-1) है। अन्य मात्रक सेंटीमीटर प्रति सेकंड (cms^-1) व किलोमीटर प्रति घंटा (kmh^-1) है।

→ यदि कोई वस्तु । समय में s दूरी तय करती है तो उसकी चाल (v) निम्न होगी

→ वायु में ध्वनि की चाल 346ms^-1 है।

→ यदि त्वरण वेग की दिशा में हो तो उसे धनात्मक लिया जाता है तथा यदि त्वरण वेग की विपरीत दिशा में हो तो उसे ऋणात्मक लिया जाता है।

→ त्वरण का SI मात्रक ms^-2 है।

→ स्वतंत्र रूप से गिर रही वस्तु की गति एकसमान त्वरित गति का उदाहरण है।

→ दूरी-समय ग्राफ में समय को X-अक्ष और दूरी को Y-अक्ष पर प्रदर्शित किया जाता है।

→ एकसमान चाल के लिए, समय के साथ तय की गई दूरी का ग्राफ एक सरल रेखा होता है।

→ एक सरल रेखा में चल रही वस्तु के वेग में समय के साथ परिवर्तन को वेग-समय ग्राफ द्वारा दर्शाया जाता है।

→ वेग-समय ग्राफ में समय को X-अक्ष पर और वेग को Y-अक्ष पर दर्शाया जाता है।

→ एकसमान त्वरण से चल रही एक वस्तु की गति की व्याख्या तीन समीकरणों के माध्यम से की जा सकती है। वे हैं

• v = u + at,
• s = ut + \(\frac{1}{2}\)at²
• 2as = v² – u²

→ यदि कोई एथलीट। त्रिज्या वाले वृत्तीय पथ का एक चक्कर लगाने में 1 सेकंड का समय लेता है तो वेग (v) = \(\frac{2 \pi \mathrm{r}}{\mathrm{t}}\)

→ चाल-प्रति इकाई समय में वस्तु के द्वारा तय की गई दूरी वस्तु की चाल कहलाती है।

→ वेग–प्रति इकाई समय में हुआ विस्थापन वस्तु का वेग कहलाता है।

→ दूरी-किसी वस्तु द्वारा तय किया गया वास्तविक पथ दूरी कहलाता है।

→ विस्थापन-किसी वस्तु की प्रारंभिक व अंतिम स्थिति के बीच की न्यूनतम दूरी को वस्तु का विस्थापन कहते हैं।

→ मूल बिंदु-किसी वस्तु की स्थिति को बताने के लिए हमें एक निर्देश बिंदु की आवश्यकता होती है, जिसे मूल बिंदु कहा जाता है।

→ एकसमान गति-यदि कोई वस्तु समान समयांतराल में समान दूरी तय करे, तो उसकी गति को एकसमान गति कहते हैं।

→ असमान गति-यदि कोई वस्तु समान समयांतराल में असमान दूरी तय करे, तो उसकी गति को असमान गति कहते हैं।

→ औसत चाल-किसी वस्तु द्वारा तय की गई कुल दूरी और कुल समय के अनुपात को औसत चाल कहते हैं।
अर्थात्

→ औसत वेग-यदि किसी वस्तु का वेग समान रूप से परिवर्तित होता हो तो प्रारंभिक वेग और अंतिम वेग के अंकगणितीय माध्य को औसत वेग कहते हैं। अर्थात्

→ त्वरण-किसी वस्तु का त्वरण प्रति इकाई समय में उसके वेग में होने वाला परिवर्तन है। अर्थात्

→ एकसमान त्वरण-यदि बराबर समयांतराल में किसी वस्तु के वेग में बराबर परिवर्तन हो, तो वस्तु एकसमान त्वरण से गतिशील कहलाती है।

→ असमान त्वरण-यदि किसी वस्तु का वेग असमान रूप से बदलता हो तो उसे असमान त्वरण कहते हैं।

→ एकसमान वृत्तीय गति-यदि एक वस्तु वृत्तीय रास्ते पर एकसमान चाल से चलती है तो उसकी गति को एकसमान वृत्तीय गति कहा जाता है।

Haryana State Board HBSE 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1

Question 1.
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting ?) Represent this situation algebraically and graphically.
Solution:
Let the age of Aftab be x years and age of his daughter be y years.
Seven years ago Aftab’s age = (x – 7) years
Seven years ago his daughter’s age = (y – 7) years
According to question,
x – 7 = 7 (y – 7)
⇒ x – 7 = 7y – 49
⇒ x – 7y = – 49 + 7 = – 42 ………………(1)
After three years Aftab’s age = (x + 3) years
After three years his daughter’s age = (y + 3) years
According to question
x + 3 = 3(y + 3)
⇒ x + 3 = 3y + 9
⇒ 3y = 9 – 3 = 6 …………..(2)
The algebraic representation of this situation is :
x – 7y = – 42 and x – 3y = 6
For representation of these equations graphically, we draw the graphs of these equations as follows :
x – 7y = – 42
⇒ – 7y = – 42 – x
⇒ y = \(\frac{42+x}{7}\)
We put the different values of x in this equation then we get different values of y and we prepare the table of x, y for the equation x – 7y = – 42.

and x – 3y = 6
⇒ 3y = x – 6
⇒ y = \(\frac{x-6}{3}\)
We put the different values of x in this equation then we get different values of y and we prepare the table of x, y for the equation x – 3y = 6.

Now, we plot the values of x and y from table 1 and 2 on the graph paper and we draw the graphs of the equations 1 and 2, those passes through these values.

Observe that we get two straight lines which intersect each other at point (42, 12).

Question 2.
The coach of a cricket team buys 3 bats and 6 balls for ‘ 3900. Later, he buys another bat and 3 more balls of the same kind for 1300. Represent this situation algebraically and geometrically.
Solution :
Let the price of 1 bat be ₹ x and price of 1 ball be ₹ y.
According to question,
3x + 6y = 3900
x + 2y = 1300 ………………(1)
and x + 3y = 1300 ……………..(2)
The algebraic representation of this situation is :
x + 2y = 1300
and x + 3y = 1300
For representation of these equations graphi-cally, we draw the graphs of these equations as follows :
x + 2y = 1300
⇒ 2y = 1300 – x
⇒ y = \(\frac{1300-x}{2}\)
We put the different values of x in this equation then we get different values of y and we prepare the table of x, y for the equation x + 2y = 1300.

and x + 3y = 1300
⇒ 3y = 1300 – x
⇒ y = \(\frac{1300-x}{3}\)
We put the different values ofx in this equation then we get different values of y and we prepare the table of x, y for the equation x + 3y = 1300.

Now, we plot the values of x andy on the graph paper from table 1 and 2 and we draw the graphs of equations 1, 2, those passes through these values.

Observe that we get two straight lines which intersect each other at point (1300, 0).

Question 3.
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be ₹ 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹ 300. Represent the situation algebraically and geometrically.
Solution :
Let the cost of 1 kg. apples be ₹ x and cost of 1 kg. of grapes be ₹ y
According to question,
2x + y = 160 ……………….(1)
and 4x + 2y = 300
⇒ 2x + y = 150 ……………..(2)
The algebraic representation of this situation
2x + y = 160
and 2x + y = 150
For representation of these equations graphically, we draw the graphs of these equations as follows:
2x + y = 160
y = 160 – 2x
We put the different values of x in this equation then we get different values of y and we prepare the table of x, y for the equation 2x + y = 160.

2x + y = 150
⇒ y = 150 – 2x

We put the different values of x in this equation then we get different values of y and we prepare the table of x, y for the equation 2x + y = 150.

Now, we plot the values of x, y on the graph paper from table 1 and 2 and we draw the graphs of equations (1) and (2) which passes through these values.

Observe that we get two straight lines which are parallel to each other.

Haryana State Board HBSE 9th Class Maths Solutions Chapter 14 Statistics Ex 14.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 14 Statistics Exercise 14.2

Question 1.
The blood groups of 30 students of Class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
Represent this data in the form of a frequency distribution table. Which is the most common, and which is the rarest, blood group among these students?
Solution:
The frequency distribution table is given below :
Frequency distribution of blood groups

Most common blood group is O and rarest blood group is AB.

Question 2.
The distance (in km) of 40 engineers from their residence to their place of work were found as follows:

Construct a grouped frequency distribution table with class size 5 for the data given above taking the first interval as 0 – 5 (5 is not included). What main features do you observe from this tabular representation?
Solution :
Minimum and maximum observations are 2 and 32. And class size is 5, first class interval is 0 – 5.
So, class intervals of same size are 0 – 5, 5 – 10, 10 – 15, 15 – 20, 20 – 25, 25 – 30 and 30 – 35. The frequency distribution table is given below
Frequency distribution of distance

We observe that:
(i) The residence of 36 engineers are within 5 km to 20 km.
(ii) The residence of 4 engineers are within 20 km to 35 km.

Question 3.
The relative humidity (in %) of a certain city for a month of 30 days was as follows:

(i) Construct a grouped frequency distribution table with classes 84 – 86, 86 – 88, etc.
(ii) Which month or season do you think this data is about?
(iii) What is the range of this data?
Solution :
Minimum and maixmum observations are 84.9 and 99.2 respectively.
∴ Class intervals of same size are 84 – 86, 86 – 88, 88 – 90, 90 – 92, 92 – 94, 96 – 98 and 98 – 100.
Frequency distribution table of relative humidity is given below :
(i) Frequency distribution of relative humidity :

(ii) The data appears to be taken in the rainy season as the relative humidity is high.
(iii) Range = 99.2 – 84.9 = 14.3.

Question 4.
The heights of 50 students, measured to the nearest centimeters, have been found to be as follows:

(i) Represent the data given above by a grouped frequency distribution table, taking the class intervals as 160 – 165, 165 – 170 etc.
(ii) What can you conclude about their heights from the table?
Solution :
Minimum and maximum observations are 150 and 173 respectively. So, class intervals of same size are
150 – 155, 155 – 160, 160 – 165, 165 – 170 and 170 – 175
The frequency distribution table of heights of 50 students is given below.
(i) Frequency distribution of heights.

(ii) One conclusion that we can draw from the above table is that more than 50% of students are shorter than 165 cm. Ans.

Question 5.
A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows:

(i) Make a ground frequency distribution table for this data with class intervals as 0.00 – 0.04, 0.04 – 0.08 and so on.
(ii) For how many days, was the concentration of sulphur dioxide more than 0.11 parts per million?
Solution :
Minimum and maximum observations are 0.01 and 0.22.
Class intervals of same size are 0.00 – 0.04, 0.04 – 0.08, 0.08 – 0.12, 0.12 – 0.16, 0.16 – 0.20 and 0.20 – 0.24.
Frequency distribution table of concentration of sulphur dioxide in the air is given below :
(i) FREQUENCY DISTRIBUTION OF CONCENTRATION OF SULPHUR DIOXIDE

(ii) The concentration of sulphur dioxide was more than 0.11 ppm for 8 days.

Question 6.
Three coins were tossed 30 times simultaneously. Each time the number of heads occurring was noted down as follows :

Prepare a frequency distribution table for the data given above.
Solution :
Frequency distribution table for the given data is given below :
Frequency distribution table of coins

Question 7.
The value of π up to 50 decimal places is given below :
3.14159265358979323846264338327950288419716939937510
(i) Make a frequency distribution of the digits from 0 to 9 after the decimal point.
(ii) What are the most and the least frequently occurring digits?
Solution:
(i) Frequency distribution table of digits from 0 to 9 after the decimal point is given below:
Frequency distribution of digit from 0 to 9

(ii) The most frequently occurring digits are 3 and 9. The least occurring is 0.

Question 8.
Thirty children were asked about the number of hours they watched TV programmes in the previous week. The results were found as follows:

(i) Make a grouped frequency distribution table for this data, using class width 5 and one of the class intervals as 5 – 10.
(ii) How many children watched television for 15 or more hours a week?
Solution :
Minimum and maximum observations are 1 and 17 respectively.
Class width = 5 and one of the class interval is 5 – 10.
So, class intervals of the following data are 0 – 5, 5 – 10, 10 – 15 and 15 – 20.
(i) Frequency distribution table of hours of T.V. programme is given below :
Frequency distribution of hours of T.V. programme

(ii) Number of children watched television for 15 or more hours a week = 2.

Question 9.
A company manufactures car batteries of a particular type. The lives (in years) of 40 such batteries were recorded as follows:

Construct a grouped frequency distribution table for this data, using class intervals of size 0.5 starting from the interval 2 – 2.5.
Solution :
The minimum and maximum observations of the data are 2.2 and 4.6 respectively.
Class size = 0.5 and one of the class interval is 2 – 2.5.
So, class intervals of the following data are :
2 – 2.5, 2.5 – 3.0, 3.0 – 3.5, 3.5 – 4.0, 4.0 – 45 and 4.5 – 5.0.
The frequency distribution table of car batteries is given below :
Frequency distribution of car batteries

Haryana State Board HBSE 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2

Question 1.
Form the pair of linear equations in the following problems, and find their solutions graphically.

(i) 10 students of class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost ₹ 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Solution :
(i) Let the number of boys in the class be x and number of girls be y.
According to question,
x + y = 10 ……………..(1)
and y = x + 4
⇒ – x + y = 4 ……………(2)
∴ Linear equations are :
x + y = 10
– x + y = 4
Now, we draw the graphs of linear equations as follows :
x + y = 10
⇒ y = 10 – x
We put the different values of x in this equation, then we get different values of y and we prepare the table of x, y for equation x + y = 10

and – x + y = 4
y = 4 – x

We put the different values of x in this equation, then we get different values of y and we prepare the table of x, y for equation – x + y = 4

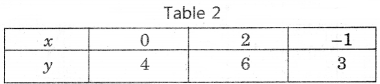
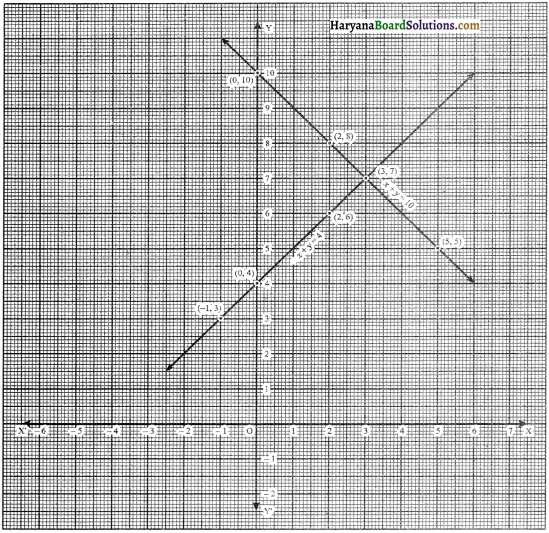
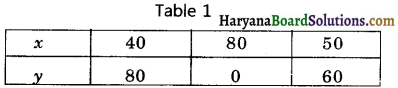
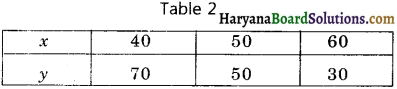
Now, we plot the points (2, 8), (5, 5) and (0, 10) on the graph paper and we draw a graph which passes through these points.
∴ We get a graph of a linear equation x + y = 10
Again, we plot the points (0, 4), (2, 6) and (- 1, 3) on the graph paper and we draw a graph which passes through these points.
∴ We get a graph of a linear equation – x + y = 4.
We observe that the graphs of the linear equations x + y = 10 and – x + y = 4, intersect each other at the point (3, 7). Hence x = 3, y = 7 is the solution of the linear equations.
Therefore, pair of linear equations is, x + y = 10, – x + y = 4 and number of boys = 3, and number of girls = 7.

(ii) Let the cost of 1 pencil be ₹ x
and the cost of 1 pen be ₹ y
According to question,
5x + 7y = 50 ……………………(1)
and 7x + 5y = 46 …………………..(2)
∴ Linear equations are:
5x + 7y = 50
7x + 5y = 46
Now, we draw the graphs of linear equations as follows :
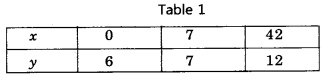
5x + 7y = 50
⇒ 7y = 50 – 5x
⇒ y = \(\frac{50-5 x}{7}\)
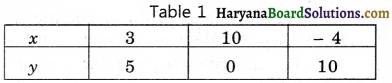
We put the different values of x in this equation, then we get different values of y and we prepare the table of x, y for equation 5x + 7y = 50

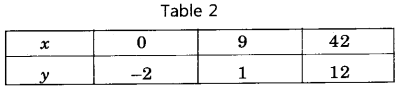
and 7x + 5y = 46
5y = 46 – 7x
y = \(\frac{46-7 x}{5}\)
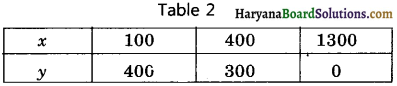
We put the different values of x in this equation, then we get different values of y and we prepare the table of x, y for equation 7x + 5y = 46

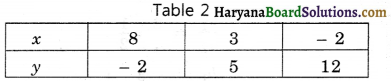
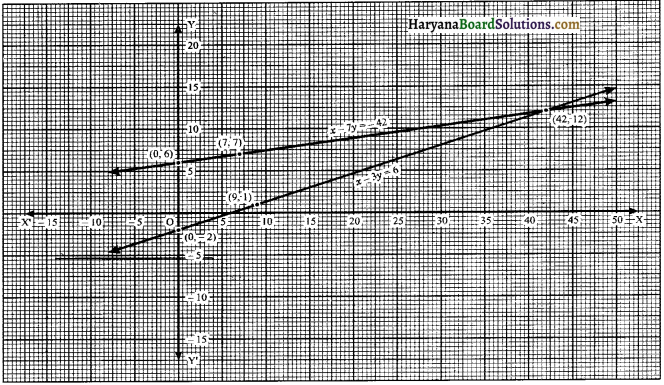
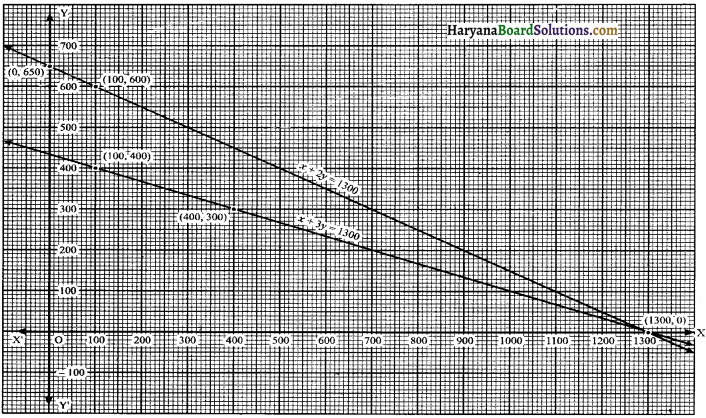
Now, we plot the points (3, 5), (10, 0), (- 4, 10) on the graph paper and we draw a graph which passes through these points.
∴ We get a graph of linear equation 5x + 7y = 50.
Again, we plot the points (8, – 2), (3, 5) and (- 2, 12) on the graph paper and we draw a graph which passes through these points.
∴ We get a graph of linear equation 7x + 5y = 46.

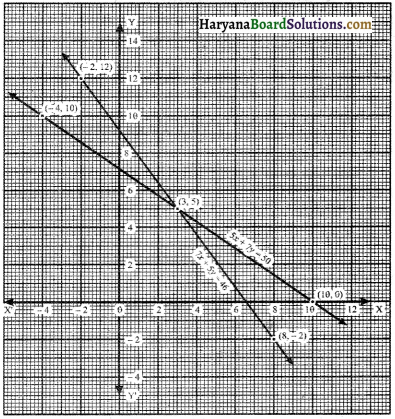
We observe that the graphs of equations 5x + 7y = 50, 7x + 5y = 46; intersect each other at point (3, 5). Hence, x = 3, y = 5 is the solution of linear equations.
Therefore, the pair of linear equations are :
5x + 7y = 50,
7x + 5y = 46
and the cost of 1 Pencil is ₹ 3 and the cost of 1 pen is ₹ 5.

Question 2.
On comparing the ratios \(\frac{a_1}{a_2}\), \(\frac{b_1}{b_2}\) and \(\frac{c_1}{c_2}\) find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0

(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0

(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0.
Solution :
(i) On comparing the linear equations 5x – 4y + 8 = 0, 7x + 6y – 9 = 0 with the general form of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
a₁ = 5, b₁ = – 4, c₁ = 8, a₂ = 1, b₂ = 6, c₂ = – 9
\(\frac{a_1}{a_2}=\frac{5}{7}\)

and \(\frac{c_1}{c_2}=\frac{8}{-9}=\frac{-8}{9}\)

Since, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
Therefore, the given lines intersect at a point.

(ii) On comparing the linear equations 9x + 3y + 12 = 0 and 18x + 6y + 24 = 0 with the general form of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
a₁ = 9, b₁ = 3, c₁ = 12, a₂ = 18, b₂ = 6, c₂ = 24
\(\frac{a_1}{a_2}=\frac{9}{18}=\frac{1}{2}\)

and \(\frac{c_1}{c_2}=\frac{12}{24}=\frac{1}{2}\)

Since, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Therefore, the given lines are coincident lines.

(iii) On comparing the linear equations 6x – 3y + 10 = 0 and 2x – y + 9 = 0 with the general form of linear equations :
a₁x + b₁y + c₁= 0
and a₂x + b₂y + c₂ = 0, we get
a₁ = 6, b₁ = – 3, c₁ = 10,
a₂ = 2, b₂ = – 1, c₂ = 9

\(\frac{a_1}{a_2}=\frac{6}{2}\) = 3

\(\frac{b_1}{b_2}=\frac{-3}{-1}\) = 3

and \(\frac{c_1}{c_2}=\frac{10}{9}\)

Since, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

Therefore, the given lines are parallel lines.

Question 3.
On comparing the ratios \(\frac{a_1}{a_2}\), \(\frac{b_1}{b_2}\) and \(\frac{c_1}{c_2}\), find out whether the following pair of linear equations are consistent, or inconsistent:
(i) 3x + 2y = 5
2x – 3y = 7

(ii) 2x – 3y = 8
4x – 6y = 9

(iii) \(\frac{3}{2}\) x + \(\frac{5}{3}\) y = 7
9x – 10y = 14

(iv) 5x – 3y = 11
– 10x + 6y = – 22

(v) \(\frac{4}{3}\)x + 2y = 8
2x + 3y = 12.
Solution :
(i) We can write the given linear equations in the form of :
3x + 2y – 5 = 0
2x – 3y – 7 = 0
On comparing these equations with the general form of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c = 0, we get
a₁ = 3, b₁ = 2, c₁ = – 5, a₂ = 2, b₂ = – 3, c₂ = – 7

Since, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

Therefore, the pair of linear equations has unique solution. So, the equations are consistent.

(ii) We can write the given linear equations in the form of :
2x – 3y – 8 = 0
4x – 6y – 9 = 0
On oemparing these equations with the general form of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
a₁ = 2, b₁ = – 3, c₁ = – 8, a₂ = 4, b₂ = – 6, c₂ = – 9
\(\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}\)

and \(\frac{c_1}{c_2}=\frac{-8}{-9}=\frac{8}{9}\)

Since, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Therefore, the pair of linear equations are parallel lines. So, the equations are inconsistent.

(iii) We can write the given linear equations in the form of:
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y – 7 = 0
9x – 10y – 14 = 0
On comparing these equations with the general form of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
a₁ = \(\frac{3}{2}\), b₁ = \(\frac{5}{3}\), c₁ = – 7, a₂ = 9, b₂ = – 10, c₂ = – 14
\(\frac{a_1}{a_2}=\frac{\frac{3}{2}}{9}=\frac{3}{2} \times \frac{1}{9}=\frac{1}{6}\)

Since \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

Therefore, the pair of linear equations has a unique solution. So, the equations are consistent.

(iv) We can write the given linear equations in the form of:
5x – 3y – 11 = 0
– 10x + 6y + 22 = 0
On comparing these equations with the general form of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
a₁ = 5, b₁ = – 3, c₁ = – 11, a₂ = – 10, b₂ = 6, c₂ = 22

and \(\frac{c_1}{c_2}=-\frac{11}{22}=\frac{-1}{2}\)

Since, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Therefore, the given linear equations are coincident lines. So, the equations are consistent.

(v) We can write the given linear equations in the form of:
\(\frac{4}{3}\)x + 2y – 8 = 0
2x + 3y – 12 = 0
On comparing these equations with the general form of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
a₁ = \(\frac{4}{3}\), b₁ = 2, c₁ = – 8, a₂ = 2, b₂ = 3, c₂ = – 12

and \(\frac{c_1}{c_2}=\frac{-8}{-12}=\frac{2}{3}\)

Since, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

Therefore, the given linear equations are coincident lines. So, the equations are consistent.

Question 4.
Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
(i) x + y = 5
2x + 2y = 10

(ii) x – y = 8
3x – 3y = 16

(iii) 2x + y – 6 = 0
4x – 2y – 4 = 0

(iv) 2x – 2y – 2 = 0
4x – 4y – 5 = 0
Solution:
(i) We can write the given linear equations in the form of:
x + y – 5 = 0
2x + 2y – 10 = 0
On comparing these equations with the general form of linear equations a₁x + by + c = 0 and ax + by + c = 0, we get
a₁ = 1, b₁ = 1, c₁ = – 5, a₂ = 2, b₂ = 2, c₂ = – 10
\(\frac{a_1}{a_2}=\frac{1}{2}\), \(\frac{b_1}{b_2}=\frac{1}{2}\)

and \(\frac{c_1}{c_2}=\frac{-5}{-10}=\frac{1}{2}\)

Since \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

Therefore, the given linear equations are coincident lines. So, the equations are consistent.

Graphical solution :
We draw the graphs of given linear equations as follows:
x + y – 5 = 0
⇒ y = 5 – x
We put the different values of x in this equation then we get different values of y and we prepare the table of x, y for equation x + y – 5 = 0.

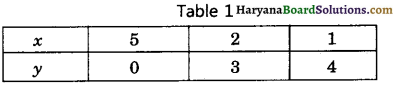
and 2x + 2y – 10 = 0
2y = 10 – 2x
⇒ y = \(\frac{10-2 x}{2}\)
⇒ y = 5 – x
The table of (x, y) for equation 2x + 2y – 10 = 0

Now, we plot the points (5, 0), (2, 3) and (1, 4) from table 1 and 2. Then we draw the graphs of linear equations x + y – 5 = 0 and 2x + 2y – 10 = 0 which passes through these points.

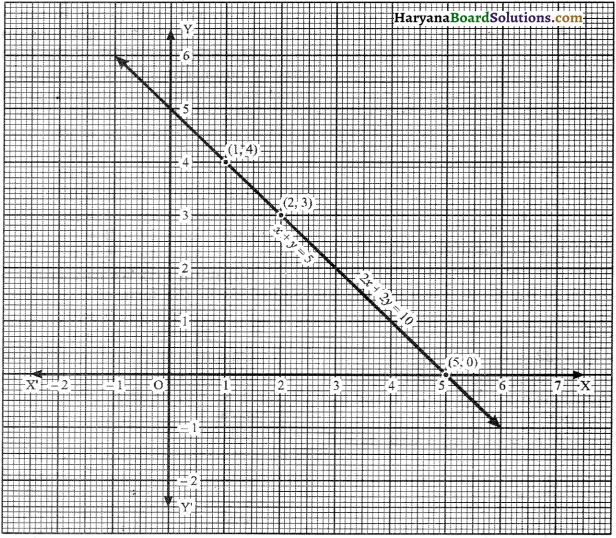
We observe that the graphs of linear equations are coincident lines which overlap each other so, it has infinitely manv solutions. Solutions are (5, 0), (2, 3) and (1, 4).

(ii) We can write the given linear equations in the form of :
x – y – 8 = 0
3x – 3y – 16 = 0
On comparing these equations with the general form of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
a₁ = 1, b₁ = – 1, c₁ = – 8, a₂ = 3, b₂ = – 3, c₂ = – 16
\(\frac{a_1}{a_2}=\frac{1}{3}\), \(\frac{b_1}{b_2}=\frac{-1}{-3}=\frac{1}{3}\)

and \(\frac{c_1}{c_2}=\frac{-8}{-16}=\frac{1}{2}\)

Since, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Therefore, the given linear equations are parallel lines. So, the equations are inconsistent.

(iii) On comparing the linear equations 2x + y – 6 = 0 and 4x – 2y – 4 = 0 with the general form oflinear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
a₁ = 2, b₁ = 1, c₁ = – 6, a₂ = 4, b₂ = – 2, c₂ = – 4
\(\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}\),

and \(\frac{c_1}{c_2}=\frac{-6}{-4}=\frac{3}{2}\)

Since, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
Therefore, the given linear equations intersect each other at a point. So, the equations are consistent.

Graphical solution :
We draw the graphs of linear equations as follows :
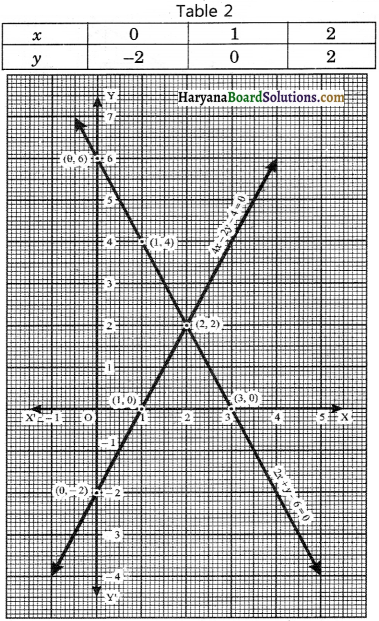
2x + y – 6 = 0
⇒ y = 6 – 2x
We put the different values of x in this equation then we get different values of y and we prepare the table of x, y.

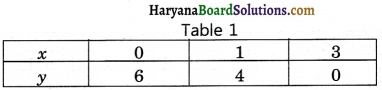
and 4x – 2y – 4 = 0
⇒ 2y = 4x – 4
⇒ y = \(\frac{4 x-4}{2}\)
y = 2x – 2
We put the different values of x in this equation, then we get different values of y and we prepare the table of x, y.

Therefore, the given linear equations are coincident lines. So, the equations are consistent.

Now, we plot the points (0, 6), (1, 4) and (3, 0) on the graph paper and we draw a graph which passes through these points.
∴ We get a graph of linear equation 2x + y – 6 = 0.
Again, we plot the points (0, – 2), (1, 0) and (2, 2) on the graph paper and we draw a graph which passes through these points.
∴ We get a graph of linear equation 4x – 2y – 4 = 0.
We observe that the graphs of linear equations 2x + y – 6 = 0 and 4x – 2y – 4 = 0 intersect each other at point (2, 2). Hence, x = 2, y = 2 is the solution of the given linear equations.

(iv) On comparing the linear equations 2x – 2y – 2 = 0 and 4x – 4y – 5 = 0, with the general form of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we get
a₁ = 2, b₁ = – 2, c₁ = – 2, a₂ = 4, b₂ = – 4, c₂ = – 5
\(\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}\)

and \(\frac{c_1}{c_2}=\frac{-2}{-5}=\frac{2}{5}\)

Since, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Therefore, the given linear equations are parallel lines. So, the equations are inconsistent.

Question 5.
Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Solution:
Let the length of rectangular garden be x m and width be y m.
According to question,
\(\frac{2(x+y)}{2}\) = 36
x + y = 36 …………………(1)
and x = y + 4
⇒ x – y = 4 ……………….(2)
We draw the graphs of these equations as follows :
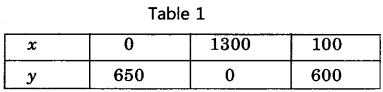
x + y = 36
⇒ y = 36 – x
We put the different values of x in this equation then we get different values of y and we prepare the table of x, y for equation x + y = 36

x – y = 4
⇒ y = x – 4
We put the different values of x in this equation then we get different values of y and we prepare the table of x, y for equation x – y = 4

Now, we plot the points (10, 26), (20, 16) and (12, 24) on the graph paper and we draw a graph which passes through these points.
∴ We get a graph of linear equation x + y = 36.
Again, we plot the points (20, 16), (2, – 2) and (4, 0) on the graph paper and we draw a graph which passes through these points.
∴ We get a graph of linear equation x – y = 4.

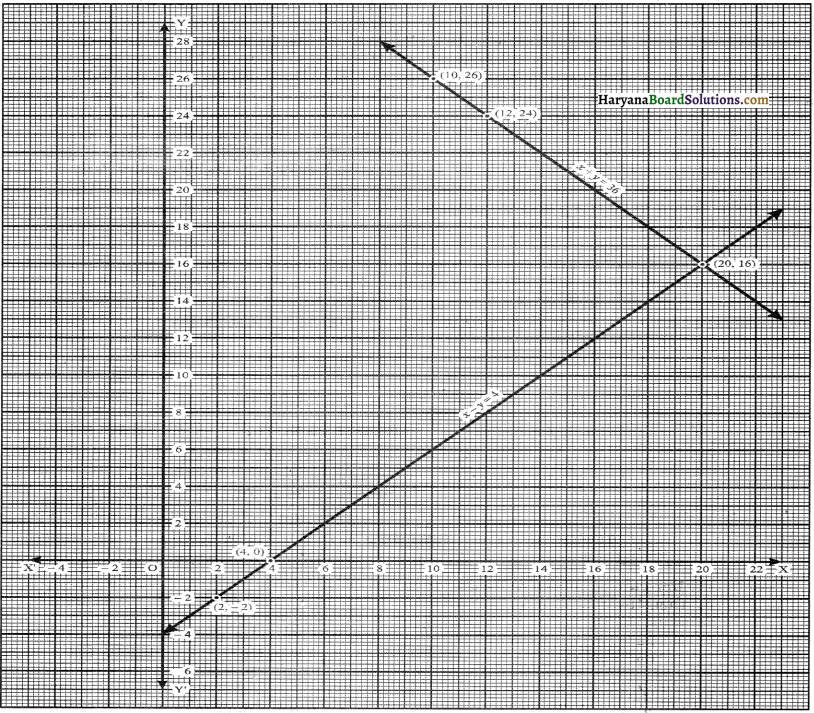
We observe that the graphs of linear equations x + y = 36 and x – y =4 intersect each other at point (20, 16). Hence, x = 20, y = 16 is the solution of given linear equations.
Therefore, Length of garden = 20 m
Width of garden = 16 m.

Question 6.
Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is :
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines.
Solution :
On comparing the given linear equation 2x + 3y – 8 = 0 with the general form of linear equation ax + by + c = 0, we get
a = 2, b = 3, c = – 8
(i) When a pair of linear equations are intersecting lines, then condition is :
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

⇒ \(\frac{2}{a_2} \neq \frac{3}{b_2}\)

⇒ \(\frac{a_2}{b_2} \neq \frac{2}{3}\)

Hence, required possible another linear equation is 3x + 2y – 10 = 0.

(ii) When a pair of linear equations are parallel lines, then condition is :

Hence, required possible another linear equation is 2x + 3y – 12 = 0.

(iii) When the pair of linear equations are coincident lines, then the condition is :
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

Let \(\frac{a_2}{2}=\frac{b_2}{3}=\frac{c_2}{-8}\) = k [Where k is constant]

a₂ = 2k
b₂ = 2k
and c₂ = – 8k

Hence, the required linear equation is : 2kx + 3ky – 8k = 0 [Where k is constant].
Therefore, the required possible linear equation is 4x + 6y – 16 = 0.

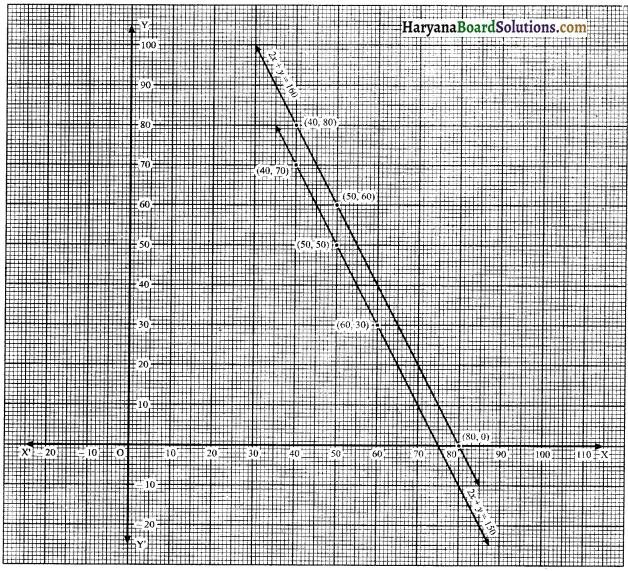
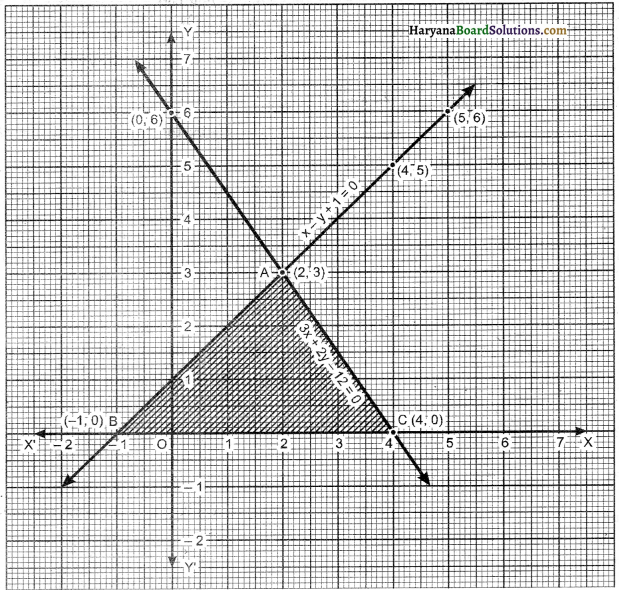
Question 7.
Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x- axis and shade the triangular region.
Solution:
We draw the graph of given linear equations as follows :
x – y + 1 = 0
y = x + 1
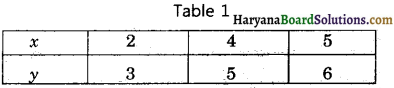
We put the different values of x in this equation, then we get different values of y and we prepare the table of x, y for equation x – y + 1 = 0

and 3x + 2y – 12 = 0
⇒ 2y = 12 – 3x
⇒ y = \(\frac{12-3 x}{2}\)

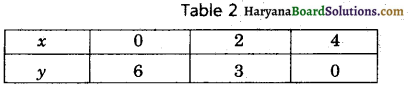
We put the different values of x m this equation then we get different values of y and we prepare the table of x, y for equation 3x + 2y – 12 = 0

Now, we plot the points (2, 3), (4, 5) and (5, 6) on the graph paper and we draw a graph which passes through these points.
∴ We get a graph of linear equation x – y + 1 = 0.
Again, we plot the points (0, 6), (2, 3) and (4,0) on the graph paper and we draw a graph, which passes through these points.
∴ We get a graph of linear equation 3x + 2y – 12 = 0.

Haryana State Board HBSE 9th Class Science Solutions Chapter 4 परमाणु की संरचना Textbook Exercise Questions and Answers.

Haryana Board 9th Class Science Solutions Chapter 4 परमाणु की संरचना

HBSE 9th Class Science परमाणु की संरचना Intext Questions and Answers
(पृष्ठ संख्या-53)
प्रश्न 1.
केनाल किरणें क्या हैं?
उत्तर:
ई० गोल्डस्टीन ने 1886 ई० में धनावेशित विकिरण की खोज की, जिन्हें केनाल किरणें कहा जाता है।

प्रश्न 2.
यदि किसी परमाणु में एक इलेक्ट्रॉन और एक प्रोटॉन है, तो इसमें कोई आवेश होगा या नहीं?
उत्तर:
यदि किसी परमाणु में एक इलेक्ट्रॉन व एक प्रोटॉन हो तो उस पर कोई आवेश नहीं होगा क्योंकि प्रोटॉन और इलेक्ट्रॉन परस्पर आवेशों को संतुलित करते हैं।

(पृष्ठ संख्या -56)

प्रश्न 1.
परमाणु उदासीन है, इस तथ्य को टॉमसन के मॉडल के आधार पर स्पष्ट कीजिए।
उत्तर:
टॉमसन के मॉडल अनुसार परमाणु धन आवेशित गोले का बना होता है तथा इलेक्ट्रॉन उसमें धंसे होते हैं। इस प्रकार ऋणात्मक और धनात्मक आवेश परिमाण समान होने के कारण परमाणु वैद्युतीय रूप से उदासीन होता है।

प्रश्न 2.
रदरफोर्ड के परमाणु मॉडल के अनुसार, परमाणु के नाभिक में कौन-सा अवपरमाणुक कण विद्यमान है?
उत्तर:
रदरफोर्ड के परमाणु मॉडल के अनुसार, परमाणु के नाभिक में प्रोटॉन अवपरमाणुक कण विद्यमान है क्योंकि वह अल्फा कण को विक्षेपित करता है।

प्रश्न 3.
तीन कक्षाओं वाले बोर के परमाणु मॉडल का चित्र बनाइए।
उत्तर

प्रश्न 4.
क्या अल्फा कणों का प्रकीर्णन प्रयोग सोने के अतिरिक्त दूसरी धातु की पन्नी से संभव होगा?
उत्तर:
हाँ, अल्फा कणों का प्रकीर्णन प्रयोग सोने के अतिरिक्त किसी भी दूसरी धातु की पन्नी से संभव होगा।

(पृष्ठ संख्या – 56)

प्रश्न 1.
परमाणु के तीन अवपरमाणुक कणों के नाम लिखें।
उत्तर:
परमाणु के तीन अवपरमाणुक कण इलेक्ट्रॉन, प्रोटॉन व न्यूटॉन हैं।

प्रश्न 2.
हीलियम परमाणु का परमाणु द्रव्यमान 4u है और उसके नाभिक में दो प्रोटॉन होते हैं। इसमें कितने न्यूट्रॉन होंगे?
उत्तर:
हीलियम परमाणु का परमाणु द्रव्यमान = 4u
हीलियम के परमाणु नाभिक में उपस्थित प्रोटॉन = 2
हीलियम के परमाणु नाभिक में उपस्थित न्यूट्रॉन = परमाणु द्रव्यमान – प्रोटॉन
= 4 – 2 = 2

(पृष्ठ संख्या-57)

प्रश्न 1.
कार्बन और सोडियम के परमाणुओं के लिए इलेक्ट्रॉन-वितरण लिखिए।
उत्तर:
1. कार्बन
द्रव्यमान संख्या = 12
परमाणु संख्या = 6
इसलिए प्रोटॉनों की संख्या = 6
इलेक्ट्रॉनों की संख्या = 6
न्यूट्रॉनों की संख्या = 12 – 6 = 6
इलेक्ट्रॉन वितरण = K = 2, L=4

2. सोडियम
द्रव्यमान संख्या = 23
परमाणु संख्या = 11
इसलिए प्रोटॉनों की संख्या = 11
इलेक्ट्रॉनों की संख्या = 11
न्यूट्रॉनों की संख्या = 23 – 11 = 12
इलेक्ट्रॉन वितरण = K = 2
L = 8
M = 1

प्रश्न 2.
अगर किसी परमाणु का K और L कोश भरा है, तो उस परमाणु में इलेक्ट्रॉनों की संख्या क्या होगी? उत्तर
कोश K = 2 इलेक्ट्रॉन
कोश L = 8 इलेक्ट्रॉन
अतः परमाणु में कुल इलेक्ट्रॉन = 2 + 8 = 10 इलेक्ट्रॉन .

(पृष्ठ संख्या-58)

प्रश्न 1.
क्लोरीन, सल्फर और मैग्नीशियम की परमाणु संख्या से आप इनकी संयोजकता कैसे प्राप्त करेंगे?
उत्तर:
(1) क्लोरीन की परमाणु संख्या 17 है इसलिए इसका इलेक्ट्रॉन वितरण निम्न होगा
K = 2 इलेक्ट्रॉन
L = 8 इलेक्ट्रॉन
M = 7 इलेक्ट्रॉन
इस प्रकार क्लोरीन को अपना अष्टक पूरा करने के लिए (8-7) = 1 इलेक्ट्रॉन की आवश्यकता है। अतः क्लोरीन की संयोजकता 1 है।

(2) सल्फर की परमाणु संख्या 16 है इसलिए इसका इलेक्ट्रॉन वितरण निम्न होगा
K = 2 इलेक्ट्रॉन
L = 8 इलेक्ट्रॉन
M = 6 इलेक्ट्रॉन
इस प्रकार सल्फर को अपना अष्टक पूरा करने के लिए (8 – 6) = 2 इलेक्ट्रॉनों की आवश्यकता है। अतः सल्फर की संयोजकता 2 है।

(3) मैग्नीशियम की परमाणु संख्या 12 है। इसलिए इसका इलेक्ट्रॉन वितरण निम्न होगा
K = 2 इलेक्ट्रॉन
L = 8 इलेक्ट्रॉन
M = 2 इलेक्ट्रॉन
इस प्रकार मैग्नीशियम को अपना बाह्य अष्टक पूरा करने के लिए 2 इलेक्ट्रॉनों को त्यागना आसान है। अतः मैग्नीशियम की संयोजकता 2 है।

(पृष्ठ संख्या – 59)

प्रश्न 1.
यदि किसी परमाणु में इलेक्ट्रॉनों की संख्या 8 है और प्रोटॉनों की संख्या भी 8 है तब,
(a) परमाणु की परमाणुक संख्या क्या है?
(b) परमाणु का क्या आवेश है?
उत्तर:
परमाणु में इलेक्ट्रॉनों की संख्या = 8
परमाणु में प्रोटॉनों की संख्या = 8
परमाणु में प्रोटॉनों की संख्या = इलेक्ट्रॉनों की संख्या
= 8
(a) परमाणु की परमाणुक संख्या = परमाणु में प्रोटॉनों तथा इलेक्ट्रॉन की संख्या
= 8 + 8 = 16

(b) इलेक्ट्रॉन वितरण = K = 2, L = 6
अतः परमाणु के बाह्यतम कोश को पूरा करने के लिए 2 इलेक्ट्रॉनों की आवश्यकता है। इसलिए आवेश -2 है।

प्रश्न 2.
पाठ्यपुस्तक की सारणी 4.1 की सहायता से ऑक्सीजन और सल्फर-परमाणु की द्रव्यमान संख्या ज्ञात कीजिए।
उत्तर:
दी गई सारणी अनुसार
(1) ऑक्सीजन में परमाणु संख्या = 8
ऑक्सीजन में प्रोटॉनों की संख्या = 8
ऑक्सीजन में न्यूट्रॉनों की संख्या = 8
द्रव्यमान संख्या = प्रोटॉनों की संख्या + न्यूट्रॉनों की संख्या
= 8 + 8 = 16

(2) सल्फर में परमाणु संख्या = 16
सल्फर में प्रोटॉनों की संख्या = 16
सल्फर में न्यूट्रॉनों की संख्या = 16
द्रव्यमान संख्या = प्रोटॉनों की संख्या + न्यूट्रॉनों की संख्या
= 16 + 16 = 32

(पृष्ठ संख्या – 60)

प्रश्न 1.
चिह्न H, D और T के लिए प्रत्येक में पाए जाने वाले तीन अवपरमाणुक कणों को सारणीबद्ध कीजिए।
उत्तर:
(1) चिह्न H प्रोटियम का प्रतीक है अर्थात ,\({ }_1 \mathrm{H}^1\)
परमाणु संख्या = 1
द्रव्यमान संख्या = 1
इलेक्ट्रॉनों की संख्या = 1
प्रोट्रॉनों की संख्या = 1
न्यूट्रॉनों की संख्या = 1 – 1 = 0

(2) चिह्न D ड्यूटीरियम का प्रतीक है अर्थात \({ }_1 \mathrm{H}^2\)
परमाणु संख्या = 1
द्रव्यमान संख्या = 2
इलेक्ट्रॉनों की संख्या = 1
प्रोट्रॉनों की संख्या = 1
न्यूट्रॉनों की संख्या = 2 – 1 = 1

(3) चिह्न T ट्राइटियम का प्रतीक है अर्थात \({ }_1 \mathrm{H}^3\)
परमाणु संख्या = 1
द्रव्यमान संख्या = 3
इलेक्ट्रॉनों की संख्या = 1
प्रोट्रॉनों की संख्या = 1
न्यूट्रॉनों की संख्या = 3 – 1 = 2

प्रश्न 2.
समस्थानिक और समभारिक के किसी एक युग्म का इलेक्ट्रॉनिक विन्यास लिखिए।
उत्तर:
(i) समस्थानिक युग्म क्लोरीन \({ }_{17} \mathrm{Cl}^{35}\) व \({ }_{17} \mathrm{Cl}^{37}\) का इलेक्ट्रॉनिक विन्यास निम्नलिखित होगा

(ii) समभारिक युग्म कैल्शियम तथा आर्गन का इलेक्ट्रॉनिक विन्यास निम्न होगा
(1) कैल्शियम \({ }_{20} \mathrm{Cl}^{40}\)
e = 20
P = 20
N = 40 – 20 – 20

(2) आर्गन ₁₈Ar⁴⁰
e = 18
P = 18
N = 40 – 18 = 22

HBSE 9th Class Science परमाणु की संरचना Textbook Questions and Answers

प्रश्न 1.
इलेक्ट्रॉन, प्रोटॉन और न्यूट्रॉन के गुणों की तुलना कीजिए।
उत्तर:

प्रश्न 2.
जे.जे. टॉमसन के परमाणु मॉडल की क्या सीमाएँ हैं?
उत्तर:
जे.जे. टॉमसन के परमाणु मॉडल ने परमाणु के उदासीन होने की व्याख्या की जिसके अनुसार परमाणु धन आवेशित गोले का बना होता है और इलेक्ट्रॉन उसमें धंसे होते हैं, परंतु यह मॉडल न्यूट्रॉनों के बारे में तथा इलेक्ट्रॉनों की स्थिति के बारे में कुछ भी नहीं बताता जो दूसरे वैज्ञानिकों द्वारा बाद में स्पष्ट किया गया।

प्रश्न 3.
रदरफोर्ड के परमाणु मॉडल की क्या सीमाएँ हैं?
उत्तर:
अरनेस्ट रदरफोर्ड के परमाणु मॉडल की मुख्य सीमा यह थी कि यह परमाणु की स्थिरता का वर्णन नहीं करता। उसके मॉडल अनुसार, इलेक्ट्रॉन नाभिक के चारों ओर वृत्तीय पथ में चक्कर काटते हैं जिसका परिणाम उनकी त्वरित गति होता है। अतः यह ऊर्जा को विकरित करके वृत्तीय पथ के नाभिक आकार को छोटा कर देगा। परिणामस्वरूप इलेक्ट्रॉन नाभिक में गिर जाएँगे और परमाणु को अस्थिर कर देंगे, परंतु वास्तव में परमाणु अस्थिर नहीं है। चित्र 4.8 : रदरफोर्ड के परमाणु मॉडल की कमी

प्रश्न 4.
बोर के परमाणु मॉडल की व्याख्या कीजिए।
उत्तर:
नील्स बोर के परमाणु मॉडल के अनुसार
(1) इलेक्ट्रॉन केवल कुछ निश्चित कक्षाओं में ही चक्कर लगा सकते हैं, जिन्हें इलेक्ट्रॉन की विविक्त कक्षा कहते हैं।
(2) जब इलेक्ट्रॉन इस विविक्त कक्षा में चक्कर लगाते हैं, तो उनकी ऊर्जा का विकिरण नहीं होता। इन कक्षाओं (या कोशों) को ऊर्जा-स्तर कहते हैं। चित्र में एक परमाणु के ऊर्जा स्तर को दिखाया गया है।

प्रश्न 5.
इस अध्याय में दिए गए सभी परमाणु मॉडलों की तुलना कीजिए।
उत्तर:
इस अध्याय में दिए गए विभिन्न परमाणु मॉडलों की तुलना निम्नलिखित प्रकार से हैं-
1. टॉमसन के परमाणु मॉडल अनुसार
(1) परमाणु धन आवेशित गोले का बना होता है और इलेक्ट्रॉन उसमें धंसे होते हैं।
(2) ऋणात्मक और धनात्मक आवेश परिणाम में समान होते हैं। इसलिए परमाणु वैद्युतीय रूप से उदासीन होते हैं।

2. रदरफोर्ड के परमाणु मॉडल अनुसार
(1) परमाणु का केंद्र धनावेशित होता है जिसे नाभिक कहा जाता है। एक परमाणु का लगभग संपूर्ण द्रव्यमान नाभिक में होता है।
(2) इलेक्ट्रॉन नाभिक के चारों ओर निश्चित कक्षाओं में चक्कर लगाते हैं।
(3) नाभिक का आकार परमाणु के आकार की तुलना में काफी कम होता है।

3. बोर मॉडल के अनुसार
(1) इलेक्ट्रॉन केवल कुछ निश्चित कक्षाओं में ही चक्कर लगा सकते हैं, जिन्हें इलेक्ट्रॉन की विविक्त कक्षा कहते हैं।
(2) जब इलेक्ट्रॉन इस विविक्त कक्षा में चक्कर लगाते हैं, तो उनकी ऊर्जा का विकिरण नहीं होता है। इन कक्षाओं को ऊर्जा स्तर कहते हैं।

प्रश्न 6.
पहले अठारह तत्त्वों के विभिन्न कक्षों में इलेक्ट्रॉन वितरण के नियम को लिखिए।
उत्तर:
पहले अठारह तत्त्वों के विभिन्न कक्षों में इलेक्ट्रॉन वितरण के लिए बोर और बरी द्वारा निम्न नियम प्रस्तुत किए गए
(1) किसी कक्षा में उपस्थित अधिकतम इलेक्ट्रॉनों की संख्या को सूत्र 2n² से दर्शाया जाता है, जहाँ ‘n’ कक्ष की संख्या या ऊर्जा स्तर है। इसलिए इलेक्ट्रॉनों की अधिकतम संख्या पहले कक्ष या K कोश में (2 x 1²) = 2 होगी, दूसरे कक्ष या L सेल में (2 x 2²) = 8 होगी, तीसरे कक्ष या M सेल में होगी = (2 x 3²)= 18, चौथे कक्ष या N सेल में होगी = (2 x 4²)= 32.

(2) सबसे बाहरी कोश में इलेक्ट्रॉनों की अधिकतम संख्या 8 हो सकती है।

(3) किसी परमाणु के अगले कोश में इलेक्ट्रॉन तब तक स्थान नहीं लेते हैं जब तक कि उससे पहले वाले भीतरी कोश पूर्ण रूप से भर नहीं जाता। इससे स्पष्ट होता है कि कक्षाएँ क्रमानुसार भरती हैं।

प्रश्न 7.
सिलिकॉन और ऑक्सीजन का उदाहरण देते हुए संयोजकता की परिभाषा दीजिए।
उत्तर:
परमाणु के बाह्यतम कक्ष में इलेक्ट्रॉनों के अष्टक बनाने के लिए जितनी संख्या में इलेक्ट्रॉनों की साझेदारी या स्थानांतरण होता है, वह उस तत्त्व की संयोजकता कहलाती है। जैसे

(1) सिलिकॉन \(({ }_{14} \mathrm{Si}^{28})\) में इलेक्ट्रॉनों का वितरण निम्न होगा
K = 2
L = 8
M = 4
अतः यह अपना अष्टक पूरा करने के लिए 4 इलेक्ट्रॉन स्थानांतरित कर सकता है। इसलिए इसकी संयोजकता 4 है।

(2) ऑक्सीजन (\(({ }_{8} \mathrm{Si}^{16})\)) में इलेक्ट्रॉनों का वितरण निम्न होगा
K = 2
L = 6
अतः इसे अपना अष्टक पूरा करने के लिए (8 – 6) = 2 इलेक्ट्रॉनों की साझेदारी करनी होगी। इसलिए इसकी संयोजकता 2 है।

प्रश्न 8.
उदाहरण के साथ व्याख्या कीजिए-परमाणु संख्या, द्रव्यमान संख्या, समस्थानिक और समभारिक समस्थानिकों के कोई दो उपयोग लिखिए।
उत्तर:
परमाणु संख्या-परमाणु के नाभिक में उपस्थित कुल प्रोटॉनों की संख्या उसकी परमाणु संख्या (Z) कहलाती है; जैसे ऑक्सीजन की परमाणु संख्या 8 व कार्बन की परमाणु संख्या 6 है।

द्रव्यमान संख्या – परमाणु के नाभिक में उपस्थित प्रोटॉनों और न्यूट्रॉनों की कुल संख्या के योग को द्रव्यमान संख्या (A) कहते हैं। जैसे ऑक्सीजन की द्रव्यमान संख्या 16u तथा कार्बन की द्रव्यमान संख्या 12u है।

समस्थानिक – एक ही तत्त्व के ऐसे परमाणु जिनकी परमाणु संख्या समान हो, परंतु द्रव्यमान संख्या भिन्न हो तत्त्व के समस्थानिक कहलाते हैं। जैसे हाइड्रोजन के तीन समस्थानिक प्रोटियम \(({ }_{1} \mathrm{H}^{1})\), ड्यूटीरियम \(({ }_{1} \mathrm{H}^{2})\) व ट्राइटियम \(({ }_{1} \mathrm{H}^{3})\) तथा कार्बन के दो समस्थानिक \(({ }_{6} \mathrm{C}^{12})\) व \(({ }_{6} \mathrm{C}^{14})\) हैं।

समभारिक – समभारिक वे परमाणु होते हैं जिनकी द्रव्यमान संख्या समान लेकिन परमाणु संख्या भिन्न-भिन्न होती है; जैसे कैल्शियम \(({ }_{20} \mathrm{Ca}^{40})\) तथा आर्गन \(({ }_{18} \mathrm{Ar}^{40})\) समभारिक हैं।

समस्थानिकों के उपयोग
(1) यूरेनियम के एक समस्थानिक (U-235) का उपयोग परमाणु भट्टी (reactor) में ईंधन के रूप में होता है।
(2) कैंसर के उपचार में कोबाल्ट के समस्थानिक का उपयोग होता है।
(3) पेंघा रोग के इलाज में आयोडीन के समस्थानिक का उपयोग होता है।

प्रश्न 9.
Na⁺ के पूरी तरह से भरे हुए Ka L कोश होते हैं व्याख्या कीजिए। उत्तर-सोडियम परमाणु की परमाणु संख्या 11 होती है। इसलिए सोडियम परमाणु में इलेक्ट्रॉनों की संख्या = 11 अतः सोडियम परमाणु का इलेक्ट्रॉनिक वितरण होगा
K = 2
L = 8
M = 1
यह सोडियम परमाणु स्थाई संरचना प्राप्त करने के लिए एक इलेक्ट्रॉन त्याग कर Na (सोडियम आयन) बन जाएगा जिस कारण इसका इलेक्ट्रॉनिक वितरण K = 2 तथा L = 8 होगा अर्थात K और L कोश पूर्ण भरे होंगे।

प्रश्न 10.
अगर ब्रोमीन परमाणु दो समस्थानिकों \({ }_{35}^{79} \mathrm{Br}\)(49.7%) तथा \({ }_{35}^{81} \mathrm{Br}\) (50.3%)] के रूप में है, तो ब्रोमीन परमाणु के औसत परमाणु द्रव्यमान की गणना कीजिए।
उत्तर:
ब्रोमीन परमाणु दो समस्थानिकों \({ }_{35} \mathrm{Br}^{79}\) और \({ }_{35} \mathrm{Br}^{81}\) के रूपों में पाया जाता है जिनका द्रव्यमान क्रमशः 49.7% व 50.3% है।
इसलिए ब्रोमीन का औसत परमाणु द्रव्यमान होगा
\(\left(79 \times \frac{49.7}{100}+81 \times \frac{50.3}{100}\right)\)
\(\left(\frac{79 \times 497}{1000}+\frac{81 \times 503}{1000}\right)\)
\(\left(\frac{39263}{1000}+\frac{40743}{1000}\right)\) = 39.263 + 40.743 = 80.006 = 80u

प्रश्न 11.
एक तत्त्व X का परमाणु द्रव्यमान 16.2u है तो इसके किसी एक नमूने में समस्थानिक \({ }_{8}^{16} \mathrm{X}\) और \({ }_{8}^{18} \mathrm{X}\) का प्रतिशत क्या होगा?
हल
माना समस्थानिक \({ }_{8} \mathrm{X}^{16}\) का प्रतिशत = x
तो \({ }_{8} \mathrm{X}^{18}\) का प्रतिशत = 100 – x
तत्त्व X का औसत परमाणु द्रव्यमान = 16.2u
\(\frac{16 \times x}{100}+\frac{18 \times(100-x)}{100}\) = 16.2
दोनों ओर 100 से गुणा करने पर
16x + 1800 – 18x = 1620
या -2x = 1620 – 1800
या -2x = -180
या x = \(\frac{-180}{-2}\) = 90
अतः नमूने (सैंपल) में \({ }_8 \mathrm{X}^{16}\) का प्रतिशत = 90%
तथा \({ }_8 \mathrm{X}^{18}\) का प्रतिशत = 100 — 90 = 10%

प्रश्न 12.
यदि तत्त्व का Z= 3 हो तो तत्त्व की संयोजकता क्या होगी? तत्त्व का नाम भी लिखिए।
हल
तत्त्व की परमाणु संख्या (Z) = 3
तत्त्व में इलेक्ट्रॉनों की संख्या = 3
इलेक्ट्रॉन वितरण
K = 2
L = 1
अतः तत्त्व के बाह्यतम कोश में 1 इलेक्ट्रॉन है। यह स्थाई विन्यास प्राप्त करने के लिए एक इलेक्ट्रॉन का त्याग कर सकता है। इसलिए तत्त्व की संयोजकता 1 है। अतः तत्त्व लीथियम (Li) है।

प्रश्न 13.
दो परमाणु स्पीशीज़ के केंद्रकों का संघटन नीचे दिया गया है

X और Y की द्रव्यमान संख्या ज्ञात कीजिए। इन दोनों स्पीशीज़ में क्या संबंध है?
हल–परमाणु x के लिए
प्रोटॉनों की संख्या = 6
न्यूट्रॉनों की संख्या = 6
द्रव्यमान संख्या = प्रोटॉनों की संख्या + न्यूट्रॉनों की संख्या
= 6+6
= 12
परमाणु Y के लिए
प्रोटॉनों की संख्या = 6
न्यूट्रॉनों की संख्या = 8
द्रव्यमान संख्या = प्रोटॉनों की संख्या + न्यूट्रॉनों की संख्या
= 6+ 8
= 14
ये दोनों स्पीशीज \({ }_6 X^{12}\) और \({ }_6 Y^{14}\) समस्थानिक हैं।

प्रश्न 14.
निम्नलिखित वक्तव्यों में गलत के लिए F और सही के लिए T लिखें।
(a) जे.जे. टॉमसन ने यह प्रस्तावित किया था कि परमाणु के केंद्रक में केवल न्यूक्लीयॉन्स होते हैं।
(b) एक इलेक्ट्रॉन और प्रोटॉन मिलकर न्यूट्रॉन का निर्माण करते हैं इसलिए यह अनावेशित होता है।
(c) इलेक्ट्रॉन का द्रव्यमान प्रोटॉन से लगभग \(\frac{1}{2000}\) गुना होता है।
(d) आयोडीन के समस्थानिक का इस्तेमाल टिंक्चर आयोडीन बनाने में होता है। इसका उपयोग दवा के रूप में होता है।
उत्तर:
(a) F,
(b) F
(c) T,
(d) F

नोट-प्रश्न संख्या 15, 16 और 17 में सही के सामने (√ ) का चिह्न और गलत के सामने (X) का चिह्न लगाइए।

प्रश्न 15.
रदरफोर्ड का अल्फा कण प्रकीर्णन प्रयोग किसकी खोज के लिए उत्तरदायी था?
(a) परमाणु केंद्रक
(b) इलेक्ट्रॉन
(c) प्रोटॉन
(d) न्यूट्रॉन
उत्तर:
(a) परमाणु केंद्रक (√),
(b) इलेक्ट्रॉन (x),
(c) प्रोटॉन (x),
(d) न्यूट्रॉन (x)

प्रश्न 16.
एक तत्त्व के समस्थानिक में होते हैं
(a) समान भौतिक गुण
(b) भिन्न रासायनिक गुण
(c) न्यूट्रॉनों की अलग-अलग संख्या
(d) भिन्न परमाणु संख्या
उत्तर:
(a) समान भौतिक गुण (x),
(b) भिन्न रासायनिक गुण (x),
(c) न्यूट्रॉनों की अलग-अलग संख्या (√),
(d) भिन्न परमाणु संख्या (x)।

प्रश्न 17.
Cl^– आयन में संयोजक इलेक्ट्रॉनों की संख्या है
(a) 16
(b) 8
(c) 17
(d) 18
उत्तर:
(a) 16 (x)।
(b) 8 (√)।
(c) 17 (x)।
(d) 18 (x)।

प्रश्न 18.
सोडियम का सही इलेक्ट्रॉनिक विन्यास निम्न में कौन-सा है?
(a) 2, 8
(b) 8, 2, 1
(c) 2, 1, 8
(d) 2, 8, 1
उत्तर:
सोडियम का सही इलेक्ट्रॉनिक विन्यास
(d) 2, 8, 1 है।

प्रश्न 19.
निम्नलिखित सारणी को पूरा कीजिए

उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 14 Statistics Ex 14.3 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 14 Statistics Exercise 14.3

Question 1.
A survey conducted by an organisation for the cause of illness and death among the women between the ages 15 – 44 (in years) worldwide, found the following figures (in %):

(i) Represent the information given above graphically.
(ii) Which condition is the major cause of women’s ill health and death world-wide ?
(iii) Try to find out, with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
Solution :
(i) We draw the bar graph of this data in the following steps :
(a) We draw a horizontal and vertical line.
(b) We represent the causes of death on horizontal axis, choosing any scale. We take equal widths for all bars and maintain equal gaps in between. Let one head be represented by one unit.
(c) We represent the female fatality rate on the vertical axis. Let 1 unit = 4%.
(d) To represent first head i.e., reproductive health conditions, we draw a rectangular bar with width 1 unit and height 7.95 units.
(e) Similarly, other heads are represented leaving a gap of 1 unit in between two consecutive bars.

(ii) Reproductive health conditions is the major cause of women’s ill health and death world wide.
(iii) Two factors which play a major role is :
(a) There are unqualified doctors in a maternity hospitals, where the pregnant women did not get better treatment.
(b) Unwanted female child.

Question 2.
The following data on the number of girls (to the nearest ten) per thousand boys in different sections of Indian society is given below :

(i) Represent the information above by a bar graph.
(ii) In the classroom discuss what conclusions can be arrived at from the graph.
Solution :
(i) We draw the bar graph of this data in the following steps :
(a) We draw a horizontal and vertical line.
(b) We represent section of society on horizontal axis, choosing any scale. We take equal widths for all bars and maintain equal gaps in between. Let one head be represented by one unit.
(c) We represent the number of girls (to nearest ten) per thousand boys on the vertical axis. Let 1 unit = 10 girls.
(d) To represent the first head i.e., scheduled caste (8.c.), we draw a rectangular bar with width 1 unit and height 4 units.
(e) Similarly, other heads are represented leaving a gap of 1 unit in between two consecutive bars.

(ii) From the graph, we observe that the number of girls to the nearest ten per thousand boys are maximum in scheduled tribe but minimum in urban.

Question 3.
Given below are the seats won by different political parties in the polling outcome of a state assembly elections :

(i) Draw a bar graph to represent the polling results.
(ii) Which political party won the maximum number of seats?
Solution:
(i) We draw the bar graph of the given data in the following steps:
(a) We draw a horizontal and vertical line.
(b) We represent political party on the horizontal axis, choosing any scale. We take equal widths for all bars and maintain equal gaps in between. Let one political party represented by 1 unit.

(c) We represent the number of seats won on the vertical axis. Let 1 unit = 10 seats.
(d) To represent the political party A, we draw a rectangular bar with width 1 unit and height 7.5 units.
(e) Similarly, other political parties we represented leaving a gap of 1 unit in between two consecutive bars.
(ii) Party A won the maximum number of seats.

Question 4.
The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table :

(i) Draw a histogram to represent the given data.
[Hint : First make the class intervals continuous]
(ii) Is there any other suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long ? Why?
Solution :
(i) The given frequency distribution is in inclusive form. So, first we convert it into exclusive form,
The difference between the lower limit of a class and upper limit of preceding class (h)= 1.
To convert the given frequency distribution into exclusive frequency distribution, we subtract \(\frac{h}{2}=\frac{1}{2}\) =0.5 from each of lower limit and add 0-5 to each upper limit. The exclusive frequency distribution table obtained as follows:

We represent the length (in mm) along x-axis on a suitable scale and the corresponding frequencies along y-axis on a suitable scale.
We construct rectangles with class intervals as bases and the corresponding frequencies as heights.
Thus, we obtain a histogram as shown below :

(ii) Frequency polygon is the another method of representing this data graphically.
(iii) No, it is not correct to conclude that maximum number of leaves are 153 mm long because number of leaves having length 153 mm or less than 153 mm = 3 + 5 + 9 + 12 = 29 and number of leaves having length more than 153 mm = 5 + 4 + 2 = 11. But there might be no leave of length 153 mm.

Question 5.
The following table gives the life times of 400 neon lamps :

(i) Represent the given information with the help of a histogram.
(ii) How many lamps have a lifetime of more than 700 hours?
Solution:
(i) The given frequency distribution is in the exclusive form. So we represent the lifetime (in hours) along x-axis on a suitable scale and the corresponding frequencies along y-axis on a suitable scale. We construct rectangles with class intervals as bases and corresponding frequencies as heights. Thus, we obtain a histogram as shown below :

(ii) Number of lamps having lifetime more than 700 hrs = 74 + 62 + 48 = 184.

Question 6.
The following table gives the distribution of students of two sections according to the marks obtained by them :

Represent the marks of the students of both the sections on the same graph by two frequency polygons. From the two polygons compare the performance of the two sections.
Solution :
To represent the frequency polygon, we need the class marks of given classes. For class interval (0 – 10), the upper limit is 10 and lower limit is 0.
So, the class mark = \(\frac{10+0}{2}\) = 5
Continuing in the same manner, we find the class marks of the other classes as well. So, we obtained the following table :

We represent class marks along the x-axis on a suitable scale and the corresponding frequency along the y-axis on a suitable scale. To obtain the frequency polygon of section A, we plot the points (5, 3), (15, 9), (25, 17),(35, 12), (45, 9) and join thuse points by line segments.
To obtain the frequency polygon of section B, we plot the points (5, 5), (15, 19), (25, 15), (35, 10) and (45, 1) on the same scale and join these points by dotted line segments.
The two frequency polygons are shown given figure.

Question 7.
The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:

Represent the data of both the teams on the same graph by frequency polygons.
(Hint First make the class intervals continuous.)
Solution:
Here the class intervals are discontinuous. So, we convert it into continuous class intervals. For this, we subtract \(\frac{h}{2}=\frac{1}{2}\) = 0.5 from each of lower limit and add 0.5 to each upper limit. So, continuous class intervals obtained as follows:

To represent the frequency polygon, we need the class marks of the given classes. For class interval (0-5 -6.5), the upper limit is 65 and lower limit is 0.5.
So, the class mark = \(\frac{6.5+0.5}{2}\) = 3.5
Continuing in the same manner, we find the class marks of the other classes as well. So, we obtained the following table :

We represent the class marks along x-axis on a suitable scale and the corresponding frequencies along y-axis on a suitable scale.
To obtain the frequency polygon of team A, we plot the points (3.5, 2), (9.5, 1), (15.5, 8), (21.5, 9), (27.5, 4), (33.5, 5), (39.5, 6), (45.5, 10), (51.5, 6) and (57.5, 2) and join these points by line segments.
To obtain the frequency polygon of team B, we plot the points (3.5, 5), (9.5, 6), (15.5, 2), (21.5, 10), (27.5, 5), (33.5, 6), (39.5, 3), (45.5, 4), (51.5, 8) and (57.5, 10) on the same scale and join these points by dotted line segments.
The two frequency polygons are shown given figure.

Question 8.
A random survey of the number of children of various age groups playing in a park was found as follows:

Draw a histogram to represent the data above.
Solution :
Here the class intervals are not same size. Here, minimum class size is 1, then lengths of the rectangles are modified to be proportionate to the class size 1. Lengths of rectangles are computed as follows in the given table :

We represent the ages of children along x-axis on a suitable scale and number of children along y-axis on a suitable scale. We construct rectangles with class intervals as bases and corresponding frequencies as heights.

Question 9.
100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:

(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.
Solution:
(i) Here the class iņtervals are not same size and minimum class size is 2, then lengths of the rectangles are modified to be proportionate to the class size 2.
Lengths of the rectangles are computed as follow in the given table :

We represent the number of letters along x-axis on a suitable scale and number of surnames along y-axis on a suitable scale. We construct rectangles with class intervals as bases and corresponding frequencies as heights.

(ii) The maximum surnames lies in the class interval 6 – 8.

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 वृत्त Ex 10.5 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 वृत्त Exercise 10.5

प्रश्न 1.
आकृति में, केंद्र O वाले एक वृत्त पर तीन बिंदु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60° है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिंदु है, तो ∠ADC ज्ञात कीजिए।

हल :
प्रश्नानुसार,
∠BOC = 30° …..(i)
∠AOB = 60° ….(ii)
समीकरण (i) तथा (ii) को जोड़ने पर,
∠AOB + ∠BOC = 60° + 30°
∠AOC = 90°
चाप AC केंद्र पर ∠AOC तथा शेष वृत्त पर ∠ADC बनाती है।
∴ ∠AOC = 2∠ADC
90° = 2∠ADC
∠ADC = \(\frac{90^{\circ}}{2}\)
∠ADC = 45° उत्तर

प्रश्न 2.
किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिंदु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात कीजिए।
हल :

माना PQ, एक जीवा है। OP तथा OQ को मिलाया।
दिया है : PQ = OP = OQ [∵ जीवा = त्रिज्या]
∴ ΔOPQ एक समबाहु त्रिभुज है।
∠POQ = 60°
∴ क्योंकि चाप PBQ वृत्त के केंद्र पर परावर्तन ∠POQ = 360° – 60° = 300° बनाती है तथा ∠PBQ वृत्त के लघु चाप पर बनाती है।
∠PBQ = \(\frac{1}{2}\) × परावर्तन ∠POQ
= \(\frac{1}{2}\) × 300° = 150°
इसी प्रकार, ∠PAQ = \(\frac{1}{2}\)(∠POQ) [∵ वृत्त के शेष भाग पर बना कोण केंद्र पर बने कोण का आधा होता है]
∴ = \(\frac{1}{2}\) × 60° = 30°
अतः जीवा द्वारा लघु चाप पर बनाया गया कोण 150° तथा दीर्घ चाप पर बनाया गया कोण = 30°

प्रश्न 3.
आकृति में, ∠PQR = 100° है, जहां P,Qतथा R, केंद्र O वाले एक वृत्त पर स्थित बिंदु हैं। ∠OPR ज्ञात कीजिए।

हल :
क्योंकि एक चाप द्वारा केंद्र पर बनाया गया कोण, उसी चाप द्वारा बनाई गई शेष परिधि के बिंदु पर कोण का दोगुना होता है।
∴ परावर्तन ∠POR = 2∠PQR
या परावर्तन ∠POR = 2 × 100° = 200°
∠POR = 360° – 200° = 160°
ΔOPR में,
या OP = OR [एक ही वृत्त की त्रिज्याएं]
∠OPR = ∠ORP [बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
तथा ∠POR = 160° [प्रमाणित]
अतः ∠OPR = ∠ORP = \(\frac{1}{2}\)(180° – 160°)
= \(\frac{1}{2}\) × 20° = 10°
∠OPR = 10° उत्तर

प्रश्न 4.
आकृति में, ∠ABC = 69° और ∠ACB = 31° हो, तो ∠BDC ज्ञात कीजिए। [B.S.E.H. March, 2020]

हल :
ΔABC में,
∠A + ∠ABC + ∠ACB = 180°
∠A + 69° + 31° = 180° (∵ ∠ABC = 69° व ∠ACB = 319)
या ∠A = 180° – 69° – 31° = 180° – 100° = 80°
परंतु ∠A = ∠BDC [एक ही वृत्तखंड में बने कोण]
अतः
∠BDC = 80° उत्तर

प्रश्न 5.
आकृति में, एक वृत्त पर A, B, C और D चार बिंदु हैं। AC और BD एक बिंद्र E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° तथा ∠ECD = 20° है। ∠BAC ज्ञात कीजिए।

हल:
∠BEC + ∠DEC = 180° (रैखिक युग्म]
⇒ 130° + ∠DEC = 180° [∵ ∠BEC = 130°]
या ∠DEC = 180° – 130°
या ∠DEC = 50°
अब ΔDEC में,
∠DEC + ∠DCE + ∠D = 180°
या 50° + 20° + ∠D = 180° [त्रिभुज के कोणों का योग]
या ∠D = 180° – 50° – 200
∠D = 180° – 70° = 110°
परंतु ∠BAC = ∠D [एक ही वृत्तखंड में बने कोण]
अतः ∠BAC = 110° उत्तर

प्रश्न 6.
ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिंदु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD ज्ञात कीजिए। पुनः यदि AB = BC हो, तो ∠ECD ज्ञात कीजिए।
हल :

∠BDC = ∠BAC [एक ही वृत्तखंड में बने कोण]
परंतु ∠BAC = 30°
∠BDC = 300
अब ΔBCD में,
या ∠BDC + ∠DBC + ∠BCD = 180° [त्रिभुज के कोणों का योग]
या 30° + 70° + ∠BCD = 180° [∵ ∠DBC = 70°, ∠BDC = 30°]
∠BCD = 180° – 30° – 70° = 180° – 100° = 80°
यदि AB = BC, तब ∠BCA = ∠BAC = 30° [बराबर भुजाओं के सम्मुख कोण]
अब ∠ECD = ∠BCD – ∠BCE
= 80° – 30° = 50°
अतः ∠BCD = 80° व ∠ECD = 50° उत्तर

प्रश्न 7.
यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से होकर जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
हल :

दिया है : एक चक्रीय चतुर्भुज ABCD जिसमें विकर्ण AC और BD एक ही वृत्त के व्यास हैं।
सिद्ध करना है : चतुर्भुज ABCD एक आयत है।
प्रमाण : ∵ एक वृत्त की सभी त्रिज्याएं बराबर होती हैं।
∴ OA = OB = OC = OD
या OA = OC = \(\frac{1}{2}\)AC
OB = OD = \(\frac{1}{2}\)BD
या AC = BD
∴ चक्रीय चतुर्भुज ABCD के विकर्ण बराबर हैं तथा एक-दूसरे को समद्विभाजित करते हैं।
अतः चक्रीय चतुर्भुज ABCD एक आयत है। [इति सिद्धम]

प्रश्न 8.
यदि एक समलंब की असमांतर भुजाएं बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
हल :

दिया है : एक समलंब ABCD में AB || CD तथा AD = BC.
सिद्ध करना है : समलंब ABCD चक्रीय है।
रचना : DL ⊥ AB व CM ⊥ AB खींचो।
प्रमाण : ΔADL व ABCM में,
AD = BC [दिया है]
DL = CM [दिया है]
∠DLA = ∠CMB [प्रत्येक 90°]
∴ ΔADL ≅ ΔBCM [समकोण-कर्ण-भुजा सर्वांगसमता]
⇒ ∠A = ∠B [सर्वांगसम त्रिभुजों के संगत भाग]
∵ AB || CD [दिया है]
∠ADC + ∠A = 180° [तियर्क रेखा के एक ओर बने कोण]
या ∠ADC + ∠B = 180° [∵ ∠A = ∠B]
अतः ABCD एक चक्रीय समलंब है।
[इति सिद्धम]

प्रश्न 9.
दो वृत्त दो बिंदुओं B और C पर प्रतिच्छेद करते हैं। B से जाने वाले दो रेखाखंड ABD और PBQ वृत्तों को A, D और P, Q पर क्रमशः प्रतिच्छेद करते हुए खींचे गए हैं। (आकृति अनुसार)। सिद्ध कीजिए कि ∠ACP = ∠QCD है।

हल :
दिया है : दो वृत्त दो बिंदुओं B व C पर प्रतिच्छेद करते हैं। B से जाने वाले दो रेखाखंड ABD व PBQ वृत्तों को क्रमशः A,D और P, Q पर प्रतिच्छेद करते हैं।
सिद्ध करना है : ∠ACP = ∠QCD
प्रमाण : क्योंकि एक ही वृत्तखंड के कोण बराबर होते हैं।
∴ ∠ACP = ∠ABP ……(i)
∠QCD = ∠QBD ……(ii)
∠ABP = ∠QBD ……(iii)
[शीर्षाभिमुख कोण]
∴ समीकरण (i), (ii) एवं (iii) से,
∠ACP = ∠QCD [इति सिद्धम]

प्रश्न 10.
यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएं, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिंदु तीसरी भुजा पर स्थित है।
हल :

दिया है : ΔABC की भुजाओं AB तथा AC को व्यास लेते हुए दो वृत्त बनाए गए हैं। वृत्त एक-दूसरे को A तथा D बिंदुओं पर प्रतिच्छेदित करते हैं।
सिद्ध करना है : D, BC पर स्थित है।
रचना : A तथा D को मिलाओ।
प्रमाण : ∵ AB तथा AC दो वृत्तों के व्यास हैं। [दिया है]
∴ ∠ADB = 90° [अर्द्धवृत्त में बना कोण]
तथा ∠ADC = 90° [अर्द्धवृत्त में बना कोण]
जोड़ने पर,
∠ADB + ∠ADC = 90° + 90° = 180° या.
या BDC एक सीधी रेखा है।
अतः D, BC पर स्थित है। [इति सिद्धम]

प्रश्न 11.
उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध कीजिए कि ∠CAD = ∠CBD है।
हल :

दिया है : कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं अर्थात ∠B = ∠D = 90°
सिद्ध करना है : ∠CAD = ∠CBD.
रचना : बिंदु B और D को मिलाओ। प्रमाण:
∠ABC = 90° …(i) [दिया है]
∠ADC = 90° …(ii) [दिया है]
समीकरण (i) तथा (ii) को जोड़ने पर
∠ABC + ∠ADC = 180°
अतः ABCD एक चक्रीय चतुर्भुज है।
∴ ∠CAD = ∠CBD [एक ही वृत्तखंड में बने कोण]
[इति सिद्धम]

प्रश्न 12.
सिद्ध कीजिए कि चक्रीय समांतर चतुर्भुज आयत होता है।
हल :

दिया है : एक चक्रीय समांतर चतुर्भुज ABCD है।
सिद्ध करना है : ABCD एक आयत है।
प्रमाण : क्योंकि ABCD एक चक्रीय समांतर चतुर्भुज है।
∴ ∠A + ∠C = 180° [चक्रीय चतुर्भुज के सम्मुख कोण]
∠A = ∠C (समांतर चतुर्भुज के सम्मुख कोण]
∴ ∠A = ∠C = 90°
यदि किसी समांतर चतुर्भुज का एक कोण 90° हो जाए तो वह आयत होता है।
∴ चक्रीय समांतर चतुर्भुज ABCD एक आयत है। [इति सिद्धम]

Haryana State Board HBSE 9th Class Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.3 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Exercise 9.3

प्रश्न 1.
आकृति में, ΔABC की एक माध्यिका AD पर स्थित E कोई बिंदु है। दर्शाइए कि ar (ABE) = ar (ACE) है।

हल :
दिया है : AD, ΔABC की माध्यिका है तथा E, AD पर स्थित कोई बिंदु है।
सिद्ध करना है : ar (ΔABE) = ar (ΔACE)
प्रमाण : ΔABC में AD इसकी माध्यिका है।
∴ ar (ΔABD) = ar (ΔACD) ……(i)
इसी प्रकार, ΔEBC में ED इसकी माध्यिका है।
∴ ar (ΔBED) = ar (ΔCED) ……(ii)
समीकरण (i) व (ii) को घटाने पर
ar (ΔABD) – ar (ΔBED) = ar (ΔACD) – ar (ΔCED)
या ar (ΔABE) = ar (ΔACE) [इति सिद्धम]

प्रश्न 2.
ΔABC में, E माध्यिका AD का मध्य-बिंदु है। दर्शाइए कि ar (BED) = \(\frac{1}{4}\)ar (ABC) है।
हल :

दिया है : एक ΔABC में, E माध्यिका AD का मध्य-बिंदु है।
सिद्ध करना है : ar (BED) = \(\frac{1}{4}\)ar (ABC)
प्रमाण : ∵ AD त्रिभुज ABC की माध्यिका है।
∴ ar (ABD) = ar (ADC)
⇒ ar (ABD) = \(\frac{1}{2}\)ar (ABC) …..(1)
ΔABD में, BE माध्यिका है।
∴ ar (BED) = ar (BAE) ……(ii)
⇒ ar (BED) = \(\frac{1}{2}\)ar (ABD)
या ar (BED) = \(\frac{1}{2}\) × \(\frac{1}{2}\)ar (ABC) [समीकरण (i) से]
या ar (BED) = \(\frac{1}{4}\)ar (ABC) [इति सिद्धम]

प्रश्न 3.
दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
हल :
दिया है : एक समांतर चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर बिंदु O पर काटते हैं।

सिद्ध करना है : ar (ΔAOB) = ar (ΔBOC) = ar (COD) = ar (ΔAOD)
प्रमाण : हम जानते हैं कि समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं। अर्थात् OA = OC व OB= OD।
अब ΔACD में OD माध्यिका है।
∴ ar (ΔAOD) = ar (ΔCOD) ……(i)
इसी प्रकार हम सिद्ध कर सकते हैं कि
ar (ΔCOD) = ar (ΔBOC) …..(ii)
व ar (ΔBOC) = ar (ΔAOB) …..(iii)
समीकरण (i), (ii) व (iii) की तुलना में,
ar (ΔAOB) = ar (ΔBOC) = ar (ΔCOD) = ar (ΔAOD) [इति सिद्धम]

प्रश्न 4.
आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखंड CD रेखाखंड AB से बिंदु 0 पर समद्विभाजित होता है, तो दर्शाइए कि ar (ABC) = ar (ABD) है।

हल :
दिया है : ΔABC और ΔABD एक ही आधार AB पर बने हैं। रेखाखंड CD, रेखाखंड AB से बिंदु 0 पर समद्विभाजित होता है।
सिद्ध करना है : ar (ΔABC) = ar (ΔABD)
प्रमाण : ΔACD, AO माध्यिका है। (∵ OC = OD दिया है)
ar (ΔAOC) = ar (ΔAOD) …….(i)
इसी प्रकार, ΔBCD में OB माध्यिका है।
∴ ar (ΔBOC) = ar (ΔBOD) …….(ii)
समीकरण (i) व (ii) को जोड़ने पर,
ar (ΔAOC) + ar (ΔBOC) = ar (ΔAOD) + ar (ΔBOD)
⇒ ar (ΔABC) = ar (ΔABD) [इति सिद्धम]

प्रश्न 5.
D, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं। दर्शाइए कि
(i) BDEF एक समांतर चतुर्भुज है।
(ii) ar (DEF) = \(\frac{1}{4}\)ar (ABC)
(iii) ar (BDEF) = \(\frac{1}{2}\)ar (ABC)
हल :

दिया है : ΔABC की भुजाओं BC, CA व AB के मध्य-बिंदु क्रमशः D, E व F हैं।
सिद्ध करना है : (i) BDEF एक समांतर चतुर्भुज है।
(ii) ar (ΔDEF) = \(\frac{1}{4}\)ar (ΔABC)
(iii) ar (BDEF) = \(\frac{1}{2}\)ar (ΔABC)
प्रमाण : (i) ΔABC में F तथा E क्रमशः AB तथा AC के मध्य-बिंदु हैं।
∴ EF || BC …….(i)
इसी प्रकार
DE || AB ……..(ii)
समीकरण (i) व (ii) से,
BDEF एक समांतर चतुर्भुज है। [इति सिद्धम]
इसी प्रकार हम सिद्ध कर सकते हैं कि AFDE तथा CDFE भी समांतर चतुर्भुज हैं।
(ii) || चतुर्भुज BDEF में DF इसका विकर्ण हैं।
ar (ΔBDF) = ar (ΔDEF) …..(i)
इसी प्रकार ar (ΔAFE) = ar (ΔDEF) …(ii)
तथा ar (ΔCDE) = ar (ΔDEF)…(iii)
समीकरण (i), (ii) व (iii) की तुलना से,
ar (ΔBDF) = ar (ΔAFE) = ar (ΔCDE) = ar (ΔDEF)
ar (ΔABC) = ar (ΔAFE) + ar (ΔBDF) + ar (ΔCDE) + ar (ΔDEF)
= ar (ΔDEF) + ar (ΔDEF) + ar (ΔDEF) + ar (ΔDEF)
ar (ΔABC) = 4 ar (ΔDEF)
⇒ ar (ΔDEF) = \(\frac{1}{4}\)ar (ΔABC) …(iv) [इति सिद्धम]
(iii) अब
ar (|| चतुर्भुज BDEF) = ar (ΔBDF) + ar (ΔDEF)
= ar (ΔDEF) + ar (ΔDEF)
= 2ar (ADEF)
= 2[\(\frac{1}{4}\)ar(ΔABC)] [समीकरण (iv) से]
= \(\frac{1}{2}\)ar(ΔABC) [इति सिद्धम]

प्रश्न 6.
आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदू 0 पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है, तो दर्शाइए कि
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है।

हल :
दिया है : एक चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB= OD है तथा भुजा AB = भुजा CD है।
सिद्ध करना है : (i) ar (ΔDOC) = ar (ΔAOB)
(ii) ar (ΔDCB) = ar (ΔACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है।
रचना : DN ⊥ AC तथा BM ⊥ AC खींचो।

प्रमाण : (i) ΔDON और ΔBOM में,
∵ ∠DNO = ∠BMO [प्रत्येक = 90°]
∠DON = ∠BOM [शीर्षाभिमुख कोण]
तथा OD = OB [दिया है]
∴ ΔDON ≅ ΔBOM [कोण-कोण-भुजा सर्वांगसमता]…(1)
DN = BM [सर्वांगसम त्रिभुजों के संगत भाग]
अब ΔDCN और ΔBAM में,
∵ ∠DNC = ∠BMA [प्रत्येक = 90°]
DC = AB [दिया है]
तथा DN = BM [प्रमाणित]
∴ ΔDCN ≅ ΔBAM [समकोण-कर्ण-भुजा-सर्वांगसमता]…(2)
क्योंकि हम जानते हैं कि सर्वांगसम त्रिभुजों का क्षेत्रफल बराबर होता है।
∴ समीकरण (1) से,
ar (ΔDON) = ar (ΔBOM) …..(3)
समीकरण (2) से,
ar (ΔDCN) = ar (ΔBAM) …..(4)
समीकरण (3) व (4) को जोड़ने पर,
ar (ΔDON) + ar (ΔDCN) = ar (ΔBOM) + ar (ΔBAM)
ar (DOC) = ar (ΔAOB)…..(5) [इति सिद्धम]

(ii) समीकरण (5) में दोनों तरफ त्रिभुज BOC का क्षेत्रफल जोड़ने पर,
ar (ΔDOC) + ar (ΔBOC) = ar (ΔAOB) + ar (ΔBOC)
या ar (ΔDCB) = ar (ΔACB) [इति सिद्धम]

(iii) क्योंकि ADCB और ΔACB के क्षेत्रफल समान हैं तथा दोनों एक ही आधार BC पर है। अतः ये एक ही समांतर रेखाओं के बीच होगें।
अर्थात DA || CB या ABCD एक समांतर चतुर्भुज है। [इति सिद्धम]

प्रश्न 7.
बिंदु D और E क्रमशः AABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar (DBC) = ar (EBC) है। दर्शाइए कि DE || BC है।
हल :

दिया है : AABC की भुजाओं AB और AC पर क्रमशः बिंदु D और E इस प्रकार स्थित हैं कि ar (ΔDBC) = ar (ΔEBC)
सिद्ध करना है : DE || BC
प्रमाण : क्योंकि ar (ΔDBC) = ar (ΔEBC) तथा दोनों, एक ही आधार BC पर स्थित हैं।
∴ दोनों एक ही समांतर रेखाओं BC और DE के बीच स्थित होगें।
अर्थात DE || BC [इति सिद्धम]

प्रश्न 8.
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है। यदि BE || AC और CF || AB रेखा XY से क्रमशः E और F पर मिलती हैं, तो दर्शाइए कि :
ar (ABE) = ar (ACF)
हल :

दिया है : ΔABC की भुजा BC के समांतर एक रेखा XY है। यदि BE || AC व CF || AB रेखा XY को क्रमशः E व F पर प्रतिच्छेदित करते हैं।
सिद्ध करना है : ar (ΔABE) = ar (ΔACF)
प्रमाण : BE || CM [∵ BE || AC दिया है]
EM || BC [∵ XY || BC दिया है]
∴ BCME एक || चतुर्भुज है।
इसी प्रकार BCFL एक || चतुर्भुज है।
अब ΔAEB तथा || चतुर्भुज EBCM एक ही आधार EB व एक ही समांतर रेखाओं AC तथा EB के मध्य स्थित हैं।
∴ ar (ΔABE) = \(\frac{1}{2}\)ar (|| चतुर्भुज EBCM) …(i)
इसी प्रकार ΔACF तथा || चतुर्भुज BCFL एक ही आधार CF व एक ही समांतर रेखाओं AB तथा CF के मध्य स्थित है।
∴ ar (ΔACF) = \(\frac{1}{2}\)ar (|| चतुर्भुज BCFL) …(ii)
परन्तु || चतुर्भुज EBCM तथा || चतुर्भुज BCFL एक ही आधार BC पर है तथा एक ही || रेखाओं EF तथा BC के मध्य में हैं।
∴ ar (समांतर चतुर्भुज EBCM) = ar (समांतर चतुर्भुज BCFL) …..(iii)
समीकरण (i), (ii) व (iii) की तुलना से,
ar (ΔABE) = ar (ΔACF) [इति सिद्धम]

प्रश्न 9.
समांतर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढ़ाया गया है। A से होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है (देखिए आकृति)। दर्शाइए कि ar (ABCD) = ar (PBQR) है।
(संकेत : AC और PQ को मिलाइए। अब ar (ACQ) और ar (APQ) की तुलना कीजिए।)

हल :

दिया है : समांतर चतुर्भुज ABCD की एक भुजा AB को बिंदु P तक बढ़ाया गया है। A से होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है। इस प्रकार चतुर्भुज PBQR प्राप्त होता है।
सिद्ध करना है : ar (चतुर्भुज ABCD) = ar (चतुर्भुज PBQR)
रचना : AC और PQ को मिलाओ।
प्रमाण : क्योंकि AC और PQ क्रमशः समांतर चतुर्भुज ABCD और समांतर चतुर्भुज PBQR के विकर्ण हैं।
∴ ar (ΔABC) = \(\frac{1}{2}\)ar (ABCD)….(i)
और ar (ΔPBQ) = \(\frac{1}{2}\)ar (PBRQ)….(ii)
परन्तु, ΔACQ और ΔAQP समान आधार AQ और समान समांतर रेखाओं AQ और CP के मध्य स्थित हैं।
ar (ΔACQ) = ar (AQP)
दोनों और ΔABQ का क्षेत्रफल घटाने पर,
ar (ΔACQ) – ar (ΔABQ) = ar (ΔAQP) – ar (ΔABQ)
⇒ ar (ΔABC) = ar (ΔBPQ)
⇒ \(\frac{1}{2}\)ar (ABCD) = \(\frac{1}{2}\)ar (PBRO) [समीकरण (i) एवं (ii) से]
⇒ ar (ABCD) = ar (PBRQ) [इति सिद्धम]

प्रश्न 10.
एक समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ar (AOD) = ar (BOC) है।
हल :
दिया है : एक समलंब ABCD में AB || DC तथा विकर्ण AC व BD परस्पर O पर प्रतिच्छेद करते हैं।
सिद्ध करना है : ar (ΔAOD) = ar (ΔBOC)
प्रमाण : ΔABD व ΔABC एक ही आधार AB तथा समांतर रेखाओं AB तथा DC के मध्य स्थित हैं।
∴ ar (ΔABD) = ar (ΔABC)
दोनों ओर से ar (ΔAOB) घटाने पर,
ar (ΔABD) – ar (ΔAOB) = ar (ΔABC) – ar (ΔAOB)
⇒ ar (ΔAOD) = ar (ΔBOC) [इति सिद्धम]

प्रश्न 11.
आकृति में, ABCDE एक पंचभुज है। B से होकर AC के समांतर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है। दर्शाइए कि
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)

हल :
दिया है : एक पंचभुज ABCDE में B से होकर AC के समांतर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है।
सिद्ध करना है : (i) ar (ΔACB) = ar (ΔACF)
(ii) ar (AEDF) = ar (ABCDE)
प्रमाण : (i) ΔACB व ΔACF एक ही आधार AC तथा एक ही समांतर रेखाओं AC तथा BF के मध्य में हैं।
∴ ar (ΔACB) = ar (ΔACF) [इति सिद्धम]
(ii) चतुर्भुज ACDE का क्षेत्रफल दोनों ओर जोड़ने पर,.
ar (ΔACB) + ar (चतुर्भुज ACDE) = ar (ΔACF) + ar (चतुर्भुज ACDE)
ar (ABCDE) = ar (AEDF) [इति सिद्धम]

प्रश्न 12.
गांव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गांव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहां एक स्वास्थ्य केंद्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबंध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
हल :

माना इतवारी के पास ABCD एक चतुर्भुजाकार मँखड है।
D से DE || CA खींचो जो BA को बढ़ाने पर E पर मिले।
∴ इस प्रकार, ΔEAC और ΔADC एक ही आधार CA तथा एक ही समांतर रेखाओं DE और CA के बीच स्थित हैं।
ar (AEAC) = ar (ΔADC) …(i)
अब ar (ABCD) = ar (ΔABC)+ ar (ΔACD)
= ar (ΔABC) + ar (ΔEAC) [समीकरण (1) से]
= ar (ΔEBC)
अर्थात चतुर्भुज ABCD = ΔEBC

प्रश्न 13.
ABCD एक समलंब है, जिसमें AB || DC है। AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ar (ADX) = ar (ACY) है।
हल :

दिया है : ABCD एक समलंब है जिसमें AB || DC है। AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेदित करती है।
सिद्ध करना है : ar (ΔADX) = ar (ACY)
रचना : DX व CX को मिलाओ। इसी प्रकार AY को मिलाओ।
प्रमाण : क्योंकि ΔADX व ΔAXC एक ही आधार AX तथा एक ही समांतर रेखाओं AB और CD के मध्य स्थित हैं।
∴ ar (ΔAXD) = ar (ΔAXC) …(i)
अब ΔACX तथा ΔACY एक ही आधार AC तथा एक ही समांतर रेखाओं XY तथा AC के मध्य स्थित हैं।
∴ ar (ΔACX) = ar (ΔACY)
समीकरण (i) व (ii) से,
ar (ΔAXD) = ar (ΔACY) [इति सिद्धम]

प्रश्न 14.
आकृति में, AP || BQ || CR है। सिद्ध कीजिए कि ar (AQC) = ar (PBR) है।

हल :
दिया है : समलंब APRC में AP || BQ || CR है।
सिद्ध करना है : ar (ΔAQC) = ar (ΔPBR)
प्रमाण : क्योंकि ΔABQ और ΔPBQ एक ही आधार BQ तथा एक ही समांतर रेखाओं BQ और AP के मध्य स्थित हैं।
∴ ar (ΔABQ) = ar (ΔPBQ) …(i)
इसी प्रकार ΔCBQ तथा ΔRBQ एक ही आधार BQ तथा एक ही समांतर रेखाओं BQ और CR के मध्य स्थित हैं।
∴ ar (ΔCBQ) = ar (ΔRBQ) …(ii)
समीकरण (i) व (ii) जोड़ने पर,
ar (ΔABQ) + ar (ΔCBQ) = ar (ΔPBQ) + (ΔRBQ)
⇒ ar (ΔAQC) = ar (ΔPBR) [इति सिद्धमा]

प्रश्न 15.
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु 0 पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD)= ar (BOC) है। सिद्ध कीजिए कि ABCD एक समलंब है।
हल :

दिया है : चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु पर इस प्रकार प्रतिच्छेद करते हैं कि ar (ΔAOD)= ar (ΔBOC)
सिद्ध करना है : ABCD एक समलंब है अर्थात् AB || CD
प्रमाण : चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि
ar (ΔAOD) = ar (ΔBOC)
दोनों और ΔAOB का क्षेत्रफल जोड़ने पर,
ar (ΔAOD) + ar (ΔAOB) = ar (ΔBOC) + ar (ΔAOB)
⇒ ar (ΔABD) = ar (ΔABC)
परन्तु ΔABD और ΔABC एक ही आधार AB पर है तथा क्षेत्रफल में समान हैं।
∴ AB || DC
अतः ABCD एक समलंब है। [इति सिद्धम]

प्रश्न 16.
आकृति में, ar (DRC) = ar (DPC) है और ar (BDP) = ar (ARC) है। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब हैं।

हल :
दिया है : आकृति ABPR में,
ar (ΔDRC) = ar (ΔDPC)
और ar (ΔBDP) = ar (ΔARC)
सिद्ध करना है : (i) चतुर्भुज ABCD एक समलंब है।
(ii) चतुर्भुज DCPR एक समलंब है।
प्रमाण : (i) क्योंकि ΔDRC तथा ΔDPC एक ही आधार DC पर हैं तथा क्षेत्रफल में समान हैं।
∴ ये समांतर रेखाओं के मध्य में हैं।
∴ DC || RP
अतः DCPR एक समलंब है। [इति सिद्धम]

(ii) अब ar (ΔBDP) = ar (ΔARC) …….(1)
ar (ΔDPC) = ar (ΔDRC) ……..(2)
समीकरण (1) में से (2) को घटाने पर,
ar (ΔBDP) – ar (ΔDPC) = ar (ΔARC) – ar (ΔDRC)
∴ ar (ΔDCB) = ar (ADCA)
ΔDCB तथा ΔDCA एक ही आधार DC पर हैं तथा इनके क्षेत्रफल समान हैं। (प्रमाणित)
∴ DC || AB
अतः ABCD एक समलंब है। [इति सिद्धम]

Haryana State Board HBSE 10th Class Maths Solutions Chapter 1 Real Numbers Ex 1.3 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 1 Real Numbers Exercise 1.3

Question 1.
Prove that √5 is an irrational.
Solution :
Let us assume, that √5 is a rational. It can be expressed in the form of \(\frac{a}{b}\), where a and b are coprime positive integers and b ≠ 0.
∴ √5 = \(\frac{a}{b}\) (Where a and b are coprime ∴ HCF of a and b is 1)
Squaring on both sides
5 = \(\frac{a^2}{b^2}\)
5b² = a² ………….(i)
Therefore, 5 divides a². It follows that 5 divides a . [By theorem 1.3]
Let a = 5c and put this value in equation (i)
[Where c is any positive integer]
5b² = (5c)²
5b² = 25c²
⇒ \(\frac{25}{5}\) c² = b²
⇒ 5c² = b² ……….(ii)
It means b² is divisible by 5. It follows that b is divisible by 5 [By theorem 1.3]
From equations (i) and (ii) we say that 5 is a common factor of both a and b. But this contradicts the fact that a and b are coprime so, they have no common factor. So, our assumption that √5 is a rational number is wrong.
Therefore, √5 is an irrational number.

Question 2.
Prove that 3 + 2√5 is an irrational.
Solution :
Let us assume 3 + 2√5 is a rational. It can be expressed in the form of \(\frac{a}{b}\), where a and b are coprime positive integers and b ≠ 0.
∴ 3 + 2√5 = \(\frac{a}{b}\)
\(\frac{a}{b}\) – 3 = 2√5
\(\frac{a-3 b}{b}\) = 2√5
\(\frac{a-3 b}{2 b}\) = √5
\(\frac{a-3 b}{2 b}\) = rational
(∵ a and b are positive integers)
So, from equation (i) √5 is a rational.
But this contradicts the fact √5 is an irrational. So, our assumption that 3 + 2√5 is a rational, is wrong.
Hence, 3 + 2√5 is an irrational number.

Question 3.
Prove that the following are irrationals:
(i) \(\frac{1}{\sqrt{2}}\)
(ii) 7√5
(iii) 6 + √2
Solution:
(i) Let us assume, that \(\frac{1}{\sqrt{2}}\) is a rational. It can be expressed in the form of \(\frac{a}{b}\), where a and b are coprime positive integer.
∴ \(\frac{1}{\sqrt{2}}=\frac{a}{b}\)
(Where HCF of a and b is 1 and b ≠ 0)
\(\frac{1}{2}=\frac{a^2}{b^2}\) (Squaring both sides)
⇒ b² = 2a² …………….(i)
It means b² is divisible by 2. It follows that b, is divisible by 2 [By theorem 1.3]
Let b = 2c (Where c is any positive integer).
And put b = 2c in equation (i)
(2c)² = 2a²
⇒ 4c² = a²
⇒ 2c² = a² …………….(ii)
It means a² is divisible by 2. It follows that a, is divisible by 2. [By theorem 1.3]
From (i) and (ii) we say that 2 is the common factor of a and b. But this contradicts the fact that a and b are coprime. So, our assumption that \(\frac{1}{\sqrt{2}}\) is a rational, is wrong.
Hence, \(\frac{1}{\sqrt{2}}\) is an irrational number.

(ii) Let us assume, that 7√5 is a rational.
It can be expressed in the form of \(\frac{a}{b}\), where a and b are coprime positive integer and b ≠ 0.
∴ 7√5 = \(\frac{a}{b}\) (Where HCF of a and b is 1)
√5 = \(\frac{a}{7 b}\)
∵ a and b are positive integers.
∴ \(\frac{a}{7 b}\) is a rational.
Therefore, √5 is a rational.
But this contradicts the fact that √5 is an irrational. So, our assumption that 7√5 is a srational, is wrong.
Hence, 7√5 is an irrational number.

(iii) Let us assume, that 6 + √2 is a rational.
It can be expressed in the form of \(\frac{a}{b}\), where a and b are coprime positive integer and b ≠ 0.
∴ 6 + √2 = \(\frac{a}{b}\) (Where HCF’ of a and b is 1)
⇒ √2 = \(\frac{a}{b}\) – 6
⇒ √2 = \(\frac{a-6 b}{b}\)
∵ a and b are positive integers.
∴ \(\frac{a-6 b}{b}\) is a rational.
Therefore, √2 is a rational.
But this contradicts the fact that √2 is an irrational. So, our assumption that 6 + √2 is a rational, is wrong
Hence, 6 + √2 is an irrational number.

Haryana State Board HBSE 9th Class Science Notes Chapter 7 जीवों में विविधता Notes.

Haryana Board 9th Class Science Notes Chapter 7 जीवों में विविधता

→ हमारी पृथ्वी पर लगभग 10 करोड़ प्रकार के जीव पाए जाते हैं, जिनमें से लगभग 17 लाख विभिन्न प्रकार की जातियों का वर्गीकरण किया गया है।

→ जीवों का वर्गीकरण इनमें समानता, विभिन्नता तथा उनके आपसी संबंधों के आधार पर किया गया है।

→ जीव विज्ञान की वह शाखा जो जीवों का वर्गीकरण करती है, वर्गिकी कहलाती है। यह शब्द डी० केंडोली ने दिया।

→ जीवों के वर्गीकरण से जीवों का अध्ययन करना आसान हो गया है।

→ केरोलस लीनियस वर्गीकरण का जनक है। उसने द्विनाम पद्धति विकसित की।

→ द्विनाम पद्धति में जीव को नाम देने के लिए नाम के दो घटक पहला जीनस (जेनेटिक नाम) तथा दूसरा जातीय नाम होता है।

→ जीवों के वर्गीकरण की विभिन्न श्रेणियाँ-जगत, फाइलम, क्लास, आर्डर, फैमिली, वंश तथा जाति हैं।

→ समूचे जीव-जगत को दो समूहों में बाँटा गया है-वनस्पति जगत तथा प्राणी जगत।

→ जीवों को पाँच जगत में वर्गीकृत करने के लिए निम्न विशेषताओं को ध्यान में रखा जाता है

→ कोशिकीय संरचना-प्रोकैरियोटी अथवा यूकैरियोटी।

→ जीव का शरीर एककोशिक अथवा बहुकोशिक है। बहुकोशिक जीवों की संरचना जटिल होती है।

→ कोशिका भित्ति की उपस्थिति तथा स्वपोषण की क्षमता।

→ उपर्युक्त आधार पर सभी जीवों को पाँच जगत में बाँटा गया है मोनेरा, प्रोटिस्टा, कवक (फंजाइ), प्लांटी और एनिमेलिया।

→ जीवों का वर्गीकरण उनके विकास से संबंधित है।

→ ्लांटी और एनिमेलिया को उनकी शारीरिक जटिलता के आधार पर वर्गीकृत किया गया है।

→ पौधों को पाँच वर्गों में बाँटा गया है-शैवाल, ब्रायोफाइटा, टेरिडोफाइटा, जिम्नोस्पर्म और एंजियोस्पर्म।

→ जंतुओं को दस फाइलम में बाँटा गया है-पोरीफेरा, सीलेंटरेटा, प्लेटीहेल्मिन्थीज, निमेटोडा, एनीलिडा, आर्थोपोडा, मोलस्का, इकाइनोडर्मेटा, प्रोटोकॉर्डेटा और वर्टीब्रेटा।

→ जैव विविधता-जीवों के गुण-धर्मों में पाई जाने वाली विविधता जैव विविधता कहलाती है।

→ वर्गीकरण-समानता और भिन्नता के आधार पर जीवों को बाँटना वर्गीकरण कहलाता है।

→ जैव विकास-जीवों में निरंतर बदलावों की प्रक्रिया के परिणामस्वरूप बेहतर जीवन-यापन जैव विकास कहलाता है।

→ मेगाडाइवर्सिटी क्षेत्र पृथ्वी पर कर्क और मकर रेखा के बीच जीवों में काफी विविधता पाई जाती है, इसलिए इसे मेगाडाइवर्सिटी क्षेत्र कहते हैं।

→ मोनेरा-एक कोशिकीय प्रोकैरियोटिक जीव, जिनमें कोशिका भित्ति पाई जाती है, मोनेरा कहलाते हैं।

→ प्रोटिस्टा-एक कोशिकीय यूकैरियोटिक जीव प्रोटिस्टा कहलाते हैं।

→ फंजाई-विषमपोषी यूकैरियोटिक जीव, जो मृत गले-सड़े कार्बनिक पदार्थों से भोजन ग्रहण करें, फंजाई कहलाते हैं।

→ प्लांटी-कोशिका भित्ति वाले बहुकोशिक यूकैरियोटिक स्वपोषी जीव प्लांटी कहलाते हैं।

→ एनिमेलिया-बहुकोशिकीय यूकैरियोटिक जीव, जिसमें कोशिका भित्ति नहीं पाई जाती, एनिमेलिया कहलाते हैं।

→ थैलोफाइट जिन पादपों में विशेष संरचना थैलस पाया जाता है।

→ ब्रायोफाइटा-पादप वर्ग के उभयचर वर्ग को ब्रायोफाइटा कहते हैं।

→ क्रिप्टोगैम्स-जिन पादपों में बीज उत्पन्न करने की क्षमता न हो, वे क्रिप्टोगैम्स होते हैं।

→ जिम्नोस्पर्म-नग्न बीज उत्पन्न करने वाले पौधे जिम्नोस्पर्म कहलाते हैं।

→ एंजियोस्पर्म-ढके हुए बीजों वाले पौधे एंजियोस्पर्म कहलाते हैं।

→ कशेरुकी-जिन जीवों में रीढ़ की हड्डी पाई जाती है, कशेरुकी कहलाते हैं।

→ अकशेरुकी जिन जीवों में रीढ़ की हड्डी न पाई जाए, अकशेरुकी कहलाते हैं।

Haryana State Board HBSE 9th Class Science Notes Chapter 6 ऊतक Notes.

Haryana Board 9th Class Science Notes Chapter 6 ऊतक

→ कोशिका विभाजन जीव के विकास और वृद्धि के लिए आवश्यक है।

→ एक कोशिका जीवों में सभी जैव प्रक्रियाएँ एक कोशिका के द्वारा ही की जाती हैं।

→ बहुकोशिका जीवों में अलग-अलग कोशिकाओं के समूह भिन्न कार्य करते हैं, इसे श्रम विभाजन कहते हैं।

→ समान उद्भव, रचना और समान कार्य करने वाली कोशिकाओं के समूह को ऊतक कहते हैं।

→ पौधे और जंतु भिन्न-भिन्न गुणों वाले जीव हैं।

→ पौधों और जंतुओं में रचना और कार्य के आधार पर भिन्न-भिन्न ऊतक पाए जाते हैं।

→ पौधों में दो प्रकार के ऊतक पाए जाते हैं

• विभज्योतक तथा
• स्थायी ऊतक।

→ विभज्योतक पौधे के शीर्ष एवं जड़ की चोटी पर ही पाया जाता है।

→ स्थायी ऊतक भी विभज्योतक से ही बनते हैं।

→ सरल ऊतक तीन प्रकार के होते हैं पैरेन्काइमा, कॉलेन्काइमा तथा स्क्लेरेन्काइमा।

→ स्क्लेरेन्काइमा (दृढ़ोत्तक) पौधे के भागों को दृढ़ता प्रदान करता है।

→ दृढ़ोत्तक ही रक्षी ऊतक में बदल जाता है।

→ स्टोमेटा (वातरंध्र) पौधे के लिए गैसों का आदान-प्रदान व वाष्पोत्सर्जन करता है।

→ जाइलम व फ्लोएम ऊतक जटिल ऊतकों के उदाहरण हैं।

→ ज़ाइलम व फ्लोएम संवहन ऊतक हैं।

→ एपिथीलियमी ऊतक रक्षी अस्तर जंतु ऊतक है।

→ पेशीय ऊतक, प्रमुख रूप से तीन प्रकार का होता है-रेखित पेशी (कंकाल या ऐच्छिक), अरेखित पेशी (चिकनी पेशी या अनैच्छिक पेशी) तथा हृदय पेशी।

→ रुधिर और अस्थि संयोजी ऊतक के प्रकार हैं।

→ रुधिर एक तरल ऊतक है।

→ अस्थि दृढ़ होती है, जबकि उपास्थि में लचीलापन होता है।

→ मस्तिष्क, मेरुरज्जु तथा तंत्रिकाएँ सभी तंत्रिका ऊतक हैं।

→ स्थायी ऊतकों में विभाजन क्षमता नहीं होती।

→ तंत्रिका ऊतक की इकाई न्यूरॉन है। यह एक संदेशवाहक है।

→ विभज्योतक में लगातार विभाजन होता रहता है।

→ ऊतक-समान उद्भव, रचना और कार्य करने वाली कोशिकाओं के समूह को ऊतक कहते हैं।

→ विभज्योतक-विभाजन की क्षमता वाले ऊतक विभज्योतक कहलाते हैं।

→ विभेदीकरण ऊतकों द्वारा विशिष्ट कार्य करने के लिए स्थाई रूप और आकार लेने की क्रिया को विभेदीकरण कहते हैं।

→ स्थायी ऊतक-विभज्योतक विभाजन की क्षमता खोकर जो ऊतक बनते हैं, उन्हें स्थायी ऊतक कहते हैं।

→ सरल ऊतक-एक ही प्रकार की कोशिकाओं से बने ऊतकों को सरल ऊतक कहते हैं।

→ जटिल ऊतक-भिन्न प्रकार की रचना और कार्य करने वाली कोशिकाओं के समूह को जटिल ऊतक कहते हैं।

→ संरक्षी ऊतक-पौधे के शरीर की रक्षा करने वाले संरक्षी ऊतक कहलाते हैं।

→ फ्लोएम-जीवित संवाहक ऊतक को फ्लोएम कहते हैं।

→ उपकला ऊतक-जंतुओं में आवरणी ऊतक को उपकला ऊतक कहते हैं।

→ पेशीय ऊतक-जिन संरचनाओं से पेशियाँ बनी होती हैं, उन्हें पेशीय ऊतक कहते हैं।

→ संयोजी ऊतक-शरीर के विभिन्न अंगों को आपस में जोड़ने या आधार देने का कार्य करने वाले ऊतकों को संयोजी ऊतक कहते हैं।

→ तंत्रिका ऊतक-संवेदनाओं को एक स्थान से दूसरे स्थान पर भेजने वाले ऊतक तंत्रिका ऊतक कहलाते हैं।