Class 9

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.6 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.6

[नोट-जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।]

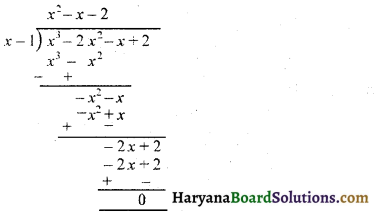
प्रश्न 1.
एक बेलनाकार बर्तन के आधार की परिधि 132 सें०मी० और उसकी ऊंचाई 25 सें०मी० है। इस बर्तन में कितने लीटर पानी आ सकता है ? (1000 सें०मी०³ = 1 लीटर)
हल :
यहां पर,
बेलनाकार बर्तन की ऊंचाई (h) = 25 सें०मी०
बेलनाकार बर्तन के आधार की परिधि = 132 सें०मी०
⇒ 2πr = 132
⇒ 2 × \(\frac{22}{7}\) × r = 132
या r = \(\frac{132 \times 7}{2 \times 22}\) = 21 सें०मी०
∴ बेलनाकार बर्तन का आयतन (V) = πr²h
= \(\frac{22}{7}\) × 21 × 21 × 25 सें०मी०³
= 34650 सें०मी०³
अतः बर्तन में जितने लीटर पानी आ सकता है = \(\frac{34650}{1000}\) लीटर
= 34.65 लीटर उत्तर

प्रश्न 2.
लकड़ी के एक बेलनाकार पाइप का आंतरिक व्यास 24 सें०मी० है और बाहरी व्यास 28 सें०मी० है। इस पाइप की लंबाई 35 सें०मी० है। इस पाइप का द्रव्यमान ज्ञात कीजिए, यदि 1 सें०मी०³ लकड़ी का द्रव्यमान 0.6 ग्राम है।
हल :
यहां पर,
बेलनाकार पाइप का अंतः व्यास (d) = 24 सें०मी०
बेलनाकार पाइप की अंतः त्रिज्या (r) = \(\frac{24}{2}\) = 12 सें०मी०
बेलनाकार पाइप का बाह्य व्यास (D) = 28 सें०मी०
बेलनाकार पाइप की बाह्य त्रिज्या (R) = \(\frac{28}{2}\) = 14 सें०मी०
बेलनाकार पाइप की लंबाई (h) = 35 सें०मी०
इस प्रकार पाइप में लगी लकड़ी का आयतन (V) =
बाह्य आयतन – आंतरिक आयतन = πh (R² – r²)
= \(\frac{22}{7}\) × 35 [(14)² – (12)²] सें०मी०³
= 110 [196 – 144] सें०मी०³
= 110 × 52 = 5720 सें०मी०³
1 सें०मी०³ लकड़ी का द्रव्यमान = 0.6 ग्राम
अतः 5720 सें०मी०³ पाइप का द्रव्यमान = 5720 × 0.6 ग्राम = 3432 ग्राम
= 3.432 किलोग्राम उत्तर

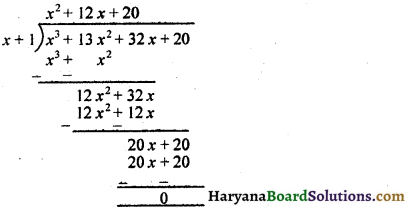
प्रश्न 3.
एक सोफ्ट ड्रिंक (soft drink) दो प्रकार के पैकों में उपलब्ध है : (i) लंबाई 5 सें०मी० और चौड़ाई 4 सें०मी० वाले एक आयताकार आधार का टिन का डिब्बा जिसकी ऊंचाई 15 सें०मी० है और (ii) व्यास 7 सें०मी० वाले वृत्तीय आधार और 10 सें०मी० ऊंचाई वाला एक प्लास्टिक का बेलनाकार डिब्बा। किस डिब्बे की धारिता अधिक है और कितनी अधिक है ?
हल :
यहां पर,
आयताकार आधार वाले डिब्बे की लंबाई (l) = 5 सें०मी०
आयताकार आधार वाले डिब्बे की चौड़ाई (b) = 4 सें०मी०
आयताकार आधार वाले डिब्बे की ऊंचाई (h) = 15 सें०मी०
∴ आयताकार आधार वाले डिब्बे का आयतन (V) = l × b × h = 5 × 4 × 15 = 300 सें०मी०³
बेलनाकार डिब्बे की ऊंचाई (h) = 10 सें०मी०
बेलनाकार डिब्बे के आधार का व्यास (d) = 7 सें०मी०
बेलनाकार डिब्बे के आधार की त्रिज्या (r) = \(\frac{7}{2}\) = सें०मी०
∴ बेलनाकार डिब्बे का आयतन (V) = πr²h
\(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 10 सें०मी०³
= 385 सें०मी०³
∵ 385 > 300 ∴ बेलनाकार डिब्बे की धारिता अधिक है।
अतः बेलनाकार डिब्बे की धारिता जितनी अधिक है = 385 – 300 सें०मी०³
= 85 से०मी०³ उत्तर

प्रश्न 4.
यदि एक बेलन का पार्श्व पृष्ठीय क्षेत्रफल 94.2 सें०मी०² है और उसकी ऊंचाई 5 सें०मी० है, तो ज्ञात कीजिए:
(i) आधार की त्रिज्या,
(ii) बेलन का आयतन (70 = 3.14 लीजिए)।
हल :
(i) यहां पर,
बेलन की ऊंचाई (h) = 5 सें०मी०
बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 94.2 सें०मी०²
⇒ 2πrh = \(\frac{942}{10}\) सें०मी०²
या 2 × 3.14 × r × 5 = \(\frac{942}{10}\)
या \(\frac{2 \times 314 \times r \times 5}{100}\) = \(\frac{942}{10}\)
या \(\frac{314 r}{10}\) = \(\frac{942}{10}\)
या r = \(\frac{942}{10} \times \frac{10}{314}\) = 3 सें०मी०
अतः बेलन के आधार की त्रिज्या (r) = 3 सें०मी० उत्तर

(ii) बेलन का आयतन = πr²h
= 3.14 × 3 × 3 × 5 सें०मी०³
= 3.14 × 45 = 141.3 सें०मी०³ उत्तर

प्रश्न 5.
10m गहरे एक बेलनाकार बर्तन की आंतरिक वक्र पृष्ठ को पेंट कराने का व्यय 2200 रुपए है। यदि पेंट कराने की दर ₹ 20 प्रति मी०² है, तो ज्ञात कीजिए :
(i) बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल,
(ii) आधार की त्रिज्या,
(iii) बर्तन की धारिता।
हल :
(i) बेलनाकार बर्तन के आंतरिक वक्र पृष्ठ पर पेंट कराने का व्यय = ₹ 2200
बेलनाकार बर्तन के आंतरिक वक्र पृष्ठ पर पेंट कराने की दर = ₹ 20 प्रति मी०²
अतः बेलनाकार बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल
= \(\frac{2200}{20}\) मी०²
= 110 मी०² उत्तर

(ii) बेलनाकार बर्तन की गहराई (h) = 10 मी०
बेलनाकार बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल = 110 मी०²
⇒ 2πrh = 110
या 2 × \(\frac{22}{7}\) × r × 10 = 110
या \(\frac{440}{7}\)r = 110
या r = \(\frac{110 \times 7}{440}=\frac{7}{4}\) मी० = 1.75 मी०
अतः बेलनाकार बर्तन के आधार की त्रिज्या (r) = 1.75 मी० उत्तर

(iii) बेलनाकार बर्तन का आयतन (V) = πr²h
= \(\frac{22}{7} \times \frac{7}{4} \times \frac{7}{4}\) × 10 मी०³ = 96.25 मी०³
अतः बेलनाकार बर्तन की धारिता = 96.25 किलोलीटर (∵ 1 मी०³ = 1 kl) उत्तर

प्रश्न 6.
ऊंचाई 1 मी० वाले एक बेलनाकार बर्तन की धारिता 15.4 लीटर है। इसको बनाने के लिए कितने वर्ग मीटर धातु की शीट की आवश्यकता होगी ? [B.S.E.H. March, 2020]
हल :
यहां पर,
बेलनाकार बर्तन की ऊंचाई (h) = 1 मी०
बेलनाकार बर्तन की धारिता = 15.4 लीटर
बेलनाकार बर्तन का आयतन (V) = \(\frac{154}{10 \times 1000}\)मी०³

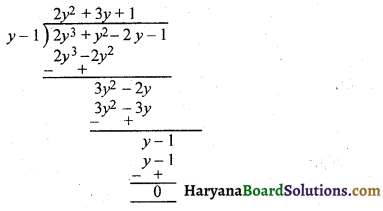
प्रश्न 7.
सीसे की एक पेंसिल (lead pencil) लकड़ी के एक बेलन के अभ्यंतर में ग्रेफाइट (graphite) से बने ठोस बेलन को डालकर बनाई गई है। पेंसिल का व्यास 7 मि०मी० है और ग्रेफाइट का व्यास 1 मि०मी० है। यदि पेंसिल की लंबाई 14 सें०मी० है, तो लकड़ी का आयतन और ग्रेफाइट का आयतन ज्ञात कीजिए।
हल :
यहां पर,
पेंसिल का व्यास (d) = 7 मि०मी०
पेंसिल की त्रिज्या (r) = \(\frac{7}{2}\) मि०मी० = \(\frac{7}{20}\) सें०मी०
पेंसिल की लंबाई (h) = 14 सें०मी०
अतः पेंसिल का आयतन (V) = πr²h
= \(\frac{22}{7} \times \frac{7}{20} \times \frac{7}{20}\) × 14 सें०मी०³
= \(\frac{539}{100}\) सें०मी०³
= 5.39 सें०मी०³
ग्रेफाइट के सिक्के का व्यास (d) = 1 मि०मी०
ग्रेफाइट के सिक्के की त्रिज्या (r₁) = \(\frac{1}{2}\) मि०मी० = \(\frac{1}{20}\) सें०मी०
ग्रेफाइट के सिक्के का आयतन (V) = πr₁²h
= \(\frac{22}{7} \times \frac{1}{20} \times \frac{1}{20}\) × 14 सें०मी०³
= \(\frac{11}{100}\) सें०मी०³
= 0.11 सें०मी०³
इस प्रकार पेंसिल में लगी लकड़ी का आयतन = 5.39 – 0.11 = 5.28 सें०मी०³ उत्तर

प्रश्न 8.
एक अस्पताल (hospital) के एक रोगी को प्रतिदिन 7 सें०मी० व्यास वाले एक बेलनाकार कटोरे में सूप (soup) दिया जाता है। यदि यह कटोरा सूप से 4 सें०मी० ऊंचाई तक भरा जाता है, तो इस अस्पताल में 250 रोगियों के लिए प्रतिदिन कितना सूप तैयार किया जाता है ?
हल :
यहां पर,
बेलनाकार कटोरे का व्यास (d) = 7 सें०मी०
बेलनाकार कटोरे की त्रिज्या (r) = \(\frac{7}{2}\) सें०मी०
कटोरे में सूप की ऊंचाई (h) = 4 सें०मी०
कटोरे में सूप का आयतन = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 4
= 154 सें०मी०³
1 रोगी को दिया जाने वाला सूप = 154 सें०मी०³
250 रोगियों को दिया जाने वाला सूप = 154 × 250 सें०मी०³
= 38500 सें०मी०³
= \(\frac{38500}{1000}\) = 285 लीटर (∵ 1000 सें०मी०³ = 1 लीटर)
अतः अस्पताल में प्रतिदिन जितने लीटर सूप तैयार होता है = 38.5 लीटर उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 2 बहुपद Ex 2.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 2 बहुपद Exercise 2.2

प्रश्न 1.
निम्नलिखित पर बहुपद 5x – 4x² + 3 के मान ज्ञात कीजिए
(i) x = 0 (ii) x = – 1 (iii) x = 2
हल :
(i) यहाँ पर बहुपद = 5x – 4x² + 3
x = 0 रखने पर
5x – 4x² + 3 = 5(0) – 4(0)² + 3
= 0 – 0 + 3 = 3 उत्तर

(ii) यहाँ पर x = – 1 रखने पर
बहुपद = 5x – 4x² + 3
5x – 4x² + 3 = 5(-1) – 4(-1)² + 3
= – 5 – 4(1) + 3
= – 5 – 4 + 3
= – 9 + 3 = – 6 उत्तर

(iii) यहाँ पर
x = 2 रखने पर
बहुपद = 5x – 4x² + 3
5x – 4x² + 3 = 5 (2) – 4(2)² +3
= 10 – 4(4) + 3
= 10 – 16 + 3
= 13 – 16 = – 3 उत्तर

प्रश्न 2.
निम्नलिखित बहुपदों में से प्रत्येक बहुपद के लिएp p(0), P (1) और p (2) ज्ञात कीजिए-
(i) p(y) = y² – y + 1
(ii) p(t) = 2 + t + 2t² – t³
(iii) p(x) = x³
(iv) P(x) = (x – 1) (x + 1)
हल :
(i) यहाँ पर
P(y) = y² – y + 1
y = 0 रखने पर
P (0) = (0)² – (0) + 1
= 0 – 0 + 1 = 1 उत्तर

y = 1 रखने पर
P(1) = (1)² – (1) + 1
= 1 – 1 + 1 = 1 उत्तर

y = 2 रखने पर
p(2) = (2)² – (2) + 1
= 4 – 2 + 1
= 5 – 2 = 3 उत्तर

(ii) यहाँ पर
p(t) = 2 + t + 2t² – t³
= – t³ + 2t² + t + 2
t = 0 रखने पर
p(0) = – (0)³ + 2(0)³ + (0) + 2
= – 0 + 0 + 0 + 2 = 2 उत्तर
t = 1 रखने पर
p(1) = -(1)³ + 2 (1)² + (1) + 2
= – 1 + 2 + 1 + 2
= – 1 + 5 = 4 उत्तर

t = 2 रखने पर
p(2) = – (2)³ + 2(2)² + (2) + 2
= – 8 + 8 + 2 + 2
= – 8 + 12 = 4 उत्तर

(iii) यहाँ पर p(x) = x³
x = 0 रखने पर
p(0) = (0)³ = 0 उत्तर
x = 1 रखने पर
p(1) = (1)³ = 1 उत्तर
x = 2 रखने पर
p(2) = (2)³ = 2 × 2 × 2 = 8 उत्तर

(iv) यहाँ पर
P(x) = (x – 1) (x + 1)
= (x)² – (1)² = x² – 1
x = 0 रखने पर
p(0) = (0)² – 1 = – 1 उत्तर
x = 1 रखने पर
p(1) = (1)² – 1 = 1 – 1 = 0 उत्तर
x = 2 रखने पर
P (2) = (2)² – 1 = 4 – 1 = 3 उत्तर

प्रश्न 3.
सत्यापित कीजिए कि दिखाए गए मान निम्नलिखित स्थितियों में संगत बहुपद के शून्यक हैं
(i) p(x) = 3x + 1; x = – \(\frac {1}{3}\)
(ii) p(x) = 5x – π, x = \(\frac {4}{5}\)
(iii) p(x) = x² – 1; x = 1, – 1
(iv) p(x) = (x + 1) (x – 2), x = – 1, 2
(v) p (x) = x², x = 0
(vi) p(x) = lx + m; x = –\(\frac {m}{l}\)
(vii) p(x) = 3x² – 1; x = –\(\frac{1}{\sqrt{3}}, \frac{2}{\sqrt{3}}\)
(viii) p(x) = 2x + 1, x = \(\frac {1}{2}\)
हल :
(i) यहाँ पर
P(x) = 3x + 1
x = – \(\frac {1}{3}\) रखने पर
p(- \(\frac {1}{3}\)) = 3(- \(\frac {1}{3}\)) + 1
= – 1 + 1 = 0
अतः –\(\frac {1}{3}\) बहुपद 3x + 1 का शून्यक है। उत्तर

(ii) यहाँ पर
p(x) = 5x – π
x = \(\frac {4}{5}\) रखने पर
p(\(\frac {4}{5}\)) = 5(\(\frac {4}{5}\)) – π
= 4 – π ≠ 0
अतः \(\frac {4}{5}\) बहुपद 5x – π का शून्यक नहीं है। उत्तर

(iii) यहाँ पर
p(x) = x² – 1
x = 1 रखने पर p(1) = (1)² – 1 = 1 – 1 = 0
x = – 1 रखने पर p(-1) = (-1)² -1 = 1 – 1 = 0
अतः 1 व – 1 बहुपद x² – 1 के शून्यक हैं। उत्तर

(iv) यहाँ पर
p(x) = (x + 1) (x – 2)
= x² + x – 2x – 2
= x² – x – 2
x = – 1 रखने पर
P(-1) = (-1)² – (-1) – 2
= 1 + 1 – 2 = 2 – 2 = 0
x = 2 रखने पर
p(2) = (2)² – (2) – 2
= 4 – 2 – 2 = 4 – 4 = 0
अतः – 1 व 2 बहुपद (x + 1) (x – 2) के शून्यक हैं। उत्तर

(v) यहाँ पर
P(x) = x²
x = 0 रखने पर
P(0) = (0)² = 0
अतः 0 बहुपद x² का शून्यक है। उत्तर

(vi) यहाँ पर
p(x) = lx + m
x = – \(\frac {m}{l}\) रखने पर
p(-\(\frac {m}{l}\)) = l (-\(\frac {m}{l}\)) +m
= – m + m = 0
अतः –\(\frac {m}{l}\) बहुपद lx + m का शून्यक है। उत्तर

(vii) यहाँ पर
p(x) = 3x² – 1

(viii) यहाँ पर
p(x) = 2x + 1
x = \(\frac {1}{2}\) रखने पर
p(\(\frac {1}{2}\)) = 2(\(\frac {1}{2}\)) + 1
= 1 + 1
= 2 ≠ 0
अतः \(\frac {1}{2}\) बहुपद 2x + 1 का शून्यक नहीं है। उत्तर

प्रश्न 4.
निम्नलिखित स्थितियों में से प्रत्येक स्थिति में बहुपद का शून्यक ज्ञात कीजिए –
(i) p(x) = x + 5
(ii) P(x) = x – 5
(iii) P(x) = 2x + 5
(iv) p(x) = 3x – 2
(v) p(x) = 3x
(vi) P(x) = ax; a ≠ 0
(vii) P(x) = cx + d; c ≠ 0, c, d वास्तविक संख्याएँ हैं।
हल :
बहुपद का शून्यक ज्ञात करने के लिए आवश्यक है-
P(x) = 0
(i) x + 5 = 0
या x = 0 – 5 = – 5
अतः बहुपद x + 5 का शून्यक = – 5 उत्तर

(ii) x – 5 = 0
या x = 0 + 5 = 5
अतः बहुपद x – 5 का शून्यक = 5 उत्तर

(iii) 2x + 5 = 0
⇒ 2x = 0 – 5 = – 5
या x = – \(\frac {5}{2}\)
अतः बहुपद 2x + 5 का शून्यक = – \(\frac {5}{2}\) उत्तर

(iv) 3x – 2 = 0
⇒ 3x = 0 + 2 = 2
या x = \(\frac {2}{3}\)
अतः बहुपद 3x – 2 का शून्यक = \(\frac {2}{3}\) उत्तर

(v) 3x = 0
या x = \(\frac {0}{3}\) = 0
अतः बहुपद 3x का शून्यक = 0 उत्तर

(vi) ax = 0
या x = \(\frac {0}{a}\) = 0
अतः बहुपद ax का शून्यक = 0 उत्तर

(vii) cx + d = 0
या cx = 0 – d = – d
या x = –\(\frac {d}{c}\)
अतः बहुपद cx + d का शून्यक = – \(\frac {d}{c}\) उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Exercise 4.2

प्रश्न 1.
निम्नलिखित विकल्पों में कौन-सा विकल्प सत्य है, और क्यों?
y = 3x + 5 का
(i) एक अद्वितीय हल है
(ii) केवल दो हल हैं
(iii) अपरिमित रूप से अनेक हल हैं
हल :
विकल्प (iii) सत्य है क्योंकि x के प्रत्येक मान के लिएy का एक संगत मान होता है तथा विलोमतः भी सत्य है।

प्रश्न 2.
निम्नलिखित समीकरणों में से प्रत्येक समीकरण के चार हल लिखिए :
(i) 2x + y = 7
(ii) πx + y = 9
(iii) x = 4y
हल :
(i) यहां पर,
2x + y = 7
या y = 7 – 2x
यदि x = 0, तो y = 7 – 2 (0) = 7 – 0 = 7
यदि x = 1, तो y = 7 – 2 (1) = 7 – 2 = 5
यदि x = 2, तो y = 7 – 2 (2) = 7 – 4 = 3
यदि x = 3, तो y = 7 – 2 (3) = 7 – 6 = 1
अतः अभीष्ट चार हल हैं : (0, 7), (1, 5), (2, 3), (3, 1) उत्तर

(ii) यहां पर,
πx + y = 9
या y = 9 – πx
यदि x = 0, तो y = 9 – π(0) = 9 – 0 = 9
यदि x = 1, तो y = 9 – π(1) = 9 – π
यदि x = 2, तो y = 9 – π(2) = 9 – 2π
यदि x = – 1, तो y = 9 – π(-1) = 9 + π
अतः अभीष्ट चार हल हैं : (0, 9), (1, 9 – π), (2, 9 – 2π), (-1, 9 + π) उत्तर

(iii) यहां पर,
x = 4y
यदि y = 0, तो x = 4(0) = 0
यदि y = 1, तो x = 4(1) = 4
यदि y = -1, तो x = 4(-1) = -4
यदि y = 2, तो x = 4(2) = 8
अतः अभीष्ट चार हल हैं : (0, 0), (4, 1), (-4, -1), (8, 2) उत्तर

प्रश्न 3.
बताइए कि निम्नलिखित हलों में कौन-कौन समीकरण.x – 2y = 4 के हल हैं और कौन-कौन हल नहीं हैं:
(i) (0, 2)
(ii) (2, 0)
(iii) (4, 0)
(iv) (\(\sqrt{2}\), 4\(\sqrt{2}\))
(v) (1, 1)
हल :
(i) यहां पर, x – 2y = 4
समीकरण में x = 0, y = 2 रखने पर,
0 – 2(2) = 4
या 0 – 4 = 4 या
या – 4 = 4 (जो कि असत्य है।)
∴ (0, 2) समीकरण का हल नहीं है। उत्तर

(ii) यहां पर,
x – 2y = 4
समीकरण में x = 2, y = 0 रखने पर,
2 – 2(0) = 4
या 2 – 0 = 4
या 2 = 4 (जो कि असत्य है।)
∴ (2, 0) समीकरण का हल नहीं है। उत्तर

(iii) यहां पर,
x – 2y = 4
समीकरण में x = 4, y = 0 रखने पर
4 – 2 (0) = 4
या 4 – 0 = 4
या 4 = 4 (जो कि सत्य है।)
∴ (4, 0) समीकरण का हल है। उत्तर

(iv) यहां पर,
x – 2y = 4
समीकरण में x = \(\sqrt{2}\), y= 4\(\sqrt{2}\) रखने पर,
\(\sqrt{2}\) – 2(4\(\sqrt{2}\)) = 4
या \(\sqrt{2}\) – 8\(\sqrt{2}\) = 4
या – 7\(\sqrt{2}\) = 4 (जो कि असत्य है।)
∴ (\(\sqrt{2}\), 4\(\sqrt{2}\)) समीकरण का हल नहीं है। उत्तर

(v) यहां पर,
x – 2y = 4
समीकरण में x = 1,y = 1 रखने पर,
1 – 2(1) = 4
या 1 – 2 = 4
या – 1 = 4 (जो कि असत्य है।)
∴ (1, 1) समीकरण का हल नहीं है। उत्तर

प्रश्न 4.
k का मान ज्ञात कीजिए जबकि x = 2, y = 1 समीकरण 2x + 3y = k का एक हल हो।
हल :
यहां पर, 2x + 3y = k
समीकरण में x = 2,y = 1 रखने पर,
2(2) + 3 (1) = k
या 4 + 3 = k
या k = 7 उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Exercise 4.1

प्रश्न 1.
एक नोटबुक की कीमत एक कलम की कीमत से दोगुनी है। इस कथन को निरूपित करने के लिए दो घरों वाला एक रैखिक समीकरण लिखिए।
हल :
माना एक नोटबुक की कीमत = x रुपये
तथा एक कलम की कीमत = y रुपये
प्रश्नानुसार,
एक नोटबुक की कीमत = 2 × एक कलम की कीमत
⇒ x = 2y
या x – 2y = 0 उत्तर

प्रश्न 2.
निम्नलिखित रैखिक समीकरणों को ax + by + c = 0 के रूप में व्यक्त कीजिए और प्रत्येक स्थिति में a, b और के मान बताइए
(i) 2x + 3y = \(9.3 \overline{5}\)
(ii) x – \(\frac {y}{5}\) – 10 = 0
(iii) – 2x + 3y = 6
(iv) x = 3y
(v) 2x = – 5y
(vi) 3x + 2 = 0
(vii) y – 2 = 0
(viii) 5 = 2x
हल :
(i) 2x + 3y = \(9.3 \overline{5}\)
⇒ 2x + 3y – \(9.3 \overline{5}\) = 0
∴ a = 2, b = 3, c = – \(9.3 \overline{5}\) उत्तर

(ii) x – \(\frac {y}{5}\) – 10 = 0
∴ a = 1, b = \(\frac {-1}{5}\), c = – 10 उत्तर

(iii) -2x + 3y = 6
⇒ -2x + 3y – 6 = 0
∴ a = – 2, b = 3, c = – 6 उत्तर

(iv) x = 3y
⇒ x – 3y + 0 = 0
∴ a = 1, b = – 3, c = 0 उत्तर

(v) 2x = – 5y
⇒ 2x + 5y + 0 = 0
∴ a = 2, b = 5, c = 0 उत्तर

(vi) 3x + 2 = 0
⇒ 3x + (0)y + 2 = 0
∴ a = 3, b = 0, c = 2 उत्तर

(vii) y – 2 = 0
⇒ (0) x + (1)y – 2 = 0
∴ a = 0, b = 1, c = – 2 उत्तर

(viii) 5 = 2x
⇒ – 2x + (0)y + 5 = 0
∴ a = – 2, b = 0, c = 5 उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 वृत्त Ex 10.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 वृत्त Exercise 10.2

प्रश्न 1.
याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएं बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएं उनके केंद्रों पर बराबर कोण अंतरित करती हैं।
हल :
दिया है : दो सर्वांगसम वृत्त जिनके केंद्र O तथा O’ हैं। AB व CD दो समान जीवाएं हैं।
सिद्ध करना है : ∠AOB = ∠CO’D

ΔAOB तथा ΔCO’D में,
OA = O’C [सर्वांगसम वृत्तों की त्रिज्याएं]
OB = O’D [सर्वांगसम वृत्तों की त्रिज्याएं]
AB = CD [दिया है]
ΔAOB ≅ ΔCO’D [भुजा-भुजा-भुजा सर्वांगसमता]
∠AOB = ∠CO’D [सर्वांगसम त्रिभुजों के संगत भाग]
[इति सिद्धम]

प्रश्न 2.
सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएं उनके केंद्रों पर बराबर कोण अंतरित करें, तो जीवाएं बराबर होती हैं।
हल :
दिया है : दो सर्वांगसम वृत्त जिनके केंद्र O तथा O’ हैं। दो जीवाएं AB और CD इस प्रकार हैं कि ∠AOB = ∠CO’D.
सिद्ध करना है : जीवा AB = जीवा CD.

ΔAOB तथा ΔCO’D में,
OA = O’C [सर्वांगसम वृत्तों की त्रिज्याएं]
OB = O’D [सर्वांगसम वृत्तों की त्रिज्याएं]
∠AOB ≅ ∠CO’D [दिया है]
∴ ΔAOB = ΔCO’D [भुजा-कोण-भुजा सर्वांगसमता]
∴ जीवा AB = जीवा CD [सर्वांगसम त्रिभुजों के संगत भाग]
[इति सिद्धम]

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 वृत्त Ex 10.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 वृत्त Exercise 10.1

प्रश्न 1.
खाली स्थान भरिए :
(i) वृत्त का केंद्र वृत्त के ………………….. में स्थित है।
(ii) एक बिंदु, जिसकी वृत्त के केंद्र से दूरी त्रिज्या से अधिक हो, वृत्त के ……………… में स्थित होता है।
(iii) वृत्त की सबसे बड़ी जीवा वृत्त का …………….. होता है।
(iv) एक चाप ……………………… होता है, जब इसके सिरे एक व्यास के सिरे हों।
(v) वृत्तखंड एक चाप तथा ……………………….. के बीच का भाग होता है।
(vi) एक वृत्त, जिस तल पर स्थित है, उसे …………….. भागों में विभाजित करता है।
उत्तर :
(i) अभ्यंतर
(ii) बहिर्भाग
(iii) व्यास
(iv) अर्द्धवृत्त
(v) जीवा
(vi) तीन।

प्रश्न 2.
लिखिए, सत्य या असत्य। अपने उत्तर के कारण दीजिए।
(i) केंद्र को वृत्त पर किसी बिंदु से मिलाने वाला रेखाखंड वृत्त की त्रिज्या होती है।
(ii) एक वृत्त में समान लंबाई की परिमित जीवाएं होती हैं।
(ii) यदि एक वृत्त को तीन बराबर चापों में बांट दिया जाए, तो प्रत्येक भाग दीर्घ चाप होता है।
(iv) वृत्त की एक जीवा, जिसकी लंबाई त्रिज्या से दोगुनी हो, वृत्त का व्यास है।
(v) त्रिज्यखंड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
(vi) वृत्त एक समतल आकृति है।
उत्तर :
(i) सत्य : क्योंकि वृत्त की परिधि पर स्थित सभी बिंदु केंद्र से समान दूरी पर होते हैं, जिसे वृत्त की त्रिज्या कहते हैं।
(ii) असत्य : क्योंकि वृत्त की परिधि पर अनेक बिंदु होते हैं जिन्हे मिलाने से अपरिमित जीवाएं प्राप्त की जा सकती हैं।
(iii) असत्य : क्योंकि एक वृत्त को तीन बराबर चापों में बांट देने पर प्रत्येक भाग समान चाप कहलाता है।
(iv) सत्य : क्योंकि व्यास सबसे बड़ी जीवा होती है, जिसकी लंबाई त्रिज्या से दोगुनी होती है।
(v) असत्य : क्योंकि चाप और दो त्रिज्याओं के बीच का क्षेत्र (केंद्र को चाप के बिंदु से मिलाने वाला) त्रिज्यखंड कहलाता है। आकृति में OAB त्रिज्यखंड है।

(vi) सत्य : क्योंकि वृत्त एक बिंदु का बिंदुपथ होता है, जो एक तल में स्थित होता है।

Haryana State Board HBSE 9th Class Maths Solutions Chapter 11 रचनाएँ Ex 11.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 11 रचनाएँ Exercise 11.2

प्रश्न 1.
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 7 cm, ∠B = 750 और AB + AC = 13 cm हो।
हल :
रचना के चरण-

1. एक किरण BX खींचिए तथा इसमें से एक रेखाखंड BC = 7 cm लीजिए।
2. बिंदु B पर ∠YBX = 75° बनाओ।
3. BY से BD = 13 cm काटो।
4. D को C से मिलाओ।
5. CD का लंब समद्विभाजक खींचिए जो BD को A पर प्रतिच्छेद करें।
6. A को C से मिलाइए।
7. इस प्रकार ABC अभीष्ट त्रिभुज है।

प्रश्न 2.
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 8 cm, ∠B = 45° और AB – AC = 3.5 cm हो। [B.S.E.H. 2017, 2018, 2020]
हल :
रचना के चरण-

1. एक किरण BX खींचिए तथा इसमें से एक रेखाखंड BC = 8 cm लीजिए।
2. अब बिंदु B पर ∠YBC = 45° बनाओ।
3. BY से BD = 3.5 cm काटो।
4. D को C से मिलाओ।
5. CD का लंब समद्विभाजक RS खींचो जो BY को A पर प्रतिच्छेद करता है।
6. A को C से मिलाइए।
7. इस प्रकार ABC अभीष्ट त्रिभुज है।

प्रश्न 3.
एक त्रिभुज PQR की रचना कीजिए, जिसमें QR = 6 cm, ∠Q = 60° और PR – PQ = 2 cm हो।
हल :
रचना के चरण-

1. एक किरण QX खींचिए तथा इसमें से एक रेखाखंड QR = 6 cm लीजिए।
2. बिंदु Q पर ∠YQX = 60° बनाओ।
3. YQ को Y’ तक आगे बढ़ाकर QY’ में से QS = 2 cm काटो।
4. R को S से मिलाओ।
5. RS का लंब समद्विभाजक AB खींचिए जो QY को P पर काटे।
6. P को R से मिलाइए।
7. इस प्रकार PQR अभीष्ट त्रिभुज है।

प्रश्न 4.
एक त्रिभुज XYZ की रचना कीजिए, जिसमें ∠Y =30°, ∠Z = 90° और XY + YZ + ZX = 11 cm हो।
हल :
रचना के चरण-

1. एक रेखाखंड PQ = 11 cm खींचिए।
2. P पर एक किरण PL खींचिए जिससे कि ∠LPQ = \(\frac{1}{2}\) × 30° = 150
3. Q पर, एक किरण QM खींचिए जिससे कि ∠MQP = \(\frac{1}{2}\) × 90° = 45० जो PL को X पर काटे।
4. PX का लंब समद्विभाजक AB खींचिए जो PQ को Y पर प्रतिच्छेद करे।
5. QX का लंब समद्विभाजक CD खींचिए जो PQ को Z पर प्रतिच्छेद करे।
6. XY तथा Xz को मिलाओ।
7. इस प्रकार XYZ अभीष्ट त्रिभुज है।

प्रश्न 5.
एक समकोण त्रिभुज की रचना कीजिए, जिसका आधार 12 cm और कर्ण तथा अन्य भुजा का योग 18 cm है।
हल :
रचना के चरण-

1. एक रेखाखंड BC = 12 cm खींचिए।
2. बिंदु B पर ∠YBC = 90° बनाओ तथा BD = 18 cm काटो।
3. DC को मिलाओ।
4. अब DC का लंबार्धक PQ खींचो जो DB को A पर प्रतिच्छेद करे।
5. AC को मिलाओ।
6. इस प्रकार ABC अभीष्ट त्रिभुज है।

Haryana State Board HBSE 9th Class Maths Solutions Chapter 2 बहुपद Ex 2.4 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 2 बहुपद Exercise 2.4

प्रश्न 1.
बताइए कि निम्नलिखित बहुपों में से किस बहुपद का एक गुणनखंड x + 1 है
(i) x³ + x² + x + 1
(ii) x³ + x³ + x² + x + 1
(iii) x⁴ + 3x³ + 3x² + x + 1
(iv) x³ – x² – (2 + \(\sqrt{2}\))x + \(\sqrt{2}\)
हल :
(i) x + 1 का शून्यक – 1 है
माना,
p (x) = x³ + x² + x + 1
अब p(-1) = (-1)³ + (-1)² + (-1) + 1
= 1 + 1 – 1 + 1
= 2 – 2 = 0
अतः गुणनखंड प्रमेय के अनुसार x + 1, x³ + x² + x + 1 का एक गुणनखंड है। उत्तर

(ii) x + 1 का शून्यक – 1 है
माना, P(x) = x⁴ + x³ + x² + x + 1
अब P(-1) = (-1)⁴ + (-1)³ + (-1)² + (-1) + 1
= 1 – 1 + 1 – 1 + 1
= 3 – 2 = 1 ≠ 0
अतः गुणनखंड प्रमेय के अनुसार x + 1, x⁴ + x³ + x² + x + 1 का एक गुणनखंड नहीं है। उत्तर

(iii) x + 1 का शून्यक -1 है
माना, p(x) = x⁴ + 3x³ + 3x² + x + 1
अब
p(-1) = (-1) +3 (-1) +3(-1) + (-1)+1
= 1+3 (-1)+3 (1) -1+1 = 1-3+3-1+1
= 5-4 = 120 अतः गुणनखंड प्रमेय के अनुसार x + 1, x* + 3x + 3x + x + 1 का एक गुणनखंड नहीं है। उत्तर

(iv) x + 1 का शून्यक – 1 है
माना,
p (x) = x³ + x² – (2 + \(\sqrt{2}\)) x + \(\sqrt{2}\)
अब
p(-1) = (-1)³ – (-1)² – (2 + \(\sqrt{2}\))(-1) + \(\sqrt{2}\)
= – 1 – 1 + 2 + \(\sqrt{2}\) + \(\sqrt{2}\)
= – 2 + 2 + 2\(\sqrt{2}\)
= 2\(\sqrt{2}\) ≠ 0
अतः गुणनखंड प्रमेय के अनुसार x + 1, x³ – x²(2 + \(\sqrt{2}\)) x + \(\sqrt{2}\) का एक गुणनखंड नहीं है। उत्तर

प्रश्न 2.
गुणनखंड प्रमेय लागू करके बताइए कि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में g (r), p (x) का एक गुणनखंड है या नहीं-
(i) p(x) = 2x³ + x² – 2x – 1, g(x) = x + 1
(ii) p(x) = x³ + 3x² + 3x + 1, g(x) = x + 2 .
(iii) p(x) = x³ – 4x² + x + 6, g(x) = x – 3
हल :
(i) x + 1 का शून्यक – 1 है
माना,
p (x) = 2x³ + x² – 2x – 1
अब
p(-1) = 2(-1)³ + (-1)² – 2(-1) – 1
= 2(-1) + (1) + 2 – 1
= – 2 + 1 + 2 – 1
अतः गुणनखंड प्रमेय के अनुसार g (x), p(x) का एक गुणनखंड है। उत्तर

(ii) x + 2 का शून्यक – 2 है
माना,
P(x) = x³ + 3x² + 3x + 1
अब
P(-2) = (-2)³ + 3 (-2)² + 3 (-2) + 1
= (-8) + 3(4) + 3(-2) + 1
= – 8 + 12 – 6 + 1
= 13 – 14 = – 1 ≠ 0
अतः गुणनखंड प्रमेय के अनुसार g(x), p(x) का एक गुणनखंड नहीं है। उत्तर

(iii) x – 3 का शून्यक है
माना,
P(x) = x³ – 4x² + x + 6
अब
p(3) = (3)³ – 4(3)² + (3) + 6
= 27 – 36 + 3 + 6
= 36 – 36 = 0
अतः गुणनखंड प्रमेय के अनुसार g(x), p(x) का एक गुणनखंड है। उत्तर

प्रश्न 3.
k का मान ज्ञात कीजिए जबकि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में (x – 1), p(x) का एक गुणनखंड हो
(i) P(x) = x² + x + k
(ii) p(x) = 2x² + kx + \(\sqrt{2}\)
(iii) P(x) = kx² – \(\sqrt{2}\)x + 1
(iv) P(x) = kx² – 3x + k
हल :
(i) क्योंकि x – 1, p (x) का एक गुणनखंड है
∴ P (1) = 0
⇒ (1)² + (1)² + k = 0
या 1 + 1 + k = 0
या 2 + k = 0
या k = – 2 उत्तर

(ii) क्योंकि x – 1, p (x) का एक गुणनखंड है
∴ P(1) = 0
⇒ 2(1)² + k(1) + \(\sqrt{2}\) = 0
या 2 + k + \(\sqrt{2}\) = 0
या k = -(2 + \(\sqrt{2}\)) उत्तर

(iii) क्योंकि x – 1, p (x) का एक गुणनखंड है
∴ p(1) = 0
⇒ k(1)² – \(\sqrt{2}\)(1) + 1 = 0
या k – \(\sqrt{2}\) + 1 = 0
या k = \(\sqrt{2}\) – 1 उत्तर

(iv) क्योंकि x – 1, p (x) का एक गुणनखंड है
∴ p(1) = 0
⇒ k (1)² – 3 (1) + k = 0
या k – 3 + k = 0
या 2k = 3
या k = \(\frac {3}{2}\) उत्तर

प्रश्न 4.
गुणनखंड ज्ञात कीजिए –
(i) 12x² – 7x + 1
(ii) 2x² + 7x + 3
(iii) 6x² + 5x – 6
(iv) 3x² – x – 4
हल :
(i) 12x² – 7x + 1 = 12x² – 4x – 3x + 1
= 4x (3x – 1) – 1 (3x – 1)
= (3x – 1) (4x – 1) उत्तर

(ii) 2x² + 7x + 3 = 2x² + 6x + x + 3
= 2x(x + 3) + 1(x + 3)
= (x + 3) (2x + 1) उत्तर

(iii) 6x² + 5x – 6 = 6x² + 9x – 4x – 6
= 3x (2x + 3) – 2(2x +3)
= (2x + 3) (3x – 2) उत्तर

(iv) 3x² – x – 4 = 3x² – 4x + 3x – 4
= x (3x – 4) + 1 (3x – 4)
= (3x – 4) (x + 1) उत्तर

प्रश्न 5.
गुणनखंड ज्ञात कीजिए
(i) x³ – 2x² – x + 2
(ii) x³ – 3x² – 9x – 5
(iii) x³ + 13x² + 32x + 20 [2017]
(iv) 2y³ + y² – 2y – 1
हल :
(i) माना p(x) = x³ – 2x² – x + 2
यहाँ पर अचर पद 2 है जिसके गुणनखंड ± 1, ± 2 है।
x = 1 रखने पर
p(1) = (1)³ – 2(1)² – (1) + 2
= 1 – 2 – 1 + 2
= 3 – 3 = 0
अतः x – 1, P(x) का एक गुणनखंड है।
अब

अतः
x³ – 2x² – x + 2 = (x – 1) (x² – x – 2)
= (x – 1) (x² – 2x + x – 2)
= (x – 1) [x(x – 2) + 1 (x – 2)]
= (x – 1) (x – 2) (x + 1) उत्तर

(ii) माना p(x) = x³ – 3x² – 9x – 5
यहाँ पर अचर पद – 5 है जिसके गुणनखंड ± 1, ± 5 है।
x = 1 रखने पर
P(1) = (1)³ – 3(1)² – 9(1) – 5
= 1 – 3 – 9 – 5
= 1 – 17 = -16 ≠ 0
x= – 1 रखने पर
p(-1) = (-1)³ – 3(-1))² – 9(-1) – 5
= – 1 – 3 + 9 – 5
= 9 – 9 = 0
अतः x + 1, p(x) का एक गुणनखंड है।
अब

अतः
x³ – 3x² – 9x – 5 = (x + 1) (x² – 4x – 5)
= (x + 1) (x² – 5x + x – 5)
= (x + 1) [x(x – 5) + 1 (x – 5)]
= (x + 1) (x – 5) (x + 1) उत्तर

(iii) माना p(x) = x³ + 13x² + 32x + 20
यहाँ पर अचर पद 20 है जिसके गुणनखंड ±1, ±2, ±4, ±5 हैं।
x=1 रखने पर
p(1) = (1)³ + 13(1)² + 32(1) + 20
= 1 + 13 + 32 + 20
= 66 ≠ 0

x = – 1 रखने पर
P(-1) = (-1)³ + 13(-1)² + 32 (-1) + 20
= -1 + 13 – 32 + 20
= 33 – 33 = 0
अतः x + 1, p(x) का एक गुणनखंड है।
अब

अतः
x³ + 13x² + 32x + 20 = (x + 1) (x² + 12x + 20)
= (x + 1) (x² + 10x + 2x + 20)
= (x + 1) [x(x + 10) + 2 (x + 10)]
= (x + 1) (x + 10) (x + 2) उत्तर

(iv) माना p(y) = 2y³ + y² – 2y – 1
यहाँ पर अचर पद – 1 है जिसके गुणनखंड ± 1 हैं।
y = 1 रखने पर
P(1) = 2 (1)³ + (1)² – 2(1) – 1
= 2 + 1 – 2 – 1
= 3 – 3 = 0
अतः y – 1, p(y) का एक गुणनखंड है।

अतः
2y³ + y² – 2y – 1 = (y – 1) (2y² + 3y + 1)
= (y – 1) (2y² + 2y + y + 1)
= (y – 1) [2y(y + 1) + 1 (y + 1)]
= (y – 1) (y + 1) (2y + 1) उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 3 निर्देशांक ज्यामिति Ex 3.3 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 3 निर्देशांक ज्यामिति Exercise 3.3

प्रश्न 1.
किस चतुर्थांश में या किस अक्ष पर बिंदु (-2, 4), (3, -1), (-1, 0), (1, 2) और (-3, -5) स्थित हैं ? कार्तीय तल पर इनका स्थान निर्धारण करके अपने उत्तर सत्यापित कीजिए।
हल :

(i) बिंदु (-2, 4) चतुर्थांश II में है।
(ii) बिंदु (3, -1) चतुर्थाश IV में है।
(iii) बिंदु (-1, 0) ऋण x-अक्ष पर है।
(iv) बिंदु (1, 2) चतुर्थाश I में है।
(v) बिंदु (-3, -5) चतुर्थाश III में है।
दिए गए बिंदु आकृति में निर्धारित कर दिए गए हैं।

प्रश्न 2.
अक्षों पर दूरी का उपयुक्त एकक लेकर नीचे सारणी में दिए गए बिंदुओं को तल पर आलेखित कीजिए:

हल :
संलग्न आकृति में बिंदुओं की स्थितियां बिंदुओं (dots) द्वारा दर्शाई गई हैं जोकि, A(-2, 8), B(-1, 7), C(0, – 1.25), D (1, 3) व E (3,-1) हैं।

Haryana State Board HBSE 9th Class Maths Solutions Chapter 3 निर्देशांक ज्यामिति Ex 3.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 3 निर्देशांक ज्यामिति Exercise 3.2

प्रश्न 1.
निम्नलिखित प्रश्नों में से प्रत्येक प्रश्न का उत्तर दीजिए:
(i) कार्तीय तल में किसी बिंदु की स्थिति निर्धारित करने वाली क्षैतिज और ऊर्ध्वाधर रेखाओं के क्या नाम हैं?
(ii) इन दो रेखाओं से बने तल के प्रत्येक भाग के नाम बताइए।
(iii) उस बिंदु का नाम बताइए जहां ये दो रेखाएं प्रतिच्छेदित होती हैं। [B.S.E.H, March, 2018]
हल :
(i) कार्तीय तल में किसी बिंदु की स्थिति निर्धारित करने वाली क्षैतिज और ऊध्वाधर रेखाओं के नाम क्रमशः x-अक्ष तथा y-अक्ष होते हैं।
(ii) वैतिज तथा ऊर्ध्वाधर रेखाओं से बने तल के प्रत्येक भाग को चतुर्थांश कहते हैं। जो चार होते हैं।
(iii) x-अक्ष व y-अक्ष रेखाओं के प्रतिच्छेदित बिंदु को मूलबिंदु (0, 0) कहते हैं।

प्रश्न 2.
आकृति देखकर निम्नलिखित को लिखिए :
(i) B के निर्देशांक
(ii) C के निर्देशांक
(iii) निर्देशांक (- 3, – 5) द्वारा पहचाना गया बिंदु
(iv) निर्देशांक (2, – 4) द्वारा पहचाना गया बिंदु
(v) D का भुज
(vi) बिंदु H की कोटि
(vii) बिंदु L के निर्देशांक
(viii) बिंदु M के निर्देशांक

हल :
आकृति अनुसार,
(i) B के निर्देशांक (- 5, 2) हैं।
(ii) C के निर्देशांक (5, – 5) हैं।
(iii) निर्देशांक (- 3, – 5) द्वारा पहचाना गया बिंदु E है।
(iv) निर्देशांक (2, – 4) द्वारा पहचाना गया बिंदु है।
(v) D का भुज = 6
(vi) बिंदु H की कोटि – 3 है।
(vii) बिंदु के निर्देशांक (0, 5) हैं।
(vii) बिंदु M के निर्देशांक (-3 , 0) हैं।

Haryana State Board HBSE 9th Class Maths Solutions Chapter 3 निर्देशांक ज्यामिति Ex 3.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 3 निर्देशांक ज्यामिति Exercise 3.1

प्रश्न 1.
एक अन्य व्यक्ति को आप अपने अध्ययन मेज पर रखे टेबल लैंप की स्थिति किस तरह बताएंगे?
हल :
हम लैंप को एक बिंदु तथा मेज को एक समतल मान लेते हैं। अब मेज के कोई भी दो लंब कोर लीजिए। बड़े कोर से लैंप की दूरी माप लीजिए। मान लीजिए यह दूरी 25 सें०मी० है। अब, छोटे कोर से लैंप की दूरी मापिए और मान लीजिए यह दूरी 30 सें०मी० है। जिस क्रम में आपने लैंप रखा है उसके अनुसार उसकी स्थिति को (30, 25) या (25, 30) लिख सकते हैं।

प्रश्न 2.
(सड़क योजना): एक नगर में दो मुख्य सड़कें हैं, जो नगर के केंद्र पर मिलती हैं। ये दो सड़कें उत्तर-दक्षिण की दिशा और पूर्व-पश्चिम की दिशा में हैं। नगर की अन्य सभी सड़कें इन मुख्य सड़कों के समांतर परस्पर 200 मीटर की दूरी पर हैं। प्रत्येक दिशा में लगभग पांच सड़कें हैं। 1 सेंटीमीटर – 200 मीटर का पैमाना लेकर अपनी नोट बुक में नगर का एक मॉडल बनाइए। सड़कों को एकल रेखाओं से निरूपित कीजिए।

आपके मॉडल में एक-दूसरे को काटती हुई अनेक क्रॉस-स्ट्रीट (चौराहे) हो सकती हैं। एक विशेष क्रॉस-स्ट्रीट दो सड़कों से बनी है, जिनमें से एक उत्तर-दक्षिण दिशा में जाती है और दूसरी पूर्व-पश्चिम की दिशा में। प्रत्येक क्रॉस-स्ट्रीट का निर्देशन इस प्रकार किया जाता है। यदि दूसरी सड़क उत्तर-दक्षिण दिशा में जाती है और पांचवीं सड़क पूर्व-पश्चिम दिशा में जाती है और ये एक क्रॉसिंग पर मिलती हैं, तब इसे हम क्रॉस-स्ट्रीट (2, 5) कहेंगे। इसी परंपरा से यह ज्ञात कीजिए कि
(i) कितनी क्रॉस-स्ट्रीटों को (4, 3) माना जा सकता है।
(ii) कितनी क्रॉस-स्ट्रीटों को (3, 4) माना जा सकता है।
हल :
सड़क मार्ग योजना नीचे दी गई आकृति में दिखाई गई है –

दोनों के क्रॉस मार्ग ऊपर की आकृति में चिहनित किए गए हैं। ये अद्वितीयतः प्राप्त किए जाते हैं, क्योंकि दो संदर्भ रेखाओं में हमने स्थान निर्धारण के लिए दोनों का प्रयोग किया है अर्थात केवल एक क्रॉस-स्ट्रीट को (4, 3) तथा एक क्रॉस-स्ट्रीट को (3, 4) माना जा सकता है।