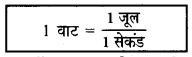Author name: Bhagya

Haryana State Board HBSE 10th Class Maths Solutions Chapter 4 Quadratic Equations Ex 4.4 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 4 Quadratic Equations Ex 4.4

Question 1.
Find the nature of the roots of the following quadratic equations. If the real roots exist, find them :
(i) 2x² – 3x + 5 = 0
(ii) 3x² – 4√3x + 4 = 0
(iii) 2x² – 6x + 3 = 0
Solution :
(i) The given equation is :
2x² – 3x + 5 = 0
Comparing the given equation with the general
form of quadratic equation, ax² + bx + c = 0, we get
a = 2, b = – 3, c = 5
∴ D = b² – 4ac
⇒ D = (- 3)² – 4 × 2 × 5
⇒ D = 9 – 40
⇒ D = – 31.
∵ D < 0
The real roots do not exist.

(ii) The given equation is :
3x² – 4√3x + 4 = 0
Comparing the given equation with the general form of quadratic equation, ax² + bx + c = 0, we get
a = 3, b = – 4√3 , c = 4
∴ D = b² – 4ac
⇒ D = (- 4√3)² – 4 × 3 × 4
⇒ D = 48 – 48
⇒ D = 0
The roots of the equation are real and equal.
x = \(-\frac{b}{2 a} \text { and }-\frac{b}{2 a}\)
x = \(\frac{4 \sqrt{3}}{2 \times 3} \text { and } \frac{4 \sqrt{3}}{2 \times 3}\)
x = \(\frac{2}{\sqrt{3}} \text { and } \frac{2}{\sqrt{3}}\)
Hence, the roots of the equation are \(\frac{2}{\sqrt{3}} \text { and } \frac{2}{\sqrt{3}}\)

(iii) The given equation is :
2x² – 6x + 3 = 0
Comparing the given equation with the general form of quadratic equation ax2 + bx + c = 0, we get a = 2, b = – 6, c = ∴ D = b² – 4ac
⇒ D = (- 6)² – 4 × 2 × 3
⇒ D = 36 – 24
⇒ D = 12
∵ D > 0
The roots of the equation are real and distinct.

Hence, the roots of the equation are \(\frac{3+\sqrt{3}}{2}\) and \(\frac{3-\sqrt{3}}{2}\).

Question 2.
Find the values of k for each of the following quadratic equations, so that they have two equal roots :
(i) 2×2 + kx + 3 = 0
(ii) kx(x – 2) + 6 = 0.
Solution:
(i) The given equation is :
2x² + kx + 3 = 0
Comparing the given equation with general form of the quadratic equation ax2 + bx + c = 0, we get
a = 2, b = k, c = 3
D = b² – 4ac
⇒ D = k² – 4 × 2 × 3
⇒ D = k² – 24
Since, the roots of the given equation are equal.
Therefore, D = 0
⇒ k² – 24 = 0
⇒ k² = 24
⇒ k = ± √24
⇒ k = ± 2√6
Hence, k = ± 2√6

(ii) The given equation is : kx (x – 2) + 6 = 0
⇒ kx² – 2kx + 6 = 0
Comparing the given equation with the general form of quadratic equation ax² + bx + c = 0, we get
a = k, b = – 2k, c = 6
D = b² – 4ac
⇒ D = (- 2k)² – 4 × k × 6
⇒ D= 4k² – 24k
Since the roots of the given equation are equal.
Therefore, D = 0
⇒ 4k² – 24k = 0
⇒ 4k(k – 6) = 0
⇒ 4k = 0 or & k – 6 = 0
⇒ k = 0 or k = 6
But k = 0 [Not possible]
Hence, k = 6.

Question 3.
Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m²? If so, find its length and breadth.
Solution:
Let the breadth of the rectangular grove be x m.
Then length of rectangular grove = 2x m
According to question,
2x × x = 800
[∵ Area of rectangle = Length × Breadth]
⇒ 2x² = 800
⇒ x² = \(\frac{800}{2}\)
⇒ x² = 400
⇒ x = √400
⇒ x = ± 20
Reject x = – 20
[∵ Breadth cannot be negative.]
∴ x = 20
Hence, the rectangular grove is possible and its breadth = 20 m
and length 2 × 20 = 40 m.

Question 4.
Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution :
Let the present age of first friend be x years.
Then present age of second friend = (20 – x) years
Four years ago age of first friend = (x – 4) years
Four years ago age of second friend = (20 – x – 4) years = (16 – x) years
According to question,
(x – 4)(16 – x) = 48
⇒ 16x – x² – 64 + 4x = 48
⇒ – x² + 20x – 64 – 48 = 0
⇒ – x² + 20x – 112 = 0
⇒ x² – 20x + 112 = 0
Here, a = 1, b = – 20, c = 112
∴ D = b² – 4ac
⇒ D = (- 20)² – 4 × 1 × 112
D = 400 – 448
⇒ D = – 48
∵ D < 0
∴ The equation has no real value of x. Hence, the situation is not possible.

Question 5.
Is it possible to design a rectangular park of perimeter 80 m and area 400 m2 ? If so, find its length and breadth.
Solution:
Let the breadth of rectangular park be x m.
Perimeter of rectangular park= 2 (length + breadth)
⇒ 80 = 2(length + x)
⇒ \(\frac{80}{2}\) = length + x
⇒ 40 = length + x
⇒ length = (40 – x) m
Now, according to question,
Area of rectangular park = Length × Breadth
400 = (40 – x) × x
⇒ 400 = 40x – x²
⇒ x² – 40x + 400 = 0
Here, a = 1, b = – 40, c = 400
D = b² – 4ac
⇒ D = (- 40)² – 4 × 1 × 400
⇒ D = 1600 – 1600
⇒ D = 0
The equation has real and equal roots.
⇒ x = 20 and 20
Hence, the rectangular park is possible and its length = 20 m and breadth = 20 m.

Haryana State Board HBSE 10th Class Maths Solutions Chapter 2 Polynomials Ex 2.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 2 Polynomials Exercise 2.2

Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x
(iv) 4u² + 8u
(v) t² – 15
(vi) 3x² – x – 4.
Solution :
(i) We have, f(x) = x² – 2x – 8
= x² – (4 – 2)x – 8
= x² – 4x + 2x – 8
= (x² – 4x) + (2x – 8)
= x(x – 4) + 2(x – 4)
= (x – 4) (x + 2)
To find the zeroes of the polynomial f(x), put f(x) = 0
⇒ (x – 4) (x + 2) = 0
⇒ x = 4, – 2
Therefore, the zeroes of polynomial f(x) are : α = 4, β = – 2.
Now, Sum of the zeroes = α + β = (4 – 2)
= 2 = \(\frac{-(-2)}{1}\)
= \(\frac{\text { – Coefficient of } x}{\text { Coefficient of } x^2}\)

Product of zeroes = α × β
= 4 × (- 2) = \(-\frac{8}{1}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)
Hence, zeroes of the polynomial f(x) are 4, – 2.

(ii) We have,
f(s) = 4s² – 4s + 1
= 4s² – (2 + 2)s + 1
= 4s² – 2s – 2s + 1
= (4s² – 2s) – (2s – 1)
= 2s (2s – 1) – 1 (2s – 1)
= (2s – 1) (2s – 1)
To find the zeroes of the polynomial f(s), put f(s) = 0.
⇒ (2s – 1) (2s – 1) = 0
⇒ s = \(\frac{1}{2}\), \(\frac{1}{2}\)
Therefore, zeroes of the polynomial f(s) are α = \(\frac{1}{2}\), β = \(\frac{1}{2}\).
∴ It has equal roots.
Now, Sum of zeroes = α + β
= \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1
= \(\frac{-(-4)}{4}\)
= \(\frac{\text { – Coefficient of } s}{\text { Coefficient of } s^2}\)

Product of zeroes = α × β
= \(\frac{1}{2}\) × \(\frac{1}{2}\) = \(\frac{1}{4}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } s^2}\)
Hence, zeroes of polynomial f(s) = \(\frac{1}{2}\), \(\frac{1}{2}\).

(iii) We have,
p(x) = 6x² – 3 – 7x
= 6x² – 7x – 3
= 6x² – (9 – 2) x – 3
= 6x² – 9x + 2x – 3
= 3x (2x – 3) + 1 (2x – 3)
= (2x – 3) (3x + 1)
To find the zeroes of the polynomial p(x)
put p(x) = 0
⇒ (2x – 3) (3x + 1) = 0
⇒ x = \(\frac{3}{2}\), – \(\frac{1}{3}\)
Therefore, zeroes of the polynomial p(x) are : α = \(\frac{3}{2}\), β = – \(\frac{1}{3}\)
Now, Sum of zeroes = α + β
= \(\frac{3}{2}\) – \(\frac{1}{3}\)
= \(\frac{9-2}{6}=\frac{7}{6}=\frac{-(-7)}{6}\)
= \(\frac{\text { – Coefficient of } x}{\text { Coefficient of } x^2}\)

Product of zeroes = α × β
= \(\frac{3}{2} \times\left(-\frac{1}{3}\right)=-\frac{3}{6}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)
Hence, zeroes of the polynomial p(x) = \(\frac{3}{2}\), – \(\frac{1}{3}\)

(iv) We have,
f(u) = 4u² + 8u
= 4 u(u + 2)
To find the zeroes of the polynomial f(u), put f(u) = 0
⇒ 4 u(u + 2) = 0
⇒ u = 0, – 2.
Therefore, zeroes of the polynomial f(u) are : α = 0, and β = – 2.
Now, Sum of zeroes = α + β
= 0 + (- 2) = – 2 = \(\frac{-8}{4}\)
= \(\frac{\text { – Coefficient of } u}{\text { Coefficient of } u^2}\)

Product of zeroes = α × β
= 0 × (- 2)
= \(\frac{0 \times(-8)}{4}=\frac{0}{4}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } u^2}\)
Hence, zeroes of the polynomial f(u) = 0, – 2.

(v) We have,
f(t) = t² – 15
= (t)² – (√15)²
= (t + √15) (t – √15)
To find the zeroes of polynomial f(t), put f(t) = 0.
⇒ (t + √15) (t – √15) = 0.
⇒ t = – √15, √15
Therefore, zeroes of polynomial f(t) are :
α = – √15 and β = √15
Now, Sum of zeroes = α + β
= – √15 + √15 = 0 = – \(\frac{0}{1}\)
= \(\frac{\text { – Coefficient of } t}{\text { Coefficient of } t^2}\)

Product of zeroes = α × β
= – √15 × √15
= \(\frac{\text { Constant term }}{\text { Coefficient of } t^2}\)
Hence, zeroes of the polynomial f(t) = – √15 , √15

(vi) We have,
f(x) = 3x² – x – 4
= 3x² – (4 – 3)x – 4
= 3x² – 4x + 3x – 4
= x(3x – 4) + 1 (3x – 4)
= (3x – 4) (x + 1)
To find the zeroes of the polynomial f(x),
put f(x) = 0
⇒ (3x – 4) (x + 1) = 0
⇒ x = \(\frac{4}{3}\), – 1
Therefore, zeroes of the polynomial f(x) are : α = \(\frac{4}{3}\) and β= – 1
Now, Sum of zeroes = α + β
= \(\frac{4}{3}\) – 1
= \(\frac{4-3}{3}=\frac{1}{3}=\frac{-(-1)}{3}\)
= \(\frac{\text { – Coefficient of } x}{\text { Coefficient of } x^2}\)

Product of zeroes = α × β
= \(\frac{4}{3}\) × (- 1)
= – \(\frac{4}{3}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)
Hence, zeroes of polynomial f(x) = \(\frac{4}{3}\) , – 1.

Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) \(\frac{1}{4}\), – 1
(ii) √2, \(\frac{1}{3}\)
(iii) 0, √5
(iv) 1, 1
(v) – \(\frac{1}{4}\), \(\frac{1}{4}\)
(vi) 4, 1.
Solution :
(i) We have,
Sum of zeroes = (α + β) = \(\frac{1}{4}\)
Product of zeroes = α × β = – 1
So, the required quadratic polynomial is f(x) = x² – (α + β)x + α × β
= x² – \(\frac{1}{4}\) x – 1
= \(\frac{1}{4}\) (4x² – x – 4)
∴ Quadratic polynomial = 4x² – x – 4.

(ii) We have,
Sum of zeroes = (α + β) = √2
Product of zeroes = α × β = \(\frac{1}{3}\)
So, the required quadratic polynomial is :
p(x) = x² – (α + β)x + α × β
= x² – √2x + \(\frac{1}{3}\)
= \(\frac{1}{3}\) (3x² – 3√2x + 1)
∴ Quadratic polynomial = 3x² – 3√2x + 1

(iii) We have,
Sum of zeroes = (α + β) = 0.
Product of zeroes = α × β = √5
So, the required quadratic polynomial is
f(x) = x² – (α + β)x + α × β
= x² – 0 × x + √5
= x² +√5

(iv) We have,
Sum of zeroes = α + β = 1
Product of zeroes = α × β = 1
So, the required quadratic polynomial is f(x) = x² – (α + β)x + α × β
= x² – 1.x + 1
= x² – x + 1

(v) We have,
Sum of zeroes = α + β = – \(\frac{1}{4}\)
Product of zeroes = α × β = \(\frac{1}{4}\)
So, the required quadratic polynomial is f(x) = x² – (α + β)x + α × β
= x² – (- \(\frac{1}{4}\)) x + \(\frac{1}{4}\)
= x² + \(\frac{1}{4}\) x + \(\frac{1}{4}\)
= \(\frac{1}{4}\) (4x² + x + 1)
∴ Quadratic polynomial = 4x² + x + 1.

(vi) We have,
Sum of zeroes = α + β = 4
Product of zeroes = α × β = 1
So, the required polynomial is
f(x) = x² – (α + β)x + α × β
= x² – 4x + 1

Haryana State Board HBSE 10th Class Maths Solutions Chapter 2 Polynomials Ex 2.1 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 2 Polynomials Exercise 2.1

Question 1.
The graphs of y = p(x) are given in the figure (A) as shown below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

Solution :
(i) The graph is parallel to x-axis. It does not intersect the x-axis. So the number of zeroes is 0.
(ii) The graph intersects the x-axis at one point. So, the number of zeroes is 1.
(iii) The graph intersects the x-axis at three points. So, the number of zeroes is 3.
(iv) The graph intersects the x-axis at two points. So, the number of zeroes is 2.
(v) The graph intersects the x-axis at four points. So, the number of zeroes is 4.
(vi) The graph intersects the x-axis at three points. So, the number of zeroes is 3.

Haryana State Board HBSE 9th Class Science Solutions Chapter 12 ध्वनि Textbook Exercise Questions and Answers.

Haryana Board 9th Class Science Solutions Chapter 12 ध्वनि

HBSE 9th Class Science ध्वनि Intext Questions and Answers
(पृष्ठ संख्या-182)

प्रश्न 1.
किसी माध्यम में ध्वनि द्वारा उत्पन्न विक्षोभ आपके कानों तक कैसे पहुँचता है?
उत्तर:
माध्यम में ध्वनि द्वारा उत्पन्न विक्षोभ माध्यम के द्वारा हमारे कानों तक पहुँचता है।

(पृष्ठ संख्या-182)

प्रश्न 1.
आपके विद्यालय की घंटी, ध्वनि कैसे उत्पन्न करती है?
उत्तर:
विद्यालय की घंटी कंपन के द्वारा ध्वनि उत्पन्न करती है क्योंकि जब घंटी को हथौड़े से पीटा जाता है तो घंटी में कंपन उत्पन्न होता है।

प्रश्न 2.
ध्वनि तरंगों को यांत्रिक तरंगें क्यों कहते हैं?
उत्तर:
ध्वनि की तरंगें माध्यम के कणों की गति द्वारा अभिलक्षित की जाती हैं, जिनके द्वारा यांत्रिक कार्य करना संभव है। इसीलिए ध्वनि तरंगों को यांत्रिक तरंगें कहते हैं।

प्रश्न 3.
मान लीजिए आप अपने मित्र के साथ चंद्रमा पर गए हुए हैं। क्या आप अपने मित्र द्वारा उत्पन्न ध्वनि को सुन पाएँगे?
उत्तर:
नहीं, क्योंकि ध्वनि संचरण के लिए माध्यम की आवश्यकता होती है। चंद्रमा पर माध्यम उपलब्ध नहीं है, इसीलिए चंद्रमा पर ध्वनि का संचरण न होने के कारण, ध्वनि सुनाई नहीं देती।

(पृष्ठ संख्या-186)

प्रश्न 1.
तरंग का कौन-सा गुण निम्नलिखित को निर्धारित करता है
(a) प्रबलता,
(b) तारत्व।
उत्तर:
(b) तारत्व।

प्रश्न 2.
अनुमान लगाइए कि निम्न में से किस ध्वनि का तारत्व अधिक है?
(a) गिटार,
(b) कार का हॉर्न।
उत्तर:
(b) कार के हॉर्न का।

(पृष्ठ संख्या -186)

प्रश्न 1.
किसी ध्वनि तरंग की तरंगदैर्ध्य, आवृत्ति, आवर्तकाल तथा आयाम से क्या अभिप्राय है?
उत्तर:

• तरंगदैर्ध्य दो क्रमागत संपीडनों अथवा दो क्रमागत विरलनों के बीच की दूरी तरंगदैर्ध्य कहलाती है। इसे ग्रीक अक्षर 2 (लैम्डा) से निरूपित किया जाता है।
• आवृत्ति प्रति सेकंड दोलनों की संख्या आवृत्ति कहलाती है।
• आवर्तकाल-एक दोलन में लिया गया समय आवर्तकाल कहलाता है।
• आयाम-लोलक में मध्य बिंदु (स्थिति) के किसी भी ओर अधिकतम दूरी आयाम कहलाती है।

प्रश्न 2.
किसी ध्वनि तरंग की तरंगदैर्ध्य तथा आवृत्ति उसके वेग से किस प्रकार संबंधित है?
उत्तर:
υ = λ v या
वेग = तरंगदैर्ध्य x आवृत्ति

प्रश्न 3.
किसी दिए हुए माध्यम में एक ध्वनि तरंग की आवृत्ति 220 Hz तथा वेग 440 m/s है। इस तरंग की तरंगदैर्ध्य की गणना कीजिए।
हल:
तरंग की आवृत्ति, (v) = 220 Hz
तरंग का वेग (υ) = 440 m/s
जबकि υ = λ x v
440 m/s = λ x 220 Hz
λ = \(\frac { 440 }{ 220 } \) = 2m
λ = 2m उत्तर

प्रश्न 4.
किसी ध्वनि स्रोत से 450m दूरी पर बैठा हुआ कोई मनुष्य 500Hz की ध्वनि सुनता है। स्रोत से मनुष्य के पास तक पहुँचने वाले दो क्रमागत संपीडनों में कितना समय अंतराल होगा?
हल
तरंग की आवृत्ति (v) = 500 Hz
समय (T) = ?
हम जानते हैं कि
(v) = \(\frac { 1 }{ T } \)
T = \(\frac { 1 }{ v } \)
T = \(\frac { 1 }{ 500 } \) = 0.002 सेकंड
T = 0.002 सेकंड उत्तर

(पृष्ठ संख्या-187)

प्रश्न 1.
ध्वनि की प्रबलता और तीव्रता में अंतर बताइए।
उत्तर:
ध्वनि की प्रबलता-ध्वनि की उत्तेजना के दर्जे को ध्वनि की प्रबलता कहते हैं। यह हल्के और तेज कंपनों पर निर्भर करती है। ध्वनि की तीव्रता-किसी एकांक क्षेत्रफल से एक सेकंड में गुजरने वाली ध्वनि ऊर्जा को ध्वनि की तीव्रता कहते हैं।

(पृष्ठ संख्या-188)

प्रश्न 1.
वायु, जल या लोहे में से किस माध्यम में ध्वनि सबसे तेज चलती है?
उत्तर:
लोहे में ध्वनि सबसे तेज चलती है। 25°C पर वायु में ध्वनि की चाल 346 m/s, जल में 1531 m/s और लोहे में 5950 m/s है।

(पृष्ठ संख्या-189)

प्रश्न 1.
कोई प्रतिध्वनि 3s पश्चात् सुनाई देती है। यदि ध्वनि की चाल 342 ms^-1हो तो स्रोत तथा परावर्तक सतह के बीच कितनी दूरी होगी?
हल:
यहाँ पर
ध्वनि का वेग (v) = 342 m/s
प्रतिध्वनि सुनने में लगा समय (t) = 3s
ध्वनि द्वारा तय दूरी = वेग x समय
= 342 x 3 m = 1026 m
अतः ध्वनि स्रोत व परावर्तक तल के बीच दूरी = \(\frac { 1026 }{ 2 } \) m = 513 m उत्तर

(पृष्ठ संख्या-190)

प्रश्न 1.
कंसर्ट हॉल की छतें वक्राकार क्यों होती हैं?
उत्तर:
कंसर्ट हॉल की छतें वक्राकार इसलिए होती हैं ताकि ध्वनि परावर्तन के बाद हॉल के सभी भागों में पहुँच सके।

(पृष्ठ संख्या-191)

प्रश्न 1.
सामान्य मनुष्य के कानों के लिए श्रव्यता परास क्या है?
उत्तर:
20 Hz से 20,000 Hz.

प्रश्न 2.
निम्न से संबंधित आवृत्तियों का परास क्या है?

• अवश्रव्य ध्वनि,
• पराश्रव्य ध्वनि।

उत्तर:

• अवश्रव्य ध्वनि का परास = 20 Hz से कम।
• पराश्रव्य ध्वनि का परास = 20 kHz से अधिक।

(पृष्ठ संख्या-193)

प्रश्न 1.
एक पनडुब्बी सोनार स्पंद उत्सर्जित करती है, जो पानी के अंदर एक खड़ी चट्टान से टकराकर 1.02 s के पश्चात् वापस लौटता है। यदि खारे पानी में ध्वनि की चाल 1531 m/s हो, तो चट्टान की दूरी ज्ञात कीजिए।
हल:
यहाँ पर
प्रेषण तथा संसूचन में लगा समय (t) = 1.02 s
खारे पानी में ध्वनि की चाल (v) = 1531m/s
पराध्वनि द्वारा तय की गई कुल दूरी = 2x पनडुब्बी से चट्टान की दूरी
= 2d
जहाँ d = पनडुब्बी से चट्टान की दूरी
कुल दूरी (20) = चाल x समय = 1531m/s x 1.02 = 1561.62 m
d = \(\frac { 1561.62 }{ 2 } \) = 780.81 m
d = 780.81 m उत्तर

HBSE 9th Class Science ध्वनि Textbook Questions and Answers

प्रश्न 1.
ध्वनि क्या है और यह कैसे उत्पन्न होती है?
उत्तर:
ध्वनि-ऊर्जा का वह रूप जिससे हमें सुनाई दे, ध्वनि कहलाती है। ध्वनि के पैदा होने के लिए किसी वस्तु में कंपन का पैदा होना जरूरी है। उदाहरण के तौर पर जब हम बोलते हैं तो हमारे गले में स्वर-तंत्र कांपते हैं। जब सितार या सारंगी बजती है तो उसकी तारें कांपती हैं। जब घंटी बजती है तो उसमें भी कंपन पैदा होता है। घंटी में कंपन को हाथ लगाकर महसूस किया जा सकता है। इस प्रकार ध्वनि कंपन पैदा होने से पैदा होती है।

प्रश्न 2.
एक चित्र की सहायता से वर्णन कीजिए कि ध्वनि के स्रोत के निकट वायु में संपीडन तथा विरलन कैसे उत्पन्न होते हैं?
उत्तर:

ध्वनि स्रोत अपने सामने की वायु को धक्का देकर संपीडित करती है और इस प्रकार उच्च दाब का क्षेत्र संपीडन बनता है। यह संपीडन वस्तु से दूर आगे की ओर गति करता है, जब कंपमान वस्तु पीछे की ओर कंपन करती है तो निम्न दाब का क्षेत्र विरलन बनता है। अतः वस्तु के कंपन से वायु में लगातार संपीडन और विरलन होते हैं। इन्हीं संपीडन और विरलन से तरंग बनती हैं।

प्रश्न 3.
किस प्रयोग से यह दर्शाया जा सकता है कि ध्वनि संचरण के लिए एक द्रव्यात्मक माध्यम की आवश्यकता होती है?
उत्तर:
ध्वनि एक यांत्रिक तरंग है। इसके संचरण के लिए माध्यम की आवश्यकता होती है। इसे निम्नलिखित प्रयोग द्वारा सिद्ध किया जा सकता है प्रयोग-चित्र में दिखाए अनुसार एक विद्युत घंटी को एक बेलजार में कार्क के द्वारा लटकाओ। बेलजार को एक निर्वात पंप से जोड़ो। विद्युत घंटी का स्विच ऑन करो। घंटी की आवाज सुनाई देती है। अब निर्वात पंप से बेलजार की वायु धीरे-धीरे निकालो। हमें घंटी की आवाज धीरे-धीरे ही कम होती अनुभव होती है। बेलजार में पूर्ण निर्वात होने पर घंटी की आवाज सुनाई देनी बंद हो जाती है। अतः प्रयोग से सिद्ध होता है कि निर्वात में ध्वनि संचरण नहीं होता। ध्वनि संचरण के लिए माध्यम की आवश्यकता होती है। बेलजार में वायु माध्यम था। इसीलिए विद्युत घंटी की ध्वनि सुनाई दे रही थी।

प्रश्न 4.
ध्वनि तरंगों की प्रकृति अनुदैर्ध्य क्यों है?
उत्तर:
ध्वनि की तरंगों में माध्यम के कणों का विस्थापन विक्षोभ के संचरण की दिशा के समांतर होता है। कण एक स्थान से दूसरे स्थान तक गति नहीं करते। वे केवल अपनी विराम अवस्था के आगे-पीछे दोलन करते हैं। इसीलिए ध्वनि तरंगें अनुदैर्ध्य होती हैं।

प्रश्न 5.
ध्वनि का कौन-सा अभिलक्षण किसी अन्य अंधेरे कमरे में बैठे आपके मित्र की आवाज पहचानने में आपकी सहायता करता है?
उत्तर:
ध्वनि का तारत्व। किसी उत्सर्जित ध्वनि की आवृत्ति को हमारा मस्तिष्क किस प्रकार अनुभव करता है, उसे तारत्व कहते हैं। तारत्व ही ध्वनि को पहचानने में हमारी मदद करता है।

प्रश्न 6.
तड़ित की चमक तथा गर्जन साथ-साथ उत्पन्न होते हैं। लेकिन चमक दिखाई देने के कुछ सेकंड पश्चात् गर्जन सुनाई देती है, ऐसा क्यों होता है?
उत्तर:
सामान्य ताप पर ध्वनि की चाल 344 मीटर प्रति सेकंड और प्रकाश का वेग 3 लाख कि०मी० प्रति सेकंड है। तड़ित और गर्जन दोनों एक ही समय में उत्पन्न होते हैं, परंतु दोनों की चाल में अंतर के कारण, चमक पहले और गर्जन बाद में सुनाई देती है।

प्रश्न 7.
किसी व्यक्ति का औसत श्रव्य परास 20 Hz से 20 kHz है। इन दो आवृत्तियों के लिए ध्वनि तरंगों की तरंगदैर्ध्य ज्ञात कीजिए। वायु में ध्वनि का वेग 344 m/s लीजिए।
हल:
वायु में ध्वनि का वेग (υ) = 344 m/s
मनुष्य की पहली आवृत्ति, (v₁) = 20 Hz
मनुष्य की दूसरी आवृत्ति, (v₂) = 20 kHz = 20,000 Hz
पहली तरंगदैर्ध्य (λ₁) = \(\frac{v}{v_1}\) = \(\frac { 344 }{ 20 } \)
= 17.2 m उत्तर
दूसरी तरंगदैर्ध्य (λ₂) = \(\frac{v}{v_2}\) = \(\frac { 344 }{ 20,000 } \)m उत्तर

प्रश्न 8.
दो बालक किसी ऐलुमिनियम पाइप के दो सिरों पर हैं। एक बालक पाइप के एक सिरे पर पत्थर से आघात करता है। दूसरे सिरे पर स्थित बालक तक वायु तथा ऐलुमिनियम से होकर जाने वाली ध्वनि तरंगों द्वारा लिए गए समय का अनुपात ज्ञात कीजिए।
हल:
माना पाइप की लंबाई = 1 मी०
सामान्य ताप पर ध्वनि की वायु में चाल (υ₁) = 346 m/s
वायु में लिया गया समय = = \(\frac { 1m }{ 346m } \)s = 1/346s ………………(i)
सामान्य ताप पर ध्वनि की ऐलुमिनियम में चाल (υ₂) = 6420 m/s
ऐलुमिनियम में लिया गया समय = = \(\frac { 1m }{ 6420m } \)S = 1/6420s ……………….(ii)
दोनों समयों में अनुपात = \(\frac { 1 }{ 346 } \) : \(\frac { 1 }{ 6420 } \) = 18.55 : 1 उत्तर

प्रश्न 9.
किसी ध्वनि स्रोत की आवृत्ति 100 Hz है। एक मिनट में यह कितनी बार कंपन करेगा?
हल:
ध्वनि की आवृत्ति (v) = 100 Hz
1 सेकंड में तय कंपनों की संख्या = 100
60 सेकंड में तय कंपनों की संख्या = 100 x 60 = 6000 उत्तर

प्रश्न 10.
क्या ध्वनि परावर्तन के उन्हीं नियमों का पालन करती है जिनका कि प्रकाश की तरंगें करती हैं। इन नियमों को बताइए।
उत्तर:
हाँ, ध्वनि परावर्तन के नियमों का प्रकाश की तरह ही पालन करती है। ध्वनि ठोस या द्रव की सतह से परावर्तित होती है। नियम –
(1) परावर्तक सतह पर खींचे गए अभिलंब और ध्वनि के आपतन होने की दिशा तथा परावर्तित होने की दिशा के बीच बने कोण आपस में बराबर होते हैं।

(2) आपतित ध्वनि, अभिलंब और परावर्तित ध्वनि की दिशा एक ही तल में होती है। ध्वनि परावर्तन के लिए पालिश किए हुए या खुरदरे बड़े आकार के अवरोधकों की आवश्यकता होती है।

प्रश्न 11.
ध्वनि का एक स्रोत किसी परावर्तक सतह के सामने रखने पर उसके द्वारा प्रदत्त ध्वनि तरंग की प्रतिध्वनि सुनाई देती है। यदि स्रोत तथा परावर्तक सतह की दूरी स्थिर रहे तो किस दिन प्रतिध्वनि अधिक शीघ्र सुनाई देगी-

• जिस दिन तापमान अधिक हो,
• जिस दिन तापमान कम हो?

उत्तर:
जिस दिन तापमान अधिक हो।

प्रश्न 12.
ध्वनि तरंगों के परावर्तन के दो व्यावहारिक उपयोग लिखिए।
उत्तर:
ध्वनि तरंगों के परावर्तन के दो व्यावहारिक उपयोग निम्नलिखित हैं

• रात्रि के समय चमगादड़ ध्वनि परावर्तन के द्वारा ही अपने गमन पथ का एहसास करते हैं।
• पराध्वनि का उपयोग गुर्दे की छोटी पत्थरी को बारीक कणों में तोड़ने के लिए किया जाता है।

प्रश्न 13.
500 मीटर ऊंची किसी मीनार की चोटी से एक पत्थर मीनार के आधार पर स्थित एक पानी के तालाब में गिराया जाता है। पानी में इसके गिरने की ध्वनि चोटी पर कब सुनाई देगी? (g = 10 ms^-2 तथा ध्वनि की चाल = 340 ms^-1)।
हल:
यहाँ पर u= 0, s = 500 m, g= 10 m/s²
परन्तु s =ut + \(\frac { 1 }{ 2 } \)gt² = 0 + \(\frac { 1 }{ 2 } \) x 10 x t² = 5t²
= 500 या 1 = 10s
पानी के तल से मीनार की चोटी की दूरी = 500 m
ध्वनि की चाल = 340 m/s
समय = = \(\frac { 500 }{ 340 } \) = 1.47s
= 1.47s
ध्वनि को ऊपर आने में लगा कुल समय = 10 + 1.47 = 11.47s उत्तर

प्रश्न 14.
एक ध्वनि तरंग 339 m/s की चाल से चलती है। यदि इसकी तरंगदैर्ध्य 1.5 cm हो, तो तरंग की आवृत्ति कितनी होगी? क्या ये श्रव्य होंगी?
हल:
यहाँ पर
ध्वनि तरंग की चाल = 339 m/s
तरंगदैर्ध्य = 1.5 cm = \(\frac { 15 }{ 10 } \) = \(\frac { 15 }{ 1000 } \)m
आवृत्ति = = \(\frac { 339 }{ 15 } \) x 1000 = 22600 Hz
यह ध्वनि अवश्रव्य है क्योंकि मनुष्य 20,000 Hz से ऊपर की ध्वनि को नहीं सुन सकता। उत्तर

प्रश्न 15.
अनुरणन क्या है? इसे कैसे कम किया जा सकता है?
उत्तर:
अनुरणन-बारंबार परावर्तन, जिसके कारण ध्वनि निर्बंध होता है, अनुरणन कहलाता है। कम करने के उपाय-सभा भवन की छतों तथा दीवारों पर ध्वनि अवशोषक पदार्थों; जैसे संपीडित फाइबर बोर्ड, खुरदरे प्लास्टर, पर्दे, गत्ता, घास-फूस की दीवारों का उपयोग कर अनुरणन कम किया जा सकता है। सीटों के पदार्थों का उचित चुनाव भी ध्वनि अवशोषण का कार्य करता है।

प्रश्न 16.
ध्वनि की प्रबलता से क्या अभिप्राय है? यह किन कारकों पर निर्भर करती है?
उत्तर:
ध्वनि की उत्तेजना के दर्जे को ध्वनि की प्रबलता कहते हैं। यह उत्तेजना का दर्जा स्रोत के तेज या हल्के कंपनों पर निर्भर करता है। जब कंपन अधिक तेज होते हैं, तब ध्वनि प्रबलता अधिक तथा जब कंपन हल्के होते हैं तो ध्वनि प्रबलता भी कम होती है। ध्वनि की प्रबलता अथवा मृदुता मूलतः उसके आयाम से ज्ञात की जाती है। अधिक ऊर्जा वाली ध्वनि में प्रबलता भी अधिक होती है।

प्रश्न 17.
चमगादड़ अपना शिकार पकड़ने के लिए पराध्वनि का उपयोग किस प्रकार करता है? वर्णन कीजिए।
उत्तर:
चमगादड़, उच्च आवृत्ति के स्पंदों (अल्प समय के ध्वनि संकेत) को उत्सर्जित करते हैं। वे अपने रास्ते में आने वाले अवरोधों या कीटों से उत्पन्न प्रतिध्वनि को सुनते हैं। प्रतिध्वनि को पहुंचने में लगने वाले समय से वे परावर्तक स्रोत की दूरी का अनुमान लगा लेते हैं। इस प्रकार चमगादड़ अपना भोजन खोजने में ध्वनि का उपयोग करते हैं।

प्रश्न 18.
वस्तुओं को साफ करने के लिए पराध्वनि का उपयोग कैसे करते हैं?
उत्तर:
वस्तुओं को साफ करने के लिए उन्हें मार्जन विलयन में रखकर विलयन में पराध्वनि तरंगों को प्रेषित किया जाता है। तरंगों की उच्च आवृत्ति के कारण, धूल, चिकनाई तथा गंदगी के कण अलग होकर नाचे गिर जाते हैं और वस्तु साफ हो जाती है। इस विधि द्वारा ऐसी वस्तुओं को भी साफ किया जाता है, जिन्हें उनके विषम आकार के कारण साफ करना आसान न हो।

प्रश्न 19.
सोनार की कार्य-विधि तथा उपयोगों का वर्णन कीजिए।
उत्तर:
कार्य-विधि-SONAR-Sound Navigation And Ranging ऐसी युक्ति है, जिसमें ध्वनि तरंगें उत्पन्न कर तथा परावर्तित कर ध्वनि तरंगों का लघु समयांतर कर मापा जाता है। इस तकनीक में पराध्वनि तरंगों का उपयोग किया जाता है। सोनार में एक प्रेषित व संसूचक होता है। इसे जहाज या नाव की तली पर लगाया जाता है। प्रेषित द्वारा ध्वनि तरंगें उत्पन्न व प्रेषित की जाती हैं और जल में गमन करती हुई पिंड से टकराकर संसूचक द्वारा ग्रहण कर ली जाती हैं। ध्वनि तरंगों के प्रेषण और अभिग्रहण में लगे समय की गणना कर, ज्ञात ध्वानि चाल के द्वारा पिंड की स्थिति का अनुमान लगा लिया जाता है।

उपयोग-इसके उपयोग निम्नलिखित हैं-

1. समुद्र की गहराई व तेल कुएँ की गहराई ज्ञात करने में।
2. मछलियों के झुंडों की दूरी ज्ञात करने में।
3. शत्रु की पनडुब्बी या टारपीडों का पता लगाने के लिए।
4. उद्योगों में विशाल गार्डरों, ब्लॉकों तथा शीटों में संभावित दरारों या दोषों का पता लगाने में।
   इनमें सोनार-युक्ति का उपयोग किया जाता है। डूबे हुए जहाज का भी इसके द्वारा पता लगाया जा सकता है।

प्रश्न 20.
एक पनडुब्बी पर लगी एक सोनार-युक्ति संकेत भेजती है और उनकी प्रतिध्वनि 5s पश्चात् ग्रहण करती है। यदि पनडुब्बी से वस्तु की दूरी 3625 s हो तो ध्वनि की चाल की गणना कीजिए।
हल:\(\)
पनडुब्बी से वस्तु की दूरी (d) = 3625 m
प्रतिध्वनि दुगुना रास्ता तय करती है
2d = 2 x 3625 = 7250 m
समय (t) = 5 s
जल में ध्वनि की चाल = \(\frac{2 d}{\mathrm{t}}\) = = \(\frac{7250}{5}\) =1450 m/s
अतः जल में ध्वनि की चाल = 1450 m/s उत्तर

प्रश्न 21.
किसी धातु के ब्लॉक में दोषों का पता लगाने के लिए पराध्वनि का उपयोग कैसे किया जाता है? वर्णन
उत्तर:
पराध्वनि का उपयोग धातु के ब्लॉकों (पिंडों) में दरारों तथा अन्य दोषों का पता लगाने के लिए किया जा सकता है। धातु के ब्लॉकों में विद्यमान दरार या छिद्र जो बाहर से दिखलाई नहीं देते, भवन या पुल की संरचना की मजबूती को कम कर देते दूरी हैं। पराध्वनि तरंगें धातु के ब्लॉक से गुजारी जाती हैं और प्रेषित तरंगों का पता लगाने के लिए संसूचकों का उपयोग किया जाता

है। दोष होने पर पराध्वनि तरंगें परावर्तित हो जाती हैं। इस कार्य के लिए इन ध्वनि तरंगों का सीधे उपयोग नहीं किया जा सकता, जिनकी तरंगदैर्ध्य अधिक हो क्योंकि ये तरंगें दोषयुक्त स्थान के कोनों से मुड़कर संसूचक तक पहुँच जाती हैं और दोष का पता लगाने के स्थान पर भ्रम की स्थिति बन जाती है।

प्रश्न 22.
मनुष्य का कान किस प्रकार कार्य करता है? विवेचन कीजिए।
उत्तर:
मनुष्य का बाह्य कान परिवेश से ध्वनि तरंगों को एकत्रित कर मध्य कान के पर्दे पर पहुँचा देता है, जिसके कारण पर्दे के बाहर की ओर लगने वाला दाब बढ़ जाता है। अंदर की ओर दाब कम होता है। इस दाब के अंतर के कारण कान का पर्दा कंपन करने लगता है। मध्य कान में तीन अस्थियाँ-मुग्दरक, निहाई, वलयक इन कंपनों को कई गुणा बढ़ाकर आंतरिक कान में संचरित कर देती हैं। आंतरिक कान में कर्णावत द्वारा इन कंपनों को विद्युत संकेतों में बदल कर श्रवण तंत्रिका द्वारा मस्तिष्क में भेज दिया जाता है, जिसे मस्तिष्क ध्वनि संदेश में पहचान लेता है।

Haryana State Board HBSE 9th Class Science Solutions Chapter 11 कार्य तथा ऊर्जा Textbook Exercise Questions and Answers.

Haryana Board 9th Class Science Solutions Chapter 11 कार्य तथा ऊर्जा

HBSE 9th Class Science कार्य तथा ऊर्जा Intext Questions and Answers
(पृष्ठ संख्या-164)

प्रश्न 1.
किसी वस्तु पर 7N का बल लगता है। मान लीजिए बल की दिशा में विस्थापन 8 m है (चित्र 11.1)। मान लीजिए वस्तु के विस्थापन के समय लगातार वस्तु पर बल लगता रहता है। इस स्थिति में किया गया कार्य कितना होगा?

हल-यहाँ पर
बल (F) = 7N
विस्थापन (s) = 8 m
किया गया कार्य (W) = ?
किया गया कार्य (w) = बल (F) x विस्थापन (s)
= 7 x 8 N.m
= 56 J उत्तर

(पृष्ठ संख्या-165)

प्रश्न 1.
हम कब कहते हैं कि कार्य किया गया है?
उत्तर:
जब किसी वस्तु पर बल लगाने से वस्तु विस्थापित हो तो कार्य किया गया माना जाता है, अर्थात्
किया गया कार्य (W) = बल (F) – विस्थापन (s)

प्रश्न 2.
जब किसी वस्तु पर लगने वाला बल इसके विस्थापन की दिशा में हो तो किए गए कार्य का व्यंजक लिखिए।
उत्तर:
जब किसी वस्तु पर लगने वाला बल इसके विस्थापन की दिशा में हो तो कार्य का व्यंजक निम्नलिखित होगा
किया गया कार्य (W) = बल (F) x विस्थापन (s)
अर्थात् जब बल विस्थापन की दिशा में लगता है तो किया गया कार्य धनात्मक होता है।

प्रश्न 3.
1J कार्य को परिभाषित कीजिए।
उत्तर:
यदि एक वस्तु पर 1 न्यूटन बल लगाने पर वह वस्तु बल की दिशा में 1 मीटर विस्थापित हो तो वस्तु पर किया गया कार्य 1 जूल कहलाता है। अर्थात्
1 J = 1 N x 1 m

प्रश्न 4.
बैलों की एक जोड़ी खेत जोतते समय किसी हल पर 140 N बल लगाती है। जोता गया खेत 15 m लंबा है। खेत की लंबाई को जोतने में कितना कार्य किया गया?
हल-यहाँ पर
बल (F) = 140 N
विस्थापन (s) = 15 m
:. किया गया कार्य (w) = F x s
= 140 x 15 N.m.
= 2100 J उत्तर

(पृष्ठ संख्या – 169)

प्रश्न 1.
किसी वस्तु की गतिज ऊर्जा क्या होती है?
उत्तर:
किसी वस्तु में उसकी गति के कारण निहित ऊर्जा को गतिज ऊर्जा कहते हैं। जैसे v वेग से गतिशील किसी m द्रव्यमान की वस्तु की गतिज ऊर्जा \(\frac { 1 }{ 2 } \)mv² के बराबर होती है।

प्रश्न 2.
किसी वस्तु की गतिज ऊर्जा के लिए व्यंजक लिखो। उत्तर-m द्रव्यमान तथा एक समान वेग v से गतिशील वस्तु की गतिज ऊर्जा का मान निम्नलिखित होगा
गतिज ऊर्जा (E) = \(\frac { 1 }{ 2 } \)mv²

प्रश्न 3.
5 ms^-1 के वेग से गतिशील किसी m द्रव्यमान की वस्तु की गतिज ऊर्जा 25 Jहै। यदि इसके वेग को दोगुना कर दिया जाए तो इसकी गतिज ऊर्जा कितनी हो जाएगी? यदि इसके वेग को तीन गुना बढ़ा दिया जाए तो इसकी गतिज ऊर्जा कितनी हो जाएगी?
उत्तर:
5 ms^-1 के वेग से गतिशील किसी m द्रव्यमान की वस्तु की गतिज ऊर्जा 25J है। यदि इसके वेग को दो गुना (10 ms^-1) कर दिया जाए तो इसकी गतिज ऊर्जा (22) चार गुना बढ़ जाएगी अर्थात् 100 J हो जाएगी। परंतु यदि इसके वेग को तीन गुना (15 ms^-1) कर दिया जाए तो इसकी गतिज ऊर्जा (32) नौ गुना बढ़ जाएगी अर्थात् 225 J हो जाएगी।

(पृष्ठ संख्या – 174)

प्रश्न 1.
शक्ति क्या है?
उत्तर:
कार्य करने की दर या ऊर्जा रूपांतरण की दर को शक्ति कहते हैं। यदि कोई अभिकर्ता (एजेंट) t समय में W कार्य करता हो तो उसकी शक्ति का मान होगा

शक्ति का मात्रक वाट (W) है।

प्रश्न 2.
1 वाट शक्ति को परिभाषित कीजिए।
उत्तर:
1 वाट उस अभिकर्ता की शक्ति होती है जो 1 सेकंड में 1 जूल कार्य करता है अर्थात्

प्रश्न 3.
एक लैंप 1000 J विद्युत ऊर्जा 10s में व्यय करता है। इसकी शक्ति कितनी है?
हल-यहाँ पर
किया गया कार्य (W) = 1000 J
समय (t) = 10s
शक्ति (P) = ?
हम जानते हैं कि
P = \(\frac { W }{ t } \)
= \(\frac { 1000 }{ 10 } \) Js^-1
= 100 W (वाट) उत्तर

प्रश्न 4.
औसत शक्ति को परिभाषित कीजिए।
उत्तर:
कुल उपयोग हुई ऊर्जा और कुल दिए गए समय के अनुपात को, औसत शक्ति कहते हैं अर्थात्

HBSE 9th Class Science कार्य तथा ऊर्जा Textbook Questions and Answers

प्रश्न 1.
निम्न सूचीबद्ध क्रियाकलापों को ध्यान से देखिए। अपनी कार्य शब्द की व्याख्या के आधार पर तर्क दीजिए कि इनमें कार्य हो रहा है अथवा नहीं।

1. सूमा एक तालाब में तैर रही है।
2. एक गधे ने अपनी पीठ पर बोझा उठा रखा है।
3. एक पवन चक्की (विंड मिल) कुएँ से पानी उठा रही है।
4. एक हरे पौधे में प्रकाश संश्लेषण की प्रक्रिया हो रही है।
5. एक इंजन ट्रेन को खींच रहा है।
6. अनाज के दाने सूर्य की धूप में सूख रहे हैं।
7. एक पाल-नाव पवन ऊर्जा के कारण गतिशील है।

उत्तर:

1. सूमा के तालाब में तैरने पर कार्य हो रहा है, क्योंकि वह बल की दिशा में विस्थापित हो रही है।
2. एक गधे द्वारा पीठ पर बोझा उठाने से कार्य नहीं हुआ माना जाता है क्योंकि उसका विस्थापन शून्य है।
3. किसी पवन चक्की द्वारा कुएँ से पानी उठाने में कार्य हुआ माना जाता है ककि वह बल की दिशा में विस्थापित होती है।
4. किसी हरे पौधे में प्रकाश संश्लेषण की प्रक्रिया होने पर कार्य शून्य माना जाता है क्योंकि विस्थापन शून्य है।
5. ट्रेन को खींच रहे इंजन की दशा में कार्य हुआ माना जाता है क्योंकि ट्रेन इंजन की दिशा में विस्थापित हो रही होती है।
6. अनाज के दानों के सूर्य की धूप में सूखने पर किया गया कार्य शून्य माना जाता है क्योंकि इस दशा में भी विस्थापन शून्य होता है।
7. जो पाल-नाव पवन ऊर्जा के कारण गतिशील है उसके द्वारा किया गया कार्य माना जाता है क्योंकि पाल-नाव वायु द्वारा बल लगाने पर बल की दिशा में विस्थापित हो रही है।

प्रश्न 2.
एक पिंड को धरती से किसी कोण पर फेंका जाता है। यह एक वक्र पथ पर चलता है और वापस धरती पर आ गिरता है। पिंड के पथ के प्रारंभिक तथा अंतिम बिंदु एक ही क्षैतिज रेखा पर स्थित हैं। पिंड पर गुरुत्व बल द्वारा कितना कार्य किया गया?
उत्तर:
पिंड पर गुरुत्व बल द्वारा किया गया कार्य शून्य माना जाता है क्योंकि पिंड का विस्थापन शून्य है।

प्रश्न 3.
एक बैटरी बल्ब जलाती है। इस प्रक्रम में होने वाले ऊर्जा परिवर्तनों का वर्णन कीजिए।
उत्तर:
एक बैटरी द्वारा बल्ब जलने पर रासायनिक ऊर्जा विद्युत ऊर्जा में परिवर्तित होती है।

प्रश्न 4.
20 kg द्रव्यमान पर लगने वाला कोई बल इसके वेग को 5 ms^-1 से 2 ms^-1 में परिवर्तित कर देता है। बल द्वारा किए गए कार्य का परिकलन कीजिए। हल यहाँ पर
वस्तु का द्रव्यमान (m) = 20 kg
वस्तु का प्रारंभिक वेग (u) = 5 ms^-1
वस्तु का अंतिम वेग (v) = 2 ms^-1
वस्तु की प्रारंभिक गतिज ऊर्जा (E₁) = \(\frac { 1 }{ 2 } \)mu²
= \(\frac { 1 }{ 2 } \) x 20 x (5)²
= 250 J
वस्तु की अंतिम गतिज ऊर्जा (E₂) = \(\frac { 1 }{ 2 } \)m (v)²
= \(\frac { 1 }{ 2 } \) x 20 (2)²J
= 40 J
अतः किया गया कार्य = गतिज ऊर्जा में परिवर्तन
= E₁ – E₂
= 250 J – 40 J = 210 J उत्तर

प्रश्न 5.
10 kg द्रव्यमान का एक पिंड मेज पर Aबिंदु पर रखा है। इसे B बिंदु तक लाया जाता है। यदि A तथा B को मिलाने वाली रेखा क्षैतिज है तो पिंड पर गुरुत्व बल द्वारा किया गया कार्य कितना होगा? अपने उत्तर की व्याख्या कीजिए।
हल:
यहाँ पर
पिंड का द्रव्यमान (m) = 10 kg
गुरुत्व बल (g) = 9.8 ms^-2
ऊँचाई (h) = 0
:. गुरुत्व बल द्वारा किया गया कार्य (W) = mgh
= 10 x 9.8 x 0
= 0 उत्तर
अतः गुरुत्व बल द्वारा किया गया कार्य शून्य है क्योंकि विस्थापन क्षैतिज है।

प्रश्न 6.
मुक्त रूप से गिरते एक पिंड की स्थितिज ऊर्जा लगातार कम होती जाती है। क्या यह ऊर्जा संरक्षण नियम का उल्लंघन करती है? कारण बताइए।
उत्तर:
मुक्त रूप से गिरते एक पिंड की स्थितिज ऊर्जा लगातार कम होती जाती है, परंतु यह ऊर्जा संरक्षण नियम का उल्लंघन नहीं है क्योंकि यह ऊर्जा गतिज ऊर्जा के रूप में परिवर्तित होती रहती है। पृथ्वी के बिल्कुल निकट पूर्ण स्थितिज ऊर्जा, गतिज ऊर्जा में बदल जाती है तथा पृथ्वी पर पहंचते ही फिर स्थितिज ऊर्जा में परिवर्तित हो जाती है।

प्रश्न 7.
जब आप साइकिल चलाते हैं तो कौन-कौन से ऊर्जा रूपांतरण होते हैं?
उत्तर:
जब हम साइकिल चलाते हैं तो हमारी मांसपेशीय ऊर्जा गतिज ऊर्जा में परिवर्तित होती है तथा मांसपेशीय ऊर्जा हमें भोजन से रासायनिक ऊर्जा में परिवर्तित होने के बाद प्राप्त होती है।

प्रश्न 8.
जब आप अपनी सारी शक्ति लगाकर एक बड़ी चट्टान को धकेलना चाहते हैं और इसे हिलाने में असफल हो जाते हैं तो क्या इस अवस्था में ऊर्जा का स्थानांतरण होता है? आपके द्वारा व्यय की गई ऊर्जा कहाँ चली जाती है?
उत्तर:
जब हम अपनी सारी शक्ति लगाकर एक बड़ी चट्टान को धकेलना चाहते हैं और इसे हिलाने में असफल हो जाते हैं तो इस अवस्था में ऊर्जा का स्थानांतरण घर्षण के विरुद्ध नष्ट हो जाता है जिस कारण किया गया कार्य शून्य माना जाता है।

प्रश्न 9.
किसी घर में एक महीने में ऊर्जा की 250 “यूनिटें” व्यय हुईं। यह ऊर्जा जूल में कितनी होगी?
हल:
यहाँ पर
व्यय ऊर्जा = 250 यूनिट
= 250 kWh
= 250 x 1000 W x 3600 s
= 900000000 ws
= 9 x 10°J उत्तर

प्रश्न 10.
40 kg द्रव्यमान का एक पिंड धरती से 5 m की ऊँचाई तक उठाया जाता है। इसकी स्थितिज ऊर्जा कितनी है ? यदि पिंड को मुक्त रूप से गिरने दिया जाए तो जब पिंड ठीक आधे रास्ते पर है उस समय इसकी गतिज ऊर्जा का परिकलन कीजिए। (g= 10 ms^-2)
हल:
यहाँ पर
पिंड का द्रव्यमान (m) = 40 kg
पिंड की पृथ्वी से ऊँचाई (h) = 5 m
गुरुत्वीय त्वरण (g) = 10 ms^-2
पिंड की स्थितिज ऊर्जा (w) = mgh
= 40 x 5 x 10 J
= 2000 J
जब पिंड को मुक्त रूप से गिरने दिया जाए तो आधे रास्ते में पिंड की आधी स्थितिज ऊर्जा गतिज ऊर्जा में परिवर्तित हो जाएगी। इसलिए आधे रास्ते में पिंड की गतिज ऊर्जा = \(\frac { 2000 }{ 2 } \) = 1000 J होगी। उत्तर

प्रश्न 11.
पृथ्वी के चारों ओर घूमते हुए किसी उपग्रह पर गुरुत्व बल द्वारा कितना कार्य किया जाएगा? अपने उत्तर को तर्कसंगत बनाइए।
उत्तर:
पृथ्वी के चारों ओर घूमते हुए किसी उपग्रह पर गुरुत्व बल द्वारा किया गया कार्य शून्य माना जाएगा क्योंकि दोनों का विस्थापन शून्य है।

प्रश्न 12.
क्या किसी पिंड पर लगने वाले किसी भी बल की अनुपस्थिति में, इसका विस्थापन हो सकता है? सोचिए। इस प्रश्न के बारे में अपने मित्रों तथा अध्यापकों से विचार-विमर्श कीजिए।
उत्तर:
किसी पिंड पर बल की अनुपस्थिति में विस्थापन नहीं हो सकता है क्योंकि विस्थापन हमेशा असंतुलित बल के कारण होता है।

प्रश्न 13.
कोई मनुष्य भूसे के एक गट्ठर को अपने सिर पर 30 मिनट तक रखे रहता है और थक जाता है। क्या उसने कुछ कार्य किया या नहीं? अपने उत्तर को तर्कसंगत बनाइए।
उत्तर:
मनुष्य द्वारा भूसे के एक गट्ठर को अपने सिर पर 30 मिनट तक रखे रहने से किया गया कार्य शून्य माना जाता है क्योंकि इसमें विस्थापन शून्य है।

प्रश्न 14.
एक विद्युत-हीटर (ऊष्मक) की घोषित शक्ति 1500 W है। 10 घंटे में यह कितनी ऊर्जा उपयोग करेगा ?
हल:
यहाँ पर
विद्युत-हीटर की शक्ति (P) = 1500 w
समय (t) = 10 घंटे
ऊर्जा (W) = P x t
= 1500 W x 10 h
= 15000 Wh
= \(\frac { 15000 }{ 1000 } \)
= 15 kWh उत्तर

प्रश्न 15.
जब हम किसी सरल लोलक के गोलक को एक ओर ले जाकर छोड़ते हैं तो यह दोलन करने लगता है। इसमें होने वाले ऊर्जा परिवर्तनों की चर्चा करते हुए ऊर्जा संरक्षण के नियम को स्पष्ट कीजिए। गोलक कुछ समय पश्चात विराम अवस्था में क्यों आ जाता है? अंततः इसकी ऊर्जा का क्या होता है? क्या यह ऊर्जा संरक्षण नियम का उल्लंघन है?
उत्तर:
गोलक अथवा पेंडुलम को जब हम उसकी मध्य स्थिति से एक ओर, माना बाईं ओर कुछ ऊपर तक ले जाते हैं तो हमारे द्वारा किया गया कार्य उसमें स्थितिज ऊर्जा के रूप में संचित हो जाता है।

जब गोलक को छोड़ दिया जाता है तो बाएँ-से-दाएँ से मध्य स्थिति तक पहुँचते-पहुँचते गोलक की सारी स्थितिज ऊर्जा गतिज ऊर्जा में बदल जाती है। यह गतिज ऊर्जा गोलक को दाईं ओर उसी ऊँचाई तक ले जाती है जिससे उसकी गतिज ऊर्जा फिर से स्थितिज ऊर्जा में बदल जाती है। इस स्थितिज ऊर्जा के कारण गोलक फिर से दाएँ से मध्य स्थिति की ओर गति करने लगता है। यह क्रम चलता रहता है तथा गोलक या पेंडुलम से दाएँ-बाएँ गति करता रहता है।

कुछ समय पश्चात् गोलक विरामावस्था में आ जाता है क्योंकि इस पर वायु का घर्षण बल कार्य करता है जिसके विरुद्ध कार्य करने में ऊर्जा नष्ट होती रहती है। यह ऊर्जा संरक्षण का उल्लंघन नहीं है।

प्रश्न 16.
m द्रव्यमान का एक पिंड एक नियत वेग v से गतिशील है। पिंड पर कितना कार्य करना चाहिए कि यह विराम अवस्था में आ जाए?
उत्तर:
m द्रव्यमान का एक पिंड एक नियत वेग v से गतिशील है, इसलिए इसकी गतिज ऊर्जा \(\frac { 1 }{ 2 } \)mv² है। इसे विराम अवस्था में लाने के लिए गतिज ऊर्जा जितना कार्य करना पड़ेगा।

प्रश्न 17.
1500 kg द्रव्यमान की कार को जो 60 km/n के वेग से चल रही है, रोकने के लिए किए गए कार्य का परिकलन कीजिए।
हल:
यहाँ पर
कार का द्रव्यमान (m) = 1500kg
कार का वेग (v) = 60 km/h
= \(\frac{60 \times 1000}{3600} \mathrm{~ms}^{-1}\)
= \(\frac { 50 }{ 3 } \)ms^-1
अतः कार की गतिज ऊर्जा
= \(\frac { 1 }{ 2 } \)mv²
= 2 x 1500 x \(\frac { 50 }{ 3 } \) x \(\frac { 50 }{ 3 } \)J
ऊर्जा (W) = P x t
= 1500 W x 10 h
= 15000 Wh
= \(\frac { 15000 }{ 1000 } \) kWh
= 15 kWh उत्तर

प्रश्न 15.
जब हम किसी सरल लोलक के गोलक को एक ओर ले जाकर छोड़ते हैं तो यह दोलन करने लगता है। इसमें होने वाले ऊर्जा परिवर्तनों की चर्चा करते हुए ऊर्जा संरक्षण के नियम को स्पष्ट कीजिए। गोलक कुछ समय पश्चात विराम अवस्था में क्यों आ जाता है? अंततः इसकी ऊर्जा का क्या होता है? क्या यह ऊर्जा संरक्षण नियम का उल्लंघन है?
उत्तर:
गोलक अथवा पेंडुलम को जब हम उसकी मध्य स्थिति से एक ओर, माना बाईं ओर कुछ ऊपर तक ले जाते हैं तो हमारे द्वारा किया गया कार्य उसमें स्थितिज ऊर्जा के रूप में संचित हो जाता है।

जब गोलक को छोड़ दिया जाता है तो बाएँ-से-दाएँ से मध्य स्थिति तक पहुँचते-पहुँचते गोलक की सारी स्थितिज ऊर्जा गतिज ऊर्जा में बदल जाती है। यह गतिज ऊर्जा गोलक को दाईं ओर उसी ऊँचाई तक ले जाती है जिससे उसकी गतिज ऊर्जा फिर से स्थितिज ऊर्जा में बदल जाती है। इस स्थितिज ऊर्जा के कारण गोलक फिर से दाएँ से मध्य स्थिति की ओर गति करने लगता है। यह क्रम चलता रहता है तथा गोलक या पेंडुलम से दाएं-बाएँ गति करता रहता है।

कुछ समय पश्चात् गोलक विरामावस्था में आ जाता है क्योंकि इस पर वायु का घर्षण बल कार्य करता है जिसके विरुद्ध कार्य करने में ऊर्जा नष्ट होती रहती है। यह ऊर्जा संरक्षण का उल्लंघन नहीं है।

प्रश्न 16.
m द्रव्यमान का एक पिंड एक नियत वेग v से गतिशील है। पिंड पर कितना कार्य करना चाहिए कि यह विराम अवस्था में आ जाए?
उत्तर:
m द्रव्यमान का एक पिंड एक नियत वेग v से गतिशील है, इसलिए इसकी गतिज ऊर्जा \(\frac { 1 }{ 2 } \)mv² है। इसे विराम अवस्था में लाने के लिए गतिज ऊर्जा जितना कार्य करना पड़ेगा।

प्रश्न 17.
1500 kg द्रव्यमान की कार को जो 60 km/h के वेग से चल रही है, रोकने के लिए किए गए कार्य का परिकलन कीजिए।
हल:
यहाँ पर
कार का द्रव्यमान (m) = 1500kg
कार का वेग (v) = 60 km/h
= \(\frac{60 \times 1000}{3600} \mathrm{~ms}^{-1}\)
= \(\frac { 50 }{ 3 } \)ms^-1
अतः कार की गतिज ऊर्जा
= \(\frac { 1 }{ 2 } \)mv²
= \(\frac { 1 }{ 2 } \) x 1500 x \(\frac { 50 }{ 3 } \) x \(\frac { 50 }{ 3 } \) J
= 208333.3 J
इस प्रकार कार को रोकने के लिए किया जाने वाला कार्य = 208333.3J उत्तर

प्रश्न 18.
निम्न में से प्रत्येक स्थिति में m द्रव्यमान के एक पिंड पर एक बल F लग रहा है। विस्थापन की दिशा पश्चिम से पूर्व की ओर है जो एक लंबे तीर से प्रदर्शित की गई है। चित्रों को ध्यानपूर्वक देखिए और बताइए कि किया गया कार्य ऋणात्मक है, धनात्मक है या शून्य है।

उत्तर:
प्रथम अवस्था में किया गया कार्य शून्य है, दूसरी अवस्था में धनात्मक तथा तीसरी अवस्था में ऋणात्मक है।

प्रश्न 19.
सोनी कहती है कि किसी वस्तु पर त्वरण शून्य हो सकता है, चाहे उस पर कई बल कार्य कर रहे हों। क्या आप उससे सहमत हैं? बताइए क्यों?
उत्तर:
हाँ, हम सोनी की बात से सहमत हैं, क्योंकि जब किसी वस्तु पर कई संतुलित बल लग रहें हो तो बल का कुल प्रभाव शून्य हो जाता है अर्थात् F= 0 इससे पता चलता है कि ma = 0, परंतु कभी शून्य नहीं होता। इसलिए त्वरण शून्य हो सकता है।

प्रश्न 20.
चार युक्तियाँ, जिनमें प्रत्येक की शक्ति 500W है 10 घंटे तक उपयोग में लाई जाती हैं। इनके द्वारा व्यय की गई ऊर्जा kWh में परिकलित कीजिए।
हल:
यहाँ पर चार युक्तियों की कुल शक्ति (P) = 500 W x 4
= 2000 w
समय (t) = 10 घंटे
व्यय ऊर्जा = शक्ति समय
= 2000 W x 10h
= 20000 Wh
= \(\frac { 20000 }{ 1000 } \) kWh
= 20kWh उत्तर

प्रश्न 21.
मुक्त रूप से गिरता एक पिंड अंततः धरती तक पहुँचने पर रुक जाता है। इसकी गतिज ऊर्जा का क्या होता है?
उत्तर:
इसकी गतिज ऊर्जा स्थितिज ऊर्जा में परिवर्तित हो जाती है।

Haryana State Board HBSE 9th Class Maths Solutions Chapter 14 Statistics Ex 14.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 14 Statistics Exercise 14.1

Question 1.
Give five examples of data that you can collect from your day-to-day life.
Solution :
Five examples of data that we can gather from our day to day life are :
(i) Number of students in your class.
(ii) Number of chairs in your class
(iii) Electricity bills of your house for last three years.
(iv) Election results obtained from television or newspapers.
(v) Literacy rate figures obtained from Educational survey.

Question 2.
Classify the data in Q. 1 above as primary or secondary data.
Solution :
(i) Primary data
(ii) Primary data
(iii) Primary data
(iv) Secondary data
(v) Secondary data.

Haryana State Board HBSE 9th Class Science Solutions Chapter 3 परमाणु एवं अणु Textbook Exercise Questions and Answers.

Haryana Board 9th Class Science Solutions Chapter 3 परमाणु एवं अणु

HBSE 9th Class Science परमाणु एवं अणु Intext Questions and Answers
(पृष्ठ संख्या-36)
प्रश्न 1.
एक अभिक्रिया में 5.3g सोडियम कार्बोनेट एवं 6.0g एसीटिक अम्ल अभिकृतं होते हैं। 2.2g कार्बन … डाइऑक्साइड, 8.2g सोडियम एसीटिक एवं 0.9g जल उत्पाद के रूप में प्राप्त होते हैं। इस अभिक्रिया द्वारा दिखाइए कि यह परीक्षण द्रव्यमान संरक्षण के नियम के अनुरूप है।
सोडियम कार्बोनेट + एसीटिक अम्ल → सोडियम एसीटिक + कार्बन डाइऑक्साइड + जल
हल-यहाँ पर
अभिकारकों का कुल द्रव्यमान = (सोडियम कार्बोनेट + एसीटिक अम्ल) का द्रव्यमान
= 5.3g + 6.0g = 11.3g
उत्पादों का कुल द्रव्यमान = (कार्बन डाइऑक्साइड + सोडियम एसीटिक + जल) का द्रव्यमान
= 2.2g + 8.2g + 0.9g
= 11.3g
क्योंकि अभिकारकों का कुल द्रव्यमान उत्पादों के कुल द्रव्यमान के समान है इसलिए यह परीक्षण द्रव्यमान संरक्षण नियम के अनुरूप है। उत्तर

प्रश्न 2.
हाइड्रोजन एवं ऑक्सीजन द्रव्यमान के अनुसार 1:8 के अनुपात में संयोग करके जल निर्मित करते हैं। 3g हाइड्रोजन गैस के साथ पूर्ण रूप से संयोग करने के लिए कितने ऑक्सीजन गैस के द्रव्यमान की आवश्यकता होगी?
हल-यहाँ पर
हाइड्रोजन का द्रव्यमान : ऑक्सीजन का द्रव्यमान = 1:8
अतः 3g हाइड्रोजन गैस के साथ पूर्ण रूप से संयोग ।
करने के लिए आवश्यक ऑक्सीजन का द्रव्यमान = 3g x 8 = 24g उत्तर

प्रश्न 3.
डॉल्टन के परमाणु सिद्धांत का कौन-सा अभिग्रहीत द्रव्यमान के संरक्षण के नियम का परिणाम है?
उत्तर:
डॉल्टन के परमाणु सिद्धांत का अभिग्रहीत है कि परमाणु अविभाज्य सूक्ष्मतम कण होते हैं जो रासायनिक अभिक्रिया में न तो सृजित होते हैं, न ही उनका विनाश होता है। यह द्रव्यमान के संरक्षण के नियम का परिणाम है।

प्रश्न 4.
डॉल्टन के परमाणु सिद्धांत का कौन-सा अभिग्रहीत निश्चित अनुपात के नियम की व्याख्या करता है?
उत्तर:
डॉल्टन के परमाणु सिद्धांत का अभिग्रहीत, किसी भी यौगिक में परमाणुओं की सापेक्ष संख्या एवं प्रकार निश्चित होते हैं। यह निश्चित अनुपात के नियम की व्याख्या करता है।

(पृष्ठ संख्या-40)
प्रश्न 1.
परमाणु द्रव्यमान इकाई को परिभाषित कीजिए।
उत्तर:
कार्बन-12 समस्थानिक के एक परमाणु द्रव्यमान के 1/12वें भाग को मानक परमाणु द्रव्यमान इकाई के रूप में लेते हैं। कार्बन-12 समस्थानिक के एक परमाणु द्रव्यमान के सापेक्ष सभी तत्त्वों के परमाणु द्रव्यमान प्राप्त किए गए।

प्रश्न 2.
एक परमाणु को आँखों द्वारा देखना क्यों संभव नहीं होता है?
उत्तर:
परमाणु का आकार बहुत छोटा होने के कारण इसे आँखों द्वारा नहीं देखा जा सकता। इसका आकार इतना छोटा होता है कि इसकी त्रिज्या को नेनोमीटर (nm) में मापा जाता है। जहाँ 1nm = 10^-9 m के बराबर होता है। अब हम आधुनिक तकनीकों की सहायता से तत्त्वों की सतहों के आवर्धित प्रतिबिंबों को दिखा सकते हैं, जिनमें उपस्थित परमाणु स्पष्ट दिखाई देते हैं।

(पृष्ठ संख्या-44)

प्रश्न 1.
निम्न के सूत्र लिखिए-
(i) सोडियम ऑक्साइड,
(ii) ऐलुमिनियम क्लोराइड,
(iii) सोडियम सल्फाइड,
(iv) मैग्नीशियम हाइड्रॉक्साइड।
उत्तर:
(i) सोडियम ऑक्साइड का सूत्र

अतः सोडियम ऑक्साइड का सूत्र Na₂o है।

(ii) ऐलुमिनियम क्लोराइड का सूत्र

अतः ऐलुमिनियम क्लोराइड का सूत्र AICl₃, है।

(iii) सोडियम सल्फाइड का सूत्र

अतः सोडियम सल्फाइड का सूत्र Na₂s है।

(iv) मैग्नीशियम हाइड्रॉक्साइड

अतः मैग्नीशियम हाइड्रॉक्साइड का सूत्र Mg(OH)₂ है।

प्रश्न 2.
निम्नलिखित सूत्रों द्वारा प्रदर्शित यौगिकों के नाम लिखिए
(i) AI₂ (SO)₃
(ii) CaCl₂
(iii) K₂SO₄
(iv) KNO₃
(v) Caco₃
उत्तर

प्रश्न 3.
रासायनिक सूत्र का क्या तात्पर्य है?
उत्तर:
किसी यौगिक का रासायनिक सूत्र उसके संघटक का प्रतीकात्मक निरूपण होता है।

प्रश्न 4.
निम्न में कितने परमाणु विद्यमान हैं?
(1) H₂S अणु एवं
(ii) \(\mathrm{PO}_4^{3-}\) आयन
उत्तर:
(i) H₂S अणु में परमाणुओं की संख्या = 2 + 1 = 3
(ii) \(\mathrm{PO}_4^{3-}\) आयन में परमाणुओं की संख्या = 1 + 4 = 5

(पृष्ठ संख्या-46)

प्रश्न 1.
निम्न यौगिकों के आण्विक द्रव्यमान का परिकलन कीजिए
H₂, 0₂, Cl₂, CO₂, CH₄, C₂H₆, C₂H₄, NH₃, एवं CH₃OH
हल-
(1) हाइड्रोजन का परमाणु द्रव्यमान = 1u.
H₂, में हाइड्रोजन के दो परमाणु हैं।
H₂, का आण्विक द्रव्यमान = 2 x 1 = 2u

(2) ऑक्सीजन का परमाणु द्रव्यमान = 16u
O₂ में ऑक्सीजन के दो परमाणु हैं।
O₂ का आण्विक द्रव्यमान = 2 x 16 = 32u

(3) क्लोरीन का परमाणु द्रव्यमान = 35.5u .
Cl₂, में क्लोरीन के दो परमाणु हैं।
CI₂, का आण्विक द्रव्यमान = 2 x 35.5 = 71u

(4) कार्बन का परमाणु द्रव्यमान = 12u
ऑक्सीजन का परमाणु द्रव्यमान = 16u अतः
CO₂, जिसमें एक परमाणु कार्बन एवं दो परमाणु ऑक्सीजन होते हैं।
CO₂, का आण्विक द्रव्यमान = 1 x 12 + 2 x 16
= 12 + 32 = 44u

(5) कार्बन का परमाणु द्रव्यमान = 12u
हाइड्रोजन का परमाणु द्रव्यमान = 1u
अतः CH₄. जिसमें एक परमाणु कार्बन तथा चार परमाणु हाइड्रोजन होते हैं।
CH₄, का आण्विक द्रव्यमान = 1 x 12 + 4 x 1 = 12 + 4 = 16u

(6) कार्बन का परमाणु द्रव्यमान = 12u
हाइड्रोजन का परमाणु द्रव्यमान = lu
अतः C₂H₆, जिसमें दो परमाणु कार्बन तथा छः परमाणु हाइड्रोजन के होते हैं।
C₂H₆ का आण्विक द्रव्यमान = 2 x 12 + 6 x 1
= 24+ 6 = 30u

(7) कार्बन का परमाणु द्रव्यमान = 12u
हाइड्रोजन का परमाणु द्रव्यमान = 1u अतः
C₂H₄, जिसमें दो परमाणु कार्बन तथा चार परमाणु हाइड्रोजन होते हैं।
C₂H₄, का आण्विक द्रव्यमान = 2 x 12 +4 x 1
= 24+4 = 28u

(8) नाइट्रोजन का परमाणु द्रव्यमान = 14u
हाइड्रोजन का परमाणु द्रव्यमान = lu
अतः NH₃, जिसमें एक परमाणु नाइट्रोजन तथा तीन परमाणु हाइड्रोजन होते हैं।
NH₃, का आण्विक द्रव्यमान = 1 x 14 +3 x 1
= 14+3 = 17u

(9) कार्बन का परमाणु द्रव्यमान = 12u
हाइड्रोजन का परमाणु द्रव्यमान = 1u
ऑक्सीजन का परमाणु द्रव्यमान = 16u
अतः CH₃OH जिसमें एक परमाणु कार्बन, चार परमाणु हाइड्रोजन व एक परमाणु ऑक्सीजन हैं।
CH₃OH का आण्विक द्रव्यमान = 1 x 12 + 4 x 1 + 16 x 1
= 12 + 4 + 16
= 32u

प्रश्न 2.
निम्न यौगिकों के सूत्र इकाई द्रव्यमान का परिकलन कीजिएZnO, Na₂0 एवं K₂CO₃ दिया गया है
Zn का परमाणु द्रव्यमान = 65u
Na का परमाणु द्रव्यमान = 23u
K का परमाणु द्रव्यमान = 39u
C का परमाणु द्रव्यमान = 12u एवं
O का परमाणु द्रव्यमान = 16u है।
उत्तर:
(1) ZnO का सूत्र इकाई द्रव्यमान = 1 x 65u + 1 x 16u
= 65u + 16u
81u

(2) Na₂O का सूत्र इकाई द्रव्यमान = 2 x 23u + 1 x 16u
= 46u + 16u
= 62u.

(3) K₂CO₃ का सूत्र इकाई द्रव्यमान = 2 x 39u + 1 x 12u + 3 x 16u
= 78u + 12u + 48u = 138u

(पृष्ठ संख्या-48)

प्रश्न 1.
यदि कार्बन परमाणुओं के एक मोल का द्रव्यमान 12g है तो कार्बन के एक परमाणु का द्रव्यमान क्या होगा?
हल-यहाँ पर
कार्बन का मोलर द्रव्यमान = 12g
1 मोल = 6.022 x 10²³ परमाणु
अर्थात् 6.022 x 10²³ परमाणु कार्बन का द्रव्यमान = 12g
1 परमाणु कार्बन का द्रव्यमान = \(\frac{12}{6.022 \times 10^{23}} \mathrm{~g}\)
= 1.993 x 10^-23g उत्तर

प्रश्न 2.
किसमें अधिक परमाणु होंगे- 100g सोडियम अथवा 100g लोहा (Fe) ? (Na का परमाणु द्रव्यमान = 23u, Fe का परमाणु द्रव्यमान = 56u)
सोडियम का मोलर द्रव्यमान = 23g
1 मोल = 6.022 x 10²³ परमाणु
अतः 23g सोडियम में परमाणुओं की संख्या = 6.022 x 10²³
1g सोडियम में परमाणओं की संग = \(\frac{6.022 \times 10^{23}}{23}\)
100g सोडियम में परमाणुओं की संख्या = \(\frac{6.022 \times 10^{23}}{23}\) x 100
= 26.18 x 10²³
लोहे का मोलर द्रव्यमान = 56g
1 मोल = 6.022 x 10²³
अतः 56g लोहे में परमाणुओं की संख्या = 6.022 x 10²³
1g लोहे में परमाणुओं की संख्या = \(\frac{6.022 \times 10^{23}}{23}\)
100g लोहे में परमाणओं की संख्या = \(\frac{6.022 \times 10^{23}}{23}\) x 100
= 10.75 x 10²³
इस प्रकार 100g सोडियम में 100g लोहे की अपेक्षा अधिक परमाणु होंगे। उत्तर

HBSE 9th Class Science परमाणु एवं अणु Textbook Questions and Answers

प्रश्न 1.
0.24g ऑक्सीजन एवं बोरॉन युक्त यौगिक के नमूने में विश्लेषण द्वारा यह पाया गया कि उसमें 0.096g बोरॉन एवं 0.144g ऑक्सीजन है। उस यौगिक के प्रतिशत संघटन का भारात्मक रूप में परिकलन कीजिए।
हल
0.24g यौगिक में बोरॉन की मात्रा = 0.096g
1g यौगिक में बोरॉन की = \(\frac{0.096}{0.24}\)g
100g यौगिक में बोरॉन की मात्रा = \(\frac{0.096}{0.24}\) x 100
= 40g
अतः यौगिक में बोरॉन की मात्रा = 40% उत्तर
0.24g यौगिक में ऑक्सीजन की मात्रा = 0.144g
1g यौगिक में ऑक्सीजन की मात्रा = \(\frac{0.144}{0.24}\)g
100g यौगिक में ऑक्सीजन की मात्रा = \(\frac{0.144}{0.24}\) x 100 = 60g
अतः यौगिक में ऑक्सीजन की मात्रा = 60% उत्तर

प्रश्न 2.
3.0g कार्बन, 8.00g ऑक्सीजन में जलकर 11.00g कार्बन डाइऑक्साइड निर्मित करता है। जब 3.00g कार्बन को 50.00g ऑक्सीजन में जलाएंगे तो कितने ग्राम कार्बन डाइऑक्साइड का निर्माण होगा? आपका उत्तर रासायनिक संयोजन के किस नियम पर आधारित होगा?
उत्तर:
3.0g कार्बन, 8.00g ऑक्सीजन में जलकर 11.00g कार्बन डाइऑक्साइड निर्मित करता है तो 3.00g कार्बन को 50.00g ऑक्सीजन में जलाने पर 53.00g कार्बन डाइऑक्साइड का निर्माण होगा जोकि रासायनिक संयोजन के द्रव्यमान संरक्षण नियम पर आधारित है।

प्रश्न 3.
बहुपरमाणुक आयन क्या होते हैं? उदाहरण दीजिए।
उत्तर:
परमाणुओं का वह समूह जो आयन की तरह व्यवहार करते हैं, बहुपरमाणुक आयन कहलाते हैं; जैसेबहुपरमाणुक आयन संकेत अमोनियम

प्रश्न 4.
निम्नलिखित के रासायनिक सूत्र लिखिए
(a) मैग्नीशियम क्लोराइड,
(b) कैल्शियम क्लोराइड,
(c) कॉपर नाइट्रेट,
(d) ऐलुमिनियम क्लोराइड,
(e) कैल्शियम कार्बोनेट।
उत्तर:
(a) मैग्नीशियम क्लोराइड का सूत्र

अतः मैग्नीशियम क्लोराइड का सूत्र = MgCl₂,

(b) कैल्शियम क्लोराइड का सूत्र ।

अतः कैल्शियम क्लोराइड का सूत्र = CaCl₂,

(c) कॉपर नाइट्रेट का सूत्र

अतः कॉपर नाइट्रेट का सूत्र = Cu (NO₃)₂,

(d) ऐलुमिनियम क्लोराइड का सूत्र

अतः ऐलुमिनियम क्लोराइड का सूत्र = AlCl₃,

(e) कैल्शियम कार्बोनेट का सूत्र ।

अतः कैल्शियम कार्बोनेट का सूत्र = Caco₃,

प्रश्न 5.
निम्नलिखित यौगिकों में विद्यमान तत्त्वों का नाम दीजिए
(a) बुझा हुआ चूना
(b) हाइड्रोजन ब्रोमाइड
(c) बेकिंग पाउडर (खाने वाला सोडा)
(d) पोटैशियम सल्फेट
उत्तर:
(a) बुझा हुआ चूना = Ca (OH)₂,
अतः बुझे हुए चूने में विद्यमान तत्त्व कैल्शियम (Ca), ऑक्सीजन (O) व हाइड्रोजन (H) हैं।

(b) हाइड्रोजन ब्रोमाइड = HBr
अतः हाइड्रोजन ब्रोमाइड में विद्यमान तत्त्व हाइड्रोजन (H) व ब्रोमीन (Br) हैं।

(c) बेकिंग पाउडर (खाने वाला सोडा) = NaHCO,
अतः बेकिंग पाउडर में विद्यमान तत्त्व सोडियम (Na), हाइड्रोजन (H), कार्बन (C) तथा ऑक्सीजन (O) हैं।

(d) पोटैशियम सल्फेट = K₂SO₄.
अतः पोटैशियम सल्फेट में विद्यमान तत्त्व पोटैशियम (K), सल्फर (S) तथा ऑक्सीजन (O) हैं।

प्रश्न 6.
निम्नलिखित पदार्थों के मोलर द्रव्यमान का परिकलन कीजिए
(a) एथाइन, C₂H₂
(b) सल्फर अणु, S₈
(c) फॉस्फोरस अणु, P₄ (फॉस्फोरस का परमाणु द्रव्यमान = 31)
(d) हाइड्रोक्लोरिक अम्ल, HCI
(e) नाइट्रिक अम्ल, HNO₃
हल-हम
जानते हैं कि C = 12, H = 1, S = 32, P = 31, CI = 35.5, N = 14, 0 = 16

(a) एथाइन (C₂H₂) का मोलर द्रव्यमान = 2 x 12 + 2 x 1
= 24 +2
= 26g उत्तर

(b) सल्फर अणु (S₈) का मोलर द्रव्यमान = 8 x 32 = 256g उत्तर

(c) फॉस्फोरस अणु (P₄) का मोलर द्रव्यमान = 4 x 31 = 124g उत्तर

(d) हाइड्रोक्लोरिक अम्ल (HCI) का मोलर द्रव्यमान = 1 x 1 + 1 x 35.5
= 1+ 35.5 = 36.5g उत्तर

(e) नाइट्रिक अम्ल (HNO₃) का मोलर द्रव्यमान = 1 x 1 + 1 x 14 + 3 x 16
= 1 + 14 + 48
= 63g उत्तर

प्रश्न 7.
निम्न का द्रव्यमान क्या होगा
(a) 1 मोल नाइट्रोजन परमाणु?
(b) 4 मोल ऐलुमिनियम परमाणु (ऐलुमिनियम का परमाणु द्रव्यमान = 27)?
(c) 10 मोल सोडियम सल्फाइट (Na₂so₃) ?
हल
(a) 1 मोल नाइट्रोजन परमाणु का द्रव्यमान = 14g उत्तर
(b) 1 मोल ऐलुमिनियम परमाणु का द्रव्यमान = 27g
4 मोल ऐलुमिनियम परमाणु का द्रव्यमान = 4 x 27 = 108g उत्तर
(c) 1 मोल सोडियम सल्फाइट (Na,So,)
का द्रव्यमान = 2 x 23 + 1 x 32+3 x 16
= 46 + 32+ 48
= 126g उत्तर
10 मोल सोडियम सल्फाइट (Na₂so₃) का द्रव्यमान = 10 x 126g
= 1260g उत्तर

प्रश्न 8.
मोल में परिवर्तित कीजिए
(a) 12g ऑक्सीजन गैस,
(b) 20g जल,
(c) 22g कार्बन डाइऑक्साइड।
हल
(a) हम जानते हैं कि 1 मोल ऑक्सीजन (O₂) = 2 x 16 = 32g
अतः 32g ऑक्सीजन = 1 मोल
1g ऑक्सीजन = 1 मोल
12g ऑक्सीजन = 12 = 0.375 मोल उत्तर

(b) हम जानते हैं कि 1 मोल जल (H₂O) = (2 x 1 + 1 x 16)g
= (2 + 16)g
= 18g
अतः 18g जल = 1 मोल
1g जल = \(\frac { 1 }{ 18 }\) मोल
20g जल = \(\frac { 1 }{ 18 }\) x 20 = 1.11 मोल उत्तर

(c) हम जानते हैं कि 1 मोल कार्बन डाइऑक्साइड (CO₂) = (1 x 12 + 2 x 16)g
= (12 + 32)g = 44g
अतः 44g कार्बन डाइऑक्साइड = 1 मोल
1g कार्बन डाइऑक्साइड = \(\frac { 1 }{ 44 }\) मोल
22g कार्बन डाइऑक्साइड = \(\frac { 1 }{ 44 }\) x 22 = 0.5 मोल उत्तर

प्रश्न 9.
निम्न का द्रव्यमान क्या होगा
(a) 0.2 मोल ऑक्सीजन परमाणु?
(b) 0.5 मोल जल अणु?
हल
(a) 1 मोल ऑक्सीजन परमाणु का द्रव्यमान = 16g
0.2 मोल ऑक्सीजन परमाणु का द्रव्यमान = 16 x 0.2g
= 3.2g उत्तर

(b) 1 मोल जल अणु (H₂O) का द्रव्यमान = (2 x 1 + 1 x 16)g
= (2 + 16)g = 18g
0.5 मोल जल अणु का द्रव्यमान = 0.5 x 18 = 9.0g उत्तर प्रश्न

प्रश्न 10.
16g ठोस सल्फर में सल्फर (S₈) के अणुओं की संख्या का परिकलन कीजिए।
हल
सल्फर S₈ का अणु द्रव्यमान = 8 x 32 = 256g
1 मोल = 6.022 x 10²³ अणु
अतः 256g सल्फर में अणुओं की संख्या = 6.022 x 10²³
1g सल्फर में अणुओं की संख्या = \(\frac{6.022 \times 10^{23}}{256}\)
16g सल्फर में अणुओं की संख्या = \(\frac{6.022 \times 10^{23}}{256}\) x 16
= 3.76 x 10²²
अतः 16g ठोस सल्फर में 3.76 x 10²² अणु होंगे।

प्रश्न 11.
0.051g ऐलुमिनियम ऑक्साइड (AI₂O₃) में ऐलुमिनियम आयन की संख्या का परिकलन कीजिए।
(संकेतः किसी आयन का द्रव्यमान उतना ही होता है जितना कि उसी तत्त्व के परमाणु का द्रव्यमान होता है। ऐलुमिनियम का परमाणु द्रव्यमान = 27u है।)
हल:
1 मोल ऐलुमिनियम ऑक्साइड (AI₂O₃) का द्रव्यमान = (2 x 27 + 3 x 16)g
= (54+ 48)g = 102g
102g ऐलुमिनियम ऑक्साइड = 1 मोल
0.051g ऐलुमिनियम ऑक्साइड = \(\frac { 1 }{ 102 }\) x 0.051
= 5 x 10^-4 मोल
1 मोल AI₂O₃ में A1 आयनों की संख्या = 2 x 6.022 x 10²³
5 x 10^-4 मोल AI₂O₃ में आयनों की संख्या = 2 x 6.022 x 10²³ x 5 x 10^-4
= 6.022 x 10²⁰ उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 15 Probability Ex 15.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 15 Probability Exercise 15.1

Question 1.
In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
Solution:
Number of balls thrown = 30
∴ Total number of possible outcomes = 30
Number of times, the boundary is hit by the ball = 6
Number of times, the boundary is not hit by the ball= 30 – 6 = 24
∴ Number of favourable outcomes = 24
Let E be event that the boundary is not hit by the ball
∴ P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{24}{30}\) = \(\frac{4}{5}\)
Hence, P(E) = \(\frac{4}{5}\)

Question 2.
1500 families with 2 children were selected randomly, and the following data were recorded :

Compute the probability of a family, chosen at random, having :
(i) 2 girls
(ii) 1 girl
(iii) No girl.
Also check whether the sum of these probabilities is 1.
Solution:
Total number of families = 1500
∴ Total number of possible outcomes = 1500
(i) Number of families having 2 girls = 475
∴ Number of favourable outcomes = 475
Let E₁ be event that the selected family has 2 girls, then
P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{475}{1500}\) = \(\frac{19}{60}\)

(ii) Number of families having 1 girl = 814
∴ Number of favourable outcomes = 814
Let E₂ be the event that the selected family has 1 girl, then
P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{814}{1500}\) = \(\frac{407}{750}\)

(iii) Number of families having no girl = 211
∴ Number of favourable outcomes = 211
Let E₃ be the event that the selected family has no girl; then
P(E₃) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{211}{1500}\)

(iv) Sum of the probabilities
= \(\frac{19}{60}+\frac{407}{750}+\frac{211}{1500}\)
= \(\frac{475+814+211}{1500}\)
= \(\frac{1500}{1500}\) = 1
Hence, (i) P(E₁) = \(\frac{19}{60}\), (ii) P(E₂) = \(\frac{407}{750}\) (iii) P(E₃) = \(\frac{211}{1500}\) (iv) Sum of the probabilities = 1.

Question 3.
In a particular section of class IX, 40 students were asked about the month of their birth and the following graph was prepared for the data so obtained :

Find the probability that a student of the class was born in August.
Solution :
Total number of students = 40
∴ Total number of possible outcomes = 40
Number of students was born in August = 6
∴ Number of favourable outcomes = 6
Let E be the event that a student of the class was born in August, then
P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{6}{40}\) = \(\frac{3}{20}\)
Hence, P(E) = \(\frac{3}{20}\)

Question 4.
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes :

If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Solution :
Total number of tosses of three coins simultaneously = 200
∴ Total number of possible outcomes = 200
Number of outcomes of 2 heads = 72
∴ Number of favourable outcomes = 72
Let E be the event of 2 heads coming up, then
P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{72}{200}\) = \(\frac{9}{25}\)
Hence, P(E) = \(\frac{9}{25}\)

Question 5.
An organisation selected 2400 families at random and surveyed them to determine their income level and the number of vehicles in a family. The information gathered is listed in the table below :

Suppose a family is chosen. Find the probability that the family chosen is :
(i) earning Rs. 10000 – 13000 per month and owning exactly 2 vehicles.
(ii) earning Rs. 16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than Rs. 7000 per month and does not own any vehicle.
(iv) earning Rs. 13000 – 16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
Solution:
The total number of families = 2400
∴ Total number of possible outcomes= 2400
(i) Number of families earning Rs. 10000 – 13000 per month and owning exactly 2 vehicles = 29
∴ Number of favourable outcomes = 29
Let E₁ be the event that a family’s earning 10000 – 13000 per month and owning exactly 2 vehicles, then
P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{29}{2400}\)

(ii) Number of families earning Rs. 16000 or more per month and owning exactly 1 vehicle = 579
∴ Number of favourable outcomes = 579
Let E₂ be the event that a family’s earning Rs. 16000 or more per month and owning exactly 1 vehicle, then
P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{579}{2400}\)

(iii) Number of families earning less than Rs. 7000 per month and does not own any vehicle = 10
∴ Number of favourable outcomes = 10
Let E₃ be the event that a family’s earning less than Rs. 7000 per month and does not own any vehicle, then
P(E₃) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{10}{2400}\) = \(\frac{1}{240}\)

(iv) Number of families earning Rs. 13000 – 16000 per month and owning more than 2 vehicles = 25
∴ Number of favourable outcomes = 25
Let E₄ be the event that a family’s earning Rs. 13000 – 16000 per month and owning more than 2 vehicles, then
P(E₄) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{25}{2400}\) = \(\frac{1}{96}\)

(v) Number of families owning not more than 1 vehicle = 10 + 0 + 1 + 2 + 1 + 160 + 305 + 535 + 469 + 579
= 2062
∴ Number of favourable outcomes= 2062
Let E₅ be the event that a family owning not more than 1 vehicle, then
P(E₅) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{2062}{2400}\) = \(\frac{1031}{1200}\)
Hence,
(i) P(E₁) = \(\frac{29}{2400}\);
(ii) P(E₂) = \(\frac{579}{2400}\)
(i) P(E₃) = \(\frac{1}{240}\)
(iv) P(E₄) = \(\frac{1}{96}\)
(v) P(E₅) = \(\frac{1031}{1200}\)

Question 6.
A teacher wanted to analyse the performance of two sections of students in a mathematics test of 100 marks. A data of their performances is given below in the table :

(i) Find the probability that a student obtained less than 20% marks in the mathematics test.
(ii) Find the probability that a student obtained marks 60 or above.
Solution:
Total number of students = 90
∴ Total number of possible outcomes = 90
(i) Number of students who obtained less than 20% marks in the test = 7
∴ Number of favourable outcomes = 7
Let E₁ be the event of a student obtaining less than 20% marks in the test.
P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{7}{90}\)

(ii) Number of students who obtained marks 60 or above in the test = 15 + 8 = 23
∴ Number of favourable outcomes = 23
Let E₂ be the event of a student obtaining 60 or above marks in the test.
P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{23}{90}\)
Hence, (i) P(E₁) = \(\frac{7}{90}\),
(ii) P(E₂) = \(\frac{23}{90}\)

Question 7.
To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table :

Find the probability that a student chosen at random :
(i) likes statistics,
(ii) does not like it.
Solution:
Total number of students = 200
∴ Total number of possible outcomes = 200
(i) Number of students who likes statistics = 135
∴ Number of favourable outcomes = 135
Let E₁ be the event of a student likes statistics, then
P(E₁) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{135}{200}\) = \(\frac{27}{40}\)

(ii) Number of students who dislikes statistics = 65
∴ Number of favourable outcomes = 65
Let E₂ be the event of a student dislikes statistics, then
P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{65}{200}\) = \(\frac{13}{40}\)
Hence, (i) P(E₁) = \(\frac{27}{40}\) (ii) P(E₂) = \(\frac{13}{40}\)

Question 8.
The distance (in km) of 40 engineers from their residence to their place of work were found as follows:

Construct a grouped frequency distribution table with class size 7 for the data given above taking the first interval as 0-7 (7 is not included).
What is the empirical probability that an engineer lives :
(i) less than 7 km from her place of work?
(ii) more than or equal to 7 km from her place of work ?
(iii) within \(\frac{1}{2}\) km from her place of work?
Solution:
First we construct the frequency distribution table taking class interval 0 – 7, 7 – 14, 14 – 21, … as follows :

Total number of engineers = 40
∴ Total number of possible outcomes = 40
(i) Number of engineers who live at a distance less than 7 km from their place of work = 9
∴ Number of favourable outcomes = 9
Let E₁ be the event of a engineer lives at a distance less than 7 km from their place, then
P(E₁) = \(\frac{9}{40}\)
(ii) Number of engineers who live at a distance more than or equal to 7 km from their place of work = 17 + 11 + 1 + 2 = 31
∴ Number of favourable outcomes = 31
Let E₂ be the event of a engineer lives at a distance more than or equal to 7 km from their place, then
P(E₂) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{31}{40}\)

(iii) Number of engineers who live within \(\frac{1}{2}\) km from their place of work = 0
Number of favourable outcomes = 0
Let E₃ be the event of a engineer lives within \(\frac{1}{2}\) km from their place of work.
P(E₃) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{0}{40}\) = 0
Hence, (i) P(E₁) = \(\frac{9}{40}\), P(E₂) = \(\frac{31}{40}\), (iii) P(E₃) = 0.

Question 9.
Activity: Note the frequency of two wheelers, three-wheelers and four-wheelers going past during a time interval, in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two-wheeler.
Solution :
Collect the data according to activity and find the required probability.

Question 10.
Activity: Ask all the students in your class to write a 3-digit number. Choose any student from the room at random. What is the probability that the number written by her/him is divisible by 3? Remember that a number is divisible by 3, if the sum of its digits is divisible by 3.
Solution :
According to activity, collect the data and find required probability

Question 11.
Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg):
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Solution:
Total number of bags = 11
∴ Total number of possible outcomes = 11
Number of bags containing more than 5 kg of flour = 7
∴ Number of favourable outcomes = 7
P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{7}{11}\)
Hence, P(E) = \(\frac{7}{11}\)

Question 12.
A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows :

make a grouped frequency distribution table for this data with class intervals as 0.00 – 0.04, 0.04 – 0·08 and so on. Using this table, find the probability of the concentration of sulphur dioxide in the interval 0.12 – 0.16 on any of these days.
Solution :
First we construct frequency distribution table taking class intervals as 0.00 – 0.04, 0.04 – 0.08, …, as follows:

Total number of days = 30
∴ Total number of possible outcomes = 30
Concentration of sulphur dioxide in the interval 0.12 – 0.16 on any day = 2
∴ Number of favourable outcomes = 2
Let E be the event of concentration of sulphur dioxide in the interval 0·12 – 0.18 on any day. Then,
P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{2}{30}\) = \(\frac{1}{15}\)
Hence, P(E) = \(\frac{1}{15}\)

Question 13.
The blood groups of 30 students of class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
Represent this data in the form of a frequency distribution table. Use this table to determine the probability that a student of this class, selected at random, has blood group AB.
Solution :
First prepare the frequency distribution table as follows :

Total number of students = 30
∴ Total number of possible outcomes = 30
Number of students having blood group AB = 3
∴ Number of favourable outcomes = 3
Let E be event of a student having blood group AB, then
P(E) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{3}{30}\) = \(\frac{1}{10}\)
Hence, P(E) = \(\frac{1}{10}\)

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.1

Question 1.
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet, determine :
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1 m² cost of Rs. 20.
Solution:
We have,
Length of the plastic box (l) = 1.5 m
Breadth of the plastic box (b)= 1.25 m
Depth of the plastic box (h)= 65 cm = \(\frac{65}{100}\)
m = 0.65 m
(i) The area of the sheet required for making the box = lb + 2(l + b) × h
= 1.5 × 1.25 + 2(1.5 + 1.25) × 0.65
= 1.875 + 2(2:75) × 0.65
= 1.875 +3.575
= 5.45m²

(ii) Cost of 1 m² sheet = Rs. 20
Cost of 5.45 m² sheet = Rs. (20 × 5.45)
= Rs. 109
Hence, (i) The area of the sheet required = 5.45 m²
(ii) Cost of sheet = Rs. 109.

Question 2.
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of Rs. 7.50 per m².
Solution:
We have,
Length of a room (l) = 5 m
Breadth of a room (b) = 4 m
Height of a room (h) = 3 m
Area for white washing = Area of four walls of a room + Area of ceiling of a room
= 2(l + b) × h + l × b
= 2(5 + 4) × 3 + 5 × 4
= 2 × 9 × 3 + 20
= 54 + 20 = 74 m²
Rate of white washing = Rs. 7.50 m²
Cost of white washing = Area × rate of white washing
= 74 × 7.50 = Rs. 555
Hence,cost of white washing = Rs. 555.

Question 3.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of Rs. 10 per m² is Rs. 15000, find the height of the hall.
[Hint : Area of the four walls = Lateral surface area.]
Solution:
We have,
Perimeter of a rectanglar hall = 250 m
⇒ 2(l + b) = 250 m …(1)
Let height of the hall be h m.
Area of four walls of a hall = 2(l + b) × h
Area of four walls of a hall = 250 × h, [using(1)] …(2)
Rate of painting = Rs. 10 per m² (given)
Total cost of painting = Rs. 15000
∴ Area of four walls of a hall = \(\frac{\text { Total cost }}{1 m^2 \cos t}\)
⇒ Area of four walls of a hall = \(\frac{15000}{10}\)
⇒ Area of four walls of a hall = Rs. 1500 m² …..(3)
From (2) and (3), we have
250 × h = 1500
⇒ h = \(\frac{1500}{250}\)
⇒ h = 6 m
Hence, height of the hall = 5 m.

Question 4.
The paint in a certain container is sufficient to paint an area equal to 9.375 m². How many bricks of dimensions 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
Solution:
We have,
Length of brick (l) = 22.5 cm
Breadth of brick (b) = 10 cm
Height of brick (h) = 7.5 cm
Surface area of one brick = 2(lb + bh + hl)
= 2(22.5 × 10 + 10 × 7.5 + 7.5 × 22.5)
= 2(225 + 75 + 168.75)
= 2(468.75) = 937.5 cm²
= \(\frac{937.5}{10000}\) m²
= 0.09375 m²
Area for which the paint is just sufficient = 9.375 m² (given)
∴ Number of bricks that can be painted with the available paint
= \(\frac{9.375}{0.09375}=\frac{937500}{9375}\)
Hence, number of bricks that can be painted = 100.

Question 5.
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
(i) Which box has the greater lateral surface area and by how much?
(ii) Which box has the smaller total surface area and by how much?
Solution:
We have,
Each edge of cubical box = 10 cm
Cuboidal box length (l) = 12.5 cm
Cuboidal box breadth (b) = 10 cm
Cuboidal box height (h) = 8 cm
(i) Lateral surface area of the cubical box =
4a² = 4 × (10)²
= 4 × 100 = 400 cm²
Lateral surface area of the cuboidal box = 2(l + b) × h
= 2(12.5 + 10) × 8
= 2 × 22.5 × 8 = 360 cm²
Thus, lateral surface area of the cubical box is greater and is more (400 – 360) cm²
i.e., 40 cm².
(ii) Total surface area of cubical box = 6a²
= 6 × (10)²
= 6 × 100 = 600 cm²
Total surface area of the cuboidal box = 2(lb + bh + hl)
= 2(12.5 × 10 + 10 × 8 + 8 × 12.5)
= 2(125 + 80 + 100)
= 2(305) = 610 cm²
Thus, total surface area of cubical box is smaller by (610-600) i.e., 10 cm².
Hence, (i) Lateral surface area of the cubical box is greater by 40 cm².
(ii) Total surface area of the cubical box is smaller by 10 cm².

Question 6.
A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.
(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges ?
Solution:
The shape of the greenhouse is cuboid.
Length of the greenhouse (l) = 30 cm
Breadth of the greenhouse (b) = 25 cm
Height of the greenhouse (h) = 25 cm
(i) Area of the glass of the greenhouse=2(lb + bh + hl)
= 2(30 × 25 + 25 × 25 + 25 × 30)
= 2(750 + 625 + 750)
= 2(2125) = 4250 cm²
(ii) Length of required tape = Sum of length of 12 edges :
= 4l + 4b + 4h
= 4 × 30 + 4 × 25+ 4 × 25
= 120 + 100 + 100
= 320 cm
Hence, (i) Area of the glass = 4250 cm²
(i) Length of required tape = 320 cm.

Question 7.
Shanti Sweets Stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm × 20 cm × 5 cm and the smaller of dimensions 15 cm × 12 cm × 5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is Rs. 4 for 1000 cm², find the cost of cardboard required for supplying 250 boxes of each kind.
Solution:
Dimensions of the bigger box are
L = 25 cm, B = 20 cm and H = 5 cm
Surface area of cardboard for bigger box
= 2(LB + BH + HL)
= 2(25 × 20 + 20 × 5 + 5 × 25)
= 2(500 + 100 + 125)
= 2(725) = 1450 cm²
Surface area of the cardboard for 250 bigger box
= 1450 × 250
= 362500 cm²
Dimensions of the smaller box are l = 15 cm, b = 12 cm and h = 5 cm
Surface area of the cardboard for smaller box
= 2(lb + bh + hl)
= 2(15 × 12 + 12 × 5 + 5 × 15)
= 2(180 + 50 + 75)
= 2 × 315
= 630 cm²
Surface area of the cardboard for 250 smaller boxes
= 630 × 250 = 157500 cm²
Required total area of cardboard sheet
= 362500 + 157500
= 520000 cm²
Area of overlaps = 5% of total area of cardboard sheet
= 5% of 520000
= \(\frac{5}{100}\) × 520000
= 26000 cm²
Total area of the sheet including overlapping area of sheet
= 520000 + 26000
= 546000 cm²
∵ 1000 cm² cardboard sheet cost = Rs. 4
∴ 1 cm² cardboard sheet cost = Rs. \(\frac{4}{1000}\)
∴ 546000 cm² cardboard sheet cost
= Rs. \(\frac{4}{1000}\) × 546000
= Rs. 2184.
Hence, cost of required cardboard sheet = Rs. 2184.

Question 8.
Parveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m, with base dimensions 4 m × 3 m?
Solution:

Dimensions of the base of car’s shelter are
l = 4 m and b = 3 m
Height of car’s shelter (h) = 2.5 m
Required area of the trapaulin for the shelter of the car
= 2(l + b) × h + l × b
= 2(4 + 3) 2.5 + 4 × 3
= 2 × 7 × 2.5 + 12
= 35 + 12 = 47 m²
Hence, required area of the trapaulin for the shelter of the car = 47 m².

Haryana State Board HBSE 10th Class Maths Solutions Chapter 4 Quadratic Equations Ex 4.2 Textbook Exercise Questions and Answers.

Haryana Board 10th Class Maths Solutions Chapter 4 Quadratic Equations Ex 4.2

Question 1.
Find the roots of the following quadratic equations by factorisation :
(i) x² – 3x – 10 = 0
(ii) 2x² + x – 6 = 0
(iii) √2x² + 7x + 5√2 = 0
(iv) 2x² – x + \(\frac{1}{8}\) = 0
(v) 100x² – 20x + 1 = 0.
Solution :
(i) The given equation is :
x² – 3x – 10 = 0
x² – (5 – 2)x – 10 = 0
[∵ 1 × – 10 = – 10
5 × – 2 = – 10
5 – 2 = – 3]
⇒ x² – 3x + 2x – 10 = 0
⇒ x(x – 5) + 2(x – 5) = 0
⇒ (x – 5)(x + 2) = 0
⇒ x – 5 = 0 or x + 2 = 0
⇒ x = 5 or x = – 2
Hence, x = 5 and x = – 2 are the roots of the given quadratic equation.

(ii) The given equation is :
2x² + x – 6 = 0
⇒ 2x² + (4 – 3)x – 6 = 0
[∵ – 6 × 2 = – 12
– 3 × 4 = – 12
4 – 3 = 1]
⇒ 2x² + 4x – 3x – 6 = 0
⇒ 2x(x + 2) – 3(x + 2) = 0
⇒ (x + 2)(2x – 3) = 0
⇒ x + 2 = 0 or 2x – 3 = 0
⇒ x = – 2 or x = – \(\frac{3}{2}\)
Hence, x = – 2 and x = – \(\frac{3}{2}\) are the roots of the given quadratic equation.

(iii) The given equation is :
√2x² + 7x + 5√2 = 0
√2x² + (2 + 5)x + 5√2 = 0
[∵ 5√2 × √2 = 10
2 × 5 = 10
2 + 5 = 7]
√2x² + 2x + 5x + 5√2 = 0
√2x(x + √2) + 5(x + √2) = 0
(x + √2)(√2x + 5) = 0
x + √2 = 0 or √2x + 5 = 0
x = – √2or x = – \(\frac{5}{\sqrt{2}}\)
Hence, x = – √2 and x = – \(\frac{5}{\sqrt{2}}\) are the roots of the given quadratic equation.

(iv) The given equation is:
2x² – x + \(\frac{1}{8}\) = 0
16x² – 8x + 1 = 0
[∵ 1 × 16 = 16
4 × 4 = 16
4 + 4 = 8]
16x² – 8x + 1 = 0
16x² – (4 + 4)x + 1 = 0
16x² – 4x – 4x + 1 = 0
4x(4x – 1) – 1(4x – 1) = 0
(4x – 1)(4x – 1) = 0
4x – 1 = 0 or 4x – 1 = 0
x = \(\frac{1}{4}\) or x = \(\frac{1}{4}\)
Hence, x = \(\frac{1}{4}\) and x = \(\frac{1}{4}\) are the roots of given quadratic equation.

(v) The given equation is :
100x² – 20x + 1 = 0
⇒ 100x² – (10 + 10)x +1 = 0
[∵ 100 × 1 = 100
10 × 10 = 100.
10 + 10 = 20]
⇒ 100x² – 1ox – 10x + 1 = 0
⇒ 10x (10x – 1) – 1 (10x – 1) = 0
⇒ (10x – 1) (10x – 1) = 0
⇒ 10x – 1 = 0 or 10x – 1 = 0
⇒ x = \(\frac{1}{10}\) or x = \(\frac{1}{10}\)
Hence, x = \(\frac{1}{10}\) and x = \(\frac{1}{10}\) are the roots of the given quadratic equation.

Question 2.
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.

(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in ₹) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was ₹ 750. We would like to find out the number of toys produced on that day.
Solution :
(i) Let the number of marbles John has be x.
Then, the number of marbles Jivanti has = 45 – x.
The number of marbles left with John, when he lost 5 marbles = x – 5
and the number of marbles left with Jivanti, when she lost 5 marbles = 45 – x – 5 = 40 – x
According to question,
(x – 5) (40 – x) = 124
⇒ 40x – x² – 200 + 5x = 124
⇒ – x² + 45x – 200 – 124 = 0
⇒ – x² + 45x – 324 = 0
⇒ x² – 45x + 324 = 0
⇒ x² – (36 + 9)x + 324 = 0
⇒ x² – 36x – 9x + 324 = 0
[∵ 324 × 1 = 324
36 × 9 = 324
36 + 9 = 45]
⇒ x(x – 36) – 9(x – 36) = 0
⇒ (x – 36)(x – 9) = 0
⇒ x – 36 = 0 or x – 9 = 0
x = 36 or x = 9
Hence, either John had 36 marbles and Jivanti had 9 marbles or vice-versa.

(ii) Let the number of toys produced on that day be x.
Therefore, the cost of production of each toy = ₹ (55 – x)
So, the total cost of production on that day = ₹ x(55 – x)
According to question,
x(55 – x) = 750
⇒ 55x – x² = 750
⇒ – x² + 55x – 750 = 0
⇒ x² – 55x + 750 = 0
⇒ x² – (25 + 30)x + 750 = 0
⇒ x² – 25x – 30x + 750 = 0
[∵ 750 × 1 = 750
25 × 30 = 750
25 + 30 = 55]
⇒ x(x – 25) – 30(x – 25) = 0
⇒ (x – 25)(x – 30) = 0
⇒ x – 25 = 0 or x – 30 = 0
⇒ x = 25 or x = 30
Hence, the number of toys produced on that day = 25 or 30.

Question 3.
Find two numbers whose sum is 27 and product is 182.‘
Solution :
Let 1st number be x, then 2nd number = 27 – x
According to question,
x(27 – x) = 182
⇒ 27x – x² = 182
⇒ – x² + 27x – 182 = 0
⇒ x² – 27x + 182 = 0
⇒ x² – (14 + 13)x + 182= 0
[∵ 182 × 1 = – 182
14 × – 13 = – 182
14 – 13 = 1]
⇒ x² – 14x – 13x + 182 = 0
⇒ x(x – 14) – 13(x – 14) = 0
⇒ (x – 14)(x – 13) = 0
⇒ x – 14 = 0 or x – 13
⇒ x = 14 or x = 13
Hence, the numbers are 14, 13 or 13, 14.

Question 4.
Find two consecutive positive integers, sum of whose squares is 365.
Solution:
Let the consecutive positive integers be x and x + 1.
According to question,
x² + (x + 1)² = 365
⇒ x² + x² + 2x + 1 = 365
⇒ 2x² + 2x + 1 – 365 = 0
⇒ 2x² + 2x – 364 = 0
⇒ x² + x – 182 = 0
[∵ 182 × 1 = 182
14 × 13 = 182
14 + 13 = 27]
⇒ x² + x (14 – 13) – 182 = 0
⇒ x(x + 14) – 13(x + 14) = 0
⇒ (x + 14)(x – 13) = 0
⇒ x + 14 = 0 or x – 13 = 0
⇒ x = – 14 or x = 13
Since, x is a positive integer, it cannot be negative.
Therefore, x = 13.
Hence, the consecutive positive integers are 13, 14.

Question 5.
The Edtitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Solution:
Let base of a right trismgle be x cm.
then altitude of the right triangle = (x – 7) cm
and hypotenuse = 13 cm (given)
In a right ∆ABC,

By Pythagoras theorem, we get
AC² = BC² + AB²
⇒ 13² = x² + (x – 7)²
⇒ 169 = x² + x² – 14x + 49
2x² – 14x + 49 – 169
⇒ 2x² – 14x – 120 = 0
[∵ – 60 × 1 = – 60
12 × – 5 = – 60
12 – 5 = 7]
⇒ x² – 12x + 5x – 60 = 0
⇒ x(x – 12) + 5(x – 12) = 0
⇒ (x – 12)(x + 5) = 0
⇒ x – 12 = 0 or x + 5 = 0
⇒ x = 12 or x = – 5
Since, x is length of base, it cannot be negative.
Therefore, x = 12.
Hence, the base of triangle = 12 cm
and altitude of triangle = 12 – 7 = 5 cm.

Question 6.
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in Rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was 90. Find the number of articles produced and the cost of each article.
Solution:
Let the number of articles produced in a day be x,
then cost of one Eirticle = ₹ (2x + 3)
According to question,
x(2x + 3) = 90
⇒ 2x² + 3x = 90
⇒ 2x² + 3x – 90 = 0
[∵ 2 × (- 90) = – 180
15 × (- 12) = – 180
15 – 12 = 3]
⇒ 2x² + (15 – 12)x – 90 = 0
⇒ 2x² + 15x – 12x – 90 = 0
⇒ x(2x + 15) – 6(2x + 15) = 0
⇒ (2x + 15)(x – 6) = 0
⇒ 2x + 15 = 0
or x – 6=0
⇒ x = – \(\frac{15}{2}\) or x = 6
Since, x is number of articles. It cannot be negative.
Therefore, x = 6
Hence,the number of articles = 6
Cost of each article = ₹ 2 × 6 + 3 = ₹ 15

Haryana State Board HBSE 9th Class Science Important Questions Chapter 12 ध्वनि Important Questions and Answers.

Haryana Board 9th Class Science Important Questions Chapter 12 ध्वनि

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
ध्वनि क्या है?
उत्तर:
ध्वनि एक प्रकार की ऊर्जा है, जो कंपन द्वारा उत्पन्न होती है।

प्रश्न 2.
ध्वनि उत्पन्न कर रही वस्तु किस अवस्था में होती है?
उत्तर:
कंपन अवस्था में।

प्रश्न 3.
वायु में ध्वनि संचरण कैसे होता है?
उत्तर:
वायु में ध्वनि संचरण संपीडन व विरलन के रूप में होता है।

प्रश्न 4.
ध्वनि की गति ठोस, द्रव और गैसों में से किसमें अधिक होती है?
उत्तर:
ठोसों में।

प्रश्न 5.
वायु में 0°C पर ध्वनि का वेग कितना होता है?
उत्तर:
331 मीटर प्रति सेकंड।

प्रश्न 6.
वायु में 22°C पर ध्वनि का वेग कितना होता है?
उत्तर:
344 मीटर प्रति सेकंड।

प्रश्न 7.
आसुत जल में 25°C पर ध्वनि का वेग कितना होता है?
उत्तर:
1498 मीटर प्रति सेकंड।

प्रश्न 8.
ध्वनि का वेग 20°C पर 5100 मीटर प्रति सेकंड किसमें होता है-
(1) स्टील
(2) ऐलुमिनियम
(3) ऐल्कोहॉल
(4) पारा।
उत्तर:
(2) ऐलुमिनियम।

प्रश्न 9.
प्रकाश का वेग कितना है?
उत्तर:
3 x 10⁸ मीटर प्रति सेकंड।

प्रश्न 10.
ऊर्जा के दो रूप के नाम बताओ।
उत्तर:

1. ऊष्मा ऊर्जा
2. प्रकाश ऊर्जा।

प्रश्न 11.
माध्यम किसे कहते हैं?
उत्तर:
द्रव्य या पदार्थ में जिससे होकर ध्वनि संचरित होती है माध्यम कहलाता है।

प्रश्न 12.
ध्वनि संचरण में माध्यम के कण आगे बढ़ते हैं या विक्षोभ आगे बढ़ता है?
उत्तर:
विक्षोभ आगे बढ़ता है।

प्रश्न 13.
ध्वनि तरंगें यांत्रिक तरंगें क्यों कहलाती हैं?
उत्तर:
क्योंकि ध्वनि की तरंगें माध्यम के कणों द्वारा अभिलक्षित की जाती हैं, इसीलिए ध्वनि तरंगें यांत्रिक तरंगें कहलाती हैं।

प्रश्न 14.
संपीडन किसे कहते हैं?
उत्तर:
माध्यम में उच्च दाब का क्षेत्र संपीडन (C) कहलाता है।

प्रश्न 15.
विरलन किसे कहते हैं?
उत्तर:
माध्यम में निम्न दाब का क्षेत्र विरलन (R) कहलाता है।

प्रश्न 16.
स्वरित्र द्विभुज (ट्यूनिंग फोक) पर 256 लिखा होने का क्या अर्थ है?
उत्तर:
स्वरित्र द्विभुज पर 256 लिखा होने का अर्थ है कि उसकी आवृत्ति 256 हज़ है।

प्रश्न 17.
विद्युत् चुंबकीय तरंग क्या होती है?
उत्तर:
वह तरंग जो बिना किसी माध्यम के गमन कर सकती है, विद्युत् चुंबकीय तरंग कहलाती है।

प्रश्न 18.
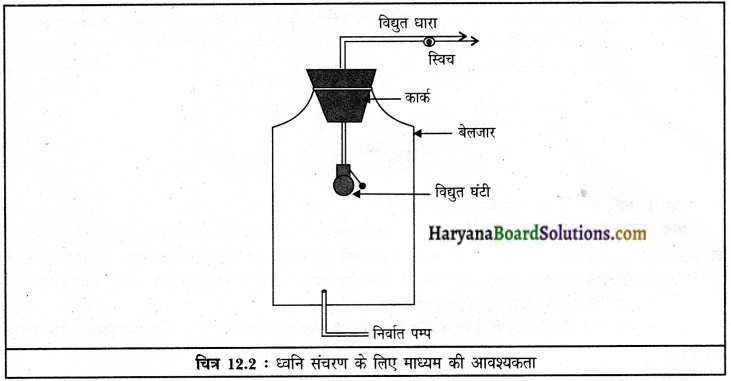
क्या निर्वात में भी ध्वनि तरंगें संचरण कर सकती हैं?
उत्तर:
नहीं, निर्वात में ध्वनि तरंगें संचरण नहीं कर सकतीं।

प्रश्न 19.
कौन-सी तरंगों द्वारा चंद्रमा पर अंतरिक्ष यात्री आपस में बातचीत करते हैं?
उत्तर:
रेडियो तरंगों द्वारा चंद्रमा पर अंतरिक्ष यात्री आपस में बातचीत करते हैं।

प्रश्न 20.
तरंग के वेग की परिभाषा दीजिए।
उत्तर:
इकाई समय में तरंग द्वारा चली गई दूरी को तरंग का वेग कहते हैं।

प्रश्न 21.
आवृत्ति तथा आवर्तकाल में क्या संबंध है?
उत्तर:
आवृत्ति आवर्तकाल के विलोम के बराबर है अर्थात् v = \(\frac { 1 }{ T }\)

प्रश्न 22.
किसी तरंग के वेग, तरंगदैर्ध्य और आवृत्ति में क्या संबंध है?
उत्तर:
तरंग का वेग, आवृत्ति और तरंगदैर्ध्य के गुणनफल के बराबर है, अर्थात् υ = vi.

प्रश्न 23.
स्लिंकी कितने प्रकार की तरंगें उत्पन्न कर सकती है?
उत्तर:
स्लिंकी तीन प्रकार की तरंगें उत्पन्न कर सकती है

• अनुप्रस्थ तरंगें।
• अनुदैर्ध्य तरंगें।
• आवर्ती तरंगें।

प्रश्न 24.
तरंगें किस भौतिक राशि का संचरण करती हैं?
उत्तर:
तरंगें ऊर्जा का संचरण करती हैं।

प्रश्न 25.
आवृत्ति की S.I. इकाई क्या है?
उत्तर:
आवृत्ति की S.I. इकाई हर्ट्ज़ है।

प्रश्न 26.
तरंगदैर्ध्य की S.I. इकाई क्या है?
उत्तर:
तरंगदैर्ध्य की S.I. इकाई मीटर है।

प्रश्न 27.
तरंग के वेग की S.I. इकाई क्या है?
उत्तर:
तरंग के वेग की S.I. इकाई मीटर/सेकंड है।

प्रश्न 28.
स्पंद किसे कहते हैं?
उत्तर:
अल्पकालिक तरंगों को स्पंद कहते हैं।

प्रश्न 29.
जब कोई तरंग गति करती है तो माध्यम के कणों पर क्या प्रभाव पड़ता है?
उत्तर:
जब कोई तरंग गति करती है तो माध्यम के कण केवल दोलन गति करते हैं, तरंग के साथ गति नहीं करते।

प्रश्न 30.
अनुदैर्ध्य तरंगें किसे कहते हैं?
उत्तर:
वे तरंगें जिनमें माध्यम के कण तरंग की गति की दिशा में कंपन करते हैं, अनुदैर्ध्य तरंगें कहलाती हैं।

प्रश्न 31.
तरंगें कितनी प्रकार की होती हैं?
उत्तर:
तरंगें तीन प्रकार की होती हैं-

• अनुप्रस्थ तरंगें
• अनुदैर्ध्य तरंगें
• आवर्ती तरंगें।

प्रश्न 32.
निम्नलिखित में से अनुदैर्ध्य तरंगें कौन-सी हैं?
(1) तालाब के जल की लहरें
(2) ध्वनि तरंगें
(3) प्रकाश तरंगें।
उत्तर:
(2) ध्वनि तरंगें।

प्रश्न 33.
अनुप्रस्थ तरंगें किसे कहते हैं?
उत्तर:
वे तरंगें जिनमें माध्यम के कण तरंग के संचरण की दिशा के लंबवत् दिशा में दोलन करते हैं, अनुप्रस्थ तरंगें कहलाती हैं।

प्रश्न 34.
ध्वनि का संचरण कौन-सी तरंग का उदाहरण है?
उत्तर:
ध्वनि का संचरण अनुदैर्ध्य तरंग का उदाहरण है।

प्रश्न 35.
तालाब के जल पर उत्पन्न उर्मियाँ कौन-सी तरंगें हैं?
उत्तर:
तालाब के जल पर उत्पन्न उर्मियाँ अनुप्रस्थ तरंगें हैं।

प्रश्न 36.
अनुदैर्ध्य तरंगें कैसे गति करती हैं?
उत्तर:
अनुदैर्ध्य तरंगें संपीडन तथा विरलन के रूप में गति करती हैं।

प्रश्न 37.
गर्त किसे कहते हैं?
उत्तर:
आवर्ती तरंगों के ग्राफ में Y-अक्ष में ऋणात्मक दिशा की ओर अधिकतम विस्थापन को गर्त कहते हैं।

प्रश्न 38.
तारत्व किसे कहते हैं?
उत्तर:
किसी उत्सर्जित ध्वनि की आवृत्ति को मस्तिष्क किस प्रकार अनुभव करता है, उसे तारत्व कहते हैं।

प्रश्न 39.
स्वर किसे कहते हैं?
उत्तर:
अनेकों आवृत्तियों के मिश्रण से उत्पन्न ध्वनि को स्वर कहते हैं।

प्रश्न 40.
ध्वनियों में अंतर होने का क्या कारण होता है?
उत्तर:
ध्वनियों में अंतर का मुख्य कारण ध्वनि प्रबलता, गुणता, ध्वनि तारत्व तथा आवृत्ति हैं।

प्रश्न 41.
हमारे कानों की श्रव्यता परिसर कितनी है?
उत्तर:
20 हर्ट्ज़ से 20,000 हज़ं।

प्रश्न 42.
पराश्रव्य ध्वनि से क्या अभिप्राय है?
उत्तर:
20,000 हर्ट्ज़ से अधिक आवृत्ति वाली ध्वनि को पराश्रव्य ध्वनि कहते हैं।

प्रश्न 43.
भूकंप व ज्वालामुखी विस्फोट के समय किस आवृत्ति की ध्वनियाँ उत्पन्न होती हैं?
उत्तर:
20 हज़ से कम आवृत्ति की ध्वनियाँ उत्पन्न होती हैं।

प्रश्न 44.
20 हर्ट्ज़ से कम आवृत्ति की ध्वनियाँ उत्पन्न करने वाले दो प्राणियों के नाम लिखो।
उत्तर:

• व्हेल
• हाथी।

प्रश्न 45.
पराश्रव्य ध्वनि उत्पन्न करने वाले दो जीवों के नाम लिखो।
उत्तर:

• चमगादड़
• कुत्ते।

प्रश्न 46.
चमगादड़ों को कौन-सी ध्वनि से अपने गमन पथ का आभास होता है?
उत्तर:
पराश्रव्य ध्वनि से।

प्रश्न 47.
अनुरणन किसे कहते हैं?
उत्तर:
ध्वनि का बारम्बार परावर्तन जिसके कारण ध्वनि निबंध हो जाती है, अनुरणन कहलाता है।

प्रश्न 48.
पराध्वनिक चाल से क्या अभिप्राय है?
उत्तर:
जब कोई पिंड ध्वनि की चाल से अधिक चाल से गति करता है तब उसकी चाल को पराध्वनिक चाल कहा जाता है।

प्रश्न 49.
कौन-से वायुयान वायु में प्रघाती तरंगें उत्पन्न करते हैं?
उत्तर:
पराध्वनिक वायुयान वायु में प्रघाती तरंगें उत्पन्न करते हैं।

प्रश्न 50.
पराध्वनिक वायुयानों द्वारा तेज गति के कारण उत्पन्न धमाके की ध्वनि को क्या कहते हैं?
उत्तर:
ध्वनि बूम।

प्रश्न 51.
ध्वनि परावर्तन से क्या अभिप्राय है?
उत्तर:
ध्वनि का किसी सतह से टकराकर दिशा बदलना; ध्वनि परावर्तन कहलाता है।

प्रश्न 52.
गहरे कुँओं, बड़ी इमारतों, पहाड़ों आदि में ध्वनि उत्पन्न करने पर मूल ध्वनि के अतिरिक्त थोड़ी देर बाद जो ध्वनि सुनाई पड़ती है, उसे क्या कहते हैं?
उत्तर:
प्रतिध्वनि (Echo)।

प्रश्न 53.
मेगाफोन किस सिद्धांत पर कार्य करता है?
उत्तर:
मेगाफोन ध्वनि-परावर्तन के सिद्धांत पर कार्य करता है।

प्रश्न 54.
प्रतिध्वनि सुनने के लिए मूल ध्वनि तथा प्रतिध्वनि के बीच कम-से-कम कितना समय होना चाहिए?
उत्तर:
0.1 सेकंड अर्थात् \(\frac { 1 }{ 10 }\) सेकंड।

प्रश्न 55.
प्रतिध्वनि सुनने के लिए परावर्तक वस्तु ध्वनि के स्रोत से कम-से-कम कितनी दूर होनी चाहिए?
उत्तर:
17.2 मीटर।

प्रश्न 56.
ध्वनि द्वारा तय की गई कम-से-कम दूरी कितनी होनी चाहिए ताकि प्रतिध्वनि सुनाई दे सके?
उत्तर:
34.4 मीटर।

प्रश्न 57.
सोनार (Sonar) क्या है?
उत्तर:
सोनार (Sound Navigation and Ranging) का अर्थ है-ध्वनि द्वारा संचालन तथा परिसर निर्धारण करना।

प्रश्न 58.
सोनार का उपयोग कहाँ किया जाता है?
उत्तर:
सोनार का उपयोग समुद्र में डूबी वस्तुओं का पता लगाने में किया जाता है।

प्रश्न 59.
सोनार की कार्य-प्रणाली में किन तरंगों का उपयोग किया जाता है?
उत्तर:
पराश्रव्य तरंगों का।

प्रश्न 60.
चमगादड़ कितनी आवृत्ति तक की पराश्रव्य ध्वनियाँ उत्पन्न कर सकता है?
उत्तर:
चमगादड़ 120 किलो-हर्ट्ज़ आवृत्ति तक की पराश्रव्य ध्वनियाँ उत्पन्न कर सकता है।

प्रश्न 61.
शरीर के पीड़ाग्रस्त जोड़ों को किन तरंगों से उद्भाषित करने पर मालिश के समान सुखद अनुभूति होती है?
उत्तर:
पराश्रव्य तरंगों से उद्भाषित करने पर।

प्रश्न 62.
एक्स-रे किरणों के स्थान पर शरीर के अंदर का चित्र लेने के लिए पराश्रव्य ध्वनि का उपयोग क्यों लाभकारी होता है?
उत्तर:
क्योंकि पराश्रव्य ध्वनि के प्रयोग से ऊत्तकों तथा कोशिकाओं पर प्रभाव नहीं पड़ता।

प्रश्न 63.
अल्ट्रासोनोग्राफी से क्या अभिप्राय है?
उत्तर:
पराश्रव्य ध्वनि तरंगों की सहायता से त्रिविमीय चित्र प्राप्त करने की तकनीक को अल्ट्रासोनोग्राफी कहते हैं।

प्रश्न 64.
आंखों में ट्यूमर का पता लगाने तथा उसका इलाज करने में कौन-सी तरंगें प्रयोग की जाती हैं?
उत्तर:
पराश्रव्य तरंगें।

प्रश्न 65.
पराश्रव्य ध्वनि का कौन-सा गुण फोटोग्राफी फिल्म बनाने में काम आता है?
उत्तर:
पराश्रव्य ध्वनि द्वारा अमिश्रणीय द्रवों को मिश्रित करने का गुण फोटोग्राफी फिल्म बनाने में काम आता है।

प्रश्न 66.
श्वसन थरेपी में किन ध्वनि तरंगों का उपयोग होता है?
उत्तर:
पराश्रव्य ध्वनि तरंगों का।

लघूत्तरात्मक प्रश्न

पूश्न 1.
सिद्ध करो कि यनि ऊर्जा का रूप है।
उत्तर:
जब हम अधिक समय तक बोलते हैं या ऊँचा बोलते हैं तो थक जाते हैं। बोलते समय हम अपनी ऊर्जा खर्च करते हैं। यह ऊर्जा गले में कंपन पैदा करती है। इससे यह सिद्ध होता है कि ध्वनि ऊर्जा का रूप है।

प्रश्न 2.
संपीडन और विरलन किसे कहते हैं? ध्वनि तरंगों के कारण वायु के परमाणुओं के घनत्व को ग्राफ द्वारा प्रदर्शित करो।
उत्तर:
संपीडन-ध्वनि संचरण के दौरान वायु के अणु जिन स्थानों पर इकट्ठे हो जाते हैं, उन्हें संपीडन कहते हैं। विरलन-ध्वनि संचरण के दौरान जिन स्थानों पर वायु के अणुओं की संख्या बहुत कम हो जाती है, उन्हें विरलन कहते हैं। ध्वनि के लिए इकाई अंतराल में वायु के घनत्व तथा दूरी के बीच ग्राफ खींचा जा सकता है।

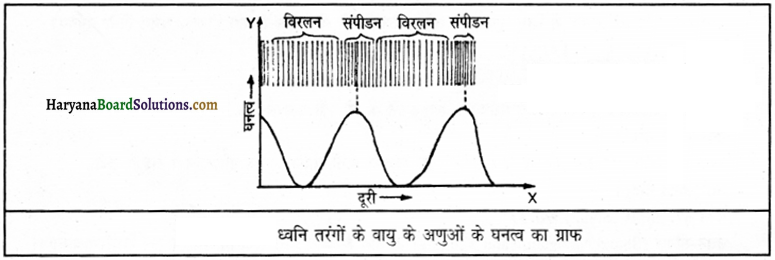
चित्र में ध्वनि तरंग के संचरण से वायु के अणुओं के वितरण की किसी व्यवस्था का स्वरूप प्रदर्शित किया गया है। घनत्व तथा दूरी के बीच ग्राफ भी दिखाया गया है।

प्रश्न 3.
एक प्रयोग द्वारा समझाओ कि कंपित वस्तु के पास बने संपीडन और विरलन माध्यम में कैसे गति करते हैं?
उत्तर:
प्रयोग-एक सर्पिलाकार कमानी लीजिए। जैसा कि चित्र में दिखाया गया है। कमानी के एक सिरे को अपने हाथ से एक समान रूप से धीरे-धीरे दबाओ और छोड़ दो। हम देखते हैं कि कमानी में संपीडन और विरलन बन जाते हैं और वे कमानी के एक सिरे से दूसरे सिरे तक संचरित हो जाते हैं। संपीडन और विरलन की इस संचरण गति को तरंग गति कहते हैं। ठीक इसी प्रकार से वायु में भी उत्पन्न संपीडन तथा विरलन वायु की एक परत से दूसरी परत में संचरित होते हैं और इस प्रकार ध्वनि एक स्थान से दूसरे स्थान तक पहुँच जाती है।

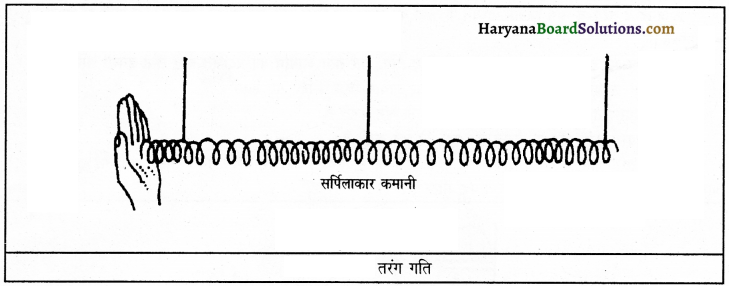
प्रश्न 4.
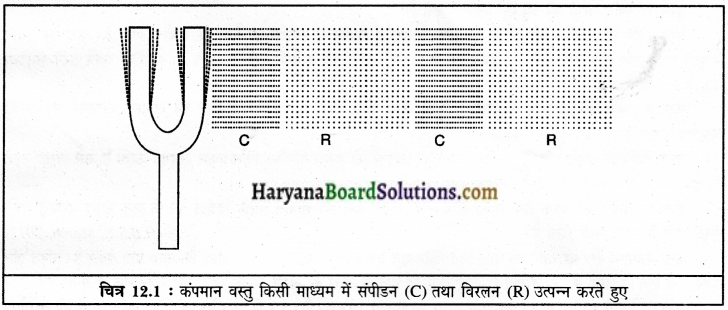
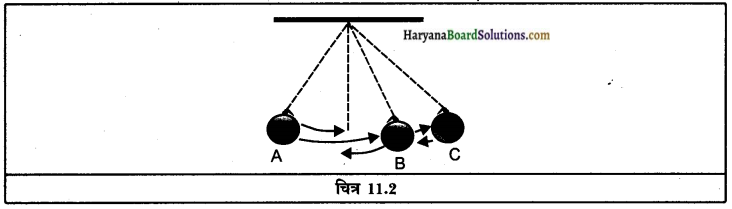
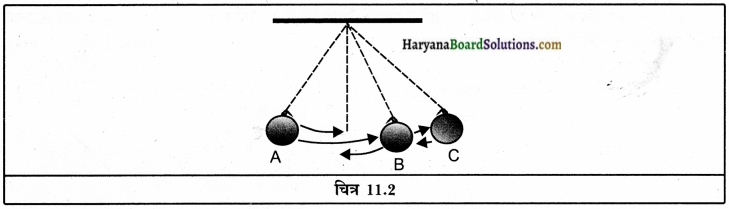
वायु में ध्वनि प्रक्रिया को स्वरित्र द्विभुज की सहायता से स्पष्ट करो।
उत्तर:
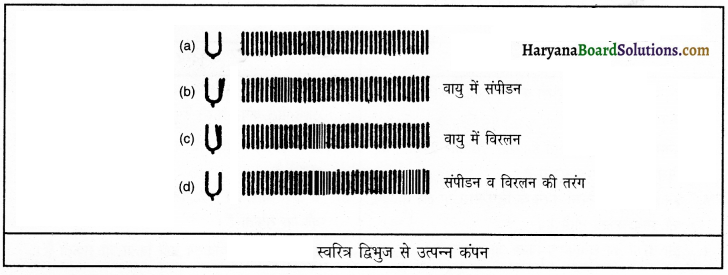
स्वरित्र द्विभुज को रबड़ पैड पर मारने से इसकी भुजाएँ कंपन करने लगती हैं। कंपित भुजा वायु के कणों पर दबाव डालकर उन्हें विस्थापित करती है। वायु के कण विरामावस्था से गति में आते हैं और निकटवर्ती कणों को विस्थापित करने के पश्चात् स्वयं अपनी मूल अवस्था में आ जाते हैं। वायु में जिस क्षेत्र के कण कंपन के दबाव के कारण पास आ जाते हैं।

वहाँ उच्च दाब का क्षेत्र संपीडन बनता है और कंपन का दबाव हटने पर वायु के कण दूर-दूर अपनी मूल अवस्था में आ जाते हैं। इस क्षेत्र को निम्न दाब का क्षेत्र विरलन कहते हैं। माध्यम के कण स्वयं आगे नहीं बढ़ते, बल्कि संपीडन और विरलन से कणों का विक्षोभ आगे बढ़ता है इसे ही ध्वनि की तरंग कहते हैं। ध्वनि संचरण के लिए वायु सबसे अधिक सामान्य माध्यक है।

प्रश्न 5.
क्या ध्वनि एक प्रकाश धब्बे को नृत्य करा सकती है। स्पष्ट करो।
उत्तर:
एक दोनों सिरों से खुला डिब्बा लो। गुब्बारे की झिल्ली को एक सिरे पर तानकर बांध दो। समतल दर्पण का एक छोटा टुकड़ा लो और इसे गुब्बारे की झिल्ली पर ऐसे चिपकाओ कि इसकी चमकदार सतह ऊपर की ओर हो और एक झिरी से आने वाले प्रकाश की किरणें दर्पण पर पड़ें और परावर्तन के पश्चात् प्रकाश का धब्बा दीवार पर पड़े। डिब्बे के खुले सिरे से जोरदार आवाज लगाइए। आप देखेंगे कि दीवार पर धब्बा नाचता हुआ नजर आएगा।

कारण आवाज के कंपन से झिल्ली और इस पर लगा दर्पण कंपन करता है जिसके कारण दीवार पर बनने वाला प्रतिबिंब हिलता हुआ नजर आता है। आवाज लगानी बंद करो। धब्बा एक जगह पर स्थिर नजर आएगा क्योंकि झिल्ली का कंपन बंद हो गया है।

प्रश्न 6.
अनुप्रस्थ और अनुदैर्ध्य तरंगों की परिभाषाएँ लिखो।
उत्तर:

• अनुप्रस्थ तरंगें वे तरंगें जिनमें माध्यम के कण तरंग के संचरण की दिशा के लंबवत् दिशा में दोलन करते हैं, अनुप्रस्थ तरंगें कहलाती हैं।
• अनुदैर्ध्य तरंगें वे तरंगें जिनके माध्यम के कणों की दोलन की दिशा तथा संचरण की दिशा एक ही होती है, अनुदैर्ध्य तरंगें कहलाती हैं।

प्रश्न 7.
ग्राफ द्वारा एक अनुप्रस्थ तरंग के लिए श्रृंग, गर्त तथा आयाम को प्रदर्शित करो तथा इनकी परिभाषा दो।
उत्तर:
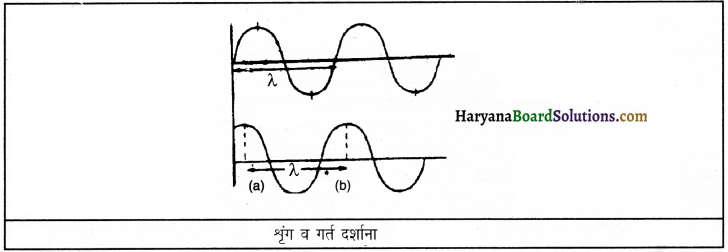
एक अनुप्रस्थ तरंग के लिए शृंग, गर्त तथा आयाम चित्र में दिए गए हैं।

• श्रृंग-अनुप्रस्थ तरंग गति के दौरान बने उभारों को शृंग कहते हैं।
• गर्त-अनुप्रस्थ तरंग गति के दौरान बने गड्ढों को गर्त कहते हैं।
• आयाम-तरंग गति के दौरान माध्यम के कणों द्वारा अपनी मध्य स्थिति से, कंपन करते समय, चली गई अधिकतम दूरी आयाम कहलाती है। आयाम का मानक मात्रक मीटर है।
  

प्रश्न 8.
अनुप्रस्थ तथा अनुदैर्ध्य तरंगों में क्या अंतर है?
उत्तर:
अनुप्रस्थ तथा अनुदैर्ध्य तरंगों में निम्नलिखित अंतर हैं-

प्रश्न 9.
निम्नलिखित के विषय में आप क्या जानते हो?
(1) ध्वनि की प्रबलता
(2) तारत्व
(3) आवृत्ति।
अथवा
ध्वनि तरंग की प्रबलता तथा तारत्व में दो अंतर लिखिए।
उत्तर:
(1) ध्वनि की प्रबलता-ध्वनि की उत्तेजना के दर्जे को ध्वनि की प्रबलता कहते हैं। यह उत्तेजना का दर्जा स्रोत के तेज या हल्के कंपनों पर निर्भर करता है। जब कंपन अधिक तेज होते हैं तब ध्वनि प्रबलता अधिक तथा जब कंपन हल्के होते हैं, तो ध्वनि प्रबलता भी कम होती है।

(2) तारत्व-यह ध्वनि की वह विशेषता है जिससे हम मोटी व पतली आवाज़ को पहचानते हैं। यह विशेषता ध्वनि स्रोत की आवृत्ति (प्रति सेकंड कंपन संख्या) पर निर्भर करती है। जब ध्वनि स्रोत की आवृत्ति अधिक होती है तब तारत्व भी अधिक होता है।

(3) आवृत्ति-किसी वस्तु द्वारा एक सेकंड में पूर्ण किए गए कंपनों की संख्या को आवृत्ति कहते हैं।

प्रश्न 10.
मच्छर की आवाज तथा शेर की आवाज में क्या अंतर है?
उत्तर:
मच्छर की आवाज (ध्वनि) की प्रबलता कम होती है, परंतु आवृत्ति अधिक होती है जबकि शेर की आवाज की प्रबलता अधिक होती है, परंतु आवृत्ति कम होती है। इसलिए मच्छर की आवाज शेर की आवाज से तीखी होती है।

प्रश्न 11.
ग्राफीय चित्र द्वारा दिखाओ कि ध्वनि तरंग जब किसी माध्यम में गति करती है तो घनत्व और दाब में कैसे परिवर्तन होता है?
उत्तर:

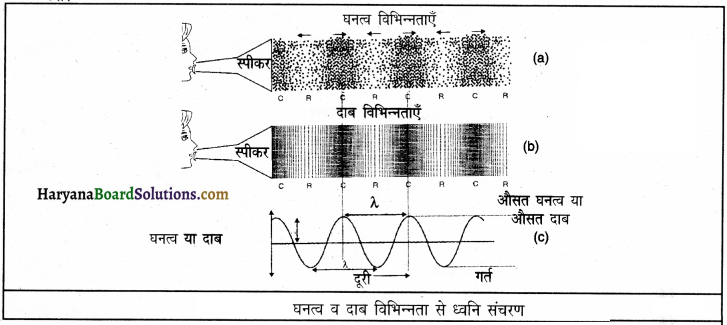
किसी निश्चित समय पर माध्यम का घनत्व तथा दाब दोनों ही उनके औसत मान से ऊपर और नीचे दूरी के साथ परिवर्तित होते हैं। चित्र में संपीडन उच्च दाब क्षेत्र और विरलन निम्न दाब क्षेत्र दिखाया गया है। चित्र में शिखर को तरंग का शृंग तथा घाटी को गर्त कहते हैं।

प्रश्न 12.
किसी आरकेस्ट्रा में वायलन और बांसुरी की ध्वनि में क्या अंतर है?
उत्तर:
वायलन और बांसुरी दोनों एक माध्यम में चलती हैं, दोनों एक ही समय में कानों तक पहुँचती हैं, दोनों की चाल एक समान हैं, परंतु दोनों ध्वनियाँ अलग-अलग अभिलक्षणों के साथ प्राप्त की जाती हैं। वह भिन्न अभिलक्षण हैं-तारत्व। किसी उत्सर्जित ध्वनि की आवृत्ति को मस्तिष्क किस प्रकार अनुभव करता है, उसे तारत्व कहते हैं। इसीलिए वायलन और बांसुरी की ध्वनि अलग-अलग प्रकार से सुनाई देती है।

प्रश्न 13.
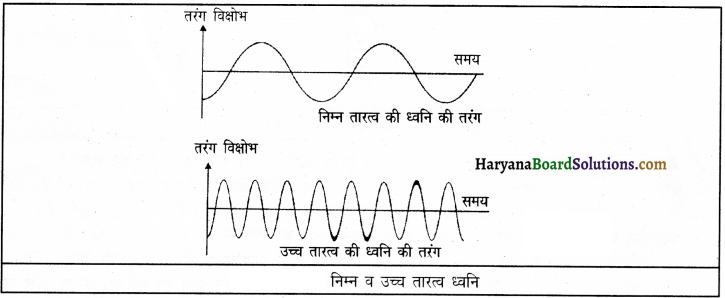
ग्राफ चित्र द्वारा निम्न व उच्च तारत्व की ध्वनि में अंतर स्पष्ट करो।
उत्तर:

प्रश्न 14.
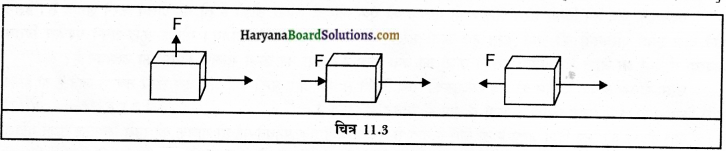
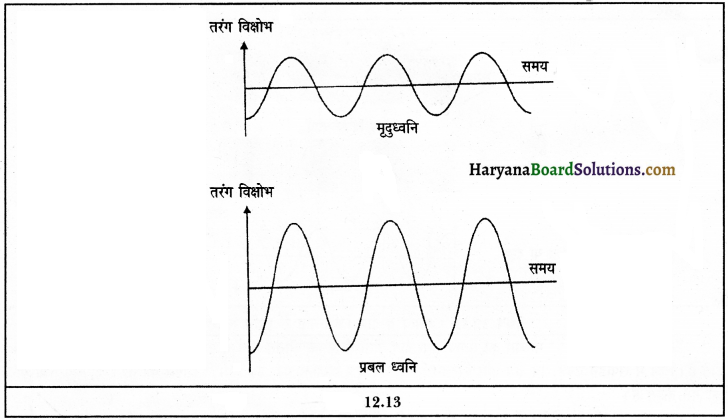
मृदु और प्रबल ध्वनि में प्रमुख कारण क्या है? इसे ग्राफ चित्र द्वारा स्पष्ट करो।
उत्तर:
ध्वनि की मृदुता और प्रबलता उसके आयाम पर निर्भर करती है। जैसे दरवाजे को धीरे-धीरे खटखकाने से कम आयाम की ध्वनि और जोर से खटखकाने से उच्च आयाम की ध्वनि उत्पन्न होती है। कम आयाम में कम ऊर्जा और उच्च आयाम में अधिक ऊर्जा संबद्ध होती है। यही कारण है कम आयाम की ध्वनि कम दूरी और उच्च आयाम की ऊर्जा अधिक दूरी तय करती है।

प्रश्न 15.
एक प्रयोग द्वारा समझाओ कि ध्वनि की गति वायु की अपेक्षा द्रवों में अधिक होती है।
उत्तर:
पानी से भरा एक गुब्बारा लो और इसकी सतह को धीरे-से अपने हाथ से रगड़ो तो हमें ध्वनि सुनाई पड़ेगी। अब गुब्बारे को अपने कान के समीप रखो और गुब्बारे की दूसरी सतह को धीरे से अपने हाथ से रगड़ो। हमें ध्वनि स्पष्ट और अधिक सुनाई देगी। इससे सिद्ध होता है कि ध्वनि की गति वायु की अपेक्षा द्रवों में अधिक होती है।

प्रश्न 16.
रेलवे लाइन के साथ कान लगाकर हम बहुत दूर से आती रेलगाड़ी की आवाज़ कैसे सुन सकते हैं?
उत्तर:
हम जानते हैं कि सामान्य तापमान पर लोहे में ध्वनि का वेग लगभग 5950 मीटर प्रति सेकंड है। इसलिए हम रेलवे लाइन, जो कि लोहे के गार्डरों की बनी होती है, से कान लगाकर बहुत दूर से आती हुई गाड़ी की आवाज़ सुन सकते हैं।

प्रश्न 17.
ध्वनि के परावर्तन को दर्शाने के लिए किसी एक प्रयोग का वर्णन कीजिए।
उत्तर:
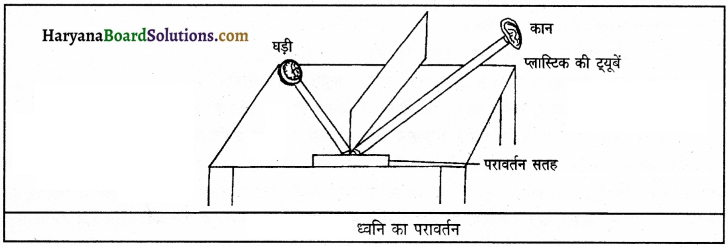
प्लास्टिक या गत्ते की बनी दो एक जैसी चौड़ी ट्यूबें लीजिए। धातु या प्लाईवुड की एक चादर भी लीजिए। चित्र के अनुसार इन्हें व्यवस्थित कीजिए। इनमें से किसी एक ट्यूब के एक सिरे पर टिक-टिक करने वाली एक घड़ी रख दीजिए। जैसा कि चित्र में दिखाया गया है। दूसरी ट्यूब के सिरे के पास अपना कान रखिए।

दोनों ट्यूबों के बीच में एक मोटा पर्दा रखिए जिससे कि घड़ी की टिक-टिक की ध्वनि आपके कानों तक सीधे न पहुँच पाए। दूसरी ट्यूब के कोण को तब तक समायोजित कीजिए जब तक कि आपको टिक-टिक की स्पष्ट ध्वनि सुनाई न देने लगे। आप देखेंगे कि इस स्थिति में दोनों ट्यूबें अभिलंब के सामान कोण बनाती है। इससे सिद्ध होता है कि ध्वनि का परावर्तन होता है।

प्रश्न 18.
ध्वनि के परावर्तन से आप क्या समझते हैं? ध्वनि परावर्तन का कान उपयोग समुद्र की गहराई को मापने में कैसे किया जाता है?
उत्तर:
ध्वनि का किसी सतह से टकराकर दिशा बदलना ध्वनि परावर्तन कहलाता है; जैसे जब किसी कुएँ के मुंह पर कोई ध्वनि उत्पन्न की जाती है तो उत्पन्न मूल ध्वनि की तरंगें कुएँ के अंदर जाती हैं और वे कुछ समय बाद पानी के तल से परावर्तित होकर फिर ऊपर कुएँ के मुंह तक आ जाती हैं और मूल ध्वनि की भांति प्रतिध्वनि के रूप में दोबारा सुनाई पड़ती हैं।

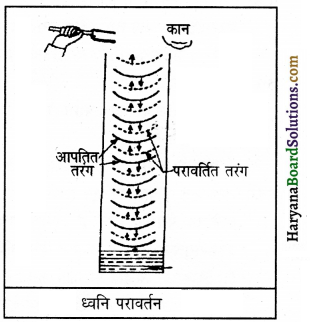
ध्वनि परावर्तन से समुद्र की गहराई मापना-समुद्र की गहराई ‘थाईमापी’ नामक यंत्र द्वारा ज्ञात की जाती है। इस यंत्र द्वारा पहले जलयान से ध्वनि संकेत समुद्र की तह तक भेजा जाता है। यह संकेत समुद्र की तली से परावर्तन के बाद इसी यंत्र में लौट आता है। इस प्रकार जलयान से सतह पर पहुँचने और परावर्तित होकर वापस आने में लगे समय को माप लेते हैं। समुद्र के पानी में ध्वनि की गति से समुद्र की गहराई ज्ञात कर ली जाती है। अब समय तथा समुद्र के पानी में ध्वनि की गति के ज्ञान से समुद्र की गहराई की गणना कर ली जाती है।

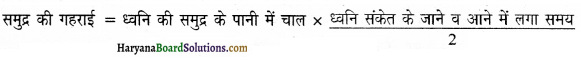
प्रश्न 19.
पराश्रव्य ध्वनि और प्रतिध्वनि में क्या अंतर है?
उत्तर:
पराश्रव्य ध्वनि-20,000 कंपन प्रति सेकंड से अधिक आवृत्ति की ध्वनि को पराश्रव्य ध्वनि कहते हैं। यह ध्वनि हमें सुनाई नहीं पड़ती। कुछ पशुओं; जैसे कुत्तों में पराश्रव्य ध्वनि सुनने की क्षमता होती है। चमगादड़ों में पराश्रव्य ध्वनि को पैदा करने तथा इसे सुनने की क्षमता होती है।

प्रतिध्वनि-गहरे कुंओं, बड़ी इमारतों, पहाड़ों आदि में ध्वनि उत्पन्न करने पर मूल ध्वनि के अतिरिक्त थोड़ी देर बाद वैसी ही ध्वनि दोबारा सुनाई पड़ती है, जिसे प्रतिध्वनि (Echo) कहते हैं। प्रतिध्वनि हम तभी सुन सकते हैं जब मूल ध्वनि और परावर्तित ध्वनि के हमारे कानों तक पहुंचने में कम-से-कम 1/10 सेकंड का अंतर हो।

प्रतिध्वनि सुनने के लिए ध्वनि द्वारा चली गई दूरी कम-से-कम 34.4 मीटर होनी चाहिए। अतः वस्तु ध्वनि के स्रोत से 17.2 मीटर या उससे अधिक दूरी पर होनी चाहिए क्योंकि 22°C पर ध्वनि की चाल 344 m/s होती है। ध्वनि को अवरोधक तक जाने और वापिस श्रोता तक 1/10 सेकंड में पहुंचनी चाहिए। हमारे मस्तिष्क में ध्वनि की संवेदना 1/10 सेकंड तक बनी रहती है।

प्रश्न 20.
विभिन्न जंतुओं में श्रव्यता का परास क्या है?
उत्तर:
भिन्न-भिन्न जंतुओं में श्रव्यता का परास भिन्न-भिन्न है, जैसे-

• मनुष्य में 20 Hz से 20,000 Hz तक।
• कुत्ता व 5 वर्ष से कम आयु के बच्चों में 25 kHz तक।
• राइनोसिरस (गेंडा) में 5 Hz तक।
• व्हेल और हाथी में अवश्रव्य परास की ध्वनियाँ भी।
• डालफिन, चमगादड़, पॉरपॉइज में 20 kHz से अधिक आवृत्ति वाली ध्वनियाँ।
• शलभ में चमगादड़ों द्वारा उच्च आवृत्ति की चींची की ध्वनियाँ भी सुन सकते हैं।

प्रश्न 21.
क्या कारण है कि हम भूकंप से उत्पन्न तरंगों को नहीं सुन पाते जबकि चमगादड़ या कुत्ते सुन सकते हैं?
उत्तर:
हमारा कान 20 हर्ट्ज़ से 20,000 हज़ तक की आवृत्तियाँ वाली तरंगों को सुन सकता है। आवृत्ति का यह परास श्रवण परास (Audible Range) कहलाता है। भूकंप द्वारा पैदा हुई तरंगों की आवृत्ति इस परास (Range) में नहीं होती। इसीलिए हम इन तरंगों को नहीं सुन सकते, परंतु चमगादड़ और कुत्ते के कान भूकंप द्वारा पैदा हुई तरंगों के प्रति संवेदनशील होते हैं। इसीलिए वे इन तरंगों को सुन सकते हैं।

प्रश्न 22.
अवश्रव्य तरंगें, श्रव्य परास व पराश्रव्य तरंगें क्या हैं?
उत्तर:

• अवश्रव्य तरंगें-वे तरंगें जिनकी आवृत्ति 20 हर्ट्ज़ से कम हो, उन्हें अवश्रव्य तरंगें कहते हैं। इन्हें हम नहीं सुन सकते; जैसे भूकंप से निकली तरंगें।
• श्रव्य परास या श्रवण परास-वे तरंगें जिनकी आवृत्ति 20 हर्ट्ज़ से 20,000 हर्ट्ज़ के बीच हो, उन्हें श्रव्य परास कहते हैं। इन्हें हम सुन सकते हैं।
• पराश्रव्य तरंगें-वे तरंगें जिनकी आवृत्ति 20,000 हर्ट्ज़ से अधिक हो, उन्हें पराश्रव्य तरंगें कहते हैं। इन्हें भी हम नहीं सुन सकते। इन्हें कुत्ते व चमगादड़ सुन सकते हैं।

प्रश्न 23.
पराश्रव्य ध्वनि के उपयोग लिखो।
उत्तर:
पराश्रव्य ध्वनि के उपयोग निम्नलिखित हैं-

• रेडार इसी सिद्धांत पर कार्य करता है।
• इससे प्रभावित दूध अधिक समय तक खराब नहीं होता।
• इससे प्रभावित अनाज में अंकुरण अधिक होता है।
• इसके द्वारा ढाली गई धातु की चादरों में दरारों का पता लगाया जाता है।
• चमगादड़ इसी पराश्रव्य ध्वनि से अपने शिकार का पता लगा लेते हैं।
• इसके प्रयोग से आधुनिक थाईमापी द्वारा समुद्र की गहराई मापी जा सकती है।
• कपड़ों व प्लेटों को धोने में इसका प्रयोग होता है।
• शरीर के भागों में कैंसर का पता लगाने में इसका प्रयोग होता है।
• यह कठोर पदार्थों को काटने व ऐलुमिनियम आदि को जोड़ने के काम आती है।

प्रश्न 24.
एक व्यक्ति को ऐसे कमरे में बंद कर दिया गया है जिसके दरवाजे व खिड़कियाँ कांच के बने हैं। जब वह व्यक्ति कमरे के अंदर आवाज़ लगाता है तो कोई नहीं सुनता, परंतु जब वह खिड़की को खटखटाता है तो बाहर के व्यक्तियों को खटखटाहट सुनाई दे जाती है। ऐसा क्यों होता है?
उत्तर:
जब कमरे में बंद व्यक्ति अंदर से आवाज़ लगाता है तो उससे उत्पन्न तरंगों का कांच द्वारा परावर्तन हो जाता है। इससे कांच में क्षीण कंपन उत्पन्न होते हैं जो कमरे के बाहर की वायु को कंपित करने में असमर्थ होते हैं। फलतः आवाज़ बाहर सुनाई नहीं देती।

इसके विपरीत खिड़की के कांच को खटखटाने से उत्पन्न तरंग कांच के बाह्य पृष्ठ पर पहुंचकर उसके संपर्क की वायु को कंपित कर देती है। परिणामस्वरूप खटखटाने की आवाज़ व्यक्तियों को सुनाई दे जाती है।

प्रश्न 25.
ध्वनि बूम से क्या अभिप्राय है? इससे क्या हानि हो सकती है?
उत्तर:
पराध्वनिक वायुयान वायु में प्रघाती तरंगें उत्पन्न करते हैं। ये प्रघाती तरंगें, पराध्वनिक चाल से चलती हैं और इनमें बहुत अधिक ऊर्जा होती है। इस प्रकार की प्रघाती तरंगों से संबद्ध वायुदाब में अत्यधिक परिवर्तन एक प्रकार का प्रस्फोट या कड़क ध्वनि उत्पन्न करता है, जिसे ‘ध्वनि बूम’ कहते हैं।

यह अप्रिय ध्वनि बूम, जो आप किसी पराध्वनिक वायुयान के निकट होने पर सुन सकते हैं, आसपास रखी कांच की प्लेटों, खिड़कियों के शीशों और यहाँ तक कि भवनों को भी क्षति पहुँचा सकता है। कई बार ध्वनि बूम से इतनी प्रबलता का शोर हो सकता है जो हमारी सहनशक्ति की सीमा से परे हो। ऐसे शोर से हमारे कानों में पीड़ा हो सकती है। याद रखिए, जब तक पराध्वनिक वायुयान उड़ता रहता है, वह निरंतर अपने चारों ओर के माध्यम में ध्वनि बूम उत्पन्न करता रहता है।

प्रश्न 26.
मरमर श्रावी गैलरी पर संक्षिप्त टिप्पणी कीजिए।
उत्तर:
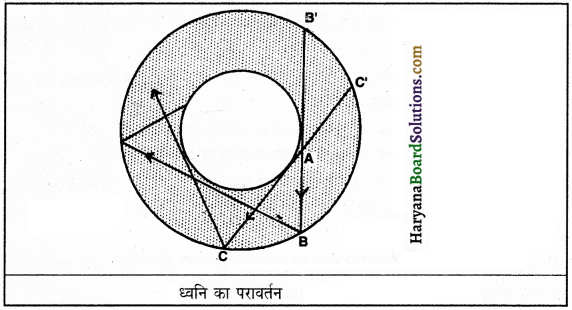
लंदन में सैंट पॉल गिरजाघर के गुंबद की मरमर श्रावी गैलरी बहुत प्रसिद्ध है तथा यह ध्वनि के परावर्तन का एक रोचक उदाहरण प्रस्तुत करती है। यह गैलरी गुंबद के भीतर के चारों ओर वृत्तीय रूप में है। जब आप इस गैलरी की दीवारों के निकट किसी बिंदु पर कोई कानाफूसी करते हैं तो उत्पन्न ध्वनि गैलरी की दीवारों द्वारा सभी स्थानों पर परावर्तित हो जाती है।

दीवारों के निकट किसी भी स्थान पर यह ध्वनि स्पष्ट सुनाई देती है, किंतु केंद्र की ओर कुछ ही दूरी पर, जैसे बिंदु A पर, यह ध्वनि कदाचित् सुनाई नहीं देती। इस प्रकार की गैलरी भारत में भी कई ऐतिहासिक स्थानों पर देखी जा सकती है।

प्रश्न 27.
सोनार (SONAR) से क्या तात्पर्य है? इसके उपयोग बताइए।
उत्तर:
सोनार-वह उपकरण, जो ध्वनि तरंगें उत्पन्न करता है तथा परावर्तित ध्वनि तरंगों का लघु समयांतर मापता है, सोनार कहलाता है।
उपयोग-

• समुद्र की गहराई मापने में।
• मछलियों के झुण्डों की दूरी ज्ञात करने में।
• पनडुब्बी एवं शत्रु के टारपीडो की स्थिति निर्धारण में।
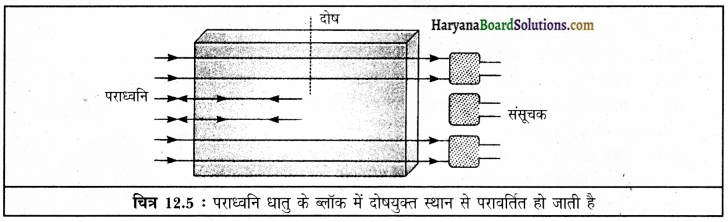
• उद्योगों में धातु के विशाल गार्डरों, ब्लॉकों अथवा शीटों में संभावित दरारों अथवा अन्य दोषों का पता लगाने में।

प्रश्न 28.
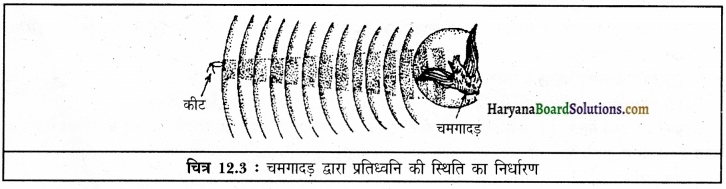
सोनार के सिद्धांत का उपयोग कर गहन अंधकार में भी चमगादड़ कैसे मुक्त रूप से उड़ सकता है?
उत्तर:
सोनार के सिद्धांत का उपयोग चमगादड़ों द्वारा प्राकृतिक रूप में किया जाता है। चमगादड़ 120 kHz अथवा 1.2 x 10⁵ Hz आवृत्ति तक की पराश्रव्य ध्वनियाँ उत्पन्न कर सकता है तथा उन्हें सुन सकता है। इतनी उच्च आवृत्तियों की संगत पराश्रव्य तरंगों की वायु में तरंगदैर्ध्य बहुत कम, लगभग 0.29 cm होती है। चमगादड़ वास्तव में दृष्टिहीन होता है, परंतु गहन अंधकार में उड़ते हुए अवरोधों से आसानी से बचता हुआ चलता है।

यह पराश्रव्य तरंगों का उपयोग अपने भोजन को खोजने में भी करता है। उड़ान के समय चमगादड़ उच्च आवृत्ति के पराश्रव्य स्पंदों को अल्प समय अंतराल में क्रम से उत्सर्जित करता है। ये स्पंद चमगादड़ के आसपास के पिंडों से टकराकर परावर्तित होते हैं। चमगादड़ के शरीर में उच्च-कोटि के अभिग्राही जैसी संरचना होती है जिसके द्वारा वह अपने समीप के पिंडों की उपस्थिति एवं अवस्थितियों का संसूचन कर लेता है। अतः चमगादड़, पराश्रव्य तरंगों द्वारा किसी पिण्ड से परावर्तित होकर वापस लौटने में लगे समय का संसूचन कर लेता है। इस प्रकार, गहन अंधकार में भी चमगादड़ मुक्त रूप से उड़ान भर सकता है।

प्रश्न 29.
ध्वनि की चाल कौन-कौन से कारकों पर निर्भर करती है?
उत्तर:
ध्वनि की चाल निम्नलिखित कारकों पर निर्भर करती है-

• माध्यम के घनत्व पर-ध्वनि की चाल माध्यम के घनत्व के समानुपाती होती है अर्थात् घनत्व बढ़ने से चाल बढ़ती है तथा घनत्व कम होने से चाल घटती है।
• ताप पर-ताप बढ़ने पर ध्वनि की चाल बढ़ जाती है।
• तरंगदैर्ध्य-ध्वनि की चाल तरंगदैर्ध्य के समानुपाती होती है।
• माध्यम की अवस्था ध्वनि की चाल ठोस में सबसे अधिक, द्रवों में उससे कम तथा गैसों में सबसे कम होती है।

प्रश्न 30.
सुनने योग्य सीमा से क्या भाव है? इस सीमा से अधिक आवृत्ति की ध्वनियों के नाम लिखो तथा इनके कोई दो उपयोग लिखो।
उत्तर:
सुनने योग्य सीमा मनुष्य 20 हर्ट्ज़ से 20,000 हर्ट्ज़ आवृत्ति की तरंगों को सुन सकता है। इस सीमा को सुनने योग्य श्रव्यता का परिसर कहते हैं।

20,000 हर्ट्ज़ से अधिक आवृत्ति की ध्वनि को पराश्रव्य तरंगें या पराध्वनि कहते हैं। इसके उपयोग निम्नलिखित हैं-

• इसके सिद्धांत पर रेडार बनाए जाते हैं।
• शरीर के भागों में कैंसर का पता लगाने में इसका उपयोग होता है।

प्रश्न 31.
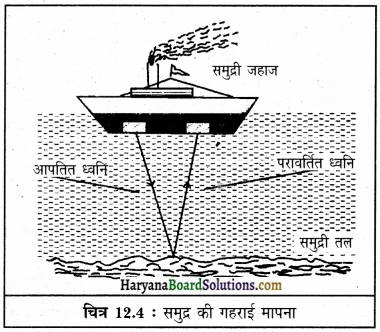
समुद्र तल की गहराई को हम किस प्रकार निर्धारित कर सकते हैं?
उत्तर:
समुद्र तल की गहराई मापने के लिए जहाज पर एक यंत्र लगा होता है जो समुद्र तल में पराश्रव्य तरंगें भेजता है। ये तरंगें समुद्र तल से परावर्तित होकर वापिस आ जाती हैं तथा जहाज पर स्थित रिसीवर इन परावर्तित किरणों को प्राप्त कर लेता है।

पराश्रव्य तरंगों को जहाज से समुद्र तल की यात्रा के लिए तथा जहाज पर वापिस आने का समय t तथा ध्वनि तरंगों के वेग υ से जहाज और समुद्र तल के मध्य की दूरी d की गणना की जा सकती है। हम जानते हैं कि
वेग = \(\frac { दूरी }{ समय }\)
या दूरी = वेग x समय यह एक निश्चित स्थान पर समुद्र की गहराई होगी।

निबंधात्मक प्रश्न

प्रश्न 1.
ध्वनि क्या है? प्रयोगों द्वारा सिद्ध करो कि ध्वनि कंपन द्वारा उत्पन्न होती है।
उत्तर:
ध्वनि-ध्वनि एक प्रकार की ऊर्जा है जो हमारे कानों में सुनने की संवेदना पैदा करती है। ध्वनि कंपन द्वारा उत्पन्न होती है। इसे निम्नलिखित प्रयोगों द्वारा सिद्ध कर सकते हैं-

प्रयोग 1.
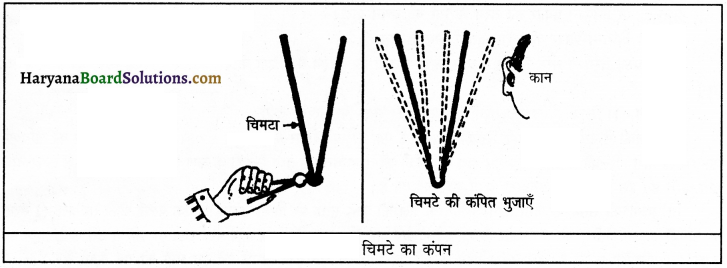
एक चिमटा लो। इसे मुड़े हुए सिरे से पकड़कर इसकी एक भुजा को फर्श या पत्थर पर मारकर उठा लो। चिमटे की भुजाएँ हिलती हुई दिखाई देंगी। चिमटे की भुजाओं का हिलना ही कंपन कहलाता है। इसी कंपन के कारण चिमटे के हिलने की ध्वनि सुनाई देती है। यह क्रिया दोबारा दोहराओ तथा चिमटे को कान के निकट लाओ। चिमटे की ध्वनि साफ सुनाई देगी।

प्रयोग 2.
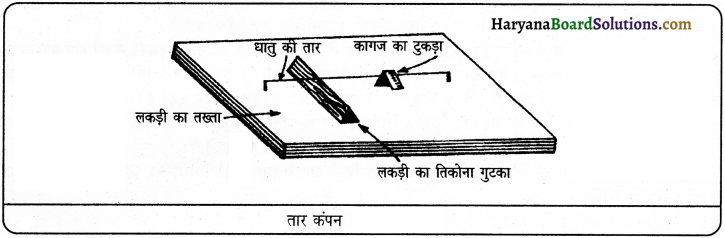
एक लकड़ी के तख्ते पर दो कीलें गाढ़ो और दोनों के बीच में एक बारीक तार कसो। तार के नीचे एक लकड़ी का तिकोना टुकड़ा रखो। अब तार को पकड़कर थोड़ा ऊपर खींचकर छोड़ दो। ध्वनि सुनाई देगी। यदि एक कागज़ का टुकड़ा तार पर रखकर तार को खींचकर छोड़ें तो कंपन के कारण यह कागज़ का टुकड़ा नीचे गिर जाता है जो सिद्ध करता है कि ध्वनि कंपन द्वारा उत्पन्न होती है।

प्रयोग 3.
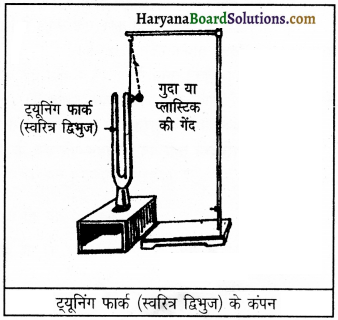
एक स्वरित्र द्विभुज या ट्यूनिंग फार्क लो। इसकी एक चोट कार्क या रबड़ पैड पर मारो। अब इसको मेज पर सीधा खड़ा कर दो। ध्वनि उत्पन्न होगी। यह ध्वनि हमें सुनाई देगी। अब स्टैंड से लटकी एक गुदे की गुहिका या प्लास्टिक की हल्की गेंद को कंपित भुजाओं के किनारों के पास लाओ।

स्वरित्र द्विभुज की भुजा से गेंद बार-बार टकराती है। यह स्वरित्र द्विभुज की भुजा के कंपित होने का प्रमाण है। यदि इसकी भुजा को हम अंगुली के समीप लाएँ, तो इसका कंपन अनुभव होगा। छूने पर ध्वनि आनी बंद हो जाएगी जो सिद्ध करता है कि ध्वनि कंपन द्वारा उत्पन्न होती है।

प्रश्न 2.
दो विभिन्न प्रकार की तरंग गतियों का वर्णन करो।
उत्तर:
दो विभिन्न प्रकार की तरंग गतियाँ निम्नलिखित हैं-
1. अनुप्रस्थ तरंगें-वे तरंगें जिनमें माध्यम के कण तरंग के संचरण की दिशा के लंबवत् दिशा में दोलन करते हैं, अनुप्रस्थ तरंगें कहलाती हैं।

उदाहरण-

• स्लिंकी में उत्पन्न तरंगें
• पानी की सतह पर उत्पन्न तरंगें।

(1) स्लिंकी में उत्पन्न तरंगें-एक स्लिंकी लो। इसके एक सिरे को दीवार में लगे हुक से बांध दो। अब दूसरे सिरे को खींचकर एक झटका मारो। स्लिंकी में उत्पन्न विक्षोभ हाथ से स्लिंकी की तरफ चलते हैं तथा स्लिंकी के कण अपनी मध्य स्थिति से ऊपर-नीचे गति करते हैं। इस प्रकार यह अनुप्रस्थ तरंगों का उदाहरण है।

(2) पानी की सतह पर बनी तरंगें तालाब के जल की शांत सतह पर किसी ऊंचाई से एक पत्थर फेंको तो जल की सतह पर उर्मियाँ उत्पन्न होती हैं जो चारों ओर फैलती हुई दिखाई देती हैं। उन उर्मियों पर कोई पत्ता रखो तो उर्मियाँ उसे उसी स्थान पर ऊपर-नीचे गतिशील करती हैं। इस प्रकार तरंग के उठे हुए भाग को शृंग तथा निचले दबे हुए भाग को गर्त कहते हैं।

2. अनुदैर्ध्य तरंगें-वे तरंगें जिनके माध्यम के कणों की दोलन की दिशा तथा तरंग के संचरण की दिशा एक ही होती है, अनुदैर्ध्य तरंगें कहलाती हैं।

उदाहरण-

• स्लिंकी में उत्पन्न तरंगें
• वायु में संचारित तरंगें।

(1) स्लिंकी में उत्पन्न तरंगें-स्लिंकी द्वारा अनुदैर्ध्य तरंगें भी उत्पन्न की जा सकती हैं। स्लिंकी के एक सिरे को दीवार पर लगे हुक से बांधों और दूसरे सिरे को हाथ से पकड़कर खींचो। अब स्लिंकी के हाथ के सिरे के पास किसी छोटे-से भाग में निहित कुंडलियों को अंगुलियों के बीच दबाकर छोड़ दो। संपीडन स्लिंकी के दूसरे सिरे तक पहुँच जाता है।

(2) वायु में संचरित तरंगें-एक स्वरित्र द्विभुज लो। इसे रबड़ के पैड से बलपूर्वक टकराओ। इसकी भुजाएँ दाएँ-बाएँ कंपन करने लगेंगी। इसकी एक भुजा कांपते हुए जब दाएँ ओर जाती है तो वायु के कणों को दबा देती है जिससे वायु के कण दाईं ओर संपीडित होते चले जाते हैं जिससे वायु के कणों के बीच की दूरी कम हो जाती है।

इसे संपीडन कहते हैं। कांपते समय स्वरित्र की भुजा जब वापस बाईं ओर जाती है तो दाईं ओर आंशिक निर्वात उत्पन्न हो जाता है जिसके भरने के लिए वायु के कण दाईं ओर खुल जाते हैं जिससे वायु के कणों के बीच की दूरी अधिक हो जाती है, जिसे विरलन कहते हैं।

प्रश्न 3.
आवर्ती तरंगों की विशेषताएँ कौन-कौन-सी हैं? किसी आवर्ती तरंग के लिए तरंग-वेग, आवृत्ति तथा तरंग-लंबाई में संबंध स्थापित कीजिए।
उत्तर:
आवर्ती तरंगों की विशेषताएँ निम्नलिखित हैं-
1. आयाम-कंपन करने वाले कण की मध्य स्थिति से अधिकतम विस्थापन को दोलन का आयाम कहते हैं।

2. आवर्त काल-एक दोलन पूरा करने में किसी कण द्वारा लगा समय आवर्त काल कहलाता है।

3. आवृत्ति कंपन करने वाला कण, एक सेकंड में जितनी बार कंपन करता है, उसे तरंग की आवृत्ति कहते हैं। इसको ‘V’ द्वारा दशति हैं, इसका मात्रक हज़ (Hz) है।

4. तरंगदैर्ध्य-जितने समय में माध्यम के कण एक कंपन पूरा करते हैं, उतने ही समय में तरंग द्वारा चली गई दूरी तरंगदैर्ध्य कहलाती है। इसे λ (ग्रीक अक्षर लैम्डा) द्वारा दर्शाते हैं।

5. वेग-इकाई समय में तरंग द्वारा चली गई दूरी तरंग का वेग कहलाती है। इसे ‘υ’ द्वारा व्यक्त करते हैं।
आवृत्ति, तरंगदैर्ध्य तथा वेग में संबंध-परिभाषा के अनुसार,
T सेकंड में तरंग द्वारा तय की गई दूरी = λ
1 सेकंड में तय की गई दूरी = \(\frac { λ }{ T }\)
परंतु 1 सेकंड में तरंग द्वारा तय की गई दूरी = वेग (υ)
∴ υ = \(\frac { λ }{ T }\) … (i)
यदि एक कंपन में लगा समय T हो तो
T सेकंड में होने वाले कंपनों की संख्या = 1
1 सेकंड में होने वाले कंपनों संख्या = \(\frac { 1 }{ T }\)
लेकिन 1 सेकंड में होने वाले कंपनों की संख्या को आवृत्ति (v) कहते हैं।
∴ V = \(\frac { 1 }{ T }\)
v का मान समीकरण (i) में रखने पर,
υ = \(\frac { λ }{ T }\) = λ\(\frac { 1 }{ T }\) = λv (∵\(\frac { 1 }{ T }\) = v)
अतः υ = v λ
वेग = आवृत्ति x तरंगदैर्ध्य

प्रश्न 4.
ध्वनि के परावर्तन से क्या अभिप्राय है? इसके कोई तीन उपयोग लिखो।
उत्तर:
ध्वनि परावर्तन-ध्वनि का किसी सतह से टकराकर दिशा बदलना ध्वनि का परावर्तन कहलाता है।

ध्वनि परावर्तन के उपयोग-ध्वनि के परावर्तन के व्यावहारिक उपयोग निम्नलिखित हैं-
1. मेगाफोन-आपने मेलों या पर्यटन स्थलों पर एकत्रित भीड़ को संबोधित | करने के लिए मेगाफोन का प्रयोग करते हुए देखा होगा। मेगाफोन, सींग के आकार की एक नली है। इसके भीतरी पृष्ठों से बार-बार परावर्तन द्वारा ध्वनि की मेगाफोन तरंगें बाहर फैलने से रुक जाती हैं और नली के भीतर की वायु तक ही सीमित रहती हैं। यही कारण है कि लाउडस्पीकरों के मुख भी सींग के आकार के ही बनाए जाते हैं।

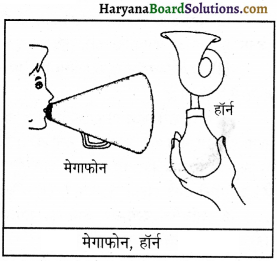
2. कर्ण तूर्य या श्रवण सहाय-यह ऐसी युक्ति है जिसे वे लोग काम में लाते हैं, जिन्हें कम सुनाई देता है। किसी तूर्य या तुरही के चौड़े सिरे पर पड़ने वाली ध्वनि तरंगें परावर्तित होकर अपसाहत अत्यधिक संकीर्ण क्षेत्र में एकत्र होकर कान में पहुँचती हैं। इससे कान के अंदर की वायु की परतों के कंपन का आयाम बढ़ जाता है और ध्वनि की प्रबलता में वृद्धि के कारण सुनने में सहायता मिलती है।

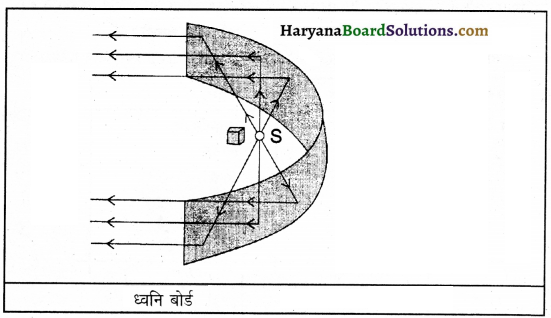
3. ध्वनि-पट्ट-ध्वनि का परावर्तन वक्राकार पृष्ठों से भी हो सकता है। इस तथ्य का उपयोग बड़े हॉलों में ध्वनि को पूरे हॉल में समान रूप से फैलाने में किया जाता है। इसके लिए ध्वनि-पट्टों को काम में लाया जाता है। वक्ता S ध्वनि-पट्ट के फोकस पर अवस्थित है।

अवतल परावर्तक ध्वनि पट्टों को बड़े हॉलों या सभा भवनों चित्र 12.22 की भांति वक्ता के पीछे रखा जाता है, ध्वनि-पट्ट ध्वनि को विभिन्न दिशाओं में फैलने से रोकते हैं। यह फोकस पर स्थित वक्ता की ध्वनि की तरंगों को श्रोताओं की ओर परावर्तित कर देता है, इनसे दूर बैठे श्रोताओं को भी वक्ता का भाषण स्पष्ट सुनाई देने में सहायता मिलती है।

प्रश्न 5.
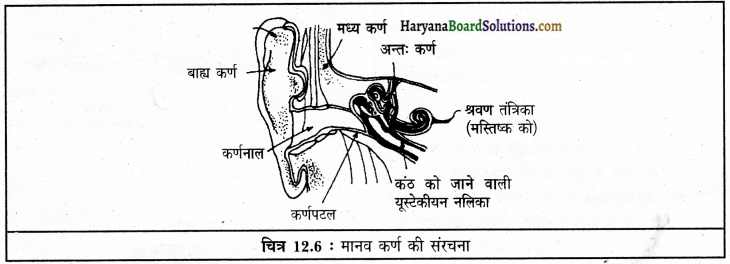
मानव कर्ण के विभिन्न भागों का वर्णन कीजिए।
उत्तर:
मानव कर्ण के मुख्य तीन भाग होते हैं-
1. बाह्य कर्ण-यह वह भाग है जो बाहर से दिखाई देता है। यह उपास्थि तथा मांसपेशियों का बना अर्धचंद्राकार भाग है। इसका निचला भाग लचीला व नर्म होता है।

बाह्य कर्ण के निम्नलिखित तीन भाग होते हैं-

• पिन्ना
• कर्णनाल
• कर्णपट।

(1) पिन्ना-यह उपास्थि एवं मांसपेशियों का बना होता है। इसका निचला भाग लचीला और नर्म होता है। पिन्ना ध्वनि की तरंगों को इकट्ठा करने तथा उनको दिशा प्रदान करने का कार्य करता है। पिन्ना कर्णनाल से जुड़ा होता है।

(2) कर्णनाल-कर्णनाल लगभग 3-4 सें०मी० लंबी तिरछी नली होती है। इस नली की त्वचा में बाल एवं सूक्ष्म ग्रंथियाँ होती हैं जिनमें कुछ अर्धद्रव पदार्थ निकलता रहता है। इसे कर्ण मोम या कान का मैल कहते हैं। यह कान को धूल कण व कीड़ों से बचाता है।

(3) कर्णपट-कर्णनाल के अंतिम सिरे पर झिल्ली का बना पर्दा होता है जिसे कर्णपट कहते हैं। यह ध्वनि की तरंगों को मध्य कान में पहुँचाता है।

2. मध्य कर्ण-मध्य कर्ण एक ऐसे कक्ष के समान है जिसमें हवा भरी रहती है। मध्य कर्ण एक नली द्वारा कंठ के साथ मिला रहता है। इस नली को यूस्टेकीयन नली कहते हैं। यह नली कर्णपट के दोनों ओर वायु के दबाव को बराबर रखती है। मध्य कर्ण में कान के पर्दे की अंदर की सतह की ओर तीन-तीन छोटी-छोटी हड्डियों की लाइन होती है जो कि भीतरी कान के साथ जुड़ी रहती है। इन छोटी-छोटी हड्डियों के नाम हैं-

• मैलियस
• इन्कस तथा
• स्टेपस।

3. आंतरिक कर्ण-यह कान का सबसे भीतरी भाग है और इसके मुख्य तीन भाग हैं-

• कौकिल्या
• कर्ण कुटी
• अर्ध-वृत्ताकार नलिकाएँ।

(1) सैकुलस अथवा कौकिल्या-ये घोंघे के कवच तथा शंख के आकार का होता है। इसके अंदर एक तरल पदार्थ होता है, जिसे एंडोलिंफ कहते हैं। यह श्रवण क्रिया में सहायक होता है।

(2) कर्ण कुटी-यह एक छोटी-सी कोष्ठिका है जो सामने से कौकिल्या से तथा पीछे से अर्ध-वृत्ताकार नलियों से जुड़ा रहता है।

(3) अर्ध-वृत्ताकार नलिकाएँ यह संख्या में तीन होती हैं और एक-दूसरे के साथ समकोण बनाती हैं। इनके अंदर भी एंडोलिंफ भरा रहता है। ये शरीर का संतुलन बनाए रखने में सहायता करती हैं। एंडोलिंफ के अंदर श्रवण तंत्रिकाओं के सिरे तैरते रहते हैं।

महत्त्वपूर्ण सारणी
सारणी : विभिन्न माध्यमों में 25°C पर ध्वनि की चाल

गणनात्मक प्रश्न

महत्त्वपूर्ण सूत्र एवं तथ्य:
(1) T = 2π\(\sqrt{\frac{L}{g}}\) (जहाँ g = 9.8m/s², L = लोलक की लंबाई, T = आवर्त काल)

(2) आवृत्ति v = \(\frac { 1 }{ T }\)

(3) यदि आवृत्ति = v (न्यू), तरंग वेग = υ, आवर्तकाल = T, तरंगदैर्ध्य = λ (लैम्डा) तो

• v = \(\frac { 1 }{ T }\)
• υ = v x λ
• υ = \(\frac { λ }{ T }\)
  तरंग संख्या = \(\frac { 1 }{ λ }\)

प्रश्न 1.
किसी ध्वनि तरंग की आवृत्ति 2kHz और उसकी तरंगदैर्ध्य 25 cm है। यह 1.5 km दूरी चलने में कितना समय लेगी?
हल:
दिया हुआ है,
आवृत्ति (v) = 2 kHz = 2000 Hz
तरंगदैर्ध्य (λ) = 25 cm = 0.25 m
हम जानते हैं, तरंग वेग (υ) = तरंगदैर्ध्य x आवृत्ति
υ = λ v
υ = 0.25 m x 2000 Hz = 500 m/s
तरंग को 1.5 km दूरी तय करने में लगने वाला समय
t = \(\frac{\mathrm{d}}{v}=\frac{1.5 \times 1000 \mathrm{~m}}{500 \mathrm{~m} / \mathrm{s}}=\frac{15}{5} \mathrm{~s}\)=3s
ध्वनि 1.5 km दूरी चलने में 3s समय लेगी।

प्रश्न 2.
एक मनुष्य किसी खड़ी चट्टान के पास ताली बजाता है और उसकी प्रतिध्वनि 6s के पश्चात् सुनाई देती है। यदि ध्वनि की चाल 346ms^-1 ली जाए, तो चट्टान तथा मनुष्य के बीच की दूरी कितनी होगी?
हल:
ध्वनि की चाल (υ) = 346ms^-1
प्रतिध्वनि सुनने में लिया गया समय (t) = 6s
ध्वनि द्वारा चली गई दूरी = υ x t = 346 m/s x 6s = 2076m
6s में ध्वनि ने चट्टान तथा मनुष्य के बीच की दुगुनी दूरी तय की। अतएव चट्टान तथा मनुष्य के बीच
की दूरी = \(\frac { 2076 }{ 2 }\)m = 1038m उत्तर

प्रश्न 3.
एक जहाज पराध्वनि उत्सर्जित करता है तो समुद्र तल से परावर्तित होकर 3.42s के पश्चात् संसूचित की जाती है। यदि समुद्र जल में पराध्वनि की चाल 1531m/s हो, तो समुद्र तल से जहाज की कितनी दूरी होगी?
हल:
प्रेषण तथा संसूचन के बीच लगा समय (t) = 3.42s
समुद्र जल में पराध्वनि की चाल (υ) = 1531m/s
पराध्वनि द्वारा चली गई दूरी = 2 x समुद्र की गहराई = 2d
जहाँ 2d = ध्वनि की चाल x समय
= 1531m/s x 3.42s = 5236m
d = 5236 m/2 = 2618m
अतः जहाज से समुद्र तल की दूरी = 2618m या 2.62km है।

प्रश्न 4.
दो बालक किसी लोहे के दो विपरीत सिरों पर हैं। एक बालक नलिका के एक सिरे को पत्थर से ठोकता है। ध्वनि के लोहे और वायु से होकर दूसरे बालक तक जाने में लगे समयों का अनुपात ज्ञात कीजिए।
[यदि वायु में ध्वनि का वेग 344 m/s तथा लोहे में ध्वनि का वेग 5130 m/s है।]
हल:
माना नलिका की लंबाई = L मीटर
वायु में ध्वनि का वेग (υ₁) = 344 m/s
लोहे में ध्वनि का वेग (υ₂) = 5130 m/s
∴ वायु में ध्वनि के गमन में लगा समय (T₁) = \(\frac{\mathrm{L}}{v_1}=\frac{\mathrm{L}}{344}\) सेकंड
और लोहे में ध्वनि के गमन में लगा समय (T₂) = \(\frac{\mathrm{L}}{v_2}=\frac{\mathrm{L}}{5130}\) सेकंड
∴ दोनों समय में अनुपात = \(\frac{\mathrm{T}_1}{\mathrm{~T}_2}=\frac{\frac{\mathrm{L}}{344}}{\frac{\mathrm{L}}{5130}}\)
= \(\frac{\mathrm{L}}{344} \times \frac{5130}{\mathrm{~L}}\)
= \(\frac{14.9}{1}\)
⇒ T₁ : T₂ = 14.9 : 1 उत्तर

प्रश्न 5.
किसी लंगर (खड़ी नाव) से जल तरंगें लगातार टकरा रही हैं। यदि इन तरंगों के दो क्रमागत शृंगों के बीच की – 100 m तथा जल में तरंगों का वेग 20 m/s है तो तरंगों के नाव से टकराने की आवृत्ति क्या है?
हल:
यहाँ पर तरंग के दो क्रमागत शृंगों के बीच की दूरी = तरंगदैर्ध्य (λ)
= 100 m
तरंग का वेग (υ) = 20 m/s
∴ तरंग की आवृत्ति (v) = \(\frac{υ}{λ}\) = \(\frac{20}{100}\)Hz
= 0.2 Hz (हर्ट्ज़) उत्तर

प्रश्न 6.
कोई तरंग-स्रोत 0.4 सेकंड में 40 शृंग और 40 गर्त उत्पन्न करता है। तरंग की आवृत्ति ज्ञात कीजिए।
हल:
यहाँ पर
तरंग के शृंगों की संख्या = तरंग के गर्तों की संख्या = 40
समय = 0.4 सेकंड
∴ प्रति सेकंड शृंगों की संख्या = प्रति सेकंड गर्मों की संख्या =\(\frac{40}{0.4}\)
= 100
अतः तरंग की आवृत्ति = 100 हर्ट्ज़ उत्तर

प्रश्न 7.
सोनार द्वारा पानी के पृष्ठ पर ध्वनि स्पंद उत्सर्जित किए जाते हैं। ये स्पंद पानी की तली से परावर्तन के पश्चात् संसूचित किए जाते हैं। यदि उत्सर्जन व संसूचन के बीच समय अंतराल 2 सेकंड है, तो पानी की गहराई कितनी है? (संकेत : पानी में ध्वनि का वेग 1498 m/s लीजिए)
हल:
पानी में ध्वनि का वेग (υ) = 1498 m/s
स्पंद पैदा होकर जाने तथा आने में लगा समय = 2 सेकंड
अतः स्पंद के जाने में लगा समय = \(\frac{2}{2}\) = 1 सेकंड
∴ पानी की गहराई = वेग x समय
= 1498 x 1 = 1498 मीटर उत्तर

प्रश्न 8.
कोई बच्चा किसी शक्तिशाली पटाखे के फटने के 4 सेकंड बाद उसकी किसी खड़ी चट्टान के कारण प्रतिध्वनि सुनता है। बच्चे से चट्टान की दूरी क्या है?
हल:
ध्वनि के जाने तथा आने में लगा कुल समय = 4 सेकंड
∴ ध्वनि के जाने में लगा समय = \(\frac{4}{2}\) = 2 सेकंड
वायु में ध्वनि का वेग = 344 m/s
∴ अतः बच्चे व चट्टान के बीच की दूरी = वेग x समय
= 344 x 2 = 688 मीटर उत्तर

प्रश्न 9.
कोई पत्थर किसी 44.1 मीटर गहरे कुएँ में डाला जाता है। यदि पत्थर के पानी से टकराने पर उत्पन्न ध्वनि, पत्थर गिराने के 3.13 सेकंड बाद सुनाई देती है, तो ध्वनि का वायु में वेग ज्ञात कीजिए। हल:
यहाँ पर
कुएँ की गहराई (s) = 44.1 मीटर
माना पत्थर को कुएँ के पानी तक पहुँचने में लगा समय = t₁ सेकंड
तथा ध्वनि को पानी से ऊपर तक आने में लगा समय = t₂ सेकंड
प्रश्नानुसार t₁ + t₂ = 3.13 सेकंड, u = 0, g = 9.8 m/s²
हम जानते हैं कि

प्रश्न 10.
यदि एक स्वरित्र द्विभुज 512 हज़ की आवृत्ति के साथ कंपन करके ऐसी ध्वनि तरंगें उत्पन्न करता है जो 330 मीटर प्रति सेकंड के वेग से चलती हैं तो उनकी तरंगदैर्ध्य क्या होगी?
हल:
यहाँ पर
आवृत्ति (v) = 512 हर्ट्ज़
तरंग वेग (υ) = 330 मीटर/सेकंड
तरंगदैर्ध्य (λ) = ?
हम जानते हैं कि
υ = vλ
या λ = \(\frac { υ }{v }\) = \(\frac { 330 }{512 }\) m = 0.645 m उत्तर

प्रश्न 11.
यदि किसी जल तरंग की तरंगदैर्ध्य 20 सें०मी० तथा आवृत्ति 20 हर्ट्ज़ हो तो उसका वेग क्या होगा?
हल:
यहाँ पर
तरंगदैर्ध्य (λ) = 20 सें०मी० = \(\frac { 20 }{ 100 }\) मीटर
= 0.2 मीटर
आवृत्ति (v) = 20 हज़
तरंग वेग (υ) = ?
हम जानते हैं कि
υ = vλ
= 20 x 0.2
= 4 मीटर/सेकंड उत्तर

प्रश्न 12.
किसी तरंग का आवर्तकाल 0.02 सेकंड हो तो उसकी आवृत्ति ज्ञात करो।
हल:
यहाँ पर
आवर्तकाल (λ) = 0.02 सेकंड
आवृत्ति (v) = ?
हम जानते हैं कि
v = \(\frac { 1 }{ T }\) = \(\frac { 1 }{ 0.02 }\)
= \(\frac { 100 }{ 2 }\) = 50 हर्ट्ज़ उत्तर

प्रश्न 13.
यदि किसी स्वरित्र द्विभुज की आवृत्ति 400 Hz है तथा हवा में ध्वनि की चाल 320 m/s है तो ध्वनि द्वारा तय की गई दूरी ज्ञात कीजिए जब स्वरित्र द्विभुज 20 कंपन पूरे करता है।
हल:
यहाँ पर
तरंग वेग (υ) = 320 मीटर/सेकंड
आवृत्ति (v) = 400 हर्ट्ज़
हज़ हम जानते हैं कि
υ = vλ
या λ = \(\frac { υ }{ v }\) = \(\frac { 320 }{ 400 }\) = 0.8 मीटर
अतः 1 कंपन में तय की दूरी = 0.8 मीटर
20 कंपनों में तय की गई दूरी = 20 x 0.8 = 16 मीटर उत्तर

प्रश्न 14.
एक वस्तु 1 मिनट में 6000 कंपन करती है। यदि वायु में उत्पन्न ध्वनि का वेग 330 m/s हो तो निम्नलिखित ज्ञात कीजिए।
(a) कंपनों की आवृत्ति
(b) उत्पन्न तरंगों की तरंगदैर्ध्य।
हल:
(a) 1 मिनट = 60 सेकंड में तय कंपनों की संख्या = 6000
∴ 1 सेकंड में तय कंपनों की संख्या = \(\frac { 6000 }{ 60 }\) = 100
अतः आवृत्ति (v) = 100 हर्ट्ज़

(b) यहाँ पर
तरंग वेग (υ) = 330 m/s
आवृत्ति (v) = 100 हज़
तरंगदैर्ध्य (λ) = ?
हम जानते हैं कि
υ = v λ
या λ = \(\frac { υ }{ v }\) = \(\frac { 330 }{ 100 }\) = 3.3 मीटर उत्तर

प्रश्न 15.
प्रकाशीय तरंग का वेग 3 x 10⁵ km/s है तथा तरंगदैर्ध्य 6 x 10^– मीटर है। इसकी आवृत्ति ज्ञात कीजिए।
हल:
यहाँ पर
तरंग वेग (υ) = 3 x 10⁵ km/s
= 3 x 10⁵ x 1000 m/s
= 3 x 10⁸ m/s
तरंगदैर्ध्य (λ) = 6 x 10^-7 m
आवृत्ति (v) = ?
हम जानते हैं कि
υ = v λ
या v = \(\frac{v}{\lambda}=\frac{3 \times 10^8}{6 \times 10^{-7}}\)
= 0.5 x 10¹⁵ हर्ट्ज़ उत्तर
अतः आवृत्ति 0.5 x 10¹⁵ हर्ट्ज़ है।

प्रश्न 16.
एक प्रेक्षक चट्टान के सामने 200 मीटर दूर खड़ा होता है। वह सीटी बजाता है। अगर ध्वनि 332 मीटर प्रति सेकंड के वेग से चलती हो तो वह सीटी की प्रतिध्वनि कितनी देर बाद सुन सकेगा?
हल:
चट्टान से प्रेक्षक की दूरी = 200 मीटर
इसलिए प्रतिध्वनि सुनने के लिए ध्वनि द्वारा
तय की गई कुल दूरी = 200 + 200 = 400 मीटर
ध्वनि की चाल = 332 मीटर प्रति सेकंड
समय =\(\frac { दूरी }{ चाल }\)
= \(\frac { 400 }{ 332 }\) सेकंड
= 1.2 सेकंड उत्तर
अतः प्रेक्षक अपनी ध्वनि उत्पन्न करने के 1.2 सेकंड बाद प्रतिध्वनि सुन सकेगा।

प्रश्न 17.
एक नाव से एक ध्वनि संकेत भेजा गया। यह संकेत समुद्र की तली से परावर्तन होने के 0.8 सेकंड के बाद नाव पर लौट आया। पानी में ध्वनि का वेग ज्ञात करो यदि समुद्र की गहराई 600 मीटर हो।
हल:
समुद्र की गहराई = 600 मीटर
इसलिए संकेत द्वारा समुद्र की तली से परावर्तित
होकर वापस आने में तय की गई कुल दूरी = 600 + 600 = 1200 मीटर
समय = 0.8 सेकंड
पानी में ध्वनि का वेग = \(\frac { दूरी }{ समय }\)
= \(\frac { 1200 }{ 0.8 }\) मीटर प्रति सेकंड
υ = 1500 मीटर प्रति सेकंड उत्तर

प्रश्न 18.
एक नाव से एक ध्वनि संकेत भेजा गया। यह संकेत समुद्र की तली से परावर्तन होने के 0.8 सेकंड के बाद नाव पर लौट आया। यदि पानी में ध्वनि का वेग 1500 मीटर प्रति सेकंड हो तो समुद्र की गहराई ज्ञात करो।
हल:
पानी में ध्वनि का वेग = 1500 मीटर प्रति सेकंड
लगा समय = 0.8 सेकंड ध्वनि द्वारा कुल तय दूरी = ध्वनि का वेग x समय
= 1500 x 0.8 = 1200 मीटर
अतः समुद्र की गहराई = \(\frac { 1200 }{ 2 }\) = 600 मीटर उत्तर

प्रयोगात्मक कार्य

क्रियाकलाप 1.
स्वरित्र द्विभुज द्वारा उत्पन्न कंपनों का अध्ययन करना।
कार्य-विधि-

• एक छोटी हल्की प्लास्टिक की गेंद को धागे से बांध कर लटकाओ।
• पहले कंपन न करते हुए स्वरित्र द्विभुज को गेंद के पास ले जाओ तथा स्थिति का अवलोकन करो।
• अब कंपन करते हुए स्वरित्र द्विभुज को गेंद के पास ले जाओ तथा स्थिति का अवलोकन करो।

पहली स्थिति में गेंद स्वरित्र द्विभुज से दूर नहीं भागती जबकि दूसरी स्थिति में गेंद स्वरित्र द्विभुज को पास ले जाने पर दूर भागती है क्योंकि कंपन करने से स्वरित्र द्विभुज की भुजा गेंद पर बल लगाकर पीछे की ओर धकेलती है।

क्रियाकलाप 2.
वाद्य यंत्रों में कंपन करने वाले भागों का अध्ययन करना।
कार्य-विधि-सुविधानुसार विद्यालय के संगीत कक्ष में जाओ और विभिन्न वाद्य यंत्रों में ध्वनि (संगीत) कैसे पैदा होती है अर्थात् किस भाग से होती है, के बारे में संगीत अध्यापक से जानो, जैसे

• ढोल में झिल्ली में कंपन के द्वारा।
• सितार में-तार में कंपन द्वारा।
• एकतारा में तार में कंपन द्वारा।
• बांसुरी में वायु स्तंभ द्वारा।
• जल तरंग में जल द्वारा।

क्रियाकलाप 3.
स्लिंकी द्वारा अनुदैर्ध्य तरंग उत्पन्न करना।

कार्य-विधि-

• एक स्लिंकी लो और इसका एक सिरा किसी विद्यार्थी को पकड़ाओ।
• विद्यार्थी की ओर स्लिंकी को तेजी से धक्का दो। बार-बार ऐसा करने पर विशेष गति स्लिंकी में दिखाई देगी। स्लिंकी पर एक स्थान पर चिह्न लगाओ और एक बार फिर क्रिया को दोहराओ। स्लिंकी पर लगा चिह्न विक्षोभ के संचरण की दिशा के समानांतर आगे-पीछे गति करता है। यही अनुदैर्ध्य तरंग है।

अध्याय का तांत्र अध्ययन

1. घंटी की ध्वनि ……….. है।
(A) यांत्रिक ऊर्जा
(B) ध्वनि ऊर्जा
(C) ऊष्मीय ऊर्जा
(D) प्रकाश ऊर्जा
उत्तर:
(B) ध्वनि ऊर्जा

2. ध्वनि निम्नलिखित के कारण उत्पन्न होती है-
(A) टकराने से
(B) कंपन से
(C) पीटने से
(D) रगड़ने से
उत्तर:
(B) कंपन से

3. ध्वनि संचरण नहीं होता है-
(A) ठोसों में
(B) द्रवों में
(C) गैसों में
(D) निर्वात में
उत्तर:
(D) निर्वात में

4. तरंग एक ………………… है।
(A) विक्षोभ
(B) संपीडन
(C) विरलन
(D) कंपन
उत्तर:
(A) विक्षोभ

5. उच्च दाब का क्षेत्र कहलाता है-
(A) तरंग
(B) संपीडन
(C) विरलन
(D) विक्षोभ
उत्तर:
(B) संपीडन

6. निम्नलिखित में से किसमें ध्वनि की गति सर्वाधिक होगी?
(A) शुष्क वायु में
(B) स्टील में
(C) आर्द्र वायु में
(D) जल में
उत्तर:
(B) स्टील में

7. ध्वनि संचरण के लिए सबसे अधिक सामान्य माध्यम कौन-सा है?
(A) जल
(B) पृथ्वी
(C) वायु
(D) अंतरिक्ष
उत्तर:
(C) वायु

8. जल में उत्पन्न तरंगें कौन-सी होती हैं?
(A) अनुदैर्ध्य
(B) अनुप्रस्थ
(C) (A) व (B) दोनों
(D) इनमें से कोई नहीं
उत्तर:
(B) अनुप्रस्थ

9. तरंग संचरण में स्थानांतरण होता है-
(A) द्रव्यमान का
(B) ऊर्जा का
(C) द्रव्यमान व ऊर्जा दोनों का
(D) इनमें से कोई नहीं
उत्तर:
(B) ऊर्जा का

10. तरंग वेग का SI मात्रक है-
(A) m
(B) m/s
(C) km
(D) km/s
उत्तर:
(B) m/s

11. निम्नलिखित में से किसको λ (लैम्डा) द्वारा प्रदर्शित किया जाता है?
(A) तरंगदैर्ध्य
(B) तरंग वेग
(C) आवृत्ति
(D) आयाम
उत्तर:
(A) तरंगदैर्ध्य

12. अनुदैर्ध्य तरंगें उत्पन्न होती हैं-
(A) ठोसों में
(B) द्रवों में
(C) गैसों में
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

13. अनुप्रस्थ तरंगें उत्पन्न होती हैं-
(A) ठोस व द्रवों में
(B) द्रव व गैसों में
(C) गैस व ठोसों में
(D) उपर्युक्त सभी
उत्तर:
(A) ठोस व द्रवों में

14. प्रकाश …………………….. तरंग है।
(A) अनुप्रस्थ
(B) यांत्रिक
(C) अनुदैर्ध्य
(D) विद्युत चुंबकीय
उत्तर:
(A) अनुप्रस्थ

15. किसी ध्वनि स्रोत की आवृत्ति 100 Hz है। आधे घंटे में यह कितनी बार कंपन करेगा?
(A) 1,80,000
(B) 90,000
(C) 60,000
(D) 1,00,000
उत्तर:
(A) 1,80,000

16. निम्नलिखित में से किसके बीच की दूरी तरंगदैर्ध्य कहलाती है?
(A) दो क्रमागत संपीडनों
(B) दो क्रमागत विरलनों
(C) एक संपीडन व एक विरलन
(D) (A) और (B) दोनों
उत्तर:
(D) (A) और (B) दोनों

17. तरंगदैर्ध्य का SI मात्रक …………………….. है।
(A) मीटर
(B) जूल
(C) अर्ग
(D) न्यूटन
उत्तर:
(A) मीटर

18. ध्वनि तरंग की आवृत्ति का मात्रक क्या है?
(A) हर्ट्ज़
(B) मी०
(C) अर्ग
(D) जूल
उत्तर:
(A) हर्ट्ज़

19. आवर्तकाल का SI मात्रक है-
(A) हज़
(B) मी०
(C) सेकंड
(D) Nm
उत्तर:
(C) सेकंड

20. किसी माध्यम में मूल स्थिति के दोनों ओर अधिकतम विक्षोभ को तरंग का/की …………………. कहते हैं।
(A) आवृत्ति
(B) आयाम
(C) वेग
(D) इनमें से कोई नहीं
उत्तर:
(B) आयाम

21. A के द्वारा किसको निरूपित किया जाता है?
(A) आवृत्ति
(B) वेग
(C) आयाम
(D) आवर्तकाल
उत्तर:
(C) आयाम

22. एकल आवृत्ति की ध्वनि को …………………. कहते हैं।
(A) स्वर
(B) टोन
(C) शोर
(D) इनमें से कोई नहीं
उत्तर:
(B) टोन

23. ………………. से कम आवृत्ति की ध्वनियों को अवश्रव्य ध्वनि कहते हैं।
(A) 20 Hz
(B) 200 Hz
(C) 2000 Hz
(D) 20000 Hz
उत्तर:
(A) 20 Hz

24. एकांक क्षेत्रफल से एक सेकंड में गुजरने वाली ध्वनि ऊर्जा को ध्वनि की ………………. कहते हैं।
(A) प्रबलता
(B) तीव्रता
(C) तारत्व
(D) आवृत्ति
उत्तर:
(B) तीव्रता

25. किस माध्यम में 25°C पर ध्वनि की चाल सर्वाधिक होती है?
(A) कांच
(B) स्टील
(C) ऐलुमिनियम
(D) निकेल
उत्तर:
(C) ऐलुमिनियम

26. किस द्रव में 25°C पर ध्वनि की चाल सर्वाधिक होती है?
(A) समुद्री जल
(B) आसुत जल
(C) इथेनॉल
(D) मीथेनॉल
उत्तर:
(A) समुद्री जल

27. किस गैस में ध्वनि की चाल 25°C पर सर्वाधिक होती है?
(A) ऑक्सीजन
(B) वायु
(C) हाइड्रोजन
(D) हीलियम
उत्तर:
(C) हाइड्रोजन

28. एकांक समय में होने वाले दोलनों की कुल संख्या को ………………. कहते हैं।
(A) आयाम
(B) तरंगदैर्ध्य
(C) आवर्ती
(D) आवर्तकाल
उत्तर:
(C) आवर्ती

29. ………………. को कम करने के लिए भवनों की दीवारों व छतों पर ध्वनि अवशोषक पदार्थ लगाए जाते हैं।
(A) प्रतिध्वनि
(B) ध्वनि परावर्तन
(C) अनुरणन
(D) पराध्वनि
उत्तर:
(C) अनुरणन

30. स्पष्ट प्रतिध्वनि सुनने के लिए परावर्तक स्रोत की न्यूनतम दूरी होनी चाहिए-
(A) 172 m
(B) 17.2 m
(C) 344 m
(D) 34.4 m
उत्तर:
(B) 17.2 m

31. ध्वनि परावर्तन सिद्धांत का उपयोग है-
(A) मेगाफोन व हॉर्न में
(B) स्टेथोस्कोप में
(C) कंसर्ट हॉल, सिनेमा हॉलों में
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

32. मनुष्य में ध्वनि की श्रव्यता का परिसर कितना है? (लगभग)
(A) 10^-15 Hz
(B) 20-20,000 Hz
(C) 30,000 Hz से-40,000 Hz
(D) 45,000 Hz-50,000 Hz तक
उत्तर:
(B) 20-20,000 Hz

33. किसी ध्वनि तरंग की तरंगदैर्ध्य तथा आवृत्ति उसके वेग से किस प्रकार संबंधित है?
(A) λ = vυ
(B) v = \(\frac { υ }{ λ }\)
(C) υ = λ v²
(D) v = υ λ
उत्तर:
(D) v = υ λ