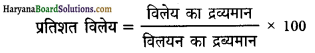Class 9

Haryana State Board HBSE 9th Class Maths Solutions Chapter 11 Constructions Ex 11.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 11 Constructions Exercise 11.2

Question 1.
Construct a triangle ABC in which BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Solution:
Steps of construction:
Step – I: Draw a line segment BC of length 7 cm.
Step – II: At B construct ∠CBX = 75° with BC.

Step – III: Cut BD = 13 cm from BX and join CD.
Step – IV: Draw the perpendicular bisector of CD intersecting BD at A.
Step – V: Join AC, then ABC is the required triangle.

Question 2.
Construct a triangle ABC in which BC = 8 cm, ∠B = 45° and AB – AC = 3.5 cm.
Solution:
Steps of construction:
Step – I: Draw a line segment BC = 8 cm.
Step – II: At point B construct ∠CBX = 45° with BC.

Step – III: Cut BD = 3.5 cm from BX and join CD.
Step – IV: Draw the perpendicular bisector of CD intersecting BX at point A.
Step – V: Join AC, then ABC is the required triangle.

Question 3.
Construct a triangle PQR in which QR = 6 cm, ∠Q = 60° and PR – PQ = 2 cm.
Solution:
Steps of construction:
Step – I: Draw a line segment QR = 6 cm.
Step – II: At the point Q construct ∠RQX = 60° with QR.

Step – III: Extend XQ to S to opposite side of QR such that QS = 2 cm.
Step – IV: Join SR and draw the perpendicular bisector of SR intersecting QX at P.
Step – V: Join PR, then PQR is the required triangle.

Question 4.
Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Solution:
Steps of construction:
Step – I: Draw a line segment PQ = 11 cm (= XY + YZ + ZX).
Step – II: At the point P construct ∠QPR = 30° and at the point Q construct ∠PQS = 90°.

Step – III: Draw the bisectors of ∠QPR and ∠PQS intersecting at point X.
Step – IV: Draw the perpendicular bisectors KL of PX and MN of XQ intersecting PQ at Y and Z respectively.
Step – V: Join XY and XZ, then XYZ is the required triangle.

Question 5.
Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.
Solution:
Steps of construction:

Step – I: Draw a line segment BC = 12 cm.
Step – II: At the point B, construct ∠CBP = 90° with BC.
Step – III: Cut BD = 18 cm from BP and join CD.
Step – IV: Draw the perpendicular bisector of CD intersecting BD at point A.
Step – V: Join AC, then ABC is the required triangle.

Haryana State Board HBSE 9th Class Science Important Questions Chapter 14 प्राकृतिक सम्पदा Important Questions and Answers.

Haryana Board 9th Class Science Important Questions Chapter 14 प्राकृतिक सम्पदा

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
प्राकृतिक संपदा किसे कहते हैं?
उत्तर:
प्रकृति में उपलब्ध उपयोगी पदार्थ, प्राकृतिक संपदा कहलाते हैं।

प्रश्न 2.
प्राकृतिक संपदाओं के उदाहरण दो।
उत्तर:
वायु, जल, मृदा, खनिज, वन आदि।

प्रश्न 3.
जीवन के लिए आवश्यक कारक कौन-कौन से हैं?
उत्तर:
परिवेश, ताप, पानी और भोजन।

प्रश्न 4.
स्थलमंडल किसे कहते हैं?
उत्तर:
पृथ्वी की सबसे बाहरी परत को स्थलमंडल कहते हैं।

प्रश्न 5.
पृथ्वी के कितने भाग पर जल है?
उत्तर:
75 प्रतिशत भाग पर।

प्रश्न 6.
जलमंडल किसे कहते हैं?
उत्तर:
पृथ्वी के जिस भाग पर जल पाया जाता है, जलमंडल कहलाता है।

प्रश्न 7.
वायुमंडल की परिभाषा लिखो।
उत्तर:
पृथ्वी को वायु का एक आवरण ढके रहता है, वह आवरण वायुमंडल कहलाता है।

प्रश्न 8.
जीवमंडल किसे कहते हैं?
उत्तर:
वायुमंडल, स्थलमंडल और जलमंडल एक-दूसरे से मिलकर जीवन को संभव बनाते हैं, इसे जीवमंडल कहते हैं।

प्रश्न 9.
जीवमंडल के निर्जीव घटकों के नाम लिखो।
उत्तर:
हवा, जल, मिट्टी।

प्रश्न 10.
वायु किसे कहते हैं?
उत्तर:
पृथ्वी पर पाए जाने वाली विभिन्न गैसों, जलवाष्पों व धूलकणों का मिश्रण वायु कहलाता है।

प्रश्न 11.
शुक्र और मंगल ग्रहों पर CO₂ की कितनी प्रतिशत मात्रा पाई जाती है?
उत्तर:
95 से 97 प्रतिशत।

प्रश्न 12.
क्या शुक्र और मंगल ग्रहों पर ऑक्सीजन पाई जाती है?
उत्तर:
नहीं।

प्रश्न 13.
पृथ्वी के वायुमंडल में CO₂ की प्रतिशत मात्रा कितनी है?
उत्तर:
0.033%।

प्रश्न 14.
क्या चंद्रमा की सतह पर वायुमंडल है?
उत्तर:
नहीं।

प्रश्न 15.
पवनें किसे कहते हैं?
उत्तर:
बहती हुई वायु को पवन या समीर कहते हैं।

प्रश्न 16.
वायु प्रदूषण किसे कहते हैं?
उत्तर:
वायु में अवांछनीय पदार्थों का मिलना वायु प्रदूषण कहलाता है।

प्रश्न 17.
वायु प्रदूषकों के नाम लिखो।
उत्तर:
अपशिष्ट गैसें (CO₂, नाइट्रोजन व सल्फर के ऑक्साइड, हाइड्रोकार्बन आदि) जलवाष्प, धूलकण आदि।

प्रश्न 18.
धूम कोहरा किसे कहते हैं?
उत्तर:
सर्दी के मौसम में जब पानी भी हवा के साथ संघनित हो जाए तो, इसे धूम कोहरा कहते हैं।

प्रश्न 19.
वायु प्रदूषण से होने वाली बीमारियों के नाम लिखो।
उत्तर:
श्वास रोग, कैंसर, हृदय रोग, एलर्जी।

प्रश्न 20.
मुख्य रूप से जल कितने प्रकार का होता है?
उत्तर:
दो, खारा और मीठा (अलवणीय)।

प्रश्न 21.
पृथ्वी की सबसे बाहरी परत को क्या कहते हैं?
उत्तर:
भू-पृष्ठ।

प्रश्न 22.
मृदा कैसे बनती है?
उत्तर:
चट्टानों के टूटने से।

प्रश्न 23.
ह्यूमस किसे कहते हैं?
उत्तर:
मृत जीवों के गलने-सड़ने से बने पदार्थ को ह्यूमस या जीवांश कहते हैं।

प्रश्न 24.
मृदा प्रदूषण किसे कहते हैं?
उत्तर:
मृदा में अवांछनीय पदार्थों का मिलना, मृदा प्रदूषण कहलाता है।

प्रश्न 25.
मृदा अपरदन को रोकने में सर्वाधिक सहायक कौन है?
उत्तर:
पेड़-पौधे।

प्रश्न 26.
भूमिगत जल को कैसे प्राप्त करते हैं?
उत्तर:
कुएँ खोद कर।

प्रश्न 27.
हमारे वायुमंडल में कितने प्रतिशत नाइट्रोजन है?
उत्तर:
78%।

प्रश्न 28.
ग्रीन हाउस प्रभाव के लिए सबसे अधिक कौन-सी गैस उत्तरदायी है?
उत्तर:
CO₂

प्रश्न 29.
ओजोन परत के ह्रास का प्रमुख कारक लिखो।
उत्तर:
क्लोरोफ्लोरो कार्बन (CFC)।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
प्राकृतिक संपदाएँ किसे कहते हैं?
उत्तर:
प्रकृति में अनेकों मनुष्योपयोगी पदार्थ पाए जाते हैं, जिन्हें प्राकृतिक संपदाएँ कहते हैं; जैसे वायु, जल, मृदा, वन खनिज और जीव-जंतु।

प्रश्न 2.
वायुमंडल किसे कहते हैं? वायुमंडल का जीवों के लिए क्या महत्त्व है?
उत्तर:
पृथ्वी के चारों ओर वायु का एक अदृश्य आवरण पाया जाता है, जिसे वायुमंडल कहते हैं। वायुमंडल पृथ्वी तल से 40 कि०मी० की ऊँचाई तक फैला है। समस्त वायु का 99% भाग इसी क्षेत्र में पाया जाता है। पृथ्वी से 1,000 कि०मी० ऊँचाई में भी वायु की कुछ मात्रा पाई जाती है। जलवाष्प और धूलकण केवल पृथ्वी तल के नजदीक ही पाए जाते हैं। 10-12 कि०मी० की ऊँचाई से ऊपर जलवाष्प नहीं पाए जाते। वायुमंडल में जीवन प्रदान करने वाली ऑक्सीजन गैस पाई जाती है। ओज़ोन की परत पृथ्वी को सूर्य की पराबैंगनी किरणों से बचाती है।

प्रश्न 3.
वायुमंडल में उपस्थित ऑक्सीजन के दो उपयोग लिखो।
उत्तर:
ऑक्सीजन के उपयोग निम्नलिखित हैं-

• ग्लूकोज़ अणुओं को तोड़कर उससे ऊर्जा प्राप्त करने में ऑक्सीजन का उपयोग होता है।
• दहन क्रिया में ऑक्सीजन का उपयोग होता है और कार्बन डाइऑक्साइड का उत्पादन होता है।

प्रश्न 4.
हवाओं का असमान विधि से गर्म होने के अतिरिक्त, चलने के अन्य क्या कारण हैं?
उत्तर:
पृथ्वी पर हवाएँ असमान विधि से गर्म होने के कारण चलती हैं परंतु इसके अन्य दो और भी कारण हैं-

• पृथ्वी की घूर्णन गति
• हवा के मार्ग में आने वाली पर्वत श्रृंखलाएँ।

प्रश्न 5.
वर्षा कैसे होती है? ओलावृष्टि किसे कहते हैं?
उत्तर:
दिन के समय विभिन्न जल-स्रोतों व वनस्पतियों का जल वाष्प बनकर वायु में मिल जाता है। गर्म हवा जलवाष्पों को अपने साथ ऊपर ले जाती है, जहाँ ठंड के कारण जलवाष्प संघनित होकर जल की बूंदें बन जाते हैं। यही पानी की बूंदें बड़ी होकर भारी हो जाती हैं। यही बूंदें वर्षा के रूप में पृथ्वी पर बरसती हैं। कई बार जल की बूंदें और ठंडी होकर ठोस बर्फ बन जाती हैं, जिन्हें ओले कहते हैं और ओलों की वर्षा ओलावृष्टि कहलाती है।

प्रश्न 6.
वायु प्रदूषण किसे कहते हैं? इसके कारकों का उल्लेख कीजिए।
उत्तर:
वायु प्रदूषण-अवांछित पदार्थों का वायु में मिलकर उसे जीवों के लिए हानिकारक बना देना, वायु प्रदूषण कहलाता है। वायु प्रदूषण के कारक-वायु प्रदूषण के प्राकृतिक कारक निम्नलिखित हैं-

• ज्वालामुखी क्रियाओं के साथ निकली गैसें तथा कण।
• आंधियाँ।
• जंगलों में लगने वाली आग से उत्पन्न धुआँ और गैसें।
• दलदलों से उत्पन्न मीथेन गैस।
• पौधों तथा जंतुओं का अपघटन तथा परागकण आदि।

वायु प्रदूषण के कृत्रिम कारक निम्नलिखित हैं-

• वाहनों का धुआँ।
• ईंधन का जलना।
• औद्योगिक धुएँ और वाष्पशील पदार्थ।
• धातु-निष्कर्षण क्रियाएँ।
• खनिजों के खनन से।
• कीटनाशक दवाइयाँ।
• परमाणु ऊर्जा उत्पन्न करते समय उत्सर्जित रेडियो विकिरण।

प्रश्न 7.
धूम कोहरा क्या है? इसके कुप्रभाव बताओ।
उत्तर:
धुएँ तथा धूलकणों का कोहरे में उपस्थित जल की बूंदों के साथ संयोग होने से धूम कोहरा बनता है। इसमें घरों, कारखानों तथा वाहनों में प्रयुक्त ईंधनों के दहन में बनी विषैली गैसें भी मिली होती हैं।
धुआँ तथा धूल + कोहरा तथा विषैली गैसें → धूम कोहरा
धूम कोहरे में उपस्थित विषैली गैसें सल्फर डाइऑक्साइड (SO₂) या परऑक्सी ऐसिटिल नाइट्रेट (PAN) होती है। यह धूम कोहरा वायुमंडल में ऊँचा नहीं उठता, परंतु महासागर के ऊपर एक प्रकार का बादल बना देता है। यह सामान्यतः शीतकाल में अधिक बनता है।

कुप्रभाव-धूम कोहरे के कुप्रभाव निम्नलिखित हैं-

• यह यातायात में बाधा डालता है क्योंकि इसके कारण बहुत कम दूरी तक दिखाई देता है।
• यह आँख, नाक तथा गले में जलन उत्पन्न करता है।
• धूम कोहरा उन सभी जीवों के लिए हानिकारक है, जिनके शरीर में यह सांस द्वारा प्रवेश कर सकता है। इससे दमा व हृदय संबंधी रोग उत्पन्न हो जाते हैं।
• पौधों की वृद्धि तथा विकास पर इसका बुरा प्रभाव पड़ता है।

प्रश्न 8.
अम्लीय वर्षा किसे कहते हैं?
उत्तर:
वातावरण में मिलने वाली अम्लीय गैसें; जैसे सल्फर डाइऑक्साइड, नाइट्रोजन डाइऑक्साइड, हाइड्रोजन क्लोराइड आदि वर्षा के जल की बूंदों में घुलकर अम्ल बनाती हैं, इन्हीं अम्लों की वर्षा अम्लीय वर्षा कहलाती है। अम्लीय वर्षा ऐतिहासिक इमारतों, चट्टानों एवं वनस्पति पेड़-पौधों के लिए हानिकारक होती है।

प्रश्न 9.
प्राकृतिक जल के मुख्य स्रोतों का वर्णन करो।
उत्तर:
प्राकृतिक जल के मुख्य स्रोत निम्नलिखित हैं-
1. वर्षा का जल-यह प्राकृतिक जल का सबसे शुद्ध रूप है। वर्षा का जल स्वाद रहित होता है। फिर भी, पृथ्वी तक पहुँचने के दौरान वर्षा के जल में वायु में उपस्थित ऑक्सीजन, नाइट्रोजन तथा कार्बन डाइऑक्साइड जैसी कुछ गैसें घुल जाती हैं। पृथ्वी की सतह पर पहुँचने वाला वर्षा का जल अशुद्ध होता है।

2. झरनों या कुओं का जल-वर्षा का जल रिसकर पृथ्वी के नीचे चला जाता है। इस प्रकार वर्षा का जल भू-तल से बहुत नीचे संगृहीत हो जाता है। यह भूमिगत जल काफी साफ होता है। इसमें बहुत कम निलंबित ठोस उपस्थित होते हैं।

3. नदियों का जल-पहाड़ों पर पड़ी बर्फ जब पिघलती है तो पानी बन जाता है। पहाड़ों से यह पानी नदियों में आता है। इस जल में पर्याप्त मात्रा में निलंबित मिट्टी के कण विद्यमान होते हैं। नदियों के पानी का प्रयोग सिंचाई के लिए किया जाता है।

4. समुद्रीय जल-समस्त नदियों का पानी अंततः समुद्र में पहुंचता है। जहां नदी समुद्र से मिलती है, उस स्थान पर नदी द्वारा लाई गई मिट्टी तथा तलछट एकत्रित हो जाते हैं। नदियों के जल में घुले पदार्थ विशेषकर लवण समुद्र के पानी में पहुँच जाते हैं।

प्रश्न 10.
जल प्रदूषण किसे कहते हैं? जल प्रदूषण के कारण लिखो।
उत्तर:
जल प्रदूषण-जल में अवांछनीय पदार्थों का मिलना जल प्रदूषण कहलाता है। जल प्रदूषण के निम्नलिखित कारण हैं-

• उद्योग-धंधों से निकला कचरा व रासायनिक पदार्थ आदि।
• कृषि अपशिष्ट; जैसे उर्वरक, कीटनाशक, पीड़कनाशी, खरपतवारनाशी आदि।
• घरेलू गंदगी व सीवेज मल-जल; जैसे कूड़ा-कचरा, पॉलिथीन आदि।
• तापीय गंदगी; जैसे विद्युत ताप घरों का गर्म जल आदि।
• रेडियोधर्मी अपशिष्ट; जैसे रेडियो एक्टिव पदार्थों का कचरा।
• सामाजिक-धार्मिक अपशिष्ट, मेलों का अपशिष्ट, मृत मनुष्यों के शव, मृत पशु आदि को नदियों में डालना।
• प्राकृतिक स्रोत; जैसे खनन, आँधी-तूफान, आपदाओं आदि से निकला कचरा व अपशिष्ट मल, मृत पशु आदि।

प्रश्न 11.
ह्यूमस की उपयोगिता लिखो।
उत्तर:
ह्यूमस की उपयोगिता निम्नलिखित है-

• मिट्टी में ह्यूमस मिलने से मिट्टी सरंध्र बन जाती है, जो हवा और पानी को भूमि के भीतर जाने में मदद करता है।
• ह्यूमस में पौधों के लिए आवश्यक पोषक तत्व पाए जाते हैं।
• ह्यूमस से अनेकों जीव पोषण ग्रहण करते हैं जैसे; केंचुआ।
• रेतीली मिट्टी में ह्यूमस मिलाने से मिट्टी में जल धारण करने की क्षमता बढ़ जाती है।
• रेतीली मिट्टी में ह्यूमस मिलने से मृदा अपरदन भी कम होता है।

प्रश्न 12.
मृदा प्रदूषण के चार सामान्य स्रोत लिखें।
उत्तर:
मृदा प्रदूषण के चार सामान्य स्रोत निम्नलिखित हैं-

• मृदा में उर्वरकों का अत्यधिक प्रयोग करना।
• मृदा पर फसलों को बचाने के लिए अत्यधिक कीटनाशकों व पीड़कनाशकों का छिड़काव करना।
• मृदा में रसोई घर तथा घर के अन्य कूड़े-कचरे को मिलाना।
• उद्योगों से निकले अपशिष्ट पदार्थों को मृदा में मिलने देना।

प्रश्न 13.
जल-चक्र के विषय में आप क्या जानते हो?
उत्तर:
पृथ्वी पर जल के विभिन्न स्रोत तालाब, झील, नदी तथा सागर हैं। जल-चक्र के अनुसार इन स्रोतों का पानी वाष्पित होकर जलवाष्प बनाता है। ये जलवाष्प बादल बनाते हैं। ठंडे होने पर बादल संघनितं होकर जल की बूंदें बनाते हैं। वर्षा के रूप में जल पुनः पृथ्वी तल पर वापिस आ जाता है। जल के इस चक्र को ‘जल-चक्र’ कहते हैं।

प्रश्न 14.
नाइट्रोजन किन-किन पदार्थों में पाया जाता है?
उत्तर:
नाइट्रोजन प्रमुख रूप से प्रोटीन, न्यूक्लिक अम्ल, डी०एन०ए०, आर०एन०ए०, विटामिन आदि में पाया जाता है। ऐल्केलाइड और यूरिया में भी नाइट्रोजन पाया जाता है।

प्रश्न 15.
पृथ्वी पर कार्बन कौन-कौन सी अवस्थाओं में पाई जाती है?
उत्तर:
पृथ्वी में कार्बन मूल रूप से हीरा व ग्रेफाइट में, यौगिक रूप में कार्बन डाइऑक्साइड, कार्बोनेट्स में, कार्बन आधारित अवयवों कार्बोहाइड्रेट्स, वसा, न्यूक्लिक अम्ल और विटामिनों में पाई जाती है। कार्बन सभी उन उत्पादों में भी पाई जाती है, जो प्रकाशसंश्लेषण क्रिया से बनते हैं; जैसे मंड, ग्लूकोस आदि।

प्रश्न 16.
हरे पौधे किस प्रकार मंड का निर्माण करते हैं?
उत्तर:
पौधे कार्बन डाइऑक्साइड के रूप में वायुमंडल से कार्बन ग्रहण करते हैं। सूर्य के प्रकाश से प्राप्त ऊर्जा के द्वारा पौधे इस कार्बन डाइऑक्साइड का संयोग जल के अणुओं से करते हैं, जिसके फलस्वरूप कार्बोहाइड्रेट और वसा के अणुओं का निर्माण होता है।

ये कार्बोहाइड्रेट तथा वसा ही जीवधारियों को ऊर्जा प्रदान करते हैं, जिससे जीवधारियों की जीवन प्रक्रियाएँ संपन्न होती हैं।

प्रश्न 17.
ग्रीन हाउस प्रभाव के दो लाभ लिखो।
उत्तर:
ग्रीन हाउस प्रभाव के दो लाभ निम्नलिखित हैं-

• ग्रीन हाउस प्रभाव सूर्य की अवरक्त विकिरणों को प्रगृहीत करके पृथ्वी की सतह तथा वायुमंडल का ताप बढ़ा देता है, जिससे ठंडी जलवायु में भी जीवन बना रहता है।
• ग्रीन हाउस प्रभाव के कारण पर्वतों की बर्फीली चोटियों पर पड़ी बर्फ धीरे-धीरे पिघलती रहती है, जिससे नदियों में सारा वर्ष पानी बना रहता है।

प्रश्न 18.
पृथ्वी पर ऑक्सीजन किन रूपों में पाई जाती है?
उत्तर:
हमारे वायुमंडल में ऑक्सीजन 21 प्रतिशत पाई जाती है। यौगिक रूप में कार्बन डाइऑक्साइड में ऑक्सीजन विद्यमान है। पटल में धातुओं और सिलिकॉन के ऑक्साइड, कार्बोनेट, सल्फेट, नाइट्रेट और कुछ अन्य खनिजों में भी ऑक्सीजन पाई जाती है। जैविक अणु; जैसे कार्बोहाइड्रेट्स, प्रोटीन, न्यूक्लिक अम्ल और वसा में भी ऑक्सीजन विद्यमान है।

प्रश्न 19.
क्या होगा यदि वायुमंडल से ओजोन परत लुप्त हो जाए?
उत्तर:
पृथ्वी की सतह से 15 कि०मी० की ऊँचाई पर ओज़ोन-(O₃) की परत है। यह ऊँचाई के साथ-साथ मोटी होती जाती है। 23 कि०मी० की ऊँचाई पर यह सबसे अधिक मोटी है। यह परत सूर्य के प्रकाश में उपस्थित पराबैंगनी प्रकाश को अवशोषित र लेती है। यह पराबैंगनी प्रकाश जीवों में त्वचा कैंसर उत्पन्न कर देता है।

इसलिए यदि वायुमंडल से ओज़ोन परत लुप्त हो जाए तो एक रक्षात्मक आवरण समाप्त हो जाएगा। हानिकारक पराबैंगनी प्रकाश हम तक पहुँचकर हममें व अन्य जीवों में त्वचा कैंसर उत्पन्न कर देगा। इससे वायुमंडल को भारी नुकसान होगा। साथ ही पराबैंगनी विकिरण मोतियाबिंद और ताप दाह रोग का कारण बनेगा। पेड़-पौधों की कोशिकाओं का विभाजन भी रुक जाएगा।

निबंधात्मक प्रश्न

प्रश्न 1.
प्रकृति में जल-चक्र किस प्रकार संपन्न होता है?
उत्तर:
जल, पर्यावरण में लगातार परिवहित होता रहता है। इसको जलीय चक्र (Hydrological Cycle) कहते हैं।

जल में मुख्य तत्त्व हाइड्रोजन है जिसका चक्रण पानी के यौगिक के रूप में प्रवाहित होने के साथ होता है। जलाशयों (सागर, समुद्र, झील, नदियाँ) तथा जैव जीवों के शरीर की सतह से जल का लगातार वाष्पन होता रहता है तथा वायु में मिलता रहता है। इसके अतिरिक्त पौधों द्वारा भूमि में से अवशोषित जल भी वाष्पोत्सर्जन द्वारा (पत्तों के रंध्रों से) वायु में मिलता रहता है।

जंतुओं द्वारा भोजन के साथ ग्रहण किया गया जल भी श्वसन क्रिया द्वारा वाष्पों के रूप में वायुमंडल में मिलता रहता है। इस प्रकार विभिन्न स्रोतों से जल वाष्पों के रूप में वायुमंडल में मिलता रहता है। वायुमंडल में उपस्थित जलवाष्प न्यून ताप पर संघनित होकर जल की बूंदें बनाते हैं। ये बूंदें वर्षा अथवा हिम के रूप में बरसती हैं और इस प्रकार जल पुनः पृथ्वी (मृदा एवं जलाशय) पर वापिस आ जाता है। इस प्रकार जीवमंडल में जल-चक्र चलता रहता है।

प्रश्न 2.
नाइट्रोजन चक्र का संक्षिप्त विवरण कीजिए।
उत्तर:
प्रोटीन नाइट्रोजन के यौगिक हैं। ये पौधे तथा प्राणियों के शरीर का एक मुख्य अंग हैं। प्रोटीन की कमी से पौधों तथा जंतुओं की वृद्धि रुक जाती है, क्योंकि प्रोटीन से ही जीवों में वृद्धि होती है। जंतु पौधों से भोजन प्राप्त करते हैं। इसमें प्रोटीन भी होती है। जब पौधे तथा जंतु मरकर गलते-सड़ते हैं तो विशेष प्रकार के अपघटक जीवाणु व कवक (Saprophytic Bacteria) इन्हें अमोनिया के लवणों में बदल देते हैं।

इन लवणों को नाइट्रेट बनाने वाले जीवाणु (Nitrifying Bacteria) नाइट्रेट में बदल देते हैं। इन नाइट्रेटों का कुछ भाग तो पौधों की जड़ों के रोम ग्रहण करके उन्हें प्रोटीन में बदल देते हैं। शेष नाइट्रेट विनाइट्रीकारक जीवाणुओं द्वारा नाइट्रोजन में बदल जाते हैं। इस प्रकार नाइट्रोजन पुनः वायुमंडल में आ जाती है। वायुमंडलीय नाइट्रोजन को स्थिर करने वाले जीवाणु मिट्टी तथा अन्य फलीदार पौधों (लैग्यूम) की जड़ों में पाई जाने वाली मूल-ग्रंथियों में पाए जाते हैं।

ये जीवाणु स्वतंत्र नाइट्रोजन को इसके यौगिकों में बदल देते हैं, जिन्हें पौधे ग्रहण कर लेते हैं। वायुमंडलीय नाइट्रोजन का कुछ भाग आकाशीय बिजली द्वारा भूमि में स्थिर होता रहता है। फैक्ट्रियों में बनाए जाने वाले उर्वरक भी नाइट्रोजन का स्थिर रूप हैं। यह नाइट्रोजन पौधों द्वारा अवशोषित होकर नाइट्रोजन खाद्य जाल में से गुजरती है। इस प्रकार प्रकृति में यह नाइट्रोजन चक्र लगातार चलता रहता है।

प्रश्न 3.
जीवमंडल में कार्बन चक्र किस प्रकार संपन्न होता है? विवरण दीजिए।
उत्तर:
कार्बन सभी जीवों के शरीर का एक मुख्य तत्त्व है। जीवों में यह कार्बोहाइड्रेट्स, वसा, प्रोटीन तथा न्यूक्लिक अम्लों के रूप में पाया जाता है। इसका स्थानांतरण आहार श्रृंखला के माध्यम से होता है। वायुमंडल में यह CO₂ के रूप में पाई जाती है। महासागरों में यह जैव कार्बन व कार्बोनेटों के रूप में मिलती है। हरे पौधे प्रकाशसंश्लेषण की विधि में CO₂ का उपयोग करके कार्बोहाइड्रेट्स का निर्माण करते हैं।

ये कार्बोहाइड्रेट्स फिर जंतुओं में स्थानांतरित हो जाते हैं। अपघटक इन्हें फिर से पर्यावरण में मुक्त कर देते हैं। सभी जीव अपनी श्वसन प्रक्रिया के दौरान CO₂ उत्पन्न करते हैं। कार्बन-युक्त ईंधनों के दहन से भी वायुमंडल में CO₂ की मात्रा बढ़ती है। ज्वालामुखी विस्फोट भी CO₂ की प्राप्ति का मुख्य साधन है।

प्रश्न 4.
प्रकृति में ऑक्सीजन चक्र का एक नामांकित चित्र बनाइए।
उत्तर:
प्रकृति में ऑक्सीजन वायुमंडल के गैसीय घटकों का लगभग 21% भाग है। यह जल भंडारों में घुली होती है, जिसका उपयोग जलीय जीव श्वसन में करते हैं। यह जैव शरीरों में CO₂ तथा H₂O के यौगिक रूप में प्रवेश और निर्गम करती है। जीवमंडल में ऑक्सीजन उपलब्ध कराने वाले प्रमुख स्रोत हरे पौधे हैं। ऑक्सीजन चक्र के दो चरण अग्रलिखित हैं-

1. ऑक्सीजन का वायुमंडल में आगमन-विभिन्न माध्यमों से पहुँची कार्बन डाइऑक्साइड का उपयोग हरे पौधे प्रकाशसंश्लेषण क्रिया में करते हैं। प्रकाशसंश्लेषण क्रिया में ऑक्सीजन सह-उत्पाद के रूप में उत्पन्न होती है।

2. ऑक्सीजन का वायुमंडल से निर्गमन-वायुमंडलीय ऑक्सीजन का उपयोग सभी जीवधारी श्वसन में करते हैं.और CO₂ के रूप में वायुमंडल में छोड़ते हैं। इसी प्रकार जल भंडारों में विलेय ऑक्सीजन का उपयोग जलीय जीव करते हैं और CO₂ के रूप में जल में ही छोड़ते हैं।
कोयला, लकड़ी तथा अन्य ईंधनों के दहन में भी वायुमंडलीय ऑक्सीजन का उपयोग किया जाता है और CO₂ के रूप में वायुमंडल में छोड़ दी जाती है।
इस प्रकार वायुमंडल में ऑक्सीजन के आगमन और निर्गमन से वायुमंडलीय संतुलन बना रहता है।

प्रयोगात्मक कार्य

क्रियाकलाप 1.
संवहन धाराओं का अध्ययन करना।
कार्य-विधि-एक बीकर में एक मोमबत्ती रख कर जलाएँ और एक अगरबत्ती को जलाकर बीकर के मुँह के पास ले जाओ। और अवलोकन करो

• अगरबत्ती को बीकर के मुँह के पास ले जाने पर धुआँ पीछे को जाता है क्योंकि गर्म हवा बाहर निकल रही है।
• अगरबत्ती को मोमबत्ती के ऊपर रखने से धुआँ एकदम ऊपर की ओर जाता है क्योंकि मोमबत्ती की ज्वाला से ऊपर की वायु तेजी से गर्म होकर सीधी ऊपर की ओर जाती है।
• दूसरे भागों में अगरबत्ती को रखने पर धुआँ पीछे की ओर ही जाता है क्योंकि बीकर के अंदर की सारी वायु गर्म होकर बाहर निकल रही है।

क्रियाकलाप 2.
कोहरा बनने की प्रक्रिया का अध्ययन करना।
कार्य-विधि-

• पतले प्लास्टिक के बोतल में 5 से 10 मि०ली० पानी लेकर ढक्कन बंद कर दें।
• इसे अच्छी तरह हिलाएँ और एक जलती अगरबत्ती का थोड़ा धुआँ, ढक्कन खोलकर अंदर जाने दें। ढक्कन बंद कर दें।
• बोतल को हथेलियों के बीच रखकर जोर से दबाएँ। थोड़ी देर के बाद पुनः बोतल को दबाएँ और अवलोकन करें। जलवाष्प संतप्त होने और दबाव बढ़ने पर बोतल में कोहरा बनता है और बोतल को थोड़ी देर रखने पर कोहरा समाप्त हो जाता है। बोतल को हिलाने या दबाने पर बोतल में दाब बढ़ जाता है। अगरबत्ती के धुएँ के कणों के चारों तरफ जलवाष्प एकत्रित होने पर ही कोहरा बना।

क्रियाकलाप 3.
वर्षामापन यंत्र बनाना तथा अपने नगर व राज्य की सबसे अधिक वर्षा का समय नोट करना।
कार्य-विधि-काँच के बीकर के मुँह के आकार की एक काँच की कीप को बीकर के मुँह में अच्छे से फिट करो तथा बीकर की दीवार पर चिह्न लगाकर पैमाना बनाओ।

वर्षामापन-वर्षा शुरू होते ही वर्षामापन यंत्र को ऐसे स्थान पर रखो, जहाँ बिना किसी बाधा के वर्षा जल कीप में गिरे। वर्षा की समाप्ति पर पाठ्यांक नोट करो। इस यंत्र द्वारा निर्धारित समय (महीनों) की प्रतिदिन की वर्षा की मात्रा को नोट करो। इस प्रकार सर्वाधिक वर्षा वाला दिन मालूम हो जाएगा।

किसी राज्य की सर्वाधिक वर्षा नोट करने के लिए राज्य के प्रमुख नगरों में वर्षा की मात्रा नोट कर औसत वर्षा ज्ञात की जाती है।

अध्याय का तीव्र अध्ययन

1. शुक्र और मंगल के वायुमंडल से भिन्न हमारे वायुमंडल में पाई जाने वाली गैस है-
(A) कार्बन डाइऑक्साइड
(B) ऑक्सीजन
(C) ऑर्गन
(D) नाइट्रोजन
उत्तर:
(B) ऑक्सीजन

2. वायु प्रवाह का कारण होता है-
(A) दाब अंतर
(B) ताप अंतर
(C) घनत्व अंतर
(D) सतह अंतर
उत्तर:
(A) दाब अंतर

3. निम्नलिखित में से कौन वायु को प्रदूषित करते हैं?
(A) जीवाश्म ईंधनों का जलना
(B) वाहनों का चलना
(C) कारखानों का धुआँ
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

4. शुद्ध जल का स्रोत होता है-
(A) वर्षा
(B) तालाब
(C) नदियाँ
(D) झीलें
उत्तर:
(A) वर्षा

5. केंचुए किस कार्य में सहायक होते हैं?
(A) नाइट्रोजन बनाने में
(B) ह्यूमस बनाने में
(C) उर्वरता कम करने में
(D) उपर्युक्त सभी
उत्तर:
(B) ह्यूमस बनाने में

6. वर्षा का पैटर्न किस कारक पर निर्भर करता है?
(A) पवन पैटर्न पर
(B) जंगल पैटर्न पर
(C) वाष्पन पैटर्न पर
(D) लोगों के रहन-सहन पैटर्न पर
उत्तर:
(A) पवन पैटर्न पर

7. मिट्टी का निर्माण होता है-
(A) चट्टानों के टूटने-फूटने से
(B) वर्षा से
(C) वायु से
(D) जल से
उत्तर:
(A) चट्टानों के टूटने-फूटने से

8. मिट्टी अपरदन के प्रमुख कारण हैं-
(A) बाढ़ें
(B) तेज हवाएँ
(C) वनों की कटाई
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

9. जैविक रूप में महत्त्वपूर्ण दो यौगिक जिनमें ऑक्सीजन और नाइट्रोजन दोनों हैं-
(A) नाइट्रेट्स और नाइट्राइट्स
(B) अमोनिया व कार्बन डाइऑक्साइड
(C) नाइट्रोजन डाइऑक्साइड व अमोनिया
(D) यूरिया व अमोनिया
उत्तर:
(A) नाइट्रेट्स और नाइट्राइट्स

10. वायुमंडल में उपस्थित CO₂ द्वारा पृथ्वी तल से परावर्तित अवरक्त प्रकाश को अवशोषित कर वायुमंडल का ताप बढ़ना कहा जाता है-
(A) ओजोन छिद्र
(B) ग्रीन हाउस प्रभाव
(C) पराबैंगनी प्रभाव
(D) अवशोषण प्रभाव
उत्तर:
(B) ग्रीन हाउस प्रभाव

11. जीवन के लिए वायुमंडल से हमें प्राप्त होती है-
(A) CO₂
(B) O₃
(C) O₂
(D) N₂
उत्तर:
(C) O₂

12. प्राकृतिक संपदाएँ हैं-
(A) वायु
(B) जल
(C) खनिज
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

13. पृथ्वी की सबसे बाहरी परत को कहा जाता है-
(A) जलमंडल
(B) स्थलमंडल
(C) वायुमंडल
(D) ओज़ोन मंडल
उत्तर:
(B) स्थलमंडल

14. पृथ्वी के लगभग कितने भाग पर जल है?
(A) 75%
(B) 25 %
(C) 50%
(D) 20 %
उत्तर:
(A) 75%

15. जीवमंडल के निर्जीव घटक हैं-
(A) हवा
(B) जल
(C) मिट्टी
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

16. दहन क्रिया में उत्पन्न होने वाली गैस है-
(A) ऑक्सीजन
(B) नाइट्रोजन
(C) कार्बन डाइऑक्साइड
(D) हीलियम
उत्तर:
(C) कार्बन डाइऑक्साइड

17. ओजोन का सूत्र होता है
(A) O₂
(B) O₃
(C) O₄
(D) O₅
उत्तर:
(B) O₃

18. प्रकाशसंश्लेषण के लिए आवश्यक है-
(A) सूर्य का प्रकाश
(B) क्लोरोफिल
(C) जल व कार्बन डाइऑक्साइड
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

19. नाइट्रोजन और सल्फर के ऑक्साइड उपस्थित होते हैं
(A) अम्लीय वर्षा में
(B) क्षारीय वर्षा में
(C) सामान्य वर्षा में
(D) उपर्युक्त सभी
उत्तर:
(A) अम्लीय वर्षा में

20. पृथ्वी के वायुमंडल में CO₂ की प्रतिशत मात्रा है-
(A) 78%
(B) 21%
(C) 0.33%
(D) 0.033%
उत्तर:
(D) 0.033%

21. दिन के समय हवा की दिशा होती है-
(A) समुद्र से स्थल की ओर
(B) स्थल से समुद्र की ओर
(C) उत्तर से पश्चिम की ओर
(D) पश्चिम से उत्तर की ओर
उत्तर:
(A) समुद्र से स्थल की ओर

22. वायु प्रदूषक है-
(A) CO
(B) NO₂
(C) SO₂
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

23. मृदा में अवांछनीय पदार्थों का मिलना कहलाता है-
(A) जल प्रदूषण
(B) वायु प्रदूषण
(C) मृदा प्रदूषण
(D) ध्वनि प्रदूषण
उत्तर:
(C) मृदा प्रदूषण

24. जीवाणुओं द्वारा वायुमंडल की नाइट्रोजन को नाइट्रेट्स व नाइट्राइट्स में बदलना कहलाता है-
(A) ऑक्सीजन स्थिरीकरण
(B) विनाइट्रीकरण
(C) नाइट्रोजन स्थिरीकरण
(D) अमोनीकरण
उत्तर:
(C) नाइट्रोजन स्थिरीकरण

25. वायुमंडल में ऑक्सीजन की प्रतिशत मात्रा है-
(A) 78 प्रतिशत
(B) 21 प्रतिशत
(C) 0.033 प्रतिशत
(D) 0.01 प्रतिशत
उत्तर:
(B) 21 प्रतिशत

26. ओजोन परत सौर प्रकाश के कौन-से घटक को अवशोषित करती है?
(A) दृश्य प्रकाश को
(B) अवरक्त विकिरण को
(C) पराबैंगनी विकिरण को
(D) इनमें से कोई नहीं
उत्तर:
(C) पराबैंगनी विकिरण को

27. मृदा एक प्राकृतिक संपदा होती है जो
(A) पौधों को आवश्यक पोषक तत्त्व प्रदान करती है
(B) जीवित रहने के लिए व विकास के लिए आवश्यक है
(C) खाद्य-पदार्थों को प्रदान करती है
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

28. ऊर्जा का नवीकरणीय स्रोत है-
(A) मिट्टी का तेल
(B) कोयला
(C) प्राकृतिक गैस
(D) बायोगैस
उत्तर:
(D) बायोगैस

29. किस ग्रह पर जीवन विद्यमान है?
(A) मंगल पर
(B) पृथ्वी पर
(C) बुध पर
(D) शुक्र पर
उत्तर:
(B) पृथ्वी पर

30. जीवमंडल के जैविक घटक होते हैं-
(A) निर्जीव
(B) सजीव
(C) हवा
(D) जल
उत्तर:
(B) सजीव

31. शुक्र ग्रह पर 95% से 97% के लगभग होती है-
(A) नाइट्रोजन गैस
(B) ऑक्सीजन गैस
(C) कार्बन डाइऑक्साइड गैस
(D) ऑर्गन गैस
उत्तर:
(C) कार्बन डाइऑक्साइड गैस

32. रात के समय हवा की दिशा होती है-
(A) समुद्र से स्थल की ओर
(B) स्थल से समुद्र की ओर
(C) उत्तर से पश्चिम की ओर
(D) पश्चिम से उत्तर की ओर
उत्तर:
(B) स्थल से समुद्र की ओर

33. समुद्रों में सामान्यतः कैसा पानी मिलता है?
(A) शुद्ध
(B) अशुद्ध
(C) (A) व (B) दोनों
(D) (A) व (B) दोनों में से कोई नहीं
उत्तर:
(B) अशुद्ध

34. कीटनाशकों और उर्वरकों के अधिक प्रयोग से बढ़ावा मिलता है-
(A) वायु प्रदूषण को
(B) ध्वनि प्रदूषण को
(C) जल प्रदूषण को
(D) इनमें से किसी को भी नहीं
उत्तर:
(C) जल प्रदूषण को

35. ओजोन परत में छिद्र किस स्थान पर देखा गया?
(A) विषुवत रेखा के ऊपर
(B) प्रशांत महासागर के ऊपर
(C) अंटार्कटिका के ऊपर
(D) हिंद महासागर के ऊपर
उत्तर:
(C) अंटार्कटिका के ऊपर

36. अम्लीय वर्षा का निम्न में से कौन-सा कारण है?
(A) वायु में नाइट्रोजन व सल्फर के ऑक्साइड
(B) वायु में लटके हुए कणों की मात्रा बढ़ना
(C) वायु में हाइड्रोकार्बन की अधिक मात्रा
(D) वायु में CO₂ गैस की अधिक मात्रा होना
उत्तर:
(A) वायु में नाइट्रोजन व सल्फर के ऑक्साइड

37. निम्नलिखित में से कौन-सा एक कथन जल प्रदूषण के बारे में सही नहीं है?
(A) जलाशयों में अनैच्छिक पदार्थों का मिलना
(B) पानी में घुली हुई ऑक्सीजन कम होना
(C) पानी के तापमान में परिवर्तन
(D) आक्सी-श्वसन जीवाणु (ऐरोबिक बैक्टीरिया) की संख्या बढ़ना
उत्तर:
(D) आक्सी-श्वसन जीवाणु (ऐरोबिक बैक्टीरिया) की संख्या बढ़ना

38. ग्रीन हाउस प्रभाव का निम्नलिखित में कौन-सा एक कारण है?
(A) हरे पौधे
(B) अवरक्त किरणें
(C) पैराबैंगनी (UV) किरणें
(D) एक्स (X) किरणें
उत्तर:
(C) पैराबैंगनी (UV) किरणें

39. ओजोन परत के अवक्षय का कारण है-
(A) CO₂
(B) O₂
(C) CFC
(D) N₂
उत्तर:
(C) CFC

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 Circles Ex 10.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 Circles Exercise 10.2

Question 1.
Recall that two circles are congruent if they have the same radü. Prove that equal chords of congruent circles subtend equal angles at their centres.
Solution:
Given: AB and CD are two equal chords of two congruent circles C(O, r) and C(O’, r) respectively.

To prove:
∠AOB = ∠CO’D.
Proof: In ΔAOB and ΔCO’D, we have
OA = O’C [Equal radii of congruent circles]
OB = O’D [Equal radii of congruent circles]
AB = CD (given)
∴ ΔAOB ≅ ΔCO’D (By SSS congruence rule)
∠AOB = ∠CO’D (CPCT)
Hence proved.

Question 2.
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Solution:
Given: AB and CD are two chords of congruent circles C(O, r) and C(O’, r) such that ∠AOB = ∠CO’D.

To prove : AB = CD.
Proof: In ΔAOB and ΔCO’D, we have
AO = O’C [Equal radii of congruent circles]
∠AOB = ∠CO’D (given)
OB = O’D [Equal radii of congruent circles]
∴ ΔAOB ≅ ΔCO’D [By SAS congruence rule]
⇒ AB = CD (CPCT)
Hence proved.

Haryana State Board HBSE 9th Class Maths Solutions Chapter 10 Circles Ex 10.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 10 Circles Exercise 10.1

Question 1.
Fill in the blanks:
(i) The centre of a circle lies in ……………… of the circle. (exterior/interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in …………….. of the circle. (exterior/ interior)
(iii) The longest chord of a circle is a ……………………. of the circle.
(iv) An arc is a …………………… when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and. ………………..of the circle.
(vi) A circle divides the plane, on which it lies, …………………… parts.
Answer:
(i) Interior
(ii) Exterior
(iii) Diameter
(iv) Semicircle
(v) The chord
(vi) Three.

Question 2.
Write True or False: Give reasons for your answers :
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Answer:
(i) True
(ii) False
(ii) False
(iv) True
(v) False
(vi) True.

Haryana State Board HBSE 9th Class Maths Solutions Chapter 12 Heron’s Formula Ex 12.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 12 Heron’s Formula Exercise 12.2

Question 1.
A parks, in the shape of a quadrilateral ABCD has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Solution:
In right ΔBCD, we have
BD² = BC² + CD²
(By Pythagoras theorem)
⇒ BD² = 12² + 5²
⇒ BD² = 144 + 25
⇒ BD² = 169
⇒ BD = \(\sqrt{169}\)
⇒ BD = 13 m

Area of ΔBCD = \(\frac{1}{2}\) × BC × CD
= \(\frac{1}{2}\) × 12 × 5
= 30 m²
In ΔABD, we have
AB = 9 m, AD = 8 m and BD = 13 m
So, a = 9 m, b = 8 m and c = 13 m
∴ s = \(\frac{a+b+c}{2}\)
s = \(\frac{9+8+13}{2}\)
s = \(\frac{30}{2}\) = 15 m
By Heron’s formula, we have
Area of ΔABD = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{15(15-9)(15-8)(15-13)}\)
= \(\sqrt{15 \times 6 \times 7 \times 2}\)
= \(\sqrt{3 \times 5 \times 3 \times 2 \times 7 \times 2}\)
= 2 × 3\(\sqrt{35}\) = 6 × 5.916
= 35.5 m² (approx.)
area of quadrilateral ABCD = area of ΔBCD + area of ΔABD
= 30 + 35.5
= 65.5 m² (approx.)
Hence, area of quadrilateral ABCD = 65.5 m² (approx.).

Question 2.
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Solution:
The sides of ΔABC are a = 3 cm, b = 4 cm and c = 5 cm.
s = \(\frac{a+b+c}{2}\)
s = \(\frac{3+4+5}{2}\)
s = \(\frac{12}{2}\) = 6 cm

By Heron’s formula, we have
Area of ΔABC = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{6(6-3)(6-4)(6-5)}\)
= \(\sqrt{6 \times 3 \times 2 \times 1}\)
= \(\sqrt{2 \times 3 \times 3 \times 2 \times 1}\)
= 2 × 3 = 6 cm²
The sides of a triangle ACD are
a= 5 cm, b = 4 cm and c = 5 cm
s = \(\frac{a+b+c}{2}\)
s = \(\frac{5+4+5}{2}\)
s = \(\frac{14}{2}\) = 7 cm
By Heron’s formula
Area of ΔACD = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{7(7-5)(7-4)(7-5)}\)
= \(\sqrt{7 \times 2 \times 3 \times 2}\) = 2\(\sqrt{21}\)
= 2 × 4.58 = 9.16 cm²
= 9.2 cm²
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD
= 6 + 9.2
= 15.2 cm² (approx.)
Hence, area of quadrilateral ABCD = 15.2 cm² (approx.).

Question 3.
Radha made a picture of an aeroplane with coloured paper as shown in Fig. 12.15. Find the total area of the paper used.

Solution:
There are five parts in the picture of an aeroplane.
The part I is the shape of a triangle. Sides of this triangle are
a = 5 cm, b = 5 cm and c = 1 cm
s = \(\frac{a+b+c}{2}\)
s = \(\frac{5+5+1}{2}\)
s = \(\frac{11}{2}\) = 5.5 cm
By Herous formula, we have
Area of part I = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{5.5(5.5-5)(5.5-5)(5.5-1)}\)
= \(\sqrt{5.5 \times 0.5 \times 0.5 \times 4.5}\)
= \(\sqrt{11 \times 0.5 \times 0.5 \times 0.5 \times 3 \times 3 \times 0.5}\)
= 0.5 × 0.5 × 3\(\sqrt{11}\)
= 0.75 × 3.32
= 2.49 cm²
Part II is the shape of rectangle.
Dimensions of the rectangle are
Length = 6.5 cm and Breadth = 1 cm
Area of part II = Length × Breadth
= 6.5 × 1
= 6.5 cm²
Part III is in the shape of trapezium as shown in figure.
Draw CE || AD and CF ⊥ EB.
∴ CE = AD = 1 cm,
AE = CD = 1 cm
∴ EB = AB – AE
⇒ EB = 2 – 1 = 1 cm

So, ΔCEB is an equilateral triangle.
Area of ΔCEB = \(\frac{\sqrt{3}}{4} \times(1)^2\)
= \(\frac{\sqrt{3}}{4}\) cm²
Again,
area of ΔCEB = \(\frac{1}{2}\) × EB × CF
\(\frac{\sqrt{3}}{4}\) = \(\frac{1}{2}\) × 1 × CF
\(\frac{2 \sqrt{3}}{4}\) = CF
CF = \(\frac{\sqrt{3}}{2}\)
∴ Area of trapezium (part III) = \(\frac{1}{2}\) (sum of parallel sides) × distance between them
= \(\frac{1}{2}(2+1) \times \frac{\sqrt{3}}{2}\)
= \(\frac{3 \sqrt{3}}{4}\)
= 1.299 cm² = 1.30 cm²
Part IV is the shape of right triangle.
Sides of this triangle are
Base = 1.5 cm and height = 6 cm
∴ Area of right triangle = \(\frac{1}{2}\) × base × height
⇒ Area of part IV = \(\frac{1}{2}\) × 1.5 × 6
= 4.5 cm²
Part V is in the shape of right triangle.
Sides of part V are same as part IV.
So, area of part V = 4.5 cm²
Total area of paper used = Area of part I + Area of part II + Area of part III + Area of part IV + Area of part V
= 2.49 + 6.5 + 1.30 + 4.5 +4.5
= 19.29 cm²
= 19.30 cm²
Hence, total area of paper used = 19.30 cm² (approx.)

Question 4.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Solution:
Sides of the triangle are
∴ a = 26 cm, b = 28 cm and c = 30 cm
s = \(\frac{a+b+c}{2}\)
⇒ s = \(\frac{26+28+30}{2}\)
⇒ s = \(\frac{84}{2}\) = 42 cm
By Heron’s formula, we have
Area of the triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{42(42-26)(42-28)(42-30)}\)
= \(\sqrt{42 \times 16 \times 14 \times 12}\)
= \(\sqrt{2 \times 3 \times 7 \times 4 \times 4 \times 2 \times 7 \times 2 \times 2 \times 3}\)
= 2 × 2 × 3 × 4 × 7
= 336 cm²
Base of parallelogram = 28 cm
Since,area of parallelogram = area of triangle, (given)
⇒ base × height = 336
⇒ 28 × height = 336
height = \(\frac{336}{28}\)
height = 12 cm
Hence, height of the parallelogram = 12 cm.

Question 5.
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Solution:
Each side of rhombus shaped field = 30 m.
We know that diagonals of a rhombus bisect each other at right angle.
∴ BO = OD
Let BO = OD = x m
and AO = OC = \(\frac{48}{2}\) = 24 m
In right triangle AOB, we have
AB² = AO² + OB²
(By Pythagoras theorem)

30² = 24² + x²
⇒ 30² – 24² = x²
⇒ (30 + 24) (30 – 24) = x²
⇒ 54 × 6 = x²
⇒ 324 = x²
⇒ x = \(\sqrt{324}\)
⇒ x = 18 m
So, BD = 2 × 18 = 36 m
Area of rhombus ABCD = \(\frac{1}{2}\) × Product of diagonals
= \(\frac{1}{2}\) × 48 × 36
= 864 m²
∵ 18 cows graze the area = 864 m²
∴ 1 cow grazes the area = \(\frac{864}{18}\) = 48 m²
Hence, each cow grazes the area = 48 m².

Question 6.
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see Fig. 12.16), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

Solution:
Sides of the triangular piece are
a= 50 cm, b = 50 cm and c = 20 cm
s = \(\frac{a+b+c}{2}\)
⇒ s = \(\frac{50+50+20}{2}\)
⇒ s = \(\frac{120}{2}\) = 60 cm
By Heron’s formula, we have
Area of 1 triangular piece = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{60(60-50)(60-50)(60-20)}\)
= \(\sqrt{60 \times 10 \times 10 \times 40}\)
= \(\sqrt{20 \times 3 \times 10 \times 10 \times 2 \times 20}\)
= 10 × 20\(\sqrt{6}\)
= 200\(\sqrt{3}\) cm²
Hence, area of cloth of each colour for five triangular pieces = 5 × 200\(\sqrt{6}\) = 1000\(\sqrt{6}\) cm².

Question 7.
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in Fig. 12.17. How much paper of each shade has been used in it?

Solution:
Since diagonals of a square are equal and bisect each other at right angle. Therefore,
AO = OC = OB = OD
\(\frac{32}{2}\) = 16 cm
Area of part I = \(\frac{1}{2}\) base × height
= \(\frac{1}{2}\) × AC × OD
\(\frac{1}{2}\) × 32 × 16 = 256 cm²

Similarly,
area of part II = 256 cm²
Sides of the part III (ΔBEF) are
a = 6 cm, b = 6 cm and c = 8 cm
⇒ s = \(\frac{6+6+8}{2}\),
= \(\frac{20}{2}\) = 10 cm
By Heron’s formula, we have
Area of part III (ΔBER)
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{10(10-6)(10-6)(10-8)}\)
= \(\sqrt{10 \times 4 \times 4 \times 2}\)
= \(\sqrt{2 \times 5 \times 4 \times 4 \times 2}\)
= 2 × 4\(\sqrt{5}\) = 8\(\sqrt{5}\)
= 8 × 2.24 = 17.92 cm²
Hence, paper used in parts I, II and III = 256 cm², 256 cm² and 17.92 cm².

Question 8.
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see Fig. 12.18). Find the cost of polishing the tiles at the rate of 50 paisa per cm².

Solution:
Lengths of the sides of a tile are
a = 28 cm, b = 9 cm and c = 35 cm
⇒ s = \(\frac{a+b+c}{2}\)
⇒ s = \(\frac{28+9+35}{2}\)
⇒ s = \(\frac{72}{2}\) = 36 cm
By Heron’s formula, we have
Area of 1 triangular tile = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{36(36-28)(36-9)(36-35)}\)
= \(\sqrt{36 \times 8 \times 27 \times 1}\)
= \(\sqrt{6 \times 6 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3}\)
= 2 × 3 × 6\(\sqrt{6}\)
= 36\(\sqrt{6}\)
Area of 16 triangular tiles = 16 × 36\(\sqrt{6}\)
= 1410.91 cm²
Cost of polishing the tiles at the rate of 50 paisa i.e., Rs. \(\frac{1}{2}\) per cm²
= 1410.91 × \(\frac{1}{2}\)
= Rs. 705.45
Hence, cost of polishing of the tiles = Rs. 705.45.

Question 9.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The nonparallel sides are 14 m and 13 m. Find the area of the field.
Solution:
Through vertex C draw CE || AD intersecting AB at E. Draw CF ⊥ EB.
∵ AE || CD and AD || CE
∴ AECD is a parallelogram.
CE = AD = 14 m
AE = CD = 10 m
BE = AB – AE
BE = 25 – 10 = 15 m
Sides of the ΔCEB are
a = 14 m, b = 13 m and c = 15 m
s = \(\frac{a+b+c}{2}\)
⇒ s = \(\frac{14+13+15}{2}\)
⇒ s = \(\frac{42}{2}\)
⇒ s = 21 m
By Heron’s formula, we have
area of ΔCEB = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{21(21-14)(21-13)(21-15)}\)
= \(\sqrt{21 \times 7 \times 8 \times 6}\)
= \(\sqrt{3 \times 7 \times 7 \times 2 \times 2 \times 2 \times 2 \times 3}\)
= 2 × 2 × 3 × 7
= 84 m²
Again, area of ΔCEB = \(\frac{1}{2}\) × base × height
84 = \(\frac{1}{2}\) × BE × CF
84 = \(\frac{1}{2}\) × 15 × CF
\(\frac{84 \times 2}{15}\) = CF
\(\frac{56}{5}\) = CF
CF = \(\frac{56}{5}\) cm
Now, area of trapezium ABCD = \(\frac{1}{2}\) (sum of parallel sides) × distance between them
= \(\frac{1}{2}\)(25 + 10) × \(\frac{56}{5}\)
= \(\frac{35}{2} \times \frac{56}{5}\)
= 7 × 28
= 196 m²
Hence, area of trapezium ABCD = 196 m².

Haryana State Board HBSE 9th Class Science Important Questions Chapter 2 क्या हमारे आस-पास के पदार्थ शुद्ध हैं Important Questions and Answers.

Haryana Board 9th Class Science Important Questions Chapter 2 क्या हमारे आस-पास के पदार्थ शुद्ध हैं

अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
शुद्धिकरण किसे कहते हैं?
उत्तर:
लाभदायक पदार्थों को अनावश्यक तथा हानिकारक पदार्थों से अलग करना, शुद्धिकरण कहलाता है।

प्रश्न 2.
किन्हीं चार शुद्ध पदार्थों के नाम लिखें।
उत्तर:

1. चीनी
2. साधारण नमक
3. सोना
4. पारा।

प्रश्न 3.
किन्हीं चार तत्त्वों के नाम लिखें।
उत्तर:

1. सोना
2. चाँदी
3. पारा
4. गंधक।

प्रश्न 4.
किन्हीं चार यौगिकों के नाम लिखें।
उत्तर:

1. जल
2. कपूर
3. चीनी
4. कार्बन डाइऑक्साइड।

प्रश्न 5.
किन्हीं चार मिश्रणों के नाम लिखें।
उत्तर:

1. मिट्टी
2. वायु
3. तालाब का जल
4. सेंधा नमक (चट्टानी नमक)।

प्रश्न 6.
जल में विलेय दो पदार्थों के नाम बताओ जो दैनिक जीवन में काम आते हैं।
उत्तर:

1. साधारण नमक
2. चीनी।

प्रश्न 7.
दो द्रवीय मिश्रणों के नाम लिखें।
उत्तर:

1. तालाब या नदी का जल
2. सोडा जल।

प्रश्न 8.
एक गैसीय मिश्रण का उदाहरण दें।
उत्तर:
वायु।

प्रश्न 9.
पृथक्करण किसे कहते हैं?
उत्तर:
मिश्रण में से एक पदार्थ को दूसरे पदार्थ से पृथक् करना, पृथक्करण कहलाता है।

प्रश्न 10.
मिश्रण में कितने अवयव होते हैं?
उत्तर:
मिश्रण में दो या दो से अधिक अवयव होते हैं।

प्रश्न 11.
हम वायु में से किस लाभदायक अवयव को सांस के रूप में प्रयोग करते हैं?
उत्तर:
हम वायु में से ऑक्सीजन को सांस के रूप में प्रयोग करते हैं।

प्रश्न 12.
चुंबकीय पृथक्करण में चुंबक के किस गुण का उपयोग किया जाता है?
उत्तर:
चुंबक लोहे को अपनी ओर आकर्षित करता है।

प्रश्न 13.
भारण का सिद्धांत क्या है?
उत्तर:
छोटे-छोटे कणों के मिलने से बड़ा तथा भारी कण बनता है।

प्रश्न 14.
विलयन किसे कहते हैं?
उत्तर:
दो या दो से अधिक पदार्थों का समांगी मिश्रण विलयन कहलाता है।

प्रश्न 15.
मिश्र धातुओं से क्या अभिप्राय है?
उत्तर:
वे धातुओं के समांगी मिश्रण, जिन्हें भौतिक क्रियाओं द्वारा अवयवों से अलग नहीं किया जा सकता, मिश्र धातुएँ कहलाती हैं।

प्रश्न 16.
विलायक को परिभाषित करें।
उत्तर:
विलयन का वह घटक (जिसकी मात्रा दूसरे से अधिक होती है) जो दूसरे घटक को विलयन में मिलाता है, विलायक कहलाता है।

प्रश्न 17.
विलेय से क्या अभिप्राय है?
उत्तर:
विलयन का वह घटक जो कि विलायक में घुला होता है, उसे विलेय कहते हैं।

प्रश्न 18.
चीनी और जल के विलयन में विलेय व विलायक बताएँ।
उत्तर:
विलेय-चीनी, विलायक-जल।

प्रश्न 19.
टिंक्चर आयोडीन से क्या अभिप्राय है?
उत्तर:
आयोडीन और ऐल्कोहॉल का विलयन टिंक्चर आयोडीन कहलाता है।

प्रश्न 20.
टिंक्चर आयोडीन में विलेय और विलायक लिखें।
उत्तर:
विलेय-आयोडीन, विलायक-ऐल्कोहॉल।

प्रश्न 21.
सोडा जल व कोक में विलेय व विलायक लिखें।
उत्तर:
विलेय कार्बन डाइऑक्साइड, विलायक-जल।

प्रश्न 22.
ठोस में ठोस विलयन के दो उदाहरण दें।
उत्तर:

1. सोने और चाँदी का मिश्रण
2. कॉपर और सोने का मिश्रण।

प्रश्न 23.
दो जलीय विलयनों के उदाहरण दीजिए।
उत्तर:

1. चीनी व जल का विलयन
2. नमक व जल का विलयन।

प्रश्न 24.
दो अजलीय विलयनों के उदाहरण दीजिए।
उत्तर:

1. ऐल्कोहॉल व आयोडीन का घोल
2. सल्फर व कार्बन डाइऑक्साइड का घोल।

प्रश्न 25.
गैस में गैस के विलयन का उदाहरण दें।
उत्तर:
वायु गैस में गैस का विलयन है।

प्रश्न 26.
वायु के मुख्य घटक कौन-से हैं?
उत्तर:
वायु के मुख्य घटक नाइट्रोजन (78%) व ऑक्सीजन (21%) हैं।

प्रश्न 27.
वायु में कौन-से घटक को विलायक माना जाता है?
उत्तर:
वायु में नाइट्रोजन गैस को विलायक माना जाता है।

प्रश्न 28.
विलयन के कणों का व्यास कितना होता है?
उत्तर:
विलयन के कणों का व्यास 1nm (10^-9m) से भी छोटा होता है।

प्रश्न 29.
असंतृप्त विलयन से क्या अभिप्राय है?
उत्तर:
यदि किसी विलयन में विलेय पदार्थ की मात्रा संतृप्तता से कम हो तो उसे असंतृप्त विलयन कहते हैं।

प्रश्न 30.
अतिसंतृप्त विलयन से क्या अभिप्राय है?
उत्तर:
यदि विलयन में विलेय पदार्थ की सांद्रता संतृप्त सांद्रता से अधिक हो तो उसे अतिसंतृप्त विलयन कहते हैं।

प्रश्न 31.
जल को सार्वत्रिक विलायक क्यों कहते हैं?
उत्तर:
जल को सार्वत्रिक विलायक इसलिए कहते हैं, क्योंकि इसमें अत्यधिक पदार्थ घुल जाते हैं।

प्रश्न 32.
समुद्री जल को घरेलू उपयोग में क्यों नहीं लाया जा सकता?
उत्तर:
क्योंकि समुद्री जल में खनिज लवणों की सांद्रता अधिक होती है।

प्रश्न 33.
किसी विलयन की सांद्रता को व्यक्त करने का सूत्र लिखो।
उत्तर:

प्रश्न 34.
10% ग्लूकोज़ का क्या अर्थ है?
उत्तर:
10% ग्लूकोज़ से अभिप्राय है कि 100 ग्राम विलयन में 10 ग्राम ग्लूकोज़ है।

प्रश्न 35.
निलंबन के कणों का आकार कितना होता है?
उत्तर:
निलंबन के कणों का आकार 100 nm (10^-7m) से बड़ा होता है।

प्रश्न 36.
निलंबन के कणों को किस विधि द्वारा पृथक् किया जा सकता है?
उत्तर:
निलंबन के कणों को छानना विधि द्वारा अलग किया जा सकता है।

प्रश्न 37.
कोलाइडल विलयन समांगी होता है अथवा विषमांगी?
उत्तर:
कोलाइडल विलयन विषमांगी होता है।

प्रश्न 38.
दैनिक जीवन में प्रयुक्त होने वाले चार कोलाइड विलयनों के उदाहरण दीजिए।
उत्तर:

1. दूध
2. शेविंग क्रीम
3. टूथपेस्ट
4. जेली।

प्रश्न 39.
टिनडल प्रभाव क्या है?
उत्तर:
कोलाइड कणों के बड़े आकार के कारण विसर्जन माध्यम से गुज़रने वाले दृश्य प्रकाश का प्रकीर्णन (बिखराव) हो जाता है, इस परिघटना को टिनडल प्रभाव कहते हैं।

प्रश्न 40.
कोलाइड के कणों का आकार कितना होता है?
उत्तर:
कोलाइड के कणों का आकार Inm से 100 nm के बीच होता है।

प्रश्न 41.
टिनडल प्रभाव का कोई एक उदाहरण दीजिए।
उत्तर:
जब एक प्रकाश की संकीर्ण किरण पुंज छत के एक छोटे छिद्र से कमरे में आती है तो टिनडल प्रभाव देखा जा सकता है, क्योंकि कमरे की वायु में धूल व धुआँ प्रकाश का प्रकीर्णन (बिखराव) कर देता है।

प्रश्न 42.
क्या कोलाइडी कण नग्न आंखों द्वारा देखे जा सकते हैं?
उत्तर:
नहीं।

प्रश्न 43.
प्रकृति में एक सामान्य कोलाइड का नाम बताइए।
उत्तर:
प्रकृति में एक सामान्य कोलाइड कोहरा है, जो वायु में जल की बूंदों से बना होता है।

प्रश्न 44.
कोलाइडों के वर्गीकरण का मुख्य आधार क्या है?
उत्तर:
कोलाइडों के वर्गीकरण का मुख्य आधार-परिक्षेपण माध्यम की अवस्था तथा परिक्षिप्त प्रावस्था की अवस्था है।

प्रश्न 45.
कोलाइडों के दो उपयोग लिखें।
उत्तर:
कोलाइडों का औषधि बनाने में तथा औद्योगिक प्रक्रमों को समझने में प्रयोग होता है।

प्रश्न 46.
क्या जल और सरसों के तेल को छानकर अलग कर सकते हैं?
उत्तर:
नहीं। इन्हें वाष्पीकरण या निथारना विधि द्वारा अलग कर सकते हैं।

प्रश्न 47.
चालन का सिद्धांत क्या है?
उत्तर:
बारीक ठोस पदार्थ को मोटे ठोस पदार्थ से किसी छिद्रयुक्त उपकरण की सहायता से अलग करने की विधि को चालन कहते हैं। इसमें द्रव का प्रयोग नहीं किया जाता।

प्रश्न 48.
नदी के गंदले जल को किस विधि द्वारा निथारा जा सकता है?
उत्तर:
नदी के गंदले जल को भारण विधि द्वारा निथारा जा सकता है।

प्रश्न 49.
किसी पदार्थ का द्रवणांक अथवा क्वथनांक किस प्रकार लाभदायक है?
उत्तर:
किसी पदार्थ के शुद्ध या अशुद्ध होने का पता इन लाक्षणिक गुणों के द्वारा लगाया जा सकता है।

प्रश्न 50.
द्रव में विलेय पदार्थों को पृथक् करने की सबसे अच्छी विधि कौन-सी है?
उत्तर:
द्रव में विलेय पदार्थों को पृथक् करने की सबसे अच्छी विधि आसवन विधि है।

प्रश्न 51.
ऊर्ध्वपातन किसे कहते हैं?
उत्तर:
जिस क्रिया में ठोस सीधे गैसीय अवस्था में बदल जाते हैं, उसे ऊर्ध्वपातन कहते हैं।

प्रश्न 52.
दो ऊर्ध्वपातित पदार्थों के नाम लिखो।
उत्तर:
कपूर और नौसादर ऊर्ध्वपातित पदार्थ हैं।

प्रश्न 53.
जल और मिट्टी के तेल के मिश्रण को कैसे अलग-अलग किया जा सकता है?
उत्तर:
जल और मिट्टी के तेल के मिश्रण को पृथक्करण कीप द्वारा अलग-अलग किया जा सकता है।

प्रश्न 54.
दूध से क्रीम (मक्खन) किस विधि द्वारा अलग की जा सकती है?
उत्तर:
दूध से क्रीम अपकेंद्रण विधि द्वारा अलग की जा सकती है।

प्रश्न 55.
आसुत जल किस प्रक्रम द्वारा प्राप्त किया जाता है?
उत्तर:
आसुत जल आसवन प्रक्रम द्वारा प्राप्त किया जा सकता है।

प्रश्न 56.
नौसादर और रेत के मिश्रण का पृथक्करण किस विधि द्वारा किया जा सकता है?
उत्तर:
नौसादर और रेत के मिश्रण का पृथक्करण ऊर्ध्वपातन विधि द्वारा किया जा सकता है।

प्रश्न 57.
घरों में जल किसं विधि द्वारा साफ किया जाता है?
उत्तर:
घरों में जल फिल्टरीकरण विधि द्वारा साफ किया जाता है।

प्रश्न 58.
पेट्रोल में मिलावट किस विधि द्वारा देखी जा सकती है?
उत्तर:
पेट्रोल में मिलावट वाष्पीकरण विधि द्वारा देखी जा सकती है।

प्रश्न 59.
जल और एसीटोन के मिश्रण को किस विधि द्वारा पृथक् किया जाता है?
उत्तर:
जल और एसीटोन के मिश्रण को आसवन विधि द्वारा पृथक् किया जा सकता है।

प्रश्न 60.
आसवन विधि कहाँ प्रयोग की जाती है?
उत्तर:
जब दो घुलनशील द्रवों के मिश्रण के घटकों के क्वथनांकों के बीच काफी अंतर होता है।

प्रश्न 61.
पेट्रोलियम उत्पादों के विभिन्न घटकों को किस विधि द्वारा पृथक्कीकृत किया जाता है?
उत्तर:
पेट्रोलियम उत्पादों के विभिन्न घटकों को प्रभाजी आसवन विधि द्वारा पृथक्कीकृत किया जाता है।

प्रश्न 62.
प्रभाजी आसवन विधि कब प्रयोग में लाई जाती है?
उत्तर:
जब दो या दो से अधिक घुलनशील द्रवों के क्वथनांकों का अंतर 25K से कम होता है।

प्रश्न 63.
वायु के विभिन्न घटकों को किस विधि द्वारा पृथक् किया जा सकता है?
उत्तर:
वायु के विभिन्न घटकों को प्रभाजी आसवन विधि द्वारा पृथक् किया जा सकता है।

प्रश्न 64.
ऑक्सीजन का क्वथनांक कितना होता है?
उत्तर:
ऑक्सीजन का क्वथनांक-183°C होता है।

प्रश्न 65.
जब वायु के घटकों को ठंडा किया जाता है तो कौन-सा घटक पहले द्रव में परिवर्तित होता है?
उत्तर:
ऑक्सीजन।

प्रश्न 66.
कॉपर सल्फेट के एक अशुद्ध नमूने में से शुद्ध कॉपर सल्फेट किस विधि द्वारा प्राप्त किया जाता है?
उत्तर:
क्रिस्टलीकरण विधि द्वारा।

प्रश्न 67.
भौतिक परिवर्तनों से क्या अभिप्राय है?
उत्तर:
भौतिक परिवर्तनों में पदार्थों के रूप में परिवर्तन होता है न कि रासायनिक रूप में अर्थात् इन परिवर्तनों में पदार्थ को । पुनः प्राप्त किया जा सकता है।

प्रश्न 68.
किन्हीं दो भौतिक परिवर्तनों के उदाहरण दें।
उत्तर:

1. चीनी व जल का विलयन
2. नमक व जल का विलयन।

प्रश्न 69.
क्या चीनी के विलयन में से चीनी प्राप्त की जा सकती है?
उत्तर:
हां, चीनी के विलयन में से जल को वाष्पीकृत करने से चीनी प्राप्त की जा सकती है।

प्रश्न 70.
रासायनिक परिवर्तन से क्या अभिप्राय है?
उत्तर:
रासायनिक परिवर्तन में, एक या एक से अधिक प्रकार के पदार्थ एक या अनेक नए पदार्थों में परिवर्तित हो जाते हैं अर्थात् इन परिवर्तनों में पदार्थ को पुनः प्राप्त नहीं किया जा सकता।

प्रश्न 71.
दैनिक जीवन में प्रयुक्त होने वाले दो रासायनिक परिवर्तन कौन-से हैं?
उत्तर:

1. दूध का दही बनना
2. भोजन का पाचन।

प्रश्न 72.
तत्त्व क्या है?
उत्तर:
तत्त्व द्रव्य का वह आधारभूत रूप है जिसे रासायनिक अभिक्रियाओं द्वारा सरल पदार्थों में नहीं तोड़ा जा सकता।

प्रश्न 73.
तत्त्व का कोई एक विशेष गुण लिखें।
उत्तर:
एक तत्त्व केवल एक ही प्रकार के परमाणुओं से बना होता है।

प्रश्न 74.
कमरे के ताप पर कितने तत्त्व गैसीय अवस्था में पाए जाते हैं? किन्हीं दो के नाम लिखें।
उत्तर:
कमरे के ताप पर 11 तत्त्व गैसीय अवस्था में पाए जाते हैं; जैसे हाइड्रोजन व ऑक्सीजन।

प्रश्न 75.
कमरे के ताप पर द्रव अवस्था में मिलने वाली एक धातु तथा एक अधातु का नाम लिखें।
उत्तर:
धातु-पारा। अधातु-ब्रोमीन।

प्रश्न 76.
उपधातु से क्या अभिप्राय है?
उत्तर:
धातु और अधातु के बीच के गुण दर्शाने वाले तत्त्व उपधातु कहलाते हैं।

प्रश्न 77.
किन्हीं दो उपधातुओं के नाम लिखें।
उत्तर:

1. बोरॉन
2. सिलिकॉन।

प्रश्न 78.
यौगिक से क्या अभिप्राय है?
उत्तर:
दो या दो से अधिक तत्त्वों के समान अनुपात में रासायनिक तौर पर मिलने से बना पदार्थ यौगिक कहलाता है।

प्रश्न 79.
वायु मुख्यतः किन दो गैसों का समांगी मिश्रण है?
उत्तर:
वायु मुख्यतः ऑक्सीजन व नाइट्रोजन गैसों का समांगी मिश्रण है, क्योंकि वायु में और गैसें बहुत कम मात्रा में उपस्थित होती हैं।

प्रश्न 80.
विषमांगी मिश्रण किसे कहते हैं?
उत्तर:
विषमांगी मिश्रण वह मिश्रण है जिसमें भौतिक रूप से अलग-अलग भाग होते हैं तथा प्रत्येक भाग भिन्न-भिन्न गुणधर्मों का होता है।

प्रश्न 81.
निम्नलिखित को तत्त्व, यौगिक तथा मिश्रण में वर्गीकृत करें।
(A) सोडियम
(B) मिट्टी
(C) चाँदी
(D) चीनी
(E) यूरिया
उत्तर:
तत्त्व: (A) सोडियम, (C) चाँदी
यौगिक : (D) चीनी, (E) यूरिया
मिश्रण : (B) मिट्टी

प्रश्न 82.
जब दो या दो से अधिक तत्त्व अथवा यौगिक किसी भी अनुपात में मिलते हैं तो क्या बनता है?
उत्तर:
जब दो या दो से अधिक तत्त्व अथवा यौगिक किसी भी अनुपात में मिलते हैं तो मिश्रण बनता है।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
मिश्रण किसे कहते हैं? ये कितने प्रकार के होते हैं? संक्षेप में समझाएँ।
उत्तर:
एक मिश्रण में एक से अधिक पदार्थ (तत्त्व याऔर यौगिक) होते हैं। मिश्रण को भौतिक प्रक्रम द्वारा दो या दो से अधिक पदार्थों में पृथक् कर सकते हैं। मिश्रण मुख्यतः दो प्रकार के होते हैं-
1. समांगी मिश्रण-जिस मिश्रण का संघटन सभी जगह एक समान रहता है, उसे समांगी मिश्रण कहते हैं; जैसे नमक व जल का मिश्रण; चीनी व जल का मिश्रण आदि।

2. विषमांगी मिश्रण-जिस मिश्रण में भौतिक रूप से अलग-अलग भाग होते हैं तथा प्रत्येक भाग भिन्न गुणधर्मों का होता है, उसे विषमांगी मिश्रण कहते हैं; जैसे सोडियम क्लोराइड और लोहे की छीलन का मिश्रण तथा नमक और सल्फर का मिश्रण तथा जल और तेल का मिश्रण।

प्रश्न 2.
पानी में नमक के विलयन को मिश्रण क्यों माना जाता है, यौगिक क्यों नहीं?
उत्तर:
पानी में नमक के विलयन को मिश्रण माना जाता है, यौगिक नहीं, क्योंकि-

1. नमक युक्त पानी में से नमक तथा पानी को आसवन विधि द्वारा अलग किया जा सकता है।
2. नमक युक्त पानी अपने दोनों अवयवों-जल तथा नमक के गुण दिखाता है।
3. नमक युक्त पानी का संघटन अलग होता है। नमक की भिन्न मात्रा को पानी की एक निश्चित मात्रा में घोलकर विभिन्न। संघटनों वाला नमक युक्त पानी प्राप्त किया जा सकता है।
4. नमक युक्त पानी का कोई निश्चित सूत्र नहीं होता।

प्रश्न 3.
ऐसे मिश्रण का उदाहरण दो-(1) जिसमें दोनों पदार्थ यौगिक हों। (2) जिसमें तत्त्व तथा यौगिक दोनों मिले हों। (3) जिसमें दोनों तत्त्व हों।
उत्तर:

1. ऐसा मिश्रण जिसमें दोनों पदार्थ यौगिक हों-पानी में चीनी मिलाने पर शरबत ऐसा मिश्रण बनता है जिसमें पानी और चीनी दोनों ही यौगिक हैं।
2. ऐसा मिश्रण जिसमें तत्त्व तथा यौगिक दोनों मिले हों वायु ऐसा मिश्रण है जिसमें ऑक्सीजन व नाइट्रोजन तत्त्व हैं तथा कार्बन डाइऑक्साइड और जलवाष्प दोनों यौगिक हैं।
3. ऐसा मिश्रण जिसमें दोनों तत्त्व हों-पीतल, ताँबा तथा जस्त दो तत्त्वों को मिलाने से बनता है।

प्रश्न 4.
विलयन किसे कहते हैं? विभिन्न प्रकार के विलयनों की एक सूची बनाइए।
उत्तर:
विलयन एक समांगी मिश्रण होता है जिसमें दो या दो से अधिक पदार्थ होते हैं। विभिन्न प्रकार के विलयन निम्नलिखित हैं-

प्रश्न 5.
विलयन के कोई चार गुण लिखें।
उत्तर:
विलयन के विभिन्न गुण निम्नलिखित हैं-

• विलयन एक समांगी मिश्रण होता है।
• विलयन के कण व्यास में 1nm (10^-9m) से भी छोटे होने के कारण आंख से नहीं देखे जा सकते हैं।
• अपने छोटे आकार के कारण विलयन, गुजर रही प्रकाश की किरण को फैलाते नहीं जिस कारण विलयन में प्रकाश का मार्ग दिखाई नहीं देता।
• छानने की विधि द्वारा विलेय के कणों को विलयन में से पृथक् नहीं किया जा सकता है। विलयन को शांत छोड़ देने पर भी विलेय के कण नीचे नहीं बैठते अर्थात् विलयन स्थाई होता है।

प्रश्न 6.
जलीय तथा अजलीय विलयन क्या होते हैं?
उत्तर:

1. जलीय विलयन-ये वे विलयन हैं जो पदार्थों को जल में घोलकर बनाए जाते हैं; जैसे शरबत तथा सोडावाटर आदि।
2. अजलीय विलयन-ये वे विलयन हैं जो पदार्थों को जल के अतिरिक्त अन्य विलायकों (जैसे-ऐल्कोहॉल, ऐसीटोन आदि) में घोलकर बनाए जाते हैं; जैसे टिंक्चर आयोडीन तथा नैफ्थलीन का बेंजीन में घोल।

प्रश्न 7.
विलयन में विलेय और विलायक के कणों को अलग-अलग पहचानना संभव क्यों नहीं होता है?
उत्तर:
विलेय के कण विलायक के साथ इतनी अच्छी तरह मिल जाते हैं कि उनको अलग से पहचाना नहीं जा सकता। विलयन समांगी होते हैं अर्थात् विलयन का संघटन एक समान होता है।

यदि लवण विलयन और चीनी विलयन को मिलाया जाए तो फलस्वरूप प्राप्त समांगी विलयन में दोनों विलयन भली-भांति एक-दूसरे में मिल जाते हैं और मूल विलायक और विलेय में भेद कर पाना संभव नहीं हो पाता है।

प्रश्न 8.
किसी विलयन की सांद्रता को किस प्रकार व्यक्त किया जाता है? उदाहरण देकर उसका अर्थ समझाएँ।
उत्तर:
विलयनों की सांद्रता को दिए हुए विलयन के द्रव्यमान या आयतन में उपस्थित विलेय की मात्रा अथवा दिए हुए विलायक के द्रव्यमान या आयतन में घुले विलेय की मात्रा के संदर्भ में व्यक्त करते हैं।

विलयनों की सांद्रता को विलेय के द्रव्यमान प्रतिशत जो विलयन की 100 द्रव्यमान इकाई में विलेय का द्रव्यमान देता है, के रूप में भी व्यक्त किया जा सकता है। इसकी द्रव्यमान इकाई ग्राम है।

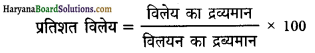
उदाहरण के लिए यदि द्रव्यमान से 10% ग्लूकोज़ (C₆H₁₂O₆) के एक विलयन को लें। इसमें 100g विलयन में 10g ग्लूकोज़ होता है। इसको 90g जल में 10g ग्लूकोज़ के रूप में भी कह सकते हैं। अगर कुछ विशिष्ट रूप में नहीं कहा गया है तो प्रतिशत का अर्थ द्रव्यमान के रूप में प्रतिशत है और उसमें जल विलायक है।

प्रश्न 9.
संतृप्त विलयन, असंतृप्त विलयन तथा अतिसंतृप्त विलयन को परिभाषित करें।
उत्तर:

1. संतृप्त विलयन-दिए हुए ताप पर किसी विलयन में जब उसकी क्षमता के अनुसार जितना अधिकतम विलेय घुल जाता है तब उसे संतृप्त विलयन कहते हैं। इस विलयन में घुले तथा बिना घुले विलेय आपस में साम्यावस्था (equilibrium) में होते हैं।
2. असंतृप्त विलयन-जब विलयन में उपस्थित विलेय की मात्रा संतृप्त स्तर से कम होती है, तब विलयन को असंतृप्त विलयन कहते हैं।
3. अतिसंतृप्त विलयन-यदि विलयन में विलेय की सांद्रता संतृप्त सांद्रता से अधिक हो तो यह विलयन अतिसंतृप्त कहलाता है।

प्रश्न 10.
एक विलयन 320g जल में 40g साधारण नमक रखता है। विलयन का द्रव्यमान बताएँ।
हल:
विलेय पदार्थ का द्रव्यमान (नमक) = 40g
विलायक का द्रव्यमान (जल) = 320g
विलयन का द्रव्यमान = विलेय पदार्थ का द्रव्यमान + विलायक का द्रव्यमान
= 40g + 320g = 360g

प्रश्न 11.
निलंबन को परिभाषित करें तथा उसके विभिन्न गण लिखें।
उत्तर:
निलंबन-निलंबन एक विषमांगी मिश्रण होता है जिसमें विलेय पदार्थ के कण घुलते नहीं, बल्कि माध्यम की समष्टि में निलंबित रहते हैं। इसके प्रमुख गुण निम्नलिखित हैं-

• यह एक विषमांगी मिश्रण होता है।
• निलंबित कण 100 nm(10^-7m) से बड़े होते हैं जिस कारण आंखों से देखे जा सकते हैं।
• ये निलंबित कण प्रकाश की किरण को फैला देते हैं, जिससे उसका मार्ग विदित हो जाता है।
• निलंबन अस्थाई होता है। छानन विधि द्वारा इसके कणों को मिश्रण से पृथक् किया जा सकता है।

प्रश्न 12.
विलयन तथा कोलाइड में क्या अंतर है?
उत्तर:
विलयन तथा कोलाइड में निम्नलिखित अंतर हैं-

प्रश्न 13.
विलयन तथा निलंबन में क्या अंतर है?
उत्तर:
विलयन तथा निलंबन में निम्नलिखित अंतर हैं-

प्रश्न 14.
क्या होता है जब कोलाइडी विलयन में से प्रकाश किरणपुंज गुजारा जाता है?
उत्तर:
जब कोलाइडी विलयन में से प्रकाश किरणपुंज को गुजारा जाता है तो इसका पथ प्रदीप्त हो जाता है, क्योंकि कोलाइडी विलयन के कणों का आकार बड़ा होता है, जिससे ये कण अपने ऊपर पड़ने
टॉर्च वाले प्रकाश को सभी दिशाओं में बिखेर देते हैं। इसे टिनडल प्रभाव कॉपर सल्फेट विलयन जल और दूध का कहते हैं।

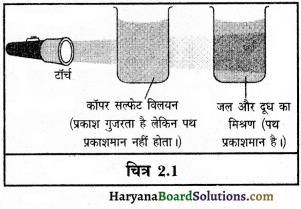
कोलाइडी विलयन तथा वास्तविक विलयन में भेद भी इसी गुण के आधार पर किया जाता है। जैसे दूध टिनडल प्रभाव दिखाता है। दैनिक जीवन में एक कमरे में छोटे छिद्र के द्वारा जब प्रकाश की किरण आती है तब वहाँ पर हम टिनडल प्रभाव देख सकते हैं।

प्रश्न 15.
ब्राऊनियन गतिशीलता से क्या अभिप्राय है?
उत्तर:
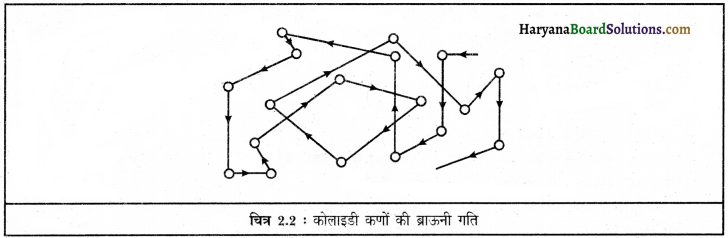
कोलाइडी कण सभी दिशाओं में सदैव आड़े-तिरछे पथों में गतिशील रहते हैं। कोलाइडी कणों की आड़े-तिरछे पथों पर कभी न रुकने वाली गतिशीलता को ब्राऊनियन गतिशीलता (Brownian movement) कहते हैं।

प्रश्न 16.
कोलाइड के गुणधर्मों का वर्णन करें।
उत्तर:
कोलाइड के विभिन्न गुणधर्म निम्नलिखित हैं-

• यह एक विषमांगी मिश्रण होता है।
• कोलाइड के कणों का आकार 1nm से 100 nm के बीच होता है तथा ये आंखों से नहीं देखे जा सकते।
• ये इतने बड़े होते हैं कि प्रकाश की किरण को फैला देते हैं और उसके मार्ग को दृश्य बनाते हैं।
• जब इनको शांत छोड़ दिया जाता है तब ये तल में नहीं बैठते हैं अर्थात् ये स्थाई होते हैं।
• ये छानन विधि द्वारा मिश्रण से पृथक् नहीं किए जा सकते हैं, परंतु अपकेंद्रीकरण तकनीक द्वारा पृथक् किए जा सकते हैं।

प्रश्न 17.
कोलाइडों को किस प्रकार वर्गीकृत किया जाता है? उदाहरण देकर स्पष्ट करें।
उत्तर:
कोलाइडों को परिक्षेपण माध्यम की अवस्था तथा परिक्षिप्त प्रावस्था की अवस्था (ठोस, द्रव या गैस) के अनुसार वर्गीकृत किया जाता है जो निम्नलिखित उदाहरणों से स्पष्ट होता है-

प्रश्न 18.
यौगिक और मिश्रण में कोई पाँच अंतर लिखें।
उत्तर:
यौगिक और मिश्रण में निम्नलिखित पाँच अंतर हैं

प्रश्न 19.
मिश्रण के अवयवों को किन-किन उद्देश्यों के लिए पृथक किया जाता है?
उत्तर:
मिश्रण के अवयवों को निम्नलिखित उद्देश्यों के लिए पृथक् किया जाता है-

• किसी अवांछनीय अवयव को अलग करने के लिए।
• किसी हानिकारक अवयव को अलग करने के लिए।
• किसी पदार्थ के शुद्ध नमूने को प्राप्त करने के लिए।
• किसी लाभदायक अवयव को प्राप्त करने के लिए।

प्रश्न 20.
निम्नलिखित को धातु, अधातु व उपधातुओं में वर्गीकृत करें।
सिलिकन, जर्मेनियम, आयोडीन, सोडियम, लोहा, कार्बन।
उत्तर:

• धातु-सोडियम, लोहा
• अधातु-आयोडीन, कार्बन
• उपधातु-सिलिकन, जर्मेनियम।

प्रश्न 21.
फटकना विधि का वर्णन करें।
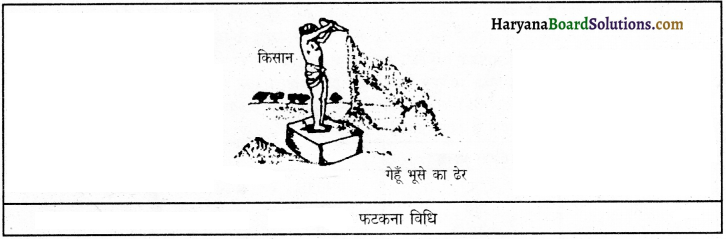
उत्तर:
किसान किसी ऊँचे स्थान पर खड़ा होकर भूसे और अनाज को अलग करने की जिस विधि को प्रयोग में लाता है, उसे फटकना कहते हैं। भूसा हल्का होने के कारण वायु के साथ दूर चला जाता है और अनाज के दाने भारी होने के कारण सीधे जमीन पर गिरते हैं।

प्रश्न 22.
‘हाथों से बीनना’ पृथक्करण विधि का संक्षिप्त वर्णन करें।
उत्तर:
गेहूँ, चावल, दालों आदि से कंकड़-पत्थर आदि अवांछनीय पदार्थों को अलग करना ही हाथों से बीनना कहलाता है। इस विधि का प्रयोग फल और सब्जियों की बिनाई करने के लिए भी किया जाता है।

प्रश्न 23.
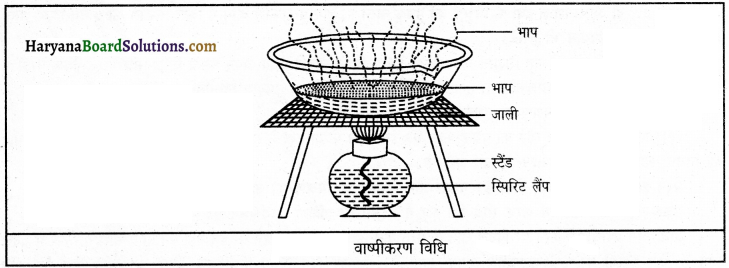
वाष्पीकरण विधि क्या है? वर्णन करें।
उत्तर:
यदि किसी द्रव में कोई अन्य विलेय पदार्थ घुला हो तथा उस मिश्रण के अवयवों को अलग-अलग करना हो तो मिश्रण को धूप में रखकर या गर्म करके वाष्पीकृत किया जाता है। द्रव वाष्प बनकर उड़ जाता है और शेष घुलनशील पदार्थ रह जाता है। इस विधि को वाष्पीकरण कहते हैं। समुद्र के जल से नमक इसी विधि से प्राप्त किया जाता है।

प्रश्न 24.
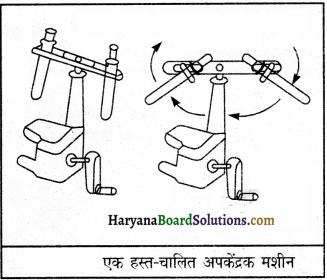
अपकेंद्रण विधि किसे कहते हैं?
उत्तर:
इस विधि में उस मिश्रण को, जिसमें अत्यधिक छोटे निलंबित कण होते हैं, एक बंद बर्तन में लेकर चारों ओर घुमाया जाता है। भारी पदार्थ तल की ओर चले जाते हैं तथा हल्के पदार्थ ऊपर रह जाते हैं। इसे अपकेंद्रण विधि कहते हैं। डेयरी में दूध से क्रीम इसी विधि द्वारा अलग की जाती है।

प्रश्न 25.
अपकेंद्रण विधि के दैनिक जीवन में उपयोगों का वर्णन करें।
उत्तर:
अपकेंद्रण विधि के दैनिक जीवन में निम्नलिखित उपयोग हैं-

• जांच प्रयोगशाला में रक्त और मूत्र के जांच में प्रयोग होता है।
• डेयरी और घर में क्रीम से मक्खन निकालने में प्रयोग होता है।
• कपड़े धोने की मशीन में भीगे हुए कपड़ों से जल निकालने में प्रयोग होता है।

प्रश्न 26.
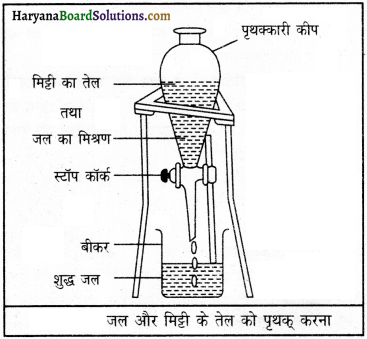
आप जल से मिट्टी का तेल किस प्रकार पृथक् करोगे?
उत्तर:
जल और मिट्टी का तेल दोनों अमिश्रणीय द्रव हैं। दोनों द्रव अलग-अलग परत बनाते हैं। मिट्टी का तेल हल्का होने के कारण जल के ऊपर अलग तैरता है। इन दोनों अवयवों को चित्रानुसार पृथक्कारी कीप की सहायता से अलग किया जा सकता है। मिश्रण को इस कीप में डालो। थोड़ी देर बाद दोनों द्रवों की अलग-अलग परतें बन जाएँगी। कीप का स्टॉप कॉर्क खोलकर नीचे बर्तन में जल अलग कर लेते हैं, जबकि मिट्टी का तेल कीप के अंदर ही रह जाएगा।

प्रश्न 27.
दो अघुलनशील द्रवों के मिश्रण को पृथक् करने के लिए पृथक्कारी कीप में किस सिद्धांत का प्रयोग किया जाता है? इसके कोई दो उपयोग भी लिखें।
उत्तर:
पृथक्कारी कीप में यह सिद्धांत काम करता है कि दो अघुलनशील द्रव अपने घनत्व के अनुसार पृथक्-पृथक् परतों में बंट जाते हैं तथा स्टॉप कॉक खोलकर अलग-अलग कर लिए जाते हैं। इसके उपयोग निम्नलिखित हैं-

• तेल और जल के मिश्रण को पृथक् करने में।
• धातुशोधन के दौरान लोहे को पृथक् करने में। इस विधि के द्वारा हल्के स्लग को ऊपर से हटा लिया जाता है और भट्टी की निचली सतह पर पिघला हुआ लोहा बच जाता है।

प्रश्न 28.
ऊर्ध्वपातन क्या होता है? नमक और नौसादर के मिश्रण को कैसे अलग करोगे?
उत्तर:
ठोस पदार्थ को गर्म करके सीधे गैस रूप में बदलने की प्रक्रिया ऊर्ध्वपातन है।
प्रायः ठोस पदार्थ गर्म करने पर पिघल जाते हैं, परंतु कुछ ठोस पदार्थ गर्म करने पर द्रव नहीं बनते। वे सीधे गैस रूप में बदल जाते हैं, ऐसे पदार्थों को ऊर्ध्वपातनशील पदार्थ कहते हैं। नौसादर (अमोनियम क्लोराइड), कपूर, आयोडीन तथा नैफ्थलीन ऊर्ध्वपातनशील पदार्थ हैं।

नमक तथा नौसादर का मिश्रण अलग करना-नमक तथा नौसादर के मिश्रण को अलग करने के लिए ऊर्ध्वपातन विधि का उपयोग किया जाता है।

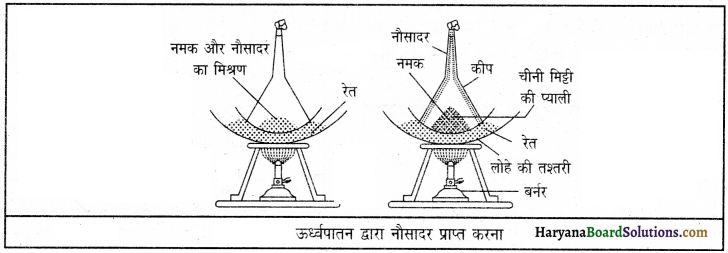
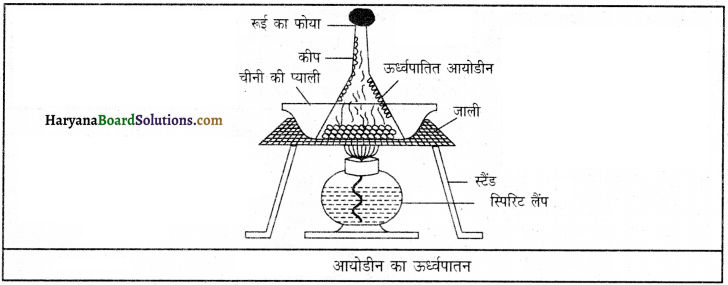
नमक तथा नौसादर के मिश्रण को चीनी की गोल प्याली में डालकर चित्र के अनुसार लोहे की एक तिपाई पर रखो। प्याली में मिश्रण के ऊपर शीशे की एक कीप चित्र की भांति उल्टी रखो। कीप की नली के छिद्र में कुछ रूई रखकर इसे बंद करो। प्याली को स्पिरिट लैंप से गर्म करो।

नौसादर गर्म होकर वाष्प में परिवर्तित हो जाएगा। नौसादर से बनी वाष्प ऊपर रखी कीप की भीतरी दीवारों के साथ लगकर पुनः ठोस रूप धारण कर लेगी तथा प्याली में नमक शेष रह जाएगा। इस विधि द्वारा नमक एवं नौसादर के मिश्रण को अलग-अलग किया जा सकता है।

प्रश्न 29.
क्रोमैटोग्राफी से आप क्या समझते हैं? इसके दैनिक जीवन में क्या उपयोग हैं?
उत्तर:
क्रोमैटोग्राफी एक ऐसी विधि है जिसका प्रयोग उन विलेय पदार्थों को पृथक् करने में होता है जो एक ही तरह के विलायक में घुले होते हैं। इनका उपयोग निम्नलिखित को पृथक् करने में किया जाता है-

• डाई में रंगों को।
• प्राकृतिक रंगों से रंग को पृथक् करने में।
• मूत्र से चीनी को पृथक् करने में।
• रक्त से दवा को पृथक् करने में।

प्रश्न 30.
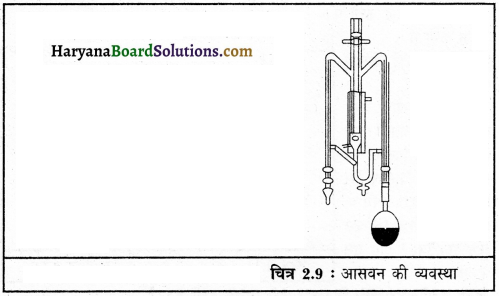
आसवन किसे कहते हैं? इसका उपयोग कहाँ किया जाता है?
उत्तर:
किसी द्रव को गर्म करके वाष्पों में बदलना और वाष्पों को पुनः ठंडा करके द्रव में बदलना आसवन कहलाता है। डॉक्टरों द्वारा प्रयोग किए जाने वाला आसुत (डिस्टील्ड) जल इसी विधि द्वारा प्राप्त किया जाता है। इस विधि का उपयोग उन दो घुलनशील द्रवों के मिश्रण को अलग करने में किया जाता है जिनके क्वथनांकों के बीच (25K से अधिक) काफी अंतर होता है।

प्रश्न 31.
प्रभाजी आसवन विधि कहाँ प्रयोग की जाती है? यह आसवन से किस प्रकार भिन्न है?
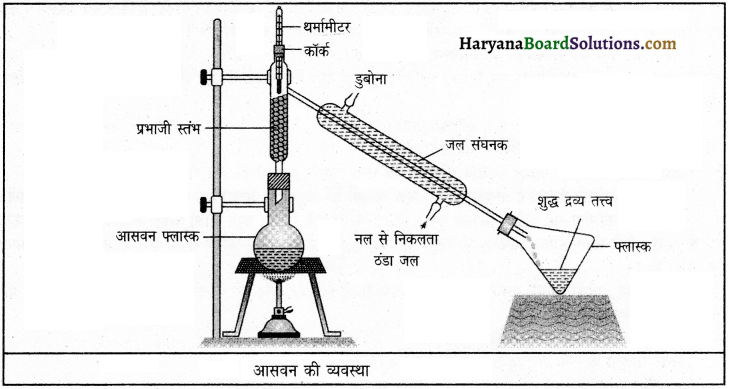
उत्तर:
जब दो या दो से अधिक घुलनशील द्रवों जिनके क्वथनांक का अंतर 25K से कम होता है, के मिश्रण को पृथक् करने के लिए प्रभाजी आसवन विधि का प्रयोग किया जाता है। उदाहरण के लिए, वायु से विभिन्न गैसों का पृथक्करण और पेट्रोलियम उत्पादों से उनके विभिन्न घटकों का पृथक्करण। इसका उपकरण साधारण आसवन विधि की तरह ही होता है। केवल आसवन फ्लास्क और संघनक के बीच एक प्रभाजी स्तंभ को लगा दिया जाता है।

साधारण प्रभाजी स्तंभ एक नली होती है जो कि शीशे के गुटके से भरी होती है। ये गुटके वाष्प को ठंडा और संघनित होने के लिए सतह प्रदान करते हैं, जैसा कि चित्र में दिखाया गया है।

प्रश्न 32.
क्रिस्टलीकरण किसे कहते हैं? इसके दो अनुप्रयोग लिखें।
उत्तर:
मिश्रण के विलयन में से ठोस पदार्थ के शुद्ध निश्चित आकार के टुकड़े प्राप्त करना क्रिस्टलीकरण कहलाता है। फिटकरी, साधारण नमक, कॉपर सल्फेट (नीला थोथा) इसी विधि द्वारा शुद्ध अवस्था में प्राप्त किए जा सकते हैं। क्रिस्टल प्राप्त करने के लिए पहले अशुद्ध नमूने को अधिक-से-अधिक मात्रा में गर्म द्रव में घोला जाता है, फिर इस विलयन को छानकर अन्य अशुद्धियाँ दूर की जाती हैं। इस विलयन को कुछ समय ठंडा करने पर शुद्ध ठोस क्रिस्टल प्राप्त हो जाते हैं।

अनुप्रयोग-

• समुद्री जल द्वारा प्राप्त नमक को शुद्ध करने में।
• अशुद्ध नमूने से फिटकरी को पृथक् करने में।

प्रश्न 33.
पिसी हुई चीनी से आप चीनी का बड़ा क्रिस्टल कैसे बनाएंगे?
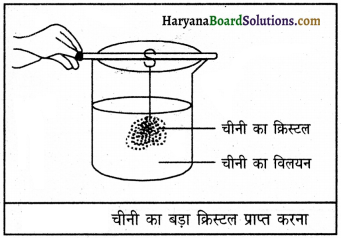
उत्तर:
चीनी के पाउडर से चीनी का बड़ा क्रिस्टल प्राप्त करने के लिए हम चीनी के पाउडर का गर्म जल में विलयन बनाते हैं। इस विलयन को ठंडा होने के लिए रख दिया जाता है। फिर विलयन को छानते हैं और धागे की सहायता से चीनी का एक क्रिस्टल इस चीनी का क्रिस्टल विलयन के अंदर लटका दिया जाता है। विलयन को कुछ समय के चीनी का विलयन लिए बिना हिलाए खुला रहने दिया जाता है। हम देखते हैं कि कुछ दिनों के बाद चीनी का क्रिस्टल बढ़ना आरंभ हो जाता है और इस प्रकार हमें चीनी का बड़ा क्रिस्टल प्राप्त हो जाता है।

प्रश्न 34.
क्रिस्टलीकरण विधि साधारण वाष्पीकरण विधि से अच्छी क्यों समझी जाती है?
उत्तर:
क्रिस्टलीकरण विधि साधारण वाष्पीकरण विधि से निम्नलिखित दो कारणों से अच्छी समझी जाती है-

• कुछ ठोस विघटित हो जाते हैं या कुछ चीनी की तरह झुलस जाते हैं।
• अशुद्ध विलेय पदार्थ को विलायक में घोलने पर विलयन में कुछ अशुद्धियाँ रह सकती हैं।

प्रश्न 35.
भौतिक और रासायनिक परिवर्तन से आप क्या समझते हैं? उदाहरण द्वारा स्पष्ट करें।
उत्तर:
भौतिक परिवर्तन-ये अस्थाई होते हैं जिनमें केवल भौतिक अवस्था में परिवर्तन होता है। इन परिवर्तनों में रासायनिक परिवर्तन नहीं होते और इन्हें मूल अवस्था में बदला जा सकता है। उदाहरण पानी को भाप या बर्फ में बदलना, चीनी को पानी में घोलना, नमक को पानी में घोलना इत्यादि।

रासायनिक परिवर्तन ये स्थाई होते हैं जिनमें भौतिक परिवर्तन के साथ रासायनिक परिवर्तन भी होते हैं। इन्हें मूल अवस्था में नहीं लाया जा सकता। उदाहरण-लोहे को जंग लगना, मैग्नीशियम तार को ऑक्सीजन की उपस्थिति में जलाना।

प्रश्न 36.
तत्त्व को परिभाषित कर विभिन्न वर्गों में बाँटो।
उत्तर:
तत्त्व पदार्थ का वह मूल रूप है जिसे रासायनिक क्रिया द्वारा छोटे टुकड़ों में नहीं बाँटा जा सकता। इसे निम्नलिखित तीन वर्गों में बांटा जा सकता है-

• धातु-सोना, चाँदी, ताँबा, लोहा, सोडियम आदि।
• अधातु-हाइड्रोजन, ऑक्सीजन, आयोडीन, कार्बन, कोल आदि।
• उपधातु-धातु और अधातु के बीच के गुणों वाले तत्त्व उपधातु कहलाते हैं; जैसे बोरॉन, सिलिकॉन।

प्रश्न 37.
आघातवर्थ्यता तथा तन्यता से आप क्या समझते हैं? किन्हीं दो आघातवर्थ्य तथा तन्य धातुओं के नाम लिखें।
उत्तर:
आघातवर्ध्यता यह धातुओं का वह गुण है जिसके कारण इन्हें पीटकर बहुत पतली चादरों के रूप में ढाला जा सकता है। सोना और चाँदी सबसे अधिक आघातवर्ध्य धातुएँ हैं। हथौड़े से पीट-पीटकर इनके कागज से भी कहीं अधिक पतले वर्क बनाए जा सकते हैं।

तन्यता-यह धातुओं का वह गुण है जिसके कारण धातुओं को खींचकर लंबी तारों के रूप में ढाला जा सकता है। चाँदी और ताँबा सबसे अधिक तन्य धातुएँ हैं।

प्रश्न 38.
धातुओं के मुख्य भौतिक गुण लिखें।
उत्तर:
धातुओं के मुख्य भौतिक गुण निम्नलिखित हैं-

• भौतिक अवस्था पारे के अतिरिक्त सभी धातुएँ साधारण ताप पर ठोस होती हैं।
• धात्विक चमक-सभी धातुओं की एक विशेष धात्विक चमक होती है।
• संरचना-धातुओं के बाह्यतम कोश में 1, 2 या 3 इलेक्ट्रॉन होते हैं।
• चालकता-धातुएँ प्रायः ऊष्मा तथा विद्युत की सुचालक होती हैं।
• आघातवर्ध्यता व तन्यता-धातुएँ प्रायः आघातवर्ध्य व तन्य होती हैं।
• कठोरता धातुएँ प्रायः कठोर होती हैं। सोडियम व पोटैशियम नरम धातुएँ होती हैं जिन्हें चाकू से काटा जा सकता है।
• घनत्व-सोडियम व पोटैशियम को छोड़कर धातुओं का घनत्व प्रायः अधिक होता है।
• द्रवणांक व क्वथनांक-धातुओं के द्रवणांक तथा क्वथनांक अपेक्षाकृत ऊँचे होते हैं।

प्रश्न 39.
अब तक ज्ञात तत्त्वों के बारे में संक्षिप्त जानकारी दें।
उत्तर:
अब तक ज्ञात तत्त्वों की संक्षिप्त जानकारी निम्नलिखित हैं-

• अभी तक ज्ञात तत्त्वों की संख्या 112 से अधिक है। इनमें से 92 तत्त्व प्राकृतिक हैं जबकि शेष मानव-निर्मित हैं।
• अधिकतर तत्त्व ठोस हैं।
• 11 तत्त्व कमरे के तापमान पर गैसें हैं।
• दो तत्त्व पारा और ब्रोमीन कमरे के तापमान पर द्रव हैं।
• गैलियम और सीसियम 303K से ऊपर द्रव के रूप में रह सकते हैं।

प्रश्न 40.
चालन विधि का वर्णन करें।
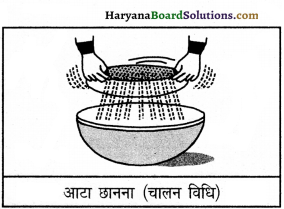
उत्तर:
जब मिश्रण के अवयवों का आकार भिन्न-भिन्न हो, तब विभिन्न प्रकार के छेदों वाली छलनियों का उपयोग करके अवयवों को अलग-अलग किया जाता है। यह विधि चालन विधि कहलाती है। आटे से चोकर अलग करना, काजू कारखानों में काजू अलग करना, स्वर्णकारों द्वारा विभिन्न आकारों के मोतियों को अलग करना तथा किसानों द्वारा विभिन्न प्रकार के अनाजों को अलग करने के लिए चालन विधि का प्रयोग किया जाता है।

प्रश्न 41.
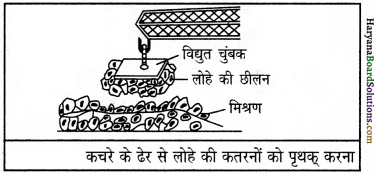
चुंबकीय पृथक्करण विधि क्या है?
उत्तर:
चुंबक के चुंबकीय गुण का उपयोग करते हुए मिश्रण में से लोहे की छीलन या लोहे के कणों को अलग करने की विधि चुंबकीय पृथक्करण विधि कहलाती है। भूमि से लौह अयस्क (खनिज) को भी इसी विधि द्वारा प्राप्त किया जाता है।

प्रश्न 42.
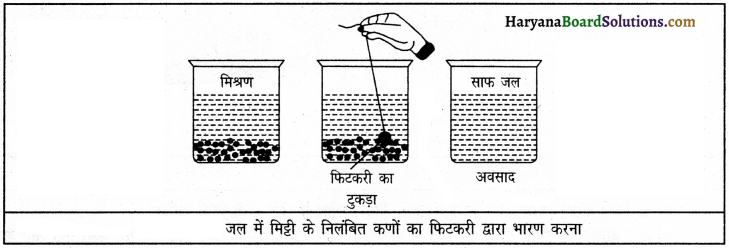
भारण विधि का संक्षिप्त वर्णन करें।
उत्तर:
कई बार तालाब या झील के गंदे जल में स्थित रेत या मिट्टी के छोटे निलंबित कण जल्दी से नीचे नहीं बैठते अर्थात् उन्हें निथारने में समय लगता है। अतः कणों को शीघ्र नीचे बैठाने के लिए या कणों को भारी करने के लिए मिश्रण में फिटकरी मिला दी जाती है और जल को शीघ्र निथार लिया जाता है। इसे भारण विधि कहते हैं। तालाब के जल को इस विधि से साफ किया जा सकता है।

निबंधात्मक प्रश्न

प्रश्न 1.
वायु से विभिन्न गैसों को प्राप्त करने की विधि का वर्णन करें।
उत्तर:
वायु विभिन्न गैसों की समांगी मिश्रण होती है और इसके घटकों को प्रभाजी आसवन विधि द्वारा पृथक् किया जा सकता है। इस विधि के विभिन्न चरण अग्र दर्शाए गए सचित्र में है-

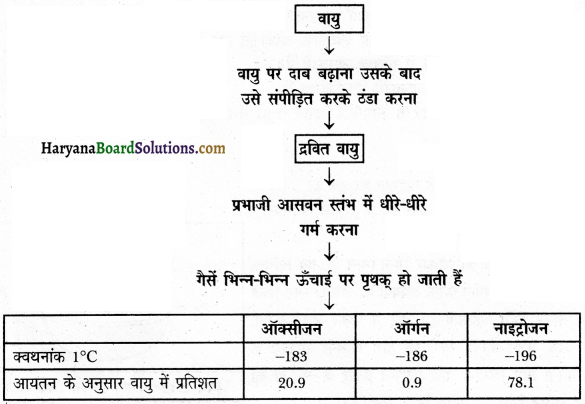
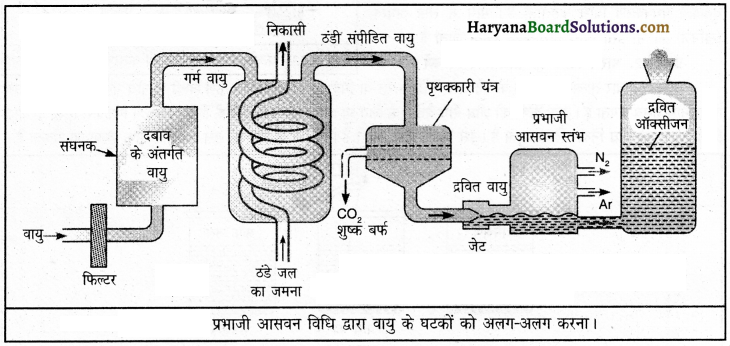
जैसे यदि हम वायु से ऑक्सीजन (चित्र अनुसार) गैस को प्राप्त करना चाहते हैं तो हमें वायु में उपस्थित दूसरी गैसों को अलग करना होगा। द्रव वायु प्राप्त करने के लिए पहले वायु पर दबाव बढ़ाया जाता है और फिर ताप को घटाकर उसे ठंडा करके संपीडित किया जाता है। इस द्रवित गैस को प्रभाजी आसवन स्तंभ में धीरे-धीरे गर्म किया जाता है, जहाँ सभी गैसें विभिन्न ऊंचाइयों पर अपने क्वथनांक के अनुसार अलग-अलग हो जाती हैं, जैसा कि चित्र में दिखाया गया है।

प्रश्न 2.
निम्नलिखित मिश्रणों को पृथक् करने के लिए उपयोग में आने वाली विधि बताइए
(1) गेहूँ , चीनी तथा भूसा, (2) चावल, चना तथा लोहे का चूर्ण, (3) रेत, उड़द तथा भूसा, (4) रेत, कपूर तथा लोहे का चूर्ण, (5) रेत, चीनी तथा लोहे का चूर्ण।
उत्तर:
(1) इस मिश्रण को अलग करने के लिए एक से अधिक विधियों का उपयोग किया जाता है। भूसे के मिश्रण को फटकना विधि द्वारा अलग किया जाता है। उसके बाद मिश्रण को जल में घोलकर छान लिया जाता है। चीनी जल में विलेयता के कारण विलयन बना लेती है तथा गेहूँ छन्ने के ऊपर रह जाता है। इनको सुखा लिया जाता है। इसके बाद विलयन को पॉर्सिलेन डिश में गर्म किया जाता है। गर्म करने पर जल भाप बनकर उड़ जाता है तथा चीनी पॉर्सिलेन डिश में रह जाती है। अतः तीन अवयव अलग हो जाते हैं।

(2) इस मिश्रण को अलग करने के लिए भी एक से अधिक विधियों का उपयोग किया जाता है। सर्वप्रथम, मिश्रण में चुंबक को घुमाओ जिससे लौह के चूर्ण चुंबक के साथ चिपककर अलग हो जाएँगे। अब शेष चावल तथा चने के मिश्रण को छानना विधि द्वारा अलग किया जा सकता है। इस विधि में चावल नीचे रह जाएँगे तथा चने ऊपर आ जाएँगे।

(3) इस मिश्रण में भूसा फटकना विधि द्वारा अलग किया जा सकता है। रेत तथा उड़द शेष रह जाएंगे। इन्हें छानना विधि द्वारा पृथक् किया जा सकता है।

(4) सर्वप्रथम, मिश्रण के ऊपर चुंबक को घुमाया जाता है। लौह-चूर्ण चुंबक के साथ चिपककर अलग हो जाता है। उसके बाद मिश्रण को ऊर्ध्वपातन की विधि द्वारा अलग किया जाता है। कपूर वाष्प में बदल जाता है, जो कीप की दीवारों पर ठंडा होकर जम जाता है तथा रेत बर्तन में बच जाती है। इस प्रकार तीन अवयव अलग-अलग हो जाते हैं।

(5) मिश्रण से लौह के चूर्ण को चुंबक का प्रयोग करके अलग कर लिया जाता है। इसके बाद मिश्रण को जल में घोलते हैं। चीनी जल में घुल जाती है। इसके बाद इसे छान लिया जाता है, चीनी विलेय होने के कारण नीचे विलयन के रूप में निकल जाती है तथा रेत ऊपर छन्ने कागज़ पर बच जाती है। फिर इस विलयन को गर्म करते हैं। गर्म करने पर जलवाष्प बनकर उड़ जाता है तथा चीनी बर्तन में रह जाती है।

प्रश्न 3.
शहरों में पेय जल वितरण प्रणाली को चित्र द्वारा समझाइए तथा बताइए इसमें कौन-सी पृथक्कीकरण विधियाँ प्रयोग की जाती हैं?
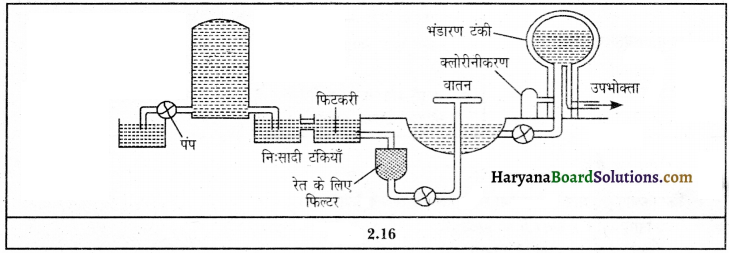
उत्तर:
शहरों में पेयजल का वितरण जल-संस्थानों (वाटर वक्स) द्वारा किया जाता है। चित्र में एक जल-संस्थान का क्रमदर्शी आरेख दर्शाया गया है। इन जल-संस्थानों में अवसादन, निथारना, भारण तथा फिल्टरन के प्रक्रमों द्वारा जल से अवांछित सामग्री को पृथक् किया जाता है। आपको भारण के प्रक्रम में फिटकरी का उपयोग अवश्य स्मरण होगा। जल-संस्थानों में हानिकारक जीवाणुओं को नष्ट करने के लिए क्लोरीन का उपयोग किया जाता है। इस साफ जल को ही पाइपों द्वारा घरों में पेयजल के रूप में पहुँचाया जाता है।

प्रश्न 4.
आसवन तथा प्रभाजी में क्या अंतर है?
उत्तर:
दोनों विधियाँ भिन्न-भिन्न क्वथनांकों वाले द्रवों के मिश्रण के अवयवों को पृथक्-पृथक् करने के लिए प्रयोग की जाती हैं। दोनों विधियों में निम्नलिखित अंतर हैं-

प्रश्न 5.
धातु और अधातु के भौतिक गुणों में अंतर बताएँ।
उत्तर:
धातु और अधातु के भौतिक गुणों में अंतर निम्नलिखित हैं-

प्रयोगात्मक कार्य

क्रियाकलाप 1.
आप प्रयोगशाला में दो समांगी मिश्रण तैयार करें।
कार्य-विधि-
(1) एक बीकर में 50 मि०ली० जल लेकर उसमें दो चम्मच नमक के मिलाएँ इस प्रकार प्राप्त मिश्रण समांगी होगा, क्योंकि इसमें विलेय और विलायक के कणों को अलग-अलग नहीं पहचाना जा सकता है।

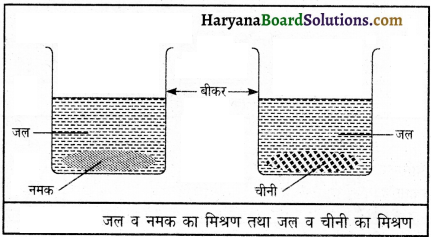
(2) एक बीकर में 50 मि०ली० जल लेकर उसमें एक चम्मच चीनी डालकर हिलाएँ। इस प्रकार घुलने से प्राप्त विलयन समांगी मिश्रण होगा क्योंकि इसमें विलेय और विलायक के कणों को अलग-अलग नहीं पहचाना जा सकता है।

क्रियाकलाप 2.
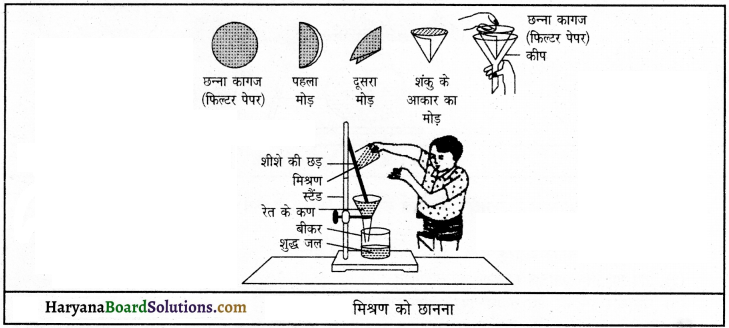
प्रयोग द्वारा सिद्ध करो कि विलयन समांगी होते हैं।
कार्य-विधि-नमक तथा पानी का एक विलयन लो। इसे छन्ना कागज़ (फिल्टर पेपर) में से छानों तथा छनित्र का स्वाद चखो। यह पहले जैसा ही नमकीन होगा। अब छन्ने कागज़ (फिल्टर पेपर) को देखें। इस पर कोई अवशेष नहीं होगा। अतः सिद्ध होता है कि विलयन समांगी होते हैं जो फिल्टर पेपर में से गुज़र जाते हैं तथा उस पर कोई अवशेष नहीं छोड़ते।

क्रियाकलाप 3.
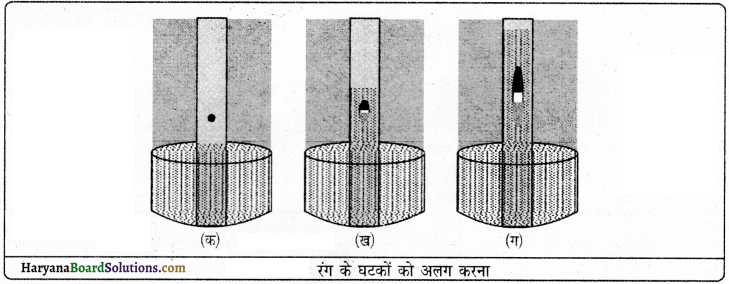
रंग (डाई) वाले घटकों को नीले अथवा काले रंग की स्याही से कैसे पृथक् किया जाता है?
कार्य-विधि-आधा बीकर जल लें तथा उसके मुख पर वाच-ग्लास रख दें जैसा कि चित्र में दिखाया गया है। कुछ बूंदें स्याही वाच-ग्लास पर डाल दें। अब बीकर को गर्म करना शुरू करें। हम स्याही को प्रत्यक्ष रूप से गर्म करना नहीं चाहते हैं।

आप देखेंगे कि वाच-ग्लास से वाष्पीकरण हो रहा है। वाष्पीकरण होने तक गर्म करना जारी रखते हैं जब वाच-ग्लास पर कोई परिवर्तन होते नहीं देखते हैं तब हम उसे गर्म करना बंद कर देते हैं। इस प्रकार वाच-ग्लास पर नीला या काला घटक शेष बच जाता है। इस प्रयोग से सिद्ध होता है कि स्याही जल में रंग का एक मिश्रण है जिसमें से जल वाष्पीकरण द्वारा वाष्पीकृत हो जाता है।

क्रियाकलाप 4.
आयोडीन तथा रेत को उनके मिश्रण से किस प्रकार पृथक् करेंगे?
कार्य-विधि-आयोडीन तथा रेत के मिश्रण को ऊर्ध्वपातन विधि के द्वारा अलग किया जाता है। इस विधि में मिश्रण को पॉर्सिलेन डिश में लेते हैं और उसके ऊपर एक कीप को उल्टी करके रख देते हैं तथा उसके खुले सिरे को रूई द्वारा बंद कर दिया जाता है। फिर मिश्रण को नीचे से गर्म किया जाता है। गर्म करने पर आयोडीन सीधे वाष्प में बदल जाती है जो ठंडा होने पर कीप की दीवारों पर जम जाती है तथा रेत डिश में शेष रह जाती है। इस प्रकार कीप में से आयोडीन को खुरच लिया जाता है। अतः मिश्रण के अंश अलग-अलग हो जाते हैं।

क्रियाकलाप 5.
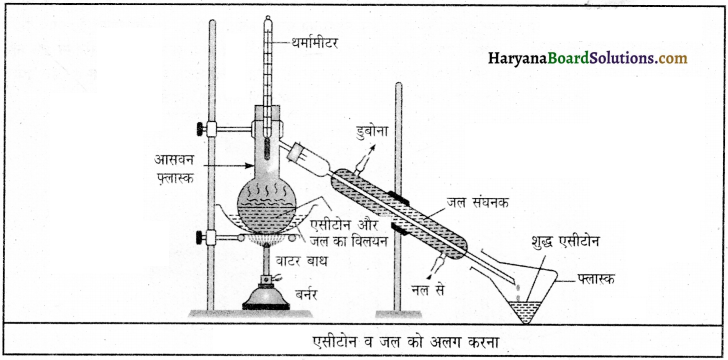
प्रयोगशाला में एसीटोन और जल को उनके क्लियन से कैसे पृथक् करें?
कार्य-विधि-

• मिश्रण को आसवन फ्लास्क में लें। इसके साथ थर्मामीटर लगा दें।
• दिए गए चित्र अनुसार उपकरण को व्यवस्थित करें।
• धीरे-धीरे गर्म करें और सावधानीपूर्वक थर्मामीटर पर नजर रखें।
• एसीटोन वाष्पीकृत होता है और संघनित होकर संघनक द्वारा बाहर निकालने पर बर्तन में एकत्रित किया जा सकता है।
• जल आसवन फ्लास्क में बच जाता है। इस प्रकार एसीटोन और जल अलग-अलग हो जाएँगे।
  

अध्याय का तीव्र अध्ययन

1. निम्नलिखित में से कौन-सा शुद्ध पदार्थ है-
(A) चीनी
(B) दूध
(C) वायु
(D) तालाब का जल
उत्तर:
(A) चीनी

2. कोलाइड में कणों का आकार होता है-
(A) 10^-5m से 10^-4m
(B) 10^-6m से 10^-5m
(C) 10^-9m से 10^-7m
(D) 10^-7m से अधिक
उत्तर:
(C) 10^-9m से 10^-7m

3. निलंबन का उदाहरण है-
(A) नमक का घोल
(B) स्याही
(C) पेंट
(D) दूध
उत्तर:
(C) पेंट

4. निम्नलिखित में से समांगी मिश्रण है-
(A) जल में चीनी का मिश्रण
(B) वायु
(C) आइसक्रीम
(D) तालाब का गंदला पानी
उत्तर:
(A) जल में चीनी का मिश्रण

5. 293 K ताप पर 36g NaCl को, 100g जल में घोला गया इसकी सांद्रता होगी-
(A) 36%
(B) 26.47%
(C) 24%
(D) इनमें से कोई नहीं
उत्तर:
(B) 26.47%

6. दही से मक्खन को अलग किया जाता है-
(A) अपकेंद्रण विधि द्वारा
(B) प्रभाजी आसवन विधि द्वारा
(C) वाष्पीकरण विधि द्वारा
(D) क्रिस्टलीकरण विधि द्वारा
उत्तर:
(A) अपकेंद्रण विधि द्वारा

7. नमक और कपूर के मिश्रण में से कपूर व नमक को अलग किया जाता है-
(A) वाष्पीकरण विधि द्वारा
(B) अपकेंद्रण विधि द्वारा
(C) ऊर्ध्वपातन विधि द्वारा
(D) पृथक्करण कीप विधि द्वारा
उत्तर:
(C) ऊर्ध्वपातन विधि द्वारा

8. जल और तेल के मिश्रण में से जल और तेल को अलग-अलग किया जाता है-
(A) पृथक्करण कीप द्वारा
(B) ऊर्ध्वपातन द्वारा
(C) वाष्पीकरण द्वारा
(D) छानना विधि द्वारा
उत्तर:
(A) पृथक्करण कीप द्वारा

9. निम्नलिखित मिश्रणों में विलयन है-
(A) समुद्री जल
(B) सोडा जल
(C) वायु
(D) तालाब का जल
उत्तर:
(B) सोडा जल

10. वायु में नाइट्रोजन की प्रतिशत मात्रा है-
(A) 20
(B) 78
(C) 0.01
(D) इनमें से कोई नहीं
उत्तर:
(B) 78

11. निम्नलिखित में से यौगिक नहीं है-
(A) रक्त
(B) CO
(C) मिथेन
(D) साबुन
उत्तर:
(A) रक्त

12. तालाब का गंदला पानी साफ हो जाता है-
(A) संगलन द्वारा
(B) भारण द्वारा
(C) अपकेंद्रण द्वारा
(D) पृथक्करण द्वारा
उत्तर:
(B) भारण द्वारा

13. टिंक्चर आयोडीन में उपस्थित विलायक का नाम है-
(A) जल
(B) गुलाब जल
(C) कार्बन डाइऑक्साइड
(D) ऐल्कोहॉल
उत्तर:
(D) ऐल्कोहॉल

14. वायु में ऑक्सीजन की प्रतिशत मात्रा है-
(A) 3
(B) 11
(C) 18
(D) 21
उत्तर:
(D) 21

15. जल और एसीटोन के मिश्रण को अलग-अलग किया जा सकता है-
(A) ऊर्ध्वपातन द्वारा
(B) वाष्पीकरण द्वारा
(C) आसवन द्वारा
(D) भारण द्वारा
उत्तर:
(C) आसवन द्वारा

16. ज्ञात तत्त्वों की संख्या है-
(A) 92
(B) 108
(C) 112
(D) 118
उत्तर:
(C) 112

17. निम्नलिखित में से भौतिक परिवर्तन है-
(A) पानी का भाप बनना
(B) आटे की रोटी बनाना
(C) फल का पकना
(D) लोहे को जंग लगना
उत्तर:
(A) पानी का भाप बनना

18. आयोडीन और रेत के मिश्रण को किस विधि द्वारा अलग-अलग किया जा सकता है?
(A) अपकेंद्रण
(B) निथारना
(C) ऊर्ध्वपातन
(D) छानना
उत्तर:
(C) ऊर्ध्वपातन

19. निम्नलिखित में से भौतिक परिवर्तन नहीं है-
(A) पानी का भाप बनना
(B) फलों का सलाद बनाना
(C) लोहे को जंग लगना
(D) इनमें से कोई नहीं
उत्तर:
(C) लोहे को जंग लगना

20. आटे से चोकर किस विधि से अलग किया जाता है?
(A) छंटाई
(B) भारण
(C) चालन
(D) फटकना
उत्तर:
(C) चालन

21. धातुओं के बाह्यतम कोश में इलेक्ट्रॉनों की संख्या नहीं होती-
(A) 1
(B) 2
(C) 3
(D) 4
उत्तर:
(D) 4

22. एक ही प्रकार के कणों से बने पदार्थ को कहा जाता है-
(A) शुद्ध पदार्थ
(B) मिश्रण
(C) विलयन
(D) अशुद्ध पदार्थ
उत्तर:
(A) शुद्ध पदार्थ

23. समांगी मिश्रण नहीं है-
(A) जल में चीनी का मिश्रण
(B) बालू व नमक का मिश्रण
(C) जल में नमक का मिश्रण
(D) जल व ऐल्कोहॉल का मिश्रण
उत्तर:
(B) बालू व नमक का मिश्रण।

24. धातु के छोटे टुकड़े को कार के इंजन ऑयल से पृथक किया जाता है-
(A) छानने की विधि द्वारा
(B) वाष्पीकरण द्वारा
(C) अपकेंद्रण द्वारा
(D) ऊर्ध्वपातन द्वारा
उत्तर:
(A) छानने की विधि द्वारा

25. भूसे से गेहूँ के दाने अलग किए जाते हैं-
(A) भारण विधि द्वारा
(B) फटकना विधि द्वारा
(C) छानना विधि द्वारा
(D) वाष्पीकरण विधि द्वारा
उत्तर:
(B) फटकना विधि द्वारा

26. प्राकृतिक तत्त्वों की संख्या है-
(A) 112
(B) 22
(C) 92
(D) 108
उत्तर:
(C) 92

27. निम्नलिखित में से कौन-सा तत्त्व नहीं है?
(A) सोडियम
(B) चाँदी
(C) टिन
(D) साबुन
उत्तर:
(D) साबुन

28. निम्नलिखित में से कौन-सा मिश्रण है?
(A) मिथेन
(B) सिलिकॉन
(C) रक्त
(D) साबुन
उत्तर:
(C) रक्त

29. निम्नलिखित में से कौन टिनडल प्रभाव को प्रदर्शित नहीं करेगा?
(A) पानी
(B) दूध
(C) कॉपर सल्फेट का विलयन
(D) उपर्युक्त सभी
उत्तर:
(C) कॉपर सल्फेट का विलयन

30. विलयन का वह घटक (जिसकी मात्रा दूसरे से अधिक होती है) जो दूसरे घटक को विलयन में मिलाता है, कहलाता है-
(A) विलायक
(B) विलेय
(C) मिश्रधातु
(D) उपधातु
उत्तर:
(A) विलायक

31. जल को छोड़कर अन्य किसी द्रव में विलेय को घोलने से प्राप्त विलयन कहा जाता है-
(A) अजलीय विलयन
(B) समांगी विलंयन
(C) असमांगी विलयन
(D) जलीय विलयन
उत्तर:
(A) अजलीय विलयन

32. यदि किसी विलयन में विलेय पदार्थ की मात्रा संतृप्तता से कम हो तो उसे कहा जाता है-
(A) संतृप्त विलयन
(B) अतिसंतृप्त विलयन
(C) असंतृप्त विलयन
(D) समांगी विलयन
उत्तर:
(C) असंतृप्त विलयन

33. धातु और अधातु के बीच के गुण दर्शाने वाले तत्त्व कहलाते हैं-
(A) धातु
(B) मिश्र धातु
(C) अधातु
(D) उपधातु
उत्तर:
(D) उपधातु

34. निम्नलिखित में से कौन-सा भौतिक परिवर्तन है?
(A) जंग लगना
(B) चीनी का जल में घुलना
(C) हाइड्रोजन का ऑक्सीजन से संयोजन
(D) कागज का जलना
उत्तर:
(B) चीनी का जल में घुलना

35. निम्नलिखित में से कौन-सी उपधातु नहीं है?
(A) बोरॉन
(B) सिलिकॉन
(C) जर्मेनियम
(D) ऑक्सीजन
उत्तर:
(D) ऑक्सीजन

36. निम्नलिखित में से कौन-सा धातु का गुण है-
(A) तन्यता
(B) आघातवर्ध्यता
(C) धात्विक चमक
(D) उपर्युक्त सभी
उत्तर:
(D) उपर्युक्त सभी

37. निम्नलिखित में से कौन-सा तत्त्व अधातु है-
(A) ब्रोमीन
(B) सोना
(C) चाँदी
(D) सोडियम
उत्तर:
(A) ब्रोमीन

38. निम्नलिखित में से कौन-सी धातु कमरे के ताप पर द्रव अवस्था में पाई जाती है
(A) सोना
(B) चांदी
(C) पारा
(D) ब्रोमीन
उत्तर:
(C) पारा

Haryana State Board HBSE 9th Class Maths Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 11 Constructions Exercise 11.1

Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:

Steps of construction:
Step – I: Draw a ray AB with initial point A.
Step – II: Taking A as centre and suitable radius, draw an arc which intersects AB at P.
Step – III: Taking P as centre and same radius as before, draw an arc intersecting previous arc at C.
Step – IV: Taking C as centre and same radius as before, draw an arc intersecting the previous, arc at D.
Step – V: Taking C and D as centres draw two arcs intersecting each other at Q.
Step – VI: Join AQ. Then ∠QAB is the required angle of measure 90°.
Justification: Join CP, AC, CD and AD.
∵ AP = CP = AC (By construction)
∴ ACP is an equilateral triangle.
⇒ ∠CAP = 60°
[∵ Each angle of equilateral triangle is 60°]
Again, AC = CD = AD
(By construction)
∴ CAD is an equilateral triangle.
⇒ ∠CAD = 60°
Since, AQ is the bisector of ∠CAD.
∴ ∠CAQ = \(\frac{1}{2}\) × 60° = 30°
Now, ∠QAB = ∠CAP + ∠CAQ
⇒ ∠QAB = 60° + 30°
⇒ ∠QAB = 90°.

Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:

Steps of construction:
Step – I: Draw ∠QAB = 90° by the following steps given in 1.
Step – II: Draw the bisector of ∠QAB.
Then ∠RAB = 45°
Justification: ∠QAB = 90° (By construction)
Since AR is the bisector of ∠QAB.
∠RAB = \(\frac{1}{2}\) × 90°
= 45°.

Question 3.
Construct the angles of the following measurements:
(i) 30°
(ii) 22°
(iii) 15°
Solution:
(i) Steps of construction:
Step – I: Draw a ray AB with initial pointA.
Step – II: Taking A as centre and suitable radius, draw an arc intersecting AB at C.
Step – III: Taking C as centre and same radius as before, draw an arc intersecting the previous arc at D.

Step – IV: Taking C and D as centres and a suitable radius more than \(\frac{1}{2}\)CD, draw two arcs intersecting each other at E.
Step – V: Join AE. Then ∠BAE = 30°.

(ii) Steps of construction:
Step – I: Draw ∠CAB = 90° as followed by the steps in 1.
Step – II: Draw the bisector AD of ∠CAB.
∠CAD = ∠BAD = \(\frac{90^{\circ}}{2}\) = 45°.

Step – III: Draw the bisector AE of ∠BAD
∴ ∠BAE = \(\frac{1}{2}\) × 45° = \(22 \frac{1}{2}^{\circ}\)

(iii) Steps of construction :
Step – I: Draw ∠CAB = 30° as followed by the steps in 3(a).

Step – II: Draw the bisector AD of ∠CAB.
∴ ∠BAD = \(\frac{1}{2}\) × 30°
= 15°

Question 4.
Construct the following angles and verify by measuring them by a protractor:
(i) 75°
(ii) 105°
(iii) 135°.
Solution:

(i) Steps of construction:
Step – I: Draw ∠CAB = 60° as followed by the steps in Construction 11.3.
Step – II: Draw ∠DAB = 90° as followed by the steps in 1. So, ∠CAD = 90° – 60° = 30°.
Step – III: Draw the bisector AE of CAD.
Then ∠EAB = 75° is required angle.
Verification: On measuring ∠EAB, with the help of protractor. We observe that ∠EAB = 75°.

(ii) Steps of construction:
Step – I:Draw a ray AB with initial point A.
Step – II:Taking A as centre and suitable radius, draw an arc intersecting AB at P.
Step – III:Taking P as a centre and same radius as before, draw an arc intersecting previous are at Q.

Step – IV: Taking Q as a centre and same radius as before, draw an arc intersecting previous arc at R.
Step – V: Draw a ray CA passing through R. Then
∠CAB = 120°
Step – VI: Draw ∠DAB = 90° as followed by the steps in 1.
∴ ∠CAD = 120° – 90° = 30°.
Step – VII: Draw the bisector AE of ∠CAD.
∠EAD = \(\frac{1}{2}\) × 30° = 15°
Then, ∠EAB = 90° + 15° = 105°
Hence, ∠EAB = 105°.
Verification: On measuring ∠EAB with the help of protractor we observe that ∠EAB = 105°.

(iii) Steps of construction :
Step – I: Draw a ray AB with initial point
Step – II: Taking A as centre and suitable radius draw an arc intersecting AB at P.
Step – III: Taking Pas centre and same radius as before, draw an arc intersecting previous arc at Q.

Step – IV: Taking Q as centre and same radius as before, draw an arc intersecting previous arc at R.
Step – V: Taking R as the centre and same radius as before, draw an arc intersecting previous arc at S. Produce BA to S. Then ∠SAB = 180°.
Step – VI: Taking Q and R as the centres and radius more than \(\frac{1}{2}\)PQ draw two arcs intersecting each other at C.
Step – VII: Join AC intersecting previous arc at M. Then ∠CAB = 90°. ∠CAS = 180° – 90° = 90°.
Step – VIII: Draw bisector AD of ∠CAS.
Then ∠CAD = \(\frac{1}{2}\) × 90o = 45°.
∴ ∠BAD = 90° + 45° = 135°.
Verification: On measuring ∠BAD with the help of protractor we osberve that ∠BAD = 135°.

Question 5.
Construct an equilateral triangle, given its side and justify the construction. Let us draw an equilateral triangle of side 3.7 cm (say).
Solution:
Steps of construction:
Step – I: Draw a line segment length 3.7 cm.
Step – II: Taking B draw an arc, that cut BC at D.
Step – III: By same radius taking D as centre, draw an arc that cut previous arc at E join BE.
Step – IV: Cut 3.7 cm from BE at A, Join ABC.

Justification:
∵ AB = BC = CA (By construction)
∴ ABC is an equilateral triangle.

Haryana State Board HBSE 9th Class Maths Solutions Chapter 2 Polynomials Ex 2.4 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 2 Polynomials Exercise 2.4

Question 1.
Determine which of the following polynomials has (x + 1) as a factor :
(i) x³ + x² + x + 1
(ii) x⁴ + x³ + x² + x + 1,
(iii) x⁴ + 3x³ + 3x² + x + 1
(iv) x³ – x² – (2 + \(\sqrt{2}\))x+ \(\sqrt{2}\).
Solution:
(i) Let
p(x) = x³ + x² + x + 1
If (x + 1) is a factor of p(x), then by factor theorem, p(-1) should be zero.
Now, p(-1) = (-1) + (-1) – 1 + 1
⇒ p(-1) = – 1 + 1 – 1 + 1
⇒ p(-1) = 2 – 2
⇒ p(-1) = 0.
Hence, (x + 1) is a factor of p(x).

(ii) Let p(x) = x⁴ + x³ + x² + x + 1
If (x + 1) is a factor of p(x), then by factor theorem, p(-1) should be zero.
Now, p(-1) = (-1)⁴ + (-1)³ + (-1)² – 1 + 1
⇒ p(-1) = 1 – 1 + 1 – 1 + 1
⇒ p(-1) = 1 ≠ 0.
Hence, (x + 1) is not a factor of p(x).

(iii) Let p(x) = x⁴ + 3x³ + 3x² + x + 1
If (x + 1) is a factor of p(x), then by factor theorem, p(-1) should be zero.
Now, p(-1) = (-1)⁴ + 3 × (-1)³ + 3 × (-1)² – 1 + 1
⇒ p(-1) = 1 – 3 + – 1 + 1
⇒ p(-1) = 1 ≠ 0.
Hence, (x + 1) is not a factor of p(x).

(iv) Let p(x) = x³ – x² – (2 + \(\sqrt{2}\))x + \(\sqrt{2}\)
If (x + 1) is a factor of p(x), then by factor theorem p(-1) should be zero.
Now, p(-1) = (-1)³ – (- 1)² – (2 + \(\sqrt{2}\))(-1) + \(\sqrt{2}\)
⇒ p(-1) = – 1 – 1 + 2 + \(\sqrt{2}\) + \(\sqrt{2}\)
⇒ p(-1) = – 2 + 2 + 2\(\sqrt{2}\)
⇒ p(-1) = 2\(\sqrt{2}\) ≠ 0.
Hence, (x + 1) is not a factor of p(x).

Question 2.
Use the factor theorem to determine, whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x³ + x² – 2x – 1; g(x) = x + 1
(ii) p(x) = x³ + 3x² + 3x + 1; g(x) = x + 2
(iii) p(x) = x³ – 4x² + x + 6; g(x) = x – 3.
Solution:
(i) We have,
p(x) = 2x³ + x² – 2x – 1
If g(x) = x + 1 is a factor of p(x), then by factor theorem, p(-1) should be zero.
Now, p(-1) = 2 × (-1)³ + (-1)² – 2 × (-1) – 1
⇒ p(-1) = – 2 + 1 + 2 – 1
⇒ p(-1)= 0.
Hence, g(x) = x + 1 is a factor of p(x).

(ii) We have, p(x) = x³ + 3x² + 3x + 1
If g(x) = 1 + 2 is a factor of p(x), then by factor theorem, p(-2) should be zero.
Now, p(-2) = (-2)³ + 3 × (-2)² + 3 × (-2) + 1
⇒ p(-2) = – 8 + 12 – 6 + 1
⇒ p(-2) = – 14 + 13
⇒ p(-2) = -1 ≠ 0.
Hence, g(x) = x + 2 is not a factor of p(x).

(iii) We have, p(x)= x³ – 4x³ + x + 6
If g(x) = x – 3 is a factor of p(x), then by factor theorem, p(3) should be zero.
Now, p(3)= (3)³ – 4 × (3)² + 3 + 6
⇒ p(3) = 27 – 36 + 3 + 6
⇒ p(3) = 36 – 36
⇒ p(3) = 0.
Hence, g(x) = x – 3 is a factor of p(x).

Question 3.
Find the value of k, if x – 1 is a factor of p(x) in each of the following cases :
(i) p(x) = x² + x + k
(ii) p(x) = 2x² + kx + \(\sqrt{2}\)
(iii) p(x) = kx² – \(\sqrt{2}\)x +1
(iv) p(x) = kx² – 3x + k.
Solution:
(i) We have,
p(x) = x² + x + k
If (x – 1) is a factor of p(x), then by factor theorem, p(1) should be zero.
⇒ p(1) = 0
⇒ (1)² + 1 + k = 0
⇒ 1 + 1 + k = 0
⇒ 2 + k = 0
⇒ k = – 2
Hence, k = -2

(ii) We have, p(x) = 2x² + kx + \(\sqrt{2}\)
If (x – 1) is a factor of p(x), then by factor theorem, p(1) should be zero.
⇒ p(1) = 0
⇒ 2 × (1)² + k × 1 + \(\sqrt{2}\) = 0
⇒ 2 + k + \(\sqrt{2}\) = 0
⇒ k = – 2 – \(\sqrt{2}\)
⇒ k = -(2 + \(\sqrt{2}\))
Hence, k= – (2 + \(\sqrt{2}\)).

(iii) We have, p(x) = kx² – \(\sqrt{2}\)x +1
If (x – 1) is a factor of p(x), then by factor theorem, p(1) should be zero.
⇒ p(1) = 0
⇒ k × (1)² – \(\sqrt{2}\) × 1 + 1 = 0
⇒ k – \(\sqrt{2}\) + 1 = 0
⇒ k = \(\sqrt{2}\) – 1
Hence,
k = \(\sqrt{2}\) – 1

(iv) We have, p(x) = kx² – 3x + k
If (x – 1) is a factor of p(x), then by factor theorem, p(1) should be zero. =
⇒ P(1) = 0
⇒ k × (1)² – 3 × 1 + k = 0
⇒ k – 3 + k = 0
⇒ 2k – 3 = 0
⇒ 2k = 3
⇒ k = \(\frac {3}{2}\)
Hence,
k = \(\frac {3}{2}\)

Question 4.
Factorise:
(i) 12x² – 7x + 1
(ii) 2x² + 7x + 3
(iii) 6x² + 5x – 6
(iv) 3x² – x – 4.
Solution:
(i) 12x² – 7x + 1 = 12x² – (4 + 3)x + 1
= 12x² – 4x – 3x + 1
= (12x² – 4x) – (3x – 1)
= 4x(3x – 1) – 1(x – 1)
= (3x – 1) (4x – 1).
Hence, 12x² – 7x + 1 = (3x – 1) (4x-1).

(ii) 2x² + 7x + 3 = 2x² + (6 + 1)x + 3
= 2x² + 6x + x + 3
= (2x² + 6x) + (x + 3)
= 2x(x + 3) + 1(x + 3)
= (x + 3) (2x + 1).
Hence, 2x² + 7x + 3 = (x + 3) (2x + 1).

(iii) 6x² + 5x – 6 = 6x² + (9 – 4)x – 6,
= 6x² + 9x – 4x – 6
= (6x³ + 9x ) -(4x + 6)
= 3x(2x + 3) – 2(2x + 3)
= (2x + 3) (3x – 2).
Hence, 6x² + 5x – 6 = (2x + 3) (3x – 2).

(iv) 3x² – x – 4 = 3x² – (4 – 3)x – 4,
= 3x² – 4x + 3x – 4
= (3x² – 4x) + (3x – 4)
= x(3x – 4) + 1(3x – 4)
= (3x – 4) (x + 1).
Hence, 3x² – x – 4 = (3x – 4)(x + 1).

Question 5.
Factorise :
(i) x³ – 2x² – x + 2
(ii) x³ – 3x² – 9x – 5
(iii) x³ + 13x² + 32x + 20
(iv) 2y³ + y² – 2y – 1.
Solution:
(i) Let
p(x) = x³ – 2x² – x + 2
Factors of + 2 are ±1, ±2.
Now, put
x = 1
∴ p(1) = (1)³ – 2 × (1)² – 1 + 2
= 1 – 2 – 1 + 2 = 0.
∴ By factor theorem, (x – 1) is a factor of p(x). Now, divide x³ – 2x² – x + 2 by (x – 1), we get

So, x³ – 2x² – x + 2 = (x – 1)(x² – x – 2)
= (x – 1)(x² – (2 – 1)x – 2)
= (x – 1)(x² – 2x + x – 2)
= (x – 1) [(x² – 2x) + (x – 2)]
= (x – 1) [x(x – 2) + 1(x – 2)]
= (x – 1)(x – 2)(x + 1).
Hence, x³ – 2x² – x + 2
= (x – 1) (x – 2) (x + 1).

(ii) Let
p(x) = x³ – 3x² – 9x – 5
Factors of – 5 are ±1, ±5.
Now, put x = – 1
∴ p(-1)=(-1)³ – 3 × (-1)² – 9 × (-1) – 5
= – 1 – 3 + 9 – 5
= – 9 + 9 = 0.
∴ By factor theorem, (x + 1) is a factor of p(x). Now, divide x³ – 3x² – 9x – 5 by (x + 1), we get

So, x³ – 3x² – 9x – 5= (x + 1) (x² – 4x – 5)
= (x + 1) (x² – (5 – 1)x – 5]
= (x + 1) [x² – 5x + x – 5]
= (x + 1) [(x² – 5x) + (x – 5)]
= (x + 1) [x(x – 5) + 1(x – 5)]
= (x + 1)(x – 5)(x + 1).
Hence, x³ – 3x² – 9x – 5
= (x + 1)(x – 5) (x + 1).

(iii) Let p(x) = x³ + 13x² + 32x + 20
Factors of 20 are = ±1, ±2, ±4, ±5, ±10 and ±20.
Now, put
x = – 1
∴ p(-1) = (-1)³ + 13 × (-1)² + 32 × (-1) + 20
= – 1 + 13 – 32 + 20
= 33 – 33 = 0.
∴ By factor theorem, (x + 1) is a factor of p(x).
Now divide x³ + 13x² + 32x + 20 by (x + 1), we get

So, x³ + 13x² + 32x +20= (x + 1) (x² + 12x + 20)
= (x + 1) (x² + (10 + 2)x +20)
= (x + 1) (x² + 10x + 2x +20)
= (x + 1) [(x² + 10x) + (2x + 20)]
= (x + 1) [x(x + 10) + 2(x + 10)]
= (x + 1)(x + 10) (x + 2).
Hence, x³ + 13x² + 32x + 20
= (x + 1) (x + 10) (x + 2).

(iv) Let p(y) = 2y³ + y² – 2y – 1
Factors of -1 = ±1
Now, put
y = 1
∴ p(1) = 2 × (1)³ + (1)² – 2 × 1 – 1
= 2 + 1 – 2 – 1
= 3 – 3 = 0
∴ By factor theorem, (y – 1) is a factor of p(y).
Now, divide 2y³ + y² – 2y – 1 by (y – 1), we get

So, 2y³ + y² – 2y – 1 = (y – 1) (2y² + 3y + 1)
= (y – 1) [2y² + (2 + 1)y + 1] [∵ 2 × 1 = 2, 2 + 1 = 3]
= (y – 1) [(2y² + 2y) + (y + 1)]
= (y – 1) (2y(y + 1)) + 1(y + 1)]
= (y – 1)(y + 1) (2y + 1)
Hence, 2y³ + y² – 2y – 1 = (y – 1) (y + 1) (2y + 1).

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.7 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.7

Assume π = \(\frac{22}{7}\), unless stated otherwise,

Question 1.
Find the volume of the right circular cone with :
(i) radius 6 cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm.
Solution:
(i) We have, Radius of cone (r) = 6 cm
Height of the cone (h) = 7 cm
∴ Volume e the cone = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times 6^2 \times 7\)
= 264 cm³.
(ii) We have,
Radius of the cone (r) = 3.5 cm
Height of the cone (h) = 12 cm
∴ Volume of the cone = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times 3.5^2 \times 12\)
= 154 cm³
Hence, volume of the cone (i) 264 cm³, (ii) 154 cm³.

Question 2.
Find the capacity in litres of a conical vessel with :
(i) radius 7 cm, slant height 25 cm
(ii) height 12 cm, slant height 13 cm.
Solution:
(i) We have, Radius of the conical vessel (r) = 7 cm
Slant height of the conical vessel (l) = 25 cm
Let the height of the conical vessel be h cm.
∴ l² = h² + r²
⇒ 25² = h² + 7²
⇒ h² = 25² – 7²
⇒ h² = (25 + 7) (25 – 7)
⇒ h² = 32 × 18
⇒ h² = 576
⇒ h= \(\sqrt{576}\)
⇒ h = 24 cm
∴ Volume of the conical vessel = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times 7^2 \times 24\)
= 1232 cm³
= \(\frac{1232}{1000}\) litres
= 1.232 litres.

(ii) We have, Slant height of the conical vessel (l) = 13 cm
Height of the conical vessel (h) = 12 cm
Let the radius of the conical vessel be r cm.
∴ l² = h² + r²
⇒ 13² = 12² + r²
⇒ r² = 13² – 12²
⇒ r² = (13 + 12) (13 – 12)
⇒ r² = 25
⇒ r = \(\sqrt{25}\)
⇒ r = 5 cm
∴ Volume of the conical vessel = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times 5^2 \times 12\)
= \(\frac{2200}{7} \mathrm{~cm}^3\)
= \(\frac{2200}{7 \times 1000} \text { litres }\)
= \(\frac{11}{35} \text { litres }\)
Hence, volume of the cone (i) 1.232 litres, (ii) \(\frac{11}{35} \text { litres }\).

Question 3.
The height of a cone is 15 cm. If its volume is 1570 cm³, find the radius of the base. (Use π = 3.14)
Solution:
Let the radius of base of a cone be r сm.
We have, Height of the cone (h) = 15 cm
volume of the cone = 1570 cm³
⇒ \(\frac{1}{3}\)πr²h = 1570
⇒ \(\frac{1}{3}\) × 3.14 × r² × 15 = 1570
⇒ 15.7 × r² = 1570
⇒ r² = \(\frac{1570}{157}\)
⇒ r² = 100
⇒ r = \(\sqrt{100}\)
⇒ r = 10 cm
Hence, radius of the base of the cone = 10 cm.

Question 4.
If the volume of a right circular cone of height 9 cm is 48π cm³, find the diameter of its base.
Solution:
Let the radius of the basse of the cone be r сm.
We have, Height of the cone (h) = 9 cm
Volume of the cone = 48π cm³
⇒ \(\frac{1}{3}\)πr²h = 48π
⇒ \(\frac{1}{3}\)π × r² × 9 = 48π
⇒ 3πr² = 48π
⇒ r² = \(\frac{48 \pi}{3 \pi}\)
⇒ r² = 16
⇒ r = \(\sqrt{16}\)
⇒ r = 4 cm
∴ Diameter of the base of the cone = 2 × 4
= 8 cm
Hence,diameter of the base of cone = 8 cm

Question 5.
A conical pit of top diameter 3.5 m is 12m deep. What is its capacity in kilolitres ?
Solution:
We have,
Depth of conical pit (h) = 12 m
Diameter of conical pit (d) = 3.5 m
∴ Radius of conical pit (r) = \(\frac{3.5}{2}\) = 1.75 m
∴ Capacity of the conical pit = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times(1.75)^2 \times 12\)
= 38.5 m³
= 38.5 kilolitres
(∵ 1 m³ = 1 kilolitres)
Hence,capacity of the conical pit = 38.5 kilolitres.

Question 6.
The volume of a right circular cone is 9856 cm³. If the diameter of the base is 28 cm, find :
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone.
Solution:
We have,
The volume of the cone = 9856 cm³
The diameter of the base of the cone (d) = 28 cm
∴ Radius of the base of the cone (r) = \(\frac{28}{2}\) cm = 14 cm
(i) Let the height of the cone be h cm.
Volume of the cone = 9856 cm³
⇒ \(\frac{1}{3}\)πr²h = 9856
⇒ \(\frac{1}{3} \times \frac{22}{7} \times 14^2 \times h\) = 9856
⇒ \(\frac{616}{3}\) × h = 9856
⇒ h = \(\frac{9856 \times 3}{616}\)
⇒ h = 480cm

(ii) Let the slant height of the cone be 1 cm, then
⇒ l² = h² + r²
⇒ l² = 48² + 14²
⇒ l² = 2304 + 196
⇒ l2 = 2500
⇒ l = \(\sqrt{2500}\)
⇒ l = 50 cm.

(iii) Curved surface of the cone = πrl
= \(\frac{22}{7}\) × 14 × 50
= 2200 cm².
Hence, (i) Height of the cone = 48 cm, (ii) Slant height of the cone = 50 cm, (iii) Curved surface area of the cone = 2200 cm².

Question 7.
A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Solution:
We have,
Sides of the triangle ABC are AB = 12 cm, BC = 5 cm and AC = 13 cm
Since ΔABC is revolved about the side AB(= 12 cm)
∴ We get a cone (AC’C) as shown in the figure.

Then,radius of the base of the cone (r) = 5 cm
and height of the cone (h) = 12 cm
∴ Volume of the cone (solid) = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × π × 5² × 12
= 100π cm³
Hence, volume of the cone so obtained = 100π cm³.

Question 8.
If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Solution:
Since ΔABC is revolved about BC(= 5 cm).
∴ We get a cone (CAA’) as shown in the figure.

Then,radius of the base of the cone (r) = 12 cm
and height of the cone (h) = 5 cm
Volume of the cone = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × π × 12² × 5
= 240π cm³
Ratio of the volumes of the two solids obtained in Q. 7 and Q. 8
= 100π : 240π = \(\frac{100 \pi}{240 \pi}\)
= \(\frac{5}{2}\) = 5 : 12
Hence,volume of the cone (solid) = 240π cm³,
and required ratio of their volumes = 5 : 12.

Question 9.
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Solution:
We have,
Height of the conical heap (h) = 3 m
Diameter of the base of the conical heap (d) = 10.5 m³

∴ Radius of the base of the conical heap (d) = \(\frac{10.5}{2}\) = 5.25 m
∴ Slant height of a conical heap (l) = \(\sqrt{h^2+r^2}\)
= \(\sqrt{3^2+(5.25)^2}\)
= \(\sqrt{9+27.56}\)
= \(\sqrt{36.56}\)
= 6.05 m
∴ Volume of the conical heap = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times(5.25)^2 \times 3\)
= \(\frac{606.375}{7}\)
= 86.625 m³
Required area of canvas = Curved surface
area of the conical heap = πrl
= \(\frac{22}{7}\) × 5.25 × 6.05
= 16.5 × 6.05
= 99.825 m²
Hence,volume of the heap = 86.625 m³ and required area of canvas = 99.825 m².

Haryana State Board HBSE 9th Class Maths Solutions Chapter 12 Heron’s Formula Ex 12.1 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 12 Heron’s Formula Exercise 12.1

Question 1.
A traffic signal board, indicating ‘SCHOOL AHEAD’ is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
Solution:
Let ABC be the signal board is shape of an equilateral triangle with side a.
s = \(\frac{a+a+a}{2}\)
⇒ s = \(\frac{3 a}{2}\)
By Heron’s formula, we have
Area of triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{\frac{3 a}{2}\left(\frac{3 a}{2}-a\right)\left(\frac{3 a}{2}-a\right)\left(\frac{3 a}{2}-a\right)}\)
= \(\sqrt{\frac{3 a}{2} \times \frac{a}{2} \times \frac{a}{2} \times \frac{a}{2}}\)
= \(\frac{a}{2} \times \frac{a}{2} \times \sqrt{3}\)
= \(\frac{a^2}{4} \times \sqrt{3}\)
= \(\frac{\sqrt{3}}{4}\) a² square units

Perimeter = 180 cm
⇒ 3a = 180
⇒ a = \(\frac{180}{3}\) = 60
∴ Area of triangle = \(\frac{\sqrt{3}}{4}\) × (60)²
= 900\(\sqrt{3}\) cm²
Hence, area of an equilateral triangle = \(\frac{\sqrt{3}}{4}\) a² square units and 900\(\sqrt{3}\) cm².

Question 2.
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 12.9). The advertisements yield an earning of Rs. 5000 per m² per year. A company hired one of its walls for 3 months. How much rent did it pay?

Solution:
Sides of a triangular wall of a flyover are 122 m, 22 m and 120 m. Here,
a = 122 m, b = 22 m and c = 120 m
s = \(\frac{122+22+120}{2}\)
⇒ s = \(\frac{264}{2}\) = 132 m
By Heron’s formula, we have
Area of side walls of flyover
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{132(132-122)(132-22)(132-120)}\)
= \(\sqrt{132 \times 10 \times 110 \times 12}\)
= \(\sqrt{11 \times 12 \times 10 \times 10 \times 11 \times 12}\)
= 10 × 11 × 12
= 1320 m²
∵ Rent paid by a company in 12 months for 1 m² = Rs. 5000
∴ Rent paid by a company in 1 month for 1 m² = Rs. \(\frac{5000}{12}\)
∴ Rent paid by company in 3 months for 1320 m² = Rs. \(\frac{5000 \times 3 \times 1320}{12}\)
= Rs. 1250 × 1320
= Rs. 1650000
Hence, rent paid by company = Rs. 1650000.

Question 3.
There is a slide in a park. One of its side walls has been painted in some colour with a message “keep the park green and clean” (see Fig. 12.10). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

Solution:
Sides of the triangular park are 15 m, 11 m and 6 m.
Here, a = 15 m, b = 11 m and c = 6 m
s = \(\frac{15+11+6}{2}\)
s = \(\frac{32}{2}\)
s = 16 m
By Heron’s formula, we have
Area of triangular park = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{16(16-15)(16-11)(16-6)}\)
= \(\sqrt{16 \times 1 \times 5 \times 10}\)
= \(\sqrt{4 \times 4 \times 1 \times 5 \times 5 \times 2}\)
= 4 × 5\(\sqrt{2}\)
= 20\(\sqrt{2}\) m²
Hence, area painted in colour of triangular park = 20\(\sqrt{2}\) m².

Question 4.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
We have,
Two sides of a triangle are a = 18 cm and b = 10 cm
and perimeter of triangle (2s) = 42 cm
We know that,
Perimeter (2s) = a + b + c
⇒ 42 = 18 + 10 + c
⇒ 42 = 28 + c
⇒ c = 42 – 28 = 14 cm
Now 2s = 42
s = \(\frac{42}{2}\) = 21 cm
By Heron’s formula, we have
Area of a triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{21(21-18)(21-10)(21-14)}\)
= \(\sqrt{21 \times 3 \times 11 \times 7}\)
= \(\sqrt{3 \times 7 \times 3 \times 11 \times 7}\)
= 3 × 7\(\sqrt{11}\)
= 21\(\sqrt{11}\) cm²
Hence,area of a triangle = 21\(\sqrt{11}\) cm².

Question 5.
Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.
Solution:
Ratio of sides of a triangle = 12 : 17 : 25 and perimeter is 540 cm.
Let sides of a triangle be 12x cm, 17x cm and 25x cm.
Perimeter = Sum of the sides of a triangle
⇒ 540 = 12x + 17x + 25x
⇒ 540 = 54x
x = \(\frac{540}{51}\) = 10
So,sides of the triangle = 12 × 10, 17 × 10, 25 × 10 = 120 cm, 170 cm, 250 cm
Here, a = 120 cm, b = 170 cm and c = 250 cm
s = \(\frac{120+170+250}{2}\)
⇒ s = \(\frac{540}{2}\)
⇒ s = 270 cm
By Heron’s formula, we have
Area of a triangler = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{270(270-120)(270-170)(270-250)}\)
= \(\sqrt{270 \times 150 \times 100 \times 20}\)
= \(\sqrt{3 \times 3 \times 30 \times 30 \times 5 \times 5 \times 20 \times 20}\)
= 3 × 5 × 20 × 30
= 9000 cm²
Hence,area of a triangle = 9000 cm².

Question 6.
An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.
Solution:
Two equal sides of an isosceles triangle are 12 cm and 12 cm and perimeter = 30 cm
Perimeter of a triangle = Sum of sides of a triangle
⇒ 30 = 12 + 12 + IIIrd side
⇒ 30 = 24 + IIIrd side
⇒ IIIrd side = 30 – 24 = 6 cm
Here, a = 12 cm, b = 12 cm and c = 6 cm
s = \(\frac{12+12+6}{2}\)
⇒ s = \(\frac{30}{2}\)
= 15 cm
By Heron’s formula, we have
Area of a triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{15(15-12)(15-12)(15-6)}\)
= \(\sqrt{15 \times 3 \times 3 \times 9}\)
= \(\sqrt{15 \times 3 \times 3 \times 3 \times 3}\)
= 3 × 3\(\sqrt{15}\)
= 9\(\sqrt{15}\) cm²
Hence, area of an isosceles triangle = 9\(\sqrt{15}\) cm².

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.9 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.9

[This exercise is not from examination point of view]

Question 1.
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see Fig. 13.31). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm² and the rate of painting is 10 paise per cm², find the total expenses required for polishing and painting the surface of the bookshelf.

Solution:
We have
External dimensions of bookshelf are
Height = 110 cm, depth = 25 cm and breadth = 85 cm
Thickness of the plank = 5 cm
∴ Internal dimensions of bookshelf are Height = 110 – 4 × 5 = 90 cm
(there are 4 plank)
Breadth = 85 – 2 × 5 = 75 cm
Depth = 25 – 5 = 20 cm
Area to be polished = (110 × 85 + 2 × 110 × 25 + 2 × 85 × 25 + 4 × 75 × 5 + 2 × 110 × 5)
= 9350 + 5500 + 4250 + 1500 + 1100
= 21700 cm²
Rate of polishing = 20 paise/cm²
Cost of polishing = Rs. 21700 × \(\frac{20}{100}\)
= Rs. 4340
Area to be painted= 6 × 75 × 20 + 2 × 90 × 20 + 75 × 90
= 9000 + 3600 + 6750
= 19350 cm²
Cost of painting = 10 paise/cm²
Cost of painting = Rs. \(\frac{19350 \times 10}{100}\)
= Rs. 1935
Total expenses = Rs. 4340 + Rs. 1935
= Rs. 6275
Hence, total expenses = Rs. 6275.

Question 2.
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in Fig. 13.32. Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm².

Fig. 13.32
Solution:
We have,
Diameter of sphere = 21 cm
∴ Radius of sphere (R) = \(\frac{21}{2}\) = 10.5 cm
Radius of cylinder (r) = 1.5 cm
Height of cylinder (h) = 7 cm
Surface area for silver paint = 8(C.S.A. of the sphere – base area of cylinder on which sphere is resting)
= 8(4πR² – πr²)
= 8π(4R² – r²)
= 8π[4 × (10.5)² – (1.5)²]
= 8 × \(\frac{22}{7}\)[4 × 110.25 – 2.25]
= 8 × \(\frac{22}{7}\)[438.75]
= 11031.43 cm² (approx.)
Rate of silver paint = 25 paise/cm²
Cost of silver paint = Rs. \(\frac{11031.43 \times 25}{100}\)
= Rs. 2757.86 (approx.)
Surface area to be black painted = 8 C.S.A. of cylinder
= 8 × 2πrh
= 8 × 2 × \(\frac{22}{7}\) × 1.5 × 7
= 528 cm²
Rate of black paint = 5 paise/cm²
Cost of black paint = Rs. \(\frac{528 \times 5}{100}\) = Rs. 26.4
Total cost of painting = 2757.86 + 26.4
= Rs. 2784.26
Hence, total cost of painting = Rs. 2784.26.

Question 3.
The diameter of a sphere is decreased by 25%. By what percent does its curved surface area decrease?
Solution:
Let the diameter of sphere be 2x.
∴ Radius of the sphere (r₁) = x
Curved surface area of sphere = 4πx²
After decreasing its diameter by 25%, then
New diameter = 2x – 25% of 2x
= \(2 x-\frac{25}{100} \times 2 x\)
= \(2 x-\frac{x}{2}=\frac{3 x}{2}\)
New radius (r₂) = \(\frac{3 x}{4}\)
Curved surface area of new sphere
= \(4 \pi r_2^2=4 \pi \times\left(\frac{3 x}{4}\right)^2\)
= \(\frac{4 \pi \times 9 x^2}{16}=\frac{9 \pi x^2}{4}\)
Decrease in curved surface area
= \(4 \pi x^2-\frac{9 \pi x^2}{4}\)
= \(\frac{16 \pi x^2-9 \pi x^2}{4}\)
= \(\frac{7 \pi x^2}{4}\)
Decrease % in curved surface area

Hence, decrease % in curved surface area = 43.75%.