Class 7

Haryana State Board HBSE 7th Class Science Solutions Chapter 14 Electric Current and its Effects Textbook Exercise Questions and Answers.

Haryana Board 7th Class Science Solutions Chapter 14 Electric Current and its Effects

HBSE 7th Class Science Electric Current and its Effects Textbook Questions and Answers

Question 1.
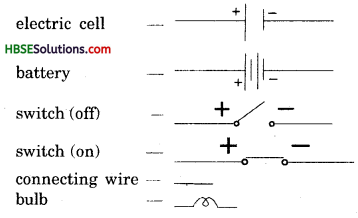
Draw in your notebook the symbols to represent the following components of electrical circuits : Connecting wires, Switch in the ‘OFF’ position. Bulb, Cell, Switch in the ‘ON’ position, and Battery.
Answer:
Draw in your notebook the synbols to represent the following components of electrical circuits :
Connecting wires — —
Switch in off position — —
Bulb — —
Cell — —
Switch in ‘on’ position — —
Battery — —

Question 2.
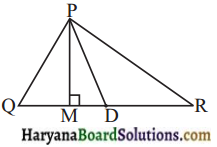
Draw the circuit diagram to represent the circuit shown in Fig. 14.1.
Answer:

Question 3.
Fig 14.2 shows four cells fixed on a board. Draw lines to indicate how you will connect their terminals with wires to make a battery of four cells.
Answer:

Question 4.
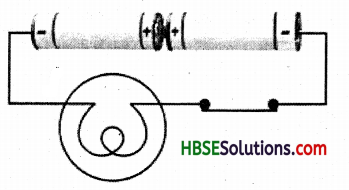
The bulb in the circuit shown in Fig 14.3 does not glow. Can you identify the problem? Make necessary changes in the circuit to make the bulbs glow.
Answer:
The problem in this circuit is that of the battery. The cells have not been arranged in right series. The correct circuit is like this.

Question 5.
Name any two effects of electric current.
Answer:
Electric current has following effects:

• Electric current can give rise to heating and lighting.
• Electric current can make a straight conductor a temporary magnet.

Question 6.
When the current is switched on through a wire, a compass needle kept nearby gets deflected from its north-south position. Explain.
Answer:
When current is passed through the wire, it deflects the compass near it from its north-south position behaving like a magnet. This is called magnetic effect of the current. As we know that needle of the compass is made up of a thin magnet, when this needle comes in contact with another magnet the like poles of the magnet repell each other and opposite poles attract each other. So the deflection is seen in the needle. In this case the wire behaves like a magnet and cause deflection in needle of the compass.

Question 7.
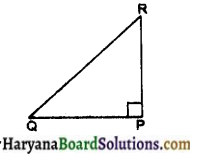
Will the compass needle show deflection when the switch in the circuit shown by Fig. 14.4 is closed?

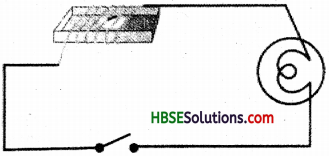
Answer:
No, because there is no source of electric current in this circuit i.e. there is no battery.

Question 8.
Fill in the blanks:
(a) Longer line in the symbol for a cell represents its _______ terminal.
(b) The combination of two or more cells is called a _______.
(c) When current is switched on in a room-heater, its _______.
(d) The safety device based on the heating effect of electric current is called a _______.
Answer:
(a) Positive
(b) Battery
(c) Element becomes red hot and emit heat
(d) Fuse.

Question 9.
Mark ‘T’ if the statement true and ‘F’ if it is false.
(a) To make a battery of two cells, the negative terminal of one cell is connected to the negative terminal of the other cell.
(b) When the electric current through the fuse exceeds a certain limit, the fuse wire melts and breaks.
(c) An electromagnet does not attract a piece of iron.
(d) An electric bell has an electromagnet.
Answer:
(a) F
(b) T
(c) F
(d) T

Question 10.
Do you think an electromagnet can be used for separating plastic bags from a garbage heap? Explain.
Answer:
No, the plastic bags do not get attracted by the magnet, so they cannot be separated by an electromagnet. Plastic bags are not magnetic materials, only magnetic materials like iron can be attracted by the magnet.

Question 11.
An electrician is carrying out some repairs in your house. He wants to replace a fuse by a piece of a wire. Would you agree? Give reasons for your response.
Answer:
No, we would not agree to allow to replace the fuse by a wire. Wires in the fuses are of specific metting points. So we should always use ISI marked fuses in our houses to save short circuits.

Question 12.
Zubeda made an electric circuit using a cell holder shown in Fig. 14.4, a switch and a bulb. When she put the switch in the ‘ON’ position, the bulb did not glow. Help Zubeda in identifying the possible defects in the circuit.
Answer:
It is important to put the cells in right series. The positive terminal of the cell should be connected with negative terminal of the second cell. The switch should be closed properly and bulb should not be fused. If Zubeda will check these then the bulb will certainly glow.

Question 13.
In the circuit shown in Fig. 14.5
(i) Would any of the bulb glow when the switch is in the ‘OFF’ position?
(ii) What will be the order in which the bulbs A, B and C will glow when the switch is moved to the ‘ON’ position?

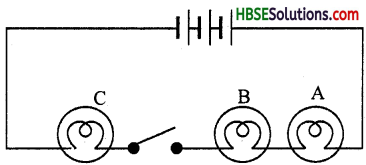
Answer:
(i) No, bulb will glow.

(ii) The bulb A will glow first, follow by B bulb and then C, because A bulb comes first in the path of electric current flowing from positive terminal towards the negative terminal of the battery.

Extended Learning-Activities and Projects

Question 1.
Set up the circuit shown in Fig. 14.6 again. Move the key to ‘ON’ position and watch carefully in which direction the compass needle gets deflected. Switch ‘OFF’ the current. Now keeping rest of the circuit intact, reverse the connections at the terminal of the cell. Again switch ‘on’ the current. Note the direction in which the needle gets deflected. Think of an explanation.
Answer:
Do it yourself.

Question 2.
Make four electromagnets with 20, 40, 60 and 80 turns. Connect them one by one to a battery of 2 cells. Bring the electromagnet near a box of pins. Count the number of pins attracted by it. Compare the strengths of the electromagnets.
Answer:
Do it yourself.

HBSE 7th Class Science Electric Current and its Effects Important Questions and Answers

Very Short Answer Type Questions

Question 1.
What is electric current?
Answer:
Flow of electrons is called electric current.

Question 2.
What is conventaional current?
Answer:
The current flowing the positive end of the conducting wire towards the negative end is called conventaional current.

Question 3.
What are the different sources of current in an electric circuit?
Answer:
Cell or a battery are the sources of elctric current in an electric circuit.

Question 4.
What role does a switch plays in an electric circuit?
Answer:
The switch regulates the flow of electric current. It allows the current to pass when it is in ‘ON’ position.

Question 5.
Write the symbols of the following : Switch (open).
Switch closed and a cell.
Answer:

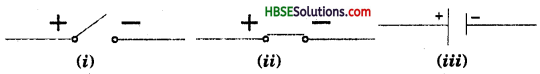
Question 6.
What is an open electric circuit?
Answer:
An electric circuit having the switch in ‘off position is called open electric circuit.

Question 7.
What is a closed electric circuit?
Answer:
An electric circuit having the switch in ‘on’ position is called a closed circuit or a complete circuit.

Question 8.
Which effect of the electric current enables the room heater to heat the room?
Answer:
The heating and lighting effect of the electric current enables the room heater to heat the room.

Question 9.
What is a fuse?
Answer:
It is a safety device used to avoid damages from short circuits and over loading in electric appliances.

Question 10.
Which effect of the electric current is used in Electric bells?
Answer:
The magnetic effect of the electric current is used in electric bells to make the sound.

Short Answer Type Questions

Question 1.
What is an electric current and electric circuit?
Answer:
Flow of electrons is called electric current. The path through which the electric current passes is called an electric circuit.

Question 2.
What are the components of the electric circuit? Name different components of the electric circuit and draw their symbols.
Answer:
Various elelments connected in the electric circuit are called components of the electric circuit. Following are some components of electric circuit and their symbols :

Question 3.
What is a cell and what is a battery?
Answer:
Cell and battery are both the sources of electric current in an electric circuit. A cell has two terminals – +ve terminal and – ve terminal. A combination of two or more than two cells is called a battery. Battery is formed by joining a positive terminal of a cell to the negative terminal of other cell.

Question 4.
What is an electric fuse? Explain its working.
Answer:
A fuse is a safety device used in household circuit to prevent damage to electric appliances due to overload and short circuit. It is the weakest part in the electric circuit. It melts and breaks the circuits when the problem arises in the circuit due to short circuiting, overloading or fluctuations of current in power supply system.

Question 5.
What is short circuit and overloaded circuit?
Answer:
Short circuit occurs when live wire and neutral wire come in direct contact. The short circuit occurs either due to melting of plastic insulation or connection of live wire with the earth wire. An overload circuit is the one through which more current passes than it can bear.

Question 6.
What is an M. C. B.?
Answer:
M.C.B. is miniature circuit breaker. This is a safety device like a fuse. It is used instead of or in addition to fuses, in household circuits. It is a switch that automatically switches off a current when it exceeds the specified maximum limit.

Question 7.
Write any three applications of the electromagnets.
Answer:
Fallowing are the applications of the electromagnets :

• Electromagnets are used to separate scrap iron from other metallic scraps.
• Used in electric motors of washing machines, fans, air conditioners etc.
• Used for preparing strong magnets.

Long Answer Type Questions

Question 1.
Explain the construction and working of an electric bell with help of a labelled diagram.
Answer:
An electric bell consists of an electromagnet, Armature, contact spring, Hammer and gong.
Electromagnet: It consists of a U-shaped soft iron rod having insulated copper wire wounded on it. One end of wire is connected to terminal T and other to the brass stud.

Armature: is a soft iron rod, suspended to brass stud. It faces the poles of the electromagnet.

Contact spring is attached to the armature and to a silver-cadmium alloy contact point. Spring is made up of steel.

Contact screw adjustment: It is a brass pillar having a brass screw passing through it. The tip of the screw is made up of silver cadmium alloy. Pillar is connected to T₂ with a copper wire.

Hammer and Gong : Hammer is made up of steel and is attached to the armature. Gong is made up of brass, and the hammer strikes the gong to make the sound.

Working : When electric current passes through T₁ and T₂, current passes from the battery to electromagnet, then to the contact screw and to T₂ completing the circuit. Electromagnet pulls the armature towards itself, the contact spring gets under tension, hammer strikes against gong thus making the sound. The whole process stops, when current stops flowing.

Electric Current and its Effects Class 7 HBSE Notes

• Flow of electrons is called electric current.
• The path in which the electric current flows is called an electric circuit.
• Conventially the current is said to flow from positive end of the conducting wire to the negative end of the conducting wire.
• There are many components which are attached to the path of the electric current. These are called the elements of the electric circuit,
• Elements like cell, battery, switch, bulb, connecting wires are represented by different symbols.
• Cell and battery are the sources of the electric current in a circuit. Battery is the combination of two or more than two cells.
• A circuit is said to be complete or closed when the switch regulating the flow of the current is in ‘on’ position when the switch is in ‘off’ position the circuit is called open.
• Flow of the electric current causes certain effects like heating and lighting and electromagnetism.
• The electric appliances like room heaters, gysers, rods etc. give out heat due to heating effect.
• When electric current passes through a magnetic substance like iron, it behaves like a temporary magnet.
• Electric bell works on this principle.
• Hans Christian Oersted found out the relation between electricity and magnetism.
• A fuse is a safety device used in house hold circuit to prevent damage to electric appliances due to over-load or short circuit.

Haryana State Board HBSE 7th Class Science Solutions Chapter 15 Light Textbook Exercise Questions and Answers.

Haryana Board 7th Class Science Solutions Chapter 15 Light

HBSE 7th Class Science Light Textbook Questions and Answers

Question 1.
Fill in the blanks :
(a) An image that cannot be obtained on a screen is called _________.
(b) Image formed by a convex _________ is always virtual and smaller in size.
(c) An image formed by a _________ mirror is always of the same size as that of the object.
(d) An image which can be obtained on a screen is called a _________ image.
(e) An image formed by a concave _________ cannot be obtained on a screen.
Answer:
(a) virtual image
(b) mirror
(c) plane
(d) real
(e) lens.

Question 2.
Mark ‘T’ if the statement is true and ‘F’ if it is false :
(a) We can obtain an enlarged and erect image by a convex mirror.
(b) A concave lens always form a virtual image.
(c) We can obtain a real, enlarged and inverted image by a concave mirror.
(d) A real image cannot be obtained on a screen.
(e) A concave mirror always form a real image.
Answer:
(a) F
(b) T
(c) T
(d) F
(e) F

Question 3.
Match the items given in Column I with one Or more items of Column II.

Answer:
(a) (v)
(b) (ii)
(c) (i)
(d) (iii)
(e) (vi)

Question 4.
State the characteristics of the image formed by a plane mirror.
Answer:

• Plane mirror forms an erect image.
• It forms a virtual image.
• Size of the image is same as that of the object.
• Image gets formed at the same distance behind the mirror as the object stands infornt of it.
• Image formed is a laterally inverted image, i.e. right hand side of the object seems to be the left hand side and vice-versa.

Question 5.
Find out the letters of English alphabet or any other language known to you in which the image formed in a place mirror appears exactly like the letter itself. Discuss your findings.
Answer:
Letters like A, H, I, M, O, T, U, V, W etc appear same when seen through a plane mirror.

Question 6.
What is a virtual image? Give one situation where a virtual image is formed.
Answer:
The image which cannot be taken on a screen is called a virtual image. When some object is placed very close to the concave mirror we do not get any image of that object on the white screen placed behind the mirror. Such image is called a virtual image.

Question 7.
State two differences between a convex and a concave lens.
Answer:

Question 8.
Give one use each of a concave and a convex mirror.
Answer:

• Use of Concave mirror: Concave mirror is used by dentists to- examine the teeth.
• Use of Convex mirror: Convex mirror is used as side view mirror in vehicles.

Question 9.
Which type of mirror can form a real image?
Answer:
Concave mirror can form a real image.

Question 10.
Which type of lens forms always a virtual image?
Answer:
Convex lens always form a virtual image.

Choose the correct option in questions 11-13

Question 11.
A virtual image larger than the object can be produced by a _________.
(i) concave lens
(ii) concave mirror
(iii) convex mirror
(iv) plane mirror
Answer:
(iii) convex mirror

Question 12.
David is observing his image in a plane mirror. The distance between the mirror and his image is 4 m. If he moves 1 m towards the mirror, then the distance between David and his image will be _________.
(i) 3 m
(ii) 5 m
(iii) 6 m
(iv) 8 m
Answer:
(i) 3 m

Question 13.
The rear view mirror of a car is a plane mirror. A driver is reversing his car at a speed of 2 m/s. The driver sees in his rear view mirror the image of a truck parked behind his car. The speed at which the image of the truck appears to approach the driver will be _________.
(i) 1m/s
(ii) 2m/s
(iii) 4mls
(iv) 8m/s
Answer:
(iii) 4mls

Extended Learning-Activities and Projects

Question 1.
Play with a mirror Write your name with a sketch pen on a thin sheet of paper, polythene or glass.

Read your name on the sheet while standing in front of a plane mirror. Now look at your image in the mirror.
Answer:
Do it yourself.

Question 2.
A burning candle in water
Take a shoe box, open on one side. Place a small lighted candle in it. Place a clear glass sheet (roughly 25 cm x 25 cm) infront of this candle (fig. 15.1). Try to locate the image of the candle behind the glass sheet. Place a glass of water as its position. Ask your friends to look at the image of the candle through the sheet of glass. Ensure that candle is not visible to your friends. Your friends will be surprised to see the candle burning in water. Try to explain the reason.
Answer:
Do it yourself.

Question 3.
Make a rainbow’.
Try to make your own rainbow. You can try this project in the morning of in the evening. Stand with your back towards the sun. Take a hosepipe or a water pipe used in the garden. Make a find spray in front of you. Your can see different colours of rainbow in the spray.
Answer:
Do it yourself.

Question 4.
Visit a laughing gallery in some science centre or a science park or a village mela. You will find some large mirrors there. You can see your distorted and funny images in these mirrors. Try to find out the kind of mirrors used there.
Answer:
Do it yourself.

Question 5.
Visit a nearby hospital. You can also visit the clinic of an ENT specialist, or a dentist. Request the doctor to show you the mirrors used for examining ear, nose,
throat and teeth. Can you recognise the kind of mirror used in these instruments?
Answer:
Do it yourseld.

Question 6.
Role play
Here is a game that a group of children can play. One child will be chosen to act as object and another will act as the image of the object. The object and the image will sit opposite to each other. The object will make movements, such as raising a hand, touching an ear, etc. The image will have to make the correct movement following the movement of the object. The rest of the group will watch the movements of the image. If the image fails to make the correct movement, she/he will be retired. Another child will take her/his place and the game will continue. A scoring scheme can be introduced. The group that scores the maximum will be declared the winner.
Answer:
Do it yourself.

HBSE 7th Class Science Light Important Questions and Answers

Very Short Answer Type Questions

Question 1.
What do you mean by rectilinear propagation of light?
Answer:
Rectilinear propagation of light means that beam of a light always travels in a straight line.

Question 2.
How can we change the direction of the light?
Answer:
We can change the direction of the light by the phenomenon called reflection.

Question 3.
What do you mean by reflection of light?
Answer:
When a ray of light falls on the surface of any mirror, it bounces back in the same medium. This is called reflection of light.

Question 4.
What is a mirror?
Answer:
Any polished or shining surface is called a mirror.

Question 5.
What do you mean by a real image?
Answer:
Image which can be obtained on a screen is called a real image.

Question 6.
What do you mean by a virtual image?
Answer:
Image which cannot be obtained on a screen is called a virtual image.

Question 7.
What is a convex mirror?
Answer:
A mirror which reflects the light from its inner polished side.

Question 8.
What is a concave mirror?
Answer:
A mirror, which reflects light from its outer polished surface.

Question 9.
What kind of image is formed by a plane mirror?
Answer:
It forms an erect, virtual and image of same size as that of the object.

Question 10.
What kind of image is formed by a concave mirror?
Answer:
It can form both real and virtual, erect or inverted image.

Question 11.
What kind of image is formed when an object is placed very close to the concave mirror?
Answer:
A virtual erect and a magnified image will be formed.

Question 12.
What kind of image is formed by a convex mirror?
Answer:
Convex mirror forms an erect, virtual and diminished image.

Question 13.
What kind of image is formed by a concave lens?
Answer:
An erect, virtual and diminished image is formed by a concave lens.

Question 14.
What happens when a beam of light enters a prism?
Answer:
The beam of light splits into seven colours.

Question 15.
What do you mean by lateral inversion?
Answer:
When right hand side of an object appears as the left hand side and vice-versa.

Short Answer Type Questions

Question 1.
What is a virtual image? Give one example of virtual image.
Answer:
Virtual image : It is an image which cannot be obtained on a screen. It is formed when the reflected rays appears to meet each other but actually do not meet in reality. It is always erect. Image formed by a plane mirror is a virtual image.

Question 2.
What is real image of an object?
Answer:
Real image is formed when two or more reflected rays actually meet. This image can be obtained on a screen. It is always inverted. Pin-hole camera forms a real image.

Question 3.
Give two uses of concave mirror.
Answer:

• It is used as a reflector in search-light and head-lights of the automobiles.
• It is used as a shaving mirror.

Question 4.
Give two uses of convex mirror.
Answer:

• It is used in the cars and scooters to get the rear view to see the traffic coming from behind.
• It is used as reflectors in street lamps so as to diverse the light over a large area.

Question 5.
What do you mean by reflection of light?
Answer:
When a beam of light is incident on a plane surface a part of it is scattered back into the same medium. The scattering back of light into the same medium is called reflection.

Question 6.
Why is silvered glass used as a mirror?
Answer:
The silvered glass has a smooth surface and the smoothness helps in forming a clear image. Silvering makes it shiny and the shiny surface helps in reducing the absorption.

Question 7.
A man walks towards a plane mirror. At what rate will his image move if :
(a) the mirror is stationary,
(b) the mirror moves towards the man.
Answer:
(a) If the mirror is stationary the image moves at the same rate as the man.
(b) When the mirror moves towards the man the image moves at twice the rate of the mirror.

Question 8.
State four characteristics of the image formed by a plane mirror.
Answer:

• The image formed is as far behind the mirror as the object.
• It is exactly of same shape and size.
• It is erect but laterally inverted.
• It is virtual.

Question 9.
Distinguish between a real image and a virtual image.
Answer:
Difference between a real and virtual image :

Question 10.
Distinguish between a concave mirror and convex mirror.
Answer:

Long Answer Type Questions

Question 1.
How would you ascertain that a given mirror is a (a) Plane mirror, (b) Concave mirror, (c) Convex mirror without touching their surface?
Answer:
Hold the given mirror in the hand near your face, see the image. If the image is upright of the same size and does not change in size by moving the mirror, then the mirror is a plane mirror.

It the image is upright, larger and becomes inverted on moving the mirror away from your face, then the given mirror is a concave mirror. If the image is upright, smaller than your face and remains upright on moving the mirror away from your face, then the given mirror is the convex mirror. In this way one can ascertain the kind of mirror, without touching its surface.

Light Class 7 HBSE Notes

1. Light is an invisible energy which casue the sensation of sight.

2. Any object that gives out light is called the source of light e.g. Sun, firefly, candle etc.

3. Sun, moon, stars etc are called natural sources of light.

4. Candle, bulb etc are called man-made sources of light.

5. Light always travels in a straight line, this property of light is called the rectilinear propagation of light.

6. When light falls on a plane mirror, it falls back. This property of turning back of light is called in the same medium is called reflection of light.

7. There are two laws of reflection :
(i) The incident ray the normal at the point of incidence and the reflected ray lie in the same plane.
(ii) The angle of reflection is equal to the angle of incidence.

8. Any polished and shining surface is called a mirror.

9. Mirrors are of two types : concave mirror and convex mirror.

10. Concave mirror form a real and inverted image of the object.

11. Convex mirror always forms a virtual erect and small image.

12. Real image is one which can be obtained on a screen.

13. Virtual image is one, which cannot be obtained on a screen.

14. Lenses are also used to form images. Lenses are used to make spectacles, microscopes, magnifying glasses and telescopes etc.

15. Lenses are of two types. Concave lens and convex lens.

16. Concave lens is also called diverging lens, because it diverge the light falling on it. Convex lens is called the converging lens because it converges the light falling on it.

17. Concave lens forms, virtual erect and diminished image.

18. Convex lens can form both real and virtual images depending upon the position of the object. It magnifies the objects, when they are placed very near the lens.

19. White light splits into seven colours when it enters a prism.

20. This phenomenon is called dispersion of light.

Haryana State Board HBSE 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.3 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.3

प्रश्न 1.
यदि m = 2 है, तो निम्नलिखित के मान ज्ञात कीजिए :
(i) m – 2
(ii) 3m – 5
(iii) 9 – 5m
(iv) 3m² – 2m – 7
(v) \(\frac{5 m}{2}\) – 4
हल :
जब m = 2, तो
(i) m – 2
= 2 – 2
= 0

(ii) 3m – 5
= 3 × 2 – 5
= 6 – 5
= 1

(iii) 9 – 5m
= 9 – 5 × 2
= 9 – 10
= -1

(iv) 3m² – 2m – 7 = 3(2)² – 2 × 2 – 7
= 3(4) – 4 – 7
= 12 – 11 = 1

(v) \(\frac{5 m}{2}\) – 4
\(\frac{5 \times 2}{2}\) – 4
= 5 – 4
= 1

प्रश्न 2.
यदि p = – 2 है, तो निम्नलिखित के मान ज्ञात कीजिए :
(i) 4p + 7
(ii) -3p² + 4p + 7
(iii) -2p³ – 3p² + 4p + 7
हल :
जब p = -2 हो तो
(i) 4p + 7 = 4(-2) + 7 = – 8 + 7 = -1
(ii) – 3p² + 4p +7 = – 3(-2)² + 4(-2) + 7
= -3(4) – 8 + 7
= 12 – 1 = – 13

(iii) – 2p³ – 3p + 4p + 7
= – 2(-2)³ – 3(-2)² + 4(-2) + 7
= -2(-8) – 3(4) – 8 + 7
= 16 – 12 – 8 + 7
= 23 – 20 = 3

प्रश्न 3.
निम्नलिखित व्यंजकों के मान ज्ञात कीजिए, जब x = -1 है:
(i) 2x – 7
(ii) – x + 2
(iii) x² + 2x + 1
(iv) 2x² – x – 2
हल :
जब x = -1 हो तो
(i) 2x – 7 = 2(-1) – 7
= – 2 – 7 = -9

(ii) – x + 2 = – (-1) + 2
1 + 2 = 3

(iii) x² + 2x + 1 = (-1)² + 2(-1) + 1
= 1 – 2 + 1
= 0

(iv) 2x² – x – 2 = 2(-1)² – (-1) – 2
= 2(1) + 1 – 2
= 2 + 1 – 2 = 1

प्रश्न 4.
यदि a = 2 और b = – 2 है, तो निम्नलिखित के मान ज्ञात कीजिए:
(i) a² + b²
(ii) a² + ab + b²
(iii) a² – b²
हल :
जब a = 2 और b = -2 हो तो
(i) a² + b² = (2)² + (-2)²
= 4 + 4
= 8

(ii) a² + ab + b²
= (2)² + (2) (-2) + (-2)²
= 4 – 4 + 4
= 4

(iii) a² – b² = (2)² – (-2)²
= 4 – 4 = 0.

प्रश्न 5.
जब a = 0 और b = – 1 है, तो दिए हुए व्यंजकों के मान ज्ञात कीजिए :
(i) 2a + 2b
(ii) 2a + b² + 1
(ii) 2a²b + 2ab² + ab
(iv) a² + ab + 2
हल :
जब a = 0 और b = -1 हो तो
(i) 2a + 2b = 2(0) + 2(-1)
= 0 – 2 = -2

(ii) 2a² + b² + 1
= 2(0)² + (-1)² + 1
= 0 + 1 + 1 = 2

(iii) 2a²b + 2ab² + ab
= 2(0)² (-1) + 2(0) (-1)² + (0) (-1)
= 0 + 0 + 0 = 0

(iv) a² + ab + 2 = (0)² + (0) (- 1) + 2
= 0 + 0 + 2 = 2

प्रश्न 6.
इन व्यंजकों को सरल कीजिए तथा इनके मान ज्ञात कीजिए, जब x का मान 2 है:
(i) x + 7 + 4(x – 5)
(ii) 3(x + 2) + 5x – 7
(iii) 6x + 5(x -2)
(iv) 4(2x – 1) + 3x + 11
हल :
(i) x + 7 + 4(x -5) = x + 7 + 4x – 20
= (x + 4x) + (7 – 20)
= 5x – 13
x = 2 रखने पर,
5x – 13 = 5(2) – 13
= 10 – 13
= -3

(ii) 3(x + 2) + 5x – 7 = 3x + 6 + 5x – 7
= (3x + 5x) + (6 – 7)
= 8x – 1
x = 2 रखने पर,
8x – 1 = 8(2) – 1 = 16 – 1 = 15

(iii) 6x + 5(x – 2) = 6x + 5x – 10
= 11x – 10
x = 2 रखने पर,
11x – 10 = 11 × 2 – 10
= 22 – 10 = 12

(iv) 4(2x – 1) + 3x + 11= 8x – 4 + 3x + 11
= (8x + 3x) + (-4 + 11)
= 11x + 7
x = 2 रखने पर,
11x + 7 = 11 × 2 + 7 = 22 + 7
= 29 उत्तर

प्रश्न 7.
इन व्यंजकों को सरल कीजिए तथा इनके मान ज्ञात कीजए, जब x = 3, a = -1 और b = -2 है:
(i) 3x – 5 – x + 9
(ii) 2 – 8x + 4x + 4
(iii) 3a + 5 – 8a + 1
(iv) 10 – 3b – 4 – 5b
(v) 2a – 2b – 4 – 5 + a
हल :
(i) 3x – 5 – x + 9 = 2x + 4
x = 3 रखने पर, 2x + 4 = 2(3) + 4
= 6 + 4 = 10

(ii) 2 – 8x + 4x + 4 = 6 – 4x
x = 3 रखने पर,
6 – 4x = 6 – 4(3)
= 6 – 12 = -6

(iii) 3a + 5 – 8a + 1 = -5a + 6
a = -1 रखने पर,
-5a + 6 = – 5(-1)+ 6
= 5 + 6 = 11

(iv) 10 – 3b – 4 – 5b = 6 – 8b
b = -2 रखने पर,
6 – 8b = 6 – 8(-2)
= 6 + 16 = 22

(v) 2a – 2b – 4 – 5 + a
= 3a – 2b – 9
a = – 1 और b = – 2 रखने पर,
3a – 2b – 9 = 3(-1) -2 (-2) – 9
= – 3 + 4 – 9
= -8

प्रश्न 8.
(i) यदि z = 10 है, तो z³ – 3(z – 10) का मान ज्ञात कीजिए।
(ii) यदि p = – 10 है, तो p² – 2p – 100 का मान ज्ञात कीजिए।
हल :
(i) जब z = 10 हो, तो
z³ – 3(z – 10) = (10)³ – 3(10 – 10)
= 1000 – 3(0)
= 1000 – 0 = 1000

(ii) जब p = – 10 हो, तो
p² – 2p – 100 = (-10)² – 2(- 10) – 100
= 100 + 20 – 100
= 20

प्रश्न 9.
यदि x = 0 पर 2x² + x – a का मान 5 के बराबर है, तो a का मान क्या होना चाहिए ?
हल:
x = 0 पर 2x² + x – a = 5 (दिया है)
2(0) + 0 – a = 5 ⇒ 0 + 0 – a = 5
-a = 5 ⇒ a = -5 उत्तर

प्रश्न 10.
व्यंजक 2(a² + ab) + 3 – ab को सरल कीजिए और इसका मान ज्ञात कीजिए, जब a = 5 और b = -3 है।
हल :
जब a = 5 और b = -3 हो, तो
2(a² + ab)+ 3 – ab = 2a² + 2ab+ 3 – ab
= 2a² + 2ab – ab + 3
= 2a² + ab + 3
जब a = 5 और b = -3 हो, तो
2a² + ab + 3 = 2(5)² + (5 × -3) + 3
= 2 × 25 + (-15) + 3
= 50 + 3 – 15
= 38

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.3 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.3

प्रश्न 1.
निम्नांकित आकृतियों में अज्ञात x का मान ज्ञात कीजिए:

हल :
त्रिभुज के तीनों कोणों का योग 180° होता है। अत:
(i) ΔABC में,
∠A + ∠B + ∠C= 180°
⇒ x + 50° + 60° = 180°
⇒ x = 180° – 50° – 60°
⇒ x = 180° – 110°
⇒ x = 70°

(ii) ΔPQR में,
∠P + ∠Q + ∠R = 180°
90° + 30° + x = 180°
x = 180° – 90° – 30°
= 180° – 120°
= 60°

(iii) ΔXYZ में
∠X + ∠Y + ∠Z = 180°
30° + 110° + x = 180°
x = 180° – 30° – 110°
= 180° – 140°
=40°

(iv) x + x + 50° = 180°
⇒ 2x + 50° = 180°
⇒ 2x = 180° – 50°
⇒ 2x = 130°
⇒ x = \(\frac {130°}{2}\)
⇒ x = 65°

(v) x + x + x = 180°
⇒ 3x = 180°
⇒ x = \(\frac {180°}{3}\)
⇒ x = 60°

(vi) x + 2x + 90° = 180°
⇒ 3x + 90° = 180°
⇒ 3x = 180° – 90°
⇒ 3x = 90°
⇒ x = \(\frac {90°}{3}\)
⇒ x = 30°

प्रश्न 2.
निम्नांकित आकृतियों में अज्ञात x और y का मान ज्ञात कीजिए:

हल :
(i) त्रिभुज में बाह्य कोण और संलग्न अंत: कोण रैखिक युग्म बनाते हैं। अतः
y + 120° = 180°
⇒ y = 180° – 120° = 60°
एक त्रिभुज में कोणों का योग 180° होता है।
∴ x + 50° + y = 180°
⇒ x = 180° – 50° – y
⇒ x = 130° – 60° = 70°.
अतः x = 70° और y = 60°

(ii) यहाँ y = 80°, [शीर्षाभिमुख कोण]
त्रिभुज में कोणों का योग 180° होता है।
∴ x + y + 50° = 180°
⇒ x + 80° + 50° = 180°, [∵ y = 80°]
⇒ x + 130° = 180°
⇒ x = 180°- 130°
⇒ x = 50°
अतः x = 50° और y = 80°

(iii) त्रिभुज के तीनों अन्तः कोणों का योग 180° होता है।
∴ y + 60° + 50° = 180°
y = 180° – 60° – 50°
y = 180° – 110°
y = 70°
बाह्य कोण (x) = 50° + 60° = 110°
अत: x = 110° और y = 70°

(iv) त्रिभुज के तीनों कोणों का योग = 180°
∴ x + y + 30° = 180°
x = 60°, (शीर्षाभिमुख कोण)
60° + y + 30° = 180°
y = 180° – 60° – 30°
= 180° – 90°
= 90°
अत: x = 60° और y = 90°

(v) त्रिभुज के तीनों अन्त: कोणों का योग 180° होता है।
∴ x + x + y = 180°
[(∵ y = 90°) शीर्षाभिमुख कोण]
2x + 90° = 180°
2x = 180° – 90°
2x = 90°
x = \(\frac {90°}{2}\) = 45°
अत: x = 45° और y = 90°

(vi) त्रिभुज के तीनों अन्त: कोणों का योग 180° होता है।
∴ x + x + y = 180°
x + x + x = 180°,
[(∵ y = x°) शीर्षाभिमुख कोण]
3x = 180°
x = \(\frac {180°}{2}\) = 60°
∴ y = 60°
अतः x = 60° और y = 60°

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.2

प्रश्न 1.
निम्न आकृतियों में अज्ञात बाह्य कोणx का मान ज्ञात कीजिए :

हल :
प्रत्येक त्रिभुज में बाह्य कोण दो अन्तः सम्मुख कोणों के योग के बराबर होता है। इसलिए
(i) x = 50° + 70° = 120°
(ii) x = 65° + 45° = 110°
(iii) x = 30° + 40° = 70°
(iv) x = 60° + 60° = 120°
(v) x = 50° + 50° = 100°
(vi) x = 30° + 60° = 90°

प्रश्न 2.
निम्न आकृतियों में अज्ञात अंत:कोण का मान ज्ञात कीजिए:

हल :
हम जानते हैं कि त्रिभुज में बाह्य कोण का मान दो अन्तः सम्मुख कोणों के योग के बराबर होता है। इसलिए
(i) x + 50° = 115°
⇒ x = 115° – 50° = 65°
(ii) x + 70° = 100°
⇒ x = 100° – 70° = 30°
(iii) x + 90° = 125°
⇒ x = 125° – 90° = 35°
(iv) x + 60° = 120°
⇒ x = 120° – 60° = 60°
(v) x + 30° = 80°
⇒ x = 80° – 30° = 50°
(vi) x + 35° = 75°
⇒ x = 75° – 35° = 40°

Haryana State Board HBSE 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.2 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.2

प्रश्न 1.
समान पदों का संयोजित (मिला) करके सरल कीजिए :
(i) 21b – 32 + 7b – 20b
(ii) -z² + 13z² – 5z + 7z³ – 15z
(iii) p – (p – q) – q – (q – p)
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
(v) 5x²y – 5x² + 3yx² – 3y² + x² – y² + 8xy² – 3y²
(vi) (3y² + 5y – 4) – (8y -y² – 4)
हल :
(i) 21b – 32 + 7b – 20b
= 21b + 7b – 20b – 32 = 8b – 32

(ii) -z² + 13z² – 5z + 7z³ – 15z
= 7z³ – z² + 13z² – 5z – 15z
= 7z³ + (-1 + 13)z² + (- 5 – 15)z
= 7z³ + 12z² – 20z

(iii) p – (p – q) – q – (q – p)
= p – p + q – q – q + p
= (p – p + p) + (q – q – q)
= p – q

(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
= 3a – 2b – ab – a + b – ab + 3ab + b – a
= 3a – a – a – 2b + b + b – ab – ab + 3ab
= (3 – 1 – 1)a + (-2 + 1 + 1)b + (- 1 – 1 + 3)ab
= a + 0b + ab = a + ab

(v) 5x²y – 5x² + 3yx² – 3y² + x² – y² + 8xy² – 3y²
= 5x²y + 3yx² – 5x² + x² – 3y² – y² – 3y² + 8xy²
= (5 + 3)x²y + (-5 + 1)x² + (- 3 – 1 – 3)y² + 8xy²
= 8x²y – 4x² – 7y² + 8xy²

(vi) (3y² + 5y – 4) – (8y – y² – 4)
= 3y² + 5y – 4 – 8y + y² + 4
= 3y² + y² + 5y – 8y – 4 + 4
= (3 + 1)y² + (5 – 8)y + (- 4 + 4)
= 4y² – 3y

प्रश्न 2.
जोड़िए:
(i) 3mn, – 5mn, 8mn, – 4mn
(ii) t – 8tz, 3tz – z, z – t
(iii) – 7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3
(iv) a + b – 3, b – a + 3, a – b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(vii) 4x²y, – 3xy², -5xy², 5x²y
(viii) 3p²q² – 4pq + 5, – 10p²q², 15 + 9pq + 7p²q²
(ix) ab – 4a, 4b – ab, 4a – 4b
(x) x² – y² – 1, y² – 1 – x², 1 – x² – y²
हल :
(i) वांछित योग
= 3mn + (-5mn) + 8mn + (-4mn)
= (3 – 5 + 8 – 4)mn
= (11 – 9)mn = 2mn

(ii) वांछित योग
= (t – 8tz) + (3tz – z) + (z – t)
= t – 8tz + 3tz – z + z – t
= t – t – 8tz + 3tz – z + z
= (1 – 1)t + (- 8 + 3)tz + (- 1 + 1)z
= (0)t + (-5)tz + (0)z
= 0 – 5tz + 0 = – 5tz

(iii) वांछित योग
= (-7mn + 5) + (12mm + 2) + (9mn – 8) + (- 2mn – 3)
= – 7mn + 5 + 12mn + 2 + 9mn + 8 – 2mn – 3
= -7mn + 12mn + 9mn -2mn + 5 + 2 – 8 – 3
= (-7 + 12 + 9 – 2)mn + (5 + 2 – 8 – 3)
= 12mn – 4

(iv) वांछित योग
= (a + b – 3) + (b – a + 3) + (a – b + 3)
= a + b – 3 + b – a + 3 + a – b + 3
= (a – a + a) + (b + b – b) + (-3 + 3 + 3)
= (1 – 1 + 1)a + (1 + 1 – 1)b + 3
= a + b + 3

(v) वांछित योग
= (14x + 10y – 12xy – 13) + (18 – 7x – 10y + 8xy) + 4xy
= 14x + 10y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
= 14x – 7x + 10y – 10y – 12xy + 8xy + 4xy – 13 + 18
= (14 – 7)x + (10 – 10)y + (- 12 + 8 + 4)xy + (- 13 + 18)
= 7x + 0y + 0xy + 5 = 7x + 5

(vi) वांछित योग
= (5m – 7n) + (3n – 4m + 2) + (2m – 3mn – 5)
= 5m – 7n + 3n -4m + 2 + 2m – 3mn – 5
= 5m – 4m + 2m – 7n + 3n – 3mn + 2 – 5
= (5 – 4 + 2)m + (- 7 + 3)n – 3mn + (2 – 5)
= 3m – 4n – 3mn – 3

(vii) वांछित योग
= 4x²y + (-3xy²) + (-5xy²) + 5x²y
= 4x²y -3xy² – 5xy²– + 5x²y
= 4x²y + 5x²y – 3xy² – 5xy²
= (4 + 5)x²y + (- 3 – 5)xy² = 9x²y – 8xy²

(viii) वांछित योग
= (3p²q² – 4pq + 5) + (-10p²q²) + (15 + 9pq + 7p²q²)
= 3p²q² – 4pg + 5 – 10p²q² + 15 + 9pq + 7p²q2
= 3p²q² – 10p²q² + 7p²q² – 4pq + 9pq + 5 + 15
= (3 – 10 + 7)p2²q² + (- 4 + 9)pq + (5 + 15)
= 0p²q² + 5pq+ 20
= 5pq + 20

(ix) वांछित योग
= (ab – 4a) + (4b – ab) + (4a – 4b)
= ab – 4a + 4b – ab + 4a – 4b
= ab – ab – 4a + 4a + 4b – 4b
= (1 – 1)ab + (- 4 + 4)a + (4 – 4)b
= (0)ab + (0)a + (0)b = 0 + 0 + 0 = 0

(x) वांछित योग
= (x² – y² – 1) + (y² – 1 – x²) + (1 – x² – y²)
= x² – y² – 1 + y² – 1 – x² + 1 – x² – y²
= x² – x² – x² – y² + y² – y² – 1 – 1 + 1
= (1 – 1 – 1)x² + (- 1 + 1 – 1)y² + (- 1 – 1 + 1)
= – x² – y² – 1

प्रश्न 3.
घटाइए :
(i) y² में से – 5y²
(ii) -12xy में से 6xy
(ii) (a + b) में से (a – b)
(iv) b(5 – a) में से a(b – 5)
(v) 4m² – 3mn + 8 में से – m² + 5mn
(vi) 5x – 10 में से – x² + 10x – 5
(vii) 3ab – 2a² – 2b² में से 5a² – 7ab + 5b²
(viii) 5p² + 3q² – pq में से 4pq – 5q² – 3p²
हल :
(i) वाछित अन्तर
y² – (-5y²) = y² + 5y²
= (1 + 5)y² = 6y²

(ii) वांछित अन्तर
(- 12xy) – 6xy = (- 12 – 6)xy
= – 18xy

(iii) वांछित अंतर
(a + b) – (a – b) = a + b – a + b
= (a – a) + (b + b)
= (1 – 1)a + (1 + 1)b
= 0a + 2b = 2b

(iv) वांछित अन्तर
b(5 – a)- a(b – 5) = 5b – ab – ab + 5a
= 5a + 5b + (- 1 – 1)ab
= 5a + 5b – 2ab

(v) वांछित अन्तर
(4m² – 3mn + 8) – (- m² + 5mn)
= 4m² – 3mn + 8 + m² – 5mn
= 4m² + m² – 3mn – 5mn + 8
= (4 + 1)m² + (- 3 – 5)mn + 8
= 5m² – 8mn +8

(vi) वांछित अन्तर
(5x – 10) – (- x² + 10x – 5)
= 5x – 10 + x² – 10x + 5
= x² + (5 – 10)x + (- 10 + 5)
=x² – 5x – 5

(vii) वांछित अन्तर
(3ab – 2a² – 2b²) – (5a² – 7ab + 5b²)
= 3ab – 2a² – 2b² – 5a² + 7ab – 5b²
=- 2a² – 5a² – 2b² – 5b² + 3ab + 7ab
= (- 2 – 5)a² + (- 2 – 5)b² + (3 + 7)ab
= -7a² – 7b² + 10ab

(viii) वांछित अन्तर
(5p² + 3q² – pg) – (4pq – 5q² – 3p²)
= 5p² + 3q² – pq – 4pq + 5q² + 3p²
= 5p² + 3p² + 3q² + 5q² – pq – 4pq
= (5 + 3)p² + (3 + 5)q² + (- 1 – 4)pq
= 8p² + 8q² – 5pq

प्रश्न 4.
(a) 2x² + 3xy प्राप्त करने के लिए, x² + xy +y में क्या जोड़ना चाहिए ?
(b) -3a + 7b + 16 प्राप्त करने के लिए, 2a + 8b + 10 में से क्या घटाना चाहिए ?
हल :
(a) 2x² + 3xy में से x² + xy + y2 को घटाने पर,
अतः वांछित व्यंजक = (2x² + 3xy) – (x² + xy +y²)
= 2x² + 3xy – x² – xy – y²
= 2x² – x² + 3xy – xy – y²
= (2 – 1)x² + (3 – 1)xy – y²
= x² + 2xy – y² उत्तर

(b) माना वांछित व्यंजकों को R से व्यक्त करें तो-
(2a + 8b + 10) – R = – 3a + 7b + 16
अत: वांछित व्यंजक R
= (2a + 8b + 10) – (- 3a + 7b + 16)
= 2a + 3a + 10 + 3a – 7b – 16
= 2a + 3a + 8b – 7b + 10 – 16
= (2 + 3)a + (8 – 7)b + (10 – 16)
= 5a + b – 6 उत्तर

प्रश्न 5.
– x² – y² + 6xy + 20 प्राप्त करने के लिए, 3x² – y² + 5xy + 20 में क्या निकाल लेना चाहिए ?
हल :
माना वांछित व्यंजक को R से व्यक्त करें तो
(3x² – 4y² + 5xy + 20) – R = – x² – y² + 6xy + 20
अत: वांछित व्यंजक R
= (3x² – 4y² + 5xy + 20) – (- x² – y² + 6xy + 20)
= 3x² – 4y² + 5xy + 20 + x² + y² – 6xy -20
= 3x² + x² – 4y² + y² + 5xy – 6xy + 20 – 20
= (3 + 1)x² + (- 4 + 1)y² + (5 – 6)xy + (20 – 20)
= 4x² – 3y² – xy उत्तर

प्रश्न 6.
(a) 3x – y + 11 और – y – 11 के योग में से 3x – y – 11 को घटाइए।
(b) 4 + 3x और 5 – 4x + 2x² के योग में से 3x² – 5x और – x² + 2x +5 के योग को घटाइए।
हल :
(a) 3x – y + 11 और – y – 11 का योग करने पर,
= (3x – y + 11) + (- y – 11)
= 3x – y + 11 – y – 11
= 3x – 2y
अब 3x – 2y में से 3x – y – 11 को घटाने पर,
= (3x – 2y) – (3x – y – 11)
= 3x – 2y – 3x + y + 11
= – y + 11 उत्तर

(b) 4 + 3x और 5 – 4x + 2x² का योग करने पर,
= (4 + 3x) + (5 – 4x + 2x²)
= 4 + 3x + 5 – 4x + 2x²
= 9 – x + 2x²
पुन: 3x² – 5x और – x² + 2x + 5 का योग करने पर,
= (3x² – 5x) + (-x² + 2x + 5)
= 3x² – 5x – x² + 2x + 5
= 2x² – 3x + 5
अब 9 – x + 2x² में से 2x² – 3x + 5 को घटाने पर
= (9 – x + 2x²) – (2x² – 3x + 5)
= 9 – x + 2x² – 2x² + 3x – 5
= 2x + 4

Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.1 Textbook Exercise Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.1

प्रश्न 1.
ΔPQR में भुजा \(\overline{Q R}\) का मध्य बिन्दु D है:
\(\overline{PM}\) …………. है।
PD ………….. है।
क्यो QM = MR ?

हल :
\(\overline{PM}\) शीर्ष लम्य है,
जो शीर्ष P से सम्मुख भुजा \(\overline{Q R}\) पर है।
PD, ΔPQR में शीर्ष Pसे सम्मुख भुजा \(\overline{Q R}\) की माध्यिका है। QM ≠ MR, क्योंकि \(\overline{Q R}\) का मध्य विन्दु M नहीं है।

प्रश्न 2.
निम्न के लिए अनुमान से आकृति खींचिए :
(a) ΔABC में, BE एक माध्यिका है।
(b) ΔPQR में, PQ तथा PR त्रिभुज के शीर्षलम्ब है।
(c) ΔXYZ में, YL एक शीर्षलंब उसके बहिर्भाग में है।
हल :
(a) ΔBC में BE एक माध्यिका की आकृति निम्न प्रकार है:

(b) ΔPQR में, PQ तथा PR त्रिभुज के शीर्ष लम्बों की आकृति निम्न प्रकार है :

(c) ΔXYZ में YL एक शीर्ष लम्ब उसके बहिर्भाग में आकति निम्न प्रकार हैं:

प्रश्न 3.
आकृति खींचकर पुष्टि कीजिए कि एक समद्विबाहु त्रिभुज में शीर्षलम्ब व माध्यिका एक ही रेखाखण्ड हो सकता है? .
हल :

एक रेखाखण्ड BC खींचते हैं। कागज के मोड़ने की विधि से \(\overline{BC}\) का लम्ब समद्विभाजक किया। मुड़ी हुई लाइन D बिन्दु पर मिलती है, जो कि BC’ का मध्य बिन्दु है।

इस लम्ब समद्विभाजक पर कोई बिन्दु लिया। AB और AC को मिलाया। इस प्रकार ΔABC एक समद्विबाहु त्रिभुज प्राप्त होगा, जिसमें AB = AC. स्पष्ट है कि \(\overline{BC}\) का मध्य बिन्दु D है। अत: AD माध्यिका है और BC का शीर्ष लम्ब AD है।

इससे सिद्ध होता है कि समद्विबाहु त्रिभुज में माध्यिका और शीर्षलम्ब एक ही होते हैं।

Haryana State Board HBSE 7th Class Maths Solutions Chapter 5 रेखा एवं कोण InText Questions and Answers.

Haryana Board 7th Class Maths Solutions Chapter 5 रेखा एवं कोण InText Questions

प्रयास कीजिए (पृष्ठ सं. 107)

प्रश्न 1.
निम्नलिखित कोणों के युग्मों में कौन-से पूरक है?

हल :
(i) इस जोड़े में दो कोणों का योग
= 70° + 20° = 90°
अतः कोणों का यह युग्म एक-दूसरे का पूरक है। उत्तर
(ii) इस जोड़े में दो कोणों का योग
= 75° + 25° = 100°
अत: कोणों का यह युग्म एक-दूसरे का पूरक नहीं है। उत्तर
(iii) इस जोड़े में दो कोणों का योग
= 48° + 52° = 100°
≠ 90°
अतः कोणों का यह युग्म एक-दूसरे का पूरक नहीं है। उत्तर
(iv) इस जोड़े में दो कोणों का योग
= 35° + 55° = 90°
अतः कोणों का यह युग्म एक-दूसरे का पूरक है। उत्तर

प्रश्न 2.
निम्नलिखित कोणों में प्रत्येक के पूरक का माप क्या है?
(i) 45° (ii) 65° (iii) 41° (iv) 54°
हल :
हम जानते हैं कि किसी कोण और इसके पूरक कोण का योग 90° होता है। अतः
(i) 45° के कोण के पूरक कोण का माप
= (90° – 45°) = 45°
(ii) 65° के कोण के पूरक कोण का माप
= (90° – 65°) = 25°
(iii) 41° के कोण के पूरक कोण का माप
= (90° -41°) = 49°
(iv) 54° के कोण के पूरक कोण का माप
= (90° – 54°) = 36°

प्रश्न 3.
दो पूरक कोणों के मापों का अंतर 12° है। कोणों के माप ज्ञात कीजिए।
हल :
माना एक कोण हैं, तो दूसरा कोण (x + 12)° होगा। अब x° और (x + 12)° पूरक कोण होंगे।
∴ x° + (x + 12)° = 90°
⇒ 2x° + 12° = 90°
⇒ 2x° = 90° – 12°
⇒ 2x° = 78°
⇒ x° = \(\frac {78°}{2}\) = 39°
अतः एक कोण = x° = 39°
औरदूसरा कोण = (x + 12)° = 39° + 12° = 51°.

पृष्ठसं 108-109

प्रश्न 1.
आकृति में सम्परक कोणों के युग्म ज्ञात कीजिए।

हल :
आकृति (i) के युग्म में,
कोणों का योग = 110° + 50° = 160° ≠ 180°
अतः ये सम्परक नहीं हैं।
आकृति (ii) के युग्म में,
कोणों का योग = 105° + 65° = 170° ≠ 180°
अतः ये सम्पूरक नहीं हैं।
आकृति (iii) के युग्म में,
कोणों का योग = 130° + 50° = 180°
अतः ये सम्पूरक हैं।
आकृति (iv) के युग्म में,
कोणों का योग = 45° + 45° = 90° ≠ 180°
अतः ये सम्पूरक नहीं हैं।

प्रश्न 2.
निम्नलिखित कोणों में प्रत्येक के सम्पूरक का माप क्या होगा?
(i) 100°
(ii) 90°
(iii) 55°
(iv) 125°
हल :
हम जानते हैं कि एक कोण और इसके सम्पुरक कोण का योग 180° होता है। इसलिए
(i) 100° के कोण का सम्पूरक कोण
= (180° – 100°) = 80°
(ii) 90° के कोण का सम्पूरक कोण
= (180° – 90°) = 90°
(iii) 550 के कोण का सम्पूरक कोण
= (180°- 55°) = 125°
(iv) 125° के कोण का सम्पूरक कोण
= (180° – 125°) = 55°

प्रश्न 3.
दो सम्पूरक कोणों में बड़े कोण का माप छोटे कोण के माप से 44° अधिक है। कोणों के माप ज्ञात कीजिए।
हल:
माना छोटा कोण = x° हो, तो
बड़ा कोण = (x + 44°)
अब और (x + 44)° सम्पूरक कोण होंगे।
x° + (x + 44)° = 180°
x° + x° + 44° = 180°
2x° + 44° = 180°
2x° = 180° – 44° = 136°
2x = 136°
x = \(\frac {136°}{2}\) = 68°
अतः छोटा कोण = x° = 68°
और बड़ा कोण = x + 44° = (68° + 44)°
= 112°

पृष्ठ सं. 110

प्रश्न 1.
क्या 1 और 2 से अंकित कोण आसन्न हैं ? [आकृति (i)-(v)] यदि ये आसन्न नहीं हैं तो बताइए, ‘क्यों ?

हल :
(i) हाँ, कोण 1 और 2 आसन्न हैं।
(ii) हाँ, कोण 1 और 2 आसन्न हैं।
(iii) नहीं, कोण 1 और 2 आसन्न नहीं है, क्योंकि इनमें उभयनिष्ठ शीर्ष नहीं हैं।
(iv) नहीं, कोण 1 और 2 आसन्न नहीं हैं, क्योंकि कोणों की अन्य भुजाएँ, उभयनिष्ठ भुजा के एक ही ओर स्थित हैं।
(v) हाँ, कोण | और 2 आसन्न हैं।

प्रश्न 2.
आकृति में, क्या निम्नलिखित कोण आसन्न हैं?

(a) ∠ZAOB और ∠BOC
(b) ∠BOD और ∠BOC
अपने उत्तर की पुष्टि कीजिए।
हल :
(a) आकृति में, ∠AOB और ∠BOC का उभयनिष्ठ शीर्ष तथा उभयनिष्ठ भुजा है। इनकी अन्य भुजा उभयनिष्ठ भुजा के विपरीत है। अत: ∠AOB और ∠BOC आसन्न कोण हैं।
(b) ∠BOD और ∠BOC आसन्न कोण नहीं हैं, क्योंकि इनकी अन्य भुजाएँ उभयनिष्ठ OB के विपरीत नहीं हैं।

पृष्ठ सं. 111

प्रश्न 1.
बताइए कोणों के निम्नलिखित युग्मों में से कौन-सा रैखिक युग्म बनाता है?


हल :
आकृति (i) में,
कोणों का योग = 140° + 40° = 180°
अत: यह युग्म रैखिक युग्म बनाता है।
आकृति (ii) में,
कोणों का योग = 60° + 90° = 150°
अत: यह युग्म रैखिक युग्म नहीं बनाता है।
आकृति (iii) में,
कोणों का योग = 90° + 40° = 130°
अत: यह युग्म रैखिक युग्म नहीं बनाता है।
आकृति (iv) में,
कोणों का योग = 65° + 115° = 180°
अत: यह युग्म रैखिक युग्म बनाता है।

पृष्ठ सं. 113

प्रश्न 1.
दी हुई आकृति में, यदि ∠1 = 30°, तो ∠2 एवं ∠3 ज्ञात कीजिए।

हल :
दो रेखाएँ एक बिन्दु पर काटती हैं।
∴ ∠1 = ∠3, (शीर्षाभिमुख कोण)
⇒ ∠1 = ∠3 = 30°
⇒ ∠3 = 30°
हम जानते हैं :
∠1 +∠2 = 180°, (रैखिक युग्म कोण)
∠2 = 180° – ∠1
∠2 = 180° – 30°
∠2 = 150°
अतः ∠2 = 150° और ∠3 = 30°.

प्रश्न 2.
अपने आस पास से शीर्षाभिमुख कोणों का एक उदाहरण दीजिए।
हल :
कैंची को खोलने पर उसके दोनों ब्लेड़ों के मध्य बनने वाले कोण।

पृष्ठ सं. 116

प्रश्न 1.
अपने आस-पास के परिवेश से ऐसे उदाहरण ज्ञात कीजिए जहाँ रेखाएँ समकोण पर प्रतिच्छेद करती हैं।
हल :
अपने आसपास के परिवेश में समकोण पर प्रतिच्छेद करने वाली रेखाओं के निम्न उदाहरण हैं:
(i) ब्लैक बोर्ड के किनारे
(ii) मेज की टाँगे ऊपर का तख्ता
(iii) कैरम बोर्ड के किनारे
(iv) पेपर शीट के किनारे।

प्रश्न 2.
एक समबाहु त्रिभुज के शीर्षों पर प्रतिच्छेदी रेखाओं द्वारा निर्मित कोणों के माप ज्ञात कीजिए।
हल :

माना ABC एक समबाहु त्रिभुज है जिसके हमें कोण ज्ञात करने हैं।
∵ समबाहु त्रिभुज के सभी कोण समान होते हैं।
∴ ∠A = ∠B = ∠C = x° (माना)
∠A + ∠B + ∠C = 180°
x + x + x = 180°
3x = 180°
x = 60°
∴ ∠A = ∠B = ∠C = 60°.

प्रश्न 3.
एक आयत खींचिए और प्रतिच्छेदी रेखाओं द्वारा निर्मित चार शीर्षों के कोणों के माप ज्ञात कीजिए।
हल :

माना ABCD एक आयत है। हमें इसके कोण ज्ञात करने हैं अर्थात् ABCD एक समान्तर चतुर्भुज है जिसमें ∠A = 90°.
हम जानते हैं कि
∠C = ∠A, [∵ समान्तर □ के प्रम्मुख कोण समान होते हैं]
= 90° [∵ ∠A = 90° (दिया है)]
पुन: ∠A + ∠B = 180°
[∵ ∠A और ∠B चतुर्भुज के आसन्न कोण हैं]
⇒ 90° + ∠B = 180°
⇒ ∠B = 180° – 90° = 90°
∴ ∠D = ∠B.
[∵ समान्तर चतुर्भुज के सम्मुख कोण समान होते हैं।]
= 90°
अत: ∠A = ∠B = ∠C = ∠D = 90°.

प्रश्न 4.
यदि दो रेखाएँ एक-दूसरे को प्रतिच्छेद करती हैं, तो क्या वे हमेशा एक-दूसरे को सम कोण पर प्रतिच्छेद करती है?
हल :
नहीं, दो रेखाएँ हमेशा एक-दूसरे को समकोण पर प्रतिच्छेद नहीं करती है।

पृष्ठ सं. 117

प्रश्न 1.
मान लीजिए दो रेखाएँ दी हुई हैं। इन रेखाओं के लिए आप कितनी तिर्यक छेदी रेखाएँ खींच सकते हैं?
हल :
दी गई दो रेखाओं के लिए असंख्य तिर्यक रेखाएँ खींच सकते हैं।

प्रश्न 2.
यदि एक रेखा तीन रेखाओं का तिर्यक छेदी रेखा है, तो बताइए कितने प्रतिच्छेदन बिन्दु हैं।
हल :
यदि तीन रेखाओं की एक तिर्यक छेदी रेखा हैं तो इनके तीन अथवा तीन से अधिक प्रतिच्छेद बिन्दु हैं।

प्रश्न 3.
अपने आस-पास कुछ तिर्यक् छेदी रेखाएँ ढूंढने का प्रयास कीजिए।
हल :
अपने आस-पास कुछ तिर्यक् छेदी रेखाओं के उदाहरण निम्न हैं :

• लोहे की सीढ़ी
• खिड़की की ग्रिल
• तौलिया स्टैण्ड आदि।

पृष्ठ सं. 118

प्रश्न 1.
प्रत्येक आकृति में कोण युग्म को नाम दीजिए :


हल :
प्रथम आकृति में : ∠1 और ∠2 संगत कोण हैं।
दूसरी आकृति में : ∠3 और ∠4 एकान्तर कोण हैं।
तीसरी आकृति में : ∠5 और ∠6 अन्त:कोण हैं।
चौथी आकृति में : ∠7 और ∠8 संगत कोण हैं।
पाँचवीं आकृति में : ∠9 और ∠10 एकांतर कोण हैं।
छठी आकृति में : ∠11 और ∠12 रैखिक युग्म हैं।

पृष्ठ सं. 121

प्रश्न 1.
(i) l || m
t एक तिर्यक छेदी रेखा है।
∠x = ?
(ii) a || b
c एक तिर्यक छेदी रेखा है।
∠y = ?
(iii) l₁, l₂ दो रेखाएँ हैं।
t एक तिर्यक छेदी रेखा है। क्या ∠1 = ∠2 हैं ?
(iv) l || m,
t एक तिर्यक छेदी रेखा है।
∠z = ?
(v) l || m,
t एक तिर्यक छेदी रेखा है।
∠x = ?
(vi) l || m, P || q, a, b, c,d ज्ञात कीजिए।

हल :
(i) आकृति में, l || m और t तिर्यक छेदी रेखा है।
∴ ∠x = 60°, (एकान्तर कोण)
(ii) आकृति में, a || b और c एक तिर्यक छेदी रेखा है।
∴ ∠y = 55°, (एकान्तर कोण)
(iii) आकृति में, l₁ और l₂ दो असमान्तर रेखाएँ हैं और t तिर्यक छेदी रेखा है।
∴ ∠1 ≠ ∠2
(iv) आकृति में, l || m और t एक तिर्यक छेदी रेखा है,।
∴ 60° + z = 180° [तिर्यक छेदी रेखा के एक ही ओर के अंत: कोणों का योग 180° होता है।
⇒ z = 180° – 60°
= 120°

(v) आकृति में, l || m और t एक तिर्यक छेदी रेखा है।
∴ ∠x = 120°, (संगत कोण)

(vi) आकृति में, p || q और l तिर्यक छेदी रेखा है।
∴ a + 60° = 180°,
(अंत:कोणों का योग 180° होता है)
⇒ a = 180° – 60° = 120°
∠1 = 60°, (एकान्तर कोण)
आकृति में, l || m और q एक तिर्यक छेदी रेखा है।
∴ ∠c = ∠1, (एकान्तर कोण)
∠c = 60°, (∵ ∠1 = 60°)
स्पष्टतः ∠b = ∠c, (शीर्षभिमुख कोण)
∴ ∠b = 60°
अब
∠d = 180° – ∠b
= 180° – 60°
= 120°
अत: ∠a = 120°, ∠b = 60°, ∠c = 60°
और ∠d = 120.

पृष्ठ सं. 122

(i) क्या l || m है ? क्यों ?

(ii) क्या l || m है ? क्यों ?

(iii) यदि l ||m, तो x क्या है?

हल :
(i) आकृति में, एकान्तर कोण बराबर हैं।
इसलिए l || m है।
(ii) आकृति में, ∠1 = 180° – 130° = 50°
∴ हम देखते हैं कि संगत कोण समान है।
इसलिए l || m.
(iii) आकृति में, l ||m और t तिर्यक छेदी रेखा है।
∴ x + 70° = 180°,
(तिर्यक रेखा के एक ओर बने अन्तः कोणों का योग 180° होता है।)
x = 180° – 70° = 110°.