Haryana State Board HBSE 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.3 Textbook Exercise Questions and Answers.
Haryana Board 7th Class Maths Solutions Chapter 6 त्रिभुज और उसके गुण Ex 6.3
प्रश्न 1.
निम्नांकित आकृतियों में अज्ञात x का मान ज्ञात कीजिए:
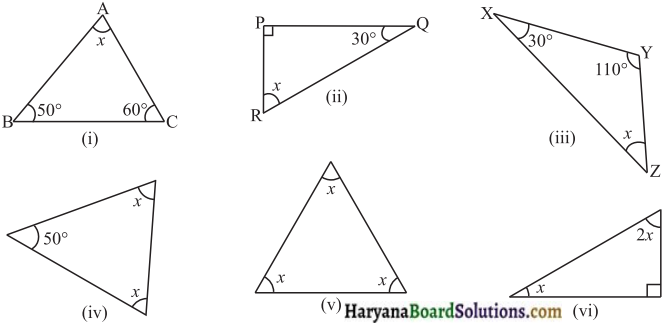
हल :
त्रिभुज के तीनों कोणों का योग 180° होता है। अत:
(i) ΔABC में,
∠A + ∠B + ∠C= 180°
⇒ x + 50° + 60° = 180°
⇒ x = 180° – 50° – 60°
⇒ x = 180° – 110°
⇒ x = 70°
(ii) ΔPQR में,
∠P + ∠Q + ∠R = 180°
90° + 30° + x = 180°
x = 180° – 90° – 30°
= 180° – 120°
= 60°
(iii) ΔXYZ में
∠X + ∠Y + ∠Z = 180°
30° + 110° + x = 180°
x = 180° – 30° – 110°
= 180° – 140°
=40°
(iv) x + x + 50° = 180°
⇒ 2x + 50° = 180°
⇒ 2x = 180° – 50°
⇒ 2x = 130°
⇒ x = \(\frac {130°}{2}\)
⇒ x = 65°
(v) x + x + x = 180°
⇒ 3x = 180°
⇒ x = \(\frac {180°}{3}\)
⇒ x = 60°
(vi) x + 2x + 90° = 180°
⇒ 3x + 90° = 180°
⇒ 3x = 180° – 90°
⇒ 3x = 90°
⇒ x = \(\frac {90°}{3}\)
⇒ x = 30°
![]()
प्रश्न 2.
निम्नांकित आकृतियों में अज्ञात x और y का मान ज्ञात कीजिए:
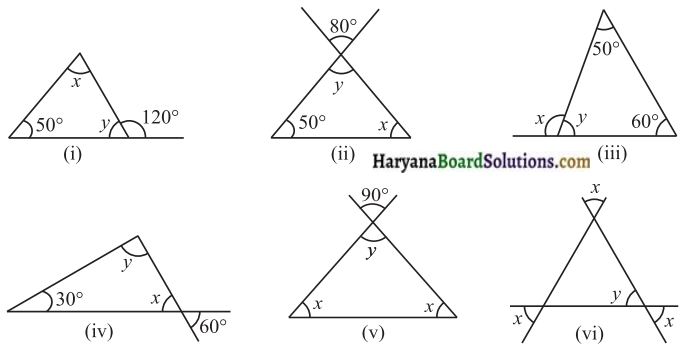
हल :
(i) त्रिभुज में बाह्य कोण और संलग्न अंत: कोण रैखिक युग्म बनाते हैं। अतः
y + 120° = 180°
⇒ y = 180° – 120° = 60°
एक त्रिभुज में कोणों का योग 180° होता है।
∴ x + 50° + y = 180°
⇒ x = 180° – 50° – y
⇒ x = 130° – 60° = 70°.
अतः x = 70° और y = 60°
(ii) यहाँ y = 80°, [शीर्षाभिमुख कोण]
त्रिभुज में कोणों का योग 180° होता है।
∴ x + y + 50° = 180°
⇒ x + 80° + 50° = 180°, [∵ y = 80°]
⇒ x + 130° = 180°
⇒ x = 180°- 130°
⇒ x = 50°
अतः x = 50° और y = 80°
(iii) त्रिभुज के तीनों अन्तः कोणों का योग 180° होता है।
∴ y + 60° + 50° = 180°
y = 180° – 60° – 50°
y = 180° – 110°
y = 70°
बाह्य कोण (x) = 50° + 60° = 110°
अत: x = 110° और y = 70°
(iv) त्रिभुज के तीनों कोणों का योग = 180°
∴ x + y + 30° = 180°
x = 60°, (शीर्षाभिमुख कोण)
60° + y + 30° = 180°
y = 180° – 60° – 30°
= 180° – 90°
= 90°
अत: x = 60° और y = 90°
(v) त्रिभुज के तीनों अन्त: कोणों का योग 180° होता है।
∴ x + x + y = 180°
[(∵ y = 90°) शीर्षाभिमुख कोण]
2x + 90° = 180°
2x = 180° – 90°
2x = 90°
x = \(\frac {90°}{2}\) = 45°
अत: x = 45° और y = 90°
(vi) त्रिभुज के तीनों अन्त: कोणों का योग 180° होता है।
∴ x + x + y = 180°
x + x + x = 180°,
[(∵ y = x°) शीर्षाभिमुख कोण]
3x = 180°
x = \(\frac {180°}{2}\) = 60°
∴ y = 60°
अतः x = 60° और y = 60°