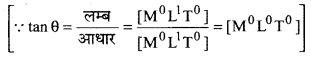Class 11

Haryana State Board HBSE 11th Class Physics Solutions Chapter 4 समतल में गति Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 4 समतल में गति

प्रश्न 4.1.
निम्नलिखित भौतिक राशियों में से बताइए कि कौन-सी सदिश हैं तथा कौन-सी अदिश?
आयतन, द्रव्यमान, चाल, त्वरण, घनत्व, मोल संख्या, वेग, कोणीय आवृत्ति, विस्थापन, कोणीय वेग।
उत्तर:
सदिश राशियाँ: त्वरण, वेग, विस्थापन तथा कोणीय वेग।
अदिश राशियाँ: आयतन द्रव्यमान, चाल, घनत्व, मोल संख्या तथा कोणीय आवृत्ति।

प्रश्न 4.2.
निम्नांकित सूची में से दो अदिश राशियों को छाँटिए:
बल, कोणीय संवेग, कार्य, धारा, रैखिक संवेग, विद्युत क्षेत्र, औसत वेग, चुम्बकीय आघूर्ण, आपेक्षिक वेग।
उत्तर:
दो अदिश राशियाँ कार्य तथा धारा हैं।

प्रश्न 4.3.
निम्नलिखित सूची में से एकमात्र सदिश राशि को छाँटिए:
ताप, दाब, आवेग, समय, शक्ति, दूरी, पथ लम्बाई, ऊर्जा, गुरुत्वीय विभव, घर्षण गुणांक, आवेश।
उत्तर:
एकमात्र सदिश राशि आवेग है।

प्रश्न 4.4.
कारण सहित बताइए कि सदिश तथा अदिश राशियों के साथ क्या निम्नलिखित बीजगणितीय संक्रियाएँ अर्थपूर्ण हैं?
(a) दो अदिशों को जोड़ना,
(b) एक ही विमाओं के एक अदिश व एक सदिश को जोड़ना,
(c) एक सदिश को एक अदिश से गुणा करना,
(d) दो अदिशों का गुणन,
(e) दो सदिशों को जोड़ना,
(f) एक सदिश के घटक को उसी सदिश से जोड़ना।
उत्तर:
(a) नहीं, दो अदिशों को जोड़ना केवल तभी अर्थपूर्ण हो सकता है. जबकि दोनों एक ही भौतिक राशि को प्रदर्शित करते हों।
(b) नहीं, सदिश को केवल सदिश के साथ तथा अदिश को केवल अदिश के साथ ही जोड़ा जा सकता है।
(c) अर्थपूर्ण है। जैसे – त्वरण सदिश को अदिश राशि द्रव्यमान गुणा करने पर बल प्राप्त होगा।
(d) अर्थपूर्ण है। जैसे – अदिश राशियाँ शक्ति P व समय को गुणा करने पर कार्य प्राप्त होगा।
(e) नहीं, केवल तभी अर्थपूर्ण होगा, जबकि दोनों एक ही भौतिक राशि को प्रदर्शित करते हों।
(f) चूँकि किसी सदिश का घटक एक सदिश होता है, जो मूल सदिश के समान भौतिक राशि को निरूपित करता है (जैसे-बल का घटक भी एक बल ही होता है)। अतः दोनों को जोड़ना अर्थपूर्ण है।

प्रश्न 4.5.
निम्नलिखित में से प्रत्येक कथन को ध्यानपूर्वक पढ़िए और कारण सहित बताइए कि यह सत्य है या असत्य
(a) किसी सदिश का परिमाण सदैव एक अदिश होता है।
(b) किसी सदिश का प्रत्येक घटक सदैव अदिश होता है।
(c) किसी कण द्वारा चली गई पथ की कुल लम्बाई सदैव विस्थापन सदिश के परिमाण के बराबर होती है।
(d) किसी कण की औसत चाल (पथ तय करने में लगे समय द्वारा विभाजित कुल पथ – लम्बाई) समय के समान अन्तराल में कण के औसत वेग के परिमाण से अधिक या उसके बराबर होती है।
(e) उन तीन सदिशों का योग जो एक समतल में नहीं हैं, कभी भी शून्य सदिश नहीं होता है।
उत्तर:
(a) सत्य, किसी भी भौतिक राशि का परिणाम एक धनात्मक संख्या है। जिसमें दिशा नहीं होती, अतः यह एक अदिश राशि है।
(b) असत्य, किसी सदिश का प्रत्येक घटक एक सदिश राशि होती
(c) असत्य, उदाहरण के लिए यदि कोई व्यक्ति R त्रिज्या के वृत्त की परिधि पर चलते हुए एक चक्कर पूर्ण करता है तो उसके द्वारा तय किए गये पथ की लम्बाई 2πR होगी, जबकि विस्थापन का परिमाण शून्य होगा।
(d) सत्य, क्योंकि औसत चाल पूर्ण पथ की लम्बाई पर तथा औसत वेग कुल विस्थापन पर निर्भर करता है, जबकि पूर्ण पथ की लम्बाई सदैव ही विस्थापन के परिमाण से अधिक अथवा बराबर होती है।
(e) सत्य, शून्य सदिश प्राप्त करने के लिए तीसरा सदिश पहले दो सदिशों के परिणामी के विपरीत दिशा में तथा परिमाण में उसके बराबर होना चाहिए। यह इस दशा में सम्भव नहीं है।

प्रश्न 4.6.
निम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिए:

इनमें समिका (समता) का चिह्न कब लागू होता है?
उत्तर:
माना OA = a, AB = b

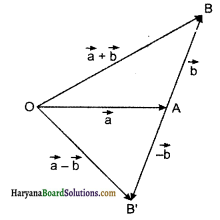
(a)
\(\vec{a}+\vec{b}\) = OA + AB
= OB
∆OAB में तीसरी भुजा, सदैव शेष दो भुजाओं के योग से बड़ी नहीं हो सकती है।
अत:
OB < OA + AB यदि \(\vec{a}\) वह \(\vec{b}\) एक ही दिशा में हों तो समता का चिह्न लागू होगा। (b) ∆OAB में, तीसरी भुजा सदैव दो भुजाओं के अन्तर से बड़ी होती है। OB > OA – AB
\(|\vec{a}+\vec{b}| \geq|\vec{a}|-|\vec{b}|\) ………..(1)
या
OB > AB – OA
\(|\vec{a}+\vec{b}| \geq|\vec{b} \vdash| \vec{a} \mid\) …….(2)
∴ समी० (1) व (2) से,
\(|\vec{a}+\vec{b}| \geq \| \vec{a}-|\vec{b}| \mid\)
यदि \vec{a} व \vec{b} है विपरीत दिशाओं में हों, तो समता का चिह्न लागू होगा।

(c) \(-\vec{b}\) = AB
∴ \(\vec{a}-\vec{b}=\vec{a}+(-\vec{b})\)
= OA + AB = OB
अत:
\(|\vec{a}-\vec{b}|\) = OB
AOAB’ में,
\(|\vec{a}-\vec{b}| \leq|\vec{a}|+|-\vec{b}|\)
या
\(|\vec{a}-\vec{b}| \leq|\vec{a}|+|\vec{b}|\)

\(\vec{a}\) व \(\vec{b}\) है विपरीत दिशा में होने पर समता चिह्न लागू होगा।
(d) त्रिभुज OAB’ में, प्रत्येक भुजा शेष दो भुजाओं के अन्तर से चाहिए।
बड़ी होती है।
OB>OA-AB
\(|\vec{a}-\vec{b}| \geq|\vec{a}|-|\vec{b}|\) ……(1)
इसी प्रकार,
\(|\vec{a}-| \geq|\vec{b}|-|\vec{a}|\) ……..(2)
समी० (1) व (2) से,
\(|\vec{a}-\vec{b}| \geq|| \vec{a} \vdash|\vec{b}| \mid\)
\(\vec{a}\) व \(\vec{b}\) है एक ही दिशा में होने पर समता चिह्न लागू होगा। अर्थात् सभी में समिका चिह्न के लिए सदिश व संरखी होने

प्रश्न 4. 7.
दिया है a + b + c + d = 0, नीचे दिए गए कथनों में से कौन-सा सही है?
(a) \(\vec{a}, \vec{b}, \vec{c}\) तथा \(\overrightarrow{\boldsymbol{d}}\) में से प्रत्येक शून्य सदिश है।
(b) \((\vec{a}+\vec{c})\) का परिमाण \((\vec{b}+\vec{d})\) का परिमाण के बराबर है।
(c) \(\vec{a}\) का परिमाण \(\vec{b}, \vec{c}\) है, \(\vec{d}\) तथा के परिमाणों के योग से कभी भी अधिक नहीं हो सकता।
(d) यदि \(\vec{a}\) तथा \(\vec{d}\) संरेखीय नहीं हैं तो \((\vec{b}+\vec{C})\) अवश्य ही \(\vec{a}\) तथा \(\vec{d}\)
के समतल में होगा और यह \(\vec{a}\) तथा \(\vec{d}\) के अनुदिश होगा, यदि वे सरेखीय हैं।
उत्तर:

प्रश्न 4.8.
तीन लड़कियाँ 200m त्रिज्या वाली वृत्तीय बर्फीली सतह पर स्केटिंग कर रही हैं। वे सतह के किनारे के बिन्दु P से स्केटिंग शुरू करती हैं तथा P के व्यासीय विपरीत बिन्दु Q पर विभिन्न पथों से होकर पहुँचती हैं, जैसा कि चित्र में दिखाया गया है। प्रत्येक लड़की के विस्थापन सदिश का परिमाण कितना है? किस लड़की के लिए यह वास्तव में स्केट किए गए पथ की लम्बाई के बराबर है?

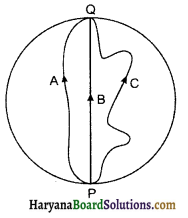
उत्तर:
∵ प्रत्येक लड़की का विस्थापन सदिश =
∴ विस्थापन सदिश का परिमाण
= व्यास PQ की लम्बाई
= 2R = 2 x 200m = 400m
∵ लड़की B द्वारा तय पथ (PQ) की लम्बाई
= 2R = 400m
∴ लड़की B के लिए विस्थापन सदिश का परिमाण वास्तव में स्केट किए गए पथ की लम्बाई के बराबर है।

प्रश्न 4.9.
कोई साइकिल सवार किसी वृत्तीय पार्क के केन्द्र 0 से चलना शुरू करता है तथा पार्क के किनारे P पर पहुँचता है। पुनः वह पार्क की परिधि के अनुदिश साइकिल चलाता हुआ 20 के रास्ते (जैसा कि चित्र में दिखाया गया है) केन्द्र पर वापस आ जाता है। पार्क की त्रिज्या 1km है। यदि पूरे चक्कर में 10 मिनट लगते हों तो साइकिल सवार का (a) कुल विस्थापन, (b) औसत वेग तथा (c) औसत चाल क्या होगी?

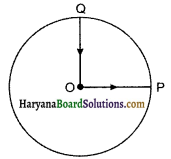
उत्तर:
(a) साइकिल सवार केन्द्र O से चलकर अन्त में पुनः केन्द्र O
पर पहुँच जाता है अतः
कुल विस्थापन = O
(b) औसत वेग
(c) कुल दूरी = त्रिज्या OP + परिधि भाग PQ + त्रिज्या QO
= 1 km + \(\frac{1}{4}\) x 2πR + 1km
= 2 + \(\frac{1}{2}\) × 3.14 × 1
= 3.57 km
समय = 10 मिनट
औसत चाल =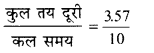
= 0.357 km / min

प्रश्न 4.10.
किसी खुले मैदान में कोई मोटर चालक एक ऐसा रास्ता अपनाता है जो प्रत्येक 500m के बाद उसके बाईं ओर 60° के कोण पर मुड़ जाता है। किसी दिए मोड़ से शुरू होकर मोटर चालक का तीसरे, छठे व आठवें मोड़ पर विस्थापन बताइए। प्रत्येक स्थिति में मोटर चालक द्वारा इन मोड़ों पर तय की गई कुल पथ लम्बाई के साथ विस्थापन के परिमाण की तुलना कीजिए।
उत्तर:
मोटर चालक द्वारा अपनाया गया मार्ग चित्रानुसार समषटभुज आकार का होगा।
(a) मोटर चालक 4 से प्रारम्भ कर तीसरे मोड़ पर बिन्दु D पर पहुँचता है।
विस्थापन = AD = 2AO
= 2AB
अतः

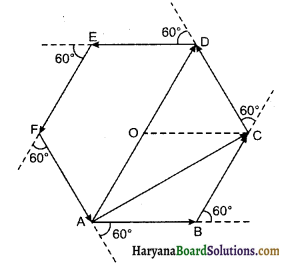
= 2x 500
= 1000m
= 1 km
कुल पथ की लम्बाई = AB + BC + CD
= 500 + 500 + 500 = 1.5 km

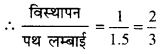
(b) मोटर चालक छठे मोड़ पर वापस शीर्ष 4 पर पहुँच जायेगा।
अतः विस्थापन = शून्य।
कुल पथ की लम्बाई = 6 × AB
= 6× 500
= 3000m = 3 km

(c) आठवें मोड़ शीर्ष C पर विस्थापन
अतः विस्थापन

कुल पथ लम्बाई = 8 x AB
= 8 × 500 = 4 km
अतः विस्थापन पथ लम्बाई = \(\frac{\sqrt{3}}{2}\) : 4
= √3 : 8

प्रश्न 4.11.
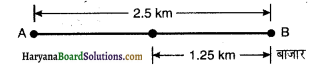
कोई यात्री किसी नए शहर में आया है और वह स्टेशन से किसी सीधी सड़क पर स्थित किसी होटल तक जो 10 किसी दूरी है, जाना चाहता है। कोई बेईमान टैक्सी चालक 23 किमी के चक्करदार रास्ते से उसे ले जाता है और 28 मिनट में होटल पहुँचता है।
(a) टैक्सी की औसत चाल और
(b) औसत वेग का परिमाण क्या होगा? क्या वे बराबर हैं?
उत्तर:
(a) टैक्सी द्वारा तय की गई कुल दूरी = 23km
समय = 28 मिनट

= 49.3 km h^-1

(b) टैक्सी का विस्थापन = 10km
समय = 28min
औसत वेग = \(\frac{10}{28}\) km/min = \(\frac{10}{28}\) × 60
= 21.4 km h^-1
औसत चाल व औसत वेग बराबर नहीं है। केवल सीधे पथों के लिए ही ये बराबर होते हैं।

प्रश्न 4.12.
वर्षा का पानी 30 ms^-1 की चाल से ऊर्ध्वाधर नीचे गिर रहा है। कोई महिला उत्तर से दक्षिण की ओर 10ms^-1 की चाल से साइकिल चला रही है। उसे अपना छाता किस दिशा में रखना चाहिए?
उत्तर:
वर्षा ऊर्ध्वाधर OA दिशा में, = 30ms^-1 वेग से गिर रही है। महिला OS दिशा में V = 10ms^-1 वेग से गति कर रही है। महिला वर्षा से बचने के लिए अपना छाता अपने सापेक्ष वर्षा के वेग की दिशा में

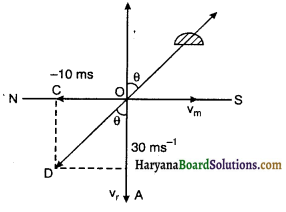
रखेगी।
वर्षा का महिला के सापेक्ष वेग
Vrw = Vr – Vw
इसलिए 10ms^-1 वेग को ऋणात्मक चिह्न में रखने पर यह ON दिशा में होगा।
∴ समान्तर चतुर्भुज OADC में,
tan θ = \(\frac{v_w}{v_r}=\frac{10}{30}=\frac{1}{3}\) = 0.33
या
θ = tan^-1 0.33
∴ θ = 18°
अतः महिला अपना छाता ऊर्ध्वाधर में 18° दक्षिण दिशा में रखेगा।

प्रश्न 4.13.
कोई व्यक्ति स्थिर जल में 4.0 km/h की चाल से तैर सकता है। उसे 1.0 km चौड़ी नदी को पार करने में कितना समय लगेगा? यदि नदी 3.0km/h की स्थिर चाल से बह रही है और वह नदी के बहाव के लम्ब दिशा में तैर रहा हो। जब वह नदी के दूसरे किनारे पर पहुँचता है तो वह नदी के बहाव की ओर कितनी दूर पहुँचेगा?
उत्तर:
बहाव का वेग Vr = 3.0 km/h
तैराक का वेग Vm = 4.0km/h
नदी को पार करने के लिए नदी के लम्ब दिशा में तय दूरी = 1 km

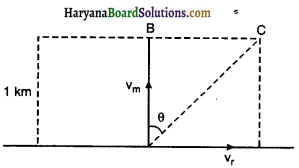
∴ नदी को पार करने में लगा समय
t =
h = 15 min
समय t में व्यक्ति नदी के बहाव की ओर BC दूरी तय कर चुका है।
अतः तय दूरी BC = बहाव का वेग x लगा समय
= 30 x \(\frac{1}{4}\) km
= 0.75 km = 750m

प्रश्न 4.14.
किसी बन्दरगाह में 72 km/h की चाल से हवा चल रही है और बन्दरगाह में खड़ी किसी नौका के ऊपर लगा झण्डा N-E दिशा में लहरा रहा है। यदि यह नौका उत्तर की ओर 51 km/h की चाल से गति करना प्रारम्भ कर दे तो नौका पर लगा झण्डा किस दिशा में लहराएगा?
उत्तर:
वायु का वेग = \(\overrightarrow{v_a}\)
नौका का वेग = \(\overrightarrow{v_b}\)
\(\overrightarrow{v_a}\) = 72 km/h (N-E) दिशा में,
\(\overrightarrow{v_b}\) = 51 km/h (N) दिशा में,
∴ वायु का नौका के सापेक्ष वेग \(\overrightarrow{v_{a b}}=\overrightarrow{v_a}-\overrightarrow{v_b}\)
झण्डा चित्रानुसार \(\overrightarrow{v_{a b}}\) दिशा में ही लहराएगा।

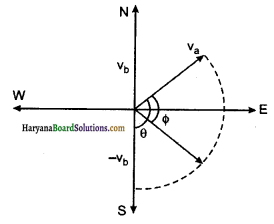
माना Vab वेग Va से \(\phi\) कोण बनाता है जबकि वेगों \(\overrightarrow{v_a}\) तथा \(\overrightarrow{v_b}\)
के बीच का कोण θ = 135° है।
∴ tan Φ = \(\frac{B \sin \theta}{A+B \cos \theta}\) सूत्र से,
∵ tan Φ = \(\frac{v_b \sin 135^{\circ}}{v_a+v_b \cos 135^{\circ}}\)
या
tan Φ = \(\frac{51 \times \frac{1}{\sqrt{2}}}{72+51 \times\left(-\frac{1}{\sqrt{2}}\right)}\)
= \(\frac{51}{72 \sqrt{2}-51} \approx 1\)
∴ Φ = 45° (लगभग)
∴ Vab द्वारा पूर्व दिशा में बनाया गया कोण
= Φ – 45°
= 45° – 45°
= 0°
अतः झण्डा लगभग पूर्व दिशा में लहरायेगा।

प्रश्न 4.15.
किसी लम्बे हाल की छत 25 m ऊँची है। वह अधिकतम क्षैतिज दूरी कितनी होगी जिसमें 40ms^-1 की चाल से फेंकी गई कोई गेंद छत से टकराये बिना गुजर जाए?
उत्तर:
अधिकतम ऊँचाई H = 25m,
वेग Vo = 40ms^-1
यदि गेंद को θ कोण पर फेंका जाये, तो
अधिकतम ऊँचाई H = \(\frac{u^2 \sin ^2 \theta}{2 g}\)
या
sin² θ = \(\frac{2 g H}{u^2}=\frac{2 \times 9.8 \times 25}{(40)^2}\)
या
sin² θ = \(\frac{49 \times 10}{(40)^2}\)
या
sin² θ = 0.30625
या
∴ sin θ = 0.553
cosθ = \(\sqrt{1-\sin ^2 \theta}\)
= \(\sqrt{1-(0.553)^2}\)
= \(\sqrt{1-0.306}\)
= \(\sqrt{0.694}\)
= 0.833
∴ अधिकतम क्षैतिज दूरी

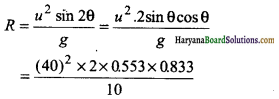
= 150.5m

प्रश्न 4.16.
क्रिकेट का कोई खिलाड़ी किसी गेंद को 100 मीटर की अधिकतम क्षैतिज दूरी तक फेंक सकता है। वह खिलाड़ी उसी गेंद को जमीन से ऊपर कितनी ऊँचाई तक फेंक सकता है?
उत्तर:
R_max = 100m, R = \(\frac{u^2 \sin 2 \theta}{g}\)
या
R_max = \(\frac{u^2}{g}\)
या
u² = R_max x g
= 100 × 10 = 1000(ms^-1)²
∴ a = \(14 \sqrt{5}\) ms^-1
गेंद को महत्तम ऊंचाई तक फेंकने के लिए θ° = 90° होना चाहिए।

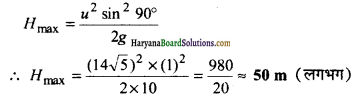
प्रश्न 4.17.
80cm लम्बे धागे के एक सिरे पर एक पत्थर बाँधा गया है और इसे किसी एक समान चाल के साथ किसी क्षैतिज वृत्त में घुमाया जाता है। यदि पत्थर 25s में 14 चक्कर लगाता है तो पत्थर के त्वरण का परिमाण और उसकी दिशा क्या होगी?
उत्तर:
R = 80cm = 0.80m
पत्थर द्वारा 1 सेकण्ड में चक्करों की संख्या

कोणीय आवृत्ति ω = 2πn = 2π x \(\frac{14}{25}\)
अभिकेन्द्रीय त्वरण
ac = ω²R
=(2 x 3.14 x 14) x 0.80
= 9.8 ms^-2
त्वरण की दिशा वृत्त के केन्द्र की ओर होगी।

प्रश्न 4.18.
कोई वायुयान 900 kmh की एक समान चाल से उड़ रहा है और 1.00 km त्रिज्या का कोई क्षैतिज लूप बनाता है। इसके अभिकेन्द्रीय त्वरण की गुरुत्वीय त्वरण के साथ तुलना कीजिए।
उत्तर:
वायुयान की चाल = 900kmh^-1
= 900 x \(\frac{1000}{60 \times 60}\)
= 250ms^-1
त्रिज्या R = 1.00km = 1000m
अभिकेन्द्रीय त्वरण ac = \(\frac{v^2}{R}=\frac{(250)^2}{1000}\)
∴ ac = 62.5ms^-2
∴
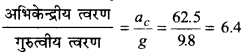
∴ अभिकेन्द्रीय त्वरण = 6.4 x गुरुत्वीय त्वरण
अतः वायुयान का त्वरण, गुरुत्वीय त्वरण का 6.4 गुना है।

प्रश्न 4.19.
नीचे दिये गये कथनों को ध्यानपूर्वक पढ़िए और कारण देकर बताइए कि वे सत्य हैं या असत्य:
(a) वृत्तीय गति में किसी कण का नेट त्वरण हमेशा वृत्त की त्रिज्या के अनुदिश केन्द्र की ओर होता है।
(b) किसी बिन्दु पर किसी कण का वेग सदिश सदैव उस बिन्दु पर कण के पथ की स्पर्श रेखा के अनुदिश होता है।
(c) किसी कण का एकसमान वृत्तीय गति में एक चक्र में लिया गया औसत त्वरण सदिश एक शून्य सदिश होता है।
उत्तर:
(a) असत्य यह कथन एक समान वृत्तीय गति के लिए ही सत्य है।
(b) सत्य है, वेग की दिशा स्पर्श रेखीय होती है।
(c) सत्य है, क्योंकि परिणामी विस्थापन शून्य है।

प्रश्न 4.20.
किसी कण का स्थिति सदिश निम्नलिखित है:
\(\vec{r}=\left(3.0 t \hat{i}-2.0 t^2 \hat{j}+4.0 \hat{k}\right)\) m
समय t सेकण्ड में है तथा सभी गुणांकों के मात्रक इस प्रकार हैं कि \overrightarrow{\boldsymbol{r}} मीटर में व्यक्त हो जाए।
(a) कण का वेग \(\overrightarrow{\boldsymbol{v}}\) तथा \(\overrightarrow{\boldsymbol{a}}\) निकालिए।
(b) t = 2.0 पर कण के वेग का परिणाम तथा दिशा कितनी होगी?
उत्तर:

प्रश्न 4.21.
कोई कण t = 0 क्षण पर मूलबिन्दु से 10 \(\hat{j}\) ms^-1 के वेग से चलना प्रारम्भ करता है तथा x-y समतल में एकसमान त्वरण \((8.0 \hat{i}+2.0 \hat{j})\) ms^-1 से गति करता है।
(a) किस क्षण कण का x- निर्देशांक 16m होगा? इसी समय इसका y-निर्देशांक कितना होगा?
(b) इस क्षण कण की चाल कितनी होगी?
उत्तर:

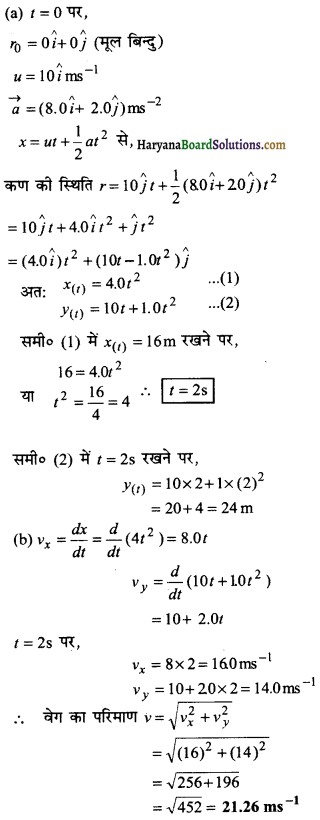
प्रश्न 4.22.
\(\hat{i}\) तथा \(\hat{i}\) क्रमश: x व y- अक्षों के अनुदिश एकांक सदिश हैं। सदिशों \(\hat{i}+\hat{j}\) तथा \(\hat{i}-\hat{j}\) का परिमाण तथा दिशाएँ क्या होंगी? सदिशों \(\vec{A}=2 \hat{i}+3 \hat{j}\) के \(\hat{i}+\hat{j}\) व \(\hat{i}-\hat{j}\) की दिशाओं के अनुदिश घटक निकालिए।
(आप ग्राफीय विधि का उपयोग कर सकते हैं।)
उत्तर:
सदिश \(\hat{i}+\hat{j}\) का परिमाण

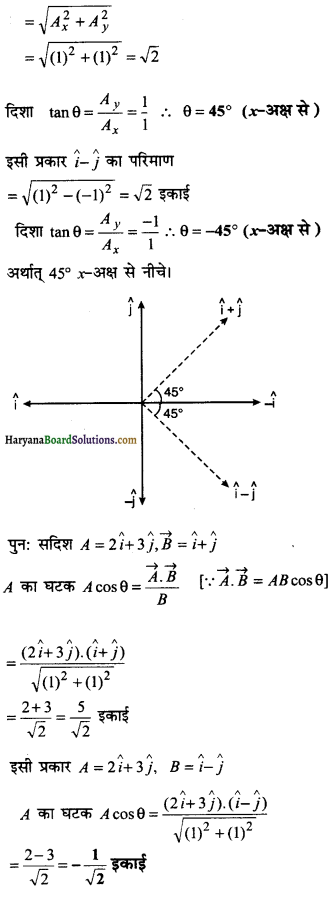
प्रश्न 4.23.
किसी दिक्स्थान पर एक स्वैच्छ गति के लिए निम्नलिखित सम्बन्धों में से कौन-सा कथन सत्य है?

यहाँ औसत का आशय समयान्तराल t2 व t1 से सम्बन्धित भौतिक राशि के औसत मान से है।
उत्तर:
(a) असत्य,
(b) सत्य,
(c) असत्य,
(d) असत्य,
(e) सत्य।
(a), (c) व (d) केवल सम त्वरित गति में लागू होते हैं।

प्रश्न 4.24.
निम्नलिखित में से प्रत्येक फलन को ध्यानपूर्वक पढ़िए तथा कारण एवं उदाहरण सहित बताइए कि क्या यह सत्य है या
असत्य:
अदिश वह राशि है, जो:
(a) किसी प्रक्रिया में संरक्षित रहती है।
(b) कभी ऋणात्मक नहीं होती।
(e) विमाहीन होती है।
(d) किसी स्थान पर एक बिन्दु से दूसरे बिन्दु के बीच नहीं बदलती।
(e) उन सभी दर्शकों के लिए एक ही मान रखती है चाहे अक्षों से उनके अभिविन्यास भिन्न-भिन्न क्यों न हों?
उत्तर:
(a) असत्य, जैसे गतिज ऊर्जा अदिश राशि है परन्तु यह संरक्षित नहीं रहती है।
(b) असत्य, जैसे ताप अदिश राशि है जो धनात्मक, शून्य या ऋणात्मक हो सकता है।
(c) असत्य, उदाहरण के लिए, किसी वस्तु का द्रव्यमान अदिश राशि है परन्तु इसकी विमा [M] है
(d) असत्य, उदाहरण के लिए, ताप एक अदिश राशि है, किसी छड़ में ऊष्मा के एकविमीय प्रवाह में, प्रवाह की दिशा में ताप बदलता जाता है।
(e) सत्य, क्योंकि अदिश राशि में दिशा नहीं होती, अतः यह प्रत्येक विन्यास में स्थित दर्शक के लिए समान मान रखती है। उदाहरण के लिए, किसी वस्तु के द्रव्यमान का मान प्रत्येक दर्शक के लिए समान होगा।

प्रश्न 4.25.
कोई वायुयान पृथ्वी से 3400m की ऊँचाई पर उड़ रहा है। यदि पृथ्वी पर किसी अवलोकन बिन्दु पर वायुयान की 10.05 की दूरी की स्थितियाँ 30° का कोण बनाती हैं, तो वायुयान की चाल क्या होगी?
उत्तर:
माना 10s के अन्तराल पर वायुयान की दो स्थितियाँ P तथा Q हैं, जबकि O प्रेक्षण बिन्दु है।
बिन्दु O से PO पर लम्ब OA डाला।
प्रश्नानुसार, OA = 3400m
तथा
∴∠POQ = 30°
∴ ∠POA = ∠QOA = 15°
tan 15° = \(\frac{A Q}{O A}\)
या
AQ = OA tan 15°

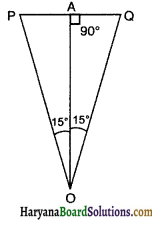
∴10s में तय दूर PQ = 24Q
= 2AO tan 15°
[ tan 15° 0.268]
= 2 x 3400m x 0.268
= 1822.4 m

= 182.22 ms^-1

अतिरिक्त अभ्यास (Additional Exercise):

प्रश्न 4.26.
किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या दिस्थान में इसकी कोई स्थिति होती है? क्या यह समय के साथ परिवर्तित हो सकता है? क्या दिक्स्थान में भिन्न स्थानों पर दो बराबर सदिशों व का समान भौतिक प्रभाव अवश्य पड़ेगा? अपने उत्तर के समर्थन में उदाहरण दीजिए।
उत्तर:
सभी संदिशों की स्थिति नहीं होती, किसी बिन्दु के स्थिति सदिश के समान कुछ सदिशों की स्थिति होती है, जबकि वेग सदिश के 5 समान कुछ सदिशों की कोई स्थिति नहीं होती है। हाँ, कोई सदिश समय के 5 साथ परिवर्तित हो सकता है। जैसे त्वरित कण का वेग सदिश समय के साथ परिवर्तित हो सकता है। आवश्यक नहीं है, उदाहरण के लिए, दो अलग-अलग बिन्दुओं पर लगे बराबर बल अलग-अलग आघूर्ण उत्पन्न करेंगे।

प्रश्न 4.27.
किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या इसका यह अर्थ है कि कोई राशि जिसका परिमाण व दिशा हो, वह अवश्य ही सदिश होगी ? किसी वस्तु के घूर्णन की व्याख्या घूर्णन अक्ष की दिशा और अक्ष के परितः घूर्णन कोण द्वारा की जा सकती है। क्या इसका यह अर्थ है कि कोई भी घूर्णन एक सदिश है?
उत्तर:
किसी राशि में परिमाण तथा दिशा होने पर उसका सदिश होना आवश्यक नहीं है। उदाहरण के लिए, प्रत्येक घूर्णन कोण एक सदिश राशि नहीं हो सकता केवल सूक्ष्म घूर्णन को ही सदिश राशि माना जा सकता है।

प्रश्न 4.28.
क्या आप निम्नलिखित के साथ कोई सदिश सम्बद्ध कर सकते हैं:
(a) किसी लूप में मोड़ी गई तार की लम्बाई,
(b) किसी समतल क्षेत्र,
(c) किसी गोले के साथ? व्याख्या कीजिए।
उत्तर:
(a) नहीं, क्योंकि वृत्तीय लूप में मोड़े गए तार की कोई निश्चित दिशा नहीं होती।
(b) दिए गए समतल पर एक निश्चित अभिलम्ब खींचा जा सकता है, अत: समतल क्षेत्र के साथ एक सदिश सम्बद्ध किया जा सकता है, जिसकी दिशा समतल पर अभिलम्ब के अनुदिश हो सकती है।
(c) नहीं, क्योंकि किसी गोले का आयतन किसी विशेष दिशा के साथ सम्बद्ध नहीं किया जा सकता।

प्रश्न 4.29.
कोई गोली क्षैतिज से 30° के कोण पर दागी गई है। और वह धरातल पर 3.0 km दूरी गिरती है। इसके प्रक्षेप्य के कोण का समायोजन करके क्या 5.0 km दूर स्थित किसी लक्ष्य का भेद किया जा सकता है? गोली की नालमुख चाल को नियत तथा वायु के प्रतिरोध को नगण्य मानिए।
उत्तर:
परास R = \(\frac{u^2 \sin 2 \theta}{g}\)
∴ R = 3km = 3000m, u = ?, θ = 30°
∴ 3000 = \(\frac{u^2 \sin 2 \theta}{g}\)
∴ u² = 2000/3g
∴ गोली की अधिकतम परास
R = \(\frac{u^2}{g}=\frac{2000 \sqrt{3} g}{g}\)
= 2000\(\sqrt{3}\)m = 3.464 km
अधिकतम परास 3.4 km है, अत: गोली 5 km दूरी पर स्थित लक्ष्य को नहीं भेद सकेगी।

प्रश्न 4.30.
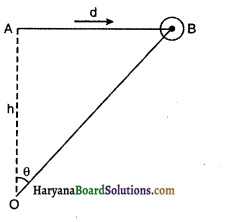
कोई लड़ाकू जहाज 1.5 km की ऊँचाई पर 720 km/h की चाल से क्षैतिज दिशा में उड़ रहा है और किसी वायुयान भेदी तोप के ठीक ऊपर से गुजरता है। ऊर्ध्वाधर से तोप की नाल का क्या कोण हो जिससे 600 ms-1 की चाल से दागा गया गोला वायुयान पर वार कर सके ? वायुयान के चालक को किस न्यूनतम ऊँचाई पर जहाज को उड़ाना चाहिए, जिससे गोला लगने से बच सके? (g = 10ms²)
उत्तर:
वायुयान की ऊँचाई 1.5 km = 1500m
चाल = 720 km/h
= 720 x \(\frac{1000}{60 \times 60}\)
= 200 ms^-1
गोले की चाल = 600ms^-1
माना जिस क्षण वायुयान B बिन्दु पर पहुँचेगा तो वह गोले से टकरायेगा।

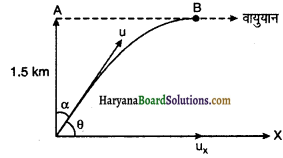
गोले के वेग का क्षैतिज घटक
u_x = ucosθ (θ = 90° – α)
या
u_x = 600cos (90° – α)
या
u_x = 600 sin α
t समय बाद गोले की क्षैतिज दूरी
x = u_xt = 600sinαt ………..(1)
समय बाद वायुयान की दूरी
x = vt = 200t ………..(2)
∴ समी० (1) व (2) से,
600sin αt = 200
sin α = \(\frac{200}{600}=\frac{1}{3}\) = 0.33
∴ α = 19.5° (ऊर्ध्वाधर से)
तोप के गोले की अधिकतम ऊँचाई

प्रश्न 4.31.
एक साइकिल सवार 27 km/h की चाल से साइकिल चला रहा है। जैसे ही सड़क पर वह 80 m त्रिज्या के वृत्तीय मोड़ पर पहुँचता है। वह ब्रेक लगाता है और अपनी चाल को 0.5m/s की एकसमान दर से कम कर लेता है। वृत्तीय मोड़ पर साइकिल सवार के नेट त्वरण का परिमाण और उसकी दिशा निकालिए।
उत्तर:
साइकिल सवार की चाल
v = 27 km/h
= 27 x \(\frac{1000}{60 \times 60}\) = 7.5ms^-1
त्रिज्या R = 80m

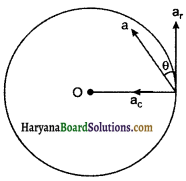
अभिकेन्द्रीय त्वरण
\(a_c=\frac{v^2}{R}=\frac{7.5 \times 7.5}{80}\)
= 0.703 ms^-2
ब्रेक लगाने पर स्पर्श रेखीय मन्दन ar = 0.5ms 2
परिणामी त्वरण
a= \(\sqrt{a_c^2+a_r^2}\)
= \(\sqrt{(0.7)^2+(0.5)^2}\)
= 0.86 ms^-2
tan θ = \(\frac{a_c}{a_T}=\frac{0.7}{0.5}\)
= 1.4 या θ = tan^-1(1.4)
∴ θ = 54.5°

प्रश्न 4.32.
(a) सिद्ध कीजिए कि किसी प्रक्षेप्य के x- अक्ष तथा उसके वेग के बीच के कोण को समय के फलन के रूप में निम्न प्रकार से व्यक्त कर सकते हैं:
θ(t) = tan^-1 \(\left(\frac{u_y-g t}{u_x}\right)\)
(b) सिद्ध कीजिए कि मूलबिन्दु से फेंके गए प्रक्षेप्य कोण का मान θ = tan^-1\(\left(\frac{4 h_m}{R}\right)\) होगा। यहाँ प्रयुक्त प्रतीकों के अर्थ सामान्य हैं।
उत्तर:
(a) माना प्रक्षेप्य के x- अक्ष तथा y-अक्ष की दिशाओं में वियोजित घटक क्रमश: ux व uy हैं।
अतः गति के समी० (1) को द्विविमीय वियोजित करने पर,

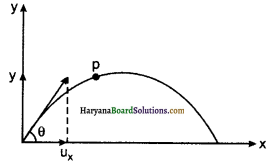
(vt = uo + at)
v_x = u_ox + a_oxt
∵ a_ox = 0
∴ v_x = u_ox
v_y = u_oy + a_oyt
∵ a_oy = -g
∴ v_y = u_oy – gt
x- अक्ष से बनाया गया कोण

Haryana State Board HBSE 11th Class Physics Solutions Chapter 3 सरल रेखा में गति Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 3 सरल रेखा में गति

प्रश्न 3.1.
नीचे दिये गये गति के कौन-कौन से उदाहरणो मे वस्तु को लगभग बिन्दु वस्तु माना जा सकता है?
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बन्दर।
(c) जमीन से टकराकर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद।
(d) किसी मेज के किनारे से फिसलकर गिरा कोई बीकर।
उत्तर:
(a) दो स्टेशनों के बीच की दूरी, रेलगाड़ी की लम्बाई की तुलना में अधिक है। अत: रेलगाड़ी को वस्तु बिन्दु माना जा सकता है।
(b) बन्दर द्वारा तय की गई दूरी अधिक है। अत: बन्दर को वस्तु बिन्दु माना जा सकता है।
(c) क्रिकेट की फिरकती गेंद द्वारा तय की गई दूरी कम होती है। अतः गेंद को वस्तु बिन्दु नहीं माना जा सकता।
(d) बीकर की मेज से नीचे गिरने की दूरी अधिक नहीं है। इसलिए इसे वस्तु बिन्दु नहीं माना जा सकता।

प्रश्न 3.2.
दो बच्चे A व B अपने विद्यालय 0 से लौटकर अपने-अपने घर क्रमश: P तथा Q को जा रहे हैं। उनके स्थिति समय (x – t) ग्राफ चित्र में दिखाये गये हैं।
नीचे लिखे कोष्ठकों में सही प्रविष्टियों को चुनिए:
(a) \(\frac{B}{A}\) की तुलना में \(\frac{A}{B}\) विद्यालय से निकट रहता है।
(b) \(\frac{B}{A}\) की तुलना में \(\frac{A}{B}\) विद्यालय से पहले चलता है।

(c) \(\frac{B}{A}\) की तुलना में \(\frac{A}{B}\) तेज चलता है।
(d) A और B घर (एक ही / भिन्न) समय पर पहुँचते हैं।
(e) \(\frac{A}{B}\) सड़क पर \(\frac{B}{A}\) से (एक बार / दो बार ) आगे हो जाते हैं।
उत्तर:
∵ OP < OQ, अत: A बच्चा, B की तुलना में विद्यालय के निकट रहता है।
(b) A मूलबिन्दु O से t = 0 पर गति प्रारम्भ करता है जबकि B, कुछ समय / पश्चात् गति प्रारम्भ करता है अतः A, B की तुलना में पहले चलता है।
(c) x – t वक्र की ढाल वेग के तुल्य होती है। अतः B, A की तुलना में तेज चलता है।
(d) A व B दोनों एक समय t पर घर पहुंचते हैं क्योंकि P व Q से ग्राफ पर खींचे गये लम्ब t समय पर मिलते हैं।
(e) B तेज चल रहा है अतः उभयनिष्ठ बिन्दु पर B एक बार A से आगे निकल जाता है।

प्रश्न 3.3.
एक महिला अपने घर से प्रातः 9.00 बजे 2.5 km दूर अपने कार्यालय के लिए सीधी सड़क पर 5 kmh^-1 चाल से चलती है। वहाँ वह सायं 5.00 बजे तक रहती है और 25 kmh^-1 की चाल से चल रही किसी ऑटो रिक्शा द्वारा अपने घर लौट आती है। उपयुक्त पैमाना चुनिये तथा उसकी गति का x – t ग्राफ भी खींचिए।
उत्तर:
घर से चलने पर तय की गई दूरी = 2.5km
चाल = 5km h^-1
कार्यालय पहुंचने में लगा समय = imm
यदि बिन्दु O को मूलबिन्दु माना जाये तब t = 9.00am पर x = 0 तथा = 9.30am पर x 2.5km, OA गति का x – t महिला अपने घर से कार्यालय के लिए चलती है।

महिला कार्यालय में 9.30am से 5.00pm तक रहती है।
अब वापस घर पहुँचने में लगा समय
= \(\frac{2.5}{25}\) = \(\frac{1}{10}h\) = 6 min
अत: 5.06p.m पर x = 2.5 km
इसे चित्र में BC रेखा द्वारा प्रदर्शित किया गया है।

प्रश्न 3.4.
कोई शराबी किसी तंग गली में 5 कदम आगे बढ़ता है। और 3 कदम पीछे आता है, उसके बाद फिर 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, और इसी तरह वह चलता रहता है। उसका हर कदम 1m लम्बा है और 1s समय लगता है। उसकी गति का x ग्राफ खींचिए ग्राफ से तथा किसी अन्य विधि से यह ज्ञात कीजिए कि वह जहाँ से चलना प्रारम्भ करता है वहाँ से 13m दूर किसी गड्ढे में कितने समय पश्चात् गिरता है?
उत्तर:
शराबी की गति का x-t ग्राफ चित्र में प्रदर्शित है।
प्रारम्भ में गड्ढे की दूरी = 13 मी
पहले 5 मी चलने में लगा समय = 5s

5 कदम आगे तथा 3 कदम पीछे चलने से तात्पर्य है कि चली गई कुल दूरी
= 5 – 3 = 2m
इस प्रक्रिया के पूरा होने में लगा समय
= 5 + 3 = 8s
अत: 8m चलने में लगा समय
= \(\frac{8 \times 8}{2}\) = 32s
अतः गड्डे तक शेष दूरी = 13 – 8 = 5m
अर्थात् शराबी अगले 5 कदमों में गड्ढे में गिर जायेगा जिसमें उसे 5s का समय और लगेगा।
अतः कुल समय 32 + 5 = 37s

प्रश्न 3.5.
कोई जेट वायुयान 500kmh^-1 की चाल से चल रहा है और यह जेट यान के सापेक्ष 1500 kmh^-1 की चाल से अपने दहन उत्पादों को बाहर निकालता है। जमीन पर खड़े किसी प्रेक्षक के सापेक्ष इन दहन उत्पादों की चाल क्या होगी?
उत्तर:
+x दिशा में जेट वायुयान का वेग
VA = 500km h^-1
दहन उत्पादों का सापेक्ष वेग (जेट वायुयान के सापेक्ष) VPA = -1500 kmh^-1
दहन उत्पादों का जेट वायुयान के सापेक्ष वेग
∵ VPA =Vp – VA
Vp = VA – 1500
= 500 – 1500 = 1000kmh^-1
यहाँ (-) चिह्न प्रदर्शित करता है कि दहन का वेग, जेट वायुयान की विपरीत दिशा में है।
∴ आपेक्षिक वेग का परिमाण = 1000kmh^-1

प्रश्न 3.6.
सीधे राजमार्ग पर कोई कार 126 kmh^-1 की चाल से चल रही है। इसे 200m की दूरी पर रोक दिया जाता है। कार के मंदन को एकसमान मानिए और इसका मान निकालिए। कार को रुकने में कितना समय लगेगा?
उत्तर:
u = 126km/h = \(\frac{126 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\)
= 35m/s
s = 200m, v = 0
गति के तीसरे समीकरण से,
v² = u² + 2as
या
a = \(\frac{v^2-u^2}{2 s}\) = \(\frac{0-(35)^2}{2 \times 200}\)
∴ a = – 3.06 ms^-2
-ve चिह्न मन्दन को प्रदर्शित करता है।
समीकरण v = u + at से,
या t = \(\frac{v-u}{a}\)
∴ t = \(\frac{0-35}{-3.06}\)
= 11.4s

प्रश्न 3.7.
दो रेलगाड़ियाँ A व B दो समान्तर पटरियों पर 72 km/h की एकसमान चाल से एक ही दिशा में चल रही है। प्रत्येक गाड़ी 400m लम्बी है और गाड़ी 4 गाड़ी B से आगे है। B का चालक 4 के आगे निकलना चाहता है तथा 1 ms^-2 से इसे त्वरित करता है। यदि 50 see के बाद B का गार्ड के चालक से आगे हो जाता है, तो दोनों के बीच आरम्भिक दूरी कितनी थी?
उत्तर:
यहाँ
u_A = 72 km/h
= 72 × \(\frac{1000}{60 \times 60}\) = 20m/s
t = 50s
S_A = u_At + \(\frac{1}{2}\) at²
= 20 x 50 + 0 = 1000m
तथा u_b = 72 km/s = 72 x \(\frac{5}{18}\) = 20m/s

a = 1 m/s²
तथा t = 50s
S_b = u_bt + \(\frac{1}{2}\) at² से,
sB = 20 x 50 + \(\frac{1}{2}\) x 1 x (50)²
= 2250m
∴ रेलगाड़ियों के बीच आरम्भिक दूरी
=2250 – 1000 = 1250 m

प्रश्न 3.8.
दो लेन वाली किसी सड़क पर कार 436kmh^-1 की चाल से चल रही है। एक-दूसरे की विपरीत दिशाओं में चलती दो कारें BTC जिनमें से प्रत्येक की चाल 54 km h^-1 है, कार 4 तक पहुँचना चाहती हैं। किसी क्षण जब दूरी AB दूरी AC के बराबर है तथा दोनों km है, कार B का चालक यह निर्णय करता है कि कार C के कार 4 तक पहुँचने के पहले ही वह कार 4 से आगे निकल जाए। किसी दुर्घटना से बचने के लिए कार B का कितना न्यूनतम त्वरण जरूरी है?
उत्तर:
कार A की चाल,
V_A = 36kmh^-1
= 36 x \(\frac{5}{18}\)
= 10ms^-1
कार B की चाल, VB = 54 kmh^-1
= 54 x \(\frac{5}{18}\) = 15ms^-1
इसी प्रकार, कार C की चाल VC = 15ms^-1

कार A के सापेक्ष कार C की आपेक्षिक चाल
= V_CA = 15 – (-10) = 25ms^-1
कार A के सापेक्ष कार B की आपेक्षिक चाल
= V_BA = 15 – 10 = 5ms^-1
∵ कार A तथा C नियत वेग से गतिमान हैं, अतः कार C का के सापेक्ष त्वरण शून्य है, а_CA =0
AB = AC = 1 km = 1000m
AC दूरी को तय करने में कार C को लगने वाला सम,
t = \(\frac{1000}{v_{A C}}\) = \(\frac{1000}{25}\)
= 40s
यदि कार B का त्वरण a है, तब चूँकि कार A का त्वरण शून्य है, अत: कार B का A के सापेक्ष त्वरण a_BA = a होगा।
कार B, कार C के कार A तक पहुँचने से पूर्व ही कार A तक पहुँच जायेगी यदि कार B, t = 40s कार A के सापेक्ष 1 km = 1000m की दूरी तय कर ले।
∴ S = ut + \(\frac{1}{2}\)at²
1000 = 5 x 40 + \(\frac{1}{2}\)a x (40)²
∴ कार B का न्यूनतम त्वरण
a = \(\frac{1000-200}{800}\)
= 1 ms^-2

प्रश्न 3.9.
दो नगर A व B नियमित बस सेवा द्वारा एक-दूसरे जुड़े हैं और प्रत्येक T मिनट के बाद दोनों तरफ बसें चलती हैं। कोई व्यक्ति साइकिल से 20 kmh^-1 की चाल से A से B की तरफ जा रहा है और यह नोट करता है कि प्रत्येक 18 मिनट के बाद एक बस उसकी गति की दिशा में तथा प्रत्येक 6 मिनट बाद उसके विपरीत दिशा में गुजरती है। बस सेवाकाल 7 कितना है और बसें सड़क पर किस चाल (स्थिर मानिए) से चलती हैं?
उत्तर:
माना प्रत्येक बस की चाल v_B तथा साइकिल सवार की चाल V_c है।
∴ साइकिल सवार की गति की दिशा में चल रही बसों की आपेक्षिक चाल = V_B – V_c
बस के गुजरने का समय = 18 मिनट = \(\frac{18}{60}\) घण्टा
∴ साइकिल सवार द्वारा पार की गयी दूरी
= आपेक्षिक चाल x समय
= (V_B – V_c) × \(\frac{18}{60}\)
चूँकि बसें प्रत्येक 7 मिनट बाद चलती हैं इसलिए दूरी V_B × \(\frac{T}{60}\) होगी।
अतः (V_B – V_c) × \(\frac{18}{60}\) = V_B × \(\frac{T}{60}\) ………..(1)
साइकिल सवार से विपरीत दिशा में प्रत्येक 6 मिनट के बाद गुजरने
वाली बसों का आपेक्षिक वेग = V_B + V_Cहै।
∴ चली गई दूरी = (V_B + V_C) × \(\frac{6}{60}\)
∴ (V_B + V_C)\(\frac{6}{60}\) = V_B × \(\frac{T}{60}\)
∴ समी० (1) से समी० (2) का भाग देने पर,
V_B = 2V_C
∵ V_C = 20 km h^-1
∴ V_B = 40 kmh^-1
समी० (1) से, [40 – 20] x \(\frac{18}{60}\) = 40 x \(\frac{T}{60}\)
T = 9 मिनट

प्रश्न 3.10.
कोई खिलाड़ी एक गेंद को ऊपर की ओर आरम्भिक चाल 29ms^-1 से फेंकता है।
(i) गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी?
(ii) इसकी गति के उच्चतम बिन्दु पर स्थान व समय को x = 0 व t = 0 चुनिये, ऊर्ध्वाधर नीचे की ओर की दिशा को X- अक्ष की धनात्मक दिशा मानिये। गेंद की ऊपर व नीचे की ओर गति के दौरान स्थिति, वेग व त्वरण के चिन्ह बताइए।
(iii) ज्ञात कीजिए कि किस ऊँचाई तक गेंद ऊपर जाती है और कितनी देर के बाद गेंद खिलाड़ी के हाथों में आ जाती है।
(g = 9.8ms^-2 तथा वायु का प्रतिरोध नगण्य है)
उत्तर:
(i) गुरुत्व के कारण त्वरण सदैव ऊर्ध्वाधर नीचे की ओर लगता है।
(ii) x = 0 व t = 0 को उच्चतम बिन्दु माना है जहाँ वेग शून्य होगा। उच्चतम बिन्दु पर त्वरण g = 9.8 m/s² (ऊर्ध्वाधर नीचे की ओर) ऊपर की ओर गति में,
स्थिति → धनात्मक (x > 0 )
वेग → ऋणात्मक (v < 0),

त्वरण → धनात्मक (∵ त्वरण 4 नीचे की ओर हैं) (a > 0)
नीचे की ओर गति में
स्थिति → धनात्मक (x > 0)
वेग → धनात्मक (v > 0)
त्वरण → धनात्मक (∵ त्वरण नीचे की ओर है) (a > 0)
(iii) ऊपर की गति के दौरान
u = – 29 m/s, a = 9.8 m/s², v =0
∴ v² = u² + 2as
0 = (-29)² + 2 × 9.8 × 8s
∴ S = \(\frac{-(-29)^2}{2 \times 9.8}\)
= -42.91m
अतः गेंद 42.91m ऊँचाई तक ऊपर जायेगी।
पुन: v = u + at से,
0 = (-29) + 9.8t
∴ t = \(\frac{29}{9.8}\) = 2.96 sec
कुल समय = 2.96 + 2.96 = 5.92 sec
(∵ जितना समय ऊपर जाने में लगता है उतना ही समय नीचे आने में लगता है।)

प्रश्न 3. 11.
नीचे दिये गये कथनों को ध्यान से पढ़िये और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य हैं या असत्य। एक विमीय गति में किसी कण की-
(a) किसी क्षण चाल शून्य होने पर उसका त्वरण अशून्य हो सकता है।
(b) चाल शून्य होने पर भी उसका वेग अशून्य हो सकता है।
(c) चाल स्थिर हो तो त्वरण अवश्य ही शून्य होना चाहिए।
(d) चाल अवश्य ही बढ़ती रहेगी, यदि उसका त्वरण धनात्मक
उत्तर:
(a) सत्य, कण की उच्चतम स्थिति में चाल शून्य होती है परन्तु त्वरण g होता है।
(b) असत्य, चाल शून्य है तो वेग का परिमाण शून्य है।
(c) असत्य, एकसमान वृत्तीय गति में चाल स्थिर रहने पर भी गति की दिशा बदलने के कारण त्वरण होता है।
(d) असत्य, जब दिशा धनात्मक होती है तो ही यह सत्य है।
वस्तु को ऊपर की ओर फेंकने पर त्वरण धनात्मक है परन्तु चाल घटती है।

प्रश्न 3.12.
किसी गेंद को 90m की ऊँचाई से फर्श पर गिराया जाता है। फर्श के साथ प्रत्येक टक्कर में गेंद की चाल \(1/10\) कम हो जाती है। इसकी गति का t = 0 से 125 के बीच चाल समय ग्राफ खींचिए।
उत्तर:
u1 = 0, s1 = 90m, a1 = 9.8 m/s²
v₁² = u₁² + 2a₁s₁
= 0 + 2 × 9.8 × 90
v₁² = 1764 → v₁ = 42m/s

∵ v₁ = u₁ + a₁t₁
42 = 0 + 9.8t₁
∴ t₁ = \(\frac{42}{9.8}\) = 4.2s
अर्थात् गेंद 4.2 sec तक नीचे आयेगी तो उसकी चाल सतत रूप से बढ़ेगी।
अतः ग्राफ सरल रेखा में होगा। इस स्थिति में अन्तिम वेग 42m/s होगा।
पुनः चाल \(\frac{1}{10}\) कम हो जाती है।
अतः
कमी = 42 x \(\frac{1}{10}\) = 4.2
∴ टकराने के पश्चात् चाल u2 = 42 – 4.2
= 37.8m/s
∵ v₂ = 0 ( उच्चतम बिन्दु पर ),
a₂ = -9.8m/s²
∴ v₂ = u₂ + a₂t₂
0 = 37.8 – 9.8 × t₂
∴ t₂ = \(\frac{37.8}{9.8}\) = 3.9 sec
कुल समय
t = t₁ + t₂ = 4.2 + 3.9 = 8.1 sec
अत: 8.1 sec पश्चात् चाल शून्य हो जायेगी।
∵ ऊपर जाने का समय = नीचे आने का समय
= 3.9 sec
t₃ = 3.9 sec, u₃ = 37.8m/s
अतः कुल समय
t = 8.1 + 3.9 = 12 sec पर चाल
= 37.8m/s

प्रश्न 3.13.
उदाहरण सहित निम्नलिखित के बीच के अन्तर को स्पष्ट कीजिए:
(a) किसी समय अन्तराल में विस्थापन के परिमाण (जिसे कभी-कभी दूरी कहा जाता है) और किसी कण द्वारा उसी अन्तराल के दौरान तय किए गए पथ की कुल लम्बाई।
(b) किसी समय अन्तराल में औसत वेग के परिमाण और उसी अन्तराल में औसत चाल (किसी समय अन्तराल में किसी कण की औसत चाल को समय अन्तराल द्वारा विभाजित की गई कुल पथ लम्बाई के रूप में परिभाषित किया जाता है)। प्रदर्शित कीजिए कि (a) व (b) दोनों में ही दूसरी राशि पहली राशि से अधिक या उसके बराबर हैं। समता का चिह्न कब सत्य होता है? (सरलता के लिए केवल एकविमीय गति पर विचार कीजिए।)
उत्तर:
(a) जब कोई वस्तु वृत्त का एक चक्कर पूर्ण करेगी तो विस्थापन शून्य होगा जबकि पथ की लम्बाई 2πr होगी।
(b) औसत चाल =
जबकि औसत वेग =
औसत चाल ≥ औसत वेग
यदि वस्तु सरल रेखा में गति करे तो औसत चाल, औसत वेग के समान होगी, तब समता का चिन्ह लगेगा।

प्रश्न 3.14.
कोई व्यक्ति अपने घर से सीधी सड़क पर 5kmh^-1 की चाल से 2.5 km दूर बाजार तक पैदल चलता है, परन्तु बाजार बन्द देखकर वह उसी क्षण वापस मुड़ जाता है तथा 7.5 kmh^-1 की चाल से घर लौट आता है।
समय अन्तराल (i) 0 – 30 मिनट, (ii) 0 – 50 मिनट, (iii) 0 – 40 मिनट की अवधि में उस व्यक्ति (a) के माध्य वेग का परिमाण तथा (b) का माध्य चाल क्या है?
उत्तर:
व्यक्ति के घर से बाजार की दूरी = 2.5 km
चाल V₁ = km/h
बाजार पहुँचने में लगा समय t₁ =
= 0.5 घण्टा = 30 मिनट
व्यक्ति की वापसी में चाल

∴ वापस आने में लगा समय, t₂ = \(\frac{2.5}{7.5}\) = 0.33h
= 0.33 × 60 = 19.8 20 मिनट
(i) 0 – 30 मिनट के अन्तराल में वस्तु द्वारा तय की गई दूरी
∆x = 2.5 km विस्थापन
अतः इस अन्तराल में औसत वेग का परिमाण, औसत चाल के तुल्य है।

(ii) 0 – 50 मिनट के अन्तराल में इस स्थिति में विस्थापन = 0
अतः
माध्य वेग = 0
कुल दूरी = 2.5 + 2.5 = 5km
कुल समय = 50 मिनट = \(\frac{50}{60}\) घण्टा
औसत चाल = \(\frac{5}{(50 / 60)}\) = \(\frac{5 \times 60}{50}\) = 6km/h
अतः यहाँ औसत वेग शून्य है जबकि औसत चाल 6km/h है।
(iii) 0 – 40 मिनट
= 30 मिनट जाने में + 10 मिनट वापस आने में व्यक्ति द्वारा 10 मिनट में तय की गई वापस दूरी
= 75 × \(\frac{10}{60}\)
= 1.25 km
∴ व्यक्ति का विस्थापन (AC)
= 2.5 km – 1.25m = 1.25km
समय = \(\frac{40}{60}\) घण्टा
∴ औसत वेग = \(\frac{1.25 \times 60}{40}\)
= 1.875 km/h
कुल तय की गई दूरी 2.5 + 1.25
AB + BC = 3.75km
∴ औसत चाल = \(\frac{3.75}{40}\) × 60
= 5.625km/h
अतः यहाँ भी औसत वेग, औसत चाल के बराबर नहीं है।

प्रश्न 3.15.
हमने अभ्यास प्रश्न 3.13 तथा 3.14 में औसत वेग के परिमाण के बीच के अन्तर को स्पष्ट किया है। यदि हम तात्क्षणिक चाल व वेग के परिमाण पर विचार करते हैं तो इस तरह का उत्तर करना आवश्यक नहीं होता। तात्क्षणिक चाल हमेशा तात्क्षणिक वेग के बराबर होती है, क्यों?
उत्तर:
हम जानते हैं कि तात्क्षणिक वेग
तात्क्षणिक चाल
अत्यन्त लघु समय अन्तरालों ∆t → 0 में वस्तु की गति की दिशा में कोई परिवर्तन नहीं माना जाता। अतः दूरी तथा विस्थापन के परिमाण में कोई अन्तर नहीं होता। एक प्रकार तात्क्षणिक चाल, सदैव तात्क्षणिक वेग के परिमाण के तुल्य होती है।

प्रश्न 3.16.
चित्र में (a) से (d) तक के ग्राफों को ध्यान से देखिए और देखकर बताइए कि इनमें से कौन-सा ग्राफ एकविमीय गति को सम्भवतः नहीं दर्शा सकता।

उत्तर:
(a) यह ग्राफ एकविमीय गति प्रदर्शित नहीं करता, क्योंकि किसी क्षण पर कण की दो स्थितियाँ होंगी, जो एकविमीय गति में सम्भव नहीं होतीं।
(b) यह ग्राफ एकविमीय गति प्रदर्शित नहीं करता, क्योंकि किसी क्षण पर कण का वेग धनात्मक तथा ऋणात्मक दोनों दिशाओं में, जो एकविमीय गति में सम्भव नहीं है।
(c) यह ग्राफ भी एकविमीय गति प्रदर्शित नहीं करता, क्योंकि यह ग्राफ कण की ऋणात्मक चाल व्यक्त कर रहा है तथा कण की चाल ऋणात्मक नहीं हो सकती।
(d) यह ग्राफ भी एकविमीय गति प्रदर्शित नहीं करता, क्योंकि यह प्रदर्शित कर रहा है कि कुल पथ की लम्बाई एक निश्चित समय के पश्चात् घट रही है, परन्तु गतिमान कण की कुल पथ- लम्बाई कभी भी समय के साथ नहीं घटती।

प्रश्न 3.17.
चित्र में किसी कण की एकविमीय गति का x – t ग्राफ दिखाया गया है। ग्राफ देखकर क्या यह कहना ठीक होगा कि यह कण t < 0 के लिए किसी सरल रेखा में और t > 0 के लिए किसी परवलीय पथ में गति करता है। यदि नहीं, तो ग्राफ के संगत किसी उचित भौतिक सन्दर्भ का सुझाव दीजिए।
उत्तर:

यह कहना ठीक नहीं होगा कि यह कण t < 0 के लिए किसी सरल रेखा में और t > 0 के लिए किसी परवलीय पक्ष में गति करता हैं, क्योंकि x- ग्राफ कण का पथ प्रदर्शित कर सकता है।
ग्राफ द्वारा t = 0 पर x = 0 प्रदर्शित है; अतः ग्राफ गुरुत्व के अन्तर्गत ऊँचाई से गिरती हुई किसी वस्तु की गति प्रदर्शित कर सकता है।

प्रश्न 3.18.
किसी राजमार्ग पर पुलिस की कोई गाड़ी 30km/h की चाल से चल रही है और यह उसी दिशा में 192 km/h की चाल से जा रही किसी चोर की कार पर गोली चलाती है। यदि गोली की नामुखी चाल 150ms^-1 है तो चोर की कार को गोली किस चाल के साथ आघात करेगी? (नोट- -उस चाल को ज्ञात कीजिए जो चोर की कार को हानि पहुँचाने में प्रासंगिक हो।)
उत्तर:
पुलिस की गाड़ी की चाल
Vp = 30km/h = 30 x \(\frac{5}{18}\) = \(\frac{25}{3}\) m/s
चोर की कार की चाल
Vt = 192km/h = 192 x \(\frac{5}{18}\) = \(\frac{160}{3}\) m/s
गोली की चाल = पुलिस की गाड़ी की चाल + गोली की नालमुखी चाल (Muzzle speed)
= (\(\frac{5}{18}\) + 150) = \(\frac{475}{3}\)m/s
∴ चोर की गाड़ी के सापेक्ष गोली का आपेक्षिक वेग
V_bt = V_b – V_t = \(\frac{475}{3}\) – \(\frac{160}{3}\) = \(\frac{315}{3}\) = 105m/s

प्रश्न 3.19.
चित्र में दिखाये गये प्रत्येक ग्राफ के लिए किसी उचित भौतिक स्थिति का सुझाव दीजिए।

उत्तर:
(a) x – t ग्राफ प्रदर्शित कर रहा है कि प्रारम्भ में x शून्य है, फिर यह एक स्थिर मान प्राप्त करता है, पुन: यह शून्य हो जाता है तथा फिर यह विपरीत दिशा में बढ़कर अन्त में एक स्थिर मान (विरामावस्था) प्राप्त कर लेता है। अतः यह ग्राफ इस प्रकार की भौतिक स्थिति व्यक्त कर सकता है जैसे एक गेंद को विरामावस्था से फेंका जाता है। वह दीवार से टकराकर लौटती है तथा कम चाल से उछलती है तथा यह क्रम इसके विराम में पहुँचने तक चलता रहता है।
(b) यह ग्राफ प्रदर्शित कर रहा है कि वेग समय के प्रत्येक अन्तराल के साथ परिवर्तित हो रहा है तथा प्रत्येक बार इसका वेग कम हो रहा है। इसलिए यह ग्राफ एक ऐसी भौतिक स्थिति को व्यक्त कर सकता है। जिसमें एक स्वतन्त्रतापूर्वक गिरती हुई गेंद (फेंके जाने पर) धरती से टकराकर कम चाल से पुन: उछलती है तथा प्रत्येक बार धरती से टकराने पर इसकी चाल कम होती जाती है।
(c) यह ग्राफ प्रदर्शित करता है कि वस्तु अल्प समय में ही त्वरित हो जाती है, अत: यह ग्राफ एक ऐसी भौतिक स्थिति को व्यक्त कर सकता है। जिसमें एकसमान चाल से चलती हुई गेंद को अत्यल्प समयान्तराल में बल्ले द्वारा टकराया जाता है।

प्रश्न 3.20.
चित्र में किसी कण की एक विमीय सरल आवर्ती गति के लिए x – t ग्राफ दिखाया गया है। समय t = 0.3s, 1.2s, -1.2s पर कण की स्थिति, वेग व त्वरण के चिन्ह क्या होंगे?

उत्तर:
(i) t = 0.3s पर ऋणात्मक, x – t वक्र की ढाल ऋणात्मक है। अतः स्थिति व वेग ऋणात्मक हैं। त्वरण a = -ω²x, अतः त्वरण धनात्मक है।
(ii) t = 1.2 s पर x स्थिति व वेग धनात्मक हैं। ऋणात्मक x-t वक्र की ढाल धनात्मक है। a = -ω²x से त्वरण धनात्मक है।
(iii) t = – 1.2 sec पर x ऋणात्मक x-t वक्र की ढाल धनात्मक है। अतः a = -ω²x से त्वरण ऋणात्मक है।

प्रश्न 3.21.
प्रस्तुत चित्र में किसी कण की एक विमीय गति का A ग्राफ दर्शाया गया। इसमें तीन समान अन्तराल दिखाए गए हैं। किस अन्तराल में औसत चाल अधिकतम है और किसमें न्यूनतम है? प्रत्येक अन्तराल के लिए औसत वेग का चिन्ह बताइए।

उत्तर:
(a) x-t वक्र की ढाल, औसत चाल व्यक्त करती है।
∴ अन्तराल (3) में ग्राफ की ढाल अधिकतम है तथा अन्तराल (2) में न्यूनतम होगी।
(c) (1) व (2) में ढाल धनात्मक है तथा अन्तराल (3) में ऋणात्मक ढाल है। अत: (1) व (2) में औसत वेग धनात्मक है परन्तु अन्तराल (3) है ऋणात्मक होगा।

प्रश्न 3.22.
चित्र में किसी नियत (स्थिर) दिशा के अनुदिश चल रहे कण का चाल – समय ग्राफ दिखाया गया है। इसमें तीन समान समय अन्तराल दिखाये गये हैं। किस अन्तराल में औसत त्वरण का परिमाण अधिकतम होगा? किस अन्तराल में औसत चाल अधिकतम होगी? धनात्मक दिशा को गति की स्थिर दिशा चुनते हुए तीनों अन्तराल में ” तथा के चिन्ह बताइए। A, B, C तथा D बिन्दुओं पर त्वरण क्या होंगे?

उत्तर:
(i) कण v-t वक्र की ढाल, औसत त्वरण प्रदर्शित करता है। ढाल (2) में अधिकतम है। अतः औसत त्वरण का परिमाण (2) में अधिकतम होगा। (3) में त्वरण का परिमाण न्यूनतम है।
(ii) औसत चाल (3) में अधिकतम तथा (1) में न्यूनतम है।
(iii) तीनों अन्तराल में धनात्मक है। (1) में त्वरण धनात्मक, (2) में त्वरण ऋणात्मक तथा (3) में त्वरण शून्य होगा क्योंकि इन बिन्दुओं पर स्पर्श रेखा समय अक्ष के समान्तर है।

अतिरिक्त अभ्यास (Additional Exercise):

प्रश्न 3.23.
कोई तीन पहिये वाला स्कूटर अपनी विरामावस्था में गति करता है। फिर 10 तक किसी सीधी सड़क पर 1ms^-2 के एकसमान त्वरण से चलता है। इसके बाद वह एक समान वेग से चलता है। स्कूटर द्वारा सेकण्ड (n = 1, 2, 3) में तय की गई दूरी को के सापेक्ष आलेखित कीजिए। आप क्या आशा करते हैं कि त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा?
उत्तर:
हम जानते हैं कि n वें Sec में तय की गई दूरी
S = u + \(\frac{a}{2}\)(2n – 1)

u = 0,a = 1
∴ n = 1
s₁ = 0 + \(\frac{1}{2}\)(2 × 1 – 1) = 0.5m
s₂ = \(\frac{1}{2}\)(2 x 2 – 1) = 1.5m
s₃ = \(\frac{1}{2}\)(2 x 3 – 1) = 2.5m
s₁₀ = \(\frac{1}{2}\)(2 × 10 – 1) = 9.5m
अतः ग्राफ से स्पष्ट है कि त्वरित गति के दौरान सरल रेखा प्राप्त होगी।

प्रश्न 3.24.
किसी स्थिर लिफ्ट में (जो ऊपर से खुली है ) कोई बालक खड़ा है। वह अपने पूरे जोर से एक गेंद ऊपर की ओर फेंकता है जिसकी प्रारम्भिक चाल 49 ms^-1 है। उसके हाथों में गेंद के वापस आने में कितना समय लगेगा? यदि लिफ्ट ऊपर की ओर 5m/s की एकसमान चाल से गति करना प्रारम्भ कर दे और वह बालक फिर गेंद को अपने जोर से फेंकता है तो कितनी देर में गेंद उसके हाथों में लौट आयेगी?
उत्तर:
यदि लिफ्ट स्थिर है, तब
h = 49m/s, a = -9.8m/s²
v = u + at
0 = 49 – 9.8t
∴ t = \(\frac{49}{9.8}\) = 5s
अतः गेंद को ऊपर जाने में 5s लगेंगे तथा 55 ही वापस आने में लगेंगे। अतः कुल समय 5 + 5 = 10s
जब लिफ्ट ऊपर की ओर एकसमान वेग से चलती है तो लिफ्ट के सापेक्ष गेंद का प्रारम्भिक वेग 49 m/s ही रहेगा। गेंद को बालक के हाथों में आने में 10s का ही समय लगेगा।

प्रश्न 3.25.
क्षैतिज में गतिमान कोई लम्बा पट्टा 4 km/h की चाल से चल रहा है। एक बालक इस पर (पट्टे के सापेक्ष) 9 km/h की चाल से कभी आगे कभी पीछे अपने माता-पिता के बीच दौड़ रहा है। माता व पिता के बीच 50m की दूरी है। बाहर किसी स्थिर प्लेटफार्म पर खड़े एक प्रेक्षक के लिए, निम्नलिखित का मान प्राप्त कीजिए।

(a) पट्टे की गति की दिशा में दौड़ रहे बालक की चाल,
(b) पट्टे की गति की दिशा के विपरीत दौड़ रहे बालक की चाल,
(c) बच्चे द्वारा (a) व (b) में लिया गया समय यदि बालक की गति का प्रेक्षण उसके माता या पिता करें तो कौन-सा उत्तर बदल जायेगा?
उत्तर:
माना \(\overrightarrow{v_B}\) = पट्टे का वेग = 4 km/h
\(\overrightarrow{v_{C B}}\) = पट्टे के सापेक्ष बालक का वेग
(a) जब बालक पट्टे की गति की दिशा में दौड़ता है:
पट्टे के सापेक्ष बालक का वेग = 9 km/h (बाएँ से दाएँ)
यदि बालक का वेग, प्लेटफार्म पर खड़े किसी प्रेक्षक के सापेक्ष \(\overrightarrow{v_C}\)
है, तो
\(\overrightarrow{v_{C B}}=\overrightarrow{v_C}-\overrightarrow{v_B}\)
VC = VC8+vg = 9+ 4 = 13km/h (बाएँ से दाएँ)
\(\overrightarrow{v_C}=\overrightarrow{v_{C B}}+\overrightarrow{v_B}\)

(b) जब बालक पट्टे की गति की दिशा के विपरीत दौड़ता है:
\(\overrightarrow{v_{C B}}\) = 9km/h (बाएँ से दाएँ)
यदि बालक का वेग किसी स्थिर प्रेक्षक के सापेक्ष \(\overrightarrow{v_C}\) है, तो
\(\overrightarrow{v_{C D}}=\overrightarrow{v_C}-\overrightarrow{v_B}\)
∴ \(\overrightarrow{v_C}=\overrightarrow{v_{C B}}+\overrightarrow{v_B}\)
= – 9+ 4 = -5km/h ( दाएँ से बाएँ)

(c) (a) अथवा (b) में लगने वाला समय

समय 20s रह जायेगा यदि माता या पिता बालक की गति का प्रेक्षण करते हैं।
माता/पिता समान बेल्ट पर हैं इसलिए उत्तर अपरिवर्तित रहेगा।

प्रश्न 3.26.
किसी 200m ऊँची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओर 15ms^-1 तथा 30ms^-1 की प्रारम्भिक चाल से फेंका जाता है। इसका सत्यापन कीजिए कि संलग्न ग्राफ पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है। वायु के प्रतिरोध को नगण्य मानिये और यह मानिये कि जमीन से टकराने के बाद पत्थर ऊपर की ओर उछलते नहीं। मान लीजिए g 10ms^-2 ग्राफ के रेखीय व वक्रीय भागों के लिए समीकरण लिखिए।

उत्तर:
पहले पत्थर के लिए,
x (0) = 200m,
v(0) = 15m/s,
a = -10m/s²
x₁(t) = x (0) + v (0)t + \(\frac{1}{2}\) at²
x₁(t) = 200 + 15t – 5t² …(1)
जब पहला पत्थर जमीन से टकराता है।
तो x₁(t) = 0
या -5t² + 15t + 2000 …….(2)
इसी प्रकार दूसरे पत्थर के लिए
x (0) = 200m, v(0) = 30m/s, a = – 10m/s²
X2(t) = 200 + 30t – 5t²
समी० (1) व समी० (2) से,
X2(t) – X1(t) = 15t
∴ x = 15t
∴ x ∝ t अर्थात् जब तक दोनों पत्थर गति करते रहेंगे उनके बीच की दूरी बढ़ती जायेगी।
∵ x व t समानुपाती हैं, अतः दोनों के मध्य ग्राफ सीधी रेखा में प्राप्त होगा।
समी० (2) से,
-5t² + 15t + 200 = 0
या 5t² – 15t – 200 = 0
या t²– 3t – 40 = 0
या t² – 8t + 5t – 40 = 0
या (t – 8) (t + 5) = 0
∴ t = 8 sec
अर्थात् 8s पश्चात् पहला पत्थर पृथ्वी पर गिर जायेगा। इसके पश्चात् एक ही पत्थर गति की अवस्था में होगा। अतः 8see पर दोनों के बीच दूरी अधिकतम होगी।
समी० (3) के अनुसार, समीकरण द्विघाती है अतः ग्राफ परवलयाकार होगा।

प्रश्न 3.27.
किसी निश्चित दिशा के अनुदिश चल रहे किसी कण का चाल-समय ग्राफ चित्र में दिखाया गया है। कण द्वारा (a) = 05 से t = 10s, (b) t = + 2s से 6s के बीच तय की गई दूरी ज्ञात कीजिए।
(a) तथा (b) में दिये गये अन्तरालों की अवधि में कण की औसत चाल क्या है?

उत्तर:
(a) t = 0 से t = 10 sec तक चली गई दूरी
= चाल-समय ग्राफ का समय अक्ष के साथ बनाया गया क्षेत्रफल
= \(\frac{1}{2}\) OC x AB
दूरी = \(\frac{1}{2}\) x 10 x 12 = 60m
औसत चाल = imm = 6m/s

(b) t = 2 sec से t = 6sec तक चली गई दूरी ज्ञात करने के लिए सर्वप्रथम t = 2 से t = 5 sec तक की दूरी ज्ञात करेंगे। इसके पश्चात् t = 5 से t = 6 sec की दूरी ज्ञात करेंगे।
∴ t = 2 से t = 5 sec के मध्य त्वरण
a = \(\frac{v-u}{t}\) = \(\\frac{12-0}{5}\)
= 2.4 m/s²
v = u + at से
u₀ = 12m/s², t = 1 sec
x = 12 × 1 – \(\frac{1}{2}\) × 24 × (1)²
= 12 – 1.2 = 10.8m
कुल दूरी = 25.2 + 10.8 = 36 m
औसत चाल = \(\frac{36}{4}\) = 9 m/s² 

प्रश्न 3.28.
एकविमीय गति में किसी कण का वेग समय ग्रांप चित्र में दिखाया गया है-नीचे दिये सूत्रों में से 12 तक के समय अन्तराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही हैं-
(i) x(t₂) = x(t₁) + v(t₁)(t₂ – t₁) + a(t₂ – t₁)²
(ii) v(t₂) = v(t₁) + a(t₂ -t₁)
(iii) aaverage = [x(t₂) – x(t₁)]\(t₂ – t₁)
(iv) aaverage = [v(t₂) – v(t₁)]\(t₂ -t₁)
(v) x(t₂) = x(t₁) + vaverage(t₂ – t₁) + aaverage(t₂ – t₁)²
(vi) x (t₂) – x (t₁) = t-अक्ष तथा दिखाई गई बिन्दुकित रेखा के बीच दर्शाए गए वक्र के अन्तर्गत आने वाला क्षेत्रफल

उत्तर:
(i) सही नहीं है, क्योंकि a का मान है t₁ तथा t₂ नियत नहीं है।
(ii) सही नहीं है, क्योंकि स्थिर नहीं है।
(iii) सही है। (iv) सही है।
(v) सही नहीं है, इसमें औसत त्वरण प्रयुक्त नहीं कर सकते हैं।
(vi) सही है।

Haryana State Board HBSE 11th Class Physics Solutions Chapter 2 मात्रक और मापन Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 2 मात्रक और मापन

प्रश्न 2.1.
रिक्त स्थान भरिए:
(a) किसी 1 cm भुजा वाले घन का आयतन …………….. m³ के बराबर है।
उत्तर:
10⁶
[संकेत: घन की भुजा L = 1 cm = \(\frac{1}{100}\) m = 10^-2 m
घन का आयतन L³ = (10²m)³ = 10⁶ m³]

(b) किसी 2 cm त्रिज्या व 10 cm ऊँचाई वाले सिलेण्डर का पृष्ठ क्षेत्रफल (mm)² के बराबर है।
उत्तर:
15 x 10⁴
[संकेत: सिलेण्डर का पृष्ठ क्षेत्रफल
= 2πr (r + h)
यहाँ,
त्रिज्या r=2cm
ऊंचाई h = 10cm
= 2 × 3.14 × 2 (2 + 10)
= 12.56 × 12
= 150.72 cm²
= 1.5 × 10⁴ mm²
[दो अंकों तक पूर्णांकित करने पर]

(c) कोई गाड़ी 18 km/h की चाल से चल रही है तो वह 1 s में …………….. m चलती है।
उत्तर:
[संकेत:
दूरी = चाल x समय
= 5 × 1 = 5m
क्योंकि
चाल = 18 km/h
= \(\frac{18 \times 1000}{3600}\) m/s = 5m/s
और
समय = 1 (सेकण्ड)]

(d) सीसे का आपेक्षिक घनत्व 11.3 है। इसका घनत्व ………….. g.cm^-3……………. kg m^-3 है।
उत्तर:
11.3, 11.3 x 10^-3
[संकेत : सीसे का घनत्व
= आपेक्षिक घनत्व x जल का घनत्व
= 11.3 x 1 = 11.3 g cm^-3
(∵ जल का घनत्व = gm cm^-3)
= 11.3 x \(\frac{10^{-3}}{\left(10^{-2}\right)^3}\) kg m^-3
= 11.3 × 10³ kgm^-3

प्रश्न 2.2.
रिक्त स्थानों को मात्रकों के उचित परिवर्तन द्वारा भरिए:
(a) 1 kgm²s^-2 = ……………… gcm²S^-2
(b) 1 m = ……………… ly
(c) 3.0 ms^-2 = ………….. km h^-2
(d) G = 6.67 × 10^-11 Nm² kg^-2
उत्तर:
(a) 10⁷
(b) 1.06 x 10¹⁶
(c) 3.9 × 10^-4
(d) 667 x 10^-8
[संकेत: (a) 1 kg m² s^-2
= 1000 gx (100 cm)² x 1s^-2
= 10⁷ g cm² s^-2

(b) 1 ly = 9.46 x 10¹⁵ m
1 m = \(\frac{1}{9.46 \times 10^{15}}\)
= 1.06 × 10^-16 ly

(c) 3.0 ms^-2 = \(\frac{3.0}{1000}\) km x (60 x 60)² h^-2
= 3.9 × 10⁴ km h^-2

(d) G = 6.67 x 10^-11 Nm²kg^-2
(∵ IN = 1kg m/s²)
= 6.67 × 10^-11 1 x m² kg^-2
= 6.67 x 10^-11 m³ s^-2 kg^-1
= 6.67 × 10^-11 x (100)³ cm³ s^-2 x \(\left(\frac{1}{1000}\right)\) g^-1
= 6.67 x 10⁸ cm³ s^-2 g^-1

प्रश्न 2.3.
ऊष्मा (परागमन में ऊर्जा) का मात्रक कैलोरी है और यह लगभग 4.2 J के बराबर है, जहाँ 1J = 1kgm² s^-2। मान लीजिए कि हम मात्रकों की कोई ऐसी प्रणाली उपप्रयोग करते हैं, जिसमें द्रव्यमान का मात्रक α kg के बराबर है, लम्बाई का मात्रक βm के बराबर है। समय का मात्रक γ s के बराबर है तो यह प्रदर्शित कीजिए कि नये मात्रकों के पदों में कैलोरी का परिमाण 4.2 α^-1 β^-2 γ² है।
उत्तर:
1 cal = 4.2 J = 4.2 kg m² s^-2
ऊर्जा का विमीय सूत्र = [ML² T ^-2]
यहाँ
m₂ =α kg, L₂ = βm, T₂ = γs
सूत्र:
n₁u₁ = n₂u₂
n₂ = n₁
= 4.2 \(\left[\frac{\mathrm{M}_1}{\mathrm{M}_2}\right]^1 \) \(\left[\frac{\mathrm{L}_1}{\mathrm{L}_2}\right]^1 \) \(\left[\frac{\mathrm{T}_1}{\mathrm{T}_2}\right]^1 \)
= 4.2 \(\left[\frac{1 \mathrm{~kg}}{\alpha \mathrm{kg}}\right]^1\) \(\left[\frac{1 \mathrm{~m}}{\beta \mathrm{m}}\right]^2\) \(\left[\frac{1 s}{\gamma s}\right]^{-2}\)
= 4.2 α^-1 β^-2 γ²
1 cal = 4.2 α^-1 β^-2 γ²
यही सिद्ध करना है

प्रश्न 2.4.
इस कथन की स्पष्ट व्याख्या कीजिए तुलना के मात्रक का विशेष उल्लेख किये बिना “किसी विमीय राशि को ‘बड़ा’ या ‘छोटा’ कहना अर्थहीन है।” इसे ध्यान में रखते हुए नीचे दिये गये कथनों को जहाँ कहीं भी आवश्यक हो, दूसरे शब्दों में व्यक्त कीजिए:
(a) परमाणु बहुत छोटे पिण्ड होते हैं।
(b) जेट वायुयान अत्यधिक गति से चलता है।
(c) बृहस्पति का द्रव्यमान बहुत ही अधिक है।
(d) इस कमरे के अन्दर वायु में अणुओं की संख्या बहुत अधिक
(e) इलेक्ट्रॉन, प्रोटॉन से बहुत भारी होता है।
(f) ध्वनि की गति प्रकाश की गति से बहुत ही कम होती है।
उत्तर:
किसी विमीय राशि को छोटा या बड़ा तुलना के आधार पर ही कहा जा सकता है। जैसे हम कह सकते हैं कि टेनिस की गेंद फुटबाल से छोटी होती है परन्तु कंचे की गोली की तुलना में बड़ी है।
(a) बाजरे के दाने की तुलना में परमाणु बहुत छोटे पिण्ड हैं।
(b) जेट वायुयान, कार की तुलना में अत्यधिक तेज चलता है।
(c) बृहस्पति का द्रव्यमान, पृथ्वी के द्रव्यमान की तुलना में बहुत अधिक है।
(d) कमरे के अन्दर वायु में अणुओं की संख्या 1 ग्राम गैस में उपस्थित अणुओं की संख्या से बहुत अधिक है।
(e) व (1) में तुलना पाठ्य पुस्तक में दी गयी है।

प्रश्न 2.5.
लम्बाई का कोई ऐसा नया मात्रक चुना गया है, जिसके अनुसार निर्वात् में प्रकाश की चाल 1 है। लम्बाई के नये मात्रक के पदों में सूर्य तथा पृथ्वी के बीच की दूरी कितनी है, प्रकाश इस दूरी को तय करने में 8 min और 20s लगाता है।
उत्तर:

समय t = 8 min 20s = 8 x 60 + 20 = 500s
∴ सूर्य तथा पृथ्वी के बीच की दूरी
= चाल x समय
= 1 x 500 = 500 मात्रक

प्रश्न 2.6.
लम्बाई मापने के लिए निम्नलिखित में से कौन-सा सबसे परिशुद्ध यन्त्र है:
(a) एक वर्नियर कैलिपर्स जिसके वर्नियर पैमाने पर 20 विभाजन
(b) एक स्क्रूगेज जिसका चूड़ी अन्तराल 1 mm और वृत्तीय पैमाने पर 100 विभाजन हैं।
(c) कोई प्रकाशिक यन्त्र जो प्रकाश की तरंगदैर्ध्य की सीमा के अन्दर लम्बाई माप सकता है।
उत्तर:
(a) यहाँ वर्नियर कैलिपर्स का अल्पतमांक

= \(\frac{0.1}{20}\)
= 0.005 cm

(b) स्क्रूगेज का अल्पतमांक

= \(\frac{0.1}{100}\)
= 0.001 cm

(c) प्रकाश की तरंगदैर्ध्य कोटि = 10^-7 m
= 10^-5 cm
अत: (a), (b) तथा (c) से स्पष्ट है कि प्रकाशिक यन्त्र की अल्पतमांक सबसे कम है। अतः यह सर्वाधिक परिशुद्ध यन्त्र है।

प्रश्न 2.7.
कोई छात्र 100 आवर्धन के एक सूक्ष्मदर्शी के द्वारा देखकर मनुष्य के बाल की मोटाई मापता है। वह 20 बार प्रेक्षण करता है और उसे ज्ञात होता है कि सूक्ष्मदर्शी के दृश्य क्षेत्र में बाल की औसत मोटाई 3.5mm है। बाल की मोटाई का अनुमान क्या है?
उत्तर:
सूक्ष्मदर्शी का आवर्धन

अतः बाल की मोटाई का अनुमान = 0.035mm

प्रश्न 2.8.
निम्नलिखित के उत्तर दीजिए:
(a) आपको एक धागा और मीटर पैमाना दिया जाता है। आप धागे के व्यास का अनुमान किस प्रकार लगायेंगे?
(b) एक स्क्रूगेज का चूड़ी अन्तराल 1.0 mm है और उसके वृत्तीय पैमाने पर 200 विभाजन हैं। क्या आप यह सोचते हैं कि वृत्तीय पैमाने पर विभाजनों की संख्या स्वेच्छा से बढ़ा देने पर स्क्रूगेज की यथार्थता में वृद्धि करना सम्भव है?
(c) वर्नियर कैलिपर्स द्वारा पीतल की किसी पतली छड़ का माध्य व्यास मापा जाना है। केवल 5 मापनों के समुच्चय की तुलना में व्यास के 100 मापनों के समुच्चय के द्वारा अधिक विश्वसनीय अनुमान प्राप्त होने की सम्भावना क्यों है?
उत्तर:
(a) सर्वप्रथम एक मीटर पैमाना लेंगे, उसके ऊपर धागे को इस प्रकार लपेटेंगे कि एक-दूसरे से सटे रहें। फेरों की संख्या l तब पैमाने की लम्बाई को नाप लेते हैं।
∴ धागे का व्यास =
इस सूत्र द्वारा धागे का व्यास ज्ञात कर लेते हैं।

(b) ∵ स्क्रूगेज का अल्पतमांक

सूत्र से स्पष्ट है कि वृत्तीय पैमाने पर कुल भाग बढ़ाने पर अल्पतमाांक कम होगा। अतः यथार्थता बढ़ेगी परन्तु व्यावहारिकता में आँखों की विभेदन क्षमता के कारण पाठ्यांक लेना कठिन होगा।

(c) ∵ प्रेक्षणों की संख्या 5 गुना करने पर त्रुटि \(\frac{1}{n}\) रह जाती है।
अतः 5 मापन से 100 मापन करने पर 20 गुना प्रेक्षण बढ़ने से त्रुटि \(\frac{1}{20}\) रह जायेगी। अतः विश्वसनीयता बढ़ जायेगी।

प्रश्न 2.9.
किसी मकान का फोटोग्राफ 35 mm स्लाइड पर 1.75 cm² क्षेत्र घेरता है। स्लाइड को किसी स्क्रीन पर प्रक्षेपित किया जाता है और स्क्रीन पर मकान का क्षेत्रफल 1.55 m² है। प्रक्षेपित पर्दा व्यवस्था का रेखीय आवर्धन क्या है?
उत्तर:
स्लाइड पर मकान का क्षेत्रफल = 1.75 cm²
स्क्रीन पर मकान का क्षेत्रफल = 1.55m²

प्रश्न 2.10.
निम्नलिखित में सार्थक अंकों की संख्या लिखिए:
(a) 0.007m²
(b) 2.64 × 10²⁴ kg
(c) 0.2370g cm^-3
(d) 6.320 J
(e) 6.032Nm^-2
(f) 0.0006032 m²
उत्तर:
( a ) 1
(b) 3
(c) 4
(d) 4
(e) 4
(f) 4

प्रश्न 2.11.
धातु की किसी आयताकार शीट की लम्बाई, चौड़ाई व मोटाई क्रमशः 4.234m 1.005m व 2.01 cm है। उचित सार्थक अंकों तक इस शीट का पृष्ठीय क्षेत्रफल व आयतन ज्ञात कीजिए।
उत्तर:
लम्बाई L = 4.234m, चौड़ाई B = 1.005m मोटाई W = 2.01 cm = 0.0201 m
∴ शीट का पृष्ठीय क्षेत्रफल
= 2 x (LB + BW + WL )
= 2 [4.234 x 1.005 + 1.005 x 0.0201 + 0.0201 × 4.234] m²
= [4.25517 + 0.0202005 + 0.0851034] m²
= 2 x 4.3604739m²
= 8.7209478 m² = 8.72 m²
(∵ मोटाई में अधिकतम सार्थक अंक तीन हैं अतः 3 अंकों तक पूर्णाकित करने पर)
आयतन = L x B x W
= 4.234 ×1.005 × 0.0201m³
=0.08552
= 0.0855 m³
(अधिकतम तीन अंकों तक पूर्णाकित करने पर)

प्रश्न 2.12.
पंसारी की तुला द्वारा मापे गये डिब्बे का द्रव्यमान 2.30 kg है। सोने के दो टुकड़े जिनके द्रव्यमान क्रमशः 20.15 g व 20.17g हैं, डिब्बे में रखे जाते हैं।
(a) डिब्बे का कुल द्रव्यमान कितना है?
(b) उचित सार्थक अंकों तक टुकड़ों के द्रव्यमान में कितना अन्तर है?
उत्तर:
डिब्बे का द्रव्यमान = 2.300kg
पहले टुकड़े का द्रव्यमान 20.15g = 0.02015 kg
दूसरे टुकड़े का द्रव्यमान = 20.17g = 0.02017 kg
∴ टुकड़े रखने के बाद डिब्बे का कुल द्रव्यमान
= 2.300 + 0.02015 + 0.02017
= 2.34032 kg
डिब्बे के द्रव्यमान में सबसे कम दशमलव के पश्चात् तीन अंक हैं। अतः तीन अंकों तक पूर्णांकित करने पर कुल द्रव्यमान = 2.340 kg

(b) ∵ सोने के टुकड़ों के द्रव्यमान में दशमलव के पश्चात् दो अंक हैं। अतः अन्तर में भी दशमलव के पश्चात् दो ही अंक तक पूर्णांकित करेंगे।
∴ टुकड़ों के द्रव्यमानों का अन्तर
= (20.17 – 20.15) g
= 0.02g

प्रश्न 2.13.
कोई भौतिक राशि P, चार प्रेक्षण योग्य राशियों a, b, c तथा से निम्न प्रकार सम्बन्धित है:
P = \(\frac{a^3 b^2}{\sqrt{c} d}\)
ab, c तथा d के मापने में प्रतिशत त्रुटियाँ क्रमशः 1%, 3%, 4% तथा 2% हैं। राशि में प्रतिशत त्रुटि कितनी है? यदि उपर्युक्त सम्बन्ध का उपयोग करके P का परिकलित मान 3.763 आता है तो आप परिणाम का किस मान तक निकटन करेंगे?
उत्तर:
P = \(\frac{a^3 b^2}{\sqrt{c} d}\)
∴ P के मान में प्रतिशत त्रुटि
= \(\frac{\Delta P \times 100}{P}\)
= 3 x \(\frac{\Delta a}{a}\) x 100% + 2 x \(\frac{\Delta b}{b}\) x 100% + \(\frac{1}{2}\) \(\frac{\Delta c}{c}\) × 100% + \(\frac{\Delta d}{d}\) x 100%
= 3 x 1% + 2 x 3% + \(\frac{1}{2}\) × 4% + 2%
= 13%
P का परिकलित मान 3.763
∵ P की % त्रुटि में दो सार्थक अंक हैं। अतः इसे दो अंकों तक पूर्णांकित करने पर P का निकटतम मान = 3.8

प्रश्न 2.14.
किसी पुस्तक में, जिसमें छपाई की अनेक त्रुटियाँ हैं, आवर्त गति कर रहे किसी कण के विस्थापन के चार भिन्न सूत्र दिये गये हैं:
(a) y = a sin \(\frac{2 \pi t}{T}\)
(b) y = asin vt
(c) y = \(\left(\frac{a}{T}\right) sin \frac{t}{a}\)
(d) y = (a√2) (sin 2πtT + cos 2πt / T)
( a = कण का अधिकतम विस्थापन, कण की चाल, 7 = गति का आवर्तकाल ) विमीय आधारों पर गलत सूत्रों को निकाल दीजिए।
उत्तर:
∵ कोण विमाहीन राशि है। अतः इस आधार पर

अतः (ii) व (iii) दोनों गलत हैं।

प्रश्न 2.15.
भौतिकी का एक प्रसिद्ध सम्बंध किसी कण के ‘चल द्रव्यमान (moving mass) ‘ m ‘विराम द्रव्यमान (rest mass) ‘ mo इसकी चाल और प्रकाश की चाल के बीच है । (यह सम्बन्ध सबसे पहले अल्बर्ट आइंस्टीन के विशेष आपेक्षिकता सिद्धान्त के परिणामस्वरूप उत्पन्न हुआ था।) कोई छात्र इस सम्बन्ध को लगभग सही याद करता है लेकिन स्थिरांक को लगाना भूल जाता है। वह लिखता है:
m = \(\frac{m_0}{\left(1-v^2\right)^{1 / 2}}\)
अनुमान लगाइए कि कहाँ लगेगा?
उत्तर:
दिया गया सम्बन्ध है:
m = \(\frac{m_0}{\left(1-v^2\right)^{1 / 2}}\)
या
(1 – v²)^1/2 = Mo/m
इस सम्बन्ध का दायाँ पक्ष विमाहीन है। अतः L. H.S. भी विमाहीन होना चाहिए।
∴ (1 – v²)^1/2 = [ M°L°T° ]
∵ L.H.S. में 1 तो विमाहीन है परन्तु v² को विमाहीन करने के लिए v² में c² का भाग देने पर \(\frac{v^2}{c^2}\) विमाहीन राशि प्राप्त होगी।
अतः
सही सूत्र m = \(\frac{m_0}{\left(1-\frac{v^2}{c^2}\right)^{1 / 2}}\)

प्रश्न 2.16.
परमाण्विक पैमाने पर लम्बाई का सुविधाजनक मात्रक एंग्स्ट्रॉम है और इसे A ( 1A = 10_-10m) द्वारा निर्दिष्ट किया जाता है। हाइड्रोजन के परमाणु का आमाप लगभग 0.54 है। हाइड्रोजन परमाणुओं के एक मोल का m’ में कुल आण्विक आयतन कितना होगा?
उत्तर:
हाइड्रोजन अणु की त्रिज्या
r = 0.5 A = 0.5 × 10^-10 m
हाइड्रोजन का अध्ययन
\(\frac{4}{3}\) πr³ = \(\frac{4}{3}\) × 3.14 × (0.5 × 10^-10)³
= 5.23 × 10^-311 m³
1 मोल हाइड्रोजन गैस में अणुओं की संख्या = 6.023 x 10²³ होती है।
∵ 1 मोल गैस का आण्विक आयतन
= अणुओं की संख्या x एक अणु का आयतन
= 6,023 × 10²³ x 5.23 x 10^-31
= 3.15 × 10⁷ m³

प्रश्न 2.17.
किसी आदर्श गैस का एक मोल (ग्राम अणुक ) मानक ताप व दाब पर 22.4 L आयतन (ग्राम अणुक आयतन) घेरता है। हाइड्रोजन के ग्राम अणुक आयतन तथा उसके मोल के परमाण्विक आयतन का अनुपात क्या है? (हाइड्रोजन के अणु की आमाप लगभग 1 A मानिए)। यह अनुपात इतना अधिक क्यों है?
उत्तर:
1 मोल हाइड्रोजन गैस का आयतन
= 22.4 L = 22.4 × 10^-3 m³
हाइड्रोजन अणु की त्रिज्या
r = 0.5 A = 0.5 × 10^-10 m
हाइड्रोजन का अध्ययन
\(\frac{4}{3}\) πr³ = \(\frac{4}{3}\) × 3.14 × (0.5 × 10^-10)³
= 5.23 × 10^-311 m³
1 मोल हाइड्रोजन गैस में अणुओं की संख्या = 6.023 x 10²³ होती है।
∵ 1 मोल गैस का आण्विक आयतन
= अणुओं की संख्या x एक अणु का आयतन
= 6,023 × 10²³ x 5.23 x 10^-31
= 3.15 × 10⁷ m³
1 मोल हाइड्रोजन गैस आण्विक आयतन = 3.15 × 10⁷ m³

∴ अभीष्ट अनुपात 7.11 x 10⁴ : 1
इसका मान अधिक इसलिए है कि गैस का आयतन उसमें उपस्थित अणुओं के वास्तविक आयतन की तुलना में बहुत अधिक होता है। इसका अर्थ है कि गैस के अणुओं के बीच बहुत अधिक खाली स्थान होता है।

प्रश्न 2.18.
इस सामान्य प्रेक्षण की स्पष्ट व्याख्या कीजिए:
यदि आप तीव्र गति से गतिमान किसी रेलगाड़ी की खिड़की से बाहर देखें तो समीप के पेड़, मकान आदि रेलगाड़ी की गति के विपरीत दिशा में तेजी से गति करते प्रतीत होते हैं, परन्तु दूरस्थ पिण्ड (पहाड़ियाँ, तारे आदि) स्थिर प्रतीत होते हैं। (वास्तव में क्योंकि आपको ज्ञात है कि आप चल रहे हैं, इसलिए ये दूरस्थ वस्तुएँ आपको अपने साथ चलती हुई प्रतीत होती हैं।)
उत्तर:
प्रेक्षक की आँखों पर समीप की वस्तु, दूर की वस्तु की तुलना में अधिक कोण बनाती है। जब प्रेक्षक गति करेगा तो समीप की वस्तु की अपेक्षा दूर की वस्तु द्वारा बने कोण में परिवर्तन कम होता है। अतः दूरस्थ वस्तु आपके साथ गतिमय प्रतीत होती है जबकि समीपस्थ वस्तु विपरीत दिशा में गतिमय प्रतीत होती है।

प्रश्न 2.19.
समीपी तारों की दूरियाँ ज्ञात करने के लिए लम्बन के सिद्धान्त का प्रयोग किया जाता है। सूर्य के परित: अपनी कक्षा में छह महीनों के अन्तराल पर पृथ्वी की अपनी दो स्थानों को मिलाने वाली, आधार रेखा AB है अर्थात् आधार रेखा पृथ्वी की कक्षा के व्यास = 3 x 10¹¹ m के लगभग बराबर है। लेकिन चूँकि निकटतम तारे भी इतने अधिक दूर हैं कि इतनी लम्बी आधार रेखा होने पर भी वे चाप के केवल 1″ ( सेकण्ड चाप का) की कोटि का लम्बन प्रदर्शित करते हैं। खगोलीय पैमाने पर लम्बाई का सुविधाजनक मात्रक पारसेक है। यह किसी पिण्ड की वह दूरी है, जो पृथ्वी से सूर्य तक की दूरी के बराबर आधार रेखा के दो विपरीत किनारों से चाप के 1″ का लम्बन प्रदर्शित करती है। मीटरों में एक पारसेक कितना होता है?
उत्तर:
चित्र में S सूर्य तथा E₁ व E₂ पृथ्वी की छ: माह के अन्तराल में स्थिति है।
बिन्दु O की पृथ्वी से दूरी 1 पारसेक है।
पृथ्वी की कक्षा का व्यास = 3 x 10¹¹ m
चाप SE1 = \(\frac{3 \times 10^{11}}{2}\) = 1.5 x 10¹¹ m
रेखाखण्ड SE बिन्दु O पर 1″ (चाप का) कोण अन्तरित करता

प्रश्न 2.20.
हमारे सौर परिवार से निकटतम तारा 4.29 प्रकाश वर्ष दूर है। पारसेक में यह दूरी कितनी है? यह तारा (ऐल्फा सेंटौरी नामक) तब कितना लम्बन प्रदर्शित करेगा। जब इसे सूर्य के परितः ‘ अपनी कक्षा में पृथ्वी के दो स्थानों से जो छः महीने के अन्तराल पर है, देखा जायेगा?
उत्तर:
तारे की सौर परिवार से दूरी
= 4.29 प्रकाश वर्ष (ly)
= 4.29 x 9.46 x 10¹⁵m
[∵ 1ly = 9.46 x 10¹⁵ m]
= \(\frac{4.29 \times 9.46 \times 10^{15}}{3 \times 10^{16}}\) पारसेक
[∵ 1 पारसेक = 3 x 10¹⁶m]
= 1.35 पारसेक

छः महीने के अन्तराल पर पृथ्वी अपनी कक्षा के व्यासत: विपरीत सिरों पर होगी।
∵ पृथ्वी का विस्थापन d = कक्षा का व्यास
= 3 x 10¹¹ m
∵ तारे की सौरमण्डल के केन्द्र सूर्य से दूरी
r = 4.29 x 9.46 x 10¹⁵ m
∴ तारे द्वारा प्रदर्शित लम्बन
θ = \(\frac{d}{r}\) = \(\frac{3 \times 10^{11}}{4.29 \times 9.46 \times 10^{15}}\)rad
= 0.0739 × 10^-4 rad
= 0.0739 × 10^-4 x \(\frac{180}{\pi}\) x 60 x 60 सेकण्ड
∴ θ = \(\frac{4.79}{3.14}\) = 1.52

प्रश्न 2.21.
भौतिक राशियों का परिशुद्ध मापन विज्ञान की आवश्यकताएँ हैं। उदाहरण के लिए, किसी शत्रु के लड़ाकू जहाज की चाल सुनिश्चित करने के लिए बहुत ही छोटे समयान्तरालों पर इसकी स्थिति का पता लगाने की कोई यथार्थ विधि होनी चाहिए। द्वितीय विश्वयुद्ध में रडार की खोज के पीछे वास्तविक प्रयोजन यही था। आधुनिक विज्ञान के उन भिन्न उदाहरणों को सोचिए जिनमें लम्बाई, समय, द्रव्यमान आदि के परिशुद्ध मापन की आवश्यकता होती है।
अन्य जिस किसी विषय में भी आप बता सकते हैं, परिशुद्धता की मात्रात्मक धारणा दीजिए।
उत्तर:
लम्बाई का मापन: विभिन्न यौगिकों के क्रिस्टलों में परमाणुओं के बीच की दूरी का मापन करते समय लम्बाई के परिशुद्ध मापन की आवश्यकता होती है।
समय का मापन: फेको की विधि द्वारा किसी माध्यम में प्रकाश की चाल ज्ञात करने के प्रयोग में समय के परिशुद्ध मापन की आवश्यकता होती है। उपग्रह प्रक्षेपण में समय का मापन परिशुद्धता से किया जाता है।
द्रव्यमान का मापन: द्रव्यमान स्पेक्ट्रमलेखी में परमाणुओं के द्रव्यमान का परिशुद्ध मापन किया जाता है। दवाइयाँ बनाने में विभिन्न साल्ट मिलाये जाते हैं, जिनका द्रव्यमान परिशुद्धता से मापन करते हैं।

प्रश्न 2.22.
जिस प्रकार विज्ञान में परिशुद्ध मापन आवश्यक है, उसी प्रकार अल्पविकसित विचारों तथा सामान्य प्रेक्षणों को उपयोग करने वाली राशियों के स्थूल आकलन कर सकना भी उतना ही महत्वपूर्ण है। उन उपायों को सोचिए जिनके द्वारा आप निम्नलिखित का अनुमान लगा सकते हैं (जहाँ अनुमान लगाना कठिन है वहाँ राशि की उपरिसीमा पता लगाने का प्रयास कीजिए)
(a) मानसून की अवधि में भारत के ऊपर वर्षांधारी मेघों का कुल द्रव्यमान।
(b) किसी हाथी का द्रव्यमान।
(c) किसी तूफान की अवधि में वायु की चाल।
(d) आपके सिर के बालों की संख्या।
(e) आपकी कक्षा के कमरे में वायु के अणुओं की संख्या।
उत्तर:
(a) सर्वप्रथम मौसम विभाग से पूरे भारत में हुई कुल वर्षा की माप की जानकारी लेंगे और वर्षा जल के आयतन को जल के घनत्व से गुणा करके वर्षा जल के द्रव्यमान की गणना कर लेंगे। इससे मेघों का द्रव्यमान ज्ञात हो जायेगा।
जैसे: बादल का द्रव्यमान
= औसत वर्षा x भारत का क्षेत्रफल पानी का घनत्व
= 1 x 3.3 x 1012 × 103 kg
= 3.3 × 1015 kg
(b) हाथी का द्रव्यमान काँटे पर भी लीवर सिद्धान्त से ज्ञात कर सकते हैं।
(c) इसके लिए एक गैस का गुब्बारा लेते हैं तथा उसे ऊपर की ओर छोड़ते हैं तथा। सेकण्ड पश्चात् उसकी स्थिति ज्ञात कर कोण θ का मापन करते हैं।

चित्र में गुब्बारा बिन्दु 0 से छोड़ा गया है, जो 1 सेकण्ड पश्चात् बिन्दु B पर पहुँचता है। गुब्बारे की ऊँचाई / ज्ञात कर विस्थापन ज्ञात करते हैं। यही विस्थापन AB = dh= θ ही तूफान में हवा की चाल होगी।
(d) मनुष्य के बालों की संख्या =
जैसे: सिर की औसत त्रिज्या R = 8cm हो, तो
सिर का क्षेत्रफल = πR² = π(8)² = 64πcm²
बाल का व्यास पेचमापी से ज्ञात करते हैं जो लगभग 5 x 10^-3cm
∴ त्रिज्या r = \(\frac{5}{2}\) x 10^-3 cm
अत; एक बाल का क्षेत्रफल = πR²
= π × \(\left(\frac{5}{2} \times 10^{-3}\right)^2\)
= π × \(\frac{25}{4}\) × 10^-6 cm²
∴ बालों की संख्या = \(\frac{64 \pi}{\pi \times \frac{25}{4} \times 10^{-6}}\)
= 10⁷

(e) ∵ NTP पर 22.4 L = 22.4 x 10^-3 m³ में अणुओं की संख्या 6.02 × 10²³ होती है।
∴ कमरे के आयतन में अणुओं की संख्या
= \(\frac{6.02 \times 10^{23}}{22.4 \times 10^{-3}}\)
यदि कमरे का आकार 5 x 4 x 3m³ = 60m³ माने तो अणुओं की संख्या 10²⁷ कोटि की प्राप्त होगी।

प्रश्न 2.23.
सूर्य एक ऊष्मा प्लाज्मा (आयनीकृत पदार्थ) है, जिसके आन्तरिक क्रोड का ताप 10⁷ K से अधिक और बाह्य पृष्ठ का ताप लगभग 6000K है। इतने अधिक ताप पर कोई भी पदार्थ ठोस या तरल प्रावस्था में नहीं रह सकता। आपको सूर्य का द्रव्यमान घनत्व किस परिसर में होने की आशा है? क्या यह ठोसों, तरलों या गैसों के घनत्वों के परिसर में है? क्या आपका अनुमान सही है, इसकी जाँच आप निम्नलिखित आँकड़ों के आधार पर कर सकते हैं? सूर्य का द्रव्यमान = 2 x 10³⁰ kg, सूर्य की त्रिज्या = 7.0 x 10⁸ m
उत्तर:
सूर्य का घनत्व
d =
= \(\frac{M}{\frac{4}{3} \pi r^3}\)
यहाँ M = 2 x 10³⁰ kg, r = 7.0 x 10⁸ m
∴ d = \(\frac{3 \times 2 \times 10^{30}}{4 \times 3.14 \times\left(7.0 \times 10^8\right)^3}\)
= 1.4 x 10³ kg/m³
सूर्य का घनत्व द्रव / ठोस के घनत्व के परिसर में होता है। यह गैसों के परिसर में नहीं होता है क्योंकि सूर्य की भीतरी परतों के कारण बाहरी परतों पर गुरुत्वाकर्षण बल के कारण प्लाज्मा का घनत्व उच्च होता है।

प्रश्न 2.24.
जब बृहस्पति ग्रह पृथ्वी से 8247 लाख किलोमीटर दूर होता है तो इसके व्यास की कोणीय माप 35.72″ का चाप है। बृहस्पति का व्यास परिकलित कीजिए।
उत्तर:
कोणीय व्यास θ =
∴ व्यास d = θ x α
कोणीय माप θ = 35.72″ = \(\frac{35.72}{60 \times 60}\) डिग्री
= \(\frac{35.72}{60 \times 60}\) x \(\frac{\pi}{180}\) rad
दूरी α = 8247 लाख किलोमीटर
= 8247 × 10⁵ km
= 8247 x 10⁸ m
∴ d = \(\frac{35.72}{60 \times 60}\) x \(\frac{3.14}{180}\) x 8247 x 10⁸ m
= 1.427 x 10⁸ m
= 1.427 x 10⁵ km

अतिरिक्त अभ्यास (Additional Exercise):

प्रश्न 2.25.
वर्षा के समय में कोई व्यक्ति चाल के साथ तेजी से चला जा रहा है। उसे अपने छाते को टेढ़ा करके ऊर्ध्वं के साथ θ कोण बनाना पड़ता है। कोई विद्यार्थी कोण 9 व ” के बीच निम्नलिखित सम्बन्ध व्युत्पन्न करता है:
tan θ = v
और वह इस सम्बन्ध के औचित्य की सीमा का पता लगाता है जैसी कि आशा की जाती है यदि। v → θ तो θ → 01 ( हम यह मान रहे हैं कि तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा ऊर्ध्वाधरत पड़ रही है।) क्या आप सोचते हैं कि यह सम्बन्ध सही हो सकता है? यदि ऐसा नहीं है तो सही सम्बन्ध का अनुमान लगाइए।
उत्तर:
दिये गये सम्बन्ध में,
बाएँ पक्ष की विमाएँ = [M°L°T° ]

जबकि दाएँ पक्ष की विमाएँ = [M°L¹T^-1]
∵ दोनों पक्षों की विमाएँ परस्पर समान नहीं हैं, अतः यह सम्बन्ध
सही नहीं हो सकता। स्पष्ट है कि सही सम्बन्ध में दाएँ पक्ष की विमाएँ भी [M°L°T° ] होनी चाहिए।
सही सम्बन्ध tan θ = v²/ rg

प्रश्न 2.26.
यह दावा किया जाता है कि यदि बिना किसी बाधा के 100 वर्षों तक दो सीजियम घड़ियों को चलने दिया जाये तो उनके समयों में केवल 0.02 (s) का अन्तर हो सकता है, मानक सीजियम घड़ी द्वारा 1 (s) के समय अन्तराल को मापने में यथार्थता के लिए इसका क्या अभिप्राय है?
उत्तर:
समय T = 100 वर्ष
= 100 x 365 x 24 x 60 x 60
त्रुटि ΔΤ = 0.02 sec
∴ 1(s) के मापन में त्रुटि
= \(\frac{\Delta T}{T} = [latex]\frac{0.02}{100 \times 365 \times 24 \times 60 \times 60}
= 6.34 × 10^-12
= 10 x 10^-12 (पूर्णांकित करने पर)
= 10^-11 = [latex]\frac{1}{10^{11}}\)
अतः सीजियम घड़ी द्वारा 1s के मापन में 10¹¹ में से 1 भाग की परिशुद्धता है।

प्रश्न 2.27.
एक सोडियम परमाणु की आमाप लगभग 2.5 A° मानते हुए उसके माध्य द्रव्यमान घनत्व का अनुमान लगाइए। (सोडियम के परमाण्वीय द्रव्यमान तथा आवोगाद्रो संख्या के ज्ञात मान का प्रयोग कीजिए।)
इस घनत्व की क्रिस्टलीय प्रावस्था में सोडियम के घनत्व 970 kg m^-3 के साथ तुलना कीजिए। क्या इन दोनों घनत्वों के परिमाण की कोटि समान है। यदि हाँ, तो क्यों?
उत्तर:
सोडियम परमाणु की आमाप 2.5 A
∴ त्रिज्या R = \(\frac{2.5}{2}\)
= 1.25 A
= 1.25 x 10^-10 m
सोडियम का ग्राम परमाणु भार
= 23g = 23 x 10^-3 kg
1 ग्राम परमाणु में परमाणुओं की संख्या = 6,023 × 10²³
∴ सोडियम के एक परमाणु का द्रव्यमान
= 3.82 × 10^-26 kg
1 परमाणु का आयतन = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) × 3.14 × (1.25 × 10^-10)³
= 8.18 × 10³⁰ m³
∴ सोडियम परमाणु का माध्य द्रव्यमान घनत्व

= 4670 kg/m³
= 4.670 × 10³ kgm
क्रिस्टलीय अवस्था में सोडियम का घनत्व = 970kgm^-3
= 0.970 × 10³ kg/m³
∴ दोनों के घनत्व की कोटि (10³) लगभग समान है क्योंकि ठोस अवस्था में परमाणु दृढ़तापूर्वक संकुचित होते हैं। अतः परमाणु द्रव्यमान घनत्व ठोस के द्रव्यमान घनत्व के लगभग बराबर होता है।

प्रश्न 2.28.
नाभिकीय पैमाने पर लम्बाई का सुविधाजनक मात्रक फर्मी (1 fm = 10^-15 m) है। नाभिकीय आमाप लगभग निम्नलिखित आनुभविक सम्बन्ध का पालन करते हैं:
r = r0A^1/3
जहाँ नाभिक की त्रिज्या, 4 इसकी द्रव्यमान संख्या और ro कोई स्थिरांक है, जो लगभग 1.2 fm के बराबर है। यह प्रदर्शित कीजिए कि इस नियम का अर्थ है कि विभिन्न नाभिकों के लिए नाभिकीय द्रव्यमान घनत्व लगभग स्थिर है। सोडियम नाभिक के द्रव्यमान घनत्व का आकलन कीजिए। प्रश्न 27 में ज्ञात किये गये सोडियम परमाणु के माध्य द्रव्यमान घनत्व के साथ इसकी तुलना कीजिए।
उत्तर:
नाभिक की त्रिज्या r = r0A^1/3
∴ नाभिक का आयतन v = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\)π(r0A^1/3)³
V = \(\frac{4}{3}\) πr³0A
माना न्यूक्लिऑन (न्यूट्रॉनों प्रोटॉनों) का द्रव्यमान m (m = 1.66 x 10^-27 kg) है।
∴ नाभिक का कुल द्रव्यमान = mA
∴ नाभिक का द्रव्यमान घनत्व =
= \(\frac{m A}{\frac{4}{3} \pi r_0^3 A}\)
= \(\frac{3 m}{4 \pi r_0^3}\)
उपर्युक्त सूत्र में द्रव्यमान संख्या नहीं है अर्थात् नाभिकीय द्रव्यमान घनत्व स्थिर है।
(b) सोडियम नाभिक का द्रव्यमान घनत्व

∵ r0 = 1.2fm
= 1.2 x 10^-15 m
m = 1.66 x 10^-27 kg
= \(\frac{3 \times 1.66 \times 10^{-27}}{4 \times 3.14 \times\left(1.2 \times 10^{-15}\right)^3}\)
= 0.3 × 10¹⁸ kg/m³

(c) क्रिस्टलीय अवस्था में सोडियम का घनत्व = 970kgm^-3
= 0.970 × 10³ kg/m³
∴ दोनों के घनत्व की कोटि (10³) लगभग समान है क्योंकि ठोस अवस्था में परमाणु दृढ़तापूर्वक संकुचित होते हैं। अतः परमाणु द्रव्यमान घनत्व ठोस के द्रव्यमान घनत्व के लगभग बराबर होता है।,
सोडियम परमाणु का माध्य घनत्व = 4.6 x 10³ kg/m³

अर्थात् सोडियम नाभिक का घनत्व, उसके परमाणु के घनत्व से 10¹⁵ गुना अधिक है। इसका अर्थ है कि परमाणु का अधिकांश भाग खोखला होता है तथा उसका अधिकांश द्रव्यमान उसके नाभिक में केन्द्रित होता है।

प्रश्न 2.29.
लेसर (Laser), प्रकाश के अत्यधिक तीव्र, एकवर्णी तथा एकदिश किरण पुंज का स्रोत है। लेसर के इन गुणों का लम्बी दूरियाँ मापने में उपयोग किया जाता है। लेसर को प्रकाश के स्रोत के रूप में उपयोग करते हुए पहले ही चन्द्रमा की पृथ्वी से दूरी परिशुद्धता के साथ ज्ञात की जा चुकी है। कोई लेसर प्रकाश किरण-पुंज चन्द्रमा के पृष्ठ से परावर्तित होकर 2.565 में वापस आ जाता है। पृथ्वी के परितः चन्द्रमा की कक्षा की त्रिज्या कितनी है?
उत्तर:
माना चन्द्रमा की कक्षा की त्रिज्या = r
∴ लेसर प्रकाश द्वारा तय की गई कुल दूरी = 2r
∴ समय t = 2.56(s)
∴ दूरी 2r = चाल (c) x समय (t)
∴ त्रिज्या r = \(\frac{c \times t}{2}\)
= \(\frac{3 \times 10^8 \times 2.56}{2}\)
= 3.84 × 10⁸ m

प्रश्न 2.30.
जल के नीचे वस्तुओं को ढूँढ़ने व उनके स्थान का पता लगाने के लिए सोनार (SONAR) में पराश्रव्य तरंगों का प्रयोग होता है। कोई पनडुब्बी सोनार से सुसज्जित है। इसके द्वारा जनित अन्वेषी तरंग और शत्रु की पनडुब्बी से परावर्तित इसकी प्रतिध्वनि की प्राप्ति के बीच काल विलम्ब 77.0 (s) है। शत्रु की पनडुब्बी कितनी दूर है? (जल में ध्वनि की चाल = 1450ms^-1)
उत्तर:
माना शत्रु की पनडुब्बी की सोनार स्टेशन से दूरी = d
∴ तरंगों द्वारा तय की गई कुल दूरी 2d
∴ दूरी 2d = चाल v x समय t
d = \(\frac{v \times t}{2}\)
= 55825 m
∴ d = 55.825 km

प्रश्न 2.31.
हमारे विभ्व में आधुनिक खगोलविदों द्वारा खोजे गये सर्वाधिक दूरस्थ पिण्ड इतनी दूर हैं कि उनके द्वारा उत्सर्जित प्रकाश को पृथ्वी तक पहुँचने में अरबों वर्ष लगते हैं। इन पिण्डों (जिन्हें क्वासर ‘Quasar’ कहा जाता है) के कई रहस्यमय लक्षण हैं। जिनकी अभी तक सन्तोषजनक व्याख्या नहीं की जा सकी है। किसी ऐसे क्वासर की km में दूरी ज्ञात कीजिए, जिससे उत्सर्जित प्रकाश को हम तक पहुँचने में 300 करोड़ वर्ष लगते हों।
उत्तर:
प्रकाश को पहुँचने में लगा समय
= 300 करोड़ वर्ष = 300 x 10⁷ वर्ष
∴ दूरी = 300 x 10⁷ प्रकाश वर्ष
प्रकाश द्वारा 1 वर्ष में तय की गई दूरी
= 9.46 x 10¹⁵ m
∴ क्वासर की दूरी = 300 x 10⁷ x 9.46 x 10¹⁵
= 28.4 × 10²⁴m = 2.84 x 10²² km 

प्रश्न 2.32.
यह एक विख्यात तथ्य है कि पूर्ण सूर्यग्रहण की अवधि में चन्द्रमा की चक्रिका सूर्य की चक्रिका को पूरी तरह ढक लेती है । चन्द्रमा का लगभग व्यास ज्ञात कीजिए। (उदाहरण 2.3 व 2.4 की सूचनाओं को प्रयुक्त कीजिए। )
उत्तर:
चन्द्रमा का कोणीय व्यास

d = \(\frac{d}{3.84 \times 10^8}\) × \(\frac{180}{\pi}\) डिग्री
d = \(\frac{d}{3.84 \times 10^8}\) × \(\frac{180}{\pi}\) × 60 × 60(s)
यहाँ चन्द्रमा की पृथ्वी से दूरी
α = 3.84 x 108 m है।
∵ चन्द्रमा की चक्रिका, सूर्य की चक्रिका को पूरी तरह ढक लेती है। अतः चन्द्रमा तथा सूर्य दोनों के कोणीय व्यास बराबर होंगे।
∴d = \(\frac{d}{3.84 \times 10^8}\) × \(\frac{180}{\pi}\) × 60 × 60 = 1920
( ∵ सूर्य का कोणीय व्यास = 1920)
d = \(\frac{1920 \times 3.84 \times 10^8 \times \pi}{180 \times 60 \times 60}\)
= 3.576 × 10⁶ m
∵ चन्द्रमा का व्यास
= 3.576 × 10³ km = 3576 km

प्रश्न 2.33.
इस शताब्दी के एक महान भौतिकविद (पी.ए.एम. डिरैक) प्रकृति के मूल स्थिरांकों (नियतांकों) के आंकिक मानों के साथ क्रीड़ा में आनन्द लेते थे। इससे उन्होंने एक बहुत ही रोचक प्रेक्षण किया । परमाण्वीय भौतिकी के मूल नियतांकों (जैसे इलेक्ट्रॉन का द्रव्यमान, प्रोटॉन का द्रव्यमान तथा गुरुत्वीय नियतांक 6) से उन्हें पता लगा कि वे एक ऐसी संख्या पर पहुँच गये हैं, जिसकी विमा समय की विमा है। साथ ही यह एक बहुत ही बड़ी संख्या थी और इसका परिमाण विश्व की वर्तमान आकलित आयु – 1500 करोड़ वर्ष) के करीब है। इस पुस्तक में दी गई मूल नियतांकों की सारणी के आधार पर यह देखने का प्रयास कीजिए कि क्या आप भी यह संख्या बना सकते हैं? यदि विश्व की आयु तथा इस संख्या में समानता महत्वपूर्ण है तो मूल नियतांकों की स्थिरता किस प्रकार प्रभावित होगी?
उत्तर:
समय की विमा t = \(\left(\frac{e^2}{4 \pi \varepsilon_0}\right) \times \frac{1}{m_p m_e^2 c^3 G}\)
∵ e = 1.6 x 10^-19C,
\(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹
c = 3 x 10⁸ m/s,
G = 6.67 × 10^-11 Nm² kg²,
mp = 1.67 x 10^-27 kg.
mg = 9 x 10^-31 kg.
मान रखने पर,
t = (1.6 × 10^-19)⁴ × (9 × 10⁹ )² × \(\frac{1}{1.67 \times 10^{-27} \times\left(9 \times 10^{-31}\right)^2}\) x (3 x 10⁸) 3 x 6.67 x 10^-11
t = 2.18 x 10¹⁶ sec
∴ यह समय ब्रह्माण्ड की आयु की कोटि का है।

Haryana State Board HBSE 11th Class Physics Solutions Chapter 1 भौतिक जगत Textbook Exercise Questions and Answers.

Haryana Board 11th Class Physics Solutions Chapter 1 भौतिक जगत

प्रश्न 1.1.
विज्ञान की प्रकृति से सम्बन्धित कुछ अत्यन्त पारंगत प्रकथन आज तक के महानतम् वैज्ञानिकों में से एक अल्बर्ट आइंस्टीन द्वारा प्रदान किये गये हैं। आपके विचार से आइंस्टीन का उस समय क्या तात्पर्य था, जब उन्होंने कहा था “संसार के बारे में सबसे अधिक अबोधगम्य विषय यह है कि यह बोधगम्य है?
उत्तर:
जब कोई घटना पहली बार देखी जाती है तो यह अबोधगम्य होती है परन्तु जब हम उस घटना से सम्बन्धित सिद्धान्त, नियम एवं तथ्यों का गहन विश्लेषण करते हैं तो वह हमारे लिए बोधगम्य हो जाती है। दूसरे शब्दों में, भौतिक जगत की जटिल प्रकृति कुछ मूलभूत नियमों के पदों में समझी जा सकती हैं। अत: आइंस्टाइन का यह कथन तर्कसंगत है।

प्रश्न 1.2.
“प्रत्येक महान भौतिक सिद्धान्त अपसिद्धान्त से आरम्भ होकर धर्म सिद्धान्त के रूप में समाप्त होता है।” इस तीक्ष्ण टिप्पणी की वैधता के लिए विज्ञान के इतिहास से कुछ उदाहरण लिखिए।
उत्तर:
समाज में स्थापित विश्वास और धर्म सिद्धान्त वैज्ञानिक सिद्धान्तों एवं प्रबुद्ध व्यक्तियों के विचारों से कई बार भिन्न होते हैं। ऐसे कुछ प्रमुख उदाहरण निम्नलिखित हैं-
1. प्राचीन काल में टॉलमी ने भूकेन्द्रीय सिद्धान्त का प्रतिपादन किया जिसके अनुसार पृथ्वी को स्थिर माना गया तथा सभी आकाशीय पिण्ड पृथ्वी के चारों और चक्कर लगाते थे। बाद में इटली के वैज्ञानिक गैलीलियो ने माना कि पृथ्वी नहीं सूर्य स्थिर है तथा पृथ्वी सहित सभी प्रह सूर्य की परिक्रमा करते हैं। तत्कालीन शासकों द्वारा गैलीलियों की संकल्पना को गलत कहा गया और इसके लिये उन्हें दण्डित भी किया गया।
2. आइंस्टीन से पहले चह माना जाता था कि द्रव्य तथा ऊर्जा अविनाशी होते हैं तथा दोनों में कुछ भी सम्बन्ध नहीं होता है। अत: दोनों ही राशियों के संरक्षण के स्वतंत्र नियम थे। आइंस्टीन ने इन दोनों स्वतंत्र नियमों के स्थान पर द्रव्यमान-ऊर्जा का संरक्षण नियम प्रस्तुत करते हुए द्रव्यमान-ऊर्जा तुल्यता समीकरण E=mc² दिया।

प्रश्न 1.3.
“सम्भव की कला ही राजनीति है।” इसी प्रकार “समाधान की कला ही विज्ञान है।” विज्ञान की प्रकृति तथा व्यवह्हार पर इस सुन्दर सूक्ति की व्याख्या कीजिए।
उत्तर:
राजनीतिज्ञ यह मानते हुए भी कि उनके द्वारा किये गये वायदों की घोषणाओं का पूरा कर पाना उनके लिए असम्भव है, बहुत से कार्यों को पूरा करने के बारे में वे स्वयं अनिश्चित होते है, लेकिन फिर भी वे उन्हे संभव करने का प्रयास करते हैं तथा प्रतिकूल परिस्थितियों को अनुकूल बनाने की संभावना निरन्तर तलाशते रहते हैं। इस प्रकार स्पष्ट है कि “संभव की कला ही राजनीति है।”
वहीं वैज्ञानिक किसी समस्या के समाधान के लिये धैर्यपूर्वक निरन्तर प्रेक्षण लेते हैं और उनके विश्लेषण से कुछ नियमों का प्रतिपादन करते हैं। उदाहरण के लिए टाइको ब्राहे ने लगभग 20 वर्षों तक ग्रहों की गति का अध्ययन किया। फैराडे ने लगभग 18 वर्षों तक चुम्बकीय क्षेत्र द्वारा विद्युत् धारा उत्पन्न करने के लिए धैर्यपूर्वक प्रयोग किये तथा इसके फलस्वरूप उन्होंने विद्युत् चुम्बकीय प्रेरण की घटना का आविष्कार किया।

प्रश्न 1.4.
यद्यषि अब भारत में विज्ञान तथा प्रौद्योगिकी का विस्तृत आधार है तथा यह तीव्रता से फैल भी रहा है, परन्तु फिर भी इसे विज्ञान के क्षेत्र में विश्ष नेता बनने की अपनी क्षमता को कायान्वित करने में काफी दूरी तय करनी है। ऐसे कुछ महत्वपूर्ण कारक लिखिए जो आपके विचार से भारत में विज्ञान के विकास में बाधक रहे हैं।
उत्तर:
भारत में विज्ञान के विकास में कई महत्वपूर्ण कारक बाधक रहे हैं। इनमें से प्रमुख बाधाएँ निम्नलिखित हैं-
1. भारत में वैज्ञानिकों को शैक्षणिक स्वतंत्रता प्राप्त नहीं है।
2. प्रारम्भिक अनुसंधान के सरकारी सुविधाओं एवं सहयोग की कमी।
3. प्रश्शिक्षित वैज्ञानिकों का देश से पलायन।
4. विज्ञान प्रबंधन पर अवैज्ञानिक और संकुचित विचारधारा वाले नौकरशाहों, राजनेताओं एवं धार्मिक संस्थानों का नियंत्रण।
5. अनुसंधान तथा प्रौद्योगिंकी में सामंजस्य का अभाव।
6. स्कूल तथा कॉलेज स्तर पर विज्ञान की शिक्षा का सही रूप में न होना।

प्रश्न 1.5.
किसी भी भौतिक विज्ञानी ने इलेक्ट्रॉन के कभी भी दर्शन नहीं किये हैं, परन्तु फिर भी सभी भौतिक विज्ञानियों का इलेक्ट्रॉन के अस्तित्व में विभ्वास है। कोई बुद्धिमान, परन्तु अन्धविश्वासी व्यक्ति इसी तुल्यस्ूपता को इस तर्क के साथ आगे बढ़ाता है कि यद्यपि किसी ने ‘ देखा ‘ नहीं है, परन्तु 4 भूतों ‘ का अस्तित्व है। आप इस तर्क का खण्डन किस प्रकार करेंगे?
उत्तर:
भातिक विज्ञानियों का इलेक्ट्रॉन के अस्तित्व में विश्वास का कारण उसकी प्रायोगिक पुष्टि जैसे, अणुओं की विभिन्न आकृतियाँ, विद्युत् धारा का प्रवाह इत्यादि है परन्तु भूतों का कोई प्रायोगिक प्रमाण नहीं है। अत: दोनों की तुलना निरर्थक है।

प्रश्न 1.6.
जापान के एक विशेष समुद्रतटीय क्षेत्र में पाये जाने वाले केकड़े के कवचों (खोल ) में से अधिकांश समुरई के अनुभुत चेहरे से मिलते-जुलते प्रतीत होते हैं। नीचे इस प्रेक्षित तथ्य की दो व्याख्याएँ दी गई हैं। इनमें से आपको कौन-सा वैज्ञानिक स्पष्टीकरण लगता है?
(i) कई शताब्दियों पूर्व किसी भयानक समुद्री दुर्घटना में एकयुवा समुरई डूब गया। उसकी बहादुरी के लिए शब्द्धांजलि के रूप में प्रकृति ने अबोधगम्य बंगों द्वारा उसके चेहरे को केकड़े के कवचों पर अंकित करके उसे उस क्षेत्र में अमर बना दिया।
(ii) समुद्री दुर्घटना के पश्शात् उस क्षेत्र के मछुआरे अपने मृत नेता के सम्मान में सद्भावना प्रदर्शन के लिए, उस हर केकड़े के कवच को जिसकी आकृति संयोगवश समुरई से मिलती-जुलती प्रतीत होती थी, उसे वापस समुब्र में फेंक देते थे। परिणामस्वरूप केकड़े के कवचों की इस प्रकार की विशेष आकृतियाँ अधिक समय तक विद्यमान रहीं और इसीलिए कालान्तर में इसी आकृति का आनुवंशतः जनन हुआ। यह कृत्रिम वरण द्वारा विकास का एक उदाहरण है।
उत्तर:
कथन (ii) वैज्ञानिक स्पष्टीकरण देने में पर्याप्त रूप समंथ है।

प्रश्न 1.7.
दो शताब्दियों से भी अधिक समय पूर्व इंग्लैण्ड तथा पश्चिमी यूरोष में जो औद्योगिक कान्ति हुई थी। उसकी चिंगारी का कारण कुछ प्रमुख वैज्ञानिक तथा प्रौद्योगिक उपलव्धियां थीं। ये उपलब्बियों क्या थीं?
उत्तर:
औद्योगिक क्रान्ति की कुछ प्रमुख वैज्ञानिक तथा प्रौद्योगिक उपलविधियाँ निम्न थी-
1. भाप इजन-इसका आविष्कार जेम्स वाट द्वारा किया गया। इसकी सहायता से औद्योगिक इकाइयों को देश के भीतरी भागों में समुद्री किनारों से दूर स्थान प्राप्त हो सका।
2. पावर लूम-इसके खोजकर्ता कार्लराइट (1785) है। इसकी सहायता से कपड़ों की बुनाई का कार्य किया जाता है।
3. वात्या भट्टी-इसकी सहायता से स्ट्रोल (इस्पात) क्षेत्र में प्रगति हुई है।
4. सेफ्टी पिन-इसका आविष्कार सर हम्फ्री डेवी ने किा इसका उपयोग कोयला खदानों में किया जाता है।
5. स्पिनिंग जिन-इसकी खोज 1765 A.D. में हारग्रीब्ज द्वारा की गयी थी। स्पिनिंग जिन ने सूत कातने का काम तेज कर दिया।

प्रश्न 1.8.
प्रायः यह कहा जाता है कि संसार अब दूसरी औद्योगिक क्रान्ति के दैर से गुजर रहा है, जो समाज में पहली क्रान्ति की भांति आमूलचूल परिवर्तन ला देगी। विज्ञान तथा प्रौद्योगिकी के उन प्रमुख समकालीन क्षेत्रों की सूची बनाइए, जो इस क्रान्ति के लिए उत्तरदायी है।
उत्तर:
दूसरी औद्योगिक क्रान्ति के लिए उत्तरदायी विज्ञान के प्रमुख क्षेत्र निम्नवत् हैं
(i) कृषि क्षेत्र में विकास,
(ii) प्रकाश विद्युत् प्रभाव,
(iii) नाभिकीय ऊर्जा का उत्पादन,
(iv) प्लाज्मा का चुम्बकीय परिरोध,
(v) कमरे के ताप पर अतिचालक पदार्थों का विकास,
(vi) प्रकाशिक रेशे,
(vii) लेसर पुंजों तथा चुम्बकीय क्षेत्रों द्वारा परमाणुओं का परिग्रहण तथा शीतलन,
(viii) अवरक्त संसूचकों का विकास,
(ix) सेटेलाइट के उपयोग एवं अंतरिक्ष विज्ञान का विकास।

प्रश्न 1.9.
बाईसवीं शताब्दी के विज्ञान तथा प्रौद्योगिकी पर अपनी निराधार कल्पनाओं को आधार मानकर लगभग 1000 शब्दों में कोई कथा लिखिए।
उत्तर:
मैं सुबह 6 बजे व्यायाम कर रहा था कि उसी समय बंगलौर से मेरे वैज्ञानिक मित्र का फोन आ गया। उसने कहा कि अनुसंधान कार्य के लिए 10 बजे तक बंगलौर आना है। मैं जल्दी से तैयार होने लगा। खाने बनाने वाली 8 बजे आती है। इसीलिए मैंने रोबोट को कमांड दी कि वह नाश्ता तैयार करे। रोबोट ने अगले 20 मिनट में नाश्ते में स्वादिष्ट पराठे तैयार कर मेरे सामने परोस दिए। में नाश्ता कर सीधे नई दिल्ली रेलवे स्टेशन कार द्वारा पहुँचा। वहाँ से 7 बजे सुपर बुलेट ट्रेन में सवार हो गया। 9 : 35 मिनट पर बुलेट ट्रेन बंगलौर पहुँच गई। जहाँ से हमें अंतरिक्ष स्टेशन पहुँचना था। वहाँ स्टेशन पर खड़ी डूाइवरलैस वायु कार के की-बोर्ड पर गन्तव्य स्थान का कोड निवेशित किया और कार का दरवाजा खुला। मैं कार में बैठ गया। कार में बैठते ही सीट बैल्ट कस गई और कार का दरवाजा बन्द हो गया। कार ने भारी ट्रैफिक होने के बावजूद मुझे ठीक समय पर अंतरिक्ष स्टेशन पहुँचा दिया। अंतरिक्ष स्टेशन पर सुरक्षा रोबोट तैनात थे। द्वार पर लगे संवेदी स्क्रीन पर हाथ रखने पर सम्बद्ध कम्य्यूटर ने मेरी पहचान की और मेरे आने की जानकारी मेंरे मित्र के मोबाइल पर पहुँच गई। मेरे मित्र ने मिलने की अनुमति दे दी। जिसका मैसेज मोबाइल से दरवाजे के संवेदी कम्प्यूटर तक पहुँचते ही दरवाजा खुल गया। अन्दर प्रवेश करते ही एक रोबोट ने हाथ मिलाकर मेरा स्वागत किया और मेरे मित्र के पास ले गया।

मेरे मित्र ने जानकारी दी कि मुझे उसके साथ मंगल ग्रह पर पिकनिक मनाने जाना है। पृथ्वी से मंगल तक यात्रा में 72 घण्टे लगना था तथा मंगलयान से अगली सुबह 7 बजे उड़ान भरनी थी। इससे पूर्व रोबोट चिकित्सकों ने हमारी चिकित्सकीय जाँच की। इस यात्रा के लिए आवश्यक सामम्मी जसे-यात्रा में पहने जाने वाले विशेष वस्त, ऑक्सीजन मॉस्क, भोजन की ट्यूब तथा कैप्सूल, पानी की ट्यूब आदि चन्द्र यात्रा का प्रबंध करने वाली एजेन्सी ने ही उपलख्ध कराये। हमें व्यक्तिगत सुरक्षा के लिए लेसरगन तथा न्यूट्रॉन गन भी उपलब्ध करायी गई।

ठीक समय पर हमने मंगलयान से उड्ान भरी और हम अन्य तीन रोबोट के साथ मंगल की सतह पर पहुँच गये। वहॉ कैम्प एक झील के किनारे प्लास्टिक की शीट से बना था, जो अति उच्च दाब सहन कर सकती थी। इसके अन्दर वायुदाब पृथ्वी के वायुदाब के बराबर रखा गया था। कैप्य अतिचालक तारों की सहायता से उत्पन्न अति उच्च तीव्रता के विद्युत् चुम्बकीय बल क्षेत्र से घिरा था, ताकि वह उल्का पिण्डों तथा शत्रु के आक्रमणों से सुरक्षित रहे। मंगलयान पर दो दिन रहने के बाद मैं दिल्ली लौट आया।

प्रश्न 1.10.
‘विज्ञान के व्यवहार’ पर अपने ‘नैतिक’ दृष्टिकोणों को रचने का प्रयास कीजिए। कल्पना कीजिए कि आप स्वयं किसी संयोगवश ऐसी खोज में लगे हैं, जो शैक्षिक दृष्टि से रोचक है परन्तु उसके परिणाम निश्चित रूप से मानव समाज के लिए भयंकर होने के अतिरिक्त कुछ नहीं होंगे। फिर भी यदि ऐसा है तो आप इस दुविधा के हल के लिए क्या करेंगे?
उत्तर:
सर्वप्रथम वैज्ञानिक खोज के गलत प्रयोग के सम्बन्ध में लोक विचार प्राप्त किये जायें। यदि समाज इसे हानिकारक मानता है तो इस प्रकार के प्रयोग रोक देने चाहिये। यदि उस प्रयोग से कुछ लाभ हो सकता है तो ही उसे आगे बढ़ाना चाहिये।

प्रश्न 1.11.
किसी भी ज्ञान की भाँति विज्ञान का उपयोग भी, उपयोग करने वाले पर निर्भर करते हुए, अच्छा अथवा बुरा हो सकता है। नीचे विज्ञान के कुछ अनुप्रयोग दिये गये हैं। विशेषकर कौन-सा अनुप्रयोग अच्छा है, बुरा है अथवा ऐसा है कि जिसे स्पष्ट रूप से वर्गबद्ध नहीं किया जा सकता। इसके बारे में अपने दृष्टिकोणों को सूचीबद्ध कीजिए:
(i) आम जनता को चेचक के टीके लगाकर इस रोग को दबाना और अन्तत: इस रोग से जनता को मुक्ति दिलाना।
(ii) निरक्षरता का विनाश करने तथा समाचारों एवं धारणाओं के जनसंचार के लिए टेलीविजन।
(iii) जन्म से पूर्व लिंग निर्धारण।
(iv) कार्यदक्षता में वृद्धि के लिए कम्प्यूटर।
(vi) पृथ्वी के परितः कक्षाओं में मानव-निर्मित उपग्रहों की स्थापना।
(vii) रासायनिक तथा जैव युद्ध की नवीन तथा शक्तिशाली तकनीकों का विकास।
(viii) पीने के लिए जल का शोधन।
(ix) प्लास्टिक शल्यक्रिया।
(x) क्लोनिंग।
उत्तर:
(i) अच्छा, क्योकि इससे जनता को चेचक के रोग से मुक्ति मिल गई।
(ii) अच्छा, टेलींविजन द्वारा अपनी बात प्रभावी रूप से सम्रेषित की जा सकती है।
(iii) बुरा, इससे लड़कियों की संख्या में गिरावट आ रही है, जिससे सामाजिक असंतुलन उत्पन्न हो रहा है।
(iv) अच्छा, कम्प्यूटर से दक्षता में वृद्धि हुई है।
(v) अच्छा, इससे संचार, अनुसंधान, मौसम का पूर्वानुमान आदि में लाभ हुआ है।
(vi) बुरा, इससे मानव-जाति के महाविनाश की स्थिति बन सकती है।
(vii) बुरा, इससे भी मानव जाति नष्ट हो सकती है।
(viii) अच्छा, इससे प्रचुर मात्रा में पीने योग्य जल उपलब्ध होगा।
(ix) अच्छा, इससे व्यक्ति की दुर्घटना आदि से उत्पन्न कुरुपता को हटाया जा सकता है।
(x) अच्छा, इसका प्रयोग अत्यन्त सावधानी से किया जाना चाहिए क्योंकि इसके उचित प्रयोग से भावी पीड़ी का सवास्थ्य बेहतर हो सकता है जबकि अनुचित प्रयोग से नुकसान भी हो सकता है।

प्रश्न 1.12.
भारत में गणित, खगोलिकी, भाषा विज्ञान, तर्क तथा नैतिकता में महान विद्वता की एक लम्बी एवं अटूट परम्परा रही है। फिर भी इसके साथ एवं समान्तर हमारे समाज में बहुत-से अन्धविश्वास तथा रूढ़िवादी दृष्टिकोण व परम्पराएँ फली फूली हैं और दुर्भाग्यवश ऐसा अभी भी हो रहा है और बहुत से शिक्षित लोगों में व्याप्त है। इन दृष्टिकोणों का विरोध करने के लिए अपनी रणनीति बनाने में आप अपने विज्ञान के ज्ञान का प्रयोग किस प्रकार करेंगे?
उत्तर:
(i) विद्यालयों में ऐसे कार्यक्रम दिखाये जायें, जिनसे छात्रों में अन्धविश्वास दूर हो सके। जैसे- सोडियम पर पानी डालकर आग उत्पन्न
करना।
(ii) वैज्ञानिक, डॉक्टर्स, शिक्षाविदों द्वारा विभिन्न घटनाओं के वास्तविक कारण व अन्धविश्वास को सही रूप से समझाएँ। जैसे – मानसिक बीमारियों के लिए जादू-टोने के इस्तेमाल को रोकना।
(iii) रेडियो, टेलीविजन, समाचार पत्र, इंटरनेट आदि जनसंचार माध्यमों का प्रयोग लोगों में व्याप्त अन्धविश्वास को दूर कर सकता है।

प्रश्न 1.13.
यद्यपि भारत में स्त्री तथा पुरुषों को समान अधिकार प्राप्त हैं, फिर भी बहुत से लोग महिलाओं की स्वाभाविक प्रकृति, क्षमता, बुद्धिमत्ता के बारे में अवैज्ञानिक विचार रखते हैं तथा व्यवहार में उन्हें गौण महत्व तथा भूमिका देते हैं। वैज्ञानिक तर्कों तथा विज्ञान एवं अन्य क्षेत्रों में महान महिलाओं का उदाहरण देकर इन विचारों को धराशायी कीजिए तथा अपने को स्वयं तथा दूसरों को भी समझाइए कि समान अवसर दिये जाने पर महिलाएँ पुरुषों के समकक्ष होती हैं।
उत्तर:
महिलाएँ भी किसी भी क्षेत्र में पुरुषों से कम नहीं हैं। मैडम क्यूरी ऐसी महिला थीं, जिन्होंने भौतिक व रसायन विज्ञान दोनों में नोबेल पुरस्कार प्राप्त किया। अन्य क्षेत्रों में भी महिलाओं ने बहुत योगदान किया। जैसे – कल्पना चावला, इन्दिरा गाँधी, बछेन्द्री पाल, लक्ष्मीबाई इत्यादि जिन्होंने अपने क्षेत्रों में असाधारण योगदान दिया। अतः महिलाएँ किसी भी क्षेत्र में पुरुषों से कम नहीं हैं।

प्रश्न 1.14.
“भौतिकी के समीकरणों में सुन्दरता होना उनका प्रयोगों के साथ सहमत होने की अपेक्षा अधिक महत्वपूर्ण है।” यह मत महान ब्रिटिश वैज्ञानिक पी०ए०एम० डिरैक का था। इस दृष्टिकोण की समीक्षा कीजिए। इस पुस्तक में ऐसे सम्बन्धों तथा समीकरणों को खोजिए जो आपको सुन्दर लगते हैं।
उत्तर:
भौतिकी में समीकरणों की सुन्दरता होना भी महत्वपूर्ण है क्योंकि समीकरण यदि सुन्दर है तो वह सरल व बोधगम्य भी होगा। जैसे – E = mc² एक सुन्दर समीकरण है, जो ऊर्जा व द्रव्यमान में सम्बन्ध बताता है।

प्रश्न 1.15.
यद्यपि उपर्युक्त प्रकथन विवादास्पद हो सकता है परन्तु अधिकांश भौतिक विज्ञानियों का यह मत है कि भौतिकी के महान नियम एक ही साथ सरल एवं सुन्दर होते हैं। डिरैक के अतिरिक्त जिन सुप्रसिद्ध भौतिक विज्ञानियों ने ऐसा अनुभव किया उनमें से कुछ के नाम इस प्रकार हैं-आइंस्टीन, बोर, हाइजेनबर्ग, चन्द्रशेखर तथा फाइनमैन। आपसे अनुरोध है कि आप भौतिकी के इन विद्वानों तथा अन्य महानायकों द्वारा रचित सामान्य पुस्तकों एवं लेखों तक पहुँचने के लिए विशेष प्रयास अवश्य करें। (पाठ्य पुस्तक के अन्त में दी गई ग्रन्थ सूची देखिए।) इनके लेख सचमुच प्रेरक हैं।
उत्तर:
भौतिकी के अति महत्वपूर्ण नियम एवं समीकरण एक साथ ही सरल तथा सुन्दर हैं। इनमें से कुछ निम्नलिखित हैं-
1. भारतीय मूल के वैज्ञानिक एस० चन्द्रशेखर ने खगोलीय पिण्डों के लिए ‘ब्लैक होल’ का सिद्धान्त देकर विश्व के सामने अनबूझे आकाशीय पिण्डों का रहस्य पता करके अपने सिद्धान्त को सरल रूप में प्रस्तुत किया।
2. इसी प्रकार फाइनमैन जिसे भौतिकी की गीता का प्रणेता कहा जाता है, ने लेजर की शक्ति का सरल, सुन्दर तथा सुग्राही भाषा में प्रतिपादन किया।
3. न्यूटन का गति विषयक द्वितीय नियम F = \(\frac{d}{d t}\)(mu) केप्लर का खगोलीय पिण्डों की गति का तीसरा नियम T² ∝ r³ भी कुछ सरल, सुन्दर तथा महत्वपूर्ण समीकरण है।
4. नील्स बोर ने परमाणु के कोणीय संवेग को छोटे से सुन्दर समीकरण L = n \(\frac{h}{2 \pi}\) द्वारा दर्शाकर एक विकट समस्या का सरल समाधान प्रस्तुत किया।
5. आइंस्टीन का द्रव्यमान ऊर्जा E = mc² अत्यन्त सरल, गूढ़ सुन्दर एवं आसानी से याद रखने वाला है।
6. डी- ब्रॉग्ली का द्रव्य तरंग के लिए सम्बन्ध λ = \(\frac{h}{p}\) = \(\frac{h}{m u}\) न केवल सरल एवं सुन्दर है, अपितु एक अत्यन्त गूढ़ तथ्य को उजागर करता है कि कण की प्रकृति द्वैती होती है।

प्रश्न 1.16.
विज्ञान की पाठ्य पुस्तकें आपके मन में यह गलत धारणा उत्पन्न कर सकती हैं कि विज्ञान पढ़ना शुष्क तथा पूर्णतः अत्यन्त गंभीर है एवं वैज्ञानिक अन्तर्मुखी, भुलक्कड़ व कभी न हँसने वाले अथवा खीसें निकालने वाले व्यक्ति होते हैं। विज्ञान एवं वैज्ञानिकों का यह चित्रण पूर्णतः आधारहीन है। अन्य समुदाय के मनुष्यों की भाँति ही वैज्ञानिक भी विनोदी होते हैं तथा बहुत से वैज्ञानिकों ने तो वैज्ञानिक कार्यों को गम्भीरता से पूरा करते हुए अत्यन्त विनोदी प्रकृति तथा साहसिक कार्य करके अपना जीवन व्यतीत किया है। गैमो तथा फाइनमैन इसी श्रेणी के दो भौतिकविद हैं। ग्रन्थ सूची में इनके द्वारा रचित पुस्तकें पढ़ने से आपको आनन्द प्राप्त होगा।
उत्तर:
समाज के अन्य व्यक्तियों की भाँति ही वैज्ञानिक भी विनोदी स्वभाव के हँसमुख व्यक्ति होते हैं तथा विज्ञान शुष्क तथा नीरस विषय नहीं है। कुछ विनोदी स्वभाव के भारतीय वैज्ञानिक हैं- होमी जहाँगीर भाभा, डी० एस० कोठारी, सी०वी० रमन, एम०एम० जोशी, ए०पी० जे० अब्दुल कलाम आदि।

Haryana State Board HBSE 11th Class Sanskrit Solutions व्याकरणम् Samasaha Prakaran समास प्रकरण Exercise Questions and Answers.

Haryana Board 11th Class Sanskrit व्याकरणम् समास प्रकरण

समास-परिचय

समास-परस्पर सम्बद्ध अर्थ वाले दो या दो से अधिक पदों को मिलाकर एक पद बनाने की क्रिया को समास कहते हैं। समास प्रक्रिया द्वारा बने हुए एक पद को समस्त पद कहा जाता है। इसमें शब्दों की पहली विभक्तियों का लोप हो जाता है; जैसे-राज्ञः पुरुषः = राजपुरुषः। यहाँ पर समस्त पद राजपुरुषः में ‘राज्ञः’ की विभक्ति का लोप करके राज (न) शब्द का प्रयोग हुआ है।

विग्रह-जब समस्त-पद के सभी शब्दों को अर्थ बोध के लिए अलग-अलग करके उपयुक्त विभक्तियाँ लगा दी जाती हैं तो उसे विग्रह कहते हैं; जैसे-रामलक्ष्मणौ = रामः च लक्ष्मणः च। समास के भेद-

1. अव्ययीभाव समास,
2. तत्पुरुष समास,
3. कर्मधारय समास,
4. द्वन्द्व समास,
5. द्विगु समास,
6. बहुव्रीहि समास। इनकी परिभाषाएँ निम्नलिखित हैं

1. अव्ययीभाव समास:
अव्ययीभाव समास में पूर्व पद का अर्थ प्रधान होता है तथा पूर्व पद अव्यय होता है। उत्तर पद संज्ञा होता है। पूर्व पद तथा उत्तर पद को मिलाकर समस्त पद भी अव्यय बन जाता है तथा वह सदा नपुंसकलिङ्ग, एकवचन में रहता है; जैसे-यथाशक्ति, प्रतिदिनम्।

2. तत्पुरुष समास:
जब उत्तर पद के अर्थ की प्रधानता होती है और समस्त पद का लिङ्ग और वचन उसी के अनुसार होते हैं तो उसे तत्पुरुष समास कहते हैं; जैसे राजपुरुषः में पुरुष के अर्थ की प्रधानता है।

3. कर्मधारय समास:
कर्मधारय ऐसे समास को कहते हैं जिसमें सभी शब्दों का आधार एक ही हो। इसके विग्रह में दोनों पदों में एक ही विभक्ति रहती है। प्रायः इसमें पूर्व पद विशेषण तथा उत्तर पद विशेष्य होता है; जैसे-कृष्णसर्पः।

4. द्वन्द्व समास:
जिस समास में पूर्व पद तथा उत्तर पद की समान रूप से प्रधानता हो, उसे द्वन्द्व समास कहते हैं; जैसे रामलक्ष्मणौ।

5. द्विगु समास:
ऐसा समानाधिकरण तत्पुरुष जिसमें पूर्व पद सङ्ख्यावाची हो, उसे द्विगु समास कहते हैं। इसका प्रयोग प्रायः समाहार या समूह अर्थ में होता है; जैसे-त्रिलोकी।

6. बहुव्रीहि समास:
जिस समास में न तो पूर्व पद प्रधान होता है, न ही उत्तर पद प्रधान होता है अपितु कोई अन्य पद ही प्रधान होता है, उसे बहुव्रीहि समास कहते हैं। बहुव्रीहि समास में दो या अधिक संज्ञा पद होते हैं तथा पदों का समास होने के उपरान्त समस्त पद से किसी अन्य ही संज्ञा का बोध होता है; जैसे-पीताम्बरः।

अव्ययीभाव समास
अव्ययीभाव समास विशेषतः जिन-जिन अर्थों में प्रयुक्त होता है, वे पाणिनि व्याकरण में एक सूत्र में परिगणित किए गए हैं। वे 16 अर्थ हैं-विभक्ति, सामीप्य, समृद्धि, अर्थाभाव, अत्यय, असम्प्रति, शब्द प्रादुर्भाव, पश्चात्, यथा, आनुपूर्व्य, यौगपद्य, सादृश्य, सम्पत्ति, साकल्य तथा अन्त। इन 16 अर्थों में वर्तमान अव्यय का सुबन्त के साथ समास होता है और उस समास को अव्ययीभाव कहते हैं।

प्रश्न-निम्नलिखित समस्त पदों का विग्रह करके समास का नाम लिखिए।

तत्पुरुष समास
जिस समास में उत्तर पद प्रधान होता है वह तत्पुरुष समास कहलाता है। यथा राज्ञः पुरुष = राजपुरुषः। यहाँ उत्तर पद ‘पुरुष’ की प्रधानता है, अतः यह तत्पुरुष समास हुआ।

तत्पुरुष समास के भेद-

1. व्यधिकरण,
2. समानाधिकरण तथा कर्मधारय तथा द्विगु तत्पुरुष।

कर्मधारय तथा द्विगु तत्पुरुष को समास के मुख्य भेदों में भी मान लिया जाता है। अतः यहाँ केवल व्यधिकरण तत्पुरुष का . ही विचार किया जाएगा।

व्यधिकरण तत्पुरुष व्यधिकरण तत्पुरुष के पुनः चार भेद हैं

1. विभक्ति तत्पुरुष,
2. अलुक् तत्पुरुष,
3. नञ् तत्पुरुष,
4. उपपद तत्पुरुष।

1. विभक्ति तत्पुरुष-विभक्ति तत्पुरुष के पुनः छः भेद हैं द्वितीया तत्पुरुष, तृतीया तत्पुरुष, चतुर्थी तत्पुरुष, पञ्चमी तत्पुरुष, षष्ठी तत्पुरुष तथा सप्तमी तत्पुरुष।

द्वितीया तत्पुरुष
द्वितीय तत्पुरुष समास में, विग्रह पूर्वपद द्वितीया विभक्ति में होता है तथा उत्तर पद में प्रायः निम्नलिखित पद रहते हैं श्रित, अतीत, पतित, गत, अत्यय, प्राप्त, आपन्न; जैसे

तृतीया तत्पुरुष
कर्त्ता और करण कारक में विद्यमान ततीया विभक्ति वाले शब्द का समान कृदन्त शब्द के साथ समास होता है; जैसे-

ततीयान्त शब्दों का खण्ड, अर्थ, पूर्व, अवर, सदृश, सम, अन, निपुण, मिश्र आदि से भी समास होता है; जैसे-

चतुर्थी तत्पुरुष
चतुर्थी विभक्ति वाले शब्दों का तदर्थ, अर्थ, बलि, हित, सुख, रक्षित आदि के साथ समास होता है; जैसे-

पञ्चमी तत्पुरुष
पञ्चमी विभक्ति अन्त वाले शब्दों का भयवाचक शब्दों (यथा भयम्, भी) के साथ तथा अपेत, मुक्त, पतित, भ्रष्ट आदि शब्दों के साथा समास होता है; जैसे-

षष्ठा तत्पुरुष
षष्ठी विभक्ति वाले शब्द का उत्तर पद के साथ समास होने से षष्ठी तत्पुरुष कहलाता है; जैसे-

सप्तमी तत्पुरुष
सप्तमी विभक्ति वाले शब्दों का जब अन्य शौण्ड, धूर्त, प्रवीण, निपुण आदि शब्दों के साथ समास होता है, तब उसे सप्तमी तत्पुरुष कहते हैं; जैसे-

अलुक् तत्पुरुष
विभक्ति का लोप न होने पर अलुक् तत्पुरुष समास होता है; जैसे-

नज् तत्पुरुष
निषेध के अर्थ को बताने के लिए नज् शब्द का किसी भी शब्द के साथ समास हो जाता है। यदि उत्तर पद का प्रथम वर्ण व्यंजन हो तो ‘नज्’ का ‘अ’ शेष रह जाता है; जैसे-न (ज्ञ) + विद्या = अविद्या।

उपपद तत्पुरुष
जब तत्पुरुष समास में किसी पद के पहले रहने के कारण किसी धातु से कोई कृत् प्रत्यय होता है, तब प्रथम पद को उपपद कहते हैं और दोनों पदों के समास को ‘उपपद तत्पुरुष’ कहते हैं; जैसे-

प्रादि तत्पुरुष
जिस समस्त पद का पूर्व भाग उपसर्ग (प्रादि) हो, उसे प्रादि तत्पुरुष कहते हैं; जैसे-

गति तत्पुरुष
कुछ शब्दों के अनन्तर क्रिया से बने अव्यय लगने पर जो तत्पुरुष समास होता है, उसे गति तत्पुरुष कहते हैं; जैसे-

कर्मधारय तत्पुरुष
कर्मधारय ऐसे समास को कहते हैं जिसमें सभी शब्दों का आधार एक ही हो। इसके विग्रह वाक्य में दोनों पदों में एक ही विभक्ति रहती है। प्रायः इसमें पूर्व पद विशेषण होता है और उत्तर पद विशेष्य होता है; जैसे-

यदि विशेषण-विशेष्य के स्थान पर पूर्व पद तथा उत्तर पद परस्पर उपमान उपमेय हों तो भी कर्मधारय समास होता है; जैसे-

द्विगु समास
यदि कर्मधारय समास का पूर्व पद सड्ख्यावाची शब्द हो तो वह द्विगु समास कहलाता है; जैसे-

द्वन्द समास
जिस समास में उभय पद (दोनों पदों) की प्रधानता होती है, उसे द्वन्द्व समास कहते हैं। द्वन्द्व समास के तीन भेद होते हैं-
(क) इतरेतर द्वन्द्ध,
(ख) समाहार द्वन्द,
(ग) एकशेष द्वन्द्व।

(क) इतरेतर द्वन्द्ध :
जहाँ सभी पद प्रधान भी होते हैं तथा अपना अस्तित्व भी बनाए रखते हैं और अन्त में सड्ख्या के अनुसार वचन होता है, उसे इतरेतर द्वन्द्व कहते हैं, जैसे-

(ख) समाहार द्वन्द्ध :
इसमें प्रत्येक पद की प्रधानता नहीं होती, अपितु उसमें एक सामूहिक अर्थ प्रकट होता है। यह समास सदा एकवचन और नपुंसकलिङ्ग में होता है; जैसे-

(ग) एकशेष द्वन्द:
जहाँ द्वन्द्व समास में केवल एक ही शब्द शेष रहे, वहाँ एकशेष द्वन्द्ध होता है; जैसे-

बहुव्रींहि समास
जिस समास में न तो पूर्व पद प्रधान होता है न उत्तर पद प्रधान होता है अपितु कोई अन्य पद ही प्रधान होता है, उसे बहुव्रीहि समास कहते हैं। बहुव्रीहि समास में दो या अधिक संज्ञा पद होते हैं तथा पदों का समास होने के उपरान्त समस्त पद से किसी अन्य ही संज्ञा का बोध होता है; जैसे-

प्रश्न:
निम्नलिखित विग्रह किए गए पदों के समस्त पद बनाकर समास का नाम लिखिए।

अभ्यासार्थ प्रश्नाः

I. 1. अव्ययीभाव समासस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
2. कर्मधारय समासस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
3. द्वन्द्व समासस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
4. तत्पुरुष समासस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
5. बहुव्रीहि समासस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।

II. अधोलिखित प्रश्नानां प्रदत्तोत्तरविकल्पेषु शुद्धविकल्पं लिखत
(निम्नलिखित प्रश्नों के दिए गए विकल्पों में से शुद्ध विकल्प लिखिए)

1. ‘देवहितम् अत्र कः समासः?
(A) अव्ययीभावः
(B) कर्मधारयः
(C) तत्पुरुषः
(D) द्वन्द्वः

2. ‘निर्मान’ अत्र कः समासः?
(A) कर्मधारयः
(B) अव्ययीभावः
(C) बहुव्रीहिः
(D) द्वन्द्वः

3. ‘अम्बरस्थः’ अत्र कः समासः?
(A) द्वन्द्वः
(B) द्विगुः
(C) कर्मधारयः
(D) तत्पुरुषः

4. ‘मृच्छकटिकम्’ अत्र कः समासः?
(A) तत्पुरुषः
(B) कर्मधारयः
(C) बहुव्रीहिः
(D) द्वन्द्वः

5. ‘प्रत्यहम्’ इति पदे कः समासः ?
(A) तत्पुरुषः
(B) अव्ययीभावः
(C) द्वन्द्वः
(D) कर्मधारयः

6. ‘महार्णवः’ इत्यस्य समास विग्रहः अस्ति
(A) महान् च असौ अर्णवः
(B) महत् च अर्णवः
(C) महान् च अर्णवः
(D) महान् च असः अर्णवः

7. ‘अहनि अहनि प्रति’ अत्र किं समस्तपदम्?
(A) प्रत्यहन्
(B) प्रतिहनि
(C) प्रत्यहः
(D) प्रत्यहम्

8. ‘सुवर्णव्यवहारः’ इति समस्तपदस्य विग्रहः अस्ति ?
(A) सुवर्णस्य व्यवहारः
(B) वर्ण व्यवहार
(C) सुवर्ण व्यवहारः
(D) सुवर्ण व्यवहारः

9. ‘भारतानां माता’ इत्यस्य समस्तपदम् अस्ति
(A) भारतांमाता
(B) भारतमाता
(C) भारतानमाता
(D) भारतान्माता

10. ‘अविरुद्धम्’ अत्र किं नाम समासः?
(A) तत्पुरुषः
(B) द्वन्द्व
(C) द्विगुः
(D) नब् तत्पुरुषः

11. ‘यथापूर्वम्’ इति पदे कः समासः?
(A) तत्पुरुषः
(B) द्विगुः
(C) अव्ययीभावः
(D) द्वन्द्वः

12. ‘सुवर्णव्यवहारः’ इति समस्तपदस्य विग्रहः अस्ति?
(A) सुवर्णस्य व्यवहारः
(B) सुवर्ण व्यवहार
(C) सौवर्ण व्यवहार
(D) सुवर्ण व्यवहारे

Haryana State Board HBSE 11th Class Sanskrit Solutions व्याकरणम् karak Prakaran कारक-प्रकरण Exercise Questions and Answers.

Haryana Board 11th Class Sanskrit व्याकरणम् कारक-प्रकरण

कारक
जब हम कोई वाक्य बोलते हैं, तो उसमें कोई-न-कोई क्रिया अवश्य होती है। बिना क्रिया का कोई वाक्य नहीं होता। उस क्रिया के कई कारण होते हैं जिनके होने से उस क्रिया का होना सम्भव होता है। क्रिया के उन कारणों को ही ‘कारक’ कहते हैं। ये कारक ही क्रिया को सिद्ध करते हैं-‘क्रिया निवर्तकं कारकम् । ‘रमेश उद्यान में वृक्ष से छड़ी से सुरेश के लिए फल ‘तोड़ता है।’

यह क्रिया पद है। ‘तोड़ना’ क्रिया के कारण (साधक) छः है। रमेश, उद्यान, वृक्ष, छड़ी, सुरेश और फल। इनमें रमेश ‘कर्ता’ कारक है। उद्यान ‘अधिकरण’ कारक है। वृक्ष ‘अपादान’ कारक है। छड़ी ‘करण’ कारक है। सुरेश ‘सम्प्रदान’ कारक है और फल ‘कर्म’ कारक है। ये छः ही ‘तोड़ना’ क्रिया के कारक हैं।

इन छः कारकों के अतिरिक्त भी वाक्य में एक वस्तु रहती है-उसे ‘सम्बन्ध’ कहते हैं। मनोज पवन के बाग में पेड़ से……..। इस प्रकार बाग के किसी स्वामी का कथन किया जा सकता है, किन्तु क्योंकि पवन अथवा किसी अन्य स्वामी का तोड़ने की क्रिया में कारणत्व अपेक्षित नहीं होता है, अतः उसे कारक नहीं माना जाता है।

दूसरे शब्दों में कहा जा सकता है कि जिसका क्रिया से सीधा सम्बन्ध रहता है, उसे ‘कारक’ कहते हैं और जिसका क्रिया से कोई सीधा सम्बन्ध नहीं है, वह कारक न होकर केवल ‘सम्बन्ध’ कहलाता है। इस प्रकार छः कारक और सम्बन्ध ये कुल सात चीजें हैं। विभक्तियों की दृष्टि से इन सातों को इस क्रम से लिखा जा सकता है। कर्ता, कर्म, करण, सम्प्रदान, अपादान, सम्बन्ध और अधिकरण। उन्हें निम्नलिखित प्रकार से देखा जा सकता है

1. प्रथमा विभक्ति (कर्ता कारक):
जो काम करने वाला होता है, उसमें प्रथमा विभक्ति का प्रयोग होता है; जैसे- रामः गच्छति। इस वाक्य में राम जाने की क्रिया का कर्ता है; इसलिए इसमें प्रथमा विभक्ति का प्रयोग किया गया है। हिन्दी में इसका चिह्न ‘ने’ होता है, किन्तु कहीं-कहीं वह चिह्न भाषा में प्रयुक्त नहीं होती; जैसे- राम घर गया। इस वाक्य में ने का प्रयोग नहीं हुआ है।

2. द्वितीया विभक्ति (कर्म कारक):
क्रिया के सम्पादन में कर्ता का जो अभीष्टतम (अत्यधिक इच्छित) होता है, वह कर्म कारक होता है। उसमें द्वितीया विभक्ति का प्रयोग होता है, जैसे- रामः वनं गच्छति (राम वन को जाता है।) इस वाक्य में राम कर्ता का अभीष्टतम कर्म है ‘वन जाना’ इसलिए इसमें द्वितीया विभक्ति का प्रयोग किया गया है। हिन्दी में इसका चिह्न ‘को’ होता है। किन्तु उसका भाषा में कई स्थानों पर प्रयोग नहीं होता अर्थात् वह चिह्न कहीं-कहीं प्रकट रूप में नहीं होता प्रच्छन्न रूप में गुप्त रूप होता है; जैसे- राम खाना खाता है। यहाँ पर हिन्दी में राम खाने को खाता है। ऐसा प्रयोग नहीं किया गया है।

3. ततीया विभक्ति (करण कारक):
जिसकी सहायता से कार्य निष्पन्न होता है या जो कार्य की निष्पत्ति में सहायक होता है, उसे करण कारक कहते हैं, जैसे- रामः हस्तेन लिखति। (राम हाथ से लिखता है) राम लेखन का कार्य हाथ से करता है। हाथ लेखन कार्य में सहायक है, अतः यहाँ तृतीया विभक्ति का प्रयोग किया गया है। तृतीया विभक्ति के लिए हिन्दी भाषा में ‘से’ या. ‘द्वारा’ चिह्नों का प्रयोग होता है।

4. चतुर्थी विभक्ति (सम्प्रदान कारक):
जिसको कोई वस्तु दी जाती है या जिसके लिए कोई कार्य किया जाता है, वह सम्प्रदान – कारक कहलाता है। इसके लिए चतुर्थी विभक्ति का प्रयोग किया जाता है; जैसे- मोहनः रामाय पुस्तकं ददाति (राम मोहन को किताब देता है) इसके लिए हिन्दी में ‘को’ या ‘के लिए’ चिह्नों का प्रयोग किया जाता है।

5. पञ्चमी विभक्ति (अपादान कारक):
जब किसी एक वस्तु का किसी अन्य वस्तु से अलग होना पाया जाए तो जिस वस्तु या स्थान से वियोग होता है, उसे अपादान कारक कहते हैं और उसमें पञ्चमी विभक्ति का प्रयोग किया जाता है, जैसे- सः प्रयागत् आगच्छति (वह प्रयाग से आता है) इसके लिए हिन्दी भाषा के ‘से’ चिह्न का प्रयोग किया जाता है।

6. षष्ठी विभक्ति (सम्बन्ध):
(इसे कारक नहीं माना जाता) जिसका किसी अन्य के साथ सम्बन्ध पाया जाता है, उसमें षष्ठी विभक्ति का प्रयोग होता है। इसके लिए हिन्दी में आवश्यकता के अनुसार का, की, के तथा रा, री, रे चिहनों का प्रयोग किया जाता है; जैसे- रामस्य भ्राता (राम का भाई) रामस्य भगिनी (राम की बहन) रामस्य भ्रातरः (राम के भाई) तव भ्राता (तेरा भाई) तव भगिनी (तेरी बहन) तव भ्रातरः (तेरे भाई) इत्यादि।

7. सप्तमी विभक्ति:
किसी वस्तु के आधार को अधिकरण कहते हैं अर्थात् जिसमें कोई वस्तु रखी जाए, उसे आधार कहते हैं। आधार ही अधिकरण कारक कहलाता है। इसमें सप्तमी विभक्ति का प्रयोग किया जाता है। इसके लिए हिन्दी में में’ और ‘पर’ चिहनों का प्रयोग होता है। जैसे- ‘आकाशे मेघाः गर्जन्ति’। (आसमान में बादल गरजते हैं।) यहाँ बादलों का आधार अधिकरण है। इसलिए इसमें सप्तमी विभक्ति का प्रयोग है। कारकों के अन्तर्गत ही उपपद विभक्ति को परिगणित किया जाता है।

उपपद विभक्ति

किसी दूसरे के पद के समीप आ जाने के कारण जिस विभक्ति का प्रयोग किया जाता है, उसे उपपद विभक्ति कहते हैं; जैसे- रामः देवेन सह विद्यालयं गच्छति। इस वाक्य में ‘सह’ के प्रयोग के कारण तृतीया विभक्ति आई है। अतः यह उपपद विभक्ति है। उपपद विभक्ति के लिए कारकों का ज्ञान अनिवार्य है। अतः उनका परिचय प्रस्तुत किया जा रहा है।

1. प्रथमा विभक्ति
सामान्यतया कर्तवाच्य के कर्ता में प्रथमा विभक्ति का प्रयोग होता है; जैसे–रामः गृहं गच्छति (राम घर जाता है)। यहाँ ‘राम’ कर्ता है। इसलिए उसमें प्रथमा विभक्ति का प्रयोग किया गया है। इसके अतिरिक्त निम्नलिखित स्थानों पर प्रथमा विभक्ति होती है

(क) सम्बोधन में प्रथमा विभक्ति का प्रयोग होता है; जैसे-
हे बालकाः! यूयं कुत्र गच्छथ? (हे बालको! तुम कहाँ जाते हो?)

(ख) कर्मवाच्य के कर्म में प्रथमा विभक्ति होती है; जैसे-
मया पाठः पठ्यते। (मेरे द्वारा पाठ पढ़ा जाता है।)
यहाँ ‘पाठ’ में प्रथमा विभक्ति का प्रयोग किया गया है।

2. द्वितीया विभक्ति
सामान्यतया कर्तृवाच्य में कर्ता में द्वितीया विभक्ति का प्रयोग होता है; जैसे-रामः वनं गच्छति (राम वन को जाता है)। यहाँ ‘वन’ कर्म है। इसलिए उसमें द्वितीया विभक्ति का प्रयोग हुआ है। इसके अतिरिक्त निम्नलिखित स्थानों पर द्वितीया विभक्ति का प्रयोग होता है

(क) अधि + शी (सोना), अधि + स्था (बैठना या रहना), अधि + आस् (बैठना) धातुओं के योग में द्वितीया विभक्ति होती है; जैसे-

• सः पर्यङ्कमधिशेते। (वह पलंग पर सोता है।)
• राजा सिंहासनमधितिष्ठति। (राजा सिंहासन पर बैठता है।)
• पुरोहितः आसनमध्यास्ते। (पुरोहित आसन पर बैठता है।)

(ख) प्रति, अनु, विना, परितः, सर्वतः, उभयतः, अभितः, धिक् इत्यादि के योग में अर्थात् इन शब्दों का प्रयोग हो तो द्वितीया विभक्ति होती है।

• प्रति (की ओर)-कृष्णः पाठशाला प्रति गच्छति। (कृष्ण पाठशाला की ओर जाता है।)
• अनु (पीछे) मातरमनुगच्छति पुत्रः। (पुत्र माता के पीछे जाता है।)
• विना (बिना)-दानं विना मुक्तिः नास्ति। (दान के बिना मुक्ति नहीं होती।)
• परितः (चारों ओर)-नगरं परितः उपवनानि सन्ति। (नगर के चारों ओर बाग है।)
• सर्वतः (सब ओर)-ग्रामं सर्वतः जलं वर्तते। (गाँव में सब ओर जल है।)
• उभयतः (दोनों ओर) गृहमुभयतः वृक्षाः सन्ति। (घर के दोनों ओर वृक्ष हैं।)
• अभितः (दोनों ओर)-ग्रामम् अभितः नदी वहति। (गाँव के दोनों ओर नदी बहती है।)
• धिक् (धिक्कार)-धिक तम् दुर्जनम्। (दुर्जन को धिक्कार है।)

3. ततीया विभक्ति
जिस साधन के द्वारा कर्ता क्रिया को सिद्ध करता है, उस साधन में ततीया विभक्ति का प्रयोग होता है। इसे करण कारक भी कहते हैं; जैसे-रामः हस्तेन लिखति (राम हाथ से लिखता है)। यहाँ पर राम द्वारा लिखने की क्रिया हाथ से बताई गई है। इसलिए लिखने के साधन ‘हाथ’ में तृतीया विभक्ति का प्रयोग किया गया है। इसके अतिरिक्त निम्नलिखित स्थानों पर भी तृतीया विभक्ति का प्रयोग होता है

(क) कर्मवाच्य तथा भाववाच्य के कर्ता में तृतीया विभक्ति होती है; जैसे-
कर्मवाच्य में रामेण रावणः हन्यते। (राम के द्वारा रावण को मारा जाता है।)
भाववाच्य में रामेण हस्यते। (राम के द्वारा हँसा जाता है।)

(ख) ‘प्रकृति’ इत्यादि शब्दों के योग में तृतीया विभक्ति होती है; जैसे-
रामः प्रकृत्या विनीतः। (राम स्वभाव से नम्र है।)
मोहनः स्वभावेन क्रूरः। (मोहन स्वभाव से क्रूर है।)

(ग) किसी शरीर के अंग-विकार में तृतीया विभक्ति होती है; जैसे-
सुरेशः नेत्रेण काणः अस्ति। (सुरेश आँख से काना है।)

(घ) सह, साकम, सार्धम्, अलम, हीनः शब्दों के योग में तृतीया विभक्ति का प्रयोग होता है

• सह (साथ) देवेन सह कृष्णः गच्छति। (देव के साथ कृष्ण जाता है।)
• साकम् (साथ) त्वया साकम् अन्यः कः आगमिष्यति? (तुम्हारे साथ अन्य कौन आएगा?)
• सार्धम् (साथ) मया सार्धम् कविता पठ। (मेरे साथ कविता पढ़ो।)
• अलम् (बस)-अलम् प्रलापेन! (प्रलाप मत करो!)
• हीनः (रहित) नरः विद्याहीनः न शोभते। (विद्या से रहित मनुष्य शोभा नहीं पाता।)

4. चतुर्थी विभक्ति
सामान्यतया सम्प्रदान में चतुर्थी विभक्ति होती है अर्थात् जिसको कुछ दिया जाए, उसमें चतुर्थी विभक्ति का प्रयोग होता है; जैसे–रामः कृष्णाय धनं यच्छति (राम कृष्ण को धन देता है)। यहाँ कृष्ण को धन देने की बात कही गई है। इसलिए ‘कृष्ण’ में चतुर्थी विभक्ति का प्रयोग किया गया है
इसके अतिरिक्त निम्नलिखित स्थानों पर चतुर्थी विभक्ति का प्रयोग होता है।

(क) नमः, स्वस्ति, स्वाहा के योग में चतुर्थी विभक्ति होती है

• नमः (नमस्कार)-देवाय नमः। (देवता को नमस्कार हो।)
• स्वस्ति (कल्याण) सर्वेभ्यः स्वस्ति अस्तु। (सबका कल्याण हो।)
• स्वाहा (आहुति डालना)-रुद्राय स्वाहा। (रुद्र के लिए स्वाहा ।)

(ख) रुच्, द्रुह् धातुओं के योग में चतुर्थी विभक्ति आती है।

• मह्यं क्षीरं रोचते। (मुझे दूध अच्छा लगता है।)
• रामः मह्यं द्रुह्यति। (राम मुझसे द्रोह करता है।)

5. पञ्चमी विभक्ति
सामान्यतया (अपादान) अलग होने के अर्थ में पञ्चमी विभक्ति का प्रयोग होता है; जैसे–अहं गृहात् आगच्छामि (मैं घर से आता हूँ)। यहाँ ‘घर’ (जहाँ से मैं आता हूँ, में अपादान है। इसलिए उसमें पञ्चमी विभक्ति का प्रयोग किया गया है। इसके अतिरिक्त अग्रलिखित स्थानों पर पञ्चमी विभक्ति का प्रयोग होता है-

(क) पूर्व, ऋते, प्रभृति, बहिर्, ऊर्ध्वम् के योग में पञ्चमी विभक्ति आती है।

• पूर्व (पहले) मोहनः दश वादनात् पूर्व पाठशालां गच्छति। (मोहन दस बजे से पहले पाठशाला जाता है।)
• ऋते (बिना) ऋते धनात् न सुखम्। (धन के बिना सुख नहीं।)
• प्रभृति (से लेकर)-जन्मनः प्रभृति स्वामी दयानन्दः ब्रह्मचारी आसीत् । (जन्म से लेकर स्वामी दयानन्द ब्रह्मचारी थे।)
• बहिर् (बाहर)-ग्रामात् बहिर् उद्यानम् अस्ति। (गाँव से बाहर बगीचा है।)
• ऊर्ध्वम् (ऊपर)-भूमे ऊर्ध्वम् स्वर्गं वर्तते। (भूमि के ऊपर स्वर्ग है।)

(ख) जुगुप्सा, विराम तथा प्रमादसूचक शब्दों के योग में पञ्चमी विभक्ति होती है।

• जुगुप्सा (घृणा)-सत्पुरुषः पापात् जुगुप्सते। (सज्जन पाप से घृणा करते हैं।)
• विरम (अनिच्छा) रामः अध्ययनात् विरमति। (राम अध्ययन से अनिच्छा करता है।)
• प्रमाद (विमुखता) स धर्मात् प्रमादयति। (वह धर्म से विमुखता करता है।)

(ग) जिससे भय होता है तथा जिससे रक्षा की जाए, उसमें पञ्चमी विभक्ति होती है।

• बालकः कुक्कुरात् बिभेति। (बालक कुत्ते से डरता है।)
• ईश्वरः मां पापात् रक्षति। (ईश्वर मुझे पाप से बचाता है।)

(घ) निवारण करना (रोकना) अर्थ वाली धातुओं के योग में पञ्चमी विभक्ति होती है।

• मोहनः स्वमित्रं पापात् निवारयति। (मोहन अपने मित्र को पाप से रोकता है।)
• कृषकः यवेभ्यः गां निवारयति। (किसान गाय को यवों से रोकता है।)

6. षष्ठी विभक्ति
सामान्यतया जिसका किसी से सम्बन्ध बताया जाए, उसमें षष्ठी विभक्ति होती है; जैसे- राज्ञः पुरुषः (राजा का पुरुष)। यहाँ पर ‘राजा’ का ‘पुरुष’ के साथ सम्बन्ध बताया गया है। इसलिए यहाँ षष्ठी विभक्ति का प्रयोग किया गया है। इसके अतिरिक्त निम्नलिखित स्थानों पर षष्ठी विभक्ति का प्रयोग होता है।

(क) ‘हेतु’ शब्द का प्रयोग होने पर षष्ठी विभक्ति का प्रयोग होता है; जैसे-
पठनस्य हेतोः सोऽत्र वसति। (पढ़ने के लिए यह यहाँ रहता है।)

(ख) अधि + इ (पढ़ना), स्मृ (स्मरण करना) के योग में षष्ठी विभक्ति होती है।

• शिष्यः गुरोरधीते। (शिष्य गुरु से पढ़ता है।)
• बालकः मातुः स्मरति। (बालक माता को स्मरण करता है।)

(ग) ‘तुल्य’ अर्थ वाले सम, सदृश इत्यादि शब्दों के योग में षष्ठी तथा तृतीया विभक्तियाँ होती है।

• तुल्य (समान)-देवः जनकस्य (जनकेन) तुल्यः । (देव पिता के समान है।)
• सदृश (समान)-सा मातुः (मात्रा) सदृशी अस्ति। (वह माता के समान है।)

7. सप्तमी विभक्ति
अधिकरण कारक में सप्तमी विभक्ति होती है। आधार को अधिकरण कहते हैं अर्थात् जो जिसका आधार होता है, उसमें सप्तमी विभक्ति होती है; जैसे–वृक्षे काकः तिष्ठति (पेड़ पर कौआ बैठा है)। इसके अतिरिक्त निम्नलिखित स्थानों पर सप्तमी विभक्ति होती है (क) जिस वस्तु में इच्छा होती है, उसमें सप्तमी विभक्ति होती है। तस्य मोक्षे इच्छा अस्ति। (उसकी मोक्ष में इच्छा है।) ) स्निह (स्नेह करना) धातु के योग में सप्तमी विभक्ति होती है। माता पुत्रे स्निह्यति। (माता पुत्र पर स्नेह करती है।) (ग) युक्तः, व्यापृतः, तत्परः, निपुणः, कुशलः इत्यादि शब्दों के योग में सप्तमी विभक्ति होती है।

• युक्तः (नियुक्त)-सः अस्मिन् कार्ये नियुक्तोऽस्ति। (वह इस काम में नियुक्त है।)
• व्यापृतः (संलग्न) मोहनः निजकार्ये व्यापृतः अस्ति। (मोहन अपने काम में संलग्न है।)
• तत्परः (प्रवृत्त)सः पठने तत्परः अस्ति। (वह पढ़ने में प्रवृत्त है।) ।
• निपुणः (निपुण)-रामः शिक्षणे निपुणः अस्ति। (राम शिक्षण में निपुण है।)
• कुशलः (दक्ष) देवः अध्ययने कुशलः अस्ति। (देव अपने अध्ययन में दक्ष है।)

संस्कृत के पाँच लकारों में वाक्य प्रयोग

1. लट् लकार (वर्तमान काल)

(1) प्रथम पुरुष

पुंल्लिंग

1. वह पढ़ता है – सः पठति।
2. वे दो पढ़ते हैं – तौ पठतः।
3. वे सब पढ़ते हैं – ते पठन्ति ।
4. आप पढ़ते हैं – भवान् पठति।
5. आप दो पढ़ते हैं – भवन्तौ पठतः।
6. आप सब पढ़ते हैं – भवन्तः पठन्ति।
7. राम पढ़ता है – रामः पठति।
8. राम और श्याम पढ़ते हैं – रामः श्यामः च पठतः। ।
9. राम, श्याम और कृष्ण पढ़ते हैं – रामः, श्यामः कृष्णः च पठन्ति।

स्त्रीलिंग

1. वह पढ़ती है – सा पठति।
2. वे दो पढ़ती हैं – ते पठतः।
3. वे सब पढ़ती हैं – ताः पठन्ति।
4. आप पढ़ती हैं – भवती पठति।
5. आप दो पढ़ती हैं – भवत्यौ पठतः।
6. आप सब पढ़ती हैं – भवत्यः पठन्ति।
7. रमा पढ़ती है – रमा पठति।
8. रमा और सीता पढ़ती हैं – रमा सीता च पठतः।
9. रमा, सीता और राधा पढ़ती हैं – रमा, सीता राधा च पठन्ति।

नपुंसकलिंग

1. फूल गिरता है – पुष्पं पतति।
2. दो फूल गिरते हैं – पुष्पे पततः।
3. बहुत से फूल गिरते हैं – पुष्पाणि पतन्ति।

(ii) मध्यम पुरुष

1. तुम पढ़ते हो, तू पढ़ता है – त्वम् पठसि।
2. तुम दोनों पढ़ते हो – युवाम् पठथः।
3. तुम सब पढ़ते हो – यूयम् पठथ।

(iii) उत्तम पुरुष

1. मैं पढ़ता हूँ – अहम् पठामि।
2. हम दोनों पढ़ते हैं – आवाम् पठावः।
3. हम सब पढ़ते हैं – वयम् पठामः।

2. लङ् लकार (भूतकाल)

(1) प्रथम पुरुष

पुंल्लिंग-

1. उसने पढ़ा – सः अपठत्।
2. उन दोनों ने पढ़ा – तौ अपठताम्।
3. उन सबने पढ़ा – ते अपठन्।
4. आपने पढ़ा – भवान् अपठत्।
5. आप दोनों ने पढ़ा – भवन्तौ अपठताम्।
6. आप सबने पढ़ा – भवन्तः अपठन्।
7. राम ने पढ़ा – रामः अपठत्।
8. राम और श्याम ने पढ़ा – रामः श्यामः च अपठताम्।
9. राम, श्याम और कृष्ण ने पढ़ा – रामः श्यामः कृष्णः च अपठन्।

स्त्रीलिंग-

1. वह पढ़ी – सा अपठत्।
2. वे दोनों पढ़ी – ते अपठताम्।
3. वे सब पढ़ी – ताः अपठन्।
4. आप पढ़ी – भवती अपठत्।
5. आप दोनों पढ़ी – भवत्यौ अपठताम्।
6. आप सब पढ़ी – भवत्यः अपठन्।
7. रमा पढ़ी – रमा अपठत्।
8. रमा और सीता पढ़ी – रमा सीता च अपठताम्।
9. रमा, सीता और राधा पढ़ती हैं – रमा, सीता राधा च अपठन्।

नपुंसकलिंग-

1. फूल गिरता है – पुष्पम् अपतत्।
2. दो फूल गिरे – पुष्पे अपतताम्।
3. बहुत से फूल गिरे – पुष्पाणि अपतन्।

(ii) मध्यम पुरुष

1. तुमने पढ़ा, तूने पढ़ा – त्वम्, अपठः।
2. तुम दोनों ने पढ़ा – युवाम् अपठतम्।
3. तुम सबने पढ़ा – यूयम् अपठत्।

(iii) उत्तम पुरुष

1. मैंने पढ़ा – अहम् अपठम्।
2. हम दोनों ने पढ़ा – आवाम् अपठाव।
3. हम सबने पढ़ा – वयम् अपठाम।

3. लृट् लकार (भविष्यत् काल)

(1) प्रथम पुरुष

पुंल्लिंग-

1. वह पढ़ेगा – सः पठिष्यति।
2. वे दो पढ़ेंगे – तौ पठिष्यतः।
3. वे सब पढ़ेंगे – ते पठिष्यन्ति।
4. आप पढ़ेंगे – भवान् पठिष्यति।

(i) प्रथम पुरुष

पुंल्लिंग-

1. उसने पढ़ा – सः अपठत्।
2. उन दोनों ने पढ़ा – तौ अपठताम्।
3. उन सबने पढ़ा – ते अपठन्।
4. आपने पढ़ा – भवान् अपठत्।
5. आप दोनों ने पढ़ा – भवन्तौ अपठताम्।
6. आप सबने पढ़ा – भवन्तः अपठन्।
7. राम ने पढ़ा – रामः अपठत्।
8. राम और श्याम ने पढ़ा – रामः श्यामः च अपठताम्।
9. राम, श्याम और कृष्ण ने पढ़ा – रामः श्यामः कृष्णः च अपठन्।

स्त्रीलिंग

1. वह पढ़ी – सा अपठत्।
2. वे दोनों पढ़ी – ते अपठताम्।
3. वे सब पढ़ी – ताः अपठन्।
4. आप पढ़ी – भवती अपठत्।
5. आप दोनों पढ़ी – भवत्यौ अपठताम्।
6. आप सब पढ़ी – भवत्यः अपठन्।
7. रमा पढ़ी – रमा अपठत्।
8. रमा और सीता पढ़ी – रमा सीता च अपठताम्।
9. रमा, सीता और राधा पढ़ती हैं – रमा, सीता राधा च अपठन्।

नपुंसकलिंग-

1. फूल गिरता है – पुष्पम् अपतत्।
2. दो फूल गिरे – पुष्पे अपतताम्।
3. बहुत से फूल गिरे – पुष्पाणि अपतन्।

(ii) मध्यम पुरुष

1. तुमने पढ़ा, तूने पढ़ा – त्वम्, अपठः।
2. तुम दोनों ने पढ़ा – युवाम् अपठतम्।
3. तुम सबने पढ़ा – यूयम् अपठत्।

(iii) उत्तम पुरुष

1. मैंने पढ़ा – अहम् अपठम्।
2. हम दोनों ने पढ़ा – आवाम् अपठाव।
3. हम सबने पढ़ा – वयम् अपठाम।

3. लृट् लकार (भविष्यत् काल)

(i) प्रथम पुरुष

पुल्लिंग-

1. वह पढ़ेगा – सः पठिष्यति।
2. वे दो पढ़ेंगे – तौ पठिष्यतः।
3. वे सब पढ़ेंगे – ते पठिष्यन्ति।
4. आप पढ़ेंगे – भवान् पठिष्यति।
5. आप दो पढ़ेंगे – भवन्तौ पठिष्यतः।
6. आप सब पढ़ेंगे – भवन्तः पठिष्यन्ति।
7. राम पढ़ेगा – रामः पठिष्यति।
8. राम और श्याम पढ़ेंगे – रामः श्यामः च पठिष्यतः।
9. राम, श्याम और कृष्ण पढ़ेंगे – रामः श्यामः कृष्णः च पठिष्यन्ति।

स्त्रीलिग-

1. वह पढ़ेगी – सा पठिष्यति।
2. वे दो पढ़ेंगी – ते पठिष्यतः।
3. वे सब पढ़ेंगी – ताः पठिष्यन्ति।
4. आप पढ़ेंगी – भवती पठिष्यति।
5. आप दो पढ़ेंगी – भवत्यौ पठिष्यतः।
6. आप सब पढ़ेंगी – भवत्यः पठिष्यन्ति।
7. रमा पढ़ेगी – रमा पठिष्यति।
8. रमा और सीता पढ़ेंगी – रमा सीता च पठिष्यतः।
9. रमा, सीता और राधा पढ़ेंगी – रमा सीता राधा च पठिष्यन्ति।

नपुंसकलिंग-

1. फूल गिरेगा – पुष्पं पतिष्यति।
2. दो फल गिरेंगे – पुष्पे पतिष्यतः।
3. बहुत से फूल गिरेंगे – पुष्पाणि पतिष्यन्ति।

(ii) मध्यम पुरुष

1. तुम पढ़ोगे, तू पढ़ेगा – त्वम् पठिष्यसि।
2. तुम दोनों पढ़ोगे – युवाम् पठिष्यथः।
3. तुम सब पढ़ोगे – यूयम् पठिष्यथ।

(iii) उत्तम पुरुष

1. मैं पढूंगा – अहम पठिष्यामि।
2. हम दो पढ़ेंगे – आवाम् पठिष्यावः।
3. हम सब पढ़ेंगे – वयम् पठिष्यामः।

4. लोट् लकार (आज्ञा अर्थ में)

(i) प्रथम पुरुष
पुंल्लिंग-

1. वह पढ़े – सः पठतु।
2. वे दो पढ़ें – तौ पठताम्।
3. वे सब पढ़ें – ते पठन्तु।
4. आप पढ़ें – भवान् पठतु।
5. आप दो पढ़ें – भवन्तौ पठताम्।
6. आप सब पढ़ें – भवन्तः पठन्तु।
7. राम पढ़े – रामः पठतु।
8. राम और श्याम पढ़ें – रामः श्यामः च पठताम्।
9. राम, श्याम और कृष्ण पढ़ें – रामः श्यामः कृष्णः च पठन्तु।

स्त्रीलिंग-

1. वह पढ़े – सा पठतु।
2. वे दो पढ़ें – ते पठताम्।
3. वे सब पढ़ें – ताः पठन्तु।
4. आप पढ़ें – भवती पठतु।
5. आप दो पढ़ें – भवत्यौ पठताम्।
6. आप सब पढ़ें – भवत्यः पठन्तु।
7. रमा पढ़े – रमा पठतु।
8. रमा और सीता पढ़ें – रमा सीता च पठताम्।
9. रमा, सीता और राधा पढ़ें – रमा, सीता, राधा च पठन्तु।

नपुंसकलिंग-

1. मित्र पढ़े – मित्रम् पठतु।
2. दो मित्र पढ़ें – मित्रे पठताम्।
3. बहुत से मित्र पढ़ें – मित्राणि पठन्तु।

(ii) मध्यम पुरुष

1. तुम पढ़ो, तू पढ़ – त्वम् पठ।
2. तुम दो पढ़ो – युवाम् पठतम्।
3. तुम सब पढ़ो – यूयम् पठत।

(iii) उत्तम पुरुष

1. मैं पढूँ – अहम् पठानि।
2. हम दो पढ़ें – आवाम् पठाव।
3. हम सब पढ़ें – वयम् पठाम।

5. विधिलिङ् लकार (चाहिए अर्थ में)

(i) प्रथम पुरुष

पुंल्लिंग:

1. उसे पढ़ना चाहिए – सः पठेत्।
2. उन दो को पढ़ना चाहिए – तौ पठेताम्।
3. उन सबको पढ़ना चाहिए
4. आपको पढ़ना चाहिए – भवान् पठेत्।
5. आप दो को पढ़ना चाहिए – भवन्तौ पठेताम्।
6. आप सबको पढ़ना चहिए – भवन्तः पठेयुः
7. राम को पढ़ना चाहिए – रामः पठेत्।
8. राम और श्याम को पढ़ना चाहिए – रामः श्यामः च पठेताम् ।
9. राम, श्याम और कृष्ण को पढ़ना चाहिए – रामः श्यामः कृष्णः च पठेयुः।

स्त्रीलिंग-

1. उसे पढ़ना चाहिए – सा पठेत्।
2. उन दो को पढ़ना चाहिए – ते पठेताम्।
3. उन सबको पढ़ना चाहिए – ताः पठेयुः।
4. आपको पढ़ना चाहिए – भवती पठेत्।
5. आप दो को पढ़ना चाहिए – भवत्यौ पठेताम् ।
6. आप सबको पढ़ना चाहिए – भवत्यः पठेयुः।
7. रमा को पढ़ना चाहिए – रमा पठेत् ।
8. रमा और सीता को पढ़ना चाहिए – रमा सीता च पठेताम्।
9. रमा, सीता और राधा को पढ़ना चाहिए – रमा सीता राधा च पठेयुः।

नपुंसकलिंग-

1. मित्र को पढ़ना चाहिए – मित्रम् पठेत्।
2. दो मित्रों को पढ़ना चाहिए – मित्रे पठेताम् ।
3. बहुत से मित्रों को पढ़ना चाहिए – मित्राणि पठेयुः।

(ii) मध्यम पुरुष

1. तुम्हें (तुझे) पढ़ना चाहिए – त्वम् पठेः।
2. तुम दो को पढ़ना चाहिए – यूवाम् पठेतम्।
3. तुम सबको पढ़ना चाहिए – यूयम् पठेत।

(iii) उत्तम पुरुष

1. मुझे पढ़ना चाहिए – अहम् पठेयम्।
2. हम दो को पढ़ना चाहिए – आवाम् पठेव।
3. हम सबको पढ़ना चाहिए – वयम् पठेम।

विभक्ति-प्रयोग के नियम

प्रथमा, सम्बोधन तथा द्वितीया विभक्ति

नियम (1) कर्ता में प्रथमा विभक्ति होती है; जैसे- राम पढ़ता है-रामः पठति।

नियम (2) किसी को सम्बोधन करने अथवा पुकारने में सम्बोधन विभक्ति होती है; जैसे- हे राम! हे हरे!

नियम (3) कर्ता जिसको (व्यक्ति, वस्तु अथवा क्रिया को) सबसे अधिक चाहता है, उसे कर्म कहते हैं तथा कर्म में द्वितीया विभक्ति होती है; जैसे-

1. राम पुस्तक पढ़ता है – रामः पुस्तकं पठति।
2. सीता राम को देखती है – सीता रामं पश्यति।
3. वे सब घर जाते हैं – ते गृहं गच्छन्ति।
4. तुम जल पीते हो – त्वमू जलं पिबसि।
5. तुम सब फल चाहते हो – यूयम् फलानि इच्छथ।
6. मैं प्रश्न पूछता हूँ – अहं प्रश्नं पृच्छामि।
7. हम दोनों गरु को नमस्कार करते हैं – आवाम गरु नमावः।

नियम (4) निम्नलिखित पदों के साथ द्वितीया विभक्ति होती है; जैसे-

1. अभितः (दोनों ओर)-नदी के दोनों ओर वृक्ष हैं-नदीम् अभितः वृक्षाः सन्ति।
2. परितः (चारों ओर)-गाँव के चारों ओर जल है-ग्रामं परितः जलम् अस्ति।
3. समया (समीप)-विद्यालय के समीप बगीचा है-विद्यालयं समया उद्यानम् अस्ति।
4. निकषा (समीप)-घर के समीप मन्दिर है-गृहं निकषा मन्दिरम् अस्ति।
5. उभयतः (दोनों ओर) मन्दिर के दोनों ओर घर हैं-मन्दिरम् उभयतः गृहाणि सन्ति।
6. सर्वतः (सब ओर)-नगर के सब ओर मार्ग हैं नगरं सर्वतः मार्गाः सन्ति।
7. उपर्युपरि (ऊपर-ऊपर) वृक्ष के ऊपर-ऊपर बन्दर हैं-वृक्षम् उपर्युपरि वानराः सन्ति।
8. अधोऽधः (नीचे-नीचे)-लता के नीचे-नीचे फूल हैं-लताम् अधोऽधः पुष्पाणि सन्ति।
9. अध्यधि (बीच-बीच में) तालाब के बीच-बीच में कमल हैं जलाशयम् अध्यधि कमलानि सन्ति।
10. हा (खेद, दुःख) दुर्जन के लिए खेद है हा दुर्जनम्।

नियम (5) समय और स्थान के दूरवाची शब्दों में द्वितीया विभक्ति होती है; जैसे-

1. समय-रमेश दस दिन तक पढ़ता है-रमेशः दश दिनानि पठति।
2. स्थान की दूरी-सीता कोस भर चलती है-सीता क्रोशं चलति।

नियम (6) निम्नलिखित धातुएं द्विकर्मक हैं। इनके साथ दो कर्म होते हैं; जैसे-

1. दुह् (दुहना)-सुरेश गाय से दूध दुहता है-सुरेशः गां पयः दोग्धि।
2. याच् (माँगना)-ब्राह्मण राजा से धन माँगता है-ब्राह्मणः नृपं धनं याचते।
3. पच् (पकाना) माता चावलों से भात पकाती है माता तण्डुलान् ओदनं पचति।
4. दण्ड् (दण्ड देना)-शासक चोर पर सौ रुपए दण्ड लगाता है-शासकः चौरं शतं दण्डयति।
5. रुध् (रोकना) वह घर में बकरी को रोकता है-सः गृहम् अजां रुणद्धि।
6. प्रच्छ् (पूछना) छात्र गुरु से प्रश्न पूछता है-छात्रः गुरुं प्रश्नं पृच्छति।
7. चि (चुनना)-तपस्वी लता से फूल चुनता है-तापसः लतां पुष्पाणि चिनोति।
8. ब्रू (बोलना)-द्रोणाचार्य दुर्योधन को धर्म बताता है-द्रोणाचार्यः दुर्योधनं धर्मं ब्रवीति।
9. शास् (बताना) पिता पुत्र को ज्ञान बताता है-पिता पुत्रं ज्ञानं शास्ति।
10. जि (जीतना) रमेश महेश से सौ रुपए जीतता है-रमेशः महेशं शतं जयति।

तृतीया विभक्ति

नियम (1) क्रिया की सिद्धि में जो सबसे अधिक सहायक होता है, उसे करण कहते हैं तथा करण में तृतीया विभक्ति होती है; जैसे-

1. बालक गेंद से खेलता है बालकः कन्दुकेन क्रीडति।
2. वृद्ध लाठी से चलता है-वृद्धः लगुडेन चलति।।

नियम (2) साथ अर्थवाची सह, साकम्, सार्थम्, समम् के साथ अप्रधान कर्ता में तृतीया होती है

1. राम सीता के साथ वन जाते हैं रामः सीतया सह वनं गच्छति।
2. पुत्र पिता के साथ विद्यालय जाता है-पुत्रः पित्रा साकं विद्यालयं गच्छति।
3. बच्चा बन्दर के साथ खेलता है-बालकः वानरैः सार्धम् क्रीडति।
4. वह किसके साथ आता है-सः केन सह आगच्छति।

नियम (3) जिस चिह्न से किसी व्यक्ति अथवा वस्तु का बोध होता है, उसमें तृतीया विभक्ति होती है; जैसे-

1. बालक पुस्तकों से छात्र प्रतीत होता है बालकः पुस्तकैः छात्रः प्रतीयते।
2. वह जटाओं से तपस्वी लगता है-सः जटाभिः तापसः।

नियम (4) प्रकृति (स्वभाव), सुख, दुःख शब्दों के साथ तृतीया विभक्ति होती है; जैसे-

1. राम स्वभाव से सज्जन है रामः स्वभावेन् सज्जनः अस्तिः।
2. रावण प्रकृति से दुर्जन है-रावणः प्रकृत्या दुर्जनः अस्ति।
3. साधु सुख से जीता है साधुः सुखेन जीवति।
4. रोगी दुःख से चलता है-रुग्णः दुःखेन चलति।

नियम (5) सादृश्यवाची सदृश, तुल्य, सम आदि शब्दों के साथ तृतीया विभक्ति होती है; जैसे-

1. गुरु पिता के समान होता है-गुरुः पित्रा सदृशः अस्ति।
2. लव राम के सदृश है-लवः रामेण तुल्यः अस्ति।

नियम (6) मत, बस अर्थवाची अलम् शब्द के साथ तृतीया विभक्ति होती है; जैसे-

1. कोलाहल मत करो–अलम् कोलाहलेन।
2. मत हँसो अलम् हसितेन।

नियम (7) शरीर के जिस अंग में विकार से व्यक्ति विकृत दिखायी दे, उसमें तृतीया विभक्ति होती है; जैसे-

1. साधु नेत्र से अंधा है साधुः नेत्राभ्याम् अन्धः अस्ति।
2. कुत्ता पैर से लँगड़ा है कुक्कुरः पादेन खञ्जः अस्ति।
3. बालक कान से बहरा है बालकः कर्णाभ्याम् बधिरः अस्ति।
4. चोर हाथ से ढूंडा है-चौरः हस्तेन लुञ्जः अस्ति।
5. धनिक सिर से गंजा है-धनिकः शिरसा खल्वाटः अस्ति।

नियम (8) हेतु अर्थात् कारण प्रकट करने वाले शब्दों में तृतीया विभक्ति होती है; जैसे-

1. कपिल पढ़ने के कारण होस्टल में रहता है कपिलः पठनेन छात्रावासे निवसति।
2. पुण्य के कारण हरि का दर्शन होता है-पुण्येन हरेः दर्शनं भवति।

नियम (9) पृथक्, विना के साथ तृतीया विभक्ति भी होती है; जैसे-

1. राम के बिना संसार नहीं है-रामेण पृथक् संसार न अस्ति।
2. धन के बिना जीवन नहीं है धनेन विना जीवनं न अस्ति।

चतुर्थी विभक्ति

नियम (1) दान आदि क्रिया जिसके लिए की जाती है उसे सम्प्रदान कहते है तथा सम्प्रदान में चतुर्थी विभक्ति होती है; जैसे-

1. राजा ब्राह्मण को धन देता है-राजा ब्राह्मणाय धनं ददाति।
2. माँ बालक को दूध देती है माता बालकाय दुग्धं यच्छति।

नियम (2) रुच् (अच्छा लगना) अर्थ वाली धातुओं के योग में चतुर्थी विभक्ति होती है; जैसे-

1. गणेश को लड्डू अच्छा लगता है गणेशाय मोदकं रोचते।
2. लड़की को फूल अच्छा लगता है बालिकायै पुष्पं रोचते।

नियम (3) क्रुधू, द्रुह, ईष्र्ण्य, असूयु अर्थ वाली धातुओं के साथ जिस पर क्रोध आदि किया जाए, उसमें चतुर्थी विभक्ति होती है; जैसे-

1. कंस कृष्ण पर क्रोध करता है कंस कृष्णाय क्रुध्यति।
2. दुर्जन सज्जन से द्रोह करता है दुर्जनः सज्जनाय द्रुह्यति।
3. निर्धन धनी से ईर्ष्या करता है निर्धनः धनिकाय ईर्ण्यति।
4. मूर्ख विद्वान् से असूया करता है मूर्खः विदुषे असूयति।

नियम (4) (ऋणी होना, उधार लेना) के योग में ऋण देने वाले व्यक्ति में चतुर्थी विभक्ति होती है; जैसे-

1. राम कृष्ण का सौ रुपए का ऋणी है-रामः कृष्णाय शतं धारयति।
2. हरि भक्त को मोक्ष देता है हरिः भक्ताय मोक्षं धारयति।

नियम (5) स्पृह (चाहना) धातु के योग में जो वस्तु चाही जाए, उसमें चतुर्थी विभक्ति होती है; जैसे-

1. पुजारी पुष्प चाहता है पूजकः पुष्पाणि स्पृह्यति।
2. लता फल चाहती है लता फलानि स्पृह्यति।

नियम (6) कथ् (कहना), निवेदय (निवेदन करना), उपदिश् (उपदेश देना), कल्पते (होना), सम्पद्यते (होना) के साथ चतुर्थी विभक्ति होती है; जैसे-

1. मुनि तपस्वी से कहता है मुनिः तापसाय कथयति।
2. प्रजा राजा से निवेदन करती है प्रजा राज्ञे निवेदयति।
3. गुरु शिष्य को उपदेश देता है-गुरुः शिष्याय उपदिशति। (उपदिश् के साथ द्वितीया भी होती है)-गुरुः शिष्यम् उपदिशति।
4. विद्या धन के लिए हैं विद्या धनाय कल्पते।
5. ज्ञान सुख के लिए है-ज्ञानं सुखाय संपद्यते।

नियम (7) जिस प्रयोजन के लिए जो वस्तु या क्रिया की जाती है, उसमें चतुर्थी विभक्ति होती है; जैसे-

1. भक्त मोक्ष के लिए हरि को भजता है भक्तः मोक्षाय हरिं भजति।

नियम (8) निम्नलिखित शब्दों के योग में चतुर्थी विभक्ति होती है; जैसे-

1. नमः (नमस्कार) गुरु को नमस्कार-गुरवे नमः।
2. स्वस्ति (आशीर्वाद)-शिष्य का कल्याण हो-शिष्याय स्वस्ति।
3. स्वाहा (आहुति)-अग्नि के लिए स्वाहा-अग्नये स्वाहा।
4. स्वधा (हवि)-पितरों के लिए हवि का दान-पितृभ्यः स्वधा।
5. अलम् (समर्थ) हरि राक्षसों के लिए समर्थ हैं हरिः दैत्येभ्यः अलम्।
6. वषट् (हवि) इन्द्र के लिए हविदान-इन्द्राय वषट् ।
7. हितम् (हित) ब्राह्मण का हित हो-ब्राह्मणाय हितं भूयात्।

पंचमी विभक्ति

नियम (1) जिससे कोई वस्तु आदि अलग होती है, उसे अपादान कहते हैं और अपादान में पंचमी विभक्ति होती है। जैसे-

1. पेड़ से फल गिरता है वृक्षात् फलं पतति।
2. घोड़े से मनुष्य गिरता है-अश्वात् मनुष्यः पतति।

नियम (2) भय और रक्षा अर्थ वाली धातुओं के साथ जिससे भय होता है, उसमें पंचमी विभक्ति होती है; जैसे-

1. बच्चा कुत्ते से डरता है बालः कुक्कुरात् बिभेति।
2. सेनापति शत्रु से राजा की रक्षा करता है-सेनापति शत्रोः नृपं रक्षति।

नियम (3) जिससे विद्या आदि पढ़ी जाए, उसमें पंचमी विभक्ति होती है। जैसे-

1. शिष्य गुरु से पढ़ता है शिष्यः गुरोः पठति।
2. रमा उपाध्याय से पढ़ती है-रमा उपाध्यायात् अधीते।

नियम (4) निम्नलिखित धातुओं के साथ पंचमी विभक्ति होती है; जैसे-

1. विरम (रुकना)-रवि अध्ययन से विराम करता है रविः अध्ययनात विरमति।
2. प्रमद् (प्रमाद करना)-दुर्जन धर्म से प्रमाद करता है-दुर्जनः धर्मात् प्रमाद्यति।
3. जुगुप्सा (घृणा करना) सज्जन पाप से घृणा करता है सज्जनः पापात् जुगुप्सते।
4. निवृ (हटाना)-भगवान भक्त को पाप से हटाता है भगवान भक्तं पापातु निवारयति
5. प्रभू (निकलना)-गंगा हिमालय से निकलती है-गंगा हिमालयात् प्रभवति।
6. उद्भ (निकलना)-अग्नि से धुआँ निकलता है-अग्नेः धूम्रः उद्भवति।
7. प्रति + दा (बदले में देना) रमा तिलों से उडद बदलती है-रमा तिलेभ्यः माषान् प्रतियच्छति।
8. जन् (उत्पन्न होना)-प्रजापति से संसार पैदा होता है प्रजापतेः संसारः जायते।
9. निली (छिपना)-चोर राजा से छिपता है-चौरः नृपात् निलीयते।

नियम (5) तुलना में जिससे तुलना की जाती है, उसमें पंचमी विभक्ति होती है; जैसे-

• धन से ज्ञान अधिक बड़ा है धनात् ज्ञानं गुरुतरम्।
• राम से कृष्ण अधिक कुशल है-रामात् कृष्णः पटुतरः ।

नियम (6) दूर और निकटवाची शब्दों में पंचमी, तृतीया तथा द्वितीया होती है; जैसे-

• विद्यालय गाँव से दूर है-विद्यालयः ग्रामस्य दूरात् (दूरेण, दूरम्)।
• घर मन्दिर के पास है-गृहं मन्दिरस्य समीपम् अस्ति।

नियम (7) निम्नलिखित शब्दों के योग में पंचमी विभक्ति होती है; जैसे-

1. अन्य (दसरा) ईश्वर से दसरा कौन रक्षक है ?-ईश्वरात अन्यः कः रक्षकः अस्ति ?
2. आरात् (समीप, दूर)-गाँव के समीप उद्यान है-ग्रामात् आरात् उद्यानम् अस्ति।
3. इतरः (अन्य) राम से अन्य कौन सत्य बोलता है-रामात् इतरः कः सत्यं वदति।
4. भिन्नः (अलावा) कृष्ण से भिन्न कौन गोपाल है-कृष्णात् भिन्नः कः गोपालः।
5. ऋते (बिना) ज्ञान के बिना मुक्ति नहीं-ज्ञानात् ऋते न मुक्तिः।
6. प्रभृति (से लेकर)-बचपन से लेकर मैं यहाँ पढ़ता हूँ-शैशवात् प्रभृतिः अहम् अत्र पठामि।
7. आरभ्य (आरम्भ करके)-यौवन से लेकर वह व्यापार करता है-यौवनात् आरभ्य सः व्यापारं करोति।
8. बहिः (बाहर)-नगर के बाहर देवालय है-नगरात् बहिः देवालयः अस्ति।
9. प्राक् (पहले, पूर्व की ओर) मन्दिर से पूर्व की ओर बगीचा है-मन्दिरात् प्राक् उद्यानम् अस्ति।
10. प्रत्यक् (पश्चिम की ओर)-बगीचे के पश्चिम की ओर कुआँ है-उद्यानात् प्रत्यक् कूपः अस्ति।
11. उदक् (उत्तर की ओर)-विद्यालय के उत्तर की ओर नदी है-विद्यालयात् उदक् नदी अस्ति।
12. दक्षिणा (दक्षिण की ओर) घर के दक्षिण की ओर वृक्ष है-गृहात् दक्षिणा वृक्षः अस्ति।

षष्ठी विभक्ति

नियम (1) सम्बन्ध का बोध कराने के लिए षष्ठी विभक्ति का प्रयोग होता है; जैसे-

• राम का घर है-रामस्य गृहम् अस्ति।
• यह मेरा पुत्र है-अयं मम पुत्रः अस्ति।

नियम (2) हेतु शब्द के साथ षष्ठी विभक्ति का प्रयोग होता है; जैसे-

• गोपाल धन के लिए यहाँ रहता है-गोपालः धनस्य हेतोः अत्र निवसति।
• राम पढ़ाई के लिए वहाँ जाता है-रामः पठनस्य हेतोः तत्र गच्छति।

नियम (3) स्मरण अर्थ की धातुओं के साथ कर्म में षष्ठी विभक्ति होती है; जैसे-

• बालक माता का स्मरण करता है-बालकः मातुः स्मरति ।
• रमेश पिता का स्मरण करता है रमेशः पितुः स्मरति।

नियम (4) बहुतों में से एक को छाँटने में जिसमें से छाँटा जाए उसमें षष्ठी तथा सप्तमी दोनों विभक्तियों का प्रयोग होता है; जैसे-

• छात्रों में कृष्ण श्रेष्ठ है-छात्राणाम् (छात्रेषु) कृष्णः श्रेष्ठः अस्ति।
• मनुष्यों में ब्राह्मण श्रेष्ठ है मनुष्याणाम् (मनुष्येषु) ब्राह्मणः श्रेष्ठः अस्ति।

नियम (5) दूर और समीपवाची शब्दों के साथ षष्ठी और पंचमी दोनों विभक्तियाँ होती हैं, जैसे-

• नदी गाँव से दूर है-नदी ग्रामस्य (ग्रामात्) दूरम् अस्ति।
• विद्यालय के पास वृक्ष हैं -विद्यालयस्य (विद्यालयात्) सकाशं वृक्षाः सन्ति।

नियम (6) तुल्यवाची शब्दों (तुल्य, सदृश, सम) के साथ षष्ठी और तृतीया दोनों विभक्तियाँ होती हैं, जैसे-

• गुरु पिता के तुल्य है-गुरुः पितुः (पित्रा) तुल्यः अस्ति।
• राम के सदृश कोई नहीं है-रामस्य (रामेण) सदृशः कोऽपि न अस्ति।

नियम (7) आशीर्वाद सूचक शब्दों के साथ षष्ठी और चतुर्थी दोनों विभक्तियाँ होती हैं; जैसे-

• राम का कुशल हो-रामस्य कुशलं भूयात् अथवा रामाय भद्रं भूयात् ।

नियम (8) निम्नलिखित शब्दों के साथ षष्ठी विभक्ति का प्रयोग होता है; जैसे-

1. उपरि (ऊपर)-नगर के ऊपर बादल हैं-नगरस्य उपरि मेघाः सन्ति।
2. उपरिष्टात् (ऊपर की ओर)-पर्व के ऊपर की ओर जाओ-पर्वतस्य उपरिष्टात् गच्छ।
3. अधः (नीचे) वृक्ष के नीचे बन्दर हैं वृक्षस्य अधः वानराः सन्ति।
4. अधस्तात् (नीचे की ओर) हरि पर्वत के नीचे की ओर जा रहा है हरिः पर्वतस्य अधस्तात् गच्छति।
5. पुरः (सामने)-गाय घर के सामने है-धेनुः गृहस्य पुरः अस्ति।
6. पुरस्तात् (सामने की ओर)-विद्यालय के सामने की ओर छात्र हैं-विद्यालयस्य पुरस्तात् छात्राः सन्ति।
7. पश्चात् (पीछे)-गाँव के पीछे वन है ग्रामस्य पश्चात् वनम् अस्ति।
8. अग्रे (आगे) घर के आगे धरती खोदता है-गृहस्य अग्रे वसुधां खनति।
9. दक्षिणतः (दक्षिण की ओर, दाहिनी ओर)-नंगर के दक्षिण की ओर मन्दिर है-नगरस्य दक्षिणतः देवालयः अस्ति।
10. उत्तरतः (उत्तर की ओर)-भवन के उत्तर की ओर वृक्ष है-भवनस्य उत्तरतः वृक्षः अस्ति।

सप्तमी विभक्ति

नियम (1) किसी वस्तु के आधार को अधिकरण कारक कहते हैं और अधिकरण कारक में सप्तमी विभक्ति होती है; जैसे-

1. सुरेश विद्यालय में पढ़ता है सुरेशः विद्यालये पठति।
2. विद्यालय में गुरु रहते हैं विद्यालये गुरवः वसन्ति ।
3. माता पतीली में पकाती है-माता स्थाल्यां पचति।

नियम (2) ‘विषय में ‘बारे में अर्थ को प्रकट करने में सप्तमी विभक्ति होती है। जैसे-

1. जनक की मोक्ष के विषय में इच्छा है-जनकस्य मोक्षे इच्छा अस्ति।

नियम (3) समय बोधक शब्दों में सप्तमी विभक्ति होती है; जैसे-

1. ‘मैं दिन में पढ़ता हूँ सायंकाल में खेलता हूँ अहं दिने पठामि, सायंकाले क्रीडामि।
2. बचपन में सब चंचल होते हैं शैशवे सर्वे चपलाः भवन्ति।

नियम (4) प्रेम, आसक्ति या आदरसूचक धातुओं और शब्दों के साथ सप्तमी विभक्ति होती है; जैसे-

1. पिता पुत्र से स्नेह करता है-पिता पुत्रे स्निह्यति।
2. हरि रमा पर अनुरक्त है हरिः रमायाम् अनुरक्ताः अस्ति ।
3. गुरु शिष्यों में आदर पाता है गुरुः शिष्येषु आद्रियते।।

नियम (5) विश्वास और श्रद्धा अर्थ वाली धातुओं और शब्दों के साथ सप्तमी विभक्ति होती है। जैसे-

1. शिष्य की गुरु में श्रद्धा होती है शिष्यस्य गुरौं श्रद्धा भवति।
2. पुत्र माता पर विश्वास करता है-पुत्रः मातरि विश्वसिति।

नियम (6) फेंकना अर्थवाची क्षिप, मुच् आदि धातुओं के साथ सप्तमी विभक्ति होती है; जैसे-

1. दशरथ मृग पर बाण छोड़ता है-दशरथः मृगे बाणं क्षिपति।।

नियम (7) संलग्न अर्थ वाले लग्नः, युक्तः आदि शब्दों तथा चतुर अर्थ वाले ‘कुशलः निपुणः’ आदि शब्दों के योग में सप्तमी विभक्ति होती है। जैसे-

1. मैं इस समय काम में लगा हूँ अहम् इदानीम् कार्ये लग्नः अस्मि।
2. चन्द्रापीड शास्त्रों में कुशल है-चन्द्रापीड़ः शास्त्रेषु कुशलः अस्ति।

नियम (8) एक क्रिया के बाद दूसरी क्रिया होने पर पहली क्रिया में सप्तमी होती है तथा उसके कर्ता में भी सप्तमी होती है; जैसे-

1. राम के वन जाने पर दशरथ मर गए-रामे वनं गते दशरथः मृतः।

अभ्यासार्थ प्रश्नाः

I. 1. करण कारकस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
2. सम्प्रदान कारकस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
3. अधिकरण कारकस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
4. कर्मकारकस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
5. अपादान कारकस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।

II. अधोलिखित प्रश्नानां प्रदत्तोत्तरविकल्पेषु शुद्धविकल्पं लिखत
(निम्नलिखित प्रश्नों के दिए गए विकल्पों में से शुद्ध विकल्प लिखिए)

1. ‘सह’ इति उपपदस्य योगे का विभक्तिः ?
(A) प्रथमा
(B) पंचमी
(C) तृतीया
(D) द्वितीया

2. ‘अलम्’ इति उपपदस्य योगे का विभक्तिः ?
(A) प्रथमा
(B) तृतीया
(C) द्वितीया
(D) चतुर्थी

3. विना’ इति उपपदस्य योगे का विभक्तिः ?
(A) प्रथमा
(B) पंचमी
(C) तृतीया
(D) द्वितीया

4. ‘नमः’ इति उपपदस्य योगे का विभक्तिः ?
(A) चतुर्थी
(B) षष्ठी
(C) पंचमी
(D) द्वितीया

5. ‘कर्म कारके’ का विभक्तिः भवति?
(A) चतुर्थी
(B) द्वितीया
(C) पंचमी
(D) सप्तमी

III. कोष्ठकाङ्कितेषु पदेषु उपयुक्तपदं चित्वा रिक्तस्थानानि पूरयत
(कोष्ठक में दिए गए शब्दों को उपयुक्त स्थान पर लिखें) ।

(क) ………………. परितः वृक्षाः सन्ति। (विद्यालयम्/विद्यालयस्य)
(ख) मोहन ……………… सः क्रीडति। (मित्रस्य मित्रेण)
(ग) …………… नमः। (देवाय देवेन)
(घ) …………… हसितेन। (अलम्/सह)
(ङ) ………………. अवकाशः आसीत्। (श्वः/ह्यः)
उत्तराणि:
(क) विद्यालयम्,
(ख) मित्रेण,
(ग) देवाय,
(घ) अलम्,
(ङ) ह्यः।

IV. उपपदम् आधृत्य उचित विभक्ति प्रयोगं कुरुत

(क) ………… नमः। (गुरवे/गुरुं)
(ख) ……….. विना न जीवनम्। (जल:/जलम्)
(ग) ………… निकषा वृक्षाः सन्ति। (विद्यालयः विद्यालयं)
उत्तराणि:
(क) गुरवे,
(ख) जलम,
(ग) विद्यालयः।

Haryana State Board HBSE 11th Class Chemistry Solutions Chapter 2 Structure of Atom Textbook Exercise Questions and Answers.

Haryana Board 11th Class Chemistry Solutions Chapter 2 Structure of Atom

Haryana State Board HBSE 11th Class Chemistry Solutions Chapter 1 Some Basic Concepts of Chemistry Textbook Exercise Questions and Answers.

Haryana Board 11th Class Chemistry Solutions Chapter 1 Some Basic Concepts of Chemistry

Haryana State Board HBSE 11th Class Biology Solutions Chapter 19 Excretory Products and their Elimination Textbook Exercise Questions and Answers.

Haryana Board 11th Class Biology Solutions Chapter 19 Excretory Products and their Elimination

Haryana State Board HBSE 11th Class Biology Solutions Chapter 18 Body Fluids and Circulation Textbook Exercise Questions and Answers.

Haryana Board 11th Class Biology Solutions Chapter 18 Body Fluids and Circulation

Haryana State Board HBSE 11th Class Biology Solutions Chapter 17 Breathing and Exchange of Gases Textbook Exercise Questions and Answers.

Haryana Board 11th Class Biology Solutions Chapter 17 Breathing and Exchange of Gases