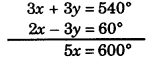Author name: Prasanna

Haryana State Board HBSE 12th Class Biology Solutions Chapter 14 Ecosystem Textbook Exercise Questions and Answers.

Haryana Board 12th Class Biology Solutions Chapter 14 Ecosystem

Haryana State Board HBSE 12th Class Biology Solutions Chapter 13 Organisms and Populations Textbook Exercise Questions and Answers.

Haryana Board 12th Class Biology Solutions Chapter 13 Organisms and Populations

Haryana State Board HBSE 12th Class Biology Solutions Chapter 12 Biotechnology and Its Applications Textbook Exercise Questions and Answers.

Haryana Board 12th Class Biology Solutions Chapter 12 Biotechnology and Its Applications

Haryana State Board HBSE 12th Class Biology Solutions Chapter 11 Biotechnology: Principles and Processes Textbook Exercise Questions and Answers.

Haryana Board 12th Class Biology Solutions Chapter 11 Biotechnology: Principles and Processes

Haryana State Board HBSE 12th Class Biology Solutions Chapter 10 Microbes in Human Welfare Textbook Exercise Questions and Answers.

Haryana Board 12th Class Biology Solutions Chapter 10 Microbes in Human Welfare

Haryana State Board HBSE 12th Class Biology Solutions Chapter 9 Strategies for Enhancement in Food Production Textbook Exercise Questions and Answers.

Haryana Board 12th Class Biology Solutions Chapter 9 Strategies for Enhancement in Food Production

Haryana State Board HBSE 12th Class Biology Solutions Chapter 8 Human Health and Diseases Textbook Exercise Questions and Answers.

Haryana Board 12th Class Biology Solutions Chapter 8 Human Health and Diseases

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 6 Lines and Angles Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 6 Lines and Angles

Very Short Answer Type Questions

Question 1.
Find the complement of the following angles :
(i) 64° 23′ 35″
(ii) 28° 25′ 48″.
Solution :
We can write,
90° = 89° 59′ 60″
(i) Complement of 64° 23′ 35″ = An angle of (90° – 64° 23′ 35″) = An angle of 25° 36′ 25″.
(ii) Complement of 28° 25′ 48″ = An angle of (90°- 28 °25′ 48″) = An angle of 61° 34′ 12″.

Question 2.
Find the measures of suppliment of the following angles :
(i) 115° 35′ 42″
(ii) 85° 15′ 59″.
Solution :
We can write,
180° = 179° 59′ 60″
(i) Supplement of 115° 35′ 42″ = An angle of (180° – 115°35′ 42″) = An angle of 64° 24′ 18″.
(ii) Suppliment of 85° 15′ 59″ = An angle of (180° – 85° 15′ 59”) = An angle of 94° 44′ 01″.

Question 3.
Find the measure of an angle which is 34° more than its complement.
Solution :
Let the complement of an angle be x° then
measure of an angle = (x + 34)°
We know that,
sum of an angle and its complement = 90°
∴ x° + (x + 34)° = 90°
⇒ 2x° + 34° = 90°
⇒ 2x° = 90° – 34°
⇒ 2x° = 56°
⇒ x° = \(\frac {56°}{2}\) = 28°
Hence,measure of an angle
= 28° + 34° = 62°.

Question 4.
Find the measure of an angle which is 26° less than its supplement.
Solution :
Let the supplement of an angle be x°
Then measure of an angle = (x – 26)°
We know that,
Sum of an angle and its supplement = 180°
∴ x° + (x – 26)° = 180°
⇒ 2x° – 26° = 180°
⇒ 2x° = 180° + 26°
⇒ 2x° = 206°
⇒ x° = \(\frac {206°}{2}\) = 103°
Hence measure of an angle = 103° – 26° = 77°.

Question 5.
Find the angle, which is 18° less than five times its complement.
Solution :
Let the complement angle be x°
Five times of complement angle = 5x°
Then angle = (5x – 18)°
We know that, Sum of an angle and its complement = 90°
∴ (5x – 18)° + x° = 90°
⇒ 6x° – 18° = 90°
⇒ 6x° = 90° + 18°
⇒ 6x° = 108°
⇒ x° = \(\frac {108°}{6}\) = 18°
Hence,measure of angle
= 5 × 18° – 18°
= 90° – 18° = 72°.

Question 6.
Find the angle, which is four times its supplement
Solution :
Let the supplement angle be x°.
Then angle = 4x°
We know that, Sum of an angle and its suppliment = 180°
∴ 4x° + x° = 180°
⇒ 5x° = 180°
⇒ x° = \(\frac {180°}{5}\) = 18°
Hence,measure of the angle
= 4 × 36° = 144°.

Question 7.
Find the measure of an angle whose supplement is three times of its complement.
Solution :
Let the angle be x°, then Supplement of an angle = (180 – x)°
Compliment of an angle = (90 – x)°
According to question,
(180 – x)° = 3(90 – x)°
⇒ 180° – x° = 270° – 3x°
⇒ – x° + 8x° = 270° – 180°
⇒ 2x° = 90°
⇒ x° = \(\frac {90°}{2}\) = 45°
Hence, the measure of the angle = 45°

Question 8.
Find the measure of an angle, if five times its complement is equal to two times of its supplement.
Solution :
Let the angle be x°, then
Complement of an angle = (90 – x)°
Supplement of an angle = (180 – x)°
According to question,
5(90 – x)° = 2(180 – x)°
⇒ 450° – 5x° = 360° – 2x°
⇒ – 5x° + 2x° = 360° – 450°.
⇒ – 3x° = – 90°
⇒ x° = \(\frac {-90°}{- 3}\) = 30°
Hence the measure of the angle = 30°.

Short Answer Type Questions

Question 1.
One of two complementary angles is seven-eighth as large as the other. How many degree are in each angle?
Solution :
Let the other complementary angle be x°.
One complimentary angle = \(\frac {7}{8}\)x°
We know that, Sum of two complementary angles = 90°

Hence, other complementary angle = 48° and one complementary angle = \(\frac {7}{8}\) × 48° = 42°.

Question 2.
In the figure, AC and BC are opposite rays. If 2x – 3y = 60°, then find the values of x and y.

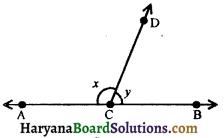
Solution :
Since, AC and BC are opposite rays. Therefore, ∠ACD + ∠BCD = 180°,
(Linear pair axiom)
⇒ x + y = 180° …(i)
2x – 3y = 60° (Given) …(ii)
Multiplying equation (i) by 3 and adding equation (i) and (ii), we get

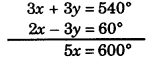
⇒ x = \(\frac {600°}{5}\) = 120°
Substituting the value of x in the equation (i), we get
120° + y = 180°
⇒ y = 180° – 120° = 60°
Hence, x = 120° and y = 60°

Question 3.
In figure, BCA is a line. Find the value of x.

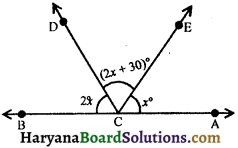
Solution :
Since, BCA is a line. Therefore ∠BCD + ∠ACD = 180°,
(Linear pair axiom)
⇒ ∠BCD + ∠DCE + ∠ACE = 180°,
[∵ ∠ACD = ∠DCE + ∠ACE]
⇒ 2x° + (2x° + 30)° + x° = 180°
⇒ 5x° + 30° = 180°
⇒ 5x° = 180° – 30°
⇒ 5x° = 150°
⇒ x° = \(\frac {150°}{5}\) = 30°
Hence, x° = 30°

Question 4.
In figure, PQR is a line. If a : b : c = 2 : 3 : 5, find the values of a, b and c.

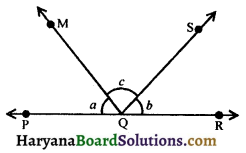
Solution :
Since, PQR is a line. Therefore ∠PQM + ∠RQM = 180°, (Linear pair axiom)
⇒ ∠PQM + ∠MQS + ∠RQS = 180°,
[∵ ∠RQM = ∠MQS + ∠RQS]
⇒ a + c + b = 180°
But a : b : c = 2 : 3 : 5
Sum of ratios = 2 + 3 + 5 = 10
∴ a = \(\frac {2}{10}\) × 180° = 36°
b = \(\frac {3}{10}\) × 180° = 54°
and c = \(\frac {5}{10}\) × 180° = 90°
Hence, a = 36°, b = 54 and c = 90°.

Question 5.
In figure, three straight lines AB, CD and EF intersect at a point o forming the angles as shown. Find the values of x, y, z and r.

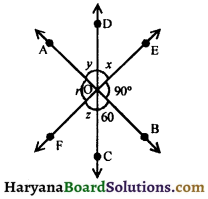
Solution:
y = 60°, (Vertically opposite angles)
r = 90° (Vertically opposite angles)
Since, AOB is a line.
∠AOE + ∠BOE = 180°
(Linear pair axiom)
⇒ ∠AOD + ∠DOE + ∠BOE = 180°
⇒ y + x + 90° = 180°
⇒ 60° + x + 90° = 180°
⇒ x + 150° = 180°
⇒ x = 180° – 150°= 30°
z = x
(Vertically opposite angles)
⇒ z = 30°
Hence,
x = 30°, y = 60°,
z = 30°, r = 90°.

Question 6.
In the figure , AB || CD, PQ || AX and ∠BAC = 70°, find ∠DPQ

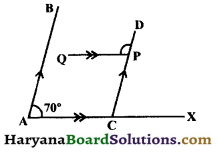
Solution :
∵ AB || CD and AX is a transversal
∴ ∠BAC + ∠ACD = 180°,
(Sum of a pair of allied angles is 180°)
⇒ 70° + ∠ACD = 180°,(∵ ∠BAC = 70°)
⇒ ∠ACD = 180° – 70°
⇒ ∠ACD = 110°
Now PQ || AX and CD is a transversal.
∠DPQ = ∠ACD, (Corresponding angles axiom)
⇒ ∠DPQ = 110°
Hence, ∠DPQ = 110°

Question 7.
In the figure, AB || CD aud m || n, find the value of x.

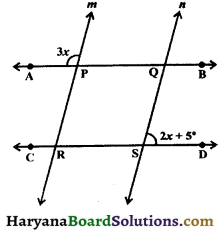
Solution :
∠QPR = 3x,
(Vertically opposite angles)
∵ AB || CD and line m is a transversal.
∴ ∠QPR + ∠PRS = 180°,
(A pair of allied angles is supplementary)
⇒ 3x + ∠PRS = 180°
⇒ ∠PRS = 180° – 3x ……(i)
Now, m || n and line CD is a transversal.
∠PRS = ∠QSD,
(Corresponding angles axiom)
⇒ 180° – 3x = 2x + 5°, [From (i), ∠PRS = 180° – 3x and ∠QSD = 2x + 5°]
⇒ 180° – 5° = 2x + 3x
⇒ 175° = 5x
⇒ \(\frac {175°}{5}\) = x
⇒ x = 35°
Hence, x = 35°

Question 8.
In the figure, AB || CD, find the value of x.

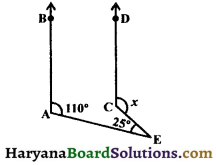
Solution :
From E, draw EF || AB || CD.
Now, AB || EF and AE is the transversal.
∴ ∠BAE + ∠AEF = 180°
(A pair of allied angles are supplementary)
⇒ 110° + ∠AEC + ∠CEF = 180°
⇒ 110° + 25° + ∠CEF = 180°
⇒ 135° + ∠CEF = 180°
⇒ ∠CEF = 180° – 135°
⇒ ∠CEF = 45°
Again CD || EF and CE is the transversal.
∴ ∠DCE + ∠CEF = 180°,
(A pair of allied angles is supplementary)
⇒ x + 45° = 180°
⇒ x = 180° – 45°
⇒ x = 135°
Hence, x = 135°

Question 9.
In the figure, AB || DE and x = y, prove that BC || EF.

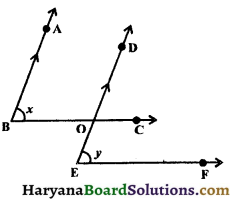
Solution :
Since AB || DE and BC is the transversal.
Therefore, ∠DOC = ∠ABC,
(Corresponding angles axiom)
⇒ ∠DOC = x
But x = y, (Given)
∴ ∠DOC = y
Thus, a pair of corresponding angles ∠DOC and y are equal. By converse of corresponding axiom, we have BC || EF. Hence proved

Question 10.
In the given figure, AB || CD, PQ || BC, ∠BAC = 52° and ∠DRS = 43°. Find the value of x.

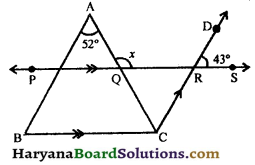
Solution :
Since, AB || CD and AC is the transversal.
∴ ∠ACD = ∠BAC,
(Alternate interior angles)
⇒ ∠ACD = 52°
⇒ ∠QCR = 52°,
(∵ ∠ACD = ∠QCR) …(i)
∠QRC = ∠DRS,
(Vertically opposite angles)
⇒ ∠QRC = 43° …….(ii)
In ΔCQR, we have
∠AQR = ∠QCR + ∠QRC,
⇒ x = 52° + 43°, [From (i) and (ii), ∠QCR = 52° and ∠QRC = 43°)
⇒ x = 95°
Hence, x = 95°

Question 11.
The sides BC, CA and AB of a triangle ABC are produced in order, forming exterior angles ∠ACD, ∠BAE and ∠CBF. Show that ∠ACD + ∠BAE + ∠CBF = 360°

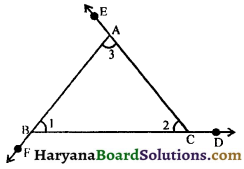
Solution :
In ΔABC, we have
∠ACD = ∠1 + ∠3 ………….(i)
∠BAE = ∠1 + ∠2 ………….(ii)
∠CBF = ∠2 + ∠3 ………….(iii)
Adding (i), (ii) and (iii), we get
∠ACD + ∠BAE + ∠CBF = ∠1 + ∠3 + ∠1 + ∠2 + ∠2 + ∠3
⇒ ∠ACD + ∠BAE + ∠CBF = 2∠1 + 2∠2 + 2∠3
⇒ ∠ACD + ∠BAE + ∠CBF = 2(∠1 + ∠2 + ∠3)
But ∠1 + ∠2 + ∠3 = 180°,
(Sum of the angles of a triangle = 180°)
∴ ∠ACD + ∠BAE + ∠CBF = 2 × 180°
⇒ ∠ACD + ∠BAE + ∠CBF = 360°
Hence proved

Question 12.
In the given figure, show that ∠A + ∠B + ∠C + ∠P + ∠Q + ∠R = 360°.

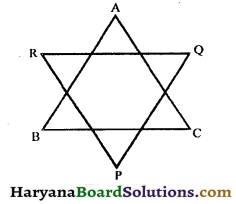
Solution :
In ΔABC, we have
∠A + ∠B + ∠C= 180°,
(Sum of angles of a triangle = 180°) …(i)
In ΔPQR, we have
∠P + ∠Q + ∠R = 180°,
(Sum of angles of a triangle = 180°) …(ii)
Adding (i) and (ii), we get
∠A + ∠B + ∠C + ∠P + ∠Q + ∠R = 180° + 180°
⇒ ∠A + ∠B + ∠C + ∠P + ∠Q + ∠R = 360°
Hence proved

Question 13.
ABC is a triangle in which ∠A = 66°, the internal bisectors of ∠B and ∠C intersect at O. Find the measure of ∠BOC.

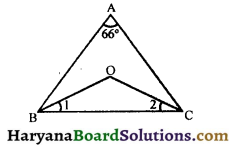
Solution :
In a triangle ΔABC, we have
∠A + ∠B + ∠C = 180°,
(Sum of angles of a triangle = 180°)
⇒ 66° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 180° – 66° = 114°
⇒ \(\frac {1}{2}\)∠B + \(\frac {1}{2}\)∠C = \(\frac {114°}{2}\) = 57°
⇒ ∠1 + ∠2 = 57° …….(i)
[∵ BO and CO are bisectors of ∠B and ∠C respectively]
Now, in ΔBOC, we have
∠1 + ∠2 + ∠BOC = 180°,
(Sum of angles of a triangle = 180°)
⇒ 57° + ∠BOC = 180°, [using (i)]
⇒ ∠BOC = 180° – 57°
⇒ ∠BOC = 123°
Hence, ∠BOC = 123°

Question 14.
The sum of two angles of a triangle is equal to its third angle. Prove that triangle is right-angled.

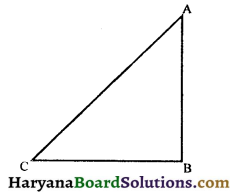
Solution :
Let the smaller angles be A and C and greater angle be B. According to question,
∠B = ∠A + ∠C ……..(i)
But, ∠A + ∠B + ∠C = 180°,
(∵ Sum of angles of a triangle = 180°)
(∠A + ∠C) + ∠B = 180°
⇒ ∠B + ∠B = 180°, [Using (i)]
⇒ 2∠B = 180°
⇒ ∠B = \(\frac {180°}{2}\)
⇒ ∠B = 90°
Hence, triangle ABC is right angled.
Proved

Question 15.
In the given figure, ∠P = ∠Q and ∠1 = ∠2. Prove that RT || PQ.

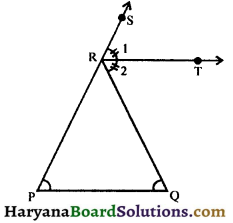
Solution :
In ΔRPQ, we have
∠SRQ = ∠P + ∠Q
⇒ ∠1 + ∠2 = ∠Q + ∠Q
(∵ It is given ∠P = ∠Q)
⇒ ∠2 + ∠2 = 2∠Q
(∵ It is given ∠1 = ∠2)
⇒ 2∠2 = 2∠Q
⇒ ∠2 = ∠Q
Thus, a pair of alternate interior angles 2 and Q are equal, then
RT || PQ. Hence proved

Question 16.
In figure, p || t and m || n. If ∠1 = 75°, prove that ∠2 = ∠1 + \(\frac {1}{3}\) of a right angle.

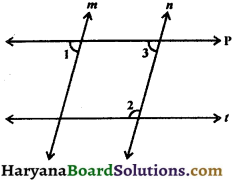
Solution :
∵ m || n and line p is a transversal
∴ ∠3 = ∠1
(Corresponding angles)
⇒ ∠3 = 75° (∴ ∠1 = 75°)
Now p || t and line n is a transversal.
∴ ∠2 + ∠3 = 180° (A pair of allied angles is supplementary)
⇒ ∠2 + 75° = 180°
⇒ ∠2 = 180° – 75°
⇒ ∠2 = 105°
⇒ ∠2 = 75° + 30°
⇒ ∠2 = ∠1 + \(\frac {1}{3}\) × 90°
(∵ ∠1 = 75°)
⇒ ∠2 = ∠1 + \(\frac {1}{3}\) of a right angle.
Hence proved

Long Answer Type Questions

Question 1.
In the figure, OP and OQ are respectively bisectors of angles ∠BOD and ∠AOC. Show that the rays OP and OQ are in the same straight line.

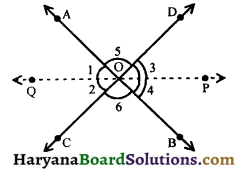
Solution :
∠1 + ∠2 + ∠6 + ∠4 + ∠3 + ∠5 = 360° …….(i)
(Sum of angles at a point = 360°)
∵ ray OP is the bisertor of ∠BOD.
∴ ∠3 = ∠4 …….(ii)
∵ ray OQ is the bisector of ∠AOC.
∴ ∠1 = ∠2 …….(iii)
∠5 = ∠6, (Vertically opposite angles) …(iv)
From (i), (ii), (iii) and (iv), we get
∠2 + ∠2 + ∠6 + ∠4 + ∠4 + ∠6 = 360°
⇒ 2∠2 + 2∠6 + 2∠4 = 360°
⇒ 2(∠2 + ∠6 + ∠4) = 360°
⇒ ∠2 + ∠6 + ∠4 = \(\frac {360°}{2}\) = 180°
⇒ ∠POQ = 180°
Hence, OP and OQ are in the same straight line.
Hence Proved

Question 2.
In the figure, AB || CD, find the value of x.

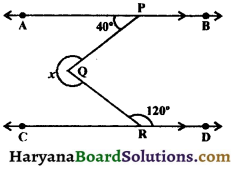
Solution :
Draw a line EF parallel to AB.

∵ AB || EF and a transversal PQ cuts them at P and Q respectively.
∴ ∠APQ + ∠EQP = 180°,
(∵ Sum of a pair of allied angles is 180°)
⇒ 40° + ∠EQP = 180°, (∵ ∠APQ = 40°)
⇒ ∠EQP = 180° – 40°
⇒ ∠EQP = 140° …….(i)
∴ AB || EF, (By construction)
and AB || CD, (Given)
∴ EF || CD, (By theorem 6.6)
∠EQR = ∠QRD,
(Alternate interior angles)
⇒ ∠EQR = 120°,
(∵ ∠QRD = 120°) …(ii)
Adding (i) and (ii), we get
∠EQP + ∠EQR = 140° + 120°
⇒ Reflex angle PQR = 260°
⇒ x = 260°
Hence, x= 260°.

Question 3.
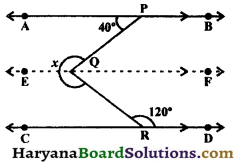
In the given figure :
(i) If x = 70°, find y and z.
(ii) If 3x = 2y, find x.
(iii) If z = 2(x + 15), find y.

Solution :
(i) ∵ CD || EF and CE is a transversal.
∴ x + z = 180° (Sum of a pair of allied angles is 180°)
⇒ 70° + z = 180°, (∵ x = 70°)
⇒ z = 180° – 70°
⇒ z = 110°
∵ AB || CD and AC is a transversal.
∴ y = z,
(Corresponding angles axiom)
⇒ y = 110°
Hence y = 110° and z = 110°.

(ii) 3x = 2y, (Given)
⇒ \(\frac {3}{2}\)x = y …….(i)
∵ AB || EF and AE is a transversal.
∴ x + y = 180° (Sum of a pair of allied angles is 180°)
⇒ x + \(\frac {3}{2}\)x = 180°
[From (i), y = \(\frac {3}{2}\)x]
⇒ \(\frac{2 x+3 x}{2}\) = 180°
⇒ 5x = 2 × 180°
⇒ x = \(\frac {360°}{5}\)
⇒ x = 72°
Hence, x = 72°.

(iii) ∵ CD || EF and CE is a transversal.
∴ x + z = 180°, (Sum of a pair of allied angle is 180°)
⇒ x + 2(z + 15) = 180,[∵ z = 2(x + 15°)
⇒ x + 2x + 30° = 180°
⇒ 3x + 30° = 180°
⇒ 3x = 180° – 30° = 150°
⇒ x = \(\frac {150°}{3}\) = 50°
Now,
z = 2(x + 15°)
⇒ z = 2(50° + 15°)
[Put x = 50°]
⇒ z = 2 × 65°
⇒ z = 130°
Now, y = z,
(Corresponding angles)
⇒ y = 130°
Hence, y = 130°

Question 4.
In the figure, PQ || RS, find the value of x.

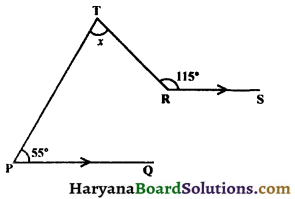
Solution :
Through T draw LTM || PQ || RS.
∵ LT || PQ and PT is the transversal.
∴ ∠LTP = ∠TPQ,
(Alternate interior angles)
⇒ ∠LTP = 55° ……..(i)
and TM || RS and TR is the transversal.
∴ ∠MTR + ∠TRS = 180°,
(A pair of allied angles is supplementary)
⇒ ∠MTR + 115° = 180°
⇒ ∠MTR = 180° – 115°
⇒ ∠MTR = 65° ……..(ii)

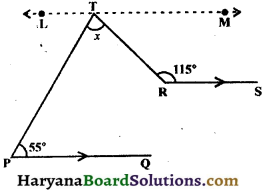
Now LTM is a line.
∴ ∠LTP + ∠PTR + ∠MTR = 180°
(Straight line)
⇒ 55° + x + 65° = 180°. [From (i) and (ii), ∠LTP = 55° and ∠MTR = 65°]
⇒ 120° + x = 180°
⇒ x = 180° – 120°
⇒ x = 60°
Hence, x = 60°.

Question 5.
In the figure, AB || CD, find the values of x, y and z.

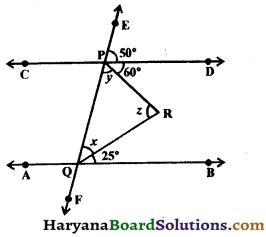
Solution :
∵ AB || CD and EF is the transversal
∴ ∠PQB = ∠EPD,
(Corresponding angles)
⇒ x + 25° = 50°
⇒ x = 50° – 25° = 25° and ∠DPQ + ∠PQB = 180°,
(A pair of allied angles is supplementary)
⇒ (y + 60°) + (x + 25°) = 180°
⇒ y + 60° + 25° + 25° = 180° (∵ x = 25°)
⇒ y + 110°= 180°
⇒ y = 180° – 110°
⇒ y = 70°
In the triangle ΔPQR, Sum of the angles of a triangle is 180°
∴ x + y + z = 180°
⇒ 25° + 70° + z = 180°
⇒ 95° + z = 180°
⇒ z = 180° – 95°
⇒ z = 85°
Hence,
x = 25°, y = 70° and z = 85°

Question 6.
In the given figure, if ΔABC right angled at B, then show that ∠x = ∠y.

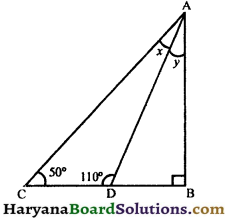
Solution :
Since, CDB is a straight line.
∠ADC + ∠ADB= 180°,(Linear pair axiom)
⇒ 110° + ∠ADB = 180°
⇒ ∠ADB = 180° – 110°
⇒ ∠ADB = 70°
In ΔABD, we have
∠ADC = ∠DAB + ∠ABD,
⇒ 110° = ∠y + 90°
⇒ 110° – 90° = ∠y
⇒ ∠y = 20° ………..(i)
Again in ΔADC, we have
∠ADB = ∠ACD + ∠DAC,
(By theorem 6.8)
⇒ 70° = 50° + ∠x
⇒ 70° – 50° = ∠x
⇒ ∠x = 20° ………..(ii)
From (i) and (ii), we get
∠x = ∠y. Hence proved

Question 7.
In the figure 6.110, AB || CD and EF is a transversal. Prove that bisectors of interior angles on the same side of transversal EF intersect at right angle. [NCERT Exemplar Problems]

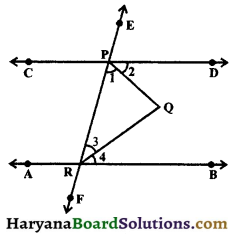
Solution :
Since AB || CD and EF is the transversal.
∠DPR + ∠PRB = 180°, (A pair of interior angles of the same side of transversal is supplementary) …(i)
⇒ ∠1 + ∠2 + ∠3 + ∠4 = 180°
But
∠1 = ∠2, (∵ PQ is the bisector of ∠DPR) …(ii) and
∠3 = ∠4, (∵ RQ is the bisector of ∠PRB) …(iii)
From (i), (ii) and (iii), we get
∠1 + ∠1 + ∠3 + ∠3 = 180°
⇒ 2∠1 + 2∠3 = 180°
⇒ 2(∠1 + ∠3) = 180°
⇒ ∠1 + ∠3 = 90° ……..(iv)
In the ΔPQR, Sum of the angles of a triangle is 180°,
∴ ∠1 + ∠3 + ∠PQR = 180°
⇒ 90° + ∠PQR = 180°,
[From (iv), ∠1 + ∠3 = 90°]
⇒ ∠PQR = 180° – 90°
⇒ ∠PQR = 90°
⇒ ∠PQR = a right angle
Hence, bisectors of interior angles on the same side of the transversal EF intersect at right angle.
Hence Proved

Question 8.
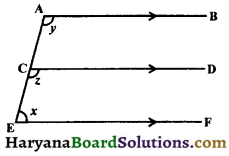
In the given figure, AD || BC, if y⁰ = \(\frac {3}{4}\)x⁰ and x⁰ = \(\frac {4}{5}\)z⁰, find the values of x⁰, y⁰, z⁰ and k⁰.

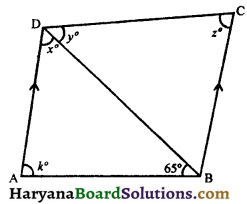
Solution :
Since, AD || BC and BD is the transversal.
∴ ∠DBC = ∠ADB,
(Alternate interior angles)
⇒ ∠DBC = x⁰
In ΔBDC, we have
x° + y° + z° = 180°, (Sum of angles of a triangle = 180°)

Now in ΔDAB,
∠DAB + ∠ADB + ∠ABD = 180°,
(Sum of angles of a triangle = 180°)
⇒ k° + x° + 65° = 180°
⇒ k° + 60° + 65° = 180° (∵ x = 60°)
⇒ k° + 125° = 180°
⇒ k° = 180° – 125°
⇒ k° = 55°
Hence,
x° = 60°, y° = 45°, z° = 75° and k° = 55°

Question 9.
The side BC of a tr iangle ΔABC is produced to D. The bisector of ∠A meets BC at M (see in figure). Prove that ∠ABC + ∠ACD = 2∠AMC.

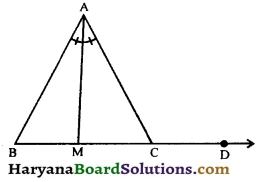
Solution :
In ΔABC, we have
∠ACD = ∠ABC + ∠BAC,
(By theorem 6.8) …(i)
But AM is the bisector of ∠BAC. (Given)
∴ ∠BAM = ∠CAM
or ∠BAC = 2∠BAM
Putting the value of ∠BAC in (i), we get
∠ACD = ∠ABC + 2∠BAM … (ii)
Again, in ΔABM, we have
∠AMC = ∠ABC + ∠BAM
⇒ 2∠AMC = 2∠ABC + 2∠BAM ……(iii)
Subtracting (ii) from (iii), we get
2∠AMC – ∠ACD = ∠ABC
⇒ 2∠AMC = ∠ABC + ∠ACD
⇒ ∠ABC + ∠ACD = 2∠AMC. Hence proved

Question 10.
If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.

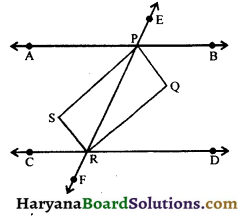
Solution :
Given : Two parallel lines AB and CD are intersected by a transversal EF at P and R respectively. PQ, RS, PS and RQ are the bisectors of the two pairs of interior angles.
To prove: PQRS is a rectangle.
Proof : ∠BPR = ∠PRC,
(A pair of alternate interior angles)
⇒ \(\frac {1}{2}\)∠BPR = \(\frac {1}{2}\)∠PRC
⇒ ∠QPR = ∠PRS
[∵ PQ and RS are bisectors of ∠BPR and ∠PRC
∴ ∠QPR = \(\frac {1}{2}\)∠BPR and ∠PRS = \(\frac {1}{2}\)∠PRC]
But these are alternate interior angles.
PQ || SR, (By theorem 6.3)
Similarly, SP || RQ
∴ PQRS is a parallelogram.
Now, ∠BPR + ∠PRD = 180°,
(Sum of a pair of allied angles = 180°)
⇒ \(\frac {1}{2}\)∠BPR + \(\frac {1}{2}\)∠PRD = \(\frac {180°}{2}\)
⇒ \(\frac {1}{2}\)∠BPR + \(\frac {1}{2}\)∠PRD = 90°
⇒ ∠QPR + ∠QRP = 90° ,
[∵ PQ and RQ are the bisectors of ∠BPR and ∠PRD respectively]
Now in ΔPQR,
∠QPR + ∠PQR + ∠QRP = 180°,
(Sum of angles of a triangle is 180°)
⇒ ∠PQR + 90° = 180°, [Using (i)]
⇒ ∠PQR = 180° – 90° = 90°
In a parallelogram PQRS, ∠PQR = 90°
Hence, PQRS is a rectangle. Hence Proved

Question 11.
In the given figure, AB = AC in ΔABC. From B, BP is drawn such that BP = BC. From P, a line PQ is drawn parallel to BC to meet AB at Q. If exterior ∠RAB = 124°, find ∠BPQ.

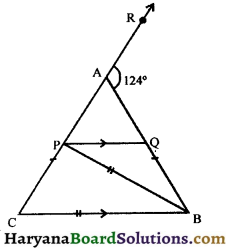
Solution :
In ΔABC, we have
AB = AC
⇒ ∠ACB = ∠ABC, (The angles opposite to equal sides of a triangle are equal)
∠RAB = ∠ACB + ∠ABC, (By theorem 6.8)
⇒ 124° = ∠ABC + ∠ABC [∵ ∠ACB = ∠ABC]
⇒ 124° = 2∠ABC
⇒ \(\frac {124°}{2}\) = ∠ABC
⇒ ∠ABC = 62°
∴ ∠ACB = ∠ABC = 62°
Now in ΔBPC, we have
BP = BC, (Given)
∠BPC = ∠PCB, (The angles opposite to equal sides of a triangle are equal)
⇒ ∠BPC = ∠PCB = 62°, (∵ ∠PCB = ∠ACB)
In ΔBPC, we have
∠BPC + ∠PCB + ∠PBC = 180°,
(Sum of angles of a triangle = 180°)
⇒ 62° + 62° + ∠PBC = 180°
⇒ 124° + ∠PBC = 180°
⇒ ∠PBC = 180° – 124°
⇒ ∠PBC = 56°
Since, PQ || BC (Given)
∴ ∠BPQ = ∠PBC (A pair of alternate interior angles are equal)
⇒ ∠BPQ = 56°
Hence, ∠BPQ = 56°

Question 12.
In figure, ∠B > ∠C and L is a point on BC such that AL is the bisector of ∠BAC. If AM ⊥ BC, prove that ∠LAM = \(\frac {1}{2}\)(∠B – ∠C). [NCERT Exemplar Problems]

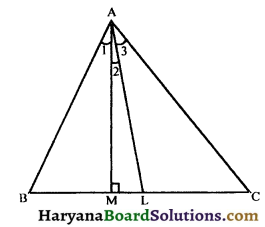
Solution :
Given : In ΔABC, AL is the bisector of ∠BAC and AM ⊥ BC.
To prove : ∠LAM = \(\frac {1}{2}\)(∠B – ∠C).
Proof : Since AL is the bisector of ∠BAC.
∴ ∠BAL = ∠CAL
⇒ ∠1 + ∠2 = ∠3 ………….(i)
In ΔAMB, ∠AMB = 90°, [∵ AM ⊥ BC]
∴ ∠ABM + ∠AMB + ∠1 = 180°,
(∵ Sum of angles of a triangle = 180°)
⇒ ∠ABM + 90° + ∠1 = 180°
⇒ ∠ABM = 180° – 90° – ∠1
⇒ ∠ABM = 90° – ∠1 ……..(ii)
Again in ΔAMC, we have
∠ACM + ∠AMC + ∠2 + ∠3 = 180°,
(∵ Sum of angles of a triangle = 180°)
⇒ ∠ACM + 90° + ∠2 + ∠3 = 180°
⇒ ∠ACM = 180° – 90° – ∠2 – ∠3
⇒ ∠ACM = 90° – ∠2 – ∠3 …….(iii)
Subtracting (iii) from (ii), we get
∠ABM – ∠ACM = 90° – ∠1 – 90° + ∠2 + ∠3
⇒ ∠B – ∠C = ∠2 + ∠3 – ∠1
⇒ ∠B – ∠C = ∠2 + (∠1 + ∠2) – ∠1,
[From (i), ∠3 = ∠1 + ∠2]
⇒ ∠B – ∠C = 2∠2
⇒ ∠2 = \(\frac {1}{2}\)(∠B – ∠C)
⇒ ∠LAM = \(\frac {1}{2}\)(∠B – ∠C).
Hence proved.

Question 13.
In figure, P and Q are two plane mirrors perpendicular to each other. Show that incident ray AB is parallel to the reflected ray CD.

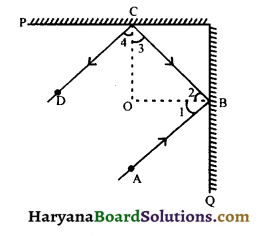
Solution :
∵ Angle of incidence = Angle of reflection
∴ ∠1 = ∠2 and ∠3 = ∠4
∴ ∠ABC = ∠1 + ∠2
= ∠2 + ∠2 = 2∠2 …(i)
and ∠DCB = ∠3 + ∠4 = ∠3 + ∠3
= 2∠3 …(ii)
Since, the two mirrors are perpendicular, the rays perpendicular to them are also perpendicular.
i.e., BO ⊥ OC or ∠BOC = 90°
In ΔBOC, we have
∠2 + ∠3 + ∠BOC= 180°,
(Sum of angles of a triangle = 180°)
⇒ ∠2 + ∠3 + 90° = 180°
⇒ ∠2 + ∠3 = 180° – 90°
⇒ ∠2 + ∠3 = 90°
⇒ 2∠2 + 2∠3 = 180°
⇒ ∠ABC + ∠DCB = 180°, [Using (i) and (ii)]
Thus, sum of a pair of co-interior angles ∠ABC and ∠DCB is 180°.
By theorem 6.5, we have
AB || CD. Hence proved

Multiple Choice Questions

Choose the correct alternative each of the following :

Question 1.
If two angles are supplementary of each other, then each angle is :
(a) a right angle
(b) an acute angle
(c) an obtuse angle
(d) a straight angle
Solution :
(a) a right angle

Question 2.
The complement of 47° 32′ 45″ is:
(a) 43° 28′ 15″
(b) 43° 27′ 15″
(c) 42° 27′ 15″
(d) 43° 27′ 15″
Solution :
(c) 42° 27′ 15″

Question 3.
The supplement of 75° 30′ 50″ is :
(a) 14° 29′ 10″
(b) 15° 30′ 10″
(c) 105° 30′ 10″
(d) 104° 29′ 10″
Solution :
(d) 104° 29′ 10″

Question 4.
The angles a triangle are in the ratio 5 : 3 : 7 The triangle is: [NCERT Exemplar Problems]
(a) an acute angled triangle
(b) an obtused angled triangle
(c) a right triangle
(d) an isosceles triangle
Solution :
(a) an acute angled triangle

Question 5.
If angles of a triangle are in the ratio 1 : 2 : 3, then the smallest angle of the triangle is :
(a) 60°
(b) 30°
(c) 90°
(d) 50°
Solution :
(b) 30°

Question 6.
If one angle of a triangle is equal to the sum of the other two angles, then triangle is : [NCERT Exemplar Problems]
(a) a right angled triangle
(b) acute angled triangle
(c) obtuse angled triangle
(d) equilateral triangle
Solution :
(a) a right angled triangle

Question 7.
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be : [NCERT Exemplar Problems]
(a) 50°
(b) 65°
(c) 145°
(d) 155°
Solution :
(d) 155°

Question 8.
In ΔPQR, side QR is produced to S such that ∠PRS = 110, if ∠P = ∠Q, then ∠Q is equal to :
(a) 70°
(b) 55°
(c) 50°
(d) 45°
Solution :
(b) 55°

Question 9.
In the figure, ∠x + ∠y + ∠z is equal to :

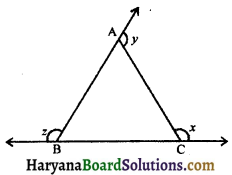
(a) 180°
(b) 90°
(c) 360°
(d) 270°
Solution :
(c) 360°

Question 10.
In the figure, ∠A + ∠B + ∠C + ∠P + ∠Q + ∠R is equal to :

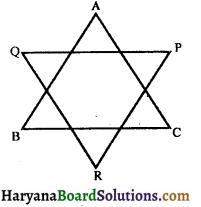
(a) 180°
(b) 270°
(c) 90°
(d) 360°
Solution :
(d) 360°

Haryana State Board HBSE 11th Class Sanskrit Solutions व्याकरणम् Samasaha Prakaran समास प्रकरण Exercise Questions and Answers.

Haryana Board 11th Class Sanskrit व्याकरणम् समास प्रकरण

समास-परिचय

समास-परस्पर सम्बद्ध अर्थ वाले दो या दो से अधिक पदों को मिलाकर एक पद बनाने की क्रिया को समास कहते हैं। समास प्रक्रिया द्वारा बने हुए एक पद को समस्त पद कहा जाता है। इसमें शब्दों की पहली विभक्तियों का लोप हो जाता है; जैसे-राज्ञः पुरुषः = राजपुरुषः। यहाँ पर समस्त पद राजपुरुषः में ‘राज्ञः’ की विभक्ति का लोप करके राज (न) शब्द का प्रयोग हुआ है।

विग्रह-जब समस्त-पद के सभी शब्दों को अर्थ बोध के लिए अलग-अलग करके उपयुक्त विभक्तियाँ लगा दी जाती हैं तो उसे विग्रह कहते हैं; जैसे-रामलक्ष्मणौ = रामः च लक्ष्मणः च। समास के भेद-

1. अव्ययीभाव समास,
2. तत्पुरुष समास,
3. कर्मधारय समास,
4. द्वन्द्व समास,
5. द्विगु समास,
6. बहुव्रीहि समास। इनकी परिभाषाएँ निम्नलिखित हैं

1. अव्ययीभाव समास:
अव्ययीभाव समास में पूर्व पद का अर्थ प्रधान होता है तथा पूर्व पद अव्यय होता है। उत्तर पद संज्ञा होता है। पूर्व पद तथा उत्तर पद को मिलाकर समस्त पद भी अव्यय बन जाता है तथा वह सदा नपुंसकलिङ्ग, एकवचन में रहता है; जैसे-यथाशक्ति, प्रतिदिनम्।

2. तत्पुरुष समास:
जब उत्तर पद के अर्थ की प्रधानता होती है और समस्त पद का लिङ्ग और वचन उसी के अनुसार होते हैं तो उसे तत्पुरुष समास कहते हैं; जैसे राजपुरुषः में पुरुष के अर्थ की प्रधानता है।

3. कर्मधारय समास:
कर्मधारय ऐसे समास को कहते हैं जिसमें सभी शब्दों का आधार एक ही हो। इसके विग्रह में दोनों पदों में एक ही विभक्ति रहती है। प्रायः इसमें पूर्व पद विशेषण तथा उत्तर पद विशेष्य होता है; जैसे-कृष्णसर्पः।

4. द्वन्द्व समास:
जिस समास में पूर्व पद तथा उत्तर पद की समान रूप से प्रधानता हो, उसे द्वन्द्व समास कहते हैं; जैसे रामलक्ष्मणौ।

5. द्विगु समास:
ऐसा समानाधिकरण तत्पुरुष जिसमें पूर्व पद सङ्ख्यावाची हो, उसे द्विगु समास कहते हैं। इसका प्रयोग प्रायः समाहार या समूह अर्थ में होता है; जैसे-त्रिलोकी।

6. बहुव्रीहि समास:
जिस समास में न तो पूर्व पद प्रधान होता है, न ही उत्तर पद प्रधान होता है अपितु कोई अन्य पद ही प्रधान होता है, उसे बहुव्रीहि समास कहते हैं। बहुव्रीहि समास में दो या अधिक संज्ञा पद होते हैं तथा पदों का समास होने के उपरान्त समस्त पद से किसी अन्य ही संज्ञा का बोध होता है; जैसे-पीताम्बरः।

अव्ययीभाव समास
अव्ययीभाव समास विशेषतः जिन-जिन अर्थों में प्रयुक्त होता है, वे पाणिनि व्याकरण में एक सूत्र में परिगणित किए गए हैं। वे 16 अर्थ हैं-विभक्ति, सामीप्य, समृद्धि, अर्थाभाव, अत्यय, असम्प्रति, शब्द प्रादुर्भाव, पश्चात्, यथा, आनुपूर्व्य, यौगपद्य, सादृश्य, सम्पत्ति, साकल्य तथा अन्त। इन 16 अर्थों में वर्तमान अव्यय का सुबन्त के साथ समास होता है और उस समास को अव्ययीभाव कहते हैं।

प्रश्न-निम्नलिखित समस्त पदों का विग्रह करके समास का नाम लिखिए।

तत्पुरुष समास
जिस समास में उत्तर पद प्रधान होता है वह तत्पुरुष समास कहलाता है। यथा राज्ञः पुरुष = राजपुरुषः। यहाँ उत्तर पद ‘पुरुष’ की प्रधानता है, अतः यह तत्पुरुष समास हुआ।

तत्पुरुष समास के भेद-

1. व्यधिकरण,
2. समानाधिकरण तथा कर्मधारय तथा द्विगु तत्पुरुष।

कर्मधारय तथा द्विगु तत्पुरुष को समास के मुख्य भेदों में भी मान लिया जाता है। अतः यहाँ केवल व्यधिकरण तत्पुरुष का . ही विचार किया जाएगा।

व्यधिकरण तत्पुरुष व्यधिकरण तत्पुरुष के पुनः चार भेद हैं

1. विभक्ति तत्पुरुष,
2. अलुक् तत्पुरुष,
3. नञ् तत्पुरुष,
4. उपपद तत्पुरुष।

1. विभक्ति तत्पुरुष-विभक्ति तत्पुरुष के पुनः छः भेद हैं द्वितीया तत्पुरुष, तृतीया तत्पुरुष, चतुर्थी तत्पुरुष, पञ्चमी तत्पुरुष, षष्ठी तत्पुरुष तथा सप्तमी तत्पुरुष।

द्वितीया तत्पुरुष
द्वितीय तत्पुरुष समास में, विग्रह पूर्वपद द्वितीया विभक्ति में होता है तथा उत्तर पद में प्रायः निम्नलिखित पद रहते हैं श्रित, अतीत, पतित, गत, अत्यय, प्राप्त, आपन्न; जैसे

तृतीया तत्पुरुष
कर्त्ता और करण कारक में विद्यमान ततीया विभक्ति वाले शब्द का समान कृदन्त शब्द के साथ समास होता है; जैसे-

ततीयान्त शब्दों का खण्ड, अर्थ, पूर्व, अवर, सदृश, सम, अन, निपुण, मिश्र आदि से भी समास होता है; जैसे-

चतुर्थी तत्पुरुष
चतुर्थी विभक्ति वाले शब्दों का तदर्थ, अर्थ, बलि, हित, सुख, रक्षित आदि के साथ समास होता है; जैसे-

पञ्चमी तत्पुरुष
पञ्चमी विभक्ति अन्त वाले शब्दों का भयवाचक शब्दों (यथा भयम्, भी) के साथ तथा अपेत, मुक्त, पतित, भ्रष्ट आदि शब्दों के साथा समास होता है; जैसे-

षष्ठा तत्पुरुष
षष्ठी विभक्ति वाले शब्द का उत्तर पद के साथ समास होने से षष्ठी तत्पुरुष कहलाता है; जैसे-

सप्तमी तत्पुरुष
सप्तमी विभक्ति वाले शब्दों का जब अन्य शौण्ड, धूर्त, प्रवीण, निपुण आदि शब्दों के साथ समास होता है, तब उसे सप्तमी तत्पुरुष कहते हैं; जैसे-

अलुक् तत्पुरुष
विभक्ति का लोप न होने पर अलुक् तत्पुरुष समास होता है; जैसे-

नज् तत्पुरुष
निषेध के अर्थ को बताने के लिए नज् शब्द का किसी भी शब्द के साथ समास हो जाता है। यदि उत्तर पद का प्रथम वर्ण व्यंजन हो तो ‘नज्’ का ‘अ’ शेष रह जाता है; जैसे-न (ज्ञ) + विद्या = अविद्या।

उपपद तत्पुरुष
जब तत्पुरुष समास में किसी पद के पहले रहने के कारण किसी धातु से कोई कृत् प्रत्यय होता है, तब प्रथम पद को उपपद कहते हैं और दोनों पदों के समास को ‘उपपद तत्पुरुष’ कहते हैं; जैसे-

प्रादि तत्पुरुष
जिस समस्त पद का पूर्व भाग उपसर्ग (प्रादि) हो, उसे प्रादि तत्पुरुष कहते हैं; जैसे-

गति तत्पुरुष
कुछ शब्दों के अनन्तर क्रिया से बने अव्यय लगने पर जो तत्पुरुष समास होता है, उसे गति तत्पुरुष कहते हैं; जैसे-

कर्मधारय तत्पुरुष
कर्मधारय ऐसे समास को कहते हैं जिसमें सभी शब्दों का आधार एक ही हो। इसके विग्रह वाक्य में दोनों पदों में एक ही विभक्ति रहती है। प्रायः इसमें पूर्व पद विशेषण होता है और उत्तर पद विशेष्य होता है; जैसे-

यदि विशेषण-विशेष्य के स्थान पर पूर्व पद तथा उत्तर पद परस्पर उपमान उपमेय हों तो भी कर्मधारय समास होता है; जैसे-

द्विगु समास
यदि कर्मधारय समास का पूर्व पद सड्ख्यावाची शब्द हो तो वह द्विगु समास कहलाता है; जैसे-

द्वन्द समास
जिस समास में उभय पद (दोनों पदों) की प्रधानता होती है, उसे द्वन्द्व समास कहते हैं। द्वन्द्व समास के तीन भेद होते हैं-
(क) इतरेतर द्वन्द्ध,
(ख) समाहार द्वन्द,
(ग) एकशेष द्वन्द्व।

(क) इतरेतर द्वन्द्ध :
जहाँ सभी पद प्रधान भी होते हैं तथा अपना अस्तित्व भी बनाए रखते हैं और अन्त में सड्ख्या के अनुसार वचन होता है, उसे इतरेतर द्वन्द्व कहते हैं, जैसे-

(ख) समाहार द्वन्द्ध :
इसमें प्रत्येक पद की प्रधानता नहीं होती, अपितु उसमें एक सामूहिक अर्थ प्रकट होता है। यह समास सदा एकवचन और नपुंसकलिङ्ग में होता है; जैसे-

(ग) एकशेष द्वन्द:
जहाँ द्वन्द्व समास में केवल एक ही शब्द शेष रहे, वहाँ एकशेष द्वन्द्ध होता है; जैसे-

बहुव्रींहि समास
जिस समास में न तो पूर्व पद प्रधान होता है न उत्तर पद प्रधान होता है अपितु कोई अन्य पद ही प्रधान होता है, उसे बहुव्रीहि समास कहते हैं। बहुव्रीहि समास में दो या अधिक संज्ञा पद होते हैं तथा पदों का समास होने के उपरान्त समस्त पद से किसी अन्य ही संज्ञा का बोध होता है; जैसे-

प्रश्न:
निम्नलिखित विग्रह किए गए पदों के समस्त पद बनाकर समास का नाम लिखिए।

अभ्यासार्थ प्रश्नाः

I. 1. अव्ययीभाव समासस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
2. कर्मधारय समासस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
3. द्वन्द्व समासस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
4. तत्पुरुष समासस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।
5. बहुव्रीहि समासस्य परिभाषां सोदाहरणं हिन्दीभाषायां लिखत।

II. अधोलिखित प्रश्नानां प्रदत्तोत्तरविकल्पेषु शुद्धविकल्पं लिखत
(निम्नलिखित प्रश्नों के दिए गए विकल्पों में से शुद्ध विकल्प लिखिए)

1. ‘देवहितम् अत्र कः समासः?
(A) अव्ययीभावः
(B) कर्मधारयः
(C) तत्पुरुषः
(D) द्वन्द्वः

2. ‘निर्मान’ अत्र कः समासः?
(A) कर्मधारयः
(B) अव्ययीभावः
(C) बहुव्रीहिः
(D) द्वन्द्वः

3. ‘अम्बरस्थः’ अत्र कः समासः?
(A) द्वन्द्वः
(B) द्विगुः
(C) कर्मधारयः
(D) तत्पुरुषः

4. ‘मृच्छकटिकम्’ अत्र कः समासः?
(A) तत्पुरुषः
(B) कर्मधारयः
(C) बहुव्रीहिः
(D) द्वन्द्वः

5. ‘प्रत्यहम्’ इति पदे कः समासः ?
(A) तत्पुरुषः
(B) अव्ययीभावः
(C) द्वन्द्वः
(D) कर्मधारयः

6. ‘महार्णवः’ इत्यस्य समास विग्रहः अस्ति
(A) महान् च असौ अर्णवः
(B) महत् च अर्णवः
(C) महान् च अर्णवः
(D) महान् च असः अर्णवः

7. ‘अहनि अहनि प्रति’ अत्र किं समस्तपदम्?
(A) प्रत्यहन्
(B) प्रतिहनि
(C) प्रत्यहः
(D) प्रत्यहम्

8. ‘सुवर्णव्यवहारः’ इति समस्तपदस्य विग्रहः अस्ति ?
(A) सुवर्णस्य व्यवहारः
(B) वर्ण व्यवहार
(C) सुवर्ण व्यवहारः
(D) सुवर्ण व्यवहारः

9. ‘भारतानां माता’ इत्यस्य समस्तपदम् अस्ति
(A) भारतांमाता
(B) भारतमाता
(C) भारतानमाता
(D) भारतान्माता

10. ‘अविरुद्धम्’ अत्र किं नाम समासः?
(A) तत्पुरुषः
(B) द्वन्द्व
(C) द्विगुः
(D) नब् तत्पुरुषः

11. ‘यथापूर्वम्’ इति पदे कः समासः?
(A) तत्पुरुषः
(B) द्विगुः
(C) अव्ययीभावः
(D) द्वन्द्वः

12. ‘सुवर्णव्यवहारः’ इति समस्तपदस्य विग्रहः अस्ति?
(A) सुवर्णस्य व्यवहारः
(B) सुवर्ण व्यवहार
(C) सौवर्ण व्यवहार
(D) सुवर्ण व्यवहारे

Haryana State Board HBSE 12th Class Biology Solutions Chapter 7 Evolution Textbook Exercise Questions and Answers.

Haryana Board 12th Class Biology Solutions Chapter 7 Evolution

Haryana State Board HBSE 12th Class Biology Solutions Chapter 6 Molecular Basis of Inheritance Textbook Exercise Questions and Answers.

Haryana Board 12th Class Biology Solutions Chapter 6 Molecular Basis of Inheritance