Class 9

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.8 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.8

Assume π = \(\frac{22}{7}\), unless stated otherwise.

Question 1.
Find the volume of a sphere whose radius is :
(i) 7 cm
(ii) 0.63 m.
Solution:
(i) We have,
Radius of sphere (r) = 7 cm
∴ Volume of sphere = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times(7)^3\)
= \(\frac{88 \times 49}{3}\)
= \(\frac{4312}{3}\)
= 4312\(\frac{1}{3}\) cm³.
Hence,volume of the spher = 4312\(\frac{1}{3}\) cm³.

(ii) We have,
Radius of the sphere (r) = 0.63 m
∴ Volume of the sphere = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times(0.63)^3\)
= 88 × 0.03 × 0.3969
= 1.0478 m³ = 1.05 m³
Hence,volume of the sphere = 1.05 m³.

Question 2.
Find the amount of water displaced by a solid spherical ball of diameter :
(i) 28 cm
(ii) 0.21 m.
Solution:
(i) We have,
Diameter of spherical ball = 28 cm
∴ Radius of the spherical ball (r) = \(\frac{28}{2}\)
= 14 cm
Amount of water displaced by spherical ball = Volume of spherical ball
= \(\frac{4}{3} \pi r^3=\frac{4}{3} \times \frac{22}{7} \times(14)^3\)
= \(\frac{4}{3} \times \frac{22}{7} \times 14 \times 14 \times 14\)
= \(\frac{88 \times 2 \times 196}{3}\)
= \(\frac{34496}{3}\)
= 11498\(\frac{2}{3}\) cm³
Amount of water displaced by spherical ball
=11498\(\frac{2}{3}\) cm³

(ii) We have,
Diameter of spherical ball = 0.21 m
∴ Radius of spherical ball (r) = \(\frac{0.21}{2}\)
= 0.105 m
Amount of water displaced by spherical ball = Volume of spherical ball
= \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times(0.105)^3\)
= \(\frac{4}{3} \times \frac{22}{7}\) × 0.105 × 0.105 × 0.105
= 88 × 0·005 × 0.011025
= 0.004851 m³
Hence, amount of water displaced by spherical ball = 0.004851 m³.

Question 3.
The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm³?
Solution:
We have,
Diameter of ball = 4.2 cm
∴ Radius of the ball (r) = \(\frac{4.2}{2}\) = 2.1 cm
Since, ball is in the shape of sphere, therefore we need to calculate the volume of sphere for its mass.
∴ Volume of spherical ball = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times(2.1)^3\)
= \(\frac{88}{21}\) × 2.1 × 2.1 × 2.1
= 8.8 × 4.41 = 38.808 cm³
mass of the ball = volume × density
= 38.808 × 8.9
= 345.39 grams (approx.)
Hence,mass of the ball = 345.39 grams (approx.)

Question 4.
The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
Solution:
Let the diameter of the earth be 2x.
∴ Radius of the earth (R) = \(\frac{2 x}{2}\) = x
According to question,
Diameter of the moon = \(\frac{1}{4}\) of diameter of the earth = \(\frac{1}{4}\) × 2x = \(\frac{x}{2}\)
∴ Radius of the moon (r) = \(\frac{x}{4}\)
Volume of the earth = \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\)πx³
Volume of the moon = \(\frac{4}{3}\)πr³ = \(\frac{4}{3} \pi\left(\frac{x}{4}\right)^3\)
= \(\frac{4}{3} \pi \frac{x^3}{64}\)

⇒ Volume of the moon = \(\frac{1}{4}\) × volume of the earth
Hence, \(\frac{1}{64}\) fraction of volume of earth is volume of the moon.

Question 5.
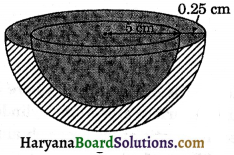
How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold.
Solution:
We have,
Diameter of hemispherical bowl = 10.5 cm
∴ Radius of hemispherical bowl (r) = \(\frac{10.5}{2}\)
= 5.25 cm
∴ Volume of the hemispherical bowl
= \(\frac{2}{3} \pi r^3\)
= \(\frac{2}{3} \times \frac{22}{7} \times(5.25)^3\)
= \(\frac{2}{3} \times \frac{22}{7}\) × 5.25 × 5.25 × 5.25
= 44 × 0.25 × 27.5625
= 303.1875 cm³
= 0.3031875 litres
= 0.303 litres (approx.)
Hence, hemispherical bowl, can hold 0.303 litres (approx.) of milk.

Question 6.
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Solution:
We have,
Inner radius of the hemispherical tank (r) = 1 m
Thickness of the iron sheet = 1 cm
= 0.01 m
∴ Outer radius of the hemispherical tank
(R) = 1 + 0.01 = 1.01 m
Volume of the iron used to make the tank = External volume – Internal volume
= \(\frac{4}{3}\)πR³ – \(\frac{2}{3}\)πr³
= \(\frac{2}{3}\)π[R³ – r³]
= \(\frac{2}{3} \times \frac{22}{7}\)[(1.01)³ – (1)³]
= \(\frac{44}{21}\)(1.030301 – 1)
= \(\frac{44}{21}\) × 0.030301
= 0·06348 m³ (approx.)
Hence, volume of the iron used to make the tank = 0·06348 m³ (approx.)

Question 7.
Find the volume of a sphere whose surface area is 154 cm².
Solution:
Let the radius of sphere be r сm.
Surface area of the sphere = 154 cm² (given)

Hence,volume of the sphere = 179\(\frac{2}{3}\) cm³.

Question 8.
A dome of a building is in the form of a hemisphere. From inside, it was whitewashed at the cost of Rs. 498.96. If the cost of the white-washing is Rs. 2.00 per square metre, find the :
(i) inside surface area of the dome,
(ii) volume of the air inside the dome.
Solution:

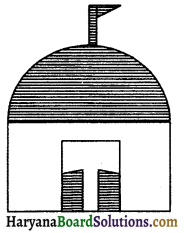
Let inner radius of dome be r m.
We have, Rate of white washed = Rs. 2.00 per m²
Total cost of white washed = Rs. 498.96
(i) Inside curved surface area of the dome
= \(\frac{\text { Total cost }}{1 m^2 \cos t}=\frac{498.96}{2}\)

(ii) We have,
Inside C.S.A. of the dome = 249.48
2πr² = 249.48
2 × \(\frac{22}{7}\) × r² = 249.48
r² = \(\frac{249.48 \times 7}{22 \times 2}\)
r² = 39.69
r = \(\sqrt{39.69}\)
r = 63 m.
Volume of air inside the dome = \(\frac{2}{3}\)πr³
= \(\frac{2}{3} \times \frac{22}{7} \times(6.3)^3\)
= \(\frac{2 \times 22}{21}\) × 6.3 × 6.3 × 6.3
= 44 × 0.3 × 39.69
= 523.908 m³
= 523.9 m³ (approx.)
Hence, (i) Curved surface area of the dome = 249.48 m²
(ii) Volume of air inside the dome = 523.9 m³ (approx.)

Question 9.
Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S’. Find the :
(i) radius r’ of the new sphere,
(ii) radio of S and S’.
Solution:
We have,
Twenty seven spheres, each of radius r and surface area S are melted to form a sphere with surface area S’.
(i) Then S = 4πr² …..(i)
Volume of one sphere = \(\frac{2}{3}\)πr³
Volume of 27 spheres = 27 × \(\frac{2}{3}\)πr³
Volume of new sphere = Volume of 27 spheres
⇒ \(\frac{4}{3} \pi r^{\prime} 3=27 \times \frac{4}{3} \pi r^3\)
⇒ \(r^{\prime 3}=\frac{27 \times \frac{4}{3} \pi r^3}{\frac{4}{3} \pi}\)
⇒ r’³ = 27r³ = (3r)³
⇒ r’= 3r
(ii) Surface area of new sphere (S’) = 4πr’²
= 4π × (3r)² = 4π × 9r²
= 36πr²
Now, \(\frac{S}{S^{\prime}}=\frac{4 \pi r^2}{36 \pi r^2}\)
⇒ \(\frac{S}{S^{\prime}}=\frac{1}{9}\)
⇒ S : S’ = 1 : 9
Hence (i)Radius of new sphere (r’) = 3r
(ii) S : S’ = 1 : 9.

Question 10.
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm³) is needed to fill this capsule?
Solution:
We have,
Diameter of spherical capsule = 3.5 mm
∴ Radius of spherical capsule (r) = \(\frac{3.5}{2}\)
= 1.75 mm
Volume of the capsule = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times(1.75)^3\)
= \(\frac{4}{3} \times \frac{22}{7}\) × 1.75 × 1.75 × 1.75
= \(\frac{88 \times 0.25 \times 3.0625}{3}\)
= \(\frac{67.375}{3}\)
= 22.46 mm³ (approx.)
Hence, volume of medicine in the capsule = 22.46 mm³ (approx.)

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.6 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.6

Assume π = \(\frac{22}{7}\), unless stated otherwise.

Question 1.
The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1000 cm³ = 11)
Solution:
We have,
Height of cylindrical vessel (h) = 25 cm
Circumference of the base of the cylindrical vessel = 132 cm …..(1)
Let the radius of the base of the cylindrical vessel be r сm, then
Circumference of the base of the cylindrical vessel = 2πr
⇒ 132 = 2 × \(\frac{22}{7}\) × r [Using (1)]
⇒ \(\frac{132 \times 7}{2 \times 22}=r\)
⇒ r = 21 cm
∴ volume of the water in the vessel = πr2h
\(\frac{22}{7}\) × (21)² × 25
= 34650 cm³
= \(\frac{34650}{1000}\)
= 34.65 litres
Hence, volume of the water in the vessel = 34.65 litres.

Question 2.
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm³ of wood has a mass of 0.6 g.
Solution:
We have,
Length of the cylindrical pipe (h) = 35 cm
Inner diameter of the cylindrical pipe = 24 cm
∴ Inner radius of the cylindrical pipe (r) = \(\frac{24}{2}\) = 12 cm
and outer diameter of the cylindrical pipe = 28 cm
∴ Outer radius of the cylindrical pipe (R) = \(\frac{28}{2}\) = 14 cm
∴ Volume of wooden used in making the pipe
= π(R² – r²) × h
= \(\frac{22}{7}\)(14² – 12²) × 35
= \(\frac{22}{7}\)(14 + 12)(14 – 12) × 35
= 110 × 26 × 2 = 5720 cm³
∵ Weight of 1 cm³ wood = 0·6 gram
∴ Weight of 5720 cm³ wood = 0·6 × 5720 gram
= 3432 gram
= \(\frac{3432}{1000}\) kg = 3.432
Hence,mass of the wooden pipe = 3.432 kg.

Question 3.
A soft drink is available in two packs – (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
Solution:
(i) We have,
Length of rectangular tin (l) = 5 cm
Breadth of rectangular tin (b) = 4 cm
Height of rectangular tin (h) = 15 cm
∴ Volume of the rectangular tin = l × b × h
= 5 × 4 × 15 = 300 cm³

(ii) Diameter of the base of the plastic cylinder (d) = 7 cm
∴ Radius of the base of the plastic cylinder (r) = \(\frac{7}{2}\) = 3.5 cm
and height of the plastic cylinder (h) = 10 cm
∴ Volume of the plastic cylinder = πr²h
= \(\frac{22}{7}\) × (3.5)² × 10
= 385 cm³
Hence, plastic cylinder has greater capacity and it is equal (385 – 300) cm³ = 85 cm³.

Question 4.
If the lateral surface of a cylinder is 94.2 cm² and its height is 5 cm, then find :
(i) radius of its base
(ii) its volume. (Use π = 3.14)
Solution:
We have,
Height of the cylinder (h) = 5 cm
Let radius of the cylinder be r сm.
and lateral surface of the cylinder = 94.2 cm²
⇒ 2πrh = 94.2
⇒ 2 × 3.14 × r × 5 = 94.2
⇒ 31.4 × r = 94.2
⇒ r = \(\frac{94.2}{31.4}\)
⇒ r = 3 cm
(ii) Volume of the cylinder = πr²h
= 3.14 × (3)² × 5
= 141.3 cm³
Hence, (i)Radius of the cylinder = 3 cm
(ii) Volume of the cylinder = 141.3 cm³.

Question 5.
It costs Rs. 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of Rs. 20 per m², find :
(i) inner curved surface area of the vessel,
(ii) radius of the base,
(iii) capacity of the vessel.
Solution:
We have,
Depth of the cylindrical vessel (h) = 10 m
cost of painting = Rs. 20 per m²
Total cost of painting = Rs. 2200
(i) Inner curved surface area of the vessel = \(\frac{\text { Total cost }}{\text { Cost of painting }}=\frac{2200}{20}\) = 110 m²
(ii) Let the radius of the base of vessel ber m.
Curved surface area of the vessel = 110 m²,
[As solved in (i)]
⇒ 2πrh = 110
⇒ 2 × \(\frac{22}{7}\) × r × 10 = 110
⇒ \(\frac{440}{7}\) × r = 110
⇒ r = \(\frac{110 \times 7}{440}\)
⇒ r = 1.75 m.
(iii) Capacity of the vessel = πr²h
= \(\frac{22}{7}\) × (175)² × 10
= 96.25 m³ = 96.25 kl
Hence, (i) Inner curved surface area of the vessel = 110 m²
(ii) Radius of the base = 1.75 m
(iii) Capacity of the vessel = 96.25 m³ or 96.25 kl.

Question 6.
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
Solution:
We have,
Height of the cylindrical vessel (h) = 1 m
and volume of the cylindrical vessel = 15.4 litres …..(1)
Let the radius of the cylindrical vessel be r m, then
Volume of the cylindrical vessel = πr²h
⇒ 15.4 litres = \(\frac{22}{7}\) × r² × 1[Using (1)]
⇒ \(\frac{15.4}{1000} \mathrm{~m}^3=\frac{22}{7} r^2\)
⇒ \(\frac{15.4 \times 7}{1000 \times 22}=r^2\)
⇒ 0.0049 = r²
⇒ r = \(\sqrt{0.0049}\)
⇒ r = \(\sqrt{\frac{49}{10000}}\)
r = \(\frac{7}{100}\)
Required area of the metal sheet = Total surface area of the cylindrical vessel
= 2πrh + 2πr²
= 2 \(\frac{22}{7}\) × 1 + 2 × \(\frac{22}{7} \times\left(\frac{7}{100}\right)^2\)
= \(\frac{44}{100}\) + 0.0308
= 0.44 + 0.0308
= 0.4708 m²
Hence, area of the metal sheet required to make the vessel = 0.4708 m².

Question 7.
A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
Solution:
We have,
Length of the cylindrical pencil (h)= 14 cm
Diameter of the cylindrical pencil = 7 mm
= \(\frac{7}{10}\) cm
∴ Radius of the cylindrical pencil (R) = \(\frac{7}{20}\) cm
and diameter of the cylindrical graphite
= 1 mm = \(\frac{1}{10}\) cm
∴ Radius of the cylindrical graphite (r) = \(\frac{1}{10}\)
∴ Volume of the cylindrical pencil = πR²h
= \(\frac{22}{7} \times\left(\frac{7}{20}\right)^2 \times 14\)
= 5.39 cm³
and volume of the cylindrical graphite = πr²h
= \(\frac{22}{7} \times\left(\frac{1}{20}\right)^2 \times 14\)
= 0·11 cm³
Volume of the wood = Volume of the pencil – Volume of the graphite
= 5.39 – 0·11 = 5.28 cm³
Hence, volume of the wood = 5.28 cm³ and volume of the graphite = 0·11 cm³.

Question 8.
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Solution:
We have,
Height of the cylidrical bowl filled with soup (h) = 4 cm
Diameter of the cylindrical bowl (d) = 7 cm
∴ Radius of the cylindrical bowl (r) = \(\frac{7}{2}\) cm
Volume of the soup for 1 patient = πr²h
= \(\frac{22}{7} \times\left(\frac{7}{2}\right)^2 \times 4\)
= 154 cm³
Volume of the soup for 250 patients
= 154 × 250 = 38500 cm³
= \(\frac{38500}{1000}\) litres
= 38.5 litres
Hence, volume of the soup for 250 patients = 38500 cm³ or 38.5 litres.

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.4 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.4

Assume π = \(\frac{22}{7}\), unless stated otherwise.

Question 1.
Find the surface area of a sphere of radius:
(i) 10.5 cm (ii) 5.6 cm (iii) 14 cm.
Solution:
(i) We have,
Radius of sphere (r) = 10.5 cm
∴ Surface area of a sphere = 4πr²
= 4 × \(\frac{22}{7}\) × (10.5)²
= \(\frac{9702}{7}\) cm² Ans.
Hence,surface area of a sphere = 1386 cm².

(ii) We have,
Radius of sphere (r) = 5.6 cm²
∴ Surface area of a sphere = 4πr²
= 4 × \(\frac{22}{7}\) × (5.6)²
= \(\frac{2759.68}{7}\)
= 394.24 cm²
Hence,surface area of a sphere
= 394.24 cm².

(iii) We have,
Radius of sphere (r) = 14 cm
∴ Surface area of a sphere = 4πr²
= 4 × \(\frac{22}{7}\) × (14)²
\(\frac{17248}{7}\) = 2464 cm²
Hence, surface area of a sphere = 2464 cm².

Question 2.
Find the surface area of a sphere of diameter :
(i) 14 cm
(ii) 21 cm
(iii) 3.5 m.
Solution:
(i) We have,
Diameter of a sphere (d) = 14 cm
∴ Radius of a sphere (r) = \(\frac{14}{2}\) = 7 cm
∴ Surface area of a sphere = 4πr²
= 4 × \(\frac{22}{7}\) × (7)²
= \(\frac{4312}{7}\)
= 616 cm²
Hence,surface area of a sphere = 616 cm².

(ii) We have,
Diameter of a sphere (d) = 21 cm
∴ Radius of a sphere (r) = \(\frac{21}{2}\) = 10.5 cm
∴ Surface area of a sphere = 4πr²
= 4 × \(\frac{22}{7}\) × (10.5)²
= \(\frac{9702}{7}\) cm² = 1386 m²
Hence,surface area of a sphere = 1386 cm².

(iii) We have,
Diameter of a sphere (d) = 3.5 m
∴ Radius of a sphere (r) = \(\frac{3.5}{2}\) = 1.75 m
∴ Surface area of a sphere = 4πr²
= 4 × \(\frac{22}{7}\) × (1.75)²
= \(\frac{269.5}{7}\)
= 38.5 m²
Hence,surface area of a sphere= 38.5 m².

Question 3.
Find the total surface area of a hemisphere of radius 10 cm. (Use π = 3.14)
Solution:
We have, Radius of a hemisphere (r) = 10 cm
∴ Total surface area of a hemisphere= 3πr²
= 3 × 3.14 × (10)²
= 942 cm²
Hence, total surface area of a hemisphere = 942 cm².

Question 4.
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Solution:
We have,
Radius of a spherical balloon (r₁) = 7 cm
∴ Surface area of a spherical balloon (S₁) = 4π(r₁)² = 4 × \(\frac{22}{7}\) × (7)²
= 616 cm²
and increased radius of a spherical ballon (r₂)= 14 cm
∴ Surface area of a spherical ballon in this case (S₂) = 4π(r₁)²
= 4 × \(\frac{22}{7}\) × (14)²
= 2464 cm²
Now,
\(\frac{S_1}{S_2}=\frac{616}{2464}\)
⇒ \(\frac{S_1}{S_2}=\frac{1}{4}\)
⇒ S₁ : S₂ = 1 : 4
Hence, required ratio of the balloon in two cases = 1 : 4.

Question 5.
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs. 16 per 100 cm².
Solution:
We have,
Diameter of hemispherical bowl
(d) = 10.5 cm
∴ Radius of the hemispherical bowl (r) = \(\frac{10.5}{2}\) = 5.25 cm
∴ Inner curved surface area of the bowl = 2πr²
= 2 × \(\frac{22}{7}\) × (5.25)²
= \(\frac{44 \times 27.5625}{7}\)
= 173.25 cm²
Rate of tin-plating = Rs. 16 per 100 cm²
∴ Cost of tin-plating inside of bowl = \(\frac{173.25 \times 16}{100}\)
= Rs. 27.72
Hence, cost of tin-plating the inside of a bowl = Rs. 27.72.

Question 6.
Find the radius of a sphere whose surface area is 154 cm².
Solution:
Let the radius of a sphere be r cm.
Surface area of a sphere = 154 cm², (given)
⇒ 4πr² = 154
⇒ 4 × \(\frac{22}{7}\) × r² = 154
⇒ \(\frac{88}{7}\) × r² = 154
⇒ r² = \(\frac{154 \times 7}{88}\)
⇒ r² = \(\frac{7 \times 7}{4}\)
⇒ r = \(\sqrt{\frac{7 \times 7}{2 \times 2}}\)
⇒ r = \(\frac{7}{2}\) = 3.5 cm
Hence, radius of the sphere = 3.5 cm.

Question 7.
The diameter of the Moon is approximately one fourth of the diameter of the Earth. Find the ratio of their surface areas.
Solution:
Let diameter of the Earth be 2x.
∴ Radius of the Earth (R) = x
∴ Surface area of the Earth (S₁) = 4πR² = 4πx²
According to question,
Diameter of the Moon = \(\frac{1}{4}\) × diameter of the Earth
= \(\frac{1}{4}\) × 2x = \(\frac{x}{4}\)
∴ Radius of the Moon (r) = \(\frac{\frac{x}{2}}{2}=\frac{x}{4}\)
∴ Surface area of the Moon (S₂) = 4πr²

Hence, required ratio of the their surface areas = 1 : 16.

Question 8.
A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Solution:
We have,
Inner radius of the bowl = 5 cm
and thickness of the bowl = 0.25 cm

Fig. 13.34
∴ Outer radius of the bowl (r) = 5 + 0.25
= 5.25 cm
∴ Outer curved surface area of the bowl = 2πr²
= 2 × \(\frac{22}{7}\) × (5.25)²
= \(\frac{44 \times 27.5625}{7}\)
= 44 × 3.9375
= 173.25 cm²
Hence, outer curved surface area of the bowl = 173.25 cm².

Question 9.
A right circular cylinder just encloses a sphere of radius r (see Fig. 13.35). Find :
(i) surface area of the sphere, (ii) curved surface area of the cylinder, (iii) ratio of the areas obtained in (i) and (ii).

Fig. 13.35
Solution:
We have,
(i) Radius of sphere = r
∴ Surface area of the sphere (S₁) = 4πr².
(ii) Radius of the cylinder = radius of the sphere = r.
Height of the cylinder (h) = 2 × r = 2r
∴ Curved surface area of the cylinder
(S₂) = 2πrh = 2π × r × 2r
= 4πr²

Hence, (i) surface area of sphere = 4πr²
(ii) curved surface area of the cylinder = 4πr²
(iii) required ratio of the areas obtained in (i) and (ii) = 1 : 1.

Haryana State Board HBSE 9th Class Science Solutions Chapter 15 खाद्य संसाधनों में सुधार Textbook Exercise Questions and Answers.

Haryana Board 9th Class Science Solutions Chapter 15 खाद्य संसाधनों में सुधार

HBSE 9th Class Science खाद्य संसाधनों में सुधार Intext Questions and Answers

(पृष्ठ संख्या – 229)

प्रश्न 1.
अनाज, दाल, फल तथा सब्जियों से हमें क्या प्राप्त होता है?
उत्तर:
अनाज; जैसे गेहूँ, चावल, मक्का , बाजरा व ज्वार से कार्बोहाइड्रेट; दालों; जैसे चना, मटर, उड़द, मूंग, अरहर, मसूर से प्रोटीन; फलों व सब्जियों से विटामिन व खनिज लवण, कुछ मात्रा में प्रोटीन, वसा व कार्बोहाइड्रेट भी प्राप्त होते हैं। ये सभी तत्त्व हमारे विकास, वृद्धि तथा स्वास्थ्य के लिए होते हैं।

(पृष्ठ संख्या – 230)

प्रश्न 1.
जैविक व अजैविक कारक किस प्रकार फसल उत्पादन को प्रभावित करते हैं?
उत्तर:
जैविक कारक; जैसे रोग, कीट तथा निमेटोड और अजैविक कारक; जैसे सूखा, क्षारता, जलाक्रांति, गर्मी, ठंड व पाला आदि से फसल उत्पादन कम हो जाता है।

प्रश्न 2.
फसल सुधार के लिए ऐच्छिक सस्य विज्ञान गुण क्या हैं?
उत्तर:
चारे वाली फसलों के लिए सघन शाखाएँ ऐच्छिक गुण हैं। अन्न के लिए बौने पौधे उपयुक्त हैं ताकि इन फसलों को उगाने के लिए कम पोषकों की आवश्यकता हो। इस प्रकार सस्य विज्ञान वाली किस्में अधिक उत्पादन करने में सहायक होती हैं।

(पृष्ठ संख्या-231)

प्रश्न 1.
वृहत् पोषक क्या हैं और इन्हें वृहत् पोषक क्यों कहते हैं?
उत्तर:
वृहत् पोषक-ऐसे पोषक जिनकी पौधों को अधिक मात्रा में आवश्यकता हो, वृहत् पोषक कहलाते हैं। इनकी अधिक मात्रा में आवश्यकता के कारण इन्हें वृहत् पोषक कहते हैं; जैसे सल्फर, नाइट्रोजन, फास्फोरस, पोटैशियम, कैल्शियम व मैग्नीशियम।

प्रश्न 2.
पौधे अपना पोषक कैसे प्राप्त करते हैं?
उत्तर:
पौधे भूमि से घोल के रूप में इन पोषकों को ग्रहण करते हैं। खाद और उर्वरक में भी यही पोषक होते हैं जिन्हें पौधे आसानी से और अधिक मात्रा में ग्रहण कर लेते हैं।

(पृष्ठ संख्या-232)

प्रश्न 1.
मिट्टी की उर्वरता को बनाए रखने के लिए खाद तथा उर्वरक के उपयोग की तुलना कीजिए।
उत्तर:
मिट्टी की उर्वरता को बनाए रखने के लिए खाद तथा उर्वरक की उपयोगिता में अंतर निम्नलिखित है

खाद

1. इसकी अधिक मात्रा की आवश्यकता पड़ती है।
2. इसका सतत उपयोग हानिकारक नहीं है।
3. इनके उपयोग से उत्पादन हमेशा बढ़ता है।
4. इनके उपयोग और उत्पादन प्राप्त करने में समय अधिक लगता है।
5. इनका उपयोग करना महंगा नहीं।
6. इनका स्थानान्तरण व भण्डारण असुविधाजनक होता है।

उर्वरक

1. इसकी कम मात्रा की आवश्यकता पड़ती है।
2. इसका सतत उपयोग हानिकारक है।
3. इनके अनावश्यक उपयोग से उत्पादन घट सकता है।
4. इनके उपयोग से अधिक उत्पादन कम समय में मिल सकता है।
5. इनका उपयोग करना महंगा है।
6. इनका स्थानांतरण व भण्डारण सुविधाजनक होता है।

(पृष्ठ संख्या – 235)

प्रश्न 1.
निम्नलिखित में से कौन-सी परिस्थिति में सबसे अधिक लाभ होगा? क्यों?

• किसान उच्च कोटि के बीज का उपयोग करें, सिंचाई ना करें अथवा उर्वरक का उपयोग ना करें।
• किसान सामान्य बीजों का उपयोग करें, सिंचाई करें तथा उर्वरक का उपयोग करें।
• किसान अच्छी किस्म के बीज का प्रयोग करें, सिंचाई करें, उर्वरक का उपयोग करें तथा फसल सुरक्षा की विधियाँ अपनाएँ।

उत्तर:
उपरोक्त तीनों परिस्थितियों में तीसरी परिस्थिति (c) ही उत्तम है क्योंकि इसमें बीजों की गुणवत्ता भी उत्तम है अर्थात् उच्च उत्पादन देने वाली है।

सिंचाई पौधों के पोषण के लिए सहायक है, उर्वरक पौधों के पोषकों की आपूर्ति करते हैं जो पौधे के विकास, वृद्धि और उत्पादन के लिए आवश्यक है। फसल संरक्षण, फसलों को हानियों से बचाता है और निःसंदेह इससे फसल उत्पादन बढ़ता है। अतः (c) परिस्थिति ही किसान के लिए श्रेष्ठ है।

(पृष्ठ संख्या- 235)

प्रश्न 1.
फसल की सुरक्षा के लिए निरोधक विधियाँ तथा जैव नियंत्रण क्यों अच्छा समझा जाता है?
उत्तर:
फसल की सुरक्षा के लिए निरोधक विधियाँ; जैसे समय पर फसल उगाना, उचित क्यारियाँ तैयार करना, अंतराफसलीकरण तथा फसल-चक्र खरपतवार के नियंत्रण में सहायक होती हैं। किसी प्रकार के कीटनाशक, खरपतवार नाशक आदि जहरीले रसायनों का इस्तेमाल नहीं किया जाता।

जैव नियंत्रण विधियों में प्रतिरोध क्षमता वाली किस्मों का उपयोग तथा ग्रीष्मकाल में हल चलाकर हानिकारक कीटों व अन्य जीवों को मारा जाता हैं। इस प्रकार मृदा प्रदूषण नहीं होता और इन विधियों पर अतिरिक्त खर्च भी नहीं करना पड़ता। अतः आर्थिक दृष्टि से भी ये उपयोगी हैं।

प्रश्न 2.
भंडारण की प्रक्रिया में कौन-से कारक अनाज की हानि के लिए उत्तरदायी हैं?
उत्तर:
भंडारण की प्रक्रिया में दो प्रकार के कारक अनाज की हानि के लिए उत्तरदायी होते हैं

• जैविक कारक-जैसे कीट, कृंतक, कवक, चिंचड़ी और जीवाणु आदि।
• अजैविक कारक-भण्डारण के स्थान पर उपयुक्त नमी व ताप का अभाव।

(पृष्ठ संख्या – 236)

प्रश्न 1.
पशुओं की नस्ल सुधार के लिए प्रायः कौन-सी विधि का उपयोग किया जाता है और क्यों?
उत्तर:
पशुओं की नस्ल सुधार के लिए संकरण विधि का प्रयोग किया जाता है ताकि संकर पशु का दुग्धस्रवण काल व रोगों की प्रतिरोधकता बढ़ जाए।

(पृष्ठ संख्या – 237)

प्रश्न 1.
निम्नलिखित कथन की विवेचना कीजिए – “यह रुचिकर है कि भारत में कुक्कुट, अल्प रेशे के खाद्य पदार्थों को उच्च पोषकता वाले पशु प्रोटीन आहार में परिवर्तन करने के लिए सबसे अधिक सक्षम है। अल्प रेशे के खाद्य पदार्थ मनुष्यों के लिए उपयुक्त नहीं होते हैं।”
उत्तर:
कुक्कुट में यह गुण है कि ऐसे खाद्य पदार्थ जिनमें रेशेदार पदार्थ कम हों और जो मनुष्य के उपयोग के लिए अच्छे नहीं माने जाते अर्थात् गुणवत्ता के आधार पर ये पदार्थ मानव उपयोग के लिए अधिक उपयोगी नहीं होते, उन्हें उच्च प्रोटीन वाले पशु प्रोटीन में बदलने की क्षमता रखते हैं। कुक्कुट के अंडे व मांस प्रोटीन से भरपूर होते हैं और ये मानव के लिए उच्च कोटि का प्रोटीन आहार माना जाता है।

(पृष्ठ संख्या – 238)

प्रश्न 1.
पशुपालन तथा कुक्कुट पालन के प्रबंधन प्रणाली में क्या समानता है?
उत्तर:
पशुपालन तथा कुक्कुट पालन के प्रबंधन प्रणाली में काफी समानता है

• दोनों को साफ-सुथरे, हवादार व नमी रहित आवास की आवश्यकता होती है।
• दोनों को उचित व संतुलित आहार दिया जाता है।
• दोनों को बीमारियाँ लगती हैं जिनका उपयुक्त समय पर टीकाकरण किया जाता है और बीमारी होने पर चिकित्सकों द्वारा . उपचार किया जाता है।
• दोनों का आधार आर्थिक महत्त्व है अर्थात् दोनों को आर्थिक लाभ पाने के लिए पाला जाता है।
• दोनों की उच्च उत्पादी नस्लों को पाला जाता है ताकि उत्पादन अधिक मिले। अतः दोनों में प्रबंधन प्रणाली के आधार पर काफी समानता है।

प्रश्न 2.
ब्रौलर तथा अडे देने वाली लेअर में क्या अंतर है? इनके प्रबंधन के अंतर को भी स्पष्ट करें।
उत्तर:
ब्रौलर को मांस के लिए पाला जाता है, जबकि लेअर को अंडे पाने के लिए पाला जाता है। दोनों में यही प्रमुख अंतर है। ब्रौलर की अच्छी वृद्धि तथा अच्छी आहार दक्षता के लिए इन्हें प्रोटीन, वसा व विटामिन से भरपूर भोजन दिया जाता है। भोजन इनके मांस, पंख व कम मृत्यु दर को ध्यान में रखकर दिया जाता है, जबकि लेअर में इस प्रकार के भोजन की कम आवश्यकता होती है। ब्रौलर की आवास पोषण और पर्यावरणीय आवश्यकताएँ अंडे देने वाली मुर्गियों से भिन्न होती हैं।

(पृष्ठ संख्या – 239)

प्रश्न 1.
मछलियाँ कैसे प्राप्त करते हैं?
उत्तर:
मछलियाँ प्राप्त करने की दो विधियाँ हैं

• प्राकृतिक स्रोत से,
• मछली पालन या मछली संवर्धन से।

मछलियाँ ताजे जल (अलवणीय जल) और समुद्री जल (लवणीय जल) दोनों में पाई जाती हैं। ताजे पानी में पाई जाने वाली मछलियाँ कटला, रोहु, मुलेट, मिलिटस आदि हैं जबकि समुद्री मछलियों में पॉमफ्रेट, मैकर्ल, टुना, सारडाइन, बाम्बेडक आदि हैं। समुद्री जल में मुलेट, भेटकी, पर्लस्पॉट, प्रॉन, मस्सल और ऑएस्टर का संवर्धन किया जाता है। मछली पालन ताजे जल या अलवणीय जल में किया जाता है।

प्रश्न 2.
मिश्रित मछली संवर्धन के क्या लाभ हैं?
उत्तर:
मिश्रित मछली संवर्धन से अधिक मछली संवर्धन किया जाता है। इस संवर्धन में अकेले तालाब में 5 या 6 मछलियों की स्पीशीज़ का उपयोग किया जाता है। इन मछलियों का चयन इस आधार पर किया जाता है कि आहार के लिए इनमें संघर्ष न हो और आहार पाने की आदत अलग-अलग हो

• तालाब के हर भाग में स्थित आहार का उपयोग हो जाता है।
• मिश्रित मछली संवर्धन से खरपतवार का जैविक विधि से नियंत्रण हो जाता है।
• बिना स्पर्धा के भोजन लेने के कारण तालाब में मछली उत्पादन बढ़ता है।

(पृष्ठ संख्या-240)

प्रश्न 1.
मधु उत्पादन के लिए प्रयुक्त मधुमक्खी में कौन-से ऐच्छिक गुण होने चाहिएँ?
उत्तर:
मधु उत्पादन वाली मधुमक्खी में यह ऐच्छिक गुण होना स्वाभाविक है कि वह मधु उत्पादन बढ़ाने में सक्षम हो। इटेलियन मक्खी में मधु एकत्रित करने व छत्ते की सुरक्षा दोनों गुण पाए जाते हैं। यह निर्धारित छत्ते में काफी समय तक रहती हुई प्रजनन तेजी के साथ करती है इससे मधु उत्पादन बढ़ता है।

प्रश्न 2.
चरागाह क्या है और ये मधु उत्पादन से कैसे संबंधित है?
उत्तर:
चरागाह ऐसा प्राकृतिक घास का मैदान होता है जहाँ पशुओं के लिए घास व अन्य फूलों वाले पौधे काफी मात्रा में उगते हैं। इन्हीं फूलों से मधुमक्खियाँ मकरंद व पराग को एकत्रित कर शहद बनाती हैं। चरागाह में उगने वाले फूलों के द्वारा शहद का स्वाद निर्धारित होता है; जैसे ब्रूस के फूलों का शहद, नीम के फूलों का शहद और यूक्लिपटिस के फूलों का शहद । स्वाद के आधार पर मधु की गुणवत्ता भी निर्धारित की जाती है।

HBSE 9th Class Science खाद्य संसाधनों में सुधार Textbook Questions and Answers

प्रश्न 1.
फसल उत्पादन की एक विधि का वर्णन करो जिससे अधिक पैदावार प्राप्त हो सके।
उत्तर:
उच्च फसल उत्पादन संकरण विधि द्वारा प्राप्त किया जा सकता है। पादप संकरण का मुख्य उद्देश्य वांछित गुणों वाली ऐसी नई किस्मों का विकास एवं उपयोग करना है, जो पादप-रोगों तथा पीड़कों के प्रतिरोधी हों। प्रजनक इन उन्नत किस्मों को विकसित करते हैं। इसमें कृत्रिम विधियों से पहले ही उपलब्ध दो भिन्न किस्मों में परस्पर क्रॉस-प्रजनन (Cross-Breeding) कराया जाता है।

इस तकनीक द्वारा एक किस्म के वांछित गुणों को दूसरी किस्म में संचारित कर सकते हैं। उदाहरण के लिए, यदि हमारे पास दो फसलें हैं, जिनमें से एक फसल में पीड़कों के प्रति प्रतिरोधक क्षमता है, जबकि दूसरी किस्म में भारी उत्पादन क्षमता है, अर्थात् उसके हर पौधे से अच्छी उपज होती है।

जब पीड़क प्रतिरोधी पौधे का अच्छी उपज वाले पौधे से क्रॉस अथवा संकरण करते हैं, तो संतति पौधे में पहली दोनों किस्मों के गुणों का समावेश हो जाता है। इस प्रकार हमारे पास उच्च उपज देने वाले संकर बीज प्राप्त हो जाते हैं जिनका उपयोग कर अधिक फसल उत्पादन प्राप्त किया जा सकता है। हरित क्रांति में संकर बीजों का महत्त्वपूर्ण योगदान रहा है।

प्रश्न 2.
खेतों में खाद तथा उर्वरक का उपयोग क्यों करते हैं?
उत्तर:
खाद और उर्वरक में कोई वृहत् पोषक अवश्य होता है। फसलें भूमि से लगातार पोषकों को ग्रहण करती रहती हैं जिससे भूमि में इन पोषकों की कमी आ जाती है। इन्हीं पोषकों की कमी को पूरा करने के लिए खेतों में खाद और उर्वरक मिलाए जाते हैं। यदि इस कमी को पूरा न किया जाए तो भूमि की उपजाऊ शक्ति घट जाती है और धीरे-धीरे भूमि बंजर बन जाती है। भूमि में इन पोषकों की कमी फसल चक्रण द्वारा भी पूरी की जा सकती है।

प्रश्न 3.
अंतराफसलीकरण तथा फसल-चक्र के क्या लाभ हैं?
उत्तर:
अंतराफसलीकरण व फसल-चक्र के लाभ निम्नलिखित हैं

• भूमि की उर्वरा शक्ति बनी रहती है अर्थात् भूमि बंजर नहीं बनती।
• एक ही समय में एक से अधिक फसल उत्पाद मिल सकते हैं।
• पीड़क और खरपतवार नष्ट हो जाते हैं।
• फसल उत्पादन बढ़ने से किसान की आय बढ़ जाती है।
• फसल उत्पादन असफल होने का जोखिम भी घट जाता है।

प्रश्न 4.
आनुवंशिक फेरबदल क्या है? कृषि प्रणालियों में ये कैसे उपयोगी हैं?
उत्तर:
फसलों की उच्च पैदावार, इनकी नस्लों के गुणों पर निर्भर करती है। यदि फसलों की नस्लों में सुधार लाना है तो ऐच्छिक गुणों वाले जीन डाले जाते हैं क्योंकि जीन ही निर्धारित करते हैं कि पौधों के गुण क्या होंगे अर्थात् इनकी उपज अधिक होगी या कम। अतः जीन में परिवर्तन आनुवंशिक फेरबदल कहलाता है। इसकी तकनीक के द्वारा आज उन्नत किस्म के बीज तैयार कर कृषि प्रणाली में पैदावार कई गुणा बढ़ाई जा सकी है। विशेषकर इस तकनीक का किसानों और बागवानों को अत्यधिक लाभ पहुंचा है।

प्रश्न 5.
भंडार गृहों (गोदामों) में अनाज की हानि कैसे होती है?
उत्तर:
भंडार गृहों में अनाज को हानि पहुँचाने वाले कारक निम्नलिखित हैं
(क) जैविक कारक
1. कृतक, पक्षी तथा अन्य जंतु-चूहे, गिलहरी आदि खेतों, घरों तथा गोदामों में रखे खाद्यान्नों को हानि पहुँचाते हैं। इनके बालों, पंखों तथा मल-मूत्र से खाद्यान्नों को नुकसान पहुंचता है।

2. सूक्ष्मजीव-विभिन्न जीवाणु तथा फफूंदी खाद्यान्नों में रासायनिक परिवर्तन के फलस्वरूप उनकी संरचना में परिवर्तन कर देते हैं और इस प्रकार ये अनाज को हानि पहुंचाते हैं।

3. कीट-कई प्रकार के कीट कच्चे खाद्यान्न; जैसे अनाज, दालों आदि को क्षति पहुँचाते हैं। वे इन्हें अपने मल-मूत्र से दूषित कर देते हैं।

4. एंजाइम ये जैव उत्प्रेरक हैं, जो कोशिकाओं में पाए जाते हैं। ये अधिक समय तक भंडारित किए गए फल, सब्जियों आदि को खराब कर देते हैं।

(ख) अजैविक कारक-भंडारित अनाज को हानि पहुँचाने वाले अजैविक कारक निम्नलिखित है

1. नमी – भंडारण करते समय खाद्य पदार्थ में अधिक नमी नहीं होनी चाहिए। खाद्य पदार्थ में नमी की मात्रा उसके भार के 14% से अधिक नहीं होनी चाहिए। खाद्यान्नों में अधिक नमी होने पर

• इसके दानों का आकार बढ़ जाता है।
• सूक्ष्मजीव तथा एंजाइम बहुत अधिक सक्रिय हो जाते हैं।
• कीटों द्वारा संक्रमण की संभावना बढ़ जाती है।
• नमी वाली वायु में फफूंदी आदि के उगने की संभावना अधिक होती है।

2. तापमान कम ताप पर एंजाइम, कीट तथा अन्य सूक्ष्मजीव अधिक सक्रिय नहीं होते। इस कारण विकारी खाद्य पदार्थों को शीत भंडारों में रखते हैं।

3. भंडारण के लिए बर्तन-भंडारण में प्रयुक्त बर्तन सीसा, धातु या तांबे के बने हुए नहीं होने चाहिएँ, क्योंकि ये विषैले होते हैं तथा इनसे खाद्यान्न के विषाक्त होने की संभावना बढ़ जाती है।

प्रश्न 6.
किसानों के लिए पशुपालन प्रणालियाँ कैसे लाभदायक हैं?
उत्तर:
पशुपालन प्रणालियाँ किसानों के लिए निम्नलिखित प्रकार से लाभदायक होती हैं

• किसान को दुधारू पशुओं से दूध की प्राप्ति होती है।
• पशुपालन द्वारा प्राप्त ड्राफ्ट पशु बोझा ढोने व कृषि कार्यों में सहायक होते हैं।
• पशुपालन से किसानों को आर्थिक लाभ होने के कारण व्यावसायिक कार्य मिलता है।
• पशु कृषि से किसानों की अतिरिक्त व वर्ष भर आय होती रहती है।
• किसान द्वारा पाले गए पशुओं से प्राप्त गोबर व मूत्र से बायोगैस व जैविक खाद तैयार की जाती है।
• पशुपालन से ऊन, मांस, खालें व हड्डियाँ प्राप्त होती हैं।

प्रश्न 7.
पशुपालन के क्या लाभ हैं?
उत्तर:
पशुपालन के दो प्रमुख लाभ निम्नलिखित हैं
1. खाद्य पदार्थों को प्राप्त करना-पशुपालन का प्रमुख उद्देश्य खाद्य उत्पादन करना है जिसमें दूध और मांस का उत्पादन प्रमुख है। इसके अतिरिक्त पशुपालन से ऊन, खालें व हड्डियों की भी प्राप्ति होती है। इस प्रकार पशुपालन का यह उद्देश्य आर्थिक कारणों से जुड़ा है।

2. कृषि कार्य में सहायता करना-पशुपालन का दूसरा प्रमुख उद्देश्य कृषि कार्य में सहायता प्रदान करना है। बैल, ऊंट, खच्चर आदि पश कृषि कार्यों जैसे हल जोतने व बोझा ढोने के काम आते हैं। छोटे किसान कृषि कार्यों के लिए आज भी पशुओं पर आधारित हैं।

प्रश्न 8.
उत्पादन बढ़ाने के लिए कुक्कुट पालन, मत्स्य पालन तथा मधुमक्खी पालन में क्या समानताएँ हैं?
उत्तर:
कुक्कुट पालन, मछली पालन और मधुमक्खी पालन में एक प्रमुख समानता यही है कि पैदावार देने वाले जंतुओं में रोग प्रतिरोधात्मक क्षमता, पर्यावरण के अनुकूल और उच्च पैदावार देने वाली नस्ल के हों। तीनों प्रकार के जीव पालन का मुख्य उद्देश्य उच्च उत्पादन के द्वारा अधिक धनार्जन करना है। तीनों को कृषि कार्य के साथ सहायक व्यवसाय के रूप में प्रयोग किया जाता है जिससे कृषक को अतिरिक्त आमदनी होती है और इसमें अलग से पूरा समय देने की आवश्यकता नहीं होती।

प्रश्न 9.
प्रग्रहण मत्स्यन, मेरीकल्चर तथा जल संवर्धन में क्या अंतर है?
उत्तर:
कुछ आर्थिक महत्त्व वाली समुद्री जल मछलियों को समुद्र में संवर्धन किया जाता है ताकि मछलियों की मांग को पूरा किया जा सके। इसे प्रग्रहण मत्स्यन ‘मेरीकल्चर’ कहते हैं। तालाबों में प्राकृतिक वातावरण प्रदान किये जाने वाला मत्स्य पालन ‘जल संवर्धन’ कहलाता है। तालाबों में मछलियाँ अलवणीय जल या ताजे जल में पाली जाती हैं। जबकि समुद्री संवर्धन में मछलियाँ लवणीय जल में पाली जाती हैं।

Haryana State Board HBSE 9th Class Science Solutions Chapter 10 गुरुत्वाकर्षण Textbook Exercise Questions and Answers.

Haryana Board 9th Class Science Solutions Chapter 10 गुरुत्वाकर्षण

HBSE 9th Class Science गुरुत्वाकर्षण Intext Questions and Answers
(पृष्ठ संख्या – 149)

प्रश्न 1.
गुरुत्वाकर्षण का सार्वत्रिक नियम बताइए।
उत्तर:
गुरुत्वाकर्षण का सार्वत्रिक नियम-विश्व का प्रत्येक पिंड अन्य पिंड को एक बल से आकर्षित करता है, जो दोनों पिंडों के द्रव्यमानों के गुणनफल के समानुपाती तथा उनकी बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह बल दोनों पिंडों को मिलाने वाली रेखा की दिशा में लगता है।

मान लीजिए M तथा m द्रव्यमान के दो पिंड A तथा B एक-दूसरे से d दूरी पर स्थित हैं जैसा कि चित्र में दिखाया गया है। मान लीजिए दोनों पिंडों के बीच आकर्षण बल F है। गुरुत्वाकर्षण के सार्वत्रिक नियम के अनुसार, दोनों पिंडों के बीच लगने वाला बल उनके द्रव्यमानों के गुणनफल के समानुपाती है। अर्थात्
F α M x m ……………(i)
तथा दोनों पिंडों के बीच लगने वाला बल उनकी बीच की दूरी के वर्ग के व्युत्क्रमानुपाती है, अर्थात्
F α \(\frac{1}{d^2}\) ………………(ii)
समीकरणों (i) तथा (ii) से हमें प्राप्त होगा
F α \(\frac{\mathrm{M} \times \mathrm{m}}{\mathrm{d}^2}\) …………………(iii)
या F = G\(\frac{\mathrm{M} \times \mathrm{m}}{\mathrm{d}^2}\) …………….(iv)
जहाँ G एक आनुपातिकता स्थिरांक है और इसे सार्वत्रिक गुरुत्वीय स्थिरांक कहते हैं।

प्रश्न 2.
पृथ्वी तथा उसकी सतह पर रखी किसी वस्तु के बीच लगने वाले गुरुत्वाकर्षण बल का परिमाण ज्ञात करने का सूत्र लिखिए। हल
माना पृथ्वी का द्रव्यमान = Me
पृथ्वी पर रखी वस्तु का द्रव्यमान = m
पृथ्वी का अर्धव्यास = R
तो पृथ्वी तथा उसकी सतह पर रखी वस्तु के बीच लगने वाला
गुरुत्वाकर्षण बल (F) = \(\frac{\mathrm{Me} \times \mathrm{m}}{\mathrm{R}^2}\) (जहाँ G गुरुत्वीय स्थिरांक है।) उत्तर

(पृष्ठ संख्या -152)

प्रश्न 1.
मुक्त पतन से आप क्या समझते हैं?
उत्तर:
जब वस्तुएँ पृथ्वी की ओर केवल गुरुत्वीय बल के कारण गिरती हैं, तब कहा जाता है कि वस्तुएँ मुक्त पतन में हैं।

प्रश्न 2.
गुरुत्वीय त्वरण से आप क्या समझते हैं?
उत्तर:
जब भी कोई वस्तु पृथ्वी की ओर गिरती है, त्वरण कार्य करता है। यह त्वरण पृथ्वी के गुरुत्वीय बल के कारण होता है। इसलिए इस त्वरण को पृथ्वी के गुरुत्वीय बल के कारण त्वरण या गुरुत्वीय त्वरण कहते हैं। इसे g से प्रदर्शित किया जाता है तथा इसका मात्रक ms^-2 है।

(पृष्ठ संख्या-153)

प्रश्न 1.
किसी वस्तु के द्रव्यमान तथा भार में क्या अंतर है?
उत्तर:
किसी वस्तु के द्रव्यमान तथा भार में निम्नलिखित अंतर हैं

प्रश्न 2.
किसी वस्तु का चंद्रमा पर भार पृथ्वी पर इसके भार का \(\frac { 1 }{ 6 } \) गुना क्यों होता है?
उत्तर:
हम जानते हैं कि पृथ्वी पर गुरुत्वीय त्वरण (g) का मान 9.8 m/s² है। चंद्रमा पर (g) का मान पृथ्वी पर (g) के मान का = गुना है, इसलिए चंद्रमा पर वस्तुओं का भार पृथ्वी की तुलना में कम होता है अर्थात् \(\frac { 1 }{ 6 } \) गुना होता है।

(पृष्ठ संख्या-157)

प्रश्न 1.
एक पतली तथा मजबूत डोरी से बने पट्टे की सहायता से स्कूल बैग को उठाना कठिन होता है, क्यों?
उत्तर:
एक पतली तथा मजबूत डोरी से बने पट्टे की सहायता से स्कूल बैग को उठाना कठिन होता है क्योंकि उसका प्रणोद एक छोटे क्षेत्रफल (डोरी के मध्य में) को प्रभावित करता है।

प्रश्न 2.
उत्प्लावकता से आप क्या समझते हैं?
उत्तर:
जब किसी वस्तु को किसी तरल में डुबोया जाता है तो तरल उस वस्तु पर ऊपर की ओर एक बल लगाता है जिसे उत्प्लावन बल कहते हैं। उत्प्लावन बल का परिमाण तरल के घनत्व पर निर्भर करता है। इस घटना को उत्प्लावकता कहते हैं।

प्रश्न 3.
पानी की सतह पर रखने पर कोई वस्तु क्यों तैरती या डूबती है?
उत्तर:
पानी के घनत्व से कम घनत्व की वस्तुएँ पानी पर तैरती हैं जबकि पानी के घनत्व से अधिक घनत्व की वस्तुएँ पानी में डूबती हैं। उदाहरणतया समान द्रव्यमान की कील और कार्क को पानी पर रखने से कील पानी में डूब जाएगी क्योंकि उसका घनत्व पानी से अधिक है जबकि कार्क तैरता रहेगा क्योंकि उसका घनत्व पानी के घनत्व से कम है।

(पृष्ठ संख्या-158)

प्रश्न 1.
एक तुला (weighing machine) पर आप अपना द्रव्यमान 42 kg नोट करते हैं। क्या आपका द्रव्यमान 42 kg से अधिक है या कम?
उत्तर:
किसी तुला द्वारा मापने पर यदि द्रव्यमान 42 kg आता है तो हमारा द्रव्यमान 42 kg ही होगा क्योंकि द्रव्यमान स्थिर रहता है।

प्रश्न 2.
आपके पास एक रुई का बोरा तथा एक लोहे की छड़ है। तुला पर मापने पर दोनों 100 kg द्रव्यमान दर्शाते हैं। वास्तविकता में एक-दूसरे से भारी हैं। क्या आप बता सकते हैं कि कौन-सा भारी है और क्यों?
उत्तर:
दोनों में लोहे की छड़ भारी है क्योंकि लोहे का घनत्व रुई की अपेक्षा अधिक होता है।

HBSE 9th Class Science गुरुत्वाकर्षण Textbook Questions and Answers

प्रश्न 1.
यदि दो वस्तुओं के बीच की दूरी को आधा कर दिया जाए तो उनके बीच गुरुत्वाकर्षण बल किस प्रकार बदलेगा?
उत्तर:
यदि दो वस्तुओं के बीच की दूरी को आधा कर दिया जाए तो उनके बीच गुरुत्वाकर्षण बल चार गुना बढ़ जाएगा क्योंकि गुरुत्वाकर्षण बल उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।

प्रश्न 2.
सभी वस्तुओं पर लगने वाला गुरुत्वीय बल उनके द्रव्यमान के समानुपाती होता है। फिर एक भारी वस्तु हल्की वस्तु के मुकाबले तेजी से क्यों नहीं गिरती?
उत्तर:
सभी वस्तुओं पर लगने वाला गुरुत्वीय बल उनके द्रव्यमान के समानुपाती होता है फिर भी एक भारी वस्तु हल्की वस्तु के मुकाबले तेजी से नहीं गिरती क्योंकि वस्तुओं का द्रव्यमान पृथ्वी के द्रव्यमान की तुलना में नगण्य होता है।

प्रश्न 3.
पृथ्वी तथा उसकी सतह पर रखी किसी 1 kg की वस्तु के बीच गुरुत्वीय बल का परिमाण कितना होगा? (पृथ्वी का द्रव्यमान 6 x 1024 kg है तथा पृथ्वी की त्रिज्या 6.4 x 10°m है।)
हल:
यहाँ पर
पृथ्वी का द्रव्यमान (M.) = 6 x 10²⁴kg
वस्तु का द्रव्यमान (m) = 1 kg
पृथ्वी की त्रिज्या (R) = 6.4 x 10⁶ m
गुरुत्वीय स्थिरांक (G) = 6.673 x 10^-11 Nm²/kg²
गुरुत्वीय बल (g) = ?
हम जानते हैं कि
गुरुत्वीय बल (g) = \(\frac{\text { G. } \mathrm{M}_{\mathrm{e}} \times \mathrm{m}}{\mathrm{R}^2}\)
= \(\frac{6.673 \times 10^{-11} \times 6 \times 10^{24} \times 1}{\left(6.4 \times 10^6\right)^2}\)
= 9.8 N उत्तर

प्रश्न 4.
पृथ्वी तथा चंद्रमा एक-दूसरे को गुरुत्वीय बल से आकर्षित करते हैं। क्या पृथ्वी जिस बल से चंद्रमा को आकर्षित करती है वह बल, उस बल से जिससे चंद्रमा पृथ्वी को आकर्षित करता है बड़ा है या छोटा है या बराबर है? बताइए क्यों?
उत्तर:
पृथ्वी, चंद्रमा को अधिक बल से आकर्षित करती है क्योंकि पृथ्वी का द्रव्यमान चंद्रमा की तुलना में अधिक है।

प्रश्न 5.
यदि चंद्रमा पृथ्वी को आकर्षित करता है, तो पृथ्वी चंद्रमा की ओर गति क्यों नहीं करती?
उत्तर:
चंद्रमा पृथ्वी को आकर्षित करता है, परंतु पृथ्वी चंद्रमा की ओर गति नहीं करती क्योंकि चंद्रमा का द्रव्यमान पृथ्वी की तुलना में काफी कम है।

प्रश्न 6.
दो वस्तुओं के बीच लगने वाले गुरुत्वाकर्षण बल का क्या होगा, यदि
(i) एक वस्तु का द्रव्यमान दुगुना कर दिया जाए?
(ii) वस्तुओं के बीच की दूरी दुगुनी तथा तीन गुनी कर दी जाए?
(iii) दोनों वस्तुओं के द्रव्यमान दुगुने कर दिए जाएँ?
उत्तर:
(i) यदि एक वस्तु का द्रव्यमान दुगुना कर दिया जाए तो दो वस्तुओं के बीच लगने वाला गुरुत्वाकर्षण बल भी दुगुना हो जाएगा क्योंकि गुरुत्वाकर्षण बल द्रव्यमान के समानुपाती होता है।

(ii) यदि वस्तुओं के बीच की दूरी दुगुनी कर दी जाए तो गुरुत्वाकर्षण बल \(\frac { 1 }{ 4 } \) गुना हो जाएगा तथा यदि वस्तुओं के बीच की दूरी तीन गुनी कर दी जाए तो गुरुत्वाकर्षण बल \(\frac { 1 }{ 9 } \) गुना हो जाएगा क्योंकि गुरुत्वाकर्षण बल दूरी के वर्ग के व्युत्क्रमानुपाती होता है।

(iii) यदि दोनों वस्तुओं के द्रव्यमान दुगुने कर दिए जाएँ तो उनके बीच लगने वाला गुरुत्वाकर्षण बल चार गुना हो जाएगा क्योंकि गुरुत्वाकर्षण बल द्रव्यमानों से समानुपाती होता है।

प्रश्न 7.
गुरुत्वाकर्षण के सार्वत्रिक नियम के क्या महत्त्व हैं?
उत्तर:
गुरुत्वाकर्षण के सार्वत्रिक नियम के निम्नलिखित महत्त्व हैं

• यह बल हमें पृथ्वी से बांधे रखता है।
• यह बल पृथ्वी के चारों ओर चंद्रमा को गति में रखता है।
• इसी बल के कारण सूर्य के चारों ओर ग्रह गति में रहते हैं।
• चंद्रमा तथा सूर्य के इस बल के कारण ज्वार-भाटे आते हैं।

प्रश्न 8.
मुक्त पतन का त्वरण क्या है?
उत्तर:
जब भी कोई वस्तु पृथ्वी की ओर गिरती है, त्वरण कार्य करता है। यह त्वरण पृथ्वी के गुरुत्वीय बल के कारण होता है। इसलिए इस त्वरण को पृथ्वी के गुरुत्वीय बल के कारण त्वरण या गुरुत्वीय त्वरण (g) कहते हैं। इसका मान 9.8 m/s² होता है।

प्रश्न 9.
पृथ्वी तथा किसी वस्तु के बीच गुरुत्वीय बल को हम क्या कहेंगे?
उत्तर:
पृथ्वी तथा किसी वस्तु के बीच गुरुत्वीय बल को हम वस्तु का भार कहते हैं।

प्रश्न 10.
एक व्यक्ति A अपने एक मित्र के निर्देश पर ध्रुवों पर कुछ ग्राम सोना खरीदता है। वह इस सोने को विषुवत वृत्त पर अपने मित्र को देता है। क्या उसका मित्र खरीदे हुए सोने के भार से संतुष्ट होगा? यदि नहीं, तो क्यों?
(संकेत : ध्रुवों पर g का मान विषुवत् वृत्त की अपेक्षा अधिक है।)
उत्तर:
नहीं, उसका मित्र खरीदे गए सोने के भार से संतुष्ट नहीं होगा क्योंकि सोने का भार विषवुत् वृत्त पर ध्रुवों की अपेक्षा कम होता है।

प्रश्न 11.
एक कागज की शीट, उसी प्रकार की शीट को मरोड़ कर बनाई गई गेंद से धीमी क्यों गिरती है?
उत्तर:
एक कागज की शीट, उसी प्रकार की शीट को मरोड़ कर बनाई गेंद से धीमी गिरती है क्योंकि शीट का क्षेत्रफल, गेंद के क्षेत्रफल से अधिक होता है जिस कारण दाब कम हो जाता है।

प्रश्न 12.
चंद्रमा की सतह पर गुरुत्वीय बल, पृथ्वी की सतह पर गुरुत्वीय बल की अपेक्षा 1/6 गुना है। एक 10 kg की वस्तु का चंद्रमा पर तथा पृथ्वी पर न्यूटन में भार क्या होगा?
हल:
यहाँ पर
वस्तु का पृथ्वी पर द्रव्यमान (m) = 10 kg
पृथ्वी पर गुरुत्वीय त्वरण (g) = 9.8 m/s²
:. वस्तु का पृथ्वी पर भार (W) = m xg
= 10 x 9.8 N
= 98 N
उत्तर:
वस्तु का चंद्रमा पर द्रव्यमान (m) = 10 kg
चंद्रमा पर गुरुत्वीय त्वरण (g₁) = 3 m/s²
:. वस्तु का चंद्रमा पर भार (W) = m g₁
= 10 x \(\frac { 9.8 }{ 6 } \) N
= 16.3 N उत्तर

प्रश्न 13.
एक गेंद ऊर्ध्वाधर दिशा में ऊपर की ओर 49 m/s के वेग से फेंकी जाती है। परिकलन कीजिए
(i) अधिकतम ऊँचाई जहाँ तक कि गेंद पहुँचती है।
(ii) पृथ्वी की सतह पर वापस लौटने में लिया गया कुल समय।
हल:
यहाँ पर
गेंद का प्रारंभिक वेग (u) = 49 m/s
गेंद का अंतिम वेग (v) = 0 m/s
गुरुत्वीय त्वरण (g) = – 9.8 m/s²

(i) हम जानते हैं कि
v² – u² = 2gs.
= \(\frac{\mathrm{v}^2-\mathrm{u}^2}{2 \mathrm{~g}}\) = \(\frac{(0)^2-(49)^2}{2(-9.8)}\)
= \(\frac{-49 \times 49}{-19.6}\) = 122.5 m
अतः गेंद अधिकतम 122.5 m ऊँचाई तक जाएगी। उत्तर

(ii) जाने में लगा समय (t) = \(\frac { v-u }{ g } \)
= \(\frac { 0-49 }{ -9.8 } \)
अतः पृथ्वी पर आने में लगा समय = 5s + 5s = 10s उत्तर

प्रश्न 14.
19.6 m ऊँची एक मीनार की चोटी से एक पत्थर छोड़ा जाता है। पृथ्वी पर पहुँचने से पहले इसका अंतिम वेग ज्ञात कीजिए।
हल:
यहाँ पर
पत्थर का प्रारंभिक वेग (u) = 0 m/s
पत्थर का अंतिम वेग (v) = ?
मीनार की चोटी की ऊँचाई (s) = 19.6 m
गुरुत्वीय त्वरण (g) = 9.8 m/s²
हम जानते हैं कि
v² – u² = 2gs
v² – (0)² = 2 x 9.8 x 19.6
या v² = 19.6 x 19.6
या v = \( \sqrt{19.6 × 19.6} \) = 19.6 m/s
अतः पत्थर का अंतिम वेग 19.6 m/s होगा। उत्तर

प्रश्न 15.
कोई पत्थर ऊर्ध्वाधर दिशा में ऊपर की ओर 40 m/s के प्रारंभिक वेग से फेंका गया है। g = 10 m/s² लेते हुए ग्राफ की सहायता से पत्थर द्वारा चली गई अधिकतम ऊँचाई ज्ञात कीजिए। नेट विस्थापन तथा पत्थर द्वारा चली गई कुल दूरी कितनी होगी?
हल:
यहाँ पर
पत्थर का प्रारंभिक वेग (u) = 40 m/s
पत्थर का अंतिम वेग (v) = 0 m/s
गुरुत्वीय त्वरण (g) = -10 m/s²
हम जानते हैं कि
v² – u² = 2gs
या s = \(\frac{v^2-u^2}{2 g}\) = \(\frac{(0)^2-(40)^2}{2(-10)}\)
= \(\frac{-40 \times 40}{-2 \times 10}\) = 80 m
अतः पत्थर द्वारा चली गई अधिकतम ऊँचाई = 80 m
पत्थर द्वारा चली गई कुल दूरी = 80 m + 80 m
+ 10 = 160 m उत्तर
पत्थर का नेट विस्थापन = शून्य उत्तर

प्रश्न 16.
पृथ्वी तथा सूर्य के बीच गुरुत्वाकर्षण बल का परिकलन कीजिए। दिया है, पृथ्वी का द्रव्यमान = 6 x 10²⁴ kg तथा सूर्य का द्रव्यमान = 2 x 10³⁰ kg । दोनों के बीच औसत दूरी 1.5 x 10¹¹ m है।
हल:
यहाँ पर
पृथ्वी का द्रव्यमान (M_e) = 6 x 10²⁴ kg
सूर्य का द्रव्यमान (M_s) = 2 x 10³⁰ kg
पृथ्वी व सूर्य के बीच की औसत दूरी (R_s) = 1.5 x 10¹¹ m
गुरुत्वीय स्थिरांक (G) = 6.673 x 10^-11 Nm²/kg²
:. पृथ्वी तथा सूर्य के बीच लगने वाला गुरुत्वाकर्षण बल (Fs) = \(\frac{\mathrm{GM}_{\mathrm{e}} \mathrm{M}_{\mathrm{s}}}{\left(\mathrm{R}_{\mathrm{s}}\right)^2}\) = \(\frac{6.673 \times 10^{-11} \times 6 \times 10^{24} \times 2 \times 10^{30}}{\left(1.5 \times 10^{11}\right)^2} \mathrm{~N}\)
= \(\frac{6.673 \times 12 \times 10^{43}}{2.25 \times 10^{22}}\) N
= 35.59 x 10²¹ N उत्तर

प्रश्न 17.
कोई पत्थर 100 m ऊँची किसी मीनार की चोटी से गिराया गया और उसी समय कोई दूसरा पत्थर 25 m/s के वेग से ऊर्ध्वाधर दिशा में ऊपर की ओर फेंका गया। परिकलन कीजिए कि दोनों पत्थर कब और कहाँ मिलेंगे?
हल:
माना दोनों पत्थर ऊपर x m दूरी पर मिलते हैं। ऊपर से फेंके जाने वाले पत्थर के लिए
प्रारंभिक वेग (u) = 0 m/s
गुरुत्वीय त्वरण (g) = 9.8 ms^-2
तय दूरी (s) = x m
हम जानते हैं कि
s = ut + \(\frac { 1 }{ 2 } \)gt²
x = (0) (t) + + (9.8)t²
x = 4.9t²
नीचे से फेंके जाने वाले पत्थर के लिए
प्रारंभिक वेग (u) = 25 m/s²
गुरुत्वीय त्वरण (g) = – 9.8 m/s²
तय दूरी (s) = (100 – x)m
हम जानते हैं कि
s = ut+ agt²
100 – x = 25 t+ \(\frac { 1 }{ 2 } \) (-9.8)t²
या 100 – 4.9t² = 25t – 4.9t²
या 100 = 25t
या t = \(\frac { 100 }{ 25 } \) = 4s
अतः दोनों पत्थर 4s के बाद मिलेंगे उत्तर
ऊपर से दूरी (x) = 4.9 (4)²
= 4.9 x 16 = 78.4 m उत्तर
:. नीचे से दूरी = 100 – 78.4 = 21.6 m उत्तर

प्रश्न 18.
ऊर्ध्वाधर दिशा में ऊपर की ओर फेंकी गई एक गेंद 6s के पश्चात् फेंकने वाले के पास लौट आती है। ज्ञात कीजिए
(a) यह किस वेग से ऊपर फेंकी गई?
(b) गेंद द्वारा पहुँची गई अधिकतम ऊँचाई।
(c) 4s पश्चात् गेंद की स्थिति।
हल:
यहाँ पर
प्रारंभिक वेग (u) = ?
अंतिम वेग (v) = 0 m/s
गेंद द्वारा अधिकतम ऊँचाई तय करने में लगा समय (t) = \(\frac { 6s }{ 2 } \) = 3s
ऊपर जाते समय गुरुत्वीय त्वरण (g) = – 9.8 m/s²
(a) हम जानते हैं कि
v = u + gt
या u = v-gt
= 0 – ( – 9.8) (3)
= 29.4 m/s
अतः गेंद का प्रारंभिक वेग (u) = 29.4 m/s उत्तर

(b) हम जानते हैं कि
s = ut + \(\frac { 1 }{ 2 } \) gt²
= (29.4) (3) + \(\frac { 1 }{ 2 } \) (-9.8) (3)²
= 88.2 – 44.1 = 44.1 m
अतः अधिकतम 44.1 m की ऊँचाई तय करेगी। उत्तर

(c) इस अवस्था के लिए ऊपर से नीचे की दूरी ज्ञात करेंगे।
u = 0
t = 4s – 35 = 1s
g = 9.8 m/s²
s = ut + \(\frac { 1 }{ 2 } \) gt²
= 0 (1) + \(\frac { 1 }{ 2 } \) (9.8) (1)²
= 4.9 m
अतः गेंद ऊपर से 4.9 m की दूरी पर होगी।
नीचे से गेंद की ऊँचाई = 44.1 – 4.9
= 39.2 m उत्तर

प्रश्न 19.
किसी द्रव में डुबोई गई वस्तु पर उत्प्लावन बल किस दिशा में कार्य करता है?
उत्तर:
किसी द्रव में डुबोई गई वस्तु पर उत्प्लावन बल ऊपर की ओर कार्य करता है।

प्रश्न 20.
पानी के भीतर किसी प्लास्टिक के गुटके को छोड़ने पर यह पानी की सतह पर ऊपर क्यों आ जाता है?
उत्तर:
पानी के भीतर किसी प्लास्टिक के गुटके को छोड़ने पर यह पानी की सतह पर पानी द्वारा ऊपर की ओर लगाए गए उत्प्लावन बल के कारण आता है।

प्रश्न 21.
50 g के किसी पदार्थ का आयतन 20 cm³ है। यदि पानी का घनत्व 1g cm^-3 हो, तो पदार्थ तैरेगा या डूबेगा ?
हल:
यहाँ पर
पदार्थ का द्रव्यमान = 50 g
पदार्थ का आयतन = 20 cm³
:. पदार्थ का घनत्व =
द्रव्यमान आयतन
= \(\frac { 50 }{ 20 } \) g cm^-3
= 2.5 g cm^-3
क्योंकि पदार्थ का घनत्व, पानी के घनत्व से अधिक है। इसलिए पदार्थ पानी में डूबेगा। उत्तर

प्रश्न 22.
500g के एक मोहरबंद पैकेट का आयतन 350 cm³ है। पैकेट 1g cm^-3 घनत्व वाले पानी में तैरेगा या डूबेगा? इस पैकेट द्वारा विस्थापित पानी का द्रव्यमान कितना होगा?
हल:
यहाँ पर
पैकेट का द्रव्यमान = 500 g
पैकेट का आयतन = 350 cm³
:. पैकेट का घनत्व =
= \(\frac { 500 }{ 350 } \) g cm^-3
= 1.43 g cm^-3
क्योंकि पैकेट का घनत्व पानी के घनत्व (1 g cm^-3) से अधिक है। इसलिए पैकेट पानी में डूबेगा। इस प्रकार पैकेट द्वारा विस्थापित पानी का द्रव्यमान = आयतन – घनत्व
= 350 x 1 g
= 350 g उत्तर

Haryana State Board HBSE 9th Class Science Solutions Chapter 9 बल तथा गति के नियम Textbook Exercise Questions and Answers.

Haryana Board 9th Class Science Solutions Chapter 9 बल तथा गति के नियम

HBSE 9th Class Science बल तथा गति के नियम Intext Questions and Answers
(पृष्ठ संख्या – 131)

प्रश्न 1.
निम्न में किसका जड़त्व अधिक है
(a) एक रबड़ की गेंद एवं उसी आकार का पत्थर ।
(b) एक साइकिल एवं एक रेलगाड़ी।
(c) पाँच रुपए का एक सिक्का एवं एक रुपए का सिक्का।
उत्तर:
(a) एक रबड़ की गेंद एवं उसी आकार के पत्थर में पत्थर का जड़त्व अधिक होगा।
(b) एक साइकिल एवं एक रेलगाड़ी में रेलगाड़ी का जड़त्व अधिक होगा।
(c) पाँच रुपए के एक सिक्के एवं एक रुपए के एक सिक्के में से पाँच रुपए के सिक्के का जड़त्व अधिक होगा।

प्रश्न 2.
नीचे दिए गए उदाहरण में गेंद का वेग कितनी बार बदलता है, जानने का प्रयास करें। “फुटबॉल का एक खिलाड़ी गेंद पर किक लगाकर गेंद को अपनी टीम के दूसरे खिलाड़ी के पास पहुँचाता है। दूसरा खिलाड़ी उस गेंद को किक लगाकर गोल की ओर पहुँचाने का प्रयास करता है। विपक्षी टीम का गोलकीपर गेंद को पकड़ता है और अपनी टीम के खिलाड़ी की ओर किक लगाता है।” इसके साथ ही उस कारक की भी पहचान करें जो प्रत्येक अवस्था में बल प्रदान करता है।
उत्तर:
फुटबॉल के एक खिलाड़ी द्वारा गेंद पर किक मारने पर उसका वेग परिवर्तित होगा तथा उसी टीम के खिलाड़ी द्वारा गेंद को गोल की ओर किक मारने पर उसका वेग पुनः परिवर्तित होगा। इसके बाद विपक्षी टीम के गोलकीपर द्वारा गेंद को पकड़ने . पर गेंद का वेग शून्य हो जाएगा तथा फिर उसके द्वारा अपनी टीम के खिलाड़ी की ओर मारने पर चौथी बार गेंद का वेग परिवर्तित होगा। प्रत्येक अवस्था में मनुष्य द्वारा लगाया गया बाह्य बल गेंद को वेग प्रदान करता है।

प्रश्न 3.
किसी पेड़ की शाखा को तीव्रता से हिलाने पर कुछ पत्तियाँ झड़ जाती हैं। क्यों?
उत्तर:
किसी पेड़ की शाखा को तीव्रता से हिलाने पर कुछ पत्तियाँ झड़ जाती हैं क्योंकि पेड़ की शाखा को हिलाने पर शाखा गति अवस्था में आ जाती है परंतु जड़त्व के कारण पत्तियाँ स्थिर अवस्था में रहने की चेष्टा करती हैं, जिस कारण पत्तियाँ झड़ जाती हैं।

प्रश्न 4.
जब कोई गतिशील बस अचानक रुकती है, तो आप आगे की ओर झुक जाते हैं और जब विरामावस्था से गतिशील होती है तो पीछे की ओर जाते हैं, क्यों?
उत्तर:
जब कोई गतिशील बस अचानक रुकती है तो हमारा नीचे का हिस्सा विरामावस्था में आ जाता है, परंतु ऊपरी हिस्सा गति जड़त्व के कारण गति करने की चेष्टा करता है, जिस कारण हम आगे की ओर झुक जाते हैं। परंतु जब कोई बस विरामावस्था से चलना शुरू करती है तो हमारा निचला हिस्सा बस के साथ गतिज अवस्था में आ जाता है, परंतु ऊपरी हिस्सा स्थिर जड़त्व के कारण स्थिर रहने की चेष्टा करता है, जिस कारण हम पीछे की ओर झुक जाते हैं।

(पृष्ठ संख्या-140)

प्रश्न 1.
यदि क्रिया सदैव प्रतिक्रिया के बराबर है, तो स्पष्ट कीजिए कि घोड़ा गाड़ी को कैसे खींच पाता है ?
उत्तर:
गति के तीसरे नियम के अनुसार क्रिया सदैव प्रतिक्रिया के समान होती है। जब घोड़ा किसी गाड़ी को खींचता है तो वह पृथ्वी पर किसी बल माना F से क्रिया करता है तो पृथ्वी द्वारा उसे R प्रतिक्रिया दी जाती है जिसके दो घटक R cos A तथा R sin A हो जाते हैं। इनमें R cos A क्षैतिज भाग गाड़ी को आगे की ओर खींचने का काम करता है, जबकि R sin A ऊर्ध्वाधर भाग गाड़ी और सड़क के बीच घर्षण बल को कम करने का काम करता है। इस प्रकार गाड़ी को घोड़ा खींच पाता है।

प्रश्न 2.
एक अग्निशमन कर्मचारी को तीव्र गति से बहुतायत मात्रा में पानी फेंकने वाली रबड़ की नली को पकड़ने में कठिनाई क्यों होती है, स्पष्ट करें।
उत्तर:
गति के तीसरे नियम के अनुसार क्रिया और प्रतिक्रिया समान और विपरीत दिशा में होती है। जब फायर ब्रिगेड के किसी पाइप से तीव्र गति से अत्यधिक मात्रा व उच्च वेग से पानी निकलता है तो वह उस पाइप को उतने ही वेग से पीछे की ओर धकेलता है, जिस कारण अग्निशमन कर्मचारी को वह पाइप संभालना कठिन होता है।

प्रश्न 3.
एक 50g द्रव्यमान की गोली 4kg द्रव्यमान की राइफल से 35 ms^-1 के प्रारंभिक वेग से छोड़ी जाती है। राइफल के प्रारंभिक प्रतिक्षेपित वेग की गणना कीजिए।
हल:
यहाँ पर
गोली का द्रव्यमान (m₁) = 50 g = 0.05 kg
राइफल का द्रव्यमान (m₂) = 4 kg
गोली का प्रारंभिक वेग (u₁) तथा राइफल का प्रारंभिक वेग (u₂) क्रमशः शून्य है।

अर्थात् u₁ = u₂ = 0
गोली का अंतिम वेग (v₁) = + 35 m/s
गोली की दिशा बाएँ से दाएँ परिपाटी के अनुसार चित्र में धनात्मक ली गई है।
माना राइफल का प्रतिक्षेपित वेग = v m/s
गोली छूटने से पहले गोली व राइफल का कुल संवेग = (4 + 0.05) kg x 0 m/s
= 0 kg ms^-1
गोली छूटने के बाद गोली का संवेग = 0.05 kg x 35 ms^-1 = 1.75 kg ms^-1
गोली छूटने के बाद राइफल का संवेग = 4 kg x v ms^-1
गोली छूटने के बाद गोली व राइफल का कुल संवेग = (1.75 + 4 v) kg ms^-1
संवेग संरक्षण के नियमानुसार
गोली छूटने के बाद का कुल संवेग = गोली छूटने से पहले का कुल संवेग
1.75 + 4v = 0
\(\frac { -1.75 }{ 4 } \) = – 0.44 ms^-1 उत्तर
ऋणात्मक चिह्न दर्शाता है कि राइफल गोली की विपरीत दिशा में अर्थात दाईं से बाईं ओर प्रतिक्षेपित होगी।

प्रश्न 4.
100 g और 200 g द्रव्यमान की दो वस्तुएँ एक ही रेखा के अनुदिश एक ही दिशा में क्रमशः 2 ms^-1 और 1 ms^-1 के वेग से गति कर रही हैं। दोनों वस्तुएँ टकरा जाती हैं। टक्कर के पश्चात् प्रथम वस्तु का वेग 1.67 ms^-1 हो जाता है, तो दूसरी वस्तु का वेग ज्ञात करें। हल-यहाँ पर
पहली वस्तु का द्रव्यमान (m₁) = 100 g = 0.1 kg
दूसरी वस्तु का द्रव्यमान (m₂) = 200 g = 0.2 kg
पहली वस्तु का प्रारंभिक वेग (u₁) = 2 ms^-1
दूसरी वस्तु का प्रारंभिक वेग (u₂) = 1 ms^-1
अतः टक्कर से पहले दोनों वस्तुओं का कुल संवेग = m₁ x u₁ + m₂ x u₂
= (0.1 x 2 + 0.2 x 1) kg ms^-1
= 0.4 kg ms^-1
टक्कर के बाद पहली वस्तु का वेग (v₁) = 1.67 ms^-1
माना टक्कर के बाद दूसरी वस्तु का वेग (v₂) = v ms^-1
अतः टक्कर के बाद दोनों वस्तुओं का कुल संवेग = m₁v₁ + m₂V₂
= [0.1 x 1.67 + 0.2 x v₂] kg ms^-1
= [0.167 + 0.2 v₂] kg ms^-1
संवेग संरक्षण के नियम के अनुसार
टक्कर के बाद कुल संवेग = टक्कर से पहले कुल संवेग
0.167 + 0.2 v₂ = 0.4
या 0.2 v₂ = 0.4 – 0.167
या v₂ = = \(\frac { 1.233 }{ 0.2 } \) = 1.165ms^-1
अतः टक्कर के बाद दूसरी वस्तु का वेग = 1.165 ms^-1 उत्तर

HBSE 9th Class Science बल तथा गति के नियम Textbook Questions and Answers

प्रश्न 1.
कोई वस्तु शून्य बाह्य असंतुलित बल अनुभव करती है। क्या किसी भी वस्तु के लिए अशून्य वेग से गति करना संभव है? यदि हाँ, तो वस्तु के वेग के परिमाण एवं दिशा पर लगने वाली शर्तों का उल्लेख करें। यदि नहीं, तो कारण स्पष्ट करें।
उत्तर:
यहाँ पर वस्तु पर लगने वाला बाह्य असंतुलित बल (F) शून्य है अर्थात्
F = 0
ma = 0
परंतु m ≠ 0 इसलिए a = 0
इस अवस्था में गति करना संभव है परंतु गति सीधे पथ पर एक ही परिमाण व एक दिशा में होगी।

प्रश्न 2.
जब किसी छड़ी से एक दरी (कार्पेट) को पीटा जाता है, तो धूल के कण बाहर आ जाते हैं। स्पष्ट करें।
उत्तर:
जब किसी दरी या कार्पेट को छड़ी से पीटा जाता है तो दरी अपने स्थान से हट जाती है तथा धूल के कण जड़त्व के कारण अपनी स्थिति बनाए रखना चाहते हैं, जिस कारण धूल के कण बाहर आ जाते हैं तथा दरी साफ हो जाती है।

प्रश्न 3.
बस की छत पर रखे सामान को रस्सी से क्यों बाँधा जाता है?
उत्तर:
बसों अथवा कारों की छतों पर रखे सामान को रस्सी से बाँधना बुद्धिमानी माना जाता है, क्योंकि चलती हुई बसों अथवा कारों के अचानक रुकने या दिशा बदलने पर जड़त्व के कारण सामान गिरने से बच जाता है।

प्रश्न 4.
किसी बल्लेबाज द्वारा क्रिकेट की गेंद को मारने पर गेंद ज़मीन पर लुढ़कती है। कुछ दूरी चलने के पश्चात् गेंद रुक जाती है। गेंद रुकने के लिए धीमी होती है, क्योंकि
(a) बल्लेबाज ने गेंद को पर्याप्त प्रयास से हिट नहीं किया है।
(b) वेग गेंद पर लगाए गए बल के समानुपाती है।
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है।
(d) गेंद पर कोई असंतुलित बल कार्यरत नहीं है, अतः गेंद विरामावस्था में आने के प्रयासरत है। (सही विकल्प का चयन करें)
उत्तर:
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है।

प्रश्न 5.
एक ट्रक विरामावस्था से किसी पहाड़ी से नीचे की ओर नियत त्वरण से लुढ़कना शुरू करता है। यह 20 s में 400 m की दूरी तय करता है। इसका त्वरण ज्ञात करें। अगर इसका द्रव्यमान 7 टन है तो उस पर लगने वाले बल की गणना करें। (1 टन = 1000 kg)
हल:
यहाँ पर पहली अवस्था में प्रारंभिक वेग (u) = 0
तय की गई दूरी (s) = 400 m
त्वरण (a) = ?
समय (t) = 20s
सूत्रानुसार s = ut + \(\frac { 1 }{ 2 } \) at²
ut + \(\frac { 1 }{ 2 } \) at² = s
0 x (20) + \(\frac { 1 }{ 2 } \)a x (20)² = 400
0 + \(\frac { 1 }{ 2 } \)a x 400 =
200 a = 400
a = \(\frac { 400 }{ 200 } \) = 2 m/s² उत्तर
दूसरी अवस्था में द्रव्यमान (m) = 7 टन
= 7 x 1000 = 7000 kg ( 1 टन = 1000 kg)
बल (F) = mx a
= 7000 kg x 2 m/s²
= 14000 N उत्तर

प्रश्न 6.
1 kg द्रव्यमान के एक पत्थर को 20 ms^-1 के वेग से झील की जमी हुई सतह पर फेंका जाता है। पत्थर 50 m की दूरी तय करने के बाद रुक जाता है। पत्थर और बर्फ के बीच लगने वाले घर्षण बल की गणना करें।
हल:
यहाँ पर
पत्थर का द्रव्यमान (m) = 1 kg
पत्थर का प्रारंभिक वेग (u) = 20 ms^-1
पत्थर का अंतिम वेग (v) = 0
पत्थर द्वारा तय दूरी (s) = 50 m
त्वरण (a) = ?
हम जानते हैं कि
v² – u² = 2as
2 = \(\frac{\mathrm{v}^2-\mathrm{u}^2}{2 \mathrm{~s}}\) = \(\frac{(0)-(20)^2}{2(50)}\)
= \(\frac { -400 }{ 100 } \) = -4 m/s²
ऋणात्मक चिह्न दर्शाता है कि त्वरण गति के विरुद्ध कार्य कर रहा है।
अतः बर्फ व पत्थर के बीच लगने वाला घर्षण बल = 1 x (-4) = – 4N उत्तर

प्रश्न 7.
एक 8000 kg द्रव्यमान का रेल इंजन प्रति 2000 kg द्रव्यमान वाले पाँच डिब्बों को सीधी पटरी पर खींचता है। यदि इंजन 40000 N का बल आरोपित करता है तथा यदि पटरी 5000 N का घर्षण बल लगाती है, तो ज्ञात करें
(a) नेट त्वरण बल तथा
(b) रेल का त्वरण।
हल:
यहाँ पर
रेल इंजन का द्रव्यमान (m₁) = 8000 kg
पांच डिब्बों का द्रव्यमान (m₂) = 2000 kg x 5
= 10000 kg
डिब्बों सहित रेल इंजन का द्रव्यमान (m) = m₁ + m₂
= (8000 + 10000) kg = 18000 kg
इंजन द्वारा डिब्बों पर आरोपित बल (F₁) = 40000 N
पटरी द्वारा डिब्बों पर आरोपित घर्षण बल (F₂) = 5000 N
नेट त्वरण बल (F) = F₁ – F₂
= 40000 N – 5000 N
= 35000 N उत्तर

(a) नेट त्वरण बल = F₁ – F₂
= 40000N – 5000N
= 35000Nउत्तर

(b) रेल का त्वरण (a) = \(\frac{\mathrm{F}}{\mathrm{m}_2}\) = \(\frac{35000}{10000} \mathrm{~ms}^{-2}\)
= 3.5 ms^-2 उत्तर

प्रश्न 8.
एक गाड़ी का द्रव्यमान 1500 kg है। यदि गाड़ी को 1.7 ms^-2 के ऋणात्मक त्वरण (अवमंदन) के साथ विरामावस्था में लाना है, तो गाड़ी तथा सड़क के बीच लगने वाला बल कितना होगा? हल:
यहाँ पर
गाड़ी का द्रव्यमान (m) = 1500 kg
गाड़ी पर लगने वाला त्वरण (a) = – 1.7 ms^-2
अंतिम वेग (v) = 0
गाड़ी व सड़क के बीच लगने वाला बल (F) = m x a
= 1500 x (-1.7) N = -2550 N उत्तर
ऋणात्मक चिह्न दर्शाता है कि बल गाड़ी की गति की दिशा के विपरीत कार्य करेगा।

प्रश्न 9.
किसी m द्रव्यमान की वस्तु जिसका वेग v है का संवेग क्या होगा?
(a) (mv)²
(b) mv²
(c) (\(\frac { 1 }{ 2 } \)) mv²
(d) mv
(उपरोक्त में से सही विकल्प चुनें।)
उत्तर:
(d) mv।

प्रश्न 10.
हम एक लकड़ी के बक्से को 200 N बल लगाकर उसे नियत वेग से फर्श पर धकेलते हैं। बक्से पर लगने वाला घर्षण बल क्या होगा?
उत्तर:
यदि हम एक लकड़ी के बक्से को 200 N बल लगाकर उसे नियत वेग से फर्श पर धकेलते हैं तो बक्से पर लगने वाला घर्षण बल भी 200 N होगा।

प्रश्न 11.
दो वस्तुएँ, प्रत्येक का द्रव्यमान 1.5 kg है, एक ही सीधी रेखा में एक-दूसरे के विपरीत दिशा में गति कर रही हैं। टकराने के पहले प्रत्येक का वेग 2.5 ms^-1 है। टकराने के बाद यदि दोनों एक-दूसरे से जुड़ जाती हैं, तब उनका सम्मिलित वेग क्या होगा?
उत्तर:
यहाँ पर दोनों वस्तुओं का द्रव्यमान तथा वेग समान है परंतु दोनों विपरीत दिशाओं में गतिशील होने के कारण टकराने के बाद जुड़ जाती हैं। इसलिए इनका सम्मिलित वेग शून्य (0) होगा।

प्रश्न 12.
गति के तृतीय नियम के अनुसार जब हम किसी वस्तु को धक्का देते हैं, तो वस्तु उतने ही बल के साथ हमें भी विपरीत दिशा में धक्का देती है। यदि वह वस्त एक ट्रक है जो सड़क के किनारे खड़ा है; संभवतः हमारे द्वारा बल आरोपित करने पर भी गतिशील नहीं हो पाएगा। एक विद्यार्थी इसे सही साबित करते हुए कहता है कि दोनों बल विपरीत एवं बराबर हैं जो एक-दूसरे को निरस्त कर देते हैं। इस तर्क पर अपने विचार दें और बताएँ कि ट्रक गतिशील क्यों नहीं हो पाता?
उत्तर:
किसी सड़क के किनारे खड़े ट्रक पर हमारे द्वारा बल लगाने पर ट्रक गतिशील नहीं हो पाएगा क्योंकि हमारे द्वारा लगाया गया बल, ट्रक द्वारा ट्रक व सड़क के बीच लगने वाले घर्षण बल से काफी कम होगा। यदि हमारा बल, घर्षण बल से बढ़ जाएगा तो ट्रक गतिशील हो जाएगा।

प्रश्न 13.
200 g द्रव्यमान की एक हॉकी की गेंद 10 ms^-1 से गति कर रही है। यह एक हॉकी स्टिक से इस प्रकार टकराती है कि यह 5 ms^-1 के वेग से अपने प्रारंभिक मार्ग पर वापस लौटती है। हॉकी स्टिक द्वारा आरोपित बल द्वारा हॉकी की गेंद में आये संवेग परिवर्तन के परिमाप का परिकलन कीजिए।
हल:
यहाँ पर
हॉकी गेंद का द्रव्यमान (m) = 200g = 0.2 kg
हॉकी गेंद का प्रारंभिक वेग (v₁) = 10 ms^-1
प्रारंभिक संवेग = mv₁
हॉकी गेंद वेग (v₂) के साथ विपरीत दिशा में जाती है = -5 ms^-1
अंतिम संवेग = mv₂
संवेग परिवर्तन = mv₁ – mV₂
= 0.2 [10 – (-5)] = 0.2 (15) = 3kg ms^-1
अतः हॉकी गेंद का संवेग परिवर्तन 3kg ms^-1 है।

प्रश्न 14.
10 g द्रव्यमान की एक गोली सीधी रेखा में 150 ms^-1 की वेग से चलकर एक लकड़ी के गुटके (टुकड़े) से टकराती है और 0.03 s के बाद रुक जाती है। गोली लकड़ी को कितनी दूरी तक भेदेगी? लकड़ी के गुटके (टुकड़े) द्वारा गोली पर लगाए गए बल के परिमाण की गणना करें। हल-यहाँ पर
गोली का द्रव्यमान (m) = 10g
= \(\frac { 10 }{ 1000 } \)kg = 0.01 kg
गोली का प्रांरभिक वेग (u) = 150 ms^-1
गोली का अंतिम वेग (v) = 0 ms^-1
समय (t) = 0.03 s
त्वरण (a) = ?
दूरी (s) = ?
हम जानते हैं कि
= \(\frac{v-u}{t}\) = \(\frac{0-150}{0.30}\)ms^-2
= – 5000 ms^-2
s = ut + \(\frac { 1 }{ 2 } \) at^-2
= (150) (0.03) + \(\frac { 1 }{ 2 } \) x (-5000) x (0.03)²
= 4.5 – 2.25 = 2.25 m उत्तर
बल (F) = ma
= 0.01 x ( – 5000) N
= – 50 N उत्तरी
ऋणात्मक चिह्न दर्शाता है कि बल गति की विपरीत दिशा में कार्य करता है।

प्रश्न 15.
एक वस्तु जिसका द्रव्यमान 1kg है, 10 ms^-1 की वेग से एक सीधी रेखा में चलते हुए विरामावस्था में रखे 5kg द्रव्यमान के एक लकड़ी के गुटके (टुकड़े) से टकराती है। उसके बाद दोनों साथ-साथ उसी सीधी रेखा में गति करते हैं। संघट्ट के पहले तथा बाद के कुल संवेगों की गणना करें। आपस में जुड़े हुए संयोजन के वेग की भी गणना करें।
हल:
यहाँ पर
वस्तु का द्रव्यमान (m) = 1 kg
वस्तु का वेग (v₁) = 10 ms^-1
:. संघटन से पहले संवेग = m x v₁
= 1 x 10 kg ms^-1
= 10 kg ms^-1
संघटन के बाद भी संवेग होगा = 10 kg ms^-1
वस्तु और लकड़ी के टुकड़े का संयुक्त द्रव्यमान (m₁) = 1 +5
= 6 kg
माना वस्तु और लकड़ी के टुकड़े का अंतिम वेग = v₂ ms^-1
संवेग संरक्षण नियमानुसार
m₁v₂ = 10
या 6 x V₂ = 10
या v₂ = \(\frac { 10 }{ 6 } \) ms^-1 = 5 ms^-1 उत्तर

प्रश्न 16.
100 kg द्रव्यमान की एक वस्तु का वेग समान त्वरण से चलते हुए 6s में 5 ms^-1 से 8 ms^-1 हो जाता है। वस्तु के पहले और बाद के संवेगों की गणना करें। उस बल के परिमाण की गणना करें जो उस वस्तु पर आरोपित है। हल-यहाँ पर
वस्तु का द्रव्यमान (m) = 100 kg
प्रारंभिक वेग (u) = 5 ms^-1
अंतिम वेग (v) = 8 ms^-1
समय (t) = 6s
पहले संवेग = mu = 100 x 5 = 500 kg ms^-1 उत्तर
बाद में संवेग = mv = 100 x 8 = 800 kg ms^-1 उत्तर हम जानते हैं कि
a = \(\frac { v-u }{ t } \) = \(\frac { 8-5 }{ 6 } \) = \(\frac { 3 }{ 6 } \) = 0.5ms^-2
वस्तु पर आरोपित बल (F) = m x a
= 100 x 0.5 N= 50 N उत्तर

प्रश्न 17.
अख्तर, किरण और राहुल किसी राजमार्ग पर बहुत तीव्र गति से चलती हुई कार में सवार हैं कि अचानक उड़ता हुआ कोई कीड़ा, गाड़ी के सामने के शीशे से आ टकराया और वह शीशे से चिपक गया। अख्तर और किरण इस स्थिति पर विवाद करते हैं। किरण का मानना है कि कीड़े के संवेग-परिवर्तन का परिमाण कार के संवेग परिवर्तन के परिमाण की अपेक्षा बहुत अधिक है (क्योंकि कीड़े के वेग में परिवर्तन का मान कार के वेग में परिवर्तन के मान से बहुत अधिक है।) अख्तर ने कहा कि चूंकि कार का वेग बहुत अधिक था। अतः कार ने कीड़े पर बहुत अधिक बल लगाया जिसके कारण कीड़े की मौत हो गई। राहुल ने एक नया तर्क देते हुए कहा कि कार तथा कीड़ा दोनों पर समान बल लगा और दोनों के संवेग में बराबर परिवर्तन हुआ। इन विचारों पर अपनी प्रतिक्रिया दें।
उत्तर:
अख्तर का विचार सही है क्योंकि कार का वेग और द्रव्यमान दोनों अधिक होने के कारण कार का संवेग उड़ते हुए कीड़े की अपेक्षा अधिक था। इसलिए कार ने उड़ते हुए कीड़े पर अधिक बल लगाया जिस कारण कीड़े की मौत हो गई।

प्रश्न 18.
एक 10 kg द्रव्यमान की घंटी 80 cm की ऊँचाई से फर्श पर गिरी। इस अवस्था में घंटी द्वारा फर्श पर स्थानांतरित संवेग के मान की गणना करें। परिकलन में सरलता हेतु नीचे की ओर दिष्ट त्वरण का मान 10 ms^-2 लें।
हल:
यहाँ पर
घंटी का द्रव्यमान (m) = 10 kg
घंटी का प्रारंभिक वेग (u) = 0 m/s
घंटी का अंतिम वेग (v) = ?
घंटी की ऊँचाई (s) = 80 cm = 0.8 m
त्वरण (a) = 10 ms^-2
हम जानते हैं कि
v² – u² = 2as
v² – (0)² = 2 (10) (0.8)
या v² = 16
या v = \(\sqrt{16}\) = 4 ms^-1
अतः घंटी द्वारा फर्श पर स्थानांतरित संवेग (p) = m.v.
= 10 x 4 = 40 kg ms^-1 उत्तर

अतिरिक्त अभ्यास के प्रश्न

प्रश्न 1.
एक वस्तु की गति की अवस्था में दूरी-समय सारणी निम्नवत है

(a) त्वरण के बारे में आप क्या निष्कर्ष निकाल सकते हैं? क्या यह नियत है? बढ़ रहा है? घट रहा है? शून्य है?
(b) आप वस्तु पर लगने वाले बल के बारे में क्या निष्कर्ष निकाल सकते हैं?
हल:
(a) दूरी-समय सारणी से स्पष्ट होता है कि त्वरण लगातार बढ़ रहा है।
(b) वस्तु पर त्वरण बढ़ने के कारण बल भी बढ़ रहा है।

प्रश्न 2.
1200 kg द्रव्यमान की कार को एक समतल सड़क पर दो व्यक्ति समान वेग से धक्का देते हैं। उसी कार को तीन व्यक्तियों द्वारा धक्का देकर 0.2 ms^-2 का त्वरण उत्पन्न किया जाता है। कितने बल के साथ प्रत्येक व्यक्ति कार को धकेल पाते है? (मान लें कि सभी व्यक्ति समान पेशीय बल के साथ कार को धक्का देते हैं।)
हल:
यहाँ पर
कार का द्रव्यमान (m) = 1200 kg
तीन व्यक्तियों द्वारा धक्का लगाने पर उत्पन्न त्वरण (a) = 0.2 ms^-2
:. प्रत्येक व्यक्ति द्वारा कार पर लगाया गया बल (F) = ma
= 1200 x 0.2 N
= 240 N उत्तर

प्रश्न 3.
500 g द्रव्यमान के एक हथौड़े द्वारा 50 ms^-1 के वेग से एक कील पर प्रहार किया जाता है। कील द्वारा हथौड़े को बहुत कम समय 0.01 s में ही रोक दिया जाता है। कील के द्वारा हथौड़े पर लगाए गए बल की गणना करें।
हल:
यहाँ पर
हथौड़े का द्रव्यमान (m) = 500 g = \(\frac { 500 }{ 1000 } \) kg
= 0.5 kg
हथौड़े का प्रारंभिक वेग (u) = 50 ms^-1
समय (t) = 0.01s
हथौड़े का अंतिम वेग (v) = 0
त्वरण (a) = \(\frac { v-u }{ t } \) = \(\frac { 0-50 }{ 0.01 } \) ms^-2
= -5000 ms^-2
ऋणात्मक चिह्न दर्शाता है त्वरण मंदन का कार्य करता है।
कील के द्वारा हथौड़े पर लगाया गया बल (F)
= m x a
= 0.5 x (5000) N
= 2500 N उत्तर

प्रश्न 4.
एक 1200 kg द्रव्यमान की मोटरकार 90 km/h की वेग से एक सरल रेखा के अनुदिश चल रही है। उसका वेग बाहरी असंतुलित बल लगने के कारण 45 में घटकर 18 km/h हो जाता है। त्वरण और संवेग में परिवर्तन का परिकलन करें। लगने वाले बल के परिमाण का भी परिकलन करें।
हल:
यहाँ पर
मोटरकार का द्रव्यमान (m) = 1200 kg
प्रारंभिक वेग (u) = 90 km/h
\(\frac { 90 x 1000 }{ 3600 } \) = 25ms^-1
अंतिम वेग (v) = 18 km/h = \(\frac { 18 x 1000 }{ 3600 } \) = 5 ms^-1
3600 समय (t) = 4s
त्वरण (a) = \(\frac { v-u }{ t } \) = \(\frac { 5-25 }{ 4 } \) = \(\frac { -20 }{ 4 } \)
= -5 ms^-2 उत्तर
संवेग में परिवर्तन = mv – mu
= m (v-u)
= 1200 (5 – 25) = 1200 x (-20)
= – 24000 kg ms^-1
लगने वाले बल का परिमाण (F) = m.a.
= 1200 x 5 = 6000 N उत्तर

Haryana State Board HBSE 9th Class Science Solutions Chapter 8 गति Textbook Exercise Questions and Answers.

Haryana Board 9th Class Science Solutions Chapter 8 गति

HBSE 9th Class Science गति Intext Questions and Answers
(पृष्ठ संख्या – 110)

प्रश्न 1.
एक वस्तु के द्वारा कुछ दूरी तय की गई। क्या इसका विस्थापन शून्य हो सकता है? अगर हाँ, तो अपने उत्तर को उदाहरण के द्वारा समझाएँ।
उत्तर:
हाँ, किसी वस्तु द्वारा कुछ दूरी तय करने पर विस्थापन शून्य हो सकता है; जैसे माना कोई व्यक्ति चित्र में दिखाए अनुसार मूल बिंदु O से चलकर एक सरल रेखा के साथ बिंदु A तक 55 कि०मी० दूरी तय करता है तथा वापिस A से फिर O तक 55 कि०मी० दूरी तय करता है तो इस अवस्था में

व्यक्ति द्वारा तय की गई दूरी = 55 कि०मी० + 55 कि०मी०
= 110 कि०मी०
विस्थापन = शून्य

प्रश्न 2.
एक किसान 10 मीटर की भुजा वाले एक वर्गाकार खेत की सीमा पर 40 सेकंड में चक्कर लगाता है। 2 मिनट 20 सेकंड के बाद किसान के विस्थापन का परिमाण क्या होगा?
हल:

वर्गाकार खेत ABCD की भुजा = 10 मीटर
वर्गाकार खेत ABCD का परिमाप = 4 x भुजा
= 4 x 10 = 40 मीटर
सीमा का एक चक्कर लगाने में लिया गया समय = 40 सेकंड
कुल समय = 2 मिनट 20 सेकंड = (2 x 60 + 20) सेकंड = 140 सेकंड
अब 40 सेकंड में किसान द्वारा तय दूरी = 40 मीटर
1 सेकंड में किसान द्वारा तय दूरी = \(\frac { 40 }{ 40 } \) मीटर = 1 मीटर
140 सेकंड में किसान द्वारा तय दूरी = 1 x 140 = 140 मीटर
यदि किसान मूल बिंदु A से चलना शुरू करता है तो वह 140 मीटर की दूरी तय करने के बाद बिंदु C पर होगा। इस प्रकार व्यक्ति का विस्थापन AC (वर्ग का विकर्ण होगा) अतः
∴ AC = \(\sqrt{(\mathrm{AB})^2+(\mathrm{BC})^2}\)
= \(\sqrt{(10)^2+(10)^2}\)
= \(\sqrt{100+100}\)
= \(\sqrt{200}\)
= \(\sqrt{2 \times 100}\)
= 10\(\sqrt{2}\) m
= 10 × 1.414 = 14.14 मी० उत्तर

प्रश्न 3.
विस्थापन के लिए निम्न में कौन सही है?

• यह शून्य नहीं हो सकता है।
• इसका परिमाण वस्तु के द्वारा तय की गई दूरी से अधिक होता है।

उत्तर:
विस्थापन के लिए

• और
• दोनों गलत हैं।

(पृष्ठ संख्या – 112)

प्रश्न 1.
चाल एवं वेग में अंतर बताइए। उत्तर-चाल तथा वेग में अंतर निम्नलिखित हैं

प्रश्न 2.
किस अवस्था में किसी वस्तु के औसत वेग का परिमाण उसकी औसत चाल के बराबर होगा?
उत्तर:
यदि कोई वस्तु एक निश्चित दिशा में समान गति से गतिमान हो तो उस वस्तु के औसत वेग का परिमाण उसकी चाल के बराबर होगा।

प्रश्न 3.
एक गाड़ी का ओडोमीटर क्या मापता है?
उत्तर:
गाड़ी का ओडोमीटर गाड़ी द्वारा चली गई दूरी को मापता है।

प्रश्न 4.
जब वस्तु एकसमान गति में होती है तब इसका मार्ग कैसा दिखाई पड़ता है?
उत्तर:
जब कोई वस्तु एकसमान गति में होती है तो उसका मार्ग एक सरल रेखीय दिखाई देता है।

प्रश्न 5.
एक प्रयोग के दौरान, अंतरिक्षयान से एक सिग्नल को पृथ्वी पर पहुँचने में 5 मिनट का समय लगता है। पृथ्वी पर स्थित स्टेशन से उस अंतरिक्षयान की दूरी क्या है? (सिग्नल की चाल = प्रकाश की चाल = 3 x 108 ms-1)
हल:
अंतरिक्षयान से पृथ्वी तक सिग्नल पहुँचने में लगा समय = 5 मिनट
= 5 x 60 = 300 सेकंड
सिग्नल की चाल = 3 x 10⁸ ms^-1
अंतरिक्षयान की पृथ्वी से दूरी = चाल x समय
= 3 x 10⁸ x 300 m
= 9 x 10¹⁰m उत्तर

(पृष्ठ संख्या – 114)

प्रश्न 1.
आप किसी वस्तु के बारे में कब कहेंगे कि,

1. वह एकसमान त्वरण से गति में है?
2. वह असमान त्वरण से गति में है?

उत्तर:

1. एकसमान त्वरण-यदि बराबर समयांतराल में किसी वस्तु के वेग में बराबर परिवर्तन हो तो वस्तु एकसमान त्वरण से गतिशील कहलाती है।
2. असमान त्वरण-यदि किसी वस्तु का वेग असमान रूप से बदलता हो, तो उसे असमान त्वरण से गतिशील कहते हैं।

प्रश्न 2.
एक बस की गति (चाल) 5s में 80 kmh^-1 से घटकर 60 kmh^-1 रह जाती है। बस का त्वरण ज्ञात कीजिए।
हल:
बस की प्रारंभिक चाल (u) = 80 kmh^-1
= = \(\frac{80 \times 1000}{3600}\)ms^-1 = \(\frac{200}{9}\)ms^-1
बस की अंतिम चाल (v) = 60 kmh^-1
= \(\frac{60 \times 1000}{3600}\)ms^-1
= \(\frac{50}{3}\)ms^-1
समय (t) = 5s
बस का त्वरण (a) = \(\frac{v-u}{t}\) = \(\frac{\left(\frac{50}{3}-\frac{200}{9}\right) \mathrm{ms}^{-1}}{5 \mathrm{~s}}\) = \(\frac{150-200}{9 \times 5}\)ms^-2
\(\frac{-50}{45}=\frac{-10}{9}\)ms^-2
= -1.1 ms^-2 उत्तर

प्रश्न 3.
एक रेलगाड़ी स्टेशन से चलना प्रारंभ करती है और एकसमान त्वरण के साथ चलते हुए 10 मिनट में 40 kmh^-1 की चाल प्राप्त करती है। इसका त्वरण ज्ञात कीजिए।
हल
रेलगाड़ी की प्रारंभिक चाल (u) = O
रेलगाड़ी की अंतिम चाल (v) = 40 kmh^-1
= \(\frac{40 \times 1000}{3600}\)
= \(\frac{40 \times 1000}{3600}\)ms^-1
समय (t) = 10
मिनट = 10 x 60s = 600s
∴ त्वरण (a) = \(\frac{v-u}{t}\) = \(\frac{\frac{100}{9}-0}{600}\)ms^-1
= \(\frac{100}{9 \times 600}=\frac{1}{54}\) ~ 0.02 ms^-2

(पृष्ठ संख्या -118)

प्रश्न 1.
किसी वस्तु के एकसमान व असमान गति के लिए समय-दूरी ग्राफ की प्रकृति क्या होती है?
उत्तर:
एकसमान गति के लिए समय के साथ तय की गई दूरी का ग्राफ एक सरल रेखा होती है। ग्राफ में OB भाग यह दर्शाता है कि दूरी, एकसमान दर से बढ़ रही है।

असमान गति के लिए समय के साथ तय की गई दूरी का ग्राफ आरेखीय परिवर्तन दर्शाता है जैसे कि संलग्न चित्र में ग्राफ समय-दूरी की असमान गति दर्शाता है।

प्रश्न 2.
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका समय-दूरी ग्राफ समय अक्ष के समानांतर एक सरल रेखा है?
उत्तर:
यदि किसी वस्तु का समय-दूरी ग्राफ समय अक्ष के समानांतर एक सरल रेखा हो तो वस्तु की गति स्थिर होती है।

प्रश्न 3.
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका चाल-समय ग्राफ समय अक्ष के समानांतर एक सरल रेखा है?
उत्तर:
यदि किसी वस्तु का चाल-समय ग्राफ समय अक्ष के समानांतर एक सरल रेखा हो तो वह वस्तु एकसमान चाल से गतिमान होगी।

प्रश्न 4.
वेग-समय ग्राफ के नीचे के क्षेत्र से मापी गई राशि क्या होती है?
उत्तर:
वेग-समय ग्राफ के नीचे के क्षेत्र से मापी गई राशि वस्तु द्वारा तय दूरी दर्शाती है।

(पृष्ठ संख्या-121)

प्रश्न 1.
कोई बस विरामावस्था से चलना प्रारंभ करती है तथा 2 मिनट तक 0.1 ms^-2 के एकसमान त्वरण से चलती है। परिकलन कीजिए-(a) प्राप्त की गई चाल तथा (b) तय की गई दूरी।
हल:
यहाँ पर
बस की प्रारंभिक चाल (u) = 0
बस की अंतिम चाल (v) = ?
त्वरण (a) = 0.1 ms^-2
समय (t) = 2 मिनट = 2 x 60 s = 120 s
(a) बस की अंतिम चाल (v) = u + at
= 0 + 0.1 (120)
= 12 ms^-1 उत्तर

(b) बस द्वारा तय की गई दूरी (s) = ut + \(\frac { 1 }{ 2 } \) at²
= 0 (120) + \(\frac { 1 }{ 2 } \) (0.1) (120)²
= \(\frac { 1 }{ 2 } \) x \(\frac { 1 }{ 10 } \) x 120 x 120 m
= 720 m उत्तर

प्रश्न 2.
कोई रेलगाड़ी 90 kmh^-1 की चाल से चल रही है। ब्रेक लगाए जाने पर वह – 0.5 ms^-2 का एकसमान त्वरण उत्पन्न करती है। रेलगाड़ी विरामावस्था में आने से पहले कितनी दूरी तय करेगी?
हल:
यहाँ पर
रेलगाड़ी की प्रारंभिक चाल (u) = 90 kmh^-1
= \(\frac{90 \times 1000}{3600}\) ms-1
= 25 ms^-1
रेलगाड़ी की अंतिम चाल (v) = 0
त्वरण (a) = – 0.5 ms^-2
दूरी (s) = ?
हम जानते हैं कि
v² – u² = 2as
s = \(\frac{\mathrm{v}^2-\mathrm{u}^2}{2 \mathrm{a}}\)
= \(\frac{(0)^2-(25)^2}{2(-0.5)}\) = \(\frac{-625}{-1.0}\)
= 625 m उत्तर
अतः रेलगाड़ी विरामावस्था में आने से पहले 625 m की दूरी तय करेगी।

प्रश्न 3.
एक ट्रॉली एक आनत तल पर 2 ms^-2 के त्वरण से नीचे जा रही है। गति प्रारंभ करने के 3s के पश्चात् उसका वेग क्या होगा?
हल:
यहाँ पर
ट्रॉली की प्रारंभिक चाल (u) = 0
ट्रॉली की अंतिम चाल (v) = ?
त्वरण (a) = 2 ms^-2
समय (t) = 3s
हम जानते हैं कि
v = u+ at
= 0 + 2 (3)
= 6 ms^-1 उत्तर
अतः 3s के पश्चात् ट्रॉली का वेग 6 ms^-1 होगा।

प्रश्न 4.
एक रेसिंग कार का एकसमान त्वरण 4 ms^-2 है। गति प्रारंभ करने के 10s के पश्चात् वह कितनी दूरी तय करेगी?
हल:
यहाँ पर
कार की प्रारंभिक चाल (u) = 0
त्वरण (a) = 4 ms^-2
समय (t) = 10s
दूरी (s) = ?
हम जानते हैं कि
s = ut + \(\frac { 1 }{ 2 } \)at²
= 0 x (10) + \(\frac { 1 }{ 2 } \) (4) (10)²
= \(\frac { 1 }{ 2 } \) x 4 x 100 = 200 m उत्तर
अतः तय दूरी 200 m होगी।

प्रश्न 5.
किसी पत्थर को ऊर्ध्वाधर ऊपर की ओर 5 ms^-1 के वेग से फेंका जाता है। यदि गति के दौरान पत्थर का नीचे की ओर दिष्ट त्वरण 10 ms^-2 है, तो पत्थर के द्वारा कितनी ऊँचाई प्राप्त की गई तथा उसे वहाँ पहुँचने में कितना समय लगा?
हल:
यहाँ पर
पत्थर का प्रारंभिक वेग (u) = 5 m/s
पत्थर का अंतिम वेग (v) = 0
त्वरण (a) = -10 m/s²
अधिकतम ऊँचाई (s) = ?
अधिकतम ऊँचाई तक पहुँचने में पत्थर द्वारा लिया गया समय (t) = ?
हम जानते हैं कि v² – u² = 2as
s = \(\frac{\mathrm{v}^2-\mathrm{u}^2}{2 \mathrm{a}}\) = \(\frac{(0)^2-(5)^2}{2(-10)}\)
= \(\frac{-25}{-20}\) = 1.25 m
v = u + at
t = \(\frac { v – u }{ a } \) = \(\frac { 0 – 5 }{ -10 } \) = 0.5 सेकंड उत्तर

HBSE 9th Class Science गति Textbook Questions and Answers

प्रश्न 1.
एक एथलीट वृत्तीय रास्ते पर, जिसका व्यास 200m है का एक चक्कर 40s में लगाता है। 2 मिनट 20 सेकंड के बाद वह कितनी दूरी तय करेगा और उसका विस्थापन क्या होगा?
हल:

यहाँ पर
वृत्तीय रास्ते का व्यास = 200 m
वृत्तीय रास्ते की त्रिज्या (r) = \(\frac { 200 }{ 2 } \) = 100 m
वृत्तीय रास्ते की परिधि = 2πr
= 2 x \(\frac { 22 }{ 7 } \) x 100m
= \(\frac { 4400 }{ 7 } \) m
कुल समय = 2 मिनट 20 सेकंड
= (2 x 60 + 20) s = (120 + 20)s = 140s
अतः एथलीट द्वारा 40s में तय दूरी = \(\frac { 4400 }{ 7 } \) m

एथलीट द्वारा 1s में तय दूरी = \(\frac { 4400 }{ 7 x 40 } \)

एथलीट द्वारा 140s में तय दूरी = \(\frac { 4400 }{ 7 x 40 } \) x 140m

= 2200 m उत्तर

यहाँ पर कुल समय 140s है इसमें एथलीट 3 पूर्ण चक्कर व एक आधा चक्कर पूरा करेगा यदि वह परिधि के एक बिंदु A से चलता है तो B बिंदु पर पहुंचेगा।
इस प्रकार विस्थापन (AB) = वृत्तीय रास्ते का व्यास
= 200 m उत्तर

प्रश्न 2.
300 m सीधे रास्ते पर जोसेफ जॉगिंग करता हुआ 2 min 50 s में एक सिरे A से दूसरे सिरे B पर पहुँचता है और घूमकर 1 min में 100 m पीछे बिंदु C पर पहुँचता है। जोसेफ की औसत चाल व औसत वेग क्या होंगे?
(a) सिरे A से सिरे B तक तथा
(b) सिरे A से सिरे C तक
हल-
(a) बिंदु A से B तक तय की गई कुल दूरी = 300 m
बिंदु A से B तक लिया गया कुल समय = 2 मिनट (min) 50 सेकंड (s)
= (2 x 60 + 50) सेकंड = 170 सेकंड
बिंदु A से B तक कुल विस्थापन = 300 – 0 = 300 m


= \(\frac { 300 }{ 170 } \) = 1.76 मिनट/सेकंड उत्तर

कुल विस्थापन – 300 मिनट
लिया गया कुल समय 170 सेकंड

(b) बिंदु A से C तक तय की गई कुल दूरी = AB + BC
= (300 + 100) m = 400 m
बिंदु A से C तक लिया गया कुल समय = 2 मिनट 30 सेकंड + 1 मिनट
= (2 x 60 + 30)s + 60s
= (150 + 60)s = 210s
बिंदु A से C तक कुल विस्थापन = 300 – 100 = 200 m

= \(\frac { 400m }{ 210s } \) = 1.90ms^-1उत्तर

= \(\frac { 200m }{ 210s } \) = 0.952ms^-1उत्तर

प्रश्न 3.
अब्दुल गाड़ी से स्कूल जाने के क्रम में औसत चाल को 20 kmh^-1 पाता है। उसी रास्ते से लौटने के समय वहाँ भीड़ कम है और औसत चाल 40 kmh^-1 है। अब्दुल की इस पूरी यात्रा में औसत चाल क्या है?
हल
माना घर से स्कूल की दूरी = x km
स्कूल जाते समय औसत चाल = 20 kmh^-1
स्कूल से आते समय औसत चाल = 40 kmh^-1
स्कूल जाने में लगा समय = = \(\frac { x }{ 20 } \)h
स्कूल से आने में लगा समय = = \(\frac { x }{ 40 } \)h
जाने व आने से तय कुल दूरी = x + x = 2x km
जाने व आने में लगा कुल समय = \(\left(\frac{x}{20}+\frac{x}{40}\right)\)h
= \(\frac { 3x }{ 40 } \)h

= \(\frac{\frac{2 x}{3 x}}{40}\) = \(\frac{2 x \times 40}{3}\) = \(\frac { 80 }{ 3 } \)
= 26.67 km/h उत्तर

प्रश्न 4.
कोई मोटरबोट झील में विरामावस्था से सरल रेखीय पथ पर 3.0 ms^-2 के नियत त्वरण से 8.0 s तक चलती है। इस समय अंतराल में मोटरबोट कितनी दूरी तय करती है?
हल:
यहाँ पर मोटरबोट की झील में प्रारंभिक चाल (u) = 0
त्वरण (a) = 3.0 ms^-2
समय (t) = 8.0 s
दूरी (s) = ?
हम जानते हैं कि
s = ut + \(\frac { 1 }{ 2 } \)at²
= 0(8) + \(\frac { 1 }{ 2 } \) (3) (8)²
= \(\frac { 1 }{ 2 } \) x 3 x 64 = 96m
अतः मोटरबोट झील में 96 m की दूरी तय कर लेगी। उत्तर

प्रश्न 5.
किसी गाड़ी का चालक 52 kmh^-1 की गति से चल रही कार में ब्रेक लगाता है तथा कार विपरीत दिशा में एकसमान दर से त्वरित होती है। कार 5s में रुक जाती है। दूसरा चालक 30 kmh^-1 की गति से चलती हुई दूसरी कार पर धीमे-धीमे ब्रेक लगाता है तथा 10s में रुक जाता है। एक ही ग्राफ पेपर पर दोनों कारों के लिए चाल-समय ग्राफ आलेखित करें। ब्रेक लगाने के पश्चात् दोनों में से कौन-सी कार अधिक दूरी तक जाएगी?
हल:
दोनों चालकों का चाल-समय ग्राफ चित्र में दिखाया गया है।
माना कि पहला चालक बिंदु A से तथा दूसरा चालक बिंदु B से चलना प्रारंभ करता है।
विराम की अवस्था से पहले पहली कार द्वारा चली गई दूरी,
= ∆AOC का क्षेत्रफल
= \(\frac { 1 }{ 2 } \) x आधार x ऊँचाई
= \(\frac { 1 }{ 2 } \) x 5s x 52km/h
= \(\frac { 1 }{ 2 } \) x \(\frac{5}{3600}\) x 52km
= \(\frac { 1 }{ 2 } \) x \(\frac{5}{3600}\) x 52 x 1000km
= 36.11m

इसी प्रकार विरामावस्था में आने से पहले दूसरी कार द्वारा
चली गई दूरी = ∆BOD का क्षेत्रफल
= \(\frac { 1 }{ 2 } \) x आधार x ऊँचाई
= \(\frac { 1 }{ 2 } \) x 10s x 30 km/h
= \(\frac { 1 }{ 2 } \) x \(\frac{10}{3600}\) x 30km
= \(\frac { 1 }{ 2 } \) x \(\frac{10}{3600}\) x 30 x 1000km/h
= 41.67 m
अतः उपर्युक्त हल से स्पष्ट है कि ब्रेक लगाने के बाद दूसरी कार अधिक दूरी तय करती है। उत्तर

प्रश्न 6.
चित्र में तीन वस्तुओं A, B तथा C के लिए दूरी-समय ग्राफ प्रदर्शित हैं। ग्राफ का अध्ययन करके निम्नलिखित
प्रश्नों के उत्तर दीजिए
(a) तीनों में से कौन सबसे तीव्र गति से गतिमान है?
(b) क्या ये तीनों किसी भी समय सड़क के एक ही बिंदु पर | होंगे?
(c) जिस समय B, A से गुज़रती है उस समय तक C कितनी दूरी तय कर लेती है?
(d) जिस समय B, C से गुज़रती है उस समय तक यह कितनी दूरी तय कर लेती है?
उत्तर:

(a) B सबसे तीव्र गति से गतिमान है, क्योंकि इसके समय-दूरी ग्राफ का ढाल A तथा C की अपेक्षा अधिक है।
(b) तीनों सड़क पर एक स्थान पर तभी मिल सकते हैं यदि उनको दर्शाने वाले समय-दूरी के ग्राफ एक बिंदु पर मिलें, परंतु ऐसा नहीं है। तीनों ग्राफ किसी एक बिंदु पर नहीं मिलते।
(c) जिस समय B, A से गुज़रती है उस समय C, 9 km की दूरी | तय कर लेती है।
(d) जब B, C से गुजरती है तो उस समय B, 6 km दूरी तय कर लेती है।

प्रश्न 7.
20 मीटर की ऊँचाई से एक गेंद को गिराया जाता है। यदि उसका वेग 10 ms^-2 की एकसमान त्वरण की दर से बढ़ता है तो यह किस वेग से धरातल से टकराएगी? कितने समय पश्चात् वह धरातल से टकराएगी?
हल:
यहाँ पर
गेंद का प्रारंभिक वेग (u) = 0
ऊंचाई (s) = 20 m
त्वरण (a) = 10 ms^-2
गेंद का अंतिम वेग (v) = ?
समय (t) = ?
हम जानते हैं कि
v² – u² = 2as
v² = u² + 2as
= (0)² + 2(10) (20) = 400
1400 = 20 m/s
या v = \(\sqrt{400}\) = 20m/s
अब a = \(\frac { v – u }{ t } \)
या t = \(\frac { v – u }{ a } \) = \(\frac { 20 – 0 }{ 10 } \)
= 2s

अतः धरातल पर टकराने से पहले गेंद का वेग 20 m/s होगा तथा वह 2s में धरातल से टकराएगी। उत्तर

प्रश्न 8.
किसी कार का चाल-समय ग्राफ चित्र में दर्शाया गया है

(a) पहले 4s में कार कितनी दूरी तय करती है? इस अवधि में कार द्वारा तय की गई दूरी को ग्राफ में छायांकित क्षेत्र द्वारा दर्शाइए।
(b) ग्राफ का कौन-सा भाग कार की एकसमान गति को दर्शाता है?
उत्तर:
(a) पहले 4s में कार द्वारा तय दूरी का क्षेत्र OAB है। जो कि लगभग एक समकोण त्रिभुज है इसलिए पहले 4s में कार द्वारा तय दूरी = \(\frac { 1 }{ 2 } \) x OA x AB = \(\frac { 1 }{ 2 } \) x 4 x 6 = 12 m कार द्वारा तय दूरी चित्र में OAB छायांकित है।

(b) ग्राफ में 6s के बाद की चाल कार की एकसमान गति को दर्शाती है।

प्रश्न 9.
निम्नलिखित में से कौन-सी अवस्थाएँ संभव हैं और प्रत्येक के लिए एक उदाहरण दें
(a) कोई वस्तु जिसका त्वरण नियत हो, परंतु वेग शून्य हो।
(b) कोई वस्तु किसी निश्चित दिशा में गति कर रही हो तथा त्वरण उसके लंबवत् हो।
उत्तर:
(a) हाँ, यह स्थिति संभव है। जब किसी वस्तु को पृथ्वी तल से ऊपर की ओर फेंका जाता है तो अधिकतम ऊँचाई पर वस्तु का वेग शून्य होता है परंतु त्वरण (पृथ्वी का गुरुत्वीय त्वरण) स्थिर रहता है।
(b) हाँ, यह स्थिति भी संभव है। वृत्तीय पथ पर एकसमान वेग से चल रही वस्तु इसका एक उदाहरण है।

प्रश्न 10.
एक कृत्रिम उपग्रह 42250 km त्रिज्या की वृत्ताकार कक्षा में घूम रहा है। यदि वह 24 घंटे में पृथ्वी की परिक्रमा करता है तो उसकी चाल का परिकलन कीजिए।
हल:
यहाँ पर
कृत्रिम उपग्रह की वृत्ताकार कक्षा की त्रिज्या (r) = 42250 km
पृथ्वी की परिक्रमा करने में उपग्रह द्वारा लिया गया समय (t) = 24 घंटे
= 24 x 3600 s
= 86400s
कृत्रिम उपग्रह की चाल = \(\frac { 2πr }{ t } \)
= \(\frac{2 \times 3.14 \times 42250}{86400}\) km/s
= 3.07 km/s उत्तर

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.5 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.5

Question 1.
A matchbox measures 4 cm × 2.5 cm × 1.5 cm. What will be the volume of a packet containing 12 such boxes?
Solution:
Dimensions of the matchbox are 4 cm × 2.5 cm × 1.5 cm. Since a matchbox is in the shape of a cuboid.
∴ Volume of the 1 matchbox = 4 × 2.5 × 1.5 = 15 cm³
∴ Volume of a packet containing 12 such boxes = 15 × 12 = 180 cm³
Hence, volume of a packet containing 12 such boxes = 180 cm³.

Question 2.
A cuboidal water tank is 6 m long, 5 m wide and 4.5 m deep. How many litres of water can it hold? (1 m³ = 1000 ?)
Solution:
Length of cuboidal water tank (l) = 6 m
Breadth of cuboidal water tank (b) = 5 m
and depth of cuboidal water tank (h) = 4.5 m
∴ Volume of the cuboidal water tank = l × b × h
= 6 × 5 × 4.5
= 135 m³
= 135 × 1000 litres
= 135000 litres
Hence,water tank can hold volume of water = 135000 litres.

Question 3.
A cuboidal vessel is 10 m long and 8 m wide. How high must it be made to hold 380 cubic metres of a liquid?
Solution:
We have,
Length of cuboidal vessel (l) = 10 m
Breadth of cuboidal vessel (b)= 8 m
Let the height of cuboidal vessel be h m and volume of cuboidal vessel = 380 m³
⇒ l × b × h = 380
⇒ 10 × 8 × h = 380
⇒ 80 × h = 380
⇒ h = \(\frac{380}{80}\)
⇒ h = 4.75 m
Hence,height of the cuboidal vessel = 4.75 m.

Question 4.
Find the cost of digging a cuboidal pit 8 m long, 6 m broad and 3 m deep at the rate of Rs. 30 per m³.
Solution:
We have, Length of cuboidal pit (l) = 8 m
Breadth of cuboidal pit (b) = 6 m
and depth of cuboidal pit (h) = 3 m
∴ Volume of the cuboidal pit = l × b × h
= 8 × 6 × 3 = 144 m³
Rate of the digging the pit = Rs. 30 per m³
∴ Cost of digging the pit = Rs. 144 × 30
= Rs. 4320
Hence,cost of digging the pit = Rs. 4320.

Question 5.
The capacity of a cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its length and depth are respectively 2.5 m and 10 m.
Solution:
We have,
Length of cuboidal tank (l) = 2.5 m
Depth of cuboidal tank (h) = 10 m
Let the breadth of cuboidal tank be b m.
and capacity of cuboidal tank = 50000 litres
⇒ l × b × h = \(\frac{50000}{1000}\)
⇒ 2.5 × 6 × 10 = 50 m³
⇒ b = \(\frac{50}{2.5 \times 10}\)
⇒ b = 2 m
Hence,breadth of the cuboidal tank = 2 m.

Question 6.
A village, having a population of 4000, requires 150 litres of water per head per day. It has a tank measuring 20 m × 15 m × 6 m. For how many days will the water of this tank last?
Solution:
Dimensions of the water tank are 20 m × 15 m × 6 m.
Volume of the water tank = 20 × 15 × 6
= 1800 m³
Requirement of water per head per day = 150 litres = \(\frac{150}{1000}\) m³
Requirement of water for population of 4000 per day
= \(\frac{150 \times 4000}{1000}\)
∵ 600 m³ water is sufficient for 4000 persons = 1 day
∴ 1800 m³ water is sufficient for 400 persons = \(\frac{1 \times 1800}{600}\) = 3 days
Hence, water of tank is sufficient for days = 3.

Question 7.
A godown measures 40 m × 25 m × 10 m. Find the maximum number of wooden crates each measuring 1.0 m × 1.25 m × 0.5 m that can be stored in the godown.
Solution:
Dimensions of the godown are 40 m × 25 m × 10 m.
∴ Volume of the godown = 40 × 25 × 10
= 10000 m³
Dimension of each wooden crate is 1.0 m × 1.25 m × 0.5
∴ Volume of each wooden crate = 1.0 × 1.25 × 0.5
= 0.625 m³
= \(\frac{\text { Volume of the godown }}{\text { Volume of } 1 \text { wooden crate }}\)
\(\frac{10000}{0.625}\) = 16000
Hence,number of wooden crates = 16000.

Question 8.
A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas.
Solution:
We have,
Edge of big cube (a) = 12 cm
∴ Volume of big cube = a³ = (12)³ = 1728 cm³
∵ It cut into eight cubes of equal volume.
∴ Volume of new (small) cube = \(\frac{1728}{8}\)
= 216 cm³
Let the edge of new cube be x cm.
∴ Volume of new cube = x³
⇒ 216 = x³
⇒ \(\sqrt[3]{216}\) = \(\sqrt[3]{x^3}\)
⇒ \(\sqrt[3]{6 \times 6 \times 6}\) = x
⇒ x = 6 cm
Surface area of new cube = 6x² = 6 × (6)²
= 216 cm²
Surface area of big cube = 6a² = 6 × (12)²
= 864 cm²
\(\frac{\text { Surface area of big cube }}{\text { Surface area of a new cube }}=\frac{864}{216}=\frac{4}{1}\)
Hence side of the cube = 6 cm.
Surface area of big cube: Surface area of new cube = 4 : 1.

Question 9.
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in one minute?
Solution:
We have,
Depth of river (h) = 3 m
Width of river (b)= 40 m
Speed of water = 2 km/hr = \(\frac{2000}{60}\) m/min.
∴ The length of water flow in 1 min.
(l) = \(\frac{2000}{60}=\frac{100}{3} \mathrm{~m}\)
Thus,required volume of water = l × b × h
= \(\frac{100}{3}\) × 40 × 3
= 4000 m³
Hence,required volume of water = 4000 m³.

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.3 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.3

Assume π = \(\frac{22}{7}\), unless stated otherwise:

Question 1.
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
Solution:
We have,
Slant height of the cone (l) = 10 cm
and diameter of the base of a cone = 10.5 cm
∴ Radius of the base of a cone (r) = \(\frac{22}{7}\)
= 5.25 cm
∴ Curved surface area of the cone = πrl
= \(\frac{22}{7}\) × 5.25 × 10
= 165 cm²
Hence, curved surface area of the cone = 165 cm²

Question 2.
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Solution:
We have,
Slant height of a cone (l) = 21 m
and diameter of base of a cone = 24 m
∴ Radius of base of a cone (r) = \(\frac{24}{2}\) = 12 m
∴ Total surface area of a cone (r) = πr(l + r)
= \(\frac{22}{7}\) × 12(21 + 12)
= \(\frac{22}{7}\) × 12 × 33
= 1244.57 m² (approx.).
Hence, total surface area of a cone = 1244.57 m² (approx.).

Question 3.
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find : (i) radius of the base and (ii) total surface area of the cone.
Solution:
We have,
Slant height of a cone (l) = 14 cm
Let radius of the base of a cone be r сm.
(i) curved surface area of a cone = 308 cm²
⇒ πrl = 308
⇒ \(\frac{22}{7}\) × r × 14 = 308
⇒ 44r = 308
⇒ r = \(\frac{308}{44}\)
⇒ r = 7 cm.

(ii) Total surface area of the cone = πr(l + r)
= \(\frac{22}{7}\) × 7(14 + 7)
= 22 × 21
= 462 cm²
Hence, (i) radius of the base of a cone = 7 cm
(ii) total surface area of a cone = 462 cm².

Question 4.
A conical tent is 10 m high and the radius of its base is 24 m. Find :
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m² canvas is Rs. 70.
Solution:
We have,
Height of the conical tent (h) = 10 m
and radius of the base of conical tent (r) = 24 m
(i) Let slant height of the cone be l m.
∴ l = \(\sqrt{h^2+r^2}\)
⇒ l = \(\sqrt{10^2+24^2}\)
⇒ l = \(\sqrt{100+576}\)
⇒ l = \(\sqrt{676}\)
⇒ l = 26 m
(ii) Required area of canvas to make the conical tent = Curved surface area of the cone
= πrl = \(\frac{22}{7}\) × 24 × 26
= \(\frac{13728}{7}\) m²
∵ 1 m² canvas cost = Rs. 70
∴ \(\frac{13728}{7}\) m² canvas cost = Rs. \(\frac{70 \times 13728}{7}\)
= Rs. 137280
Hence, (i) Slant height of the tent = 26 m
(ii) Cost of canvas = Rs. 137280.

Question 5.
What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (Use π = 3.14)
Solution:
We have, Height of the conical tent (h) = 8 m
Radius of base of conical tent (r) = 6 m
∴ l = \(\sqrt{h^2+r^2}\)
⇒ l = \(\sqrt{8^2+6^2}\)
⇒ l = \(\sqrt{64+36}\)
⇒ l = \(\sqrt{100}\)
⇒ l = 10 m
Area of tarpaulin required to make the conical tent = Curved surface area of the cone
= πrl = 3.14 × 6 × 10
= 188.4 m²
∵ Width of tarpaulin = 3 m.
∴ Length of tarpaulin = \(\frac{\text { Area of tarpaulin }}{\text { Width of tarpaulin }}\)
\(\frac{188\cdot4}{3}\) = 62.8 m
Wastage in cutting = 20 cm = 0.20 m
Total length of tarpaulin = 62.8 + 0.20
= 63 m
Hence,length of tarpualin = 63 m.

Question 6.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of whitewashing its curved surface at the rate of Rs. 210 per 100 m²
Solution:
We have,
Slant height of a conical tomb (l) = 25 m
and diameter of a conical tomb = 14 m
∴ Radius of a conical tomb (r) = \(\frac{14}{2}\) = 7m

∴ Curved surface area of the conical tomb = πrl
= \(\frac{22}{7}\) × 7 × 25
= 550 m²
∵ Cost of white washing of 100 m² of tomb
= Rs. 210
∴ Cost of white washing of 550 m² of tomb
= Rs \(\frac{210 \times 550}{100}\)
= Rs. 1155
Hence,cost of white washing of tomb = Rs. 1155.

Question 7.
A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Solution:
We have,
Radius of conical cap (r) = 7 cm
and height of the conical cap (h) = 24 cm

∴ l = \(\sqrt{h^2+r^2}\)
⇒ l = \(\sqrt{24^2+7^2}\)
⇒ l = \(\sqrt{576+49}\)
⇒ l = \(\sqrt{625}\)
⇒ l = ±25
⇒ l = 25
∴ Curved surface area of a cap = πrl
= \(\frac{22}{7}\) × 7 × 25 = 550 cm²
Curved surface area of 10 such caps = 550 × 10 = 5500 cm²
Hence, required area of sheet to make 10 such caps = 5500 cm².

Question 8.
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard, Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cone is to be painted and the cost of painting is Rs. 12 per m², what will be the cost of painting all these cones? (Use π = 3.14 and take \(\sqrt{1.04}\) = 1.02)
Solution:
We have,
Height of a cone (h) = 1 m = 100 cm
and diameter of a cone (d) = 40 cm
∴ Radius of a cone (r) = \(\frac{40}{2}\) = 20 cm
∴ l = \(\sqrt{h^2+r^2}\)
⇒ l = \(\sqrt{100^2+20^2}\)
⇒ l = \(\sqrt{10000+400}\)
⇒ l = \(\sqrt{10400}\)
⇒ l = 101.98
⇒ l = 102 (approx.)
Outer surface area of 1 cone = πrl = 3.14 × 20 × 102 = 6405.6 cm²
Outer surface area of 50 cones= 6405.6 × 50 = 320280 cm²
\(\frac{320280}{10000}\) m²
= 32.028 m²
Cost of painting of 1 m² = Rs. 12
Cost of painting of 32.028 m² = Rs. 12 × 32.028
= Rs. 384.336
= Rs. 384.34
Hence, cost of painting of 50 cones = Rs. 384.34.

Haryana State Board HBSE 9th Class Science Solutions Chapter 14 प्राकृतिक सम्पदा Textbook Exercise Questions and Answers.

Haryana Board 9th Class Science Solutions Chapter 14 प्राकृतिक सम्पदा

HBSE 9th Class Science प्राकृतिक सम्पदा Intext Questions and Answers

(पृष्ठ संख्या-217)

प्रश्न 1.
शुक्र और मंगल ग्रहों के वायुमंडल से हमारा वायुमंडल कैसे भिन्न है?
उत्तर:
हमारे वायुमंडल में जीवन वायु (प्राण वायु-ऑक्सीजन) के घटक विद्यमान हैं जबकि शुक्र और मंगल पर इसका अभाव है।

प्रश्न 2.
वायुमंडल एक कंबल की तरह कैसे कार्य करता है?
उत्तर:
वायुमंडल में स्थित वायु कुचालक है, जो वायुमंडल के औसत तापमान को दिन-रात व वर्ष-भर नियंत्रित रखती है; जैसे कंबल शरीर की गर्मी को बाहर जाने से रोकता है। ठीक उसी प्रकार वायुमंडल पृथ्वी की सतह की गर्मी को बाहर जाने से रोकता है और न ही तापमान को अचानक बढ़ने देता है। अतः वायुमंडल कंबल की तरह कार्य करता है।

प्रश्न 3.
वायु प्रवाह (पवन) के क्या कारण हैं?
उत्तर:
पृथ्वी के वायुमंडल के असमान विधियों से गर्म होने के कारण कहीं पर उच्च दाब का क्षेत्र और कहीं पर निम्न दाब का क्षेत्र विकसित हो जाता है। दाब के इस अंतर के कारण वायु प्रवाह होता है, इसे पवन या समीर कहते हैं।

प्रश्न 4.
बादलों का निर्माण कैसे होता है?
उत्तर:
वायुमंडल में जलवाष्प जब ठंडे क्षेत्रों से गुजरते हैं तो जलवाष्प पानी की बूंदों के रूप में संघनित हो जाते हैं। जल की यही बूंदें जमा होकर बादल बनाती हैं।

प्रश्न 5.
मनुष्य के तीन क्रियाकलापों का उल्लेख करें जो वायु प्रदूषण में सहायक हैं।
उत्तर:
मनुष्य के निम्नलिखित क्रियाकलापों से वायु प्रदूषण होता है

• जीवाश्म ईंधन के जलने से प्रदूषक बनते हैं, जो वायु में मिलकर वायु को प्रदूषित करते हैं।
• वाहनों से निकलने वाले धुएँ से भी वायु प्रदूषित होती है।
• मनुष्य द्वारा स्थापित कल-कारखानों से निकलने वाली गैसें वायु में मिलकर वायु को प्रदूषित करती हैं।

(पृष्ठ संख्या-219)

प्रश्न 1.
जीवों को जल की आवश्यकता क्यों होती है?
उत्तर:
जल प्रत्येक सजीव की मूलभूत आवश्यकता है। प्रत्येक जीव के शरीर का 75 प्रतिशत भाग जल होता है। जल से ही जीवों के शरीर में जैव रासायनिक प्रक्रियाएँ संचालित होती हैं। सभी कोशिकीय प्रक्रियाओं के लिए जलीय माध्यम का होना अनिवार्य है। जीवों के शरीर में पदार्थों का संवहन जल के माध्यम से होता है और उत्सर्जन का कार्य भी जल के द्वारा होता है। स्थलीय जीवों को जीवित रहने के लिए मीठे जल की आवश्यकता होती है। अनेकों जीवों का वास स्थान जल ही है।

प्रश्न 2.
जिस गाँव/शहर/नगर में आप रहते हैं वहाँ पर उपलब्ध शुद्ध जल का मुख्य स्रोत क्या है?
उत्तर:
गाँव, नगर और शहरों में उपलब्ध शुद्ध जल के स्रोत भूमिगत जल, तालाब, झील और नदियाँ हैं। विशेषकर पर्वतों से आने वाली नदियों में बर्फ के पिघलने से जल मिलता है। तालाब, झीलों आदि में भी अधिकतर वर्षा का ही जल होता है।

प्रश्न 3.
क्या आप किसी क्रियाकलाप के बारे में जानते हैं जो इस जल के स्रोत को प्रदूषित कर रहा है?
उत्तर:
सीवर का मल-जल अधिकतर जल-स्रोतों (नदियों, नहरों, झीलों) में डाल दिया जाता है, जिससे जल प्रदूषित होता है। नदियों के किनारे बसे बड़े-बड़े शहरों और नगरों के सीवर मल-जल, सीधे नदियों के जल में डाल दिए जाते हैं। इसी प्रकार गंगा के किनारे बसे लोग अधजले शव या बिना जले शवों को गंगा के जल में फेंक देते हैं, जिससे गंगा का जल प्रदूषित हो रहा है।

(पृष्ठ संख्या-222)

प्रश्न 1.
मृदा (मिट्टी) का निर्माण किस प्रकार होता है?
उत्तर:
चट्टानों के टूटने व पिसने-घिसने से मृदा या मिट्टी का निर्माण होता है। मिट्टी के निर्माण में चट्टानों के छोटे-छोटे टुकड़े, ताजी व गली-सड़ी पत्तियाँ, मृत जीव अवशेष व रेत के कण आदि मिलने से होता है। मृदा की ऊपरी परत को बनने में कम-से-कम 300 से 800 वर्ष का समय लगा है। मृदा निर्माण की प्रक्रिया सतत् है।

प्रश्न 2.
मृदा अपरदन क्या है?
उत्तर:
मिट्टी का किन्हीं भी कारणों से कट जाना या बह जाना, मिट्टी का अपरदन कहलाता है। मिट्टी अनेकों कारणों से कटती है; जैसे

1. बाद मृदा अपरदन का प्रमुख कारण बाढ़ है, जिसके कारण मृदा एक स्थान से दूसरे स्थान पर बह जाती है।
2. तेज हवाएँ-मृदा अपरदन का दूसरा प्रमुख कारण तेज गति से बहती हवाएँ हैं।
3. वनों की कटाई-बढ़ती जनसंख्या तथा औद्योगीकरण के कारण वनों की कटाई अधिक होती है, जिस कारण मृदा-अपरदन बढ़ता है।
4. अनियंत्रित तथा अत्यधिक पशुओं की चराई-अनियंत्रित तथा अत्यधिक पशुओं की चराई से मृदा-अपरदन बढ़ता है।
5. खेती के अवैज्ञानिक तरीकों से अधिकतर किसान खेतों में लगातार एक ही प्रकार की फसल उगाते रहते हैं, जिससे उपजाऊ शक्ति कम होने के कारण मृदा का अपरदन बढ़ता है।
6. खेती के लिए भूमि की गहरी जुताई से-खेती के लिए भूमि की गहरी जुताई से भी मृदा अपरदन बढ़ता है।

प्रश्न 3.
अपरदन को रोकने और कम करने के कौन-कौन से तरीके हैं?
उत्तर:
अपरदन को रोकने के निम्नलिखित तरीके हैं
1. घास लगाकर-घास के पत्ते तथा जड़ें पानी की गति को कम कर देते हैं, जिससे जल मिट्टी के कणों को बहाकर नहीं ले जा पाता।

2. खेत समतल करके ढलवाँ जगह को छोटे-छोटे समतल टुकड़ों में बाँटकर खेती करने से भी पानी की गति कम हो जाती है, जिससे भूमि का कटाव नहीं होता है।

3. वृक्ष लगाकर-वृक्षों की जड़ें मिट्टी को बाँधे रखती हैं, जिससे पानी मिट्टी को बहाकर नहीं ले जा पाता।

4. खेती के उचित ढंग ढलान की दिशा में हल न चलाकर दाएँ-बाएँ हल चलाने से जल की गति कम हो जाती है, जिससे मिट्टी नहीं कटती।

5. बाँध बनाकर-ढलान पर बने बाँध तेजी से बहते हुए पानी के वेग को कम करते हैं, जिससे कटाव नहीं होता।

6. सीढ़ीनुमा खेत बनाकर-पहाड़ी प्रदेशों में ढलान के विरुद्ध सीढ़ियाँ बनाकर खेती करनी चाहिए।

7. खाद डालकर-भूमि में खाद डालने से भूमि की जल रोकने की शक्ति बढ़ जाती है, जिससे कटाव नहीं होता।

8. वायुरोधक लगाकर-जहाँ रेतीली भूमि हो तथा तेज हवाएँ चलती हों, वहाँ खेत के चारों ओर घने पौधे लगा देने चाहिएँ ताकि तेज वायु मिट्टी के कणों को उड़ाकर न ले जा सके।

9. खेतों की मेड़ों को ऊँचा बनाकर खेतों की मेड़ें ऊँची हो जाने से खेतों का पानी खेतों से बाहर नहीं जा पाता और भूमि का कटाव भी नहीं हो पाता।

10. विशेष फसलें उगाकर-मूंगफली जैसी विशेष फसलों को उगाकर भी भूमि कटाव को कम किया जा सकता है।

(पृष्ठ संख्या-226)

प्रश्न 1.
जल-चक्र के क्रम में जल की कौन-कौन सी अवस्थाएँ पाई जाती हैं?
उत्तर:
जल-चक्र के क्रम में जल की निम्नलिखित तीन अवस्थाएँ पाई जाती हैं

• द्रव अवस्था में जल,
• वाष्प अवस्था में जल तथा,
• ठोस अवस्था में बर्फ।

वाष्पों से बादल बनते हैं, यही बादल वर्षा के रूप में पृथ्वी पर बरसते हैं और कई बार बादलों का जल जमकर बर्फ अर्थात् ओलों का रूप ले लेता है। पहाड़ों की चोटियों पर पड़ी बर्फ भी ठोस रूप में जल ही है, जो पिघलकर द्रव अवस्था में नदियों में आती है और वाष्प बनकर वायु में मिल जाती है।

प्रश्न 2.
जैविक रूप से महत्त्वपूर्ण दो यौगिकों के नाम दीजिए जिनमें ऑक्सीजन और नाइट्रोजन दोनों पाए जाते हों।
उत्तर:
नाइट्रेट्स और नाइट्राइट्स।

प्रश्न 3.
मनुष्य की किन्हीं तीन गतिविधियों को पहचानें जिनसे वायु में कार्बन डाइऑक्साइड की मात्रा बढ़ती है।
उत्तर:
मनुष्य की गतिविधियों से वायु में कार्बन डाइऑक्साइड की मात्रा निम्नलिखित प्रकार से बढ़ती है

• ईंधन के दहन द्वारा।
• वाहनों में पेट्रोलियम पदार्थों के इस्तेमाल से।
• श्वसन क्रिया में भी CO₂ उत्पन्न होती है।

प्रश्न 4.
ग्रीन हाउस प्रभाव क्या है?
उत्तर:
पृथ्वी सूर्य से विभिन्न तरंगदैर्यों का प्रकाश प्राप्त करती है। वायुमंडल की ओज़ोन परत पराबैंगनी विकिरणों को सोखकर अन्य तरंगदैर्यों को जाने देती है, परंतु पृथ्वी की सतह पर पड़ने वाले प्रकाश में से कुछ भाग अवरक्त प्रकाश के रूप में परावर्तित होकर वापस चला जाता है।

CO₂ के अणुओं में पृथ्वी की सतह से परावर्तित अवरक्त विकिरणों को सोख लेने की क्षमता है। अतः वायुमंडल में उपस्थित कार्बन डाइऑक्साइड किसी कंबल के समान अवरक्त प्रकाश को प्रगृहीत कर सकती है, जिसके कारण वायुमंडल गर्म हो जाता है। वायुमंडल के इस प्रकार गर्म होने को ग्रीन हाउस प्रभाव या पौधा घर प्रभाव कहते हैं।

प्रश्न 5.
वायुमंडल में पाए जाने वाले ऑक्सीजन के दो रूप कौन-कौन से हैं?
उत्तर:
O₂ (ऑक्सीजन) तथा O₃ (ओज़ोन)।

HBSE 9th Class Science प्राकृतिक सम्पदा Textbook Questions and Answers

प्रश्न 1.
जीवन के लिए वायुमंडल क्यों आवश्यक है?
उत्तर:
जीवन वायुमंडल पर ही आधारित है क्योंकि

• वायुमंडल पृथ्वी के औसत तापमान को बनाए रखता है।।
• वायुमंडल में जीवन वायु के रूप में ऑक्सीजन पाई जाती है।
• वायुमंडल की ओज़ोन परत सूर्य की हानिकारक पराबैंगनी किरणों से पृथ्वी को बचाती है।
• वायुमंडल उल्काओं से पृथ्वी को बचाता है, जिससे जीवन की भी सुरक्षा होती है।
• हरे पौधों के लिए प्रकाशसंश्लेषण क्रिया में प्रयुक्त होने वाली CO₂ गैस भी वायुमंडल में ही पाई जाती है।
• वायुमंडल में जल, जलवाष्पों के रूप में पाया जाता है, जो जीवन का आधार है। अतः वायुमंडल जीवन के लिए आवश्यक है।

प्रश्न 2.
जीवन के लिए जल क्यों अनिवार्य है?
उत्तर:
जीवन के लिए जल अनिवार्य है क्योंकि मनुष्य की सभी कोशिकीय प्रक्रियाएँ जलीय माध्यम में होती हैं।

प्रश्न 3.
जीवित प्राणी मृदा पर कैसे निर्भर हैं? क्या जल में रहने वाले जीव संपदा के रूप में मृदा से पूरी तरह स्वतंत्र हैं?
उत्तर:
मिट्टी जीवन का आधार है। सभी जीवधारी मिट्टी पर प्रत्यक्ष या अप्रत्यक्ष रूप से निर्भर करते हैं। पौधे मिट्टी से पोषण प्राप्त करते हैं जिनमें खनिज और जल प्रमुख हैं और सभी जंतु पौधों पर निर्भर करते हैं। पौधों से ही जंतुओं को भोजन व सांस लेने के लिए ऑक्सीजन मिलती है। पौधों के बिना प्राणियों का जीवन संभव ही नहीं है और पौधे मिट्टी के बिना जीवित नहीं रह सकते। जलीय जीव भी मिट्टी पर निर्भर करते हैं क्योंकि पौधों से ही ये अपने जीवन की आवश्यकताएँ पूरी करते हैं।

प्रश्न 4.
आपने टेलीविजन पर और समाचार-पत्र में मौसम संबंधी रिपोर्ट को देखा होगा। आप क्या सोचते हैं कि हम मौसम के पूर्वानुमान में सक्षम हैं?
उत्तर:
हाँ, मौसम के पूर्वानुमान में हम सक्षम हैं। मौसम संबंधी आँकड़े भू-कक्षा में स्थापित कृत्रिम उपग्रहों के माध्यम से प्राप्त कर, आने वाले समय में मौसम का अनुमान सहज से लगाया जा सकता है। INSAT- 1B के द्वारा प्रत्येक आधे-आधे घंटे पश्चात् चित्र व सूचनाएँ प्राप्त की जाती हैं। इन्हीं चित्रों से मौसम की भविष्यवाणी की जाती है, जो काफी कारगर सिद्ध हुई हैं।

प्रश्न 5.
हम जानते हैं कि बहुत-सी मानवीय गतिविधियाँ वायु, जल एवं मृदा के प्रदूषण-स्तर को बढ़ा रहे हैं। क्या आप सोचते हैं कि इन गतिविधियों को कुछ विशेष क्षेत्रों में सीमित कर देने से प्रदूषण के स्तर को घटाने में सहायता मिलेगी?
उत्तर:
हाँ, मानव की इन गतिविधियों को कुछ विशेष क्षेत्रों में सीमित कर देने से प्रदूषण स्तर को घटाने में मदद मिलेगी; जैसे

• वाहनों को जीवाश्म ईंधन पेट्रोलियम पर न चलाकर सौर ऊर्जा पर आधारित बैटरी से चलाने पर वायु प्रदूषण कम होगा।
• घरों में कोयले व एल०पी०जी० जैसे ईंधनों के उपयोग के स्थान पर सौर ऊर्जा का उपयोग भोजन पकाने, पानी को गर्म करने में, आदि से प्रदूषण नहीं होगा।
• कृषि क्षेत्र में रासायनिक उर्वरकों के स्थान पर कंपोस्ट खाद का उपयोग करने से मृदा प्रदूषण नहीं होगा।
• उद्योग-धंधों का कचरा सीधे जल-स्रोतों में मिलाने की बजाए ट्रीटमैंट प्लांट के द्वारा केवल उपयोगी पदार्थ उपयोग करने से जल प्रदूषण कम होगा।

प्रश्न 6.
जंगल वायु, मृदा तथा जलीय स्रोत की गुणवत्ता को कैसे प्रभावित करते हैं?
उत्तर:
जंगल पर्यावरण संतुलन में महत्त्वपूर्ण घटक हैं। जंगल वायु की रचना (78% नाइट्रोजन, 21% ऑक्सीजन) को संतुलित करते हैं। जंगलों के अभाव में यह संतुलन बिगड़ जाता है। वायु में CO₂ और ठोस कणों की मात्रा बढ़ने से तापमान बढ़ जाता है, जबकि अधिक वन होने से वायु शुद्ध और शीतल रहती है। वन प्रदूषण घटता है।

वन मृदा अपरदन को रोकने के साथ-साथ मिट्टी की उर्वरा शक्ति को बढ़ाकर गुणवत्ता में सुधार लाते हैं। वनों के कटने से भूमि बंजर बन जाती है। वातावरण का तापमान बढ़ जाता है।

अधिक वनों से वर्षा भी अधिक होती है। जल-स्रोतों में जल की मात्रा बढ़ती है और उपयोगी मृदु जल अधिक मात्रा में उपलब्ध होता है। भूमिगत जल-स्तर में सुधार आता है। अतः जंगल वायु, मृदा और जलीय स्रोतों की गुणवत्ता सुधारते हैं।

Haryana State Board HBSE 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.2 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.2

Assume π = \(\frac{22}{7}\), unless stated otherwise.

Question 1.
The curved surface area of a right circular cylinder of height 14 cm is 88 cm². Find the diameter of the base of the cylinder.
Solution:
We have, height of the cylinder (h) = 14 cm
Let radius of the cylinder be r cm and curved surface area of the cylinder = 88 cm²
⇒ 2πrh = 88
⇒ 2 × \(\frac{22}{7}\) × r × 14 = 88
⇒ r = \(\frac{88 \times 7}{2 \times 22 \times 14}\)
⇒ r = 1 cm
Diameter = 2 × 5 = 2 × 1 = 2 cm
Hence,diameter of the base of the cylinder = 2 cm.

Question 2.
It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square metres of the sheet are required for the same?
Solution:
We have,
Base diameter of the cylinder (d) = 140 cm
∴ Radius of the cylinder (r) = \(\frac{140}{2}\) = 70 cm
and height of the cylinder (h) = 1 m = 100 cm
Required metal sheet to make a closed cylindrical tank = Total surface area of the cylinder
= 2πr(h + r)
= 2 × \(\frac{22}{7}\) × 70(100 + 70)
= 440(170) = 74800 cm²
= \(\frac{74800}{10000}\) m² = 7.48 m²
Hence, area of the required sheet = 7.48 m².

Question 3.
A metal pipe is 77 cm long. The inner diameter of a cross section is 4 cm, the outer diameter being 4.4 cm (see Fig. 13.15). Find its : (i) inner curved surface area, (ii) outer curved surface area, (iii) total surface area.

Solution:
We have, Length of cylindrical pipe (h) = 77 cm
Inner diameter of the cross section = 4 cm.
∴ Inner radius of the cross section (r) = \(\frac{4}{2}\)
= 2 cm
and outer diameter of the cross section = 4.4 cm
∴ outer radius of the cross section
(R) = \(\frac{4.4}{2}\) = 2.2 cm
(i) Inner curved surface area = 2πrh
= 2 × \(\frac{22}{7}\) × 2 × 77
= 968 cm²
(ii) Outer curved surface area = 2πRh
= 2 × \(\frac{22}{7}\) × 2.2 × 77
= 44 × 2.2 × 11
= 1064.8 cm²
(iii) Surface area of the two bases = 2 × π
(R² – r²) = 2 × \(\frac{22}{7}\) [(2.2)² – (2)²]
= \(\frac{44}{7}\)(2.2 + 2) (2.2 – 2)
= \(\frac{44}{7}\) × 4.2 × 0.2
= 44 × 0.6 × 0.2
= 5.28 cm²
∴ Total surface area= Inner curved surface area + outer curved surface area + surface area of the two bases
= 968 + 1064.8 +5.28
= 2038.08 cm²
Hence, inner C.S.A., outer C.S.A. and T.S.A. of the metal pipe are 968 cm², 1064.8 cm² and 2038.08 cm² respectively.

Question 4.
The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in m².
Solution:
We have,
length of roller (h)= 120 cm
and diameter of roller = 84 cm
∴ Radius of the roller (r) = \(\frac{84}{2}\) = 42 cm
Area covered by roller in 1 revolution = curved surface area of roller
= 2πrh
= 2 × \(\frac{22}{7}\) × 42 × 120
= 22 × 12 × 120
= 31680 cm²
Area covered by roller in 500 revolutions = 31680 × 500
= 15840000 cm²
= \(\frac{15840000}{10000}\) m²
= 1584 m²
Hence,area of the playground = 1584 m².

Question 5.
A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of Rs. 12.50 per m².
Solution:
We have, Height of the cylindrical pillar (h) = 3.5 m
= 350 cm
and diameter of the cylindrical pillar = 50cm
∴ Radius of the cylindrical pillar (r) = \(\frac{50}{2}\)
= 25 cm
Curved surface area of the cylindrical pillar
= 2πrh
= 2 × \(\frac{22}{7}\) × 25 × 350
= 44 × 25 × 50
= 55000 cm²
= \(\frac{55000}{10000}\) m² = 5.5 m²
Rate of the painting = Rs. 12.50 per m²
Cost of painting the curved surface area of the pillar
= 5.5 × 12.50 = Rs. 68.75
Hence, cost of the painting the C.S.A. of the pillar = Rs. 68.75.

Question 6.
Curved surface area of a right circular cylinder is 4.4 m². If the radius of the base of the cylinder is 0.7 m, find its height.
Solution:
We have,
Radius of the circular cylinder (r) = 0.7 m
Let height of the circular cylinder be h m andcurved surface area of a right circular cylinder= 4.4 m²
⇒ 2πrh = 4.4
⇒ 2 × \(\frac{22}{7}\) × 0.7 × h = 4.4
⇒ \(\frac{44}{10}\) × h = 4.4
⇒ h = \(\frac{4.4 \times 10}{44}\)
⇒ h = 1m
Hence, height of the right circular cylinder = 1m.

Question 7.
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find :
(i) its inner curved surface area.
(ii) the cost of plastering this curved surface at the rate of Rs. 40 per m².
Solution:
We have,
Depth of the circular well (h) = 10 m
and inner diameter of the circular well (d) = 3.5 m
∴ Inner radius of the circular well (r) = \(\frac{3.5}{2}\) m
Inner curved surface area of the wall = 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{3.5}{2}\) × 10
= 110 m²
Rate of plastering the curved surface area of the well= Rs. 40 per m²
∴ Cost of plastering the inner curved surface of the well= 110 × 40 = Rs. 4400
Hence, (i)Inner curved surface area of the well = 110 m²
(ii) cost of plastering the inner curved surface = Rs. 4400.

Question 8.
In a hot water het ing system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.
Solution:
We have,
Length of cylindrical pipe (h) = 28 m
and diameter of cylindrical pipe = 5 cm
∴ Radius of cylindrical pipe (r) = \(\frac{5}{2}\) cm
= \(\frac{5}{200}\) m
The total radiating surface in the system = Curved surface area of the pipe
= 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{5}{200}\) × 28
= \(\frac{88 \times 5}{100}\) = 4.4 m²
Hence, total radiating surface in the system = 4.4 m²

Question 9.
Find :
(i) the lateral or curved surface area of a closed cylindrical petrol storage tank that is 4.2 m in diameter and 4.5 m high.
(ii) how much steel was actually used, if \(\frac{1}{12}\) of the steel actually used was wasted in making the tank.
Solution:
We have, Height of cylindrical petrol tank (h) = 4.5 m
and diameter of cylindrical petrol tank = 4.2 m
∴ Radius of the cylindrical petrol tank
(r) = \(\frac{4.2}{2}\) = 2.1 m
Curved surface area of the cylindrical petrol tank = 2πrh
= 2 × \(\frac{22}{7}\) × 2.1 × 4.5
= 9 × 6.6 = 59.4 m²
Steel used to make the tank = Total surface area of the tank
= 2πr(h + r)
= 2 × \(\frac{22}{7}\) × 2.1(4.5 + 2.1)
= 13.2 × 6.6
= 87.12 m² …(i).
Let the area of the actual steel used to make the tank be x m².
Area of steel which wasted to make the tank
= \(\frac{1}{2}\) of x = \(\frac{x}{2}\) m²
Steel used to make the tank = x – \(\frac{x}{12}=\frac{11 x}{12}\) ….(ii)
From (i) and (ii), we get
\(\frac{11 x}{12}\) = 87.12
⇒ x = \(\frac{87\cdot12 \times 12}{11}\)
⇒ x = 95.04 m²
Hence, (i) curved surface area of the petrol tank = 59.4 m²
(ii) area of the actual steel used = 95.04 m².

Question 10.
In Fig. 13.16, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.

Solution:
Diameter of the base of a cylindrical lampshade = 20 cm
∴ Radius of the base of a cylindrical lampshade (r) = \(\frac{20}{2}\) = 10 cm
and height of the cylindrical lampshade = 30 cm
Margin for folding over the top and bottom of the cylindrical lampshade = 2.5 cm
∴ Total height of cloth for covering the cylindrical lampshade = 30 + 2 × 2.5 = 35 cm
Area of cloth required for covering the lampshade = Curved surface area of the cylindrical lampshade
= 2πrh
= 2 × \(\frac{22}{7}\) × 10 × 35
= 220 × 10 = 2200 cm²
Hence, area of cloth required for covering the lampshade = 2200 cm².

Question 11.
The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
Solution:
We have,
Radius of base of cylindrical penholder (r) = 3 cm
Height of the cylindrical pen holder (h) = 10.5 cm
Required area of cardboard for one pen holder = Total surface area
= 2πrh + πr² [∵ penholder is open at top]
= 2 × \(\frac{22}{7}\) × 3 × 10.5 + \(\frac{22}{7}\) × 3 × 3
= \(\frac{66}{7}\)[21 +3]
= \(\frac{1584}{7}\) cm²
Required area of cardboard for 35 penholders = \(\frac{1584}{7}\) × 35
= 7920 cm²
Hence, required area of cardboard for 35 penholders = 7920 cm².