Author name: Bhagya

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 5 युक्लिड के ज्यामिति का परिचय Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 5 युक्लिड के ज्यामिति का परिचय

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
सिद्ध कीजिए कि एक दिए हुए रेखाखंड पर एक समबाहु त्रिभुज की रचना की जा सकती है।
हल :
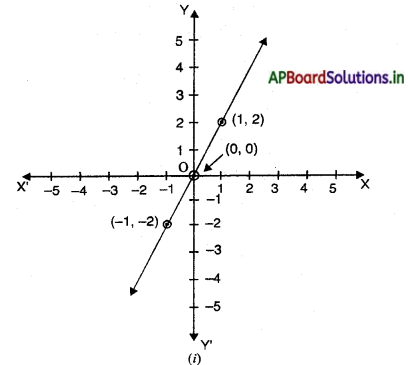
एक दी हुई लंबाई का एक रेखाखंड, मान लीजिए, AB दिया है [आकृति (i) अनुसार]

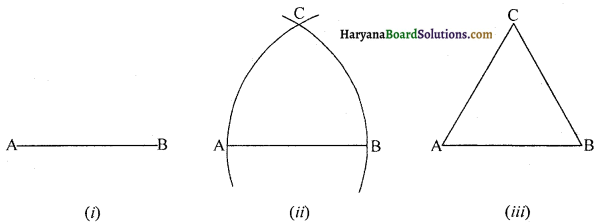
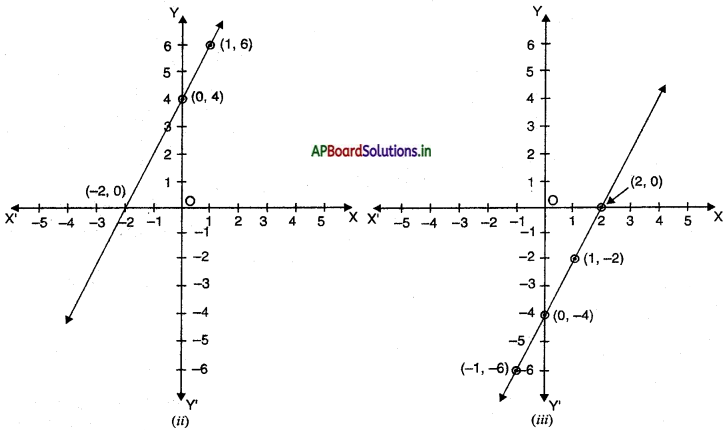
यूक्लिड की अभिधारणा (3) का प्रयोग करके, आप बिंदु A को केंद्र और AB त्रिज्या लेकर एक वृत्त खींच सकते हैं [आकृति (ii) अनुसार] । इसी प्रकार, B को केंद्र मानकर और BA त्रिज्या लेकर एक अन्य वृत्त खींचा जा सकता है। ये दोनों वृत्त बिंदु C पर मिलते हैं। अब रेखाखंडों AC और BC खींचकर AABC बनाइए। [आकृति (iii) अनुसार]
अब सिद्ध करना है कि यह त्रिभुज एक समबाहु त्रिभुज है; अर्थात् AB = AC = BC है।
क्योंकि AB = AC है, क्योंकि ये एक वृत्त की त्रिज्याएँ हैं। …………….(1)
इसी प्रकार, AB = BC (एक ही वृत्त की त्रिज्याएँ) …………….(2)
यूक्लिड के पहले अभिगृहीत अनुसार वे वस्तुएँ जो एक ही वस्तु के बराबर होती हैं एक-दूसरे के बराबर होती हैं। इससे निष्कर्ष निकलता है कि AB = BC = AC है।
अतः ∆ABC एक समबाहु त्रिभुज है।

प्रश्न 2.
निम्नलिखित को परिभाषित करें-
(i) समांतर चतुर्भुज,
(ii) आयत।
हल :
(i) समांतर चतुर्भुज-समांतर चतुर्भुज एक विशेष प्रकार का चतुर्भुज होता है जिसकी सम्मुख भुजाएँ समांतर होती हैं तथा बराबर भी होती हैं।
(ii) आयत-आयत एक ऐसा समांतर चतुर्भुज होता है जिसका एक कोण समकोण होता है।

Multiple Choice Questions with Answers:

प्रश्न 1.
यदि A, B और C एक रेखा पर स्थित तीन बिंदु हों और B बिंदु A और C के मध्य स्थित हो तो कौन-सा कथन सत्य है ?
(A) AB + BC = AC
(B) AB – BC = AC
(C) AB + AC = BC
(D) AB + BC = AB
उत्तर-
(A) AB + BC = AC

प्रश्न 2.
केवल एक दिए हुए रेखाखंड पर रचना की जा सकती है-
(A) समबाहु त्रिभुज की
(B) विषमबाहु त्रिभुज की
(C) समद्विबाहु त्रिभुज की
(D) समकोण त्रिभुज की
उत्तर-
(A) समबाहु त्रिभुज की

प्रश्न 3.
निम्नलिखित कथनों में से कौन-सा कथन सत्य है ?
(A) एक बिंदु से होकर केवल एक ही रेखा खींची
(B) दो भिन्न बिंदुओं से होकर जाने वाली असंख्य जा सकती है रेखाएँ हैं
(C) एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है
(D) यदि दो वृत्त बराबर हों, तो उनकी त्रिज्याएँ भिन्न-भिन्न होती हैं
उत्तर-
(C) एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है

प्रश्न 4.
यदि दो रेखाएँ अनिश्चित रूप से बढ़ाने पर कहीं नहीं मिलती तो उन्हें क्या कहा जाता है ?
(A) प्रतिच्छेदी रेखाएँ
(B) असमांतर रेखाएँ
(C) समांतर रेखाएँ
(D) लंब रेखाएँ
उत्तर-
(C) समांतर रेखाएँ

प्रश्न 5.
यदि एक सरल रेखा दूसरी सरल रेखा पर इस प्रकार खड़ी हो कि उनके बीच का कोण समकोण हो तो उन्हें कहा जाता है-
(A) समांतर रेखाएँ
(B) असमांतर रेखाएँ
(C) लंब रेखाएँ
(D) प्रतिच्छेदी रेखाएँ
उत्तर-
(C) लंब रेखाएँ

प्रश्न 6.
दो निश्चित बिंदुओं के बीच स्थित रेखा को कहा जाता है-
(A) सरल रेखा
(B) किरण
(C) रेखाखंड
(D) इनमें से कोई नहीं
उत्तर-
(C) रेखाखंड

प्रश्न 7.
वृत्त की परिधि पर स्थित दो बिंदुओं को मिलाने वाला रेखाखंड जो केंद्र से गुजरता है, क्या कहलाता है?
(A) अर्धव्यास
(B) व्यास
(C) चाप
(D) वृत्तखंड
उत्तर-
(B) व्यास

प्रश्न 8.
वृत्त के केंद्र को वृत्त की परिधि पर स्थित किसी बिंदु से मिलाने पर प्राप्त रेखाखंड कहलाता है(A) त्रिज्या
(B) व्यास
(C) चाप
(D) वृत्तखंड
उत्तर-
(A) त्रिज्या

प्रश्न 9.
एक बिंदु से होती हुई खींची जा सकती हैं-
(A) दो रेखाएँ
(B) तीन रेखाएँ
(C) परिमित रेखाएँ
(D) अपरिमित रेखाएँ
उत्तर-
(D) अपरिमित रेखाएँ

प्रश्न 10.
एक सांत रेखा को बढ़ाया जा सकता है-
(A) निश्चित रूप से
(B) अनिश्चित रूप से
(C) बढ़ाया नहीं जा सकता
(D) कुछ सीमा तक बढ़ाया जा सकता है
उत्तर-
(B) अनिश्चित रूप से

प्रश्न 11.
यदि a || b, b || c तो कौन-सा कथन सत्य है?
(A) a ⊥ c
(B) a ⊥ b
(C) a || c
(D) b ⊥ c
उत्तर-
(C) alc

प्रश्न 12.
चार भुजाओं से घिरी बंद आकृति को कहा जाता है-
(A) त्रिभुज
(B) चतुर्भुज
(C) पंचभुज
(D) षट्भुज
उत्तर-
(B) चतुर्भुज

प्रश्न 13.
चार भुजाओं से घिरी बंद आकृति. जिसकी सभी भुजाएँ समान हों और प्रत्येक कोण 90° का हो, उसे कहा जाता है-
(A) वर्ग
(B) आयत
(C) समांतर चतुर्भुज
(D) त्रिभुज
उत्तर-
(A) वर्ग

प्रश्न 14.
समबाहु त्रिभुज का प्रत्येक कोण होता है-
(A) 30° का
(B) 45° का
(C) 60° का
(D) 90° का
उत्तर-
(C) 60° का

प्रश्न 15.
यदि दो बिंदुओं A और B के बीच एक बिंदु C इस प्रकार हो कि AC = BC तो निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) AC = \(\frac{1}{2}\) BC
(B) BC = \(\frac{1}{2}\) AC
(C) BC = \(\frac{1}{3}\) AB
(D) AC = \(\frac{1}{2}\) AB
उत्तर-
(D) AC = \(\frac{1}{2}\) AB

प्रश्न 16.
तीन भुजाओं से घिरी बंद आकृति को क्या कहा जाता है ?
(A) त्रिभुज
(B) चतुर्भुज
(C) पंचभुज
(D) षट्भुज
उत्तर-
(A) त्रिभुज

प्रश्न 17.
दो भिन्न बिंदुओं से होकर
(A) केवल एक रेखा खींची जा सकती है
(B) दो रेखाएँ खींची जा सकती हैं।
(C) कोई रेखा नहीं खींची जा सकती है
(D) अनंत रेखाएँ खींची जा सकती हैं
उत्तर-
(A) केवल एक रेखा खींची जा सकती है

प्रश्न 18:
एक बिन्दु वह है जिसका :
(A) कोई भाग नहीं होता
(B) चौड़ाई रहित लम्बाई होती है
(C) किनारे होते हैं
(D) इनमें से कोई नहीं
उत्तर-
(D) कोई भाग नहीं होता

प्रश्न 19.
दो समांतर रेखाओं में उभयनिष्ठ बिंदुओं की संख्या होती है-
(A) शून्य
(B) 1
(C) 2
(D) अनंत
उत्तर-
(A) शून्य

प्रश्न 20.
आकृति में यदि AC = BD हो तो निम्नलिखित में से कौन-सा कथन सत्य है?

(A) AB = BD
(B) BC = CD
(C) AB = CD
(D) AB = BC
उत्तर-
(C) AB = CD

प्रश्न 21.

आकृति में यदि AB = PQ और PQ = XY हो तो निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) AB ≠ XY
(B) AB = XY
(C) AB ⊥ XY
(D) (A), (B), (C) में से कोई नहीं
उत्तर-
(B) AB = XY

प्रश्न 22.
पूर्ण अपने भाग से _____________ होता है।
(A) छोटा
(B) बराबर
(C) बड़ा
(D) छोटा या बराबर
उत्तर-
(C) बड़ा

प्रश्न 23.
यदि दो बिंदुओं A और B के बीच एक बिंदु C ऐसा स्थित है कि AC = 3BC तो निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) BC = \(\frac{3}{4}\) AB
(B) BC = \(\frac{1}{4}\) AB
(C) BC = \(\frac{1}{2}\) AB
(D) BC = \(\frac{1}{4}\) AC
उत्तर-
(B) BC = \(\frac{1}{4}\) AB

प्रश्न 24.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) दो भिन्न रेखाओं में एक से अधिक बिंदु उभयनिष्ठ नहीं हो सकते हैं
(B) दो भिन्न रेखाओं में एक से अधिक बिंदु उभयनिष्ठ हो सकते हैं
(C) दो भिन्न रेखाओं में अनंत बिंदु उभयनिष्ठ हो सकते हैं
(D) दो समांतर रेखाओं में एक उभयनिष्ठ बिंदु होता है
उत्तर-
(A) दो भिन्न रेखाओं में एक से अधिक बिंदु उभयनिष्ठ नहीं हो सकते हैं

प्रश्न 25.
किसी रेखाखंड में-
(A) दो मध्य-बिंदु होते हैं
(B) केवल एक मध्य-बिंदु होता है
(C) तीन मध्य-बिंदु होते हैं
(D) कोई मध्य-बिंदु नहीं होता
उत्तर-
(B) केवल एक मध्य-बिंदु होता है

प्रश्न 26.
किसी वर्ग की विशेषता होती है.
(A) प्रत्येक भुजा समान
(B) प्रत्येक समान कोण 90°
(C) प्रत्येक विकर्ण समान
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी

प्रश्न 27.
निम्नलिखित में कौन-सा कथन सत्य है ?
(A) एक वर्ष में 13 महीने होते हैं
(B) एक सप्ताह में 8 दिन होते हैं
(C) पृथ्वी का एक चंद्रमा है
(D) फरवरी में केवल 28 दिन होते हैं
उत्तर-
(C) पृथ्वी का एक चंद्रमा है

प्रश्न 28.
निम्नलिखित में से कौन-सा कथन असत्य है ?
(A) एक चतुर्भुज के अंतः कोणों का योग 350° होता है
(B) समचतुर्भुज एक समांतर चतुर्भुज होता है
(C) दो सम संख्याओं का योग सम होता है
(D) किसी भी वास्तविक संख्या x के लिए x² ≥ 0 है
उत्तर-
(A) एक चतुर्भुज के अंतः कोणों का योग 350° होता है

प्रश्न 29.
निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) 1 से बड़ी प्रत्येक विषम संख्या अभाज्य होती है
(B) सभी अभाज्य संख्याएँ विषम होती हैं
(C) एक त्रिभुज के अंतः कोणों का योग 180° होता है
(D) दो विषम पूर्णांकों का गुणनफल सम होता है
उत्तर-
(C) एक त्रिभुज के अंतः कोणों का योग 180° होता है

प्रश्न 30.
यदि दो बिंदुओं P और Q के बीच एक बिंदु R ऐसा स्थित हो कि PR = 5QR तो निम्नलिखित में से कौन-सा कथन सत्य है ?
(A) PR = \(\frac{1}{6}\) PQ
(B) PR = \(\frac{5}{6}\) PQ
(C) PR = \(\frac{5}{6}\) QR
(D) PR = \(\frac{1}{6}\) QR
उत्तर-
(B) PR = \(\frac{5}{6}\) PQ

प्रश्न 31.
एक ही वस्तुओं के दुगुने परस्पर __________ होते हैं।
(A) बराबर
(B) असमान
(C) बड़े
(D) छोटे
उत्तर-
(A) बराबर

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 4 दो चरों वाले रैखिक समीकरण Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 4 दो चरों वाले रैखिक समीकरण

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
निम्नलिखित में से प्रत्येक को दो चरों वाले समीकरणों के रूप में व्यक्त कीजिए :
(i) x = – 5
(ii) y = 2
(iii) 2x = 3
(iv) 5y = 2
हल :
(i) x = – 5 को (1)x + (0)y = – 5, या (1) x + (0). y + 5 = 0 के रूप में लिखा जा सकता है।
(ii) y = 2 को (0)x + (1)y = 2 या (0)x + (1)y – 2 = 0 के रूप में लिखा जा सकता है।
(iii) 2x = 3 को 2x + (0)y = 3 या 2x + (0)y – 3 = 0 के रूप में लिखा जा सकता है।
(iv) 5y = 2 को (0)x + 5y = 2 या (0)x + 5y – 2 = 0 के रूप में लिखा जा सकता है।

प्रश्न 2.
समीकरण x + 2y = 6 के चार हल ज्ञात करें।
हल :
यहां पर
x + 2y = 6
x = 6 – 2y
(i) यदि y = 1, तो x = 6 – 2(1) = 6 – 2 = 4
(ii) यदि y = 2, तो x = 6 – 2(2) = 6 – 4 = 2
(iii) यदि y = 0, तो x = 6 – 2(0) = 6 – 0 = 6
(iv) यदि y = – 1, तो x = 6 – 2(- 1) = 6 + 2 = 8
∴ अभीष्ट चार हल हैं : (4, 1), (2, 2), (6, 0), (8, – 1)

प्रश्न 3.
समीकरण 2x + 1 = x – 3 को हल कीजिए और हल को
(i) संख्या रेखा
(ii) कार्तीय तल पर निरूपण कीजिए।
हल :
2x + 1 = x – 3 को हल करने पर यह प्राप्त होता है-
2x – x = – 3 – 1 अर्थात्
x = – 4
(i) संख्या रेखा पर हल के निरूपण को आकृति में दिखाया गया है, जहाँ x = – 4 को एक चर वाला समीकरण माना गया है।

(ii) हम चर x तथा y वाले रैखिक समीकरण के रूप में x = – 4 को x + 0.y = – 4 के रूप में लिख सकते हैं। इसे एक रेखा से निरूपित किया जाता है। अब y के सभी मान मान्य होते हैं, क्योंकि 0.y सदा ही शून्य होता है। फिर भी x को संबंध x = – 4 को अवश्य संतुष्ट करना चाहिए। अतः दिए हुए समीकरण के दो हल x = – 4, y = 0 और x = – 4, y = 2 हैं।
आलेख AB, y-अक्ष के समांतर एक रेखा है जो इसके बाईं ओर 4 एकक की दूरी पर है।
इसी प्रकार, y = 3 या 0.x + 1.y = 3 के प्रकार के समीकरणों के संगत, हम x-अक्ष के समांतर एक रेखा प्राप्त कर सकते हैं।

प्रश्न 4.
आकृति में दिए गए प्रत्येक आलेख को ध्यान से देखिए और नीचे के प्रत्येक आलेख के विकल्पों से आलेख में। दिए गए समीकरण का चयन कीजिए : (a) आकृति (i) के लिए,
(i) x + y = 0 (ii) y = 2x (iii) y = x (iv) y = 2x + 1

(b) आकृति (ii) के लिए,
(i) x + y = 0 (ii) y = 2x (iii) y = 2x + 4 (iv) y = x – 4

(c) आकृति (iii) के लिए,
(i) x + y = 0 (ii) y = 2x (iii) y = 2x + 1 (iv) y = 2x – 4

हल :
(a) आकृति (1) में रेखा पर बिंदु (-1,- 2), (0, 0), (1, 2) हैं। जांच करने पर इस आलेख का संगत समीकरण y = 2x है।
जांध :
y = 2x
(- 1, – 2) के लिए
– 2 = 2 × (- 1)
⇒ – 2 = – 2

y = 2x
(0, 0) के लिए
0 = 2 × 0
⇒ 0 = 0

y = 2x
(1, 2) के लिए
2 = 2 × 1
⇒ 2 = 2

(b) आकृति (ii) में रेखा पर बिंदु (- 2, 0), (0, 4), (1, 6) हैं। जांच करने पर आलेख के बिंदुओं के निर्देशांक समीकरण y = 2x + 4 को संतुष्ट करते हैं। अतः y = 2x + 4 आकृति (ii) के आलेख का संगत समीकरण है।

जांच :
y = 2x + 4
(- 2, 0) के लिए
0 = 2 × (- 2) + 4
0 = – 4 + 4
⇒ 0 = 0

y = 2x +4
(0, 4) के लिए
4 = 2 × 0 + 4
4 = 0 + 4
⇒ 4 = 4

y = 2x + 4
(1, 6) के लिए
6 = 2 × 1 + 4
6 = 2 + 4
⇒ 6 = 6

(c) आकृति (iii) में, रेखा पर बिंदु (- 1, – 6), (0, – 4), (1, – 2), (2, 0) हैं। जांच करने पर हम कह सकते हैं कि y= 2x – 4 दिए हुए आलेख का संगत समीकरण है।

जांच :
y = 2x – 4
(- 1, – 6) के लिए
– 6 = 2 × (- 1) – 4
– 6 = – 2 – 4
⇒ – 6 = – 6

y = 2x – 4
(0, 4) के लिए
– 4 = 2 × 0 – 4
– 4 = 0 – 4
⇒ – 4 = – 4

y = 2x – 4
(1, – 2) के लिए
– 2 = 2 × 1 – 4
– 2 = 2 – 4
⇒ – 2 = – 2

y = 2x – 4
(2, 0) के लिए
0 = 2 × 2 – 4
0 = 4 – 4
⇒ 0 = 0.

Multiple Chpice Questions with Answers:

प्रश्न 1.
यदि a, b और c वास्तविक संख्याएँ हों तो निम्नलिखित में से कौन-सा समीकरण दो चरों वाला रैखिक समीकरण होगा-
(A) ax = 0
(B) by = 0
(C) ax = – c
(D) ax + by + c = 0
उत्तर-
(D) ax + by + c = 0

प्रश्न 2.
दो चरों वाले रैखिक समीकरण के हलों की संख्या होती है-
(A) एक
(B) दो
(C) अपरिमित रूप से अनेक
(D) परिमित
उत्तर-
(C) अपरिमित रूप से अनेक

प्रश्न 3.
दो चरों वाले प्रत्येक रैखिक समीकरण का आलेख होता है-
(A) सरल रेखा
(B) वक्र रेखा
(C) चाप आकार
(D) U आकार
उत्तर-
(A) सरल रेखा

प्रश्न 4.
2x +3y = \(9.3 \overline{5}\) को रैखिक समीकरण ax + by + c = 0 के रूप में व्यक्त करने पर c का मान होगा-
(A) \(9.3 \overline{5}\)
(B) – \(9.3 \overline{5}\)
(C) 2
(D) 3
उत्तर-
(B) – \(9.3 \overline{5}\)

प्रश्न 5.
समीकरण x – \(\frac{y}{5}\) – 10 = 0 की तुलना ax + by + c = 0 से करने पर b का मान होगा-
(A) 1
(B) \(\frac{1}{5}\)
(C) – \(\frac{1}{5}\)
(D) – 10
उत्तर-
(C) – \(\frac{1}{5}\)

प्रश्न 6.
समीकरण 4 = 5x – 3y को ax + by + c = 0 के रूप में लिखिए व c का मान बताइए।
(A) 5
(B) – 3
(C) 0
(D) – 4
उत्तर-
(D) – 4

प्रश्न 7.
समीकरण 2x = – 5y का ax + by + c = 0 रूप होगा-
(A) 2x – 5y + 0 = 0
(B) 2x + 5y + 0 = 0
(C) – 2x + 5y + 0 = 0
(D) – 2x – 2y + 0 = 0
उत्तर-
(B) 2x + 5y+ 0 = 0

प्रश्न 8.
समीकरण 3x + 2 = 0 की तुलना ax + by + c = 0 से करने पर b का मान होगा-
(A) 3
(B) 2
(C) – 2
(D) शून्य
उत्तर-
(D) शून्य

प्रश्न 9.
समीकरण y – 2 = 0 को रैखिक समीकरण ax + by + c = 0 के रूप में व्यक्त करने पर aव b के मान क्रमशः होंगे-
(A) 0, 1
(B) 0, – 2
(C) 1, – 2
(D) 0, – 1
उत्तर-
(A) 0, 1

प्रश्न 10.
x = – 5 को दो चरों वाले समीकरण के रूप में लिखा जा सकता है-
(A) (1)x + (1) y + 5 = 0
(B) (1)x + (0)y + 5 = 0
(C) (1)x + 0(1) – 5 = 0
(D) (1)x + 1(y) – 5 = 0
उत्तर-
(B) (1) x + (0) y + 5 = 0

प्रश्न 11.
5y = 2 को दो चरों वाले समीकरण के रूप में लिखा जा सकता है-
(A) (0) (x) + 5 y + 2 = 0
(B) 5x + 5y-2 = 0
(C) (0) x + 5y — 2 = 0
(D) 5x + 5y + 2 = 0
उत्तर-
(C) (0) x + 5y – 2 = 0

प्रश्न 12.
निम्नलिखित विकल्पों में से कौन-सा विकल्प सत्य है- y = 3x + 5 का
(A) एक अद्वितीय हल है
(B) केवल दो हल हैं
(C) अपरिमित रूप से अनेक हल हैं
(D) परिमित हल
उत्तर-
(C) अपरिमित रूप से अनेक हल हैं

प्रश्न 13.
समीकरण 2x + y = 7 में x = 1 के लिए y का मान होगा-
(A) 7
(B) 5
(C) 3
(D) 1
उत्तर-
(B) 5

प्रश्न 14.
समीकरण 2x + y = 7 में y = 1 के लिए x का मान होगा-
(A) शून्य
(B) 1
(C) 2
(D) 3
उत्तर-
(D) 3

प्रश्न 15.
समीकरण πx + y = 9 में x = 1 के लिए एका मान होगा-
(A) 9 – 3π
(B) 9 – 2π
(C) 9 – π
(D) 9
उत्तर-
(C) 9 – π

प्रश्न 16.
समीकरण x = 4y का अभीष्ट हल है-
(A) (0, 0)
(B) (4, 1)
(C) (- 4, – 1)
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी

प्रश्न 17.
निम्नलिखित हलों में से कौन-सा समीकरण x – 2y = 4 का अभीष्ट हल है-
(A) (4, 0)
(B) (0, 2)
(C) (2, 0)
(D) (1, 1)
उत्तर-
(A) (4, 0)

प्रश्न 18.
यदि x = 2, y = 1 समीकरण 2x + 3y = k का एक अभीष्ट हल हो तो k का मान होगा-
(A) 8
(B) 7
(C) 6
(D) 5
उत्तर-
(B) 7

प्रश्न 19.
समीकरण 4x + 3y = 12 का अभीष्ट हल है-
(A) (3, 0)
(B) (0, 4)
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों नहीं
उत्तर-
(C) (A) और (B) दोनों

प्रश्न 20.
समीकरण 2x + 5y = 0 का अभीष्ट हल है-
(A) (1, 1)
(B) (2, 2)
(C) (3, 3)
(D) (0, 0)
उत्तर-
(D) (0,0)

प्रश्न 21.
समीकरण 3y + 4 = 0 का अभीष्ट हल है-
(A) (0, \(\frac{-4}{3}\))
(B) (\(\frac{-4}{3}\), 0)
(C) (\(\frac{-4}{3}\), \(\frac{-4}{3}\))
(D) (A) और (C) दोनों
उत्तर-
(D) (A) और (C) दोनों

प्रश्न 22.
यदि x = 2,y = 2 समीकरण x + 2y = k का एक अभीष्ट हल हो तो k का मान होगा-
(A) 4
(B) 5
(C) 6
(D) 8
उत्तर-
(C) 6

प्रश्न 23.
यदि बिन्दु (3, 4) समीकरण 3y = ax + 7 के आलेख पर स्थित हो तो a का मान होगा-
(A) \(\frac{5}{3}\)
(B) \(-\frac{5}{3}\)
(C) \(\frac{3}{5}\)
(D) \(\frac{-3}{5}\)
उत्तर-
(A) \(\frac{5}{3}\)

प्रश्न 24.
एक नगर में टैक्सी का पहले किलोमीटर का किराया 8 रुपये है और उसके बाद की दूरी के लिए प्रति किलोमीटर का किराया 5 रुपये है। यदि तय की गई दूरी x किलोमीटर हो और कुल किराया रुपये हो, तो इसका एक रैखिक समीकरण होगा-
(A) 5x – 3 = y
(B) 5x + 3 = y
(C) 5y + 3 = x
(D) 8x + 3 = y
उत्तर-
(B) 5x + 3 = y

प्रश्न 25.
बिन्दु (2, 14) से होकर जाने वाली रेखाओं की संख्या होगी-
(A) केवल एक
(B) दो
(C) चार
(D) अनन्तः अनेक
उत्तर-
(D) अनन्तः अनेक

प्रश्न 26.
निम्न आलेख के लिए उचित समीकरण होगा-

(A) y = x
(B) x + y = 0
(C) y = 2x
(D) 2 + 3y = 7x
उत्तर-
(B) x + y = 0

प्रश्न 27.
निम्न आलेख के लिए उचित समीकरण होगा-

(A) x + y = 0
(B) y = x
(C) y = 2x
(D) y = 2x + 1
उत्तर-
(C) y = 2x

प्रश्न 28.
एक विद्यालय की कक्षा IX की छात्राएं यामिनी और फातिमा ने मिलकर भूकंप पीड़ित व्यक्तियों की सहायता के लिए प्रधानमंत्री राहत कोष में 100 रुपये अंशदान दिया। इसके लिए उचित रैखिक समीकरण होगा-
(A) x + y = 100
(B) x – y = 0
(C) 2x – y = 100
(D) x – 2y = 0
उत्तर-
(A) x + y = 100

प्रश्न 29.
F = \(\frac{9}{5}\) C + 32 फारेनहाइट को सेल्सियस में रूपांतरित करने वाला एक रैखिक समीकरण है। यदि तापमान 30°C हो तो फारेनहाइट में तापमान होगा-
(A) 84°F
(B) 86°F
(C) 88°F
(D) 22°F
उत्तर-
(B) 86°F

प्रश्न 30.
F = \(\frac{9}{5}\) C + 32 फारेनहाइट को सेल्सियस में रूपांतरित करने वाला एक रैखिक समीकरण है। यदि तापमान 95°F हो तो सेल्सियस में तापमान होगा-
(A) 49°C
(B) 42°C
(C) 28°C
(D) 35°C
उत्तर-
(D) 35°C

प्रश्न 31.
प्रश्न 30 की समीकरण में यदि तापमान 0°C हो तो फारेनहाइट में तापमान होगा-
(A) 32°F
(B) – 32°F
(C) 0°F
(D) 41°F
उत्तर-
(A) 32°F

प्रश्न 32.
x-अक्ष का समीकरण होता है-
(A) x = 0
(B) y = 0
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों नहीं
उत्तर-
(B) y = 0

प्रश्न 33.
y-अक्ष का समीकरण होता है-
(A) x = 0
(B) y = 0
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों नहीं
उत्तर-
(A)x = 0

प्रश्न 34.
x = a का आलेख होता है-
(A) x-अक्ष के समान्तर सरल रेखा
(B) x-अक्ष वाली सरल रेखा
(C) y-अक्ष के समान्तर सरल रेखा
(D) y-अक्ष वाली सरल रेखा
उत्तर-
(C) y-अक्ष के समान्तर सरल रेखा

प्रश्न 35.
y=a का आलेख होता है-
(A) y-अक्ष के समान्तर सरल रेखा
(B) y-अक्ष वाली सरल रेखा
(C) x-अक्ष वाली सरल रेखा
(D) x-अक्ष के समान्तर सरल रेखा
उत्तर-
(D) x-अक्ष के समान्तर सरल रेखा

Haryana State Board HBSE 9th Class Maths Important Questions Chapter 3 निर्देशांक ज्यामिति Important Questions and Answers.

Haryana Board 9th Class Maths Important Questions Chapter 3 निर्देशांक ज्यामिति

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:

प्रश्न 1.
संलग्न आकृति को देखकर निम्नलिखित कथनों को पूरा कीजिए:

(i) बिंदु B का भुज और कोटि क्रमशः __________ और __________ हैं। अतः B के निर्देशांक (__________, __________) हैं।
(ii) बिंदु M के x-निर्देशांक और y-निर्देशांक क्रमशः __________ और __________ हैं। अतः Mके निर्देशांक (__________, __________) हैं।
(iii) बिंदु L के x-निर्देशांक और y-निर्देशांक क्रमशः __________और __________ है। अतः L के निदेशाक (__________, __________) हैं।
(iv) बिंदु के x-निर्देशांक और y-निर्देशांक क्रमशः __________ और __________ हैं। अतः के निर्देशांक (__________, __________) हैं।
हल :
आकृति अनुसार,
(i) बिंदु B का भुज और कोटिं क्रमशः 4 और 3 हैं। अतः B के निर्देशांक (4, 3) हैं।
(ii) बिंदु M के x-निर्देशांक और y-निर्देशांक क्रमशः – 3 और 4 हैं। अतः M के निर्देशांक (- 3, 4) हैं।
(iii) बिंदु L के x-निर्देशांक और y-निर्देशांक क्रमशः – 5 और – 4 हैं। अतः L के निर्देशांक (- 5, – 4) हैं।
(iv) बिंदु s के x-निर्देशांक और y-निर्देशांक क्रमशः 3 और – 4 हैं। अतः S के निर्देशांक (3, – 4) हैं।

प्रश्न 2.
अक्षों पर दूरी का उपयुक्त एकक लेकर नीचे सारणी में दिए गए बिंदुओं को तल पर आलेखित कीजिए-

हल :
संलग्न आकृति में बिंदुओं की स्थितियाँ बिन्दुओं द्वारा दर्शाई गई हैं जोकि, A (- 2, 5), B(- 1, – 3), C(0, 4) व D(2, – 3) हैं।

प्रश्न 3.
निम्नलिखित संख्या युग्मों को कार्तीय तल के बिन्दुओं के रूप में आलेखित कीजिए-

हल :
आकृति में बिन्दुओं की स्थितियाँ बिन्दुओं (dots) द्वारा दर्शाई गई हैं जो कि A(- 2, – 3), B(- 3, 7), C(3, – 1) व D(0, – 1.5) हैं।

प्रश्न 4.
बिंदुओं A(2,0), B (2, 2) व C (0, 2) को खींचिए तथा रेखाखंड OA,AB, BC तथा CO को मिलाइए। इससे हमें कौन-सी आकृति प्राप्त होती है?

हल :
बिंदुओं A (2, 0), B (2, 2), C (0, 2) व O (0, 0) को आकृति में दर्शाया गया है। OA, AB, BC तथा CO को मिलाने पर पता चलता है कि OA = AB = BC = CO = 2 इकाई ।
तथा ∠A = ∠B = ∠C = 90°
अतः OABC एक वर्ग है।

प्रश्न 5.
बिंदु (1, – 1) और (3, 3) को कार्तीय तल में खींचिए और इनसे गुजरती हुई एक सरल रेखा खींचिए। अब एक अन्य बिंदु (- 3, 3) खींचकर ज्ञात कीजिए क्या ये सरल रेखा पर है या नहीं।
हल :

कार्तीय तल A (1, – 1) व B (3, 3) बिंदु हैं, जिन्हें मिलाने पर रेखा AB प्राप्त होती है। अब C बिंदु (- 3, 3) खींचा गया है जो आकृति से स्पष्ट होता है कि सरल रेखा पर नहीं है।

Multiple Choice Questions with Answers:

प्रश्न 1.
y-अक्ष से किसी बिन्दु की दूरी को कहा जाता है-
(A) x-निर्देशांक
(B) y-निर्देशांक
(C) शून्य-निर्देशांक
(D) z-निर्देशांक
उत्तर-
(A) x-निर्देशांक

प्रश्न 2.
x-अक्ष से किसी बिन्दु की दूरी को कहा जाता है-
(A) x-निर्देशांक
(B) y-निर्देशांक
(C) शून्य-निर्देशांक
(D) z-निर्देशांक
उत्तर-
(B) y-निर्देशांक

प्रश्न 3.
x-अक्ष और -अक्ष के प्रतिच्छेद बिन्दु को कहा जाता है-
(A) शून्य बिन्दु
(B) x-बिन्दु
(C) y-बिन्दु
(D) मूल बिन्दु
उत्तर-
(D) मूल बिन्दु

प्रश्न 4.
मूल बिन्दु के निर्देशांक होते हैं-
(A) x,0
(B) 0, x-अक्ष
(C) 0,0
(D) xy
उत्तर-
(C) 0,0

प्रश्न 5.
x-अक्ष पर किसी बिन्दु के निर्देशांक होते हैं-
(A) x, 0
(B) 0, y
(C) 0, 0
(D) x, y
उत्तर-
(A) x, 0

प्रश्न 6.
y-अक्ष पर किसी बिन्दु के निर्देशांक होते हैं-
(A) x, 0
(B) 0, y
(C) 0, 0
(D) x, y
उत्तर-
(B) 0,

प्रश्न 7.
कार्तीय तल में किसी बिन्दु की स्थिति निर्धारित करने वाली क्षैतिज रेखा को कहा जाता है-
(A) y-अक्ष
(B) शून्य अक्ष
(C) x-अक्ष
(D) मूल-अक्ष
उत्तर-
(C) x-अक्ष

प्रश्न 8.
x-अक्ष कार्तीय तल में किसी बिन्दु की स्थिति निर्धारित करने वाली ऊर्ध्वाधर रेखा को कहा जाता है-
(A) y-अक्ष
(B) शून्य अक्ष
(C) x-अक्ष
(D) मूल-अक्ष
उत्तर-
(A) y-अक्ष

प्रश्न 9.
y-निर्देशांक का दूसरा नाम होता है-
(A) कोटि
(B) भुज
(C) चतुर्थांश
(D) मूलांश
उत्तर-
(A) कोटि

प्रश्न 10.
x-निर्देशांक का दूसरा नाम होता है-
(A) कोटि
(B) भुज
(C) चतुर्थांश
(D) मूलांश
उत्तर-
(B) भुज

प्रश्न 11.
संलग्न आकृति में B का भुज है-
(A) 3
(B) 7
(C) 4
(D) 1

उत्तर-
(C) 4

प्रश्न 12.
प्रश्न 11 की आकृति में M की कोटि है-
(A) 4
(B) 3
(C) – 4
(D) – 3
उत्तर-
(A) 4

प्रश्न 13.
प्रश्न 11 की आकृति में M के निर्देशांक हैं-
(A) (3, 4)
(B) (3, – 4)
(C) (- 3, – 4)
(D) (- 3, 4)
उत्तर-
(D) (- 3, 4)

प्रश्न 14.
प्रश्न 11 की आकृति में L के निर्देशांक हैं-
(A) (5, 4)
(B) (- 5, – 4)
(C) (- 5, 4)
(D) (5, – 4)
उत्तर-
(B) (- 5, – 4)

प्रश्न 15.
प्रश्न 11 की आकृति में विन्दु s के x-निर्देशांक तथा y-निर्देशांक क्रमशः हैं-
(A) 3, 4
(B) – 3, 4
(C) 3, – 4
(D) – 3, – 4
उत्तर-
(C) 3, – 4

प्रश्न 16.
प्रश्न 11 की आकृति में चतुर्थांश-I में स्थित बिन्दु का नाम है-
(A) B
(B) M
(C) L
(D) S
उत्तर-
(A) B

प्रश्न 17.
प्रश्न 11 की आकृति में L बिन्दु किस चतुर्थांश में आता है?
(A) चतुर्थांश I में
(B) चतुर्थांश II में
(C) चतुर्थांश III में
(D) चतुर्थांश IV में
उत्तर-
(C) चतुर्थांश III में

प्रश्न 18.
बिन्दु (- 2, 4) कार्तीय तल के किस चतुर्थांश में स्थित होगा?
(A) चतुर्थांश I में
(B) चतुर्थांश II में
(C) चतुर्थांश III में
(D) चतुर्थांश IV में
उत्तर-
(B) चतुर्थांश II में

प्रश्न 19.
बिन्दु (3, -1) कार्तीय तल के किस चतुर्थांश में स्थित होगा?
(A) चतुर्थांश I में ।
(B) चतुर्थांश I में
(C) चतुर्थांश III में
(D) चतुर्थांश IV में
उत्तर-
(D) चतुर्थांश IV में

प्रश्न 20.
निर्देशांक (- 6, 4) में भुज का मान क्या है?
(A) 4
(B) 0
(C) – 6
(D) इनमें से कोई नहीं
उत्तर-
(C) – 6

प्रश्न 21.
बिन्दु (- 3, -10) कार्तीय तल के किस चतुर्थांश में स्थित होगा-
(A) चतुर्थांश I में
(B) चतुर्थांश II में
(C) चतुर्थांश III में
(D) चतुर्थांश IV में
उत्तर-
(C) चतुर्थांश III में

प्रश्न 22.
बिन्दु (- 1, 0) स्थित होगा-
(A) धन -अक्ष पर
(B) ऋण -अक्ष पर
(C) धन x-अक्ष पर
(D) ऋण x-अक्ष पर
उत्तर-
(D) ऋण x-अक्ष पर

प्रश्न 23.
निम्नलिखित में से कौन-सा बिन्द्र :-अक्ष पर स्थित होगा-
(A) 1, 0
(B) 0, 2
(C) 0, – 1
(D) 0, 7
उत्तर-
(A) 1, 0

प्रश्न 24.
निम्नलिखित में से कौन-सा बिन्दु x-अक्ष पर स्थित नहीं होगा-
(A) 1, 0
(B) 0, 0
(C) – 1, 0
(D) 0, – 7
उत्तर-
(D) 0, – 7

प्रश्न 25.
बिंदु (- 6, 7) किस चतुर्थांश में स्थित है?
(A) पहले
(B) दूसरे
(C) तीसरे
(D) चौथे
उत्तर-
(B) दूसरे

प्रश्न 26.
निम्नलिखित में से कौन-सा बिन्दु y-अक्ष पर स्थित होगा-
(A) 0, 2
(B) 0, – 1
(C) 0, – 5
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी

प्रश्न 27.
निम्नलिखित में से कौन-सा बिन्दु y-अक्ष पर स्थित नहीं होगा-
(A) 0, -3
(B) 0, 4
(C) – 4, 0
(D) 0, – 4
उत्तर-
(C) – 4, 0

Haryana State Board HBSE 10th Class Maths Notes Chapter 5 Arithmetic Progressions Notes.

Haryana Board 10th Class Maths Notes Chapter 5 Arithmetic Progressions

Introduction
We must have observed that in nature, many things follow a certain pattern, such as the petals of a sunflower, the grains on a maize cob, the holes of a honeycomb, the spirals on a pineapple etc.

Many times we come across certain specific patterns of numbers, e.g.
3, 6, 9, 12, 15, 18, ……..
9, 16, 25, 36, 49, ……..
2, 4, 6, 8, 10, 12, ……..
– 60, – 50, – 40, – 30, – 20, …….. etc.
These patterns are generally known as sequences. Hence, a sequence may be defined as an arrangement of numbers in some definite order and according to some rule.
The various numbers appearing in a sequence are called its terms. For example, in the first sequence 3 is the first term, it is denoted by a₁, 6 is the second term, it is denoted by a₂, 9 is the third term, it is denoted by a, and so on.
Generally, we denoted the terms of a sequence by a₁, a₂, a₃, a₄, …… etc. or x₁, x₂, x₃, x₄, …….. etc.

In general, the number at the place is called the n^th term of the sequences and it is denoted by an is also called the general term of the sequence. In this chapter, we shall study special type of sequence in which succeeding terms are obtained by adding, a field number to the preceding terms.

Arithmetic Progressions
Consider the following patterns :
1. 1, 2, 3, 4, 5, …..
2. 10, 20, 30, 40, 50, ….
3. 90. 80. 70. 60. 50 ……
4. -10.5, -11, -11.5, -12, -12.5, …
Each of the numbers in the pattern is called a term.
We observe that:
In Pattern (1) : each term is 1 more than the term preceding it.
In Pattern (2) : each term is 10 more than the term preceding it.
In Pattern (3) : each term is 10 less than the term preceding it.
In Pattern (4) : each term is 0.5 less than the term preceding it.
So, an arithmetic progression is a list of numbers in which each term is obtained by adding or subtracting a fixed number to the preceding term except the first term.
The fixed number is called the common difference of the AP. It is denoted by d. It can be positive, negative or zero.
So, d = a₂ – a₁ = a₃ – a₂ = ….. = a_n – a_n-1
Therefore, the AP with first term a and common difference d is:
a, a + d, a + 2d, a + 3d, a + 4d, …
In other words, sequence a₁, a₂, a₃, …… a_n… is called an arithmetic progression is the difference of a term and preceding term is always constant. This constant is called the common difference of the AP.
Finite AP : An AP containing finite number of terms is called finite AP.
Infinite AP : An AP containing infinite number of terms is called infinite AP.
If a, b, c are in AP, then \(\frac{a+c}{2}\) and b is called arithmetic mean of a and c.

n^th Term of an AP
n^th term of an AP from the start
Let a₁, a₂, a₃, a₄, …… be an AP whose first term is a1 and the common difference is d.
Then a₁ = a = a + (1 – 1)d ……(1)
a₂ = a + d = a + (2 – 1)d … (2)
a₃ = a₂ + d
= (a + d) + d
= (a + 2d)
= a + (3 – 1)d …..(3)
a₄ = a₃ + d
= (a + 2d) + d
= a + 3d
= a + (4 – 1)d ……(4)
Observing the pattern in equations (1), (2), (3), (4), we find that : a_n = a + (n – 1)d
So, the n^th term a_n of the AP with first terma and common difference is given by :
an = a + (n – 1)d
If there are m terms in the AP then am represents the last term which is also denoted by l.
n^th Term of an AP from the end.
(1) If there are m terms in an AP whose first term is a and common difference is d, then
n^th term from the end = a + (m – n)d
(2) If l is the last term of the AP then, n^th term from the end is the n^th term of an AP whose first term is l and common difference is – d.
n^th term from the end = last term + (n – 1) (n – d)
= l – (n – 1)d

Sum of first n terms of an AP
Let a₁, a₂, a₃, …… be an AP whose first term a and common difference is d. Then
a₁ = a, a₂ = a + d, a₃ = a + 2d, a₄ = a + 3d, …… a_n = a + (n – 1)d.
Now, S_n = a₁ + a₂ + a₃ + a₄ + … + a_n-1 + a_n
⇒ S_n = a + (a + d) + (a + 2d) + (a + 3d) + …… [a + (n – 2)d] + [a + (n – 1)d] … (1)
Writing the above series in reverse order, we get
S_n = a + [a + (n – 1)d] + [a + (n – 2)d] + …… + (a + d) + a …(2)
Adding the corresponding terms of equation (1), and (2), we get
⇒ 2S_n = a + [a + (n – 1)d] + (a + d) + [a + (n – 2d] + … + [a + (n – 1) d] + a
⇒ 2S_n = [2a + (n – 1)d] + [2a + (n – 1)d] + … + [2a + (n – 1)d]
∵ 2a + (n – 1)d repeats n times.
∴ 2S_n = n[2a + (n – 1)d]
⇒ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
Now, if l is the last term n^th term = n^th term = a + (n – 1)d.
Then
S_n = \(\frac{n}{2}\)[a + a + (n − 1)d]
S_n = \(\frac{n}{2}\)[a + l]
Hence, the sum of the first n terms of AP is given by :
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
or S_n = \(\frac{n}{2}\)[a + l]
where l = last term.
Important Results:
(i) Three numbers in AP considered as (a – d), a, (a + d).
(ii) Four numbers in AP considered as (a – 3d), (a – d), (a + d), (a + 3d).
(iii) Five numbers in AP considered as (a – 2d), (a – d), a, (a + d), (a + 2d).