Haryana State Board HBSE 9th Class Maths Important Questions Chapter 4 दो चरों वाले रैखिक समीकरण Important Questions and Answers.
Haryana Board 9th Class Maths Important Questions Chapter 4 दो चरों वाले रैखिक समीकरण
परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न:
प्रश्न 1.
निम्नलिखित में से प्रत्येक को दो चरों वाले समीकरणों के रूप में व्यक्त कीजिए :
(i) x = – 5
(ii) y = 2
(iii) 2x = 3
(iv) 5y = 2
हल :
(i) x = – 5 को (1)x + (0)y = – 5, या (1) x + (0). y + 5 = 0 के रूप में लिखा जा सकता है।
(ii) y = 2 को (0)x + (1)y = 2 या (0)x + (1)y – 2 = 0 के रूप में लिखा जा सकता है।
(iii) 2x = 3 को 2x + (0)y = 3 या 2x + (0)y – 3 = 0 के रूप में लिखा जा सकता है।
(iv) 5y = 2 को (0)x + 5y = 2 या (0)x + 5y – 2 = 0 के रूप में लिखा जा सकता है।
प्रश्न 2.
समीकरण x + 2y = 6 के चार हल ज्ञात करें।
हल :
यहां पर
x + 2y = 6
x = 6 – 2y
(i) यदि y = 1, तो x = 6 – 2(1) = 6 – 2 = 4
(ii) यदि y = 2, तो x = 6 – 2(2) = 6 – 4 = 2
(iii) यदि y = 0, तो x = 6 – 2(0) = 6 – 0 = 6
(iv) यदि y = – 1, तो x = 6 – 2(- 1) = 6 + 2 = 8
∴ अभीष्ट चार हल हैं : (4, 1), (2, 2), (6, 0), (8, – 1)
![]()
प्रश्न 3.
समीकरण 2x + 1 = x – 3 को हल कीजिए और हल को
(i) संख्या रेखा
(ii) कार्तीय तल पर निरूपण कीजिए।
हल :
2x + 1 = x – 3 को हल करने पर यह प्राप्त होता है-
2x – x = – 3 – 1 अर्थात्
x = – 4
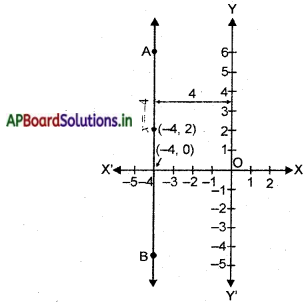
(i) संख्या रेखा पर हल के निरूपण को आकृति में दिखाया गया है, जहाँ x = – 4 को एक चर वाला समीकरण माना गया है।

(ii) हम चर x तथा y वाले रैखिक समीकरण के रूप में x = – 4 को x + 0.y = – 4 के रूप में लिख सकते हैं। इसे एक रेखा से निरूपित किया जाता है। अब y के सभी मान मान्य होते हैं, क्योंकि 0.y सदा ही शून्य होता है। फिर भी x को संबंध x = – 4 को अवश्य संतुष्ट करना चाहिए। अतः दिए हुए समीकरण के दो हल x = – 4, y = 0 और x = – 4, y = 2 हैं।
आलेख AB, y-अक्ष के समांतर एक रेखा है जो इसके बाईं ओर 4 एकक की दूरी पर है।
इसी प्रकार, y = 3 या 0.x + 1.y = 3 के प्रकार के समीकरणों के संगत, हम x-अक्ष के समांतर एक रेखा प्राप्त कर सकते हैं।
![]()
प्रश्न 4.
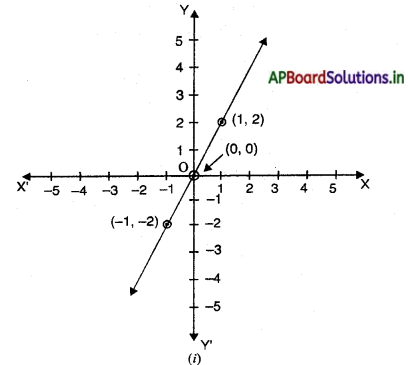
आकृति में दिए गए प्रत्येक आलेख को ध्यान से देखिए और नीचे के प्रत्येक आलेख के विकल्पों से आलेख में। दिए गए समीकरण का चयन कीजिए : (a) आकृति (i) के लिए,
(i) x + y = 0 (ii) y = 2x (iii) y = x (iv) y = 2x + 1
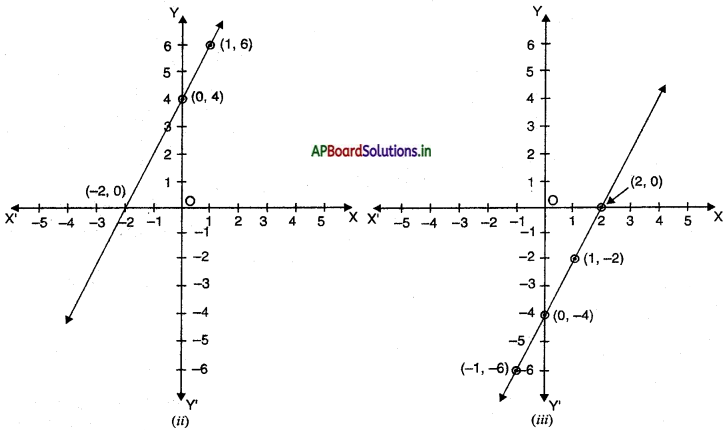
(b) आकृति (ii) के लिए,
(i) x + y = 0 (ii) y = 2x (iii) y = 2x + 4 (iv) y = x – 4
(c) आकृति (iii) के लिए,
(i) x + y = 0 (ii) y = 2x (iii) y = 2x + 1 (iv) y = 2x – 4
हल :
(a) आकृति (1) में रेखा पर बिंदु (-1,- 2), (0, 0), (1, 2) हैं। जांच करने पर इस आलेख का संगत समीकरण y = 2x है।
जांध :
y = 2x
(- 1, – 2) के लिए
– 2 = 2 × (- 1)
⇒ – 2 = – 2
y = 2x
(0, 0) के लिए
0 = 2 × 0
⇒ 0 = 0
y = 2x
(1, 2) के लिए
2 = 2 × 1
⇒ 2 = 2
(b) आकृति (ii) में रेखा पर बिंदु (- 2, 0), (0, 4), (1, 6) हैं। जांच करने पर आलेख के बिंदुओं के निर्देशांक समीकरण y = 2x + 4 को संतुष्ट करते हैं। अतः y = 2x + 4 आकृति (ii) के आलेख का संगत समीकरण है।
जांच :
y = 2x + 4
(- 2, 0) के लिए
0 = 2 × (- 2) + 4
0 = – 4 + 4
⇒ 0 = 0
y = 2x +4
(0, 4) के लिए
4 = 2 × 0 + 4
4 = 0 + 4
⇒ 4 = 4
y = 2x + 4
(1, 6) के लिए
6 = 2 × 1 + 4
6 = 2 + 4
⇒ 6 = 6
(c) आकृति (iii) में, रेखा पर बिंदु (- 1, – 6), (0, – 4), (1, – 2), (2, 0) हैं। जांच करने पर हम कह सकते हैं कि y= 2x – 4 दिए हुए आलेख का संगत समीकरण है।
जांच :
y = 2x – 4
(- 1, – 6) के लिए
– 6 = 2 × (- 1) – 4
– 6 = – 2 – 4
⇒ – 6 = – 6
y = 2x – 4
(0, 4) के लिए
– 4 = 2 × 0 – 4
– 4 = 0 – 4
⇒ – 4 = – 4
y = 2x – 4
(1, – 2) के लिए
– 2 = 2 × 1 – 4
– 2 = 2 – 4
⇒ – 2 = – 2
y = 2x – 4
(2, 0) के लिए
0 = 2 × 2 – 4
0 = 4 – 4
⇒ 0 = 0.
![]()
Multiple Chpice Questions with Answers:
प्रश्न 1.
यदि a, b और c वास्तविक संख्याएँ हों तो निम्नलिखित में से कौन-सा समीकरण दो चरों वाला रैखिक समीकरण होगा-
(A) ax = 0
(B) by = 0
(C) ax = – c
(D) ax + by + c = 0
उत्तर-
(D) ax + by + c = 0
प्रश्न 2.
दो चरों वाले रैखिक समीकरण के हलों की संख्या होती है-
(A) एक
(B) दो
(C) अपरिमित रूप से अनेक
(D) परिमित
उत्तर-
(C) अपरिमित रूप से अनेक
प्रश्न 3.
दो चरों वाले प्रत्येक रैखिक समीकरण का आलेख होता है-
(A) सरल रेखा
(B) वक्र रेखा
(C) चाप आकार
(D) U आकार
उत्तर-
(A) सरल रेखा
![]()
प्रश्न 4.
2x +3y = \(9.3 \overline{5}\) को रैखिक समीकरण ax + by + c = 0 के रूप में व्यक्त करने पर c का मान होगा-
(A) \(9.3 \overline{5}\)
(B) – \(9.3 \overline{5}\)
(C) 2
(D) 3
उत्तर-
(B) – \(9.3 \overline{5}\)
प्रश्न 5.
समीकरण x – \(\frac{y}{5}\) – 10 = 0 की तुलना ax + by + c = 0 से करने पर b का मान होगा-
(A) 1
(B) \(\frac{1}{5}\)
(C) – \(\frac{1}{5}\)
(D) – 10
उत्तर-
(C) – \(\frac{1}{5}\)
प्रश्न 6.
समीकरण 4 = 5x – 3y को ax + by + c = 0 के रूप में लिखिए व c का मान बताइए।
(A) 5
(B) – 3
(C) 0
(D) – 4
उत्तर-
(D) – 4
![]()
प्रश्न 7.
समीकरण 2x = – 5y का ax + by + c = 0 रूप होगा-
(A) 2x – 5y + 0 = 0
(B) 2x + 5y + 0 = 0
(C) – 2x + 5y + 0 = 0
(D) – 2x – 2y + 0 = 0
उत्तर-
(B) 2x + 5y+ 0 = 0
प्रश्न 8.
समीकरण 3x + 2 = 0 की तुलना ax + by + c = 0 से करने पर b का मान होगा-
(A) 3
(B) 2
(C) – 2
(D) शून्य
उत्तर-
(D) शून्य
प्रश्न 9.
समीकरण y – 2 = 0 को रैखिक समीकरण ax + by + c = 0 के रूप में व्यक्त करने पर aव b के मान क्रमशः होंगे-
(A) 0, 1
(B) 0, – 2
(C) 1, – 2
(D) 0, – 1
उत्तर-
(A) 0, 1
प्रश्न 10.
x = – 5 को दो चरों वाले समीकरण के रूप में लिखा जा सकता है-
(A) (1)x + (1) y + 5 = 0
(B) (1)x + (0)y + 5 = 0
(C) (1)x + 0(1) – 5 = 0
(D) (1)x + 1(y) – 5 = 0
उत्तर-
(B) (1) x + (0) y + 5 = 0
![]()
प्रश्न 11.
5y = 2 को दो चरों वाले समीकरण के रूप में लिखा जा सकता है-
(A) (0) (x) + 5 y + 2 = 0
(B) 5x + 5y-2 = 0
(C) (0) x + 5y — 2 = 0
(D) 5x + 5y + 2 = 0
उत्तर-
(C) (0) x + 5y – 2 = 0
प्रश्न 12.
निम्नलिखित विकल्पों में से कौन-सा विकल्प सत्य है- y = 3x + 5 का
(A) एक अद्वितीय हल है
(B) केवल दो हल हैं
(C) अपरिमित रूप से अनेक हल हैं
(D) परिमित हल
उत्तर-
(C) अपरिमित रूप से अनेक हल हैं
प्रश्न 13.
समीकरण 2x + y = 7 में x = 1 के लिए y का मान होगा-
(A) 7
(B) 5
(C) 3
(D) 1
उत्तर-
(B) 5
प्रश्न 14.
समीकरण 2x + y = 7 में y = 1 के लिए x का मान होगा-
(A) शून्य
(B) 1
(C) 2
(D) 3
उत्तर-
(D) 3
![]()
प्रश्न 15.
समीकरण πx + y = 9 में x = 1 के लिए एका मान होगा-
(A) 9 – 3π
(B) 9 – 2π
(C) 9 – π
(D) 9
उत्तर-
(C) 9 – π
प्रश्न 16.
समीकरण x = 4y का अभीष्ट हल है-
(A) (0, 0)
(B) (4, 1)
(C) (- 4, – 1)
(D) उपरोक्त सभी
उत्तर-
(D) उपरोक्त सभी
प्रश्न 17.
निम्नलिखित हलों में से कौन-सा समीकरण x – 2y = 4 का अभीष्ट हल है-
(A) (4, 0)
(B) (0, 2)
(C) (2, 0)
(D) (1, 1)
उत्तर-
(A) (4, 0)
प्रश्न 18.
यदि x = 2, y = 1 समीकरण 2x + 3y = k का एक अभीष्ट हल हो तो k का मान होगा-
(A) 8
(B) 7
(C) 6
(D) 5
उत्तर-
(B) 7
![]()
प्रश्न 19.
समीकरण 4x + 3y = 12 का अभीष्ट हल है-
(A) (3, 0)
(B) (0, 4)
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों नहीं
उत्तर-
(C) (A) और (B) दोनों
प्रश्न 20.
समीकरण 2x + 5y = 0 का अभीष्ट हल है-
(A) (1, 1)
(B) (2, 2)
(C) (3, 3)
(D) (0, 0)
उत्तर-
(D) (0,0)
प्रश्न 21.
समीकरण 3y + 4 = 0 का अभीष्ट हल है-
(A) (0, \(\frac{-4}{3}\))
(B) (\(\frac{-4}{3}\), 0)
(C) (\(\frac{-4}{3}\), \(\frac{-4}{3}\))
(D) (A) और (C) दोनों
उत्तर-
(D) (A) और (C) दोनों
प्रश्न 22.
यदि x = 2,y = 2 समीकरण x + 2y = k का एक अभीष्ट हल हो तो k का मान होगा-
(A) 4
(B) 5
(C) 6
(D) 8
उत्तर-
(C) 6
![]()
प्रश्न 23.
यदि बिन्दु (3, 4) समीकरण 3y = ax + 7 के आलेख पर स्थित हो तो a का मान होगा-
(A) \(\frac{5}{3}\)
(B) \(-\frac{5}{3}\)
(C) \(\frac{3}{5}\)
(D) \(\frac{-3}{5}\)
उत्तर-
(A) \(\frac{5}{3}\)
प्रश्न 24.
एक नगर में टैक्सी का पहले किलोमीटर का किराया 8 रुपये है और उसके बाद की दूरी के लिए प्रति किलोमीटर का किराया 5 रुपये है। यदि तय की गई दूरी x किलोमीटर हो और कुल किराया रुपये हो, तो इसका एक रैखिक समीकरण होगा-
(A) 5x – 3 = y
(B) 5x + 3 = y
(C) 5y + 3 = x
(D) 8x + 3 = y
उत्तर-
(B) 5x + 3 = y
प्रश्न 25.
बिन्दु (2, 14) से होकर जाने वाली रेखाओं की संख्या होगी-
(A) केवल एक
(B) दो
(C) चार
(D) अनन्तः अनेक
उत्तर-
(D) अनन्तः अनेक
प्रश्न 26.
निम्न आलेख के लिए उचित समीकरण होगा-
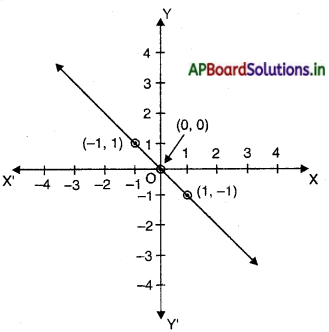
(A) y = x
(B) x + y = 0
(C) y = 2x
(D) 2 + 3y = 7x
उत्तर-
(B) x + y = 0
![]()
प्रश्न 27.
निम्न आलेख के लिए उचित समीकरण होगा-
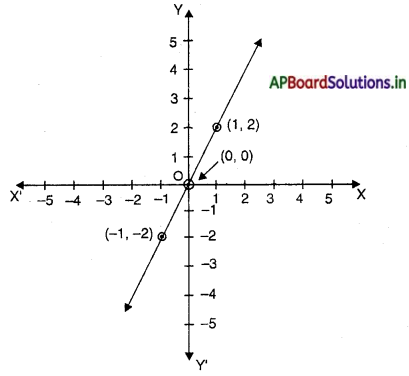
(A) x + y = 0
(B) y = x
(C) y = 2x
(D) y = 2x + 1
उत्तर-
(C) y = 2x
प्रश्न 28.
एक विद्यालय की कक्षा IX की छात्राएं यामिनी और फातिमा ने मिलकर भूकंप पीड़ित व्यक्तियों की सहायता के लिए प्रधानमंत्री राहत कोष में 100 रुपये अंशदान दिया। इसके लिए उचित रैखिक समीकरण होगा-
(A) x + y = 100
(B) x – y = 0
(C) 2x – y = 100
(D) x – 2y = 0
उत्तर-
(A) x + y = 100
प्रश्न 29.
F = \(\frac{9}{5}\) C + 32 फारेनहाइट को सेल्सियस में रूपांतरित करने वाला एक रैखिक समीकरण है। यदि तापमान 30°C हो तो फारेनहाइट में तापमान होगा-
(A) 84°F
(B) 86°F
(C) 88°F
(D) 22°F
उत्तर-
(B) 86°F
प्रश्न 30.
F = \(\frac{9}{5}\) C + 32 फारेनहाइट को सेल्सियस में रूपांतरित करने वाला एक रैखिक समीकरण है। यदि तापमान 95°F हो तो सेल्सियस में तापमान होगा-
(A) 49°C
(B) 42°C
(C) 28°C
(D) 35°C
उत्तर-
(D) 35°C
![]()
प्रश्न 31.
प्रश्न 30 की समीकरण में यदि तापमान 0°C हो तो फारेनहाइट में तापमान होगा-
(A) 32°F
(B) – 32°F
(C) 0°F
(D) 41°F
उत्तर-
(A) 32°F
प्रश्न 32.
x-अक्ष का समीकरण होता है-
(A) x = 0
(B) y = 0
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों नहीं
उत्तर-
(B) y = 0
प्रश्न 33.
y-अक्ष का समीकरण होता है-
(A) x = 0
(B) y = 0
(C) (A) और (B) दोनों
(D) (A) और (B) दोनों नहीं
उत्तर-
(A)x = 0
प्रश्न 34.
x = a का आलेख होता है-
(A) x-अक्ष के समान्तर सरल रेखा
(B) x-अक्ष वाली सरल रेखा
(C) y-अक्ष के समान्तर सरल रेखा
(D) y-अक्ष वाली सरल रेखा
उत्तर-
(C) y-अक्ष के समान्तर सरल रेखा
![]()
प्रश्न 35.
y=a का आलेख होता है-
(A) y-अक्ष के समान्तर सरल रेखा
(B) y-अक्ष वाली सरल रेखा
(C) x-अक्ष वाली सरल रेखा
(D) x-अक्ष के समान्तर सरल रेखा
उत्तर-
(D) x-अक्ष के समान्तर सरल रेखा