HBSE 9th Class Maths Solutions Chapter 2 Polynomials Ex 2.3

Haryana State Board HBSE 9th Class Maths Solutions Chapter 2 Polynomials Ex 2.3 Textbook Exercise Questions and Answers.

Haryana Board 9th Class Maths Solutions Chapter 2 Polynomials Exercise 2.3

Question 1.
Find the remainder when x³ + 3x² + 3x + 1 is divided by:
(i) x + 1
(ii) x – \(\frac {1}{2}\)
(iii) x
(iv) x + π
(v) 5 + 2x.
Solution:
Let p(x) = x³ + 3x² + 3x + 1
(i) We know that when p(x) is divided by (x + 1), the remainder is p(- 1).
(By Remainder Theorem)
So, p(-1) = (-1)³ + 3 x (-1)2 + 3 x (-1) + 1
= – 1 + 3 – 3 + 1 = 0
Hence, required remainder = 0.

(ii) We know that when p(x) is divided by (x – \(\frac {1}{2}\)), the remainder is p(\(\frac {1}{2}\))
(By Remainder Theorem)

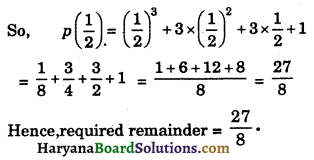
(iii) We know that when p(x) is divided by x, the remainder is p(0).
[By Remainder Theorem]
So, p(0) = (0)³ + 3 × (0)² + 3 × 0 + 1
= 0 + 0 + 0 + 1 = 1
Hence,required remainder = 1.

(iv) We know that when p(x) is divided by (x + π), the remainder is p(-π).
(By Remainder Theorem)
So, p(-π) = (-π)³ + 3 × (-π)² + 3 × (-π) + 1
= – π³ + 3π² – 3π + 1
Hence,required remainder = – π³ + 3π² – 3π + 1.

(v) We know that when p(x) is divided by (5 + 2x), the remainder is p(\(\frac {-5}{2}\))
[By Remainder Theorem]

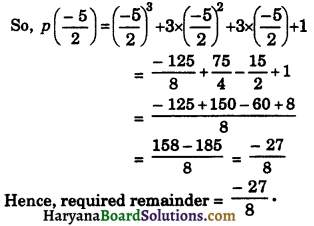
Question 2.
Find the remainder when x³ – ax³ + 6x – a is divided by x – a.
Solution :
Let p(x) = x³ – ax² + 6x – a
We know that when p(x) is divided by (x – a), the remainder is p(a).
[By Remainder Theorem]
So, p(a)=(a)³ – a × (a)² + 6 × a – a
= a³ – a³ + 6a – a = 5a
Hence required remainder = 5a.

Question 3.
Check whether 7 + 3x is a factor of 3x³ + 7x.
Solution :
Letp(x) = 3x³ + 7x
We know that, if 7 + 3x is a factor of p(x), then it is divisible by (7 + 3x) with leaving no
remainder i.e., remainder [p(\(\frac {-7}{3}\))] will be zero. (By Factor Theorem)

Since, remainder p(\(\frac {-7}{3}\)) ≠ 0. Therefore, (7 + 3x) is not a factor of p(x)